Discovering Doily in PG(2,5)

Preprint

Article

Discovering Doily in PG(2,5)

Altmetrics

Downloads

117

Views

Comments

A peer-reviewed article of this preprint also exists.

Stefano Innamorati^*

This version is not peer-reviewed

Submitted:

17 April 2023

Posted:

17 April 2023

You are already at the latest version

Alerts

Abstract

W. L. Edge proved that the internal points of a conic in PG(2,5), together with the collinear triples on the non-secant lines, form the Desargues configuration. M. Saniga showed an intimate connection between Desargues configurations and the generalized quadrangles of order two, GQ(2,2), whose representation has been dubbed “the doily” by Stan Payne in 1973. In this paper we prove that the external points of a conic in PG(2,5), together with the collinear and non-collinear triples on the non-tangent lines, form the generalized quadrangle of order two.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction and Motivation

W. L. Edge [2] proved that the internal points of a conic in PG(2,5) together with the non-secant lines form a Desargues configuration. M. Saniga [7] showed an intimate connection between Desargues configurations and the generalized quadrangle of order two, GD(2,2). The two results motivate the writing of this note. By using the Singer representation of PG(2,5), we provide a short proof of W. L. Edge result and, believing it is novel, we prove that the external points of a conic of PG(2,5) define the generalized quadrangle of order two, GD(2,2). The reason for deciding to conduct a detailed investigation of this special case is the charm of small projective planes, cf. [1,3,5,6,9,10].

2. The Singer Representation of PG(2,5)

Let ω be a primitive element of

F_{5^{3}}

over F₅ and let

f (x) = - a_{0} - a_{1} x - a_{2} x^{2} + x^{3}

be its minimal polynomial over F₅. The companion matrix

C (f)

of f is given by

C (f) = (\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ a_{0} & a_{1} & a_{2} \end{matrix})

and it induces a Singer cycle γ of PG(2,5), cf. [8]. Let’s us consider the minimal polynomial f(x)=4+4x+x³ over F₅. The companion matrix

C (f)

of f

C (f) = (\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{matrix})

gives the 31 points of this plane as follows, cf. [4]. If the first point is

ω^{0} = (x_{0}, x_{1}, x_{2}) = (\begin{matrix} 1 & 0 & 0 \end{matrix})

, we get

ω^{1} = ω^{0} T = (\begin{matrix} 1 & 0 & 0 \end{matrix}) (\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{matrix}) = (\begin{matrix} 0 & 1 & 0 \end{matrix});

ω^{2} = ω^{0} T^{2} = ω^{1} T (\begin{matrix} 0 & 1 & 0 \end{matrix}) (\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{matrix}) = (\begin{matrix} 0 & 0 & 1 \end{matrix});

ω^{3} = ω^{0} T^{3} = ω^{2} T (\begin{matrix} 0 & 0 & 1 \end{matrix}) (\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{matrix}) = (\begin{matrix} 1 & 1 & 0 \end{matrix});

ω0=(1,0,0)
ω1=(0,1,0)	ω2=(0,0,1)	ω3=(1,1,0)	ω4=(0,1,1)	ω5=(1,1,4)	ω6=(1,2,1)
ω7=(1,0,3)	ω8=(1,4,0)	ω9=(0,1,4)	ω10=(1,1,1)	ω11=(1,0,4)	ω12=(1,2,0)
ω13=(0,1,2)	ω14=(1,1,2)	ω15=(1,3,2)	ω16=(1,3,1)	ω17=(1,0,2)	ω18=(1,3,0)
ω19=(0,1,3)	ω20=(1,1,3)	ω21=(1,4,3)	ω22=(1,4,2)	ω23=(1,3,3)	ω24=(1,4,4)
ω25=(1,2,4)	ω26=(1,2,2)	ω27=(1,3,4)	ω28=(1,2,3)	ω29=(1,4,1)	ω30=(1,0,1)

Let us denote the points represented by

ω^{i}

simply by i. So, the Singer group is isomorphic to the additive group

Z_{31}

, the integers modulo 31. Now select any line: for example, we choose the line x₁=x₂, which contains the points: l₀={0,4,10,23,24,26}. The remaining lines of the plane are found by adding 1 to each point of the preceding line beginning with l₀ and using addition modulo 31. For convenience, we represent the projective plane of order 5 as a set of orthogonal arrays of the affine plane of order 5 with the intersection point of the member of each parallel class indicated to the right of the row array and at the bottom of the column array. We do this by using the Singer difference set defining PG(2,5) as the line at infinity, designated by l_∞. Thus, let l_∞={0,4,10,23,24,26}. The remaining lines of the plane are found by adding 1 to each point of the preceding line beginning with l_∞ as l₀ and using addition modulo 31. The pencil of lines on the point 4 is then intersected by the pencil of lines on the point 0 to form the first array. Thus, each row (column) plus its point at infinity represents a line of the plane. Now, let us take into account the Singer representation

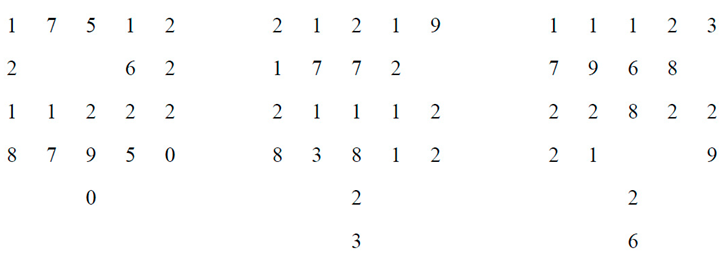
Moreover, by the Singer representation, since all conics in PG(2,5) are projectively equivalent, see [4], let us consider the conic C=−l_∞={−0,−4,−10,−23,−24,−26}={0,5,7,8,21,27},

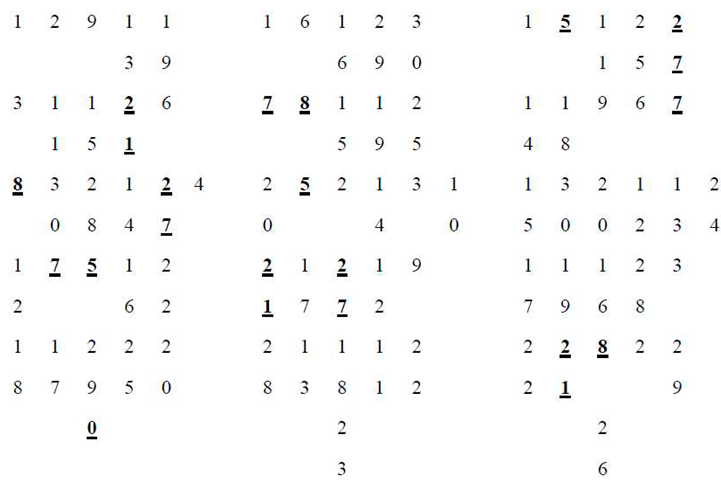
by taking into account the points not on C and not on the tangent lines, we get the 10−set I of the internal points of the conic I={1,12,13,17,19,22,25,28,29,30}. Now, taking into account the triples on the external lines

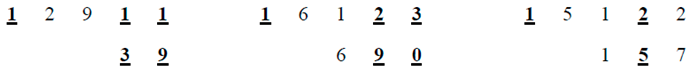
We get {{1,13,19},{1,17,22},{1,29,30},{12,13,30},{12,19,29},{12,25,28},{13,22,28},{17,19,28}, {17,25,29},{22,25,30}}. Let us now consider the point-line incidence geometry (I,T) where the point-set I is the 10−set of the internal points of the conic I={1,12,13,17,19,22,25,28,29,30}, and the line-set T is the union of the triples of collinear points on the external lines:

T={{1,13,19},{1,17,22},{1,29,30},{12,13,30},{12,19,29},{12,25,28},{13,22,28},{17,19,28}, {17,25,29},{22,25,30}}

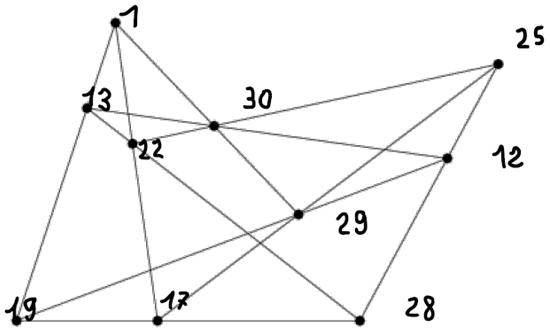
A brief inspection of the above Figure confirms that the geometry (I,T) is the Desargues configuration, as W. L. Edge proved in [2].

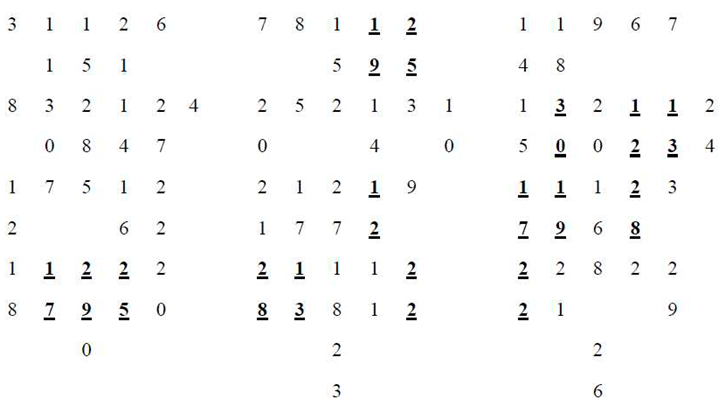
Now, by taking into account the points non on C, but on the tangent lines,

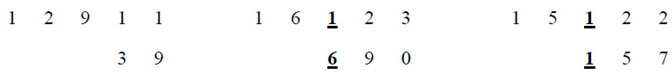
We get the 15−set of external points of the conic E={2,3,4,6,9,10,11,14,15,16,18,20,23,24,26}, cf. [4]. Now, taking into account the triples on the external lines and the triples of non-collinear points of the triangles of the 2-lines:

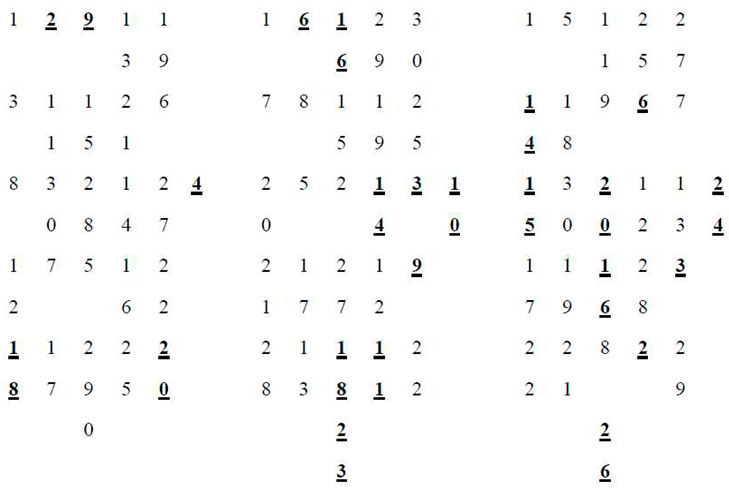
We get the sets T₁={{2,4,9},{2,6,26},{3,9,23},{3,16,24},{4,18,20},{6,10,16},{10,11,18}, {11,14,23},{14,15,26},{15,20,24}} and T₂={{2,11,24},{3,18,26},{4,14,16},{6,20,23},{9,10,15}}

Let us now construct the point-line incidence geometry (E,L) where the point-set E is the 15−set of the external points of the conic, and the line-set L=T₁∪T₂

A brief inspection of the under Figure confirms that this geometry is isomorphic to GD(2,2).

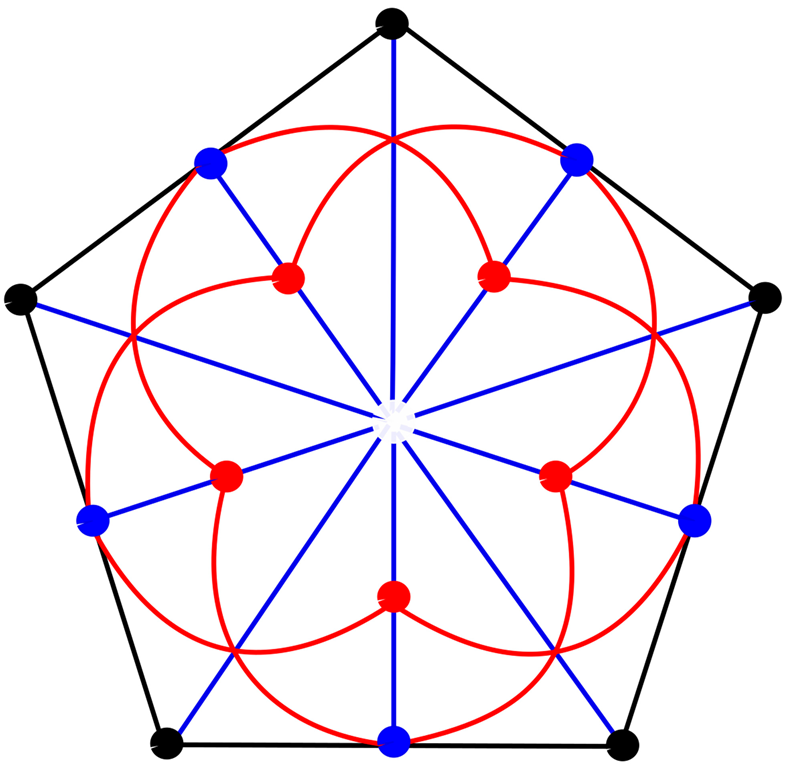
3. Conclusion

This note confirms the intimate connection between Desargues configurations and the generalized quadrangles of order two.

References

Beutelspacher, A., A defense of the honour of an unjustly neglected little geometry or a combinatorial approach to the projective plane of order five. J. Geom. 30, 182-195 (1987). [CrossRef]
Edge, W. L., 31-point Geometry, Math. Gaz. 39 (1955), 113-121.
Havlicek, H., Lenz, H. Another simple proof for the existence of the small Witt design. Elem. Math. 56 89-94 (2001). [CrossRef]
Hirschfeld, J. W. P., Projective geometries over finite fields, Clarendon Press, Oxford, Second Edition, 1998.
Innamorati, S., Tondini, D., The yin-yang structure of the affine plane of order four, Ars Combin. 110 (2013), 193-197.
Mancini, C., Zannetti, M., 21=9+12: PG(2,4)=AG(2,3)+DAG(2,3), Ars Combin. 135 (2017), 103-108.
Saniga, M., Geometric Hyperplanes: Desargues Encodes Doily, HAL, Volume 2010, (2010) n. 0. http://gdmltest.u-ga.fr/item/hal-00550447/.
Singer, J., A theorem in finite projective geometry and some applications to number theory, Trans. Am. Math. Soc. 43 (1938), 377-385.
Tondini, D., An excursion in finite geometry, J. Interdiscip. Math. 22 (8) (2019), 1589-1595. [CrossRef]
Tondini, D., The type of a point and a characterization of the set of external points of a conic in PG(2,q), q odd, J. Discrete Math. Sci. Cryptogr. 23 (5) (2020), 1077-1083. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.