Preprint
Article
Real-World Urban Light Emission Functions and Quantitative Comparison With Spacecraft Measurements
Altmetrics
Downloads
159
Views
58
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
17 April 2023
Posted:
18 April 2023
You are already at the latest version
Alerts
Abstract
We provide quantitative results from GIS-based modelling of urban emission functions for a range of representative low- and mid-rise locations, ranging from individual streets to residential communities within cities as well as entire towns and city regions with the aim of whether lantern photometry or built environment has the dominant effect on light pollution. We demonstrate the scalability of our work by providing results for the largest urban area modelled to date, comprising the central 117 km2 area of Dublin City and containing nearly 42,000 public lights. Our results show a general similarity in the shape of the azimuthally-averaged emission function for all areas examined, with differences in total light output distribution depending primarily on the nature of the lighting and, to a smaller extent, on the obscuring environment including seasonal foliage effects. A comparison with global satellite observations shows that they are consistent with the deduced angular emission function for other low-rise areas worldwide. We further validate our approach by comparing results for a range of urban locations by the close agreement observed in a detailed comparison of with calibrated imagery from the International Space Station. To our knowledge, this is the first such detailed quantitative verification of light loss calculations.
Keywords:
Subject: Environmental and Earth Sciences - Remote Sensing
1. Introduction
Our goal in this work is to address a number of topics of relevance to energy and light pollution measurement. The emission function, i.e. the amount of light emitted in different directions is, a priori, unknown for complex situations involving different numbers and types of lighting in urban environments and needs to be calculated through analysis of ground-based scattering observations [1,2,3], or by means of theoretical models using either analytic simplifications or more detailed models requiring complex and time consuming high performance computing approaches, e.g. [4,5,6,7]. As a particular example of a worldwide approach to modelling, Falchi et al. developed a globally representative emission function based on their study of zenithal light emission measurements taken around and outside a sample of urban areas and then used this model to predict light pollution at sites remote from the emitting source [8].
As discussed in Paper 1 [9], our method to obtain the emission function involves an innovative, semi-empirical, GIS-based approach in that we model the emission data from the ground upwards using information about public lighting, including the angular photometry of the individual lanterns, as well as elevation data at 1-2 metre spatial resolution to provide detailed information on obstructions and we refer the reader to that paper for details. The output of this approach is a representative emission function which includes both direct and diffuse emission and which can be readily tailored to account for differences in light sources, surface reflectivity etc. Although GIS-based approaches using estimated light locations coupled with ground measurements of illumination, to our knowledge there have been no integration of lighting and obstruction information to produce a comprehensive picture – see, e.g. [10].
In this paper we develop this work to show applications to specific areas of increasing area and complexity to produce representative emission functions for urban areas, i.e. a general description how much light is emitted at differing azimuth and zenith angles. Such emission functions have utility as they can be used for application to studies of light pollution’s impact on urban areas themselves as well as on the wider environment and, additionally, provide a means to interpret satellite observations. Our specific aim in this paper is to study a range of representative residential and general urban areas to determine their emission functions and assess the relative importance of lighting photometry compared with areal geometry, i.e. the relative importance of the number and distribution of both public lighting compared with the number and type of buildings or trees. Irish building heights are relatively low and predominantly in the low- to mid-rise class, as there is a 26 metre high limit in the centre of Dublin with lower levels in suburban areas and outside the capital. In the areas of study chosen for this paper building heights are typically two to three stories.
2. Materials and Methods
2.1. Selection of areas
We have sampled a range of local environments defined as low- to mid-rise buildings and also within the categories of continuous or discontinuous urban fabric as defined by the EU Corine landuse categorisation. To span a wide range of environments we have chosen areas ranging from suburban residential, through complete towns, to city centre locations. We include the areas already introduced in Paper 1 together with a range of new locations and apply our study to additional elevation datasets which have come available. Note that our models only include public lighting as the information from local authorities enables us to have a complete and detailed inventory to metre level accuracy, though we aim to extend our work in the future to include other light sources. The date range modelled is the period 2015-2017 as this is the date range covered by our public lighting databases as well as the digital elevation data. For this period public lighting was predominantly of the low or high pressure sodium type, which we will refer to as LPS and HPS, respectively. For ease of intercomparison, in all cases we adopt a surface reflectivity of 10% as representative of urban roadways.
2.2. Data and locations
Our work makes use of a number of input datasets including light detection and ranging (LiDAR) digital elevation datasets which map buildings and trees, and we couple this with information on public lighting types and locations, all at metre-scale precision. Basic information regarding the datasets is given in Table 1. In the following sections we will discuss the test regions in rough order of their size, from individual residential areas to towns and larger city areas. In all models we use a surface reflectivity of 10%, representative of urban areas.
In Table 2 below we present a summary of the characteristics for all areas studied in this paper. Besides the basic information for each location, included in the table are a number of parameters related to light output, including a parameter an indication of the relative impact of foliage on the total light emitted in the upward hemisphere. The two columns labelled “% to zenith” and “output relative to Lambertian” are intended to summarise the results of each set of calculations from the point of view of air- or space-borne observations. Under the assumption that a series of near-nadir (within 20° of nadir) observations of a given location are made and fitted with a Lambertian model, i.e. interpreted as being due to purely Lambertian (diffuse) emission, the first number indicates what fraction the resulting emission integral is of the total light which would be emitted upwards from a uniformly flat location without obstacles. The second number indicates the magnitude of the correction required to bring the assumed Lambertian emission into agreement with the total emission to the upward hemisphere. For comparison, the equivalent correction factor for a similar approximation to the model adopted by Falchi et al. ([8]) is 12% larger than the Lambertian integral normalised to the near-nadir.
The large output of the residential models is biased by the presence of many low wattage LPS lanterns in these areas which, as noted earlier, produce a larger amount of upward light compared with more modern units. For the city centre areas, there is both a reduction in the amount of LPS lighting and a lower foliage correction value for these areas. The latter is to be expected in these less vegetated environs, as there are only a few relatively low wattage lights bordering park areas, and relatively few large trees which can shield higher output units which tend to be placed around 8-10 metres above road level.
3. Results
3.1. Dublin residential areas
For the residential areas we chose locations where various types of LPS lighting dominated as these older units have the widest distribution of light and so the largest proportion of direct to diffuse emission, with up to 10% of the lamp output being directly emitted above the horizontal for LPS 55W prismatic lens units [9]. Our aim is also to model locations which can be readily compared with spacecraft data, and the relatively monochromatic light provided by LPS units facilitates calculations to convert from lumens to watts, which are the more usual units for earth observation.
We used colour imagery obtained from the International Space Station (ISS) in conjunction with our public lighting databases to identify contiguous areas with predominantly LPS lighting and similar wattage throughout – either 55W, 90W, or 135W, depending on location. Additionally, we used the ISS imagery to identify areas which were uncontaminated by neighbouring lighting such as commercial or architectural floodlighting. In this regard the ability to determine both intensity and colour from the ISS camera data proved useful in distinguishing useful areas as these locations are easily distinguishable in the imagery and – for the wattages used in our study – at intensities where the camera response is linear. Our chosen areas lie at distances ranging from two to nine kilometres from the centre of Dublin, with the bulk being beyond four kilometres.
The representative residential areas chosen were sufficiently large to contain tens to one hundred lanterns (see Table 2). In terms of general environment, residential streets had roadways of 6 to 8 metres wide, with tree-lined pavements and an average building height (ABH) – defined as height above roadway of 3 meters or more, to exclude walls, trees etc. – of 7.1 metres, with a standard deviation (SDBH) of 2.36 metres. The residential public lighting lanterns were located 6 to 7 metres above the ground, while higher wattage lighting was located at 8 to 10 metres above the roadway on busier roads which were up to 11 metres wide. The geometry of the individual areas varied from housing estates to single streets and are classed as discontinuous urban fabric in the EU Corine 2018 land cover database. Modelling of the areas to produce azimuthally-averaged emission functions followed the procedure outlined in Paper 1. A point to note for all results reported in this work is that, although the lantern photometry only provides data for a discrete set of angles, we have fitted a sixth order polynomial to the calculated values in order to produce a smooth curve for both display and also numerical integration purposes.
The results presented in Figure 1 show that the azimuthally-averaged radiant intensity emission functions. Each curve is normalised to its zenithal value so that the relative behaviour of the curves can be readily seen. The data fall into two broad categories, dependent on the nature of the lantern: the lanterns with the highest emission correspond to locations where there is a large component of emission to intermediate angles from 55W LPS lanterns with prism lenses. The local environment is a secondary effect which generates the spread of results within both broad categories, though the direct emission from the 55W lanterns exaggerates this behaviour.
To illustrate the importance of direct emission in these cases we show in Figure 1 (b) the reflected component only which illustrates that there is little difference between any of the areas in this respect. This plot also indicates the expected behaviour when these lanterns are replaced with more modern units with better light control and the improvement can be seen in Table 2 where the integrated light ratio is shown under the column “Direct/Total”.
3.2. Irish towns
We also studied whole rural Irish towns, comprising the towns in the Cork area introduced in Paper 1 supplemented by larger towns selected on the basis of available digital elevation models – details are presented in Table 2. As for the residential areas, Irish towns are generally low- to midrise in height with a mix of street widths: for market towns there is a wider street or square, but narrower streets elsewhere. For these locations the lighting is again predominantly of LPS and HPS type, though not as uniform in wattage as the Dublin residential areas which were chosen to be near-uniform in character. Additionally, when moving to larger urban areas there may be a range of road sizes and also a mix of public and commercial lighting. The current work does not intend to provide a complete model for these towns in terms of all lighting components, but rather to test our model over larger areas and to study the influence of larger scale environments. The intended goal is to determine whether there are any commonalities in terms of emission function for these locations and to study how the wider environment may influence the emission of light into the surrounding countryside and to space.
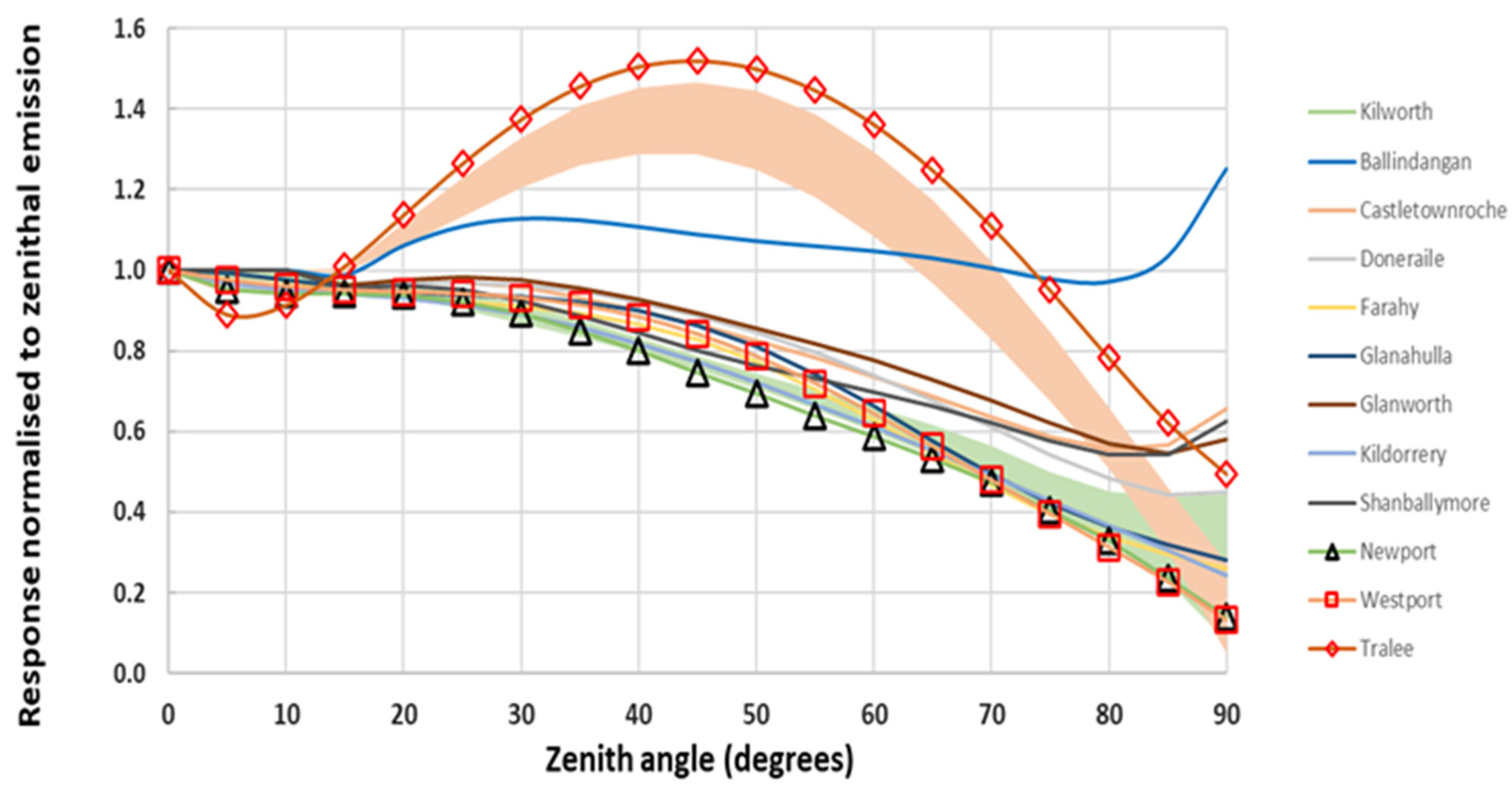
For the largest town modelled, Tralee County Kerry – the administrative centre of the county – there are over 5,000 public lights within an area of 19 km2. As a test case we modelled the entire town assuming that all public lighting was of the worst controlled type, i.e. the LPS 55W lanterns present in the residential areas described above and discussed in Paper 1. Our results are shown in Figure 3 where the towns from Paper 1 are shown as lines, while the new towns are shown with lines and open symbols. It is readily apparent that the results for Tralee follow the same trend as the residential cases containing this type of lantern but, since all the lighting is set to this one type, the model output is at the upper bound of the previous results and can be taken as the worst case scenario in terms of light pollution. We note that the diffuse component for this town follows almost exactly a pure Lambertian distribution although, as noted in Table 2, the upward emission from all areas is diminished to varying extents relative to an obstruction-free landscape. The worst-case example from Paper 1 is seen as the line trending to higher output at the largest zenith angles and is again the worst example of all towns modelled.
Figure 2.
Azimuthally-averaged results for the towns modelled in Paper 1 together with model results for three additional towns shown by the lines and open symbols. The shaded regions show the range of values for the residential areas discussed above. See text for details.
Figure 2.
Azimuthally-averaged results for the towns modelled in Paper 1 together with model results for three additional towns shown by the lines and open symbols. The shaded regions show the range of values for the residential areas discussed above. See text for details.
3.3. Dublin City
To compare our results with those for more urbanised areas we analysed the Dublin test area presented in Paper 1. This area lies approximately one kilometre from the City Centre and consists mainly of mid-rise commercial buildings set along wide streets with narrower streets off them. Within the area are a number of enclosed public parks and there are also a few boulevard areas. The 1 metre resolution LiDAR data presented previously were obtained in March 2015 when the trees were in leaf, while the 2 metre resolution data presented here were obtained between December 2011 and February 2012. The model output for these two datasets is indicated in Figure 3 by the curves marked “NYU” as the original dataset was taken as part of an New York University programme. There is very good agreement between the models based on the two seasonal datasets with less than 1% difference between the results for both the total emission and its dominant diffuse component, and only a 3% increase in the weaker direct emission component between the summer and winter dataset. These results are, perhaps, to be expected as there is generally little tree cover aside from along the margins of the public parks where some lights are located, and also only relatively few cases where there are trees bordering the roadways.
In keeping with our previous observation that the biggest difference between models is due to the photometry of the predominant lantern type, we find that our result for the inner city area is roughly similar to that expected from one of the smaller residential areas with better controlled lighting, consistent with the small proportion of 55W LPS lanterns present in the inner city, which is dominated by higher wattage HPS lighting (see Table 2 for numbers). In the same figure we also plot the curve derived by Falchi et al. [8] from their inversion of global skyglow measurements and it is heartening to see the close agreement between the two sets of results derived by different means. We interpret this finding as follows: although other locations may have high-rise structures, it would be expected that the bulk of the emission at near-horizontal angles that contributes to skyglow in surrounding regions comes from the low- and mid-rise areas. We also expect that the bulk of public lighting in the areas studied by Falchi et al. would now be of HPS type with better lighting control.
Also included in Figure 3 is a test of our modelling approach to the entire Dublin City Council (DCC) area, amounting to over one hundred square kilometres and over 40,000 lanterns of both LPS and HPS types. The intention of this model was twofold: to see if the code would work efficiently with such a large area and number of lanterns, and also to get an estimate of what the entire City Emission Function looks like for the case of well-controlled lanterns with no (or very little) direct emission above the horizontal. We thus restricted the model to a diffuse component only and the model, including the generation of the base map of light pools around each light location and also the grid of shading models, ran in less than two hours on a modern 3.6 GHz CPU. It is notable that this model is almost identical with a Lambertian distribution although, as seen in Table 2 the emission to space is reduced relative to a model with no obstructions.
We calculated a version of the Li et al. ([11]) “blocking index” for the whole of the DCC area for the case of the two azimuthal angles from which city of Dublin is viewed by the SUOMI satellite, viz. 99° and 289°. Our approach differs from that of the Li et al. paper in that we used the GIS plugin for shadow depth to generate a raster masked to show the visible areas from a given azimuth and elevation. A final output raster was generated in which each pixel contains the value of the elevation when it first becomes visible, i.e. the blocking index value. Our approach has the advantage that it includes all obstructions over the entire mapped area simultaneously.
As the lit areas are also available, we can use these to weight the blocking index raster to select areas of relevance to the lit model. This has two advantages: firstly that the numbers derived are for the individual locations, rather than random points along the street and, secondly, that better lit locations receive a higher weighting, so the angle derived is more representative of the installed lighting. From our analysis, the minimum elevation angle required for a pixel to become visible is similar for both azimuths and equivalent to a zenith angle of 64°, although for an inner 2 km radius around the commercial heart of the city the zenith angle is smaller by 6° relative to the value for the entire Dublin City Council area due to the presence of higher structures. This finding indicates why the poorer lighting control of the 55W LPS units is reduced towards higher zenith angles, such as shown in Figure 3. This reduction is important as light emission in the range 80° < zenith angle < 90° is the dominant contributor to rural skyglow, e.g. [12]. In comparison, the relatively unobstructed emission at lower zenith angles contributes predominantly to the urban skyglow. Through integration of the light in these ranges we find that the ratio of light in the “rural” to “urban” range is marginally lower in the 55W LPS dominated residential areas due to the increased proportion of light to lower zenith angles and, for all regions, increases from 4% in the winter data to 8% in the summer months, though this is also influenced by the restriction in light towards the zenith by tree canopies. For comparison, the ratio for towns (summer data only) ranges from 4% to 6%, so 6-7% is a representative value for all locations examined over the summer months.
3.4. Comparison with SUOMI satellite measurements
It has been pointed out by other authors ([11,13,14]) that the SUOMI satellite observations of cities taken at different nadir angles show discrepancies in the observed radiance, indicative of variations in light output with angle that differ from a simple Lambertian assumption. There are two general effects which can be observed: a light distribution in which the observed radiance decreases with increasing zenith angle, and a distribution where the where there is an increase with zenith angle. The former behaviour is ascribed to the effect of high-rise buildings obstructing emission towards the horizon, and the latter occurs where low-rise buildings are present. While there are relatively few high-rise buildings in Irish cities, we can compare our predicted light to that observed for other worldwide locations using the fits reported in Li et al. [14].
For comparison with the Li et al. fits, in Figure 4 we plot our model results in terms of radiance, i.e. with a correction for areal projection effects, consistent with the way data from the SUOMI or NOAA-20 VIIRS DNB instruments are processed and reported. Plotted like this, a true Lambertian response will follow a horizontal line of unity, as is the case for the citywide diffuse-only model for Dublin (marked DCC). A reasonable upper limit is provided by the uppermost line which represents the results for the town of Tralee, modelled assuming the worst-case 55W LPS lanterns.
The plot also shows that the majority of our results lie within the boundaries and follow the trend of the satellite observations which suggests that our models have generic application. In the Irish cases we are limited to relatively low building heights so we cannot comment on how our model compares with the high-rise urban centres found in other countries, but we aim to address this once suitable international data is identified.
3.5. Seasonal effects
Although the impact of the high reflectivity of snow on light pollution has been discussed for other locations snow events are relatively unimportant in the mild Irish climate. The effect of snow on the ground is to increase the ground reflectivity, while leaving the direct emission unaffected, so we expect that for lanterns with relatively poor lighting control the total detected output under such conditions will more closely approximate Lambertian emission.
Other than snow, a relatively large seasonal effect in temperate latitudes results from the change in vegetation levels over the year [15]. Such effects can also be examined in our models as datasets covering a range of dates are available. For the case of Dublin, the higher resolution dataset was obtained in the months of May 2013 and June 2018, while the lower resolution dataset was obtained in the period mid-December 2011 to early February 2012. We return to the residential areas discussed above as these consist of relatively open areas of two-storey housing with differing amounts of trees lining the roads and compare the two datasets to determine typical ranges in light output. In Paper 1 we noted that aggregating digital elevation data from 1 metre to 2 metre pixels does not affect the overall emission results and we appeal to this finding when comparing these two datasets to determine the seasonal effects of foliage cover on the emission function.
In Figure 5 we plot two extreme cases of behaviour due to seasonal effects, normalised to the winter zenithal emission in both cases. The upper (winter) curves for both locations agrees with a Lambertian model to a high degree, but there is a noticeable reduction of light output during the summer months which differs between the sites. The region with the largest effect is a straight road with fully mature tree canopies up to 13 metres high, while the lanterns are at 10 metres above the roadway – see Figure 6 for an illustration of the proximity of the tree canopies.
By comparing the two datasets taken at different seasons for each area we find a range of behaviour as exemplified in the Figure Figure 5, with a maximum decrease in total output by 38% between winter and summer which compares favourably with the 31% value reported for tree-lined streets in Cambridge Massachusetts [16]. Their result was obtained from sky visibility analysis derived from Google Street View imagery, though we note that our approach is much less computationally intensive.
3.6. Azimuthal photometry
Our work to this point has made use of azimuthally-averaged emission functions based on similarly-averaged luminaire photometry and these functions enable the calculation of total emission to space and the surrounding environment. The justification for this is that for relatively large numbers of light sources, sampling of viewpoints to each light location should be (relatively) random, so azimuthally-averaged values would be sufficient to provide relatively robust results. However, when we want to study small numbers of lights and/or the emission along a particular line-of-sight, such as in an individual spacecraft image, then we need to consider that the lantern photometry is non-uniform in azimuth and elevation, particularly at low elevation angles (large zenith angles) where the type of light distribution of the lantern is important. For most streetlights the lighting distribution is chosen to produce the maximum amount of light across and along the street i.e., in lighting photometric terms along the direction 0° < C < 180° (see Appendix A.1 for an illustration), with the maxima towards the extremes of this range. At high elevations (low zenith angles) the published photometry is fairly uniform with azimuth, hence we find little difference between the two approaches for zenith angles less than approximately 50° as shown in the examples in Figure 6.
Figure 6.
There can be quite large differences between the single line-of-sight model and the azimuthally-averaged values at large zenith angles, i.e. near-horizontal emission, however the differences are negligible at zenith angles below 50° for the case of these low-rise environments as the lantern photometry is more symmetric for these angles. The plots show the difference between the use of azimuth-averaged values (shown as the darker line in all plots) and the azimuth specific values (shown with a lighter line) for the case of a) a housing estate with many street orientations; b) a single road orientated roughly perpendicular to the line-of-sight; c) a single road orientated roughly along the line-of-sight.
Figure 6.
There can be quite large differences between the single line-of-sight model and the azimuthally-averaged values at large zenith angles, i.e. near-horizontal emission, however the differences are negligible at zenith angles below 50° for the case of these low-rise environments as the lantern photometry is more symmetric for these angles. The plots show the difference between the use of azimuth-averaged values (shown as the darker line in all plots) and the azimuth specific values (shown with a lighter line) for the case of a) a housing estate with many street orientations; b) a single road orientated roughly perpendicular to the line-of-sight; c) a single road orientated roughly along the line-of-sight.
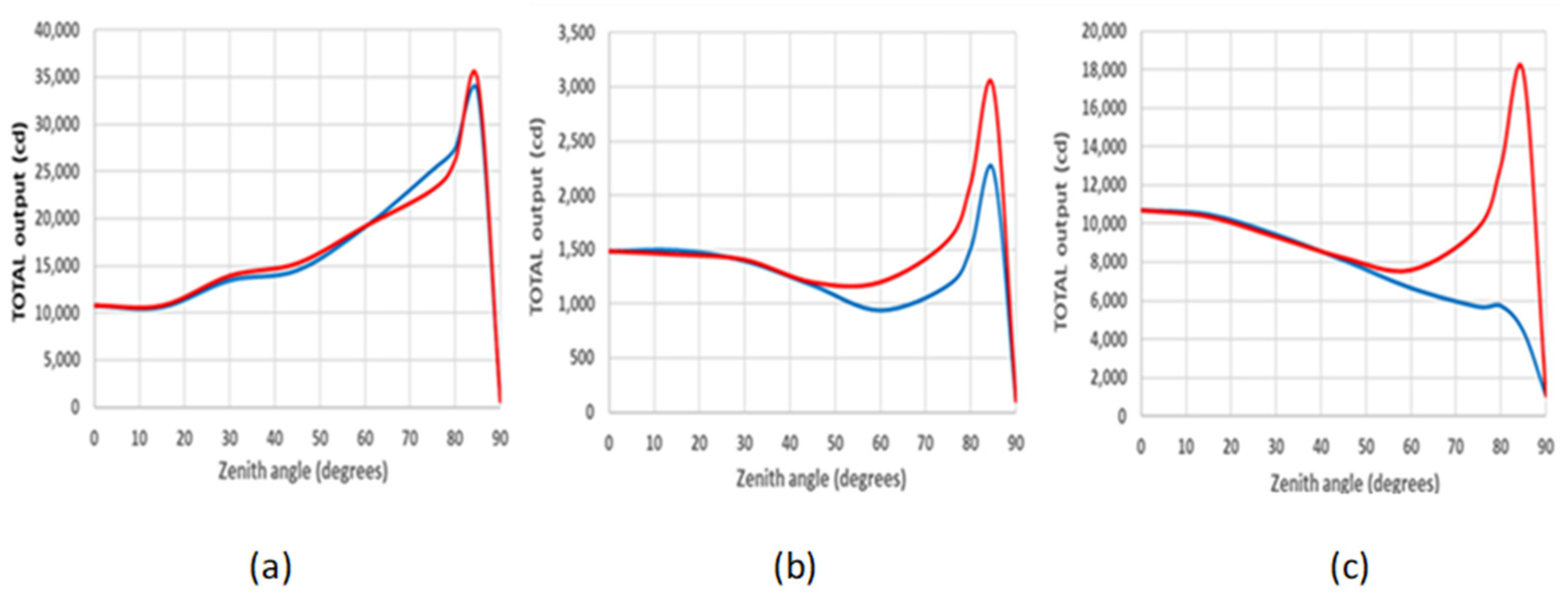
Note that the results from the averaged and correct calculation of azimuth shown in Figure 6 (a) are very similar as there are a range of orientations of the roads within the housing estate, but that differences can be much larger where the number of lights is small and/or a single road is modelled with a restricted range of lantern orientations relative to the line-of-sight. Such differences need to be borne in mind when modelling or when comparing areas of different size and/or range of orientations.
3.7. Quantitative Comparison to ISS Data
We have updated our model to include this angular dependence by incorporating OpenStreetMap data to determine the azimuth of the road segment closest to each light. A suitable change of reference then provides the C-angle appropriate to a viewpoint from due North, which is easily modified to deal with any given line-of-sight azimuth. Finally, by referencing the photometric tables appropriate to each luminaire we can include the appropriate direct emission in our calculations.
We located an image of Dublin (ISS045-E-170140) taken from the International Space Station in winter 2015 which had both good resolution and was roughly contemporaneous with the digital elevation and public lighting data. This image was georeferenced, calibrated to radiance units and corrected for atmospheric absorption and scattering. We used the radiance-calibrated images in the G band as these are roughly coincident with the photopic band used for determining our model radiances and facilitated comparison with our model output. We used the information available in the NASA image footprint calculator to determine the location of the viewpoint relative to the ground spreadsheet at and so determine the appropriate azimuth and nadir angle to model.1
By using vector shapefiles of the test regions we were able to extract both model and observed radiances for each of the residential areas and compare them directly. We have used a uniform reflectance of 10% for all areas and not adjusted the model output to account for any differences in environment or orientation beyond the selection of the appropriate azimuthal photometry for the observation geometry. Finally, the model results were converted from lux to watts per square metre by using the known wavelength of the sodium emission and the luminous efficacy for that value. The results can be seen in Figure 7 together with the best-fit linear model to the data. From the correlation coefficient of 0.93 it can be seen that there is a very good agreement between the model output and the observations, with a slope close to unity and a high level of significance given the stringent nature of the test, with no other free parameters. While our model results are slightly offset to higher values, we note that we have not attempted to account for degradation in light output due to total failure of individual lamps, nor for the progressive decrease in output due to lamp degradation and/or dirty lantern lenses, i.e. the maintenance factor has been set to unity for all locations.
4. Discussion
We have presented a collection of results from our modelling of low- and mid-rise locations in Ireland using realistic photometric data. From our modelling we find that the main difference in normalised emission function between low-rise locations is due to lantern photometry, with obstructions such as foliage causing a secondary effect. Our results are generally similar with the light distributions found for similarly low-rise developments worldwide, based on SUOMI satellite observations. While details will necessarily vary, this generality is important for the understanding of artificial light at night propagation and also inferences from satellite data for similar locations worldwide, including informal developments in the developing world, though more work needs to be done to determine the fraction of light emitted upward for those locations. We also showed that the emission function developed from skyglow data by Falchi and coworkers is a good approximation to these data [8].
A related finding is that the production of a VIIRS Black Marble output product based on data taken within 20° of nadir is a good choice in terms of limiting the variation between observations and also between sites. Although the resulting mean radiance does not directly enable the true value of emission to be determined, processed data will, at least, be consistent in that the assumption of a Lambertian dependence is closely met over the range. With the continued move to better controlled lighting this should only improve, as has been shown in the results of [187].
We have demonstrated and quantified the effect of seasonal foliage on the light emission from a range of areas and show that it is consistent with that found independently for a similar area using a different technique. The accuracy and wide-area coverage of digital elevation data enables such calculations to be performed quickly and completely and is much less computational intense than the approach of Li and co-workers [11].
A development of our model to use more detailed photometric data to calculate the radiance towards a single point-of-view produces results in very good quantitative agreement with calibrated space imagery, suggesting that our models can be developed to enable approximate calibrations for public lighting as imaged with ISS data, hence obviating atmospheric corrections.
Our results have implications for other ALAN workers, including those working in the fields of environment and health studies as the use of satellite imagery to determine the nature and amount of night-time light currently depends on assumptions of the light distribution at low angles that may vary markedly from simple assumptions.
As in Paper 1 we have focussed on modelling public lighting which accounts for all, or a large part of the emission in the regions modelled. While this is not a complete picture, it enables us to compare the influence of environments directly without additional complications. For the residential areas, as noted earlier, we used the ISS data as a guide to the selection of public lighting dominated emission. We are working to add additional lighting sources to our model such as floodlighting in order to more completely represent other significant sources of light pollution and, in particular, of light that peaks close to the horizontal and hence will be of importance in terms of its impact both within urban areas and also on the peri-urban environment.
Author Contributions
Conceptualization, B.E.; Methodology, Software & Validation, B.E., X.Y. and K.P.; Formal Analysis, B.E.; Investigation, X.X.; Resources, X.X.; Data Curation, B.R.; Writing – Original Draft Preparation, Review & Editing, Visualization: B.E.; Supervision, Project Administration & Funding Acquisition, B.E.
Funding
We gratefully acknowledge funding provided by the Sustainable Energy Authority of Ireland (SEAI)
Data Availability Statement
All data other than the 1 metre resolution data for Dublin City are publicly available from the Irish government web portal https://data.gov.ie. LiDAR data from this site is © Government of Ireland. These datasets were created for and are the property of the Office of Public Works and this copyrighted material is licensed for re-use under the Creative Commons Attribution 4.0 International licence. Commercial elevation data for our study areas was obtained with the kind assistance of Prof. Gerald Mills of University College Dublin. Esri imagery was utilised in the production of this work and obtained via. QGIS QuickMapServices - ArcGIS® software by Esri. ArcGIS® and ArcMap™ are the intellectual property of Esri and are used herein under license. Copyright © Esri. All rights reserved. ISS imagery was provided by the Earth Science and Remote Sensing Unit, NASA Johnson Space Center and our thanks go to Alejandro Sanchez de Miguel of Complutense University of Madrid for providing the radiance calibration. We made use of the EU Corine database which is © European Union, Copernicus Land Monitoring Service 2018, European Environment Agency (EEA). Figure A1 is adapted from Figure 2 of Skarżyński, Żagan and Krajewski (2021) available under Creative Commons License CC BY 4.0
Acknowledgments
We acknowledge Pat Caden, Executive Engineer (retired), Dublin City Council, for providing the lighting database for the city, and also the Irish Road Management Office (RMO) for providing data for the areas outside Dublin City. Finally, our thanks go to Peter McEnroe for his undergraduate project work in finding suitable urban test areas and producing the initial shapefiles.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
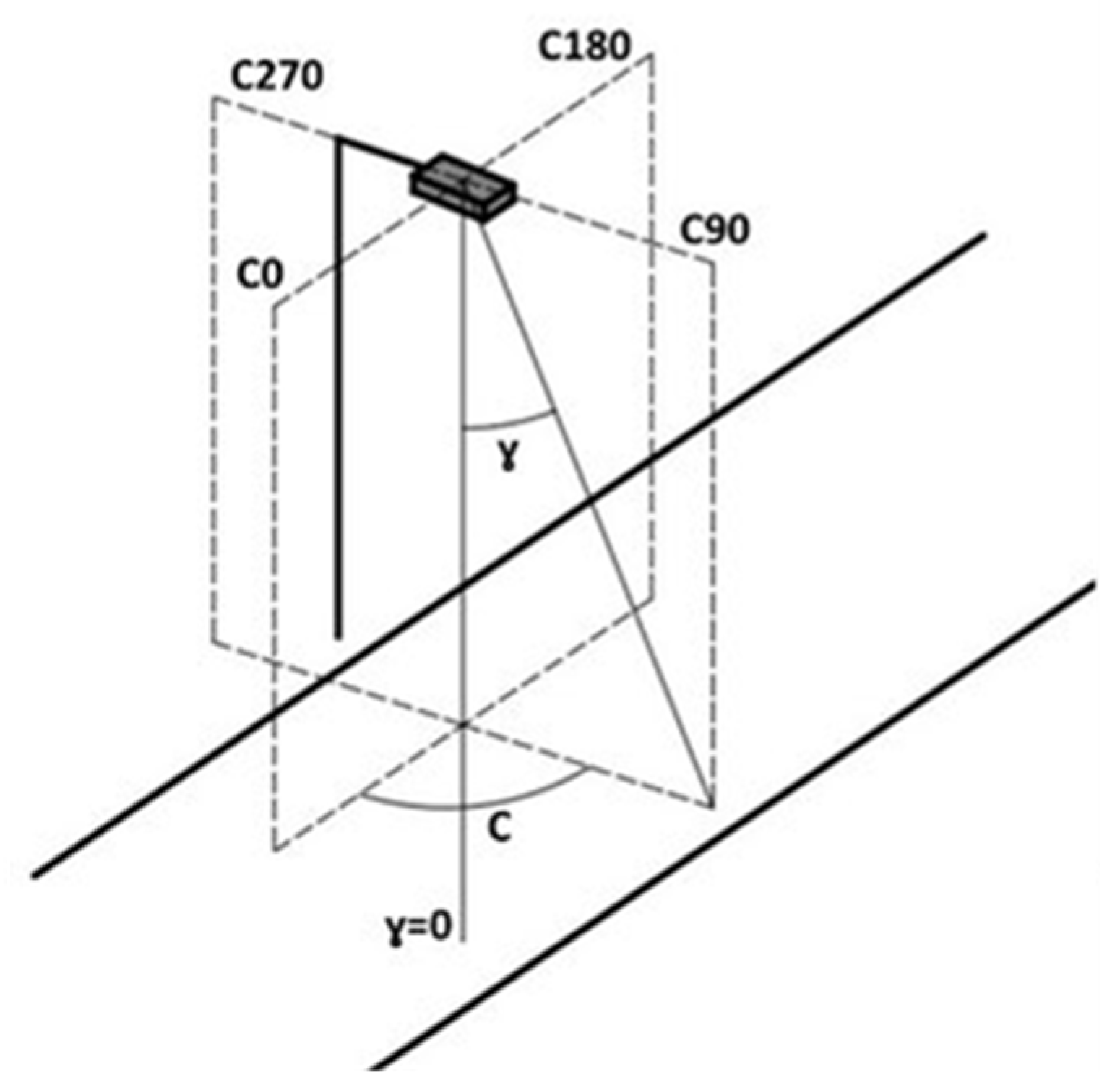
Lantern photometric measurements provided by manufacturers contain data in both the horizontal and vertical plane and a realistic model of light output should take this into account, particularly where the numbers of lanterns are small so that statistical averaging does not apply. In particular, linear features such as roadways result in a distant point-of-view having only a limited number of viewing angles, expressed in terms of the angle of the observer to the road perpendicular, which is also the axis of the photometry in the C-Gamma system which is orientated as shown in Figure A1.
An elegant solution for the problem of obtaining lantern azimuths can be found by utilizing OpenStreetMap (OSM) data. Using the OSM database it is possible to download highways information for a given area and to obtain the alignment of a road in the vicinity of a given lantern. The azimuth from each lantern to the closest road segment for a large number of lanterns can then be determined in a matter of minutes. As the shortest distance line is perpendicular to the road axis, the lantern orientation (in photometric terms the C-angle) can be easily found from this number as the origin is at right angles, and to the right of, this line (see Figure below). By tagging each lantern in the database with this azimuth, the orientation of a lantern to the line-of-sight is easily found by adding any given observation azimuth to the stored lantern value.
Figure A1.
Diagram illustrating the definition of the (C, γ) angle definitions used in streetlight photometry. The figure is adapted from that found in.
Figure A1.
Diagram illustrating the definition of the (C, γ) angle definitions used in streetlight photometry. The figure is adapted from that found in.
Appendix B
Li et al have made use of a visibility angle for each pixel location based on the blocking nature of buildings [11]. In their approach they calculate the minimum elevation angle required to see the sky from the ground for all azimuths around every pixel location out to a used-defined radius. This is a computationally intense calculation with large rasters and, in our case of the Dublin City Council data amounts to nearly thirty million pixels. We have developed a more efficient GIS-based approach to calculate results for all pixels in the image based through casting shadows. For this we again make use of the QGIS Terrain Shading plugin. As noted above, this plugin generates a shadow raster for which the value at each pixel is the depth below a sharp shadow. By mapping the range of values to a binary mask – i.e., translating to a simple image illustrating locations lying above or below the shadow line – a virtual raster image can be efficiently generated for the entire image in one pass which takes into account all objects, including tall buildings far away from the reference location or, for example, relatively low obstructions such as trees for sightlines near the horizontal. As the code runs, a check is made if a given point becomes visible, i.e. when the depth below the sightline ceases to be negative and that zenith angle is recorded in a raster frame that is written out on completion of the run.
Since the viewpoint of the SUOMI and NOAA-20 satellites is of interest in light pollution studies, and these satellites have a restricted range of azimuths from any given location, it is possible to efficiently generate a shadow map for a range of elevation angles for the entire image at one time. In our implementation we calculated a grid of models for the relevant azimuthal angles (mean angles of 99° and 289° degrees for the Irish case) at 5° elevation increments. We can then access the location of individual lights to determine the viewpoint statistics or even use an OpenStreetMap vector road map to calculate the minimum visibility angle along all roads within the area of interest.
References
- Cinzano, P.; Falchi, F. The propagation of light pollution in the atmosphere. Mon Not R Astron Soc, 2012, 427, 3337–3357. [Google Scholar] [CrossRef]
- Kolláth, Z.; Kránicz, B. On the feasibility of inversion methods based on models of urban sky glow. JQSRT 2014, 139, 27–34. [Google Scholar] [CrossRef]
- Kocifaj, M.; Solano-Lamphar, H.A.; Gorden Videen, G. Night-sky radiometry can revolutionize the characterization of light-pollution sources globally. PNAS 2018, 116, 7712–7717. [Google Scholar] [CrossRef] [PubMed]
- Garstang, R.H. Model for artificial night-sky illumination. Publications of the Astronomical Society of the Pacific. 1986, 98, 364. Available at: https://iopscience.iop.org/article/10.1086/131768. [Google Scholar] [CrossRef]
- Luginbuhl, C.B.; Duriscoe, D.M.; Moore, C.W.; Richman, A.; Lockwood, G.W.; and Davis, D.R. From the Ground Up II: Sky Glow and Near-Ground Artificial Light Propagation in Flagstaff, Arizona. Publ. Astr. Soc. Pacific 2009, 121, 204–212 Available at:. [Google Scholar] [CrossRef]
- https://iopscience.iop.org/article/10.1086/597626.
- Aubé, M.; Kocifaj, M. Using two light-pollution models to investigate artificial sky radiances at Canary Islands observatories. Mon Not R Astron Soc. 2012, 422, 819–830. [Google Scholar] [CrossRef]
- Aubé, M.; Simoneau, A. New features to the night sky radiance model Illumine: Hyperspectral support, improved obstacles and cloud reflection. JQSRT 2018, 211, 25–34. [Google Scholar] [CrossRef]
- Falchi, F.; Cinzano, P.; Duriscoe, D.; Kyba, C.; Elvidge, C.; Baugh, K.; Portnov, B.; Rybnikova, N.; Furgoni, R. The new world atlas of artificial night sky brightness. Science Advances 2016, 2, e1600377. [Google Scholar] [CrossRef]
- Espey, B.R. Empirical Modelling of Public Lighting Emission Functions. Remote Sens. 2021, 13, 3827. [Google Scholar] [CrossRef]
- Bruehlmann, S.M. Measuring and Mapping Light Pollution at a Local Scale. MSc thesis submitted to Vrije Universiteit Amsterdam 2014. Available at: https://spinlab.vu.nl/websites/unigis/downloads/msc/SBruehlmann_MSc_DarkSky_141120_FinalPublication.pdf. (accessed on 13 April 2023).
- Li, X.; Shang, X.; Zhang, Q.; Li, D.; Chen, F.; Jia, M.; Wang, Y. Using radiant intensity to characterize the anisotropy of satellite-derived city light at night. Remote Sens. Environ. 2022, 271, 112920. [Google Scholar] [CrossRef]
- Baddiley, C.J. http://www.baddileysuniverse.net/ModelResults.aspx. (accessed on 13 April 2023).
- Tong, K.P., Kyba, C, Heygster, G., Kuechly, HU, Nothalt, J., Kolláth, Z. Angular distribution of upwelling artificial light in Europe as observed by Suomi–NPP satellite. Journal of Quantitative Spectroscopy and Radiative Transfer. 2020, 249, 107009. [CrossRef]
- Li, X.; Ma, R.; Zhang, Q.; Li, D.; Liu, S.; He, T. et al. Anisotropic characteristic of artificial light at night systematic investigation with VIIRS DNB multi-temporal observations. Remote Sens. Environ. 2019, 233, 111357. [Google Scholar] [CrossRef]
- Levin, N.; Zhang, Q. A global analysis of factors controlling VIIRS nighttime light levels from densely populated areas. Remote Sens. Environ. 2017, 190, 366–382. [Google Scholar] [CrossRef]
- Li, X.; Duarte, F.; Ratti, C. Analyzing the obstruction effects of obstacles on light pollution caused by street lighting system in Cambridge, Massachusetts. EPB: Urban Analytics and City Science 2021, 48, 216–230. [Google Scholar] [CrossRef]
- Wang, Z.; Román, M.O.; Kalb, V. NASA’s Black Marble Multiangle Nighttime Lights Temporal Composites. IEEE Geoscience and Remote Sensing Letters 2022, 19, 2505105, Available at: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9779217. (accessed on 13 April 2023). [Google Scholar] [CrossRef]
| 1 |
Figure 1.
Azimuthally-averaged radiant intensity results for the Dublin residential areas containing LPS lighting. In order to compare the areas the radiances have been normalised to the zenithal emission in each case. In Figure (a) the upper curves are for areas with the largest emission due to 55W units with prismatic lenses which contribute to excess emission in the upper hemisphere. Figure (b) shows the good agreement between all areas when only the diffuse (reflected) component is considered.
Figure 1.
Azimuthally-averaged radiant intensity results for the Dublin residential areas containing LPS lighting. In order to compare the areas the radiances have been normalised to the zenithal emission in each case. In Figure (a) the upper curves are for areas with the largest emission due to 55W units with prismatic lenses which contribute to excess emission in the upper hemisphere. Figure (b) shows the good agreement between all areas when only the diffuse (reflected) component is considered.
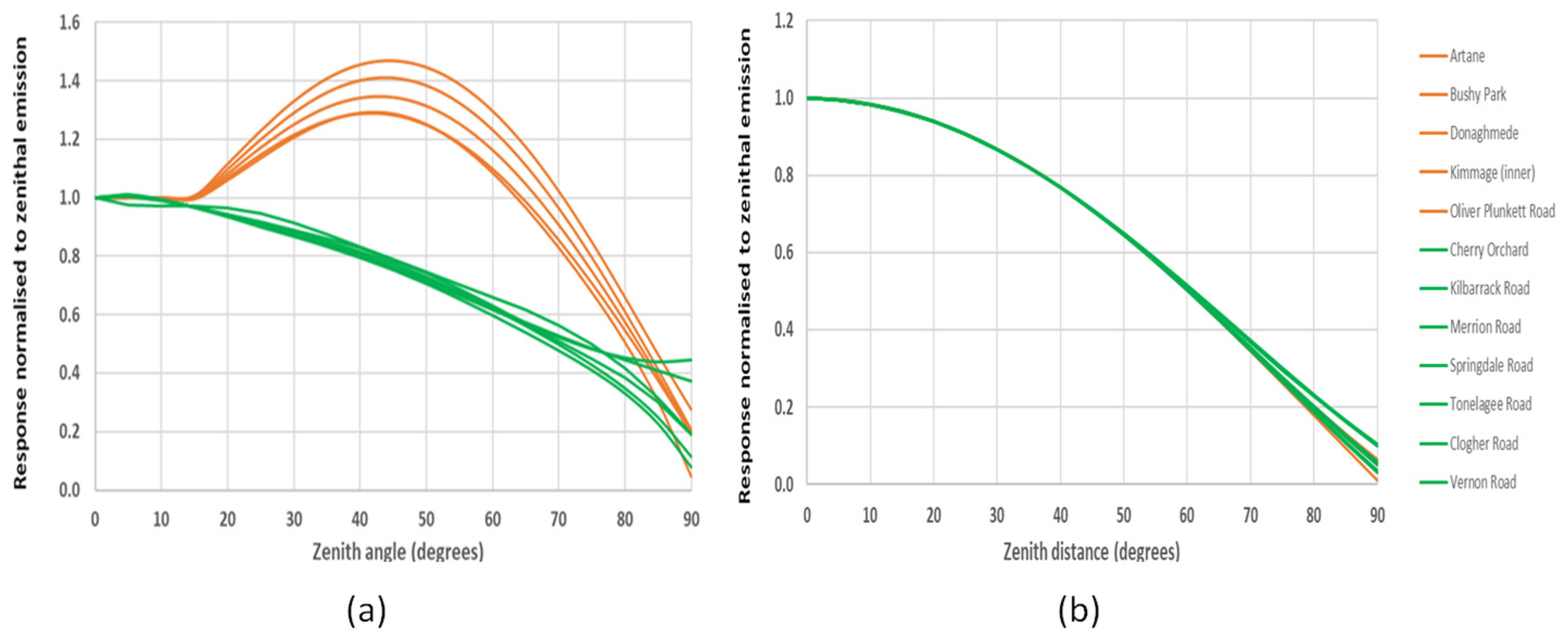
Figure 3.
Radiant intensity plot showing results for the central city area presented in Paper 1 for summer and winter datasets (filled circles), both of which lie above the band of better-controlled residential lighting and are indistinguishable on this plot. Also shown is a model of the diffuse-only emission from the entire Dublin City Council region (squares) which is well approximated by a Lambertian model. The dashed curve with circles represents the model used for the 2015 World Atlas of light pollution. For comparison, the ranges of data for the residential areas previously described are indicated by the shaded areas.
Figure 3.
Radiant intensity plot showing results for the central city area presented in Paper 1 for summer and winter datasets (filled circles), both of which lie above the band of better-controlled residential lighting and are indistinguishable on this plot. Also shown is a model of the diffuse-only emission from the entire Dublin City Council region (squares) which is well approximated by a Lambertian model. The dashed curve with circles represents the model used for the 2015 World Atlas of light pollution. For comparison, the ranges of data for the residential areas previously described are indicated by the shaded areas.
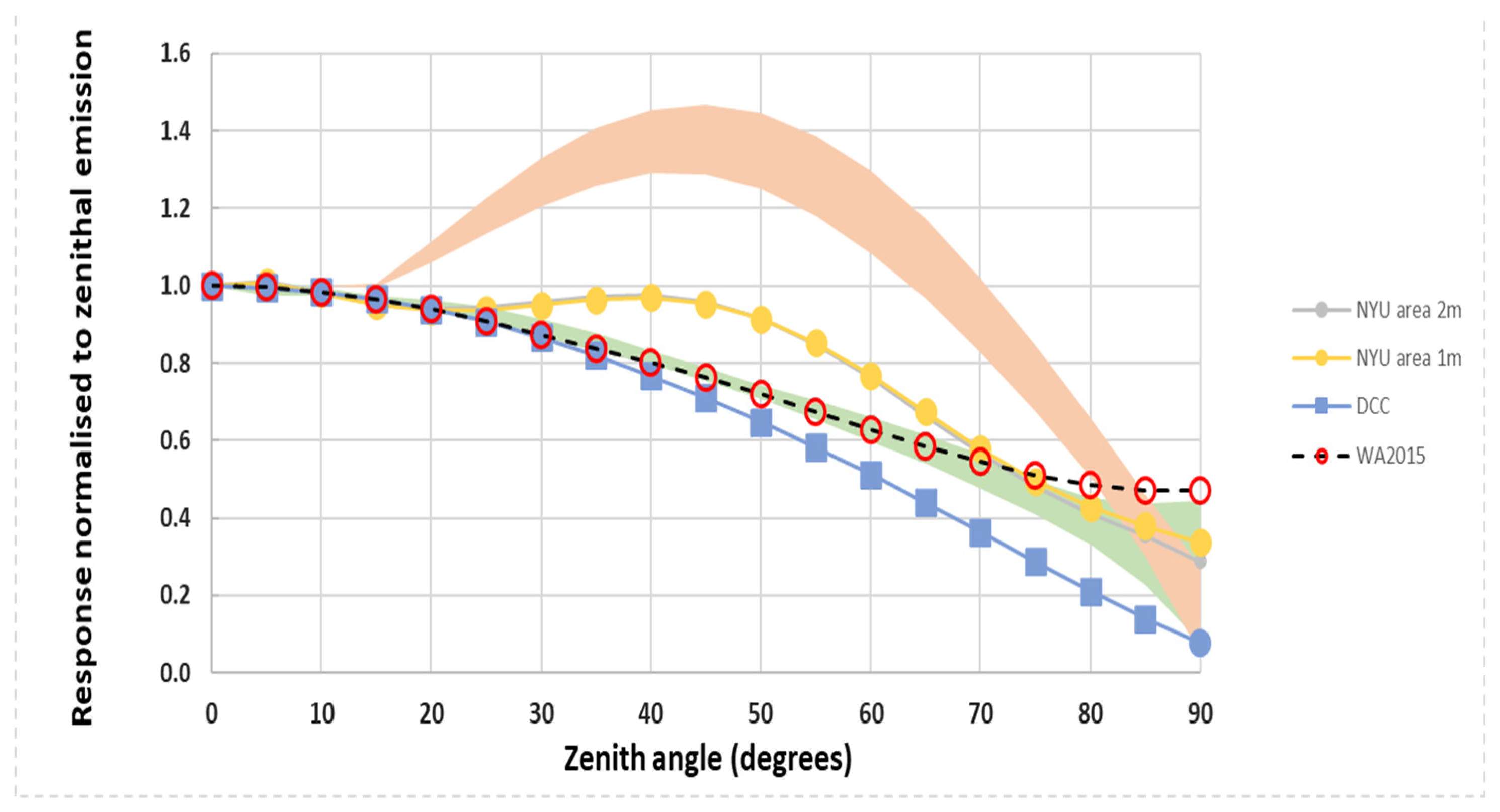
Figure 4.
Model outputs for all urban areas reported in this paper are overlaid on the range of results for SUOMI VIIRS/DNB observations of worldwide cities reported by Li et al. [14]. The range of reported global values are indicated by the cream shaded region (identified as low-rise neighbourhoods) and light blue (identified as high-rise neighbourhoods). For references to colour see the on-line version of the paper. Note that the limited range of angles plotted is as a result of limitations on the SUOMI satellite viewing angle.
Figure 4.
Model outputs for all urban areas reported in this paper are overlaid on the range of results for SUOMI VIIRS/DNB observations of worldwide cities reported by Li et al. [14]. The range of reported global values are indicated by the cream shaded region (identified as low-rise neighbourhoods) and light blue (identified as high-rise neighbourhoods). For references to colour see the on-line version of the paper. Note that the limited range of angles plotted is as a result of limitations on the SUOMI satellite viewing angle.
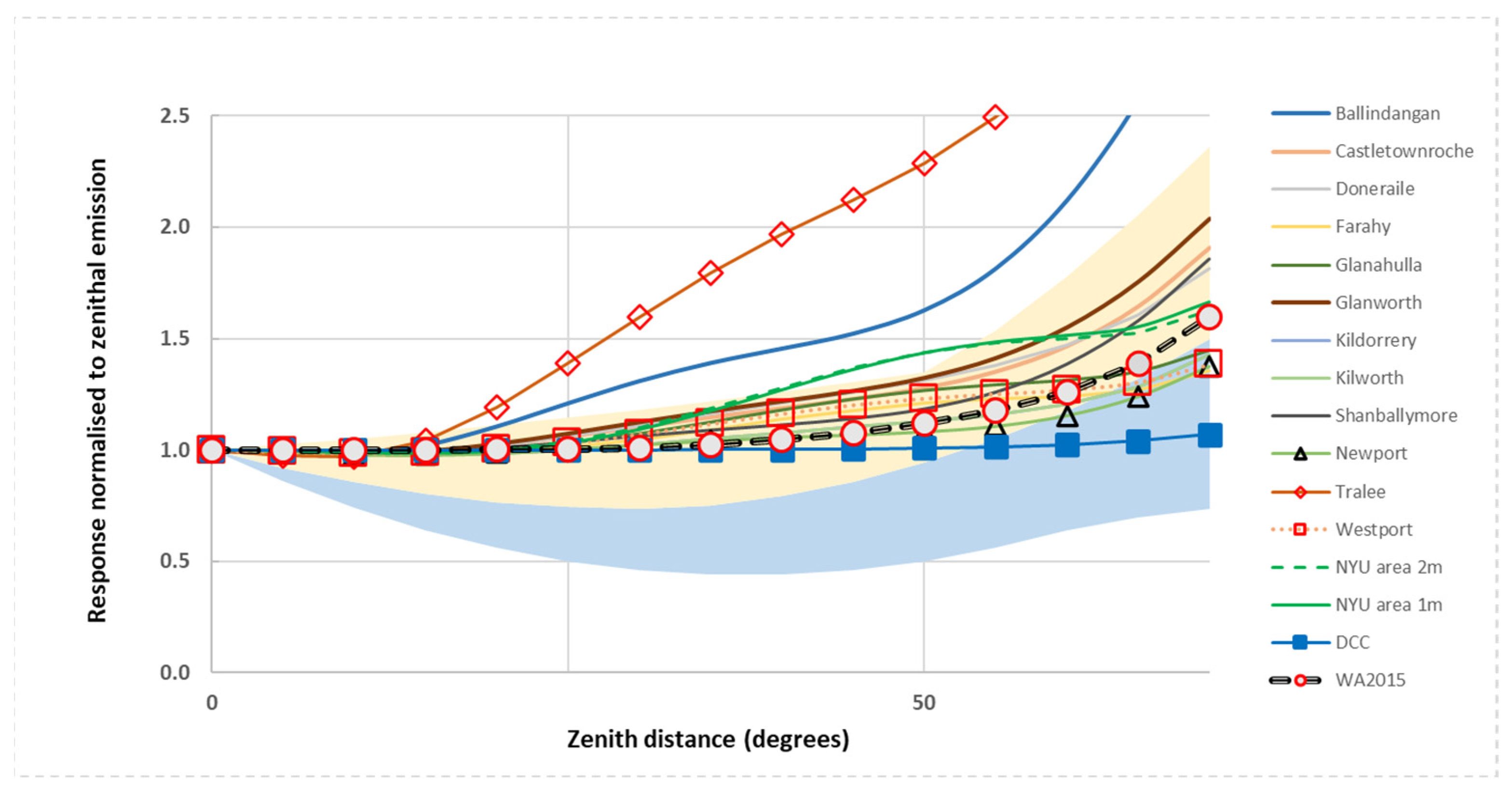
Figure 5.
The emission function of the diffuse (reflected) component alone is shown to illustrate the effects of foliage in two extreme examples found in our residential sample areas. We have normalised the curves to the zenithal maximum of the winter emission for each location so that the relative decrease in summer months can be more clearly seen. The winter emission function is almost identical for both and has a pure Lambertian response, but the decrease due to summer foliage differs between the two locations. See text for details.
Figure 5.
The emission function of the diffuse (reflected) component alone is shown to illustrate the effects of foliage in two extreme examples found in our residential sample areas. We have normalised the curves to the zenithal maximum of the winter emission for each location so that the relative decrease in summer months can be more clearly seen. The winter emission function is almost identical for both and has a pure Lambertian response, but the decrease due to summer foliage differs between the two locations. See text for details.
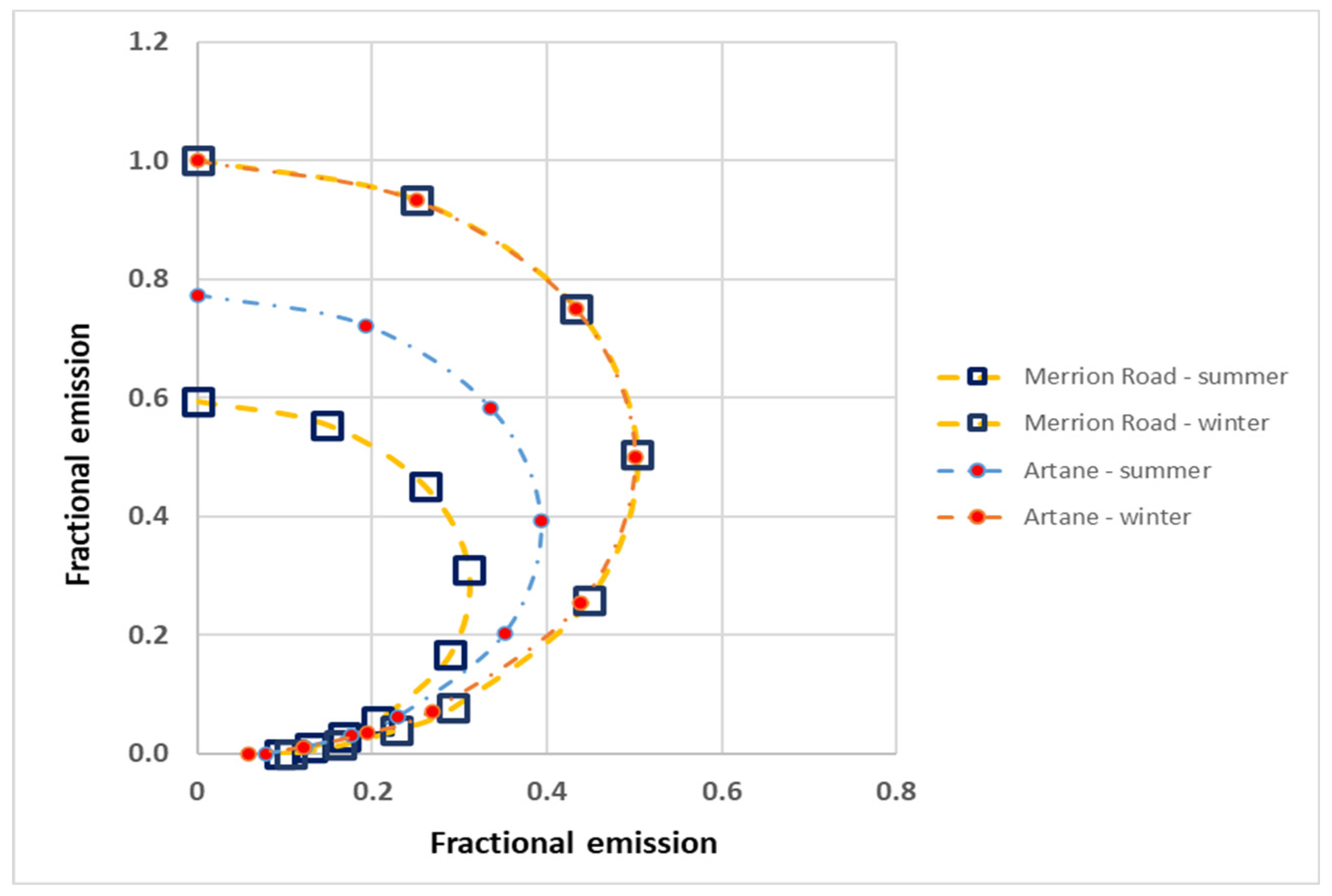
Figure 6.
One of the residential locations from our survey is the Merrion Road region which consists of a road with lined by mature trees. In (a) the selected area is shown outlined on imagery from the QGIS ESRI basemap and this outline was also used for the extraction of data from both our raster output files and the calibrated ISS imagery. It can be seen from this plot that the locations of the light poles (open circles) quite often lie beside or in the canopy of deciduous trees. In (b) the location of two lanterns are outlined indicating how close they are to the tree canopies which rise several metres higher than the lighting poles.
Figure 6.
One of the residential locations from our survey is the Merrion Road region which consists of a road with lined by mature trees. In (a) the selected area is shown outlined on imagery from the QGIS ESRI basemap and this outline was also used for the extraction of data from both our raster output files and the calibrated ISS imagery. It can be seen from this plot that the locations of the light poles (open circles) quite often lie beside or in the canopy of deciduous trees. In (b) the location of two lanterns are outlined indicating how close they are to the tree canopies which rise several metres higher than the lighting poles.

Figure 7.
Comparison of the extracted output from the radiance-calibrated imagery with our model predictions for the same areas. We have converted the LPS output from lux to watts using a photopic-weighted curve. The dotted line is the best-fit linear model while, for comparison, the dashed line indicates a line of unity slope.
Figure 7.
Comparison of the extracted output from the radiance-calibrated imagery with our model predictions for the same areas. We have converted the LPS output from lux to watts using a photopic-weighted curve. The dotted line is the best-fit linear model while, for comparison, the dashed line indicates a line of unity slope.
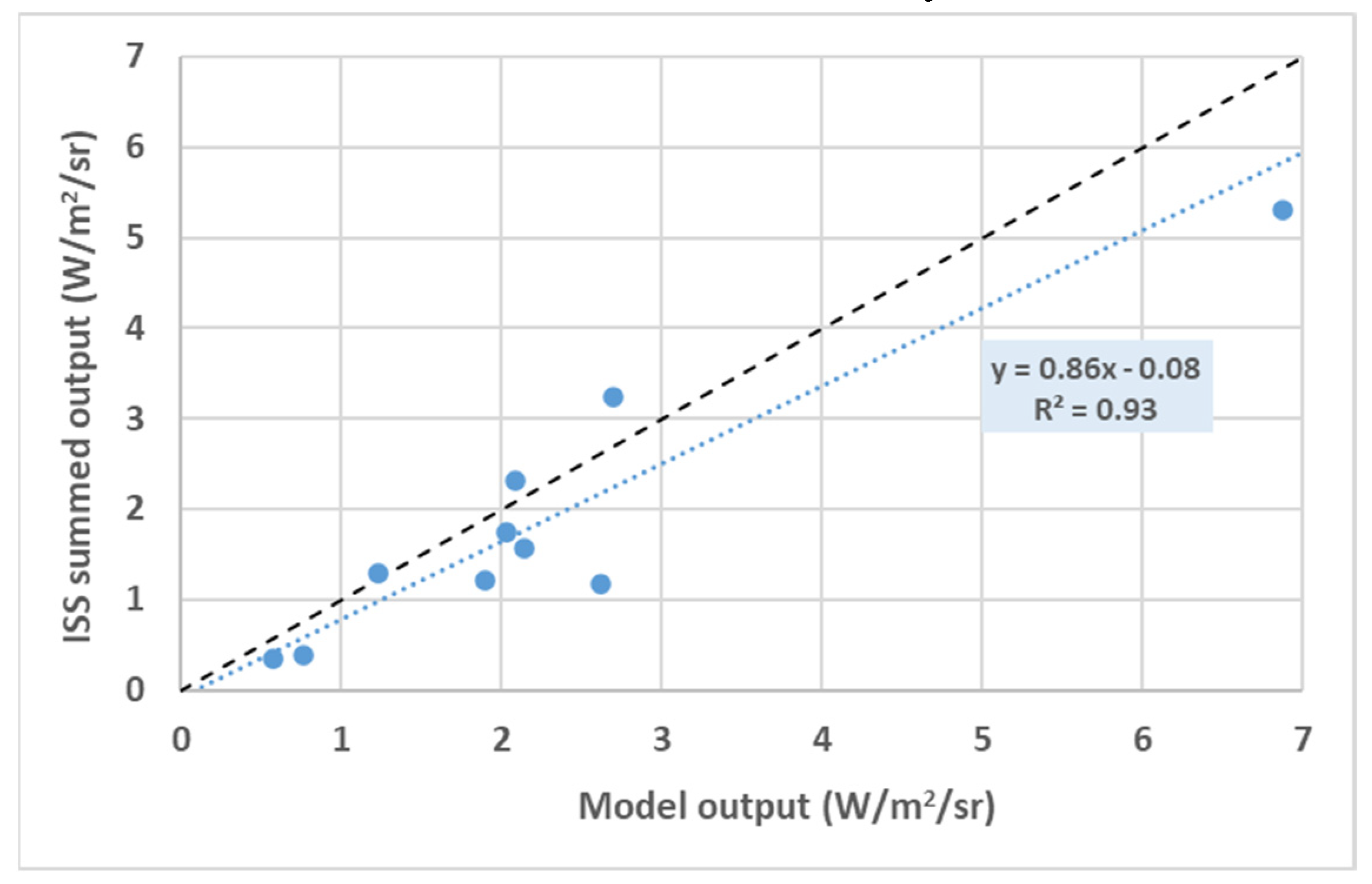
Table 1.
LiDAR DEM datasets used in this work. Data generally have a vertical rms accuracy of 20 cm. Note that datasets cover a range of seasons.
Table 1.
LiDAR DEM datasets used in this work. Data generally have a vertical rms accuracy of 20 cm. Note that datasets cover a range of seasons.
| Origin | Spatial resolution | Area | Date obtained |
| NYU | 1 m | Dublin | Mar 2015 |
| Commercial | 1 m | Dublin | May – Jun 2018 |
| OPW | 1 m | Cork towns | Nov – Dec 2015 |
| OPW | 2 m | Newport, Westport, Tralee | Aug 2012 |
| OPW | 2 m | data | Dec 2011 – Feb 2012 |
Table 2.
Summary table of the parameters for a range of areas reported in this paper. The column headed “S/W %” indicates the change between summer and winter data; “% LPS” indicates the proportion of lanterns modelled that were of the LPS type; “Direct/Total” indicates the proportion of light emitted skyward that is due to the direct emission from the lantern itself, the rest of the emission being diffuse, i.e. reflected from the surroundings; “% to zenith” indicate the upward emission relative to the unobstructed model; the “LAMFIT” column represents the scaling of the total emission relative to the amount estimated from fitting a Lambertian curve to the near-nadir observations.
Table 2.
Summary table of the parameters for a range of areas reported in this paper. The column headed “S/W %” indicates the change between summer and winter data; “% LPS” indicates the proportion of lanterns modelled that were of the LPS type; “Direct/Total” indicates the proportion of light emitted skyward that is due to the direct emission from the lantern itself, the rest of the emission being diffuse, i.e. reflected from the surroundings; “% to zenith” indicate the upward emission relative to the unobstructed model; the “LAMFIT” column represents the scaling of the total emission relative to the amount estimated from fitting a Lambertian curve to the near-nadir observations.
| Location | Pixel size | Area (km2) | S/W % | # Lights modelled | % LPS median | Direct/Total median | % to zenith median | LAMFIT |
| Residential LPS 55W | 1 m, 2m | 0.04 – 0.2 | 83% | 12 – 112 | 99% | 68% | 80% | 3.2 |
| Residential other | 1 m, 2m | 0.01– 0.06 | 0.01 – 0.06 | 7 – 47 | 100% | 10% | 88% | 1.1 |
| Cork towns | 1 m | 0.3 – 3.9 | a | 9 – 149 | 35% | 21% | 77% | 1.2 |
| New towns | 2 m | 1 8 19 |
a | 135 1,098 5,121 |
0% 13% 100% |
9% | 73% | 1.1 |
| Dublin NYU | 1 m | 1.5 | 100% | 1,012 | 13% | 24% | 59% | 1.3 |
| DCC | 1 m, 2m | 117 | 89* | 41,763 | 51% | b | 80% | 1.0 |
a Only one DSM dataset was available for these areas so no comparison could be made; b DCC area was modelled without direct emission component.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







