Prerpints.org logo
Preprint
Article

Structure, Optical, and Dielectric Properties of Cu1-xAgxAlO2 Nanoparticles

Altmetrics

Downloads

156

Views

53

Comments

0

This version is not peer-reviewed

Submitted:

18 April 2023

Posted:

19 April 2023

You are already at the latest version

Alerts
Abstract
The solid-state technique was utilized to make a single phase of delafossite CuAlO2, along with 1%, 2%, 3% and 4% silver doped CuAlO2 samples in this study. The content of the samples was investigated using energy dispersive X-ray spectroscopy (EDS) equipped with a field emission scanning electron microscope (FE-SEM). The polycrystalline nature of all of the analyzed cases was confirmed by structural analyses utilizing an X-ray diffraction (XRD) pattern with a simple typical peak of CAO rhombohedral phase. Raman, FT-IR and UV–Vis spectroscopy were used to study the structural, and optical energy band gap (Eg) of Ag doped CuAlO2 nanoparticles. The Kubelka–Munk function was used to calculate the optical band gap of ACAO alloys using diffuse reflectance spectra, and it altered as the Ag ion concentration increased. A. c. impedance spectroscopy was used to investigate the dielectric characteristics of Ag doped CuAlO2 nanoparticles.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

In these days, a highly attractive topic is the fabrication of transparent TE devices with transparent p-n junctions for generating electricity and ultraviolet (UV) absorption in smart infrastructure systems [1]. Presently, significant attention is given to Cu-delafossites because these structures combine strong electrical conductivity with excellent visible light transparency. The outstanding properties of the CuAlO2 based materials, such as their wide band gap, high electrical conductivity, optical transparency, and interesting thermal and chemical stabilities, have drawn considerable interest [2,3,4,5,6,7,8]. A wide range of technical options are also made possible by these materials' modifiable conductivity and transparency. Understanding a material's optical and electrical properties requires knowledge of its band gap energy. Any variation in the band gap at the nanoscale directly affects the property of the material [9]. As a result, when studying and developing nanomaterials, energy band gap values should be taken into account. In particular, their optoelectric, electric, and thermoelectric properties can be adjusted by doping with the appropriate elements. Doped CuAlO2 compositions are interesting possibilities for a range of applications thanks to the tuning of these characteristics. The copper aluminate lattice is subjected to the proper dopants, which alters the structure and defect density of the material and, in turn, alters its physical characteristics, including its electrical (dielectric), optical, and thermoelectric capabilities. This motivates us to study the interplay between the microstructure and optoelectric properties of copper aluminate based material for incorporating this system into technological applications such as thermoelectric devices, smart windows, transparent solar cells, electromagnetic shielding, transparent heat sources, light emitting diodes, and other optoelectronic devices [10]. Due to the mixed valency nature of Cu cations, doping of Ag ions at Cu sites are predicted to distort the host lattice which leads to the change in optical and dielectric properties.
For device applications in microelectronics, the dielectric properties of the materials are very important where information about localized and free band conduction, ac conductivity as function of frequency and interior region are provided [11].
Recently, it is reported that defect density in this type of materials plays key role in modification of its application properties which can be used to develop the next generation of multifunctional devices [12]. These defects can be intrinsic (oxygen vacancies) and extrinsic (dopant). Therefore, knowledge of the dielectric properties in the present material is very important for the development of devices in microelectronics. The Complex Impedance Spectroscopy (CIS) is a non-destructive and effective technique to characterize intragranular and interfacial properties and also the interrelations between them. This technique is very useful to separate the contributions due to grain, grain boundary and interfaces and enable us to separate the real and imaginary components of complex electrical parameters to analyze the electrical response of polycrystalline materials [13].
In view of the importance of dielectric and optical characterization, the present paper describes a detailed analysis of electrical (dielectric) and optical properties which have been carried out on silver substituted copper aluminate (CAO).

2. Experimental details

A series of samples with chemical formula Cu1-xAgx AlO2 (x = 0.00, 0.01, 0.02, 0.03, and 0.04) was prepared from the mixture of stoichiometric amounts of highly pure powder of CuO, Al2O3, and Ag2O (Sigma-Aldrich, Inc., 99%) which were thoroughly mixed using agate mortar, by means of solid-state reaction technique. The solid-state reaction method is more suitable for synthesizing oxide materials rather than other methods. Foremost is the readily availability of starting materials, suitability for the preparation of high purity, degree of homogenization achieved on mixing, intimacy of contact between the grains and accurately stoichiometric compounds by optimizing the processing and synthesis parameters that have a large influence on the properties of final products [14]. The mixture was cold pressed into circular pellets inside a stainless steel die under 5 ton cm-2 and subsequently sintered at 1373K for 24h in flowing air. This thermal treatment was followed by natural furnace cooling.
The prepared samples were characterized by various techniques. The X-ray diffraction (XRD) patterns on the samples were taken using a PANalytical X’Pert PRO diffractometer at room temperature with Cu (Kα) radiation (λ=1.5406Å), with scan step increment of 0.02o and counting time of 1 s/step for phase identification, in the 2θ range from 10o to 90o. Energy dispersive spectroscopy (EDS) was used to check chemical purity of the samples. Raman studies were performed using Perkin Elmer, Raman spectrometer with an excitation wavelength at 514.5 nm using an Ar laser. Perkin Elmer's Fourier transform infrared (FTIR) spectrometer was used to examine the presence of different functional groups. The FTIR spectra from the powders were obtained by the usual method of pressing them into KBr pellets. Room temperature diffusion reflection spectra were recorded on a UV–vis spectroscopy (Perkin Elmer's LAMBDA 950 spectrophotometer) through the Kubelk-Munk function. Frequency dependent dielectric parameters were performed at room temperature using (LCR) meter (HP4284A) in the frequency range of 75 kHz–10 MHz. For dielectric measurements, the surfaces of the samples were ground and polished followed by application of a silver conducting paste on two opposite surfaces of the sample.

3. Results and discussion

3.1. EDS and XRD analyses

It is well known that the properties of the materials depend strongly on their chemical composition, microstructure and impurities present in them. Hence, the investigated samples have been examined by using an energy dispersive spectroscopy (EDS) and X-ray diffraction (XRD) at room temperature to study the composition, phase and crystal structure of them. To analyze the chemical composition of Cu1-xAgxAlO2 specimens, EDS was employed to characterize the powders. The results can be seen in Figure 1a,b. EDS spectra confirmed the presence of Cu, Al and O that are the basic elements of the pure CuAlO2 system, while Ag peaks were observed in Ag-doped CuAlO2 samples. Furthermore, the percentage of the dopant element was found to be similar to the nominal concentration that was used through the calculations procedure and samples growth. Hence, EDS spectra affirmed the Ag atoms were indeed incorporated in the matrix of the host material. The consistent and sharp peaks with cupper aluminate and silver-cupper aluminate demonstrated that both synthesized nanoparticles were crystalline in nature. Hence, the present NPs were obtained in their pure forms.
In other words, the elements (Cu, Ag, Al, and O) concentrations in the samples can be quantitatively estimated using the EDS analysis of the patterns. These values are in good agreement with the calculated weight percentages of all the elements present based on their empirical formula, indicating that the materials obtained were solely those intended for the intended compositions.
X-ray diffraction measurements of the silver doped copper aluminate samples with various silver concentrations (x = 0.00, 0.01, 0.02, 0.03 and 0.04) are illustrated in Figure 2. The data reveal that, silver free CuAlO2 compound is crystalized in a single structure form with rhombohedral delafossite-type crystal system according to R 3 ¯ m S.G. No 166. Moreover, all the peaks in CuAlO2 (i.e. 006, 101, 012, 104, 015, 009, 107, 018, 110, 0012, 1012, and 1010) are in a good match with the JCPDS file No. 00-041-1401 [15]. Doping with the so small Ag2O concentrations keeps rhombohedral crystal system after doping where copper atoms partially replaced by silver atoms, and no other phases or nondelafossites (impurities) were detected. In other words, this may suggest that the dopant is dissolved into CuAlO2 with no impurity peak of Ag or its oxide. By increasing Ag concentration in CuAlO2, the intensity as well as the broadening and shifting of the peaks are affected. This can be ascribed to the change in the lattice distortion and the crystallite size. Moreover, the shift of XRD peaks causes variation in lattice constants with dopant content, indicating a structural modification due to lattice distortion caused by molar variation. Unit cell parameters (a, c and V) were calculated from the relation between inter planar spacing of (hkl) planes and lattice constants of hexagonal crystal structure described elsewhere [16]. It is found that the calculated lattice parameters of the given material depend on the increase of the amount of Ag content. As indicated in Table 1, the calculated lattice distance of Ag0 specimen for the a-axis and the c-axis is confirmed as the previous work [17], respectively, which agrees with the standard file of ICDD-PDF 35-1401. Moreover, the incorporation of Ag dopant in CuAlO2 does not change the a-axis length, whereas the c-axis length increases with the Ag substitution. Such an increment in the c-axis length can be attributed to the larger radius of Ag1+ (0.67 Å) substituting the Cu1+ (0.46 Å) [18].
The crystallite size δ of Ag-doped CuAlO2 compounds is deduced from the strongest peak broadening. After correcting for instrumental broadening [19], the average crystallite size (δ) shown in Table 1 was calculated using Sherrer's equation. With different ratios of silver, particle size increases. The calculated crystalline size from XRD patterns for the silver free copper aluminate is found to be 45 nm and increases with adding silver to 92 nm to this compound. Furthermore, as particle size is increased, the dislocation density ( ε = 1 δ 2 ) decreases. Once the dislocation density is relatively low, it is proposed that the presence of dislocations causes a reduce in the semiconductor material's band gap, given that the dislocations are isolated by a substantial degree than the interatomic distance [20].

3.2. Vibrational analysis

According to the aforementioned findings, the delafossite structure of the samples may be maintained when Cu is replaced with Ag in the examined concentration range. Doping does, however, create regional alterations. Raman spectroscopy, which has superior local probe properties compared to XRD, makes these changes much more noticeable than they would be in XRD. Therefore, Raman spectroscopy was performed on the investigated samples in order to learn more about the impact of doping on these localized variations. Raman spectra of the prepared samples are presented in Figure 3.
In the case of Ag=0 sample, observed vibration peaks around 209 cm-1, 441 cm-1, 535 cm-1, and 693 cm-1 were ascribed to recorded, but with different intensities. According to Figure 3, the CuAlO2 and Ag doped CuAlO2 samples' room temperature Raman scattering spectra exhibit many photonic bands of the delafossite structure. From Raman spectrum of Ag0 sample, Raman modes present around 209 cm-1, 441 cm-1, 535 cm-1, and 693 cm-1, in agreement with earlier results on CuAlO2 [21,22]. Observed modes identified as A1g at 693 cm-1, Eg at 441 cm-1, and Ag at 209 cm-1, in addition to band at 535 cm-1 are the bands that make up this pattern. Moreover, the mode at 535 cm-1 is attributed to relaxation of selection rules by defects such as Cu vacancies, interstitial oxygen’s or tetrahedrally coordinated Al on the Cu site [23]. It implies that these vibrations could be linked to the spectrum characteristics of the edge-sharing AlO6 octahedra and perhaps the O-Cu-O linear bond. It suggests that these vibrations may be associated with the spectral features of the edge-sharing AlO6 octahedra and possibly the O-Cu-O linear bond. The substitution of Cu by Ag induces a change in frequency and inline width of A1g and Eg modes. Moreover, the A1g depicts the vibrations of the Cu-O bonds along the c-axis while the Eg mode is describes the atomic vibrations perpendicular to c-axis [24,25]. In other words, Cu is replaced with Ag, which results in a change in the frequency and inline width of the A1g and Eg modes. The observed lattice expansion along various axes and the difference in ionic radii between Cu and Ag are both compatible with the two frequencies' shift to shorter wavenumbers, which denotes a weak (Cu, Ag)-O bonding. Particularly, the A1g mode is displaced up 33, and the A1g mode frequency is highly dependent on the oxygen bonding properties of the (Cu, Ag)-site atoms. We also observe a sharp decline in the intensity of the initially prominent band at 535 cm-1 for these Ag-doped materials, as well as a reversal in the A1g-Eg mode magnitude ratio. The peak at 535 cm-1 is thought to result from the presence of a prohibited non-zero wavevector phonon, which shows a breakdown in the translational symmetry of the crystal and relaxes the Raman selection rules, indicating the presence of crystal structure defects. Several delafossites have also shown comparable forbidden modes, which may have similar causes, such as interstitials, vacancies, and substitutional defects [26]. We contend that the decline in disorder and intensity are connected. Consequently, it can be deduced that the Raman spectrum are affected by the existence of number of defects (oxygen vacancies, stacking faults, antisite disorder, structural inhomogeneities, etc.) that are introduced into the CuAlO2 lattice structure during the simultaneous Ag-doping. All the observed changes in the Raman spectra of the samples are consistent with the results of XRD analysis, which further confirm the successful Cu-site substitution with Ag and the structural distortion. The Raman modes show that increasing the concentration of x from 0.00 to 0.04 results in the emergence of peak shifting and broadening along with the change in intensity and the disappearance of mode at 535 cm-1. This variation might be due to the lattice distortion induced by Ag ions into the host lattice of copper aluminate.
Our results demonstrate that the substitution of Cu by Ag in the studied concentration range of Cu1-xAgxAlO2 compound can be made without changing the delafossite structure. However, local changes do occur, and they are much more relevant in Raman spectroscopy, that is a local probe, more than X-ray diffraction, where the impacts of cationic composition changes are averaged and mostly seen as peak variation.
FTIR analysis
FT-IR spectra in the wavenumber range of 400 – 4000 cm-1 for Cu1-xAgxAlO2 nanoparticles with x=0, 0.01, 0.02, 0.03, and 0.04 are presented in Figure 4. A small amount of water vapour, CO2 and N2 are absorbed on CuAlO2 powder from atmosphere. In the case of Ag=0 sample, broad band at 3467 cm-1 is due to the stretching vibration of hydroxyl groups attached on the surface of nanocrystalline powders, indicating the existence of water absorbed on the surfaces of grains [27], the ranging band from 2356 cm-1 is assigned to C-H stretching, and a peak near 1560 cm-1 appears due to CO2 adsorbed on the surface, which might have been incorporated from the atmosphere [28]. The peak around 1400 cm-1 is associated to nitrate groups [29], and 1016 cm-1 attributed to C-O stretching [30]. The bands originated at the region below 1000 cm-1 demonstrate the mixed vibrations of metal and oxygen molecules due to the formation of Cu-O, Al-O, and Ag-O stretching bonds [22,31]. FTIR spectra of Cu1-xAgxAlO2 close agree with those previously reported for this material [32].

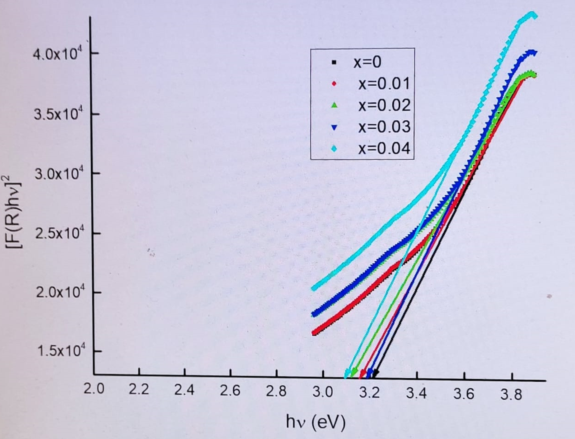
3.3. Uv-vis. analysis

The specimens were subjected to diffuse reflectance spectroscopy (DRS) at 300 K in order to examine the impact of Ag substitution on the band gap of Cu1-xAgxAlO2. At room temperature, Figure 5 displays the optical reflection spectra of the Cu1-xAgxAlO2 powder samples at x= 0, 0.01,0.02, 0.03, and 0.04 as a function of wavelengths. As the wavelengths were raised, the diffused reflectance of pure and doped samples significantly rose. In addition, the incorporation of Ag dopant into the host copper aluminate reduces diffused reflectance.
Pure, 1%, 2%, 3%, and 4% Ag-doped Cu1-xAgxAlO2 have absorption edges that begin below 400 nm. Doping causes a change in the absorption edge, which implies a change in the band structure. The Kubelka-Munk method [33] converts the reflectivity into the absorption coefficient (α). The absorption coefficient α of an indirect/direct semiconductor near the absorption threshold can be expressed by the following relation [34]:
α =   β   ( h ϑ −   E g o p t ) n h ϑ
where Egopt is the band gap (eV) of indirect allowed transition for n = 2 and of direct allowed transition for n = 1 2 , h is the Planck’s constant in (J s), β is the absorption constant, and ν is the frequency of the light (s-1). In the present case, n = 1 2 that is for direct allowed transition. The intercept of the plot between F R * h ν 2 vs. h ν gives the optical band gap energy. By extrapolating the linear portions of these plots to the x-axis (photon energy) i.e. h ν = 0 , values of the optical band gap for pure and Ag-doped CuAlO2 were obtained. The band gap energy values obtained for CuAlO2 is 3.22 eV and for the 1, 2, 3 and 4 mol % Ag doped CuAlO2 is 3.19, 3.16, 3.12 and 3.09 eV respectively. It is noticed that there is red shifted in the optical band gap with doping concentration. This behavior in band gap with Ag concentration can be attributed either to the increasing particle size or to strain present in the samples [35]. Moreover, the variation of optical band gap is attributed to the higher concentrations of carriers which leads to a rise of Fermi level within the conduction band producing electrically degenerate semiconductors [36]. Moreover, a plausible explanation for this change in Egopt with respect to the size and the shape of the particle is that the properties of the electrons in small particles should be dependent upon the crystallite size due to quantized motion of the electron and hole in a confined space. Generally, the Egopt value of delafossites is possible influenced by a particle size and shape. From the literature [37], the small particle size sample seems to have the higher Egopt value than a big particle size sample. The dependency of the band gap on its dimension is due to the fact that the band gap is a function of the lattice parameters. Because the lattice parameters increase as the diameter of the particle decreases, the gaps between the bands widen [9]. As a result, the band gap decreases and the band edges shift. The larger particle size, the redder shift [38]

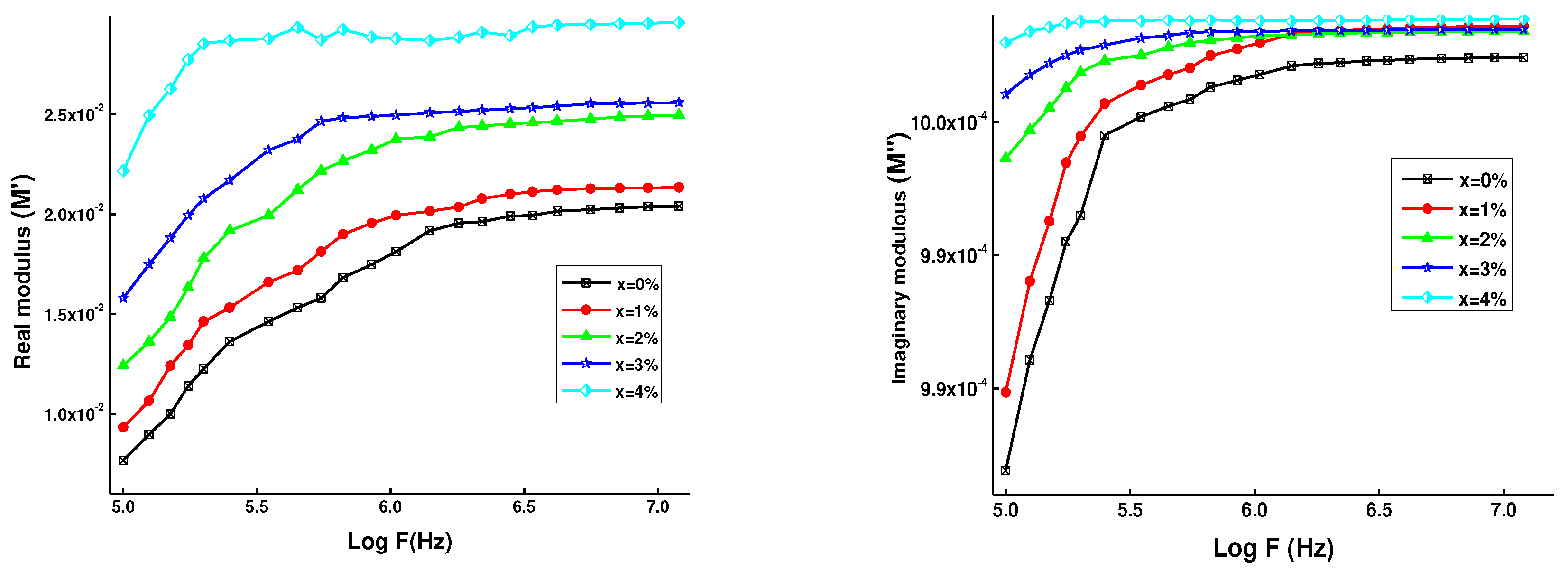
3.4. Dielectric analysis

The electrical impedance of a material can reveal a lot about its dielectric characteristics. Grain structure, conductivity type, frequency, and temperature all influence the electrical impedance. Impedance spectroscopy (IS) can be used to intuitively examine the impedance and conduction process. (IS) is an effective tool for characterization of the electrical/dielectric mechanisms occurring inside the materials [39] where it is enormously beneficial to determine the various mechanisms of conduction [40].
Frequency variation of the complex impedance parameter (Z*) for Cu1-xAgxAlO2 (x=0, 0.01, 0.02, 0.03 and 0.04) NPs was measured at room temperature and the results are presented in Figure 7a. The impedance was found to decrease as the frequency increases while Z* increases with increase in Ag concentration. Impedance analysis was performed by calculating the resultant complex impedance parameter Z* = Z' + j Z" [41] where the real and imaginary components of the complex impedance function are denoted by Z' and Z", respectively. Both components are determined from the measured impedance (Z*) and phase angle (θ) and represented by the following mathematical equations: Z ' = │ Z * │ cos ⁡ θ and Z ' ' = │ Z * │ sin ⁡ θ Figure 7b shows the alternations of the real component of impedance (Z') as a function of frequency at various dopant content (0–4%).
Z' drops with greater frequency, reflecting that the ac conductivity of the samples increases with frequency. At higher frequencies, the magnitude of Z' tends to be constant for all samples, indicating the possibility of space charges dissipating due to a reduction in material barrier quantities [42]. With increasing the concentration of Fe dopant, Z' magnitude increases indicating a decrease in the conductivity of the samples. Figure 7c presents the variation of the imaginary part impedance (Z") vs. frequency for all samples. It can be seen that the curves display a trend similar to that of Z'.
To get the real (ɛʹ) and imaginary (ɛ″) parts of permittivity from the impedance data, the following equations are used [43]: ε ' = Z " 2 π f C 0 [ Z ' 2 + Z " 2 ] and ε " = Z ' 2 π f C 0 [ Z ' 2 + Z " 2 ] , where Co is the geometrical capacitance connected to vacuum permittivity εo (8.854×10−14 F/cm) through the εoA/d relationship (A is the effective area of the electrode and d is the distance between the two electrodes). The real part of permittivity (ɛʹ) vs. frequency (f) curves for undoped and Ag-doped CuAlO2 nanoparticles are presented in Figure 8a. ɛʹ decreases with increasing frequency which can be explained according to the type of polarization mechanism that dominates within a certain range of the applied frequency. At relatively lower range of frequency, the total contribution of polarization arises from the electronic displacement, ionic displacement, dipole orientation and space charge displacement. Imaginary part of permittivity (ɛ″) versus frequency is shown in Figure 8b where it decreases with increasing frequency and Ag doping concentration in CuAlO2, suggesting an ability of using these materials in high frequency application. The decrease in the ɛ″ value with increasing Ag concentration may be attributed to larger molecules relaxation time with delayed polarization processes.
The nearly constant values of ε′ and ε´´ (dielectric dispersion) in the higher frequency range can be explained using the Maxwell and Wagner’s bilayer model and Koops phenomenological theory [44]. Basing on these model, the space charge polarization is caused by the material's heterogeneous dielectric nature, which is made up of two layers: well-conducting grains separated by a layer of poor-conducting grain boundaries. The sintering process, in which high temperature promotes the oxidation of crystallites and a reduction in the grains surface area, is known to generate grain boundaries in the material [45]. Existence of the grain boundaries with their poor conductance among the high conductive grains results in a reduced dielectric constant at higher frequencies. Consequently, one can conclude that the grain boundaries and their volume percentage influenced the dielectric constant's behavior of our samples [46].
The loss of electrical energy in the dielectric material is described by the term dissipation factor tan δ = Z'/Z" [47], where δ is the phase difference between the material's induced current and the applied field. Figure 8c shows the variation of tan δ as a function of frequency up to 10 MHz. It is observed that tan δ decreases as the frequency increases with a fast rate of drop in the low frequency range and a nearly frequency-independent decrease in the higher one. It is also observed that doping with Ag decreases the dissipation factor. The resistive loss and relaxation loss are the two major components that contribute to the dissipation factor. In the case of resistive loss, energy is used by the mobile charges, whereas in the case of relaxation loss energy is dissipated due to dipole relaxation [48]. The space charge polarization, which can be explained by Shockley-Read mechanism, causes significant dielectric losses at lower frequencies [49]. According to this mechanism, impurities and imperfections in the crystal lattice will catch surface electrons at low and intermediate frequencies resulting in space charge polarization. The reduced dielectric loss at higher frequencies could be related to the production of defect dipoles caused by a modification in the cations valence state [50].
AC conductivity (σac), which provides information on the type of charge carriers, is computed using an empirical formula [51]: σ a c = Z ' Z ' 2 + Z " 2 Figure 8d depicts σac vs. f plots of the undoped and Ag-doped CuAlO2 NPs. σac of all samples increases with f suggesting an enhancement in the charge carriers hopping [52]. Also Khan et al., attributes the increase of σac with f to series resistance effect [53]. In low-frequency range pure and doped compounds have essentially identical σac behavior, indicating that charge carriers hopping is an explicit and instinctive process in all materials. In high-frequency regime, the pristine specimen has lower σac values compared to doped samples. Because the AC conductivity of materials is highly influenced by the presence of weakly bound charge carriers, the high σac of doped samples at higher frequencies could arise from the development of charged particles (electrons) in extrinsic specimens, which are valuable in the electrical conduction [54]. AC conductivity is changed due to the dielectric relaxation which corresponds to the immobile charge carriers that can be described by AC power’s relationship [55]: σ a c = B ω n where temperature and material intrinsic properties affect the coefficient B and the exponent n; B denotes conductivity units, while n is a dimensionless quantity [47]. To evaluate whether the conduction is frequency-independent (n = 0) or frequency-dependent (0 < n < 1) [56], the numerical value of n is calculated from the slope of the log σac vs. log f . Undoped, 1%, 2%, 3%, and 4% Ag doped CuAlO2 NPs have n values of 0.827, 0.831, 0.835, 0.833, and 0.836, respectively. The results suggest that the current NPs' conduction mechanism is highly frequency-dependent.
In order to obtain more precise information regarding the role of grains and grain boundaries on conductivity properties of Ag (0%, 1%, 2%, 3%, and 4%) doped CuAlO2 NPs, the electrical modulus was explored. The modulus formalism is a powerful technique for suppressing the electrode effect on electric conductivity because it takes into consideration the effect of grain and grain boundary capacitance [57]. The sum of real (M') and imaginary (M") constituents yields the complex electric modulus (M*). The real and imaginary modulus in the current system have been calculated using real and imaginary dielectric permittivity variables and are provided by [58] M * = M ' + j M " = ε ' ε ' 2 + ε " 2 + j ε " ε ' 2 + ε " 2 The frequency dependent M' and M" is shown in Figure 9 for all samples. It is observed that M' increases by increasing frequency and becomes independent at high frequencies. Also, similar behavior has been observed for M". As the Fe doping level rises, the overall behavior of the real (M') and imaginary (M") components increases.

Conclusion

Nanocrystalline samples of Cu1-xAgxAlO2 (0.00 ≤ x ≤ 0.04) were successfully fabricated by conventional solid state technique within crystallite size of 45-92 nm and they are formed in the rhombohedral crystal structure form with R 3 ¯ m (166) space group. Raman spectra revealed that phonon frequency shifted to lower wavenumber and line width broadened with increase in silver content, indicating a weakening of Al-O bonding. The optical band energy for the direct optical band transition was determined to be 3.22-3.09 eV, exhibiting transparency in the visible region. The results suggest that the current NPs' conduction mechanism is highly frequency-dependent. The dielectric constant and dielectric loss decrease while the ac conductivity increases as the frequency increase which has been explained on the basis of space charge polarization according to Maxwell and Wagner’s two-layer model. The real and imaginary dielectric constant as well as the ac conductivity decrease with increasing the Ag content in CuAlO2 NPs. On the basis of this research study, it can be concluded that the effect of small Ag substitution into CuAlO2 improves the optical parameters and dielectric properties.

Acknowledgments

The authors would like to express their Gratitude’s to the ministry of education and the deanship of scientific research-Najran University-Kingdom of Saudi Arabia for their financial and Technical support under code number (NU/NRP/SERC/11/30).

References

  1. S. Gotbi, et al., Infrastructures, 7 (2022) 97.
  2. S. Yanagiya, et al., Materials 3 (2010) 318.
  3. M. V. Lalic, et al., Braz. J. Phys. 34 (2004) 611.
  4. C. K. Ghosh, et al., J. Mater. Sci. 46 (2011) 1613.
  5. K. Park, K.Y. Ko, W.-S. Seo, J. Euro. Ceram. Soc. 25 (2005) 2219–2222.
  6. M. V. Lalic, et al., J. Phys. Cond. Mater. 14 (2002) 5517.
  7. J. Cai, H. Gong, J. Appl. Phys. 98 (2005) 033707.
  8. H. Kawazoe, et al., Nature 389 (1997) 939–942.
  9. B. J. Abdullah, Mater. Sci. Semicond. Proc. 137 (2022) 106214.
  10. J. F. H. L. Monteiro, et al., Ceramic Inter. 44 (2018) 14101-14107.
  11. P.P. Sahay, et al., Curr. Appl. Phys. 13 (2013) 479-486.
  12. Zulfiqar, et al., Ceram. Int. 42 (2016)17128.
  13. T. Sahu, B. Behera, J. Mater. Sci.: Mater. Electron. 29 (2018) 7412–7424.
  14. N. Dodiya, D. Varshney, J. Molecular Structure 1031 (2013) 104–109.
  15. S. Pantian, et al., Current Apllied Physics 17 (2017) 1264-1270.
  16. E.M.M. Ibrahim et al., J. Alloy. Compd. 804 (2019) 272-280.
  17. K. Park et al., Mater. Sci. Eng. B 129 (2006) 1–7.
  18. S. Shibasaki, et al., Phys. Rev. B 74 (2006) 235110.
  19. S.A. Saleh, J. Taibah Uni. Sci., 16 (2022) 280-287.
  20. S.A. Saleh, Mate. Sci. Appl. 2 (2011) 950.
  21. J. Pellicer-Porres, et al., Phys. Rev. B 74 (2006) 184301.
  22. D. Bhattacharya et al., Ceramics International 47 (2021) 9907-9922.
  23. N. P. Salke, et al., Vibrational Spectroscopy 81 (2015) 112-118.
  24. M. Aziziha, et al., J. Phys. Chem. C 123 (2019) 30604-30612.
  25. A. Yassin, et al., J. Phys. D Appl. Phys. 46 (2013).
  26. Aktas, et al., J. Phys-Condens Mat, (2012) 24.
  27. R. Seoudi, et al., J. Electron. Mater. 44 (2015) 3367-3374.
  28. T. Prakash, et al., J. Nanosc. Nanotechnol., 8 (2008) 4273-4278.
  29. M. Aqeel, et al., Appl. Nanoscience 10 (2020) 2045-2055.
  30. P.O. Offor, et al., J. Solid State Electrochem 21 (2017) 2687-2697.
  31. Y. Chuai, et al., J. Mater. Sci. 51 (2016) 3592-3599.
  32. B. Saha et al., Mater. Lett. 63 (2009) 394-396.
  33. H.M. Ali, and S.A. Saleh, Thin Solid Films 556 (2013) 552-559.
  34. S.A. Saleh, et al, Physica Scripta 84 (2011) 015604.
  35. B. Nandan, et al, J Nanopart Res 15 (2013) 1999.
  36. V. Senthilkumara, et al, Philo. Mag. Lett. 90 (5), (2010) 337.
  37. S. Traiphop, et al., Chiang Mai J. Sci., 49 (2022) 205-216.
  38. S.T. Hayle, and G.G. Gonfa, Amer. J. Nanosci. Nanotechn., 2 (2014) 1.
  39. N. Ahmad, et al., Ceram. Int. 44 (2018)15972–15980.
  40. W. Ben Soltan, et al., J. Mater. Sci. Mater. Electron. 28 (2017) 6649-6656.
  41. S.T. Dadami et al. Ceramics International 43 (2017) 16684–16692.
  42. S. Mohanty, et al., J Mater Sci: Mater Electron (2015) 26:9640–9648.
  43. K.P. Padmasree, A.F. Fuentes, Mater. Chem. Phys. 223 (2019) 466–472.
  44. T. Bhasin et al., J. Alloys Compd. 748 (2018) 1022-1030.
  45. M. Javed Iqbal, et al., J. Appl. Phys. 111 (2012).
  46. S. Naseem et al., J. Magn. Magn. Mater. 447 (2018) 155–166.
  47. M. Mehedi Hassan et al., Mater. Res. Bull. 47 (2012) 3952–3958.
  48. H.B. Sharma, et al., J. Alloy. Compd. 599 (2014) 32–39.
  49. W. Shockley, W.T. Read, Phys. Rev. 87 (1952) 835–42.
  50. S. Mehraj and M.S. Ansari, Phys. E Low-dimensional Syst. Nanostructures 65 (2015) 84–92.
  51. Md. R. Islam et al., J. Alloys Compd. 735 (2018) 2584-2596.
  52. K. Rajwali, et al., Chinese Phys. B 24 (2015) 127803.
  53. R. Khan, et al., J. Mater. Sci. Mater. Electron. 27 77 (2016) 25–30.
  54. N. Ahmad, S. Khan, M.M.N. Ansari, Mater. Res. Express 5 (2018) 035045.
  55. M.A. El-Hiti, J. Phys. D: Appl. Phys. 29 (1996) 501–504.
  56. Saleh et al., J. nanoparticles research, 22 (2020) 4763.
  57. P.T. Phong et al., Ceramics International 42 (2016) 7414–7421.
  58. D. Xu et al., J. Alloys Compd. 773 (2019) 853-859.
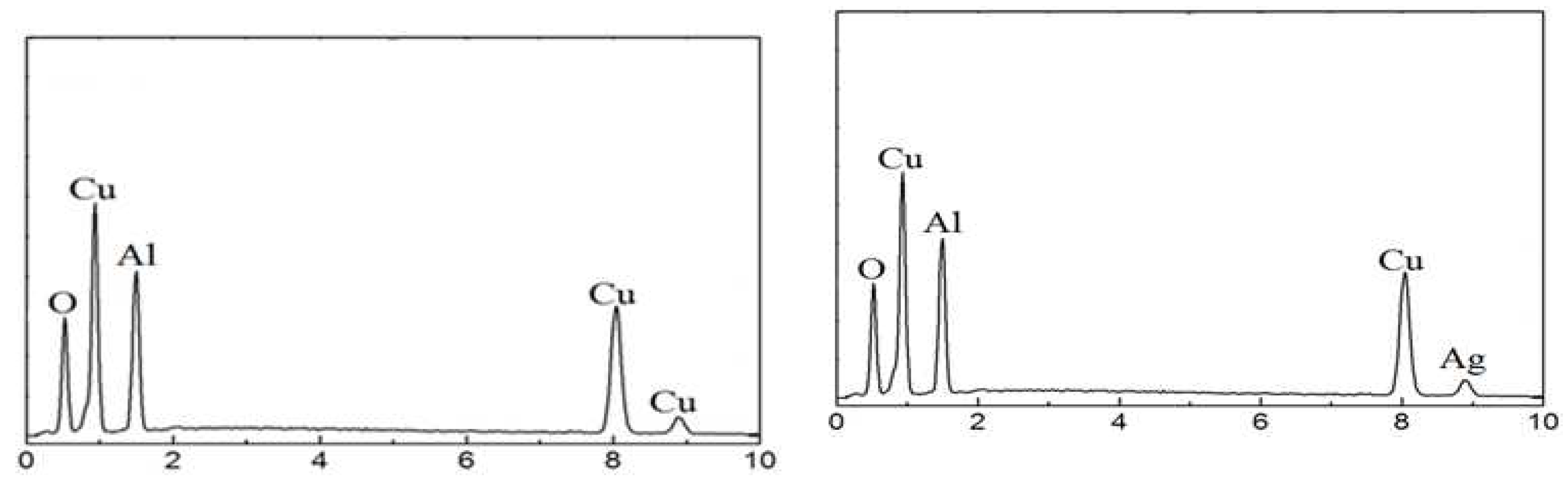
Preprints 71307 g001
Figure 1. The EDS patterns of (a) CuAlO2 and (b) Cu0.97Ag0.03AlO2 samples.
Figure 1. The EDS patterns of (a) CuAlO2 and (b) Cu0.97Ag0.03AlO2 samples.
Preprints 71307 g001
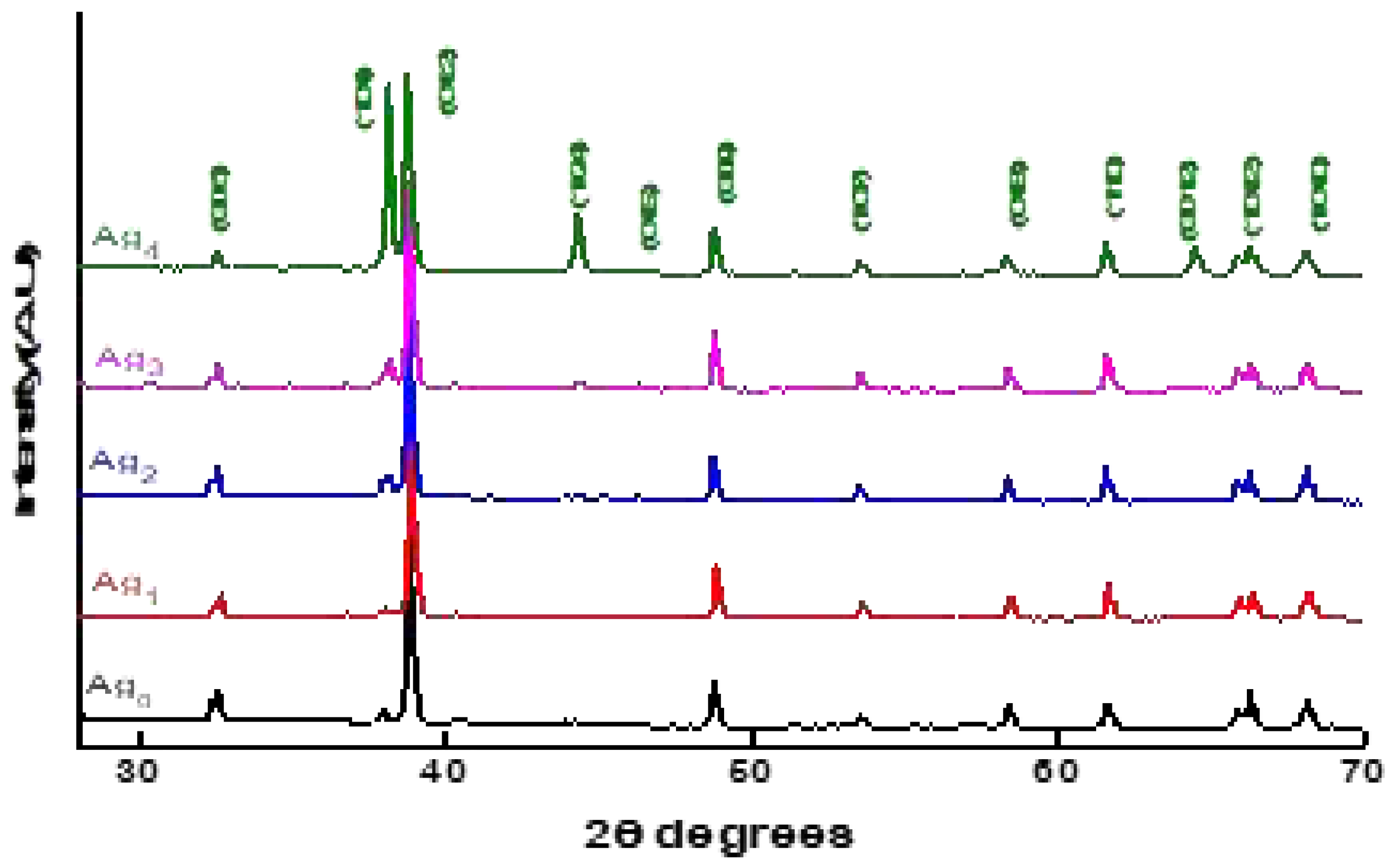
Preprints 71307 g002
Figure 2. XRD patterns of Cu1-xAgxAlO2 powders with Ag contents of x = 0, 0.01, 0.02, 0.03 and 0.04.
Figure 2. XRD patterns of Cu1-xAgxAlO2 powders with Ag contents of x = 0, 0.01, 0.02, 0.03 and 0.04.
Preprints 71307 g002
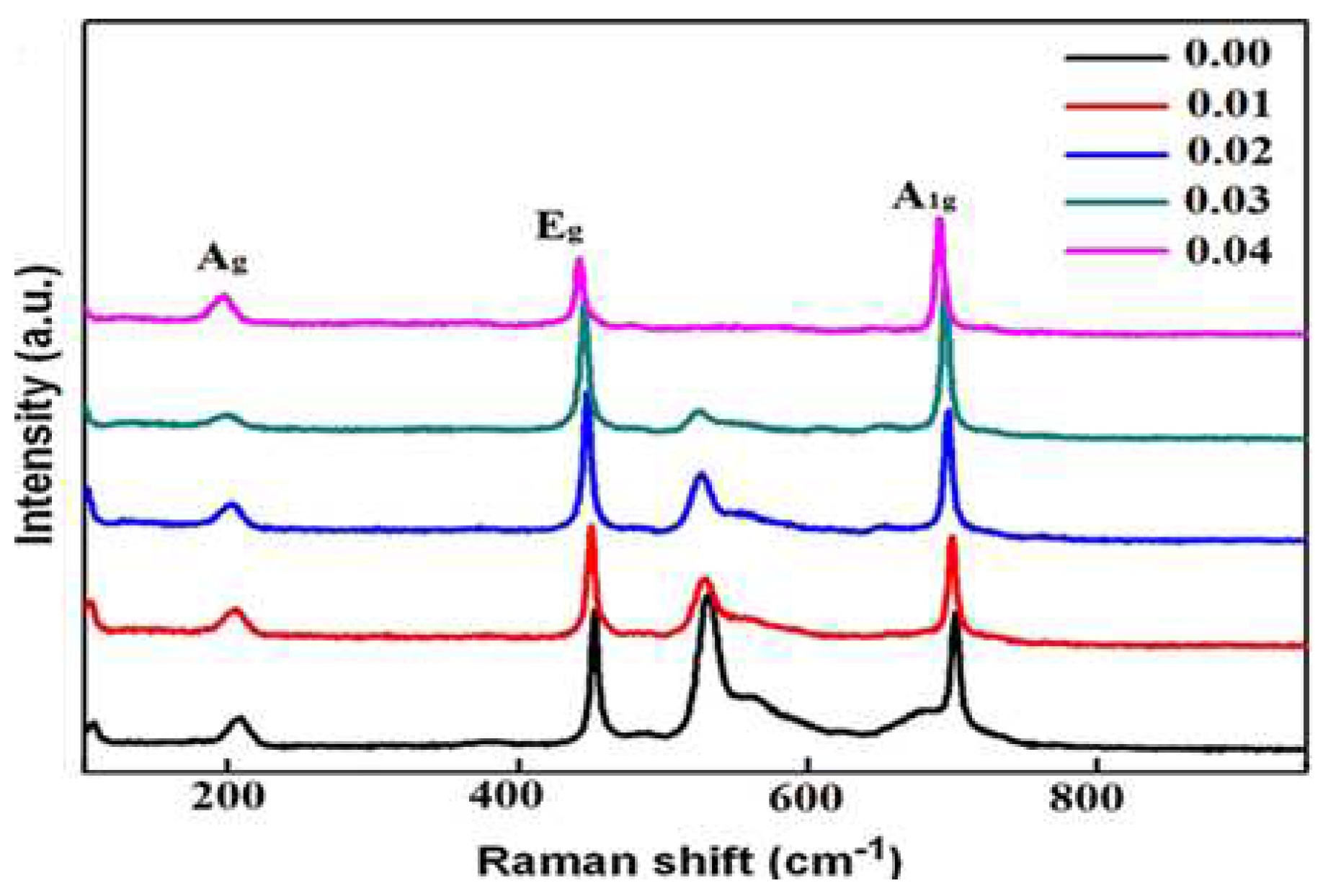
Preprints 71307 g003
Figure 3. Raman scattering of all samples.
Figure 3. Raman scattering of all samples.
Preprints 71307 g003
Preprints 71307 g004
Figure 4. FT-IR of five samples.
Figure 4. FT-IR of five samples.
Preprints 71307 g004
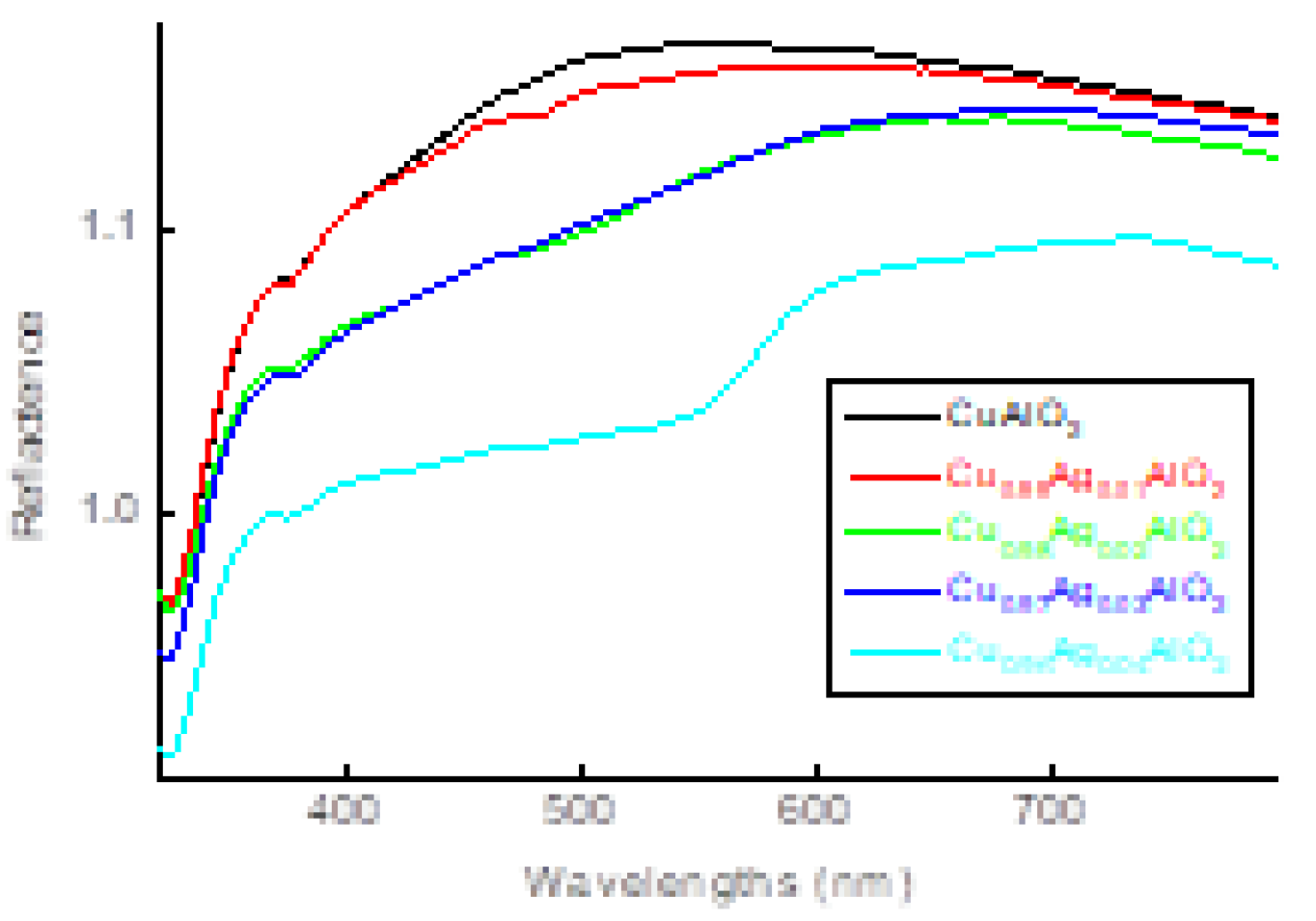
Preprints 71307 g005
Figure 5. DRS spectra of investigated samples.
Figure 5. DRS spectra of investigated samples.
Preprints 71307 g005
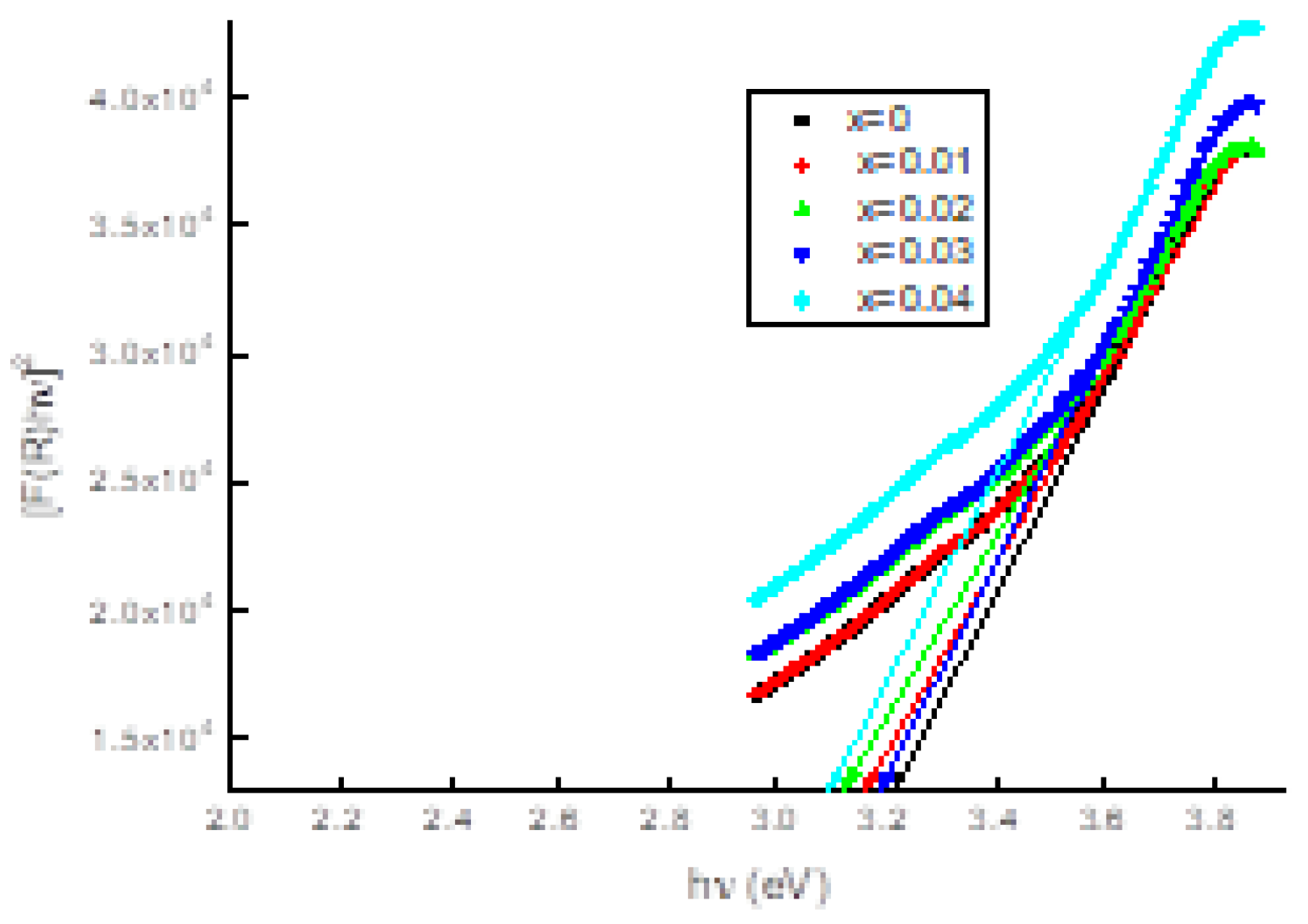
Preprints 71307 g006
Figure 6. Extracted Egopt of prepared samples.
Figure 6. Extracted Egopt of prepared samples.
Preprints 71307 g006
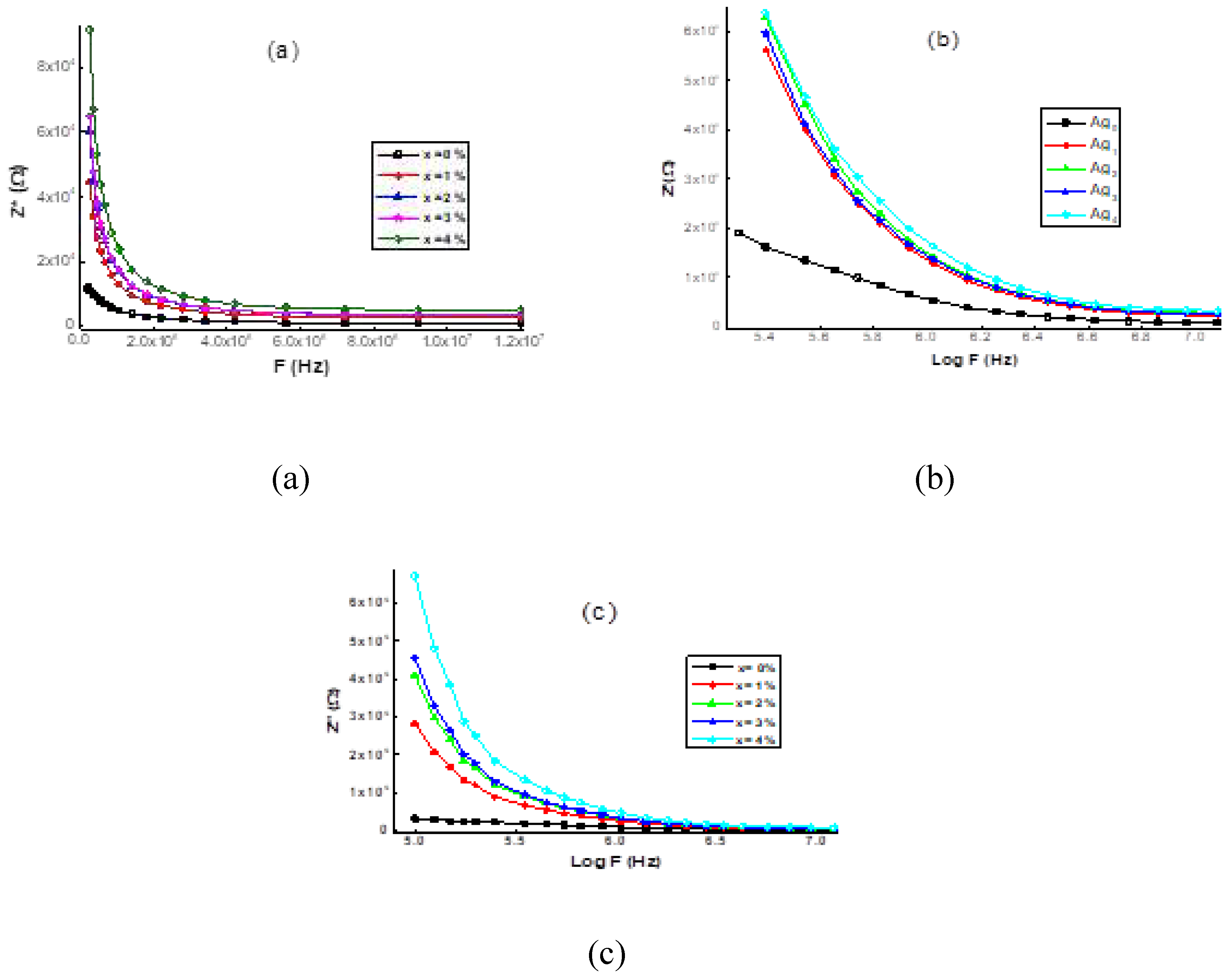
Preprints 71307 g007
Figure 7. The frequency dependence of (a) complex impedance, (b) real component of impedance and (c) imaginary component.
Figure 7. The frequency dependence of (a) complex impedance, (b) real component of impedance and (c) imaginary component.
Preprints 71307 g007
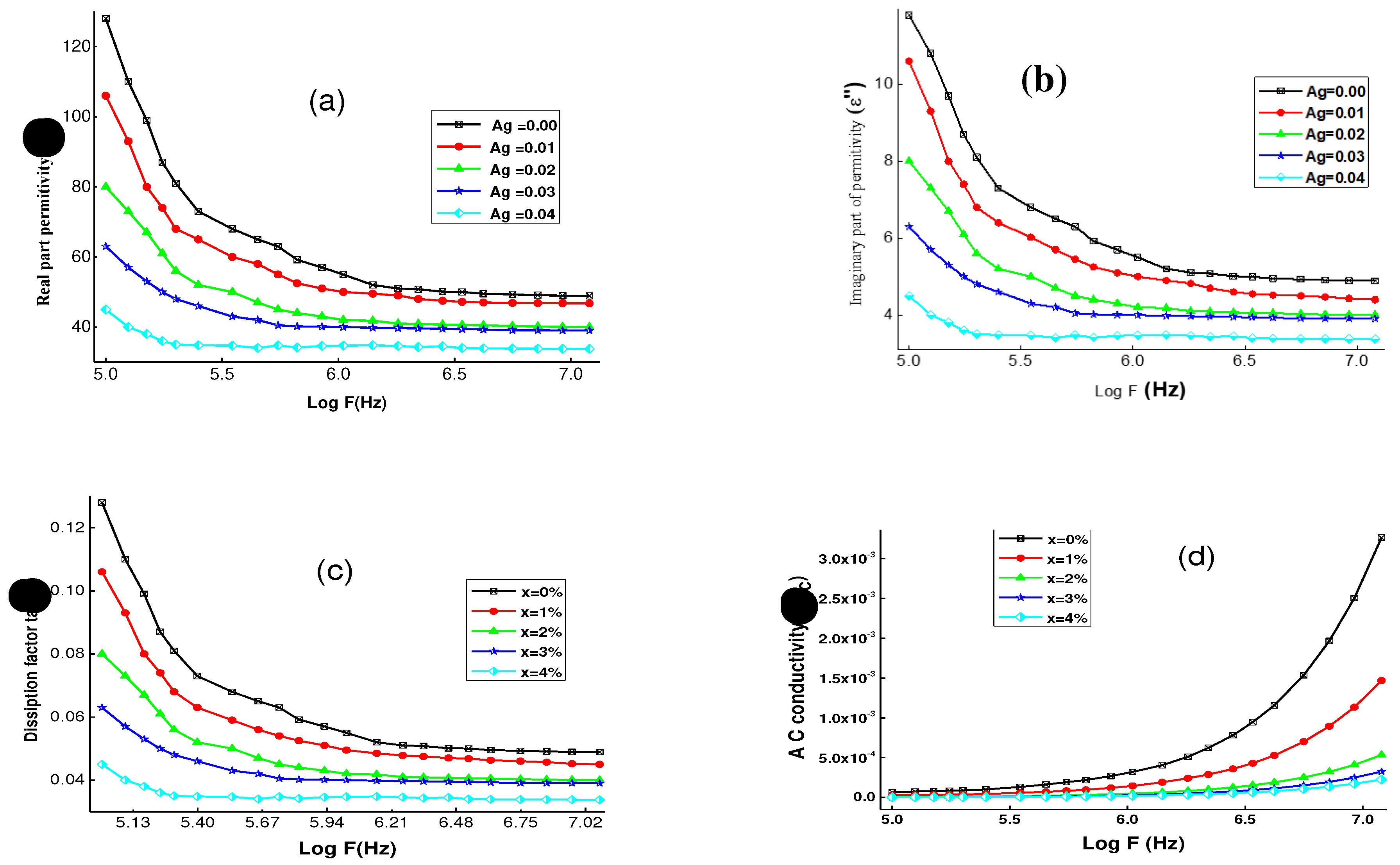
Preprints 71307 g008
Figure 8. Real (a) and imaginary (b) permittivity, dissipation factor (C), and AC conductivity (σac) of Cu1-xAgxAlO2 NPs (d).
Figure 8. Real (a) and imaginary (b) permittivity, dissipation factor (C), and AC conductivity (σac) of Cu1-xAgxAlO2 NPs (d).
Preprints 71307 g008
Preprints 71307 g009
Figure 9. Real (a) and imaginary (b) electrical modulus of Cu1-xAgxAlO2 NPs.
Figure 9. Real (a) and imaginary (b) electrical modulus of Cu1-xAgxAlO2 NPs.
Preprints 71307 g009
Table 1. Some parameters of investigated samples.
Table 1. Some parameters of investigated samples.
name δ (nm) ε∗1012 (cm-2) a-axis length (Å) c-axis length (Å) V (Å3) EOpt.(eV)
CuAlO2 45 4.94 3.0586 17.169 139.09 3.22
Cu0.99Ag0.01AlO2 49 4.17 3.0590 17.185 139.26 3.19
Cu0.98Ag0.02AlO2 60 2.78 3.0596 17.223 139.63 3.16
Cu0.97Ag0.03AlO2 78 1.64 3.0589 17.266 139.91 3.12
Cu0.96Ag0.04AlO2 92 1.18 3.0587 17.298 140.14 3.09
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated