Prerpints.org logo
Preprint
Article

Two-Lane DNN Equalizer using Balanced Random-Oversampling for W-Band PS-16QAM RoF Delivery over 4.6km

Altmetrics

Downloads

121

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 April 2023

Posted:

19 April 2023

You are already at the latest version

Alerts
Abstract
For W-band long-range mm-wave wireless transmission systems, nonlinearity issues resulting from photoelectric devices, optical fiber, and wireless power amplifiers can be handled by deep learning equalization algorithms. Besides, the PS technique is considered an effective measure to further increase the capacity of the modulation-constraint channel. However, since the proba-bilistic distribution of m-QAM varies with the amplitude, there have been difficulties in learning valuable information from the minority class. This limits the gain of nonlinear equalization. To overcome the imbalanced machine learning problem, we propose a novel two-lane DNN (TLD) equalizer with the random over-sampling (ROS) technique in this paper. The combination of PS at the transmitter and ROS at the receiver improves the overall performance of the W-band wireless transmission system, and our 4.6-km ROF delivery experiment verifies its effectiveness for the W-band mm-wave PS-16QAM system. Based on our proposed equalization scheme, we realize single-channel 10-Gbaud W-band PS-16QAM wireless transmission over 100 m optical fiber link and 4.6-km wireless air-free distance. The results show that compared with the typical TLD without ROS, the TLD-ROS can improve the receiver sensitivity by 1dB. Furthermore, a reduction of 45.6% in complexity is realized, and training samples can be reduced by 15.5%. Considering the actual wireless physical layer with its requirements, there is much to be gained from the joint use of deep learning and balanced data pre-processing techniques.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

With the advancement of 5G mobile communication, millimeter band systems can provide higher data rates and less wireless interference, even in high mobility environments [1,2,3,4,5,6,7,8,9,10,11]. Moreover, as wireless communications develop, the wider bandwidth expansion is driven by the growing demand for capacity in next-generation 6G mobile networks, which is expected to lead to ultra-high data rates [12,13]. Recently, W-band (75–110 GHz) has received more and more attention, with its wide bandwidth, relatively low atmospheric loss，and good directionality. It has been considered as a potential candidate for long-distance mobile communication [14,15,16,17]. Photonics-aided W-band signal generation is a critical technology in long-distance radio-over-fiber (ROF) transmission systems. And it breaks the bottleneck of the bandwidth limitation of traditional electrical equipment and can achieve cost-effective and stable high-frequency millimeter-wave signals [18,19,20,21].
To further enlarge the capacity of the modulation-constraint channel, the probabilistic shaping (PS) technique is introduced into optical fiber communication systems [22]. Moreover, with the development of the PS technique, significant breakthroughs can be achieved in expanding transmission distance and improving spectral efficiency [23]. However, simultaneously, photoelectric and electronic devices usually introduce nonlinear impairment. This impairment is not only in the optical fiber system but also in the photonics-aided mm-wave ROF system [24], which is a significant constraint factor of W-band ROF transmission systems. In most recent research, neural networks (NN) have been proven to be one of the most effective equalizers for RoF delivery [25,26,27]. Recently, we [28]design a dual gated recurrent unit neural network based nonlinear equalizer (dual-GRU NLE), in the W-band mm-wave transmission over 10-km SMF and 1.2-m wireless link. It has been proven that two-lane DNN equalizers made up of two-lane independent Real-valued DNNs dealing with in-phase and quadrature component training data have superiority in nonlinear compensation, and training paradigms in multi-classification usually employ a real-valued (RV) input, a RV active function, and RV weights by discarding the inherent phase content [29,30]. However, overly complex models, including too many parameters, can lead to over-fitting suppression. Besides, introducing of the PS algorithm can cause a severe skew in the generalization of the PS-16QAM data. Such bias in the training dataset may result in a machine learning imbalance, which leads to inadequate training of the minority class. Several studies have shown that this problem can be overcome by randomly resampling the training dataset, which can be achieved by under-sampling or oversampling [31]. Random under-sampling deletes the length of the training dataset from the majority class and thus may lead to the loss of useful information, which further results in capacity reduction. In contrast, random oversampling (ROS) is prone to increasing the training dataset of the minority class, which has been demonstrated to be an effective way to overcome machine learning imbalance.
In this paper, to our knowledge, we demonstrate a two-lane DNN (TLD) equalizer combined with ROS (TLD-ROS) for the first time, which is adaptive to the PS technique especially employed in long-distance ROF transmission systems. We experimentally realize single-channel 10-Gbaud W-band PS-16QAM transmission over a 100 m optical link and 4.6-km wireless link. In terms of the receiver sensitivity, the PS-16QAM signal using TLD-ROSQAM equalizers shows a 1dB gain over typical NN equalizers without balancing ROS when the BER reaches the HD-FEC threshold of 3.8×10-3. Compared with the traditional nonlinear DNN equalizer and Volterra-series, it has a better performance in good training accuracy, less training size demand, and computation complexity.

2. Principle

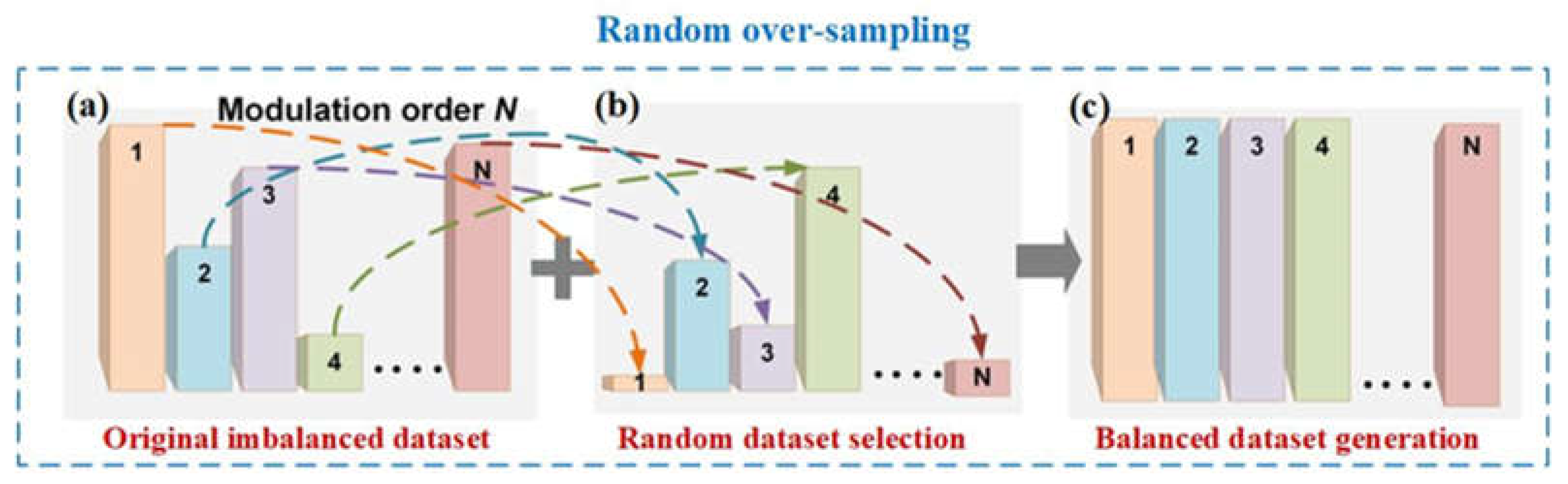
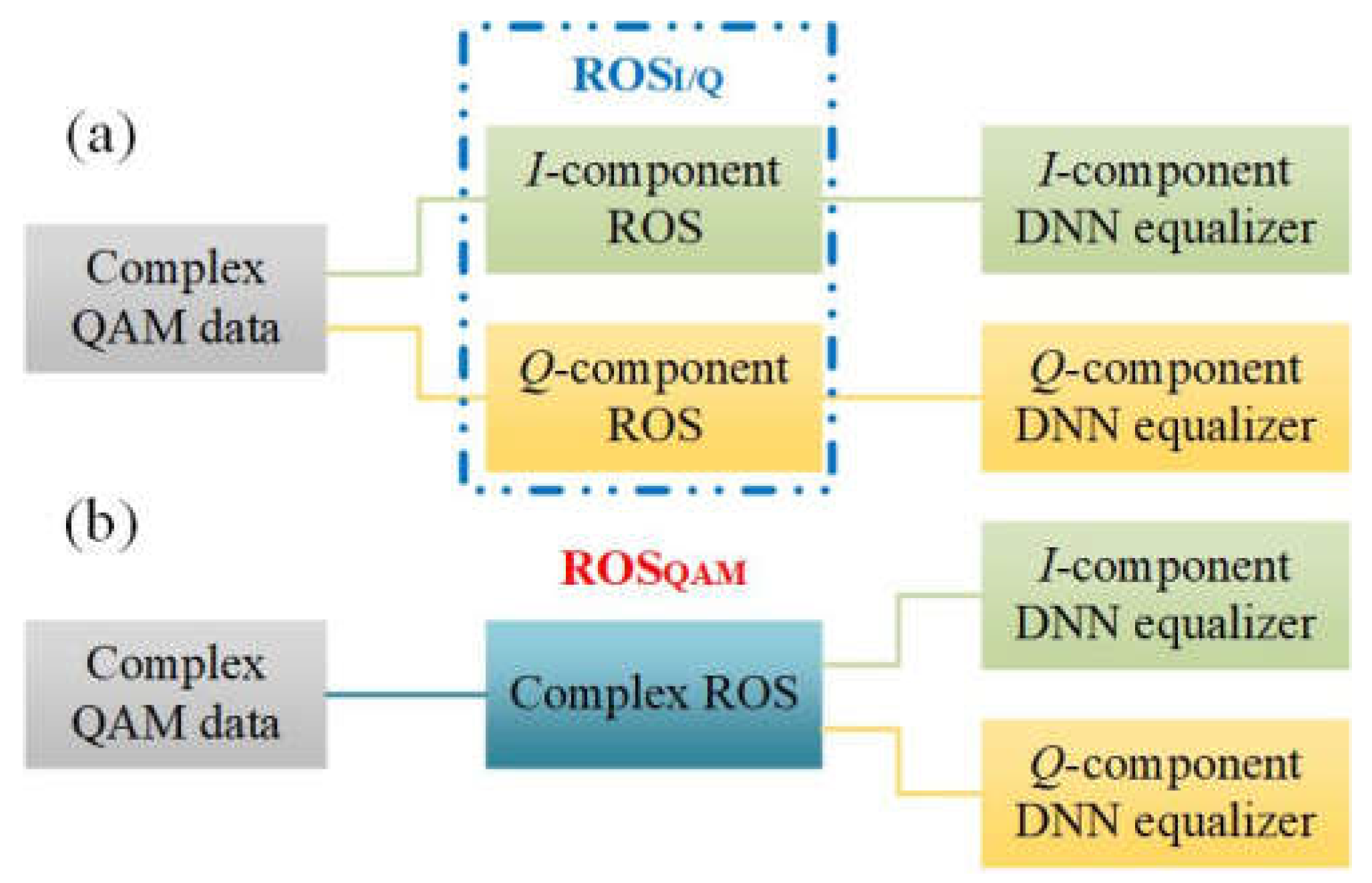
2.1. Random over-sampling (ROS)

For the NN classification algorithm, a class imbalance will occur when the number of samples in some classes is more than that of instances in other classes. Here, we define the larger data set as the majority class and the smaller one as the minority class. For long-range high-speed wireless channels influenced by nonlinearity, phase noises, and high loss, it is difficult to learn from the samples of the minority class in the presence of serious class overlapping. The random over-sampling (ROS) algorithm’s main function is to overcome the imbalance problem by redistributing the training dataset. We employed the ROS technique on the Rx side of the W-band PS-16QAM RoF delivery in our work. The basic principle of ROS is shown in Figure 1. As we know, N-order modulation signal equalization is regarded as N-classification. The PS technique will introduce a severe skew in the class distribution of the baseband PS-16QAM data, causing the generation of the majority class in inner rings and a few minority classes in outer rings, which can result in the original imbalanced dataset, as shown in Figure 1(a). The core idea of the ROS algorithm is to randomly extract samples from the minority classes and make multiple replications in order to balance the class distribution of the training set [32,33]. The procedure of the classic ROS algorithm to generate a training set S ' is described as follows:
Step 1. For an original training dataset S , the data size in the smallest minority class is counted as N − . Meanwhile, the data size in the biggest majority class is written as N + , and the sample rate is SR. Here N + + N − = N and N + N − × S R is the length of the final training dataset for every classification. The imbalance ratio is λ = N + N − .
Step 2. For one specific minority classification and the biggest majority classification, all their original samples construct the original minority class training set S − and majority class training set S + , respectively.
Step 3. For i = 1 : N − × S R , we randomly choose numbers from [ 1 , N − ] , and find the corresponding sample set x ' from S − .
Step 4. Add the selected samples to the minority class set S − = S − + x ' .
Step 5. Then get the generated training set S ' = S + ∪ S − .
Step 6. For all minority classifications, we repeat the operations above and obtain a large number of samples. Also, for majority classifications, we extract only a small subset of samples from the imbalanced dataset. Finally, we get the balanced dataset generation.

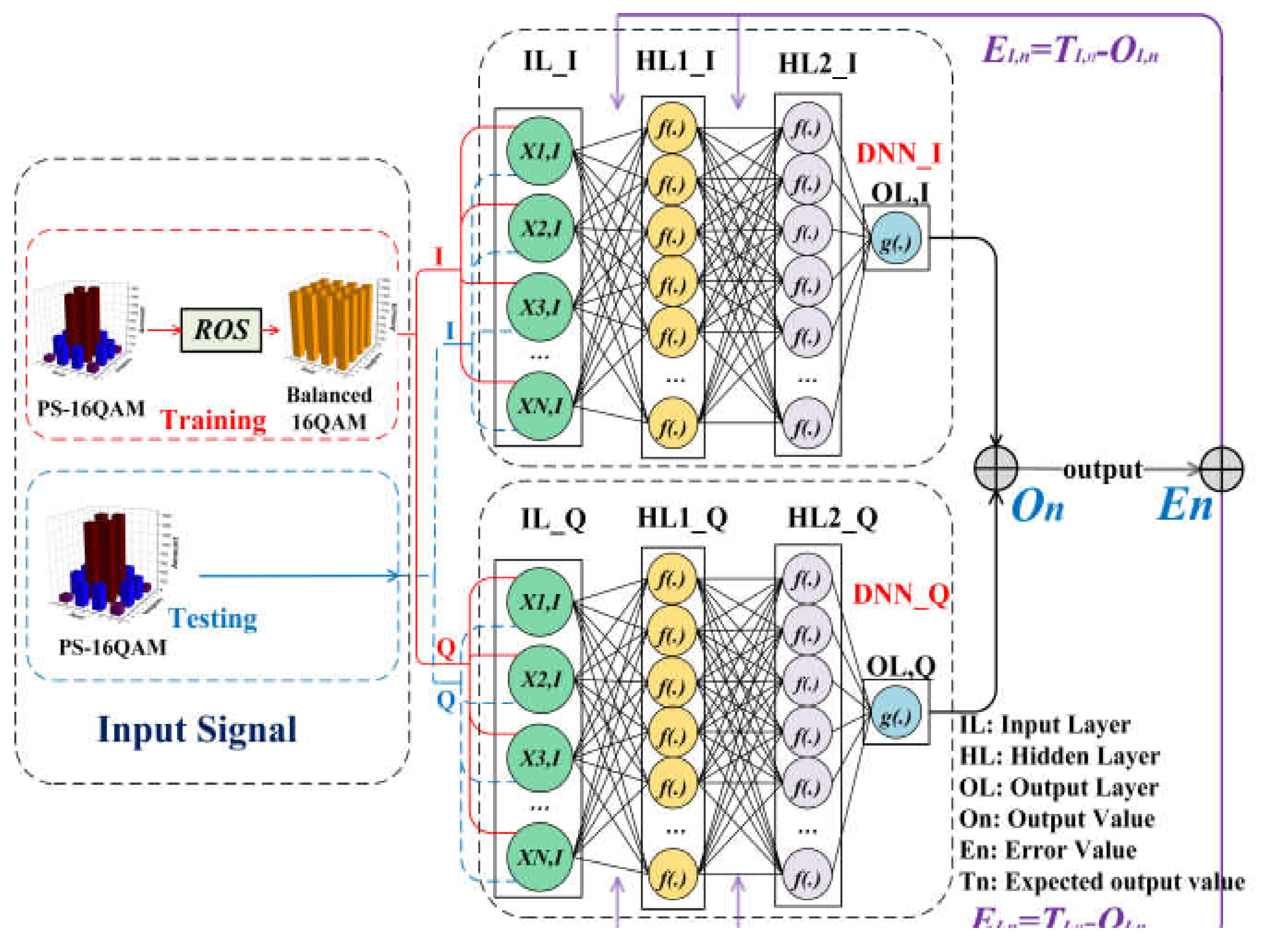
2.2. Two-lane DNN (TLD) Equalizer

A two-lane DNN (TLD) equalizer has been employed in our experiment to mitigate the nonlinear impairment. The so-called “two-lane DNN” represents that such an equalizer is composed of two DNNs, one designed to process real signal sequences, and the other is applied for imaginary signal sequences since our modulated signal is a 16QAM signal, a complex signal. Figure 2 shows the schematic diagram of the TLD equalizer combined with ROS.
In the training process, our proposed TLD equalizer is trained via two steps. In the first step, the training dataset is randomly oversampled to generate the balance 16QAM signals. In the second step, the equalizer is trained with the help of the training balanced 16QAM sequence, and the weight value of the TLD equalizer will be further optimized until the target error value is achieved. In the testing process, differently, 30% of the original received PS-16QAM signal used as the testing dataset is directly input into the well-trained TLD neural network. Finally, the BER decision can be implemented according to the equalized testing signals. Therefore, it is worth noting that ROS is only implemented to the training data, and the TLD network is well trained with the help of balanced training data.
In general, a NN is made up of an input layer, several hidden layers, and an output layer. Our proposed TLD equalizer has one input layer, L (set as 2 in our experiment) hidden layers, and one output layer. w I , m j k and w Q , m j k are the weight values of two lanes, respectively, which link the hidden layers and the output layer, where I or Q denotes the I or Q lane of signals it deals with, respectively, k represents the current k-th layer,(0-th for the input layer, and 3-th for the output layer), and m and j represent the m-th node in the former hidden layer and the j-th node in the current layer, respectively. Firstly, the weight value randomization ( w I , m j k and w Q , m j k ∈ − 1,1 ) initializes their TLD equalizer, learning rate, and iterative learning epoch setting. Secondly, the over-sampled PS-16QAM dataset is separated into I and Q two-lane vectors, respectively, and then send to the input layer with a length of n 0 . As is shown in Figure 2, the input vectors can be written as X I n = x I n , x I n − 1 … , x I n − n 0 + 1 and X Q n = x Q n , x Q n − 1 … , x Q n − n 0 + 1 ,and then be multiplied by weight values w I , m j 1 and w Q , m j 1 in the first hidden layer, respectively. Because the neurons between the layers are fully connected, the output of the j-th neurons in the first hidden layer can be described as follow, respectively:
h 1 I , j = f ( ∑ m = 1 n 0 w 1 I , m j x I , m )
h 1 Q , j = f ( ∑ m = 1 n 0 w 1 Q , m j x Q , m )
where n i denotes the number of nodes in the i-th layer, with n 0 and n M defining the numbers of nodes in the input layer and output layer, respectively. Based on the training feed-forward process, the output of the l-th neuron in the 2-th hidden layer can be calculated as follow, respectively:
h L I , l = f ( ∑ m = 1 n 1 w L I , m l ⋅ h L − 1 I , m )
h L Q , l = f ( ∑ m = 1 n 1 w L Q , m l ⋅ h L − 1 Q , m )
Here, as mentioned above, L is set to 2. And n 1 is the number of nodes in the 1-th hidden layer. Take w L I , m l in the DNN dealing with I-lane signals as an example, it represents the weight value in the 2-th hidden layer of the m-th node in L-1-th hidden layer to the l-th node in the current layer. h L I , m and h L Q , m denotes the output of the m-th neuron in the L-th hidden layer for the I-lane DNN and Q-lane DNN, respectively. It is worth noting that f (.) denotes the nonlinear active function between hidden layers. In DNN, there are several common active functions like “sigmoid” and “tanh” functions, taking gradient explosion and gradient vanishing into consideration, we chose the “ReLu” function, which can be described as:
f x = r e l u x = max ⁡ 0 , x
Meanwhile, the transformation from the hidden layer to the output layer is linear, contrary to that from the input layer to the hidden layer, which is nonlinear. Considering this, we thus chose “purelin” function as the active function g (.) in the output layer, and the final equalized output result is given as:
O n = g ( ∑ m = 1 n 2 w L + 1 I , m j h L I , m ) + i ⋅ g ( ∑ m = 1 n 2 w L + 1 Q , m j h L Q , m )
We note that the weight values are adaptively updated based on least mean squares (LMS) error function, which can be given as:
J n = 1 2 ∑ n = 1 T T n − O n 2
Where T refers to the length of the training dataset X n . Then we subtract the predetermined expected output value T N from the obtained output result O n to get the error value e n which is fed back to TLD equalizers to participate in the calculation. With the aid of BP algorithms, the weight values w I , m j k and w Q , m j k will get updated constantly, until reaching the preset epoch or error value. The process of iterations can be given as:
w k + 1 I , m j = w k I , m j − △ w k I , m j = w k I , m j − η ∂ r e a l J n w k I , m j
∂ r e a l J n ∂ w I , m j k = r e a l e n ⋅ ∂ r e a l O n ∂ w I , m j k ⋅ ∂ h I , j L ∂ h I , j L − 1 … ∂ h I , j k ∂ w I , m j k
w k + 1 Q , m j = w k Q , m j − △ w k Q , m j = w k Q , m j − η ∂ i m a g J n w k Q , m j
∂ i m a g J n ∂ w Q , m j k = i m a g e n ⋅ ∂ i m a g O n ∂ w Q , m j k ⋅ ∂ h Q , j L ∂ h Q , j L − 1 … ∂ h Q , j k ∂ w Q , m j k
Here, η denotes the learning rate and the Δ symbol refers to calculations of the gradients. In our proposed TLD-ROS equalization scheme, the original received PS-16QAM signal is firstly processed by deployed ROS, and then the target output is corresponding modified. Finally, the average distributed 16QAM is put into the TLD classifier to obtain the optimum network parameters.

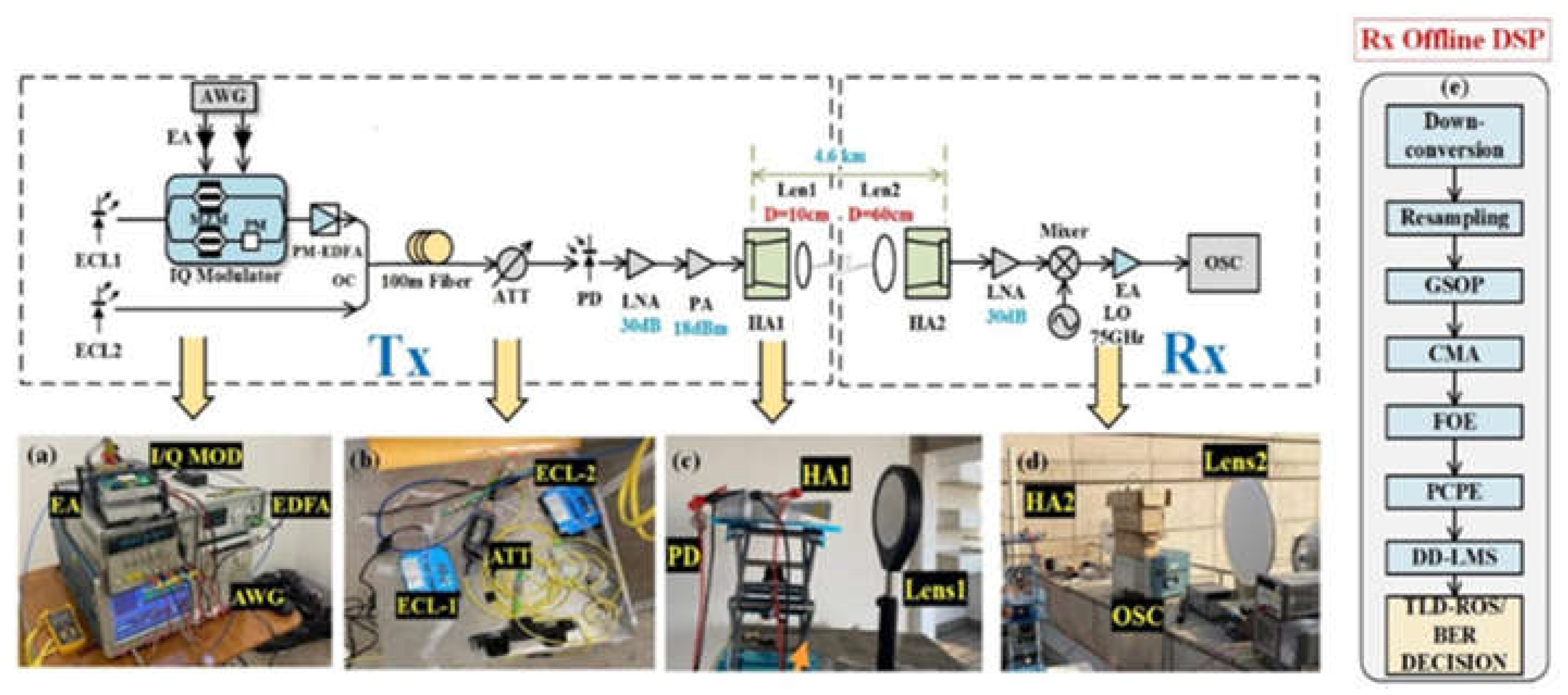
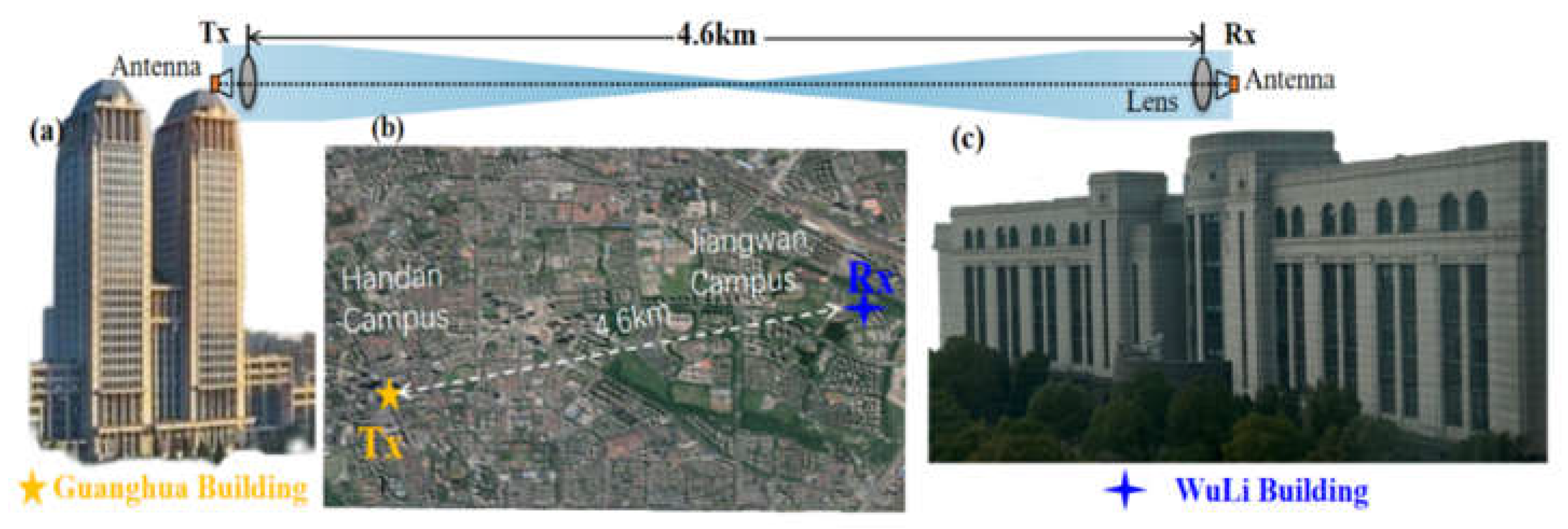
3. Experimental Setup

Figure 3 shows the experimental setup of our presented W-band PS-16QAM delivery over a 4.6- km free space wireless transmission system. As the transmitter side shown in Figure 3(a), an 88.5 GHz frequency space is generated by two individual external cavity lasers (ECLs) based on optical heterodyne beating. The baseband PS-16QAM signal is firstly generated via offline Matlab software, and then digital-to-analog converted (DAC) by the arbitrary wave generator (AWG) with a sampling rate of 100GSa/s. Boosted by two parallel electrical amplifiers (EAs), the baseband I and Q component of the PS-16QAM signal created by the PRBS sequence with a length of 2 20 -1 is used to drive the I/Q modulator, respectively. In order to avoid the overfitting in the equalization process, we used the PRBS of order 20 to generate the transmitted sequence. The periodic length of a PRBS-20 is 1048575 (220-1 =1048575 bits). The total transmitted I/Q length is 16384 (16384 symbols = 65536 bits) extracted from the generated PRBS-20 sequence, which is much less than 1048575 and avoids repetition of pseudo-random numbers effectively. The external cavity laser (ECL1) at 1550 nm with a line width of 100 kHz and an average power of 16 dBm as a signal light source is modulated to carry transmitted PS-16QAM data by I/Q modulator with a 3 dB optical bandwidth of 30 GHz, a half-wave voltage of 2.7 V at 1 GHz. And then the optical beam is amplified by a Polarization Maintaining Erbium-doped Fiber Amplifier (PM-EDFA). Then the ECL2 at the center wavelength of 1549.3 nm, operated as a local oscillator (LO), which has a frequency space of 88.5 GHz with the ECL1 light, is used to generate W-band mm-wave signals. After being delivered over 100 m standard single mode fiber (SSMF), the optical power of the combined beam is adjusted by an attenuator (ATT) to obtain the optimum input power into the photodiode (PD), and PD is implemented with the frequency range of 10∼170 GHz at −2 V DC bias, and the output power of −7 dBm.
As depicted in Figure 3(a), at the transmitter, the output 88.5 GHz PS-16QAM signal is amplified by a low-noise amplifier (LNA) with a 30dB gain and a cascaded power amplifier (PA, saturated output 18 dBm), and then the boosted W-band signal is fed into the W-band horn antenna (HA) with a 30 dBi gain. A pair of the identical lens (Lens 1 and Lens 2) whose diameter and focal length are 10 cm and 60 cm, respectively, is designed to amplify mm-wave signals thereby improving SNR. The pair of the lens is placed just between the transmitted HAs to focus the wireless mm-wave signal at the position of the received W-band HA.
Figure 4 shows the photos of the long-distance radio-over-fiber delivery of PS-16QAM signal over 4.6-km on Fudan campus. The Tx-side of the W-band 4.6-km wireless transmission system is at the Guanghua Building on the Handan Campus of Fudan University, and the Rx-side is located at the WuLi Building on the Jiangwan Campus of Fudan University. The distance between them is 4.6-km on the satellite map. At the receiver, the received signal by HA is firstly boosted by a low-noise amplifier (LNA) with a 30-dB gain, and then down-converted into a 13.5 GHz intermediate frequency (IF) signal via a commercial mixer, driven by a radio frequency (RF) signal with a frequency of 75 GHz. And the amplified IF signal after an EA with a gain of 26 dB is finally captured by a digital storage oscilloscope with a sampling rate of 100 GSa/s and an electrical bandwidth of 45 GHz. As shown in Figure 4, the offline DSP at the Rx-side is followed by down-conversion, resampling, Gram-Schmidt orthogonalization procedure (GSOP), constant modulus algorithm (CMA), frequency offset estimation (FOE), carrier phase estimation (CPE), decision directed-least mean squares (DD-LMS), and nonlinear equalization. Here, the nonlinear equalization methods we compared include typical Volterra series, TLD, TLD equalizers combined with ROS (TLD-ROS).

4. Experimental results and discussions

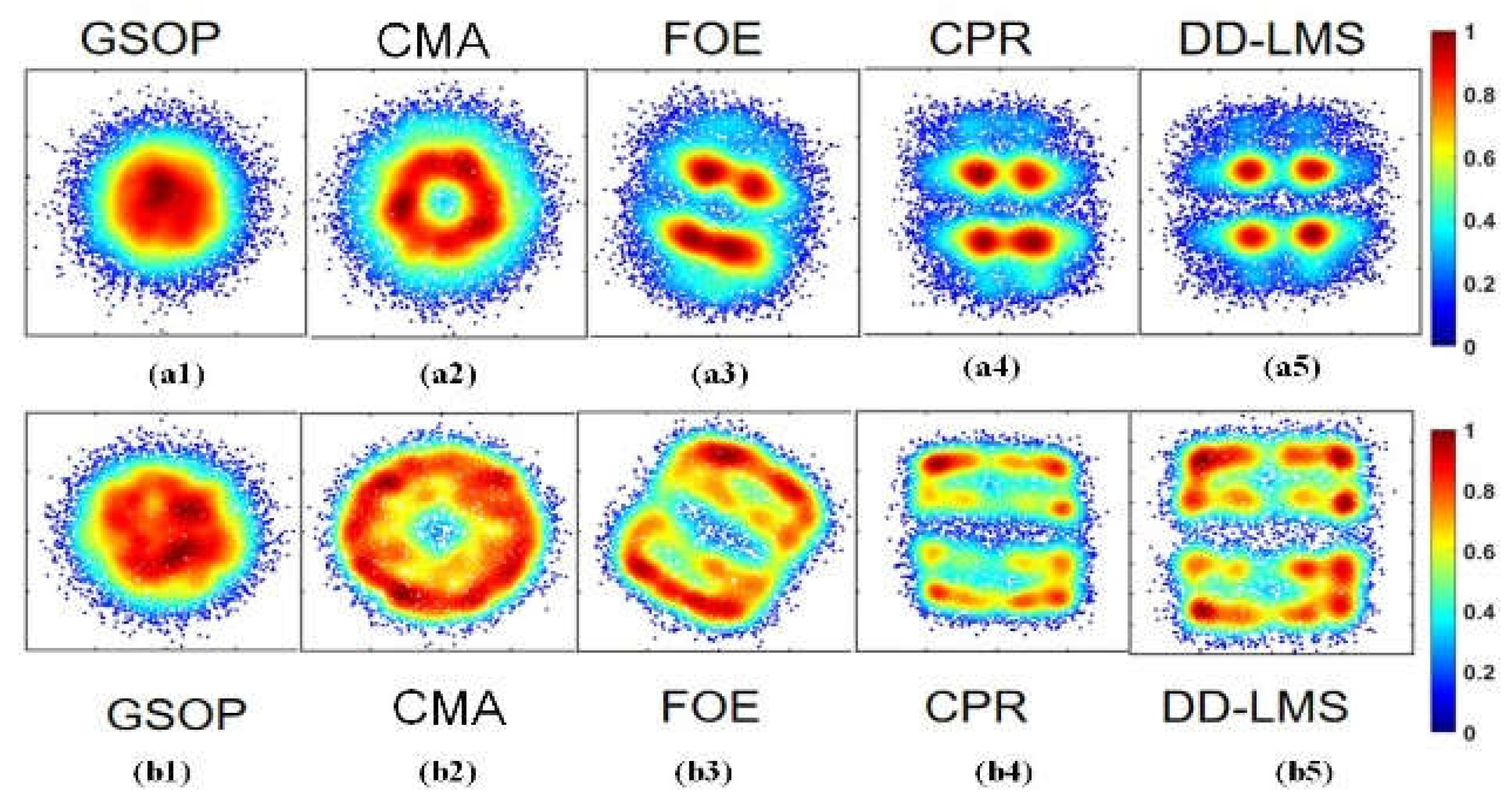
4.1. Traditional DSP Algorithm

Figure 5(a1) -(a5) give the density distribution of PS-16QAM constellation diagrams after successive DSP algorithms such as GSOP, CMA, FOE, CPR, and DD-LMS. As seen in Figs. 5(a2), the constellation diagrams are circles after the CMA algorithm, but after the FOE algorithms, the frequency offset noise can be mitigated. And by employing carrier phase recovery (CPR), the problem of phase offset is solved. After the DD-LMS algorithm, four points in the inner circle can be identified from complex-valued fuzzy signals. However, the remaining constellation points are widely scattered in Figure 5(a5). It implies that noises with a higher SNR requirement easily affect the signals in outer circles. Meanwhile, in Figure 5(b1) -(b5), the complex-value16QAM signals can be successfully separated into real and imaginary parts after the above DSP algorithms. However, they are still fuzzy since these steps are linear algorithms and useless for nonlinear noises. For the 16QAM constellation diagram in Figure 5(b5), the recovered signals after DD-LMS are evenly distributed and relatively concentrated around the 16 points. It proves that PS-16QAM does not have the same density distribution as 16QAM, as PS-16QAM has a severe skew in the class distribution of constellation diagrams due to the PS algorithm. In order to conquer the uneven distribution problem, a pre-processing data method of ROS is considered a simple and valid approach to achieving balance learning.

4.2. Results of ROS processing

As seen in Figure 6(a), the distribution of the transmitted PS-16QAM has an uneven change with the information entropy. Such imbalance is severe when the information entropy becomes smaller. Here is the process of the ROS method. The information entropy in our experiment is set as 5.6 bit/symbol. First, we oversampled the original unbalanced PS-16QAM training dataset. Thus, the corresponding target output has an equal distribution in Figure 6(b). The constellation diagrams of PS-16QAM before ROS cannot be separated into 16 points totally in Figure 6(c), while in Figure 6(d), they can be divided into 16 parts equally after ROS.
There are two ways of ROS. In the first approach, called “ROSI/Q” in Figure 7(a), the complex QAM sequence is firstly divided into the real-valued (RV) I and Q parts and then randomly oversampled separately. The I and Q components after ROSI/Q are finally trained through the TLD equalizer, respectively. In the other approach, denoted as “ROSQAM” in Figure 7(b), the density of the complex QAM signal is directly flattened via the complex-valued ROS and then split into real and imaginary parts as the input dataset sent into the two independent DNN equalizers, respectively. In our experiment, we assumed that 70% of the received symbols after DD-LMS are constructed as the training samples. Therefore, when transmitting 16384 symbols, the length of the training data is set around 11000 ( 16384 × 70 % ≈ 11000 )，and the length of the testing set is around 5000 ( 16384 × 30 % ≈ 5000 ). For the ROSI/Q scheme, the size of the generated balanced training dataset for the I-branch and Q-branch is 17208 and 17108, respectively, caused by the difference between the I- and Q-distribution. For the ROSQAM scheme, assuming that the lengths of the original and repeated samples are 11000 and 15864 symbols, respectively, the same target output numbers for the I-branch and Q-branch are 26864 symbols (11000+15864=26864).
Then the category values Y (∈ [1,16]) are converted to standard complex 16QAM signals with I data (∈ [-3, -1,1,3]) and Q data (∈ [-3,-1,1,3]). Furthermore, the generated ROS samples are fed into TLD with MSE loss, where the weight value on the I- and Q-path is updated, respectively, until the threshold error value or iteration number is reached.

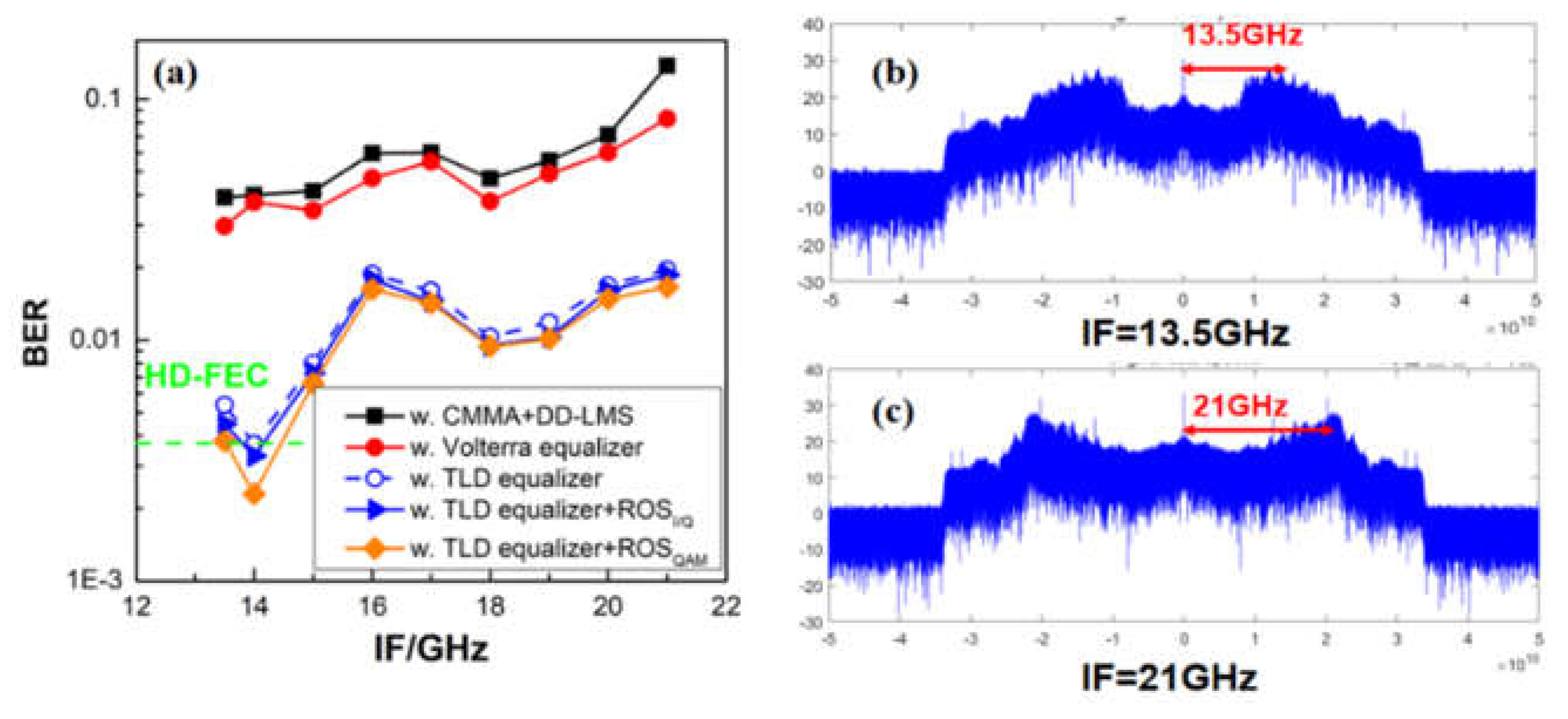
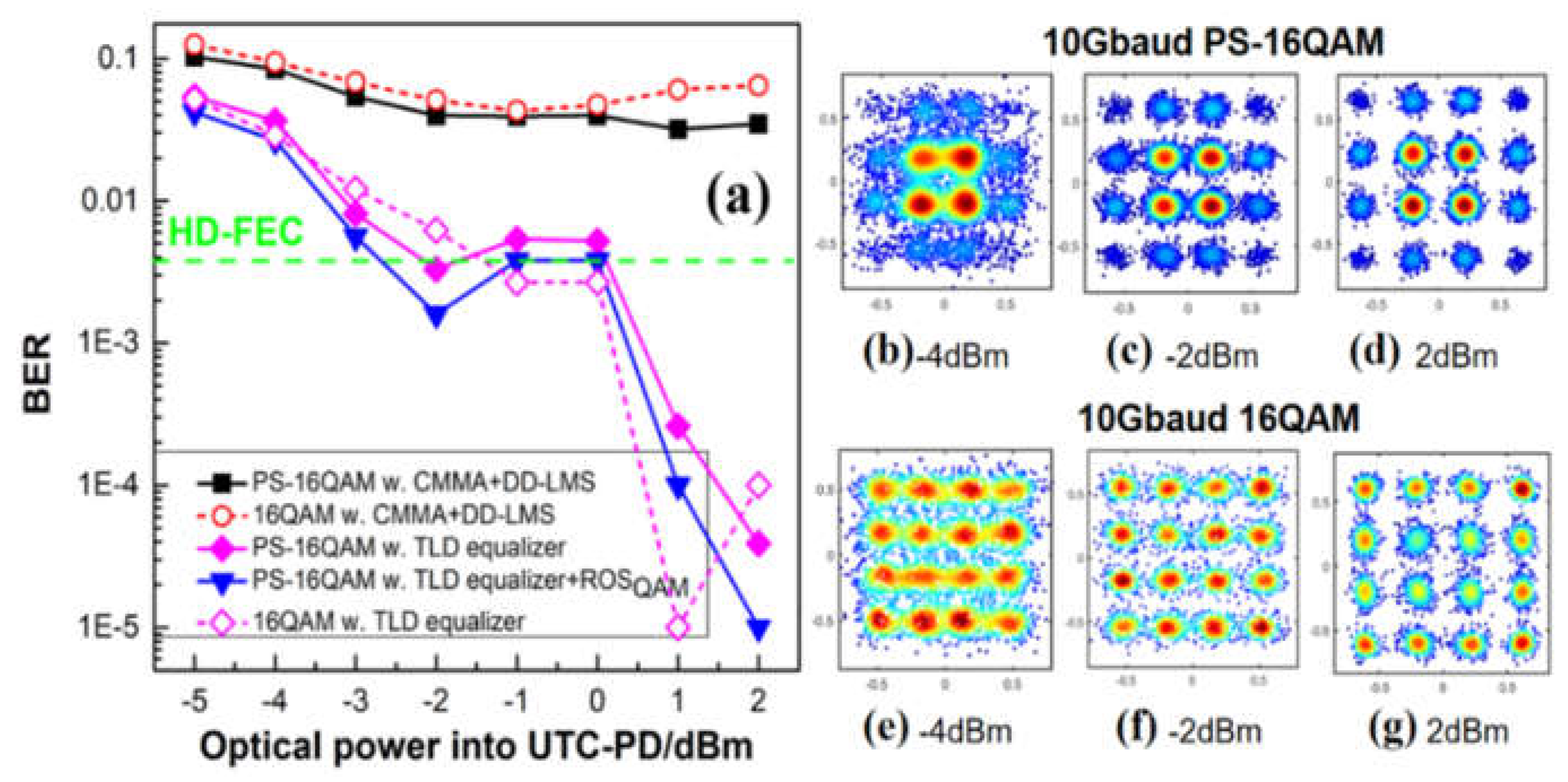
4.3. BER performances using TLD equalizer with/without ROS preprocessing

Moreover, we compare the BER performance versus the intermediate frequency (IF) after down-conversion for10-Gbaud PS-16QAM signals when the optical power into UTC-PD is fixed as -1dBm. It can be found that the BER increases with IF increasing, and when the IF is 21GHz, there is a steep fading in the high-frequency part of the electrical spectrum for the PS-16QAM signal, which severely affects the BER performance. In our experiment setup, the IF is optimized as 14 GHz. Meanwhile, we compare the BER performances of PS-16QAM signals employing only TLD equalizers and the two different TLD-ROS equalizer schemes. It is obvious that the TLD-ROS equalizer schemes offer great help to the drop of BER compared with the TLD equalizer. Moreover, it is worth noting that in this case, the PS-16QAM signal is firstly shaped into a “flat” 16-QAM constellation and then trained by the neural network model, where a “perfect” ROS is carried out, namely, equiprobable symbols without repetition.
Figure 9(a) illustrates the BER performance versus the input optical power for the PS-16QAM signal and the 16QAM signal, respectively. All nonlinear NN equalizers have the same neural structure [180-300-300-1], where 180 defines the memory length of the input layer. It is evident that when employing the traditional DSP algorithms, PS-16QAM has a better BER performance than 16QAM since it has a lower demand for SNR. However, linear CMMA and DD-LMS DSP algorithms are ineffective against the nonlinear problem. Differently, with the aid of TLD equalizers, the BER performances improve significantly. Whereas there is a BER difference between 16QAM signals and PS-16QAM signals employing TLD equalizers. When the optical input power is less than -1 dBm, the BER performance of PS-16QAM is better than 16QAM by employing TLD equalizers, because PS-16QAM is better adapted to channel transmission when the SNR is low. Contrarily, when optical input power is larger than -1dBm, 16QAM outperforms PS-16QAM. Because the larger input power meets the higher SNR requirement of 16QAM. Moreover, the outer ring constellation points of PS-16QAM signals are minority classes, which suffers inadequate training during the machine learning phase. Therefore, PS-16QAM may not perform as well as 16QAM when the optical input power is larger than -1dBm. It is essential to deploy ROS technique to overcome the imbalance learning issue of PS-16QAM. With the help of ROS, the receiver sensitivity of PS-16QAM signals equalized by TLD-ROS is improved as 1dB at BER of FEC-HD threshold of 3.8×10-3 compared with 16QAM signals only employing TLD equalizer.

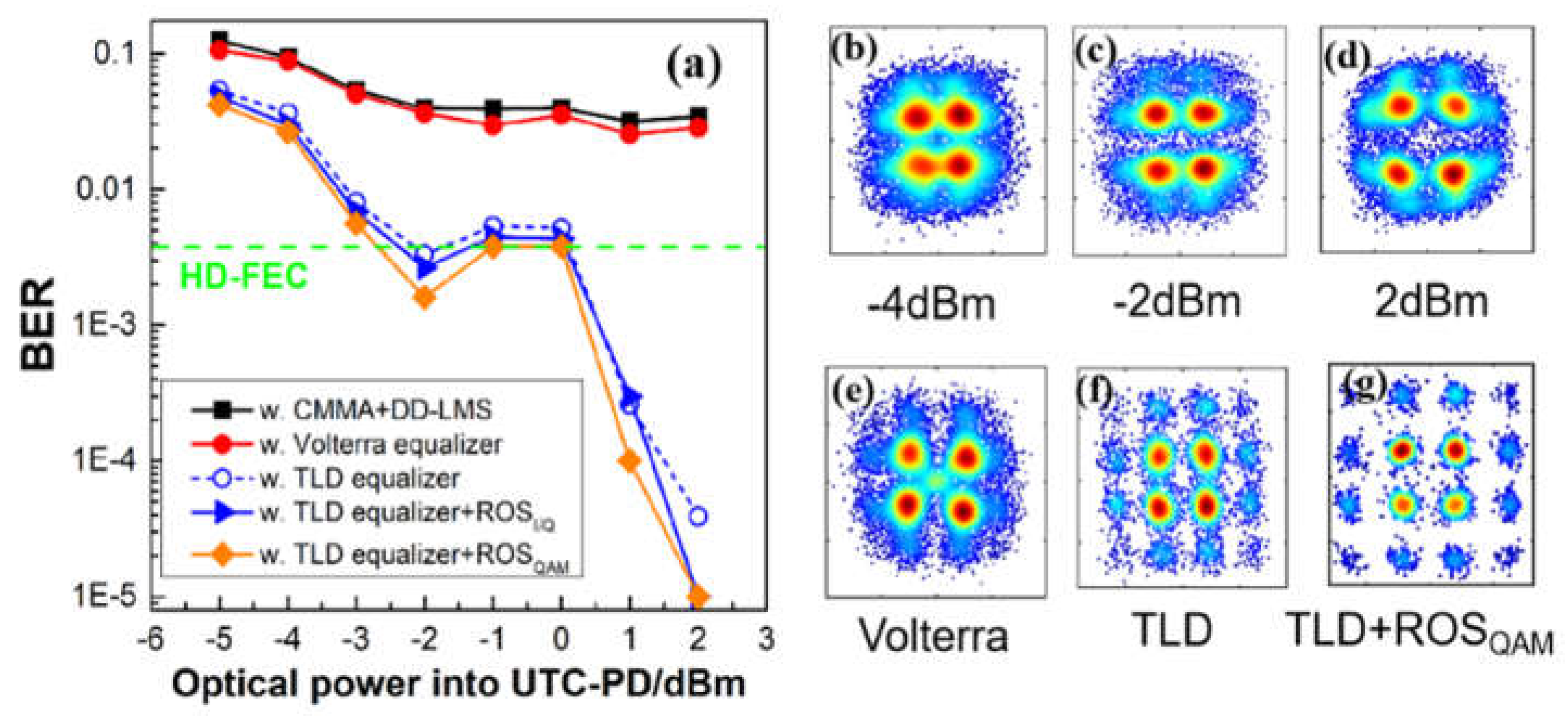
4.4. BER performance comparison using different equalizer schemes

4.4.1. Training Accuracy

For the implementation of DSP followed by carrier phase recovery, we deployed different schemes of various linear and nonlinear equalizers, including a linear 21-tap CMMA equalizer combined with 223-tap DD-LMS, 321-2nd tap Volterra equalizer, TLD equalizer with the same structure as [180-300-300-1] with 180 units in the input layer, 300 cells for both two hidden layers, and one neuron in the output layer, as well as the TLD equalizer combined with ROS balancing method when the transmission speed of PS-16QAM signal is 10-Gbaud. As given in Figure 10(a), it can be found that the BER performance improves with a larger optical power. We can see clearly from Figs. 10(b), (c), and (d) that with the increase of optical power into UTC-PD, the recovered constellation diagrams after DD-LMS becomes more and more clear, although still cannot be separated into 16 parts. When fixing the input optical power at 0 dBm, we find that the recovered constellation diagrams after the Volterra equalizer is still fuzzy and focused on four areas, and TLD equalizers perform better than Volterra-series in terms of learning accuracy because it helps constellation points separate into 16 parts and shows a better BER performance. The BER further drops by employing our proposed TLD-ROS, and the constellation diagram becomes clearer. Moreover, it is worth noting that in this case, the PS-16QAM signal is firstly shaped into a “flat” 16-QAM constellation and then trained by the neural network model, where a “perfect” ROS is carried out, namely, equiprobable symbols without repetition. Moreover, we compare two TLD-ROS schemes. As seen from the BER result in Figure 9(a), we come to the conclusion that the TLD-ROSQAM scheme performs better than the former one, with a relatively lower BER. And it is verified that ROS is an effective algorithm for handling the imbalance learning problem. In particular, ROSQAM is more suitable for handling imbalance caused by PAS. In terms of the receiver sensitivity, the PS-16QAM signal using TLD-ROSQAM equalizers shows a 1dB gain over typical TLD equalizers without balancing ROS at the BER of 3.8×10-3.

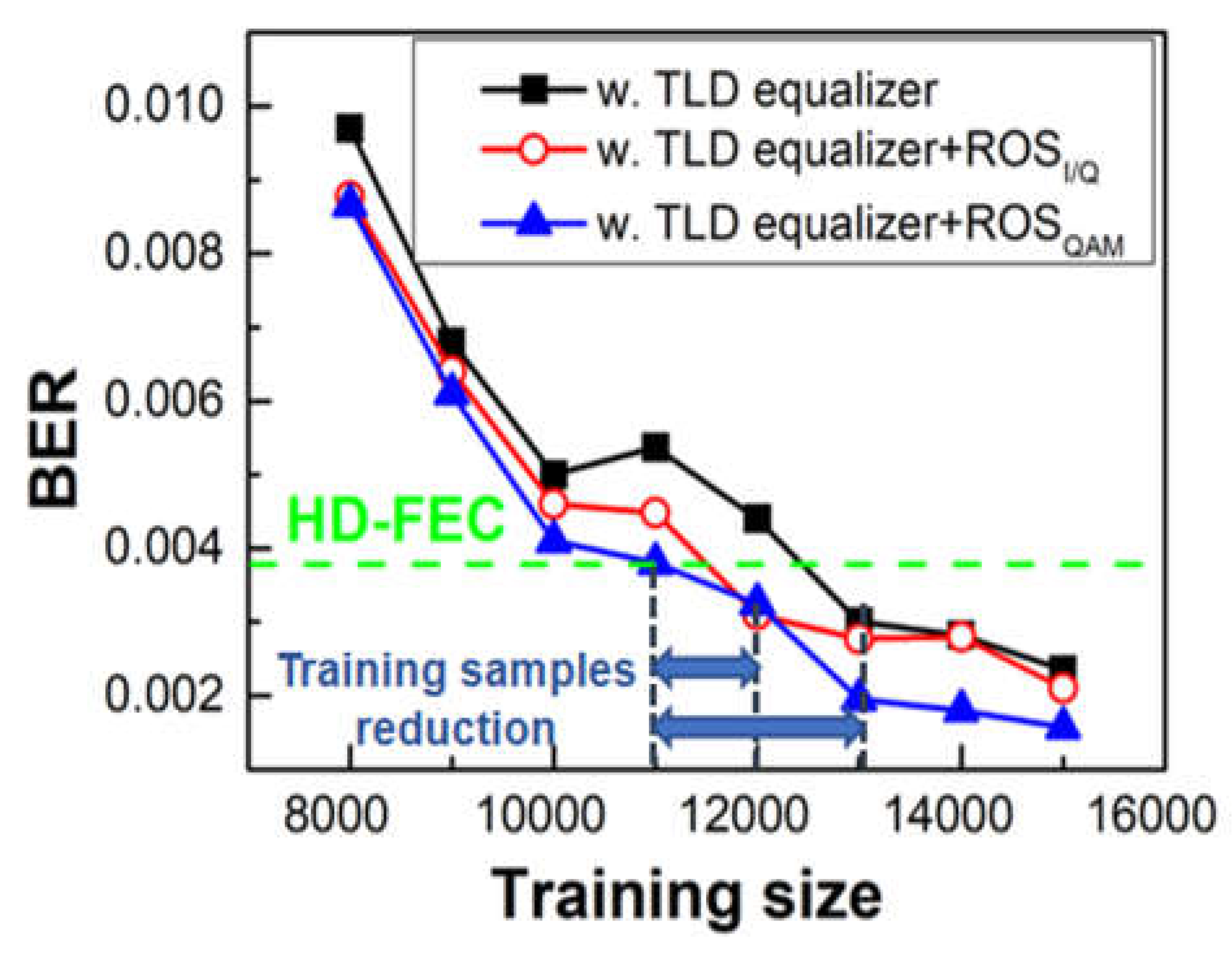
4.4.2. Training Data Size

Next, we compare the BER curves of PS-16QAM versus different training sizes of TLD schemes in Figure 11 when the optical input power is fixed at -1 dBm. It can be concluded that a longer training dataset is beneficial to BER reduction though at the expense of efficient system capacity. Besides, it is obvious that the BER of PS-16QAM employing TLD-ROSQAM equalizer performs the best, and it is reduced below 3.8 × 10 - 3 when the length of the training set exceeds 11000. In contrast, the TLD-ROSI/Q equalizer needs 1000 extra training samples, and 2000 extra training samples for the TLD equalizer. It means the ROS method is not only helpful to the adequate training of minority categories but also has a superiority in training sample reduction. Although the training size is increased based on ROS, the demand for training capacity is decreased. In the following discussion, the training data size is set as 11000 samples.

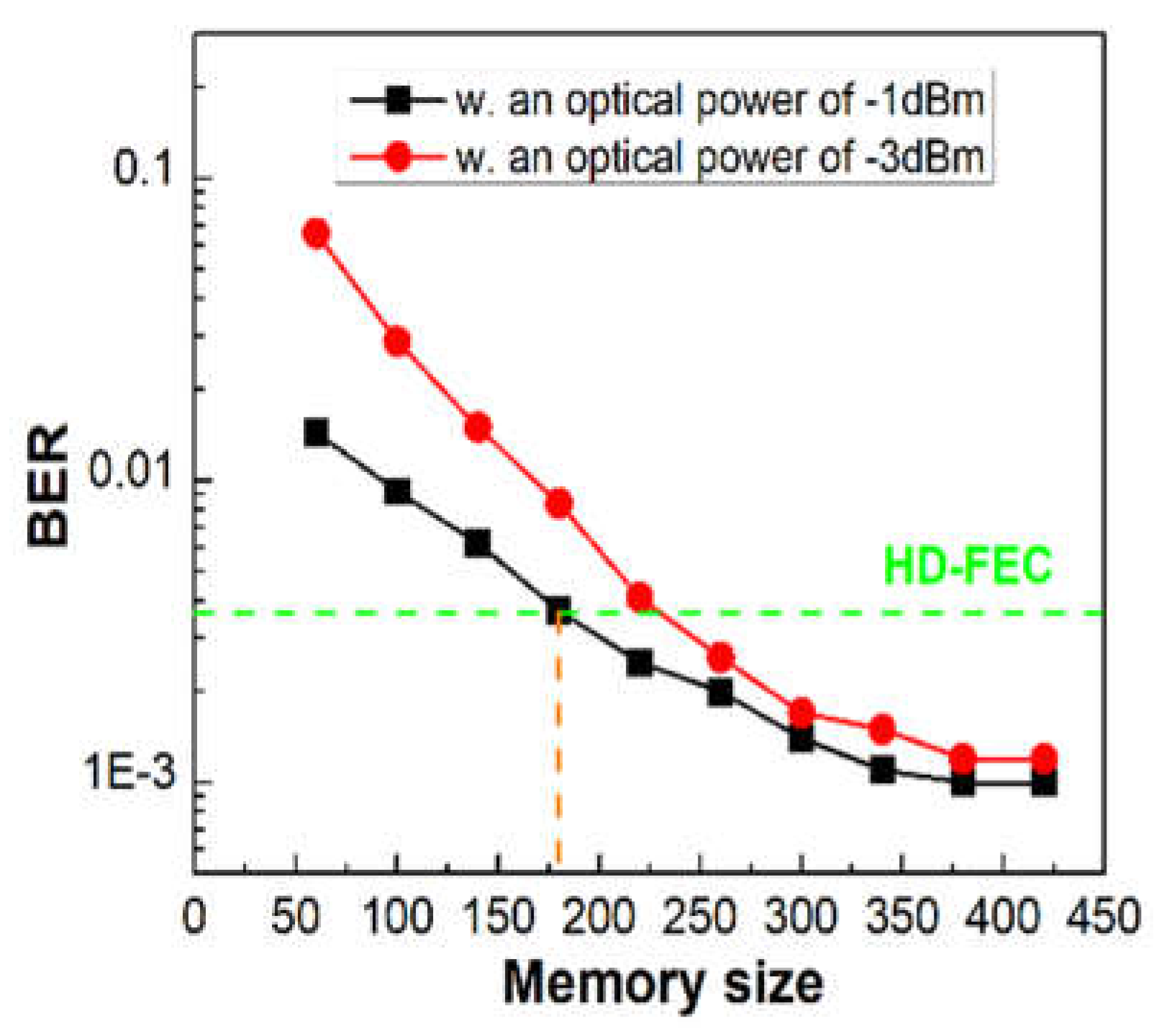
4.4.3. Memory Size in Input Layer

Furthermore, we compare the BER performance of PS-16QAM signals with different optical input powers versus memory sizes of the NN model. The BER performance significantly improves with the increase of the system’s SNR. As seen in Figure 12, it is evident that the HD-FEC threshold of 3.8×10-3 cannot be met for PS-16QAM signals when the system’s SNR is low with -3dBm optical input power until the memory size of the NN model exceeds 220. The HD-FEC threshold is reached with only 180 memory size when the optical input power is -1dBm. However, BER performances improve with the increase in memory sizes despite the expense of computational complexity. Additionally, when the memory size is more than 180, the BER curve decreases slowly since the overfitting effect occurs when the parameters of NN are too complicated. In light of those mentioned above, 180 is the experiment’s preferred memory size for the NN model.

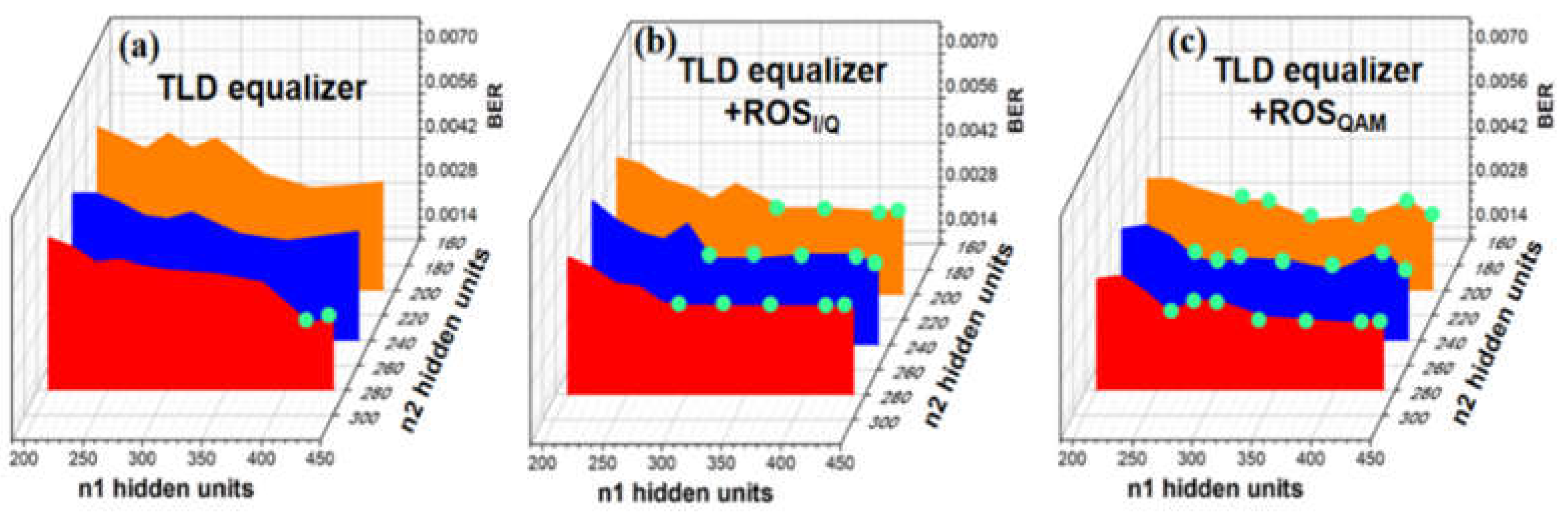
4.4.4. Neuron Number in Hidden Layer

Moreover, we further compare the BER performance with an input optical power of -1 dBm versus the amounts of neural cells n1, and n2 in hidden layer1 and hidden layer2, respectively. The amounts of neurons n0, and n M in the input layer and the output layer is 180 and 1, respectively, for all TLD schemes. Here, the green dots mark when the BER is 3.8×10-3. As shown in Figure 13, for TLD equalizers, the minimum data pair is 410 and 280. And for TLD-ROSI/Q equalizers, the minimum data pairs are 280-240 or 320-200 while 270-200 for TLD-ROSQAM equalizers. Results imply that the BER performance can get improved with the increase of n1 or n2.
Furthermore, we compare the complexity of different TLD schemes in Table 1, where the n1 and n2 data pair mark BER reaching the HD-FEC threshold with such hidden layer parameters. Besides, we also listed the complexity of the optimal 2nd Volterra equalizer in the same Table, despite its BER not reaching the HD-FEC threshold in the same conditions. The complexity in a typical M-layer NN is described as C M L P = n 0 n 1 + n 1 n 2 + n 2 n M [34], where n i denotes the number of nodes in the i-th layer, with n 0 and n M defining the numbers of nodes in the input layer and output layer, respectively. 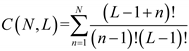Moreover, for a traditional Volterra equalizer, the total number of multiplications offers the complexity measure: Preprints 71152 i001[35], with N representing the Volterra order and L denoting the memory length. According to Table. 1, the complexity of the optimal 2nd Volterra with 321 taps is close to that of TLD-ROS equalizers, whereas its effect on nonlinear compensation is far less than TLD-ROS equalizers. Therefore, it can further prove the superiority of a TLD-ROSQAM equalizer because it reaches the HD-FEC threshold with the simplest structure.
According to our test, the Adam Optimizer is used, the batch size is 128, and the network requires 30 epochs to converge. In our proposed TLD-ROSQAM equalization scheme, the trained neural network (NN) got plenty of selective over-sampled data on which to train its few classification models. It implies that these samples in the minority class get more training epochs than those in the majority class. Instead, the computation burden does not increase in our well-trained neural network. Besides, the complexity can be decreased by decreasing the amounts of neural cells, and we see a complexity reduction of 45.6% for TLD-ROSQAM compared with a typical TLD equalizer without balancing ROS.

5. Conclusions

In this paper, we propose a novel equalization scheme applying two-lane DNN combined with balancing ROS to improve the overall W-band long-range wireless transmission performance. Moreover, its effectiveness is verified by PS-16QAM 4.6-km ROF delivery experiment results. In our proposed nonlinear equalization scheme, we employ ROS before TLD classification to avoid the class imbalance problem introduced by the PS technique. The experiment demonstrates that the ROS algorithm could enhance system performance without increasing the prediction phase complexity. In terms of the receiver sensitivity, the PS-16QAM signal using TLD-ROSQAM equalizers shows a 1dB gain over typical NN equalizers without balancing ROS when the BER reaches the HD-FEC threshold of 3.8×10-3. Besides, we compare the performance regarding training accuracy, sample size requirement, and network structure complexity between TLD, TLD-ROSI/Q, and TLD- ROSQAM schemes. We find that there is less demand for sample capacity and network structure depth by using TLD-ROSQAM, which realizes leaning imbalance mitigation. Besides, we can see a complexity reduction of 45.6% for TLD-ROS compared with a typical TLD equalizer without balancing ROS. Considering actual wireless physical layer with its requirements, there is much to be gained from the joint use of deep learning and balancing data pre-processing technique.

Author Contributions

Conceptualization, S.X.; methodology, B.S.; software, B.S.; validation, S.X. and L.Z.; formal analysis, L.Z.; investigation, S.X.; resources, S.X.; data curation, S.X.; writing—original draft preparation, S.X.; writing—review and editing, L.Z.; visualization, B.S.; supervision, L.Z.; project administration, S.X.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.

Funding

National Key Research and Development Program of China (2018YFB1801703), National Natural Science Foundation of China (61720106015, 61835002 and 62127802).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The raw/processed data required to reproduce these findings cannot be shared at this time as the data also forms part of an ongoing study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Y. Takahashi, K. Muraoka, J. Mashino, S. Suyama and Y. Okumura, “5G downlink throughput performance of 28 GHz band experimental trial at 300 km/h”, 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC, 2018), pp. 1140-1141.
  2. N. Nonaka, K. Muraoka, T. Okuyama, S. Suyama, Y. Okumura, T. Asai, and Y. Matsumura, “28 GHz-Band experimental trial at 283 km/h using the Shinkansen for 5G evolution”, 2020 IEEE 91st Vehicular Technology Conference (VTC, 2020), pp. 1-5.
  3. T. Okuyama, S. Suyama, N. Nonaka, Y. Okumura and T. Asai, “Two millimeter-wave base station cooperation technologies in high-mobility environments for 5G evolution,” 2020 IEEE 91st Vehicular Technology Conference (VTC, 2020), pp. 1-5.
  4. T. Okuyama, S. Suyama, N. Nonaka and T. Asai, “Outdoor experimental trials of 28 GHz band base station cooperation in high-mobility environment of multiple mobile stations, ” 2021 IEEE 94th Vehicular Technology Conference (VTC, 2021), pp. 1-5.
  5. A. Hirata, T. Kosug, H. Takahashi, R. Yamaguchi, F. Nakajima, T. Furuta, H. Ito, H. Sugahara, and Y. Sat, “120-GHz-band millimeter-wave photonic wireless link for 10-Gb/s data transmission,” IEEE Trans. Microw. Theory Tech. 54(5), 1937-1944 (2006). [CrossRef]
  6. ClarkS.Durrant-WhyteH., “Autonomous land vehicle navigation using millimeter wave radar,” in IEEE International Conference on Robotics and Automation (IEEE, 1998), pp. 3697-3702.
  7. W. Zhou, and C. Qin, “Simultaneous generation of 40, 80 and 120 GHz optical millimeter-wave from one Mach-Zehnder modulator and demonstration of millimeter-wave transmission and down-conversion,” Opt. Commun.398, 101-106 (2017). [CrossRef]
  8. H. Zheng, S. Liu, X. Li, W. Wang, and Z. Tian, “Generation and transmission simulation of 60 G millimeter-wave by using semiconductor optical amplifiers for radio-over-fiber systems,” Opt. Commun.282(22), 4440-4444 (2009). [CrossRef]
  9. P. T. Shih, J. Chen, C. T. Lin, W. J. Jiang, H. Huang, P. Peng, and S. Chi, “Optical millimeter-wave signal generation via frequency 12-tupling,” J. Lightwave Technol. 28(1), 71-78(2010). [CrossRef]
  10. X. Li, J. Xiao, Y. Xu, L. Chen, J. Yu. “Frequency-doubling photonic vector millimeter-wave signal generation from one DML,” IEEE Photon. J. 7(6), 1-7 (2015). [CrossRef]
  11. X. Li, J. Xiao, J. Yu. “W-band vector millimeter-wave signal generation based on phase modulator with photonic frequency quadrupling and precoding, “ J. Lightwave Technol. 35 (13), 2548-2558 (2017). [CrossRef]
  12. Press release from NTT DOCOMO on, Jan. 2020, [online] Available: https://www.nttdocomo.co.jp/english/info/media_center/pr/2020/0124_00.html.
  13. S. Suyama, T. Okuyama, Y. Kishiyama, S. Nagata and T. Asai, “A study on extreme wideband 6G radio access technologies for achieving 100 Gbps data rate in higher frequency bands”, IEICE Trans. Commun.E104-B (9), 992-999 (2021). [CrossRef]
  14. J. Xiao, J. Yu, X. Li, Y. Xu and Z. Zhang, “20-Gb/s PDM-QPSK signal delivery over 1.7-km wireless distance at W-band”, 2015 Optical Fiber Communications Conference and Exhibition (OFC, 2015), pp. 1-3.
  15. X. Li, J. Yu, J. Xiao, Z. Zhang, Y. Xu and L. Chen, “Field trial of 80-Gb/s PDM-QPSK signal delivery over 300-m wireless distance with MIMO and antenna polarization multiplexing at W-band”, 2015 Optical Fiber Communications Conference and Exhibition (OFC, 2015), pp. 1-3.
  16. J. A. Nanzer, P. T. Callahan, M. L. Dennis, T. R. Clark, D. Novak and R. B. Waterhouse, “Millimeter-wave wireless communication using dual-wavelength photonic signal generation and photonic upconversion”, IEEE Trans. Microw. Theory Tech. 50(12), 3522-3530(2011). [CrossRef]
  17. J. Xiao, X. Li, J. Yu, Y. Xu, Z. Zhang and L. Chen, “40-Gb/s PDM-QPSK signal transmission over 160-m wireless distance at W-band”, Opt. Lett 40(6), 998-1001 (2015). [CrossRef]
  18. X. Li, J. Xiao and J. Yu, “Long-Distance Wireless mm-Wave Signal Delivery at W-Band,” J. Lightwave Technol. 34(2), pp. 661-668 (2016). [CrossRef]
  19. X. Li, J. Yu, J. Zhang, F. Li, Y. Xu, Z. Zhang, and J. Xiao, “Fiber-wireless-fiber link for 100-Gb/s PDM-QPSK signal transmission at W-band.” IEEE Photonics Technology Letters 26(18), 1825-1828 (2014). [CrossRef]
  20. Yu, Jianjun, Xinying Li, and Nan Chi. “Faster than fiber: over 100-Gb/s signal delivery in fiber wireless integration system.” Opt. express 21(19), 22885-22904 (2013). [CrossRef]
  21. J. Yu, Z. Jia, L. Yi, Y. Su, G. K. Chang and T. Wang, “Optical millimeter-wave generation or up-conversion using external modulators,” in IEEE Photonics Technology Letters 18(1), 265-267 (2006). [CrossRef]
  22. W. Idler, F. Buchali, L. Schmalen, E. Lach, R. Braun, G. Boecherer, P. Schulte and F. Steiner, “Field Demonstration of 1 Tbit/s Super-Channel Network Using Probabilistically Shaped Constellations,” 2016 42nd European Conference on Optical Communication (ECOC, 2016), pp. 1-3.
  23. Q. Xu, L. Wang, D. Wang, X. Chen and S. Sun, “Probabilistic Shaping QC-LDPC Coded Modulation Scheme for Optical Fiber Systems,” 2018 Conference on Lasers and Electro-Optics Pacific Rim (CLEO-PR, 2018), pp. 1-2.
  24. K. M. Gharaibeh, Nonlinear Distortion in Wireless Systems: Modeling and Simulation with Matlab (Wiley-IEEE Press, 2012).
  25. K. B. Petrov, C. Mathieu, T. Felix, T. A. Eriksson, B. Henning, L. Domanic, B. Polina and S. Laurent, “End-to-End Deep Learning of Optical Fiber Communications,” J. Lightwave Technol. 36(20), 4843 – 4855 (2018). [CrossRef]
  26. S. Guob, G Peng, A Yangd and Y Qiaoe, “Deep Neural Network Based Chromatic Dispersion Estimation With Ultra-Low Sampling Rate for Optical Fiber Communication Systems,” IEEE Access 7, 84155-84162 (2019). [CrossRef]
  27. W. Wang and B. Chang, “Graph-based Dependency Parsing with Bidirectional LSTM,” in Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Academic, 2016), pp. 2306-2315.
  28. C. Liu, C. Wang, W. Zhou, F. Wang, M. Kong, and J. Yu, “81-GHz W-band 60-Gbps 64-QAM wireless transmission based on a dual-GRU equalizer,” Opt. Express 30, 2364-2377 (2022). [CrossRef]
  29. R. Liu, Y. Guo and S. Zhu, “Modulation Recognition Method of Complex Modulation Signal Based on Convolution Neural Network,” in Proc. 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC, 2020), pp. 1179-1184.
  30. Al-Nuaimi, Dhamyaa H., Muhammad F. Akbar, Laith B. Salman, Intan S. Zainal Abidin, and Nor Ashidi Mat Isa, “AMC2N: Automatic Modulation Classification Using Feature Clustering-Based Two-Lane Capsule Networks,” Electronics 10(1), 76 (2021). [CrossRef]
  31. A. Ghazikhani, H. S. Yazdi and R. Monsefi, “Class imbalance handling using wrapper-based random oversampling,” 20th Iranian Conference on Electrical Engineering (ICEE, 2012), pp. 611-616.
  32. S. Wang and X. Yao, “Multiclass Imbalance Problems: Analysis and Potential Solutions,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 42(4), 1119-1130 (2012). [CrossRef]
  33. S. Choirunnisa and J. Lianto, “Hybrid Method of Undersampling and Oversampling for Handling Imbalanced Data,” in Proc. 2018 International Seminar on Research of Information Technology and Intelligent Systems (ISRITI, 2018), pp. 276-280.
  34. P. J. Freire, Y. Osadchuk, B. Spinnler, A. Napoli, W. Schairer, N. Costa, J. E. Prilepsky, and S. K. Turitsyn, “Performance Versus Complexity Study of Neural Network Equalizers in Coherent Optical Systems,” J. Lightwave Technol. 39(19), 6085-6096 (2021). [CrossRef]
  35. J. Tsimbinos and K. V. Lever, “The computational complexity of nonlinear compensators based on the Volterra inverse,” Proceedings of 8th Workshop on Statistical Signal and Array Processing (Academic, 1996), pp. 387-390.
Preprints 71152 g001
Figure 1. The principle of random over-sampling and the corresponding target output of (a) original imbalanced dataset, (b) random over-sampled dataset and (c) balanced dataset.
Figure 1. The principle of random over-sampling and the corresponding target output of (a) original imbalanced dataset, (b) random over-sampled dataset and (c) balanced dataset.
Preprints 71152 g001
Preprints 71152 g002
Figure 2. The schematic diagram of a two-lane DNN (TLD) equalizer combined with ROS. IL: Input Layer. HL: Hidden Layer. OL: Output Layer. On: Output Value. En: Error Value. Tn: Expected output value.
Figure 2. The schematic diagram of a two-lane DNN (TLD) equalizer combined with ROS. IL: Input Layer. HL: Hidden Layer. OL: Output Layer. On: Output Value. En: Error Value. Tn: Expected output value.
Preprints 71152 g002
Preprints 71152 g003
Figure 3. The ROF experimental setup for W-band PS-16QAM RoF delivery over 4.6-km and photos of (a) the I/Q modulator, EA, PM-EDFA, and AWG; (b)ECLs and the ATT; (c) the PD, HA, and lens at the Tx-side (d) the PD, HA, and lens at the Rx-side; (e) the block diagram of Rx DSP.
Figure 3. The ROF experimental setup for W-band PS-16QAM RoF delivery over 4.6-km and photos of (a) the I/Q modulator, EA, PM-EDFA, and AWG; (b)ECLs and the ATT; (c) the PD, HA, and lens at the Tx-side (d) the PD, HA, and lens at the Rx-side; (e) the block diagram of Rx DSP.
Preprints 71152 g003
Preprints 71152 g004
Figure 4. (a) the experimental photo of the transmitter, (b) Satellite map of W-band PS-16QAM mm-wave signal long distance radio-over-fiber delivery on Fudan campus, (c)the experimental photo of the receiver.
Figure 4. (a) the experimental photo of the transmitter, (b) Satellite map of W-band PS-16QAM mm-wave signal long distance radio-over-fiber delivery on Fudan campus, (c)the experimental photo of the receiver.
Preprints 71152 g004
Preprints 71152 g005
Figure 5. The density distribution of PS-16QAM constellation diagrams after (a1) GSOP; (a2) CMA (a3) FOE; (a4) CPR; (a5)DD-LMS, and the density distribution of 16QAM constellation diagrams after (b1)GSOP; (b2) CMA (b3) FOE; (b4) CPR; (b5)DD-LMS.
Figure 5. The density distribution of PS-16QAM constellation diagrams after (a1) GSOP; (a2) CMA (a3) FOE; (a4) CPR; (a5)DD-LMS, and the density distribution of 16QAM constellation diagrams after (b1)GSOP; (b2) CMA (b3) FOE; (b4) CPR; (b5)DD-LMS.
Preprints 71152 g005
Preprints 71152 g006
Figure 6. Transmitted PS-16QAM amount distribution (a) before ROS, (b) after ROS, and the density distribution of received PS-16QAM constellation diagrams (c) before ROS, (d) after ROS.
Figure 6. Transmitted PS-16QAM amount distribution (a) before ROS, (b) after ROS, and the density distribution of received PS-16QAM constellation diagrams (c) before ROS, (d) after ROS.
Preprints 71152 g006
Preprints 71152 g007
Figure 7. The scheme of TLD equalizers combined with ROS. (a) TLD equalizer combined with ROSI/Q; (b) TLD equalizer combined with ROSQAM.
Figure 7. The scheme of TLD equalizers combined with ROS. (a) TLD equalizer combined with ROSI/Q; (b) TLD equalizer combined with ROSQAM.
Preprints 71152 g007
Preprints 71152 g008
Figure 8. (a) The BER performance vs. the intermediate frequency after down-conversion for10-Gbaud PS-16QAM signals, and the electrical spectrum when the received IF is (b)13.5GHz, (c)21GHz.
Figure 8. (a) The BER performance vs. the intermediate frequency after down-conversion for10-Gbaud PS-16QAM signals, and the electrical spectrum when the received IF is (b)13.5GHz, (c)21GHz.
Preprints 71152 g008
Preprints 71152 g009
Figure 9. (a) BER performance vs. the input optical power of PD for 88.5 GHz PS-16QAM signals and 88.5GHz 16QAM signals at 10-Gbaud by employing 45-tap CMMA equalizer combined with 301-tap DD-LMS, nonlinear TLD equalizers, and TLD equalizers combined with ROS respectively. And the recovered constellation diagrams of the PS-16QAM signal using TLD equalizers when the input optical power of PD is (b)-4dBm; (c) -2dBm; (d)2dBm; and that of the 16QAM signal when the input optical power of PD is (e) -4dBm; (f) -2dBm; (g)2dBm.
Figure 9. (a) BER performance vs. the input optical power of PD for 88.5 GHz PS-16QAM signals and 88.5GHz 16QAM signals at 10-Gbaud by employing 45-tap CMMA equalizer combined with 301-tap DD-LMS, nonlinear TLD equalizers, and TLD equalizers combined with ROS respectively. And the recovered constellation diagrams of the PS-16QAM signal using TLD equalizers when the input optical power of PD is (b)-4dBm; (c) -2dBm; (d)2dBm; and that of the 16QAM signal when the input optical power of PD is (e) -4dBm; (f) -2dBm; (g)2dBm.
Preprints 71152 g009
Preprints 71152 g010
Figure 10. (a) The BER performance vs. the input optical power of PD for 88.5 GHz PS-16QAM signals at 10-Gbaud by using traditional DSP algorithms, Volterra equalizers, and different TLD-ROS nonlinear equalizer schemes with MSE loss function. And the recovered constellation diagrams of the PS-16QAM signal after DD-LMS when the input optical power of PD is (b)-4dBm; (c) -2dBm; (d)2dBm; and when the input optical power of PD is fixed at 0dBm,different constellation performances of the PS-16QAM signal after (e)the Volterra equalizer; (f) the TLD equalizer; (g)TLD+ROSQAM scheme. .
Figure 10. (a) The BER performance vs. the input optical power of PD for 88.5 GHz PS-16QAM signals at 10-Gbaud by using traditional DSP algorithms, Volterra equalizers, and different TLD-ROS nonlinear equalizer schemes with MSE loss function. And the recovered constellation diagrams of the PS-16QAM signal after DD-LMS when the input optical power of PD is (b)-4dBm; (c) -2dBm; (d)2dBm; and when the input optical power of PD is fixed at 0dBm,different constellation performances of the PS-16QAM signal after (e)the Volterra equalizer; (f) the TLD equalizer; (g)TLD+ROSQAM scheme. .
Preprints 71152 g010
Preprints 71152 g011
Figure 11. the corresponding BER vs. the training data size for 10Gbaud PS-16QAM signals.
Figure 11. the corresponding BER vs. the training data size for 10Gbaud PS-16QAM signals.
Preprints 71152 g011
Preprints 71152 g012
Figure 12. The BER performances of PS-16QAM signals with different optical power versus the memory size of the NN model.
Figure 12. The BER performances of PS-16QAM signals with different optical power versus the memory size of the NN model.
Preprints 71152 g012
Preprints 71152 g013
Figure 13. The BER performance for PS-16QAM signals vs. the neural cells n1 in hidden layer1 and those n2 in hidden layer 2 when the optical power into PD is -1 dBm for (a)TLD equalizer, (b)TLD equalizer combined with ROSI/Q (c) TLD equalizer combined with ROSQAM.
Figure 13. The BER performance for PS-16QAM signals vs. the neural cells n1 in hidden layer1 and those n2 in hidden layer 2 when the optical power into PD is -1 dBm for (a)TLD equalizer, (b)TLD equalizer combined with ROSI/Q (c) TLD equalizer combined with ROSQAM.
Preprints 71152 g013
Table 1. Network parameters of various TLD schemes
Table 1. Network parameters of various TLD schemes
type Training size n1/tap n2/tap Minimum multiplication Complexity reduction
TLD 13000 410 280 377760 0%
TLD-ROSI/Q 12000 320 200 243600 35.5%
TLD-ROSQAM 11000 270 200 205600 45.6%
2nd Volterra 13000 321 321 207366 45.1%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated