Prerpints.org logo
Preprint
Article

Damage Degree Assessment of Steel Products Based on the Statistical Processing of Acoustic Emission Signal Flow

Altmetrics

Downloads

141

Views

45

Comments

0

Submitted:

20 April 2023

Posted:

20 April 2023

You are already at the latest version

Alerts
Abstract
This research is aimed to develop the method for damage degree evaluation in metals and alloys during their deformation and destruction based on acoustic emission (AE) technique. Experimental studies were carried out on tensile specimens of high-strength steel with simultaneous registration of AE signals in tested material. It was shown that the time-dependent AE primary parameters, such as the AE signal maximum amplitudes and AE activity, do not have a clear relationship with the material damage degree. This fact makes it difficult to use standard methods for assessing the damage degree of acoustic signal sources, including defects. It was proposed to use the Kolmogorov-Smirnov criterion to differ the processes of metal plastic deformation and crack propagation during the rupture. The possibility of estimating the material damage degree by high-energy AE hits share was shown. Besides, a particular expression was obtained for evaluating the damage degree for the material under study.
Keywords: 
Subject: Engineering  -   Safety, Risk, Reliability and Quality

1. Introduction

Determining the material damage degree during its operation is one of the most urgent tasks in industrial diagnostics. Currently, both periodic survey (for example, ultrasonic, eddy current and magnetic testing systems) and industrial monitoring systems based on permanent diagnostic signals recording during operation are used to detect damage in different types of products, structures and equipment.
The most promising method that allows a real-time detection of material damage is the acoustic emission (AE) [1,2,3]. The AE method is based on the registration of signals caused by irreversible displacements in the material due to structure changes or the defects formation. Any violation of atomic structure in metallic material generates AE signals of different shape and spectrum. These characteristics of AE signals reflect the energy and temporal parameters of the possible destruction [4]. As a result of the AE data processing, the identification, localization and damage degree assessment of propagating defects are carried out [5,6,7,8,9,10].
According to the results obtained in [11,12,13], to estimate the damage degree of materials by investigating the parameters of the registered AE signals, an assessment of the correlation dependence between the primary AE signal parameters and the level of the applied load should be made. The values of amplitude um, AE activity Ń, and energy E of acoustic signals were used as primary AE parameters. Based on the values of the above parameters, the stages of elastic and plastic deformation of materials under control may be defined.
For a more accurate damage degree assessment, a comprehensive analysis of AE data is usually performed. Thus, complex AE parameters were applied in [5,11,12,13,14]. For instance, the ratio of the rise time to the maximum amplitude of the AE signal, the ratio of the spikes number to the AE signal duration, as well as the slope of the linear function approximating the shape of the AE signal amplitude distribution were used. The proposed approaches make it possible to assess the damage degree of products under control in real-time and are effective for AE monitoring of their state with a small spread in AE parameters generated in the processes of the material plastic deformation and crack-like defects propagation.
It is known from fracture mechanics that in case of ductile metallic materials static failure, the fracture process begins with the formation of a plastic deformation zone near the stress concentrator. At this moment, an active plastic shear in the crystal lattice is occurred. Then this process is supplemented by crack propagation to a certain depth [15,16]. Next, a new zone of elastic-plastic deformation is formed nearby the crack tip, and the process of crack propagation proceeds further along the specimen cross-section.
Such processes (plastic shear and detachment of atomic bonds) are different in nature and generate AE signals that are noticeably different in their energy and temporal parameters. The number of AE signals generated by plastic shear accompanied by dislocations movement or a local change in the sample shape under loading is several times greater compared with the amount of AE signals recorded during structural bonds break. However, their energy is noticeably lower than that released in the result of destruction. Moreover, according to the results presented in [3,4,5,7,8], low-amplitude AE signals were recorded during plastic deformation of the material. At the same time, a significant increase in energy and the average frequency of recorded AE signals was noted during the process of crack growth.
Thus, an important task of AE diagnostics is to pick out the pulses corresponding to the crack propagation and the pulses corresponding to the plastic deformation zone development from AE signal flow. In this case, it becomes technically possible to assess the intensity of the crack formation and damage accumulation in the material, followed by the evaluation of its degree of damage. This study is devoted to experimental research of the most informative and valuable AE parameters recorded during tensile testing of steel specimens in order to monitor its damage degree. Tensile testing of cracked specimens with a side notch was used to evaluate the change in the AE parameters of the acoustic signal flow during plastic deformation of a specimen at the top of the stress concentrator and the crack growth. The statistical analysis of experimental data allowed differentiating these processes, identifying the characteristic stages of destruction, determining time intervals corresponding to crack growth, and establishing correlations between the energy parameters of acoustic signals and the damage degree of steel specimens.

2. Materials and Methods

Tensile testing of flat specimens with a side notch with simultaneous registration of AE signals was conducted. The 30KhGSA high-strength alloyed steel was chosen as a studied material because it is widely used in welding and manufacturing of highly loaded parts. Table 1 presents the chemical composition of the 30KhGSA steel determined in this research using the LAES Matrix atomic emission spectrometer and the Metavak-CS sulfur and carbon analyzer.
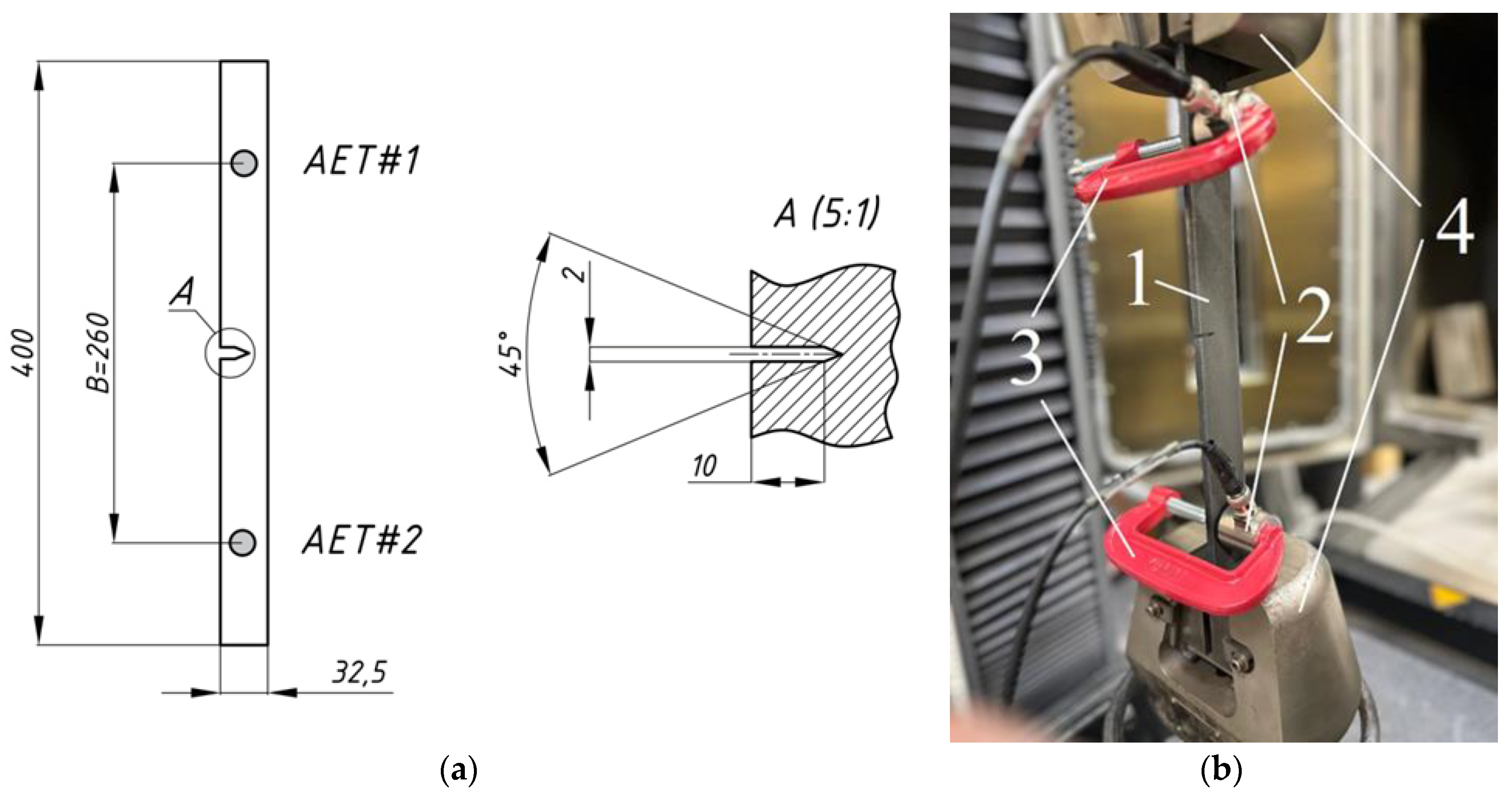
Flat specimens with a side notch were cut from a 6 mm thick steel sheet. The shape and dimensions of the specimens are shown in Figure 1a. The width of the specimens was chosen as 20 mm to provide perfect contact between the specimen side surface and the AE transducers of 18 mm diameter. The total length of the specimen was large enough (400 mm) to build a map of the AE sources linear location accurately.
The specimen was placed in the grips of the Instron 5982 universal testing machine. A pair of quasi-resonant sensors VS150-RIC with a built-in preamplifier with a gain of 34 dB was used as AE transducers (AETs). AE transducers (AET#1 and AET#2) were installed on the side surface of each specimen at a distance of 130 mm on the both sides of the side notch. The transducers were fixed with clamps through a layer of contact lubricant providing a good acoustic contact with the specimen surface. Thus, a formation of location zone with a size B = 260 mm was ensured. A photo of the specimen with installed AETs is represented in Figure 1b. Registration of AE signals arising in the process of tension was carried out using a Vallen AMSY-5 system for storing and processing acoustic signals. Tensile testing was conducted with strain rate of 2 mm/min. AE signals were recorded throughout all stages of loading till failure.
At the initial stage of experimental studies, the optimal parameters of the Vallen AMSY-5 acoustic system were determined. Based on the maximum noise amplitude recorded by the AE transducers, the threshold level uth = 36 dB of AE signals was defined. It was calculated according to the equation uth ≥ un + 6 dB (un is the maximum noise amplitude). The bandwidth of the digital filters was chosen to be Δfp = 95-850 kHz.
Linear location coordinates of AE sources were obtained to filter the noise signals arising in the process of mechanical friction of the specimen in the testing machine grips. For this purpose, the wave velocity of AE signals Vg was estimated. The calculation of Vg was carried out according to the results of preliminary tests consisting in the registration of acoustic signals generated in the process of breaking of a pencil lead (Hsu–Nielsen test) near one of the AETs outside the location zone. According to the results of preliminary tests, the wave velocity was Vg = 3300 m/s.
After determining the optimal parameters of the Vallen AMSY-5 system, the main batch of specimens was tested with AE signals registration. The method for processing the AE signal flow during static tension of steel specimens before failure included the combined use of statistical analysis models, digital signal processing, and fracture mechanics.
In this paper the material damage parameter is described by the scalar value j, which is equal to the relation of the relative elongation value of the steel specimen ε to the value of relative total elongation at the moment of failure εr:
Preprints 71436 i001
For the specimen without any damage j = 0. An increase in the concentration of micro- and macro damages during the loading process leads to a monotonous rise in j parameter [17]. When the ultimate strain values are reached, the parameter of the damage degree corresponds to j = 1.
Empirical distribution functions F W ∗ for both primary and complex AE parameters were studied to analyze the AE signal flow generated during the accumulation of internal damage in the specimen material [18]. The calculation of empirical distribution functions F W ∗ for a specimen based on AE parameters was carried out using a sliding window W = 100 hits. The F W ∗ function was evaluated using the equation below:
Preprints 71436 i002
where W – window size; I – the number of AE parameters that satisfy the condition Xi < y; Xi – value of the AE parameter from the sample X = (X1,…,Xi,…,Xw); y – threshold value of the AE parameter in the range y ∈ [Xmin,…Xmax]; Xmin and Xmax – the minimum and maximum values of the AE parameter from the sample, respectively.
To identify the moment of disorder in the flow of AE parameters caused by an AE source occurrence of different nature, the calculation of the two-sample Kolmogorov-Smirnov criterion [19] was applied based on a comparison of two empirical distribution functions:
Preprints 71436 i003
where Dw – maximum difference between empirical distribution functions of AE parameters calculated for (i-1) and i step of sliding window displacement with a size W.
If the Kolmogorov-Smirnov Dw statistics is significant, then the hypothesis of the two empirical distribution functions similarity of the AE parameters is rejected. The significance of the criterion was estimated according to the condition:
Preprints 71436 i004
where α =0.1 – the chosen level of significance; λα – critical value of the Kolmogorov-Smirnov statistics corresponding to the significance level α.
To determine the similarity degree of the empirical distribution functions of AE parameters, the probabilistic criterion Kα(λ) was evaluated, the values of which were selected from reference data [19]. When the empirical distribution functions of the AE parameters were similar, the criterion parameter Kα(λ) was close to zero. When there was a disorder in the parameters of the AE signal flow, which occurs when acoustic signals were generated by AE sources of different nature, the value of Kα(λ) parameter increased. In this regard, as a result of applying the statistical analysis technique discussed above, it was possible to differentiate the AE signal flow into two characteristic processes: 1) plastic deformation of the steel specimen at the top of the stress concentrator, characterized by a flow of low-energy AE signals; 2) the growth of a crack-like defect, distinguished by a flow of high-energy AE signals [20,21].
Application of the method discussed above contributed to assess the damage degree of the controlled product based on the correlation dependence between the activity of high-energy AE signals recorded at the stage of crack-like defect propagation and the values of the j parameter.

3. Results and Discussion

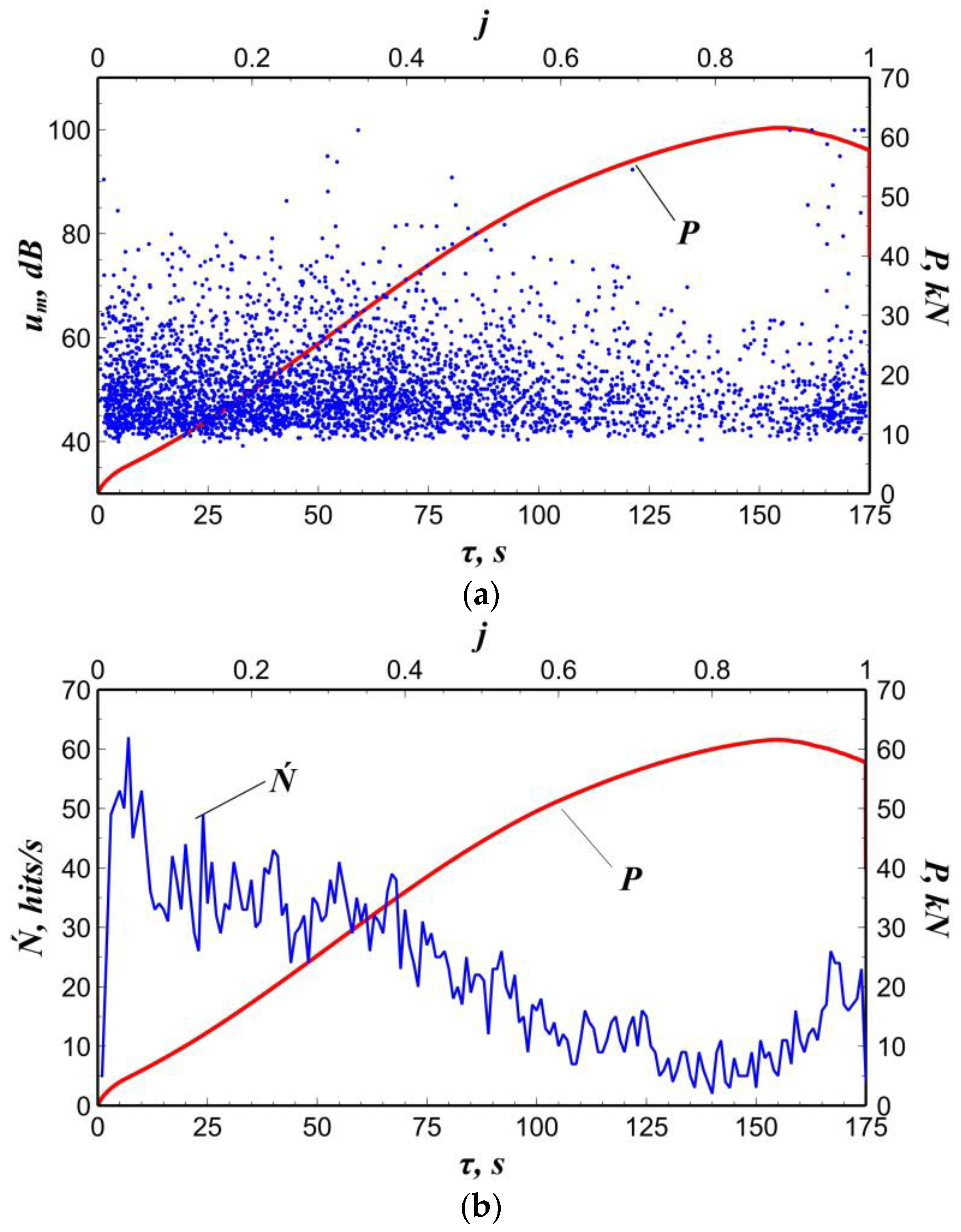
When processing the experimental data, the change in the primary AE parameters was estimated depending on the level of the applied load P during tensile testing. To demonstrate the fact that characteristics of the acoustic signal flow are non-stationary during specimen tension, the results of amplitudes um and activity Ń of AE signals were superimposed on the tension curve (Figure 2).
When analyzing the kinetics of changes in the maximum amplitude um(τ) and activity Ń(τ) during tension, the following results were obtained. At the initial stage of a steel specimen loading (τ < 10 s; j ≤ 0.06), a flow of high-amplitude AE signals was recorded, the activity of which reached 62 hits/s. Basically, it is typical for the microdamages scattered accumulation throughout the entire volume of the controlled specimen. A further increase in the applied load (10 < τ ≤ 120 s; 0.06 < j ≤ 0.70) leads to localization of the material deformation region in the notch area and a decrease in the amplitude and activity to the values of um = 75 dB and Ń = 17 hits/s, respectively. In the time interval from 120 to 160 seconds (0.70 < j ≤ 0.93), the moment of “acoustic calm” was recorded [22]. It is characterized by a growth in the intensity of plastic deformation at the crack tip and a decline in the maximum amplitude and activity to the values of um = 63 dB and Ń = 11 hits/s, respectively. When the specimen reached the pre-destruction state (160 < τ ≤ 172 s; 0.93 < j ≤ 1), a significant rise in the maximum amplitude up to um = 100 dB was noted. Moreover, the AE activity at the moment of destruction corresponded to the value Ń = 26 hits/s, which is 2.4 times less than the value of AE activity at the initial stage of specimen loading.
An analysis of the time-dependent functions of the maximum amplitude um(τ) and activity Ń(τ) during tensile testing (Figure 2) shows that it is impossible to unambiguously determine their relation with the damage degree of the steel specimen. This fact makes it difficult to use standard methods for assessing the damage degree caused by acoustic signal sources.
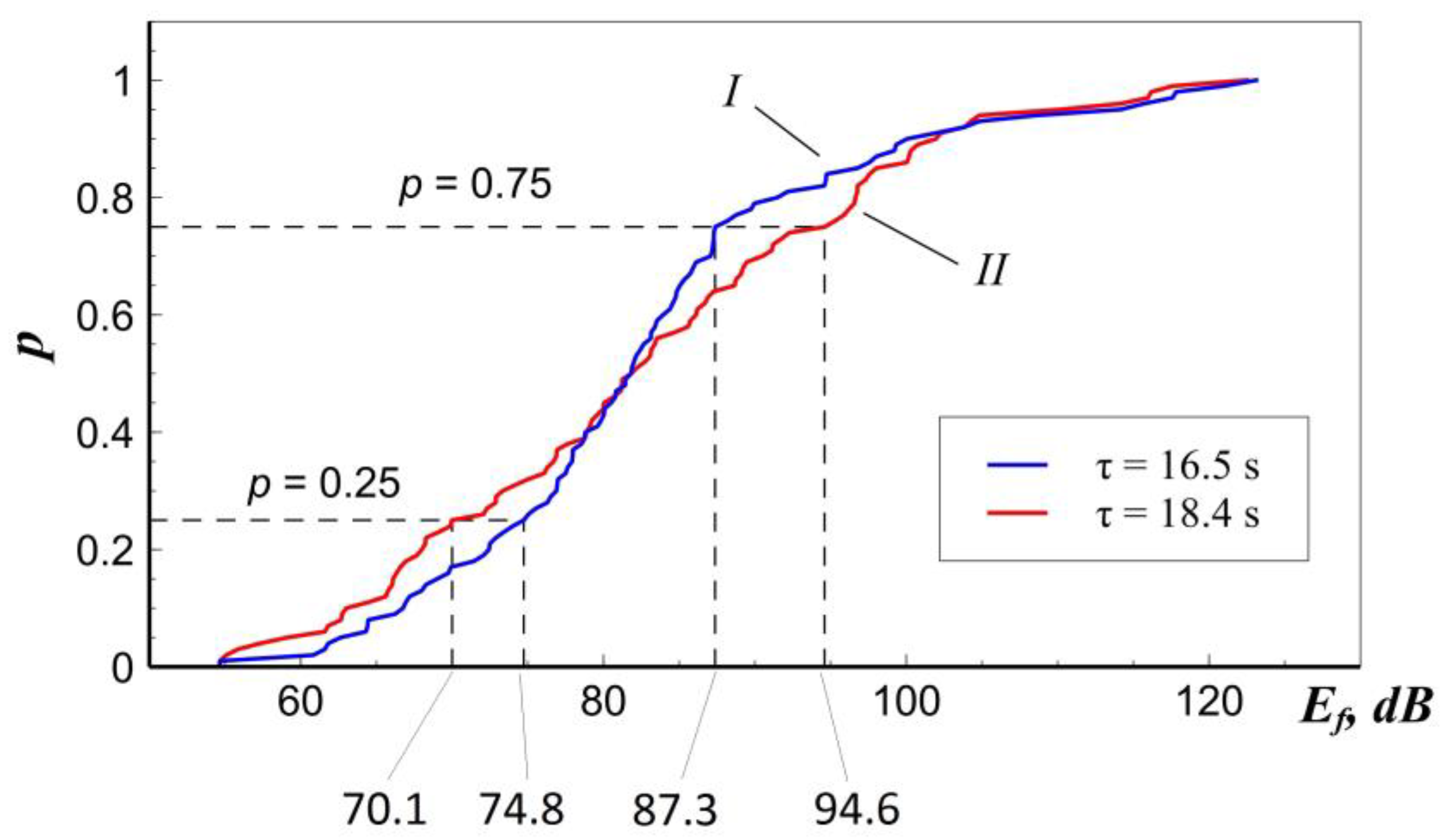
To improve the validity of AE monitoring results, not only the primary parameters, but also the statistical characteristics of the acoustic signal flow during tensile testing were evaluated. It was proposed to consider two charts of energy distribution of AE signals leading edge Ef for two adjacent recording times of specimen tension. As an example, two close time points τ = 16.5 s and τ = 18.4 s were chosen. The energy values of the AE signal leading edge Ef were calculated by the formula:
Preprints 71436 i005
where uμV – AE signal amplitude (µV), τf – AE signal rise time (μs).
The results are shown in Figure 3.
As shown in Figure 3, at time τ = 16.5 s (curve I), the lower (p = 0.25) and upper (p = 0.75) quartiles of the empirical distribution energy function of the AE signals leading edge correspond to the values of Ef (p = 0.25) = 74.8 dB and Ef (p = 0.75) = 87.3 dB, respectively. At time τ = 18.4 s (curve II), there is a rise in the activity of high-energy AE signals Ef > 80 dB, which manifests in the upper quartile increase up to Ef (p = 0.75) = 94.6 dB. Thus, the nature of the AE signal flow can change significantly even over a short time interval τ = 16.5 – 18.4 s. This is consistent with the known researches results of ductile and brittle fractures of the structural steels at all scale levels [22,23]. In this case, it can be assumed that a strong difference in the AE parameters at adjacent times indicates the different intensity of processes of plastic deformation and crack propagation at each time. For a numerical assessment of these processes in the material, the two-sample Kolmogorov-Smirnov criterion was used, the application of which is described in the previous section of the article. The statistical criterion was estimated based on the results of the energy empirical distribution functions of the AE signal leading edge Ef. The calculated Kolmogorov-Smirnov statistical criterion Kα calculated by Ef parameter is provided in Figure 4.
Figure 4 shows the probabilistic statistics (Kα) describing the similarity of the empirical distribution function F W i + 1 ( y ) and the test sample F W i ( y ) . The scalar value of the probabilistic statistics Kα changes in the range [0 - 1] and takes on a zero value at Dw = 0.
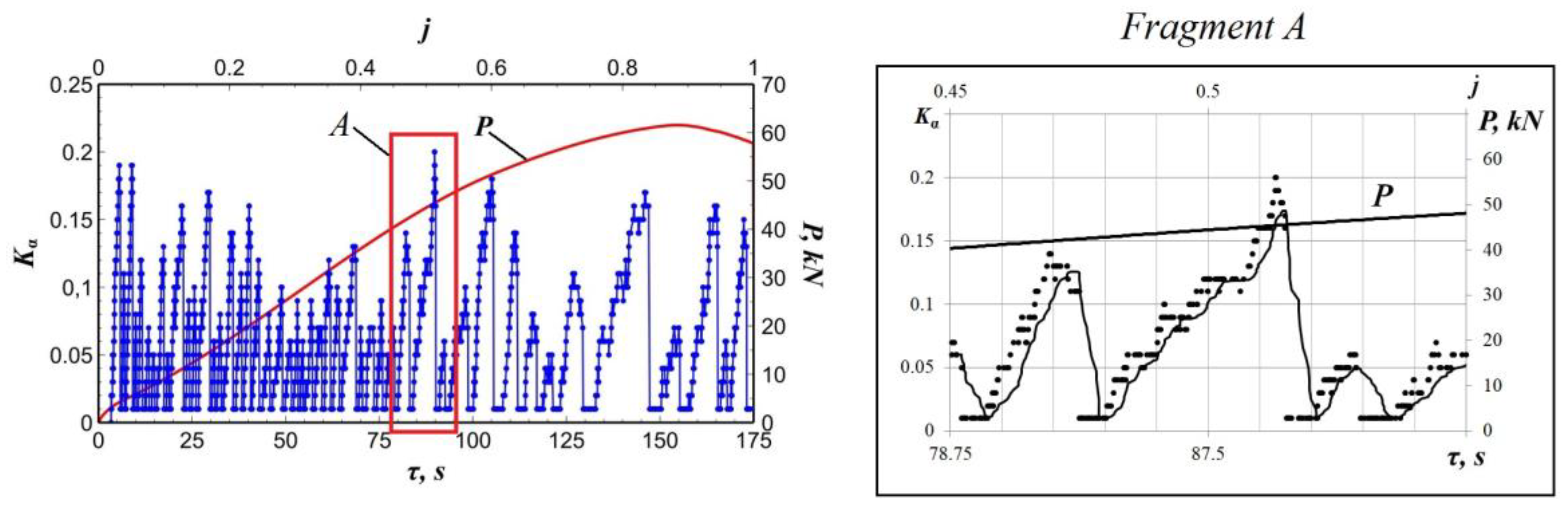
As an example, the change in the characteristics of the high-energy AE signal flow recorded with an increase in load from P = 45.4 kN (j = 0.51) to P = 47.7 kN (j = 0.54) is shown in Figure 4 (Fragment A). A rise in the applied load leads to the crack-like defect propagation and to an increase in the proportion of high-energy AE signals. A change in the energy characteristics of the AE signal flow has a considerable effect on the form of the empirical distribution function of the Ef parameter. In this regard, there is an increase in the statistical criterion from Kα = 0.01 to Kα = 0.20. With a further growth in the applied load, a local maximum of the Kα(τ) function at j = 0.51 appears, which characterizes the change in the energy characteristics of the AE signal flow. A decrease in the Kα is explained by a decline in the activity of high-energy AE signals. It indicates a transition from the stage of crack-like defect propagation to the plastic deformation of metal in the stress concentration zone.
It should be noted that the activity of the local maximums of the Kα(τ) function decreases with a growth in the applied load and damage degree, especially when j > 0.7. It can be explained by the appearance of a main crack in the region of the side notch of the steel specimen. Thus, the application of the Kolmogorov-Smirnov statistical criterion makes it possible to divide the main stages of damage development during tensile testing.
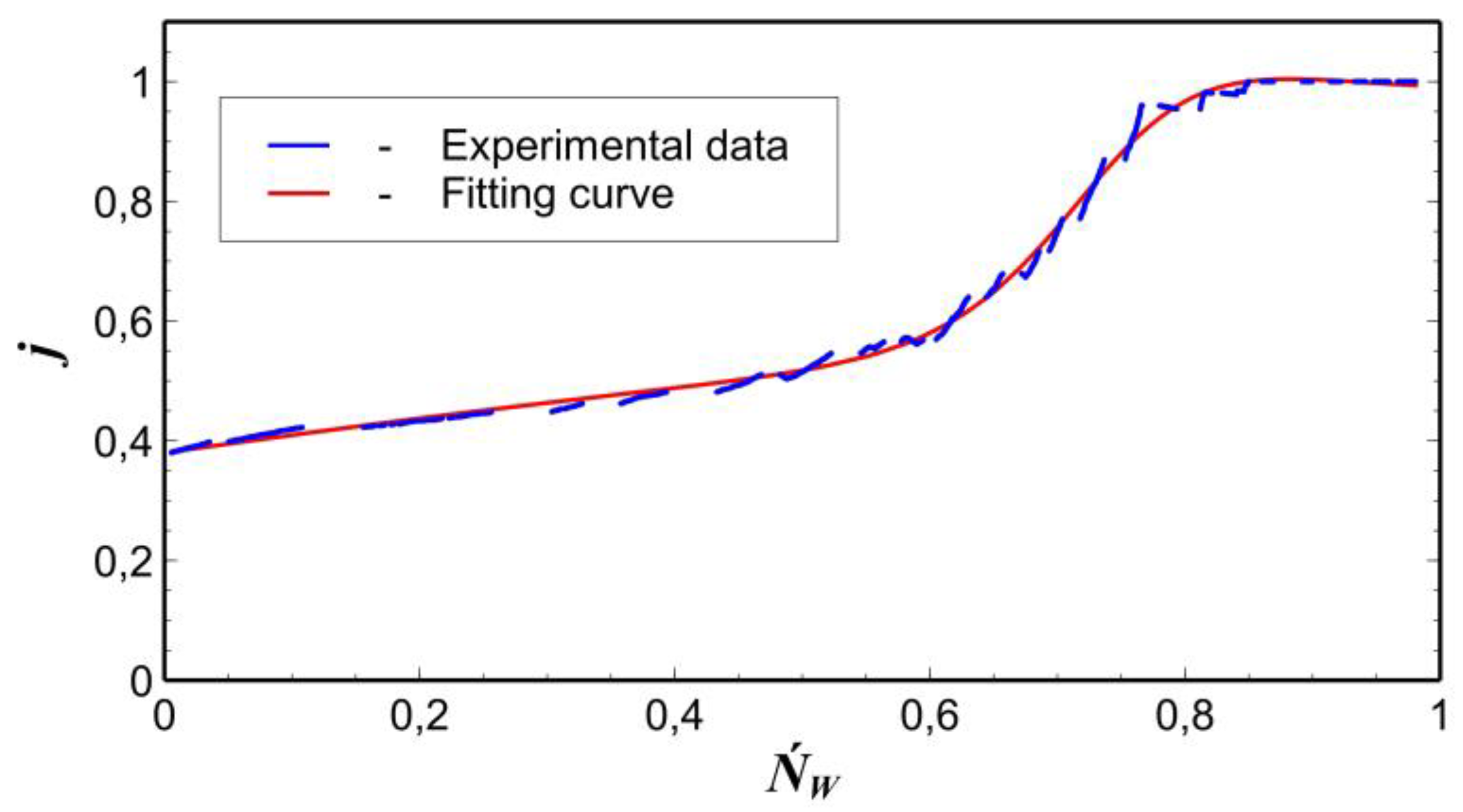
At the final stage of the research, the synthesis of an empirical relation for assessing the damage degree j of the product under control based on the statistical processing of AE signals recorded during experimental studies was carried out. The high-energy AE signals content (ṄW=N(Ef ≥ 80 db)/W) in the flow of acoustic signals corresponding to the propagation of a crack-like defect was chosen as a dependent variable. Figure 5 presents the correlation dependence of the damage degree j of the steel specimen on the values of the criterion ṄW.
At the initial stage of specimen tension, a high activity of the Kα(τ) function local maxima appearance was recorded. It interfered the process of AE sources division of different nature. Therein, an unambiguous differ of the AE signal flow into two processes using the proposed technique is possible only for the damage degree of the specimen is j ≥ 0.37. Polynomial approximation of the j = f(Ńw) empirical function was performed using the least squares method (please, see “Fitting curve” in Figure 5):
Preprints 71436 i006
The high accuracy of the approximation results was confirmed by the determination coefficient R2 = 0.988, which is close to 1.

4. Conclusions

A series of experimental studies consisting in AE signals recording during tensile testing of a steel specimen with a side notch was carried out in this study. Statistical analysis of the AE signal flow made it possible to identify the most informative parameters of AE pulses, which can be used to identify the periods of crack propagation and damage accumulation in the material and to assess the damage degree of the object under control.
1.
The dependences of the AE amplitudes um and the AE activity Ń during all loading stages of the specimen were obtained. It was established that the temporal dependencies functions um(τ) and Ń(τ) cannot be used for unambiguously determination of their relation with the damage degree of the steel specimen.
2.
The energy distribution of AE signals leading edge Ef can be an effective tool to differentiate the processes of plastic deformation and crack propagation in the tested material. To differ these processes by the parameters of the AE flow, the authors proposed a method for detecting the moment of discord in the acoustic signals flow. It was performed based on the calculation of the Kolmogorov–Smirnov (Kα) statistical criterion. As a result of calculating this statistical criterion, local maxima of the Kα(τ) function were determined and their period of occurrence was correlated with the damage degree of the steel specimen.
3.
The analytical dependence Preprints 71436 i007 may be used as a numerical criterion for assessing the damage degree j of the investigated specimens made of 30KhGSA high strength steel using the calculated values of high-energy AE signals content ṄW. It should be noted that the high accuracy of the results applied by the developed technique is ensured when the damage degree of the specimen is j ≥ 0.37.
At the next step in the development of the proposed approach, it is necessary to improve the accuracy of estimating the damage degree at low j values (j < 0.37). Perhaps it would be efficient to use artificial neural networks to solve this task of high scientific interest. As input data for neural networks, it is supposed to apply not only energy, but also spectral characteristics of the recorded AE flow.

Author Contributions

Conceptualization, A.M. and D.C.; methodology, D.C. and I.V.; validation, D.C., T.K. and E.K.; formal analysis, A.P.; investigation, A.M. and D.C.; data curation, I.V.; writing—original draft preparation, D.C.; writing—review and editing, A.M., D.Z. and I.V.; visualization, D.Z.; supervision, A.M.; project administration, D.Z.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.

Funding

The reported study was funded by the Russian Science Foundation (project No. 21-79-00232).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

This research was carried out in National Research University “Moscow Power Engineering Institute”. The experimental results were obtained using the equipment provided by the center "Science-intensive technologies for creating machines of the future" (IMASH RAS).

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Lukonge, A.; Cao, X. Leak detection system for long-distance onshore and offshore gas pipeline using acoustic emission technology. A review. Trans. Indian Inst. Met. 2020, 73, 1715–1727. [Google Scholar] [CrossRef]
  2. Livadiotis, S.; Sitaropoulos, K.; Ebrahimkhanlou, A.; Salamone, S. Acoustic emission monitoring of corrosion in steel pipes using Lamb-type helical waves. Struct. Health Monit. 2023, 22, 1225–1236. [Google Scholar] [CrossRef]
  3. Shehadeh, M.; Osman, A.; Elbatran, A.A.; Steel, J.; Reuben, R. Experimental Investigation Using Acoustic Emission Technique for Quasi-Static Cracks in Steel Pipes. Assessment. Machines 2021, 9, 73. [Google Scholar] [CrossRef]
  4. Louda, P.; Sharko, A.; Stepanchikov, D. An Acoustic Emission Method for Assessing the Degree of Degradation of Mechanical Properties and Residual Life of Metal Structures under Complex Dynamic Deformation Stresses. Mater. 2021, 14, 2090. [Google Scholar] [CrossRef] [PubMed]
  5. Matvienko, Y.G.; Vasil’ev, I.E.; Chernov, D.V. Damage and failure of unidirectional laminate by acoustic emission combined with video recording. Acta Mech. 2021, 232, 1889–1900. [Google Scholar] [CrossRef]
  6. Yang, L.; Xu, F. A Novel Acoustic Emission Sources Localization and Identification Method in Metallic Plates Based on Stacked Denoising Autoencoders. IEEE Access. 2020, 8, 141123–141142. [Google Scholar] [CrossRef]
  7. Marchenkov, A.; Vasiliev, I.; Chernov, D.; Zhgut, D.; Moskovskaya, D.; Mishchenko, I.; Kulikova, E. Estimation of Acoustic Source Positioning Error Determined by One-Dimensional Linear Location Technique. Appl. Sci. 2022, 12, 224. [Google Scholar] [CrossRef]
  8. Matvienko, Y.G.; Vasil’ev, I.E.; Chernov, D.V.; Ivanov, V.I.; Elizarov, S.V. Problems of Locating Acoustic Emission Sources. Russ. J. Nondestruct. Test. 2021, 57, 769–778. [Google Scholar] [CrossRef]
  9. Uhlmann, E.; Holznagel, T.; Clemens, R. Practical Approaches for Acoustic Emission Attenuation Modelling to Enable the Process Monitoring of CFRP Machining. J. Manuf. Mater. Process. 2022, 6, 118. [Google Scholar] [CrossRef]
  10. Sofer, M.; Kucera, P.; Mazancova, E.; Krejci, L. Acoustic Emission and Fractographic Analysis of Seamless Steel Pressure Cylinders with Artificial Flaws under Hydrostatic Burst Testing. J. Nondestruct. Eval. 2019, 38, 84. [Google Scholar] [CrossRef]
  11. Li, P.; Zhang, W.; Ye, Z.; Wang, Y.; Yang, S.; Wang, L. Analysis of Acoustic Emission Energy from Reinforced Concrete Sewage Pipeline under Full-Scale Loading Test. Appl. Sci. 2022, 12, 8624. [Google Scholar] [CrossRef]
  12. D'Angela, D.; Ercolino, M. Acoustic emission entropy: An innovative approach for structural health monitoring of fracture-critical metallic components subjected to fatigue loading. FFEMS 2021, 44, 1041–1058. [Google Scholar] [CrossRef]
  13. Aggelis, D.G.; Kordatos, E.Z.; Matikas, T.E. Acoustic emission for fatigue damage characterization in metal plates, Mech. Res. Commun. 2011, 38, 106–110. [Google Scholar]
  14. Makhutov, N.A.; Matvienko, Y.G.; Vasil’ev, I.E.; Chernov, D.V.; Ivanov, V.I. Rupture Tests of Reinforcing Fibers and a Unidirectional Laminate Using Acoustic Emissions. Instrum. Exp. Tech. 2022, 65, 305–313. [Google Scholar] [CrossRef]
  15. Sun, Ya.; Edwards, M.G.; Chen, B.; Li, C. A state-of-the-art review of crack branching. Eng. Fract. Mech. 2021, 257, 108036. [Google Scholar] [CrossRef]
  16. Ritchie, R.O. Mechanisms of fatigue-crack propagation in ductile and brittle solids. Int. J. Fract. 1999, 100, 55–83. [Google Scholar] [CrossRef]
  17. Stepanova, L.V.; Igonin, S.A. Rabotnov damage parameter and description of delayed fracture: Results, current status, application to fracture mechanics, and prospects. J. Appl. Mech. Tech. Phys. 2015, 56, 282–292. [Google Scholar] [CrossRef]
  18. Lagutin, M.B. Visual mathematical statistics, 2nd ed.; Binom: Moscow, Russia, 2009; 472p. [Google Scholar]
  19. Bolshev, L.N. , Smirnov, N.V. Tables of mathematical statistics; Nauka: Moscow, Russia, 1983; 416p. [Google Scholar]
  20. Salita, D.S.; Polyakov, V.V. Acoustic Emission during Plastic Deformation of Pb–Sn Alloys. Phys. Mesomech. 2020, 23, 593–600. [Google Scholar] [CrossRef]
  21. Lependin, A.A.; Polyakov, V.V. Scaling of the Acoustic Emission Characteristics during Plastic Deformation and Fracture. Tech. Phys. 2014, 59, 1041–1045. [Google Scholar] [CrossRef]
  22. Tyutin, M.R. , Botvina, L.R., Levin, V.P., Beletskii, E.N., Sinev, I.O., Petersen, T.B. Kinetics of Damage Accumulation in a D16CH Alloy During Static Loading. Rus. Metallurgy (Metally) 2022, 2022(4), 444–451. [Google Scholar] [CrossRef]
  23. Zavodchinskaya, E.B. General patterns and criteria for the destruction of solids at different scale levels under long-term loading. Industr. laboratory. Mater. diagn. 2022, 7, 48–62. [Google Scholar] [CrossRef]
Preprints 71436 g001
Figure 1. Scheme of the tested tensile specimen with a side notch (а) and photo of the specimen in the testing machine grips (b): 1 – tensile specimen with a side notch; 2 – quasi-resonant AE transducers VS150-RIC; 3 – clamps for AE transducers; 4 – testing machine grips.
Figure 1. Scheme of the tested tensile specimen with a side notch (а) and photo of the specimen in the testing machine grips (b): 1 – tensile specimen with a side notch; 2 – quasi-resonant AE transducers VS150-RIC; 3 – clamps for AE transducers; 4 – testing machine grips.
Preprints 71436 g001
Preprints 71436 g002
Figure 2. Time-dependent functions of the amplitude um (а) and activity Ń (b) of AE signals recorded during tensile testing.
Figure 2. Time-dependent functions of the amplitude um (а) and activity Ń (b) of AE signals recorded during tensile testing.
Preprints 71436 g002
Preprints 71436 g003
Figure 3. Empirical distribution energy functions of the AE signals leading edge, recorded at the time moment τ = 16.5 s (I) и τ = 18.4 s (II).
Figure 3. Empirical distribution energy functions of the AE signals leading edge, recorded at the time moment τ = 16.5 s (I) и τ = 18.4 s (II).
Preprints 71436 g003
Preprints 71436 g004
Figure 4. Disorder of the AE signal flow according to the results of the calculated Kolmogorov-Smirnov statistical criterion Kα.
Figure 4. Disorder of the AE signal flow according to the results of the calculated Kolmogorov-Smirnov statistical criterion Kα.
Preprints 71436 g004
Preprints 71436 g005
Figure 5. Assessment of the damage degree j of a steel specimen using the high-energy AE signals content criterion ṄW.
Figure 5. Assessment of the damage degree j of a steel specimen using the high-energy AE signals content criterion ṄW.
Preprints 71436 g005
Table 1. Chemical composition of 30KhGSA high-strength alloyed steel under study.
Table 1. Chemical composition of 30KhGSA high-strength alloyed steel under study.
Element C Cr Mn Si Ni Cu S P
Content, wt. % 0.29 0.9 1.0 1.0 < 0.1 < 0.1 0.003 0.008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated