Survey of Optimization Algorithms in Modern Neural Networks

Preprint

Review

Survey of Optimization Algorithms in Modern Neural Networks

Altmetrics

Downloads

537

Views

155

Comments

A peer-reviewed article of this preprint also exists.

Ruslan Abdulkadirov^*

Pavel Lyakhov

Nikolay Nagornov

Ruslan Abdulkadirov^*

Pavel Lyakhov

Nikolay Nagornov

This version is not peer-reviewed

Submitted:

20 April 2023

Posted:

20 April 2023

You are already at the latest version

Alerts

Abstract

Creating self-learning algorithms, developing deep neural networks and improving other methods that "learn" for various areas of human activity is the main goal of the theory of machine learning. It helps to replace the human with a machine, aiming to increase the quality of production. The theory of artificial neural networks, which already have replaced the humans in problems of detection of moving objects, recognition of images or sounds, time series prediction, big data analysis and numerical methods remains the most dispersed branch of the theory of machine learning. Certainly, for each area of human activity it is necessary to select appropriate neural network architectures, methods of data processing and some novel tools from applied mathematics. But the universal problem for all these neural networks with specific data is the achieving the highest accuracy in short time. Such problem can be resolved by increasing sizes of architectures and improving data preprocessing, where the accuracy rises with the training time. But there is a possibility to increase the accuracy without time growing, applying optimization methods. In this survey we demonstrate existing optimization algorithms of all types, which can be used in neural networks. There are presented modifications of basic optimization algorithms, such as stochastic gradient descent, adaptive moment estimation, Newton and quasi-Newton optimization methods. But the most recent optimization algorithms are related to information geometry, for Fisher-Rao and Bregman metrics. This approach in optimization extended the theory of classic neural networks to quantum and complex-valued neural networks, due to geometric and probabilistic tools. There are provided applications of all introduced optimization algorithms, what delighted many kinds of neural networks, which can be improved by including any advanced approaches in minimization of the loss function. Afterwards, we demonstrated ways of developing optimization algorithms in further researches, engaging neural networks with progressive architectures. Classical gradient based optimizers can be replaced by fractional order, bilevel and, even, gradient free optimization methods. There is a possibility to add such analogues in graph, spiking, complex-valued, quantum and wavelet neural networks. Besides the usual problems of image recognition, time series prediction, object detection, there are many are other tasks for modern theory of machine learning, such as solving problem of quantum computations, partial differential and integro-differential equations, stochastic processes and Brownian motion, making decisions and computer algebra.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

Notations

$θ$	weight
$α$	learning rate
$f (θ)$	loss function
$g_{t}$	gradient $\nabla f (θ_{t})$
$λ$	weight decay parameter, $L^{2}$ regularization factor
$μ$	momentum
$G_{t}$	sum of gradients $G_{t + 1} = G_{t} + \nabla f (θ_{t - 1})$
$m_{t}$	exponential moving average of $g_{t}$
$v_{t}$	horizontal direction converging, exponential moving average of $g_{t}^{2}$
$E {[g^{2}]}_{t}$	running average $E {[g^{2}]}_{t} = γ E {[g^{2}]}_{t - 1} + (1 - γ) g_{t}^{2}$ , where $ρ$ is a decay rate parameter $\in (0, 1) .$
$η_{t}$	schedule multiplier
$ν$	immediate discount factor
$β$	momentum buffer’s discount factor
$β_{0}, β_{1}, β_{2}$	moments
$ρ_{t}$	variance $ρ_{t} = ρ_{\infty} - \frac{2 t β_{2}^{t}}{1 - β_{2}^{t}}$
$r_{t}$	variance rectification
$ξ$	DiffGrad friction coefficient (DFC)
$H e s s (θ_{t})$	Hessian matrix $H e s s (θ_{t}) = \nabla^{2} f (θ_{t})$
$H_{t}$	inverse BFGS Hessian approximation
$(s_{t}, y_{t})$	curvature pairs
$D_{t}$	Hessian diagonal matrix
${\bar{D}}_{t}$	Hessian diagonal matrix with momentum
$(M^{n}, g)$	Riemannian manifold with n-dimensional topological space $M^{n}$ and metric g
∇	affine connection, gradient
$T M^{n}$	tangent bundle
$Φ (\cdot, \cdot)$	proximity function
$B (\cdot, \cdot)$	Bregman

1. Introduction

The question of rising the accuracy of neural networks remains actual. There are many approaches applied for solving this problem: data augmentation [1], improving the mathematical model of neurons [2], adding complement neural network [3] and so on. Indeed, all this approaches resolve the problem of increasing the accuracy of neural networks particularly. But there exist universal methods for improving the quality of various types of networks, and one of them is the optimization of the loss function. The problem of minimization of such functions, which contain local extremes, is a descent to the neighborhood of the global minimum, which remains important in machine learning. First attempts to achieve the minimal value were realized by using stochastic gradient descent (SGD) [4]. Such approach is still widely used in modern neural networks and belongs to set of first order optimization methods. Later, there was stochastic gradient descent with momentum and Nesterov condition (SGDM Nesterov) [5], which increased the rate of convergence and gave the high accuracy for less number of iterations.

According to the structure of SGD, there were proposed AdaGrad [6], RMSProp [7], Adadelta [8] and Adam [9], which allow to attain the minimum of functions that contain little number of local extremes. But in case of Rastrigin, Rosenbrouck and Ackley functions from [10] these approaches are not able to reach the global minimum. It is explained by achieving the minimum taking into account only directions of gradients. Even presence of exponential moving averages in Adam do not suffice for minimization such test functions. The same technique is used in modifications of Adam and SGD. Adam-type algorithms, which updates the exponential moving averages of the gradient, were build to improve the process of minimization for multi-extreme functions. The advantage of these approaches is that the initialization of biases can be easily counteracted, resulting in bias-corrected estimates. However, they are able to minimize the loss function, but not always in global minimum. Using Adam-type algorithms, it is possible to receive required accuracy without big time consumption. Therefore, for attaining higher accuracy one needs to apply second order optimization algorithms.

The main goal of second order optimization algorithms [11] is the achieving global minimum for short number of iterations, because, usually, they are slower compared with first order optimization algorithms. It can be explained by the fact, that second order algorithms take into account not only directions of gradients, but the convexity (curvature) of objective functions by Hessian matrix. Computations of inverted Hessian matrix make the second optimization more complex. This approach is called Newton optimization method [12]. In machine learning, where number of neurons can attain over one hundred, Newton optimization is an ineffective tool, but the approximation of inverted Hessian matrix makes possible to minimize the loss function for required time consumption. Such technique is called quasi-Newton optimization method [13]. Quasi-Newton optimization algorithms analyze the loss function from functional point of view, which allows to avoid local minimums and rapidly converge in global minimum. For increasing the quality of minimization, it is possible to observe the objective function from geometric and probabilistic points of view.

First attempt to geometrically minimize smooth functions was applied in [14], where authors engaged the properties of Rimannian geometry. Such optimization used the gradient flow for receiving the global minimum. Later, there was an idea to engage information geometry in [15], which is an intersection of Riemannian geometry and probability theory. Such approach is divided in two branches, which utilize Fisher-Rao [16] and Bregman [17] metrics, respectively. The optimization with Fisher-Rao metrics (Fisher information matrix) is called a natural gradient descent. In case of utilizing Bregman metrics, one receives the mirror descent. These optimization algorithms proved their abilities in image recognintion [18], time series prediction [19]. The main application they find in physics-informed neural networks [20], which are devoted to solve partial differential and integro-differential equations.

In this paper the main goal is the classification of optimization algorithms, which are used in machine learning, identification their properties, which allow to increase the rate of convergence for certain neural network, and providing ways of developing minimization methods in further researches. After gradient-based optimization methods, we will demonstrate alternative approaches in minimization of loss function: gradient-free and bilevel optimization.

All provided above optimization algorithms are presented in the Figure 1, which constructs the contests of this paper.

The remainder of the paper is organized as follows. Section 2 is devoted to first order optimization algorithms, which are described in 3 subsections: SGD-type, Adam-type and PNM-type optimization algorithms. Section 3 presents second order optimization techniques, such as Newton and Quasi-newton algorithms. Section 4 consists of representation of information-geometric methods, which are divided on Fisher-Rao and Bregman metrics. Such Part of this paper contains the most progressive approaches in modern theory of optimization methods. Section 5 represents applications of all optimization algorithms, introduced in Section 2, Section 3 and Section 4. In Section 6, we report the conclusions of the provided optimization algorithms and suggestions for their improving and further exploitation in neural networks.

2. First Order Optimization Algorithms

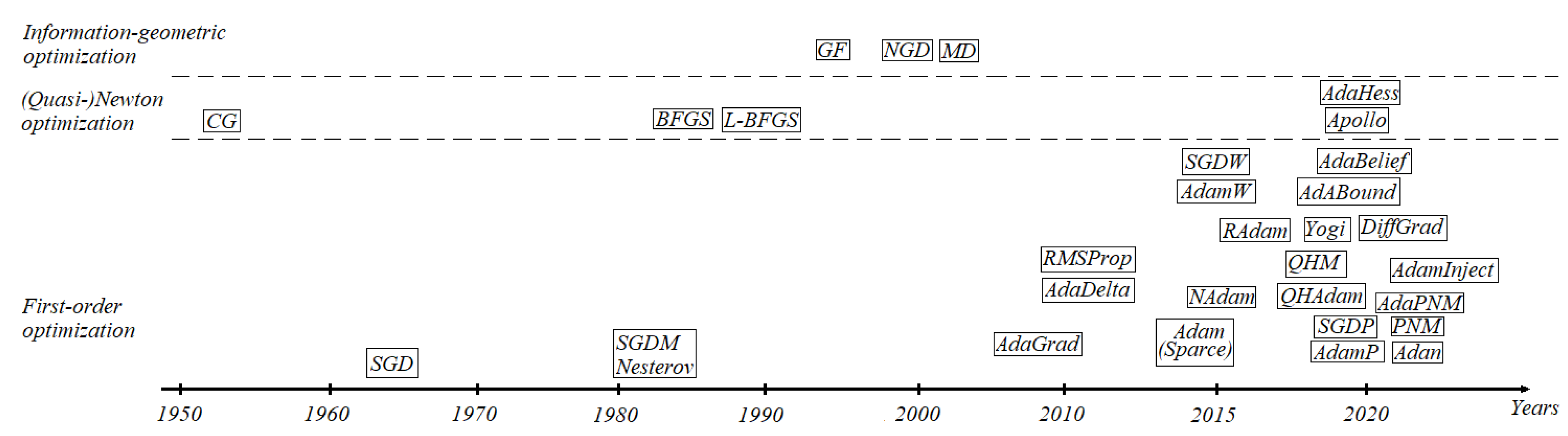
2.1. SGD-Type Algorithms

How can we see from Figure 1, the earliest first order optimization algorithm is SGD [4], which can be described by the iterative formula

θ_{t + 1} = θ_{t} - α_{t} \nabla f (θ_{t}),

(1)

where

θ_{t}

denotes weight,

f (θ_{t})

is a loss function with its gradient

\nabla f (θ_{t})

and

α_{t}

is a learning rate. Later such approach was modified to SGDM with Nestreov condition [5] presented by

θ_{t + 1} = θ_{t} - α_{t} (\nabla f (θ_{t}) + μ b_{t + 1}),

(2)

where

θ_{0}

is an initial point,

b^{(k + 1)} = μ b^{(k)} + (1 - τ) (\nabla f (θ^{(k)}) + λ θ^{(k)})

, where

τ

is a damping parameter and

μ

is a momentum. The algorithm of SGDM with Nesterov condition is constructed in [22]. This optimization method is still used in approximation theory and machine learning. Various back propagation methods ([23,24,25,26]) are based on calculating of local partial derivatives, which rectify the value of weights of neural networks using (2). But such approach can be modified to others more effective versions, which converge to minimum faster. Therefore, because of relatively small rate of convergence of SGDM with Nesterov condition and its step-size updating, There was introduced Adaptive gradient method (AdaGrad) in [6].

AdaGrad differs from SGDM with Nesterov condition by the adaptive step-size. This advantage allows to increase learning rate and, simultaneously, reduce time consumption. AdaGrad is described by the following formula

θ_{t + 1} = θ_{t} - \frac{α_{t}}{\sqrt{G_{t + 1} + ϵ}} \nabla f (θ_{t}),

where the sum of gradients is presented as

G_{t + 1} = G_{t} + \nabla f (θ_{t - 1}) .

As was noted above, AdaGrad updates the stepsize

α_{t}

on the given information of all previous gradients observed along the way. But its disadvantage is similar, like in SGD, where minimization is based on directions of the gradients and step-size regulation, which does not guarantee the convergence in the neighborhood of global minimum. Afterwards, Adagrad was equipped with the gradient norm information, which improves the convergence rate. Such modification is called AdaGrad-Norm [6], presented as follows:

θ_{t + 1} = θ_{t} - \frac{α}{1 + (t - 1) η} \frac{g_{t}}{\sqrt{G_{t}} + ϵ} .

(3)

AdaGrad and AdaGrad-Norm adapt the step-size more accurately, compared with SGD and SGDM with Nesterov condition, what allows to increase the learning rate for growing the probability of reaching the global minimum. But accumulation of previous gradients does not resolve the problem of convergence in the neighborhood of global minimum. This approach, like SGD, descends towards negative directions of gradients. Such disadvantage caused researchers to come up with idea of adapting of the step-size using mean moments, what implied the root mean square propagation (RMSProp) optimization algorithm.

The RMSprop optimizer [7] partially uses the same technique as SGDM and limits the oscillations in the upright direction, what allows to increase the learning rate. It makes possible to take fast substantial step-sizes in the horizontal direction converging

v_{t}

. Such approach is described as

v_{t} = γ v_{t - 1} + (1 - γ) g_{t}^{2},

θ_{t + 1} = θ_{t} - α_{t} \frac{g_{t}}{\sqrt{v_{t}} + ϵ},

(4)

where

γ \in (0, 1)

is a moment. RMSProp is still actual algorithm in many neural networks, like SGDM with Nesterov condition, because it contains prerequisites of exponential moving averages, which later will have a lot of modifications, that give an opportunity to avoid some local minimums. Moreover, according to techniques in AdaGrad and RMSProp, there was introduce AdaDelta [8].

AdaDelta is a modification, based on techniques in SGD, RMSProp and AdaGrad, that separate dynamic learning rate per-dimension, requires no manual setting of a learning rate and takes minimal computation over gradient descent. Additionaly, it is insensitive to hyperparemeters and robust to blow-up gradient, noise and architecture choice. Unlike Adagrad such method reduces aggressive, monotonically decreasing learning rate. Adadelta restricts the window of accumulated past gradients to a fixed size, instead of accumulating all past squared gradients. The running average

E {[g^{2}]}_{t}

depends only on the previous average and current gradient. Initial accumulation variables

E {[g^{2}]}_{0}

E {[Δ θ^{2}]}_{0}

are equal to 0. AdaDelta algorithms is described as follows. Accumulate gradient:

E {[g^{2}]}_{t} = ρ E {[g^{2}]}_{t - 1} + (1 - ρ) g_{t}^{2},

where

ρ

is a decay rate paremeter. Compute update:

Δ θ_{t} = - \frac{R M S {[Δ θ]}_{t - 1}}{R M S {[g]}_{t}} g_{t},

where

R M S {[g]}_{t} = \sqrt{E {[g^{2}]}_{t} + ϵ} .

Accumulate updates:

E {[Δ θ^{2}]}_{t} = ρ E {[Δ θ^{2}]}_{t - 1} + (1 - ρ) Δ θ_{t}^{2},

θ_{t + 1} = θ_{t} + Δ θ_{t} .

(5)

The stochastic gradient descent was modified in other variations, which, like AdaGrad, AdaDelta and RMSProp, increase the test accuracy and accelerate the implementation of algorithm. Such modifications can improve the process of recognition, prediction, generation and making decision, what develops the theory of neural networks. But in deep convolutional neural networks modification (2)-(5) does not achieve the higher accuracy compared with SGDM with Nesterov condition, how can be seen in [27], where only some modified algorithms presented in next subsection give higher test accuracy of recognition. Therefore, one needs algorithms, which take into account gradient directions and values weight. First very important modification of SGDM is Nesterov Accelerated Gradient (NAG), presented in [28].

Nesterov’s accelerated gradient descent is widely used in practice for training deep networks and other supervised learning models, because it often provides significant improvements over SGDM with Nesterov condition. Rigorously speaking, “fast gradient” methods have provable ammendments over gradient descent only for the deterministic case, where the gradients are exact. In the stochastic case, "fast gradients" partially mimic their exact gradient counterparts, resulting in some practical gain. Such approach is described as

v_{t} = μ v_{t - 1} + α f (θ - μ v_{t - 1}),

θ_{t} = θ_{t - 1} + v_{t} .

(6)

As said before, there is an efficient technique of utilizing Lebesgue norm on weight of neurons for improving resulting test accuracy. Such approach is called

L^{2}

regularization. It is well described and tested on SGDM with Nesterov condition in [29].

Proposed

L^{2}

regularization in [30] acts similarly with the usual weight decay, which is used in SGD. Indeed, both approaches evaluate weights closer to zero with the same rate. The

L^{2}

regularized SGD (SGDW) is a modification of usual SGD, which differs by recovering original weight decay using decoupling weight decay from the optimization steps with respect to the loss function. However, for adaptive gradient algorithms the main difference is a presence of adapted sums of gradients of the loss function and the regularizer, whereas with decoupled weight decay, only gradients of the loss function are adapted. With

L^{2}

regularization both types of gradients are normalized by their typical summed magnitudes, and therefore weights with large typical gradient magnitude are regularized by a smaller relative amount than other weights. The introduced SGDW method is described by the following iterative formula

g_{t} = \nabla f (θ_{t}) + λ θ_{t - 1},

where

λ

is a weight decay parameter (

L_{2}

regularization factor),

m_{t} = β_{1} m_{t - 1} + η_{t} α g_{t},

θ_{t} = θ_{t - 1} - m_{t} - η_{t} λ θ_{t - 1},

(7)

where

η_{t}

is a schedule multiplier. Unfortunately, such SGDW does not significantly improve usual SGD, especially in deep neural networks, auto-encoders and graph-neural networks. Because the architecture of these neural networks confuses the

L^{2}

regularization and make the process of minimization too difficult for SGDW. But there are two techniques, which can improve the quality of minimization of the loss function using projection [31] and hyper-parameter methods [32].

Before introducing the projection technique for SGD, it is necessary to recall a batch normalization [33]. In practise, normalization techniques, such as batch normalization, play an important role in for modern deep learning. They allow weights converge more rapid with better generalization performances. The normalization-induced scale invariance among the weights gives advantages to SGD, such as the effective step-size automatic regularization and stabilizing the training procedure. In practise, one can notice that the including momentum in SGD-type optimizers reduces much step-sizes for scale-invariant weights. Such phenomenon is not yet studied and causes unwanted side effects in the process of minimization. This is a crucial issue because the vast majority of modern deep neural networks consist of SGD- and Adam-type optimizer, which contain momentum, and scale-invariant parameters. Therefore, there was proposed SGD with projection (SGDP), which removes the radial component, or the norm-increasing direction, at each optimizer step. Because of the scale invariance, this modification only alters the effective step-sizes without changing the effective update directions, thus satisfying the original convergence properties of GD optimizers.

SGDP can be presented as following iterative formulas:

\begin{matrix} p_{t} = μ p_{t - 1} + \nabla f (θ_{t - 1}), \\ θ_{t} = θ_{t - 1} - α p_{t} . \end{matrix}

(8)

This approach, compared with SGDW, increases the rate of convergence, but it is not enough to significantly advance the process of minimization of the loss function in global minimum. what can be seen in experiments of minimizing Rastrigin function in (https://github.com /jettify/pytorch-optimizer). But the problem of avoiding the local minimums was solved by introducing the hyper-parameter methods, which is called quasi-hyperbolic momentum algorithm (QHM).

Momentum-based acceleration of SGD is widely used in deep learning. There is presented QHM as an extremely simple alteration of momentum SGD, averaging a plain SGD step with a momentum step, what presented in [34]. This approach introduces the immediate discount factor

ν

, encapsulating plain SGD (

ν = 0

) and momentum (

ν = 1

). A self-evident interpretation of QHM is a

ν

-weighted average of the momentum update step and the plain SGD update step. The expressive power of QHM intuitively comes from decoupling the momentum buffer’s discount factor

β

from the current gradient’s contribution to the update rule

1 - ν β

. In contrast, momentum tightly couples the discount factor

β

and the current gradient’s contribution

1 - β

Let us present QHM as the following iterative process:

g_{t} = β g_{t - 1} + (1 - β) {\hat{g}}_{t},

θ_{t} = θ_{t - 1} - α [(1 - ν) \cdot {\hat{g}}_{t} + ν g_{t}] .

(9)

Such method lets surmount the local minimums. This approach has no disadvantages, compared with demonstrated above algorithms. But, like others, it QHM does not suffice for achieving the highest accuracy in deep neural networks, because it still takes into account the direction of gradients and amendments with parameters and gradient normalization.

Before drawing conclusions, it should be noted that for any smooth objective function

f : R^{n} \to R

provided optimization methods in above have almost the same regret bound [35,36]

R (T) = \sum_{t = 1}^{T} f_{t} (x_{t}) - min_{x \in R^{n}} \sum_{t = 1}^{T} f_{t} (x),

(10)

which measures the convergence rate and belongs to set of

O (\sqrt{T})

. Presented above algorithms can be improved by performing their regret bounds to

O (log T)

, which was done in [37] and. Such algorithms are called strongly convex.

SGD-type algorithms are used in convolutional, recurrent, autoencoder, graph neural networks. But their huge disadvantage is insufficient information about the properties of loss function to reach the global minimum. SGD is led by the direction of gradient, which is not enough for increasing the test accuracy. In modern neural networks more preferred approaches are Adam and its modifications (Adam-type algorithms), which contain exponential moving averages of gradient and squared gradient, that significantly improves the quality of training neural networks. These methods improve the optimization by estimation of moments, which gives more information of about the global minimum. Moreover, such improvement allows to increase the accuracy of image recognition, time series prediction and object classification.

2.2. Adam-Type Algorithms

The adaptive moment estimate (Adam) [39] algorithm is a continuation of developing gradient based optimization, which significantly increases the accuracy in neural networks. Taking into account directions of gradients and means of moments, minimization of loss function with higher frequency converges in the neighborhood of global minimum. The iterative formula is presented as

m_{t} = β_{1} m_{t - 1} + (1 - β_{1}) g_{t},

v_{t} = β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2},

{\hat{m}}_{t} = m_{t} / (1 - β_{1}^{t}), {\hat{v}}_{t} = v_{t} / (1 - β_{2}^{t}),

θ_{t} = θ_{t - 1} - α {\hat{m}}_{t} / (\sqrt{{\hat{v}}_{t}} + ϵ) .

(11)

Note that

β_{1}, β_{2}

are called moments,

m_{t}

and

v_{t}

are exponential moving averages of

g_{t}

and

g_{t}^{2}

, respectively.

According to the adaptive moment estimate algorithm (11), there were provided modified versions, which distinct by step-size adaptation and manipulation with exponential moving averages. Like SGDW, there was provided a modification in [40], which is called Adam algorithm with

L^{2}

regularization. In the case of usual Adam, weights, that tend to have large gradients of f, are not regularized as much as they would with decoupled weight decay, since the gradient of the regularizer is scaled. AdamW with the same exponential moving averages can be described as the following iteration formula:

θ_{t} = θ_{t - 1} - η + t [α \cdot {\hat{m}}_{t} / (\sqrt{{\hat{v}}_{t}} + ϵ) + λ θ_{t}],

(12)

where

η_{t}

is a schedule multipliers and

λ

is a

L^{2}

regularization factor. There is proved fact, that such modification with decoupled weight decay yields substantially better generalization performance than the common implementation of Adam with

L^{2}

regularization, in [41]. Another approach for modification of Adam algorithms is projected Adam, which is called AdamP [42].

AdamP, like SGDP in (8), is based on projection of the sum of gradient and momentum vectors onto the tangent space of weights. Such approach allows to accelerate effective step sizes for scale-invariant weights. This technique with its applications is described in [43] and has the following representation:

g_{t} = \nabla f (θ_{t - 1}) + λ θ_{t - 1},

m_{t} = β_{1} m_{t - 1} + (1 - β_{1}) g_{t},

v_{t} = β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2},

p_{t} = \frac{m_{t}}{\sqrt{v_{t}} + ϵ} .

Then, according to cosine condition we obtain

i f cos (g_{i}) < δ / \sqrt{d i m (θ)} : q_{i} = p_{i} - (\frac{θ}{{∥ θ ∥}_{2}} \cdot p_{i}) \frac{θ}{{∥ θ ∥}_{2}}

e l s e : q_{i} = p_{i}

Afterwards, one obtain

θ_{t} = θ_{t - 1} - η_{t} (\frac{α m_{t}}{\sqrt{v_{t}} + ϵ} + λ θ_{t - 1}) .

(13)

According to notes in [44], it implies that momentum-based optimizers induce an excessive growth of the scale-invariant weight norms, which prematurely decay the effective optimization steps, leading to sub-optimal performances. The resulting AdamP, like SGDP in Section 2.1, successfully suppresses the weight norm growth and train a model at an unobstructed speed. Another approach to accelerate the convergence rate is the applying the quasi-hyperbolic momentum, like it was made for QHM in (9).

As for QHM, there was proposed QHAdam [45], which replaces both of Adam’s moment estimators with quasi-hyperbolic terms. This approach is described as

g_{t + 1} = β_{1} g_{t} + (1 - β_{1}) \nabla f (θ_{t}), g_{t + 1}^{'} = {(1 - β_{1}^{t + 1})}^{- 1} g_{t + 1},

s_{t + 1} = β_{2} s_{t} + (1 - β_{2}) {(\nabla f (θ_{t}))}^{2}, s_{t + 1}^{'} = {(1 - β_{2}^{t + 1})}^{- 1} s_{t + 1},

θ_{t + 1} = θ_{t} - α [\frac{(1 - ν_{1}) \nabla f (θ_{t}) + ν_{1} g_{t + 1}^{'}}{\sqrt{(1 - ν_{2} {(\nabla f (θ_{t}))}^{2}) + ν_{2} s_{t + 1}^{'}} + ϵ}]

(14)

As was noted in previous subsection, there exist Nesterov trick NAG, which accelerates usual SGD in [46]. The same modification propagates to Adam and transform it to NAdam [47]. This technique with higher frecuency converge to the neighborhood of global minimum for less number of iteration, compared with Adam and its previous modifications, and constructed more simple than AdamW, AdamP and QHAdam. But for cases of Rastrigin functions and Rosenbrock functions, (11)-(13) do not converge in neighborhood of global minimum. As was said in Section 2.1,

L^{2}

regularization, projection and quasi-hyperbolic parameters techniques influence to step-size, taking into account gradient directions. In cases, when included moment estimation, such modifications can accelerate the process of convergence, but not necessary in the neighborhood of global minimum. But there are two techniques, which make the process of minimization ’smoother’. Such approaches are called Nesterov-accelerated (NAdam) and Rectified (RAdam) adaptive moment estimation.

Let us present the iterative formula of NAdam:

θ_{t + 1} = θ_{t} - \frac{η}{\sqrt{{\hat{v}}_{t}} + ϵ} (β_{1} {\hat{m}}_{t} + \frac{(1 - β_{1}) g_{t}}{1 - β_{1}^{t}})

(15)

This method is a continuation of NAG due to the added exponential moving averages. Compared with Adam and its previous modifications, NAdam increases the accuracy of converging in deep convolutional neural networks and, simultaneously, make the minimization process faster by ’smoothing’ the descent. But such technique is ineffective in physics-informed neural networks, because of the smoothing descent trajectory, which for partial differential equation solution gives more deviations. Such disadvantage was resolved by rectified Adam (RAdam).

Proposed in [48], RAdam differs from other optimization method by introducing a term to rectify the variance of the adaptive language modeling and learning rate. This modification proved its ability to receive higher test accuracy. Such optimization method has the following iterative formula:

ρ_{t} = ρ_{\infty} - 2 t β_{2}^{t} / (1 - β_{2}^{t})

ρ_{\infty} = \frac{2}{1 - β_{2}} - 1

If the variance is tractable (

ρ_{t} > 4

) then the adaptive learning rate is computed as:

l_{t} = \sqrt{(1 - β_{2}^{t}) / v_{t}},

the variance rectification term is calculated as:

r_{t} = \sqrt{\frac{(ρ_{t} - 4) (ρ_{t} - 2) ρ_{\infty}}{(ρ_{\infty} - 4) (ρ_{\infty} - 2) ρ_{t}}}

and we update parameters with adaptive momentum:

θ_{t} = θ_{t - 1} - α_{t} r_{t} {\hat{m}}_{t} l_{t} .

(16)

If the variance is not tractable we update instead with:

θ_{t} = θ_{t - 1} - α_{t} {\hat{m}}_{t} .

(17)

Such method overtake NAdam and other algorithms, especilly in deep neural networks [49], such as AlexNet [50], ResNet [51], InceptionNet [52], GoogleNet [53] and Res-Next [54]. But RAdam adapts the learning rate too complex and, like previous analogues, can not converge in the neighborhood of global minimum of Rastrigin function. Moreover, there exist other simple ways to adjust the learning rate and make the process of minimization faster. One of them is difference gradient approach, which is called DiffGrad [55].

The difference gradient approach is based on moment estimate technique and, instead of complex manipulations with learning rate and weights, calculate only additional coefficient, which is called DiffGrad friction coefficient (DFC). The main distinction of DiffGrad is that such approach is based on the change in short-term gradients and controls the learning rate based on the need of dynamic adjustment of learning rate. This means that diffGrad follows the norm that the parameter update should be smaller in low gradient changing regions. The friction coefficient diffGrad (DFC) is designed to control the learning rate using information about the short-term behavior of the gradient. The DFC is represented by

ξ_{t}

and defined as

ξ_{t} = \frac{1}{1 + exp - | Δ g_{t} |},

(18)

where

Δ g_{t}

is the change between previous and current gradients, given as

Δ g_{t} = g_{t - 1} - g_{t} .

In the proposed DiffGrad optimization method, the steps up to the computation of bias-corrected 1-st order moment

m_{t}

and bias-corrected 2-nd order moment

v_{t}

are the same as those of Adam optimization [38]. The DiffGrad optimization method updates

θ_{t + 1}

, using the following update rule:

θ_{t + 1} = θ_{t} - \frac{α_{t} ξ_{t} {\hat{m}}_{t}}{\sqrt{{\hat{v}}_{t}} + ϵ} .

(19)

DiffGrad generate a high learning rate if the gradient change is more (i.e., the optimization is far from the optimum solution), and a low learning rate if the gradient changes minimally (i.e., the optimization is near to the optimum solution). Moreover, such technique lets to avoid some local minimums, which can be seen in minimization of Rastrigin and Rosenbrock functions [56]. This approach is suitable for deep convolutional neural networks due to moment estimation, analysing past and current gradient. Also, DiffGrad adjusts the learning rate very accurately for avoiding overshooting of the global minimum and reducing oscillation around it. Such algorithms is tested with the ResNet50 model for an image categorization task over the CIFAR10 and CIFAR100 datasets in [57]. According to result of recognition, it became clear that DiffGrad works better, compared with SGDM (2), AdaDelta (5) and Adam (11). But this approach does not guarantee the high accuracy in other neural networks, especially in quantum, spiking, complex valued and physics-informed neural networks. Such disadvantage is explained by the lack of analyzing the curvature of minimizing loss function. For that reason, there was introduced progressive optimization algorithm in [58], which is called Yogi.

The Yogi algorithms, like Adam, relies on scaling gradients down by the square root of exponential moving averages of past squared gradients and controls the increase in effective learning rate, leading to even better performance with similar theoretical guarantees on convergence in [59]. It allows to solve the problem of convergence failure in simple convex optimization settings, which Adam-type algorithms, like AdamW, AdamP, QHAdam, NAdam and RAdam, can not handle. The difference between

v_{t}

and

v_{t - 1}

and its magnitude depend on

v_{t - 1}

and

g_{t}^{2}

. When

v_{t - 1}

is much larger than

g_{t}^{2}

, Yogi, like Adam, increase the effective learning rate, but such procedure is more controllable. This approach has the following describtion:

m_{t} = β_{1} m_{t - 1} + (1 - β_{1}) g_{t},

v_{t} = v_{t - 1} - (1 - β_{2}) s i g n (v_{t - 1} - g_{t}^{2}) g_{t}^{2},

{\hat{m}}_{t} = m_{t} / (1 - β_{1}^{t}), {\hat{v}}_{t} = v_{t} / (1 - β_{2}^{t}),

θ_{t} = θ_{t - 1} - γ {\hat{m}}_{t} / (\sqrt{{\hat{v}}_{t}} + ϵ) .

(20)

This method shows better results in deep convolutional neural networks, compared with DiffGrad and other previous Adam-type algorithms. But authors from [60,61] defined new optimization methods for deep learning such as AdaBelief and AdaBound.

The main feature of AdaBelief is adapting the learning rate, according to the "belief" in the current gradient direction. There is a difference between AdaBelief and Adam in parameters

v_{t}

and

s_{t}

, which are defined as exponential moving averages of

g_{t}^{2}

and

{(g_{t} - m_{t})}^{2}

, respectively. According to

s_{t}

as the prediction of the gradient at the next time step, if the observed gradient greatly deviates from the prediction, then one distrust the current observation and take a small step; if the observed gradient is close to the prediction, therefore one trust it and take a large step. This allows to achieve the high test accuracy in convolutional neural networks, that was presented in [61] on ImageNet and CIFAR10.

m_{t} = β_{1} m_{t - 1} + (1 - β_{1}) g_{t},

s_{t} = β_{2} s_{t - 1} + (1 - β_{2}) {(g_{t} - m_{t})}^{2} + ϵ,

\hat{m_{t}} = \frac{m_{t}}{1 - β_{1}^{t}}, \hat{s_{t}} = \frac{s_{t}}{1 - β_{2}^{t}},

θ_{t} = θ_{t - 1} - γ {\hat{m}}_{i} / (\sqrt{{\hat{s}}_{i}} + ϵ) .

(21)

It should be noticed that such approach has a modified version with fast gradient sign method (FGSM) presented in [62,63].

The AdaBound method gives an opportunity to restrict the learning rate between upper and lower continuous functions, which are called clips. Such technique reduces the probability of vanishing and blow-up gradient. This approach is defined as

m_{t} = β_{1} m_{t - 1} + (1 - β_{1}) g_{t},

v_{t} = β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2} a n d V_{t} = d i a g (v_{t}),

{\hat{η}}_{t} = C l i p (α / \sqrt{V_{t}}, η_{l} (t), η_{u} (t)) a n d η_{t} = {\hat{η}}_{t} / \sqrt{t},

θ_{t + 1} = θ_{t} - η_{t} {\hat{m}}_{t} / (\sqrt{{\hat{v}}_{i}} + ϵ) .

(22)

This approach is more complex, compared with DiffGrad, Yogi and AdaBelief, but it is capable to converge in the neighborhood of global minimum. There were made experiments of minimization of Rastrigin and Rosenbrock functions (https://github.com/jettify/pytorch-optimizer), where AdaBound achieved the highest accuracy, converging in the neighborhood of global minimum. But such approach is too complex for optimization and there exists much simple method, which is called AdamInject [64]. It reduces time consumption, preserving convergence rate.

AdamInject is one of the most recent approaches in first order optimization algorithms, which, unlike the AdaBelief algorithm, modifies

m_{t}

, which is the exponential moving average of

g_{t}

, into

s_{t}

. Such parameter is equipped with the difference between the previous parameters

θ_{t - 1}

and

θ_{t - 2}

. AdamInject has the following description.

t = 1

s_{t} = β_{1} s_{t - 1} + (1 - β_{1}) g_{t} .

Else:

Δ θ = θ_{t - 2} - θ_{t - 1}

s_{t} = β_{1} s_{t - 1} + (1 - β_{1}) (g_{t} + Δ g_{t}^{2}) / k .

Afterwards, one make usual calculations

v_{t} = β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2}

\hat{s_{t}} = \frac{s_{t}}{1 - β_{1}^{t}}, \hat{v_{t}} = \frac{v_{t}}{1 - β_{2}^{t}}

θ_{t} = θ_{t - 1} - γ \hat{s_{t}} / (\sqrt{\hat{v_{t}}} + ϵ)

This algorithms was tested on Rastrigin and Rosenbrock functions. Afterwards, there were trained on CIFAR10 VGG 16, ResNet, ResNext, SENet and DenseNet equipped with AdamInject, which presented the best results, compared with known analogues.

Introduced Adam-type optimization algorithms are used in deep convolutional neural networks, like Res-Net, Res-Next, InceptionNet, GoogleNet and so on. Also they find an application in recurrent and spiking neural networks due to their described above advantages, which SGD-type algorithms does not have. But in quantum, complex-valued and quaternion-valued neural networks such approaches loses in accuracy to usual SGDM with Nesterov condition. This problem caused researches in [65] come up with extending the number of moment from 2 to 3. This approach is called positive-negative momentum (PNM)

2.3. Positive-Negative Momentum

Developing SGD- and Adam-types optimization algorithms can not be infinite, there have to another approaches and techniques for extending class of first-order methods. This issue made the researches to consider the methods, which allow more than two exponential moving averages

m_{t}

and

v_{t}

. Because step-size regularization, according to moment estimation and introduced modification in Section 2.1 and Section 2.2, has its limits, what can be seen in convolutional neural networks, such as ResNet18, GoogLeNet and DenseNet. In this cases there have to additional exponential moving average, that let descend to neighborhood of global minimum.

In the paper [66] introduced conventional momentum method, also called Heavy Ball (HB), which is described in [67]. Later there was proposed positive-negative momentum (PNM) optimization algorithms. In this approach the main feature is a positive-negative averaging, which is analogue of exponential moving average in Adam. This averaging is described as follows:

m_{t} = \sum_{k = 0}^{t} β_{3} β_{1}^{t - k} g_{k} .

Inspired by this simple idea, there were proposed the combining the positive-negative averaging with the conventional momentum method in [66]. The positive-negative average is described as

m_{t} = (1 + β_{0}) m_{t}^{(o d d)} + β_{0} m_{t}^{e v e n} = (1 + β_{0}) \sum_{k = 1, 3, . . ., t} β_{3} β_{0}^{t - k} g_{k} + β_{0} \sum_{k = 0, 2, . . ., t} β_{3} β_{0}^{t - k} g_{k} .

The stochastic gradient descent equipped with the conventional momentum estimates, which adjust the learning rate and value of the gradient, is written in the following formula

m_{t} = β_{1}^{2} m_{t - 2} + (1 - β_{1}^{2}) g_{t},

θ_{t + 1} = θ_{t} - \frac{η}{\sqrt{{(1 + β_{0})}^{2} + β_{0}^{2}}} [(1 + β_{0}) m_{t} - β_{0} m_{t - 1}] .

(23)

This approach is an analogue of SGD-type algorithm, which differs by presence of positive-negative average

m_{t}

and step-size adaptation. There is also proposed Adam-type analogue of PNM algorithm, which is called AdaPNM, described as

m_{t} = β_{1}^{2} m_{t - 2} + (1 - β_{1}^{2}) g_{t},

{\hat{m}}_{t} = \frac{(1 + β_{0}) m_{t} - β_{0} m_{t - 1}}{1 - β_{1}^{t}},

v_{t} = β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2},

v_{max} = max (v_{t}, v_{max}), {\hat{v}}_{t} = \frac{v_{max}}{1 - β_{2}^{t}},

θ_{t + 1} = θ_{t} - \frac{η}{\sqrt{{(1 + β_{0})}^{2} + β_{0}^{2}}} {\hat{m}}_{t} .

(24)

The advantage of PNM and AdaPNM can be seen in [68], where were tested deep neural networks, such as ResNet, VGG, DenseNet and GoogleNet on image bases CIFAR10 and CIFAR100. These approaches gives higher test accuracy, compared with advances Adam-type optimization algorithms, like Yogi and AdaBound. If one equips AdaPNM and PNM with techniques contained in known analogues with two exponential moving averages, then it can improve the quality of optimization process. Besides these algorithms, there exists the extension of NAG and Nadam, which is called adaptive Nesterov momentum Algorithm (Adan).

In [69] proposed the Adaptive Nesterov momentum algorithm is devoted to effectively accelerate the training of deep neural networks. Adan first reformulates the vanilla Nesterov acceleration to develop a new Nesterov momentum estimation method, which reduces extra computations and memory overhead of computing gradient at the extrapolation point. Adan adopts the first and second order moments of the gradient in adaptive gradient algorithms for convergence acceleration. This approach has the following form:

m_{t} = (1 - β_{0}) m_{t - 1} + β_{0} g_{t},

v_{t} = (1 - β_{1}) v_{t - 1} + β_{1} (g_{t} - g_{t - 1}),

n_{t} = (1 - β_{2}) n_{t - 1} + β_{2} {[g_{t} + (1 - β_{1}) (g_{t} - g_{t - 1})]}^{2},

η_{t} = η / (\sqrt{n_{t} + ϵ}),

θ_{t + 1} = {(1 + λ η)}^{- 1} [θ_{t} - η_{t} (m_{t} + (1 - β_{1})) v_{t}] .

(25)

This method is the same generalization of SGD, Adam and NAdam. There is presented the advantage of this approach over AdaBelief, which shew third result of test accuracy after usual SGD. Regardless the modifications of Adam-type algorithms, usual SGD can give even better results, what claims to search other methods, that approve their modifications.

First order optimization methods are suitable for problem of image recognition, time series prediction and object classification. They do not consume much time of execution and power, what makes them actual in modern neural networks. But first order optimization algorithms, except PNM, AdaPNM and Adan, can not significantly increase the accuracy in neural networks with complex architecture, such as graph, complex-valued and quantum neural networks. In the solving differential equations they can not overtake the results of Adam, because physics-informed neural networks contain automatic differentiation, which work after multilayer perceptron.. Therefore, one needs second order optimization algorithms, which are able to significantly improve the process of minimization of the loss function.

3. Second Order Optimization Algorithms

First order optimization algorithms are not the most effective for receiving the global minimum of objective smooth function. Such approaches of minimization generally take into account the directions of gradient in every iterations. The customization and performing of class of first order optimization algorithms can only increase the accuracy and avoid some local minimums. Therefore, for improving the quality of minimization there are provided second order optimization algorithms. They reach the minimum taking into account not only directions of gradients, but the convexity (curvature) of objective function, which is measured with the Hessian. Such approach is called as Newton method.

3.1. Newton Algorithms

The main idea of the Newton optimization method [70] is based on gradient descent, containing the calculation of inverse Hessian of smooth objective function. Such approach increases the accuracy of minimization of functions with multiple number of local minimums. Newton optimization algorithm is described as

θ_{t + 1} = θ_{t} - H e s s {(θ_{t})}^{- 1} \nabla f (θ_{t}),

(26)

where

t = 0, . . ., M > 0

and

H e s s (θ_{t}) = \nabla^{2} f (θ_{t}) .

(27)

This iterative formula is received from second order Taylor expansion.

In [71] were introduced Newton-Minimum-Residual (Newton-MR) optimization method, which calculates the Hessian matrix by Moore-Penrose inverse [72] operator

{[\cdot]}^{†}

such as

θ_{t + 1} = θ_{t} + p_{t} = θ_{t} + {[\nabla^{2} f (θ_{t})]}^{†} \nabla f (θ_{t}) .

(28)

According to Newton and Newton-MR methods, there were suggested OverSketch Newton Fast convex optimization. Such approach is described in [73] with proper algorithms, which compute the update direction, taking into account the case of strongly-convexity. But there are other modifications of Newton’s optimization methods, that differs by their simplicity in realization and implementation in neural networks.

There are Krylov methods, such as conjugate gradients (CG) [74], the minimal residual method (MINRES) [75], and the generalized minimal residual method (GMRES) [76]. GMRES applies to indefinite matrices, MINRES applies to symmetric indefinite matrices. Besides GD, MINRES and GMRES, there exists a generic stochastic inexact Newton-Krylov method, described in [77]. Such approach can be implemented and applied in physics-informed neural networks, because of suitable approximations for time-dependent equations with divergence operator

(\nabla \cdot)

. But for vast majority of neural networks CG is the most preferred.

One of the most dispersed Newton’s optimization method is conjugate gradient. This approach comprises a class of unconstrained optimization algorithms, characterized by low memory requirements and strong local and global convergence properties. Such optimization algorithms is described as the following iterative formula:

θ_{t + 1} = θ_{t} + η_{t} d_{t},

d_{t + 1} = - g_{t + 1} + β_{t} d_{t}, d_{0} = - g_{0} .

The main part of this formula is

β_{t}

, which is called CG update parameter, which are presented in Table 1.

Despite the increasing the accuracy of minimization, Newton method optimization is slower comparing with the first order optimization. This disadvantage significantly impacts on time consumption, that slows the training of deep neural networks. For accelerating minimization process, there are developed many approximations of Hessian matrix. Second order optimization algorithms, which contain the approximation of Hessian matrix, are called quasi-Newton.

3.2. Quasi-Newton Algorithms

The class of quasi-Newton optimization algorithms shows approximately the same accuracy as Newton optimization algorithms, but ability to converge faster makes them useful in machine learning. Ones of the first quasi-newton optimization algorithms are BFGS [87], and L-BFGS [88].

BFGS method and its limited memory version, at the t-th iteration, is presented as the following iterative formula:

θ_{t + 1} = θ_{t} - α_{t} H_{t} \nabla f (θ_{t}),

(29)

where

α_{t}

is the step length,

\nabla f (θ_{t})

is the gradient and

H_{t}

is the inverse BFGS Hessian approximation, that is updated at every iteration by means of the formula

H_{t + 1} = V_{k}^{T} H_{t} V_{t} + ρ_{t} s_{t} s_{t}^{T},

(30)

ρ_{t} = \frac{1}{y_{t}^{T} s_{t}}, V_{t} = I - ρ_{t} y_{t} s_{t}^{T},

(31)

where the curvature pairs

(s_{t}, y_{t})

are defined as

s_{t} = θ_{t} - θ_{t - 1}, y_{t} = \nabla f (θ_{t}) - \nabla f (θ_{t - 1}) .

(32)

The curvature pairs

(s_{t}, y_{t})

are constructed sequentially at every iteration, and inverse Hessian approximation at the t-th iteration

H_{t}

depends on iterate and gradient information from past iterations.

The inverse BFGS Hessian approximations have to satisfy secant and curvature conditions:

H_{t + 1} y_{t} = s_{t}, s_{t}^{T} y_{t} > 0,

(33)

Consequently, as a result, as long as the initial inverse Hessian approximation is positive definite, then all subsequent inverse BFGS Hessian approximations are also positive definite. Note, the inverse Hessian approximation

H_{k + 1}

differs from the approximation

H_{k}

by a rank-2 matrix.

In the limited memory version, the matrix

H_{k}

is defined at each iteration, as the result of applying m BFGS updates to a multiple of the identity matrix, using the set of m most recent curvature pairs

{s_{t}, y_{t}}

kept in storage. As a result, one does not need store four dense inverse Hessian matrices approximation, rather one can store two

m \times d

matrices and compute the matrix-vector product via the two-loop recursion [89]. After the step has been computed, the oldest pair

(s_{t}, y_{t})

is discarded and the new curvature pair is stored.

Analogically, there were proposed symmetric rank-one (SR-1) [90] formula and its limited memory version in [91]. At the t-th iteration, the SR1 method computes a new iterate by the formula

θ_{k + 1} = θ_{k} + p_{k},

(34)

where

p_{k}

is the minimizer of the following equation

min_{p} m_{k} (p) = f (θ_{k}) + \nabla f {(θ_{k})}^{T} p + \frac{1}{2} p^{T} B_{k} p,

(35)

{∥ p ∥}_{2} \leq Δ_{k},

where

Δ_{k}

is the trust region and

B_{k}

is the SR1 Hessian approximation computed as

B_{k + 1} = B_{k} + \frac{(y_{k} - B_{k} s_{k}) {(y_{k} - B_{k} s_{k})}^{T}}{{(y_{k} - B_{k} s_{k})}^{T} s_{k}} .

(36)

Similar to L-BFGS, in the limited memory version of SR1 the matrix

B_{k}

is defined at each iteration as the result of applying m SR1 updates to a multiple of the identity matrix, using a set of m correction pairs

{s_{i}, y_{i}}

kept in storage.

Provided BFGS and SR-1 with their low memory versions preserve the rate of convergence and reduce the computational complexity. But this methods remain ineffective in deep neural networks, which makes calculations of matrices of extremely large dimension. Therefore, one needs to come with simplified versions of quasi-Newton methods. One of the most used quasi-Newton optimization method in neural networks is Apollo [92]. Apollo is a quasi-Newton method for nonconvex stochastic optimization, which dynamically incorporates the curvature of the loss function by approximating the Hessian via a diagonal matrix. Importantly, the update and storage of the diagonal approximation of Hessian is as efficient as adaptive first-order optimization methods with linear complexity for both time and memory. To handle nonconvexity, there is replaced the Hessian with its rectified absolute value, which is guaranteed to be positive definite. Experiments on deep neural networks, which recognize images from Cifar10 and ImageNet, show that Apollo achieves significant improvements over other stochastic optimization methods, including SGD and variants of Adam, in terms of both convergence speed and generalization performance. Such approach is described as:

g_{t + 1} = \nabla f (θ_{t}),

m_{t + 1} = \frac{β (1 - β^{t})}{1 - β^{t + 1}} m_{t} + \frac{1 - β}{1 - β^{t + 1}} g_{t + 1},

α = \frac{d_{t}^{T} (m_{t + 1} - m_{t}) + d_{t}^{T} B_{t} d_{t}}{(∥ d_{t} {∥_{4} + ϵ)}^{4}},

B_{t + 1} = B_{t} - α \cdot d i a g (d_{t}^{2}),

D_{t + 1} = r e c t i f y (B_{t + 1}, 1),

d_{t + 1} = D_{t + 1}^{- 1} m_{t + 1},

θ_{t + 1} = θ_{t} - η_{t + 1} d_{t + 1},

(37)

Apollo is a method, which is devoted to accelerate the process of minimization. But there is a problem of losing accuracy for achieving lower time consumption. Because of this disadvantage, authors in [93] proposed another often used quasi-Newton optimization method in neural networks, which is called AdaHessian.

AdaHessian is a second order stochastic optimization algorithm which dynamically incorporates the curvature of the loss function via adaptive estimates of the Hessian. Second order algorithms are among the most powerful optimization algorithms with superior convergence properties as compared to first order methods such as SGD and Adam. The main disadvantage of traditional second order methods is their heavier per-iteration computation and poor accuracy as compared to first order methods. But AdaHessian includes a fast Hutchinson based method to approximate the curvature matrix with low computational overhead, root-mean-square exponential moving average to smooth out variations of the Hessian diagonal across different iterations and a block diagonal averaging to reduce the variance of Hessian diagonal elements. This approximation of Hessian matrix makes the process of learning faster, preserving the reta of convergence.

Before presenting AdaHessian algorithm, it needs to note that gradient

g_{t} = \nabla f (θ_{t})

and Hessian

H_{t} = \nabla^{2} f (θ_{t})

. Let present the following matrix diagonalization of Hessian matrix as

D_{t} = d i a g (H) = E [θ_{t} ⊙ (H_{t} θ_{t})],

where ⊙ is a componentwise multiplication of vector. Perform a simple spatial averaging on the Hessian diagonal as follows:

D^{(s)} [i b + j] = \frac{1}{b} \sum_{k = 1}^{b} D [i b + k],

for

1 \leq j \leq b

0 \leq i \leq \frac{d}{b} - 1

. Hessian diagonal with momentum:

{\bar{D}}_{t} = \sqrt{\frac{(1 - β_{2}) \sum_{i = 1}^{t} β_{2}^{t - i} D_{i}^{(s)} D_{i}^{(s)}}{1 - β_{2}^{t}}},

m_{t} = \frac{(1 - β_{1}) \sum_{i = 1}^{t} β_{1}^{t - i} g_{i}}{1 - β_{1}^{t}},

v_{t} = {({\bar{D}}_{t})}^{k},

θ_{t} = θ_{t - 1} - η m_{t} / v_{t} .

(38)

Second order optimization algorithms have higher rate of convergence, especially in the neighborhood of global minimum. Unfortunately, they are not suitable in deep convolutional, recurrent and spiking neural networks, because of their high complexity. Therefore, one needs methods that satisfy the high rate of convergence and low time consumption. In 2012 there were proposed developing second order optimization algorithms using the smooth manifolds in [94]. But in [95] authors came up with idea of using probability distribution manifolds, instead of smooth. Such technique appeared on the intersection of geometry, probability, statistics and optimization.

4. Information-Geometric Optimization Methods

Second order optimization methods converge faster to the neighborhood of global minimum, compared with first order methods. But their time consumption is not fast enough for deep neural networks. Therefore, it is necessary to make quasi-Newton optimization algorithms faster. The most recent way is applying the information geometry. In this section we present a concise and modern view of the basic structures of information geometry, and report some applications in machine learning (statistical mixture clustering).

Initially, idea of using means of geometry in problems of optimization takes its beginning sicne 2010 in [96]. Hessian matrix, presented in second order optimization algorithms, does not contain full information about surface of the loss function, moreover, it makes process of descent too complex from computational point of view. But taking into account the geometric structure of the surface and corresponding spaces (Euclidean, hyperbolic, parabolic) allows to define the shortest way for descent and can reduce unnecessary computations. In [97] authors for defining shortest way applied gradient flow, that improved the quality of searching global minimum. This method applied smooth manifolds and generalized definition of gradient. But later, researches came up with idea to use probability distribution manifolds, which prove their advantage over smooth manifolds in problem of optimization. The intersection of probability theory and statistics with Riemannian geometry produces information geometry.

Analogically to information theory, considering the communication of messages over noisy transmission channels, one defines information sciences as the fields of studying connection between data and families of models, i.e. information sciences create methods to transform information from data to models. Such transformation is made by means of probability, statistics and geometry, that allows to include it in the theory of machine learning.

There is another definition of information geometry given by F. Nielson in [98] as the geometry of decision making. It includes model fitting (inference) which can be interpreted as a decision problem, namely, deciding which model parameter to choose from a family of parametric models. This framework was advocated by Abraham Wald [99,100] who considered all statistical problems as statistical decision problems. Dissimilarities (also loosely called distances among others) play a crucial role not only for measuring the goodness-of-fit of data to model (likelihood in statistics, classifier loss functions in machine learning, objective functions in mathematical programming or operations research, etc.) but also for measuring the discrepancy (or deviance) between models.

In this section we show two distinguish optimization algorithms, based on means of information geometry – natural gradient descent [101] and mirror descent [102]. These methods differ from any other optimization algorithms by their ability to measure distances in non-Euclidean domains using Kullback-Leibler and Bregman divergences, resperctively.

4.1. Natural Gradient Descent

Initially, there was proposed gradient descent with gradient flow in [103]. This approach is a generalization of second-order optimization method on Riemannian manifolds, which, particularly, can be Euclidead or non-Euclidean. Let

(M^{n}, g)

be a Riemannian manifold, where

M^{n}

is a topological space, which can be expressed in local coordinate system of an atlas

A = {(U_{i}, x_{i})}_{i}

of charts

(U_{i}, x_{i})

, and for tangent bundle

T M^{n}

Riemannian metric

g : T M^{n} \otimes T M^{n} \to R

The Riemannian gradient glow dynamics

θ (t)

for the optimization problem

{min}_{θ \in M^{n}} f (θ)

, obtained by seeking an infinitesimal change in

θ (t)

that would lead to the best improvement in objective value, while controlling the length of the change in terms of the manifold geometry, that is,

θ (t + d t) = a r g m i n_{θ} f (θ) d t + \frac{1}{2} d θ^{T} g (θ, θ + d θ) d θ .

(39)

For

d t

, utilizing

d θ (t) = θ (t + d t) - θ (t)

, one can substitute

f (θ (t)) + 〈 d θ, \nabla f (θ (t)) 〉

instead of

f (θ)

and receive

d θ (t) = a r g m i n_{d θ} 〈 d θ, \nabla f (θ (t)) 〉 d t + \frac{1}{2} d θ^{T} g (θ, θ + d θ) d θ .

Solving for

d θ

, one get:

\frac{d θ (t)}{d t} = - g {(θ, θ + d θ)}^{- 1} \nabla f (θ (t)) .

(40)

For better understanding, there are provided examples of Riemannian metric is the standard Euclidean manifold has the corresponding metric

g = I

, that reduces the gradient flow to usual gradient descent. But there is another very important example – probability distribution manifold with K-L divergence metric ([104,105]), that put the beginning of quantum neural networks.

There is noted the advantage of using probability distribution manifolds in [106], which can be equipped not necessary with KL-divergence, but Bergman, Jensen and others. There are presented extension of Rimannian manifolds with Levi-Civita connection

(M^{n}, g, \nabla_{L C})

to conjugate connection manifolds

(M^{n}, g, \nabla, \nabla^{*})

, where

\nabla_{L C} = \frac{\nabla + \nabla^{*}}{2}

. Conjugate connection manifolds are the private case of divergence manifolds, denoted as

(M^{n}, D^{g}, \nabla^{D}), \nabla^{* D}

. In such manifolds D can be Kullback-Leibler or Bregman divergences. There are two ways to imply natural gradient descent using direct K-L divergence, like in [95], and more fundamental way, presented in [98]. Let

f \in C^{\infty} (M^{n})

be a smooth loss function,

{exp}_{θ} : T_{θ} M^{n} \to M^{n}

be the Riemannian exponential map for updating the sequence of points

θ_{t}

on the manifold as follows:

θ_{t + 1} = {exp}_{θ_{t}} (- α_{t} \nabla_{M} f (θ_{t})),

(41)

where

\nabla_{M} f (θ) = \nabla_{v} (f ({exp}_{θ} (v))) |_{v = 0} = lim_{h \to 0} \frac{f (θ + h v) - f (θ)}{h} .

(42)

Returning to the formula of gradient flow, we receive:

θ_{t + 1} = R_{θ_{t}} (- α_{t} \nabla_{θ} f (θ_{t})) .

Using the retraction

R_{θ} (v) = θ + v

which corresponds to a first-order Taylor approximation of the exponential map, one implies the natural gradient descent:

θ_{t + 1} = θ_{t} - α_{t} g^{- 1} (θ, θ + d θ) \nabla_{θ} f (θ_{t}) .

(43)

Here

g (θ, θ + d θ) = F (θ_{t})

is called Fisher information matrix the natural gradient is defined as follows:

\nabla^{N G} f (θ) = F^{- 1} (θ) \nabla_{θ} f (θ) .

(44)

Afterwards, we come to natural gradient descent:

θ_{t + 1} = θ_{t} - α_{t} \nabla_{θ}^{N G} f (θ_{t}) .

(45)

Natural gradient descent differs from the first- and second-order optimization algorithms presented in Section 2 and Section 3, respectively, by ability to converge in global minimum for time consumption, suitable for deep learning. As was said, such approach created new branch in the theory of artificial intelligence – quantum machine learning. Application of neural networks for training quantum circuits required new structure of mathematical model of neurons, appropriate for quantum computations. Afterwards, vanilla natural gradient descent was replaced with quantum in [107]. Such networks are part of developing quantum information theory and quantum computers, that makes the process of training significantly faster. But in actual researches, vanilla natural gradient descent with Dirichlet distributions is already tested on Rastrigin and Rosebrock functions in [108] and exploited in convolutional, recurrent neural networks in [109]. The important thing in this method is selecting appropriate probability distribution, which can increase the rate of convergence and even accelerate learning process. There are presented probability distributions in Table 2, which can improve the quality of minimization of the loss functions.

As can be seen, this is second order optimization algorithm. But selecting appropriate probability distribution, like Gauss and Dirichelt, we can reduce the variable

θ

in Fisher infromation matrix, what makes possible to avoid its calculation in every iteration. Such approach is realized in [108,109,110,111]. The natural gradient descent, based on Fisher-Rao metrics, can replace second order optimization algorithms, due to their rate of convergence and time consumption. But there is another approach, that uses Bregman metrics, which is called mirror descent.

4.2. Mirror Descent

Bregman metrics, as an alternative for Fisher-Rao metrics, is based on dual Hessian manifolds. This approach takes into account not only gradient direction, curvature of the minimizing loss function, but the duality. Dual spaces are defined as the set of maps from the topological spaces to their underlying field, which is usually presented as

R

. This feature impacted on the name of such method. This technique is a reason continuation of second order optimization algorithms towards the information geometry. Moreover, this method contains a potential in the theory of quantum and complex-valued neural networks. Also it can be used in the physics-informed neural networks, where dual averaging procedure can increase the accuracy of final solutions.

Recall that the gradient descent can be extended by proximity function

Φ (\cdot, \cdot)

as follows:

θ_{t + 1} = a r g m i n_{θ} \{〈 θ, \nabla f (θ_{t}) 〉 + \frac{1}{α_{t}} Φ (θ, θ_{t})\} .

(46)

Φ (θ, θ_{t}) = \frac{1}{2} {∥ θ - θ_{t} ∥}_{2}^{2}

then we obtain usual gradient descent. For Bregman divergence the proximity function

Φ (θ, θ_{t}) = D_{ψ} (θ, θ_{t})

and we get mirror descent

θ_{t + 1} = a r g m i n_{θ} \{〈 θ, \nabla f (θ_{t}) 〉 + \frac{1}{α_{t}} D_{ψ} (θ, θ_{t})\},

(47)

where

D_{ψ} (θ, θ_{t}) = ψ (θ) - ψ (θ_{t}) - 〈 θ - θ_{t}, \nabla ψ (θ_{t}) 〉 .

(48)

According to presented above divergence manifolds, it is possible to imply the equivalence between natural gradient descent and mirror descent. Also, this fact was proven in [98], but without geometric tools. The mirror descent can be interpreted as a natural gradient descent as follows: Bregman mirror descent on the Hessian manifold

(M, g = \nabla^{2} F (θ))

is equivalent to natural gradient descent on the dual Hessian manifold

(M, g^{*} = \nabla^{2} F (η))

, where F is a Bregman generator,

η = \nabla F (θ)

and

θ = \nabla F^{*} (η)

Indeed, the mirror descent rule yields the following natural gradient update rule:

N G^{*} : ξ_{t + 1} = ξ_{t} - η {(g_{ξ}^{*})}^{- 1} (ξ_{t}) \nabla_{ξ} f_{θ} (θ (ξ_{t})),

(49)

N G^{*} : ξ_{t + 1} = ξ_{t} - η {(g_{ξ}^{*})}^{- 1} (ξ_{t}) \nabla_{ξ} f_{ξ} (ξ_{t})

where

g_{ξ}^{*} (ξ) = \nabla^{2} F^{*} (ξ) = {(\nabla_{θ}^{2} F (θ))}^{- 1}

and

θ (ξ) = \nabla F^{*}

The method is called mirror descent because of performing the gradient step in the dual space, which plays the role of ’mirror’. It means that mirror descent search the global minimum, according to duality of probability distribution manifold, which is equivalent to Fisher infomration matrix for natural gradient descent.

Besides the usual mirror descent, there is proposed stochastic mirror descent (SMD) by Nemirovski and Yudin in [113]. This method presented high accuracy on ResNet18 recognising images from Cifar10. For a strictly convex differentiable function

ψ (\cdot)

, called the potential (proximity) function, stochastic mirror descent is presented by the following iterative formula

\nabla ψ (θ_{t + 1}) = \nabla ψ (θ_{t}) - η \nabla f (θ_{t}),

(50)

which is equivalent to the following expression

θ_{t + 1} = arg min_{θ} \{η θ_{t}^{T} \nabla f (θ_{t}) + D_{ψ} (θ, θ_{t})\},

(51)

where Bregman divergence can be presented as

D_{ψ} (θ, θ_{t}) = ψ (θ) - ψ (θ_{t}) - \nabla ψ {(θ_{t})}^{T} (θ - θ_{t})

(52)

is the Bregman divergence with respect to the potential function

ψ

. Note that

D_{ψ}

is nonnegative, convex in its first argument, and that, due to strict convexity,

D_{ψ} (θ, θ^{'}) = 0

if and only if

θ = θ^{'}

Different choices of the potential function

ψ

yield different optimization algorithms, which will potentially have different implicit biases. A few examples follow in Table 3.

Potentially, this method can improve the process of minimization of the loss function in convolutional, graph and recurrent neural networks with huge architectures. Also mirror descent can be equipped with the adaptive moment estimation and other modifications proper for first-order optimization methods.

5. Application of Optimization Methods in Modern Neural Networks

Introduced optimization methods find their applications in various architectures of artificial neural networks. All presented above optimization algorithms show good results in some determined problems, which can be solved by means of machine learning.

First order optimization methods are reliable in problems of image recognition, time series prediction, voice detection and text analysis. In such cases one needs deep convolutional and recurrent neural networks, which can be equipped with meta-data [114]. Provided architectures train neural networks too long even with GPU, therefore one needs first optimization methods, which are classified in SGD- and Adam-type algorithms. Such approaches do not consume much time and power, that simplify the process of training. For convolutional neural networks, such as AlexNet, GoogleNet, ResNet, SqueezeNet [115] and VGG [116] it suffice to use SGD-type algorithms for achieving high test accuracy. In case of DenseNet [117], Xception [118], ShuffleNet [119] and GhostNet [120] it is necessary to use advanced Adam-type algorithms, such as DiffGrad, Yogi, AdaBelief, AdaBound, AdamInject and AdaPNM. The more complex deep neural network applied in problem of recognition, the more advanced first order optimization methods it requires. The same proposition holds for recurrent neural networks, where for SVR [121], XGBoost [122], LSTM [123] and GRU [124] is enought to apply SGD-type and Adam-type algorithms, such as Adam, RAdam, NAdam and QHAdam. Recurrent neural networks, containing CNN-LSTM [125], CNN-GRU [126], TCN-LSTM [127] layers, need advanced Adam-type algorithms.

Second-order optimization methods have a higher rate of convergence in the neighborhood of global minimum, but their time consumption grows. Even quasi-Newton methods, which are dedicated to reduce time consumption, preserving the rate of convergence, still consume more time resources compared with first-order optimization algorithms. But they can be used in some convolutional neural networks, such as AlexNet, Res-Net, VGG and SqueezeNet. For these architectures time and power consumption is not critical. The most appropriate algorithms for this architectures are Apollo and AdaHessian. In recurrent neural networks second-order optimization algorithms show better results, compared with first-order, but they rise time of training. But second order methods are good in physics-informed neural networks (PINN). In the problem of finding solution of some partial differential equation with initial and boundary conditions one needs to extensively analyse the loss function. In this case L-BFGS, SR1, Apollo and AdaHessian can reach higher accuracy compared with first-order optimization methods. Simple PINN, DeepONet [128], MFNN [129] are not large like CNN, what allows to use second-order optimization methods, which gives solution with the high accuracy. For Riemannian neural networks, which rise the accuracy by determining the geodesic, one prefers to apply Apollo and AdaHessian, because with gradient directions they analyze the curvature of loss function. But for cases of Riemannian convolutional neural networks [130] they can not reduce time and power consumption, and applying first-oder optimization algorithm one loses the test accuracy. Therefore, it is necessary to engage algorithms based on information geometry.

Optimization methods based on information geometry have advantages in speed and accuracy. They can be used in convolutional, recurrent, physics-informed and Rimannian neural networks. Moreover, according to their principle of work there are provided quantum neural networks, which correlate with complex-valued neural network. Natural gradient descent and mirror descent are able to achieve the same accuracy and consume low time resources, as second- and first-order optimization methods, respectively. Such possibilities allows to include such algorithms in convolutional, recurrent, graph and auto-encoder neural networks. Moreover, natural gradient and mirror descent extended the application of neural network in quantum computations, where vanilla natural gradient descent is modified into its quantum analogue. For physics-informed neural networks opportunity to converge in the neighborhood of global minimum, consuming time and power similar to first-order methods, can improve the process of solving partial differential and integral equations. This allows to compete with traditional finite difference, element and volume methods.

The summarizing of the above areas of applications is contained in Table 4.

Note, that CNN, RNN, GNN, PINN, SNN, CVNN, QNN are convolutional, recurrent, graph, physics-informed, spiking, complex-valued and quantum neural networks, respectively. These neural networks proved their ability to solve vast majority of problems, related to recognition, prediction, generation, processing, detecting and so on. All of them belong to set of neural networks with gradient based architectures. Recall, that machine learning is the theory, which studies self-learning algorithms, which also can be classified by means of learning. Gradient based neural networks present one of classes in machine learning. Meanwhile, there are many other ways train, which are advanced gradient and gradient free learning methods.

6. Challenges and Potential Research

Despite the advanced optimization methods, there exist problems, which concern the fundamental theory of machine learning. All algorithms presented above are utilizable for neural networks with gradient backpropagation, which is not the unique way to rectify weights. There are presented potential methods in [173], which let reduce gradient calculation, i.e. make the gradient-free error backpropagation process. Therefore, for minimizing loss function one needs to engage alternative optimization methods. On example Alternating Direction Method of Multipliers in [174] or ensemble neural network in [175], where gradient is reduced. For such models one need to use the following gradient free optimization methods in Table 5.

Gradient free optimization methods attract the interest of many researches, because of their computational simplicity, absence of unwanted differentiation operators and convergence rate, that is not less compared with usual gradient descent. Such approach makes mathematicians to develop alternative mathematical models of neural networks, which show their effectiveness over gradient based neural networks in [193]. But it does not say, that one needs to refuse from the gradient-based optimization algorithms. They have worthy continuation, which is an engaging fractional derivatives for computing the gradient.

Fractional calculus, which is a reason continuation of classical calculus, put significant influence in theories of partial differential and integral equations, approximations, signal processing and optimizations. Attempts to generalize differential operators implied many various properties and helpful propositions, which concern the theory of machine learning. It can be seen by extending gradient based optimization methods by fractional derivatives. Let in Table 6 summarize all known fractional derivatives [194], which can improve the process of minimization of loss functions in neural networks.

Fractional optimization methods have proved their efficiency in [195], but there is a question: that chain rule for fractional derivatives makes the modeling of error propagation more complex? No, because there are implied generalized chain and Leibniz rules in [196], which do not differ much from usual versions. Therefore, it is possible to generalize first order optimization methods from SGD- to Adam-type algorithms.

Simultaneously, there is the problem of developing neural networks, containing bilevel optimization [197]. For neural networks equipped with meta-learning, utilization of provided optimization methods does not suffice. There have to be used bilevel optimization algorithms, such as BSA [198], TTSA [199], HOAG [200], AID-FP [201], AID-CG [202] and stocBiO [203]. Such approaches provide the theoretical guarantee in hyperparameter optimization and meta-learning. Potentionaly, these methods can be improved by means of information geometry or techniques from advanced first order optimization algorithms. Moreover, these algorithms can be useful in physics-informed neural networks.

Another problem in physics-informed neural networks is their extension on delay differential equations. The problem of solving such kind of equations with various type of delay is not solved yet, whereas there is found a model for solving fractional differential equations in [204]. In this case one rises the question about using different activation functions, what, consequently, impact on process of optimization of the loss function. Therefore, one can use optimizers based on information geometry. Afterwards, they can be modified in advanced algorithms, which can guarantee the higher accuracy for minimal number of iterations. Especially, information-geometric methods are actual for complex-valued neural networks.

Complex-valued neural networks shew their efficiency in engineering areas such as antenna design, radar imaging, optical/lightwave information processing and quantum devices such as superconductive devices. All these areas of applications contain the mathematical models with rotational point, wave functions and integral transforms such as Fourier, Laplace and Hilbert. This kind of models suggest the future realization of intrinsically non-von Neumann computers including pattern-information representing devices. Conventional quantum computation is strictly limited in its treatable problems. Contrarily, CVNN-based quantum computation can deal with more general problems, which leads to wider applications of quantum computer science. Therefore, one needs to imply optimization methods, based on quantum and tensor computations. On example techniques, used in shampoo [205], can perform the optimization on tensor level.

Quantum neural networks start to attract attention of many researches, who research and develop advanced methods of machine learning. With appearance of quantum computers it was necessary to expand the theory of neural networks on quantum devices, which let to analyze quantum processes, and tensor-network circuits. For problems of image recognition, time series prediction and moving object detection one needs to use quanvolutional neural networks [206], which engage quantum natural gradient. This optimization algorithms presents a quantum analogue of vanilla natural gradient descent, but it uses the Fubini-Study tensor instead of the Fisher information matrix. Unlike the usual Fisher and Hessian matrices, such tensor considers quantum computations with wave functions, bra- and ket-vectors. Such method, can be equipped with exponential moving and positive-negative averages, that can increase the test accuracy for quantum neural networks. There are proposition of equipping the quantum neural networks with spiking neurons in recent researches, what will causes other tasks for developing optimization methods with memory.

Recall that neural networks of third generation are based on weights with memory. Such approach is more close model to biological neuron networks, what makes the process of training more accurate. Potentially, for such models one can use corresponding memory-based optimization algorithms, such as mixed stochastic gradient descent, denoted MEGA I and MEGA II in [207]. The ability of remembering past experiences while being trained on a continuum of tasks makes possible to significantly rise the test accuracy of spiking neural networks. This kind of neural networks experienced the extension from multi-layer perceptrons to various advanced networks, such as Feedback SNN, attice map SNN, deep convolutional SNN, spike timing dependent plasticity and many other networks. But one of the most recent architectures are graph networks, which without spiking neurons can successfully train the models.

Graph neural networks, which structure reminds the simple graph, are utilized in many tasks related to medicine and biology. As can be seen in neuroscience resource, biological neural networks do not present the linear, sequential and organized in determined order model, but construct another more progressive connections, which significantly impacted in mathematical model of neurons. If it is possible to create the model with corresponding structure, then one receives the network without unwanted layers and computations. But such model rise the problem of error propagation, which definitely differs from classical error backpropagation. Afterwards, there were proposed alternative error rectification methods, which are called neighbor aggregation and information update in [208]. For this methods are suitable to apply presented above first order optimization methods, which are based on information geometry, on example mirror descent. Such algorithms can be modified with new proximal functions, and extended version of Bregman divergence in further researches. Neverless, there are exists other divergence formulas, which can produce new information-geometric optimization methods. But, for modifying the structure of neural networks, one may use wavelet decompositions, which potentially can process input data more accurately.

Neural networks, based on wavelet, are dispersed in the problems of signal processing. Moreover, such tool is already utilized in numerical solving partial differential equations, which seems as an important advance of physics-informed neural networks. Wavelet decomposition was used in convolution, LSTM and GRU layers, what made the data processing more accurate, especially in cases of scaling input information. Moreover, there is presented model of graph-wavelet neural networks, which gave the best results of node classification in [209], compared with spectral CNN, ChebyNet, GCN and MoNet. For wavelet neural networks one can use algorithms presented in talbe 4, but there are presented two new approaches, which are called whale and butterfly optimization methods, in [210]. Also for such kind of network researches often utilize particle swarm method, which is gradient free. Therefore, there is a possibility in comparing gradient free optimization methods between each other and developing new approaches.

In summary, one needs to say, that developing of optimization algorithms correlates with evolution of architectures of neural network and challenges, posed before researches. Also such relation works in backward, what can be seen in case of quantum natural gradient descent and quantum neural networks. Note that improving neural network can be infinite on the problems of image recognition, therefore one needs to consider the problem of moving detection. In case of time series predictions, it should to consider the stochastic process and Brownian motion, which comes from statistical physics and thermodynamics. Such kind of challenges have a big influence to the theory not just neural networks, but the theory of artificial intelligence.

7. Conclusions

In conclusion of this review, we can say, that fundamental developing of the theory of neural networks allows to simplify the work of human in more scales. The developing of optimization methods in machine learning allowed to achieve not only higher test accuracy for short time, but to imply necessary features and disadvantages of existing models, what through the time made researches to provide advanced architectures. First order optimization algorithms, presented in section 2, were improving and changing simultaneously with growing of neural networks in sizes and qualities. There were described every SGD-, Adam- and PNM-type algorithms, their approaches in optimization process, improving techniques and evolution. In section 3, we provided second order optimization algorithms, which are divided on Newton and quasi-Newton methods. There were described their applications in neural networks, simplifying their computation complexity by means of approximation theory, which produced other useful modifications and variations. Such approximation led to changing the Hessian by gradient flow tensor, and then by Fisher information matrix. This modification brought us to information geometry, that allowed to provide natural gradient and mirror descents, which equivalence was introduced in section 4. Afterwards, we summarized in Table 4 all type of neural networks, suitable for introduced optimization methods. There are provided modern networks, which already have used introduced optimization algorithms and those, that could have been used for increasing test accuracy. In section 6, we demonstrated ways of further developing and applications of optimization methods. There are provided gradient-free, fractional order and bilevel optimization algorithms, their existing versions and potentials for rising test accuracy for various type of neural networks. In the end, this survey can demonstrate to readers all type of existing optimization methods, their modifications, applications, which can help researches to comprehend the state of modern theory of optimization and machine learning. Such information allows to create advanced fundamental modifications and extend the area of applications for modern neural networks of all types.

Author Contributions

Conceptualization, R.A.; Formal analysis, R.A.; Funding acquisition, P.L., R.A. and N.N.; Investigation, R.A.; Methodology, P.L. and N.N.; Project administration, P.L.; Resources, R.A.; Supervision, P.L.; Writing—original draft, R.A.; Writing—review and editing, P.L. and N.N. All authors have read and agreed to the published version of the manuscript.

Funding

The section 2 is supported by North-Caucasus Center for Mathematical Research under agreement No 075-02-2022-892 with the Ministry of Science and Higher Education of the Russian Federation. The research in section 3 was supported by the Russian Science Foundation (Project No. 21-71-00017). The research in section 4 was supported by the Russian Science Foundation (Project No. 22-71-00009).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to thank the North-Caucasus Federal University for supporting in the contest of projects competition of scientific groups and individual scientists of the North-Caucasus Federal University.

Conflicts of Interest

The authors declare no conflict of interest.

References

Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
Qian, K.; Pawar, A.; Liao, A. et al. Modeling neuron growth using isogeometric collocation based phase field method. Sci Rep 2022, 12, 8120. [Google Scholar] [CrossRef] [PubMed]
Liu, Y.; Shi, Y.; Mu, F.; Cheng, J.; Li, C.; Chen, X. Multimodal MRI Volumetric Data Fusion With Convolutional Neural Networks. IEEE Transactions on Instrumentation and Measurement 2022, 71, 1–15. [Google Scholar] [CrossRef]
Li, Q.; Xiong, D.; Shang, M. Adjusted stochastic gradient descent for latent factor analysis. Information Sciences 2022, 588, 196–213. [Google Scholar] [CrossRef]
Dogo, E. M.; Afolabi, O.J.; Nwulu, N.I.; Twala, B.; Aigbavboa, C.O. A Comparative Analysis of Gradient Descent-Based Optimization Algorithms on Convolutional Neural Networks. 2018 International Conference on Computational Techniques, Electronics and Mechanical Systems (CTEMS), Belgaum, India, 2018, pp. 92-99. [CrossRef]
Ward, R.; Wu, X.; Bottou, L. AdaGrad stepsizes: sharp convergence over nonconvex landscapes. The Journal of Machine Learning Research 2020, 21, 9047–9076. [Google Scholar]
Xu, D.; Zhang, S.; Zhang, H.; Mandic, D.P. Convergence of the RMSProp deep learning method with penalty for nonconvex optimization. Neural Networks 2021, 139, 17–23. [Google Scholar] [CrossRef] [PubMed]
Zeiler, M.D. Adadelta: an adaptive learning rate method. aeXiv 2012, arXiv:1212.5701. [Google Scholar]
Singarimbun, R. N; Nababan, E.B.; Sitompul, O.S. Adaptive Moment Estimation To Minimize Square Error In Backpropagation Algorithm.2019 International Conference of Computer Science and Information Technology (ICoSNIKOM), Medan, Indonesia, 2019, pp. 1-7. [CrossRef]
Seredynski, F.; Zomaya, A.Y.; Bouvry, P. Function Optimization with Coevolutionary Algorithms. Intelligent Information Processing and Web Mining. Advances in Soft Computing 2003, 22, 13–22. [Google Scholar]
Osowski, S.; Bojarczak, P.; M. Stodolskia, M. Fast Second Order Learning Algorithm for Feedforward Multilayer Neural Networks and its Applications. Neural Networks 1996, 9, 1583–1596. [Google Scholar] [CrossRef]
Tyagi, K.; Rane, C.; Irie, B. et al. Multistage Newton’s Approach for Training Radial Basis Function Neural Networks. SN COMPUT. SCI. 2021, 2, 366. [Google Scholar] [CrossRef]
Likas, A.; Stafylopatis, A. Training the random neural network using quasi-Newton methods. European Journal of Operational Research 2000, 126, 331–339. [Google Scholar] [CrossRef]
Arbel, M.; Korba, A.; Salim, A.; Gretton, A. Maximum Mean Discrepancy Gradient Flow. arXiv 2019, arXiv:1906.04370. [Google Scholar]
Ay, N.; Jost, N.J.; Lê, H.V.; Schwachhöfe, L. Information Geometry; Springer: Berlin, Heidelberg, Germany, 2008. [Google Scholar]
Gattone, S.A.; Sanctis, A.D.; Russo, T.; Pulcini, D. A shape distance based on the Fisher–Rao metric and its application for shapes clustering. Physica A: Statistical Mechanics and its Applications 2017, 487, 93–102. [Google Scholar] [CrossRef]
Hua, X.; Fan, H.; Cheng, Y.; Wang, H.; Qin, Y. Information Geometry for Radar Target Detection with Total Jensen–Bregman Divergence. Entropy 2018, 20, 256. [Google Scholar] [CrossRef] [PubMed]
Osawa, K.; Tsuji, Y.; Ueno, Y.; A. Naruse, A.; Foo. C. -S; Yokota, R. Scalable and Practical Natural Gradient for Large-Scale Deep Learning. IEEE Transactions on Pattern Analysis and Machine Intelligence 2022, 44, 404–415. [Google Scholar] [CrossRef] [PubMed]
Orabona, F.; Crammer, K.; Cesa-Bianchi, N. A generalized online mirror descent with applications to classification and regression. Mach Learn 2015, 99, 411–435. [Google Scholar] [CrossRef]
Lu, L.; Pestourie, R.; Yao, W.; Wang, Z.; Verdugo, F.; Johnson, S.G. Physics-Informed Neural Networks with Hard Constraints for Inverse Design. SIAM Journal on Scientific Computing 2021, 43, 1105–1132. [Google Scholar] [CrossRef]
Shi, C.; Tan, C.; Wang, T.; Wang, L. A Waste Classification Method Based on a Multilayer Hybrid Convolution Neural Network. Appl. Sci. 2021, 11, 8572. [Google Scholar] [CrossRef]
Hacker, C.; Aizenberg, I.; Wilson, J. Gpu simulator of multilayer neural network based on multi-valued neurons. 2016 International Joint Conference on Neural Networks (IJCNN), 2016, 4125–4132. 4125. [Google Scholar] [CrossRef]
Chen, S.; McLaughlin, S.; Mulgrew, B. Complex-valued radial basis function network, part i: Network architecture and learning algorithms. Signal Process. 1994, 35, 19–31. [Google Scholar] [CrossRef]
Suzuki, Y.; Kobayashi, M. Complex-valued bidirectional auto-associative memory. he 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 2013, pp. 1-7. [CrossRef]
Traore, C; Pauwels, E. Sequential convergence of AdaGrad algorithm for smooth convex optimization. Operations Research Letters 2021, 49, 452–458. [Google Scholar] [CrossRef]
Dogo, E.M.; Afolabi, O.J.; Nwulu, N.I.; Twala, B.; Aigbavboa, C.O. A Comparative Analysis of Gradient Descent-Based Optimization Algorithms on Convolutional Neural Networks. 2018 International Conference on Computational Techniques, Electronics and Mechanical Systems (CTEMS), Belgaum, India, 2018, pp. 92-99. [CrossRef]
Gu, P.; Tian, S.; Chen, Y. Iterative Learning Control Based on Nesterov Accelerated Gradient Method. IEEE Access 2019, 7, 115836–115842. [Google Scholar] [CrossRef]
Van Laarhoven, T. L₂ Regularization versus Batch and Weight Normalization. arXiv 2017, arXiv:1706.05350. [Google Scholar]
Byrd, J.; Lipton, Z.C. What is the Effect of Importance Weighting in Deep Learning? Proceedings of the 36th International Conference on Machine Learning, PMLR, 2019, 97, 872–881. [Google Scholar]
Vrbančič, G.; Podgorelec, V. Efficient ensemble for image-based identification of Pneumonia utilizing deep CNN and SGD with warm restarts. Expert Systems with Applications 2022, 187, 115834. [Google Scholar] [CrossRef]
Heo, B.; Chun, S.; Oh, S.J.; Han, D.; Yun, S.; Kim, G.; Uh, Y.; Ha, J.-W. AdamP: Slowing Down the Slowdown for Momentum Optimizers on Scale-invariant Weights. arXiv 2021, arXiv:2006.08217. [Google Scholar]
Sun, J.; Yang, Y.; Xun, G.; Zhang, A. Scheduling Hyperparameters to Improve Generalization: From Centralized SGD to Asynchronous SGD. ACM Transactions on Knowledge Discovery from Data (accepted paper). [CrossRef]
Wu, S. et al. "L₁ -Norm Batch Normalization for Efficient Training of Deep Neural Networks. IEEE Transactions on Neural Networks and Learning Systems 2019, 30, 2043–2051. [Google Scholar] [CrossRef] [PubMed]
Yu, Z.; Sun, G.; Lv, J. A fractional-order momentum optimization approach of deep neural networks. Neural Comput and Applic 2022, 34, 7091–7111. [Google Scholar] [CrossRef]
Gokcesu, K.; Gokcesu, H. Regret Analysis of Global Optimization in Univariate Functions with Lipschitz Derivatives. arXiv 2021, arXiv:2108.10859. [Google Scholar]
Gower, R.M.; Loizou, N.; Qian, X.; Sailanbayev, A.; Shulgin, E.; Richtárik, P. SGD: General Analysis and Improved Rates. Proceedings of Machine Learning Research 2019, 97, 5200–5209. [Google Scholar]
Mukkamala, M.C.; Hein, M. Variants of RMSProp and Adagrad with Logarithmic Regret Bounds. Proceedings of Machine Learning Research 2017, 70, 2545–2553. [Google Scholar]
Wang, G.; Lu, S.; Tu, W.; Zhang, L. Sadam: A variant of adam for strongly convex functions. arXiv 2019, arXiv:1905.02957. [Google Scholar]
Kingma, D.P. ; Ba. J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
&lt, *!!! REPLACE !!!*; i&gt, *!!! REPLACE !!!*; Kalfaoglu, M.E.; Kalkan, S.; Alatan, A.A. (2020). Late Temporal Modeling in 3D CNN Architectures with BERT for Action Recognition. Computer Vision – ECCV 2020 Workshops. ECCV 2020. Lecture Notes in Computer Science, 2020, 12539, 731–747. ,. [CrossRef]
Herrera-Alcántara, O. Fractional Derivative Gradient-Based Optimizers for Neural Networks and Human Activity Recognition. Appl. Sci. 2022, 12, 9264. [Google Scholar] [CrossRef]
Jia, X.; Feng, X.; Yong, H.; Meng, D. Weight Decay With Tailored Adam on Scale-Invariant Weights for Better Generalization. IEEE Transactions on Neural Networks and Learning Systems 2022, 1–12. [Google Scholar] [CrossRef]
Heo, B.; Chun, S.; Oh, S.J.; Han, D.; Yun, S.; Kim, G.; Uh, Y.; Ha, J.-W. AdamP: Slowing Down the Slowdown for Momentum Optimizers on Scale-invariant Weights. arXiv 2021, arXiv:2006.08217v3. [Google Scholar]
Ma, J.; Yarats, D. Quasi-hyperbolic momentum and Adam for deep learning. arXiv 2019, arXiv:1810.06801v4. [Google Scholar]
Tang, S.; Shen, C.; Wang, D.; Li, S.; Huang, W.; Zhu, Z. Adaptive deep feature learning network with Nesterov momentum and its application to rotating machinery fault diagnosis. Neurocomputing 2018, 305, 1–14. [Google Scholar] [CrossRef]
Li, L.; Xu, W.; Yu, H. Character-level neural network model based on Nadam optimization and its application in clinical concept extraction. Neurocomputing 2020, 414, 182–190. [Google Scholar] [CrossRef]
Melinte, D.O.; Vladareanu, L. Facial Expressions Recognition for Human–Robot Interaction Using Deep Convolutional Neural Networks with Rectified Adam Optimizer. Sensors 2020, 20, 2393. [Google Scholar] [CrossRef]
Gholamalinejad, H,; Khosravi, H. Whitened gradient descent, a new updating method for optimizers in deep neural networks. Journal of AI and Data Mining 2022, 10, 467–477.
Shanthi, T.; Sabeenian, R.S. Modified Alexnet architecture for classification of diabetic retinopathy images. Computers and Electrical Engineering 2019, 76, 56–64. [Google Scholar] [CrossRef]
Wu, Z.; Shen, C.; Van Den Hengel, A. Wider or Deeper: Revisiting the ResNet Model for Visual Recognition. Pattern Recognition 2019, 90, 119–133. [Google Scholar] [CrossRef]
Das, D.; Santosh, K.C.; Pal, U. Truncated inception net: COVID-19 outbreak screening using chest X-rays. Phys Eng Sci Med 2020, 43, 915–925. [Google Scholar] [CrossRef] [PubMed]
Tang, P.; Wang, H.; Kwong, S. G-MS2F: GoogLeNet based multi-stage feature fusion of deep CNN for scene recognition. Neurocomputing 2017, 225, 188–197. [Google Scholar] [CrossRef]
Lin, L.; Liang, L.; Jin, L. R2-ResNeXt: A ResNeXt-Based Regression Model with Relative Ranking for Facial Beauty Prediction. 2018 24th International Conference on Pattern Recognition (ICPR), pp. 85-90, 2018. [CrossRef]
Dubey, S.R.; Chakraborty, S.; Roy,S.K.; Mukherjee, S.; Singh, S.K.; Chaudhuri, B.B. "diffGrad: An Optimization Method for Convolutional Neural Networks. IEEE Transactions on Neural Networks and Learning Systems 2020, 31, 4500–4511. [CrossRef]
Panait, L.; Luke, S. A comparison of two competitive fitness functions. GECCO’02: Proceedings of the 4th Annual Conference on Genetic and Evolutionary ComputationJuly 2002, pp. 503–511.
Khan, W.; Ali, S.; Muhammad, U.S.K.; Jawad, M.; Ali, M.; Nawaz, R. AdaDiffGrad: An Adaptive Batch Size Implementation Technique for DiffGrad Optimization Method. 2020 14th International Conference on Innovations in Information Technology (IIT), Al Ain, United Arab Emirates, 2020, pp. 209-214. [CrossRef]
Valova, I.; Harris, C.; Mai, T.; Gueorguieva, N. Optimization of Convolutional Neural Networks for Imbalanced Set Classification. Procedia Computer Science 2020, 176, 660–669. [Google Scholar] [CrossRef]
Zaheer, M.; Reddi, S.; Sachan, D.; Kale, S.; Kumar, S. Adaptive Methods for Nonconvex Optimization. Advances in Neural Information Processing Systems 2018, 31. [Google Scholar]
Zhuang, J.; Tang, T.; Ding, Y.; Tatikonda, S.C.; Dvornek, N. Papademetris, X.; Duncan, J. AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients. Advances in Neural Information Processing Systems 2020, 33.
Liu, J.; Kong, J.; Xu, D.; Qi, M.; Lu, Y. Convergence analysis of AdaBound with relaxed bound functions for non-convex optimization. Neural Networks 2022, 145, 300–307. [Google Scholar]
Wang, Y.; Liu, J.; Chang, X.; Wang, J.; Rodríguez, R.J. AB-FGSM: AdaBelief optimizer and FGSM-based approach to generate adversarial examples. Journal of Information Security and Applications 2022, 68, 103227. [Google Scholar] [CrossRef]
Wang, Y.; Liu, J.; Chang, X. Generalizing Adversarial Examples by AdaBelief Optimizer. arXiv 2021, arXiv:2101.09930v1. [Google Scholar]
Dubey, S.R.; Basha, S.H.S.; Singh, S.K.; Chaudhuri, B.B. AdaInject: Injection Based Adaptive Gradient Descent Optimizers for Convolutional Neural Networks. IEEE Transactions on Artificial Intelligence 2022, 1–10. [Google Scholar] [CrossRef]
Li, G. A Memory Enhancement Adjustment Method Based on Stochastic Gradients. 2022 41st Chinese Control Conference (CCC), Hefei, China, 2022, pp. 7448-7453. [CrossRef]
Xie, Z.; Yuan, L.; Zhu, Z.; Sugiyama, M. Positive-Negative Momentum: Manipulating Stochastic Gradient Noise to Improve Generalization. Proceedings of the 38th International Conference on Machine Learning, PMLR, 2021, 139, 11448-11458.
Zavriev, S.; Kostyuk, F. Heavy-ball method in nonconvex optimization problems. Computational Mathematics and Modeling 1993, 4, 336–341. [Google Scholar] [CrossRef]
Wright, L.; Demeure, N. Ranger21: a synergistic deep learning optimizer. arXiv 2021, arXiv:2106.13731v2. [Google Scholar]
Xie, X.; Zhou, P.; Li, H.; Lin, Z.; Yan, S. Adan: Adaptive Nesterov Momentum Algorithm for Faster Optimizing Deep Models. arXiv 2022, arXiv:2208.06677v3. [Google Scholar]
Burke, J.V.; Ferris, M.C. A Gauss—Newton method for convex composite optimization. Mathematical Programming 1995, 71, 179–194. [Google Scholar] [CrossRef]
Berahas, A.S.; Bollapragada, R.; Nocedal, J. An investigation of Newton-Sketch and subsampled Newton methods. Optimization Methods and Software 2020, 35, 661–680. [Google Scholar] [CrossRef]
Hartmann, W.M.; Hartwig, R.E. Computing the Moore–Penrose Inverse for the Covariance Matrix in Constrained Nonlinear Estimation. SIAM Journal on Optimization 1996, 6, 727–747. [Google Scholar] [CrossRef]
Gupta, V.; Kadhe, S.; Courtade, T.; Mahoney, M.W.; Ramchandran, K. OverSketched Newton: Fast Convex Optimization for Serverless Systems. 2020 IEEE International Conference on Big Data (Big Data), 2020, 288-297. [CrossRef]
Yang, Z. Adaptive stochastic conjugate gradient for machine learning. Expert Systems with Applications 2022, 206, 117719. [Google Scholar] [CrossRef]
Faber, V.; Joubert, W.; Knill, E.; Manteuffel, T. Minimal Residual Method Stronger than Polynomial Preconditioning. SIAM Journal on Matrix Analysis and Applications 1996, 17, 707–729. [Google Scholar] [CrossRef]
Jia, Z.; Ng, M.K. Structure Preserving Quaternion Generalized Minimal Residual Method. SIAM Journal on Matrix Analysis and Applications 2021, 42, 616–634. [Google Scholar] [CrossRef]
Mang, A.; Biros, G. An Inexact Newton–Krylov Algorithm for Constrained Diffeomorphic Image Registration. SIAM Journal on Imaging Sciences 2015, 8, 1030–1069. [Google Scholar] [CrossRef] [PubMed]
Hestenes, M.R.; Stiefel, E.L. Methods of conjugate gradients for solving linear systems. J. Research Nat. Bur. Standards 1952, 49, 409–436. [Google Scholar] [CrossRef]
Fletcher, R.; Reeves, C. Function minimization by conjugate gradients. Comput. J 1964, 7, 149–154. [Google Scholar]
Daniel, J.W. The conjugate gradient method for linear and nonlinear operator equations. SIAM J. Numer. Anal. 1967, 4, 10–26. [Google Scholar] [CrossRef]
Polak, E.; Ribiere, G. Note sur la convergence de directions conjuge´es. Rev. Francaise Informat Recherche Opertionelle, 3e Ann´ee 16, 1969, 35–43.
Polyak, B.T. The conjugate gradient method in extreme problems. USSR Comp. Math.Math. Phys. 1969, 9, 94–112. [Google Scholar] [CrossRef]
Fletcher, R. Practical Methods of Optimization vol. 1: Unconstrained Optimization; John Wiley and Sons: New York, USA, 1987. [Google Scholar]
Liu, Y.; Storey, C. Efficient generalized conjugate gradient algorithms. J. Optim. Theory Appl. 1991, 69, 129–137. [Google Scholar] [CrossRef]
Dai, Y.H.; Yuan, Y. A nonlinear conjugate gradient method with a strong global convergence property. SIAM J. Optim. 1999, 10, 177–182. [Google Scholar] [CrossRef]
Hager, W.W.; Zhang, H. A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM J. Optim. 2005, 16, 170–192. [Google Scholar] [CrossRef]
Dai, Y.-H. Convergence Properties of the BFGS Algoritm. SIAM Journal on Optimization 2002, 13, 693–701. [Google Scholar] [CrossRef]
Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Mathematical Programming 1989, 45, 503–528. [Google Scholar] [CrossRef]
Shi, H.-J. M.; Xie, Y.; Byrd, R.; Nocedal, J. A Noise-Tolerant Quasi-Newton Algorithm for Unconstrained Optimization. SIAM Journal on Optimization 2022, 32, 29–55. [Google Scholar]
Byrd, R.H.; Khalfan, H.F.; Schnabel, R.B. Analysis of a Symmetric Rank-One Trust Region Method. SIAM Journal on Optimization 1996, 6, 1025–1039. [Google Scholar] [CrossRef]
Rafati, J.; Marcia, R.F. Improving L-BFGS Initialization for Trust-Region Methods in Deep Learning. 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), 2018, 501-508. [CrossRef]
Ma, X. Apollo: An Adaptive Parameter-wise Diagonal Quasi-Newton Method for Nonconvex Stochastic Optimization. arXiv 2021, arXiv:2009.13586v6. [Google Scholar]
Yao, Z.; Gholami, A.; Shen, S.; Mustafa, M.; Keutzer, K.; Mahoney, M. ADAHESSIAN: An Adaptive Second Order Optimizer for Machine Learning. Proceedings of the AAAI Conference on Artificial Intelligence 2021, 35, 10665–10673. [Google Scholar] [CrossRef]
Shen, J.; Wang, C.; Wang, X.; Wise, S.M. Second-order Convex Splitting Schemes for Gradient Flows with Ehrlich–Schwoebel Type Energy: Application to Thin Film Epitaxy. SIAM Journal on Numerical Analysis 2012, 50, 105–125. [Google Scholar] [CrossRef]
Martens, J. New insights and perspectives on the natural gradient method. Journal of Machine Learning Research 2020, 21, 5776–5851. [Google Scholar]
Amari, Si. Information geometry in optimization, machine learning and statistical inference. Front. Electr. Electron. Eng. China 2010, 5, 241–260. [Google Scholar] [CrossRef]
Wang, S.; Teng, Y.; Perdikaris, P. Understanding and Mitigating Gradient Flow Pathologies in Physics-Informed Neural Networks. SIAM Journal on Scientific Computing 2021, 43, 3055–3081. [Google Scholar] [CrossRef]
Nielsen, F. An Elementary Introduction to Information Geometry. Entropy 2020, 22, 1100. [Google Scholar] [CrossRef] [PubMed]
Wald, A. Statistical decision functions. Ann. Math. Stat. 1949, 165–205. [Google Scholar] [CrossRef]
Wald, A. Statistical Decision Functions; Wiley: Chichester, UK, 1950. [Google Scholar]
Rattray, M.; Saad, D.; Amari, S. Natural Gradient Descent for OnLine Learning. Phys. Rev. Lett. 1998, 81, 5461–5464. [Google Scholar] [CrossRef]
Duchi, J.C.; Agarwal, A.; Johansson, M.; Jordan, M.I. Ergodic Mirror Descent. SIAM Journal on Optimization 2012, 22, 1549–1578. [Google Scholar] [CrossRef]
Wang, Y.; Li, W. Accelerated Information Gradient Flow. J. Sci. Comput. 2022, 90, 11. [Google Scholar] [CrossRef]
Goldberger; Gordon; Greenspan. An efficient image similarity measure based on approximations of KL-divergence between two gaussian mixtures. Proceedings Ninth IEEE International Conference on Computer Vision 2003, 1, 487-493. [CrossRef]
Joyce, J.M. Kullback-Leibler Divergence. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin, Heidelberg, Germany, 2011. [Google Scholar]
Nielsen, F. Statistical Divergences between Densities of Truncated Exponential Families with Nested Supports: Duo Bregman and Duo Jensen Divergences. Entropy 2022, 24, 421. [Google Scholar] [CrossRef]
Stokes, J.; Izaac, J.; Killoran, N.; Carleo, G. Quantum Natural Gradient. Open journal for quantum science 2020, 4, 269–284. [Google Scholar] [CrossRef]
Abdulkadirov, R.; Lyakhov, P.; Nagornov, N. Accelerating Extreme Search of Multidimensional Functions Based on Natural Gradient Descent with Dirichlet Distributions. Mathematics 2022, 10, 3556. [Google Scholar] [CrossRef]
Abdulkadirov, R.I.; Lyakhov, P.A. A new approach to training neural networks using natural gradient descent with momentum based on Dirichlet distributions. Computer Optics 2023, 2023. 47, 160–170. [Google Scholar]
Lyakhov, P,; Abdulkadirov, R. Accelerating Extreme Search Based on Natural Gradient Descent with Beta Distribution. 2021 International Conference Engineering and Telecommunication (En&T), Dolgoprudny, Russian Federation, 2021, pp. 1-5. [CrossRef]
Abdulkadirov, R.I.; Lyakhov, P.A. Improving Extreme Search with Natural Gradient Descent Using Dirichlet Distribution. Mathematics and its Applications in New Computer Systems. MANCS 2021. Lecture Notes in Networks and Systems 2022, 424, 19–28. [Google Scholar]
Kesten, H.; Morse, N. A Property of the Multinomial Distribution. The Annals of Mathematical Statistics 1959, 30, 120–127. [Google Scholar] [CrossRef]
D’Orazio, R.; Loizou, N.; Laradji, I.; Mitliagkas, I. Stochastic Mirror Descent: Convergence Analysis and Adaptive Variants via the Mirror Stochastic Polyak Stepsize. arXiv 2021, arXiv:2110.15412v2. [Google Scholar]
Gessert, N.; Nielsen, M.; Shaikh, M.; Werner, R.; Schlaefer, A. Skin lesion classification using ensembles of multi-resolution EfficientNets with meta data. MethodsX 2020, 7, 100864. [Google Scholar] [CrossRef] [PubMed]
Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0. 5MB model size. arXiv 2016, arXiv:1602.07360v4. [Google Scholar]
Ke, H.; Chen, D.; Li, X.; Tang, Y.; Shah, T.; Ranjan, R. Towards Brain Big Data Classification: Epileptic EEG Identification With a Lightweight VGGNet on Global MIC. IEEE Access 2018, 6, 14722–14733. [Google Scholar] [CrossRef]
Zhu, Y.; Newsam, S. DenseNet for dense flow. 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 2017, pp. 790-794. [CrossRef]
Chollet, F. Xception: Deep Learning With Depthwise Separable Convolutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 1251-1258. [CrossRef]
Zhang, X.; Zhou, X.; Lin, M.; Sun, J. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018, pp. 6848-6856. [CrossRef]
Paoletti, M.E.; Haut, J.M.; Pereira, N.S.; Plaza, J.; Plaza, A. Ghostnet for Hyperspectral Image Classification. IEEE Transactions on Geoscience and Remote Sensing 2021, 59, 10378–10393. [Google Scholar] [CrossRef]
Liu, Y. Novel volatility forecasting using deep learning–Long Short Term Memory Recurrent Neural Networks. Expert Systems with Applications 2019, 132, 99–109. [Google Scholar] [CrossRef]
Lai, CH.; Liu, DR.; Lien, KS. A hybrid of XGBoost and aspect-based review mining with attention neural network for user preference prediction. Int. J. Mach. Learn. and Cyber. 2021, 12, 1203–1217. [Google Scholar] [CrossRef]
Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Physica D: Nonlinear Phenomena 2020, 404, 132306. [Google Scholar] [CrossRef]
Lynn, H.H.; Pan, S.B.; Kim, P. A Deep Bidirectional GRU Network Model for Biometric Electrocardiogram Classification Based on Recurrent Neural Networks. IEEE Access 2019, 7, 145395–145405. [Google Scholar] [CrossRef]
Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
Sajjad, M. et al. A Novel CNN-GRU-Based Hybrid Approach for Short-Term Residential Load Forecasting. IEEE Access 2020, 8, 143759–143768. [Google Scholar]
Hu, C.; Cheng, F.; Ma, L.; Li, B. State of Charge Estimation for Lithium-Ion Batteries Based on TCN-LSTM Neural Networks. Journal of The Electrochemical Society 2022, 169, 0305544. [Google Scholar] [CrossRef]
Lu, L.; Jin, P.; Pang, G. et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat Mach Intell 2021, 3, 218–229. [Google Scholar]
Meng, X.; Karniadakis, G.T. A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems. Journal of Computational Physics 2020, 401, 109020. [Google Scholar] [CrossRef]
Gao, C.; Lui, W.; Yang, X. Convolutional neural network and riemannian geometry hybrid approach for motor imagery classification. Neurocomputing 2022, 2022, 180–190. [Google Scholar] [CrossRef]
Hosseini, M.S.; Tuli, M.; Plataniotis, K.N. Exploiting Explainable Metrics for Augmented SGD. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022, pp. 10296-10306. [CrossRef]
Singh, H.; Bhatt, P.; Jacob, S.; Kaur, A.; Vashist, A. ; Vij. D. Stock Prediction on Historical Data based on SGD and LSTM. 2022 2nd International Conference on Innovative Practices in Technology and Management (ICIPTM), 2022, pp. 200-204. [CrossRef]
Mu, Z.; Tang, S.; Zong, C.; Yu, D.; Zhuang, Y. Graph neural networks meet with distributed graph partitioners and reconciliations. Neurocomputing 2023, 518, 408–417. [Google Scholar] [CrossRef]
Li, J.; Chen, J.; Li, B. Gradient-optimized physics-informed neural networks (GOPINNs): a deep learning method for solving the complex modified KdV equation. Nonlinear Dyn 2022, 107, 781–792. [Google Scholar] [CrossRef]
Volinski, A. Volinski, A.; Zaidel,Y.; Shalumov, A.; DeWolf, T.; Supic, L.; Tsur, E.E. Data-driven artificial and spiking neural networks for inverse kinematics in neurorobotics. Patterns 2022, 3, 100391. [Google Scholar] [CrossRef]
Wang, R.; Liu, Z.; Zhang, B. et al. Few-Shot Learning with Complex-Valued Neural Networks and Dependable Learning. Int J Comput Vis 2023, 131, 385–404. [Google Scholar] [CrossRef]
Chen, M.; Shi, X.; Zhang, Y.; Wu, D.; Guizani, M. Deep Feature Learning for Medical Image Analysis with Convolutional Autoencoder Neural Network. IEEE Transactions on Big Data 2021, 7, 750-758. IEEE Transactions on Big Data 2021, 7, 750–758. [Google Scholar] [CrossRef]
Taqi, A.M.; Awad, A.; Al-Azzo, F.; Milanova, M. The Impact of Multi-Optimizers and Data Augmentation on TensorFlow Convolutional Neural Network Performance. 2018 IEEE Conference on Multimedia Information Processing and Retrieval (MIPR), 2018, pp. 140-145. [CrossRef]
Qu, Z.; Yuan, S.; Chi, R.; Chang, L.; Zhao, L. Genetic Optimization Method of Pantograph and Catenary Comprehensive Monitor Status Prediction Model Based on Adadelta Deep Neural Network. IEEE Access 2019, 7, 23210–23221. [Google Scholar] [CrossRef]
Huang, Y.; Peng, H.; Liu, Q.; Yang, Q.; Wang, J.; Orellana-Martin, D.; Perez-Jimenez, M.J. Attention-enabled gated spiking neural P model for aspect-level sentiment classification. Neural Networks 2023, 157, 437–443. [Google Scholar] [CrossRef] [PubMed]
Taqi, A.M.; Awad, A.; Al-Azzo, F.; Milanova, M. The Impact of Multi-Optimizers and Data Augmentation on TensorFlow Convolutional Neural Network Performance. 2018 IEEE Conference on Multimedia Information Processing and Retrieval (MIPR), 2018, pp. 140-145. [CrossRef]
Huk, M. Stochastic Optimization of Contextual Neural Networks with RMSprop. Lecture Notes in Computer Science 2020, 12034, 343–352. [Google Scholar]
Gautam, A.; Singh, V. CLR-based deep convolutional spiking neural network with validation based stopping for time series classification. Appl Intell 2020, 50, 830–848. [Google Scholar] [CrossRef]
Liu, B.; Zhang, Y.; He, D.; Li, Y. Identification of Apple Leaf Diseases Based on Deep Convolutional Neural Networks. Symmetry 2018, 10, 11. [Google Scholar] [CrossRef]
Kisvari, A.; Lin, Z.; Liu, X. Wind power forecasting – A data-driven method along with gated recurrent neural network. Renewable Energy 2021, 163, 1895–1909. [Google Scholar] [CrossRef]
Kim, K.-S.; Choi, Y.-S. HyAdamC: A New Adam-Based Hybrid Optimization Algorithm for Convolution Neural Networks. Sensors 2021, 21, 4054. [Google Scholar] [CrossRef] [PubMed]
Shankar, K.; Kumar, S.; Dutta, A.K.; Alkhayyat, A.; Jawad, A.J.M.; Abbas, A.H.; Yousif, Y.K. An Automated Hyperparameter Tuning Recurrent Neural Network Model for Fruit Classification. Mathematics 2022, 10, 2358. [Google Scholar] [CrossRef]
Wu, J.; Chua, Y.; Zhang, M.; Yang, Q.; Li, G.; Li, H. Deep Spiking Neural Network with Spike Count based Learning Rule. 2019 International Joint Conference on Neural Networks (IJCNN), 2019, pp. 1-6. [CrossRef]
Gong, M.; Zhou, H.; Qin, A.K.; Liu, W.; Zhao, Z. Self-Paced Co-Training of Graph Neural Networks for Semi-Supervised Node Classification. IEEE Transactions on Neural Networks and Learning Systems 2022, 1–14. [Google Scholar] [CrossRef]
Bararnia, H.; Esmaeilpour, M. On the application of physics informed neural networks (PINN) to solve boundary layer thermal-fluid problems. International Communications in Heat and Mass Transfer 2022, 132, 105890. [Google Scholar] [CrossRef]
Lu, S.; Sengupta, A. Exploring the Connection Between Binary and Spiking Neural Networks. Front. Neurosci. 2020, 14, 535. [Google Scholar] [CrossRef] [PubMed]
Freire, P.J. et al. Complex-Valued Neural Network Design for Mitigation of Signal Distortions in Optical Links. Journal of Lightwave Technology 2021, 39, 1696–1705. [Google Scholar] [CrossRef]
Jiang, J.; Ren, H.; Zhang, M. A Convolutional Autoencoder Method for Simultaneous Seismic Data Reconstruction and Denoising. IEEE Geoscience and Remote Sensing Letters 2022, 19, 1-5. IEEE Geoscience and Remote Sensing Letters 2022, 19, 1–5. [Google Scholar]
Khan, W.; Ali, S.; Muhammad, U.S.K.; Jawad, M.; Ali, M.; Nawaz, R. AdaDiffGrad: An Adaptive Batch Size Implementation Technique for DiffGrad Optimization Method. 2020 14th International Conference on Innovations in Information Technology (IIT), 2020, pp. 209-214. [CrossRef]
Sun, W.; Wang, Y.; Chang, K.; Meng, K. IdiffGrad: A Gradient Descent Algorithm for Intrusion Detection Based on diffGrad. 2021 IEEE 20th International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), 2021, pp. 1583-1590. [CrossRef]
Roy, S.K.; Manna, S.; Dubey, S.R.; Chaudhuri, B.B. LiSHT: Non-parametric linearly scaled hyperbolic tangent activation function for neural networks. arXiv 2022, arXiv:1901.05894v3, Yogi. [Google Scholar]
Valova, I.; Harris, C. Valova, I.; Harris, C.; Mai,T.; Gueorguieva, N. Optimization of Convolutional Neural Networks for Imbalanced Set Classification. Procedia Computer Science 2020, 176, 660–669. [Google Scholar] [CrossRef]
Yogi, S.C.; Tripathi, V.K.; Behera, L. Adaptive Integral Sliding Mode Control Using Fully Connected Recurrent Neural Network for Position and Attitude Control of Quadrotor. IEEE Transactions on Neural Networks and Learning Systems 2021, 32, 5595–5609. [Google Scholar] [CrossRef]
Shi, H.; Wang, L.; Scherer, R.; Woźniak, M.; Zhang, P.; Wei, W. Short-Term Load Forecasting Based on Adabelief Optimized Temporal Convolutional Network and Gated Recurrent Unit Hybrid Neural Network. IEEE Access 2021, 9, 66965–66981. [Google Scholar] [CrossRef]
Guo, J.; Liu, Q.; Guo, H.; Lu, X. Ligandformer: A Graph Neural Network for Predicting Ligand Property with Robust Interpretation. arXiv 2022, arXiv:2202.10873v3, AdaBound. [Google Scholar]
Wu, D.; Yuan, Y.; Huang, J.; Tan, Y. Optimize TSK Fuzzy Systems for Regression Problems: Minibatch Gradient Descent With Regularization, DropRule, and AdaBound (MBGD-RDA). IEEE Transactions on Fuzzy Systems 2020, 28, 1003–1015. [Google Scholar] [CrossRef]
Demertzis, K.; Iliadis, L.; Pimenidis, E. Large-Scale Geospatial Data Analysis: Geographic Object-Based Scene Classification in Remote Sensing Images by GIS and Deep Residual Learning. Proceedings of the International Neural Networks Society 2020, 2, 274–291. [Google Scholar]
Wang, C. et al. Distributed Newton Methods for Deep Neural Networks. Neural Computation 2018, 30, 1673–1724. [Google Scholar] [CrossRef]
Kim, H., Wang, C.; Byun, H.; Hu, W.; Kim, S.; Jiao, Q.; Lee, T.H. Variable three-term conjugate gradient method for training artificial neural networks.Neural Networks 2022(accepted paper). [CrossRef]
Peng, C.-C.; Magoulas, G.D. Adaptive Nonmonotone Conjugate Gradient Training Algorithm for Recurrent Neural Networks. 19th IEEE International Conference on Tools with Artificial Intelligence(ICTAI 2007), 2007, pp. 374-381. (L-)BFGS. [CrossRef]
Franklin, T.S.; Souza, L.S.; Fontes, R.M.; Martins, M.A.F. A Physics-Informed Neural Networks (PINN) oriented approach to flow metering in oil wells: an ESP lifted oil well system as a case study. Digital Chemical Engineering 2022, 5, 100056. [Google Scholar] [CrossRef]
Koshimizu, H.; Kojima, R.; Kario, K.; Okuno, Y. Prediction of blood pressure variability using deep neural networks. International Journal of Medical Informatics 2020, 136, 104067. [Google Scholar] [CrossRef] [PubMed]
Osawa, K.; Tsuji, Y.; Ueno, Y.; Naruse, A.; Foo, C.-S.; Yokota, R. Scalable and Practical Natural Gradient for Large-Scale Deep Learning. IEEE Transactions on Pattern Analysis and Machine Intelligence 2022, 44, 404–415. [Google Scholar] [CrossRef] [PubMed]
Sun, F.; Sun, J.; Zhao, Q. A deep learning method for predicting metabolite–disease associations via graph neural network. Briefings in Bioinformatics 2022, 23. [Google Scholar] [CrossRef]
Boso, F.; Tartakovsky, D.M. Information geometry of physics-informed statistical manifolds and its use in data assimilation. Journal of Computational Physics 2022, 467, 111438. [Google Scholar] [CrossRef]
Becker, S.; Li, W. Quantum Statistical Learning via Quantum Wasserstein Natural Gradient. J Stat Phys 2021, 182, 1–26. [Google Scholar] [CrossRef]
You, J.-K.; Cheng, H.-C.; Li, Y.-H. Minimizing Quantum Rényi Divergences via Mirror Descent with Polyak Step Size. 2022 IEEE International Symposium on Information Theory (ISIT), 2022, pp. 252-257. [CrossRef]
Chen, Y.; Chang, H.; Meng, J.; Zhang, D. Ensemble Neural Networks (ENN): A gradient-free stochastic method. Neural Networks 2019, 110, 170–185. [Google Scholar] [CrossRef]
Han, D.; Yuan, X. A Note on the Alternating Direction Method of Multipliers. J Optim Theory Appl 2012, 155, 227–238. [Google Scholar] [CrossRef]
Zhang, S.; Liu, M.; Yan, J. The Diversified Ensemble Neural Network.Advances in Neural Information Processing Systems 33, 2020.
Dominic, S.; Das, R.; Whitley, D.; Anderson, C. Genetic reinforcement learning for neural networks. IJCNN-91-Seattle International Joint Conference on Neural Networks 1991, 2, 71–76. [Google Scholar]
Kanwar, S.; Awasthi, L.K.; Shrivastava, V. Feature Selection with Stochastic Hill-Climbing Algorithm in Cross Project Defect Prediction. 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), pp. 632-635, 2022. [CrossRef]
Sexton, R.S.; Dorsey, R.E.; Johnson, J.D. Optimization of neural networks: A comparative analysis of the genetic algorithm and simulated annealing. European Journal of Operational Research 1999, 114, 589–601. [Google Scholar] [CrossRef]
Maehara, N.; Shimoda, Y. Application of the genetic algorithm and downhill simplex methods (Nelder–Mead methods) in the search for the optimum chiller configuration. Applied Thermal Engineering 2013, 61, 433–442. [Google Scholar] [CrossRef]
Huang, G.B.; Chen, L. Enhanced random search based incremental extreme learning machine. Neurocomputing 2008, 71, 3460–3468. [Google Scholar] [CrossRef]
Pontes, F.J.; Amorim, G.F.; Balestrassi, P.P.; Paiva, A.P.; Ferreira, J.R. Design of experiments and focused grid search for neural network parameter optimization. Neurocomputing 2016, 186, 22–34. [Google Scholar] [CrossRef]
Farfán, J.F.; Cea, L. Improving the predictive skills of hydrological models using a combinatorial optimization algorithm and artificial neural networks. Model. Earth Syst. Environ. 2022. [Google Scholar] [CrossRef]
Zerubia, J.; Chellappa, R. Mean field annealing using compound Gauss-Markov random fields for edge detection and image estimation. IEEE Transactions on Neural Networks 1993, 4, 703–709. [Google Scholar] [CrossRef]
Ihme, M.; Marsden, A.L.; Pitsch, H. Generation of Optimal Artificial Neural Networks Using a Pattern Search Algorithm: Application to Approximation of Chemical Systems. Neural Computation 2008, 20, 573–601. [Google Scholar] [CrossRef] [PubMed]
Vilovic, I.; Burum, N.; Sipus, Z. Design of an Indoor Wireless Network with Neural Prediction Model. The Second European Conference on Antennas and Propagation, EuCAP 2007, pp. 1-5, 2007. [CrossRef]
Bagherbeik, M.; Ashtari, P.; Mousavi, S.F.; Kanda, K.; Tamura, H.; Sheikholeslami, A. A Permutational Boltzmann Machine with Parallel Tempering for Solving Combinatorial Optimization Problems. Lecture Notes in Computer Science 2020, 12269, 317–331. [Google Scholar]
Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell 2007, 1, 33–57. [Google Scholar] [CrossRef]
Wang, Q.; Perc, M.; Duan, Z.; Chen, G. Delay-enhanced coherence of spiral waves in noisy Hodgkin–Huxley neuronal networks. Physics Letters A 2008, 372, 5681–5687. [Google Scholar] [CrossRef]
Fernandes Jr, F.E.; Yen, G.G. Pruning deep convolutional neural networks architectures with evolution strategy. Information Sciences 2021, 552, 29–47. [Google Scholar] [CrossRef]
Cho, H.; Kim, Y.; Lee, E.; Choi, D.; Lee, Y.; Rhee, W. Basic Enhancement Strategies When Using Bayesian Optimization for Hyperparameter Tuning of Deep Neural Networks. IEEE Access 2020, 8, 52588–52608. [Google Scholar] [CrossRef]
Pauli, P.; Koch, A.; Berberich, J.; Kohler, P.; Allgöwer, F. Training Robust Neural Networks Using Lipschitz Bounds. IEEE Control Systems Letters 2022, 6, 121–126. [Google Scholar] [CrossRef]
Rong, G.; Li, K.; Su, Y.; Tong, Z.; Liu, X.; Zhang, J.; Zhang, Y.; Li, T. Comparison of Tree-Structured Parzen Estimator Optimization in Three Typical Neural Network Models for Landslide Susceptibility Assessment. Remote Sens. 2021, 13, 4694. [Google Scholar] [CrossRef]
Chen, Y.; Chang, H.; Meng, J.; Zhang, F. Ensemble Neural Networks (ENN): A gradient-free stochastic method. Neural Networks 2019, 110, 170–185. [Google Scholar] [CrossRef] [PubMed]
Yang, X.-J. General Fractional Derivatives. Theory, Methods and Applications; CRC Press, Taylor and Francis Group: Boca Raton, 2019. [Google Scholar]
Wang, J.; Wen, Y.; Gou, Y.; Ye, Z.; Chen, H. Fractional-order gradient descent learning of BP neural networks with Caputo derivative. Neural Networks 2017, 89, 19–30. [Google Scholar] [CrossRef] [PubMed]
Sales Teodoro, G.; Tenreiro Machado, J.A.; Capelas de Oliveira, E. A review of definitions of fractional derivatives and other operators. Journal of Computational Physics 2019, 388, 195–208. [Google Scholar] [CrossRef]
Louati, H.; Bechikh, S.; Louati, A.; Hung, C.C.; Said, L.B. Deep convolutional neural network architecture design as a bi-level optimization problem. Neurocomputing 2021, 439, 44–62. [Google Scholar] [CrossRef]
Yang, J.; Ji, K.; Liang, Y. Provably Faster Algorithms for Bilevel Optimization. Part of Advances in Neural Information Processing Systems 34, 2021. .
Hong, M.; Wai, H.T.; Wang, Z.; Yang, Z. A two-timescale framework for bilevel optimization: Complexity analysis and application to actor-critic. arXiv 2020, arXiv:2007.05170. [Google Scholar] [CrossRef]
Khanduri, P.; Zeng, S.; Hong, M.; Wai, H.-T.; Wang, Z.; Yang, Z. A Near-Optimal Algorithm for Stochastic Bilevel Optimization via Double-Momentum, Part of Advances in Neural Information Processing Systems 34, 2021. .
Grazzi, R.; Franceschi, L.; Pontil, M.; Salzo, S. On the iteration complexity of hypergradient computation. In International Conference on Machine Learning (ICML), pp. 3748–3758, 2020.
Sow, D.; Ji, K.; Liang, Y. Es-based jacobian enables faster bilevel optimization. arXiv 2021, arXiv:2110.07004. [Google Scholar]
Ji, K.; Yang, J.; Liang, Y. Bilevel Optimization: Convergence Analysis and Enhanced Design. Proceedings of the 38th International Conference on Machine Learning, PMLR, 2021, 139, 4882-4892.
Pang, G.; Lu, L.; Karniadakis, G.E. fPINNs: Fractional physics-informed neural networks. SIAM Journal on Scientific Computing 2019, 41, 2603–2626. [Google Scholar] [CrossRef]
Gupta, V.; Koren, T.; Singer, Y. Shampoo: Preconditioned Stochastic Tensor Optimization. Proceedings of Machine Learning Research 2018, 80, 1842–1850. [Google Scholar]
Henderson, M.; Shakya, S.; Pradhan, S. et al. Quanvolutional neural networks: powering image recognition with quantum circuits. Quantum Mach. Intell. 2020, 2, 2. [Google Scholar] [CrossRef]
Guo, Y.; Liu, M.; Yang, T.; Rosing, T. Improved Schemes for Episodic Memory-based Lifelong Learning. Part of Advances in Neural Information Processing Systems 33, 2020. .
Zhang, D.; Liu, L.; Wei, Q.; Yang, Y.; Yang, P.; Liu, Q. Neighborhood Aggregation Collaborative Filtering Based on Knowledge Graph. Appl. Sci. 2020, 10, 3818. [Google Scholar] [CrossRef]
Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
Wang, G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput and Applic 2019, 31, 1995–2014. [Google Scholar] [CrossRef]

Figure 1. The historical tree of developing optimization algorithms from 1950 to 2022.

Table 1. List of conjugate gradient update parameters.

CG Update Parameter	Authors	Year
$β_{t}^{H S} = \frac{g_{t + 1}^{T} y_{t}}{d_{t}^{T} y_{t}}$	Hestenes and Stiefel [78]	1952
$β_{t}^{F R} = \frac{∥ g_{t + 1} ∥_{2}^{2}}{∥ g_{t} ∥_{2}^{2}}$	Fletcher and Reeves [79]	1964
$β_{t}^{D} = \frac{g_{t + 1}^{T} \nabla^{2} f (θ_{t}) d_{t}}{d_{t}^{T} \nabla^{2} f (θ_{t}) d_{t}}$	Daniel [80]	1967
$β_{t}^{P R P} = \frac{g_{t + 1}^{T} y_{t}}{∥ g_{t} ∥_{2}^{2}}$	Polak and Ribière [81] and by Polyak [82]	1969
$β_{t}^{C D} = \frac{∥ g_{t + 1} ∥_{2}^{2}}{- d_{t}^{T} g_{t}}$	Fletcher [83], CD stands for “Conjugate Descent”	1987
$β_{t}^{L S} = \frac{g_{t + 1}^{T} y_{t}}{- d_{t}^{T} g_{t}}$	Liu and Storey [84]	1991
$β_{t}^{D Y} = \frac{∥ g_{t + 1} ∥_{2}^{2}}{d_{t}^{T} g_{t}}$	Dai and Yuan [85]	1999
$β_{t}^{N} = {(y_{t} 2 d_{t} \frac{∥ y_{t +} ∥_{2}^{2}}{d_{t}^{T} g_{t}})}^{T} \frac{g_{t + 1}}{d_{t}^{T} y_{t}}$	Hager and Zhang [86]	2005

Table 2. List of Fisher information matrices for different probability distributions.

Probability Density Function	Fisher Information Matrix	Probability Distribution
$p (x; μ, σ) = \frac{2 π^{- \frac{n}{2}}}{\sqrt{σ_{1}^{2} . . . σ_{n}^{2}}} e^{- \frac{{(x - μ)}^{T} d i a g {(σ_{1}^{2}, . . ., σ_{n}^{2})}^{- 1} (x - μ)}{2}}$	$F_{G} = (\begin{matrix} \frac{1}{σ_{1}^{2}} & 0 & . . . & 0 & 0 \\ 0 & \frac{2}{σ_{1}^{2}} & . . . & 0 & 0 \\ . . . & . . . & . . . & . . . & . . . \\ 0 & 0 & . . . & \frac{1}{σ_{n}^{2}} & 0 \\ 0 & 0 & . . . & 0 & \frac{2}{σ_{n}^{2}} \end{matrix})$	Gauss [110]
$p (x; t) = \frac{n!}{x_{1}! . . . x_{n}!} t_{1}^{x_{1}} . . . t_{n}^{x_{n}}$	$F_{M} = (\begin{matrix} \frac{t_{1} + t_{n}}{t_{1} t_{n}} & \frac{1}{t_{n}} & . . . & \frac{1}{t_{n}} \\ \frac{1}{t_{n}} & \frac{t_{2} + t_{n}}{t_{2} t_{n}} & . . . & \frac{1}{t_{n}} \\ . . . & . . . & . . . \\ \frac{1}{t_{n}} & \frac{1}{t_{n}} & . . . & \frac{t_{1} + t_{n}}{t_{n - 1} t_{n}} \end{matrix})$	Multinomial [111]
	$F_{D}^{i i} = ψ^{'} (α_{i}) - ψ^{'} (\sum_{i} α_{i}),$
$p (x; α) = \frac{1}{B (α)} \prod_{i = 1}^{n} x_{i}^{α_{i} - 1}, B (α) = \frac{\prod_{i} Γ (α_{i})}{Γ (\sum_{i} α_{i})}$	$F_{D}^{i j} = - ψ^{'} (\sum_{i} α_{i})$	Dirichlet [108,112]
	$i \neq j, i = 1, . ., n$
$p (x; α, β) = \prod_{i = 1}^{n} \frac{x_{i}^{α_{i} - 1}}{B (α_{i}, β_{i})} {(1 - \sum_{j = 1}^{i} x_{j})}^{γ_{i}}$	$F_{G D} = d i a g (F_{D} (α_{1}, β_{1}), . . ., F_{D} (α_{1}, β_{1}))$
$γ_{i} = β_{i} - α_{i + 1} - β_{i + 1}$ for $i = 1, . . ., n - 1$		Generalized Dirichlet [108]
and $γ_{n} = β_{n - 1}$	$O$ -zero matrix

Table 3. Potential function with corresponding Bregman divergences.

Potential Function $ψ (θ)$	Bregman Divergence $D_{ψ} (θ, θ^{'})$	Algorithm
$\frac{1}{2} {∥ θ ∥}_{2}^{2}$	$\frac{1}{2} {∥θ - θ^{'}∥}_{2}^{2}$	Gradient Descent
$\sum_{j} θ_{j} log θ_{j}$	$\sum_{j} θ_{j} log \frac{θ_{j}}{θ_{j}^{'}} - \sum_{j} θ_{j} + \sum_{j} θ_{j}^{'}$	Exponentiated Gradient Descent

Table 4. Applications of optimization algorithm, divided in 4 types.

Type of Optimization Algorithm	Optimizer	Application
SGD-type		CNN [131], RNN [132], GNN [133],
	SGD	PINN [134], SNN [135], CVNN [136],
		AE [137]
	AdaGrad	CNN [138]
	AdaDelta	CNN[139], RNN [139], SNN [140]
	RMSProp	CNN [141], RNN [142], SNN [143]
	SGDW	CNN [30]
	SGDP	CNN [31]
	QHM	CNN [32]
	NAG	CNN [144], RNN [145]
Adam-type		CNN [146], RNN [147], SNN [148],
	Adam	PINN [150], GNN [151],
		CVNN [152]
	AdamW	CNN [40]
	AdamP	CNN [42]
	QHAdam	CNN [45]
	Nadam	CNN [47]
	Radam	CNN [48]
	DiffGrad	CNN [154], RNN [155], GNN [156]
	Yogi	CNN [157], RNN [158]
	AdaBelief	CNN [159], RNN [159], GNN [160]
	AdaBound	CNN [161], RNN [162]
	AdamInject	CNN [64]
PNM-type	PNM	CNN [68]
	AdaPNM	CNN [68]
	Adan	CNN [69]
Newton	Newton approach	CNN [163]
Newton	CG	CNN [164], GNN [165]
Quasi-Newton	(L-)BFGS	PINN [166]
	SR1	CNN [167]
	Apollo	CNN [92]
	AdaHessian	CNN [93]
Information geometry		CNN [168], RNN [109],
	NGD	GNN [169], PINN [170],
		QNN [170]
	MD	CNN, RNN [172]

Table 5. Types of gradient free optimization algorithm.

Type of Optimization Algorithm	Optimizer
Local optimization	Hill Climbing [176],
	Stochastic Hill Climbing [177],
	Simulated Annealing [178],
	Downhill Simplex Optimization [179]
Global optimization	Random Search [180],
	Grid Search [181],
	Random Restart Hill Climbing [182],
	Random Annealing [183],
	Pattern Search [184],
	Powell’s Method [185]
Population-based optimization	Parallel Tempering [186],
	Particle Swarm Optimization [187],
	Spiral Optimization [188],
	Evolution Strategy [189]
Sequential model-based optimization	Bayesian Optimization [190],
	Lipschitz Optimization [191],
	Tree of Parzen Estimators [192]

Table 6. Types of fractional derivatives on finite interval

[a, b]

for gradient descent.

Table 6. Types of fractional derivatives on finite interval

[a, b]

for gradient descent.

Type of fractional derivatives	Formulas
Riemann-Liouville	$(_{R L} D_{a +}^{α} f) (t) = \frac{1}{Γ (n - α)} {(\frac{d}{d t})}^{κ} \int_{a}^{t} \frac{f (τ)}{{(τ - t)}^{α - κ + 1}} d τ$ ,
	$(_{R L} D_{b -}^{α} f) (t) = \frac{1}{Γ (n - α)} {(\frac{d}{d t})}^{κ} \int_{t}^{b} \frac{f (τ)}{{(τ - t)}^{α - κ + 1}} d τ$ ,
	where $R e (α) > 0$
Liouville-Sonine-Caputo	$(_{L S C} D_{a +}^{α} f) (t) = \frac{1}{Γ (κ - α)} \int_{a}^{t} \frac{f^{(κ)} (τ)}{{(τ - t)}^{α - κ + 1}} d τ$ ,
	$(_{L S C} D_{b -}^{α} f) (t) = \frac{{(- 1)}^{κ}}{Γ (κ - α)} \int_{t}^{b} \frac{f^{(κ)} (τ)}{{(τ - t)}^{α - κ + 1}} d τ$ ,
	where $R e (α) > 0$ and $κ = [R e (α)] + 1$
Tarasov	$(_{T} D_{a +}^{α} f) (t) = \frac{α}{Γ (1 - α)} \int_{0}^{\infty} \frac{f (τ) - f (t - τ)}{{(τ)}^{α + 1}} d τ$ ,
	$(_{T} D_{b -}^{α} f) (t) = \frac{α}{Γ (1 - α)} \int_{0}^{\infty} \frac{f (τ) - f (t + τ)}{{(τ)}^{α + 1}} d τ$ ,
	where $0 < α < 1$ and $a = 0$ , $b = \infty$
Hadamard	$(_{H} D_{a +}^{α} f) (t) = \frac{1}{Γ (α)} {(t \frac{d}{d t})}^{κ} \int_{a}^{t} {(log \frac{t}{τ})}^{σ} f (τ) \frac{d τ}{t a u}$ ,
	$(_{H} D_{b -}^{α} f) (t) = \frac{1}{Γ (α)} {(t \frac{d}{d t})}^{κ} \int_{a}^{t} {(log \frac{τ}{t})}^{σ} f (τ) \frac{d τ}{τ}$ ,
	where $R e (α) > 0$ , $σ \in C$ and $κ = [R e (α)] + 1$
Marchaud	$(_{M} D_{+}^{α} f) (t) = \frac{α}{Γ (1 - α)} \int_{- \infty}^{t} \frac{f (t) - f (τ)}{{(t - τ)}^{α + 1}} d τ$ ,
	$(_{M} D_{-}^{α} f) (t) = \frac{α}{Γ (1 - α)} \int_{t}^{\infty} \frac{f (t) - f (τ)}{{(t - τ)}^{α + 1}} d τ$ ,
	where $0 < R e (α) < 1$
Liouville-Weyl	$(_{L W} D_{+}^{α} f) (t) = \frac{1}{Γ (κ - α)} \frac{d^{κ}}{d t^{κ}} \int_{- \infty}^{t} \frac{f (τ)}{{(t - τ)}^{α - κ + 1}} d τ$ ,
	$(_{L W} D_{+}^{α} f) (t) = \frac{1}{Γ (κ - α)} \frac{d^{κ}}{d t^{κ}} \int_{t}^{\infty} \frac{f (τ)}{{(τ - t)}^{α - κ + 1}} d τ$ ,
	where $0 < R e (α)$ and $- \infty < x < b < \infty$
Sabzikar-Meerschaert-Chen	$(_{S M C} D_{+}^{α, λ} f) (t) = \frac{α}{Γ (1 - α)} \int_{0}^{\infty} \frac{e^{- λ τ} (f (t) - f (t - τ))}{τ^{α + 1}} d τ$ ,
	$(_{S M C} D_{+}^{α, λ} f) (t) = \frac{α}{Γ (1 - α)} \int_{0}^{\infty} \frac{e^{- λ τ} (f (t) + f (t - τ))}{τ^{α + 1}} d τ$ ,
	where $0 < R e (α)$ and $λ \in C$
Katugampola	$(_{K} D_{a +, σ}^{α, λ} f) (t) = \frac{σ^{α - κ + 1} e^{λ t}}{Γ (κ - α)} {(t^{1 - σ} \frac{d}{d t})}^{κ} \int_{a}^{t} \frac{τ^{σ - 1} e^{- λ τ} f (τ)}{{(t^{σ} - τ^{σ})}^{α - κ + 1}}$ ,
	$(_{K} D_{b -, σ}^{α, λ} f) (t) = \frac{σ^{α - κ + 1} e^{λ t}}{Γ (κ - α)} {(t^{1 - σ} \frac{d}{d t})}^{κ} \int_{t}^{b} \frac{τ^{σ - 1} e^{- λ τ} f (τ)}{{(τ^{σ} - t^{σ})}^{α - κ + 1}}$ ,
	where $0 < R e (α)$ and $λ \in C$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Survey of Optimization Algorithms in Modern Neural Networks

Abstract

Notations

1. Introduction

2. First Order Optimization Algorithms

2.1. SGD-Type Algorithms

2.2. Adam-Type Algorithms

2.3. Positive-Negative Momentum

3. Second Order Optimization Algorithms

3.1. Newton Algorithms

3.2. Quasi-Newton Algorithms

4. Information-Geometric Optimization Methods

4.1. Natural Gradient Descent

4.2. Mirror Descent

5. Application of Optimization Methods in Modern Neural Networks

6. Challenges and Potential Research

7. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe