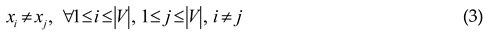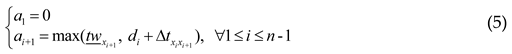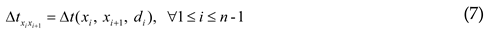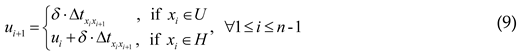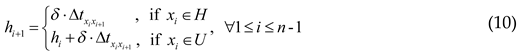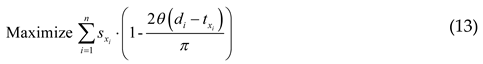Palace: A Parallel Adaptive Local-Search Algorithm Based on Competition and Evolution for Orienteering Problems and Variants

Preprint

Article

Palace: A Parallel Adaptive Local-Search Algorithm Based on Competition and Evolution for Orienteering Problems and Variants

Altmetrics

Downloads

138

Views

Comments

Haiwei Lei^*,Yonghao Du,

Lining Xing,Yingwu Chen

Haiwei Lei^*,Yonghao Du,

Lining Xing,Yingwu Chen

This version is not peer-reviewed

Submitted:

20 April 2023

Posted:

21 April 2023

You are already at the latest version

Alerts

Abstract

A number of challenging combinatorial optimization problems in logistics, transportations, aeronautics, and astronautics can be modeled as orienteering problems (OPs). To address the classic OP and its real-world variants, a parallel adaptive local-search algorithm based on competition and evolution (Palace) is proposed in this paper. In this algorithm, the parallelism runs proper local-search metaheuristics and operators to obtain the population per generation; then the competition grades those metaheuristics and operators to highlight the outperforming and eliminate the underperforming; also, the evolution explores large solution space and reproduces the best solutions for next generation. In this manner, the parallelism, competition, and evolution are organized in an easy-to-use algorithm and enable the expansibility, adaptivity, and exploration abilities, respectively. The Palace is examined on the classic and real-world Benchmarks about the OP, the time-dependent/independent OP with time windows, and the unmanned aerial vehicle and agile earth observation satellite planning. As a result, the Palace shows good performance in applicability and effectiveness in comparison with the state-of-the-art algorithms.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction

In recent decades, many challenging combinatorial optimization problems in logistics, transportations, aeronautics, and astronautics were modeled as orienteering problems (OPs). The OP was first introduced by Golden et al. [1], which was named according to an outdoor sport game of orienteering. In the OP, a subset of vertices should be selected and ordered, aiming at maximizing the total rewards of the selected vertices; hence, the OP is often viewed as a combination of the knapsack and traveling salesman problem (TSP) [2,3]. In contrast to the TSP, not all the vertices in an OP are required to be visited since the total travel time throughout those vertices is additionally constrained. Therefore, the OP is also known as the selective TSP and is of more general significance to real-world applications.

To meet the real-world requirements, several variants of the OP have been studied. For example, considering the constraint that requires the vertices can only be visited within predefined time windows, the OP with time windows (OPTW) was raised and studied [4]-[7]. Based on the OPTW, the changeable travel time among vertices that depends on the departure time of a travel is also introduced [8]-[10] in the time-dependent OPTW (TD-OPTW). The OP, OPTW, and TD-OPTW were all proven NP-hard [1,8], and have many other interesting applications. An aeronautics application of the OP is the unmanned aerial vehicle (UAV) mission planning, where the UAV is constrained by the fuel capacity [11]. In addition, astronautic mission planning problems of the earth-observation satellite (EOS) and the agile EOS (AEOS) can also be modeled as the OPTW and the TD-OPTW, respectively, which maximize the total valued targets that are observed by satellites within orbital time windows [12]. These OPs and variants are the important optimization problems to be addressed in related real-world fields, and an easy-to-use algorithm that can well address these problems is required.

There have been many efforts to apply evolutionary algorithms (EAs) and local-search metaheuristics to OPs and variants. For example, Sevkli and Sevilgen [13,14], Muthuswamy and Lam [15], and Dang et al. [16] and Vincent et al. [17] applied different strengthened versions of particle swarm optimization to the OPs and contributed many best-known solutions in Benchmarks. Marinakis et al. [18] and Abbaspour and Samadzadegan [19] adopted genetic algorithms and well addressed the OP and TD-OPTW. Gambardella et al. [20] and Verbeeck et al. [21,22] introduced ant colony systems into the optimization of the OPTW and TD-OPTW. Cura [23] and Martín-Moreno et al. [24] introduced artificial bee colony into the optimization of the OPTW and multi-objective OP. Literature show that EAs are usually equipped with good diversity and implicit parallelism, which result in good performance of solution exploration and acceleration. Also, the sequence-based encoding of the OPs is very applicable for EAs. However, it is also acknowledged that EAs often present underperformance in terms of solution exploitation in comparison with local-search metaheuristics, especially when addressing complex and strongly constrained problems. Therefore, a hybridized version of EA named memetic algorithm (MA) was introduced and applied to OPs in recent studies [25]-[28], where the EA is followed by local-search operators on offspring per generation. Many other studies indicated that the local-search metaheuristics often work well with EAs in MAs.

Regarding the local-search metaheuristics, they often present a good ability of exploitation due to the neighborhood-based optimization framework. The simulated annealing (SA) [29]-[32] is a popular one for OPs and variants, where the annealing acceptance rule plays a very important role in global optimization. To further strengthen the exploration ability for global optimization, two extended local-search metaheuristics named iterated local-search (ILS) [33]-[37] and adaptive large neighborhood-search (ALNS) [38]-[40] were also developed, where special operators were designed to perturb, destroy, and repair the OP solutions to construct much larger neighborhoods. These local-search metaheuristics well addressed the OPs and variants in cases of inventory optimization, UAV planning, AEOS planning, and others. However, for the sake of a better exploration ability, those operators in the ILS or ALNS should be specifically designed based on the characteristics of the studied problem; otherwise, the ILS or ALNS might be inefficient since the destroyed solutions cannot be well repaired. Alternatively, the crossover operators of EAs are qualified for perturbing, destroying, and repairing the sequence-based encoded solutions in OPs and variants in an easy and well acceptable manner. Thereby, another MA framework that is looped by local-search metaheuristics and adopts EA operators for solution exploration is likely to be a great choice for OPs and variants. Admittedly, the exploration ability of EAs should be supported by enough diversified solutions, so some other mechanisms that improve the diversity of local-search metaheuristics in this MA framework are also needed.

With the development of computer hardware, a great many local-search metaheuristics were designed in a parallel and competitive manner [41]-[45]. In this manner, the computing abilities of computer threads can be fully used, and the outperforming algorithms, operators or solutions will be selected adaptively. Obviously, it is not economical to use those algorithms that leave many threads unused in real-world applications. Given the same computing time, the parallel threads that run different algorithms or operators are qualified for producing much more diversified solutions, which also satisfy the required diversity by the EAs or MAs mentioned above. Therefore, the advantage and appropriateness of this manner provide the motivation for developing a hybrid framework based on local-search parallelism, evolution, and competition for the OP and variants in this paper. Combining the traditional local-search metaheuristics and EAs with a well-designed parallel and competitive framework will most likely result in better overall performance.

To address the OP and its variants including the OPTW, TD-OPTW, UAV-OP, and AEOS planning problem, a parallel adaptive local-search algorithm based on competition and evolution (Palace) is proposed in this paper. Parallelism, competition, and evolution are the three keywords in the Palace, where: (1) The parallelism runs proper local-search metaheuristics and operators to obtain diversified high-quality solutions. (2) The competition grades those metaheuristics and operators with respect to the obtained solutions, so as to highlight the outperforming ones and eliminate the underperforming ones. (3) The evolution further explores large solution space and reproduces the best solutions for next generation. The contribution of this paper is the easy-to-use hybrid optimization framework for addressing the OP and variants, where the parallelism, competition, and evolution enable the expansibility, adaptivity, and exploration abilities, respectively. In cases of different applications, experiment studies of Benchmarks validate the applicability and effectiveness of the Palace.

The remainder of the paper is organized as follows: In Section 2, the OP and its four variants are described and formulized. In Section 3, the framework of the Palace along with the inner phases are explained. Then, the Palace is examined on the Benchmarks of the OP and variants in Section 4, in comparison with the state-of-the-art algorithms. Finally, the paper ends with the discussions and conclusions in Section 5 and Section 6, respectively.

2. The orienteering problem and variants

In this section, the description and the mathematical model of the OP are first given. Based on this model, the extended properties and constraints of its variants, including the OPTW, TD-OPTW, UAV-OP, and AEOS planning problem, are also presented. Regarding the nonlinearity of some constraints in those problems and the metaheuristic design in this paper, those problems are all modeled in constraint satisfaction problem (CSP) formations.

2.1. The OP

Given a set of vertices V = {1, 2, …, |V|}, where each vertex is rewarded with a score, a subset of those vertices should be selected and ordered in the OP. The objective of the OP is to maximize total rewards of the selected vertices in the subset, while the total travel time among those vertices cannot exceed the limit. The OP was usually formulated as an integer programming (IP) model, which concentrated on the decision variables that activate the visits among vertices and the path connectivity. Other than the commonly used IP model for the OP, the CSP model that directly determines an ordered subset of vertices is given here and will be extended for other OP variants. Meanwhile, the CSP model can well guide the neighborhood design and encoding of the Palace in the following section.

Two integer decision variables are defined in the CSP model:

n: which ranges from 2 to |V| and determines the total number of vertices in the subset, namely, the number of the vertices that will be visited (including the starting and ending ones).

x_i: which ranges from 1 to |V| and determines the i^th vertex in the subset, so that an ordered visit path of vertices can be obtained.

In this regard, the objective function that accumulates and maximizes score s_x_i of vertex x_i in the subset can be expressed by Eq. (1).

Also, the model is constrained by some other equations: Eq. (2), which shows that the starting vertex and the ending vertex in the OP are predesignated; Eq. (3), which requires that there is no revisited vertex in the subset; and Eq. (4), which requires that the sum of travel time Δt_x_it_x_i₊₁ between vertex x_i and x_i₊₁, namely, the total travel time throughout the selected vertices cannot exceed the limit of T_max. Notably, all the notations in this paper are numbered from 1.

In this way, the OP is modeled as a briefer formation than the commonly used IP model, and other properties and constraints can be easily added regarding different OP variants. The Palace in the following section will be directly encoded depending on the valued decision variables in this model.

2.2. The OPTW

The OPTW is a classic extension of the OP, which was first introduced by Kantor and Rosenwein [4]. In addition to the aforementioned OP model, given the set of vertices V = {1, 2, …, |V|} in the OPTW, each vertex x_i∈V is also associated with a required service time t_x_i and a time window [tw_x_i,

\overset{____}{t w}

_x_i]. In other words, the OPTW additionally requires that the visit to each vertex x_i should be followed by a stay between time tw_x_i and

\overset{____}{t w}

_x_i. To address the OPTW, another continuous integer decision variable is defined in addition to the two others given in the OP:

d_i, which ranges from time tw_x_i + t_x_i to

\overset{____}{t w}

_x_i and determines the departure time at vertex x_i, so that the service stay at this vertex will be located within the required time window between time tw_x_i and

\overset{____}{t w}

_x_i.

Also, in addition to the OP constraints expressed in Eq. (2) to (4), the OPTW is constrained by some more equations: Eq. (5) sequentially calculates arrival time a_i₊₁ at vertex x_i₊₁ on the basis of departure time d_i at vertex x_i. Even if vertex x_i₊₁ can be visited before its time window, the required stay cannot be started until the time window opens at tw_x_i₊₁. Eq. (6) requires that service time t_x_i at each vertex x_i should be reserved between the arrival and departure.

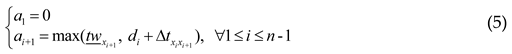
Notably, if the travel time is first in first out (FIFO), an earlier departure from vertex x_i will result in an earlier arrival at vertex x_i₊₁ [22]. Since the travel time among vertices remain constant in the OPTW, which is FIFO, departure time d_i can be directly set to the minimum value that satisfies Eq. (6) here. However, in many real-world situations, the travel time among vertices is changeable and depends on the departure time of the travel; hence, a further OP variant that introduces the time-dependent travel time into the OPTW was also raised.

2.3. The TD-OPTW

The TD-OPTW was first introduced by Fomin and Lingas [8]. The difference between the OPTW and TD-OPTW is that the travel time in the former is constant while that in the latter is time-dependent. In the TD-OPTW, any Δt_x_ix_i₊₁ travel time between two vertices not only depends on the connected vertices x_i and x_i₊₁, but also depends on departure time d_i from vertices x_i. Therefore, time-dependent travel time Δt_x_ix_i₊₁ in the TD-OPTW can be expressed in Eq. (7), where Δt represents the function to obtain this time.

In this regard, the decision variables and constraints in the TD-OPTW remain those in the OPTW. The TD-OPTW was also modeled as the mixed IP (MIP) model in previous studies [3,22], where time slots are defined to assist in the linear formulization of constraints. In comparison, the CSP model in this section is presented more briefly with a small change to the OPTW model.

Although the travel time among vertices is changeable in the TD-OPTW, the FIFO characteristic still remains in some conditions. Verbeeck et al. [22] pointed out that when changing rate of the travel time vs. time ranges from -1.5 to 1.5, the travel time in the TD-OPTW will be FIFO as well. Thereby, departure time d_i can also be set to the minimum value that satisfies Eq. (6) here in these conditions.

Since the time windows and time-dependent travel time are usually constrained in real-world applications, the TD-OPTW can be viewed as an application-oriented variant of the OP. Many challenging combinatorial optimization problems in logistics, transportations, aeronautics, and astronautics can be modeled as the TD-OPTW, possibly with some other problem-specific constraints. In the following two subsections, the CSP model of the TD-OPTW is reused and further extended, so as to describe the real-world UAV-OP and AEOS planning problem.

2.4. The UAV-OP

In recent decades, the UAV has become a useful and well-accepted tool in many fields. It is acknowledged that, for all kinds of UAV missions, navigation is required but navigation errors are always inevitable. When the UAV’s flight path is too long to ensure safe navigation errors, the timely error-corrections throughout the flight path must be done. Under such circumstances, the UAV should visit a series of error-correction points to zero the accumulated navigation error, and then the OP characteristic appears. To be specific, the UAV-OP studied in this subsection is to determine a subset of vertices (error-correction points) at which the UAV errors always within the limits.

The CSP model of the OP can be reused, and some additional constraints concerning the UAV-OP are required. First, the score of each vertex is marked by -1 here, so that the objective function in Eq. (1) is namely to minimize the error-correction vertices throughout a feasible UAV path. Then, the navigation errors of the UAV are divided into the vertical and the horizontal, and they can only be zeroed by the vertical error-correction vertices in set U and horizontal error-correction vertices in set H, respectively. In Eq. (8), it is assumed that vertical error u₁ and horizontal error h₁ at the starting vertex are both 0. On the one hand, in Eq. (9), if the UAV departs from a vertical error-correction vertex x_i, the vertical error will be zeroed at vertex x_i and then the accumulated vertical error u_i₊₁ at vertex x_i₊₁ will only be produced by the flight between vertices x_i and x_i₊₁, where δ represents the additional UAV error per unit travel time. On the other hand, if the UAV departs from a horizontal error-correction vertex x_i, the vertical error u_i at vertex x_i will not be zeroed and should be accumulated to the next vertex. In a similar way, Eq. (10) indicates the corrections of horizontal errors. Finally, the corrections at any vertex can be successful only if the accumulated vertical and horizontal errors are within the respective limits, as Eq. (11) and (12) show.

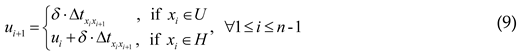
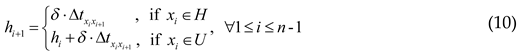
2.5. The AEOS planning problem

The EOS and AEOS have become important space-based platforms in many aspects, and the planning problems of the EOS or AEOS are needed to be addressed in satellite monitoring departments every day. Take the EOS planning problem as an example first: Given a set of targets to be observed by the EOS, which can be viewed as a set of vertices V = {1, 2, …, |V|} to be visited in the OP, each target (vertex x_i) is associated with a score, as well as a time window [tw_x_i,

\overset{____}{t w}

_x_i] only in which the target is visible to the EOS. Without considering other constraints, the EOS planning problem can be modeled as the OPTW in this regard.

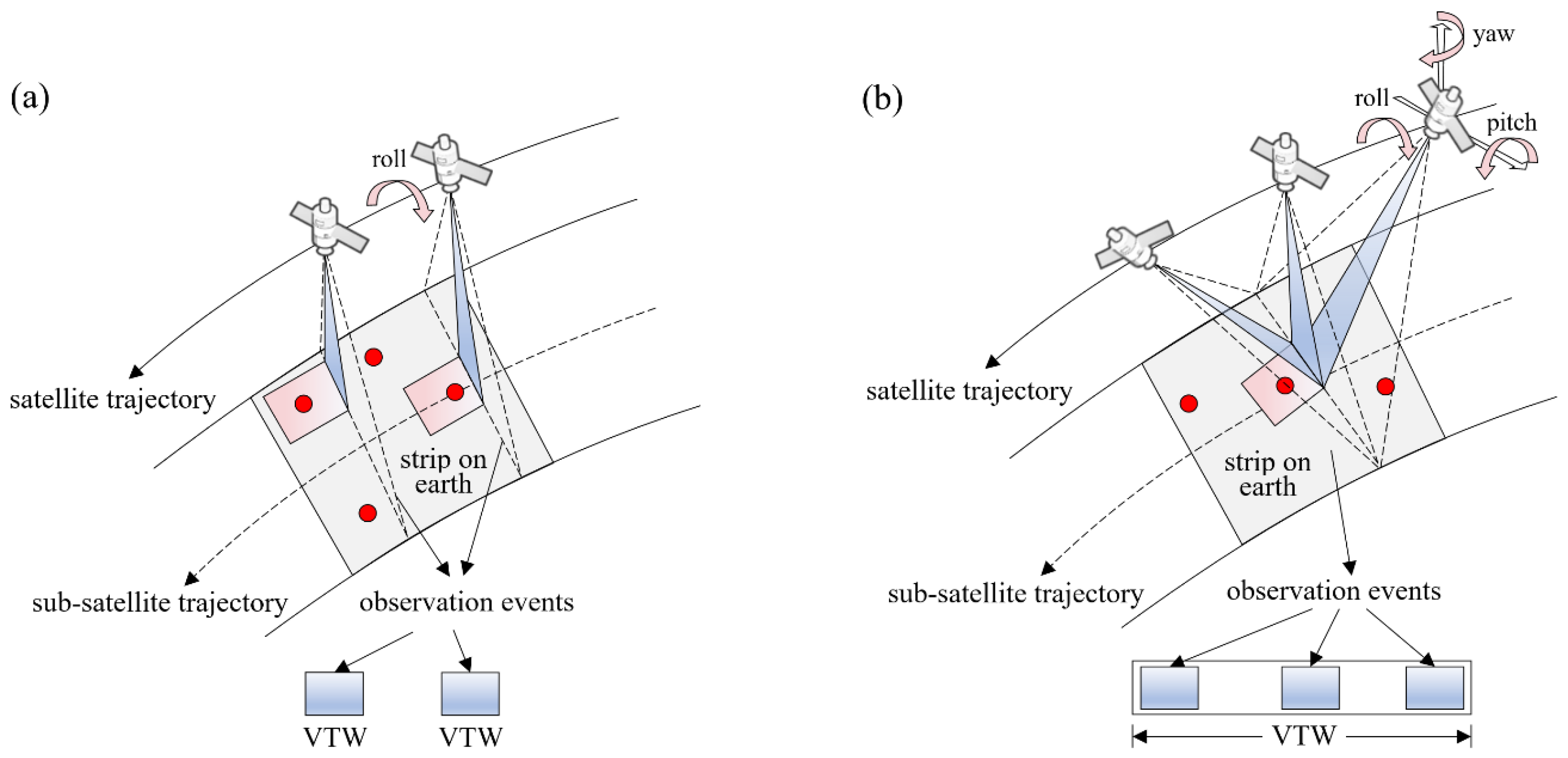
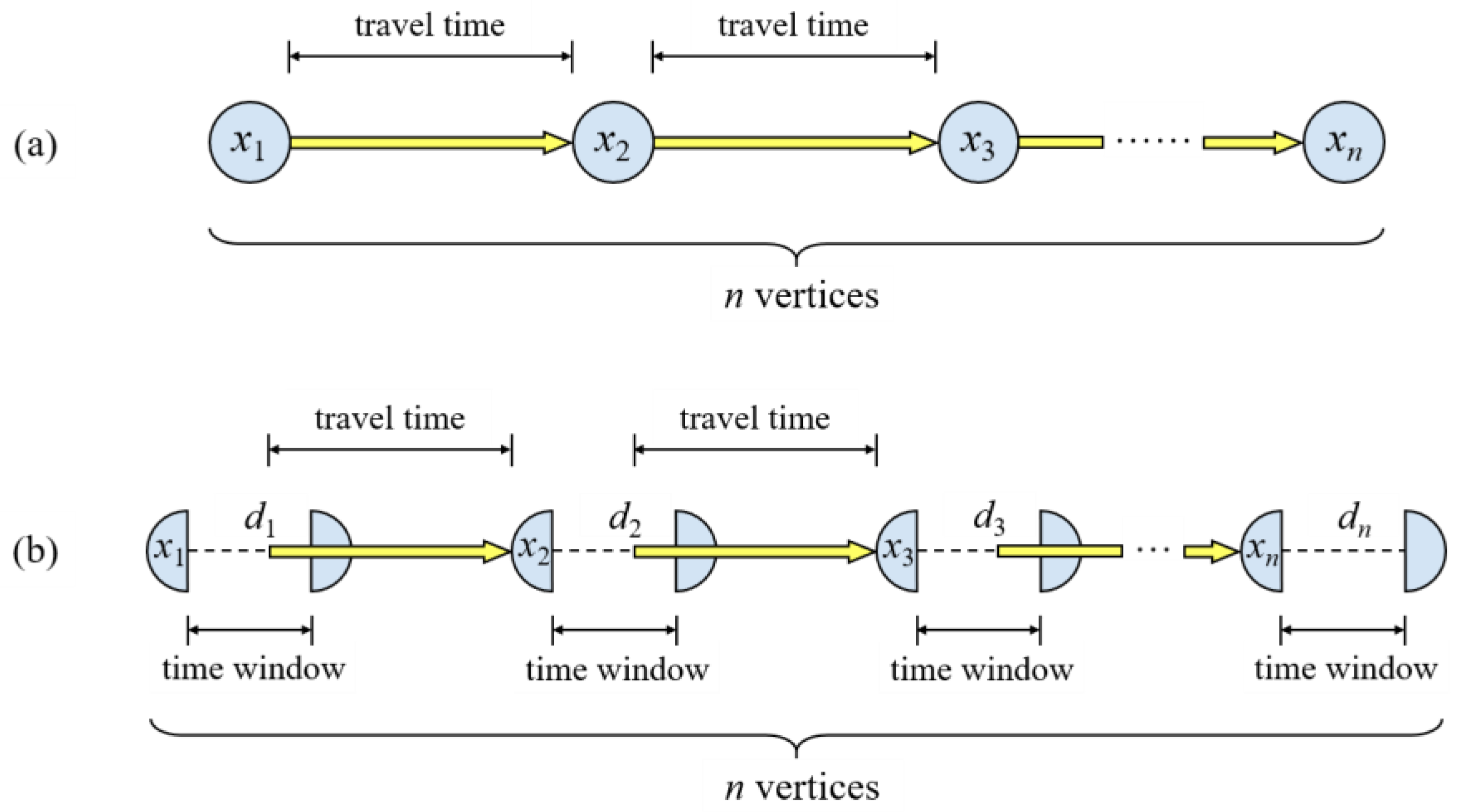
The AEOS is an ability-strengthened version of the EOS, which is additionally equipped with pitching and yawing imaging abilities. These abilities give the time-dependent characteristic to the AEOS planning problem. As shown in Figure 1 (a), an EOS can only roll around the satellite trajectory and observe targets that are vertically distributed along the sub-satellite trajectory, so the executed observation will exactly fill its visible time window (VTW). When it comes to the AEOS in Figure 1 (b), the pitching and yawing abilities enable an observation before or after its upright pass, so the duration of the VTW will be much longer, and the observation can be executed at any time in the VTW. However, the required transition (travel) time of the AEOS between two observations depends on their orbital attitudes, which namely depends on the time when they are executed. Thereout, the time-dependent characteristic appears in the AEOS planning problem.

In this case, the AEOS planning problem can be modeled as the TD-OPTW with the same decision variables and constraints in the previous subsection: The duration and ending time of the observation for target (vertex x_i) can be viewed as service time t_x_i and departure time d_i in the TD-OPTW model, respectively. Besides, this observation should be started at time d_i - t_x_i, namely arrival time a_i. Based on the starting and ending time of two observations, the transition (travel) time of the AEOS can be obtained by the time-dependent function given by Peng et al. [12], while ending time can also be determined in the dynamic programming manner in Ref. [12].

Moreover, another type of time-dependent characteristic also remains in the AEOS planning problem. Peng et al. [12] have introduced that the scores of observed targets in the AEOS planning problem are also time-dependent since different observations within a time window of the AEOS will result in different qualities. Using starting time d_i - t_x_i at each target (vertex x_i), the objective function in the TD-OPTW should be modified by Eq. (13), where θ(d_i - t_x_i) obtains the pitch angle of the AEOS when starting this observation at time d_i - t_x_i.

To summarize, the CSP models of the OP and its variants, including the OPTW, TD-OPTW, UAV-OP, and AEOS planning problem are given in this section, as listed in Table 1. In comparison with MIP models, the CSP ones present much briefer formations and closer relations to the follow-up design of metaheuristics. Based on these given models, a parallel and hybrid structured metaheuristic algorithm named Palace will be proposed in the following section.

3. The Palace

To address the OP and its variants, an easy-to-use algorithm named Palace, which well organizes parallelism, competition, and evolution is proposed. In this section, the framework and encoding of the Palace are given first. Then, the inner phases of the parallelism, competition, and evolution are explained in detail.

3.1. The framework

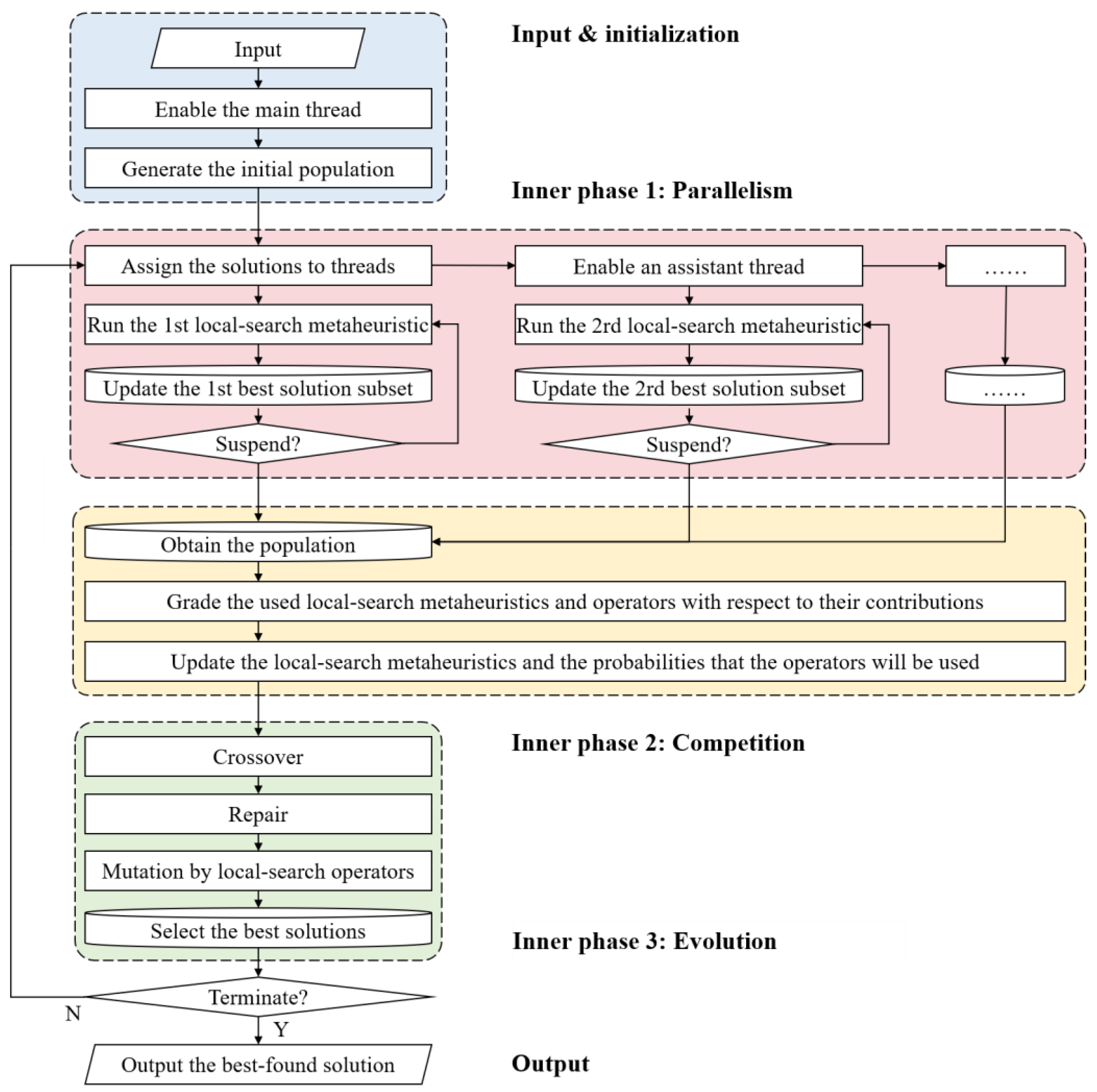
Parallelism, competition, and evolution are the keywords in the Palace designed in this paper. As shown in Figure 2, the framework of the Palace that addresses these keywords are organized as follows:

Input & initialization: Given the required parameters to the Palace, the main thread of the computer will be enabled, and an initial population will be randomly generated. The best-found solution in the population will play the initial one of follow-up local-search metaheuristics. Also, the encoding formation for both local-search metaheuristics and evolution will be unified here.

Inner phase 1: Parallelism: In a parallel manner, each given local-search metaheuristic with proper operators will be run on an independent thread. Simultaneously, a subset will record the recent best-found solutions per thread. After the local-search optimization, those threads will be suspended and amalgamate all their best-found subsets into a population set.

Inner phase 2: Competition: Local-search metaheuristics and operators will be graded according to the number of solutions they obtained in the population. With these grades, the local-search metaheuristics and the using probabilities of the operators will be updated. In a word, the more solutions the metaheuristics or operators obtained, the higher they will be graded, and the more frequently they will be used in the next generation.

Inner phase 3: Evolution: Based on the obtained population, the evolution will be performed so as to explore better solutions. After that, the reproduced best solutions will be chosen and re-play the initial ones of the updated local-search metaheuristics in the next generation.

Output: When the termination criteria are met, the best-found solution will be outputted.

The advantages of the Palace can also be stated in terms of its keywords:

The evolution enables the exploration ability of the Palace. Regarding the combination of evolution and local-search metaheuristics, the Palace is also a type of MA. In contrast to the most commonly used MAs that originate from Moscato [46], which is looped and strengthened in exploitation by EAs and local-search operators, respectively, the Palace is looped and strengthened in exploration by local-search metaheuristics and evolution, respectively. In this way, the Palace can not only extend the common advantages in exploitation and exploration of MAs, but also show better performance in addressing the constrained OP and variants by the more general local-search loops. Besides, the evolution can be viewed as a general mechanism that perturbs, destroys, and repairs solutions in the ILS and ALNS, which is of more general significance to real-world applications.

The competition enables the diversity and adaptivity of the Palace. The competition among local-search metaheuristics provides the diversity required by the evolution. Also, the grading and updating of the metaheuristics and operators per generation contribute to the adaptivity, where after the outperforming ones will be highlighted and underperforming ones will be eliminated.

The parallelism enables the acceleration and expansibility of the Palace. On the one hand, local-search metaheuristics that run in a parallel manner will decrease the computing time. On the other hand, a new competitor that adopts other metaheuristics, operators or parameters can easily join in the competition by enabling a new thread. In other words, the parallelism is the hardware-based means to make the best use of the Palace.

3.2. The encoding

For general use in both local-search metaheuristics and evolution, a unified encoding formation is required. Considering the characteristic of sequential optimization in the studied OP and variants, a sequence-based encoding formation that matches the decision variables in the previous section is given here.

The encoding formation for the OP and UAV-OP is shown in Figure 3 (a), where n vertices are connected end-to-end and the i^th one of them is marked by vertex x_i given in the problem. In this way, a visiting path among the vertices can be easily represented in codes with respect to the predefined decision variables n and x_i. Because of the FIFO characteristic in the OP, given the travel time among vertices, the arrival and departure time at each vertex x_i can also be obtained in this sequence.

Regarding the OPTW, TD-OPTW, and AEOS planning problem, in which another decision variable d_i in addition to n and x_i should also be addressed; hence, an extended encoding formation for these problems is given, as shown in Figure 3 (b). Decision variable d_i determines the departure time at each vertex x_i within the required time window, which used to be obtained in the FIFO way in Figure 3 (a). Then, given the travel time among vertices, the arrival time can also be obtained easily according to Eq. (5).

Therefore, the encoding formations are qualified to represent a special visiting path in the studied OP and variants. The advantages of those formations are the uniformity to the decision variables in CSP models, as well as the applicability for both local-search metaheuristics and evolution. Based on this, local-search and evolutionary operators can then be designed and implemented.

3.3. The parallelism

During the inner phase of parallelism in the Palace, local-search metaheuristics will be run parallelly so as to obtain diversified high-quality solutions. In this subsection, some basic local-search metaheuristics and operators are introduced into the Palace, so as to present an easy-to-use way for addressing the studied OP and variants in this paper. In addition to those introduced in this paper, the parallelism in the Palace is also accessible to any other specially designed metaheuristics and operators.

3.3.1. Local-search metaheuristics

Some simple and effective metaheuristics such as tabu search (TS), simulated annealing (SA), and late acceptance (LA) are very commonly used and have shown good performance in applications. For the required parallelism in the Palace for the OP and variants in this paper, five types of metaheuristics, including TS, SA, LA, tabu simulated annealing (TSA), and tabu late acceptance (TLA) are employed. In other words, five threads that run these metaheuristics will be enabled in a parallel manner. In this subsection, the pseudo-codes of the TS, TSA, and TLA are given in Algorithm 1, Algorithm 2, and Algorithm 3, respectively. Also, the SA and LA can be viewed as the simplified versions of the TSA and TLA without the tabu list, respectively. In these pseudo-codes, S denotes a solution that is encoded by the aforementioned formation, and f(S) denotes the objection function of this solution.

Hybridizing the TS with the SA and LA here is due to their different acceptance rules. As the pseudo-codes show, the TS tabus local optimal solutions, while the SA and LA accept unimproved solutions occasionally; hence, the tabu list of the TS can be well incorporated into the SA and LA for recoding local optima. In this manner, under the local-search framework, the hybrid TSA and TLA can be strengthened in terms of escaping from local optima, which will assist in the global optimization in the Palace. In addition, the performance of these metaheuristics also depends on local-search operators, the operators that join the parallelism will be explained in the next subsection.

Algorithm 1: Tabu search metaheuristic
Input: Given initial solution S⁰, an empty FIFO tabu list L^T with length l^T, neighborhood exploration times N^T
Output: An improved solution S
1:	S_cur ← S⁰ {S_cur is the current solution whose neighborhood is explored}
2:	S^* ← S⁰{S^* is the best-found untabued solution in the neighborhood of S_cur}
3:	S ←S⁰ {S is the best-found solution}
4:	while not suspended do
5:	for n ← 1, 2, …. N^T do
6:	S' ← perform a local-search operator on S_cur
7:	if f(S') > f(S) then
8:	S ← S' {accept S' as the new best-found solution}
9:	S^* ← S' {accept S' as the new untabued best-found solution}
10:	else if S' ∉ L^T and f(S') > f(S^) then*
11:	S^* ← S' {accept S' as the new untabued best-found solution considering the tabu list}
12:	end if
13:	end for
14:	S_cur ← S^* {move to the untabued best-found solution}
15:	insert S^* into tabu list L^T and update S^*
16:	end while
17:	return S

Algorithm 2: Tabu simulated annealing metaheuristic
Input: Given initial solution S⁰, initial temperature T₀, an empty FIFO tabu list L^T with length l^T
Output: An improved solution S
1:	S ← S⁰, T ← T⁰
2:	while not suspended do
3:	S' ← perform a local-search operator on S
4:	if f(S') > f(S) then
5:	S ← S'
6:	else if S' ∉ L then
7:	T ← T > 0 ? T - 1 : 0
8:	p ← exp[ ( f(S') - f(S) ) / T ]
9:	r ← random number uniformly distributed in [0, 1]
10:	if r < p then
11:	S ← S'
12:	end if
13:	end if
14:	insert S into tabu list L^T
15:	end while
16:	return S

Algorithm 3: Tabu late acceptance metaheuristic
Input: Given initial solution S⁰, an empty FIFO Tabu list L^T with length l^T, an empty FIFO late list L^L with length l^L
Output: An improved solution S
1:	S ← S⁰
2:	while not suspended do
3:	S' ← perform a local-search operator on S
4:	if f(S') > f(S) then
5:	S ← S'
6:	else if f(S') = f(S) & S' ∉ L^T then
7:	S ← S'
8:	else if f(S') ≥ f(S^L) & S' ∉ L^T {S^L is the earliest solution in late list L^L} then
9:	S ← S'
10:	end if
11:	insert S into tabu list L^T and late list L^L
12:	end while
13:	return S

3.3.2. Local-search operators

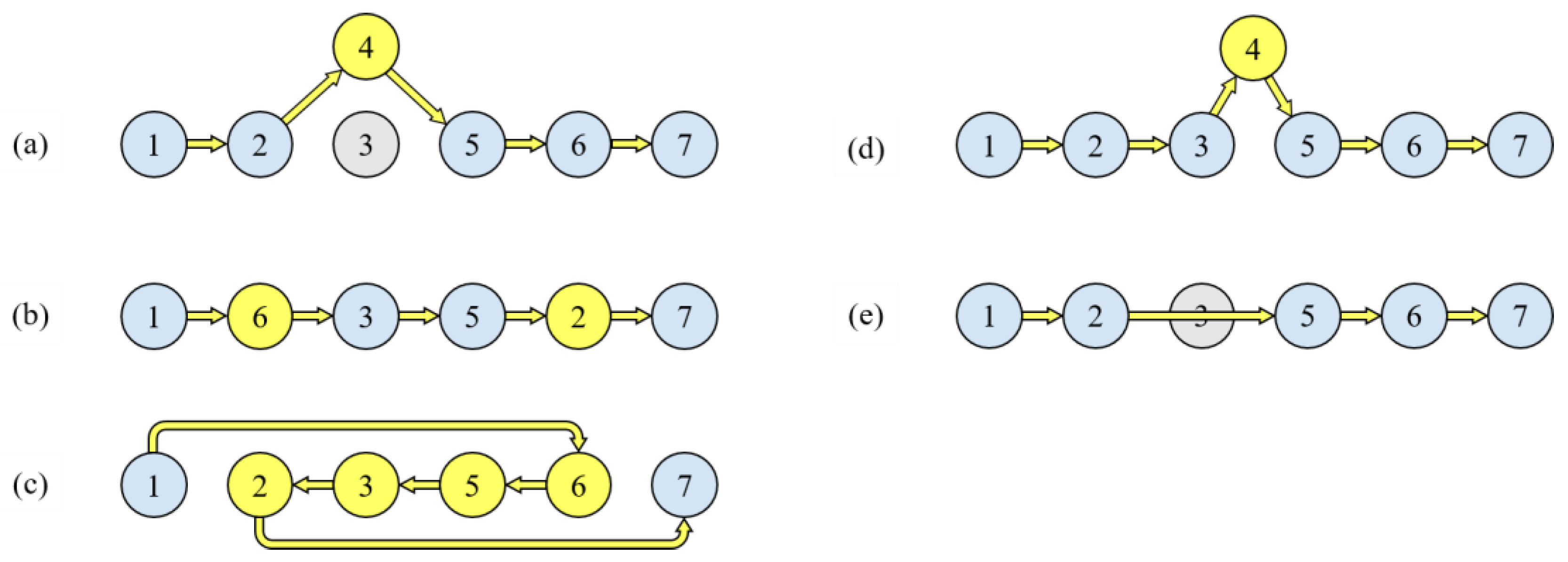
On the basis of the encoding formations for the OP and variants, seven kinds of local-search operators are entered into the parallelism in the Palace, as shown in Figure 4. They are: (1) Vertex-change operator, which randomly changes decision variable x_i in the encoded solution. (2) Vertex-swap operator, which randomly swaps decision variables x_i and x_j in the encoded solution. (3) Vertices-reverse operator, which randomly selects several connected vertices in the encoded solution and reverses all decision variables x_i of them. (4) Departure-change operator, which randomly changes decision variable d_i at the i^th vertex in the encoded solution. (5) Departure-swap operator, which randomly swaps decision variables d_i and d_j in the encoded solution. (6) Insert operator, which randomly inserts a vertex into the encoded solution (decision variable n+1), along with decision variables x_i and d_i. (7) Remove operator, which randomly removes a vertex from the encoded solution (decision variable n-1), along with decision variables x_i and d_i.

It can be seen that, these local-search operators are highly linked with the decision variables defined in the CSP models; hence, a much more direct guidance from the mathematical model to the algorithm is presented in this paper. Besides, since decision variable d_i is only defined in the OPTW, TD-OPTW, and AEOS planning problem, the operators that address d_i will not work on the OP and UAV-OP.

With these operators, local-search metaheuristics will be run in a parallel manner in the Palace. All metaheuristics and operators that join in the parallelism will be graded per generation, and each of them will be accordingly updated so as to achieve stronger overall performance of the Palace in the next generation.

3.4. The competition

To distinguish the performance of local-search metaheuristics and operators and select outperforming ones for further generations, the competition among them is required. During the parallelism in the Palace, each best-found solution will also be marked by the local-search metaheuristic and the operator that obtain this solution. After the parallelism, all the subsets that record the best-found solutions obtained in different threads will be amalgamated, and the best ones of them will be chosen as the population per generation. In other words, the solutions in the population may differ in terms of the local-search metaheuristics and operators that obtain them; hence, the contributions of these metaheuristics and operators can then be quantized.

Define that P is the population set of solutions per generation, and M_i and O_i are the solution subsets obtained by the i^th local-search metaheuristic and operator, respectively. Therefore, the i^th local-search metaheuristic and operator can be graded by the contribution rate m_i and o_i of them, respectively, as shown in Eq. (14).

After the grading, the local-search metaheuristics and operators should be updated so as to obtain stronger overall performance in the next generation. It is reasonable that the more solutions they obtained, the more frequently they should be used. Therefore, two aspects of updating are defined here: (1) Local-search metaheuristic updating, if the grade of a metaheuristic is smaller than threshold m_min for n_filter generations, it will be removed from the competition and replaced by that with the highest grade. (2) Local-search operator updating, the using probability of the i^th operator will be set to its grade o_i, no smaller than threshold o_min. Also, if an operator is set by the under-threshold probability for n_filter generations, it will be removed from the competition.

In a word, the competition in the Palace assists in highlighting outperforming local-search metaheuristics and operators and eliminating the underperforming ones. Nonetheless, all the solutions are searched in a local-search manner, which often outperforms in terms of solution exploitation but underperforms in terms of exploration, in comparison with the evolutionary manner. In this regard, population-based evolution is also designed after competition, which is aimed at strengthening the exploration ability of the Palace.

3.5. The evolution

Different from the competition that is held among local-search metaheuristics and operators, the evolution in the Palace is directly performed on best-found solutions. The evolution not only takes charge of reproducing higher-quality solutions, but also plays a large neighborhood constructor, which is similar to the perturb, destroy, or repair operator in the ILS and ALNS. In this way, the concerned underperformance in terms of the exploration can be well overcome in the Palace. The evolution includes the following steps:

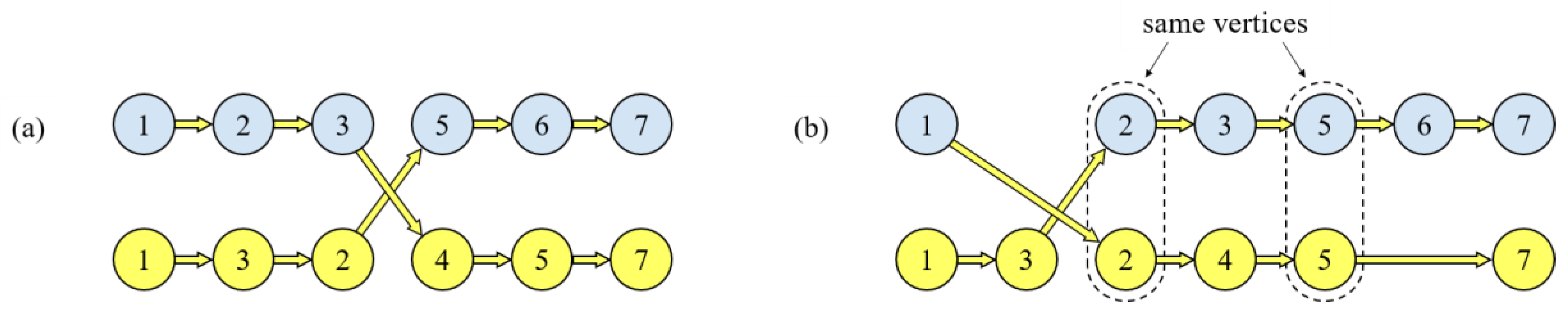
(1) Crossover: Based on the encoding formations of the Palace, two crossover operators are designed: random single-vertex crossover, which randomly selects a vertex position in two encoded solutions and exchanges the follow-up vertices, as shown in Figure 5 (a); and random same-vertices crossover, which randomly selects the position that is marked by the same vertices in two encoded solutions, and then exchanges the follow-up vertices, as shown in Figure 5 (b). The difference between these two operators is that the only the positions that are marked by the same vertices will be selected by the random same-vertices crossover; hence, given two feasible solutions, the travel time to the selected vertices will not be changed and the related constraints will be still met.

(2) Repair: Since some other constraint may still be violated after crossover, the repairing of infeasible solutions after crossover is necessary. To obtain feasible solutions in an easy manner, the follow-up vertices after crossover and their departure time will be re-determined by the FIFO rule. If no proper departure time of a vertex can be determined under the constraints, this vertex will be removed.

(3) Mutation: The mutation will then be performed on each solution after crossover. The local-search operators that are used in the parallelism will take charge of this work, and the mutation probabilities will be set to the updated probabilities of those local-search operators.

After all, the reproduced solutions will be sorted in the quality-decreasing order, and the higher-quality ones will be assigned to the higher-graded local-search metaheuristics. These assigned solutions will re-play the initial ones of those local-search metaheuristics in the next generation of the Palace.

In summary, the framework of the Palace that successively adopts parallelism, competition, and evolution is given in this section. During each generation in the Palace: (1) The parallelism runs proper local-search metaheuristics and operators to obtain diversified high-quality solutions. (2) The competition grades those metaheuristics and operators with respect to the obtained solutions, so as to highlight outperforming ones and eliminate underperforming ones. (3) The evolution further explores large solution space and reproduces the best solutions for next generation. In the next section, the Palace will be implemented and examined on the Benchmarks of the OP and its variants.

4. Experiment study on Benchmarks

4.1. Experiment setup

To examine the performance of the Palace proposed in this paper, the open access datasets of the OP, OPTW, TD-OPTW, UAV-OP, and AEOS planning problem were experimented. The datasets of the OP, OPTW, and TD-OPTW can be accessed from https://www.mech.kuleuven.be/en/cib/op, and those of the UAV-OP and AEOS planning problem can be accessed from https://cpipc.chinadegrees.cn/cw/hp/4 and https://github.com/duyonghao15/Benchmarks-for-AEOS-1, respectively. Based on these datasets, quantitative comparison of the solutions obtained by the Palace and the state-of-the-art algorithms in previous studies will be present in this section.

The parameters in the Palace are listed in Table 2, where many parameters were set in percentage of number |V| of the vertices given in the OP and variants. In this way, the parameters of the Palace will be adaptive to the problem size. Also, in light of the framework that well organizes the parallelism, competition, and evolution, the Palace will not be sensitive to the parameters; hence, those percentages and other parameters were all set in easy-going manners and fixed in the experiments. On this basis, the Palace was coded in Visual Studio 2013, and all the experiments were run 10 times independently using an Intel (R) Core (TM) i7-8550U CPU at 1.80 GHz under Windows 10 with 8 GB RAM.

4.2. Experiment results

4.2.1. The OP results

After the runs of the Palace on the OP dataset from Chao et al. [47] Marinakis et al. [18], the results are listed in Table 3, where the best results from Chao et al. [47] were obtained by a fast and effective heuristic (OH) and acknowledged as the optima in the recent study [18]. The table shows that, regarding the best results, the Palace proposed in this paper performs identically with the OH in all cases. In each case, the mean value and standard deviation (SD) indicate that the Palace achieves the same results after 10 runs. Simultaneously, the Palace costs much less time than the OH. In a word, the Palace proposed in this paper shows great performance in both optimization and speed in addressing the OP.

4.2.2. The OPTW results

After the runs of the Palace on the OPTW dataset from Verbeeck et al. [22], the results are listed in Table 4, where the best and mean results from Verbeeck et al. [22] were obtained by the CPLEX and a 5-run ant colony system (ACS), respectively. Notably, some cases (marked by stars) in the dataset could not be solved by the CPLEX within 72 hours by the high-performance computing system, so their best results in Table 4 were those best-found results after 72-hour runs. The mean results are deduced by the given gaps between the best and mean values in their study. Also, the system showed considerably greater performance than common computers, of which the computing time cannot be used for comparison directly [48]; hence, the computing time of the ACS is not studied here.

The table shows that, regarding the best results, the Palace outperforms the CPLEX in 5 cases (marked in bold) by 0.2% to 4.0%, which are the marked ones that cannot be solved by the CPLEX. In other words, the Palace has updated 5 best-known results of this dataset. In all other cases, the Palace obtains the same best results, and results in average outperformance of 0.3% in this dataset. Regarding the mean results, the Palace outperforms in 6 cases by 0.3% to 6.7% (marked in bold), resulting in average outperformance of 0.5%. Also, the average SD among the 10 runs of the Palace is as low as 0.2. Therefore, it can be summarized that the Palace outperforms the state-of-the-art algorithm in both optimization and statistics in addressing the OPTW.

4.2.3. The TD-OPTW results

After the runs of the Palace on the TD-OPTW dataset from Verbeeck et al. [22], the results are listed in Table 5, where the results from Verbeeck et al. [22] were obtained by the 5-run ACS. The table shows that, regarding the best results, the Palace outperforms the ACS in 5 cases (marked in bold) by 0.4% to 2.7%, but underperforms in 3 cases (underlined) by 0.3% to 1.1%, resulting in average outperformance of 0.1% in this dataset. Regarding the mean values, the Palace outperforms in 12 cases (marked in bold) by 0.1% to 2.7%, but underperforms in 1 case (underlined) by 0.3%, resulting in average outperformance of 0.3% here. Also, the average SD among the 10 runs of the Palace is as low as 0. Admittedly, the Palace may not always obtain the best results of the state-of-the-art algorithm, but it still updates 5 best-known results in the TD-OPTW dataset and shows slight outperformance in both optimization and statistics in addressing this problem. In addition, the ACS was designed for the TD-OPTW with specific insert and replace operators, but the Palace proposed this paper is not equipped with problem-specific operators; hence, the Palace shows more advantages in applicability and easy usability.

4.2.4. The UAV-OP results

After the runs of the Palace on the UAV-OP dataset, the results are listed in Table 6, where the optimal results were obtained by the CPLEX. Considering that there are only two open access cases (Case 1 and 2) in this dataset, ten more similar cases (Case 3 to 12) were imitated with randomly distributed vertices. The table shows that the Palace can achieve the optima within a much shorter time than the CPLEX in all cases. Also, the Palace shows great statistic performance since the SD is as low as 0 per case. As a result, the Palace proposed in this paper is qualified for addressing the UAV-OP in an easy and quick manner.

4.2.5. The AEOS planning results

After the runs of the Palace on the dataset from Peng et al. [12], the AEOS planning results only with time-dependent travel and that with both time-dependent travel time and scores are listed in Table. 7 and Table. 8, respectively. Although whether scores are time-dependent or not is important to the model and algorithm from Peng et al. [12], it will not affect the Palace proposed in this paper; hence, these two datasets are studied together here. In the tables, the mean results from Peng et al. [12] were obtained by the 5-run iterated local search (ILS), and suffix -A and -W in case names mean that the AEOS targets were distributed nationally and worldwide, respectively.

In all nationally distributed (-A) cases in Table 7 and Table 8, the Palace outperforms the ILS by 0.1% to 7.9%, resulting in average outperformance of both 1.8% in two datasets. When it comes to the worldwide distributed (-W) cases, the Palace outperforms in 2 cases (marked in bold) by 0.1% to 0.2%, but underperforms in 6 cases (underlined) by 0.1% to 0.7%. Nonetheless, it is also acknowledged that the nationally distributed (-A) cases are much more difficult to be optimized than worldwide distributed (-W) ones. Simultaneously, the Palace costs much less time than the ILS and presents satisfying SDs. Therefore, it can be summarized that the Palace can show competitive overall performance in comparison with the state-of-the-art algorithm in addressing the AEOS planning problems.

Another advantage of the Palace is that it requires no additional strategies to address the time-dependent characteristics in the AEOS planning problems, which is implemented in a much easier manner than the ILS. In other words, the Palace gives an applicable and easy way to address the AEOS planning problems, whatever they are time-dependent in terms of score, travel time or other else.

5. Discussions

Many challenging combinatorial optimization problems in logistics, transportations, aeronautics, and astronautics were modeled as the OPs and variants in recent years, and these problems still require addressing in related real-world fields. To provide an easy-to-use algorithm for these problems, the parallelism, competition, and evolution are organized in a local-search optimization framework; thereby, the Palace is highlighted in this paper and the Benchmark studies validate its applicability and effectiveness.

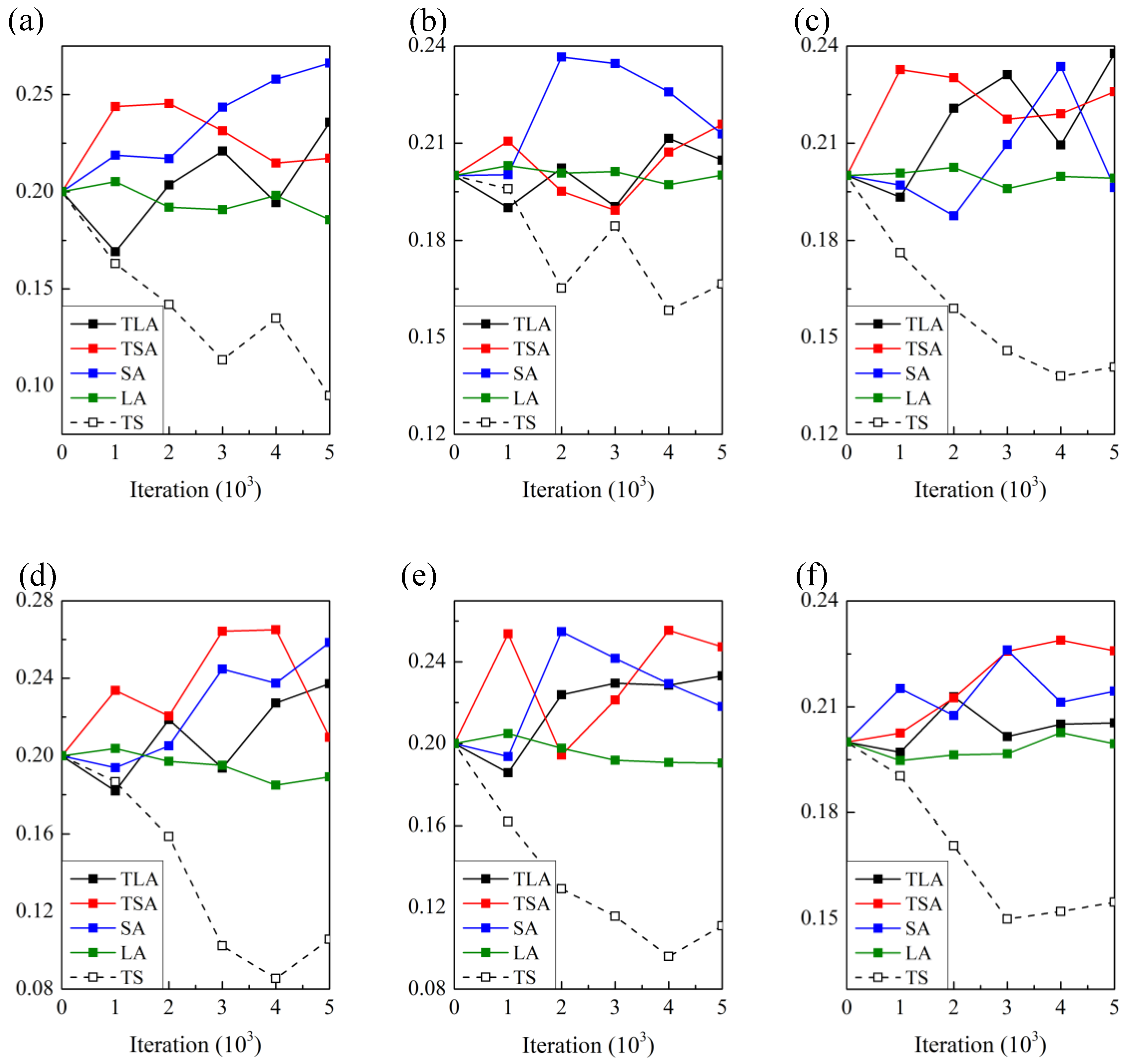
For a view of the competition among the parallel local-search metaheuristics in the Palace, the mean contributions (percent of the solutions obtained in the population) per 1000 iterations of those metaheuristics are shown in Figure 6. The cases in Figure 6 are all the largest-scale in the datasets of OP, OPTW, TD-OPTW, UAV-OP, and AEOS planning problem. It can be seen, five local-search metaheuristics are initially graded by 0.2 at the beginning but differ in their contributions as the iteration increases; hence, the competition properly works throughout the Palace. Herein, the SA (marked in blue) and TSA (marked in red) often contribute a lot but the TS (dotted) often makes increasingly smaller contributions. Nonetheless, the different performance of the metaheuristics in competition can also assist in the solution diversity required by the evolution in the Palace.

In summary, the outperformance of the Palace should be attributed to the following three reasons: (1) The easy-to-use hybrid optimization framework that well organizes the parallelism, competition, and evolution, so that the advantages of different methods can be made the best use. (2) The general sequence-based encoding formations for both local-search metaheuristics and evolution, which enable the feasibility of this hybridization. (3) The parallel running of the optimization, which further accelerates the algorithm.

In addition, it is also worthwhile to apply the Palace to other types of challenging combinatorial optimization problems with orienteering or routing requirements, for example, the vehicle routing problem and its variants, the coverage path planning problems and the satellite range scheduling problem. Since the idea of hybridization and the encoding formations are also suitable for those problems, the Palace is most likely to present satisfying performance as well.

Future work will include more real-world examinations of the Palace and a system development for more than 30 satellites. Also, more outperforming algorithms will be transplanted and engineered in the Palace for easy and friendly use.

6. Conclusions

This paper proposes a parallel adaptive local-search algorithm based on competition and evolution named Palace for addressing the OP and its variants. The CSP models of those problems and the associated encoding formations for the Palace is also given. In cases of classic and real-world OP Benchmarks, the Palace shows good performance in applicability and effectiveness in comparison with the state-of-the-art algorithms.

The main contribution of this paper is the easy-to-use hybrid optimization framework in the Palace, where the parallelism, competition, and evolution enable the expansibility, adaptivity, and exploration abilities, respectively. Furthermore, the Palace is also accessible to any other specially designed local-search metaheuristics and operators, which can also be applied to other challenging orienteering or routing problems with different backgrounds.

Acknowledgments

This study is supported by the National Natural Science Foundation of China (61773120, 61873328), the National Natural Science Fund for Distinguished Young Scholars of China (61525304), the Foundation for the Author of National Excellent Doctoral Dissertation of China (2014-92), the Hunan Postgraduate Research Innovation Project (CX2018B022), and the China Scholarship Council-Leiden University Scholarship.

References

Golden, B. L., Levy, L., & Vohra, R. (1987). The orienteering problem. Naval Research Logistics. 34(3), 307–318.
Vansteenwegen, P. , Souffriau, W., & Van Oudheusden, D. (2011). The orienteering problem: A survey. European Journal of Operational Research, 209 (1), 1-10. [CrossRef]
Gunawan, A. , Lau, H. C., & Vansteenwegen, P. (2016). Orienteering Problem: A survey of recent variants, solution approaches and applications. European Journal of Operational Research, 255 (2), 315-332. [CrossRef]
Kantor, M. G., & Rosenwein, M. B. (1992). The orienteering problem with time windows. Journal of the Operational Research Society. 43(6), 629–635. [CrossRef]
Vansteenwegen, P. , Souffriau, W., Vanden Berghe, G., & Van Oudheusden, D. (2009). Iterated local search for the team orienteering problem with time windows. Computers & Operations Research, 36(12), 3281-3290. [CrossRef]
Gunawan, A. , Lau, H. C., & Lu, K. (2015). An iterated local search algorithm for solving the orienteering problem with time windows. In G. Ochoa, & F. Chicano (Eds.), Evolutionary computation in combinatorial optimization. Lecture Notes in Computer Science: vol. 9026(pp. 61-73). Springer.
Duque, D. , Lozano, L., & Medaglia, A. L. (2015). Solving the orienteering problem with time windows via the pulse framework. Computers & Operations Research, 54, 168-176. [CrossRef]
Fomin, F. V. , & Lingas, A. (2002). Approximation algorithms for time-dependent orienteering. Information Processing Letters, 83, 57-62. [CrossRef]
Varakantham, P. , & Kumar, A. (2013). Optimization approaches for solving chance constrained stochastic orienteering problems. In P. Perny, M. Pirlot, & A. Tsoukiàs (Eds.), Algorithmic decision theory. In Lecture Notes in Computer Science: vol. 8176(pp. 387-398). Springer.
Verbeeck, C. , Sörensen, K., Aghezzaf, E. H., & Vansteenwegen, P. (2014). A fast solution method for the time-dependent orienteering problem. European Journal of Operational Research, 236(2), 419-432. [CrossRef]
Mufalli, F. , Batta, R., & Nagi, R. (2012). Simultaneous sensor selection and routing of unmanned aerial vehicles for complex mission plans. Computers & Operations Research, 39(11), 2787-2799. [CrossRef]
Peng, G. , Dewil, R., Verbeeck, C., Gunawan, Aldy., Xing, L., & Vansteenwegen, P. (2019). Agile earth observation satellite scheduling: An orienteering problem with time-dependent profits and travel times. Computers & Operations Research, 111, 84-98. [CrossRef]
Sevkli, Z., & Sevilgen, F. E. (2010). Discrete particle swarm optimization for the orienteering problem. In Proceedings of the IEEE congress on evolutionary computation (CEC 2010), Barcelona, Spain(pp. 3234-3241).
Sevkli, Z. , & Sevilgen, F. E. (2010). StPSO: Strengthened particle swarm optimization. Turkish Journal of Electrical Engineering & Computer Sciences, 18(6), 1095-1114. [CrossRef]
Muthuswamy, S., & Lam, S. S. (2011). Discrete particle swarm optimization for the team orienteering problem. Memetic Computing. 3(4), 287–303. [CrossRef]
Dang, D. C. , Guibadj, R. N., & Moukrim, A. (2013). An effective PSO-inspired algorithm for the team orienteering problem. European Journal of Operational Research, 229 (2), 332-344. [CrossRef]
Vincent, F. Y. , Redi, A. P., Jewpanya, P., & Gunawan, A. (2019). Selective discrete particle swarm optimization for the team orienteering problem with time windows and partial scores. Computers & Industrial Engineering, 138, 106084. [CrossRef]
Marinakis, Y. , Politis, M., Marinaki, M., & Matsatsinis, N. (2015). A memetic-grasp algorithm for the solution of the orienteering problem. In Modelling, Computation and Optimization in Information Systems and Management Sciences (pp. 105-116). Springer, Cham.
Abbaspour, R. A. , & Samadzadegan, F. (2011). Time-dependent personal tour planning and scheduling in metropolises. Expert Systems with Applications, 38(10), 12439-12452. [CrossRef]
Gambardella, L. M., Montemanni, R., & Weyland, D. (2012). Coupling ant colony systems with strong local searches. European Journal of Operational Research. 220(3), 831–843. [CrossRef]
Verbeeck, C. , Sörensen, K., Aghezzaf, E. H., & Vansteenwegen, P. (2014). A fast solution method for the time-dependent orienteering problem. European Journal of Operational Research, 236(2), 419-432. [CrossRef]
Verbeeck, C. , Vansteenwegen, P., & Aghezzaf, E-H. (2017). The time-dependent orienteering problem with time windows: A fast ant colony system. Annals of Operations Research, 254(1-2), 481-505. [CrossRef]
Cura, T. (2014). An artificial bee colony algorithm approach for the team orienteering problem with time windows. Computers & Industrial Engineering, 74, 270-290. [CrossRef]
Martín-Moreno, R. , & Vega-Rodríguez, M. A. (2018). Multi-objective artificial bee colony algorithm applied to the bi-objective orienteering problem. Knowledge-Based Systems, 154, 93-101. [CrossRef]
Bouly, H., Dang, D. C., & Moukrim, A. (2010). A memetic algorithm for the team orienteering problem. 4OR. 8(1), 49–70. [CrossRef]
Labadie, N., Mansini, R., Melechovsky, J., & Wolfler Calvo, R. (2011). Hybridized evolutionary local search algorithm for the team orienteering problem with time windows. Journal of Heuristics. 17(6), 729–753. [CrossRef]
Marinakis, Y. , Politis, M., Marinaki, M., & Matsatsinis, N. (2015). A memetic-GRASP algorithm for the solution of the orienteering problem. In H. A. Le Thi, T. P. Dinh, & N. T. Nguyen (Eds.), Modelling, computation and optimization in information systems and management sciences. In Advances in Intelligent Systems and Computing: 360(pp. 105-116). Springer.
Vincent, F. Y. , Jewpanya, P., Lin, S. W., & Redi, A. P. (2019). Team orienteering problem with time windows and time-dependent scores. Computers & Industrial Engineering, 127, 213-224. [CrossRef]
Lin, S. W., & Yu, V. F. (2012). A simulated annealing heuristic for the team orienteering problem with time windows. European Journal of Operational Research. 217(1), 94–107. [CrossRef]
Hu, Q. , & Lim, A. (2014). An iterative three-component heuristic for the team orienteering problem with time windows. European Journal of Operational Research, 232(2), 276-286. [CrossRef]
Gunawan, A., Lau, H. C., & Lu, K. (2015b). SAILS: hybrid algorithm for the team orienteering problem with time windows. In Proceedings of the 7th multidisciplinary international scheduling conference (MISTA 2015), Prague, Czech Republic (pp. 276-295).
Lin, S. W. , & Vincent, F. Y. (2017). Solving the team orienteering problem with time windows and mandatory visits by multi-start simulated annealing. Computers & Industrial Engineering, 114, 195-205. [CrossRef]
Souffriau, W. , Vansteenwegen, P., Vanden Berghe, G., & Van Oudheusden, D. (2013). The multiconstraint team orienteering problem with multiple time windows. Transportation Science, 47(1), 53-63. [CrossRef]
Lu, Y., & Shahabi, C. (2015). An arc orienteering algorithm to find the most scenic path on a large-scale road network. In Proceedings of the 23rd ACM SIGSPATIAL international conference on advances in geographic information systems, Washington, USA. [CrossRef]
Vansteenwegen, P. , & Mateo, M. (2014). An iterated local search algorithm for single-vehicle cyclic inventory. European Journal of Operational Research, 237(3), 802-813. [CrossRef]
Avci, M. , & Avci, M. G. (2017). A GRASP with iterated local search for the traveling repairman problem with profits. Computers & Industrial Engineering, 113, 323-332. [CrossRef]
Gunawan, A. , Lau, H. C., & Lu, K. (2018). ADOPT: Combining parameter tuning and Adaptive Operator Ordering for solving a class of Orienteering Problems. Computers & Industrial Engineering, 121, 82-96. [CrossRef]
Salazar-Aguilar, M. A. , Langevin, A., & Laporte, G. (2014). The multi-district team orienteering problem. Computers & Operations Research, 41, 76-82. [CrossRef]
Palomo-Martínez, P. J. , Salazar-Aguilar, M. A., & Laporte, G. (2017). Planning a selective delivery schedule through Adaptive Large Neighborhood Search. Computers & Industrial Engineering, 112, 368-378. [CrossRef]
Karabulut, K. , & Tasgetiren, M. F. (2019). An evolution strategy approach to the team orienteering problem with time windows. Computers & Industrial Engineering, 106109. [CrossRef]
Groenwold, A. A., & Hindley, M. P. (2002). Competing parallel algorithms in structural optimization. Structural and Multidisciplinary Optimization. 24(5), 343–350. [CrossRef]
Behnamian, J. (2014). A parallel competitive colonial algorithm for JIT flowshop scheduling. Journal of Computational Science, 5(5), 777-783. [CrossRef]
Deng, J. , Wang, L., Wang, S. Y., & Zheng, X. L. (2016). A competitive memetic algorithm for the distributed two-stage assembly flow-shop scheduling problem. International Journal of Production Research, 54(12), 3561-3577. [CrossRef]
Deng, J. , & Wang, L. (2017). A competitive memetic algorithm for multi-objective distributed permutation flow shop scheduling problem. Swarm and Evolutionary Computation, 32, 121-131. [CrossRef]
Kiziloz, H. E. , & Dokeroglu, T. (2018). A robust and cooperative parallel tabu search algorithm for the maximum vertex weight clique problem. Computers & Industrial Engineering, 118, 54-66. [CrossRef]
Moscato, P. (1989). On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. Caltech concurrent computation program, C3P Report, 826, 1989.
Chao, I. M., Golden, B. L., & Wasil, E. A. (1996). A fast and effective heuristic for the orienteering problem. European journal of operational research. 88(3), 475–489. [CrossRef]
He, L. , de Weerdt, M., & Yorke-Smith, N. (2019). Time/sequence-dependent scheduling: the design and evaluation of a general purpose tabu-based adaptive large neighbourhood search algorithm. Journal of Intelligent Manufacturing. [CrossRef]

Figure 1. The difference between observations of the EOS and AEOS: (a) An observation of the EOS. (b) An observation of the AEOS.

Figure 2. The framework of the Palace.

Figure 3. Encoding formations of the Palace: (a) The encoding formation for the OP and UAV-OP. (b) The encoding formation for the OPTW, TD-OPTW, and AEOS planning problem.

Figure 4. The local-search operators that join the parallelism in the Palace, where the vertices are marked by 1, 2, 3, 5, 6, 7 originally: (a) Vertex-change and departure-change operators. (b) Vertex-swap and departure-swap operators. (c) Vertices-reverse operator. (d) Insert operator. (e) Remove operator.

Figure 5. The crossover operators: (a) Random single-vertex crossover. (b) Random same-vertices crossover.

Figure 6. The mean contributions per 1000 iterations of local-search metaheuristics that join in the competition. (a) Case 3.20 of the OP. (b) Case 100.4.3 of the OPTW. (c) Case 100.4.3 of the TD-OPTW. (d) Case 1 of the UAV-OP. (e) Case 600_A of the AEOS planning only with time-dependent travel time. (f) Case 600_A of the AEOS planning results with both time-dependent travel time and scores.

Table 1. A summary of the CSP models for the OP and its variants.

Problem	Decision variables	Objective function	Constraints
OP	n and x_i	Eq. (1)	Eq. (2), (3), and (4)
OPTW	n, d_i, and x_i	Eq. (1)	Eq. (2), (3), (4), (5), and (6)
TD-OPTW	n, d_i, and x_i	Eq. (1)	Eq. (2), (3), (4), (5), (6), and (7)
UAV-OP	n and x_i	Eq. (1)	Eq. (2), (3), (4), (8), (9), (10), (11), and (12)
AEOS planning problem	n, d_i, and x_i	Eq. (1) for time-independent scores;Eq. (13) for time-dependent scores	Eq. (2), (3), (4), (5), (6), and (7)

Table 2. The parameters in the Palace.

Inner phase	Parameter	Setting
Parallelism	Length l^T of the tabu list in the TS, TSA, and TLA	0.3\|V\|
	Neighborhood exploration times N^T in the TS	0.5\|V\|
	Initial temperature T₀ in the SA and TSA	2\|V\|
	Length l^T of the late list in the LA and TLA	10\|V\|
Competition	Threshold m_min of the grades on local-search metaheuristics	0.1
	Threshold o_min of the grades on local-search operators	0.1
	Number n_filter of the generations after that under-threshold competitors will be replaced	10
Evolution	The population size	100
	The crossover probability	0.8
	The mutation probability	1.0
Overall framework	The number of enabled threads	5
Overall framework	The number of total generations	5000

Table 3. The results of the OP dataset.

Case	The OH from Chao et al. [47]		The Palace
Case	Best	CPU (s)	Best	Mean	SD	CPU (s)
1.1	10	0.7	10	10	0.0	0.9
1.2	15	0.8	15	15	0.0	0.8
1.3	45	2.3	45	45	0.0	1.1
1.4	65	17.5	65	65	0.0	1.1
1.5	90	9.0	90	90	0.0	0.9
1.6	110	31.9	110	110	0.0	1.2
1.7	135	25.3	135	135	0.0	1.3
1.8	155	16.7	155	155	0.0	0.9
1.9	175	21.6	175	175	0.0	1.3
1.10	190	24.9	190	190	0.0	1.0
1.11	205	24.7	205	205	0.0	0.8
1.12	225	24.3	225	225	0.0	1.3
1.13	240	23.3	240	240	0.0	1.2
1.14	260	25.1	260	260	0.0	1.3
1.15	265	25.2	265	265	0.0	1.0
1.16	270	28.5	270	270	0.0	1.2
1.17	280	26.8	280	280	0.0	1.1
1.18	285	21.7	285	285	0.0	1.1
2.1	120	1.3	120	120	0.0	0.5
2.2	200	2.2	200	200	0.0	0.6
2.3	210	4.5	210	210	0.0	0.4
2.4	230	5.7	230	230	0.0	0.7
2.5	230	6.4	230	230	0.0	0.6
2.6	265	6.2	265	265	0.0	0.5
2.7	300	7.2	300	300	0.0	0.6
2.8	320	7.8	320	320	0.0	0.6
2.9	360	6.8	360	360	0.0	0.6
2.10	395	7.1	395	395	0.0	0.6
2.11	450	0.6	450	450	0.0	0.5
3.1	170	4.4	170	170	0.0	1.3
3.2	200	5.2	200	200	0.0	1.2
3.3	260	9.4	260	260	0.0	1.0
3.4	320	10.0	320	320	0.0	1.3
3.5	390	15.4	390	390	0.0	1.1
3.6	430	18.7	430	430	0.0	1.3
3.7	470	26.8	470	470	0.0	1.3
3.8	520	28.7	520	520	0.0	1.1
3.9	550	30.3	550	550	0.0	1.2
3.10	580	27.7	580	580	0.0	1.3
3.11	610	25.0	610	610	0.0	1.0
3.12	640	29.8	640	640	0.0	1.3
3.13	670	29.3	670	670	0.0	1.3
3.14	710	30.1	710	710	0.0	1.4
3.15	740	28.3	740	740	0.0	1.3
3.16	770	24.4	770	770	0.0	1.1
3.17	790	22.3	790	790	0.0	1.3
3.18	800	0.7	800	800	0.0	1.4
3.19	800	0.6	800	800	0.0	1.4
3.20	800	0.7	800	800	0.0	1.5

Table 4. The results of the OPTW dataset.

Case	The ACS and CPLEX from Verbeeck et al. [22]		The Palace
Case	Best	Mean	Best	Outperform	Mean	Outperform	SD	CPU (s)
20.1.1	177	177	177	0.0%	177	0.0%	0.0	0.8
20.1.2	193	193	193	0.0%	193	0.0%	0.0	0.9
20.1.3	201	201	201	0.0%	201	0.0%	0.0	0.8
20.2.1	213	213	213	0.0%	213	0.0%	0.0	0.9
20.2.2	219	219	219	0.0%	219	0.0%	0.0	0.9
20.2.3	211	211	211	0.0%	211	0.0%	0.0	0.9
20.3.1	306	306	306	0.0%	306	0.0%	0.0	0.9
20.3.2	262	262	262	0.0%	262	0.0%	0.0	0.8
20.3.3	286	286	286	0.0%	286	0.0%	0.0	0.9
20.4.1	293	293	293	0.0%	293	0.0%	0.0	1.0
20.4.2	299	299	299	0.0%	299	0.0%	0.0	1.0
20.4.3	283	283	283	0.0%	283	0.0%	0.0	0.9
50.1.1	314	314	314	0.0%	314	0.0%	0.0	6.9
50.1.2	290	290	290	0.0%	290	0.0%	0.0	6.6
50.1.3	316	316	316	0.0%	316	0.0%	0.0	7.8
50.2.1	322	322	322	0.0%	322	0.0%	0.0	6.8
50.2.2	347	347	347	0.0%	347	0.0%	0.0	7.9
50.2.3	346	346	346	0.0%	346	0.0%	0.0	6.4
50.3.1	380	380	380	0.0%	380	0.0%	0.0	8.4
50.3.2	444	444	444	0.0%	444	0.0%	0.0	9.4
50.3.3*	403	403	403	0.0%	403	0.0%	0.0	8.5
50.4.1	498	498	498	0.0%	498	0.0%	0.0	9.6
50.4.2*	463	463	464	0.2%	463	0.0%	1.1	9.9
50.4.3*	479	479	493	2.9%	493	2.9%	0.0	10.0
100.1.1	297	297	297	0.0%	297	0.0%	0.0	59.5
100.1.2	320	320	320	0.0%	320	0.0%	0.0	53.2
100.1.3	373	373	373	0.0%	373	0.0%	0.0	54.9
100.2.1	397	397	397	0.0%	397	0.0%	0.0	54.3
100.2.2*	393	393	397	1.0%	396.8	1.0%	0.6	55.6
100.2.3	394	394	394	0.0%	394	0.0%	0.0	58.1
100.3.1	490	490	490	0.0%	490	0.0%	0.0	64.0
100.3.2*	511	511	511	0.0%	511	0.0%	0.0	59.8
100.3.3	525	523.4	525	0.0%	525	0.3%	0.0	65.5
100.4.1*	505	489.3	525	4.0%	522.3	6.7%	0.9	78.7
100.4.2*	543	529.4	552	1.7%	552	4.3%	0.0	77.6
100.4.3*	590	581.7	590	0.0%	588.3	1.1%	3.1	82.5
Average				0.3%		0.5%	0.2

Table 5. The results of the TD-OPTW dataset.

Case	The ACS from Verbeeck et al. [22]		The Palace
Case	Best	Mean	Best	Outperform	Mean	Outperform	SD	CPU (s)
20.1.1	159	159	159	0.0%	159	0.0%	0.0	0.9
20.1.2	173	173	173	0.0%	173	0.0%	0.0	0.9
20.1.3	183	183	184	0.5%	184	0.5%	0.0	0.8
20.2.1	188	188	188	0.0%	188	0.0%	0.0	0.9
20.2.2	201	201	201	0.0%	201	0.0%	0.0	0.9
20.2.3	195	195	195	0.0%	195	0.0%	0.0	0.9
20.3.1	277	277	277	0.0%	277	0.0%	0.0	1.0
20.3.2	245	245	246	0.4%	246	0.4%	0.0	0.8
20.3.3	259	259	259	0.0%	259	0.0%	0.0	0.9
20.4.1	274	274	274	0.0%	274	0.0%	0.0	1.0
20.4.2	275	275	275	0.0%	275	0.0%	0.0	1.0
20.4.3	268	268	268	0.0%	268	0.0%	0.0	0.9
50.1.1	288	288	288	0.0%	288	0.0%	0.0	7.1
50.1.2	274	274	274	0.0%	274	0.0%	0.0	6.5
50.1.3	289	289	289	0.0%	289	0.0%	0.0	7.5
50.2.1	298	298	298	0.0%	298	0.0%	0.0	6.9
50.2.2	310	310	310	0.0%	310	0.0%	0.0	8.2
50.2.3	340	340	340	0.0%	340	0.0%	0.0	6.5
50.3.1	339	339	346	2.1%	346	2.1%	0.0	8.3
50.3.2	404	404	415	2.7%	415	2.7%	0.0	9.6
50.3.3	366	366	366	0.0%	366	0.0%	0.0	8.5
50.4.1	478	476.6	478	0.0%	478	0.3%	0.0	9.3
50.4.2	441	439.8	441	0.0%	441	0.3%	0.0	10.0
50.4.3	450	450	450	0.0%	450	0.0%	0.0	10.3
100.1.1	275	275	275	0.0%	275	0.0%	0.0	61.8
100.1.2	278	278	278	0.0%	278	0.0%	0.0	53.6
100.1.3	343	343	342	-0.3%	342	-0.3%	0.0	55.7
100.2.1	352	351.2	352	0.0%	351.1	0.0%	0.3	55.4
100.2.2	367	366.6	367	0.0%	367	0.1%	0.0	54.2
100.2.3	370	370	370	0.0%	370	0.0%	0.0	55.5
100.3.1	437	436	437	0.0%	437	0.2%	0.0	61.4
100.3.2	454	446.6	454	0.0%	454	1.7%	0.0	62.0
100.3.3	468	467	470	0.4%	470	0.6%	0.0	63.2
100.4.1	484	480	480	-0.8%	480	0.0%	0.0	80.6
100.4.2	497	494.6	497	0.0%	497	0.5%	0.0	75.5
100.4.3	538	526.8	532	-1.1%	532	1.0%	0.0	84.7
Average				0.1%		0.3%	0.0

Table 6. The results of the UAV-OP dataset.

Case	CPLEX		The Palace
Case	Optimal	CPU (s)	Best	Mean	SD	CPU (s)
1	103516	180.5	103516	103516	0.0	1.2
2	109342	176.9	109342	109342	0.0	1.0
3	112629	146.4	112629	112629	0.0	1.3
4	112944	119.6	112944	112944	0.0	1.3
5	113475	157.1	113475	113475	0.0	1.5
6	112716	163.0	112716	112716	0.0	1.1
7	112973	141.9	112973	112973	0.0	1.2
8	112989	132.6	112989	112989	0.0	1.4
9	113042	223.8	113042	113042	0.0	1.2
10	113310	128.0	113310	113310	0.0	1.0
11	112829	170.2	112829	112829	0.0	1.1
12	112756	146.7	112756	112756	0.0	1.2

Table 7. The AEOS planning results only with time-dependent travel time.

Case	The ILS from Peng et al. [12].		The Palace
Case	Mean	CPU (s)	Mean	Outperform	SD	CPU (s)
100_A	568.4	13.7	569.2	0.1%	2.7	1.6
200_A	894	69.2	910.8	1.9%	23.1	8.4
300_A	998.6	147.1	1037.6	3.9%	24.9	13.3
400_A	1162.8	260.3	1224.7	5.3%	57.4	21.1
500_A	1297.6	398.6	1345.8	3.7%	53.4	31.3
600_A	1399.8	478.5	1510.2	7.9%	63.1	33.5
100_W	550	5.8	550.0	0.0%	0.0	2.3
200_W	1004	10.4	997.4	-0.7%	3.4	3.3
300_W	1622	25.8	1619.7	-0.1%	2.3	5.9
400_W	2263	45.7	2255.4	-0.3%	3.7	8.8
500_W	2686	74.1	2691.3	0.2%	2.4	12.5
600_W	3122	103.0	3122.2	0.0%	1.9	14.2
Average				1.8%	19.9

Table 8. The AEOS planning results with both time-dependent travel time and scores.

Case	The ILS from Peng et al. [12].		The Palace
Case	Mean	CPU (s)	Mean	Outperform	SD	CPU (s)
100_A	491.1	8.8	492.3	0.2%	2.5	1.8
200_A	747.6	33.1	763.0	2.1%	24.0	8.8
300_A	854.9	50.9	889.2	4.0%	22.3	14.3
400_A	1053.2	100.9	1102.1	4.6%	48.3	23.4
500_A	1153.7	166.8	1197.8	3.8%	49.6	31.3
600_A	1260.1	228.0	1360.1	7.9%	47.2	29.1
100_W	528.0	11.2	528.0	0.0%	0.0	2.4
200_W	973.9	16.0	971.3	-0.3%	2.1	3.2
300_W	1557.1	32.3	1550.2	-0.4%	1.7	6.6
400_W	2149.9	49.7	2141.2	-0.4%	3.6	9.8
500_W	2558.4	75.0	2561.0	0.1%	2.2	15.6
600_W	2847.4	89.9	2847.8	0.0%	1.5	19.3
Average				1.8%	17.1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Palace: A Parallel Adaptive Local-Search Algorithm Based on Competition and Evolution for Orienteering Problems and Variants

Abstract

1. Introduction

2. The orienteering problem and variants

2.1. The OP

2.2. The OPTW

2.3. The TD-OPTW

2.4. The UAV-OP

2.5. The AEOS planning problem

3. The Palace

3.1. The framework

3.2. The encoding

3.3. The parallelism

3.3.1. Local-search metaheuristics

3.3.2. Local-search operators

3.4. The competition

3.5. The evolution

4. Experiment study on Benchmarks

4.1. Experiment setup

4.2. Experiment results

4.2.1. The OP results

4.2.2. The OPTW results

4.2.3. The TD-OPTW results

4.2.4. The UAV-OP results

4.2.5. The AEOS planning results

5. Discussions

6. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe