Preprint
Article
mech2d: An Efficient Tool for High-Throughput Calculation of Mechanical Properties for Two-Dimensional Materials
Altmetrics
Downloads
214
Views
99
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
21 April 2023
Posted:
21 April 2023
You are already at the latest version
Alerts
Abstract
Two-dimensional (2D) materials have been a research hot topic in the passed decades due to their unique and fascinating properties. Among them, mechanical properties plays an important role for their application. However, there lacks an effective tool for high-throughput calculating, analysing and visualizing the mechanical properties of 2D materials. In this work, we present, mech2d package, a highly automated toolkit for calculating and analysing second-order elastic constants (SOECs) tensor and relevant properties of 2D materials with considering their symmetry. In the mech2d, the SOECs can be fitted by both strain-energy and stress-strain approach, where the energy or strain can be calculated by first-principles engine, such as VASP. As a key feature, the mech2d package can automatically submit and collect the tasks from local or remote machine with robust fault-tolerant ability, make it suitable for high-throughput calculation. The present code has been validated by several common 2D materials, including graphene, black phosphorene, GeSe2 and so on.
Keywords:
Subject: Physical Sciences - Condensed Matter Physics
1. Introduction
The mechanical properties of 2D materials, such as graphene [1], hexagonal boron nitride [2], transition metal dichalcogenide [3] and phosphorene [4] are crucial for determining their potential applications and performance. These materials have unique mechanical properties, such as proper strength and stiffness [5,6], which make them suitable for a wide range of applications, including electronics [7], energy storage [8], catalyst [9], sensors [10] and magnetic devices [11]. The mechanical behavior of 2D materials can be influenced by various factors, including their structure [12], defects [13], and interfaces with other materials [14]. Accurately characterizing the mechanical properties of 2D materials is therefore essential for understanding and optimizing their performance in different applications. In particular, the second-order elastic constants (SOECs) tensor [15], which describes the material’s response to an applied strain, is a key factor in determining the mechanical properties of 2D materials.
The calculation of SOECs and relevant mechanical properties of 2D materials via first principles simulation is a tedious and time-consuming task, which requires considering different symmetries of materials and configuring efficient computational resources [16]. Previous research has proposed algorithms and tools, such as ELASTool [17], MECHELASTIC [18], ElATools [19] and vaspkit [20], to reduce computational complexity and analyze mechanical properties. However, research gaps still exist in the field of calculating and analyzing the mechanical properties of two-dimensional materials. A clear mathematical principle for SOEC calculation of 2D materials is missing, and the presented tools lack the basic functions for task submission, monitoring, and data collection, which are crucial for high-throughput calculations [21,22]. Therefore, it is important to present mathematical principles of 2D SOECs calculation and develop an automated tool that can quickly and efficiently calculate and analyze SOECs tensor and other relevant mechanical properties of 2D materials.
In this work, we design mech2d, a highly automated toolkit for calculation, analysis and visualization the mechanical properties of 2D materials. To be specific, Mech2d allows for the calculation of SOECs using both the strain-energy approach and the stress-strain approach, utilizing first-principles engines such as Vienna ab initio simulation package (VASP)[23,24]. The strain-energy approach (SE) concerns calculating the total energy of the system as a quadratic function of strain, while the stress-strain approach (SS) involves calculating the stress as a linear function of strain. Both approaches can be used to evalute the mechanical properties of 2D materials. Particularly, mech2d support to automatically submit and collect tasks from local or remote machines, making it suitable for high-throughput calculations [21,22]. This is particularly useful for evaluating the mechanical properties of a large number of 2D materials as it allows for efficient and robust calculations without the need for manual intervention [13]. The effectiveness of mech2d has been demonstrated based on the validation on several common 2D materials, including graphene [1], black phosphorene [4], and GeSe2[25] et al.
2. Methods
According to the Lagrangian theory of elasticity, solid can be viewed as a homogeneous and an-isotropic elastic medium [15]. The fundamental relationship between physical stress tensor (in this work all of the bold font letter present the matrix or vector) and physical strain tensor of the solid crystalline body within the linear regime is connected by generalized Hook’s law [15]:
According to the generalized Hook’s law, it can be found that physical stress tensor is a linear function of physical strain tensor , where the proportionality coefficient is forth-rank elastic tensor . Generally, it is more convenient to use Lagrangian stress tensor and Lagrangian strain tensor , the corresponding generalized Hook’s law also has the similar formula:
The relationship between Lagrangian stress tensor and physical stress tensor is defined as
where, is the determinant of matrix, is the identity matrix and the physical stress tensor can be calculated by second order differentiation of the total energy E:
where V is the volume of the crystal. The Lagrangian strain tensor expression is
As a center physical quantity, the elastic tensor can be approached in many different ways. From experiment aspect, the elastic tensor can be obtained based on sound velocity with very high precision. From theoretical aspect, elastic constant can be calculated by either the energy-strain or stress-strain approach [26] since most of popular DFT engines can calculate energy and stress precisely. According to the Taylor’s series, the total energy E of a crystal can be expressed as the summation of a power series of the Lagrangian strain :
where and are the energy and volume of the equilibrium structure. By using the Voigt notation (, , , , and ) , the Equation (6) can be simplified as:
In similar way, the Equation (3) can be read as:
Therefore, under strain-energy approach, the elastic constant can be expressed as
and for stress-strain approach, the expression is
As for 2D materials, we assume that the crystal lies in the plane; therefore, all of the elements with subscript including z will be zero. To simplify the formula, we may rewrite total energy E and generalize Hook’s law in matrix format:
and
As can be seen, the maximum number of independent elastic constants of 2D materials has been reduced to 6 compared with their bulk counterpart ( 21). Considering that symmetry plays an important role in elastic properties, the number of independent elastic constants of different 2D crystal structure can be further reduced according to their lattice type. Specifically, the independent elastic constants and Born stability conditions for five 2D plan Bravais (see Figure 1) lattice are listed as follow [27]:
1) Hexagonal lattice
2) Square lattice
3) Rectangular and centered rectangular lattice
4) Oblique lattice
After the theoretical introduction, we pay our attention to how to calculate elastic constant C via state-of-art DFT calculation. Here, we take square lattice as an example to show how to calculate the independent elastic constant based on energy-strain approach. It should be noted that the nature of this problem is to solve the linear equation. For squared lattice, there are 3 independent elastic constant (, and ), which means that we need at least 3 equations to solve this problem.
1) Energy-strain approach: By substituting Equation (14) to Equation (11), the elastic energy can be written as below:
To simplify the above equation, a set of deformation needs to be applied. The full sets of deformation types that are used in the mech2d are listed in Table 1.
As for square lattice, the required deformation set is , and . When the bi-axial strain is applied, the above Equation can be simplified as:
Similarly, is obtained by using uni-axial strain :
Also, is calculated by using the shear strain :
To calculate elastic constant according to the above equation, a series of deformed structures with different Lagrangian strain (e.g., ) will be generated and evaluated by DFT engines to calculate the corresponding strain energy . Then the quadratic coefficients are determined by polynomial fitting of strain energy and Lagrangian Strain. Generally speaking, a 4-6 order polynomial fitting with and 9-11 deformed structures is a reasonable setting [15]. Finally, the second order elastic constants can be obtained by solving the system of linear equations consisted by Equations (18)–(20).
One thing deserved to be noted is that Lagrangian strain for 2D materials is defined as
and the corresponding the physical strain is
Once the Lagrangian strain is defined, the physical strain can be solved iteratively. Furthermore, the lattice vector of deformed structure can be calculated according to the physical strain and equilibrium lattice vector by following equation:
So far, we have presented the energy-strain approach that is used for calculating the square lattice 2D materials. For other lattice type, the corresponding deformation type can be found in the Table 2.
2) Stress-strain approach: In this part, we take rectangular lattice as an example to demonstrate how to calculate the independent elastic constant based on stress-strain approach. For rectangular lattice, there are 4 independent elastic constant (, , , and ), which means that we need at least 4 equations to solve this problem. Similar to energy-stress approach, by substituting Equation (14) to Equation (12), the generalized Hook’s law can be written as below:
It is obviously that for given and , 3 linear equation can be obtained according to the above matrix equation, which is not enough to calculate the 4 elastic constants. To solve this problem, at least 2 sets of deformation are needed. For rectangular lattice, the required deformation set is and . Therefore, the corresponding equation can be written as:
Furthermore, we may rewrite the above equation as:
where
The above over-determined equation can be solved by least square method, namely:
Likewise, a series of deformed structures (by using Equation (23)) with different Lagrangian strain (e.g., ) will be generated and evaluated by DFT engines to give the corresponding physical stress and calculate the Lagrangian stress by using Equation (3). Then the linear coefficients are determined by polynomial fitting of Lagrangian stress and Lagrangian Strain. Finally, the second order elastic constants can be obtained according to Equation (28). Similarly, the second order elastic constants of other lattice type can be calculated by using the corresponding deformation type, which is listed in Table 3.
3. Results
3.1. mech2d Design
The workflow of mech2d code is shown in Figure 2. Implemented with Python, mech2d is designed in a loosely coupled mode, which is considered easy to extend and maintain. Specifically, the workflow of mechanical properties calculation is divided into three stage, including: init, run and post. For the init stage, the initialization works are carried out. Firstly, the equilibrium crystal structure is read from configuration file, such as POSCAR, cif, XSF format and so on. Then the symmetry of 2D Bravais lattice will be determined. Finally, the deformed structures will be generated according to the required parameters, including number of deformation, maximum strain amplitude, lattice type and calculation approach. In the run stage, all of DFT tasks will be submitted to local or remote machine without manually writing the submitting script. As is known, fault-tolerant is a key problem for high-throughput calculation. In the mech2d package, the basic errors of VASP during the mechanical properties calculation will be automatically fixed and resubmitted to the server. Once all of the DFT tasks are finished, the calculation results will be collected to working direction from local or remote machine. In addition, the time consuming run stage supports the task to restart. Specifically, tasks that are interrupted for external reasons will be submitted automatically, while those tasks already finished or still running will not be submitted. For post stage, an internal DFT validator will be used to check the validity of results. Once passed the results checking, the elastic constant or stress strain curve will be calculated and the corresponding results will be output to texts and figures. Based on object oriented design rule, the mech2d mainly includes 4 classes as detailed below.
Elastic class: As the core class of mech2d, Elastic class is written in mechanics.py file. The Elastic class is used to initialize the mechanical properties calculation, including symmetry detection, Lagrangian strain set selection, Lagrangian strain and physical strain conversion, deformed structure generation, and so on. In addition, the post processing of mechanical properties calculation is also employed by Elastic class, such as stress-strain fitting and energy-strain fitting.
Calculation class: This class focuses on the DFT task initialization, running and result parsing. Three files are included in the calculation sub-folder, including calculator.py, vasp.py and runtask.py. The Calculator class in the calculator.py file is the base class that defines the basic method that should be implemented in the subclass. The VASP class in the vasp.py file is a subclass of Calculator, which is used to prepare the VASP calculation tasks and to parse the energy and stress from vasprun.xml file. As for runtask.py file, it contains the RunTasks class. The RunTasks class is a wrapper of open source code dpdispatcher, which is part of our previous work [28] that is used to operate large scale tasks managements in machine learning potential development. As a key component, the job management framework is employed by custodian, a open source code that performs error checking, job management and error recovery.
Analysis class: This class is used to calculate the main mechanical properties of 2D materials, such as , , , , , orientation dependent Young’s modulus and Poisson’s ratio. In addition, the Born stability condition will be calculated according to the lattice type.
Plot class: This class is responsible for data visualization, including energy-stress fitting curve, stress-strain fitting curve, stress-strain curve under tensile strength and polar plot of orientation dependent Young’s modulus and Poisson’s ratio.
This main features of mech2d are listed as follows:
- (1)
- Easy to install (see below).
- (2)
- Loosely coupled mode, which is considered easy to extend and maintain.
- (3)
- Support for any symmetry of 2D materials.
- (4)
- Support for the popular DFT engine VASP. It can be easily extended to other DFT calculators by implementing the corresponding input writer and output parser.
- (5)
- Automatically task submission, error correction and collection on both local or remote machine.
3.2. Installation
Developed by python, the simplest way to install the mech2d is using pip. The mech2d code can be installed by downloading and decompressing the code, and then run the following command “pip install .” in the source code directory. One thing deserves to be noted is that 3 necessary libraries should be installed firstly, including:
- pymatgen
- dpdispatcher
- custodian
3.3. Running of Code
mech2d provides a user-friendly interface, which can be started via a single line of command. For example, the help information can be obtained by following command (more details see in the Supporting Information):
- m2d~-h
- usage: m2d [-h] [-v] {init,run,post} ...
- Desctiption:
- ------------
- mech2d is a convenient script that use to calculate the mechanical
- properties of 2D materials, including Stress-Strain Curve, elastic
- constants and relevant properties. The~script works based on several
- sub-commands with their own options. To~see the options for the
- sub-commands, type ``m2d sub-command~-h’’.
- positional arguments:
- {init,run,post}
- init Generating initial data for elastic systems.
- run Run the DFT calculation for deformed structures.
- post Post processing for elastic~calculation.
- optional arguments:
- -h, --help show this help message and exit
- -v, --version Display version
The initialization of the calculation of elastic constant calculation by using stress-strain approach can be specified by following command:
- m2d init -c POSCAR -m 0.05 -n 9 -a stress -p elc
After running the above command, the corresponding deformed structures will be generated in elc_stress folder.
To run the DFT calculations, the follow command can be used:
- m2d run -a stress input.yaml
Here, the input.yaml parameter specifies the input file name. In this file, the machine that uses to conduct the calculation, the queue system of machine, the resources of hardware information and DFT code input information are supplied. An example of input.yaml is supplied in the Supporting Information.
To post process the mechanical properties calculation, the follow command can be used:
- m2d post -a stress --plot
3.4. Examples
In this section, we present some results of mechanical properties of some typical 2D materials calculated by our mech2d code. There are 6 test cases in this work, including graphene, , penta-graphene, , black phosphorene and . The energies and stresses are calculated by the VASP software package [23,24]. The generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) exchange correlation functional [29] and plane wave basis set are used to describe the valence electrons with the cutoff set to 520 eV [30]. The energy convergence criteria for static calculation is set to be eV. The geometry optimization is converged when the force on each atom is smaller than 1 eV.
Table 4 shows the calculation details for these cases in the present work.
The Table 5 presents the in-plane elastic constants of various 2D materials, including graphene, , penta-graphene, , alpha-phosphorene, and . The calculation results suggest that the values for the elastic constants reported in this work are consistent with previous studies. For example, in graphene, the values for and reported in this work are in good agreement with those reported in Refs. [20,25,31,32,33,34,35]. One thing deserves to be noted is that there are slight differences in value between our work and references, which may be due to differences in simulation accuracy and methods. Overall, the values for the elastic constants reported in this work are in agreement with previous studies, validating the work.
4. Conclusions
In this work we design a python-based open-source software, mech2d, for calculating the SOECs and relevant mechanical properties of 2D materials. The package allows the calculation of SOECs with the assistant of strain-energy approach and the stress-strain approach via first-principles engines. One essential feature of mech2d is its ability to automatically submit and collect tasks from local or remote machines, making it suitable for high-throughput calculations. This is particularly useful for evaluating the mechanical properties of a large number of 2D materials, as it allows for efficient and robust calculations without the need for manual intervention. The effectiveness of mech2d has been demonstrated through its validation on several common 2D materials, including graphene, black phosphorene, et al.
The mech2d package represents a valuable resource for researchers in terms of studying the mechanical properties of 2D materials. It provides method for calculating SOECs and other relevant mechanical properties with high efficiency, and its automation capabilities make it suitable for high-throughput calculations. This can greatly facilitate the understanding and optimization of 2D materials for a wide range of applications, such as electronics, energy storage, and structural materials. Further research and development of the mech2d package may result in even greater capabilities and applications in the field of 2D material mechanics.
Author Contributions
Conceptualization, Haidi Wang, Zhongjun Li and Jinlong Yang; methodology, Haidi Wang; software, Haidi Wang; validation, Haidi Wang, Tao Li, Xiaofeng Liu, Weiduo Zhu and Zhao Chen; investigation, Haidi Wang, Tao Li, Xiaofeng Liu, Weiduo Zhu and Zhao Chen; writing—original draft preparation, Haidi Wang, Tao Li, Xiaofeng Liu, Weiduo Zhu and Zhao Chen; writing—review and editing, Haidi Wang, Tao Li, Xiaofeng Liu, Weiduo Zhu and Zhao Chen; supervision, Jinlong Yang; project administration, Haidi Wang; funding acquisition, Haidi wang, Zhongjun Li and Jinlong Yang. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partly supported by the National Natural Science Foundation of China (22203026, 22203025, 22288201 and 12174080), the National Key R&D Program of China (2022YFA1602601), the Fundamental Research Funds for the Central Universities (JZ2022HGTA0313 and JZ2022HGQA0198), and the Anhui Provincial Natural Science Foundation (2208085QB44). This work also supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (XDB0450101), by the Anhui Initiative in Quantum Information Technologies (AHY090400), by the Innovation Program for Quantum Science and Technology (2021ZD0303306).
Institutional Review Board Statement
Not applicable
Data Availability Statement
The code can be found at https://gitee.com/haidi-hfut/mech2d.
Acknowledgments
The authors thanks the Hefei University of Technology the University of Science and Technology of China and for providing the computational resources. We also thank the chatGPT model for refining our manuscript.
Conflicts of Interest
The authors declare no conflict of interest
Abbreviations
The following abbreviations are used in this manuscript:
| 2D | Two-dimensional |
| SS | stress-strain |
| ES | energy-strain |
| DFT | Density functional theory |
| SOEC | second-order elastic constants |
Appendix A. Help Information
Appendix A.1. Init Help Information
- usage: m2d init [-h] [-c CONFIG] [-a {stress,energy}] [-m MAXS] [-n NUMBER]
- [-d {xx,yy,bi,xy} [{xx,yy,bi,xy} ...]]
- [-r RANGES [RANGES ...]] [-p {elc,ssc}] [-v] [-b]
- optional arguments:
- -h, --help show this help message and exit
- -c CONFIG, --config CONFIG
- The structure filename. Supported format:
- [’.vasp’,’POSCAR’,’.cif’,’.xsf’]
- -a {stress,energy}, --approach {stress,energy}
- Support ’Energy’ or ’Stress’ approach.
- -m MAXS, --maxs MAXS For elastic constant calculation, it stands for the
- maximum Lagrangian strain, suggested value is [0.030,
- 0.150] for Energy approach, [0.0010, 0.0050] for
- Stress approach; for stress strain cuver calcuation,
- this value has no above limitation.
- -n NUMBER, --number NUMBER
- The number of the deformed structures [odd number >
- 4].
- -d {xx,yy,bi,xy} [{xx,yy,bi,xy} ...], --direction {xx,yy,bi,xy} [{xx,yy,bi,xy} ...]
- The direction used for stress strain curve, default
- value: ’xx’. ’xx’ for ’x’ direction; ’yy’ for ’y’
- direction; ’bi’ for bi-Axis strain and ’xy’ for shear
- strain.
- -r RANGES [RANGES ...], --ranges RANGES [RANGES ...]
- The Lagrangian strain range used for stress-strain
- curve calculation. e.g.,~0.0 0.2
- -p {elc,ssc}, --properties {elc,ssc}
- What do you want to calcuation? elastic constant or
- stress strain curve? default value: ’elc’.
- -v, --verbose print verbose information or not.
- -b, --back Whether back the old folder? default value: False.
Appendix A.2. Run Help Information
- usage: m2d run [-h] [-a {stress,energy}] [-p {elc,ssc}] [--manual] [-v] input
- positional arguments:
- input input file for supplying information about DFT calculation,
- json/yaml format. The~’machine’, ’tasks’,’code’, and~
- ’resources’ should be~supplied.
- optional arguments:
- -h, --help show this help message and exit
- -a {stress,energy}, --approach {stress,energy}
- Support ’Energy’ or ’Stress’ approach.
- -p {elc,ssc}, --properties {elc,ssc}
- What do you want to calcuation? elastic constant or
- stress strain curve? default value: ’elc’.
- --manual Manual model, only for generating the input files without runing
- -v, --verbose Print verbose information or not.
Appendix A.3. Post Help Information
- usage: m2d init [-h] [-c CONFIG] [-a {stress,energy}] [-m MAXS] [-n NUMBER]
- [-d {xx,yy,bi,xy} [{xx,yy,bi,xy} ...]]
- [-r RANGES [RANGES ...]] [-p {elc,ssc}] [-v] [-b]
- optional arguments:
- -h, --help show this help message and exit
- -c CONFIG, --config CONFIG
- The structure filename. Supported format:
- [’.vasp’,’POSCAR’,’.cif’,’.xsf’]
- -a {stress,energy}, --approach {stress,energy}
- Support ’Energy’ or ’Stress’ approach.
- -m MAXS, --maxs MAXS For elastic constant calculation, it stands for the
- maximum Lagrangian strain, suggested value is [0.030,
- 0.150] for Energy approach, [0.0010, 0.0050] for
- Stress approach; for stress strain cuvrve calculation,
- this value has no above limitation
- -n NUMBER, --number NUMBER
- The number of the deformed structures [odd number >
- 4].
- -d {xx,yy,bi,xy} [{xx,yy,bi,xy} ...], --direction {xx,yy,bi,xy} [{xx,yy,bi,xy} ...]
- The direction used for stress strain curve, default
- value: ’xx’. ’xx’ for ’x’ direction; ’yy’ for ’y’
- direction; ’bi’ for bi-axis strain and ’xy’ for shear
- strain.
- -r RANGES [RANGES ...], --ranges RANGES [RANGES ...]
- The Lagrangian strain range used for stress-strain
- curve calculation. e.g.,~0.0 0.2
- -p {elc,ssc}, --properties {elc,ssc}
- What do you want to calculation? elastic constant or
- stress strain curve? default value: ’elc’.
- -v, --verbose print verbose information or not.
- -b, --back Whether back the old folder? default value: False.
Appendix B. input.yaml for mech2d
The input file is supplied by YAML format, which is easy to read and write.
- ---
- machine:
- batch_type: Slurm
- context_type: LocalContext
- local_root: ``./work’’
- remote_root: ``./work’’
- remote_profile:
- hostname: localhost
- username: wang
- port: 22
- timeout: 10
- resources:
- number_node: 1
- cpu_per_node: 48
- gpu_per_node: 0
- queue_name: batch
- task_max: 10
- group_size: 1
- custom_flags:
- - ``ulimit -s unlimited’’
- module_list:
- - ``vasp/5.4.1’’
- #source_list:
- # - ``/opt/intel/parallel_studio_xe_2020.2.108/psxevars.sh intel64’’
- #envs:
- # PATH: ``/opt/soft/vasp541:$PATH’’
- tasks:
- command: ``mpirun -np 48 vasp_std’’
- task_work_path:
- forward_files:
- - INCAR
- - KPOINTS
- - POTCAR
- - POSCAR
- backward_files:
- - runlog
- - errlog
- - OUTCAR
- - OSZICAR
- - vasprun.xml
- - CONTCAR
- outlog: runlog
- errlog: errlog
- code:
- name: vasp
- input:
- INCAR: ``./INCAR’’
- #KPOINTS: ``./KPOINTS’’
- KPOINTS:
- kspacing: 5000
- kgamma: false
- POTCAR: ``./POTCAR’’
- #vdw_kernel: vdw_kernel.bindat
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.E.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef]
- Manzeli, S.; Ovchinnikov, D.; Pasquier, D.; Yazyev, O.V.; Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2017, 2, 17033. [Google Scholar] [CrossRef]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef]
- Wei, Q.; Peng, X. Superior mechanical flexibility of phosphorene and few-layer black phosphorus. Appl. Phys. Lett. 2014, 104, 251915. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Pomerantseva, E.; Gogotsi, Y. Two-dimensional heterostructures for energy storage. Nat. Energy 2017, 2, 17089. [Google Scholar] [CrossRef]
- Deng, D.; Novoselov, K.S.; Fu, Q.; Zheng, N.; Tian, Z.; Bao, X. Catalysis with two-dimensional materials and their heterostructures. Nat. Nanotechnol. 2016, 11, 218–230. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Liu, Z.; Yang, J. ψ-Phosphorene: A new allotrope of phosphorene. Phys. Chem. Chem. Phys. 2017, 19, 2402–2408. [Google Scholar] [CrossRef]
- Ahn, E.C. 2D materials for spintronic devices. Npj 2D Mater. Appl. 2020, 4, 17. [Google Scholar] [CrossRef]
- Akinwande, D.; Brennan, C.J.; Bunch, J.S.; Egberts, P.; Felts, J.R.; Gao, H.; Huang, R.; Kim, J.S.; Li, T.; Li, Y.; Liechti, K.M.; Lu, N.; Park, H.S.; Reed, E.J.; Wang, P.; Yakobson, B.I.; Zhang, T.; Zhang, Y.W.; Zhou, Y.; Zhu, Y. A review on mechanics and mechanical properties of 2D materials—Graphene and beyond. Extrem. Mech. Lett. 2017, 13, 42–77. [Google Scholar] [CrossRef]
- Li, X.; Cai, W.; An, J.; Kim, S.; Nah, J.; Yang, D.; Piner, R.; Velamakanni, A.; Jung, I.; Tutuc, E.; others. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 2009, 324, 1312–1314. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.H.; Jang, C.; Xiao, S.; Ishigami, M.; Fuhrer, M.S. Intrinsic and extrinsic performance limits of graphene devices on SiO2. Nat. Nanotechnol. 2008, 3, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Golesorkhtabar, R.; Pavone, P.; Spitaler, J.; Puschnig, P.; Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comput. Phys. Commun. 2013, 184, 1861–1873. [Google Scholar] [CrossRef]
- de Jong, M.; Chen, W.; Angsten, T.; Jain, A.; Notestine, R.; Gamst, A.; Sluiter, M.; Krishna Ande, C.; van der Zwaag, S.; Plata, J.J.; Toher, C.; Curtarolo, S.; Ceder, G.; Persson, K.A.; Asta, M. Charting the complete elastic properties of inorganic crystalline compounds. Sci. Data 2015, 2, 150009. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.L.; Ekuma, C.; Li, W.Q.; Yang, J.Q.; Li, X.J. ElasTool: An automated toolkit for elastic constants calculation. Comput. Phys. Commun. 2022, 270, 108180. [Google Scholar] [CrossRef]
- Singh, S.; Lang, L.; Dovale-Farelo, V.; Herath, U.; Tavadze, P.; Coudert, F.X.; Romero, A.H. MechElastic: A Python library for analysis of mechanical and elastic properties of bulk and 2D materials. Comput. Phys. Commun. 2021, 267, 108068. [Google Scholar] [CrossRef]
- Yalameha, S.; Nourbakhsh, Z.; Vashaee, D. ElATools: A tool for analyzing anisotropic elastic properties of the 2D and 3D materials. Comput. Phys. Commun. 2022, 271, 108195. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Jain, A.; Hautier, G.; Moore, C.J.; Ping Ong, S.; Fischer, C.C.; Mueller, T.; Persson, K.A.; Ceder, G. A high-throughput infrastructure for density functional theory calculations. Comput. Mater. Sci. 2011, 50, 2295–2310. [Google Scholar] [CrossRef]
- Pizzi, G.; Cepellotti, A.; Sabatini, R.; Marzari, N.; Kozinsky, B. AiiDA: Automated interactive infrastructure and database for computational science. Comput. Mater. Sci. 2016, 111, 218–230. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, Z.; Wang, H. Two-dimensional auxetic GeSe2 material with ferroelasticity and flexoelectricity. J. Phys. Chem. C 2021, 125, 19666–19672. [Google Scholar] [CrossRef]
- Paweł, T. Jochym. Elastic.
- Maździarz, M. Comment on ‘The Computational 2D Materials Database: high-throughput modeling and discovery of atomically thin crystals’. 2D Mater. 2019, 6, 48001. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Chen, W.; Zeng, J.; Zhang, L.; Wang, H.; E, W. DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun. 2020, 253, 107206. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Wei, X.; Fragneaud, B.; Marianetti, C.A.; Kysar, J.W. Nonlinear elastic behavior of graphene: Ab initio calculations to continuum description. Phys. Rev. B 2009, 80, 205407. [Google Scholar] [CrossRef]
- Liu, Z.L. High-efficiency calculation of elastic constants enhanced by the optimized strain-matrix sets. arXiv 2020, arXiv:2002.00005. [Google Scholar]
- Haastrup, S.; Strange, M.; Pandey, M.; Deilmann, T.; Schmidt, P.S.; Hinsche, N.F.; Gjerding, M.N.; Torelli, D.; Larsen, P.M.; Riis-Jensen, A.C.; others. The Computational 2D Materials Database: High-throughput modeling and discovery of atomically thin crystals. 2D Mater. 2018, 5, 042002. [Google Scholar] [CrossRef]
- Wang, L.; Kutana, A.; Zou, X.; Yakobson, B.I. Electro-mechanical anisotropy of phosphorene. Nanoscale 2015, 7, 9746–9751. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372–2377. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Five types of 2D Bravais lattice.
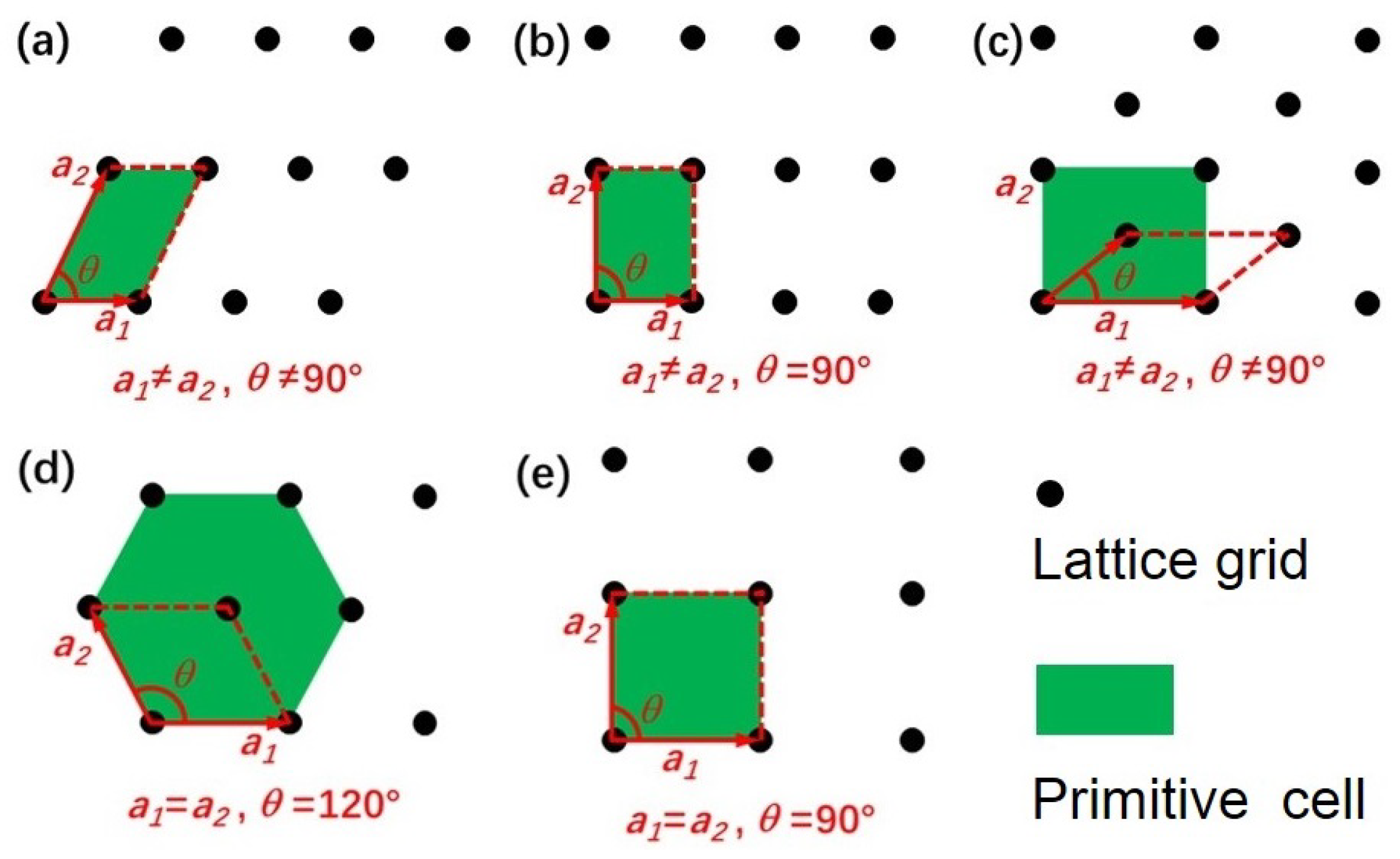
Figure 2.
Workflow of mech2d code.

Figure 3.
The direction-dependent Young’s modulus (a) and Poisson’s ratio (b) of 2D material. Green circles denote positive values and red circles stand for negative ones for Poisson’s ratio.
Figure 3.
The direction-dependent Young’s modulus (a) and Poisson’s ratio (b) of 2D material. Green circles denote positive values and red circles stand for negative ones for Poisson’s ratio.
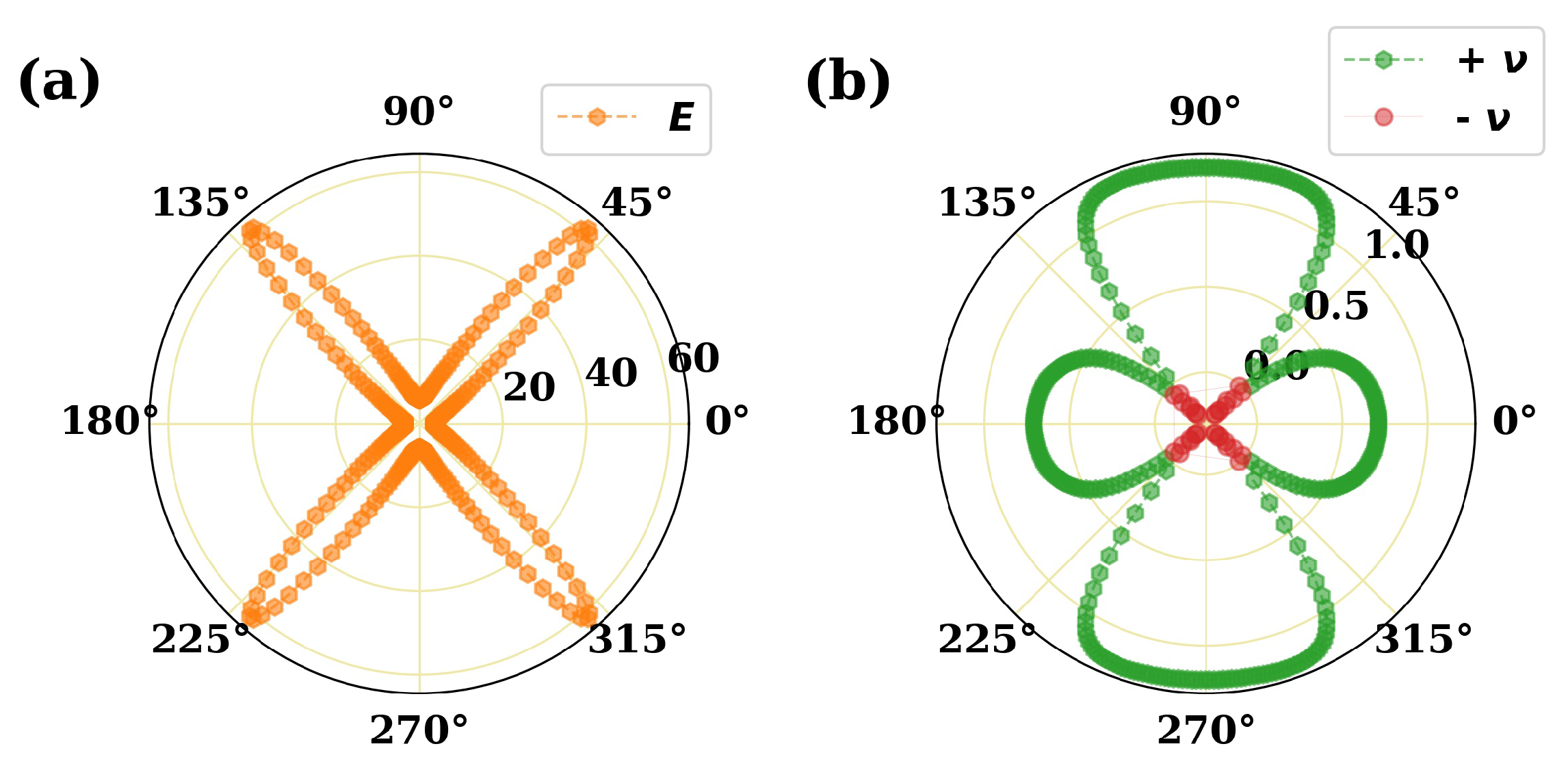
Table 1.
Deformation types that are used in mech2d with Voigt notation. The generic (i-th) Lagrangian strain tensor is represented as a vector: . In the table we only list , and .
Table 1.
Deformation types that are used in mech2d with Voigt notation. The generic (i-th) Lagrangian strain tensor is represented as a vector: . In the table we only list , and .
| 0 | 0 | ||
| 0 | |||
| 0 | 0 | ||
| 0 | 0 | ||
| 0 | |||
| 0 |
Table 2.
Lagrangian strain sets used for different 2D Bravais lattice in the energy-strain approach. The deformation list is shown in Table 1.
Table 2.
Lagrangian strain sets used for different 2D Bravais lattice in the energy-strain approach. The deformation list is shown in Table 1.
| Lattice type | Number of Deformation | Deformation lists |
| Hexagonal | 2 | , |
| Square | 3 | ,, |
| Rectangular | 4 | ,,, |
| Oblique | 6 | ,,,,, |
Table 3.
Lagrangian strain sets used for different 2D Bravais in the stress-strain approach. The deformation list is shown in Table 1.
Table 3.
Lagrangian strain sets used for different 2D Bravais in the stress-strain approach. The deformation list is shown in Table 1.
| Lattice type | Number of Deformation | Deformation lists |
|---|---|---|
| Hexagonal | 1 | |
| Square | 1 | |
| Rectangular | 2 | , |
| Oblique | 3 | , , |
Table 4.
The lattice type, lattice parameters and k-points for 2D test cases.
| System | Lattice type | a(Å) | b(Å) | K-points | |
| graphene | Hexagonal | 2.468 | 2.468 | 120 | 24×24×1 |
| Hexagonal | 3.180 | 3.180 | 120 | 21×21×1 | |
| penta-graphene | Square | 3.631 | 3.631 | 90 | 17×17×1 |
| Square | 3.671 | 3.671 | 90 | 18×18×1 | |
| Rectangular | 3.297 | 3.297 | 90 | 25×15×1 | |
| Centered-Rectangular | 4.906 | 5.571 | 90 | 15×12×1 |
Table 5.
The 2D in-plane elastic constants (N/m) of 2D systems in comparison with references. SS stands for stress-strain approach and ES stands for energy-strain approach.
Table 5.
The 2D in-plane elastic constants (N/m) of 2D systems in comparison with references. SS stands for stress-strain approach and ES stands for energy-strain approach.
| system | sources | approach | |||||
| graphene | our work | ES | 354.1 | 67.5 | |||
| our work | SS | 353.2 | 63.1 | ||||
| Ref. [20] | ES | 349.1 | 60.3 | ||||
| Ref. [31] | ES | 358.1 | 60.4 | ||||
| Ref. [32] | SS | 353.2 | 63.7 | ||||
| our work | ES | 132.6 | 32.8 | ||||
| our work | SS | 134.4 | 34.6 | ||||
| Ref. [32] | SS | 136.9 | 33.1 | ||||
| Ref. [33] | SS | 131.4 | 32.6 | ||||
| Ref. [20] | ES | 128.9 | 32.6 | ||||
| penta-graphene | our work | ES | 269.5 | -20.1 | 151.4 | ||
| our work | SS | 270.1 | -18.6 | 151.4 | |||
| Ref. [35] | ES | 265.0 | -18.0 | / | |||
| our work | ES | 58.4 | 20.5 | 38.3 | |||
| our work | SS | 62.4 | 25.7 | 36.9 | |||
| Ref. [32] | SS | 58.2 | 22.7 | 38.1 | |||
| -phosphorene | our work | ES | 103.8 | 17.1 | 24.4 | 22.7 | |
| our work | SS | 103.4 | 17.8 | 23.9 | 22.6 | ||
| Ref. [34] | ES | 105.2 | 18.4 | 26.2 | 22.4 | ||
| Ref. [20] | ES | 104.4 | 21.6 | 34.0 | 27.4 | ||
| Ref. [32] | SS | 103.4 | 18.0 | 24.6 | 21.8 | ||
| our work | ES | 23.2 | 28.1 | 39.4 | 31.6 | ||
| our work | SS | 23.7 | 28.3 | 39.4 | 31.5 | ||
| Ref. [25] | ES | 23.0 | 27.4 | 37.8 | 31.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






