Prerpints.org logo
Preprint
Review

Fuzzy Random Option Pricing in Continuous Time: A Systematic Review and an Extension of Vasicek’s Equilibrium Model of the Term Structure

Altmetrics

Downloads

146

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 April 2023

Posted:

23 April 2023

You are already at the latest version

Alerts
Abstract
This paper has a twofold objective. The first aim is to present a comprehensive bibliographical analysis of journal articles and book chapters on fuzzy-random option pricing (FROP) over the WoS and SCOPUS databases. It follows PRISMA criteria and takes special care of developments in continuous time. Thus, we described the principal findings about the research streams, outlets and authors of this topic and lets us suggest further research. The second contribution is motivated by the fact that the bibliographical revision has identified a lack of developments on equilibrium models on the yield curve. This question motivates extending Vasicek’s yield curve equilibrium model to introduce fuzziness in the parameters that govern interest rate movements (speed of reversion, equilibrium short-term interest rate, and volatility). Likewise, this paper develops an empirical application on the term structure of fixed income public bonds with the highest credit rating in the Euro area.
Keywords: 
Subject: Business, Economics and Management  -   Finance

MSC:  62A88; 91G20; 91G30

1. Introduction

Option pricing mathematics started its development at the end of the 19th century [1,2] and has been an active research field since the second half of the 20th century [3]. The Black-Scholes-Merton option pricing model [4,5] (BSM hereinafter) is commonly considered a milestone, not only in the constrained field of option pricing but also in the financial arena [3]. The value of the works [4,5] is twofold. From a strict perspective of options on financial asset pricing, the BSM model provides a very operational formula, as the parameters required for its implementation are easy to obtain and do not depend on subjective risk attitude. From the more general setting of pricing any asset, valuation through the so-called "arbitrage argument", which is generalized by the concepts of "risk-neutral valuation" and "equivalent martingale measure", allows for valuing any asset as the mathematical expectation of the present value of its future cash flows [6].
Thus, the BSM model can be applied to options on stocks but also to any asset that includes some type of optionality. Therefore, it can be used to determine the price of assets such as convertible bonds and develop formulas for new types of options such as exotic options or novel derivative assets such as catastrophe bonds [3]. Additionally, that analytical ground has also been applied to traditional assets such as mortgage-backed loans [7], life insurance policies with guaranteed returns [8], and real assets by using real option theory [9]. In fact, while [4] explicitly state in their work that their formula can be used to value companies, [10] proposes using the formula to value credit risk.
The analytical framework of BSM has been particularly productive in modelling the term structure of interest rates with arbitrage-based models, providing a solid mathematical foundation for pricing interest rate derivative instruments such as bond options, caps, floors, or options but also to assess the dynamics of the yield curve. Following [11], it can be differentiated into models whose parameters do not depend on time [12,13,14,15] and those with time-varying parameters [16,17,18]. The first type of development, while providing a valuable analytical framework for conducting economic analysis on the yield curve, does not capture its empirical shapes especially well. Thus, due to their parsimony, they are very useful to make a great deal of financial and economic analysis, but in the setting of valuing interest rate derivatives, their usefulness is limited [11]. On the other hand, time-dependent parameter models are calibrated based on actually observed prices of zero-coupon instruments, resulting in perfect adherence to the observed temporal structure forms, but they suffer from a lack of parsimony.
Option valuation models, since their early stages in the late 19th century, have been grounded in the analytical framework of statistics and stochastic calculus. Therefore, they assume a strict risk environment where probabilities of alternative event realizations can be established. Undoubtedly, these models provide a valuable analytical framework. However, financial activities are conducted with information that involves different degrees of knowledge and can combine risk with other sources of uncertainty, such as imprecision or vagueness. Fuzzy set theory (FST) has provided tools for option pricing for modelling nonprobabilistic uncertainty, such as fuzzy measures, fuzzy numbers, or fuzzy regression [19]. While stochastic models provide rigorous analytical groundwork, the addition of fuzzy tools can improve their results by allowing for the introduction of additional sources of uncertainty to risk [19,20].
Among the various ways in which FST has been applied to option valuation (FOP), the most fruitful is what we can label fuzzy random option pricing (FROP) [19]. This set of contributions extends conventional option valuation models to the hypothesis that knowledge of the parameters governing financial asset price movements is not crisp, as they could be affected by issues such as fuzziness or imprecision [20]. The uncertainty existing in these parameters, such as volatility, observed price of the underlying asset, or discount rates, is modelled using fuzzy numbers [20]. Thus, FROP can be applied to continuous-time models by using the BSM framework or discrete-time models taking as a groundwork the binomial model by Cox, Ross, & Rubinstein [21]. The first approach, which is the main object of this paper, will be referred to as FROP in continuous time (FROPCT).
This work has two contributions. It first presents the results of a systematic literature review on FROP from the first work up to March 2023 in Web of Knowledge (WoS) and SCOPUS. In any case, we focus especially on contributions related to FROPCT. We feel that this systematic review should provide a useful perspective on the main contributions and developments of FROPCT. It also serves to motivate the second contribution of the work. We observed that FROPCT has achieved significant development in the context of equity and real options, but on the other hand, extensions to the context of fixed income markets and interest rate-sensitive instruments are much scarcer.
Thus, the second contribution of this work is developing an FROP extension of Vasicek's yield curve model [12]. In this regard, we will assume that the uncertainty about the parameters governing interest rates (mean-reverting rate, long-term mean, and volatility) is modelled with fuzzy numbers. Our extension will be applied to the zero-coupon curve published by the European Central Bank for bonds with the highest credit rating of the Euro area.

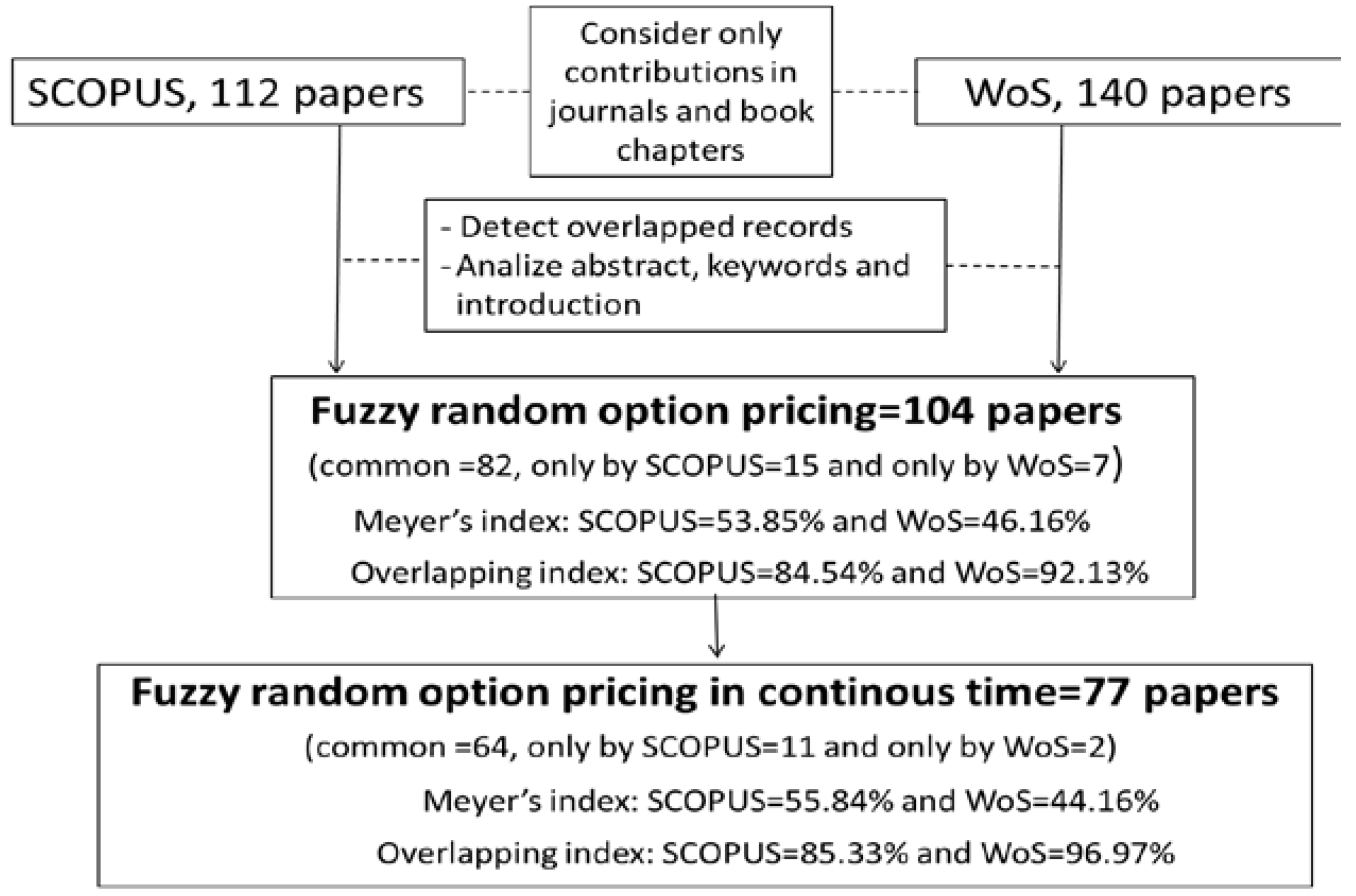
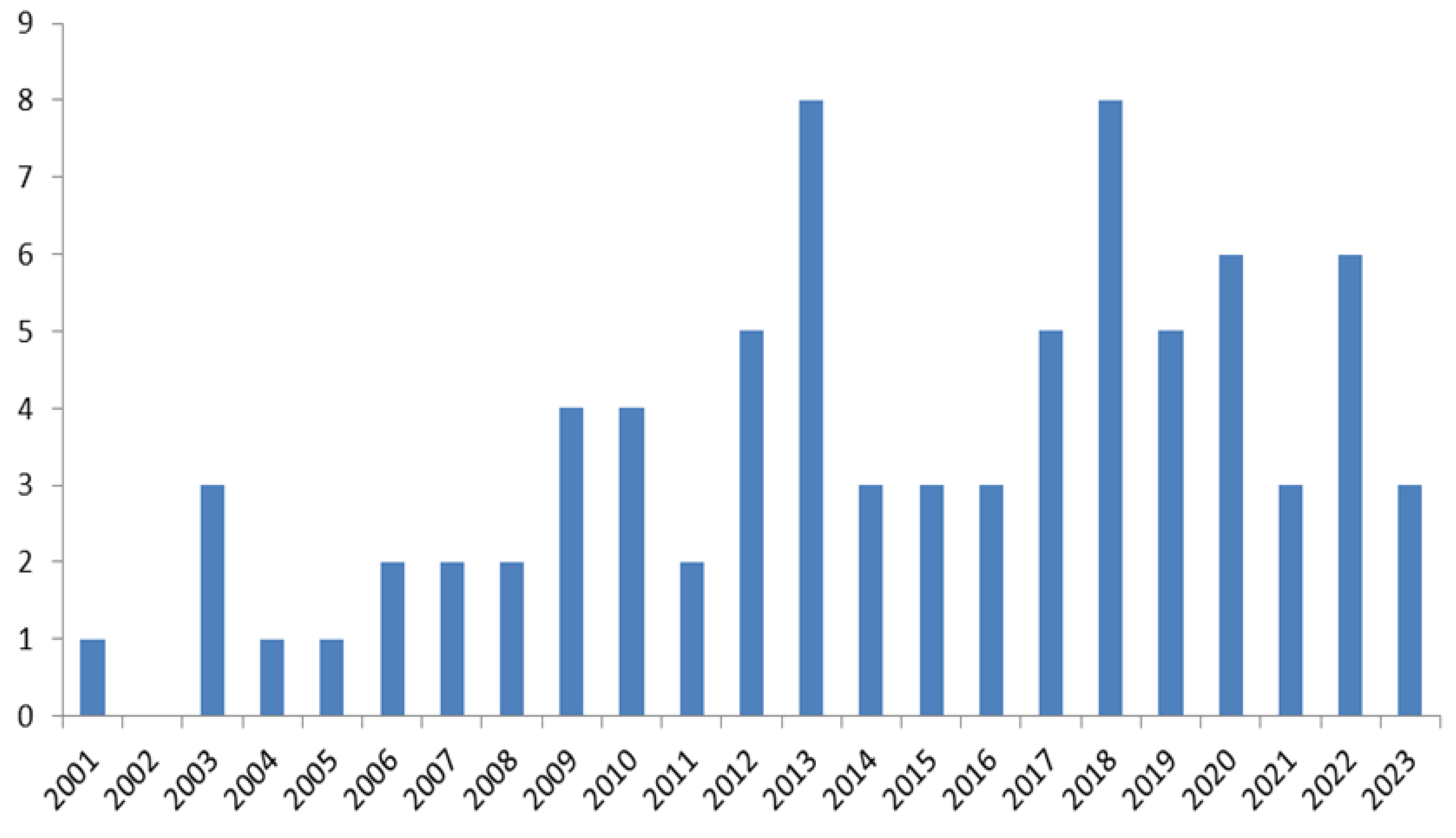
2. Bibliographical Analysis

2.1. Methodology

The bibliographic review was conducted following the PRISMA guidelines [22]. Its implementation requires specifying the methodology used to search for the documents to be reviewed, the databases where these documents should be found, the types of documents that will be considered, etc. Subsequently, it must be indicated how the obtained documents have been compiled. The next step is to classify the papers identifying the sources, authors, and main areas of application of FROP in continuous time.
Regarding eligible studies, we only considered articles written in English and published as journal articles or book chapters until March 31, 2023. We did not consider other types of documents that are typically categorized as "grey literature," such as conference proceedings or documents in digital repositories. The reason is that normally, after a peer review process, these types of contributions are usually published as articles or book chapters. Additionally, we only analysed works written in English. We chose to combine two databases, SCOPUS and WoS, in this review, as they are commonly used in bibliographic reviews, and it is recommended to combine more than one bibliographic source when the topic is not very broad [22].
The search was executed on titles, abstracts, and keywords using the following search: ("option pricing" OR "arbitrage model" OR "risk neutral pricing" OR "equivalent martingale measure") AND ("fuzzy sets" OR "fuzzy mathematics" OR "fuzzy numbers"). Figure 1 graphically shows how we proceeded.
There were a total of 117 documents reported by SCOPUS and 144 by WoS. We eliminated duplicate works and examined the title, abstract, keywords, and, if necessary, the full document to ensure that the papers were effectively related to FROP.
Finally, we identified 104 documents related to FROP. We found 83 documents common to both databases; 7 were exclusively provided by WoS, and SCOPUS provided 15. At this stage, Meyer's index, which quantifies the level of coverage attributable to each database, recorded a rate of 46.15% for WoS and 53.85% for SCOPUS. The degree of overlap, i.e., the redundancy rate of a database, was 92.13% for WoS and 84.54% for SCOPUS.
Our bibliographic exploration showed that FROPCT was developed in 77 articles. Within these documents, 2 come exclusively from the WoS database and 11 from SCOPUS. Therefore, 64 documents were common to both SCOPUS and WoS. At this step, Meyer's index was 55.84% for SCOPUS and 44.16% for WoS. We verified an overlap level of 85.33% for SCOPUS and 96.97% for WoS.

2.2. Classification

Table 1 displays all the works reviewed in this article. These have been classified, by columns, according to the stochastic process that serves as the basis for fuzzy extension. It can be observed that the majority of works (45) assume a single underlying asset and geometric Brownian motion. Thus, the majority is based on the application of the Black-Scholes-Merton (BSM) model. However, there are several nuances to consider in this regard. For example, [68,69] extend FROPCT to currency options using the analytical framework provided by Garman and Kolhagen [99], and [73] extends the Asian option valuation formula of Kemma and Vorst [100]. Additionally, within the framework of geometric Brownian, there are 6 works that assume that various parameters of the Margabre exchange valuation model [101] and Geske's compound option model pricing formula [101] are given by fuzzy numbers.
In the framework of more complex stochastic models, Fractional Brownian motion (7 works) and the more general Levy modelling (11 works) have been extensively addressed. It is also worth mentioning that Merton's jump-diffusion model [103] and the Heston formula [104] have been objects of attention in the FROPCT literature.
In most cases, the analysed topics are technical aspects that emerge from the juxtaposition of stochastic calculus with fuzzy mathematics. The most common mathematical issue is the application of fuzzy arithmetic, which quantifies certain parameters of the generalized option formula. Without being exhaustive, we can indicate that [62,63,70] do so in the context of BSM, [27,29] in a multiple underlying asset options framework but governed by Brownian motion, [92] in the framework of a diffusion and jump model, [77] in the fuzzification of the Heston model [104], [75] in fuzzy-fractional models, or in the fuzzy extension to Levy stochastic processes [85,93]. In some cases, especially in articles that are based on the standard BSM model, issues associated with fuzzy analysis are refined. These issues may embed, such as defuzzification [33,36,56,57,68,71] or the construction of membership functions for the inputs of the pricing formula or the final price of the asset [25,31,32,36,40,50,51,52].
The first row of Table 1 indicates that the modelling of uncertainty in the parameters of the valuation formula is usually done by using type-1 fuzzy numbers (i.e., conventional fuzzy numbers). Exceptions are [59,90], which model uncertain parameters with type-2 fuzzy numbers, and [67], which uses intuitionistic fuzzy numbers. In most cases, the assumed form of the fuzzy magnitude is linear, i.e., triangular or trapezoidal. However, within type-1 fuzzy numbers, the literature has also used other shapes, such as adaptive fuzzy numbers [36,56,57], Gaussian fuzzy numbers [35], or parabolic fuzzy numbers [94]. The parameters that are considered crisp and those that are considered fuzzy are established ad hoc depending on the problem being addressed. In options on financial assets traded in financial markets, volatility (always), risk-free interest rate, and underlying asset value (in most cases) are assumed to be estimated with fuzzy numbers. However, the strike price and expiration are crisp parameters because they are clearly defined in the contract. However, in real options, the strike price [33] or even the expiration [19] may not be known with precision and, therefore, are susceptible to be quantified with fuzzy numbers.
Starting from the second row (included), relevant topics in financial pricing addressed by concrete papers are indicated. A great proportion of papers price European options. However, other types of options, such as American [47,71,72,94], binary [47,49,55,89], exchange [26,27,29,61], or compound [60,91,98] options, have been analysed. Sensitivity analysis of option prices from the perspective of the BSM model has been the subject of attention by various authors [35,36,41,46,69]. Likewise, while fuzzy Malliavin calculus has been applied in [43,80], [25] shows that the use of Greeks can be useful in the linear approximation of the membership functions of fuzzy option prices.
We must acknowledge that empirical applications of FROPCP are relatively scarce [19,20]. Within this group of works, we can highlight [31,32], which propose the use of congruent probability-possibility transformations [105] to model the volatility of options based on empirical data, and [71,72,73], which use fuzzy regression models to estimate the volatility, kurtosis, and skewness of asset returns. Papers [24,25] observe good adherence of the fuzzy version of the standard BSM formula to traded prices on the Spanish stock index IBEX-35. Furthermore, [77], in its extension of [104], and [93,94], in their fuzzy-Levy modelling, perform comprehensive empirical applications for options on Standard & Poor indexes.
Beyond options on stocks or indexes traded on stock exchanges, a very fruitful field of FROPCT has been real options. In a sense, it is logical since in this type of option, the underlying asset is usually an investment project, and data on it are often given by subjective estimates from experts that can be well represented through trapezoidal or triangular numbers [26,33,61]. While the simplest real options can be valued using a fuzzy version of the BSM formula [33,34,37,39,45,58,59], other works [26,27,29,53,60,61,91,98] extend more complex option valuation frameworks to real asset-related optionality.
Other residual applications of FROPCT to asset valuation include assessing firms’ value [74], as suggested by the seminal work of Black and Scholes [4], credit default swaps [66,67], bank deposit insurance [65], catastrophe bonds [88], and forward contracts in energy markets [84].
Figure 2 shows the evolution of the production of FROPCT by year of publication. The first works were published in the years 2001-2003, which means that the introduction of fuzzy numbers in option valuation started in the beginning of the 21st century. We can observe a trend until 2013 that, although not monotonic, is clearly increasing. In that year, the maximum number of published works (8) was reached. From that year, works on FROPCT remained within a fluctuation range of 3 to 8 annual contributions. Therefore, although FROP is not a mainstream topic in fuzzy mathematics, it can be considered a consolidated topic within the applications of fuzzy logic.
Table 2 shows the main outlets where contributions on FROPCT have been published. We only include journals with two or more contributions. Undoubtedly, the main journal is Fuzzy Sets and Systems (10 contributions), which is one of the principal academic references in fuzzy mathematics. Other journals whose scope is fuzzy logic and where FROP has had significant impact are the International Journal of Fuzzy Systems (4 contributions), IEEE Transactions on Fuzzy Systems, Fuzzy Optimization and Decision Making, Journal of Intelligent & Fuzzy Systems (2 contributions). Other types of journals that collect a large part of the contributions of FROPCP are more generalist journals dedicated to computing and/or soft computing (for example, Journal of Computational and Applied Mathematics, 4 contributions; Soft Computing, 3 contributions, or International Journal of Intelligent Systems, 2 contributions). Likewise, generalist journals of operational research have also been a vehicle with relevant production on FROPCP (e.g., European Journal of Operational Research with 4 contributions; International Journal of Information Technology & Decision Making and Journal of Applied Mathematics and Statistics with 2 contributions).
Tables 3a and 3b list the most relevant works according to the WoS (Table 3a) and SCOPUS (Table 3b) databases. We determined the relevance based on the number of citations, and we included works referenced at least 25 times. We can observe that both databases essentially include the same works, and the ordering, although not identical, is very similar. It can also be noted that works are usually more cited in SCOPUS than in WoS, which was expected since the SCOPUS database is more comprehensive. The most cited works are usually the oldest works that fall between 2001 and 2010 and are all within the framework of the BSM formula.
Within the WoS database (Table 3a), the most cited paper is [33], which applies a fuzzy version of BSM to real options, followed by [63,70], which develop the valuation of European-style options with BSM on stocks. The papers [36,56,57,63,64,70,74] also fall within the scope of the BSM model and value European-style options, but some of them introduce new nuances related to nonlinear fuzzy numbers [36,57], defuzzification [56], sensitivity analysis of prices [36], or valuation of companies [74]. It was not until the tenth work, [85], that we observed an analytical framework different from that provided by the geometric Brownian, specifically a more general Levy stochastic process. In the eleventh cited contribution, [55], a different type of option from the European binary options is evaluated. In later positions, there are several contributions in more alternative fuzzy-stochastic modelling to geometric Brownian, such as [92,96] that addressed jump-diffusion processes and [87] that uses fuzzy-Levy processes. Additionally, noteworthy are the contributions [52] that apply fuzzy regression in the adjustment of implied volatility and [20] that provides a review in fuzzy random option pricing in both continuous and discrete time. The patterns observed in the SCOPUS database are very similar to those in WoS, although there may be small changes. Changes in the ranking are not very pronounced in any case. The top three most cited works continue to be [33], [70], and [63]. However, starting from the fourth work, the order may undergo subtle modifications. For example, in the SCOPUS database, [74] is the fifth most referenced work instead of the fourth. On the other hand, [64] goes from being the fifth in SCOPUS to the fourth in WoS.
Table 3a. Papers with at least 25 citations in the WoS database.
Table 3a. Papers with at least 25 citations in the WoS database.
Year Authors Article Title Source Title Citations
2003 Carlsson, C; Fuller, R. [33] A fuzzy approach to real option valuation Fuzzy Sets and Systems 168
2003 Yoshida, Y. [70] The valuation of European options in uncertain environment European Journal of Operational Research 119
2004 Wu, HC. [63] Pricing European options based on the fuzzy pattern of Black-Scholes formula Computers & Operations Research 105
2001 Zmeskal, Z. [74] Application of the fuzzy-stochastic methodology to appraising the firm value as a European call option European Journal of Operational Research 81
2007 Wu, HC. [64] Using fuzzy sets theory and Black-Scholes formula to generate pricing boundaries of European options Applied Mathematics and Computation 80
2009 Chrysafis, KA.; Papadopoulos, BK. [36] On theoretical pricing of options with fuzzy estimators Journal of Computational and Applied Mathematics 50
2009 Thavaneswaran, A.; Appadoo, S. S.; Paseka, A. [56] Weighted possibilistic moments of fuzzy numbers with applications to GARCH modeling and option pricing Mathematical and Computer Modelling 50
2007 Thiagarajah, K.; Appadoo, S.S.; Thavaneswaran, A.[57] Option valuation model with adaptive fuzzy numbers Computers & Mathematics With Applications 49
2005 Wu, HC [62] European option pricing under fuzzy environments International Journal of Intelligent Systems 36
2010 Nowak, P.;
Romaniuk, M. [85]		 Computing option price for Levy process with fuzzy parameters European Journal of Operational Research 35
2013 Thavaneswaran, A.; Appadoo, S. S.; Frank, J. [55] Binary option pricing using fuzzy numbers Applied Mathematics Letters 33
2015 Muzzioli, S.; Ruggieri, A.; De Baets, B. [52] A comparison of fuzzy regression methods for the estimation of the implied volatility smile function Fuzzy Sets And Systems 31
2009 Xu, W.; Wu, C.;
Xu, W.; Li, H. [92]		 A jump-diffusion model for option pricing under fuzzy environments Insurance Mathematics & Economics 31
2014 Nowak, P.;
Romaniuk, M. [87]		 Application of Levy processes and Esscher transformed martingale measures for option pricing in fuzzy framework Journal of Computational and Applied Mathematics 29
2012 Zhang, LH; Zhang, WG; Xu, WJ;
Xiao, WJ [96]		 The double exponential jump diffusion model for pricing European options under fuzzy environments Economic Modelling 29
2017 Muzzioli, S.;
De Baets, B. [20]		 Fuzzy Approaches to Option Price Modeling IEEE Transactions on Fuzzy Systems 28
Table 3b. Papers with at least 25 citations in the Scopus database.
Table 3b. Papers with at least 25 citations in the Scopus database.
Year Author Tittle Source Tittle Citations
2003 Carlsson, C., Fullér, R. [33] A fuzzy approach to real option valuation Fuzzy Sets and Systems 195
2003 Yoshida, Y. [70] The valuation of European options in uncertain environment European Journal of Operational Research 122
2004 Wu, HC. [63] Pricing European options based on the fuzzy pattern of Black-Scholes formula Computers and Operations Research 112
2007 Wu, HC. [64] Using fuzzy sets theory and Black-Scholes formula to generate pricing boundaries of European options Applied Mathematics and Computation 76
2001 Zmeškal, Z. [74] Application of the fuzzy-stochastic methodology to appraising the firm value as a European call option European Journal of Operational Research 73
2009 Thavaneswaran, A., Appadoo, S.S., Paseka, A. [56] Weighted possibilistic moments of fuzzy numbers with applications to GARCH modeling and option pricing Mathematical and Computer Modelling 55
2009 Chrysafis, K.A., Papadopoulos, B.K. [36] On theoretical pricing of options with fuzzy estimators Journal of Computational and Applied Mathematics 51
2007 Thiagarajah, K., Appadoo, S.S., Thavaneswaran, A. [57] Option valuation model with adaptive fuzzy numbers Computers and Mathematics with Applications 51
2005 Wu, HC., [62] European option pricing under fuzzy environments International Journal of Intelligent Systems 46
2015 Muzzioli, S.; Ruggieri, A.;
De Baets, B. [52]		 A comparison of fuzzy regression methods for the estimation of the implied volatility smile function Fuzzy Sets And Systems 31
2010 Nowak, P.,
Romaniuk, M., [85]		 Computing option price for Levy process with fuzzy parameters European Journal of Operational Research 36
2017 Muzzioli, S., De Baets, B. [20] Fuzzy Approaches to Option Price Modeling IEEE Transactions on Fuzzy Systems 32
2009 Xu, W., Wu, C.,
Xu, W., Li, H. [92]		 A jump-diffusion model for option pricing under fuzzy environments Insurance: Mathematics and Economics 32
2013 Thavaneswaran, A.,
Appadoo, S.S., Frank, J. [55]		 Binary option pricing using fuzzy numbers Applied Mathematics Letters 31
2014 Nowak, P.,
Romaniuk, M. [87]		 Application of Levy processes and Esscher transformed martingale measures for option pricing in fuzzy framework Journal of Computational and Applied Mathematics 29
2012 Zhang, L.-H., Zhang, W.-G., Xu, W.-J., Xiao, W.-L. [96] The double exponential jump diffusion model for pricing European options under fuzzy environments Economic Modelling 29
2011 Guerra, M.L., Sorini, L., Stefanini, L. [41] Option price sensitivities through fuzzy numbers Computers and Mathematics with Applications 27
Table 4 shows that the authors who, as of March 2023, had the highest indexed production in WoS and SCOPUS in the field of FROPCT are Nowak (7 contributions), followed by Muzzioli, Romaniuk, and Guerra (4 contributions). These four authors are followed by 11 authors with 3 papers.
Table 4. Authors with at least 3 items.
Table 4. Authors with at least 3 items.
Author Country items Author Country items
Nowak, P. Poland 7 Liu, S. China 3
Muzzioli, S. Italy 4 Pawlowski, M. Poland 3
Romaniuk, M. Poland 4 Sorini, L. Italy 3
Guerra, M.L. Italy 4 Stefanini, L. Italy 3
Andres-Sanchez, J. Spain 3 Thavaneswaran, A. Canada 3
Appadoo, S.S. Canada 3 Vilani, G. Italy 3
de Baets, B. Belgium 3 Wu, H.C. Taiwan 3
Figa-Talamanca, G. Italy 3

3. Fuzzy-Random Extension to Vasicek’s Equilibrium Term Model

3.1. The Equilibrium Model of the Yield Curve by Vasicek

Table 1 shows that the mainstreams of fuzzy-random option pricing in continuous time are focused on options on stocks, often of European style, and real options. We have not retrieved any fuzzy-random approach to equilibrium models of yield rates and to the option pricing formulas that can be derived from these models. We can only outline [68], which assumes a crisp modelling of the term structure with the model by Cox-Ingersoll and Ross [15] to free the risk interest rate in the evaluation of credit default swaps, but the observed short rate is a fuzzy number. This fact motivates the extension developed in this section for the one-factor model for the yield curve model by Vasicek [12] to the presence of fuzziness in the parameters. As with any one-factor model,[12] it is assumed that the stochastic variability comes from short-term interest rate ( r ) fluctuations. The ultimate goal of equilibrium models is to obtain the price that would be agreed upon at t for a risk-free zero-coupon bond that pays one monetary unit (u.m) at   T ≥ t , P ( t , T ) . In term structure models, stochastic variation does not directly apply to P ( t , T ) , as in the case of stocks, but rather to the interest rate   r , which is directly connected to P ( t , T ) . In general, one-factor models suppose that r follows an Ito process such as [12]:
d r = m r , t d t + σ r , t d z ,
where m ( r , t ) and r , t   are the instantaneous drift and variance, respectively, and d z is a Wiener process with standard deviation d t . The price of any asset affected by r (bonds, derivatives on fixed income assets, etc. ), P , must accomplish:
∂ P ∂ t + m r , t ∂ P ∂ r d t + 1 2 ∂ 2 P ∂ r 2 σ 2 r , t = r P ,
and thus, to obtain P ( t , T ) , we have to consider the condition P T , T = 1 .
Among the many models proposed for d r (see Hull [106]), we extend the classical Vasicek’s model [12]. It supposes that the fluctuations of the short interest rate follow a mean-reverting process:
d r = a b − r d t + α d z ,
where a ≥ 0 is the reversion rate, i.e., the speed at which interest rates return to equilibrium and the b equilibrium short rate. By naming r T to the short interest rate in year T and r t to that rate in t ≤ T , the expectation of r T in t   E t r T is:
E t r T = b + b − r t e − a T − t ,
and the variance V t r T
V t r T = σ 2 2 a 1 − e − 2 a T − t .
Note that for ⟶ ∞ ,   E t r T = b , i.e., r T is increasing with respect to b . Likewise, (4b) suggests that the variance of the short-term rate is affected by an exponential decay at rate a . That decreasing behaviour can be easily checked in the limit because if T ⟶ ∞ ,   V t r T = σ 2 2 a and the long-term variance is decreasing respect a and, of course, decreasing respect σ .
Therefore, in a mean-reverting groundwork (3), the general equation (2) becomes:
∂ P ∂ t + a b − r ∂ P ∂ r d t + 1 2 ∂ 2 P ∂ r 2 σ 2 = r C .
Thus, for the zero coupon bond, we find
P t , T , a , b , σ , r t = A t , T , a , b , σ exp ⁡ − B t , T , a · r t ,
where:
B t , T , a = 1 − e x p − a T − t a ,
A t , T , a , b , σ = e x p B t , T , a − T + t a 2 b − σ 2 2 a 2 − σ 2 B 2 t , T , a 4 a .
Note that the fact that b and r t are the discount rates of the zero coupon bond implies that the partial derivatives must be ∂ P ∂ b < 0 and ∂ P ∂ r t < 0 . Likewise, the price of a bond is a decreasing function of interest rate volatility because its profit is positively linked with volatility [107]. Therefore, ∂ P ∂ σ < 0 and ∂ P ∂ a > 0 since a basically negatively affects the volatility of the short-term interest rate (see (4b)).

3.2. An Extension of Vasicek’s Yield Curve with Fuzzy Parameters

In the following, we will suppose that with the exception of maturities t and T , all the parameters of (6a)-(6c) are imprecise and are given by means of fuzzy numbers (FNs). An FN is a fuzzy set f   ~ defined on the reference set R and is normal, (i.e., m a x x ∈ R μ f ( x ) = 1 , where μ f ( x ) is its membership function) and convex, i.e., all its α-cuts are convex and compact sets. Therefore, they can be represented as confidence intervals (so-called α-cuts or α-level sets) f α = f α _ , f α ¯ , where   f α _ ( f α ¯ ) are continuously increasing (decreasing) functions of α. An FN can be interpreted as a fuzzy quantity approximately equal to the value x ∈ R whose membership function is 1, f 1 .
Therefore, the parameters a , b , σ and r t are now the imprecise quantities a ~ , b ~ , σ ~ and r t ~ whose α-cuts are denoted as a α = a α _ , a α ¯ ,   b α = b α _ , b α ¯ , σ α = σ α _ , σ α ¯ and r t α = r t α _ , r t α ¯ .
Therefore, under our hypothesis, the mean-reverting process (3) turns into a fuzzy random process where the parameters that rule interest rate movements are fuzzy numbers. In the fuzzy-random approach setting of the FOP, the differential equation (5) has fuzzy parameters but a crisp boundary condition   P T , T = 1 .
FROPCT literature obtains fuzzy option prices by evaluating the crisp pricing formula that comes from the assumed stochastic process (e.g., BSM after accepting that a geometrical Brownian motion explains price movements of subjacent asset), with fuzzy numbers, by using the rules in [108]. This procedure is theoretically supported by the concept of the solution of differential equations with fuzzy coefficients [109]. Thus, in our case, the assumption of fuzzy parameters in (3) leads to the need to solve (6a)-(6c) with FNs. Therefore, the price of a zero-coupon bond turns into a fuzzy number P ~ t , T = P t , T , a ~ , b ~ , σ ~ , r t ~   whose α-levels P t , T α = P t , T _ α , P t , T ¯ α can be obtained by evaluating (6a)-(6c) in a α ,   b α ,   σ α and r t α :
P t , T α = { x | x = P t , T , a , b , σ , r t = A t , T , a , b , σ exp ⁡ − B t , T , a · r t , a ∈ a α , b ∈ b α , σ ∈ σ α , σ ∈ σ α , r t ∈ r t α , }
and given that ∂ P ∂ b < 0 ,   ∂ P ∂ r t < 0 ,   ∂ P ∂ σ < 0 and ∂ P ∂ a > 0 we can obtain the extremes of the α-cuts by evaluating (6a)-(6c) in the extremes of a α ,   b α ,   σ α and r t α as:
P t , T _ α = P t , T , a α _ , b α ¯ , α α ¯ , r t α ¯ = A t , T , a α _ , b α ¯ , α α ¯ exp ⁡ − B t , T , a α _ , · r t α ¯ ,
and:
P t , T ¯ α = P t , T , a α ¯ , b α _ , α α _ , r t α _ = A t , T , a α ¯ , b α _ , α α _ exp ⁡ − B t , T , a α ¯ · r t α _ .

3.3. Empirical Application of Fuzzy Vasicek’s Model in the Public Debt Bond Market of Euro Area

The empirical application developed in this work estimates the theoretical yield curve using the Vasicek model [12] for European public bonds with the highest rating (AAA) on April 18, 2023. The data we work with have been obtained from the website of the European Central Bank (https://www.ecb.europa.eu/home/html/index.en.html). The short-term interest rate considered is the 3-month interest rate, which is the lowest term published in the public bond market by the European Central Bank.
We will fit the parameters in (3) as the fuzzy numbers a ~ , b ~ , σ ~ by following a consistent possibility of probability-possibility transformation exposed in [110] in which these FN will be modelled by means of symmetrical fuzzy numbers, which we will also suppose triangular. A triangular symmetrical fuzzy number (TSFN) can be represented as f   ~ = f C , f R , where f C is the centre of the FN and f R is the spread. Its membership function is μ f ( x ) = max ⁡ 0 , x − f C f R , and its α-cut representation f α = f α _ , f α ¯ = f C − f R 1 − α , f C + f R 1 − α . Therefore, its support is f 0 = f 0 _ , f 0 ¯ = f C − f R , f C + f R . For example, the equilibrium short-term rate b ~ = ( 3 % , 0.5 % ) can be interpreted that the most reliable value for that rate is 3%, but deviations of approximately 0.5% are viewed as possible.
To fit the parameters, we use the ground of the conventional AR(1) model that serves as the basis to empirically estimate (3) [11]. Therefore, the time-series model to fit is [11]:
r t + 1 = α + β r t + ϵ t + 1 , t = 1 , 2 , … , n
where α is the intercept, β the slope and ϵ t + 1 is white noise normally and i.i.d. with mean 0 and standard deviation σ ε . A commonly used methodology to adjust (8) is ordinary least squares. In this regard, it is easy to check that the relations between the parameters of (3), (4a) and (8) are a = − ln β · h , b = α 1 − β and σ = σ ε h , where h is the frequency of data. Thus, for daily data, h = 252 .
To fit the temporal structure in the calendar date m, we adjust (8) in the moments i=1,2,…,m and, in all cases, by using n observations. Therefore, for the ith adjustment of (8), we obtain point estimates in (8) α ^ ( i ) ,   β ^ ( i ) ,   σ ε ^ ( i ) , i=1,2,…,m and, consequently, a ^ ( i ) ,   b ^ ( i ) ,   σ ^ ( i ) , i=1,2,….,m.
After fitting the m AR(1) models (8), we can fit for every parameter an empirical probability distribution that for the parameter f , we symbolize as f ^ , whose outcomes are f ^ ( i ) ,   i = 1,2 , … , m . Therefore, we can calculate the mean and the standard deviation of f simply as:
f ^ m e a n = ∑ i f ^ ( i ) m a n d f ^ s d = ∑ i f ^ ( i ) − f m e a n 2 m .
A natural way to adjust a fuzzy number to a unimodal probability distribution f with mean f m e a n and standard deviation f s d is to state an STFM f   ~ = f C , f R with centre f C = f m e a n and fit the spread f R by considering the Chebychev inequality [110]. Concretely, given that,
P x ∈ f m e a n − k · f s d , f m e a n + k · f s d ≥ 1 − 1 2.25 · k 2 ,   k ≥ 1 ,
where P · is a probability measure, we choose f R in such a way that P x f m e a n − f R , f m e a n + f R ≥ 1 − 1 2.25 · k 2 . Therefore, after fixing · k , f R = k · f s d .
In our empirical application, to implement the set of regressions (8), we have considered n=50 and s=25 so that all the observations from the year 2023 until April 18 have been used. The data used have a daily periodicity, so h=252. Figures 3a-3c show the estimated empirical distribution functions for the parameters ruling the model. Table 5 shows the centre of the a ~ , b ~ y σ ~ and their possible spreads for k=2,3,4 taking into account (9). Table 6 shows the observed prices of zero coupon bonds (with facial value 100) from 3 months to 20 years and the fuzzy estimations of these prices by the proposed extension to Vasicek’s model [12]. At that date, the 3-month interest rate was r0=2.877%. We can observe that despite the few parameters needed to build the model (only 3) is able to produce predictions of zero coupon bonds containing the observed prices. That is, [12] could be useful to explain term structure equilibria and to develop economic analyses that need a parametric and parsimonious estimation of yield rates.
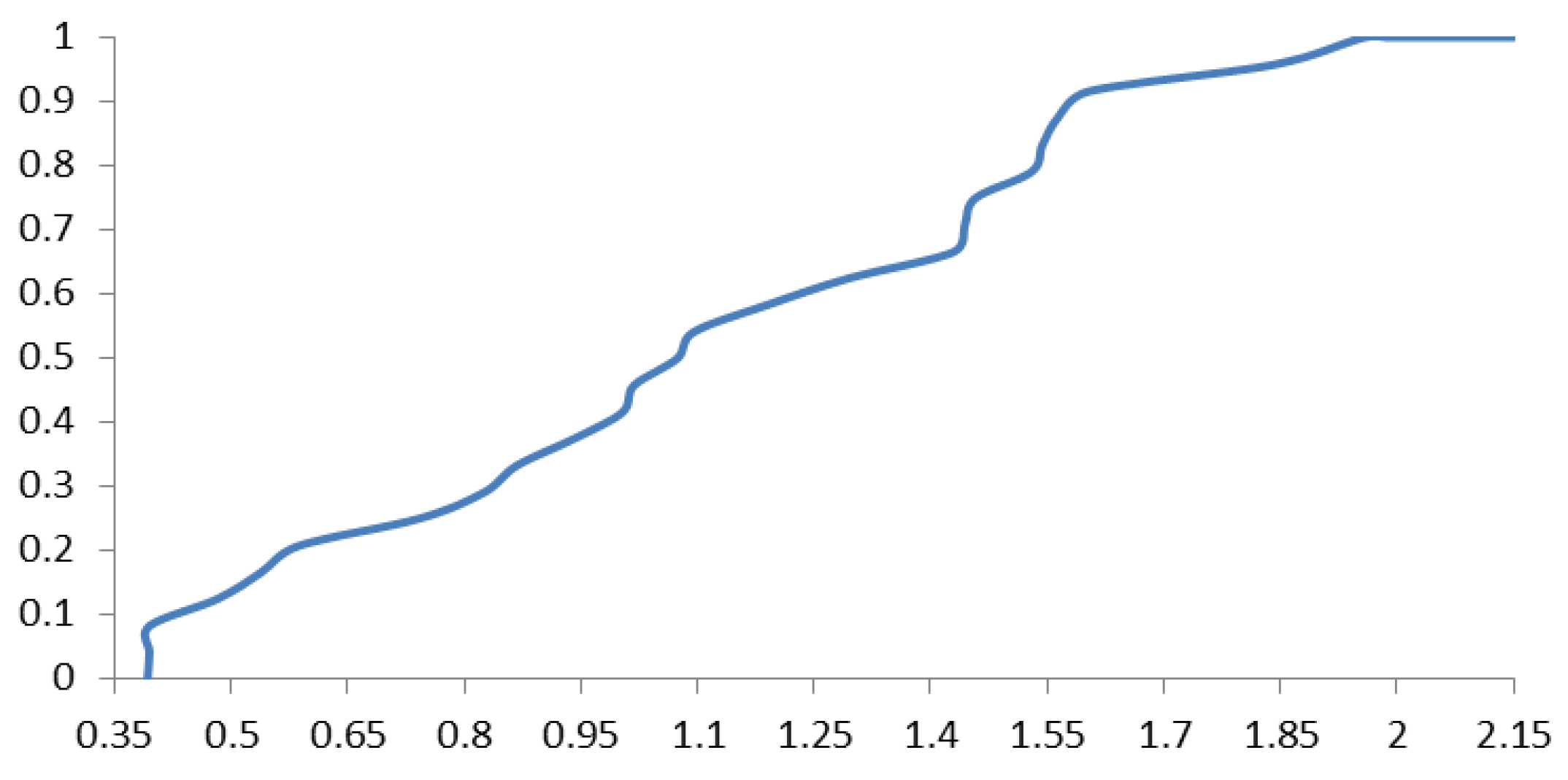
Preprints 71582 g003
Figure 3a. Empirical distribution function of the speed of adjustment rate a.
Figure 3a. Empirical distribution function of the speed of adjustment rate a.
Preprints 71582 g003
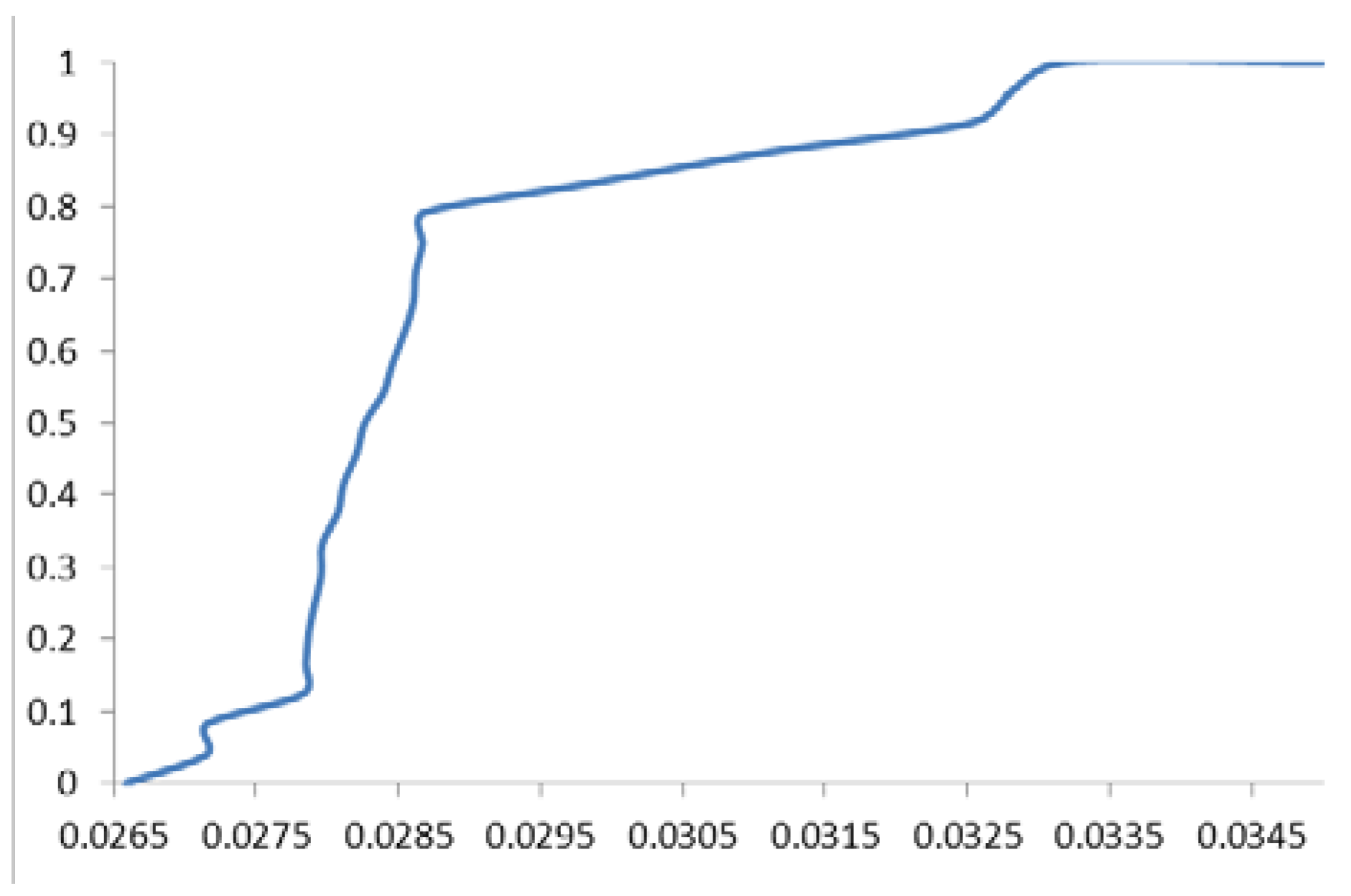
Preprints 71582 g004
Figure 3b. Empirical distribution function of the equilibrium interest rate b.
Figure 3b. Empirical distribution function of the equilibrium interest rate b.
Preprints 71582 g004
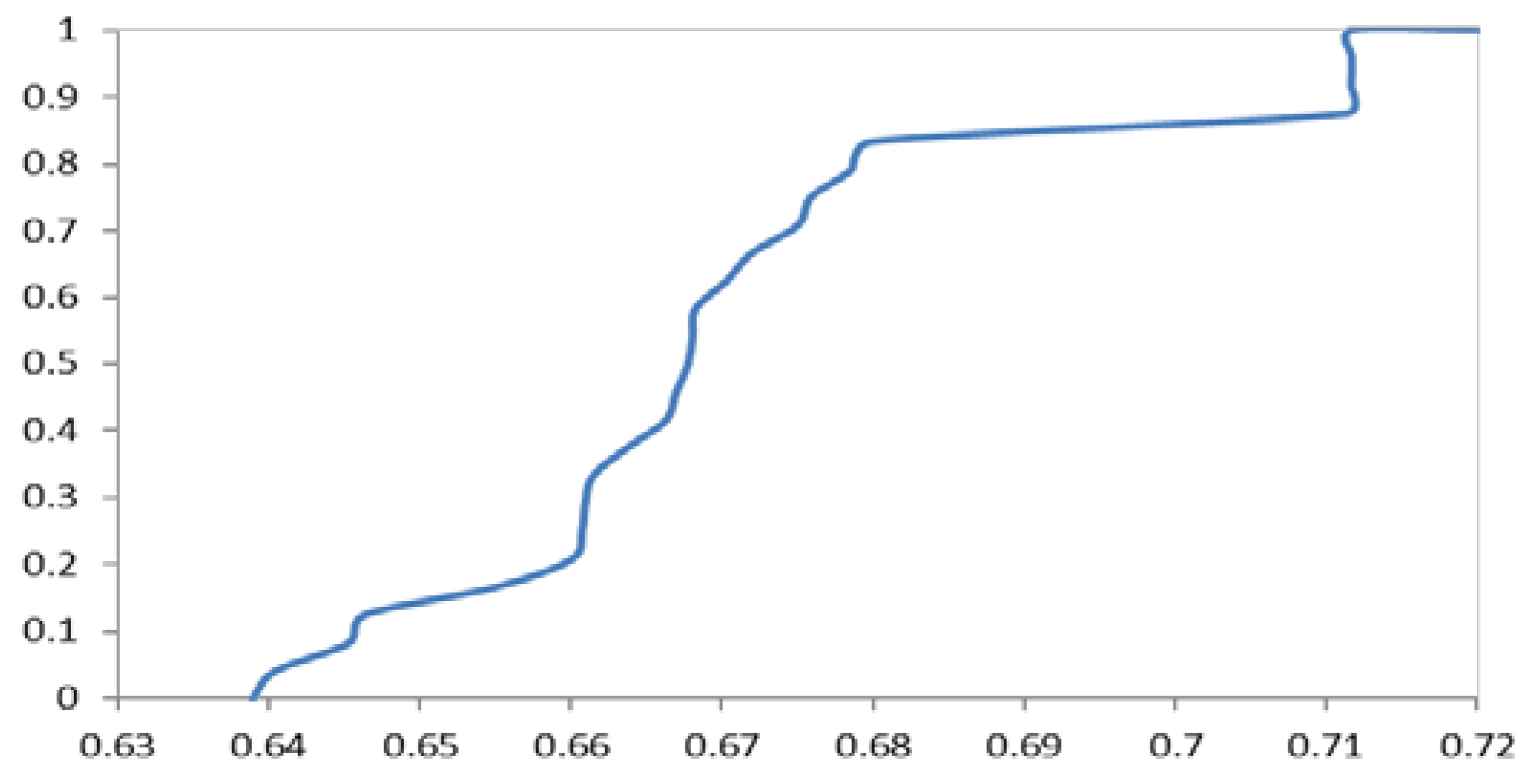
Preprints 71582 g005
Figure 3c. Empirical distribution function of the parameter σ.
Figure 3c. Empirical distribution function of the parameter σ.
Preprints 71582 g005

4. Conclusions and Further Research

This paper presents a double contribution. On the one hand, it has systematically reviewed a set of contributions that we can label as fuzzy-random option price in continuous time (FROPCT), which is the dominant approach within fuzzy option pricing [19]. On the other hand, we have extended the fuzzy-random approach to model the term structure with an equilibrium model. We have concretely extended the classical model [12] to the existence of imprecise parameters in the mean-reverting process.
We have checked that journals of soft computing and fuzzy mathematics are the most burgeoning outlets of FROPCT. However, journals devoted to the wider fields of computational mathematics and operational research have also actively published papers on FROPCT. We have checked that the contributions to FROPCT grew continuously from early 2000 to 2013. From middles 2010 contributions by literature has reached a no growing constant production in such a way that FROPCT can be labelled as a small but well stablished branch of fuzzy mathematics.
The mainstream of FROPCT models imprecise knowledge of parameters that govern subjacent random movements of subjacent assets with type-1 fuzzy numbers that are often triangular and trapezoidal. More complex forms of uncertain quantities such as type-2 fuzzy numbers or intuitionistic fuzzy numbers are rarely applied. Of course, the application of such more complex fuzzy numbers in FROPCP may be a natural and fruitful research field. However, it must also be taken into account that the introduction of these more sophisticated forms of imprecise quantities could also be a source of drawbacks. Note that defining their shape requires estimating more parameters than for conventional fuzzy numbers, and their arithmetical handle is less parsimonious in such a way that the developments of FROPCP with this type of uncertainty may be more difficult to put into practice.
The main applications of FROPCP have focused on the development of the valuation of stocks on stock and stock market indices. Most developments take as a reference the analytical framework of the Black-Scholes-Merton (BSM) formula [4,5], which is based on the consideration of a geometric Brownian motion of the subjacent asset price. However, the literature has also provided other approaches with more complex stochastic processes such as jump-diffusion [81,92,96], stochastic variance [77,79], fractional stochastic movements (e.g., [75,78,89]) or Levy-processes (e.g., [76,82,93]). The development of real options with fuzziness in the parameters has been another relevant stream of FROPCT. The reviewed developments of fuzzy real options are based on the assumption of conventional geometric Brownian motion. Thus, in the modelling of the simplest options, the FROPCT literature uses the BSM framework (e.g., [32,33]), but in the case of options on options or for compound options, the analytical frameworks that support contributions such as [26,27,29,53,60,61] are option pricing models [101,102].
The no-arbitrage approach to option valuation initiated in [3,4] has been particularly fruitful in modelling the term structure of interest rates [11,106]. Surprisingly, we have observed that developments by the FROPCT literature in this setting have been scarce, if not nonexistent. In this regard, we can outline [111] it does not use a fuzzy random approach but rather uncertain Liu processes. This lack has motivated the second contribution of the paper, in which we have extended the equilibrium model of the yield rate curve by Vasicek [12] to fuzziness in the reverting rate, long-term equilibrium short-term rate and volatility. The fuzzy-random extension of the model [12] has been applied in an empirical application in the European market for public debt bonds with the highest credit rating. We are aware that one of the main criticisms of [12] is that it allows negative interest rates that, from an economic perspective, have no meaning. However, the empirical evidence in European fixed income markets, such as that of public debt assets, contradicts this alleged disadvantage because in 2010, the internal rate of returns was consistently negative.
The empirical application developed in the European public debt market suggests that the extension of model [12] can reasonably capture the prices of zero-coupon bonds for all analysed maturities (up to 20 years) using only the fuzzy-random modelling of the 3-month interest rate as the input with a fuzzy-stochastic process with mean reversion and constant volatility. Of course, there are better alternatives to equilibrium term structure models if the only objective is to obtain the best adjustment of the yield curve. For example, econometric models usually provide better results, and some of them have been implemented with fuzzy regression [111,112]. However, in our empirical application, we were interested in demonstrating that the extension of the FROPCT in [12], which is a parsimonious parametric model, can be useful in further analytical developments, not only because of its good properties and ease of interpretation but also because it is coherent with empirical evidence.
A key aspect in the fuzzy-random modelling of asset prices is the calibration of the fuzzy parameters that govern their variation [11]. Naturally, since the parameters that govern the movements of short-term interest rates have a clear economic interpretation, it could be assumed that they can be set intuitively by experts. Alternatively, following [31,32,36,52,77,94], we can adjust the parameters that are assumed to be fuzzy numbers based on existing evidence in financial markets. Likewise, it should be noted that the existence of studies that empirically apply FROPCP developments is relatively scarce [19,20]. Both considerations motivate the parameter adjustment methodology of the mean reversion process outlined in this study. The speed of return to equilibrium, the asymptotic short-term interest rate, and the volatility are fitted using symmetric triangular fuzzy numbers that are obtained by combining the conventional autoregressive modelling of the Ornstein-Uhlenbeck process [11] and the application of a consistent probability-possibility transformation criterion [110].
A natural extension of this paper involves extending the possibility of fuzziness in the coefficients that govern the movement of interest rates to other yield curve models based on arbitrage arguments, which can be either single-factor [14,15,16,17] or multifactorial [18], and in continuous time, such as [12], or in discrete time [16,17,18]. It should be noted that while models with fixed parameters such as [12,13,14,15], which are built simply on the basis of a no-arbitrage argument, do not necessarily provide a perfect fit for the term structure, they are very useful in a wide variety of economic and financial analyses. Conversely, models referred to as consistent, with variable parameters [16,17,18], require estimating a greater number of parameters, allowing them to perfectly fit the zero-coupon yield curve existing on a particular date; however, they are less parsimonious, and their application is usually limited to the valuation of interest rate-sensitive instruments such as swaptions, options on bonds, cap and floor options, etc.

Author Contributions

This paper has uniquely one author.

Funding

This research received no external funding.

Data Availability Statement

The data used in this paper is freely available at https://www.ecb.europa.eu/home/html/index.en.html..

Conflicts of Interest

Author declare no conflict of interest.

References

  1. A Dotsis, G. (2020). Option pricing methods in the City of London during the late 19th century. Quantitative Finance, 20, 5, 709-719. [CrossRef]
  2. Zimmermann, H., & Hafner, W. (2007). Amazing discovery: Vincenz Bronzin’s option pricing models. Journal of Banking & Finance, 31, 2, 531-546. [CrossRef]
  3. Merton, R. C. (1998). Applications of option-pricing theory: twenty-five years later. The American Economic Review, 88, 3, 323-349. http://www.jstor.org/stable/116838.
  4. Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities, Journal of Political Economy, 81, 3, 637-654. http://www.jstor.org/stable/1831029.
  5. Merton, R.C. (1973). Theory of rational option pricing. The Bell Journal of Economics and Management Science, 4, Spring, 141-183. [CrossRef]
  6. Broadie, M., & Detemple, J. B. (2004). Option pricing: Valuation models and applications. Management Science, 50, 9, 1145-1177. [CrossRef]
  7. Merton, R. C. (1977). An analytic derivation of the cost of deposit insurance and loan guarantees an application of modern option pricing theory. Journal of Banking & Finance, 1, 1, 3-11. [CrossRef]
  8. Brennan, M. J., & Schwartz, E. S. (1976). The pricing of equity-linked life insurance policies with an asset value guarantee. Journal of Financial Economics, 3,3, 195-213. [CrossRef]
  9. Trigeorgis, L., & Reuer, J. J. (2017). Real options theory in strategic management. Strategic Management Journal, 38, 1, 42-63. [CrossRef]
  10. Merton, R. C. (1974). On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance, 29, 2, 449-470. [CrossRef]
  11. Chen, R. R. (1996). Understanding and managing interest rate risks (Vol. 1). World Scientific.
  12. Vasicek, O. (1977). "An equilibrium characterization of the term structure". Journal of Financial Economics. 5 (2): 177–188. CiteSeerX 10.1.1.164.447. [CrossRef]
  13. Brennan, M. J., & Schwartz, E. S. (1979). “A continuous time approach to the pricing of bonds”. Journal of Banking & Finance, 3(2), 133-155. [CrossRef]
  14. Dothan, L. U. (1978). On the term structure of interest rates. Journal of Financial Economics, 6(1), 59-69. [CrossRef]
  15. Cox, J. C., Ingersoll Jr, J. E., & Ross, S. A. (1985). An intertemporal general equilibrium model of asset prices. Econometrica, 53, 2, 363-384. [CrossRef]
  16. Ho, T. S., & Lee, S. B. (1986). Term structure movements and pricing interest rate contingent claims. The Journal of Finance, 41(5), 1011-1029.
  17. Black, F., Derman, E., & Toy, W. (1990). A one-factor model of interest rates and its application to treasury bond options. Financial Analysts Journal, 46(1), 33-39. [CrossRef]
  18. Hull, J., & White, A. (1993). One-factor interest-rate models and the valuation of interest-rate derivative securities. Journal of Financial and Quantitative Analysis, 28(2), 235-254. [CrossRef]
  19. Andrés-Sánchez, J. (2023). A systematic review of the interactions of fuzzy set theory and option pricing. Expert Systems with Applications, 223, 119868. [CrossRef]
  20. Muzzioli, S., & De Baets, B. (2016). Fuzzy approaches to option price modelling. IEEE Transactions on Fuzzy Systems, 25, 2, 392-401. [CrossRef]
  21. Cox, J., Ross, S., & Rubinstein, M. (1979). Option Pricing: A Simplified Approach. Journal of Financial Economics, 7, pp. 229-26. [CrossRef]
  22. Belle, A. B., & Zhao, Y. (2023). Evidence-based decision-making: On the use of systematicity cases to check the compliance of reviews with reporting guidelines such as PRISMA 2020. Expert Systems with Applications, 119569. [CrossRef]
  23. Zupic, I., & Čater, T. (2015). Bibliometric methods in management and organization. Organizational Research Methods, 18, 3, 429-472. [CrossRef]
  24. Andres-Sanchez, J. (2017) An empirical assessment of fuzzy Black and Scholes pricing option model in Spanish stock option market. Journal of Intelligent & Fuzzy Systems, 33, 2509-2521. [CrossRef]
  25. Andres-Sanchez, J. (2018). Pricing European Options with Triangular Fuzzy Parameters: Assessing Alternative Triangular Approximations in the Spanish Stock Option Market. International Journal of Fuzzy Systems 20, 5, 1624-1643. [CrossRef]
  26. Anzilli, L., & Villani, G. (2022). Cooperative R&D investment decisions: A fuzzy real option approach. Fuzzy Sets and Systems. [CrossRef]
  27. Anzilli, L., & Villani, G. (2021). Real R&D options under fuzzy uncertainty in market share and revealed information. Fuzzy Sets and Systems, 434, 117-134. [CrossRef]
  28. Buckley, J.J., & Eslami, E. (2008). Pricing Options, Forwards and Futures Using Fuzzy Set Theory. Fuzzy Engineering Economics With Applications, 233, 339- 357. [CrossRef]
  29. Biancardi, M., & Villani, G. (2017) A fuzzy approach for R&D compound option valuation Fuzzy Sets and Systems 310, 108-121. [CrossRef]
  30. Buckley J.J., & Eslami E., (2008) Pricing stock options using black-scholes and fuzzy sets. New Mathematics and Natural Computation, 4,02, 165-176. [CrossRef]
  31. Capotorti A., & Figà-Talamanca G. (2020) SMART-or and SMART-and fuzzy average operators: A generalized proposal. Fuzzy Sets and Systems, 395, 1-20. [CrossRef]
  32. Capotorti, A., & Figa-Talamanca, G. (2013). On an implicit assessment of fuzzy volatility in the Black and Scholes environment. Fuzzy Sets and Systems, 223, 59-71. [CrossRef]
  33. Carlsson, C., & Fuller, R. (2003). A fuzzy approach to real option valuation. Fuzzy Sets and Systems 139, 2, 297-312. [CrossRef]
  34. Carlsson, C., Heikkila, M., & Fuller, R. (2010). Fuzzy Real Options Models for Closing/Not Closing a Production Plant. Production Engineering And Management Under Fuzziness (pp. 537-560). Springer, Berlin, Heidelberg.
  35. Chen, HM., Hu, CF., & Yeh, WC. (2019). Option pricing and the Greeks under Gaussian fuzzy environments. Soft Computing, 23-24, 13351-13374. [CrossRef]
  36. Chrysafis, KA., & Papadopoulos, BK. (2009). On theoretical pricing of options with fuzzy estimators. Journal of Computational and Applied Mathematics, 223, 2, 552-566. [CrossRef]
  37. Collan M., Carlsson C., & Majlender P. (2003). Fuzzy Black and Scholes real options pricing. Journal of Decision Systems 12, 3-4, 391-416. [CrossRef]
  38. Dash, JK., Panda, S., & Panda, GB (2022). A new method to solve fuzzy stochastic finance problem Journal of Economic Studies. 49, 2, 243-258. [CrossRef]
  39. Gao, H., Ding, X.H., & Li, S.C. (2018). EPC renewable project evaluation: a fuzzy real option pricing model. Energy Sources Part B - Economics Planning and Policy, 13, 9-10, 404-413. [CrossRef]
  40. Guerra M.L., Sorini L., (2012). Incorporating uncertainty in financial models. Applied Mathematical Sciences, 6,76, 3785-3799.
  41. Guerra, ML., & Sorini, L., Stefanini, L (2011). Option price sensitivities through fuzzy numbers. Computers & Mathematics with Applications, 61, 3, 515-526. [CrossRef]
  42. Guerra, ML., Sorini, L., & Stefanini, L. (2017). Value Function Computation in Fuzzy Models by Differential Evolution. International Journal of Fuzzy Systems, 19, 4, 1025-1031. [CrossRef]
  43. Jafari, H. (2022). Sensitivity of option prices via fuzzy Malliavin calculus. Fuzzy Sets and Systems, 434, 98-116. [CrossRef]
  44. Kim, Y., & Lee, EB. (2018). Optimal Investment Timing with Investment Propensity Using Fuzzy Real Options Valuation. International Journal of Fuzzy Systems, 20, 6, 1888-1900. [CrossRef]
  45. Li H., Ware A., Di L., Yuan G., Swishchuk A., & Yuan S. (2018). The application of nonlinear fuzzy parameters PDE method in pricing and hedging European options. Fuzzy Sets and Systems, 331, 14-25. [CrossRef]
  46. Liu S., Liu E., & Huang L. (2013). Fuzzy random European call option pricing model. Journal of Theoretical and Applied Information Technology, 48, 2, 1003-1013.
  47. Liu S., Liu E., Huang L., Chai Z., & Chang Y. (2013). American option pricing in fuzzy random environment. International Journal of Applied Mathematics and Statistics, 45, 15, 111-118.
  48. Liu S., Xu W., Hou J., Zhao M., & Sun Q. (2013). Option valuation based on fuzzy theory in risk management. International Journal of Applied Mathematics and Statistics, 48,18, 414-422.
  49. Miyake, M., Inoue, H., Shi, J.M., & Shimokawa, T. (2014). A Binary Option Pricing Based on Fuzziness. International Journal Of Information Technology & Decision Making. 13,6,1211-1227. [CrossRef]
  50. Muzzioli, S., Gambarelli, L., & De Baets, B. (2018). Indices for Financial Market Volatility Obtained Through Fuzzy Regression. International Journal Of Information Technology & Decision Making, 17, 6, 1659-1691. [CrossRef]
  51. Muzzioli, S., Gambarelli, L., & De Baets, B. (2020). Option implied moments obtained through fuzzy regression. Fuzzy Optimization and Decision Making, 19, 2, 211-238. [CrossRef]
  52. Muzzioli, S., Ruggieri, A., & De Baets, B. (2015). A comparison of fuzzy regression methods for the estimation of the implied volatility smile function. Fuzzy Sets and Systems, 266, 131-143. [CrossRef]
  53. Tang W., Cui Q., Zhang F., & Chen Y. (2019). Urban Rail-Transit Project Investment Benefits Based on Compound Real Options and Trapezoid Fuzzy Numbers. Journal of Construction Engineering and Management, 145, 1, 05018016.
  54. Teran, P. (2006). A note on Yoshida's optimal stopping model for option pricing. European Journal of Operational Research, 170, 2, 672-676. [CrossRef]
  55. Thavaneswaran, A., Appadoo, S.S., & Frank, J. (2013). Binary option pricing using fuzzy numbers. Applied Mathematics Letters, 26,1,65-72. [CrossRef]
  56. Thavaneswaran, A., Appadoo, S.S., & Paseka, A. (2009). Weighted possibilistic moments of fuzzy numbers with applications to GARCH modelling and option pricing. Mathematical and Computer Modelling, 49, 1-2, 352-368. [CrossRef]
  57. Thiagarajah, K., Appadoo, S.S., & Thavaneswaran, A. (2007). Option valuation model with adaptive fuzzy numbers. Computers & Mathematics with Applications, 53, 5, 831-841. [CrossRef]
  58. Tolga, A. Ç., Kahraman, C., & Demircan, M. L. (2010). A Comparative Fuzzy Real Options Valuation Model using Trinomial Lattice and Black-Scholes Approaches: A Call Center Application. Journal of Multiple-Valued Logic & Soft Computing, 16, 1-2, 135-154.
  59. Tolga,A.C. (2020). Real options valuation of an IoT based healthcare device with interval Type-2 fuzzy numbers. Socio-Economic Planning Sciences, 69, 100693. [CrossRef]
  60. Wang, X.D., He, J.M., & Li, S.W. (2014). Compound Option Pricing under Fuzzy Environment. Journal Of Applied Mathematics, 2014, 875319. [CrossRef]
  61. Wang Q., Hipel K.W., & Kilgour D.M. (2009). Fuzzy real options in brownfield redevelopment evaluation. Journal of Applied Mathematics and Decision Sciences, 2009. 817137. Margrabre. [CrossRef]
  62. Wu, HC. (2005). European option pricing under fuzzy environments. International Journal of Intelligent Systems, 20, 1, 89-102. [CrossRef]
  63. Wu, H.C. (2004). Pricing European options based on the fuzzy pattern of Black-Scholes formula. Computers & Operations Research, 31, 7, 1069-1081. [CrossRef]
  64. Wu, HC. (2007). Using fuzzy sets theory and Black-Scholes formula to generate pricing boundaries of European options. Applied Mathematics and Computation,185,1, 136-146. [CrossRef]
  65. Wu, SL., Yang, S.G., Wu, Y.F., & Zhu, S.Z. (2020). Interval Pricing Study of Deposit Insurance in China. Discrete Dynamics in Nature and Society, 2020, 1531852. [CrossRef]
  66. Xu, J.X., Tan, Y.H., Gao, J.G., & Feng, E.M. (2013). Pricing Currency Option Based on the Extension Principle and Defuzzification via Weighting Parameter Identification. Journal of Applied Mathematics, 2013, 623945 . [CrossRef]
  67. Wu, L., Liu, J.F., Wang, J.T., & Zhuang, Y.M. (2016). Pricing for a basket of LCDS under fuzzy environments. SpringerPlus, 5, 1747. Intuicionistico. Merton. [CrossRef]
  68. Wu, L., Mei, X.B., & Sun, JG. (2018). A New Default Probability Calculation Formula an Its Application under Uncertain Environments. Discrete Dynamics in Nature and Society, 2018, 3481863. Introduce fuzziness in interests rates: r borroso pero los parámentros CIR son ciertos. Borrosos triangulares. [CrossRef]
  69. Xu, W.J., Xu, W.D., Li, H.Y., & Zhang, W.G. (2010). A study of Greek letters of currency option under uncertainty environments. Mathematical and Computer Modelling, 51, 5-6, 670-681. [CrossRef]
  70. Yoshida, Y. (2003). The valuation of European options in uncertain environment. European Journal of Operational Research, 145,1,221-229. [CrossRef]
  71. Yoshida, Y., Yasuda, M., Nakagami, J.I., & Kurano, M. (2006). A new evaluation of mean value for fuzzy numbers and its application to American put option under uncertainty. Fuzzy Sets and Systems, 157, 19, 2614-2626. [CrossRef]
  72. Zhang, W.G., Shi, Q.S., & Xiao, W.L. (2011). Fuzzy Pricing of American Options on Stocks with Known Dividends and Its Algorithm. International Journal of Intelligent Systems, 26, 2,169-85. [CrossRef]
  73. Zhang, W.G., Xiao, W.L., Kong, W.T., & Zhang, Y. (2015). Fuzzy pricing of geometric Asian options and its algorithm. Applied Soft Computing, 28, 360-367. [CrossRef]
  74. Zmeskal, Z. (2001). Application of the fuzzy-stochastic methodology to appraising the firm value as a European call option. European Journal of Operational Research, 135, 2, 303-310. [CrossRef]
  75. Bian, L., & Li, Z. (2021). Fuzzy simulation of European option pricing using subfractional Brownian motion. Chaos Solitons & Fractals, 153, 111442. [CrossRef]
  76. Feng, Z.Y., Cheng, J.T.S., Liu, Y.H., & Jiang, I.M. (2015). Options pricing with time changed Levy processes under imprecise information. Fuzzy Optimization and Decision Making, 65, 8, 2348-2362. [CrossRef]
  77. Figa-Talamanca, G., Guerra, M.L., & Stefanini, L. (2012). Market Application of the Fuzzy-Stochastic Approach in the Heston Option Pricing Model. Finance a Uver-Czech Journal of Economics and Finance. 62, 2, 162-179. [CrossRef]
  78. Ghasemalipour, S., & Fathi-Vajargah, B. (2019). Fuzzy simulation of European option pricing using mixed fractional Brownian motion. Soft Computing, 23, 13205–13213. [CrossRef]
  79. Lia, H., Wareb, A., & Swishchukb, A. (2012). Nonlinear PDE approach for option pricing with stochastic volatility by using fuzzy sets theory. Journal of Theoretical and Applied Information Technology, 45, 2, 508-514. [CrossRef]
  80. Liu, K., Chen, J., Zhang, J., & Yang, Y. (2023). Application of fuzzy Malliavin calculus in hedging fixed strike lookback option. AIMS Mathematics, 8(4), 9187-9211. [CrossRef]
  81. Liu, W.Q., & Li, S.H. (2013). European option pricing model in a stochastic and fuzzy environment. Applied Mathematics-a Journal Of Chinese Universities Series B, 28, 3, 321-334. [CrossRef]
  82. Nowak, P., & Pawlowski, M. (2017). Option Pricing With Application of Levy Processes and the Minimal Variance Equivalent Martingale Measure Under Uncertainty. IEEE Transactions on Fuzzy Systems, 25, 2, 402-416. [CrossRef]
  83. Nowak, P., & Pawlowski, M. (2019). Pricing European options under uncertainty with application of Levy processes and the minimal L-q equivalent martingale measure. Journal of Computational and Applied Mathematics, 345, 416-433. [CrossRef]
  84. Nowak, P., & Pawłowski, M. (2023). Application of the Esscher Transform to Pricing Forward Contracts on Energy Markets in a Fuzzy Environment. Entropy, 25(3), 527. ; [CrossRef]
  85. Nowak, P., & Romaniuk, M. (2010). Computing option price for Levy process with fuzzy parameters. European Journal of Operational Research, 201, 1, 206-210. [CrossRef]
  86. Nowak, P., & Romaniuk, M. (2013). A fuzzy approach to option pricing in a Levy process setting. International Journal of Applied Mathematics and Computer Science, 23, 3, 613-622. [CrossRef]
  87. Nowak, P., & Romaniuk, M. (2014). Application of Levy processes and Esscher transformed martingale measures for option pricing in fuzzy framework. Journal of Computational and Applied Mathematics, 263, 129-151. [CrossRef]
  88. Nowak, P., & Romaniuk, M. (2017). Catastrophe bond pricing for the two-factor Vasicek interest rate model with automatized fuzzy decision making. Soft Computing, 21, 2575-2597. [CrossRef]
  89. Qin, X.Z., Lin, X.W., & Shang, Q. (2020). Fuzzy pricing of binary option based on the long memory property of financial markets. Journal Of Intelligent & Fuzzy Systems, 38, 4, 4889-4900. [CrossRef]
  90. Wang, T., Zhao, P.P., & Song, AM. (2022). Power Option Pricing Based on Time-Fractional Model and Triangular Interval Type-2 Fuzzy Numbers. Complexity, 2022, 5670482. [CrossRef]
  91. Wang, X.D., & He, J.M. (2016). A geometric Levy model for n-fold compound option pricing in a fuzzy framework. Journal of Computational and Applied Mathematics, 306, 248-264. [CrossRef]
  92. Xu, W.D., Wu, C.F., Xu, W.J., & Li, H.Y. (2009). A jump-diffusion model for option pricing under fuzzy environments. Insurance Mathematics & Economics, 44, 3, 337-344. [CrossRef]
  93. Zhang, H.M., & Watada, J. (2018). A European call options pricing model using the infinite pure jump levy process in a fuzzy environment. IEEJ Transactions on Electrical and Electronic Engineering, 13, 10, 1468-1482. [CrossRef]
  94. Zhang, H.M., & Watada, J. (2018). Fuzzy Levy-GJR-GARCH American Option Pricing Model Based on an Infinite Pure Jump Process. IEICE Transactions on Information and Systems, E101D, 7, 1843-1859. [CrossRef]
  95. Zhang, J.K., Wang, Y.Y., & Zhang, S.M. (2022). A New Homotopy Transformation Method for Solving the Fuzzy Fractional Black-Scholes European Option Pricing Equations under the Concept of Granular Differentiability. Fractal and Fractional, 6, 6, 286. [CrossRef]
  96. Zhang, L.H., Zhang, W.G., Xu, W.J., & Xiao, W.L. (2012). The double exponential jump diffusion model for pricing European options under fuzzy environments. Economic Modelling, 29, 3, 780-786. [CrossRef]
  97. Zhang, W.G., Li, Z., Liu, Y.J., & Zhang, Y. (2021). Pricing European Option Under Fuzzy Mixed Fractional Brownian Motion Model with Jumps. Computational Economics, 58, 2, 483-515. [CrossRef]
  98. Zhao, P.P., Wang, T., Xiang, K.L., Chen, P.M. (2022). N-Fold Compound Option Fuzzy Pricing Based on the Fractional Brownian Motion. International Journal of Fuzzy Systems, 24, 6, 2767-2782. [CrossRef]
  99. Garman, M. B., & Kohlhagen, S. W. (1983). Foreign currency option values. Journal of International Money and Finance, 2,3, 231-237. [CrossRef]
  100. A.G.Z. Kemma, A.C.F. Vorst, A pricing method for options based on average asset values, J. Bank. Financ. 4 (1990) 121–168.
  101. Margrabe, W. (1978) The value of an exchange option to exchange one asset for another, Journal of Finance, 33 ,1, 177–186. [CrossRef]
  102. Geske, R. The valuation of compound options, Journal of Financial Economics, 7 (1979): 63-81.
  103. Merton, R. C. (1976). Option pricing when underlying stock returns are discontinuous. Journal of Financial Economics, 3(1-2), 125-144. [CrossRef]
  104. Heston, S.L. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. The Review of Financial Studies, 6,2, 327-343. [CrossRef]
  105. Dubois, D., Folloy, L., Mauris, G., & Prade, H. (2004). Probability–possibility transformations, triangular fuzzy sets, and probabilistic inequalities, Reliability Computing, 10, 273–297. [CrossRef]
  106. Hull, J.C. (2008). Options futures and other derivatives. Pearson Education India.
  107. Longstaff, F. A., & Schwartz, E. S. (1993). Interest rate volatility and bond prices. Financial Analysts Journal, 49(4), 70-74. [CrossRef]
  108. Buckley, J.J., & Qu, Y. (1990). On using α-cuts to evaluate fuzzy equations. Fuzzy Sets and Systems, 38 ,3, 309–312. [CrossRef]
  109. Buckley, J.J., & Feuring, T. (2000). Fuzzy differential equations. Fuzzy Sets and Systems, 110,1, 43-54. [CrossRef]
  110. Dubois, D., Folloy, L., Mauris, G., & Prade, H. (2004). Probability–possibility transformations, triangular fuzzy sets, and probabilistic inequalities, Reliability Computing, 10, 273–297. [CrossRef]
  111. Bo, L., You, C. (2020). Fuzzy Interest Rate Term Structure Equation. Int. J. Fuzzy Syst. 22, 999–1006 . [CrossRef]
  112. Shapiro, A. F. (2004, November). Fuzzy regression and the term structure of interest rates revisited. In Proceedings of the 14th international AFIR colloquium (Vol. 1, pp. 29-45).
  113. Andres-Sanchez, J., & Gómez, A.T. (2003). Estimating a term structure of interest rates for fuzzy financial pricing by using fuzzy regression methods. Fuzzy Sets and Systems, 139(2), 313-331. [CrossRef]
Preprints 71582 g001
Figure 1. Protocol used to select articles on FROP and FROPCT for review..
Figure 1. Protocol used to select articles on FROP and FROPCT for review..
Preprints 71582 g001
Preprints 71582 g002
Figure 2. Evolution of the papers on fuzzy-random option pricing in continuous time published during 2003-2023.
Figure 2. Evolution of the papers on fuzzy-random option pricing in continuous time published during 2003-2023.
Preprints 71582 g002
Table 1. Revised papers on fuzzy stochastic option pricing in continuous time.
Table 1. Revised papers on fuzzy stochastic option pricing in continuous time.
Log-normal (BSM) Log-normal (more than one asset) Other Brownian processes Jump-diffusion Heston Fractional Levy
All revised papers [24,25,28,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,54,55,56,57,58,59,62,63,64,65,66,67,68,69,70,71,72,73,74] [26,27,29,53,60,61] [67,80] [81,92,96] [77,79] [75,78,89,90,95,97,98] [76,82,83,84,85,86,87,88,91,93,94]
Fuzzy numbers of higher degree [59,66] [67] [90]
Non-European options [47,49,55,71,72,73] [26,27,29,53,60,61] [89,90] [91,94,98]
Hedging [35,36,41,43,46,69] [80]
Application to financial markets [31,32,50,51,52] [77] [93,94]
Real Options [33,34,37,39,45,58,59] [26,27,29,53,60,61] [80]
Other financial applications [65,66,74] [67] [88,94]
Table 2. Principal outlets of fuzzy random option pricing in continuous time.
Table 2. Principal outlets of fuzzy random option pricing in continuous time.
Journal Number of items
Fuzzy Sets and Systems 10
Journal of Computational and Applied Mathematics 4
International Journal of Fuzzy Systems 4
European Journal of Operational Research 4
Soft Computing 3
IEEE Transactions on Fuzzy Systems 2
Fuzzy Optimization and Decision Making 2
Journal of Intelligent & Fuzzy Systems 2
Computers & Mathematics with Applications 2
Discrete Dynamics in Nature and Society 2
International Journal of Information Technology & Decision Making 2
International Journal of Intelligent Systems 2
International Journal of Applied Mathematics and Statistics 2
Journal of Applied Mathematics 2
Table 5. Estimates of a ~ , b ~ and σ ~ on April 18th, 2023.
Table 5. Estimates of a ~ , b ~ and σ ~ on April 18th, 2023.
k a ^ b ^ σ ^
mean 1.117 0.02882 0.0067075
std. dev. 0.245 0.00174 0.0002121
a ~ b ~ σ ~
centre 1.117 0.02882 0.0067075
2 spread 0.491 0.00349 0.0004242
3 spread 0.736 0.00523 0.0006363
4 spread 0.982 0.00697 0.0008484
Table 6. Spot prices of zero coupon bonds with face value 100 monetary units on April 18th, 2023, in the European Union public debt market and α-cuts of the estimates (α=0,0.5,1) with fuzzy Vasicek’s model.
Table 6. Spot prices of zero coupon bonds with face value 100 monetary units on April 18th, 2023, in the European Union public debt market and α-cuts of the estimates (α=0,0.5,1) with fuzzy Vasicek’s model.
Estimated by Vasicek’s model
Observed 1-cut 0.5-cut 0-cut
T P 0 , T P 0 , T 1 P 0 , T _ 0.5 P 0 , T ¯ 0.5 P 0 , T _ 0 P 0 , T ¯ 0
3 months 99.29 99.28 99.27 99.29 99.25 99.29
1 year 97.04 97.16 97.00 97.26 96.79 97.28
2 years 94.62 94.40 93.96 94.72 93.44 94.81
3 years 92.57 91.72 90.98 92.31 90.16 92.52
4 years 90.56 89.12 88.09 89.98 86.99 90.37
5 years 88.49 86.59 85.29 87.72 83.93 88.32
6 years 86.36 84.13 82.58 85.53 80.98 86.35
7 years 84.20 81.74 79.96 83.39 78.14 84.45
8 years 82.02 79.42 77.42 81.31 75.39 82.61
9 years 79.86 77.17 74.96 79.28 72.74 80.82
10 years 77.73 74.98 72.57 77.30 70.18 79.07
11 years 75.64 72.85 70.27 75.37 67.72 77.37
12 years 73.61 70.78 68.03 73.48 65.34 75.70
13 years 71.64 68.77 65.87 71.65 63.04 74.08
14 years 69.73 66.82 63.78 69.86 60.82 72.49
15 years 67.90 64.92 61.75 68.12 58.69 70.93
16 years 66.13 63.08 59.79 66.41 56.62 69.41
17 years 64.44 61.29 57.89 64.76 54.63 67.93
18 years 62.82 59.55 56.05 63.14 52.71 66.47
19 years 61.27 57.86 54.27 61.56 50.86 65.05
20 years 59.79 56.22 52.54 60.03 49.07 63.65
Note: The spread of parameters used in the estimation of prices has been stated with k=4. Likewise, the 3-month rate at that date was 2.877%.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated