Preprint
Article
Phase Field Modeling of Crack Growth with Viscoplasticity
Altmetrics
Downloads
161
Views
45
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 April 2023
Posted:
24 April 2023
You are already at the latest version
Alerts
Abstract
Fracture of viscoplastic materials is a complex process due to its time-dependent and plastic responses. Numerical simulation for fracture plays a significant role in crack prediction and failure analysis. In recent years, the phase field model is becoming a competitive approach to predict crack growth and has been extended to inelastic materials such as elasto-plastic, viscoelastic and viscoplastic materials, etc. However, the contribution of inelastic energy to crack growth is seldom studied. For this reason, we implement the phase field model coupled with a viscoplastic constitutive in finite element framework, in which the elastic energy and inelastic energy are used as crack driving energy. The implicit algorithm for a viscoplastic constitutive is presented, this procedure is suitable for other viscoplastic constitutive relations. The strain rate effect, creep effect, stress relaxation effect and cyclic loading responses are tested using a single element model with different inelastic energy contributions; A titanium alloy plate specimen and a stainless-steel plate specimen under tension are studied compared with the experimental observations in existing literature. The results show that the above typical damage phenomenon and fracture process can be well reproduced; The inelastic energy significantly affects the force-displacement responses but has slight effect on the crack paths.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Numerical simulation methods for fracture failure can be generally classified into two categories: discrete and continuum approaches [1] depending on how to describe the interfacial discontinuity. The former includes cohesive element [2], node splitting [3] and hybrid discrete finite element method [4], etc. These methods require additional crack initiation and growth criteria. In the finite element framework, the displacement is discontinuous at the cracking locations, thus the crack will propagate along or between elements, which leads to a mesh-dependent crack path [5]. To overcome this problem, XFEM [6,7] and some re-meshing strategies [8,9] were developed; However, tracking complicated fracture surfaces is still a difficult task in numerical computations [10]. The continuum approaches such as GTN model [11], Lemaitre damage model [12] and gradient damage model [13] are widely used for simulating ductile fracture. While the continuum methods cannot describe crack propagation phase after damage localization, the crack propagation phase is still dealt with by discrete methods, for instance, re-meshing or embedding techniques [14], meanwhile the continuum approaches usually need to calibrate many model parameters [15].
As a competitive method to simulate cracking processes, the phase field model has attracted widespread attention for nearly two decades. This diffuse crack model has advantages in predicting complex topologies including crack branching, coalescence, or 3D crack paths. The phase field model origins from the Griffith’s [16] energy theory of fracture. But Griffith’s theory was unable to predict crack initiation, path jumping or branching. Francfort and Marigo [17] proposed a variational approach to overcome this problem, and then Bourdin [18] regularized this approach. Also the extension to fracture simulations in inelastic materials such as elasto-plastic materials [1,5,10,19], viscoelastic materials [20,21,22], and viscoplastic materials [23,24] has been studied. Borden et al. [25] first introduced two weight parameters to control the contribution of elastic energy and plastic energy to crack growth in a rate-independent phase field model. Hojjat et al. [23] presented a rate-dependent ductile phase field model incorporating these two weight parameters. However, they did not discuss the influence of the weight parameters on fracture behavior, and two weight parameters are more complex to be calibrated. Shen et al. [20] modified the phase field model for fracture of viscoelastic solid, in which only one weight parameter was used to quantify the viscos crack driving energy. The weight parameter is considered to reflect the influence of temperature, humidity and aging on material damage implicitly. And the influence of the weight parameter on viscoelastic fracture response was studied. Nevertheless, the value of weight parameter has not been calibrated against relevant experiments.
Therefore, based on the existing researches, we implemented the phase field model incorporating viscoplastic constitutive, in which one weight parameter is used to control the inelastic energy that contributes to crack growth. The structure of this paper is as follows: Section 2 presents the viscoplastic phase field model and numerical algorithm. Section 3 provides some numerical examples of few typical viscos tests and two metal plate specimens to discuss the effect of inelastic energy contributions on fracture response of viscoplastic solid. Section 4 gives some conclusions.
2. Viscoplastic phase field model
2.1. Viscoplastic constitutive
To simplify the illustration, the uniaxial tensile state is taken as an example. The uniaxial stress considering viscoplasticity is defined as [26]
where is the yield stress, is the hardening stress, and the effective plastic strain rate . and are material constants related to the viscous behavior.
By rearranging Eq. (1), the expression of can be given
In viscoplasticity, Eq. (2) is used to replace the consistency condition in time-independent plasticity. For a von-Mises material, the normality hypothesis is written as
Here is the inelastic strain (including plastic strain and viscos strain) rate tensor, the yield function is
where is the von-Mises stress.
Substituting Eq. (4) into Eq. (3) gives,
in which is the deviatoric stress tensor.
The Hooke’s law in terms of the elastic strain rate tensor is written as
in which G is the shear modulus, the Lame constant. In viscoplasticity, the strain decomposition still holds
Here is the total strain rate tensor, is the elastic strain rate tensor.
2.2. Viscoplastic phase field model
Figure 1 shows an arbitrary domain with external boundary .
Here is the surface traction, applied on the Neumann boundary, is the displacement constraint, applied on the Dirichlet boundary. in Figure 1(a) represents a set of discrete cracks. The diffuse approximation of the crack through a phase field d is depicted in Figure 1(b), where the value d = 0 indicates intact material, d = 1 represents broken material. is the length scale parameter. The total energy functional for viscoplastic materials can be written as
where the second integral of the right side is the approximation of fracture energy. is elastic strain energy density, is the inelastic strain energy density, is the elastic strain tensor. is the critical energy release rate. is the stiffness degradation function. A common form is , in which k is a tiny value to keep a residual stiffness in fully broken conditions.
According to the minimizing of the total energy functional
The stress equilibrium equation and the phase field governing equation are given
In order to control the state at which the inelastic energy starts to drive the crack growth, the energy density threshold is introduced. is a parameter to weight the contribution of inelastic energy to fracture. The Macaulay bracket operators are defined as
To prevent the crack healing due to elastic energy release, The elastic history field is introduced by Miehe et al. [27]
where denotes the time in a loading process. Since the inelastic energy is monotonically increasing, it does not need to consider the crack growth irreversibility. Therefore, the history field in this paper is expressed as,
Substituting Eq. (13) into Eq. (10), the phase field governing equation turns into,
2.3. Implicit Integration for Viscoplasticity
Here we implement the implicit integration for linear isotropic hardening viscoplasticity with the radial return implicit backward Euler integration method. Regardless of the temperature effect, the sinh-type viscoplastic constitutive equation can be written as [26],
and are material constants. In order to implement the viscoplastic constitutive in incremental form using for Newton’s iterative solution. Eq. (15) is taken to be a function of hardening stress and equivalent inelastic strain increment , which is given by,
All quantities are given at the end of each time increment, that is at time . The procedure of updating stresses and strains of viscoplasticity is as follows.
(Ⅰ).Calculate the elastic trial stress
(Ⅱ).Check for viscoplastic flow
(Ⅲ). Solve the effective inelastic strain increment by Newton-Raphson iterative method
If the yielding is not active, .
(Ⅳ).Update inelastic strain, elastic strain and undegraded stress increment tensors
(Ⅴ).Update undegraded stress tensors and effective inelastic strain and degraded stress tensors
(Ⅵ).Exit
2.4. Numerical implementation
Algorithmically, solving phase field problem can be classified into monolithic and staggered methods [28]. The monolithic method is more efficient while the staggered method has proved to be more robust [30]. In order to get a better convergence for viscoplastic fracture problem, we adopted the staggered method to solve the phase field problem. Finite element spatial discretization is given as below
where and are the shape functions associated with node i, and are the corresponding values at node i. is the number of nodes of element. Taking derivative of and
where and are the gradient operators of the shape functions. The test functions and corresponding derivatives are given by
According to the previous definitions, the residual vectors of equilibrium equation and phase field evolution equation are expressed as
The Newton iteration equations is written as
where
Since the tangential stiffness only affect the convergence rate [25] but does not affect the solution accuracy, and generally, the explicit expression of Jacobian is hard to obtained for viscoplastic constitutive. Hence the elastic stiffness is used for simplicity. The above equations are implemented in Abaqus subroutines UEL and UMAT using Fortran language. Some implementation details can be found in [10,28,29,31].
3. Numerical examples
3.1. Viscoplastic test of unbroken model
In this section, a single element is modeled to study the effect of β on crack driving energy and phase field evolution. The model is 1 × 1 × 1 mm element as shown in Figure 2. The axial displacement load and constraint are applied on the bottom and top surface respectively. Table 1 shows the material and phase field parameters.
3.1.1. Strain rate test
Viscoplasticity describes the rate-dependent behavior of materials, and the strain rate affects the mechanical response of viscoplastic solid. Thus, in this subsection, four strain rate loads are selected to illustrate the rate-dependent behavior with the presented phase field model. The stress-strain and phase field-strain relations under different strain rate loads for β=0.1 and β=0.3 are shown in Figure 3 and Figure 4. Comparing Figure 3(a) with Figure 4(a), the stress-strain curve becomes greater with increasing strain rate, which exhibits obvious viscoplastic characteristic. A larger value of β may causes greater damage to the stress, resulting from larger inelastic energy contribution. In Figure 3(b) with Figure 4(b), the phase field curve increases with the increasing strain rate. That’s because higher stress may cause more driving energy to be produced under the same strain condition, then resulting in greater damage.
3.1.2. Creep test
In the creep test, a force load is applied to the top of the model from zero to a fixed value within the first 100s and then stay constant. Figure 5a,b show the curves of axial strain and phase field versus time for different values of β. The strain increases gradually under a constant force load, which is usually called creep phenomenon. The axial strain and phase field increase with the increase of . The model tends to be fully broken when .
In this creep process, the force does work on the model continually, resulting in continuous phase field evolution. In order to show the evolution of driving energies, we plotted the elastic driving energy , inelastic driving energy and total driving energy , which are defined as below
The evolution curves of driving energies for and are plotted in Figure 6a,b. There is little difference between the elastic driving energies. Whereas the inelastic driving energy for is significantly larger than that for . For , the inelastic energy surpasses the elastic energy in a relatively long time (about 250s); however, for , the inelastic energy surpasses the elastic energy in a relatively short time (about 180s). This means that a larger value of can accelerate the phase field evolution. Whether or , once the inelastic energy begins to accumulate, it grows significantly faster than elastic energy. It indicates that the inelastic energy is dominant in driving phase field evolution.
3.1.3. Stress relaxation test
The response of stress relaxation is tested in this subsection. The displacement load increases from zero to a fixed value within the first 100s and then stay constant. Figure 7a,b show the curves of axial stress and phase field evolution with time for different values of . Figure 8a,b show the corresponding driving energies evolution curves. In Figure 7(a), within the first 100s, the axial stresses increase rapidly in the elastic stage and then yield with the increase of displacement. In the stage where the displacement remains constant, the stress decreases gradually to a finite value, this phenomenon is called stress relaxation. In this process, part of the elastic strain converts to inelastic strain, the elastic energy decreases and the inelastic energy increases which can be observed in Figure 8a,b. The history field will increase as the inelastic energy increases, correspondingly, the phase field also increases after 100s which can be seen in Figure 7(b). Additionally, large value of causes greater damage, it is due to that more inelastic energy contributes to the phase field evolution.
3.1.4. Cyclic load test
Sinusoidal displacement loads of low and high frequency are applied to the single element model. and are selected, the simulation durations are 1000s and 1s, and the load curves are shown in Figure 9. The axial strains and phase field evolution with time subjected to low and high frequency cyclic loads for different values of are plotted in Figure 10 and Figure 11. For this single element model subjected to displacement-controlled load, the axial strain is not affected by , therefore the elastic and inelastic strains only for are plotted as a representative in Figure 10(a) and Figure 11(a). When loading, the driving energy increases to exceed the previous history field, the phase field will increase continually, whereas the phase field remains unchanged when unloading, which is controlled by the irreversibility. Comparing Figure 10(a) with Figure 11(a), the inelastic strain of the model under low frequency cyclic load is larger than that under high frequency cyclic load, that’s because the viscoplastic response has more time to develop for low frequency. Comparing Figure 10(b) with Figure 11(b), a larger value of can produce more inelastic driving energy, then leads to greater damage. And the effect of β on phase field evolution is more significant for low frequency cyclic load.
The elastic, inelastic and total driving energies are plotted for low frequency and high frequency cyclic load respectively in Figure 12a,b. Under low frequency cyclic load,the inelastic energy is larger than elastic energy, the inelastic energy plays a dominant role in driving phase field evolution; whereas under high frequency cyclic load, the inelastic energy is smaller than elastic energy, the elastic energy plays a dominant role in driving phase field evolution.
3.2. Stainless-steel plate tensile test
In this section, the fracture of a stainless-steel plate specimen with thickness of 1.5mm is studied using the presented phase field model. The tensile experiment used for comparison is taken from literature [33]. The specimen was produced by additive manufacturing method using the austenitic stainless-steel 316L powder. The material and phase field parameters of the specimen are given in Table 2. The geometry and finite element discretization are illustrated in Figure 13. The effective element size in the area of crack growth is 0.1mm. The displacement loading rate is 2×10-3mm/s. The reaction force curves for different values of are plotted in Figure 14, in which the curve for agrees well with the experimental result, and a large value of can accelerate the fracture process. Figure 15 shows the final crack paths of the specimen for different values of . It is observed that the crack paths for different values of are similar, has no influence on crack path for this stainless-steel plate specimen.
3.3. Titanium alloy plate tensile test
In order to illustrate the influence of β in the present phase field model on crack growth. The fracture behavior of a thin titanium alloy plate under tension load is studied in this subsection. The experiment of this specimen was presented by Verleysen et al. [34]. The material and phase field parameters of titanium alloy Ti6Al4V are shown in Table 3. The geometry and mesh of the specimen are depicted in Figure 16, in which the left end is fixed and the displacement load is imposed on the right end. The thickness of the specimen is 0.6mm. The geometry is meshed using 12280 brick reduced integration elements. The effective size of the elements in the refined region is 0.06mm. The average strain rate of loading is 360/s.
The force-displacement curves of the titanium alloy plate specimen for different values of are shown in Figure 17. With the increase of parameter , the force drops faster after reaching the maximum force. For , the force-displacement curve matches the experiment result. Figure 18(a) shows the crack paths of the titanium alloy plate specimen for different values of , in which the red color indicates crack. The cracks start from the middle of the specimen, then propagate perpendicular to the loading direction (this section of the crack is named straight crack), finally develop diagonally to rupture (this section of the crack is named inclined crack). The length of the straight crack increase with the increasing . The angle between the inclined crack and loading direction is 55.2°, it is very close to the angle 54.7° of the inclined crack obtained in the experimental observation.
4. Conclusions
The phase field model with viscoplastic constitutive was implemented using Abaqus subroutines. The strain rate, creep, stress relaxation and cyclic loading test are studied using a single element model. The results show that significantly accelerates the evolution of phase field of viscoplastic materials. For cyclic loadings, the acceleration effect for low frequency is more significant than high frequency. The fracture response of a stainless-steel plate and a titanium alloy plate subjected to tension load are studied. The influence of on the force-displacement curve mainly occurs after reaching the maximum force point. for titanium alloy plate and for stainless-steel plate are calibrated through comparison of force-displacement curves. For the modeⅠfracture of stainless-steel plate specimen, has no influence on the crack path. For the mixed fracture of titanium alloy plate specimen, the angle of the inclined crack path agrees well with the observation in experiment, however, higher value of results in a longer straight crack. Based on the specimens tested in this paper, the inelastic energy has significant effect on post-critical behavior, but has slight effect on the crack path. In future work, more complex fracture processes need to be tested to study the influence of inelastic energy on fracture response of viscoplastic material.
Author Contributions
Writing – original draft, Software, Methodology, Investigation, Q.S. Writing – review & editing, Supervision, Conceptualization, H.Y. Writing – review & editing, X. W. Supervision, Funding acquisition, Data curation, L.G. Writing – review & editing, Funding acquisition, K.H. Writing – review, Funding acquisition, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by National Key R&D Program of China (Grant No. 2020YFA0714402), Natural Science Foundation of China (NSFC) (Grant Nos. 12172103, 11972134, 12020101001 and 12002106), Natural Science Foundation of Heilongjiang Province of China (Grant No. JJ2023TD0005), Heilongjiang Touyan Innovation Team Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.
References
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Zhou, F.; Molinari, J.F. Dynamic crack propagation with cohesive elements: a methodology to address mesh dependency. Int. J. Numer. Meth. Eng. 2004, 59, 1–24. [Google Scholar] [CrossRef]
- Peng, G.L.; Wang, Y.H. A Node Split Method for Crack Growth Problem, in: Applied Mechanics and Materials. Trans. Tech. Publ. 2012, 182, 1524–1528. [Google Scholar]
- Azevedo, N.M.; Lemos, J. Hybrid discrete element/finite element method for fracture analysis. Comput. Methods Appl. Mech. Eng. 2006, 195, 4579–4593. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Li, J.; Liu, Q.; Wu, C.; Sun, G. Phase field fracture in elasto-plastic solids: variational formulation for multi-surface plasticity and effects of plastic yield surfaces and hardening. Int. J. Mech. Sci. 2019, 156, 382–396. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Meth. Eng. 1999, 46(1), 131–150. [Google Scholar] [CrossRef]
- Moës, N.; Gravouil, A.; Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets. Part I: Mechanical model. Int. J. Numer. Meth. Eng. 2002, 53(11), 2549–2568. [Google Scholar] [CrossRef]
- Mueller, R.; Maugin, G.A. On material forces and finite element discretizations. Comput. Mech. 2002, 29, 52–60. [Google Scholar] [CrossRef]
- Miehe, C.; Gürses, E.; Birkle, M. A computational framework of configurational-force-driven brittle fracture based on incremental energy minimization. Int. J. Fract. 2007, 145(4), 245–259. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Rabczuk, T.; Wu, C.; Ma, C.; Sun, G.; Li, Q. Phase field fracture in elasto-plastic solids: Abaqus implementation and case studies, Theor. Appl. Fract. Mech. 2019, 103, 102252. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Metallurgica. 1984, 32(1), 157–169. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. ASME. J. Eng. Mater. Technol. 1985, 107(1), 83–89. [Google Scholar] [CrossRef]
- Peerlings, R.; Borst, R.; Brekelmans, W.; Vree, J.; Spee, I. Some observations on localisation in non-local and gradient damage models. Eur. J. Mech. A-Solids 1996, 15(6), 937–953. [Google Scholar]
- Ambati, M.; Kruse, R.; Lorenzis, L.D. A phase-field model for ductile fracture at finite strains and its experimental verification. Comput. Mech. 2016, 57, 149–167. [Google Scholar] [CrossRef]
- Oh, Y.R.; Nam, H.S.; Kim, Y.J.; Naoki, M. Application of the GTN model to ductile crack growth simulation in through-wall cracked pipes. Int. J. Pres. Ves. Pip. 2018, 159, 35–44. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flows in solids. Phil. Trans. R. Soc. Lond. A 1921, 221, 163–198. [Google Scholar]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids. 1998, 46.8, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. Numerical experiments in revisited brittle fracture. Mech. Phys. Solids. 2000, 48.4, 797–826. [Google Scholar] [CrossRef]
- Shi, Q.; Yu, H.; Guo, L.; Hao, L.; Huang, K. A phase field model with plastic history field for fracture of elasto-plastic materials. Eng. Fract. Mech. 2022, 268, 108447. [Google Scholar] [CrossRef]
- Shen, R.; Waisman, H.; Guo, L. Fracture of viscoelastic solids modeled with a modified phase field method. Comput. Methods Appl. Mech. Eng. 2019, 346, 862–890. [Google Scholar] [CrossRef]
- Yin, B.; Kaliske, M. Fracture simulation of viscoelastic polymers by the phase-field method. Comput. Mech. 2020, 65, 293–309. [Google Scholar] [CrossRef]
- Huang, K.; Yan, J.; Shen, R.; Wan, Y.; Li, Y.; Ge, H. Investigation on fracture behavior of polymer-bonded explosives under compression using a viscoelastic phase-field fracture method. Eng. Fract. Mech. 2022, 266, 108411. [Google Scholar]
- Hojjat, B.; Elahe, E.; Mohammed, M. A phase field model for rate-dependent ductile fracture. Metals 2017, 7(5), 180. [Google Scholar]
- Gmati, H. Phase field modelling of fracture of elastic and elasto-viscoplastic solid materials. Mechanics of materials [physics.class-ph]. HESAM Université, 2020. English.
- Borden, M.J.; Hughes, T.J.; Landis, C.M.; Anvari, A.; Lee, I.J. A phase-field formulation for fracture in ductile materials: finite deformation balance law derivation, plastic degradation, and stress triaxiality effects. Comput. Methods Appl. Mech. Eng. 2016, 312, 130–166. [Google Scholar] [CrossRef]
- Dunne, F. Introduction to computational plasticity; Oxford University Press; p. 2005.
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids. 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Liu, G.; Li, Q.; Msekh, M.A.; Zuo, Z. Abaqus implementation of monolithic and staggered schemes for quasi-static and dynamic fracture phase-field model. Comput. Mater. Sci. 2016, 121, 35–47. [Google Scholar] [CrossRef]
- Jeong, H.; Signetti, S.; Han, T.S.; Ryu, S. Phase field modeling of crack propagation under combined shear and tensile loading with hybrid formulation. Comput. Mater. Sci. 2018, 155, 483–492. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Msekh, M.A.; Sargado, J.M.; Jamshidian, M.; Areias, P.M.; Rabczuk, T. Abaqus implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Kang, G.; Kan, Q. Constitutive modeling for uniaxial time-dependent ratcheting of SS304 stainless steel. Mechanics of Materials 2007, 39(5), 488–499. [Google Scholar] [CrossRef]
- Azinpour, E.; Cruz, D.J.; Cesar de Sa, J.M.A.; Santos, A. Phase-field approach in elastoplastic solids: application of an iterative staggered scheme and its experimental validation. Comput. Mech. 2021, 68, 255–269. [Google Scholar] [CrossRef]
- Verleysen, P.; Peirs, J. Quasi-static and high strain rate fracture behaviour of Ti6Al4V. Int. J. Impact Eng. 2017, 108, 370–388. [Google Scholar] [CrossRef]
Figure 1.
Crack representation of the phase field model: (a) sharp crack model, (b) diffuse crack model.
Figure 1.
Crack representation of the phase field model: (a) sharp crack model, (b) diffuse crack model.
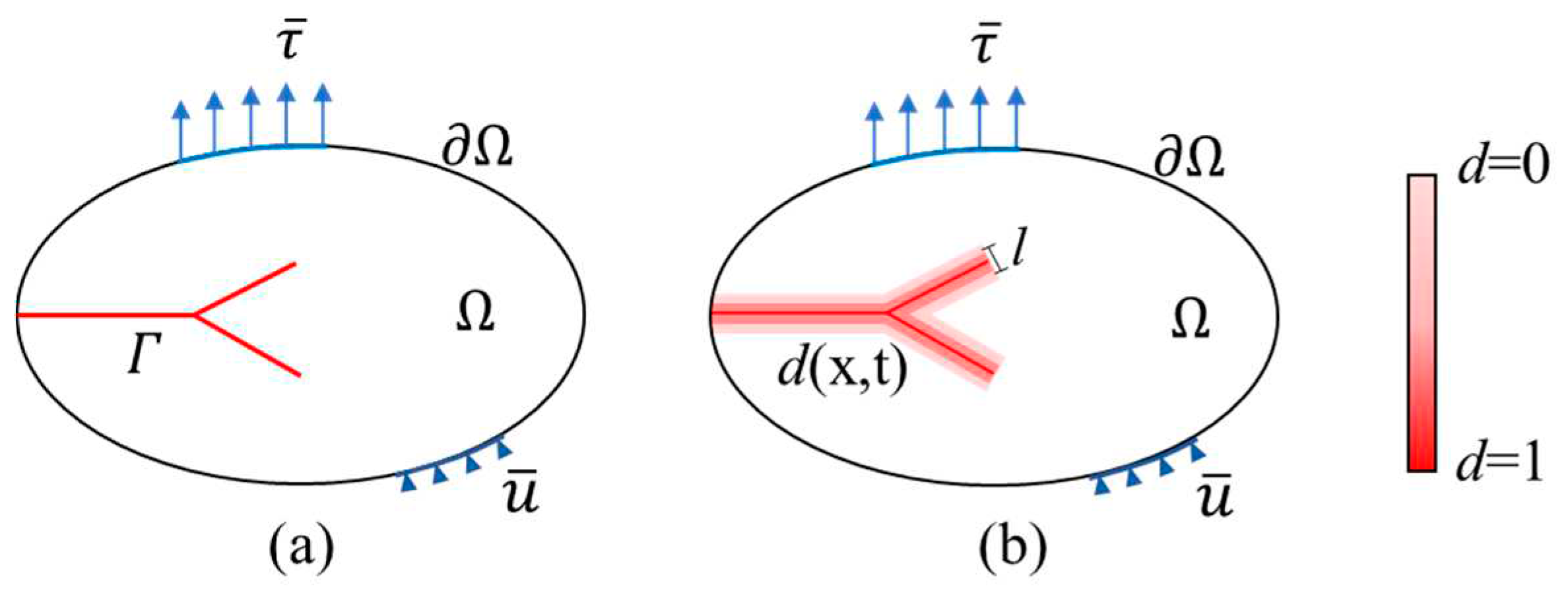
Figure 2.
Single element model and boundary condition.
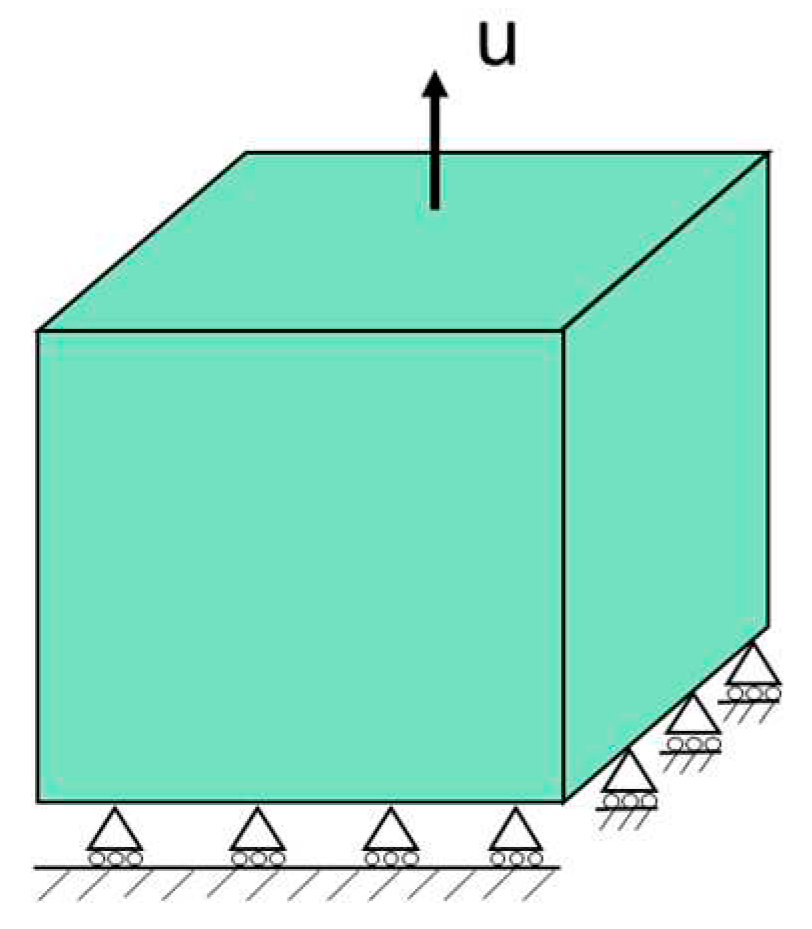
Figure 3.
Response of the viscoplastic material under various strain rate loads for β=0.1: (a) stress-strain relation and (b) phase field-strain relation.
Figure 3.
Response of the viscoplastic material under various strain rate loads for β=0.1: (a) stress-strain relation and (b) phase field-strain relation.
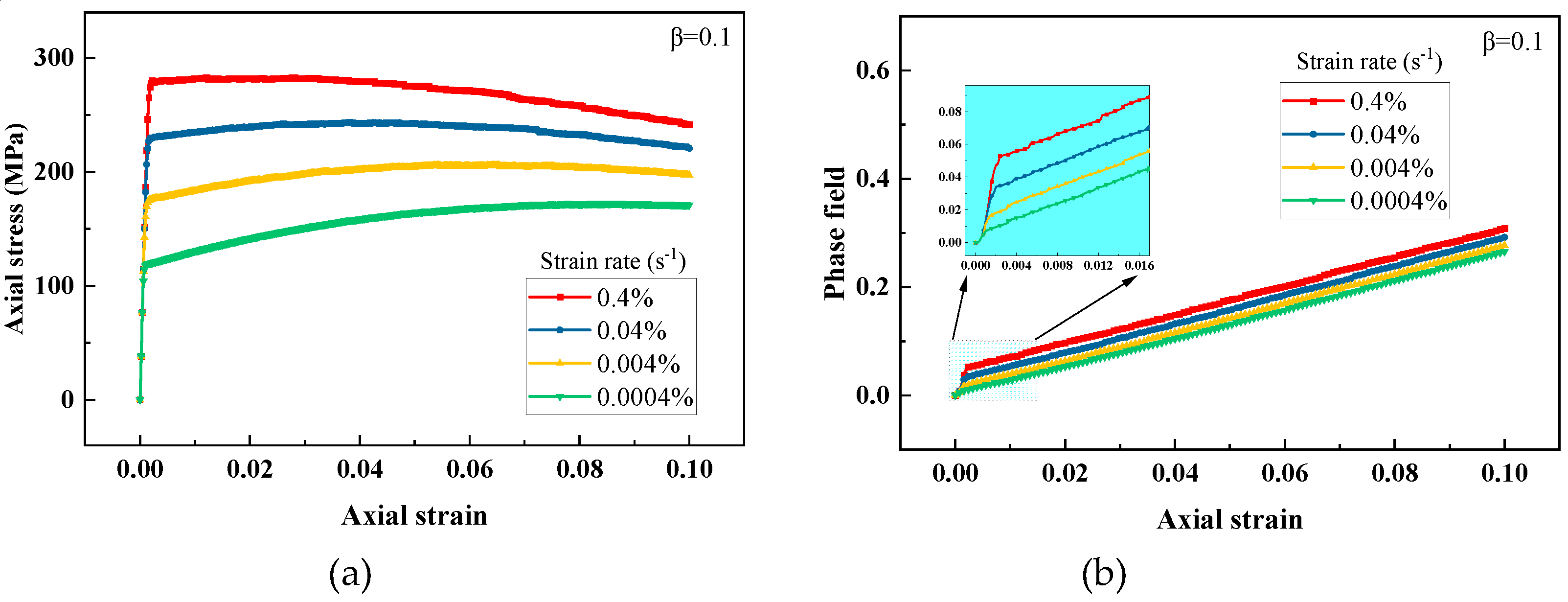
Figure 4.
Response of the viscoplastic material under various strain rate loads for β=0.3: (a) stress-strain relation, (b) phase field-strain relation.
Figure 4.
Response of the viscoplastic material under various strain rate loads for β=0.3: (a) stress-strain relation, (b) phase field-strain relation.
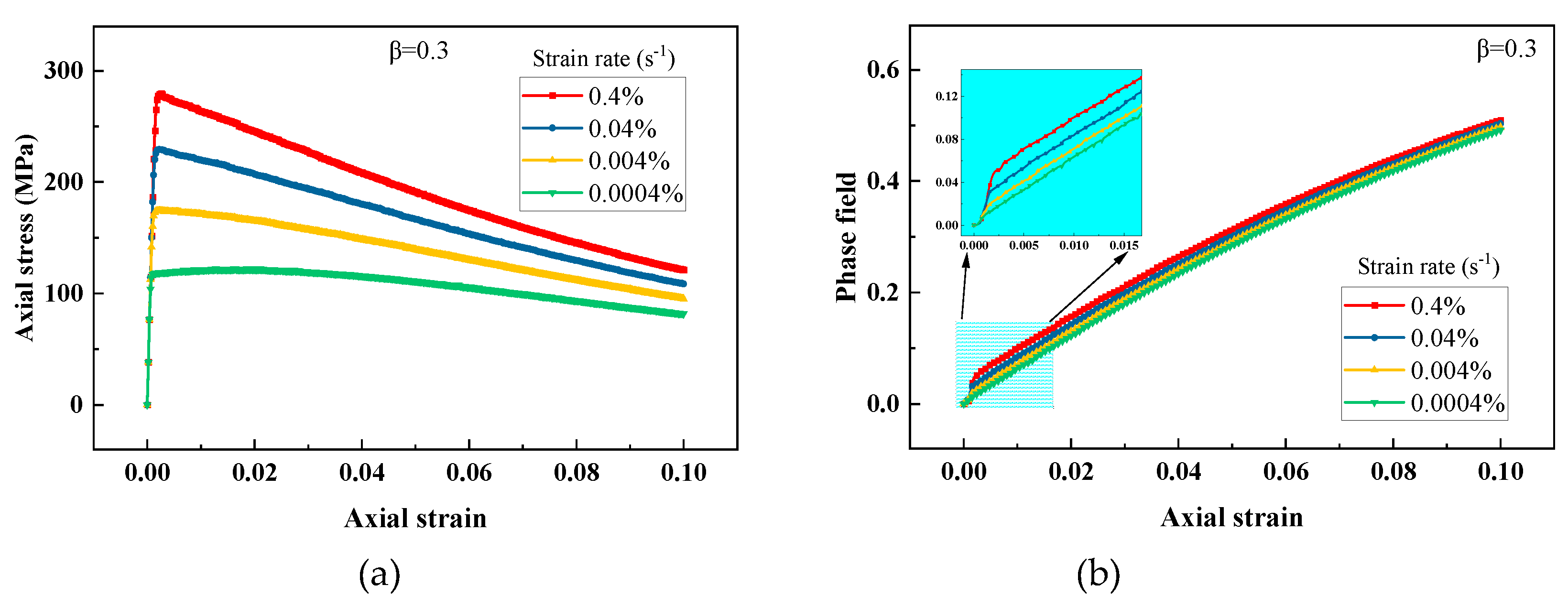
Figure 5.
Response of the viscoplastic material under creep load for different values of : (a) strain-time relation, (b) phase field-time relation.
Figure 5.
Response of the viscoplastic material under creep load for different values of : (a) strain-time relation, (b) phase field-time relation.
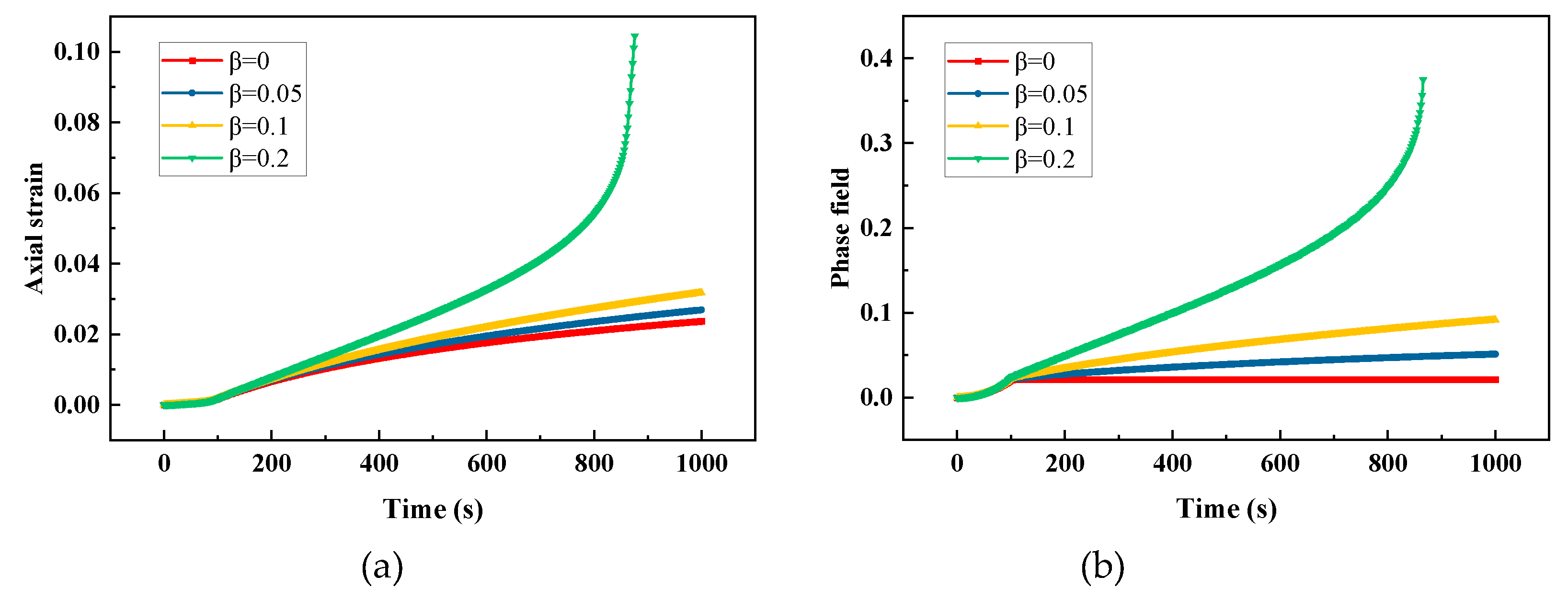
Figure 6.
Driving energies of the viscoplastic material under creep load.
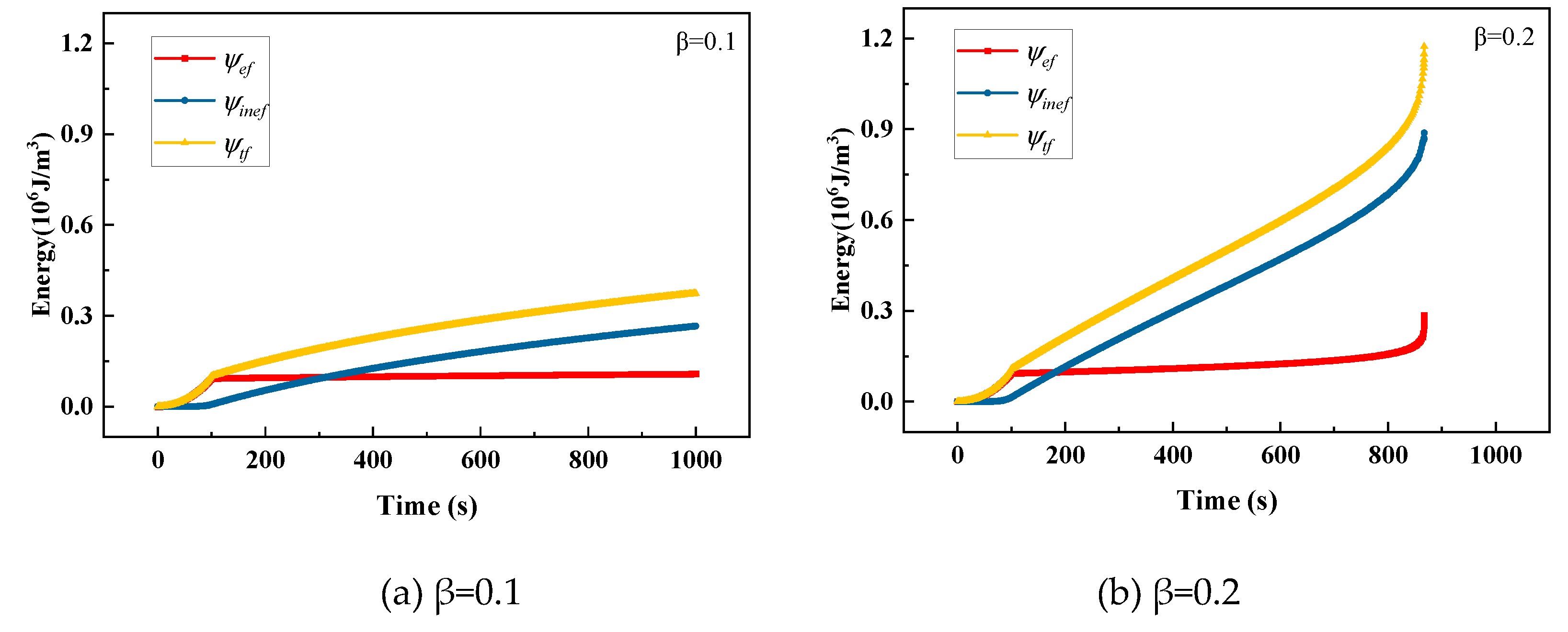
Figure 7.
Response of the viscoplastic material under relaxation load for different values of : (a) stress-time relation, (b) phase field-time relation.
Figure 7.
Response of the viscoplastic material under relaxation load for different values of : (a) stress-time relation, (b) phase field-time relation.
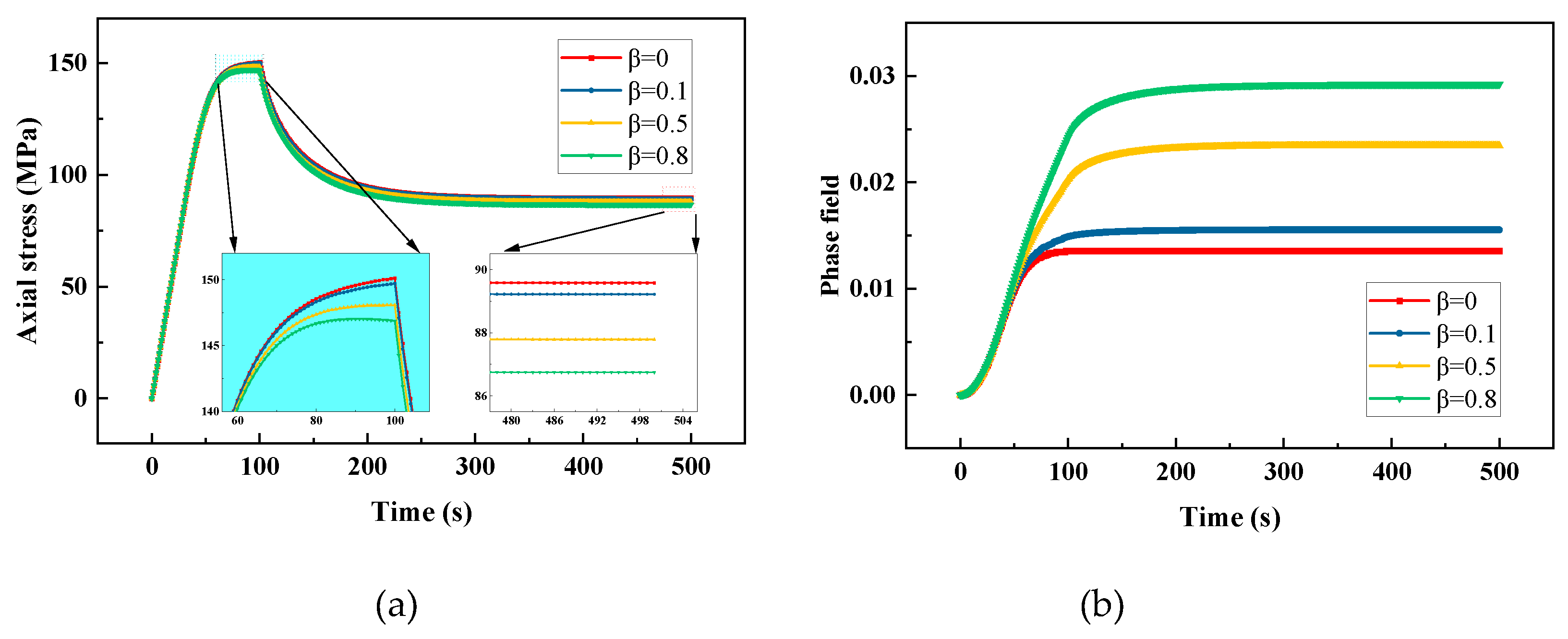
Figure 8.
Driving energies of the viscoplastic solid subject to relaxation load.
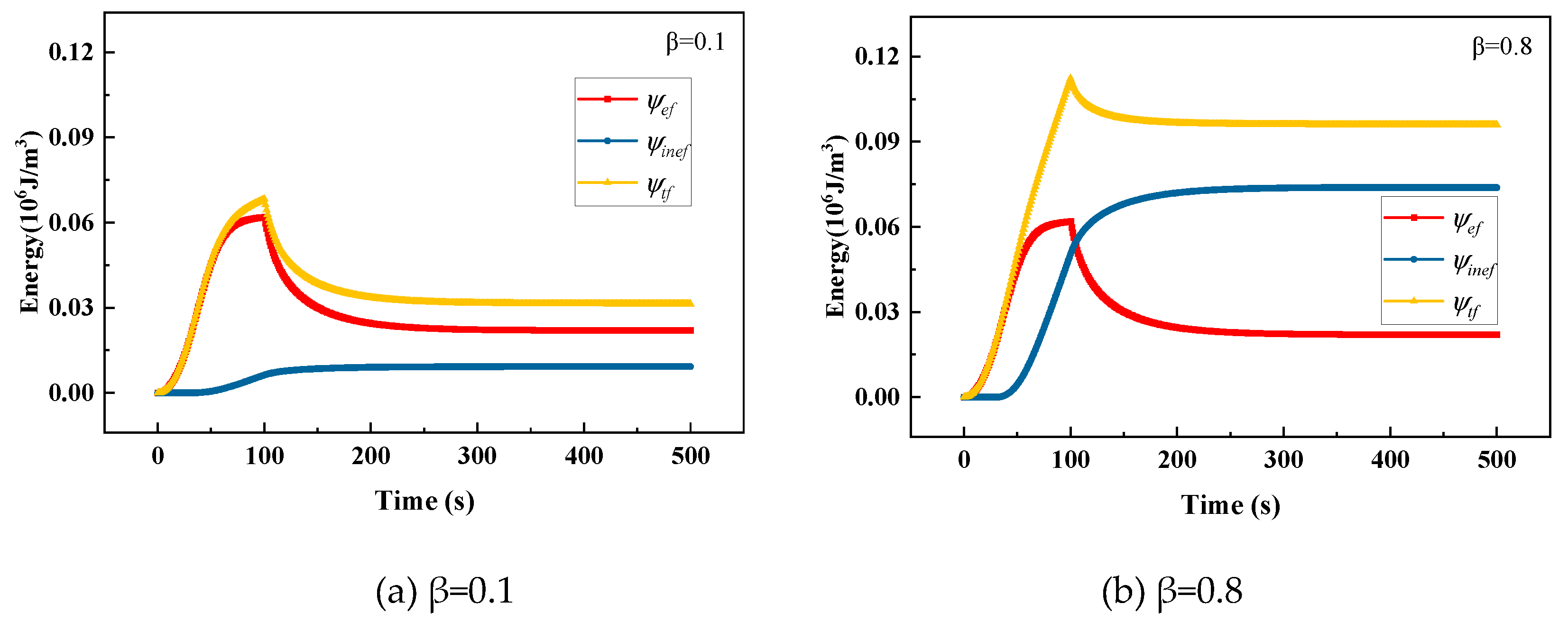
Figure 9.
Sinusoidal displacement loads: (a) low frequency, (b) high frequency.
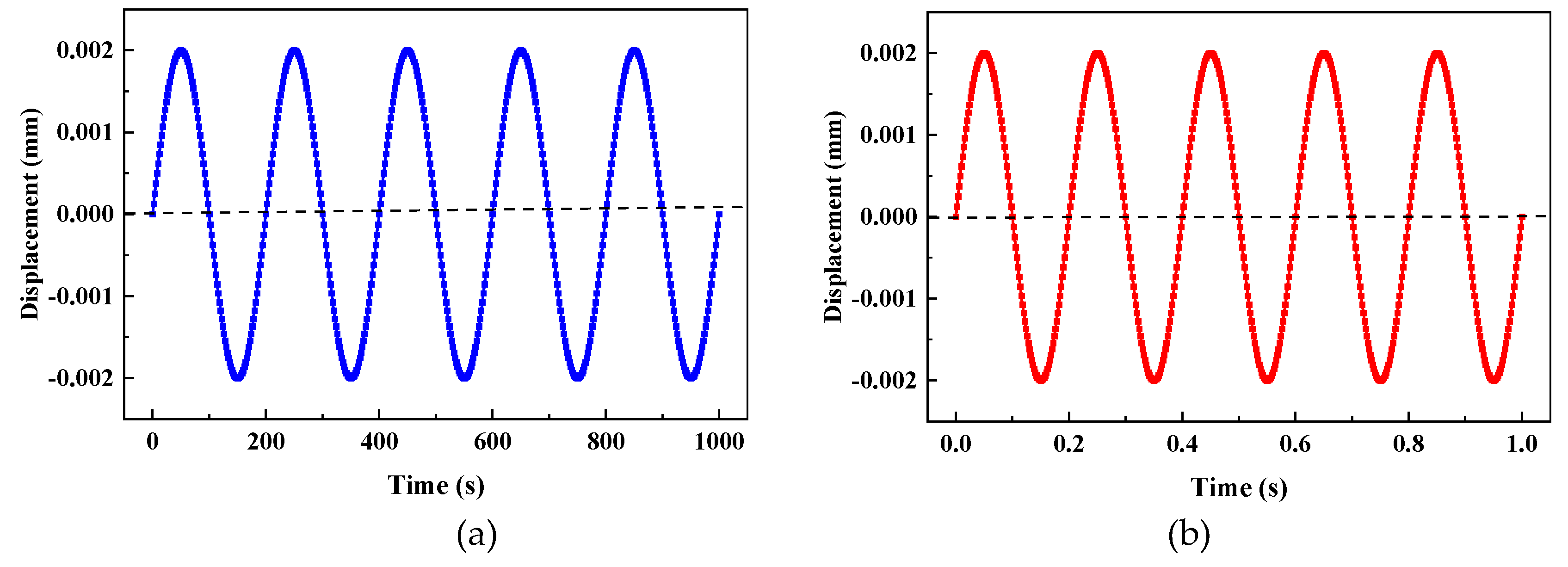
Figure 10.
Response of the viscoplastic material under low frequency cyclic load: (a) strain-time relation for , (b) phase field-time relation for different values of .
Figure 10.
Response of the viscoplastic material under low frequency cyclic load: (a) strain-time relation for , (b) phase field-time relation for different values of .
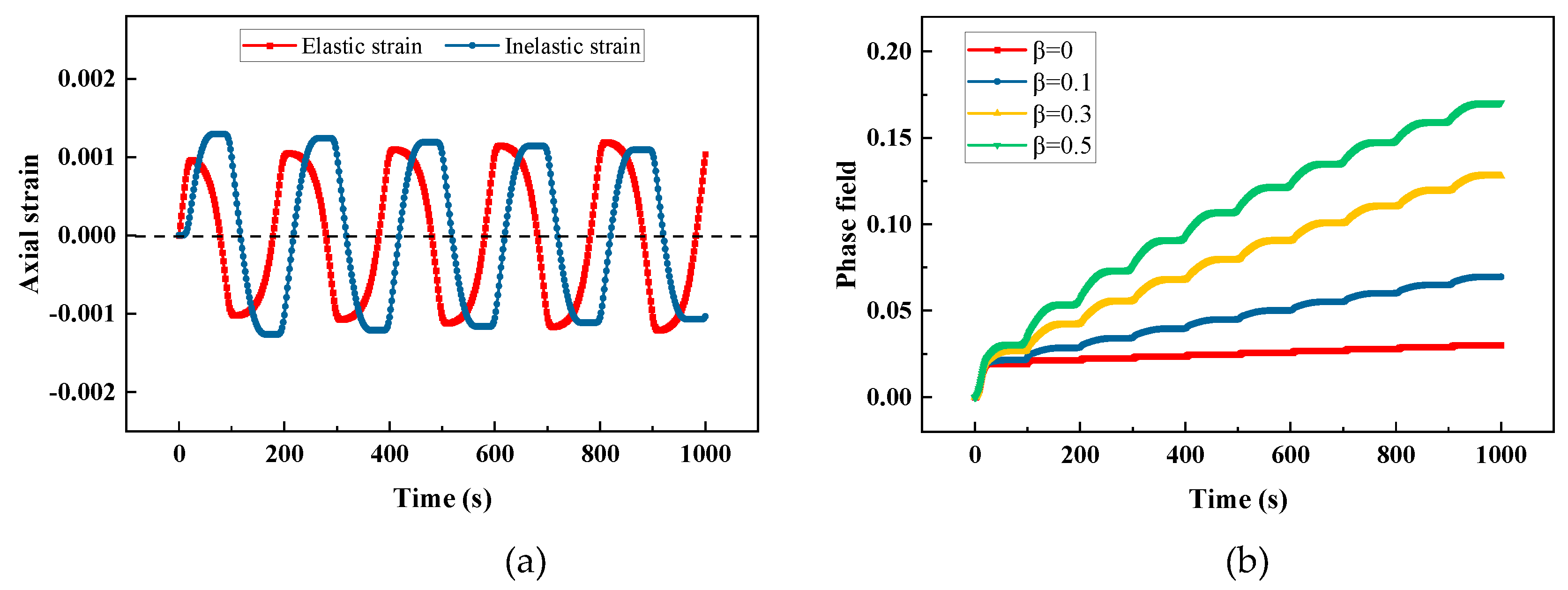
Figure 11.
Response of the viscoplastic material under high frequency cyclic load: (a) strain-time relation for , (b) phase field-time relation for different values of β.
Figure 11.
Response of the viscoplastic material under high frequency cyclic load: (a) strain-time relation for , (b) phase field-time relation for different values of β.
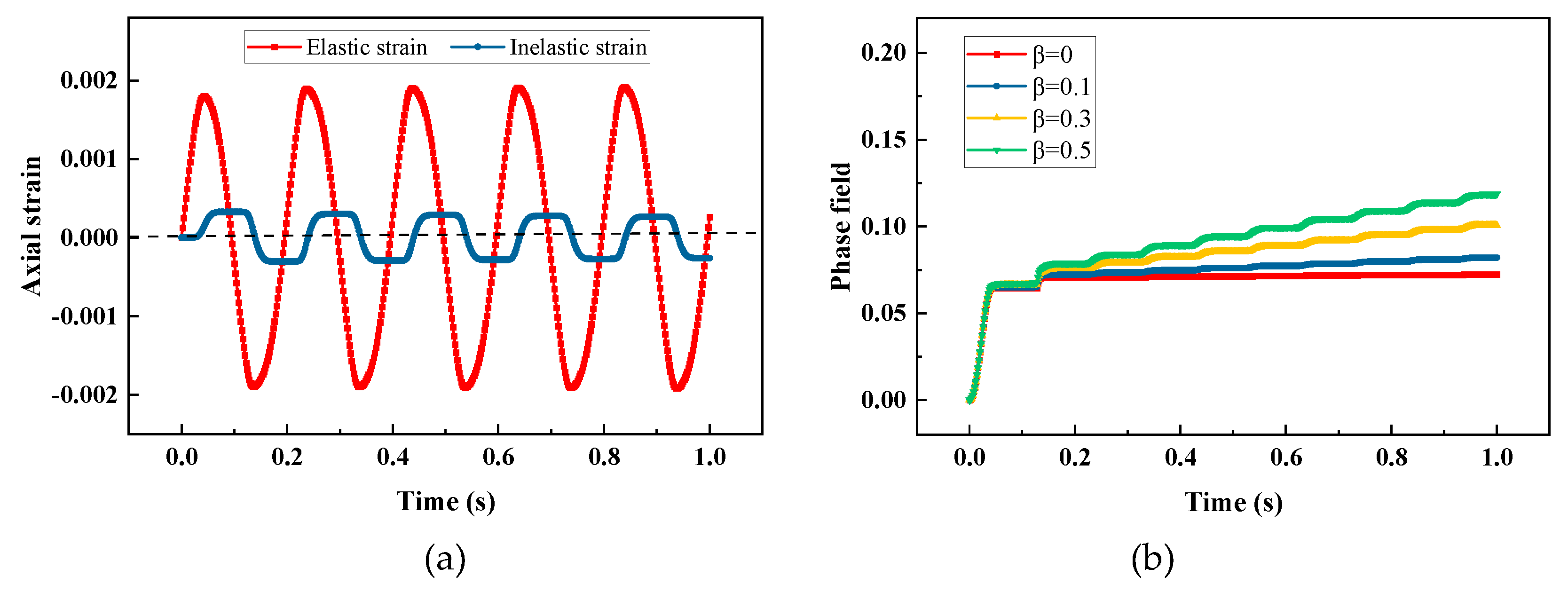
Figure 12.
Driving energies of the viscoplastic material under (a) low frequency and (b) high frequency cyclic load for different values of β.
Figure 12.
Driving energies of the viscoplastic material under (a) low frequency and (b) high frequency cyclic load for different values of β.
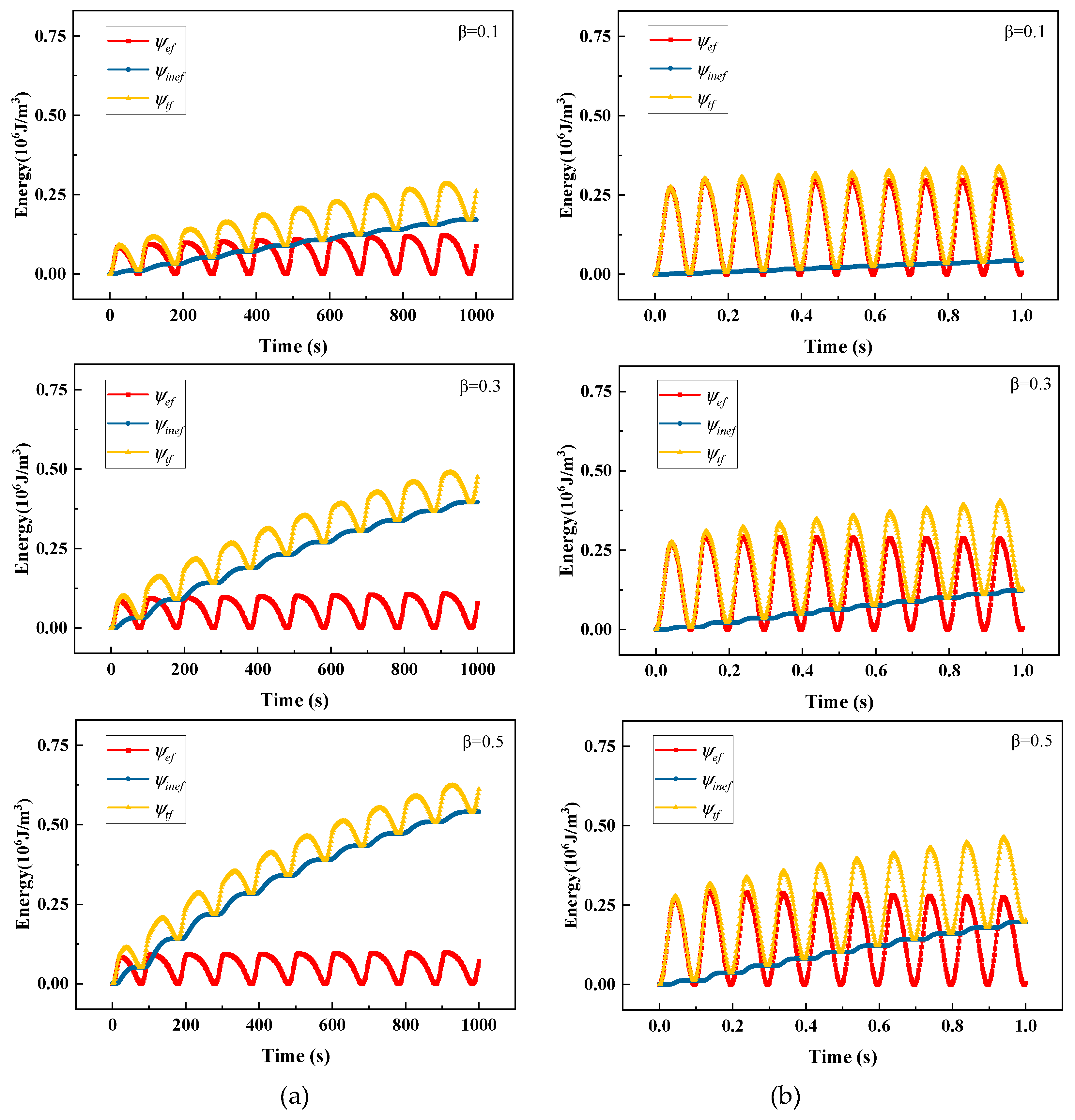
Figure 13.
Stainless-steel plate specimen: (a) geometry (b) finite element discretization.
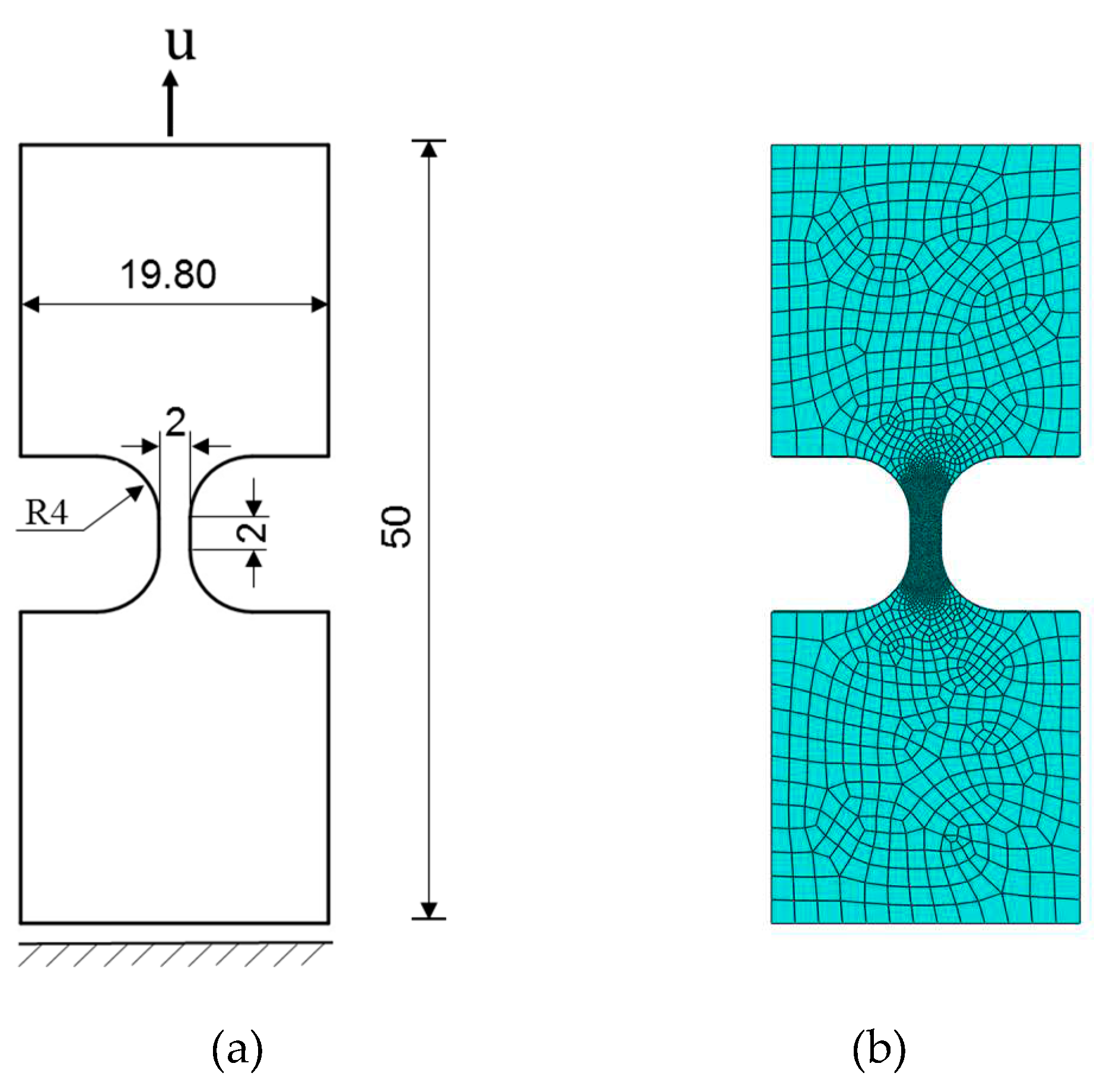
Figure 14.
Force-displacement curves of the stainless-steel plate specimen for different values of β.
Figure 14.
Force-displacement curves of the stainless-steel plate specimen for different values of β.
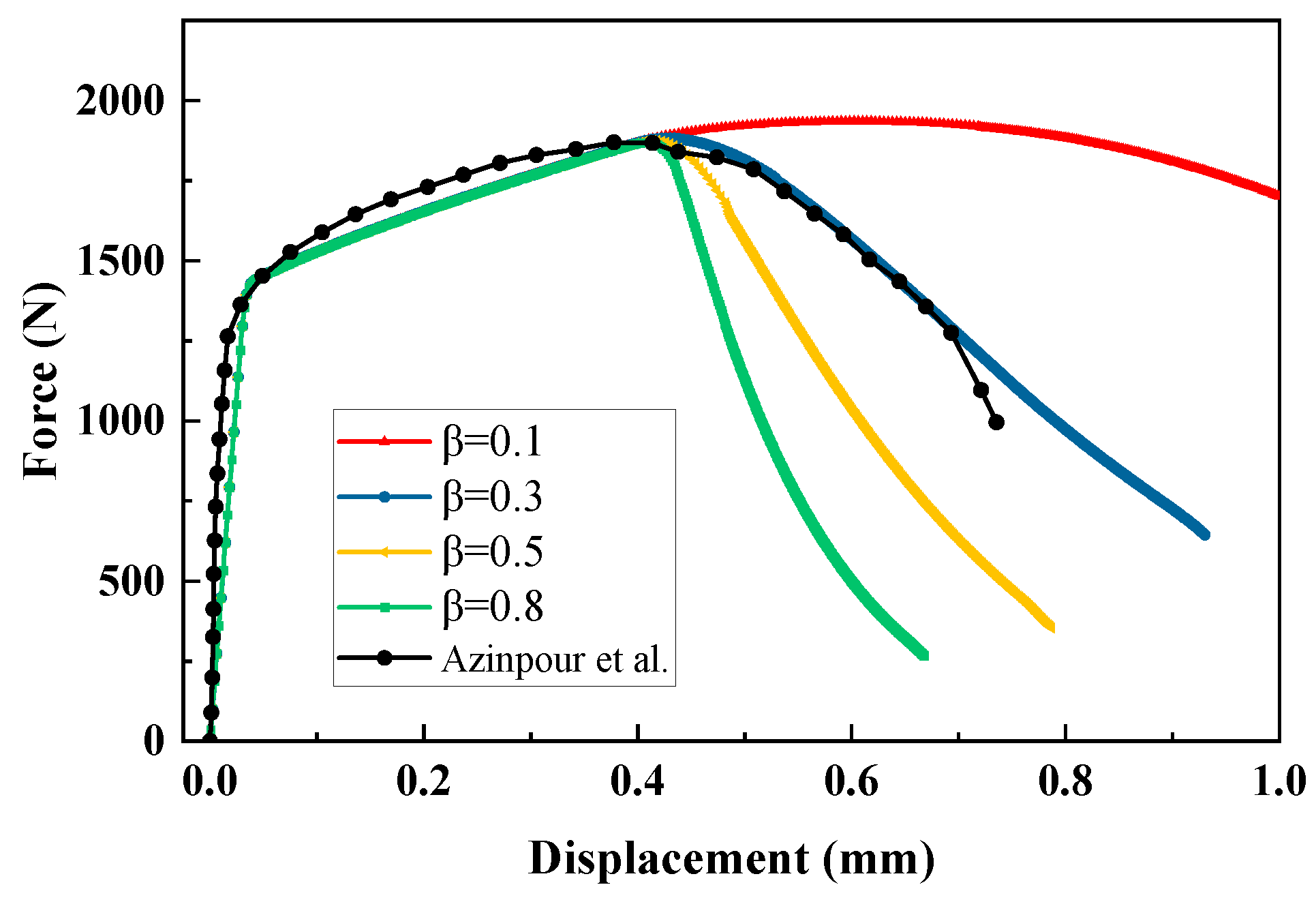
Figure 15.
Fracture of the stainless-steel plate specimen: (a) simulation results, (b) experimental observation in literature [33].
Figure 15.
Fracture of the stainless-steel plate specimen: (a) simulation results, (b) experimental observation in literature [33].
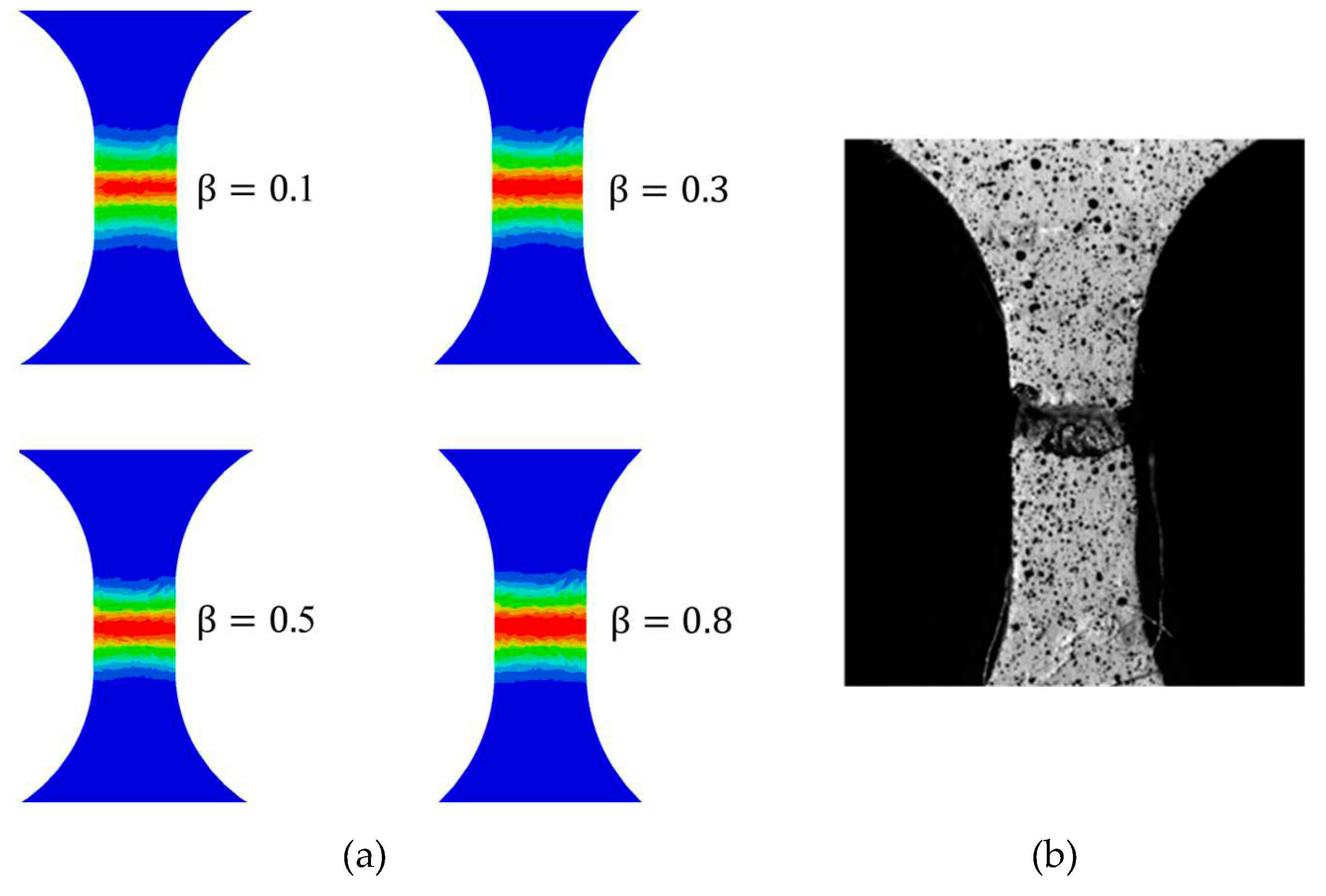
Figure 16.
Titanium alloy plate specimen: (a) geometry and boundary condition, (b) finite element mesh.
Figure 16.
Titanium alloy plate specimen: (a) geometry and boundary condition, (b) finite element mesh.
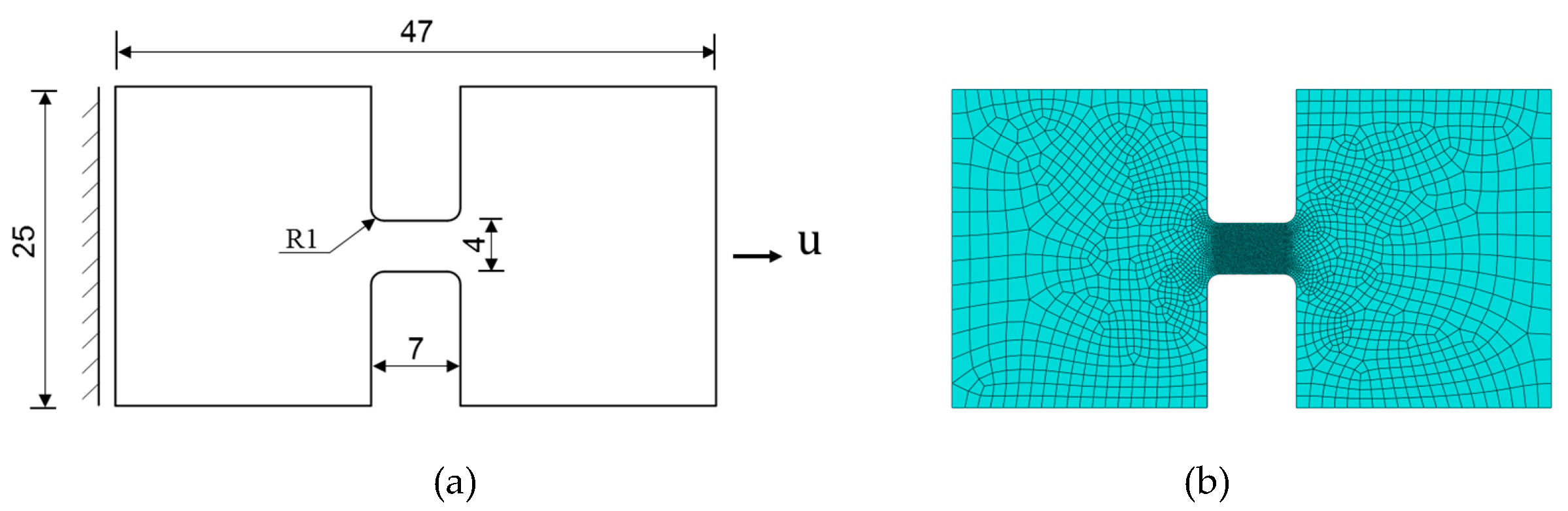
Figure 17.
Force-displacement curves of the titanium alloy plate specimen for different values of β.
Figure 17.
Force-displacement curves of the titanium alloy plate specimen for different values of β.

Figure 18.
Crack paths of the titanium alloy plate specimen: (a) results of simulation, (b) experimental observation in literature [34].
Figure 18.
Crack paths of the titanium alloy plate specimen: (a) results of simulation, (b) experimental observation in literature [34].
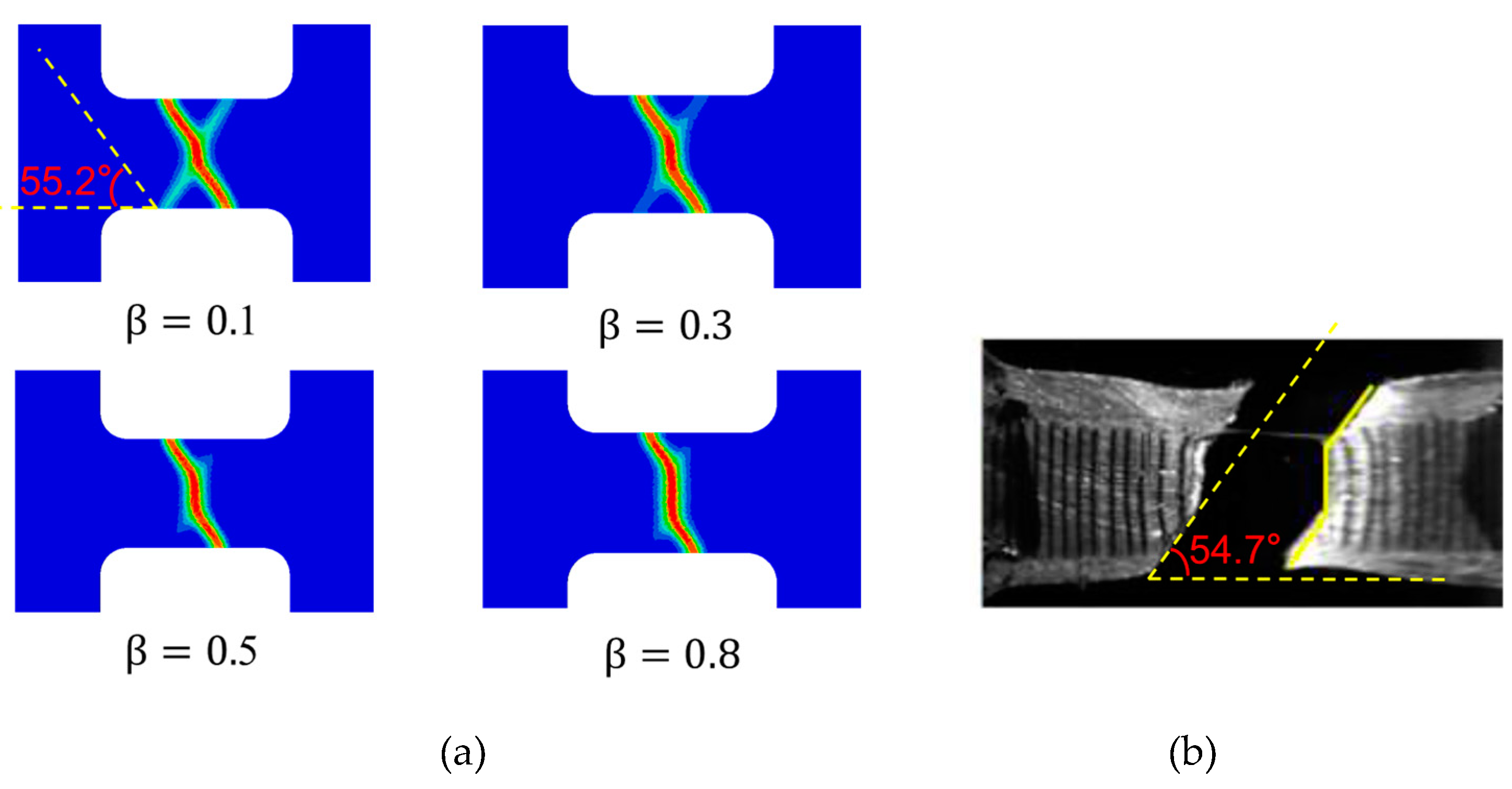
Table 1.
Material parameters for single element[32].
Table 1.
Material parameters for single element[32].
| Parameter | Name | Values |
| E | Young’ modulus | 192(GPa) |
| Poisson’ ratio | 0.33 | |
| Initial yield stress | 90(MPa) | |
| h | Hardening modulus | 2001.09(MPa) |
| Gc | Critical energy release rate | 18(N/mm) |
| A | Material constant | 3.16×10-6 |
| B | Material constant | 0.03572 |
| W0 | Energy density threshold | 0(MPa) |
| l | Length scale | 2mm |
Table 2.
Material parameters of 316L [33].
Table 2.
Material parameters of 316L [33].
| Parameter | Name | Values |
| E | Young’ modulus | 192(GPa) |
| Poisson’ ratio | 0.33 | |
| Initial yield stress | 402(MPa) | |
| h | Hardening modulus | 1708(MPa) |
| Gc | Critical energy release rate | 25(N/mm) |
| A | Material constant | 6.1×10-4 |
| B | Material constant | 0.04 |
| W0 | Energy density threshold | 40(MPa) |
| l | Length scale | 0.2mm |
Table 3.
Material parameters of Ti6Al4V [34].
Table 3.
Material parameters of Ti6Al4V [34].
| Parameter | Name | Values |
| E | Young’ modulus | 117(GPa) |
| Poisson’ ratio | 0.3 | |
| Initial yield stress | 951(MPa) | |
| h | Hardening modulus | 40(MPa) |
| Gc | Critical energy release rate | 50(N/mm) |
| A | Material constant | 1.3×10-4 |
| B | Material constant | 0.055 |
| W0 | Energy density threshold | 120(MPa) |
| l | Length scale | 0.12mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






