Preprint
Article
Fuzzy Adaptive Parameter in the Dai-Liao Optimization Method Based on Neutrosophy
Altmetrics
Downloads
126
Views
36
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
23 April 2023
Posted:
24 April 2023
You are already at the latest version
Alerts
Abstract
The influence of neutrosophy in the previous period is constantly growing in many areas of science and technology. Moreover, various applications of the neutrosophic approach have become more common in recent years. Our goal in this research is to utilize the neutrosophy to improve the performance of the Dai-Liao conjugate gradient (CG) method. Specifically, in this research, we propose and investigate a new neutrosophic logic system to calculate the key parameter t involved in the Dai–Liao CG iterations. Theoretical analysis and numerical experience indicate that the efficiency and robustness of the new rule for determining t. Combining the neutrosophy and the Dai-Liao conjugate gradient method, we propose and explore a new Dai-Liao CG iterations for solving large-scale unconstrained optimization models. The global convergence is established under common assumptions and the backtracking line search. Finally, by conducting numerical experiments, computational evidence demonstrates that the new fuzzy neutrosophic Dai-Liao conjugate gradient method is computationally effective and robust.
Keywords:
Subject: Computer Science and Mathematics - Applied Mathematics
MSC: 90C70; 90C30; 65K05
1. Introduction and Background Results
Numerous iterative methods have been developed to solve the large-scale unconstrained optimization problem
in which is a continuously differentiable function and bounded below. Continuing well established notation, stands for the gradient vector of f at the actual iterative point , and further and . Utilizing the extended conjugacy condition
Dai and Liao in [1] suggested the conjugate gradient (CG) iterations
where the is the last calculated iteration, is a new iterative point, is a positive step size parameter defined as the output of an inexact line search, and is a descent direction. The search directions are created by the recurrent regulation
where is the CG coefficient which describes the type of CG method by the general rule
wherein is an appropriate scalar. The Dai–Liao (DL) method guarantees global convergence for uniformly convex objective functions. These results have attracted a lot of attention, leading to the creation of several methods based on various patterns for defining . Most of these methods were developed by modifying the conjugate gradient parameter [2,3,4,5,6,7,8,9]. For more details, see the survey on the DL family of nonlinear CG methods in [10]. One of rules for defining is denoted as and defined in [7] by
such that and is as in (5).
Due to the large influence of the size t on numerical results generated by the DL class of CG methods [11], one of the most common issues is the determination of an appropriate value t. We can distinguish two research directions based on the previous results in determining proper values t in the DL established CG iterations. The first direction of research consists of a group of DL methods that aim to find a suitable constant value for t[1,2,6,7,8] during iterations, while the second direction consists of a group of DL methods that propose a suitable control in recalculating t in each iteration. In this research, we prioritize the second research stream: find values t that changes appropriately accros iterations. The quantity t determined in kth iterative step will be denoted by , where i is a variant of the algorithm for defining t.
Some of the most important adaptive choices for the DL parameter will be presented in the rest of this section. Hager and Zhang in [12,13] suggested the CG-DESCENT method, which is classified into the group of the DL CG methods (5) defined by and
Dai and Kou suggested DK method in [14] where the CG coefficient is of the form
In the equality (8), the parameter is defined utilizing the self-scaling memoryless BFGS method. It is also obvious from (8) that the DK method is involved into the DL CG class of methods where is defined by
Andrei in [16] originated a new DL class, denoted DLE, where is defined by
A special place in the DL iterations is occupied by the DL method with
where is a constant, has been defined according to the sufficient descent condition
such that is a constant independent of the cost function convexity and the line search rules (for more details see [17]).
Ivanov et al. in [19] proposed a variant of the Dai-Liao CG method (6), known as the Effective Dai-Liao (EDL) CG method, where is determined as
The experiments performed in [19] verify that the EDL iterations outperform many existing CG variants.
The basics of neutrosophy. Neutrosophic logic was applied in [20] in regulating proper step sizes for a class of accelerated gradient-descent optimization methods. The approach in [20] assumes an additional fuzzy parameter which stabilizes the behavior of an important class of gradient-descent family. Motivated by that approach, in this research we apply neutrosophy in order to enhance performances of DL methods. Based on the review and analysis of the class of DL methods, we propose a new method for determining . The proposed method defines as the output produced by an appropriate neutrosophic logic controller (NLC). Our idea is to replace the classical parameter by an adaptive neutrosophic logic parameter , determined as the output of the NLC. Since our decision is to define as the value of , without additional parameters.
A fuzzy set theory utilizes a membership function (MF) in the universe that defines the degree of membership of in [21]. The intuitionistic fuzzy set (IFS) is established using both degrees of membership and non-membership function [22], which are mutually corelated by and . The IFS theory was originally generalized in [23,24] by the the neutrosophic theory. The background of the neutrosophic logic is the utilization of the indeterminacy . In that direction, entries of a neutrosophic set are determined by three independent MFs [23,24]: the truth-MF , the indeterminacy-MF , and the falsity-MF . Due to the indeterminacy-MF, the neutrosophic logic is based on the symmetry involved in the ordered triple of MFs and the inequality if all three MFs are independent. Clearly, is the symmetric pole to its opposite pole with respect to , which represents an axis of the symmetry between and [25]. The same observation is valid for refined neutrosophic set that assumes the refined indeterminacies and between and [26]. The MFs of a neutrosophic set satisfy , which which based on their independence implies , and enables a symmetry between them. In [27], the authors originated a neutrosophic-based multiple criteria decision-making procedure based on previously introduced symmetry measure.
The benefits of the NL approach over the FL and IFL are discussed in [20].
Motivation and highlights of main results. Our task in this paper is to improve the behavior of DL class for solving unconstrained nonlinear optimization problems with the support of an appropriate neutrosophic logic system. The principal results obtained in this paper are presented as follows.
- (1)
- We examine the application of NL in determining the parameter t in the Dai-Liao CG method (5).
- (2)
- A theoretical analysis is accomplished to confirm the global convergence of the proposed method.
- (3)
- A numerical comparison is given between the proposed FDL algorithm and other known DL algorithms.
The sections of the paper are arranged as follows. Introduction, motivation and a brief review of obtained results are presented in Section 1. A neutrosophic-based control for defining appropriate changeable values is proposed in Section 2. Moreover, we present details of the FDL method. The global convergence behavior of the FDL method is examined in Section 3. Numerical comparison of the FDL method with main standard DL methods is presented in Section 4, and a comparison with some known variations of the DL class of methods, is also given. Final conclusions are presented in the concluding section.
2. Fuzzy Neutrosophic Dai-Liao Conjugate Gradient Method
The fuzzy neutrosophic Dai-Liao CG method is defined as a modification of the Dai-Liao CG method (3), where the search directions are calculated by the recurrence rule
where the CG coefficient is defined by
such that is a proper fuzzy neutrosophic parameter. Our intention is to define as a function of i.e., . More precisely, is defined subject to the following constraint
It is know that reduces (2) into
Hence, the equation (22) can be considered as a reflection of the conjugacy condition, which in conjuction with (4) determines the HS parameter [28]
Alternatively, for , the equation (2) is considered as a conjugacy condition that implicitly satisfies the quasi-Newton characteristics. For more details on these cases, see [1,10].
The idea for defining a new parameter in the Dai-Liao CG method (5) comes from the neutrosophic logic. According to this decision, our intention is to define inside the interval according to neutrosophic principles.
The generic layout of the fuzzy neutrosophic Dai-Liao CG method is given in the diagram in Figure 1.
The input of the NLC presented in Figure 1 is and the output is the desired step size . This means that our basic idea is to define based on two consecutive values of the objective function f. On the other hand, the backtracking line search is reponsible for appropriate step lengths in (3) and then the descent direction by (19). Using it is possible to compute in (20). Finally, (3) generates new iterative point .
To develop the FDL method, it is necessary to plan three global steps: neutrosophistication, neutrosophic inference engine, and de-neutrosophistication (score function).
- (1)
-
Neutrosophication maps the input into neutrosophic ordered triplets . The MFs are defined with the aim to improve the CG iterative rule exploiting numerical experience. The sigmoid function with the slope defined by at the crossover point is a proper choice for :A proper choice for is the following sigmoid function:The Gaussian function with the standard deviation and the mean defines the indeterminacy :
- (2)
-
Neutrosophic inference between an input fuzzy set and an output fuzzy set is based on the subsequent “IF–THEN” regulations:Fuzzy sets and point, respectively, to positive or negative errors. Applying the unification , we define , , where ∘ denotes the fuzzy transformation. In addition, for a fuzzy vector , it follows , , where ⋀ and ⋁ denote the and operator, respectively. In this research, the centroid defuzzification method is utilized to generate a vector of crisp outputs :
- (3)
- De-neutrosophication is based on the transformation resulting in a crisp value and suggested as:
The diagram of Figure 2 presents the NLC based on the neutrosophic rules.
The settings in the NLC employed in numerical testing are arranged in Table 1.
Our imperative requirement is , requested in (21). This statement is verified in Lemma 1.
Lemma 1.
Proof.
In order to prove (21), we need to replace the MFs (24), (25), and (26) in (27). After applying the parameters from Table 1, we get
Elementary calculation gives
Graphs of are displayed in Figure 3a. The fulfilment of the requirements (21) in the NLC output generated throughout the described de-neutrosophication is illustrated in Figure Figure 3b.
Remark 1.
The objective function decreases with the flow of iterations and tends to the minimal value, which means , i.e., . Such behavior leads to as the minimum of f approaches, so the impact of the proposed neutrosophic strategy decreases and disappears, which agrees with our goal.
Remark 2.
Obviously, larger values of lead to increasing values approaching to 1, which will be denoted as . In addition, based on the limit , we anticipate smaller values approaching 0, i.e., in final iterations. As a result, is suitable as an adjustable regulator for the quantity t in the Dai–Liao CG method.
The backtracking line search from [29] begins from and generates further step sizes which ensure decrease of the goal function in each iteration. Algorithm 1, restated from [30], is used to define the primary step size .
| Algorithm 1 The backtracking line search. |
 |
Algorithm 2 of the FDL method is described as follows:
| Algorithm 2 Fuzzy neutrosophic Dai-Liao (FDL) conjugate gradient method. |
 |
3. Convergence Examination
The subsequent assumptions are necessary during the theoretical examination of the FDL algorithm.
Assumption 1.
The level set of the iterative process (3) is bounded.
The objective f is continuously differentiable in a neighborhood of ℧ with the Lipschitz continuous gradient . Such assumption initiates the existence of a constant such that
The Assumption 1 provides the existence of quantities and such that
and
If Assumption 1 holds, in view of the uniform convexity of f, there exists satisfying
or equivalently,
The inequality (36) implies
Taking into account and the last inequality, we conclude
Lemma 2.
Lemma 3.
Proof.
Theorem 1 confirms the global convergence of the FDL flow.
Theorem 1.
Proof.
Suppose the opposite. Since (45) is not valid, we conclude the existence of satisfying
Squaring both sides of (19) one derives
Taking into account (20), we obtain
Now from (42), it follows
Now, an application of (20) initiates


The inequalities in (53) imply
Therefore, causes a contradiction with Lemma 2. □
4. Numerical Results
In this section, numerical results obtained by the FDL method are analyzed and compared with the numerical results generated by the EDL [19] and DL [1] methods.
All the algorithms were written in Matlab R2017a and ran on a 64-bit Lenovo laptop (Intel Core i3 GHz, RAM 8 GB) with the Windows 10 operating system. The implementation of the FDL method is based on Algorithm 2, while EDL and DL implementation are based on algorithms given in [19] and [1], respectively.
The numerical testing is performed on 50 test functions collected in [33,34], with dimensions from the range . All three tested methods used start from the same initial point for each test function. Each case in testing is evaluated 10 times with gradually increased dimensions , , , and .
The uniform terminating criteria for observed DL, EDL, and FDL algorithms are
We are going to evaluate the efficiency of the FDL method and compare it with the EDL and DL methods under the backtracking search based on the parameters and .
Summary numerical results for DL, FDL, and EDL methods, performed on 50 test functions, are shown in Table 2, where `Test function’, `Nitr’, `Nfe’, and `Tcpu’ represent the name of the tested function, the total number of iterations, the total number of function evaluations, and the running time, respectively.
To visually compare the performance of tested methods, we used the performance profiles technique [35] on numerical results corresponding to Nitr, Nfe, and Tcpu criteria generated by DL, FDL, and EDL methods. An upper graph in a performance profile corresponds to the method that shows better performance. The vertical axis of each performance profile in figures undicates the percentage of test functions for which the considered method is the winner between compared methods, whereby the right-hand side corresponds to the percentage of successfully solved test functions.
Figure 4 and Figure 5 plot the performance profiles for the data in Table 2. Graphs in Figure 4 illustrate the performance profiles Nitr and Nfe for DL, FDL, and EDL iterations based on the data from Table 2. In Figure 4a, it is noticeable that DL, FDL, and EDL methods are able to solve all tested functions, wherein the FDL method produces the best results in % (27 out of 50) of test functions compared with DL (% (13 out of 50)) and EDL (% (19 out of 50)). From Figure 4a, it is observed that the FDL graph reaches the top first, so FDL is the best relative to other examined methods with respect to the Nitr criterion.
Figure 4b indicates that the FDL graph is the most efficient and successfully solves all test cases. In addition, the obtained numerical results confirm that FDL performs well in most cases. Most specifically, FDL is the fastest because it solves about (24 out of 50) of tested functions with the least Nfe compared to the DL and EDL methods. Meanwhile, the DL and EDL are superior for solving (11 out of 50) and (15 out of 50) test functions, respectively. Hence, the numerical behavior of FDL is superior compared to the DL and EDL methods for the given test functions.
Figure 5 shows Tcpu performance profiles graphs of DL, FDL, and EDL methods. It is observable that DL, FDL, and EDL are able to solve all tested functions. Further examination leads to the conclusion that the FDL method is the best in % (37 out of 50) of the test cases compared with DL (% (6 out of 50)) and EDL (% (8 out of 50)). Analysing the graphs in Figure 5, a clear conclusion is that the FDL graph comes to the top first, which confirms its dominance in terms of Tcpu.
By analyzing the results shown in Figure 4, Figure 5 and in Table 2, we conclude that the FDL method achieved better results. This observation leads us to the final conclusion that the proposed FDL method is effective for solving unconstrained optimization problems in terms of all three criteria (iterations, function evaluations, and processor time).
5. Conclusions
In current research, we propose a novel approach to determining the parameter t in the Dai-Liao CG iterations. New approach is based on finding suitable values for a non-negative parameter t in the DL method using neutrosophic logic. Utilizing in (5), an original strategy in defining the Dai-Liao CG parameter is proposed and a novel fuzzy neutrosophic Dai-Liao (FDL) CG method is presented.
Numerical experiments and comparisons with some well-known CG methods and the theoretical convergence analysis show effectiveness of the method. The numerical testing and initiated comparison are based on standard performance profiles, such as the total number of iterations (Nitr), the total number of function evaluations (Nfe), and the running time (Tcpu) performances for each function and each method. Analysis of the obtained numerical results revealed that the FDL method is the most efficient.
We are convinced that the obtained results will be a motivation for further research in defining improved DL methods strengthened by the neutrosophic logic.
Future scientific research in this direction can be continued in in several directions. Previous research has shown the effectiveness of the neutrosophic principle in scaled gradient descent methods and DL class of CG methods. The challenge is to apply such a principle to other non-linear optimization methods. On the other hand, there is a wide variety of different possibilities for defining the principles of neutrosophication and de-neutrosophication, which can be considered in future research. Finally, there is a great opportunity in improving the Neutrosophic inference engine used in this research.
Author Contributions
Conceptualization, P.S.S. and B.D.I; methodology, P.S.S., V.N.K., and L.A.K.; software, B.D.I..; validation, D.S., V.N.K., P.S.S., and L.A.K.; formal analysis, D.S., P.S.S., V,N,K. and D.K.; investigation, P.S.S., D.S., V.N.K., and L.A.K. ; resources, B.D.I., D.K. and S.D.M.; data curation, B.D.I. and D.S..; writing-original draft, P.S.S., B.D.I., and D.S.; writing-review and editing, P.S.S., D.K., and D.S.; visualization, B.D.I. and D.S. All authors have read and agreed to the published version of the manuscript..
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2022-1121).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data and code will be provided on request to authors.
Acknowledgments
Predrag Stanimirović is supported by the Science Fund of the Republic of Serbia, (No. 7750185, Quantitative Automata Models: Fundamental Problems and Applications - QUAM).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dai, Y.-H.; Liao, L.-Z. New conjugacy conditions and related nonlinear conjugate gradient methods. Appl. Math. Optim. 2001, 43, 87–101. [Google Scholar] [CrossRef]
- Cheng, Y.; Mou, Q.; Pan, X.; Yao, S. A sufficient descent conjugate gradient method and its global convergence. Optim. Methods Softw. 2016, 31, 577–590. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. A descent Dai-Liao conjugate gradient method based on a modified secant equation and its global convergence. ISRN Computational Mathematics 2012, 2012, Article ID 435495. [Google Scholar] [CrossRef]
- Peyghami, M.R.; Ahmadzadeh, H.; Fazli, A. A new class of efficient and globally convergent conjugate gradient methods in the Dai-Liao family. Optim. Methods Softw. 2015, 30, 843–863. [Google Scholar] [CrossRef]
- Yabe, H.; Takano, M. Global convergence properties of nonlinear conjugate gradient methods with modified secant condition. Comput. Optim. Appl. 2004, 28, 203–225. [Google Scholar] [CrossRef]
- Yao, S.; Qin, B. A hybrid of DL and WYL nonlinear conjugate gradient methods. Abstr. Appl. Anal. 2014, 2014, Article ID 279891. [Google Scholar] [CrossRef]
- Yao, S.; Lu, X.; Wei, Z. A conjugate gradient method with global convergence for large-scale unconstrained optimization problems. J. Appl. Math. 2013, 2013, Article ID 730454. [Google Scholar] [CrossRef]
- Zheng, Y.; Zheng, B. Two new Dai-Liao-type conjugate gradient methods for unconstrained optimization problems. J. Optim. Theory Appl. 2017, 175, 502–509. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, L. A nonlinear conjugate gradient method based on the MBFGS secant condition. Optim. Methods Softw. 2006, 21, 707–714. [Google Scholar] [CrossRef]
- Babaie-Kafaki, S. A survey on the Dai-Liao family of nonlinear conjugate gradient methods. RAIRO-Oper. Res. 2023, 57, 43–58. [Google Scholar] [CrossRef]
- Andrei, N. Open problems in nonlinear conjugate gradient algorithms for unconstrained optimization. Bull. Malays. Math. Sci. Soc. 2011, 34, 319–330. [Google Scholar]
- Hager, W.W.; Zhang, H. A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM J. Optim. 2005, 16, 170–192. [Google Scholar] [CrossRef]
- Hager, W.W.; Zhang, H. Algorithm 851: CG DESCENT, a conjugate gradient method with guaranteed descent. ACM Transactions on Mathematical Software 2006, 32, 113–137. [Google Scholar] [CrossRef]
- Dai, Y.-H.; Kou, C.-X. A nonlinear conjugate gradient algorithm with an optimal property and an improved wolfe line search. SIAM. J. Optim. 2013, 23, 296–320. [Google Scholar] [CrossRef]
- Babaie-Kafaki, S.; Ghanbari, R. The Dai-Liao nonlinear conjugate gradient method with optimal parameter choices. Europ. J. Oper. Res. 2014, 234, 625–630. [Google Scholar] [CrossRef]
- Andrei, N. A Dai-Liao conjugate gradient algorithm with clustering of eigenvalues. Numer. Algor. 2018, 77, 1273–1282. [Google Scholar] [CrossRef]
- Babaie-Kafaki, S. On the sufficient descent condition of the Hager-Zhang conjugate gradient methods. 4OR-Q. J. Oper. Res. 2014, 12, 285–292. [Google Scholar] [CrossRef]
- Lotfi, M.; Hosseini, S.M. An efficient Dai–Liao type conjugate gradient method by reformulating the CG parameter in the search direction equation. J. Comput. Appl. Math. 2020, 371, Article–112708. [Google Scholar] [CrossRef]
- Ivanov, B.; Stanimirović, P.S.; Shaini, B.I.; Ahmad, H.; Wang, M.-K. A Novel Value for the Parameter in the Dai-Liao-Type Conjugate Gradient Method. J. Funct. Spaces 2021, 2021, Article ID 6693401, 10 pages. [Google Scholar] [CrossRef]
- Stanimirović, P.S.; Ivanov, B.; Stanujkić, D.; Katsikis, V.N.; Mourtas, S.D.; Kazakovtsev, L.A.; Edalatpanah, S.A. Improvement of Unconstrained Optimization Methods Based on Symmetry Involved in Neutrosophy. Symmetry 2023, 15, 250. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics, Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, NM, USA, 1999. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistructure 2010, 4, 410–413. [Google Scholar]
- Smarandache, F. Special Issue "New types of Neutrosophic Set/Logic/Probability, Neutrosophic Over-/Under-/Off-Set, Neutrosophic Refined Set, and their Extension to Plithogenic Set/Logic/Probability, with Applications". Symmetry 2019, https://www.mdpi.com/journal/symmetry/special_issues/Neutrosophic_Set_Logic_Probability.
- Mishra, K.; Kandasamy, I.; Kandasamy W.B., V.; Smarandache, F. A novel framework using neutrosophy for integrated speech and text sentiment analysis. Symmetry 2020, 12, 1715. [Google Scholar] [CrossRef]
- Tu, A.; Ye, J.; Wang, B. Symmetry measures of simplified neutrosophic sets for multiple attribute decision-making problems. Symmetry 2018, 10, 144. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E.L. Methods of conjugate gradients for solving linear systems. J. Res. Nat. Bur. Standards. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Andrei, N. An acceleration of gradient descent algorithm with backtracking for unconstrained optimization. Numer. Algorithms 2006, 42, 63–73. [Google Scholar] [CrossRef]
- Stanimirović, P.S.; Miladinović, M.B. Accelerated gradient descent methods with line search. Numer. Algorithms 2010, 54, 503–520. [Google Scholar] [CrossRef]
- Cheng, W. A two-term PRP-based descent method. Numer. Funct. Anal. Optim. 2007, 28, 1217–1230. [Google Scholar] [CrossRef]
- Zoutendijk, G. Nonlinear Programming, Computational Methods. In: J. Abadie (eds.): Integer and Nonlinear Programming, North-Holland, 37–86, Amsterdam, 1970.
- Andrei, N. An unconstrained optimization test functions collection. Adv. Model. Optim. 2008, 10, 147–161. [Google Scholar]
- Bongartz, I.; Conn, A.R.; Gould, N.; Toint, P.L. CUTE: constrained and unconstrained testing environments. ACM Trans. Math. Softw. 1995, 21, 123–160. [Google Scholar] [CrossRef]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
Figure 1.
The global structure of the fuzzy neutrosophic Dai-Liao CG method.
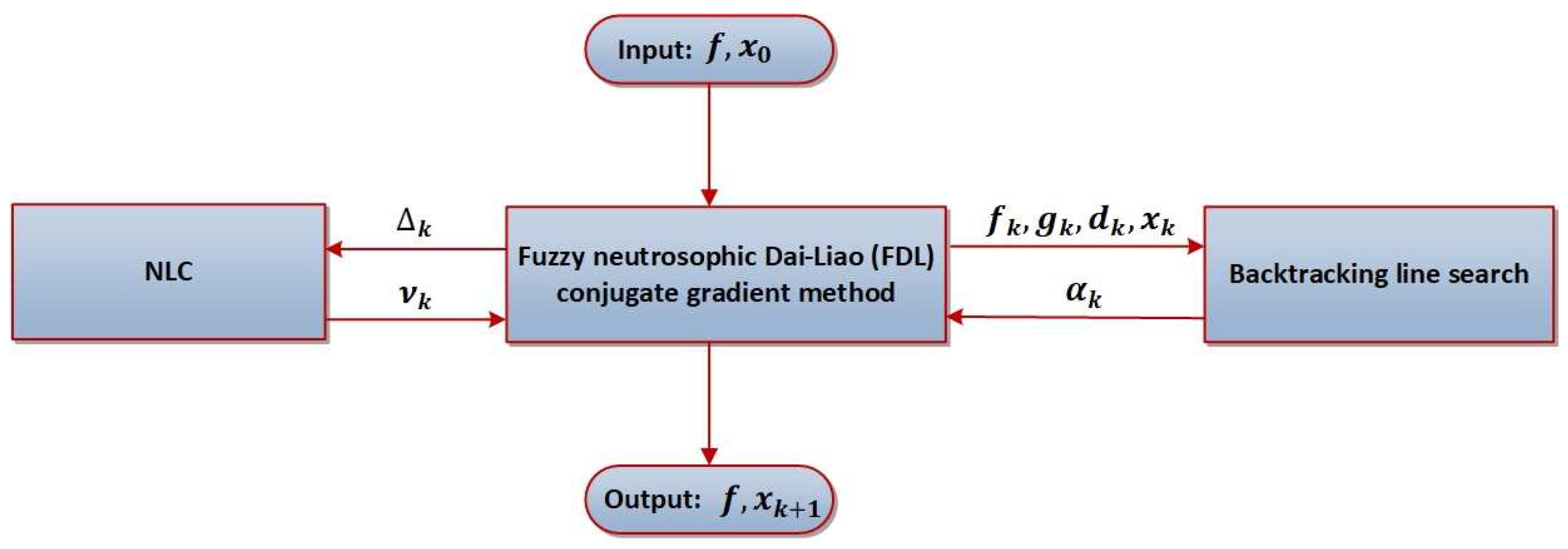
Figure 2.
The NLC design based on the neutrosophy.
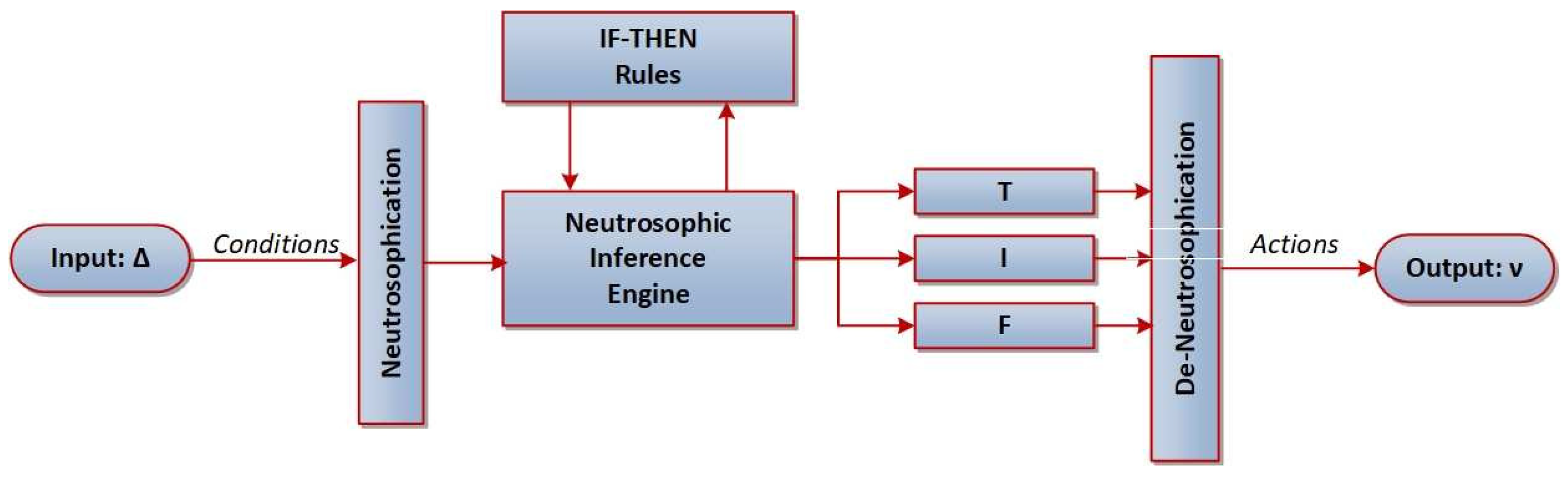
Figure 3.
Neutrosophication (24)–(26) and de-neutrosophication (27) guided by the parameters in Table 1.
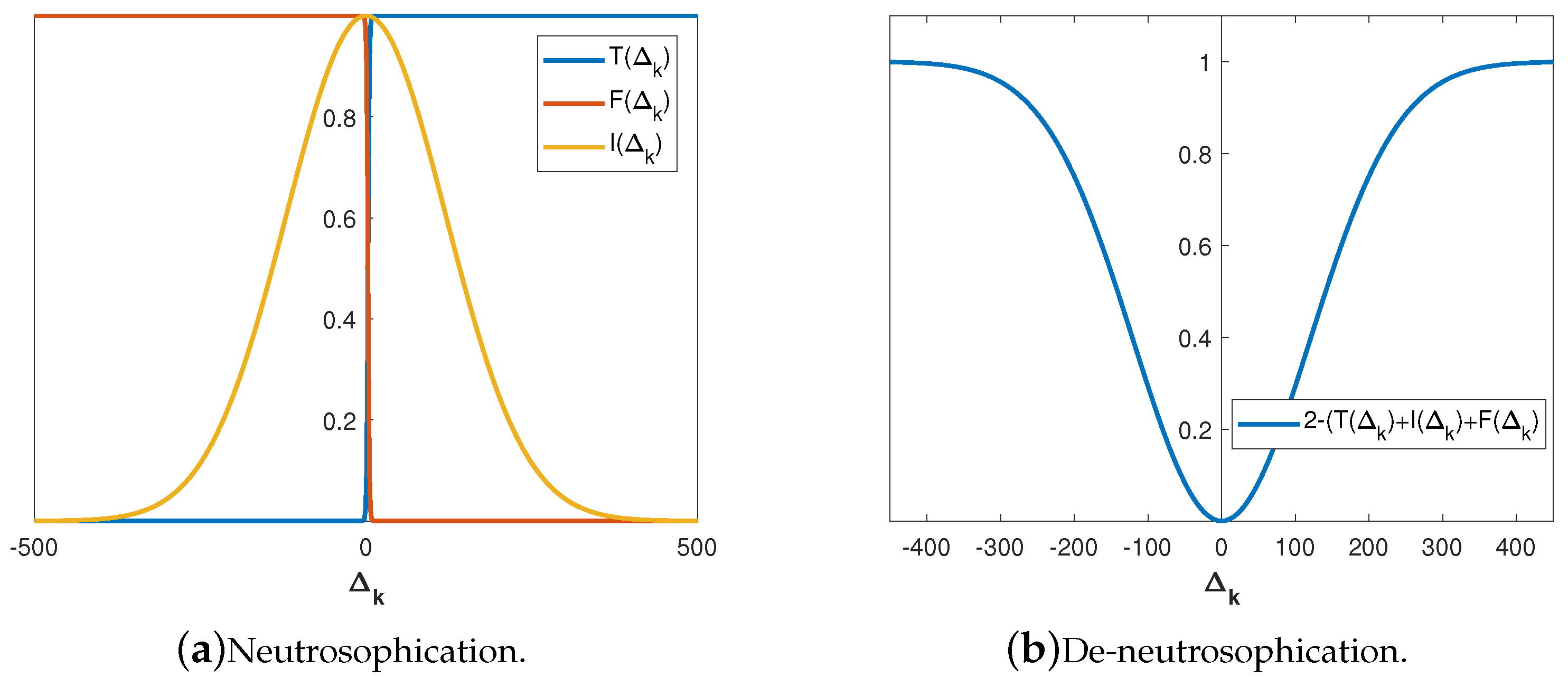
Figure 4.
Performance profile for DL, FDL, and EDL methods.
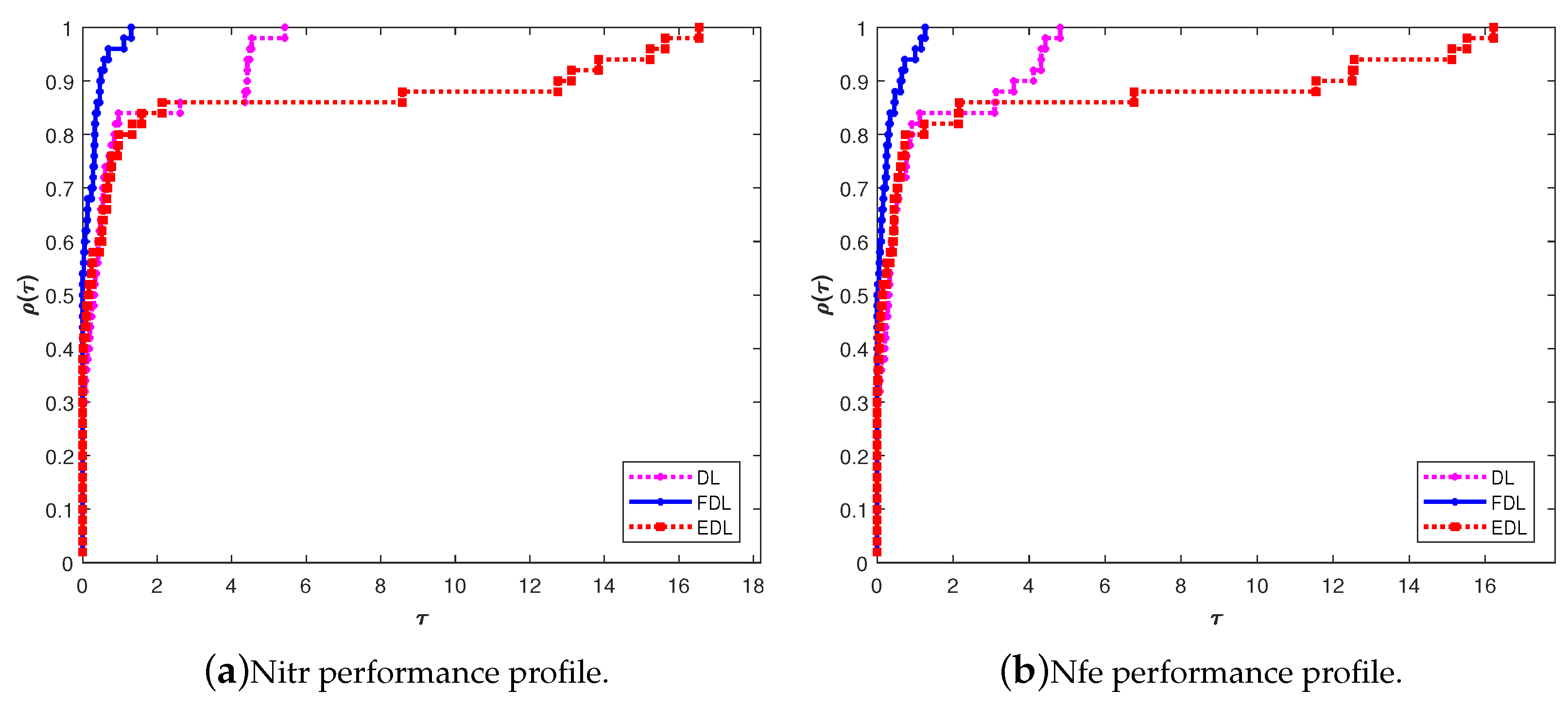
Figure 5.
Tcpu performance profile for DL, FDL, and EDL methods.
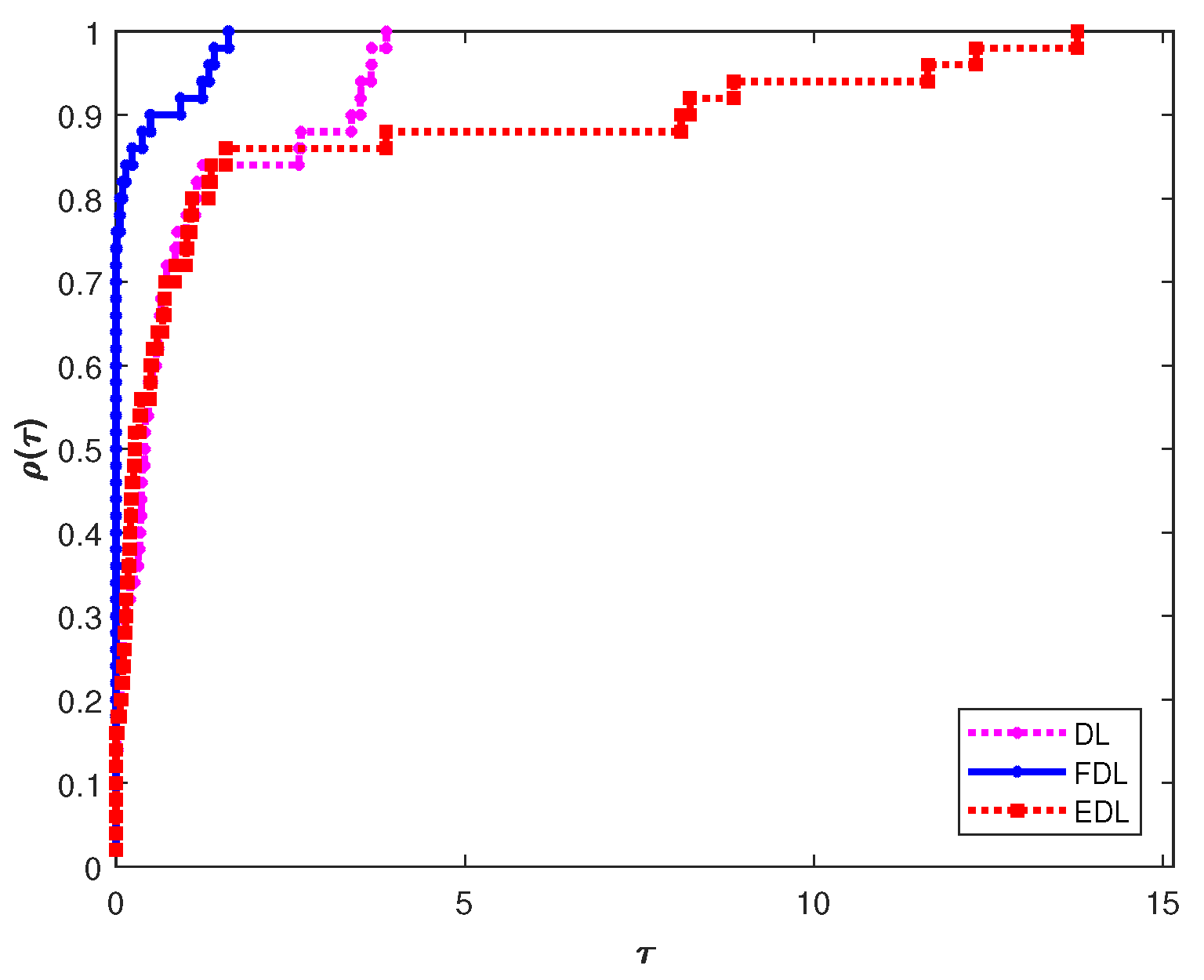
Table 1.
Recommended parameters in NLC.
| Set | Membership Function | Weight | ||
|---|---|---|---|---|
| Input | Sigmoid function (24) | 1 | 3 | 1 |
| Sigmoid function (25) | 1 | 3 | 1 | |
| Gaussian function (26) | 120 | 0 | 1 | |
| Output | Score function (27) | - | - | 1 |
Table 2.
Summary numerical results on unconstrained problems of DL, FDL, and EDL methods for the Nitr, Nfe, and Tcpu.
Table 2.
Summary numerical results on unconstrained problems of DL, FDL, and EDL methods for the Nitr, Nfe, and Tcpu.
| Test function | DL | FDL | EDL |
|---|---|---|---|
| Nitr/Nfe/Tcpu | Nitr/Nfe/Tcpu | Nitr/Nfe/Tcpu | |
| Extended Penalty | 1905/77578/32.438 | 1610/62534/24.266 | 2304/82602/39.344 |
| Perturbed Quadratic | 14555/606750/379.359 | 10800/440213/206.5 | 10012/408474/248.5 |
| Raydan 1 | 4337/114595/98.984 | 5497/122843/76.813 | 4194/109164/96.938 |
| Raydan 2 | 1427/2864/3.188 | 67/144/0.281 | 2572540/5145090/894.453 |
| Diagonal 1 | 5809/223750/245.578 | 5488/212491/227.781 | 4673/178295/219.109 |
| Diagonal 3 | 5247/196745/423.766 | 4531/168162/307.594 | 4596/171636/366.203 |
| Hager | 1742/31516/103.672 | 1242/22799/47.063 | 1940/33206/98.766 |
| Generalized Tridiagonal 1 | 2058/32313/49.5 | 2160/32033/27.5 | 2161/33285/44.703 |
| Extended Tridiagonal 1 | 310/2932/8.391 | 182/2501/6.297 | 308/4129/12.766 |
| Extended TET | 1140/9840/11.031 | 619/5808/5.484 | 749/6362/5.969 |
| Diagonal 5 | 1394/2798/6.938 | 60/130/0.609 | 3053907/6107824/3124.875 |
| Extended Himmelblau | 50/2431/1.016 | 51/2602/0.813 | 50/2413/0.938 |
| Perturbed quadratic diagonal | 1837/69156/18.453 | 1261/36785/13.875 | 2157/86977/34.797 |
| Quadratic QF1 | 13895/526995/187.313 | 21989/846402/376.156 | 10199/379554/122.844 |
| Extended quadratic penalty QP1 | 1080/17440/9.922 | 1524/23840/8.25 | 1157/18043/9.109 |
| Extended quadratic penalty QP2 | 218/9479/11.047 | 112/5513/4.953 | 218/9194/8.906 |
| Quadratic QF2 | 19211/847031/348.781 | 18861/816310/225.891 | 15555/689736/250.891 |
| Extended quadratic exponential EP1 | 1254/3443/3.172 | 56/404/0.516 | 21431/43829/7.531 |
| Extended Tridiagonal 2 | 22468/998473/549.484 | 3668/114169/87.438 | 10989/510713/93.609 |
| TRIDIA (CUTE) | 33278/1647913/967.234 | 40156/1977068/950.547 | 29133/1428866/675.422 |
| ARWHEAD (CUTE) | 1624/81625/44.875 | 1529/72379/31.594 | 1219/57140/28.672 |
| Almost Perturbed Quadratic | 14904/621925/259.797 | 19675/829784/357.359 | 13201/543372/188.047 |
| LIARWHD (CUTE) | 30/2705/1.281 | 30/2732/1.25 | 30/2739/1.438 |
| POWER (CUTE) | 532442/44419504/16742.672 | 580790/48609979/17435.609 | 629342/52431424/23630.781 |
| ENGVAL1 (CUTE) | 2489/33103/13.781 | 2400/32299/10.719 | 1975/27260/12.922 |
| INDEF (CUTE) | 21/1924/2.125 | 26/2238/2.5 | 30/2610/4.266 |
| Diagonal 6 | 1583/3197/4.531 | 74/185/0.359 | 7052401/14105032/5037.219 |
| DIXON3DQ (CUTE) | 320921/1775846/1083.281 | 229757/1368033/727.172 | 257451/1517252/1045.328 |
| COSINE (CUTE) | 20/1600/1.891 | 20/1697/1.891 | 20/1700/2 |
| BIGGSB1 (CUTE) | 249919/1400798/832.375 | 259475/1549293/810.766 | 236612/1389720/945.672 |
| Generalized Quartic | 866/11273/3.984 | 1099/8951/4.063 | 959/10662/3.125 |
| Diagonal 7 | 1453/4564/6.875 | 68/162/0.469 | 469477/940686/140.172 |
| Diagonal 8 | 1371/3962/5.359 | 67/199/0.422 | 594522/1193760/195.094 |
| Full Hessian FH3 | 2237/6202/7.125 | 52/513/0.688 | 767988/1537759/188.469 |
| Diagonal 9 | 3312/138545/225.719 | 5344/217150/224.906 | 4520/189307/260.453 |
| HIMMELH (CUTE) | 20/1690/4.797 | 20/1758/4.531 | 20/1760/4.891 |
| FLETCHCR (CUTE) | 303212/10189775/5073.688 | 300227/10011849/4704.125 | 289670/9702961/4411.453 |
| Extended BD1 (Block Diagonal) | 1597/16783/7.625 | 1227/15639/5.875 | 1200/12605/6.625 |
| Extended Maratos | 72/3366/1.188 | 50/2069/0.719 | 40/1975/0.75 |
| Extended Cliff | 234/2992/2.078 | 217/6000/4.891 | 950/13187/6.188 |
| Extended Hiebert | 70/7215/1.938 | 70/7220/1.828 | 70/7228/1.859 |
| NONDIA (CUTE) | 33/3066/1.375 | 30/2829/1.266 | 32/3031/1.625 |
| NONDQUAR (CUTE) | 58/4652/18.047 | 45/3666/17.219 | 86/4989/19.016 |
| DQDRTIC (CUTE) | 3456/87105/26.453 | 2327/59047/16.406 | 3637/92315/34.953 |
| Extended Freudenstein and Roth | 1376/46597/10.734 | 3390/111830/28.516 | 2018/66654/16.172 |
| Generalized Rosenbrock | 282948/8410218/4125.516 | 280440/8335396/4088.547 | 281792/8373946/4055.172 |
| Extended White and Holst | 76/5794/9.219 | 50/3171/7.281 | 59/4022/11.563 |
| Extended Beale | 118/6791/14.047 | 72/3118/5.906 | 181/4748/6.75 |
| EG2 (CUTE) | 507/29388/47.547 | 697/48512/119.875 | 811/39769/122.469 |
| EDENSCH (CUTE) | 1694/23160/89.453 | 2089/27821/83.266 | 1684/22731/116.844 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated











