Preprint
Article
Magnetic Heating Effect for Quarter-Wave Resonator (QWR) Superconducting Cavities
Altmetrics
Downloads
156
Views
49
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 April 2023
Posted:
25 April 2023
You are already at the latest version
Alerts
Abstract
The magnetic heating effect for the superconducting quarter-wave resonator (QWR) cavities is investigated, and the Q slopes of the superconducting cavities are measured with an increasing accelerating field. Physical phenomena for zero-temperature limit are introduced. Bardeen–Cooper–Schrieffer (BCS) resistance and Casimir force are calculated for the zero-temperature limit. The vertical test is shown for the performance test of the quarter-wave resonator (QWR) cavities. The parameters for the quarter-wave resonator (QWR) cavity are presented. The Q slopes are measured as a function of an accelerating electric field at 4.2 K. The surface resistance of the superconducting cavity increases with an increasing peak magnetic field. The magnetic defects cause the degradation for the quality factor. From the magnetic degradation, we can find the magnetic moments of the superconducting cavities. All the quarter-wave resonator (QWR) cryomodules are installed in the tunnel, and beam commissioning is performed successfully.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction
Superconducting cavities are an important component of a heavy ion accelerator. The superconducting cavities are operated at low temperatures, such as 4.2 K and 2 K. Reducing field emission sites, electric defects sites, and magnetic defects sites as much as possible is important to maintain the high quality factor of the superconducting cavity. The performance of the superconducting cavity, which includes quality factor, Lorentz force detuning (LFD), pressure sensitivity, x-ray emission, and resonance frequency, is tested at operation temperature, which is called the vertical test. A vertical test facility which includes a hanging booth, pits, a solid state power amplifier (SSPA), control racks, and a control room was designed, constructed, and used in order to test the superconducting cavities [1,2,3,4]. The field emission, which shows electron emission under a local strong electric field, and the thermionic emission, which shows electron emission under a local high temperature, were investigated [5,6,7,8,9,10,11]. The field emission and thermionic emission were studied in terms of dimensions [12,13,14], and the unified theory for the field emission and thermionic emission was also studied [15,16]. The field emission sites of the superconducting cavity were investigated [17,18,19,20], and reducing the outgassing and the RF processing of the pulsed high peak power for the superconducting cavity were used to reduce the field emission in order to achieve a high-quality cavity [21,22]. The RAON accelerator was designed [23], the cavity was tested with liquid nitrogen [24], the quarter-wave resonator (QWR) and the half-wave resonator (HWR) were developed [25,26,27,28], and the half-wave resonator (HWR) cryomodule was tested at 2 K [29,30]. The high-beta cavity for the quarter-wave resonator (QWR) was tested [31], and both the electric and magnetic field-dependent surface resistances were studied on a superconducting niobium accelerating cavity [32,33,34]. For superconducting cavities, medium-temperature furnace baking was performed to improve the quality factor [35] and electro-polishing (EP) was conducted to achieve a high gradient [36]. The Casimir force between type-II superconducting plates was calculated [37].
In this research, we show the vertical test and get the Q slopes for the quarter-wave resonators (QWRs) as a function of an accelerating electric field. The Q factors are shown as a function of the applied peak magnetic field. The magnetic defects cause the Q factor degradation. The magnetic moments caused by magnetic defects are obtained by fitting the surface resistance data with Bardeen–Cooper–Schrieffer (BCS) resistance, in which the band gap is reduced by magnetic defects. Physical phenomena at the zero-temperature limit are studied, and the beam commissioning for QWR cryomodules is presented.
2. Magnetic Effect on Superconducting Cavity
The quality factor of a cavity is defined as the ratio of the stored energy in the resonator to the dissipated energy per cycle by damping processes. The quality factor for the cavity is
where is the quality factor of the cavity, is the angular frequency of the cavity, U is the stored energy of the cavity, T is the period of the cycle, and is the dissipated power in the cavity surface, called the RF surface. The RF power is mainly dissipated in the cavity surface, while some RF power leaves through the input power coupler and transmitted pickup coupler. The quality factor for the input power coupler is defined as
where is the quality factor of the emitted or input power coupler and is the emitted power through the input power coupler.
The quality factor of the transmitted power coupler is defined as
where is the quality factor of the transmitted power coupler and is the transmitted power through the pickup power coupler.
The loaded quality factor is expressed as
where represents the total power losses in the cavity system. Here is the total power, is the dissipated power in the cavity walls, is the emitted power, and is the transmitted power.
The stored cavity energy when the RF power is turned off decays according to the differential equation
From Equation (5), the stored energy is expressed as
where represents the initial stored energy. The decay time becomes
The comes from the measurement of the decay time. The cavity quality factor of can be obtained by defining the quality factors of the couplers as
where is the total RF power, is the dissipated RF power in the cavity, is the emitted RF power, and is the transmitted RF power.
From Equation (8), the quality factors are expressed as
The quality factors of Equation (9) become
where and .
The can be expressed as
where is the forward power, is the dissipated power in the cavity walls, and is the reflected power. The cavity is over-coupled for where the upper sign is used, the cavity is under-coupled for where the lower sign is used, and the cavity is critical-coupled for .
The can be expressed as
where is the transmitted RF power and is the dissipated RF power on the cavity surface.
The quality factors of Equation (10) becomes
By controlling the variable power coupler, the beta can be set up with the critical coupling of. The is very small value in which is much bigger than . The decay time is measured at the critical coupling, and the loaded quality factor can be expressed as
The accelerating field depends on cavity parameters as well. The accelerating electric field can be expressed as
where the geometric shunt impedance of is the shunt impedance divided by , which measures the beam acceleration efficiency per unit stored energy U at a resonance frequency, and is the effective length of the cavity. The and are found by CST-MWS simulation. The geometric shunt impedance of , which depends only on the cavity’s shape, needs to be maximized for cavity design. RF dissipation is reduced by maximizing both the geometric shunt impedance of and the geometry factor of G.
The accelerating electric field of Equation (15) is expressed as
where R/Q is the geometric shunt impedance of the cavity and is the effective length of the cavity. The accelerating electric field of Equation (16) is written as
where is the kappa of the cavity.
The quality factor of Equation (1) is also expressed as
where , and represent the forward RF power, the reflected RF power, and the transmitted RF power, respectively.
The quality factor of the cavity becomes [38]
where is the quality factor of the cavity, is the resonance frequency of the cavity, is the magnetic field, is the magnetic permeability, is the cavity volume, and is the cavity surface area.
The cavity quality factor is expressed as
where is the cavity quality factor, is the cavity geometry factor, and is the cavity surface resistance.
The surface resistance of the superconducting cavity can be expressed as
where is the surface resistance of the superconducting cavity, is the residual resistance of the superconducting cavity, and is the Bardeen–Cooper–Schrieffer (BCS) resistance of the superconducting cavity. The Bardeen–Cooper–Schrieffer (BCS) resistance depends on temperature, and the residual resistance is the leftover resistance at zero temperature.
Magnetic flux is quantized, and the magnetic flux in the superconductor is quantized with the magnetic flux quantum [39,40]. The trapped magnetic flux, which is the multiple of the magnetic flux quantum in Nb superconducting cavity, can be expressed as
where n is the integer number, and h is the Planck constant. The magnetic defect comes from the trapped magnetic flux of Equation (22). The superconducting current surrounds the quantized magnetic flux, in which the core of the vortex corresponds to its normal state.
The action in nature is expressed as , in which S is the action, L is the Lagrangian, and is the reduced Planck constant. The physical meaning of the reduced Planck constant is the minimum action in nature. The reduced Planck constant () or Planck constant (h) is related to the origin of quantization, which includes magnetic flux quantum (h/2e), conductance quantum (2e2/h), inverse conductance quantum (h/2e2), von Klitzing constant (h/e2), Josephson constant (2e/h), photon (hf), etc.
The dissipated power in the superconducting cavity walls is the product of the local surface resistance and the local magnetic field squared over all of the RF surface. The dissipated power is expressed as
where is the dissipated power in the superconducting cavity, is the local surface resistance of the superconducting cavity, is the local magnetic field over the superconducting cavity surface, and is the surface area of the superconducting cavity. According to Equation (23), the dissipated power increases as the surface resistance and the trapped magnetic field are increased.
The Cooper pairs in a superconductor show zero resistance for DC current, while they show some resistance for AC current due to finite momentum. When the temperature is less than half of niobium’s critical temperature , the BCS surface resistance is approximated by [41]
where T is the temperature in Kelvin, C is the material-dependent constant, is the band gap of the superconducting material, which represents half of the energy required to break a Cooper pair, andis the resonance frequency of the superconducting cavity.
The Bardeen–Cooper–Schrieffer (BCS) resistance is changed by the presence of magnetic defects in the superconducting cavity, which reduces the band gap energy with [42]. From Equation (24), the Bardeen–Cooper–Schrieffer (BCS) resistance is expressed as
where is the initial band gap, M is the magnetic moment of the superconducting cavity, and is the applied peak magnetic field. The surface resistance of Equation (21) can also be expressed as
where is the surface resistance, M is the magnetic moment, B is the magnetic field, and is the residual resistance. Magnetic defects cause magnetic heating, which causes the pair-breaking of the superconducting current density and the increased density of normal-state electrons. The Bardeen–Cooper–Schrieffer (BCS) resistance decreases as the temperature decreases from 4.2 K to 2 K. The surface resistance of Equation (26) shows that the residual resistance and the magnetic resistance coming from magnetic flux remain at zero temperature. The Bardeen–Cooper–Schrieffer (BCS) resistances of Nb for 81.25, 162.5, and 325 MHz at 4.2 K are about 2, 8, 32 nΩ, respectively. The Bardeen–Cooper–Schrieffer (BCS) resistances of Nb for 81.25, 162.5, and 325 MHz at 2 K are below nΩ.
3. Physical Phenomena at the Zero-Temperature Limit
The following are the physical phenomena for the zero-temperature limit: Blackbody radiation stops at 0 K. Materials’ resistivity is different according to their properties as the temperature goes down to 0 K. Figure 1 shows the resistivity as a function of temperature for different material types. Insulator is a material with a very high resistivity that is almost independent of temperature. Semiconductor is a material with an intermediate-range resistivity. The resistivity of the semiconductor increases as the temperature is decreased. Electrons move through the bandgap in semiconductors. Metal is a material with very low resistivity. The resistivity of the metal increases as the temperature is increased. The electron-phonon scattering of the metal increases with increasing temperature. A superconductor is a material whose resistance is similar to that of a metal at high temperatures but whose direct current (DC) resistance drops to zero below a critical temperature. The Bardeen–Cooper–Schrieffer (BCS) theory of the superconductor shows the electron-phonon coupling.
The surface resistance of the superconducting cavity is reduced to the residual resistance and the flux-trapped resistance at 0 K because the Bardeen–Cooper–Schrieffer (BCS) resistance goes down to zero as the temperature is reduced to 0 K. Figure 2 shows the Bardeen–Cooper–Schrieffer (BCS) resistance of Nb as a function of temperature for different cavity frequencies. From Equation (24), the Bardeen–Cooper–Schrieffer (BCS) resistance for the Nb superconducting cavity decreases to 8.3 n, 0.17 n, and 0, respectively, as the temperature is reduced to 4.2, 2, and 0 K for 162.5 MHz. The Bardeen–Cooper–Schrieffer (BCS) resistance for the Nb superconducting cavity decreases to 2.1 n, 0.004 n, and 0, respectively, as the temperature is reduced to 4.2, 2, and 0 K for 81.25 MHz.
The Casimir effect works well at zero temperature. Particles and antiparticles are created and annihilated in a vacuum at zero temperature, which is called vacuum fluctuation. The Casimir effect is the motion of two parallel conducting plates in the vacuum. The plates are closed together because only small fluctuations fit in between and larger modes are excluded. The boundary condition is that the electric field is zero on the conducting plates. The larger modes exert a total force greater than the smaller modes. Thus, the plates are attracted to each other. The Casimir force is
where F is the Casimir force, A is the surface area of the plates, and d is the distance between the conducting plates.
The Casimir force per unit area with temperature correction for is [43]
where T is the temperature.
Figure 3 shows the Casimir force per unit area as a function of distance. The Casimir force is very powerful at small distances below micrometers, which is inversely proportional to the fourth power of the distance between the plates. The Casimir force at 0 K is higher than that at 300 K. The temperature effect is very small in the range of the distance below a micrometer.
Zero-point energy can be found in many areas of physics. The radiation energy is expressed as
where is the frequency.
Phonon energy in one dimension is expressed as
where n is an integer number. From Equation (29) and Equation (30), we can find the zero-point energy,. The zero-point energy exists for all gases because the uncertainty principle works for all atoms. For the most gases, the zero-point energy is lower than the potential energy, so gases are transformed to solids at 0 K. All gases except helium become solid at 0 K because the zero-point energy of the liquid helium is high compared to its potential energy. The helium gas stays liquid at 0 K as long as the pressure is below 25 bars. For solid materials, the phonon shows the zero-point vibration, and the electrons in metal fill up to Fermi energy. The zero-point motion, or vibration, exists in all solids and quantum fluids.
Four fundamental forces, which include gravitational force, electromagnetic force, strong nuclear force, and weak nuclear force, work at zero temperature. Their potential energies do not depend on temperature, while their kinetic energies do. The zero temperature approximation is assumed in high energy physics such as strong nuclear force because the room temperature effect is very small and can be negligible compared to the strong nuclear energy.
4. Experimental Procedures
The residual-resistivity ratio (RRR) 300-grade niobium is used to fabricate superconducting cavities. Figure 4 shows the pictures of the Nb raw materials. The thickness of the Nb sheet is 3 mm. The dimensions, mechanical properties, and electrical properties of Nb sheet are checked. The resistivity of Nb was measured as a function of temperature [44]. Young’s modulus is measured for mechanical properties.
The components of the cavity are made by electrical discharge machining (EDM) wire cutting, deep drawing, press forming, and brazing. The resonance frequency of the superconducting cavity is checked in the stack-up test. The electron beam welding is performed with a vacuum pressure below mbar. A visual inspection is performed for weld beads. The dimensions and resonance frequency for the cavity are checked, and then a teak test is performed.
Ultrasonic cleaning is used to clean the cavity surface. First, 1% of liquinox is used at 50 oC for more than half an hour. Second, deionized (DI) water is used at 50 oC for more than half an hour. Buffered chemical polishing (BCP) is performed. The etchant is 49%HF+69%HNO3+85%H3PO4 (1:1:2 in volume ratio). The etch rate is below 1 µm/min and the total amount of the etching is around 120 µm. The etching temperature is controlled at less than 15 oC because the etching rate increases rapidly as the temperature is increased. The concentration of Nb in the acid solution needs to be less than 15 g/l. The etchant is supplied from the bottom of the quarter-wave resonator (QWR) cavity to the top of the quarter-wave resonator (QWR) cavity, in which the flow direction is opposite that of gravity. The etchant comes out of the top of the quarter-wave resonator (QWR) cavity, which is the closed loop circulation. Once the etching is finished, the cavity is turned upside down. Then deionized (DI) water is supplied to the bottom of the QWR cavity, where it moves from the bottom to the top of the cavity. The deionized (DI) water comes out of the top of the quarter-wave resonator (QWR) cavity, which is also the closed loop circulation.
The inner surface of the cavity is inspected after the buffered chemical polishing (BCP). A uniform and smooth surface is important to prevent a rough surface in the cavity. The rough surface can be a field emission site. High-temperature baking at 600 oC for 10 hours is performed in a high-vacuum furnace. The resistivity of deionized (DI) water should be higher than 17at 25 oC. High-pressure rinsing (HPR) is used to remove the leftover particles on the cavity surface. The filter size of the high-pressure rinsing is 0.5 μm, and the water pressure is about 100 bars. The diameter of the nozzle is 0.5 mm, and the speed of the nozzle’s rotation is around 20 rpm. The total rinsing time for each cavity is over 10 hours, of which the rinsing time for each step is over 2 hours.
A liquid helium vessel or jacket is attached on the outside of the cavity, and then additional light buffered chemical polishing (BCP) and high-pressure rinsing (HPR) are performed after attaching the jacket. The minimum distance between the outside of the cavity and the jacket is 1 cm, in which liquid helium flows.
5. Experimental Setup
The RAON accelerator was designed [23], and the cavity was tested with liquid nitrogen [24]. The quarter-wave resonator (QWR) and the half-wave resonator (HWR) cavity were developed [25,26,27,28]. The performance of the quarter-wave resonator (QWR) cavities is tested at the vertical test facility. Figure 5 shows the schematic diagram for the magnetic shielding in cryostat. The mumetal and cryophy are used to reduce the external magnetic field. The x-ray detector is located outside of the cryostat.
Figure 6 shows the cryostat and magnetic shielding. The design of the cryostat, the magnetic shielding such as mumetal and cryophy, and the top view of the vertical test are shown in Figure 6. Two quarter-wave resonator (QWR) cavities can be simultaneously tested in the cryostat. The measured static heat load of the cryostat is 8 W. The Mag-03MSB100 Three-Axis Magnetic Field Sensor, from Bartington Instruments, is used to measure the magnetic field strength. The magnetic field strength for the position of the cavity is measured below 6 mG by applying the mumetal and cryophy.
Table 1 shows the parameters of the quarter-wave resonator (QWR) cavity. The geometry factor of G is 18.1 Ω for the quarter-wave resonator (QWR) cavity. For the accelerating electric field of Equation (16), and are found for the parameters of the QWR cavity. For the accelerating electric field of Equation (17), the kappa is also found for the parameters of the QWR cavity.
The resonance frequency for the quarter-wave resonator (QWR) cavity is 81.25 MHz. Figure 7 shows the picture of the quarter-wave resonator (QWR) cavities during vertical test preparation. The temperature sensors, consisting of calibrated Cernox sensors, are attached with kapton tape on the QWR jacket cavities. The physical property measurement system (PPMS) is used to calibrate the Cernox sensors in the temperature range from 350 to 1.9 K. These temperature sensors monitor the temperature of the quarter-wave resonator (QWR) cavities. Two liquid helium level meters are used to monitor the liquid helium level in the cavity.
The quarter-wave resonator (QWR) cavities are baked at 120 oC for 48 hours while a dry pump and a turbo molecular pump (TMP) are used for cavity pumping, which is called the low-temperature baking. The low-temperature baking removes the water from the cavity and is very effective in getting rid of multipacting. The low-temperature baking is also necessary for a high Q factor in a high-accelerating electric field.
A x-ray detector is placed outside of the cryostat. The FHZ 632 L-10 gamma detector is used to detect the x-ray radiation. The liquid nitrogen and then the liquid helium are supplied to do the vertical test. The superconducting cavities get cooled down fast, which takes about an hour from 150 K to 50 K.
Cable calibration is performed at 4.2 K. Both the forward and reflected power are measured by keeping the input power at 18 dBm. The drive frequency of the Solid State Power Amplifier (SSPA) with 200 W is 81.25 MHz for the quarter-wave resonator (QWR) cavities. The directional coupler and circulator should work well for 81.25 MHz. The S11, S21, and S22 for each cavity are measured with the Keysight ENA Network Analyzer E5080A.
RF conditioning can be started at 4.2 K. The RF conditioning is a process to clean the RF surface of the superconducting cavity in order to make the highest possible quality factor in the range of all possible accelerating fields. The RF conditioning starts at over-coupled, in which a variable coupler is maximally inserted into the inside of the cavity. By watching the transmitted power, we change the forward power and the phase of the Low Level Radio Frequency (LLRF) with Self Excited Loop (SEL) mode to increase the transmitted power. The forward power and transmitted power increase together after finishing the RF conditioning. It takes from about 2 hours to about 8 hours to do the RF conditioning for the quarter-wave resonator (QWR) cavity. The RF power is used from about mW to about 100 W to do the RF conditioning. The RF power must be below 50 W for a high-quality cavity. Pulsed RF conditioning and continuous wave (CW) RF conditioning are used. The pulsed RF conditioning is used for a pulse width of 0.2 s at 1 Hz. The pulsed RF conditioning requires more RF power compared to the continuous wave (CW) RF conditioning. The reflected RF power goes down to zero when the variable coupler is pulled out to the critical coupling.
The decay time at the critical coupling is measured at 1 MV/m. The decay time for the quarter-wave resonator (QWR) cavities is about 1 s. X-rays and multipacting should not be generated while the decay time is measured. When there is multipacting, the decay time becomes very short, such as microseconds. The quality factor of
, obtained by using the decay time measurement, is about 1011.
The Q slope of the quarter-wave resonator (QWR) cavities is measured from 1 MV/m to the maximum accelerating field such as 8 MV/m. The quality factor and x-ray radiation are simultaneously measured as functions of the accelerating field. The Q value of the quarter-wave resonator (QWR) cavities decreases as the accelerating field increases.
6. Discussions
The quarter-wave resonator (QWR) is made of Nb, whose phase transition temperature is 9.25 K [44]. The magnetic field trapping coming from the magnetic defects on the RF surface of the superconducting cavity occurs as its temperature decreases and crosses the phase transition temperature of 9.25 K. Therefore, we try to reduce the external earth magnetic field strength while the quarter-wave resonator (QWR) cavities are tested.
Figure 8 shows the measurement of the magnetic field strength for the cryostat. The magnetic field strength inside the cryostat is measured from the bottom at a height of 0 cm to the top at a height of 200 cm. The quarter-wave resonator (QWR) cavity is located between 40 and 140 cm. The mumetal is installed outside of the cryostat, the cryophy is installed inside of the cryostat, and the top plate containing the mumetal and the cryophy is installed on top of the cryostat. The cryophy is effective at low temperatures, while the mumetal is ineffective. The magnetic field strength is measured by installing the mumetal, the mumetal and cryophy, and the mumetal, cryophy, and top plate. The mumetal is also installed on the bottom of the cryostat. The magnetic field strength at the location of the quarter-wave resonator (QWR) cavity decreases to under 6 mG by installing the mumetal, the cryophy, and the top plate. The external magnetic field strength causes increased surface resistance of the Nb superconducting cavity due to trapped magnetic flux. The surface resistance is linearly proportional to the external magnetic field strength [45]. In general, the external magnetic field strength for vertical tests is recommended to be below 10 mG. Therefore, the 6 mG is good enough to do a vertical test.
The Q slopes are measured with increasing accelerating electric fields for the quarter-wave resonator (QWR) cavities in Figure 9. The Q factor decreases with increasing accelerating fields. The Q factor decreases more rapidly above the accelerating field in which x-ray radiation appears. The field emission effect on the superconducting cavity was investigated [30]. The local temperature of the field emission site increases due to Joule heating, and the electrons emitted from the field emission are accelerated and generate Bremsstrahlung radiation by consuming the RF energy. Therefore, the quality factor of the superconducting cavity decreases with increasing field emission and x-ray generation.
Figure 10 shows the surface resistance measurement as a function of the peak magnetic field strength for the quarter-wave resonator (QWR) cavities. The surface resistance increases with an increasing peak magnetic field.
The quarter-wave resonator (QWR) cavities are made of niobium, which is a type II superconductor. Type I and Type II superconductors are classified by their superconducting coherence length and London magnetic field penetration depth. The superconductor becomes the type I superconductor for , while the superconductor becomes the type II superconductor for . The type I superconductors, or soft superconductors, showing zero resistance under DC fields, expel magnetic field perfectly, which is known as the Meissner effect. The type II superconductors, or hard superconductors, show the Meissner state below the RF critical magnetic field of Hc1, the vortex state, or magnetic flux trapping state, in the range of magnetic field between Hc1 and Hc2, and the normal conducting state in the range of magnetic field above Hc2. According to Equation (23), the dissipated power is proportional to the trapped magnetic field squared. In order to reduce the magnetic heating, it is important to increase the critical magnetic field of Hc1. The niobium material has a residual-resistivity ratio (RRR) value of 300 for the quarter-wave resonator (QWR) cavities. The niobium material has various defects, which include tantalum, molybdenum, tungsten, titanium, hafnium, zirconium, carbon, nitrogen, oxygen, and hydrogen [46,47]. The critical magnetic field of Hc1 decreases as the defect size increases and the surface roughness increases [48,49,50]. The oxide layer on the niobium surface works as the magnetic flux pinning sites [51]. Electron-beam welding (EBW) is used to fabricate the quarter-wave resonator (QWR) cavities. The electron-beam welding (EBW) should be performed in a high-vacuum environment. The electron-beam welding (EBW) was studied to measure the residual-resistivity ratio (RRR) value of Nb as a function of distance from the welding site in terms of the vacuum level, welding power, and welding speed [52]. The defects, such as oxygen, can cause the magnetic field trapping while the electron-beam welding (EBW) is performed in a low vacuum environment. The smooth surface of the E-beam welding sites should be kept; otherwise, the rough surface of the welding site can cause magnetic field trapping.
The surface resistance for the quarter-wave resonator (QWR) cavities is shown as a function of peak magnetic field in Figure 11. According to Equation (23), the dissipated power coming from the magnetic heating depends on the surface resistance and magnetic field on the superconducting surface. The magnetic heating causes a decreased quality factor. The surface resistances for the quarter-wave resonator (QWR) cavities are fitted with the magnetic heating of Equation (26). The magnetic moments for the QWR from 1 through 6 are , , , , , and [J/T], respectively. The magnetic moments for the QWR cavities are comparable to the magnetic moments of [J/T] obtained from the research work [42]. The magnetic defects of the superconducting quarter-wave resonator (QWR) cavities cause magnetic heating, which causes pair-breaking of the superconducting current density and increases the density of normal-state electrons. The magnetic defects causing the trapped magnetic flux can come from welding sites, material defects, surface particles, a rough surface, etc. In order to fabricate a high-quality superconducting cavity, the magnetic defects should be reduced as much as possible.
All 22 quarter-wave resonator (QWR) cavities are qualified in the vertical test, and the QWR cryomodules made of the quarter-wave resonator (QWR) cavities are also qualified in the horizontal test. The static heat load, dynamic heat load, pressure sensitivity, Lorentz force detuning (LFD), cavity alignment, x-ray emission, and RF control are measured in the horizontal test. The cavity alignment is within 1 mm in the horizontal test. Following the horizontal test, all of the quarter-wave resonator (QWR) cryomodules are installed in the RAON SCL3 tunnel.
It is very important to reduce microphonics to control the superconducting cavity with radio frequency (RF). The liquid helium pressure of the QWR cryomodule is around 1.3 bars in the superconducting cavity at 4.5 K. The fluctuation of helium pressure goes down by changing the flow rate, supply pressure, return pressure, cryogenic valve control speed, etc. The low-level radio frequency (LLRF) with self-excited loop (SEL) mode is used to get the performance test of the superconducting cavity in the vertical test. The low-level radio frequency (LLRF) can control the cavity with generator-driven resonator (GDR) controller mode for beam experiment. The external QL of the forward power coupler is around 5⨯105, the external Qt of the pickup is around 1⨯1011, the bandwidth of the QWR cavity is about 150 Hz, the pressure sensitivity is around 5 Hz/mbar, and Lorentz force detuning (LFD) is around -15 Hz/(MV/m)2. The quality factor requirement for the QWR cavity is 2.4⨯108 at 6.1 MV/m. The total heat load for the QWR cryomodule at 6.1 MV/m is around 12 W, in which the static heat load is about 4.5 W. The tuner is used to control the resonance frequency of the cavity and changes the frequency to 81.25 MHz. The tuner is only used to change the frequency when the frequency is off by more than 20 Hz from the resonance frequency of 81.25 MHz. For the first time, the amplitude and phase of the cavity are controlled for one minute. Later, the amplitude and phase of the cavity are controlled for one hour by reducing the fluctuation of the liquid helium pressure under 5 mbar in 20 seconds. The superconducting cavities have different pressure sensitivities, so the cavities respond differently to the helium pressure fluctuation. The amplitude and phase of the cavity can be stabilized as the helium pressure fluctuation decreases. The amplitude fluctuation is less than 1% and the phase fluctuation is also less than 1 degree for more than an hour for beam commissioning.
Figure 12 shows the pictures of the quarter-wave resonator (QWR) cryomodules and RAON SCL3 tunnel. For the first beam commissioning, the quarter-wave resonator (QWR) cryomodules from 1 through 5 are used and the beam energy of Ar+9 is increased from 0.5 to 0.7 MeV/u with 30 µA. The second beam commissioning is performed for all quarter-wave resonator (QWR) cryomodules from 1 through 22 in RAON SCL3, in which the energy of Ar 9+ is increased from 0.5 to 2.45 MeV/u with 30 µA. The two quarter-wave resonator (QWR) cryomodules (CMs) for 3 and 20 are excluded because the quarter-wave resonator (QWR) cryomodule (CM) 3 shows the unstable RF control and the the quarter-wave resonator (QWR) cryomodule (CM) 20 shows the off resonance frequency even if the tuner is used at maximum range. The beam energy is determined by the time of flight measurement. For each quarter-wave resonator (QWR) cavity in the quarter-wave resonator (QWR) cryomodule, the accelerating amplitude and phase are determined one by one during beam commissioning. The accelerating field and phase for each cavity are kept during beam commissioning.
This research can be useful for the fabrication and testing of superconducting cavities and for understanding the magnetic degradation of the superconducting cavities.
7. Conclusions
We have measured the Q slopes for the quarter-wave resonator (QWR) cavities and shown the magnetic heating effect for the Q factor degradation. Physical phenomena at the zero-temperature limit are introduced. The Bardeen–Cooper–Schrieffer (BCS) resistance is calculated as a function of temperature for different frequencies, and the Casimir force is calculated with temperature correction for the zero-temperature limit. The magnetic shielding is applied in the cryostat in order to reduce the magnetic heating of the superconducting cavity coming from an external magnetic field, such as the earth’s the magnetic field. The magnetic field is reduced below 6 mG in the cryostat by installing both mumetal and cryophy. The manufacturing processes for the quarter-wave resonator (QWR) cavity are shown, and the vertical test is performed for the quarter-wave resonator (QWR) cavities. The parameters for the quarter-wave resonator (QWR) cavities are presented. The Q slopes of the quarter-wave resonator (QWR) cavities are measured with increasing accelerating field. The data of the Q slope is changed to the surface resistance, so the surface resistance is expressed as a function of the peak magnetic field. The magnetic heating causes degradation of the quality factors in the superconducting cavities. From the magnetic degradation, we can find the magnetic moments for the quarter-wave resonator (QWR) cavities. The medium magnetic moment is obtained as [J/T]. The Q slope degradation of the quarter-wave resonator (QWR) cavities is reasonably explained by the magnetic defects having magnetic moments. All quarter-wave resonator (QWR) cryomodules are installed in the tunnel, and beam commissioning is successfully performed, during which the energy of Ar 9+ is increased from 0.5 to 2.45 MeV/u.
Author Contributions
Heetae Kim: Conceptualization, Data curation, Investigation, Writing – original draft, Writing – review & editing. Sungmin Jeon: Data curation, Investigation, Validation. Yoochul Jung: Investigation, Validation. Juwan Kim: Investigation, Validation.
Funding
This research was supported by the Rare Isotope Science Project (RISP) of Institute for Basic Science (IBS) funded by the Ministry of Science and ICT and National Research Foundation of Korea (2013M7A1A1075764).
Acknowledgments
The authors would like to thank the low-temperature technical supporters and beam experimental researchers of RAON.
Conflicts of Interest
The authors declare no conflict of interest.
References
- H. Kim, Y. H. Kim, Y. Jung, J. Shin, S. Kim, W.K. Kim, G.T. Park, S. Lee, Y.W. Jo, S. Nam, D. Jeon, RAON superconducting radio frequency test facility construction, Proceedings of Linac 2014, Geneva, Switzerland, TUPP086, 2014, 625.
- D. Zhou, S. D. Zhou, S. Quan, J. Hao, L. Lin, L. Feng, F. Wang, F. Zhu, H. Xie, D. Zhuang, W. Cheng, K. Liu, J. Chen, Vertical test system for superconducting RF cavities at Peking University, 18th International Conference on RF Superconductivity SRF2017, Lanzhou, China, TUPB099, 2017, 631.
- Reschke, D.; Gubarev, V.; Schaffran, J.; Steder, L.; Walker, N.; Wenskat, M.; Monaco, L. Performance in the vertical test of the 832 nine-cell 1.3 GHz cavities for the European X-ray Free Electron Laser. Phys. Rev. Accel. Beams 2017, 20, 042004. [Google Scholar] [CrossRef]
- Ge, R.; Sun, L.; Xu, M.; Ye, R.; Zhang, X.; Sang, M.; Han, R.; Zhang, Z.; Zhang, J.; Bian, L.; et al. 2 K superfluid helium cryogenic vertical test system for superconducting cavity of ADS Injector I. Radiat. Detect. Technol. Methods 2020, 4, 131–138. [Google Scholar] [CrossRef]
- Richardson, On the Negative Radiation from Hot Platinum, Proc. Camb. Philos. Soc. 1901, 11, 286.
- Fowler, R.H.; Nordheim, L. Electron emission in intense electric fields. Proc. R. Soc. London. Ser. A, Contain. Pap. a Math. Phys. Character 1928, 119, 173–181. [Google Scholar] [CrossRef]
- Gomer, R. Field emission and field ionization in condensed phases. Accounts Chem. Res. 1972, 5, 41–48. [Google Scholar] [CrossRef]
- de Heer, W.A.; Châtelain, A.; Ugarte, D. A Carbon Nanotube Field-Emission Electron Source. Science 1995, 270, 1179–1180. [Google Scholar] [CrossRef]
- J. -M. Bonard, H. Kind, T. Stockli, L.-O. Nilsson, Field emission form carbon nanotubes: the first five years, Solid State Electron 2001, 45, 893. [CrossRef]
- Wei, X.; Chen, Q.; Peng, L. Electron emission from a two-dimensional crystal with atomic thickness. AIP Adv. 2013, 3. [Google Scholar] [CrossRef]
- Chouhan, V.; Noguchi, T.; Kato, S. Field emission from optimized structure of carbon nanotube field emitter array. J. Appl. Phys. 2016, 119, 134303. [Google Scholar] [CrossRef]
- Ang, Y.S.; Yang, H.Y.; Ang, L.K. Universal Scaling Laws in Schottky Heterostructures Based on Two-Dimensional Materials. Phys. Rev. Lett. 2018, 121, 056802. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.-K. Generalized Thermionic Emission for Arbitrary Dimension. J. Korean Phys. Soc. 2019, 74, 701–706. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.-K.; Park, C.-S. Generalized n-dimensional field emission. J. Korean Phys. Soc. 2021, 79, 363–368. [Google Scholar] [CrossRef]
- Kim, H.; Yu, S.J. Numerical calculation study on the generalized electron emission phenomenon. J. Inf. Disp. 2009, 10, 158–163. [Google Scholar] [CrossRef]
- Kim, H.; Lee, S. Unified theory of thermionic and field emission for two-dimensional conducting materials. J. Korean Phys. Soc. 2022, 80, 167–174. [Google Scholar] [CrossRef]
- D. Moffat, P. D. Moffat, P. Barnes, T. Flynn, J. Graber, L. Hand, W. Hartung, T. Hayes, J. Kirchgessner, J. Knobloch, R. Noer, H. Padamsee, D. Rubin, J. Sears, Studies on the Nature of Field Emission Sites, Conf. RF Superconductivity (SRF'91), SRF91D02, 1991, 245.
- Sakai, H.; Cenni, E.; Enami, K.; Furuya, T.; Sawamura, M.; Shinoe, K.; Umemori, K. Field emission studies in vertical test and during cryomodule operation using precise x-ray mapping system. Phys. Rev. Accel. Beams 2019, 22, 022002. [Google Scholar] [CrossRef]
- Léger, Field emission from a superconductor, J. Phys. France 1968, 29, 646.
- J. Tan, Field emission studies at saclay and orsay, Particle Accelerators 1996, 53, 1.
- Shu, Q.; Gendreau, K.; Hartung, W.; Kirchgessner, J.; Moffat, D.; Noer, R.; Padamsee, H.; Rubin, D.; Sears, J. Influence of condensed gases on field emission and the performance of superconducting RF cavities. 25, 1868. [Google Scholar] [CrossRef]
- J. Graber 1, C. Crawford 2, J. Kirchgessner, H. Padamsee, D. Rubin, P. Sctimueser, Reduction of field emission in superconducting cavities with high power pulsed RF, Nucl. Instrum. Methods Phys. Res. A: Accel. Spectrom. Detect. Assoc. Equip. 1994, 350, 572.
- Jeon, D.; Hong, I.S.; Kim, H.J.; Bodenstein, R.M.; Cha, H.J.; Choi, S.J.; Choi, O.R.; Do, H.; Choi, B.H.; Choi, C.J.; et al. Design of the RAON accelerator systems. J. Korean Phys. Soc. 2014, 65, 1010–1019. [Google Scholar] [CrossRef]
- Choi, S.; Park, G.-T.; Kim, H. Vacuum Test of Cavity with Liquid Nitrogen. Appl. Sci. Converg. Technol. 2015, 24, 132–135. [Google Scholar] [CrossRef]
- H. Kim, J. W. H. Kim, J. W. Choi, Y. W. Jo, Y. Jung, W. Kim, Y. Kim, M.K. Lee, Development of RAON QWR cryomodule for linac demonstration, Proceedings of Linac 2016, Michigan USA, TUPLR073, 2016, 588.
- G.T. Park, H.
- G. T. Park, W.K. Kim, Y. Jung, H.J. Cha and H. Kim, Fabrication of the Prototype β = 0.12 Half Wave Resonator at Rare Isotope Science Project (RISP), J. Korean Phys. Soc. 2015, 67, 1293. [CrossRef]
- W. K. Kim, H. Kim, H. J. Kim, Y. Kim, M. K. Lee, G.T. Park, Design and Assembly of QWR and HWR Cryomodules, Special Issue on the 18th International Conference on Accelerators and Beam Utilizations, J. Korean Phys. Soc. 2015, 67, 1287. [CrossRef]
- Kim, H.; Kim, Y.; Lee, M.K.; Park, G.-T.; Kim, W. Low Temperature Test of HWR Cryomodule. Appl. Sci. Converg. Technol. 2016, 25, 47–50. [Google Scholar] [CrossRef]
- S. Jeon, H. Kim, Y. Jung, J. Kim, J. Lee, M. Kim, H.I. Kim, M. Lee, Field emission and x-ray effect on RAON HWR superconducting cavity performance, Curr. Appl. Phys. 2022, 38, 67. [CrossRef]
- Zhang, P.; Zhang, X.; Li, Z.; Dai, J.; Guo, L.; Lin, H.; Ma, Q.; Huang, T.; Mi, Z.; Wang, Q.; et al. Development and vertical tests of a 166.6 MHz proof-of-principle superconducting quarter-wave beta = 1 cavity. Rev. Sci. Instruments 2019, 90, 084705. [Google Scholar] [CrossRef] [PubMed]
- J. Vines, Y. J. Vines, Y. Xie, H. Padamsee, Systematic Trends for the Medium Field Q-Slope, Proceedings of SRF2007, TUP27, 2007, 178.
- W. Weingarten, R. W. Weingarten, R. Eichhorn, Field-dependent surface resistance for superconducting niobium accelerating cavities: the case of N-doping, Proceedings of SRF2015, MOPB010, 2015, 95.
- H. Kim, S. H. Kim, S. Jeon, Y. Jung, J. Kim, H. Kim, Understanding Q slope of superconducting cavity with magnetic defect and field emission, Linac 2022 Liverpool, United Kingdom, MOPOGE24, 2022, 208. [CrossRef]
- Sha, P.; Pan, W.; Zhai, J.; Mi, Z.; Jin, S.; Liu, B.; Dong, C.; He, F.; Ye, L.; He, X.; et al. Quality Factor Enhancement of 650 MHz Superconducting Radio-Frequency Cavity for CEPC. Appl. Sci. 2022, 12, 546. [Google Scholar] [CrossRef]
- Jin, S.; Sha, P.; Pan, W.; Zhai, J.; Mi, Z.; He, F.; Dong, C.; Ye, L.; He, X. Development and Vertical Tests of CEPC 650-MHz Single-Cell Cavities with High Gradient. Materials 2021, 14, 7654. [Google Scholar] [CrossRef]
- Inui, N. Casimir Effect between Superconducting Plates in the Mixed State. Quantum Rep. 2021, 3, 731–745. [Google Scholar] [CrossRef]
- H. S. Padamsee, Superconducting Radio-Frequency Cavities, Annu. Rev. Nucl. Part. 2014, 64, 175. [CrossRef]
- Byers, N.; Yang, C.N. Theoretical Considerations Concerning Quantized Magnetic Flux in Superconducting Cylinders. Phys. Rev. Lett. 1961, 7, 46–49. [Google Scholar] [CrossRef]
- Okada, T.; Kako, E.; Masuzawa, M.; Sakai, H.; Ueki, R.; Umemori, K.; Tajima, T. Observation of quenching-induced magnetic flux trapping using a magnetic field and temperature mapping system. Phys. Rev. Accel. Beams 2022, 25, 082002. [Google Scholar] [CrossRef]
- K. Saito, Q slope analysis of Niobium SC RF cavities, Proceedings of the 11th Workshop on RF Superconductivity, ThP17, 2004, 643.
- Miyazaki, W. Venturini Delsolaro, Two different origins of the Q-slope problem in superconducting niobium film cavities for a heavy ion accelerator at CERN, Phys. Rev. Accel. Beams. 2019, 22, 073101. [Google Scholar] [CrossRef]
- Brevik, I.; Høye, J.S. Temperature dependence of the Casimir force. Eur. J. Phys. 2013, 35, 15012. [Google Scholar] [CrossRef]
- H. Kim, Y. H. Kim, Y. Jung, J.W. Choi, Y.W. Jo, M. Lee, M. S. Kim, J. Kim, Y. Kim, H. Jung, Temperature measurement of cryomodules, HB2018 (Proceedings of the 61st ICFA Advanced Beam Dynamics Workshop on High-Intensity and High-Brightness Hadron Beam), WEP2PO016, 2018, 299.
- Ginsburg, C.M.; Reid, C.; Sergatskov, D.A. Magnetic Shielding for the Fermilab Vertical Cavity Test Facility. IEEE Trans. Appl. Supercond. 2009, 19, 1419–1422. [Google Scholar] [CrossRef]
- Sankar, M.; Mirji, K.; Prasad, V.S.; Baligidad, R.; Gokhale, A. Purification of Niobium by Electron Beam Melting. High Temp. Mater. Process. 2015, 35, 621–627. [Google Scholar] [CrossRef]
- Casalbuoni, S.; Knabbe, E.; Kötzler, J.; Lilje, L.; von Sawilski, L.; Schmüser, P.; Steffen, B. Surface superconductivity in niobium for superconducting RF cavities. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2005, 538, 45–64. [Google Scholar] [CrossRef]
- Zhang, P.; Lau, Y.Y.; Gilgenbach, R.M. Analysis of radio-frequency absorption and electric and magnetic field enhancements due to surface roughness. J. Appl. Phys. 2009, 105, 114908. [Google Scholar] [CrossRef]
- H. Sara, An Analytical Approach for Calculating the Quench Field in Superconducting Cavities, Proceedings of the 1995 Workshop on RF Superconductivity, SRF95C10, 1995, 413.
- H. Safa, Statistical analysis of the quench fields in scrf cavities, Proceedings of the 1997 Workshop on RF Superconductivity, SRF97C11, 1997, 503.
- Padamsee, H.; Knobloch, J.; Hays, T.; Wilson, P.B. RF superconductivity for Accelerators, Wiley-VCH Verlag GmbH&Co. KGaA, 2011. Phys. Today 1999, 52, 54–54. [Google Scholar] [CrossRef]
- Y. Jung, H. Kim, W. K. Kim, J. Lee, J. Seo, Status of RRR analysis for RAON accelerator, Proceedings of LINAC2016, TUP10 6004, 2016, 594.
Figure 1.
Resistivity as a function of temperature for different material types.
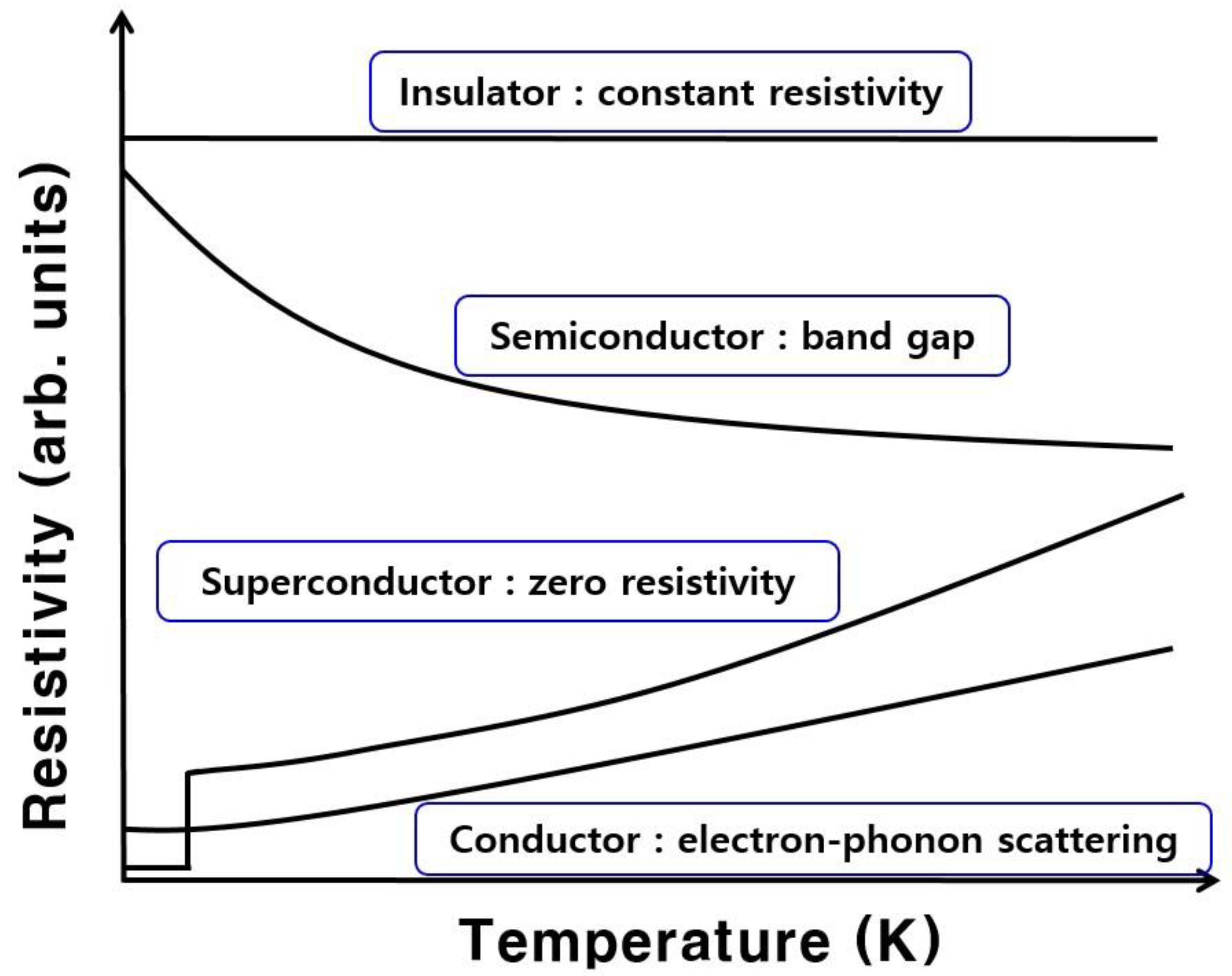
Figure 2.
Bardeen–Cooper–Schrieffer (BCS) resistance of Nb as a function of temperature for different frequencies. The Bardeen–Cooper–Schrieffer (BCS) resistance decreases as the temperature decreases. The corresponding frequencies of the Bardeen–Cooper–Schrieffer (BCS) resistances, from the bottom to the top, are 81.25 MHz, 162.5 MHz, 325 MHz, 500 MHz, and 1.5 GHz, respectively.
Figure 2.
Bardeen–Cooper–Schrieffer (BCS) resistance of Nb as a function of temperature for different frequencies. The Bardeen–Cooper–Schrieffer (BCS) resistance decreases as the temperature decreases. The corresponding frequencies of the Bardeen–Cooper–Schrieffer (BCS) resistances, from the bottom to the top, are 81.25 MHz, 162.5 MHz, 325 MHz, 500 MHz, and 1.5 GHz, respectively.
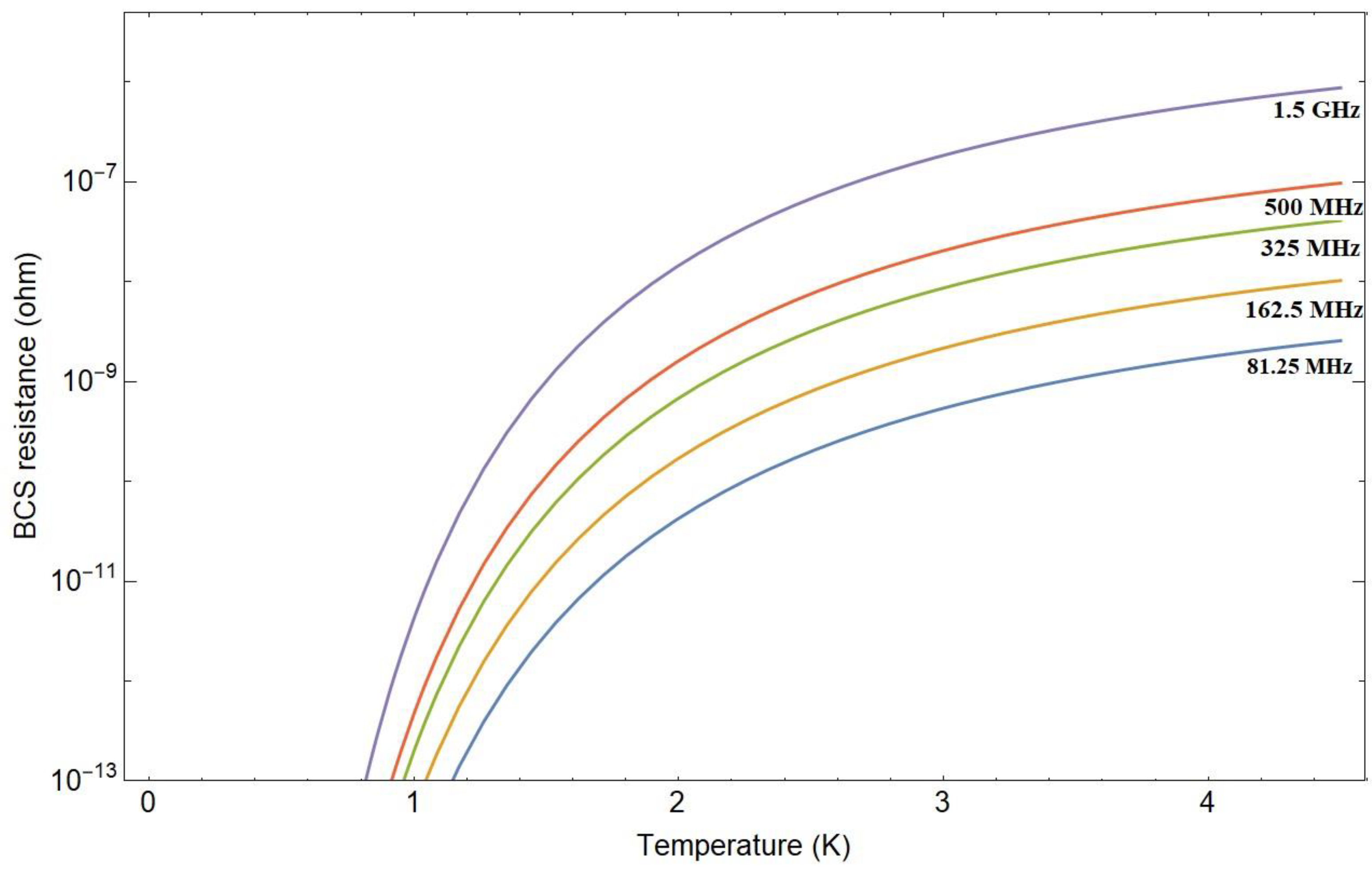
Figure 3.
Casimir force per unit area as a function of distance. The Casimir force increases as the distance between two parallel plates is decreased. The Casimir force for the 0 K, Equation (27), and that for the 300 K correction, Equation (28), are shown as functions of distance. The Casimir force for the zero-temperature is higher than that for the room temperature of 300 K. .
Figure 3.
Casimir force per unit area as a function of distance. The Casimir force increases as the distance between two parallel plates is decreased. The Casimir force for the 0 K, Equation (27), and that for the 300 K correction, Equation (28), are shown as functions of distance. The Casimir force for the zero-temperature is higher than that for the room temperature of 300 K. .
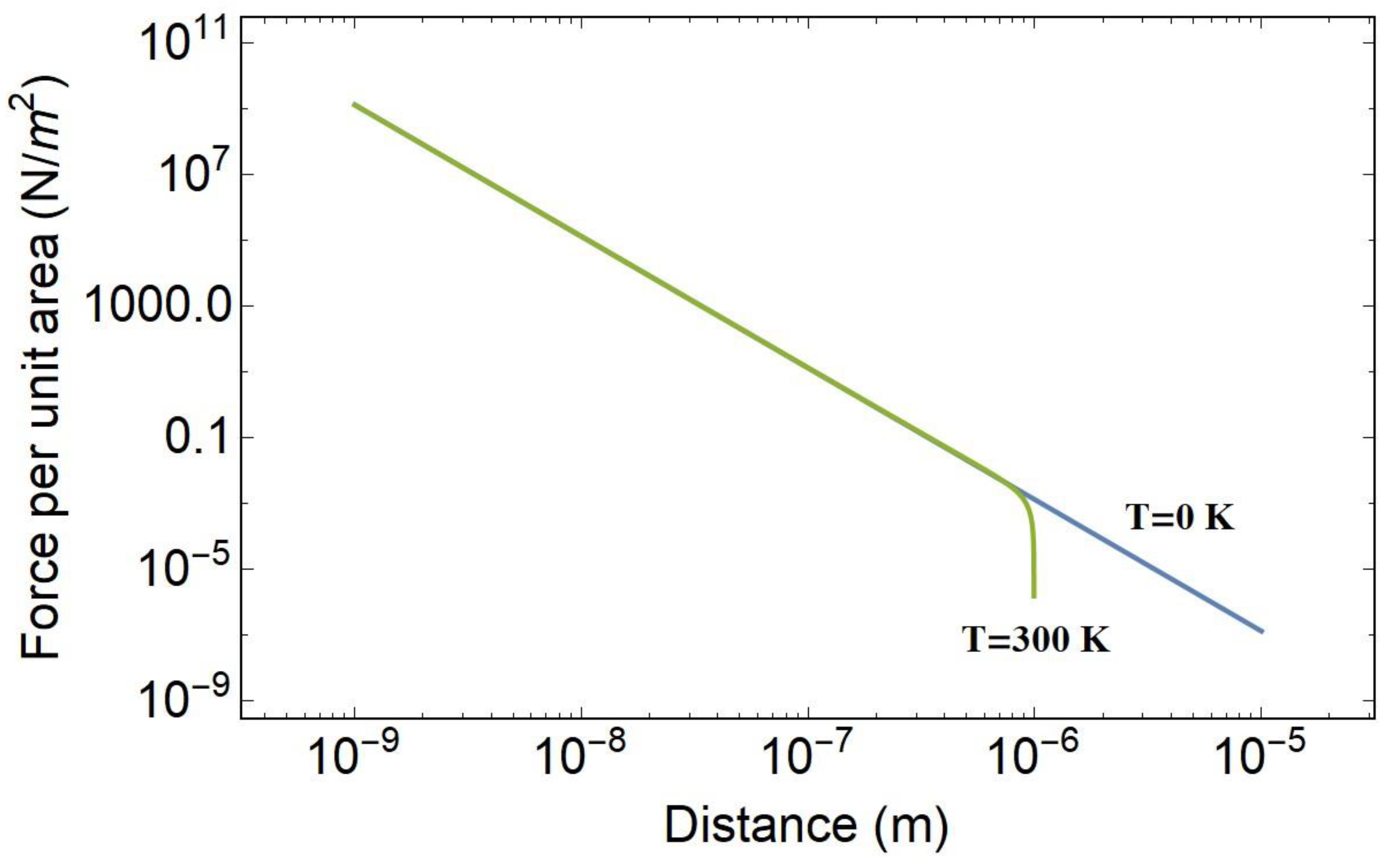
Figure 4.
Pictures of Nb raw materials. (a,b) show the raw materials of Nb.

Figure 5.
Schematic diagram for magnetic shielding in a cryostat. The mumetal and cryophy are used to reduce the external magnetic field for the quarter-wave resonator (QWR) cavity test.
Figure 5.
Schematic diagram for magnetic shielding in a cryostat. The mumetal and cryophy are used to reduce the external magnetic field for the quarter-wave resonator (QWR) cavity test.
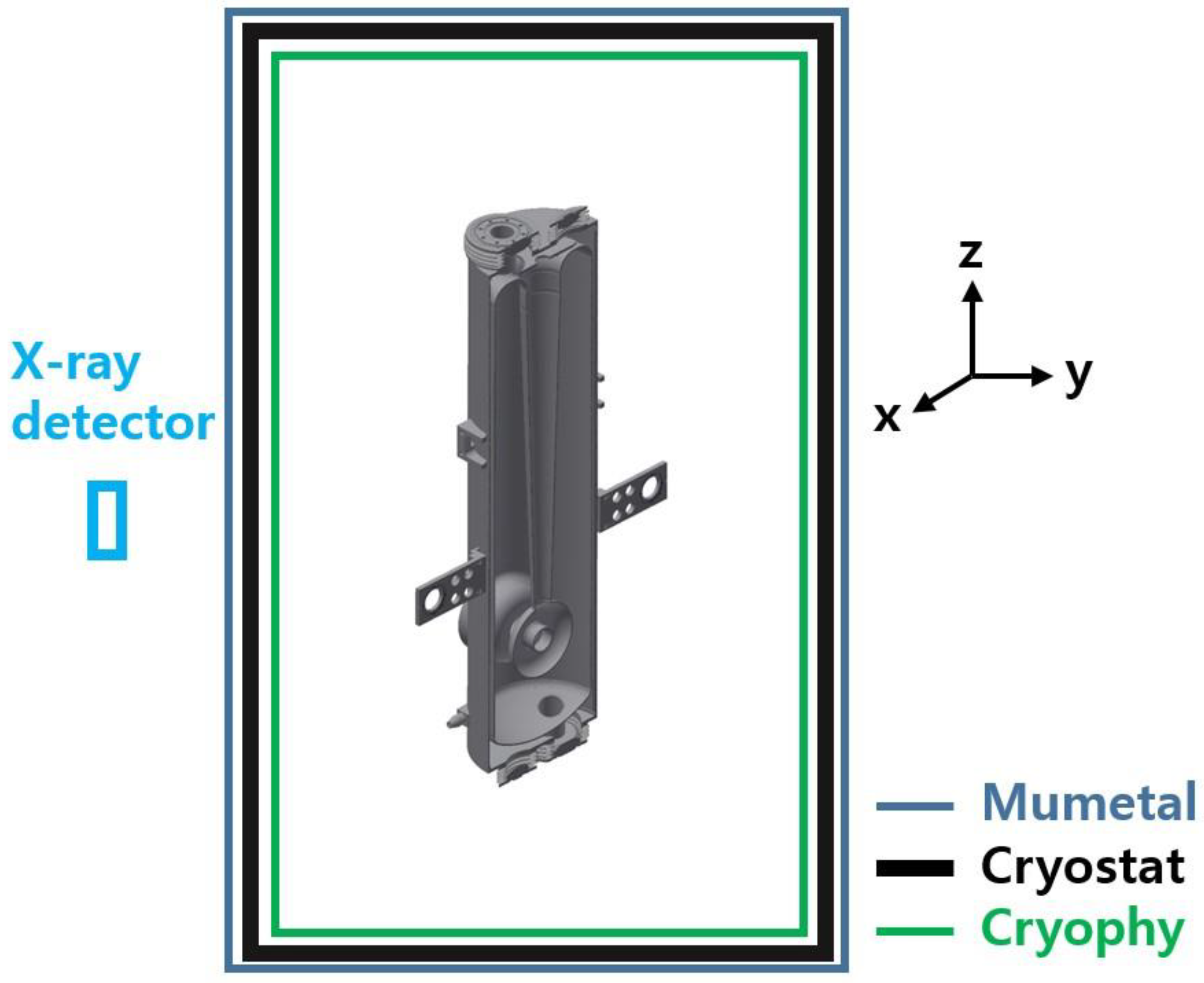
Figure 6.
Cryostat and magnetic shielding. (a) shows the design of the cryostat, (b) shows the picture of the mumetal and cryostat, (c) shows the top view of mumetal, cryostat, and cryophy from the outside of the cryostat, and (d) shows the top view of the vertical test.
Figure 6.
Cryostat and magnetic shielding. (a) shows the design of the cryostat, (b) shows the picture of the mumetal and cryostat, (c) shows the top view of mumetal, cryostat, and cryophy from the outside of the cryostat, and (d) shows the top view of the vertical test.

Figure 7.
A picture of the quarter-wave resonator (QWR) cavities. Two QWR jacket cavities are shown in the hanging booth. The high pressure rinsing (HPR) ports, liquid helium level meters, temperature sensors, beam ports, vacuum lines, and variable couplers are indicated. Here, temperature sensors are attached under kapton tape on the QWR jacket cavities.
Figure 7.
A picture of the quarter-wave resonator (QWR) cavities. Two QWR jacket cavities are shown in the hanging booth. The high pressure rinsing (HPR) ports, liquid helium level meters, temperature sensors, beam ports, vacuum lines, and variable couplers are indicated. Here, temperature sensors are attached under kapton tape on the QWR jacket cavities.

Figure 8.
Measurement of the magnetic field strength for the cryostat.
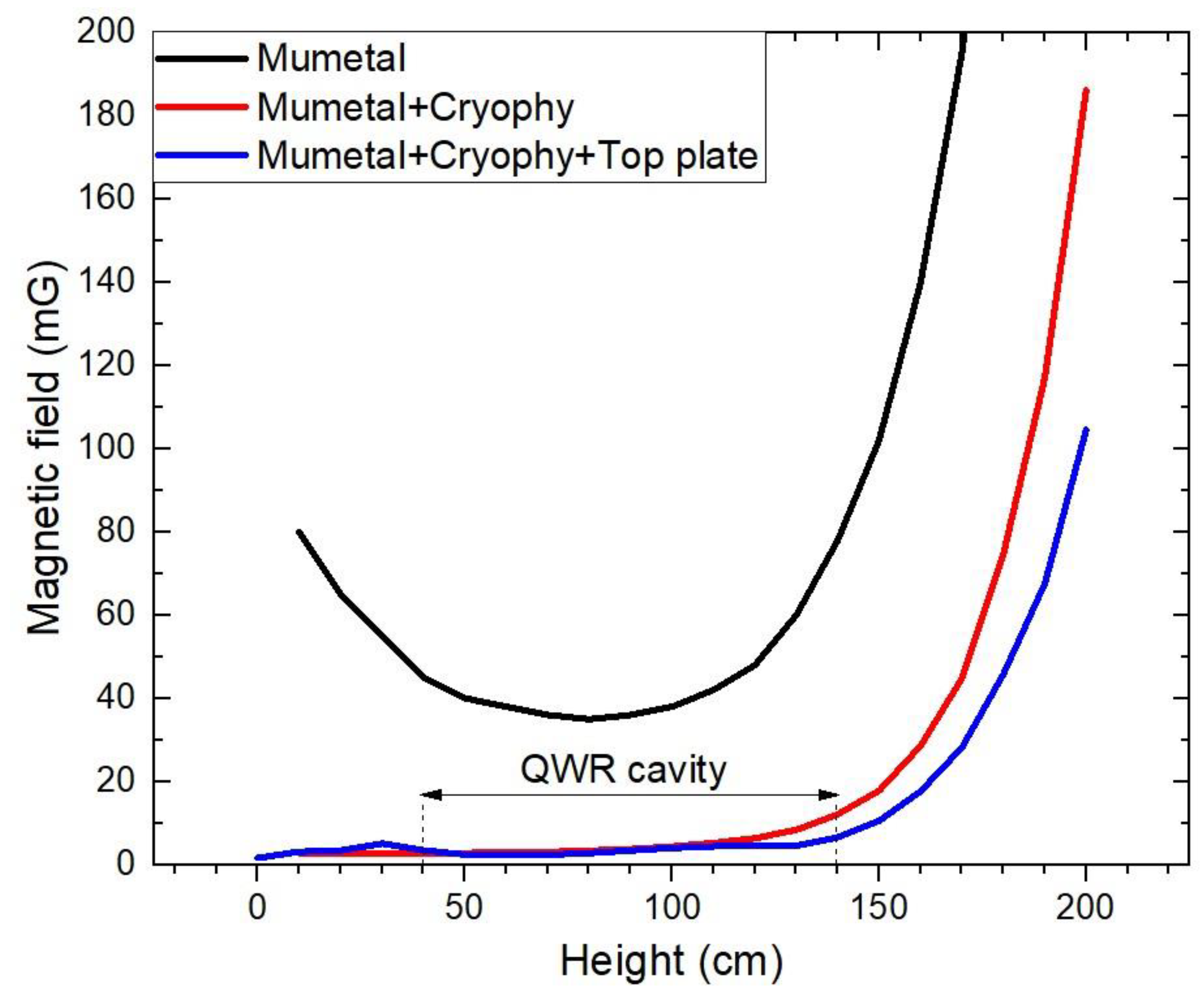
Figure 9.
Q slope measurement with increasing accelerating fields for the quarter-wave resonator (QWR) cavities. The quality factor of the superconducting cavity decreases with increasing field emission and x-ray generation.
Figure 9.
Q slope measurement with increasing accelerating fields for the quarter-wave resonator (QWR) cavities. The quality factor of the superconducting cavity decreases with increasing field emission and x-ray generation.
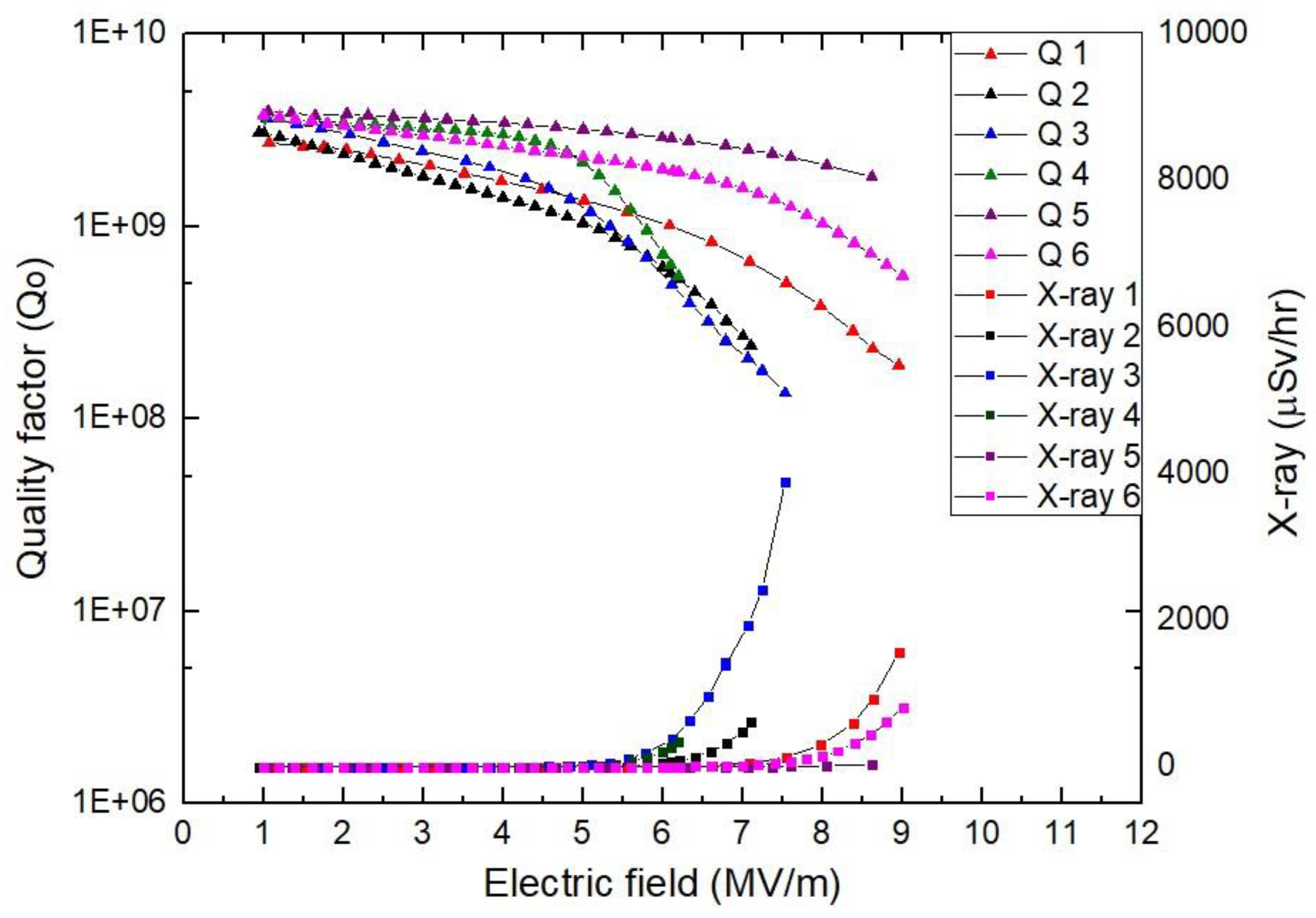
Figure 10.
Surface resistance measurement as a function of peak magnetic field strength for quarter-wave resonator (QWR) cavities.
Figure 10.
Surface resistance measurement as a function of peak magnetic field strength for quarter-wave resonator (QWR) cavities.
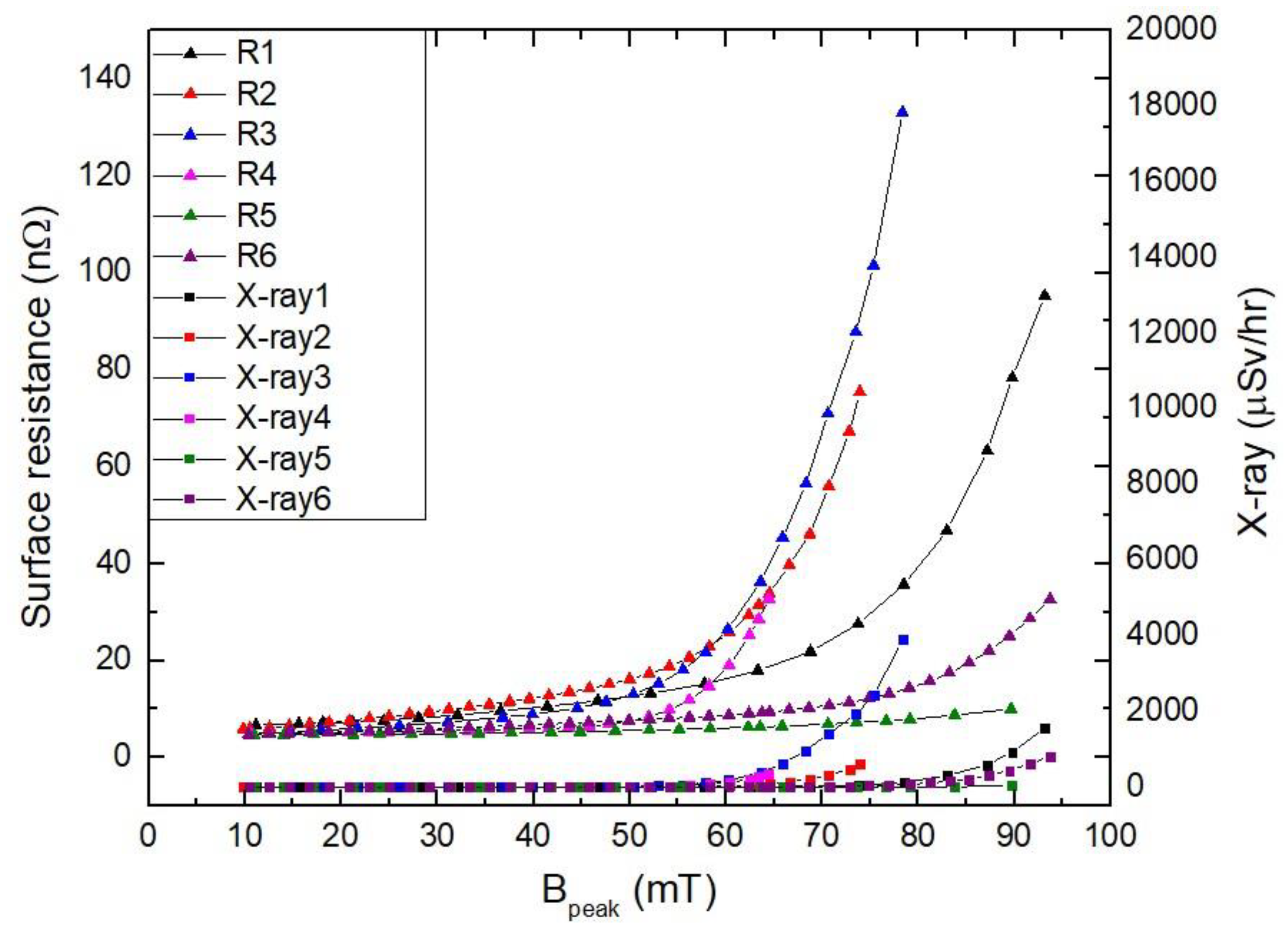
Figure 11.
Surface resistance as a function of peak magnetic field. According to Equation (23), the dissipated power coming from magnetic heating depends on the surface resistance and magnetic field on the superconducting surface. The surface resistances are fitted with the magnetic heating of Equation (26), and the magnetic moments can be obtained for the cavities.
Figure 11.
Surface resistance as a function of peak magnetic field. According to Equation (23), the dissipated power coming from magnetic heating depends on the surface resistance and magnetic field on the superconducting surface. The surface resistances are fitted with the magnetic heating of Equation (26), and the magnetic moments can be obtained for the cavities.
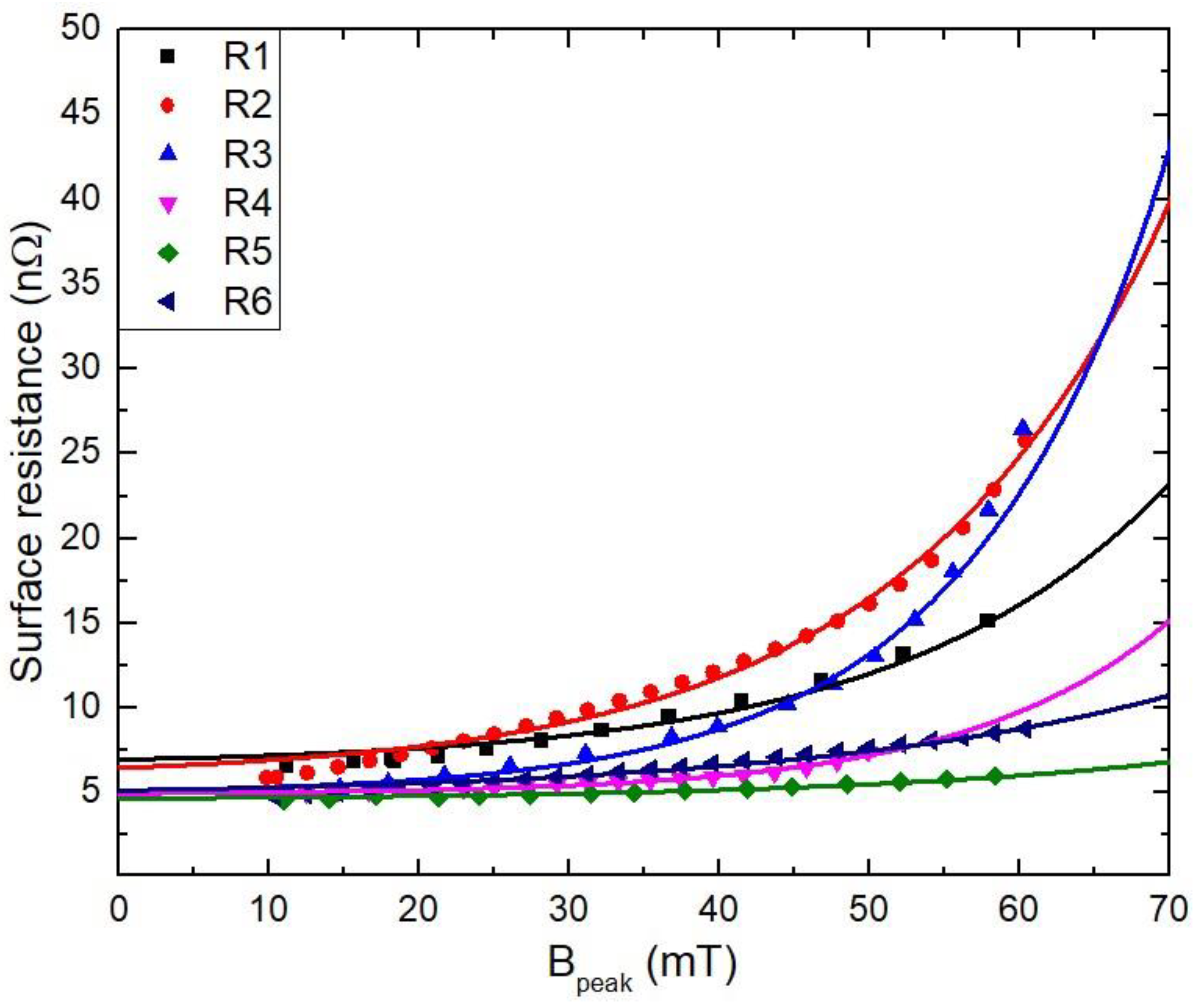
Figure 12.
Pictures of quarter-wave resonator (QWR) cryomodules. (a) shows the QWR cryomodule in the horizontal test bunker, (b) shows the installed quarter-wave resonator (QWR) cryomodules on the front side, (c) shows the solid state power amplifier (SSPA) for cryomodules, (d) shows the RAON SCL3 tunnel, and (e) shows the main control screen during beam commissioning.
Figure 12.
Pictures of quarter-wave resonator (QWR) cryomodules. (a) shows the QWR cryomodule in the horizontal test bunker, (b) shows the installed quarter-wave resonator (QWR) cryomodules on the front side, (c) shows the solid state power amplifier (SSPA) for cryomodules, (d) shows the RAON SCL3 tunnel, and (e) shows the main control screen during beam commissioning.

Table 1.
Parameters for the quarter-wave resonator (QWR) cavity.
| Parameter | QWR |
|---|---|
| Optimum | 0.047 |
| f [MHz] | 81.25 |
| 173.5 | |
| R/Q [ | 469 |
| 5.7 | |
| [mT/(MV/m)] | 10.4 |
| [MV/m] | 6.1 |
| [MV] | 1.06 |
| Stored Energy [J] | 4.7 |
| Q[ | 18.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






