Preprint
Article
Improved Algorithms of Data Processing for Dispersive Interferometry using Optical Frequency Comb
Altmetrics
Downloads
147
Views
56
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
25 April 2023
Posted:
25 April 2023
You are already at the latest version
Alerts
Abstract
Two algorithms of data processing are proposed to shorten the unmeasurable dead-zone close to the zero-position of measurement, i.e., the minimum working distance of a dispersive interferometer using optical frequency comb, which is a critical issue in millimeter-order short-range absolute distance measurement. After demonstrating the limitation of the conventional data processing algorithm, the principles of the proposed algorithms, namely the spectral fringe algorithm, and the combined algorithm that combines the spectral fringe algorithm with the excess fraction method, are presented, together with simulation results for demonstrating the possibility of the proposed algorithms for shortening the dead-zone with a high accuracy. An experimental setup of dispersive interferometer is also constructed for implementing the proposed data processing algorithms over spectral interference signals. Experimental results demonstrate that the dead-zone by the proposed algorithms can be as small as half of that by the conventional algorithm while the measurement accuracy can be further improved with the combined algorithm.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Absolute distance measurement with a high resolution is important in the field of dimensional metrology. The use of light waves as a length ruler, which was proposed by Michelson in 1893, revolutionized distance measurement by determining the phase shift of a signal after it traveled a certain distance with a subwavelength resolution. However, this method has its limitations, as it can only determine relative distance changes and cannot directly measure the absolute value of the target distance [1,2,3]. Moreover, the phase shift information repeats every fringe, making it difficult to implement measurements beyond λ/2 because the unknown integer fringe order cannot be determined by the Michelson Interferometer itself [4,5]. Since its invention in the end of the 20th century [6,7,8], the optical frequency comb (OFC) has been widely employed to broaden the horizon for optical metrology, including measurement of optical frequency [9,10,11], distance [12,13,14,15,16], angle [17,18,19,20,21,22], and etc. An optical frequency comb (OFC), which provides numerous ultra-narrow linewidth wavelengths over a broad optical spectral range, is the Fourier transform of femtosecond ultrashort pulses from a mode-locked laser in the time domain. It enables versatile advanced absolute distance measurement methods, including synthetic wavelength interferometry (SWI) [12,23,24,25], multi-wavelength interferometry (MWI) [26,27,28,29,30], dispersive interferometry (also known as spectrally resolved interferometry, SRI) [31,32,33,34], dual-comb interferometry [35,36,37,38,39], and time-of-flight (TOF) measurement [40,41,42,43,44]. Compared with other methods, the dispersive interferometry can achieve a high resolution of distance measurement.
In 2006, Joo et al. first proposed to use the dispersive interference of a mode-locked femtosecond laser to achieve an absolute distance measurement over a range of 0.89 m with a resolution of 7 nm, in which the target distance was obtained by the first-order derivation of unwrapped phase, while the existence of the direct-current item in the transferred time domain data generated a certain range of unmeasurable dead-zone close to the zero-position of measurements, i.e., the minimum working distance, in this configuration [14,45]. In 2012, van den Berg et al. made refinement by combining dispersive and homodyne interferometry based on a virtually imaged phase array (VIPA) and a grating in an optical setup, achieving a non-ambiguous range of 15 cm with an accuracy of λ/30, in which the homodyne interferometry is just an auxiliary and cannot output the target distance independently and the phase is obtained by the cosine fit rather than the wrapped phase [46]. In 2019, Tang et al. proposed a non-filtered and differential envelope phase demodulation method based on dispersive interferometry, where the phase value was obtained by taking the arccosine of a demodulated spectral interference signal [47]. However, the measurement accuracy is influenced by that of the demodulation process for removing the upper and lower envelopes of the spectral interference signal. In addition, the focus of the previous research was on long absolute distance measurement, rather than on shortening the unmeasurable dead-zone close to the zero-position of measurement, which is a critical issue for short-range absolute distance measurement.
In this paper, after a demonstration of the mechanism for generating the dead-zone in the conventional data processing algorithm for dispersive interferometry, two new data processing algorithms are proposed to shorten the dead-zone for millimeter-order short-range absolute distance measurement. The first one is named as the spectral fringe algorithm, which is then combined with the excess fraction method [48,49] as the second algorithm. The latter is named as the combined algorithm for clarity. The feasibility of the proposed algorithms is then confirmed by simulation and experiment through comparison with the results of the conventional algorithm.
2. Principles of the Data-Processing Algorithms
2.1 Proposed Algorithm 1: The Spectral Fringe Algorithm
The dispersive interferometry using OFC is typically implemented by a Michelson interferometer-type configuration, whereby the optical path difference (OPD) between the reference and measurement arms can be accurately determined by analyzing the interference spectrum with a proper data processing algorithm [45]. In this subsection, the conventional data processing algorithm is re-visited according to literature [47,50,51], based on which an improved data processing algorithm, namely the spectral fringe algorithm, is proposed.
When a laser beam emits from an OFC source, it will be separated by a beam splitter into two beams, which are reflected by mirrors in the reference arm and the measurement arm, respectively. The recombined beams interfere with each other to produce a spectral interference signal, which is subsequently detected by an optical spectrum analyzer (OSA). An OSA has a set of discrete spectral output data. For simplicity, the kth spectral output of OSA is assumed to correspond to the frequency fk and the wavelength λk. Practically, it is difficult to ensure that the splitting ratio (αR, αM) of the beam splitter and the reflective index (rR, rM) of the mirrors in the two arms are exactly equal to each other. Therefore, the electric fields of the reference beam and the measurement beam, which correspond to the kth spectral output of the OSA, i.e., the kth mode of the optical frequency comb if the OSA has enough resolving power, can be expressed as:

Here, τ is the time delay caused by the optical path difference 2n(f)L between the reference beam and the measurement beam, which is explicitly given as τ = 2n(f)L/c where n and c are the refractive index of air and the light speed in a vacuum, respectively. The intensity of the corresponding interference signal can be written as:
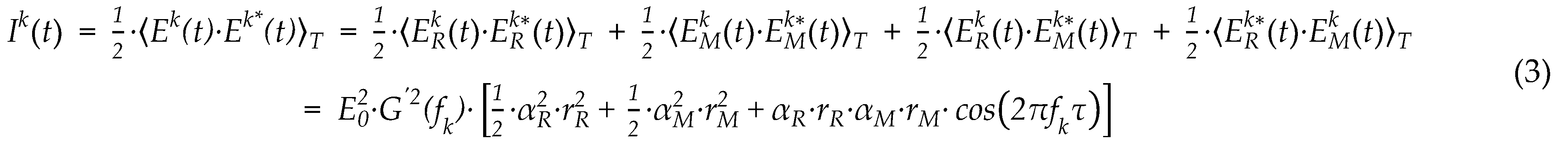
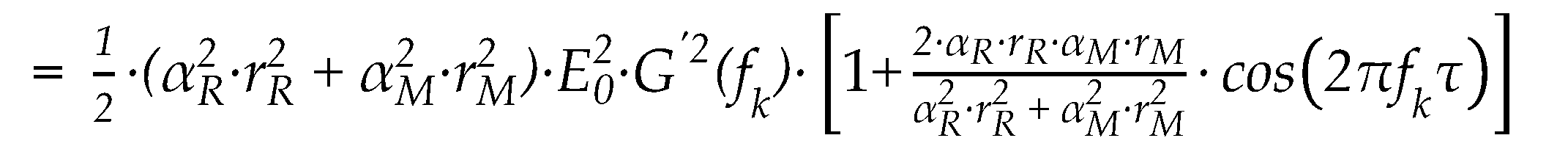
For simplicity, S(fk), which corresponds to the power spectrum of the OFC source, is referred to as the envelope component. The term in the brackets includes 1 and a cosine function, which is referred to as the interference fringe component with its unwrapped phase and amplitude defined by (fk) and A, respectively. S(fk), (fk) and A can be written as follows:
where φ() is the wrapped phase, and n is an integer showing the period number of the spectral interference fringe component. Consequently, the intensity of the spectral interference signal output from the OSA, which is a Fourier transform of Equation (3), can be rewritten as:
In the conventional data processing algorithm, the spectral interference signal shown in Equation (7) is directly inverse Fourier transformed into a time-domain function i(t) as follows:
where is a unit impulse function, and s(t) is the inverse Fourier transform of S(f). Assuming the OFC source has a Gaussian-like power spectrum, both S(f) and s(t) will have Gaussian-like shapes. Three Gaussian-like pulses can then be observed in i(t), with their peaks located at -τ, 0, τ and amplitudes of ∙, A∙, ∙, respectively. The pulse at τ is subsequently picked out by utilizing a time-window centered at τ. Then, the picked-up pulse is Fourier transformed into the frequency domain as follows:
The wrapped phase φ(f) can then be calculated by the arctangent function as:
Since the wrapped phase φ(f) changes periodically within the range of [-π/2, +π/2] with the increase or decrease of the target distance L, L cannot be obtained directly from φ(f) due to the ambiguity in period number n in Equation (5). Therefore, it is necessary to calculate L by taking the first-order derivation of the wrapped or the unwrapped phase values as follows:
where = n(f) + (dn(f)/df)∙f, is the group refractivity of air determined by the central frequency of the source, and n(f) is the phase refractivity of air. L can then be obtained as:
As can be seen above, in the conventional data processing algorithm for dispersive interferometry, the spectral interference signal from OSA shown in Equation (7) is directly inverse Fourier transformed into the time-domain function i(t) shown in Equation (8). In this conventional algorithm, the dead-zone, which is the unmeasurable distance range, is determined by the width of the pulse function s(t). Since is proportional to the target distance L, when L is smaller than a certain value, the three pulses of i(t) will overlap with each other. In this case, the time-window for selecting the pulse does not function well, which prevents the measurement of the distance.
On the other hand, in the proposed spectral fringe algorithm, the envelope component S(f) and the 1 in the brackets of Equation (7) are removed to leave only the cosine function, i.e., the interference fringe component as a modified spectral interference signal Im(f) = . Consequently, the inverse Fourier transform of the modified Im(f) will generate a modified time function of im(t) with only two impulse-shaped pulses at -τ and τ, instead of the three Gaussian-like pulses at -τ, 0, τ in the conventional data processing algorithm. As a result, the distance between two pulses in im(t) by the spectral fringe algorithm is doubled due to the removal of the central pulse compared with that in i(t) by the conventional algorithm. In addition, the width of the impulse-shaped pulses im(t) is much narrower than that of the Gaussian-like pulses in i(t). These two effects can significantly shorten the dead-zone, which is the fundamental concept of the proposed spectral fringe algorithm shown below.
In the spectral fringe algorithm, the upper and lower envelopes of the detected spectral interference signal in Equation (7) are first evaluated based on Ref. [47] as follows:

The modified spectral interference signal Im() can then be obtained by:
where
Subsequently, an inverse Fourier transforming of Equation (15) gives rise to modified time function im(t) as follows:
Differing from the conventional data processing algorithm, only two impulse-shaped pulses exist in the time domain, which are located at -τ and τ with an intensity of ∙ and ∙, respectively. The distance between the two pulses is twice of that in the conventional algorithm, which shortens the dead-zone to be half for the same pulse width. In addition, the width of the impulse-shaped pulses by the proposed spectral fringe algorithm is much narrower than that of the Gaussian-like pulses by the conventional algorithm, which further shortens the dead-zone. In other words, the impulse-shaped pulse at τ can be selected more easily and precisely by a time-window with a much narrower bandwidth for calculating the target distance based on Equations (9)-(12) with a significantly shortened dead-zone.
It should be noted that although the way of calculating the upper and lower envelopes of the spectral interference signal is similar, the proposed spectral fringe algorithm is different from that of Ref. [47] from the point of view of the phase calculation method. In Ref. [47], the phase of the spectral interference signal is directly obtained from taking arccosine of the modified spectral interference signal Im(f) based on Equation (15) for the purpose of improving the performance of dispersive interferometry in long absolute distance measurement. On the other hand, in the proposed spectral fringe algorithm, the phase is obtained from Equations (9) and (10) by using the time-windowed impulse-shaped pulse of the modified time function im(t) in Equation (18) for the purpose of shortening the dead-zone close to the zero-position of measurement, which is a critical issue in millimeter-order short-range absolute distance measurement.
2.2 Proposed Algorithm 2: The Combined Algorithm
The spectral fringe algorithm is combined with the excess fraction method [52] as the combined algorithm. In a dispersive interferometer using OFC, the relationship between the kth OSA output of wavelength λk (λk = c/(2π)) and the target distance L can be given by ni∙L = (mk + εk)∙λk, in which mk is an integer, εk is the excess fraction part of the wavelength λk, and ni is the refractive index. The excess fraction part εk can be calculated by the wrapped phase φ(fk), which is εk = [φ(fk) + 0.5π]/π. The uncertain integer number mk can be obtained from the excess fraction part εk based on the excess fraction method.
The excess fraction method is an effective approach to determine the absolute target length L by employing the measured excess fraction values of multiple wavelengths λ1>λ2>…>λi [53]. For the dispersive interferometer with OFC, multiple discrete spectral outputs of OSA with a narrow linewidth determined by the wavelength resolution of OSA, which can be as small as 0.02 nm [54], can be employed for the excess fraction method. The relationship between the target distance L and the used wavelengths can be expressed as:
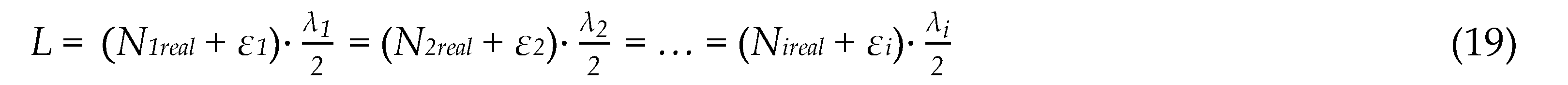
where Nireal is the unknown integer part of the wavelength order for each wavelength λi, εi is the measured fractional fringe value whose value is within the interval of [0, 1], and the subscript i is the wavelength number. Similarly, the nominal length measured by another method with an error range of can be expressed as:
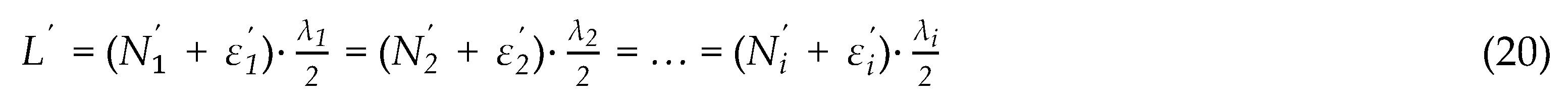
Here, and represent the calculated integer part and the excess fraction part of the wavelength order, respectively. can be calculated by:
in which function INT(x) means to obtain the integer part value of x. The difference c between the real length L and the nominal length is:
where the first term mi = (Nireal - ) means the integer part of the difference c, and its value is varied by adjusting the desired value of . The second term δi(εi - ) is stable and means the excess fractional part of c.
Now the issue of determining the integer part of the wavelength order Nireal is transformed to determining the value of c. The maximum adjustment value ∆NiT for the calculated integer part is:
where means the error range of the nominal length. Hence, the acceptable adjustment integer value mij for the integer part of c is within the interval:
-∆NiT ≤ mij = j ≤ ∆NiT
As a result, the value for difference c can be adjusted by a variable mij,
Considering the same adjusted difference value of cj when using another wavelength λi+1, the fractional part of wavelength order caused by cj can be calculated by:
Hence, the fractional part of +cj with using the wavelength λi+1 can be given by:
Finally, when the difference value between ε(i+1)j and ε(i+1) reach the minimum, the corresponding cJ is the optimum adjusted value, and the real length L of the target distance can be calculated by:
Figure 1 illustrates the detailed procedure of selecting the optimum difference cJ and the relationship between those above-mentioned parameters in the excess fraction method.
It is worth mentioning that similar to Ref. [46], the target distance L is given by ni∙L = (mk + εk)∙λk. However, the approach in the proposed combined algorithm for determining the integer and excess fraction part of wavelength λk is different from that of Ref. [46]. In Ref. [46], the phase φ(λk) for a specific wavelength λk, is obtained from a cosine fit of the interference signal, and the integer number of the wavelength mk is determined by the result of dispersive interferometry. In addition, the aim of using the integer and excess fraction part of wavelength λk in Ref. [46] is not to measure the absolute distance L directly and make a comparison with the result of the dispersive interferometry, but to refine the final value of the distance L by averaging the results of different wavelengths.
3. Simulation and experiment Results
3.1 Simulation Results
Simulation results of the interference spectrum detected by OSA with different target distances of 1 mm, 2 mm, and 3 mm without considering the inequality of laser power in the two arms are shown in Figure 2. In the simulation process, parameters of the femtosecond laser source are set as center frequency fc = 192.175 THz, repetition frequency frep = 100 MHz, and full width as half maximum FWHM = 2.5 THz.
It can be seen from Figure 2 that with increasing target distance from 1 mm to 3 mm, the density of the interference fringes dramatically raises. If the target distance continuously stretches to a certain threshold, the interference fringes will become too dense to be distinguished due to the limited resolution of the OSA. To expand the applicable range for dispersive interferometry, decreasing the fringes density at large distances is the key point, which can be performed by several approaches. For instance, employing a Fabry-Perot Etalon (FPE) before the spectrometer to trim down the incident combs’ density or just choosing a femtosecond source with a higher repetition frequency which has a larger comb interval.
In an actual experiment, it is impossible to ensure the optical power in the reference and measurement arms of a Michelson-type interferometer are exactly equal to each other. Therefore, it is critical to clarify the impact derived from modulated parameter A, which reflects the inequality of the optical power in the two arms. For a certain target distance of L = 1 mm, simulation results of different values of modulated parameter A = 0.25, 0.5, and 0.75 are shown in Figure 3.
Compared to Figure 2a where the modulated parameter A is set to 1, i.e., the optical power in the two arms is equal, a decreasing value of A leads to an increasing inflation of the lower envelope away from the zero line and a significant reduction in the visibility V of the interference fringes.
3.1.1 Simulation Results of Conventional Data Processing Algorithm
Based on the interference spectrum with a target distance of 1 mm shown in Figure 2a, the data processing procedure of the conventional algorithm is shown in Figure 4. Inverse Fourier transforming, time-window selecting, and phase unwrapping processes are operated to generate the desired distance by Equation (12) with a result of 1.0005 mm. The deviation of 0.5 μm between the simulated result and the ideal target distance may be caused by the error or signal loss in the time-window selecting and phase unwrapping, which is also verified by other researchers [55]. It is worth mentioning that for the inverse Fourier transforming in Figure 4a, the target distance can be evaluated coarsely by the time peak position, 2L = c∙X(t = τ), and the modulated parameter A can be assessed coarsely by the ratio of A = Y(t = 0)/2Y(t = τ).
3.1.2 Simulation Results of the Spectral Fringe Algorithm
An interference spectrum with a target distance of 1 mm and a modulated parameter A = 0.5 is employed in the simulated data processing procedure of the spectral fringe algorithm. Firstly, extracting the upper and lower envelopes to obtain the modified spectral interference signal Im(), and then operating inverse Fourier transforming to achieve two sharp peaks in the time domain. Subsequently, obtaining the wrapped phase from the Fourier Transform results of the time-window filtered peak, and finally, the target distance is developed by the first-order deviation of the unwrapped phase, as illustrated in Figure 5.
3.1.3 Simulation Results of the Combined Algorithm
The simulated data processing procedure of the combined algorithm is started by obtaining the wrapped phase φ(fk) in the spectral fringe algorithm, as shown in Figure 6. The excess fraction εk is then calculated by εk = [φ(fk) + 0.5π]/π. Two arbitrary points of excess fraction value in Figure 6b, Point A (190.519 THz, 0.253494) and Point B (191.988 THz, 0.845917) are selected to achieve the desired target length based on the excess fraction method by Equation (28) with a result of 0.99995 mm. The deviation between the simulated result and the ideal target distance decreases to 0.05 μm. Besides, it is also possible to select several excess fraction values within the OSA working range to calculate the target distance individually and average their results to improve the accuracy and stability of the final result.
3.2 Experimental Setup
An overview of the experimental setup is shown in Figure 7. A homemade femtosecond fiber laser source with a center frequency fc of 192.175 THz is exploited as the frequency comb for the experiment [56]. Its frep and fceo are locked at 100 MHz and 10.5 MHz to a rubidium frequency standard (Stanford Research System, FS725). About 5 mW power of laser is sent into the beam splitter (OptoSigma, NPCH-10-15500) via a single-mode fiber. Two square-protected silver mirrors (Thorlabs, PFSQ05-03-P01) are utilized to reflect the light in the reference and measurement beam, separately. The mirror in the measurement beam is mounted on a single-axis motorized stage (Saruka Seiki, KXC04015-CA), making it can be moved linearly in the optical path direction within a travel range of ±7 mm. Besides, a laser encoder (Renishaw, RLD10-3R) is employed as an external reference to calibrate the moving distance of the stage. The interference optical signal is subsequently analyzed by an optical spectrum analyzer (Yokogawa, AQ6370D) with a wavelength resolution of 0.02 nm.
3.3 Experimental Results and Discussion
In the experiment, the target mirror in the measurement arm is moved continuously from -1 mm to +10 mm with a step of 10 μm, and the interference signal within the frequency range of 191 THz to 193 THz is recorded by OSA at the same time. The laser encoder is set to zero at the initial position to calibrate the movement distance of the motorized stage. The experimental interference spectrum at various positions is shown in Figure 8, in which it is easy to find that the visibility of the interference signal decreases, and the interference fringes density increases with increasing target distance, complying with the simulation results of Section 3.1.
Furthermore, all the detected interference spectrum at different positions is processed by the conventional data processing algorithm, the spectral fringe algorithm, and the combined algorithm, respectively. Comparisons of the measurement results of these three algorithms are presented in Figure 9, Figure 10, Figure 11 and Figure 12.
Both the conventional data processing algorithm and the spectral fringe algorithm reveal a good agreement with the reference distance for a target distance from +1 mm to +10 mm, as illustrated in Figure 9. There is little manifest difference in the measurement results of these two algorithms when the target distance is not a short one because of the stretched pulse interval in the time domain. Meanwhile, for a target distance from +1 mm to +10 mm, the measurement results of the combined algorithm are also highly consistent with the reference distance, as shown in Figure 10a. However, Figure 10b illustrates that the difference between the measurement results and referenced distance of the combined algorithm is nearly two times smaller than that of the conventional and the spectral fringe one, which is ~1.8 μm and ~4.2 μm, respectively. In other words, the combined algorithm can improve the accuracy of the conventional data processing algorithm owing to utilizing the wrapped phase directly.
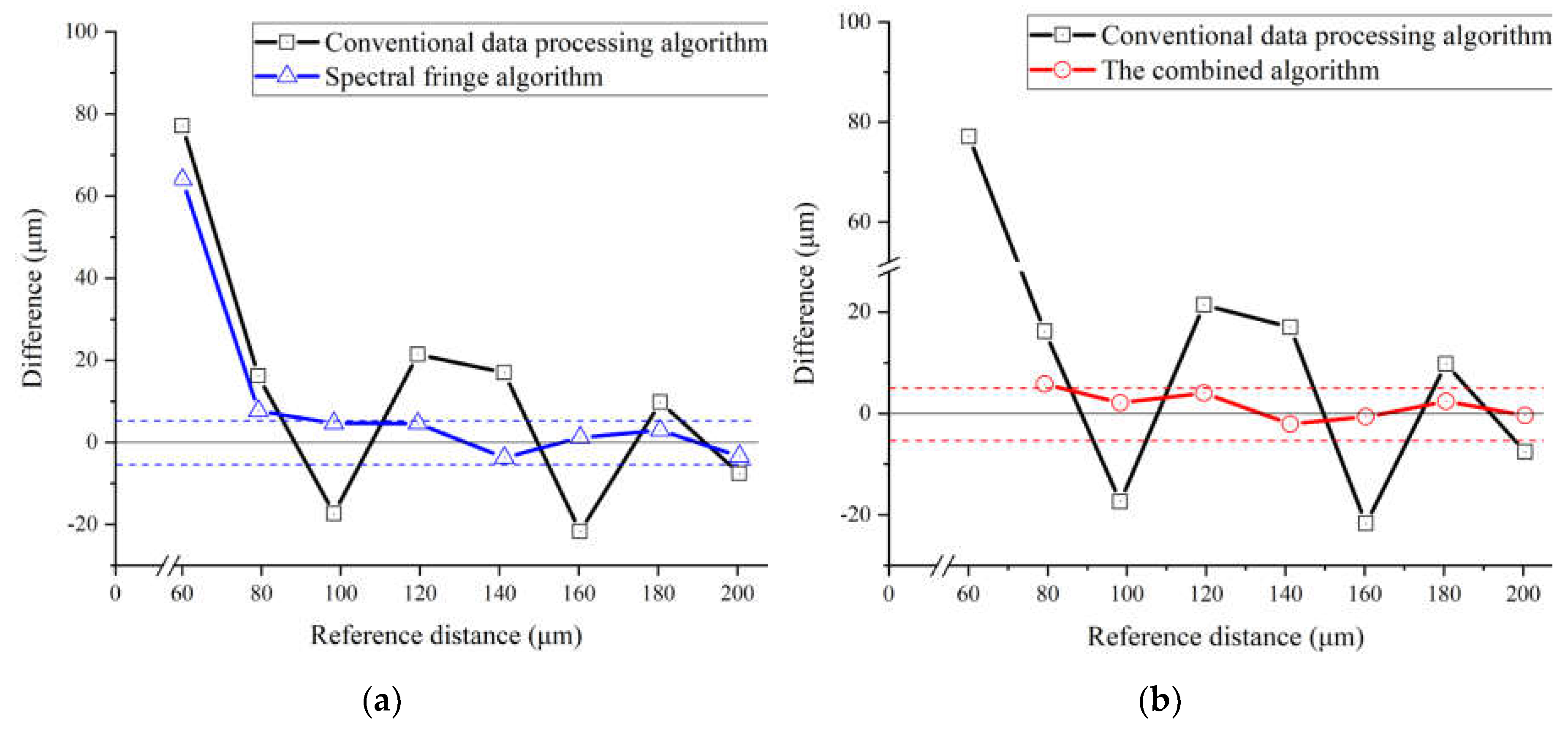
The performance of the conventional data processing algorithm dramatically decreases when the target distance is smaller than 1 mm. The measurement results of the conventional data processing algorithm from -1 to +1 mm are shown in Figure 11, in which an undetectable region emerges near zero distance highlighted in a red box, whose amplified details are shown in Figure 11b. The dead zone of the conventional data processing algorithm is approximately 200 μm, in which reliable and accurate value of the target distance cannot be obtained by this conventional algorithm. However, the spectral fringe algorithm can reach a more precise result within the dead zone of the conventional algorithm, as shown in Figure 12a. The minimum working distance achieved by the spectral fringe algorithm is approximately 100 μm, while that of the conventional one is only around 200 μm, which indicates the spectral fringe algorithm can significantly shorten the dead-zone two times smaller than that of the conventional one benefiting from the vanished central pulse in the time domain and more sharped shape as theoretically analyzed. Moreover, the combined algorithm can achieve an accuracy-improved result in the conventional algorithm’s dead zone, as shown in Figure 12b. The average difference of the combined algorithm with a target distance from 100 to 200 μm is 2.49 μm, which is approximately 40% smaller than the spectral fringe algorithm of 4.02 μm.
4. Conclusions
In this paper, two improved data processing algorithms have been proposed for shortening the dead-zone close to the zero-position of measurement, i.e., the minimum working distance of dispersive interferometry using an optical frequency comb, which is a critical issue in millimeter-order short-range absolute distance measurement. The principles of the proposed algorithms, namely, the spectral fringe algorithm and the combined algorithm, have been derived. Meanwhile, we have clarified the impact of the modulated parameter A and the data processing procedure of these proposed algorithms by simulation. An experimental setup has been established to carry out short-range absolute distance measurement by dispersive interferometry. The results of the conventional data processing algorithm and those of the proposed algorithms have been compared. It was verified the dead-zone by the proposed algorithms was shortened to half of that by the conventional algorithm. Furthermore, owing to the employment of the wrapped phase information directly, the combined algorithm was demonstrated to have a better measurement accuracy than the spectral fringe algorithm.
Author Contributions
Conceptualization, W.G. and H.M.; methodology, W.G., J.W. and T.L.; software, A.S. and T.L.; validation, J.W. and R.S.; formal analysis, T.L. and R.S.; investigation, A.S. and T.L.; resources, W.G. and H.M.; data curation, J.W., A.S. and T.L.; writing—original draft preparation, T.L.; writing—review and editing, W.G., H.M. and R.S.; visualization, J.W., H.M. and T.L.; supervision, W.G.; project administration, W.G.; funding acquisition, W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Japan Society for the Promotion of Science (JSPS), grant number 20H00211.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The paper is financially supported by Japan Society for Promotion of Science. Tao Liu would like to thank the Chinese Scholarship Council (CSC) for living cost support.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Michelson, A.A.; Pease, F.; Pearson, F. Repetition of the Michelson-Morley experiment. JOSA 1929, 18, 181–182. [Google Scholar] [CrossRef]
- Straube, G.; Fischer Calderón, J.S.; Ortlepp, I.; Füßl, R.; Manske, E. A Heterodyne Interferometer with Separated Beam Paths for High-Precision Displacement and Angular Measurements. Nanomanufacturing and Metrology 2021, 4, 200–207. [Google Scholar] [CrossRef]
- Gao, W. Precision Nanometrology: Sensors and Measuring Systems for Nanomanufacturing, 1st ed.; Springer: London, UK, 2010; pp: 69-107. [Google Scholar]
- Gao, W.; Haitjema, H.; Fang, F.Z.; Leach, R.K.; Cheung, C.F.; Savio, E.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. CIRP Annals 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Gao, W. Surface Metrology for Micro-and Nanofabrication, 1st ed.; Elsevier: Oxford, UK, 2021; pp: 1-32. [Google Scholar]
- Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical frequency metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef]
- Hall, J.L. Nobel Lecture: Defining and measuring optical frequencies. Reviews of modern physics 2006, 78, 1279. [Google Scholar] [CrossRef]
- Hänsch, T.W. Nobel lecture: passion for precision. Reviews of Modern Physics 2006, 78, 1297. [Google Scholar] [CrossRef]
- Jones, D.J.; Diddams, S.A.; Ranka, J.K.; Stentz, A.; Windeler, R.S.; Hall, J.L.; Cundiff, S.T. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 2000, 288, 635–640. [Google Scholar] [CrossRef]
- Fortier, T.; Baumann, E. 20 years of developments in optical frequency comb technology and applications. Communications Physics 2019, 2, 131–147. [Google Scholar] [CrossRef]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Coherent multiheterodyne spectroscopy using stabilized optical frequency combs. Phys Rev Lett 2008, 100, 013902. [Google Scholar] [CrossRef]
- Minoshima, K.; Matsumoto, H. High-accuracy measurement of 240-m distance in an optical tunnel by use of a compact femtosecond laser. Appl Opt 2000, 39, 5512–5517. [Google Scholar] [CrossRef]
- Kim, S.W. Combs rule. Nature Photonics 2009, 3, 313–314. [Google Scholar] [CrossRef]
- Jang, Y.S.; Kim, S.W. Distance Measurements Using Mode-Locked Lasers: A Review. Nanomanufacturing and Metrology 2018, 1, 131–147. [Google Scholar] [CrossRef]
- Sato, R.; Shimizu, Y.; Shimizu, H.; Matsukuma, H.; Gao, W. Confocal probe based on the second harmonic generation for measurement of linear and angular displacements. Optics Express 2023, 31. [Google Scholar] [CrossRef]
- Gao, W.; Shimizu, Y. Optical Metrology for Precision Engineering, 1st ed.; De Gruyter: Berlin/Boston, 2021; pp: 379-423. [Google Scholar]
- Chen, Y.L.; Shimizu, Y.; Kudo, Y.; Ito, S.; Gao, W. Mode-locked laser autocollimator with an expanded measurement range. Opt Express 2016, 24, 15554–15569. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Kudo, Y.; Chen, Y.L.; Ito, S.; Gao, W. An optical lever by using a mode-locked laser for angle measurement. Precision Engineering 2017, 47, 72–80. [Google Scholar] [CrossRef]
- Chen, Y.L.; Shimizu, Y.; Tamada, J.; Kudo, Y.; Madokoro, S.; Nakamura, K.; Gao, W. Optical frequency domain angle measurement in a femtosecond laser autocollimator. Opt Express 2017, 25, 16725–16738. [Google Scholar] [CrossRef]
- Chen, Y.L.; Shimizu, Y.; Tamada, J.; Nakamura, K.; Matsukuma, H.; Chen, X.; Gao, W. Laser autocollimation based on an optical frequency comb for absolute angular position measurement. Precision Engineering 2018, 54, 284–293. [Google Scholar] [CrossRef]
- Dwi Astuti, W.; Matsukuma, H.; Nakao, M.; Li, K.; Shimizu, Y.; Gao, W. An Optical Frequency Domain Angle Measurement Method Based on Second Harmonic Generation. Sensors (Basel) 2021, 21. [Google Scholar] [CrossRef]
- Shin, D.W.; Matsukuma, H.; Sato, R.; Gao, W. Fabry-Perot angle sensor using a mode-locked femtosecond laser source. Opt Express 2022, 30, 46366–46382. [Google Scholar] [CrossRef]
- Doloca, N.R.; Meiners-Hagen, K.; Wedde, M.; Pollinger, F.; Abou-Zeid, A. Absolute distance measurement system using a femtosecond laser as a modulator. Measurement Science and Technology 2010, 21. [Google Scholar] [CrossRef]
- Jang, Y.S.; Lee, K.; Han, S.; Lee, J.; Kim, Y.J.; Kim, S.W. Absolute distance measurement with extension of nonambiguity range using the frequency comb of a femtosecond laser. Optical Engineering 2014, 53. [Google Scholar] [CrossRef]
- Wu, G.; Liao, L.; Xiong, S.; Li, G.; Cai, Z.; Zhu, Z. Synthetic wavelength interferometry of an optical frequency comb for absolute distance measurement. Sci Rep 2018, 8, 4362. [Google Scholar] [CrossRef]
- Dändliker, R.; Salvadé, Y.; Zimmermann, E. Distance measurement by multiple-wavelength interferometry. Journal of Optics 1998, 29, 105–114. [Google Scholar] [CrossRef]
- Towers, C.E.; Towers, D.P.; Reid, D.T.; MacPherson, W.N.; Maier, R.R.; Jones, J.D. Fiber interferometer for simultaneous multiwavelength phase measurement with a broadband femtosecond laser. Opt Lett 2004, 29, 2722–2724. [Google Scholar] [CrossRef] [PubMed]
- Hyun, S.; Kim, Y.J.; Kim, Y.; Kim, S.W. Absolute distance measurement using the frequency comb of a femtosecond laser. CIRP Annals 2010, 59, 555–558. [Google Scholar] [CrossRef]
- Salvade, Y.; Schuhler, N.; Leveque, S.; Le Floch, S. High-accuracy absolute distance measurement using frequency comb referenced multiwavelength source. Appl Opt 2008, 47, 2715–2720. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Jang, Y.S.; Hyun, S.; Chun, B.J.; Kang, H.J.; Yan, S.; Kim, S.W.; Kim, Y.J. Absolute positioning by multi-wavelength interferometry referenced to the frequency comb of a femtosecond laser. Opt Express 2015, 23, 9121–9129. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.J.; Zhang, H.Y.; Li, Y.; Wei, H.Y. Absolute group refractive index measurement of air by dispersive interferometry using frequency comb. Opt Express 2015, 23, 33597–33607. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhang, F.; Liu, T.; Li, J.; Qu, X. Absolute distance measurement with correction of air refractive index by using two-color dispersive interferometry. Opt Express 2016, 24, 24361–24376. [Google Scholar] [CrossRef]
- Niu, Q.; Song, M.; Zheng, J.; Jia, L.; Liu, J.; Ni, L.; Nian, J.; Cheng, X.; Zhang, F.; Qu, X. Improvement of Distance Measurement Based on Dispersive Interferometry Using Femtosecond Optical Frequency Comb. Sensors (Basel) 2022, 22. [Google Scholar] [CrossRef]
- Liang, X.; Wu, T.; Lin, J.; Yang, L.; Zhu, J. Optical Frequency Comb Frequency-division Multiplexing Dispersive Interference Multichannel Distance Measurement. Nanomanufacturing and Metrology 2023, 6. [Google Scholar] [CrossRef]
- Schiller, S. Spectrometry with frequency combs. Opt Lett 2002, 27, 766–768. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, H.; Wu, X.; Yang, H.; Li, Y. Absolute distance measurement by dual-comb nonlinear asynchronous optical sampling. Opt Express 2014, 22, 6597–6604. [Google Scholar] [CrossRef]
- Wu, G.; Xiong, S.; Ni, K.; Zhu, Z.; Zhou, Q. Parameter optimization of a dual-comb ranging system by using a numerical simulation method. Opt Express 2015, 23, 32044–32053. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Wu, Z.; Cao, H.; Shi, Y.; Li, R.; Tian, H.; Song, Y.; Hu, M. Dual-comb absolute distance measurement of non-cooperative targets with a single free-running mode-locked fiber laser. Optics Communications 2021, 482. [Google Scholar] [CrossRef]
- Zhu, Z.; Wu, G. Dual-Comb Ranging. Engineering 2018, 4, 772–778. [Google Scholar] [CrossRef]
- Ye, J. Absolute measurement of a long, arbitrary distance to less than an optical fringe. Opt Lett 2004, 29, 1153–1155. [Google Scholar] [CrossRef] [PubMed]
- Balling, P.; Kren, P.; Masika, P.; van den Berg, S.A. Femtosecond frequency comb based distance measurement in air. Opt Express 2009, 17, 9300–9313. [Google Scholar] [CrossRef]
- Wei, D.; Takahashi, S.; Takamasu, K.; Matsumoto, H. Time-of-flight method using multiple pulse train interference as a time recorder. Opt Express 2011, 19, 4881–4889. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Matsumoto, H. Measurement accuracy of the pulse repetition interval-based excess fraction (PRIEF) method: an analogy-based theoretical analysis. Journal of the European Optical Society: Rapid Publications 2012, 7. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.; Lee, S.; Kim, S.W.; Kim, Y.J. High precision laser ranging by time-of-flight measurement of femtosecond pulses. Measurement Science and Technology 2012, 23. [Google Scholar] [CrossRef]
- Joo, K.N.; Kim, S.W. Absolute distance measurement by dispersive interferometry using a femtosecond pulse laser. Opt Express 2006, 14, 5954–5960. [Google Scholar] [CrossRef] [PubMed]
- van den Berg, S.A.; Persijn, S.T.; Kok, G.J.; Zeitouny, M.G.; Bhattacharya, N. Many-wavelength interferometry with thousands of lasers for absolute distance measurement. Phys Rev Lett 2012, 108, 183901. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Qu, X.; Zhang, F.; Zhao, X.; Peng, B. Absolute distance measurement based on spectral interferometry using femtosecond optical frequency comb. Optics and Lasers in Engineering 2019, 120, 71–78. [Google Scholar] [CrossRef]
- de Groot, P.J. Extending the unambiguous range of two-color interferometers. Appl Opt 1994, 33, 5948–5953. [Google Scholar] [CrossRef] [PubMed]
- Falaggis, K.; Towers, D.P.; Towers, C.E. Optimum wavelength selection for the method of excess fractions. In Proceedings of the Optical Engineering Applications, San Diego, California, United States; 2008. [Google Scholar]
- Cui, M.; Zeitouny, M.G.; Bhattacharya, N.; van den Berg, S.A.; Urbach, H.P. Long distance measurement with femtosecond pulses using a dispersive interferometer. Opt Express 2011, 19, 6549–6562. [Google Scholar] [CrossRef]
- van den Berg, S.A.; van Eldik, S.; Bhattacharya, N. Mode-resolved frequency comb interferometry for high-accuracy long distance measurement. Sci Rep 2015, 5, 14661. [Google Scholar] [CrossRef]
- Aoki, H. Revised Precision Measurement, 1st ed.; Corona Publishing: Tokyo, Japan, 1957; pp: 62-67. [Google Scholar]
- Falaggis, K.; Towers, D.P.; Towers, C.E. Method of excess fractions with application to absolute distance metrology: theoretical analysis. Appl Opt 2011, 50, 5484–5498. [Google Scholar] [CrossRef]
- Corporation, Y.T.M. AQ6370D Telecom Optical Spectrum Analyzer 600 - 1700 nm. Available online: https://tmi.yokogawa.com/solutions/products/optical-measuring-instruments/optical-spectrum-analyzer/aq6370d-optical-spectrum-analyzer/#Documents-Downloads____downloads_9 (accessed on July 2022).
- Xu, Y. Study on Absolute Distance Measurement Technology Based on Femtosecond Optical Frequency Comb. Doctoral, Huazhong University of Science and Technology, Wuhan, China, , 2012. 23 October.
- Inaba, H.; Daimon, Y.; Hong, F.L.; Onae, A.; Minoshima, K.; Schibli, T.R.; Matsumoto, H.; Hirano, M.; Okuno, T.; Onishi, M.; et al. Long-term measurement of optical frequencies using a simple, robust and low-noise fiber based frequency comb. Opt Express 2006, 14, 5223–5231. [Google Scholar] [CrossRef]
Figure 1.
Theoretical analysis of the excess fraction method. (a) excess fraction εi of wavelength λi periodically varies with increasing target distance L, and the other two horizontal axes in the middle represent the acceptable integer part Ni and the acceptable adjustment range for the integer part mi, respectively. (b) excess fraction value εi+1 of λi+1 periodically varies with increasing target distance L. The four small blue circles mean the excess fraction ε(i+1)j of +cj in wavelength λi+1, and the magenta square box represents the ε(i+1)j which is the closest to ε(i+1), whose corresponding cJ is the optimum one.
Figure 1.
Theoretical analysis of the excess fraction method. (a) excess fraction εi of wavelength λi periodically varies with increasing target distance L, and the other two horizontal axes in the middle represent the acceptable integer part Ni and the acceptable adjustment range for the integer part mi, respectively. (b) excess fraction value εi+1 of λi+1 periodically varies with increasing target distance L. The four small blue circles mean the excess fraction ε(i+1)j of +cj in wavelength λi+1, and the magenta square box represents the ε(i+1)j which is the closest to ε(i+1), whose corresponding cJ is the optimum one.
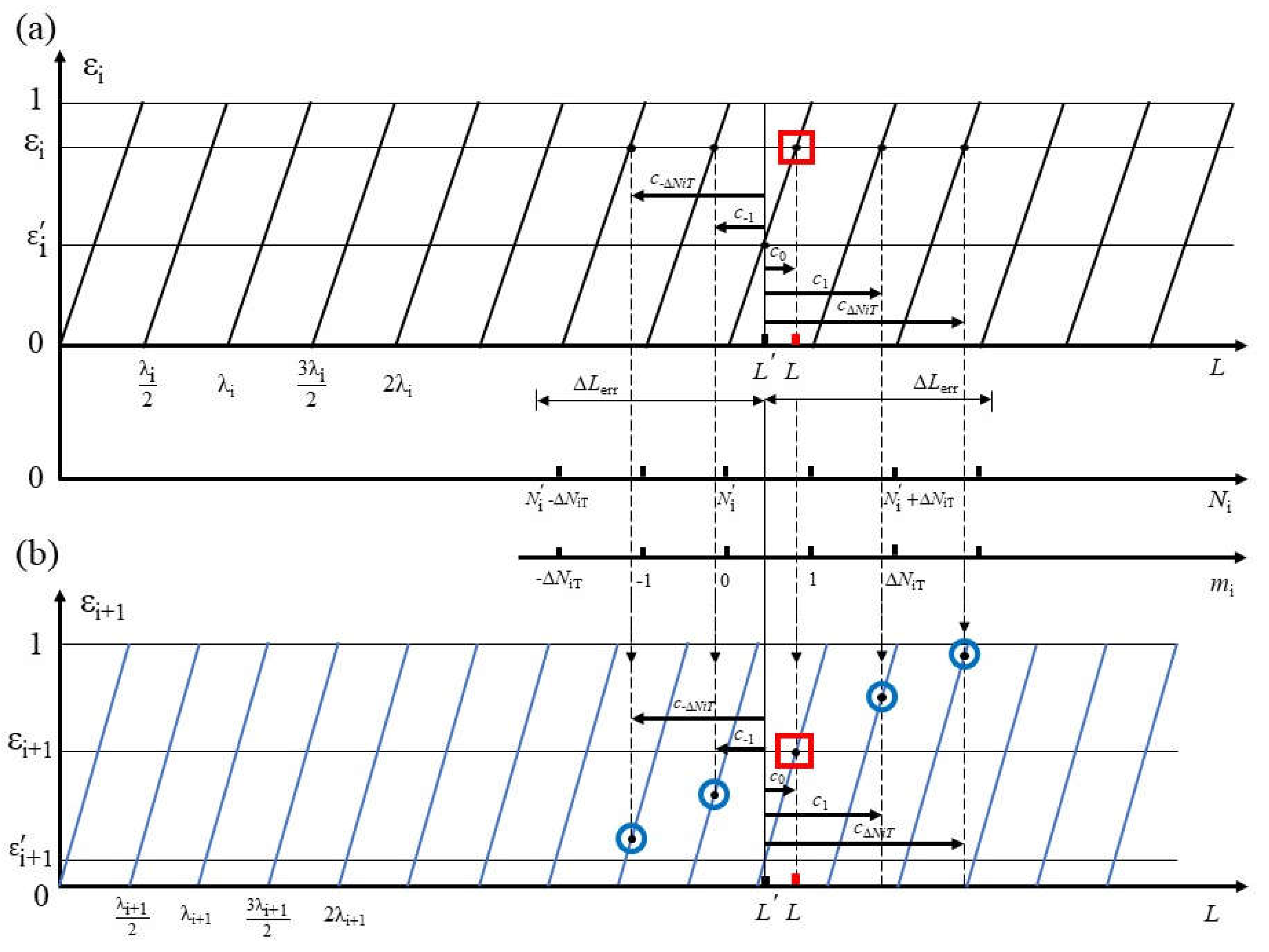
Figure 2.
Interference spectrum with different target distance L. (a) L = 1 mm; (b) L = 2 mm; (c) L = 3 mm.
Figure 2.
Interference spectrum with different target distance L. (a) L = 1 mm; (b) L = 2 mm; (c) L = 3 mm.
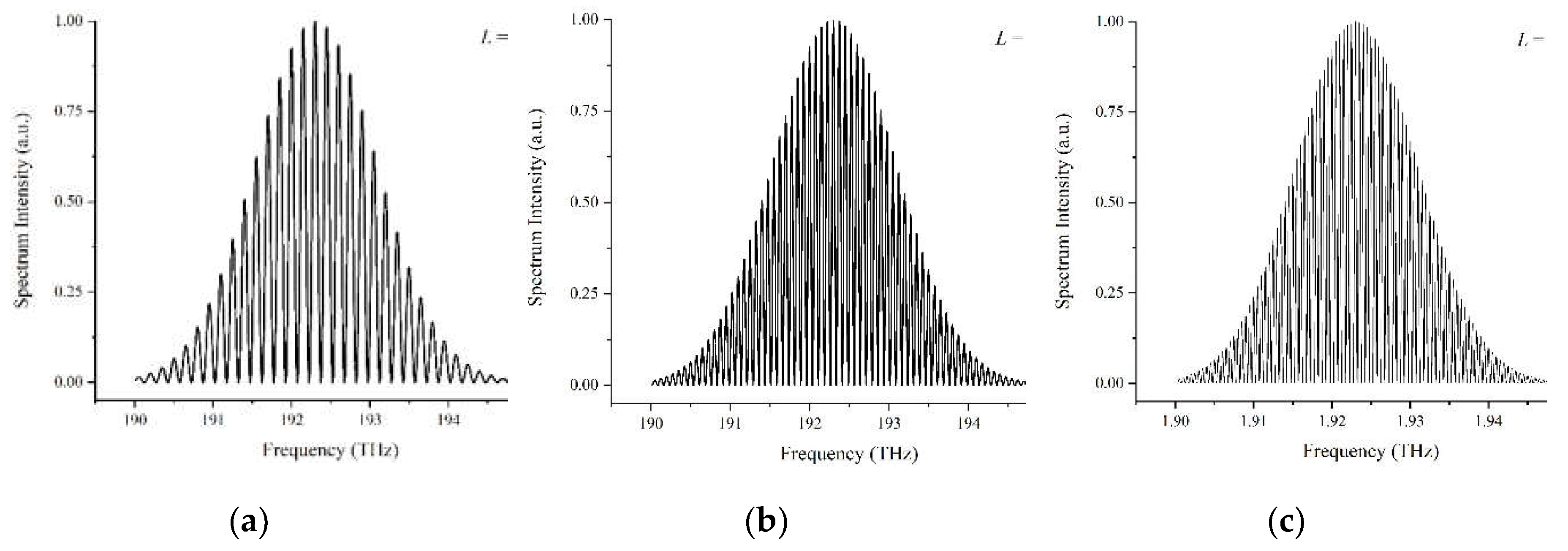
Figure 3.
Interference spectrum with different values of modulated parameter A for a target distance of L = 1 mm. (a) A = 0.25; (b) A = 0.5; (c) A = 0.75.
Figure 3.
Interference spectrum with different values of modulated parameter A for a target distance of L = 1 mm. (a) A = 0.25; (b) A = 0.5; (c) A = 0.75.
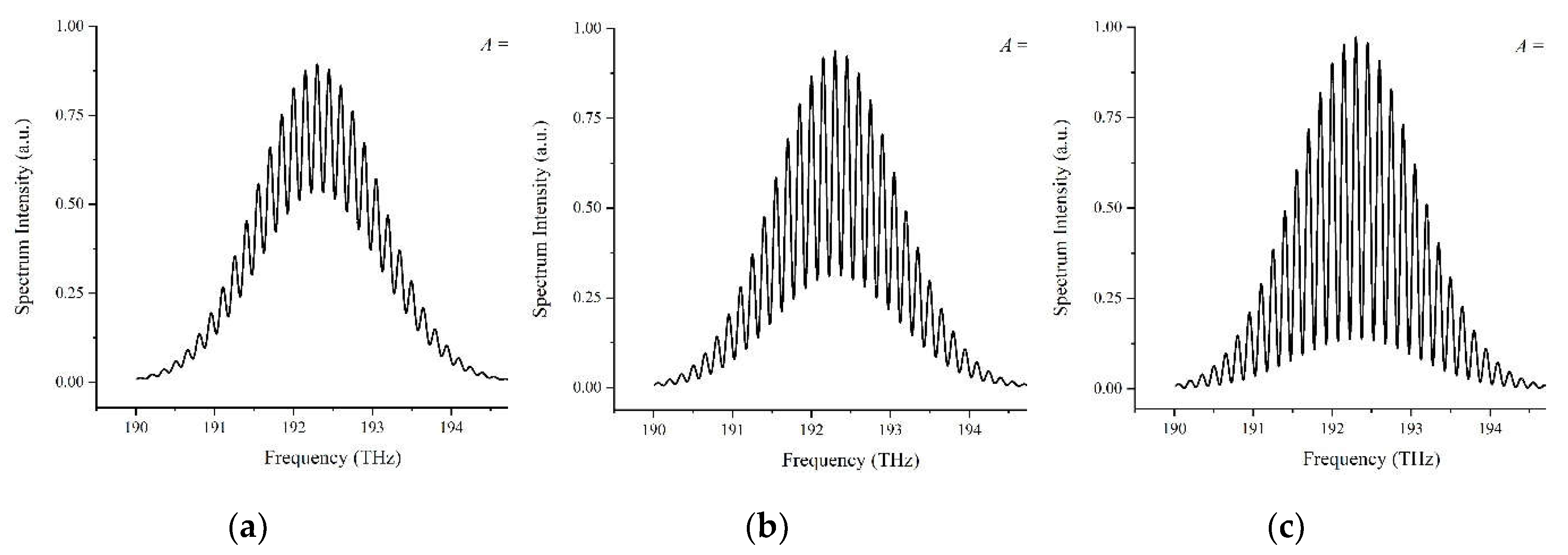
Figure 4.
The data processing procedure of the conventional data processing algorithm. (a) inverse Fourier transforming interference spectrum into the time domain, leading to a rough time delay of 6.67×10-12 s; (b) wrapped phase; (c) unwrapped phase.
Figure 4.
The data processing procedure of the conventional data processing algorithm. (a) inverse Fourier transforming interference spectrum into the time domain, leading to a rough time delay of 6.67×10-12 s; (b) wrapped phase; (c) unwrapped phase.
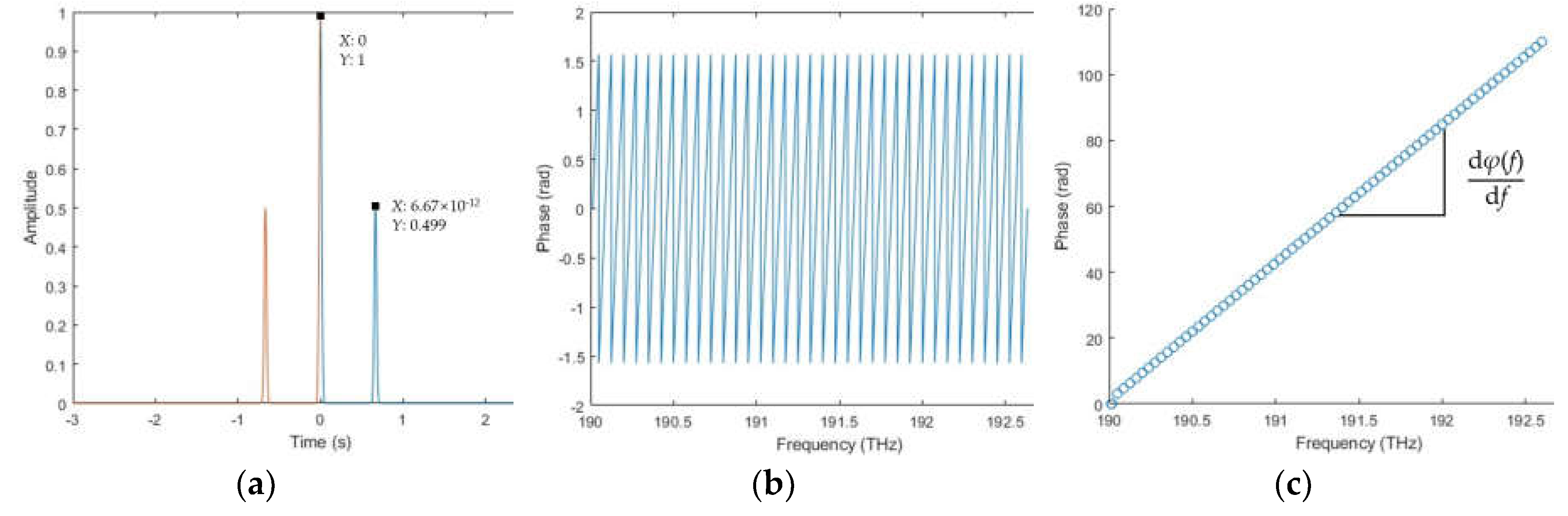
Figure 5.
The data processing procedure of the spectral fringe algorithm. (a) extracting the upper and lower envelopes of the interference spectrum, where the red line is the upper envelope, the green line is the lower envelope, and the middle blue line is the spectrum of the source; (b) modified spectral interference signal Im(); (c) inverse Fourier transforming and only two sharp peaks can be found; (d) time-window filtered peak; (e) wrapped phase; (f) unwrapped phase.
Figure 5.
The data processing procedure of the spectral fringe algorithm. (a) extracting the upper and lower envelopes of the interference spectrum, where the red line is the upper envelope, the green line is the lower envelope, and the middle blue line is the spectrum of the source; (b) modified spectral interference signal Im(); (c) inverse Fourier transforming and only two sharp peaks can be found; (d) time-window filtered peak; (e) wrapped phase; (f) unwrapped phase.
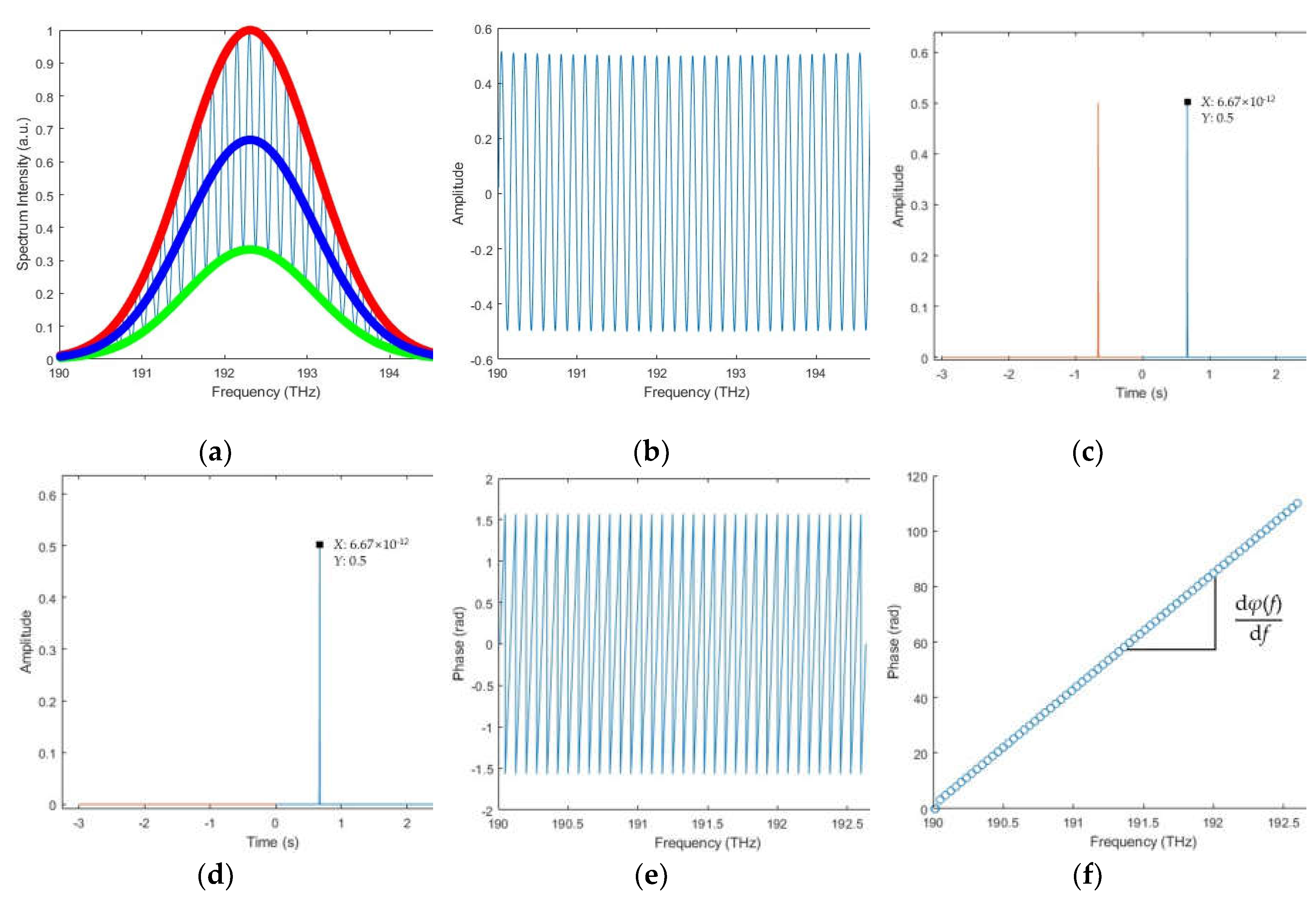
Figure 6.
The data processing procedure of the combined algorithm. (a) wrapped phase; (b) excess fraction value.
Figure 6.
The data processing procedure of the combined algorithm. (a) wrapped phase; (b) excess fraction value.
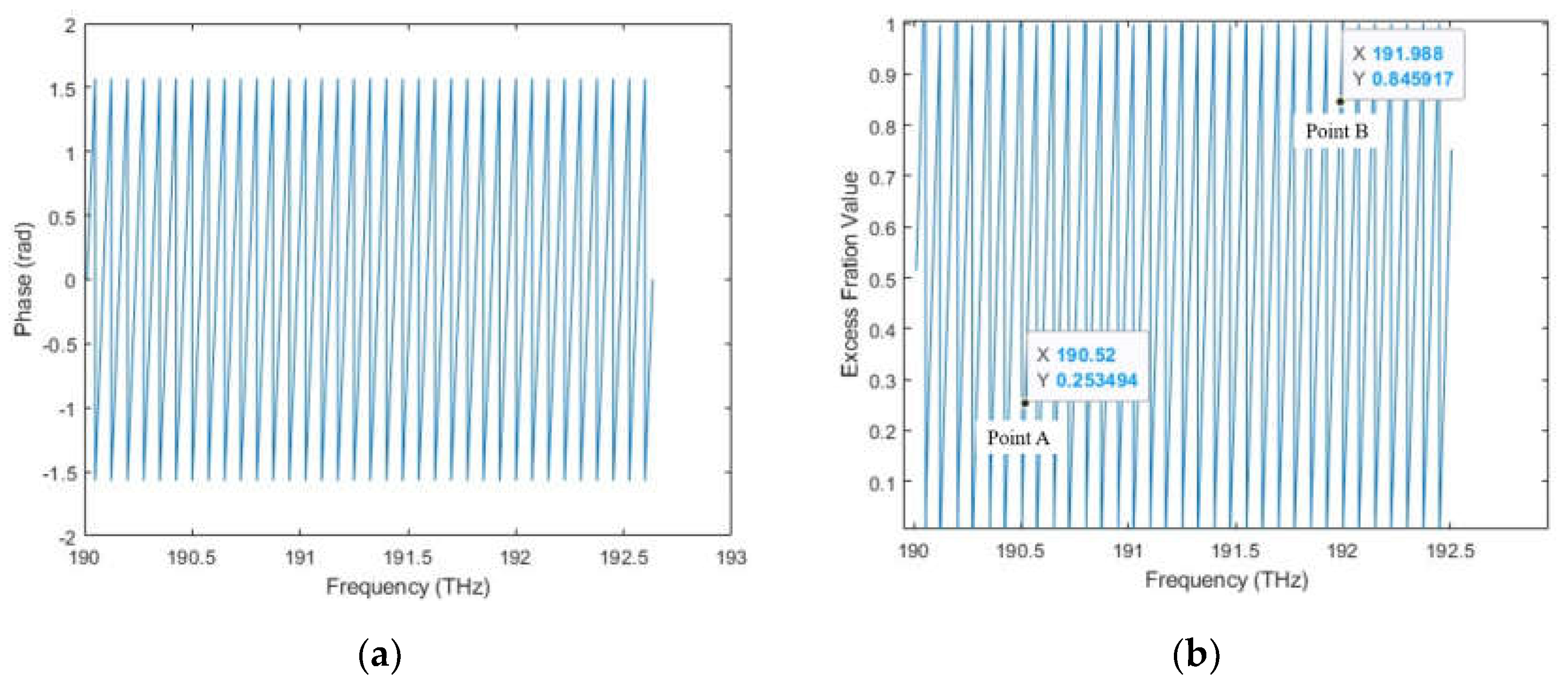
Figure 7.
A schematic to show the dispersive interferometry experiment setup.
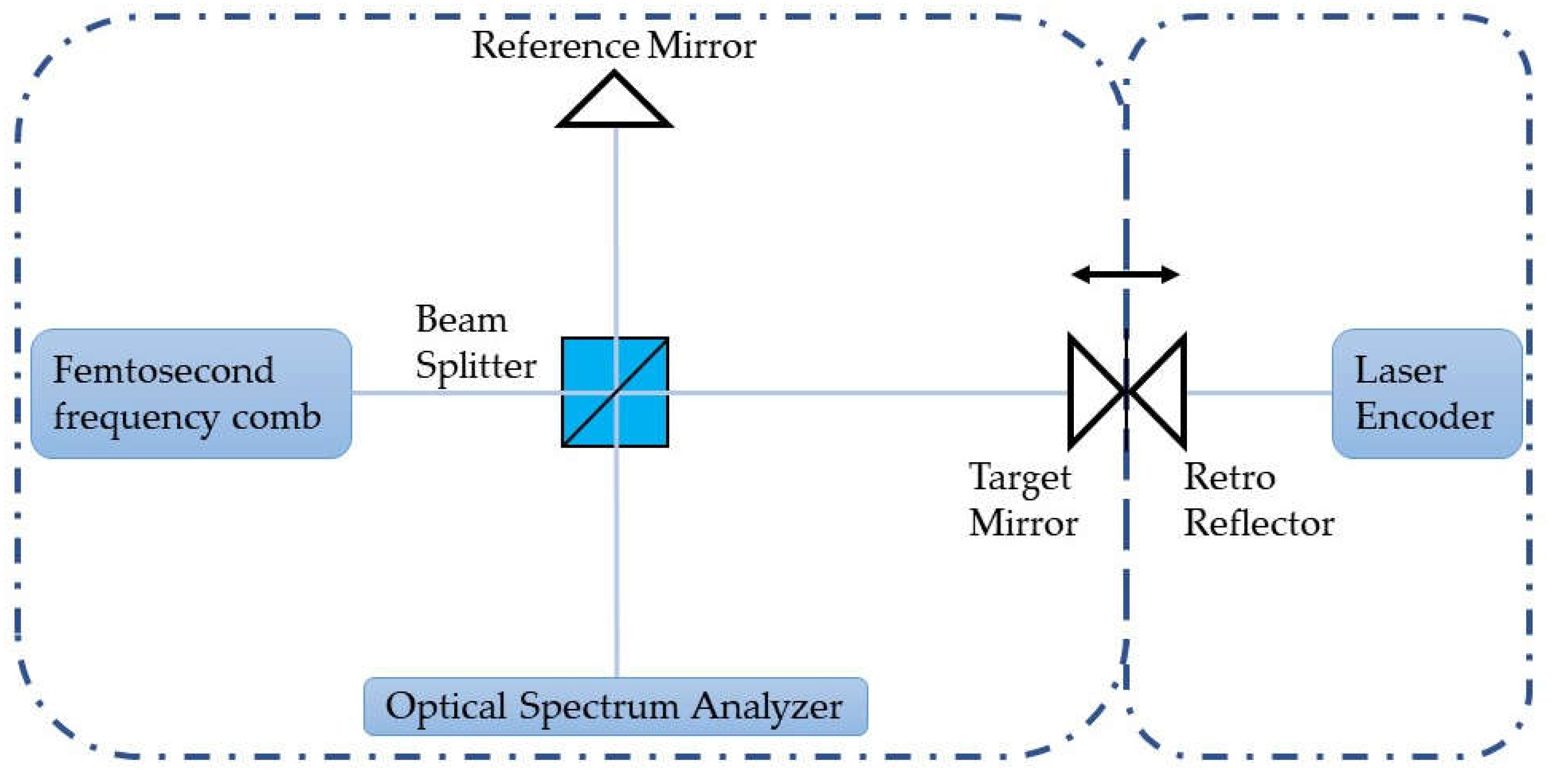
Figure 8.
Interference spectrum at different positions. (a) the interference spectrum at 1 mm; (b) the interference spectrum at 2 mm; (c) the interference spectrum at 3 mm.
Figure 8.
Interference spectrum at different positions. (a) the interference spectrum at 1 mm; (b) the interference spectrum at 2 mm; (c) the interference spectrum at 3 mm.
Figure 9.
A comparison of the measurement results by the conventional data processing algorithm (black) and the spectral fringe algorithm (blue). (a) the measurement result from 1 mm to 10 mm with a step of 1 mm; (b) the difference between the measurement results and referenced distance.
Figure 9.
A comparison of the measurement results by the conventional data processing algorithm (black) and the spectral fringe algorithm (blue). (a) the measurement result from 1 mm to 10 mm with a step of 1 mm; (b) the difference between the measurement results and referenced distance.
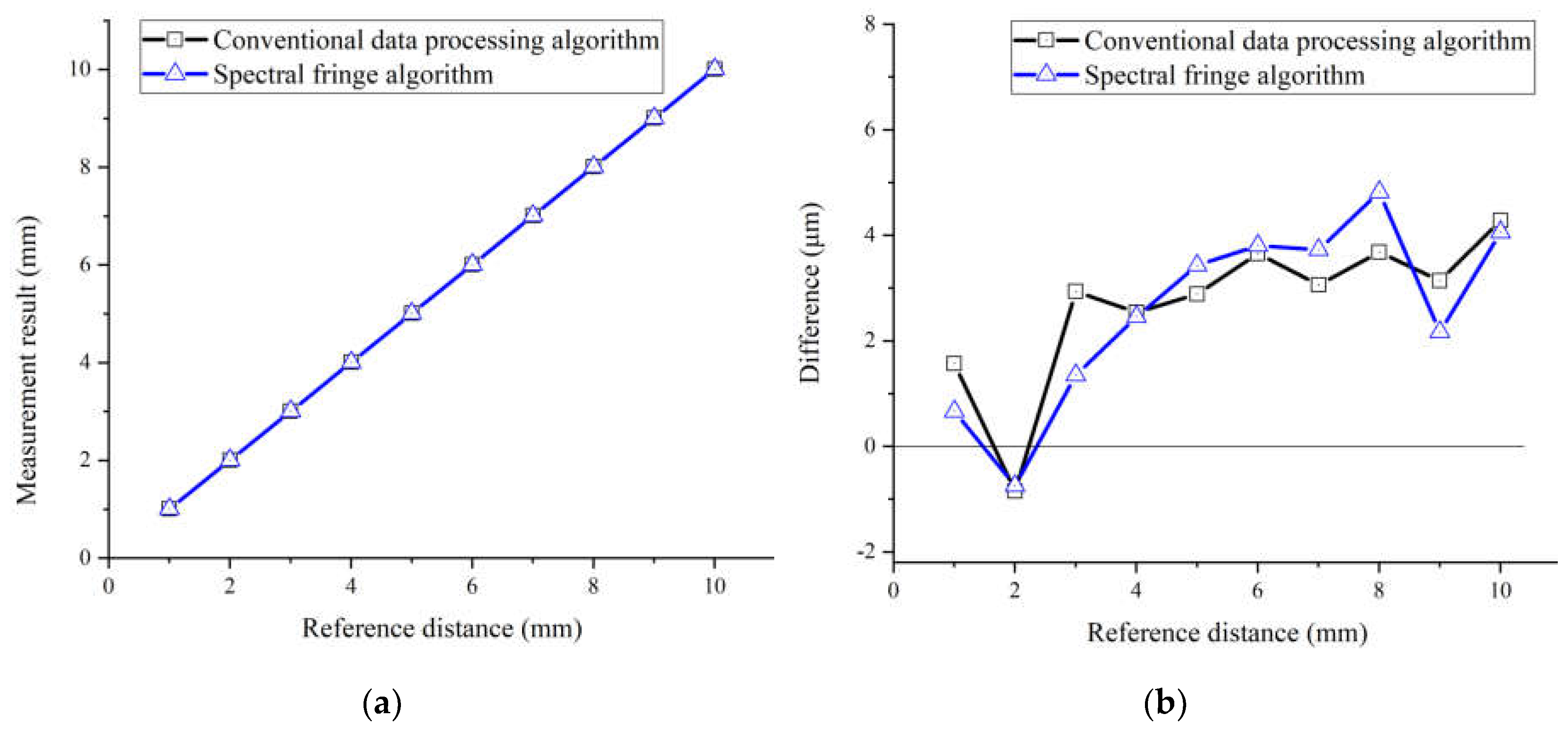
Figure 10.
A comparison of the measurement results by the conventional data processing algorithm (black) and the combined algorithm (red). (a) the measurement result from 1 mm to 10 mm; (b) the difference between the measurement results and referenced distance.
Figure 10.
A comparison of the measurement results by the conventional data processing algorithm (black) and the combined algorithm (red). (a) the measurement result from 1 mm to 10 mm; (b) the difference between the measurement results and referenced distance.
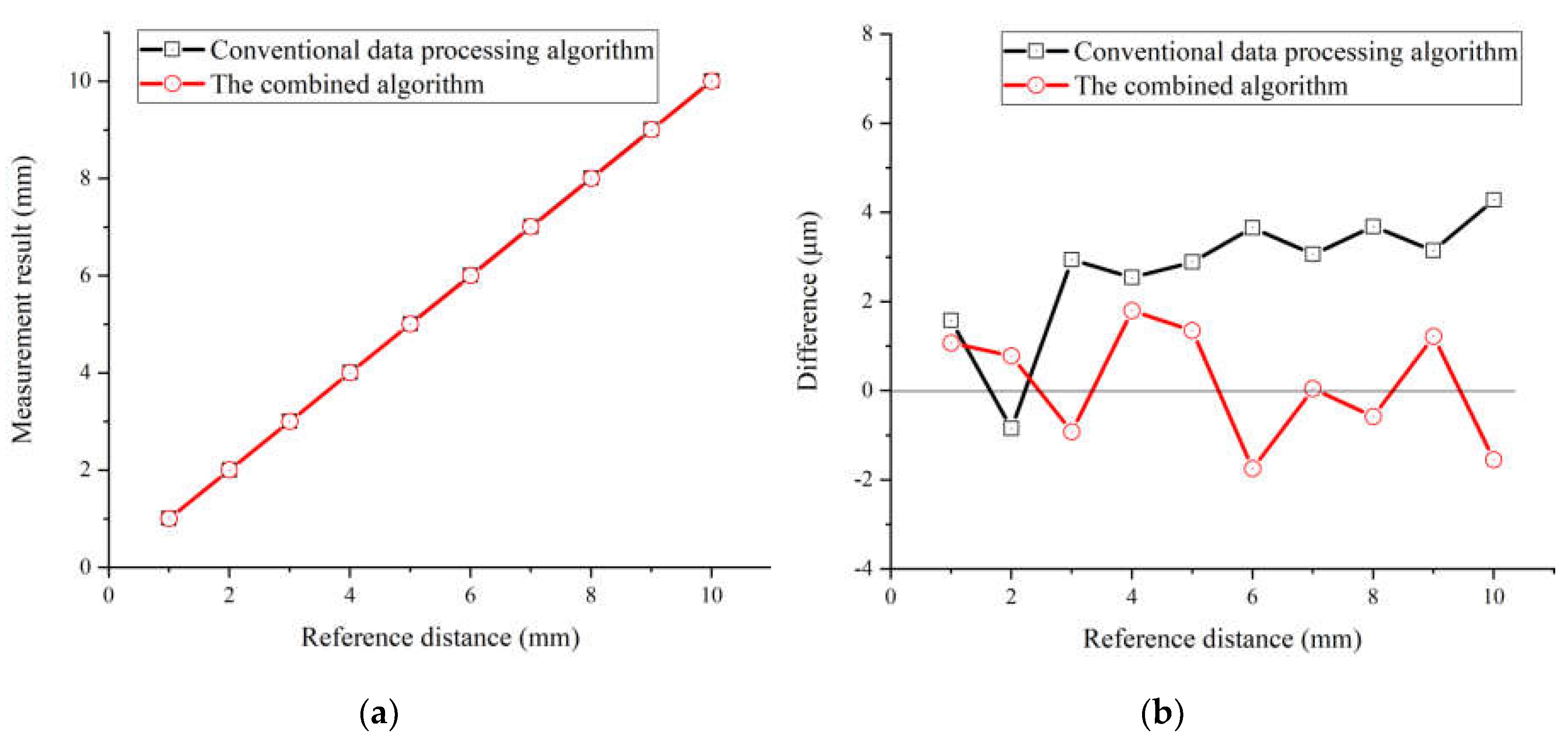
Figure 11.
The dead zone of the conventional data processing algorithm. (a) measurement results of the conventional algorithm from -1 mm to +1 mm with a step of 1 μm; (b) amplification of the red box labeled region in the left figure (a).
Figure 11.
The dead zone of the conventional data processing algorithm. (a) measurement results of the conventional algorithm from -1 mm to +1 mm with a step of 1 μm; (b) amplification of the red box labeled region in the left figure (a).
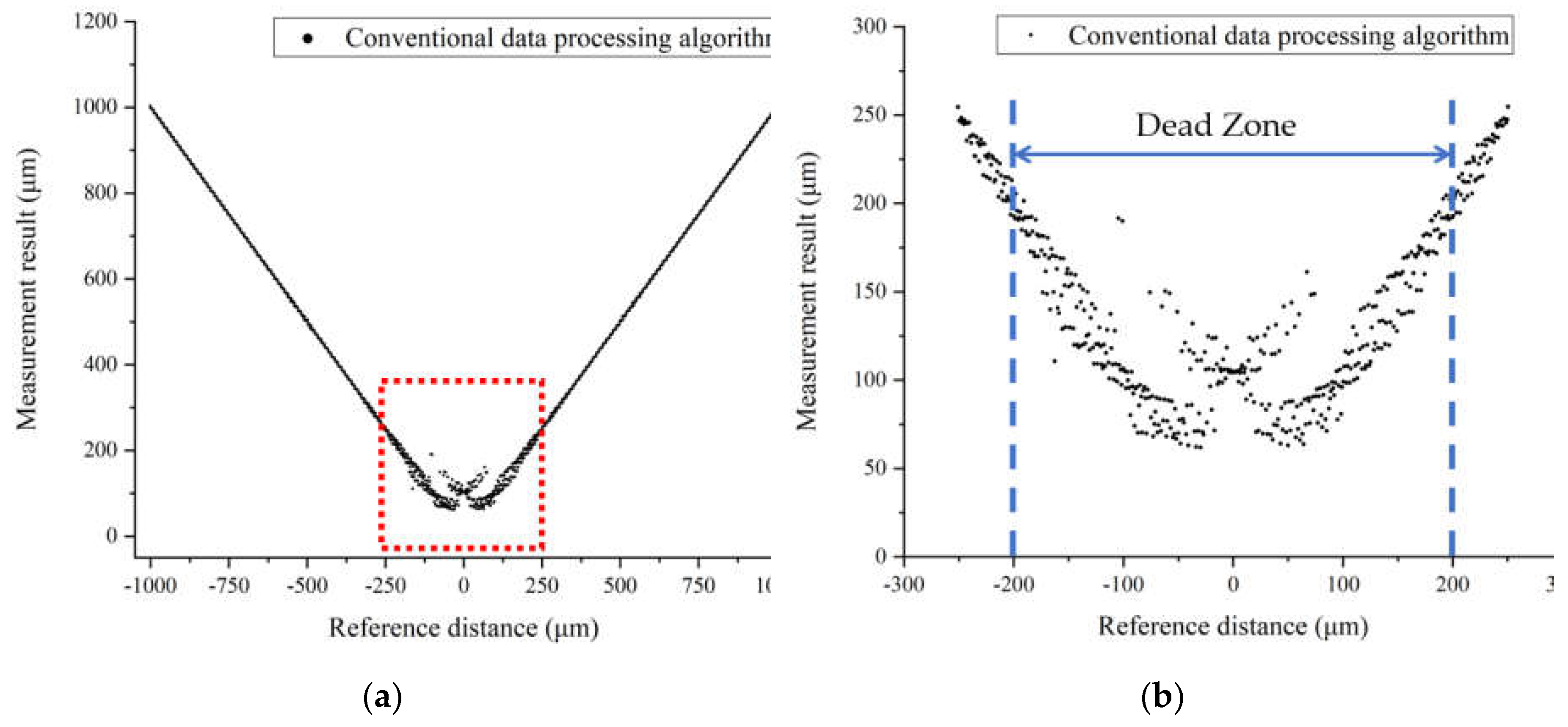
Figure 12.
Measurement results of the conventional data processing algorithm, the spectral fringe and the combined algorithm from +60 to +200 μm. (a) a comparison of the conventional algorithm (black) and the spectral fringe algorithm (blue); (b) a comparison of the conventional algorithm (black) and the combined algorithm (red).
Figure 12.
Measurement results of the conventional data processing algorithm, the spectral fringe and the combined algorithm from +60 to +200 μm. (a) a comparison of the conventional algorithm (black) and the spectral fringe algorithm (blue); (b) a comparison of the conventional algorithm (black) and the combined algorithm (red).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






