Prerpints.org logo
Preprint
Article

Microwave Humidity Sensor for Early Detection of Sweat and Urine Leakage

Altmetrics

Downloads

134

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 April 2023

Posted:

26 April 2023

You are already at the latest version

Alerts
Abstract
A planar microwave sensor devoted to the detection of humidity in underwear and clothes in general is proposed. The ultimate goal of the sensor is to detect the presence of liquids in fabrics, of interest to aid patients that suffer from certain pathologies, such as hyperhidrosis and enuresis. The main target in the design of the sensor, considering the envisaged application, is simplicity. Thus, the sensor operates at a single frequency, and the working principle is the variation in the mag-nitude of the transmission coefficient of a matched line loaded with an open-ended quar-ter-wavelength sensing stub resonator. The stub, which must be in contact with the so-called fabric under test (FUT), generates a notch in the transmission coefficient with a resonance frequency that depends on the humidity level of the fabric. By designing the stub with a moderately high quality factor, the variation in the resonance frequency causes a significant change in the magnitude level at the operating frequency, the resonance frequency when the sensing stub is loaded with the dry fabric, and the presence of liquid can be detected by means of an amplitude detector. A prototype device is proposed and experimentally validated.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Planar microwave technology is of the highest interest for the implementation of a wide variety of sensors [1,2]. Among their advantages, planar microwave sensors exhibit low cost and profile, and they can be implemented in many different types of substrates, including rigid substrates (such as low-cost FR4, or low-loss microwave substrates), or flexible substrates (including polymeric substrates, organic substrates, e.g., paper, or fabric, among others). Planar microwave sensors can be fabricated by means of either subtractive (e.g., photoetching or milling) or additive (e.g., inkjet-printing, screen-printing, or 3D-printing) processes. Moreover, planar microwave sensors are compatible with many other technologies such as microfluidics, micromachining, textiles, etc., and can be equipped with functional films, that make these sensors of interest in applications as diverse as liquid sensing [3,4,5,6,7], bio-sensing [8,9], gas sensing [10,11,12,13,14,15,16], wearables [17,22], measurement of physical variables (such as temperature or ambient humidity [23,24,25]), etc. Nevertheless, the most canonical application of planar microwave sensors is the dielectric characterization of materials (permittivity measurements [7,26,27,28]). Microwave sensors are sensitive to the dielectric properties of the material surrounding the sensitive element (typically, a transmission line section or a planar resonator). Thus, the permittivity of such material, or any other variable related to it, can be retrieved. The sensor to be developed in this paper is based on the change in the permittivity of fabric (the fabric under test—FUT) caused by liquid absorption (sweat or urine in real environment). Such change will modify the electrical characteristics of the sensitive element (capacitance, characteristic impedance, electrical length, etc.), which in turn will generate a variation in the output variable of the sensor (resonance frequency, quality factor, group delay, phase and/or magnitude of the reflection or transmission coefficient, etc.).
Planar microwave sensors can be categorized according to the output variable as frequency-variation sensors [7,8,9,26,27,28,29,30,31,32,33,34,35], frequency-splitting sensors [4,22,36,37,38,39], magnitude variation sensors (or coupling modulation sensors [40,41,42,43,44,45,46,47,48,49,50,51]), and phase-variation sensors [52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69]. Nevertheless, in some cases, two combined output variables are used. For example, for the determination of the complex permittivity of materials, resonant sensors that exploit the resonance frequency variation (mainly correlated with the dielectric constant of the material under test) and the magnitude of the notch or peak in the frequency response (mainly correlated with the loss tangent), have been used [7,26,27,28]. Frequency-variation and frequency-splitting sensors are robust against electromagnetic interference (EMI) and noise (as corresponds to frequency measurements), but such sensors need wideband sweeping interrogation signals for sensing, covering the output dynamic range (an aspect that complicates the implementation of the associated electronics in real environment). The solution to this issue is given by the so-called single-frequency sensors, fed by a harmonic (single-tone) interrogation signal. Coupling-modulation and phase-variation sensors belong to this class of sensors. Phase-variation sensors, additionally, are robust against EMI and noise (similar to frequency-variation sensors) and result very attractive for sensing. Nevertheless, retrieving the phase of either the reflection or the transmission coefficient in operational environment (i.e., without the use of a vector network analyzer), in general, is not as simple as inferring the magnitude [70]. Magnitude measurements are more prone to the effects of EMI and noise, but the simplicity of the associated electronics is important in certain applications, in particular, the intended application in this work (the detection of liquid absorption in fabric). Note that a simple amplitude detector suffices to convert the magnitude of the transmission coefficient in a voltage variable (an easy measurable magnitude) [49,50,51]. Thus, in the present paper, we exploit the magnitude of the transmission coefficient at a single frequency for sensing, with an eye towards sensor simplicity.
The proposed sensing device is a resonant sensor, where the sensitive element is an open-ended quarter-wavelength stub resonator that must be in contact with the FUT. Such element is the load of a matched transmission line, and the output variable is the magnitude of the transmission coefficient at the operational frequency, the resonance frequency of the open-ended stub (given by the notch in the transmission coefficient) when it is loaded with the dry FUT. When the FUT absorbs liquid (urine or sweat in a real scenario), the frequency response shifts downwards (because the effective dielectric constant “seen” by the stub increases), and the magnitude of the transmission coefficient at the operational frequency varies. Thus, liquid absorption by the fabric can be detected with this method.
The work is organized as follows. Section 2 presents the proposed humidity sensor and the working principle in detail. The specific sensor design is the subject of Section 3, where validation at simulation level is included. Experimental validation is carried out in Section 4, by considering fabric, and different levels of water absorption. Finally, the main conclusions of the work are highlighted in Section 5.

2. The Proposed Sensor and Working Principle

The topology and perspective view of the proposed sensor is depicted in Figure 1. It consists of a transmission line loaded with an open-ended quarter-wavelength stub resonator, the sensitive element. The transmission line is matched to the reference impedance of the ports (Z0 = 50 Ω), namely, its characteristic impedance is Zc = Z0. The design variables are the length and width of the sensitive stub. The length determines the resonance frequency (notch frequency) of the sensor, whereas the width is related to the characteristic impedance of the stub, Zs. In turn, Zs is the key parameter that determines the quality factor of the stub resonator. An extreme (i.e., very high or very low) quality factor, should be avoided. The reason is that if the quality factor is very small, a soft variation in the magnitude of the transmission coefficient at the resonance of the stub loaded with the dry FUT (the reference FUT) is expected. By contrast, if the quality factor is very high, tuning to the resonance frequency of the stub when it is loaded with the dry FUT is not absent of certain difficulty. Thus, a tradeoff is necessary.
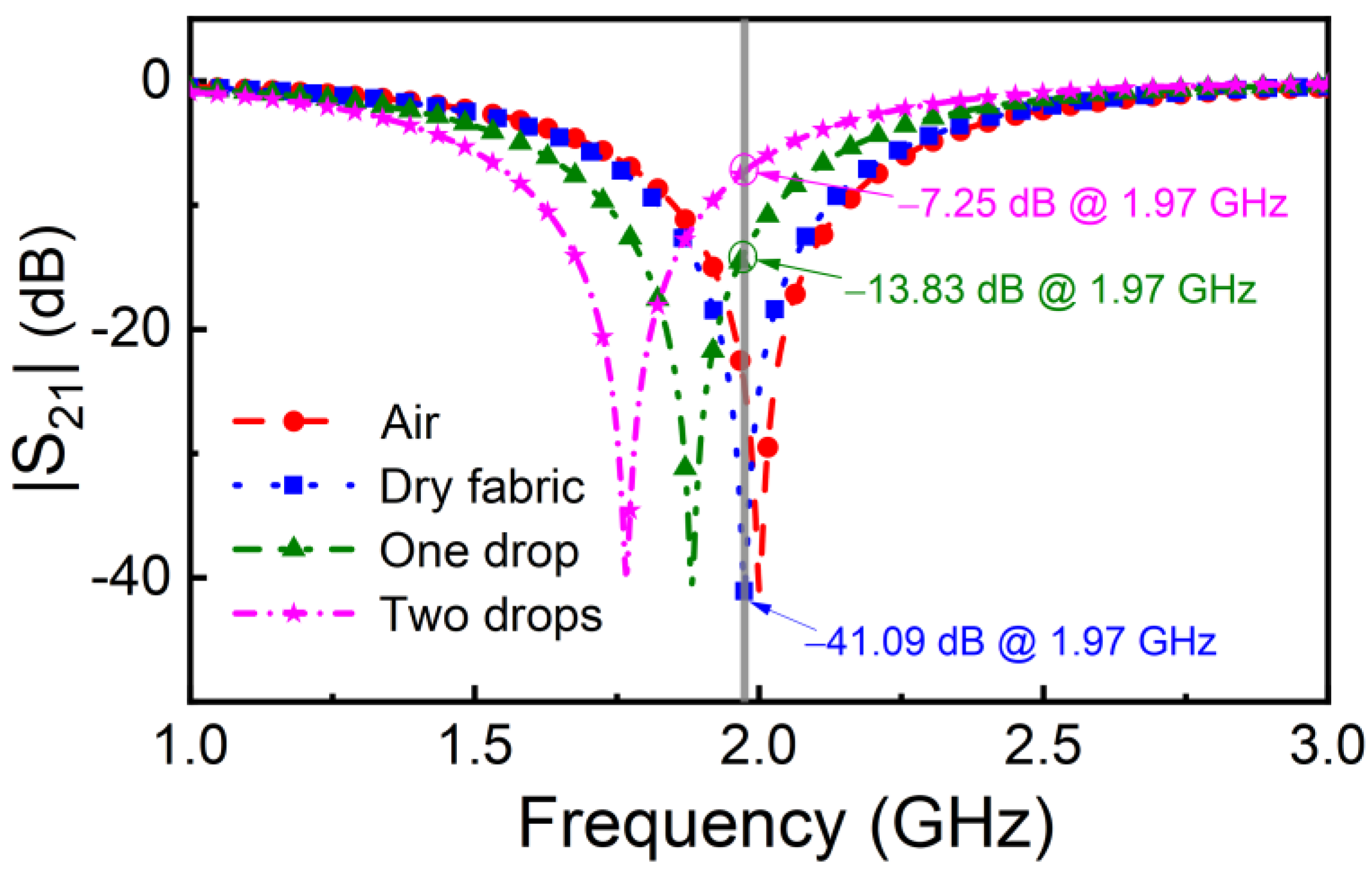
The working principle of the sensor is the shift in the frequency response (magnitude of the transmission coefficient) when the FUT absorbs a certain liquid. This modifies the dielectric constant of the FUT, and the resonance frequency of the stub shifts down (Figure 2). As consequence, the magnitude of the transmission coefficient at f0 (the resonance frequency of the sub loaded with the reference-dry-FUT), varies (increases), and liquid absorption is thereby detected. The output variable in the proposed sensor is thus the magnitude of the transmission coefficient at f0, whereas the input variable is the dielectric constant of the FUT, intimately related to the level of liquid absorption by the FUT.
Preprints 71822 g001
Figure 1. Topology (a) and perspective view (b) of the proposed sensor. The sensing region is indicated by the dashed rectangle. The ground plane in (a) is depicted in soft grey color.
Figure 1. Topology (a) and perspective view (b) of the proposed sensor. The sensing region is indicated by the dashed rectangle. The ground plane in (a) is depicted in soft grey color.
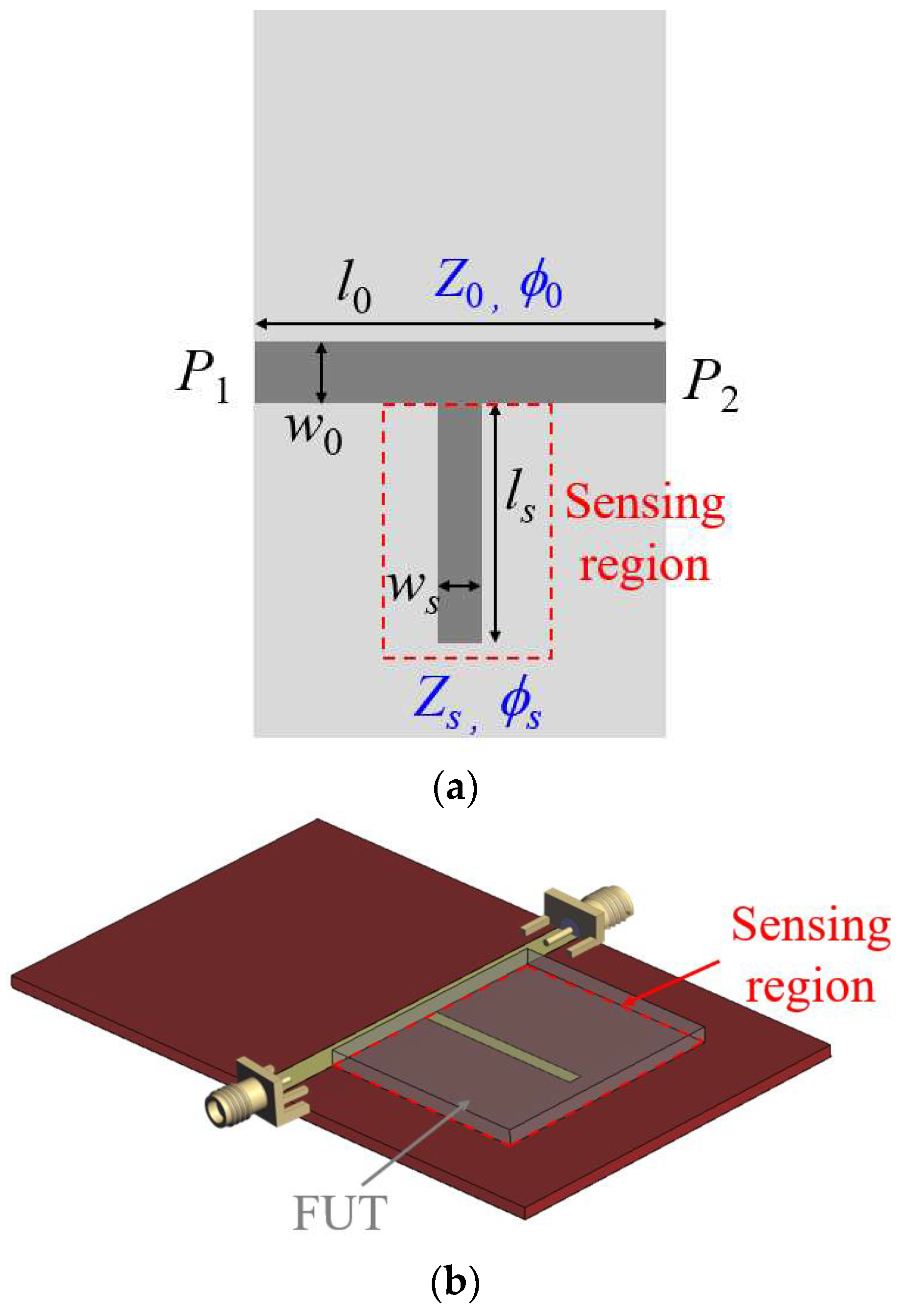
Preprints 71822 g001
Preprints 71822 g002
Figure 2. Simulated results from ANSYS HFSS simulator showing the working principle of the humidity sensor. Note that the dry fabric is set with thickness 0.3 mm and dielectric constant 1.5; and the one drop and two drops of liquid in the fabric are emulated by changing the dielectric constant to 4 and 9, respectively, just for indictive purpose. The open-ended stub has characteristic impedance of 70 Ω when it is empty (surrounded by air), and it resonates at 2 GHz.
Figure 2. Simulated results from ANSYS HFSS simulator showing the working principle of the humidity sensor. Note that the dry fabric is set with thickness 0.3 mm and dielectric constant 1.5; and the one drop and two drops of liquid in the fabric are emulated by changing the dielectric constant to 4 and 9, respectively, just for indictive purpose. The open-ended stub has characteristic impedance of 70 Ω when it is empty (surrounded by air), and it resonates at 2 GHz.
Preprints 71822 g002

3. Sensor Design

The proposed sensor is designed to exhibit a resonance frequency of 2GHz when the stub is in contact with air (bare sensor). The frequency of operation, f0, is expected to be slightly smaller since it should be tuned to the resonance frequency of the stub coated with the reference (dry) FUT. Nevertheless, the dielectric constant of fabric is expected to be very close to that of air, and hence f0 should not vary excessively from the resonance frequency of the bare sensor (2 GHz). The considered substrate for sensor implementation is the Rogers 4003C substrate with dielectric constant εr = 3.55, thickness h = 1.524 mm and loss factor tanδ = 0.0022. With the considered substrate, the width of the 50-Ω host line is W = 3.36 mm. For the stub, let us consider three different values of the characteristic impedance, Zs,1 = 25 Ω, Zs,2 = 50 Ω, and Zs,3 = 70 Ω. The corresponding widths, with the considered substrate, are Ws,1 = 9.04 mm, Ws,2 = 3.36 mm, and Ws,3 = 1.85 mm. We have adjusted the length of the open stub in all three cases, in order to generate a notch (bare sensor) at 2 GHz, as indicated. The lengths are not identical, since the effective dielectric constant of the stub depends on its width, but the values are very similar (ls,1 = 21.03 mm, ls,2 = 22.15 mm, and ls,3 = 22.45 mm). The responses of the bare sensors (magnitude of the reflection and transmission coefficient) for all three cases, inferred from full wave electromagnetic simulation using the ANSYS HFSS commercial software, are depicted in Figure 3. The length of the host line has been set to 50 mm in all cases, but this length does not affect the magnitude of the reflection and transmission coefficient, since the impedance of that line coincides with the reference impedance of the ports. The stop band bandwidth, or quality factor of the stub, varies with its characteristic impedance. According to the previously mentioned tradeoff, we consider that the stub with impedance Zs,3 = 70 Ω (and width Ws,3 = 1.85 mm) is appropriate for our purposes since it exhibits a moderate quality factor. Therefore, the sensor will be implemented by considering such stub impedance and width.
Before experimental validation (left for the next section), let us anticipate the behavior of the sensor by electromagnetic simulation. For that purpose, let us consider that the sensing region is coated with a hypothetical material, with varying dielectric constant, that emulates the FUT with different levels of liquid absorption. The considered thickness of that material is 0.3 mm since this thickness can be comparable to the one of fabric, such as underwear or clothes made of cotton. We have varied the dielectric constant of the FUT between εFUT = 1 (the value of air and expected to be very close to the dielectric constant of dry fabric) and εFUT = 21 (a relatively high value, as expected in situations where significant liquid absorption by the fabric occurs). Note that this maximum value of εFUT is somehow arbitrary, since the actual value (in a real environment) is expected to depend on the specific liquid (sweat, urine, etc.). Nevertheless, it is a representative value providing a reasonable input dynamic range, useful to qualitatively predict the behavior of the sensor. We have carried out the simulations parametrized by the loss tangent of the FUT (by considering values of 0.001, 0.01 and 0.1). The simulated frequency responses are depicted in Figure 4, whereas Figure 5 depicts the dependence of the magnitude of the transmission coefficient at f0 (2GHz) with the dielectric constant of the FUT, for the different considered values of the loss tangent. According to Figure 5, the transmission coefficient at f0 varies significantly with εFUT for the three considered values of the loss tangent of the FUT. Nevertheless, the variation (and hence the sensitivity) is more pronounced for small values of the loss tangent. Note also that the sensitivity for small values of εFUT degrades as the loss tangent of the FUT increases. However, for moderate and high values of εFUT, the sensitivity does not depend on the loss tangent of the FUT. These simulation results reveal that the intended sensor can work to detect the presence of liquid absorption in fabric, an aspect to be discussed in the next section, where the sensor is experimentally validated.

4. Experimental Validation

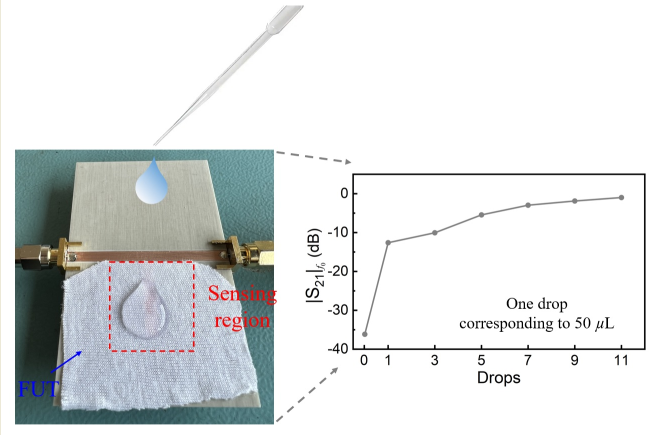
For experimental validation, we have fabricated the sensor with dimensions and substrate corresponding to the simulations of Figs. 4 and 5. The sensor was fabricated by means of the LPKF H100 drilling machine, available in our laboratory (the photograph is depicted in Figure 6). The measured frequency response of the bare sensor and the one of the sensor loaded with the reference (dry) FUT, depicted in Figure 7, and inferred by means of the Keysight N5221A vector network analyzer, reveal that the dielectric constant of the dry FUT is very similar to the one of air, as anticipated (note that the responses are very similar). Indeed, the notch frequency of the sensor loaded with the dry FUT is slightly inferior to the one of the bare sensor, and it is the considered operating frequency of the sensor, f0 = 2 GHz. The FUT is a piece of cotton underwear, which has been cut in a rectangular shape to accommodate it to the dimensions of the sensing region.
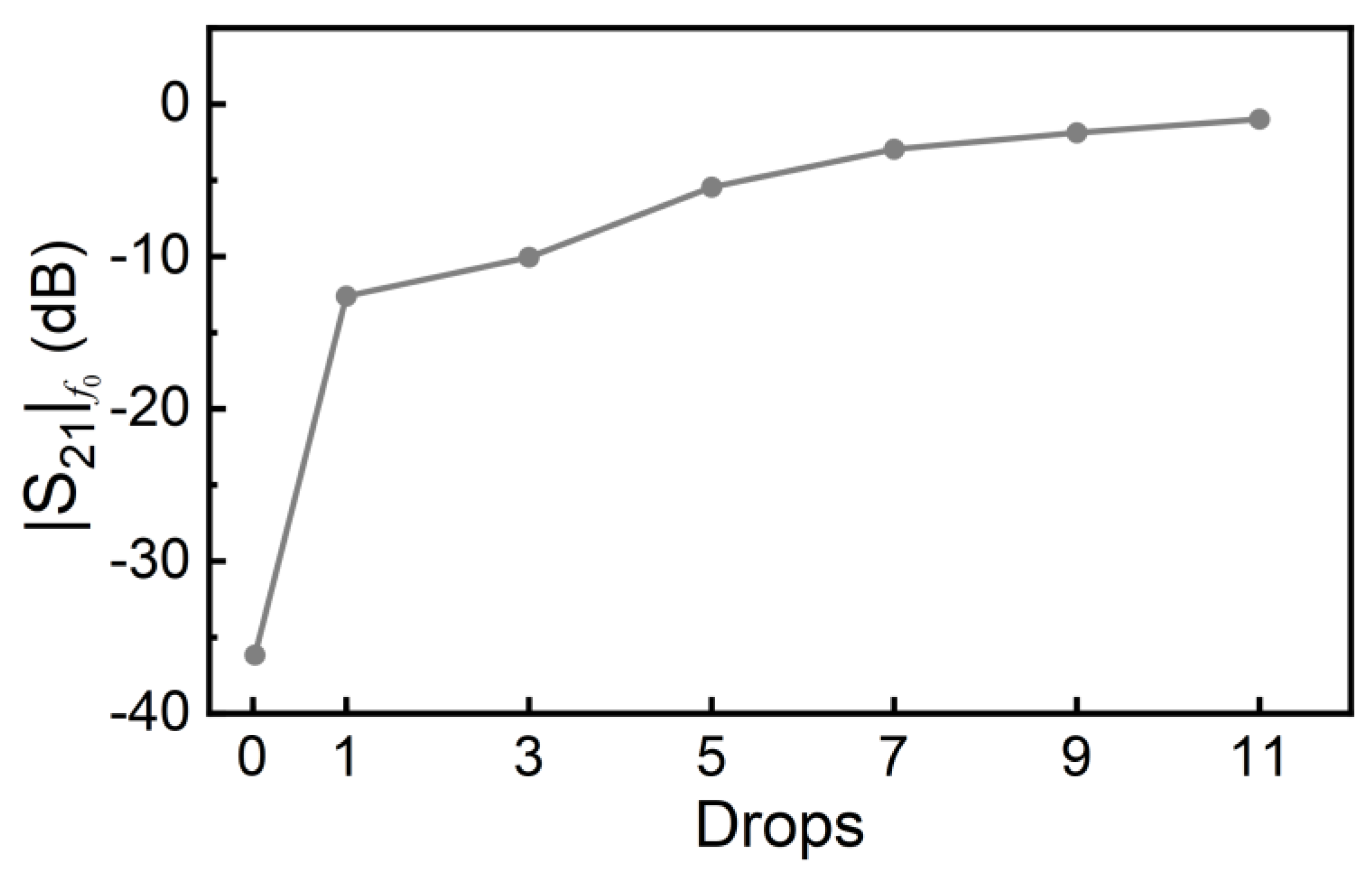
Next, we have emulated sweat or urine absorption by the fabric by dropping DI water with a pipette on top of it. Specifically, we have sequentially added a water drop on top of the fabric and made the measurement of the frequency response after each drip. The results, also included in Figure 7, reveal that, as the number of accumulated drops in the fabric increase, the frequency response progressively shifts down. The result is an increase of the magnitude of the transmission frequency at f0, S 21 f 0 . The variation of S 21 f 0 with the accumulated number of drops is depicted in Figure 8. (It follows a similar trend to that of Figure 5). According to the results of Figure 8, the presence of water in the fabric can be detected, and therefore the sensor is experimentally validated.
Preprints 71822 g007
Figure 7. Frequency responses of the bare sensor, sensor loaded with the reference (dry) FUT, and sensor loaded with the FUT with water absorbed (indicated with the number of drops). Note that the volume of water of one drop from the pipette is 50 μL.
Figure 7. Frequency responses of the bare sensor, sensor loaded with the reference (dry) FUT, and sensor loaded with the FUT with water absorbed (indicated with the number of drops). Note that the volume of water of one drop from the pipette is 50 μL.
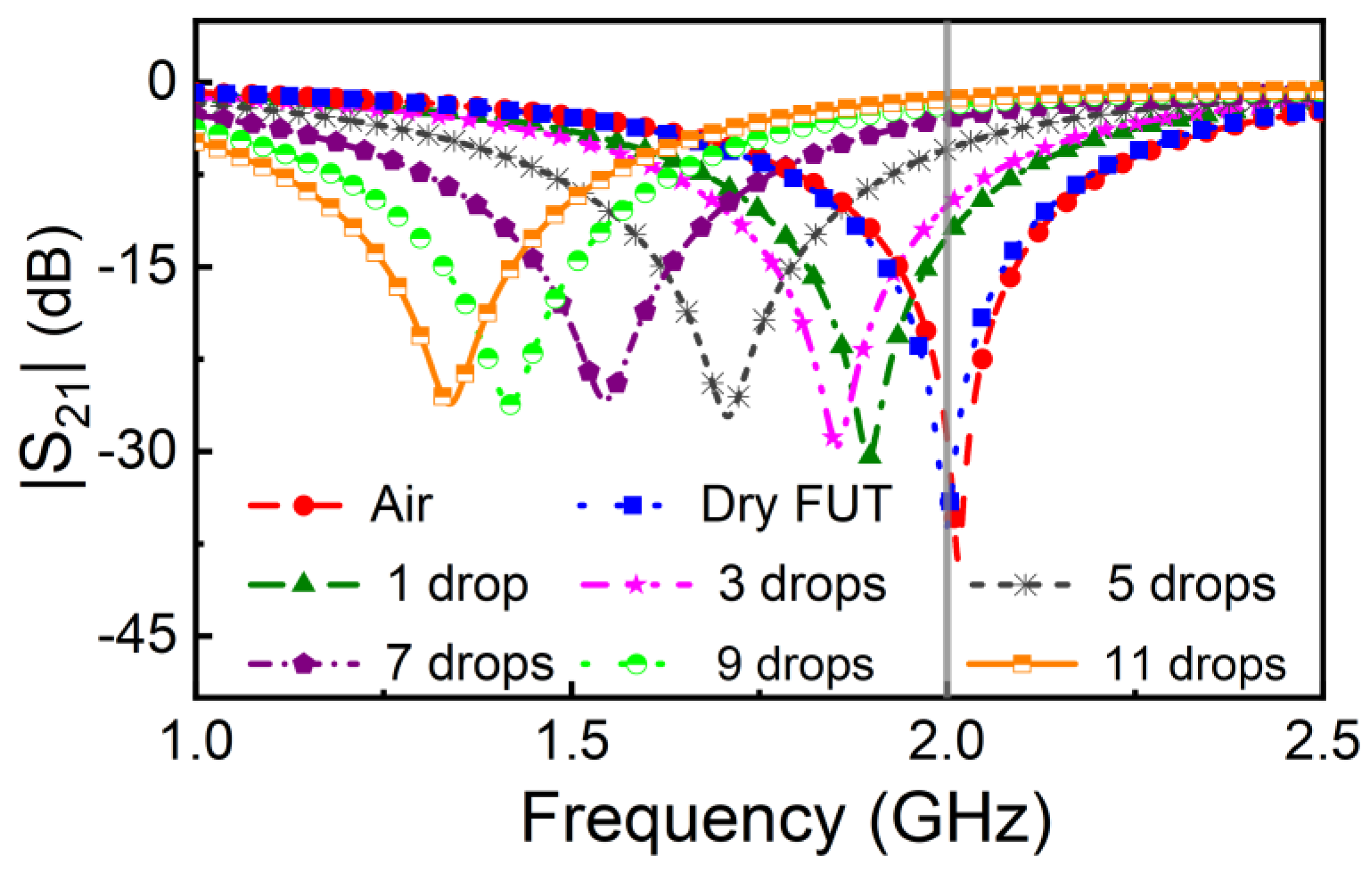
Preprints 71822 g007
Preprints 71822 g008
Figure 8. Dependence of the magnitude of the transmission coefficient at f0 with the number of cumulative water drops deposited on the FUT.
Figure 8. Dependence of the magnitude of the transmission coefficient at f0 with the number of cumulative water drops deposited on the FUT.
Preprints 71822 g008

5. Conclusions

In conclusion, it has been experimentally demonstrated that humidity in fabric (particularly, cotton of underwear clothes) can be detected by means of a simple planar microwave sensor consisting in a microstrip line loaded with an open-ended quarter-wavelength resonant stub, the sensitive element. For simplicity, it has been considered that the output variable is the magnitude of the transmission coefficient measured at a specific frequency, i.e., the resonance frequency of the stub when it is coated with the dry fabric. Thus, the sensor works at a single frequency, an important aspect for operation in real environment, where vector network analyzers used at laboratory level should be replaced with signal generators and detectors (in the considered structure, a narrow band voltage-controlled oscillator and an amplitude detector would suffice). According to the obtained experimental results, a single drop (with estimated volume of 50 μL) generates a magnitude variation in the transmission coefficient of the sensor at the operating frequency of roughly 25 dB, more than enough to detect the presence of small amounts of water in fabric. Thus, with these results, it can be envisaged that the reported sensor can be applied to the detection of sweet in fabric or urine leakage in underwear. In next future, the focus will be the direct implementation of the sensor in a fabric substrate, more compatible with the intended application.

Author Contributions

Conceptualization, Ferran Martín; Funding acquisition, Ferran Martín; Methodology, Lijuan Su and Paris Vélez; Project administration, Ferran Martín; Software, Lijuan Su and Paris Vélez; Supervision, Ferran Martín; Validation, Lijuan Su, Paris Vélez, Pau Casacuberta and Jonathan Muñoz-Enano; Writing—original draft, Lijuan Su and Ferran Martín; Writing—review & editing, Lijuan Su, Paris Vélez, Pau Casacuberta, Jonathan Muñoz-Enano and Ferran Martín.

Funding

This work was supported by MCIN/AEI 10.13039/501100011033, Spain, through projects PID2019-103904RB-I00 (ERDF European Union) and PDC2021-121085-I00 (European Union Next Generation EU/PRTR), by Generalitat de Catalunya through project 2021SGR-00192, and by ICREA. P. Casacuberta acknowledges the Ministerio de Universidades, Spain, for the FPU grant (Ayudas para la formación de profesorado universitario), ref. FPU20/05700. L. Su acknowledges the Juan de la Cierva Program for the support through the project IJC2019-040786-I.

Data Availability Statement

The article contains the necessary data to verify the results (circuit dimensions and substrate used, as well as setup conditions). Text-based files containing the S-parameter data obtained in simulations and measurement can be requested to the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Martín, F.; Vélez, P.; Muñoz-Enano, J.; Su, L. Planar Microwave Sensors; Wiley/IEEE Press: Hoboken, NJ, USA, 2022. [Google Scholar]
  2. Abdolrazzaghi, M.; Nayyeri, V.; Martín, F. Techniques to Improve the Performance of Planar Microwave Sensors: A Review and Recent Developments. Sensors 2022, 22, 6946. [Google Scholar] [CrossRef]
  3. Grenier, K.; Dubuc, D.; Poleni, P.E.; Kumemura, M.; Toshiyoshi, H.; Fujii, T.; Fujita, H. New Broadband and Contact Less RF/Microfluidic Sensor Dedicated to Bioengineering. In Proceedings of the 2009 IEEE MTT-S International Microwave Symposium Digest, Boston, MA, USA, 7–12 June 2009; pp. 1329–1332. [Google Scholar]
  4. Vélez, P.; Su, L.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martín, F. Microwave Microfluidic Sensor Based on a Microstrip Splitter/Combiner Configuration and Split Ring Resonators (SRRs) for Dielectric Characterization of Liquids. IEEE Sens. J. 2017, 17, 6589–6598. [Google Scholar] [CrossRef]
  5. Ebrahimi, A.; Scott, J.; Ghorbani, K. Ultrahigh-Sensitivity Microwave Sensor for Microfluidic Complex Permittivity Measurement. IEEE Trans. Microw. Theory Techn. 2019, 67, 4269–4277. [Google Scholar] [CrossRef]
  6. Chuma, E.L.; Iano, Y.; Fontgalland, G.; Roger, L.L.B. Microwave Sensor for Liquid Dielectric Characterization Based on Metamaterial Complementary Split Ring Resonator. IEEE Sens. J. 2018, 18, 9978–9983. [Google Scholar] [CrossRef]
  7. Su, L.; Mata-Contreras, J.; Vélez, P.; Fernández-Prieto, A.; Martín, F. Analytical Method to Estimate the Complex Permittivity of Oil Samples. Sensors 2018, 18, 984. [Google Scholar] [CrossRef]
  8. Puentes, M.; Maasch, M.; Schubler, M.; Jakoby, R. Frequency Multiplexed 2-Dimensional Sensor Array Based on Split-Ring Resonators for Organic Tissue Analysis. IEEE Trans. Microw. Theory Techn. 2012, 60, 1720–1727. [Google Scholar] [CrossRef]
  9. Puentes, M.; Maasch, M.; Schüssler, M.; Damm, C.; Jakoby, R. Analysis of Resonant Particles in a Coplanar Microwave Sensor Array for Thermal Ablation of Organic Tissue. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014. [Google Scholar]
  10. Yang, L.; Zhang, R.; Staiculescu, D.; Wong, C.P.; Tentzeris, M.M. A Novel Conformal RFID-Enabled Module Utilizing Inkjet-Printed Antennas and Carbon Nanotubes for Gas-Detection Applications. IEEE Ant. Wirel. Propag. Lett. 2009, 8, 653–656. [Google Scholar] [CrossRef]
  11. Yang, L.; Staiculescu, D.; Zhang, R.; Wong, C.P.; Tentzeris, M.M. A Novel “Green” Fully-Integrated Ultrasensitive RFID-Enabled Gas Sensor Utilizing Inkjet-Printed Antennas and Carbon Nanotubes. In Proceedings of the 2009 IEEE Antennas and Propagation Society International Symposium, North Charleston, SC, USA, 1–5 June 2009. [Google Scholar]
  12. Occhiuzzi, C.; Rida, A.; Marrocco, G.; Tentzeris, M.M. Passive Ammonia Sensor: RFID Tag Integrating Carbon Nanotubes. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation (APSURSI), Spokane, WA, USA, 3–8 July 2011; pp. 1413–1416. [Google Scholar]
  13. Occhiuzzi, C.; Rida, A.; Marrocco, G.; Tentzeris, M.M. CNT-Based RFID Passive Gas Sensor. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011. [Google Scholar]
  14. Occhiuzzi, C.; Rida, A.; Marrocco, G.; Tentzeris, M. RFID Passive Gas Sensor Integrating Carbon Nanotubes. IEEE Trans. Microw. Theory Techn. 2011, 59, 2674–2684. [Google Scholar] [CrossRef]
  15. Baccarelli, R.; Orecchini, G.; Alimenti, F.; Roselli, L. Feasibility Study of a Fully Organic, CNT Based, Harmonic RFID Gas Sensor. In Proceedings of the 2012 IEEE International Conference on RFID-Technologies and Applications (RFID-TA), Nice, France, 5–7 November 2012; pp. 419–422. [Google Scholar]
  16. Vena, A.; Sydänheimo, L.; Tentzeris, M.M.; Ukkonen, L. A Novel Inkjet Printed Carbon Nanotube-Based Chipless RFID Sensor for Gas Detection. In Proceedings of the 2013 European Microwave Conference, Nuremberg, Germany, 6–10 October 2013; pp. 9–12. [Google Scholar]
  17. Yilmaz, T.; Foster, R.; Hao, Y. Detecting Vital Signs with Wearable Wireless Sensors. Sensors 2010, 10, 10837–10862. [Google Scholar] [CrossRef] [PubMed]
  18. Elgeziry, M.; Costa, F.; Tognetti, A.; Genovesi, S. Wearable Textile-Based Sensor Tag for Breath Rate Measurement. IEEE Sens. J. 2022, 22, 22610–22619. [Google Scholar] [CrossRef]
  19. Elsheikh, D.; Eldamak, A.R. Microwave Textile Sensors for Breast Cancer Detection. In Proceedings of the 2021 38th National Radio Science Conference (NRSC), Mansoura, Egypt, 27–29 July 2021; pp. 288–294. [Google Scholar]
  20. Martínez-Estrada, M.; Gil, I.; Fernández-García, R. An Alternative Method to Develop Embroidery Textile Strain Sensors. Textiles 2021, 1, 504–512. [Google Scholar] [CrossRef]
  21. Nejad, H.R.; Punjiya, M.P.; Sonkusale, S. Washable Thread Based Strain Sensor for Smart Textile. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 1183–1186. [Google Scholar]
  22. Vélez, P.; Martín, F.; Fernández-García, R.; Gil, I. Embroidered Textile Frequency-Splitting Sensor Based on Stepped-Impedance Resonators. IEEE Sens. J. 2022, 22, 8596–8603. [Google Scholar] [CrossRef]
  23. Amin, E.M.; Bhuiyan, M.S.; Karmakar, N.C.; Winther-Jensen, B. Development of a Low Cost Printable Chipless RFID Humidity Sensor. IEEE Sens. J. 2014, 14, 140–149. [Google Scholar] [CrossRef]
  24. Abdulkawi, W.M.; Sheta, A.F.A. Chipless RFID Sensors Based on Multistate Coupled Line Resonators. Sens. Act. A Phys. 2020, 309, 112025. [Google Scholar] [CrossRef]
  25. Yeo, J.; Lee, J.I.; Kwon, Y. Humidity-Sensing Chipless RFID Tag with Enhanced Sensitivity Using an Interdigital Capacitor Structure. Sensors 2021, 21, 6550. [Google Scholar] [CrossRef]
  26. Boybay, M.S.; Ramahi, O.M. Material Characterization Using Complementary Split-Ring Resonators. IEEE Trans. Instrum. Meas. 2012, 61, 3039–3046. [Google Scholar] [CrossRef]
  27. Lee, C.S.; Yang, C.L. Complementary Split-Ring Resonators for Measuring Dielectric Constants and Loss Tangents. IEEE Microw. Wireless Compon. Lett. 2014, 24, 563–565. [Google Scholar] [CrossRef]
  28. Yang, C.L.; Lee, C.S.; Chen, K.W.; Chen, K.Z. Noncontact Measurement of Complex Permittivity and Thickness by Using Planar Resonators. IEEE Trans. Microw. Theory Techn. 2016, 64, 247–257. [Google Scholar] [CrossRef]
  29. Puentes, M.; Weiß, C.; Schüßler, M.; Jakoby, R. Sensor Array Based on Split Ring Resonators for Analysis of Organic Tissues. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011. [Google Scholar]
  30. Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Abbott, D. High-Sensitivity Metamaterial-Inspired Sensor for Microfluidic Dielectric Characterization. IEEE Sens. J. 2014, 14, 1345–1351. [Google Scholar] [CrossRef]
  31. Schueler, M.; Mandel, C.; Puentes, M.; Jakoby, R. Metamaterial Inspired Microwave Sensors. IEEE Microw. Mag. 2012, 13, 57–68. [Google Scholar] [CrossRef]
  32. Su, L.; Mata-Contreras, J.; Vélez, P.; Martín, F. Estimation of the Complex Permittivity of Liquids by means of Complementary Split Ring Resonator (CSRR) Loaded Transmission Lines. In Proceedings of the 2017 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Pavia, Italy, 20–22 September 2017. [Google Scholar]
  33. Jha, A.K.; Delmonte, N.; Lamecki, A.; Mrozowski, M.; Bozzi, M. Design of Microwave-Based Angular Displacement Sensor. IEEE Microw. Wireless Compon. Lett. 2019, 29, 306–308. [Google Scholar] [CrossRef]
  34. Saadat-Safa, M.; Nayyeri, V.; Khanjarian, M.; Soleimani, M.; Ramahi, O.M. A CSRR-Based Sensor for Full Characterization of Magneto-Dielectric Materials. IEEE Trans. Microw. Theory Techn. 2019, 67, 806–814. [Google Scholar] [CrossRef]
  35. Muñoz-Enano, J.; Vélez, P.; Gil, M.; Martín, F. Frequency-Variation Sensors for Permittivity Measurements Based on Dumbbell-Shaped Defect Ground Structures (DB-DGS): Analytical Method and Sensitivity Analysis. IEEE Sens. J. 2022, 22, 9378–9386. [Google Scholar] [CrossRef]
  36. Naqui, J.; Damm, C.; Wiens, A.; Jakoby, R.; Su, L.; Mata-Contreras, J.; Martín, F. Transmission Lines Loaded with Pairs of Stepped Impedance Resonators: Modeling and Application to Differential Permittivity Measurements. IEEE Trans. Microw. Theory Techn. 2016, 64, 3864–3877. [Google Scholar] [CrossRef]
  37. Su, L.; Mata-Contreras, J.; Velez, P.; Martin, F. Splitter/Combiner Microstrip Sections Loaded with Pairs of Complementary Split Ring Resonators (CSRRs): Modeling and Optimization for Differential Sensing Applications. IEEE Trans. Microw. Theory Techn. 2016, 64, 4362–4370. [Google Scholar] [CrossRef]
  38. Ebrahimi, A.; Scott, J.; Ghorbani, K. Differential Sensors Using Microstrip Lines Loaded with Two Split-Ring Resonators. IEEE Sens. J. 2018, 18, 5786–5793. [Google Scholar] [CrossRef]
  39. Ebrahimi, A.; Beziuk, G.; Scott, J.; Ghorbani, K. Microwave Differential Frequency Splitting Sensor Using Magnetic-LC Resonators. Sensors 2020, 20, 1066. [Google Scholar] [CrossRef] [PubMed]
  40. Naqui, J.; Durán-Sindreu, M.; Martín, F. Novel Sensors Based on the Symmetry Properties of Split Ring Resonators (SRRs). Sensors 2011, 11, 7545–7553. [Google Scholar] [CrossRef]
  41. Naqui, J.; Durán-Sindreu, M.; Martín, F. Alignment and Position Sensors Based on Split Ring Resonators. Sensors 2012, 12, 11790–11797. [Google Scholar] [CrossRef]
  42. Horestani, A.K.; Fumeaux, C.; Al-Sarawi, S.F.; Abbott, D. Displacement Sensor Based on Diamond-Shaped Tapered Split Ring Resonator. IEEE Sens. J. 2013, 13, 1153–1160. [Google Scholar] [CrossRef]
  43. Horestani, A.K.; Abbott, D.; Fumeaux, C. Rotation Sensor Based on Horn-Shaped Split Ring Resonator. IEEE Sens. J. 2013, 13, 3014–3015. [Google Scholar] [CrossRef]
  44. Naqui, J.; Martín, F. Transmission Lines Loaded with Bisymmetric Resonators and their Application to Angular Displacement and Velocity Sensors. IEEE Trans. Microw. Theory Techn. 2013, 61, 4700–4713. [Google Scholar] [CrossRef]
  45. Naqui, J.; Martín, F. Angular Displacement and Velocity Sensors Based on Electric-LC (ELC) Loaded Microstrip Lines. IEEE Sens. J. 2014, 14, 939–940. [Google Scholar] [CrossRef]
  46. Horestani, A.K.; Naqui, J.; Abbott, D.; Fumeaux, C.; Martín, F. Two-Dimensional Displacement and Alignment Sensor Based on Reflection Coefficients of Open Microstrip Lines Loaded with Split Ring Resonators. Elec. Lett. 2014, 50, 620–622. [Google Scholar] [CrossRef]
  47. Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.F.; Abbott, D. Metamaterial-Inspired Rotation Sensor with Wide Dynamic Range. IEEE Sens. J. 2014, 14, 2609–2614. [Google Scholar] [CrossRef]
  48. Naqui, J.; Coromina, J.; Karami-Horestani, A.; Fumeaux, C.; Martín, F. Angular Displacement and Velocity Sensors Based on Coplanar Waveguides (CPWs) Loaded with S-Shaped Split Ring Resonators (S-SRR). Sensors 2015, 15, 9628–9650. [Google Scholar] [CrossRef]
  49. Mata-Contreras, J.; Herrojo, C.; Martin, F. Application of Split Ring Resonator (SRR) Loaded Transmission Lines to the Design of Angular Displacement and Velocity Sensors for Space Applications. IEEE Trans. Microw. Theory Techn. 2017, 65, 4450–4460. [Google Scholar] [CrossRef]
  50. Mata-Contreras, J.; Herrojo, C.; Martin, F. Detecting the Rotation Direction in Contactless Angular Velocity Sensors Implemented with Rotors Loaded with Multiple Chains of Resonators. IEEE Sens. J. 2018, 18, 7055–7065. [Google Scholar] [CrossRef]
  51. Velez, P.; Munoz-Enano, J.; Ebrahimi, A.; Herrojo, C.; Paredes, F.; Scott, J.; Ghorbani, K.; Martin, F. Single-Frequency Amplitude-Modulation Sensor for Dielectric Characterization of Solids and Microfluidics. IEEE Sens. J. 2021, 21, 12189–12201. [Google Scholar] [CrossRef]
  52. Muñoz-Enano, J.; Vélez, P.; Su, L.; Gil, M.; Casacuberta, P.; Martín, F. On the Sensitivity of Reflective-Mode Phase-Variation Sensors Based on Open-Ended Stepped-Impedance Transmission Lines: Theoretical Analysis and Experimental Validation. IEEE Trans. Microw. Theory Techn. 2021, 69, 308–324. [Google Scholar] [CrossRef]
  53. Damm, C.; Schüßler, M.; Puentes, M.; Maune, H.; Maasch, M.; Jakoby, R. Artificial Transmission Lines for High Sensitive Microwave Sensors. In Proceedings of the 2009 IEEE Sensors, Christchurch, New Zealand, 25–28 October 2009; pp. 755–758. [Google Scholar]
  54. Ferrández-Pastor, F.J.; García-Chamizo, J.M.; Nieto-Hidalgo, M. Electromagnetic Differential Measuring Method: Application in Microstrip Sensors Developing. Sensors 2017, 17, 1650. [Google Scholar] [CrossRef]
  55. Munoz-Enano, J.; Velez, P.; Barba, M.G.; Martin, F. An Analytical Method to Implement High-Sensitivity Transmission Line Differential Sensors for Dielectric Constant Measurements. IEEE Sens. J. 2020, 20, 178–184. [Google Scholar] [CrossRef]
  56. Gil, M.; Velez, P.; Aznar-Ballesta, F.; Munoz-Enano, J.; Martin, F. Differential Sensor Based on Electroinductive Wave Transmission Lines for Dielectric Constant Measurements and Defect Detection. IEEE Trans. Ant. Propag. 2020, 68, 1876–1886. [Google Scholar] [CrossRef]
  57. Munoz-Enano, J.; Velez, P.; Barba, M.G.; Mata-Contreras, J.; Martín, F. Differential-Mode to Common-Mode Conversion Detector Based on Rat-Race Hybrid Couplers: Analysis and Application to Differential Sensors and Comparators. IEEE Trans. Microw. Theory Techn. 2020, 68, 1312–1325. [Google Scholar] [CrossRef]
  58. Coromina, J.; Muñoz-Enano, J.; Vélez, P.; Ebrahimi, A.; Scott, J.; Ghorbani, K.; Martín, F. Capacitively-Loaded Slow-Wave Transmission Lines for Sensitivity Improvement in Phase-Variation Permittivity Sensors. In Proceedings of the 2020 50th European Microwave Conference (EuMC), Utrecht, Netherlandsd, 12–14 January 2021; pp. 491–494. [Google Scholar]
  59. Ebrahimi, A.; Coromina, J.; Munoz-Enano, J.; Velez, P.; Scott, J.; Ghorbani, K.; Martin, F. Highly Sensitive Phase-Variation Dielectric Constant Sensor Based on a Capacitively-Loaded Slow-Wave Transmission Line. IEEE Trans. Circ. Syst. I Reg. Papers 2021, 68, 2787–2799. [Google Scholar] [CrossRef]
  60. Su, L.; Munoz-Enano, J.; Velez, P.; Casacuberta, P.; Gil, M.; Martin, F. Phase-Variation Microwave Sensor for Permittivity Measurements Based on a High-Impedance Half-Wavelength Transmission Line. IEEE Sens. J. 2021, 21, 10647–10656. [Google Scholar] [CrossRef]
  61. Jha, A.K.; Lamecki, A.; Mrozowski, M.; Bozzi, M. A Highly Sensitive Planar Microwave Sensor for Detecting Direction and Angle of Rotation. IEEE Trans. Microw. Theory Techn. 2020, 68, 1598–1609. [Google Scholar] [CrossRef]
  62. Su, L.; Munoz-Enano, J.; Velez, P.; Casacuberta, P.; Gil, M.; Martin, F. Highly Sensitive Phase Variation Sensors Based on Step-Impedance Coplanar Waveguide (CPW) Transmission Lines. IEEE Sens. J. 2021, 21, 2864–2872. [Google Scholar] [CrossRef]
  63. Casacuberta, P.; Muñoz-Enano, J.; Vélez, P.; Su, L.; Gil, M.; Martín, F. Highly Sensitive Reflective-Mode Defect Detectors and Dielectric Constant Sensors Based on Open-Ended Stepped-Impedance Transmission Lines. Sensors 2020, 20, 6236. [Google Scholar] [CrossRef]
  64. Su, L.; Muñoz-Enano, J.; Vélez, P.; Gil-Barba, M.; Casacuberta, P.; Martin, F. Highly Sensitive Reflective-Mode Phase-Variation Permittivity Sensor Based on a Coplanar Waveguide Terminated with an Open Complementary Split Ring Resonator (OCSRR). IEEE Access 2021, 9, 27928–27944. [Google Scholar] [CrossRef]
  65. Casacuberta, P.; Vélez, P.; Muñoz-Enano, J.; Su, L.; Barba, M.G.; Ebrahimi, A.; Martín, F. Circuit Analysis of a Coplanar Waveguide (CPW) Terminated with a Step-Impedance Resonator (SIR) for Highly Sensitive One-Port Permittivity Sensing. IEEE Access 2022, 10, 62597–62612. [Google Scholar] [CrossRef]
  66. Horestani, A.K.; Shaterian, Z.; Martin, F. Rotation Sensor Based on the Cross-Polarized Excitation of Split Ring Resonators (SRRs). IEEE Sens. J. 2020, 20, 9706–9714. [Google Scholar] [CrossRef]
  67. Munoz-Enano, J.; Velez, P.; Su, L.; Gil-Barba, M.; Martín, F. A Reflective-Mode Phase-Variation Displacement Sensor. IEEE Access 2020, 8, 189565–189575. [Google Scholar] [CrossRef]
  68. Casacuberta, P.; Vélez, P.; Muñoz-Enano, J.; Su, L.; Martín, F. Highly Sensitive Reflective-Mode Phase-Variation Permittivity Sensors Using Coupled Line Sections. IEEE Trans. Microw. Theory Techn. 2023. accepted. [Google Scholar] [CrossRef]
  69. Casacuberta, P.; Vélez, P.; Muñoz-Enano, J.; Su, L.; Gil, M.; Martín, F. Reflective-Mode Phase-Variation Permittivity Sensors Based on Coupled Resonators. In Proceedings of the 2022 IEEE Sensors, Dallas, TX, USA, 30 October 2022–2 November 2022. [Google Scholar]
  70. Vélez, P.; Paredes, F.; Casacuberta, P.; Elgeziry, M.; Su, L.; Muñoz-Enano, J.; Costa, F.; Genovesi, S.; Martín, F. Portable Reflective-Mode Phase-Variation Microwave Sensor Based on a Rat-Race Coupler Pair and Gain/Phase Detector for Dielectric Characterization. IEEE Sens. J. 2023, 23, 5745–5756. [Google Scholar] [CrossRef]
Preprints 71822 g003
Figure 3. Simulated frequency response of the bare sensor for different stub impedances (and widths).
Figure 3. Simulated frequency response of the bare sensor for different stub impedances (and widths).
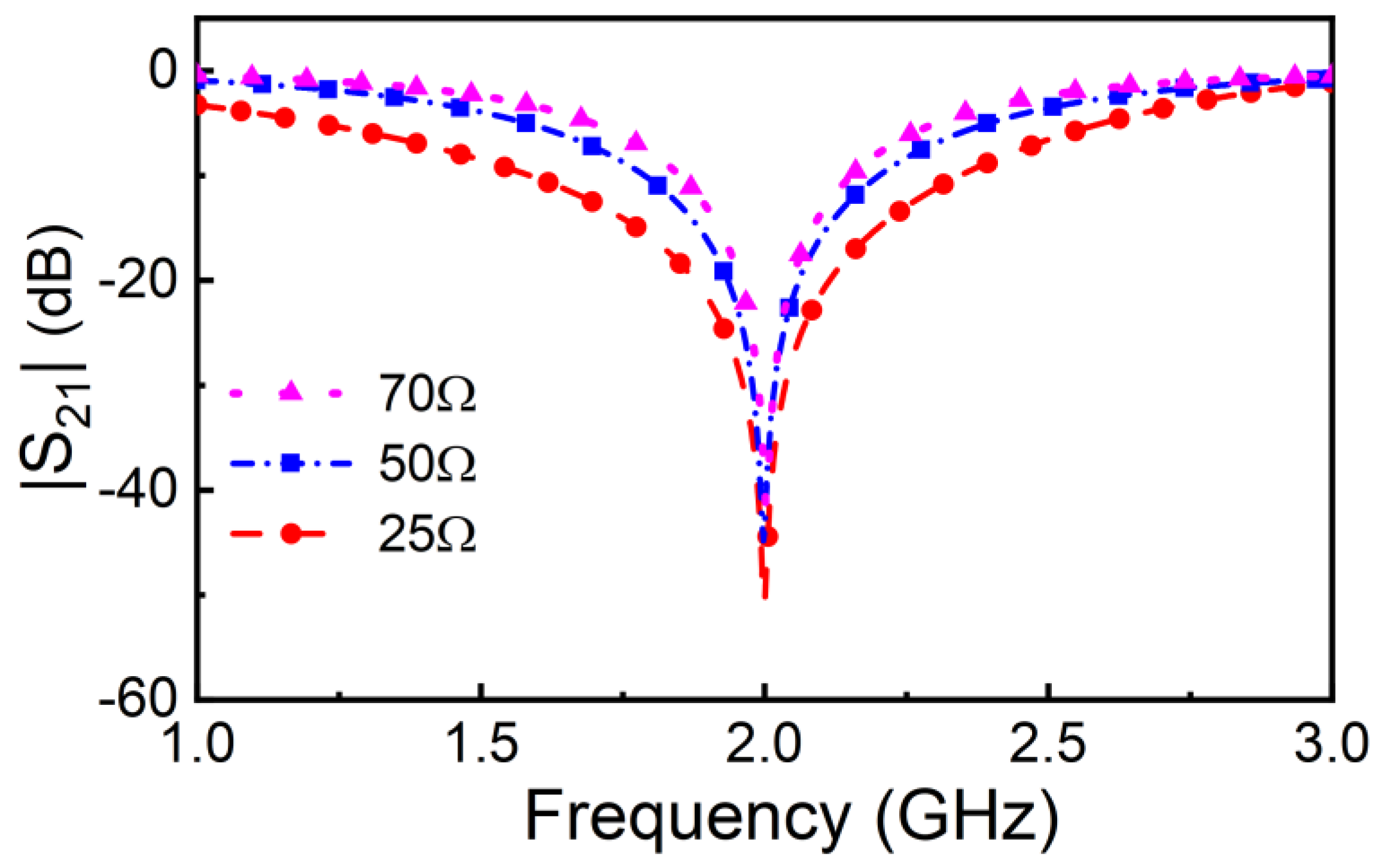
Preprints 71822 g003
Preprints 71822 g004
Figure 4. Simulated frequency responses of the sensor for different values of the dielectric constant of the FUT, and loss tangent of the FUT set to 0.001 (a), 0.01 (b) and 0.1 (c).
Figure 4. Simulated frequency responses of the sensor for different values of the dielectric constant of the FUT, and loss tangent of the FUT set to 0.001 (a), 0.01 (b) and 0.1 (c).
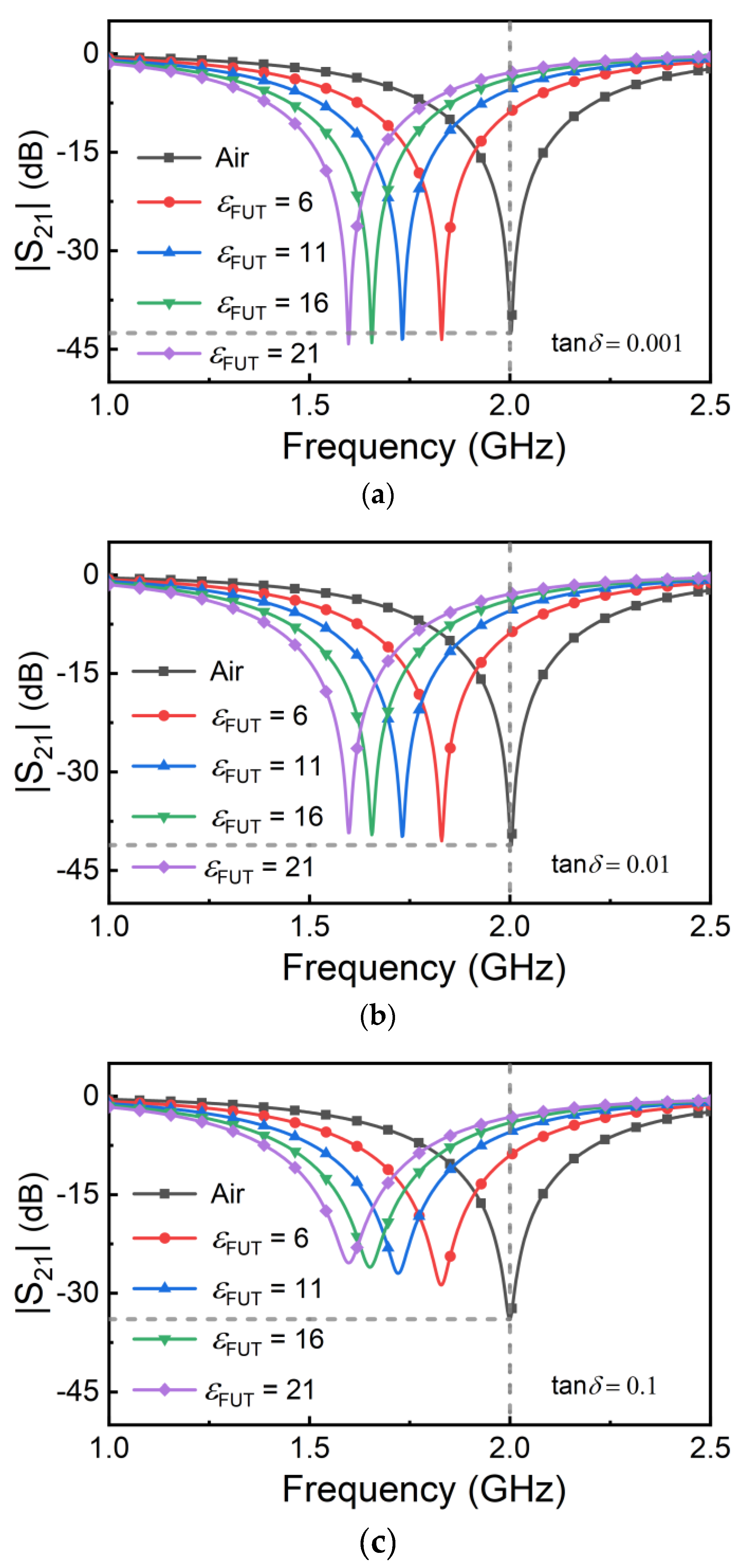
Preprints 71822 g004
Preprints 71822 g005
Figure 5. Dependence of the magnitude of the transmission coefficient at f0 = 2 GHz with the dielectric constant of the FUT for different values of the loss tangent of the LUT.
Figure 5. Dependence of the magnitude of the transmission coefficient at f0 = 2 GHz with the dielectric constant of the FUT for different values of the loss tangent of the LUT.
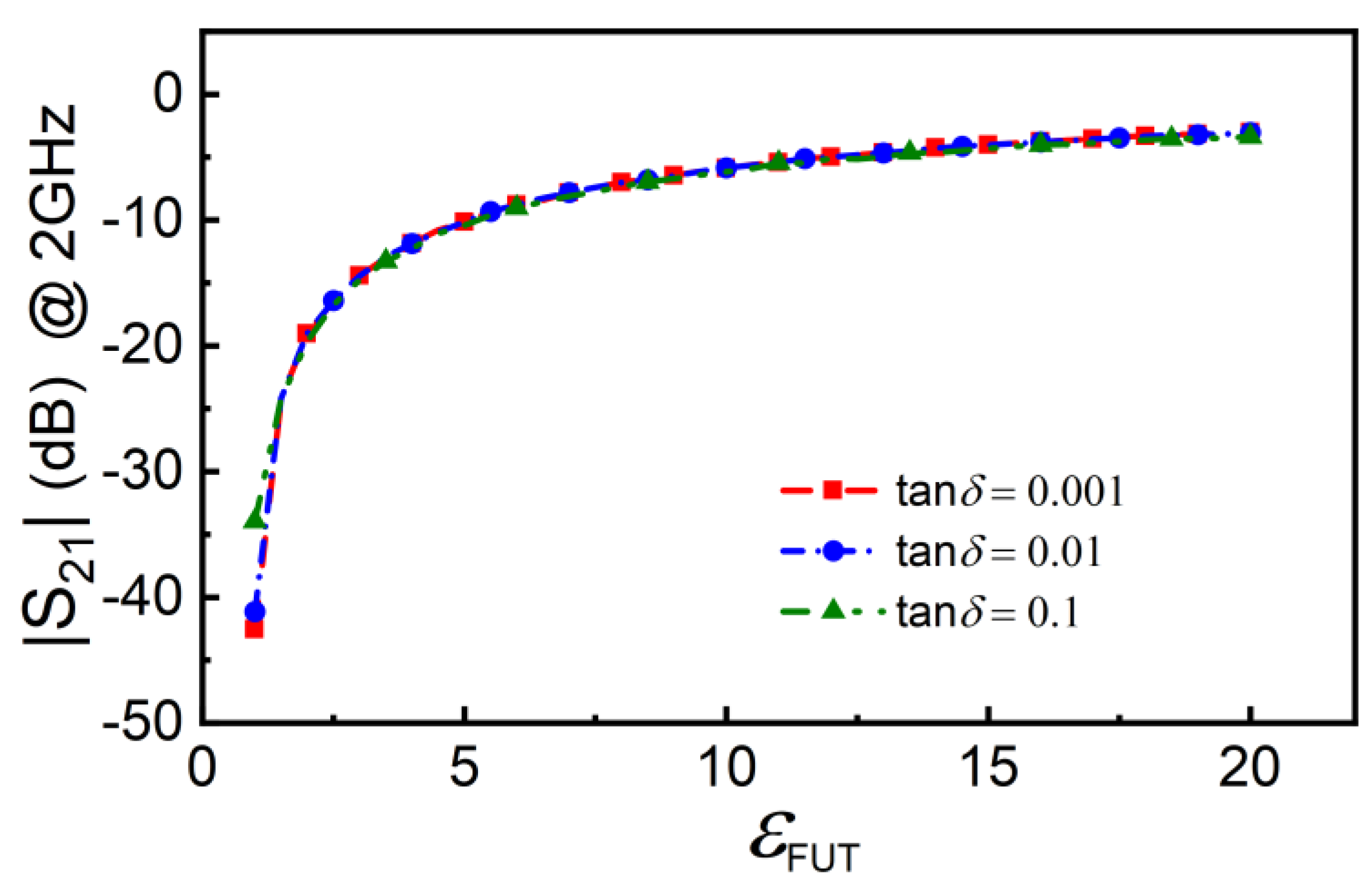
Preprints 71822 g005
Preprints 71822 g006
Figure 6. Measurement setup of the fabricated sensor.
Figure 6. Measurement setup of the fabricated sensor.
Preprints 71822 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated