Propagation Law of Hydraulic Fracture across the Coal-Rock Interface under the Co-Effect of Natural Fractures and Tectonic Stress

Indirect fracturing from roof rock to coal using a horizontal well is a new and promising technology for coalbed methane surface exploitation in soft and low-permeability coal seams. In order to study the propagation law of hydraulic fracture across the coal-rock interface, a pore pressure cohesive element is used to establish a numerical model for indirect fracturing. Combined with practical engineering in 3# coal seam in Xinjing mine in China, the propagation behavior of hydraulic fracture across the coal-rock interface was researched, and the range of horizontal well position for indirect fracturing was determined. The results show that: (1) the pore pressure cohesive element can be used to simulate accurately the interaction between hydraulic fracture and natural fracture, and the propagation of hydraulic fracture across the coal-rock interface. (2) As the vertical distance between the horizontal well and coal-rock interface decreases, the breakdown pressure of perforation decreases; while the injection pressure increases when the hydraulic fracture crosses the coal-rock interface. (3) For the indirect fracturing engineering in 3# coal seam in Xinjing mine, the vertical distance between the horizontal well and coal-rock interface should not be larger than 2.0m to make the hydraulic fracture propagate into the coal seams.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Coalbed methane (CBM) resource in China at buried depths shallower than 2000m were approximately 36.81 trillion m³ [1], while most coal seams in mining area are characterized by low saturation, low permeability, low reservoir pressure and high metamorphism [2,3], resulting in the difficulty in the efficient and industrial development of CBM. In addition, the main coal-bearing basins in China have experienced long-term intense squeezing, shearing and deformation [4,5,6], which may result in the problems such as hole collapse, stuck drilling and plugging when directly fracturing the coal seam. Therefore, the indirect fracturing technology has been widely used in CBM extraction in recent years. The core idea of this technology is that the horizontal well is drilled in the roof or the floor, and the hydraulic fracture initiating in the roof or floor propagates into the coal seam. To date, the indirect fracturing technology has been successfully applied in Luling mine of Huaibei and in Zhaozhuang mine of Jincheng in China [7].

The concept of indirect fracturing for CBM extraction was firstly proposed by Olsen et al. [8,9] at the beginning of this century, and many scholars have done lots of work aimed at the propagation law of hydraulic fracture across the coal-rock interface. Tan et al. [10] experimentally studied the fracture propagation behaviour in tight sandstone-coal interbedded formations. Jiang et al. [11] experimentally studied the effect of interfacial friction and in-situ stress difference on the propagation law of hydraulic fracture across the coal-rock interface. Liu et al. [12] experimentally studied the effect of injection rate of the fracturing fluid on the dynamic propagation of hydraulic fracture across the coal-rock interface. Wan et al. [13] studied transition zone’s influence on the fracture vertical propagation behaviour for coal measure strata. Then the effect of fracture initiation position and fluid viscosity on the fracture propagation in multi-layered coal strata were experimentally investigated [14]. He et al. [15] found that compared with hydraulic fracturing, the stress difference between the vertical stress and the minimum horizontal principal stress for cracks to penetrate through the coal–rock interface is larger in supercritical CO₂ fracturing.

As for the simulation work, Zhao et al. [16] established a composite criterion to predict subsequent intersection behavior between a hydraulic fracture and a natural fracture. Huang et al. [17,18] using the block discrete element method to explore the influence of engineering parameters on the behaviour process of hydraulic fractures penetrating bedding planes. Li et al. [19] studied the propagation law of hydraulic fracture across the coal-rock interface based on Plasticity Fracture-Seepage (PF-S) model, and found that the in-situ stress and the interfacial shear strength are the dominant factor controlling the propagation of hydraulic fracture across the coal-rock interface. Escobar et al. [20] studied the effect of stress interference on the penetration ability of multiple fractures using XFEM method, and the results showed that stress shadowing facilitate the propagation of hydraulic fracture from shale into roof rock.

To sum up, the current researches about the indirect fracturing for CBM extraction using horizontal well mainly focus on the in-situ stress, rock mechanical parameters, interfacial strength, and fracturing operation parameters such as injection rate, interval distance between fracturing stages and so on. However, it has little consideration on the natural fractures, and the considered in-situ stresses are restricted to the conventional normal faulting stress regime, i.e., the vertical in-situ stress is the largest stress. While the strike-slip faulting stress regime in the Qinshui basin is widely distributed, i.e., the horizontal in-situ stress is larger than the vertical in-situ stress [21,22]. In addition, it is well known that the coal measure strata contains many natural fractures. Therefore, it is of practical importance to study the propagation law of hydraulic fracture across the coal-rock interface under the co-effect of natural fractures and tectonic stress.

In this paper, the applicability of the pore pressure cohesive element to the simulation of the interaction between hydraulic fracture and natural fracture and the propagation of hydraulic fracture across the coal-rock interface is validated. Then, considering the natural fracture distribution and tectonic stress field of 3# coal seams of Xinjing mine in Shanxi province in China, we established the numerical model for indirect fracturing from the roof to coal, using which the propagation law of hydraulic fracture across the coal-rock interface was studied, and the required location of the horizontal well in roof for the hydraulic fracture propagating into the coal from the roof was determined. This research can provide theoretical basis for the CBM extraction in natural fractured coal seam with tectonic stress field using indirect fracturing.

2. Cohesive element model for hydraulic fracturing

As a special finite element, the cohesive element has been widely used to simulate the fracture propagation. In terms of hydraulic fracturing simulation, the pore pressure cohesive element with zero thickness is used to pre-define the propagation path of hydraulic fracture. As shown in Figure 1, the fracture process zone (FPZ, i.e., the unbroken cohesive zone) at the tip of hydraulic fracture is simulated using a partially damaged cohesive element with non-zero traction T, while the visible fracture (i.e., the broken cohesive zone) is simulated using the completely damaged cohesive element with the traction T of zero. The mathematic crack tip refers to the point which is yet to separate, the cohesive crack corresponds to the damage initiation point where the traction T reaches the tensile strength T_max and the separation δ between the top and bottom surface of the cohesive element reaches the critical value δ₀, and the material crack tip is the completely damaged point where the δ reaches the critical value δ_f and the cohesive strength just vanishes [23,24,25].

2.1. Equations governing the solid deformation

The linear elastic constitutive relation is adopted in to describe the coal and rock deformation. Specifically, T represents the nominal traction vector subjected to the top and bottom surfaces of the cohesive element. For 2D numerical model, T consists two components, i.e., the one perpendicular to the surface of cohesive element and the one parallel to the surface of cohesive element, which are denoted by T_n and T_s, respectively. The corresponding separations between the top and bottom surfaces of cohesive element are denoted by δ_n and δ_s, respectively. The initial constitutive thickness of cohesive element is denoted by h₀, and then the nominal normal strain and shear strain can be defined as

\begin{array}{l} ε_{n} = \frac{δ_{n}}{h_{0}} \\ ε_{s} = \frac{δ_{s}}{h_{0}} \end{array}

(1)

Correspondingly, the linear elastic constitutive relation can be written as

T = {\begin{cases} T_{n} \\ T_{s} \end{cases}} = [\begin{matrix} E_{n n} & E_{n s} \\ E_{n s} & E_{s s} \end{matrix}] {\begin{cases} ε_{n} \\ ε_{s} \end{cases}} = E ε

(2)

As the default value of h₀, 1.0 is used in following simulation, so E in Equation. (2) is the stiffness matrix, and T_n and T_s are the normal stress tn and shear stress ts, respectively.

2.2. Equations governing the solid deformation

The irreversible bilinear traction-separation law [26] is adopted to simulate the damage process of cohesive element, as shown in Figure 2. K₀ is the initial stiffness of cohesive element without damage (δ<δ₀). When δ=δ₀, the cohesive element damage occurs, and the traction T reaches to the peak value equal to the material tensile/shear strength. When δ>δ₀, the cohesive element experiences damage evolution, and D is the damage factor. When δ increases to δ_f, the cohesive element fails completely, forming a visible fracture. Therefore, δ_f is the fracture displacement and the area under the solid red line is equal to the fracture energy G_c.

The maximum nominal stress criterion is adopted to define the damage initiation in this work. This criterion assumes that the damage is to initiate when the maximum nominal stress ratio (as defined in the expression below) reaches 1.0 and can be written as

\max {\frac{〈 T_{n} 〉}{T_{n}^{0}}, \frac{T_{s}}{T_{s}^{0}}} = 1

(3)

Where

T_{n}^{0}

and

T_{s}^{0}

represent the peak values of the nominal stress when the deformation is either purely normal to the interface or purely in the shear direction, respectively.

Two types of simplified criteria based on the fracture displacement δ_f and fracture energy G_c are used to determine the tensile failure of cohesive element, and the linear friction law written as in Equation (4) is used to determine the shear failure of the cohesive element.

| τ_{s} | = {\begin{cases} f σ_{n} f σ_{n} \leq τ_{\max} \\ τ_{\max} f σ_{n} > τ_{\max} \end{cases}

(4)

Where f is the coefficient of friction, σ_n is the normal compressive stress, τ_s is the frictional shear stress, and τ_max is shear stress limit on the contacting surfaces.

2.3. Equations governing the fluid flow

The fluid constitutive response within the gap between the cohesive surfaces comprises the tangential flow and the normal flow (i.e., leakage flow), as shown in Figure 3. The fracturing fluid is assumed to be incompressible Newtonian fluid, and its flow can be characterized using the Reynolds lubrication equation as [25,27,28]

\frac{\partial w}{\partial t} + c_{t} (p_{i} - p_{t}) + c_{b} (p_{i} - p_{b}) = \frac{1}{12 μ} \nabla (w^{3} \nabla p_{i}) + Q (t) δ (x)

(5)

where w(x, t) is the crack width, t is the injection time, x is the distance to the wellbore, c_t and c_b are fluid leak-off coefficients for the top and bottom surfaces of cohesive element, respectively. p_i is the fluid pressure, and p_t and p_b are the pore pressures in the adjacent pore fluid material on the top and bottom surfaces of the cohesive element, respectively. μ is the fluid viscosity, Q(t) is the injection rate, and δ(x) is the Dirac delta function.

3. Model verification

3.1. Comparison with Blanton’s criteria

Aimed at the interaction between the hydraulic fracture and the pre-existing fracture shown in Figure 4, Blanton [29,30] proposed the criteria for the opening of pre-existing fracture and the arrest of hydraulic fracture, respectively.

The opening criterion can be written as

σ_{\max} - σ_{\min} = {[\frac{π E G_{c}}{4 (1 - ν^{2}) S}]}^{1 / 2} \cdot \frac{1}{\sin^{2} θ}

(6)

and the arrest criterion can be written as

σ_{\max} - σ_{\min} = {[\frac{π E G_{c}}{4 (1 - ν^{2}) S}]}^{1 / 2} \cdot \frac{2 f}{2 f \cdot \sin^{2} θ - \sin 2 θ}

(7)

Where S is the horizontal distance between the wellbore and the pre-existing fracture, and θ is the intersection angle.

The numerical model setup is shown in Figure 5 and the major input parameters are listed in Table 1. In the series of simulations, the horizontal distance between the injection node and the pre-existing fracture is fixed as 7.5 m, the length of the pre-existing fracture is fixed as 6 m, and the initial length of the hydraulic fracture is fixed as 7 m.

The three typical interaction model, i.e., the natural fracture opening, the hydraulic fracture arrest, and the hydraulic fracture crossing, can be simulated successfully using the pore pressure cohesive element, as shown in Figure 6. The comparison between the numerical results and the Blanton’s criteria is shown in Figure 7, from which it can be found that the numerical results are in good agreement with the analytic solution. Therefore, the pore pressure cohesive element can accurately simulate the interaction between the hydraulic fracture and the natural fracture.

3.2. Comparison with indirect fracturing experiment

Using the coal-cement blocks with interfaces lubricated by oil grease or Vaseline, Jiang et al. [11] studied the effect of the stress difference and the interfacial friction on the hydraulic fracture propagation across the coal-rock interface. The physical and mechanics parameters of coal and cement blocks are listed in Table 2. According to Jiang’s experiment, the numerical model is set as Figure 8 and the input parameters are listed in Table 3. Note that, in our simulation, the shear strength of the coal-cement interface was input based on the linear friction law, and elastic modulus of the interface was input equating to half of the sum of that of the coal and the cement.

3.1.1. S

Bulleted lists

The comparison between the numerical results and the experiment results is listed in Table 4. Note that the boldly highlighted cells show the cases at which the numerical results do not agree with the laboratory work. It can be found that the numerical results agree well with the experiment results indicating the applicability of the pore pressure cohesive element to the simulation of the hydraulic fracture propagation across the coal-rock interface.

4. Engineering application

4.1. Numerical model for CBM extraction using indirect fracturing

The site measurement results shows that the Xinjing mine of Shanxi province in China belongs to Strike-slip faulting stress regime, i.e., σ_H＞σ_v＞σ_h. The mean in-situ stress is σ_v=8.74MPa，σ_H=11.34MPa，σ_h=3.55MPa. The samples including coal, roof and floor are obtained from the 3# coal seam, the coal was cut using wire cutting machine to analyze the natural fracture distribution, as shown in Figure 9, and the statistical result of the natural fractures in coal is listed in Table 5.

Combined with the geological condition of the 3# coal, the numerical model for indirect fracturing from the roof to the coal is established, as shown in Figure 10. Note that the natural fractures are embedded into the numerical model using python language based on the statistical result shown in Table 5. The perforation depth is set as 0.6m, and the propagation law of hydraulic fracture across the coal-rock interface is studied by changing the distance between the horizontal well and the coal, i.e., H. To minimize the dependence of fracture propagation path on the embedded location of pore pressure cohesive element and reflect truly the fracture propagation process, the pore pressure cohesive elements were globally embedded between all the solid elements.

The mechanical parameters of coal, roof and floor were obtained using the uniaxial compression test, Brazilian split test, and semi-circular specimens under three-point bending test. In addition, the height of hydraulic fracture was estimated as 5m and the injection rate in the simulation was set as 0.001m³/s. Considering the actual fracturing parameters with perforation interval of 3m and perforation density of 10 in 1m, the injection rate of 0.001m³/s in simulation is correspond to that of 9m³/s in actual engineering. The specific input parameters for the numerical model are listed in Table 6.

4.2. Results analysis

The propagation paths of hydraulic fracture for different values of H are shown in Figure 11, from which it can be found that, when H=0.7m, 1.0m, and 1.5m, the hydraulic fracture can propagate into the coal from the roof, when H≥0.7m, the hydraulic fracture can not propagate into the coal. Therefore, in terms of the indirect fracturing for CBM extraction in 3# coal of Xinjing mine, the distance between the horizontal well in the roof and the coal should be smaller than 2.0m.

The injection pressure-injection time curve under different horizontal well drilling position was extracted, as shown in Figure 12, from which the perforation breakdown pressure and the crossing pressure (i.e., the injection pressure at the time when the hydraulic fracture just propagates to the interface) were recorded in Table 7, respectively.

It can be found from Figure 11 and Table 7 that the perforation breakdown pressure increases with increasing H and this phenomenon is more obvious when H is small (H=0.7m, 1.0m and 1.5m). The mechanical mechanism for this phenomenon is that the incompatible deformation between roof and coal induces the tensile internal stress when fracturing, and the induced tensile stress increases with decreasing H. Therefore, as the horizontal well drilling position H increases, the breakdown pressure increases but increment decreases.

It can be found from Tabel 7 that, for H=0.7m, 1.0m and 1.5m, the hydraulic fracture can propagate into the coal but the crossing pressure decreases with increasing H, the reason for this is that when H is large, the released elastic strain energy due to the roof fracture is more, the part of the elastic strain energy is transformed into the surface energy of hydraulic fracture, and the other is consumed to overcome the fracture propagation resistance, keeping the continuous propagation of hydraulic fracture in coal.

Conclusion

1. Pore pressure cohesive element can be used to accurately simulate the propagation of the hydraulic fracture across the coal-rock interface in coal measure strata and the interaction between hydraulic fracture and natural fracture.

2. As the horizontal well drilling position decreases, the perforation breakdown pressure decreases while the crossing pressure increases. The mechanical mechanism for this phenomenon is that the incompatible deformation between roof and coal induces the tensile internal stress when fracturing, and the induced tensile stress increases with decreasing H.

3. Considering the co-effect of natural fractures and tectonic stress in 3# coal of Xinjing mine of Shanxi province in China, it is suggested that the horizontal well drilling position is smaller than 2.0m when indirectly fracturing the coal from roof, the hydraulic fracture can propagate into the coal successfully.

Author Contributions

Conceptualization, D.Z.; methodology, D.Z.; software, D.Z.; validation, W.L.; investigation, D.N.; resources, H.C.; writing—original draft preparation, D.Z.; supervision, W.L.; project administration, X.S.; funding acquisition, X.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Basic Research Program of Shanxi Province, China (No. 202103021224059), Taiyuan University of Technology-Huayang new material technology group CO.,LTD. Cooperation Project (No. 2020007899), Science and Technology Major Project Shanxi Province (No. 20201102002), Basic Research Program of Shanxi Province, China (No. 20210302124664).

Data Availability Statement

Data is contained in the article.

Acknowledgments

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Qin, Y.; Moore, T.A.; Shen, J.; Yang, Z.; Shen, Y.; Wang, G. Resources and geology of coalbed methane in China: a review. Int. Geol. Rev. 2017, 60, 777–812. [Google Scholar] [CrossRef]
Yuan, L.; Xue, J.; Zhang, N.; Lu, P. Development orientation and status of key technology for mine underground coal bed methane drainage as well as coal and gas simultaneous mining. Coal Science and Technology, 2013,41(9): 6-11.
Lau, H.C.; Li, H.; Huang, S. Challenges and Opportunities of Coalbed Methane Development in China. Energy Fuels 2017, 31, 4588–4602. [Google Scholar] [CrossRef]
Li, L.; Liu, D.; Cai, Y.; Wang, Y.; Jia, Q. Coal Structure and Its Implications for Coalbed Methane Exploitation: A Review. Energy Fuels 2020, 35, 86–110. [Google Scholar] [CrossRef]
Cheng, Y.; Pan, Z. Reservoir properties of Chinese tectonic coal: A review. Fuel 2019, 260, 116350. [Google Scholar] [CrossRef]
Cheng, Y.; Lei, Y. Causality between tectonic coal and coal and gas outbursts. Journal of China Coal Society, 2021,46(1): 180-198.
Li, H.; Liang, W.; Jiang, Y.; Wu, P.; Wu, J.; He, W. Numerical Study on the Field-Scale Criterion of Hydraulic Fracture Crossing the Interface Between Roof and Broken Low-Permeability Coal. Rock Mech. Rock Eng. 2021, 54, 4543–4567. [Google Scholar] [CrossRef]
Olsen, T. N.; Bratton, T. R.; Donald, A.; Koepsell, R.; Tanner, K. Application of indirect fracture for efficient stimulation of coalbed methane. SPE Rocky Mountain Oil ＆ Gas Technology Symposium, Denver, Colorado. 16-18 April, 2007.
Olsen, T. N.; Brenize, G.; Frenzel, T. Improvment process of coalbed natural gas completion and stimulation. SPE Annual Technical Conference and Exhibition, Denver, Colorado. 5-8 October, 2003.
Tan, P.; Jin, Y.; Yuan, L.; Xiong, Z.-Y.; Hou, B.; Chen, M.; Wan, L.-M. Understanding hydraulic fracture propagation behavior in tight sandstone–coal interbedded formations: an experimental investigation. Pet. Sci. 2019, 16, 148–160. [Google Scholar] [CrossRef]
Jiang, Y.; Lian, H.; Nguyen, V.P.; Liang, W. Propagation behavior of hydraulic fracture across the coal-rock interface under different interfacial friction coefficients and a new prediction model. J. Nat. Gas Sci. Eng. 2019, 68, 102894. [Google Scholar] [CrossRef]
Liu, J.; Yao, Y.; Liu, D.; Xu, L.; Elsworth, D.; Huang, S.; Luo, W. Experimental simulation of the hydraulic fracture propagation in an anthracite coal reservoir in the southern Qinshui basin, China. J. Pet. Sci. Eng. 2018, 168, 400–408. [Google Scholar] [CrossRef]
Wan, L.; Hou, B.; Tan, P.; Chang, Z.; Muhadasi, Y. Observing the effects of transition zone properties on fracture vertical propagation behavior for coal measure strata. J. Struct. Geol. 2019, 126, 69–82. [Google Scholar] [CrossRef]
Wan, L.; Hou, B.; Meng, H.; Chang, Z.; Muhadasi, Y.; Chen, M. Experimental investigation of fracture initiation position and fluid viscosity effect in multi-layered coal strata. J. Pet. Sci. Eng. 2019, 182. [Google Scholar] [CrossRef]
He, W.; Lian, H.; Liang, W.; Wu, P.; Jiang, Y.; Song, X. Experimental Study of Supercritical CO2 Fracturing Across Coal–Rock Interfaces. Rock Mech. Rock Eng. 2022, 56, 57–68. [Google Scholar] [CrossRef]
Zhao, Y.; Zhang, Y.F.; He, P.F. A composite criterion to predict subsequent intersection behavior between a hydraulic fracture and a natural fracture. Eng. Fract. Mech. 2019, 209, 61–78. [Google Scholar] [CrossRef]
Huang, L.; Dontsov, E.; Fu, H.; Lei, Y.; Weng, D.; Zhang, F. Hydraulic fracture height growth in layered rocks: Perspective from DEM simulation of different propagation regimes. Int. J. Solids Struct. 2021, 238, 111395. [Google Scholar] [CrossRef]
Zheng, Y.; He, R.; Huang, L.; Bai, Y.; Wang, C.; Chen, W.; Wang, W. Exploring the effect of engineering parameters on the penetration of hydraulic fractures through bedding planes in different propagation regimes. Comput. Geotech. 2022, 146, 104736. [Google Scholar] [CrossRef]
Li, H.; Liang, W.; Jiang, Y.; Wu, P.; Wu, J.; He, W. Numerical Study on the Field-Scale Criterion of Hydraulic Fracture Crossing the Interface Between Roof and Broken Low-Permeability Coal. Rock Mech. Rock Eng. 2021, 54, 4543–4567. [Google Scholar] [CrossRef]
Escobar, R.G.; Sanchez, E.C.M.; Roehl, D.; Romanel, C. Xfem modeling of stress shadowing in multiple hydraulic fractures in multi-layered formations. J. Nat. Gas Sci. Eng. 2019, 70. [Google Scholar] [CrossRef]
Zhang, P.; Meng, Z.; Jiang, S.; Chen, X. Characteristics of in-situ stress distribution in Zhengzhuang Region, Southern Qinshui Basin, China and its stress path during depletion. Eng. Geol. 2019, 264, 105413. [Google Scholar] [CrossRef]
Hou, X.; Liu, S.; Li, G.; Zhu, Y.; Liu, A. Quantifying and Modeling of In Situ Stress Evolutions of Coal Reservoirs for Helium, Methane, Nitrogen and CO2 Depletions. Rock Mech. Rock Eng. 2021, 54, 3701–3719. [Google Scholar] [CrossRef]
Chen, Z.; Bunger, A.; Zhang, X.; Jeffrey, R.G. Cohesive zone finite element-based modeling of hydraulic fractures. Acta Mech. Solida Sin. 2009, 22, 443–452. [Google Scholar] [CrossRef]
Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical investigation of hydraulic fracture propagation in a layered reservoir using the cohesive zone method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
Tan, P.; Jin, Y.; Pang, H. Hydraulic fracture vertical propagation behavior in transversely isotropic layered shale formation with transition zone using XFEM-based CZM method. Eng. Fract. Mech. 2021, 248. [Google Scholar] [CrossRef]
Tomar, V.; Zhai, J.; Zhou, M. Bounds for element size in a variable stiffness cohesive finite element model. Int. J. Numer. Methods Eng. 2004, 61, 1894–1920. [Google Scholar] [CrossRef]
Peirce, A.; Detournay, E. An implicit level set method for modeling hydraulically driven fractures[J]. Computer Methods in Applied Mechanics and Engineering, 2008,197: 2858-2885.
Detournay, E. Propagation regimes of fluid-driven fractures in impermeable rocks[J]. International Journal of Geomechanics, 2004,4(1): 35-45.
Blanton, T. L. An experimental study of interaction between hydraulically induced and pre-existing fractures. SPE/DOE Unconventional Gas Recovery Symposium of the Society of Petroleum Engineers, Pittsburgh, PA. 16-18 May, 1982.
Zhang, Q.; Zhang, X.-P.; Sun, W. A review of laboratory studies and theoretical analysis for the interaction mode between induced hydraulic fractures and pre-existing fractures. J. Nat. Gas Sci. Eng. 2020, 86, 103719. [Google Scholar] [CrossRef]

Figure 1. Cohesive element model for hydraulic fracturing.

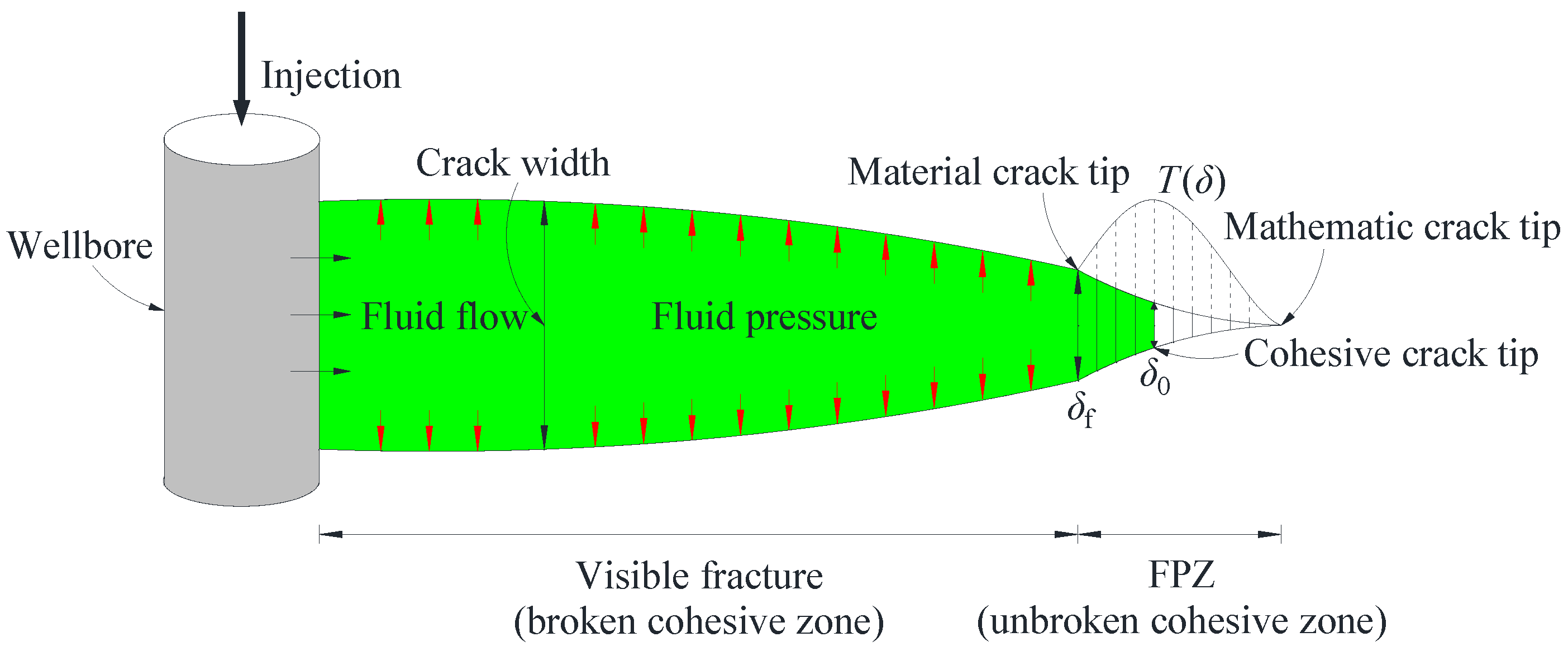
Figure 2. Irreversible bilinear traction-separation law.

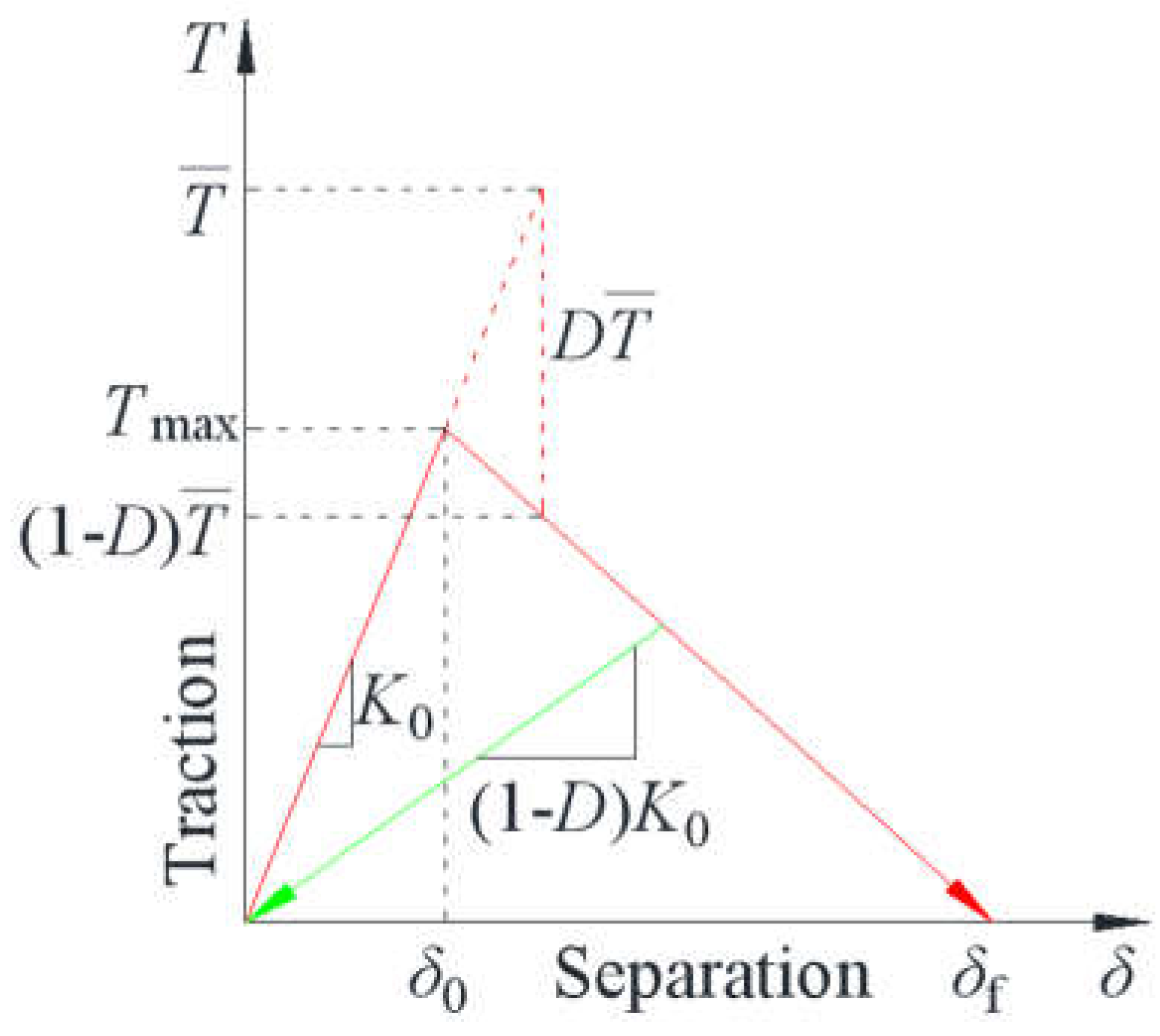
Figure 3. Fluid flow within cohesive elements.

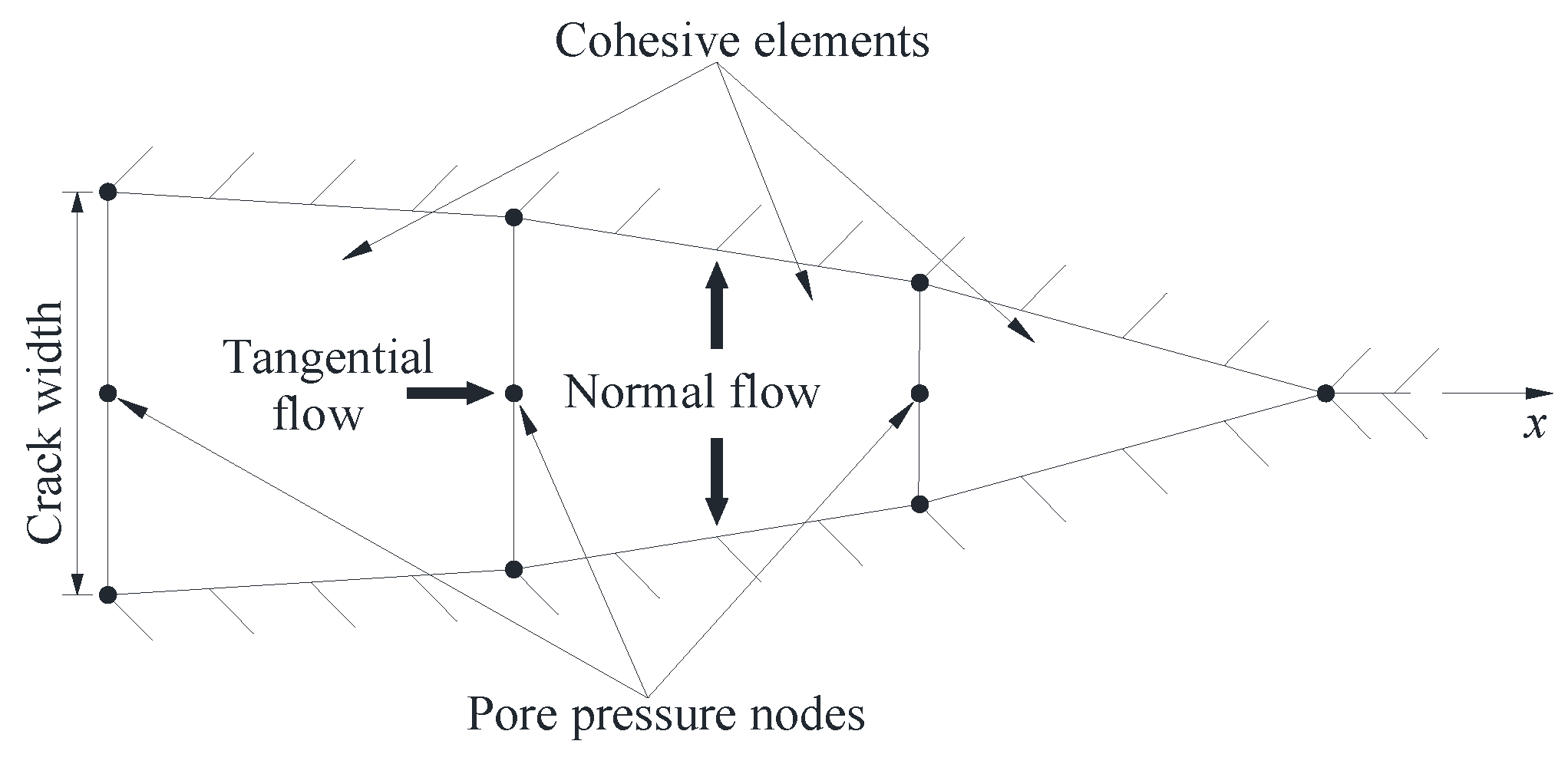
Figure 4. Diagram of hydraulic fracture intersecting pre-existing fracture.

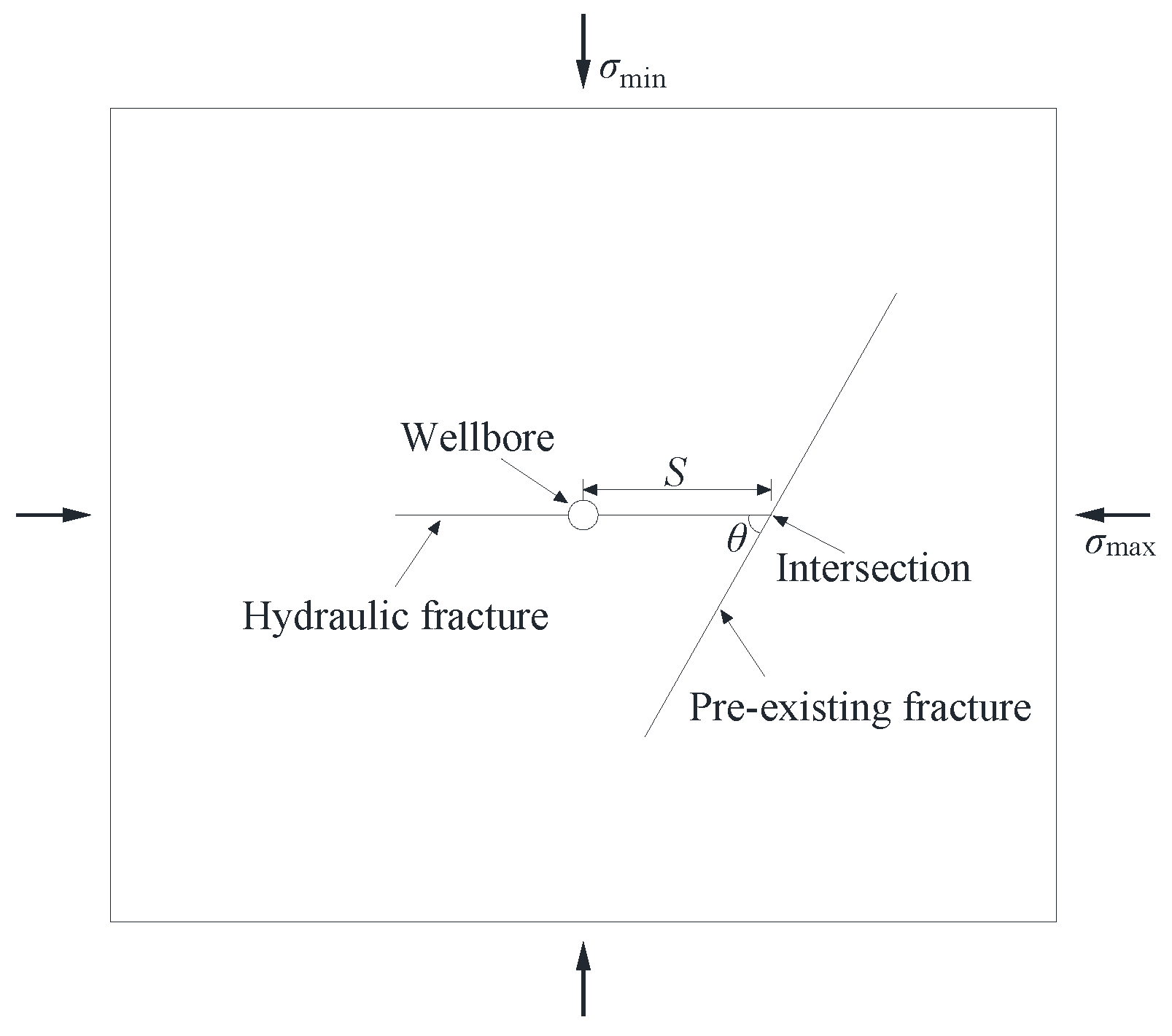
Figure 5. Model setup for interaction between hydraulic fracture and natural fracture.

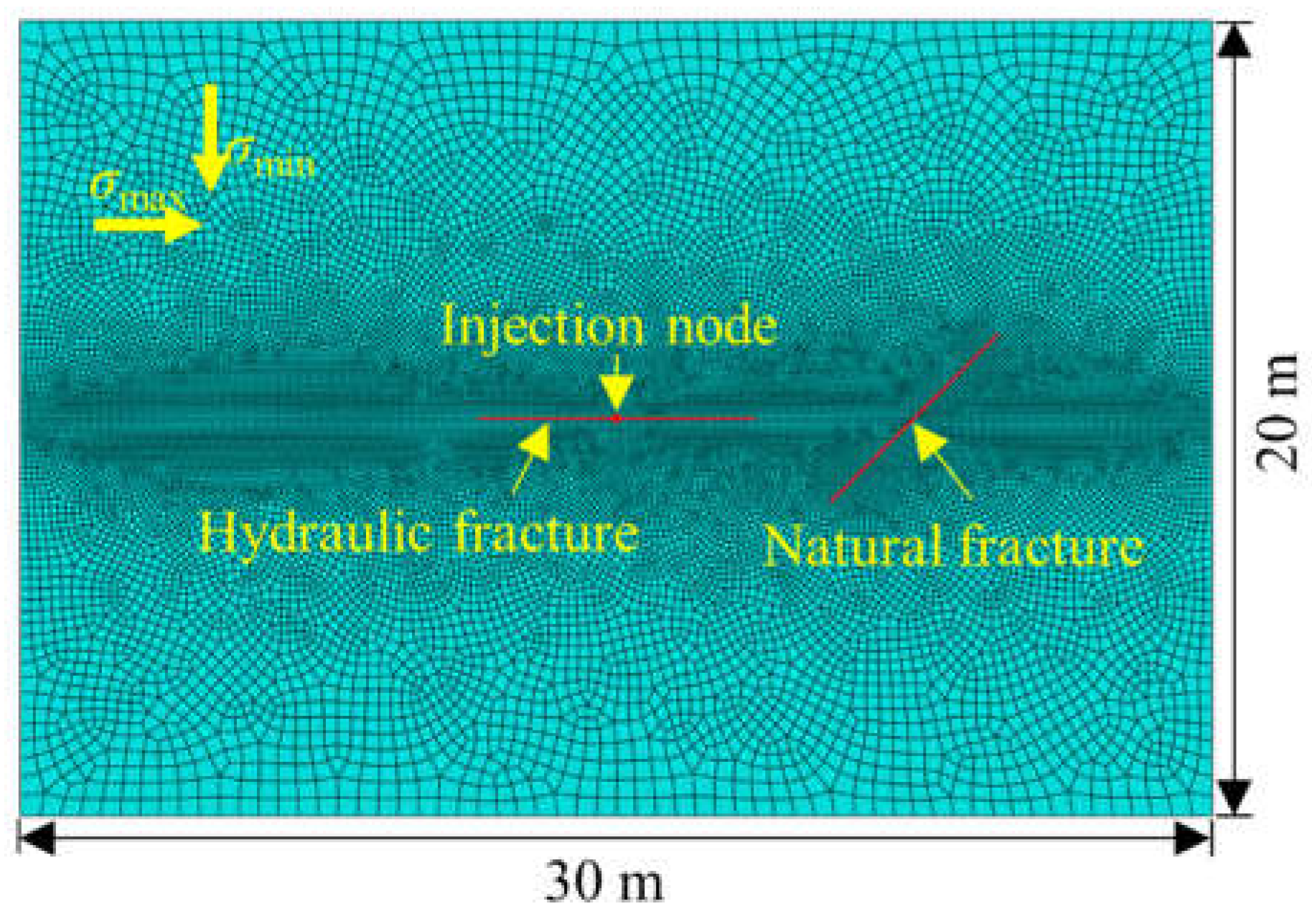
Figure 6. Interaction between hydraulic fracture and natural fracture from the present model; (a) σ_max - σ_min = 0MPa, θ = 15°; (b) σ_max - σ_min = 2MPa, θ = 45°; (c) σ_max - σ_min = 4MPa, θ = 75°.

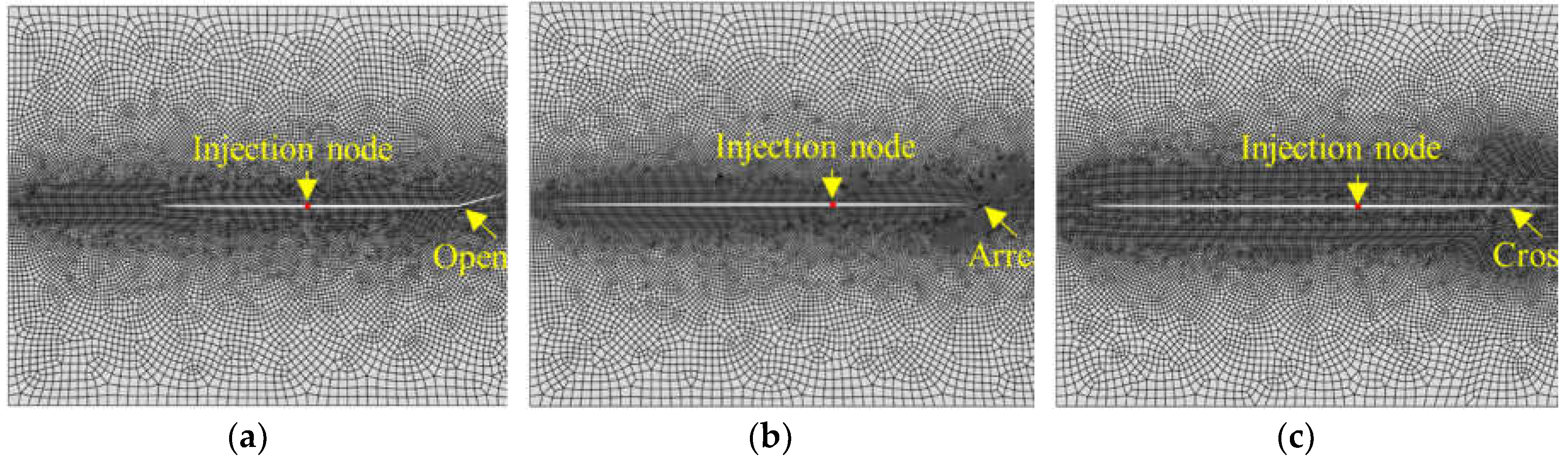
Figure 7. Comparison between numerical results and Blanton’s criteria.

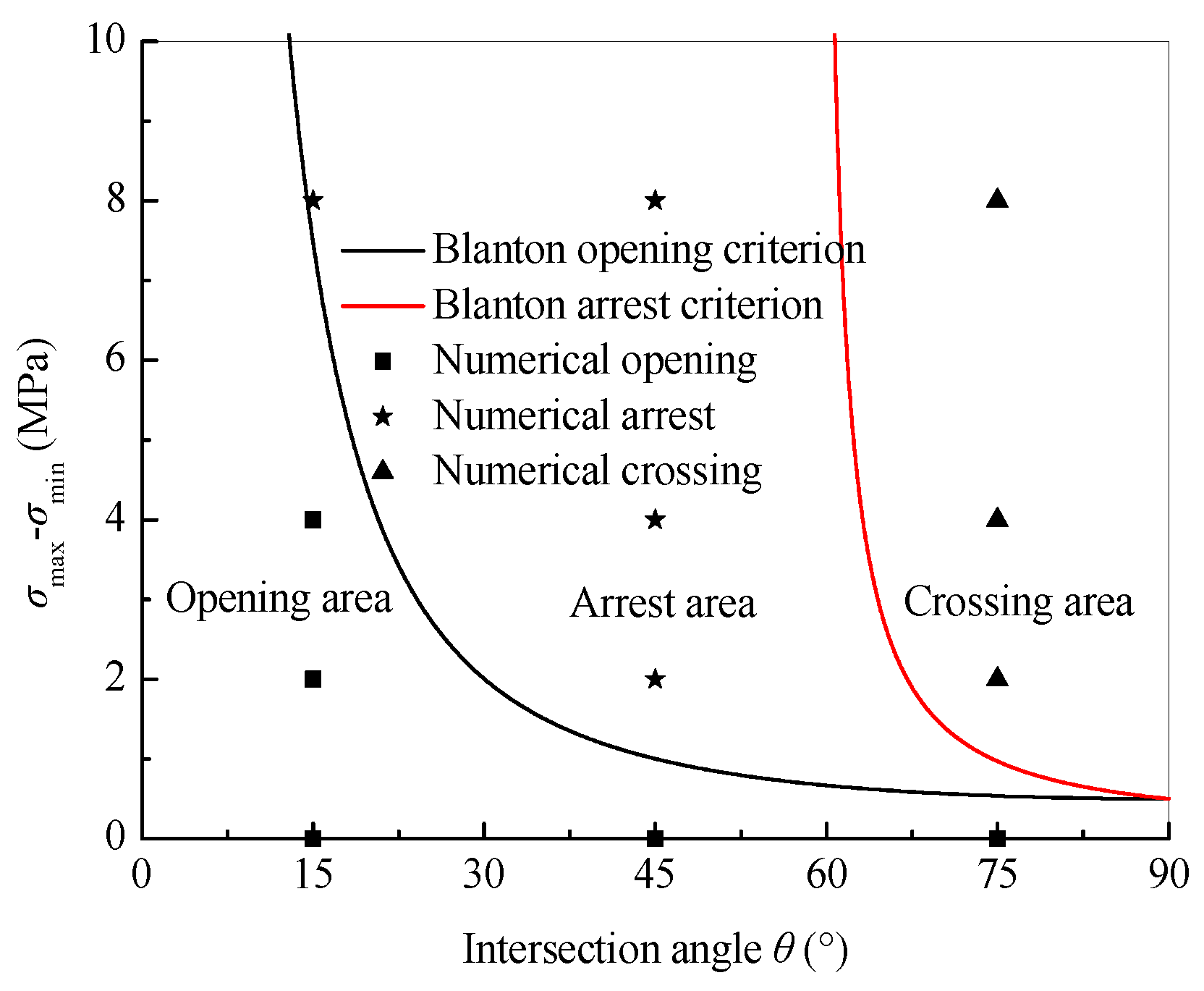
Figure 8. Model setup for indirect fracturing from cement to coal.

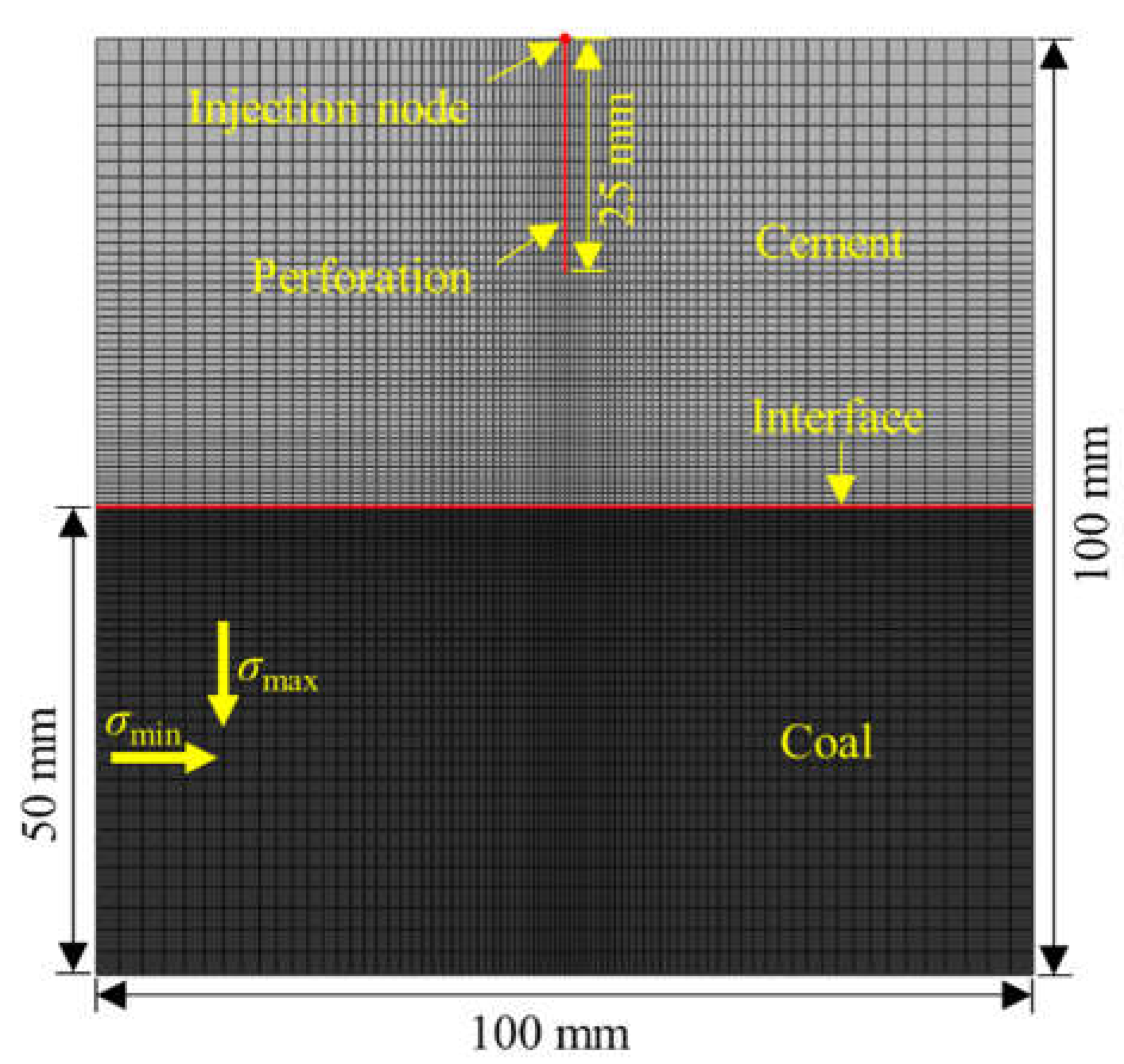
Figure 9. Natural fractures distribution in coal.

Figure 10. Model setup for CBM extraction using indirect fracturing.

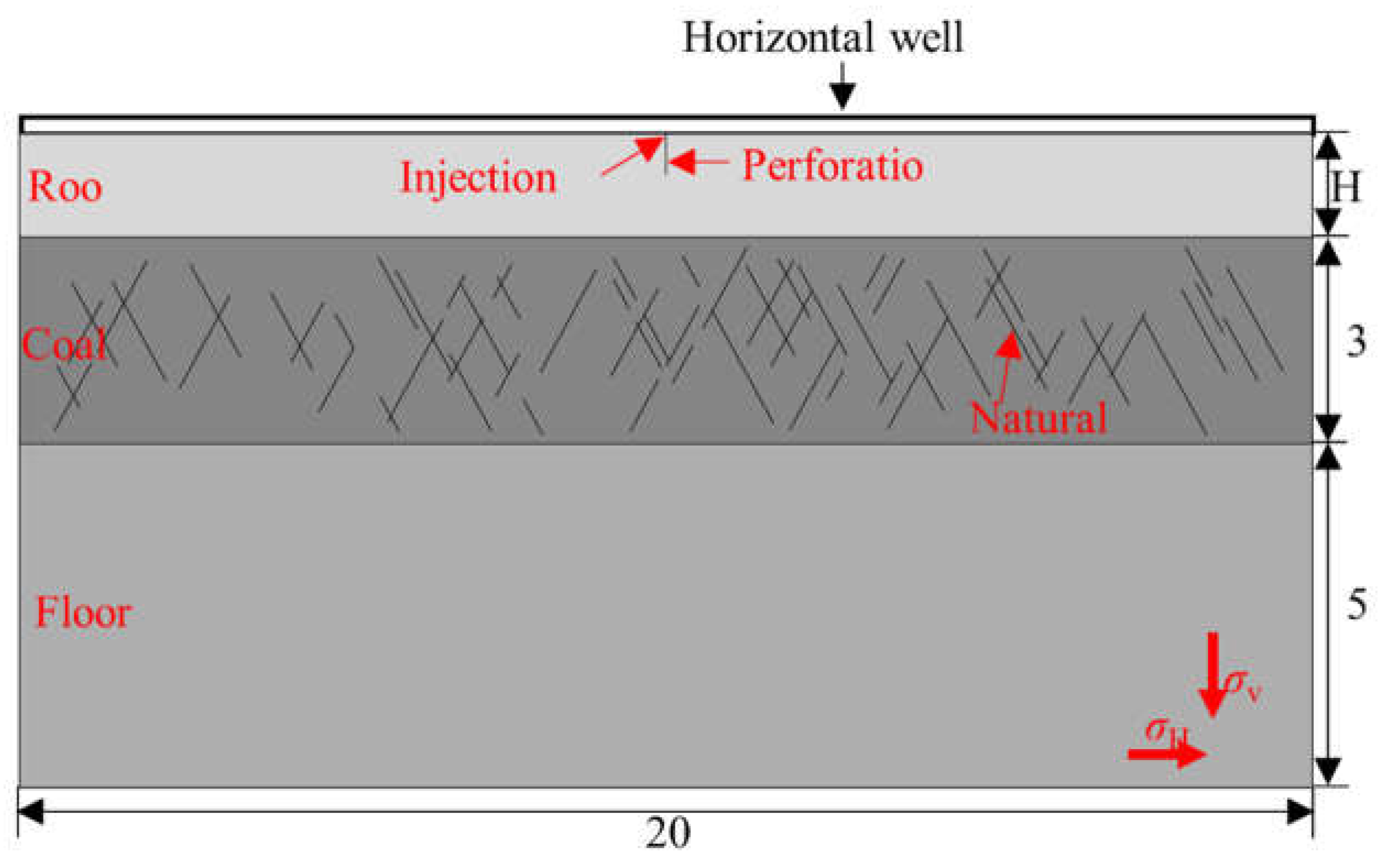
Figure 11. Propagation path of hydraulic fracture under different horizontal well drilling position.

Figure 12. Injection pressure under different horizontal well drilling position.

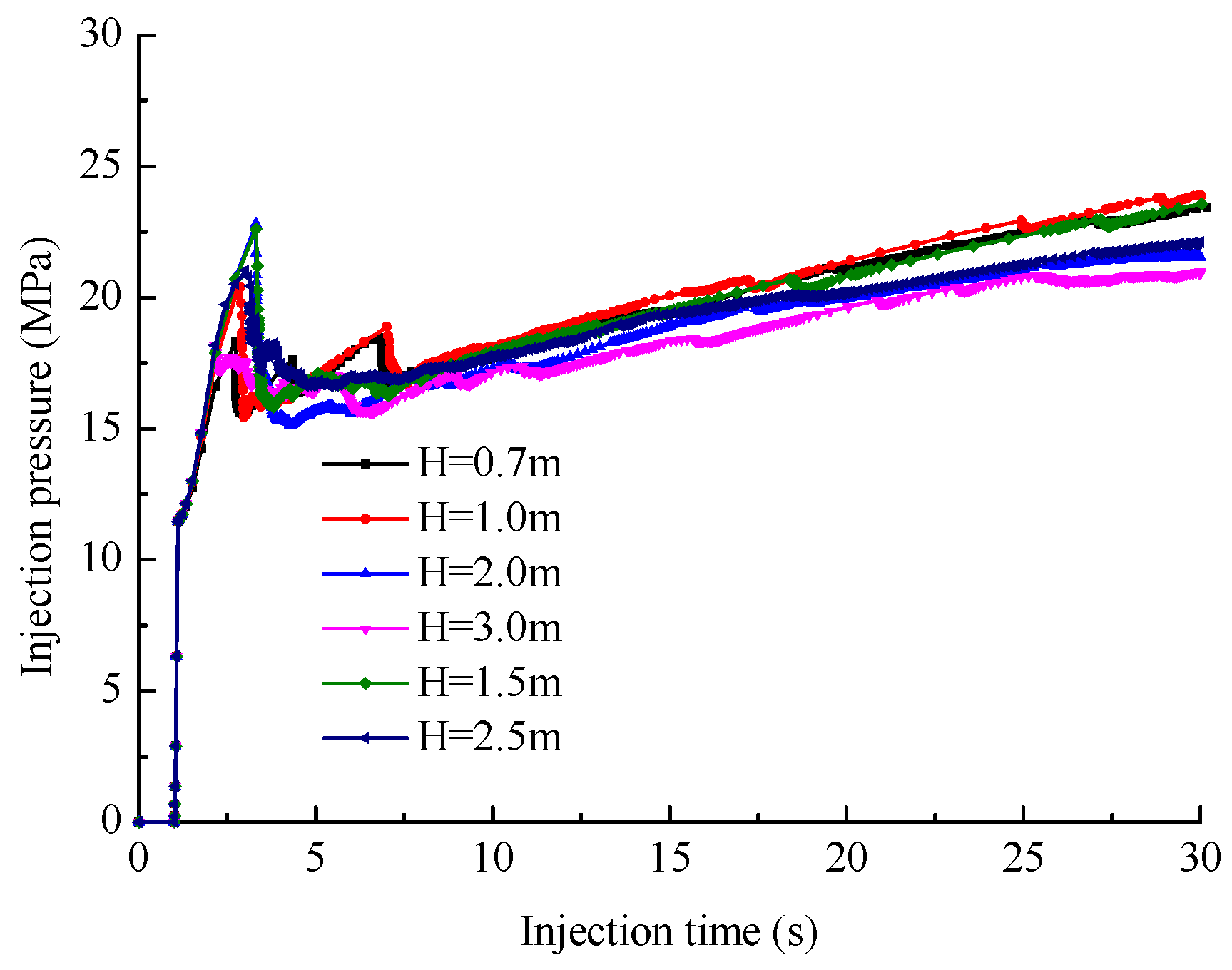
Table 1. Model parameters for interaction between hydraulic fracture and natural fracture.

Input parameters	Value	Unit
Young’s modulus	15	GPa
Poisson’s ratio	0.25	Nondimensionless
Fluid viscosity	1	cP
Tensile strength of rock	6	MPa
Shear strength of rock	20	MPa
Tensile strength of pre-existing fracture	2	MPa
Shear strength of pre-existing fracture	10	MPa
Formation permeability	10	mD
Injection rate	0.001	m3/s
Specific weight of fluid	9800	N/m3
Initial pore pressure	0	MPa
Tensile critical fracture energy for rock	150	J/m2
Tensile critical fracture energy for natural fracture	25	J/m2
Leak-off coefficient	1e-14	m/(Pa·s)
Porosity	0.1	Nondimensionless
Friction coefficient	0.6	Nondimensionless

Table 2. Physical and mechanics parameters of Jiang’s laboratory experiment [11].

Parameters	Coal	Cement
Porosity	0.089	0.079
Permeability (10⁻¹⁵ m2)	0.014	0.0039
Elastic modulus (GPa)	3.48	6.58
Poisson ratio	0.23	0.19
Tensile strength (MPa)	1.69	4.56
Mode-I fracture toughness (MPa·m0.5)	0.20	0.98

Table 3. Model parameters for indirect fracturing from cement to coal.

Input parameters	Coal	Cement	Interface
Porosity	0.089	0.079	—
Permeability (mD)	0.014	0.0039	—
Elastic modulus (GPa)	3.48	6.58	5.03
Poisson’s ratio	0.23	0.19	—
Tensile strength (MPa)	1.69	4.56	0
Shear strength (MPa)	20	30	linear friction law
Tensile critical fracture energy (J/m²)	10.89	140.69	0
Leak-off coefficient (m/(Pa·s))	1e-13	1e-14	Top 1e-14
Leak-off coefficient (m/(Pa·s))	1e-13	1e-14	Bottom 1e-13
Specific weight of fluid (N/m³)	9800
Initial pore pressure (MPa)	0
Injection rate (m³/s)	3.33e-6
Fluid viscosity (cP)	1

Table 4. Comparison between numerical simulation and Jiang’s experiment.

σ_mid (MPa)	σ_min (MPa)	σ_max (MPa)	Interfacial friction coefficient	Interfacial shear strength (MPa)	Experiment results	Numerical results
5	3	6	0.7200	4.32	No crossing	No crossing
5	3	7		5.04	No crossing	No crossing
5	3	8		5.76	No crossing	Crossing
5	3	9		6.48	Crossing	Crossing
5	3	6	0.4976	2.99	No crossing	No crossing
5	3	7		3.48	No crossing	No crossing
5	3	8		3.98	No crossing	No crossing
5	3	11		5.47	Crossing	Crossing
5	3	11	0.2557	2.81	No crossing	No crossing
5	3	12		3.07	No crossing	No crossing
5	3	13		3.32	No crossing	Crossing
5	3	14		3.58	No crossing	Crossing
5	3	15		3.84	Crossing	Crossing

Table 5. Statistical result of the natural fractures in coal.

Geometric parameters	value	Unit
Angle between natural fracture and σ_min direction	60, 120	°
Length of natural fracture	0.5~2	m
Interval of natural fractures along the length direction	0.1~1	m
Interval of natural fractures vertical the length direction	0.1~1	m

Table 6. Model parameters for CBM extraction using indirect fracturing.

Input parameters	Roof	Coal	Floor
Elastic modulus (GPa)	5.65	1.35	19.57
Poisson’s ratio	0.25	0.3	0.2
Permeability (mD)	0.1	1	1
Porosity	0.1	0.2	0.1
Tensile strength (MPa)	3.51	0.6	4.44
Shear strength (MPa)	25	20	30
Tensile strength of natural fracture (MPa)	—	0.001	—
Shear strength of natural fracture (MPa)	—	10	—
Fracture displacement (m)	0.001	0.0015	0.0005
Fracture displacement of natural fracture (m)	—	0.00075	—
Leak-off coefficient (m/(Pa·s))	1e-14	1e-13	1e-14
Specific weight of fluid (N/m³)	9800
Fluid viscosity (cP)	1
Injection rate (m³/s)	0.001
Initial pore pressure (MPa)	5.62

Table 7. Fracturing characteristic parameters under different horizontal well drilling position.

Horizontal well drilling position H (m)	Perforation breakdown pressure (MPa)	Crossing pressure (MPa)
0.7	16.60	17.55
1.0	17.55	16.54
1.5	17.91	16.06
2.0	18.02	—
2.5	18.17	—
3.0	18.18	—

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer