Prerpints.org logo
Preprint
Article

Real-Time Pipe Structure Change Detection and Classification using Distributed Acoustic Fiber Sensors Based on Convolutional Neural Network (CNN) Models

Altmetrics

Downloads

232

Views

93

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 April 2023

Posted:

26 April 2023

You are already at the latest version

Alerts
Abstract
This study proposes a machine-learning-based framework for detecting mechanical damage in pipelines, utilizing physics-informed datasets collected from simulations for mechanical damage. The framework provides an effective workflow from dataset generation to damage detection and identification for three types of pipeline events: welds, clamps, and corrosion defects. While the study initially focused on optimizing the CNN structure using various advanced optimizers, it also investigated the impact of sensing systems on data classification and the effect of noise on classification performance. The study's analysis highlights the importance of selecting the appropriate sensing system for the specific application. The authors also found that the proposed framework is robust to experimentally relevant levels of noise, suggesting its applicability in real-world scenarios where noise is present. Overall, this study contributes to the development of a more reliable and effective method for detecting mechanical damage in pipelines. The proposed framework provides an effective workflow for damage detection and identification, and the findings on the impact of sensing systems and noise on classification performance add to its robustness and reliability.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Pipelines are critical for the transportation and distribution of liquid and gaseous fuel in various industrial sectors, including oil, gas, and petrochemical. However, these pipelines have been laid across diverse and often harsh terrains, making it challenging to maintain their structural integrity. To safeguard national security and economic growth, it is important to study and develop comprehensive monitoring methods that can detect and mitigate external threats, such as sabotage, unauthorized access, construction accidents, and natural disasters, as well as internal structural degradation caused by various factors such as corrosion, erosion, fatigue, and material degradation due to environmental and operational factors.
Different technology-driven and human-operated evaluation programs have been employed to protect pipeline infrastructure for many years. Currently, structure health monitoring (SHM) is a novel technology that integrates sophisticated sensor systems with intelligent algorithms to assess “health” of a structure. This approach has the potential to enhance reliability and safety, optimize performance, increase automation capabilities, and decrease overall lifecycle costs. As such, SHM has garnered significant interest in recent years and is now recognized as a promising solution for improving the structural integrity of civil infrastructure, aerospace, and mechanical systems. In these applications, damage detection by guided-wave nondestructive testing has attracted widespread interest. Ultrasonic sensors can detect the backscattering acoustic response, which provides data for identifying different events, such as structural damage, or changes in the structure, like the addition of clamps or the presence of welds within the structure.
Elastic perturbations known as guided waves are capable of propagating over extended distances in thin-walled structures while experiencing minimal amplitude loss. Laboratory experiments [1] have demonstrated the efficiency of using guided acoustic waves to detect and locate pipeline anomalies in critical areas that are susceptible to defects. To excite a cylindrical structure and propagate UGWs, an appropriate signal is chosen, which will then propagate through the structure and encounter any damage or other material discontinuities. Traditionally, by analyzing the resulting changes in the waveform, the location and severity of the damage can be quantified. It is important to note that UGWs can experience dispersion as they propagate, which can affect the accuracy of damage detection. To analyze the dispersion of UGWs, a MATLAB toolbox package named PCDISP [24] is commonly used. 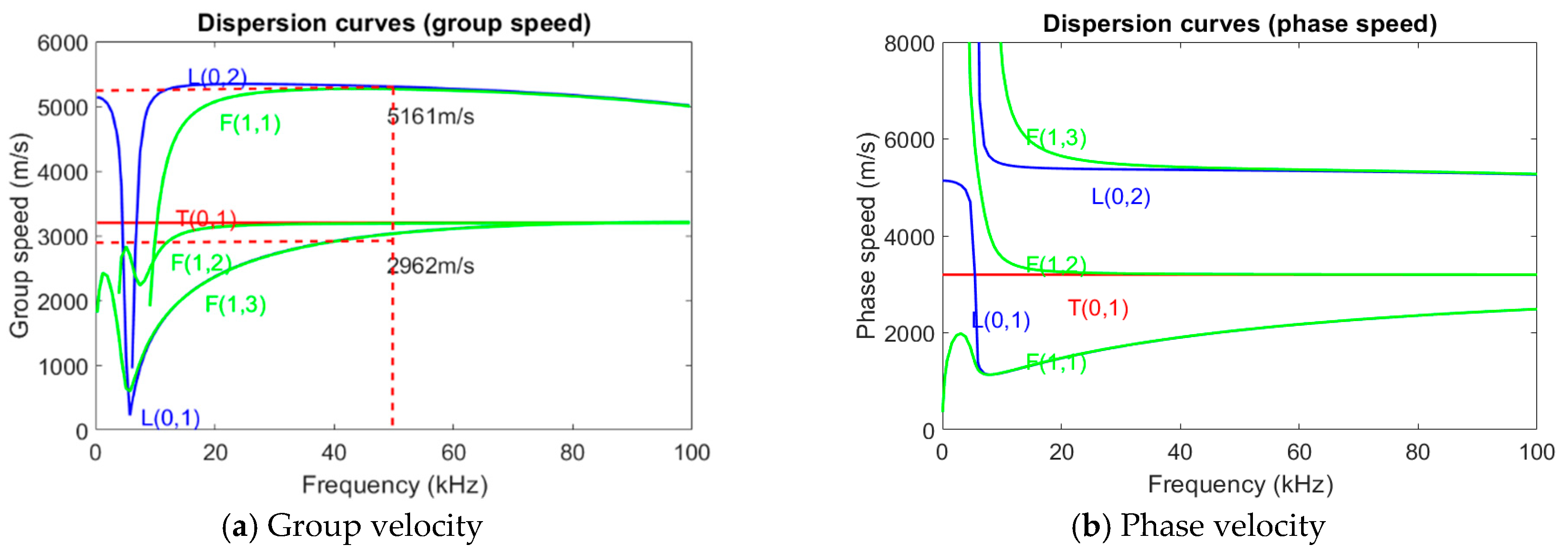This toolbox utilizes Navier Lame's equation [19], which describes the behavior of elastic waves in solid bodies, to calculate the dispersion curves of different guided wave modes. The use of PCDISP allows for a more accurate analysis of the dispersion and ultimately a more accurate identification of the location and severity of the damage. By utilizing the appropriate excitation signal, analyzing the resulting changes in the waveform, and utilizing tools such as PCDISP, it is possible to effectively detect and quantify damage in the structure. Wave phase velocities and group velocities of a steel pipeline with an outside diameter of 12 inches and wall thickness of 0.5 inches are shown in Figure 1a,b.
Also, guided wave NDE has potential to significantly decrease the number of sensors necessary for monitoring a structure. Specifically, guided wave NDE technology is a promising method for structural health monitoring (SHM), but one of the main limitations is the size, cost, and practical constraints of deploying conventional NDE sensors ubiquitously. In guided acoustic wave sensing, the exciting transducer is therefore typically also used as the measurement sensor, thereby measuring the backscattered acoustic wave. Such an installation scenario can be highly limiting in terms of investigating damage over large distances and in remote locations, and the amount of information that can be extracted is also limited by what can be measured at the excitation location. The use of distributed fiber optic sensors as alternative measurement transducers has been proposed as an alternative solution, and they can be placed at multiple points along a pipeline to monitor for damage. Practical limitations of permanently mounting conventional NDE sensors on structures have been widely discussed [2]. Assuming sufficiently high frequency bandwidth can be achieved, distributed fiber optic sensors are promising candidates for guided acoustic wave detection schemes because they are able to detect acoustic signatures generated by external events or alternatively scattered by defects within a pipeline segment with high spatial and temporal resolution [3,4,5].
In the past decades, distributed fiber vibration/acoustic sensor technology has gained increasing attention and tremendous growth. The quasi-distributed/point fiber vibration/acoustic sensor technologies include fiber Bragg grating (FBG) [3], Fabry–Pérot [4], and Multimodal interference [5]. Various interferometric configurations include; the Sagnac interferometer [6], the Mach–Zehnder interferometer (MZI) [7], and polarization-OTDR (POTDR) [8]. Fiber optic sensors are known for being resilient in harsh environments and capable of distributed interrogation. They have a unique ability to perform distributed strain, and acoustic measurements using backscattered light phenomena in unmodified telecommunications fibers or fibers that have been modified to enhance the scattering, resulting in high sensing performance with improved spatial resolution measurements [9,10]. The most common distributed acoustic sensing modality involves a technique referred to as phase–optical time domain reflectometry (φ – OTDR) as discussed in our recent review of distributed optical fiber sensing [11]. The Φ-OTDR system utilizes the interference effects within pump pulses generated by a narrow linewidth (usually <10 kHz) laser source. The Φ-OTDR system demodulates the backscattered Rayleigh signal amplitude/phase to acquire acoustic signals. The Rayleigh signal amplitude varies with the strain on the sensing fiber induced by the surrounding acoustic signals. In the use of a fiber-optic-based distributed acoustic sensing (DAS) system, the fiber-optic cable is used as the sensor; in which a pulsed laser is used to excite the fiber and backscattered light is detected and processed using appropriate optical interrogator hardware.
However, the limitation behind the traditional guided wave based NDE technology is that the number of transducers is limited and typically located at the source of the ultrasonic guided wave. Currently, for raw data acquired based on fiber acoustic sensing, machine learning (ML)-based data analysis techniques can offer advantages in classification, pattern recognition, prediction, and system optimization, especially when there is no explicit mathematical model to describe the relationship between inputs and outputs [12]. A great deal of research has been pursued seeking to improve the dynamic range, spatial resolution, and sensitivity of the DAS system hardware and signal processing methods. However, the ability of event recognition is typically the goal when considering the limitation of performance in field application. High nuisance alarm rates can occur due to complex environmental interferences and benign artificial disturbances, leading to false alarms. To address this, signal feature extraction methods have been proposed to accurately identify the events [13]. Feature-based methods can achieve high recognition rate if carefully implemented but require careful feature selection and relatively complex real-time processing to extract signal features. Different disturbances also cause unique effects in spatial and temporal domains. In their work, Sun and colleagues [14] proposed a method for recognizing events through the extraction of morphological features from a time-space data matrix. They employed correlation techniques to classify three distinct events, namely manual excavation, walking, and vehicle passing.
A key barrier to the wide adoption of machine learning based data analysis for SHM, is that the procurement of training datasets of damage/failure events of real-world structural system of interest are both expensive and time consuming. While it is relatively straightforward to gather data for events such as humans walking or vehicles passing, obtaining real-time sensor data for pipeline structural damage or failure events is exceedingly challenging. Further, pipelines can undergo a wide variety of damage events, further complicating ML model training and degrading ML model performance.
This challenge can be addressed by training ML models on simulated sensor datasets. Such simulations fuse (i) a sensor measurement model (e.g., distributed acoustic sensor measurement model) with (ii) a high-fidelity physics-based numerical model simulation of the structural degradation event (e.g., ultrasonic vibrations of a pipeline with corrosion damage). Hence, the high-fidelity numerical model response is filtered through a suitable sensor model to simulate sensor measurements. This simulation strategy can be systematically deployed to simulate sensor datasets for various pipeline degradation events. Next, an ML classifier can be trained on these diverse and rich simulated datasets to predict structural degradation events of interest. The ML classifier can further be improved by supplementing training data with available experimental measurements. This concept is known as domain adaptation in ML literature and is increasingly adopted in SHM [15].
In this paper, we propose a CNN-based classification method that directly uses a time-space data matrix for the full distributed sensor system. Deep learning, specifically Convolutional Neural Networks (CNNs), has shown superior performance over traditional machine learning (ML) algorithms in many applications, including pipeline structural health monitoring (SHM) and defect identification using distributed acoustic sensing (DAS) data. The use of CNNs in combination with DAS systems can greatly enhance the accuracy of SHM by providing real-time data analysis for detecting and identifying defects in pipelines. Unlike traditional ML algorithms, CNNs can automatically extract features from raw data and identify patterns that are difficult for humans or conventional algorithms to recognize. This capability is particularly beneficial for processing large amounts of data generated by DAS systems in real-time. CNN-based SHM systems can also adapt to changing conditions and automatically adjust their parameters to optimize performance, making them well-suited for complex environments where conventional approaches may be less effective. In summary, the use of CNNs in combination with DAS systems have the potential to significantly improve pipeline SHM and defect identification by providing accurate and timely analysis of large amounts of sensor data [12].
The datasets used in this study were generated through finite element simulation of guided wave propagation on the surface of a pipeline, which included various types of damage severities and shapes relevant to common corrosion modes in pipelines. The simulations also incorporated varying levels of noise to emulate real-world conditions during sensor deployment. Our objective was to develop a comprehensive learning framework for guided-wave-based damage recognition, covering the entire process from dataset collection to feature extraction and selection. For model training and prediction, we utilized a Convolutional Neural Network (CNN) algorithm. In this study, various CNN models with different structures and activation functions will be considered to test the prediction performance under diverse configurations. The focus of the study is not on the specific architecture of the model, but rather on demonstrating the effectiveness of the overall learning framework in processing simulated sensor data and building machine learning models for pipeline damage recognition. By exploring different CNN architectures, we aim to understand how the choice of model structure and activation functions may impact the performance of the learning framework for this particular application.

2. Enhancing Guided Wave Approaches with Machine Learning Techniques

The current study aims to demonstrate machine-learning-enriched methods for damage detection based upon physics informed data sets relevant for distributed fiber optic sensing. As illustrated in Figure 2, the learning framework consists of the following:
a)
Datasets collected from simulation for mechanical damage/defects.
b)
Pre-processing of data and consideration of noise.
c)
A prediction formulated by learning model training for knowledge discovery associated with mechanical damage detection and identification for test data applied.
In our future work, we plan to conduct designed experiments to be compared against the framework's simulation predictions to further validate and extend the proposed methodologies to include experimental results in an integrated and synergistic based approach.

3. Generating Datasets using Guided Ultrasonic Wave (UGW) Approaches

3.1. The Excitation Concept of Guided Ultrasonic Waves (UGWs)

Structural health monitoring (SHM) is a crucial approach to detecting and quantifying damage in structures. One of the effective ways to accomplish this is by using UGWs, a non-destructive testing technique that is based on the analysis of changes in the waveform of an excited signal. A guided wave propagating along a hollow cylindrical shell as a pattern, as illustrated in Figure 2a,b, while different damage location and severity could cause wave scattering in form of mode conversion as well as reflection and transmission. Cylindrical structures are particularly suitable for this approach because they can support different types of UGWs, such as axisymmetric and longitudinal (L mode), axisymmetric and torsional (T mode), and non-axisymmetric and flexural modes (F mode) [16]. As a result, linking changes of wave modes with associated damage types, localization and severity make it flexible for damage identification. Much research [17,18] has demonstrated that the certain guided wave modes are highly sensitive to minor damage, including damage that is difficult to detect by other non-destructive detection methods. In addition, guided waves are used for damage identification as an elastic vibration in thin plate-like structures due to low attenuation rate, high penetration capability, ease of generation, and ease of use, and are also highly sensitive to damage in small-sized structures [18,19]. Since guided waves generate stresses over the entire thickness of the plate, it is possible to interrogate the entire plate thickness. This means that defects starting at the surface of the plate as well as internal defects can be detected. As guided waves can have more than one propagation mode, and even when a single mode guided wave interacts with a structural defect, the received signal usually contains more than one mode, at which point the proportion of different modes present in the wave depends on the mode transition and other impedance changes at the defect which impact received signals [20].
To excite a cylindrical structure and propagate UGWs, an appropriate signal is chosen, which will then propagate through the structure and encounter any damage or other material discontinuities. It is important to note that UGWs can experience dispersion as they propagate, which can affect the accuracy of damage detection.
The L (0,2) mode is selected for excitation, due to its high sensitivity to circumferential cracks and low identification difficulties [21]. This mode is known to have a faster velocity than L (0,1) at 50kHz and is reported to be more sensitive to the circumferential size of pipeline defects. The selected frequency for the L (0,2) mode allows for flat dispersion curves as illustrated in Figure 2, minimizing dispersion during propagation. The excitation signal used for this purpose is a 50 kHz, 5 cycle sinusoidal signal modulated with a Hanning window in the axial direction, with an amplitude of 0.003 inches, representative of a typical excitation achievable with a guided wave collar:
u t = u ¯ a m p 1 − c o s 2 π f c t n sin ⁡ 2 π f c t ;
Where u ¯ a m p is amplitude of the signal, f c is frequency. Specifically, in this equation provided, n is the number of cycles of the signal that should be included in the excitation (based upon the Hanning window (period)). The assumed excitation amplitude is 0.003 inches, based on calibration between piezo actuator voltage and simulation excitation displacement from past work [8,9]. This signal was defined in ANSYS to simulate the effects of an actuator, which is a representative excitation waveform when compared with existing commercial ultrasonic acoustic NDE technologies [21,23]. The excitation signals in time and frequency domain are shown in Figure 3a,b, respectively.

3.2. Finite Element Modeling and Wave Propagation Analysis of Steel Pipe Structure

To construct the finite element model of the steel pipe structure, the dimensions and material properties of the pipe and excitation source are established, and then calibrated based on previous research by P.S. Lowe. [24]. Table 1 and Table 2 show the dimensional and material parameters for the pipe structure that was tested. Figure 4a shows the overall schematic setup of the finite element simulation, as well as an example of the visualization of the finite element simulation of the investigated pipe. In addition, the Figure shows that the guided wave propagates along the pipe from the left side to the right and produces dispersion phenomena. When utilizing NDT technology that combines ultrasonic wave guides with fiber optic sensors, the information is transmitted to the signal receiver by the sensor while the excitation signal is passing through.
The model featured a 96-inch long nominal 96-inch schedule 40 steel pipe, with an outer diameter of 12 inches and a wall thickness of 0.5 inches. The assumed material properties for steel are presented in Table 2. In the current simulation setup, our study focuses on a single material steel pipeline structure, and we assume negligible damping for simplicity due to strong dependence upon the details of the experimental configuration. For boundary conditions, both ends of the pipeline were assumed to be fixed, leading to zero displacements and rotation at those points. To simulate sensor data, the displacement component of the pipeline was extracted from the numerical simulations. This information was then used to recreate sensor readings along the pipeline, providing valuable insights into the pipeline's response to various types of excitations and damage scenarios.
An averaging scheme was employed to generate sensor data from the displacement values obtained from the simulation. In this method, the sensor signal is calculated as an average over specific segments to ensure a more accurate representation of the sensor readings, consistent with a first-order approximation to the measured sensor response of an optical fiber distributed sensor “gauge length” or a quasi-distributed sensor active sensing length. This averaging process takes into consideration potential variations in the data due to noise, sensor positioning, and other factors. A detailed discussion of this approach can be found in Section 3.4. In the current analysis, guided wave damping attenuation is not considered due to the complexities involved in modeling, with the focus being on the proof of concept and feasibility of the modeling approach. However, the effectiveness of structural detection will ultimately rely on the damping characteristics and their spectral response to target damage. Future investigations will incorporate damping based on comparisons with experiments, specifically tailored to scenarios related to pipe installation (e.g., buried in soil, secured with clamps, etc.), as elaborated in Section 3.5.

3.2.1. Analysis Setup and Parameter Design:

To explore the characteristics of waves generated by the assumed excitation signal and to understand wave propagation, a 3D model was constructed using ANSYS Finite Element (FE) software [25]. For the numerical simulation of guided wave-based pipe structures, the selection of analysis steps and time increments relies on the system properties (including dimensions and excitation signal), as well as the sampling interval and frequency of detection signals. The Transient Structural Module, which is a dynamic implicit analysis step in ANSYS, was chosen to examine the problem of integrating damage identification for pipe structures with fiber optic sensor deployment [26]. The guided wave propagation can be derived from the Navier-Lame equation [16]:
μ ∇ 2 u + λ + μ ∇ ( ∇ · u ) = ρ ∂ 2 u ∂ t 2 ,
where u is the displacement, t is the time, ρ is density, ∇ 2 is the 3-dimensional Laplace operator, λ and μ are Lame’s constant. Guided wave generation and propagation in a cylindrical structure can be simulated using numerical methods. The equation of motion can be expressed in matrix form:
M u ¨ + C u ˙ + K u = F ,
In equation (3), M represents the structural mass, C represents the damping, and K represents the stiffness, all in matrix form. F is a vector of excitation or loaded force. It is worth noting that u ˙ , and u ¨ are the first- and second-time derivatives of displacement, respectively. In our case, the damping factor is not considered. The Equation (3) can be solved by the Newmark time increment method. The time step, Δ t is the step size in Equation (3) and the smaller the time step, the higher the accuracy of the model. For a trade-off between accuracy and calculation time [27], the rule of time step is expressed:
Δ t < 1 20 f m a x
Here, ∆t denotes the time increment and f m a x represent the highest frequency of the excitation signal. So, the maximum time increment should be smaller than 1/20 of the excitation signal period corresponding to the highest frequency. In this paper, the highest frequency of the excitation signal is 50 kHz, so it can be obtained that the time increment should be equal or less than 1 µs by equation (4). Considering the accuracy of the analytical results, 1 µs is chosen as the increment.
To ensure the accuracy of the calculation and consider the influence of calculation efficiency, in this paper, the general mesh size should be smaller than 1/20 [21] of the minimum wavelength along the pipeline body, as shown in Equation (5)
l m < λ m i n 20  
Where l m means the size of the mesh elements and λ m i n denotes the minimum wavelength of the guided wave. Considering Equation (5) and considering the structure of pipeline, this requires that the mesh size should be smaller than 3.93 inches and the thickness of pipeline should include a minimum of between 2 to 3 elements. Therefore, the meshing size of the pipeline is set to 0.2 inches and the meshing method is set to sweeping with edge division to ensure the pipe mesh has three layers of mesh in the thickness direction. In addition to the general setting for healthy structures, the element size for defect regions should be less than one third of minimum defect geometry parameter.

3.1. Wave Propagation Analysis of Steel Pipe Structure

Finite element analysis has been performed to investigate the nature of the excited modes from the assumed excitation signal. Given the frequency range of excitation and the assumed longitudinal displacement direction of the excitation signal as well as the symmetric nature of the signal around the pipe circumference, the L(0,1) and L(0,2) modes are anticipated to be the dominant excited modes. Prior literature [21,24] describes the potential of isolated excitation of L modes as preferred for defect identification with conventional ultrasonic guided NDE application. Longitudinal mode guided waves were reported to be sensitive to circumferential dimensions of pipe defects. When the circumferential length of the defect increases, all else the same, the signal reflection area increases, which enhances the reflected signal. The L(0,2) wave mode shows predominantly axial displacement character, and the L(0,1) wave mode exhibits a dominant radial displacement with lower axial displacement [28].
Commercially available UGW transducers (axially aligned) can therefore be used to excite the L (0,2) based upon prior work [24]. Predicted waveforms are labelled based on the time-of-flight information extracted from dispersion curves shown in Figure 2. The FE model was performed to study the waveform generated by excitation consistent with current commercially available UGW transducers by applying the vibration longitudinally as in Figure 4a. Figure 4b shows the predicted time-domain data from FE and the displacement caused by the axial excitation. To validate the simulation setup described in the study, the authors reference the work of P.S. Lowe. Lowe conducted experiments on an 8-inch schedule 40 steel pipe, with an outer diameter of 12 inches and a wall thickness of 0.5 inches. A ten-cycle Hanning-windowed 40kHz pulse was used as the excitation signal, and the generated waveform was captured 1 meter away from the point of excitation. To compare the results of their simulation with these experimental results, the authors used the same simulation setup and assumed excitation signal. Results of the simulation are shown in Figure 4c and demonstrate good agreement with experiment, as indicated by the close match between predicted results from the finite element (FE) simulation (represented by the blue line) and experimental results (represented by the red line) in [18].

3.4. Sensor Measurement Model

A quasi-distributed acoustic sensing system uses a fiber-optic cable as a sensor to measure local dynamic straining along the length of the fiber. A pulsed laser excites the fiber and backscattered light is detected and processed using an optical interrogator, typically using phase-optical time domain reflectometry (φ - OTDR). The smallest resolvable spatial resolution of the optical fiber segment is referred to as the "gauge length", which can be adjusted to optimize the signal-to-noise ratio (SNR) and frequency resolution. Unlike fully distributed acoustic sensing systems, quasi-distributed systems are not able to resolve acoustic signals along the entire length of the fiber. In prior studies, the ratio of gauge length and spatial wavelength of the acoustic excitation signal for fully distributed acoustic sensors was used to achieve a trade-off between SNR and frequency distortion.
When we consider fiber optic-based distributed acoustic sensing system in our simulation work, the concept of gauge length needs to be incorporated into the development of the sensor measurement model. In optical fiber, fully distributed optical sensing involves monitoring the intensity and phase of the backscattered light and analyzing as a function of time to allow measurement of local dynamic strain along the length of the fiber. The minimum resolvable spatial resolution of the fiber segment is dictated by the physical hardware limitations as well as the signal processing scheme applied and is referred to as the "gauge length". The measurement length of a given distributed fiber optic sensor can be adjusted over reasonable limits, and the selection of an optimized gauge length is an important aspect of data acquisition and processing. For example, the gauge length has a significant effect on the signal-to-noise ratio (SNR) of the data and on the accurate resolution of an acoustic wave within the frequency domain. Dean et al. [29] presented an approach which discussed an explicit trade-off between the maximum SNR and the estimated measurement wavelength by setting an optimum gauge length G L o p t :
G L o p t = R υ f p
where R denotes ratio of gauge length and spatial wavelength of acoustic excitation signal, 𝑣 donates acoustic velocity (m/s), and 𝑓𝑝 is peak frequency (Hz); In our simulation, the resulting signal is extracted using an assumed gauge length of 2.21 inches with R equal to 0.49 and a target wave mode velocity of 5161 m/s to achieve a trade-off between signal-noise ratio and frequency distortion, see detail in T. Dean and T. Cuny (2017) [30] .
Based on the resolution limit we cited and the assumed gauge length in our simulation, the resulting signal can be treated as an averaged strain value over a certain fiber segment. Specifically, the averaging strain value can be expressed as the integral of the local dynamic strain over the segment length L, divided by the segment length L. This averaging operation is necessary to ensure that the signal is representative of the entire segment, and to minimize the effects of noise and frequency distortion:
  ϵ a v g = 1 L ∫ x x + L ϵ x d x
Here, ϵ a v g is the averaged strain value, x is the spatial coordinate along the fiber and ϵ x is the local dynamic strain at the point x. Additionally, typical gauge lengths of fully distributed interrogation systems and limitations in upper frequency bandwidth are not optimized for features we are trying to measure, due to short wavelength and high frequency of UGW (ultrasonic guided waves). Hence, our simulations assume a quasi-distributed sensing scheme based on Fiber Bragg Gratings, in-line Fabry Perot interferometers, or other interferometric structures, which can achieve smaller gauge lengths, better optimization for measuring UGW features, and higher bandwidth acoustic frequency sensing as required for UGW monitoring [30,31].

3.5. Simulation Collection for Pipeline Structure Changes

Structural discontinuities can arise from variations in material properties, such as a structure that is partially embedded in a surrounding medium. To represent practical scenarios, this study considers three types of pipeline events: welds, clamps, and corrosion defects. The weld is modeled as a narrow cylinder with a constant inside diameter that protrudes through the weld and connects to the pipe, with an outside diameter larger than that of the pipe. The clamps on the pipeline are modeled with a specific surface connected to the pipe and a stiffness ratio determined by constraint of the clamps. The categorization of corrosion used in the work is based on the classification proposed by M. Askar [23], which includes three main types: localized, general, and pitting corrosion. These corrosion types will be described in more detail in the following sections. As Figure 5 shows, localized corrosion is mainly due to damage to the surface in the form of mass removal in selected areas, resulting in formation of pits, cracks, and grooves. Pitting is a form of localized corrosion damage that results in the formation of small defects or pits. We differentiate between types of corrosion due to their significant differences in size. Pitting corrosion typically has a size in the hundreds of micrometers range, making it a challenge for finite element analysis (FEA) models due to need for fine meshing in proximity to the defect and relatively weak scattering signature. General corrosion is another type that occurs in a relatively large area caused by several electrochemical processes occurring consistently over the entire surface under consideration. In this type, key characteristics are the loss of metal thickness and unit weight, both of which can have a measurable signature in an acoustic signal to reflect specific characteristics.
By conducting multiple simulation runs for various types of defects in pipelines across five groups – Clamp, Welding, Localized Corrosion, General Corrosion, and Pitting – we will be able to gather valuable data for each group, with varying variables as specified in the Table 3.
  • Clamp: Elastic support loaded by clamps; varying axial length (0.02-0.2 inches) and stiffness factor (5e+06-6.5e+06 N/m).
  • Welding: Discontinuity and material property changes between pipeline and welded portion; varying axial length (0.02-0.2 inches), depth (0.05-0.2 inches).
  • Localized Corrosion: Presence of a rectangular notch on the pipeline's inner surface; varying axial length (1-8 inches) and depth (0.01-0.45 inches).
  • General Corrosion: Even reduction in pipeline thickness; varying axial length (0.5-5 feet) and depth (0.05-0.45 inches).
  • Pitting: Micrometer-scale localized corrosion (pitting); varying radius (0.5-10 inches) and depth (0.05-0.45 inches).
By performing these simulations, we can gain a deeper understanding of the different types of defects in pipelines and their effects on pipeline integrity. Additionally, the data collected from these simulations can be used to build a comprehensive training dataset for further defect classification and prediction work. This dataset can then be leveraged to develop more accurate and reliable diagnostic tools, ultimately helping to improve pipeline safety and maintenance practices.
Here, Figure 6 illustrates a quasi-distributed sensing scheme consisting of five fiber sensing regions arranged in a 1200 (time) × 5 (sensor) matrix. Comparison of the acoustic waveform from these sensors includes information about attenuation and reflection shown in Figure 6. Pitting corrosion shows only a relatively weak signal due to small dimensions of the assumed defect, which can be a significant practical challenge in pipeline health detection. Of the five events, the reflection signal generated by welding is the most pronounced. In contrast, generalized and localized corrosion produces a range of reflected waves due to structural discontinuities. Based on the results of our analysis, we observed that the presence of clamps in the blue region of the pipeline led to a reduction in the amplitude of the resulting signal. This reduction can be attributed to the elastic support provided by the clamps, which helps to suppress the reflection or distortion of the wave. However, we also observed some weak echo signals in the resulting signal, indicating that there may still be some scattering or reflection of the wave occurring in the clamped region. In the following sections of the paper, the authors will describe specific methods and processes used to apply neural networks and training techniques to identify pipe events through analysis of guided wave interactions. This will involve pre-processing training data to ensure that it is suitable for use in the neural network model. The study will evaluate impacts of different optimizers on the accuracy of the machine learning model and investigate the robustness of the damage classification approach under high noise levels. The aim is to illustrate how supervised learning-based neural networks can effectively identify and classify pipeline events, and to highlight a proof-of-concept for the proposed method to be further developed in future work.

3.6. Data Pre-Processing

The accuracy of fiber optic sensors can be negatively impacted by noise, which can arise from various factors such as the light source, the coupling efficiency, and the signal processing amongst other sources [32]. To mitigate the effects of noise, it is important to identify and analyze different sources of noise and take appropriate measures to minimize their impact. While a detailed analysis of each contributing factor can be valuable, it may also be possible in some cases to define a reasonable noise level based on experimental data. This can be achieved through experimentation and validation of the chosen noise level to ensure accurate and reliable results. In the present study, the challenge of real-world noise in data collected from an acoustic fiber sensor experiment was addressed, considering various random processes such as source noise, detector noise, and background noise. Current fully distributed DAS interrogation systems are not capable of operating at frequencies of 30-50kHz. So, in the current study we use a representative example of the magnitude of experimental noise derived from a previously demonstrated experimental set-up having sufficient frequency bandwidth for ultrasonic acoustic guided wave monitoring, and its resulting signal with a 32kHz excitation as illustrated in Figure 7a,b [5]. In this case, a quasi-distributed multimode interferometric structure is assumed. In future studies, deeper investigation of noise levels will be conducted for fully and various quasi-distributed acoustic fiber optic sensing schemes.
The sensor structure assumed here is comprised of a multimode interferometer using a DFB laser with an output power of 45 mW as a laser source, and a single wavelength laser output split into N paths using a 1×N fiber coupler. Validation of the sensor signal derived experimentally in past work on a 50-foot length of pipeline theoretically is also presented in Figure 7c for comparison. We use the experimental data to extract a rough estimate of noise from the sensor signal resulting in an estimated value of approximately 9.63dB. Based upon this estimate, the basic noise model of additive white Gaussian noise (AWGN) was used in training data and compared to data without noise introduced. The noise in decibels (dB) is defined as a logarithmic representation of signal-to-noise ratio:
S N R d B = 10 l o g 10 P s i g n a l P n o i s e
Here, Psignal is the experimental signal after passband filtering the raw data set as per our prior publications [5,33]. The noise signal, Pnoise, can be extracted from the received signal by applying wavelet transformation to isolate different frequency components, followed by bandpass filtering to further remove unwanted frequency components outside the specified range. This processed signal can then be used to estimate noise and calculate signal-to-noise ratio. Figure 8 shows how the simulated signal is affected with application of background noise, in this case noise extracted from recently completed experimental measurement of guided acoustic waves on a pipeline by a quasi-distributed sensor.
After generating the simulated data, we construct a training data matrix by considering each time-domain signal of a fiber segment along a specific spatial resolution limit as a separate row. This spatial resolution limit, also referred to as the minimum resolvable distance or the spatial sampling interval, functions as a low-pass filter for the data that can be acquired. This process can be generalized for both fully distributed and quasi-distributed sensing systems. In the data matrix, the spatial domain is represented by the vertical column, while the time domain is represented by the horizontal row. Figure 9 illustrates the temporal-spatial data matrix for a healthy pipeline. Figure 9a,c display the signal matrix from a fully distributed fiber sensor with and without noise interference (SNR=9.63dB), respectively. For Figure 9b,d, the received data from the quasi-distributed sensing system has the same matrix size as the fully distributed sensor signal contour. Along the pipeline, there are 12 sensor segments, corresponding to 12 signal channels in the signal matrix plot. The invalid area in the sensor fiber, depicted as a blue segment in Figure 9, is filled with zero values in the dataset.
The data for each pipeline segment is represented as a matrix with a size of 96-inch in the spatial domain and 1.2ms (1200 time steps) in the temporal domain. These matrices are converted into grayscale images with a size of 46 x 1200 pixels before being fed into the Convolutional Neural Network (CNN) in the case of both training and test data. Resultant grayscale images represent different events, such as welds, clamps, and corrosion, and are shown in Figure 10.

4. Event Recognition

4.1. Comparison of Common CNNs

Convolutional neural networks (CNNs) have gained significant popularity in recent years due to their remarkable effectiveness in processing and classifying signals, such as time-series data from sensors or audio signals. This can be attributed to the unique ability of CNNs to capture local patterns and time dependencies in the input data while maintaining robustness to changes in the timing and amplitude of the signal. As a result, they are particularly well-suited for processing complex and noisy signals that are frequently encountered in real-world applications.
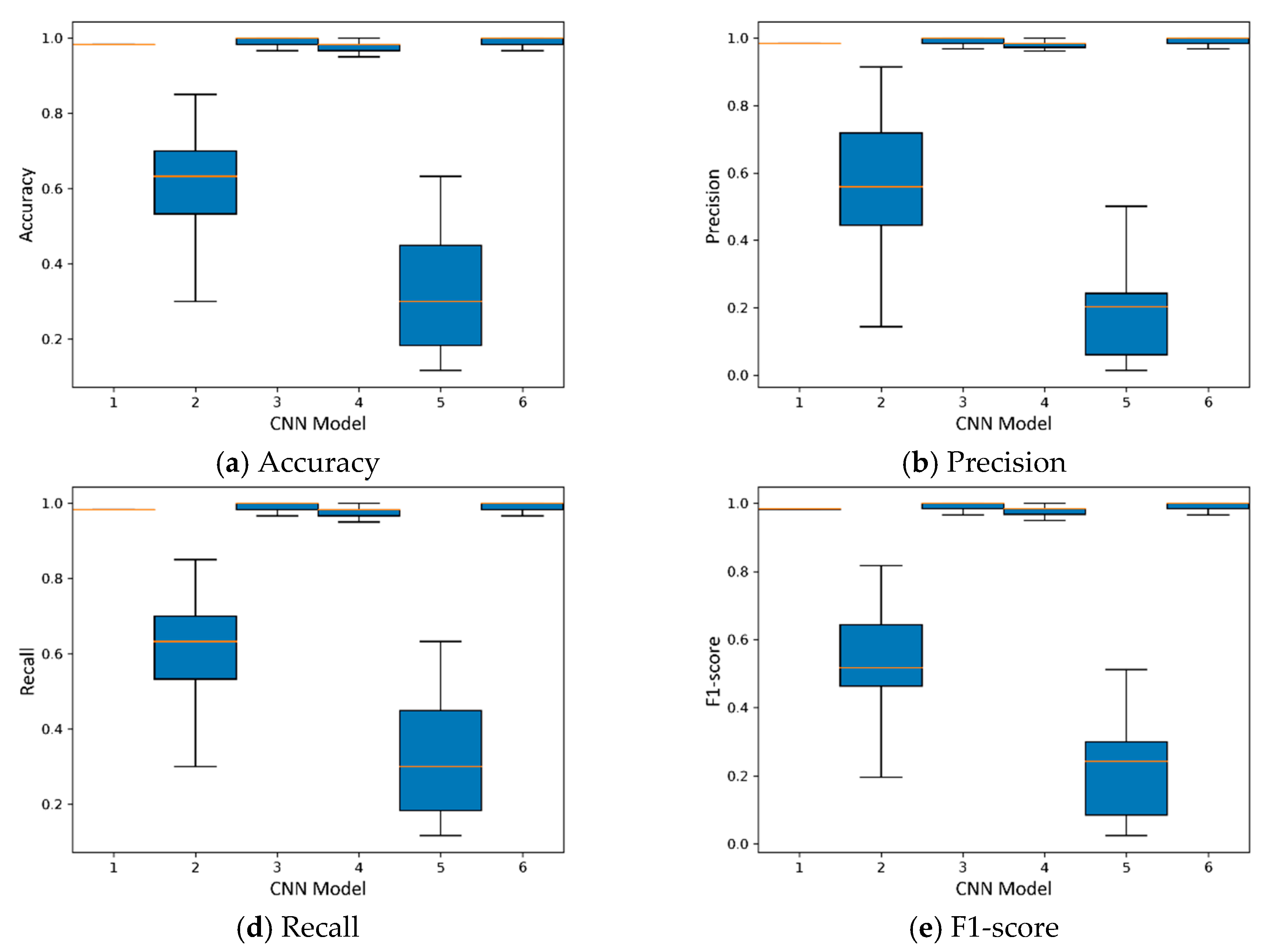
In this study, our primary objective is to compare the performance of various CNN models in the task of classifying pipeline signals into six distinct categories using a relatively small dataset. To accomplish this, we considered three crucial variables in our CNN models: the number of layers, kernel size, and activation function. Specifically, we trained six different CNN models with either 1 or 2 layers, a fixed kernel size of 10, and one of three activation functions: "relu", "sigmoid", or "tanh", as presented in Table 4.
In Figure 11, we showed an example as one of these CNN model candidates, which is a relatively shallow CNN architecture for classifying signals based on their waveform patterns. As mentioned above, our dataset consists of 150 samples, each with dimensions of 46 (space) x 1200 (time points), and no noise interference. While the dataset may be limited in size, we adopted a systematic approach to ensure reliability and validity of our results, accounting for constraints imposed by available data. First, we carefully pre-processed the dataset, normalizing the input features and removing any potential outliers or inconsistencies. To account for the small dataset size, we employed a stratified sampling approach to maintain the distribution of the six different types of pipeline signals when splitting the data into training and testing sets. In order to account for potential variations in model performance due to random initialization and other factors, we repeated the training process for each CNN model using a large number of iterations (1000) to strike a balance between computational feasibility and reliable performance estimation. This allowed us to observe the distribution of prediction accuracy across multiple runs, providing a robust estimation of each model's performance. Additionally, we employed cross-validation techniques, such as k-fold cross-validation, to further ensure the generalizability of our results, given the limited dataset size. This approach helps to mitigate the risk of overfitting and provides a more reliable estimation of model performance.
To ensure the reliability of our findings, we repeated the training process 1000 times for each model to examine the distribution of prediction accuracy. Figure 12 shows the prediction accuracy distribution for each CNN model. Our results showed that among the 6 CNN models tested, K-fold iteration test of model 3 and model 6 shows good robust properties and high accuracy. Here, we select CNN model 3, which is the one with 1 layer, kernel size of 10, and 'tanh' activation function. This CNN model consistently achieved the highest test accuracy across multiple repetitions of the training process.

4.2. The Impacts of classification accuracy due to sensing system to the Robustness of Data Classification

In this section, we compare the classification accuracy of two different acoustic sensing systems: a fully distributed acoustic sensing (DAS) system and a quasi-distributed acoustic sensing (qDAS) system. The DAS system provides continuous measurements along the entire length of the pipeline, while the qDAS system uses a limited number of sensors placed at discrete locations along the pipeline. We evaluate accuracy of these systems in classifying the condition of the pipeline based on six different defect types. It is noted that fully distributed sensing capability is currently limited for ultrasonic guided wave acoustic monitoring due to both the large gauge length in current standard commercial systems (~1m) and the limited acoustic frequency bandwidth (~10kHz). Nevertheless, we include hypothetical fully distributed sensing schemes for completeness.
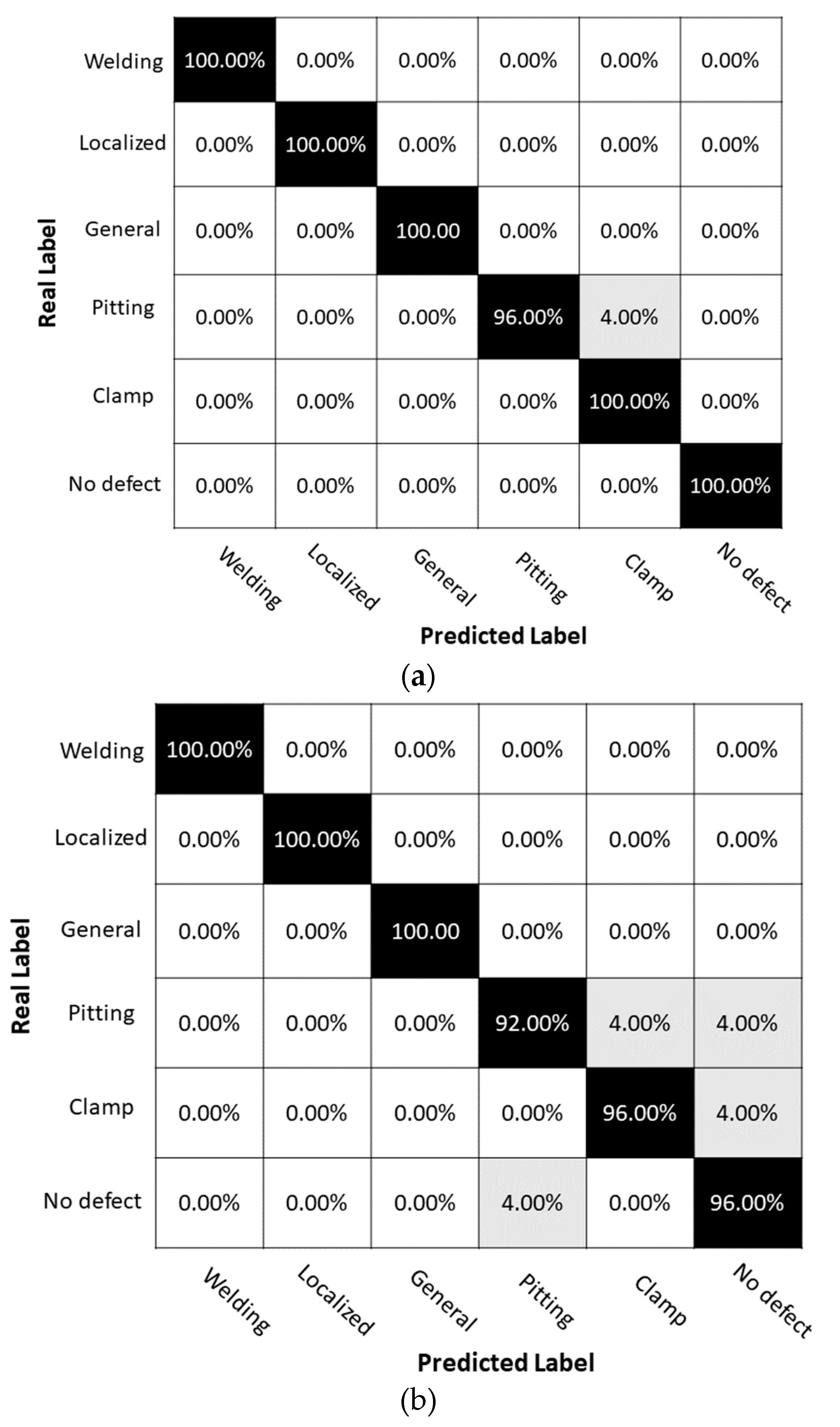
The confusion matrix and classification report for the DAS system without introduced noise indicates near-perfect accuracy for all defect types, with an overall accuracy of 99%. This suggests that the DAS system is highly effective in capturing the subtle differences in acoustic signals associated with different types of pipeline defects and can reliably classify the condition of the pipeline. However, limitations of existing DAS system prevent realization of such a distributed sensor network in practice.
In contrast, the confusion matrix and classification report for the quasi-distributed system indicate a slight reduction in accuracy across different defect types, with an overall accuracy of 96%. Specifically, in Figure 13, the system performs well in detecting general corrosion, localized corrosion, and weldings, but shows lower accuracy for clamps and pitting corrosion, which is likely due to the weaker associated scattering amplitudes and the relatively small spatial extent. Overall, these results suggest that the choice of sensing system can have a significant impact on accuracy of pipeline defect classification, with fully distributed systems providing higher accuracy compared to a quasi-distributed system in case of sensors without introduced noise. Sensor network optimization subject to realities of available performance of existing and emerging DAS and qDAS systems is an important topic for further investigation in future studies.
The results of the confusion matrices based on the fully distributed acoustic sensing system and the quasi-distributed acoustic sensing system show high classification accuracy for all pipeline features, as shown in Figure 13 and Table 5. Both systems correctly classified welding, localized corrosion, general corrosion, and no defect features with a precision and recall of 1.0. However, the results for pitting corrosion are lower than for other features, especially in the quasi-distributed sensing system, which has a recall of only 0.92. This can be attributed to the relatively weak amplitude of acoustic scattering associated with pitting corrosion and need for careful meshing to accurately capture this feature. It is essential to consider spatial resolution and sensitivity of sensing systems when detecting subtle features like pitting corrosion for accurate classification.
In summary, the results demonstrate the high classification accuracy of both fully distributed and quasi-distributed acoustic sensing systems for various pipeline features. While both systems show similar performance in detecting most types of defects, the detection of subtle features like pitting corrosion requires careful consideration of the modeling strategy in simulation and the spatial resolution of the sensing system.

4.3. Analysis of Classification Performance with noise effect

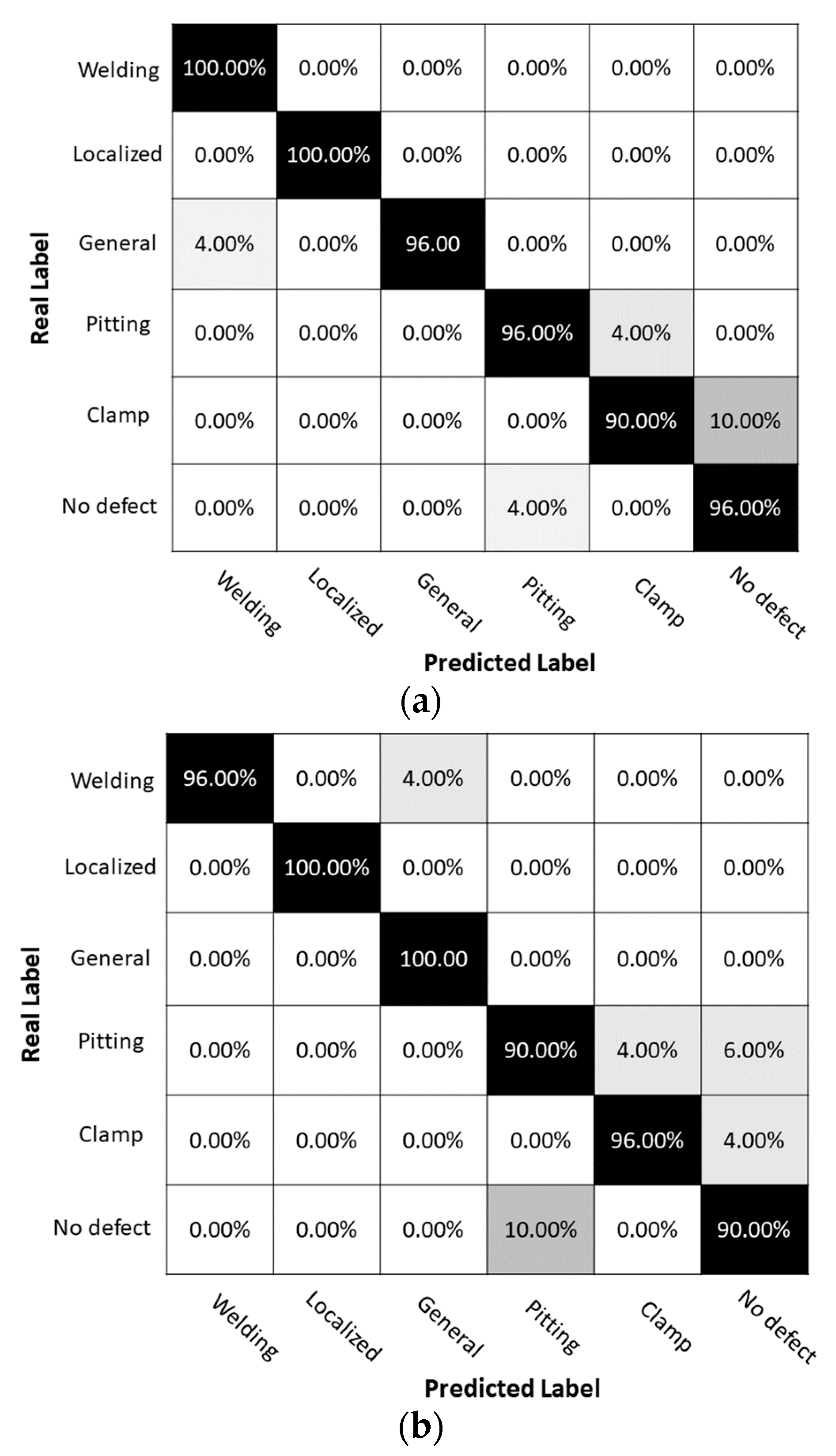
In this scenario we introduce noise, and again present two confusion matrices and classification reports for a fully distributed sensor system and a quasi-distributed sensor system (Figure 14). Sensor systems are affected by Gaussian noise with a signal-to-noise ratio of 9.63dB. The training dataset for CNN model is shown in Figure 9c,d.
The confusion matrices and classification reports show performance of sensor systems in classifying six different types of defects in a pipeline condition monitoring application. Comparing two confusion matrices, it is evident that the fully distributed system has a higher overall accuracy of 98% compared to quasi-distributed system's accuracy of 96%. This result is consistent with the fully distributed system demonstrating a higher precision and recall for most of the classes. For example, in Figure 14 and Table 6, the fully distributed system has a higher recall and precision for welding, localized corrosion and pitting corrosion, indicating that it correctly classified all instances belonging to those classes. In contrast, the quasi-distributed system has lower recall values for these classes, but there is improved performance for localized corrosion, general corrosion, and clamps. The fully distributed system also demonstrates a higher precision and recall for pitting. On the other hand, the quasi-distributed system showed improved performance for localized corrosion and general corrosion, which could be due to introduced noise affecting the fully distributed system more significantly than the quasi-distributed system. Detailed investigations of various sensor networks and configurations is an important aspect of optimizing the performance for a particular sensing objective of the sensor system.

4.4. Analysis of Classification Performance with noise and varying quasi-distributed sensing

In this study, we have explored the performance of quasi-distributed acoustic sensing systems compared to fully distributed systems. Quasi-distributed systems utilize a limited number of strategically placed sensors to provide a balance between performance and resource utilization. We conducted a comprehensive analysis of the prediction accuracy of quasi-distributed systems at different sensor configurations, investigating the impact of sensor segments on prediction accuracy.
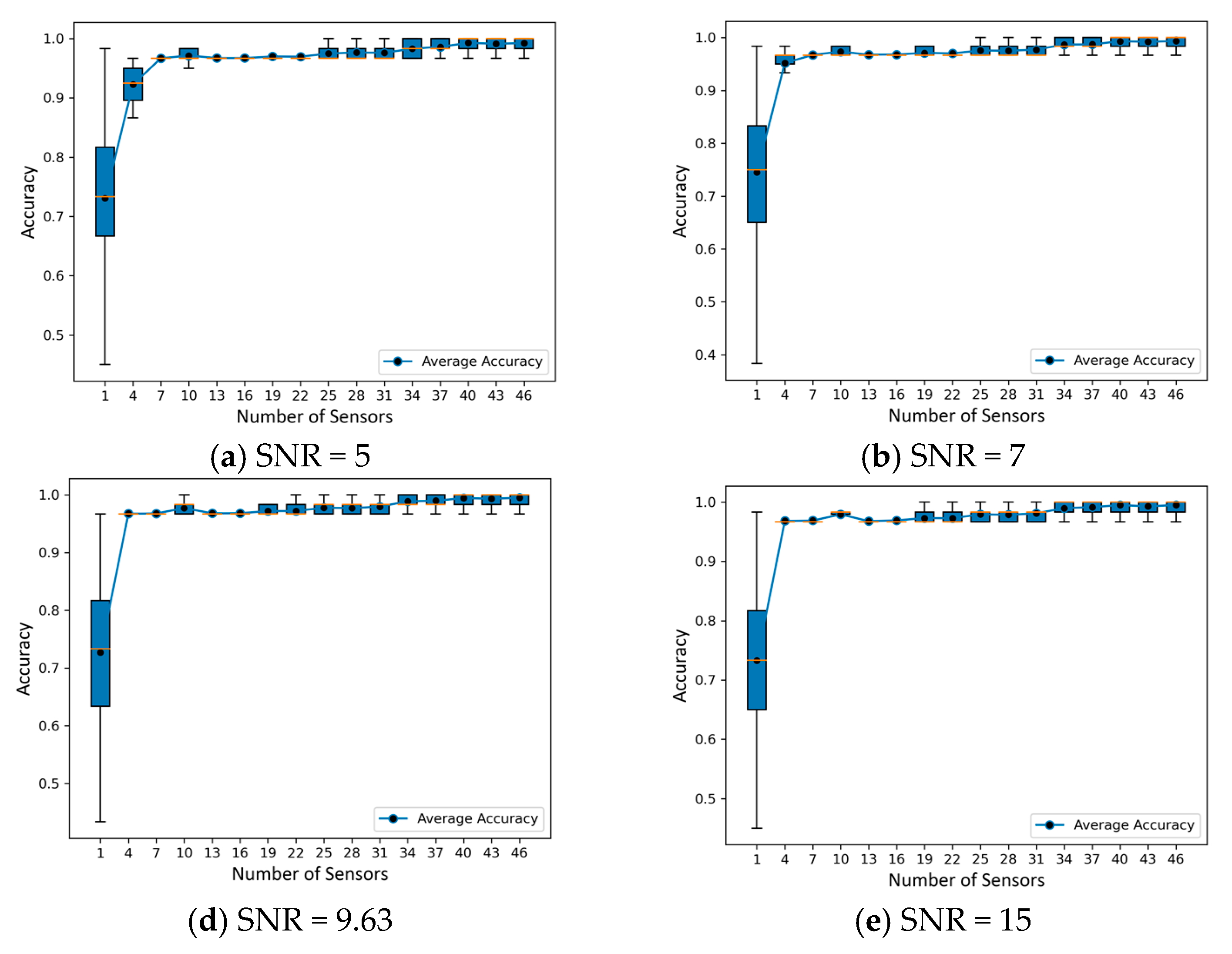
To investigate the machine learning classifier based on ultrasonic guided acoustic wave and fiber optic sensor fusion in more detail, we consider the possibility of varying positions and number of quasi-distributed sensors, which can be adjusted as shown in Figure 15 as red segments of 1, 4, 7, 10, 13, …,40, 43,46 (Continuous DAS) at an assumed noise level (SNR = 9.63dB). The configuration shows a fiber sensor that completely covers the pipe with measurement units evenly distributed along its length. To evaluate their performance, a series of tests were conducted, and the results are presented in Figure 16 and described in more detail below.
In addition to the total sensor segment numbers, we also explored the effect of sparse sampling on the acoustic sensing system's ability to withstand variations in sensor positioning. To evaluate the influence of sensor positioning at varying signal-to-noise ratios, we uniformly selected sensor segments for a specific sensor count and carried out the selection procedure 10000 times at a consistent noise level. We examined 16 distinct sensor numbers, ranging from 1 to 46, with sparse sampling playing a role in this selection. By creating boxplots of the dataset, we could visually appraise the distribution of prediction accuracy across various SNR and sensor numbers.
These visualizations offer insight into the performance fluctuations for each configuration and the system's ability to withstand alterations in sensor placement, with sparse sampling potentially contributing to the observed variations.
Figure 16 shows the impact of randomly down spatial sampling of received signals on classification prediction using a CNN under various levels of background noise. Our results demonstrate that as the level of background noise increases, the prediction accuracy becomes less stable, with an increased variance and more outliers. Furthermore, as the sampling size increases, the diversity of random sampling decreases, thereby improving the robustness of multiple predictions. However, increasing the spatial size of the sampling from 16 to 46 sensor segments did not significantly improve prediction accuracy, and in some cases, a specific small subset of the training set achieved higher accuracy than a fully sampled (46 sensor segments) training set.
Our findings reveal a trade-off between the number of sensor segments and prediction accuracy in the context of sparse sampling. However, this improvement becomes less significant as the number of sensors rises. Engineers can effectively tailor the design of quasi-distributed acoustic sensing systems for diverse applications by considering the signal-to-noise ratios and the number of sensors to achieve an optimum between predictive accuracy and reduced system intricacy and resource requirements using sparse sampling.
Furthermore, our findings align with the work of Jingwen Hu (2015) [34], who suggested that scene classification is composed of various scenes, ranging from simple to complex. Under hardware limitations, a random sampling strategy is recommended due to its robustness, good performance, and lower spatial complexity. However, random sampling may not meet specific requirements for sampling and lacks interpretability.
Down-sampling or sparse-sampling has been investigated in several studies, with consistent and interesting results. For instance, Cohen et al. (2018) [35] demonstrated the advantages of spatial and temporal down-sampling in event-based visual classification, while Kang et al. (2020) [36] examined the effects of uniform down-sampling in a deep CNN-based ground vibration monitoring scheme for MEMS sensed data. Similarly, Naagome et al. (2020) [37] showed that down-sampling increased the accuracy of RNNs in decoding gait from EEG data. These studies emphasize the importance of down-sampling as a preprocessing technique for improving the efficiency and accuracy of neural networks in various applications.
Our research can be extended in future work to optimize sparse sensor placement for classification and transition from sparse to dense sampling in compressed measurements [38]. By leveraging these insights, researchers and engineers can develop more cost-effective and efficient systems for a range of applications, while optimizing resource allocation.

5. Conclusions

This proof-of-concept study explores the potential of machine learning to accelerate the classification of damage size and orientation in guided-wave-based damage detection methods by combining ultrasound acoustic guided-wave-based non-destructive evaluation methods with distributed/quasi-distributed fiber optic acoustic sensing. The proposed learning framework provides an efficient workflow and identifies potential areas of improvement to develop a robust and experimentally validated framework. The investigation explores the impact of noise interference, mixed data types, and various features and corrosion defects on the efficacy of the proposed method.
This study has demonstrated the effectiveness of various CNN models in classifying pipeline signals into six distinct categories using a relatively small dataset. By carefully considering crucial variables in the CNN models, such as the number of layers, kernel size, and activation function, we were able to identify the most suitable model for this task. Specifically, the CNN model with 1 layer, a kernel size of 10, and 'tanh' activation function consistently achieved the highest test accuracy and exhibited good robust properties. Our systematic approach, which involved data preprocessing, stratified sampling, multiple training iterations, and cross-validation, ensured reliability and validity of results despite the limited dataset size. The findings of this study highlight the potential of CNNs as a powerful tool for classifying complex and noisy signals in real-world applications, while also emphasizing the importance of selecting the optimal model architecture and hyperparameters for achieving reliable and accurate classification performance.
The effect of noise on the prediction accuracy and sensor type (fully vs. quasi) of the sensor system was also investigated and shows significant differences in performance depending upon the specific assumptions. Our results show that fully distributed acoustic sensing systems exhibit higher overall accuracy and precision compared to quasi-distributed systems. In addition, the presence of experimentally relevant noise levels adversely impacted the overall accuracy and precision but did not preclude a high level of performance. The performance gap narrows specifically for detecting specific types of defects, with the quasi-distributed systems investigated being particularly effective for localized corrosion and general corrosion even in the presence of experimentally relevant noise.
Regarding the sensor location and its effect on accuracy, our results show that the performance of quasi-distributed acoustic sensing systems can be significantly affected by the sensor location and number. In general, the first few additional sensor elements improve classification framework accuracy significantly, and eventually the additional improvement becomes limited or even negligible for sufficiently large numbers of sensors approaching a fully distributed sensing configuration. Sparse sampling strategies can be effectively utilized to balance prediction accuracy with reduced system complexity and resource requirements. Understanding trade-offs and optimizing sensor networks is an area in which additional future work can be pursued, as understanding the impact of noise and sensor placement on the performance of fully distributed and quasi-distributed systems is critical to optimizing sensor network configurations and achieving reliable, robust, and accurate data classification in pipeline monitoring applications.

Acknowledgments

We express our profound gratitude to the United States Department of Energy for their generous financial support through the Natural Gas Infrastructure FWP (FWP-1022424). Additionally, we appreciate the funding assistance received from the Advanced Research Projects Agency-Energy (ARPA-E) REPAIR project, under contract DE-AR00001332, titled "Innervated Pipelines: A Novel Technological Platform for In-Situ Repair and Embedded Intelligence." Furthermore, we acknowledge the financial backing from the Nuclear Energy University Program (NEUP) project, under contract DE-NE0009210, entitled "Integration of Distributed Fiber Optics, Acoustic Nondestructive Evaluation, and Physics-Based Artificial Intelligence for Spent Fuel Monitoring." The author also recognizes the invaluable technical contributions made by research scientists at the National Energy Technology Laboratory (NETL), as well as Sandeep Reddy's insightful recommendations on data sampling methodologies.

References

  1. Rezaei, D.; Taheri, F. A Novel Application of a Laser Doppler Vibrometer in a Health Monitoring System. J. Mech. Mater. Struct. 2010, 5, 289–304. [Google Scholar] [CrossRef]
  2. Pallarés, F.J.; Betti, M.; Bartoli, G.; Pallarés, L. Structural health monitoring (SHM) and Nondestructive testing (NDT) of slender masonry structures: A practical review. Constr. Build. Mater. 2021, 297, 123768. [Google Scholar] [CrossRef]
  3. P. R. Ohodnicki et al., “Fusion of Distributed Fiber Optic Sensing, Acoustic NDE, and Artificial Intelligence for Infrastructure Monitoring,” in 27th International Conference on Optical Fiber Sensors, in Technical Digest Series. Alexandria, Virginia: Optica Publishing Group, Aug. 2022, p. Tu1.1. [CrossRef]
  4. Zhang, P.; Venketeswaran, A.; Wright, R.; Denslow, K.; Babaee, H.; Ohodnicki, P.R., Jr. Feature extraction for pipeline defects inspection based upon distributed acoustic fiber optic sensing data. In Fiber Optic Sensors and Applications XVIII; SPIE, 2022; pp. 14–29.
  5. Stajanca, P.; Chruscicki, S.; Homann, T.; Seifert, S.; Schmidt, D.; Habib, A. Detection of Leak-Induced Pipeline Vibrations Using Fiber—Optic Distributed Acoustic Sensing. Sensors 2018, 18, 2841. [Google Scholar] [CrossRef]
  6. Lu, P.; Chen, Q. Fiber Bragg grating sensor for simultaneous measurement of flow rate and direction. Meas Sci Technol 2008, 19, 125302. [Google Scholar] [CrossRef]
  7. Gao, X.-X.; Cui, J.-M.; Ai, M.-Z.; Huang, Y.-F.; Li, C.-F.; Guo, G.-C. An Acoustic Sensor Based on Active Fiber Fabry–Pérot Microcavities. Sensors 2020, 20. [Google Scholar] [CrossRef]
  8. Lalam, N.; Wright, R.F.; Ohodnicki, P.R. Pipeline monitoring based on ultrasonic guided acoustic wave and fiber optic sensor fusion. In Proceedings of the Fiber Optic Sensors and Applications XVIII; Lieberman, R.A., Sanders, G.A., Scheel, I.U., Eds.; SPIE, 2022; Vol. 12105; p. 1210509. [Google Scholar]
  9. Choban, T.; Zhirnov, A.; Stepanov, K.; Khan, R.; Koshelev, K.; Pnev, A.; Karasik, V. Sensitivity of Distributed Acoustic Sensor Based on Sagnac Interferometer. presented at the 2022 International Conference Laser Optics (ICLO); IEEE; 2022; pp. 01–01. [Google Scholar]
  10. Zhu, W.; Li, D.; Liu, J.; Wang, R. Membrane-free acoustic sensing based on an optical fiber Mach–Zehnder interferometer. Appl. Opt. 2020, 59, 1775–1779. [Google Scholar] [CrossRef] [PubMed]
  11. Tong, Y.; Dong, H.; Wang, Y.; Sun, W.; Wang, X.; Bai, J.; Yuan, H.; Zhu, N.; Liu, J. Distributed incomplete polarization-OTDR based on polarization maintaining fiber for multi-event detection. Opt. Commun. 2015, 357, 41–44. [Google Scholar] [CrossRef]
  12. Liokumovich, L.B.; Ushakov, N.A.; Kotov, O.I.; Bisyarin, M.A.; Hartog, A.H. Fundamentals of optical fiber sensing schemes based on coherent optical time domain reflectometry: Signal model under static fiber conditions. J. Light. Technol. 2015, 33, 3660–3671. [Google Scholar] [CrossRef]
  13. Shatalin, S.V.; Treschikov, V.N.; Rogers, A.J. Interferometric optical time-domain reflectometry for distributed optical-fiber sensing. Appl. Opt. 1998, 37, 5600–5604. [Google Scholar] [CrossRef] [PubMed]
  14. Lu, P.; Lalam, N.; Badar, M.; Liu, B.; Chorpening, B.T.; Buric, M.P.; Ohodnicki, P.R. Distributed optical fiber sensing: Review and perspective. Appl. Phys. Rev. 2019, 6, 041302. [Google Scholar] [CrossRef]
  15. Venketeswaran, A.; Lalam, N.; Wuenschell, J.; Ohodnicki, P.R.; Badar, M.; Chen, K.P.; Lu, P.; Duan, Y.; Chorpening, B.; Buric, M. Recent Advances in Machine Learning for Fiber Optic Sensor Applications. Adv. Intell. Syst. 2022, 4, 2100067. [Google Scholar] [CrossRef]
  16. Rizzo, P.; di Scalea, F.L. Feature Extraction for Defect Detection in Strands by Guided Ultrasonic Waves. Struct. Health Monit. 2006, 5, 297–308. [Google Scholar] [CrossRef]
  17. Sun, Q.; Feng, H.; Yan, X.; Zeng, Z. Recognition of a Phase-Sensitivity OTDR Sensing System Based on Morphologic Feature Extraction. Sensors 2015, 15, 15179–15197. [Google Scholar] [CrossRef] [PubMed]
  18. Gardner, P.; Liu, X.; Worden, K. On the application of domain adaptation in structural health monitoring. Mech. Syst. Signal Process. 2020, 138, 106550. [Google Scholar] [CrossRef]
  19. Gazis, D.C. Three-dimensional investigation of the propagation of waves in hollow circular cylinders. I. Analytical foundation. J. Acoust. Soc. Am. 1959, 31, 568–573. [Google Scholar] [CrossRef]
  20. Giurgiutiu, V. Structural health monitoring: with piezoelectric wafer active sensors; Elsevier, 2007; ISBN 0-08-055679-5.
  21. Ahmed, M.N. A study of guided ultrasonic wave propagation characteristics in thin aluminum plate for damage detection; The University of Toledo, 2014; ISBN 1-321-09923-1.
  22. SU, Z.; Ye, L. 7 - Lamb wave-based quantitative identification of delamination in composite laminates. In Delamination Behaviour of Composites; Sridharan, S., Ed.; Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing, 2008; pp. 169–216 ISBN 978-1-84569-244-5.
  23. Gresil, M.; Shen, Y.; Giurgiutiu, V. Predictive modeling of ultrasonics SHM with PWAS transducers. In Proceedings of the 8th international workshop on structural health monitoring; 2011. [Google Scholar]
  24. Yan, S.; Li, Y.; Zhang, S.; Song, G.; Zhao, P. Pipeline Damage Detection Using Piezoceramic Transducers: Numerical Analyses with Experimental Validation. Sensors 2018, 18. [Google Scholar] [CrossRef] [PubMed]
  25. Zhang, Z.; Pan, H.; Wang, X.; Lin, Z. Machine Learning-Enriched Lamb Wave Approaches for Automated Damage Detection. Sensors 2020, 20, 1790. [Google Scholar] [CrossRef] [PubMed]
  26. Mahajan, H.; Banerjee, S. A machine learning framework for guided wave-based damage detection of rail head using surface-bonded piezo-electric wafer transducers. Mach. Learn. Appl. 2022, 7, 100216. [Google Scholar] [CrossRef]
  27. Lowe, P.S.; Sanderson, R.; Pedram, S.K.; Boulgouris, N.V.; Mudge, P. Inspection of Pipelines Using the First Longitudinal Guided Wave Mode. Phys. Procedia 2015, 70, 338–342. [Google Scholar] [CrossRef]
  28. by Gabriel, J. DeSalvo and John A. Swanson ANSYS engineering analysis system user’s manual; Houston, Pa. : Swanson Analysis Systems, 1985, 1985. [Google Scholar]
  29. Moser, F.; Jacobs, L.J.; Qu, J. Modeling elastic wave propagation in waveguides with the finite element method. NDT E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]
  30. Wilcox, P.D.; Lowe, M.J.S.; Cawley, P. Mode and Transducer Selection for Long Range Lamb Wave Inspection. J. Intell. Mater. Syst. Struct. 2001, 12, 553–565. [Google Scholar] [CrossRef]
  31. Dean, T.; Cuny, T.; Hartog, A.H. The effect of gauge length on axially incident P-waves measured using fibre optic distributed vibration sensing. Geophys. Prospect. 2017, 65, 184–193. [Google Scholar] [CrossRef]
  32. Dean, T.; Cuny, T.; Hartog, A.H. The effect of gauge length on axially incident P-waves measured using fibre optic distributed vibration sensing. Geophys. Prospect. 2017, 65, 184–193. [Google Scholar] [CrossRef]
  33. Ohodnicki, P.R.; Zhang, P.; Lalam, N.; Karki, D.; Venketeswaran, A.; Babaee, H.; Wright, R. Fusion of Distributed Fiber Optic Sensing, Acoustic NDE, and Artificial Intelligence for Infrastructure Monitoring. In Proceedings of the 27th International Conference on Optical Fiber Sensors; Optica Publishing Group: Alexandria, Virginia, 2022; p. 1. [Google Scholar]
  34. Ölçer, İ.; Öncü, A. Adaptive temporal matched filtering for noise suppression in fiber optic distributed acoustic sensing. Sensors 2017, 17, 1288. [Google Scholar] [CrossRef] [PubMed]
  35. N. Lalam; P. S. Westbrook; J. Li; P. Lu; M. P. Buric Phase-Sensitive Optical Time Domain Reflectometry With Rayleigh Enhanced Optical Fiber. IEEE Access 2021, 9, 114428–114434. [Google Scholar] [CrossRef]
  36. J. Hu; G. -S. Xia; F. Hu; H. Sun; L. Zhang A comparative study of sampling analysis in scene classification of high-resolution remote sensing imagery. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS); 2015; pp. 2389–2392. [CrossRef]
  37. G. Cohen; S. Afshar; G. Orchard; J. Tapson; R. Benosman; A. van Schaik Spatial and Temporal Downsampling in Event-Based Visual Classification. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5030–5044. [CrossRef] [PubMed]
  38. J.-M. Kang; I. -M. Kim; S. Lee; D. -W. Ryu; J. Kwon A Deep CNN-Based Ground Vibration Monitoring Scheme for MEMS Sensed Data. IEEE Geosci. Remote Sens. Lett. 2020, 17, 347–351. [CrossRef]
  39. Nakagome, S.; Luu, T.P.; He, Y.; Ravindran, A.S.; Contreras-Vidal, J.L. An empirical comparison of neural networks and machine learning algorithms for EEG gait decoding. Sci. Rep. 2020, 10, 4372. [Google Scholar] [CrossRef]
  40. Brunton, B.W.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Sparse Sensor Placement Optimization for Classification. SIAM J. Appl. Math. 2016, 76, 2099–2122. [Google Scholar] [CrossRef]
Preprints 71861 g001
Figure 1. Dispersion curves for a 0.5 inches thickness and 12 inches outside diameter pipeline model a) group velocity; and b) phase velocity.
Figure 1. Dispersion curves for a 0.5 inches thickness and 12 inches outside diameter pipeline model a) group velocity; and b) phase velocity.
Preprints 71861 g001
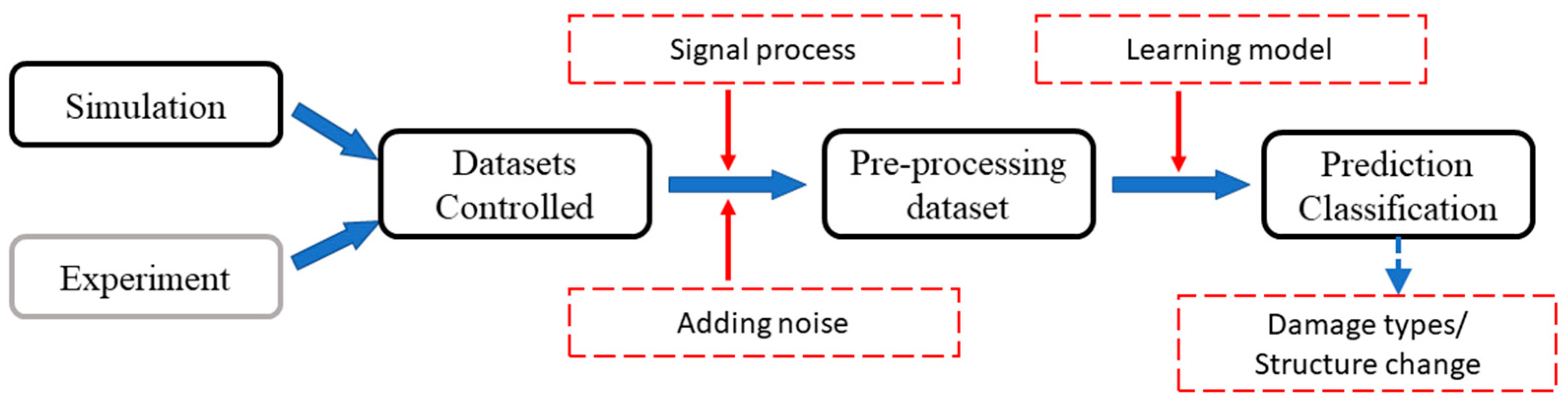
Preprints 71861 g002
Figure 2. The framework for the machine learning-enhanced method of structure change detection consists of the above components.
Figure 2. The framework for the machine learning-enhanced method of structure change detection consists of the above components.
Preprints 71861 g002
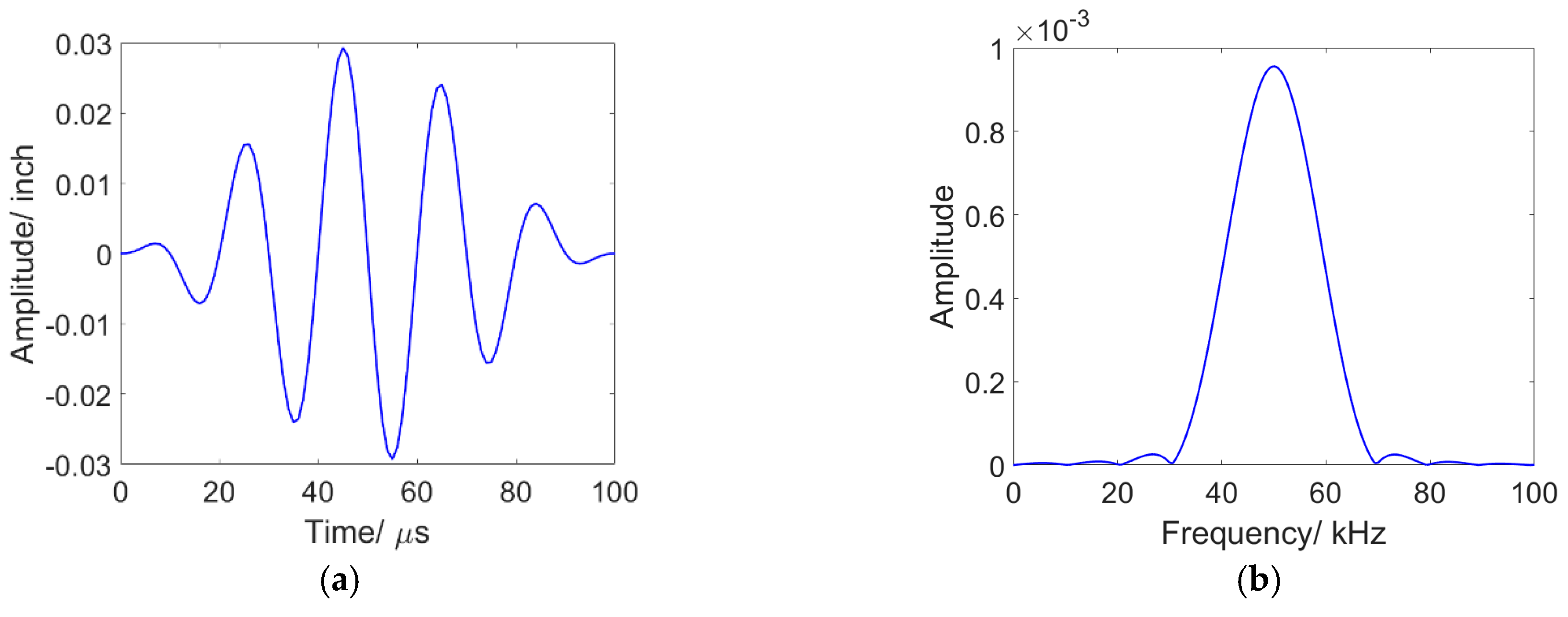
Preprints 71861 g003
Figure 3. The excitation signal assumed in the simulation; a) The waveform in the time domain; b) The corresponding wave in the frequency domain.
Figure 3. The excitation signal assumed in the simulation; a) The waveform in the time domain; b) The corresponding wave in the frequency domain.
Preprints 71861 g003
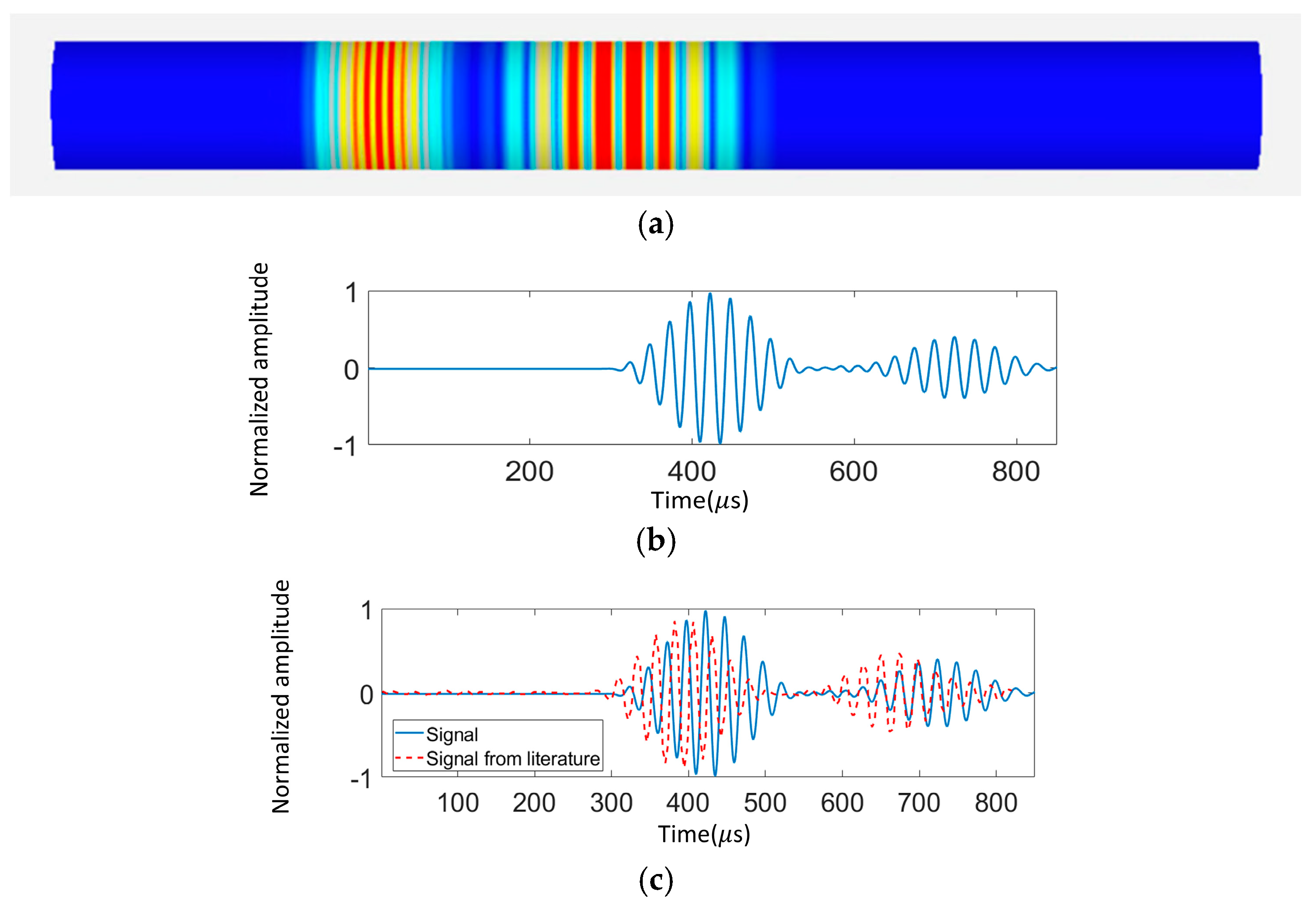
Preprints 71861 g004
Figure 4. Comparison of the literature result [28] and the excitation signal dispersion from the proposed simulation work. (a) Excitation signal dispersion contour from the proposed simulation, (b) Dispersive time domain signal from the proposed simulation, (c) Comparison of the dispersive signals from the literature [24] and the proposed simulation. (Excitation: (a, b) A five-cycle Hann-windowed 50kHz signal; (c) A ten-cycle Hann-windowed 40kHz signal).
Figure 4. Comparison of the literature result [28] and the excitation signal dispersion from the proposed simulation work. (a) Excitation signal dispersion contour from the proposed simulation, (b) Dispersive time domain signal from the proposed simulation, (c) Comparison of the dispersive signals from the literature [24] and the proposed simulation. (Excitation: (a, b) A five-cycle Hann-windowed 50kHz signal; (c) A ten-cycle Hann-windowed 40kHz signal).
Preprints 71861 g004
Preprints 71861 g005
Figure 5. Illustration of pipe structure type classification: (a) Clamp (~inch); (b) Welding (~inch); (c) Localized Corrosion(~inch); (d) General Corrosion(~feet); (e) Pitting Corrosion (Radius: ~200µm).
Figure 5. Illustration of pipe structure type classification: (a) Clamp (~inch); (b) Welding (~inch); (c) Localized Corrosion(~inch); (d) General Corrosion(~feet); (e) Pitting Corrosion (Radius: ~200µm).
Preprints 71861 g005
Preprints 71861 g006
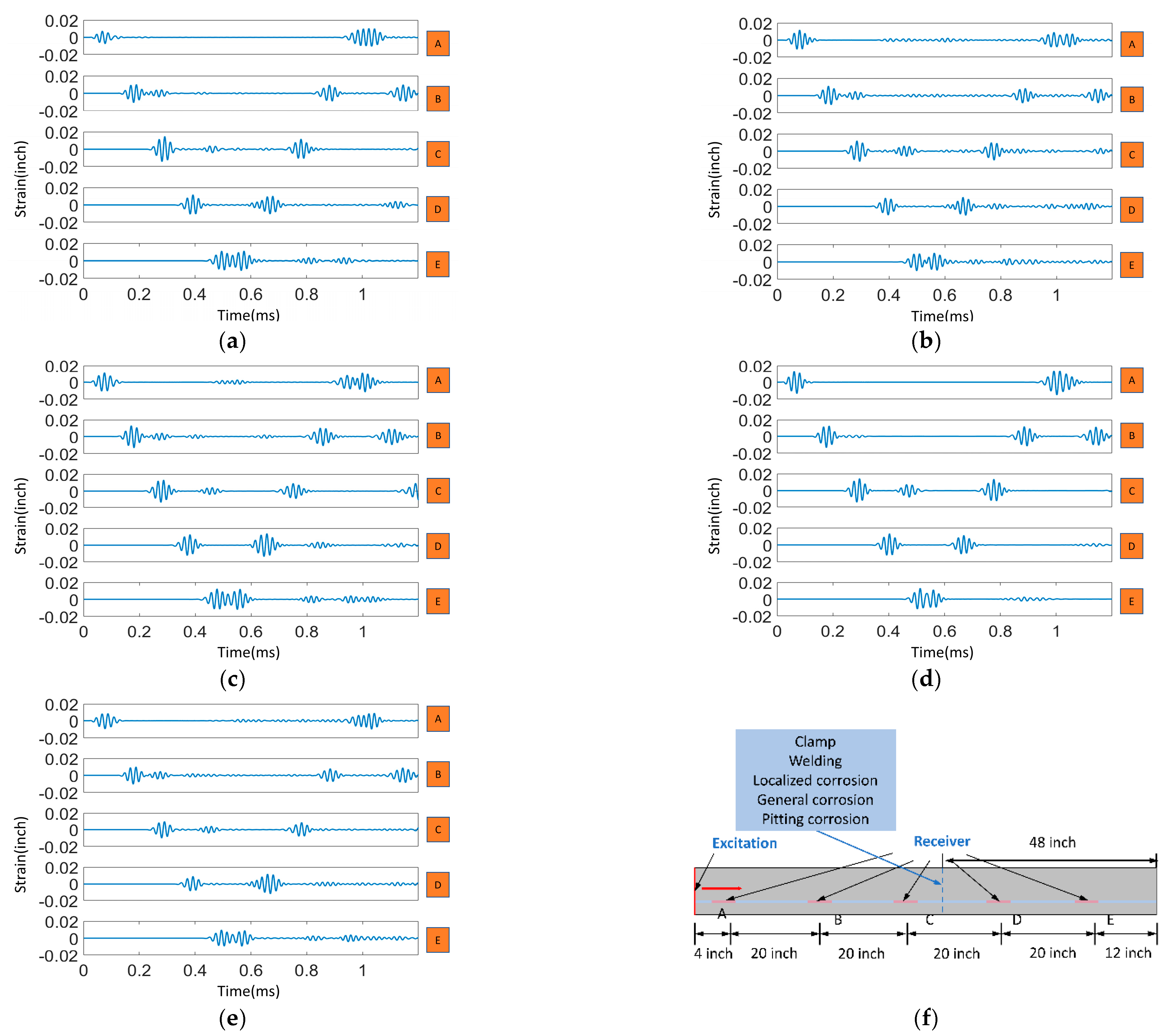
Figure 6. The time-domain acoustic waveforms from 5 sensors (A-E) by the excitation and the typical reflected signals of the five types of damage: (a) echoes of clamp; (b) echoes of welding; (c) echoes of localized corrosion; (d) echoes of general corrosion; (e) echoes of pitting corrosion; and (f) the schematic diagram of fiber optic acoustic sensors positions for pipeline structure monitoring.
Figure 6. The time-domain acoustic waveforms from 5 sensors (A-E) by the excitation and the typical reflected signals of the five types of damage: (a) echoes of clamp; (b) echoes of welding; (c) echoes of localized corrosion; (d) echoes of general corrosion; (e) echoes of pitting corrosion; and (f) the schematic diagram of fiber optic acoustic sensors positions for pipeline structure monitoring.
Preprints 71861 g006
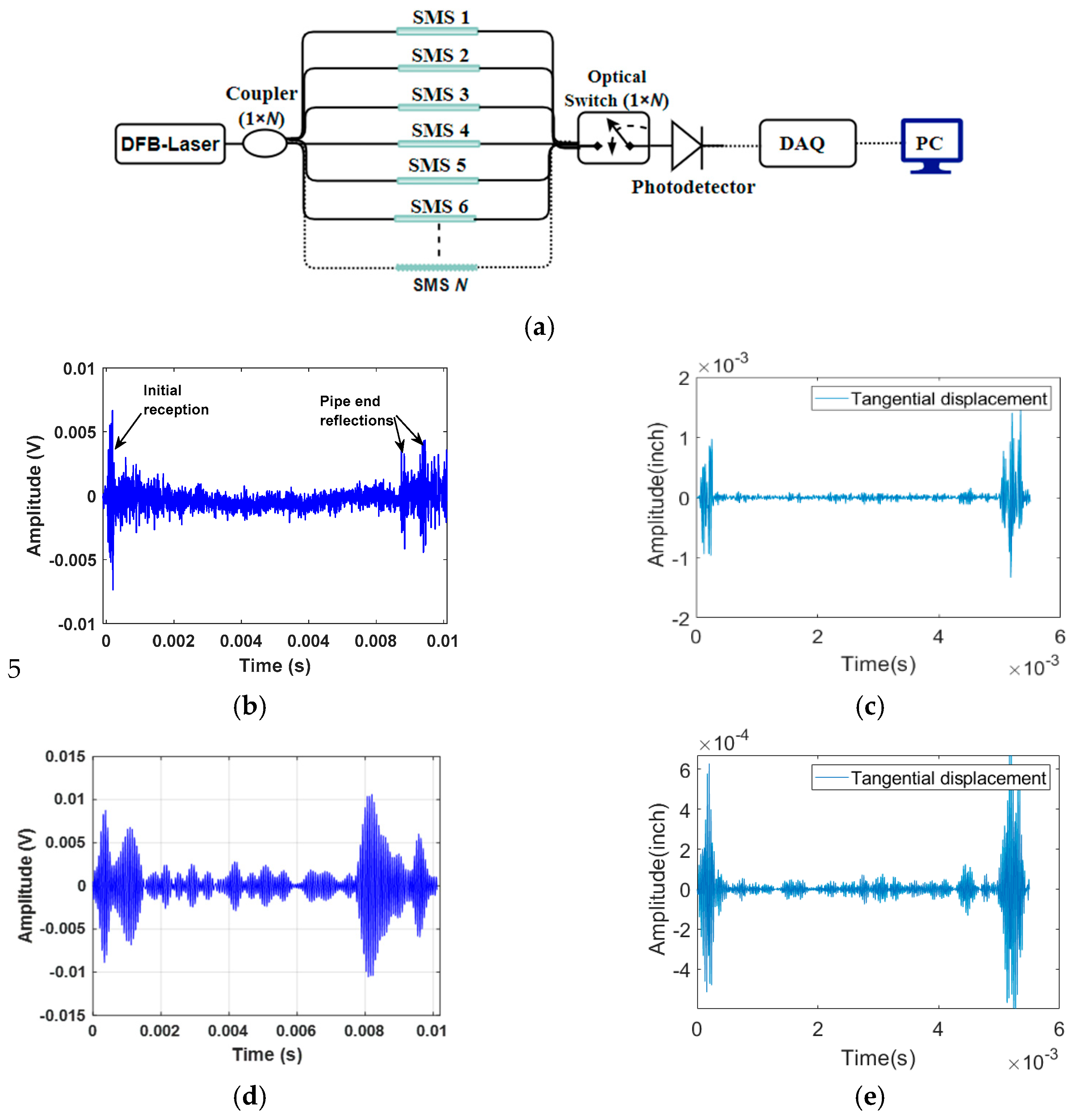
Preprints 71861 g007
Figure 7. Comparative Analysis of Experimental and Simulated Results for a 32 kHz Quasi-Distributed SMS Fiber Sensor: (a) Multiplexed Interrogator Schematic; (b) Received Signal with 32 kHz Excitation; (c) Simulated 32 kHz, 5-Cycle Sinusoidal Signal for Validation at Same Location as Experiment; (d) Time-Domain Signal after Passband Filtering (26-36 kHz); (e) Filtered Simulated 32 kHz, 5-Cycle Sinusoidal Signal (26-36 kHz).
Figure 7. Comparative Analysis of Experimental and Simulated Results for a 32 kHz Quasi-Distributed SMS Fiber Sensor: (a) Multiplexed Interrogator Schematic; (b) Received Signal with 32 kHz Excitation; (c) Simulated 32 kHz, 5-Cycle Sinusoidal Signal for Validation at Same Location as Experiment; (d) Time-Domain Signal after Passband Filtering (26-36 kHz); (e) Filtered Simulated 32 kHz, 5-Cycle Sinusoidal Signal (26-36 kHz).
Preprints 71861 g007
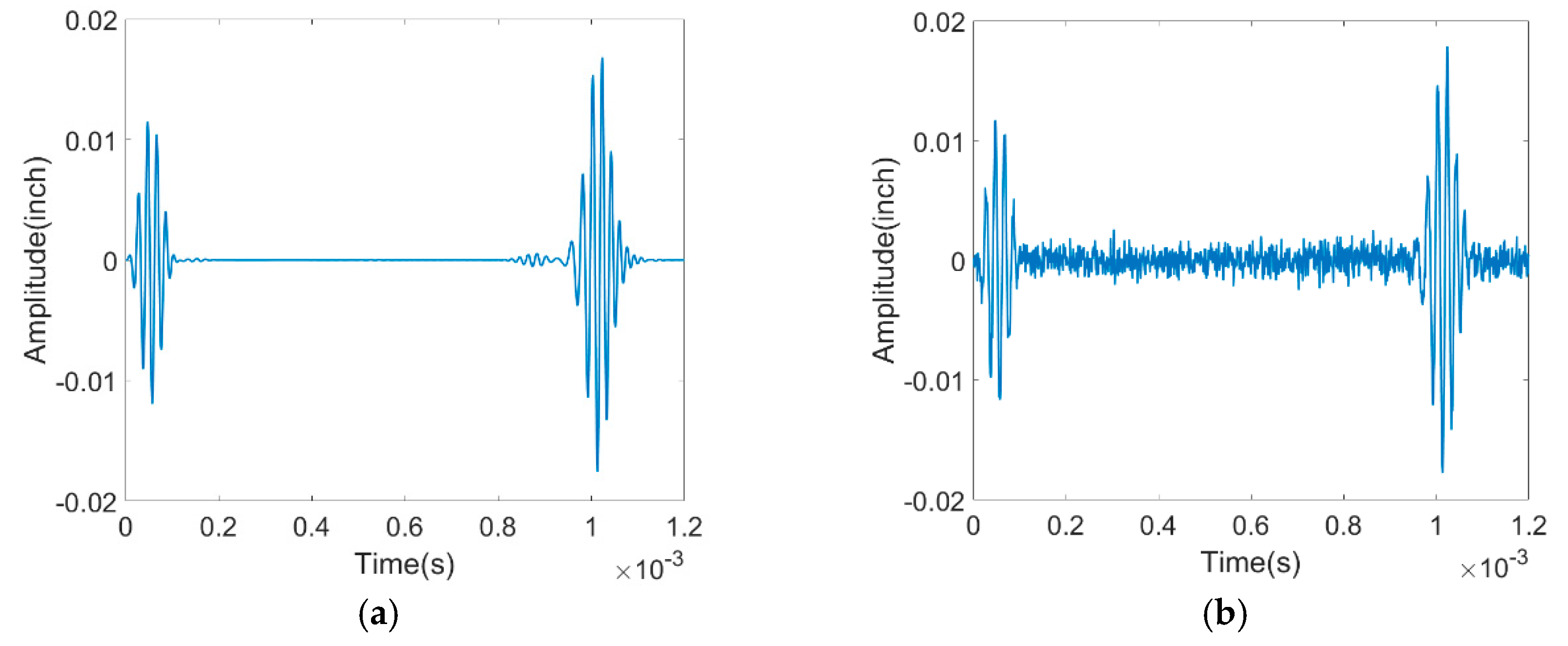
Preprints 71861 g008
Figure 8. (a) Simulated Pure Signal - Original signal without any noise interference, (b) Signal with 9.63 dB Noise Added - The pure signal is altered by introducing a 9.63 dB noise component to simulate real-world conditions.
Figure 8. (a) Simulated Pure Signal - Original signal without any noise interference, (b) Signal with 9.63 dB Noise Added - The pure signal is altered by introducing a 9.63 dB noise component to simulate real-world conditions.
Preprints 71861 g008
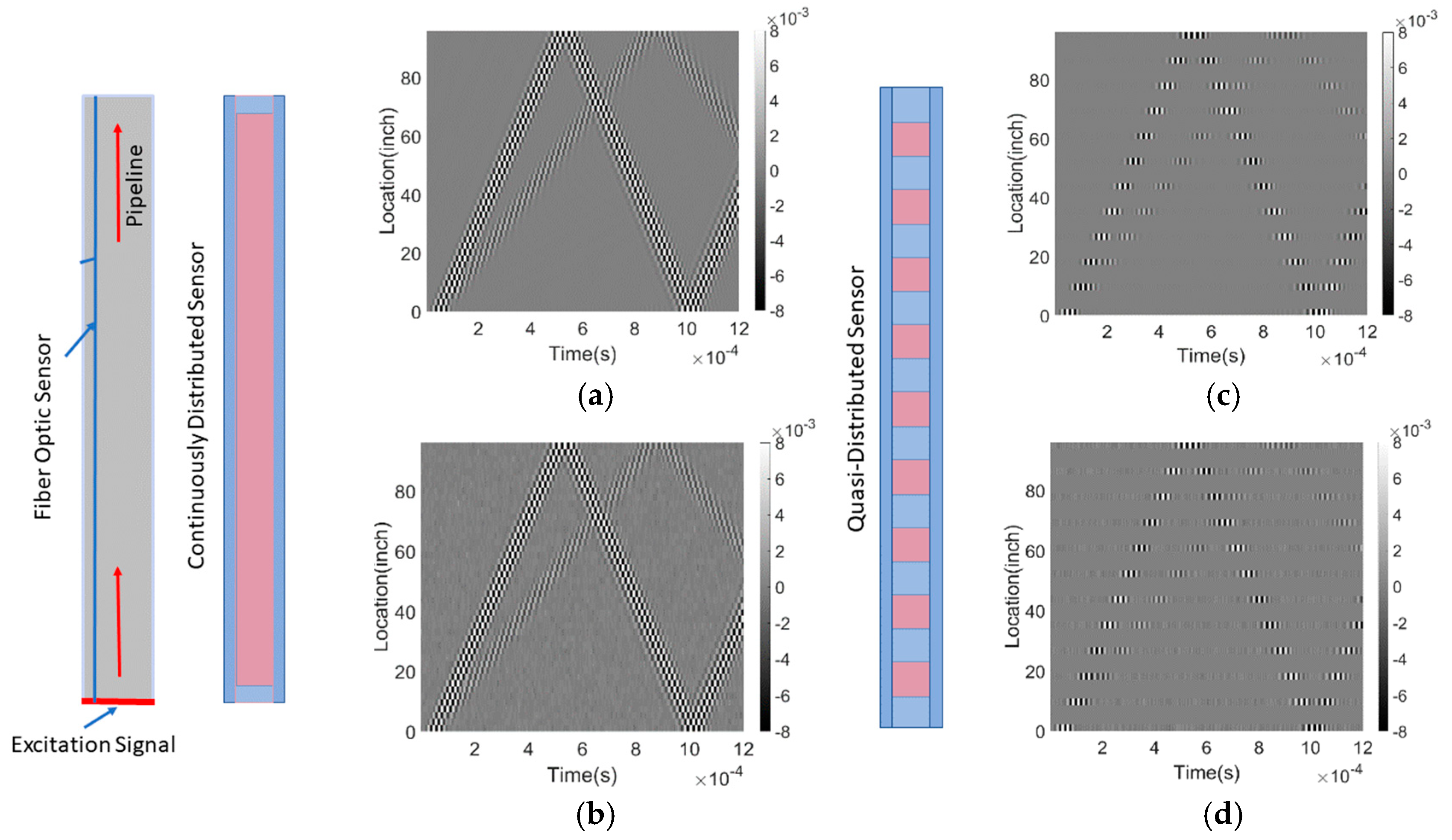
Preprints 71861 g009
Figure 9. Resulting signal for a healthy pipeline based on distributed sensing system (a) without noise and (b) with Gaussian noise (SNR=9.63dB); and the resulting signal based on quasi-distributed sensing system(12 signal channels) (c) without noise and (d) with Gaussian noise (SNR=9.63dB). The resulting signal is shown as a 2D time-space plot, where the x-axis represents time, and the y-axis represents the length of the pipeline.
Figure 9. Resulting signal for a healthy pipeline based on distributed sensing system (a) without noise and (b) with Gaussian noise (SNR=9.63dB); and the resulting signal based on quasi-distributed sensing system(12 signal channels) (c) without noise and (d) with Gaussian noise (SNR=9.63dB). The resulting signal is shown as a 2D time-space plot, where the x-axis represents time, and the y-axis represents the length of the pipeline.
Preprints 71861 g009
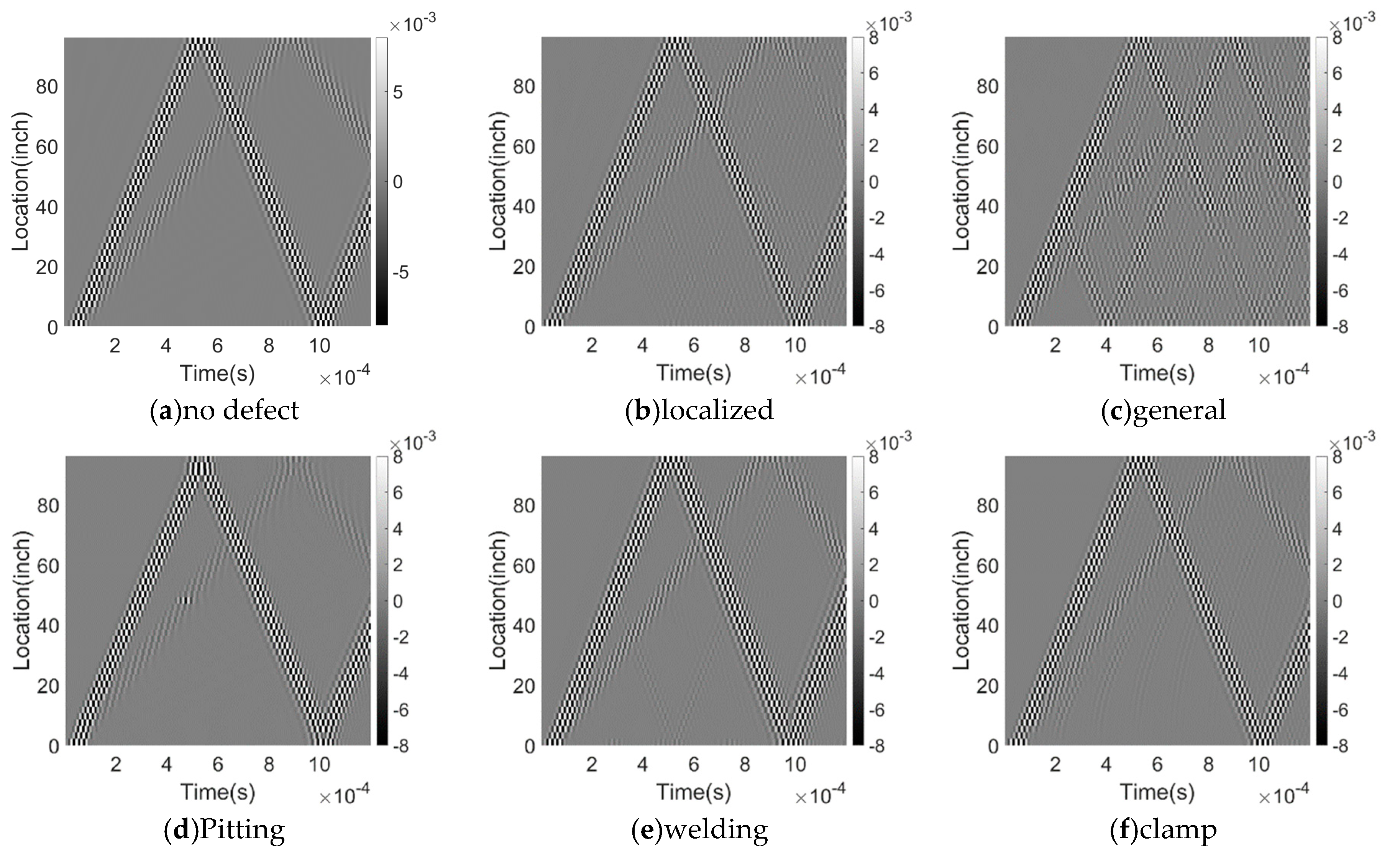
Preprints 71861 g010
Figure 10. Time-space plots for a pipeline with (a) no defect, (b) localized corrosion, (c) general corrosion, (d) pitting corrosion, (e) welding, and (f) clamp. Each plot shows the resulting signal from a different type of defect or feature. The x-axis represents time, and the y-axis represents the spatial location along the pipeline. The color scale indicates the amplitude of the signal.
Figure 10. Time-space plots for a pipeline with (a) no defect, (b) localized corrosion, (c) general corrosion, (d) pitting corrosion, (e) welding, and (f) clamp. Each plot shows the resulting signal from a different type of defect or feature. The x-axis represents time, and the y-axis represents the spatial location along the pipeline. The color scale indicates the amplitude of the signal.
Preprints 71861 g010
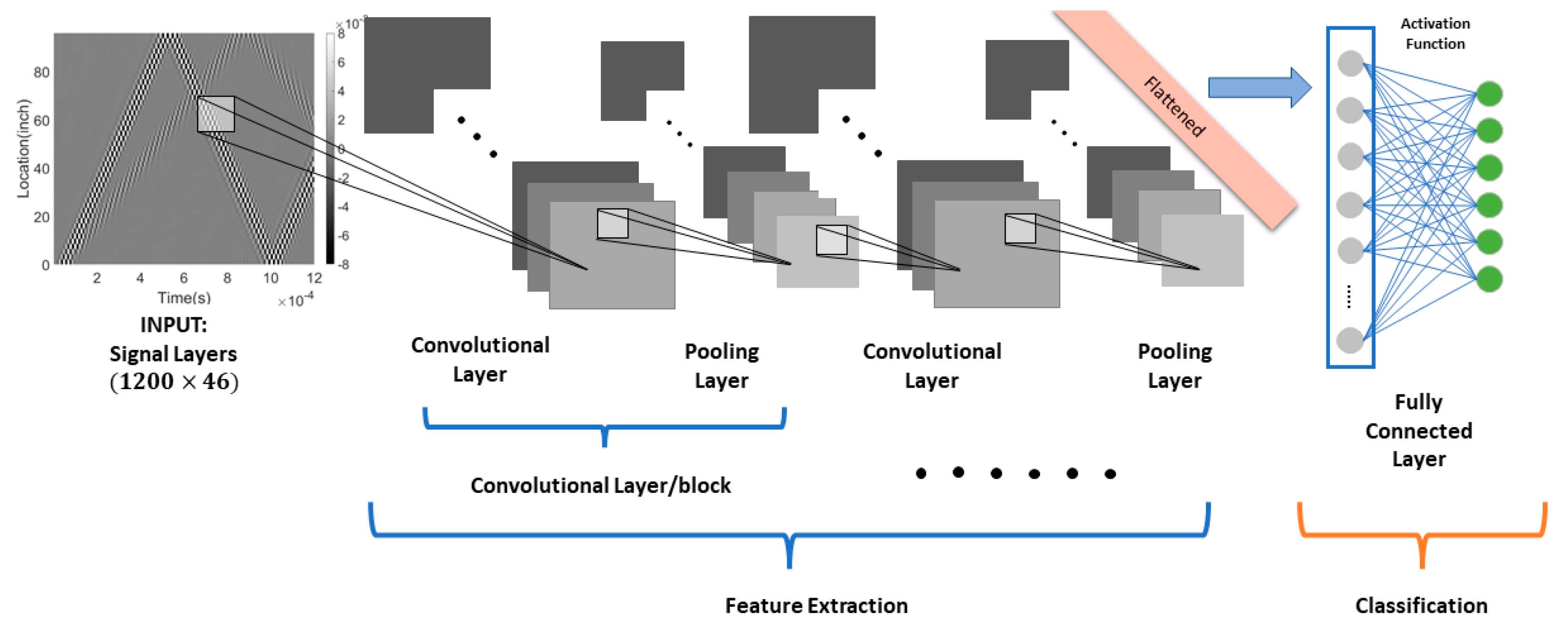
Preprints 71861 g011
Figure 11. Two-Layer CNN for Signal Classification: Input data is a 2D tensor of size (batch size, 1200, 46). The network consists of two convolutional layers (16 and 32 filters, kernel size of 10), followed by max pooling layers (pool size of 2), two fully connected layers (64 and 6 neurons) for multi-class classification.
Figure 11. Two-Layer CNN for Signal Classification: Input data is a 2D tensor of size (batch size, 1200, 46). The network consists of two convolutional layers (16 and 32 filters, kernel size of 10), followed by max pooling layers (pool size of 2), two fully connected layers (64 and 6 neurons) for multi-class classification.
Preprints 71861 g011
Preprints 71861 g012
Figure 12. Comparing test accuracy distributions of 6 CNN models with different layer number and activation function for pipeline signal classification.
Figure 12. Comparing test accuracy distributions of 6 CNN models with different layer number and activation function for pipeline signal classification.
Preprints 71861 g012
Preprints 71861 g013
Figure 13. matrix for pipeline condition classification using (a) fully distributed acoustic sensing (DAS) system and (b) quasi-distributed acoustic sensing (qDAS) system with 12 sensor segments. The confusion matrix shows the number of true positives, true negatives, false positives, and false negatives for each pipeline condition class. The classification accuracy for fully DAS system is 99% and for quasi-DAS system is 96%. The results suggest that the fully DAS system achieved higher classification accuracy compared to the qDAS system, particularly in distinguishing between different types of corrosion.
Figure 13. matrix for pipeline condition classification using (a) fully distributed acoustic sensing (DAS) system and (b) quasi-distributed acoustic sensing (qDAS) system with 12 sensor segments. The confusion matrix shows the number of true positives, true negatives, false positives, and false negatives for each pipeline condition class. The classification accuracy for fully DAS system is 99% and for quasi-DAS system is 96%. The results suggest that the fully DAS system achieved higher classification accuracy compared to the qDAS system, particularly in distinguishing between different types of corrosion.
Preprints 71861 g013
Preprints 71861 g014
Figure 14. Comparison of Confusion Matrices for (a) Fully Distributed and (b) Quasi-Distributed Sensor Systems with Gaussian Noise and SNR=9.63dB.
Figure 14. Comparison of Confusion Matrices for (a) Fully Distributed and (b) Quasi-Distributed Sensor Systems with Gaussian Noise and SNR=9.63dB.
Preprints 71861 g014
Preprints 71861 g015
Figure 15. The sensor system is configured as a fiber sensor that covers the pipe, with the measurement units evenly distributed along its length.
Figure 15. The sensor system is configured as a fiber sensor that covers the pipe, with the measurement units evenly distributed along its length.
Preprints 71861 g015
Preprints 71861 g016
Figure 16. The prediction accuracy changes with different sensor numbers under different signal-noise ratio.
Figure 16. The prediction accuracy changes with different sensor numbers under different signal-noise ratio.
Preprints 71861 g016
Table 1. Dimensional parameters of the steel pipeline model.
Table 1. Dimensional parameters of the steel pipeline model.
Length   ( i n c h ) Outside   Diameter   ( i n c h ) Wall   thickness   ( i n c h )
96 12 0.5
Table 2. Material property parameters of the steel pipeline model.
Table 2. Material property parameters of the steel pipeline model.
Material   ( i n c h ) Density   ( k g / m 3 ) Young ’ s   Modules   ( P a ) Poisson   Ratio   ( μ )
96 7850 21 × 10 10 0.32
Table 3. Dimensional parameters of pipeline feature types.
Table 3. Dimensional parameters of pipeline feature types.
Pipe
feature		 Clamp Welding Localized
Corrosion		 General
Corrosion		 Pitting
Variable Axial Length:
(0.02~0.2 inch)
Stiffness factor:
(5e+06~6.5e+06N/m)		 Axial length:
(0.02~0.2 inch)
Depth:
(0.05~0.2 inch)		 Axial length:
(1~8 inch), Depth:
(0.01 ~0.45 inch)		 Axial length:
(0.5~5 feet)
Depth:
(0.05~0.45inch)		 Radius:
(0.5~10 inch)
Depth:
(0.05~0.45 inch)
Case
number		 20 30 40 40 25
Description The elastic support loaded by clamps (blue region); The discontinuity and material property changes between the pipeline and the welded portion A rectangular notch on the inner surface of the pipeline, indicating presence of corrosion in a specific area. Evenly reduction in pipeline thickness Micrometer-scale localized corrosion of a specific type
1 Based on the table, we will conduct multiple simulation runs for various types of defects in batches, where each group's variables - such as the defect width or material properties of the clamp part - will be randomly altered according to the table's specifics.
Table 4. The training and validation accuracy comparison of different optimizers.
Table 4. The training and validation accuracy comparison of different optimizers.
CNN_model CNN structure
Model 1 1 Layer + ‘relu’
Model 2 1 Layer + ‘sigmoid’
Model 3 1 Layer + ‘tanh’
Model 4 2 Layer + ‘relu’
Model 5 2 Layer + ‘sigmoid’
Model 6 2 Layer + ‘tanh’
Table 5. Comparison of Classification Performance Metrics for Fully Distributed and Quasi-Distributed Sensor Systems with Gaussian Noise, SNR = 9.63 db.
Table 5. Comparison of Classification Performance Metrics for Fully Distributed and Quasi-Distributed Sensor Systems with Gaussian Noise, SNR = 9.63 db.
Fully Distributed Quasi-Distributed
Classification report Precision Recall Precision Recall
Welding 100.00% 100.00% 100.00% 100.00%
Localized corrosion 100.00% 100.00% 100.00% 100.00%
General corrosion 100.00% 100.00% 100.00% 100.00%
Pitting corrosion 100.00% 96.00% 95.83% 92.00%
Clamp 96.15% 100.00% 96.00% 96.00%
No defect 100.00% 100.00% 92.31% 96.00%
Table 6. Comparison of Classification Performance Metrics for Fully Distributed and Quasi-Distributed Sensor Systems with Gaussian Noise, SNR = 9.63dB.
Table 6. Comparison of Classification Performance Metrics for Fully Distributed and Quasi-Distributed Sensor Systems with Gaussian Noise, SNR = 9.63dB.
Fully Distributed Quasi-Distributed
Classification report Precision Recall Precision Recall
Welding 96.15% 100.00% 100.00% 96.00%
Localized corrosion 100.00% 100.00% 100.00% 100.00%
General corrosion 100.00% 96.00% 96.15% 100.00%
Pitting corrosion 96.00% 96.00% 90.00% 90.00%
Clamp 95.74% 90.00% 96.00% 96.00%
No defect 90.57% 96.00% 90.00% 90.00%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated