Traceability of the Micro Scale Pipe Viscometer for Traceable Calibration of Dynamic Viscosity

Calibration of flow devices is important in several areas of pharmaceutical, flow chemistry and microfluidic applications where dosage of process liquids or accurate measurement of the flow rate is important. The process-oriented liquid itself might influence the performance of the flow device and the simultaneous determination of the dynamic viscosity under flow conditions might be a valuable information for the process parameters. To offer the simultaneous calibration of the dynamic viscosity of the process-oriented liquid at the corresponding flowrate, METAS has built a pipe viscometer for the traceable in-line measurement of the dynamic viscosity in the current flow facilities for low flow rates from 1 L/min to 150 mL/min and pressure drops up to 10 bar. The traceability of all the measuring quantities as well as the geometrical dimensions of the micro tube guarantee the traceability of the pipe viscometer to SI units. The most challenging part is the traceable determination of the inner diameter of the micro tube. This can be achieved by measuring the pressure drop as a function of flow rate with the pipe viscometer and applying the law of Hagen-Poiseuille with a traceable dynamic viscosity of a reference liquid (water) or perform the measurements with the micro-CT at METAS, which determines the inner diameter by x-ray diffraction. The validation of the stated measurement uncertainty of the pipe viscometer has been performed by means of calibration of the dynamic viscosity of several reference liquids with traceable density and kinematic viscosity. The setup of the facility, the traceability as well as the uncertainty calculation of the pipe viscometer for the in-line measurement of the dynamic viscosity are discussed in this paper.

Keywords:

Subject: Physical Sciences - Applied Physics

1. Introduction

Calibration of flow devices is important in several areas of pharmaceutical, flow chemistry and HPLC applications where dosage of process liquids or accurate measurement of flow rate are important. The process-oriented liquid itself might influence the performance of the flow meter. Coriolis flow meter are rather insensitive to the viscosity of the liquid and the flow profile in the piping. Thermal flow meter might be sensitive to the flow profile of the liquid inside the tube, but they are obviously extremely sensitive to the thermal properties of the liquids [1]. Therefore, the calibration of the flow meter with the process-oriented liquid is important and the simultaneous determination of the dynamic viscosity under flow conditions is a valuable information for viscosity dependent flow metering methods or other process parameters [1,2]. Pipe viscometers are widely used in industrial and research applications for the measurement of the dynamic viscosity of the liquids [3,4,5,6]. Various instruments are available for the determination of the dynamic viscosity as a function of shear rate for piping dimensions of tens of millimeters [5,7,8,9]. Another option is to determine the dynamic viscosity with glass capillary viscometers, which requires sampling of the liquid. The sampling of the liquid is not always an advantage in production processes. Several commercially available instruments exist for the in-line measurements of the dynamic viscosity and the density of the process liquid [10,11], which fulfill the advantages of an in-line measurement in small pipes. To monitor the accuracy of these sensors over time, they could be calibrated by a traceable pipe viscometer with any liquids to determine the deviations to reference values traceable to SI units at a given time interval.

To offer the simultaneous calibration of the dynamic viscosity of the process-oriented liquid at the corresponding flowrate, METAS has built a pipe viscometer for the traceable in-line measurement of the dynamic viscosity in the current flow facilities for low flow rates from 1 μL/min to 150 mL/min and pressure drops up to 10 bar [12]. Several micro tubes have been implemented into the pipe viscometer and characterization tests have been performed to test the influence of different materials. Characterization of the inner diameter of the micro tube has been performed by means of the μ-CT at METAS, which determines the inner diameter by x-ray diffraction [13,14]. It turned out that glass micro tubes are most suitable for the pipe viscometer as the inner diameter is circular and the cross section reveals an excellent roundness. Another method for the determination of the inner diameter is the measurement of the pressure drop as a function of flow rate and applying the law of Hagen-Poiseuille with a well known liquid (water), which is called flow calibration method in this paper. A detailed analysis of both methods is described later in this paper for a soda glass and a stainless steel micro tube.

2. Materials and Methods

2.1. Experimental setup of pipe viscometer

The current flow facility at METAS [15] has been modified to include a section with a pipe viscometer as can be seen in Figure 1 and Figure 2. The pipe viscometer consists of a micro tube with temperature and pressure sensors upstream and downstream of the micro tube.

Measuring the flow rate, the pressure drop, the temperature and including the geometrical specifications of the micro tube allows the calculation of the dynamic viscosity of the liquid according to the Hagen-Poisseuille equation (1):

\begin{matrix} η = \frac{Δ P \cdot π \cdot r^{4}}{8 \cdot Q \cdot L} \end{matrix}

(1)

where η is the dynamic viscosity, ΔP is the pressure drop over the micro tube, Q is the volumetric flow rate, L is the length of the micro tube and r is the inner radius of the micro tube.

2.2. Calibration of all the sensors mesuring physical quantities

To guarantee the traceability of the pipe viscometer, all the sensors or instruments measuring physical quantities have to be calibrated and therefore be traceable to SI units. In the next section, the different sensors or instruments are described and their traceability discussed.

2.2.1. Piston prover

The piston prover generates the volume flow rate, which is traceable to time and length [15]. The inner diameter of conventional glass syringes ILS from WICOM International GmbH or homemade stainless steel pistons are calibrated by the length laboratory at various positions and an average inner diameter with the corresponding uncertainty is determined [16,17]. The position of the plunger of the piston is measured by the linear measuring system LMS-LIMES80-130 of the high precision linear stage LIMES 80-130-Hi00 from OWIS GmbH, which is calibrated by interferometry to get traceability. The linear measuring system sends pulses that are counted by a FPGA and a timestamp of the FPGA is recorded in order to form a pair of values being the position and the corresponding timestamp. The real time speed is then determined by a linear fit of the position as a function of time. The counter clock on the FPGA is calibrated and thus the timestamps are traceable getting the speed of the piston and the calculated volume flow rate traceable to length and time.

2.2.2. Pressure sensor

The pressure is measured by pressure transducer UC2 from Endress+Hauer AG with a pressure range of 0 – 10 bar(g) and an analog output signal of 4 – 20 mA. The pressure sensors are calibrated regularly with a traceable pressure controller PPC3 from Fluke Calibration in order to include repeatability, drift of the sensor and hysteresis effect in the measurement uncertainty calculation of the sensor. With this knowledge the operation range of the pressure difference to fulfill the measurement uncertainty can be defined being 0.4 bar(g) – 10 bar(g).

2.2.3. Temperature sensor

The temperature sensors are NTC sensors R2152-F (10kOhm@25°C) from Moser TMT AG. The outer diameter of the tubing of the sensor part is 3.175 mm (1/8”). The sensor part is mounted in a Swagelok T-junction (1/8” connectors), where the inner diameter has been perforated slightly larger than 1/8” allowing the sensor part to be surrounded by the flowing liquid. The temperature sensors are calibrated regularly by the traceable field metrology well from Fluke Calibration. Repeatability, drift of the sensor and hysteresis effect are included in the measurement uncertainty calculation of the temperature sensors.

2.3. Calibration of the geometrical dimensions of the micro tube

The length and the inner diameter of the micro tube have to be calibrated. The calibration of the length is daily business for the length metrology [18]. However, the calibration of the inner diameter of the micro tube is more challenging. One method is to calibrate the inner diameter of the micro tube by means of the μ-CT at METAS, which determines the inner diameter by x-ray diffraction [13,14]. The other method is the flow calibration method, where the pressure drop is measured as a function of the flow rate with a reference liquid with known dynamic viscosity in order to calculate the inner diameter of the micro tube according to law of Hagen-Poisseuille. Both methods were used to determine the inner diameter of the soda glass and the stainless steel micro tube, whereas only the flow calibration method was applied for the determination of the inner diameter of the PEEK beige micro tube (Table 1). The methods are described in the next paragraphs.

2.3.1. CT method

The μ-CT method has been used for the calibration of the inner diameter of the soda glass micro tube and the stainless steel micro tube in order to compare it to the flow calibration method and validate the latter method.

µ-CT measurements were performed on the high-accuracy METAS-CT system [13,14]. The measurement conditions are provided in Table 2. Grey value volumes were analysed in VG Studio MAX (Volume Graphics) as follows: Gradient based surface determination and subsequent least-squares fitting of cylindrical primitives to determine the mean diameter for the soda glass micro tube and threshold-based segmentation and volume determination to derive an equivalent diameter of the steel micro tube. Measurement uncertainties were estimated using a hybrid approach, which combines reference measurements and a CT simulation of the actual workpiece [13].

2.3.2. Flow calibration method

Another method for the calibration of the inner diameter of the micro tubes is the flow calibration method in the laminar regime. A reference liquid with known dynamic viscosity is used to measure the pressure drop as a function of the flow rate and to calculate the inner diameter of the micro tube according to equation (2).

\begin{matrix} r = \sqrt[4]{\frac{8 \cdot η \cdot Q \cdot L}{π \cdot Δ P}} \end{matrix}

(2)

where η is the dynamic viscosity, ΔP is the pressure drop over the micro tube, Q is the volumetric flow rate, L is the length of the micro tube and r is the inner radius of the micro tube.

The reference liquid chosen is pure water as the viscosity and the density formulas as a function of temperature are well established and these quantities can be determined by measuring the temperature of the pure water. The dynamic viscosity and the density of the pure water are calculated according to the equations from the NIST database [19] by measuring the temperature in the tubing before and after the micro tube. Measurements are performed in the corresponding flow rate range to obtain pressure drops in the range from 0.5 bar to 8.0 bar. Thus, the pressure drop over the micro tube as a function of flow rate can be fitted linearly in the laminar regime to obtain the slope ΔP/Q and then calculate the inner diameter of the micro tube.

For the determination of the inner diameter of the micro tubes with the flow calibration method, the following values of the dynamic viscosity and density of pure water were taken from the NIST database [19] (listed in Table 3), which is based on the IAPWS R12-08 [20].

The values at 1 bar absolute pressure are applied, which corresponds roughly to the ambient pressure of the laboratory conditions. The change rate of the dynamic viscosity as a function of the pressure is -4^.10^-5 mPa^.s/bar. As the measurements are performed for pressure drops in the range from 0.5 bar to 8.0 bar the maximum average pressure in the liquid over the full capillary is half of the maximum pressure drop being 4.0 bar. This implies a maximum change in the dynamic viscosity of 1.6^.10^-4 mPa^.s, which corresponds to 0.016 % of the dynamic viscosity at ambient conditions. This contribution is negligible as we assume the uncertainty contribution from the calculation of the dynamic viscosity of pure water with the measured temperature as 0.5 % (see Table 4).

2.4. Measurement uncertainty of the flow calibration method

Several contributions to the measurement uncertainty have already been mentioned in the text above. In this paragraph, an overview of the contributions to the uncertainty is listed in Table 4 for the flow calibration method determining the inner diameter of the micro tube in the pipe viscometer with a liquid of known dynamic viscosity.

The main contribution is related to the determination of the dynamic viscosity of water, where the temperature of the water is measured and the viscosity value is calculated from the known formula of the dynamic viscosity as a function of temperature and pressure [19]. The expanded uncertainty of the temperature measurement is 0.2 °C leading to an extended uncertainty contribution of the dynamic viscosity of 0.5 %. Additionally, the uncertainty of the formula is stated being 0.5 % [21], which lead to an extended uncertainty contribution of 0.71 % for the dynamic viscosity of water. The other important contribution is the pressure measurements upstream and downstream of the micro tube leading to an extended uncertainty of 0.28 % for the pressure drop measurement larger than 0.4 bar(g). Therefore, the extended uncertainty of the determination of the inner diameter is 0.20 % (k=2).

2.5. Measurement uncertainty of the pipe viscometer

Now that the extended uncertainty of the inner diameter of the micro tube is determined, the uncertainty contributions of the pipe viscometer are known and are listed in Table 5. Three main contributions can be identified. The largest contribution is the measurement of the pressure drop at the micro tube with an uncertainty contribution of 0.28 % for pressure drops larger than 0.4 bar(g). Other important contributions are the uncertainty of the inner diameter of the micro tube being 0.20 % and the uncertainty of the single point analysis for the determination of the dynamic viscosity being 0.20 %. The latter one has been determined empirically by analyzing several sets of data, where the linear fit method and the single point analysis have been used for the determination of the dynamic viscosity and the additional contribution to it. Therefore, the expanded uncertainty is set to 0.90 % for the pipe viscometer build with the glass micro tube.

3. Results and discussion

3.1. Calibration of the inner diameter of the micro tube

3.1.1. Soda glass micro tube using the μ-CT method

Figure 3 shows the cross section of the soda glass micro tube with a nominal inner diameter of 0.130 mm determined by means of the μ-CT method. The surface of the cylindrical hole is identified to determine the inner diameter of the micro tube as can be seen in Figure 4. The average inner diameter of the soda glass micro tube measured at 9 different positions is (0.1269 ± 0.0010) mm.

3.1.2. Stainless steel micro tube using the μ-CT method

The stainless steel micro tube with a nominal inner diameter being 0.150 mm has also been characterized with the μ-CT method. It reveals non-circular cross sections as shown in Figure 5. Therefore, the surface areas of the cross sections are determined and an equivalent inner diameter is calculated being (0.144 ± 0.010) mm. The uncertainty is dominated by the variation of the equivalent diameter along the micro tube. This result is close to the nominal diameter specified by the manufacturer.

3.1.3. Glass, stainless steel and PEEK micro tube using the flow calibration method

The flow calibration method shows laminar flow behavior over the full range of the generated flow rates as shown in Figure 6 for the glass, stainless steel and PEEK beige micro tube. The data are fitted with a linear fit with forced zero intercept to obtain the slope ΔP/Q. As mentioned earlier, the inner diameter is then calculated according to Equation (2) by taking into account the slope of the fit ΔP/Q, the dynamic viscosity of pure water obtained by the calculation with the measured temperature and the length of the micro tube. The results are listed in Table 6.

It is important to mention here that the two pressure drops of the connectors between the ends of the micro tube and the pressure sensors have to be taken into account if they are not negligible compared to the main pressure drop over the micro tube. Otherwise, the inner diameter will be underestimated. This correction has been applied in these measurements although the nominal inner diameter of the micro tubes are of the order of 0.13 mm – 0.15 mm and much smaller than the inner diameter of the connectors (more than 2 mm for this setup). Thus, the corrections due to the pressure drop of the connectors are negligible compared to the main pressure drop over the micro tube.

The results of the inner diameter of the soda glass micro tube obtained with both methods are in perfect agreement. For the case of the stainless steel micro tube, the structure of the cross sections lead to the assumption that the hydrodynamic diameter has to be smaller as the structure represents more a random surface with a high surface roughness instead of a circular cross section with smooth surface roughness. Thus, both methods show different results, as it would have been expected. Therefore, the stainless steel micro tube is less feasible for the pipe viscometer.

3.2. Validation of the pipe viscometer with reference liquids

The pipe viscometer has then been validated by measuring the dynamic viscosity of reference liquids. These reference liquids have certificates for the density and dynamic viscosity as a function of temperature and are traceable to SI-units [22]. Three reference liquids with dynamic viscosities in the range from 1.5 mPa^.s to 4.0 mPa^.s have been measured at the liquid temperature of 21.3 °C and their dynamic viscosities and densities are listed in Table 7. The certificates of the reference liquids contain the reference values at the temperatures of 20 °C, 23 °C, 25 °C, 30 °C and 40 °C. A linear fit of the first order has been applied to the data of the density and a linear fit of the second order has been applied to the date of the dynamic viscosity to obtain the values at the measurement temperature of 21.3 °C, which corresponds to the liquid temperature in the tubing being measured by several temperature sensors.

The three reference liquids “2AW”, “2BW” and “5AW” have been calibrated with the pipe viscometer with the three micro tubes of Table 4 and the results are listed in Table 8. The measurement data with the pipe viscometer including the soda glass micro tube are shown in Figure 7, where the pressure drop is shown as a function of the flow rate. The data are fitted with a linear fit with forced zero intercept to obtain the slope ΔP/Q. The dynamic viscosity is then calculated according to Equation (1) by taking into account the slope of the fit ΔP/Q, the length and the inner diameter of the micro tube. The calibration results are consistent with the reference values (Table 7) within the expanded uncertainty of this pipe viscometer being 0.90 %. The calibration results of the three reference liquids lead to a deviation in respect to the reference values between +0.42 % and +0.43 %, which seems to be a systematic deviation as the deviation is nearly the same for all three reference liquids. However, the deviations are smaller than the stated measurement uncertainty of 0.90 %.

The pipe viscometer with the stainless steel micro tube and the PEEK beige micro tube show larger deviations for all three reference liquids and are not consistent within the measurement uncertainties with the reference values. The non-circular shape of the stainless steel micro tube is probably one of the reasons for the large deviations as the inner surface of the micro tube shows large irregularities, which do not meet the requirements for the law of Hagen-Poisseuille. The reason for the large deviations of the PEEK beige micro tube are not that obvious and further investigations are needed to fully understand these results.

All these measurement results show that the soda glass micro tube is the most suitable micro tube. Therefore, the single measurement point analysis is investigated for the pipe viscometer including the soda glass micro tube.

3.3. Single measurement point analysis

The linear fit with forced zero intercept over a range of pressure drops as a function of flow rate is one method to obtain the quotient ΔP/Q. The reason to force the intercept being zero is to compare this result from the linear fit over the measured flow rate range in the laminar regime to the results obtained by the single measurement point analysis. This means that the quotient ΔP/Q is calculated from a single measurement. The results of the single measurement point analysis of the measurement with the pipe viscometer including the soda glass micro tube and the reference liquid “2BW” are listed in Table 9. The single measurement point analysis results are very consistent with the result from the linear fit analysis. Although, the result for the lowest pressure drop of 0.56 bar shows a larger deviation, it is still consistent within the measurement uncertainty with the result of the linear fit over the full range.

Note that the pressure measurement downstream of the micro tube is performed with a pressure sensor of maximum 10 bar and measures pressures of the order of tens of mbar with an uncertainty of 10 mbar. This might be the reason for the larger deviation at the lowest pressure drop. One option for improvement is the use of a pressure sensor downstream of the micro tube with a lower maximum pressure of the order of 0.5 bar. Additionally, measurements at zero flow leading to zero pressure drop for the verification of the indication of the pressure sensors can be performed to investigate if there are systematic deviations due to short time drift.

3.4. Comparison with glass capillary viscometers

The measurement uncertainty of the micro pipe viscometer has also been validated by a comparison between several metrology institutes, which use either a pipe viscometer or a glass capillary viscosity meter to determine the dynamic viscosity or the kinematic viscosity, which is transformed into the dynamic viscosity with the measured density of the liquid [2,23]. Eight different liquids were used and all the details of the comparison can be found in the references mentioned above. Only the results of two liquids measured by three pipe viscometers (METAS, RISE and NEL) and two glass capillary viscosity meters (NQIS/EIM and KRISS) with the corresponding reference value for the dynamic viscosity of the liquids are listed in Table 10. Liquid C is a 10 %wt glucose solution and liquid E is a solution of 0.22 %wt NaCl and 5.55 %wt glucose. The calculation of the reference value and the consistency check of the results is explained in detail in [2]. The results shown here are consistent within the measurement uncertainty and strengthen the stated measurement uncertainty of the pipe viscometer described in this paper.

5. Conclusions

Extensive investigations for the characterization of the pipe viscometer for the traceable in-line measurement of the dynamic viscosity for flow rates from 1 μL/min to 150 mL/min and pressure drops up to 10 bar have been presented. The glass micro tube is the best option and is therefore integrated in the pipe viscometer leading to the extended uncertainty of the pipe viscometer being 0.90 %. The stated measurement uncertainty has been validated with measurements of three traceable reference liquids for the dynamic viscosity and a comparison with other pipe viscometers and glass capillary viscosity meters. The measurements showed consistent results with the reference values within the stated uncertainties. Additionally, the glass micro tube has been characterized by means of the μ-CT at METAS. These measurements showed also consistent results for the inner diameter compared to the flow calibration method. Therefore, the measurement of the inner diameter of the glass micro tube has been validated by the μ-CT measurements and the measurements of the dynamic viscosity of the various liquids.

The determination of the dynamic viscosity with the linear fit method over several measurement data or the single point method with a single measurement is possible as long as the pressure drop is not too small compared to the resolution of the pressure sensors installed.

Author Contributions

Conceptualization, H.B.; methodology, H.B. and B.B.; validation, B.B., S.N. and H.B.; formal analysis, B.B. and S.N.; investigation, B.B. S.N. and H.B.; writing—original draft preparation, H.B.; writing—review and editing, H.B., B.B. and M.H.; supervision, M.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. Most of the relevant data are already presented in tables.

Conflicts of Interest

The authors declare no conflict of interest.

References

Bissig, H.; Tschannen, M.; de Huu, M. Liquid properties effects on Coriolis and thermal mass flow meters at very low flow rates. In Proceedings of Flomeko 2016, Sydney, Australia, 26th Sept 2016. [Google Scholar]
Bissig, H.; Büker, O.; Stolt, K.; Graham, E. et al. In-line measurements of the physical and thermodynamic properties of single and multicomponent liquids. Biomedical Engineering / Biomedizinische Technik 2023, vol. 68, no. 1, pp. 39-50. [CrossRef]
Richter, M.; Woias, P.; Weiss, D. (1997) Microchannels for applications in liquid dosing and flow-rate measurement. Sensors and Actuators A: Physical 1997, 62, 480-483. [CrossRef]
Draad, A.A.; Kuiken, G.D.C.; Nieuwstadt, F.T.M. Laminar-turbulent transition in pipe flow for Newtonian and non-Newtonian fluids. J Fluid Mech 1998, 377, 267–312. [Google Scholar] [CrossRef]
Haavisto, S.; Liukkonen, J.; Jäsberg, A.; Koponen, A.; Lille, M.; Salmela, J. Laboratory scale pipe rheometry: A study of a microfibrillated cellulose suspension. Paper Conference and Trade Show 2011, 357–370, https://www.tappi.org/content/events/11papercon/documents/330.350.pdf. [Google Scholar]
Salipante, P.F.; Dharmaraj, V.L.; Hudson, S.D. Entrance effects and high shear rate rheology of shear-banding wormlike micelle fluids in a microcapillary flow. Journal of Rheology 2020, 64, 481. [Google Scholar] [CrossRef]
Ouriev, B.; Windhab, E. Rheological study of concentrated suspensions in pressure-driven shear flow using a novel in-line ultrasound Doppler method. Experiments in Fluids 2002, 32, 204–211. [Google Scholar] [CrossRef]
Birkhofer, B.; Debacker, A.; Russo, S.; Ricci, S.; Lootens, D. In-Line Rheometry Based on Ultrasonic Velocity Profiles: Comparison of Data Processing Methods. Applied Rheology 2012, 22–44701. [Google Scholar] [CrossRef]
Wiklund, J.; Shahram, I.; Stading, M. Methodology for in-line rheology by ultrasound Doppler velocity profiling- and pressure difference technique. Chemical Engineering Science 2007, 62, 4277 – 4293. [CrossRef]
VLO-M1 sensor from TrueDyne Sensors AG, https://www.truedyne.com/viscosity_sensors_for_liquids/vlo-m1-for-liquids/?lang=en.
DVM sensor from Rheonics GmbH, https://rheonics.com/products/hpht-pvt-density-meter-viscometer-dvm/.
Neuhaus, S.; Bissig, H.; Bircher, B.A.; de Huu, M. Presentation of the METAS pipe viscometer. In Proceedings of Flomeko 2022, Chongqing, China, 17th Oct 2022. [Google Scholar]
Bircher, B.A.; Meli, F.; Küng, A.; Thalmann, R. METAS-CT: Metrological X-ray computed tomography at sub-micrometre precision. In Proceedings of euspen’s 20th International Conference & Exhibition, Geneva, Switzerland, 8th June 2020. [Google Scholar]
Bircher, B.A.; Meli, F.; Küng, A.; Thalmann, R. X-ray source tracking to compensate focal spot drifts for dimensional CT measurements. In Proceedings of 10th Conference on Industrial Computed Tomography, Wels, Austria, 4th Feb 2020. [Google Scholar]
Bissig, H.; Tschannen, M.; de Huu, M. (2016) Recent Innovations in the field of traceable calibration of liquid milli-flow rates with liquids other than water. In Proceedings of Flomeko 2016, Sydney, Australia, 26th Sept 2016. [Google Scholar]
METAS, Laboratory “Length, Nano- and Microtechnology”, Metrological X-ray computed tomography (XCT), METAS-CT, https://www.metas.ch/metas/en/home/fabe/laenge/computed-tomography.html.
METAS, Laboratory “Length, Nano- and Microtechnology”, Nano- and microtechnology, micro coordinate metrology, https://www.metas.ch/metas/en/home/fabe/laenge/nano-and-microtechnology.html.
METAS, Laboratory “Length, Nano- and Microtechnology”, Length and Form, https://www.metas.ch/metas/en/home/fabe/laenge/length-and-form.html.
Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 10.0, National Institute of Standards and Technology, Standard Reference Data Program, Gaithersburg, 2018. [CrossRef]
IAPWS R12-08 (2008) Release on the IAPS Formulation 2008 for the Viscosity of Ordinary Water Substance. International Association for the Properties of Water and Steam, Berlin, Germany.
Huber, M.L.; Perkins, R.A.; Laesecke, A.; Friend, D.G. New International Formulation for the viscosity of H₂O. J. Phys. Chem. Ref. Data 2009, 38, 101. [Google Scholar] [CrossRef]
ZMK Zentrum für Messen und Kalibrieren & ANALYTIK GmbH, Bitterfeld-Wolfen, Germany. www.zmk-wolfen.de.
EURAMET. Validation of the pipe viscometers (primary standards) for the in-line measurement of the dynamic viscosity of Newtonian liquids. Report A2.1.4, EURAMET, Braunschweig 2022, www.drugmetrology.com.

Figure 1. Schematic setup of the pipe viscometer with temperature and pressure sensors upstream and downstream of the micro tube.

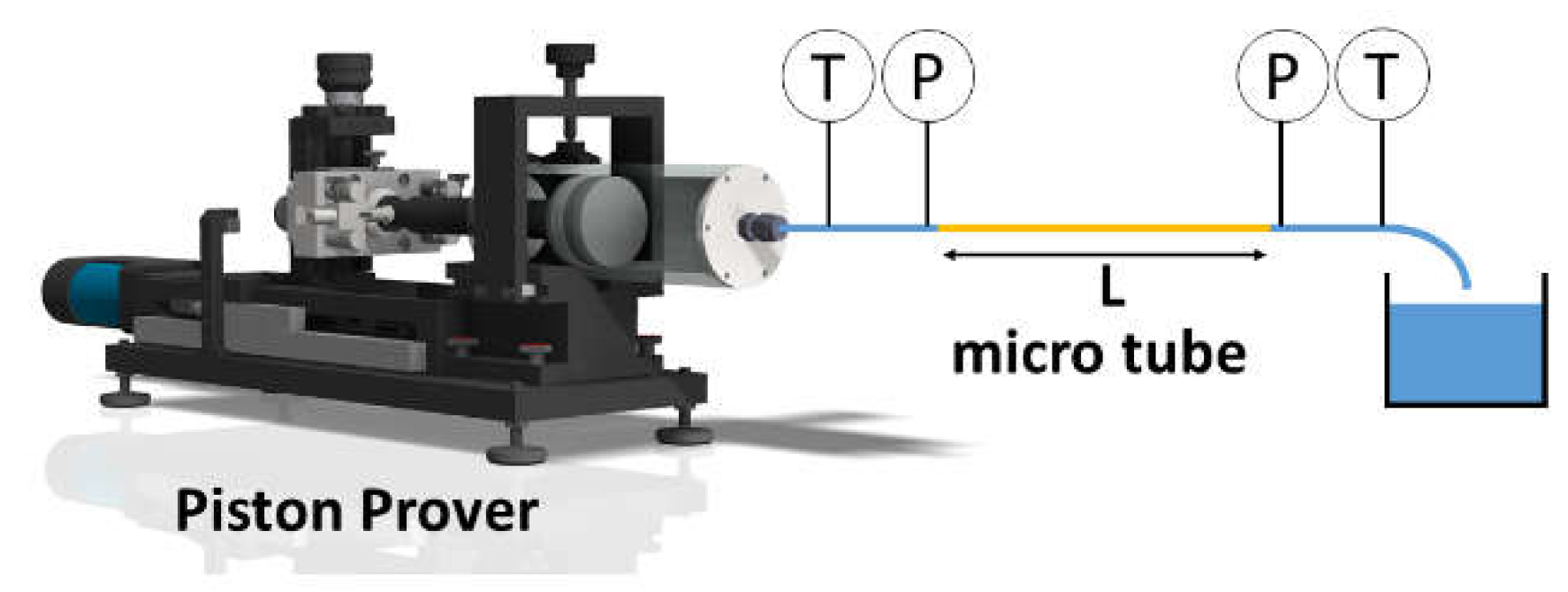
Figure 2. The micro pipe viscometer at METAS: (A) piston prover, (B) temperature sensors, (C) pressure sensors and (D) the glass micro tube with an inner diameter of 0.13 mm and a length of 200 mm.

Figure 3. Cross section of the glass micro tube determined by means of the μ-CT.

Figure 4. Zoom into the cross section of the micro tube shown in Figure 3 for the determination of the inner diameter by the μ-CT method. The average inner diameter of the soda glass micro tube measured at nine different positions is (0.1269 ± 0.0010) mm.

Figure 5. Cross section of the stainless steel micro tube determined by means of the μ-CT. Due to the non-circular shape of the cross sections the volumes are determined to calculate an equivalent inner diameter being (0.144 ± 0.010) mm.

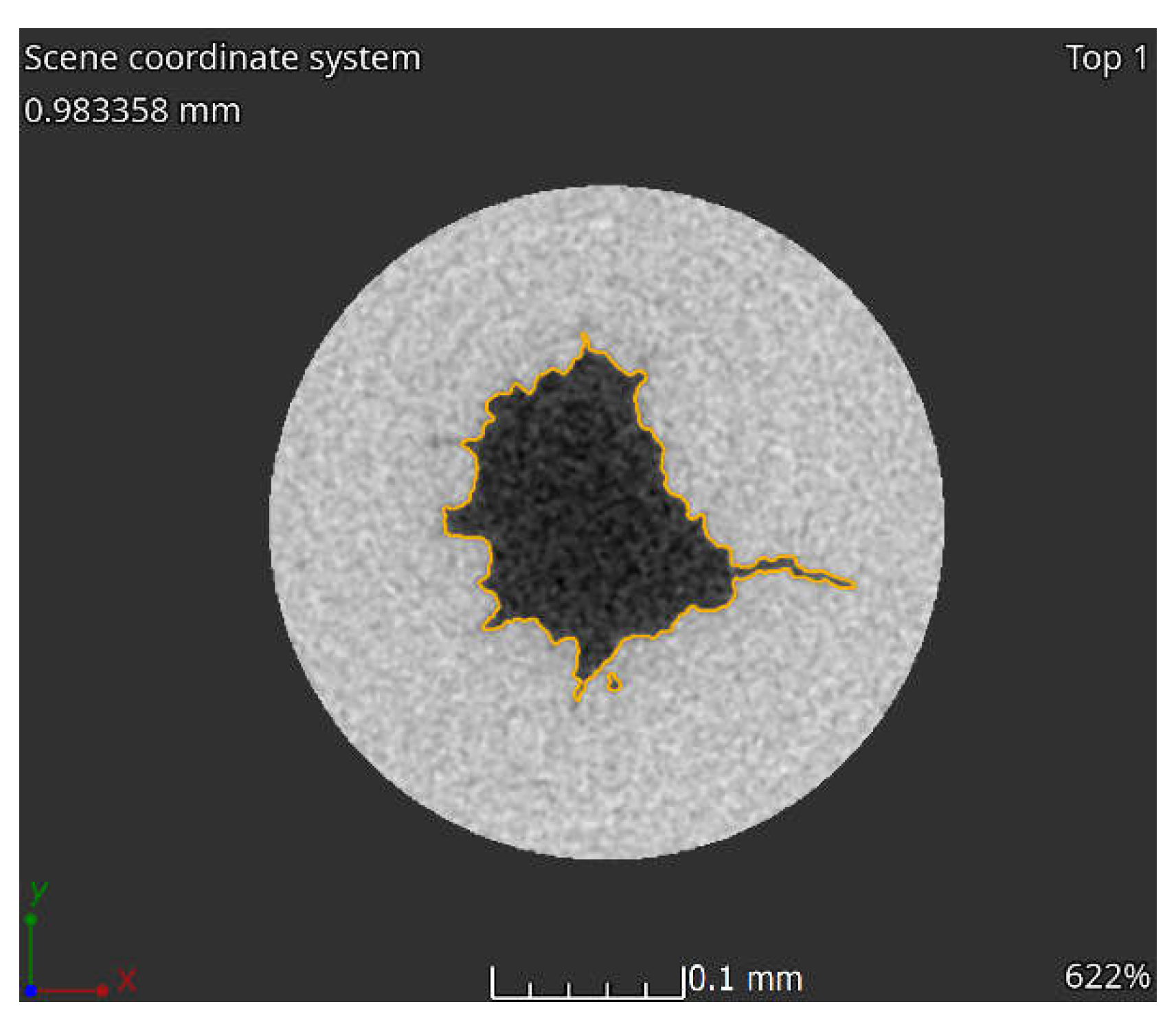
Figure 6. Pressure drop as a function of flow rate for the laminar flow of water through the soda glass micro tube (light blue circle), stainless steel micro tube (black triangles,) and PEEK Beige micro tube (beige diamonds).

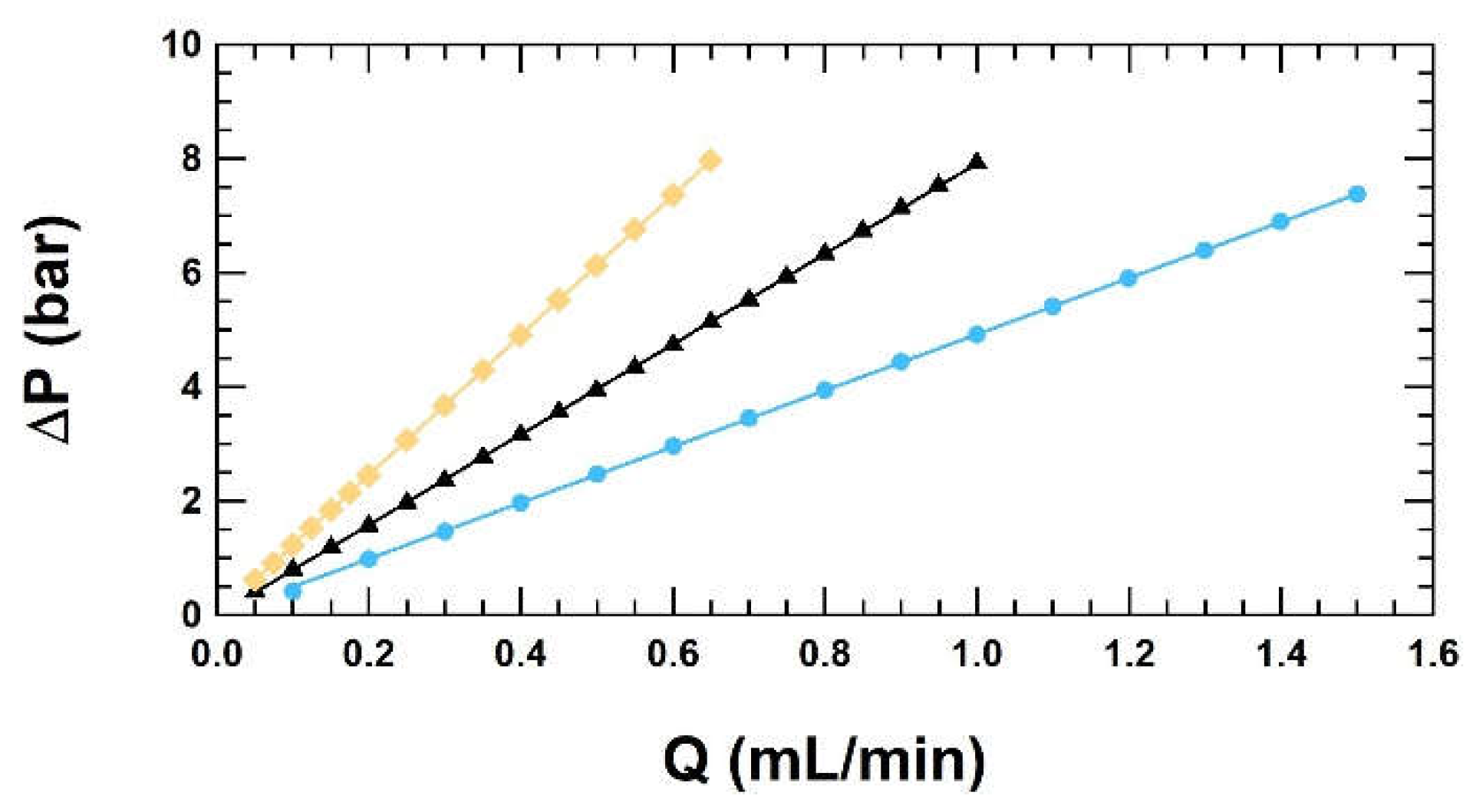
Figure 7. Pressure drop as a function of flow rate flow through the glass micro tube of reference liquid 2AW (blue open circles), reference liquid 2BW (violet solid squares) and reference liquid 5AW (dark blue open squares) with the corresponding linear fit with forced zero intercept.

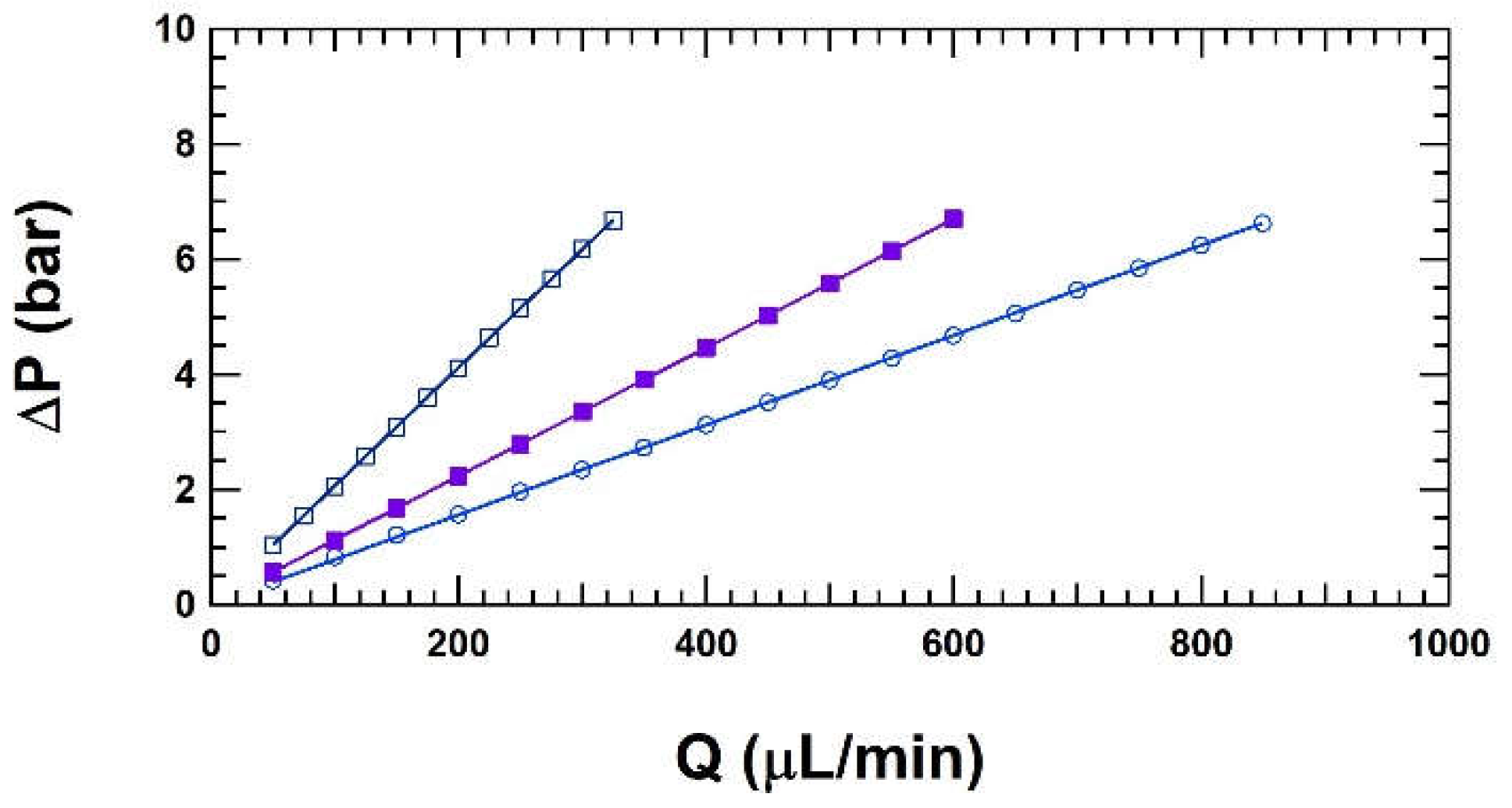
Table 1. The materials and dimensions of the different tested micro. The length and the inner diameter are nominal values from the specifications of the manufacturers.

Material	Length (mm)	Nominal inner diameter (mm)
Soda glass	200.0	0.130
Stainless steel	300.0	0.150
PEEK beige	981.0	0.150

Table 2. µ-CT measurement conditions.

Parameter	Soga glass micro tube	Stainless steel micro tube
Positions	9	2
X-ray tube voltage	100 kV	160 kV
Target power	10 W	5 W
X-ray filter	0.03 mm Al	0.1 mm Cu
Exposure time	1.3 s	5.5 s
Projections	800	800
Voxel size	2.8 mm	1.0 mm

Table 3. Density and dynamic viscosity of water according to the NIST database [19] at a temperature of 21.3 °C and several values of absolute pressure.

Reference liquid	Absolute pressure (bar a)	Dynamic viscosity (mPa^.s)	Density (kg/m³)
H₂O	1.0	0.97052	997.93
H₂O	2.0	0.97048	997.97
H₂O	4.0	0.97041	998.07
H₂O	8.0	0.97026	998.25

Table 4. Uncertainty contributions for the determination of the inner diameter of the micro tube with water as reference liquid. All these values are either direct uncertainties from calibration certificates and/or empiric estimations.

Contribution	Uncertainty (k=2)	Coefficient
Piston prover for the generation of flow	0.10 %	0.25
Length measurement of the micro tube	0.01 %	0.25
Pressure difference measured by 2 sensors of maximum pressure at 10 bar in the range of 0.4 bar(g) to 10.0 bar(g).	0.28 %	0.25
Dynamic viscosity of water calculated according to [19] by measuring the temperature and pressure. Uncertainty of temperature measurement is 0.2 °C leading to an uncertainty contribution of 0.50 % of the dynamic viscosity. Uncertainty from the formula is 0.50 % [20,21].	0.71 %	0.25

Table 5. Uncertainty contributions of the pipe viscometer for the determination of the dynamic viscosity. All these values are either direct uncertainties from calibration certificates and/or empiric estimations.

Contribution	Uncertainty (k=2)	Coefficient
Piston prover for the generation of flow	0.10 %	1.0
Length measurement of the micro tube	0.01 %	1.0
Pressure difference measured by 2 sensors of maximum pressure at 10 bar in the range of 0.4 bar(g) to 10.0 bar(g).	0.28 %	1.0
Inner diameter of micro tubes determined with the pipe viscometer and the reference liquid water.	0.20 %	4.0
Single point analysis at each flow rate for a given pressure drop vs Linear Regression over the flow rate range.	0.20 %	1.0

Table 6. Determination of the inner diameter by means of the flow calibration method and μ-CT method. The results include the expanded uncertainty (k=2).

Material	Flow calibration method (mm)	m-CT method (mm)
Soda glass	0.1267 ± 0.0003	0.1269 ± 0.0010
Stainless steel	0.1257 ± 0.0003	0.144 ± 0.010
PEEK beige	0.1515 ± 0.0004	Not applied

Table 7. Reference liquids [22] with traceable density and dynamic viscosity at a temperature of 21.3 °C with the stated expanded (k=2) uncertainty of 0.20 % for the dynamic viscosity and 0.1 kg/m³ for the density.

Reference liquid name	Dynamic viscosity (mPa^.s)	Density (kg/m³)
2AW	1.5319 ± 0.0031	751.2 ± 0.1
2BW	2.1913 ± 0.0044	764.7 ± 0.1
5AW	4.0393 ± 0.0081	785.3 ± 0.1

Table 8. The determination of the dynamic viscosities of reference liquids 2AW, 2BW, 5AW [22] by means of the pipe viscometer in the laminar regime. The uncertainty (k=2) of the pipe viscometer is 0.90 %.

Material		2AW	2BW	5AW
Soda glass	Dynamic viscosity (mPa^.s)	1.5384	2.2005	4.0563
	Deviation incl. uncertainty (%)	+0.43 ± 0.90	+0.42 ± 0.90	+0.43 ± 0.90
Stainless steel	Dynamic viscosity (mPa^.s)	1.5090	2.1517	3.9797
	Deviation incl. uncertainty (%)	-1.50 ± 0.90	-1.81 ± 0.90	-1.48 ± 0.90
PEEK beige	Dynamic viscosity (mPa^.s)	1.5141	2.1671	3.9928
	Deviation incl. uncertainty (%)	-1.16 ± 0.90	-1.10 ± 0.90	-1.15 ± 0.90

Table 9. Dynamic viscosity η of the reference liquid “2BW” determined by the pipe viscometer with the soda glass micro tube.

Method / pressure drop (bar)	η @ 21.3 °C (mPa^.s)	Deviation to reference (%)
Linear fit / full range ΔP = 0.56 – 6.70	2.201 ± 0.020	0.42 ± 0.90
Single point / ΔP = 6.70	2.203 ± 0.020	0.54 ± 0.90
Single point / ΔP = 6.15	2.200 ± 0.020	0.39 ± 0.90
Single point / ΔP = 5.58	2.199 ± 0.020	0.33 ± 0.90
Single point / ΔP = 5.02	2.200 ± 0.020	0.41 ± 0.90
Single point / ΔP = 4.46	2.202 ± 0.020	0.47 ± 0.90
Single point / ΔP = 3.91	2.202 ± 0.020	0.48 ± 0.90
Single point / ΔP = 3.35	2.193 ± 0.020	0.08 ± 0.90
Single point / ΔP = 2.78	2.195 ± 0.020	0.16 ± 0.90
Single point / ΔP = 1.67	2.197 ± 0.020	0.27 ± 0.90
Single point / ΔP = 1.11	2.195 ± 0.020	0.19 ± 0.90
Single point / ΔP = 0.56	2.219 ± 0.020	1.27 ± 0.90

Table 10. Dynamic viscosity of the liquids measured by means of pipe viscometers and glass capillary viscometers at temperature of 22 °C [2,23].

Facility	Liquid C	Liquid E
METAS	1.810 ± 0.017	1.110 ± 0.010
RISE	1.800 ± 0.037	1.112 ± 0.023
NEL	1.795 ± 0.018	1.123 ± 0.012
NQIS/EIM	1.823 ± 0.019	1.119 ± 0.012
KRISS	1.803 ± 0.036	1.107 ± 0.023
Reference value	1.809 ± 0.009	1.116 ± 0.006

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer