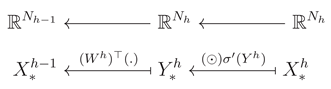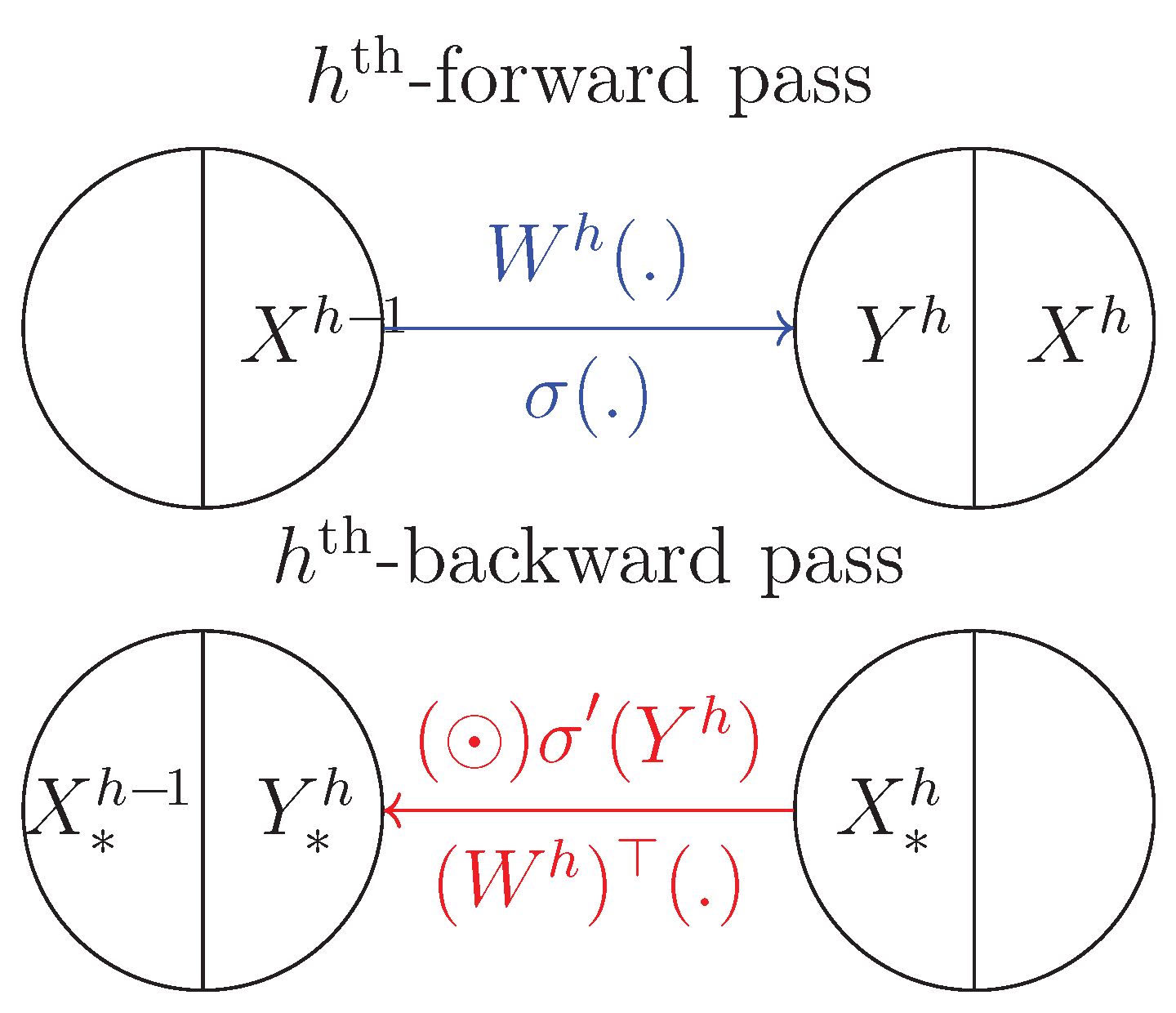1. Introduction
An Artificial Neural Network (ANN) is a mathematical model which is intended to be a universal function approximator which learns from data (cf. McCulloch and Pitts, [
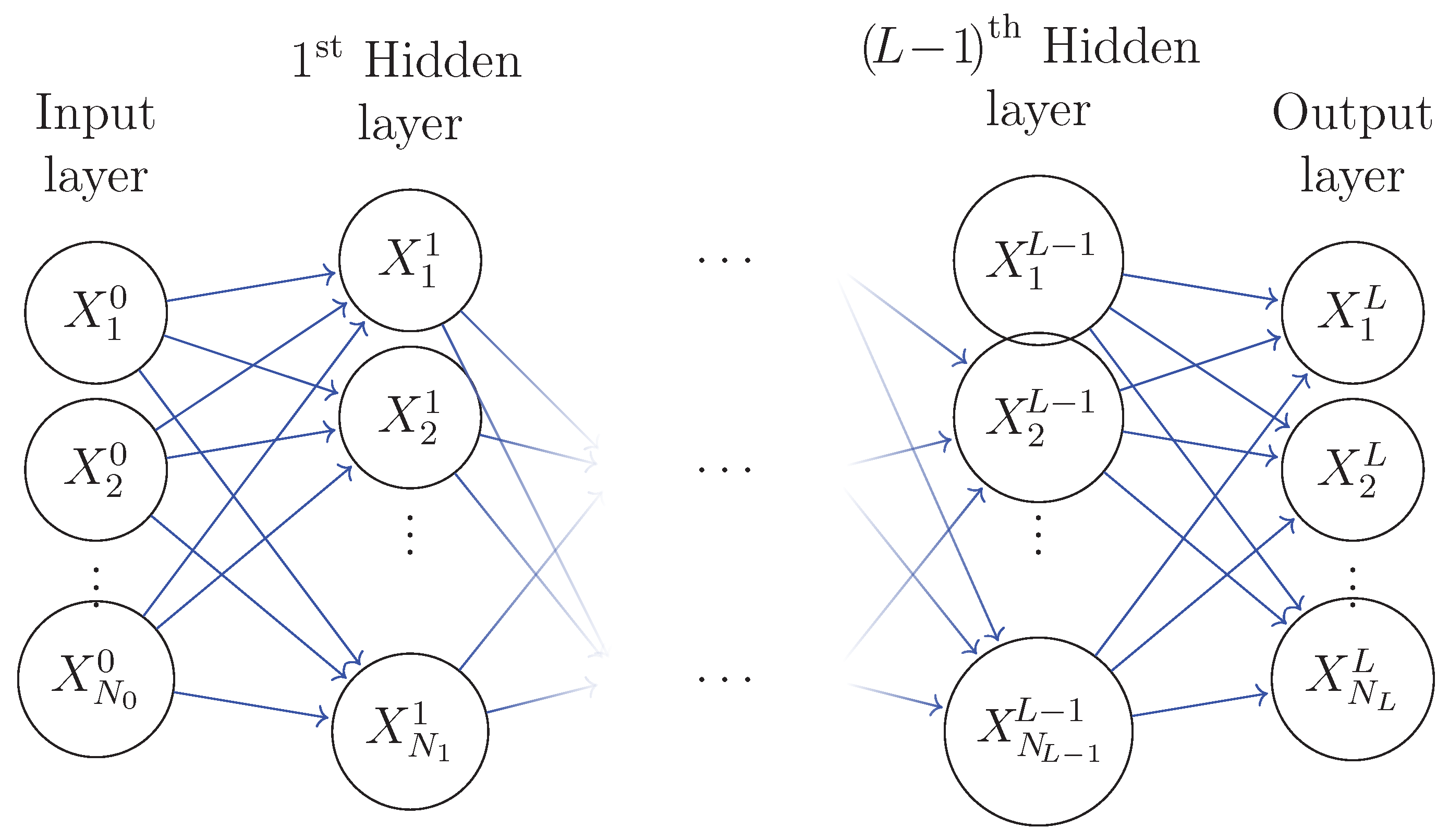
1]). In general, an ANN consists of a number of units called artificial neurons, which are a composition of affine mappings, and non-linear (activation) mappings (applied element wise), connected by weighted connections and organized into layers, containing an input layer, one or more hidden layers, and an output layer.The neurons in an ANN can be connected in many different ways. In the simplest cases, the outputs from one layer are the inputs for the neurons in the next layer. An ANN is said to be a feedforward ANN, if outputs from one layer of neurons are the only inputs to the neurons in the following layer. In a fully connected ANN, all neurons in one layer are connected to all neurons in the previous layer (cf. page 24 of [
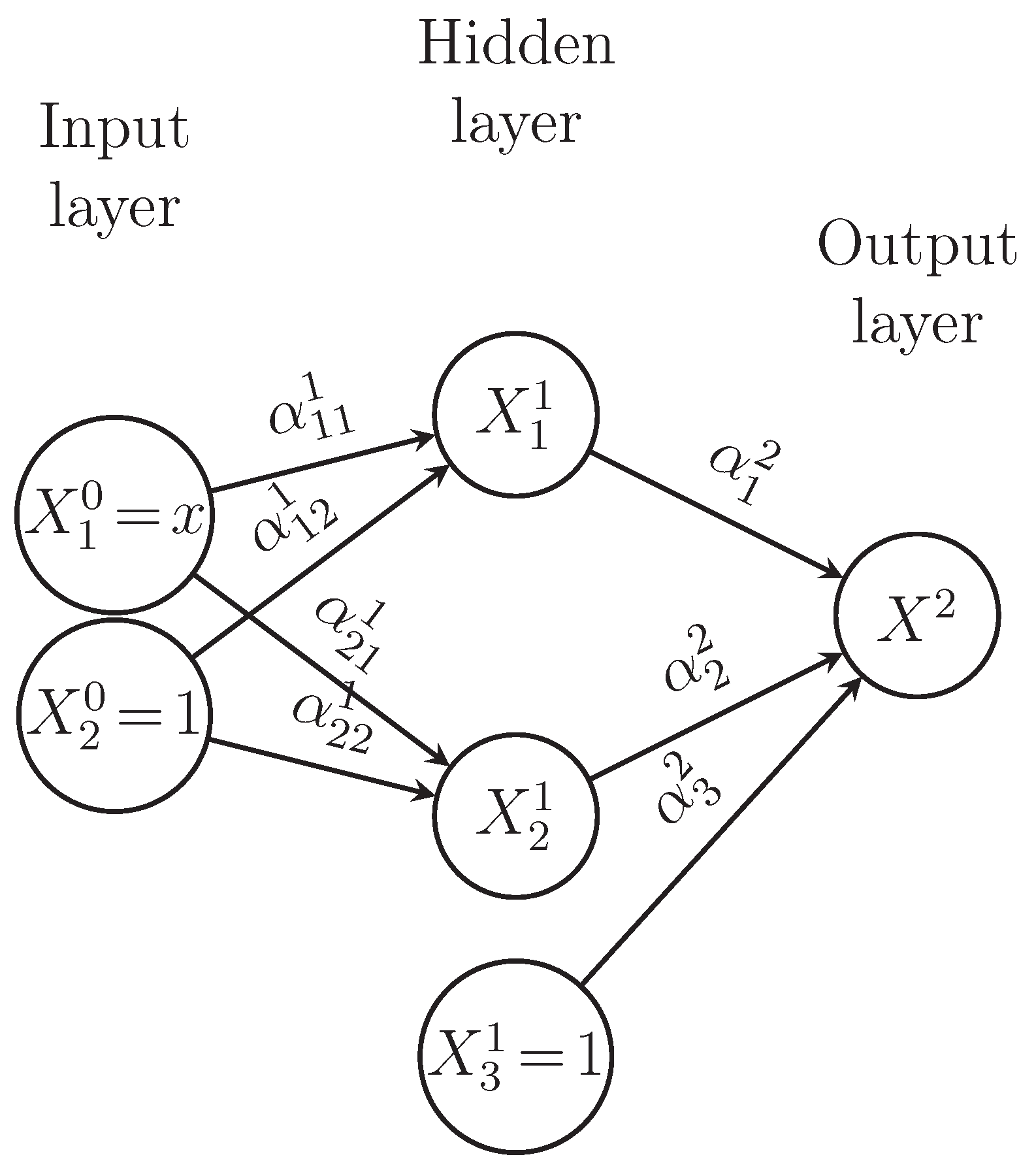
2]). An example of a fully connected feedforward network is presented in
Figure 1.
In the present work we focus essentially on feed-forward artificial neural networks, with
L hidden layers and a transfer (or activation) function
, and the corresponding supervised learning problem. Let us define a simple artificial neural network as follows:
where
is the input to the network,
h indexes the hidden layer and
is the weight matrix of the
h-th hidden layer. In what follows we shall refer to the two equations of (
1) as the two-step recursive forward formula. The two-step recursive forward formula is very useful in obtaining the outputs of the feed-forward deep neural networks.
A major empirical issue in the neural networks is to estimate the unknown parameters
with a sample of data values of targets and inputs. This estimation procedure is characterized by the recursive updating or the learning of estimated parameters. This algorithm is called the backpropagation algorithm. As reviewed by Schmidhuber [
3], back-propagation was introduced and developed during the 1970’s and 1980’s and refined by Rumelhart et al. [
4]). In addition, it is well known that the most important algorithms of artificial neural networks training is the back-propagation algorithm. From mathematical point view, back-propagation is a method to minimize errors for a loss/cost function through gradient descent. More precisely, an input data is fed to the network and forwarded through the so-called layers ; the produced output is then fed to the cost function to compute the gradient of the associated error. The computed gradient is then back-propagated through the layers to update the weights by using the well known gradient descent algorithm.
As explained in [
4], the goal of back-propagation is to compute the partial derivatives of the cost function
J. In this procedure, each hidden layer
h is assigned teh so-called delta error term
. For each hidden layer, the delta error term
is derived from the delta error terms
; thus the concept of error back-propagation. The output layer
L is the only layer whose error term
has no error dependencies, hence
is then given by the following equation
where ⊙ denotes the element-wise matrix multiplication (the so-called Hadamard product, which is exactly the element-wise multiplication
in Python). For the error term
, this term is derived from matrix multiplying
with the weight transpose matrix
and subsequently multiplying (element-wise) the activation function derivative
with respect to the preactivation
. Thus, one has the following equation
Once the layer error terms have been assigned, the partial derivative
can be computed by
In particular, we deduce that the back-propagation algorithm is uniquely responsible for computing weight partial derivatives of
J by using the recursive equations (
4) and (
3) with the initialization data given by (
2). This procedure is often called "the generalized delta rule". The key question to which we address ourselves in the present work is the following: how could one reformulate this "generalized delta rule" in two-step recursive backward formula as (
1) ?
In the present work, we shall provided a concise mathematical answer to the above question. In particular, we shall introduce the so-called two-step rule for back-propagation, recently proposed by the author in [
5], similar to the one for forward propagation. Moreover, we explore some mathematical concepts behind the two-step rule for backpropagation.
The rest of the paper is organized as follows.
Section 2 outlines some notations, setting and ANN framework. In
Section 3 we recall and develop the two-step rule for back-propagation. In
Section 4 we introduce the concepts of F-propagation and the associated F-adjoint and rewrite the two-step rule with these notions. In
Section 5 we provide some application of this method to study some simple cases. In
Section 6 conclusion, related works and mention future work directions are given.
2. Notations, Setting and the ANN
Let us now precise some notations. Firstly, we shall denote any vector
, is considered as columns
and for any family of transfer functions
, we shall introduce the coordinate-wise map
by the following formula
This map can be considered as an “operator” Hadamard multiplication of columns
and
, i.e.,
Secondly, we shall need to recall some useful multi-variable functions derivatives notations. For any
and any differentiable function with respect to the variable
x
we use the following notations associated to the partial derivatives of
F with respect to
x
In adfdition, for any
and any differentiable function with respect to the matrix variable
we shall use the so-called
denominator layout notation (see page 15 of [
6]) for the partial derivative of
F with respect to the matrix
X
In particular, this notation leads to the following useful formulas: for any
and any matrix
we have
when
with
one has
where
is the matrix
W whose last column is removed (this formula is highly useful in practice). Moreover, for any matrix
we have
Then, by the chain rule one has for any
and any differentiable function with respect to the matrices variables
:
Furthermore, for any differentiable function with respect to
Y
we have
Throughout this paper, we consider layered feedforward neural networks and supervised learning tasks. Following [
2] (see (2.18) in page 24), we will denote such an architecture by
where
is the size of the input layer,
is the size of hidden layer
h, and
is the size of the output layer;
L is defined as the depth of the ANN, then the neural network is called as Deep Neural Network (DNN). We assume that the layers are fully connected, i.e., neurons between two adjacent layers are fully pairwise connected, but neurons within a single layer share no connections.
In the next section we shall recall, develop and improve the two-scale rule for backpropagation, recently introduced by the author in [
5].
3. Two-step rule for backpropagation
First, let us mention that the two-step rule for backpropagation is very useful in obtaining some estimation of the unknown parameters
with a sample of data values of targets and inputs (see some examples given in [
5]).
Now, let
denote the weight connecting neuron
j in layer
to neuron
i in hidden layer
h and let the associated transfer function denoted
. In general, in the application two different passes of computation are distinguished. The first pass is referred to as the forward pass, and the second is referred to as the backward pass. In the forward pass, the synaptic weights remain fixed throughout the network, and the output
of neuron
i in hidden layer
h is computed by the following recursive-coordinate form :
In two-step recursive-matrix form, one may rewrite the above formulas as
with
Let us assume that for all
,
, where
is a fixed activation function, and define a simple artificial neural network as follows:
where
is the input to the network.
To optimize the neural network, we compute the partial derivatives of the cost
w.r.t. the weight matrices
. This quantity can be computed by making use of the chain rule in the back-propagation algorithm. To compute the partial derivative with respect to the matrices variables
, we put
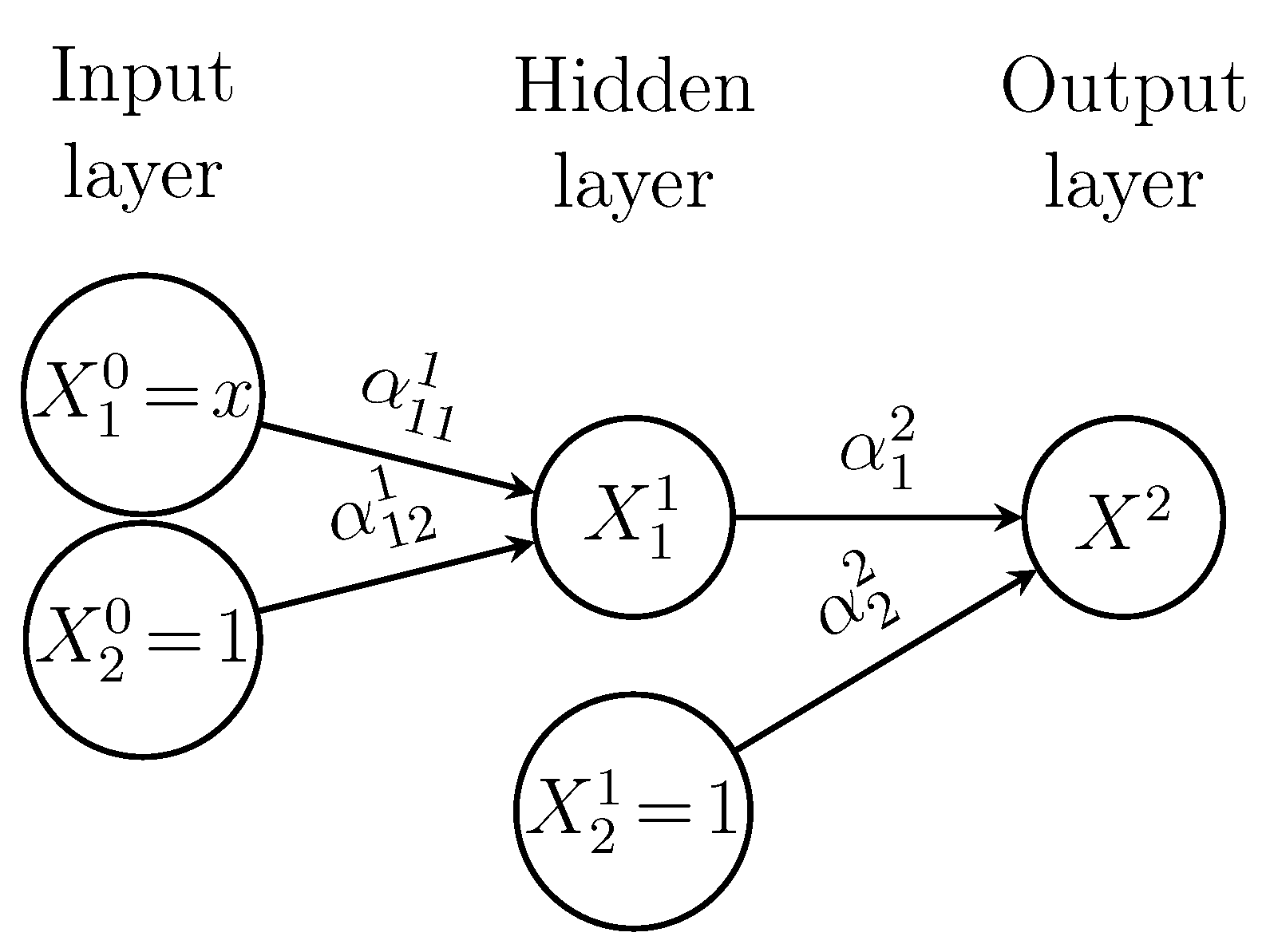
Figure 1.
Example of an architechture.
Figure 1.
Example of an architechture.
Let us notice that the forward pass computation between the two adjacent layers and h may be represented mathematically as the composition of the following two maps:
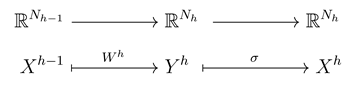
The backward computation between the two adjacent layers h and may be represented mathematically as follows:
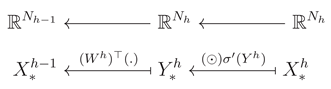
One may represent those maps as a simple mapping diagrams with
and
as inputs and the respective outputs are
and
(see
Figure 2).
Remark 1. It is crucial to remark that, if we impose the following setting on and :
-
1.
all input vectors have the form for all ;
-
2.
the last functions in the columns for all are constant functions equal to 1.
Then, the neural network will be equivalent to a -layered affine neural network with -dimensional input and -dimensional output. Each hidden layer h will contain “genuine” neurons and one (last) “formal”, associated to the bias; the last column of the matrix will be the bias vector for the h-th layer (For more details, see the examples given in Section 5).
Figure 2.
Mapping diagrams associated to the forward and backward passes between two adjacent layers.
Figure 2.
Mapping diagrams associated to the forward and backward passes between two adjacent layers.
Now, we state our first main mathematical result to answer the above question, in the following theorem.
Theorem 1 (The two-step rule for backpropagation).
Let L be the depth of a Deep Neural Network and the number of neurons in the h-th hidden layer. We denote by the inputs of the network, the weights matrix defining the synaptic strengths between the hidden layer h and its preceding . The output of the hidden layer h are thus defined as follows:
Where is a point-wise differentiable activation function. We will thus denote by its first order derivative, is the input to the network and is the weight matrix of the h-th layer. To optimize the neural network, we compute the partial derivatives of the loss w.r.t. the weight matrices , with and y are the output of the DNN and the associated target/label respectively. This quantity can be computed similarly by the following two-step rule:
Once is computed, the weights update can be computed as
Hereafter, the two-step recursive formulae given in (
22) and (
23) will be referred to as "the two-step rule for back-propagation" (see the mapping diagram represented by
Figure 3.). In particular, this rule provide us a simplified formulation of the so-called "generalized delta rule" similarly to (
1). Thus, we have answered our key question.
Proof.
Firstly, for any let us recall the simplified notations introduced by (
20):
Secondly, for fixed ,
, then (
14)
implies that
thus
On the other hand, , thus
by vertue of (
13).
As consequence,
Equations (
24) and (
25)
implies immediately (
22).
Moreover, we apply again (
13)
to the cost function J and the relation , we deduce that
This end the proof of the Theorem 1. Furthermore, in the practical setting mentioned in Remark 1, one should replace by
by vertue of (
11).
Thus, we have for all
and then the associated two-step rule is given by
□
4. The F-propagation and F-adjoint
Based on the above idea of two-scale rule for back-prpagation, we shall introduce the following two natural definitions :
Definition 1 (An F-propagation).
Le be a given data, σ be a coordinate-wise map from into and for all . We say that we have a two-step recursive F-propagation F through the DNN if one has the following family of vectors
Before going further, let us point that in the above definition the prefix "F" stands for "Feed-forward".
Definition 2 (The F-adjoint of an F-propagation).
Let be a given data and a two-step recursive F-propagation F through the DNN . We define the F-adjoint of the F-propagation F as follows
Remark 2.
It is immediately seen that if for every , is an orthogonal matrix i.e. , and one has
also, by recurrence we get
Consequently, we obtain and we refer to this property as F-symmetric. We may conjecture that under the following assumption : for all vector X, , a DNN is F-symmetric if and only if , i.e. for all , is an orthogonal matrix.
Similarly to the note at the end of the proof of Theorem 1, if we are in the practical setting mentioned in Remark 1, one should replace
by
by vertue of (
11) and (
30) by the following relations :
Now, following these definitions, we can deduce our second main mathematical result.
Theorem 2 (The backpropagation is an F-adjoint of the associated F-propagation).
Let be a Deep Neural Network and let an F-propagation through , with weights matrix and fixed point-wise activation , .
Let be the input to this network and be the loss function, with and y are the output of the DNN and the associated target/label respectively.
Then the associated backpropagation pass is computed with the F-adjoint of F with , that is . Moreprecisely, for all
Before proving the Theorem 2, let us as remark that this mathematical result is a simplified version of Theorem 1 based on the notion of F-adjoint introduced in Definition 2.
Proof.
By definition of the F-adjoint one has for all
Moreover, by the two-step rule for backpropagation, we have
As consequence, we deduce that the backpropagation is exactely determined by the F-adjoint relatively to the choice of . Here we present a new proof of Theorem 1 of [
5]
which is simpler than the original one. □
6. Related works and Conclusion
To the best of our knowledge, in literature, the related works to this paper are [
7] and [
8]. In particular, in the first paper the authors uses some decomposition of the partial derivatives of the cost function, similar to the two-step formula (cf. (
22)), to replace the standard back-propagation. In addition, they show (experimentally) that for specific scenarios, the two-step decomposition yield better generalization performance than the one based on the standard back-propagation. But in the second article, the authors find some similar update equation similar to the one given by (
22) that report similarly to standard back-propagation at convergence. Moreover, this method discovers new variations of the back-propagation by learning new propagation rules that optimize the generalization performance after a few epochs of training.
In conclusion, we have provided a two-step rule for back-propagation similar to the one for forward propagation and a new mathematical notion called F-adjoint which is combined by the two-step rule for back-propagation describes, in a simple and direct way, the computational process given by the back-propagation pass. We hope that, the power and simplicity of the F-adjoint concept may inspire the exploration of novel approaches for optimizing some artificial neural networks training algorithms and investigating some mathematical properties of the F-propagation and F-adjoint notions. As future work, we envision to explore some mathematical results regarding the F-adjoint for deep neural networks with respect to the choice of the activation function.