In physics, quantum field theory (QFT) was developed to describe structureless elementary particles (e.g., electrons, quarks, photons, etc.), their interaction with each other and with their environment [1-3]. A graphical technique to account for physical processes in QFT (e.g., scattering) is by using diagrams known as the Feynman diagrams. These consist of points (vertices) connected by lines (propagators) [4-5]. The lines represent free propagation of elementary particles and the points represent the interaction among particles meeting at those points. One way to represent free scalar particles in QFT is to utilize solutions of the Klein-Gordon wave equation in 3+1 dimensional Minkowski space-time that reads where m is the rest mass of the scalar particle and we have adopted the relativistic units $\hslash =c=1$. Recently, a formulation of QFT for elementary particles that have internal structure was developed in which the quantum field operator $\Psi (t,\overrightarrow{r})$ is written as Fourier expansion over the energy domain consisting of continuous and discrete components:

The integral over $\Omega$ represents the continuous energy spectrum of the particle whereas the sum represents its structure, which is resolved in the energy and of size $N+1$. This formulation of QFT is referred to by the acronym SAQFT that stands for “Structural Algebraic QFT” and could be useful in treating elementary particles that are thought to be structureless at low energy scale [6]. We take $\Omega$ to stand for the single energy interval $E^2\ge m^2$ and take $0\le E_j^2<m^2$. The objects $a\left(E\right)$ and $a_j$ are field operators (the vacuum annihilation operators) that satisfy the conventional commutation relations: $\left[a\left(E\right),a^{†}\left(E^{’}\right)\right]=\delta (E-E^{’})$ and $\left[a_i,a_j^{†}\right]={\delta }_{i,j}$. The continuous and discrete Fourier energy components in (2) are written as the following pointwise convergent series where $z=E^2-m^2$, $z_j=E_j^2-m^2$ and $\left\{{\varphi }_n\left(\overrightarrow{r}\right)\right\}$ is a complete set of functions, which for scalar particles satisfy the following differential equation where $\left\{{\alpha }_n,{\beta }_n\right\}$ are real constants that are independent of z and such that ${\beta }_n\ne 0$ for all n. Using (4) in the free Klein-Gordon wave equation (1) gives the following algebraic relation for $n=\mathrm{1,2},3,..$. This is a symmetric three-term recursion relation that makes $\left\{p_n\left(z\right)\right\}$ a sequence of polynomials in z with the two initial values $p_0\left(z\right)=1$ and $p_1\left(z\right)=\frac{z-{\alpha }_0}{{\beta }_0}$. Favard theorem (a.k.a. the spectral theorem; see Section 2.5 in [7]) dictates that the polynomial solutions of Eq. (5) satisfy the following general orthogonality relation [7,8,9] where $\rho \left(z\right)$ is the continuous component of the weight function and $\xi \left(z_j\right)$ is the discrete component. These weight functions are positive definite and related to the energy functions $A\left(E\right)$ and $B\left(E\right)$ as $A^2\left(E\right)dE=\rho \left(z\right)dz$ (with $\frac{dz}{dE}>0$ for $E\in \Omega$) and $B^2\left(E_j\right)=\xi \left(z_j\right)$.

In conventional QFT, the propagators in the Feynman diagrams are tagged with the energy-momentum four-vector $(E,\overrightarrow{k})$. However, in SAQFT these propagators are tagged with the spectral parameter z. For free scalar particles, $E^2>m^2$ making z positive. However, doing scattering calculation with the Feynman diagrams in closed loops, one should integrate and sum over all possible values of the real energy in $\Omega \cup {\left\{E_j\right\}}_{j=0}^N$ (i.e., $E^2\ge 0$) making the values of these spectral parameters z greater than or equal to $-m^2$. At each vertex in the Feynman diagrams, the energy-momentum 4-vector is conserved. 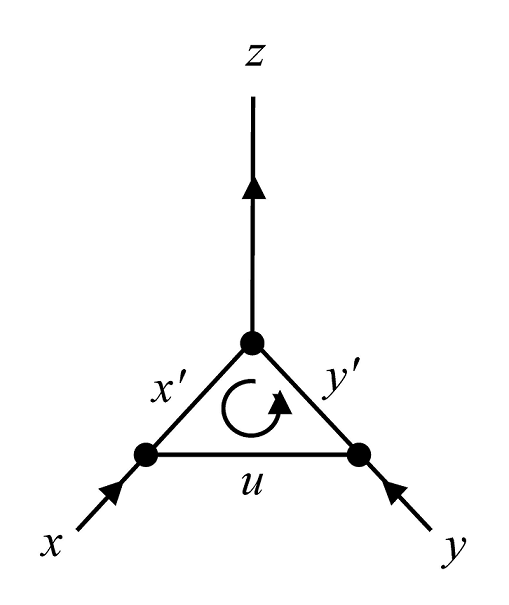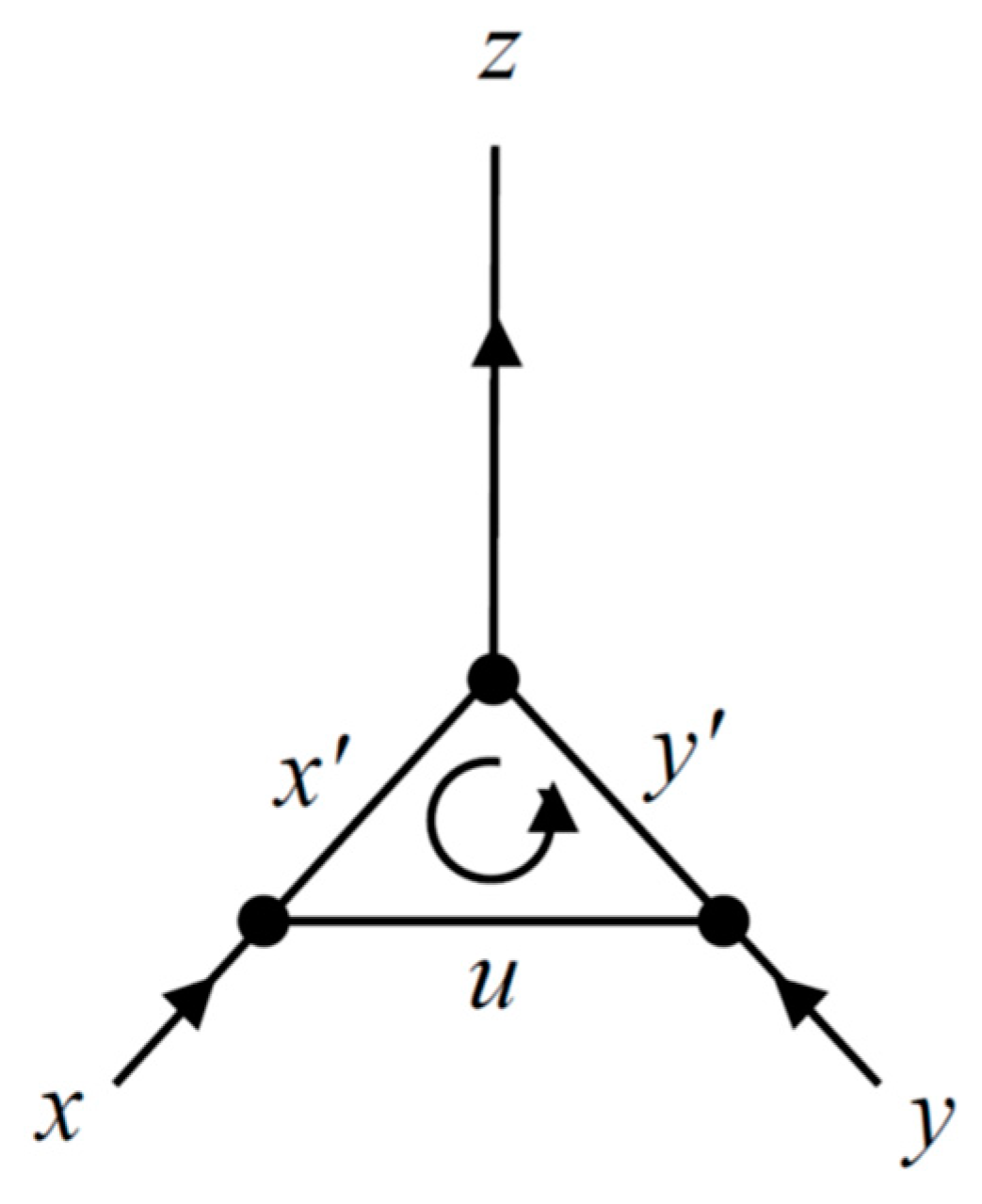For example, when calculating the first order correction to the three-particle interaction vertex, we encounter loop diagrams similar to that shown in Figure 1 where the spectral parameters $\left\{x,x^{’},y,y^{’},z,u\right\}$ are indicated on their respective propagators. Choosing a counterclockwise loop, the three energy conservation equations are: $E\left(x\right)=E\left(u\right)-E(x’)$, $E\left(y\right)=E(y’)-E\left(u\right)$, and $E\left(z\right)=E\left(y^{’}\right)-E\left(x^{’}\right)=E\left(x\right)+$ $E\left(y\right)$, where $E\left(a\right)=\pm \sqrt{a+m^2}$. This leads to a special rule for adding and subtracting spectral parameters. For example, $E\left(z\right)=E\left(x\right)+E\left(y\right)$ gives where “sgn” is ±, which is the product of the signs of the two energies $E\left(x\right)$ and $E\left(y\right)$. Moreover, the sign of the energy $E\left(z\right)$ is the sign of $E\left(x\right)+E\left(y\right)$. Therefore, for the spectral parameters to contain full physical information, they must carry the sign of their corresponding energies. Hence, we associate with each spectral parameter a ± parity, which will be indicated as superscript on the parameter. For example, the parity of z in (7) is the sign of $\sigma \sqrt{x+m^2}+$ $\tau \sqrt{y+m^2}$ where σ is the sign of the energy $E\left(x\right)$ (i.e., parity of x) and τ is the sign of the energy $E\left(y\right)$ (i.e., parity of y). Thus, we rewrite (7) properly as follows where ρ is the (nonzero) sign of the energy $E\left(z\right)$ (i.e., parity of z). This equation defines the operation of addition of the spectral parameters. Repeating the same for the energy conservation equation $E\left(z\right)=E(y’)-E(x’)$, we obtain the following rule for the subtraction of spectral parameters where ρ is the (nonzero) sign of $\tau \sqrt{y^{’}+m^2}-\sigma \sqrt{x^{’}+m^2}$. The parity of each spectral parameter $\left\{x,x’,y,y’,z,u\right\}$ in the figure (not shown) is the sign of the corresponding energy.

Interested readers are referred to Ref. [6] for further details on the scattering calculation in SAQFT that utilizes this algebraic system. In the following section, we make a proper and rigorous mathematical definition of the underlying algebraic structure emerging from the physics of scattering with scalar particles in SAQFT as outlined above and detailed in Ref. [6].

The novel algebraic system emerging from the physical application in QFT presented in the previous section and exhibited by the addition and subtraction rules of the spectral parameters as shown by Eq. (8) and (9) will now be given a proper mathematical definition.

Define operations $\oplus$ and $\otimes$ on ${\mathbb{R}}^r$ by where $z=\sigma \sqrt{x-r}+\tau \sqrt{y-r}$ and $w=\sigma \tau \sqrt{(x-r)(y-r)}$.

Note that the multiplicative identity of ${\mathbb{R}}^r$ is g(1), i.e. $(1+r,1)$, and that the additive and multiplicative inverses of $x^{\sigma }$ are $g\left(-f\left(x^{\sigma }\right)\right)$ and $g\left(\frac{1}{f\left(x^{\sigma }\right)}\right)\left(\mathrm{for}x\ne r\right),$ respectively, i.e. $x^{s\left(-\sigma \sqrt{x-r}\right)}$ and ${\left(\frac{1}{x-r}+r\right)}^{\sigma }$.

If we denote subtraction on ${\mathbb{R}}^r$ by $\ominus$, i.e. $x^{\sigma }\ominus y^{\tau }=g\left(f\left(x^{\sigma }\right)-f\left(y^{\tau }\right)\right)$, then where $z=\sigma \sqrt{x-r}-\tau \sqrt{y-r}$, so that

(note that $\ominus$ is not commutative since $x^{\sigma }\ominus y^{\tau }$ and $y^{\tau }\ominus x^{\sigma }$ may have different parities).

Other properties of $\mathbb{R}$ are also inherited by ${\mathbb{R}}^r$ via the bijection f above. For example, $({\mathbb{R}}^r,d)$ where $d(x^{\sigma },y^{\tau })=\left|f\left(x^{\sigma }\right)-f\left(y^{\tau }\right)\right|$ is a metric space.

As shown in Section 1 and detailed in Ref. [6], this algebraic system is very useful in relativistic scattering calculations using Feynman diagrams in SAQFT if we take the real constant $r=-m^2$. In that case, $f\left(x^{\sigma }\right)=\sigma \sqrt{x+m^2}$ becomes the relativistic energy of the particle associated with the spectral parameter $x^{\sigma }$. Finally, it is worth noting that ${\mathbb{R}}^r$ together with addition $\oplus$ and a scalar multiplication * defined by $a*x^{\sigma }={\left(a^2(x-r)+r\right)}^{s\left(a\sigma \sqrt{x-r}\right)}$, for each real number a, will turn ${\mathbb{R}}^r$ into a real vector space. This extra structure could have a physical interpretation and might be useful for certain applications in QFT.