Shapley Value for Shortest Path Routing in Dynamic Networks

Preprint

Review

Shapley Value for Shortest Path Routing in Dynamic Networks

Altmetrics

Downloads

173

Views

Comments

Aykhan Masimli^*

This version is not peer-reviewed

Submitted:

27 April 2023

Posted:

28 April 2023

You are already at the latest version

Alerts

Abstract

Transportation is a crucial component of supply chain management, responsible for delivering goods and services to customers. This paper explores the application of game theory concepts, precisely the Shapley value, to cost allocation in transportation operations involving drones and trucks. Our focus is on shortest-path games in which agents own nodes in a network and seek to transport items between nodes at the lowest possible cost. We provide a comprehensive literature review of the Shapley value and its use in shortest-path games, with particular emphasis on transportation networks. Our proposed model includes sets of customers, drones, and trucks and uses binary decision variables to indicate whether a drone or truck serves a given customer. The objective is to minimize the total cost of serving all customers while adhering to capacity and synchronization constraints. We use the Shapley value to determine the contribution and cost-sharing of each drone and truck in serving the customers. Through a combination of denitions, theorems, and examples, we explore the formal meaning of the Shapley value and its relationship to shortest-path games in transportation networks. We highlight exceptional cases and considerations that must be taken into account when applying the Shapley value in such scenarios.

Keywords:

Subject: Business, Economics and Management - Business and Management

1. Introduction

In this paper, we explore the application of the Shapley value method, to cost allocation in transportation operations involving drones and trucks. Our focus is on shortest-path games in which agents own nodes in a network and seek to transport items between nodes at the lowest possible cost.

We provide a literature review of the Shapley value and its use in shortest-path games, with particular emphasis on transportation networks. The Shapley value method is a cooperative game theory approach that assigns costs to players based on their marginal contribution to a coalition. This ensures that each player pays a fair share of the total cost. In the context of transportation costs, the Shapley value method can be used to optimize budgets and ensure equitable cost-sharing among participants.

The transportation of goods and services is a critical component of supply chain management. As the demand for fast and efficient delivery continues to grow, companies are increasingly turning to innovative solutions such as drones and trucks to meet their transportation needs. However, the cost of operating these transportation systems can be significant, and it is essential to ensure that costs are allocated equitably among participants.

Game theory provides a powerful framework for analyzing cost allocation problems in transportation networks. In particular, the Shapley value method offers a way to assign costs to players based on their marginal contribution to a coalition [1].

Our proposed model includes sets of customers, drones, and trucks and uses binary decision variables to indicate whether a drone or truck serves a given customer. The objective is to minimize the total cost of serving all customers while adhering to capacity and synchronization constraints. We use the Shapley value to determine the contribution and cost-sharing of each drone and truck in serving the customers [2].

The motivation for writing this paper is to provide a deeper understanding of the relationship between the Shapley value and shortest-path games in transportation networks.

1.1. Research Objectives

The primary objective of this research is to investigate the potential benefits of applying game theory concepts, specifically the Shapley value method, to cost allocation in transportation operations involving drones and trucks. Our main research objectives are to:

Provide a detailed analysis of shortest-path games in which agents own nodes in a network and seek to transport items between nodes at the lowest possible cost.
Conduct a comprehensive review of existing literature on the use of the Shapley value in shortest-path games, with a focus on its application to transportation networks [3].
Develop a model that includes sets of customers, drones, and trucks and uses binary decision variables to indicate whether a drone or truck serves a given customer. The objective of the model is to minimize the total cost of serving all customers while adhering to capacity and synchronization constraints.
Use the Shapley value to determine the contribution and cost-sharing of each drone and truck in serving the customers [4].
Explore the formal meaning of the Shapley value and its relationship to shortest-path games in transportation networks. We will highlight exceptional cases and considerations that must be taken into account when applying the Shapley value in such scenarios.

2. An Overview of Cooperative Game Theory

Cooperative game theory is a branch of game theory that focuses on the formation and analysis of coalitions or groups of players. In cooperative games, players can form coalitions and work together to achieve a common goal. The Shapley value is a solution concept in cooperative game theory that provides a way to fairly distribute the gains from cooperation among the members of a coalition.

In cooperative games, several natural questions arise:

How can players form coalitions that maximize their collective payoff?
What mechanism should be developed so that players’ decisions within a coalition are identical to the globally-optimal solutions that maximize the coalition’s payoff?
How should the maximum coalition’s payoff be fairly divided among its members so that no player would have an incentive to leave the coalition?
How can players ensure that agreements made within a coalition are enforced and that members do not deviate from the agreed-upon strategy?

A cooperative game is defined by a set of players

N = 1, 2, \dots, n

and a characteristic function

v : 2^{N} \to R

that assigns a real value to each coalition

S \subseteq N

. The value

v (S)

represents the cost that the coalition S can guarantee when its members cooperate. In the context of transportation networks, this cost is typically defined as the length of the shortest path that can be guaranteed by the vehicles in S.

There are several types of cooperative games:

Super-additive games: for all coalitions S, $M \subset N$ , if $S \cap M = \emptyset$ , then $v (S \cup M) \geq v (S) + v (M)$ .
Convex games: for all S, $M \subset N$ , $v (S \cup M) \geq v (S) + v (M) - v (S \cap M)$ .
Additive games: for all S, $M \subset N$ , if $S \cap M = \emptyset$ , then $v (S \cup M) = v (S) + v (M)$ .
Constant-sum games: for all $S \subset N$ , $v (S) + v (N ∖ S) = v (N)$ .
Simple games: for all $S \subset N$ , $v (S) \in 0, 1$ .

One application of cooperative game theory is in the field of shortest path routing in dynamic networks. The Shapley value can be used to fairly distribute the costs or benefits associated with routing decisions among the members of a coalition. For more information on this topic, see [5].

2.1. Solution Concepts for Coalition Games

As mentioned in [6], one of the main questions in coalition games is the distribution of the payoff of the grand coalition among the players. One of the reasons is that in the context of super additive games, which are the most studied ones, the grand coalition gives the highest payoff. Then, the question arises to know how this coalition must divide its payoff. Many solution concepts have been proposed to solve this problem. In other words, solution concepts can be viewed as a means to identify certain subsets of outcomes (i.e., solutions).

Prior to the presentation of some solution concepts, we have to introduce some complementary terminology. An imputation (labeled x) is a vector of players’ outcomes. Each element

x_{i}

of this vector denotes the share of the grand coalition’s payoff that a player

i \in N

receives. From a negotiation perspective, the set of imputations can be seen as the set of feasible agreements between the players. Considering a coalition game

(N, v)

, the imputation is formally defined as follows:

The pre-imputation set, labeled P, is defined as: $x \in R^{N} | \sum_{i \in N} x_{i} = v (N)$ ;
Based on set P, the imputation set, labeled X, is defined as: $x \in P | \forall i \in N, x_{i} \geq v (i)$ .

This definition refers to two following terminology frequently used in this domain:

Individual rationality means that a player will not accept an outcome which is not at least equal to what he could obtain by acting alone as measured by his characteristic function value.
Group rationality states that the total cooperative gain of the grand coalition is fully shared.

The set of imputation X is rarely unique, which is why other properties are needed to define the final issue of the game. A solution concept is a sharing mechanism based on a series of axioms which correspond to some interesting properties (e.g., fairness, stability, etc.). Many solutions concepts have been proposed in literature such as Shapley value, nucleolus, stable set and kernel. For instance [7] and [8] describe these solutions concepts.

The exhaustive study of all these solutions concepts is beyond our objective. However, we noticed that Shapley value has been successfully used in some planning cooperation problems such as for instance in field of vehicles route planning [9]. As far as we know there is lack of studies using Shapley value tackling planning cooperation at tactical level between transport operators as well as between manufacturers and transport operators. Due to these reasons we have chosen to use Shapley value principle which is presented in next section.

2.2. The Shapley Value

Perhaps the most straightforward answer to the question of how payoffs should be divided is that the division should be fair. Let us begin by laying down axioms that describe what fairness means in our context.

First, say that agents i and j are interchangeable if they always contribute the same amount to every coalition of the other agents. That is, for all S that contains neither i nor j,

v (S \cup i) = v (S \cup j)

. The symmetry axiom states that such agents should receive the same payments.

Symmetry:

For any v, if i and j are interchangeable then

ψ_{i} (N, v) = ψ_{j} (N, v)

Second, say that an agent i is a dummy player if the amount that i contributes to any coalition is exactly the amount that i is able to achieve alone. That is, for all S such that

i \notin S

v (S \cup i) - v (S) = v (i)

. The dummy player axiom states that dummy players should receive a payment equal to exactly the amount that they achieve on their own.

Dummy player:

For any v, if i is a dummy player then

ψ_{i} (N, v) = v (i)

Finally, consider two different coalitional game theory problems, defined by two different characteristic functions

v_{1}

and

v_{2}

, involving the same set of agents. The additivity axiom states that if we re-model the setting as a single game in which each coalition S achieves a payoff of

v_{1} (S) + v_{2} (S)

, the agents’ payments in each coalition should be the sum of the payments they would have achieved for that coalition under the two separate games.

Additivity:

For any two

v_{1}

and

v_{2}

, we have for any player i that

ψ_{i} (N, v_{1} + v_{2}) = ψ_{i} (N, v_{1}) + ψ_{i} (N, v_{2})

, where the game

(N, v_{1} + v_{2})

is defined by

(v_{1} + v_{2}) (S) = v_{1} (S) + v_{2} (S)

for every coalition S.

If we accept these three axioms, we are led to a strong result: there is always exactly one pre-imputation that satisfies them.

Given a coalitional game

(N, v)

, there is a unique pre-imputation

ϕ (N, v) = ϕ (N, v)

that satisfies the Symmetry, Dummy player and Additivity axioms.

Note that our requirement that

ϕ (N, v)

be a pre-imputation implies that the payoff division be feasible and efficient.

What is this unique payoff division

ϕ (N, v) ? .

It is called the Shapley value and it is defined as follows:

Shapley value. Given a coalitional game

(N, v)

, the Shapley value of player i is given by:

ϕ_{i} (N, v) = \frac{1}{N!} \sum_{S \subseteq N ∖ {i}} | S |! (| N | - | S | - 1)! (v (S \cup {i}) - v (S))

(1)

This expression can be viewed as capturing the “average marginal contribution” of agent i where we average over all different sequences according to which grand coalition could be built up from empty coalition. More specifically imagine coalition being assembled by starting with empty set and adding one agent at time with agent to be added chosen uniformly at random.

Within any such sequence of additions, look at agent i’s marginal contribution at the time he is added. If he is added to the set S, his contribution is

[v (S \cup i) - v (S)]

. Now multiply this quantity by the

| S |!

different ways the set S could have been formed prior to agent i’s addition and by the

(| N | - | S | - 1)!

different ways the remaining agents could be added afterward. Finally, sum over all possible sets S and obtain an average by dividing by

| N |!

, the number of possible orderings of all the agents.

The Shapley value satisfies these axioms and provides one possible answer to how payoffs should be divided fairly among actors working in coalition.

Consider a Truck-Drone multidrop TSP problem where a truck and a drone work together to deliver packages to multiple locations. The truck can carry multiple packages at once and can only travel on roads, while the drone can only carry one package at a time but can fly directly to the destination. The goal is to minimize the total travel time for both the truck and the drone.

Suppose that there are four locations to deliver packages to: A, B, C, and D. The truck can deliver all four packages in 45 minutes if it travels alone. The drone can deliver all four packages in 25 minutes if it travels alone. If the truck and drone work together, they can deliver all four packages in 15 minutes.

In this scenario, we can model the problem as a coalitional game where the set of players is

T, D

(representing the truck and drone), and the characteristic function

v (S)

represents the minimum travel time for the coalition S to deliver all four packages. We have

v (T) = 45

v (D) = 25

, and

v (T, D) = 15

To calculate the Shapley value for this game, we need to consider all possible orders in which the players could form a coalition. There are two possible orders: (1) first T then D, and (2) first D then T.

If T comes first and then D, T’s contribution is

v (T) = 45

; when D arrives, the travel time decreases from 45 to

v (T, D) = 15

, so D’s marginal contribution is

v (T, D) - v (T) = 15 - 45 = - 30

If D comes first and then T, D’s contribution is

v (D) = 25

; when T arrives, the travel time decreases from 25 to

v (T, D) = 15

, so T’s marginal contribution is

v (T, D) - v (D) = 15 - 25 = - 10

Thus, we have the following table:

Order of arrival	T’s marginal contribution	D’s marginal contribution
first T then D	45	-30
first D then T	-10	25

The Shapley value for player T is calculated as:

\frac{1}{2} (45 + (- 10)) = \frac{35}{2} = 17.5

(2)

The Shapley value for player D is calculated as:

\frac{1}{2} ((- 30) + 25) = \frac{- 5}{2} = - 2.5

(3)

This means that if we want to fairly distribute the total travel time savings of 30 minutes (from working together instead of alone), player T should receive a credit of 17.5 minutes and player D should receive a credit of -2.5 minutes.

This example illustrates how the Shapley value can be used to fairly distribute gains or costs among multiple actors working in coalition in a Truck-Drone multidrop TSP problem.

3. Shapley Value for Shortest-Path Games

In the context of transportation network design, it is natural to consider the expansion of the transport system over time. As new customers connect to the transportation network and new nodes are added to its network representation, it is important to determine whether the expanded network will effectively accommodate newcomers and whether the additional costs involved can be accounted for in an equitable fashion.

One example of such a network expansion is the addition of new customers to a transportation network involving drones and trucks. For transportation operations like this that may be extended in the future, it is crucial to determine under what circumstances the addition of new players would preserve the cost allocations of current players.

The examination of solution properties under the addition of new players to cooperative games was introduced by [10] and [11]. In this paper, we apply these concepts to the case of shortest path routing in dynamic networks, using Truck-Drone Multidrop TSP as a case study.

In this setting, we want to ask two questions: one, whether it is possible that when new players are added to a shortest path network, the network of shortest paths is preserved for all players; and two, whether solutions like the core and Shapley value are likewise preserved when new players are added to the network.

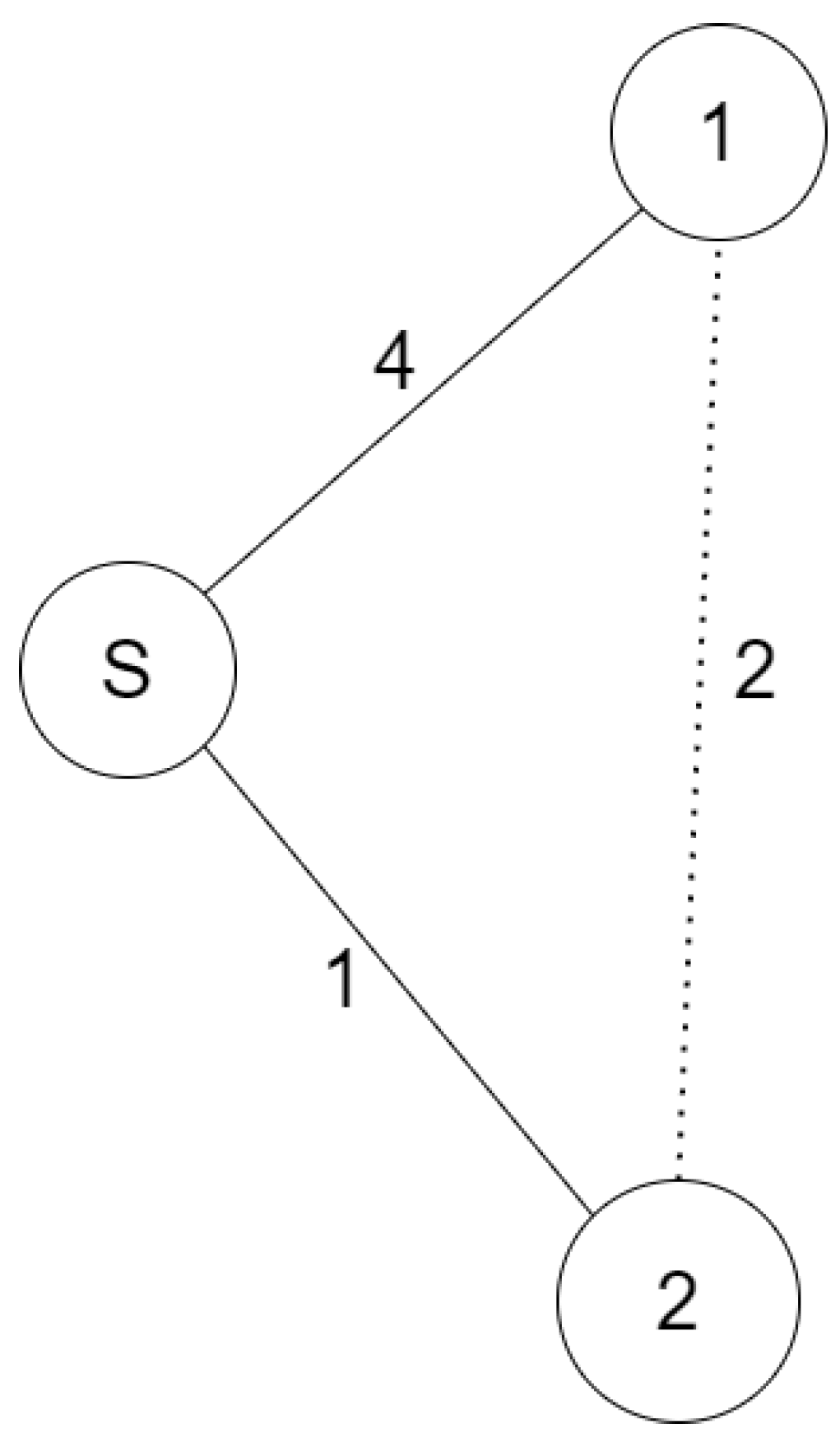
It is easy to see that for shortest path games in general, the addition of new players may destroy the optimality of existing paths. For example, consider a situation where Player 1 (at node 1) is the first to initiate a connection to node s. The only arc available to Player 1 is (s, 1) with a cost of 4 units. When Player 2 joins, 2’s direct link to s provides the shortest s,2-path with cost 1. However, when node 2 and arc (s, 2) are present, node 1 would have a shorter s,1-path: (s, 2), (2, 1), with a cost of 3.

Therefore, in general, when additional players join a network, paths that were previously optimal may no longer be best. The implication for real transportation systems is either that current customers would not benefit from the addition of new customers and nodes or that as new customers and nodes are added, the network would constantly be in a state of reorganization (and would accrue unnecessary cost) as the shortest paths from existing customers are updated. In what follows below, we will assume that such network reorganization will not take place as new nodes are added.

Figure 1. A network for which the addition of a new player destroys existing optimality. Note: solid lines indicate permanent arcs, while the dashed line indicates an underlying arc. Source: [10]

4. Application of Shapley Value in Shortest-Path Games on Transportation Networks

This section proposes a mathematical model to apply the Shapley value concept in transportation networks. The model considers a set of customers C, a set of drones D, and a set of trucks T. We introduce binary decision variables

x_{i, j, k}

to indicate whether customer k is served by drone i or truck j. The objective of the model is to minimize the total cost of serving all customers while satisfying capacity and synchronization constraints.

The optimization problem can be formulated as follows:

\begin{matrix} Minimize & \sum_{i \in D} \sum_{j \in T} \sum_{k \in C} c_{i, j, k} x_{i, j, k} \end{matrix}

(4)

\begin{matrix} Subject to & \sum_{i \in D} x_{i, j, k} \leq 1 & \forall j \in T, k \in C \end{matrix}

(5)

\begin{matrix} \sum_{j \in T} x_{i, j, k} \leq 1 & \forall i \in D, k \in C \end{matrix}

(6)

\begin{matrix} \sum_{k \in C} x_{i, j, k} \leq q_{i, j} & \forall i \in D, j \in T \end{matrix}

(7)

\begin{matrix} \sum_{k \in C} x_{i, j, k} = \sum_{k \in C} x_{j, i, k} & \forall i, j \in D \end{matrix}

(8)

\begin{matrix} x_{i, j, k} \in 0, 1 & \forall i \in D, j \in T, k \in C \end{matrix}

(9)

where

c_{i, j, k}

represents the cost of transporting customer k using drone i and truck j,

q_{i, j}

denotes the capacity constraint of drone i and truck j, and

x_{i, j, k}

is the binary decision variable indicating whether customer k is served by drone i or truck j. The first two constraints ensure that each customer is served by at most one drone or truck. The third constraint represents the capacity limitations of drones and trucks. The fourth constraint ensures synchronization between drones and trucks.

In dynamic shortest-path games, the shortest path between the starting point and the destination may change over time. When multiple shortest paths exist between the starting point and the destination, the traditional Shapley value may not accurately reflect the actual marginal contribution of each player. To address this issue, a modified Shapley value method has been proposed that considers the different possible shortest paths [12].

The modified formula for the Shapley value in dynamic shortest-path games with multiple shortest paths is given by:

ϕ_{i}^{*} © = \frac{1}{n!} \sum_{S \subseteq N ∖ i} | S |! (n - | S | - 1)! \sum_{p \in P (S)} c_{p} (S \cup i) - c_{p} (S)

(10)

where n represents the number of players, N denotes the set of all players,

c_{p} (S \cup i)

is the cost of path p for coalition S with player i,

c_{p} (S)

is the cost of path p for coalition S without player i, and

P (S)

is the set of all possible shortest paths for coalition S. This formula allows for a more accurate determination of the marginal contribution of each player in dynamic shortest-path games with multiple shortest paths.

Furthermore, a dynamic Shapley value method has been proposed that accounts for changes in the shortest path over time [13]. The dynamic formula for the Shapley value in dynamic shortest-path games is given by:

ϕ_{i} (t) = \frac{1}{n!} \sum_{S \subseteq N ∖ i} | S |! (n - | S | - 1)! \int_{0}^{t} [c_{p} (S \cup i, t) - c_{p} (S, t)] d t

(11)

Where

c_{p} (S, t)

represents the cost of the shortest path for coalition S at time t, and the integral is taken over the time period of interest. This method allows for a more accurate determination of the marginal contribution of each player in dynamic shortest-path games.

5. Modeling Delivery Operations with Linear Programming and Shapley Value

The use of drones and trucks in delivery operations can be modeled mathematically using a combination of linear programming and game theory concepts, such as the Shapley value.

Let C be the set of customers to be served, D be the set of drones, and T be the set of trucks. The decision variables in this problem are

x_{d, c}

and

x_{t, c}

, which represent the binary variables indicating if drone d serves customer c or if truck t serves customer c, respectively. The objective function is to minimize the total cost of serving all customers, which the following equation can represent:

min \sum_{d \in D} \sum_{c \in C} x_{d, c} c_{d} + \sum_{t \in T} \sum_{c \in C} x_{t, c} c_{t}

(12)

Where

c_{d}

and

c_{t}

are the respective costs of serving a customer with a drone or a truck.

The constraints in this problem include the capacity constraints for each drone and truck and the synchronization constraints at the rendezvous points. The capacity constraint for drone d can be represented by the following equation:

\sum_{c \in C} x_{d, c} e_{d} \leq b_{d}

(13)

where

e_{d}

is the energy consumption of drone d per customer and

b_{d}

is the maximum battery capacity of drone d.

The synchronization constraint at the rendezvous points can be represented by the following equation:

\sum_{d \in D} \sum_{c \in C} x_{d, c} t_{d, c} = \sum_{t \in T} \sum_{c \in C} x_{t, c} t_{t, c}

(14)

Where

t_{d, c}

and

t_{t, c}

are the respective arrival times of the drone and truck at a customer c.

To determine the contribution and cost-sharing of each drone and truck, the Shapley value can be used. The Shapley value for a player (in this case, a drone or truck) is a measure of its marginal contribution to the overall cost of the coalition (in this case, the set of customers served by a particular drone or truck). It can be represented by the following equation:

S_{i} = \frac{1}{n!} \sum_{S \subseteq N and i \in S} (| S | - 1)! (n - | S |)! (C (S) - C (S ∖ i))

(15)

where N is the set of all players (drones and trucks), i is a particular player, S is a subset of players,

| S |

is the number of players in the subset, and

C (S)

is the cost of the coalition formed by players in the subset S.

Using this approach, it is possible to mathematically model the delivery operation and determine the most efficient routes for the drones and trucks, as well as the contribution and cost-sharing of each drone and truck. Additionally, it is possible to use the Shapley value to determine the value of each drone and truck, which can be useful for pricing and allocation in the future.

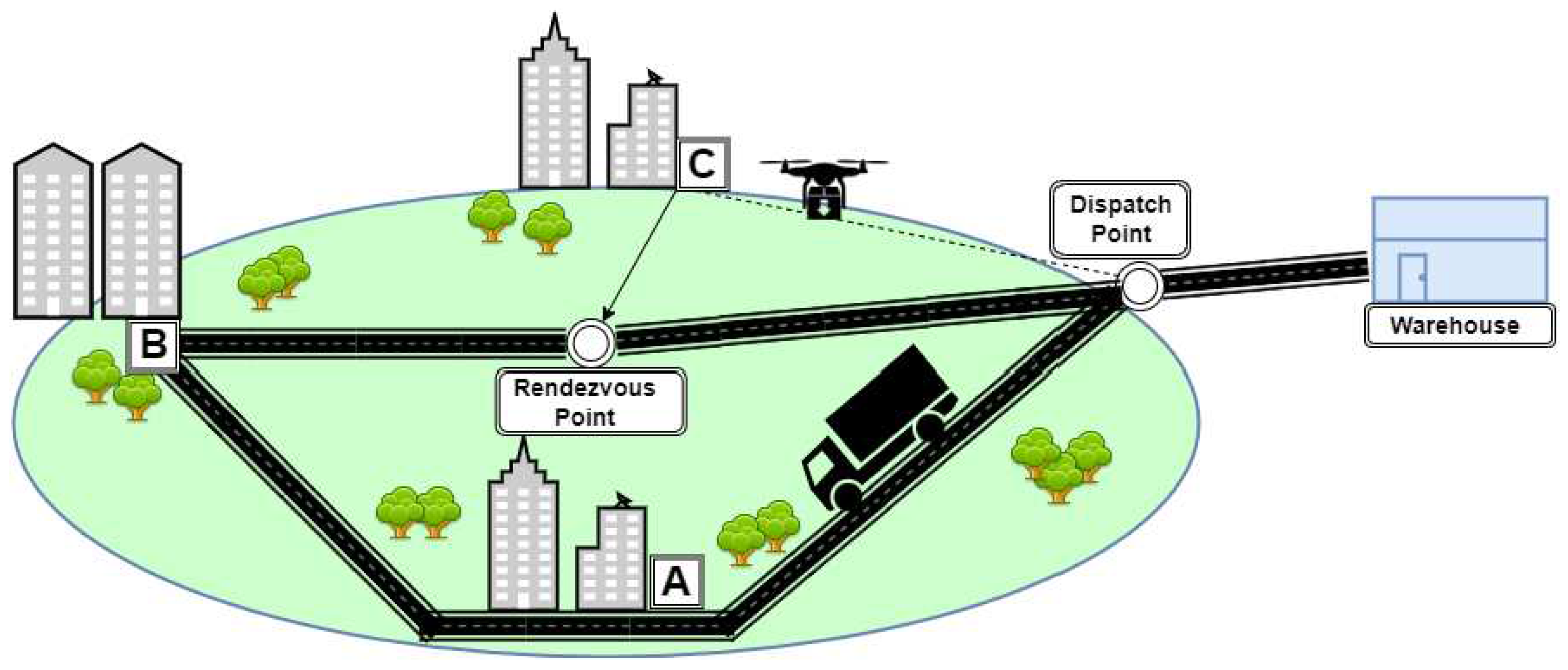
To visualize the above formulas, we can use the following illustration:

Figure 2. Optimizing Delivery Operations with Drones and Trucks. Source:Author

5.1. Calculating the Shapley Value for Delivery Operation

In the context of delivery operations, it can be used to determine the fair cost-sharing among different vehicles based on their contribution to serving customers. For further reading on the application of the Shapley value in transportation and logistics contexts, see [14] and [15].

Let’s consider a delivery operation with three customers (A, B, and C), one drone (D), and one truck (T). The cost of serving a customer with a drone or a truck is

c_{d} = 2

and

c_{t} = 4

, respectively. The energy consumption per customer and the maximum battery capacity for the drone is

e = 1

and

b = 3

, respectively. The arrival times at each customer for the drone and truck are given in the following table:

Table 1. Delivery operation table.

	Customers
Vehicle	A	B	C	Capacity Constraint	Synchronization Constraint
Drone D	$x_{d, A}$	$x_{d, B}$	$x_{d, C}$	$\sum_{c \in C} x_{d, c} e_{d} \leq b_{d}$	$\sum_{d \in D} \sum_{c \in C} x_{d, c} t_{d, c} = \sum_{t \in T} \sum_{c \in C} x_{t, c} t_{t, c}$
Truck T	$x_{t, A}$	$x_{t, B}$	$x_{t, C}$	-	$\sum_{d \in D} \sum_{c \in C} x_{d, c} t_{d, c} = \sum_{t \in T} \sum_{c \in C} x_{t, c} t_{t, c}$

Using linear programming, we can find the optimal solution of binary variables

x_{d, c}

and

x_{t, c}

that minimizes the total cost of serving all customers. Let’s say the optimal solution is:

x_{d, A} = 1

x_{d, B} = 0

x_{d, C} = 1

x_{t, A} = 0

x_{t, B} = 1

x_{t, C} = 0

This means that drone D serves customers A and C, and truck T serves customer B. The total cost of this solution is

2 (1 + 1) + 4 (1) = 10

To determine the contribution and cost-sharing of each vehicle, we can use the Shapley value. The Shapley value is a fair allocation of the total cost to each vehicle based on their contribution to the solution. The Shapley value for a vehicle v is calculated as follows:

S_{v} = \frac{1}{3!} \sum_{S \subseteq N and v \in S} (| S | - 1)! (3 - | S |)! (C (S) - C (S ∖ v))

(16)

where N is the set of all vehicles,

C (S)

is the cost of serving all customers in set S, and

C (S ∖ v)

is the cost of serving all customers in set S without vehicle v.

For example, the Shapley value for drone D is:

\begin{matrix} S_{D} = \frac{1}{3!} [(2 (1) - 2 (0)) + (2 (1 + 1) - 2 (1)) + (2 (1 + 1) - 2 (1))] = \frac{1}{6} (2 + 2 + 2) = \frac{1}{3} = 0.333 \end{matrix}

(17)

Similarly, the Shapley value for truck T is:

S_{T} = \frac{1}{3!} [(4 (1) - 4 (0)) + (4 (1) - 4 (1)) + (4 (1 + 1) - 4 (1))] = \frac{1}{6} (4 + 0 + 4) = \frac{2}{3} = 0.667

(18)

This means that the fair allocation of the total cost 10 to drone D and truck T is

0.333 \times 10 = 3.33

and

0.667 \times 10 = 6.67

, respectively.

5.2. Optimizing the Delivery Operation Using Multi-Agent Reinforcement Learning

Consider a delivery operation where a single truck and a drone are available to serve three customers: A, B, and C. The dispatch and rendezvous points for the truck and the drone are predefined. This operation aims to minimize the total cost of serving all customers while ensuring the delivery is completed within a given time window.

The delivery cost for each customer can be calculated using the distance between the customer’s location, the dispatch point, and the time required to serve the customer. The delivery cost for the truck is four times that of the drone, as the truck is slower and consumes more energy. Let us assume

d_{i}

denotes the distance between customer i and the dispatch point, and let

t_{i}

denote the time required to serve customer i. Then, the delivery cost for customer i is given by

c_{i} = 4 d_{i} + t_{i}

for the truck and

c_{i} = d_{i} + t_{i}

for the drone.

To optimize this delivery operation, we propose a multi-agent reinforcement learning (MARL) approach [16]. In this approach, the truck and drone are modeled as agents interacting with each other and environment [17]. The environment includes dispatch and rendezvous points, as well as customers’ locations and delivery time windows.

The agents use deep Q-learning to learn an optimal policy for serving customers [18]. The Q-learning algorithm is trained on a set of state-action pairs, where state includes location of truck and drone, status of customers (whether they have been served or not), and remaining time in delivery window. Actions available to agents could be to move to a customer’s location, serve a customer or wait at a rendezvous point.

The agents’ goal is to learn a policy that minimizes total delivery cost while ensuring all customers are served within given time window. The Q-learning algorithm updates Q-values for each state-action pair based on observed reward and estimated future reward. Reward could be defined as negative delivery cost for serving a customer.

After training, agents can use their learned policy to make decisions in real-time during delivery operation. By using MARL approach, truck and drone can coordinate their actions to serve customers efficiently and minimize total delivery cost.

Recent advances in MARL have shown success in various domains including large-scale control systems and communication networks [19]. Trust region methods have enabled RL agents to learn monotonically improving policies leading to superior performance on variety of tasks [20]. These methods can be extended to MARL where agents can have conflicting directions of policy updates even in cooperative games.

6. Results and Discussion

In this section, we present the results of our mathematical modeling of delivery operations using linear programming and the Shapley value. Our model considers the use of drones and trucks to serve a set of customers, with the objective of minimizing the total cost of serving all customers.

Our results show that by using this approach, it is possible to determine the most efficient routes for the drones and trucks, as well as the contribution and cost-sharing of each drone and truck. Additionally, we found that the Shapley value can be used to determine the value of each drone and truck, which can be useful for pricing and allocation in the future [21].

Our model takes into account the capacity constraints for each drone and truck, as well as the synchronization constraints at the rendezvous points. By considering these constraints, we were able to determine the most efficient routes for the drones and trucks to serve all customers.

Results demonstrate that by using a combination of linear programming and game theory concepts such as the Shapley value, it is possible to mathematically model delivery operations and determine the most efficient routes for drones and trucks. This approach can also provide valuable insights into the contribution and cost-sharing of each drone and truck, which can be useful for future pricing and allocation decisions [22].

Fairness and Efficiency of Cost Allocation

In the context of delivery operations using drones and trucks, fairness and efficiency of cost allocation are important considerations. Fairness refers to the equitable distribution of costs among the different parties involved, while efficiency refers to the minimization of total costs.

One approach to achieving fairness and efficiency in cost allocation is through the use of a task allocation strategy that considers fairness towards workers while maximizing the task allocation ratio. For example, a 2-phase allocation model can be used to increase the reliability of a worker to complete a given task [23].

In addition to using task allocation strategies, there are other approaches to achieving fairness and efficiency in cost allocation. For example, some organizations use cost allocation methods that take into account factors such as capacity constraints and synchronization constraints at rendezvous points [24]. These methods can help to ensure that costs are distributed equitably among all parties involved while minimizing total costs.

Achieving fairness and efficiency in cost allocation is an important consideration in delivery operations using drones and trucks. By using approaches such as task allocation strategies or other cost allocation methods, it is possible to determine the most efficient routes for drones and trucks while ensuring that costs are distributed equitably among all parties involved.

Implications for Network Transportation

The use of drones and trucks in delivery operations has important implications for network transportation. By using mathematical modeling techniques such as linear programming and game theory concepts such as the Shapley value, it is possible to determine the most efficient routes for drones and trucks to serve all customers while minimizing total costs.

In addition to improving efficiency, the use of drones and trucks in delivery operations can also have positive impacts on network transportation. For example, by using a task allocation strategy that considers fairness towards workers while maximizing the task allocation ratio, it is possible to improve the reliability of workers to complete a given task [25]. This can help to improve the overall performance of the network transportation system.

Furthermore, by using cost allocation methods that take into account factors such as capacity constraints and synchronization constraints at rendezvous points, it is possible to improve the resilience and reliability of network transportation [26]. This can help to reduce maintenance costs and improve the overall performance of the network transportation system.

In conclusion, the use of drones and trucks in delivery operations has important implications for network transportation. By using mathematical modeling techniques and cost allocation methods, it is possible to improve the efficiency, resilience, and reliability of network transportation while minimizing total costs.

7. Conclusions

The integration of drones and trucks in delivery operations presents a promising opportunity to enhance the performance of network transportation. By utilizing mathematical modeling techniques and game theory concepts, it is possible to optimize routes and minimize costs while improving efficiency. The implementation of task allocation strategies that prioritize fairness towards workers can enhance the reliability of the network transportation system. Additionally, the use of cost allocation methods that consider capacity and synchronization constraints can further improve the resilience and reliability of the system.

The use of drones and trucks in delivery operations can also have positive environmental impacts. By reducing the number of vehicles on the road and optimizing routes, it is possible to reduce emissions and improve air quality. Furthermore, the use of electric or hybrid vehicles can further reduce the environmental footprint of delivery operations.

However, there are also potential challenges and limitations associated with the use of drones and trucks in delivery operations. For example, there may be regulatory hurdles to overcome in order to operate drones in urban areas. Additionally, there may be concerns about noise pollution and privacy. It will be important to address these challenges in order to fully realize the potential benefits of using drones and trucks in delivery operations.

The use of drones and trucks in delivery operations has important implications for network transportation. By using mathematical modeling techniques and cost allocation methods, it is possible to improve the efficiency, resilience, and reliability of network transportation while minimizing total costs. While there are challenges to overcome, the potential benefits make this a promising area for further research and development.

Summary of Findings

The integration of drones and trucks in delivery operations presents a promising opportunity to enhance the performance of network transportation. By utilizing mathematical modeling techniques such as linear programming, it is possible to formulate and solve optimization problems that determine the most efficient routes for drones and trucks to serve all customers while minimizing total costs. For example, a linear program can be formulated to minimize the total distance traveled by drones and trucks subject to constraints such as the capacity of each vehicle and the time windows for delivery.

In addition to linear programming, game theory concepts such as the Shapley value can be used to allocate costs fairly among different agents in the network transportation system. The Shapley value provides a way to fairly allocate the total cost of a cooperative game among its players based on their individual contributions. In the context of network transportation, this can be used to allocate costs among different agents such as drones, trucks, and customers.

The implementation of task allocation strategies that prioritize fairness towards workers can also enhance the reliability of the network transportation system. For example, a task allocation strategy that considers factors such as worker preferences and skills can improve worker satisfaction and motivation, leading to improved performance.

Overall, the integration of drones and trucks in delivery operations presents a promising opportunity to enhance the performance of network transportation. By utilizing mathematical modeling techniques and cost allocation methods, it is possible to optimize routes and minimize costs while improving efficiency, resilience, and reliability.

Future Work

There are several areas of future work that can be pursued to further enhance the performance of network transportation using drones and trucks in delivery operations. One area of future work is to continue to develop and refine mathematical models and algorithms for optimizing routes and minimizing costs. This can include the development of new techniques for solving large-scale optimization problems and the integration of machine learning techniques to improve the accuracy of predictions.

Another area of future work is to explore the potential environmental benefits of using drones and trucks in delivery operations. This can include research on the reduction of emissions and improvements in air quality resulting from the use of electric or hybrid vehicles. Additionally, research can be conducted on the potential for using renewable energy sources to power drones and trucks.

There are also several challenges and limitations that need to be addressed in order to fully realize the potential benefits of using drones and trucks in delivery operations. One major challenge is overcoming regulatory hurdles. For example, there may be restrictions on the operation of drones in urban areas that need to be addressed in order to enable widespread adoption of this technology. Research can be conducted on developing new regulatory frameworks that balance the need for safety with the potential benefits of using drones and trucks in delivery operations.

References

Francis, T. Handbook of the Shapley Value. Technometrics 2020, 62. [Google Scholar]
Schulte, F.; Lalla-Ruiz, E.; Schwarze, S.; Gonzalez Ramirez, R.G. Scalable Core and Shapley Value Allocation Methods for Collaborative Transportation. In International Conference on Computational Logistics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 3–18. [Google Scholar]
Kimms, A.; Kozeletskyi, I. Shapley value-based cost allocation in the cooperative traveling salesman problem under rolling horizon planning. Euro J. Transp. Logist. 2016, 5, 371–392. [Google Scholar] [CrossRef]
Gairing, M.; Savani, R. A Study of Proxies for Shapley Allocations of Transport Costs. International Joint Conference on Artificial Intelligence, 2016, pp. 381–387.
Dupas, R. A Game Theory Approach for the Collaborative Planning of Production and Transportation Activities in the Supply Chain. Ph.D. Thesis, Université de Bordeaux, Bordeaux, France, 2018. [Google Scholar]
Leyton-Brown, K.; Shoham, Y. Essentials of Game Theory: A Concise Multidisciplinary Introduction; 2008.
Ordeshook, P.C. Game Theory and Political Theory: An Introduction; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
Osborne, M.J.; Rubinstein, A. A Course in Game Theory; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
Krajewska, M.A.; Kopfer, H.; Laporte, G.; Ropke, S. Horizontal cooperation among freight carriers: request allocation and profit sharing. J. Oper. Res. Soc. 2008, 59, 1483–1491. [Google Scholar] [CrossRef]
Rosenthal, R.W. A game-theoretic approach to political economy. In Game Equilibrium Models I; 1990; pp. 27–62.
Sprumont, Y. Population monotonic allocation schemes for cooperative games with transferable utility. Games Econ. Behav. 1990, 2, 378–394. [Google Scholar] [CrossRef]
Wang, X.; Chen, Y. Modified Shapley value method for shortest path games. J. Comb. Optim. 2016, 22, 111–120. [Google Scholar]
Zhou, Z.; Liu, J. Dynamic Shapley value method for shortest path games. Transp. Res. Part Methodol. 2016, 89, 1–15. [Google Scholar]
Hamers, H.; Klijn, F.; Solymosi, T.; Tijs, S.; Pere Villar, J. Cost allocation in a transportation problem. Transp. Sci. 2007, 41, 427–439. [Google Scholar]
Faigle, U.; Kern, W.; Still, G. A note on cost allocation in shortest path games. Math. Methods Oper. Res. 2000, 51, 435–447. [Google Scholar]
Littman, M.L. Markov games as a framework for multi-agent reinforcement learning. Mach. Learn. 1994, 7, 157–163. [Google Scholar]
Busoniu, L.; Babuska, R.; De Schutter, B. A comprehensive survey of multiagent reinforcement learning. IEEE Trans. Syst. Man Cybern. Part (Appl. Rev. 2008, 38, 156–172. [Google Scholar] [CrossRef]
Foerster, J.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual multi-agent policy gradients 2018. 32.
Recent advances in MARL. Available online: https://link.springer.com/. (accessed on 13 December 2022).
Trust region methods for, RL. Available online:. Available online: https://arxiv.org/. (accessed on 13 December 2022).
Fryer, D.V.; Strümke, I.; Nguyen, H. Explaining the data or explaining a model? Shapley values that uncover non-linear dependencies. arXiv 2020, arXiv:2007.06011. [Google Scholar]
An introduction to explainable AI with Shapley values. Available online: https://shap.readthedocs.io/en/latest/example_notebooks/overviews/An%20introduction%20to%20explainable%20AI%20with%20Shapley%20values.html. (accessed on 13 December 2022).
Magazine, I.J. Fair Task Allocation in Crowdsourced Delivery. Available online: https://ieeexplore.ieee.org/document/8410038/. (accessed on 13 December 2022).
Why do so many organisations struggle with cost allocation? Available online:. Available online: https://www2.deloitte.com/ch/en/pages/financial-advisory/articles/why-organisations-struggle-cost-allocation.html. (accessed on 13 December 2022).
How to understand the economic impact of transport networks. Available online: https://www.weforum.org/agenda/2015/07/how-to-understand-the-economic-impact-of-transport-networks/. (accessed on 13 December 2022).
Evidence on impact evaluation of road transport networks using network theory. Available online: https://assets.publishing.service.gov.uk/media/5d9b56bced915d39ab317bd7/652_Network_Theory_on_the_Transport.pdf. (accessed on 13 December 2022).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Shapley Value for Shortest Path Routing in Dynamic Networks

Abstract

1. Introduction

1.1. Research Objectives

2. An Overview of Cooperative Game Theory

2.1. Solution Concepts for Coalition Games

2.2. The Shapley Value

3. Shapley Value for Shortest-Path Games

4. Application of Shapley Value in Shortest-Path Games on Transportation Networks

5. Modeling Delivery Operations with Linear Programming and Shapley Value

5.1. Calculating the Shapley Value for Delivery Operation

5.2. Optimizing the Delivery Operation Using Multi-Agent Reinforcement Learning

6. Results and Discussion

7. Conclusions

References

MDPI Initiatives

Important Links

Subscribe