Prerpints.org logo
Preprint
Article

Stark Effect for Donors in Rolled-Up Quantum Well

Altmetrics

Downloads

102

Views

23

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 April 2023

Posted:

28 April 2023

You are already at the latest version

Alerts
Abstract
We calculate energies of shallow donors confined in a rolled-up quantum well in the presence of the electric field by solving numerically the Schrödinger equation in natural curvilinear coordinates. It is found that the curves of density of states (DOS) are very sensitive to the variation of the donor position, the geometry of the spiral and the applied electric field value. Novel results for dependencies of donor’s dipole moment and its polarizability on the electric field strength and its orientation, for different donor positions are presented. Also, we found that anisotropic Stark effect of the first order provides in this structure a dependency of the polarizability on the external electric field in a spike-like shape, giving rise to a sharp variation of the dipole moment.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Electronic properties of a 2D semiconductor and a semiconductor bulk differs substantially. As the semiconductor film’s thickness reduces to a nanometric range the ratio between number of surface and bulk atoms is increased substantially providing a drastic variation of its electronic properties. Semiconductor quantum well (QW), a layer of nanometric thickness, sandwiched between two layers of a different semiconductor material, today enjoy widespread use in different optoelectronic applications. Progress achieved at last years in manufacturing of nanostructures have allowed for fabricating layers with topologically nontrivial surfaces such as a twisted single crystalline NbSe3 ribbon in a form of a one-sided Mobius strip [1] or rolled-up quantum wells (RUQWs), in the form of spirals [2,3,4,5,6,7,8,9].
RUQW is a structure consisting of semiconductor layer of nanometer thickness curls up after being released from the substrate as a result of the relaxation of elastic stresses. Both sides of the layer are cylindrical surfaces whose cross sections have the form of spirals. The curvature of this structure and its optoelectronic properties depend strongly on the thickness of the layer and the lattice mismatch of the substrate and the layer. Due to existence of a variable curvature along the spiral cross section, electronic properties of RUQWs have characteristic features, which distinguishes them from planar quantum wells and nanotubes. In the last two decades this rolled-up semiconductors have sparked great attentions and been widely used as optical resonators [10,11,12,13,14,15,16,17] to realize laser structures [18,19,20], and the alteration of energy band in self-rolled nanomembranes containing G a A s / A l 0.26 G a 0.74 A s quantum wells (QWs) has been investigated [21]. Spectral analyses reveal that the small strain change in structures with different curvatures the optical transitions and the light emission intensity of the GaAs QW layer are essentially influenced by the strain evolution. In addition, the first order Stark effect revealed in these structures opens an opportunity for the fabrication of high performance rolled-QW infrared photo-detectors.
Wide scopes for RUQWs of InGaAs/GaAs heterostructures applications as optical materials for quantum information technology are discussed previously in ref. [22], where it has been found an essential modification of the band structure of InGaAs semiconductor quantum wells by changing their geometrical configuration. Particularly, the photoluminescence demonstrates a strong energy shift of the valence-band states in comparison to flat structures due to an inversion of the heavy-hole with the light-hole states in a rolled-up InGaAs quantum well, which in addition conduces to a strong change in the optical selection rules for the rolled-up quantum wells. Previously, the relation between the photoluminescence characteristics and curvature for rolled-up GaAs quantum wells has been studied in ref. [23]. It has been revealed that the room-temperature photoluminescence (PL) characteristics of rolled-up RUQWs show dramatic PL intensity enhancement compared to their planar counterparts. Systematic shift of PL peak position as a function of tube curvature, attributed to strain induced band structure change, is established.
In this work, we analyze theoretically an effect of a possible increase of the probability of the carriers tunneling between adjacent spiral wings in the presence of the external electric field, enabled by a special topology of RUQW, that could be a possible source of other novel useful properties. In order to analyze this effect, one should solve a boundary value problem for the Schrodinger equation inside of a domain, which represents a waveguide formed by a semiconductor tape rolled up around z-axis. In the case, when the tape thickness is essentially smaller in comparison to the separations between wings, the motion across the waveguide is considerably faster than along it, that opens a chance for application the well-known adiabatic approximation (AA) to separate the corresponding coordinates of the electron’s motions along and across the spiral waveguide. Such approach has been used earlier in references [24,25] for analyzing the energy spectrum of the free electron confined in infinite-barrier RUQW in a form of the Archimedean spiral. It has been found an effective one-dimensional Schrödinger equation that describes in curvilinear coordinates slow motion of the electron inside the waveguide. In this paper, we use a similar formalism to derive an effective wave equation in curvilinear coordinates corresponding to the low-lying energy levels of the electron bound to the shallow donor. Unlike of a similar problem for a free electron, the movements of the electron bound to the donor at Z-direction and along the spiral no longer can be separated and the corresponding effective wave equation is two-dimensional. In our numerical work, to solve it we use the double Fourier series expansion method.
Our calculations for donors with different locations show that energies shiftings in the presence of the external electric field depend heavily on the geometry of the spiral, the strength, and the orientation of the applied field, inducing in some especial cases a permanent dipole moments. We believe that our numerical procedure gives an efficient tool for the study of impurity-related phenomena in RUQWs. The article is organized as follows. In Section 2, we describe the formalism, in which we solve in natural coordinates for electron and donor wave equation in RUQW and determine low-lying energies as functions of the external electric field. In Section 3, we present results of calculations and discussion of the Stark effect for shallow donor confined in RUQW. Finally, the conclusion is drawn in Section 4.

2. Theoretical model

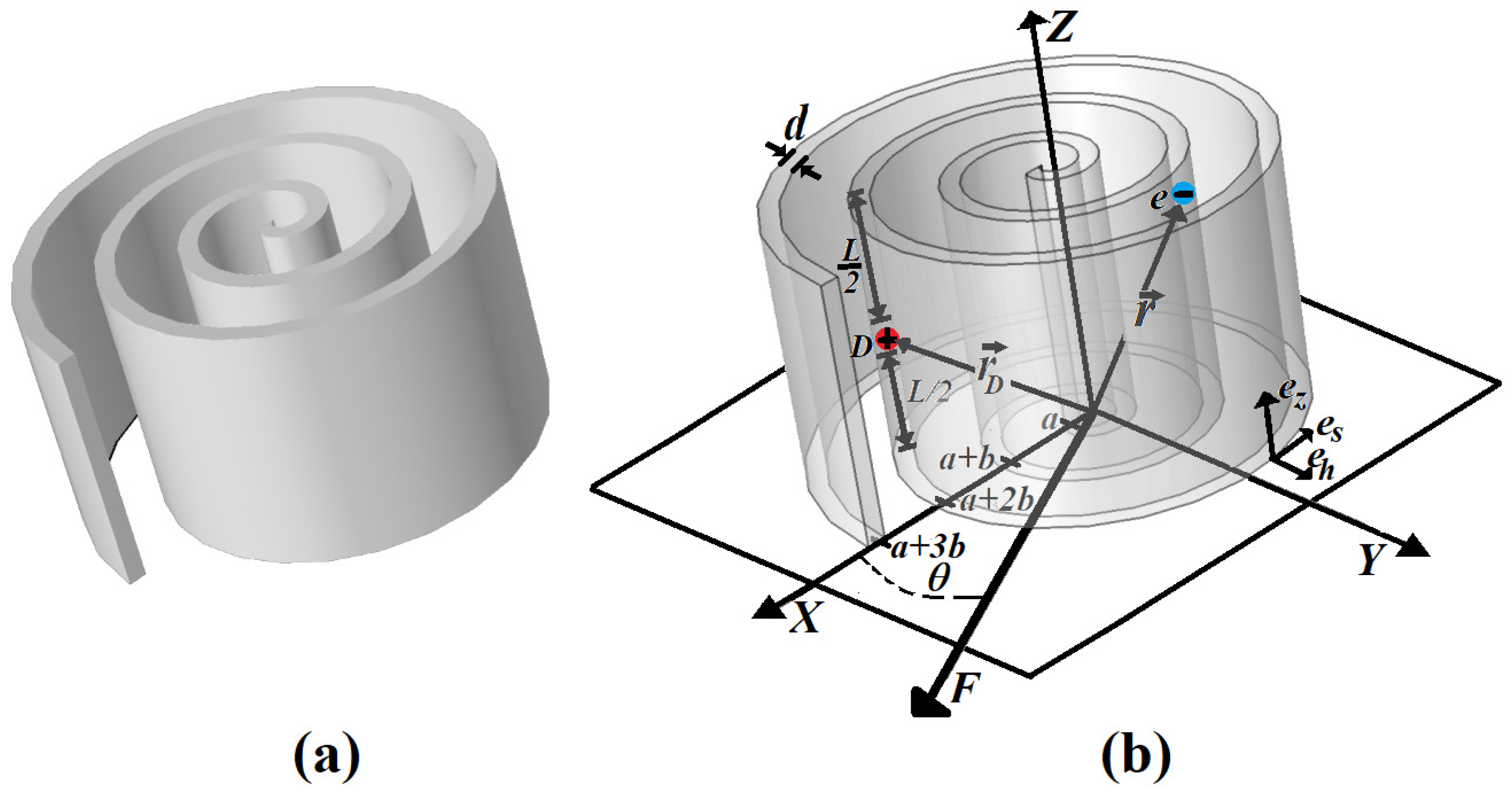
To analyze the features of RUQW’s electronic properties related to their curvature, let us to consider a model of the homogeneous rolled-up QW represented schematically in Figure 1, flat at z-direction and rolled-up in x-y plane. We assume that the structure along Z-axis is very long and therefore the free electron wave function depends on the z coordinate as in a plane wave. It allows us to reduce the one-particle problem to study of the movement of an electron only inside helical waveguide. In addition, if the QW’s thickness is very small, the electron movement transversely the waveguide is faster than along it, and one can use an advantage of the well-known adiabatic approximation to separate coordinates corresponding to these two degrees of freedom. For this purpose, it is appropriate to describe the RUQW geometry in natural coordinates given by unit vectors ( e → s , e → h , e → z ) shown in Figure 1. The vector e → s describes the tangential direction for the curvilinear coordinate s corresponding to the arc length measured from the beginning of the spiral ( 0 < s < s F ), the vector e → h describes the normal direction and the corresponding coordinate h measures the distance from the exterior border of the QW along the normal, while the vector e → z describes the vertical direction with corresponding to the coordinate z that gives the distance from the bottom of the structure ( 0 < z < L ). Here and in what follows, we denote as s F the spiral length, as d and L the thickness and the height of the QW, respectively. In addition, we assume that in the adiabatic limit ( d → 0 ) the normal coordinate h = 0 and positions of the donor and electron are defined by vectors r → D = ( S D , 0 , L / 2 ) and r → e = ( S , 0 , z ) , respectively. The external electric field is applied in plane XOY along the line that forms the angle θ with the X-axis.
We assume that cross-sections of the RUQW’s along XOY plane are spirals, whose equations in polar coordinates correspond approximately to a generalized Archimedean equation r ( φ ) = a + b φ / 2 π ; 0 < φ < φ F . The arc length s and the curvature radius R s of this curve depend on the polar angle as follows:
s ( φ ) = ∫ 0 φ R s ( φ ) d φ ; R s ( φ ) = ( a + b φ / 2 π ) 2 + ( b / 2 π ) 2
In our numerical work, we first found the dependence of the polar angle on the arc length, φ = φ ˜ ( s ) by using the inverse cubic spline-interpolation procedure. Once such dependence is found, then one can define similar dependencies for the Cartesian and polar coordinates of the electron and donor positions:
r ˜ ( s ) = a + b ( ˜ φ ( s ) ) / 2 π ; x ˜ ( s ) = r ˜ ( s ) cos φ ( s ) ; y ˜ ( s ) = r ˜ ( s ) sin φ ( s )
Below, we use the effective Bohr radius a 0 * as a dimensionless unit of the distance, and the effective Rydberg, R y * as a dimensionless unit of the energy. In these units, the effective 2D potential energy of the donor confined in a RUQW is given by the following expression [24,25,26]:
V ( s , z ) = π d 2 − 1 4 R s 2 ( s ) + α r ˜ ( s ) cos [ ϑ − φ ( s ) ] − 2 r ˜ e D 2 ( s , s D ) + ( z − z D ) 2 α = e F a 0 * R y * ; r ˜ e D 2 ( s , s D ) = [ x ˜ ( s ) − x ˜ ( s D ) ] 2 + [ y ˜ ( s ) − y ˜ ( s D ) ] 2
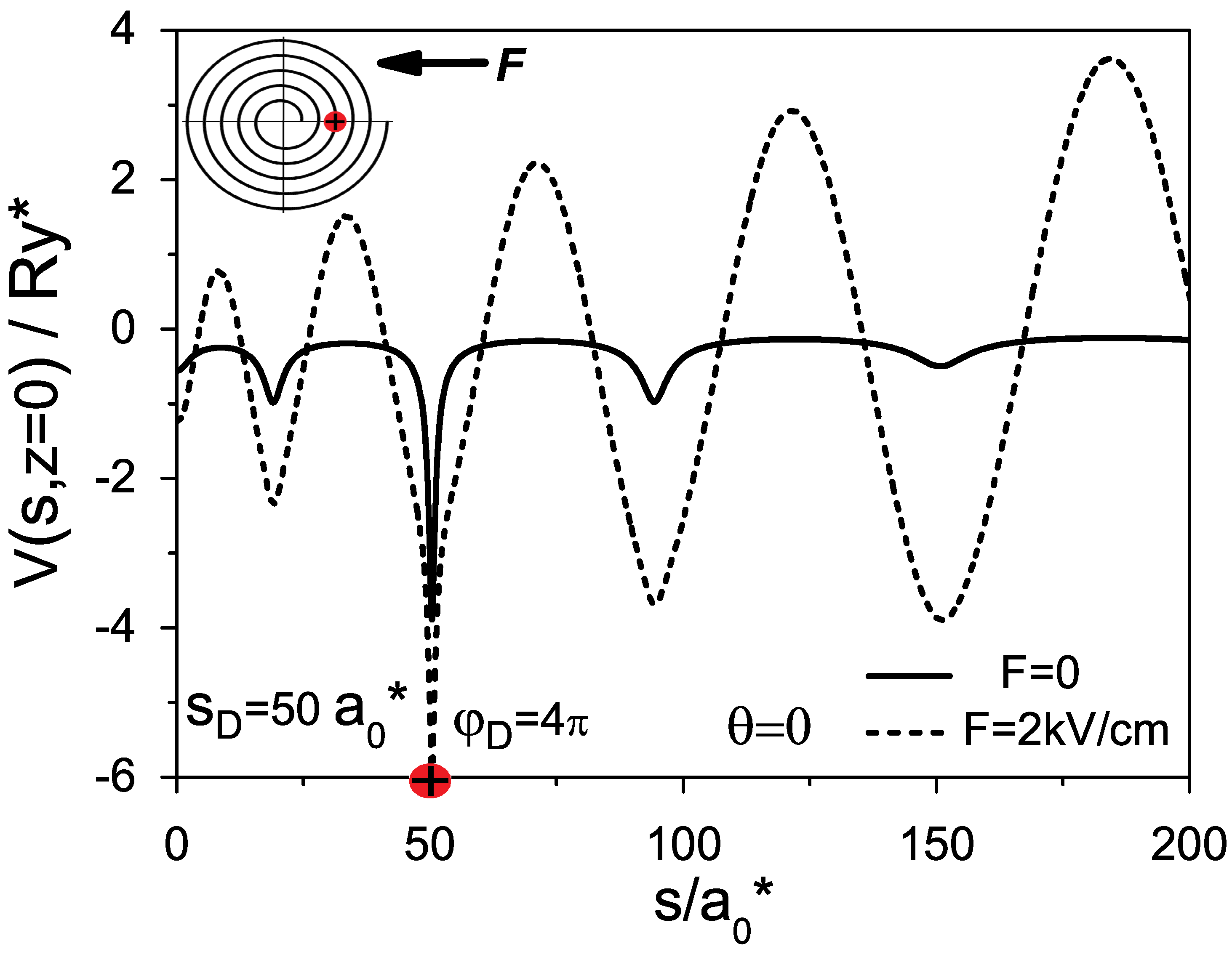
The Four terms in Equation (3) correspond to the contribution to the potential energy from the lateral confinement inside the nanolayer, from the curvature variation along the spiral [25,26], from the external electric field and from the electron-donor attraction, respectively. In Figure 2, we show curves of potential energies along the Archimedean spiral with parameters a = b = a 0 * , φ F = 10 π and with the donor located at the point with polar coordinate φ D = 4 π as functions of the arc length, given by the relations (1)–(3) for the zero-electric field (solid line) and for the case F = 2 k V / c m (dash line). One can see in Figure 2 that the curve of the potential energy undergoes an essential change in the presence of the external electric field obtaining a form of oscillation with increasing amplitude. Such transformation of the potential along the spiral can provide a strong polarizability and the formation a giant dipole moment in the ground state of the shallow donor.
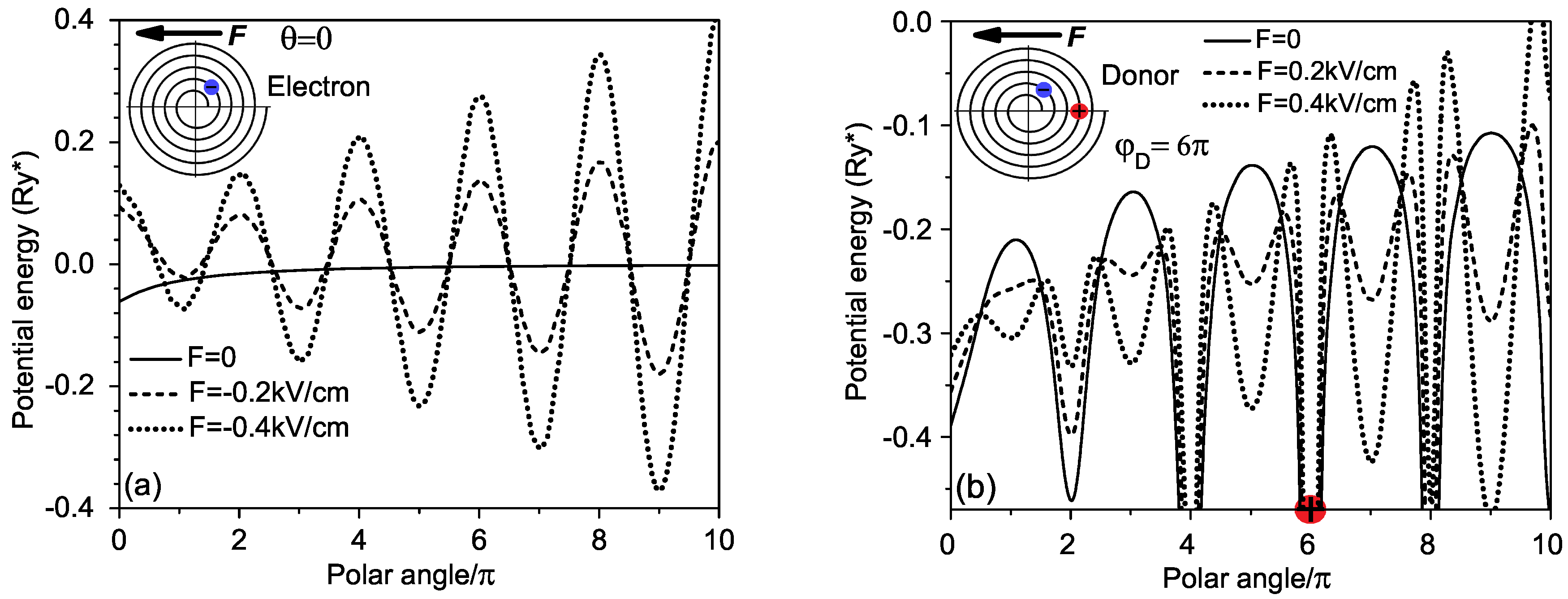
To clarify why the external electric field applied the X-axis can induce a permanent giant moment in a donor we present in Figure 3 some plots, which demonstrate the successive evolution of the potential curves along the spiral at the cross-section z = 0 under increasing electric field for the electron (a) and for the donor (b).
The curve of the free electron’s potential in Figure 3a for the zero electric field case (solid line) is smooth and it has a shallow minimum at the initial point of the spiral ( s = 0 ), where the curvature of the spiral is the largest. In the presence of the external electric field directed toward initial spiral point along X-axis, this potential is transformed to a set of periodically arranged quantum wells with successively increasing depth at the radial direction (dash and dot lines). Bottoms and tops of quantum wells are located at points of corresponding wings with polar coordinates φ k = ( 2 k + 1 ) π and φ k = 2 k π , respectively. As the electric field grows the bottoms of all wells descend, while their heights are increased. It is seen that larger is the electric field, the bigger should be the displacement of the electron from the initial point of the spiral.
Similar potential curves for the donor placed inside RUQW at the position with polar angle are presented in Figure 3b. As F = 0 (solid line), the main deepest minimum is situated at the donor location while other minima with lesser deep are located at points of nearest wings with polar angles φ k = 2 k π , situated at the same side of spiral. With an increase in the electric field, additional minima appear on both sides of the main minimum at points with polar angles φ k = ( 2 k − 1 ) π , at that the minima on the right side are deeper than those on the left. The larger the electric field, the deeper are additional quantum wells (cf. dashed and dotted curves). One can expect that such alteration of the potential curves under increasing electric field could lead to an instability of the donor ground state when the energy a similar state of one of additional minima at right side becomes lower than of the main minimum and the electron jumps from the wing with the donor toward the right side of the spiral. Such transition can be accompanied by an origination of a giant dipole moment and a strong polarizability of the donor. The final 2D wave equation in dimensionless units for the electron inside a two-dimensional surface with the potential energy (3) has in natural coordinates the following form [7]:
− ∂ 2 Φ ( s , z ) ∂ s 2 − ∂ 2 Φ ( s , z ) ∂ z 2 + V ( s , z ) Φ ( s , z ) = E ( s , z ) Φ ( s , z ) ; 0 < s < s F ; 0 < z < L Φ ( 0 , z ) = Φ ( s F , z ) = Φ ( s , 0 ) = Φ ( s , L )
Here we assume that z D = L / 2 , i.e., the donor is located at the middle along the Z-axis of the structure (depreciated surface states). In our numerical work, we solve the boundary value problem (4) by using the double Fourier series expansion method, in which the wave function is represented as follows:
Φ ( s , z ) = ∑ n , m = − ∞ ∞ C n , m χ m , n ( s , z ) ; χ m , n ( s , z ) = 2 S F L sin π m s S F sin π n z L ; n , m = 1 , 2 , . . . ;
The functions χ m , n ( s , z ) present an orthogonal and normalized basis, which satisfy the boundary conditions. Substituting (5) in (4) one can reduce the eigenvalue problem (4) to the following secular equation:
∑ n , m = − ∞ ∞ H m , m ’ , n , n ’ − E ˜ δ m , m ’ δ n , n ’ C m ’ , n ’ = 0 ; H m , m ’ , n , n ’ = π 2 m 2 S F 2 + n 2 L 2 δ m , m ’ δ n , n ’ + U m , m ’ ( 1 ) δ n , n ’ + U m , m ’ , n , n ’ ( 2 )
U m , m ’ ( 1 ) = 2 S F ∫ 0 S F π d 2 ( s ) − 1 4 R s 2 ( s ) + α r ˜ ( s ) [ cos ϑ cos φ ˜ ( s ) − sin ϑ sin φ ˜ ( s ) ] sin π m s S F sin π m ’ s S F d s
U m , m ’ , n , n ’ ( 2 ) = 4 S F L ∫ 0 S F sin π m s S F sin π m ’ s S F d s ∫ 0 L 2 r ˜ e D 2 ( s , s D ) + ( z − L / 2 ) 2 sin π n z L sin π n ’ z L d z

3. Results

In this section, we present results of calculations for the energy spectrum of donors confined in an infinite barrier GaAs RUQW’s cylindrical surface of the height L = 50 a 0 * , and the homogeneous thickness d = 0.5 a 0 * , whose cross-section along the plane perpendicular to the axis Z is the finite Archimedean spiral, given in polar coordinates by the relation r = a + b φ , with a = b = 2 a 0 * , 0 < φ < φ F and φ F = 10 π , S F = s ( φ F ) ≈ 220 a 0 * . In addition, we show below results corresponding to the donor position with coordinates φ D = 6 π , z D = 0 , and for the direction of the applied electric field given by the polar angle ϑ = π .
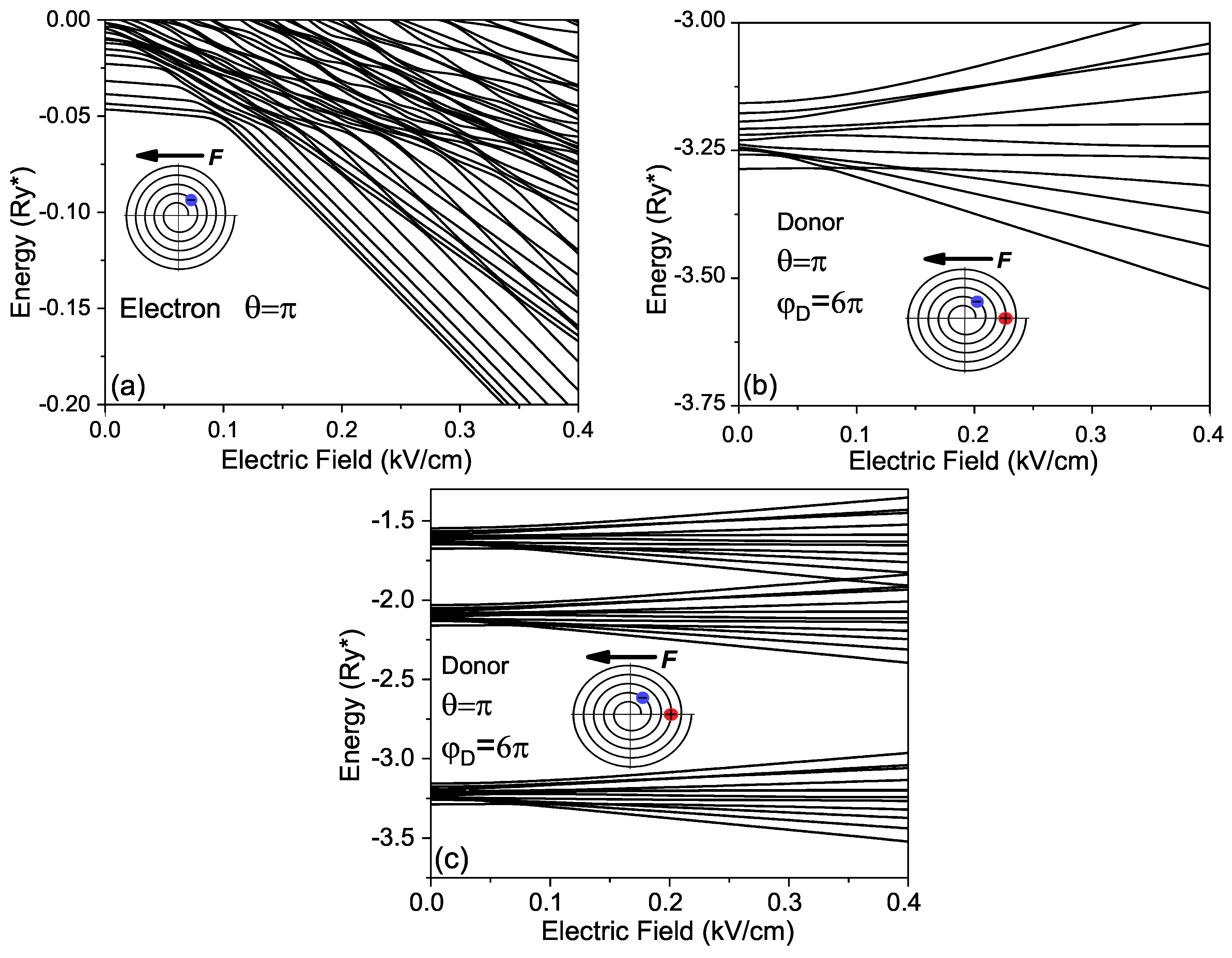
Energies dependencies on the electric field presented in Figure 4 demonstrate significant differences of the corresponding curves for the electron and the donor. In the contrast to the electron energy spectrum in Figure 4a, which is quasi-continuous, the corresponding spectrum of the donor in Figure 4c is splits in bands with decreasing gaps as the of band number grows typically for of Coulomb-like potentials spectra. Also, one can observe in Figure 4a,b multiple crossovers of the curves corresponding to the lower energies, which originate a sharp jump of the slope ground state energy dependency for electric field value about 0.1 kV/cm.
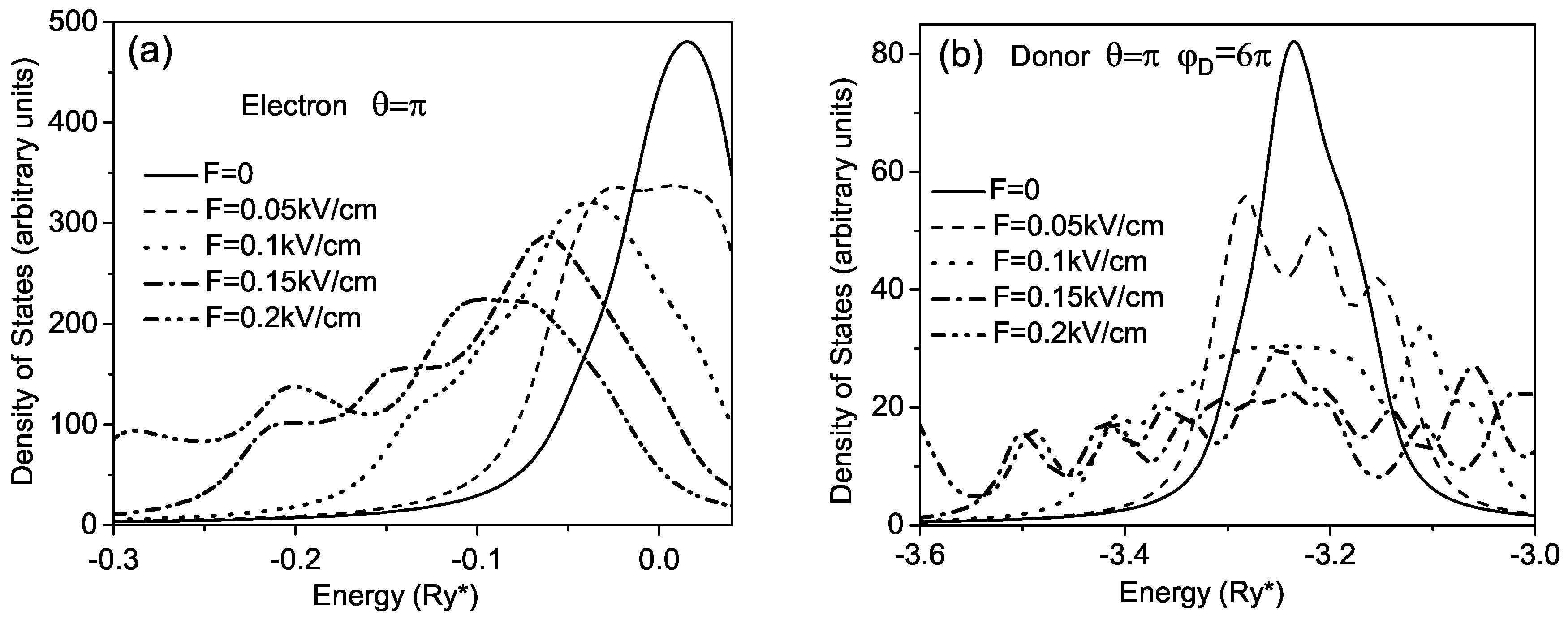
Both for the electron and the donor gaps between energies inside the subbands corresponding to states of the electron localized in wings of the spiral, remote from the donor position are very small and therefore, it is more appropriate the description of the energy spectrum in terms of the density of the electronic states (DOS) ρ ( E ) . In Figure 5, we show curves of the DOS for different values of the electric field both for the electron and for the donor. In both cases one can observe a consecutive broadening of the principal peak of the DOS with increasing of the electric field. But for the donor, this broadening is almost symmetrical in contrast to the electron, for which the broadening of the peak is accompanied by its shifting to the red end of the spectrum. In addition, in the case of the electron the increase of the electric field induces the fine structure in the curve of the DOS.
One can also observe in Figure 4 that ground state energies dependencies on the external electric field E 0 ( F ) in both cases as for the electron and for the donor have critical points, in which their slopes are changed abruptly. Such a feature in behavior of the curves can be related to a jump of the electron between two adjacent wings of the spiral induced by the external electric field, which should be accompanied by a sharp variation of the dipole moment of the donor p, defined by the relation p = d E 0 ( F ) / d F .
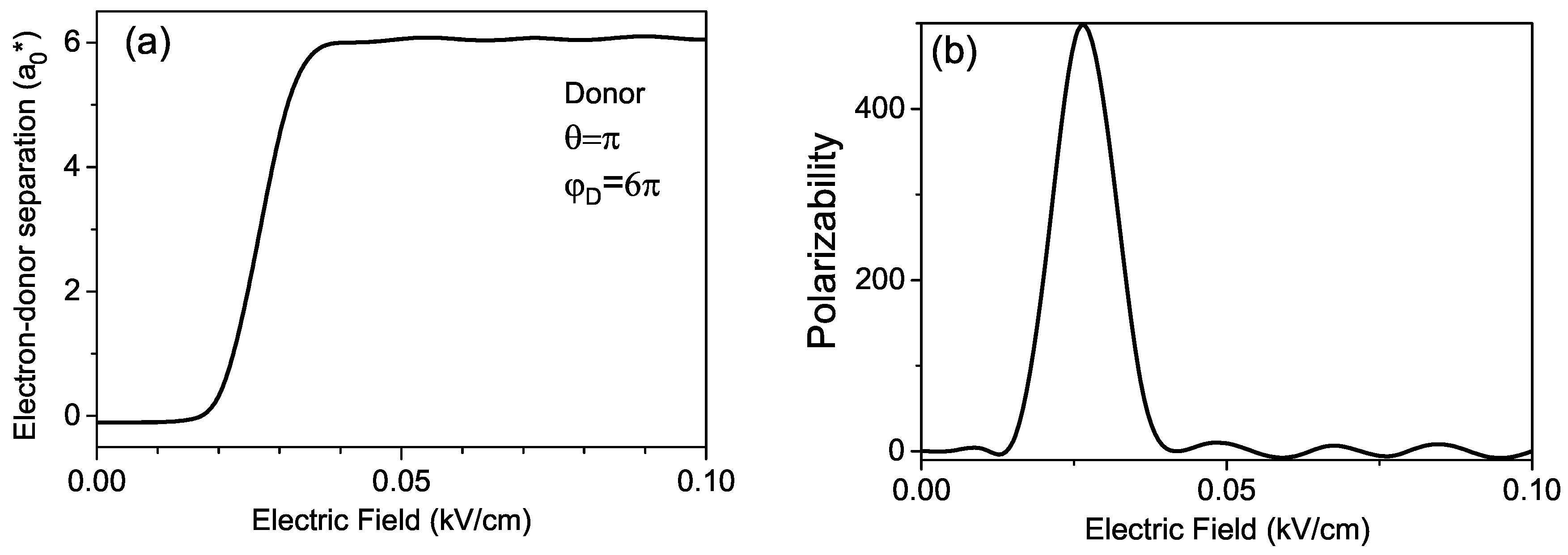
In Figure 6a we display the values of the averaged distance between electron and donor, characterizing the induced dipole moment of donor confined in the rolled-up QW calculated as a function of the external electric field. As the electric field increasing becomes larger than 0.1 k V / c m the electron-donor separation changes its sign and it grows by jump. The explanation of this effect is given in Figure 6b, where we present the density of the electron distribution before and after the jump. It is seen that before the jump the electron is located mainly at the same wing where is placed the donor, while after the jump it is displaced toward the adjacent wing and it is mainly located at opposite sides of the spiral.
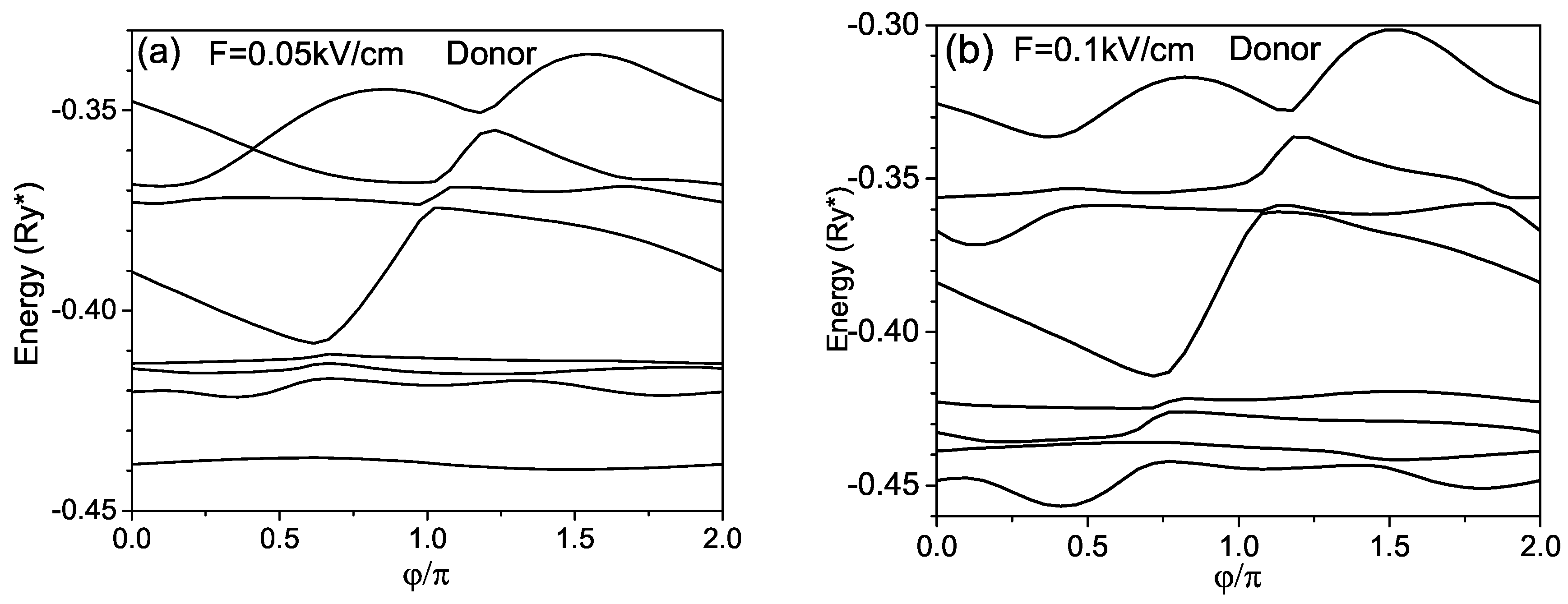
Finally, Figure 7, we present the energies of the donor of as a function of the angle θ between electric field direction and X axis. It is seen that for a weak electric field as the donor dipole moment is small, the lower energies in Figure 7a almost does not depend on the electric field orientation, because these state are strongly bound to thed donor. The behaviour of the lower levels in Figure 7b is essentially changed as the electric field is equal to 0.1 kV/cm and the electron-donor separaion is large according to the results presented in Figure 6a. The energies of the ground and of first excited states become sensitive to the orientation of the electric field in contrasst to the corresponding dependencies in Figure 7a.

4. Conclusions

Low-dimensional systems based on semiconductors have been the subject of interest for last decades. Quantum properties of these systems offer the possibility of analyzing the physical behavior in the nanoscale; and numerous possible applications. Among other uses, they can be used, for example, as an active surface in heterogeneous catalysis, for the growth of other low-dimensional materials. Donor impurities confined inside a thin semiconductor film of nanometer scale has a spectral properties similar to an artificial two-dimensional hydrogen-like atom studied previously in detail for thin plane films. However, a greater diversity of spectral properties could be expected from donors confined in thin films with curvature. In a particular case of a thin semiconductor film in a form of a spiral, the donor confined in such a structure cannot be no longer considered nor as a two-dimensional hydrogen-like atom neither as a three-dimensional, due to long-range interaction between electron and donor located at different adjacent wings of the spiral. In this work, we propose a simple method, which allows us to analyze effect of impurity doping on the spectral properties of a spirally rolled-up quantum wells in the presence of the external electric field, applied at a direction perpendicular to spiral axis. Considering as an example an Archimedean shape of the spiral, we have investigated theoretically the effect of the curvature and the location of a single shallow donor, the intensity and the orientation of the external electric field on the donor energies. We present novel curves of the electron and donor energies dependencies on the intensity y orientation of the electric field and of the density of the corresponding states. We have found a high sensitivity of all curves of the energies dependencies both for the electron and the donor on the external electric field, which is characterized by abruptly change the dipole moment und the polarizability of the structure, related to the electron translations between adjacent wings of the spiral. Our method should be applicable to a variety of complex quasi-two-dimensional structures with curvature for which more rigorous approaches requires extensive numerical calculations.

Author Contributions

L.F.G.R.: proposed the problem and was responsible of the formal analysis, and writing of the manuscript, I.D.M.: was responsible of the methodology, analytical and numerical calculations, and formal analysis, R.A.E.C.: was responsible of formal analysis and writing of the manuscript, J.S.-O.: was responsible of numerical calculations, formal analysis and writing of the manuscript, G.E.E.S.: was responsible of the formal analysis and writing of the manuscript, original draft preparation, review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financed by the Universidad del Magdalena and Universidad Popular del Cesar through Vicerrectoría de Investigación, and the Universidad Industrial de Santander (UIS) through Vicerrectoría de Investigación y Extensión, DIEF de Ciencias.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Tanda, S.; Tsuneta, T.; Okajima, Y.; Inagaki, K.; Yamaya, K.; Hatakenaka, N. A Möbius strip of single crystals. Nature 2002, 417, 397. [Google Scholar] [CrossRef] [PubMed]
  2. Prinz, V.Y.; Seleznev, V.A.; Gutakovsky, A.K.; Chehovskiy, A.V.; Preobrazhenskii, V.V.; Putyato, M.A.; Gavrilova, T.A. Free-standing and overgrown InGaAs/GaAs nanotubes, nanohelices and their arrays. Physica E: Low-Dimensional Systems and Nanostructures 2000, 6, 828. [Google Scholar] [CrossRef]
  3. Schmidt, O.G.; Deneke, C.; Kiravittaya, S.; Songmuang, R.; Heidemeyer, H.; Nakamura, Y.; Zapf-Gottwick, R.; Muller, C.; Jin-Phillipp, N.Y. Self-Assembled Nanoholes, Lateral Quantum-Dot Molecules, and Rolled-up Nanotubes. IEEE Journal of Selected Topics in Quantum Electronics 2002, 8, 1025–1034. [Google Scholar] [CrossRef]
  4. Schmidt, O. G.; Schmarje, N.; Deneke, C.; Muller, C.; JinPhillipp, N.Y. Three-Dimensional Nano-Objects Evolving from a Two-Dimensional Layer Technology. Advanced Materials 2001, 13, 756–759. [Google Scholar] [CrossRef]
  5. Wang, J.; Song, E.; Yang, C.; Zheng, L.; Mei, Y. Fabrication and whispering gallery resonance of self-rolled up gallium nitride microcavities. Thin Solid Films 2017, 627, 77–81. [Google Scholar]
  6. Schulz, K.M.; Vu, H.; Schwaiger, S.; Rottler, A.; Korn, T.; Sonnenberg, D.; Kipp, T.; Mendach, S. Controlling the Spontaneous Emission Rate of Quantum Wells in Rolled-Up Hyperbolic Metamaterials. Physical Review Letters 2016, 117, No. 085503. [Google Scholar] [CrossRef]
  7. Deneke, C.; Songmuang, R.; Jin-Phillipp, N.Y.; Schmidt, O.G. The Structure of Hybrid Radial Superlattices. Journal of Physics D: Applied Physics 2009, 42, No. 103001. [Google Scholar] [CrossRef]
  8. Wang, H.; Zhen, H.; Li, S.; Jing, Y.; Huang, G.; Mei, Y.; Lu, W. Self-rolling and light-trapping in flexible quantum well–embedded nanomembranes for wide-angle infrared photodetectors. Science Advances 2016, 2, e1600027. [Google Scholar] [CrossRef]
  9. Deng, J.; Lu, X.; Liu, L.; Zhang, L.; Schmidt, O.G. Introducing Rolled-Up Nanotechnology for Advanced Energy Storage Devices. Advanced Energy Materials 2016, 6, 1600797. [Google Scholar] [CrossRef]
  10. Wang, J.; Yin, Y.; Yang, Y.-D.; Hao, Q.; Tang, M.; Wang, X.; Saggau, C. N.; Karnaushenko, D.; Yan, X.; Huang, Y.-Z.; Ma, L.; Schmidt, O.G. Deterministic Yet Flexible Directional Light Emission from Spiral Nanomembrane Cavities. ACS Photonics 2019, 6, 2537–2544. [Google Scholar] [CrossRef]
  11. Huang, G.S.; Kiravittaya, S.; Quinones, V.A.B.; Ding, F.; Benyoucef, M.; Rastelli, A.; Mei, Y.F.; Schmidt, O.G. Optical Properties of Rolled-up Tubular Microcavities from Shaped Nanomembranes. Applied Physics Letters. 2009, 94, 141901. [Google Scholar]
  12. Strelow, C.; Rehberg, H.; Schultz, C. M.; Welsch, H.; Heyn, C.; Heitmann, D.; Kipp, T. Optical Microcavities Formed by Semiconductor Microtubes Using a Bottlelike Geometry. Physical Review Letters 2008, 101, 127403. [Google Scholar] [CrossRef]
  13. Kipp, T.; Strelow, C.; Welsch, H.; Heyn, C.; Heitmann, D. In Optical Microtube Ring Resonators, AIP Conference Proceedings; American Institute of Physics 2007, 1127–1128. [Google Scholar]
  14. Songmuang, R.; Rastelli, A.; Mendach, S.; Deneke, C.; Schmidt, O. G. From Rolled-up Si Microtubes to SiOx/Si Optical Ring Resonators. Microelectron. Microelectronic Engineering 2007, 84, 1427–1430. [Google Scholar] [CrossRef]
  15. Kipp, T.; Welsch, H.; Strelow, C.; Heyn, C.; Heitmann, D. Optical Modes in Semiconductor Microtube Ring Resonators. Physical Review Letters 2006, 96, 077403. [Google Scholar] [CrossRef] [PubMed]
  16. Hosoda, M.; Kishimoto, Y.; Sato, M.; Nashima, S.; Kubota, K.; Saravanan, S.; Vaccaro, P.O.; Aida, T.; Ohtani, N. Quantum-Well Microtube Constructed from a Freestanding Thin Quantum-Well Layer. Applied Physics Letters. 2003, 83, 1017–1019. [Google Scholar] [CrossRef]
  17. Chai, Z.; Wang, Q.; Cao, J.; Mao, G.; Liu, H.; Ren, X.; Maleev, N.A.; Vasil’ev, A.P.; Zhukov, A.E.; Ustinov, V.M. Optically Pumped Lasing in a Rolled-up Dot-in-a-Well (DWELL) Microtube via the Support of Au Pad. Applied Physics B 2018, 124, 21. [Google Scholar] [CrossRef]
  18. Yang, S.; Wang, Y.; Sun, H. Advances and Prospects for Whispering Gallery Mode Microcavities. Advanced Optical Materials 2015, 3, 1136–1162. [Google Scholar] [CrossRef]
  19. Chen, X. An Analytical Model to Investigate the Resonant Modes of the Self-Rolled-up Microtube Using Conformal Transformation. Optics Express 2014, 22, 16363–16376. [Google Scholar] [CrossRef]
  20. Li, F.; Mi, Z.T. Optically Pumped Rolled-up InGaAs/GaAs Quantum Dot Microtube Lasers. Optics Express 2009, 17, 19933–19939. [Google Scholar] [CrossRef]
  21. Zhang, F.; Huang, G.; Nie, X.; Cao, X.; Ma, Z.; Ding, F.; Di, Z.; Zhen, H.; Mei, Y. Energy band modulation of GaAs/Al0.26Ga0.74As quantum well in 3D self-assembled nanomembranes. Physics Letters A 2019, 383, 2938–2942. [Google Scholar] [CrossRef]
  22. Rodrigues, L.N.; Scolfaro, D.; da Conceição, L.; Malachias, A.; Odilon, D.; Couto Jr, D.; Iikawa, F.; Deneke, C. Rolled-Up Quantum Wells Composed of Nanolayered InGaAs/GaAs Heterostructures as Optical Materials for Quantum Information Technology. ACS Applied Nano Materials 2021, 4, 3140–3147. [Google Scholar] [CrossRef]
  23. Wang, H.; Zhen, H.; Li, S.; Jing, Y.; Huang, G.; Mei, Y.; Lu, W. Self-rolling and light-trapping in flexible quantum well–embedded nanomembranes for wide-angle infrared photodetectors. Science Advances 2016, 2, e1600027. [Google Scholar] [CrossRef] [PubMed]
  24. Vedernikov, A.I. Chaplik, A.V. Two-dimensional electrons in spirally rolled-up quantum wells. Journal of Experimental and Theoretical Physics 2000, 90, 397–399. [Google Scholar] [CrossRef]
  25. Ortix, C.; Van Den Brink, J. Effect of curvature on the electronic structure and bound-state formation in rolled-up nanotubes. Physical Review B 2010, 81, 2–6. [Google Scholar] [CrossRef]
  26. Castro, D.Y.; Mikhailov, I.D. Shallow donor in spirally rolled-up quantum well. IOP Conference Series: Journal of Physic 2019, 1247, 012004. [Google Scholar] [CrossRef]
Preprints 71964 g001
Figure 1. Characteristics of the model: (a) Image of a rolled-up quantum well considered in this work, (b) 3D image of donor confined in a rolled-up QW, where the electron and donor positions, and the orientation of applied electric field are indicated.
Figure 1. Characteristics of the model: (a) Image of a rolled-up quantum well considered in this work, (b) 3D image of donor confined in a rolled-up QW, where the electron and donor positions, and the orientation of applied electric field are indicated.
Preprints 71964 g001
Preprints 71964 g002
Figure 2. Alteration of the donor’s potential energy along the spiral, under external electric field.
Figure 2. Alteration of the donor’s potential energy along the spiral, under external electric field.
Preprints 71964 g002
Preprints 71964 g003
Figure 3. Potential energies along the spiral at the cross-section for (a) the electron and (b) the donor located at the position with polar coordinate φ D = 6 π , for different values of the external electric field applied along X-axis.
Figure 3. Potential energies along the spiral at the cross-section for (a) the electron and (b) the donor located at the position with polar coordinate φ D = 6 π , for different values of the external electric field applied along X-axis.
Preprints 71964 g003
Preprints 71964 g004
Figure 4. Lowest energies of (a) electron, (b) donor and (c) some excited states of donor in rolled-up QW as functions of the external electric field.
Figure 4. Lowest energies of (a) electron, (b) donor and (c) some excited states of donor in rolled-up QW as functions of the external electric field.
Preprints 71964 g004
Preprints 71964 g005
Figure 5. Density of states for (a) electron and (b) donor in rolled-up QW for different values of the electric field.
Figure 5. Density of states for (a) electron and (b) donor in rolled-up QW for different values of the electric field.
Preprints 71964 g005
Preprints 71964 g006
Figure 6. Dependencies of (a) the averaged electron-donor separation and (b) the donor polarizability on the external electric field.
Figure 6. Dependencies of (a) the averaged electron-donor separation and (b) the donor polarizability on the external electric field.
Preprints 71964 g006
Preprints 71964 g007
Figure 7. Energies of donor in rolled-up QW as functions of the angle applied electric field.
Figure 7. Energies of donor in rolled-up QW as functions of the angle applied electric field.
Preprints 71964 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated