Preprint
Article
Nonlinear Electrоmagnetic Properties of Thinfilm Nanocomposites (CoFeZr)x(MgF2)100-x
Altmetrics
Downloads
86
Views
34
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
28 April 2023
Posted:
29 April 2023
You are already at the latest version
Alerts
Abstract
The aim of this work is a comprehensive study of the effect of variable atomic composition and structural-phase state of (CoFeZr)x(MgF2)100-x nanocomposites (NCs) on their nonlinear electronic and magnetic/magneto-optical properties.
Micrometer-thick nanocomposites layers on the glass substrates were obtained by ion-beam sputtering of a composite target in the argon atmosphere in a wide range of compositions x=9-51at.%
The value of the resistive percolation threshold xper=34 at.%, determined from the concentration dependences of the electrical resistance of NCs, coincides with the beginning of nucleation of metallic nanocrystals CoFeZr in MgF2 dielectric matrix.
The absolute value of maximum magnetoresistance of NCs is 2.4 % in a magnetic field of 5.5 kOe at x=25 at.%, up to the percolation threshold.
Two maxima appear in the concentration dependences of magneto-optical transversal Kerr effect, one of which at x = 34 at.% corresponds to the formation of CoFeZr alloy nanocrystals of a hexagonal structure, and the second one at x=45 at.% corresponds to the phase transition of nanocrystals from a hexagonal to a cubic body-centered structure.
The magnetic percolation threshold in (CoFeZr)x(MgF2)100-x system at xfm=34 at.% with the appearance of a hysteresis loop and a coercive force of Hc≈ 8 Oe, coincides with the resistive percolation threshold xper=34 at.%.
Concentration dependence of the coercive force showed that at low contents of metallic alloy x<30 at.% NCs are superparamagnetic (Hc=0). With an increase of the alloy content, in the region of magnetic and resistive percolation thresholds NCs exhibit a magnetically soft ferromagnetic character and do not change it far beyond the percolation threshold with the maximum value of the coercive force Hc< 30 Oe. Decrease in magnetic order and soft ferromagnetic are influenced by the diamagnetic phase FeF2 that we discovered at the interface of magnetic nanocrystals CoFeZr with a dielectric matrix MgF2 by the Mössbauer spectroscopy.
Keywords:
Subject: Physical Sciences - Condensed Matter Physics
1. Introduction
Metal-dielectric magnetic nanocomposites (NCs) have a number of unique physical properties that are promising for their use in spintronics, information recording and storage technologies, shielding coatings, sensitive magnetic sensors, and other devices.
For the first time the tunnel type of giant magnetoresistance (GMR) in metal-dielectric Ni-SiO2 films was discovered in [1,2,3]. Later, the authors of [4] obtained sputtered Co-based CoAlO granular alloy thin films, which were characteristic in exhibiting GMR of about 8% accompanying a large specific electrical resistivity of the order of 10-2Ω*cm, due to a weak tunnel conductance in the metal-nonmetal granular structure of this alloy. It was found [4] that GMR changes in a dependence on Co content and shows a maximum near the percolation threshold where transition from metallic conductance to the tunnel one takes place in Co-Al-O granular alloy thin films. In addition, superparamagnetic behavior in the magnetic field and temperature dependencies of magnetization have been found for the GMR alloy films. The observations support the spin-dependent tunneling effect for this new GMR.
Next, the problem of the influence of the phase composition and atomic structure of granular composites metal-dielectric, which were realized in the process of self-organization during their preparation, on the electrical, magnetic, and magneto-optical properties became a challenge subject of intensive experimental and theoretical studies [5,6,7,8,9,10]. All of these properties of composites depend nonlinearly on the phase composition and atomic structure, in particular, on the concentration of the magnetic metal phase, the shape and size of metal granules, and their distribution over the bulk of the sample. In this regard, electroresistive, magnetic, and magneto-optical (MO) studies, which are sensitive to the characteristic sizes, shapes, and topology of metal particles, are of a considerable interest [5,6,7,8,9,10,11].
For granular composites, there is the concept of the percolation threshold xper, i.e. such a value of the concentration of the metal component, at which the final "conductive network" of contacting metal particles is formed in the entire volume of the sample. One can say that the percolation region is an intermediate state during the transition from electrically nonconductive to the electrically conductive state, where metal granules start coming into contact between each other. In this region, all the unique physical properties that are inherent in granular metal-dielectric composites are manifested to a greater extent [4,11].
Thus, in granular metal-dielectric composites, depending on the value of the volume fraction of the metal component x, two types of conductivity are possible. When this fraction is large, the metal granules come into contact and form a conductive network so that electrons can flow directly through the connected metal channels, and the composite exhibits metallic conductivity. When the volume fraction of the metal component is small, well below the percolation threshold, then the granules of the metal are distributed as separate dispersed metal particles in the insulating matrix. The electrical conductivity in this state is determined by the hopping conductivity of electrons tunneling from one metal particle to another through the dielectric regions. Tunneling conductivity is retained up to xc (xper>x>xc), where the metal-dielectric transition occurs. In this concentration range, unusual transport phenomena, such as the tunneling anomalous Hall effect and the logarithmic temperature dependence of the conductivity, were detected [12]. It has been experimentally established that, for a large number of granular metal–dielectric composites, the percolation threshold is close to the interval xper≈0.5–0.6 [11].
The behavior of magnetic properties in a ferromagnetic metal-insulator NCs is even more complex. In the region of low concentrations of the metal component x<xper, NC exhibits superparamagnetic properties, while in the region of high metal concentrations x>xper it demonstrates ferromagnetic properties. Most often, the magnetic percolation threshold xfm does not coincide with the transport one [13] and is usually less than xper, since the ferromagnetic order FM can arise without physical contact between the granules as a result of the exchange interaction. Therefore, xfm can be defined as the concentration at which the magnetization sharply increases and a coercive force arises in nanocomposites.
The main methods for producing composite films are thermal, cathode and ion-plasma sputtering. Each of these methods has its own advantages and disadvantages, depending on the sputtered material and the purpose of using NC. Monograph [11] analyzes the existing methods for obtaining granular composites, and it is concluded that the most universal method is ion-plasma magnetron sputtering, when the separation of the condensing medium into two components (metal and dielectric) is carried out as a result of their self-organization in a single precipitation process. As a magnetic component of film composites, ferromagnetic metals Fe, Co, Ni and their alloys are usually applied, which are often amorphized under additions of boron or zirconium. Most of the known metal-dielectric composite systems are obtained using oxide dielectrics SiO2, Al2O3, MgO, TiO2, ZrO2. At the same time, due to oxygen presence in a condensing medium, a significant oxidation of the surface of metal granules occurs, which affects the electrical, magnetic, and magneto-optical (MO) characteristics of the composites.
Recently, the studies of composites with oxygen-free dielectrics have been realized. For example, in [14], when studying the magnetotransport properties of (Fe51Co49)32(MgF2)68 film with Fe51Co49 alloy distributed in MgF2 dielectric matrix, a giant magnetoresistance of 13.3% at 10 kOe was found at room temperature. In [15], the frequency dependence of the tunnel-type magnetodielectric effect in Cox(MgF2)1-x superparamagnetic nanostructures was demonstrated with an exact change in x in the range from 0.06 to 0.2.
In [16,17] the electrical and magnetoresistive properties of Cox(MgF2)100-x thin films were studied in a wide range of metal phase concentrations (14 ≤ x, at.% ≤ 62) in the initial state and after thermal annealing in vacuum. The percolation threshold for this system is set in the range x=30-36 at.% Co. The magnetoresistive effect of the studied samples attained 7% in a field of 10 kOe at cobalt concentration x=25 at. %. When samples are heated up to 250°C, in the composites containing cobalt up to the percolation threshold, the magnitude of the magnetoresistance increases, while in composites above the percolation threshold, it decreases. It has been found that the matrix of the MgF2 system is resistant to thermal heating up to 250°C. Raising the temperature to 350°C leads to the disappearance of the magnetoresistive effect.
In [18,19], we studied in details the features of the atomic structure, phase formation and substructure of the same Cox(MgF2)100-x nanocomposites depending on the ratio of metal and dielectric components using X-ray diffraction (XRD), X-ray photoelectron spectroscopy (XPS), and infrared spectroscopy (IR). It was found that when the content of cobalt Co x< 29 at. %, metal is in the X-ray amorphous state in the form of clusters in the MgF2 nanocrystalline matrix. With an increase in the cobalt content up to x=42 at.% on a glass substrate, already in the amorphous dielectric matrix MgF2 cobalt nanocrystals of hexagonal syngony with the sizes of about 10 nm are formed, predominantly oriented in the plane of the basis of the hexagonal lattice (001) α-Co.
Then in [20] we studied the effect of atomic composition and structural-phase state of Cox(MgF2)100-x nanocomposites on their nonlinear transport and magnetic/magneto-optical properties. It was shown that the beginning of Co nanocrystals formation coincides with the attainment of electric and magnetic percolation thresholds at x = 37 at.% and is accompanied by a transition from a superparamagnetic to a soft ferromagnetic state, which under an increase in the metal content (x>42 at. %) acquires a magnetohardness with a coercive force of up to 95 Oe.
At the same time, we conducted a study of nanocomposites of a more complex atomic composition with a three-element magnetic alloy CoFeZr in the same oxygen-free dielectric matrix MgF2 [21,22]
The studies of nanocomposites of variable composition (CoFeZr)x(MgF2)100-x by X-ray diffraction XRD, X-ray electron spectroscopy XPS, and infrared spectroscopy IR showed that the relative content of the CoFeZr metal alloy in the oxygen-free nanocomposite in the most significant way affects its atomic structure, substructure [21], conductivity and magneto-optical properties of the material [22].
The aim of this work is to show the influence of the atomic composition and structural-phase changes of (CoFeZr)x(MgF2)100-x nanocomposites on their nonlinear electronic and magnetic/magneto-optical properties.
To demonstrate this relationship to the fullest extent, we used in this paper some results of structural and magneto-optical studies of (CoFeZr)x(MgF2)100-x nanocomposites from our previous works [21,22] in the form of Figure 1 (Section 3.1) and Figure 5, Figure 6 and Figure 7 (Section 3.3). This is due to the fact that the Mössbauer spectra presented in this paper (Section 3.2) made it possible to explain the softer magnetic properties of (CoFeZr)x(MgF2)100-x NCs compared to the harder magnetic properties of Cox(MgF2)100-x NCs [20].
2. Materials and Methods
Composite films with different content of metallic alloy CoFeZr in the MgF2 dielectric matrix were obtained using an original ion-beam deposition setup described in [11]. The composite target consisted of the Co45Fe45Zr10 amorphous metal alloy plate with an uneven and asymmetric placement of the dielectric MgF2 inserts, as a result of which a given concentration gradient is formed in the sputtered material in a single cycle within the argon atmosphere at the operating pressure of ~ 5.10-4Torr on glass substrates [11,22].
The phase composition of nanocomposites formed as a result of self-organization of two components, metallic and dielectric in different ratios, was studied by X-ray diffraction (XRD) with DRON-4 diffractometer applying Co-Kα radiation in the step-by-step scanning mode (Russia)[20]. СoFeZr concentration in atomic % and thicknesses of film composites were determined using electron probe X-ray spectral microanalysis with an attachment to a JEOL JSM-6380LV scanning electron microscope (Japan); the error did not exceed 1.5% of the content of the measured element. The thicknesses of the investigated films of nanocomposites on glass substrates vary in the range of 0.9–3.4 μm in accordance with an increase in the CoFeZr alloy content (х,at.%) in the range of x =9–51 at.%.
The study of the magnetoresistive effect was carried out by direct measurement of the electrical resistance of the samples with a change in the external constant magnetic field using the four-probe method at an ECOPIA HMS-3000 setup. The device package included a certified magnetic attachment with a magnetic induction of B=5.5 kG
The impedance was measured applying alternative signal using an Elins Z-1500J impedancemeter. The studies were carried out at room temperature in the frequency range from 1 MHz to 3 MHz. The amplitude of the alternating measuring signal did not exceed 100 mV. The measurement error did not exceed 5%. The analysis of the impedance spectra was carried out within the framework of the model of serially connected parallel equivalent circuits using the procedure for processing experimental data with the modern software.
To study the magnetic properties of nanocomposites, we used an automated Lake Shore 7404 VSM vibrating magnetometer with a sensitivity of 10-5 - 10-7 G*cm3. Magneto-optical (MO) properties of the nanocomposites were studied in the geometry of the transversal Kerr effect (TKE) with an automated MO spectrometer in the incident light energy range E from 0.5 to 4 eV at room temperature [22]. The amplitude of the applied alternating magnetic field attained 3 kOe. The spectral, field, and concentration dependences of the TKE were measured in the dynamic mode, when the sample under study is in an alternating magnetic field. This method allows the use of a differential measurement scheme, and an increase accuracy in measuring the relative light intensity to ~ 10-5.
3. Results and discussions
3.1. Structural-Phase Composition of Nanocomposites Depending on the Alloy Content in the Dielectric Matrix
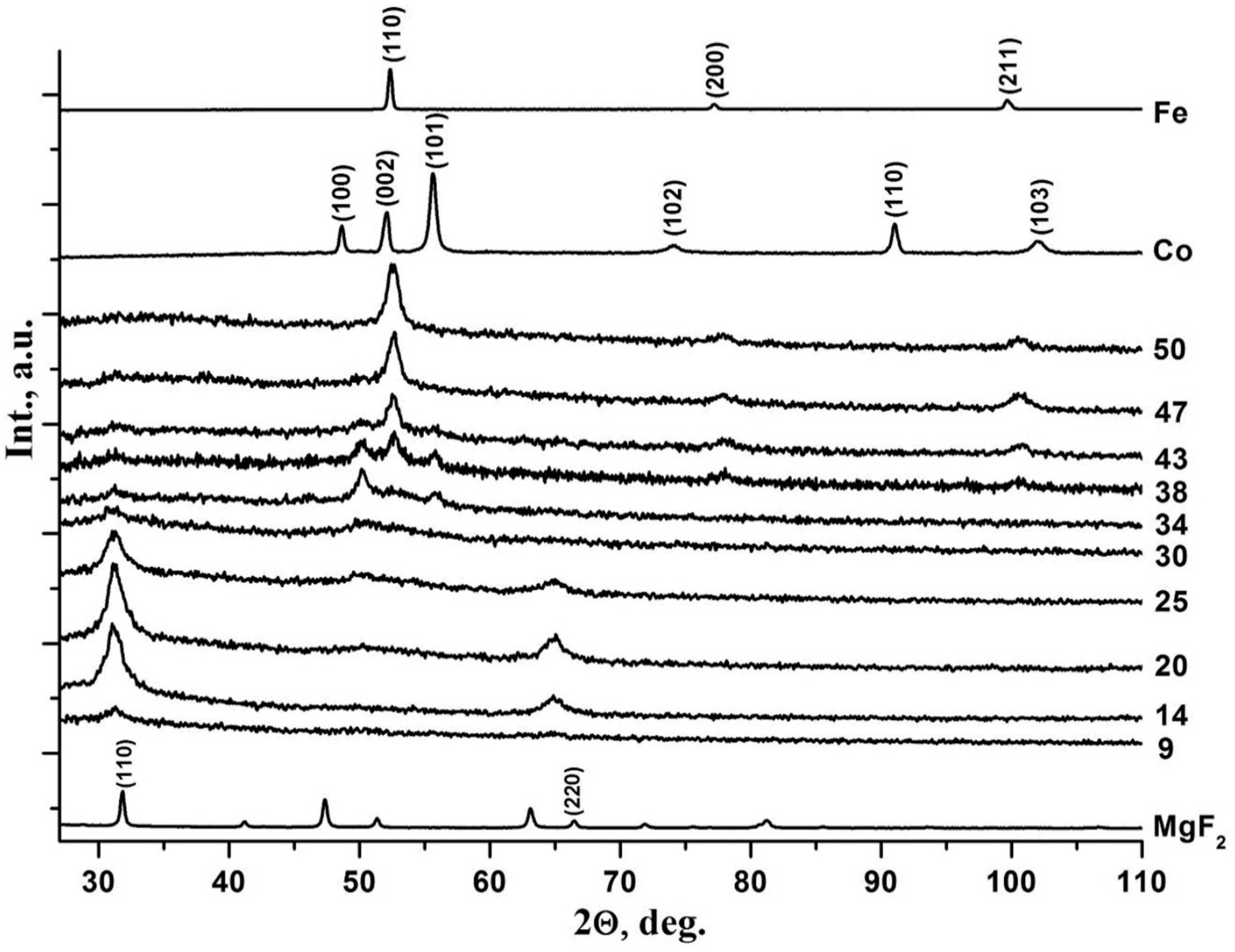
In Figure 1, we reproduce the diffraction patterns of nanocomposite samples from our previous work [21] with different alloy content x at.%, which is shown to the right of each diffraction pattern. For comparison, polycrystalline samples of cubic BCC iron α-Fe and hexagonal cobalt α-Co are presented on the two upper diffractograms, and powder of tetragonal MgF2 is presented on the lower diffractogram.
Obtained in [21] XRD data shows, that in the region of low concentrations (x≤25at.%) the metal alloy CoFeZr is in the X-ray amorphous state in the form of metal clusters distributed in MgF2 nanocrystalline matrix, represented in diffraction patterns by two wide reflections (110) and (220.
The first phase transition in the composites is the formation of a nanocrystalline CoFeZr phase based on a hexagonal α-Co lattice thus correlating with the relative content of the metal component x ~ 35 at.% in the amorphous dielectric matrix MgF2.
The second phase transition from the hexagonal structure of CoFeZr nanocrystals to the cubic bcc structure in the amorphous dielectric matrix MgF2 occurs with an increase in the relative alloy content in the range x = 40-45 at.%, beyond the percolation threshold xper=34 at.%
The average sizes of metallic nanocrystals, calculated by the Debye-Scherrer formula, increase from 10 nm at x = 34 at.% to 20 nm at x = 50 at.%.
Thus, as a result of self-organization under non-equilibrium conditions of ion-plasma sputtering at certain concentration ratios of the metal and dielectric components of nanocomposites, mutually inverse (antibate) phase transitions occur from the amorphous to the nanocrystalline state of the metal alloy with an increase in its content in the composite and the reverse transition of the MgF2 dielectric phase from the nanocrystalline to the amorphous state.
At the same time, XRD showed, that MgF2 nanocrystals of the dielectric matrix in the composites have slightly increased interplanar distances d110 and d220 as compared to the reference microcrystalline MgF2 [21]. Wherein two other methods of diagnosing the phase composition of materials with a complex atomic composition, XPS and IR spectroscopy, which we used in [21], could not establish unambiguously the cause of these changes.
Figure 1.
Diffractograms of nanocomposites with different compositions.(CoFeZr)x (MgF2)100-x on the glass substrates.
Figure 1.
Diffractograms of nanocomposites with different compositions.(CoFeZr)x (MgF2)100-x on the glass substrates.
3.2. Determination of chemical bonds of iron atoms in a nanocomposite (CoFeZr)51(MgF2)49 by the nuclear gamma resonance method of Mössbauer spectroscopy.
Since the increased values of the interplane distances d110 and d220 of the nanocrystals of the dielectric matrix of the MgF2 were closer to the corresponding values in the iron and cobalt fluorides FeF2 and CoF2, that we had not previously detected by IR spectroscopy and XPS X-ray electron spectroscopy [21], we attempted to detect the interaction of iron atoms with fluorine by the Mössbauer nuclear spectroscopy.
Figure 2 shows two Mössbauer spectra, the calibration spectrum from α-Fe (left) and the spectrum from the sample (CoFeZr)51(MgF2)49 with the maximum magnetic alloy content x=51 at. % (right).
The total amount of accumulation of statistics in the Mössbauer spectrum from this sample was more than 500 hours.
In the Mössbauer spectrum of the sample (CoFeZr)51(MgF2)49 an intense magnetic sextet (hyperfine magnetic splitting) is isolated with parameters (Is = -0.08 mm/s, Q = 0 mm/s G = 0.70mm/s, H = 339 kE) close to α-Fe (see left calibration spectrum in Fig.2), which we refer to iron in the composition of nanocrystals of the CoFeZr alloy with the BCC structure α-Fe.
However, along with the magnetic sextet, the spectrum of the nanocomposite contains a paramagnetic quadrupole doublet related to iron fluoride FeF2 with parameters (Is = -0.85 mm/s, Q = 1.92 mm/s). The ratio of the areas of these two spectra from the phases in the nanocomposite sample (magnetic alloy CoFeZr and paramagnetic phase FeF2) is 82:18 with a total area of 100 for NC (CoFeZr)51(MgF2)49 (Table 1).
Figure 2.
Mössbauer spectra: Calibration α-Fe (left) and nanocomposite (CoFeZr)51(MgF2)49 (right).
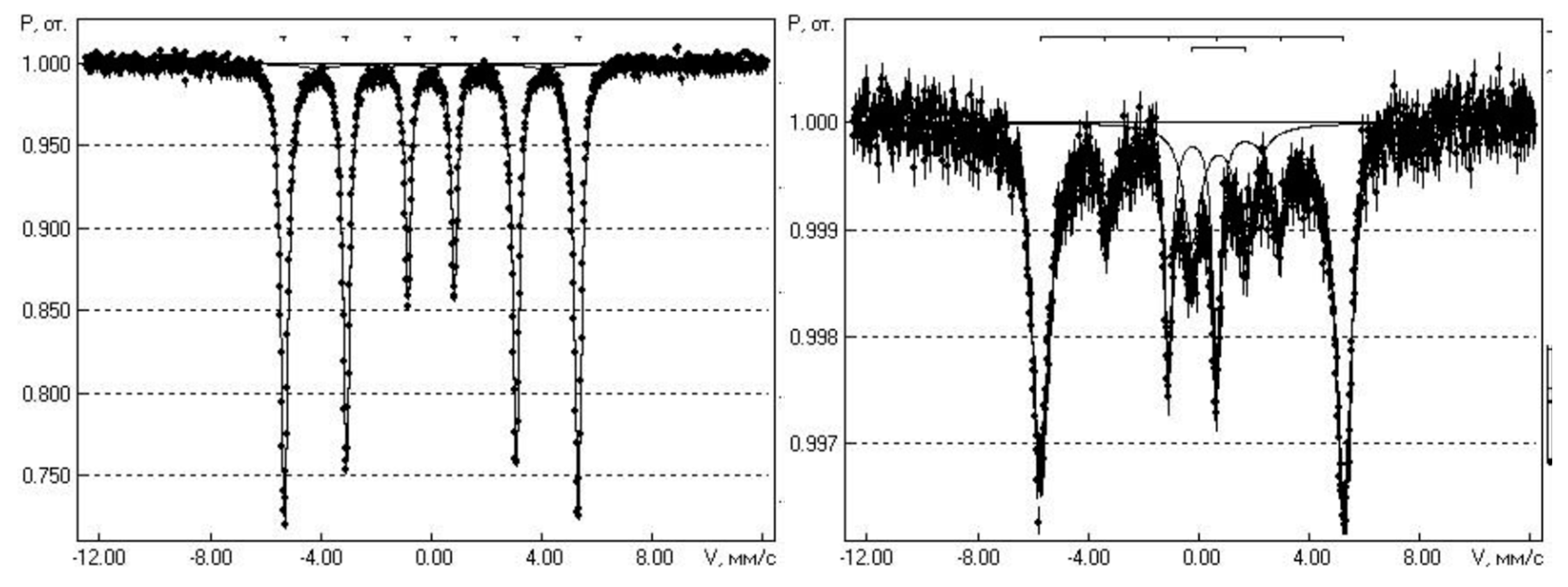
Thus, the appearance of an additional doublet from the paramagnetic phase FeF2 in the Mössbauer spectrum of the nanocomposite (CoFeZr)51(MgF2)49 indicates that at the interfacial boundaries of nanocrystals of a magnetic alloy CoFeZr with a dielectric MgF2, the boundary iron atoms interact with the fluorine atoms of the dielectric matrix to form the paramagnetic phase of iron fluoride FeF2. This circumstance can significantly affect the magnetic properties of the studied nanocomposites.
3.3. Concentration dependences of electrical resistance and magnetoresistance
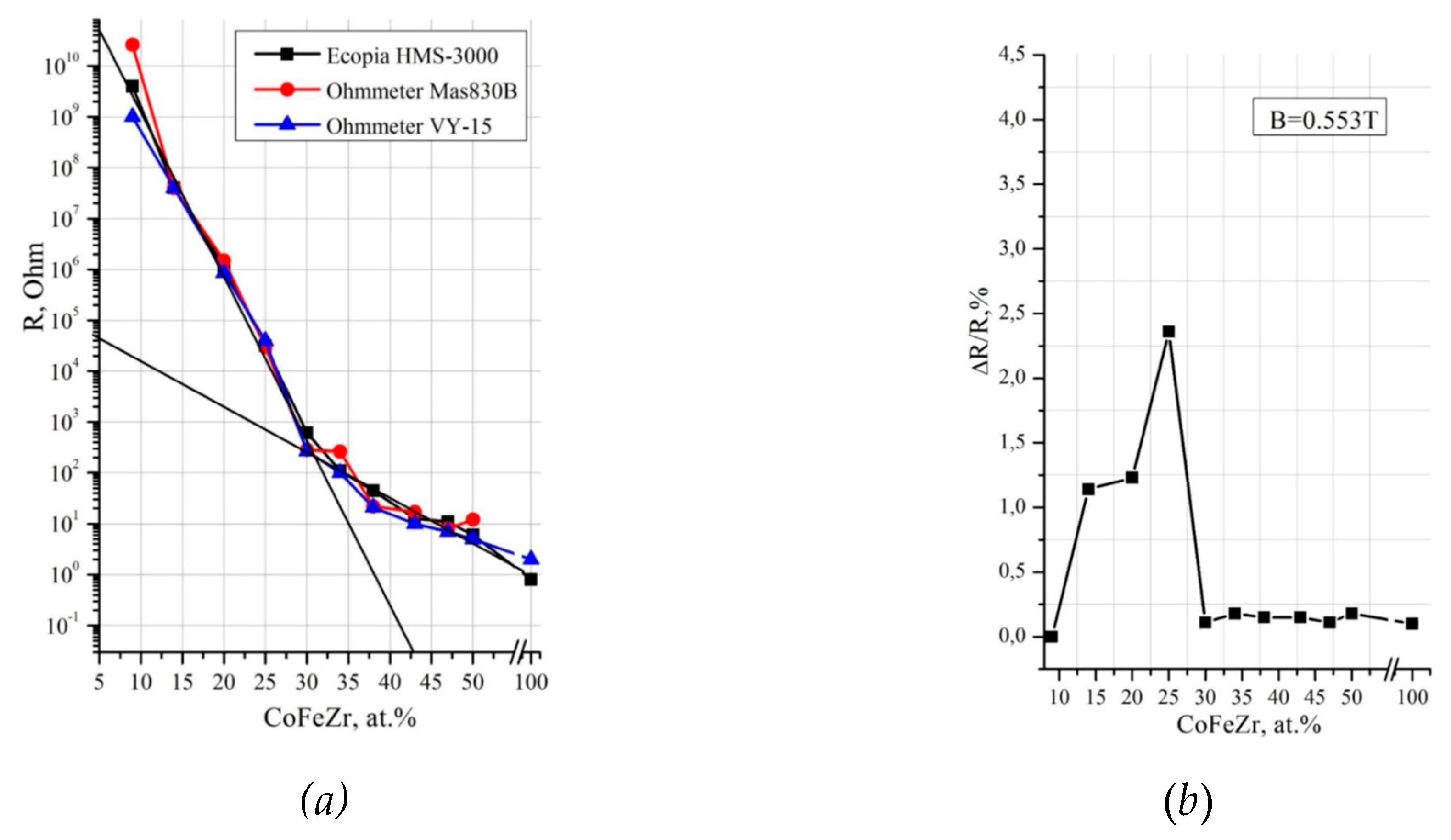
Concentration dependence of the electrical resistance of nanocomposites (CoFeZr)x (MgF2)100-x with different alloy content x (at.%) is shown in Figure 3a and in Table 3. This dependence of the resistivity of the studied nanocomposites is characterized by nonlinear pattern of metal-dielectric composites behavior, when the electric transfer mechanism changes with variations in the relative content of metal and dielectric components [11,23,24,25,26,27,28,29]].
The Figure 3a and Table 3 shows, that in the range of x = 9 - 25 at.% the resistance of nanocomposites (CoFeZr)x (MgF2)100-x falls by five orders of magnitude from 4*109 to 3*104, but remains characteristic of dielectrics. With a further increase in the alloy content from 35 to 50 at.% the resistance of nanocomposites drops sharply to values characteristic of that on for alloys and even some metals.
In the graph of the concentration dependence (Figure 3a), we draw two extrapolation lines with different angles of inclination. The range of intersection of these lines in the region (30-35 at.%) corresponds to the percolation threshold. Two straight lines on the concentration dependence indicate different current flow mechanisms before and after the percolation threshold along the high-resistance and low-resistance pathways. The obtained experimental data correlate well with the data for similar systems of composites with dielectrics of barium fluoride, calcium fluoride and aluminum oxide [23,24,25,26,27,28,29].
The absolute values of the tunneling giant magnetic resistance (GMR) were determined in accordance with the expression:
where R(H) is the resistance of the sample in the presence of an external magnetic field H, R(0) is the resistance of the composite in the absence of an external magnetic field.
Figure 3b shows the concentration dependence of magnetoresistance for the samples of the system (CoFeZr)x(MgF2)100-x. The resulting concentration dependence of magnetoresistance is extremely nonmonotonic. In the dielectric region of composites, small values of magnetoresistance are recorded far from the percolation threshold. With an increase relative to the content of the metal component in the range of 9<x<27, the GMR increases abruptly to the maximum value of ΔR/R(0) = 2.4%. With a further increase in the proportion of the metal component (x > 27 at. %) GMR is also sharply reduced.
The obtained concentration dependence of the magnetoresistive effect is fully consistent with the general model of tunneling magnetoresistance [25,26,27,28,29,30], according to which the number of electrons tunneling through the dielectric barrier increases with decreasing distance between neighboring alloy nanocrystals. Near the percolation threshold, the morphology of composites is such that the dielectric layer between the nanocrystals has a minimum thickness. The appearance of an exchange interaction between alloy nanocrystals/granules with decreasing distance follows from the analysis of Slonchevsky model [30].
Figure 3.
Concentration dependences of electrical resistance (a) and magnetoresistance (b) of (CoFeZr)x(MgF2)100-x nanocomposites.
Figure 3.
Concentration dependences of electrical resistance (a) and magnetoresistance (b) of (CoFeZr)x(MgF2)100-x nanocomposites.
Thus, with an increase in the content of CoFeZr alloy in the nanocomposite, the average size of nanocrystals increases from 10 to 20 nm [21], and the distance between them decreases. This leads to the mechanical contact of neighboring nanocrystals and the formation of extended fractal-like metal clusters. As a result, the number of energy barriers decreases and the mechanism of electric transfer through the nanocomposite starts to change from tunneling to Ohmic one (Table 1).
3.4. Capacitive/inductive nature of the resistance of (CoFeZr)x(MgF2)100–x nanocomposites according to impedancemetry data
One of the most accessible methods for studying electrophysical processes is impedance spectroscopy [34,35].
Impedance is ,
where i = √–1, ω is the cyclic frequency, С is the total capacitance of the composite. Z' = R is the real resistance component, is the imaginary resistance component.
The hodograph of the impedance Z (impedance diagrams) is a graphical dependence of the imaginary component of the impedance Z" on the real Z'.
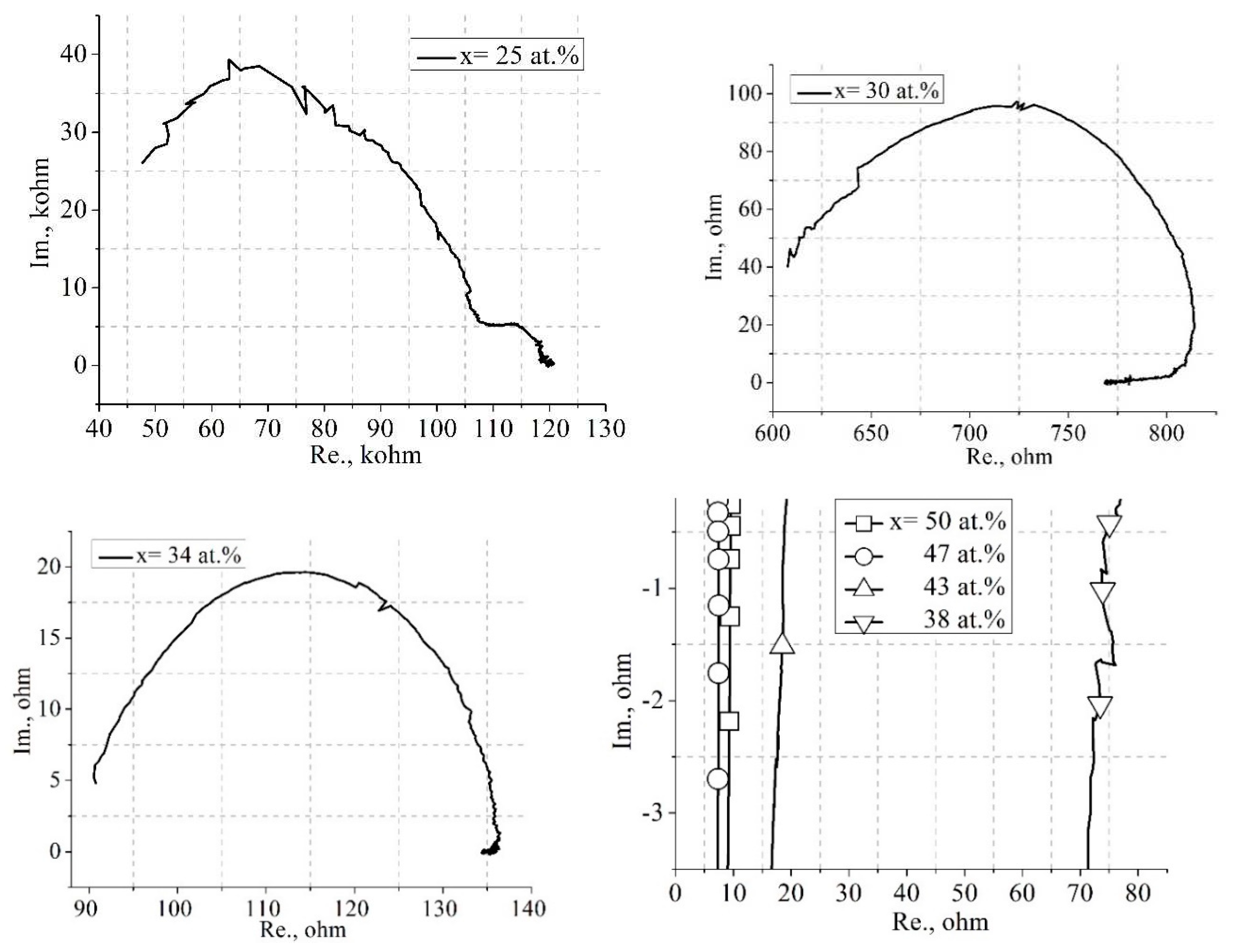
For (CoFeZr)x(MgF2)100–x nanocomposites, impedancemetry data in Fig.4 show two different types of hodographs before percolation threshold and after the percolation threshold. On the hodograph for a nanocomposite with an alloy content up to the percolation threshold x≥34 at.%, a semicircle is observed, which corresponds to the typical behavior of the RC chain of metal clusters in a dielectric matrix[35]. At the percolation threshold x≥35 at.%, the hodograph takes the form of an inclined line, and then, as x increases beyond the percolation threshold, the hodographs become vertical lines, indicating the metallic nature with the ohmic character of conduction [35].
Figure 4.
Impedance diagrams (hodographs) for nanocomposites(CoFeZr)x(MgF2)100-x of different compositions.
Figure 4.
Impedance diagrams (hodographs) for nanocomposites(CoFeZr)x(MgF2)100-x of different compositions.
The resistance and capacitance values of the nanocomposites according to the impedancemetry data given in Table 2 show that the capacitance of the nanocomposites in the prepercolation region does not exceed several picofarads. And only in the region of the percolation threshold (xper=35 at. %) the capacitance increases by three orders of magnitude up to two nanofarads. This increase in capacitance value is due to the beginning of formation of metallic nanocrystals and the remaining dielectric interlayers between them.
The presented data correlate well with the capacitive properties of a similar system (CoFeZr)x(PZT)100-x from [36].
Table 4.
Concentration dependence of the total electric resistance R and capacitance C of the nanocomposites (CoFeZr)x(MgF2)100-x.
Table 4.
Concentration dependence of the total electric resistance R and capacitance C of the nanocomposites (CoFeZr)x(MgF2)100-x.
| x, at.% | R, Ohm | C, f |
| 20 | 13*106 | 6*10-12 |
| 25 | 25*104 | 4*10-12 |
| 30 | 830 | 4*10-9 |
| 34 | 136 | 1.2*10-9 |
| 38 | 75 | - |
| 43 | 16 | - |
| 47 | 8 | - |
| 50 | 8 | - |
3.5. Magneto-optical and magnetic properties of (CoFeZr)x(MgF2)100–x nanocomposite
The magneto-optical Kerr effect in transversal geometry [6,7,8,9], transversal Kerr effect (TKE), consists in changing the intensity of linearly polarized light reflected by a sample magnetized perpendicular to the plane of the incident light. The value and sign of TKE are defined as the ratio of the difference between the intensities of the light reflected by the sample in the magnetized (I) and demagnetized (I0) states to the light intensity I0:
δ=(I- I0)/I0 =ΔI/I0
The absolute value of TKE depends on the amount of the metal phase in the composite. Its increase leads to an increase in the TKE modulus, which attains maximum at a concentration corresponding to the percolation threshold.
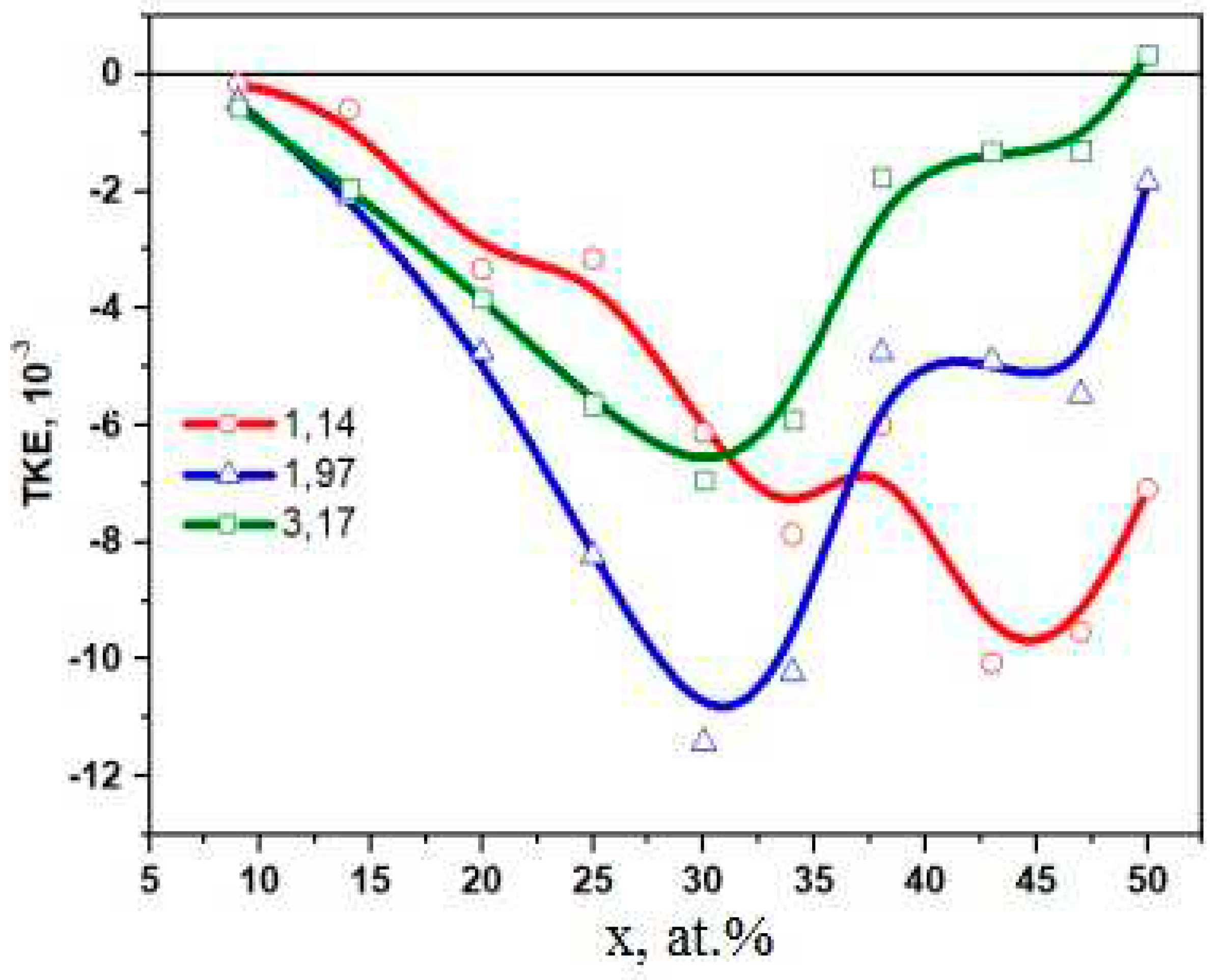
Figure 4 from our previous work [22] shows the concentration dependences of TKE for (CoFeZr)x(MgF2)100-x nanocomposites at three values of the incident light photon energy of Е=1.14 eV; 1.97 eV and 3.17 eV. The concentration dependences of TKE in the NC (CoFeZr)x(MgF2)100 – x system showed two maxima, one of which at х =30-34 at.% corresponded to the formation of hexagonal nanocrystals of the CoFeZr alloy and the second maximum at x=45 at. % corresponded to the phase transition of the hexagonal structure to the cubic BCC structure α-Fe.
Thus, magneto-optical spectra respond to changes in the composition, atomic structure, and magnetic order of a complex heterophase systems.
Figure 5.
Concentration dependencies of transversal Kerr effect (TKE) for nanocomposites (CoFeZr)x(MgF2)100-x at different values of the incident light energy.
Figure 5.
Concentration dependencies of transversal Kerr effect (TKE) for nanocomposites (CoFeZr)x(MgF2)100-x at different values of the incident light energy.
Since the magnetic percolation threshold xfm is defined as the concentration of the metal phase when the magnetization sharply increases and a coercive force arises in nanocomposites, further, in Figure 6 we present the dependences of magnetizations on the magnetic field arising parallel and perpendicular to the sample plane, which show the first appearance of a hysteresis loop with coercive force Нс≈18 Oe in a (CoFeZr)34(MgF2)66 sample for the alloy content x=34 at.%.
Figure 6.
Appearance of hysteresis in (CoFeZr)34(MgF2)66 and its absence in (CoFeZr)30(MgF2)70.
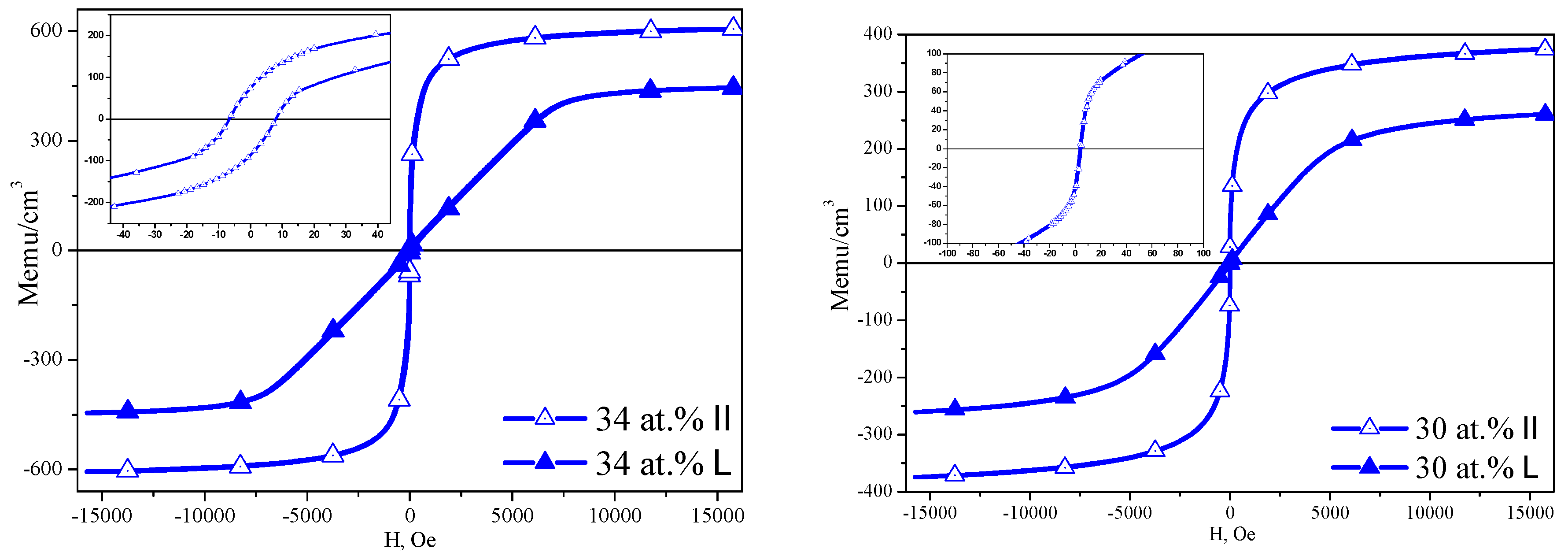
It means that the magnetic percolation threshold in the (CoFeZr)x(MgF2)100-x system at xfm=34 at.% coincides with the resistive percolation threshold xper=34 at.% due to the exchange interaction between electrons and spins of the formed hexagonal CoFeZr nanocrystals.
Figure 7 shows the dependence of coercive force Hc on the concentration of the metal component for nanocomposites (CoFeZr)x(MgF2)100-x on the glass. The measurements of the NCs magnetic properties with a vibration magnetometer showed that the value of the coercive force Hc in all of the nanocomposites at x≤30 at.% is equal to zero.
Thus, in concentration region of x≤30 at.%, nanocomposites (CoFeZr)x(MgF2)100-x are superparamagnets, and the critical magnetic percolation threshold for this system is xfm=34 at.%. However, as the x value increases, hysteresis loops with non-zero Hc values appear in the samples.
Figure 7.
Concentration dependence of the coercive force Hc for (CoFeZr)x(MgF2)100-х. nanocomposites.
Figure 7.
Concentration dependence of the coercive force Hc for (CoFeZr)x(MgF2)100-х. nanocomposites.
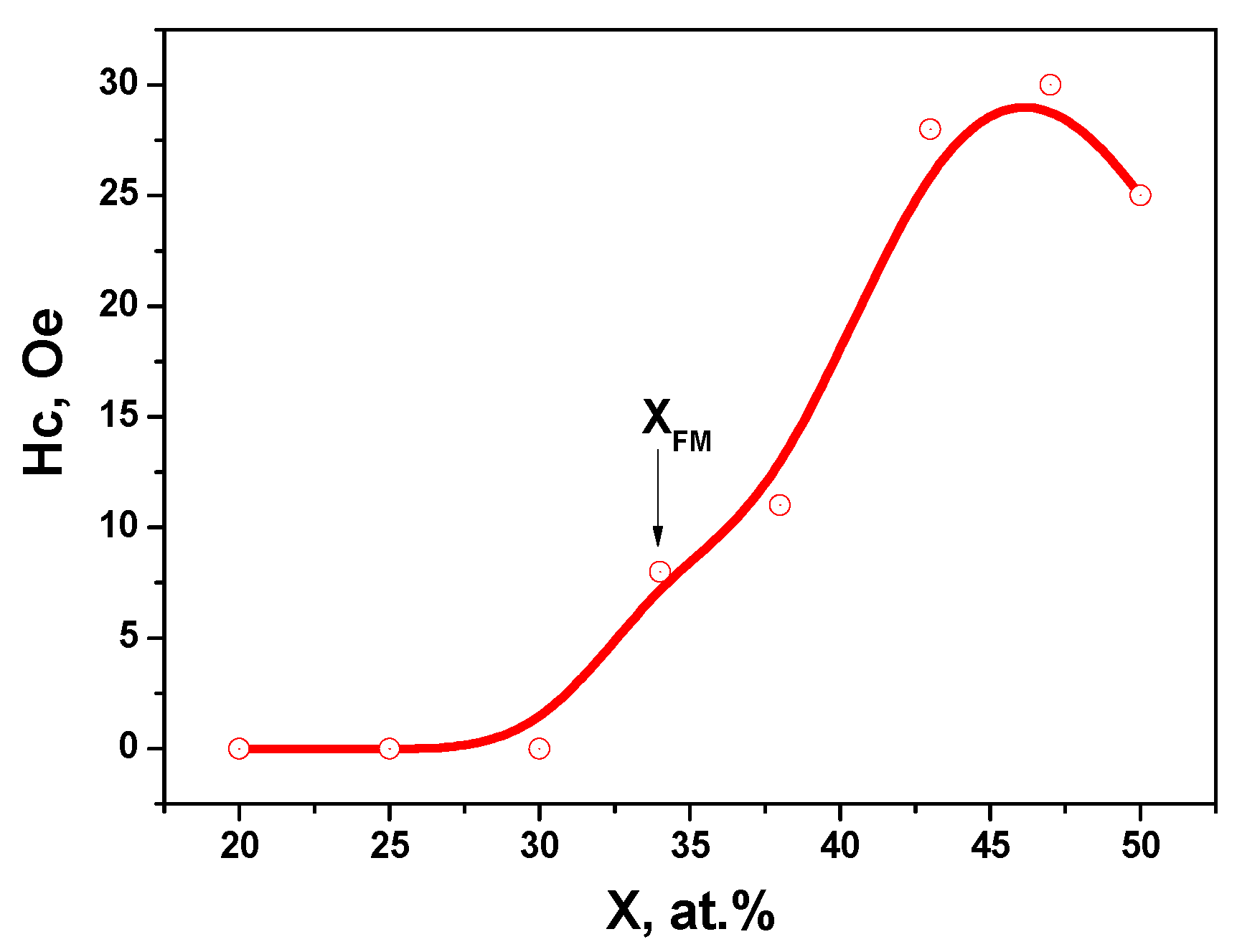
According to the magnitude of the coercive force Nс, magnetic materials are divided into magnetically hard and magnetically soft. Materials with values of Nс < 50 Oe are soft magnetic, and materials with Nс > 50 Oe are magnetic hard (GOST 19693 – 74). Based on this classification, the studied nanocomposites (CoFeZr)x(MgF2)100-x should be attributed to soft magnetic materials with a maximum value of Нс < 30 Oe (Figure 7).
It should be noted that the nanocomposites of less complex composition Cox(MgF2)100-x studied by us recently [20] exhibit a more hard magnetic character at approximately the same concentrations of cobalt with a maximum value of the coercive force about 90Oe. Apparently, the decrease in magnetic order in NCs (CoFeZr)x(MgF2)100-x is influenced by the diamagnetic phase FeF2 that we discovered at the interface of magnetic nanocrystals CoFeZr with a dielectric matrix MgF2 by the Mössbauer spectroscopy.
4. Conclusion
Thus, the results of comprehensive studies of the structural-phase, electrical resistive, and electromagnetic properties of thin-film samples of heterogeneous metal-dielectric system (CoFeZr)x(MgF2)100-x with variable composition, obtained by ion-plasma sputtering on glass substrates, show that in a wide range of the studied compositions x =9-51 at.% nanocomposite consists of one X-ray amorphous phase and one nanocrystalline phase.
Which of the two components, metallic CoFeZr or dielectric MgF2, forms nanocrystals in the composite depends on the relative alloy content x: at x<34 at.%, the metal phase is X-ray amorphous, and the MgF2 dielectric matrix is nanocrystalline, while at x>34 at.% metallic alloy is formed hexagonal nanocrystals, and the dielectric matrix becomes X-ray amorphous. Starting from x=43 at.%, the crystal structure of CoFeZr nanocrystals is rearranged into a cubic volume-centered phase based on α-Fe with a predominant orientation of (110), like that of α-Fe.The average size of CoFeZr alloy nanocrystals increases within 10-20 nm.
At the metal-insulator interfaces in (CoFeZr)x (MgF2)100-x, the formation of Fe-F chemical bonds between iron and fluorine atoms with the formation of a paramagnetic FeF2 phase by the Mössbauer spectroscopy was found.
The value of the percolation threshold of nanocomposites xper=34 at.%, determined from the concentration dependences of the electrical resistance of nanocomposites, coincides with the beginning of the nucleation of metal CoFeZr hexagonal nanocrystals in the MgF2 dielectric matrix.
The absolute value of the maximum negative magnetoresistance in the investigated NCs is 2.4% in the field of 5.5 kOe at alloy concentration of x=25 at. %, up to the percolation threshold.
The magnetic percolation threshold in the (CoFeZr)x(MgF2)100-x system occurs at xfm=34 at.% with the appearance of a hysteresis loop and a coercive force Hc≈18 Oe, coinciding with the resistive percolation threshold xper=34 at.% and with beginning of the CoFeZr hexagonal nanocrystals nucleation.
In the concentration dependences of the magneto-optical transversal Kerr effect in the (CoFeZr)x(MgF2)100-x NCs, two maxima appear, one of which corresponds to the formation of CoFeZr alloy nanocrystals of a hexagonal structure (x = 34at.%), and the second maximum at x=45 at.% corresponds to the phase transition of nanocrystals from hexagonal structure to a cubic body-centered structure.
Electric and magnetic percolation thresholds in (CoFeZr)x(MgF2)100-x NCs at x = 34 at.% coincides with the formation of CoFeZr nanocrystals. Below this value x < 34 at.%, nanocomposites exhibit superparamagnetic properties.
At large values of x > 34 at.% (CoFeZr)x(MgF2)100-x NCs become magnetically soft materials and remain so far beyond the percolation thresholds with the maximum value of the coercive force
Hc< 30 Oe. Apparently, the decrease in magnetic order and soft ferromagnetic are influenced by the diamagnetic phase FeF2 that we discovered at the interface of magnetic nanocrystals CoFeZr with a dielectric matrix MgF2 by the Mössbauer spectroscopy.
Author Contributions
Conceptualization, E.P.D.; methodology, E.P.D., A.V.S. and E.A.G.; validation, E.A.G. and P.V.S.; formal analysis, E.P.D.; investigation, S.A.I., S.V.R., D.L.G., Yu.G.S.; writing—original draft preparation, E.P.D., S.A.I. and E.A.G.; writing—review and editing, E.P.D. and S.A.I.; supervision, E.P.D.; project administration, P.V.S.; funding acquisition, All authors have read and agreed to the published version of the manuscript.E.D. and E.G. conceived and designed the experiments, analyzed the data; S.I., P.S., D.G., K.B., Yu.S.and S.R. conceived and designed the experiments; A.S. contributed materials. All authors have read and agreed to the published version of the manuscript.
Funding
The work was partially supported by the Ministry of Science and Higher Education of the Russian Federation as part of the state task for Universities in the field of scientific activity, project No. FZGU-2023-006 and the Agreement N 075-15-2021-1351 in part of the electronic properties.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Gittleman, J.L., Goldstain J., Borowski S. Magnetic Properties of Granular Nikel Films. Phys. Rev. B. 1972. V.B5. P.3609-3621. [CrossRef]
- Helman J.S., Abeles B. Tunneling of Spin-Polarized Electrons and Magnetoresistance in Granular Ni Films. Phys. Rev. Lett.1976. V. 37. N.21. P.1429-1433 . [CrossRef]
- Abeles B., Sheng P., Coutts M. D., Arie Y. Structural and electrical properties of granular metal films. Adv.Phys. 1975. V.24. N.3. P.407–461. [CrossRef]
- Fujimori, H.; Mitani, S.; Ohnuma, S. Tunnel-type GMR in metal-nonmetal granular alloy thin films. Materials Science and Engineering B 1995, 31, 219-223. [CrossRef]
- Zvezdin, A.K.; Kotov, V.A. Modern Magnetooptics and Magnetooptical Materials; Institute of Physics Publishing Ltd.: London, UK, 1997.
- Gan’shina, E.; Granovsky, A.; Gushin, V.; Kuzmichev, M.; Podrugin, P.; Kravetz, A.; Shipil, E. Optical and Magneto-Optical Spectra of Magnetic Granular Alloys. Physika A 1997, 241(1-2), 45-51. [CrossRef]
- Kravets, V.G.; Petford-Long, A.K.; Kravets, A.F. Optical and magneto-opticalproperties of (CoFe)x(HfO21)1-x magnetic granular films. J. Appl. Phys. 2000, 87,1762-1768. [CrossRef]
- Gan'shina E.A.; Kim, C.G.; Kim, C.O.; Kochneva, M.Yu.; Perov, N.Yu.; Sheverdyaeva, P.A. Magnetostatic and magneto-optical properties of Co-based amorphous ribbons. Journal of Magnetism and Magnetic Materials 2002, 239, 484-486. [CrossRef]
- Gan'shina, E.A.;Vashuk, M.V.;Vinogradov, A.N. et al. Evolution of optical and magneto-optical properties in amorphous metal-dielectric nanocomposites. Journal of Experimental and Theoretical Physics 2004, 125(5), 1172-1183. [CrossRef]
- Buravtsova, V.E.; Guschin, V.S.; Kalinin, Yu.E. et al. Magnetooptical properties and FMR in granular nanocomposites (Co84Nb14Ta2)x(SiO2)100−x.CEJP 2004, 2(4), 566-578. [CrossRef]
- Gridnev, S.A.; Kalinin, Yu.E.;Sitnikov, A.V.;Stogney, O.V. and Gridnev, S.A. Nonlinear Phenomena in Nano—and Microheterogeneous Systems; BINOM Knowledge Laboratory: Moscow,Russia, 2015.
- Rylkov, V.V.; Nikolaev, S.N.; Chernoglazov, K.Y. et. al. Tunneling anomalous Hall effect in the nanogranular CoFeB-AlO films near metal-insulator transition. Phys. Rev. B 2017, 95, 144402. [CrossRef]
- Bedanta, S.; Kleemann, W. Superparamagnetism. J. Phys. D 2009, 42, 013001. [CrossRef]
- Kobayashi, N.; Ohnuma, S.;Masumoto, T.;Fujimori, H. (Fe–Co)–(Mg-fluoride) insulating nanogranular system with enhanced tunnel-type giant magnetoresistance. J. Appl. Phys. 2001, 4159-4162. [CrossRef]
- Cao, Y.; Umetsu, A.; Kobayashi, N.; Ohnuma, S.; Masumoto, H.Tunable frequency response of tunnel-type magneto-dielectric effect In CoхMgF2 granular films with different content of Co. Appl. Phys. Lett.2017, 111, 122901. [CrossRef]
- Tregubova, T.; Stognei, O.; Kirpan, V. Magnetotransport properties of Cox(MgF2)100-x oxygen-free nanocomposites. EPJ Web of Conferences. Moscow International Symposium on Magnetism, 2018, 01014. [CrossRef]
- Tregubova, T.V.; Stogney, O.V.; Tregubov, I.M.; Kirpan, V.V.; et al. Electrical and magnetoresistive properties of oxygen-free composites Cox(MgF2)100-x. Vestnik of Voronezh State Technical University 2017, 13 (6), 122-127. [CrossRef]
- Domashevskaya, E.P.; Ivkov, S.A.; Sitnikov, A.V.; Stogney, O.V.;Kozakov, A.T.; Nikolsky, A.V. Formation of nanocrystals of a metal or dielectric component depending on their relative content in Cox(MgF2)1-x composites. Solid State Physics, 2019, 61(2), 211-219. [CrossRef]
- Domashevskaya, E.P.; Ivkov, S.A.; Stogney, O.V.; Sitnikov, A.V. Mutual influence of the relative content of the metallic and dielectric component on the phase composition and substructure of nanocomposites Cox(MgF2)1-x. 8th International Conference on Nanotechnology and materials science, Netherlands, Amsterdam, April 24-26, 2019, 81.
- Ivkov, S.A., Barkov, K.A., Domashevskaya, E.P. et al. Nonlinear Transport and Magnetic/Magneto-Optical Properties of Cox(MgF2)100-x Nanostructures. Appl. Sci. 2023, 13(5), 2992; [CrossRef]
- E.P. Domashevskaya, S.A. Ivkov, A.V. Sitnikov, et al. The features of CoFeZr alloy nanocrystals formation in film composites of (CoFeZr)x(MgF2)100-x. Journal of Alloys and Compounds 870 (2021) 159398. [CrossRef]
- E.A. Ganshina, S.A. Ivkov, E.P. Domashevskaya et al. Effect of phase transformations of a metal component on the magneto-optical properties of thin-films nanocomposites (CoFeZr)x(MgF2)100-x. Nanomaterials 11 (2021) 1666. [CrossRef]
- Kalinin, Y.E.; Sitnikov, A.V.; Stognei, O.V.; Zolotukhin, I.V. Electrical properties and giant magnetoresistance of the CoFeB-SiO2 amorphous granular composites. Mater. Sci. Eng. A 2001, 304(306), 941–945. [CrossRef]
- Stogneĭ, O.V.; Sitnikov, A.V.; Kalinin, Y.E.; Avdeev, S.F.; Kopytin, M.N. Isotropic positive magnetoresistance in Co-Al2On nanocomposites. Physics of the Solid State 2007, 49(1), 164-170. [CrossRef]
- Nikiruy, K.E., Iliasov, A.I., Emelyanov, A.V., Sitnikov, A.V., et al. Memristors Based on Nanoscale Layers LiNbO3 and (Co40Fe40B20) x (LiNbO3) 100–x. Physics of the Solid State. 2020. 62(9), 1732-1735. [CrossRef]
- Nikiruy, K.E., Emelyanov, A.V., Demin, V.A., Sitnikov, A.V. Dopamine-like STDP modulation in nanocomposite memristors. AIP Advances. 2019. V.9, №6 P.065116. [CrossRef]
- Kijima-Aoki, H., Cao, Y., Kobayashi, N., Takahashi, S. Large magnetodielectric effect based on spin-dependent charge transfer in metal-insulator type Co-(BaF2) nanogranular films. J. Appl. Phys. 2020. Vol. 128, № 13. [CrossRef]
- Cao, Y., Kobayashi, N., Zhang, Y.W., Ohnuma, S., Masumoto, H. Enhanced spin-dependent charge transport of Co-(Al-fluoride) granular nanocomposite by co-separate sputtering. J. Appl. Phys. 2017. Vol. 122, № 13. P. 1–7. [CrossRef]
- Mitani, S., Fujimori, H., Ohnuma, S. Spin-dependent tunneling phenomena in insulating granular systems. J. Magn. Magn. Mater. 1997. Vol. 165, № 1–3. P. 141–148. [CrossRef]
- Moodera, J.S., Mathon, G. Spin polarized tunneling in ferromagnetic junctions. J. Magn. Magn. Mater. 1999. Vol. 200, № 1–3. P. 248–273. [CrossRef]
- Slonczewski, J.C. Conductance and exchange coupling of two ferromagnets separated by a tunneling barrier. Phys. Rev. B. 1989. Vol. 39, № 10. P. 6995–7002. [CrossRef]
- Stogney, O.V., Sitnikov, A.V. Anisotropy of amorphous nanogranulated composites CoNbTa-SiO. Solid State Physics. 2010. Vol. 52. № 12. P.2356.
- Németh, R., Mühlschlegel, B. Hopping conductivity in granular systems. Zeitschrift für Phys. B Condens. Matter. 1988. Vol. 70, № 2. P. 159–162. [CrossRef]
- Barsoukov, Ed.E.; Macdonald, J.R. Impedance spectroscopy:theory, experiment, and applications. N.Y., Willey 2005, 606 р. [CrossRef]
- Poklonsky, N.A.; Gorbachuk, N.I. Fundamentals of impedance spectroscopy of composites: a course of lectures. Minsk: Belaruce State University, 2005, 130 p.
- Koltunowicz, T. N., Zukowski, P., Boiko, O., Czarnacka, K. Capacitive properties of nanocomposite (FeCoZr)x(PZT)(100−x) produced by sputtering with the use of argon and oxygen ions beam. J. Mater. Sci. Mater. Electron. Springer US, 2016. Vol. 27, № 2. P. 1171–1176. [CrossRef]
Table 1.
Parameters of the Mössbauer spectra of CoFeZr and FeF2 phases in the composition of the sample (CoFeZr)51(MgF2)49 : S − magnetic sextet, D − paramagnetic doublet; Is− isomeric shift; Q − quadrupole splitting; H − effective magnetic field on α-Fe; G − line width; A − area of the component under the spectrum.
Table 1.
Parameters of the Mössbauer spectra of CoFeZr and FeF2 phases in the composition of the sample (CoFeZr)51(MgF2)49 : S − magnetic sextet, D − paramagnetic doublet; Is− isomeric shift; Q − quadrupole splitting; H − effective magnetic field on α-Fe; G − line width; A − area of the component under the spectrum.
 |
Table 3.
Concentration dependence of the electrical resistance of nanocomposites. (CoFeZr)x (MgF2)100-x
Table 3.
Concentration dependence of the electrical resistance of nanocomposites. (CoFeZr)x (MgF2)100-x
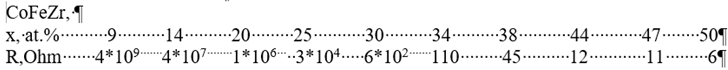 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








