Prerpints.org logo
Preprint
Article

Description of Mesoscale Static and Fatigue Analysis of 2D Woven Roving Plates with Convex Holes and Subjected to Axial Tension

Altmetrics

Downloads

204

Views

85

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 March 2024

Posted:

10 April 2024

You are already at the latest version

Alerts
Abstract
Abstract—The static and fatigue analysis of plates with holes, made of 2D woven roving composites, is conducted. The parametrization of convex holes is proposed. Experimental results of specimens without holes and with different shapes of notches are discussed. The fatigue behaviour is considered with the use of the low cycle fatigue method. The analysis is supplemented by the numerical finite element modeling. The present work is an extension of the results discussed in the literature. The finite element modeling of plates with holes is presented in details in Ref [1-3] including also the problems of the accuracy. The experimental results and the form of specimens are shown in Ref [4]. Two parametrical description of static and fatigue behaviour of plates with holes characterizes the goal and the novelty of the paper. The fuzzy approach is employed to reduce the number of experimental data [5].
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The present state of art in materials engineering is directly connected and determined with the application of composites in various areas of mechanical or building sciences (e.g. wind turbine blades, aerospace, automotive). It relates to the use of both:
š
classical composites such as: chopped fibers (nonwovens), long fibers grouped together and assembled into fabrics, called as tows or yarns and constitute unidirectional laminates, (wovens, braids or knits), 2D woven fabrics – the yarns are divided into two components, i.e. the warp and the weft running in the cross direction to the warp, 2.5D and 3D fabrics – the definitions and figures of those composites are presented by Gowayed [6]; Each type of fabrics has its own advantages and disadvantages and they are illustrated in details in Ref. [7], and
š
non-classical composites such as: nanostructural reinforcements (nanoplatelets, nanoribbons, various forms of graphens – hexagonal nanostructures), functionally graded materials, or piezoelectric being sensors or actuators – the detailed discussion of their material properties is illustrated in Refs [8,9,10].
Constructions of structures made of composite materials take the classical forms dealing with beams, plates, shells and 3D structures. Each of the physical problems is subjected to different boundary and loading conditions. As it is shown in Figure 1 various physical problems can be formulated and solved.
Due to the variety of problems and the number of works published in the literature the review of the literature should be limited to the indications of the most significant references in this area. Since the present work is devoted to the analysis of stress concentrations of 2D composite structures the discussion of the literature should be limited to the presentation of the most significant papers in the area of failure damage for 2D, 2.5D and 3D composites..
In general for composites, the notch sensitivity and stress concentration around the holes problems can be divided into four categories:
š
Strength (static and fatigue) performance of laminated unidirectional constructions [3,11,12,13,14,15,16,17] – the failure morphology depends on fibre orientations, stacking sequences and forms of holes
š
2-D woven and braided composite structures [17,18,19,20,21] – the failure occurs also at the perpendicular directions to tensile loads; the failure is characterized by fibre and matrix damage
š
2.5-D woven roving composites Guo et al. [22], Song et al. [23] – yarn debonding is observed
š
3-D woven roving composites [24,25,26,27,28] – depending on the fibre alignement and the size of the hole different response and damage accumulation are observed.
The investigations in each of the above mentioned areas tend to introduce the more accurate description of numerical modeling to experimental results. The standard method used in the experimental analysis are discussed in Ref. [29]. Pandita et al. [4] demonstrate experimental and theoretical static strain concentrations results for circular, and vertical, and horizontal ellipsoidal centrally located holes. Guo et al. [22] describe the results for centrally located waist, slit, octagon, square, hexagon and rhombus holes. For 2D woven roving composites the analysis is also carried out for plates made of hybrid, natural (juta) material [30,31].
As it is pointed by Guo et al. [22] the present studies are mainly directed in the analysis of structures made of 3-D woven roving materials. The identical conclusions can be drawn in the literature concerning with the fatigue reliability.
The aim of the present work is to present the comparison of experimental and theoretical (numerical) studies for plates (specimens) made of 2-D woven roving composites. The analysis deals with constructions of centrally located holes and subjected to tensile loading. Since the static experimental studies demonstrate an evident material nonlinear (σ-ε) characteristics the fatigue numerical (finite element) description is carried out with the use of the low fatigue cycle (LFC) method. The experimental (static and fatigue) results illustrate essentially the occurrence of the random (probabilistic) nature of both static and fatigue cracks. The classical approach to such problems is based on the statistical (Weibull) distributions. However, in such a description, a lot of experimental data is required. Therefore, we propose to use herein the limit data (lower and higher bounds) to characterize the LFC behaviour of structures.
In the present paper we intend to discuss similarities and differences for static and fatigue behaviour of plates made of 2D woven roving composites having central holes and subjected to uniaxial tension. The analysis is conducted with the application and comparison of experimental results with the finite element computations.

2. Woven Roving Composite Materials

2.1. A Brief Description of 2-D Woven Roving Composites

The category of fiber architecture is that formed by 2-D,2.5-D or 3-D weaving, braiding, or knitting the fiber bundles or “tows” to create interlocking fibers that often have orientations slightly or fully in an orientation orthogonal to the primary structural plane. This approach is taken for a variety of reasons, including the ability to have structural, thermal, or electrical properties in the third or “out-of-plane” dimension. Another often- cited reason for using these architectures is that the “unwetted” or dry fiber preforms (fibers before any matrix is added) are easier to handle, lower in cost, and conform to highly curved shapes more readily than the highly aligned, continuous fiber form.
Three different types of 2-D woven roving composites are distinguished – Figure 2.
Woven fiber-reinforce plastics are becoming increasingly important because they have a lot of advantages over laminates made from individual layers of unidirectional material:

2.2. Design, Tooling, and Manufacturing Interaction

A draping simulation is used to generate fiber paths, identify areas of wrinkling and bridging, develop flat patterns, and allow the calculation of local ply orientations and the resulting laminate mechanical properties, such as stiffness, permeability, volume fraction, and thickness. The existing models for draping simulation fall into one of the following two categories: mapping models and mechanical models. Mapping models assume a geometric mechanism to transform an initial unit square of fabric into the corresponding draped shape. Mechanical models use the equilibrium equations that balance the internal forces in the fabric with external applied loads.
The above problems are very significant in manufacturing curved structures made of 2-D woven roving fabrics. For instance considering hemispherical shells the length of the meridian is equal to πR, and the maximal length of the circumference to 2πR, where R denotes the shell radius. The excess of the material along the circumference leads to the wrinkling of the produced curved structures. Those problems are discussed for shallow ellipsoidal domes by Gohari et al. [32], curved structures by Wang et al. [33], Potluri et al. [34], Sharma, Sutcliffe [35], torispherical shells by Galletly, Muc [36] or hemispherical domes by Muc [37]. For all cases discussed above the rectangular form of 2-D woven roving composites (e.g. Figure 2a) changes to rhombs. It leads to the unsymmetric mechanical description of the axisymmetric shell constructions. It should be included in the numerical analysis.
The use of filament winding method can eliminate the appearance of wrinkles along shells circumference both for opened or closed shells but it does not eliminate the unsymmetric deformations of axisymmetric domes.

3. Methods of the Analysis

To determine the methods of the analysis it is necessary to characterize the set of parameters required in the evaluation of results. Let us note that the present investigations deal with the analysis of structures subjected to tensile loads so that the studies are limited to description of the stress-strain relations for such loading and boundary conditions both for experimental an theoretical considerations.

3.1. Static Behaviour

Tensile testing is used to measure the force required to break a polymer composite specimen and the extent to which the specimen stretches or elongates to that breaking point. Tensile tests produce a stress-strain diagram which is used to determine tensile modulus. The specimen is a constant rectangular cross-section. The tabs are bonded to the ends to prevent gripping damage. As it is plotted in Figure 3 the holes are drilled at the center of the specimen.
To model theoretically mechanical properties of 2-D woven roving composites two possible approaches can be used – see e.g. L. Wang et al. [38]:
š
Two level modeling where at the first level the fiber bundle (tow) is represented in the microscale and at the second level the representative volume element (RVE) is illustrated and modeled in the mesoscale
š
One level modeling (mesoscale) where the mesh of composites (RVE) contains three parts: resin pocket, warp tows and fill tows – each of the part is represented by 3-D (hexahedron) finite elements
The homogenization can be also carried out for the unit cell presented in Figure 4 – see Refs [39,40]. They are dependent on the form of the cross-sections that are demonstrated in Figure 4.
The geometry of the cross-sections of 2D woven fabric have a crucial influence of the derivation of mechanical properties. The homogenized mechanical properties can be determined with the use of experimental tension tests or by the numerical finite element analysis.

3.2. Fatigue Behaviour of Woven Roving 2D Composites

Nowadays,the fatigue of structures can be approached using the following concepts – Figure 5:
š
Low cycle fatigue (LCF)
š
High (Mega) cycle fatigue (HCF) from A. Whoeler – both infinite and finite cyclic life can be analyzed, where the small strain increment results in large stress increment
Bathias [41] noticed that in metals, the fatigue damage is strongly related to the cyclic plasticity that is to say the dislocation mobility and slip systems. Due to the environment effect and the plane stress states, the initiation of fatigue damage is often localized near the surface of metals. In polymer matrix composite materials the fatigue damage is not related to plasticity. Considering only polymer-matrix composites reinforced by long fibres, it is acknowledged that the first damage that appears under loading is matrix cracks, before the fracture of the fibres. These are micro cracks with an initial thickness of one layer, and their presence constitutes the initiation of damage. Propagation will develop next, by a multiplication of cracks building to a critical density and resulting in the development of delamination, until the eventual fracture of the fibres, should arise.
At the mesoscopic level, the fatigue damage propagation in metal is a single crack perpendicular to the tension loading. This fatigue crack tip is surrounded by a plastic zone. In composites materials, the fatigue damage is multidirectional and the damage zone, much larger than the plastic zone, is related to the complex morphology of the fracture [3]. For 2D woven roving composites the results are presented in the section 4.3.
In the further part of the paper the LCF problems are investigated.
Low cycle fatigue (LCF) from Coffin [42] and Manson [43] – only finite fatigue life is possible and can be considered using the LCF criteria in such a case a small strain increment corresponds to a large stress increment – Figure 6; according to this approach, the fatigue life of a member subjected to fully reversed constant amplitude strain-controlled loading is given by an equation of the form:
ε = ε a + ε p = σ f ' E N f b + ε f ' ( N f ) c
where: ε - total strain amplitude, σ f ' - fatigue strength coefficient, b - fatigue strength exponent, ε f , - fatigue ductility coefficient, c - fatigue ductility exponent, E - modulus of elasticity, Nf - reversals to failure; the determination of coefficients is presented schematically in Figure 6 and Figure 7;
The LCF curve is defined by five coefficients. Manson proposed the method of universal slope where the equation for the method can be given as follows:
Δ ε / 2 t o t a l = 1.75 U T S / E N f − 0.12 + D 0.6 N f − 0.6
where UTS denotes the ultimate tensile strength, D is the ductility , i.e. the percentage reduce of the area.
Since the static stress-strain curves demonstrate the evident nonlinear behaviour (see the section 4) the fatigue analysis is carried out with the use of the LCF method where the static load carrying capacity is not exceeded. The form of the tensile load is illustrated in Figure 8 where Pm = 0.8 Pstatic and ΔP = 0.1 Pm.

3.3. Definition of Convex Holes

A lot of planar convex curves can be expressed in the form of the super-ellipse defined in the following way – see Muc [1]:
x a n + y b n = 1
where a, b and n are positive rational numbers. A supercircle will obviously correspond to setting a = b. For each value of n – the supercircular exponent – we obtain a different convex curve. The shapes of the supercircles for different values of n are shown in Figure 9. Evidently, n = 2 corresponds to a circle whereas n= 1 corresponds to a triangle with its sides rotated by an angle of π/4 . The case n → ∞ also corresponds to a square with its sides parallel to the axes. Finally, the curve characterizing the convex hole (the supercircle) can be represented in the form of the Fourier series:
The above relation exploits the symmetry with respect to the OX and OY axes.
Applying the form of the curve (3) one quarter of the surface closed by the superelipse can be written in the following form:
A C = a b Γ 2 ( 1 + 1 / n ) Γ ( 1 + 0.5 / n )
where Γ(…) denotes the Euler gamma function.
Assuming the constant value of the area AC one can find that the area is the function of three values a, b and n. Therefore, for the identical value of the n parameter there is an infinite number of the a and b parameters satisfying Equation (4) – see Figure 9.

4. Experimental and Numerical Results

4.1. Static Strain-Stress Relations

Figure 4a,b depict the photographs of 2D woven composites having different thicknesses of bundles corresponding to packing density of fibres.
Using the experimental results plotted in Figure 10 the average Young’s and Kirchhoff’s moduli are written in Table 1- see Ref [39,40]. The numerical (Finite Element) homogenization is also carried out for the unit cell presented in Figure 4 – see Refs [39,40]. The agreement between experimental and numerical results is very good. In addition, let us note that the values of the Young’s moduli for warp and weft directions are almost the same.
The failure modes of rectangular specimens are presented in Figure 11. The damage occurs in the perpendicular direction to the tension load. Since the thickness of the aramid specimen is very low (Figure 4 and Figure 11a) its mechanical behaviour (σ-ε curve) is almost linear and the failure is characterized by a brittle fracture. For glass woven roving the deformation (Figure 10) is nonlinear and can be described by elastic-plastic bahaviour. The failure is not localized along one line (compare Figure 11b). It is observed that failure forms is associated with delaminations illustrated by white zones.
It is mainly caused by the non-uniform thickness distributions of glass specimens. It has a significant influence on the load distributions along specimens at the particular points as it is plotted in Figure 12. The broader discussion of those problems is presented by Muc [44]. For woven roving composites the scatter of results is usually observed.
Usuallly, as it discussed in Ref [45] for 2D woven composites (fabric formed by interlacing the longitudinal yarns (warp) and the transverse yarns (weft)), such as plain, twill or satin), four types of damage mechanisms occur under static and fatigue loadings: intra-yarn cracks in yarns oriented transversely to the loading direction, inter-yarn decohesion between longitudinal and transverse yarns, fiber failure in longitudinal yarns and yarn failures. The failure forms plotted in photographs in Figure 11 are identical for fatigue problems.

4.2. Stress Concentration around Convex Holes

Figure 13 demonstrates the forms of the final damage of the specimens. As it may be seen the failures occur always in the perpendicular direction to the tensile loads similarly as for isotropic materials. However, the failure mode is associated with delaminations and the inelastic deformations of the matrix – white zones in Figure 13.
The 2-D solid elements (plane stress elements NKTP = l) in the NISA finite element package are included in the present analysis. The element may be shaped as a 4 to 12 node quadrilateral, or as a 3 or 6 node triangle depending on the selected approach. Each node has two degrees of freedom (two displacements ux, uy) and the state of stress is characterized by three components: σx , σy and σxy. In addition, the nonuniform thickness distributions at each of the nodes can be introduced. The influence of the meshing on the accuracy of computations will be discussed and illustrated later.
Using the planar finite elements it is possible to evaluate numerically the stress distributions around the holes. Figure 14 illustrates the plots of the static stress concentrations around the convex holes. The maximal stress concentrations occurs at the tip of the notch. The stresses are related to the value: P/(Wt).
As it may be noticed in Figure 14 the stress concentrations increase with the growth of the ratio a/b (see Equation (3)). The identical behavior occurs for the higher values of the n parameter (i.e. n=6), keeping the same values of the area Ac. The similar effects are obtained for plates with holes made of woven roving composites, isotropic materials or laminated composites as it is discussed by Pandita ,Nishiyabu, Verpoest [4] and Muc, Romanowicz [3]. In general, various stress criteria can be employed in the analysis. We are searching for the maximal values of:
š
The circumferential stresses
š
The Hill criterion
š
The Huber-Mises-Hencky citerion
š
The Tsai-Wu criterion
š
The Hashin 3-D or 2-D criterion
The detailed description of the above criteria is presented e. g. in Refs [46,47]. Let us note that the Hill, Tsai-Wu and the Hashin criteria are used for the description of structures where both positive and negative values of stresses occur what is not observed in the analysed problem.
Since in the present analysis and modeling 2-D bidirectional woven roving plain composite materials can be treated as isotropic materials (see Table 1 – the mesoscale analysis) the strain concentration factors can be approximated by the results valid for isotropy. The ratio between the local stresses around the hole and the nominal stresses is characterized by the stress concentration factor kt1, i.e.:
σ t i p = k t 1 σ ∞
where the nominal stress σ ∞ = P / ( W t ) , and the local stress σ t i p corresponds to the value of the σy stress component at x = a and y = 0 (the edge of the hole). The theoretical stress concentration factor is a function only of geometry and the type of loading, and can be determined either analytically (using the theory of elasticity), through finite element analysis, or through experiments.
For isotropic materials the stress concentration factor of an elliptical notch can be described in the following way:
k t 1 = 1 + 2 b a
Considering the values of the coefficients 1+2b/a one can notice that the horizontal ellipses correspond to the high concentration effects, whereas the vertical position of ellipses corresponds to the low concentration effects. The comparisons of the stress concentration factors (4) are demonstrated in Table 2.
The accuracy of the FE approximations is a function of the accuracy of meshing, however, in the present case is quite good. Pandita et al. [4] obtained the unsymmetric behaviour of failure modes. It is difficult to verify such results since it depends on too many factors.
Let us note that for the parameter n greater than 6 the area AC Equation (2) can be approximated by the value ab(1-0.5/n). Therefore, the growth of the ratio a/b and the parameter n corresponds to the increase of the stress concentration factors and/or the HMH factor (Table 2 and Figure 15).
a)   b)
Figure 16 demonstrates the non-homoheneus strain distributions around elliptical holes. The results are obtained with the use of the digital image correlation (DIC) method. They resemble the plots presented by Pandita et al. [4].

4.3. Fatigue Behaviour

Let us note that static stress-strain curves (Figure 10) have the identical form as the curve describing the low cycle fatigue in Figure 6. Therefore, it dictates the necessity of the use of the LCF criterion in the analysis of this method in the analysis of fatigue behaviour for the structures considered.
The results presented in Table 1 show that the analysed glass 2D plain weave can be treated as quasiisoptropic materials. It allows to use the Coffin-Manson description (Figure 5 and Figure 7) for isotropic materials with the material constants described by Equations (1) and (2).
For notched plates made of woven roving composites and subjected to tension the typical fatigue final form is illustrated in Figure 17. It is analogous to fatigue behaviour of isotropic (metallic) structures.
The number of cycles corresponding to the final fatigue failure are presented in Table 3. They show the scatter of results caused by the nonuniform distributions of thickness for woven roving composites that have also a great influence on distributions of stresses along the specimen length – see Figure 12.
The scatter of the critical number of cycles should be represented by the statistical or fuzzy set analysis – see the discussion presented by Muc [5]. Using the fuzzy set analysis the experimental fatigue degradation analysis (the decrease of the secant Young modulus) can be illustrated in the form drawn in Figure 18. The results are represented in the form of straight lines being the approximation (linearization) of the experimental data, where E(n) denotes the values of Young’s modulus for the prescribed values of the number of cycles n, and n=0 corresponds to the static behaviour. Nf is the number of cycles characterizing the fatigue failure – see Table 3.
In our opinion the results presented in Figure 18 are much more convenient than the classical statistical analysis since it requires less of experimental data.

4.4. Finite Element Analysis

For low cycle fatigue problems the numerical modeling is carried out in two steps:
  • Finite element modeling of structures with convex holes
  • Derivation of final number of cycles using the Coffin, Manson relation (5)
The analysis is conducted with the use of the numerical package NISA II Endure version 17.
The lowest value occurs at the tip of the circular notch (the grey colour – see Figure 19) and it corresponds to the experimental value – Table 2. The crack initiation is always characterized by the lowest value of the number of cycles. The maximal value of Nf exists in the direction of the remote tension – the axis y.
For different shapes of central notches the identical numerical analysis can be repeated. The results are illustrated in Figure 20. The dimensions of the holes are identical to those discussed for static loads. As it may be seen the distributions are almost identical to the curves plotted in Figure 11 describing the stress concentration effects for static loads.
Similarly as for the stress concentration factors the increase of the parameters a/b and n results in the increase of the critical number of cycles. The identical effects are observed in Refs [48,49].

5. Concluding Remarks

The influence of notches in 2D woven fabric composites is investigated in the mesoscale based on the ultimate stress and on fatigue loads. The stress/strain concentration under static and fatigue loads in 2D woven fabric composites with holes is influenced by the tensile loading direction and by the hole geometry and its dimension relative to the unit cell of the plain woven fabrics. For different shape parameters the strain concentration is located at the tip of holes.
For the analysed problem the similarity between the static stress-strain curves and the low fatigue cycle is observed. Therefore, the fatigue load behaviour is described by the low fatigue cycle method that is described herein both in the experimental and theoretical way.
The 2D woven roving composites have nonlinear behaviour and it has a significant influence on the final failure of static and fatigue failure. It results in the necessity of the use of statistical and fuzzy methods.
The computational finite element methods are also implemented in the paper. The comparison of experimental and numerical results is very good.
The presented results show the necessity of the use of at least two parameters (convex hole) to compare the static and fatigue behaviour of plates subjected to tension. The growth of the parameters a/b and n leads to the increase of the critical values characterizing the static and the LCS fatigue failure.

Acknowledgments

The author would like to thank Dr H. Jodłowski, Dr P. Kędziora, Dr Z. Krawiec for their help in the preparation of the experiments.

References

  1. Muc, A. Effectiveness of optimal design with respect to computational models for laminated composite structures weakened by holes. Struct. Multidiscip. Optim. 1998, 16, 58–67. [Google Scholar] [CrossRef]
  2. Muc, A.; Ulatowska, A. Local fibre reinforcement of holes in composite multilayered plates. Composite Structures 2012, 94, 1413–1419. [Google Scholar] [CrossRef]
  3. Muc, A.; Romanowicz, P. Effect of notch on static and fatigue performance of multilayered composite structures under tensile loads. Composite Structures 2017, 178, 27–36. [Google Scholar] [CrossRef]
  4. Pandita, S.D.; Nishiyabu, K.; Verpoest, I. Strain concentrations in woven fabric composites with holes. Compos. Struct. 2003, 59, 361–368. [Google Scholar] [CrossRef]
  5. Muc, A. Fuzzy approach in modeling static and fatigue strength of composite materials and structures. Neurocomputing 2019, 393, 156–164. [Google Scholar] [CrossRef]
  6. Gowayed, Y. Types of fiber and fiber arrangement in fiber-reinforced polymer (FRP) composites, 2013, Woodhead Publishing Ltd, pp. 1-16.
  7. Carpintero, A.C.D. Development and validation of numerical approaches for triaxially braided composites, Ph D Thesis, Madrid. 2019. [Google Scholar]
  8. Muc, A.; Muc-Wierzgoń, M. Effects of Material Constructions on Supersonic Flutter Characteristics for Composite Rectangular Plates Reinforced with Carbon Nano-structures. Sci. Eng. Compos. Mater. 2021, 28, 107–115. [Google Scholar] [CrossRef]
  9. Muc, A.; Muc-Wierzgoń, M. Analytical Solutions of Coupled Functionally Graded (FG) Conical Shells of Revolution, Sci. Eng. Compos. Mater. ( 2023.
  10. Muc, A.; Kędziora, P.; Stawiarski, A.; Składanowska, K. Buckling enhancement of laminated composite structures partially covered by piezoelectric actuators. Eur. J. Mech. - A/Solids 2018, 73, 112–125. [Google Scholar] [CrossRef]
  11. Divse, V.; Marla, D.; Joshi, S.S. Finite element analysis of tensile notched strength of composite laminates. Compos. Struct. 2020, 255, 112880. [Google Scholar] [CrossRef]
  12. Castanié, B.; Achard, V.; Chirol, C. Effect of milled notches on the strength of open hole, filled holes, single and double lap shear CFRP tension coupons. Compos. Struct. 2020, 254, 112872. [Google Scholar] [CrossRef]
  13. Wan, L.; Ismail, Y.; Sheng, Y.; Wu, K.; Yang, D. Progressive failure analysis of CFRP composite laminates under uniaxial tension using a discrete element method. J. Compos. Mater. 2020, 55, 1091–1108. [Google Scholar] [CrossRef]
  14. Khechai, A.; Tati, A.; Guerira, B.; Guettala, A.; Mohite, P. Strength degradation and stress analysis of composite plates with circular, square and rectangular notches using digital image correlation. Compos. Struct. 2018, 185, 699–715. [Google Scholar] [CrossRef]
  15. Flatscher, T.; Wolfahrt, M.; Pinter, G.; Pettermann, H.E. Simulations and experiments of open hole tension tests – Assessment of intra-ply plasticity, damage, and localization, Compos. Sci. Technol. 2012, 72, 1090–1095. [Google Scholar]
  16. Abisset, E.; Daghia, F.; Ladevèze, P. On the validation of a damage mesomodel for laminated composites by means of open-hole tensile tests on quasi-isotropic laminates. Compos. Part A: Appl. Sci. Manuf. 2011, 42, 1515–1524. [Google Scholar] [CrossRef]
  17. Kim, H.; Hwang, W.; Park, H.; Han, K. Notched Strength of Laminated and Woven Composites. Sci. Eng. Compos. Mater. 1994, 3, 11–22. [Google Scholar] [CrossRef]
  18. Sun, G.; Wang, L.; Chen, D.; Luo, Q. Tensile performance of basalt fiber composites with open circular holes and straight notches. Int. J. Mech. Sci. 2020, 176, 105517. [Google Scholar] [CrossRef]
  19. Hwan, C.-L.; Tsai, K.-H.; Chen, W.-L.; Chiu, C.-H.; Wu, C. Strength prediction of braided composite plates with a center hole. J. Compos. Mater. 2011, 45, 1991–2002. [Google Scholar] [CrossRef]
  20. Kumar, R.S.; Mordasky, M.; Ojard, G.; Yuan, Z.; Fish, J. Notch-strength prediction of ceramic matrix composites using multi-scale continuum damage model. Materialia 2019, 6, 100267. [Google Scholar] [CrossRef]
  21. Chauhan, M.M.; Sharma, D.S. Stresses in finite anisotropic plate weakened by rectangular hole. Int. J. Mech. Sci. 2015, 101-102, 272–279. [Google Scholar] [CrossRef]
  22. Guo, J.; Wen, W.; Zhang, H.; Cui, H. Influence of notch shape on the quasi-static tensile behavior of 2.5D woven composite structure. Thin-Walled Struct. 2021, 165. [Google Scholar] [CrossRef]
  23. Song, J.; Wen, W.; Cui, H.; Wang, Y.; Lu, Y.; Long, W.; Li, L. Warp direction fatigue behavior and damage mechanisms of centrally notched 2.5D woven composites at room and elevated temperatures. Compos. Sci. Technol. 2019, 182. [Google Scholar] [CrossRef]
  24. Dai, S.; Cunningham, P.R.; Marshall, S.; Silva, C. Open hole quasi-static and fatigue characterisation of 3D woven composites. Compos. Struct. 2015, 131, 765–774. [Google Scholar] [CrossRef]
  25. Song, J.; Liu, L.; Li, L.; Zhou, H.; Zhou, W.; Li, X.; Wen, W. Thermo-mechanical responses of notched layer-to-layer 3D angle-interlock woven composites. Compos. Part B: Eng. 2019, 176. [Google Scholar] [CrossRef]
  26. Shuangqiang, L.; Qihong, Z.; Ge, C.; Ko, F. Open hole tension and compression behavior of 3D braided composites. Polym. Compos. 2020, 41, 2455–2465. [Google Scholar] [CrossRef]
  27. M. Arshad, Damage Tolerance of 3D Woven Composites with Weft Binders, The University of Manchester, Manchester, 2014, pp. 109–130.
  28. Saleh, M.N.; Wang, Y.; Yudhanto, A.; Joesbury, A.; Potluri, P.; Lubineau, G.; Soutis, C. Investigating the Potential of Using Off-Axis 3D Woven Composites in Composite Joints’ Applications. Appl. Compos. Mater. 2016, 24, 377–396. [Google Scholar] [CrossRef]
  29. ASTM D5766/D5766M-11Standard Test Method for Open-Hole TensileStrength of Polymer Matrix CompositeLaminates, 2018.
  30. Fontes, R.S.; Bezerra, H.A.D.; Batista, A.C.M.d.C.; Tinô, S.R.L.; de Aquino, E.M.F. Failure Theories and Notch Type Effects on the Mechanical Properties of Jute-Glass Hybrid Composite Laminates. Mater. Res. 2019, 22. [Google Scholar] [CrossRef]
  31. Lau, K.-T.; Hung, P.-Y.; Zhu, M.-H.; Hui, D. Properties of natural fibre composites for structural engineering applications. Compos. Part B: Eng. 2018, 136, 222–233. [Google Scholar] [CrossRef]
  32. Gohari, S.; Sharifi, S.; Burvill, C.; Mouloodi, S.; Izadafir, M.; Thissen, P. Localized failure analysis of internally pressurized laminated ellipsoidal woven GFRP composite dome: Analytical, numerical, and experimental studies, Archives of Civil and Mechanical Engng. 2019, 19, 1235-1250.
  33. Wang, Y.; Dai, X.; Wei, K.; Guo, X. Progressive failure behaviour of composite flywheels stacked from annular plain profiling woven fabric for energy storage, Composite Structures 2018, 194, 377-387.
  34. Potluri, P.; Sharma, S.; Rangulam, R. P: drape modeling for moulding 3D textile performs, Composites, 2001; 32.
  35. Sharma, S.; Sutcliffe, M. A simplified finite element model for draping of woven material. Compos. Part A: Appl. Sci. Manuf. 2004, 35, 637–643. [Google Scholar] [CrossRef]
  36. Galletly, G.D.; Muc, A. Buckling of Fibre-Reinforced Plastic-Steel Torispherical Shells Under External Pressure. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 1988, 202, 409–420. [Google Scholar] [CrossRef]
  37. Muc, A. On the buckling of composite shells of revolution under external pressure. Composite Structures 1992, 21, 107–119. [Google Scholar] [CrossRef]
  38. Wang, L.; Wu, J.; Chen, C.; Zheng, C.; Li, B.; Joshi, S.C.; Zhou, K. Progressive failure analysis of 2D woven composites at the meso-micro scale. Compos. Struct. 2017, 178, 395–405. [Google Scholar] [CrossRef]
  39. Muc, A. 2003, Mechanics of fibrous composites, 2003, Kraków, (in Polish).
  40. Chwał, M.; Muc, A. Transversely isotropic properties of carbon nanotube/polymer composites. Composites Part B: Engineering 2016, 88, 295–300. [Google Scholar] [CrossRef]
  41. Bathias, C. An engineering point of viewaboutfatigue of polymer matrix composite materials, International Journal of Fatigue. 2006; 28, 1094–1099. [Google Scholar]
  42. Coffin, L.F., Jr. A Study of the Effects of Cyclic Thermal Stresses on a Ductile Metal,Trans. ASME 1954, 76, 931–950. [Google Scholar]
  43. Manson, S.S. Behavior of Materials under Conditions of Thermal Stress, NASA TN-2933, 1953.
  44. Muc, A.; Kędziora, P. Application of fuzzy set theory in mechanics of composite materials, Soft Computing in Textile Sciences (editors L. Sztandera, C. 2001. [Google Scholar]
  45. Kaminski, M.; Laurin, F.; Maire, J.-F.; Rakotoarisoa, C.; Hemon, E. Fatigue Damage Modeling of Composite Structures: the ONERA Viewpoint, Life Prediction Methodologies for Materials and Structures. Journal of Aerospace Lab 2015. [Google Scholar] [CrossRef]
  46. Muc, A. Introduction to mechanics of composite materials and structures. J. Composite Sciences 2020, 4, 1055705. [Google Scholar]
  47. Elshabasy, M.M.Y.B. Validating the Classical Failure Criteria for Applicability to the Notched Woven-Roving Composite Materials. J. Compos. 2014, 2014, 1–12. [Google Scholar] [CrossRef]
  48. Xiao, J.; Bathias, C. Fatigue behaviour of unnotched and notched woven glass/epoxy laminates. Compos. Sci. Technol. 1994, 50, 141–148. [Google Scholar] [CrossRef]
  49. Khan, Z.; Al-Sulaiman, F.S.; Farooqi, J.K. Fatigue Damage Characterization in Plain-Weave Carbon-Carbon Fabric Reinforced Plastic Composites. J. Reinf. Plast. Compos. 1998, 17, 1320–1337. [Google Scholar] [CrossRef]
Preprints 102455 g001
Figure 1. Possible approaches in the analysis of composite constructions.
Figure 1. Possible approaches in the analysis of composite constructions.
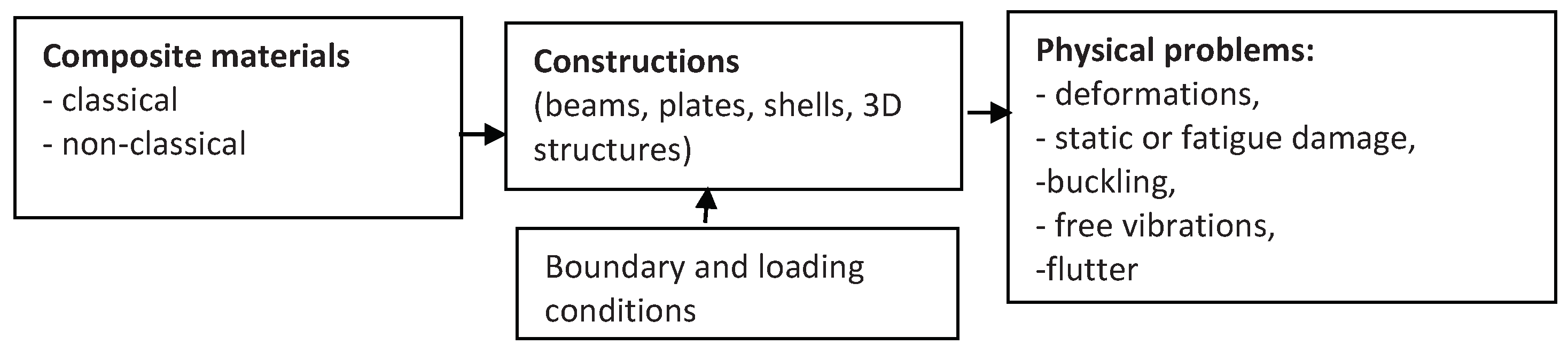
Preprints 102455 g001
Preprints 102455 g002
Figure 2. Commonly 2-D woven roving composites architecture.
Figure 2. Commonly 2-D woven roving composites architecture.
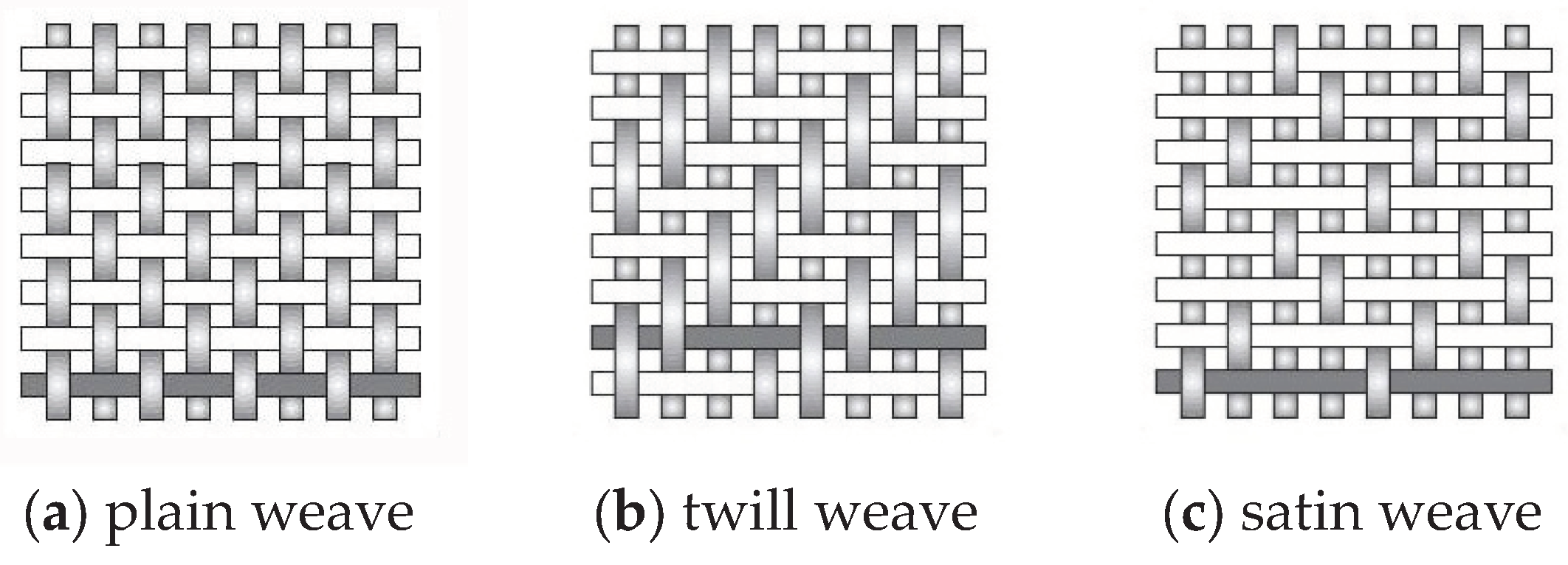
Preprints 102455 g002
Preprints 102455 g003
Figure 3. The geometry of the specimens subjected to the uniaxial tension – the lower part of the figure represents the location of the drilled hole.
Figure 3. The geometry of the specimens subjected to the uniaxial tension – the lower part of the figure represents the location of the drilled hole.
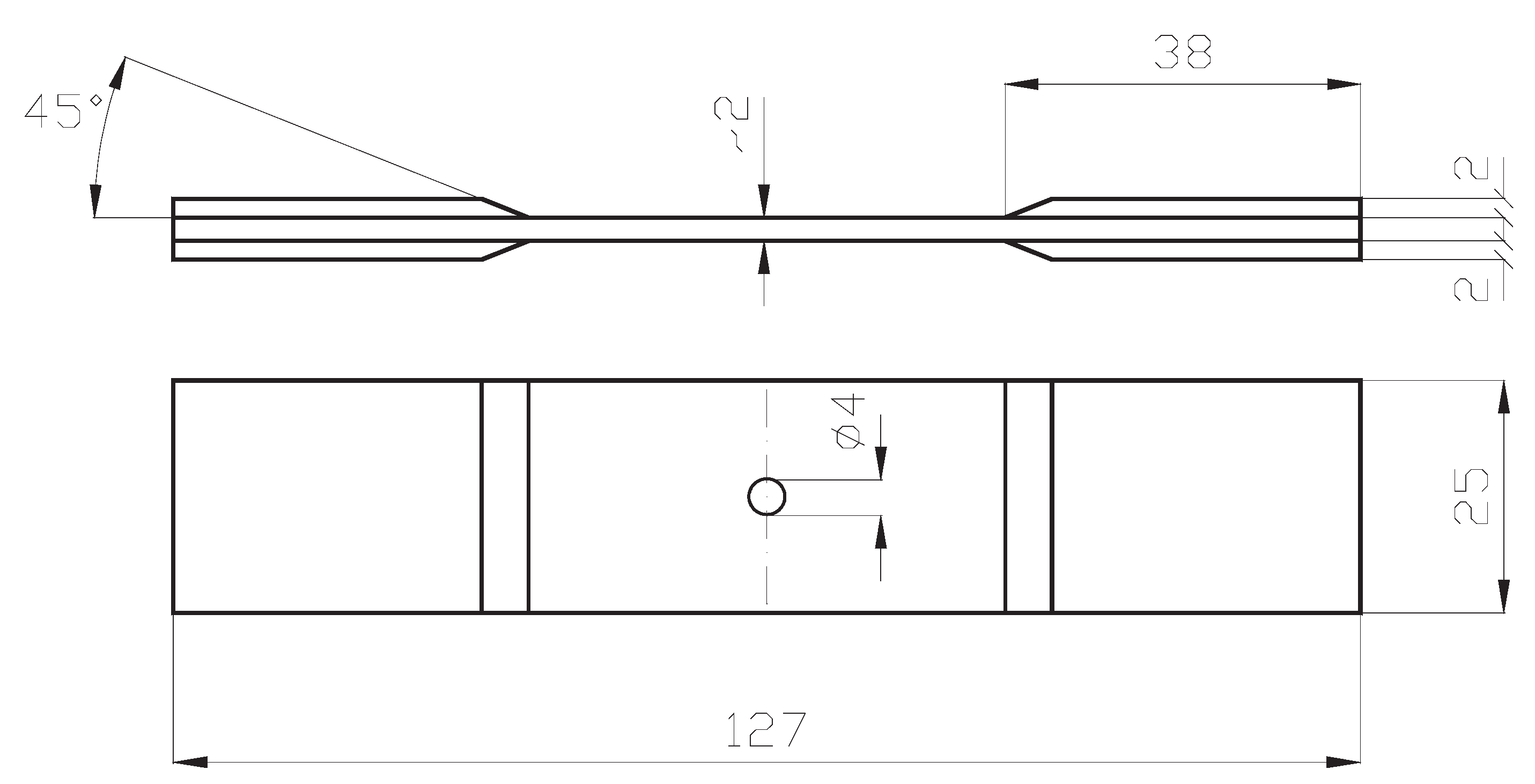
Preprints 102455 g003
Preprints 102455 g004
Figure 4. Textile 2D woven fabric (plain weave).
Figure 4. Textile 2D woven fabric (plain weave).
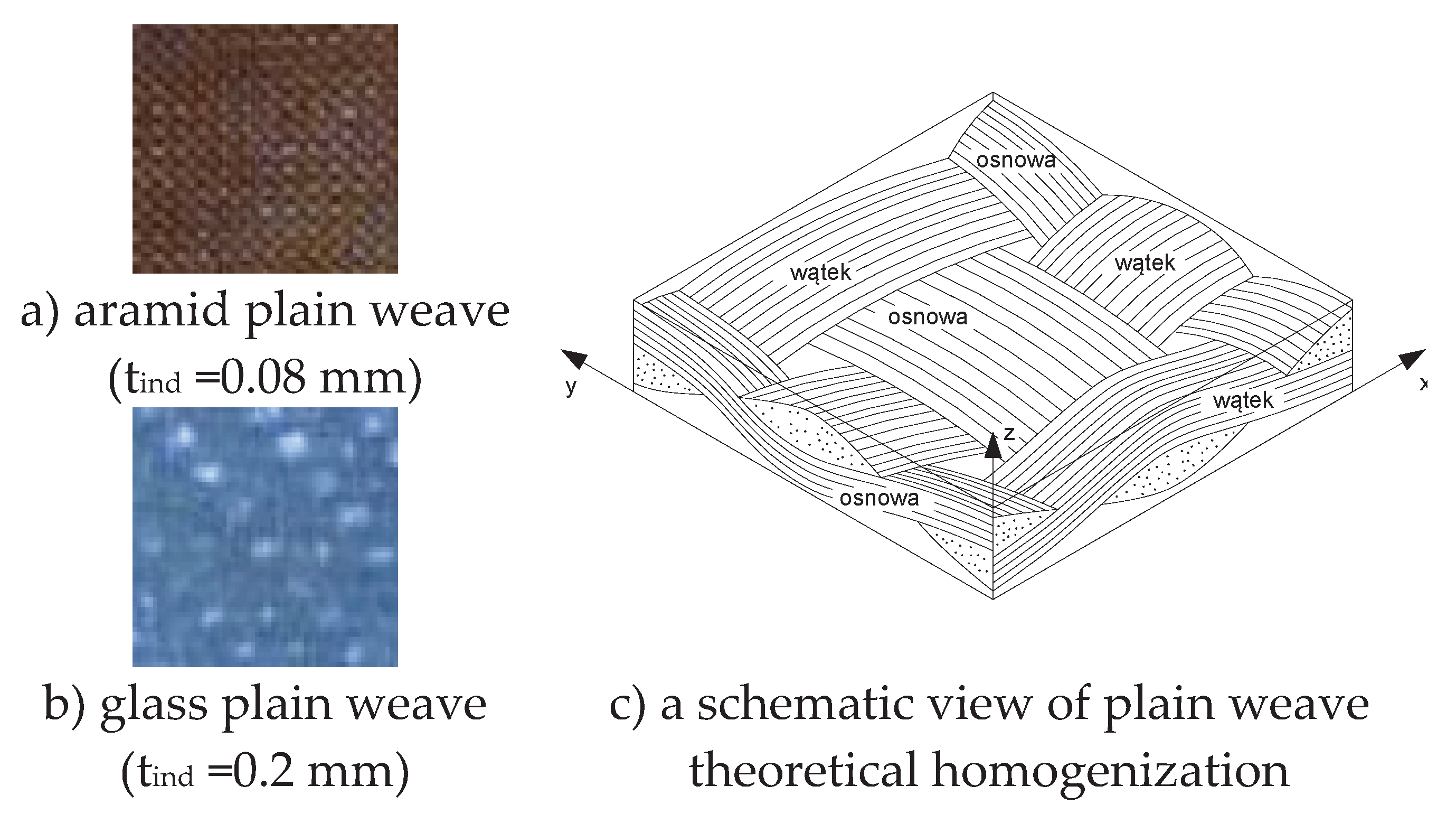
Preprints 102455 g004
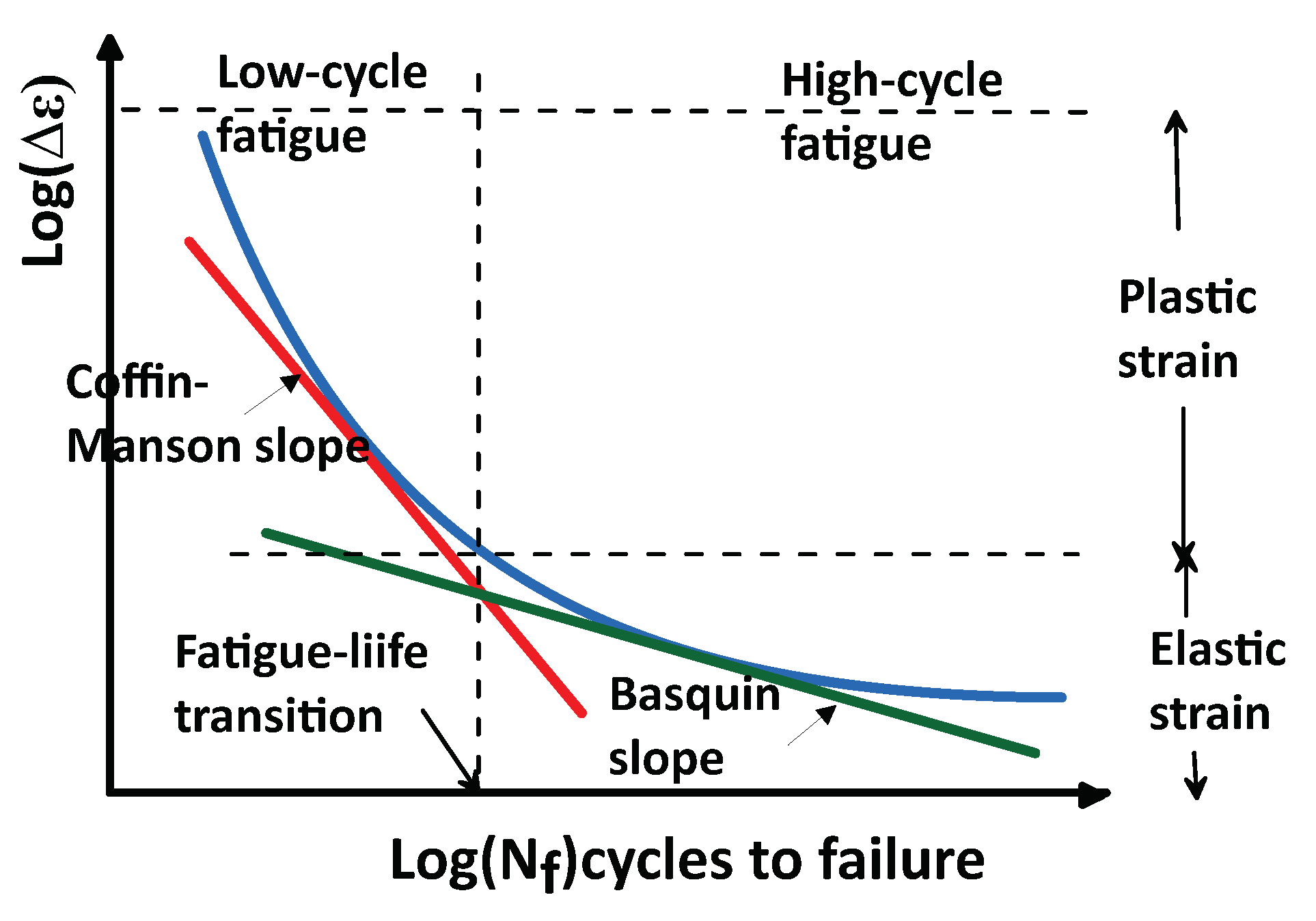
Preprints 102455 g005
Figure 5. ε-Nf curve – elastic and plastic strain curves.
Figure 5. ε-Nf curve – elastic and plastic strain curves.
Preprints 102455 g005
Preprints 102455 g006
Figure 6. Stress-strain curves for LCF.
Figure 6. Stress-strain curves for LCF.
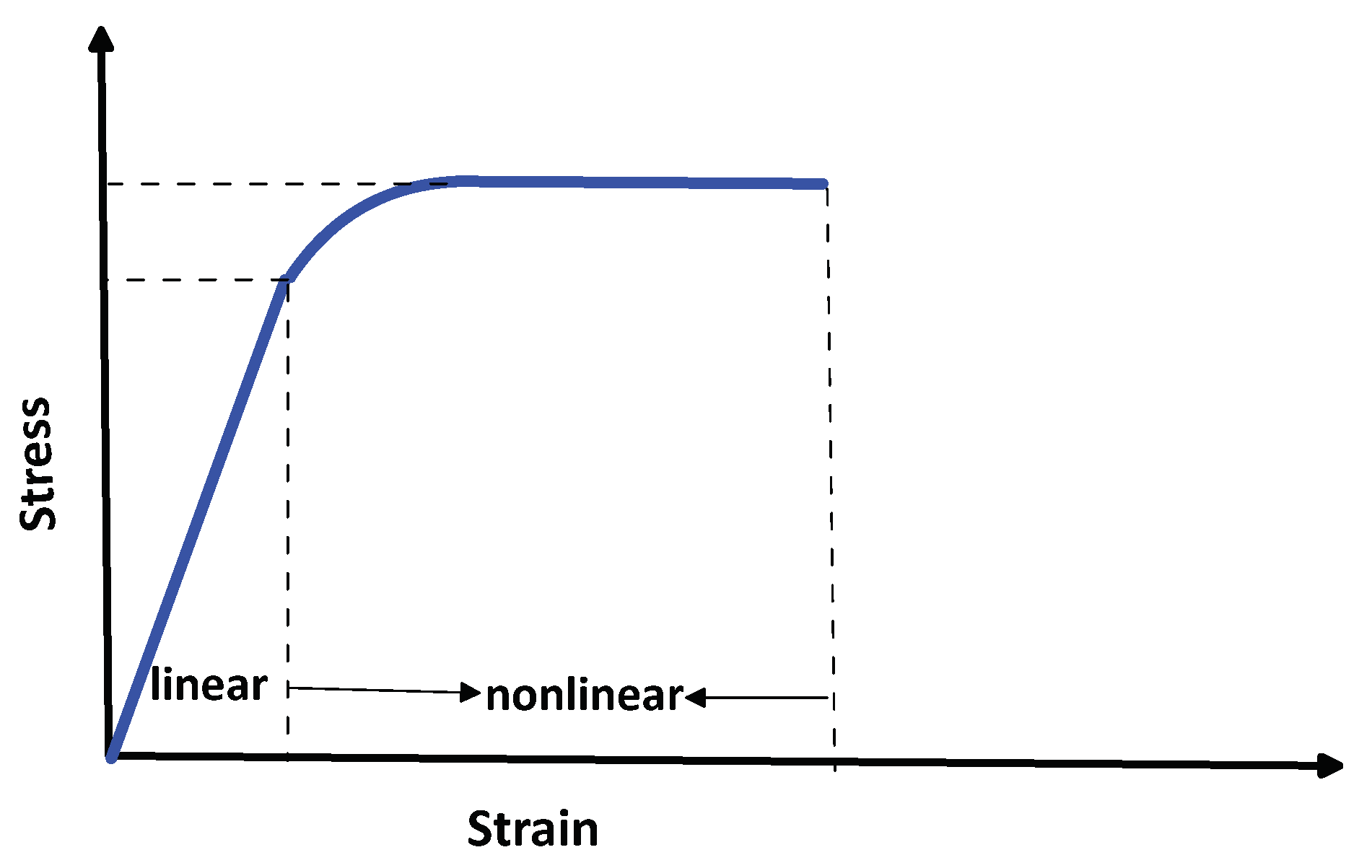
Preprints 102455 g006
Preprints 102455 g007
Figure 7. Strain life ε-N curve.
Figure 7. Strain life ε-N curve.
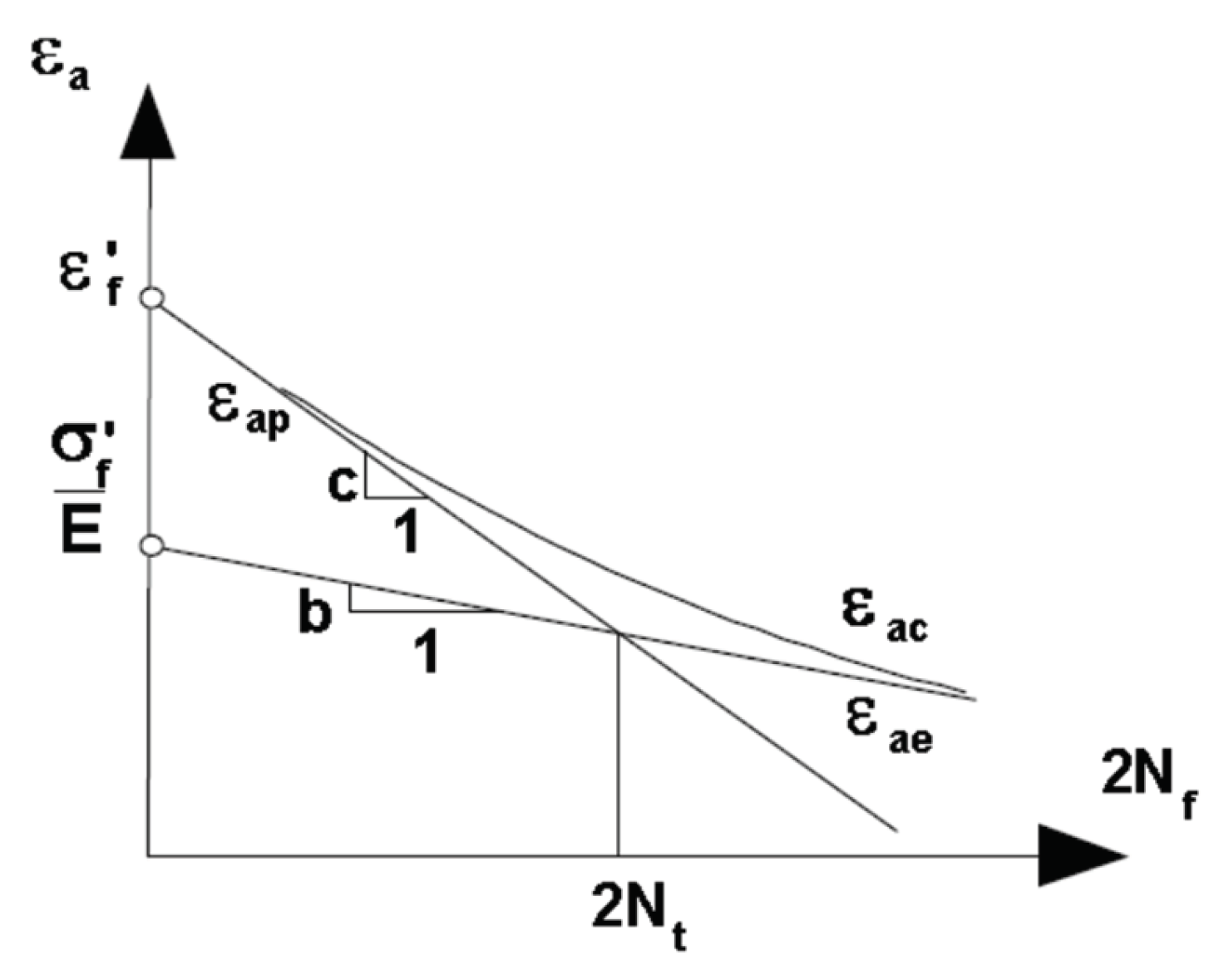
Preprints 102455 g007
Preprints 102455 g008
Figure 8. Fatigue tensile load distributions.
Figure 8. Fatigue tensile load distributions.
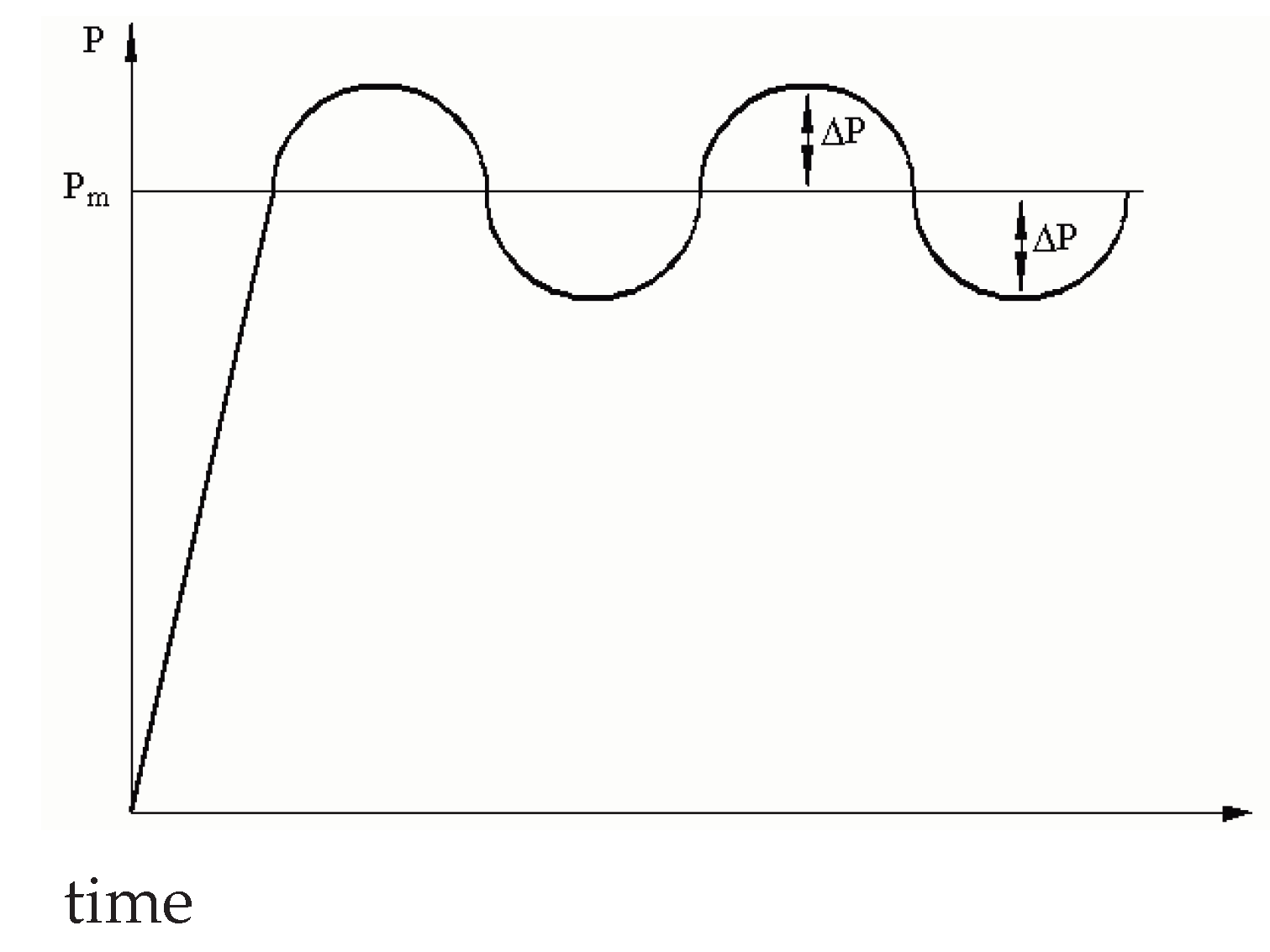
Preprints 102455 g008
Preprints 102455 g009
Figure 9. Shape of the supercircle for different values of n (the constant area).
Figure 9. Shape of the supercircle for different values of n (the constant area).
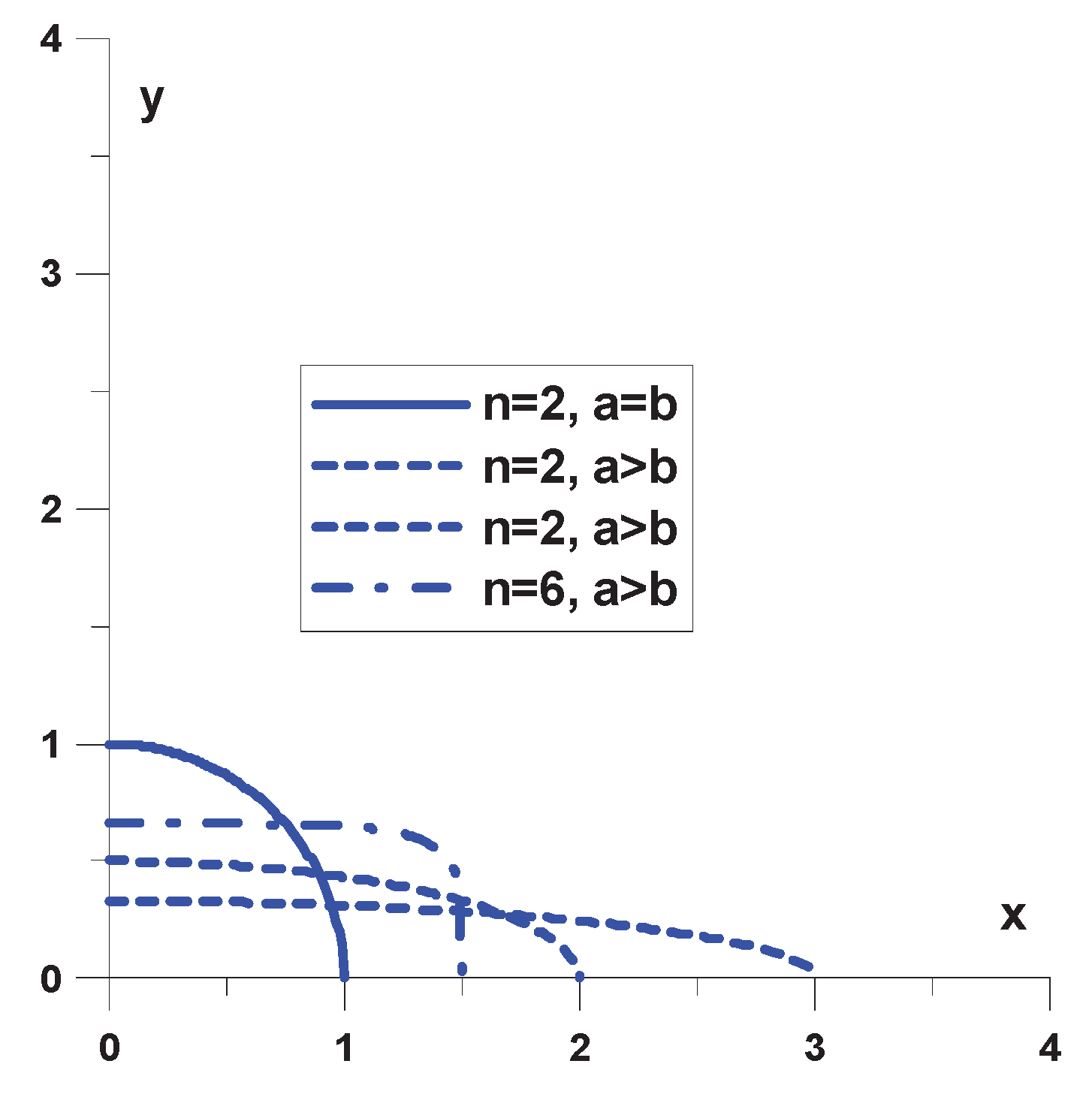
Preprints 102455 g009
Preprints 102455 g010
Figure 10. Static strength of rectangular specimens made of woven roving composites (plain 2D glass) for different warp orientations.
Figure 10. Static strength of rectangular specimens made of woven roving composites (plain 2D glass) for different warp orientations.
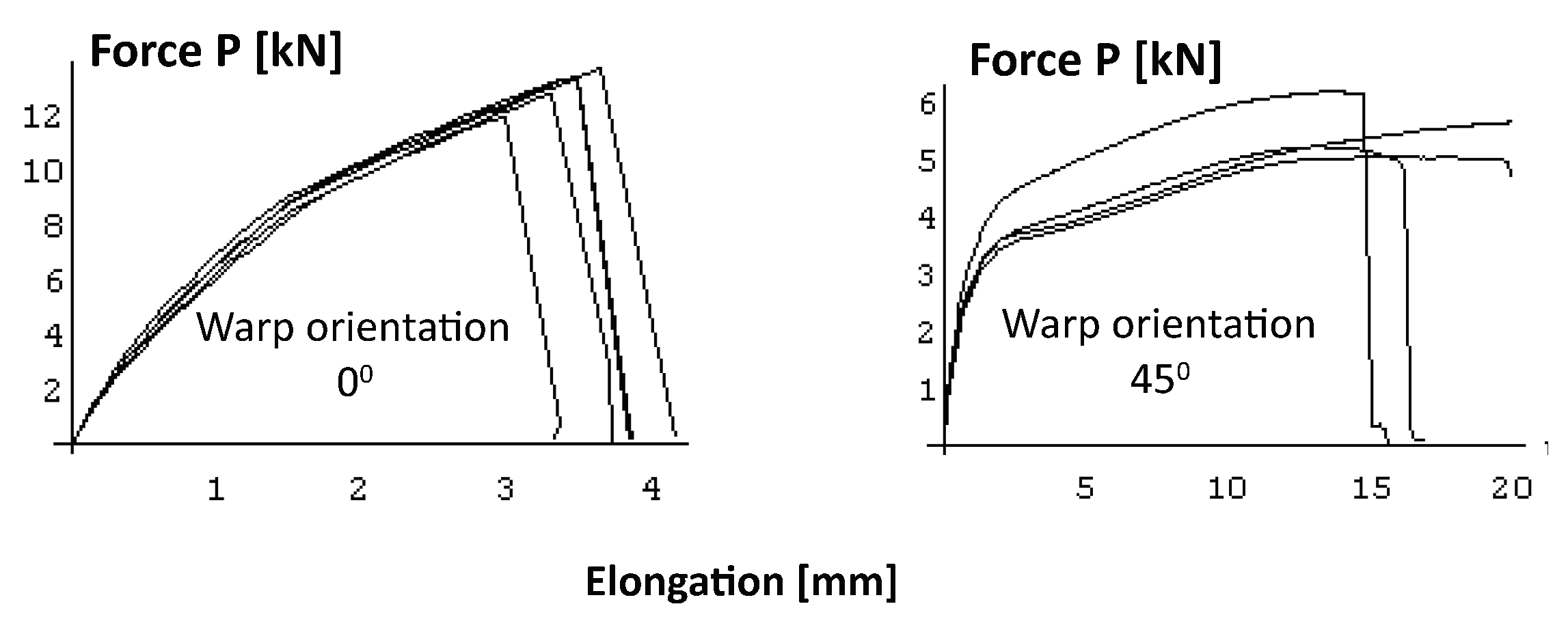
Preprints 102455 g010
Preprints 102455 g011
Figure 11. Failure modes of 2D woven roving composites subjected to tension.
Figure 11. Failure modes of 2D woven roving composites subjected to tension.
Preprints 102455 g011
Preprints 102455 g012
Figure 12. Distributions of the stresses (the vertical axes warp, the horizontal axes weft– the width) – the force 11.25 [kN] – see [5].
Figure 12. Distributions of the stresses (the vertical axes warp, the horizontal axes weft– the width) – the force 11.25 [kN] – see [5].
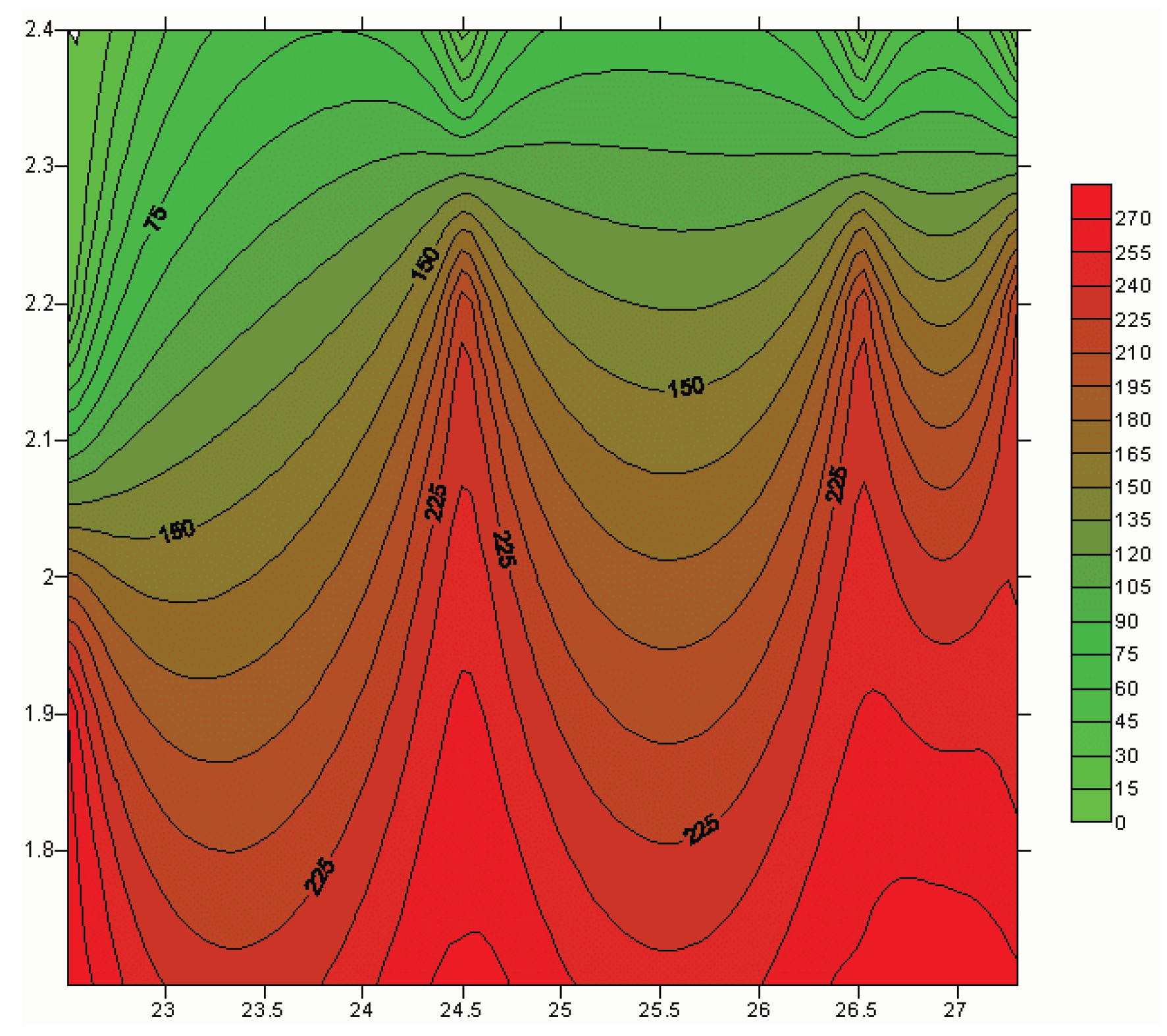
Preprints 102455 g012
Preprints 102455 g013
Figure 13. Final failure of specimens subjected to uniaxial tensile load – woven roving glass.
Figure 13. Final failure of specimens subjected to uniaxial tensile load – woven roving glass.
Preprints 102455 g013
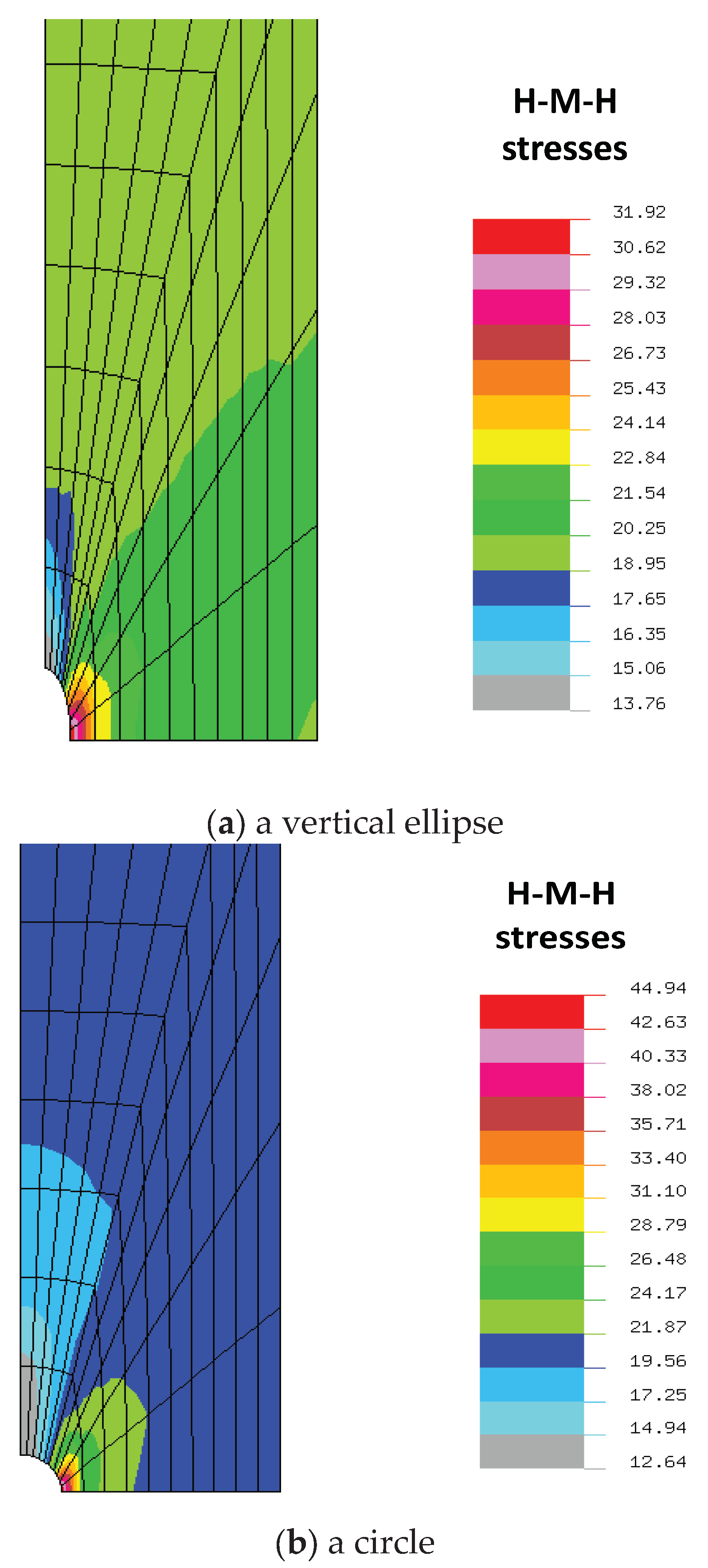
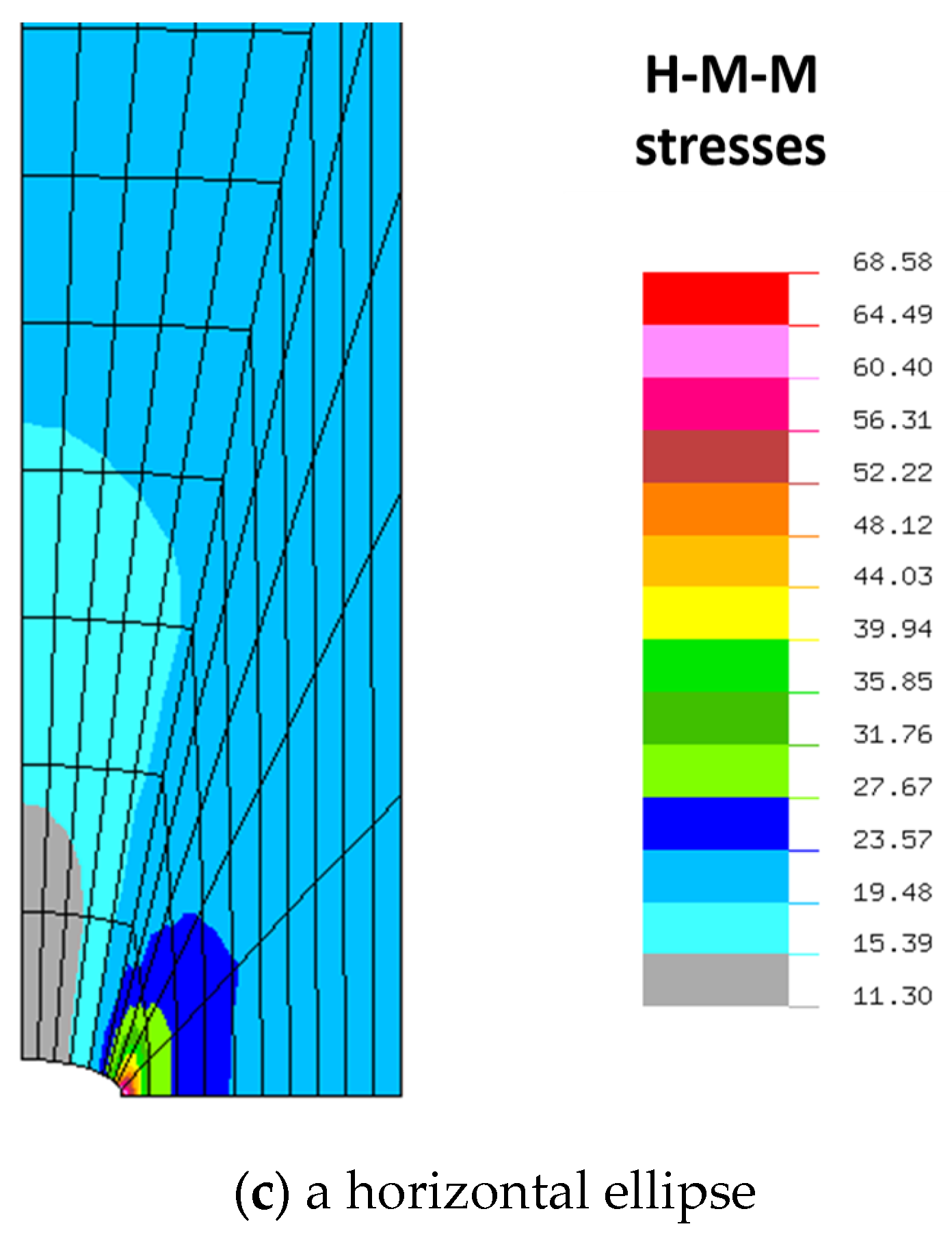
Preprints 102455 g014aPreprints 102455 g014b
Figure 14. Distributions of dimensionless the Huber-Mises-Hencky stresses for n=2 and the constant area Ac.
Figure 14. Distributions of dimensionless the Huber-Mises-Hencky stresses for n=2 and the constant area Ac.
Preprints 102455 g014aPreprints 102455 g014b
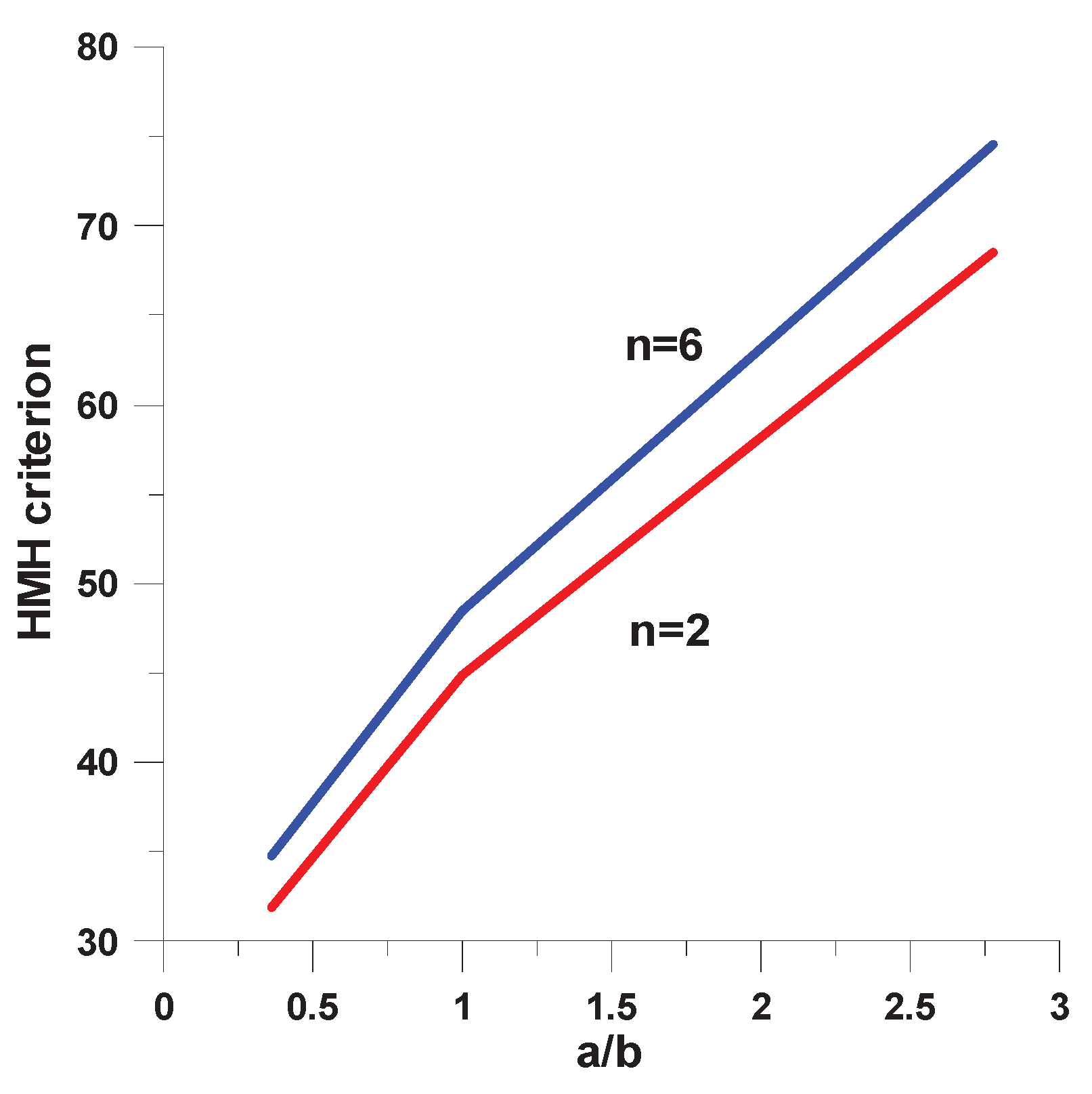
Preprints 102455 g015
Figure 15. Variations of the stress concentration around convex hole for constant area Ac.
Figure 15. Variations of the stress concentration around convex hole for constant area Ac.
Preprints 102455 g015
Preprints 102455 g016
Figure 16. Tensile strain distributions around elliptical holes – glass 2D plain weave.
Figure 16. Tensile strain distributions around elliptical holes – glass 2D plain weave.
Preprints 102455 g016
Preprints 102455 g017
Figure 17. Fatigue failure modes of stretched plates made of woven roving glass/epoxy – circular hole [3].
Figure 17. Fatigue failure modes of stretched plates made of woven roving glass/epoxy – circular hole [3].
Preprints 102455 g017
Preprints 102455 g018
Figure 18. The degradation of the stiffness for 2D woven roving composites (M – the average value, R – the highest value treated as the upper bound, L – the lowest value treated as the lower bound).
Figure 18. The degradation of the stiffness for 2D woven roving composites (M – the average value, R – the highest value treated as the upper bound, L – the lowest value treated as the lower bound).
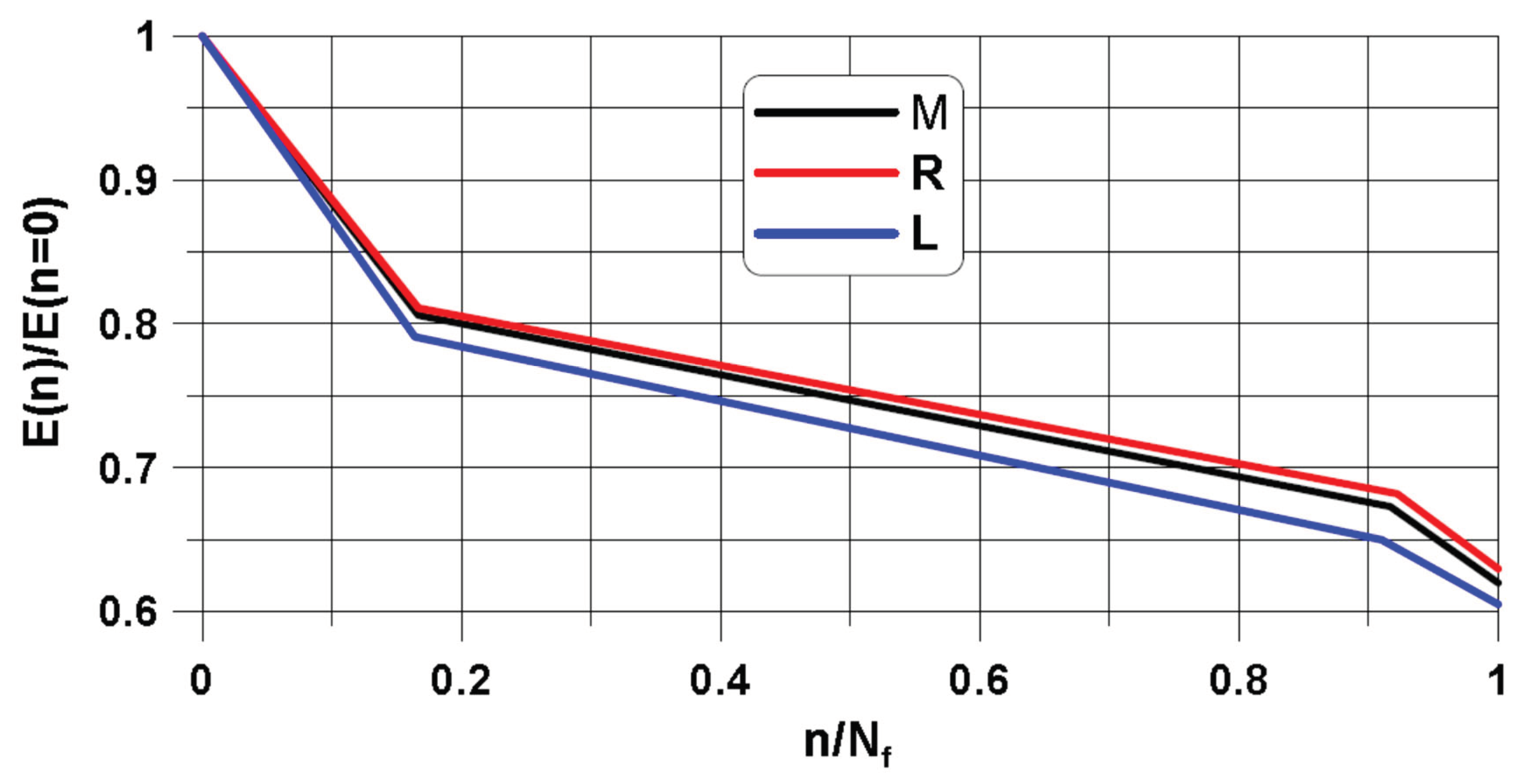
Preprints 102455 g018
Preprints 102455 g019
Figure 19. Fatigue crack initiation life contours (the logarithmic scale).
Figure 19. Fatigue crack initiation life contours (the logarithmic scale).
Preprints 102455 g019
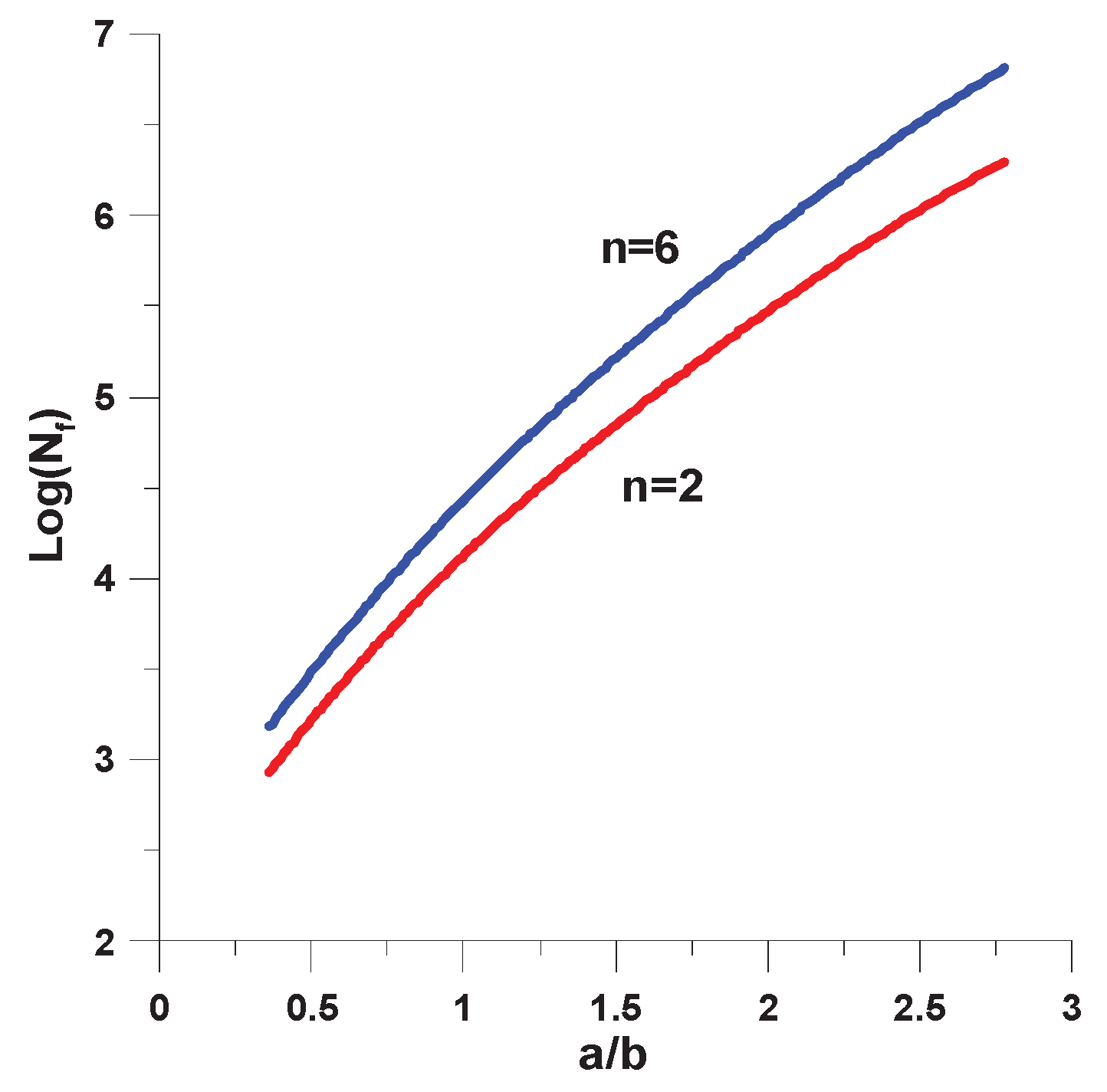
Preprints 102455 g020
Figure 20. Variations of the critical number of cycles Nf around convex hole for constant area Ac.
Figure 20. Variations of the critical number of cycles Nf around convex hole for constant area Ac.
Preprints 102455 g020
Table 1. Static mechanical properties of plain 2D glass.
Table 1. Static mechanical properties of plain 2D glass.
Young’s modulus in the warp (longitudinal) direction linear part of the curves plotted in Figure 10a in [GPa] Young’s modulus in the weft (transverse) direction [GPa] Kirchhoff’s modulus linear part of the curves plotted in Figure 10b in [GPa]
Experimental 13.142 13.004 9.621
Finite Element modeling 12.958 12.930 9.143
Table 2. The comparison of the stress concentration effects for the ellipsoidal notches – the initiation of cracks.
Table 2. The comparison of the stress concentration effects for the ellipsoidal notches – the initiation of cracks.
Stress Concentration
Factor k t 1 		Theoretical Numerical (FE) Analysis Percentage Error
( k t 1 n u m e r − k t 1 t h e o r e t ) / k t 1 t h e o r e t
b/a=2.812 6.624 6.943 10.24
b/a=1.000 3.000 3.211 12.51
b/a=0.336 1.672 1.745 13.71
Table 3. The critical number of cycles.
Table 3. The critical number of cycles.
Specimen 1 2 3 4
The length [mm] 125.0 125.0 125.05 125.04
The average thickness [mm] 2.48 2.39 2.43 2.47
Number of cycles Nf 11012 10945 15004 14617
Average number of cycles 12894.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated