Prerpints.org logo
Preprint
Review

Review of Multi-fidelity Models

Altmetrics

Downloads

179

Views

121

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 April 2023

Posted:

30 April 2023

You are already at the latest version

Alerts
Abstract
This article provides an overview of multi-fidelity modeling trends. Fidelity in modeling refers to the level of detail and accuracy provided by a predictive model or simulation. Generally, models with higher fidelity deliver more precise results but demand greater computational resources. Multi-fidelity models integrate high-fidelity and low-fidelity models to obtain fast yet accurate predictions. Their growing popularity is due to their ability to approximate high-fidelity models with high accuracy and low computational cost. This work classifies publications in multi-fidelity modeling based on various factors, including application, surrogate selection, fidelity difference, fidelity combination method, field of application, and year of publication. The study also examines the techniques used to combine fidelities, focusing on multi-fidelity surrogate models. To accurately evaluate the advantages of utilizing multi-fidelity models, it is necessary to report the achieved time savings. This paper includes guidelines for authors to present their multi-fidelity-related savings in a standard, succinct, yet thorough way to guide future users. According to a select group of publications that provided sufficient information, multi-fidelity models achieved savings of up to 90% while maintaining the desired level of accuracy. However, the savings achieved through multi-fidelity models depend highly on the problem.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Motivation

In science and engineering, high-fidelity models (HFMs) commonly refer to complex high-dimensional systems that can make highly accurate predictions. However, the cost of developing and utilizing such models is often prohibitively high, which limits their practicality for many applications. Alternatively, low-fidelity models (LFMs), their simpler and cheaper counterparts, offer a more affordable alternative. LFMs are less accurate due to dimensionality reduction, linearization, use of simpler physics models, coarser domains, or partially converged results, as depicted schematically in Figure 1. If a model is considered to have low or high fidelity can only be determined relative to another. A fully three-dimensional simulation can be considered expensive compared to an analytical function evaluation but cheap compared to actual experiments. In the early 2000s, multi-fidelity models (MFMs), which combine multiple fidelities in a single model, gained significant attention due to their potential to achieve the desired level of accuracy at a lower cost.
MFMs typically involve the construction of surrogate models (SMs) in order to reduce the computational burden associated with a large number of expensive simulations required for tasks such as optimization (e.g., [58,183]) and uncertainty quantification (UQ) (e.g., [136]). SMs are approximations created to model the behavior of the underlying system. The construction of SM architectures trained using data from different levels of fidelity is referred to as multi-fidelity surrogate modeling (MFSM), which is the primary focus of this review. SMs can also be constructed to reduce the computational cost of individual models. While it is assumed that the reader is familiar with the concept of surrogate modeling, Appendix B provides a brief overview of the most commonly used surrogate models in the context of MFMs. It should be noted that the choice of the most appropriate SM will depend heavily on the specific characteristics of the problem at hand.
In the framework of computational simulations, the process of fitting an SM to high-fidelity data may be impeded by the computational resources required to obtain just enough data for an accurate approximation. In this scenario, a possible approach to circumvent this issue is to rely on lower-cost, lower-fidelity simulations previously employed to analyze similar problems when computers were less powerful. Alternatively, SMs may be constructed to approximate LFMs, although they may be sufficiently inexpensive to warrant direct usage in some instances. A case in point is illustrated by Nguyen et al., 2013 [138].
The construction of MFSMs by integrating various fidelity levels is not mandatory for MFMs, as exemplified by Choi et al., 2008 [36]. In their paper, they employed different fidelity types proficiently through adaptive sampling without constructing an MFSM. This alternative MFM technique is known as MFHM. Figure 2 illustrates the options for constructing an MFM. The MFM, where a surrogate model is constructed to combine the fidelities, is termed an MFSM. In contrast, if no surrogate model is built, and the fidelities are combined hierarchically, the resulting technique is known as MFHM. In both techniques, HFMs and LFMs or their surrogate models are utilized.
Most of the articles reviewed in this paper have limited the construction of MFMs to two fidelities. However, it is worth noting that MFMs can be developed using more than two fidelities, as demonstrated in several studies, including Huang et al., 2006 [76], Forrester et al., 2007 [58], Qian et al., 2008 [147], Le Gratiet, 2013 [109] and Goh et al., 2013 [66].
Another survey on multi-fidelity modeling is the work of Peherstorfer et al., 2016a [145]. They focus primarily on methodologies for using MFMs in outer-loop applications, such as optimization, uncertainty propagation, and inference. In contrast, this survey focuses on the penalty and savings associated with combining multiple physics-based models, particularly when these models are fused to create MFSMs. It is worth noting that in this survey, the term multi-fidelity is used only for methods combining at least two physical models. Therefore, articles that consider a physical model and its SM as different fidelities are not seen as MFMs in this review. Methods such as multi-level methods, which replace the HFM with an LFM (with occasional accuracy checks), are not considered as MFMs in this review either. These model reduction methods speed up processes such as optimization at the cost of reduced accuracy. In contrast, MFMs aim to balance accuracy and affordability.
The development of MFM techniques offers the potential to reduce computational costs while maintaining accuracy in various scientific fields. However, it has been noted that the process of developing MFMs requires a significant investment of time and effort by the user and that the point at which the payoff justifies it remains unclear. Hence, one of the goals of this study aims to quantify the efficacy of MFM techniques in maintaining modeling accuracy while reducing its computational cost. This study also aims to comprehensively explore the use of MFMs in scientific research. MFMs will first be introduced, providing information on their field of application, simulation models, year of publication, and fidelity types gathered from the analysis of over 150 papers. The different fidelities utilized in MFMs across scientific fields are categorized. The available techniques for combining fidelities through surrogate models in MFMs are reviewed and evaluated. Sampling strategies used in constructing MFMs are also investigated. Successful combinations of fidelities that significantly improve accuracy and cost through MFMs are identified. Finally, a standard and effective reporting method is suggested to provide readers with a clear understanding of the benefits of MFMs. Papers that have reported such information to facilitate a better understanding of the potential benefits of MFMs are discussed. Overall, this study seeks to contribute to a deeper understanding of the advantages and shortcomings of MFMs in scientific research.

2. Overview

In this study, a comprehensive analysis of various MFM implementations has been carried out, and a classification scheme based on six key attributes has been constructed. The classification categories include application, fidelity type, method for constructing the MFSM (i.e., deterministic method and non-deterministic method), year of publication, paper field, and SM used. Figure 3 presents an overview of the categories in the reviewed literature.
The reviewed literature focuses on using MFMs in three main applications: optimization (including inference and inverse problems), uncertainty quantification or UQ, and optimization under uncertainty. In cases where papers describe a generic procedure without a specific application, such as analytic functions, they are classified as none. The nature of the fidelities in the model, referred to as the types of fidelity, can be classified into four categories. The first category is physics, which accounts for differences in the assumptions and considerations in the physical model. The second category is numerical solution accuracy, which accounts for different levels of discretization in space or time and partially converged solutions. The third category is numerical models, which refers to instances where the same physical model and assumptions are used, but the method of computing the results varies. Finally, the fourth category is sim+exp, which refers to the combination of simulations, usually as LFM, and experiments, usually as HFM, in constructing an MFM.
The criterion used to fit the data in the MFSM construction is referred to as the method, which can be classified into two categories: deterministic or DM and non-deterministic or NDM. Papers that use MFHMs where no MFSM is constructed are classified as none. The paper’s year of publication is referred to as the year published. The area of application of the problem addressed in the paper is referred to as the field. The most common fields observed in the reviewed literature were fluid mechanics and solid mechanics. Finally, the type of SM used to construct the MFSM is referred to as the surrogate model. Papers that use MFHMs without constructing an MFSM are classified as none.
Figure 3a shows that the most common application found for MFMs is optimization, followed by UQ and optimization under uncertainty. These applications are introduced as outer-loop applications by Peherstorfer et al., 2016a [145] and extensively discussed in sections 5, 6, and 7 of their work. The fact that optimization is the main application is understandable because UQ and optimization under uncertainty are relatively new subjects. However, it is expected that more publications will appear in these applications. Figure 3b shows the distribution of papers by the type of fidelities used; these are discussed in Section 3.
Figure 3c shows that the proportion of papers that use DMs or NDMs to construct an MFSM is similar. The category none refers to papers that present MFMs without constructing an MFSM, called MFHMs. This approach is frequently observed in fields such as optimization, where LFMs are initially utilized to narrow down the domain of interest, followed by the implementation of HFMs to achieve more accurate information about the optimum location, see Rodriguez et al., 2001 [161] and Peherstorfer et al., 2016b [144]. The most common methods used to combine fidelities in the MFM context are presented in Section 4. Section 4.3 presents a further study of the time distribution of DMs and NDMs.
Figure 3d shows that the use of MFMs seems to be expanding since its beginning in the late ’80s. Finally, the distribution of MFMs applications across various fields is presented in Figure 3e. It indicates that most of the reviewed papers implement MFMs in fluid mechanics and solid mechanics. However, other fields, such as electronics, aeroelasticity, and thermodynamics, also feature in the reviewed literature. Furthermore, some papers do not have any specific application, but rather use mathematical functions like Hartman or Rosenbrock to test the methods.
Figure 3f displays the distribution of papers by surrogate type used for constructing MFSMs. The study found that basis function regression and Kriging surrogates are the two most commonly used types for constructing an MFSM. The category others includes artificial neural networks, moving least squares, support vector machines, radial basis interpolation, and proper orthogonal decomposition, each with a usage of less than 1%. In addition, the research reveals that some MFMs do not require the construction of an MFSM, referred to as MFHM, which is included in the category none. For instance, Choi et al., 2008 [36] proposes a hierarchical MFM approach for optimization, utilizing HFMs selectively to rectify inadequacies of LFMs. As mentioned, this technique does not involve constructing MFSMs or explicitly integrating fidelities. Other examples are Kalivarapu and Winer, 2008 [84], where an MFM is used for interactive modeling of advective and diffusive contaminant transport with no MFSM construction. Giunta et al., 1995 [64], and Zahir et al., 2013 [199] are other examples of such cases.
Section 5 provides a detailed analysis of the computational cost and accuracy associated with using MFMs. Additionally, it offers guidelines for authors on how to present cost savings and accuracy improvements. Sampling methods used for MFSM construction are discussed in Appendix A, while Appendix B introduces the most commonly used surrogate methods in MFSM research.

3. Types of Fidelity

The current study aimed to review the literature and identify different types of fidelities commonly associated with three principal categories: model, accuracy and source (Figure 4). Model involves simplifying the mathematical representation of the physical phenomenon, typically by simplifying the differential equations being solved or the numerical model. Accuracy refers to changes on the discretization of the model, such as using smaller grid elements or shorter time steps for HFMs. Source is associated with the incorporation of experimental results in addition to simulations, which are regarded as having the highest level of fidelity.
Authors may explicitly state the superiority of one fidelity over another, as in the scenario involving a refined grid as opposed to a coarser grid if the same model is used. Nevertheless, in cases such as comparing a one-dimensional model with a refined grid against a three-dimensional model with a coarser grid, the comparative superiority of fidelities may not be apparent. Peherstorfer et al., 2016a [145] classified LFMs in three categories: simplified models, data-fit models, and projection-based models. Their simplified models’ category includes the differences between fidelities discussed in this study. In contrast, data-fit models and projection-based models are included in this review as surrogate modeling techniques in Appendix B.
This survey identified two main fields where MFMs are used, fluid mechanics and solid mechanics. In fluid mechanics, the primary fidelity types were analytical expressions, empirical relations, numerical linear approximations, potential flow, numerical non-linear non-viscous approximations (Euler), numerical non-linear viscous approximations (RANS), coarse vs. refined analysis, and simulations vs. experiments. A detailed listing of the papers that employed these types of fidelities as LFMs and HFMs is provided in Table 1.
Other types of fidelities, that were not included in the table, were found in the literature. These included simplifying physics found in Castro et al., 2006 [29], where an earth penetrator problem is simplified by assuming a rigid penetrator and in Goldfeld et al., 2005 [67], where the physics are simplified by assuming constant instead of variable material properties; using different geometries in Forrester et al., 2010 [56], where the LFM is a RANS simulation with simplified geometry and the HFM is a RANS simulation with full geometry; and using different numbers of Monte Carlo samples in Keane, 2012 [88]. In fluid mechanics, additional categories were also found including dimensionality (e.g., 2D/3D), coarse vs. refined analysis, simulations vs. experiments, transient vs. steady, and semiconverged vs. converged solutions (Table 2).
Several types of fidelities were identified in the literature but not included in Table 2. For instance, Castro et al., 2006 [29] simplified a physics problem by assuming a rigid penetrator, while Goldfeld et al., 2005 [67] simplified the physics by assuming constant material properties instead of variable ones. Forrester et al., 2010 [56] used RANS simulations with simplified and complete geometries for the LFM and HFM, respectively. Additionally, Keane, 2012 [88] varied the number of Monte Carlo samples used. In the field of fluid mechanics, various additional fidelity categories were also found, such as dimensionality, level of analysis refinement, simulation versus experimentation, transient versus steady states, and semiconverged versus fully converged solutions. Table 2 presents a detailed summary of these categories.
Table 3 presents the common types of fidelities employed in the domain of solid mechanics. These types comprise of mesh density, material models, and temperature. However, the investigation revealed other fidelity types that were not included in Table 3. For example, Kim et al., 2007 [91] employed isothermal and non-isothermal analyses for LFM and HFM, respectively. In addition to these, several more categories of fidelities were discovered in solid mechanics, such as dimensionality (e.g., 2D/3D), coarse vs. refined, simulations vs. experiments, and boundary condition simplification (e.g., infinite plate vs. finite plate), and are presented in Table 4.
In addition, papers from other fields such as electronics and robotics, and papers based on analytical functions were reviewed. In electronics, the most common method utilized was coarse vs. refined analysis, although some papers, such as Absi and Mahadevan, 2016 [1], employed steady vs. transient models. In robotics, Winner et al., 2000 [192], determined the fidelities based on the complexity of the robot’s resources. Several academic papers have utilized mathematical functions to examine the effectiveness of different methods, including analytical function versus analytical approximations of the function. These studies include the works of Robinson et al., 2006 [157][159], Zimmermann and Han, 2010 [206], Ng et al., 2012 [136], Le Gratiet, 2013 [110], Raissi and Seshaiyer, 2013 [149], Raissi and Seshaiyer, 2014 [150], and Goh et al., 2013 [66]. Lastly, the category of methods for uncertainty analyses with no particular application, includes Burton and Hajela, 2003 [28], Eldred, 2009 [50], Perdikaris et al., 2015 [146], Peherstorfer et al., 2016b [144], and Chaudhuri and Willcox, 2016 [32]. In Burton and Hajela, 2003, Eldred, 2009, and Perdikaris et al., 2015, the types of fidelity pertained to less and more accurate uncertainty analysis. Peherstorfer et al., 2016b [144] utilized LF models to aid in the construction of the biasing distribution for importance sampling and a small number of HF samples to obtain an unbiased estimate. Chaudhuri and Willcox, 2016 [32], employed an iterative method that used low-fidelity surrogate models (LFSMs) to estimate coupling variables and adaptively sampled the HF system to enhance the SM, while retaining a comparable level of precision in uncertainty analysis as the fully coupled HF multidisciplinary system.

4. Methods for Combining Fidelities

This section discusses different methods for combining fidelities. Fidelity refers to the level of detail and accuracy of the model or simulation, where a higher fidelity model provides more accurate results but requires more computational resources. The goal of combining fidelities is to take advantage of the strengths of each model and create an accurate, computationally efficient model. The focus will be on two main categories of methods: MFSMs and MFHMs. MFSMs use an algebraic surrogate to correct LFMs using HFM predictions, while MFHMs use different fidelities based on some criterion (see Figure 2). This survey also examines the four principal correction techniques employed in MFSMs: multiplicative correction, additive correction, comprehensive correction, and space mapping. Furthermore, this article encompasses various illustrations and applications of these techniques.

4.1. Multi-Fidelity Surrogate Models vs. Multi-Fidelity Hierarchical Models

This article provides a comparative analysis between MFSMs and MFHMs based on the literature reviewed. Out of the total of 157 papers surveyed, 67% focused on MFSMs, while the remaining 33% utilized MFHMs (see Figure 5). The latter approach combines different fidelities using a criterion to optimize a process, instead of constructing a surrogate model architecture where information from both is considered. Examples of such techniques include Burton and Hajela, 2003 [28], Choi et al., 2005 [34], and Singh and Grandhi, 2010 [168]. For instance, Christen and Fox, 2005 [37] used predictions from the LFM for Markov Chain Monte Carlo sampling and only employed the HFM when the acceptance criterion was met, whereas Rethore et al., 2011 [155] utilized simpler/faster cost functions with coarse discretization and increased the resolution of the domain and complexity of models where needed. Other examples include the work by Narayan et al., 2014 [134] which employed a stochastic collocation approach to select data points for HFM construction based on LFMs, and Peherstorfer et al., 2016b [144] which used an importance sampling method based on an LFM to choose sampling points for HFSM construction.
In their 2016 survey, Peherstorfer et al. 2016 classified techniques for integrating multiple fidelities into three categories: adaptation, fusion, and filtering. The adaptation approach improves the LFM by incorporating information from the HFM during computation, with the SM being adjusted in each iteration. Fusion methods combine information from both LFMs and HFMs by evaluating them separately, as in the case of the co-Kriging method [55]. Filtering methods, on the other hand, employ the HFM after the LFM has been evaluated by a filter, using the HFM only when the LFM is inaccurate or when the candidate point satisfies some criterion based on the LFM assessment. Peherstorfer et al., 2016 classified MFHMs under adaptation and filtering management methods. This survey’s MFSMs category, on the other hand, was included in their fusion methods category. For more information, interested readers can refer to their work [145].

4.2. Multi-Fidelity Surrogate Models

This article focuses on MFSMs that incorporate fidelities into a single SM. MFSMs utilize an algebraic SM to improve the accuracy of LFMs with the aid of HFMs. Four main correction techniques are utilized in MFSMs, namely multiplicative correction, additive correction, comprehensive correction, and space mapping. In some cases, the parameters of the LFM differ from those of the HFM, requiring problem-specific conversion from LF to HF parameters. Examples are provided in Robinson et al., 2008 [158] and Koziel et al., 2009 [101]. In conventional mathematical techniques, convergence can be ensured if the LFM and HFM meet first-order consistency (i.e., their derivatives are equal). For example, studies by Alexandrov et al., 2000 [3] and Alexandrov et al., 2001 [5] fulfill first-order consistency. If second-order consistency is obtained, convergence rates can be increased, as shown by Eldred et al., 2004 [49]. However, meta-heuristic optimization, which is not mathematically rigorous and typically has lower accuracy and slower convergence rates, is favored in global optimization, as described in Kaveh and Talatahari, 2010 [87].

4.2.1. Additive and Multiplicative Corrections

One possible approach to enhance the accuracy of LFMs is to construct a SM of the discrepancy or ratio between HFMs and LFMs. These surrogate models are known as additive or multiplicative corrections, respectively.
The MFSM, which estimates the HFM using an additive correction, can be expressed as:
y ^ H F = y L F ( x ) + δ ( x ) ,
where y L F denotes the LFM, which may be substituted with an LFSM if the cost is prohibitive. Additionally, δ ( x ) refers to an additive correction or discrepancy function, which is an SM that accounts for the difference between the HFM and the LFM.
Alternatively, the MFSM using a multiplicative correction can be expressed as:
y ^ H F = ρ ( x ) · y L F ( x ) ,
where ρ ( x ) is the multiplicative correction, which is an SM constructed using the ratio between the HFM and LFM. Note that if the LFM is not cheap enough, it can be replaced by an LFSM.
MFSMs have been widely used in aerodynamic optimization problems to reduce computational costs. Various correction techniques have been proposed to construct MFSMs, including additive and multiplicative corrections. Alexandrov et al., 2001 utilized MFSM with multiplicative corrections for aerodynamic optimization problems. Balabanov et al., 1998 compared the performance of MFSMs constructed using additive and multiplicative corrections for a similar optimization problem. Forrester et al., 2006 used an additive correction based on fully converged results to correct partially converged results. The literature provides more references to MFSMs constructed using additive and multiplicative corrections, which are presented in Table 5 and Table 6 in Section 4.3.
To illustrate the concepts of additive and multiplicative corrections, a simple algebraic one-dimensional problem is presented. Consider two analytical functions, y L F and y H F , given by Equations (3) and (4), respectively:
y L F = 5 x + sin ( 11 x ) + 12
and
y H F = 5 x + sin ( 10 x + 2 ) + exp ( x ) + 10
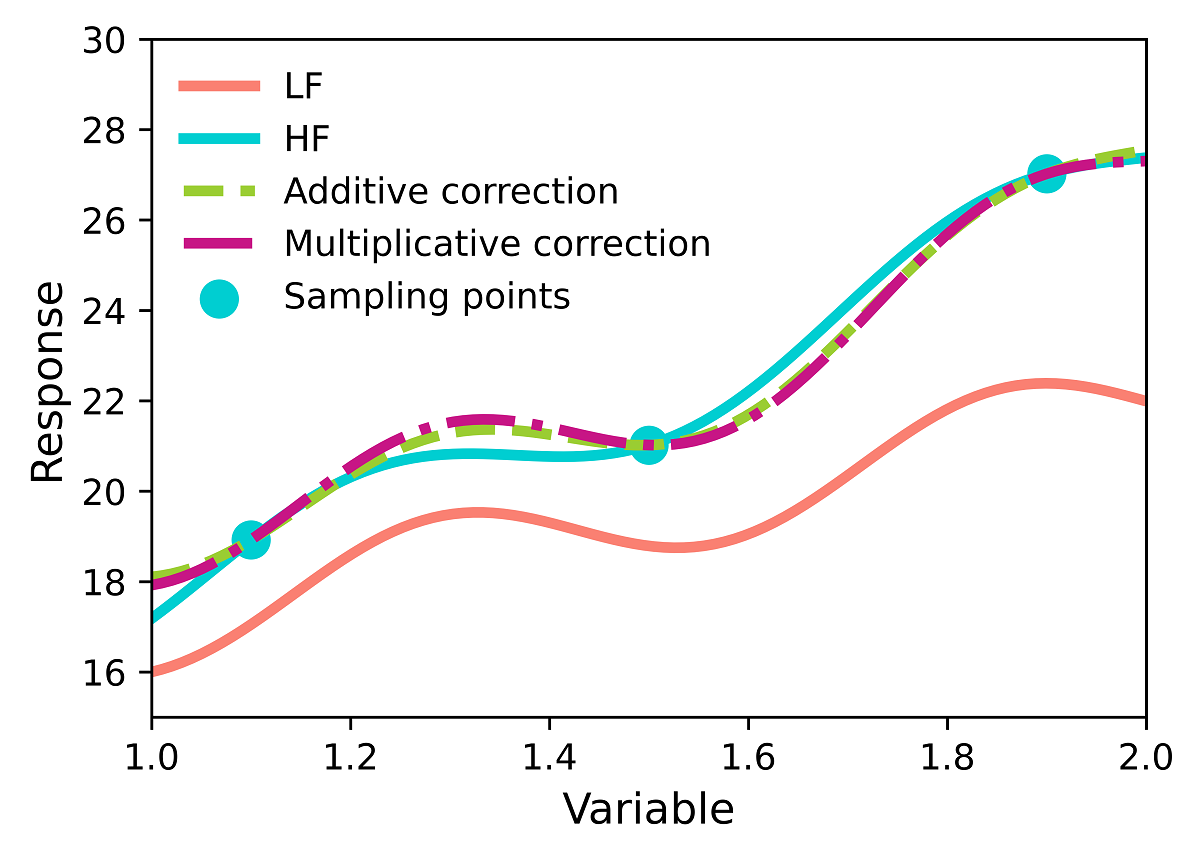
where x ∈ [ 1 , 2 ] , y H F is the HFM and y L F represents the LFM. In practice, LFM and HFM may be unavailable, and surrogate models are used instead. For this toy problem, is assumed the functions are accesible, but due to cost constraints, only three samples from the HFM can be afforded. Evenly distributed samples are chosen, specifically [ x 1 , x 2 , x 3 ] = [ 1.1 , 1.5 , 1.9 ] , from two models, and the objective is to estimate the output of the HFM while minimizing expenses by utilizing LFM for prediction. To achieve this, additive and multiplicative corrections are introduced, as shown in Figure 6. The ratio y H F / y L F or the difference y H F - y L F at the sampling points x i are used to fit the multiplicative or additive corrections, respectively. In simpler terms, the sampling points [ y H F ( x i ) / y L F ( x i ) ] for i ∈ 1 , 2 , 3 are used to fit the multiplicative correction ρ ( x ) , whereas the sampling points [ y H F ( x i ) − y L F ( x i ) ] for i ∈ 1 , 2 , 3 are used to fit the additive correction δ . The functions ρ ( x ) and δ ( x ) (Eqs. (1) and (2), respectively) are obtained using basis function regression by fitting a linear combination of second-order polynomial basis functions where the polynomial coefficients are optimized to minimize the residuals ([52,202]). Figure 6 displays the original HFM and LFM within the interval [1,2], alongside the additive and multiplicative corrections and the sample locations. Although the performance appears to be similar in this particular case, it is important to note that for more complex systems, there can be significant variations in performance that may favor one approach over the other. Additional information regarding the methodology employed to generate Figure 6 may interest readers and can be found in the supplementary material.
To further illustrate the use of correction factors, consider a scenario in which only 20 HFM and 200 LFM data points can be performed to build an MFSM. Step 1 is to build an SM to approximate the discrepancy or ratio between the LFM and HFM based on the 20 shared data points. Two options are available for Step 2: (a) building an LFSM using the 200 LFM analyses and summing or multiplying it with the surrogate from the first step (as done in the analytic example from the previous section), or (b) using the SM from the first step to estimate the discrepancy or ratio at the 180 points where only LFM data is available. Then we calculate the predicted HFM results at these 180 data points by summing or multiplying to the corresponding 180 LFM results. We now have HFM data at 20 sampling points, and we have estimated HFM data at 180 points. We treat them equally and fit an SM to the 200 points using this surrogate as an MFSM.
It is worth noting that the choice between these two options can lead to noticeable differences when using regression rather than interpolation. Specifically, the first option may result in larger differences between the MFSM predictions and the HFM data at points where HFM data is available, whereas the second option may result in smaller differences, which can be further reduced by employing a weighted least squares approach with higher weights for the HFM data.

4.2.2. Comprehensive Corrections

A comprehensive correction involves the use of both additive and multiplicative corrections in the same MFSM. One widely used comprehensive correction is defined as follows:
y ^ H F = ρ ( x ) · y L F ( x ) + δ ( x )
where ρ ( x ) represents the multiplicative correction surrogate and δ ( x ) represents the additive correction surrogate. The literature review indicates that the most common approach is to set the multiplicative factor ρ as a constant and to use an SM to approximate the additive correction, as has been demonstrated in previous studies such as Keane, 2012[88] and Perdikaris et al., 2015[146] and [202]. However, Qian et al., 2008 [147] proposed a comprehensive correction method with a non-constant ρ ( x ) .
The literature also provides a comprehensive correction technique known as the hybrid method, which was devised by Gano et al. in 2005 [59]. This method can be described as follows:
y ^ H F = w ( x ) · ρ ( x ) · y L F ( x ) + ( 1 − w ( x ) ) [ y L F ( x ) + δ ( x ) ] ,
where w ( x ) is a weight function. A weight function is employed to assign greater importance or preference to specific data points while training an SM. This technique has been widely adopted in numerous research studies, including those conducted by Zheng et al., 2013 [203] and Fischer et al., 2017 [54].
The Space Mapping technique is a comprehensive correction method that offers an alternative approach to directly modifying the output of the LFM. Instead, it involves establishing a connection between the original input variables and a new set of input variables as shown in (7). This new set of variables, when evaluated in the LFM, approximates the response of the HFM.
This approach has been shown to be a viable alternative for achieving the desired corrections. Bandler et al. [15][14] introduced Space Mapping for the first time in early ’90s. The fundamental concept behind this technique is to generate an appropriate transformation of the vector of HF input parameters, x H F , to the vector of LF input parameters, x L F , such that:
x L F = F ( x H F ) .
The purpose of this iterative process is to allow the vectors x H F and x L F to have varying dimensions. Although it is not necessary, it is desirable for F to be invertible. The objective is to ensure that the response of the HFM, y H F ( x H F ) , and the response of the LFM, y L F ( x L F ) , fulfill the following condition:
y H F ( x H F ) − y L F ( x L F ) ≤ ϵ
within some local region, where · is a suitable norm and ϵ is a tolerance setting. Space Mapping has been only been found in publications using DMs.
The first review paper of the Space Mapping method was published ten years after its implementation [17], and the second one was published two decades later [152]. The concept of Space Mapping has been expanded to include other techniques, such as Aggressive Space Mapping [16], Trust Regions [10], Artificial Neural Networks [11], Implicit Space Mapping [18], Neural-Based Space Mapping [200][201], Inverse Problems[153], Corrected Space Mapping [158], and Tuning Space Mapping [101]. Further literature regarding the utilization of Space Mapping to construct MFSMs can be found in Table 5 of Section 4.3.
In Table 5 and Table 6 presented in Section 4.3, the interested reader can locate additional references which illustrate the construction of MFSMs utilizing comprehensive corrections.

4.3. Deterministic Methods vs. Non-Deterministic Methods

The present study categorizes MFSMs into DMs and NDMs, based on the model used to estimate the MFSM parameters. DMs assume a set of basis functions and determine their coefficients by minimizing the discrepancy between the data and the function [65,186], whereas NDMs assume either the function or the coefficients to be uncertain and utilize samples to reduce the uncertainty [111]. Although DMs do not require an uncertainty structure and can be applied to any surrogate, prior research has revealed that NDMs demonstrate superior accuracy over DMs [88,142]. The schematic diagram in Figure 7 shows the differences between DMs and NDMs, depending on the assumptions made about the unknown parameters.
In the context of outer-loop applications, specifically uncertainty quantification, NDMs need a method of statistical inference in order to treat parameter uncertainties, thus avoiding the costly standard Monte Carlo simulations [156] [71]. A prevalent non-deterministic methodology in statistical inference is the Bayesian framework, which employs Bayes’ theorem to derive the posterior distribution for the model’s unknown parameters. This distribution is conditioned on both the prior distribution for the parameters and the likelihood of the observed data. Gaussian processes have become a popular and widely used class of SMs due to their flexibility and convenience in incorporating prior knowledge about the data [90]. However, alternative methods to the Gaussian process have also been proposed, such as the approach presented by Koutsourelakis, 2009 [96], where non-Gaussian distributions are used to model the uncertainties. While Gaussian process-based models have been successful in low-dimensional contexts, they are not regarded as suitable for tackling high-dimensional problems or large datasets.
In contrast, for DMs, the parameters are estimated by minimizing the difference between the predictions of the LFSM ( y ^ L F ) and the HFSM ( y ^ H F ) at the high-fidelity data points. On the other hand, NDMs such as Bayesian discrepancy or co-Kriging estimate parameters that simplify the discrepancy function δ as much as possible, even if this leads to an increase in its magnitude. By simplifying δ , the accuracy of the discrepancy surrogate can be improved beyond that achieved by simply minimizing the discrepancy [143]. This approach offers an alternative method for handling parameter uncertainties in outer-loop applications.
Calibration is a widely-used technique in engineering to enhance simulation predictions by adjusting physical parameters to attain better agreement with experiments. Numerous studies in the engineering community, such as Kosonen and Shemeikka, 1997 [95], Owen et al., 1998 [139], Lee et al., 2008 [117], McFarland et al., 2008 [126], Coppe et al., 2012 [40], and Yoo and Choi, 2013 [195], have employed calibration to improve simulation predictions. Although pure calibration is not considered an MFM, Kennedy and O’Hagan, 2001 [90] introduced a popular Bayesian calibration method that views calibration from a different perspective. Bayesian calibration involves treating calibration parameters in the same way as other non-physical hyper-parameters. It is worth noting that the calibrated physical parameters obtained through this approach may deviate from their true values. This technique, known as calibration along with comprehensive correction is considered an MFM. Several studies, including Qian et al., 2008 [147] and Biehler et al., 2015 [21], have investigated the potential applications of this methodology.
Figure 8 indicates that 55% of the studies that construct an MFSM utilize deterministic methods (DMs), while 45% employ non-deterministic methods (NDMs). Additionally, the figure provides insight into the distribution of each method employed for MFSM construction, as outlined in Section 4.2. An inference that can be made from the data is that multiplicative methods are predominantly utilized in DMs, while comprehensive corrections are the prevailing approach in NDMs.
The 20th-century publications were predominantly characterized by the use of DMs. However, there has been a notable surge in interest towards NDMs within the statistical community in the early 21st century. Several examples of NDMs that have been widely embraced include Kriging [93], which entails spatial dependence estimation in geostatistics, co-Kriging models [123], an expansion of Kriging to multiple-fidelity datasets, and related MFSMs such as Kennedy and O’Hagan’s Bayesian-based calibration models [90]. Figure 9 displays histograms illustrating the distribution of published papers related to DMs and NDMs over different yearly intervals.
In the context of MFSMs, the uncertainty prediction in Kriging surrogates can be modeled using techniques such as Generalized Least Squares or Gaussian Process (GP). A GP can be defined as a collection of random variables having the property that the joint distribution of any finite subset follows a Gaussian distribution. Kriging surrogates constructed using a GP kernel have gained popularity in recent years, as evidenced by their application in Kennedy and O’Hagan, 2000 [89], as well as in LeGratiet, 2012 [111], LeGratiet, 2013 [110], and LeGratiet, 2014 [113].
Numerous popular MFSMs, such as co-Kriging and Bayesian-based comprehensive corrections, employ GP to model each fidelity response and its corresponding prediction uncertainty. However, MFSMs are typically based on certain assumptions, and if these assumptions are not met, the accuracy of the models could be impacted. For instance, the most prevalent assumption in GP-based techniques is the independence of the predictive uncertainty among fidelities.
Table 5 and Table 6 have been designed to systematically arrange the reviewed literature that employs DMs and NDMs, respectively, within the four categories of combining methods discussed in Section 4. The four categories are additive correction, multiplicative correction, comprehensive correction and space mapping.

5. Accuracy and Cost Reporting for Multi-Fidelity Papers

5.1. Reporting Assessment

The primary objectives of employing MFMs are cost and time savings. Thus, a comprehensive account of the savings achieved is critical. Despite this, the current body of literature that reports on cost versus accuracy analyses of MFMs is somewhat limited. An exemplary instance of proficient reporting can be observed in the work conducted by Park et al., 2017 [142] on the Hartmann 6 function example. Their research findings showcase a potential for achieving cost savings while maintaining high levels of accuracy. Specifically, the study reveals that maximum cost savings of up to 86% can be achieved while ensuring the same level of accuracy. Furthermore, it was demonstrated that maximum accuracy improvements of up to 51% can be attained while maintaining the same level of cost.
However, the savings offered by MFMs are highly dependent on the problem at hand. Thus, unless one is dealing with a class of problems of similar structure, the savings that a researcher reports for one problem may differ significantly from those obtained for other problems, even when the same methodology is employed. This issue becomes even more severe when the savings are attributed not solely to the SM construction but to the entire optimization process. For example, convergence results attained with first-order corrections can ensure global convergence of some algorithms, implying that the algorithm will converge to a local optimum of a problem, regardless of the initial guess. Nonetheless, the convergence rate will depend on the relative properties of the LFM and HFM. A more detailed examination of these issues can be found in Eldred et al. [49] and Peherstorfer et al. [145].
The accuracy of SMs is a critical factor in their selection for design optimization tasks. Cross-validation error (CVE) is a popular and effective measure for SM selection, which can be applied to both DMs and NDMs. In a study by Park et al., 2017 [142], the authors evaluated the efficacy of different MFSMs for a given design of experiments using CVE and compared the results with their actual rank based on the root mean squared error (RMSE). The study investigated eleven cases of six different MFSMs, including co-Kriging and NDM calibration with and without a discrepancy function, with various options. The results of the study showed that while CVE was not a reliable measure for selecting a good MFSM candidate, it was useful in identifying the worst candidate. Another measure for SM selection is the model likelihood, which gives different weights based on the MFSM uncertainty estimation. However, this measure is only valid for an MFSM that uses NDMs, such as co-Kriging.
It would be also informative to include the accuracy of LFMs, HFMs, and MFMs obtained at equivalent computational cost, as well as the cost of HFMs and MFMs obtained for the same level of accuracy, if available. Such an analysis has been carried out by Peherstrofer et al., 2016 [144], who account for accuracy in the calculation of the quantity of interest by presenting a plot of the RMSE as a function of the number of samples used. This plot provides an answer to the question of the accuracy of the MFM relative to the LFMs and HFMs at the same computational cost. Additionally, a second plot is included in the analysis, which reports time savings for multiple sample options. This plot provides an answer to the question of the savings associated with the implementation of the MFMs relative to the HFMs for the same level of accuracy.
Notwithstanding the challenges encountered, Table 7 summarizes the cost of MFMs versus HFMs based on reported data to give readers a general idea of the savings that MFMs may offer. Furthermore, the table is divided based on the application field, enabling MFM users to identify where MFMs have been more successful.
The expectation is that computational efficiencies are enhanced when low-fidelity models LFMs incur significantly lower costs than their high-fidelity counterparts HFMs. To validate this hypothesis, an empirical investigation was carried out by analyzing data obtained from prior studies that utilized MFSMs for optimization tasks. Figure 10 presents data extracted from 18 out of 120 reviewed papers that conducted optimization procedures, wherein both the LFM/HFM cost ratio for a single analysis (LFA/HFA cost ratio) and the MFM/HFM cost ratio for a complete optimization process (MFO/HFO cost ratio) were explicitly reported. The dashed line in the figure represents the threshold, points below which do not benefit from speed ups from using MFMs.
The results depicted in Figure 10 indicate that there is no noticeable correlation between the LFA/HFA and the MFO/HFO cost ratios. This outcome may be attributed to the problem-dependent nature of savings, as previously noted, as well as to the relationship between the cost and accuracy of the LFM. Specifically, less expensive models may exhibit lower levels of precision, delaying the optimization convergence. Additionally, the complexity of the MFM model may also increase the cost of optimization.
In summary, the utilization of MFMs has the potential to enhance computational efficiency. However, the extent of benefits attained highly relies on the cost and accuracy of the LFM employed and the particularities of the optimization problem at hand. As a result, the choice of model should be made carefully, considering the trade-off between cost and accuracy and the specific attributes of the optimization problem under investigation.

5.2. Reporting Recommendations

The present study suggests that authors who employ MFMs in their research should provide a comprehensive account of cost, savings, and accuracy comparisons between said models and other models utilized in their investigations. While the inclusion of such information is occasionally present in the manuscripts, its presentation is often hidden, posing difficulties for the readers in assessing the benefits and shortcomings of implementing multi-fidelity models. As a solution to this matter, this work advised authors to consider presenting the pertinent information in a tabular format that encompasses the following constituents, when applicable:
1.
Basic information
(a)
Differentiation between low-fidelity and high-fidelity models.
(b)
Details of surrogate models constructed, if any.
(c)
Description of the process or method employed to combine fidelities.
2.
Cost
(a)
Cost comparison between low-fidelity and high-fidelity models.
(b)
Cost comparison between multi-fidelity and high-fidelity models.
(c)
Accuracy comparison between low-fidelity, high-fidelity, and multi-fidelity models at equivalent costs.
(d)
Cost comparison between multi-fidelity and high-fidelity models for the same level of accuracy.
3.
Cost-benefit analysis
(a)
Cost comparison between low-fidelity and high-fidelity surrogate models (if surrogates are constructed).
(b)
Cost comparison between high-fidelity surrogate models and high-fidelity models (if surrogates are constructed).
(c)
Time and resources invested in constructing the multi-fidelity model.

5.3. Example of Good Reporting

The implementation of MFMs has the potential to provide benefits in terms of both time savings and accuracy improvements. However, the usefulness of such implementations is often difficult to ascertain from research papers. To address this issue, Section 5.2 includes a guidance for authors on how to report of the cost, savings, and accuracy associated with the use of MFMs in their research. Padrón et al. [140] provides a thorough investigation into the optimization of an airfoil, serving as an exemplary illustration. The study employs computational fluid dynamics (CFD) RANS simulations as HFM and Eulerian CFD simulations as LFM, and the use of a stochastic polynomial chaos expansion as SM combined through additive correction. Future authors are encouraged to follow Padrón et al.’s approach and include the information presented in Table 8, which provides an overview of the essential elements that must be included in any study related to MFM.

6. Conclusions

The versatility of the multi-fidelity modeling approach makes it a promising method open to improvement and development, as evidenced by its diverse applications in various fields. This study provides an exhaustive review of multi-fidelity models and their remarkable characteristics, with optimization being the most prevalent application in 70% of the reviewed publications. Fidelity-management strategies in multi-fidelity models consist of two approaches: creating a surrogate model that blends the different fidelities or utilizing the various fidelity models in a hierarchical manner according to a specific criterion. The former method is more commonly used, as evidenced by 67% of the examined literature. In the late 1990s, deterministic methods were favored; however, non-deterministic methods are currently preferred due to their ability to provide uncertainty estimates. Gaussian Process-like surrogates have replaced basis function regression as the most common surrogate model for constructing multi-fidelity models. Despite the potential for cost and time savings, there was no clear correlation between the cost ratio of low-fidelity and high-fidelity analysis and the cost ratio of multi-fidelity and high-fidelity optimization. This lack of correlation may be attributed to the problem and model-specific characteristics of the considered analysis. Reporting of cost and time savings metrics was often absent or unclear in the reviewed literature, so this paper recommends standardizing reporting to enable better understanding of multi-fidelity model efficacy in various fields.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Funding

This work was performed under the auspices of the United States Department of Energy (DOE) by Lawrence Livermore National Laboratory under contract DE-AC52-07NA27344. This research was funded by the National Nuclear Security Administration, Defense Nuclear Nonproliferation Research and Development (NNSA, DNN R&D).

Institutional Review Board Statement

Public release number LLNL-JRNL-847790

Data Availability Statement

The data supporting this study’s findings are available from the corresponding authors upon request.

Acknowledgments

The present publication owes its existence to the invaluable guidance and support of the late Raphael T. Haftka (Rafi), who served as both a mentor and a paternal figure to me. His dedicated efforts towards the development of this manuscript are indelibly imprinted in its contents. Regrettably, his passing in 2020 precludes confirmation of his willingness to participate in this publication. Hence, while not formally acknowledged in this article, I extend my profound gratitude to Rafi for his invaluable contributions, which were pivotal in its inception and subsequent development. It is worth noting that the article was finalized in 2017, and the decision of the other two co-authors not to be included in the published version was influenced by the intervening temporal discrepancy between completion and dissemination.

Conflicts of Interest

The author declare no conflict of interest.

Nomenclature

The following abbreviations are used in this manuscript:
Analysis A single evaluation of a model, or process.
Data The outcome of multiple analyses.
Data fit Process of using available data points to construct a surrogate model.
Data point Information used to train a surrogate model. Exchangeable with sampling point.
Datum The outcome of a single analysis.
DM Deterministic method. The multi-fidelity model is constructed assuming basis functions and finding their coefficients by minimizing discrepancy between the data and the functions.
Experiment A real-world test.
Fidelity Level of accuracy.
HFA High-fidelity analysis. A single evaluation of a high-fidelity model.
HFM High-fidelity model. Model that estimates the output with the accuracy that is necessary for the current task [145].
HFSM High-fidelity surrogate model. Surrogate model constructed using a high-fidelity model. After its construction it may be also treated a high-fidelity model.
LFA Low-fidelity analysis. A single evaluation of a low-fidelity model.
LFM Low-fidelity model. Model that estimates the output with a lower accuracy than the high-fidelity model typically in favor of lower costs than the costs of the high-fidelity model [145].
LFSM Low-fidelity surrogate model. Surrogate model constructed using data points from a low-fidelity model. After its construction it may be also treated a low-fidelity model.
Model Representation of physical phenomenon using a mathematical approximation.
MFHM Multi-fidelity hierarchical model. A multi-fidelity model where no multi-fidelity surrogate model is constructed and the fidelity is chosen following a criterion 1.
MFM Multi-fidelity model. A model constructed using the information of multiple models with different levels of accuracy.
MFSM Multi-fidelity surrogate model. Surrogate model constructed using the information of multiple models with different levels of accuracy. These models can also be surrogate models by themselves. Multi-fidelity surrogate model construction in multi-fidelity modeling is optional and it can be done by using a deterministic or a non-deterministic method. After its construction it may be treated as a multi-fidelity model.
NDM Non-deterministic method. The multi-fidelity surrogate model is constructed assuming that either the function or the function coefficients are uncertain, and use samples to reduce the uncertainty.
Outer-loop application Computational application that forms outer loops around a model where in each iteration an input is received and the corresponding model output is computed, and an overall outer-loop result is obtained at the termination of the outer loop. Examples of these are optimization, uncertainty propagation, and inference [145].
Point Value that a variable can take, which is the input for an analysis, along with its correspondent output.
Response Exchangeable with analysis.
Sampling point Information used to train a surrogate model. Exchangeable with data point.
Simulation Imitation of a real-world process or system usually by running a computer code. Performing a simulation first requires the development of a model.
SM Surrogate model. Algebraic approximation fitted to available data points. They are usually built because the data is too expensive to obtain or because there are regions where the data is not available.

Appendix A. Design of Experiments Strategies for Multi-Fidelity Surrogate Models

The construction of SMs needs the adoption of a suitable sampling approach for the generation of a representative set of sample points. The choice of sampling methodology is crucial to the accuracy that the SM will attain, as illustrated in the work of Dribusch et al., 2010 [44]. Grid-based sampling methods, such as the full factorial design (FFD), entail the sampling of each factor or variable at a fixed number of levels, and are generally used for problems of low dimensionality (typically involving less than three variables), as depicted in Figure A1a. Its utilization can be observed in the work of Fernández-Godino et al., 2016 [51]. On the other hand, the central composite design (CCD) method extends the two-level FFD by augmenting it with the minimum required number of points for each variable to provide three levels, enabling the fitting of a quadratic polynomial. This method is frequently employed for problems with three to six design variables, as shown in Figure A1b. For high-dimensional problems, only a subset of the vertices of the CCD is utilized in the so-called small composite design (SCD), as described in the work of Myers and Montgomery, 1995, pp. 351-355 [132]. It should be noted that FFD, CCD, and SCD are inflexible with regard to the number of sampling points and domain shape.
Preprints 72296 g0a1
Figure A1. This is a figure, Schemes follow the same formatting. If there are multiple panels, they should be listed as: (a) Description of what is contained in the first panel. (b) Description of what is contained in the second panel. Figures should be placed in the main text near to the first time they are cited. A caption on a single line should be centered.
Figure A1. This is a figure, Schemes follow the same formatting. If there are multiple panels, they should be listed as: (a) Description of what is contained in the first panel. (b) Description of what is contained in the second panel. Figures should be placed in the main text near to the first time they are cited. A caption on a single line should be centered.
Preprints 72296 g0a1
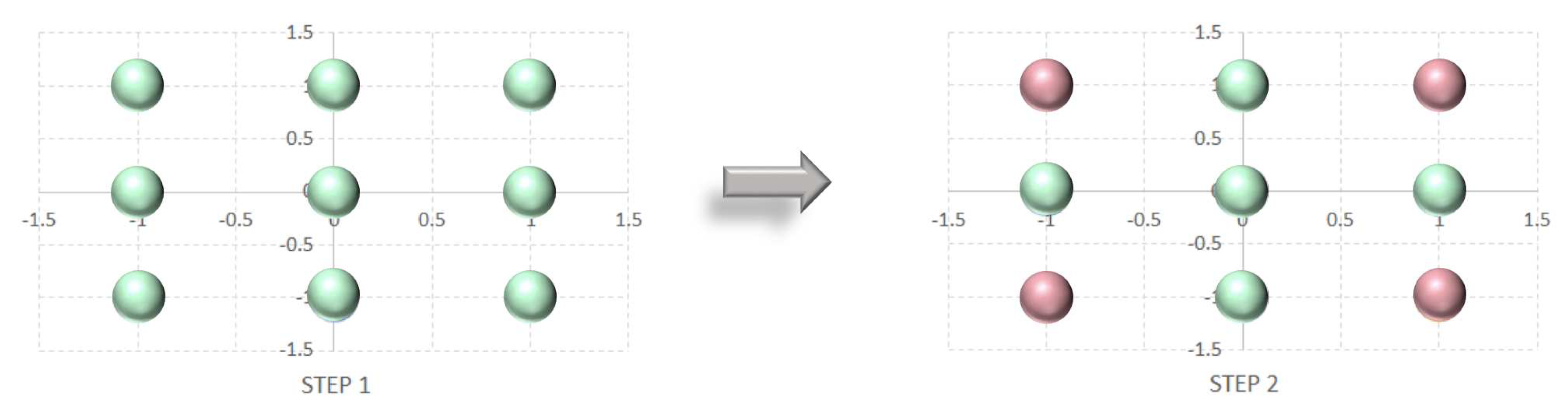
Design of experiments that allow for any number of samples are frequently based on an optimality criterion. For instance, the D-optimal design approach [42] selects a subset of a grid in any domain shape by minimizing the determinant of the Fisher information matrix [127], which reduces the impact of noise on the fitted polynomial and often results in most of the points being located at the boundary of the domain. An example of the application of the D-optimal criterion in a nested sampling design for MFMs is illustrated in Figure A2.
Space filling methods, such as Monte Carlo and Latin hypercube sampling, are more commonly employed when the noise in the data is not a concern and the points need to be more uniformly distributed in the domain. In such cases, it is preferable to use an optimality criterion method to sample near the domain boundaries. The most popular variant of Latin hypercube sampling attempts to maximize the minimum distance between points, also known as the maximin criterion [81], to promote uniformity.
When dealing with MFSMs, the relationship between the sampling points of the LFMs and HFMs is an additional issue. The nested design sampling strategy generates HFM points as a subset of LFM points or LFM points as a superset of HFM points. It was initially developed as a space filling method for generating additional datasets to complement existing ones using a criterion. For example, Jin et al., 2005 [80] used three optimality criteria: maximin distance criterion, entropy criterion, and centered L 2 discrepancy criterion.
The combination of the original sampling points and additional points results in the sampling points for an LFSM, with the additional subset reserved for the HFSM [142]. Nested design sampling has been proposed by Haaland and Quian, 2010 for categorical and mixed factors [69]. Zheng et al., 2015 compared the effects of nested and non-nested design sampling on modeling accuracy [204].
Incorporating the HFM points as a subset of LFM points simplifies the parameter estimation process for discrepancy function-based methods. However, if the HFM points are not a subset of the LFM points, the parameter estimation of the discrepancy function becomes reliant on the LFSM parameter determination. For instance, the co-Kriging method utilizes GP to model uncertainties for both the LFSM and the discrepancy function. If the design of experiments satisfies the nested sampling condition, the parameters of each GP model can be estimated independently.
Although not all MFSMs adhere to this approach, some, such as those used for combining computer simulation results, allow for the control of input settings and the satisfaction of the nested condition.
Multiple options exist for nested designs, including generating the LFM design of experiments first and then selecting a subset using a specific criterion. This approach was used in Balabanov et al., 1998, where 2107 points were generated in a 29-dimensional space using SCD for LFM sampling points, and then 101 sampling points were selected using the D-optimality criterion [12]. Another method involves generating LFM points as a superset of the HFM points.
Preprints 72296 g0a2
Figure A2. Example of a nested sampling design, where the teal colored bubbles represent LFM points and the pink colored bubbles represent HFM points selected using the D-optimal design criterion.
Figure A2. Example of a nested sampling design, where the teal colored bubbles represent LFM points and the pink colored bubbles represent HFM points selected using the D-optimal design criterion.
Preprints 72296 g0a2
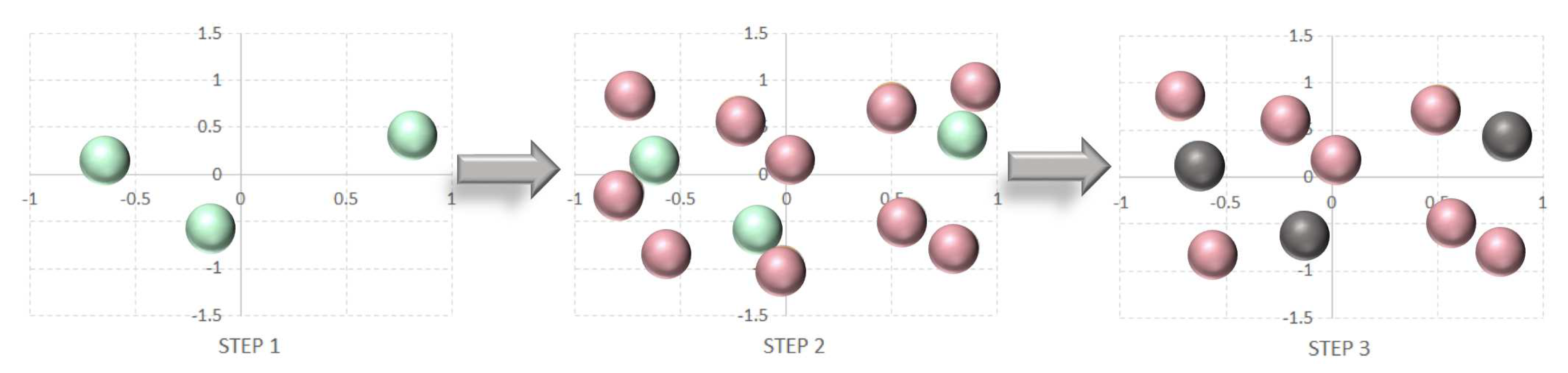
In Le Gratiet’s study from 2013 [110], the generation of sampling points from both, the LFM and HFM, were conducted independently. Subsequently, the nearest LFM point to each HFM point was moved onto their corresponding nearest neighbor, as depicted in Figure A3. This technique is commonly known as nearest neighbor sampling.
Preprints 72296 g0a3
Figure A3. Nearest neighbor sampling. High-fidelity model points (teal bubbles) and low-fidelity model points (pink bubbles) are sampled independently, then the low-fidelity model nearest neighbor point to each high-fidelity model point is moved on top of it (black bubbles)
Figure A3. Nearest neighbor sampling. High-fidelity model points (teal bubbles) and low-fidelity model points (pink bubbles) are sampled independently, then the low-fidelity model nearest neighbor point to each high-fidelity model point is moved on top of it (black bubbles)
Preprints 72296 g0a3
Adaptive sampling methods are commonly utilized SM strategies that aim to minimize the number of simulations required to construct a model to a specified accuracy by utilizing efficient interpolation and sampling techniques. These methods are widely employed and can be found in various scientific literature. Specifically, in a study by Mackman et al. in 2013 [119], two adaptive sampling strategies for generating SMs based on Kriging and radial basis function interpolation were compared. The authors found that both strategies outperformed traditional space filling methods.
Recently, the use of LFMs and reduced order methods in local searches of parameter space for optimal placement of new design points has become popular, as evidenced in studies by Robinson et al. in 2006 [157] and Raissi and Seshaiyer in 2014 [150].

Appendix B. Surrogate Models

Surrogate models are mathematical approximations developed from a set of available data that capture the relationship between input variables and the output quantity of interest. SMs are commonly utilized in MFM context to reduce computational costs. In some instances, SMs are developed for each fidelity separately in an MFHM, as seen in Nelson et al., 2007 [135], and Koziel and Leifsson, 2013 [100]. The MFM method allows for the efficient construction and application of SMs in order to achieve significant savings. Alternatively, an MFSM can include information from different types of fidelities into a single surrogate, as demonstrated in Giunta et al., 1995 [64], Qian et al., 2008 [147], and Padrón et al., 2016 [140].
Most SMs are algebraic models developed by fitting a limited set of computationally expensive simulations to predict a quantity of interest. The accuracy of an SM depends on several factors, such as the design of experiments used to select data points, the size of the domain of interest, the accuracy of the simulations at the data points, and the number of available samples used to construct the SM [167].
Peherstorfer et al. [145] provide a comprehensive review of projection-based models and data-fit models in their appendix, which enables readers to supplement their understanding of these topics.
Basis function regression, also known as response surface modeling, which are the most commonly employed surrogate modeling technique in engineering design, are the oldest form of surrogate modeling. Basis function regression are constructed via linear regression, which is simple and inexpensive as it only requires solving a set of linear algebraic equations. In this method is assumed that the functional behavior, such as a second order polynomial, is accurate, but the response data points are subject to noise. In the context of MFMs, basis function regression have been extensively utilized, as evidenced by numerous research papers, including Chang et al. [31], Burgee et al. [27], Venkatarman et al. [182], Balabanov et al. [12], Balabanov et al. [13], Mason et al. [125], Vitali et al. [185], Knill et al. [94], Vitali et al. [186], Umakant et al. [179], Venkatarman et al. [181], Choi et al. [36], Sharma et al. [165], Sharma et al. [166], Sun et al. [169], Goldsmith et al. [68], and Chen et al. [33]. Polynomial chaos expansion (PCE) has gained popularity in the 21st century as a method for analyzing aleatory uncertainties using probabilistic approaches in uncertainty quantification (UQ)[61,164,193]. This review includes PCE as a basis function regression. In PCE, a polynomial function is constructed to map uncertain inputs to the outputs of interest, and the statistics of the outputs are approximated. The chaos coefficients are estimated by projecting the system onto a set of basis functions (e.g., Hermite, Legendre, Jacobi). PCE has been applied in the context of MFM in several studies, such as Eldred, 2009 [50], Ng and Eldred, 2012 [136], Padrón et al., 2014 [141], Padrón et al., 2016 [140], and Absi and Mahadevan, 2016 [1].
Recent advances in computer power have led to the development of more expensive surrogate models (SMs) that perform better for highly nonlinear and multimodal functions. Examples of such SMs include Kriging, artificial neural networks (ANNs), moving least squares (MLS), and support vector regression. Kriging SM estimates the value of a function as the sum of a trend function (e.g., polynomial) representing low-frequency variation and a systematic departure representing high-frequency variation components [148]. Unlike basis function regression, Kriging assumes that the data points response is correct, but the functional behavior is uncertain.
Kriging has gained significant popularity as a surrogate model, particularly for applications in MFSM. This may be attributed to its uncertainty structure, which is conducive to probabilistic MFSM, as demonstrated in Section 4. Various studies have employed Kriging methods in the context of MFM, such as those by Leary et al., 2003 [114], Forrester et al., 2007 [58], Goh et al., 2013 [66], Huang et al., 2013, 2014 [77], Biehler et al., 2015 [21], and Fidkowski et al., 2014 [53].
Co-Kriging, which extends Kriging to incorporate MFMs, is regarded as a technique to combine fidelities and enable the construction of an HFM approximation enhanced by data from LFMs. Relevant studies on co-Kriging methods can be found in Chung and Alonso, 2002 [39], Forrester et al., 2008 [55], Yamazaki et al., 2010 [194], and Han et al., 2013 [73]. Laurenceau and Sagaut, 2008 [107] compared the performance of Kriging and co-Kriging.
The concept of ANNs was initially introduced in the 1980s by Rumelhart and colleagues [163]. However, ANNs have only recently gained popularity due to the increased computational power that allows the handling of the massive amount of data they require. ANNs are constructed with a layered architecture consisting of individual neurons that calculate a weighted sum of input values. Activation functions are employed to generate non-linear transformations of the output of these neurons. Note that the absence of activation functions at the output of an ANN layer would result in purely linear operations, rendering the network incapable of effectively modeling non-linearities. Minisci and Vasile, 2013 [129] provide an example of ANNs’ application in MFM, where it is used in the optimization process to correct the aerodynamic forces in the simplified LFM using CFD simulations as HFM model. The LFM is utilized to generate samples globally across the design parameter range, while the HFM is used to refine the ANN surrogate model locally in later optimization stages.
MLS surrogate is a technique first proposed by Lancaster and Salkauskas in 1981 [106] and extensively discussed by Levin in 1998 [118]. MLS is an improvement over the weighted least-squares (WLS) method, which was first introduced by Aitken in 1935 [2]. WLS recognizes that not all design points are equally important in estimating the polynomial coefficients, and thus, a WLS model is a straightforward polynomial, but with the fit biased toward points with a higher weighting. In an MLS model, the weightings are varied depending on the distance between the point to be predicted and each observed data point. Several studies have implemented MLS in MFM for various applications such as multi-point optimization [176], multi-fidelity analysis [20,197,198], and aerodynamic shape optimization [170].
Traditional SMs typically predict scalar responses, whereas some nontraditional SMs, such as proper orthogonal decomposition based SM, are used to obtain the entire solution field to a partial differential equation. Toal in 2014 [172], Roderick et al. in 2014 [160], and Mifsud et al. in 2016 [128] have explored the MFM proper orthogonal decomposition method in fluid mechanics.

References

  1. Absi, G.N.; Mahadevan, S. Multi-fidelity approach to dynamics model calibration. Mech. Syst. Signal Process. 2016, 68-69, 189–206. [Google Scholar] [CrossRef]
  2. Aitken, A.C. IV. —On Least Squares and Linear Combination of Observations. Proc. R. Soc. Edinb. 1936, 55, 42–48. [Google Scholar] [CrossRef]
  3. Alexandrov, N.; Nielsen, E.; Lewis, R.; Anderson, W. First-order model management with variable-fidelity physics applied to multi-element airfoil optimization. 8th Symposium on Multidisciplinary Analysis and Optimization. LOCATION OF CONFERENCE, U.S.ADATE OF CONFERENCE;
  4. Alexandrov, N.M.; Dennis, J.E.; Lewis, R.M.; Torczon, V. A trust-region framework for managing the use of approximation models in optimization. Struct. Multidiscip. Optim. 1998, 15, 16–23. [Google Scholar] [CrossRef]
  5. Alexandrov, N.M.; Lewis, R.M.; Gumbert, C.R.; Green, L.L.; Newman, P.A. Approximation and Model Management in Aerodynamic Optimization with Variable-Fidelity Models. J. Aircr. 2001, 38, 1093–1101. [Google Scholar] [CrossRef]
  6. Allaire, D.; Kordonowy, D.; Lecerf, M.; Mainini, L.; Willcox, K. Multifidelity DDDAS Methods with Application to a Self-aware Aerospace Vehicle. Procedia Comput. Sci. 2014, 29, 1182–1192. [Google Scholar] [CrossRef]
  7. Allaire, D.; Willcox, K. A MATHEMATICAL AND COMPUTATIONAL FRAMEWORK FOR MULTIFIDELITY DESIGN AND ANALYSIS WITH COMPUTER MODELS. Int. J. Uncertain. Quantif. 2014, 4, 1–20. [Google Scholar] [CrossRef]
  8. Allaire, D.; Willcox, K.; Toupet, O. A Bayesian-Based Approach to Multifidelity Multidisciplinary Design Optimization. 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  9. Bahrami, S.; Tribes, C.; Devals, C.; Vu, T.; Guibault, F. Multi-fidelity shape optimization of hydraulic turbine runner blades using a multi-objective mesh adaptive direct search algorithm. Appl. Math. Model. 2015, 40, 1650–1668. [Google Scholar] [CrossRef]
  10. Bakr, M.; Bandler, J.; Biernacki, R.; Chen, S.H.; Madsen, K. A trust region aggressive space mapping algorithm for EM optimization. IEEE Trans. Microw. Theory Tech. 1998, 46, 2412–2425. [Google Scholar] [CrossRef]
  11. Bakr, M. H. , Bandler, J. W., Ismail, M. A., Rayas-Sánchez, J. E., and Zhang, Q. J. (2000). Neural space mapping em optimization of microwave structures. In IEEE MTT-S International Microwave Symposium Digest, volume 2, pages 879–882.
  12. Balabanov, V. , Haftka, R. T., Grossman, B., Mason,W. H., andWatson, L. T. (1998). Multifidelity response surface model for HSCT wing bending material weight. In Proc. 7th. AIAA/USAF/NASA/ISSMO Symposium on Multidisiplinary Analysis and Optimization, pages 2–4.
  13. Balabanov, V.O.; Giunta, A.A.; Golovidov, O.; Grossman, B.; Mason, W.H.; Watson, L.T.; Haftka, R.T. Reasonable Design Space Approach to Response Surface Approximation. J. Aircr. 1999, 36, 308–315. [Google Scholar] [CrossRef]
  14. Bandler, J. (2013). Have you ever wondered about the engineer’s mysterious ‘feel’for a problem? IEEE Canadian Rev, (70):50–60.
  15. Bandler, J.W.; Biernacki, R.M.; Chen, S.H.; Grobelny, P.A.; Hemmers, R.H. Space mapping technique for electromagnetic optimization. IEEE Trans. Microw. Theory Tech. 1994, 42, 2536–2544. [Google Scholar] [CrossRef]
  16. Bandler, J.; Biernacki, R.; Chen, S.H.; Hemmers, R.; Madsen, K. Electromagnetic optimization exploiting aggressive space mapping. IEEE Trans. Microw. Theory Tech. 1995, 43, 2874–2882. [Google Scholar] [CrossRef]
  17. Bandler, J.; Cheng, Q.; Dakroury, S.; Mohamed, A.; Bakr, M.; Madsen, K.; Sondergaard, J. Space Mapping: The State of the Art. IEEE Trans. Microw. Theory Tech. 2004, 52, 337–361. [Google Scholar] [CrossRef]
  18. Bandler, J.; Cheng, Q.; Nikolova, N.; Ismail, M. Implicit Space Mapping Optimization Exploiting Preassigned Parameters. IEEE Trans. Microw. Theory Tech. 2004, 52, 378–385. [Google Scholar] [CrossRef]
  19. Bayarri, M.J.; O Berger, J.; Paulo, R.; Sacks, J.; A Cafeo, J.; Cavendish, J.; Lin, C.-H.; Tu, J. A Framework for Validation of Computer Models. Technometrics 2007, 49, 138–154. [Google Scholar] [CrossRef]
  20. Berci, M.; Gaskell, P.H.; Hewson, R.W.; Toropov, V.V. Multifidelity metamodel building as a route to aeroelastic optimization of flexible wings. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2011, 225, 2115–2137. [Google Scholar] [CrossRef]
  21. Biehler, J.; Gee, M.W.; Wall, W.A. Towards efficient uncertainty quantification in complex and large-scale biomechanical problems based on a Bayesian multi-fidelity scheme. Biomech. Model. Mechanobiol. 2014, 14, 489–513. [Google Scholar] [CrossRef]
  22. Böhnke, D. , Jepsen, J., Pfeiffer, T., Nagel, B., Gollnick, V., and Liersch, C. (2011a). An integrated method for determination of the oswald factor in a multi-fidelity design environment. In 3rd CEAS Air & Space Conference, Venice, Italy.
  23. Bohnke, D.; Nagel, B.; Gollnick, V. An approach to multi-fidelity in conceptual aircraft design in distributed design environments. 2011 IEEE Aerospace Conference. LOCATION OF CONFERENCE, USADATE OF CONFERENCE; pp. 1–10.
  24. Bradley, P.J. A MULTI-FIDELITY BASED ADAPTIVE SAMPLING OPTIMISATION APPROACH FOR THE RAPID DESIGN OF DOUBLE-NEGATIVE METAMATERIALS. Prog. Electromagn. Res. B 2013, 55, 87–114. [Google Scholar] [CrossRef]
  25. Brooks, C. J. , Forrester, A., Keane, A., and Shahpar, S. (2011). Multi-fidelity design optimisation of a transonic compressor rotor. In 9th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Istanbul, Tukey.
  26. Burgee, S.; Giunta, A.A.; Balabanov, V.; Grossman, B.; Mason, W.H.; Narducci, R.; Haftka, R.T.; Watson, L.T. A Coarse-Grained Parallel Variable-Complexity Multidisciplinary Optimization Paradigm. Int. J. Supercomput. Appl. High Perform. Comput. 1996, 10, 269–299. [Google Scholar] [CrossRef]
  27. Burgee, S.; Watson, L.; Giunta, A.; Grossman, B.; Haftka, R.; Mason, W. Parallel multipoint variable-complexity approximations for multidisciplinary optimization. IEEE Scalable High Performance Computing Conference. LOCATION OF CONFERENCE, USADATE OF CONFERENCE;
  28. Burton, S.; Hajela, P. A variable-complexity approach to second-order reliability-based optimization. Struct. Multidiscip. Optim. 2003, 25, 237–250. [Google Scholar] [CrossRef]
  29. Castro, J. P. J. , Gray, G. A., Hough, P. D., and Giunta, A. A. (2005). Developing a computationally efficient dynamic multilevel hybrid optimization scheme using multifidelity model interactions. Technical report, SAND2005-7498, Sandia National Laboratories. Albuquerque, NM.
  30. Celik, N.; Lee, S.; Vasudevan, K.; Son, Y.-J. DDDAS-based multi-fidelity simulation framework for supply chain systems. IIE Trans. 2010, 42, 325–341. [Google Scholar] [CrossRef]
  31. Chang, K.J.; Haftka, R.T.; Giles, G.L.; Kao, P.-J. Sensitivity-based scaling for approximating structural response. J. Aircr. 1993, 30, 283–288. [Google Scholar] [CrossRef]
  32. Chaudhuri, A.; Willcox, K.E. Multifidelity Uncertainty Propagation in Coupled Multidisciplinary Systems. 18th AIAA Non-Deterministic Approaches Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  33. Chen, R.; Xu, J.; Zhang, S.; Chen, C.-H.; Lee, L.H. An effective learning procedure for multi-fidelity simulation optimization with ordinal transformation. 2015 IEEE International Conference on Automation Science and Engineering (CASE). LOCATION OF CONFERENCE, SwedenDATE OF CONFERENCE; pp. 702–707.
  34. Choi, S.; Alonso, J.; Kroo, I. Multi-Fidelity Design Optimization Studies for Supersonic Jets Using Surrogate Management Frame Method. 23rd AIAA Applied Aerodynamics Conference. LOCATION OF CONFERENCE, CanadaDATE OF CONFERENCE;
  35. Choi, S. , Alonso, J. J., Kroo, I. M., andWintzer, No. AIAA 2004-4371 in AIAA Paper, 2004. 14 of 15 American Institute of Aeronautics and Astronautics. Citeseer., M. (1997). Multi-fidelity design optimization of low-boom supersonic business multi-fidelity design optimization of low-boom supersonic business jets. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. [Google Scholar]
  36. Choi, S.; Alonso, J.J.; Kroo, I.M.; Wintzer, M. Multifidelity Design Optimization of Low-Boom Supersonic Jets. J. Aircr. 2008, 45, 106–118. [Google Scholar] [CrossRef]
  37. Christen, J. A. and Fox, C. (2005). Markov chain monte carlo using an approximation. Journal of Computational and Graphical statistics, 14(4):795–810.
  38. Christensen, D. E. (2012). Multifidelity methods for multidisciplinary design under uncertainty. PhD thesis, Massachusetts Institute of Technology.
  39. Chung, H.S.; Alonso, J. Design of a Low-Boom Supersonic Business Jet Using Cokriging Approximation Models. 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization. LOCATION OF CONFERENCE, GeorgiaDATE OF CONFERENCE;
  40. Coppe, A.; Pais, M.J.; Haftka, R.T.; Kim, N.H. Using a Simple Crack Growth Model in Predicting Remaining Useful Life. J. Aircr. 2012, 49, 1965–1973. [Google Scholar] [CrossRef]
  41. Cressie, N. (1993). Statistics for Spatial Data: Wiley Series in Probability and Statistics. Wiley: New York, NY, USA.
  42. de Aguiar, P. F. , Bourguignon, B., Khots, M., Massart, D., and Phan-Than-Luu, R. (1995). D-optimal designs. Chemometrics and Intelligent Laboratory Systems, 30(2):199–210.
  43. Deblois, A.; Abdo, M. Multi-Fidelity Multidisciplinary Design Optimization of Metallic and Composite Regional and Business Jets. 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  44. Dribusch, C.; Missoum, S.; Beran, P. A multifidelity approach for the construction of explicit decision boundaries: application to aeroelasticity. Struct. Multidiscip. Optim. 2010, 42, 693–705. [Google Scholar] [CrossRef]
  45. Drissaoui, M.A.; Lanteri, S.; Leveque, P.; Musy, F.; Nicolas, L.; Perrussel, R.; Voyer, D. A Stochastic Collocation Method Combined With a Reduced Basis Method to Compute Uncertainties in Numerical Dosimetry. IEEE Trans. Magn. 2012, 48, 563–566. [Google Scholar] [CrossRef]
  46. Dufresne, S.; Johnson, C.; Mavris, D.N. Variable Fidelity Conceptual Design Environment for Revolutionary Unmanned Aerial Vehicles. J. Aircr. 2008, 45, 1405–1418. [Google Scholar] [CrossRef]
  47. Eby, D. , Averill, R., Punch III, W. F., and Goodman, E. D. (1998). Evaluation of injection island GA performance on flywheel design optimisation. In Adaptive Computing in Design and Manufacture, pages 121–136. Springer.
  48. Eldred, M. and Dunlavy, D. (2006). Formulations for surrogate-based optimization with data fit, multifidelity, and reduced-order models. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, number AIAA-2006-7117, Portsmouth, VA, volume 199.
  49. Eldred, M.; Giunta, A.; Collis, S. Second-Order Corrections for Surrogate-Based Optimization with Model Hierarchies. 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  50. Eldred, M. Recent Advances in Non-Intrusive Polynomial Chaos and Stochastic Collocation Methods for Uncertainty Analysis and Design. 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  51. Fernández-Godino, M. G. , Diggs, A., Park, C., Kim, N. H., and Haftka, R. T. (2016). Anomaly detection using groups of simulations. In 18th AIAA Non-Deterministic Approaches Conference, page 1195.
  52. Fernández-Godino, M.G.; Dubreuil, S.; Bartoli, N.; Gogu, C.; Balachandar, S.; Haftka, R.T. Linear regression-based multifidelity surrogate for disturbance amplification in multiphase explosion. Struct. Multidiscip. Optim. 2019, 60, 2205–2220. [Google Scholar] [CrossRef]
  53. Fidkowski, K. (2014). Quantifying uncertainties in radiation hydrodynamics models. Ann Arbor, 1001:48109.
  54. Fischer, C.C.; Grandhi, R.V.; Beran, P.S. Bayesian Low-Fidelity Correction Approach to Multi-Fidelity Aerospace Design. 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE;
  55. Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; Wiley: Chichester, UK, 2008. [Google Scholar]
  56. Forrester, A. I. (2010). Black-box calibration for complex-system simulation. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 368(1924):3567–3579.
  57. Forrester, A.I.; Bressloff, N.W.; Keane, A.J. Optimization using surrogate models and partially converged computational fluid dynamics simulations. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2006, 462, 2177–2204. [Google Scholar] [CrossRef]
  58. Forrester, A. I. , Sóbester, A., and Keane, A. J. (2007). Multi-fidelity optimization via surrogate modelling. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 463(2088):3251–3269.
  59. Gano, S.E.; Renaud, J.E.; Sanders, B. Hybrid Variable Fidelity Optimization by Using a Kriging-Based Scaling Function. AIAA J. 2005, 43, 2422–2433. [Google Scholar] [CrossRef]
  60. Geiselhart, K.; Ozoroski, L.; Fenbert, J.; Shields, E.; Li, W. Integration of Multifidelity Multidisciplinary Computer Codes for Design and Analysis of Supersonic Aircraft. 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  61. Ghanem, R.; Spanos, P.D. Polynomial Chaos in Stochastic Finite Elements. J. Appl. Mech. 1990, 57, 197–202. [Google Scholar] [CrossRef]
  62. Ghoman, S.S.; Kapania, R.K.; Chen, P.C.; Sarhaddi, D.; Lee, D.H. Multifidelity, Multistrategy, and Multidisciplinary Design Optimization Environment. J. Aircr. 2012, 49, 1255–1270. [Google Scholar] [CrossRef]
  63. Ghoreyshi, M.; Badcock, K.; Woodgate, M. Integration of Multi-Fidelity Methods for Generating an Aerodynamic Model for Flight Simulation. 46th AIAA Aerospace Sciences Meeting and Exhibit. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  64. Giunta, A.; Narducci, R.; Burgee, S.; Grossman, B.; Mason, W.; Watson, L.; Haftka, R. Variable-complexity response surface aerodynamic design of an HSCT wing. 13th Applied Aerodynamics Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  65. Goel, T.; Hafkta, R.T.; Shyy, W. Comparing error estimation measures for polynomial and kriging approximation of noise-free functions. Struct. Multidiscip. Optim. 2008, 38, 429–442. [Google Scholar] [CrossRef]
  66. Goh, J.; Bingham, D.; Holloway, J.P.; Grosskopf, M.J.; Kuranz, C.C.; Rutter, E. Prediction and Computer Model Calibration Using Outputs From Multifidelity Simulators. Technometrics 2013, 55, 501–512. [Google Scholar] [CrossRef]
  67. Goldfeld, Y.; Vervenne, K.; Arbocz, J.; van Keulen, F. Multi-fidelity optimization of laminated conical shells for buckling. Struct. Multidiscip. Optim. 2005, 30, 128–141. [Google Scholar] [CrossRef]
  68. Goldsmith, M.B.; Sankar, B.V.; Haftka, R.T.; Goldberg, R.K. Effects of microstructural variability on thermo-mechanical properties of a woven ceramic matrix composite. J. Compos. Mater. 2014, 49, 335–350. [Google Scholar] [CrossRef]
  69. Haaland, B. and Qian, P. Z. (2010). An approach to constructing nested space-filling designs for multi-fidelity computer experiments. Statistica Sinica, 20(3):1063.
  70. Haftka, R.T. Combining global and local approximations. AIAA J. 1991, 29, 1523–1525. [Google Scholar] [CrossRef]
  71. Hammersley, J. (2013). Monte carlo methods. Springer Science & Business Media.
  72. Han, Z.-H.; Zimmermann, R.; Görtz, S. Alternative Cokriging Method for Variable-Fidelity Surrogate Modeling. AIAA J. 2012, 50, 1205–1210. [Google Scholar] [CrossRef]
  73. Han, Z.-H.; Görtz, S.; Zimmermann, R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function. Aerosp. Sci. Technol. 2013, 25, 177–189. [Google Scholar] [CrossRef]
  74. Hevesi, J.A.; Istok, J.D.; Flint, A.L. Precipitation Estimation in Mountainous Terrain Using Multivariate Geostatistics. Part I: Structural Analysis. J. Appl. Meteorol. 1992, 31, 661–676. [Google Scholar] [CrossRef]
  75. Higdon, D.; Kennedy, M.; Cavendish, J.C.; Cafeo, J.A.; Ryne, R.D. Combining Field Data and Computer Simulations for Calibration and Prediction. SIAM J. Sci. Comput. 2004, 26, 448–466. [Google Scholar] [CrossRef]
  76. Huang, D.; Allen, T.T.; Notz, W.I.; Miller, R.A. Sequential kriging optimization using multiple-fidelity evaluations. Struct. Multidiscip. Optim. 2006, 32, 369–382. [Google Scholar] [CrossRef]
  77. Huang, L.; Gao, Z.; Zhang, D. Research on multi-fidelity aerodynamic optimization methods. Chin. J. Aeronaut. 2013, 26, 279–286. [Google Scholar] [CrossRef]
  78. Hutchison, M.G.; Unger, E.R.; Mason, W.H.; Grossman, B.; Haftka, R.T. Variable-complexity aerodynamic optimization of a high-speed civil transport wing. J. Aircr. 1994, 31, 110–116. [Google Scholar] [CrossRef]
  79. Jacobs, J.P.; Koziel, S.; Ogurtsov, S. Computationally Efficient Multi-Fidelity Bayesian Support Vector Regression Modeling of Planar Antenna Input Characteristics. IEEE Trans. Antennas Propag. 2012, 61, 980–984. [Google Scholar] [CrossRef]
  80. Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
  81. Johnson, M. E. , Moore, L. M., and Ylvisaker, D. (1990). Minimax and maximin distance designs. Journal of statistical planning and inference, 26(2):131–148.
  82. Joly, M.M.; Verstraete, T.; Paniagua, G. Integrated multifidelity, multidisciplinary evolutionary design optimization of counterrotating compressors. Integr. Comput. Eng. 2014, 21, 249–261. [Google Scholar] [CrossRef]
  83. Jonsson, I.M.; Leifsson, L.; Koziel, S.; Tesfahunegn, Y.A.; Bekasiewicz, A. Shape Optimization of Trawl-doors Using Variable-fidelity Models and Space Mapping. Procedia Comput. Sci. 2015, 51, 905–913. [Google Scholar] [CrossRef]
  84. Kalivarapu, V.; Winer, E. A multi-fidelity software framework for interactive modeling of advective and diffusive contaminant transport in groundwater. Environ. Model. Softw. 2008, 23, 1370–1383. [Google Scholar] [CrossRef]
  85. Kandasamy, M.; Peri, D.; Ooi, S.K.; Carrica, P.; Stern, F.; Campana, E.F.; Osborne, P.; Cote, J.; Macdonald, N.; de Waal, N. Multi-fidelity optimization of a high-speed foil-assisted semi-planing catamaran for low wake. J. Mar. Sci. Technol. 2011, 16, 143–156. [Google Scholar] [CrossRef]
  86. Kaufman, M. , Balabanov, V., Giunta, A., Grossman, B., Mason,W., Burgee, S., Haftka, R., andWatson, L. T. (1996). Variable-complexity response surface approximations for wing structural weight in HSCT design. Computational Mechanics, 18(2):112–126.
  87. Kaveh, A.; Talatahari, S. A novel heuristic optimization method: charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
  88. Keane, A.J. Cokriging for Robust Design Optimization. AIAA J. 2012, 50, 2351–2364. [Google Scholar] [CrossRef]
  89. Kennedy, M.; O’Hagan, A. Predicting the output from a complex computer code when fast approximations are available. Biometrika 2000, 87, 1–13. [Google Scholar] [CrossRef]
  90. Kennedy, M. C. and O’Hagan, A. (2001). Bayesian calibration of computer models. Journal of the Royal Statistical Society. Series B, Statistical Methodology, pages 425–464.
  91. Kim, H.S.; Koç, M.; Ni, J. A hybrid multi-fidelity approach to the optimal design of warm forming processes using a knowledge-based artificial neural network. Int. J. Mach. Tools Manuf. 2007, 47, 211–222. [Google Scholar] [CrossRef]
  92. Kleiber, W.; Sain, S.R.; Heaton, M.J.; Wiltberger, M.; Reese, C.S.; Bingham, D. Parameter tuning for a multi-fidelity dynamical model of the magnetosphere. Ann. Appl. Stat. 2013, 7. [Google Scholar] [CrossRef]
  93. Kleijnen, J.P. Kriging metamodeling in simulation: A review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef]
  94. Knill, D.L.; Giunta, A.A.; Baker, C.A.; Grossman, B.; Mason, W.H.; Haftka, R.T.; Watson, L.T. Response Surface Models Combining Linear and Euler Aerodynamics for Supersonic Transport Design. J. Aircr. 1999, 36, 75–86. [Google Scholar] [CrossRef]
  95. Kosonen, R. and Shemeikka, J. (1997). The use of a simple simulation tool for energy analysis. VTT Building Technology.
  96. Koutsourelakis, P.-S. Accurate Uncertainty Quantification Using Inaccurate Computational Models. SIAM J. Sci. Comput. 2009, 31, 3274–3300. [Google Scholar] [CrossRef]
  97. Koyuncu, N.; Lee, S.; Vasudevan, K.K.; Son, Y.-J.; Sarfare, P. DDDAS-based multi-fidelity simulation for online preventive maintenance scheduling in semiconductor supply chain. 2007 Winter Simulation Conference. LOCATION OF CONFERENCE, USADATE OF CONFERENCE; pp. 1915–1923.
  98. Koziel, S. (2010). Multi-fidelity multi-grid design optimization of planar microwave structures with sonnet. International Review of Progress in Applied Computational Electromagnetics, pages 26–29.
  99. Koziel, S.; Leifsson, L. Knowledge-Based Airfoil Shape Optimization Using Space Mapping. 30th AIAA Applied Aerodynamics Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  100. Koziel, S.; Leifsson, L. Multi-level CFD-based Airfoil Shape Optimization With Automated Low-fidelity Model Selection. Procedia Comput. Sci. 2013, 18, 889–898. [Google Scholar] [CrossRef]
  101. Koziel, S.; Meng, J.; Bandler, J.W.; Bakr, M.H.; Cheng, Q.S. Accelerated Microwave Design Optimization With Tuning Space Mapping. IEEE Trans. Microw. Theory Tech. 2009, 57, 383–394. [Google Scholar] [CrossRef]
  102. Koziel, S.; Ogurtsov, S. Robust multi-fidelity simulation-driven design optimization of microwave structures. 2010 IEEE/MTT-S International Microwave Symposium - MTT 2010. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE; pp. 201–204.
  103. Koziel, S.; Tesfahunegn, Y.; Amrit, A.; Leifsson, L.T. Rapid Multi-Objective Aerodynamic Design Using Co-Kriging and Space Mapping. 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  104. Kroo, I. , Willcox, K., March, A., Haas, A., Rajnarayan, D., and Kays, C. (2010). Multifidelity analysis and optimization for supersonic design. Technical report, NASA/CR-2010-216874, NASA.
  105. Kuya, Y.; Takeda, K.; Zhang, X.; Forrester, A.I.J. Multifidelity Surrogate Modeling of Experimental and Computational Aerodynamic Data Sets. AIAA J. 2011, 49, 289–298. [Google Scholar] [CrossRef]
  106. Lancaster, P. and Salkauskas, K. (1981). Surfaces generated by moving least squares methods. Mathematics of computation, 37(155):141–158.
  107. Laurenceau, J.; Sagaut, P. Building Efficient Response Surfaces of Aerodynamic Functions with Kriging and Cokriging. AIAA J. 2008, 46, 498–507. [Google Scholar] [CrossRef]
  108. Lazzara, D.; Haimes, R.; Willcox, K. Multifidelity Geometry and Analysis in Aircraft Conceptual Design. 19th AIAA Computational Fluid Dynamics. LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE;
  109. Le Gratiet, L. Bayesian Analysis of Hierarchical Multifidelity Codes. SIAM/ASA J. Uncertain. Quantif. 2013, 1, 244–269. [Google Scholar] [CrossRef]
  110. Le Gratiet, L. (2013b). Multi-fidelity Gaussian process regression for computer experiments. PhD thesis, Université Paris-Diderot-Paris VII.
  111. Le Gratiet, L. and Cannamela, C. (2012). Kriging-based sequential design strategies using fast cross-validation techniques with extensions to multi-fidelity computer codes. arXiv:1210.6187.
  112. Le Gratiet, L.; Cannamela, C. Cokriging-Based Sequential Design Strategies Using Fast Cross-Validation Techniques for Multi-Fidelity Computer Codes. Technometrics 2015, 57, 418–427. [Google Scholar] [CrossRef]
  113. Le Gratiet, L.; Cannamela, C.; Iooss, B. A Bayesian Approach for Global Sensitivity Analysis of (Multifidelity) Computer Codes. SIAM/ASA J. Uncertain. Quantif. 2014, 2, 336–363. [Google Scholar] [CrossRef]
  114. Leary, S. , Bhaskar, A., and Keane, A. (2003a). Method of generating a multifidelity model of a system. US Patent App. 10/608,042.
  115. Leary, S.J.; Bhaskar, A.; Keane, A.J. A Knowledge-Based Approach To Response Surface Modelling in Multifidelity Optimization. J. Glob. Optim. 2003, 26, 297–319. [Google Scholar] [CrossRef]
  116. Lee, S.; Kim, T.; Jun, S.O.; Yee, K. Efficiency Enhancement of Reduced Order Model using Variable Fidelity Modeling. 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  117. Lee, S.; Youn, B. Computer Model Calibration and Design Comparison on Piezoelectric Energy Harvester. 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. LOCATION OF CONFERENCE, CanadaDATE OF CONFERENCE;
  118. Levin, D. (1998). The approximation power of moving least-squares. Mathematics of Computation of the American Mathematical Society, 67(224):1517–1531.
  119. Mackman, T.J.; Allen, C.B.; Ghoreyshi, M.; Badcock, K.J. Comparison of Adaptive Sampling Methods for Generation of Surrogate Aerodynamic Models. AIAA J. 2013, 51, 797–808. [Google Scholar] [CrossRef]
  120. Madsen, J.I.; Langthjem, M. Multifidelity Response Surface Approximations for the Optimum Design of Diffuser Flows. Optim. Eng. 2001, 2, 453–468. [Google Scholar] [CrossRef]
  121. March, A.; Willcox, K. Constrained multifidelity optimization using model calibration. Struct. Multidiscip. Optim. 2012, 46, 93–109. [Google Scholar] [CrossRef]
  122. March, A.; Willcox, K. Provably Convergent Multifidelity Optimization Algorithm Not Requiring High-Fidelity Derivatives. AIAA J. 2012, 50, 1079–1089. [Google Scholar] [CrossRef]
  123. March, A.; Willcox, K.; Wang, Q. Gradient-based multifidelity optimisation for aircraft design using Bayesian model calibration. Aeronaut. J. 2011, 115, 729–738. [Google Scholar] [CrossRef]
  124. Mason, B. H. , Haftka, R. T., and Johnson, E. (1994). Analysis and design of composite curved channel frames. Proc 5th A1AA/USAF/NASA/ISSMO Syrup on Multidisciplinary Analysis and Optimization, pages 1023–1040.
  125. Mason, B.H.; Haftka, R.T.; Johnson, E.R.; Farley, G.L. Variable complexity design of composite fuselage frames by response surface techniques. Thin-Walled Struct. 1998, 32, 235–261. [Google Scholar] [CrossRef]
  126. McFarland, J.; Mahadevan, S.; Romero, V.; Swiler, L. Calibration and Uncertainty Analysis for Computer Simulations with Multivariate Output. AIAA J. 2008, 46, 1253–1265. [Google Scholar] [CrossRef]
  127. Mentré, F.; Mallet, A.; Baccar, D. Optimal design in random-effects regression models. Biometrika 1997, 84, 429–442. [Google Scholar] [CrossRef]
  128. Mifsud, M.J.; MacManus, D.G.; Shaw, S. A variable-fidelity aerodynamic model using proper orthogonal decomposition. Int. J. Numer. Methods Fluids 2016, 82, 646–663. [Google Scholar] [CrossRef]
  129. Minisci, E.; Vasile, M. Robust Design of a Reentry Unmanned Space Vehicle by Multifidelity Evolution Control. AIAA J. 2013, 51, 1284–1295. [Google Scholar] [CrossRef]
  130. Minisci, E.; Vasile, M.; Liqiang, H. Robust multi-fidelity design of a micro re-entry unmanned space vehicle. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2011, 225, 1195–1209. [Google Scholar] [CrossRef]
  131. Molina-Cristobal, A.; Palmer, P.R.; Skinner, B.A.; Parks, G.T. Multi-fidelity simulation modelling in optimization of a submarine propulsion system. 2010 IEEE Vehicle Power and Propulsion Conference (VPPC). LOCATION OF CONFERENCE, FranceDATE OF CONFERENCE; pp. 1–6.
  132. Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C. Process and product optimization using designed experiments. Response Surf. Methodol. 2002, 2, 328–335. [Google Scholar]
  133. Myers, D.E. Matrix formulation of co-kriging. J. Int. Assoc. Math. Geol. 1982, 14, 249–257. [Google Scholar] [CrossRef]
  134. Narayan, A.; Gittelson, C.; Xiu, D. A Stochastic Collocation Algorithm with Multifidelity Models. SIAM J. Sci. Comput. 2014, 36. [Google Scholar] [CrossRef]
  135. Nelson, A.; Alonso, J.; Pulliam, T. Multi-Fidelity Aerodynamic Optimization Using Treed Meta-Models. 25th AIAA Applied Aerodynamics Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  136. Ng, L.W.-T.; Eldred, M. Multifidelity Uncertainty Quantification Using Non-Intrusive Polynomial Chaos and Stochastic Collocation. 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference20th AIAA/ASME/AHS Adaptive Structures Conference14th AIAA. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  137. Ng, L.W. andWillcox, K. E. (2014). Multifidelity approaches for optimization under uncertainty. International Journal for Numerical Methods in Engineering, 100(10):746–772.
  138. Nguyen, N.-V.; Choi, S.-M.; Kim, W.-S.; Lee, J.-W.; Kim, S.; Neufeld, D.; Byun, Y.-H. Multidisciplinary Unmanned Combat Air Vehicle system design using Multi-Fidelity Model. Aerosp. Sci. Technol. 2012, 26, 200–210. [Google Scholar] [CrossRef]
  139. Owen, A.K.; Daugherty, A.; Garrard, D.; Reynolds, H.C.; Wright, R.D. A Parametric Starting Study of an Axial-Centrifugal Gas Turbine Engine Using a One-Dimensional Dynamic Engine Model and Comparisons to Experimental Results: Part 2 — Simulation Calibration and Trade-Off Study. ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition. LOCATION OF CONFERENCE, SwedenDATE OF CONFERENCE;
  140. Padron, A.S.; Alonso, J.J.; Eldred, M.S. Multi-fidelity Methods in Aerodynamic Robust Optimization. 18th AIAA Non-Deterministic Approaches Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  141. Padron, A.S.; Alonso, J.J.; Palacios, F.; Barone, M.F.; Eldred, M.S. Multi-Fidelity Uncertainty Quantification: Application to a Vertical Axis Wind Turbine Under an Extreme Gust. 15th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  142. Park, C. , Haftka, R. T., and Kim, N. H. (2017). Remarks on multi-fidelity surrogates. Structural and Multidisciplinary Optimization, 55:1029–1050.
  143. Park, C.; Haftka, R.T.; Kim, N.H. Low-fidelity scale factor improves Bayesian multi-fidelity prediction by reducing bumpiness of discrepancy function. Struct. Multidiscip. Optim. 2018, 58, 399–414. [Google Scholar] [CrossRef]
  144. Peherstorfer, B. , Cui, T., Marzouk, Y., and Willcox, K. (2016a). Multifidelity importance sampling. Computer Methods in Applied Mechanics and Engineering, 300:490–509.
  145. Peherstorfer, B.; Willcox, K.; Gunzburger, M. Survey of Multifidelity Methods in Uncertainty Propagation, Inference, and Optimization. SIAM Rev. 2018, 60, 550–591. [Google Scholar] [CrossRef]
  146. Perdikaris, P.; Venturi, D.; Royset, J.O.; Karniadakis, G.E. Multi-fidelity modelling via recursive co-kriging and Gaussian–Markov random fields. Proc. R. Soc. A: Math. Phys. Eng. Sci. 2015, 471, 20150018. [Google Scholar] [CrossRef]
  147. Qian, P.Z.G.; Wu, C.F.J. Bayesian Hierarchical Modeling for Integrating Low-Accuracy and High-Accuracy Experiments. Technometrics 2008, 50, 192–204. [Google Scholar] [CrossRef]
  148. Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Tucker, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef]
  149. Raissi, M. and Seshaiyer, P. (2013). A multi-fidelity stochastic collocation method using locally improved reduced-order models. arXiv:1306.0132.
  150. Raissi, M.; Seshaiyer, P. A MULTI-FIDELITY STOCHASTIC COLLOCATION METHOD FOR PARABOLIC PARTIAL DIFFERENTIAL EQUATIONS WITH RANDOM INPUT DATA. Int. J. Uncertain. Quantif. 2014, 4, 225–242. [Google Scholar] [CrossRef]
  151. Rajnarayan, D. , Haas, A., and Kroo, I. (2008). A multifidelity gradient-free optimization method and application to aerodynamic design. Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, Etats-Unis.
  152. Rayas-Sanchez, J.E. Power in Simplicity with ASM: Tracing the Aggressive Space Mapping Algorithm Over Two Decades of Development and Engineering Applications. IEEE Microw. Mag. 2016, 17, 64–76. [Google Scholar] [CrossRef]
  153. Rayas-Sanchez, J.; Lara-Rojo, F.; Martinez-Guerrero, E. A linear inverse space-mapping (LISM) algorithm to design linear and nonlinear RF and microwave circuits. IEEE Trans. Microw. Theory Tech. 2005, 53, 960–968. [Google Scholar] [CrossRef]
  154. Ren, J.; Leifsson, L.T.; Koziel, S.; Tesfahunegn, Y. Multi-Fidelity Aerodynamic Shape Optimization Using Manifold Mapping. 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  155. Réthoré, P.-E. , Fuglsang, P., Larsen, G. C., Buhl, T., Larsen, T. J., Madsen, H. A., et al. (2011). TopFarm: Multi-fidelity optimization of offshore wind farm. In The Twenty-first International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers.
  156. Robert, C. P. (2004). Monte carlo methods. Wiley Online Library.
  157. Robinson, T. , Eldred, M., Willcox, K., and Haimes, R. (2006a). Strategies for multifidelity optimization with variable dimensional hierarchical models. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference (2nd AIAA Multidisciplinary Design Optimization Specialist Conference), Newport, RI, pages 2006–1819.
  158. Robinson, T.D.; Eldred, M.S.; Willcox, K.E.; Haimes, R. Surrogate-Based Optimization Using Multifidelity Models with Variable Parameterization and Corrected Space Mapping. AIAA J. 2008, 46, 2814–2822. [Google Scholar] [CrossRef]
  159. Robinson, T. , Willcox, K., Eldred, M., and Haimes, R. (2006b). Multifidelity optimization for variable complexity design. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA.
  160. Roderick, O.; Anitescu, M.; Peet, Y. Proper orthogonal decompositions in multifidelity uncertainty quantification of complex simulation models. Int. J. Comput. Math. 2014, 91, 748–769. [Google Scholar] [CrossRef]
  161. Rodríguez, J.; Pérez, V.; Padmanabhan, D.; Renaud, J. Sequential approximate optimization using variable fidelity response surface approximations. Struct. Multidiscip. Optim. 2001, 22, 24–34. [Google Scholar] [CrossRef]
  162. Roux,W., Stander, N., and Haftka, R. T. (1998). Response surface approximations for structural optimization. International Journal for Numerical Methods in Engineering, 42(3):517–534.
  163. Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
  164. Sakamoto, S.; Ghanem, R. Polynomial Chaos Decomposition for the Simulation of Non-Gaussian Nonstationary Stochastic Processes. J. Eng. Mech. 2002, 128, 190–201. [Google Scholar] [CrossRef]
  165. Sharma, A.; Gogu, C.; Martinez, O.; Sankar, B.; Haftka, R. Multi-Fidelity Design of an Integrated Thermal Protection System for Spacecraft Reentry. 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 16th AIAA/ASME/AHS Adaptive Structures Conference10t. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  166. Sharma, A.; Sankar, B.; Haftka, R. Multi-Fidelity Analysis of Corrugated-Core Sandwich Panels for Integrated Thermal Protection Systems. 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  167. Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for Computer-based Engineering Design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
  168. Singh, G.; Grandhi, R.V. Mixed-Variable Optimization Strategy Employing Multifidelity Simulation and Surrogate Models. AIAA J. 2010, 48, 215–223. [Google Scholar] [CrossRef]
  169. Sun, G.; Li, G.; Stone, M.; Li, Q. A two-stage multi-fidelity optimization procedure for honeycomb-type cellular materials. Comput. Mater. Sci. 2010, 49, 500–511. [Google Scholar] [CrossRef]
  170. Sun, G.; Li, G.; Zhou, S.; Xu, W.; Yang, X.; Li, Q. Multi-fidelity optimization for sheet metal forming process. Struct. Multidiscip. Optim. 2010, 44, 111–124. [Google Scholar] [CrossRef]
  171. Thoresson, M. J. (2007). Efficient gradient-based optimisation of suspension characteristics for an off-road vehicle. PhD thesis, University of Pretoria.
  172. Toal, D.J.J. On the Potential of a Multi-Fidelity G-POD Based Approach for Optimization and Uncertainty Quantification. ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. LOCATION OF CONFERENCE, GermanyDATE OF CONFERENCE;
  173. Toal, D.J.J. Some considerations regarding the use of multi-fidelity Kriging in the construction of surrogate models. Struct. Multidiscip. Optim. 2014, 51, 1223–1245. [Google Scholar] [CrossRef]
  174. Toal, D.J.J.; Keane, A.J. Efficient Multipoint Aerodynamic Design Optimization Via Cokriging. J. Aircr. 2011, 48, 1685–1695. [Google Scholar] [CrossRef]
  175. Toal, D.J.J.; Keane, A.J.; Benito, D.; Dixon, J.A.; Yang, J.; Price, M.; Robinson, T.; Remouchamps, A.; Kill, N. Multifidelity Multidisciplinary Whole-Engine Thermomechanical Design Optimization. J. Propuls. Power 2014, 30, 1654–1666. [Google Scholar] [CrossRef]
  176. Toropov, V. , Van Keulen, F., Markine, V., and Alvarez, L. (1999). Multipoint approximations based on response surface fitting: a summary of recent developments. In Proceedings of the 1st ASMO UK/ISSMO Conference on Engineering Design Optimization, Ilkley, West Yorkshire, UK, pages 371–381.
  177. Toropov, V. V. and Markine, V. (1998). Use of simplified numerical models as approximations: Application to a dynamic optimal design problem. Proceedings of the First ISSMO/NASA Internet Conference on Approximation and Fast Reanalysis Techniques in Engineering Optimization.
  178. Turner, M.G.; Reed, J.A.; Ryder, R.; Veres, J.P. Multi-Fidelity Simulation of a Turbofan Engine With Results Zoomed Into Mini-Maps for a Zero-D Cycle Simulation. ASME Turbo Expo 2004: Power for Land, Sea, and Air. LOCATION OF CONFERENCE, AustriaDATE OF CONFERENCE; pp. 219–230.
  179. Umakant, J.; Sudhakar, K.; Mujumdar, P.M.; Rao, C.R. Ranking Based Uncertainty Quantification for a Multifidelity Design Approach. J. Aircr. 2007, 44, 410–419. [Google Scholar] [CrossRef]
  180. Variyar, A.; Economon, T.D.; Alonso, J.J. Multifidelity Conceptual Design and Optimization of Strut-Braced Wing Aircraft using Physics Based Methods. 54th AIAA Aerospace Sciences Meeting. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  181. Venkataraman, S. Reliability optimization using probabilistic sufficiency factor and correction response surface. Eng. Optim. 2006, 38, 671–685. [Google Scholar] [CrossRef]
  182. Venkataraman, S.; Haftka, R.; Johnson, T. Design of shell structures for buckling using correction response surface approximations. 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization. LOCATION OF CONFERENCE, U.S.ADATE OF CONFERENCE;
  183. Viana, F. A. , Simpson, T. W., Balabanov, V., and Toropov, V. (2014). Special section on multidisciplinary design optimization: Metamodeling in multidisciplinary design optimization: How far have we really come? AIAA Journal, 52(4):670–690.
  184. Viana, F. A. , Steffen Jr, V., Butkewitsch, S., and de Freitas Leal, M. (2009). Optimization of aircraft structural components by using nature-inspired algorithms and multi-fidelity approximations. Journal of Global Optimization, 45(3):427–449.
  185. Vitali, R.; Haftka, R.; Sankar, B. Correction response surface approximations for stress intensity factors of a composite stiffened plate. 39th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit. LOCATION OF CONFERENCE, U.S.ADATE OF CONFERENCE;
  186. Vitali, R.; Haftka, R.; Sankar, B. Multi-fidelity design of stiffened composite panel with a crack. Struct. Multidiscip. Optim. 2002, 23, 347–356. [Google Scholar] [CrossRef]
  187. Vitali, R.; Park, O.; Haftka, R.; Sankar, B. Structural optimization of a hat stiffened panel by response surface techniques. 38th Structures, Structural Dynamics, and Materials Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  188. Vitali, R.; Park, O.; Haftka, R.T.; Sankar, B.V.; Rose, C.A. Structural Optimization of a Hat-Stiffened Panel Using Response Surfaces. J. Aircr. 2002, 39, 158–166. [Google Scholar] [CrossRef]
  189. Vitali, R.; Sankar, B. Correction response surface design of stiffened composite panel with a crack. 40th Structures, Structural Dynamics, and Materials Conference and Exhibit. LOCATION OF CONFERENCE, U.S.ADATE OF CONFERENCE;
  190. Wang, P.; Zheng, Y.; Zou, Z.; Qi, L.; Zhou, Z. A novel multi-fidelity coupled simulation method for flow systems. Chin. J. Aeronaut. 2013, 26, 868–875. [Google Scholar] [CrossRef]
  191. Willis, D.; Persson, P.O.; Israeli, E.; Peraire, J.; Swartz, S.; Breuer, K. Multifidelity Approaches for the Computational Analysis and Design of Effective Flapping Wing Vehicles. 46th AIAA Aerospace Sciences Meeting and Exhibit. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  192. Winner, E. and Veloso, M. (2000). Multi-fidelity robotic behaviors: Acting with variable state information. In AAAI/IAAI, pages 872–877.
  193. Xiu, D.; Karniadakis, G.E. The Wiener--Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
  194. Yamazaki, W.; Rumpfkeil, M.; Mavriplis, D. Design Optimization Utilizing Gradient/Hessian Enhanced Surrogate Model. 28th AIAA Applied Aerodynamics Conference. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
  195. Yoo, M.Y.; Choi, J.H. Probabilistic Calibration of Computer Model and Application to Reliability Analysis of Elasto-Plastic Insertion Problem. Trans. Korean Soc. Mech. Eng. - A 2013, 37, 1133–1140. [Google Scholar] [CrossRef]
  196. Yu, K.; Yang, X.; Mo, Z. Profile Design and Multifidelity Optimization of Solid Rocket Motor Nozzle. J. Fluids Eng. 2014, 136, 031104. [Google Scholar] [CrossRef]
  197. M.Zadeh, P.; Toropov, V. M.Zadeh, P.; Toropov, V. Multi-Fidelity Multidisciplinary Design Optimization Based on Collaborative Optimization Framework. 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization. LOCATION OF CONFERENCE, GeorgiaDATE OF CONFERENCE;
  198. Zadeh, P. M. , Toropov, V. V., andWood, A. S. (2005). Use of moving least squares method in collaborative optimization. 6th World Congresses of Structural and Multidisciplinary Optimization. Rio de Janeiro Brazil.
  199. Zahir, M.K.; Gao, Z. Variable-fidelity optimization with design space reduction. Chin. J. Aeronaut. 2013, 26, 841–849. [Google Scholar] [CrossRef]
  200. Zhang, L.; Xu, J.; Yagoub, M.; Ding, R.; Zhang, Q.-J. Efficient analytical formulation and sensitivity analysis of neuro-space mapping for nonlinear microwave device modeling. IEEE Trans. Microw. Theory Tech. 2005, 53, 2752–2767. [Google Scholar] [CrossRef]
  201. Zhang, L.; Zhang, Q.-J.; Wood, J. Statistical Neuro-Space Mapping Technique for Large-Signal Modeling of Nonlinear Devices. IEEE Trans. Microw. Theory Tech. 2008, 56, 2453–2467. [Google Scholar] [CrossRef]
  202. Zhang, Y.; Kim, N.H.; Park, C.; Haftka, R.T. Multifidelity Surrogate Based on Single Linear Regression. AIAA J. 2018, 56, 4944–4952. [Google Scholar] [CrossRef]
  203. Zheng, J.; Shao, X.; Gao, L.; Jiang, P.; Li, Z. A hybrid variable-fidelity global approximation modelling method combining tuned radial basis function base and kriging correction. J. Eng. Des. 2013, 24, 604–622. [Google Scholar] [CrossRef]
  204. Zheng, J.; Shao, X.; Gao, L.; Jiang, P.; Qiu, H. Difference mapping method using least square support vector regression for variable-fidelity metamodelling. Eng. Optim. 2014, 47, 719–736. [Google Scholar] [CrossRef]
  205. Zheng, L.; Hedrick, T.L.; Mittal, R. A multi-fidelity modelling approach for evaluation and optimization of wing stroke aerodynamics in flapping flight. J. Fluid Mech. 2013, 721, 118–154. [Google Scholar] [CrossRef]
  206. Zimmermann, R.; Han, Z. Simplified cross-correlation estimation for multi-fidelity surrogate cokriging models. Advances and Applications in Mathematical Sciences 2010, 7, 181–202. [Google Scholar]
  207. Zou, Z.; Liu, J.; Zhang, W.; Wang, P. Shroud leakage flow models and a multi-dimensional coupling CFD (computational fluid dynamics) method for shrouded turbines. Energy 2016, 103, 410–429. [Google Scholar] [CrossRef]
1
Multi-fidelity surrogate models and multi-fidelity hierarchical models are called multi-fidelity management strategies by Peherstofer et al., 2016 [145] and they divide them into adaptation, fusion and filtering.
Preprints 72296 g001
Figure 1. Connection between high-fidelity and low-fidelity models is commonly observed to be attributed to one or more of the following factors: Dimensionality reduction, grid coarsening, linearization, partial convergence, reduced complexity in geometry, and simplified physics.
Figure 1. Connection between high-fidelity and low-fidelity models is commonly observed to be attributed to one or more of the following factors: Dimensionality reduction, grid coarsening, linearization, partial convergence, reduced complexity in geometry, and simplified physics.
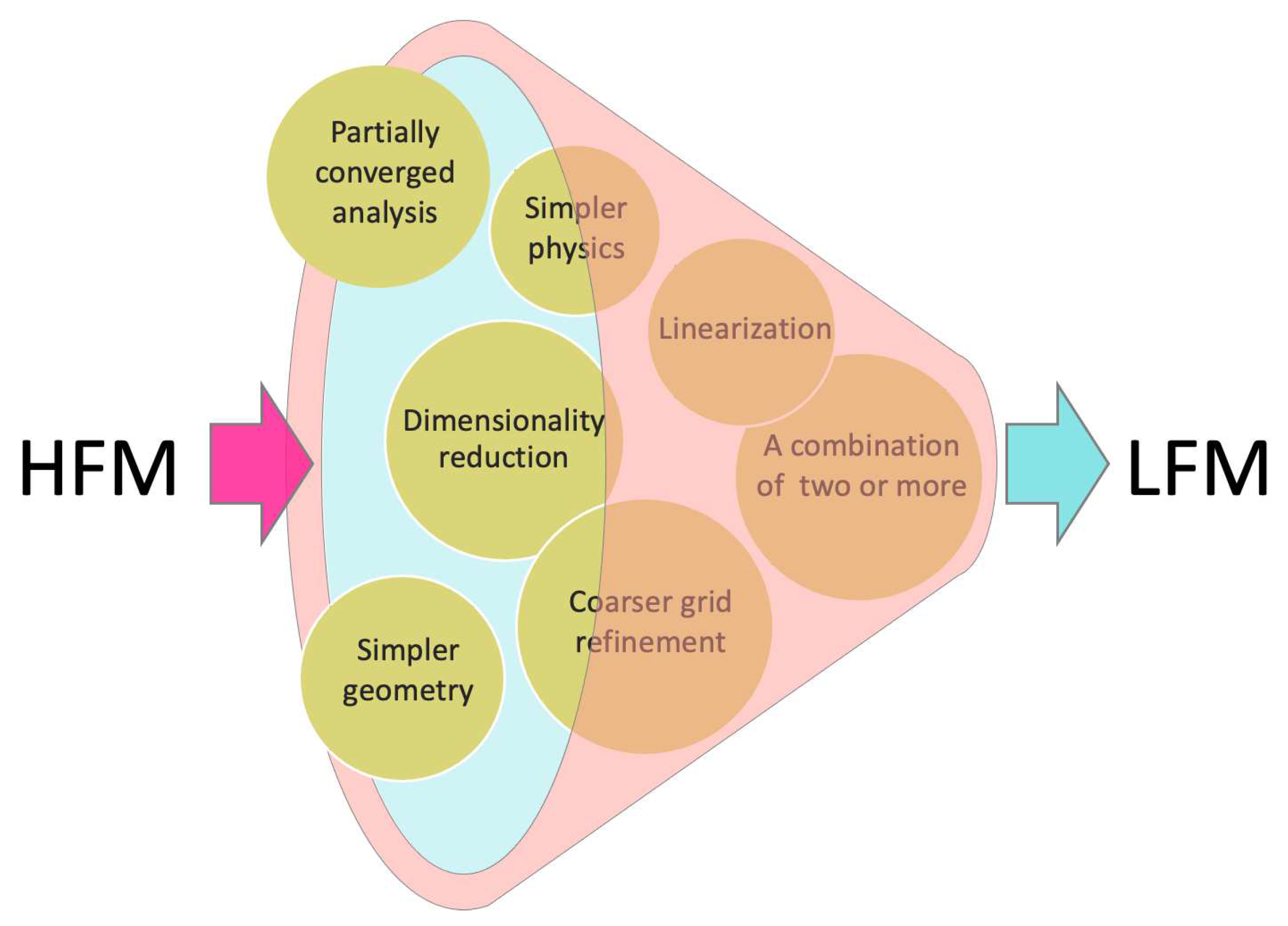
Preprints 72296 g001
Preprints 72296 g002
Figure 2. Within the frame of multi-fidelity modeling, surrogate models are commonly used to integrate information from different fidelities. When constructing a surrogate model that combines fidelities explicitly, such as co-Kriging, the resulting approach is referred to as a multi-fidelity surrogate model. In contrast, multi-fidelity hierarchical models combine fidelities without requiring an explicit multi-fidelity surrogate model architecture. Methods such as importance sampling fall under the multi-fidelity hierarchical category.
Figure 2. Within the frame of multi-fidelity modeling, surrogate models are commonly used to integrate information from different fidelities. When constructing a surrogate model that combines fidelities explicitly, such as co-Kriging, the resulting approach is referred to as a multi-fidelity surrogate model. In contrast, multi-fidelity hierarchical models combine fidelities without requiring an explicit multi-fidelity surrogate model architecture. Methods such as importance sampling fall under the multi-fidelity hierarchical category.
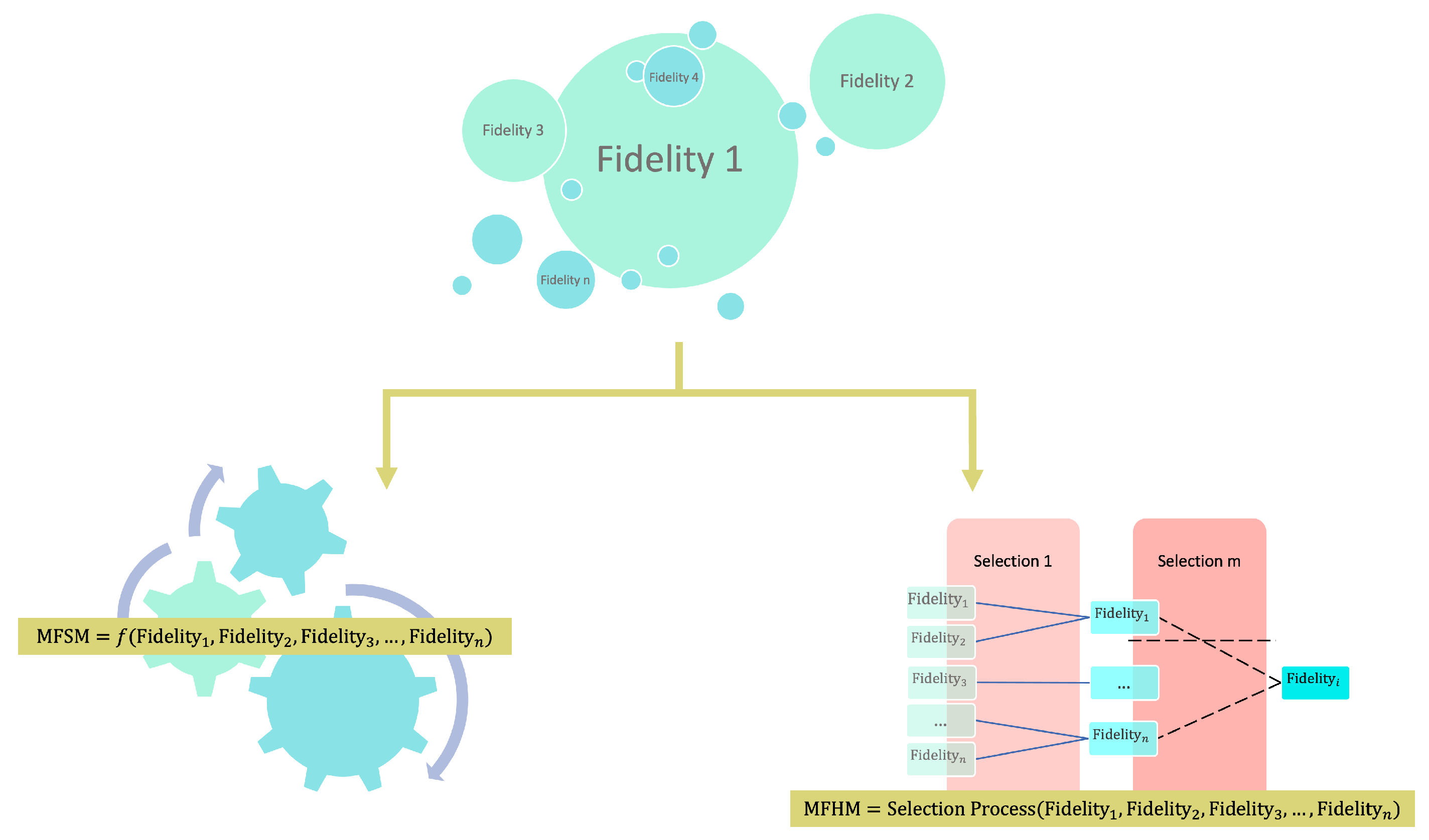
Preprints 72296 g002
Preprints 72296 g003
Figure 3. Proportion of different attributes considered in the multi-fidelity model papers reviewed, the charts are based on 157 papers.
Figure 3. Proportion of different attributes considered in the multi-fidelity model papers reviewed, the charts are based on 157 papers.
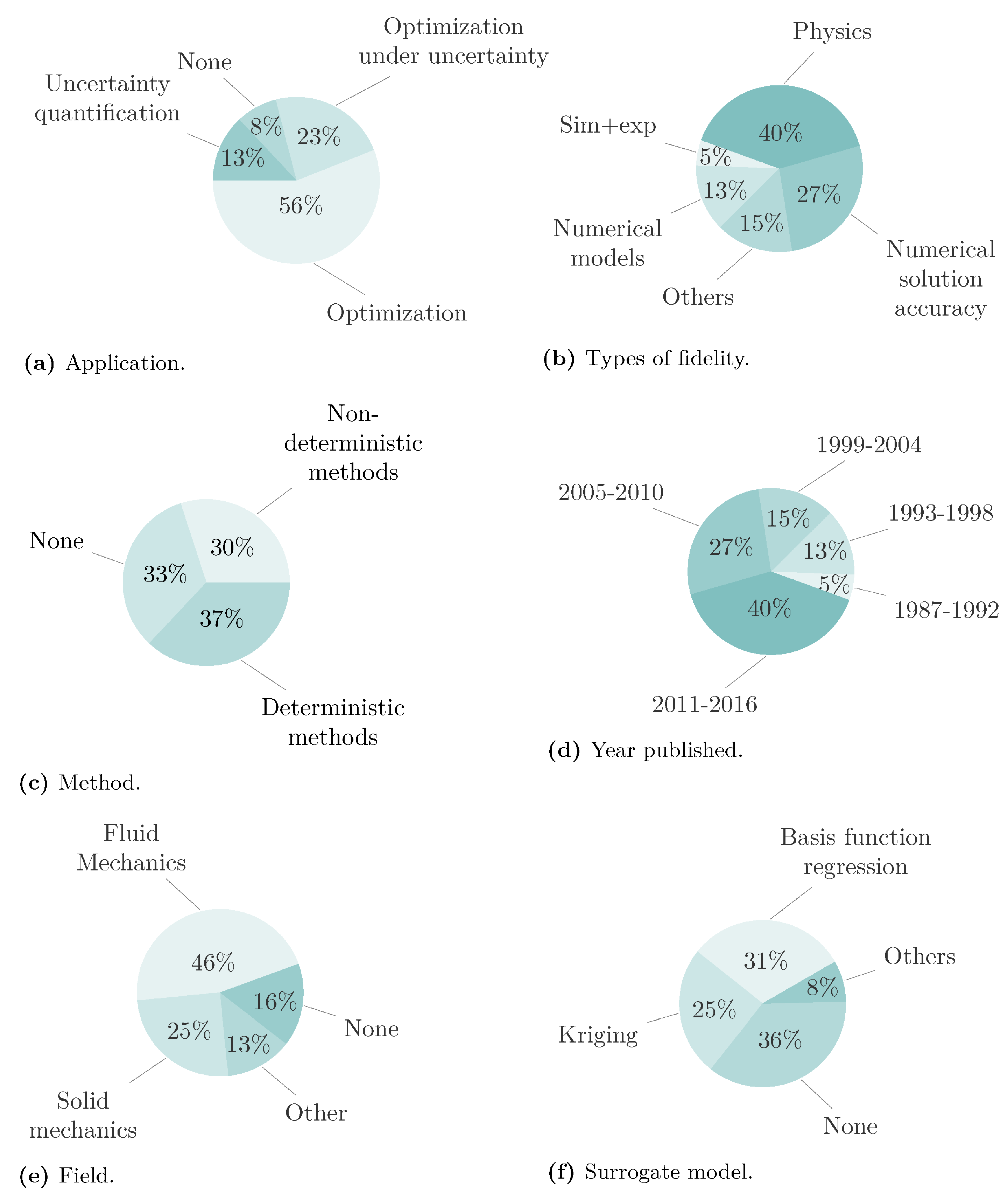
Preprints 72296 g003
Preprints 72296 g004
Figure 4. Main differences between fidelities found in the literature.
Figure 4. Main differences between fidelities found in the literature.
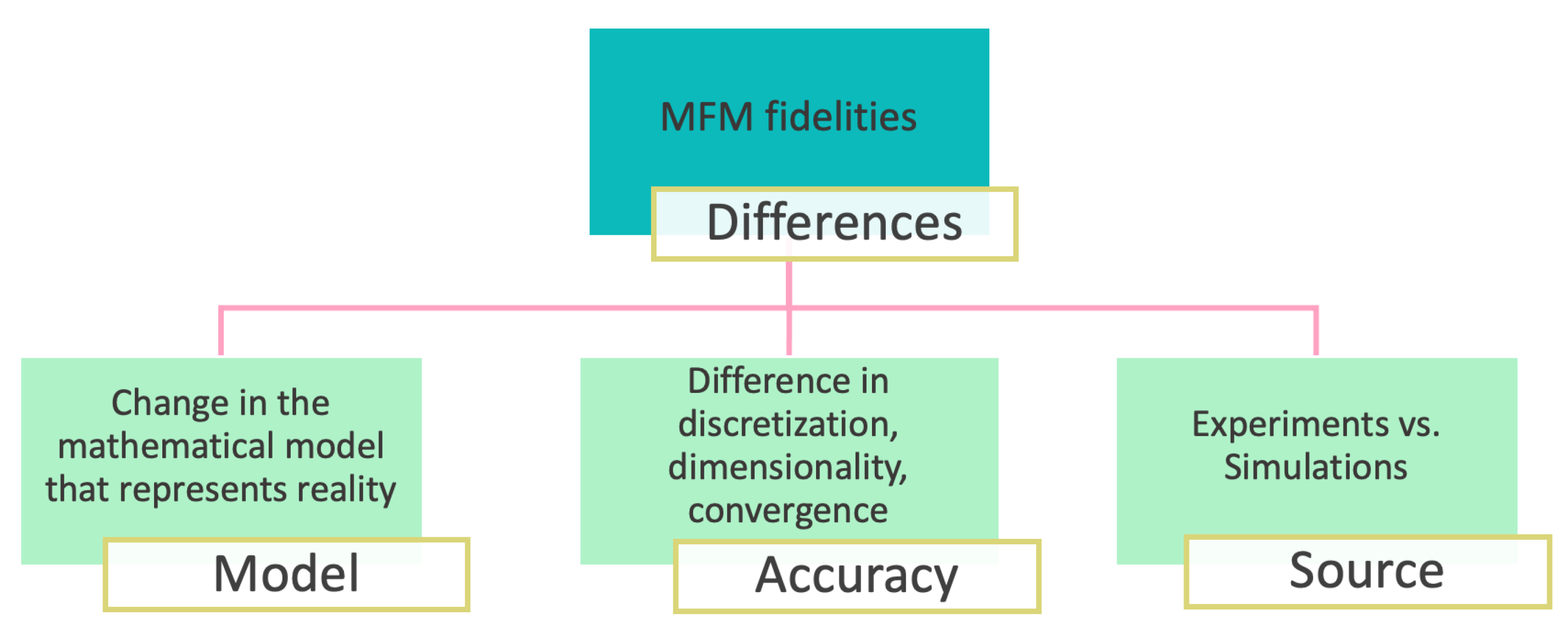
Preprints 72296 g004
Preprints 72296 g005
Figure 5. Among the 157 papers that were scrutinized, a total of 105 studies were found to have developed a multi-fidelity surrogate model that explicitly integrates the different levels of fidelities. The remaining papers, however, have introduced multi-fidelity hierarchical models.
Figure 5. Among the 157 papers that were scrutinized, a total of 105 studies were found to have developed a multi-fidelity surrogate model that explicitly integrates the different levels of fidelities. The remaining papers, however, have introduced multi-fidelity hierarchical models.
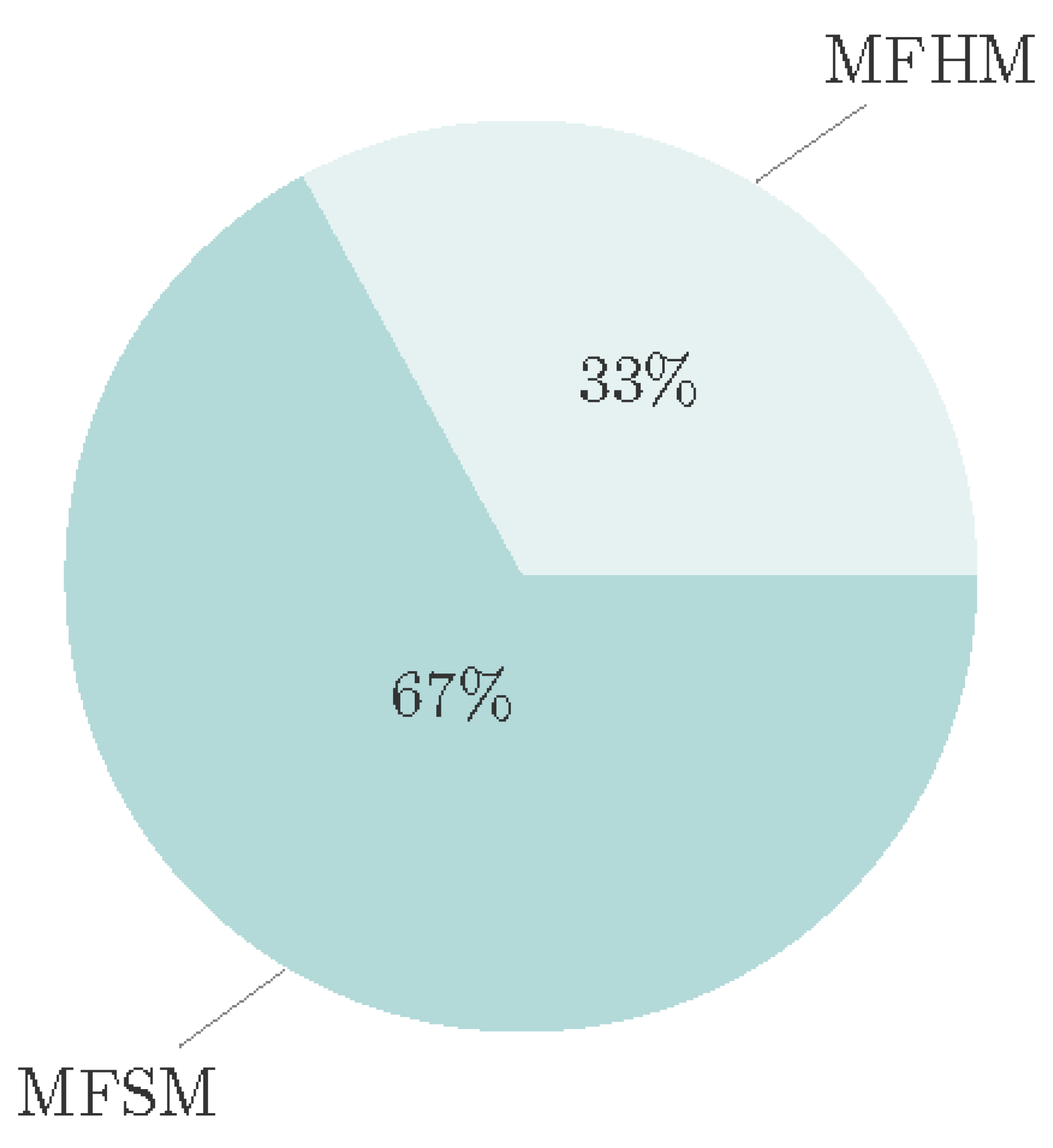
Preprints 72296 g005
Preprints 72296 g006
Figure 6. One-dimensional, analytic example that illustrates the performance of additive and multiplicative corrections.
Figure 6. One-dimensional, analytic example that illustrates the performance of additive and multiplicative corrections.
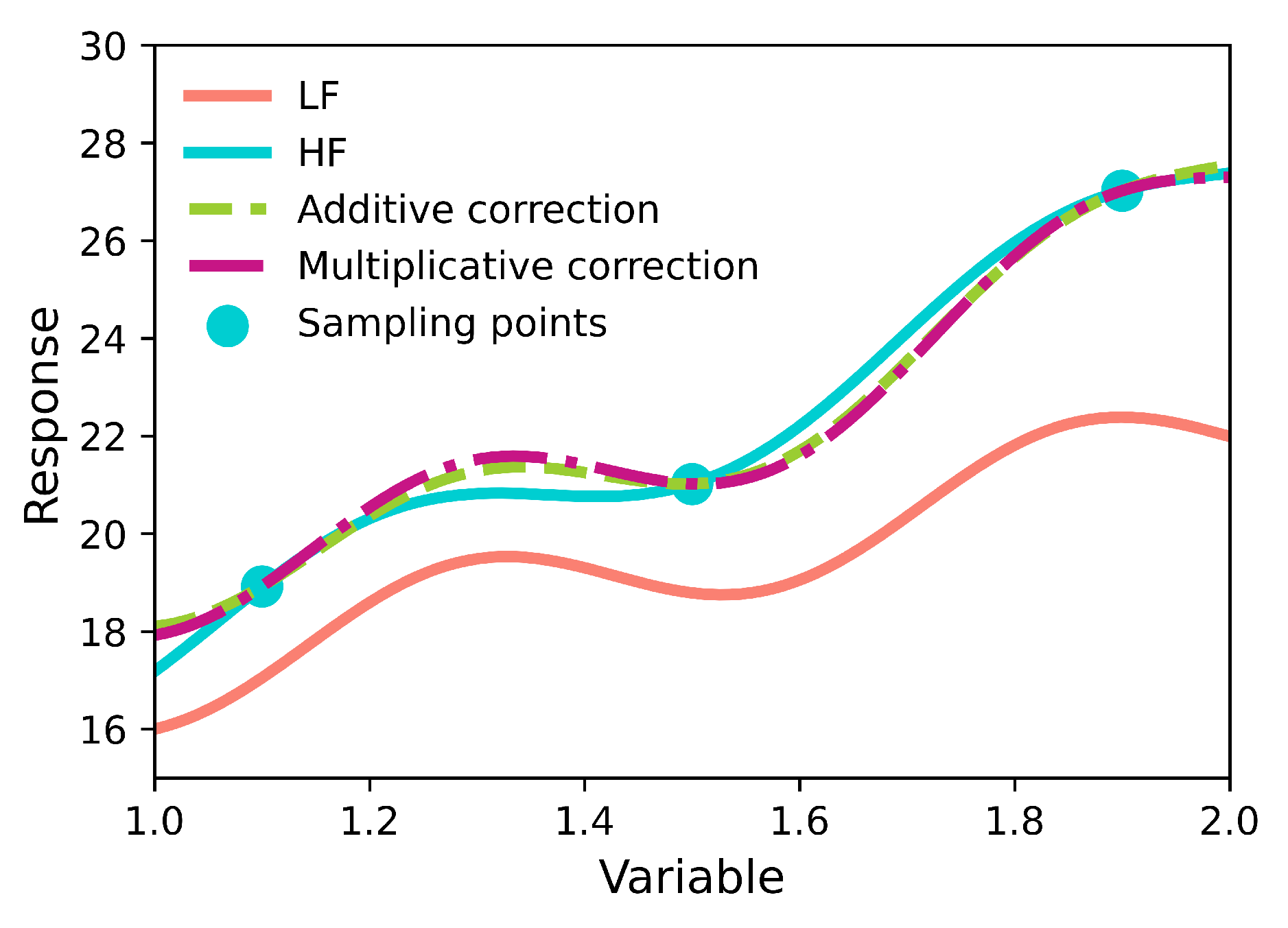
Preprints 72296 g006
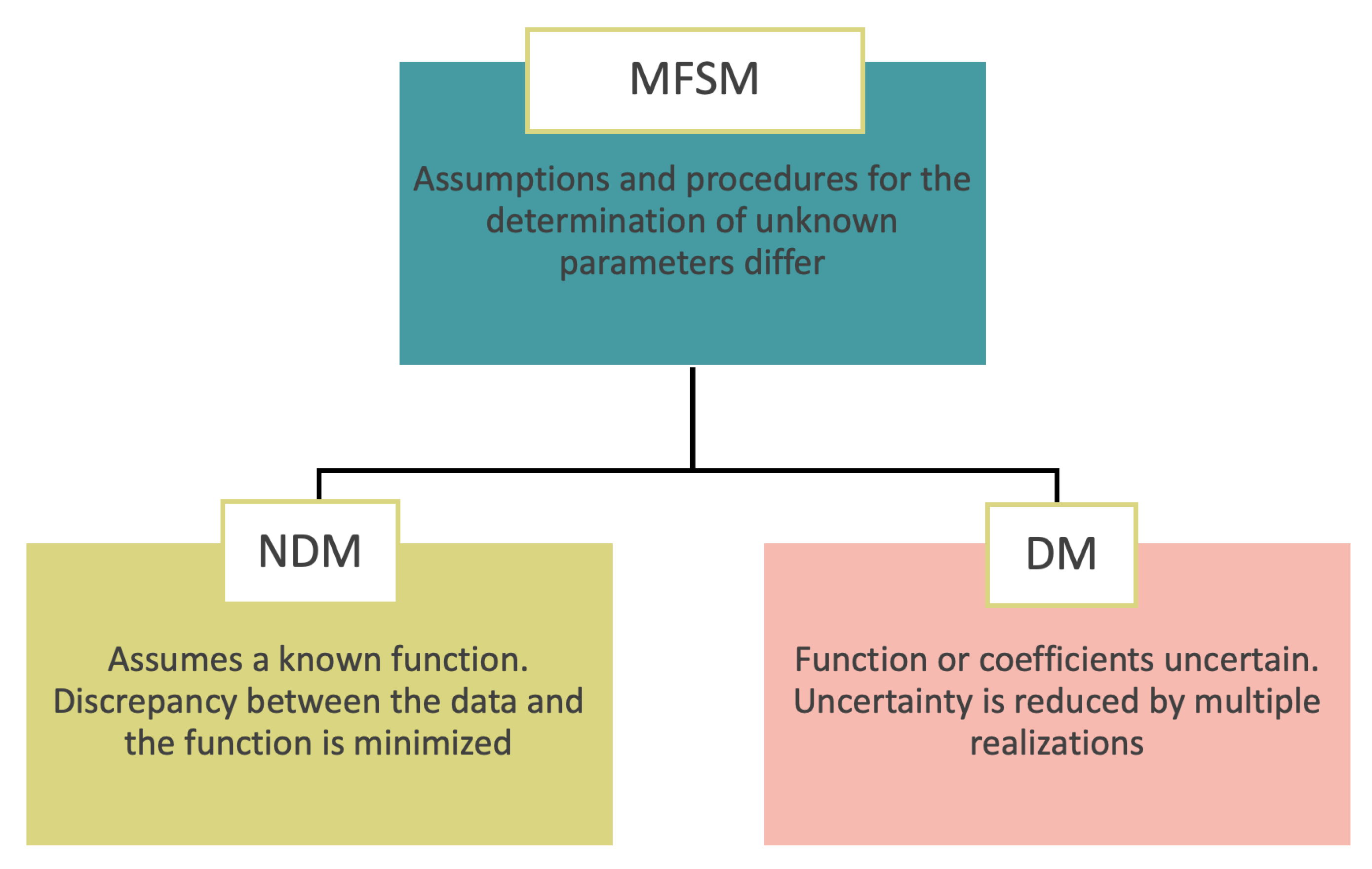
Preprints 72296 g007
Figure 7. Multi-fidelity surrogate models’ parameters are inferred utilizing either deterministic or non-deterministic methodologies contingent upon the underlying presumptions of the unknown parameters.
Figure 7. Multi-fidelity surrogate models’ parameters are inferred utilizing either deterministic or non-deterministic methodologies contingent upon the underlying presumptions of the unknown parameters.
Preprints 72296 g007
Preprints 72296 g008
Figure 8. Proportion of deterministic and non-deterministic methods utilized for the construction of multi-fidelity surrogate models based on the literature. The chart also displays the distribution of the combination methods introduced in Section 4.2 within each category, deterministic and non-deterministic methods.
Figure 8. Proportion of deterministic and non-deterministic methods utilized for the construction of multi-fidelity surrogate models based on the literature. The chart also displays the distribution of the combination methods introduced in Section 4.2 within each category, deterministic and non-deterministic methods.
Preprints 72296 g008
Preprints 72296 g009
Figure 9. Frequency of publication over time for both deterministic and non-deterministic methods.
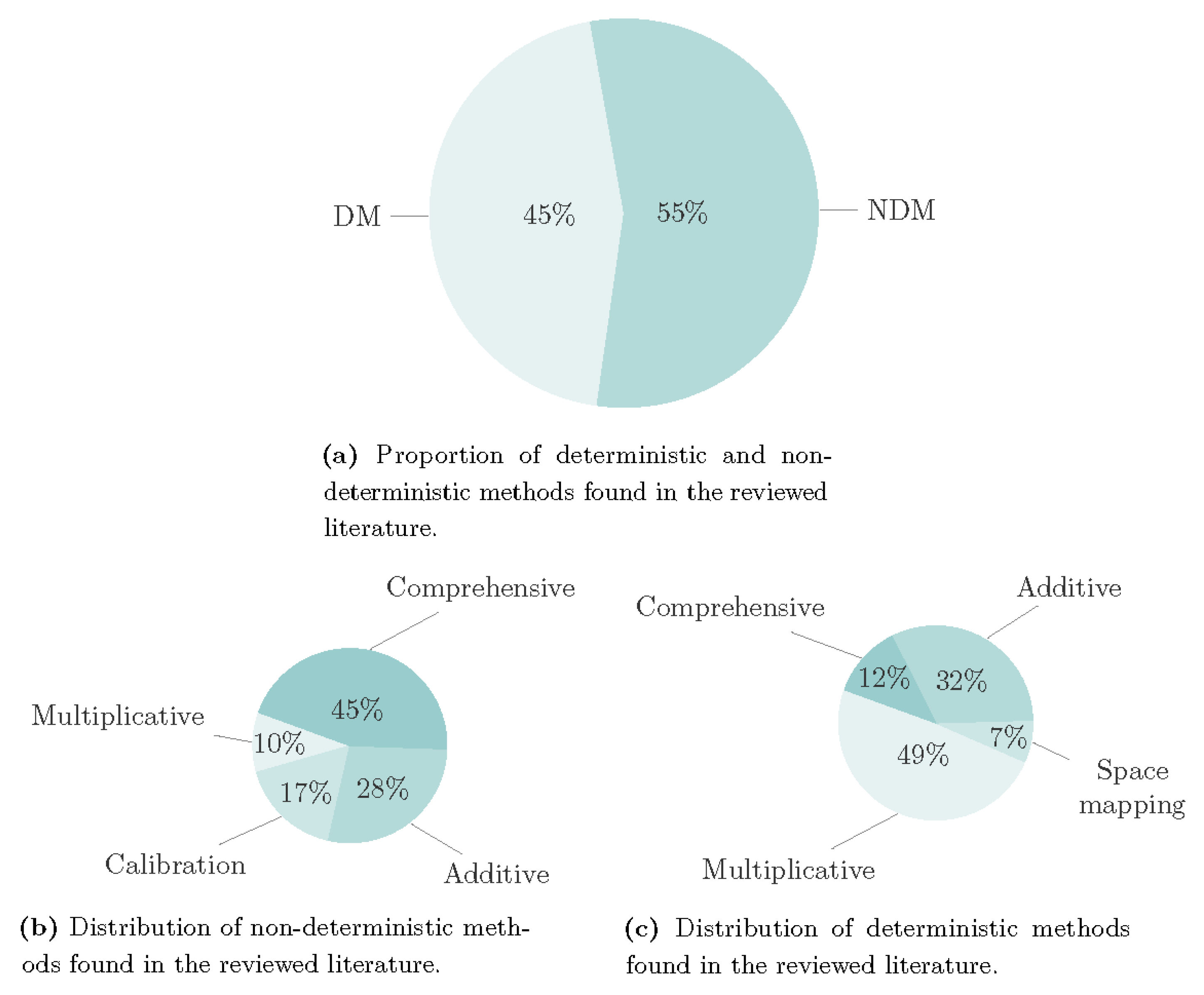
Figure 9. Frequency of publication over time for both deterministic and non-deterministic methods.
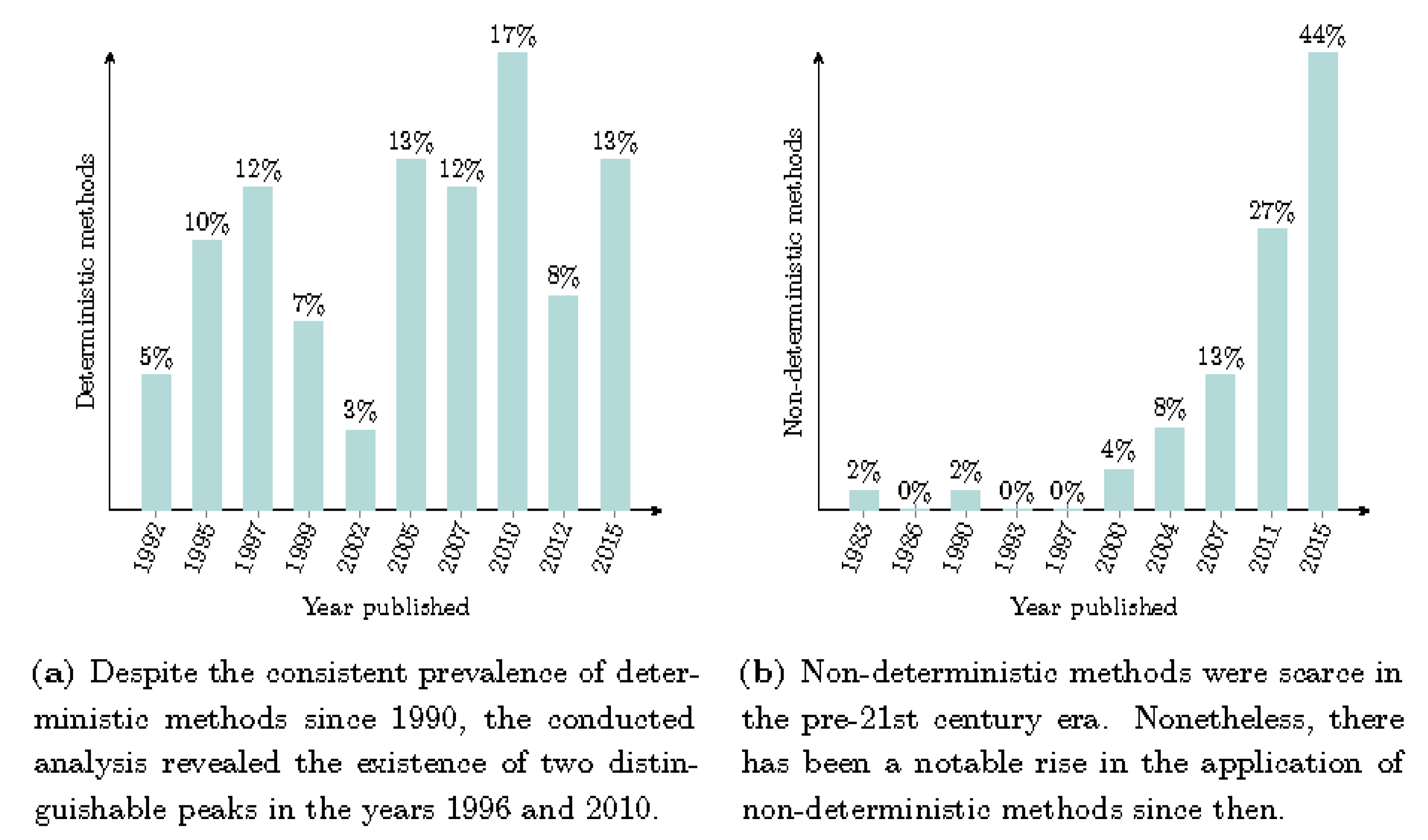
Preprints 72296 g009
Preprints 72296 g010
Figure 10. Cost ratio between a single analysis of the low-fidelity model and a single analysis of the high-fidelity model (LFA/HFA cost ratio) vs. cost ratio between the optimization process using an MFSM and the optimization process using an HFM (MFO/HFO cost ratio). The dashed line is the threshold line, below which the points indicate no speed ups from using multi-fidelity models.
Figure 10. Cost ratio between a single analysis of the low-fidelity model and a single analysis of the high-fidelity model (LFA/HFA cost ratio) vs. cost ratio between the optimization process using an MFSM and the optimization process using an HFM (MFO/HFO cost ratio). The dashed line is the threshold line, below which the points indicate no speed ups from using multi-fidelity models.
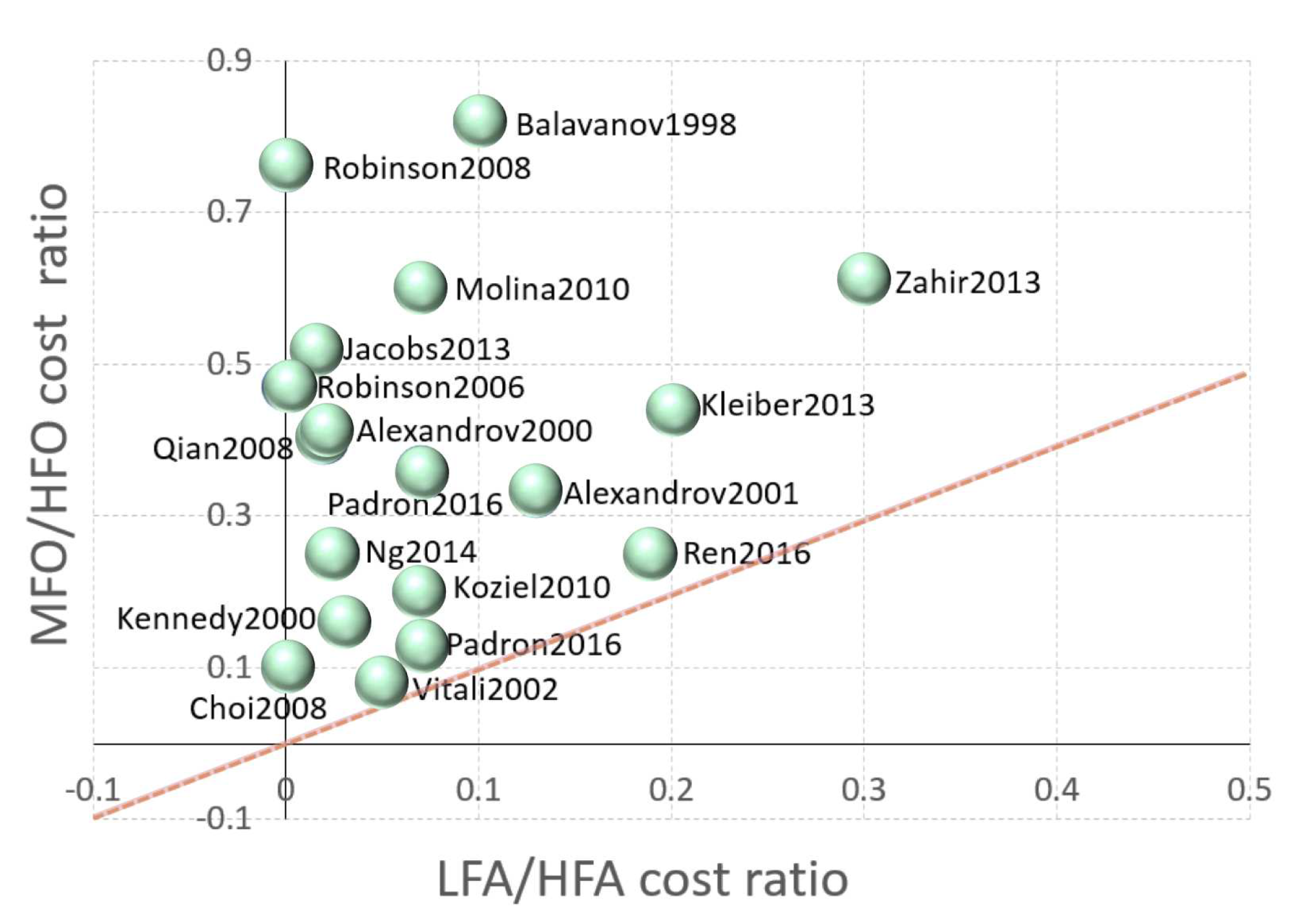
Preprints 72296 g010
Table 1. Categorization of fluid mechanics-focused papers based on the methodologies employed as high- and low-fidelity models. The analysis techniques used in these studies were analyzed and categorized into six distinct categories: analytical approach (An), empirical methods (Em), linear analysis (Li), potential flow models (PF), Euler analysis (Eu), and Reynolds-averaged Navier-Stokes techniques (RANS).
Table 1. Categorization of fluid mechanics-focused papers based on the methodologies employed as high- and low-fidelity models. The analysis techniques used in these studies were analyzed and categorized into six distinct categories: analytical approach (An), empirical methods (Em), linear analysis (Li), potential flow models (PF), Euler analysis (Eu), and Reynolds-averaged Navier-Stokes techniques (RANS).
Fluid mechanics
Reference An Em Li PF Eu RANS
[68] [179] LF - HF - - -
[7] [22] [26] [38] [57] [58] - LF HF - -
[129] [130] [138] [180] - LF - - - HF
[27] [46] [60] [94] [104] [121] [122] [141] [151] - - LF - HF -
[35] [43] [175] [204] [205] LF HF
[9] [85] [135] [191] - - - LF - HF
[3] [63] [72] [77] [140] [154] - - - LF HF
Table 2. Distinct types of fidelity implemented in research papers on fluid mechanics, which differ from those based on analysis type. The classifications include dimensionality (2D/3D), analysis resolution (coarse vs. refined), type of study (simulations vs. experiments), state of flow (transient vs. steady), and degree of solution convergence (semiconverged vs. converged). Each paper’s physical model is designated by the following abbreviations: Em (empirical), Li (linear), PF (potential flow), Eu (Euler), RANS (Reynolds-averaged Navier-Stokes), URANS (unsteady RANS), TM (turbulence method), MHD (magnetohydrodynamics), AE (aeroelastic equations), MPF (multiphase flow), and TM (thermomechanical equations).
Table 2. Distinct types of fidelity implemented in research papers on fluid mechanics, which differ from those based on analysis type. The classifications include dimensionality (2D/3D), analysis resolution (coarse vs. refined), type of study (simulations vs. experiments), state of flow (transient vs. steady), and degree of solution convergence (semiconverged vs. converged). Each paper’s physical model is designated by the following abbreviations: Em (empirical), Li (linear), PF (potential flow), Eu (Euler), RANS (Reynolds-averaged Navier-Stokes), URANS (unsteady RANS), TM (turbulence method), MHD (magnetohydrodynamics), AE (aeroelastic equations), MPF (multiphase flow), and TM (thermomechanical equations).
Fluid mechanics
Fidelity type Reference
Dimensionality [57] 2D/3D Eu, [82] 1D/3D RANS+TM, [85] 2D/3D URANS, [108] 2D/3D, [147] 1D/2D RANS, [158] 1D/2D Li, [178] 1D/3D RANS, [190] 1D/3D RANS, [207] 1D,2D/3D RANS
Coarse/Refined [5] Eu, [25] RANS, [34] Eu, [35] Eu, [36] Li/Eu, [83] RANS, [89] MPF, [92] MHD, [99] Eu, [100], Eu[103] Eu, [116] Eu, [120] RANS, [155] RANS, [173] RANS, [199] Eu/RANS
Exp./Sim. [53] Euler/MHD, [56] PF/Em, [105] RANS, [174] RANS
Semiconverged/Converged [83], RANS[100] Eu
Steady/Transient [20] AE, [62] Eu, [173] TM
Table 3. Categorization of papers within the domain of solid mechanics, according to the fidelity type employed in their analyses. The four fidelity types included are: analytical (An), empirical (Em), linear (Li), and non-linear (NL).
Table 3. Categorization of papers within the domain of solid mechanics, according to the fidelity type employed in their analyses. The four fidelity types included are: analytical (An), empirical (Em), linear (Li), and non-linear (NL).
Solid mechanics
Reference An Em Li NL
[165] LF - HF -
[181] [182] - LF HF -
[182] - LF - HF
[6] [8] [45] [78] [151] [161] [184] [187] - - LF HF
Table 4. Categorization of solid mechanics research papers according to the type of fidelity used. The fidelity categories are defined based on dimensionality (i.e., 2D/3D), degree of refinement (i.e., coarse vs. refined), and simplification of boundary conditions (i.e., infinite plate vs. finite plate). Each paper is associated with the corresponding model employed, with Li indicating the use of linear models and NL representing non-linear models.
Table 4. Categorization of solid mechanics research papers according to the type of fidelity used. The fidelity categories are defined based on dimensionality (i.e., 2D/3D), degree of refinement (i.e., coarse vs. refined), and simplification of boundary conditions (i.e., infinite plate vs. finite plate). Each paper is associated with the corresponding model employed, with Li indicating the use of linear models and NL representing non-linear models.
Solid mechanics
Fidelity type Reference
Dimensionality [111] 1D/2D Li, [113] 1D/3D, [124] 2D/3D, [125] 2D/3D Li, [166] 2D/3D Li, [168] 2D/3D NL
Coarse/Refined [12] Li, [21] NL, [23] Li, [24] NL, [31] Li, [114] Li, [123] Li, [169] NL, [170] NL, [189] Li, [197] Li, [198] Li
Boundary conditions [185] Li, [188] Li
Table 5. Papers that use deterministic methods for the construction of multi-fidelity surrogate models.
Table 5. Papers that use deterministic methods for the construction of multi-fidelity surrogate models.
Deterministic methods
Combining method Reference
Additive correction [12] [13] [27] [50] [67] [94] [141] [157] [159] [162] [165] [166] [170] [169] [177] [184] [188]
Multiplicative correction [4] [5][12] [13] [26] [27] [31] [67] [70] [74] [78] [86] [120] [125] [134] [157] [159] [165] [166] [170] [169] [177] [181] [182] [185] [187] [188] [189]
Comprehensive correction [48] [63] [91] [136] [160] [197] [198]
Space mapping [29] [83] [103] [154] [158]
Table 6. Papers that use non-deterministic methods to construct multi-fidelity surrogate models.
Table 6. Papers that use non-deterministic methods to construct multi-fidelity surrogate models.
Non-deterministic methods
Combining method Reference
Additive correction [21] [57] [72] [92] [122] [123] [144] [147] [151]
Multiplicative correction [33] [56] [121]
Comprehensive correction [7] [24] [25][58] [66] [77] [88] [89] [105] [110] [109] [111] [113] [115] [146] [172] [174] [196]
Calibration + comprehensive correction [19] [53] [75] [90]
Table 7. MFM/HFM cost ratio. The references are divided also per field, given by fluid mechanics, solid mechanics and other. Other includes electronics, aeroelasticity, thermodynamics and analytical functions.
Table 7. MFM/HFM cost ratio. The references are divided also per field, given by fluid mechanics, solid mechanics and other. Other includes electronics, aeroelasticity, thermodynamics and analytical functions.
MFM cost/HFM cost
Percentage Fluid mechanics Solid mechanics Other
0% - 20% [36] [140] [154] [137] [186] [89] [102] [144] [171]
21% - 40% [3] [5] [140] [172] [174] [28] -
41% - 60% [5] [92] [157] [159] [147] [79] [131]
61% - 80% [83] [94] [158] - [30] [199] [207]
81% - 90% - [12] [97]
Table 8. Padrón et al., 2016 [140] cost, savings and accuracy report as a model for authors.
Table 8. Padrón et al., 2016 [140] cost, savings and accuracy report as a model for authors.
Property Value a Comments
Cost LF/HF 0.07 a LF= Euler, HF= RANS
Error LF/HF 0.18 -
Cost MF/HF 0.13 a MF= 1 HF + 17 LF
Error MF/HF 0.05 -
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated