1. Introduction
Lightning disasters pose a significant threat to humanity and have been listed as "one of the ten most severe natural disasters" by the United Nations. In southern China, lightning disasters account for 82.98% of total disasters, and casualties constitute 82.94% of the total number of casualties [
1,
2]. The atmospheric electric field (AEF) is a fundamental parameter in atmospheric physics and atmospheric electricity [
3,
4]. Lightning activities are often accompanied by changes in AEF, which can be utilized for lightning warnings.
In recent years, research on lightning risk warnings based on AEF has rapidly progressed. Warning methods can be broadly divided into two categories: time-domain and frequency-domain. Time-domain methods typically employ the simple AEF threshold method for lightning risk warnings. However, these methods exhibit a low probability of detection (POD) and neglect the inherent physical characteristics of AEF. Furthermore, they fail to thoroughly explore the relationship between AEF characteristics and lightning [
5,
6]. In 2008, Murphy conducted a preliminary investigation of lightning warning using the threshold judgment method for AEF data [
7]. in 2009, Aranguren compared and analyzed the threshold method and the polarity reversal method, discovering that the first polarity reversal of AEF data was more effective in predicting lightning occurrence, with 47% accuracy [
8]; in 2015, Srivastava combined AEF data with the Markov model to achieve a POD of 66.45%, but the false alarm rate (FAR) reached 59.7%, rendering it unsuitable for practical application [
9].
Frequency-domain methods first employ spectral transform methods, such as Fourier transform, Hilbert-Huang transform (HHT), and short-time Fourier transform (STFT), to obtain features. Lightning warnings are then achieved by setting thresholds for these features. Although the warning effect has improved compared to time-domain methods, the application of AEF data remains insufficient [
10,
11]. In 2014, Kang demonstrated that AEF energy could be used as a characteristic of lightning risk warning via STFT [
12]; in 2016, Lu utilized HHT and observed that the high-frequency energy of AEF gradually increased during lightning events. A method for using energy for lightning risk warnings was also proposed [
13]. However, previous studies have failed to account for the impact of noise on the atmospheric electric field (AEF) [
14].
In this study, we address the noise of AEF and the low POD of existing methods by proposing a lightning risk warning method based on EEWT-ASG and Morpho. This method initially decomposes the AEF signal using EEWT-ASG to minimize the noise component, then extracts time-domain and frequency-domain features employing Wavelet transform (WT), and ultimately achieves lightning risk warning by setting thresholds for the features and Morpho-based trend calculation. Compared to using time-domain or frequency-domain features, the POD of warning is improved, and both MAR and FAR are reduced.
The remainder of this paper is organized as follows.
Section 2 describes the EEWT-ASG and global trend calculations based on Morpho.
Section 3 analyzes the time-frequency spectrum of the AEF for the lightning process.
Section 3 analyzes the time-frequency spectrum of the AEF for both lightning and non-lightning events. Finally,
Section 5 summarizes and discusses this study and provides a plan for future work.
2. Method
In this section, we introduce two approaches for lightning warning scenarios, aimed at mitigating the impact of noise and augmenting the generalizability of the lightning risk warning methodology.
2.1. EEWT-ASG
In 2021, Yang emphasized the importance of denoising for the study of AEFs and proposed a complementary ensemble empirical mode decomposition with adaptive noise and a Savitzky-Golay filter (CEEMDAN-SG) for AEF noise reduction [
14]. However, CEEMDAN, being an iterative signal decomposition method, demands a considerable amount of time to process intricate signals [
15], rendering it unsuitable for real-time warning requirements. In 2013, Gilles presented an empirical Wavelet transform (EWT) [
16], which offers faster processing than empirical mode decomposition (EMD). Nevertheless, the challenge with EWT lies in executing spectrum segmentation. Although Gilles proposed several solutions to this issue [
17], these methods still led to excessive spectrum segmentation, resulting in redundancy in the decomposition outcomes. In 2017, Hu investigated Gilles’ spectrum segmentation methods and introduced an enhanced empirical Wavelet transform [
18].
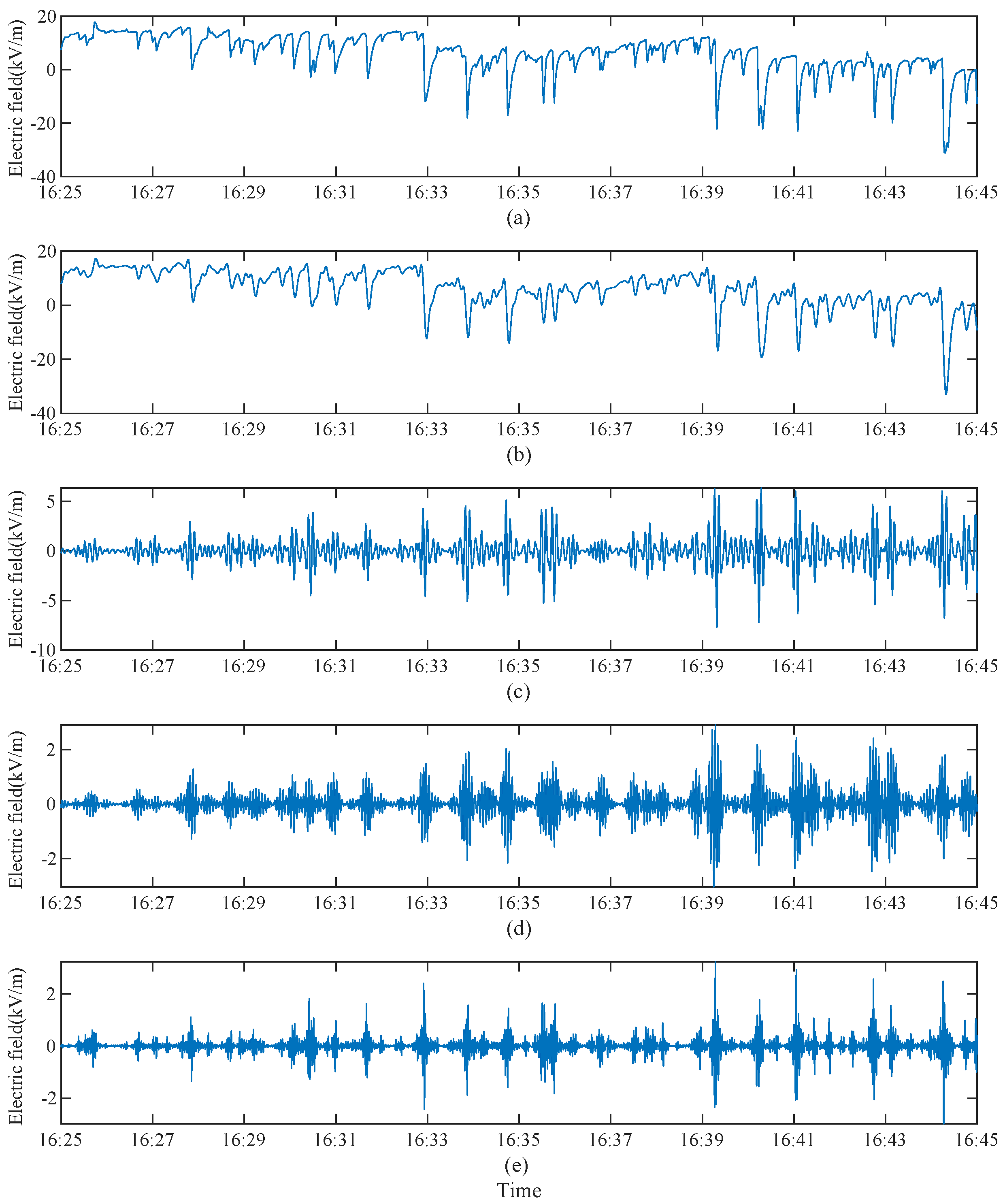
In this study, we employed EEWT to carry out the decomposition of AEF signals, with the decomposition outcomes displayed in
Figure 1. It is evident that the original AEF signal is partitioned into four modes, each displaying a progressively increasing frequency. We designated the AEF signal and the decomposed
k component signals as
and
,
, respectively, which maintain the following relationship:
Indeed, the value of
k is dictated by the inherent complexity of the processed AEF signal, which stems from the adaptive spectral analysis performed by the EEWT. The more intricate the frequency components of the AEF signal, the greater the number of decomposed modes. In order to ascertain whether each component contained noise, we employed an autocorrelation analysis, inspired by Yang, to make this determination[
14]. We computed the normalized autocorrelation function of
as follows:
At this time, the normalized autocorrelation function for all components can be obtained as :
Furthermore, the normalized autocorrelation function of the ideal Gaussian white noise was computed and denoted as
. Subsequently, the Pearson correlation coefficient [
19] was employed to gauge the similarity between
and
, as follows:
Figure 1.
The modes extracted by EEWT are displayed, with (a) representing the original signal and (b) through (e) illustrating the decomposition modes.
Figure 1.
The modes extracted by EEWT are displayed, with (a) representing the original signal and (b) through (e) illustrating the decomposition modes.
Among them,
and
denote the covariance and standard deviation, respectively. The range of
is between -1 and 1.
closer to 1 means that the correlation between
and
is better, then the more probable that
contains noise. In this study, the component signal
that contains noise is defined as follows:
An Adaptive Savitzky-Golay (ASG) filter is employed for
to smooth it [
20]. The ASG filter addresses the issue of selecting two key parameters in the SG filter: the size of the data window and the polynomial degree. If the data window is excessively wide, it may result in the loss of valuable information in the signal. Conversely, if the data window is too narrow to effectively filter the signal, opting for a large polynomial degree might introduce new noise, while selecting a small polynomial degree could cause distortion due to oversmoothing of the signal [
14,
21]. Given that the AEF signal is non-stationary, fixing both the data window size and the polynomial degree in signal smoothing could lead to the loss of original information in the signal. In [
14], Xu utilized an SG filter to address the noise in AEF and set the polynomial degree and data window size to 3 and 7, respectively. Building on Xu’s work, we adopted a polynomial degree of 3 and employed the G-FL scheme to dynamically adjust the data window size [
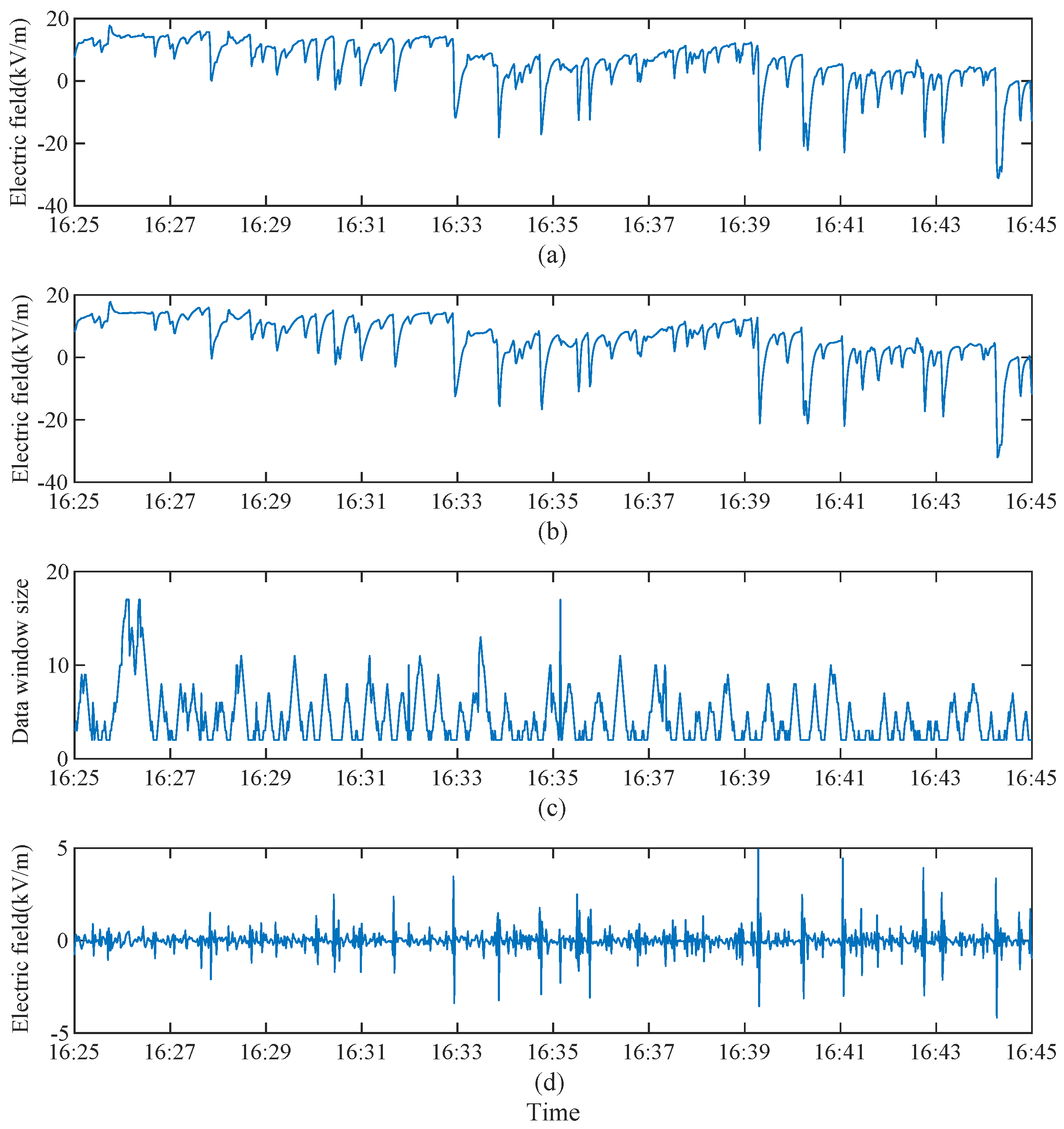
20]. The denoising results are depicted in
Figure 2.
Figure 2.
The denoising results of EEWT-ASG are presented, with (a) representing the original signal, (b) illustrating the denoised signal, (c) depicting the dynamic adjustment of the data window size using the G-FL scheme, and (d) showcasing the noisy signal.
Figure 2.
The denoising results of EEWT-ASG are presented, with (a) representing the original signal, (b) illustrating the denoised signal, (c) depicting the dynamic adjustment of the data window size using the G-FL scheme, and (d) showcasing the noisy signal.
2.2. Calculation of global trend based on Morpho
To delineate the global trend of the signal over time, drawing inspiration from Hu and Gilles’ trend computation [
18,
22], we put forth the following method to acquire the global trend based on Morphology.
Where
X is the data sequence and
is a sliding window of size
s. Euclidean distances between the local maxima of the data are calculated and denoted as
.
Prior to the Dilate and Erode calculations, data must undergo preprocessing using the mirror expansion method to ensure consistent data size [
18]. The results of Morpho are rectified through the following steps. Firstly, the first-order backward differentiation of
is calculated and denoted as
. Subsequently, the upward and downward regions in
are identified as:
Ultimately, the flat top is rectified based on the following three criteria:
Here, we calculate the global trend using equation (
13).
In equation (
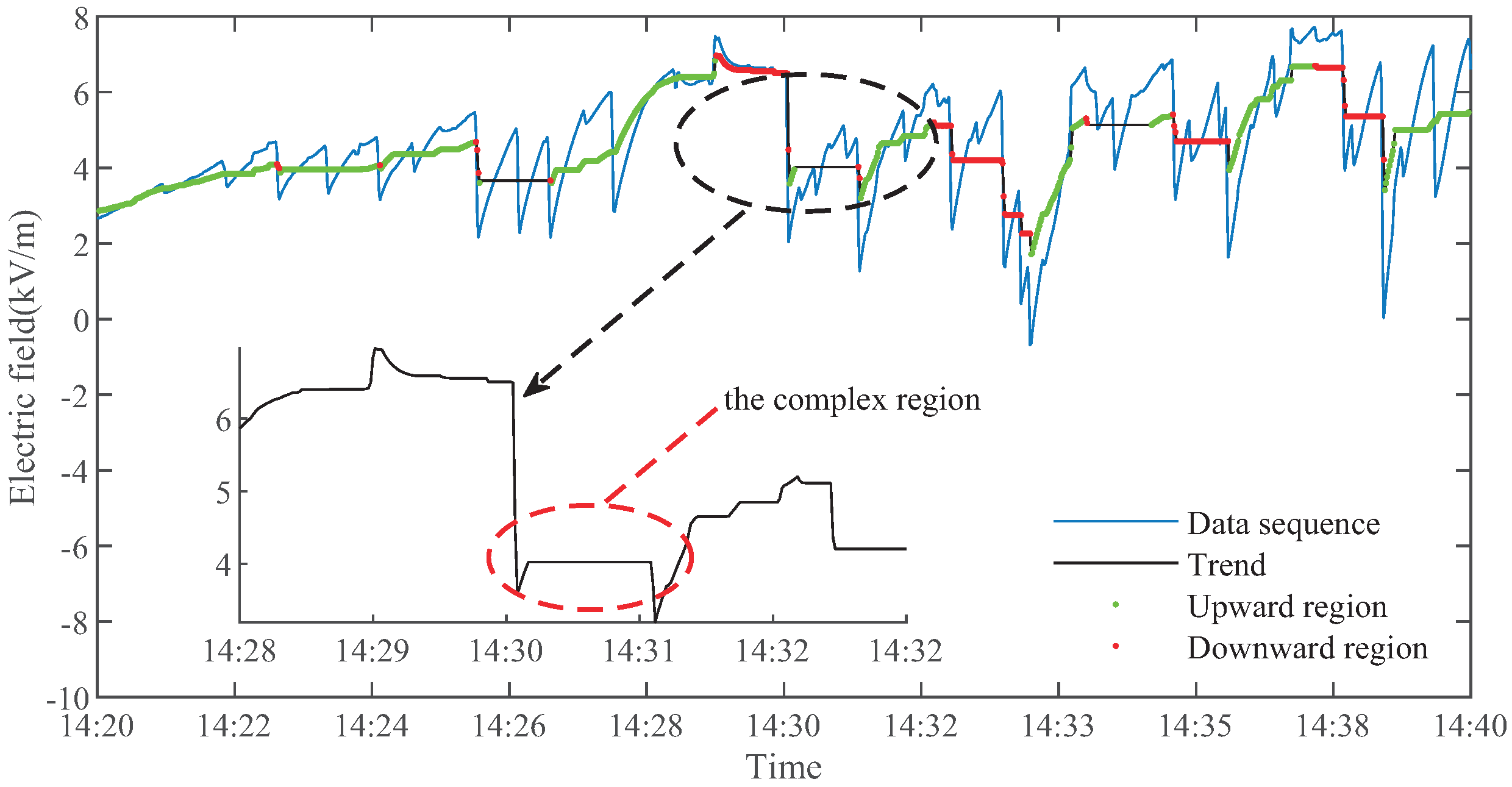
13), the global trend is represented as a ratio, which is subsequently assessed by establishing a threshold value. The selection of this threshold bears a direct influence on the efficacy of the global trend determination. We used the 22 days of lightning weather data analysed statistically in the next section and set the threshold to 0.6 by the 95th percentile method. The outcomes of the trend computations are illustrated in
Figure 3. The corrected upward (downward) trend range is depicted in green (red). By employing equation (
13), the signal in
Figure 3 is characterized as a global uptrend. This methodology provides a more holistic examination of the signal trend, as opposed to solely relying on slope for the determination of the global trend. Furthermore, the presence of a data window of size
s (equation (
8)) imparts partial resistance to interference, ensuring that substantial local signal fluctuations do not compromise the global trend determination.
Figure 3.
Global trend of the Morpho with rectification.
Figure 3.
Global trend of the Morpho with rectification.
3. Time-frequency spectrum feature statistics
The Atmospheric Electric Field (AEF) represents the magnitude of the electric field in the atmosphere at any given location and time. AEF changes are intimately connected to lightning activity, and lightning may occur when the AEF potential gradient reaches a breakdown value. Consequently, analyzing the AEF characteristics of a specific region is not only beneficial for understanding the AEF characteristics of lightning weather, but also plays a crucial role in lightning warning systems.
In this study, AEF data were obtained from a novel Microelectromechanical Systems (MEMS) Atmospheric Electric Field Meter (AEFM)[
23]. This device employs highly sensitive, low-power MEMS electric field sensor chip technology, fulfilling the requirements for real-time monitoring of lightning weather events[
24]. The AEFM was positioned atop the Guangzhou Tower at an elevation of 500 m (
). Considering the AEFM’s resolution for AEF measurements, we selected a total of 62 days of AEF data for statistical analysis, which included 22 days with lightning weather events and 40 days with non-lightning weather events. In the lightning weather cases, the initial cloud-to-ground (CG) flash locations were all within a 10 km radius of the AEFM.
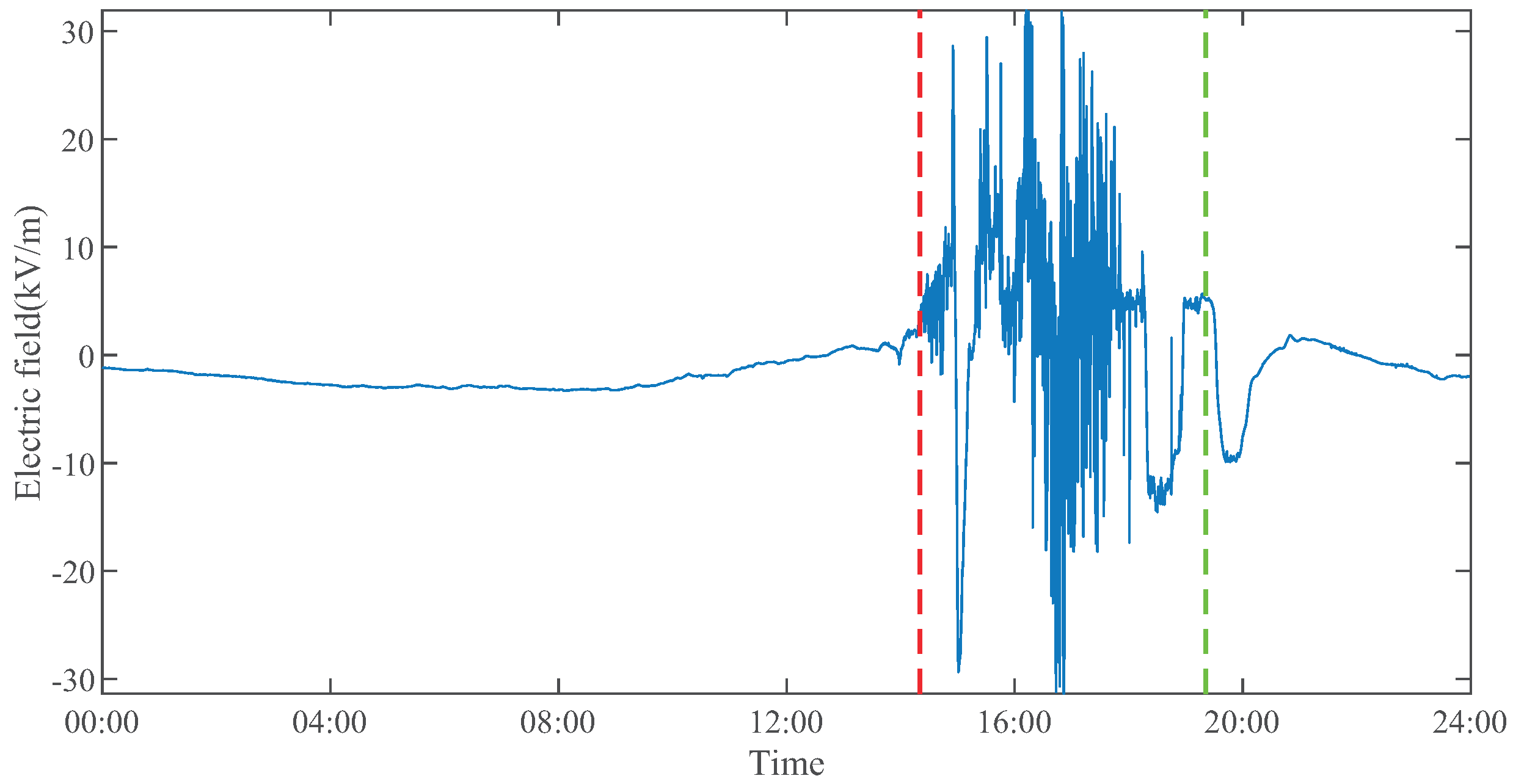
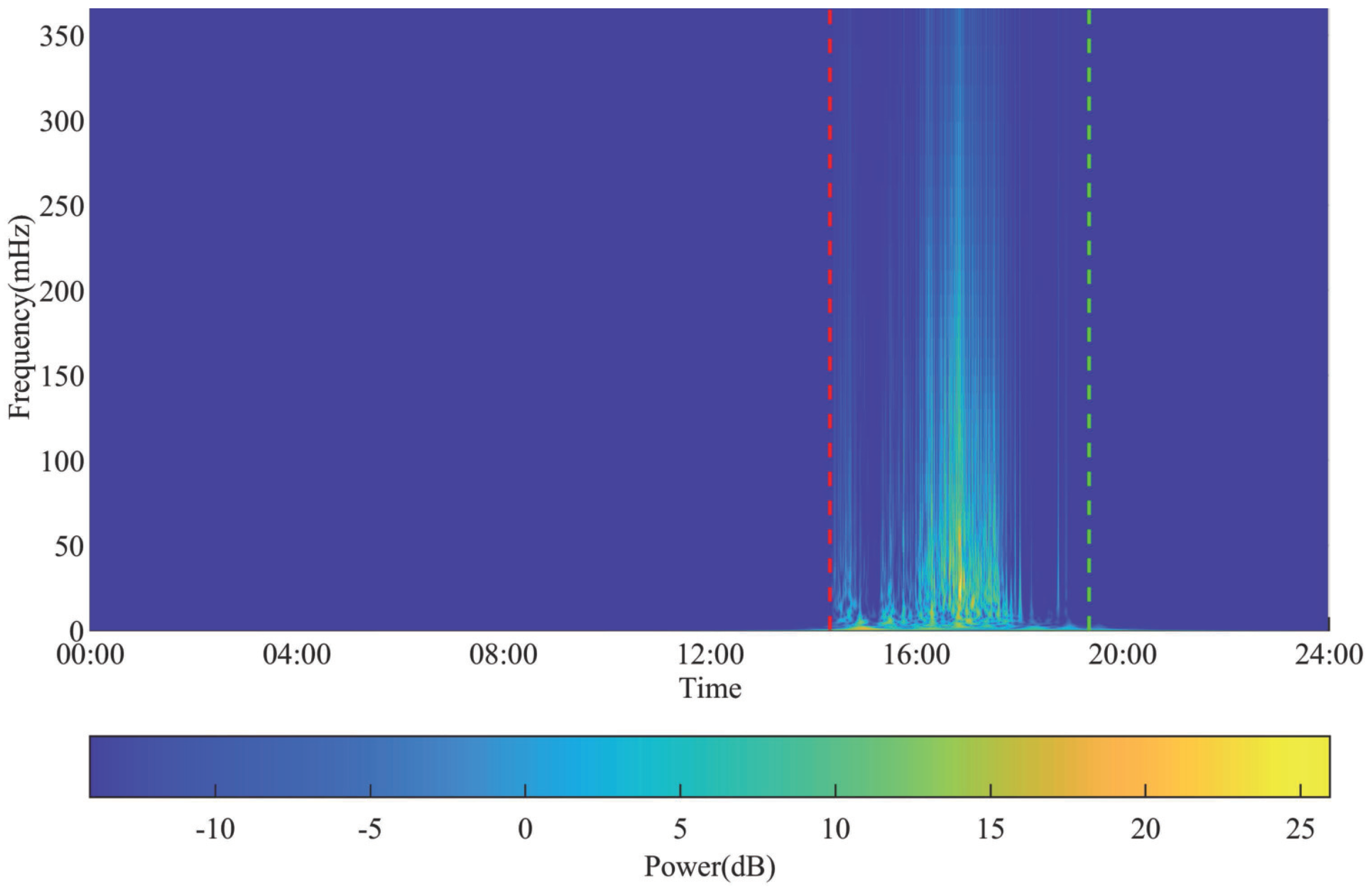
The variations in AEF and frequency spectrum during the lightning event are depicted in
Figure 4 and
Figure 5, respectively. The red and green dashed lines represent the warning time and de-warning time as determined by the Guangdong-Hong Kong-Macau Lightning Location System (GHMLLS), respectively. In 2022, data from artificially triggered lightning experiments conducted by Yue were employed to assess the performance of the GHMLLS utilized in this study. The outcomes revealed that the detection efficiencies for artificially triggered lightning and strokes were 96% and 88%, respectively. The arithmetic mean, geometric mean, and median values of location error amounted to 279 m, 193 m, and 202 m, respectively[
25].
Figure 4.
The AEF changes during a lightning event.
Figure 4.
The AEF changes during a lightning event.
Integrating
Figure 4 and
Figure 5, it is evident that the AEF data exhibited significant fluctuations around the warning time (indicated by the red dashed line), accompanied by a substantial increase in the spectral bandwidth. Consequently, we employed the manually determined warning information as the benchmark and computed the spectral bandwidth
, energy difference
, and standard deviation
of the AEF data, as presented in
Table 1 and
Table 2, respectively.
Figure 5.
Time-frequency spectrum of AEF by WT for a lightning event.
Figure 5.
Time-frequency spectrum of AEF by WT for a lightning event.
Table 1.
Spectral Bandwidth and STD statistical results of lightning and non-lightning processes.
Table 1.
Spectral Bandwidth and STD statistical results of lightning and non-lightning processes.
| Category |
Phase |
Period |
Index |
Average |
Range |
| min |
max |
| Lightning |
Warning |
Before |
|
5.51 |
0.02 |
14.46 [t] |
|
225.54 |
0 |
368.28 |
|
0 |
0 |
0 |
| STD |
1.80 |
0.21 |
6.93 [b] |
| After |
|
7.19 |
0.99 |
14.47 [t] |
|
222.83 |
62.65 |
341.84 |
|
0 |
0 |
0 |
| STD |
5.73 |
0.22 |
59.06 [b] |
| De-warning |
Before |
|
6.10 |
0.08 |
16.50 [t] |
|
212.06 |
13.88 |
368.28 |
|
0 |
0 |
0 |
| STD |
1.55 |
0.22 |
5.88 [b] |
| After |
|
3.79 |
0 |
10.89 [t] |
|
137.25 |
0 |
293.49 |
|
0 |
0 |
0 |
| STD |
1.59 |
0.18 |
6.77 [b] |
| Non-lightning |
|
|
|
0.01 |
0 |
2.64 [t] |
| |
|
|
0.24 |
0 |
144.30 |
| |
|
|
0 |
0 |
0 |
| |
|
STD |
0.06 |
0.01 |
4.80 [b] |
In
Table 1, the first-order backward differentiation of
is calculated and represented as
. Using 10 minutes of AEF data as the statistical length, we evaluated
,
,
and
under lightning and non-lightning conditions.
,
, and
represent the average, maximum, and minimum values of
, respectively. The lightning event was divided into four stages based on the warning information from the time flow: before the warning, after the warning, before the de-warning, and after the de-warning. From
Table 1, it is evident that
and
can effectively differentiate between lightning and non-lightning events, and they can be considered as features for lightning risk warning.
Table 2.
Statistical results of energy differences between warning and de-warning of the original AEF data, CEEMDAN-SG denoised data, and EEWT-ASG denoised data.
Table 2.
Statistical results of energy differences between warning and de-warning of the original AEF data, CEEMDAN-SG denoised data, and EEWT-ASG denoised data.
| Filter |
No Filter |
CEEMDAN-SG |
EEWT-ASG |
| Index |
Average |
Range |
Average |
Range |
Average |
Range |
|
12.96 |
5.33 |
38.08 |
12.23 |
4.07 |
34.94 |
12.48 |
4.07 |
34.97 |
|
27.89 |
17.01 |
57.07 |
16.14 |
16.14 |
51.82 |
27.82 |
17.79 |
52.20 |
|
1.91 |
0 |
16.72 |
2.18 |
0 |
17.21 |
2.07 |
0 |
17.48 |
|
13.54 |
5.89 |
30.82 |
12.77 |
5.11 |
28.87 |
13.8 |
5.52 |
28.40 |
|
34.36 |
20.98 |
59.54 |
31.95 |
22.23 |
54.56 |
37.39 |
25.06 |
54.77 |
|
0.75 |
0 |
5.68 |
1.20 |
0 |
8.69 |
1.03 |
0 |
9.13 |
In
Table 2, we denote the energy of the original AEF signal as
and the energy of the AEF signal with low-frequency components removed as
. Furthermore, we represent the warning and de-warning moments as
and
, respectively. The energy difference
is given by equation (
15). Similarly, we calculate the energy difference for
, denoted by
. For both
and
, we also calculate the average, maximum, and minimum values, which are denoted as
(
),
(
), and
(
), respectively.
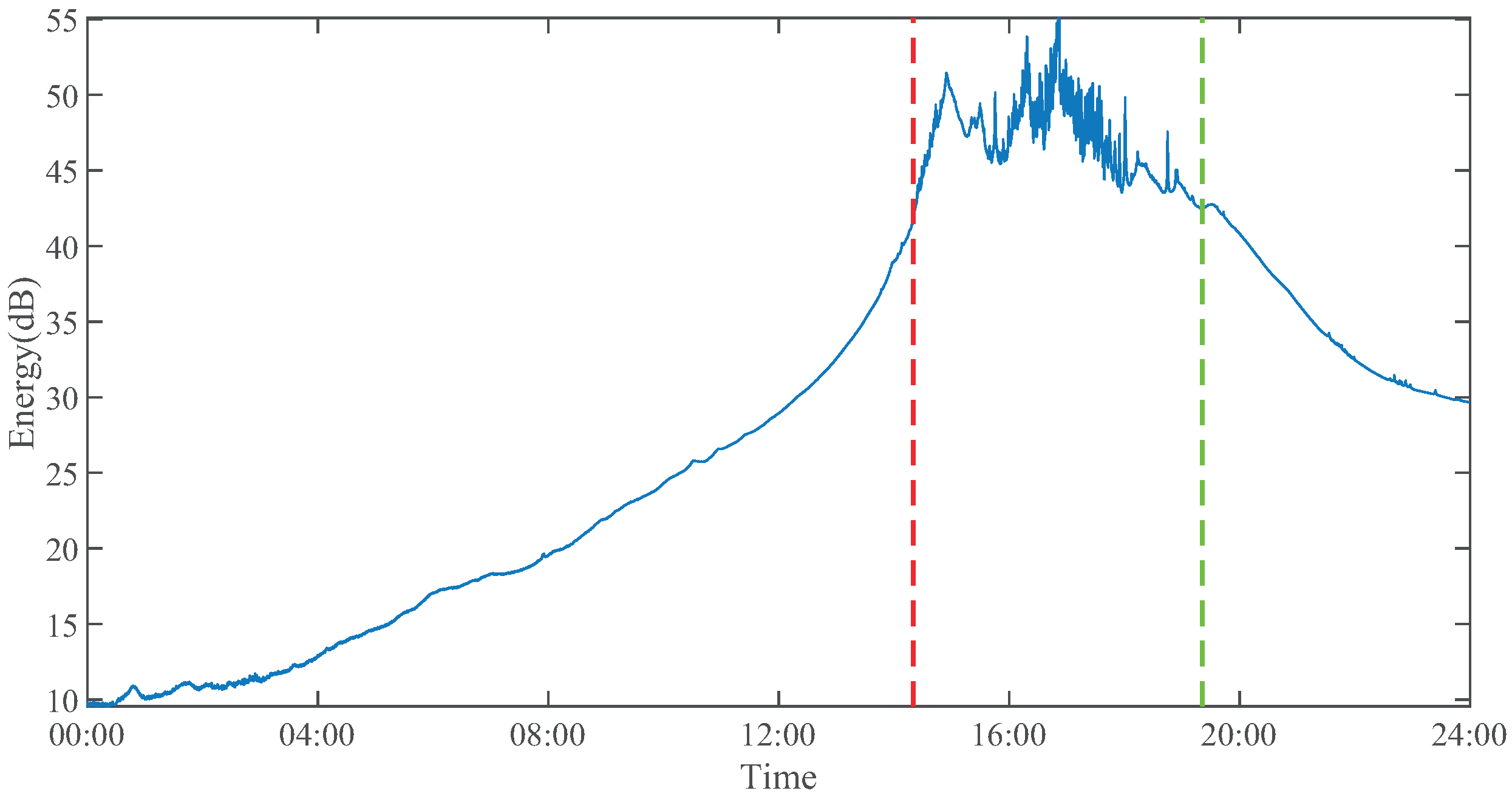
Combining
Table 2 and
Figure 6, it can be observed that the energy difference between
and
is very small. Meanwhile, owing to the slow fluctuation of the AEF (i.e., low-frequency signal) during the non-lightning process, we consider it as a disturbance in the lightning warning. After excluding the signal energy near the zero frequency,
was only approximately 1 dB; therefore, we chose
as the main feature for de-warning. Comparing the energy difference between the original and denoised signals, the ranges of
and
after denoising were reduced to different degrees.This indicates that the denoised AEF signal has a better energy correspondence between
and
, which has positive implications for lightning risk warning. The denoising effects of CEEMDAN-SG and EEWT-ASG were similar. In terms of time consumption, EEWT-ASG requires less time than CEEMDAN-SG.
Figure 6.
The AEF energy changes during a lightning process.
Figure 6.
The AEF energy changes during a lightning process.
4. Lightning risk warning method and evaluation
Building upon the time-frequency spectrum statistics for lightning and non-lightning events presented in
Section 3, we merge the two techniques from
Section 2 to develop a lightning risk warning method. Moreover, an evaluation of this risk warning method is provided to demonstrate its effectiveness.
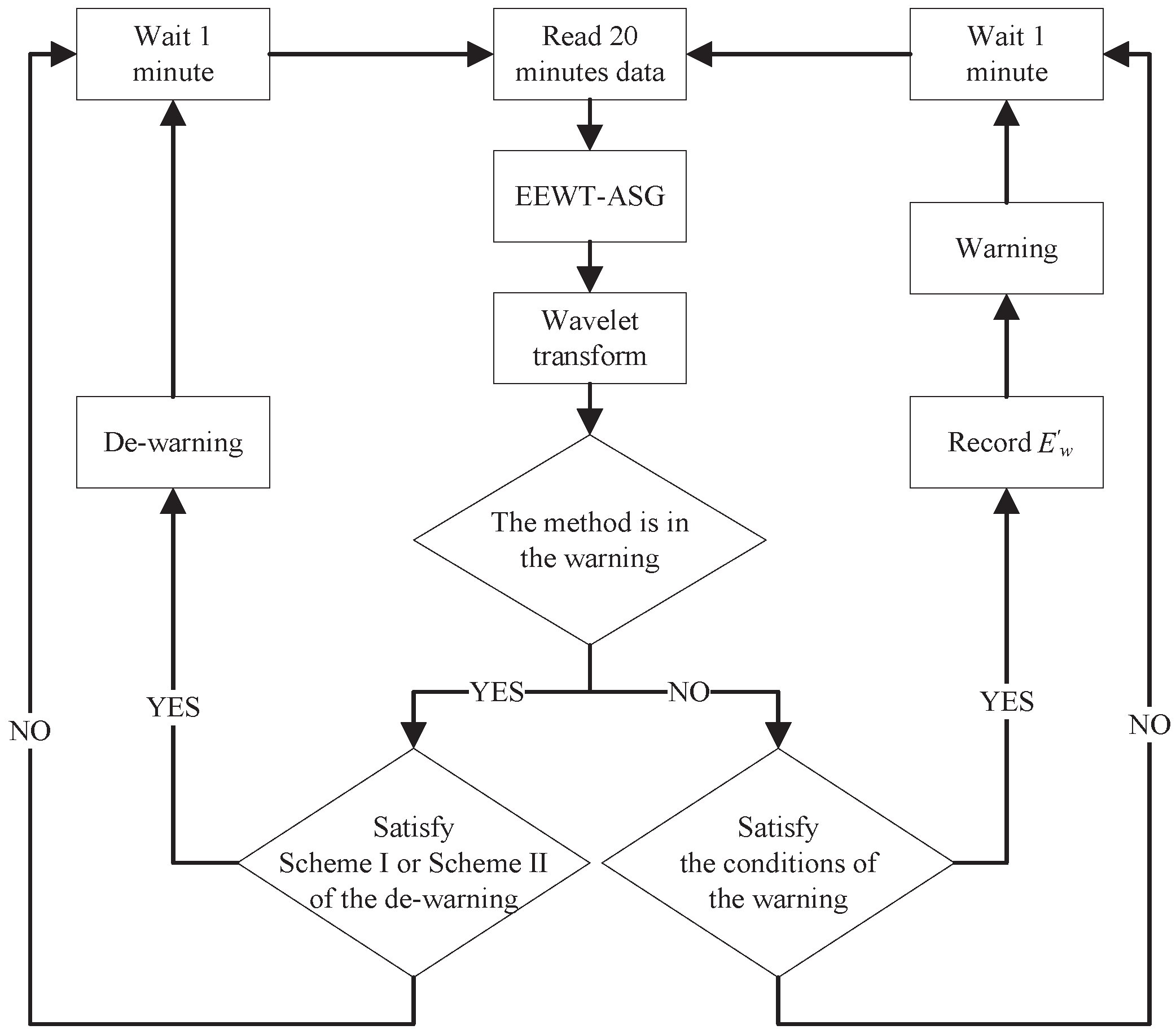
4.1. Lightning risk warning method based on AEF signal
The lightning risk warning method proposed in this paper consists of two components: warning and de-warning. The "global trend" referenced here is computed using the method detailed in
Section 2.2. The criteria for warning and de-warning are outlined below.
Warning conditions:
During the design of de-warning conditions, we found that relying solely on AEF energy at the moments of warning and de-warning led to inaccuracies in identifying the conclusion of a minor fraction of lightning events. To guarantee the smooth operation of the entire method, we devised an alternative Scheme II as a supplementary measure for the lightning risk warning method in cases where the de-warning signal is unable to be issued properly.
De-warning conditions:
Scheme I
Scheme II
In the Scheme I,
is the minimum value of
among the 10 judgments before the lightning risk warning method is judged as a warning.
changed with the value of
each time the lightning risk warning method was judged to be a warning state. A flowchart of the lightning warning method is presented in
Figure 7.
Figure 7.
Flow chart of the lightning risk warning method.
Figure 7.
Flow chart of the lightning risk warning method.
4.2. Evaluation metrics
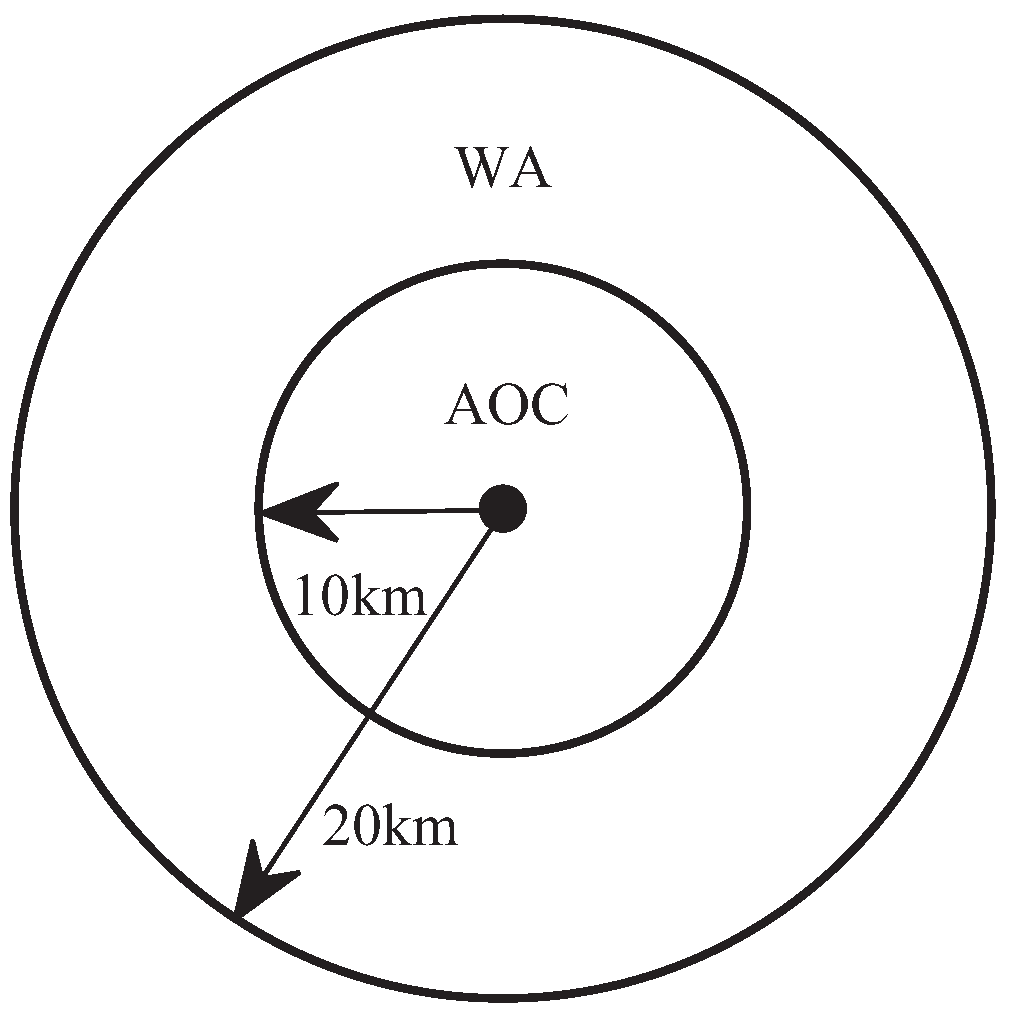
In accordance with the scholarly definitions of the Area of Concern (AOC) and Warning Area (WA) within the "Two Area Method" [
7,
26,
27], we establish the AOC and WA as illustrated in
Figure 8. Here, the circle’s center represents the location of the AEFM, while the AOC encompasses the area surrounding the AEFM that requires protection from lightning hazards. Additionally, the WA constitutes the outer region encircling the AOC.
To assess the performance of the warning behavior, we utilized five metrics: Probability of Detection (POD), Miss Alarm Rate (MAR), False Alarm Rate (FAR), Critical Success Index (CSI), and Mean Warning Lead Time (WLT). These metrics are represented by equations (
16), (
17), (
18), (
19), and (
20), respectively.
In these metrics, represents the number of effective alarms, referring to warnings issued prior to the first cloud-to-ground (CG) flash within a warning cycle. Conversely, denotes the number of failures to warn, which occur when warnings are either issued or absent after the first CG flash within a warning cycle. Additionally, signifies the number of false alarms, indicating the absence of a CG flash during a warning cycle. Lastly, and correspond to the time of the first CG flash as detected by the Guangdong-Hong Kong-Macau Lightning Location System (GHMLLS), and the warning time provided by the AEF-based lightning risk warning method, respectively.
Figure 8.
Configuration of AOC and WA.
Figure 8.
Configuration of AOC and WA.
4.3. Results and Analysis
We evaluated the lightning risk warning method proposed in this paper using AEF data with 83 lightning events, employing the evaluation metrics in
Section 4.2. In addition, using 123 days of AEF data for non-lightning events, we employed POD to evaluate the performance of the lightning risk warning method for non-lightning events. The statistical results are presented in
Table 3.
Table 3.
Statistics on the performance of different lightning risk warning methods.
Table 3.
Statistics on the performance of different lightning risk warning methods.
| Method |
Lightning |
Non-lightning |
| POD |
MAR |
FAR |
CSI |
WLT/min |
POD |
| EFAI [28] |
18.07% |
81.93% |
80.52% |
0.11 |
19.19 |
42.61% |
| EFDI [28] |
91.57% |
8.43% |
60.00% |
0.38 |
32.48 |
80.00% |
| Lu [13] |
18.07% |
81.93% |
70.59% |
0.13 |
10.04 |
98.26% |
| We proposed |
77.11% |
22.89% |
40.19% |
0.51 |
22.27 |
90.24% |
In
Table 3, we compare our proposed method with previous studies in the literature [
13,
28]. It was found that the EFDI method had the highest Probability of Detection (POD) during lightning events, but its False Alarm Rate (FAR) reached 60.00%, indicating low reliability [
29]. Lu’s method had the highest POD of 98.26% during non-lightning events, but it performed poorly with a POD of 18.07% during lightning events and failed to meet the warning goal. Our proposed method achieved the lowest FAR (40.19%) and highest Critical Success Index (CSI) (0.51) among the four methods during lightning events, while maintaining a reasonable POD. Additionally, our method also had a high POD (90.24%) during non-lightning events, although it was lower than that of Lu’s method. We also visualized the warning lead time of the warning methods in this paper (
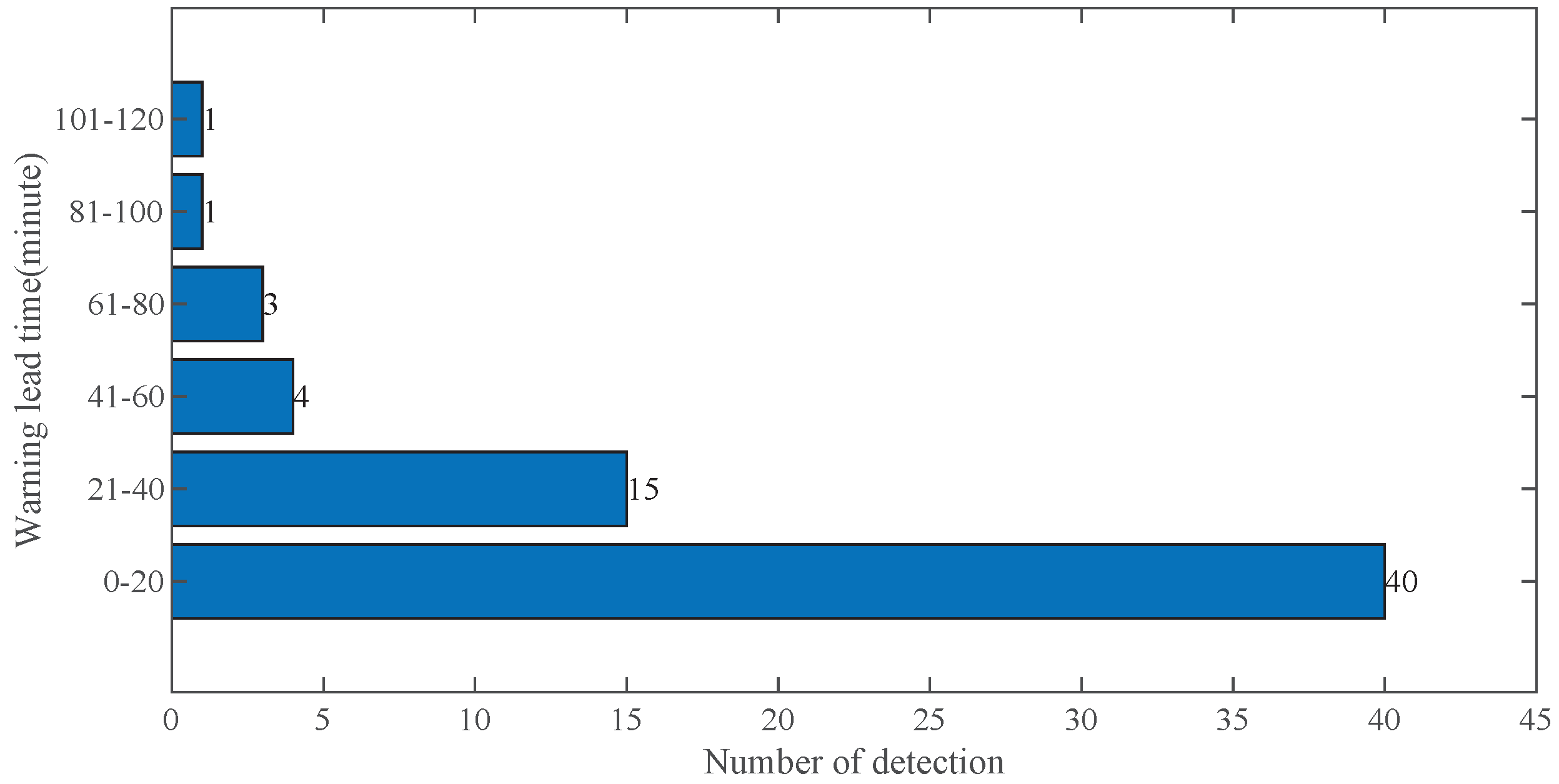
Figure 9), and it can be seen that the warning lead times are mostly within the range of 0 to 20 minutes.
Figure 9.
The distribution of warning lead time.
Figure 9.
The distribution of warning lead time.
5. Discussions and conclusions
Lightning risk warnings play a crucial role in safeguarding critical infrastructure, sensitive equipment, and various facilities from the impact of lightning strikes. In this paper, we propose a lightning risk warning method specifically tailored for the Guangzhou Tower in China, which is capable of automatically deactivating for a set period following a lightning event. The key contributions of this study can be summarized as follows:
(1) We introduced the EEWT-ASG and morpho-based global trend calculation methods, specifically designed for lightning warning scenarios.
(2) Employing Wavelet Transform (WT), we conducted a statistical analysis of the time-frequency spectral characteristics for both lightning and non-lightning events.
(3) We proposed a lightning risk warning method that utilizes features from both time and frequency domains.
In this paper, we analyze the time-frequency spectral characteristics of lightning and non-lightning events in
Section 3. Building on the results from
Section 3, we create a lightning risk warning method in
Section 4, using both techniques described in
Section 2. Additionally, we provide an evaluation of this risk warning method.
Table 1 demonstrates that
and
can effectively distinguish between lightning and non-lightning events, making them suitable for use as warning features.
For de-warning, we observe similar energy magnitudes in the AEF signal at both warning and de-warning moments (
Figure 6), which is supported by the energy difference statistics presented in
Table 2. This finding reinforces our hypothesis that, as lightning develops, the AEF signal energy progressively concentrates in the high-frequency band and eventually returns to its pre-lightning value when the lightning process concludes.
Moreover, when calculating the AEF signal energy, we exclude the low-frequency components due to the presence of slow fluctuations (i.e., low-frequency signals) in the AEF during non-lightning events, which are considered as interference. To enhance the universality of the method, we also incorporated the calculation of one-dimensional morphological global trends into the warning method, reducing the reliance on thresholds.
From
Table 2, we can observe that the ranges of
and
decrease after denoising. This reduction in range enables the threshold to be triggered more efficiently for de-warning, indicating that denoising has a positive impact on lightning warning. When comparing the performance of CEEMDAN-SG and EEWT-ASG in terms of energy features, we can see that both methods yield similar results (
Table 2). However, their theoretical foundations differ: CEEMDAN is based on an iterative approach, while EEWT relies on mathematical spectrum segmentation. Consequently, EEWT-ASG achieves a faster processing speed than CEEMDAN-SG.
We evaluated the time required to process a 20-minute AEF signal using the two filters mentioned above, and the results demonstrated that EEWT-ASG can complete the smoothing operation more quickly (121.1 seconds for CEEMDAN-SG and 5.8 seconds for EEWT-ASG). Thus, EEWT-ASG is more suitable for lightning warning scenarios.
However, the proposed method has certain limitations that must be addressed. Firstly, it does not incorporate a function for classifying lightning risks and issuing warnings. Secondly, it is necessary to reduce the false alarm rate (FAR) further. Finally, as the AEFM is a passive detection device, it lacks positional information, which can result in some errors in the warnings issued. To overcome these limitations, we are considering incorporating radar information or multiple AEFM networks into the current setup to obtain the location information of thunderstorm cloud clusters, which can be used for their localization and lightning risk warning.Additionally, we plan to conduct a thorough study of the thresholds that have been set(equations (
5), (
13)), based on the AEF data collected in this paper, in order to further improve the proposed method.
Author Contributions
Conceptualization, Q.Y.; methodology, X.L., Z.Y.; validation, Q.Y., L.Y., Z.Y. and F.Z.; formal analysis, X.L., Q.Y., and F.Z.; investigation, Q.Y.; resources, Q.Y., L.Y.; data curation, Q.Y.; writing—original draft preparation, X.L., Z.Y.; writing—review and editing, X.L., L.Y., Q.Y., Z.Y. and F.Z.; visualization, Q.Y.; supervision, Q.Y.; project administration, Q.Y.; funding acquisition, Q.Y., L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Key Laboratory of South China Sea Meteorological Disaster Prevention and Mitigation of Hainan Province (Grant No SCSF202210).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Holle, R.L. A summary of recent national-scale lightning fatality studies. Weather, Climate, and Society 2016, 8, 35–42. [Google Scholar] [CrossRef]
- Yin, Q.; Liu, H.; Fan, X.; Zhang, Y.; Zhuang, Y.; Wang, F.; Du, H.; Huang, X.; Chen, S.; Chen, L. Lightning fatalities in China, 2009-2018. Journal of Agricultural Meteorology 2021, 77, 150–159. [Google Scholar]
- Bernard, M.; Underwood, S.J.; Berti, M.; Simoni, A.; Gregoretti, C. Observations of the atmospheric electric field preceding intense rainfall events in the Dolomite Alps near Cortina d’Ampezzo, Italy. Meteorology and Atmospheric Physics 2020, 132, 99–111. [Google Scholar] [CrossRef]
- Odzimek, A.; Baranski, P.; Kubicki, M.; Jasinkiewicz, D. Electrical signatures of Nimbostratus and Stratus clouds in ground-level vertical atmospheric electric field and current density at mid-latitude station Swider, Poland. Atmospheric Research 2018, 209, 188–203. [Google Scholar] [CrossRef]
- Hoeft, R.; Wakefield, C. Evaluation of the electric field mill as an effective and efficient means of lightning detection. International Aerospace and Ground Conference on Lightning and Static Electricity, National Interagency Coordinating Group, Atlantic City, NJ, US, 1992.
- Montanya, J.; Bergas, J.; Hermoso, B. Electric field measurements at ground level as a basis for lightning hazard warning. Journal of Electrostatics 2004, 60, 241–246. [Google Scholar] [CrossRef]
- Murphy, M.J.; Holle, R.L.; Demetriades, N.W. Cloud-to-ground lightning warnings using electric field mill and lightning observations. 20th international lightning detection conference, 2008, pp. 21–23.
- Aranguren, D.; Montanya, J.; Sola, G.; March, V.; Romero, D.; Torres, H. On the lightning hazard warning using electrostatic field: Analysis of summer thunderstorms in Spain. Journal of Electrostatics 2009, 67, 507–512. [Google Scholar] [CrossRef]
- Srivastava, A.; Mishra, M.; Kumar, M. Lightning alarm system using stochastic modelling. Natural Hazards 2015, 75, 1–11. [Google Scholar] [CrossRef]
- Ying, L.I.; Wang, Z.; XIAO. FFT analysis on atmospheric electric field and the applications in thunderstorm prediction. Journal of the Meteorological Sciences 2013, 33, 66–70. [Google Scholar]
- Xu, D.; Wang, Z.; Zeng, Q.; Xue, A. EMD Based Analysis of Atmospheric Electric Field Data. Meteorological Science and Technology 2013. [Google Scholar]
- Kang, H.; Liu, C.; Jiang, X. Weather Recognition Algorithm Based on the Characteristics of Atmospheric Electric Field Signal [J]. Computer Simulation 2014, 31, 312–315. [Google Scholar]
- Lu, Y.; Zhou, Z.; Gu, S.; Wu, D.; Guo, J.; Tao, H. Research on lightning warning method based on the characteristics of atmospheric electric field. 2016 33rd International Conference on Lightning Protection (ICLP). IEEE, 2016, pp. 1–5.
- Yang, X.; Xing, H.; Zhuang, L. A thunderstorm cloud point charge localization method based on CEEMDAN and SG filtering. IEEE Access 2021, 9, 17049–17059. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. 2011 IEEE international conference on acoustics, speech and signal processing (ICASSP). IEEE, 2011, pp. 4144–4147.
- Gilles, J. Empirical wavelet transform. IEEE transactions on signal processing 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Gilles, J.; Heal, K. A parameterless scale-space approach to find meaningful modes in histograms—Application to image and spectrum segmentation. International Journal of Wavelets, Multiresolution and Information Processing 2014, 12, 1450044. [Google Scholar] [CrossRef]
- Hu, Y.; Li, F.; Li, H.; Liu, C. An enhanced empirical wavelet transform for noisy and non-stationary signal processing. Digital signal processing 2017, 60, 220–229. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. The American Statistician 1988, 42, 59–66. [Google Scholar] [CrossRef]
- John, A.; Sadasivan, J.; Seelamantula, C.S. Adaptive Savitzky-Golay filtering in non-Gaussian noise. IEEE Transactions on Signal Processing 2021, 69, 5021–5036. [Google Scholar] [CrossRef]
- Muthusivagami, R. A survey on ECG signal denoising using S-transform and SG filtering. International Journal of Advanced Research 2020, 8, 332–336. [Google Scholar] [CrossRef]
- Gilles, J.; Tran, G.; Osher, S. 2D empirical transforms. Wavelets, ridgelets, and curvelets revisited. SIAM Journal on Imaging Sciences 2014, 7, 157–186. [Google Scholar] [CrossRef]
- Yang, P.; Peng, C.; Fang, D.; Wen, X.; Xia, S. Design, fabrication and application of an SOI-based resonant electric field microsensor with coplanar comb-shaped electrodes. Journal of Micromechanics and Microengineering 2013, 23, 055002. [Google Scholar] [CrossRef]
- Yang, P.; Chen, B.; Wen, X.; Peng, C.; Xia, S.; Hao, Y. A novel MEMS chip-based atmospheric electric field sensor for lightning hazard warning applications. 2015 IEEE SENSORS. IEEE, 2015, pp. 1–4.
- Zhang, Y.; Lu, W.; Chen, L.; Wu, B.; Qi, Q.; Ma, Y.; Zhang, Y.; Zheng, D.; Yan, X.; Meng, Q. Evaluation of GHMLLS Performance Characteristics Based on Observations of Artificially Triggered Lightning. Journal of Applied Meteorological Science 2022, 33, 329–340. [Google Scholar]
- Zhou, J.; Zeng, Q.; Shah, A.B.; Jiao, X. A lighting warning algorithm using electric filed mills network and lightning locating system. 2016 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD). IEEE, 2016, pp. 1631–1635.
- Li, X.; Hayawi, K.; Chen, Y.; Chang, S.Y.; Wen, H.; Ho, P.H.; Yang, L.; Yin, Q. False Data Injection Attack on Atmospheric Electric Field in Thunderstorm Warning. 2022 International Conference on Computing, Communication, Perception and Quantum Technology (CCPQT). IEEE, 2022, pp. 219–223.
- Zeng, Q.; Wang, Z.; Guo, F.; Feng, M.; Zhou, S.; Wang, H.; Xu, D. The application of lightning forecasting based on surface electrostatic field observations and radar data. Journal of Electrostatics 2013, 71, 6–13. [Google Scholar] [CrossRef]
- Cooper, M.A.; Holle, R.L. Reducing lightning injuries worldwide; Springer, 2019.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).