Prerpints.org logo
Preprint
Article

High Resolution Profiling the Turbulence in an Atmosphere Using UAVs Flight Logs

Altmetrics

Downloads

130

Views

54

Comments

0

This version is not peer-reviewed

Advances, Innovations and Applications of UAV Technology for Remote Sensing

Submitted:

30 April 2023

Posted:

01 May 2023

You are already at the latest version

Alerts
Abstract
Capabilities of hovering unmanned aerial vehicles (UAVs) in low-altitude sensing of atmospheric turbulence with high spatial resolution are studied experimentally. The experiment was carried out at the Basic Experimental Observatory of the V.E. Zuev Institute of Atmospheric Optics SB RAS. UAV findings are compared with objective data on the state of the atmosphere that were measured by acoustic anemometers installed at weather towers at altitudes of 4, 10, and 27 m. Profiles of atmospheric turbulence were recorded with three UAVs hovering at the same heights at a distance of 5 m from the anemometers. The behavior of the longitudinal and lateral wind velocity components is studied in the frequency band 0-10 Hz before and after one-minute smoothing, which reveals long turbulent wind gusts. The discrepancy between the UAV and anemometer data is analyzed. It is found that after smoothing, the discrepancy does not exceed 0.5 m/s in 95% cases. This value meets the requirements of the World Meteorological Organization for some applications in wind velocity measurements. The spectral and correlation analysis of the UAV and anemometer measurements is carried out. The profiles of the longitudinal and lateral scales of turbulence are examined based on the UAV data and are found to be in agreement with the anemometer data to a good accuracy.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

The traditional aviation faces the necessity to monitor atmospheric vortices with a size larger than 100 m that carry high kinetic energy. In contrast to the manned aviation, the stability of a light unmanned aerial vehicle (UAV) moving in the atmosphere can be affected by relatively weak turbulent inhomogeneities with a size within 10 cm or more. The atmospheric turbulence can result in UAV control loss, flying off the intended flight path or altitude, and rapid battery drain. Recent studies show that turbulence degrades the quality of drone images [1,2]. A swarm of quadcopters may experience communication problems in the presence of significant wind gusts [3]. Thus, the knowledge of the state of turbulence allows one to predict critical flight parameters such as attitude, altitude, speed, roll, pitch, yaw, and so on. It forms the basis for development of UAV stability standards in a turbulent atmosphere, as well as standards of micrometeorological turbulence data with high spatial resolution.
The development of these standards requires the use of modern methods for diagnosing turbulent vortex formations. An analysis of the modern diagnostic methods shows [4] that in the height range needed for low-altitude sensing (up to 500 m), there are no instruments that can be used for UAV navigation under adverse meteorological conditions and have a unique characteristic in terms of high spatiotemporal resolution. For example, sodars, radars, and lidars [5,6,7,8,9,10] provide high spatial resolution, but it is insufficient for diagnostics of small high-intensity vortices to provide for navigation of small UAVs.
The capability of small copter-type UAVs to hover at a required spatial point for a considerable time allows them to be used for solution of numerous scientific and practical problems related to the physics of a turbulent atmosphere with high spatiotemporal resolution. In addition to high spatiotemporal resolution, small copter-type UAVs have unique characteristics in such criteria as mass-dimensions, reliability, cost, as well as the capability to monitor turbulence at a territory with complex orography, such as an urban environment and various types of natural landscapes (rugged terrain cut by rivers, ditches, woodlands, etc.). Thus, the development and creation of devices for low-altitude monitoring of the state of atmospheric turbulence with high spatial resolution based on copter-type UAVs is considered an urgent problem primarily in UAV aviation micrometeorology, as well as in other scientific and applied problems for which the knowledge of the state of turbulence is decisive.
Such problems include the inclusion of various types of UAVs in the Aircraft Meteorological Data Relay (AMDAR) system, one of the main tasks of which is to obtain atmospheric data for numerical weather forecasting (NWP) [11,12]. Large and expensive UAVs capable of flying at high altitudes should bridge the gap between satellite data [13] and measurements obtained from ground-based networks in global NWP. At the same time, small and inexpensive UAVs can fill the gaps in obtaining data on profiles of the turbulent atmospheric boundary layer, especially in hard-to-reach or dangerous places [14,15,16,17] for local forecasting.
The main disadvantage of small and inexpensive UAVs is the limited battery life. In addition, the use of extra sensors, such as a pitot tube or an acoustic anemometer [17,18,19,20], can significantly increase the weight and cost of a drone. Among obvious solutions of this problem is the use of the UAV itself as a detector of the state of the atmosphere. The use of such UAVs makes it possible obtaining information about the wind velocity in a turbulent atmosphere from flight logs of UAVs in a hover mode [15,17,21,22,23,24,25,26,27]. It was shown in [4,28,29,30] that the data on Euler angles of a hovering UAV can be used to obtain the longitudinal and lateral turbulence spectra and the longitudinal and lateral scales of turbulence. Thus, the scientific basis is created now for monitoring the main characteristics of a turbulent medium with high spatial resolution based on flight logs of copter-type UAVs in a hover mode without additional measuring sensors.
The possibility of measuring atmospheric turbulence profiles was noted in [4]. In this paper, we study the possibility of low-altitude sensing of atmospheric turbulence profiles with several UAVs hovering at different vertically spaced points. The measurements were carried out in the Basic Experimental Observatory (BEO) of the V.E.Zuev Institute of Atmospheric Optics SB RAS (Tomsk). Two weather towers 4 and 30 m high are located next to each other at the BEO territory. Due to this arrangement of the weather towers with acoustic anemometers installed on them, we can obtain data about the objective state of the atmosphere at several vertically spaced points and compare these data with measurements by UAV hovering near the anemometers. The orography of the BEO territory is similar to the orography of the Tsimlyansk Scientific Station of the A.M. Obukhov Institute of Atmospheric Physics. Thus, we can compare our results concerning the turbulence scales with the results reported in [31,32]
The “Materials and Methods” section considers the models of atmospheric turbulence that are used for correlation and spectral analysis of measurements obtained with UAVs and acoustic anemometers. The territory and the weather conditions of the experiment are described. In addition, the scientific instrumentation used to measure wind velocity components at different altitudes is touched.
In the “Results and Discussions” section, the UAV speed during the hovering is analyzed. The longitudinal and lateral components of the wind velocity as judged from data of UAV in the altitude hold mode are given in the comparison with the results of measurements by the acoustic anemometers. Correlation and spectral properties of atmospheric turbulence at different altitudes are investigated, and profiles of the longitudinal and lateral scales of turbulence are examined. The Conclusion summarizes the results obtained in this study.

2. Materials and Methods

This section provides the main equations of the von Karman and Dryden models of atmospheric turbulence. These models are used to analyze measurements of quadcopters and AMK-03 anemometers [33,34] installed on the weather towers. The territory of the Basic Experimental Observatory and the weather conditions of the experiment are described. The scientific instrumentation used to measure the wind velocity components at different heights is touched.

2.1. Models of atmospheric turbulence

The most commonly used models of turbulence include the von Karman, Dryden, and Kaimal models [35,36,37,38], as well as the unified turbulence model [39]. The von Karman model is used to analyze the UAV dynamics in a turbulent atmosphere. The simpler but mathematically convenient Dryden model is also a suitable approximation. The description of the von Karman and Dryden models used by us for analysis of the measurements is given below.

2.1.1. Von Karman model

The equations for the longitudinal and lateral spectra in the von Karman model have the form [35,36,37,38]
Φ u f σ u 2 = 2 L u π 1 1 + 1.339 L u · 2 π f / W 2 5 / 6 ,
Φ v f σ v 2 = 2 L v π 1 + 8 3 2.678 L v · 2 π f / W 2 1 + 2.678 L v · 2 π f / W 2 11 / 6 ,
where L u is the longitudinal turbulence scale, L v is the lateral turbulence scale, σ u 2 and σ v 2 are the turbulence intensities, and W is the average horizontal wind velocity.
One of the methods to determine the turbulence scales is to measure the maxima of the functions f Φ u f and f Φ v f [40]. For the von Karman model, the relation between the turbulence scales and the maxima takes the form
L u = 0.146 W f u , m a x ,
L v = 0.106 W f v , m a x ,
where f u , m a x is the maximum of the function f Φ u f and f v , m a x is the maximum of the function f Φ v f . These maxima can be calculated by Eqs. (1) and (2).

2.1.2. Dryden model

The equations for the longitudinal and lateral spectra in the Dryden model are as follows [35,36,37,38]:
Φ u f σ u 2 = 2 L u π W 1 1 + 2 π L u W f 2
Φ v f σ u 2 = 2 L v π W 1 + 12 2 π L u W f 2 1 + 4 2 π L u W f 2 2
The relation between the turbulence scales and the maxima of the functions f Φ u f and f Φ v f for the Dryden model takes the form
L u = 0.159 W f u , m a x ,
L v = 0.117 W f v , m a x .
where f u , m a x is the maximum of the function f Φ u f and f v , m a x is the maximum of the function f Φ v f . These maxima are calculated by Eqs. (5) and (6).
In the case of the von Karman model, the longitudinal and lateral correlation functions have a complex form and can be determined through second-kind Bessel functions of an imaginary argument [35,36,37,38]. For the Dryden model the longitudinal and lateral correlation functions have a simple analytical form
R u t = r u t σ u 2 = e − t / L u / W ,
R v t = r v t σ v 2 = 1 − t 4 L v / W e − t / 2 L v / W .
With the Taylor hypothesis of frozen turbulence [35,36,37,38], we can pass to the spatial longitudinal and lateral correlation function. Then, it follows from Eqs. (9) and (10) and ξ = W t that L u and L v have the meaning of the integral longitudinal and lateral scales of turbulence, that is, L u = σ u − 2 ∫ 0 ∞ R u ξ d ξ and L v = σ v − 2 ∫ 0 ∞ R v ξ d ξ . For the Kolmogorov-Obukhov turbulence, the equation R v ξ = R u t + ξ 2 R u ' ξ is true. This leads to the ratio of the integral turbulence scales L v / L u = 0.5 . If the ratio of the integral turbulence scales L v / L u ≠ 0.5 , this means that the turbulence observed in the atmosphere is anisotropic. Thus, the integral scales L u and L v describe the longitudinal and lateral dimensions of a turbulent structure, inside which an air vortex moves almost synchronously. The above properties of the integral scales have the general character and, in particular, are valid for the von Karman model.

2.1. General information about the experiment

The experiment was conducted on July 15, 2021, at the territory of the Basic Experimental Observatory (BEO) of the V.E. Zuev Institute of Atmospheric Optics SB RAS near Akademgorodok (Tomsk, the Russian Federation). Figure 1 shows the Google map of the BEO territory and photographs of the 30-m and 4-m weather towers. The white arrow shows the location of the weather tower on the ground, and the red arrows show the positions of AMK-03 acoustic anemometers [33,34] at heights of 4, 10, and 27 m on the weather towers. In the experiment, we used three commercial quadcopters: DJI Mini, DJI Air, and DJI Phantom 4 Pro. The starting point of the quadcopters was close to the weather tower, and hovering was carried out at a distance of 5 m from the acoustic anemometers. Table 1 gives the start, end, and hovering height for each quadcopter, as well as the wind speed profile at the studied altitude.
Strictly speaking, the BEO territory is not a flat and uniform surface. The ground surface has a slope. It borders a villa community on one side and a forest on the other side. Earlier, we noted that turbulence over such a territory may deviate from isotropic [28].
According to the data of the Tomsk International Airport located at a distance of ~10 km from BEO, the weather conditions observed during the experiment on July 15, 2021, were favorable in terms of quadcopter flight: south wind, speed of 5.0 m/s, air temperature of 17°C , air humidity of 83%, horizontal visibility range of 10 km or more, no precipitation. In contrast to the Tomsk International Airport data, the wind speed at the BEO territory was lower. This fact is explained by different terrain.

3. Results and Discussions

In this section, we consider the quadcopter velocity in the altitude hold mode. The behavior of this velocity allows us to judge how closely the experimental data correspond to ideal hovering. The longitudinal and lateral components of the wind velocity determined from the data of the quadcopters in the altitude hold mode are compared with the results of objective measurements by the AMK-03 anemometers. The correlation and spectral properties of atmospheric turbulence at different altitudes are analyzed, and the profiles of the longitudinal and transverse turbulence scales are studied.

3.1. Quadcopter velocity

Figure 2 shows the variations of the quadcopter velocity components relative to the ground along the x, y, and z axes during quadcopter hovering at altitudes of 4 (a), 10 (b), and 27 m (c) near AMK-03 anemometers installed on the weather towers. It can be seen that during the measurements, the quadcopter velocity components are equal to zero except for insignificant periods of time. It can also be seen that in insignificant time periods, the forces acting on the quadcopters exceed the capabilities of the control system and high-precision positioning is violated, but the control is soon restored and the quadcopter returns to its original position.
It was found in [4,28,29,30] that the periods, in which the positioning of the quadcopter in space is violated, can be neglected due to their insignificance, and hovering observed during the experiments can be assumed ideal. The theoretical investigations [4,28,29,30] show that in the case of ideal hover, fluctuations of the longitudinal and lateral components of the wind velocity coincide with the data of objective measurements.

3.2. Longitudinal and lateral wind velocity components

Let us consider the behavior of the longitudinal and lateral components of the wind velocity estimated from the data of quadcopters in the altitude hold mode in the turbulent atmosphere in comparison with the results of objective AMK-03 measurements. Figure 3 shows the longitudinal w r and lateral w t wind velocity measured by the quadcopter (black curve) and AMK-03 anemometer (red curve) at heights of 4 (a, b), 10 (c, d), and 27 m (e, f). The top plot for each height corresponds to measurements in the 0-10 Hz band, while the bottom one is for the same data but smoothed for 1 min. It can be seen from Figure 3 that the time series of w r and w t measured by the different methods in the 0-10 Hz band coincide, while differences are observed for high-frequency fluctuations.
When the series of longitudinal and lateral wind velocities are smoothed, a good agreement is observed between the data measured by the different methods. It is well known that the smoothing of random series leads to the averaging of high-frequency fluctuations. In the high-frequency range, the greatest discrepancy is observed in the unsmoothed data. Therefore, the discrepancy between the UAV and AMK-03 data after the smoothing procedure becomes considerably smaller, which can be well seen from Figure 3.
The discrepancy between UAV and AMK-03 data before the smoothing procedure is characterized by the parameters Δ r , p = w r D r o n t p − w r A M K − 03 t p and Δ t , p t p = w t D r o n t p − w t A M K − 03 t p and, after the smoothing, by Δ r , q = w r D r o n t q − w r A M K − 03 t q and Δ t , q = w t D r o n t q − w t A M K − 03 t q . The series of Δ r , p and Δ t , p , as well as Δ r , q and Δ t , q , are random numbers whose scatter is characterized by
σ r = 1 M − 1 ∑ p = 1 M Δ r , p 2 ,   σ t = 1 M − 1 ∑ p = 1 M Δ t , p 2 ,
σ r = 1 M − 1 ∑ q = 1 M ∆ r , q 2 ,   σ t = 1 M − 1 ∑ q = 1 M ∆ t , q 2 ,
Table 2 gives the values of the variances at heights of 4, 10, and 27 m before and after the smoothing procedure. It can be seen that before the smoothing, the variances σ r and σ t range within 0.40-0.54 m/s at these heights, and their average values fall within the range 0.45-0.49 m/s. After the smoothing of the measurement series at these heights, the values of σ r and σ t decrease significantly down to 0.11-0.21 m/s, and their average values decrease down to 0.15-0.17 m/s. Thus, the 1-min smoothing of the longitudinal and lateral wind velocities suppresses considerably high-frequency fluctuations, which leads to significant reduction of the variances.
The variance is an integral characteristic of a random process. In contrast to the variance, the histogram and total probability in per cent allows us to study the frequency distribution of random numbers Δ r , p and Δ t , p , as well as Δ r , q and Δ t , q . Figure 4 and Figure 5 show the histograms and total probabilities in per cent for the discrepancy between the UAV and AMK-03 data before and after the smoothing procedure. It follows from Figure 4 that before the smoothing procedure, the discrepancy between the AMK-03 and quadcopter data does not exceed 0.7 m/s for the longitudinal component and ~1 m/s for the lateral component in 95% of cases (this level is shown by arrows in Figure 4 and Figure 5). After the 1-min smoothing of the measurement series, the discrepancy reduces significantly. Thus, for heights of 4 and 27 m, the discrepancy between the AMK-03 and quadcopter data does not exceed 0.5 m/s for both the longitudinal and lateral wind velocity components. For a height of 10 m, the discrepancy between the data ranges from 0 to 0.5 m/s in 95% of cases.
With 1-min averaging of the wind velocity components, insufficient smoothing of natural turbulent fluctuations of the wind velocity is observed [41], as can be seen from Figure 3. Aviation and other applications often use wind velocities averaged over this averaging time, and such results are treated as long turbulent gusts. For a lot of applications, the uncertainty of wind velocity measurements should not exceed 0.5 m/s for wind speeds less than 5 m/s [41]. These values are the most common meteorological requirements of the World Meteorological Organization for wind velocity measurements [41].
During our experiment, the wind speed at the heights under study did not exceed 5 m/s and the discrepancy did not exceed 0.5 m/s in 95% of cases for the longitudinal and lateral wind velocity components after 1-min smoothing procedure. Thus, a quadcopter swarm can provide the accuracy in determining the atmospheric turbulence profile that meets the requirements of the World Meteorological Organization in monitoring of long turbulent wind gusts.

3.3. Correlation analysis

Let us analyze now the statistical correlation between the data measured with UAV and the AMK-03 acoustic anemometer. The correlation coefficient serves as a mathematical measure of the correlation between two random variables. Table 3 shows the values of the correlation coefficients for the longitudinal and lateral wind velocity components at heights of 4, 10, and 27 m before and after the smoothing procedure. We can see that the correlation coefficients before the smoothing procedure fall within the range of 0.56-0.75, while their average values are in the range of 0.66-0.71. This means that the correlation between the data is moderate. The 1-min smoothing leads to the correlation coefficients of 0.89-0.93 or to the very high correlation between the data. Thus, the suppression of high-frequency fluctuations by applying the 1-min smoothing procedure to the series of longitudinal and lateral wind velocities leads to the significantly higher correlation manifesting itself in the higher correlation coefficient between the UAV and AMK-03 measurements.
Figure 6 shows the results of calculation of the longitudinal and lateral autocorrelation functions of turbulent fluctuations of the wind velocity at heights of 4, 10, and 27 m. In addition to autocorrelation, of great interest is the cross-correlation between the quadcopter and AMK-03 acoustic anemometer data obtained at the same height. The behavior of cross-correlation functions of turbulent fluctuations at heights of 4, 10, and 27 m is shown in Figure 7.
One can see that as τ increases, the autocorrelation for both UAV and AMK-03 data drops down and then oscillates about zero. The general behavior of the autocorrelation functions of longitudinal and lateral turbulent fluctuations of wind velocity for the two measurement methods coincides within the statistical uncertainty. It follows from Figure 7 that the cross-correlation also drops down with time and then oscillates to zero. This behavior of autocorrelation and cross-correlation functions is typical for a turbulent atmosphere [40,42,43].

3.4. Spectral analysis

The spectra of turbulent wind velocity fluctuations were calculated by well-known methods using standard FFT software. It is known [35,36,37,38] that turbulence spectra change significantly with small variations of the frequency f . These changes are random fluctuations about the main regularities of the turbulence spectra. To reveal these regularities in the turbulence spectra, a moving smoothing procedure over 50 points was used. We used this procedure for calculation of turbulence spectra in [4,28,29,30].
Figure 8 and Figure 9 show the calculated smoothed longitudinal Φ u f and lateral Φ v f spectra as judged from the quadcopter and AMK-03 anemometer data, σ 2 is the normalization coefficient. The green, blue, and red curves correspond to a height of 4, 10, and 27 m, while the black curve is the Kolmogorov-Obukhov turbulence spectrum. An analysis of the turbulence spectra shows that they coincide for the data measured with the quadcopters and acoustic anemometers at different heights, while minor differences are observed in the high-frequency spectral range of the spectrum. This behavior of the turbulence spectra measured by various methods was noted earlier in [4,28,29,30].

3.5. Longitudinal and lateral scales of turbulence

It is well-known that relative turbulence spectra contain information about the longitudinal and lateral scales of turbulence. The longitudinal and lateral turbulence scales were calculated based on Eqs. (3) and (4) for the von Karman model and Eqs. (7) and (8) for the Dryden model. The spectral maxima were determined from the smoothed experimental longitudinal Φ u f and lateral Φ v f spectra obtained from both the quadcopter and AMK-03 anemometer data. Table 4 presents the profiles of the longitudinal and lateral turbulence scales. The values calculated by the von Karman and Dryden models are separated by a slash. One can see from Table 4 that the values of the longitudinal turbulence scales coincide to a good accuracy for both the quadcopter and AMK-03 anemometer data.
When analyzing the experimental data, a difference in the behavior of the ratio of turbulence scales from that in an isotropic atmosphere is marked. It follows from Table 4 that the experimentally measured value of the ratio of turbulence scales ranges within L v L u ≈ 0.59-0.74, whereas L v L u = 0.5 for isotropic turbulence. Thus, a deviation from the laws of isotropic turbulence was observed during the experiment.
We have noted earlier [28] that the same deviation from the laws of isotropic turbulence was observed in the experiment, which took place at the Basic Experimental Observatory. In the experiments [31,32], which were carried out for several years at the territory of the Tsimlyansk Research Station of the A.M. Obukhov Institute of Atmospheric Physics, it was found that the longitudinal scale, on average, 1.4 times exceeds the lateral scale or L v L u ≤ 0.71 . The territories of the Basic Experimental Observatory and the Tsimlyansk Research Station have a nearly flat underlying surface. At such territories, slight deviations from isotropic turbulence can be observed, which is also confirmed by this study.
In contrast to a territory with a flat underlying surface, stronger deviations from isotropic turbulence can be observed in an urban environment [4]. For example, measurements of the ratio of turbulence scales for the urban environment in different seasons (winter, spring, summer, and fall) provide the ratios L v L u = 0.70 − 0.79 . Thus, the obtained results on the ratio of longitudinal and lateral turbulence scales are in agreement with the conclusions of [4,28,31,32].
It follows from Table 3 that the average values of the correlation coefficients before the smoothing procedure are 0.71 for longitudinal wind velocity and 0.66 for the lateral wind velocity. The drop in the correlation down to these values can be explained by many factors, among which the turbulent atmosphere is one of the main ones.
During the experiment, the quadcopter was at a distance of ~5 m from the acoustic anemometer. This distance was chosen from safety reasons for the experiment. It follows from Table 4 that the turbulence scales varied from 10 to 17 m depending on the height. This relation of the turbulence scales and the separation between the acoustic anemometer and the quadcopter means that the measurement instruments were within the same turbulent structure, inside which an air vortex moves almost synchronously.
To quantitatively estimate the degree of synchronism in the motion of an air vortex at different points, we can use Eqs. (9) and (10) for the correlation functions. The calculations shown that the average values of the correlation function for two points spaced by 5 m are 0.8 for the longitudinal wind velocity and 0.6 for the lateral wind velocity. Thus, during the experiment, the instruments were within the same turbulent structure, but at a considerable distance. So we can only approximately speak about the synchronism of motion inside an air vortex. Actually, a closer correlation between the objective data on atmospheric turbulence and data measured with the quadcopter in the hover mode should be expected if measurements are carried out at closer distances.
The results of measurements of the autocorrelation functions allow us to estimate approximately the longitudinal and lateral turbulence scales. These scales were estimated by the least square fit method with the Dryden model as the best fit. The longitudinal and lateral correlation functions of this model have a simple analytical form described by Eqs. (9) and (10). Table 5 provides the estimates of the longitudinal and lateral scales of turbulence obtained by the least square fit method. The comparison of L u and L v in Table 4 and Table 5 shows that they coincide in the order а magnitude.

4. Conclusions

This study continues our investigations reported in [4,28,29,30]. It was noted in those papers that the simultaneous monitoring of atmospheric turbulence at different spatial points with hovering quadcopters that can provide high spatial resolution is of great scientific and practical interest. In this study, we have measured the profile of atmospheric turbulence at the territory of the Basic Experimental Observatory at altitudes of 4, 10, and 27 m using both quadcopters and AMK-03 acoustic anemometers. In the experiment, the behavior of the longitudinal and lateral components of the wind velocity was studied, and the discrepancy between the quadcopter and AMK-03 data before and after the smoothing procedure was analyzed. The spectral and correlation analysis of the quadcopter and anemometer findings was carried out. The profiles of the longitudinal and lateral scales of turbulence were studied.
Based on the results obtained, we can conclude that a swarm of quadcopters is a promising tool for determining atmospheric turbulence profiles with high spatial resolution. The use of several rotary wing UAVs in the hover mode can allow the detailed description of the state of turbulence, which significantly impacts a lot of processes occurring in the atmosphere. Detailed description of the state of atmospheric turbulence is very important for solving numerous problems, including navigation of drones under adverse meteorological conditions over territories with complex orography, such as urban environments and various types of natural landscapes, as well as in hard-to-reach or dangerous places.

Author Contributions

Conceptualization, A.S.; methodology, A.S.; software, A.A. and E.S.; validation, A.K., A.T. and A.M.; investigation, A.S. and A.A.; data curation, A.K., A.T. and A.M.; writing—original draft preparation, O.P.; writing—review and editing, A.S.; supervision, A.S.; project administration, A.S. All authors have read and agreed to the published version of the manuscript.

Funding

The study was supported by the Russian Foundation for Basic Research (project no. 19-29-06066 mk).

Acknowledgments

The authors are grateful to A.B. Gonchar for the help in preparing this paper.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Zhu, Baoyu; Qunbo, Lv; Tan, Zheng. Adaptive Multi-Scale Fusion Blind Deblurred Generative Adversarial Network Method for Sharpening Image Data. Drones 2023, 7, 96. [Google Scholar] [CrossRef]
  2. Xiao, Y.; Zhang, J.; Chen, W.; Wang, Y.; You, J.; Wang, Q. SR-DeblurUGAN: An End-to-End Super-Resolution and Deblurring Model with High Performance. Drones 2022, 6, 162. [Google Scholar] [CrossRef]
  3. Tajima, Y.; Hiraguri, T.; Matsuda, T.; Imai, T.; Hirokawa, J.; Shimizu, H.; Kimura, T.; Maruta, K. Analysis of Wind Effect on Drone Relay Communications. Drones 2023, 7, 182. [Google Scholar] [CrossRef]
  4. Shelekhov, A.; Afanasiev, A.; Shelekhova, E.; Kobzev, A.; Tel’minov, A.; Molchunov, A.; Poplevina, O. Low-Altitude Sensing of Urban Atmospheric Turbulence with UAV. Drones 2022, 6, 61. [Google Scholar] [CrossRef]
  5. Kral, S.T.; Reuder, J.; Vihma, T.; Suomi, I.; O’Connor, E.; Kouznetsov, R.; Wrenger, B.; Rautenberg, A.; Urbancic, G.; Jonassen, M.O.; et al. Innovative strategies for observations in the arctic atmospheric boundary layer (ISOBAR)—The Hailuoto 2017 campaign. Atmosphere 2018, 9, 268. [Google Scholar] [CrossRef]
  6. Stith, J.L.; Baumgardner, D.; Haggerty, J.; Hardesty, M.; Lee, W.; Lenschow, D.; Pilewskie, P.; Smith, P.L.; Steiner, M.; Vömel, H. 100 Years of progress in atmospheric observing systems. Meteorol. Monogr. 2018, 59, 2.1–2.55. [Google Scholar] [CrossRef]
  7. Hocking, W.K.; Röttger, J.; Palmer, R.D.; Sato, T.; Chilson, P.B. Atmospheric Radar; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
  8. Leosphere, Windcube, Vaisala. Available online: https://www.vaisala.com/en/wind-lidars/wind-energy/windcube/ (accessed on 30 April 2023).
  9. METEK Meteorologische Messtechnik GmbH. Available online: https://metek.de/product-group/doppler-sodar/ (accessed on 30 April 2023).
  10. Scintec. Available online: https://www.scintec.com/ (accessed on 30 April 2023).
  11. Commission for Basic Systems and Commission for Instruments and Methods of Observation: Workshop on Use of Unmanned Aerial Vehicles (UAV) for Operational Meteorology WMO; 2019. Available online: https://library.wmo.int/doc_num.php?explnum_id=9951. (accessed on 30 April 2023).
  12. AMDAR Reference Manual: Aircraft Meteorological Data Relay WMO-No.958, WMO; 2003. Available online: https://library.wmo.int/doc_num.php?explnum_id=9026. (accessed on 30 April 2023).
  13. Stoffelen, A.; et al. Wind Profile Satellite Observation Requirements and Capabilities. Bull. Amer. Meteor. Soc. 2020, 101, E2005–E2021. [Google Scholar] [CrossRef]
  14. LIAO, Xiaohan; et al. Critical Infrastructures for Developing UAVs’ Applications and Low-altitude Public Air-Route Network Planning. Bulletin of Chinese Academy of Sciences (Chinese Version) 2022, 37.7, 977–988. [Google Scholar]
  15. González-Rocha, Javier; Bilyeu, Landon; Ross, Shane D.; Foroutan, Hosein; Jacquemin, Stephen J.; Ault, Andrew P.; Schmale, David G. III. Sensing atmospheric flows in aquatic environments using a multirotor small unscrewed aircraft system (sUAS)”. Environ. Sci.: Atmos. 2023, 3, 305–315. [Google Scholar] [CrossRef]
  16. Lepikhin, A.P.; Lyakhin, Y.S.; Lucnikov, A.I. The Experience in Drone Use to Evaluate the Coefficients of Turbulent Diffusion in Small Water Bodies. Water Resour. 2023, 50, 242–251. [Google Scholar] [CrossRef]
  17. McConville, Alexander; Richardson, Thomas. High-altitude vertical wind profile estimation using multirotor vehicles. Frontiers in Robotics and AI 2023, 2023. [Google Scholar] [CrossRef]
  18. Villa, T.F.; Gonzalez, F.; Miljievic, B.; Ristovski, Z.D.; Morawska, L. An Overview of Small Unmanned Aerial Vehicles for Air Quality Measurements: Present Applications and Future Prospectives. Sensors 2016, 16, 1072. [Google Scholar] [CrossRef] [PubMed]
  19. Loubimov, G.; Kinzel, M.P.; Bhattacharya, S. Measuring Atmospheric Boundary Layer Profiles Using UAV Control Data. AIAA Scitech 2020 Forum; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2020. [CrossRef]
  20. Li, Zhengnong; Pu, Ou; Pan, Yueyue; Huang, Bin; Zhao, Zhefei; Wu, Honghua. A Study on Measuring the Wind Field in the Air Using a Multi-rotor UAV Mounted with an Anemometer. Boundary-Layer Meteorology 2023, 1–27. [Google Scholar] [CrossRef]
  21. González-Rocha, J.; De Wekker, S.F.J.; Ross, S.D.; Woolsey, C.A. Wind Profiling in the Lower Atmosphere from Wind-Induced Perturbations to Multirotor UAS. Sensors 2020, 20. [Google Scholar] [CrossRef] [PubMed]
  22. González-Rocha, J.; Woolsey, C.A.; Sultan, C.; De Wekker, S.F.J. Sensing wind from quadrotor motion. J. Guid. Control. Dyn. 2019, 42, 836–852. [Google Scholar] [CrossRef]
  23. González-Rocha, J.; Woolsey, C.A.; Sultan, C.; De Wekker, S.F. Model-based wind profiling in the lower atmosphere with multirotor UAS. Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA 2019. p. 1598. [Google Scholar]
  24. Neumann, Patrick; Bartholmai, Matthias. Real-time wind estimation on a micro unmanned aerial vehicle using its inertial measurement unit. Sensors and Actuators A: Physical. 2015, 235, 300–310. [Google Scholar] [CrossRef]
  25. Palomaki, R.T.; Rose, N.T.; van den Bossche, M.; Sherman, T.J.; De Wekker, S.F.J. Wind estimation in the lower atmosphere using multirotor aircraft. J. Atmos. Ocean. Technol. 2017, 34, 1183–1190. [Google Scholar] [CrossRef]
  26. Meier, Kilian; Hann, Richard; Skaloud, Jan; Garreau, Arthur. Wind Estimation with Multirotor UAVs. Atmosphere. 2022, 13. 551. [CrossRef]
  27. Cheng, X., Wang, Y., Cai, Z., Liu, N., Zhao, J. Wind Estimation of a Quadrotor Unmanned Aerial Vehicle. In Advances in Guidance, Navigation and Control. ICGNC 2022 Lecture Notes in Electrical Engineering; Yan, L., Duan, H., Deng, Y. Springer, Singapore, 2023, 845. [CrossRef]
  28. Shelekhov, A.; Afanasiev, A.; Shelekhova, E.; Kobzev, A.; Tel’minov, A.; Molchunov, A.; Poplevina, O. Using small unmanned aerial vehicles for turbulence measurements in the atmosphere. Izv. Atmos. Ocean. Phys. 2021, 57, 533–545. [Google Scholar] [CrossRef]
  29. Shelekhov, Alexander P.; Afanasiev, Aleksey L.; Shelekhova, Evgenia A.; et al. Profiling the turbulence from spectral measurements in the urban atmosphere using UAVs. Remote Sensing Technologies and Applications in Urban Environments VI 2021, 8. [Google Scholar] [CrossRef]
  30. Shelekhov, Alexander P.; Afanasiev, Alexey L.; Kobzev, Alexey A.; Shelekhova, Evgenia A. Opportunities to monitor the urban atmospheric turbulence using unmanned aerial system Proc. SPIE 11535, Remote Sensing Technologies and Applications in Urban Environments V 2020, 1153506. [CrossRef]
  31. Shishov, E.A.; Solenaya, O.A.; Chkhetiani, O.G.; Azizyan, G.V.; Koprov, V.M. Multipoint measurements of temperature and wind in the surface layer. Izv. Atmos. Ocean. Phys. 2021, 57, 254–263. [Google Scholar] [CrossRef]
  32. Shishov, E.A.; Solyonaya, O.A.; Koprov, B.M.; Koprov, V.M. Investigation into variations of wind directions near the surface. Izv. Atmos. Ocean. Phys. 2018, 54, 515–523. [Google Scholar] [CrossRef]
  33. Azbukin, A.A.; Bogushevich, A.Y.; Korolkov, V.A.; Tikhomirov, A.A.; Shelevoi, V.D. A field version of the AMK-03 automated ultrasonic meteorological complex. Russ. Meteorol. Hydrol. 2009, 34, 133–136. [Google Scholar] [CrossRef]
  34. Azbukin, A.A.; Bogushevich, A.Y.; Kobzev, A.A.; Korolkov, V.A.; Tikhomirov, A.A.; Shelevoy, V.D. AMK-03 Automatic weather stations, their modifications and applications. Sens. Syst. 2012, 3, 47–52. [Google Scholar]
  35. McCombs, Alexandria G.; Hiscox, April L. Always in flux: The nature of turbulence. In Conceptual Boundary Layer Meteorology; Hiscox, April L.; Academic Press, 2023, Pages 19-35. [CrossRef]
  36. Monin, A.S.; Yaglom, A.M. Statistical Hydromechanics. Part 2. In Turbulent Mechanics; Nauka: Moscow, Russia, 1967. [Google Scholar]
  37. Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989. [Google Scholar]
  38. Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows. Their Structure and Measurement; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
  39. Tieleman, H.W. Universality of velocity spectra. J. Wind Eng. Ind. Aerodyn. 1995, 56, 55–69. [Google Scholar] [CrossRef]
  40. Flay, R.G.J.; Stevenson, D.C. Integral length scales in an atmospheric boundary-layer near the Ground. 9th Australasian fluid mechanics conference, Auckland, 8-12 December, 1986.
  41. Guide to Instruments and Methods of Observation Volume I –Measurement of Meteorological Variables (WMO-No. 8) WMO, 2021 edition. Available online: https://library.wmo.int/doc_num.php?explnum_id=11386. (accessed on 30 April 2023).
  42. O’Neill, P. L.; Nicolaides, D.; Honnery, D.; Soria, J. Autocorrelation Functions and the Determination of Integral Length with Reference to Experimental and Numerical Data, 15th Australasian Fluid Mechanics Conference, The University of Sydney, Sydney, Australia 13-17 December 2004.
  43. Emes, M.J.; Arjomandi, M.; Kelso, R.M.; Ghanadi, F. Integral length scales in a low-roughness atmospheric boundary layer. Proceedings of the 18th Australasian Wind Engineering Society Workshop 2016, 1–4. [Google Scholar]
Preprints 72339 g001
Figure 1. Google map of the territory of the Basic Experimental Observatory and photographs of the 30-m and 4-m weather towers.
Figure 1. Google map of the territory of the Basic Experimental Observatory and photographs of the 30-m and 4-m weather towers.
Preprints 72339 g001
Preprints 72339 g002
Figure 2. Quadcopter velocity components along the x, y, and z axes during hovering; (a) 4 m, (b) 10 m, (c) 30 m.
Figure 2. Quadcopter velocity components along the x, y, and z axes during hovering; (a) 4 m, (b) 10 m, (c) 30 m.
Preprints 72339 g002
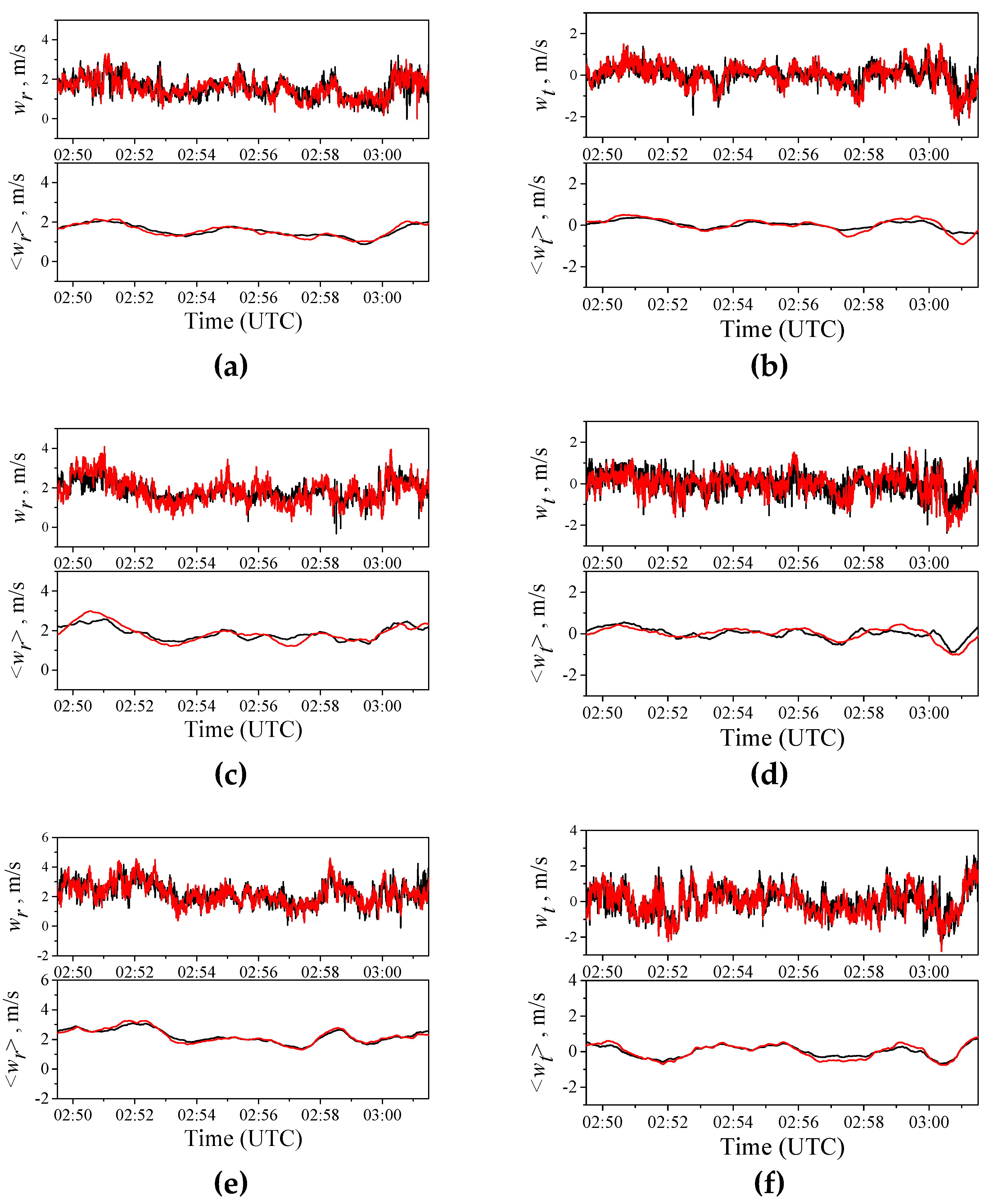
Preprints 72339 g003
Figure 3. Longitudinal and lateral wind velocities at a height of 4 (a, b), 10 (c, d), and 27 m (e, f); quadcopter (black curve) and AMK-03 acoustic anemometer (red curve) data. Top plots correspond to the values of w r and w t measured with a frequency of 10 Hz, bottom plots are for the 1-min smoothed data on w r and w t .
Figure 3. Longitudinal and lateral wind velocities at a height of 4 (a, b), 10 (c, d), and 27 m (e, f); quadcopter (black curve) and AMK-03 acoustic anemometer (red curve) data. Top plots correspond to the values of w r and w t measured with a frequency of 10 Hz, bottom plots are for the 1-min smoothed data on w r and w t .
Preprints 72339 g003
Preprints 72339 g004
Figure 4. Histograms and total probabilities in per cent for the discrepancies between UAV and AMK-03 data for Δ r (a, c, e) and Δ t (b, d, f) before the smoothing procedure at a height of 4 (a, b), 10 (c, d), and 27 m (e, f).
Figure 4. Histograms and total probabilities in per cent for the discrepancies between UAV and AMK-03 data for Δ r (a, c, e) and Δ t (b, d, f) before the smoothing procedure at a height of 4 (a, b), 10 (c, d), and 27 m (e, f).
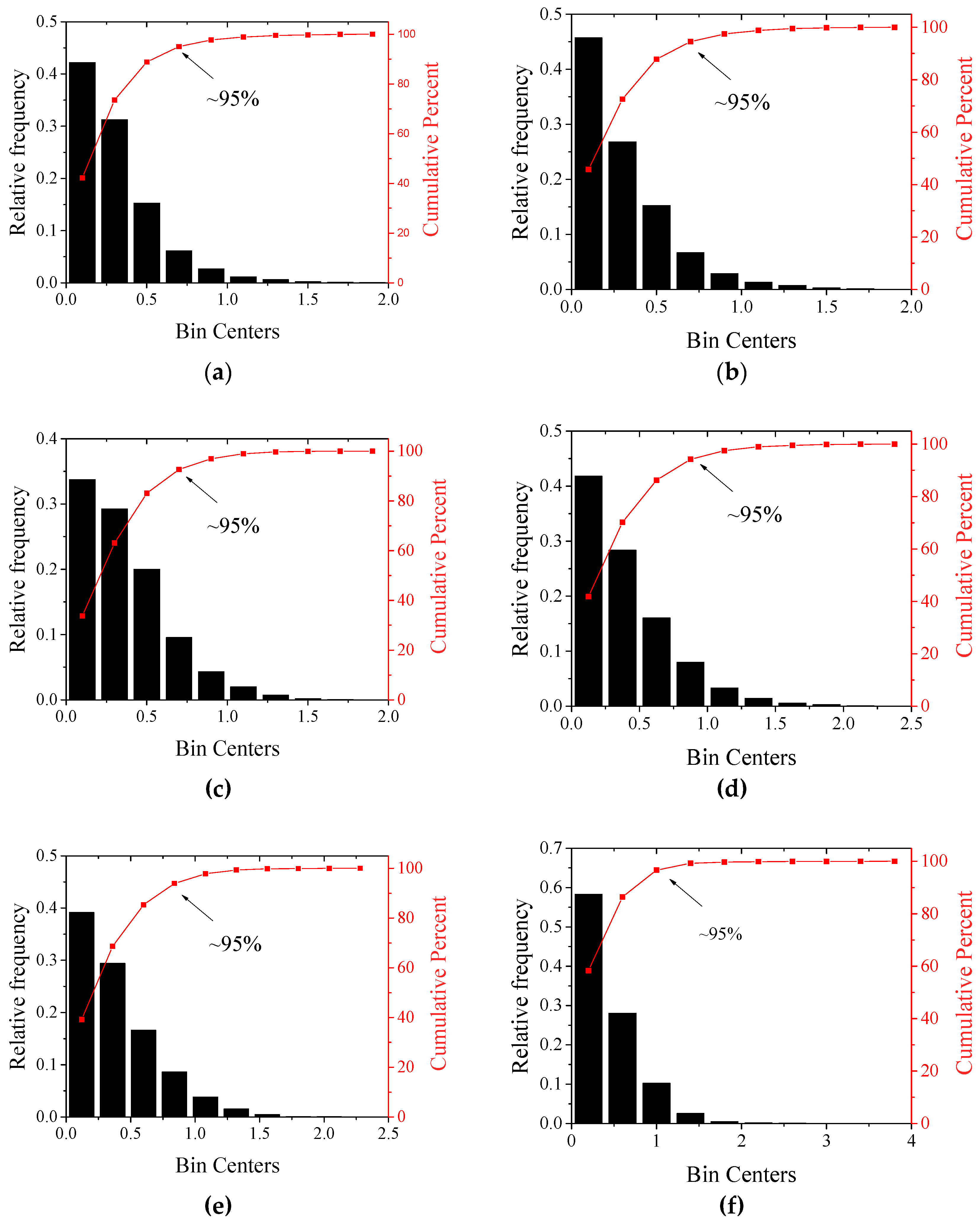
Preprints 72339 g004
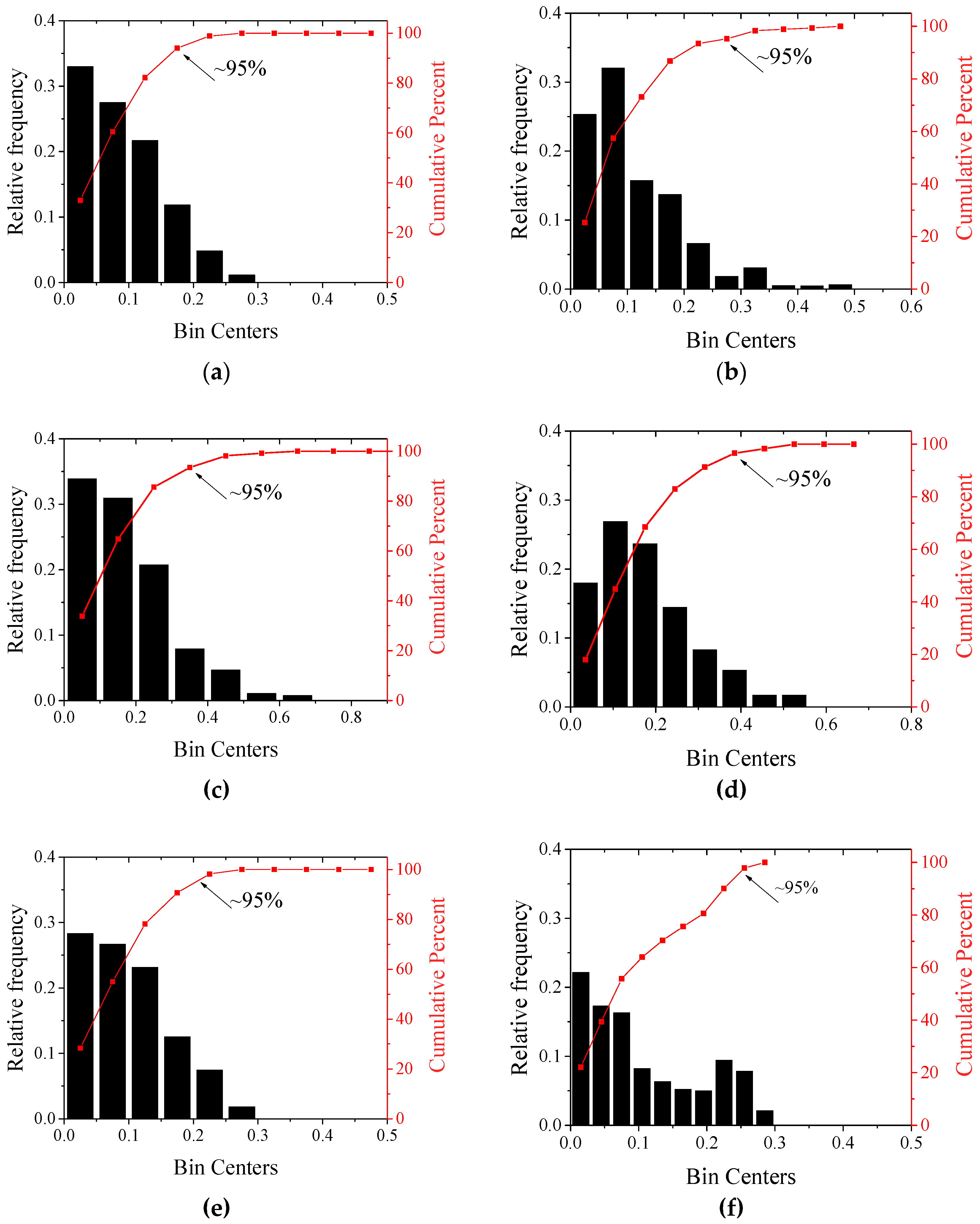
Preprints 72339 g005
Figure 5. Histograms and total probabilities in per cent for the discrepancies between UAV and AMK-03 data for Δ r (a, c, e) and Δ t   (b, d, f) after the smoothing procedure at a height of 4 (a, b), 10 (c, d), and 27 m (e, f).
Figure 5. Histograms and total probabilities in per cent for the discrepancies between UAV and AMK-03 data for Δ r (a, c, e) and Δ t   (b, d, f) after the smoothing procedure at a height of 4 (a, b), 10 (c, d), and 27 m (e, f).
Preprints 72339 g005
Preprints 72339 g006
Figure 6. Autocorrelation functions of longitudinal and lateral turbulent fluctuations of wind velocity at a height of 4 (a, b), 10 (c, d), and 27 m (e, f): AMK-03 anemometer (black curve) and UAV (red curve) data.
Figure 6. Autocorrelation functions of longitudinal and lateral turbulent fluctuations of wind velocity at a height of 4 (a, b), 10 (c, d), and 27 m (e, f): AMK-03 anemometer (black curve) and UAV (red curve) data.
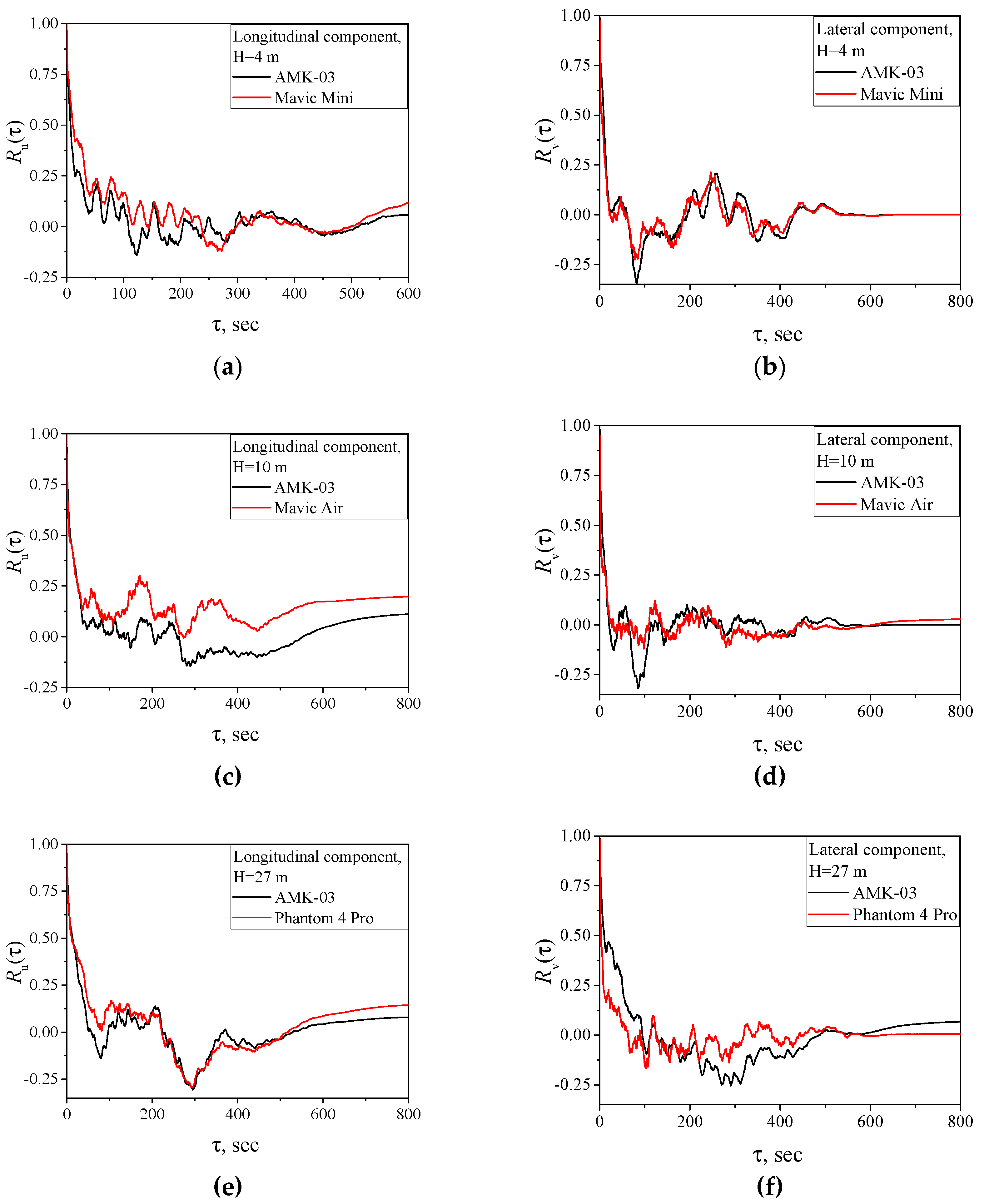
Preprints 72339 g006
Preprints 72339 g007
Figure 7. Cross-correlation functions of turbulent fluctuations at a height of 4 (green curve), 10 (blue curve), and 27 m (red curve) for the longitudinal (a) and lateral (b) wind velocity components.
Figure 7. Cross-correlation functions of turbulent fluctuations at a height of 4 (green curve), 10 (blue curve), and 27 m (red curve) for the longitudinal (a) and lateral (b) wind velocity components.
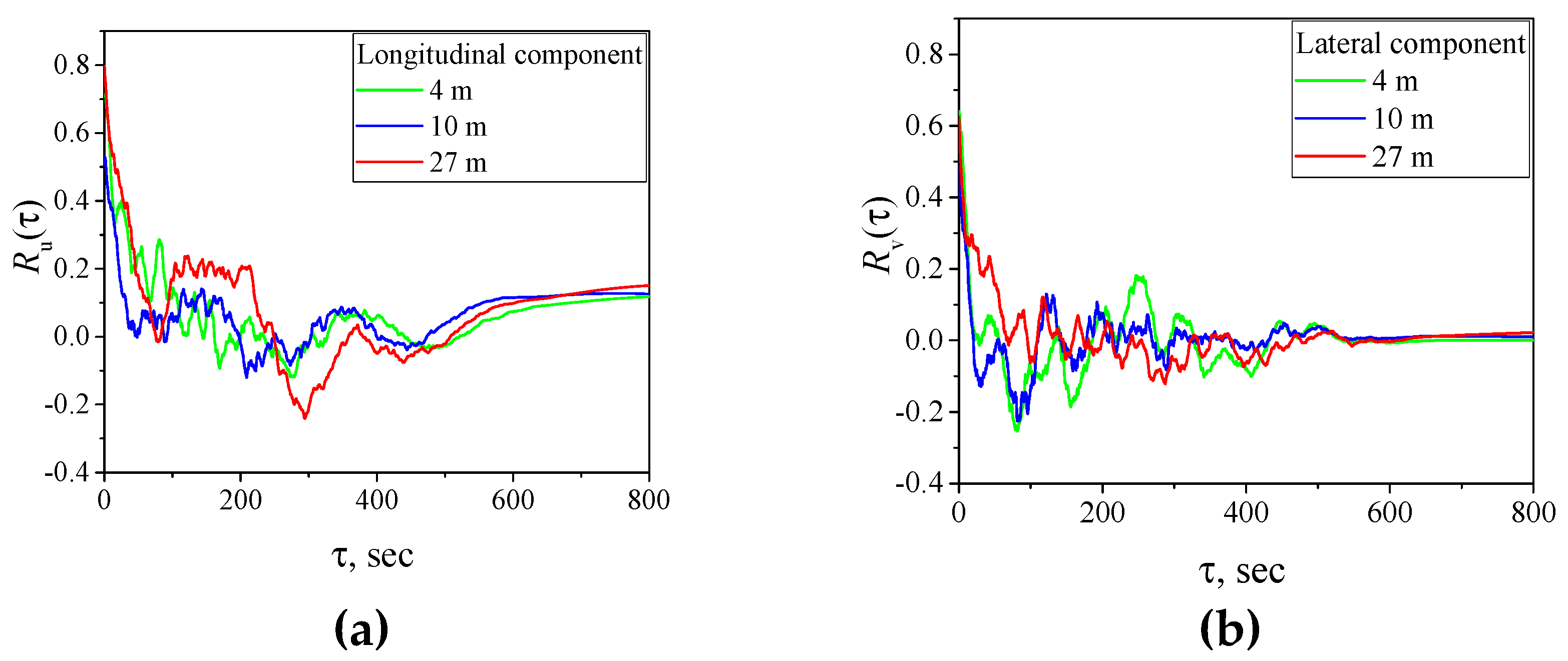
Preprints 72339 g007
Preprints 72339 g008
Figure 8. Spectra of turbulent wind velocity fluctuations from quadcopter data at 4 (green curve), 10 (blue curve), and 27 m (red curve): (a) longitudinal Φ u f and (b) lateral Φ v f spectrum.
Figure 8. Spectra of turbulent wind velocity fluctuations from quadcopter data at 4 (green curve), 10 (blue curve), and 27 m (red curve): (a) longitudinal Φ u f and (b) lateral Φ v f spectrum.
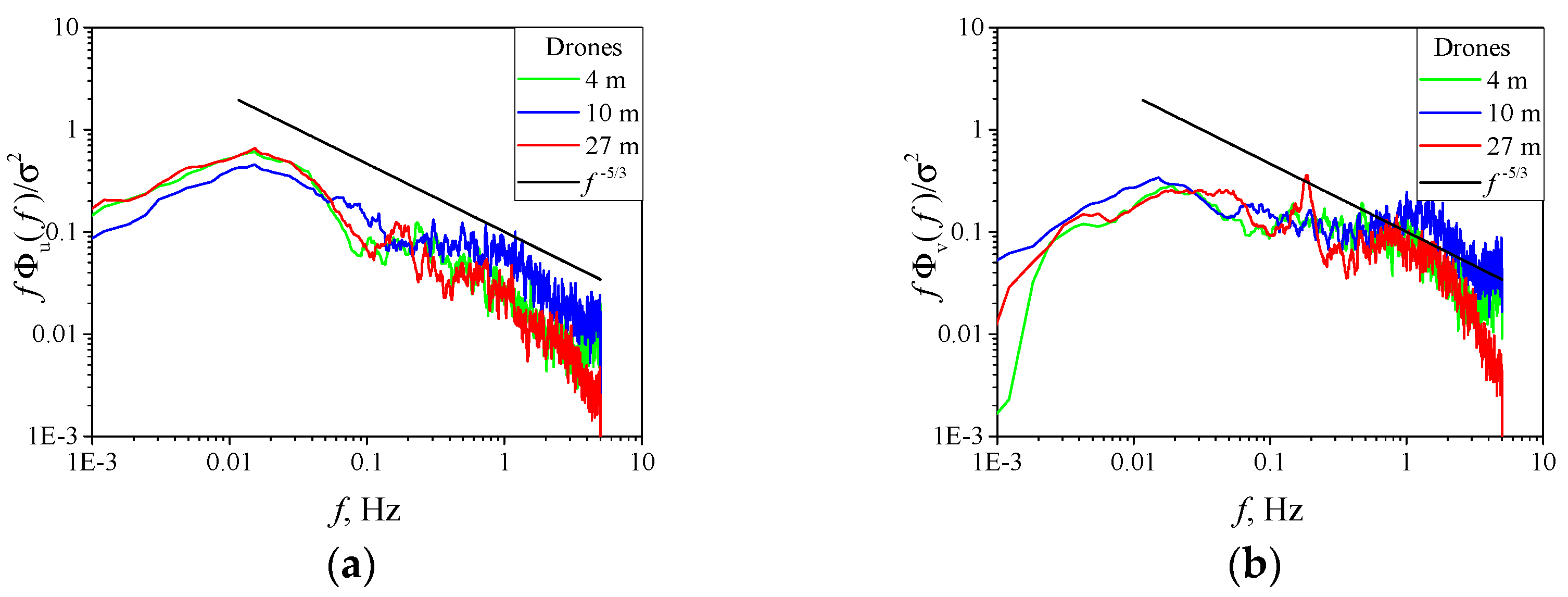
Preprints 72339 g008
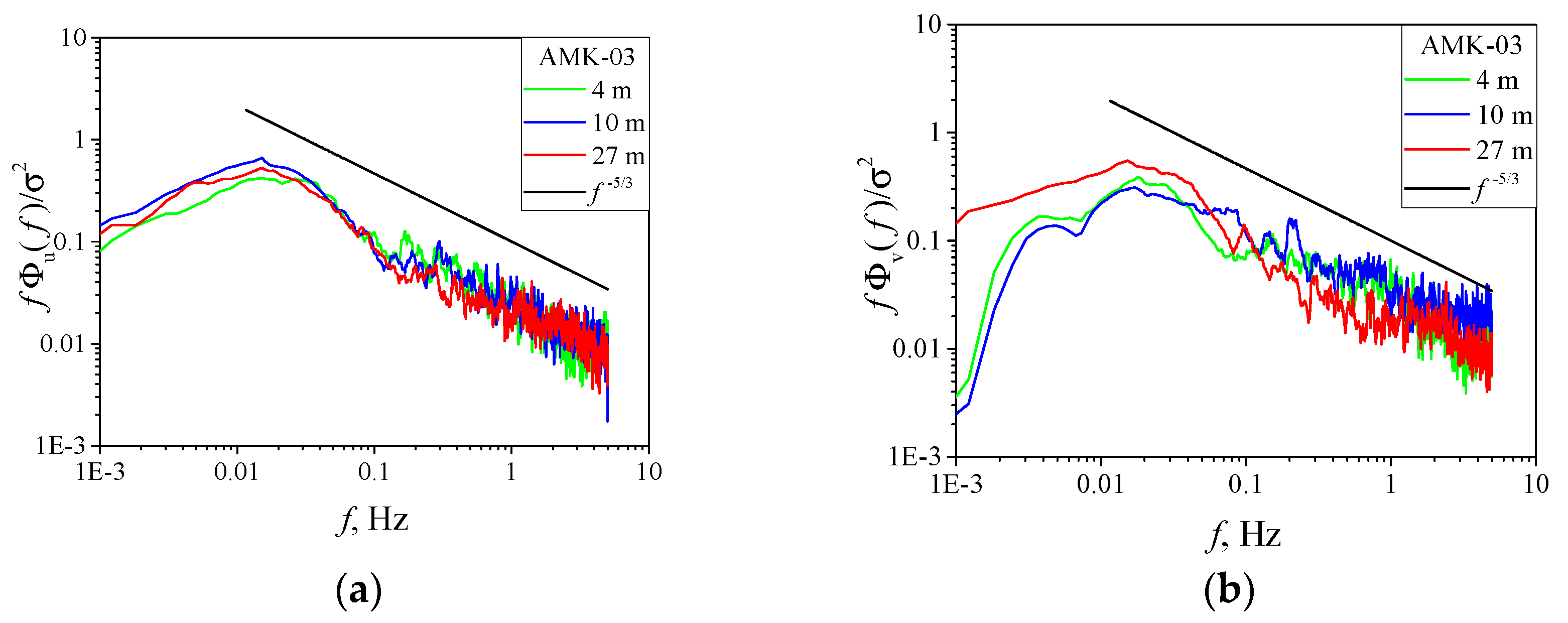
Preprints 72339 g009
Figure 9. Spectra of turbulent wind velocity fluctuations from AMK-03 anemometer data at 4 (green curve), 10 (blue curve), and 27 m (red curve): (a) longitudinal Φ u f and (b) lateral Φ v f spectrum.
Figure 9. Spectra of turbulent wind velocity fluctuations from AMK-03 anemometer data at 4 (green curve), 10 (blue curve), and 27 m (red curve): (a) longitudinal Φ u f and (b) lateral Φ v f spectrum.
Preprints 72339 g009
Table 1. UAVs used in the experiment, the start and end time, the hover height, and wind speed.
Table 1. UAVs used in the experiment, the start and end time, the hover height, and wind speed.
UAV Start, UTC End, UTC Hover height, m Wind speed, m/s
DJI Mini
DJI Air
DJI Phantom 4 Pro		 02:48 03:48 4 1.6
10 1.9
27 2.2
Table 2. Variances σ r   σ t , σ r , and σ t .
Table 2. Variances σ r   σ t , σ r , and σ t .
Height Longitudinal component Lateral component
σ r σ r σ t σ t
4 m 0.40 0.11 0.40 0.15
10 m 0.45 0.21 0.52 0.21
30 m 0.50 0.12 0.54 0.14
Average 0.45 0.15 0.49 0.17
Table 3. Correlation coefficients.
Table 3. Correlation coefficients.
Height Longitudinal component Lateral component
No smoothing Smoothing No smoothing Smoothing
4 m 0.68 0.94 0.68 0.93
10 m 0.69 0.89 0.56 0.77
30 m 0.75 0.97 0.72 0.96
Average 0.71 0.93 0.66 0.89
Table 4. Profiles of the longitudinal and lateral turbulence scales for the von Karman model and Dryden model.
Table 4. Profiles of the longitudinal and lateral turbulence scales for the von Karman model and Dryden model.
L u L v L v / L u
4 м
AMK-03 14.9/16.3* 9.0/10.0 0.61/0.61
DJI Mavic Mini 14.9/16.3 8.7/9.7 0.59/0.59
10 м
AMK-03 17.8/19.4 11.6/12.8 0.65/0.66
DJI Mavic Air 17.8/19.4 12.9/14.3 0.73/0.74
27 м
AMK-03 21.4/23.3 15.5/17.1 0.73/0.74
DJI Phantom 4 Pro 21.4/23.3 12.5/13.8 0.59/0.59
*Note. Hereinafter: von Karman model/ Dryden model.
Table 5. Longitudinal and lateral scales of turbulence.
Table 5. Longitudinal and lateral scales of turbulence.
L u L v L v / L u
4 м
AMK-03 15 11 0.7
DJI Mavic Mini 17 9 0.5
10 м
AMK-03 21 12 0.6
DJI Mavic Air 20 10 0.5
27 м
AMK-03 25 17 0.7
DJI Phantom 4 Pro 24 12 0.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated