Prerpints.org logo
Preprint
Article

Analysis of Concurrent Systems Based on Interval Order

Altmetrics

Downloads

138

Views

41

Comments

0

Yang Xu  *,
YE Chen  *
,
Chen Yi Jun  *

This version is not peer-reviewed

Submitted:

01 May 2023

Posted:

02 May 2023

You are already at the latest version

Alerts
Abstract
Studying concurrent systems is to sort the read/write and control events in the concurrent system according to the order, or in partial order, or in strict order. Because of the concurrency of events and the timeliness of writing events, there will be overlap between events, which requires interval order analysis. A single start and end sequence to represent the entire hierarchical order structure as well as all equivalent spaced order observations.a single sequence of beginnings and endings to represent the entire stratified order structures as well as all equivalent interval order observations. Mazurkiewicz traces and Comtracks are hierarchical traces, but they cannot describe interval traces. In a few sentences of this summary, we can tell the problems (petri interval traces with data), the previous work (Mazurkiewicz traces, Comtracks), the reasons that cannot be solved, and our own solutions (DPN: Petri nets with data, interval traces). This paper focuses on a BE (Beginnings and Endings) sequence representing an equivalent class of runs, or targets. Our goal is to have a BE sequence to represent the entire hierarchical order structure, that is, all equivalent observable interval orders.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

Introduction

In concurrent systems, most behavioral semantics are defined according to total order or stratified step order. If the causal relationship is considered, concurrent history is partial order [1,2,3] or Mazurkiewicz trace [4]. The Mazurkiewicz trace allows an equivalent single sequence, to represent the entire partial order. Traces provide a simple link between the observational and process semantics of concurrency systems. Another trace Comtraces represents the hierarchical sequence structure by a single step sequence, and its related observations can be obtained as a hierarchical or interval extension of the appropriate partial order [5,6]. A sequence of events that contains a causal relationship needs to be represented by a step-by-step sequence, or by a structure using a hierarchical order. An interval order structure is required when modeling the relationship, or when the observation is an interval order. Other relevant observations can be obtained as stratified or interval expansion of appropriate partial order. All observations of causality [7,8] are step sequences, which use stratified order structures. When modeling with the "no later than" relationship or all observations are interval order [9], the interval order structure should be employed to describe the observations.
When studying the behavior patterns of the concurrent system, the read and write data events in the concurrent system are sorted according to the sequence relationship, either in partial orders [10] or in total orders. Because of the concurrency of events [11,12,13] and the time required to writing events, there will be overlap between events, which requires interval order analysis. For most concurrency models, it is problematic to directly generate interval order. A very good way to represent sequences with feasible interval order is to use the beginnings and endings of events involved.
On a monoid-based model, the model will allow a sequence containing the beginning and end of written data events to represent the entire hierarchical order structure, and all equivalent observable interval orders. This completes the write data events by introducing the concept of an interval trace that combines the idea of Mazurkiewicz traces and comtrace, and proves that converting the write events into each interval trace at the beginning and end, uniquely identifies the interval order structure.
The impact of data on control flow cannot be described in ordinary Petri nets [14] or Petri nets with read arcs [10] or inhibitor arcs [15] for concurrent systems. This paper uses Petri nets with data, namely DPN, to describe the data participation in the modeling and simulation of concurrent systems [16,17,18,19,20]. This paper will also show how interval write data traces describe the interval orders semantics of Petri nets with data, so as to analyze the operation of concurrent systems. Through the analysis of the results, the interval trace is applied to the concurrent system with data Petri net description.
The main contributions are as follows:
1.Using Petri nets with data, namely DPN, to describe the data participation in the modeling and simulation of concurrent systems. 2.A BE (Beginnings and Endings) sequence representing an equivalent class of runs, or targets. The goal is to have a BE sequence to represent the entire hierarchical order structure, that is, all equivalent observable interval orders. 3.How interval write data traces describe the interval orders semantics of Petri nets with data, so as to analyze the operation of concurrent systems. Through the analysis of the results, the interval trace is applied to the concurrent system with data Petri net description.
The rest of this paper is organized as follows. Session II to III discuss the relevant concepts and modeling model work. Session II provides some basic mathematical knowledge about partial order, complete order, hierarchical order and interval order, as well as Mazurkiewicz traces and Comtraces. Then, the Petri net and the Petri network with the data are introduced in Session III. In Session Iv, the addition of beginnings and endings of writing events in DPN for description, as well as experiments performed in netDraw. In Session V, the application of the interval trajectory is discussed, and the interval trajectory is analyzed to effectively represent the abstract interval order semantics of DPN. In Session VI, we present the running results of the interval of the case, indicating that the proposed interval sequence correctly describes the analysis of the control process based on the interval order.

1. Mathematical Foundations

We will introduce some relevant mathematical symbols and concepts such as partial order, hierarchical order, interval order, Mazurkiewicz trace and Comtraces and etc.

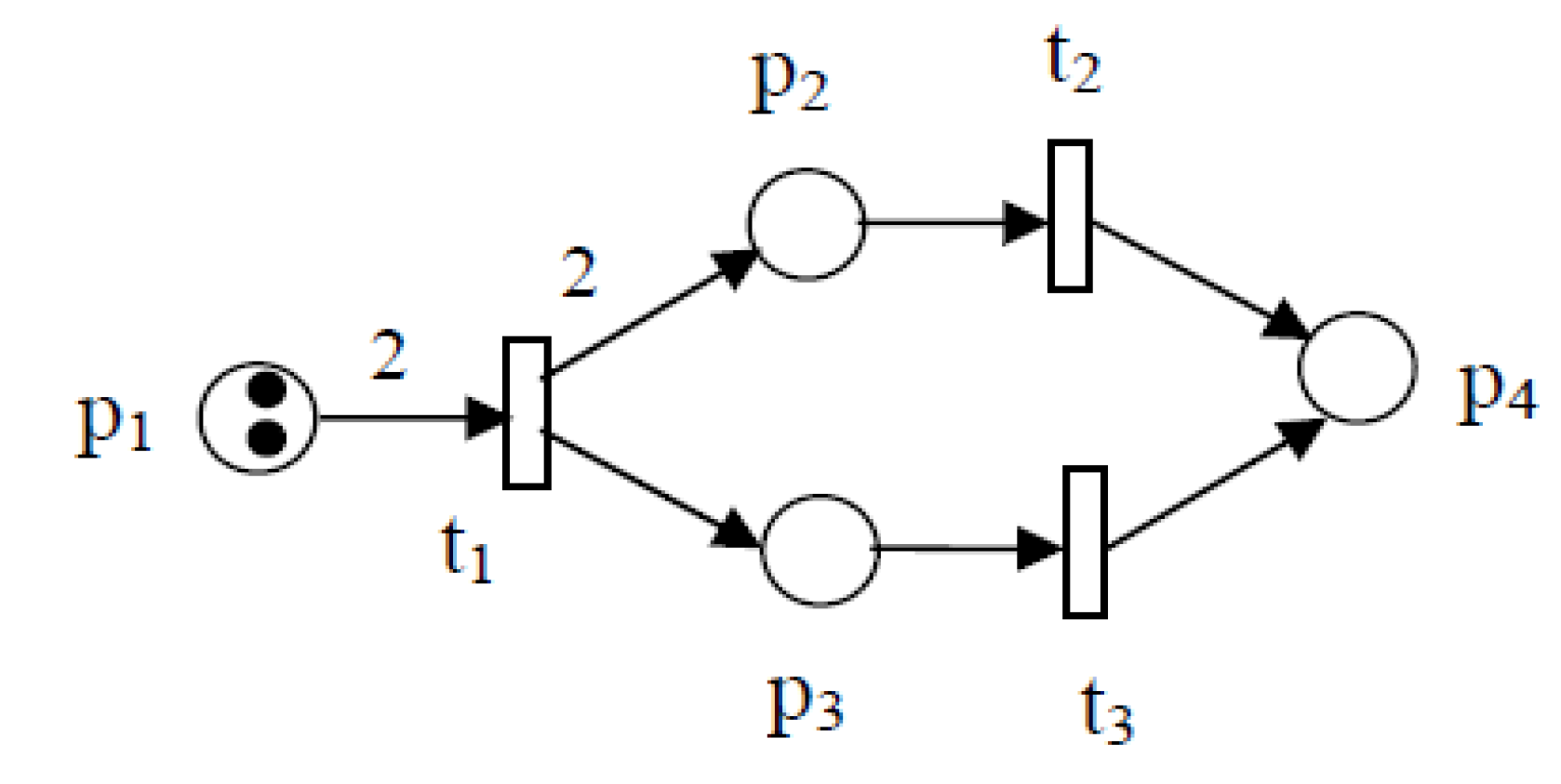
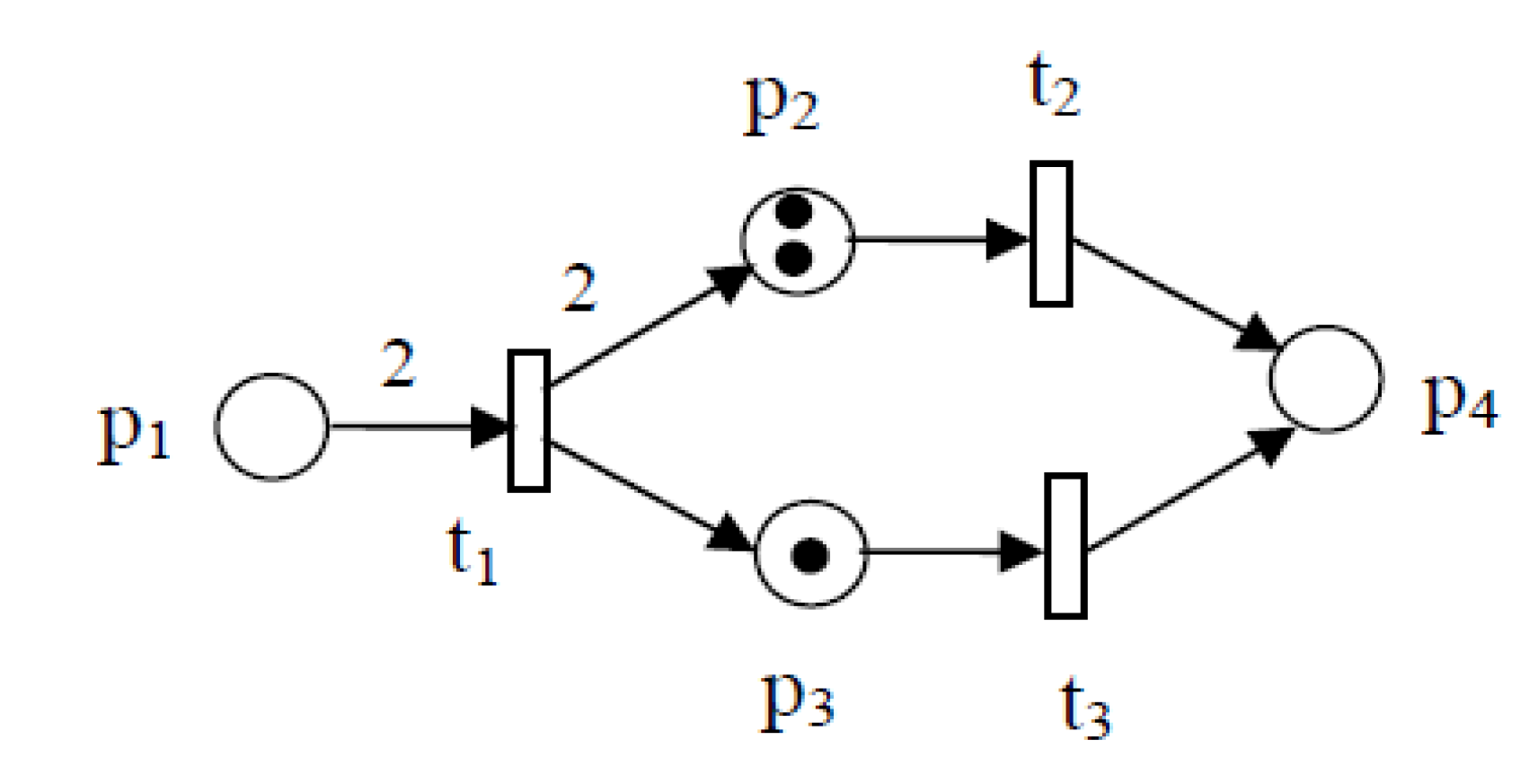
1.1. Partial orders,Stratified order and Interval order

Sort description of events running in a concurrent system, partial order is one of the tools to describe the relationship between events in a concurrent system. Will be used as a complete representation of events running in the concurrent system and a partial representation of concurrent events. There are also hierarchical sequences, complete sequences, and interval sequences, which can all sequence the events. Figure 1 presents the time-based orders. The definitions of different orders are presented as follows.
Definition 1 
(Partial Orders). The relation < ⊆ E × E is a (strict) partial order if it is transitive and irreflexive, i.e., for all e 1 , e 2 , e 3 ∈ E, e 1 < e 2 < e 3 ⇒ e 1 < e 3 . and:
1) e 1 ⌢ < e 2 ⇔ d f ¬ ( e 1 < e 2 ) ∧ ¬ ( e 2 < e 1 ) ∧ e 1 ≠ e 2 ,
2) e 1 < ⌢ e 2 ⇔ d f e 1 < e 2 ∨ e 1 ⌢ < e 2
Note that e 1 ⌢ < e 2 means e 1 and e 2 are incomparable (w.r.t.<) elements E.
Definition 2 
(Total order). For a relation R 1 ⊆ E × E , any relation R 2 ⊆ E × E is an extension of R 1 if R 1 ⊆ R 2 . we define Total ( < ) ⇔ d f { ◃ ⊆ E × E } , where ◃ is a total order and < ⊆ ◃
Definition 3 
(Stratified orders). Stratified orders are often defined in an alternative way,i.e., a partial order < on E is stratified iff there exists a total order ◃ on some n and a mapping O : m → n such that ∀ m , n ∈ E . m < n ⇔ ϕ ( m ) ◃ ϕ ( n ) . This definition is illustrated in Figure 1, where ϕ ( 1 ) = { 1 } , ϕ ( 2 ) = ϕ { 3 } = { 2 , 3 } and ϕ ( 4 ) = { 4 } .
Theorem 1.(Fishburn [1970]) A partial order < on E is interval if and only if there exists a total order ◃ on some W, and two mappings B , E : y → W such that for all a , b ∈ E :
1) B ( a ) < E ( b ) ,
2) a < b ⇔ E ( a ) ◃ B ( b ) .
Usually B ( a ) is interpreted as the beginning and E ( a ) as the end of an interval a (Such events/actions consume time). The intuition of Fishburn’s theorem is illustrated in Figure 1 with < 3 and ◃ 3 . For all a , b ∈ { 1 , 2 , 3 , 4 } , we have B ( a ) ◃ 3 E ( a ) and a < 3 b ⇔ E ( a ) ◃ 3 B ( b ) . For better readability in the future we will skip parentheses in B ( a ) and E ( a ) .
In summary, we can conclude that:
1) < is total if ⌢ < = O , In other words, for all e 1 , e 2 ∈ X , e 1 > e 2 ∨ e 2 < e 1 ∨ e 1 = e 2 . For clarity, we will reserve the symbol ◃ to denote total orders;
2) < is stratified if e 1 − < e 2 ⌢ < e 3 ⇒ e 1 ⌢ < e 3 ∨ e 1 = e 3 , i.e., the relation ⌢ < ⋃ i d X is an equivalence relation on X;
3) < is interval if for all a , b , c , d ∈ E , e 1 < e 3 ∧ e 2 < e 4 ⇒ e 1 < e 4 ∨ e 2 < e 3 .

1.2. Mazurkiewicz Traces

In 1970, Anthony Mazurkiewicz first proposed the trace theory [21,22,23,24,25,26,27] due to the generation, which was also driven by Petri Nets [28,29,30,31,32,33,34,35,36,37] and the formal language with automata. The aim is to circumvent some of the problems in the theory of concurrent computation, initially, the most popular way to deal with concurrency is interweaving. Includes interleaved and non-deterministic selection issues regarding process computational refinement. Mazurkiewicz Traces, often abbreviated as traces, correspond to a sequence of atomic actions of concurrent systems and are used to model the execution. The concurrent system can then be described by the execution set, called the language in the framework. Currently, the concept of a trace [38] is usually used to describe the non-sequential behavior of a concurrent system through its sequential observation. In this approach, concurrency is replaced by non-deterministic, where concurrent execution of actions is considered as an uncertain choice of the order of execution of these actions. The trace always represents a concurrent process in a sequence associated with a string.
For a concurrent system, the different actions executed are not formed in a linear order, but the events are arranged in partial order. Therefore, the sequential relationship of the execution events of the concurrent system is defined as the partial order.
Definition 4 
(Partia1 order set, poset). Let ( E v , ≤ , λ ) be a poset where Ev is countable.
For e ∈ Ev , we define ↓ e = { e 1 ∈ E v ∣ e 1 ≤ e } and ↑ e = { e 1 ∈ E v ∣ e ≤ e 1 } . We call ↓ e the history of the event e and ↑ e the future of the event e.
Let ≮ be the covering relation given by e 1 < e 2 if e 1 ≤ e 2 , e 1 ≠ e 2 , and for all e 3 ∈ E v , e 1 ≤ e 3 ≤ e 2 implies e 1 = e 3 or e 3 = e 2 .
Moreover, let the concurrency relation (co) be defined as e 1 co e 2 iff e 1 ≰ e 2 and e 2 ≰ e 1 .
The definition of the Mazurkiewicz trace is given below
Definition 5 
(Mazurkiewicz trace). A Mazurkiewicz trace over the independence alphabet ( Σ x , I n ) is a Σ-labeled poset T = ( E v , ≤ , λ ) satisfying:
1) For ∀ e 1 ∈ E v , ↓ e 1 is a finite set.
2) For ∀ e 1 , e 2 ∈ E v , e 1 ⋖ e 2 implies λ ( e 1 ) ⪯ λ e 2 , where ⪯ refers to dependence relation.
3) For ∀ e 1 , e 2 ∈ E v , λ ( e 1 ) ⪯ λ e 2 implies e 1 ≤ e 2 or e 2 ≤ e 1 .
The monoid of Mazurkiewicz traces are on the sequence, equivalent monoid. The application of traces in concurrency theory stems from the fact that traces are sequential representations of partial order. The theory of the traces has been used to solve problems from a number of different fields, which enables the traces to model the "true concurrency" semantics. Including combinatorial theory, graph theory, algebra theory, logic, and especially concurrency theory.

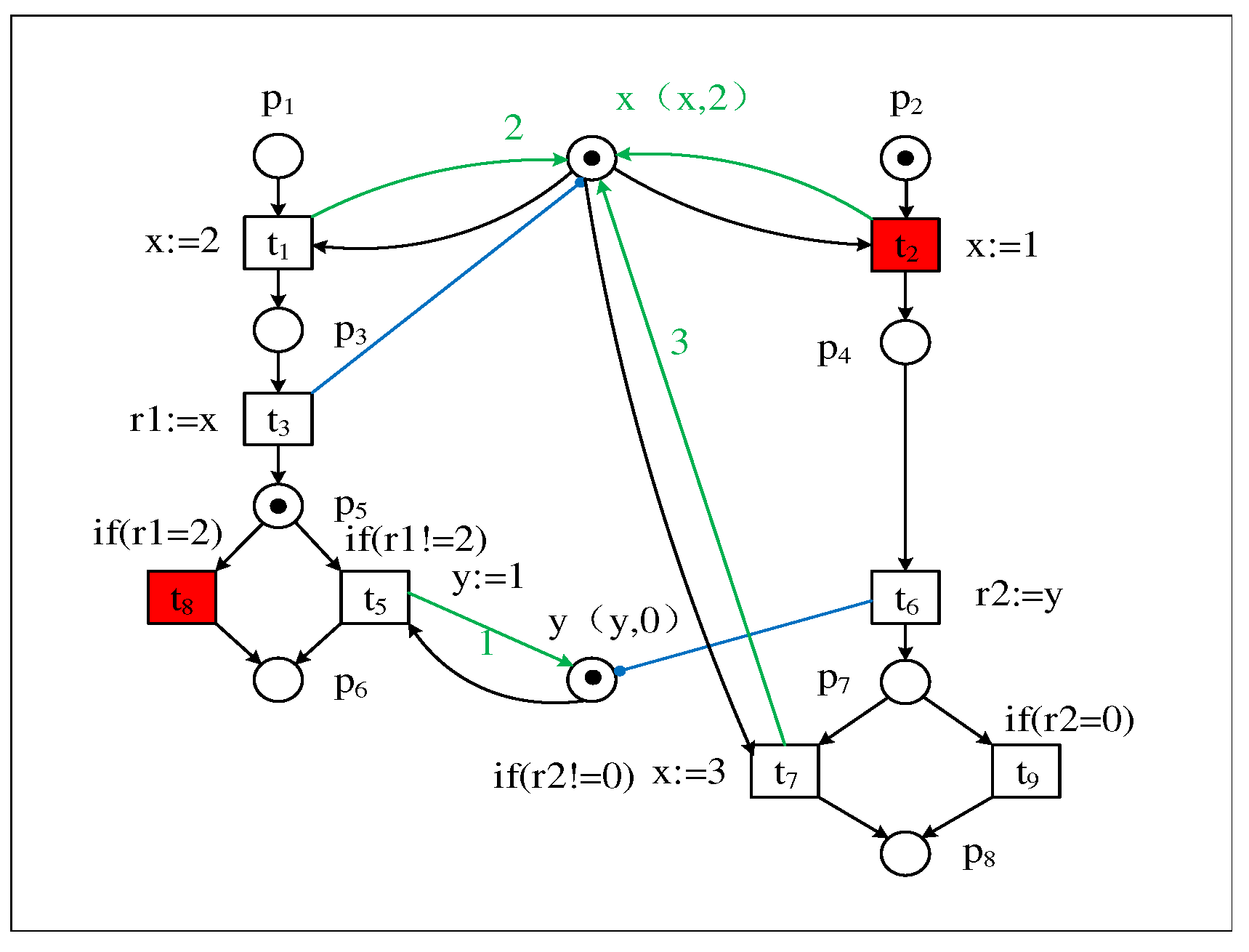
2. The proposed model

Multi-threaded concurrent system is multi-threaded in a multi-core processor, in a certain storage mode, based on the shared memory, under the operation process. Before analyzing the operation of multi-threaded system, give the semantic rules of multi-threaded system, the storage rules of running storage mode, the memory access rules and data transformation rules.

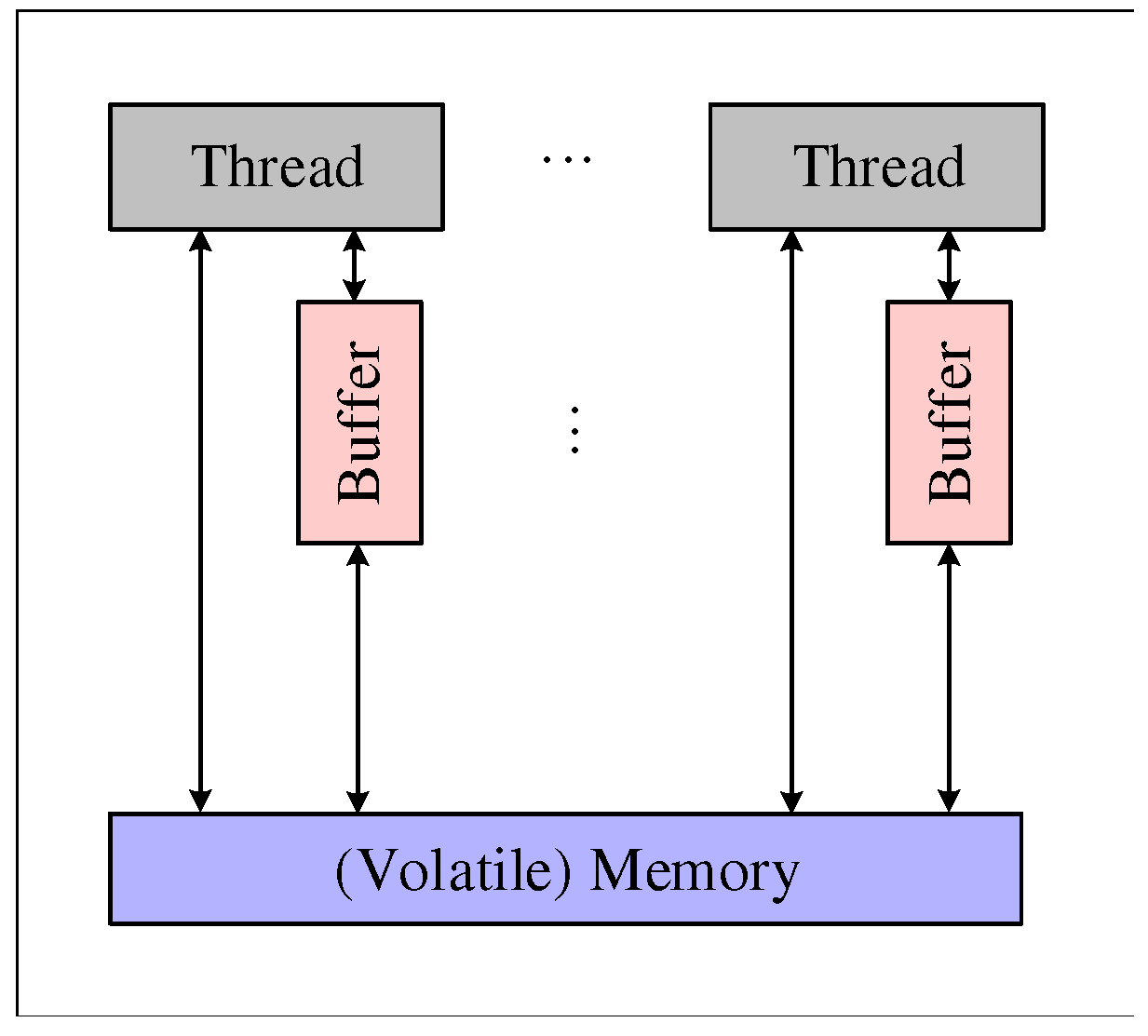
2.1. Multithreaded system

Here presents the syntax of concurrent programming language.
a , b ∈ Values o X ∈ Mod X where X ∈ { R , W } Access modes
r , s , t ∈ Loc ⊆ { r , s , … } Locations sPr ∈ SProg ≜ { 0 , 1 , … , N } → Inst Sequential programs
x ∈ Reg ⊆ { x , y , … } Registers Pr : Tid → SProg (Concurrent) programs
τ , π ∈ Tid ⊆ { T 1 , T 2 , … } Thread identifiers
e : : = r | v | e + e | e = e | e ≠ e ∣ …
Inst ∋ inst : : = r : = e ∣ if e goto pc 1 , … , pc n ∣ assert ( e )
| x . s t o r e ( e , o W ) | r : = x · load ( o R )
A finite set Loc of memory location; a finite set Reg of (local) register; a finite set Val of value; a finite set TId of thread identifier;
Owicki Gries inference logic is used for concurrency. OG inference extends Hoare’s proof rule logic and rules to infer the concurrent program form C 1 || C 2 , allowing the combination of verified programs C 1 and C 2 into a verified concurrent program, provided that the two C1 and C2 proofs do not interfere with each other:
READ:
P 1 ⇒ P 2 x v / a
〈 { P 1 , P 2 } , ⌀ 〉 ⊢ { P 1 } a : = x { P 1 } .
WRITE:
P 1 ⇒ P 1 e / x v
{ P 1 , Q 1 } , x v , e , P 1 ⊢ { P 1 } x : = e { P 1 }
SEQ:
R 2 ; G 2 ⊢ { R } c 2 { Q }
R 1 ∪ R 2 ; G 1 ∪ G 2 ⊢ { P } c 1 ; c 2 { Q }
ITE:
〈 R ; G 〉 ⊢ { P ∧ e = 0 } c 2 { Q }
〈 R ∪ { P } ; G 〉 ⊢ { P } if ( e ) then c 1 else c 2 { Q }
P ∧ e = 0 ⇒ Q P ⇒ P R ′ ⊆ R G ′ ⊆ G Q ′ ⇒ Q
WHILE:
〈 R ; G 〉 ⊢ { P ∧ e ≠ 0 } c { P }
〈 R ∪ { Q } ; G 〉 ⊢ { P } while ( e ) c { Q } .
CONSEQ:
R ′ ; G ′ ⊢ P ′ C { Q }
〈 R ∪ { P , Q } ; G 〉 ⊢ { P } C { Q }
With the advent of non-volatile memory, the presence of permanent memory in the storage system requires new storage modes to verify multithreaded concurrent systems. volatile memory storage mode of random access memory (RAM), and non-volatile permanent storage mode(NVM) have emerged in the storage system, as shown in Figure 2 and Figure 3.
In persistent memory model [39,40,41,42], Multithreaded system verification [39,43] is very important, since it is difficult to verify the correctness of a Multithreaded system [44,45] sharing variables [46,47,48,49,50,51,52,52]. Prior work fails to well consider the impact of data on control flow, which makes verification more difficult [17,18,19,20]. Figure 4 is the two multi-thread systems sharing x and y in the persistent memory mode, r 1 , r 2 are local variables, where x, y are shared variables, thread 1 and thread 2 run concurrently, thread 1 and thread 2 assign 2 and 1 respectively to x, and thread 1 reads the value of x, which may be 1 or 2. If the read value of x is 2, 1 is written to the y. thread 2 may read the value of y as 1 or 0 (initial), and judge the value of r 2 . If the read value r 2 of y is 0, Number 3 is assigned as the value of x.

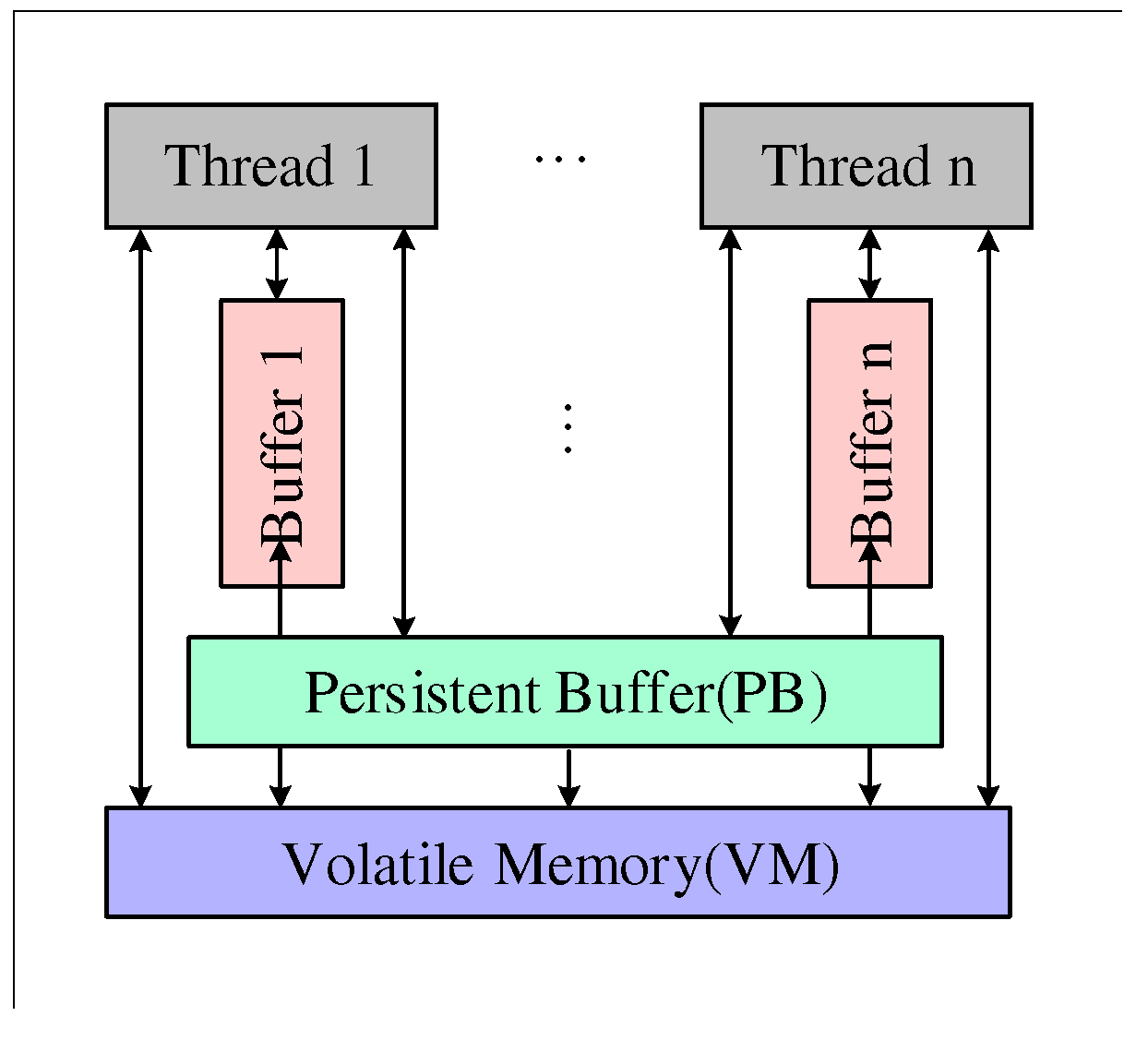
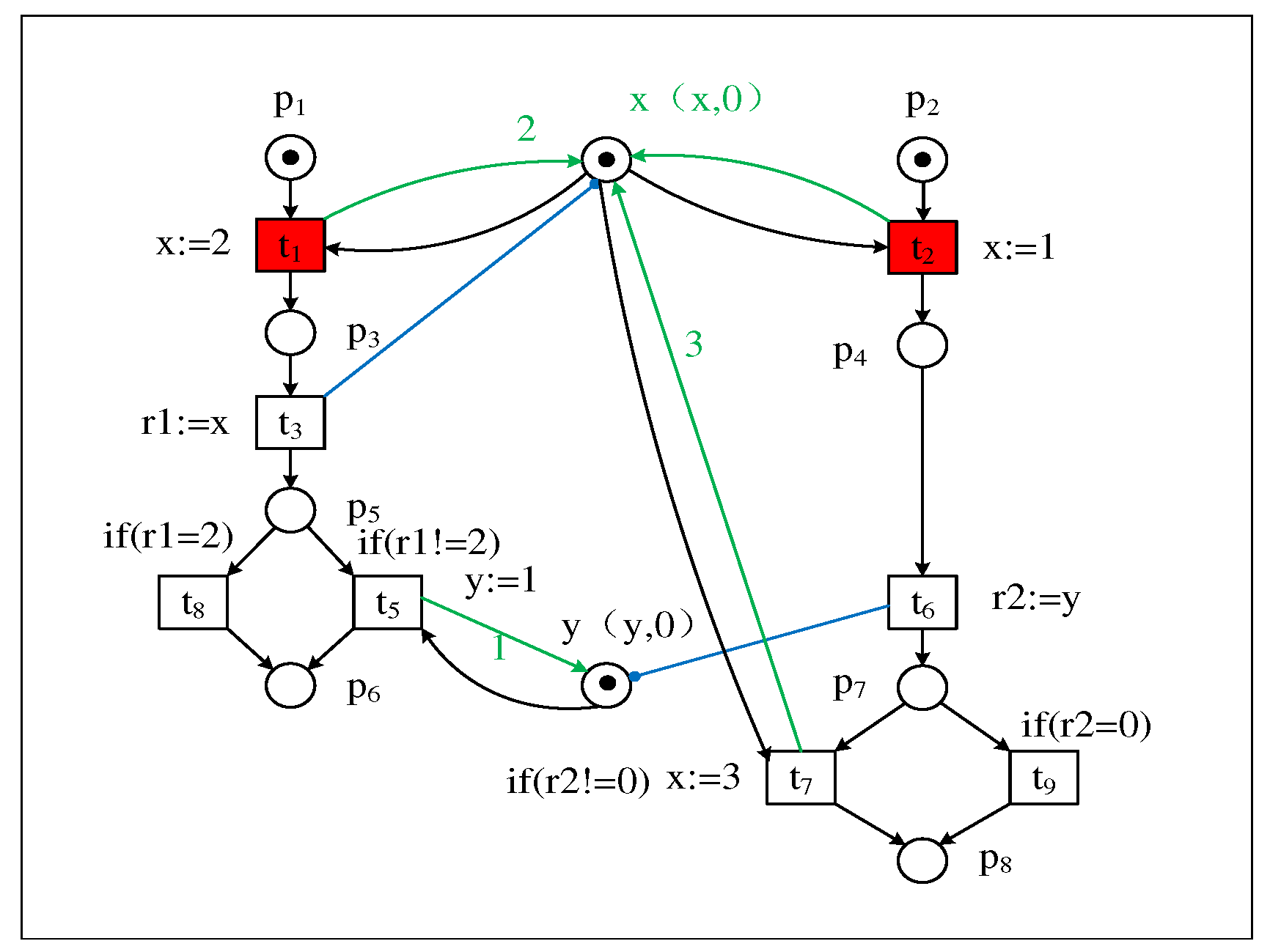
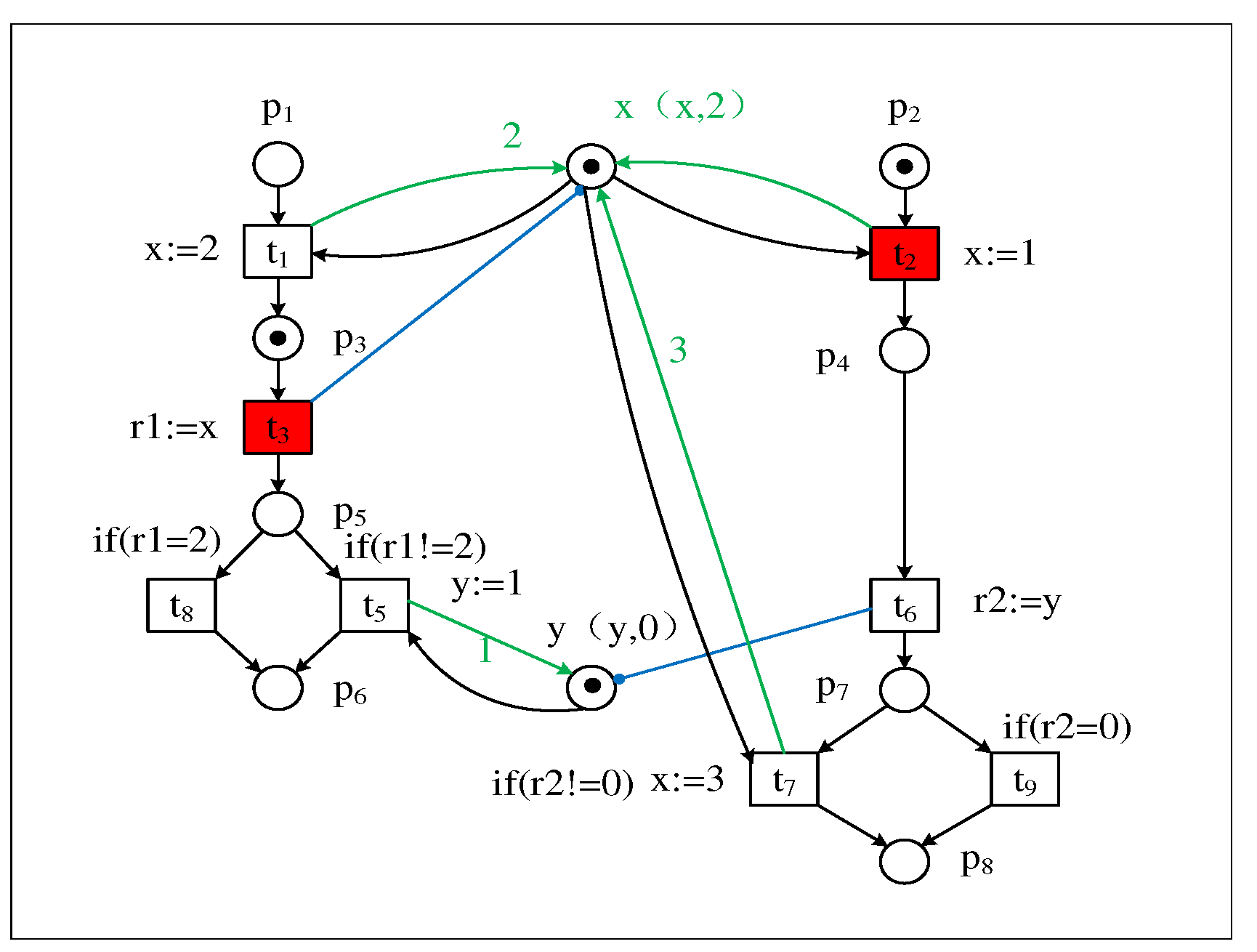
2.2. Petri net with read-write data

Definition 6 
(Petri net). Petri net [53,54] is a triplet P N i =(Pl, Tr, Fl), where Pl and Tr are respectively finite sets of places and transitions Pl ∩ Tr = ⌀ and Pl ∪ Tr ≠ ⌀ ) . while Fl ⊆ ( Pl × Tr ) ∪ ( Tr × Pl ) is a set of arcs (flow relationships). • x = { y ∈ P l ∪ T ∣ ( y , x ) ∈ F l } ; x • = { y ∈ P l ∪ T r ∣ ( x , y ) ∈ F l } . ∀ x ∈ P l ∪ T r : • x ∪ x • ≠ ⌀ .
Figure 5 is a simple example of Petri net, where T r = { t 1 , t 2 , t 3 } ; P l = { p 1 , p 2 , p 3 , p 4 } ; I n ( t 1 , p 1 ) = 2 , I n ( t 1 , p i ) = 0 for i = 2 , 3 , 4 ; O c ( t 1 , p 2 ) = 2 , O c ( t 1 , p 3 ) = 1 , O c ( t 1 , p i ) = 0 f o r i = 1 , 4 ; I n ( t 2 , p 2 ) = 1 , I n ( t 2 , p i ) = 0 for i = 1, 3, 4; O c ( t 2 , p 4 ) = 1 , O c ( t 2 , p i ) = 0 f o r i = 1 , 2 , 3 ; I n ( t 3 , p 3 ) = 1 , I n ( t 3 , p i ) = 0 f o r i = 1 , 2 , 4 ; O c ( t 3 , p 4 ) = 1 , O c ( t 3 , p i ) = 0 f o r i = 1 , 2 , 3 ; M 0 = ( 2 , 0 , 0 , 0 ) .
Definition 7 
(PN transition rules). Let P N i =(N, M) be a simple Petri net and the transition rules :
(1) For transition t 1 ∈ T i , if ∀ p i ∈ • t i : M i ( p i ) ≥ 1 , it is said that transition t i is enabled under the marking M i , which is recorded as M i [ t i 〉 ;
(2) If M i [ t i 〉 , the transition t i can take place under the marking M i ′ , and a new marking M i ′ can be obtained from the transition t i caused by the marking M i , which is marked as M i [ t i 〉 M i ′ for ∀ p i ∈ P ,
The whole state space of P N i =(N, M 0 ) is determined by its network N and initial marking M 0 . Figure 6 shows a transition t 1 firing based on Figure 5, which presents new tokens distribution of this Petri net.
We can find that under marking, M 0 = (2, 0, 0, 0). Firing of t 1 results in a new marking, i.e., M 2 . = (0, 2, 1, 0). Again , It follows the firing rule that M 1 In marking M 1 = (0, 2, 1, 0), both transitions of t 3 and t 2 are enabled. If t 3 fires, the new marking, i.e., M 3 = (0, 2, 0, 1).If t 2 fires, the new marking, i.e., M 2 = (0, 1, 1, 1).
Definition 8 
(Petri net with data: DPN). An 8-tuple D P N i = ( P c , P d , T c , T d , F c , F d , P c 0 , P d 0 ) is called Data Petri net if it meets:
(1) (Pc, Tc, Fc, P c 0 ) is a Petri net;
(2) Pd= p d 1 =[ D 1 , v a l 1 ], p d 2 = [ D 2 , v a l 2 ] . . . p d n = [ D n , v a l n ]. [ D i , v a l i ] is the data place, Pd is a finite set of elements D i , where v a l i is the value of D i , and the token of the initial p d i =1, v a l i =0.
(3) Fd : Td×Pd ∪ Pd×Td. Fd includes read data (Rd) and write data (Wr) arcs, namely Rd : Pd×Td and Wr: Td×Pd;
(4) Wr writing data transition: write the value to D i . Rd read data transition: read the value v a l i from the data place D i .
(5) Td: Td×Pd ∪ Pd×Td. Write data transition Td ⟶ F d Pd, read data transition: Pd ⟶ F d Td.
(6) Configuration: Pc → { 0 , 1 , 2 … } and Pd → { 1 } represent the configuration or state, where c = ( m , σ ) , M is the control marking, σ is the data status. P c 0 is the initial configuration of the control place, and P d 0 is the initial configuration of the data place, p d i = 1 , v a l i = 0 .
For the data place p d i ∈Pd in DPN, its value is obtained by using the function getValue(pd). For convenience, a pair of data transition functions on conversion are also provided, namely Read: getValue( D i ), Write: setValue( p d i )=value.
Definition 9 
(DPN transition rule). and set DPN=(DN,M,Σ) It is a Petri net and has the following transition rules:
(1) For transition t ∈ Tc, if ∀ p ∈ • t : M ( p ) ≥ 1 , control transition t is said to be enabled under the marking M 1 , which is recorded as M 1 [ t 〉 ;
(2) If M 1 [ t 〉 , the control transition t can occur under the marking M 1 , and the transition t caused by the marking M 1 can get a new marking M 1 ′ , which is recorded as M 1 [ t 〉 M 1 ′ ,and for ∀ p ∈ Pc ∪ Pd.
M ′ , Σ ′ = ( M ( p ) − 1 , Σ ) i f p ∈ • t − t • ( M ( p ) + 1 , Σ ′ ) i f p ∈ t • − • t M ( p ) e l s e
For the transition t ∈ T c , if ∀ p ∈ • t : M ( p ) ≥ 1 , the data transition t in marking ( M i , Σ ) is enabled, which is recorded as ( M i , Σ ) [ t 〉 ( M i ′ , Σ ) ;
(3) In the marking ( M i , Σ), if ( M i , Σ)[td〉, data transition t d ∈ T d is enabled and triggered to get a new marking ( M i ′ , Σ ′ ), i.e., ( M i , Σ ) t d > M i ′ , Σ ′ .
M ′ , Σ ′ = ( M ( p ) − 1 , Σ ) i f p ∈ • t − t • ( M ( p ) + 1 , Σ ) i f p ∈ t • − • t ∧ t ∈ P c M ( p ) + 1 , Σ ′ i f p ∈ t • − • t ∧ t ∈ P d M ( p ) ∈ e l s e
Wherein, Σ [ F d ⟶ ( D i , v a l u e ) P d > Σ ′ .
(4) Finally, the entire state space of D P N i =(DN,(M, Σ)) is determined by its network D P N i and initial marking M 0 .
In Figure 7, T 1 is the write data transition, which realizes the write data value 2 to the data place x (there is a green arrow line between the write transition and the data place office). t 8 and t 9 are control transitions. The first step is to obtain the write permission in x, i.e., the token of x. After obtaining the write permission in x, write the value 2 to x, and then return the write permission of the token to x; T 2 is the change of write data. Write the data value 1 to the data place x, and the process is the same as the change of write data t 1 . T 3 is read data transition. Read the value of data place x (there is a blue line between the data place object and the change of read data, and the end of the read data place object is a solid circle). First, judge whether data place object x has read permission, i.e., whether there is a token in x, if hold, it can be read. Read the value of x through the reading arc, if there is no token in x, x cannot be read. The semantics of read data transition t 6 are the same as that of read data transition t 3 .
In Figure 7, if P 1 has a token and the data place D x has a token, t 1 can occur. After the occurrence, the value of x(x, 2) in the data place change to number 2, and the status is shown in Figure 8; If there is a token in P 2 , and there is a token in data place x(x, 2), t 2 can occur. After t 2 transition occur, the value in data place x(x, 1) change to number 1; When P 3 has a token, and the data place has a token in x(x, 1), then t 3 transition can occur. Read the value in x(x, 1) of the data place, and the token in x(x, 1) of the data place remains unchanged, and read the value of data place x is number 1.
In Figure 8, if t 3 is triggered again (i.e., t 1 is triggered first, then t 3 is triggered), the state is shown in Figure 9.

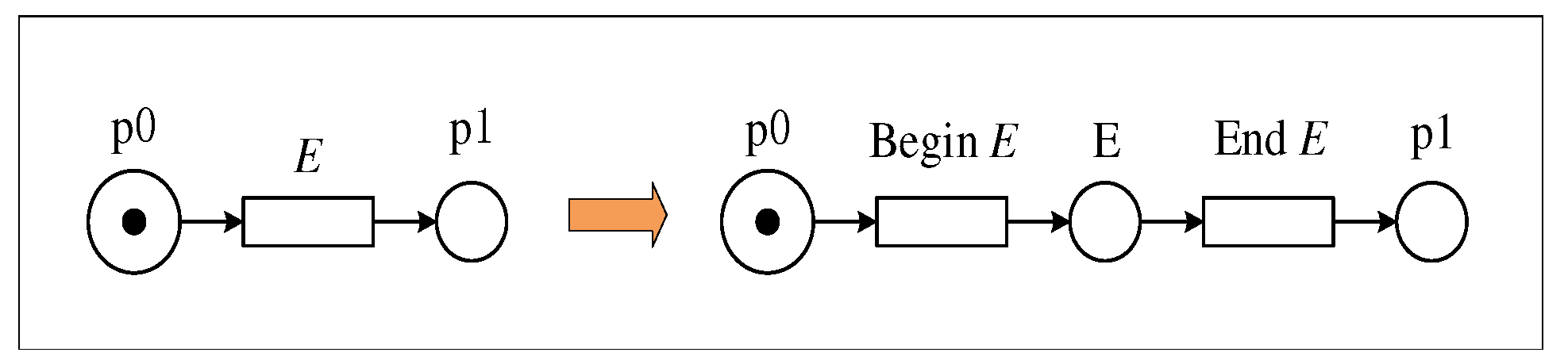
3. Convert the writing event to the Beginning and Ending event

Writing events takes time in theory, so when we study the sequence of reading and writing events, we consider the time of writing events and convert the writing events into two events: starting and ending [55,56]. BE for a given writing event Σ = {Beg a∣a∈ Σ } ⋃ {End a∣a ∈ Σ }. The write data event is converted to the Beginning and Ending events according to Figure 10. For each writing event in Σ , it is transferred into beginning and ending event following by BE Σ ={Ba∣a∈ Σ }⋃{Ea∣a∈ Σ }, where B refers to the beginning event and E refers to the ending one.
Definition 10. 
Let Petri P N i = (P, T, TR, TW, D, m 0 ) be a Petri net with data.
(1) For each t i ∈ TW,now,we define B e g − t i the beginning of t i and E n d t − t i the end of t i , and the set B e g T = { B e g t ∣ t ∈ T w } ∪ { E n d t ∣ t ∈ T w } . The elements of TW are called BE-transitions.
(2) For each t i ∈ T W , we define: (a) • B t = • t , (b) B t • = { t } , (c) • E t = { t } , (d) E t • = t • .
(3) We say that a set m ⊆ P ∪ T is an extended marking if m ∩ • m ∪ m • = ⌀ .
(4) An enabled BE-transition same enabling capacity as Petri net
(5) An extended firing sequence same enabling capacity as Data Petri net
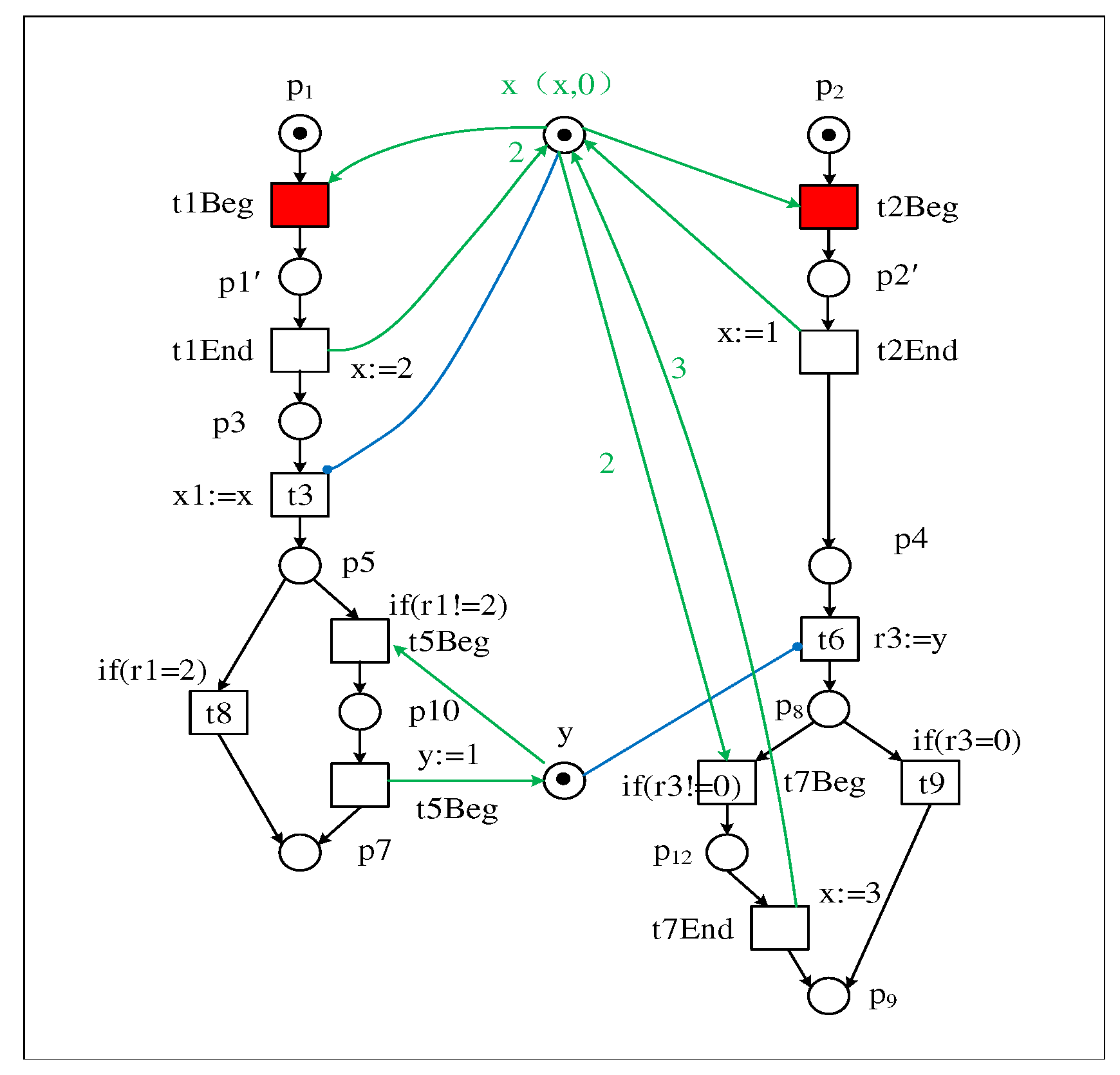
Preprints 72351 g011
Figure 11. The writing events of concurrent code in Figure 7 to beginning and ending ones.
Figure 11. The writing events of concurrent code in Figure 7 to beginning and ending ones.
Preprints 72351 g011
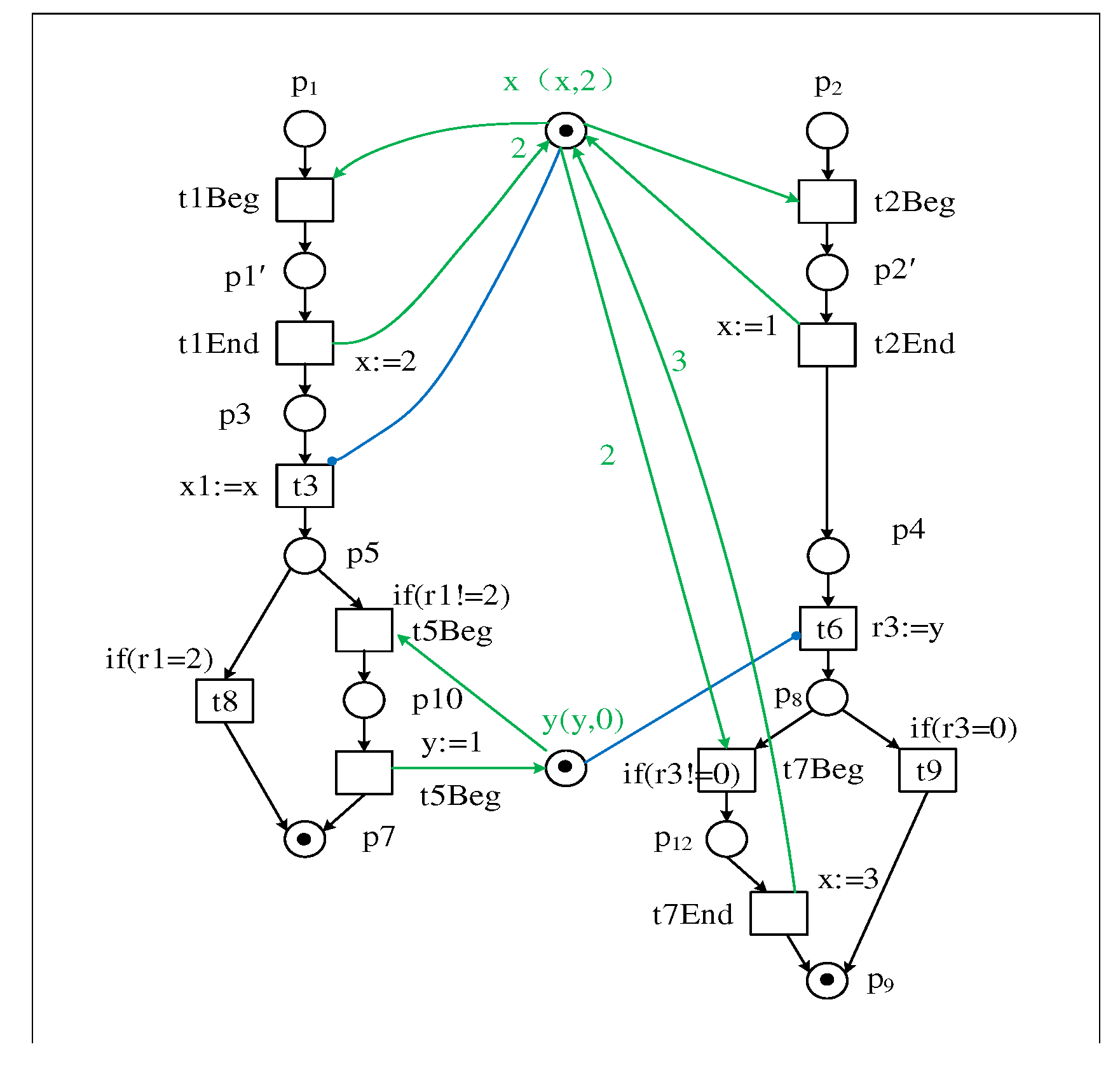
Preprints 72351 g012
Figure 12. result[x=2,y=0].
Figure 12. result[x=2,y=0].
Preprints 72351 g012
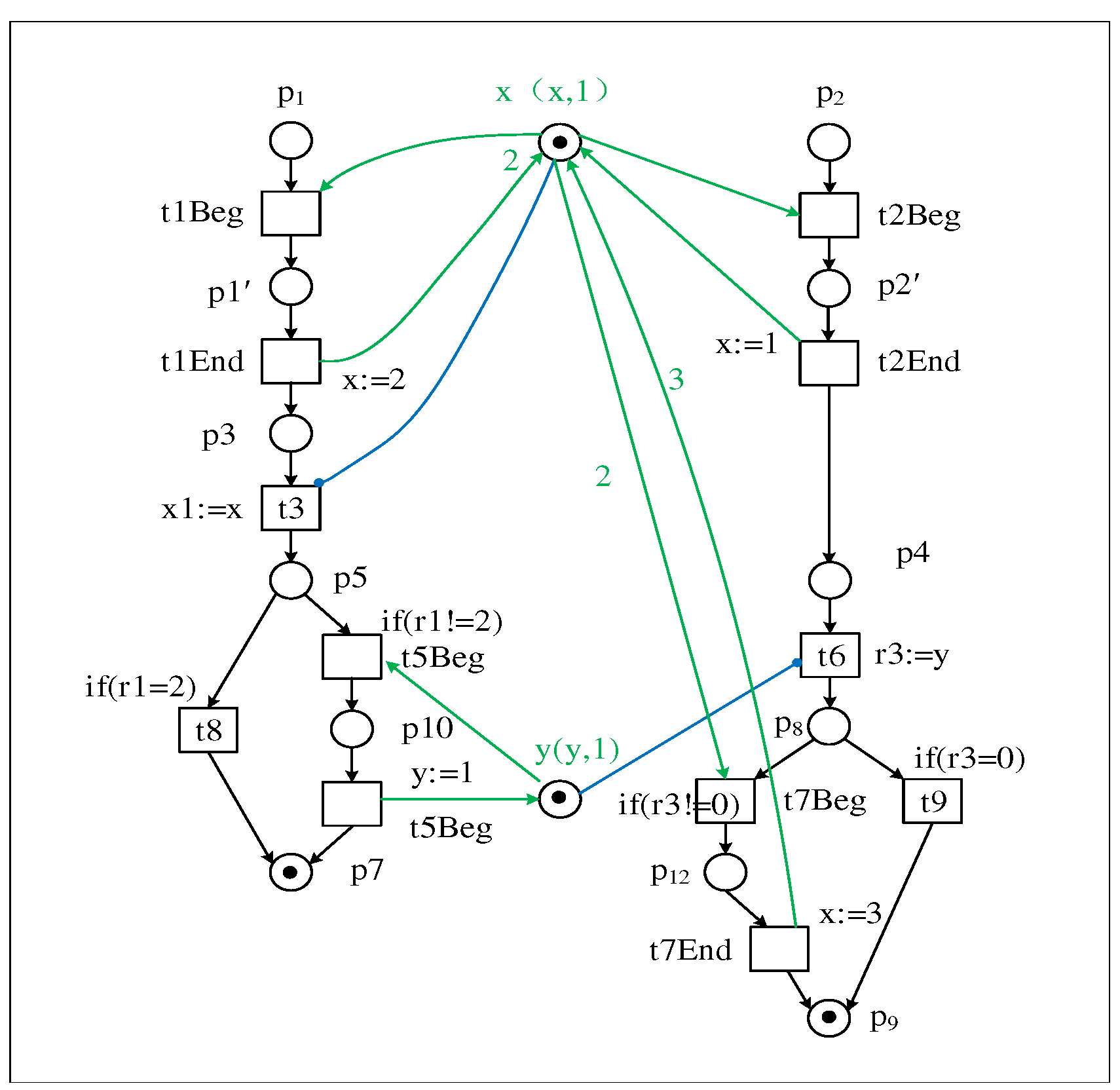
Preprints 72351 g013
Figure 13. result[x=1,y=1].
Figure 13. result[x=1,y=1].
Preprints 72351 g013
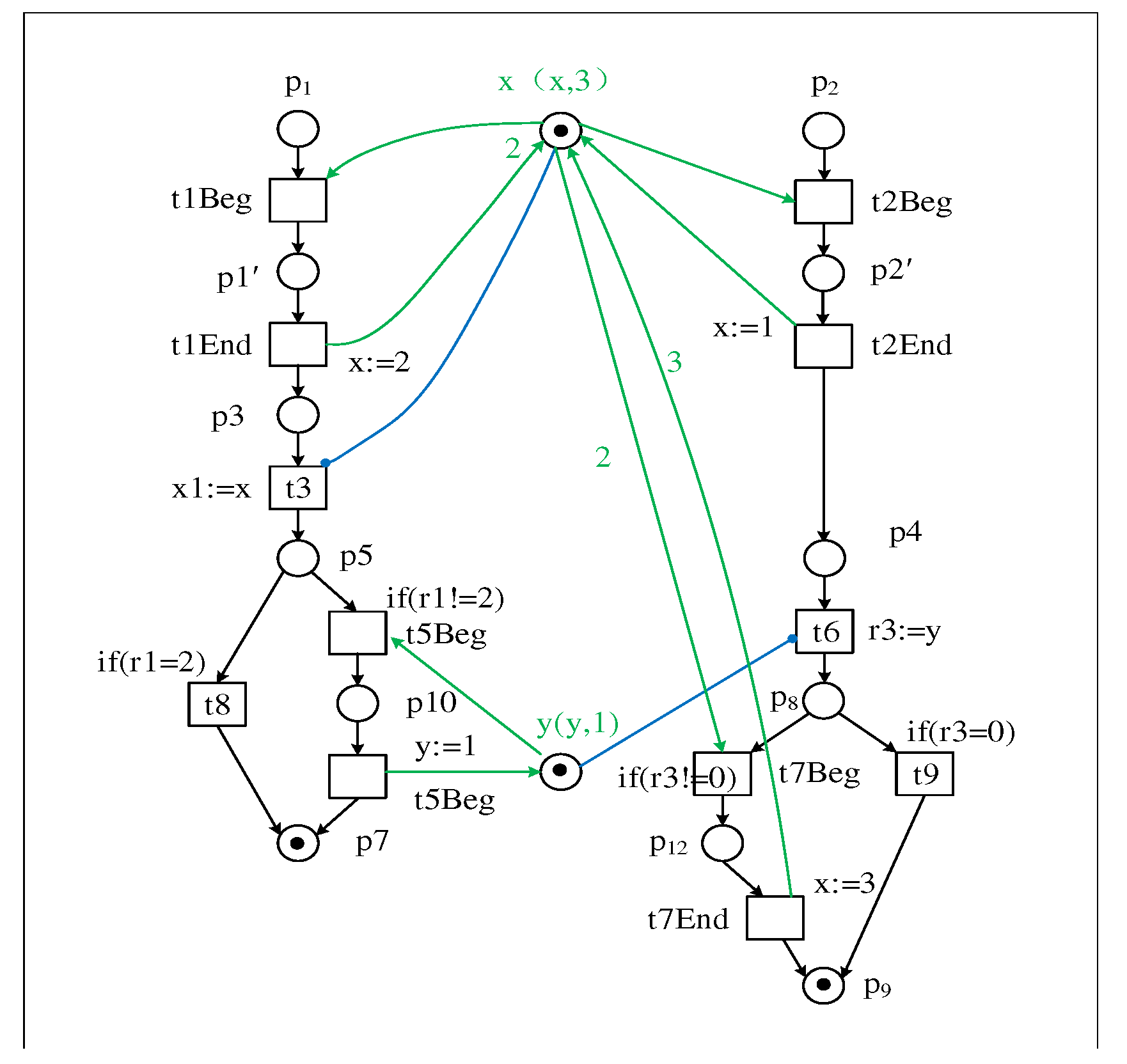
Preprints 72351 g014
Figure 14. result[x=3,y=1].
Figure 14. result[x=3,y=1].
Preprints 72351 g014
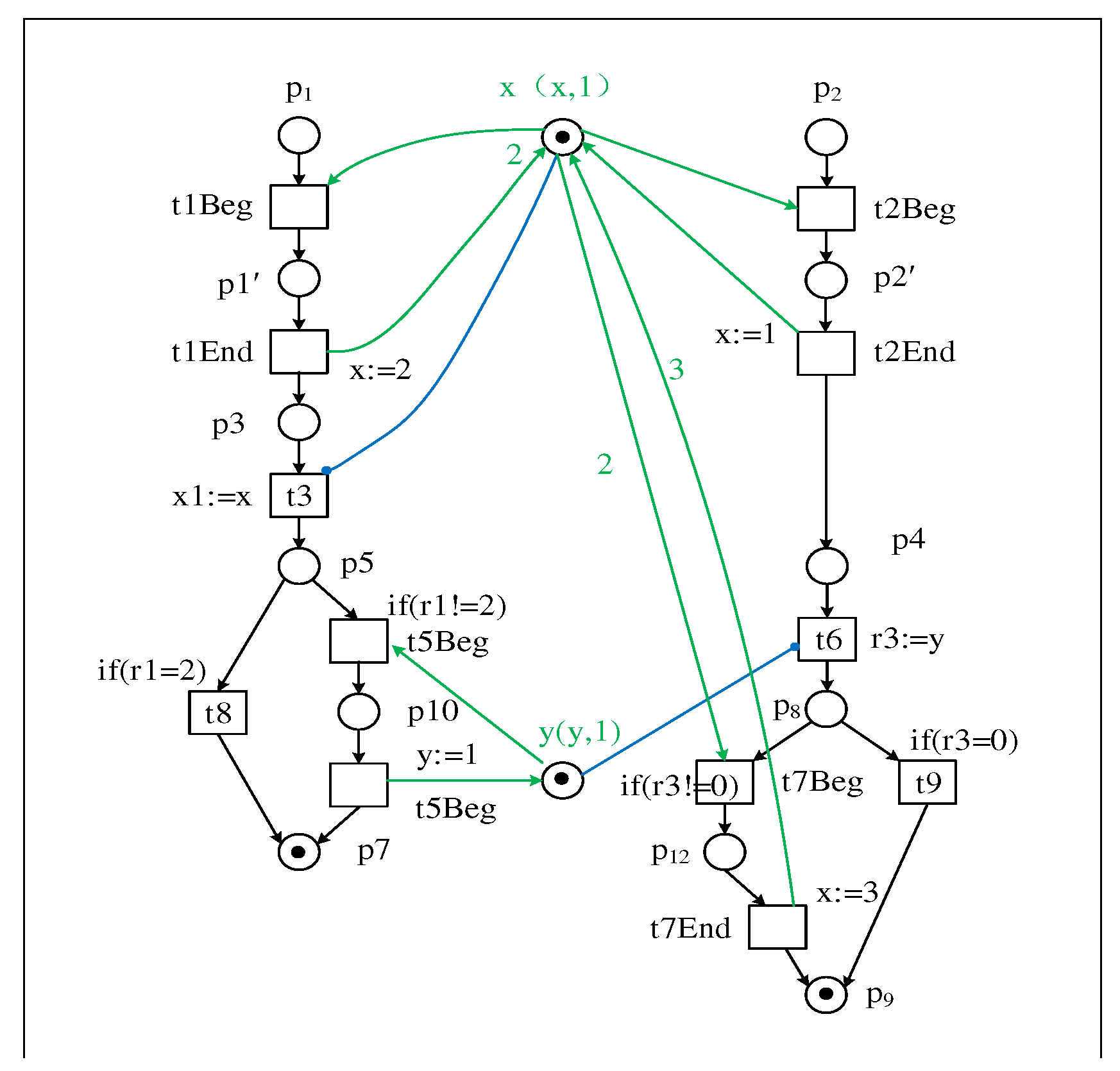
Preprints 72351 g015
Figure 15. result[x=3,y=0].
Figure 15. result[x=3,y=0].
Preprints 72351 g015
Table 1. The firing trace of transition and the final results of shared variables x and y.
Table 1. The firing trace of transition and the final results of shared variables x and y.
Firing trace of transition x , y
T1 : Bt1, Et1, Bt2, Et2, t3, Bt5, Et5, t6, Bt7, Et7 3 , 0
T 2 : B t 1 , E t 1 , B t 2 , E t 2 , t 3 , t 6 , t 8 , B t 5 , E t 5 1 , 1
T 3 : B t 1 , E t 1 , t 3 , t 4 , B t 2 , E t 2 , t 6 , t 8 1 , 1
T 5 : B t 2 , E t 2 , t 6 , B t 1 , E t 1 , t 8 , t 3 , B t 5 , E t 5 1 , 1
T 4 : B t 2 , E t 2 , t 6 , B t 1 , E t 1 , t 3 , B t 5 , E t 5 , B t 7 , E t 7 3 , 1
T 7 : B t 2 , E t 2 , B t 1 , E t 1 , t 3 , B t 5 , E t 5 , t 6 , B t 7 , E t 7 3 , 1
T 6 : B t 2 , E t 2 , t 6 , t 8 , B t 1 , E t 1 , t 3 , t 4 2 , 0

4. Conclusion

The verification of concurrent system has always been a hot topic of academic research. The verification of concurrent system based on trace realizes the detection of stateless model, which can well reduce the state space and memory consumption. The concept of trace itself is based on state equivalence classification, and again based on the equivalence of numerical traces, classification will further reduce the number of traces.
This paper first introduces the sequence of events describing the operation of a multithreaded concurrent system. The sequence of events has order, bias order, complete order, and hierarchical sequence, interval sequence. In a concurrent multi-threaded system, the events of writing the data need some time, and an interval sequence can be formed between the events of writing the written data. In order to better analyze the running of multi-threading of the concurrent system, the events of read and write data are presented as interval sequence, presented in the form of trace, describing the results of multi-threading running. With a multi-threaded case as the motivation, describe multi-threaded system as Petri net with data, in writing data event x to B (x) and E (x), the event interval sequence, gives the trajectory of the case, and present the state of the data, perfect trajectory with data.
The research [57] in this paper only realizes the interval sequence [4]of events in multi-threaded systems, and analyzed the operation results, which has achieved initial success. However, the data consistency analysis still needs further analysis, and there are still many research work to be further conducted. One is to add the time label to analyze the amount of time. Second, the new permanent storage mode brings a new storage access mode to the concurrent system, which gives new challenges to the model detection of the concurrent system. Further research will be done from the above two aspects.
The equivalence of traces is also the focus of recent research. Based on numerical equivalence trace, some studies have shown that based on numerical trace number less than M trace, especially based on read equivalent trace, less than the number of M trace, this paper has realized the numerical involved in the trace of the trace, the next step, whether can be based on read equivalence, or based on numerical equivalence applied to the Petri net trace, reduce the number of traces, is also a good research idea.

Funding

The APC was funded by National Natural Science Foundation of China (62172166).

References

  1. Alglave, J.; Deacon, W.; Grisenthwaite, R.; Hacquard, A.; Maranget, L. Armed Cats: Formal Concurrency Modelling at Arm. ACM Trans. Program. Lang. Syst. 2021, 43, 8:1–8:54. [Google Scholar] [CrossRef]
  2. Alglave, J.; Kroening, D.; Nimal, V.; Poetzl, D. Don’t Sit on the Fence: A Static Analysis Approach to Automatic Fence Insertion. ACM Trans. Program. Lang. Syst. 2017, 39, 6:1–6:38. [Google Scholar] [CrossRef]
  3. Alglave, J.; Cousot, P. Ogre and Pythia: an invariance proof method for weak consistency models. Proceedings of the 44th ACM SIGPLAN Symposium on Principles of Programming Languages, POPL 2017, Paris, France, January 18-20, 2017; Castagna, G.; Gordon, A.D., Eds. ACM, 2017, pp. 3–18. [CrossRef]
  4. Janicki, R.; Kleijn, J.; Koutny, M.; Mikulski, L. Paradigms of Concurrency - Observations, Behaviours, and Systems - a Petri Net View; Vol. 1020, Studies in Computational Intelligence, Springer, 2022. [CrossRef]
  5. Janicki, R.; Koutny, M. Operational Semantics, Interval Orders and Sequences of Antichains. Fundam. Informaticae 2019, 169, 31–55. [Google Scholar] [CrossRef]
  6. Horn, A.; Alglave, J. Concurrent Kleene Algebra of Partial Strings. CoRR 2014, abs/1407.0385.
  7. Lutz-Ley, A.; López-Mellado, E. Stability Analysis of Discrete Event Systems Modeled by Petri Nets Using Unfoldings. IEEE Trans Autom. Sci. Eng. 2018, 15, 1964–1971. [Google Scholar] [CrossRef]
  8. de Visme, M.; Winskel, G. Causal Unfoldings. 8th Conference on Algebra and Coalgebra in Computer Science, CALCO 2019, June 3-6, 2019, London, United Kingdom; Roggenbach, M.; Sokolova, A., Eds. Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2019, Vol. 139, LIPIcs, pp. 9:1–9:18. [CrossRef]
  9. Janicki, R.; Kleijn, J.; Koutny, M.; Mikulski, L. Relational structures for concurrent behaviours. Theor. Comput. Sci. 2021, 862, 174–192. [Google Scholar] [CrossRef]
  10. Rodríguez, C. Verification based on unfoldings of Petri nets with read arcs. (Vérification à l’aide de dépliages de réseaux de Petri étendus avec des arcs de lecture). PhD thesis, École normale supérieure de Cachan, Paris, France, 2013.
  11. Baldan, P.; Bruni, R.; Corradini, A.; Gadducci, F.; Melgratti, H.C.; Montanari, U. Event Structures for Petri nets with Persistence. Log. Methods Comput. Sci. 2018, 14. [Google Scholar] [CrossRef]
  12. Baldan, P.; Gorla, D.; Padoan, T.; Salvo, I. Characterising spectra of equivalences for event structures, logically. Inf. Comput. 2022, 285, 104887. [Google Scholar] [CrossRef]
  13. Baldan, P.; Corradini, A.; Gadducci, F. Concurrent semantics for fusions: Weak prime domains and connected event structures. Inf. Comput. 2021, 281, 104770. [Google Scholar] [CrossRef]
  14. Kähkönen, K.; Heljanko, K. Testing Multithreaded Programs with Contextual Unfoldings and Dynamic Symbolic Execution. 14th International Conference on Application of Concurrency to System Design, ACSD 2014, Tunis La Marsa, Tunisia, June 23-27, 2014. IEEE Computer Society, 2014, pp. 142–151. [CrossRef]
  15. Janicki, R. On Interval Semantics of Inhibitor and Activator Nets. Application and Theory of Petri Nets and Concurrency - 40th International Conference, PETRI NETS 2019, Aachen, Germany, June 23-28, 2019, Proceedings; Donatelli, S.; Haar, S., Eds. Springer, 2019, Vol. 11522, Lecture Notes in Computer Science, pp. 192–212. [CrossRef]
  16. Gondelman, L.; Gregersen, S.O.; Nieto, A.; Timany, A.; Birkedal, L. Distributed causal memory: modular specification and verification in higher-order distributed separation logic. Proc. ACM Program. Lang. 2021, 5, 1–29. [Google Scholar] [CrossRef]
  17. Coti, C.; Petrucci, L.; Rodríguez, C.; Sousa, M. Quasi-optimal partial order reduction. Formal Methods Syst. Des. 2021, 57, 3–33. [Google Scholar] [CrossRef]
  18. Schemmel, D.; Büning, J.; Rodríguez, C.; Laprell, D.; Wehrle, K. Symbolic Partial-Order Execution for Testing Multi-Threaded Programs. Computer Aided Verification - 32nd International Conference, CAV 2020, Los Angeles, CA, USA, July 21-24, 2020, Proceedings, Part I; Lahiri, S.K.; Wang, C., Eds. Springer, 2020, Vol. 12224, Lecture Notes in Computer Science, pp. 376–400. [CrossRef]
  19. Nguyen, H.T.T.; Rodríguez, C.; Sousa, M.; Coti, C.; Petrucci, L. Quasi-Optimal Partial Order Reduction. Computer Aided Verification - 30th International Conference, CAV 2018, Held as Part of the Federated Logic Conference, FloC 2018, Oxford, UK, July 14-17, 2018, Proceedings, Part II; Chockler, H.; Weissenbacher, G., Eds. Springer, 2018, Vol. 10982, Lecture Notes in Computer Science, pp. 354–371. [CrossRef]
  20. Sousa, M.; Rodríguez, C.; D’Silva, V.V.; Kroening, D. Abstract Interpretation with Unfoldings. Computer Aided Verification - 29th International Conference, CAV 2017, Heidelberg, Germany, July 24-28, 2017, Proceedings, Part II; Majumdar, R.; Kuncak, V., Eds. Springer, 2017, Vol. 10427, Lecture Notes in Computer Science, pp. 197–216. [CrossRef]
  21. Xiang, D.; Liu, G.; Yan, C.; Jiang, C. Detecting data-flow errors based on Petri nets with data operations. IEEE/CAA Journal of Automatica Sinica 2018, 5, 251–260. [Google Scholar] [CrossRef]
  22. Zhao, F.; Xiang, D.; Liu, G.; Jiang, C. A New Method for Measuring the Behavioral Consistency Degree of WF-Net Systems. IEEE Transactions on Computational Social Systems 2022, 9, 480–493. [Google Scholar] [CrossRef]
  23. Xiang, D.; Liu, G.; Yan, C.; Jiang, C. Checking the Inconsistent Data in Concurrent Systems by Petri Nets with Data Operations. 2016 IEEE 22nd International Conference on Parallel and Distributed Systems (ICPADS), 2016, pp. 501–508. [CrossRef]
  24. Huang, Z.; Xu, X.; Zhu, H.; Zhou, M. An Efficient Group Recommendation Model With Multiattention-Based Neural Networks. IEEE Transactions on Neural Networks and Learning Systems 2020, 31, 4461–4474. [Google Scholar] [CrossRef] [PubMed]
  25. Zhu, H.; Liu, G.; Zhou, M.; Xie, Y.; Kang, Q. Dandelion Algorithm With Probability-Based Mutation. IEEE Access 2019, 7, 97974–97985. [Google Scholar] [CrossRef]
  26. He, L.; Liu, G.; Zhou, M. Petri-Net-Based Model Checking for Privacy-Critical Multiagent Systems. IEEE Transactions on Computational Social Systems 2022, pp. 1–14. [CrossRef]
  27. He, L.; Liu, G. Model Checking CTLK Based on Knowledge-Oriented Petri Nets. 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; IEEE 5th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), 2019, pp. 1139–1146. [CrossRef]
  28. Tao, X.; Liu, G.; Yang, B.; Yan, C.; Jiang, C. Workflow Nets With Tables and Their Soundness. IEEE Transactions on Industrial Informatics 2020, 16, 1503–1515. [Google Scholar] [CrossRef]
  29. Yu, W.; Yan, C.G.; Ding, Z.; Jiang, C.; Zhou, M. Modeling and Verification of Online Shopping Business Processes by Considering Malicious Behavior Patterns. IEEE Transactions on Automation Science and Engineering 2016, 13, 647–662. [Google Scholar] [CrossRef]
  30. Yu, W.; Yan, C.; Ding, Z.; Jiang, C.; Zhou, M. Analyzing E-Commerce Business Process Nets via Incidence Matrix and Reduction. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2018, 48, 130–141. [Google Scholar] [CrossRef]
  31. Wang, M.; Ding, Z.; Zhao, P.; Yu, W.; Jiang, C. A Dynamic Data Slice Approach to the Vulnerability Analysis of E-Commerce Systems. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2020, 50, 3598–3612. [Google Scholar] [CrossRef]
  32. Ding, Z.; Wang, S.; Jiang, C. Kubernetes-Oriented Microservice Placement with Dynamic Resource Allocation. IEEE Transactions on Cloud Computing 2022, pp. 1–1. [CrossRef]
  33. Wang, C.; Wang, C.; Zhu, H.; Cui, J. LAW: Learning Automatic Windows for Online Payment Fraud Detection. IEEE Transactions on Dependable and Secure Computing 2021, 18, 2122–2135. [Google Scholar] [CrossRef]
  34. Cui, J.; Yan, C.; Wang, C. ReMEMBeR: Ranking Metric Embedding-Based Multicontextual Behavior Profiling for Online Banking Fraud Detection. IEEE Transactions on Computational Social Systems 2021, 8, 643–654. [Google Scholar] [CrossRef]
  35. Chen, X.; Wang, C.; Cui, J.; Yang, Q.; Teng, H.; Jiang, C. Incorporating Prior Knowledge in Local Differentially Private Data Collection for Frequency Estimation. IEEE Transactions on Big Data 2022, pp. 1–13. [CrossRef]
  36. Wang, C.; Yang, B.; Cui, J.; Wang, C. Fusing Behavioral Projection Models for Identity Theft Detection in Online Social Networks. IEEE Transactions on Computational Social Systems 2019, 6, 637–648. [Google Scholar] [CrossRef]
  37. Liang, Y.; Li, M.; Jiang, C.; Liu, G. CEModule: A Computation Efficient Module for Lightweight Convolutional Neural Networks. IEEE Transactions on Neural Networks and Learning Systems 2021, pp. 1–12. [CrossRef]
  38. Janicki, R.; Mikulski, L. Algebraic Structure of Step Traces and Interval Traces. Fundam. Informaticae 2020, 175, 253–280. [Google Scholar] [CrossRef]
  39. Lahav, O.; Boker, U. Decidable verification under a causally consistent shared memory. Proceedings of the 41st ACM SIGPLAN International Conference on Programming Language Design and Implementation, PLDI 2020, London, UK, June 15-20, 2020; Donaldson, A.F.; Torlak, E., Eds. ACM, 2020, pp. 211–226. [CrossRef]
  40. Lahav, O.; Boker, U. What’s Decidable About Causally Consistent Shared Memory? ACM Trans. Program. Lang. Syst. 2022, 44, 8:1–8:55. [Google Scholar] [CrossRef]
  41. Lahav, O.; Namakonov, E.; Oberhauser, J.; Podkopaev, A.; Vafeiadis, V. Making weak memory models fair. Proc. ACM Program. Lang. 2021, 5, 1–27. [Google Scholar] [CrossRef]
  42. Khyzha, A.; Lahav, O. Taming x86-TSO persistency. Proc. ACM Program. Lang. 2021, 5, 1–29. [Google Scholar] [CrossRef]
  43. Cho, M.; Lee, S.; Hur, C.; Lahav, O. Modular data-race-freedom guarantees in the promising semantics. PLDI ’21: 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation, Virtual Event, Canada, June 20-25, 2021; Freund, S.N.; Yahav, E., Eds. ACM, 2021, pp. 867–882. [CrossRef]
  44. Wang, P.; Ding, Z.; Jiang, C.; Zhou, M. Constraint-Aware Approach to Web Service Composition. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2014, 44, 770–784. [Google Scholar] [CrossRef]
  45. Wang, P.; Ding, Z.; Jiang, C.; Zhou, M.; Zheng, Y. Automatic Web Service Composition Based on Uncertainty Execution Effects. IEEE Transactions on Services Computing 2016, 9, 551–565. [Google Scholar] [CrossRef]
  46. Kähkönen, K.; Heljanko, K. Testing Multithreaded Programs with Contextual Unfoldings and Dynamic Symbolic Execution. 2014 14th International Conference on Application of Concurrency to System Design, 2014, pp. 142–151. [CrossRef]
  47. Lutz-Ley, A.; López-Mellado, E. Stability Analysis of Discrete Event Systems Modeled by Petri Nets Using Unfoldings. IEEE Transactions on Automation Science and Engineering 2018, 15, 1964–1971. [Google Scholar] [CrossRef]
  48. André, E.; Chatain, T.; Rodríguez, C. Preserving Partial-Order Runs in Parametric Time Petri Nets. ACM Trans. Embed. Comput. Syst. 2016, 16. [Google Scholar] [CrossRef]
  49. Xie, Y.; Liu, G.; Yan, C.; Jiang, C.; Zhou, M.; Li, M. Learning Transactional Behavioral Representations for Credit Card Fraud Detection. IEEE Transactions on Neural Networks and Learning Systems 2022, pp. 1–14. [CrossRef]
  50. Xie, Y.; Liu, G.; Yan, C.; Jiang, C.; Zhou, M. Time-Aware Attention-Based Gated Network for Credit Card Fraud Detection by Extracting Transactional Behaviors. IEEE Transactions on Computational Social Systems 2022, pp. 1–13. [CrossRef]
  51. Xiang, D.; Liu, G.; Yan, C.; Jiang, C. A Guard-Driven Analysis Approach of Workflow Net with Data. IEEE Transactions on Services Computing 2021, 14, 1650–1661. [Google Scholar] [CrossRef]
  52. Xiang, D.; Lin, S.; Wang, X.; Liu, G. Checking Missing-Data Errors in Cyber-Physical Systems Based on the Merged Process of Petri Nets. IEEE Transactions on Industrial Informatics 2022, pp. 1–10. [CrossRef]
  53. Kähkönen, K.; Heljanko, K. Testing Programs with Contextual Unfoldings. ACM Trans. Embed. Comput. Syst. 2018, 17, 23:1–23:25. [Google Scholar] [CrossRef]
  54. Kähkönen, K.; Saarikivi, O.; Heljanko, K. Unfolding based automated testing of multithreaded programs. Autom. Softw. Eng. 2015, 22, 475–515. [Google Scholar] [CrossRef]
  55. Bui, T.L.; Chatterjee, K.; Gautam, T.; Pavlogiannis, A.; Toman, V. The reads-from equivalence for the TSO and PSO memory models. Proc. ACM Program. Lang. 2021, 5, 1–30. [Google Scholar] [CrossRef]
  56. Agarwal, P.; Chatterjee, K.; Pathak, S.; Pavlogiannis, A.; Toman, V. Stateless Model Checking Under a Reads-Value-From Equivalence. Computer Aided Verification - 33rd International Conference, CAV 2021, Virtual Event, -23, 2021, Proceedings, Part I; Silva, A.; Leino, K.R.M., Eds. Springer, 2021, Vol. 12759, Lecture Notes in Computer Science, pp. 341–366. 20 July. [CrossRef]
  57. He, L.; Liu, G. Verifying Computation Tree Logic of Knowledge via the Similar Reachability Graphs of Knowledge-oriented Petri Nets. 2020 39th Chinese Control Conference (CCC), 2020, pp. 5026–5031. [CrossRef]
Preprints 72351 g001
Figure 1. Time-based orders. [5]
Figure 1. Time-based orders. [5]
Preprints 72351 g001
Preprints 72351 g002
Figure 2. Volatile Memory.
Figure 2. Volatile Memory.
Preprints 72351 g002
Preprints 72351 g003
Figure 3. Non-Volatile Memory.
Figure 3. Non-Volatile Memory.
Preprints 72351 g003
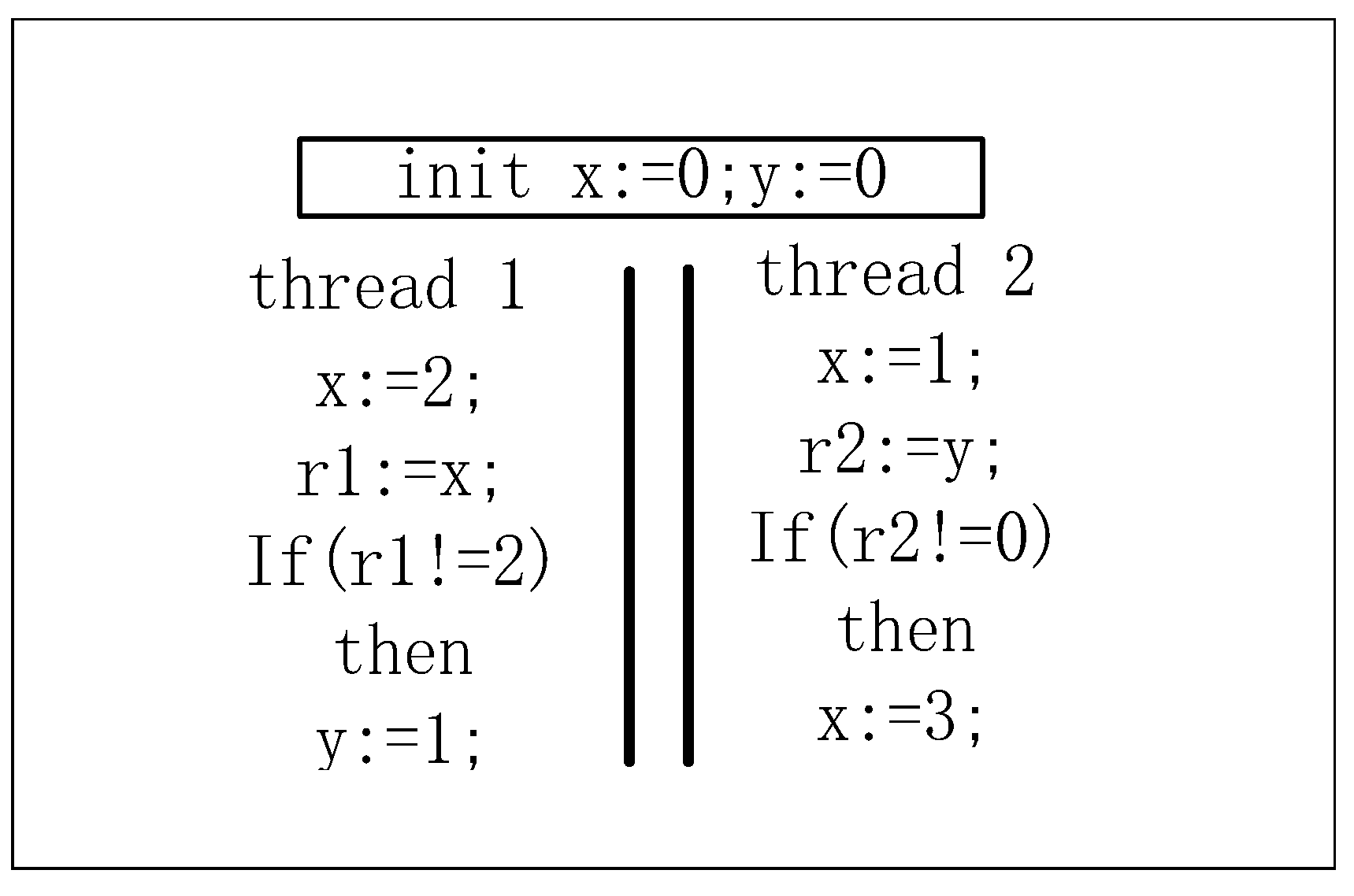
Preprints 72351 g004
Figure 4. Concurrent code.
Figure 4. Concurrent code.
Preprints 72351 g004
Preprints 72351 g005
Figure 5. A simple Petri net.
Figure 5. A simple Petri net.
Preprints 72351 g005
Preprints 72351 g006
Figure 6. Firing of transition t 1 .
Figure 6. Firing of transition t 1 .
Preprints 72351 g006
Preprints 72351 g007
Figure 7. Concurrent code of Figure 4 described in DPN.
Figure 7. Concurrent code of Figure 4 described in DPN.
Preprints 72351 g007
Preprints 72351 g008
Figure 8. Concurrent code of Figure 7 after t 1 is fired.
Figure 8. Concurrent code of Figure 7 after t 1 is fired.
Preprints 72351 g008
Preprints 72351 g009
Figure 9. Concurrent code of Figure 7 after t 1 and t 3 is fired.
Figure 9. Concurrent code of Figure 7 after t 1 and t 3 is fired.
Preprints 72351 g009
Preprints 72351 g010
Figure 10. Conversion from writing event to beginning and ending one.
Figure 10. Conversion from writing event to beginning and ending one.
Preprints 72351 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated