Preprint
Article
Implementation and Realisation of Quantum and Quantum-Inspired Stereographic K Nearest-Neighbour Clustering
Altmetrics
Downloads
308
Views
181
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
01 May 2023
Posted:
02 May 2023
Read the latest preprint version here
Alerts
Abstract
Nearest-neighbour clustering is a simple yet powerful machine learning algorithm that finds natural application in the decoding of signals in classical optical fibre communication systems. Quantum nearest-neighbour clustering promises a speed-up over the classical algorithms, but the current embedding of classical data introduces inaccuracies, insurmountable slowdowns, or undesired effects. This work proposes the generalised inverse stereographic projection into the Bloch sphere as an encoding for quantum distance estimation in k nearest-neighbour clustering, develops an analogous classical counterpart, and benchmarks its accuracy, runtime and convergence. Our proposed algorithm provides an improvement in both the accuracy and the convergence rate of the algorithm. We detail an experimental optic fibre setup as well, from which we collect 64-Quadrature Amplitude Modulation data. This is the dataset upon which the algorithms are benchmarked. Through experiments, we demonstrate the numerous benefits and practicality of using the stereographic quantum analogue k nearest-neighbour for clustering real-world optical-fibre data. This work also proves that one can achieve a greater advantage by optimising the radius of inverse stereographic projection.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction
Quantum Machine Learning, using quantum algorithms to learn quantum or classical systems, has attracted a lot of research in recent years, with some algorithms possibly gaining an exponential speedup. Since machine learning routines often push real-world limits of computing power, an exponential improvement to algorithm speed would allow for such systems with vastly greater capabilities. Google’s ’Quantum Supremacy’ experiment [1] showed that quantum computers can naturally solve certain problems with complex correlations between inputs that can be incredibly hard for traditional (“classical”) computers. Such a result naturally suggests that machine learning models executed on quantum computers could be more effective for certain applications. It seems quite possible that quantum computing could lead to faster computation, better generalization on less data, or both even, for an appropriately designed learning model. Hence it was of great interest to discover and model the scenarios in which such a “quantum advantage” could be achieved. A number of such “Quantum Machine Learning” algorithms are detailed in papers such as [2,3,4,5,6]. Many of these methods claim to offer exponential speedups over analogous classical algorithms. However, on the path from theory to technology, some significant gaps exist between theoretical prediction and implementation. These gaps result in unforeseen technological hurdles and sometimes misconceptions, necessitating more careful case-by-case studies.
In this work, we start from a theoretical abstraction of a well-known technical problem in signal processing through optic fibre communication links. Specifically, problems and opportunities are demonstrated for the k nearest-neighbour clustering algorithm when applied to the real-world problem of decoding 64-QAM data provided by Huawei. It is known from the literature that the k nearest-neighbour clustering algorithm can be applied to solve the problem of phase estimation in optical fibres [7,8].
A quantum version of this k nearest-neighbour clustering algorithm has been developed in [6], promising an exponential speedup. However, the practical usefulness of this algorithm is under debate [9]. There are claims that the speedup is reduced to only polynomial once the quantum version of the algorithm takes into account the time taken to prepare the necessary quantum states. This work builds upon several observations. First, in any classical implementation of k nearest-neighbour clustering, it is possible to vary the loss function. Second, this observation carries over to hybrid quantum-classical implementations of k-nearest neighbour algorithms which utilize quantum methods only to calculate the loss function. Third, the hitherto insurmountable impairment of existing QRAMs being unsuitable for storing quantum states over several steps in a quantum algorithm due to very poor decoherence times introduces an intractable impracticability. Fourth, the encoding of classical data into quantum states has been proven to be a complex task which significantly reduces the advantage of known quantum machine learning algorithms [9]. In this work, we, therefore, reduce the use of quantum methods to calculate distance loss functions. We thereby utilise the process of encoding classical data into quantum states by pre-processing the data. We also minimise the storage time of quantum states by encoding the states before each shot and using destructive measurements. In the case of angle embedding, the pre-processing of data before encoding using the unitary is the critical step. This work introduces a method of encoding using the inverse stereographic projection and focuses on its performance on real-world 64-QAM data. We introduce an analogous classical quantum-inspired algorithm. In the portion of this section that follows, we introduce the problem to be tackled - clustering of 64-QAM optic fibre transmission data - as well as the experimental setup used. This section also discusses the related body of work and our contribution to it. In Section 2 we introduce the preliminaries required for understanding our approach. Furthermore Section 3 introduces the developed stereographic quantum k nearest-neighbour clustering and quantum analogue k nearest-neighbour clustering algorithms. Afterwards, in Section 4, we describe the various experiments for testing the algorithms, present the obtained results, and discuss the conclusions from the experimental results. Section 5 concludes this work and proposes some directions for future research.
1.1. Quadrature Amplitude Modulation (QAM) and Clustering
Quadrature amplitude modulation (QAM) conveys multiple digital bits with each transmission by mixing both amplitude and phase variations in a carrier frequency, by changing (modulating) the amplitudes of two carrier waves. The two carrier waves (of the same frequency) are out of phase with each other by 90 i.e. they are the sine and cosine waves of a given frequency. This condition is known as orthogonality or quadrature. The transmitted signal is created by adding the two carrier waves (the sine and cosine components) together. At the receiver, the two waves can be coherently separated (demodulated) because of their orthogonality. QAM is used extensively as a modulation scheme for digital telecommunication systems, such as in 802.11 Wi-Fi standards. Arbitrarily high spectral efficiencies can be achieved with QAM by setting a suitable constellation size, limited only by the noise level and linearity of the communications channel[10]. QAM allows us to transmit multiple bits for each time interval of the carrier symbol. The term “symbol” means some unique combination of phase and amplitude [11].
In this work, each transmitted signal corresponds to a complex number :
where is the initial transmission power and is the phase of s. The case shown in Equation (1) is ideal; however, in real-world systems, noise affects the transmitted signal, distorting it and scattering it in the amplitude and phase space. For our case, the received and partially processed noisy signal can be modelled as:
where is a random noise affecting the overall value of ideal amplitude and phase. This model motivates the use of nearest neighbour clustering for cases when the noise causes the received signal to be scattered in the vicinity of the ideal signal s.
In [6] is proposed an algorithm that solves the problem of clustering N-dimensional vectors to M clusters in time on a quantum computer, compared to time for the (then) best known classical algorithm. The approach detailed in [6] requires querying the QRAM for preparing a ’mean state’, which is then projected using the SWAP test and used to find the inner product between the centroid (by default the mean point) and a given point. However, there exist some significant caveats to this approach. Firstly, this algorithm achieves an exponential speedup only when comparing the bit-to-bit processing time with the qubit-to-qubit processing time. If one compares the bit-to-bit execution times of both algorithms, the exponential speedup disappears [9,12]. Secondly, since stable enough quantum memories do not exist, a hybrid quantum-classical approach must be used in real-world applications - all the information is stored in classical memories, and the states to be used in the algorithm are prepared in real time. This process is known as ’Data Embedding’ since we are embedding the classical data into quantum states. This as mentioned before [12,13] slows down the algorithm to only a polynomial advantage over classical k-means. However, we propose an approach whereby this step of embedding can be treated as a data preprocessing step, allowing us to achieve an advantage still and make the quantum approach viable. Quantum-inspired algorithms have shown a lot of promise in achieving some types of advantage that are demonstrated by quantum algorithms [12,13,14,15], but as [5] remarks, the massive increase in runtime with rank, condition number, Frobenius norm, and error threshold make the algorithms proposed in [9,12] impractical for matrices arising from real-world applications. This observation is supported by [16]. In this work, we develop an analogous classical algorithm to our proposed quantum algorithm to overcome the many issues faced by quantum algorithms. This work focuses on (a) developing the stereographic quantum and quantum-inspired k nearest-neighbour algorithms and (b) experimentally verifying the viability of the stereographic quantum-inspired k nearest-neighbour classical algorithm on real-world 64-QAM communication data.
1.2. Experimental Setup for Data Collection
The dataset contains a launch power sweep of 80 km fibre transmission of coherent 80 GBd dual polarization (DP)-64QAM with a gross data rate of 960Gb/s. In this experiment, the channel under test (CUT) carries an 80GBd dual polarization (DP)-64QAM signal. We use 15% overhead for FEC and 3.47% overhead for pilots and training sequences, so the net bit rate is 800Gb/s (pilots and training sequences are removed in the published dataset). The experimental setup to capture this real-world database is shown in Figure 1. Four 120 GSa/s digital-to-analog converters (DACs) generate an electrical signal amplified by four 60 GHz 3dB-Bandwidth amplifiers. A tunable 100 kHz external cavity laser (ECL) source generates a continuous wave signal that is modulated by a 32 GHz DP-I/Q modulator. The receiver consists of an optical 90 -hybrid and four 100 GHz balanced photodiodes. The electrical signals are digitized using four 10-bit analog-to-digital converters (ADCs) with 256 GSa/s and 110 GHz. Subsequently, the raw signals are preprocessed by the receiver digital signal processing (DSP) blocks. The datasets were collected in a very short time, corresponding to the memory size of the oscilloscope, which is limited. This is referred to as offline processing. At the receiver, the signals were normalized to fit the alphabet. The average launch power (laser power feed into the fiber) in watts can be calculated as follows:
There are 4 sets of published data with different launch powers, corresponding to different noise levels during transmission: dBm, dBm, dBm, and dBm. Each data set consists of 3 variables:
- ’alphabet’: The initial analog values at which the data was transmitted, in the form of complex numbers i.e. for an entry (), the transmitted signal was of the form . Since the transmission protocol is 64-QAM, there are 64 values in this variable. The transmission alphabet is the same irrespective of the channel noise.
- ’rxsignal’: The received analog values of the signal by the receiver. This data is in the form of a matrix. Each datapoint was transmitted 5 times to the receiver, and so each row contains the values detected by the receiver during the different instances of the transmission of the same datapoint. The values in different rows represent unique datapoint values detected by the receiver.
- ’bits’: This is the true label for the transmitted points. This data is in the form of a matrix. Since the protocol is 64-QAM, each analog point represents 6 bits. These 6 bits are the entries in each column, and each value in a different row represents the correct label for a unique transmitted datapoint value. The first 3 bits encode the column and the last 3 bits encode the row - see Figure 2.
block/.style = draw,rounded corners, fill=white, rectangle, minimum height=2em, minimum width=6em, EDFA/.style = draw, fill=white, regular polygon, regular polygon sides=3,minimum size=1.1cm, sum/.style= draw, fill=none, circle, node distance=0.5cm,color=black,minimum size=14pt, fiber/.style= draw, fill=none, circle, node distance=2cm,color=red,minimum size=20pt,
The data as well as the noise model has been visualised in detail in the Appendix A. A few key figures have been included here as well for context. Figure 2 shows the transmission alphabets for all the different channels.
Figure 3 shows the received data (all 5 instances of transmission) for the dataset with the least noise (2.7dBm), and Figure 4 shows the received data (all 5 instances of transmission) for the dataset with most noise (10.7dBm).
One can see from these figures that as the noise in the channel increases, the points are further scattered away from the initial alphabet. In addition, the non-linear noise effects also increase, causing distortion of the ’shape’ of the data, most clearly visible in Figure 4 - especially near the ’corners’. The birefringence phase noise also increases with an increase in the channel noise causing all the points to be ’rotated’ about the origin.
Once the centroids have been found and the data has been clustered, as mentioned before, we need to ’de-map’ the analog centroid values and clusters to bit-strings. For this, we need a de-mapping alphabet which maps the analog values of the alphabet to the corresponding bit strings. The de-mapping alphabet is depicted in Figure 2. It can be seen from the figure that, as in most cases, the points are Gray coded i.e. adjacent points differ in binary translation by only 1 bit. This helps minimise the number of bit errors per symbol error in case of misclassification or exceptionally high noise. In case a point is misclassified, with the most probability it will be assigned to a neighbouring cluster. Since the surrounding clusters differ by only 1 bit, it minimises the bit error rate. Due to Gray coding, the bit error rate is approximately of the symbol error rate.
1.3. Related Work
A unifying overview of several quantum algorithms is presented in [17] in a tutorial style. An overview targeting data scientists is given in [18]. The idea of using quantum information processing methods to obtain speedups for the k-means algorithm was proposed in [19]. In general, neither the best nor even the fastest method for a given problem and problem size can be uniquely ascribed to either the class of quantum or classical algorithms, as can be seen in the detailed discussion presented in [5]. The advantages of using local (classical) processing units alongside quantum processing units in a distributed fashion are quantified in [20]. The accuracy of (quantum) K-means has been demonstrated experimentally in [21] and in [22], while quantum circuits for loading classical data into a quantum computer are described in [23].
Recent works such as [12] suggest that even the best QML algorithms, without state preparation assumptions, fail to achieve exponential speedups over their classical counterparts. In [13] it is pointed out that most QML algorithms are incomparable to classical algorithms since they take quantum states as input and output quantum states, and that there is no analogous classical model of computation where one could search for similar classical algorithms. In [13], the idea of matching state preparation assumptions with -norm sampling assumptions (first proposed in [12]) is implemented by introducing a new input model, sample and query access (SQ access). In [13] the Quantum K-Means algorithm described in [6] is ’de-quantised’ using the ’toolkit’ developed in [12], i.e. a classical algorithm is given that, with classical SQ access assumptions replacing quantum state preparation assumptions, matches the bounds and runtime of the corresponding quantum algorithm up to polynomial slowdown. From the works [12,13,24], we can conclude that the exponential speedups of many quantum machine learning algorithms that are under consideration arise not from the ’quantumness’ of the algorithms but instead from strong input assumptions, since the exponential part of the speedups vanish when classical algorithms are given analogous assumptions. In other words, in a wide array of settings, on classical data, these algorithms do not give exponential speedups but rather yield polynomial speedups.
The fundamental aspect that allowed for the exponential speedup in [12] vis-á-vis classical recommendation system algorithms is the type of problem being addressed by recommendation systems in [4]. The philosophy of recommendation algorithms before this breakthrough was to estimate all the possible preferences of a user and then suggest one or more of the most preferred objects. The quantum algorithm promised an exponential speedup but provided a recommendation without estimating all the preferences; namely, it only provided a sample of the most preferred objects. This process of sampling along with state preparation assumptions was, in fact, what gave the quantum algorithm an exponential advantage. The new classical algorithm obtains comparable speedups also by only providing samples rather than solving the whole preference problem. In [13], it is argued that the time taken to create the quantum state should be included for comparison since the time taken is not insignificant; it is also claimed that for every such linear algebraic quantum machine learning algorithm, a polynomially slower classical algorithm can be constructed by using the binary tree data structure described in [12]. Since then, more sampling algorithms have shown that multiple quantum exponential speedups are not due to the quantum algorithms themselves but due to the way data is provided to the algorithms and how the quantum algorithm provides the solutions [13,24,25,26]. Notably, in [26] it is argued that there exist competing classical algorithms for all linear algebra subroutines, and thus for many quantum machine learning algorithms. However, as pointed out in [5] and proven in [16], there exist significant caveats to these aforementioned results of quantum-inspired algorithms. The polynomial factor in these algorithms often contains a very high power of the rank and condition number, making them suitable only for sparse low-rank matrices. Matrices of real-world data are most often quite high in rank and hence unfavourable for such sampling-based quantum-inspired approaches. Whether such sampling algorithms can be used also highly depends on the specific application and whether or not samples of the solution instead of the complete data are suitable. It should be pointed out that in case such complete data is needed, quantum algorithms generally do not provide an advantage anyway.
The method of encoding classical data into quantum states contributes to the complexity and performance of the algorithm. In this work, the use of the stereographic projection is proposed. Others have explored this procedure [27,28,29] as well; however, the motivation, implementation, and use vary significantly, as well as the procedure for embedding data points into quantum states. There has also been no extensive testing of the proposed methods, especially not in an industry context. In our method, we exclusively use pure states from the Bloch sphere since this reduces the complexity of the application. Theorem 1 assures that our method with existing quantum techniques is applicable for nearest neighbour clustering. In contrast, The density matrices of mixed states and the normalised trace distance between the density matrices are used for binary classification in [27,28]. A very important thing to consider here is to distinguish the contribution of the stereographic projection from the quantum effects. We will see in Section 4 that the stereographic projection itself seems to be the most important contributing factor. In [30], it is also proposed to encode classical information into quantum states using the stereographic projection in the context of quantum generative adversarial networks. Their motivation for using the Inverse Stereographic projection is due to the fact that it is one-one and can hence be used to uniquely represent every point in the 2-D plane without any loss of information. Angle embedding, on the other hand, loses all amplitude information due to the normalisation of all points. A method to transform an unknown manifold into an n-sphere using stereographic projection is proposed in [31] - here, however, the property of their concern was the conformality of the projection since subsequent learning is performed upon the surface. In [32], a parallelised version of [6] is developed using the FF-QRAM procedure [33] for amplitude encoding and the stereographic projection to ensure a one-one embedding.
In the method of Spherical Clustering [34], the nearest neighbour algorithm is explored on the basis of the cosine similarity measure (Eq. (8) and Lemma 1). The cosine similarity is used in cases of information retrieval, text mining, and data mining to find the similarity between document vectors. It is used in those cases because the cosine similarity has low complexity for sparse vectors since only the non-zero coordinates need to be considered. For our case as well, it is in our interest to study Definitions 1 and 2 with the cosine dissimilarity. This, in particular, becomes relevant once we employ stereographic embedding to encode the data points into quantum states.
1.4. Contribution
The subject of this work is the development and testing of the quantum-analogous classical algorithm for performing k nearest neighbour clustering using the general stereographic projection (Section 3.3) and the stereographic quantum k nearest-neighbour clustering quantum algorithm (Section 3.1, Section 3.2). The main contributions of this work are (a) the development of a novel quantum embedding using the generalised stereographic projection along with proving that the ideal projection radius is not 1; (b) the development of the quantum analogue classical algorithm through a new method of centroid update which yields significant advantage and; (c) the experimental exploration and verification of the developed algorithms. The extensive testing upon the real-world, experimental QAM dataset (Section 1.2) revealed some very important results regarding the dependence of accuracy, runtime, and convergence performance upon the radius of projection, number of points, noise in the optic fibre, and stopping criteria - described in Section 4. No other work has considered a generalised projection radius for quantum embedding or studied its effect. Through our experimentation, we have verified that there exists an ideal radius greater than 1 for which accuracy performance is maximised. The advantageous implementation of the algorithm upon experimental data shows that our procedure is quite competitive. The fact that the developed quantum algorithm has a completely classical analogue (with comparable time complexity to the classical k means algorithm) is a distinct advantage in terms of in-field deployment, especially compared to [5,6,19,27,28,29,32]. The developed quantum algorithm also has another advantage with respect to NISQ realisations - it has the least circuit depth and circuit width among all candidates [5,6,29,32] - making it practical to implement with the current quantum technologies. Another important contribution is the ’Distance Loss Function’ approach, where we generalise the distance for clustering; instead of Euclidean distance, we consider other ’distances’ which might be better estimated by quantum circuits (Section 3.2.3). A somewhat similar approach was developed in parallel by [35] in the context of amplitude embedding. All previous approaches [5,6,29,32] only try to estimate the Euclidean distance. We also make the contribution of studying the relative effect of ’quantumness’ and the stereographic projection, something completely overlooked in previous works. We show that the quantum ’advantage’ in accuracy performance touted by works such as [27,28,29,32] is in reality quite suspect and achievable through classical means. We describe a generalisation of the stereographic embedding - the Ellipsoidal embedding, which we expect to give even better results.
Other contributions of our work include: the generalisation of the k nearest-neighbour problem to clearly indicate the contribution of dissimilarities and dataspace (see Section 2.1); presenting the procedure and circuit for stereographic embedding using the angle embedding procedure, which consumes only in time and resources (Section 3.1); and demonstrating that for hybrid implementations, the popular SWAP test method can be replaced by the Bell State measurement circuit (Section 3.2) saving not only a qubit but also a quantum gate.
2. Preliminaries
2.1. Nearest Neighbour Clustering Algorithm
The nearest neighbour algorithm consists of classifying data sets into clusters by associating an ’average point’ (centroid) to each cluster. In our method, the objective of the clustering algorithm is to first identify from a given set () of received signals a given number M of centroids (one for each cluster) and to then assign each signal to the ’nearest’ centroid. The second step is classification. This creates the clusters, which can then be decoded into bit signals through the process of demapping. Demapping consists of mapping the original transmission constellation (alphabet) to the current centroids, and then assigning the bitstring label associated with that initial transmission point to all the points in the cluster of that centroid. This process completes the final step of the QAM protocol, translating the analog values to bitstrings read by the receiver. The size M of the constellation is known since we know beforehand which QAM protocol is being used. We also know the “alphabet”, i.e. the initial and ideal points at which the signals were transmitted.
The criterion of assigning a cluster to a centroid in each iteration of the algorithm is defined as follows:
Definition 1
(Cluster Update). Let be a space in which the data points exist. Let be the set of data points meant to be categorized by the set of M centroids , with . Let be a centroid. A cluster is associated to a given centroid using the following relation:
where
is a lower-bounded dissimilarity measure function used to perform the nearest neighbour clustering algorithm.
Notice that does not have to be a distance metric. Also notice that this definition requires one to initialise or populate the set with initial values, i.e. the initial centroids must be defined as a starting point for the clustering algorithm. The initial centroids can be defined either randomly or given initially prior. Note that Equation (3) may lead to a single point being eligible for assignment to multiple clusters. In such cases, the assignment will be implementation dependent. This, however, is rare in practice and in general, does not affect the result by much. New centroids can then be defined at each iteration of the algorithm:
Definition 2
(Centroid Update). Let be the cluster associated to the centroid obtained after the iteration, then the centroid for the iteration is the point that minimizes the total (and therefore the average) dissimilarity within the cluster, i.e. the centroid is updated by the following expression:
Notice that Definition 2 implies that centroids are generally not part of the original data set; however, according to Definition 2 they must be restricted to the space in which the dataset is defined. Definitions involving centroids for which are possible, but are not used in this work. Again, Equation (5) does not guarantee a unique assignment of the updated centroid and the choice will be implementation dependent. In our case, we will see later in Section 3.2.4 that all choices will be equivalent. This freedom can be exploited, for example, to reduce the amount of computation.
One can see that any k nearest-neighbour clustering algorithm can be broken down into 2 steps that keep alternating until a stopping condition (a condition which when true forces the algorithm to terminate) is met: a cluster update which updates the points associated with the newly calculated centroid, and then a centroid update which recalculates the centroid based upon the new points associated to it through its cluster. For the cluster update, the value of the centroid calculated in the previous iteration is taken, and its cluster set is constructed by collecting all the points in the dataset that are ’closer’ to it than any other centroid. The ’closeness’ is computed by using a pre-defined dissimilarity function. In the next step, the centroids are updated by searching in the dataspace, for each updated cluster, a new point for which the sum of dissimilarity functions between that point and all points in the cluster is minimised.
It can also be seen that this procedure will lead to different results if one changes the dissimilarity measure and/or the space of data points. In this paper, we explore the effects of changing this measure as well as the space of data points, and we shall explain it in the context of quantum states.
2.1.1. Dissimilarity Function
It is noticeable from Equation 3 and Equation 5 that the dissimilarity function ( Equation 4) plays a central role in the clustering algorithm. The nature of this function directly controls the first step of cluster update since the dissimilarity function is what is used to compute the ’closeness’ between any two points. It is also very clear that in the second step (centroid update), if the dissimilarity function is varied, the point in the dataspace for which the function is minimised could also change.
For instance, the Euclidean dissimilarity is defined as:
The minimization of Equation 5 with reduces to the average:
where is the cardinality of the cluster set C. This is the most usual case of centroid update where the new centroid is updated as the mean point of all points in the cluster. This corresponds to the k-means clustering algorithm. The computation of the centroid through Equation 7 instead of Equation 5 reduces the complexity of the centroid update step. Almost universally, since the function is well-defined beforehand, a closed-form analytical expression for is computed. Such a reduced expression is used to compute the updated centroids () rather than searching the entire dataspace for each cluster. In this work, we project the available two-dimensional dataset (described in Section 1.2) onto a sphere via the inverse stereographic projection. After this projection, the calculation of the centroids according to Equation 7 would generally yield centroids which lie inside of the sphere instead of on the surface due to the convex nature of the sphere. This effect is a consequence of the component-wise application of Jensen’s inequality.
In our work, in order to use pure states, we restrict the dataspace to the sphere surface , forcing the centroids to lie on the surface of a sphere. This naturally leads to the question of what the proper reformulation of Equation 5 is, and whether a computationally inexpensive formula similar to Equation 7 exists for this case as well. To answer these questions, let us first define:
Definition 3
(Cosine Dissimilarity).
For two points, and in an inner-product space the cosine dissimilarity is expressed as:
where is the inner product between the 2 points expressed as vectors from the origin, is the norm of induced by the inner product, and α is the angle between and .
With this definition, we return to the question of computing a direct centroid update equation from Equation 5. We note that Equation 8 can be related to the Euclidean dissimilarity ( Equation 6) by restricting and to lie on the n-sphere of radius r. This leads to the following lemma:
Lemma 1.
Let and respectively refer to the cosine and Euclidean dissimilarities of and . If we restrict , to the n-sphere of radius r, then
Proof.
2.2. Stereographic Projection
The inverse stereographic projection, (see Figure 5) is a way to bijectively map the Euclidean space into an n-sphere in an (n+1) dimensional Euclidean space, with one point p, removed:
From this point onward, for brevity, we refer to the inverse stereographic projection simply as the stereographic projection. In our method, we are interested in studying the projection from the north pole, mapping the 2-dimensional plane to a 3-dimensional sphere . This is due to the simplicity of embedding the points on into quantum states (one can see the intuition that qubit quantum states can be represented through the unit sphere ). In this case, the stereographic projection maps a 2-dimensional point, into a three-dimensional point (see Figure 6) through the following set of transformations:
The polar and azimuthal angles are given by the expressions:
This information, particularly Equation 16 will allow us to associate each point in to a unique quantum state through the Bloch-sphere, but first, we make some observations regarding clustering within the sphere.
As noted before, Eqs. (3) and (5) can lead to different results if different dissimilarities and dataspaces are used. However, there are cases where one dissimilarity is related to another. For instance, Lemma 1 already provides a relation between the dissimilarity functions of two cases of interest. Here we show that the centroid obtained through centroid update with and with can be correlated. The dissimilarity function when is typically the Euclidean dissimilarity, while for the case of we will employ the cosine dissimilarity.
Theorem 1.
Let be a cluster on the sphere of radius r at the iteration and let and be centroids resulting after updating the centroids of the cluster , where was obtained by employing the Euclidean dissimilarity with and was obtained with the cosine (or Euclidean) dissimilarity restricted to the sphere, i.e. . Then:
Proof.
Let C be the cluster that will update the centroid to and , given that , then according to Lemma 1, the cosine dissimilarity given in Equation 8 reduces for all to:
The procedure of centroid update as stated in Definition 1 can then be summarized for the cosine dissimilarity with a Lagrangian that satisfies Equation 5 at the minimizing point. We have to find x that minimises:
subject to the restriction condition that assures that , that is:
Such Lagrangian is expressed as
where is the Lagrangian multiplier. We then proceed to calculate the centroid update by employing the derivative criterion to Equation 22.
Therefore the following holds:
Therefore, the critical point is written as
as claimed. □
We can observe that Theorem 1 implies that the centroid obtained by restricting the minimising point to lie on the surface of the sphere is the projection (from the origin) of the average point in Euclidean space (which is the minimising point in Euclidean space) onto the sphere’s surface. Theorem 1 enables us to calculate using quantum methods which we describe in Section 3.2. In other words, it allows one to state that quantum states on the Bloch-sphere can be used to perform the nearest neighbour algorithm with the cosine dissimilarity. Moreover, the centroids will be the same, safe a multiplicative scalar, as the centroids in the three-dimensional Euclidean dissimilarity measure. The quantum states can be prepared in such a way that there is a direct correlation to the classical data we wish to classify with the algorithm since we employ stereographic embedding. Later on in Section 3.2 we will show how the cosine dissimilarity arises naturally from the Bell-state measurement circuit.
3. Quantum and Quantum-Inspired k Nearest-Neighbour Clustering Using Stereographic Embedding
In this section, we describe quantum k nearest-neighbour clustering using the stereographic embedding and demonstrate an equivalent quantum-inspired version of it. Stereographic Embedding consists, in essence, of two steps: in the first step, the two-dimensional data point is mapped onto the sphere . In the second step, the resulting point on the sphere is encoded through angle embedding into a qubit. Once the embedding is done, the states are put through a Bell State measurement circuit whose output can be correlated to a quantity that we can use for classifying the datapoint. After describing this procedure, we prove that an analogous quantum-inspired version exists.
3.1. Stereographic Embedding
Distance estimation between two data points using stereographic embedding consists of preparing quantum states through a unitary operation with parameters of the transformed data point encoded in it. The two steps we use for our method are as follows:
- Then, the computed parameters and are used to map the data points into the Bloch-sphere (pure states of qubits) by performing the unitary operation:
The final quantum state is prepared by acting the unitary on the reference state :
or as a density matrix
Equation 30 corresponds to a unique point on the Bloch-Sphere, , which has the same polar angle and azimuthal angle as (which can have radius different than one), the stereographic projection of the data point . That is,
where is the vector of Pauli matrices.
If we measure the overlap of two states and as given in Equation 29, each representing a stereographically projected data point, , , with their corresponding density matrices and and data points , , the measurement would give us:
where , are the associated Bloch-vectors of , respectively. This can be verified as follows. The states are prepared as:
and we once again obtain Equation 32 as:
which implies:
where we used the trigonometric identities
In the following sections, we will prove that this procedure allows us to obtain the cosine dissimilarity directly from the Bell-state measurement and as a consequence enables us to perform the nearest neighbour algorithm employing existing quantum techniques.
3.2. Computation Engines and Distance Loss Function
A very time-consuming computational step of the k nearest-neighbour algorithm involves the repeated calculations of distances between the data set points meant to be classified and each centroid. In the case of the quantum k nearest-neighbour algorithm in [6], since angle embedding is not one-one, many steps must be spent after the calculation of the inner product to calculate the actual distance between the points using the norms. Even in [27,28], the norms of the points have to be kept track of in the density pattern matrix and this leads to much computational expense. Our method has the clear benefit of calculating the dissimilarity directly through measurements from the Bell-state preparation procedure as an alternative where quantum methods are exploited. No further calculations are required due to all points having the same norm r in the sphere, and the existence of a bijection between the stereographic projection and the original 2-D datapoints, thus saving computational time and resources.
In the previous subsection (Section 3.1), we defined the method to convert the classical data into quantum states. In what follows, we describe how these states are manipulated so that we obtain an output that can be used to perform clustering. In Section 3.2.1, we define the quantum circuit that the prepared quantum states are subjected to, and Section 3.2.2 proves that the output of this circuit can be used for dissimilarity estimation. Section 3.2.3 quantifies the end-to-end performance of the combination of stereographic embedding and the bell state measurement quantum circuit.
3.2.1. Quantum Circuit Set-Up
Here, we use the Bell-state measurement, the von-Neumann measurement of the maximally entangled basis
to measure the overlap between two quantum states. The Bell-state measurement can be used instead of the swap test when the post measurement state is not needed. The measurement is obtained by equivalently by first transforming the Bell basis in the standard basis with and then measuring the standard basis. Let us assume that the qubits are prepared in the following form
Then the state before the standard-basis measurement is
where is the identity operator acting on the second qubit .
3.2.2. Cosine Dissimilarity from the Bell-Measurement Circuit
The quantum circuit described in Section 3.2.1 can be used to recover the cosine dissimilarity directly from measuring one outcome of the circuit. If we measure the probability of detecting whenever the experiment gives output , that is, if we project the output Equation 34 with , we get:
This result, in combination with Equation 32, makes it possible to recover the cosine dissimilarity between the associated stereographically projected data points , . That is,
Note that Lemma 1 also connects Equation 37 to the Euclidean dissimilarity,
As one can see, is directly proportional to the Euclidean dissimilarity between 2 stereographically projected points. Since all the points after projection onto the sphere have equal modulus r, and each projected point corresponds to a unique 2-D data point, we can directly compare the probability of getting a on the Bell State Measurement circuit for cluster assignment. This eliminates extra steps needed during computation to account for the different moduli of points on the 2-dimensional plane.
In summary, Equation 37 and Equation 38 portray a method to measure a dissimilarity function that leads to consistent clustering involving pure states. Moreover, Theorem 1, Equation 38 and Equation 53 tell us that our method can be analogous to the standard Euclidean clustering algorithm when restricting to the data space , more of this is discussed in Section 3.3. This means that either classical data or quantum data in pure states can be used to perform the nearest neighbour algorithm by using a Hadamard gate and a controlled not gate.
One can extend the definition of quantum dissimilarity ( Equation 38) to any qubit state by taking mixed states from a convex linear combination of pure states:
where and are pure states. Calculating the trace of the product with any pure state as in Equation 32 leads to:
Therefore, the quantum dissimilarity between a pure state (corresponding to a datapoint) and a mixed state (corresponding to a quantum centroid) can be written as:
The result in Equation 41 can be interpreted as: first, repeatedly performing the Bell state measurement of each state that makes up the cluster and corresponding to the datapoint, to estimate each individual dissimilarity; and then, taking the weighted average of the dissimilarities according to the composition of the mixed state centroid. This procedure is clearly impractical experimentally and no longer correlates to the cosine dissimilarity for mixed states. A procedure can be used to make dissimilarity calculations between mixed states and pure states much simpler. From Equation 31 we know that can be expressed as . For a mixed state , will lie inside the sphere. It is well-known that since is Hermetian, one can diagonalise it such that:
where
and
Where and are orthogonal pure states corresponding to diametrically opposite points on the Bloch sphere lying on the diameter containing . Given the cluster, one can calculate and , and then find the quantum dissimilarity using:
The implementation portrayed at Equation 47 simplifies the measurement procedure of the mixed state, yet it comes with the caveat that the pure states and must be calculated and then prepared, which brings an extra layer of complexity to the state preparation process. Due to this reasons, we propose in this project an algorithm involving entirely pure states based exclusively on result Equation Section 3.2.2.
It is important to mention that this implementation destroys the quantum states, and the procedure must be repeated several times until the value of is estimated to the desired accuracy. This forces us to prepare the states and at each repetition of the experiment using the stereographic embedding procedure. To estimate the value of we use the unbiased estimator:
where and are the measurement results obtained from the repeated simultaneous measurement of the qubits of the bell state measurement test circuit. As mentioned before ( Equation Section 3.2.2), given two input states and , independent of the form of embedding, the bell state measurement circuit yields a random variable M with:
In particular, when we measure for , Equation 50 converges to Equation 37, Equation 38 when repetitions of the experiment are performed. The choice of this approach, destroying the initial states when projecting with , seems logical when looking at the capabilities of NISQ devices. Minimising the number of qubits, gate depth, and circuit area is essential in NISQ devices due to low fidelity and high difficulty of maintaining entanglement. Hence, we choose the bell state measurement circuit instead of the swap test suggested in [6], to reduce both circuit width and depth by 1 at the expense of performing a destructive measurement instead of a non-destructive measurement. Moreover, there is no current technology that enables to store quantum information for extended periods of time (QRAM). The SWAP test procedure does not destroy the quantum information of and (non-destructive measurement), enabling the reuse of and given a QRAM technology to store the states. The use of the SWAP test leads to an equivalent result as in Equation Section 3.2.2, but involving an extra ancilla qubit and a gate depth of 3 instead of 2.
3.2.3. Distance Loss Function
Now that we have described the method to embed the 2-dimensional data into quantum states and the circuit used to manipulate the states, we put together everything to show what our system finally returns given the input of 2 2-dimensional points. We call this number the distance loss function. To calculate this effective distance loss function, we substitute:
in Equation 32, Equation . For this gives us:
Hence our final distance loss function:
where is the Euclidean dissimilarity between the points (see Equation 6). It is quite illustrative to pick the point (origin) and see how the distance loss function varies as the other point varies. In this case, the distance loss function ( Equation 53) for stereographic embedding becomes:
3.2.4. Summary
Section 3.1 described the procedure for converting classical data into quantum states, which are then fed into the circuit described in Section 3.2.1, Figure 7 to give an output, which when projected, yields a quantity that can be used as a ’distance measure’ (see Section 3.2.2 Definition 3, Equation 38). The final loss function is described in Section 3.2.3. We now formally define the developed algorithm:
Definition 4
(Stereographic Quantum K Nearest-Neighbour Clustering). We define the Stereographic Quantum K Nearest-Neighbour Clustering as a nearest-neighbour clustering algorithm (as defined in Section 2.1) with the dataspace , dataset (D), dissimilarity , and initial centroids (K) - where is the original 2-dimensional dataset, is the 2-dimensional alphabet, is the inverse stereographic projection as defined in Section 2.2, is the probability of measuring ’1’ on both qubits as the output of the Bell State measurement circuit (Figure 7) with input , and are the quantum states corresponding to the points (datapoint), (centroid).
The complete process of Generalised Stereographic Quantum K Nearest Neighbour Clustering can be described in detail as follows:
- First, prepare to embed the classical data and initial centroids into quantum states using the Generalised Stereographic Embedding procedure: project the 2-dimensional datapoints and initial centroids (in our case, the alphabet) onto a sphere of radius r and calculate the polar and azimuthal angles of the points. The calculated angles will be used to create the states using angle embedding through the unitary U( Equation 28). This first step is executed entirely on a classical computer.
- Cluster Update: The polar and azimuthal angles of the updated centroids are calculated classically. The dissimilarity between the centroid and datapoint is then estimated by using the calculated polar and azimuthal angles to create the quantum state, manipulating the state through the Bell State measurement quantum circuit, and finding the probability of measuring ’1’ on both qubits. This step is entirely handled by the quantum circuit and classical controller. The controller feeds in the classical values at the appropriate times and stores the results of the various shots.
Once the centroid is updated, Step 2 (Cluster Update) is repeated, followed once again by Step 3 (Centroid Update) until a decided stopping condition is fulfilled.
3.3. A Classical Analogue to the Quantum Algorithm
Through the previous sections [Section 3.1, Section 3.2] we have detailed the developed quantum algorithm. In this section, we develop the classical analogue to this quantum algorithm - the ’quantum-inspired’ classical algorithm.
Definition 5
(Equivalence of Clustering Algorithms). Let and be clustering algorithms acting upon datasets and , respectively. The two algorithms are said to be equivalent if there exists a transformation such that for all iterations it maps the centroids, clusters and data of to the centroids, clusters and data of ; namely if:
- 1.
- ,
- 2.
- ,
- 3.
- for all .
Definition 6
(Quantum Analogue Nearest-Neighbour Clustering Algorithm). We define the Quantum Analogue Nearest-Neighbour Clustering Algorithm as a nearest-neighbour clustering algorithm (as defined in Section 2.1) with the dissimilarity function , initial centroids = (K), and dataspace acting upon the dataset (D) - where once again, is the original 2-dimensional dataset, is the 2-dimensional alphabet, and is the inverse stereographic projection as defined in Section 2.2.
Theorem 2.
The stereographic quantum k nearest-neighbour clustering (as defined in Definition 4) is equivalent (as per Definition 5) to the quantum analogue nearest-neighbour clustering algorithm (as defined in Definition 6).
Proof.
Recall that as per Definition 4 and 6 we have datasets with initial centroids , with being the 2D data points projected by and being the 2D initial centroids (in our case, the alphabet) projected by .
Let us use the notation and define the transform as , which rescales any vector to have length r. Observe that trivially for all , and thus . Therefore
Hence condition 1 of Definition 5 is satisfied, and we have the starting point for proving condition 2 by induction. Let now assume and for all .
The new centroids are and
where the first equality is by Theorem 1 and because ; which is also the reason for the equality from Equation 59 to Equation Section 3.3. Thus .
For the clusters, we prove the equivalence of the cluster updates as follows:
where Equation (67) is due to
which follows from Equation (40). Equation (67) also holds for the first cluster update, thus proving both the base case and the inductive step. Hence by induction, we satisfy conditions 2 and 3 of Definition 5 for all iterations i. □
Therefore, we have proven that k nearest-neighbour clustering with dissimilarity , initial centroids equal to the stereographic projection of the 2-dimensional alphabet, dataspace , acting upon the stereographically projected dataset is equivalent to clustering stereographically embedded pure quantum states in with dissimilarity as the probability of getting ’1’ on both qubits of the bell state measurement circuit (Figure 7), initial centroids as stereographically embedded 2-dimensional alphabet, and the centroid update in dataspace .
The following discussion provides a visual intuition of Theorem 2. This discussion will refer to Figure 12. In Figure 12, the sphere with centre origin (O) and radius r is the stereographic sphere into which the 2-dimensional points are projected, while the sphere with centre O and radius 1 is the Bloch sphere. The points are the stereographically projected points defining a cluster. The centroid is obtained with [ Equation 6], and . In contrast, the centroid is obtained with or [ Equation 8] and (either can be used since they are equivalent in a sphere [Lemma 1]). The quantum states are obtained after angle embedding the stereographically projected points , and is the quantum state obtained after angle embedding the centroid.
One can see from Equation 29, Equation 31 that O, any point on the sphere, and the point on the Bloch sphere corresponding to the angle embedded quantum state of are collinear, i.e. and lie on a line. Hence, it can be seen that in the process of quantum k nearest-neighbour clustering, the points on the sphere are projected onto the sphere of radius 1. Once the labels were assigned in the previous iteration, the centroid was computed, giving an integer multiple of the average point , which lies within the stereographic sphere (Jensen’s inequality). Crucially, when we embed the centroid into the quantum state, since we only use the polar and azimuthal angle of the point for embedding (see Equation 29), the prepared quantum state is also projected onto the surface of the Bloch sphere - or, in other words, a pure state is prepared (). Hence, we can see that all the dissimilarity calculations in the quantum k nearest-neighbour algorithm will take place on the surface of the Bloch sphere, even though the calculated classical centroid is contained within the stereographic sphere. This argument also illustrates why any point on the ray can be used for the centroid update step of the stereographic quantum k nearest-neighbour clustering algorithm; any chosen point on the ray, when embedded into a quantum state for dissimilarity calculations will reduce to .
We know from Theorem 1 that and lie on a straight line. Therefore one can see that if the Bloch sphere is scaled by r, the point on the Bloch sphere corresponding to will transform to , i.e. and are all collinear. Equation 38 shows that quantum k nearest-neighbour clustering clusters as per Euclidean dissimilarity; that implies that simply scaling the sphere makes no difference to the clustering.
Therefore, we conclude that clustering on the surface of the stereographic sphere with Euclidean dissimilarity is exactly equivalent to quantum k nearest-neighbour clustering with stereographic embedding.
To summarise, for the quantum-inspired/classical analogue stereographic k nearest-neighbour clustering algorithm:
- Stereographically project all the 2-dimensional data and initial centroids onto the sphere of radius r. Notice that the initial centroids will naturally lie on the sphere.
- Centroid Update: A closed-form expression for the centroid update was calculated in Equation 27 . This expression recalculates the centroid once the new clusters have been assigned. Once the new centroid is updated, Step 2 (cluster update) is then repeated, and so on, until a stopping condition is met.
4. Experiments and Results
We defined the procedure for performing quantum k nearest-neighbour clustering using stereographic embedding in Section 3. Section 3.1 introduces our idea for state preparation - projecting the 2-dimensional data points into a higher dimension. Section 3.2 details the hybrid quantum-quantum method used for our process and then proves that the output of the quantum circuit is not only a valid but also an excellent metric that can be used for distance estimation between 2 points. Section 3.3 describes the quantum-inspired classical algorithm that is analogous to the quantum algorithm.
These outlined methods were also tested extensively through simulation and compared to their counterparts. The objective of this section is to define the various algorithms that were tested, the various experiments and methodology of testing, detail the obtained results, and provide observations from the obtained results.
All the experiments were carried out on a server with the following specifications: 2 Intel Xeon E5-2687W v4 chips clocked at 3.0 GHz (24 cores / 48 threads), 128GB RAM. All experiments are performed on the real-world 64-QAM data provided by Huawei (see Section 1.2 and Appendix A). Some terminology used is as follows:
- Radius: the radius of the stereographic sphere onto which the 2-dimensional points are projected.
- Number of points: the number of points upon which the clustering algorithm was performed. For every experiment, the selected points were a random subset of all the 64-QAM data (of a specific noise) with cardinality equal to the required number of points.
- Accuracy: The symbol accuracy rate. As mentioned before, due to Gray encoding, the bit error rate is approximately of the symbol error rate. All accuracies are recorded as a percentage.
- Number of iterations: One iteration of the clustering algorithm occurs when the algorithm performs the cluster update followed by the centroid update (the algorithm must then perform the cluster update once again). The number of times the algorithm repeats these 2 steps before stopping is the number of iterations.
- Execution time: The amount of time taken for a clustering algorithm to give the final output (the final centroids and clusters) given the 2-dimensional data points as input, i.e. the time taken end to end for the clustering process. All times in this work are recorded in milliseconds (ms).
4.1. Candidate Algorithms
In this subsection, we define the various tested algorithms.
- Quantum Analogue: The most important candidate for our testing. The algorithm is described in Section 3.3.
- 2-D Classical: The standard classical k nearest-neighbour algorithm implemented upon the original 2-dimensional dataset. The algorithm performed Cluster Update [Definition 1] with (i.e. using the Euclidean dissimilarity) and , the phase-space plane in which the dataset exists. It performed Centroid Update [Definition 2] with the same parameters, resulting in the updated centroid being equal to the average point of the cluster. In terms of closed form expression, where. This serves as a baseline for performance comparison.
- Stereographic Classical: The standard classical k nearest-neighbour algorithm, but implemented upon the stereographically projected 2-dimensional dataset. The algorithm performed Cluster Update [Definition 1] with (i.e. using the Euclidean dissimilarity) as well, but with , the 3-dimensional space which the projected dataset occupies. It performed Centroid Update [Definition 2] with the same parameters, resulting in the updated centroid once again being equal to the average point of the cluster. In terms of closed form expression, once again, . Note that generally, this centroid will lie within the stereographic sphere. This algorithm serves as another control to see how much is the effect of just stereographically projecting the dataset, versus restricting the centroid to the surface of the sphere. It is an intermediate step between the Quantum Analogue and the 2-D classical algorithms.
4.2. Experiments
Several experiments were performed on all 3 algorithms to characterise them and quantify their performance. In all the experiments, the variable parameters were as follows:
- 2-D Classical: Number of points, dataset noise
- Quantum Analogue: Radius, Number of points, dataset noise
- Stereographic Classical: Radius, Number of points, dataset noise
4.2.1. Characterisation Experiment 1
Here, the datasets were divided into training and testing data.
First, a random subset of cardinality equal to the number of points was chosen from the dataset, and then 80% of the selected points were assigned as ’Training Data’, while the other 20% was assigned as ’Testing Data’.
The algorithms were then first run on the training data with the maximum number of possible iterations set to 50 - the training phase. The stopping criteria for all algorithms was chosen as the natural endpoint - the algorithm stopped either when the number of iterations hit 50, or when for all , i.e. when all the clusters remained unchanged even after the Centroid Update. It is the natural end-point since if the clusters do not change, the centroids will not change either in the next iteration, in turn leading to the same clusters and centroids for all future iterations. The final centroid coordinates () were recorded in the training phase, to be used for the testing phase, along with a number of performance parameters. The recorded performance parameters were the algorithm’s accuracy, the number of iterations taken and the execution time.
Once the training was over, the centroids calculated at the end of training were used as the initial centroids for the testing set datapoints, and the algorithm was run with the maximum number of iterations set to 1, i.e. the calculated centroids were then used to simply classify the remaining points as per the dissimilarity function and dataspace of each algorithm. Here, the recorded performance parameters were the algorithm’s accuracy and execution time. Once both the testing and training accuracy had been recorded, the overfitting parameter (testing accuracy−training accuracy) was also recorded.
For each set of performance variables (just the number of points for 2-D classical clustering, the radius and number of points for the quantum analogue and stereographic classical clustering), the entire experiment (training and testing) was repeated 10,000 times in batches of 100 to calculate reasonable standard deviations for every performance parameter.
As mentioned before, we usually chose the random subsets of a chosen number of points from the same transmission iteration to avoid choosing different iterations of the same datapoint. However, to test some trends, we selected data from across multiple columns. It does not make much difference due to the random nature of the noise (transmission of the same bitstring later in the column or in another row do not suffer from different kinds of noise, the distinction is purely due to the nature of the protocol). These experiments, which were used to test certain observed trends, are presented separately in the results section.
There are several reasons for this choice of experiment:
- It exhaustively covers all the parameters that can be used to quantify the performance of the algorithms. We were able to observe very important trends in the performance parameters with respect to the choice of radius and the effect of the number of points (affecting the choice of when one should trigger the clustering process on the collected received points).
- It avoids the commonly known problem of overfitting. Though this approach is not usually used in the testing of the k nearest-neighbour algorithm due to its iterative nature, we felt that from a machine learning perspective, it is useful to know how well the algorithms perform in a classification setting as well.
- Another reason that justifies the approach of training and testing (clustering and classification) is the nature of the real-world application setup. When transmitting QAM data through optic fibre, the receiver receives only one point at a time and has to classify the received point to a given cluster in real-time using the current centroid values. Once a number of datapoints have accumulated, the k means algorithm can be run to update the centroid values; after the update, the receiver will once again perform classification until some number of points has been accumulated. Hence, we can see that in this scenario the clustering, as well as classification performance of the chosen method, becomes important.
4.2.2. Characterisation Experiment 2
Based on the results obtained from the first experiment, we performed another experiment to see how the accuracy of the algorithms varies iteration by iteration. It was observed that the natural end point of the algorithm was rarely the ideal endpoint in terms of performance, and hence we wished to observe the performance of each algorithm as the number of iterations progressed.
In this experiment, the entire random subset of datapoints was used for the clustering algorithm. The algorithms were run on the dataset, and the accuracy of the algorithms at each iteration as well as the iteration number of the natural endpoint was recorded. The maximum number of iterations was once again 50. By repeating this 100 times for each number of points (and radius, if applicable), we obtained the general performance variation of each algorithm with the iteration number. The performance variables were the number of points, the radius of the stereographic sphere and the iteration number; the recorded performance parameters were the accuracy and probability of stopping.
This experiment revealed that the natural endpoint was indeed a poor choice of stopping criteria, and the that endpoint should be chosen as per some loss function. It also revealed some important trends in the performance parameters which not only emphasised the importance of the choice of radius and number of points but also gave greater insight into the disadvantaged and advantages of each algorithm.
4.3. Results of Experiments
This section details the results of Characterisation Experiments 1 and 2. Due to the extensive nature of testing and the large volume of analysis generated, we do not present all the figures in the following sections. Figures which sufficiently demonstrate general trends and observations have been included here. An exhaustive collection of all figures and other such analysis results, as well as the source code, real-world data, and raw data collected, can we obtained from the GitHub repository of the project.
4.3.1. Characterisation Experiment 1: The Overfitting experiment
This section presents the obtained results of the first experiment.
Characterisation of Quantum Analogue Algorithm:
Figure 13, Figure 14 and Figure 15 characterise the testing accuracy, i.e. classification performance of the quantum analogue algorithm acting upon the 2.7dBm dataset, while Figure 16, Figure 17 and Figure 18 characterise the training accuracy, i.e. clustering performance of the algorithm when acting upon the 2.7dBm dataset. Figure 19 and Figure 19 portray the same results in the form of a heat map, and with the focus upon the best-performing paradigm of the algorithm. These figures are representative of the trends of all 4 datasets.
Figure 20– Figure 22 characterise the convergence performance of the quantum algorithm - they show how the number of iterations required to reach the natural endpoint of the quantum analogue algorithm varies as the number of points and radius of projection changes. Once again, the figures for all the other datasets follow the same pattern as the included figures.
Performance Comparisons:
We compare here the performance of the Quantum Analogue algorithm and 3D Stereographic Classical algorithm with each other as well as the 2-dimensional classical k-means clustering algorithm.
Accuracy performance:
In all the figures in this section, the winner is chosen as the radius for which the maximum accuracy is achieved for the given number of points.
Figure 23, Figure 24, Figure 25 and Figure 26 depict the variation in testing accuracy with the number of points for all three algorithms along with error bars. As mentioned before, this characterises the performance of the algorithms in ’classification’ mode, that is, when the received points must be decoded in real time.
Figure 27, Figure 28, Figure 29 and Figure 30 portray the trend in training accuracy with the number of points for all three algorithms along with error bars. This characterises the performance of the algorithms in ’clustering’ mode, that is, when the received points must be used to update the centroid for future re-classification or if the received datapoints are stored and decoded in batches.
Figure 31Figure 31 and Figure 32Figure 32 plot the gain in testing and training accuracies respectively for the 3D stereographic classical and quantum analogue algorithms. The gain is calculated as (accuracy of candidate algorithm - accuracy of 2-dimensional classical k-means clustering algorithm), i.e. it is the increase in accuracy of the algorithm over the baseline, defined as the accuracy of the classical k-means clustering algorithm acting on the 2D dataset for those number of points. The label of the points in these figures is the radius of stereographic projection for which that accuracy gain was achieved.
Convergence Performance
We use the number of iterations required by the algorithm to reach its ’natural endpoint’ as a proxy for convergence performance. Clearly, the lesser the number of iterations performed, the faster the convergence of the algorithm. The number of iterations does not directly correspond to time performance since the time taken for one iteration differs between all algorithms.
In all the figures in this section, the winner is chosen as the radius for which the minimum number of iterations is achieved for the given number of points.
Figure 33Figure 33 show how the required number of iterations for all three algorithms varies as the number of points increases. Figure 34Figure 34 display the gain of the Quantum Analogue and 3D Stereographic Classical algorithms in the number of iterations to reach their natural endpoints. In these figures, the gain is defined as (the number of iterations of 2D k-means clustering algorithm - the number of iterations of candidate algorithm), i.e. the gain is how many fewer iterations the candidate algorithm took than the classical k-means acting upon the 2D dataset to reach their natural endpoints. The label of the points in these figures is the radius of stereographic projection for which that iteration gain was achieved.
Time Performance
In all the figures in this section, the winner is chosen as the radius for which the minimum execution time is achieved for the given number of points.
Figure 35Figure 35 put forth the dependence of testing accuracy upon the number of points for all three algorithms along with error bars. As mentioned before, these times are effectively the amount of time the algorithm takes for one iteration. This characterises the performance of the algorithms when performing direct classification decoding of the received points in real-time.
Figure 36Figure 36 reveal the trend in training accuracy with the number of points for all three algorithms along with error bars. This characterises the time performance of the algorithms when performing clustering - that is, when the received points must be used to update the centroid for future re-classification or if the received datapoints are stored and decoded in batches.
Figure 37Figure 37 and Figure 38Figure 34 graph the gains in testing and training execution times respectively for the 3D stereographic classical and quantum analogue algorithms. The gain is calculated as (the execution time of 2D classical k-means clustering algorithm - the execution time of candidate algorithm). The label of the points in these figures is the radius of stereographic projection for which that execution time gain was achieved.
All times have been recorded in milliseconds (ms).
Overfitting Performance
Figure 39Figure 39 exhibit how the overfitting parameter for the 2D classical k-means clustering, 3D stereographic classical and quantum analogue algorithms vary as the number of points changes. The overfitting parameter is defined as (accuracy of candidate algorithm in testing - accuracy of candidate algorithm at end of training).
4.3.2. Characterisation Experiment 2: the Stopping Criteria experiment
Results for Quantum Analogue algorithm
Figure 40– Figure 43 depict the dependence of the accuracy of the quantum analogue algorithm upon the iteration number and projection radius for the 2.7dBm dataset. The figures for the rest of the datasets follow the same trends and are nearly identical in shape.
Figure 45 shows the dependence of the probability of the quantum analogue algorithm reaching its natural endpoint versus the radius of projection and iteration number for the 10.7dBm dataset for 51200 number of points, while Figure 44 shows the same for the 2.7dBm dataset and 640 points. Once again, the figures for the rest of the datasets follow the same trends and their shape can be extrapolated from the presented Figure 45.
Comparison with 2D Classical K-Means Clustering:
Figure 46Figure 46 portray the gain of the Quantum Analogue and 3D Stereographic Classical algorithms in the number of iterations to reach maximum accuracy for the 2.7, 6.6, 8.6 and 10.7dBm datasets respectively. In these figures, a gain of ’g’ means that the algorithm took ’g’ fewer iterations than the classical k means acting upon the 2D dataset did to reach maximum accuracy.
Figure 47Figure 47 plot the gain of the Quantum Analogue and 3D Stereographic Classical algorithms in the maximum achieved accuracy for the 2.7, 6.6, 8.6 and 10.7dBm datasets respectively. Here a gain of ’g’ means that the algorithm was more accurate than the maximum accuracy of the classical k means acting upon the 2D dataset.
4.4. Discussion and Analysis of Experimental Results
In this section we provide an analysis based on the obtained results from the two experiments presented above.
4.4.1. Characterisation Experiment 1: the overfitting test
From Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 we can see that there is an ideal radius > 1 for which maximum accuracy is achieved. This ideal radius is usually between 2 and 5 for our datasets. For a good choice of radius (>1), the accuracy increases monotonically (with an upper bound) with the number of points, while for a poor choice of radius (<1), the accuracy nosedives as the number of points increases. This is due to the clusters getting squished together near the North pole of the stereographic sphere (the point ). If one is dealing with a large number of points, the accuracy becomes even more sensitive to the choice of radius as the decline in accuracy for a bad radius is much steeper as the number of points increases. These observations hold for both training and testing accuracy (classification and clustering), regardless of the noise in the dataset. All of these observations are also well-reflected in the heatmaps, where one can see that the best training and testing performance is for to and the maximum number of points. It would seem that choosing too large of a radius is not too harmful. This might hold true for the classical algorithms, but in the case when the quantum algorithm is deployed, all the points will be clustered around the South pole of the Bloch sphere and even minimal noise in the quantum circuit will degrade performance. Hence, there is a sweet spot of radius to be chosen.
Figure 20, Figure 21 and Figure 22 also show that there is an ideal radius > 1 for which one needs the minimum number of iterations to reach the natural endpoint. This ideal radius is once again between 2 and 5 for our datasets. As the number of points increases, the number of iterations always increases. For a good choice of radius, the increase is minimal, while for a bad choice, the convergence is very slow. For our experiments, we chose the maximum iterations as 50 hence the observed plateau at 50 iterations. If one is dealing with a large number of points, the convergence becomes more sensitive to the choice of radius. The increase in iterations for a poor choice of radius is much steeper. Quantum Analogue algorithm and 3D Stereographic Classical algorithm display near-identical performance.
From Figure 23, Figure 24, Figure 25 and Figure 26 we can see that both Quantum Analogue algorithm and 3D Stereographic Classical algorithm perform better in accuracy than the 2D classical algorithm for all datasets. The advantage becomes more definitive as the number of points increases as the increase in accuracy moves beyond the error bar. We observe the highest increase in accuracy for the 2.7dBm dataset.
Figure 27, Figure 28, Figure 29 and Figure 30 show noticeably better performance of the Quantum Analogue algorithm and 3D Stereographic Classical algorithm over the 2D classical algorithm for all datasets than in the testing case (classification mode). Once again the 2.7dBm dataset shows the maximum increase. The advantage again becomes more definitive as the number of points increases as the increase in accuracy moves beyond the error bar. The Quantum Analogue algorithm and 3D Stereographic Classical algorithm show an almost identical performance.
Figure 31Figure 31 and Figure 32– Figure 32 support the aforementioned observations. We can see that almost universally for both algorithms, the gainis greater than 0, i.e. we beat the 2D classical algorithm in nearly every case! We can also see that the best radius is almost always between 2 and 5. Another observation is that the gain in training accuracy increases with the number of points. The figures further display how similarly the 3D Stereographic Classical algorithm and Quantum Analogue algorithm perform in terms of accuracy, regardless of noise.
From Figure 33Figure 33 and Figure 34Figure 34 it can be concluded that for low noise datasets, since the number of iterations is already quite low, there is not much gain or loss; all 3 algorithms perform almost identically. For high-noise datasets, however, both the 3D Stereographic Classical algorithm and Quantum Analogue algorithm show significant improvement in performance, especially for a higher number of points. For a high number of points, the improvement is beyond the error bars and hence very significant. It can be noticed that the ideal radius for minimum iterations is once again between 2 and 5. Here also the 3D Stereographic Classical algorithm and Quantum Analogue algorithm perform similarly, with the Quantum Analogue algorithm performing slightly better in certain cases.
One learns from Figure 35Figure 35 that most importantly, the Quantum Analogue algorithm and 2D classical algorithm take nearly the same amount of time for execution in classification mode, and the Quantum Analogue algorithm in most cases beats the 3D Stereographic Classical algorithm. Here too, the gain is significant since it is much beyond the error bar. The execution time increases linearly with the number of points, as expected. These conclusions are supported by Figure 37Figure 37.
Since the Quantum Analogue algorithm takes almost the same time, and provides greater accuracy, it is an ideal candidate to replace the 2D classical algorithm for classification applications.
Figure 36Figure 36 show that all 3 algorithms take almost the same amount of time for training, i.e. in clustering mode. The 3D Stereographic Classical and Quantum Analogue algorithms once again perform almost identically, almost always slightly worse than 2D classical clustering. Figure 38– Figure 38 support these observations. Here execution time increases linearly with the number of points as well, as one would expect.
In Figure 39Figure 39, all 3 algorithms have nearly identical performance. As expected. the overfitting decreases with an increase in the number of points.
Overall observations:
- The ideal radius of projection is greater than 1 and between 2 and 5. At this ideal radius, one achieves maximum testing and training accuracy, and minimum iterations.
- In general, the accuracy performance is the same for 3D Stereographic and Quantum Analogue algorithms - this shows a significant contribution of the stereographic projection to the advantage as opposed to ’quantumness’. This is a very significant distinction, not made by any other previous work. The Quantum Analogue algorithm generally requires fewer iterations to achieve the ideal accuracy, however.
- Quantum Analogue algorithm and 3D Stereographic Classical algorithm lead to an increase in the accuracy performance in general, with the increase most pronounced for the 2.7dBm dataset.
- The Quantum Analogue algorithm and 3D Stereographic Classical algorithm give more iteration performance gain (fewer iterations required than 2D classical) high noise datasets and for a large number of points.
- Generally, increasing the number of points works in favour of the Quantum Analogue algorithm and 3D Stereographic Classical algorithm, with the caveat that a good radius must be carefully chosen.
4.4.2. Characterisation Experiment 2: Stopping Criterion
Figure 40, Figure 41, Figure 42 and Figure 43 show that once again, there is an ideal radius for which maximum accuracy is achieved. The ideal projection radius is >1, between 2 and 5. Most importantly, there is an ideal number of iterations for maximum accuracy, beyond which the accuracy reduces. As the number of points increases, the sensitivity of the accuracy to radius increases significantly. For a bad choice of radius, accuracy only falls with an increase in a number of iterations and stabilises at a very low value. For a good radius, accuracy increases to a point as iterations proceed, and then stabilises at a slightly lower value. If the allowed number of iterations is restricted, the choice of radius to achieve the best results becomes extremely important. With a good radius one can achieve nearly the maximum possible accuracy with very few iterations. As mentioned before, this holds true for all dataset noises. As the dataset noise increases, the iteration number at which maximum accuracy is achieved also expectedly increases. Since accuracy always falls after a point, it is important to choose a stopping criteria rather than wait for the algorithm to reach its natural endpoint. An idea for the stopping criteria is to record the sum of the average dissimilarity for each centroid at each iteration and stop the algorithm if that quantity increases.
Figure 44 and Figure 45 portray that for a good choice of radius, the quantum analogue algorithm approaches convergence much faster. For r < 1 the algorithm converges much slower or never converges. As the number of points increases, the rate of convergence for poor radius falls dramatically. For a radius greater than the ideal radius as well, the rate of convergence is lower. As one would expect, as dataset noise increases, the algorithm takes longer to converge. As we mentioned before, if the number of iterations is severely limited, the choice of radius becomes very important. If chosen well, the algorithm can reach its ideal endpoint in very few iterations.
Through Figure 46Figure 46 we see that for lower values of noise, both algorithms do not produce much advantage in terms of iteration gain, regardless of the number of points in the data set. However, at higher noises in the dataset and a high number of points, both algorithms significantly outperform the classical one. This effect is especially significant for the quantum analogue algorithm. For the highest noise and all the points, it saves over 20 iterations over the 2D classical algorithm - an advantage of over 50%. One of the reasons for this is that at low noises, the algorithms already perform quite well, and it is at high noise with a high number of points that the algorithm is stressed enough to reveal the difference in performance. It should be noted that these gains are much higher than when the algorithms are allowed to reach their natural endpoint, suggesting another reason for choosing an ideal stopping criteria.
Figure 47Figure 47 suggest that for all datasets and numbers of points, the 2 algorithms perform better than 2D classical clustering. The 3D Stereographic Classical algorithm and Quantum Analogue algorithm perform nearly the same, and the accuracy gain seems to stabilise with an increase in the number of points. Figure 48Figure 48 support these conclusions.
Overall observations:
- These results further stress the importance of choosing a good radius (2 to 5) and a better stopping criteria. The natural endpoint is not suitable.
- The results clearly justify the fact that the developed Quantum Analogue algorithm has significant advantages over 2D classical k-means clustering and 3D Stereographic Classical clustering.
- The Quantum Analogue algorithm performs the nearly the same as the 3D Stereographic Classical algorithm in terms of accuracy, but for iterations to achieve this max accuracy, the Quantum Analogue algorithm is better (esp. for high noise and a high number of points).
- The developed Quantum Analogue algorithm and 3D Stereographic Classical algorithm are better than the 2D classical algorithm in general - in terms of both accuracy and iterations to reach that maximum accuracy.
5. Conclusion and Further Work
This work considers the practical case of performing k-nearest neighbour clustering on experimentally acquired 64-QAM data. This work has described the problem in detail and explained how the Stereographic Quantum K Nearest-Neighbour Clustering and Quantum Analogue algorithms can be used. The proposed processes and circuits as well as the theoretical justification for the Stereographic Quantum K Nearest-Neighbour Clustering quantum algorithm and the Quantum Analogue classical algorithm have been described in detail. Finally, the simulation results on the real-world datasets have been presented, along with relevant analysis. From the analysis, one can clearly see that the Stereographic Quantum K Nearest-Neighbour Clustering and especially its classical analogue is something that should be considered for industrial implementation - the experiments provide a proof of concept. It also shows the importance of choosing the projection radius. In addition, from Section 3.2.3 one can see by the distance loss function for stereographic quantum k nearest neighbour clustering that it is expected to perform better than quantum k-means clustering with normal angle embedding. These results clearly warrant the practical implementation and testing of both quantum and classical algorithms.
Quantum and quantum-inspired computing has the potential to change the way certain algorithms are performed, with potentially significant advantages. However, as the field is still in relative infancy, finding where quantum and quantum-inspired computing fits in practice is a challenging problem. Here, we have seen that quantum and quantum-inspired computing can indeed be applied to signal-processing scenarios, and could potentially work well in the noisy quantum era as clustering algorithms that are relatively robust to noise and inaccuracy.
5.1. Future Work
One of the most important directions of future work is to experiment with more diverse datasets. More experimentation may also lead to more sophisticated methods of selecting the radius for stereographic projection. A more detailed analysis of how to choose a radius of projection through analytical methods is another important direction for future work. A comparison with ampltiude embedding is also warranted. The ellipsoidal stereographic projection (Appendix D) is another promising and novel idea that is to be explored. In this project, two different stopping criteria for the algorithm were proposed and revealed a change in its performance; yet there is plenty of room to explore more possible stopping criteria.
Further directions of study include improved oberlap estimation methods [37] and communication scenarios where the dimensionality of the data points is greatly increased. For example when multiple carriers experience identical or at least systematically correlated phase rotations.
Another future work is to benchmark against sampling-based quantum-inspired algorithms. As part of a research analysis to evaluate the best possibilities for achieving a practical speed-up, we investigated the landscape of classical algorithms inspired by the sampling in quantum algorithms. Initially, we found that such algorithms have theoretical complexity competing with quantum algorithms, however only under arguably unrealistic assumptions on the structure of the classical data. As the performance of the quantum algorithms turns out to be extremely poor, this reopens the possibility that quantum-inspired algorithms can actually yield performance improvements while we wait for quantum computers with sufficiently low noise. Thus future work will also be a practical implementation of the quantum-inspired k nearest-neighbour clustering algorithm, with the goal of testing the computational advantage over 2D classical, 3D Stereographic Classical, and Quantum Analogue algorithms.
Funding
This work was funded by the TUM-Huawei Joint Lab on Algorithms for Short Transmission Reach Optics (ASTRO). This project has received funding from the DFG Emmy-Noether program under grant number NO 1129/2-1 (JN) and by the Federal Ministry of Education and Research of Germany in the programme of ”Souveran. Digital. Vernetzt.”. Joint project 6G-life, project identification number: 16KISK002, and of the Munich Center for Quantum Science and Technology (MCQST).
Data Availability Statement
The generated experimental datasets used in this work, all source codes, analysed data, and the complete set of generated graphs are available through the publicly accessible GitHub repository at the following link: https://github.com/AlonsoViladomat/Stereographic-quantum-embedding-clustering.
Acknowledgments
We would like to acknowledge fruitful discussions with Stephen DiAdamo and Fahreddin Akalin during the initial stages of the project.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Data Visualisation
Appendix A.1. 64-QAM Data
In this appendix, the various datasets are visualised. In Figure 2, we can see the analog transmission values (alphabet) for all the different channels.
In the next 5 Figures (Figure A1–Figure A5), the data for each of the 5 iterations of transmission within the same channel ( dBm) is represented separately.
Figure A1.
The data detected by the receiver from the 10.7dBm noise channel on the first instance of transmission.
Figure A1.
The data detected by the receiver from the 10.7dBm noise channel on the first instance of transmission.
Figure A2.
The data detected by the receiver from the 10.7dBm noise channel on the second instance of transmission.
Figure A2.
The data detected by the receiver from the 10.7dBm noise channel on the second instance of transmission.
Figure A3.
The data detected by the receiver from the 10.7dBm noise channel on the third instance of transmission.
Figure A3.
The data detected by the receiver from the 10.7dBm noise channel on the third instance of transmission.
Figure A4.
The data detected by the receiver from the 10.7dBm noise channel on the fourth instance of transmission.
Figure A4.
The data detected by the receiver from the 10.7dBm noise channel on the fourth instance of transmission.
Figure A5.
The data detected by the receiver from the 10.7dBm noise channel on the fifth instance of transmission.
Figure A5.
The data detected by the receiver from the 10.7dBm noise channel on the fifth instance of transmission.
In the next 4 figures (Figure A6–Figure A9) we can observe the transmission data for all the iterations for each channel. The first transmission data is represented as blue crosses, the second transmission as orange circles, the third transmission as yellow dots, the fourth transmission as purple stars, and the fifth transmission as green pluses.
Figure A6.
The data detected by the receiver from the 2.7dBm noise channel. All 5 iterations of transmission are depicted together.
Figure A6.
The data detected by the receiver from the 2.7dBm noise channel. All 5 iterations of transmission are depicted together.
Figure A7.
The data detected by the receiver from the 6.6dBm noise channel. All 5 iterations of transmission are depicted together.
Figure A7.
The data detected by the receiver from the 6.6dBm noise channel. All 5 iterations of transmission are depicted together.
Figure A8.
The data detected by the receiver from the 8.6dBm noise channel. All 5 iterations of transmission are depicted together.
Figure A8.
The data detected by the receiver from the 8.6dBm noise channel. All 5 iterations of transmission are depicted together.
Figure A9.
The data detected by the receiver from the 10.7dBm noise channel. All 5 iterations of transmission are depicted together.
Figure A9.
The data detected by the receiver from the 10.7dBm noise channel. All 5 iterations of transmission are depicted together.
The de-mapping alphabet is depicted in Figure A10.
Figure A10.
The de-mapping alphabet.
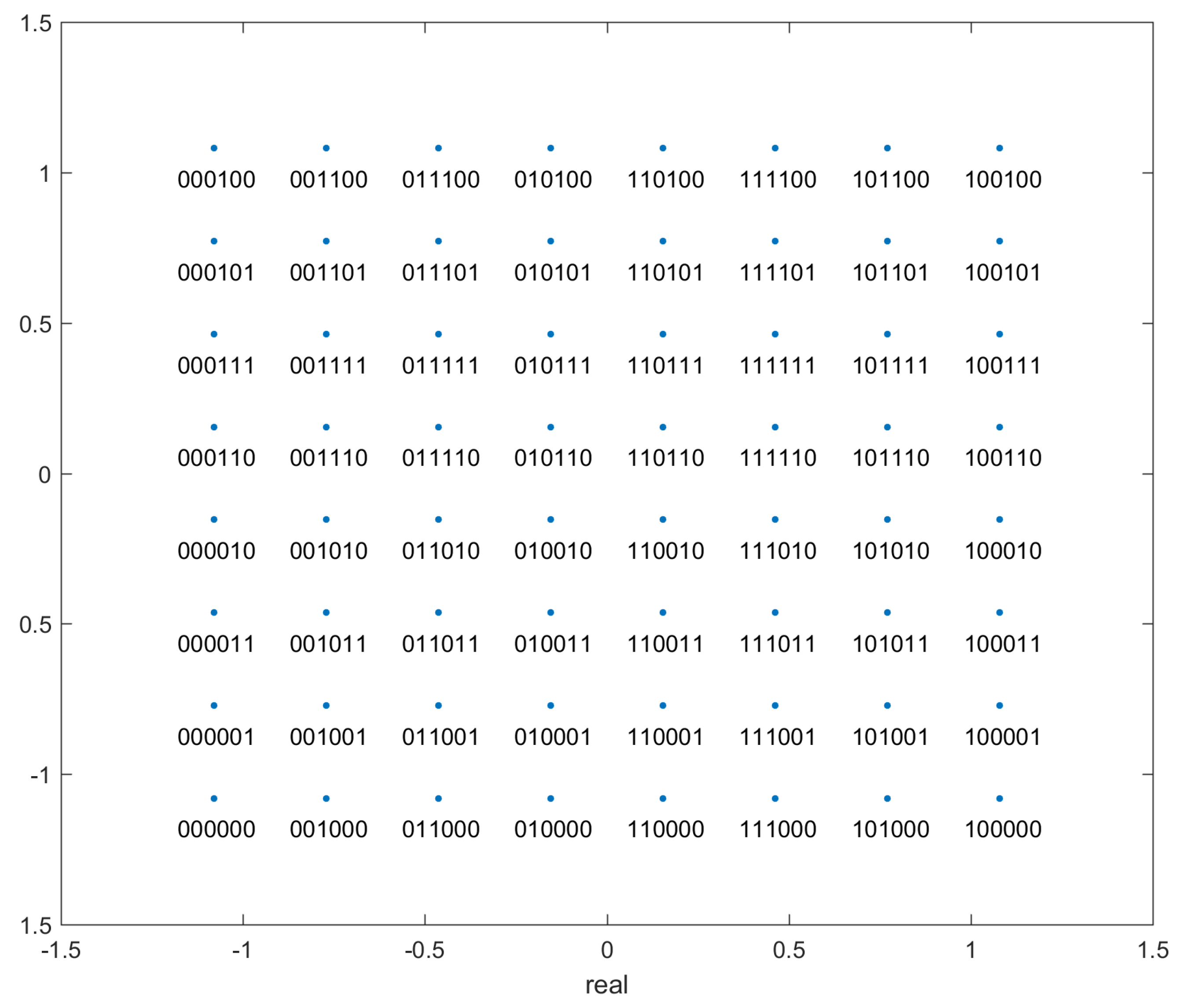
Appendix B. Data Embedding
One needs data in the form of quantum states for processing in a Quantum Computer. However, due to the instability of current qubits, data can currently only be stored for an extended period of time in classical form. Hence, the need arises to convert classical data into a quantum form. NISQ (Noisy Intermediate Scale Quantum) devices have a very limited number of logical qubits, and these qubits are stable for a very limited period of time. The first step in Quantum Machine Learning is to load classical data by encoding it into qubits. This process is called quantum data encoding or embedding. Classical data encoding for Quantum computation plays a critical role in the overall design and performance of the Quantum Machine Learning algorithms. Table A11 summarizes the various forms of data embedding.
| Embedding | Encoding | Num. qubits required | Gate Depth |
|---|---|---|---|
| Basis | per data point | ||
| Angle | |||
| Amplitude | gates | ||
| QRAM | queries |
Appendix B.1. Angle Embedding
Angle encoding is one of the most fundamental forms of encoding classical data into a quantum state. Each data point is represented as a separate qubit. The classical real number is encoded into the rotation angle of the qubit. This encoding, in its most basic form, requires N qubits to represent N dimensional data. It is quite cheap to prepare in terms of complexity – all that is needed is one rotation quantum gate for each qubit. This is one of the forms of encoding we have used in our implementation Quantum Clustering. It is generally useful for quantum neural networks. Angle encoding encodes N features into the rotation angles of n qubits where .
The rotations can be chosen as either , or gates, as defined by the rotation parameter:
- rotation=X uses the features as angles of rotations
- rotation=Y uses the features as angles of rotations
- rotation=Z uses the features as angles of rotations
As a first step, each data point of the input is normalized to the interval . To encode the data points, a rotation around the y-axis is used, for which the angle depends on the value of the normalized data point. This creates the following separable state:
It can easily be seen that one qubit is needed per data point, which is not optimal. To load the data, the rotations on the qubits can be performed in parallel; thus, the depth of the circuit is optimal [39].
The main advantage of this encoding is that it is very efficient in terms of operations – only a constant number of parallel operations are needed regardless of how many data values need to be encoded. This is not optimal from a qubit point of view (the circuit is very wide), as every input vector component requires one qubit. Another related encoding, called dense angle encoding, exploits an additional property of qubits (relative phase) to use the only qubits to encode n data points. An example of how angle encoding (using y-axis rotation) is used for state preparation is depicted in Figure A12. QRAM can be used to generate the more compact quantum state
Figure A12.
Angle Encoding [41].
Figure A12.
Angle Encoding [41].
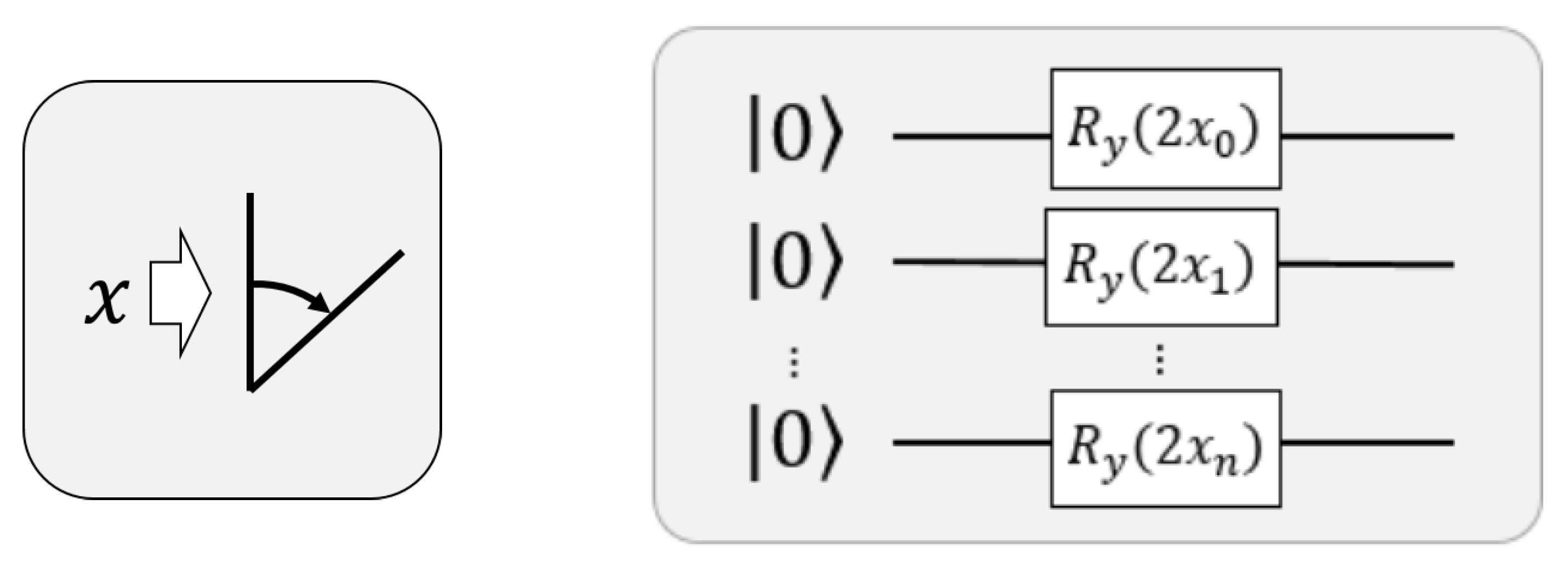
Appendix C. Stereographic Projection
Appendix C.1. Stereographic Projection for General Radius
In this appendix, the transformations for obtaining the cartesian co-ordinates of the projected point on a sphere of general radius are derived, followed by the derivation of polar and azimuthal angles of point on the sphere. First mentioned are 3 conditions that the point on the sphere must satisfy, and then follows the rest of the derivation. Refer to Figure A13 for better understanding of the conditions and calculations.
Figure A13.
Stereographic projection for a sphere of radius ’r’

Condition 1: Azimuthal angle of the original point and the projected point must be the same, i.e. the original point, projected point, and the top of the sphere (the point from which all projections are drawn) lie on the same plane, which is perpendicular to the x-y plane.
Condition 2: The projected point lies on the sphere.
Condition 3: The triangle with vertices , and is similar to the triangle with vertices , and .
Substituting in Equation A4 we get,
Hence one gets the set of transformations:
Calculating the zenith angle () and azimuthal angle ():
Appendix C.2. Equivalence of displacement and scaling
Refer to Figure A14. Here, is the point from which all the projections originate; and are the centres of the projection spheres of radius and respectively; is the point on the 2-D plane to be projected; and and are the stereographic projection of P on the spheres of radius and centre and radius and centre respectively.
Figure A14.
Stereographic projection on a sphere displaced above the plane and a sphere centred at origin
Figure A14.
Stereographic projection on a sphere displaced above the plane and a sphere centred at origin
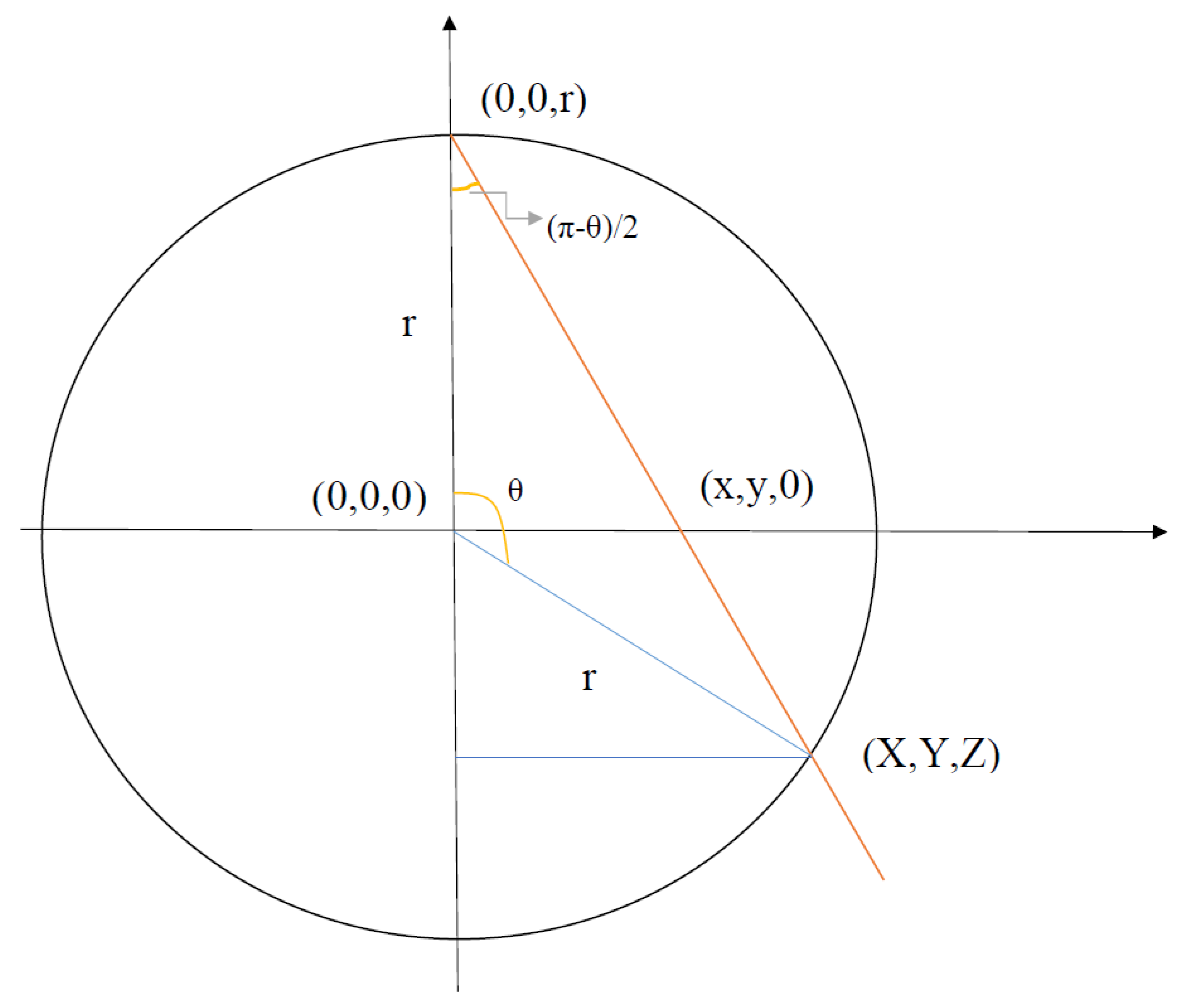
Also,
Hence
Since both and lie on the same plane, which is a vertical cross section of the sphere (plane perpendicular to the data plane and passing through the centre of both stereographic spheres), the azimuthal angle of both points is equal ().
Hence one can see that the azimuthal and the zenith angle generated by stereographic projection on a sphere of radius displaced above the 2-D plane containing the points by is the same as the azimuthal and the zenith angle generated by stereographic projection on a sphere of radius centred at origin. This reduces the effective number of parameters that can be chosen for the embedding.
Appendix D. Ellipsoidal Embedding
Here, we first derive the transformations for obtaining the cartesian co-ordinates of the projected point on a general ellipsoid, followed by the derivation of polar and azimuthal angles for the point on the ellipsoid. First mentioned are three conditions that the point on the sphere must satisfy, and then follows the rest of the derivation. Refer to Figure A15 for a better understanding of the conditions and calculations.
Figure A15.
Ellipsoidal Projection: a generalisation of the stereographic projection
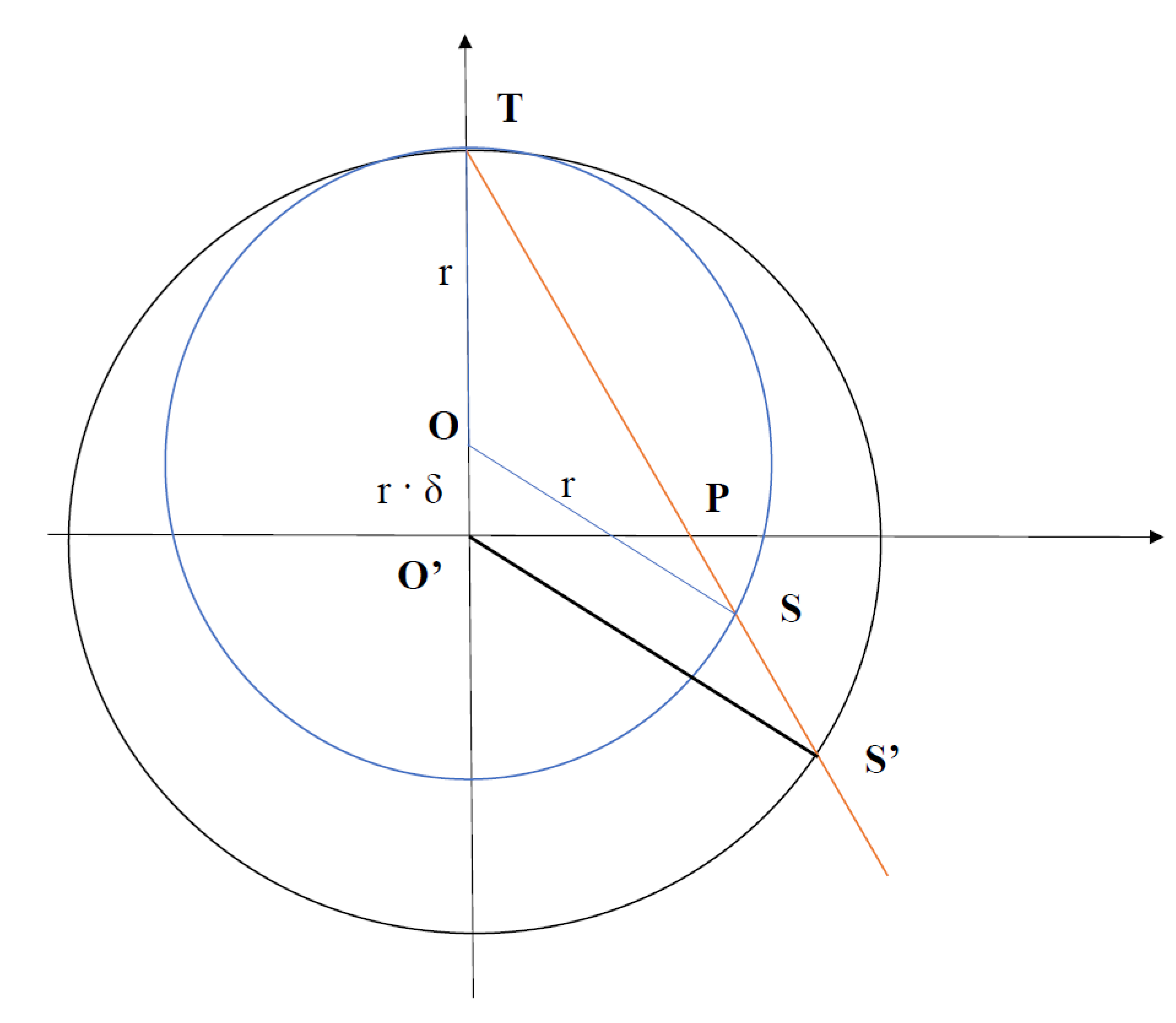
Condition 1: Azimuthal angle -
Condition 2: The projected point lies on the ellipsoid -
Condition 3: The triangle with vertices , and is similar to the triangle with vertices , and -
From the above conditions, we have
Substituting as before, we get
Hence one gets the set of transformations:
From Figure A15 one can see that
Also, as before, by the same reasoning
Now that we have these expressions, we have 2 methods of encoding the datapoint. We can either encode it as before, using the unitary which would correspond to projecting all the points on the ellipsoid to the surface of the sphere radially; or, we could use mixed states to represent the points on the surface of the ellipsoid after rescaling it to lie within the Bloch sphere.
Appendix E. Rotation Gates and the UGate
The complete expression for the unitary UGate in Qiskit is as follows:
Using the state for encoding, we have
One can see that there is no dependence of this state on . On the other hand, if we use the state for encoding, we have
One can see that the term leads only to a global phase. A global phase will not affect the observable outcome of the swap test or bell state measurement test (due to the modulus operator) - hence once again, no information can be encoded into the quantum state using .
For constructing the point () on the Bloch sphere, we can use rotation gates as well:
From Equation A27 one can see that and only differ by a global phase (). Hence, the and operations can be used interchangeably for state preparation since a global phase will not affect the observable result of the swap test.
Appendix F. Distance Estimation through the SWAP test
Figure A16.
Quantum circuit of the SWAP Test
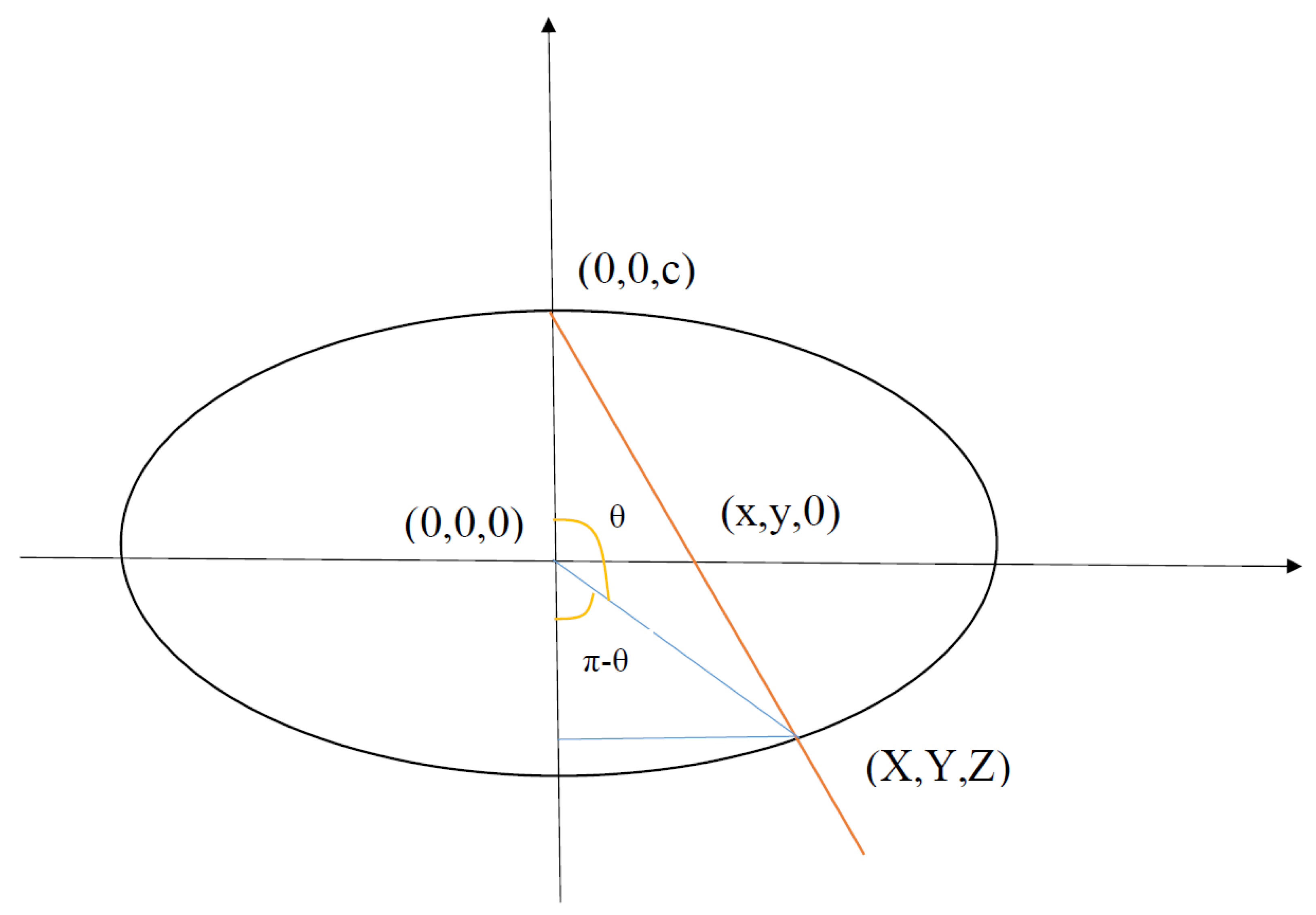
The swap test is a common procedure in quantum computing, first described in [42]. It is commonly used in quantum machine learning overlap estimation between two quantum states. The task of finding the overlap is accomplished by measuring the output of the ancilla qubit of the SWAP Test circuit many times (see Figure A16). The state of the system at the beginning of the protocol is . After the Hadamard gate, the state of the system is . The controlled SWAP gate transforms the state into . The second Hadamard gate results in
For such state, the probability of measuring the ground state is [42]:
As a consequence of Equation A33 the complementary probability is
which agrees with Equation Section 3.2.2. This procedure requires one to directly measure the ancilla qubit instead of the composite system, hence the two embedded qubits become reusable for future experiments (assuming that their quantum information is store-able). This procedure performs a non-destructive measurement as opposed to Figure 7.
It is important to mention that with current technology quantum gates and therefore state preparation are noisy. It requires time to embed the data into pure states, which leads to a drop in performance. In [13] it is claimed, in fact, that this might nullify a lot of the expected time advantage of linear algebraic quantum algorithms. This might be subject to change once more refined theoretical and experimental methods are developed.
References
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.; Buell, D.; et al. Quantum Supremacy using a Programmable Superconducting Processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Schuld, M.; Petruccione, F. Supervised Learning with Quantum Computers; Quantum Science and Technology, Springer International Publishing, 2018.
- M. Schuld, I. Sinayskiy, F.P. An introduction to quantum machine learning. arXiv:1409.3097 [quant-ph] 2014.
- Kerenidis, I.; Prakash, A. Quantum Recommendation Systems. In Proceedings of the 8th Innovations in Theoretical Computer Science Conference (ITCS 2017); Leibniz International Proceedings in Informatics (LIPIcs), Vol. 67; Papadimitriou, C.H., Ed.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2017; pp. 49–49. [Google Scholar] [CrossRef]
- Kerenidis, I.; Landman, J.; Luongo, A.; Prakash, A. q-means: A quantum algorithm for unsupervised machine learning. arXiv, 2018; arXiv:1812.03584. [Google Scholar]
- Lloyd, S.; Mohseni, M.; Rebentrost, P. Quantum algorithms for supervised and unsupervised machine learning. arXiv, 2013; arXiv:1307.0411. [Google Scholar]
- Pakala, L.; Schmauss, B. Non-linear mitigation using carrier phase estimation and k-means clustering. In Proceedings of the Photonic Networks; 2015, 16. ITG Symposium. VDE; pp. 1–5.
- Zhang, J.; Chen, W.; Gao, M.; Shen, G. K-means-clustering-based fiber nonlinearity equalization techniques for 64-QAM coherent optical communication system. Optics express 2017, 25, 27570–27580. [Google Scholar] [CrossRef]
- Tang, E. Quantum Principal Component Analysis Only Achieves an Exponential Speedup Because of Its State Preparation Assumptions. Phys. Rev. Lett. 2021, 127, 060503. [Google Scholar] [CrossRef] [PubMed]
- Microsystems, B. Digital modulation efficiencies.
- Jr., L.E.F. Electronics Explained: Fundamentals for Engineers, Technicians, and Makers, Newnes, 2018.
- Tang, E. A Quantum-Inspired Classical Algorithm for Recommendation Systems. In Proceedings of the Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing; STOC 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 217–228. [Google Scholar] [CrossRef]
- Tang, E. Quantum Principal Component Analysis Only Achieves an Exponential Speedup Because of Its State Preparation Assumptions. Physical Review Letters 2021, 127. [Google Scholar] [CrossRef] [PubMed]
- Chia, N.H.; Lin, H.H.; Wang, C. Quantum-inspired sublinear classical algorithms for solving low-rank linear systems. arXiv, 2018; arXiv:1811.04852. [Google Scholar]
- Gilyén, A.; Lloyd, S.; Tang, E. Quantum-inspired low-rank stochastic regression with logarithmic dependence on the dimension. arXiv, 2018; arXiv:1811.04909. [Google Scholar]
- Arrazola, J.M.; Delgado, A.; Bardhan, B.R.; Lloyd, S. Quantum-inspired algorithms in practice. Quantum 2020, 4, 307. [Google Scholar] [CrossRef]
- Martyn, J.M.; Rossi, Z.M.; Tan, A.K.; Chuang, I.L. A grand unification of quantum algorithms. arXiv, 2021; arXiv:2105.02859. [Google Scholar]
- Kopczyk, D. Quantum machine learning for data scientists. arXiv, 2018; arXiv:1804.10068. [Google Scholar]
- Esma Aimeur, G.B.; Gambs, S. Quantum clustering algorithms. ICML ’07: Proceedings of the 24th international conference on Machine learning June 2007, 2007; 1–8. [Google Scholar]
- Cruise, J.R.; Gillespie, N.I.; Reid, B. Practical Quantum Computing: The value of local computation. arXiv, 2020; arXiv:2009.08513. [Google Scholar]
- Johri, S.; Debnath, S.; Mocherla, A.; Singh, A.; Prakash, A.; Kim, J.; Kerenidis, I. Nearest centroid classification on a trapped ion quantum computer. npj Quantum Information 2021, 7, 122. [Google Scholar] [CrossRef]
- Khan, S.U.; Awan, A.J.; Vall-Llosera, G. K-Means Clustering on Noisy Intermediate Scale Quantum Computers. arXiv, 2019; arXiv:1909.12183. [Google Scholar]
- Cortese, J.A.; Braje, T.M. Loading classical data into a quantum computer. arXiv, 2018; arXiv:1803.01958. [Google Scholar]
- Chia, N.H.; Gilyén, A.; Li, T.; Lin, H.H.; Tang, E.; Wang, C. Sampling-based sublinear low-rank matrix arithmetic framework for dequantizing Quantum machine learning. Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing 2020. [Google Scholar] [CrossRef]
- Arrazola, J.M.; Delgado, A.; Bardhan, B.R.; Lloyd, S. Quantum-inspired algorithms in practice. Quantum 2020, 4, 307. [Google Scholar] [CrossRef]
- Chia, N.H.; Gilyén, A.; Lin, H.H.; Lloyd, S.; Tang, E.; Wang, C. Quantum-Inspired Algorithms for Solving Low-Rank Linear Equation Systems with Logarithmic Dependence on the Dimension. In Proceedings of the 31st International Symposium on Algorithms and Computation (ISAAC 2020); Leibniz International Proceedings in Informatics (LIPIcs), Vol. 181; Cao, Y.; Cheng, S.W.; Li, M., Eds.; Schloss Dagstuhl–Leibniz-Zentrum für Informatik: Dagstuhl, Germany, 2020; pp. 47–47. [Google Scholar] [CrossRef]
- Sergioli, G.; Santucci, E.; Didaci, L.; Miszczak, J.A.; Giuntini, R. A quantum-inspired version of the nearest mean classifier. Soft Computing 2018, 22, 691–705. [Google Scholar] [CrossRef]
- Sergioli, G.; Bosyk, G.M.; Santucci, E.; Giuntini, R. A quantum-inspired version of the classification problem. International Journal of Theoretical Physics 2017, 56, 3880–3888. [Google Scholar] [CrossRef]
- Subhi, G.M.; Messikh, A. Simple quantum circuit for pattern recognition based on nearest mean classifier. International Journal on Perceptive and Cognitive Computing 2016, 2. [Google Scholar] [CrossRef]
- Nguemto, S.; Leyton-Ortega, V. Re-QGAN: an optimized adversarial quantum circuit learning framework, 2022. [CrossRef]
- Eybpoosh, K.; Rezghi, M.; Heydari, A. Applying inverse stereographic projection to manifold learning and clustering. Applied Intelligence 2022, 52, 4443–4457. [Google Scholar] [CrossRef]
- Poggiali, A.; Berti, A.; Bernasconi, A.; Del Corso, G.; Guidotti, R. Quantum Clustering with k-Means: a Hybrid Approach. arXiv, 2022; arXiv:2212.06691. [Google Scholar]
- de Veras, T.M.L.; de Araujo, I.C.S.; Park, D.K.; da Silva, A.J. Circuit-Based Quantum Random Access Memory for Classical Data With Continuous Amplitudes. IEEE Transactions on Computers 2021, 70, 2125–2135. [Google Scholar] [CrossRef]
- Hornik, K.; Feinerer, I.; Kober, M.; Buchta, C. Spherical k-Means Clustering. Journal of Statistical Software 2012, 50, 1–22. [Google Scholar] [CrossRef]
- Feng, C.; Zhao, B.; Zhou, X.; Ding, X.; Shan, Z. An Enhanced Quantum K-Nearest Neighbor Classification Algorithm Based on Polar Distance. Entropy 2023, 25. [Google Scholar] [CrossRef] [PubMed]
- Ahlfors, L.V. Complex Analysis, 2 ed.; McGraw-Hill Book Company, 1966.
- Fanizza, M.; Rosati, M.; Skotiniotis, M.; Calsamiglia, J.; Giovannetti, V. Beyond the Swap Test: Optimal Estimation of Quantum State Overlap. Physical Review Letters 2020, 124. [Google Scholar] [CrossRef] [PubMed]
- Plesch, M.; Brukner, Č. Quantum-state preparation with universal gate decompositions. Physical Review A 2011, 83, 032302. [Google Scholar] [CrossRef]
- Weigold, M.; Barzen, J.; Leymann, F.; Salm, M. Expanding Data Encoding Patterns For Quantum Algorithms. In Proceedings of the 2021 IEEE 18th International Conference on Software Architecture Companion (ICSA-C); 2021; pp. 95–101. [Google Scholar] [CrossRef]
- Quantum Computing Patterns. https://quantumcomputingpatterns.org/. Accessed: 2021-10-30.
- Roy, B. All about Data Encoding for Quantum Machine Learning.https://medium.datadriveninvestor.com/all-about-data-encoding-for-quantum-machine-learning-2a7344b1dfef, 2021.
- Harry Buhrman, Richard Cleve, J.W.; de Wolf, R. Quantum fingerprinting. arXiv:quant-ph/0102001.
Figure 1.
Experimental setup over a 80 km G.652 fiber link at optimal launch power of 6.6 dBm. Chromatic disperion (CD) and carrier frequency offset (CFO) compensation, timing recovery (TR) and carrier phase estimation (CPE).
Figure 1.
Experimental setup over a 80 km G.652 fiber link at optimal launch power of 6.6 dBm. Chromatic disperion (CD) and carrier frequency offset (CFO) compensation, timing recovery (TR) and carrier phase estimation (CPE).

Figure 2.
The bitstring mapping and demapping alphabet.
Figure 3.
The data detected by the receiver from the least noisy (2.7dBm noise) channel. All 5 iterations of transmission are depicted together.
Figure 3.
The data detected by the receiver from the least noisy (2.7dBm noise) channel. All 5 iterations of transmission are depicted together.
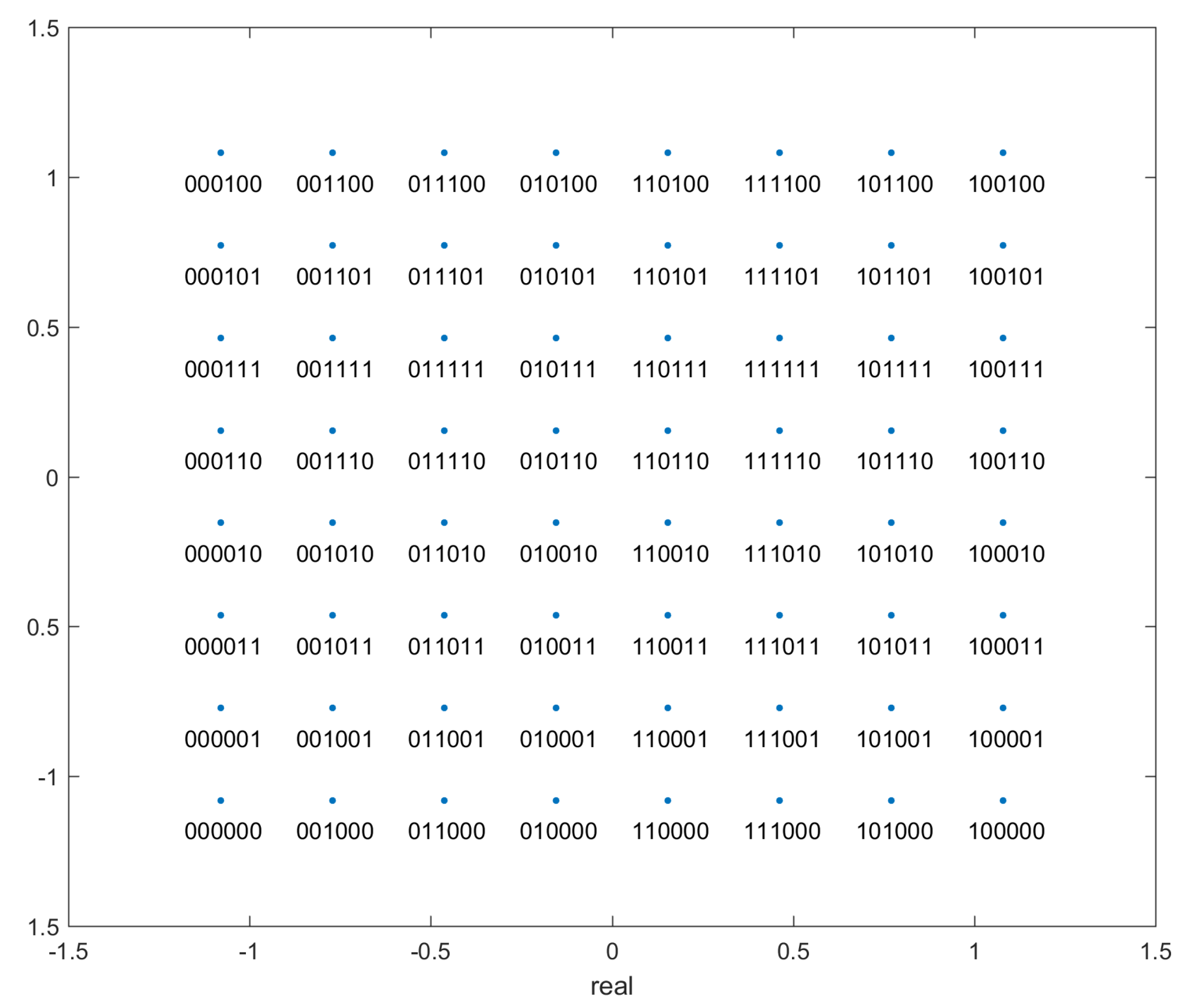
Figure 4.
The data detected by the receiver from the noisiest (10.7dBm noise) channel. All 5 iterations of transmission are depicted together.
Figure 4.
The data detected by the receiver from the noisiest (10.7dBm noise) channel. All 5 iterations of transmission are depicted together.
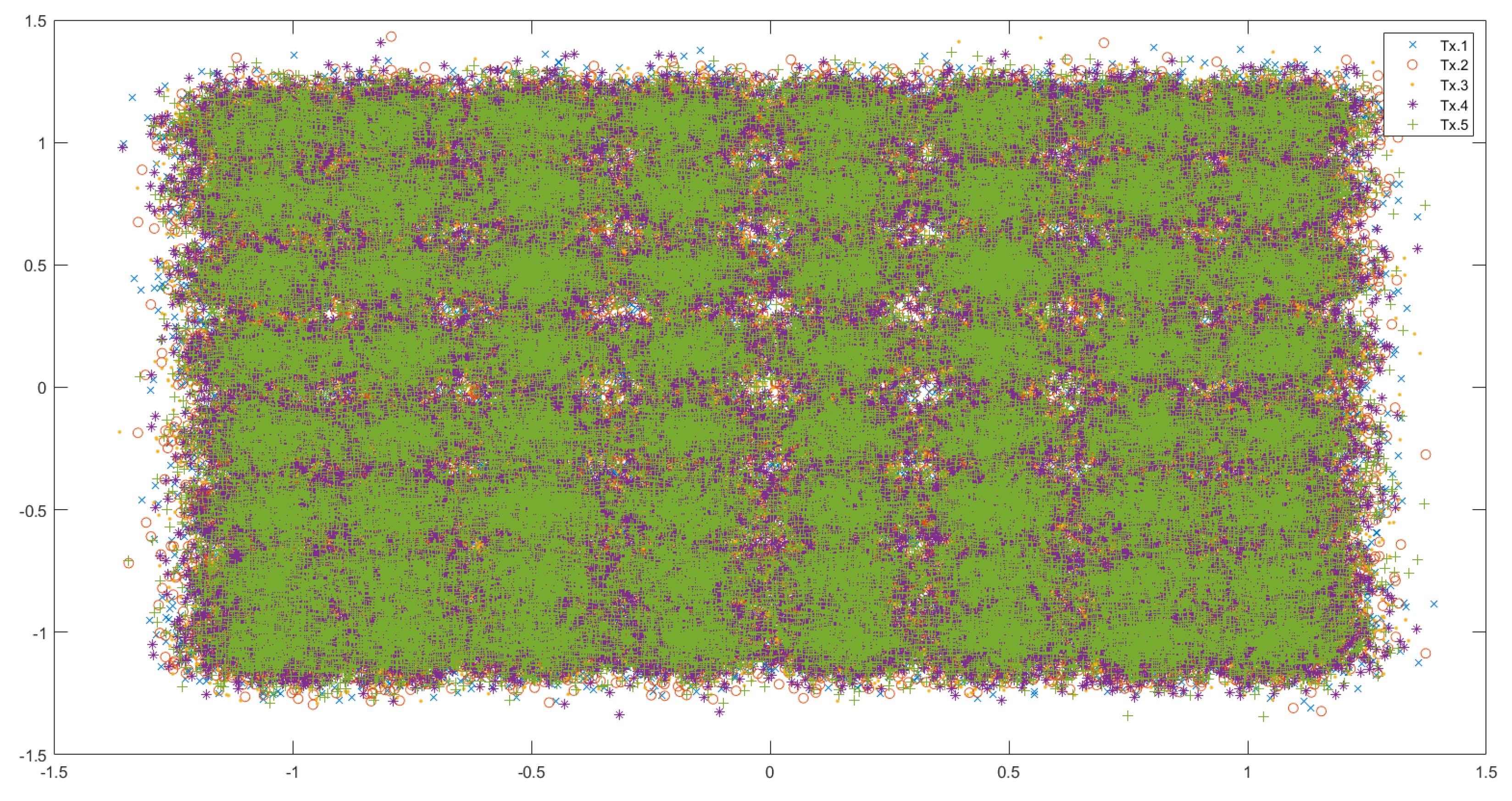
Figure 5.
Stereographic Projection [36].
Figure 5.
Stereographic Projection [36].
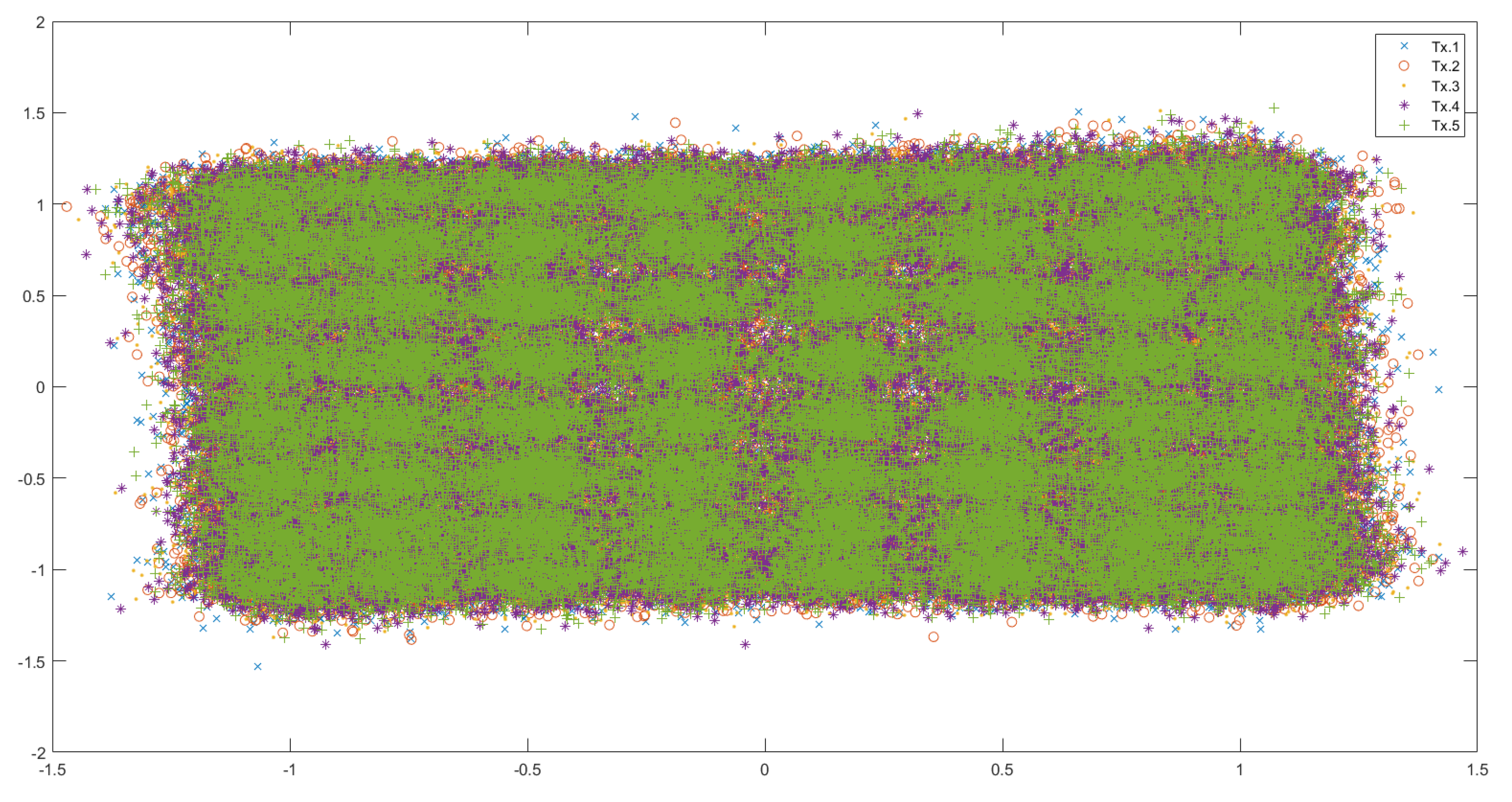
Figure 6.
Stereographic projection for a sphere of radius ’r’.
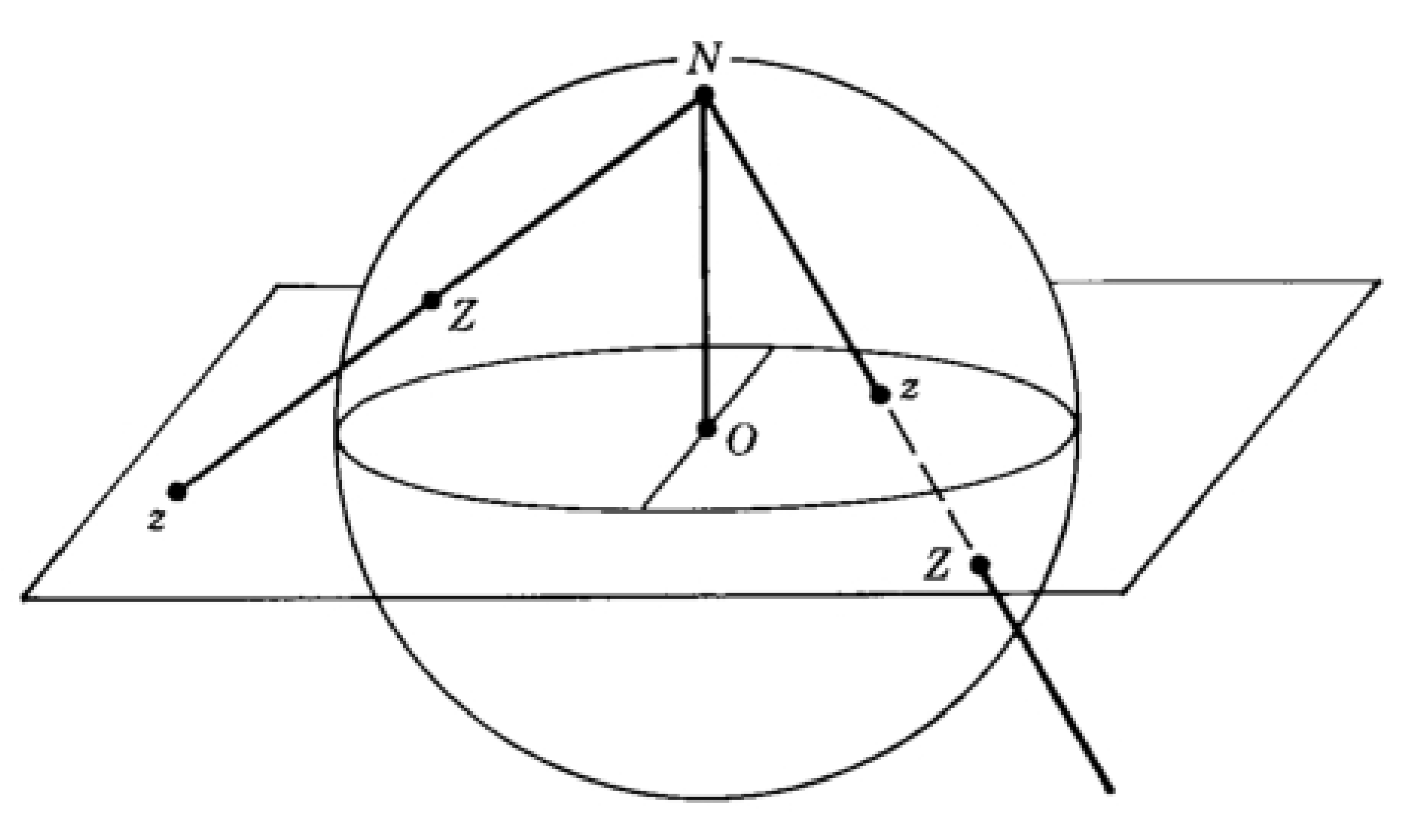
Figure 7.
Quantum circuit of the method, note that it is equivalent to the Bell state measurement set up.
Figure 7.
Quantum circuit of the method, note that it is equivalent to the Bell state measurement set up.
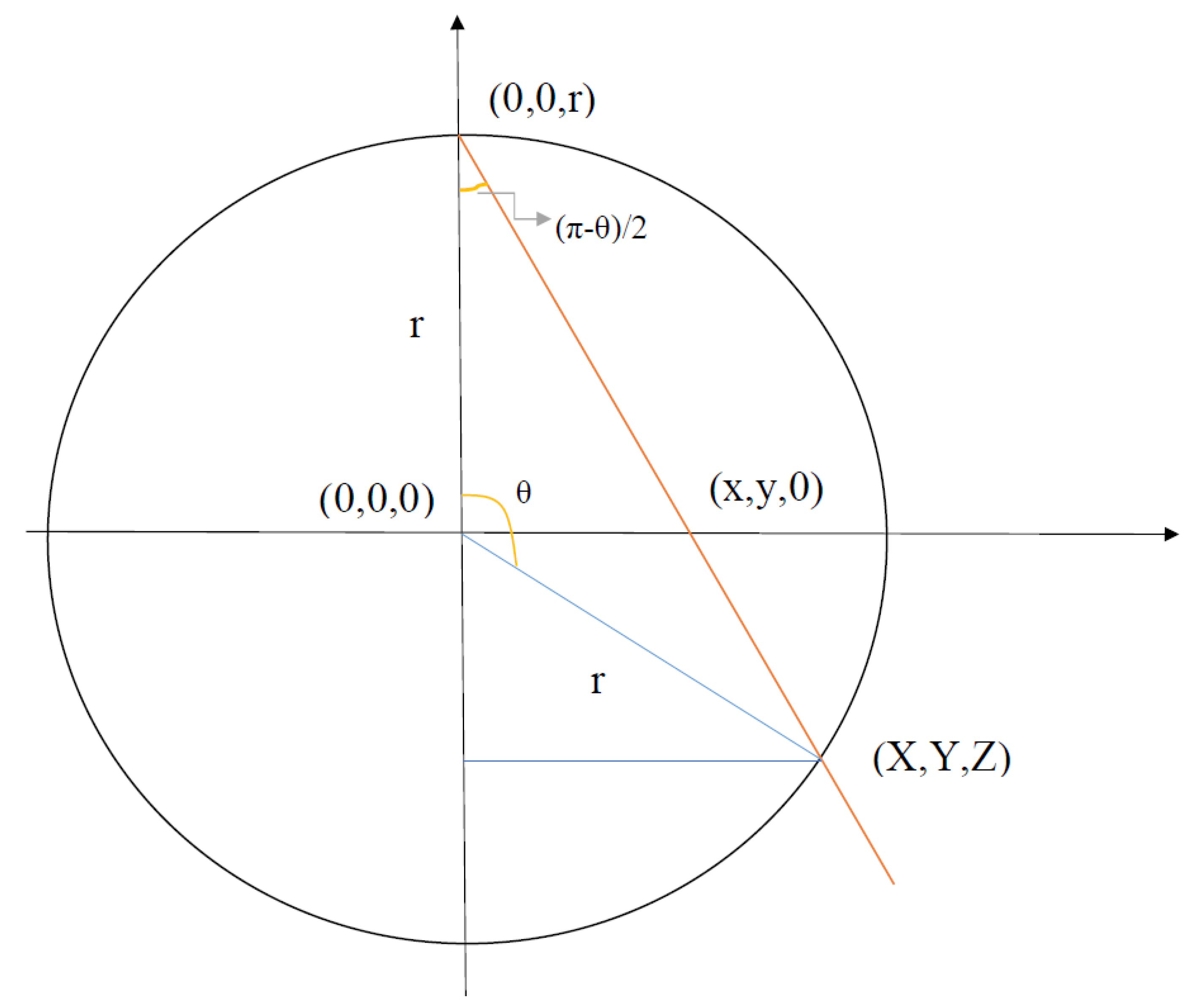
Figure 8.
Distance Loss Function for stereographic embedding with .
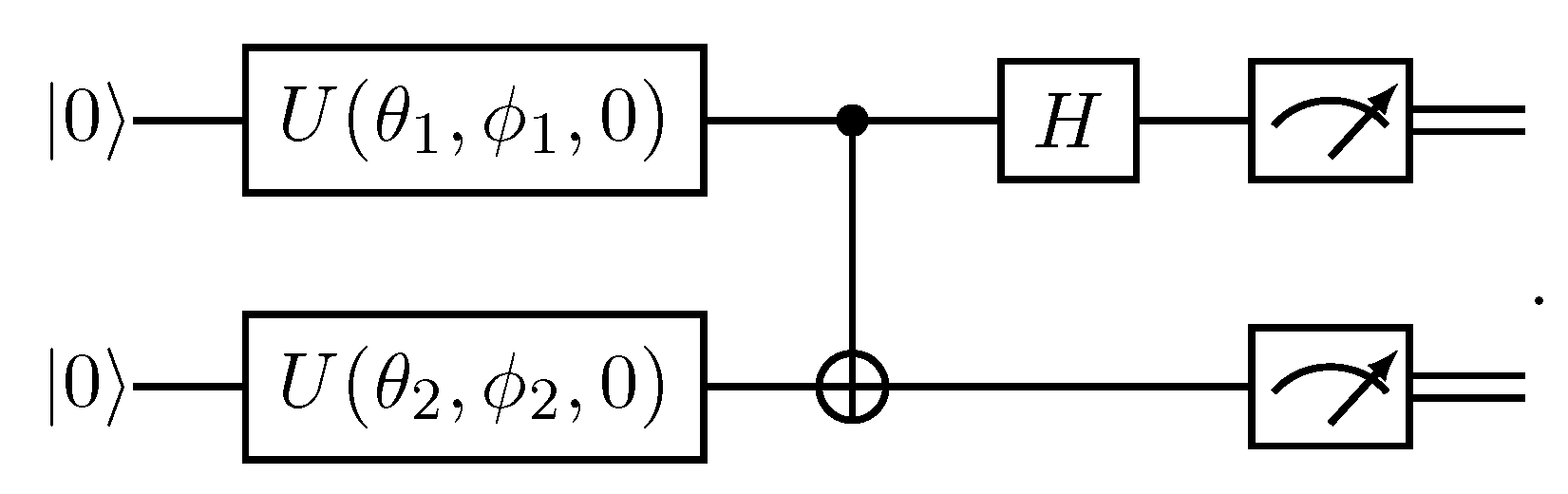
Figure 9.
Distance Loss Function for stereographic embedding with .
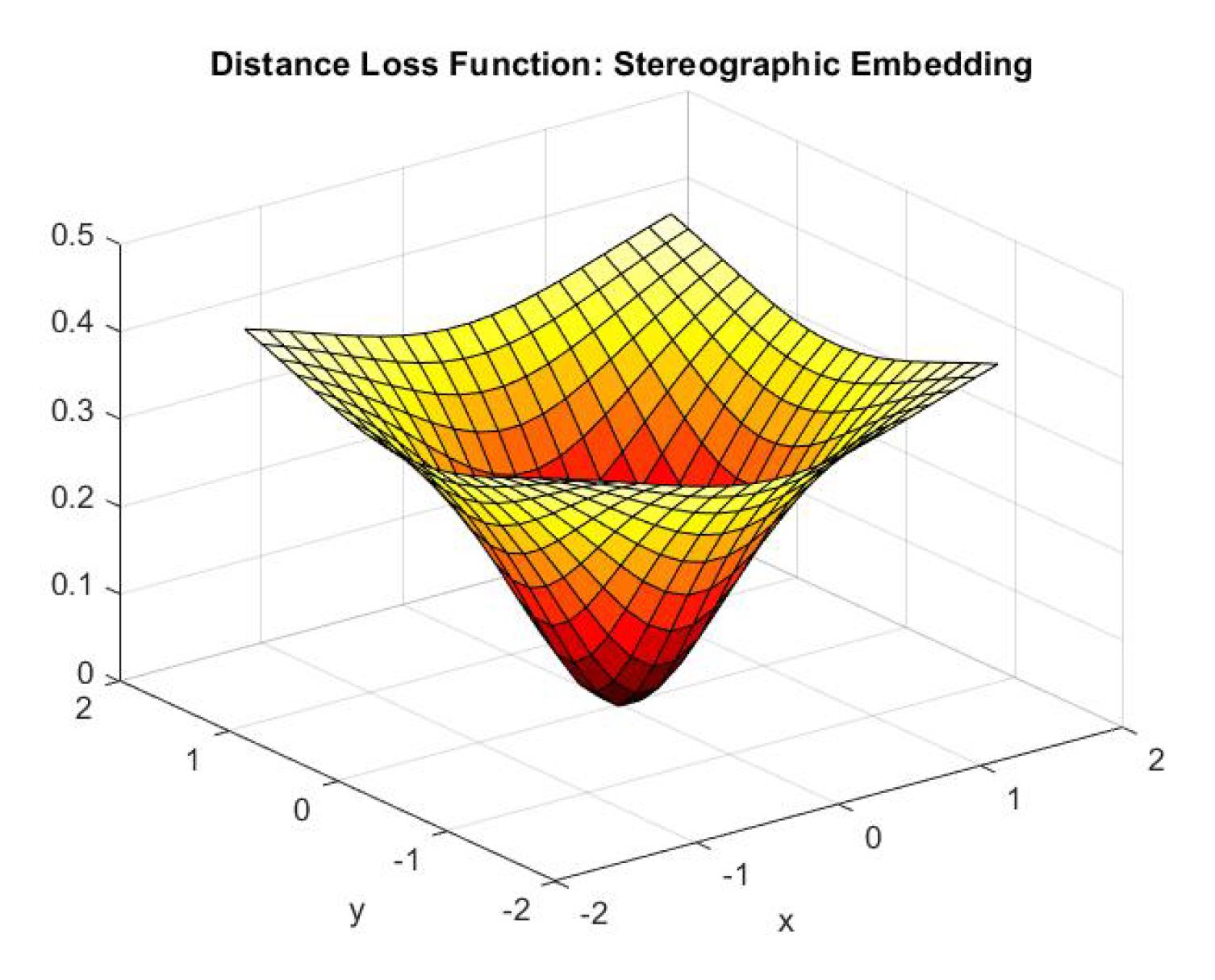
Figure 10.
Distance Loss Function for stereographic embedding with .
Figure 11.
Distance Loss Function for stereographic embedding with .
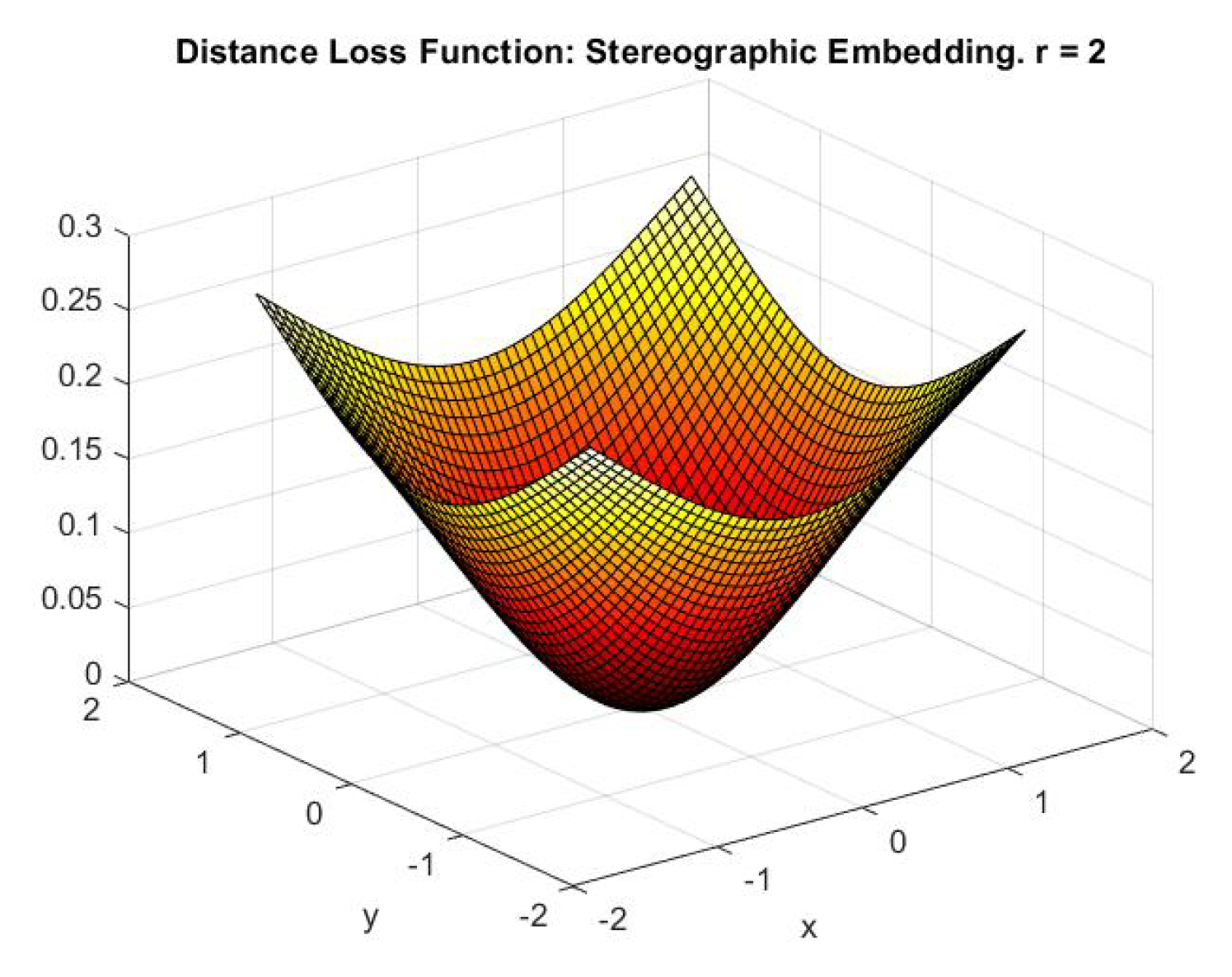
Figure 12.
A diagram providing a visual intuition for how the stereographic quantum k nearest-neighbour clustering quantum algorithm is equivalent to the quantum analogue k nearest-neighbour clustering classical algorithm.
Figure 12.
A diagram providing a visual intuition for how the stereographic quantum k nearest-neighbour clustering quantum algorithm is equivalent to the quantum analogue k nearest-neighbour clustering classical algorithm.
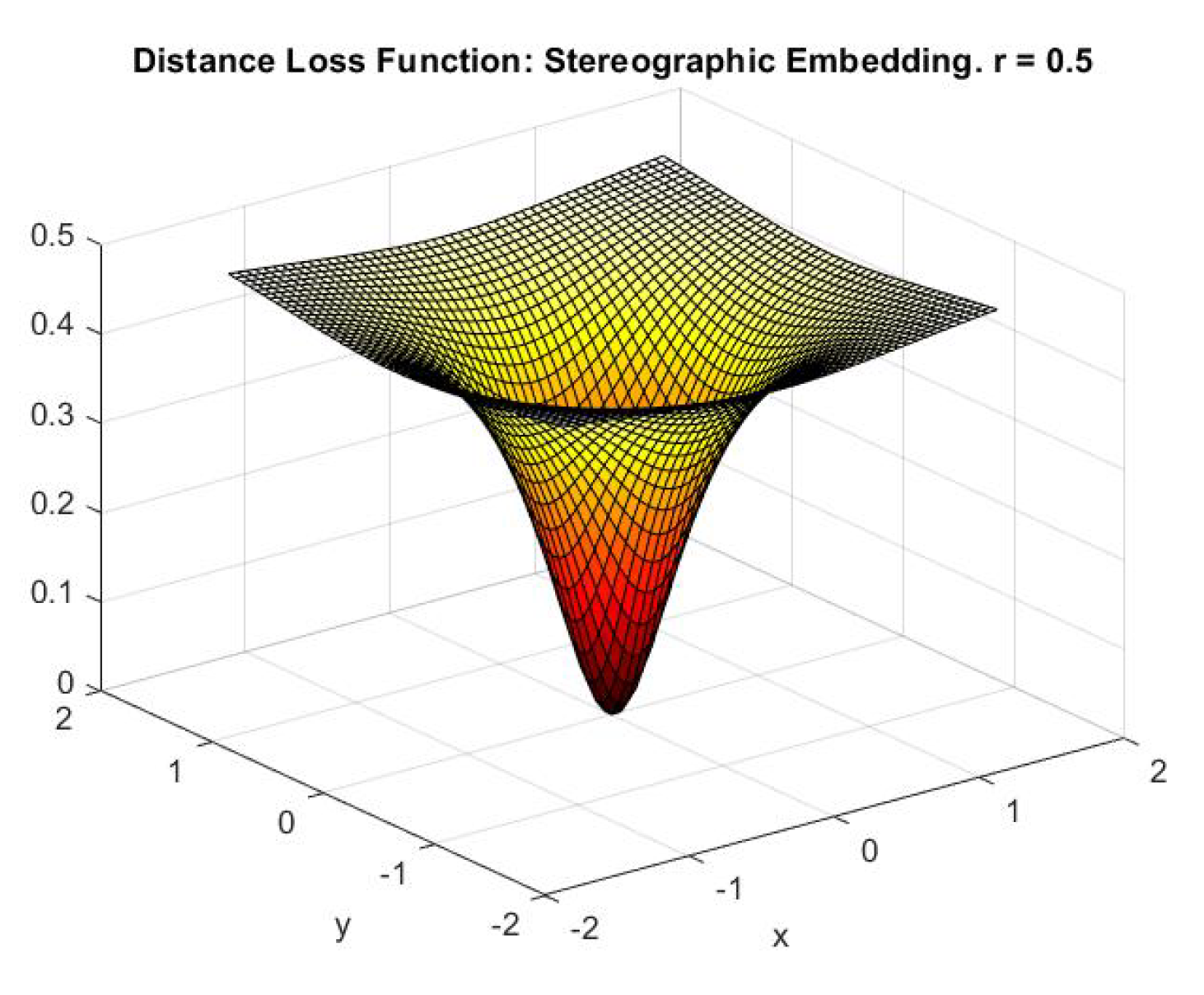
Figure 13.
Mean testing accuracy v/s ln(Number of points) v/s ln(projection radius) for the quantum analogue algorithm acting upon the 2.7 dBm dataset.
Figure 13.
Mean testing accuracy v/s ln(Number of points) v/s ln(projection radius) for the quantum analogue algorithm acting upon the 2.7 dBm dataset.
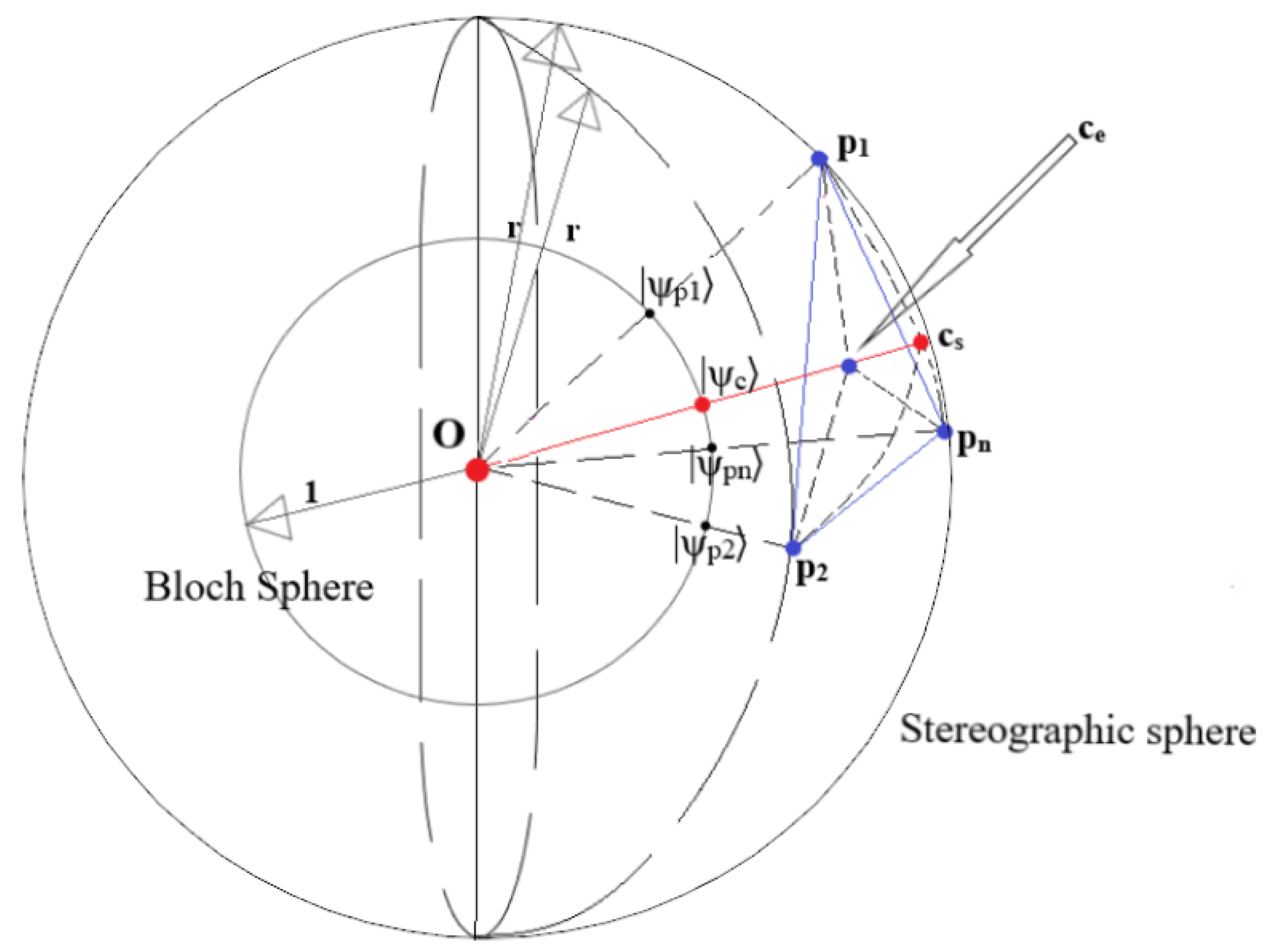
Figure 14.
Mean testing accuracy v/s ln(Number of points) v/s ln(projection radius) for the quantum analogue algorithm acting upon the 2.7 dBm dataset, another view.
Figure 14.
Mean testing accuracy v/s ln(Number of points) v/s ln(projection radius) for the quantum analogue algorithm acting upon the 2.7 dBm dataset, another view.
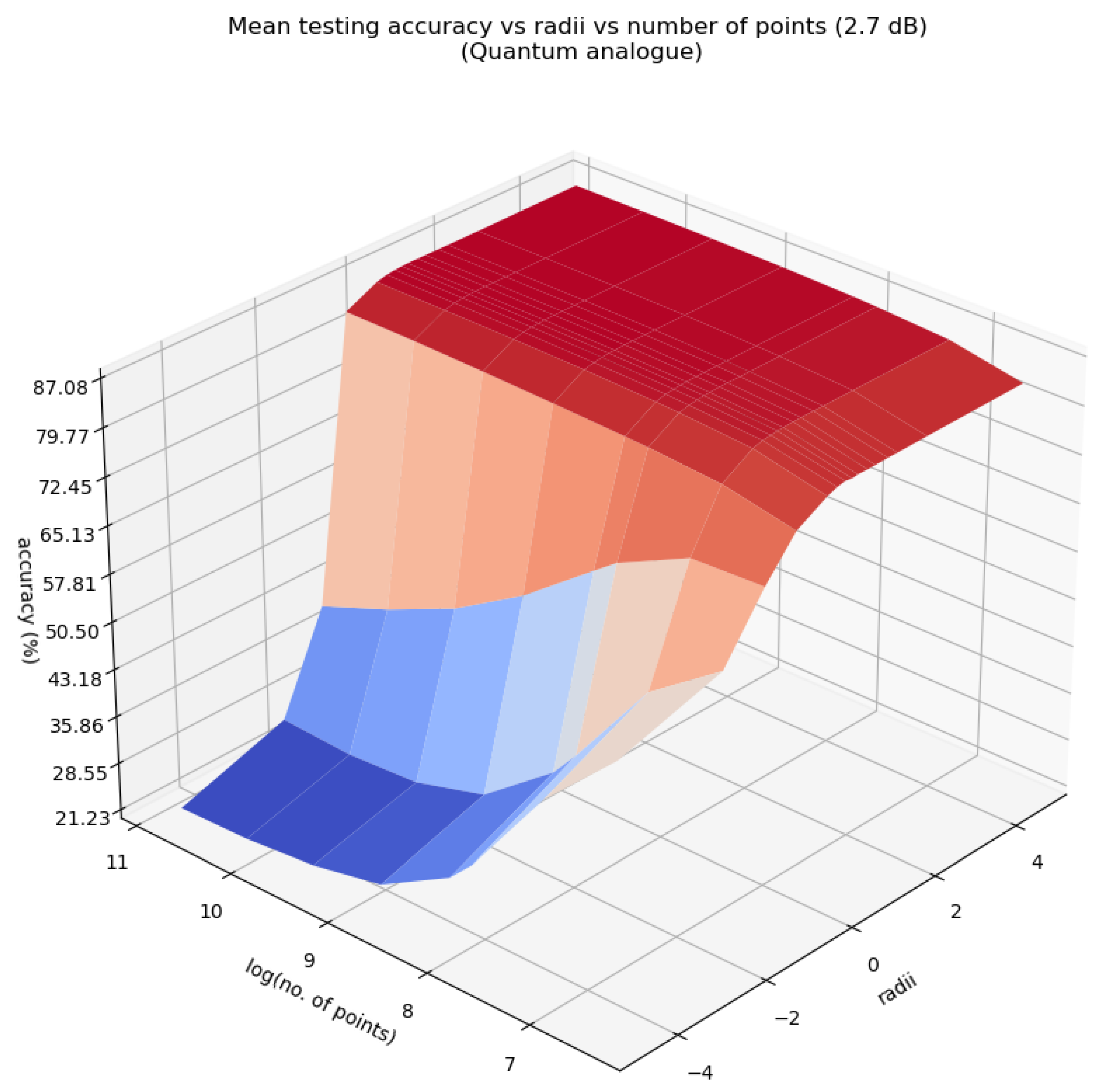
Figure 15.
Mean testing accuracy v/s ln(Number of points) v/s projection radius for the quantum analogue algorithm acting upon the 2.7 dBm dataset, close up.
Figure 15.
Mean testing accuracy v/s ln(Number of points) v/s projection radius for the quantum analogue algorithm acting upon the 2.7 dBm dataset, close up.
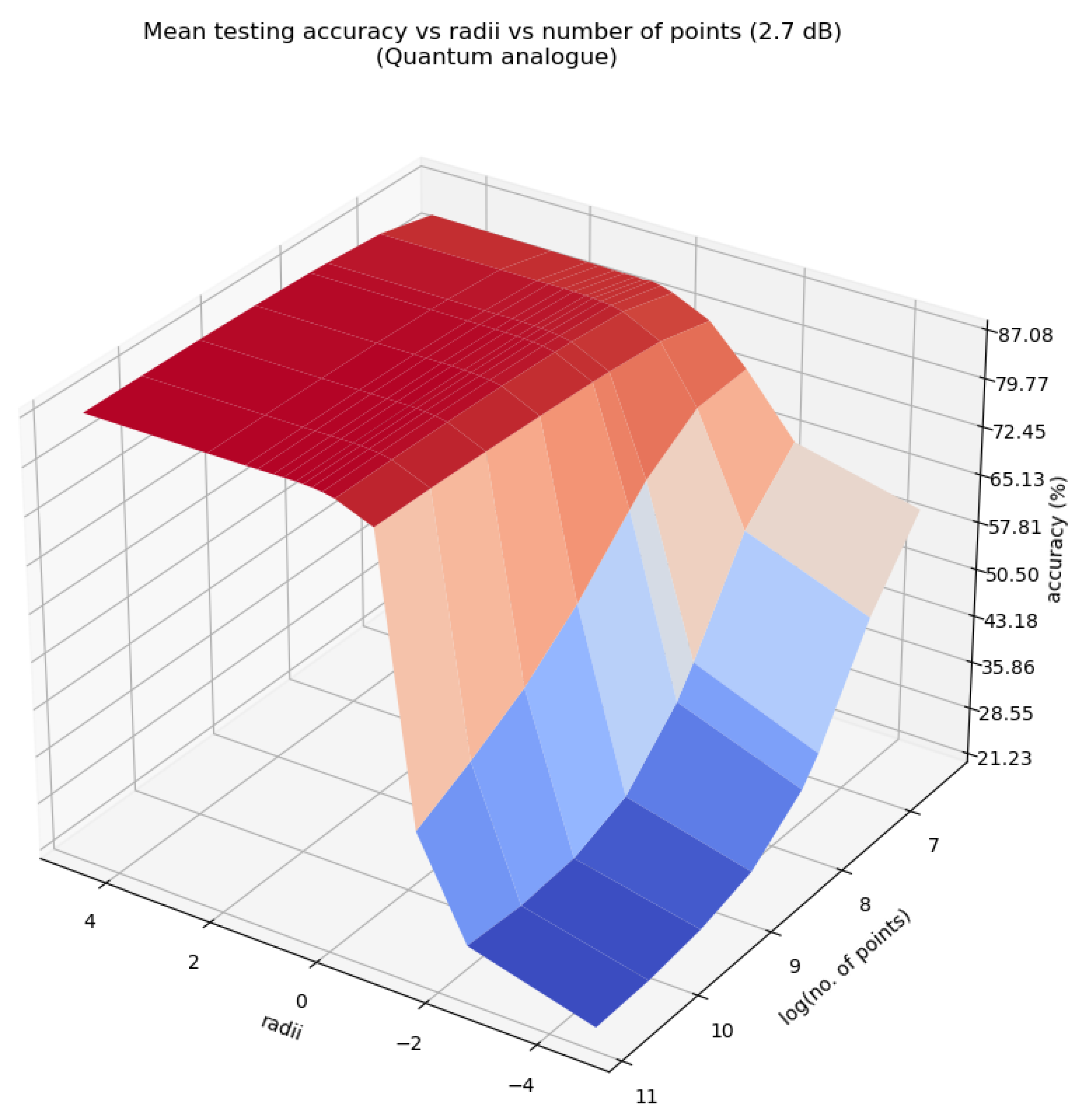
Figure 16.
Mean training accuracy v/s ln(Number of points) v/s ln(projection radius) for the quantum analogue algorithm acting upon the 2.7 dBm dataset.
Figure 16.
Mean training accuracy v/s ln(Number of points) v/s ln(projection radius) for the quantum analogue algorithm acting upon the 2.7 dBm dataset.
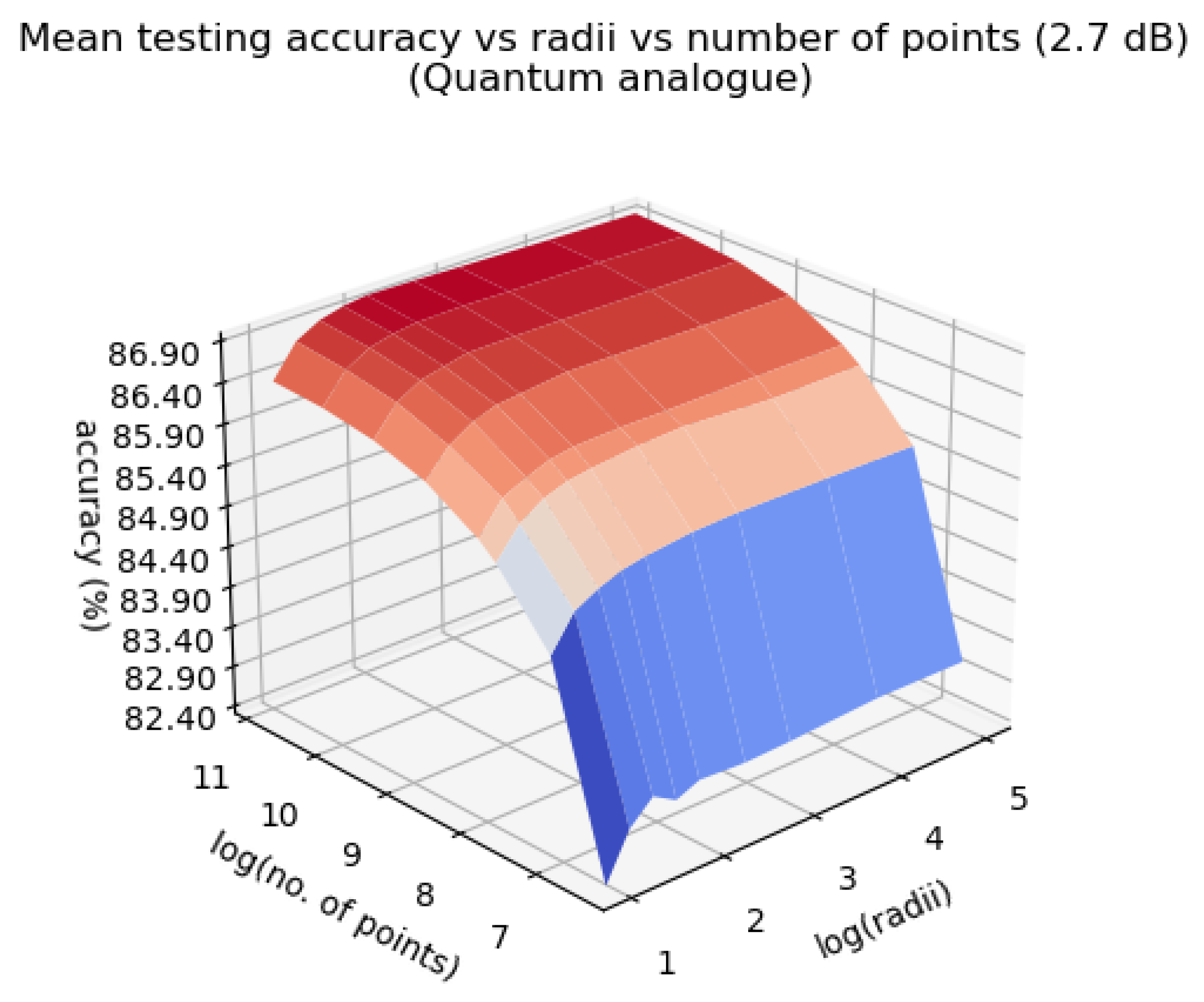
Figure 17.
Mean training accuracy v/s ln(Number of points) v/s ln(projection radius) for the quantum analogue algorithm acting upon the 2.7 dBm dataset, another view.
Figure 17.
Mean training accuracy v/s ln(Number of points) v/s ln(projection radius) for the quantum analogue algorithm acting upon the 2.7 dBm dataset, another view.
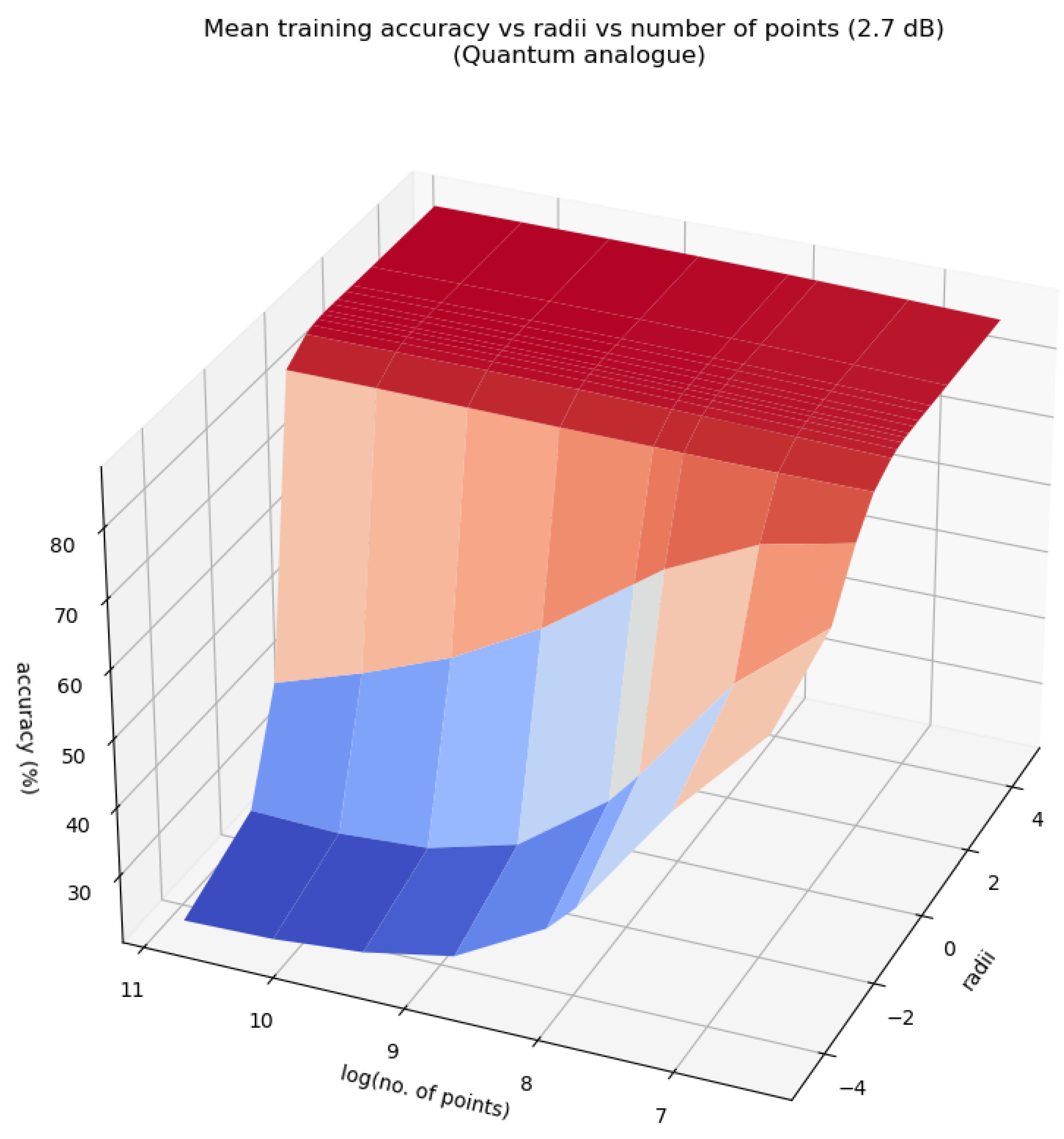
Figure 18.
Mean training accuracy v/s ln(Number of points) v/s projection radius for the quantum analogue algorithm acting upon the 2.7 dBm dataset, close up.
Figure 18.
Mean training accuracy v/s ln(Number of points) v/s projection radius for the quantum analogue algorithm acting upon the 2.7 dBm dataset, close up.
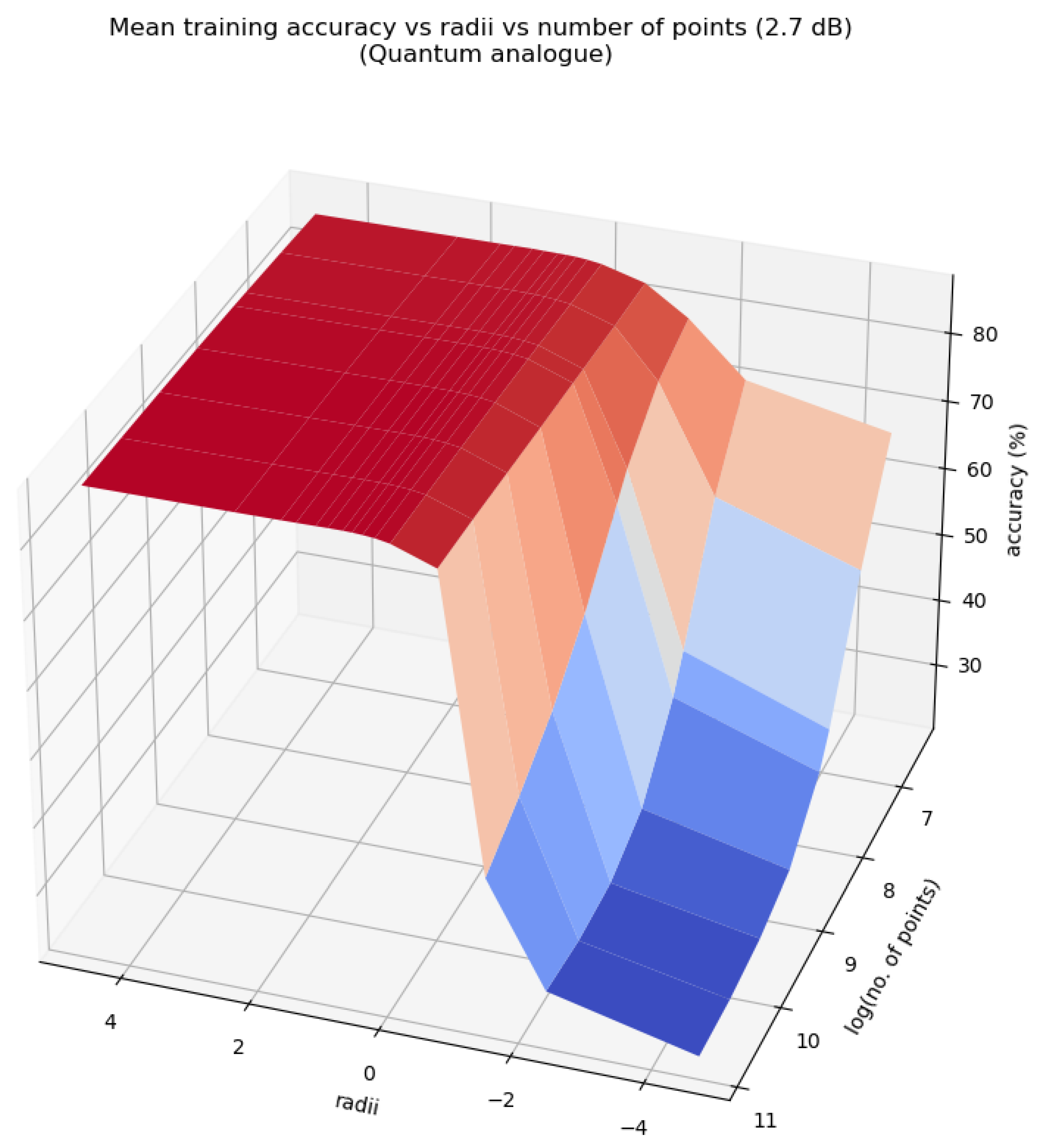
Figure 19.
Heat Map of Mean training accuracy v/s ln(Number of points) v/s projection radius for the quantum analogue algorithm acting upon the 2.7 dBm dataset
Figure 19.
Heat Map of Mean training accuracy v/s ln(Number of points) v/s projection radius for the quantum analogue algorithm acting upon the 2.7 dBm dataset
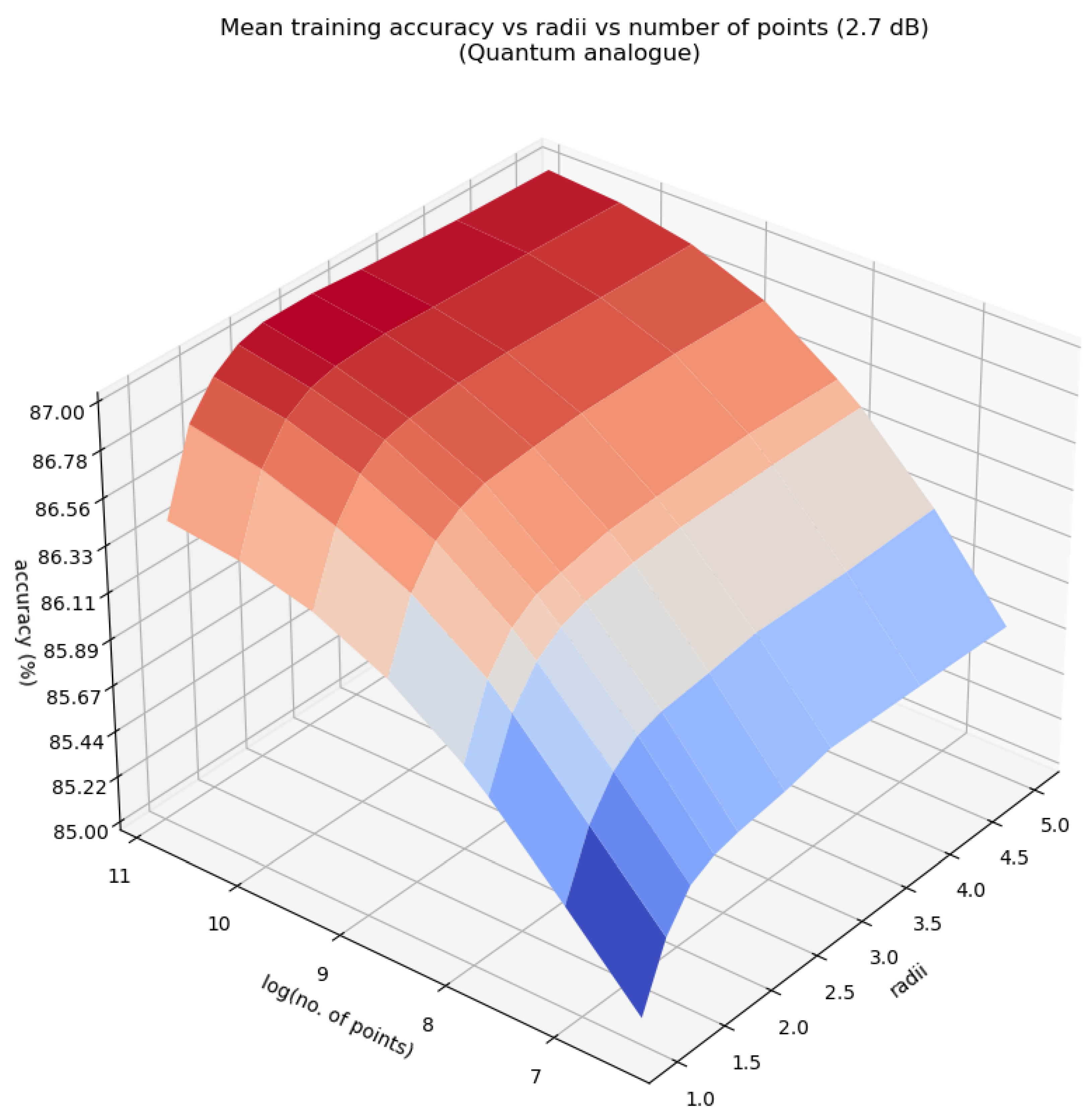
Figure 20.
Mean no. of iterations in training v/s Number of points v/s log(projection radius) for the quantum analogue algorithm acting upon the 10.7 dBm dataset.
Figure 20.
Mean no. of iterations in training v/s Number of points v/s log(projection radius) for the quantum analogue algorithm acting upon the 10.7 dBm dataset.
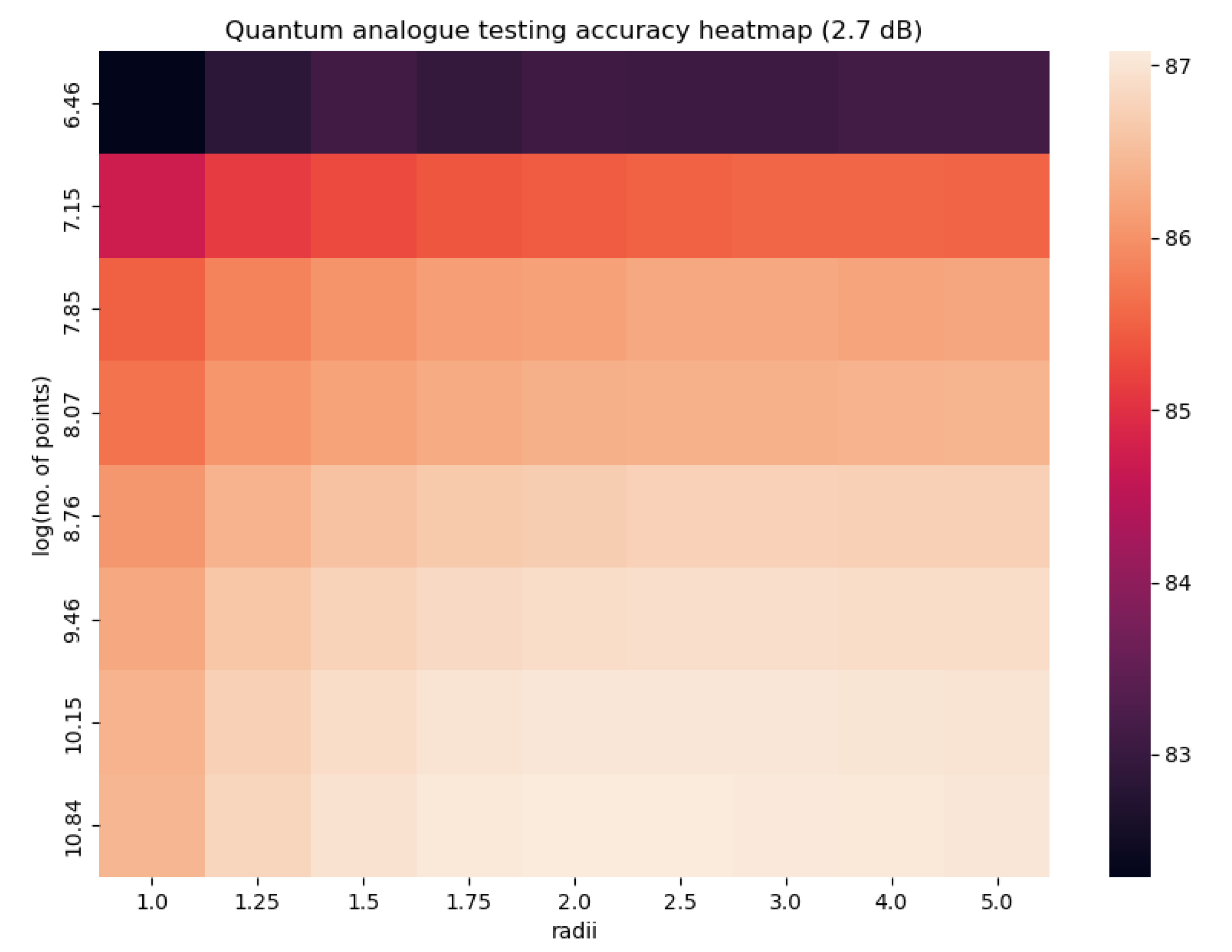
Figure 21.
Mean no. of iterations in training v/s Number of points v/s log(projection radius) for the quantum analogue algorithm acting upon the 10.7 dBm dataset, close up.
Figure 21.
Mean no. of iterations in training v/s Number of points v/s log(projection radius) for the quantum analogue algorithm acting upon the 10.7 dBm dataset, close up.
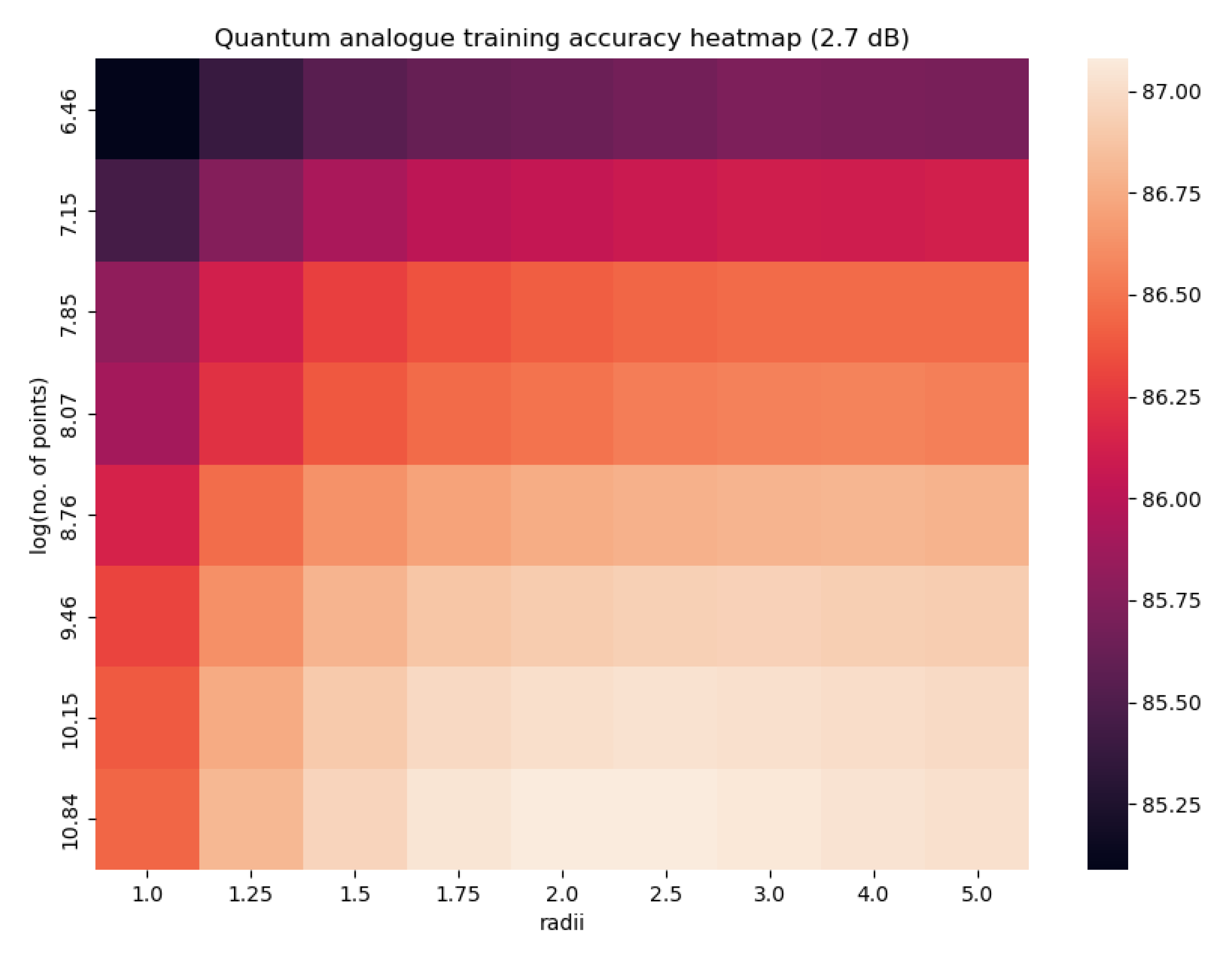
Figure 22.
Mean no. of iterations in training v/s Number of points v/s log(projection radius) for the quantum analogue algorithm acting upon the 10.7 dBm dataset, close up, another view.
Figure 22.
Mean no. of iterations in training v/s Number of points v/s log(projection radius) for the quantum analogue algorithm acting upon the 10.7 dBm dataset, close up, another view.
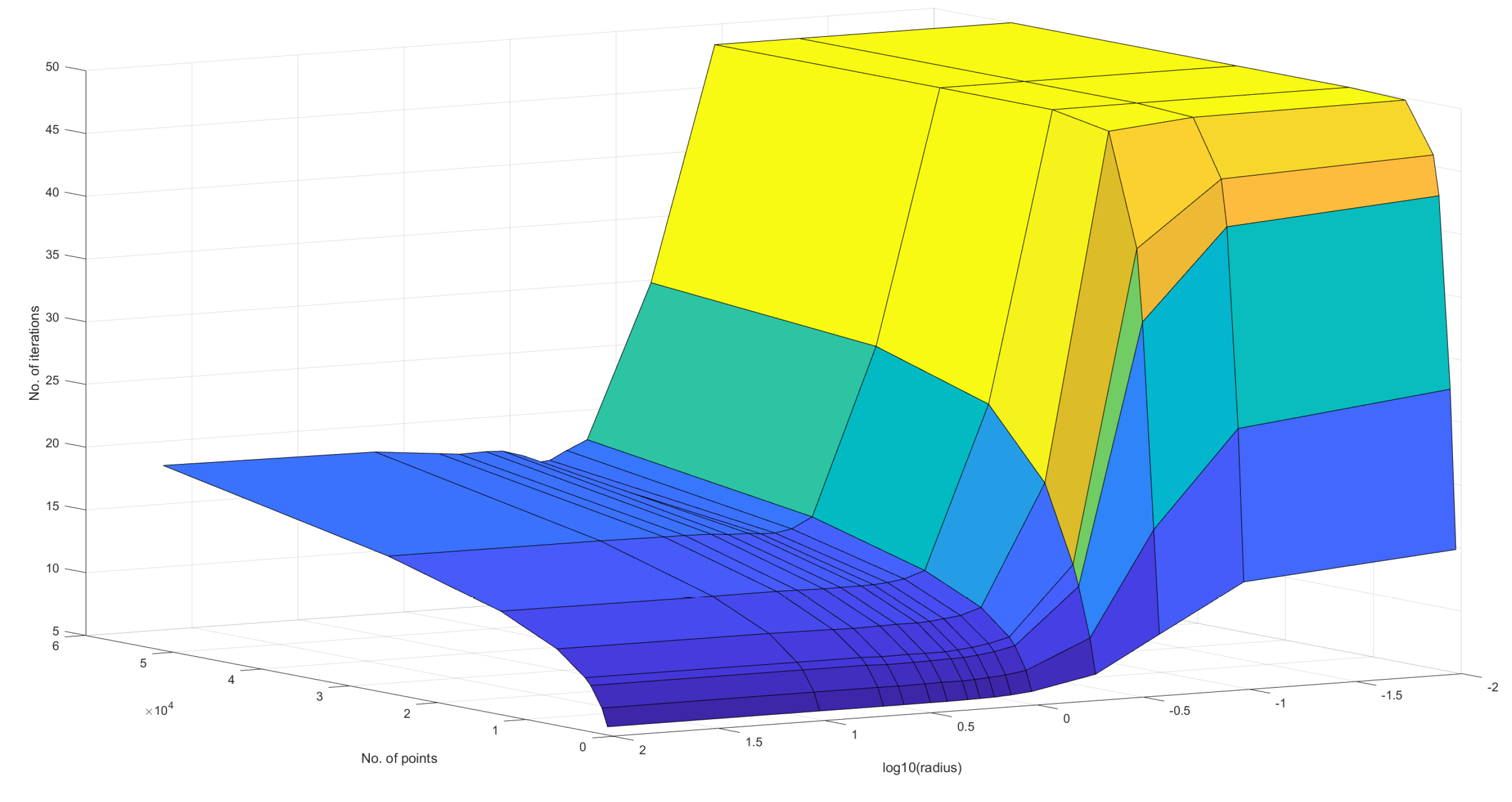
Figure 23.
Mean testing accuracy v/s the natural log of the number of points, 2.7dBm dataset.
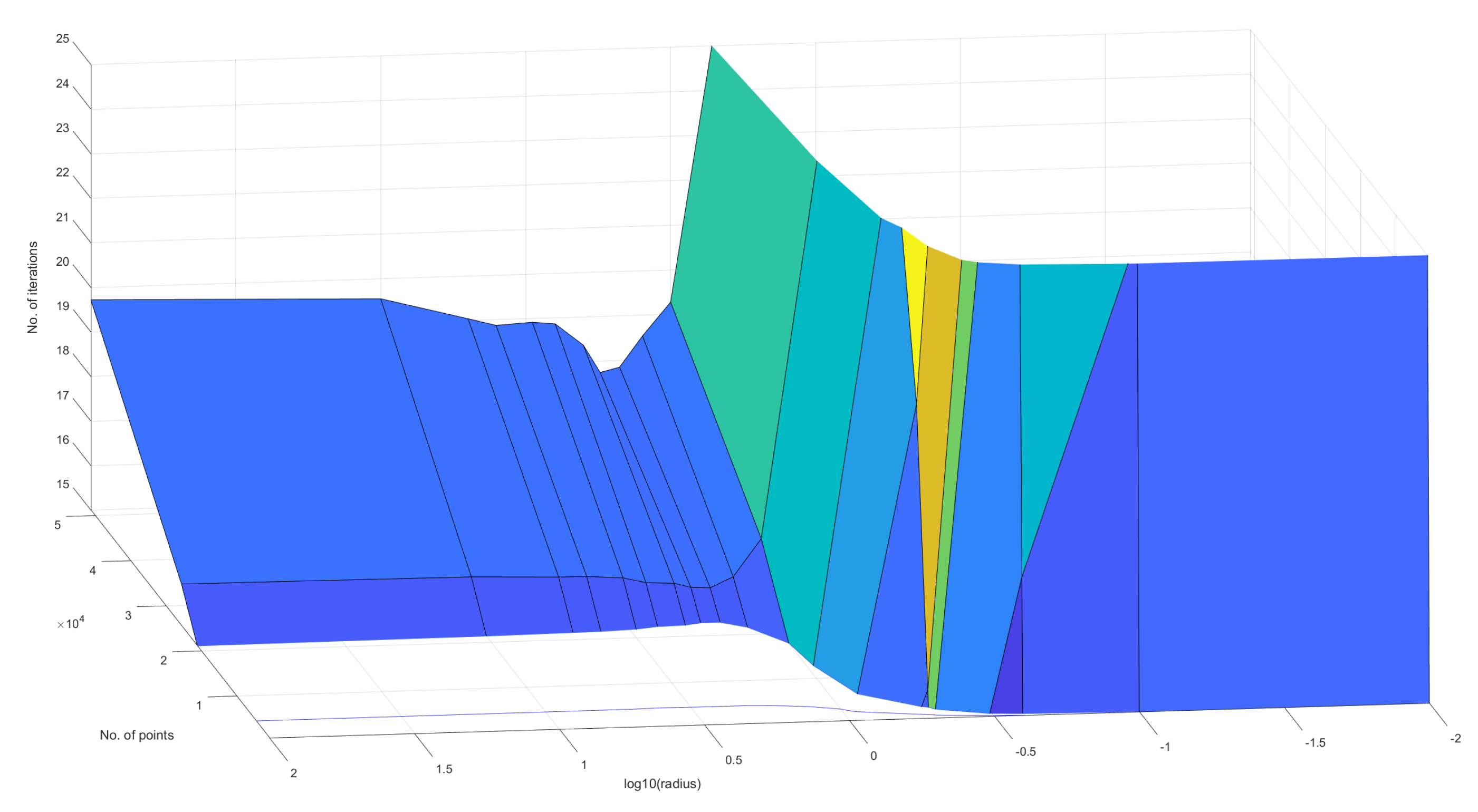
Figure 24.
Mean testing accuracy v/s the natural log of the number of points, 6.6dBm dataset.
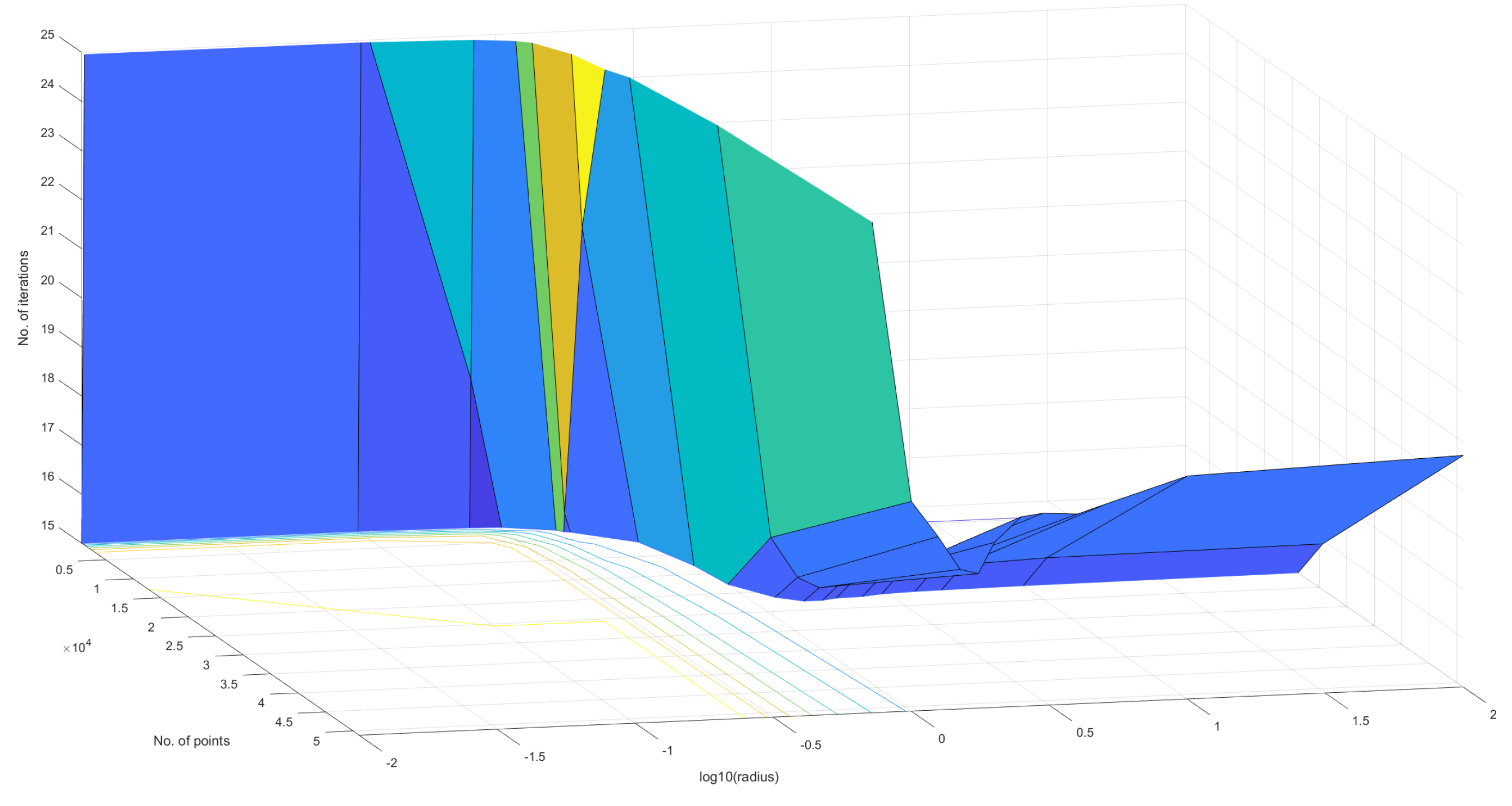
Figure 25.
Mean testing accuracy v/s the natural log of the number of points, 8.6dBm dataset.
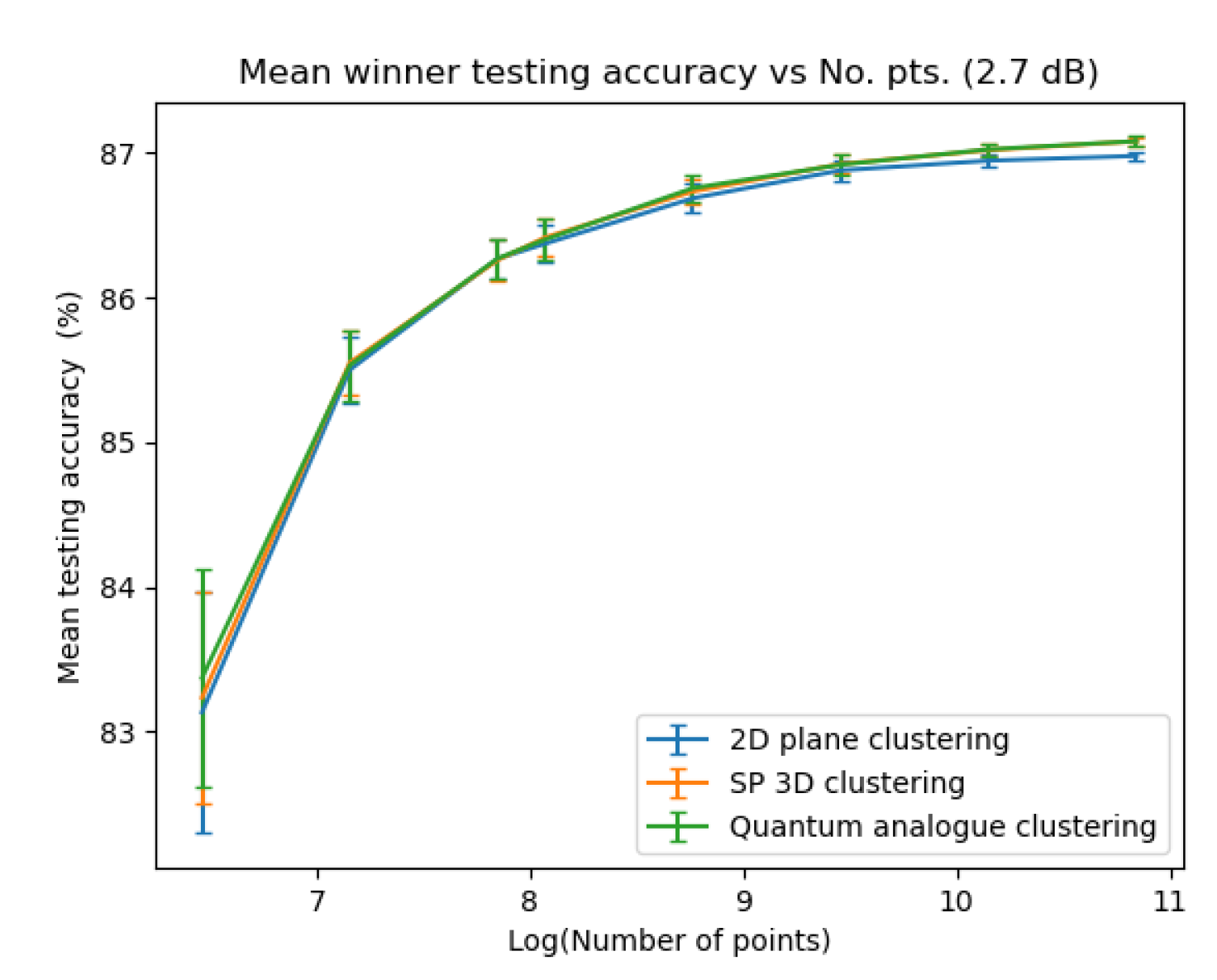
Figure 26.
Mean testing accuracy v/s the natural log of the number of points, 10.7dBm dataset.
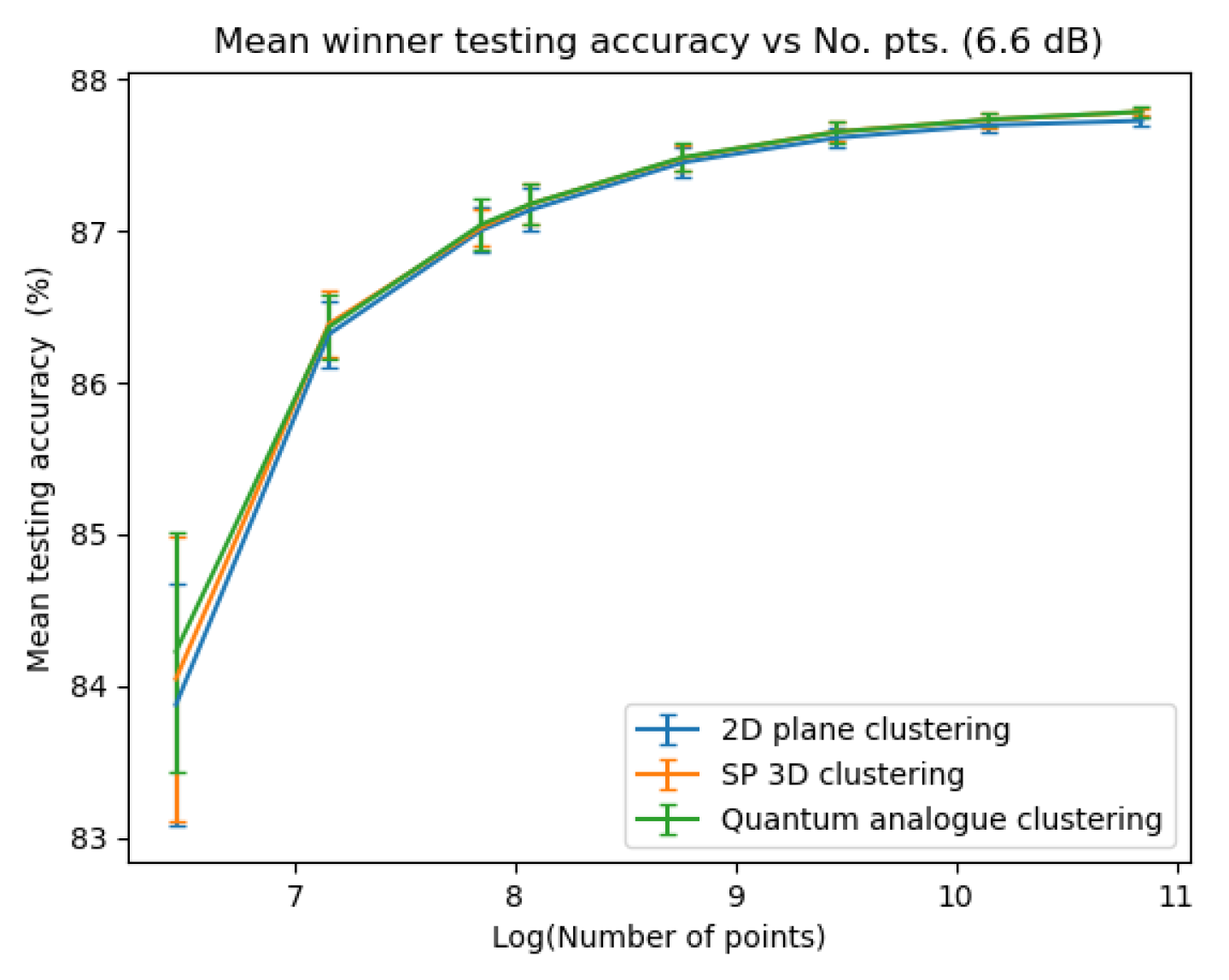
Figure 27.
Mean training accuracy v/s the natural log of the number of points, 2.7dBm dataset.
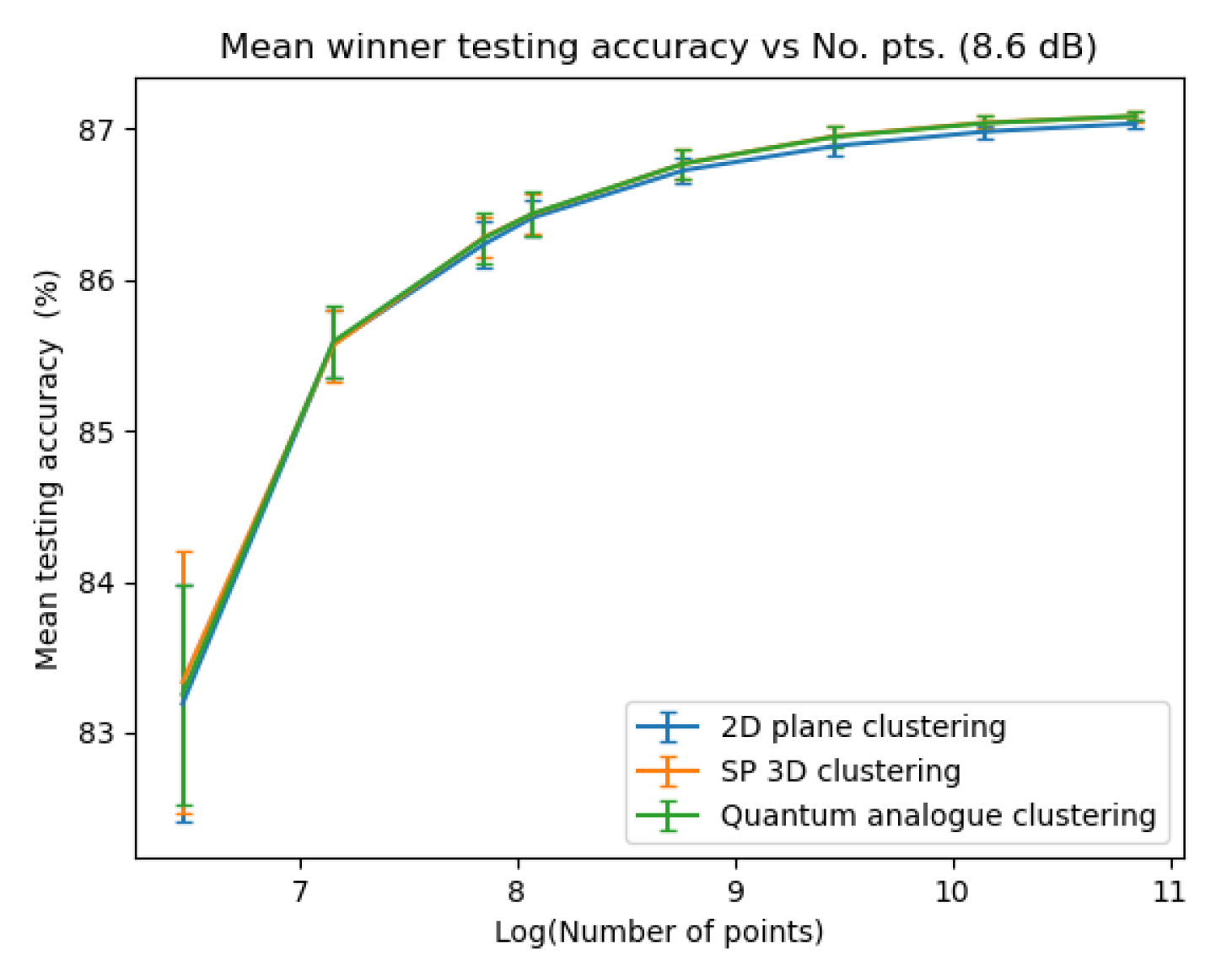
Figure 28.
Mean training accuracy v/s the natural log of the number of points, 6.6dBm dataset.
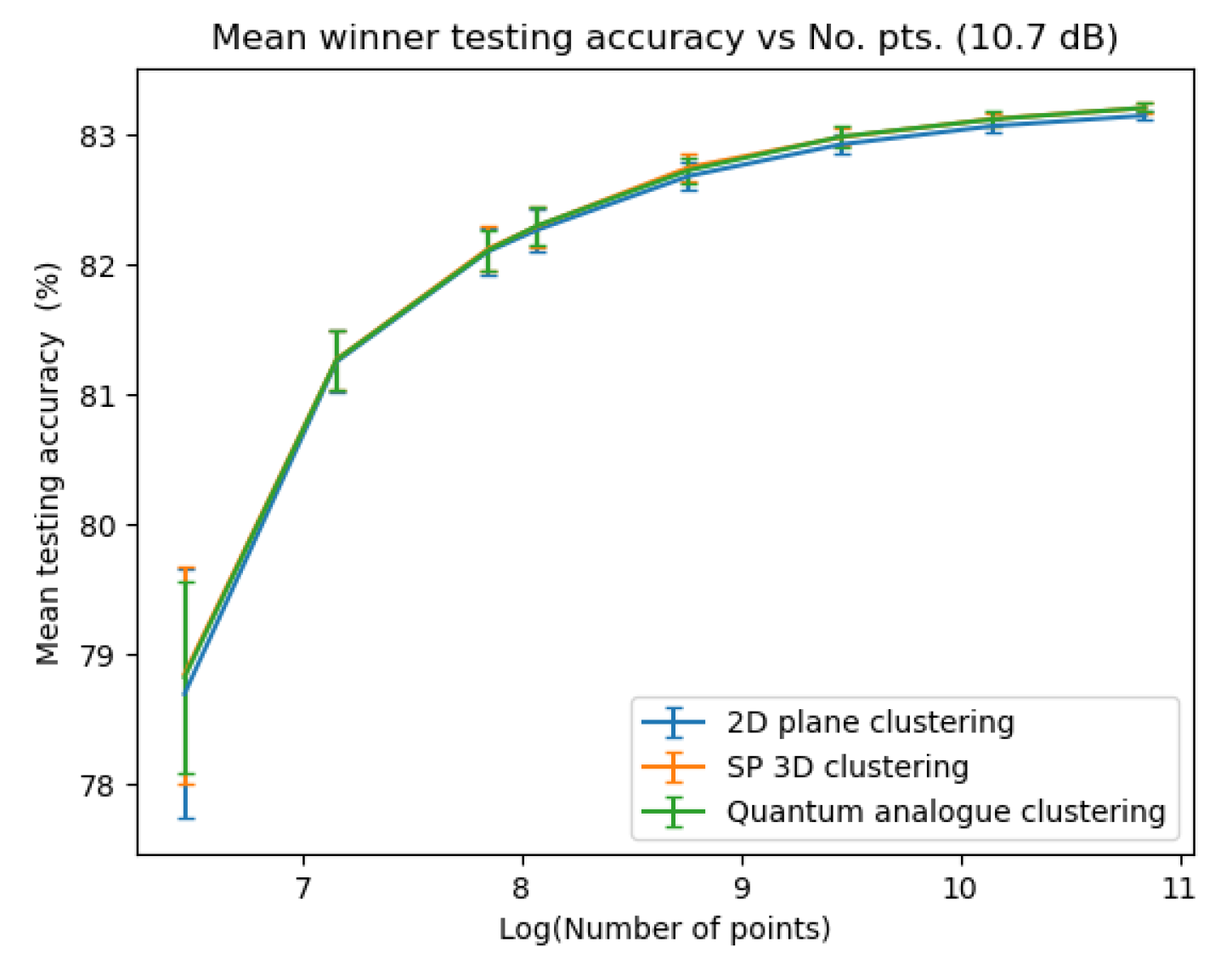
Figure 29.
Mean training accuracy v/s the natural log of the number of points, 8.6dBm dataset.
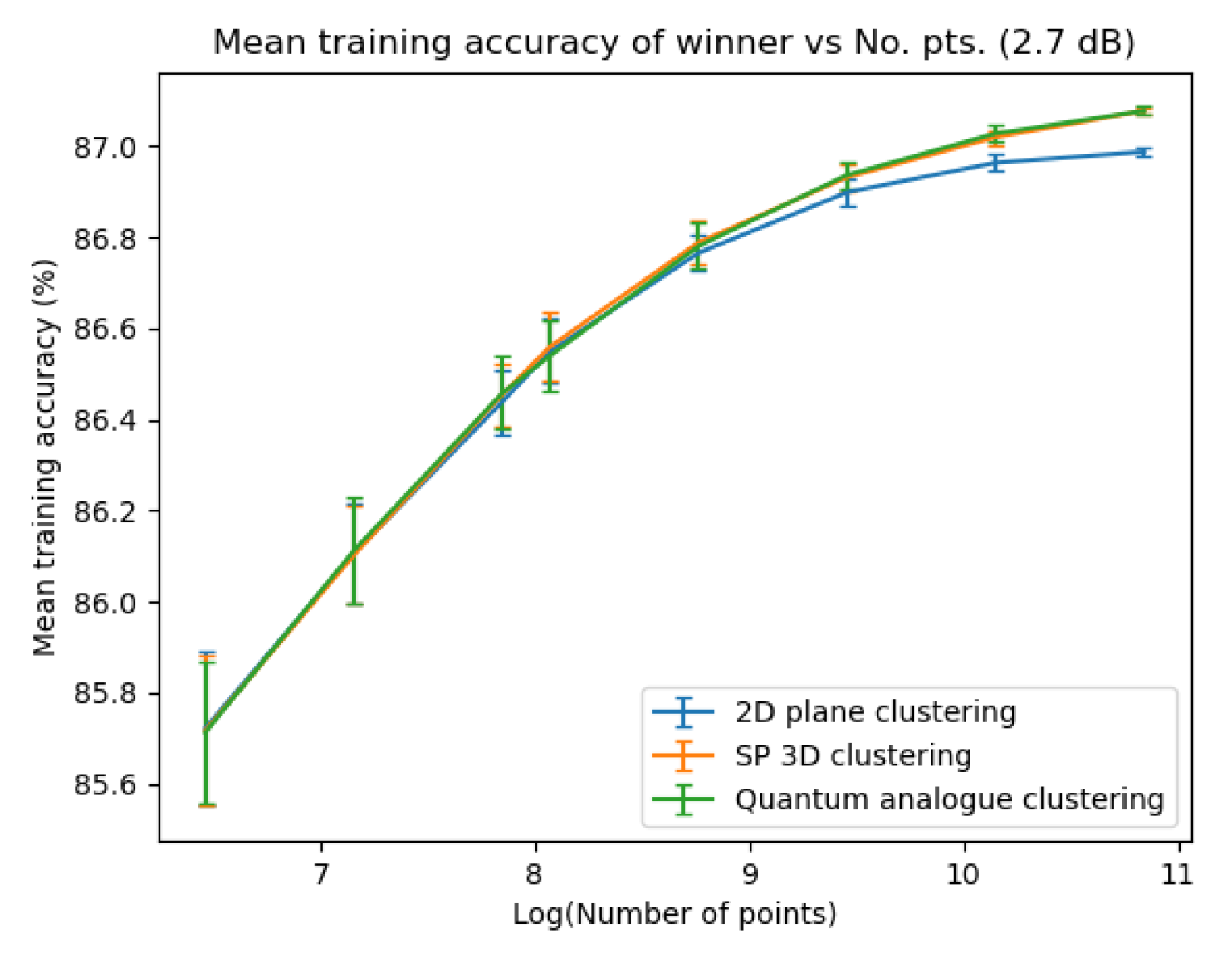
Figure 30.
Mean training accuracy v/s the natural log of the number of points, 10.7dBm dataset.
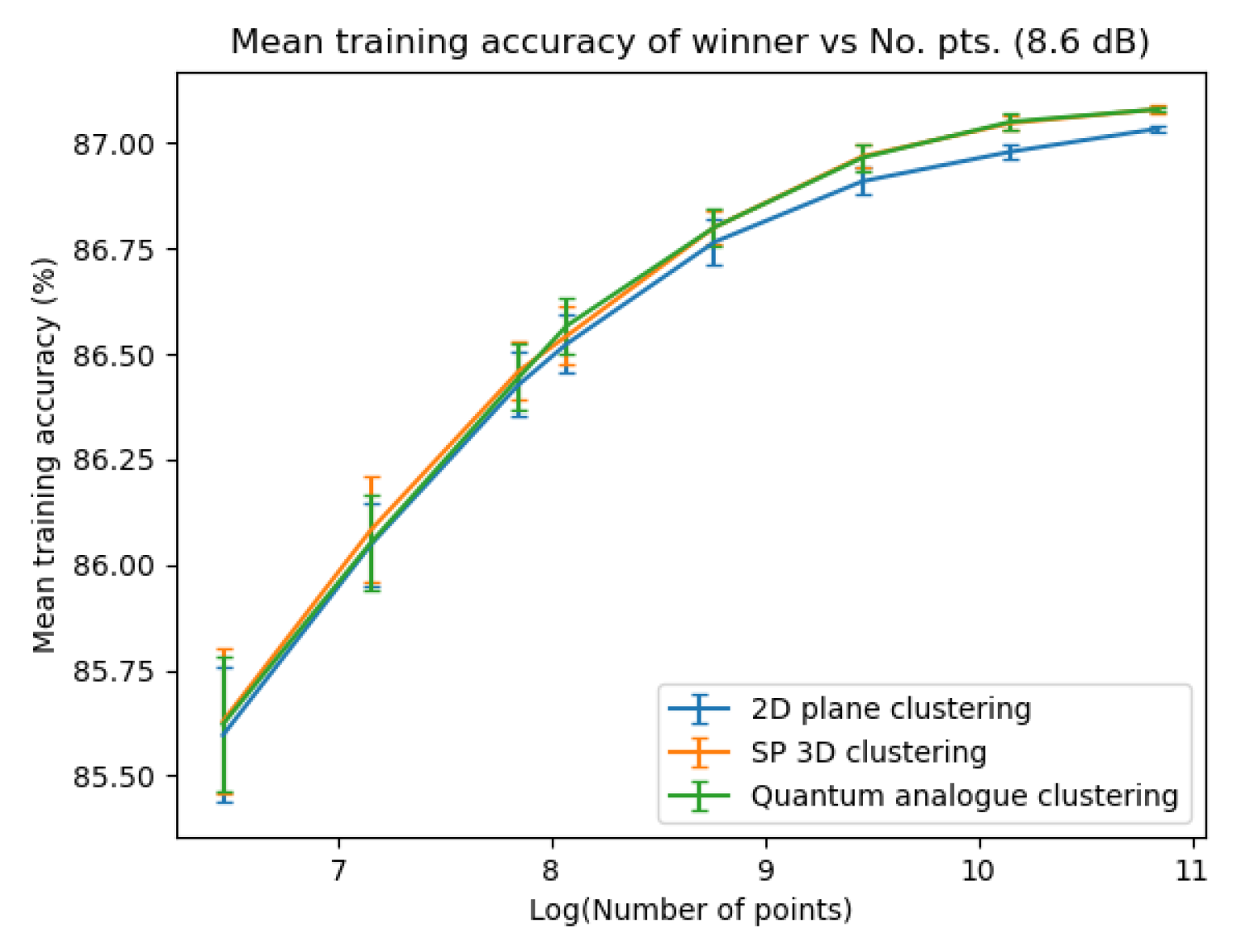
Figure 31.
Mean testing accuracy gain v/s the natural log of the number of points, 10.7dBm dataset.
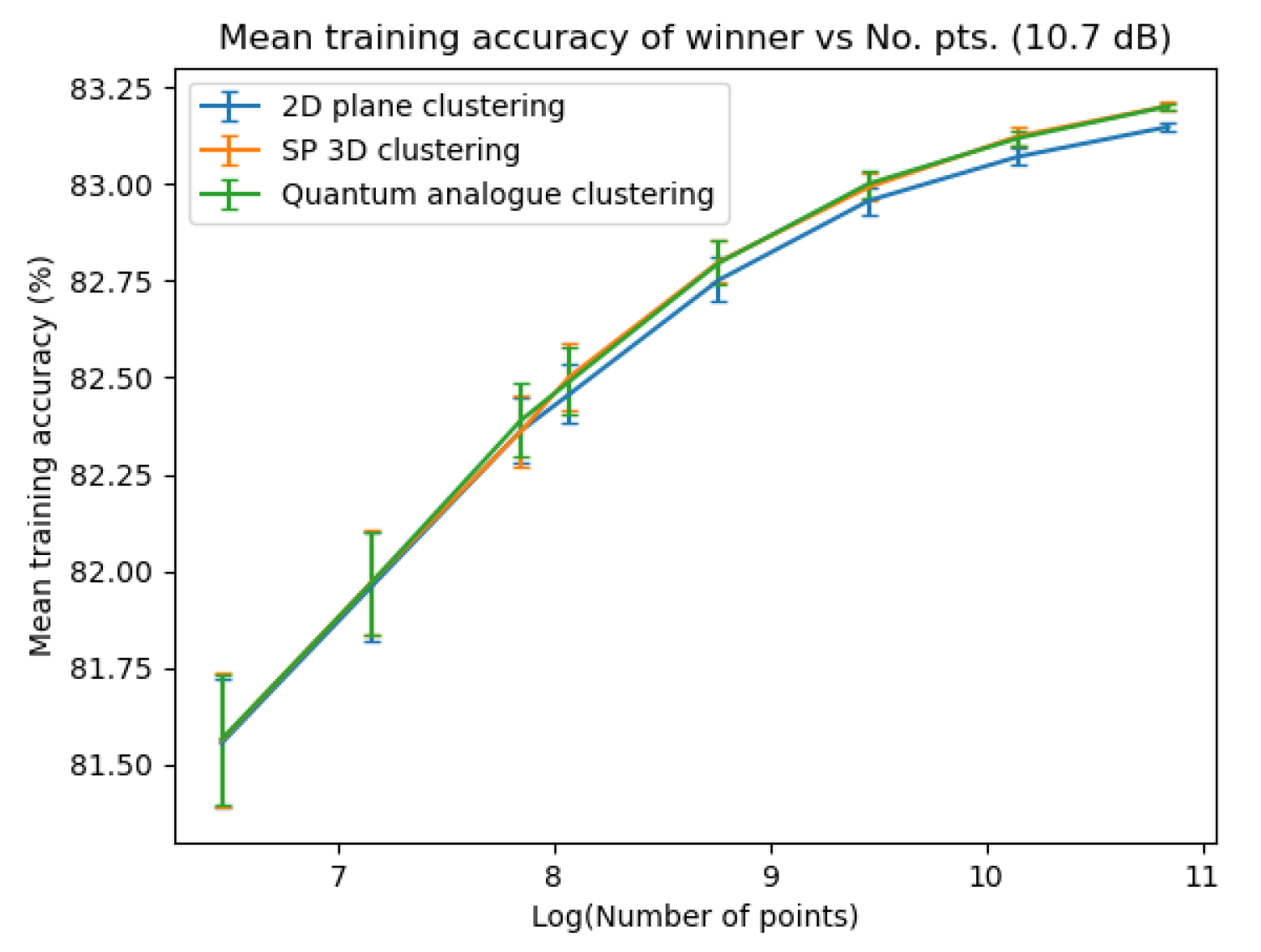
Figure 32.
Mean training accuracy gain v/s the natural log of the number of points, 10.7dBm dataset.
Figure 32.
Mean training accuracy gain v/s the natural log of the number of points, 10.7dBm dataset.
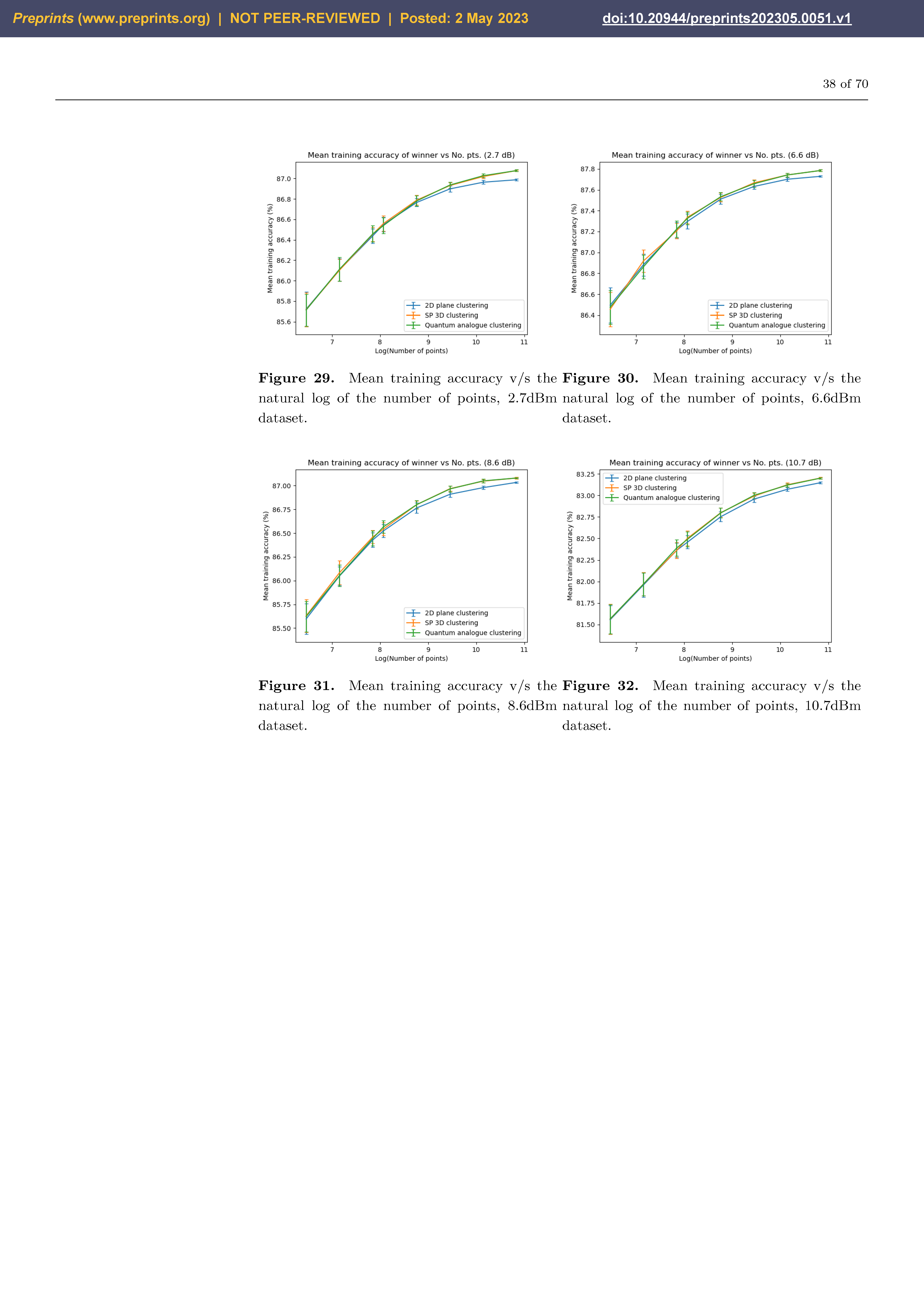
Figure 33.
Mean training iterations v/s the natural log of the number of points, 10.7dBm dataset.
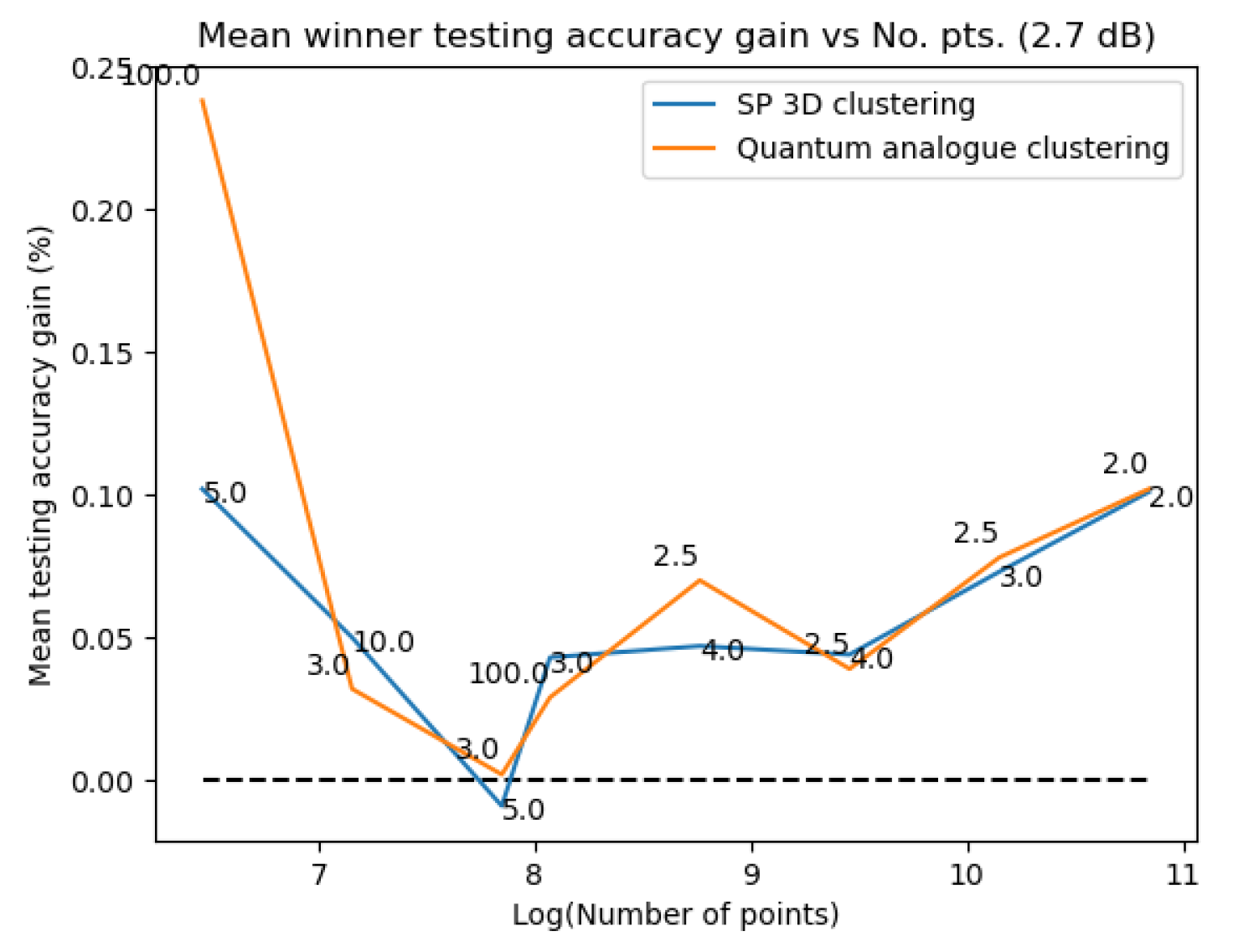
Figure 34.
Mean training iterations gain v/s the natural log of the number of points, 10.7dBm dataset.
Figure 34.
Mean training iterations gain v/s the natural log of the number of points, 10.7dBm dataset.
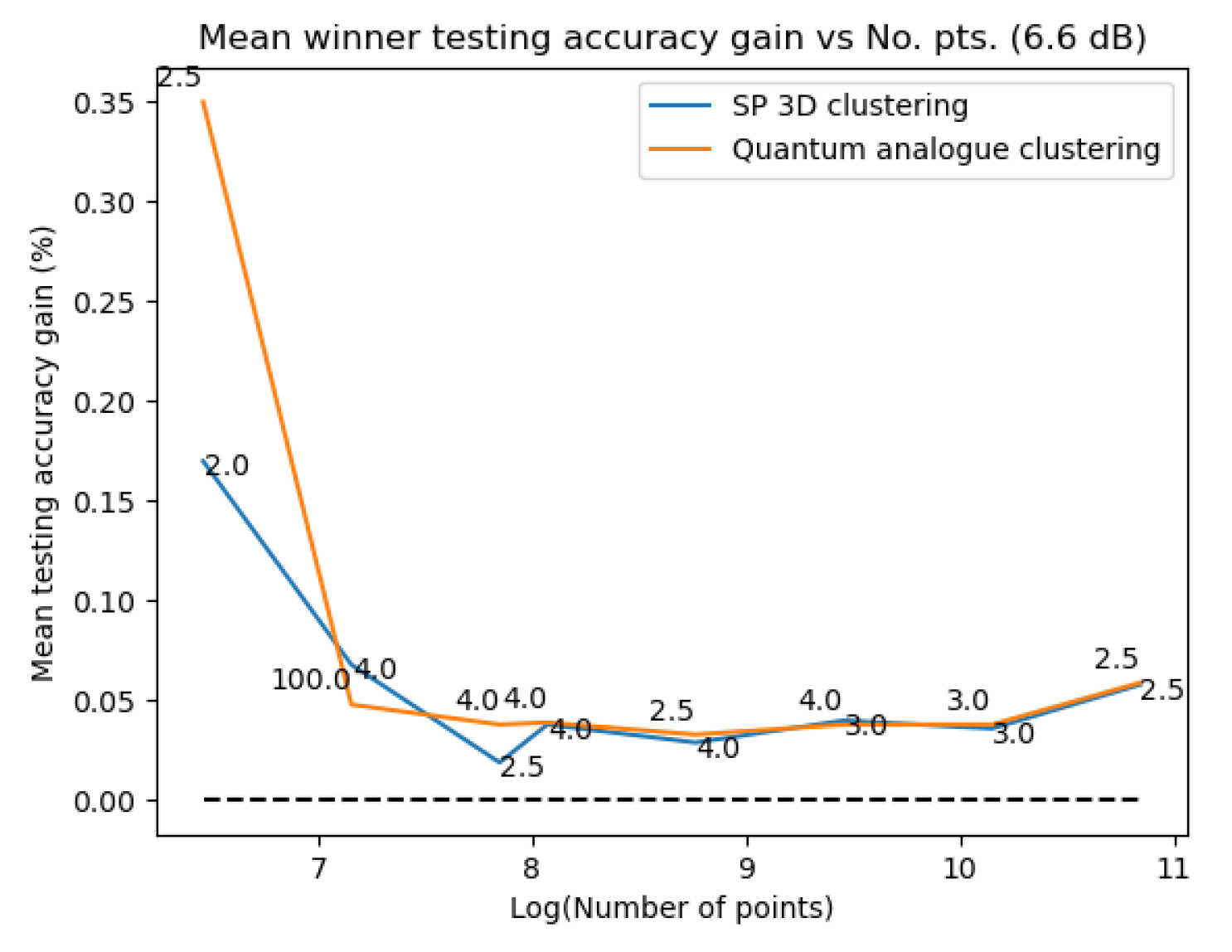
Figure 35.
Mean testing execution time v/s the natural log of the number of points, 10.7dBm dataset.
Figure 35.
Mean testing execution time v/s the natural log of the number of points, 10.7dBm dataset.
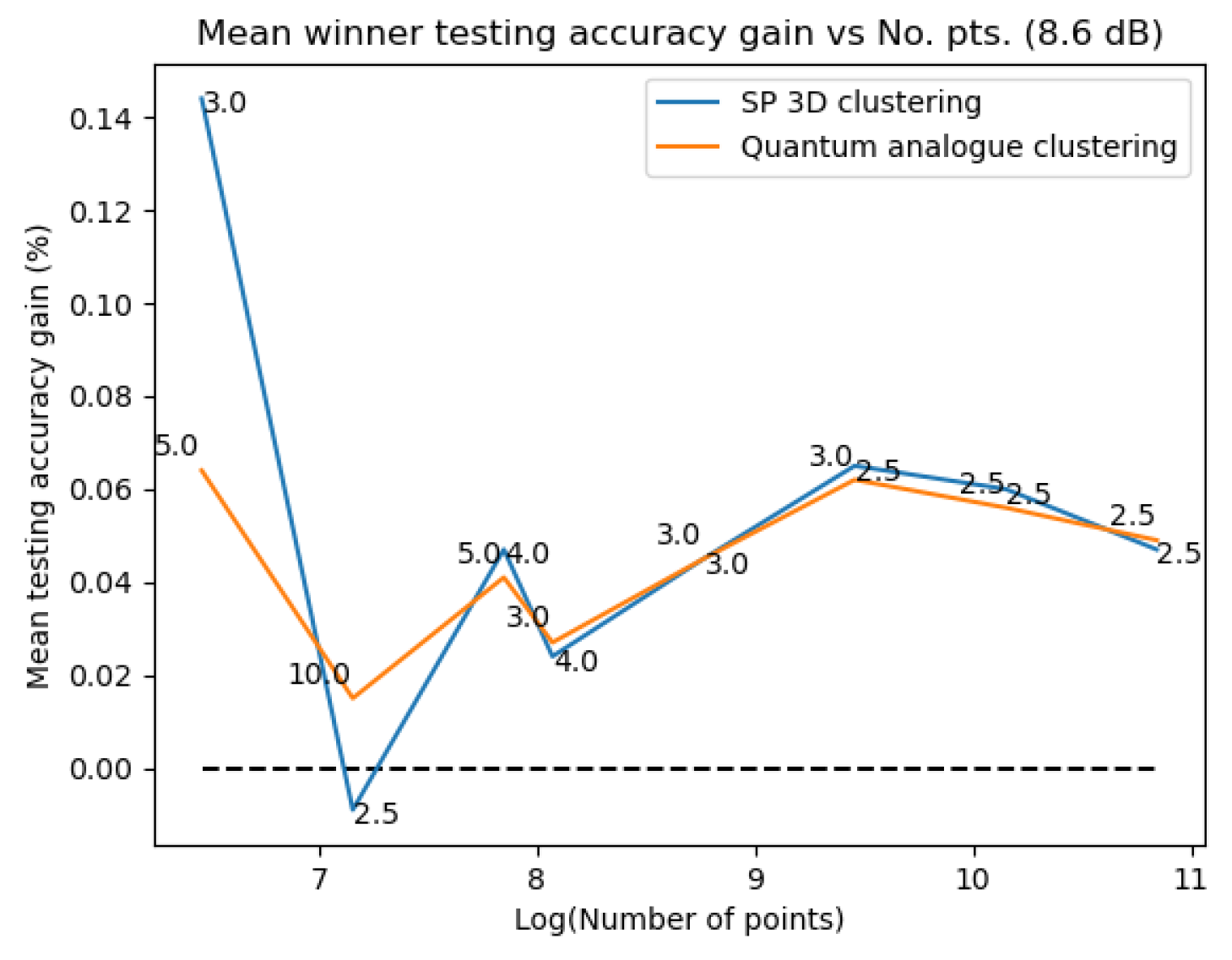
Figure 36.
Mean training execution time v/s the natural log of the number of points, 10.7dBm dataset.
Figure 36.
Mean training execution time v/s the natural log of the number of points, 10.7dBm dataset.
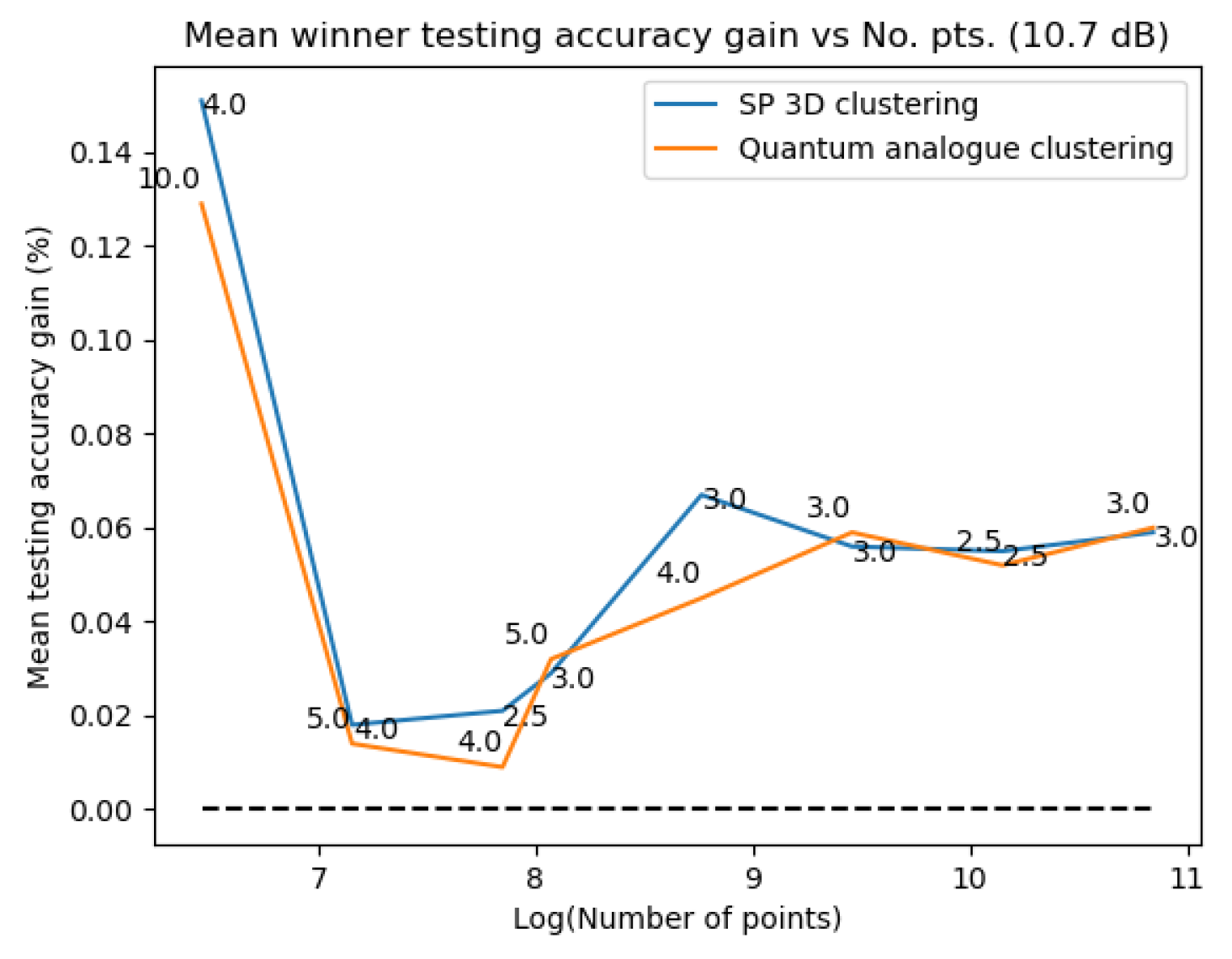
Figure 37.
Mean testing execution time gain v/s the natural log of the number of points, 10.7dBm dataset.
Figure 37.
Mean testing execution time gain v/s the natural log of the number of points, 10.7dBm dataset.
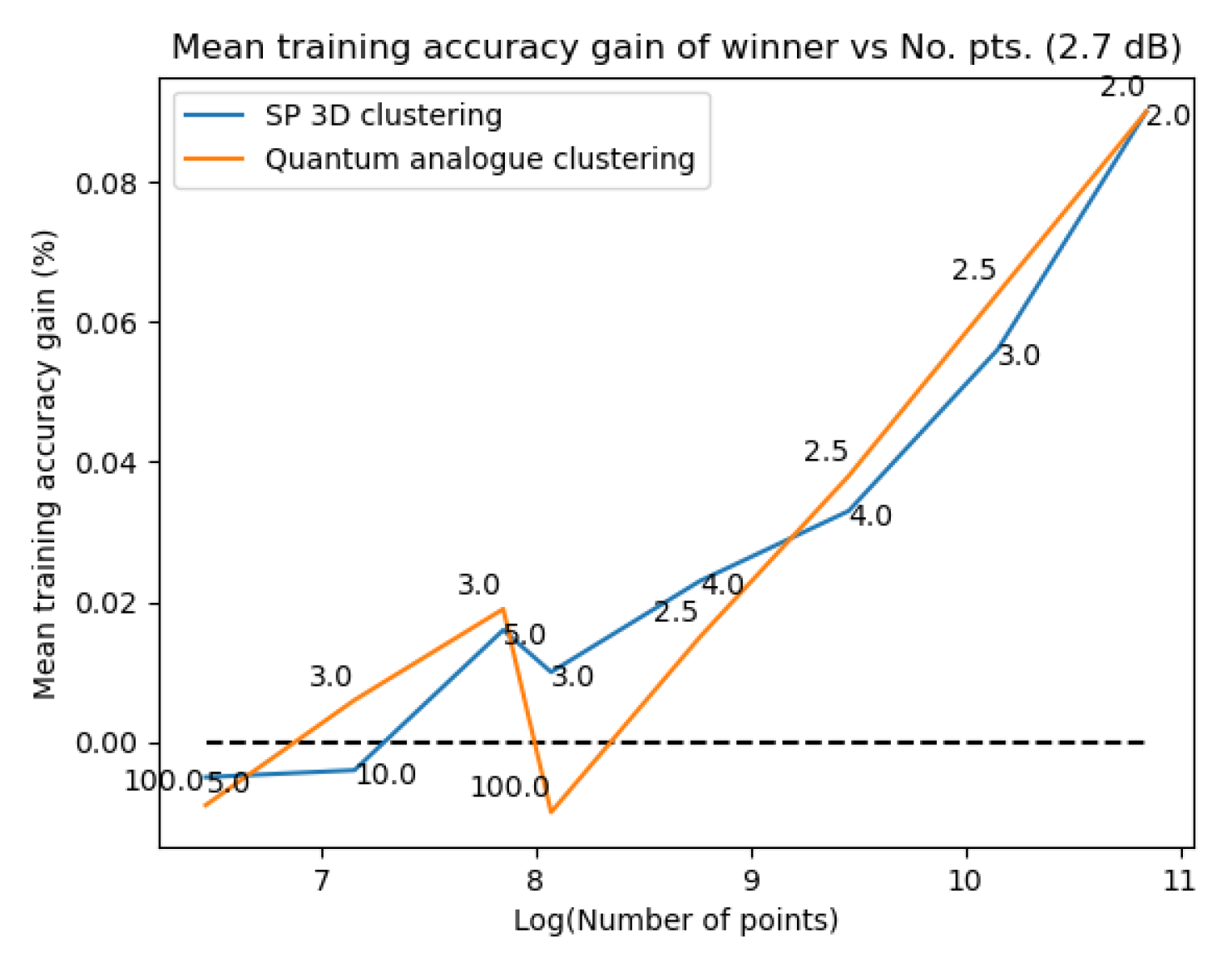
Figure 38.
Mean training execution time gain v/s the natural log of the number of points, 10.7dBm dataset.
Figure 38.
Mean training execution time gain v/s the natural log of the number of points, 10.7dBm dataset.
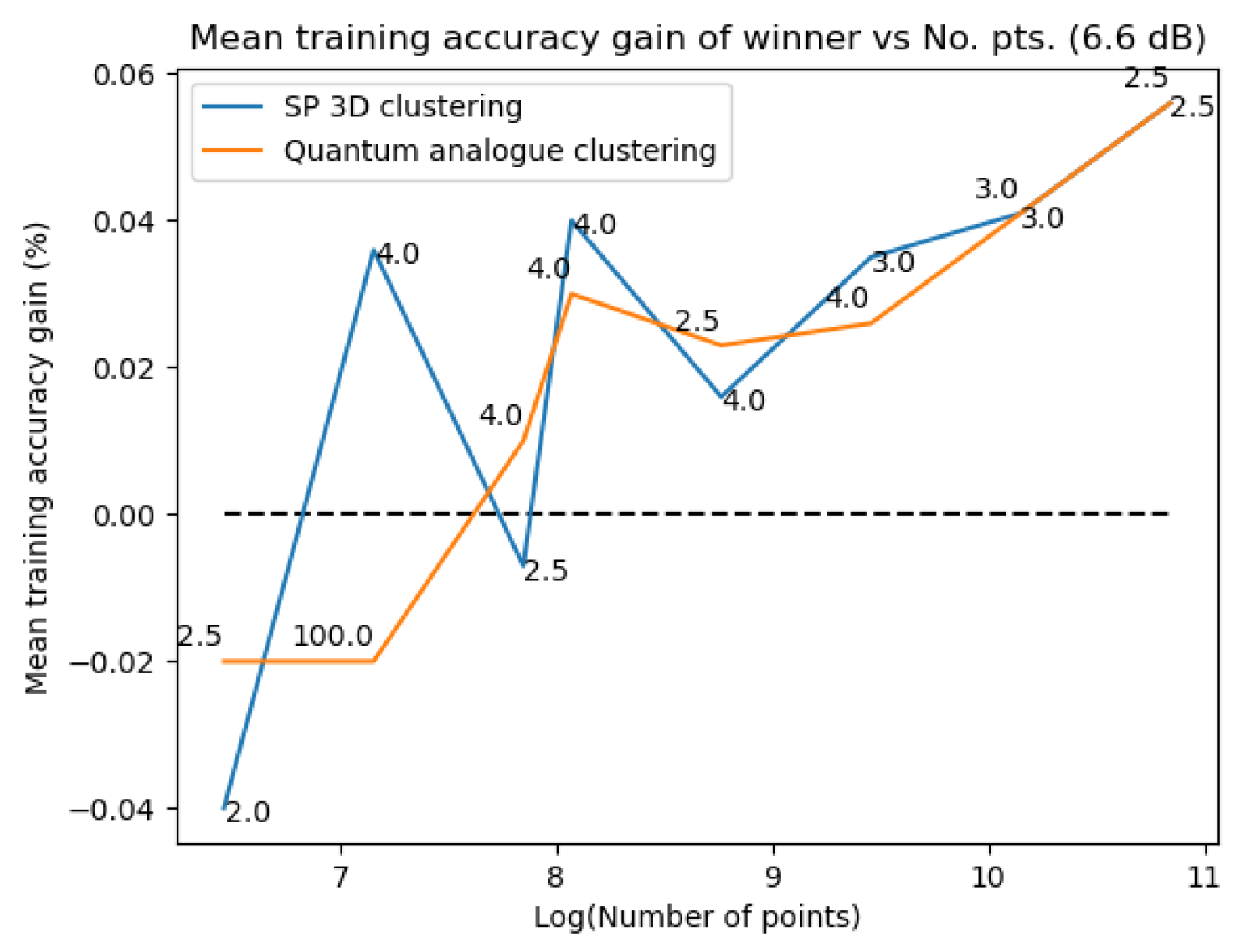
Figure 39.
Mean overfitting parameter v/s the natural log of the number of points, 10.7dBm dataset.
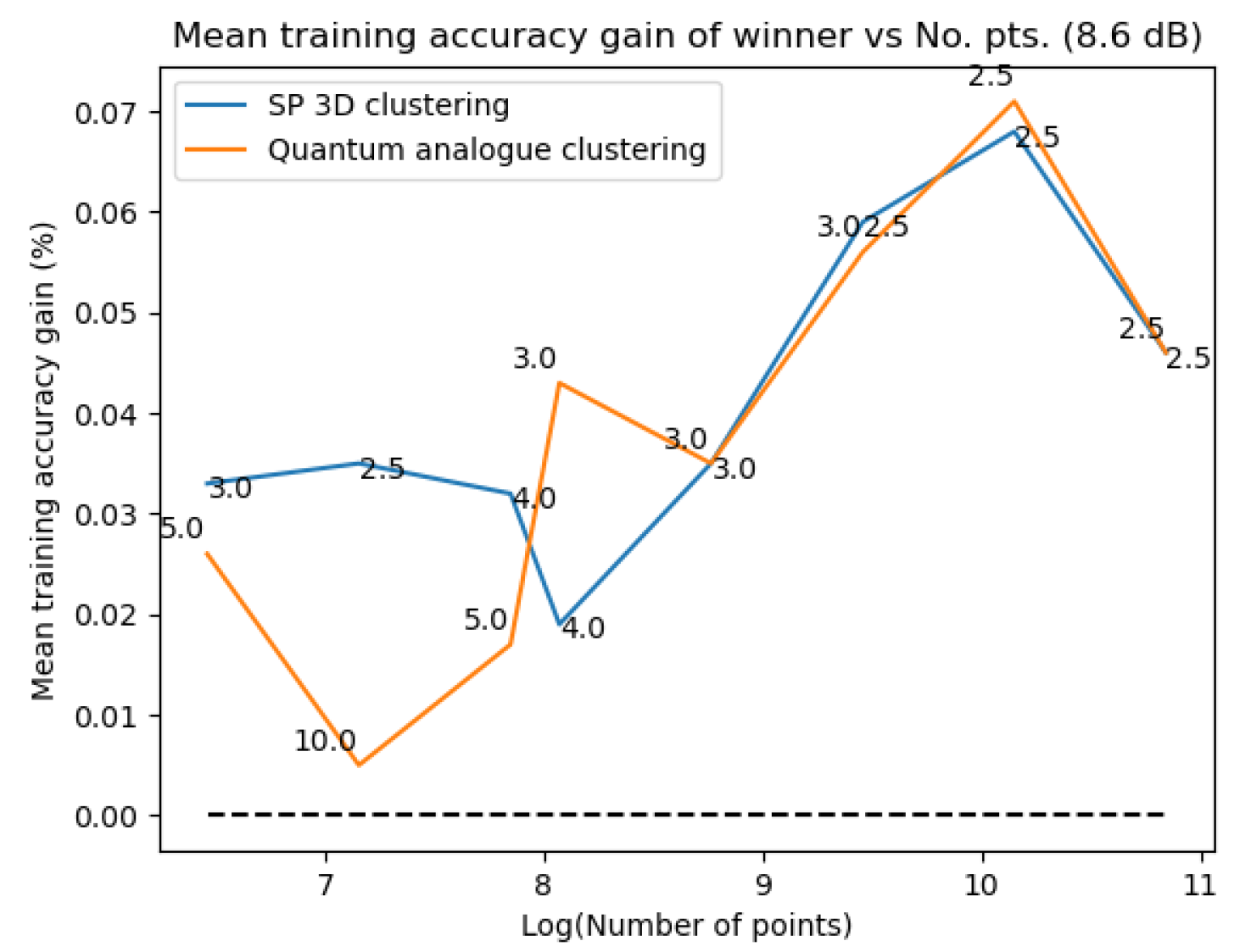
Figure 40.
Maximum Accuracy v/s iteration number v/s projection radius for the quantum analogue algorithm acting upon the 2.7 dBm dataset.
Figure 40.
Maximum Accuracy v/s iteration number v/s projection radius for the quantum analogue algorithm acting upon the 2.7 dBm dataset.
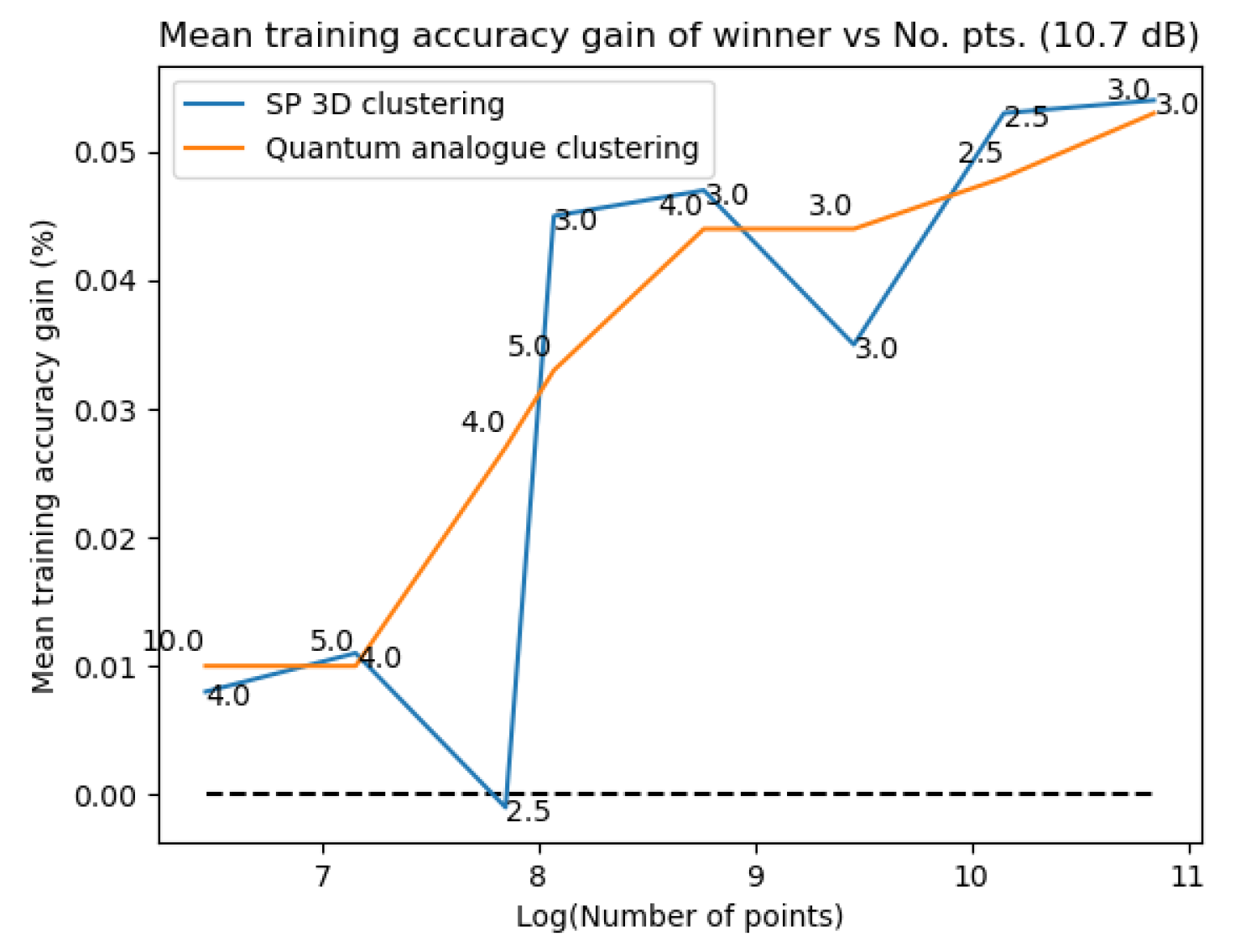
Figure 41.
Another view of Figure 40.
Figure 41.
Another view of Figure 40.
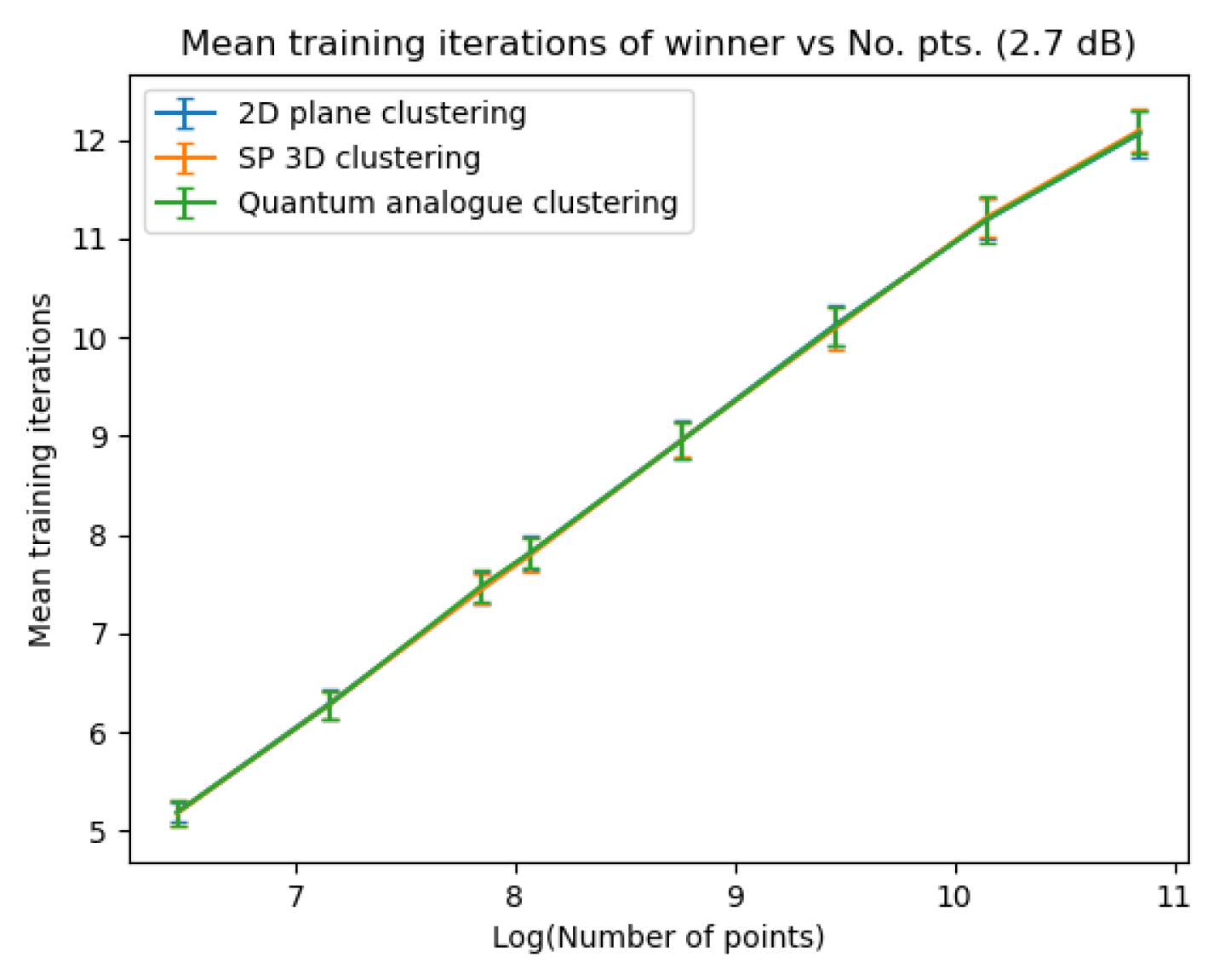
Figure 42.
A view of Figure 41 magnified to better depict the algorithm’s behaviour in the region of interest.
Figure 42.
A view of Figure 41 magnified to better depict the algorithm’s behaviour in the region of interest.
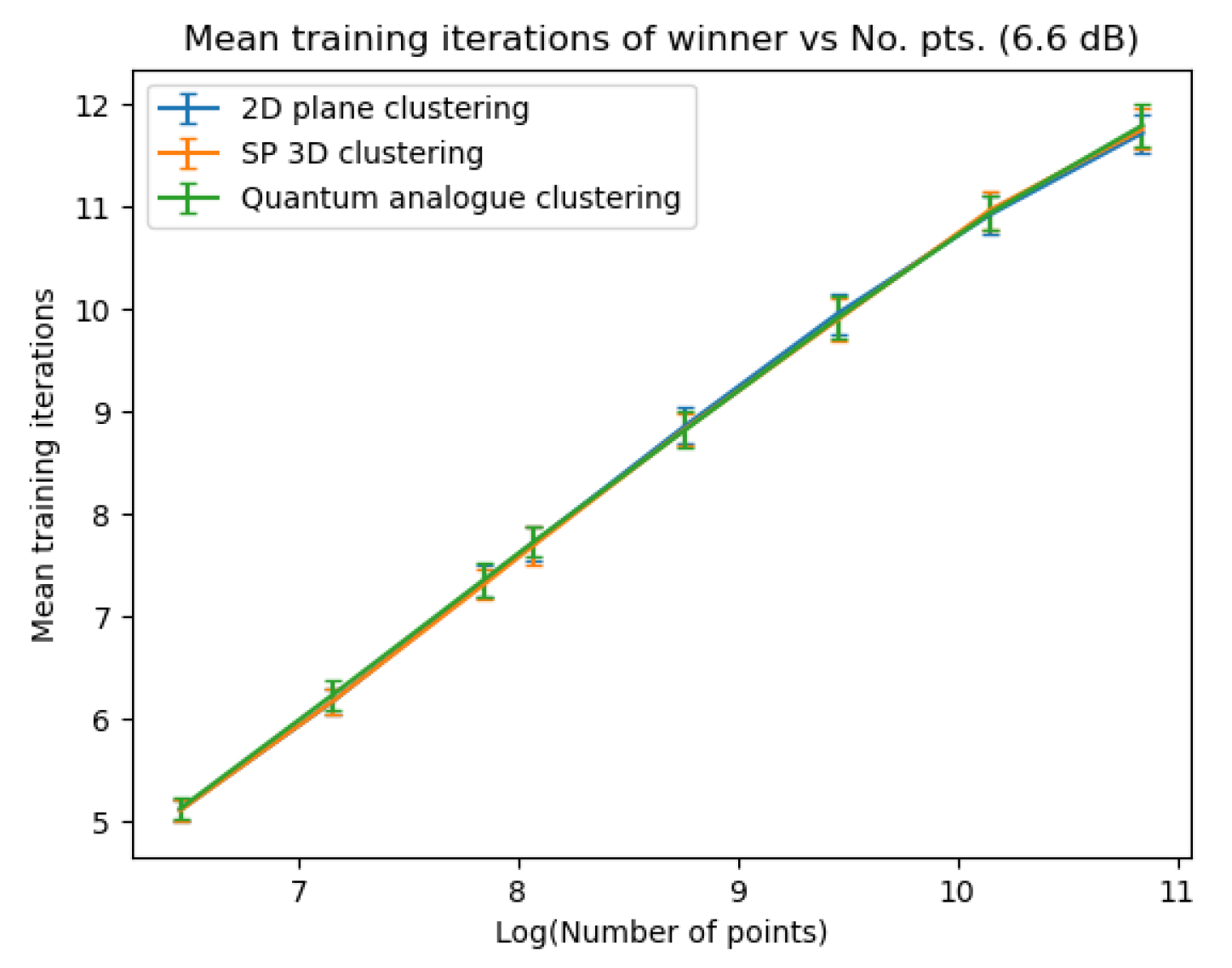
Figure 43.
Another view of Figure 42.
Figure 43.
Another view of Figure 42.
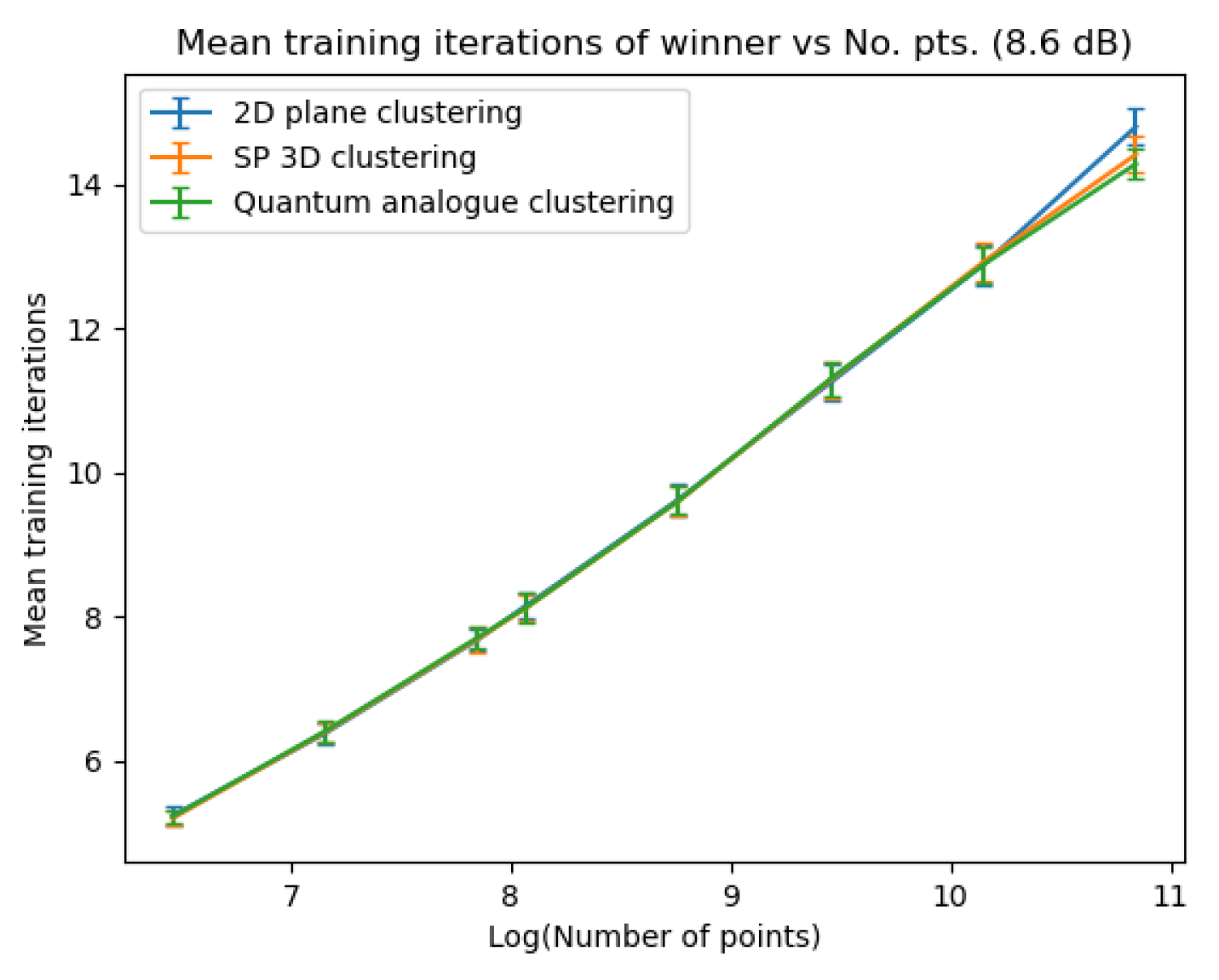
Figure 44.
Probability of stopping v/s projection radius v/s iteration number for quantum analogue algorithm acting upon the 2.7dBm dataset, and with the number of points = 640.
Figure 44.
Probability of stopping v/s projection radius v/s iteration number for quantum analogue algorithm acting upon the 2.7dBm dataset, and with the number of points = 640.
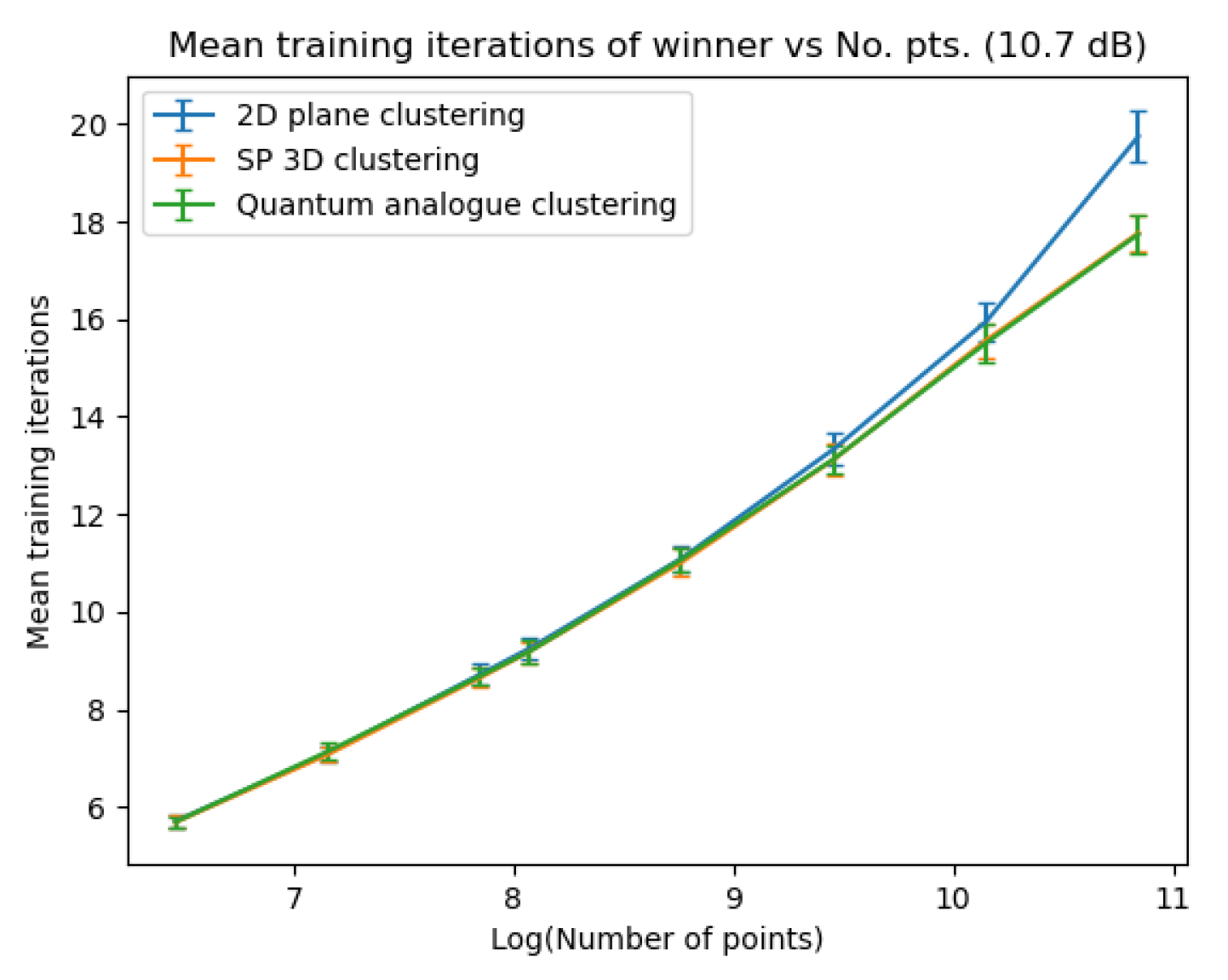
Figure 45.
Probability of stopping v/s projection radius v/s iteration number for quantum analogue algorithm acting upon the 10.7dBm dataset, and with the number of points = 51200.
Figure 45.
Probability of stopping v/s projection radius v/s iteration number for quantum analogue algorithm acting upon the 10.7dBm dataset, and with the number of points = 51200.
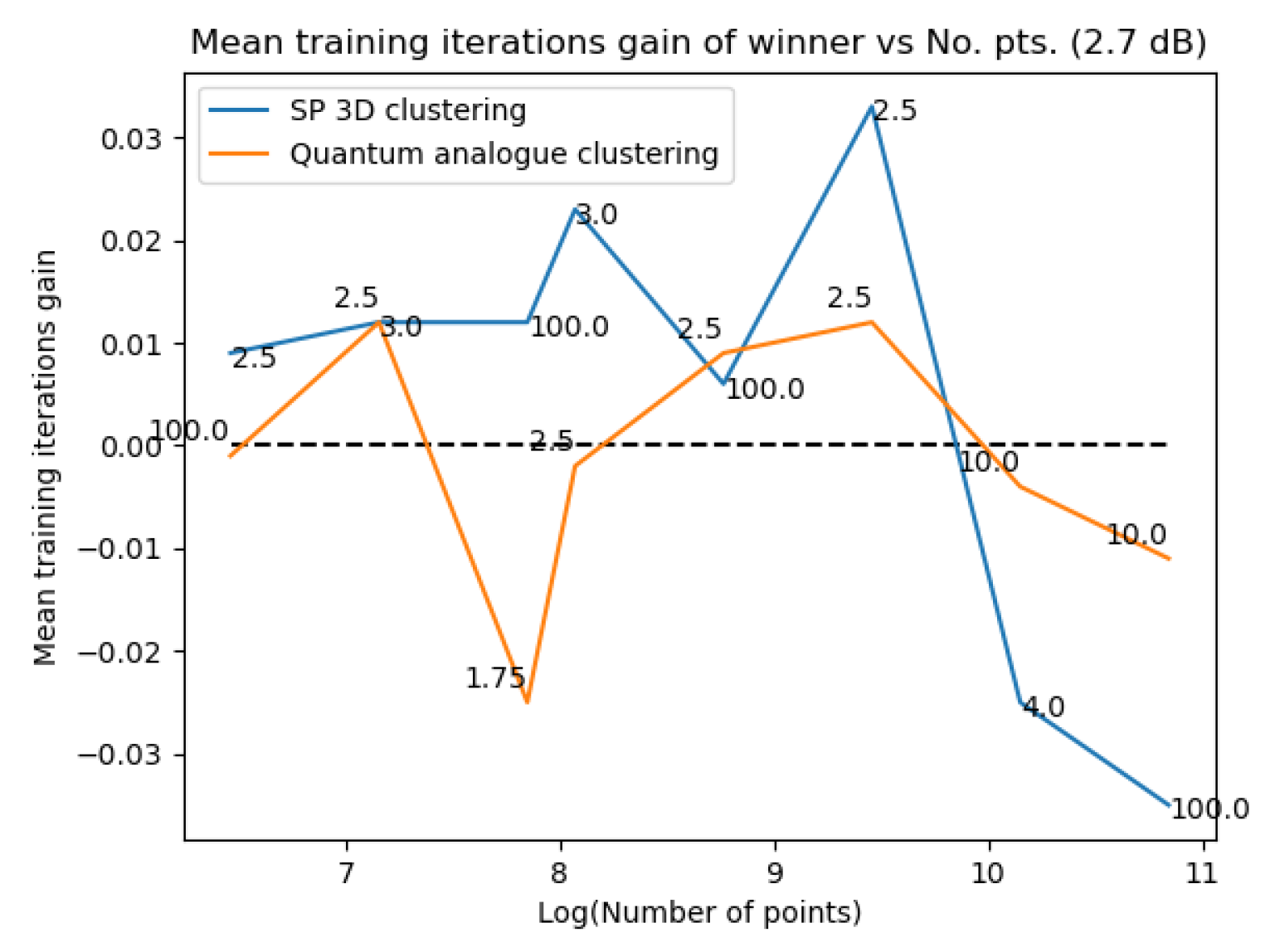
Figure 46.
Gain in iteration number for maximum accuracy v/s number of points, 10.7dBm dataset.
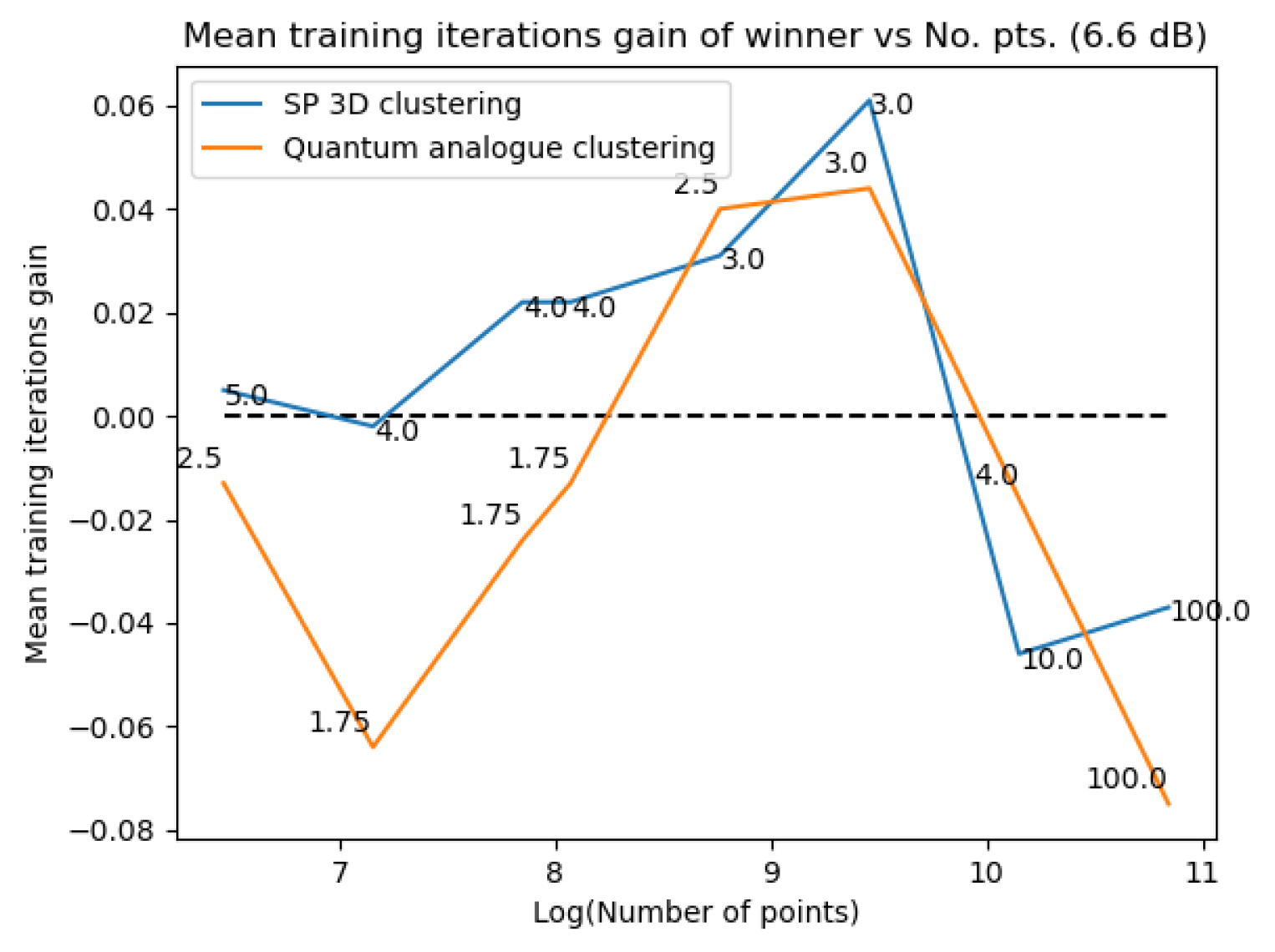
Figure 47.
Maximum accuracy gain v/s number of points, 10.7dBm dataset.
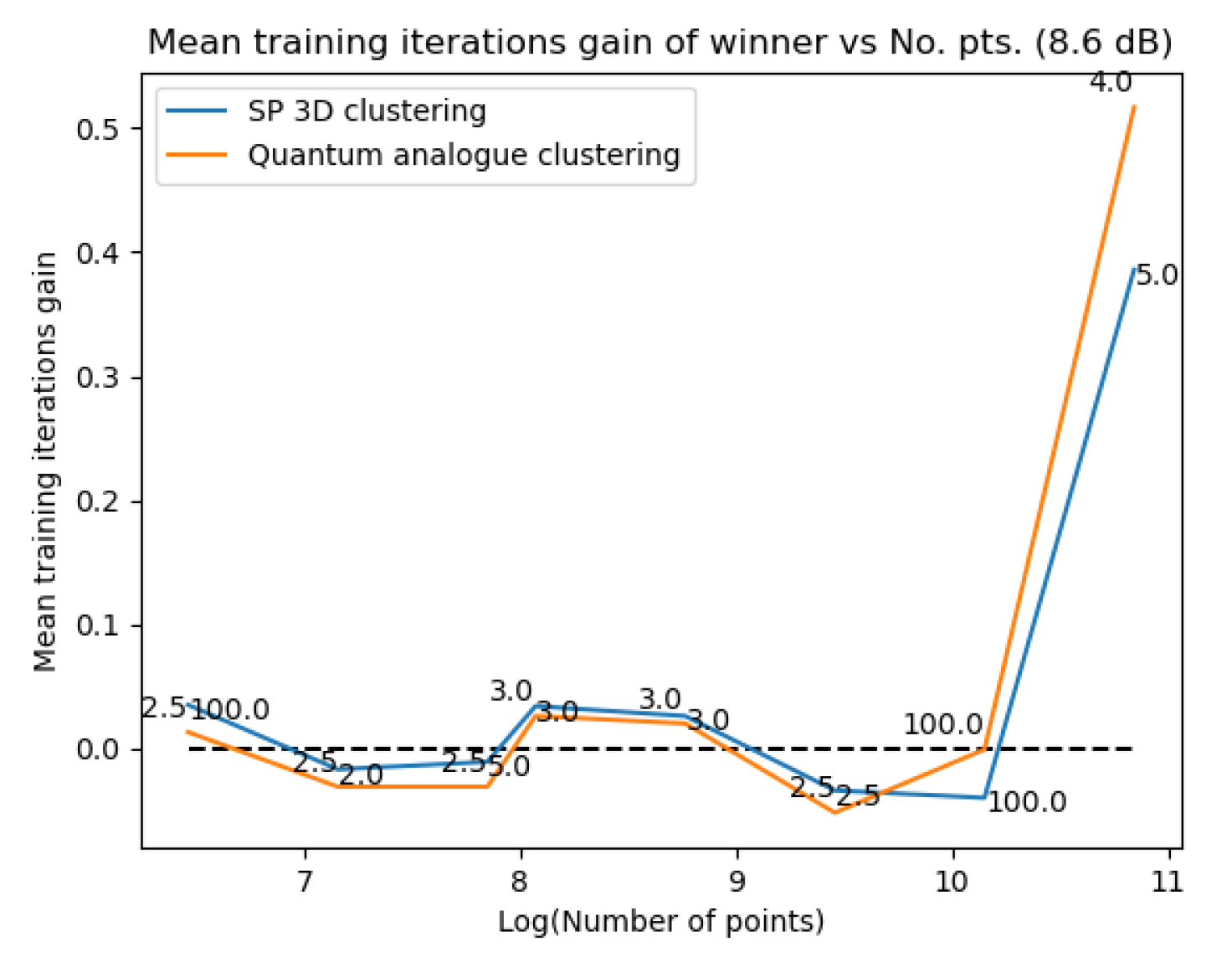
Figure 48.
Maximum accuracy v/s number of points, 10.7dBm dataset.
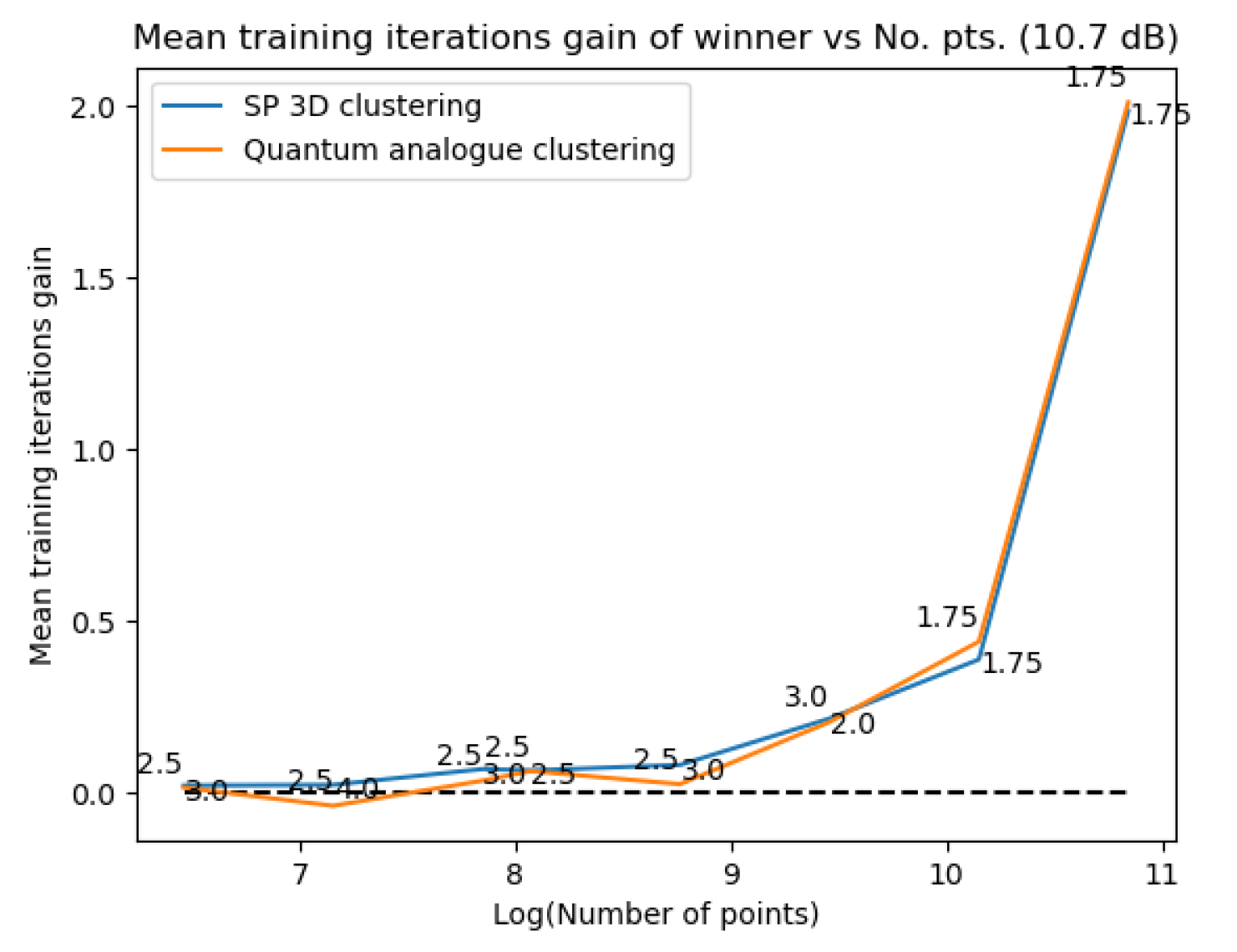
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









