Preprint
Article
Piezoresistive Behavior of a Conductive Polyurethane Based Foam for Real Time Structural Monitoring
Altmetrics
Downloads
124
Views
31
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
02 May 2023
Posted:
02 May 2023
You are already at the latest version
Alerts
Abstract
Smart flexible materials with piezoresistive property are increasingly used in sensors field. When embedded in structures, they would allow an in-situ structural health monitoring and damage assessment of impact loading such as crash, bird strikes and ballistic impacts. However, this could not be achieved without a deep characterization of the relation between piezoresistivity and mechanical behavior. The aim of this paper is to study the potential use of the piezoresistivity effect of a conductive foam made of a flexible polyurethane matrix filled with active carbon for integrated Structural Health Monitoring (SHM) and damage assessment applications. To do so, PolyUrethane Foam filled with Active Carbon, namely PUF-AC, are manufactured and tested under quasi-static compression tests and under Dynamic Mechanical Analyser (DMA) with in-situ measurement of its resistivity during tests. A relation is proposed for describing the evolution of the resistivity versus strain and stress. In addition, a demonstrative experiment of a PUF-AC sample subjected to low velocity impact assesses the interest of this type of materials for damage assessments.

Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
These last decades, composite structures have become essential in many industrial applications. As a key material for eco-design in transport industry (aeronautics, space, defense), civil engineering or even energy production (wind turbine, pipelines), they are facing a variety of loadings (collision, vibration, flexion…) during their lifetime. In this context, where safety standards are particularly drastic, numerous research works aim to improve structure performance in terms of weight, manufacturing, safety and durability. Sandwich structures made from composite materials are a representative example [1,2]. They are particularly used for their energy absorption property combined with their light weight and important stiffness. Nevertheless, these structures are vulnerable facing impacts which could create an internal damage, such as delamination or kissing bonds, with serious consequences. Even though numerical models were created [3], a total prevention of risks remains challenging. Therefore, structures in general are regularly controlled during maintenance operations with various techniques, among them Structural Health Monitoring (SHM). This technique consists in a real time identification of eventual damages by making a health state diagnostic of a structure by embedding numerous sensors (optical fibers, piezoelectric or piezoresistive sensors…) onto or within it [4]. Depending on the sensor nature and structure type, SHM operations can be complex, time-consuming and expensive, for example the immobilization of a commercial aircraft for maintenance. For those reasons, the new tendency in materials field is to create smart composite structures allowing real time monitoring. Therefore, composite materials embedding piezoelectric, capacitive, optical fibers or piezoresistive sensors in their conception have been tested [4,5,6,7,8]. The main problematic of these new structures is the sensors integration which possibly causes structure degradation. Moreover, even if traditional sensors have a good performance, they are complex to produce because they are mostly designed with metals or inorganic semiconductors which also reduce their flexibility [7,9].
Therefore, over the last decade, new soft sensors made from smart materials have been highly studied. Smart polymer-based composites such as smart textiles, piezoelectric elastomer or piezoresistive foams are solution of interest for strain/pressure sensing [9,10,11]. Thanks to their microcellular morphology and low density, foams are ultra-light and highly compressible making them valuable as low intrusive materials [10,11,12,13]. They are also economic and easy to elaborate [14]. Piezoresistive foams are composed of an insulating polymer matrix (polyurethane, polyethylene, melamine…) and filled by a nanofiller (graphene, carbon nanotubes, conductive polymers…) giving the foam an electrical conductivity property. The integration of nanofillers can be done by a simple coating method [10,13,16,17]. Piezoresistivity is a passive behavior based on the variation of electrical resistance of the foam sandwiched in a structure subjected to external loading.
The characterization of the piezoresistive response of conductive foams in quasi static regime was broadly investigated in numerous works [11,12,13,15,16,17,18,19,20]. However, dynamic characterization of such materials hasn’t really been studied especially for impact sensing [21]. This paper aims to evaluate the performance of an antistatic foam as a pressure/strain sensor made from conductive polyurethane on a large dynamic measurement range by identifying the most influent parameters.
In order to evaluate the sensing performance of the piezoresistive foam in quasi static and dynamic regime, electrical sensitivity must be considered. In scientific literature, there is no universal model quantifying the most influent parameters (foam density, filler mass fraction) over sensitivity on piezoresistive foams. The main objective of this article is to better understand the relation between mechanical and electrical behavior by identifying various parameters influencing sensitivity such as initial conditions (conductivity, mechanical environment) and foam viscoelasticity (compression velocity). Polymer based foam are mainly viscoelastic materials meaning that the elastic modulus is proportional to the strain rate. To the authors knowledge, there is a gap in research works about the influence of strain rate over sensitivity on a large-scale measurement. A direct link between those parameters would permit an effective evaluation from the foam sensor of a damage extend on a structure. To do so, the foam microstructure is analyzed by optical microscopy and samples were subjected to compressive tests with in-situ conductivity measurement at various strain-rate until 10 s-1. In addition, the piezoresistive response of a structure embedded piezoresistive foam was studied.
This paper starts by a description of material and the elaboration of tested samples. Polyurethane foam based filled with active carbon was studied. The method of measuring electrical resistance is described. Quasi-static tests are carried out in order to verify the responsiveness of the foam facing cyclic compressions. The basic electromechanical response of the foam is then analyzed. An attention is paid on the first compression analysis to compare the sensitivity of the electro-mechanical response of the foam when sample is in free and confined configuration with a closed structure. The third part aims at identifying the influence of the material viscoelasticity and the initial conductivity on the detection performance by means of a dynamic mechanical analysis. This research work ends with a conclusion and by giving some outlooks.
2. Materials and Methods
2.1. Material
The considered material is a very low density (18 ± 1 kg.m-3) polyurethane-based foam (PUF-AC) impregnated with activated carbon purchased from Industrie-Shaulm-Produkte GmbH & Co. KG under the product name of ELS-soft. The concentration ratio of carbon fillers in the foam is not communicated by the manufacturer. The foam has a three-dimensional microstructure. It consists of set of open pores which is an assembly of struts forming hexagons or pentagons of 300 μm side on average, randomly oriented in space as shown in Figure 1 obtained with the digital microscope Keyence VHX-500 series at ESTACA’LAB. Thanks to its electrical conductivity and energy absorber capacity, this kind of foam is broadly used for antistatic packaging.
2.2. Sample Elaboration and Determination of Electrical Resistance
The samples with square surfaces of 35 mm side by 12 mm thick were cut with a cutter from a 2 x 2 m plate. Depending on the position on the plate where the sample was cut, it has an intrinsic conductivity R0 varying from 1 to 10 kΩ. This dispersion of R0 measure is due to manufacturing process. Therefore, to obtain homogeneous series of samples, there are cut in the same area (center) of the plate.
In order to correctly measure the electrical resistance, electrodes made from a thin copper tape are placed on the top and bottom surfaces of the samples (Figure 3a). They cover 100% of their horizontal surface. Nevertheless, the high porosity (> 95%) and roughness (Figure 1c) of the foam make a good adhesion difficult between its surfaces and the electrodes, inducing unstable contact electrical resistance.
Therefore, top and bottom surfaces are initially covered by a thin layer of a highly conductive (silver content) varnish (LOCTITE® 3863 Circuit+™) (Figure 3a). This varnish layer thus fills some of the hollow cells of the foam surface at 1 mm maximum penetration so covering less than 10% of the total thickness (Figure 3b). Resistance contact was identified in various research works on conductive foams; electrodes made from a dense silver paint seems to be a popular solution [12,15,21].
A low direct current (30.8 µA) from a low current generator is sent to PUF-AC samples via wires which are connected to a laboratory made data acquisition system (DAQ) for measuring the tension in a 0 – 10 V voltage range with an accuracy of 15 effective bits (Figure 2). The electrical resistance is determined with the Ohm’s law considering the foam as a series of 3 variable resistances depending on mechanical parameters. Electrodes made from silver varnish assure good electrical contact so the terms Rcontact1 and Rcontact2 can be nullified in equation (1).
Rtotal = Rcontact1 + Rfoam + Rcontact2
Figure 2.
Electrical illustration of PUF-AC foam and its electrical measure setup.
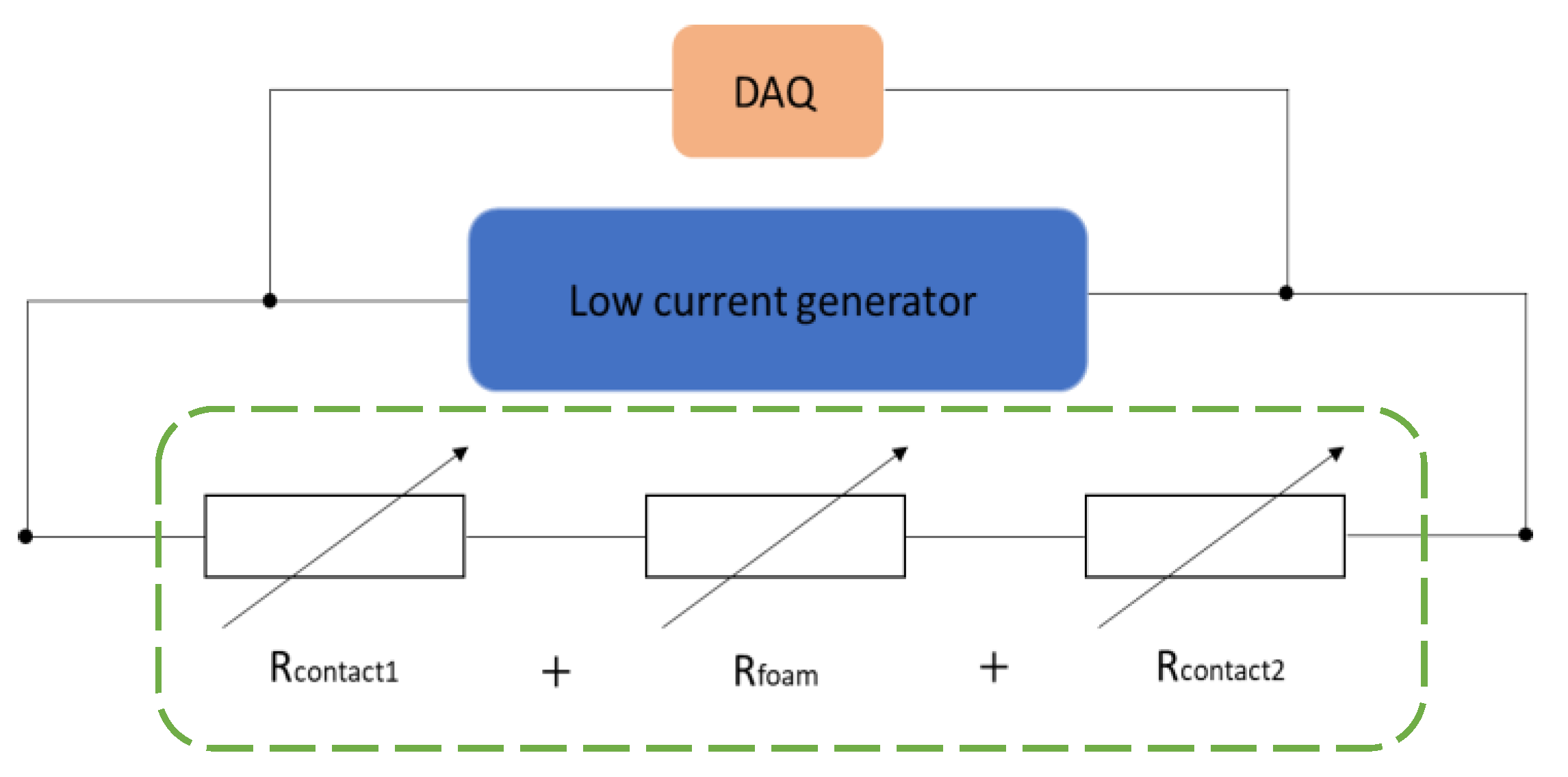
Figure 3.
Optical Microscopy photographs of the PUF-AC microstructure covered by varnish layer: (a) compression surface view; (b) thickness view.
Figure 3.
Optical Microscopy photographs of the PUF-AC microstructure covered by varnish layer: (a) compression surface view; (b) thickness view.

2.3. Quasi Static Tests : Method
The electromechanical behavior of PUF-AC is firstly characterized with cyclic uniaxial compressions, in two initial configurations (Figure 4) with a conventional testing machine, model INSTRON 3369, with cell force of 500N based at ESTACA’LAB. In free configuration, PUF-AC samples are placed between two plates recovered by Teflon (for electrical insulation) and vertically compressed at 80% of the thickness with the testing machine. A 2.5 kS/s data acquisition rate option acquires simultaneously load and strain measurement. The testing machine is operated in displacement control. A PUF-AC sensor for SHM would be likely preloaded when embedded in a structure so its performances are supposed to be modified. Therefore, a second configuration is studied. PUF-AC samples are inserted in a structure designed to assure lateral pre-loading. It is a cuboid cavity of 34 mm width, pressing lateral surfaces of foam sample (Figure 4b). In both configurations, electrical data (tension) are simultaneously acquired with mechanical data (force, strain). PUF-AC samples are compressed during 10 cycles at a compression ratio of 66%/min (8 mm/min) in relation to the sample thickness.
The evolution of conductivity Is quantified by the variation of the relative electrical resistance R expressed as (2):
R [Ω]: resistance at t time [s]
R0 [Ω]: resistance at t = 0 s
PUF-AC sensor performances are evaluated through its electrical sensitivity in relation to strain Sε (3) and stress Sσ [kPa-1] (4).
H(t) [mm]: position of top plate at t time
H0 [mm]: position of top plate at t = 0 s
e [mm]: sample thickness
Stress on PUF-AC sample is quantified from the force F(t) measured by the testing machine in relation with the sample surface S considered as constant (6).
σ(t) [kPa]: Stress at t time
F(t) [N]: Force at t time
S [mm²]: Surface of foam sample (constant)
2.4. Strain Rate Dependancy Test Method
In order to better understand the dependency of the electromechanical behavior on the strain rate, foam samples are compressed at 80% of their thickness at various strain rates (10-2, 10-1, 1, 10 s-1), in free configuration on a DMA machine (E3000, ElectroPuls® Instron 3kN, at ESTACA’LAB capable of dynamic cycle load up to 100 Hz), in displacement control mode.
Strain rate is defined as the displacement velocity of superior compression plate of the E3000 machine (Figure 5), in relation with the sample thickness e. It is simply the temporal derived expression of eq (5):
Strain rate [s-1] is a test consign so it is considered as constant during the entire test.
Compressive strain and loading data are acquired via a LVDT position sensor from E3000 and a load cell of 500 N capacity with accuracy of 10-3 N. Electrical resistance is obtained via the same method as explained in Figure 2.
2.5. Assessment of the piezoresistive response under impact test
The dynamic response of PUF-AC is analyzed by subjecting low velocity impacts (< 10 m/s). For that purpose, an impactor in Teflon of 16 cm long by a square surface of 36 mm large is dropped vertically at a various height ranging from 1 to 16 cm (Figure 6). Surface dimensions are chosen to assure an as planar compression as possible of the sample. In this test, impact energy is considered as equal to potential energy defined as:
m is mass of impactor (= 145 g) [kg],
g is earth gravity acceleration [9.81 m.s-2]
h is height of drop [m]
Electrical resistance of samples is recorded with the same method as used in quasi static tests.
Table 1.
Impact energy absorbed by PUF-AC samples with the corresponding drop height.
| Epotential (J) | Drop height (cm) |
|---|---|
| 0.014 | 1 |
| 0.028 | 2 |
| 0.057 | 4 |
| 0.114 | 8 |
| 0.171 | 12 |
| 0.227 | 16 |
3. Results and Discussion
3.1. Piezoresitive Response and Conductive Mechanism of PUF-AC
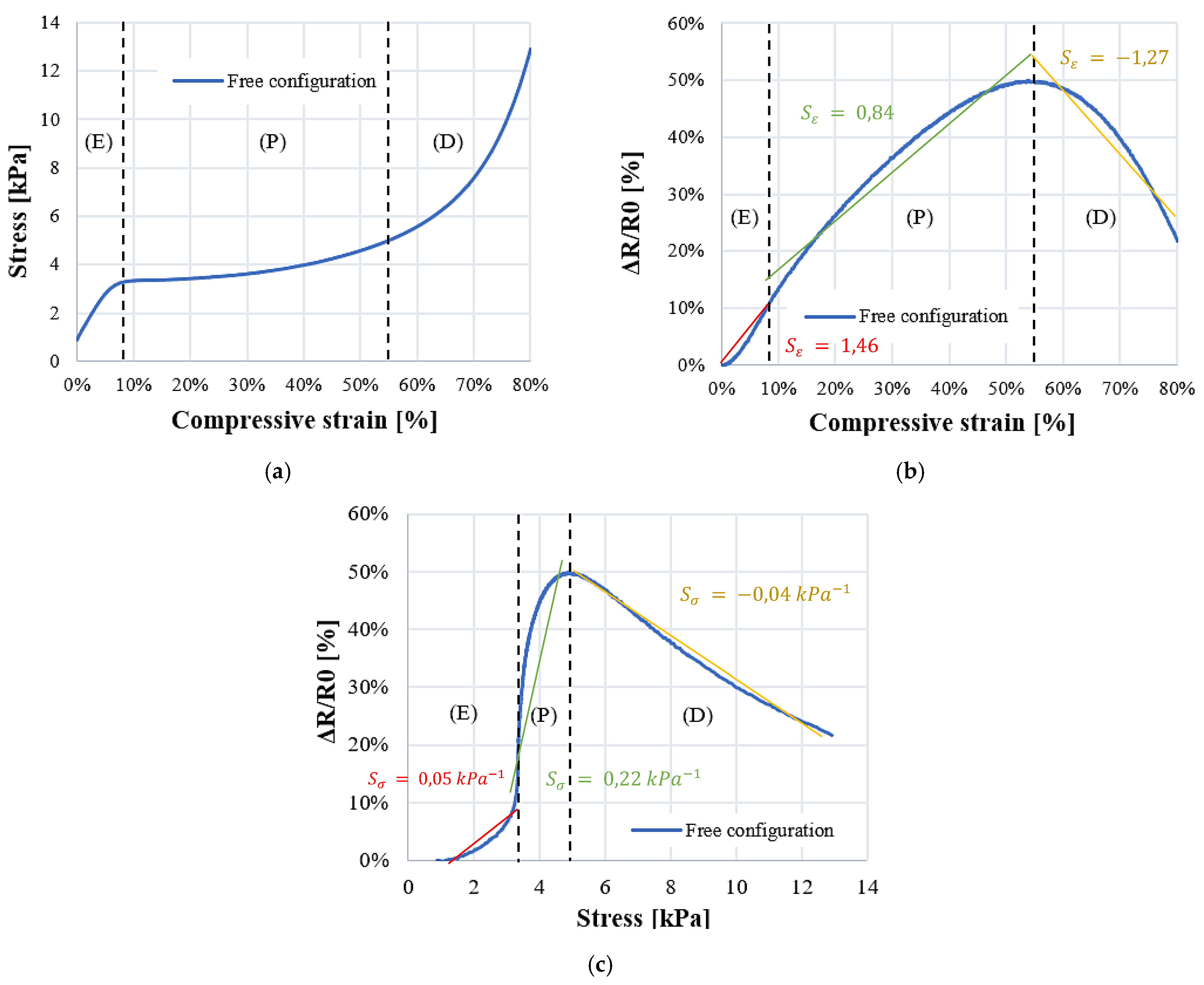
Initially, it is essential to analyze the electromechanical behavior of PUF-AC during the first compression in free configuration. On the stress/strain curve in Figure 9a, an elasto-plastic behavior is observed. It is a typical mechanical response of polymeric foams which is described by three stages: (E) elasticity (ε = 0-10%), (P) plateau (ε =10-55%) and (D) densification (ε = 55-80%). The Figure 8 shows the deformation of a cell at each compressive phase. This micro-cell pictured in Figure 8 is situated on the median horizontal line from the foam sample thickness.
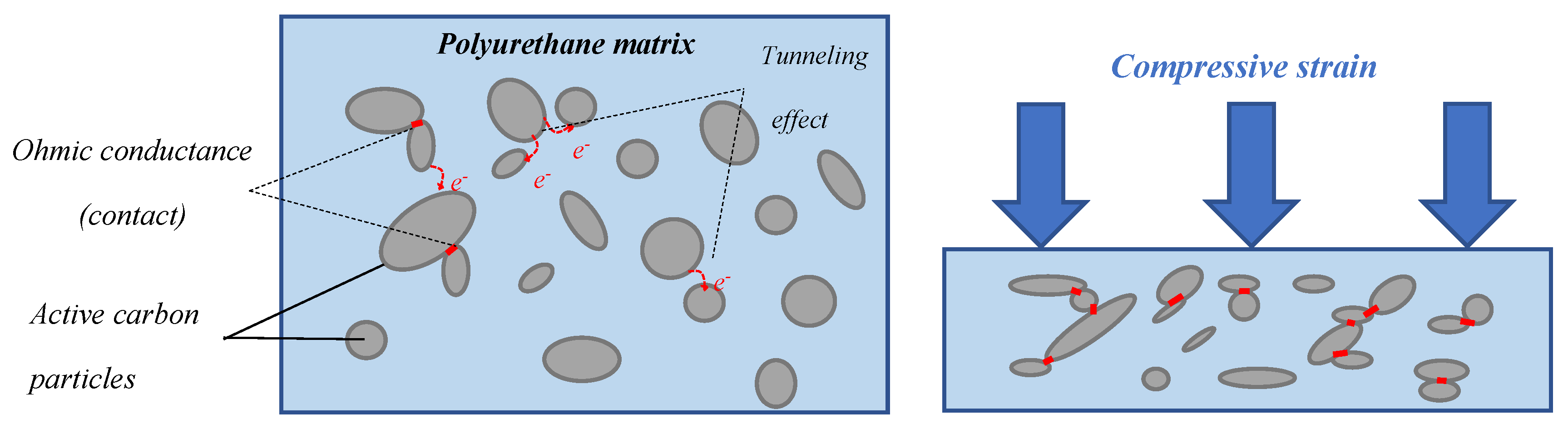
The conduction mechanism is initially based on the intrinsic resistance of the filler particles forming a conductive network. Two forms of conductance are operated in the network: tunneling effect and ohmic conductance (Figure 7). Depending on the inter-particle distance, the tunneling effect is the probability to an electron to pass from a filler particle to another through a thin layer of an insulating material (polyurethane matrix). This quantic effect is directly related to the concentration and repartition of the conductive filler into the polyurethane matrix. A higher filler concentration ratio increases the number of contact points between filler particles so reducing the influence of tunnel resistance [10].
During the elastic phase, the stress increases linearly until reaching a “plateau constraint” of 3.5 kPa approximately. Mechanical models [22] describe this phase as a linear bending of the cells struts of the foam (considered as beams). In the plateau phase, a low augmentation of stress is observed until εdensification. It is due to struts buckling, collapsing cells with low effort. It is suggested that the increasing resistance ratio observed from ε0 to εdensification is due to progressive reduction of tunneling effect influence; during deformation, the variation of tunneling distance between filler particles disturbs electrons exchange. Moreover, compression damages induced on microstructure perturb conduction network (Figure 8c).
Figure 7.
3D illustration of impact test setup.
The densification phase starts at approximately 55% of compressive strain. It corresponds to the threshold at which the foam cells collapse (Figure 8c,d). The mechanical
response shows an increasing stiffness (Figure 9a). From an electrical point of view, the conductive network is denser which reduces foam resistance (Figure 9b).
After being completely compressed, sample foam is supposed to be damaged. Partial or complete rupture of struts can be observed (Figure 8c). Consequently, the conductive network considered as an assembly of current pass ways (struts) is also damaged. Moreover, the initial conductivity R0 will be never recovered after unloading.
As represented in Figure 9b and Figure 9c, resistance ratio curve is divided accordingly into three deformation phases. By the least mean square method, each domain is approximated by a linear curve with a slope corresponding to Sε (Figure 9b) and Sσ (Figure 9c).
Figure 8.
Foam cell deformation during compression: (a) ε0 = 0; (b) εelasticity = 10%; (c) εdensification = 55%; (d) εfinal = 80%.
Figure 8.
Foam cell deformation during compression: (a) ε0 = 0; (b) εelasticity = 10%; (c) εdensification = 55%; (d) εfinal = 80%.

Figure 9.
PUF electromechanical behavior during first compression in free configuration: (a) compressive stress strain curve; (b) relative resistance as a function of compressive strain and (c) stress.
Figure 9.
PUF electromechanical behavior during first compression in free configuration: (a) compressive stress strain curve; (b) relative resistance as a function of compressive strain and (c) stress.
3.2. Cyclic Compressions: Electromechanical Hysteresis
Cyclic compressions test, performed with Instron 3369, aims to study the repeatability of the electromechanical response of PUF-AC.
Cycle 1: The mechanical behavior during cycle 1 of compression is described by a hysteresis curve on graph in Figure 9a. The diminution of stress level during unloading phase is due to Mullins effect, which is directly related to the viscoelasticity property of PUF-AC. The evolution of relative resistance is also non repeatable during unloading phase (Figure 9b,9c). Few information in scientific literature are reported to explain this observation. This work suggests that the main consequence is linked to viscoelasticity and cells damaging. Viscoelasticity can be described by a temporary residual stress in the foam sample varying stiffness. The Maxwell model represented by association of spring and dashpot well describes viscoelastic behavior of materials [23]. From a microscopic point of view, under loading, polyurethane constitutive molecules chains are temporary in movement by creating entanglements [24]. This mobility cancels tunneling effect because tunnel distance between particles are broken. In consequence, the main conduction mechanism in operation is ohmic conductance, depending only on cells contacts variation. When the sample gets its initial state back after a certain recovering time, the two conduction mechanisms (tunneling and ohmic conductance) operate again. The similar form of curves is observed after one day at rest. However, the general resistance level is increased because of irreversible damages caused by compressions (Figure 8c, Figure 8d).
Cycle 2 to 10: At the second compression cycle, an electromechanical hysteresis is observed. The relative resistance of PUF-AC sample has increased by 160% compared with the starting first cycle. As explained previously, at this time of experiment, the evolution of foam conductivity only depends on ohmic conductance so the progressive diminution of relative resistance during loading phase (Figure 10b,10c,10d) is justified. From 2nd to 10th cycle, the hysteresis effect is progressively decreasing, and the electromechanical behavior tends to be more stable (Figure 10). Along compressive cycles, polyurethane chains and filler particles are moving with the same inertia without recovery time which could explain this form of stability regarding the hysteresis behavior.
Tests in fatigue and a complete historic of foam events would permit a better interpretation of its electrical response.
3.3. Influence of Pre-Stress Condition on Performances
As explained in previous parts, PUF-AC is destined to be integrated in a structure. Foam samples would be likely pre-stressed by its implementation in a structure. The experiment aims to understand the influence of lateral pre-stress condition on its electromechanical behavior and performances.
The stress-strain curve on Figure 11a shows that samples with pre-stress condition have an elasto-plastic behavior with more stiffness. An increase of plateau constraint (+0.5 kPa) can be observed. The piezoresistive response of confined samples is broadly similar to samples in free configuration. Nevertheless, results show a lower electrical sensitivity to strain (Sε) and stress (Sσ) in elasticity phase (see Table 2) with a relative difference of 58% and 60% respectively.
The performances in terms of sensitivity would likely be diminished by the implementation of PUF-AC in a structure.
3.4. Strain-Rate Dependency
Figure 12a describes the electro-mechanical behavior of samples. The three phases of elasto-plastic behavior are still visible (at the same strain levels), but the global level of stress is proportionally increasing with strain rate, confirming the rate dependency of polymeric foams. Moreover, it can be observed that the stiffness is superior regarding the progressive augmentation of Young modulus in Table 3. At 10 s-1, stress-strain curve in plateau phase is not linear and presents a decrease at ε = 30%. This loss of rigidity is possibly due to an eventual fragilization of foam samples.
Figure 12 shows the potential relation between viscoelasticity and electrical sensitivity in PUF AC sample. Regarding Figure 12d, all set of tested samples have a homogeneous initial resistance meaning that R0 can be considered as a controlled parameter.
Elasticity and plateau phases: The progressive reduction of (ΔR/R0)max and Sε are proportional to the augmentation of strain rate (see Table 3). It is supposed to be due to the augmentation of stiffness induced by viscoelasticity which lowers tunnel resistance. Nevertheless, at sample scale, it is difficult to confirm this interpretation. Numerical simulation of foam deformation at local scale (cell) would help understanding this result. Figure 12b shows a similar electrical response and sensitivity (Sε) between tests at 1 and 10 s-1 suggesting the electrical sensitivity is more influent at lower strain rates. Regarding Figure 12c, by considering compressive stress, electrical sensitivity (Sσ) is clearly inferior between tests at 1 and 10 s-1 strain rates with a relative difference of 75%. Until densification, viscoelasticity seems to be influent on detection performances of the foam.
Densification phase: Results from Table 3 and Figure 12 show a non-influence of strain rates on electrical sensitivity (Sε, Sσ) except for Sσ at 10 s-1. This exception is due to an eventual damaging of samples at 10 s-1. From these results, it can be concluded that viscoelasticity doesn’t influence much foam sensitivity during large deformation when [ε ≥ εdensification].
In summary, a distinct variation of electromechanical sensitivity of PUF-AC is observed with the augmentation of strain velocity until the densification phase. This result is interesting because it shows the ability of the foam to detect various loading velocities which represents a potential advantage for damage assessment of a structure subjected to impact loading such as bird strikes, mechanical drop or ballistic impacts. Moreover, starting from densification phase where cells are collapsing, as explained previously, ohmic conductance is prominent. One suggests that if ohmic conductance was prominent during elastic phase, the influence of strain rate rising would be quite reduced as it is in densification. Same test method applied on samples with various filler concentration ratios would verify this hypothesis.
3.5. Electromechanical Parameter
As mentioned in material and methods part, the resulting foam conductivity is dependent of the manufacturing process. Initial resistance is directly related to filler concentration. In order to quantify R0 influence on sensitivity, PUF-AC samples with different conductivities were tested with the exact same method as strain dependency test. From Table 2 and Table 3, the maximum relative resistance (ΔR/R0)max obtained during first compression is a great indicator for sensitivity.
Figure 13 shows the piezoresistivity response as a function of R0 for different strain rates . Each ensemble of ((ΔR/R0)max ; R0) points are approximated as linear curves (Figure 13a). Moreover, when R0 value is approaching zero, conductivity tends to infinity meaning that the considered material is an electrical conductor. Therefore, (ΔR/R0)max can be considered as negligible when R0 = 0 because electrical conductors such as metals are faintly sensible to conductivity variation when subjected to loads. Each slope of linear curve is considered as a new measurement parameter that is arbitrary named electromechanical parameter (PEM), for evaluation of electrical sensitivity to strain rate (Figure 13b) considering R0. It is expressed by equation (8).
Results from Figure 13a firstly show that for a fixed strain rate, when R0 is increasing, (ΔR/R0)max is augmented, confirming the augmentation of sensitivity with R0. Secondly, referring to linear curves, for a same R0, (ΔR/R0)max is superior proportionally to strain rate. Eventually, it can be clearly observed (Figure 13b) that sensitivity to load velocity is more important when PUF-AC conductivity is lower. The PEM can be approached with a logarithmic expression of strain rate (9).
The resulting equation (10) can be expressed as below:
3.6. Piezoresistivity Behavior during Dynamic Loading
This part aims at presenting the characterization of dynamic behavior of PUF-AC subjected to light shocks. At the authors knowledge, only one publication is reported about impact sensing of piezoresistive foams [21].
Unlike quasi-static tests, samples undergo a quick compression during impact. Foam is acting as a soft spring: a part of the impact energy is absorbed by the foam and is partly redistributed to the impactor until it is immobilized on sample causing a relaxation condition.
The dynamic behavior of PUF-AC observed in Figure 14a is quite different to quasi-static response. It can be broadly described by a steep augmentation of relative resistance during impact followed by a smooth decrease until reaching a stabilization of resistance level. This form of electrical response is similar to research work of Boland et al. [21] (Eimpact ≤ 5 mJ) on PU foam filled with graphene.
However, for an impact energy superior to 114 mJ (h > 8 cm), an abrupt diminution of resistance (≈ -10%) systematically precedes the impulsion (Figure 14a). From a physical point of view, this fact can be connected to the quasi complete compression of the sample (ε ≈ 100%, densification phase) which is not reached at lower impact energies. The distance between electrodes is clearly reduced (capacitive effect) resulting in a better conductivity. From this suggestion, the first resistance impulsion is attributed to the foam response: the impactor is rebounding on the sample. It is similar to the hysteresis effect observed in quasi static tests where resistance is increasing during unloading phase of compression (Figure 10b). Moreover, after reaching (ΔR/R0)max, another rapid diminution of resistance is observed. This behavior is due to the rebound of the impactor on the sample until reaching a complete energy absorption.
In order to compare the sensitivity of PUF-AC in relation to impact energy, the maximum reached resistance (ΔR/R0)max is presented as a function of Eimpact. A good repeatability can be observed and a relation between those parameters is expressed as a power law (11):
5. Conclusion
To conclude, the aim of this work was to analyze the electromechanical behavior of an antistatic foam in quasi-static and dynamic regimes in order to evaluate its ability to monitor the severity of an impact when embedded into a structure, by characterizing its piezoresistive response. As the performances are directly linked to the electrical sensitivity to strain (Sε) or stress (Sσ) of the foam, an attention is paid to key parameters such as viscoelasticity, initial conductivity and boundary conditions. The polyurethane foam filled with active carbon (PUF-AC) shows a great responsiveness at first quasi static compression with an important electrical sensitivity at low strain (Sε = 1.46). The repeatability of this response is discussed as the conduction mechanism varies starting from the unloading phase of first compression duo to polymer viscosity and foam damages. However, from cycle 2 to 10, repeatable electromechanical hysteresis is then observed which tends to minimize with the augmentation of compression cycles.
This low-cost conductive foam shows a great detection capacity on large deformations (ε ∈ [0 ; 80%]) with a good sensitivity to low impacts (Eimpact ≤ 227 mJ). Electrical sensitivity is also linked to viscoelasticity regarding its negligible dependency to strain rate () with a maximum decrease of 40% (Sε), demonstrating the ability to PUF-AC to evaluate a damage seriousness on a structure. Nevertheless, the pre-stress configuration test aiming to anticipate the structure integration consequences on performances, shows a global diminution of sensibility. Moreover, regarding the electromechanical parameter (PEM), sensitivity variations to strain rate are amplified with a lower foam conductivity. Finally, an experimental approach is given to understand piezoresistivity behavior of conductive polymeric foams for sensing applications. An empirical parameter is defined in order to connect the strain rate with the resistivity.
Before testing the foam performances integrated in a structure, further tests are necessary to identify its detection limits. Experimentations conducted on Hopkinson bars at much higher strain rates more representative of severe impacts would provide results at higher impact energies. As presented in this article, the same tests applied on PU foam samples filled at various concentrations ratio would permit a better understanding of conduction mechanism. In parallel, a complementary numerical model at cell scale would also be pertinent to explain the suggested diminution of tunnel resistance during augmentation of strain rate.
Author Contributions
Conceptualization, A.P. ; methodology, A.P.; validation, A.P. ; formal analysis, A.P.; investigation, A.P.; resources, J-C.W; data curation, A.P.; writing—original draft preparation, A.P., N.B; writing—review and editing, A.P., N.B, J-C.W and M.A.; visualization, A.P., N.B. and J-C.W; supervision, N.B. and J-C.W., M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Acknowledgements are addressed to Geneviève Brel from ODAXOS company for project creation in 2018, ESTACA and its technical staff: Raphaël Defossez and Yoann Seiller. Authors are also grateful to ESTACA students and interns, Tanguy Pilard, Oumar Diakhate for their contribution.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Birman V.; Kardomateas G.A. Review of current trends in research and applications of sandwich structures. Composites Part B: Engineering. 2018, 142, 221-240. [CrossRef]
- Elnasri I. ; Comportement des matériaux cellulaires sous impact et de panneaux sandwichs sous perforation dynamique. Doctoral dissertation, École normale supérieure de Cachan, Cachan, 14 December 2006.
- Ivañez I.; Santiuste C.; Barbero E.; Sanchez-Saez S. Numerical modelling of foam-cored sandwich plates under high-velocity impact. Composite Structures. 2011, 93, 2392-2399. [CrossRef]
- Mesquita E.; Antunes P.; Coelho F.; André P.; Arêde A.; Varum H. Global overview on advances in structural health monitoring platforms. J Civil Struct Health Monit. 2016, 6, 461-475. [CrossRef]
- Tayebi A.; Ul Hoque M.M. Design of experiments optimization of embedded MEMS sensors in composites for structural health monitoring. Smart Structures and Materials, San Diego, CA, USA; 19 August 2003.
- Su Z.; Wang X.; Chen Z.; Ye L.; Wang D. A built-in active sensor network for health monitoring of composite structures. Smart Materials and Structures. 2006, 15, 1939-1949.
- Montazerian H.; Rashidi A.; Milani A.S.; Hoorfar M. Integrated Sensors in Advanced Composites: A Critical Review. Critical Reviews in Solid State and Materials Sciences. 2020, 45, 187-238. [CrossRef]
- Kinet D.; Mégret P.; Goossen K.; Qiu L.; Heider D.; Caucheteur C. Fiber Bragg Grating Sensors toward Structural Health Monitoring in Composite Materials: Challenges and Solutions. Sensors. 2014, 14, 7394-7419. [CrossRef]
- Meti S.; Balavalad K.; Sheeparamatti B. MEMS Piezoresistive Pressure Sensor: A Survey. IJERA. 2016, 6, 23-31.
- Liu H.; Li Q.; Zhang S.; Yin R.; Liu X.; He Y.; et al. Electrically conductive polymer composites for smart flexible strain sensors: a critical review. J Mater Chem C. 2018, 6, 12121-12141.
- Hanson R.A.; Newton C.N.; Merrell A.J.; Bowden A.E.; Seeley M.K.; Mitchell U.H.; et al. Dual-Sensing Piezoresponsive Foam for Dynamic and Static Loading. Sensors. 2023, 23, 3719. [CrossRef]
- Ding Y.; Yang J.; Tolle C.R.; Zhu Z. Flexible and Compressible PEDOT:PSS@Melamine Conductive Sponge Prepared via One-Step Dip Coating as Piezoresistive Pressure Sensor for Human Motion Detection. ACS Appl Mater Interfaces. 2018, 10, 16077-16086.
- Kordas K.; Pitkänen O. Piezoresistive Carbon Foams in Sensing Applications. Front Mater. 2019, 6, 93. [CrossRef]
- Jin F.L.; Zhao M.; Park M.; Park S.J. Recent Trends of Foaming in Polymer Processing: A Review. Polymers. 2019, 11, 953.
- Wang H.; Bernardeschi I.; Beccai L. Developing Reliable Foam Sensors with Novel Electrodes. IEEE SENSORS, Montreal, QC, Canada; 27-30 October 2019.
- Zhong W.; Ding X.; Li W.; Shen C.; Yadav A.; Chen Y.; et al. Facile Fabrication of Conductive Graphene/Polyurethane Foam Composite and Its Application on Flexible Piezo-Resistive Sensors. Polymers. 2019, 11, 8.
- Beccatelli M.; Villani M.; Gentile F.; Bruno L.; Seletti D.; Nikolaidou D.M.; Culiolo M.; Zappettini A.; Coppedè N. All-Polymeric Pressure Sensors Based on PEDOT:PSS-Modified Polyurethane Foam. ACS Applied Polymer Materials. 2021, 3, 563-572. [CrossRef]
- Kausar A. Polyurethane Composite Foams in High-Performance Applications: A Review. Polymer-Plastics Technology and Engineering. 2018, 57, 346-369. [CrossRef]
- Zhai Y.; Yu Y.; Zhou K.; Yun Z.; Huang W.; Liu H.; et al. Flexible and wearable carbon black/thermoplastic polyurethane foam with a pinnate-veined aligned porous structure for multifunctional piezoresistive sensors. Chemical Engineering Journal. 2020, 382, 122985.
- Wu X.; Han Y.; Zhang X.; Zhou Z.; Lu C. Large-Area Compliant, Low-Cost, and Versatile Pressure-Sensing Platform Based on Microcrack-Designed Carbon Black@Polyurethane Sponge for Human-Machine Interfacing. Adv Funct Mater. 2016, 26, 6246-6256.
- Boland C.S.; Khan U.; Binions M.; Barwich S.; Boland J.B.; Weaire D.; et al. Graphene-coated polymer foams as tuneable impact sensors. Nanoscale. 2018, 10, 5366-5375. [CrossRef]
- Gibson L.J.; Ashby M.F. Cellular Solids: Structure and Properties. 2nd ed.; Cambridge University Press, Cambridge, England, 1997.
- Shaw M.T.; MacKnight W.J. Introduction to polymer viscoelasticity. 3rd ed.; Wiley Hoboken, NJ, USA, 2005.
- Hanson D.E.; Hawley M.; Houlton R.; Chitanvis K.; Rae P. ; Orler E.B. ; et al. Stress softening experiments in silica-filled polydimethylsiloxane provide insight into a mechanism for the Mullins effect. Polymer. 2005, 46, 10989-10995. [CrossRef]
Figure 1.
Optical Microscopy photographs of the PUF-AC microstructure: (a) on surface; (b) at cell scale; (c) with depth representation.
Figure 1.
Optical Microscopy photographs of the PUF-AC microstructure: (a) on surface; (b) at cell scale; (c) with depth representation.

Figure 4.
PUF-AC sample in free configuration (a) and confined configuration (b).

Figure 5.
Experimental setup on E3000.

Figure 6.
3D illustration of impact test setup.

Figure 10.
Evolution of the relative resistance of the piezoelectric foam during cyclic compressions on ten cycles: (a) compressive stress strain curve; relative resistance as a function of compressive (b) strain, (c) stress and (d) time.
Figure 10.
Evolution of the relative resistance of the piezoelectric foam during cyclic compressions on ten cycles: (a) compressive stress strain curve; relative resistance as a function of compressive (b) strain, (c) stress and (d) time.

Figure 11.
Comparison of electromechanical behavior of PUF-AC samples in free and pre-stress configuration: (a) compressive stress strain curve; relative resistance as a function of compressive (b) strain, (c) stress.
Figure 11.
Comparison of electromechanical behavior of PUF-AC samples in free and pre-stress configuration: (a) compressive stress strain curve; relative resistance as a function of compressive (b) strain, (c) stress.
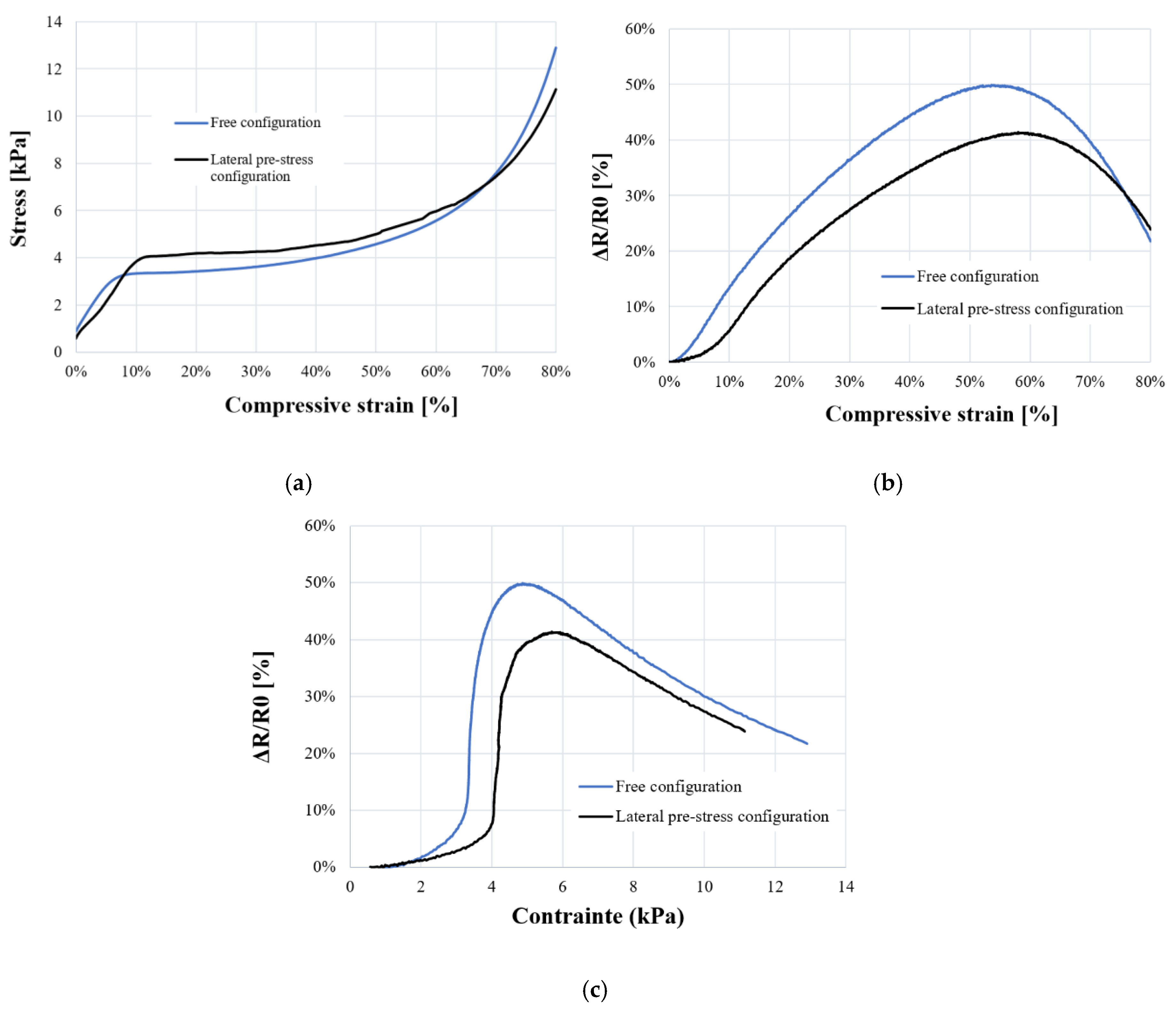
Figure 12.
Electromechanical characterization of PUF-AC at various strain rates with: (a) stress-strain curve; relative resistance as a function of (b) compressive strain and (c) stress; (d) initial resistance average of each samples set.
Figure 12.
Electromechanical characterization of PUF-AC at various strain rates with: (a) stress-strain curve; relative resistance as a function of (b) compressive strain and (c) stress; (d) initial resistance average of each samples set.
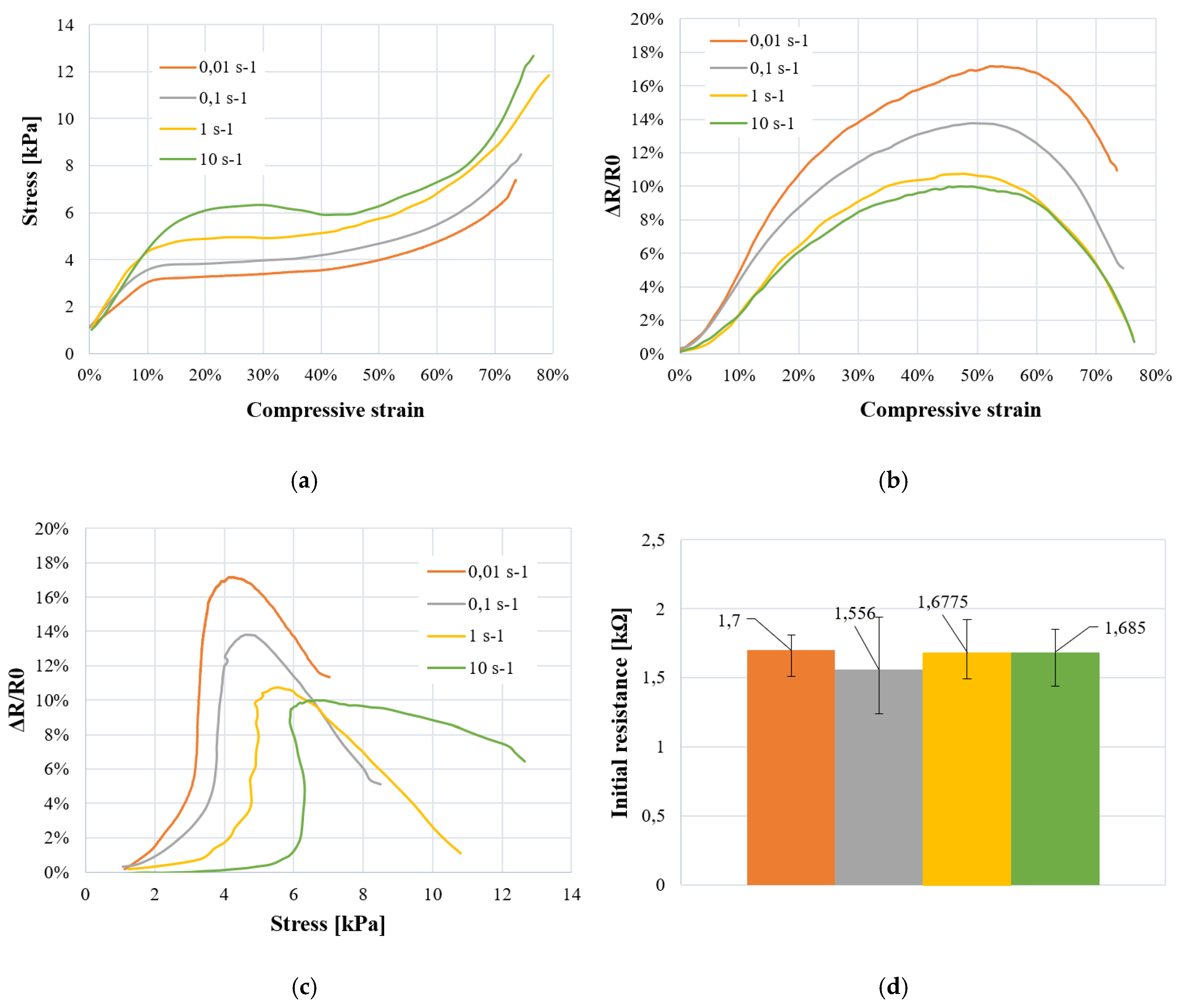
Figure 13.
Analysis of electromechanical parameter (PEM): (a) (ΔR/R0)max represented as a function of R0 for different strain rates; (b) PEM as a function of strain rate in logarithm scale.
Figure 13.
Analysis of electromechanical parameter (PEM): (a) (ΔR/R0)max represented as a function of R0 for different strain rates; (b) PEM as a function of strain rate in logarithm scale.
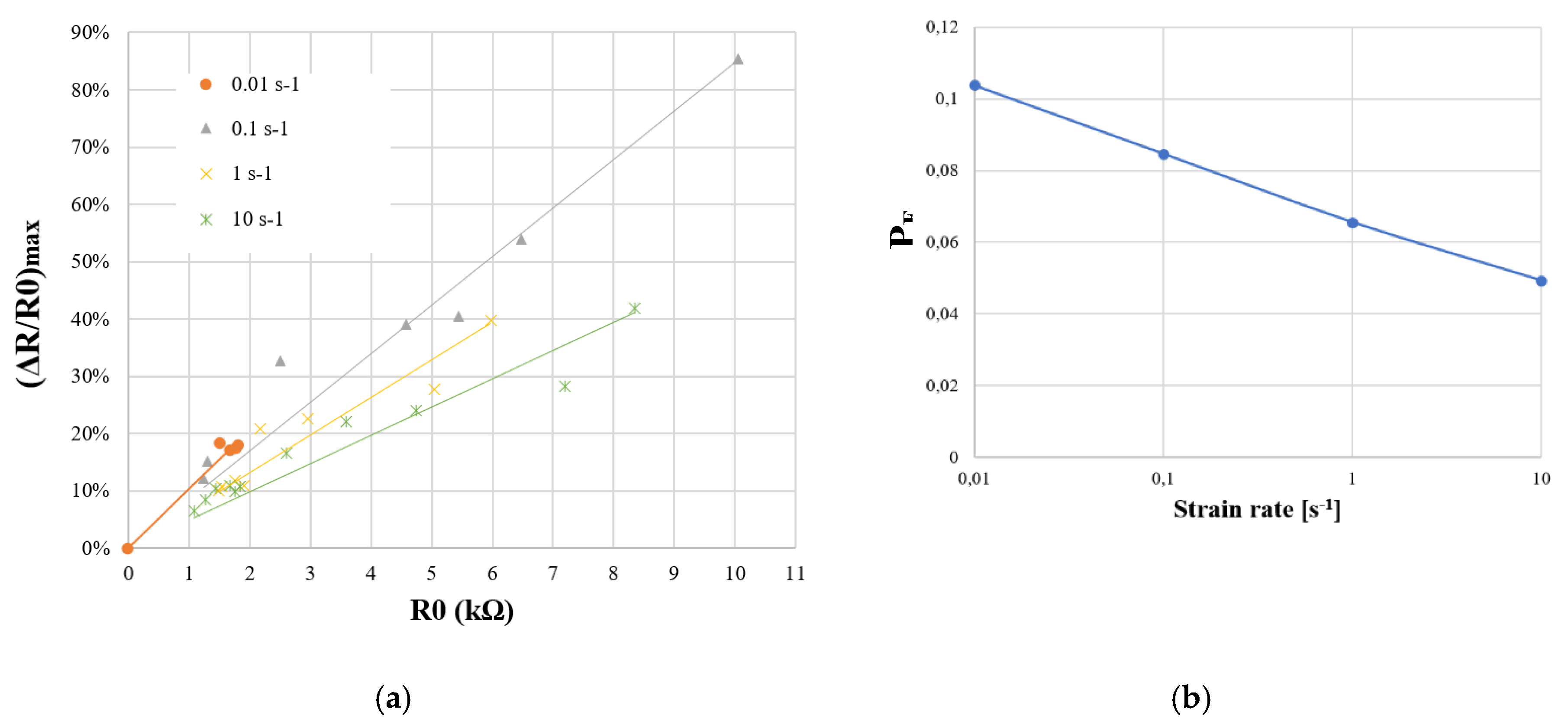
Figure 14.
Electrical response of PUF-AC during light impacts: (a) Temporal response of relative resistance at the minimum (14 mJ) and maximum (227 mJ) impact energies; (b) Maximum resistance ratio as a function of impact energy.
Figure 14.
Electrical response of PUF-AC during light impacts: (a) Temporal response of relative resistance at the minimum (14 mJ) and maximum (227 mJ) impact energies; (b) Maximum resistance ratio as a function of impact energy.
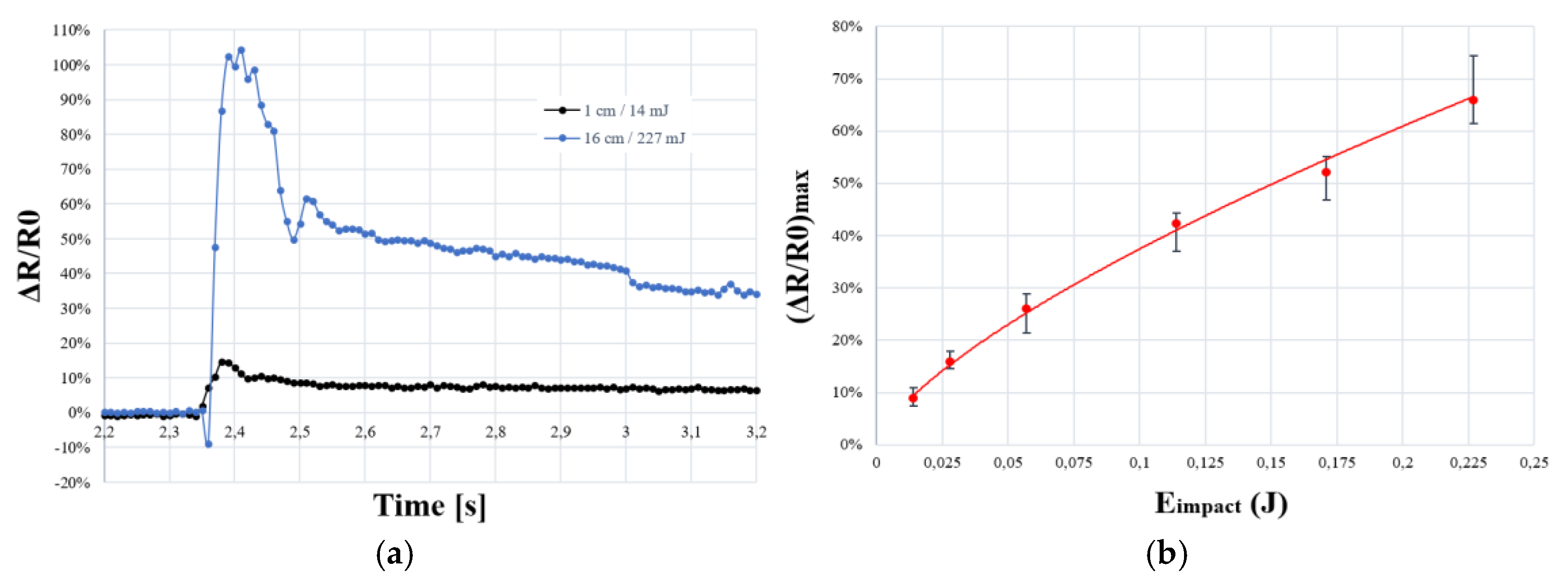
Table 2.
Comparison of electrical data between free and pre-stress configuration.
| Samples | R0 [kΩ] | (ΔR/R0)max | Elasticity | Plateau | Densification | |||
|---|---|---|---|---|---|---|---|---|
| Sε | Sσ | Sε | Sσ | Sε | Sσ | |||
| Free | 5.81 | 49.63% | 1.46 | 0.05 kPa-1 | 0.84 | 0.22 kPa-1 | - 1.27 | 0.04 kPa-1 |
| Pre-stress | 5.71 | 41.35% | 0.62 | 0.02 kPa-1 | 0.71 | 0.19 kPa-1 | - 0.86 | 0.03 kPa-1 |
Table 3.
Electromechanical response data obtained at every strain rate for the PUF AC foam.
| Strain rate [s-1] | Young modulus [kPa] | (ΔR/R)max | Elasticity | Plateau | Densification | |||
|---|---|---|---|---|---|---|---|---|
| Sε | Sσ | Sε | Sσ | Sε | Sσ | |||
| 0.01 | 19.63 | 17.17% | 0.487 | 0.025 kPa-1 | 0.223 | 0.077 kPa-1 | -0.411 | -0.026 kPa-1 |
| 0.1 | 22.881 | 13.89% | 0.446 | 0.019 kPa-1 | 0.211 | 0.074 kPa-1 | -0.454 | -0.026 kPa-1 |
| 1 | 31.058 | 10.76% | 0.334 | 0.008 kPa-1 | 0.141 | 0.037 kPa-1 | -0.436 | -0.02 kPa-1 |
| 10 | 32.35 | 9.97% | 0.287 | 0.002 kPa-1 | 0.112 | 0.044 kPa-1 | -0.413 | -0.005 kPa-1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






