Prerpints.org logo
Preprint
Article

Demonstration of Silicon Nitride Optical Waveguide Parametric Amplifiers Integrated with Graphene Oxide Films

Altmetrics

Downloads

119

Views

31

Comments

0

This version is not peer-reviewed

Submitted:

02 May 2023

Posted:

02 May 2023

You are already at the latest version

Alerts
Abstract
Optical parametric amplification (OPA) represents a powerful solution to achieve broadband amplification in wavelength ranges beyond the scope of conventional gain media, for generating high-power optical pulses, optical microcombs, entangled photon pairs and a wide range of other applications. Here, we demonstrate optical parametric amplifiers based on silicon nitride (Si3N4) waveguides integrated with two-dimensional (2D) layered graphene oxide (GO) films. We achieve precise control over the thickness, length, and position of the GO films using a transfer-free, layer-by-layer coating method combined with accurate window opening in the chip cladding using photolithography. Detailed OPA measurements with a pulsed pump for the fabricated devices with different GO film thicknesses and lengths show a maximum parametric gain of ~24.0 dB, representing a ~12.2 dB improvement relative to the device without GO. We perform a theoretical analysis of the device performance, achieving good agreement with experiment and showing that there is substantial room for further improvement. This work demonstrates a new way of achieving high photonic integrated OPA performance by incorporating 2D materials.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

Introduction

Optical amplifiers are key to many applications1-3 such as optical communications where they have been instrumental with rare-earth-doped fibers4-6 and III-V semiconductors7-9. However, these devices are restricted to specific wavelength ranges determined by the energy gaps between states1,10. In contrast, optical parametric amplification (OPA) can achieve gain across virtually any wavelength range11,12, and so is capable of achieving broadband optical amplification outside of conventional wavelength windows11,13. Since its discovery in 196514, OPA has found applications in many fields such as ultrafast spectroscopy15,16, optical communications5,13, optical imaging17,18, laser processing19,20, and quantum optics21,22. Notably, it has underpinned many new technological breakthroughs such as optical microcombs23,24 and entangled photon pairs25,26.
To achieve OPA, materials with a high optical nonlinearity are needed ‒ either second- (χ(2)) or third-order (χ(3)) nonlinearities27,28, and has been demonstrated in birefringent crystals 29-31, optical fibers10,32,33, and photonic integrated chips1,3,24,34,35. Amongst these, photonic integrated chips offer the advantages of a compact footprint, low power consumption, high stability and scalability, as well as cost reduction through large-scale manufacturing36-38. Despite silicon’s dominance as a platform for linear photonic integrated devices39,40, its significant two photon absorption (TPA) in the near infrared wavelength region and the resulting free carrier absorption lead to a high nonlinear loss3,27, making it challenging to achieve any significant OPA gain in this wavelength range. Other nonlinear integrated material platforms, such as silicon nitride (Si3N4)1,41, silicon rich nitride42,43, doped silica36,44, AlGaAs45,46, chalcogenide47,48, GaP49, and tantala50, exhibit much lower TPA at near infrared wavelengths and have made significant progress over the past decade. However, their comparatively low third-order optical nonlinearity imposes a significant limitation on the OPA gain that they can achieve.
Recently, two-dimensional (2D) materials with ultrahigh optical nonlinearities and broadband response have been integrated on photonic chips to achieve exceptional nonlinear optical performance25,51-54, highlighted by the progress in realizing OPA by exploiting the high second-order optical nonlinearities of monolayer transition metal dichalcogenides (TMDCs)25. Previously55-59, we reported an ultra-high third-order optical nonlinearity in 2D graphene oxide (GO) films that is about 4 orders of magnitude larger than silicon, together with a large bandgap (> 2 eV) that yields a linear loss more than 2 orders of magnitude lower than graphene, and perhaps most importantly, low TPA at near infrared wavelengths ‒ all of which are key to achieving high OPA. In addition, GO has demonstrated high compatibility with various integrated platforms 12,38, along with the capability to achieve precise control over its film thickness and length56,60.
In this work, we demonstrate significantly increased optical parametric gain in Si3N4 waveguides by integrating them with 2D layered GO films. We employ a transfer-free, layer-by-layer coating method to achieve precise control over the GO film thickness, and by using photolithography to open windows in the waveguide cladding we are able to accurately control the GO film length and position. We perform a detailed experimental characterization of the OPA performance of the devices with different GO film thicknesses and lengths, achieving a maximum parametric gain of ~24.0 dB, representing a ~12.2 dB improvement over the uncoated device. By fitting experimental results with theory, we analyse the influence of the applied power, wavelength detuning, and GO film thickness and length on the OPA performance, and in the process demonstrate that there is still significant potential for improved performance. These results verify the effectiveness of the on-chip integration of 2D GO films to improve the OPA performance of photonic integrated devices.

Experimental results

GO properties.Figure 1(a) illustrates the atomic structure and bandgap of GO, which is a derivative of graphene. Unlike graphene, which consists solely of sp2-hybridized carbon atoms, GO contains various oxygen-containing functional groups (OCFGs) such as hydroxyl, carboxyl, and carbonyl groups12. Some of the carbon atoms in GO are sp3-hybridized through σ-bonding with the OCFGs, resulting in a heterogeneous structure. In contrast to graphene, which has a zero bandgap, GO has an opened bandgap resulting from the isolated sp2 domains within the sp3 C–O matrix. The bandgap of GO typically falls between 2.1 eV and 3.6 eV38, resulting in both low linear light absorption and low nonlinear TPA at near-infrared wavelengths that are attractive for nonlinear optical applications54. Moreover, the material properties of GO can be tuned by manipulating the OCFGs to engineer its bandgap, which has enabled a range of photonic, electronic, and optoelectronic applications12.
Figure 1(b) illustrates the principle of signal amplification based on an optical parametric process61. In this process, when pump and idler photons travel collinearly through a nonlinear optical medium, a pump photon excites a virtual energy level. The decay of this energy level is stimulated by a signal photon, resulting in the emission of an identical second signal photon and an idler photon, while conserving both energy and momentum. In processes that involve optical absorption, such as photoluminescence and TPA, real photogenerated carriers are involved, which can alter the quiescent material nonlinear response12,27. In contrast, the optical parametric process operates by virtual excitation of carriers without creating photogenerated carriers. This makes it quasi-instantaneous, with ultrafast response times on the order of femtoseconds1,54. We note that although the parametric gain itself is almost instantaneous, when influenced by nonlinear absorption with much slower recovery times such as that induced by free carriers in silicon27, the net parametric gain can accordingly have a slow time response component.
Device design and fabrication. Figure 1(c) illustrates the schematic of a Si3N4 waveguide integrated with a single layer GO film. Compared to silicon that has a small (indirect) bandgap of ~1.1 eV27, Si3N4 has a large bandgap of ~5.0 eV36 that yields low TPA in the near-infrared region. To enable the interaction between the GO film and the evanescent field of the waveguide mode, a portion of the silica upper cladding was removed to allow for the GO film to be coated on the top surface of the Si3N4 waveguide. Figure 1(d) shows a microscopic image of the fabricated Si3N4 chip integrated with a single layer GO film. The successful coating of the GO film is confirmed by the presence of the representative D (1345 cm-1) and G (1590 cm-1) peaks in the measured Raman spectrum, as shown in Figure 1(e). First, we fabricated low-loss Si3N4 waveguides via CMOS-compatible processes (see Methods). Next, we coated the waveguides with 2D GO films using a transfer-free, solution-based coating method (see Methods). This approach allows for large-area, layer-by-layer film coating with high repeatability and compatibility with various integrated material platforms12,38,62. The thickness of the GO film, characterized via atomic force microscopy measurements, was ~2 nm. The high transmittance and excellent morphology of the fabricated device demonstrate that our GO coating method, based on self-assembly via electrostatic attachment, can achieve conformal film coating in the window opening area without any noticeable wrinkling or stretching. This offers advantages compared to film transfer techniques commonly used for coating other 2D materials like graphene and TMDCs19. The length and position of the GO films can be easily controlled by adjusting the length and position of the windows opened on the silica upper cladding, which provides high flexibility for optimizing the performance of the hybrid waveguides by altering the GO film parameters.
Figure 1(f) shows the dispersion D of the uncoated waveguide and the hybrid waveguides with 1 and 2 layers of GO, calculated with commercial mode solving software using the materials’ refractive indices measured by spectral ellipsometry. The Si3N4 waveguides in all these devices had a cross section of 1.60 μm × 0.72 μm, and the inset in Figure 1(f) depicts the transverse electric (TE) mode profile of the hybrid waveguide with 1 layer of GO. The interaction between the highly nonlinear GO film and the waveguide’s evanescent field enhances the nonlinear optical response of the hybrid waveguide, which is the foundation for improving the OPA performance. We selected TE-polarization for our subsequent measurements since it supports in-plane interaction between the waveguide’s evanescent field and the GO film, which is much stronger than the out-of-plane interaction due to the significant optical anisotropy in 2D materials63,64. In Figure 1(f), it can be observed that all three waveguides exhibit anomalous dispersion, which is crucial for reducing phase mismatch and improving the parametric gain in the optical parametric process. Upon incorporating 1 layer of GO, the hybrid waveguide shows a slightly increased anomalous dispersion compared to waveguides without GO. For the hybrid waveguides with 2 layers of GO, the anomalous dispersion is further enhanced.
Loss measurements. The coating of GO films onto Si3N4 waveguides introduces extra linear and nonlinear loss. Before the OPA measurements, we used the experimental setup in Figure S1 of the Supplementary Information to characterize the linear and nonlinear loss of the fabricated devices. Fiber-to-chip coupling was achieved via lensed fibers butt coupled to inverse-taper couplers at both ends of the Si3N4 waveguides. The coupling loss was ~4.2 dB / facet. We measured three devices, including the uncoated Si3N4 waveguide and hybrid waveguides with 1 and 2 layers of GO. The Si3N4 waveguides in these devices were all ~20 mm in length, while for the hybrid waveguides, windows with a length of ~1.4 mm were opened at a distance of ~0.7 mm from the input port. In our following discussion, the input light power quoted refers to the power coupled into the devices, with the fiber-to-chip coupling loss being excluded.
The linear loss was measured using continuous-wave (CW) light with a power of ~1 mW. Figure 2a shows the insertion loss of the fabricated devices versus wavelength. All devices exhibited nearly a flat spectral response, which suggests the absence of any material absorption or coupling loss that would generate a strong wavelength dependence. By using a cut-back method65, we obtained a propagation loss of ~0.5 dB/cm for the Si3N4 waveguides buried in silica cladding. By comparing the Si3N4 waveguides with and without opened windows in the silica cladding, we deduced a higher propagation loss of ~3.0 dB/cm for the Si3N4 waveguides in the opened window area, which can be attributed to the mitigating effect of the silica cladding on the Si3N4 surface roughness. Finally, using these values and the measured insertion loss of the hybrid waveguides, we extracted an excess propagation loss induced by the GO films of ~3.1 dB/cm and ~6.3 dB/cm for the 1- and 2-layer devices, respectively. Such a loss induced by the GO films is about 2 orders of magnitude lower than Si3N4 waveguides integrated with graphene films66,67, which can be attributed to the large bandgap of GO, resulting in low light absorption at near infrared wavelengths. This is a crucial advantage of GO in OPA applications where low loss is required to achieve a high net parametric gain.
Figure 2b shows the measured insertion loss versus input CW power at a wavelength of ~1550 nm. All devices showed no significant variation in insertion loss when the power was below 30 mW, indicating that the power-dependent loss induced by photo-thermal changes in the GO films was negligible within this range. This observation is consistent with our previous results where photo-thermal changes were only observed for average powers above 40 mW56,68.
The measurement of nonlinear loss was conducted using a fiber pulsed laser (FPL) capable of generating nearly Fourier-transform limited femtosecond optical pulses centered around 1557 nm. The pulse duration and repetition rate were ~180 fs and ~60 MHz, respectively. Figure 2c shows the measured insertion loss versus pulse peak power Ppeak. The average power of the femtosecond optical pulses was adjusted using a variable optical attenuator, ranging from 0.32 mW to 1.94 mW, which corresponds to peak powers ranging from 30 W to 180 W. The insertion loss of the hybrid waveguides decreased as the pulse peak power increased, with the 2-layer device exhibiting a more significant decrease than the 1-layer device. In contrast, the insertion loss of the uncoated Si3N4 waveguide remained constant. These results reflect that the hybrid waveguides experienced saturable absorption (SA) in the GO films, consistent with observations in waveguides incorporating graphene66,69. Additionally, we note that the loss changes observed were not present when using CW light with equivalent average powers. This suggests that the changes are specifically induced by optical pulses with high peak powers. In GO, the SA can be induced by the bleaching of the ground states that are associated with sp2 orbitals (e.g., with an energy gap of ~0.5 eV55) as well as the defect states. Figure 2d shows the SA-induced excess propagation loss (∆SA) versus pulse peak power Ppeak, which was extracted from the result in Figure 2c, with the linear propagation loss being excluded. The negative values of ∆SA indicate that there is a decrease in loss as the peak power increases in the SA process. Such decrease in loss is beneficial for increasing the pump peak power in the OPA process, which helps improve the parametric gain.
OPA experiments. We conducted OPA experiments using the same devices that were fabricated and used for the loss measurements. A schematic of the experimental setup is shown in Figure 3. To generate the pump light required for the OPA experiments, we employed the same FPL that was used for the loss measurements. On the other hand, the signal light was generated through amplification of the CW light from a tunable laser. The pulsed pump and the CW signal were combined by a broadband 50:50 coupler and sent to the device under test (DUT) for the optical parametric process. The polarization of both signals was adjusted to TE polarized using two polarization controllers (PCs). To adjust the power of the pulsed pump, a broadband variable optical attenuator (VOA) was utilized. The output after propagation through the DUT was directed towards an optical spectrum analyzer (OSA) for analysis.
Figure 4a shows the optical spectra after propagation through the uncoated Si3N4 waveguide and the hybrid waveguides with 1 and 2 layers of GO. For all three devices, the input pump peak power and signal power were kept the same at Ppeak = ~180 W and Psignal = ~6 mW, respectively. As the pump light used for the OPA experiments was pulsed, the optical parametric process occurred at a rate equivalent to the repetition rate of the FPL. As a result, both the generated idler and amplified signal also exhibited a pulsed nature with the same repetition rate as that of the FPL. The optical spectra in Figure 4a were analyzed to extract the parametric gain PG experienced by the signal light for the three devices (see Methods). The PG for the uncoated Si3N4 waveguide and the hybrid waveguides with 1 and 2 layers of GO were ~11.8 dB, ~20.4 dB, and ~24.0 dB, respectively. The hybrid waveguides exhibited higher parametric gain compared to the uncoated waveguide, and the 2-layer device had higher parametric gain than the 1-layer device. These results confirm the improved OPA performance in the Si3N4 waveguide by integrating it with 2D GO films. We also note that the hybrid devices showed greater spectral broadening of the pulsed pump caused by self-phase modulation (SPM), which is consistent with our previous observations from SPM experiments57.
The values of PG in Figure 4 are the net parametric gain, over and above the waveguide loss induced by both the GO-coated and uncoated Si3N4 waveguide segments (see Methods). This is different to the “on/off” parametric gain often quoted 11,43, where the waveguide loss is excluded, resulting in higher values of parametric gain. Here, the on-off gains for the waveguides with 0, 1, and 2 layers of GO were ~13. 2 dB, ~22.3 dB, and ~26.2 dB, respectively, which are only slightly higher than their corresponding net gains due to the low loss of the Si3N4 waveguides and the relatively short GO film length. Although the net gain can be increased closer to the on-off gain by reducing the waveguide loss via optimization of the fabrication processes, because the differences between the net and on-off gains are small in our case, there is not much incentive to do this. In the following, we focus our discussion on the net parametric gain PG. This can also ensure a fair comparison of the parametric gain improvement, as different waveguides have different waveguide loss.
Figure 4b shows the measured output optical spectra after propagation through the device with 2 layers of GO for different Ppeak. Figure 4c-i shows the signal parametric gain PG for the uncoated and hybrid waveguides versus input pump peak power, and the parametric gain improvement ∆PG for the hybrid waveguides as compared to the uncoated waveguide is further extracted and shown in Figure 4c-ii. We varied the input pump peak power from ~30 W to ~180 W, which corresponds to the same power range used in Figure 2d for loss measurements. The PG is higher for the hybrid waveguide with 1 layer of GO compared to the uncoated waveguide, and lower than the device with 2 layers of GO. In addition, both PG and ∆PG increase with Ppeak, and a maximum ∆PG of ~12.2 dB was achieved for the 2-layer device at Ppeak = ~180 W. Likewise, we observed similar phenomena when using lower-peak-power picosecond optical pulses for the pump, as shown in Figure S2 of the Supplementary Information.
To evaluate the OPA performance, we conducted experiments where we varied the wavelength detuning, CW signal power, and GO film length. Except for the varied parameters, all other parameters are the same as those in Figure 4. In Figure 5a, the measured signal parametric gain PG and parametric gain improvement ∆PG are plotted against the wavelength detuning Δλ, which is defined as the difference between the CW signal wavelength λsignal and the pump center wavelength λpump. It is observed that both the PG and ∆PG increase as Δλ changes from -12 nm to -22 nm. In Figure 5b, the PG and ∆PG are plotted against the CW signal power Psignal, showing a slight decrease as Psignal increases, which is primarily due to the fact that an increase in Psignal can result in a decrease in PG as per its definition (i.e., PG = Pout,signal / Pin,signal, see Methods). Figure 5c shows the PG and ∆PG versus GO film length. By measuring devices with various GO film lengths, ranging from ~0.2 mm to ~1.4 mm, we observed that those with longer GO films exhibited greater PG and ∆PG values. The PG achieved through the optical parametric process is influenced by several factors, such as the applied powers, optical nonlinearity, dispersion, and loss of the waveguides. These factors will be comprehensively analyzed in the following section.

Analysis and discussion

Optical nonlinearity of hybrid waveguides and GO films. We used the theory from Refs.10,58,70 to model the OPA process in the fabricated devices (see Methods). By fitting the measured PG with theory, we obtained the nonlinear parameter γ of the uncoated and hybrid waveguides. The fit γ for the uncoated Si3N4 waveguide is ~1.11 W-1m-1, which is consistent with the previously reported values in the literature58,71-82. Figure 6a shows the fit γ of the hybrid waveguides as a function of pulse peak power Ppeak. For both devices with different GO film thickness, the lack of any significant variation in γ with Ppeak indicates that the applied power has a negligible effect on the properties of the GO films. This is in contrast to the effects of light with high average optical powers, which can lead to changes in GO’s properties via photo-thermal reduction56,58. The fit values of γ for the devices with 1 and 2 layers of GO are ~14.5 and ~27.3 times greater than the value for the uncoated Si3N4 waveguide. These agree with our earlier work58,59 and indicate a significant improvement in Kerr nonlinearity for the hybrid waveguides.
Based on the fit γ for the hybrid waveguides, we further extracted the Kerr coefficient n2 of the GO films (see Methods), as shown in Figure 6b. The extracted n2 values for the films with 1 and 2 layers are similar, with the former being slightly higher than the latter. The lower n2 for thicker films is likely caused by an increase in inhomogeneous defects within the GO layers and imperfect contact between multiple GO layers. The n2 values for the films with 1 and 2 layers are about 5 orders of magnitude higher than that of Si3N4 (~2.62 × 10-19 m2/W, obtained by fitting the result for the uncoated Si3N4 waveguide), highlighting the tremendous third-order optical nonlinearity of the GO films.
We also quantitatively compare the nonlinear optical performance of the Si3N4 waveguide and the hybrid waveguides by calculating their nonlinear figure of merit FOM. The FOM is determined by balancing a waveguide’s nonlinear parameter against its linear propagation loss, and can be expressed as a function of waveguide length L given by:
FOM (L) = γ × Leff (L)
where γ is the waveguide nonlinear parameter and Leff (L) = [1 - exp (-α×L)] /α is the effective interaction length, with α denoting the linear loss attenuation coefficient. Note that the nonlinear figure of merit defined in Eq. (1) allows for comparison of the nonlinear optical performance of optical waveguides made from different materials. This is distinct from the nonlinear figure of merit commonly used for comparing the nonlinear optical performance of a single material, which is defined as n2/(λ‧βTPA)36, with n2, λ, and βTPA denoting the Kerr coefficient, wavelength, TPA coefficient, respectively.
Figure 6c shows Leff versus L for the Si3N4 waveguide and the hybrid waveguides with 1 and 2 layers of GO. The Si3N4 waveguide has a higher Leff due to its comparably lower linear propagation loss. Figure 6d shows the FOM versus L for the three waveguides. Despite having a lower Leff, the hybrid waveguides exhibit a higher FOM than the Si3N4 waveguide, owing to the significantly improved nonlinear parameter γ for the hybrid waveguides. This indicates that the impact of enhancing the optical nonlinearity is much greater than the degradation caused by the increase in loss, resulting in a significant improvement in the device’s overall nonlinear optical performance.
For the hybrid waveguides that we measured in the OPA experiments, only a specific section of the waveguides was coated with GO films. In Figure 6e,f, we compare PG and ∆PG versus waveguide length L for the hybrid waveguides uniformly coated with GO films, respectively, which were calculated based on the fit γ values (at Ppeak = ~180 W) in Figure 6a. The pump peak power, CW signal power, and wavelength detuning were Ppeak = ~180 W, Psignal = ~6 mW, and Δλ = ~-22 nm, respectively ‒ the same as those in Figure 4a. The corresponding results for the uncoated Si3N4 waveguide are also shown for comparison. The 2-layer device has higher PG and ∆PG values for L < ~5.7 mm but lower values for L > ~5.7 mm, reflecting the trade-off between the increase in optical nonlinearity and waveguide loss. At L = 1.4 mm, the 1-layer and 2-layer devices achieve PG of ~10.5 dB and ~15.6 dB, respectively. When compared to waveguides that have patterned GO films of the same length as those used in our OPA experiments, their total PG (including those provided by both the ~1.4-mm-long GO-coated section and the ~18.6-mm-long uncoated section) are ~20.4 dB and ~24.0 dB, respectively. This highlights the dominant role of the GO-coated section in providing the parametric gain, as well as the fact that a further improvement in ∆PG could be obtained by increasing the length of the GO-coated segments.
Performance improvement by optimizing parameters. Based on the OPA modeling (see Methods) and the fit parameters in Figure 6, we further investigate the margin for performance improvement by optimizing the parameters.
Figure 7a shows the calculated PG for the hybrid waveguides versus pulse peak power Ppeak and CW signal power Psignal. The corresponding results for ∆PG are shown in Figure 7b. In each figure, (i) and (ii) show the results for the devices with 1 and 2 layers of GO, respectively. The black points mark the experimental results in Figure 4, and the black crossings mark the results corresponding to the maximum values of PG or ∆PG. As can be seen, both PG and ∆PG increase with Ppeak but decrease with Psignal, showing agreement with the trends observed in the experimental results. For the device with 1 layer of GO, the maximum PG of ~32.7 dB and ∆PG of ~10.7 dB are achieved at Ppeak = 400 W and Psignal = 1 mW. Whereas for the device with 2 layers of GO, the maximum PG and ∆PG are ~36.9 dB and ~15.0 dB at the same Ppeak and Psignal, respectively. This reflects that there is a large room for improvement by further optimizing the pulse peak power and the CW signal power. In our experiments, the maximum output power of our FPL limited the applied pulse peak power. In addition, we opted to avoid using excessively low CW signal power due to two reasons. First, the CW signal power does not exert a significant influence on PG. Second, as the power of the output pulsed signal diminishes with the decrease of the input CW signal power, it becomes increasingly challenging to extract PG accurately.
Figure 8a shows the calculated PG and ∆PG versus wavelength detuning ∆λ. The dashed curves were calculated based on the fit result at ∆λ = -22 nm, and the data points mark the measured results in Figure 5a. The curves with an ‘M’ shape are consistent with the results in Refs.3,10,11, reflecting the anomalous dispersion of these waveguides. The experimental data points match closely with the simulation curves, thereby confirming the consistency between our experimental results and theory. For the device with 1 layer of GO, the maximum PG of ~34.7 dB and ∆PG of ~14.7 dB are achieved at ∆λ = ~-67 nm and ~-80 nm, respectively. Whereas for the 2-layer device, the maximum PG of ~37.6 dB and ∆PG of ~17.3 dB are achieved at ∆λ = ~-61.8 nm and ~-57.8 nm, respectively. These results highlight the significant potential for improvement through further optimization of the wavelength detuning. In our experiments, the range of wavelength detuning was limited by the operation bandwidth of the erbium-doped fiber amplifier used to amplify the CW signal power.
We also investigate the performance improvement by optimizing the GO film length LGO. Figure 8b shows the calculated PG and ∆PG versus LGO. The dashed curves were calculated based on the fit result at LGO = 1.4 mm, and the data points mark the measured results in Figure 5a. For the device with 1 layer of GO, the maximum PG of ~26.3 dB and ∆PG of ~19.9 dB are achieved at LGO = ~7 mm and ~9.7 mm, respectively. Whereas for the device with 2 layers of GO, the maximum PG of ~27.0 dB and ∆PG of ~17.2 dB are achieved at LGO = ~3.3 mm and ~3.9 mm, respectively. These results suggest that the OPA performance can be improved by further optimizing the length of the GO film. In our experiments, the lengths of the GO films were restricted by the size of the opened windows on the silica cladding (as shown in Figure 1d). Aside from optimizing the GO film length, we would anticipate even higher values of PG and ∆PG for devices with an increased number of GO layers at LGO = 1.4 mm, similar to what we observed in our previous nonlinear optics experiments56,57. This is due to the considerably increased optical nonlinearity of devices with thicker GO films. However, such an increase in optical nonlinearity is accompanied by a rise in loss, making it imperative to balance the trade-off between them.
We investigate the performance by optimizing both ∆λ and LGO simultaneously (see Figure S4 of the Supplementary Information), finding that the 1-layer device has a maximum PG of ~37.4 dB and maximum ∆PG of ~31.5 dB, while the 2-layer device reaches PG up to ~37.8 dB and ∆PG up to ~27.3 dB. In addition, by further increasing the pump peak power from 180 W to 400 W, even higher performance is achieved, with the 1-layer device reaching a maximum PG of ~43.7 dB and maximum ∆PG of ~40.1 dB, and the 2-layer device a maximum PG of ~43.8 dB and maximum ∆PG of ~37.3 dB (see Figure S5 of the Supplementary Information). According to these simulation results, it is found that if both ∆λ and LGO are optimized simultaneously, there is not much difference between the maximum PG for the 1- and 2- layer devices. However, the 1-layer device still yields a slightly higher ∆PG because of its lower loss compared with the 2-layer device. For this reason, devices coated with more GO layers will have lower maximum ∆PG.
Finally, we also investigate the improvement in PG and ∆PG by optimizing the coating position of the GO films (see Figure S6 of the Supplementary Information), as well as the influence of the SA of GO on the OPA performance (see Figure S7 of the Supplementary Information). We find that although optimizing the coating position can lead to further improvements in PG and ∆PG, the extent of these improvements is not as substantial as those achieved through optimization of Δλ and LGO. In addition, we find that the SA of GO has a positive impact on enhancing PG and ∆PG, especially for devices with thicker GO films. These results have significant implications for devices involving microcombs83-138 that require high on-chip parametric gain, as well as linear, nonlinear 139-158 and potentially quantum159-170 optical chips.

Conclusion

In summary, we experimentally demonstrate significantly improved OPA performance in Si3N4 waveguides integrated with 2D GO films compared to uncoated waveguides. We fabricate GO-Si3N4 hybrid waveguides with precise control of the thickness, length, and position of the GO films. Detailed OPA measurements are performed for the fabricated devices using a pulsed pump and CW signal. The results show that up to ~24.0 dB parametric gain is achieved for the hybrid devices, representing a ~12.2 dB improvement relative to the device without GO. Based on the experimental results, the influence of the pump / signal power, wavelength detuning, and GO film thickness / length on the OPA performance is theoretically analyzed, showing that further improvement can be achieved by optimizing these parameters. We calculate that a parametric gain of ~37.8 dB and a parametric gain improvement of ~31.5 dB should be possible by optimizing the wavelength detuning and GO film length, and even higher to 43.8 dB by increasing the pump peak power to 400 W. Our study provides valuable insights into the promising potential of on-chip integration of 2D GO films for enhancing the OPA performance of photonic integrated devices, of benefit to many nonlinear optical applications.

Materials and methods

Fabrication of Si3N4 waveguides. The Si3N4 waveguides were fabricated via CMOS compatible processes72. First, a Si3N4 film was deposited on a silicon wafer with a 3-μm-thick wet oxidation layer on its top surface, using a low-pressure chemical vapor deposition (LPCVD) method. The deposition was carried out in two steps involving a twist-and-grow process, resulting in a crack-free film. Next, waveguides were created using 248-nm deep ultraviolet lithography followed by fluorocarbon-based dry etching with CF4/CHF3/Ar, which resulted in a low sidewall surface roughness for the waveguides. After waveguide patterning, we employed a multi-step, chemical-physical, in-situ annealing sequence using H2, O2, and N2 to further reduce the loss of the Si3N4 waveguides. Subsequently, a silica upper cladding was deposited to encapsule the Si3N4 waveguides via multi-step low-temperature oxide deposition at 400 °C. This was achieved through a low-rate deposition of a liner, followed by the filling of the silica layer using high-density plasma enhanced chemical vapor deposition (HD-PECVD). Finally, we employed lithography and dry etching to create windows on the silica cladding extending to the top surface of the Si3N4 waveguides.
Synthesis and coating of GO films. Before GO film coating, a GO solution with small GO flack size (< 100 nm) was prepared by using a modified Hummers method followed by vigorous sonication via a Branson Digital Sonifier62. The coating of 2D layered GO films was then achieved by using a transfer-free method that allows for layer-by-layer GO film deposition with precise control of the film thickness, as we did previously171,172. During the coating process, four steps for in-situ assembly of monolayer GO films were repeated to construct multi-layered films on the fabricated Si3N4 chips with opened windows, including (i) immerse substrate into a 2.0% (w/v) aqueous PDDA (Sigma-Aldrich) solution; (ii) rinse with a stream of deionized distilled water and dry with N2; (iii) immerse the PDDA-coated substrate into GO solution; and (iv) rinse with a stream of deionized water and dry with N2. After the film coating, the chip was dried in a drying oven.
Extracting parametric gain from the measured optical spectra. We used the same methods as those in Refs. 11,43 to extract the signal parametric gain from the measured optical spectra we obtained through OPA experiments. The peak power of the pulsed signal after propagation through the fabricated devices was derived from the measured output optical spectra according to:
P = ∬ P signal ,   out ( λ ) d λ f rep   ×   T
where Psignal, out (λ) is the average output power spectrum of the signal as a function of wavelength λ, frep is the repetition rate of the FPL, and T is the pulse width. In our calculation of Psignal, peak, the power residing in the CW signal line was subtracted from the spectrum of Psignal, out (λ).
After deriving Psignal, peak, the signal parametric gain PG was calculated as:
PG (dB) = 10 × log10 (Psignal, peak / Psignal)
where Psignal is the CW signal power at the input of the waveguide. According to Eq. (3), the PG in our discussion is the net gain over and above the waveguide loss (including that induced by both the Si3N4 waveguide and the GO film). In contrast, the on/off parametric gain is defined as11,43
PGon-off (dB) = 10 × log10 (Psignal, peak / Psignal, out)
where Psignal,out is the CW signal power at the output of the waveguide when the pump is turned off. The parametric gain calculated using Eq. (4) is higher than that calculated using Eq. (3) since Psignal,out is lower than Psignal.
OPA Modeling. The third-order optical parametric process in the GO-coated Si3N4 waveguides was modeled based on the theory from Refs.10,58,70. Assuming negligible depletion of the pump and signal powers due to the generation of the idler, and considering only the short wavelength idler, the coupled differential equations for the dominant degenerate FWM process can be given by10,65
d A p ( z ) dz = - α p 2 A p z   + j γ p A p z 2 + 2 A s z 2 + 2 A i z 2 A p z
+ j 2 γ p A p * ( z ) A s z A i z exp ( j ∆ β z )
d A s ( z ) dz = - α s 2 A s z + j γ s A s z 2 + 2 A p z 2 + 2 A i z 2 A s z
+ j γ s A i * ( z ) A p 2 ( z ) exp ( - j ∆ β z )
d A i ( z ) dz = - α i 2 A i z + j γ i A i z 2 + 2 A p z 2 + 2 A s z 2 A i z
+ j γ i A s * ( z ) A p 2 ( z ) exp ( - j ∆ β z )  
where Ap,s,i are the amplitudes of the pump, signal and idler waves along the z axis, which is defined as the light propagation direction, αp,s,i are the loss factor including both the linear loss and the SA-induced nonlinear loss, Δβ = βs + βi – 2βp is the linear phase mismatch, with βp,s,i denoting the propagation constants of the pump, signal and idler waves, and γp,s,i are the waveguide nonlinear parameters. In our case, where the wavelength detuning range was small (≤ 10 nm), the linear loss and the nonlinear parameter are assumed to be constant, i.e., αp =αs = αi = α, γp = γs = γi = γ.
In Eqs. (5) − (7), the dispersions βp,s,i were calculated via commercial mode solving software using the refractive index n of layered GO films measured by spectral ellipsometry. Given that the photo-thermal changes are sensitive to the average power in the hybrid waveguides, which was below 2 mW for the femtosecond optical pulses studied here, they were considered negligible. By numerically solving Eqs. (5) – (7), the PG was calculated via
PG (dB) = 10 × log10[|As(L)|2/|As(0)|2]
where L is the length of the Si3N4 waveguide (i.e., 20 mm). For our devices with patterned GO films, the waveguides were divided into uncoated Si3N4 (without GO films) and hybrid (with GO films) segments with different α, γ and βp,s,i. The differential equations were solved for each segment, with the output from the previous segment as the input for the subsequent segment.
Extracting n2 of GO films. The Kerr coefficient n2 of the layered GO films is extracted from the nonlinear parameter γ of the hybrid waveguides according to:56,70
γ = 2 π λ c   ∬ D n 0 2 x ,   y n 2 x ,   y S z 2 dxdy ∬ D n 0 x ,   y S z dxdy 2
where λc is the pulse central wavelength, D is the integral of the optical fields over the material regions, Sz is the time-averaged Poynting vector calculated using Lumerical FDTD commercial mode solving software, n0 (x, y) and n2 (x, y) are the linear refractive index and n2 profiles over the waveguide cross section, respectively. The values of n2 for silica and Si3N4 used in our calculation were 2.60 × 10 –20 m2/W36 and 2.62 × 10-19 m2/W, respectively, the latter obtained by fitting the experimental results for the uncoated Si3N4 waveguide.

Conflict of Interest

The authors declare no competing financial interest.

References

  1. Riemensberger, J.; Kuznetsov, N.; Liu, J.; He, J.; Wang, R.N.; Kippenberg, T.J. A photonic integrated continuous-travelling-wave parametric amplifier. Nature 2022, 612, 56–61. [Google Scholar] [CrossRef]
  2. Liu, Y.; Qiu, Z.; Ji, X.; Lukashchuk, A.; He, J.; Riemensberger, J.; Hafermann, M.; Wang, R.N.; Liu, J.; Ronning, C.; et al. A photonic integrated circuit–based erbium-doped amplifier. Science 2022, 376, 1309–1313. [Google Scholar] [CrossRef]
  3. Foster, M.A.; Turner, A.C.; Sharping, J.E.; Schmidt, B.S.; Lipson, M.; Gaeta, A.L. Broad-band optical parametric gain on a silicon photonic chip. Nature 2006, 441, 960–963. [Google Scholar] [CrossRef]
  4. Desurvire, E.; Simpson, J.R.; Becker, P.C. High-gain erbium-doped traveling-wave fiber amplifier. Opt. Lett. 1987, 12, 888–890. [Google Scholar] [CrossRef]
  5. Temprana, E.; Myslivets, E.; Kuo, B.-P.; Liu, L.; Ataie, V.; Alic, N.; Radic, S. Overcoming Kerr-induced capacity limit in optical fiber transmission. Science 2015, 348, 1445–1448. [Google Scholar] [CrossRef]
  6. Barnard, C.; Myslinski, P.; Chrostowski, J.; Kavehrad, M. Analytical model for rare-earth-doped fiber amplifiers and lasers. IEEE J. Quantum Electron. 1994, 30, 1817–1830. [Google Scholar] [CrossRef]
  7. Stubkjaer, K. Semiconductor optical amplifier-based all-optical gates for high-speed optical processing. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1428–1435. [Google Scholar] [CrossRef]
  8. Durhuus, T.; Mikkelsen, B.; Joergensen, C.; Danielsen, S.L.; Stubkjaer, K. All-optical wavelength conversion by semiconductor optical amplifiers. J. Light. Technol. 1996, 14, 942–954. [Google Scholar] [CrossRef]
  9. Haq, B.; Kumari, S.; Van Gasse, K.; Zhang, J.; Gocalinska, A.; Pelucchi, E.; Corbett, B.; Roelkens, G. Micro-Transfer-Printed III-V-on-Silicon C-Band Semiconductor Optical Amplifiers. Laser Photon- Rev. 2020, 14, 1900364. [Google Scholar] [CrossRef]
  10. Hansryd, J.; Andrekson, P.; Westlund, M.; Li, J.; Hedekvist, P.-O. Fiber-based optical parametric amplifiers and their applications. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 506–520. [Google Scholar] [CrossRef]
  11. Liu, X.; Osgood, R.M.; Vlasov, Y.A.; Green, W.M.J. Mid-infrared optical parametric amplifier using silicon nanophotonic waveguides. Nat. Photon- 2010, 4, 557–560. [Google Scholar] [CrossRef]
  12. Wu, J.; Lin, H.; Moss, D.J.; Loh, K.P.; Jia, B. Graphene oxide for photonics, electronics and optoelectronics. Nat. Rev. Chem. 2023, 7, 162–183. [Google Scholar] [CrossRef]
  13. Marhic, M.E.; Andrekson, P.A.; Petropoulos, P.; Radic, S.; Peucheret, C.; Jazayerifar, M. Fiber optical parametric amplifiers in optical communication systems. Laser Photon- Rev. 2015, 9, 50–74. [Google Scholar] [CrossRef]
  14. Wang, C.C.; Racette, G.W. MEASUREMENT OF PARAMETRIC GAIN ACCOMPANYING OPTICAL DIFFERENCE FREQUENCY GENERATION. Appl. Phys. Lett. 1965, 6, 169–171. [Google Scholar] [CrossRef]
  15. Suh, M.-G.; Yang, Q.-F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef]
  16. Yang, Q.-F.; Shen, B.; Wang, H.; Tran, M.; Zhang, Z.; Yang, K.Y.; Wu, L.; Bao, C.; Bowers, J.; Yariv, A.; et al. Vernier spectrometer using counterpropagating soliton microcombs. Science 2019, 363, 965–968. [Google Scholar] [CrossRef]
  17. Zeng, X.; Zheng, S.; Cai, Y.; Lin, Q.; Liang, J.; Lu, X.; Li, J.; Xie, W.; Xu, S. High-spatial-resolution ultrafast framing imaging at 15 trillion frames per second by optical parametric amplification. Adv. Photon- 2020, 2, 056002. [Google Scholar] [CrossRef]
  18. Vaughan, P.M.; Trebino, R. Optical-parametric-amplification imaging of complex objects. Opt. Express 2011, 19, 8920–8929. [Google Scholar] [CrossRef]
  19. Jia, L.; Wu, J.; Zhang, Y.; Qu, Y.; Jia, B.; Chen, Z.; Moss, D.J. Fabrication Technologies for the On-Chip Integration of 2D Materials. Small Methods 2022, 6, 2101435. [Google Scholar] [CrossRef]
  20. El-Kady, M.F.; Strong, V.; Dubin, S.; Kaner, R.B. Laser Scribing of High-Performance and Flexible Graphene-Based Electrochemical Capacitors. Science 2012, 335, 1326–1330. [Google Scholar] [CrossRef]
  21. Reimer, C.; Kues, M.; Roztocki, P.; Wetzel, B.; Grazioso, F.; Little, B.E.; Chu, S.T.; Johnston, T.; Bromberg, Y.; Caspani, L.; et al. Generation of multiphoton entangled quantum states by means of integrated frequency combs. Science 2016, 351, 1176–1180. [Google Scholar] [CrossRef] [PubMed]
  22. Kues, M.; Reimer, C.; Roztocki, P.; Cortés, L.R.; Sciara, S.; Wetzel, B.; Zhang, Y.; Cino, A.; Chu, S.T.; Little, B.E.; et al. On-chip generation of high-dimensional entangled quantum states and their coherent control. Nature 2017, 546, 622–626. [Google Scholar] [CrossRef]
  23. Del’haye, P.; Schliesser, A.; Arcizet, O.; Wilken, T.; Holzwarth, R.; Kippenberg, T.J. Optical frequency comb generation from a monolithic microresonator. Nature 2007, 450, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
  24. Sun, Y.; Wu, J.; Tan, M.; Xu, X.; Li, Y.; Morandotti, R.; Mitchell, A.; Moss, D.J. Applications of optical microcombs. Adv. Opt. Photon- 2023, 15, 86–175. [Google Scholar] [CrossRef]
  25. Trovatello, C.; Marini, A.; Xu, X.; Lee, C.; Liu, F.; Curreli, N.; Manzoni, C.; Conte, S.D.; Yao, K.; Ciattoni, A.; et al. Optical parametric amplification by monolayer transition metal dichalcogenides. Nat. Photon- 2020, 15, 6–10. [Google Scholar] [CrossRef]
  26. Sciarrino, F.; Vitelli, C.; De Martini, F.; Glasser, R.; Cable, H.; Dowling, J.P. Experimental sub-Rayleigh resolution by an unseeded high-gain optical parametric amplifier for quantum lithography. Phys. Rev. A 2008, 77, 012324. [Google Scholar] [CrossRef]
  27. Leuthold, J.; Koos, C.; Freude, W. Nonlinear silicon photonics. Nat. Photon- 2010, 4, 535–544. [Google Scholar] [CrossRef]
  28. Boes, A.; Chang, L.; Langrock, C.; Yu, M.; Zhang, M.; Lin, Q.; Lončar, M.; Fejer, M.; Bowers, J.; Mitchell, A. Lithium niobate photonics: Unlocking the electromagnetic spectrum. Science 2023, 379, 379. [Google Scholar] [CrossRef]
  29. Baumgartner, R.; Byer, R. Optical parametric amplification. IEEE J. Quantum Electron. 1979, 15, 432–444. [Google Scholar] [CrossRef]
  30. Petrov, V.; Yelisseyev, A.; Isaenko, L.; Lobanov, S.; Titov, A.; Zondy, J.-J. Second harmonic generation and optical parametric amplification in the mid-IR with orthorhombic biaxial crystals LiGaS 2 and LiGaSe 2. Appl. Phys. B Laser Opt. 2004, 78, 543–546. [Google Scholar] [CrossRef]
  31. Schmidt, B.E.; Thiré, N.; Boivin, M.; Laramée, A.; Poitras, F.; Lebrun, G.; Ozaki, T.; Ibrahim, H.; Légaré, F. Frequency domain optical parametric amplification. Nat. Commun. 2014, 5, 3643. [Google Scholar] [CrossRef] [PubMed]
  32. Marhic, M.E.; Kagi, N.; Chiang, T.-K.; Kazovsky, L.G. Broadband fiber optical parametric amplifiers. Opt. Lett. 1996, 21, 573–575. [Google Scholar] [CrossRef] [PubMed]
  33. Marhic, M.; Wong, K.-Y.; Kazovsky, L. Wide-Band Tuning of the Gain Spectra of One-Pump Fiber Optical Parametric Amplifiers. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 1133–1141. [Google Scholar] [CrossRef]
  34. Razzari, L.; Duchesne, D.; Ferrera, M.; Morandotti, R.; Chu, S.; Little, B.E.; Moss, D.J. CMOS-compatible integrated optical hyper-parametric oscillator. Nat. Photon- 2009, 4, 41–45. [Google Scholar] [CrossRef]
  35. Pasquazi, A.; Park, Y.; Azaña, J.; Légaré, F.; Morandotti, R.; Little, B.E.; Chu, S.T.; Moss, D.J. Efficient wavelength conversion and net parametric gain via Four Wave Mixing in a high index doped silica waveguide. Opt. Express 2010, 18, 7634–7641. [Google Scholar] [CrossRef] [PubMed]
  36. Moss, D.; Morandotti, R.; Gaeta, A.L.; Lipson, M. New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics. Nat. Photonics 2013, 7, 597–607. [Google Scholar] [CrossRef]
  37. Arianfard, H.; Juodkazis, S.; Moss, D.J.; Wu, J. Sagnac interference in integrated photonics. Appl. Phys. Rev. 2023, 10, 011309. [Google Scholar] [CrossRef]
  38. Wu, J.; Jia, L.; Zhang, Y.; Qu, Y.; Jia, B.; Moss, D.J. Graphene Oxide for Integrated Photonics and Flat Optics. Adv. Mater. 2021, 33, e2006415. [Google Scholar] [CrossRef]
  39. Wu, J.; Xu, X.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. RF Photonics: An Optical Microcombs’ Perspective. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–20. [Google Scholar] [CrossRef]
  40. Wu, J.; Cao, P.; Pan, T.; Yang, Y.; Qiu, C.; Tremblay, C.; Su, Y. Compact on-chip 1 × 2 wavelength selective switch based on silicon microring resonator with nested pairs of subrings. Photon- Res. 2014, 3. [Google Scholar] [CrossRef]
  41. Liu, J.; Lucas, E.; Raja, A.S.; He, J.; Riemensberger, J.; Wang, R.N.; Karpov, M.; Guo, H.; Bouchand, R.; Kippenberg, T.J. Photonic microwave generation in the X- and K-band using integrated soliton microcombs. Nat. Photon- 2020, 14, 486–491. [Google Scholar] [CrossRef]
  42. Wang, T.; Ng, D.K.T.; Ng, S.; Toh, Y.; Chee, A.K.L.; Chen, G.F.R.; Wang, Q.; Tan, D.T.H. Supercontinuum generation in bandgap engineered, back-end CMOS compatible silicon rich nitride waveguides. Laser Photon- Rev. 2015, 9, 498–506. [Google Scholar] [CrossRef]
  43. Ooi, K.J.A.; Ng, D.K.T.; Wang, T.; Chee, A.K.L.; Ng, S.K.; Wang, Q.; Ang, L.K.; Agarwal, A.M.; Kimerling, L.C.; Tan, D.T.H. Pushing the limits of CMOS optical parametric amplifiers with USRN:Si7N3 above the two-photon absorption edge. Nat. Commun. 2017, 8, 13878. [Google Scholar] [CrossRef] [PubMed]
  44. Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef] [PubMed]
  45. Chang, L.; Xie, W.; Shu, H.; Yang, Q.-F.; Shen, B.; Boes, A.; Peters, J.D.; Jin, W.; Xiang, C.; Liu, S.; et al. Ultra-efficient frequency comb generation in AlGaAs-on-insulator microresonators. Nat. Commun. 2020, 11, 1–8. [Google Scholar] [CrossRef]
  46. Yan, Z.; He, H.; Liu, H.; Iu, M.; Ahmed, O.; Chen, E.; Akasaka, Y.; Ikeuchi, T.; Helmy, A.S. An Optical Parametric Amplifier via $ \chi ^{(2)}$ in AlGaAs Waveguides. J. Light. Technol. 2022, 40, 5943–5951. [Google Scholar] [CrossRef]
  47. Kim, D.-G.; Han, S.; Hwang, J.; Do, I.H.; Jeong, D.; Lim, J.-H.; Lee, Y.-H.; Choi, M.; Choi, D.-Y.; Lee, H. Universal light-guiding geometry for on-chip resonators having extremely high Q-factor. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef]
  48. Lamont, M.R.; Luther-Davies, B.; Choi, D.-Y.; Madden, S.; Gai, X.; Eggleton, B.J. Net-gain from a parametric amplifier on a chalcogenide optical chip. Opt. Express 2008, 16, 20374–20381. [Google Scholar] [CrossRef]
  49. Wilson, D.J.; Schneider, K.; Hönl, S.; Anderson, M.; Baumgartner, Y.; Czornomaz, L.; Kippenberg, T.J.; Seidler, P. Integrated gallium phosphide nonlinear photonics. Nat. Photon- 2019, 14, 57–62. [Google Scholar] [CrossRef]
  50. Jung, H.; Yu, S.-P.; Carlson, D.R.; Drake, T.E.; Briles, T.C.; Papp, S.B. Tantala Kerr nonlinear integrated photonics. Optica 2021, 8, 811–817. [Google Scholar] [CrossRef]
  51. Gu, T.; Petrone, N.; McMillan, J.F.; van der Zande, A.; Yu, M.; Lo, G.Q.; Kwong, D.L.; Hone, J.; Wong, C.W. Regenerative oscillation and four-wave mixing in graphene optoelectronics. Nat. Photon- 2012, 6, 554–559. [Google Scholar] [CrossRef]
  52. Jiang, T.; Huang, D.; Cheng, J.; Fan, X.; Zhang, Z.; Shan, Y.; Yi, Y.; Dai, Y.; Shi, L.; Liu, K.; et al. Gate-tunable third-order nonlinear optical response of massless Dirac fermions in graphene. Nat. Photon- 2018, 12, 430–436. [Google Scholar] [CrossRef]
  53. Seyler, K.L.; Schaibley, J.R.; Gong, P.; Rivera, P.; Jones, A.M.; Wu, S.; Yan, J.; Mandrus, D.G.; Yao, W.; Xu, X. Electrical control of second-harmonic generation in a WSe2 monolayer transistor. Nat. Nanotechnol. 2015, 10, 407–411. [Google Scholar] [CrossRef] [PubMed]
  54. Zhang, Y.; Wu, J.; Jia, L.; Qu, Y.; Yang, Y.; Jia, B.; Moss, D.J. Graphene Oxide for Nonlinear Integrated Photonics. Laser Photon- Rev. 2023, 17. [Google Scholar] [CrossRef]
  55. Zheng, X.; Jia, B.; Chen, X.; Gu, M. In Situ Third-Order Non-linear Responses During Laser Reduction of Graphene Oxide Thin Films Towards On-Chip Non-linear Photonic Devices. Adv. Mater. 2014, 26, 2699–2703. [Google Scholar] [CrossRef] [PubMed]
  56. Wu, J.; Yang, Y.; Qu, Y.; Jia, L.; Zhang, Y.; Xu, X.; Chu, S.T.; Little, B.E.; Morandotti, R.; Jia, B.; et al. 2D Layered Graphene Oxide Films Integrated with Micro-Ring Resonators for Enhanced Nonlinear Optics. Small 2020, 16, 1906563. [Google Scholar] [CrossRef] [PubMed]
  57. Zhang, Y.; Wu, J.; Yang, Y.; Qu, Y.; Jia, L.; Moein, T.; Jia, B.; Moss, D.J. Enhanced Kerr Nonlinearity and Nonlinear Figure of Merit in Silicon Nanowires Integrated with 2D Graphene Oxide Films. ACS Appl. Mater. Interfaces 2020, 12, 33094–33103. [Google Scholar] [CrossRef] [PubMed]
  58. Qu, Y.; Wu, J.; Yang, Y.; Zhang, Y.; Liang, Y.; El Dirani, H.; Crochemore, R.; Demongodin, P.; Sciancalepore, C.; Grillet, C.; et al. Enhanced Four-Wave Mixing in Silicon Nitride Waveguides Integrated with 2D Layered Graphene Oxide Films. Adv. Opt. Mater. 2020, 8. [Google Scholar] [CrossRef]
  59. Zhang, Y.; Wu, J.; Yang, Y.; Qu, Y.; Jia, L.; El Dirani, H.; Kerdiles, S.; Sciancalepore, C.; Demongodin, P.; Grillet, C.; et al. Enhanced Supercontinuum Generation in Integrated Waveguides Incorporated with Graphene Oxide Films. Adv. Mater. Technol. 2023, 8. [Google Scholar] [CrossRef]
  60. Wu, J.; Yang, Y.; Qu, Y.; Xu, X.; Liang, Y.; Chu, S.T.; Little, B.E.; Morandotti, R.; Jia, B.; Moss, D.J. Graphene Oxide Waveguide and Micro-Ring Resonator Polarizers. Laser Photon- Rev. 2019, 13, 1900056. [Google Scholar] [CrossRef]
  61. Boyd, R. W. Nonlinear optics. (Academic press, 2020).
  62. Yang, Y.; Lin, H.; Zhang, B.Y.; Zhang, Y.; Zheng, X.; Yu, A.; Hong, M.; Jia, B. Graphene-Based Multilayered Metamaterials with Phototunable Architecture for on-Chip Photonic Devices. ACS Photon- 2019, 6, 1033–1040. [Google Scholar] [CrossRef]
  63. Bao, Q.; Zhang, H.; Wang, B.; Ni, Z.; Lim, C.H.Y.X.C.; Wang, Y.Y.; Tang, D.Y.D.; Loh, K. Broadband graphene polarizer. Nat. Photon- 2011, 5, 411–415. [Google Scholar] [CrossRef]
  64. Lin, H.; Song, Y.; Huang, Y.; Kita, D.; Deckoff-Jones, S.; Wang, K.; Li, L.; Li, J.; Zheng, H.; Luo, Z.; et al. Chalcogenide glass-on-graphene photonics. Nat. Photonics 2017, 11, 798–805. [Google Scholar] [CrossRef]
  65. Koos, C.; Vorreau, P.; Vallaitis, T.; Dumon, P.; Bogaerts, W.; Baets, R.; Esembeson, B.; Biaggio, I.; Michinobu, T.; Diederich, F.; et al. All-optical high-speed signal processing with silicon–organic hybrid slot waveguides. Nat. Photon- 2009, 3, 216–219. [Google Scholar] [CrossRef]
  66. Demongodin, P.; El Dirani, H.; Lhuillier, J.; Crochemore, R.; Kemiche, M.; Wood, T.; Callard, S.; Rojo-Romeo, P.; Sciancalepore, C.; Grillet, C.; et al. Ultrafast saturable absorption dynamics in hybrid graphene/Si3N4 waveguides. APL Photon- 2019, 4, 076102. [Google Scholar] [CrossRef]
  67. Alexander, K.; Savostianova, N.A.; Mikhailov, S.A.; Kuyken, B.; Van Thourhout, D. Electrically Tunable Optical Nonlinearities in Graphene-Covered SiN Waveguides Characterized by Four-Wave Mixing. ACS Photon- 2017, 4, 3039–3044. [Google Scholar] [CrossRef]
  68. Qu, Y.; Yang, Y.; Wu, J.; Zhang, Y.; Jia, L.; El Dirani, H.; Crochemore, R.; Sciancalepore, C.; Demongodin, P.; Grillet, C.; et al. Photo-Thermal Tuning of Graphene Oxide Coated Integrated Optical Waveguides. Micromachines 2022, 13, 1194. [Google Scholar] [CrossRef]
  69. Wang, H.; Yang, N.; Chang, L.; Zhou, C.; Li, S.; Deng, M.; Li, Z.; Liu, Q.; Zhang, C.; Li, Z.; et al. CMOS-compatible all-optical modulator based on the saturable absorption of graphene. Photon- Res. 2020, 8, 468–474. [Google Scholar] [CrossRef]
  70. Yang, Y.; Wu, J.; Xu, X.; Liang, Y.; Chu, S.T.; Little, B.E.; Morandotti, R.; Jia, B.; Moss, D.J. Invited Article: Enhanced four-wave mixing in waveguides integrated with graphene oxide. APL Photon- 2018, 3, 120803. [Google Scholar] [CrossRef]
  71. Zhang, Y.; Wu, J.; Yang, Y.; Qu, Y.; El Dirani, H.; Crochemore, R.; Sciancalepore, C.; Demongodin, P.; Grillet, C.; Monat, C.; et al. Enhanced self-phase modulation in silicon nitride waveguides integrated with 2D graphene oxide films. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1–13. [Google Scholar] [CrossRef]
  72. El Dirani, H.; Youssef, L.; Petit-Etienne, C.; Kerdiles, S.; Grosse, P.; Monat, C.; Pargon, E.; Sciancalepore, C. Ultralow-loss tightly confining Si3N4 waveguides and high-Q microresonators. Opt. Express 2019, 27, 30726–30740. [Google Scholar] [CrossRef] [PubMed]
  73. Qu, Y.; Yang, Y.; Wu, J.; Zhang, Y.; Jia, L.; El Dirani, H.; Crochemore, R.; Sciancalepore, C.; Demongodin, P.; Grillet, C.; et al. Photo-Thermal Tuning of Graphene Oxide Coated Integrated Optical Waveguides. Micromachines 2022, 13, 1194. [Google Scholar] [CrossRef] [PubMed]
  74. Zhang, Y.; Wu, J.; Yang, Y.; Qu, Y.; Jia, L.; Jia, B.; Moss, D.J. Enhanced Spectral Broadening of Femtosecond Optical Pulses in Silicon Nanowires Integrated with 2D Graphene Oxide Films. Micromachines 2022, 13, 756. [Google Scholar] [CrossRef] [PubMed]
  75. Jia, L.; Wu, J.; Zhang, Y.; Qu, Y.; Jia, B.; Chen, Z.; Moss, D.J. Fabrication Technologies for the On-Chip Integration of 2D Materials. Small Methods 2022, 6, 2101435. [Google Scholar] [CrossRef] [PubMed]
  76. Zhang, Y.; Wu, J.; Qu, Y.; Jia, L.; Jia, B.; Moss, D.J. Design and Optimization of Four-Wave Mixing in Microring Resonators Integrated With 2D Graphene Oxide Films. J. Light. Technol. 2021, 39, 6553–6562. [Google Scholar] [CrossRef]
  77. Zhang, Y.; Wu, J.; Qu, Y.; Jia, L.; Jia, B.; Moss, D.J. Optimizing the Kerr Nonlinear Optical Performance of Silicon Waveguides Integrated With 2D Graphene Oxide Films. J. Light. Technol. 2021, 39, 4671–4683. [Google Scholar] [CrossRef]
  78. Qu, Y.; Wu, J.; Zhang, Y.; Jia, L.; Liang, Y.; Jia, B.; Moss, D.J. Analysis of Four-Wave Mixing in Silicon Nitride Waveguides Integrated With 2D Layered Graphene Oxide Films. J. Light. Technol. 2021, 39, 2902–2910. [Google Scholar] [CrossRef]
  79. Y. Qu, J. Wu, Y. Zhang, L. Jia, Y. Yang, X. Xu, S. T. Chu, B. E. Little, R. Morandotti, B. Jia, and D. J. Moss, “Graphene oxide for enhanced optical nonlinear performance in CMOS compatible integrated devices”, Paper No. 11688-30, PW21O-OE109-36, 2D Photonic Materials and Devices IV, SPIE Photonics West, San Francisco CA -11 (2021). [CrossRef]
  80. Zhang, Y.; Wu, J.; Yang, Y.; Qu, Y.; Jia, L.; Moein, T.; Jia, B.; Moss, D.J. Enhanced Kerr Nonlinearity and Nonlinear Figure of Merit in Silicon Nanowires Integrated with 2D Graphene Oxide Films. ACS Appl. Mater. Interfaces 2020, 12, 33094–33103. [Google Scholar] [CrossRef]
  81. Wu, J.; Yang, Y.; Zhang, Y.; Qu, Y.; Xu, X.; Jia, L.; Liang, Y.; Chu, S.T.; Little, B.E.; Morandotti, R.; et al. Graphene oxide waveguide polarizers and polarization selective micro-ring resonators”, Paper 11282-29, SPIE Photonics West, San Francisco, CA, 4 - 7 February (2020). [CrossRef]
  82. Wu, J.; Yang, Y.; Qu, Y.; Xu, X.; Liang, Y.; Chu, S.T.; Little, B.E.; Morandotti, R.; Jia, B.; Moss, D.J. Graphene Oxide Waveguide and Micro-Ring Resonator Polarizers. Laser Photon- Rev. 2019, 13, 1900056. [Google Scholar] [CrossRef]
  83. Xu, X.; Wu, J.; Nguyen, T.G.; Moein, T.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Photonic microwave true time delays for phased array antennas using a 49 GHz FSR integrated optical micro-comb source [Invited]. Photon- Res. 2018, 6, B30–B36. [Google Scholar] [CrossRef]
  84. Xu, X.; Tan, M.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. Microcomb-Based Photonic RF Signal Processing. IEEE Photon- Technol. Lett. 2019, 31, 1854–1857. [Google Scholar] [CrossRef]
  85. Tan, M.; Xu, X.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Mitchell, A.; Morandotti, R.; Moss, D.J. Orthogonally polarized RF optical single sideband generation with integrated ring resonators. J. Semicond. 2021, 42. [Google Scholar] [CrossRef]
  86. Tan, M.; Xu, X.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Photonic radio frequency channelizers based on Kerr optical micro-combs. J. Semicond. 2021, 42. [Google Scholar] [CrossRef]
  87. Xu, et al., “Advanced adaptive photonic RF filters with 80 taps based on an integrated optical micro-comb source,” Journal of Lightwave Technology, vol. 37, no. 4, pp. 1288-1295 (2019).
  88. Xu, X.; Wu, J.; Tan, M.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Broadband Microwave Frequency Conversion Based on an Integrated Optical Micro-Comb Source. Optical Fiber Communications Conference and Exhibition (OFC). LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE; pp. 332–338.
  89. Tan, M.; Xu, X.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. Photonic RF and microwave filters based on 49 GHz and 200 GHz Kerr microcombs. Opt. Commun. 2020, 465, 125563. [Google Scholar] [CrossRef]
  90. Xu, X.; Tan, M.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Broadband Photonic RF Channelizer With 92 Channels Based on a Soliton Crystal Microcomb. J. Light. Technol. 2020, 38, 5116–5121. [Google Scholar] [CrossRef]
  91. Xu, X.; Tan, M.; Wu, J.; Boes, A.; Corcoran, B.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Photonic RF and Microwave Integrator Based on a Transversal Filter With Soliton Crystal Microcombs. IEEE Trans. Circuits Syst. II: Express Briefs 2020, 67, 3582–3586. [Google Scholar] [CrossRef]
  92. Xu, X.; Tan, M.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. High performance RF filters via bandwidth scaling with Kerr micro-combs. APL Photon- 2019, 4, 026102. [Google Scholar] [CrossRef]
  93. Tan, M.; Mitchell, A.; Moss, D.J.; Xu, X.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; et al. Microwave and RF Photonic Fractional Hilbert Transformer Based on a 50 GHz Kerr Micro-Comb. J. Light. Technol. 2019, 37, 6097–6104. [Google Scholar] [CrossRef]
  94. Tan, M.; Xu, X.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. RF and Microwave Fractional Differentiator Based on Photonics. IEEE Trans. Circuits Syst. II: Express Briefs 2020, 67, 2767–2771. [Google Scholar] [CrossRef]
  95. Tan, M.; Xu, X.; Boes, A.; Corcoran, B.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Photonic RF Arbitrary Waveform Generator Based on a Soliton Crystal Micro-Comb Source. J. Light. Technol. 2020, 38, 6221–6226. [Google Scholar] [CrossRef]
  96. Tan, M.; Xu, X.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. RF and microwave photonic temporal signal processing with Kerr micro-combs. Adv. Physics: X 2021, 6, 1838946. [Google Scholar] [CrossRef]
  97. Xu, X.; Wu, J.; Nguyen, T.G.; Shoeiby, M.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Advanced RF and microwave functions based on an integrated optical frequency comb source. Opt. Express 2018, 26, 2569–2583. [Google Scholar] [CrossRef] [PubMed]
  98. Tan, M.; Xu, X.; Boes, A.; Corcoran, B.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Lowery, A.J.; Morandotti, R.; et al. Highly Versatile Broadband RF Photonic Fractional Hilbert Transformer Based on a Kerr Soliton Crystal Microcomb. J. Light. Technol. 2021, 39, 7581–7587. [Google Scholar] [CrossRef]
  99. Wu, J. et al. RF Photonics: An Optical Microcombs’ Perspective. IEEE Journal of Selected Topics in Quantum Electronics Vol. 24, 6101020, 1-20 (2018).
  100. Nguyen, T.G.; Shoeiby, M.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Integrated frequency comb source based Hilbert transformer for wideband microwave photonic phase analysis. Opt. Express 2015, 23, 22087–22097. [Google Scholar] [CrossRef]
  101. Xu, X.; Wu, J.; Shoeiby, M.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source. APL Photon- 2017, 2. [Google Scholar] [CrossRef]
  102. Xu, X.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Broadband RF Channelizer Based on an Integrated Optical Frequency Kerr Comb Source. International Topical Meeting on Microwave Photonics (MWP). LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE; pp. 4519–4526.
  103. Xu, X.; Wu, J.; Jia, L.; Tan, M.; Nguyen, T.G.; Chu, S.T.; E Little, B.; Morandotti, R.; Mitchell, A.; Moss, D.J. Continuously tunable orthogonally polarized RF optical single sideband generator based on micro-ring resonators. J. Opt. 2018, 20, 115701. [Google Scholar] [CrossRef]
  104. Xu, X.; Wu, J.; Tan, M.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Orthogonally Polarized RF Optical Single Sideband Generation and Dual-Channel Equalization Based on an Integrated Microring Resonator. J. Light. Technol. 2018, 36, 4808–4818. [Google Scholar] [CrossRef]
  105. Xu, X.; Tan, M.; Wu, J.; Boes, A.; Corcoran, B.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Photonic RF Phase-Encoded Signal Generation With a Microcomb Source. J. Light. Technol. 2020, 38, 1722–1727. [Google Scholar] [CrossRef]
  106. B. Corcoran, et al., “Ultra-dense optical data transmission over standard fiber with a single chip source”, Nature Communications, vol. 11, Article:2568, 2020.
  107. Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Nguyen, T.G.; Boes, A.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Photonic Perceptron Based on a Kerr Microcomb for High-Speed, Scalable, Optical Neural Networks. Laser Photon- Rev. 2020, 14. [Google Scholar] [CrossRef]
  108. Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef] [PubMed]
  109. Xu, X.; Han, W.; Tan, M.; Sun, Y.; Li, Y.; Wu, J.; Morandotti, R.; Mitchell, A.; Xu, K.; Moss, D.J. Neuromorphic Computing Based on Wavelength-Division Multiplexing. IEEE J. Sel. Top. Quantum Electron. 2022, 29, 1–12. [Google Scholar] [CrossRef]
  110. Sun, Y.; Wu, J.; Tan, M.; Xu, X.; Li, Y.; Morandotti, R.; Mitchell, A.; Moss, D.J. Applications of optical microcombs. Adv. Opt. Photon- 2023, 15, 86–175. [Google Scholar] [CrossRef]
  111. Bai, Y.; Xu, X.; Tan, M.; Sun, Y.; Li, Y.; Wu, J.; Morandotti, R.; Mitchell, A.; Xu, K.; Moss, D.J. Photonic multiplexing techniques for neuromorphic computing. Nanophotonics 2022, 12, 795–817. [Google Scholar] [CrossRef]
  112. Prayoonyong, C.; Boes, A.; Xu, X.; Tan, M.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J.; Corcoran, B. Frequency comb distillation for optical superchannel transmission. J. Light. Technol. 2021, 39, 1–1. [Google Scholar] [CrossRef]
  113. Tan, M.; Xu, X.; Wu, J.; Corcoran, B.; Boes, A.; Nguyen, T.G.; Chu, S.T.; E Little, B.; Morandotti, R.; Mitchell, A.; et al. Integral order photonic RF signal processors based on a soliton crystal micro-comb source. J. Opt. 2021, 23, 125701. [Google Scholar] [CrossRef]
  114. Yang Sun, Jiayang Wu, Yang Li, Xingyuan Xu, Guanghui Ren, Mengxi Tan, Sai Tak Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Performance analysis of microcomb-based microwave photonic transversal signal processors with experimental errors”, Journal of Lightwave Technology 41 Special Issue on Microwave Photonics (2023).
  115. Sun, Y.; Wu, J.; Li, Y.; Tan, M.; Xu, X.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Quantifying the Accuracy of Microcomb-Based Photonic RF Transversal Signal Processors. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1–17. [Google Scholar] [CrossRef]
  116. Mengxi Tan, Xingyuan Xu, Andreas Boes, Bill Corcoran, Thach G. Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Jiayang Wu, Arnan Mitchell, and David J. Moss, “Photonic signal processor for real-time video image processing at 17 Tb/s”, Communications Engineering 2 (2023).
  117. Pasquazi, A.; Peccianti, M.; Park, Y.; Little, B.E.; Chu, S.T.; Morandotti, R.; Azaña, J.; Moss, D.J. Sub-picosecond phase-sensitive optical pulse characterization on a chip. Nat. Photon- 2011, 5, 618–623. [Google Scholar] [CrossRef]
  118. Bao, C.; Xuan, Y.; Jaramillo-Villegas, J.A.; Leaird, D.E.; Qi, M.; Weiner, A.M. Direct soliton generation in microresonators. Opt. Lett. 2017, 42, 2519–2522. [Google Scholar] [CrossRef]
  119. M.Ferrera et al., “CMOS compatible integrated all-optical RF spectrum analyzer”, Optics Express, vol. 22, no. 18, 21488 - 21498 (2014).
  120. Kues, M.; Reimer, C.; Wetzel, B.; Roztocki, P.; Little, B.E.; Chu, S.T.; Hansson, T.; Viktorov, E.A.; Moss, D.J.; Morandotti, R. Passively mode-locked laser with an ultra-narrow spectral width. Nat. Photon- 2017, 11, 159–162. [Google Scholar] [CrossRef]
  121. Razzari, L.; Duchesne, D.; Ferrera, M.; Morandotti, R.; Chu, S.; Little, B.E.; Moss, D.J. CMOS-compatible integrated optical hyper-parametric oscillator. Nat. Photon- 2010, 4, 41–45. [Google Scholar] [CrossRef]
  122. Ferrera, M.; Razzari, L.; Duchesne, D.; Morandotti, R.; Yang, Z.; Liscidini, M.; Sipe, J.E.; Chu, S.; Little, B.E.; Moss, D.J. Low-power continuous-wave nonlinear optics in doped silica glass integrated waveguide structures. Nat. Photon- 2008, 2, 737–740. [Google Scholar] [CrossRef]
  123. M.Ferrera et al.“On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Opt. Express, vol. 19, (23)pp. 23153-23161 (2011).
  124. Duchesne, D.; Peccianti, M.; Lamont, M.R.E.; Ferrera, M.; Razzari, L.; Légaré, F.; Morandotti, R.; Chu, S.; Little, B.E.; Moss, D.J. Supercontinuum generation in a high index doped silica glass spiral waveguide. Opt. Express 2010, 18, 923–930. [Google Scholar] [CrossRef] [PubMed]
  125. Bao, H.; Olivieri, L.; Rowley, M.; Chu, S.T.; Little, B.E.; Morandotti, R.; Moss, D.J.; Gongora, J.S.T.; Peccianti, M.; Pasquazi, A. Turing patterns in a fiber laser with a nested microresonator: Robust and controllable microcomb generation. Phys. Rev. Res. 2020, 2, 023395. [Google Scholar] [CrossRef]
  126. Ferrera, M.; Park, Y.; Razzari, L.; Little, B.E.; Chu, S.T.; Morandotti, R.; Moss, D.J.; Azaña, J. On-chip CMOS-compatible all-optical integrator. Nat. Commun. 2010, 1, 29. [Google Scholar] [CrossRef]
Preprints 72423 g001
Figure 1. (a) Schematic of GO’s atomic structure and bandgap. The colorful balls in the atomic structure represent the diverse oxygen-containing functional groups (OCFGs). (b) Schematic of signal amplification based on optical parametric process. (c) Schematic of a Si3N4 waveguide integrated with a single layer GO film. (d) Microscopic image of the fabricated Si3N4 integrated chip coated with a single layer GO film. (e) Measured Raman spectrum of the GO-coated Si3N4 chip in (d). (f) Dispersion (D) of the uncoated waveguide (GO-0) and hybrid waveguides with 1 and 2 layers of GO (GO-1, GO-2). Inset shows TE mode profile of the Si3N4 waveguide integrated with a single layer GO film.
Figure 1. (a) Schematic of GO’s atomic structure and bandgap. The colorful balls in the atomic structure represent the diverse oxygen-containing functional groups (OCFGs). (b) Schematic of signal amplification based on optical parametric process. (c) Schematic of a Si3N4 waveguide integrated with a single layer GO film. (d) Microscopic image of the fabricated Si3N4 integrated chip coated with a single layer GO film. (e) Measured Raman spectrum of the GO-coated Si3N4 chip in (d). (f) Dispersion (D) of the uncoated waveguide (GO-0) and hybrid waveguides with 1 and 2 layers of GO (GO-1, GO-2). Inset shows TE mode profile of the Si3N4 waveguide integrated with a single layer GO film.
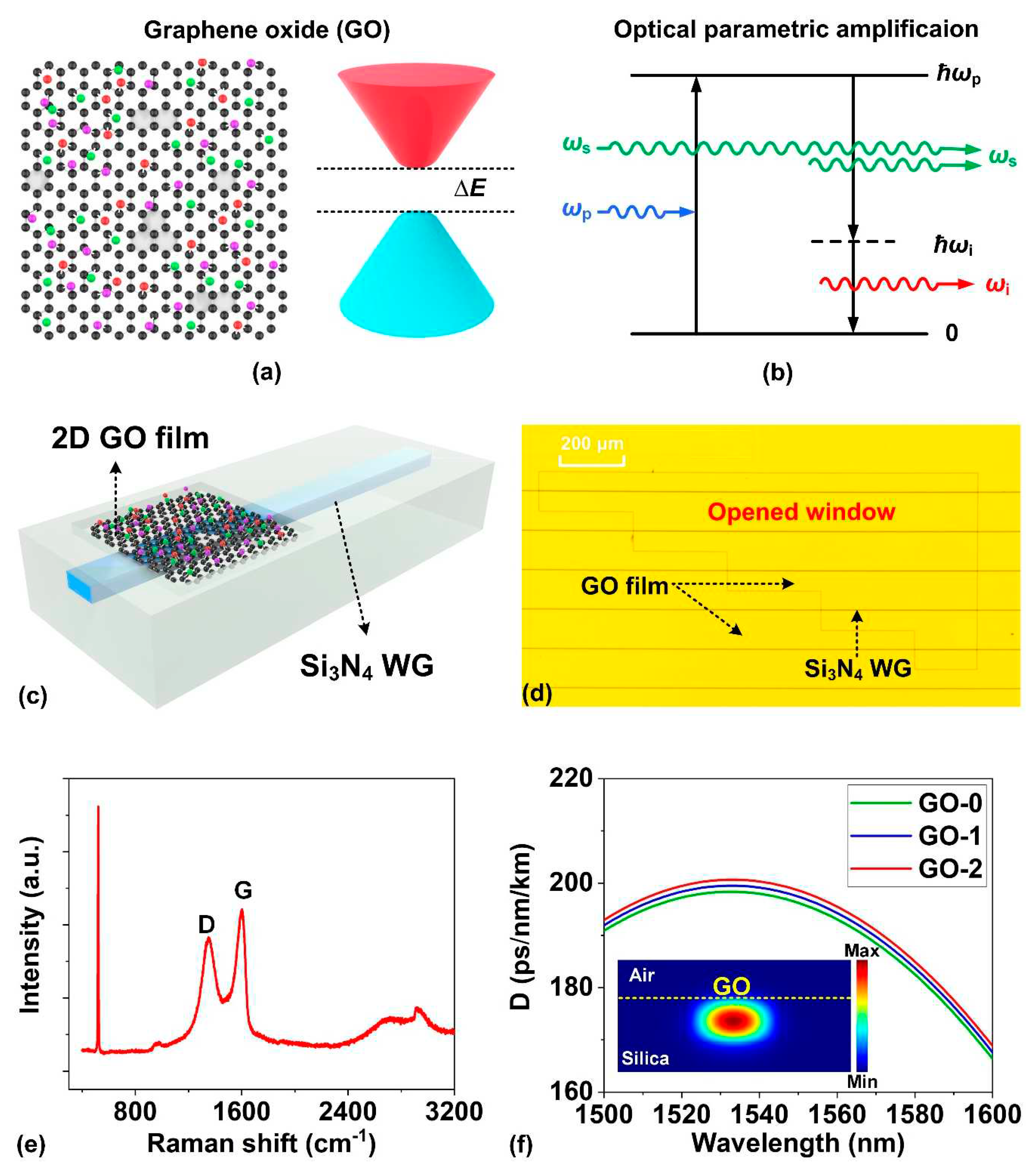
Preprints 72423 g001
Preprints 72423 g002
Figure 2. Experimental results for loss measurements. (a) Measured insertion loss versus wavelength of input continuous-wave (CW) light. The input CW power is ~1 mW. (b) Measured insertion loss versus input CW power. The input CW wavelength is ~1550 nm. (c) Measured insertion loss versus peak power Ppeak of 180-fs optical pulses. (d) Excess propagation loss induced by SA of GO ΔSA versus Ppeak extracted from (c). In (a) – (d), the curves for GO-0, GO-1, and GO-2 show the results for the uncoated Si3N4 waveguides, and the hybrid waveguides with 1 and 2 layers of GO, respectively.
Figure 2. Experimental results for loss measurements. (a) Measured insertion loss versus wavelength of input continuous-wave (CW) light. The input CW power is ~1 mW. (b) Measured insertion loss versus input CW power. The input CW wavelength is ~1550 nm. (c) Measured insertion loss versus peak power Ppeak of 180-fs optical pulses. (d) Excess propagation loss induced by SA of GO ΔSA versus Ppeak extracted from (c). In (a) – (d), the curves for GO-0, GO-1, and GO-2 show the results for the uncoated Si3N4 waveguides, and the hybrid waveguides with 1 and 2 layers of GO, respectively.
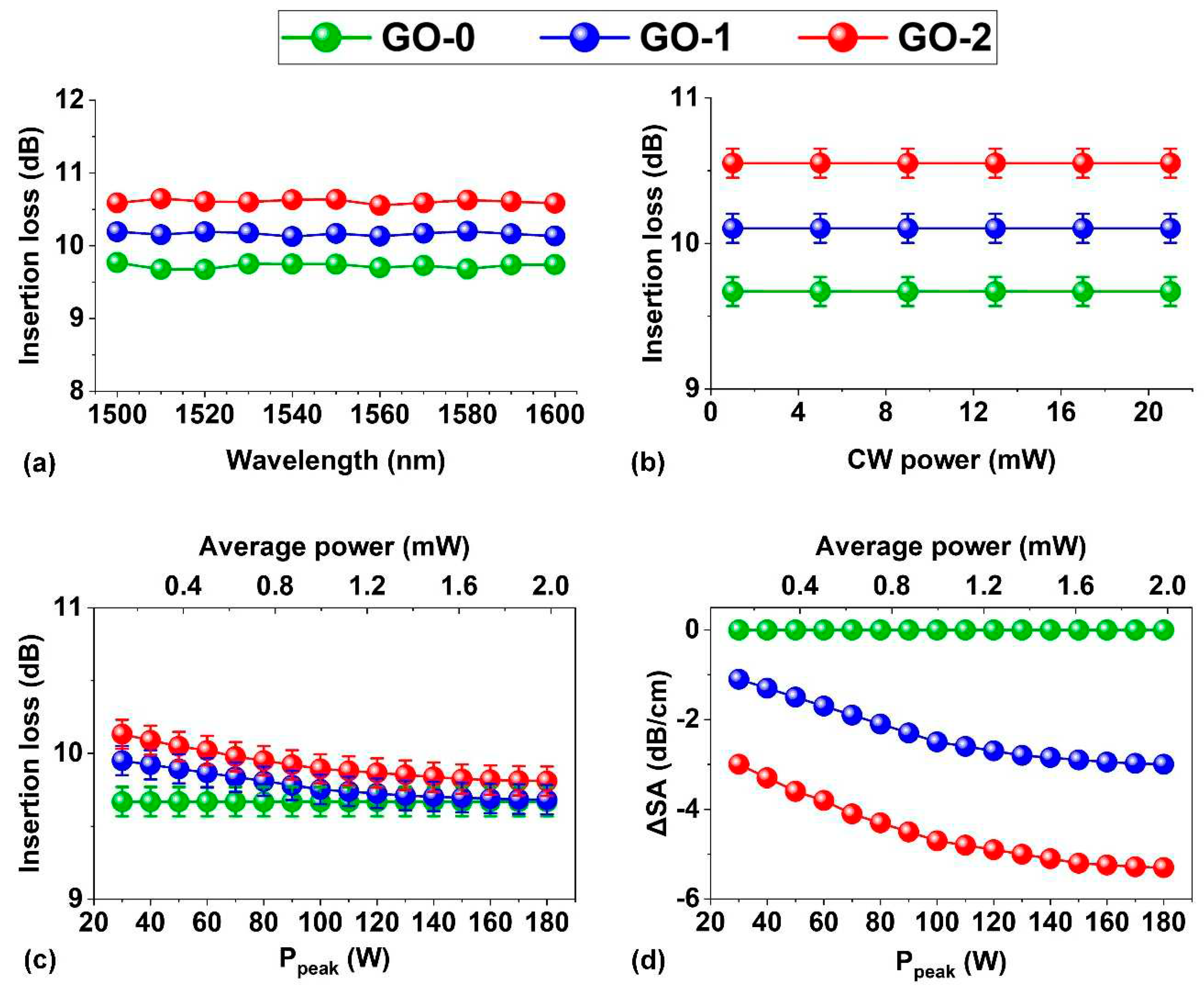
Preprints 72423 g002
Preprints 72423 g003
Figure 3. Experimental setup for OPA experiments. CW laser: continuous-wave laser. FPL: fiber pulsed laser. PC: polarization controller. EDFA: Erbium doped fiber amplifier. VOA: variable optical attenuator. OPM: optical power meter. DUT: device under test. CCD: charged-coupled device. OSA: optical spectrum analyzer.
Figure 3. Experimental setup for OPA experiments. CW laser: continuous-wave laser. FPL: fiber pulsed laser. PC: polarization controller. EDFA: Erbium doped fiber amplifier. VOA: variable optical attenuator. OPM: optical power meter. DUT: device under test. CCD: charged-coupled device. OSA: optical spectrum analyzer.
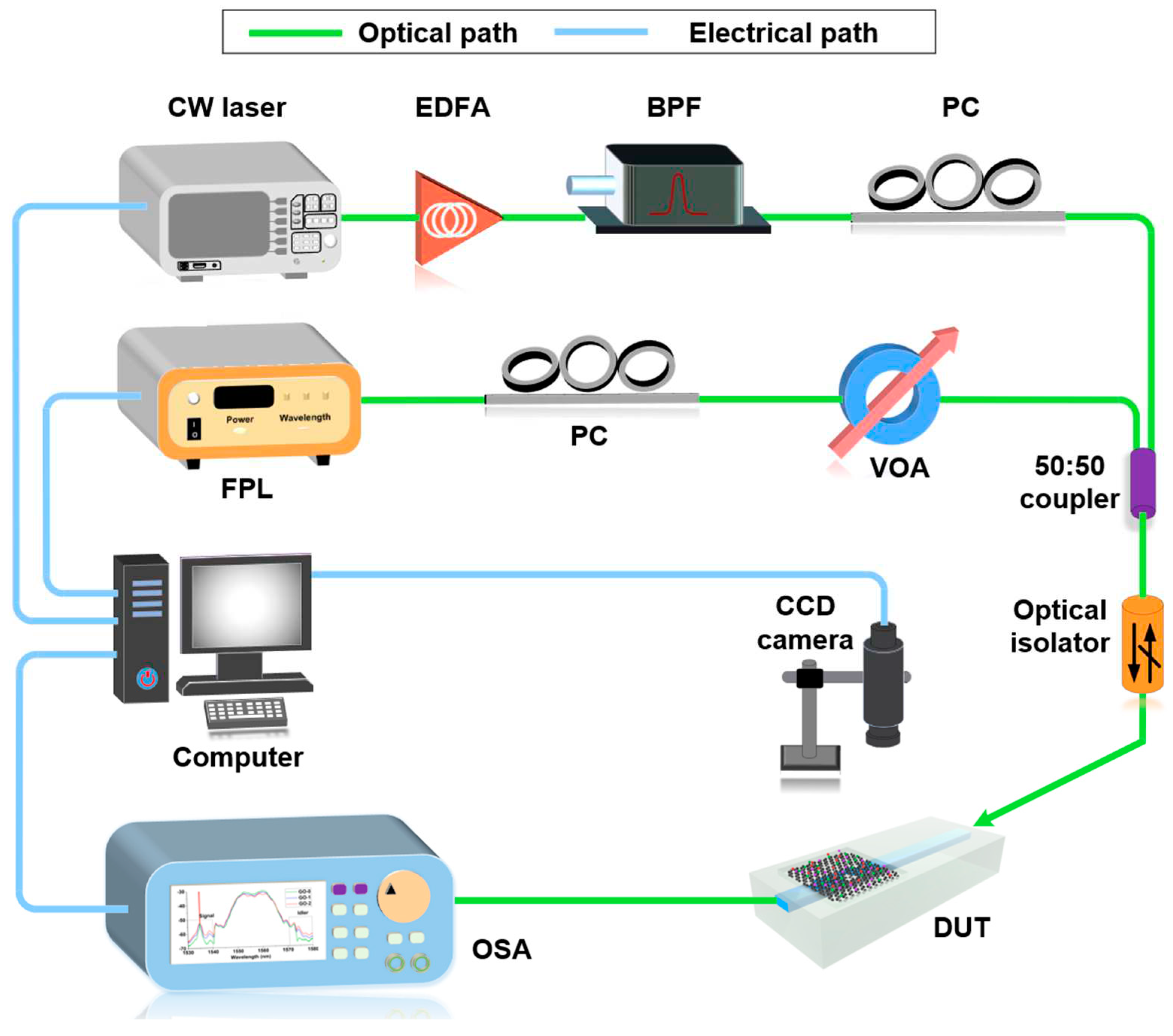
Preprints 72423 g003
Preprints 72423 g004
Figure 4. Optical parametric amplification (OPA) using a 180-fs pulsed pump and a continuous-wave (CW) signal. (a) Measured output optical spectra after propagation through uncoated (GO-0) and hybrid waveguides with 1 (GO-1) and 2 (GO-2) layers of GO. The peak power of the input pump light Ppeak was ~180 W. (b) Measured output optical spectra after propagation through the device with 2 layers of GO at different Ppeak. In (a) and (b), the power of the CW signal light was Psignal = ~6 mW, and insets show zoom-in views around the signal and idler. (c) Measured (i) parametric gain PG and (ii) parametric gain improvement ∆PG versus Ppeak. .
Figure 4. Optical parametric amplification (OPA) using a 180-fs pulsed pump and a continuous-wave (CW) signal. (a) Measured output optical spectra after propagation through uncoated (GO-0) and hybrid waveguides with 1 (GO-1) and 2 (GO-2) layers of GO. The peak power of the input pump light Ppeak was ~180 W. (b) Measured output optical spectra after propagation through the device with 2 layers of GO at different Ppeak. In (a) and (b), the power of the CW signal light was Psignal = ~6 mW, and insets show zoom-in views around the signal and idler. (c) Measured (i) parametric gain PG and (ii) parametric gain improvement ∆PG versus Ppeak. .
Preprints 72423 g004
Preprints 72423 g005
Figure 5. (a) Measured (i) parametric gain PG and (ii) parametric gain improvement ∆PG versus wavelength detuning Δλ. (b) Measured (i) PG and (ii) ∆PG versus input CW signal power Psignal. (c) Measured (i) PG and (ii) ∆PG versus GO film length LGO. In (a) ‒ (c), the peak power of the 180-fs pulsed pump centered around 1557 nm was Ppeak = ~180 W. Except for the varied parameters, all other parameters are kept the same as Δλ = ~-22 nm, Psignal = ~6 mW, and LGO = ~1.4 mm.
Figure 5. (a) Measured (i) parametric gain PG and (ii) parametric gain improvement ∆PG versus wavelength detuning Δλ. (b) Measured (i) PG and (ii) ∆PG versus input CW signal power Psignal. (c) Measured (i) PG and (ii) ∆PG versus GO film length LGO. In (a) ‒ (c), the peak power of the 180-fs pulsed pump centered around 1557 nm was Ppeak = ~180 W. Except for the varied parameters, all other parameters are kept the same as Δλ = ~-22 nm, Psignal = ~6 mW, and LGO = ~1.4 mm.
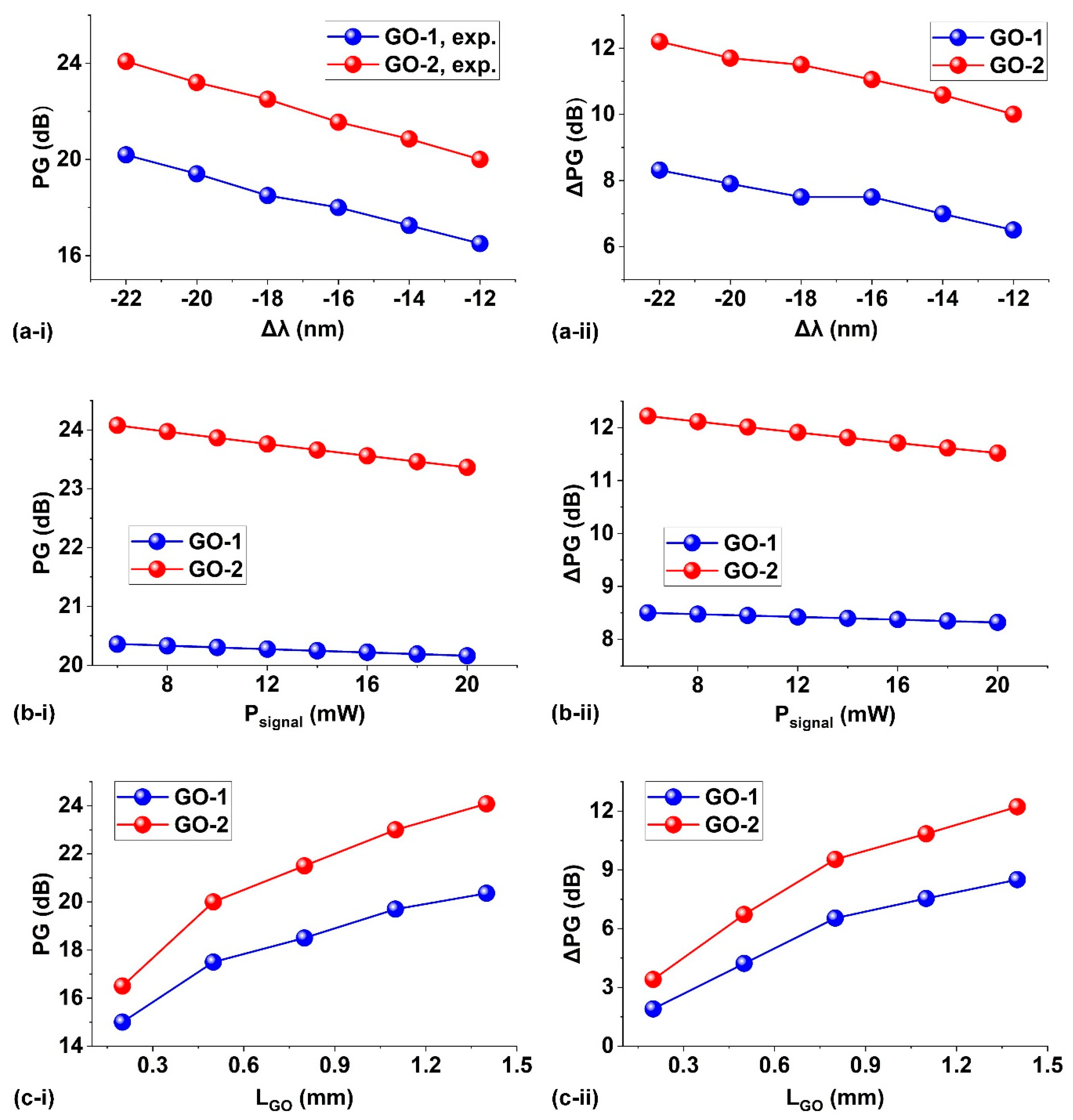
Preprints 72423 g005
Preprints 72423 g006
Figure 6. (a) Nonlinear parameter γ of hybrid waveguides with 1 (GO-1) and 2 (GO-2) layers of GO as a function of pump peak power Ppeak. (b) Kerr coefficient n2 of films with 1 (GO-1) and 2 (GO-2) layers of GO versus Ppeak. (c) Effective interaction length Leff and (d) figure of merit FOM versus waveguide length L for the uncoated (GO-0) and hybrid waveguides with 1 (GO-1) and 2 (GO-2) layers of GO. (e) Parametric gain PG and (f) parametric gain improvement ∆PG versus waveguide length L for the uncoated Si3N4 waveguide (GO-0) and the hybrid waveguides uniformly coated with 1 (GO-1) and 2 (GO-2) layers of GO. In (e) and (f), the pump peak power, CW signal power, and the wavelength detuning are Ppeak = ~180 W, Psignal = ~6 mW, and Δλ = ~-22 nm, respectively.
Figure 6. (a) Nonlinear parameter γ of hybrid waveguides with 1 (GO-1) and 2 (GO-2) layers of GO as a function of pump peak power Ppeak. (b) Kerr coefficient n2 of films with 1 (GO-1) and 2 (GO-2) layers of GO versus Ppeak. (c) Effective interaction length Leff and (d) figure of merit FOM versus waveguide length L for the uncoated (GO-0) and hybrid waveguides with 1 (GO-1) and 2 (GO-2) layers of GO. (e) Parametric gain PG and (f) parametric gain improvement ∆PG versus waveguide length L for the uncoated Si3N4 waveguide (GO-0) and the hybrid waveguides uniformly coated with 1 (GO-1) and 2 (GO-2) layers of GO. In (e) and (f), the pump peak power, CW signal power, and the wavelength detuning are Ppeak = ~180 W, Psignal = ~6 mW, and Δλ = ~-22 nm, respectively.
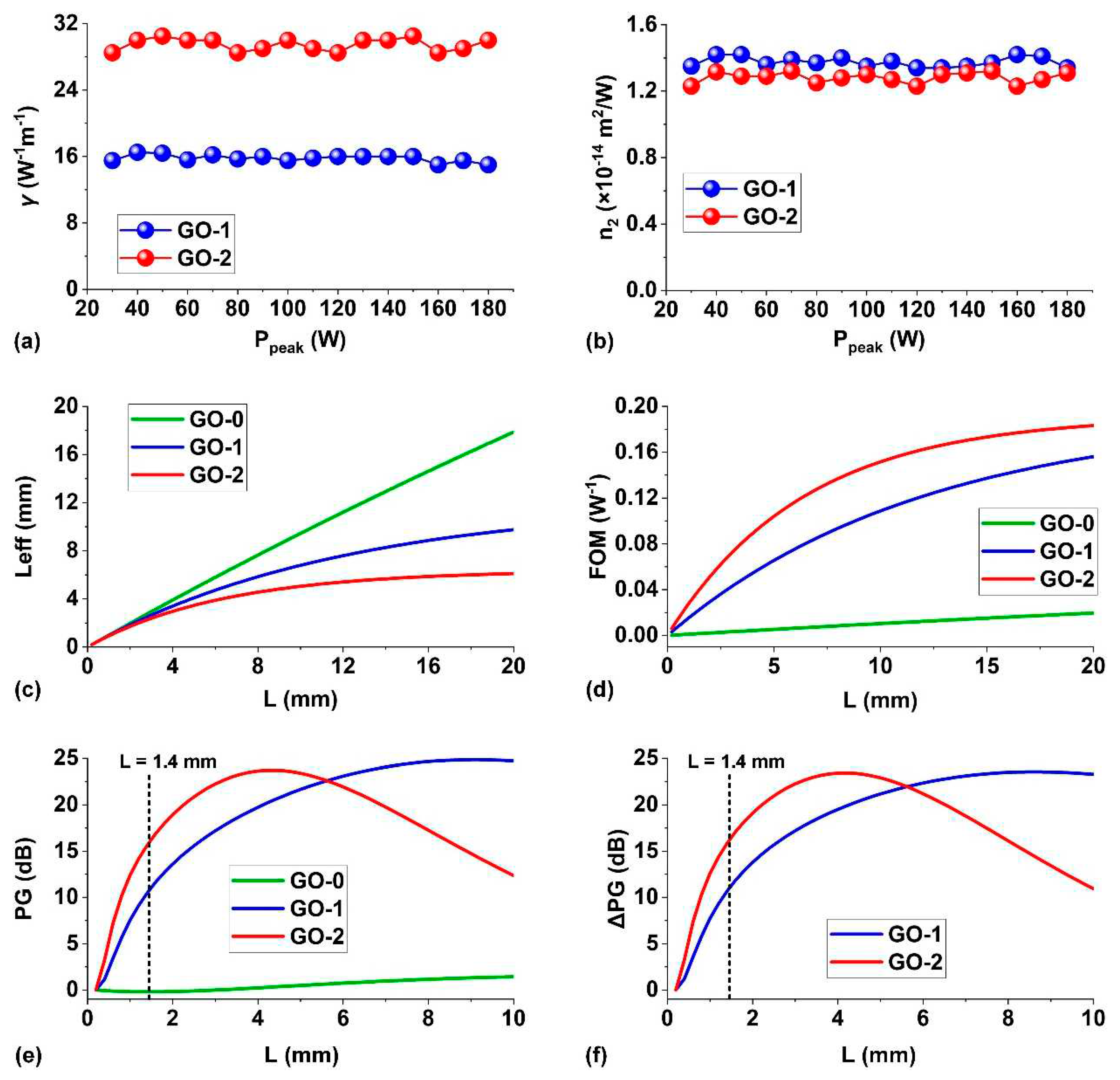
Preprints 72423 g006
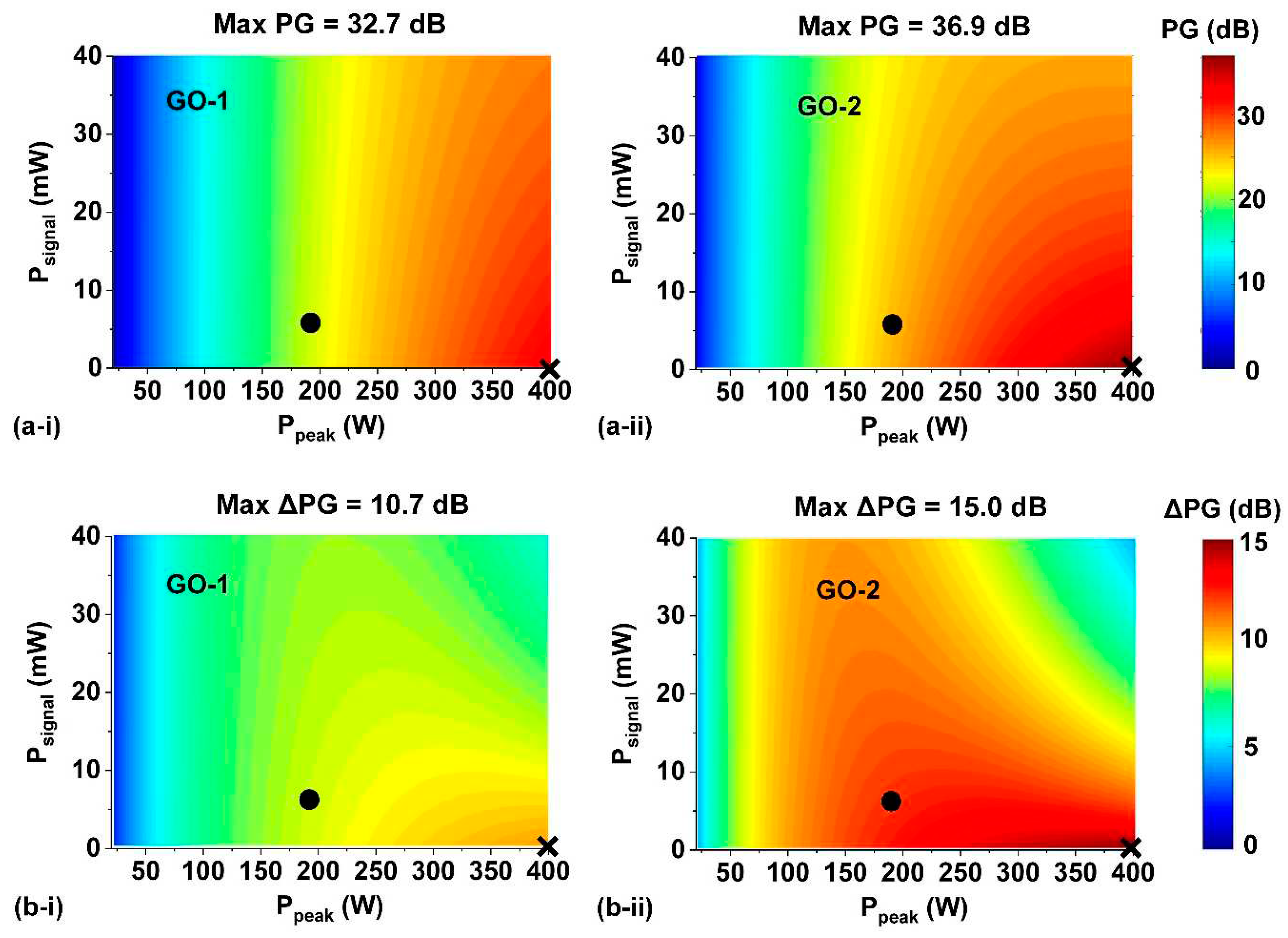
Preprints 72423 g007
Figure 7. (a) Simulated parametric gain PG versus input pump peak power Ppeak and CW signal power Psignal. (b) Simulated parametric gain improvement ∆PG versus Ppeak and Psignal. In (a) and (b), (i) and (ii) show the results for the hybrid waveguides with 1 and 2 layers of GO (GO-1, GO-2), respectively. The black points mark the OPA experimental results, and the black crossing mark the results corresponding to the maximum values of PG and ∆PG. The wavelength detuning and the GO film length are ∆λ = -22 nm and LGO = 1.4 mm, respectively.
Figure 7. (a) Simulated parametric gain PG versus input pump peak power Ppeak and CW signal power Psignal. (b) Simulated parametric gain improvement ∆PG versus Ppeak and Psignal. In (a) and (b), (i) and (ii) show the results for the hybrid waveguides with 1 and 2 layers of GO (GO-1, GO-2), respectively. The black points mark the OPA experimental results, and the black crossing mark the results corresponding to the maximum values of PG and ∆PG. The wavelength detuning and the GO film length are ∆λ = -22 nm and LGO = 1.4 mm, respectively.
Preprints 72423 g007
Preprints 72423 g008
Figure 8. (a) Simulated (i) parametric gain PG and (ii) parametric gain improvement ∆PG versus wavelength detuning ∆λ. (b) Simulated (i) PG and (ii) ∆PG versus GO coating length LGO. In (a) and (b), the measured and fit results are shown by the data points and the dashed curves, respectively. The pump peak power and the signal power are Ppeak = 180 W and Psignal = 6 mW, respectively. In (a), LGO = 1.4 mm. In (b), ∆λ = -22 nm.
Figure 8. (a) Simulated (i) parametric gain PG and (ii) parametric gain improvement ∆PG versus wavelength detuning ∆λ. (b) Simulated (i) PG and (ii) ∆PG versus GO coating length LGO. In (a) and (b), the measured and fit results are shown by the data points and the dashed curves, respectively. The pump peak power and the signal power are Ppeak = 180 W and Psignal = 6 mW, respectively. In (a), LGO = 1.4 mm. In (b), ∆λ = -22 nm.
Preprints 72423 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated