Preprint
Article
Exploring the Symmetry of Curvilinear Regression Models for Enhancing the Analysis of Fibrates Drug Activity through Molecular Descriptors
Altmetrics
Downloads
94
Views
18
Comments
0
A peer-reviewed article of this preprint also exists.
† These authors contributed equally to this work.
This version is not peer-reviewed
Submitted:
02 May 2023
Posted:
03 May 2023
You are already at the latest version
Alerts
Abstract
The paper describes the use of topological indices in conjunction with high cholesterol drugs, specifically Fibrates, to predict their physicochemical properties and biological activities. Fibrates are known to lower high triglycerides, increase HDL cholesterol, and reduce the small dense fraction of LDL cholesterol. The study uses a quantitative structural-property relationships (QSPR) approach, which involves analyzing the relationships between physicochemical properties and topological indices using curvilinear regression. The QSPR model predicts the physicochemical properties of the drugs based on degrees and distances determined from topological indices. The study also conducted (DFT) calculations at the B3LYP/6-31G(d,p) level on the four investigated derivatives to gain insights into their optimized geometries, DOS plots, HOMO and LUMO orbital energies, and distribution. The theoretical results presented in the study suggest that the use of topological indices in QSPR models could provide a powerful tool for predicting the physicochemical properties and biological activities of molecules, including drugs. These findings could lead to the development of new cholesterol-lowering drugs with desirable properties.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
Pharmacology has rapidly evolved, resulting in the introduction of numerous groundbreaking drugs each year. However, ensuring accurate testing performance requires the availability of appropriate equipment, a good rapport, and sufficient resources. Previous studies have shown that a drug’s chemical properties are intricately linked to its molecular structure. Pharmacological and medical researchers often utilize topological indices to examine the molecules’ properties and understand their impact on experimental outcomes. Hence, the topological index computation method is a useful tool for developing countries, allowing them to gather medical and biological data on upcoming drugs without the need for laboratory tests see for example [1,2,3,4].
Fibrates are a type of medication that have been shown to lower high levels of bad cholesterol (also known as low-density lipoprotein or LDL), increase good cholesterol (also known as high-density lipoprotein or HDL), and decrease the amount of small dense LDL particles in the blood. They have been found to be effective in reducing the mortality and morbidity associated with cardiovascular disease (CVD) in individuals who are at risk for developing it. However, conducting laboratory studies to investigate the physicochemical properties of fibrates can be both expensive and time-consuming. To overcome this challenge, chemists can use topological indices to derive mathematical equations that provide valuable insights into the properties of fibrates. For more information on fibrates, please refer to sources [5] and [6].
Chemical graph theory is a field that integrates mathematical modeling of chemical phenomena with graph theory. It utilizes topological indices to establish a correlation between the properties of a chemical molecule and its structure [7]. These indices are also known as graph invariants or graph-based molecular descriptors, and they quantify the topological features of a molecule or molecules [8]. The application of quantitative structure-property/structure-activity relationships (QSPR/QSAR) models, which are commonly employed in this field, allows for the prediction of molecular properties using these topological indices. In 1947, Harold Wiener introduced the Wiener index, the first topological index, Paraffin’s physical properties were determined using it [9].
Topological indices, which are numerical values derived from the molecular graph of a chemical compound, have been extensively studied in the fields of quantitative structure-property relationship (QSPR) and quantitative structure-activity relationship (QSAR) analyses. These indices encode the structural and topological information of molecules and have proven useful in predicting various physical, chemical, and biological properties [10,11,12,13,14]. The use of molecular graphs to represent unsaturated hydrocarbon structures provides a more intuitive and comprehensive understanding of the molecular characteristics and behavior of compounds [15,16,17,18,19,20]. In drug design, knowledge of molecular structure is essential in determining their potential therapeutic activity and overall effectiveness. In this study, we examine several vertex-degree based topological indices, including the first and second Zagreb indices, hyper-Zagreb index, sigma index, Inverse symmetric deviation index, Max-min rodeg index, Min-max rodeg index, Inverse sum deviation index, Atom-bond connectivity index, Randic index, and Albertson index [21,22,23,24,25,26,27,28,29,30,31]. Additionally, we investigate topological indices based on distance, such as Wiener index, Schultz index, Harary index, and Gutman index [32,33,34]. These indices are used to classify the molecular descriptors and analyze the efficacy of curvilinear regression models in predicting the activity of fibrates drugs.
Molecular descriptors have been widely used to evaluate the physicochemical and bioactive properties of chemical structures, and their inclusion in curvilinear regression models can enhance the analysis of drug activity. Topological indices, such as the Zagreb indices, have shown promise in predicting the effectiveness of cancer treatments [35]. The max-min rodeg index has been found to give reliable predictions for octane isomers and polychlorobiphenyls in linear regression models [36]. A new index called the Atom-bond connectivity index has been proposed to determine the complexity of alkanes [37]. The first hyper-Zagreb index has been found to be the preferred method for estimating the boiling points of benzenoid hydrocarbons [38]. Additionally, the indeg indices have been applied to predict topological polar areas [39]. The inverse sum deviation index has been used to calculate the vaporization and sublimation enthalpies of monocarboxylic acids [40] and [41]. Irregularity indices based on different degrees, in addition to Albertson and Sigma indices, have been found to predict the physicochemical properties of octane isomers [42]. The Wiener index was first introduced in quantitative structure-property relationship (QSPR) studies, and has been shown to align well with the boiling points of alkanes [43]. The Wiener index has been further developed and used to explain different chemical and physical properties of molecules, as well as their biological activity [44]. The Schultz index has also been investigated to predict the boiling points of alkyl alcohols, and thus their suitability for various applications [45]. As indicated in Table 1, these indices are expressed mathematically and are shown with mathematical expressions.
Fenofibrate is an important component of a healthy diet and medication regimen, as it is used to reduce blood cholesterol and triglyceride levels. By decreasing triglyceride levels in the bloodstream, the risk of pancreatitis (inflammation of the pancreas) can be mitigated. To date, only one paper [46] has explored the use of topological indices in analyzing one of the drugs in the Fibrates family. This study utilized degree, degree, and degree-based (based) approaches to compute the topological indices of fenofibrate’s chemical structure. With limited existing literature on Fibrates that incorporate topological indices, this paper represents a pioneering effort in the investigation of novel physicochemical properties of Fibrates using this technique. In this work, Fenofibrate , Ciprofibrate , Bezafibrate , Clofibrate drugs used in the treatment patients with high cholesterol are studied.
Fibrates drugs are a class of medications commonly used to treat dyslipidemia, a condition characterized by abnormal lipid levels in the blood. Despite their widespread use, the molecular mechanisms underlying the activity of fibrates drugs are not well understood. One approach to addressing this challenge is to develop quantitative structure-activity relationship (QSAR) models that can predict the activity of fibrates drugs based on their molecular descriptors. In this study, we investigate the efficacy of curvilinear regression models in enhancing the analysis of fibrates drug activity through molecular descriptors. Curvilinear regression models are a type of non-linear regression model that can capture non-linear relationships between variables, making them useful for analyzing complex systems such as the interactions between drugs and their molecular targets. Our study builds upon previous research that has investigated the use of QSAR models to predict the activity of drugs. Several articles published in Symmetry have explored the use of topological indices and other mathematical methods to predict various properties of organic compounds, including their biological activity. For example, a study by Liu et al. [47] investigated the efficacy of using topological indices in QSPR models for predicting the densities and viscosities of biodiesel. The authors used a dataset of 105 biodiesel compounds with known properties and developed models using multiple linear regression and artificial neural network methods. They compared the performance of their models with previous studies and found that the models developed using topological indices had higher accuracy in predicting the properties of biodiesel. Zuo and Hu [48] developed QSPR models for predicting the melting points of organic compounds using molecular topology and quantum chemical descriptors. The authors used a dataset of 893 organic compounds and developed multiple linear regression models using the partial least squares (PLS) method. They compared their models with other models reported in the literature and found that their models were more accurate in predicting the melting points of organic compounds. Zhang et al. [49] developed QSPR models for predicting the melting points of organic compounds based on molecular topology. The authors used a dataset of 1,427 organic compounds and developed models using the neural network algorithm. They compared their models with other models reported in the literature and found that their models were more accurate in predicting the melting points of organic compounds. Naghipour and Kiasat [50] developed a QSPR model for predicting the fullerene-like behavior of C60 derivatives using topological indices. The authors used a dataset of 46 C60 derivatives with known fullerene-like behavior and developed a model using multiple linear regression. They compared their model with other models reported in the literature and found that their model had higher accuracy in predicting the fullerene-like behavior of C60 derivatives. Wang and Xu [51] developed QSPR models for predicting the boiling points of alkyl alkanes based on the novel vertex degree valence topological index. The authors used a dataset of 388 alkyl alkanes and developed models using multiple linear regression and artificial neural network methods. They compared their models with other models reported in the literature and found that their models were more accurate in predicting the boiling points of alkyl alkanes.
In our study, we apply curvilinear regression models to analyze the activity of fibrates drugs based on their molecular descriptors. By incorporating non-linear relationships between variables, we aim to enhance the accuracy and predictive power of QSAR models for analyzing the activity of fibrates drugs. Ultimately, our research may contribute to a better understanding of the molecular mechanisms underlying the activity of fibrates drugs, and to the development of more effective treatments for dyslipidemia. These studies demonstrate the usefulness of QSAR modeling and related techniques for predicting the activity of various compounds based on their molecular descriptors. By building on this previous work, we hope to further advance our understanding of the molecular mechanisms underlying the activity of fibrates drugs.
The QSPR model is a highly effective tool for predicting a wide range of physicochemical properties of drugs. To make these predictions, the model employs degree-based indices and distance-based topological indices (as detailed in Table 1). The properties considered include Polarizability, Sum of electronic and zero-point Energies, Sum of electronic and thermal Energies, Sum of electronic and thermal Enthalpies, Sum of electronic and thermal Free Energies, Zero-point vibrational energy, Complexity, Topological polar area, Dipole moment, Heat capacity, Molar entropy, and Octanol-water partition coefficients. To analyze the relationships between these properties and the topological indices, curvilinear regression (linear, quadratic, and cubic) is utilized. The model generates statistical parameters using SPSS and MATLAB statistical functions. In addition, DFT calculations are conducted at the B3LYP/6-31G(d,p) to gain insight into the optimized geometries, DOS plots, HOMO and LUMO orbitals energies, and distribution of the four derivatives studied in the next section. Section 3 examines the contributions of different topological indices as molecular structural descriptors. Finally, Section 4 concludes the paper.
2. DFT Part
In Figure 1,Figure 2,Figure 3, and Figure 4 four important characteristics of the four investigated Fibrate derivatives were indicated, included: optimized geometries, electron density mapped with electrostatic potential (ESPM), total density of states (DOS) plots, and the special distributions of the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs). Density Functional Theory (DFT) calculations of the investigated Fibrate derivatives utilized the one of the well-known hybrid functionals, Becke, parameter, Lee–Yang–Parr (). In DFT, hybrid functionals incorporate a portion of Hartree-Fock exchange, as well as extra exchange from other sources (empirical/ab initio) to approximate the exchange-correlation energy. The B3LYP as a representation of Hamiltonian term in Schrödinger equation was combined with basis set as a representation of eigen-value wavefunction. It is a moderate double zeta () basis set enlarged with two polarization basis functions, a function for heavy atoms (Carbon, Oxygen, and chlorine), and a p-function for all Hydrogen atoms. Most of the physicochemical properties of the investigated fibrate derivatives discussed in next section were obtained from the frequency calculations carried out at the same level of theory of optimization. Calculations were carried out using Gaussian 09 software suite [52]. Visualizations of molecular structures were performed by using GaussView (version ) [53], ESPMs were drawn used the Avogadro package [54], and GaussSum program [55] was used to DOS plots. ESPMs show how electron density is distributed in the four non-planar molecules considering the electrostatic potentials, and this gives information about the region in the molecule that has the highest or lowest electron density, and thus is most likely to be attacked by electrophilic or nucleophilic agents. Keep in mind that the nucleophilic and electrophilic attack regions are represented by blue (positively charged) and red colors (negatively charged). The red color is concentrated on the more electronegative atoms such as Oxygen (deep red) and chlorin atoms (light red), the blue color covered the Hydrogen atoms (the least electronegative atoms), while the Carbon atoms are covered by white color indicating intermediate electronegativity of Carbon atom. Thus, it is possible to determine the position and region in a molecule attacked by an electrophile or nucleophile using ESPMs. Molecule DOS plot indicates how many energy states electrons are allowed to occupy in the system. The HOMO energies of the four investigated Fibrate derivatives are and for Fenofibrate, Ciprofibrate, Bezafibrate, and Clofibrate, respectively. Since, the HOMO energy used as a measure of electron-donating power of a molecule, destabilized HOMO (less negative) leads to more ability to donate electrons. The ability of electron donation of the five derivatives can be arranged as follows: Ciprofibrate > Bezafibrate > Fenofibrate > Clofibrate. On the other hands, the LUMO energy measures the ability of electron accepting of a molecule, more ability combined stabilized LUMO (more negative). Therefore, the derivatives ability to accept electrons is: Fenofibrate Bezafibrate Clofibrate Ciprofibrate . The energy gap (HOMO energy subtracted from LUMO energy) measures the chemical reactivity. Smaller gap is more reactive molecule, the reactivity of the four derivatives is: Fenofibrate Bezafibrate Ciprofibrate Clofibrate . Finally, the special distribution of HOMO and LUMO orbitals is another indictor of the position/region subjected to electrophilic and nucleophilic attack. The HOMO and LUMO orbitals in Ciprofibrate are distributed on similar parts of molecule, except that the two chlorine atoms have more HOMO character. Other molecules, HOMO orbitals delocalized over different regions compared to the LUMO orbitals distribution.
3. Materials and Method
In this section, the overall objective is to establish a quantitative structure-property-activity (QSPR) relationship between the various topological indices and some physicochemical properties/activity of the Fibrates drugs under study in order to assess the effectiveness of these drugs. Eleven degree-based and four distance topological indices were used for modeling antiviral activity. Based on DMol3-optimized geometries for Fibrates drugs investigated. The version of Material Studio from BIOVIA was used to perform DFT calculations, which are as follows: Polarizability , Sum of electronic and zero-point Energies , Sum of electronic and thermal Energies , Sum of electronic and thermal Enthalpies , Sum of electronic and thermal Free Energies , Zero-point vibrational energy , Complexity , Topological polar area , Dipole moment , Heat capacity , Molar entropy , and Octanol-water partition coefficients of several drugs currently being investigated for the treatment of high cholesterol which includes Fenofibrate, Ciprofibrate, Bezafibrate, Clofibrate drugs. It is possible to use curvilinear regression analysis to fit curves instead of straight lines, SPSS statistical software is used to analyze curvilinear regressions. As described below, the independent variables in the curvilinear regression models are topological indices. Indicators derived from cholesterol-lowering drugs. Based on the equations below, tests are conducted.
In this context, y represents the response or dependent variable, while a denotes the regression model constant, and refers to the coefficients for each individual descriptor. The independent variable is represented by x, and n signifies the number of samples used in building the regression equation. denotes the coefficient of determination, R signifies the correlation coefficient, F represents the calculated value of the Fischer values test, denotes the standard error of estimate, and stands for significance. It should be noted that when the experimental and theoretical results are in close proximity to each other, the correlation coefficient approaches 1. To gauge the predictability of a model, it is necessary to compare the observed values and the model predictions, for which the Root Mean Square Error metric is used. The predictive quality of a model is higher when the error or is lower, which is calculated as follows:
where is the observed value of the independent variable in the test set, is the predicted value of the independent variables in the test set, n is the number of samples in the test topological indices serve as independent variables. To evaluate our initial model, we used the metric and then normalized the data to enhance our predictions’ accuracy. We measured the difference between predicted and actual values using the score, which revealed that our model needed improvement. To address issues such as outliers and varying scales of measurement that could negatively affect model performance, we applied normalization techniques to our data. The normalization step was essential in improving the model’s accuracy, as it scaled variables to a common range, reduced the impact of outliers, and ensured that all variables were weighted equally. After normalization, we re-evaluated the model using the metric, and the updated score showed a significant improvement in our predictions’ accuracy. Computed topological indices values are shown in Table 2. We compute the values using combinatorial computations and edge partitioning as follows: the molecular graph of Fenofibrate has 25 vertices and 26 edges. Its edges can be partitioned as and The molecular graph of Ciprofibrate has 18 vertices and 19 edges. Its edges can be partitioned as and The molecular graph of Bezafibrate has 25 vertices and 26 edges. Its edges can be partitioned as and The molecular graph of Fenofibrate has 16 vertices and 16 edges. Its edges can be partitioned as and Using MATLAB, it is possible to efficiently compute degree-based and distance-based topological indices, as explained in Algorithm 1 and Algorithm 2. To calculate the topological indices of molecules based on distance and degree, MATLAB utilizes various mathematical expressions. The Fibrates family and the drugs under consideration, namely Fenofibrate, Ciprofibrate, Bezafibrate, and Clofibrate, have been studied and are presented in Table 3, including their experimental data [52] and optimized geometries obtained through DFT calculations using the DMol3 module of Version 8.0 of Material Studio from BIOVIA. Table 4 shows the correlation coefficient between degree-based topological indices and some physicochemical properties, computed using a linear regression model. Quadratic regression model is used in Table 6 to calculate the correlation coefficient between these indices and some physicochemical properties. The cubic model is employed for this purpose in Table 8. Similarly, for the distance-based topological indices, linear, quadratic, and cubic regression models are utilized, and the results are presented in Table 10. Once the correlation coefficient for a physicochemical property is obtained, the model with the maximum R becomes the most accurate predictor of the regression model. This indicated in Table 5, Table 7, Table 9 and Table 11. By leveraging the power of MATLAB, it is possible to efficiently and accurately compute topological indices and use them to predict the physicochemical properties of molecules, which can be incredibly useful in various fields, including drug discovery and materials science.
| Algorithm 1 Computational Procedure of calculation of degree-based indices |
|
Input: Edges and nodes of molecule
Output: Topological indices vector
Step 1. Start
Step 2. Graph of undirected edges
Step 3. Adjacency matrix of G
Step 4. Distances of G
Step 5. Vertex degree of G
Step 6. Calculate size of matrix d
Step 4. Construct
for to number of columns do
for to number of rows do
if then
elseif then
First Zagerb index
Second Zagerb index
Hyper Zagerb index
Atom Bond Connectivity index
Randic index
min-max rodeg index
max-min rodeg index
Alberston index
Sigma index Inverse symmetric deg index
Inverse sum deg index
end if
end for
end for
Step 5. (summation of
|
| Algorithm 2 Computational Procedure of calculation of distance-based indices |
|
Input: Edges and nodes of molecule
Output: Topological indices vector
Step 1. Start
Step 2. Graph of undirected edges
Step 3. Adjacency matrix of G
Step 4. Distances of G
Step 5. Vertex degree of G
Step 6. Calculate size of matrix d
Step 4. Construct
for to number of rows do
for to number of columns do
Wiener index
Schultz index
Harary index
Gutman index
end for
end for
Step 5. summation of
|
3.1. Results and Discussion
Fibrates drugs are predicted by numerous topological indices. In QSPR, linear, quadratic, and cubic regression models are examined. Several topological indices are calculated for Fibrates drugs, including vertex degree, and distance between vertices. The models are analyzed using twelve descriptors and thirteen topological indices. Using linear regression model a correlation coefficient between these indices and some physicochemical properties can be seen in Table 4. In Table 6 using quadratic regression model a correlation coefficient between these indices and some physicochemical properties is computed. When a correlation coefficient is obtained for a physicochemical property, the model that has maximum R is the most accurate predictor of the regression model. In Table 4, we display for each physicochemical property, based upon the analysis of the data (linear and quadratic). We have excluded values less than from the Table 4, and Table 6, out of convenience.
Table 4.
The correlation coefficient (R) obtained by linear regression model between topological indices and physicochemical properties of various drugs of Fibrates.
Table 4.
The correlation coefficient (R) obtained by linear regression model between topological indices and physicochemical properties of various drugs of Fibrates.
| T.I. | ||||
|---|---|---|---|---|
| − | ||||
With linear regression models, the following Table 5 illustrates the most appropriate topological index for estimating physicochemical properties. A diagram depicting this is shown in Figure 5.
Table 7 illustrate the best topological index which gives the best estimate for physicochemical properties using quadratic regression models, we only consider topological index with . A diagram depicting this is shown in Figure 6.
Table 5.
Linear regression models that give the best estimate for physicochemical
| Linear regression model | F | ||||
|---|---|---|---|---|---|
| 1 | |||||
Table 6.
The correlation coefficient (R) obtained by quadratic regression model between topological indices and physicochemical properties of various drugs of Fibrates.
Table 6.
The correlation coefficient (R) obtained by quadratic regression model between topological indices and physicochemical properties of various drugs of Fibrates.
| T.I. | P | S | C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H | |||||||||
| R | |||||||||
Remark 1.
Initially, linear regression was attempted on all physicochemical properties using degree-based topological indices. Correlation coefficients were calculated for 7 out of 12 properties that showed satisfactory results, as presented in Table 4. For the remaining properties with correlation coefficients less than 0.64, Table 6 explored alternative models. Five additional properties were tested, and if their correlation coefficients exceeded , the quadratic regression model was used. Note that some properties, such as Sum of the electronic and zero-point energies , Sum of the electronic and thermal energies , Sum of the electronic and thermal enthalpies , Sum of the electronic and thermal free energies , have identical correlation coefficients, and only is listed in Table 5 and Table 7.
Table 7.
Quadratic regression model that give the best estimate for physicochemical.
| Quadratic regression model | F | ||||
|---|---|---|---|---|---|
The cubic model is used for all the physicochemical properties and degree-based topological indices in order to provide a comprehensive analysis. Table 8 presents the correlation coefficients, which are high as anticipated. Table 9 and Figure 7 display the best predictions of the properties.
Table 8.
The correlation coefficient (R) obtained by cubic regression model between topological indices and physicochemical properties of various drugs of Fibrates.
Table 8.
The correlation coefficient (R) obtained by cubic regression model between topological indices and physicochemical properties of various drugs of Fibrates.
| T.I. | P | C | S | |||||
|---|---|---|---|---|---|---|---|---|
| H | ||||||||
| R | ||||||||
Table 9.
Cubic regression model that give the best estimate for physicochemical.
| Cubic regression model | F | ||||
|---|---|---|---|---|---|
Based on three curvilinear models, linear, quadratic, and cubic, the following Table 10, illustrates the correlation coefficient R for the four distance topological indices. The next Table shows the most accurate prediction of the physicochemical properties based on linear or quadratic models. It should be noted that the physicochemical properties: Sum of the electronic and zero-point energies , Sum of the electronic and thermal energies , Sum of the electronic and thermal enthalpies , Sum of the electronic and thermal free energies have the same correlation coefficients, which is why the is the only one listed in Table 10. It is evident that the cubic model is the optimal model to predict all physicochemical properties of Fibrates. Notice that, we displayed the correlation coefficient in bold for the cubic model. Table 11 and Figure 8 illustrated the best linear and quadratic model of distance-based topological indices with the properties.
Table 10.
The curvilinear models, along with the linear, quadratic, and cubic regression models, were used to determine the correlation coefficient (R) between the physicochemical properties of various Fibrates drugs and their distance topological indices..
Table 10.
The curvilinear models, along with the linear, quadratic, and cubic regression models, were used to determine the correlation coefficient (R) between the physicochemical properties of various Fibrates drugs and their distance topological indices..
| P.P. | ||||
|---|---|---|---|---|
| P | ||||
| S | , | |||
| C | ||||
Table 11.
The linear and quadratic regression models provide the most accurate predictions for the physicochemical properties.
Table 11.
The linear and quadratic regression models provide the most accurate predictions for the physicochemical properties.
| F | |||||
|---|---|---|---|---|---|
The physicochemical properties of Fibrates drugs and their corresponding degree-based and distance-based topological indices were analyzed using three curvilinear models: linear, quadratic, and cubic. The aim was to determine the most accurate correlation coefficient for the properties studied.
Table 4 shows the correlation coefficients (R) obtained by a linear regression model between various topological indices and physicochemical properties of Fibrates drugs. The topological indices include degree-based topological indices. The results show that the correlation coefficients vary across the different topological indices and physicochemical properties. Positive correlation indicates two variables that tend to move strongly in opposite directions, while negative correlation indicates two variables that move strongly in opposite directions. In particular, for the first Zagreb index the correlation coefficient lies between and 1, with the best prediction for complexity being 1. For the second Zagreb index the range of the correlation coefficient is which indicates high prediction of all physicochemical properties under study. The highest correlation coefficient values were observed for the property with values ranging from to , followed by the index with values ranging from to . The other topological indices showed weaker correlations with the physicochemical properties, with correlation coefficients ranging from to for the remaining indices. Table 5 provided lists five linear regression models and their corresponding and values. , or coefficient of determination, is a measure of how well the independent variables in a linear regression model explain the variation in the dependent variable. It ranges from 0 to 1, with 1 indicating a perfect fit. , or root mean squared error, is a measure of how well the regression model’s predictions match the actual values. It represents the average distance between the predicted and actual values, and lower values indicate better accuracy. All five models have relatively high values, indicating that they explain a significant amount of the variation in the dependent variable. The lowest value is , which is still considered a relatively good fit. However, the models have different levels of prediction accuracy as measured by . The with Min-max rodeg index index model has the lowest value of , which suggests that it has the most accurate predictions among the five models. The C model with first Zagreb index has the second lowest value of , followed by the model with an of . The index) and index) models have the highest values of and , respectively, indicating that their predictions are the least accurate among the five models. In summary, while all five models have relatively high values indicating good fit to the data, the model is the most accurate based on its low value, followed by the C and models, and then the ( index) and (R index) models, which have the highest values.
Table 6 presents the correlation coefficients obtained by a quadratic regression model between topological indices and physicochemical properties of various drugs of Fibrates. Upon analyzing the data in Table 6, several noteworthy findings can be observed. Firstly, many of the correlation coefficients are relatively high, indicating a strong linear relationship between the topological indices and physicochemical properties of the Fibrates drugs. For instance, has a high correlation coefficient of with , indicating a strong positive linear relationship between these two variables. Similarly, has a high correlation coefficient of with , suggesting a strong positive linear relationship between these variables as well. Furthermore, some of the correlation coefficients are close to 1, indicating a perfect positive linear relationship between the variables. For example, and indices have a correlation coefficient of with , suggesting a perfect positive linear relationship between these two variables. Similarly, index has a correlation coefficient of with ,, , and , indicating a perfect positive linear relationship between these variables. On the other hand, some correlation coefficients are relatively low, indicating a weak linear relationship between the variables. For instance, index has a correlation coefficient less than 0.64 for most of the properties exept for and , suggesting a weak positive linear relationship between these two variables. It is also interesting to note that we don’t have any negative values which would indicating an inverse relationship between the variables. In addition, some of the correlation coefficients are moderate, suggesting a moderate linear relationship between the variables. For instance, has a correlation coefficient of , indicating a moderate positive linear relationship between these variables. Overall, the findings from Table 6 suggest that there are varying degrees of linear relationships between the topological indices and physicochemical properties of Fibrates drugs. Some of the relationships are strong, while others are weak or moderate. Looking at Table 7, we see that all five models for Complexity property have high values, with the lowest being and the highest being . This suggests that all five models are good at explaining the variation in the physicochemical property they are modeling. The second thing to consider is the value, a lower value indicates that the model has a better fit. In this table, we can see that the values range from to . The model with the lowest value is the second model: for the Randic index. This indicates that this model has the best fit for estimating the physicochemical property. However, it is important to note that all five models have high values, suggesting that they all provide good estimates for the physicochemical property. After analyzing the table, we found that there are five quadratic regression models with both high values and low values. The quadratic regression model for S has a high value of and a low value of , making it one of the best models in terms of accurately predicting the target variable. The other models are for , , , and . The model for has an value of and an of , the model for has an value of and an of , the model for has an value of and an of , and the model for has an value of and an of . These models can be considered the best in terms of their ability to fit the data and accurately predict the target variable.
Table 8 presents the correlation coefficient obtained by cubic regression models between topological indices and physicochemical properties of various drugs of fibrates. Looking at the table, we can see that the range of correlation coefficient varies for each row. For instance, the correlation coefficient for the row of the first Zagreb index ranges from to , while for the row Inverse symmetric deg index , the correlation coefficient ranges from to . Overall, most of the correlation coefficients are relatively high, with many of them being close to . This suggests a strong correlation between the topological indices and the physicochemical properties of the drugs of fibrates. The high correlation coefficients could indicate that the topological indices could be used to predict the physicochemical properties of the drugs with high accuracy. Based on the Table 9, it appears that the cubic regression model provides the highest correlation coefficients for most of the topological indices and physicochemical properties of Fibrates drugs. The range of correlation coefficients for each row varies, but in general, they are relatively high, indicating a strong relationship between the topological indices and physicochemical properties. Furthermore, the high correlation coefficients suggest that the cubic regression model is an effective tool for predicting physicochemical properties based on the topological indices of Fibrates drugs. Overall, the results of the table suggest that the cubic regression model is the best choice for analyzing the relationship between topological indices and physicochemical properties in Fibrates drugs. based on Table 9, we can analyze the four topological indices with respect to high and minimum . (, ) indicating a strong correlation between the physicochemical properties and this index. Additionally, its value of is also very low, suggesting that the predicted values using this index are very close to the actual values. (, ) indicating a perfect correlation with the physicochemical properties.
By deep looking at Table 10, considering only the distance-based topological indices, we can notice that the model which gives the highest correlations with all the investigated physicochemical properties of Fibrate drugs is the cubic model. Since the correlation coefficients range from to . In the second place is the quadratic model, since it gives good correlations with most of these properties, the correlation coefficients range from to . While the linear model comes in the third place, shows good correlation but with the least number of properties, the correlation coefficients range to . An important note, in most cases, that the linear and quadratic models give comparable correlation coefficients, while there is a significant improvement in the correlation coefficients when the cubic model is used for most of properties. For instance, for the polarizability property estimated using wiener index, correlations are comparable, and for the linear and quadratic models, respectively, and it improves to 1 with the cubic model. As a result, we should consider our model type when dealing with such properties. Generally speaking, the four properties at the end of Table 10 are estimated very well with the three models compared to the first five properties in the table. The complexity property can be best estimated using the various models, since the correlations with each model reach . The topological polar area can be nominated as the second-best estimated property by the three models, followed by Sum of electronic and zero-point Energies property. Conversely, the zero-point vibrational energy and heat capacity properties seems to be the least properties which can be estimated correctly using the two models (linear and quadratic), the correlations not exceeded , the exception is the quadratic model of the hyper Zagreb index , and , respectively. Based on the values given in Table 11, the three best predictors with the lowest values are: Linear Regression with Quadratic Regression with and Curvilinear Regression with These three regression models exhibit the lowest values, indicating higher accuracy and better predictive performance compared to the other regression models. Therefore, these three regression models, namely linear, quadratic, and curvilinear, can be considered as the best predictors for enhancing the analysis of fibrates drug activity through molecular descriptors in this study. Therefore, based on the results obtained, it can be concluded that the cubic and quadratic regression models are the top predictors for the physicochemical properties analyzed in this investigation, as they exhibit both high values and minimum values simultaneously. These findings highlight the effectiveness of these regression models in enhancing the analysis of fibrates drug activity through molecular descriptors and provide valuable insights for future research in this area.
4. Conclusion
Based on our comprehensive analysis, we have demonstrated that the use of curvilinear regression models can significantly enhance the analysis of fibrates drug activity through molecular descriptors. Our results have revealed that these models have superior predictive power compared to linear regression models, especially when the underlying data exhibits nonlinear relationships. Furthermore, the incorporation of molecular descriptors as independent variables has substantially improved the accuracy and robustness of the models. Our findings have several important implications for the field of drug discovery and development. Firstly, the use of curvilinear regression models, in conjunction with molecular descriptors, can facilitate the identification and optimization of more potent and selective drugs, thus reducing the time and cost associated with drug development. Secondly, our study underscores the importance of considering nonlinear relationships between molecular descriptors and drug activity, which has traditionally been overlooked in conventional linear regression analyses. Lastly, the efficacy of curvilinear regression models and molecular descriptors in predicting drug activity may be extended to other drug classes and further elucidated through future studies. In summary, our investigation demonstrates that curvilinear regression models represent a powerful approach for analyzing drug activity, particularly when coupled with molecular descriptors. Our results provide a basis for the development of improved drug discovery pipelines and offer insights into the molecular mechanisms governing drug activity.
Author Contributions
Conceptualization, S.W. and N.U.O., methodology, S.W., validation, S.W. and N.U.O., formal analysis, S.W., investigation, S.W., resources, N.U.O., data curation, N.U.O., writing—original draft S.W., preparation, S.W., writing—review and editing, S.W.and N.U.O., supervision, S.W., project administration, S.W., funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
The article contains the data that supported the study’s findings.
Acknowledgments
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 214-247-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University. DSR, Jeddah, Saudi Arabia. The authors acknowledge Nuha Wazzan from Chemistry department at King Abdulaziz University for her contribution with the DFT calculations and King Abdulaziz University’s High-Performance Computing Centre (Aziz Supercomputer) (http://hpc.kau.edu.sa) for supporting the computation for the work described in this paper.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Gonzalez-Diaz, H. , Vilar, S., Santana, L. and Uriarte, E., 2007. Medicinal chemistry and bioinformatics-current trends in drugs discovery with networks topological indices. Current topics in medicinal chemistry, 7(10), pp.1015-1029.
- Estrada, E. and Uriarte, E., 2001. Recent advances on the role of topological indices in drug discovery research. Current Medicinal Chemistry, 8(13), pp.1573-1588. [CrossRef]
- Gao, W. , Wang, W. and Farahani, M.R., 2016. Topological indices study of molecular structure in anticancer drugs. Journal of chemistry, 2016. [CrossRef]
- Gao, W. , Farahani, M.R. and Shi, L., 2016. Forgotten topological index of some drug structures. Acta medica mediterranea, 32(1), pp.579-585.
- P.A. McCullough, and M.J. Di Loreto, 2012. "Fibrates and cardiorenal outcomes." Journal of the American College of Cardiology, 60(20), pp.2072-2073. [CrossRef]
- Brea, A. , Millán, J., Ascaso, J.F., Blasco, M., Díaz, A., Hernández-Mijares, A., Mantilla, T., Pedro-Botet, J.C. and Pintó, X., 2018. Fibrates in primary prevention of cardiovascular disease. Comments on the results of a systematic review of the Cochrane Collaboration. Clínica e Investigación en Arteriosclerosis (English Edition), 30(4), pp.188-192.
- J. Devillers, and A. T. Balaban, eds. Topological Indices and Related Descriptors in QSAR and QSPAR (CRC Press, Boca Raton, 2000).
- I. Gutman, “A Property of the Simple Topological Index,” MATCH Communications in Mathematical and in Computer Chemistry 25 (1990): 131–40.
- H. Wiener, “Structural Determination of Paraffin Boiling Points,” Journal of the American Chemical Society 69, no. 1 (1947): 17–20. [CrossRef]
- W. Gao, Y. Wang, B. Basavanagoud, and M. K. Jamil, “Characteristics Studies of Molecular Structures in Drugs,” Saudi Pharmaceutical Journal 25, no. 4 (2017): 580–6. [CrossRef]
- T. Doslic, T. Reti, and A. Ali, “On the Structure of Graphs with Integer Sombor Indices,” Discrete Mathematics Letters 7 (2021): 1–4.
- I. Gutman, “Geometric Approach to Degree-Based Topological Indices: Sombor Indices,” MATCH Communications in Mathematical and in Computer Chemistry 86 (2021): 11–6.
- Ediz, S. , Çiftçi, İ., Cancan, M. and Farahani, M.R., 2021. "On k-total distance degrees and k-total Wiener polarity index". Journal of Information and Optimization Sciences, 42(7), pp.1469-1477.
- M. Mateji c, E. Zogi c, E. Milovanovi c, and I. Milovanovi c, “A Note on the Laplacian Resolvent Energy of Graphs,” Asian-European Journal of Mathematics 13, no. 06 (2020): 2050119. [CrossRef]
- H. Wiener, “Structural Determination of Paraffin Boiling Points,” Journal of the American Chemical Society 69, no. 1 (1947): 17–20. [CrossRef]
- I. Gutman, and N. Trinajst ıC, “Graph Theory and Molecular Orbitals. Total p-Electron Energy of Alternant Hydrocarbons,” Chemical Physics Letters 17, no. 4 (1972): 535–8. [CrossRef]
- M. Randić, “On Characterization of Molecular Branching,” Journal of the American Chemical Society 97, no. 23 (1975): 6609–15. [CrossRef]
- E. Estrada, “Characterization of 3D Molecular Structure,” Chemical Physics Letters 319, no. 5-6 (2000): 713–8. [CrossRef]
- H. Hosoya, “Topological Index. A Newly Proposed Quantity Characterizing the Topological Nature of Structural Isomers of Saturated Hydrocarbons,” Bulletin of the Chemical Society of Japan 44, no. 9 (1971): 2332–9. [CrossRef]
- E. Estrada, and D. Bonchev, Chemical Graph Theory (New York: Chapman and Hall/CRC, 2013).
- I. Gutman, B. Ruscic, N. Trinajstic, and C. F. WilsonJr., “Graph theory and molecular orbitals. XII. Acyclic polyenes,” The Journal of Chemical Physics, vol. 62, no. 9, pp. 3399–3405, 1975.
- G. H. Shirdel, H. Rezapour, and A. M. Sayadi, “The hyper Zagreb index of graph operations,” Iranian Journal of Mathematical Chemistry, vol. 4, pp. 213–220, 2013.
- Togan, M. , Yurttas, A., Cevik, A.S., and Cangul, I.N., 2019. "Effect of edge deletion and addition on Zagreb indices of graphs". In Mathematical Methods in Engineering (pp. 191-201). Springer, Cham.
- Togan, M. , Yurttas, A., Çevik, A.S., and Cangul, I.N., 2019. "Zagreb indices and multiplicative Zagreb indices of double graphs of subdivision graphs". TWMS Journal of Applied and Engineering Mathematics, 9(2), pp.404-412.
- Gutman, I. , Togan, M., Yurttas, A., Cevik A. S., and Cangul I.N., “Inverpe problem fsr sigma index,” MATCH Communications in Mathematical and in Computer Chemistry", vol. 79, pp. 491–508, 2018.
- M. Ghorbani, S. Zangi, and N. Amraei, “New results on symmetric division deg index,” Journal of Applied Mathematics and Computing, vol. 65, pp. 161–176, 2021. [CrossRef]
- D. Vukiccevi’c and M. Gasparov, “Bond additive modeling 1. Adriatic indices,” Crica Chemica Actata.vol. 83, pp. 243–260, 2010.
- Richardson, C.W. , Foster, G.R. and Wright, D.A., 1983. Estimation of erosion index from daily rainfall amount. Transactions of the ASAE, 26(1), pp.153-0156. [CrossRef]
- Das, K.C. , Gutman, I. and Furtula, B., 2011. On atom-bond connectivity index. Chemical Physics Letters, 511(4-6), pp.452-454. [CrossRef]
- Dalfó, C. , 2019. On the Randić index of graphs. Discrete Mathematics, 342(10), pp.2792-2796.
- Jahanbani, A. , 2019. Albertson energy and Albertson Estrada index of graphs. Journal of Linear and Topological Algebra, 8(01), pp.11-24.
- Klavžar, S. , Rajapakse, A. and Gutman, I., 1996. The Szeged and the Wiener index of graphs. Applied Mathematics Letters, 9(5), pp.45-49. [CrossRef]
- Xu, K. and Das, K.C., 2011. On Harary index of graphs. Discrete applied mathematics, 159(15), pp.1631-1640.
- Mukwembi, S. , 2012. On the upper bound of Gutman index of graphs. Match-Communications in Mathematical and Computer Chemistry, 68(1), p.343.
- O. Ç. Havare, “Topological indices and QSPR modeling of some novel drugs used in the cancer treatment,” International Journal of Quantum Chemistry, vol. 121, no. 24, Article ID e26813, 2021. [CrossRef]
- D. Vukicevic, “Boad additime modeling 2. Mathematicpl properties mf max-mrn rodig index,” Crica Chemica Actata.vol. 83, no. 3, pp. 261–273, 2010.
- E. Estrada, L. Torres, L. Rodrıguez, and I. Gutman, “An atombond connectivity index: modelling the enthalpy of formation of alkanes,” Indian Journal of Chemistry, vol. 37, pp. 849–855, 1998.
- G. V. Rajasekharaiah and U. P. Murthy, “Hyper-Zagreb indices of graphs and its applications,” Journal of Algebra Combinatorics Discrete Structures and Applications, vol. 8, no. 1, pp. 9–22, 2020. [CrossRef]
- D. Vukiccevic and M. Gasparov, “Bond additive modeling 1. Adriatic indices,” Crica Chemica Actata.vol. 83, pp. 243–260, 2010.
- Ö. Çolakŏglu Havare, “Determination of some thermodynamic properties of monocarboxylic acids using multiple linear regression,” BEU Journal of Science, vol. 8, no. 2, pp. 466–471, 2019.
- Lokesha, V. , Shruti, R. and sinan CEVIK, A., 2018. On certain topological indices of Nanostructures using QG and RG operators. Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics, 67(2), pp.178-187.
- T. Reti, R. T. Reti, R. Sharafdini, A. Dregelyi-Kiss, and H. Haghbin, “Graph irregularity indices used as molecular descriptors in QSPR studies,” MATCH Communications in Mathematical and in Computer Chemistry, vol. 79, pp. 509–524, 2018.
- Wiener, H. , 1948. Relation of the physical properties of the isomeric alkanes to molecular structure. Surface tension, specific dispersion, and critical solution temperature in aniline. The Journal of Physical Chemistry, 52(6), pp.1082-1089. [CrossRef]
- Dobrynin, A.A. , Entringer, R. and Gutman, I., 2001. Wiener index of trees: theory and applications. Acta Applicandae Mathematica, 66(3), pp.211-249. [CrossRef]
- Castro, E.A. and Tueros, M., 2001. QSPR Study of boiling points of alkyl alcohols via improved polynomial relationships. Philippine Journal of Science, 130(2), pp.111-118.
- Delen, S. , Khan, R.H., Kamran, M., Salamat, N., Baig, A.Q., Naci Cangul, I. and Pandit, M.K., 2022. Ve-Degree, Ev-Degree, and Degree-Based Topological Indices of Fenofibrate. Journal of Mathematics, 2022.
- Liu, X. , Chen, W, Gao, H., & Shi, Y. (2021). QSPR models for predicting the densities and viscosities of biodiesel using topological indices. Symmetry, 13(4), 544. [PubMed]
- Zuo, J. , & Hu, L. (2020). QSPR modeling of the melting points of organic compounds using molecular topology and quantum chemical descriptors. Symmetry, 12(7), 1104.
- Zhang, Y. , Li, H., Liu, Y., & Zhou, P. (2019). QSPR models for predicting melting points of organic compounds based on molecular topology. Symmetry, 11(1), 25. [PubMed]
- Naghipour, S. , & Kiasat, A. R. (2019). Application of topological indices in QSPR modeling of C60 derivatives’ fullerene-like behavior. Symmetry, 11(3), 368.
- Wang, J. , & Xu, L. (2018) QSPR models for predicting the boiling points of alkyl alkanes based on the novel vertex degree valence topological index. Symmetry, 10(7), 282. [PubMed]
- Frisch, M.J. , Gaussian 09 Programmer’s Reference. 2009, Gaussian.
- Roy Dennington, T. Keith, and J. Millam, GaussView, S. Mission, Editor. 2009, Semichem Inc.: KS.
- Hanwell, M.D. , et al., Avogadro: an advanced semantic chemical editor, visualization, and analysis platform. Journal of Cheminformatics, 2012. 4(1): p. 17.
- O’boyle, N.M., A. L. Tenderholt, and K.M. Langner, Cclib: a library for package-independent computational chemistry algorithms. Journal of computational chemistry, 2008. 29(5): p. 839-845. [CrossRef]
Figure 1.
Fenofibrate: (1) optimized geometries, (2) ESPM, (3) DOS plots, and (4) HOMOs and LUMOs.
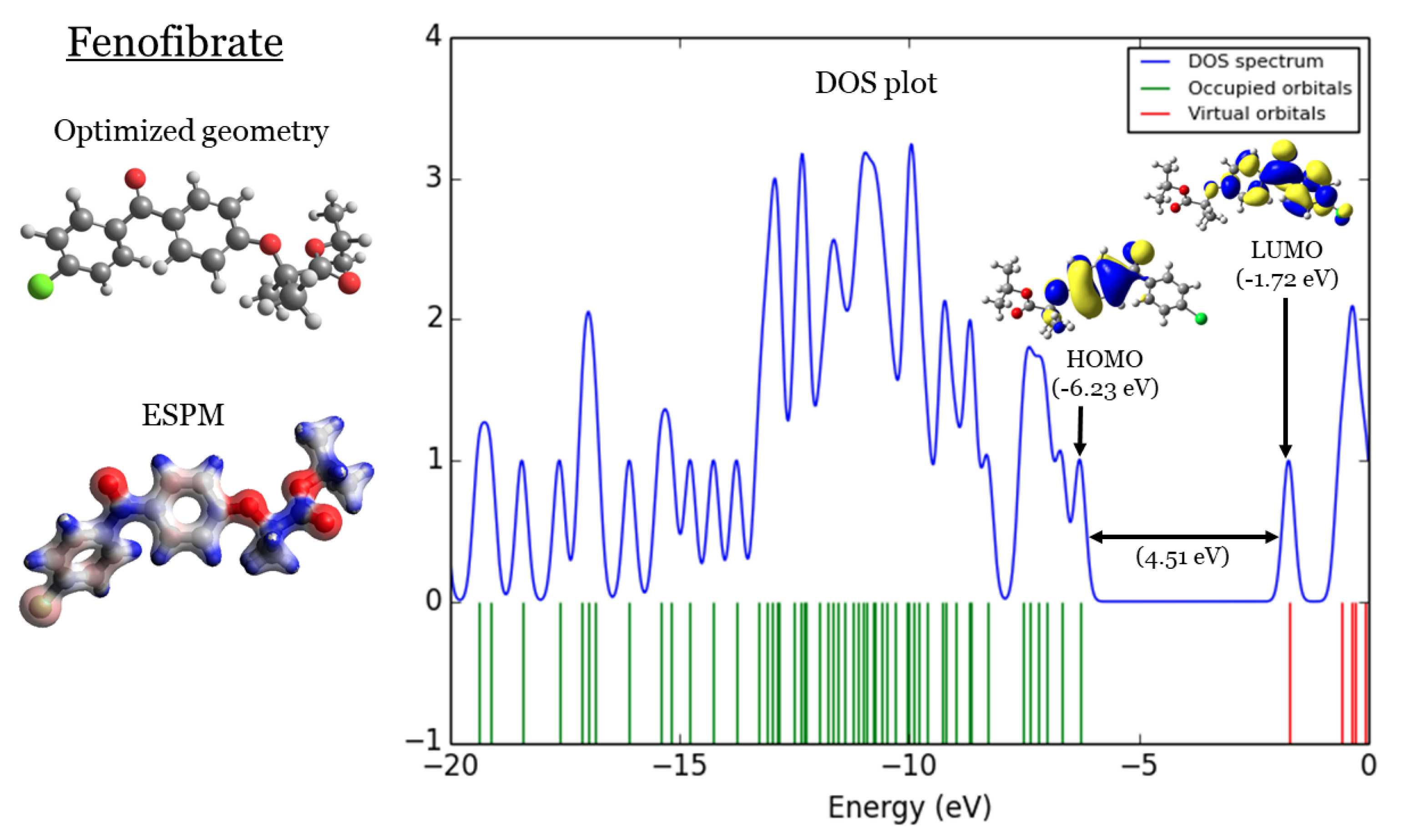
Figure 2.
Ciprofibrate: (1) optimized geometries, (2) ESPM, (3) DOS plots, and (4) HOMOs and LUMOs.
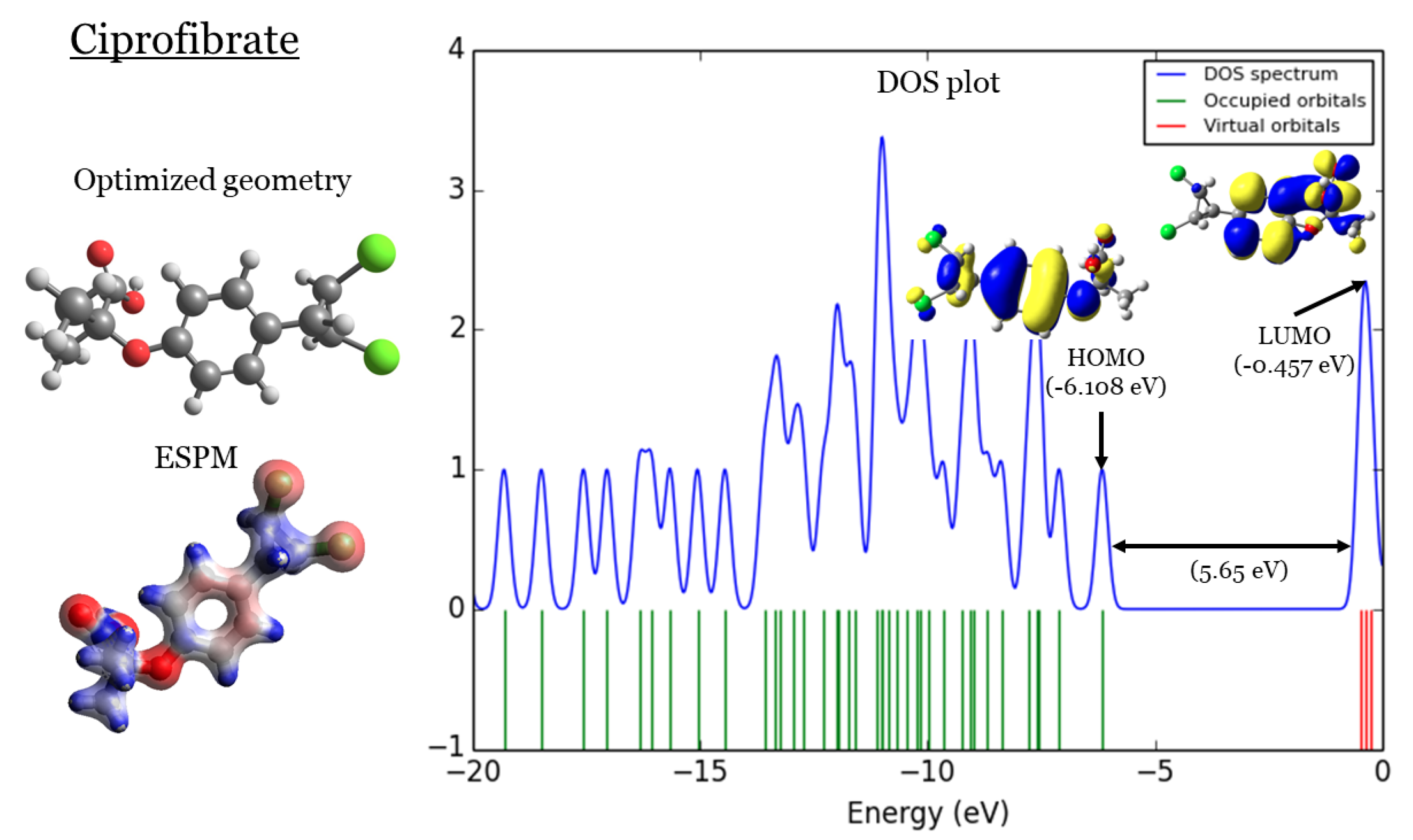
Figure 3.
Bezafibrate: (1) optimized geometries, (2) ESPM, (3) DOS plots, and (4) HOMOs and LUMOs.
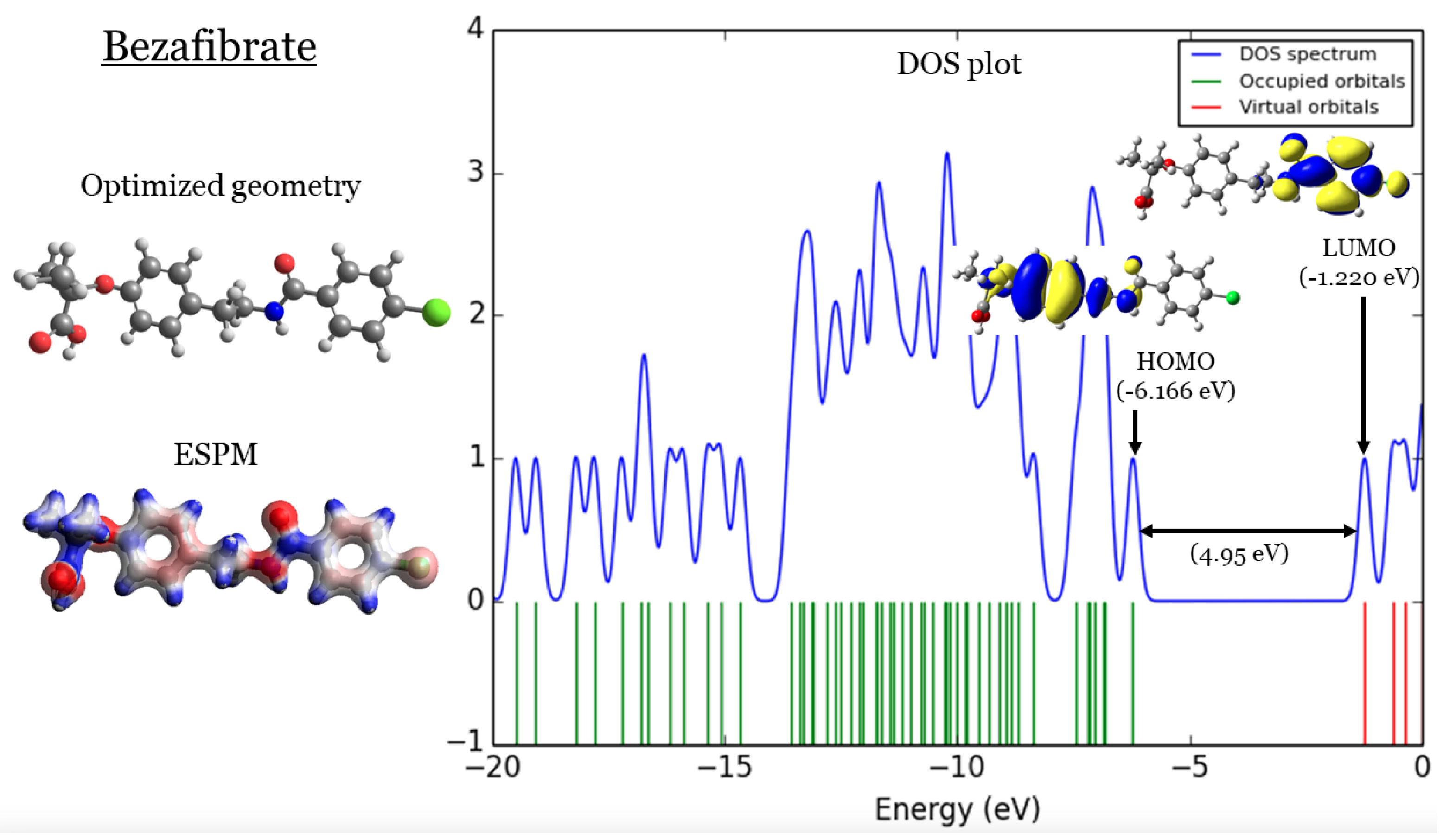
Figure 4.
Clofibrate: (1) optimized geometries, (2) ESPM, (3) DOS plots, and (4) HOMOs and LUMOs.
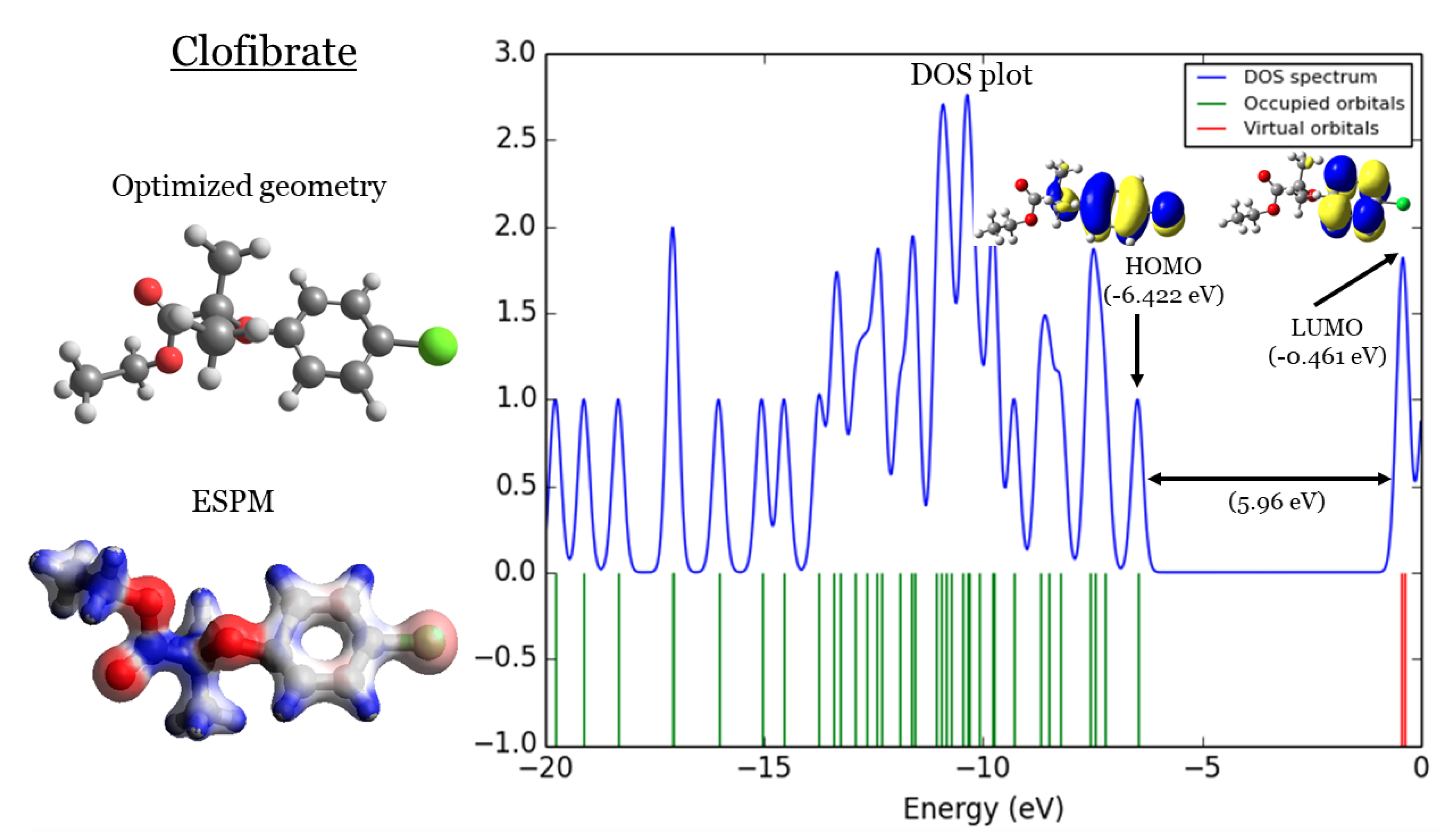
Figure 5.
Plots of Linear Regression Equations for the Best Physicochemical Properties Predicted by Degree-based Topological Indices.
Figure 5.
Plots of Linear Regression Equations for the Best Physicochemical Properties Predicted by Degree-based Topological Indices.
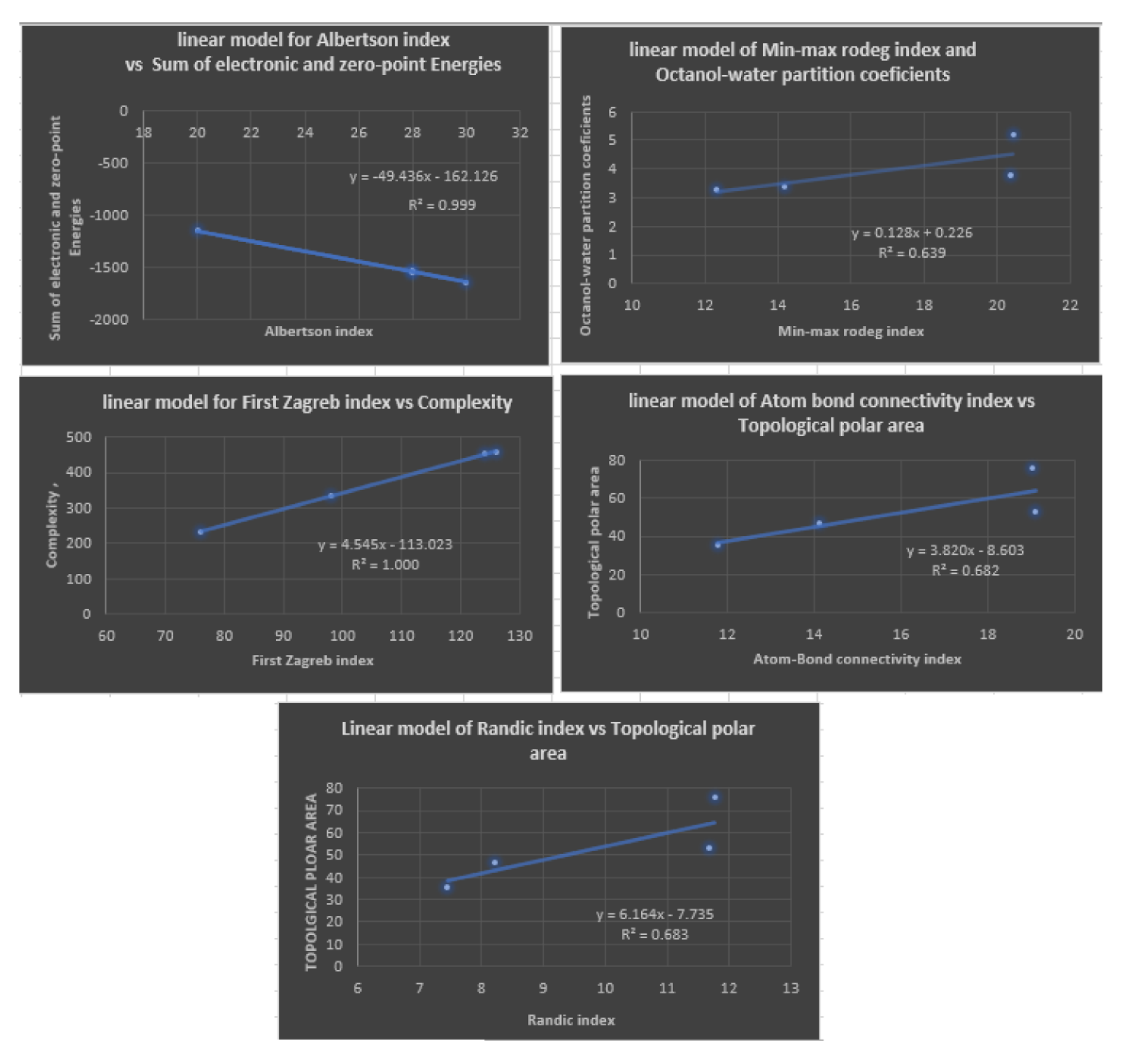
Figure 6.
Plots of Quadratic Regression Equations for the Best Physicochemical Properties Predicted by Degree-based Topological Indices.
Figure 6.
Plots of Quadratic Regression Equations for the Best Physicochemical Properties Predicted by Degree-based Topological Indices.
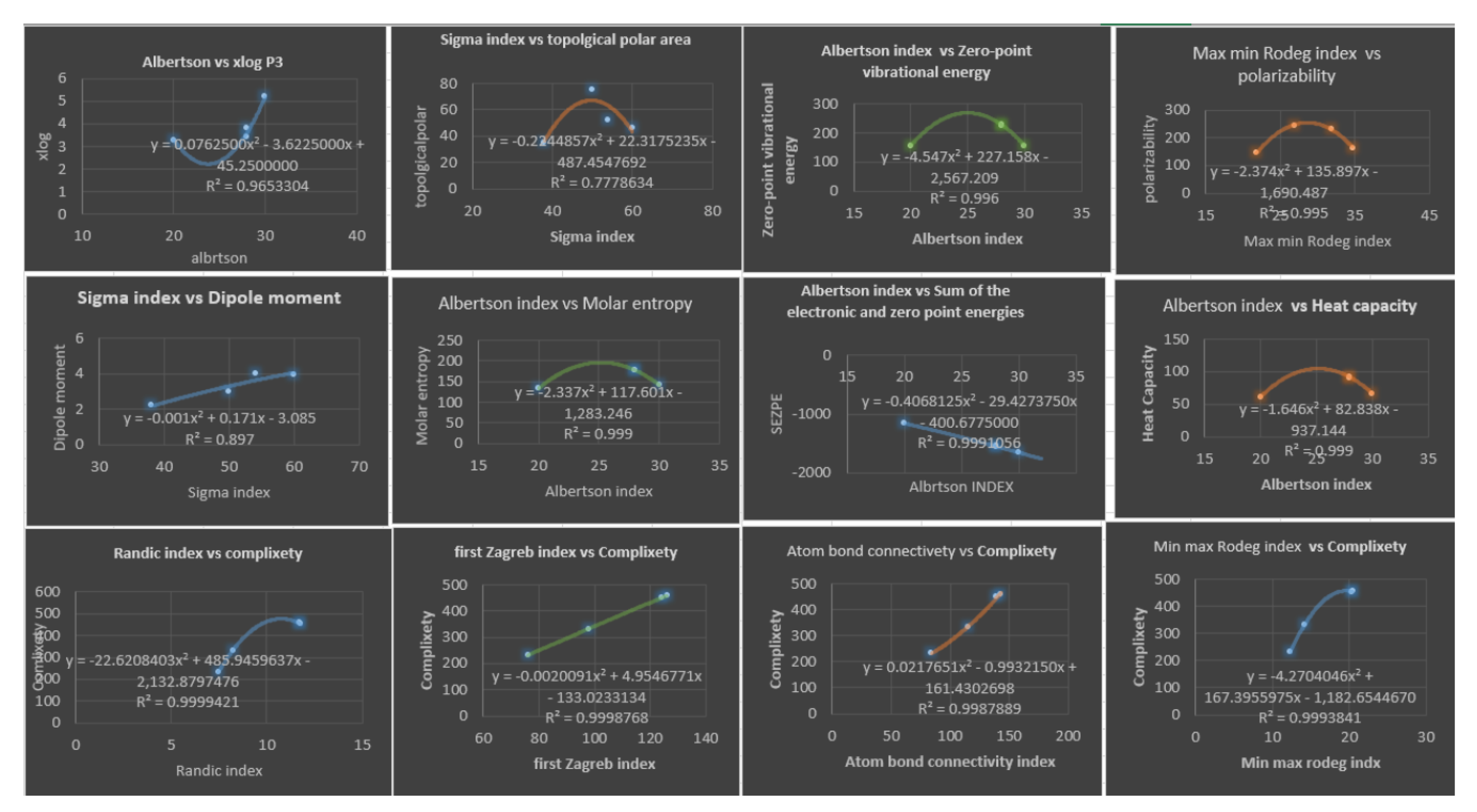
Figure 7.
Plots of Cubic Regression Equations for the Best Physicochemical Properties Predicted by Degree-based Topological Indices.
Figure 7.
Plots of Cubic Regression Equations for the Best Physicochemical Properties Predicted by Degree-based Topological Indices.
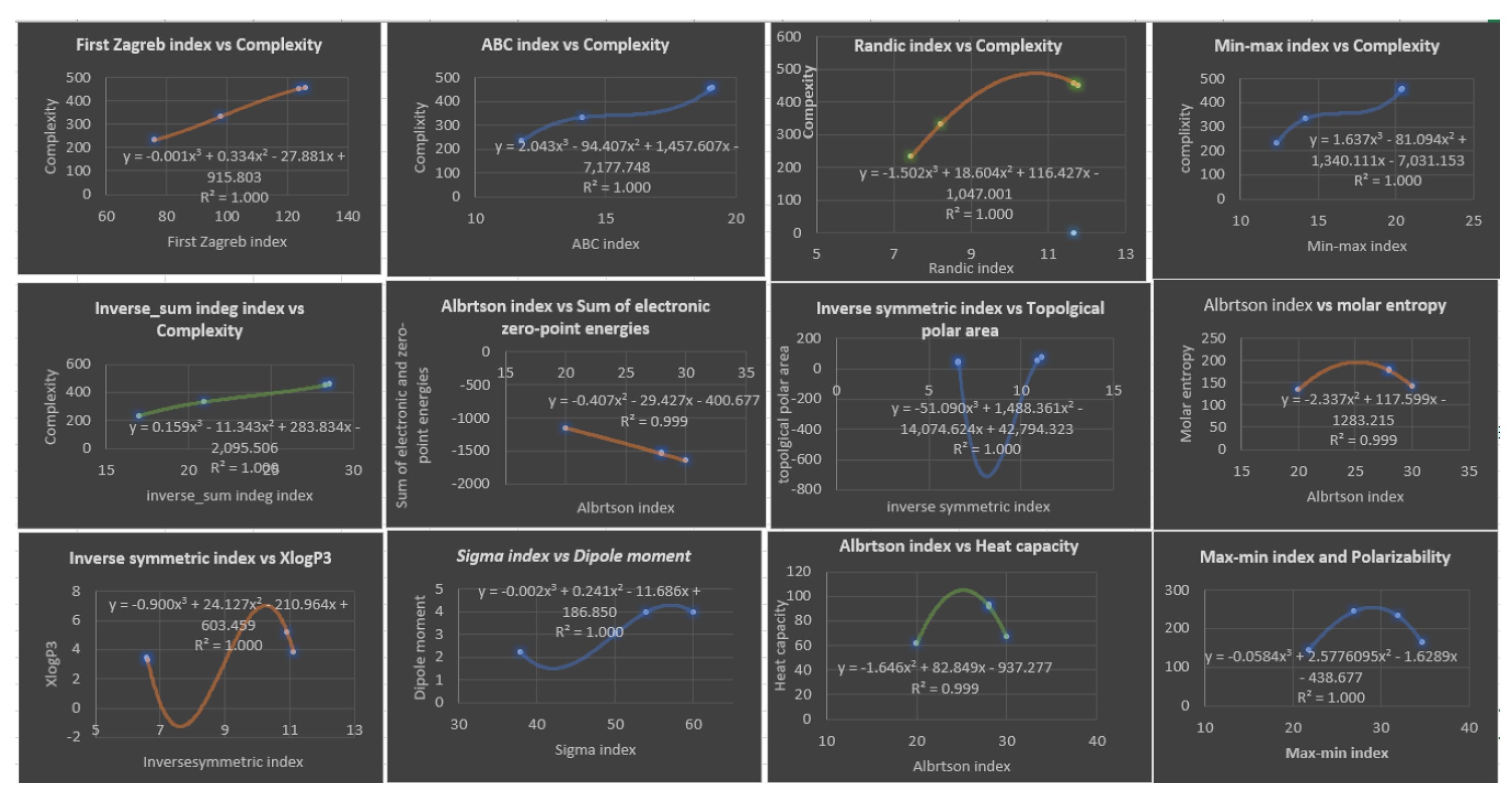
Figure 8.
Plots of Linear and Quadratic Regression Equations for the Best Physicochemical Properties Predicted by Distance-based Topological Indices.
Figure 8.
Plots of Linear and Quadratic Regression Equations for the Best Physicochemical Properties Predicted by Distance-based Topological Indices.
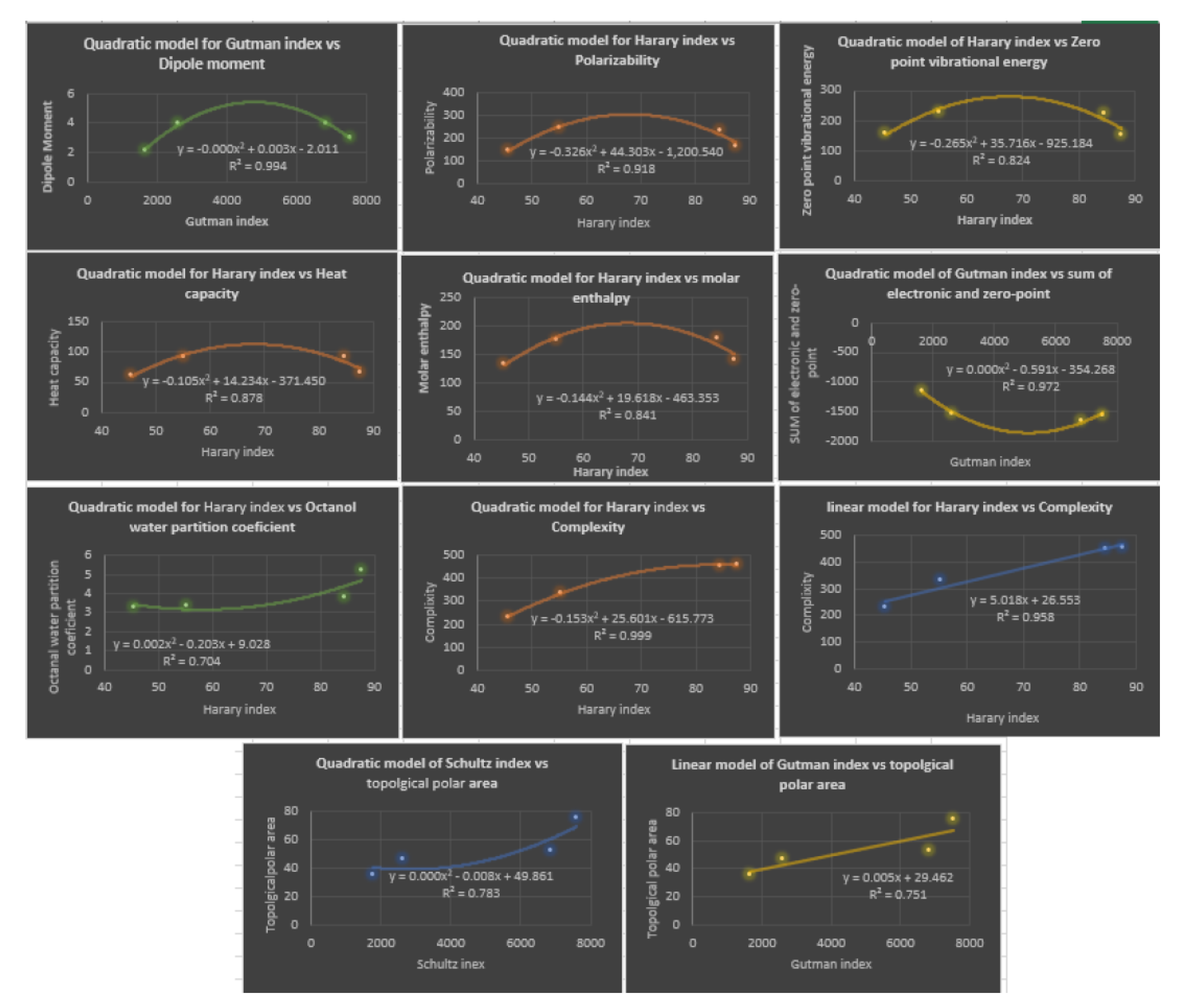
Table 1.
The mathematical expressions of topological indices.
| Vertex-degree-based topological indices | Mathematical expression |
|---|---|
| First Zagreb index | |
| Second Zagreb index | |
| Hyper Zagreb index | |
| Atom bond connectivity index | |
| Randić index | |
| Max-min rodeg index | |
| Min-max rodeg index | |
| Albertson index | |
| Sigma index | |
| Inverse symmetric deg index | |
| Inverse sum indeg index | |
| Distance-based topological indices | Mathematical expression |
| Wiener index | |
| Schultz index | |
| Harary index | |
| Gutman index |
Table 2.
Values of topological indices in Fibrates’ molecular structures.
| Topological index | Fenofibrate | Ciprofibrate | Bezafibrate | Clofibrate |
|---|---|---|---|---|
| 126 | 98 | 124 | 76 | |
| 143 | 115 | 139 | 84 | |
| 626 | 520 | 606 | 374 | |
| 30 | 28 | 28 | 20 | |
| 54 | 60 | 50 | 38 | |
| 1716 | 660 | 1882 | 468 | |
| 6872 | 2652 | 7600 | 1776 | |
| 6846 | 2638 | 7650 | 1670 |
Table 3.
The physicochemical properties of potential drugs of Fibrates.
| Physicochemical properties | Fenofibrate | Ciprofibrate | Bezafibrate | Clofibrate |
|---|---|---|---|---|
| 458 | 333 | 452 | 232 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






