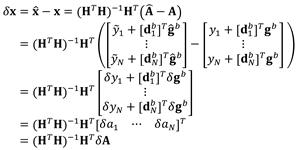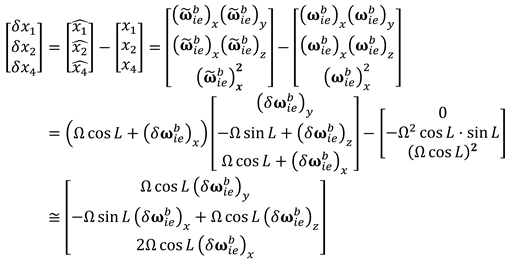Preprint

Article

Coarse Alignment of Gyro-Free Inertial Navigation System

Altmetrics

Downloads

168

Views

Comments

A peer-reviewed article of this preprint also exists.

Heyone Kim,Sang Heon Oh,

Jae Hoon Son,

Dong-Hwan Hwang^*

Heyone Kim,Sang Heon Oh,

Jae Hoon Son,

Dong-Hwan Hwang^*

This version is not peer-reviewed

Submitted:

02 May 2023

Posted:

03 May 2023

You are already at the latest version

Alerts

Abstract

In this paper, feasibility of the initial alignment of the gyro-free inertial navigation system (GF-INS) is investigated. Initial roll and initial pitch are obtained as the conventional INS since centripetal acceleration is very small. Relation between initial heading and accelerometers’ outputs of the gyro-free inertial measurement unit (GF-IMU) is derived. It is determined from the relation whether initial heading can be obtained in 15 GF-IMUs which have been presented in research literatures. The relationship between the accelerometer errors of GF-IMU and the initial heading error is derived. When gyros are additionally attached in one axis or two axes of the body frame, it is investigated that initial heading can be obtained. The initial heading error is also calculated from the accelerometer errors and the gyroscope errors. The results show that the initial heading from only accelerometer outputs of the GF-IMU cannot be used in the GF-INS since the error is too large. It can also be seen from the results that the initial heading can be used in the GF-INS if two gyroscopes are additionally attached to the roll and pitch axes of the body frame.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The inertial navigation system (INS) continuously provides attitude, velocity and position of a vehicle from specific force and angular velocity measured by an inertial measurement unit (IMU) [1,2,3]. Since the INS has high output rate and wide bandwidth, it has been widely used as a navigation system of vehicles with high dynamics such as rocket, guided missile and aircraft [4].

Initial attitude, initial velocity, and initial position must be known before the navigation is carried out since the INS calculates a navigation solution by integrating IMU measurements. The initial velocity and initial position should be provided externally. On the other hand, initial attitude can be determined in stationary state by itself from the gravity and the earth rate measured by the IMU [2]. This initial attitude determination without external aiding is called self-alignment [5]. In the gimbaled INS (GINS), the self-alignment is a procedure which aligns physically the platform with the navigation frame using gimbals. The self- alignment in the strap-down INS (SDINS) is a procedure to determine the initial attitude represented by the direction cosine matrix (DCM) between the body frame and the navigation frame or Euler angles, roll, pitch and heading.

The GF-INS is an inertial navigation system which uses only accelerometers. Shuler first proposed in 1960s the idea which measures angular motion of a vehicle using the lever-arm effect of accelerometer [6]. However, subsequent researches were not followed since quality of the accelerometer was not good enough to completely replace the gyroscope. With the development of micro-electro-mechanical system (MEMS) technology, nanotechnology and cold atomic technology from late 1990s, researchers have paid much attention to the GF-INS [7,8].

Before performing navigation, attitude should be initialized in the GF-INS as in the conventional INS. Even though self-alignment algorithm for the conventional INS is available, it cannot be used as it is since the measuring method of angular motion for a vehicle in the GF-INS is fundamentally different from that of the conventional INS.

Vaknin and Klein derived a partial coarse alignment procedure for the roll and pitch only and developed closed form expressions for the angular error of the GF-INS coarse alignment [9]. They compared the partial coarse alignment performances between different GF configurations. Vaknin and Klein claimed that a useful initial heading cannot be obtained regardless of the accelerometer grade since GF-INS is not able to directly measure the earth rate [9].

In this paper, a coarse alignment of the GF-INS is presented, and the feasibility of the initial heading is evaluated. The initial heading expression in accelerometer outputs of the GF-IMU is derived from the initial heading expression in the coarse alignment of the conventional INS. The configurations of the GF-IMU, in which the initial heading expression can be obtained, are investigated among the configurations of the GF-IMU in literatures [9,10,11,12,13,14,15]. A relation between accelerometer error and initial heading error is derived. In addition to these, initial heading expression is derived when one or two gyroscopes are added in the axes of the body frame to the GF-IMU. Relation between accelerometer of GF-IMU and gyroscope errors and initial heading error are also derived.

Organization of this paper is as follows. In section2, coarse alignment equations for the conventional INS is introduced. In section 3, the coarse alignment of the GF-INS is described. In section 4, the coarse alignment of the GF-INS is described when gyroscopes are added to the GF-IMU. Finally concluding remarks and further studies are presented in section 5.

2. Coarse Alignment of INS

2.1. Leveling

Only gravity is measured by the accelerometer when the vehicle is stationary. The measured gravity is represented in Equation (1) between the body frame and the navigation frame [16,17,18].

\begin{array}{l} f^{b} = C_{n}^{b} f^{n} = C_{3} C_{2} C_{1} f^{n} \\ = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos ϕ & \sin ϕ \\ 0 & - \sin ϕ & \cos ϕ \end{matrix}] [\begin{matrix} \cos θ & 0 & - \sin θ \\ 0 & 1 & 0 \\ \sin θ & 0 & \cos θ \end{matrix}] [\begin{matrix} \cos ψ & \sin ψ & 0 \\ - \sin ψ & \cos ψ & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} 0 \\ 0 \\ - g \end{matrix}] \\ = [\begin{matrix} \cos θ \cos ψ & \cos θ \sin ψ & - \sin θ \\ \sin ϕ \sin θ \cos ψ - \cos ϕ \sin ψ & \sin ϕ \sin θ \sin ψ + \cos ϕ \cos ψ & \sin ϕ \cos θ \\ \cos ϕ \sin θ \cos ψ + \sin ϕ \sin ψ & \cos ϕ \sin θ \sin ψ - \sin ϕ \cos ψ & \cos ϕ \cos θ \end{matrix}] [\begin{matrix} 0 \\ 0 \\ - g \end{matrix}] \\ = [\begin{matrix} g \sin θ \\ - g \sin ϕ \cos θ \\ - g \cos ϕ \cos θ \end{matrix}] = [\begin{matrix} {(f^{b})}_{x} \\ {(f^{b})}_{y} \\ {(f^{b})}_{z} \end{matrix}] \end{array}

(1)

where

ϕ

θ

and

ψ

are roll, pitch and heading, respectively.

g

denotes gravity.

f^{b}

and

f^{n}

are the specific force represented in the body frame and the navigation frame, respectively.

C_{n}^{b}

denotes the DCM between the navigation frame and the body frame.

C_{1}

C_{2}

and

C_{3}

denote DCMs between two frames when the frame is rotated

ψ

θ

, and

ϕ

around yaw, pitch, and roll axes, respectively.

Roll can be obtained as Equation (2) from Equation (1) [16,17,18].

ϕ = \tan^{- 1} (\frac{{(f^{b})}_{y}}{{(f^{b})}_{z}})

(2)

where

{(f^{b})}_{y}

and

{(f^{b})}_{z}

are the

y

axis and the

z

axis component the specific force, respectively. Pitch

θ

is obtained from Equation (3) [16,17,18].

θ = \tan^{- 1} (\frac{{(f^{b})}_{x}}{\sqrt{{(f^{b})}_{y}^{2} + {(f^{b})}_{z}^{2}}})

(3)

where

{(f^{b})}_{x}

is the

x

axis component of the specific force.

2.2. Gyrocompassing

Only the earth rate is measured by the gyroscope when the vehicle is stationary. The earth rate is represented as Equation (4) in the body frame and in the navigation frame [16,17,18].

ω_{i e}^{b} = C_{n}^{b} ω_{i e}^{n} = C_{3} C_{2} C_{1} [\begin{matrix} Ω \cos L \\ 0 \\ - Ω \sin L \end{matrix}]

(4)

where

Ω

and

L

are the magnitude of the earth rate and the latitude, respectively.

ω_{i e}^{b}

and

ω_{i e}^{n}

are the earth rate represented in the body frame and navigation frame, respectively. From Equation (4), the earth rate

ω_{i e}^{r}

represented in the frame, which is rotated from the navigation frame by the heading

ψ

, is given in Equation (5) [16,17,18].

\begin{array}{l} ω_{i e}^{r} = C_{1} ω_{i e}^{n} = [\begin{matrix} Ω \cos L \cos ψ \\ - Ω \cos L \sin ψ \\ - Ω \sin L \end{matrix}] \\ = {(C_{3} C_{2})}^{- 1} ω_{i e}^{b} = [\begin{matrix} {(ω_{i e}^{b})}_{x} \cos θ + {(ω_{i e}^{b})}_{y} \sin ϕ \sin θ + {(ω_{i e}^{b})}_{z} \cos ϕ \sin θ \\ {(ω_{i e}^{b})}_{y} \cos ϕ - {(ω_{i e}^{b})}_{z} \sin ϕ \\ - {(ω_{i e}^{b})}_{x} \sin θ + {(ω_{i e}^{b})}_{y} \sin ϕ \cos θ + {(ω_{i e}^{b})}_{z} \cos ϕ \cos θ \end{matrix}] = [\begin{matrix} {(ω_{i e}^{r})}_{x} \\ {(ω_{i e}^{r})}_{y} \\ {(ω_{i e}^{r})}_{z} \end{matrix}] \end{array}

(5)

From Equation (5), the heading is obtained from Equation (6) [16,17,18].

ψ = \tan^{- 1} (- \frac{{(ω_{i e}^{r})}_{y}}{{(ω_{i e}^{r})}_{x}}) = \tan^{- 1} (- \frac{{(ω_{i e}^{b})}_{y} \cos ϕ - {(ω_{i e}^{b})}_{z} \sin ϕ}{{(ω_{i e}^{b})}_{x} \cos θ + {(ω_{i e}^{b})}_{y} \sin ϕ \sin θ + {(ω_{i e}^{b})}_{z} \cos ϕ \sin θ})

(6)

3. Coarse Alignment of GF-INS

3.1. Roll and pitch

The

k

-th accelerometer output of the GF-IMU with

N

accelerometers is given in Equation (7) [10].

y_{k} = {[d_{k}^{b}]}^{T} f_{k}^{b} = {[d_{k}^{b}]}^{T} [a^{b} + ω_{i b}^{b} \times (ω_{i b}^{b} \times r_{k}^{b}) + {\dot{ω}}_{i b}^{b} \times r_{k}^{b} - g^{b}]

(7)

where

d_{k}^{b}

denotes the sensing direction of the

k

-th accelerometer.

f_{k}^{b}

is the specific force of the

k

-th accelerometer represented in the body frame.

a^{b}

is the acceleration at the center of the gravity of the vehicle represented in the body frame.

ω_{i b}^{b}

is the angular velocity of the body frame with respect to the inertial frame represented in the body frame.

{\dot{ω}}_{i b}^{b}

is the angular acceleration of the body frame with respect to the inertial frame represented in the body frame.

r_{k}^{b}

is the position of the

k

-th accelerometer represented in the body frame.

g^{b}

is the gravity vector represented in the body frame. If the vehicle is stationary on earth, then

a^{b} = 0

{\dot{ω}}_{i b}^{b} = 0

and

ω_{i b}^{b} = ω_{i e}^{b} + ω_{e b}^{b} = ω_{i e}^{b}

. Therefore, the

k

-th accelerometer output can be represented in Equation (8).

y_{k} = {[d_{k}^{b}]}^{T} f_{k}^{b} = {[d_{k}^{b}]}^{T} [ω_{i e}^{b} \times (ω_{i e}^{b} \times r_{k}^{b}) - g^{b}]

(8)

In Equation (8), since the magnitude of the vector

ω_{i e}^{b}

‖ω_{i e}^{b}‖

7.292115 \times 1 0^{- 5} rad /

s, the magnitude of the centripetal acceleration is much less than the gravity as Equation (9) [9].

‖ω_{i e}^{b} \times (ω_{i e}^{b} \times r_{k}^{b})‖ ≪ ‖g^{b}‖

(9)

As a result of this, Equation (9) can be represented in Equation (10) [9].

y_{k} \approx [d_{k}^{b}]^{T} f_{k}^{b} = [d_{k}^{b}]^{T} (- g^{b})

(10)

The estimated specific force

{\hat{f}}^{b}

from

N

accelerometers outputs can be obtained from Equation (11).

{\hat{f}}^{b} = {[\begin{matrix} {({\hat{f}}^{b})}_{x} & {({\hat{f}}^{b})}_{y} & {({\hat{f}}^{b})}_{z} \end{matrix}]}^{T} = - {\hat{g}}^{b} = {(D^{T} D)}^{- 1} D^{T} \tilde{Y}

(11)

where

D

is the sensing direction matrix of the accelerometers in (12).

D = {[\begin{matrix} {(d_{1}^{b})}^{T} & {(d_{2}^{b})}^{T} & \cdot \cdot \cdot & {(d_{N}^{b})}^{T} \end{matrix}]}^{T}

(12)

\tilde{Y}

is the accelerometer measurement vector in (13).

\tilde{Y} = {[\begin{matrix} {\tilde{y}}_{1} & {\tilde{y}}_{2} & \dots & {\tilde{y}}_{N} \end{matrix}]}^{T}

(13)

Inserting the specific force in Equation (11) into Equation (2) and (3), roll and pitch can be obtained.

3.2. Heading

In order to obtain heading, let's change Equation (8) to Equation (14).

\begin{array}{l} y_{k} + [d_{k}^{b}]^{T} g^{b} & = [d_{k}^{b}]^{T} f_{k}^{b} + [d_{k}^{b}]^{T} g^{b} \\ = [d_{k}^{b}]^{T} [ω_{i e}^{b} \times (ω_{i e}^{b} \times r_{k}^{b})] \\ = [d_{k}^{b}]^{T} Ω_{i e}^{b} Ω_{i e}^{b} r_{k}^{b} \\ = {[\begin{matrix} {(d_{k}^{b})}_{x} \\ {(d_{k}^{b})}_{y} \\ {(d_{k}^{b})}_{z} \end{matrix}]}^{T} [\begin{matrix} 0 & - {(ω_{i e}^{b})}_{z} & {(ω_{i e}^{b})}_{y} \\ {(ω_{i e}^{b})}_{z} & 0 & - {(ω_{i e}^{b})}_{x} \\ - {(ω_{i e}^{b})}_{y} & {(ω_{i e}^{b})}_{x} & 0 \end{matrix}] [\begin{matrix} 0 & - {(ω_{i e}^{b})}_{z} & {(ω_{i e}^{b})}_{y} \\ {(ω_{i e}^{b})}_{z} & 0 & - {(ω_{i e}^{b})}_{x} \\ - {(ω_{i e}^{b})}_{y} & {(ω_{i e}^{b})}_{x} & 0 \end{matrix}] [\begin{matrix} (r_{k}^{b})_{x} \\ (r_{k}^{b})_{y} \\ (r_{k}^{b})_{z} \end{matrix}] \\ = {[\begin{matrix} {(d_{k}^{b})}_{x} \\ {(d_{k}^{b})}_{y} \\ {(d_{k}^{b})}_{z} \end{matrix}]}^{T} [\begin{matrix} - {(ω_{i e}^{b})}_{y}^{2} - {(ω_{i e}^{b})}_{z}^{2} & {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{y} & {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{z} \\ {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{y} & - {(ω_{i e}^{b})}_{x}^{2} - {(ω_{i e}^{b})}_{z}^{2} & {(ω_{i e}^{b})}_{y} {(ω_{i e}^{b})}_{z} \\ {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{z} & {(ω_{i e}^{b})}_{y} {(ω_{i e}^{b})}_{z} & - {(ω_{i e}^{b})}_{x}^{2} - {(ω_{i e}^{b})}_{y}^{2} \end{matrix}] [\begin{matrix} (r_{k}^{b})_{x} \\ (r_{k}^{b})_{y} \\ (r_{k}^{b})_{z} \end{matrix}] \end{array}

(14)

where

{(ω_{i e}^{b})}_{x}

{(ω_{i e}^{b})}_{y}

, and

{(ω_{i e}^{b})}_{z}

are

x

y

, and

z

axis component of

ω_{i e}^{b}

, respectively.

Ω_{i e}^{b}

is the skew symmetric matrix of the vector

ω_{i e}^{b}

{(d_{k}^{b})}_{x}

{(d_{k}^{b})}_{y}

and

{(d_{k}^{b})}_{z}

are

x

y

and

z

axis component of the sensing direction of the

k

-th accelerometer, respectively.

Rearranging Equation (14), Equation (15) can be obtained.

\begin{array}{l} y_{k} + {[d_{k}^{b}]}^{T} g^{b} & = {[\begin{matrix} (r_{k}^{b})_{y} {(d_{k}^{b})}_{x} + (r_{k}^{b})_{x} {(d_{k}^{b})}_{y} \\ (r_{k}^{b})_{z} {(d_{k}^{b})}_{x} + (r_{k}^{b})_{x} {(d_{k}^{b})}_{z} \\ (r_{k}^{b})_{z} {(d_{k}^{b})}_{y} + (r_{k}^{b})_{y} {(d_{k}^{b})}_{z} \\ - (r_{k}^{b})_{y} {(d_{k}^{b})}_{y} - (r_{k}^{b})_{z} {(d_{k}^{b})}_{z} \\ - (r_{k}^{b})_{x} {(d_{k}^{b})}_{x} - (r_{k}^{b})_{z} {(d_{k}^{b})}_{z} \\ - (r_{k}^{b})_{x} {(d_{k}^{b})}_{x} - (r_{k}^{b})_{y} {(d_{k}^{b})}_{y} \end{matrix}]}^{T} [\begin{matrix} {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{y} \\ {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{z} \\ {(ω_{i e}^{b})}_{y} {(ω_{i e}^{b})}_{z} \\ {(ω_{i e}^{b})}_{x}^{2} \\ {(ω_{i e}^{b})}_{y}^{2} \\ {(ω_{i e}^{b})}_{z}^{2} \end{matrix}] \\ = [\begin{matrix} {(h_{k})}_{1} & {(h_{k})}_{2} & {(h_{k})}_{3} & {(h_{k})}_{4} & {(h_{k})}_{5} & {(h_{k})}_{6} \end{matrix}] x \end{array}

(15)

where

x

is given in Equation (16).

\begin{array}{l} x & = {[\begin{matrix} x_{1} & x_{2} & x_{3} & x_{4} & x_{5} & x_{6} \end{matrix}]}^{T} \\ = {[\begin{matrix} {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{y} & {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{z} & {(ω_{i e}^{b})}_{y} {(ω_{i e}^{b})}_{z} & {(ω_{i e}^{b})}_{x}^{2} & {(ω_{i e}^{b})}_{y}^{2} & {(ω_{i e}^{b})}_{z}^{2} \end{matrix}]}^{T} \end{array}

(16)

If all the

N

accelerometer outputs of the GF-MU are put together, Equation (17) can be obtained from Equation (15).

\begin{array}{l} A & = H x = {[\begin{matrix} a_{1} & a_{2} & \dots & a_{N} \end{matrix}]}^{T} \\ = [\begin{matrix} y_{1} + {[d_{1}^{b}]}^{T} g^{b} \\ ⋮ \\ y_{N} + {[d_{N}^{b}]}^{T} g^{b} \end{matrix}] = [\begin{matrix} {(h_{1})}_{1} & {(h_{1})}_{2} & {(h_{1})}_{3} & {(h_{1})}_{4} & {(h_{1})}_{5} & {(h_{1})}_{6} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ {(h_{N})}_{1} & {(h_{N})}_{2} & {(h_{N})}_{3} & {(h_{N})}_{4} & {(h_{N})}_{5} & {(h_{N})}_{6} \end{matrix}] x \end{array}

(17)

From Equation (17),

x

can be obtained as Equation (18).

x = {(H^{T} H)}^{- 1} H^{T} A

(18)

The heading can be obtained as Equation (19) from Equation (6) and

x

of Equation (18).

\begin{array}{l} ψ & = \tan^{- 1} (- \frac{{(ω_{i e}^{b})}_{x} {(ω_{i e}^{r})}_{y}}{{(ω_{i e}^{b})}_{x} {(ω_{i e}^{r})}_{x}}) \\ = \tan^{- 1} (- \frac{{(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{y} \cos ϕ - {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{z} \sin ϕ}{{(ω_{i e}^{b})}_{x}^{2} \cos θ + {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{y} \sin ϕ \sin θ + {(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{z} \cos ϕ \sin θ}) \\ = \tan^{- 1} (- \frac{x_{1} \cos ϕ - x_{2} \sin ϕ}{x_{4} \cos θ + x_{1} \sin ϕ \sin θ + x_{2} \cos ϕ \sin θ}) \end{array}

(19)

3.3. Accelerometer configuration and possiblity of initial heading calculation

In this section, it is investigated using Equation (19) in section 3.2 whether the initial heading can be calculated for the accelerometer arrangements of GF-IMUs which have been presented in literatures [9,10,11,12,13,14,15].

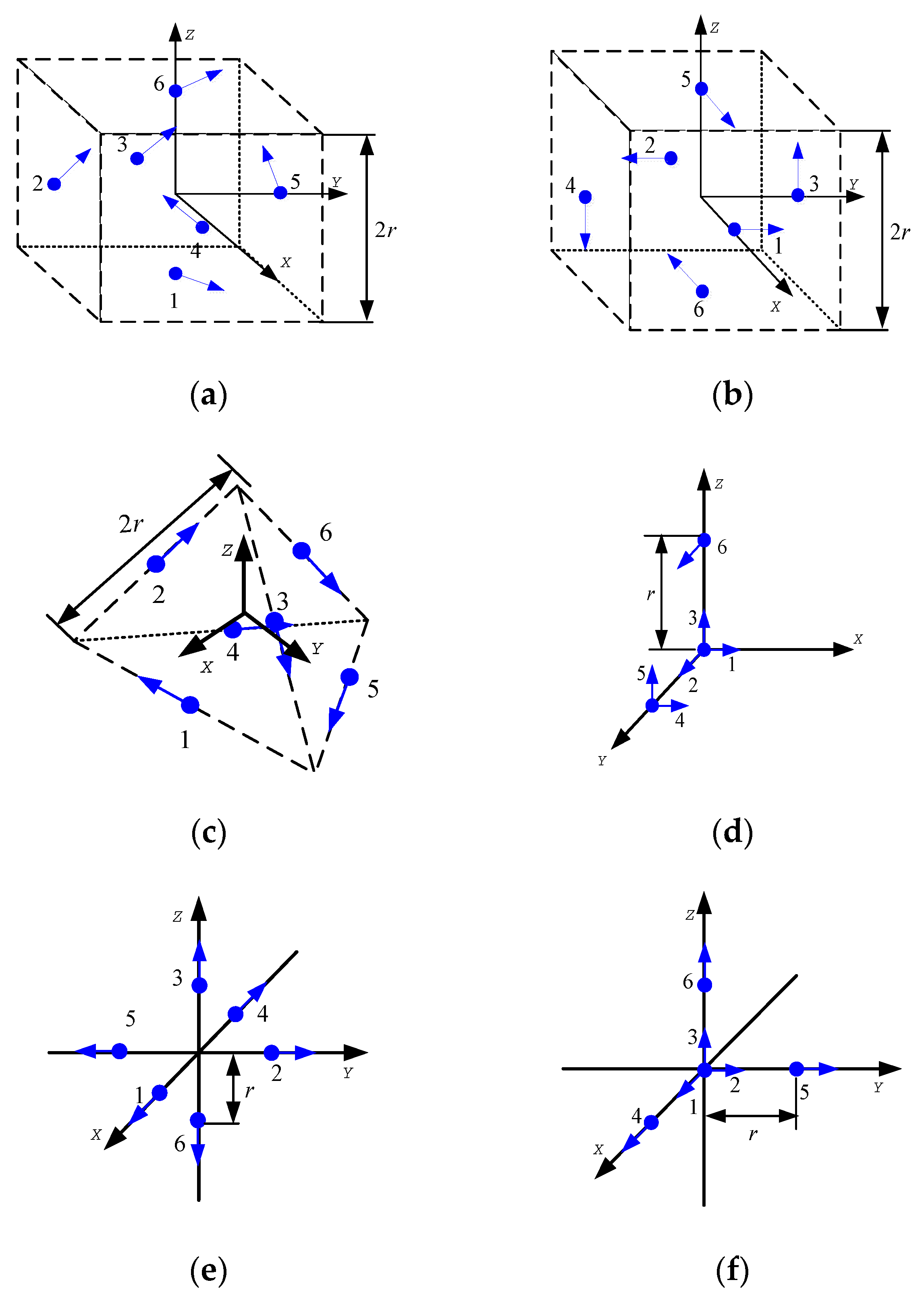
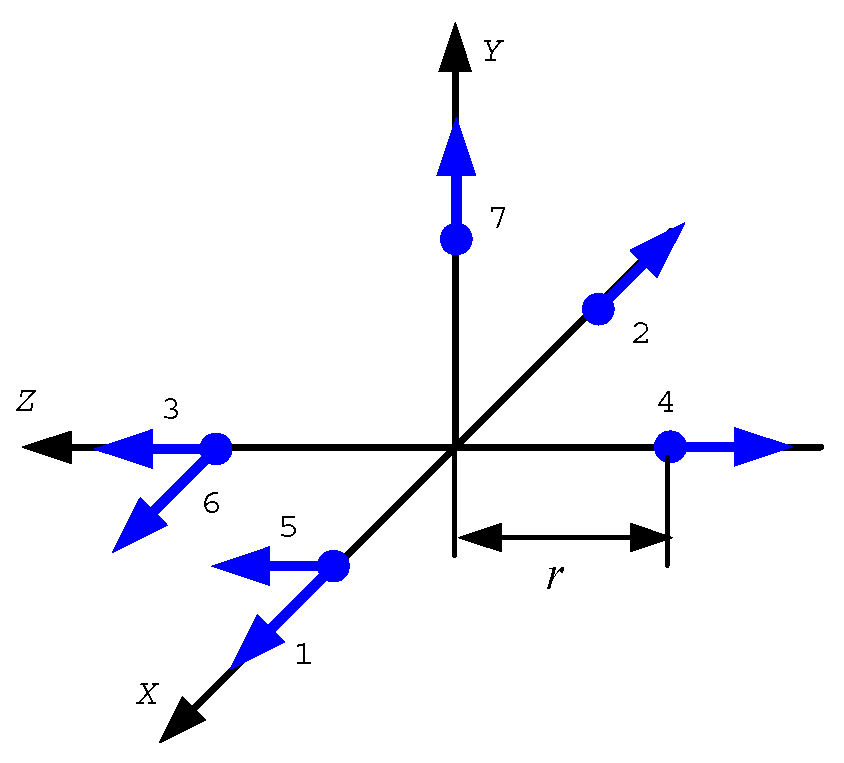
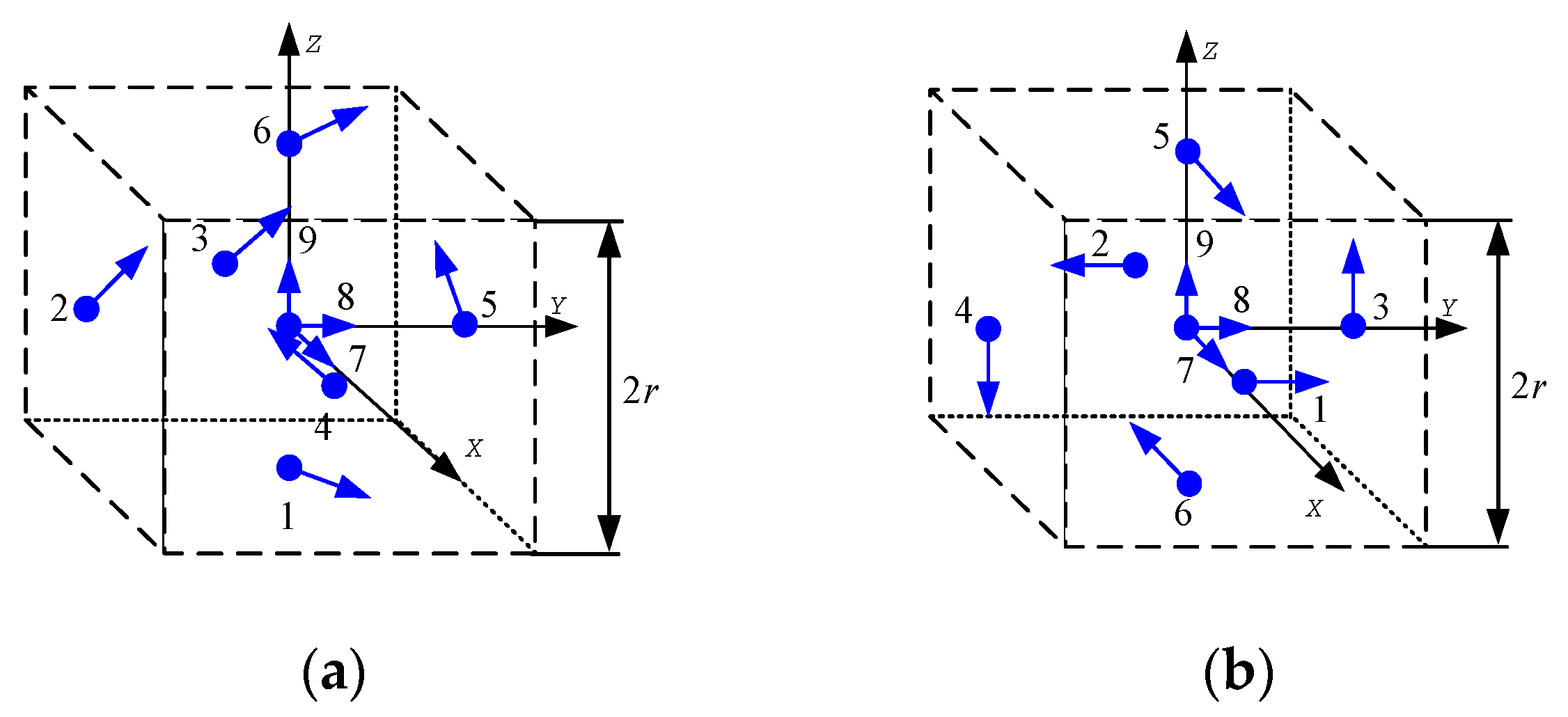
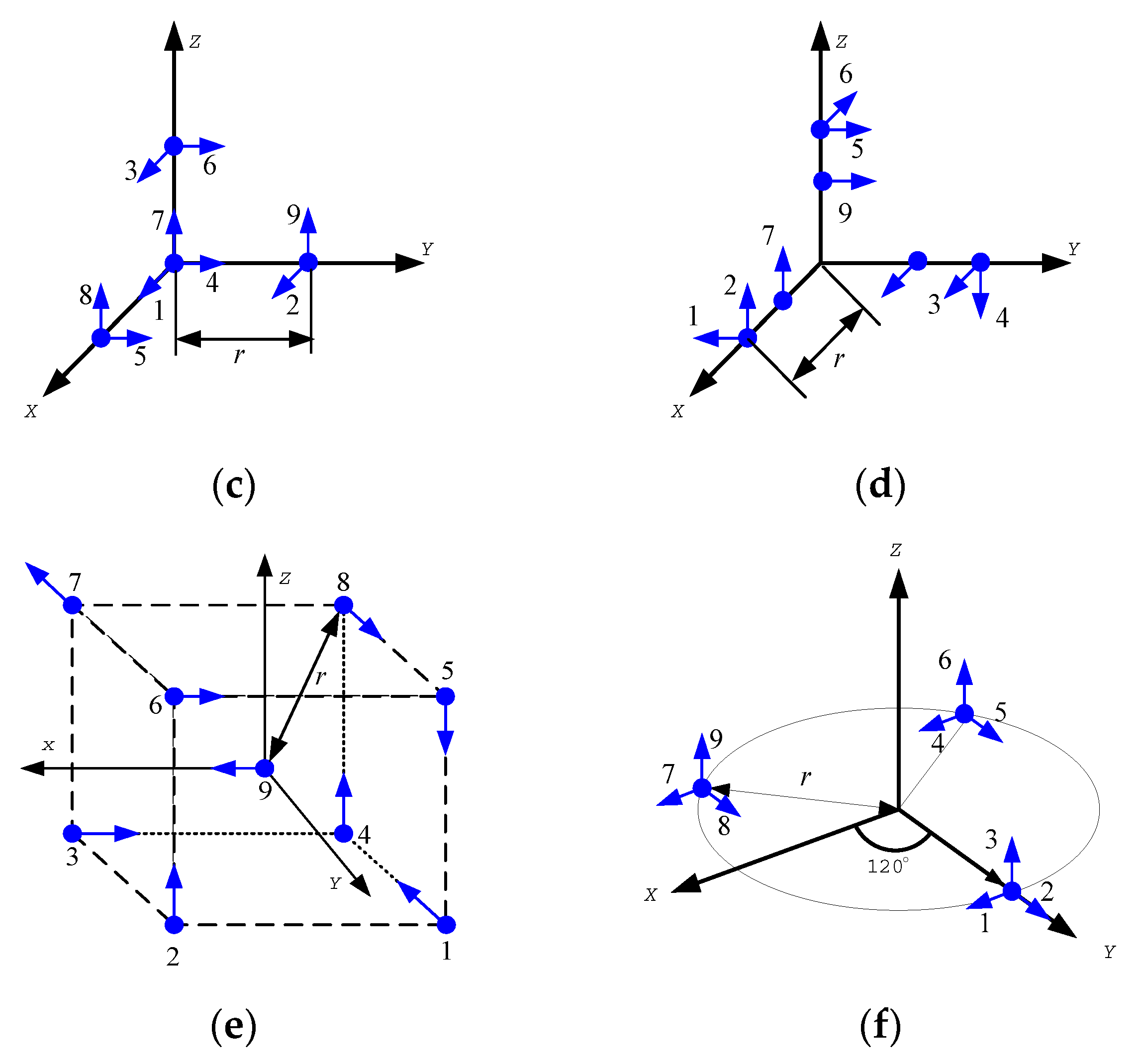
Figure 1, Figure 2, Figure 3 and Figure 4 shows 6 arrangements with 6 accelerometers, one arrangement with 7 accelerometers, 6 arrangements with 9 accelerometers and 2 arrangements with 12 accelerometers of GF-IMUs, respectively. In Figure 1, Figure 2, Figure 3 and Figure 4, black arrows indicate

x

y

, and

z

axes of the body frame, respectively. Blue dots indicate positions of accelerometers and blue arrows sensing directions of accelerometers.

x

can be obtained from Equation (18), the initial heading can be obtained from Equation (19). In order to obtain

x

, rank of the matrix

H^{T} H

should be 6. Ranks of the matrix

H^{T} H

for the arrangements in Figure 1, Figure 2, Figure 3 and Figure 4 are listed in Table 1.

It can be seen from Table 1 that the initial heading can be obtained from Equation (19) when the accelerometer arrangements are given in Figure 3e and a.

x_{1}

x_{2}

, and

x_{4}

for the initial heading calculation for the accelerometer arrangement in Figure 3e are given in Equation (20), (21), and (22), respectively.

x_{1} = \frac{\sqrt{3}}{22 r} (- 3 a_{1} - 4 a_{3} - 3 a_{4} + 3 a_{5} + 4 a_{6} - 8 a_{7} + 3 a_{8})

(20)

x_{2} = \frac{\sqrt{3}}{22 r} (- 4 a_{1} + 2 a_{3} + 7 a_{4} + 4 a_{5} - 2 a_{6} + 4 a_{7} - 7 a_{8})

(21)

x_{4} = \frac{\sqrt{3}}{22 r} (- 5 a_{1} - 3 a_{3} + 6 a_{4} - 6 a_{5} + 3 a_{6} + 5 a_{7} + 5 a_{8})

(22)

where

a_{k} (k = 1, \dots, 8)

is given in Equation (23).

r

denotes distance from the center of gravity (accelerometer 9) to the accelerometer 1 to 8.

a_{k} = y_{k} - {[d_{k}^{b}]}^{T} g^{b}

(23)

x_{1}

x_{2}

and

x_{4}

for the initial heading calculation for the accelerometer arrangement in Figure 4a are given in Equation (24), (25), and (26), respectively.

x_{1} = \frac{1}{2 r} (a_{5} + a_{7})

(24)

x_{2} = \frac{1}{2 r} (a_{6} + a_{10})

(25)

x_{4} = \frac{1}{2 r} (a_{4} - a_{8} - a_{12})

(26)

where

a_{k} (k = 4, 5, 6, 7, 8, 10, 12)

is given in Equation (23).

r

denotes distance from the center of gravity (accelerometer 1 to 3) to the accelerometer 4 to 12.

3.4. Initial heading error

Let us check the initial heading error when the initial heading is obtained using the method in section 3.3. Accelerometer output

{\tilde{y}}_{k}

can be represented in Equation (27).

{\tilde{y}}_{k} = y_{k} + δ y_{k}

(27)

where

δ y_{k}

denotes error of the

k

-th accelerometer output. If Equation (17) is used,

\hat{A}

can be represented in Equation (28) from accelerometer output

{\tilde{y}}_{k}

in Equation (27) and

{\hat{g}}^{b}

in Equation (11).

\hat{A} = [\begin{matrix} {\tilde{y}}_{1} + {[d_{1}^{b}]}^{T} {\hat{g}}^{b} \\ ⋮ \\ {\tilde{y}}_{N} + {[d_{N}^{b}]}^{T} {\hat{g}}^{b} \end{matrix}] = H \hat{x}

(28)

where

\hat{x}

is the estimate of

x

from accelerometer outputs. Error

δ x

\hat{x}

can be represented in Equation (29) from Equation (18) and Equation (28).

(29)

where

δ A

and

δ g^{b}

denote errors of

\hat{A}

and

{\hat{g}}^{b}

, respectively. Covariance of

δ x

Σ_{δ x}

can be obtained in Equation (30) from Equation (29).

Σ_{δ x} = {(H^{T} Σ_{δ A}^{- 1} H)}^{- 1}

(30)

where covariance of

δ A, Σ_{δ A}

is given in Equation (31) since

cov [δ a_{i}, δ a_{j}] = 0

i \neq j

Σ_{δ A} = [\begin{matrix} σ_{δ a_{1}}^{2} & 0 & 0 \\ 0 & ⋱ & 0 \\ 0 & 0 & σ_{δ a_{N}}^{2} \end{matrix}]

(31)

where

σ_{δ a_{k}}^{2}

denotes variance of

δ a_{k}

. Let us calculate variances of

δ x_{1}

δ x_{2}

, and

δ x_{4}

given in Equation (20) ~ (26). If accelerometers with the same specification are used, Equation (30) can be represented in Equation (32) since the condition

σ_{δ a_{1}}^{2} = \dots = σ_{δ a_{N}}^{2} = σ_{δ a}^{2}

is valid.

Σ_{δ x} = σ_{δ a}^{2} {(H^{T} H)}^{- 1}

(32)

Variances of

δ x_{1}

δ x_{2}

, and

δ x_{4}

are listed in Table 2 for Figure 3e and Figure 4a from Equation (32).

Consider the initial heading error of the generic INS alignment to check the initial heading error of the GF-INS alignment. The gyroscope output in the navigation frame can be expressed in Equation (33) when the vehicle is stationary.

{\tilde{ω}}_{i e}^{n} = C_{b}^{n} (ω_{i e}^{b} + δ ω_{i e}^{b}) = C_{b}^{n} ω_{i e}^{b} + C_{b}^{n} δ ω_{i e}^{b}

(33)

where

{\tilde{ω}}_{i e}^{n}

denotes the gyroscope output in the navigation frame and

δ ω_{i e}^{b}

the gyroscope output error in the body frame.

If roll, pitch, and heading are sufficiently small,

C_{b}^{n}

can be expressed in Equation (34).

C_{b}^{n} ≅ [\begin{matrix} 1 & - δ ψ & δ θ \\ δ ψ & 1 & - δ ϕ \\ - δ θ & δ ϕ & 1 \end{matrix}]

(34)

where

δ ϕ

δ θ

, and

δ ψ

denote sufficiently small roll, pitch, and heading, respectively. In order to make the description simple, it is assumed that the body frame and the navigation frame are the same, i.e.

ω_{i e}^{b} = ω_{i e}^{n}

. Then, Equation (33) can be written in Equation (35).

{\tilde{ω}}_{i e}^{n} = {[\begin{matrix} {({\tilde{ω}}_{i e}^{n})}_{N} & {({\tilde{ω}}_{i e}^{n})}_{E} & {({\tilde{ω}}_{i e}^{n})}_{D} \end{matrix}]}^{T} ≅ [\begin{matrix} Ω \cos L - δ θ \cdot Ω \sin L + {(δ ω_{i e}^{b})}_{x} \\ δ ψ \cdot Ω \cos L + δ ϕ \cdot Ω \sin L + {(δ ω_{i e}^{b})}_{y} \\ - δ θ \cdot Ω \cos L - Ω \sin L + {(δ ω_{i e}^{b})}_{z} \end{matrix}]

(35)

In order to obtain heading in the initial alignment, the east component of the gyroscope output (

{({\tilde{ω}}_{i e}^{n})}_{E}

) should be zero as Equation (36).

{({\tilde{ω}}_{i e}^{n})}_{E} = δ ψ \cdot Ω \cos L + δ ϕ \cdot Ω \sin L + {(δ ω_{i e}^{b})}_{y} = 0

(36)

δ ψ

can be written in Equation (37) when

δ ϕ = 0

in Equation (36)

δ ψ = - \frac{{(δ ω_{i e}^{b})}_{y}}{Ω \cos L}

(37)

It can be seen from Equation (37) that the initial heading error in the generic INS is proportional to the gyroscope error of the east direction (the pitch axis direction) and inversely proportional to

Ω \cos L

when the body frame is the same as the navigation frame. Therefore, the heading error is minimum when the vehicle is located at the equator and the heading error increases as the vehicle becomes nearer the pole (

L = \pm 90

deg).

Now, let us consider the initial heading error of the GF-INS.

{[\begin{matrix} δ x_{1} & δ x_{2} & δ x_{4} \end{matrix}]}^{T}

of Equation (29) is given in Equation (38) when the body frame is the same as the navigation frame.

(38)

Therefore, Equation (37) can be represented as Equation (39) using Equation (38).

δ ψ = - \frac{{(δ ω_{i e}^{b})}_{y}}{Ω \cos L} = - \frac{{Ω \cos L (δ ω_{i e}^{b})}_{y}}{{(Ω \cos L)}^{2}} = - \frac{δ x_{1}}{{(Ω \cos L)}^{2}}

(39)

It can be seen from Equation (39) that the heading error is proportional to

δ x_{1}

which is error of

{(ω_{i e}^{b})}_{x} {(ω_{i e}^{b})}_{y}

obtained from Equation (29) and it is impossible to get the heading at the pole as Equation (37) when the initial alignment is performed using Equation (19).

Since

δ x_{1}

depends on the grade and arrangement of accelerometers whether the initial heading of the GF-INS can be obtained is checked for the arrangements in Figure 3e and Figure 4a and accelerometers in Table 3 [19,20].

Let us obtain heading error for the accelerometers in Table 3 when

L = 0

deg and

r = 1

m. In order to check the effect of accelerometer error to the heading error,

δ x

can be expressed in accelerometer error

δ y

as Equation (40) when

{\hat{g}}^{b} = g^{b}

in Equation (29)

δ x = {(H^{T} H)}^{- 1} H^{T} {[\begin{matrix} δ y_{1} & \dots & δ y_{N} \end{matrix}]}^{T} = {(H^{T} H)}^{- 1} H^{T} δ y

(40)

Since

σ_{δ a}^{2} = σ_{δ y}^{2} {= σ}_{{δ y}_{i}}^{2} (i = 1, \dots, N

), 1

σ

δ x_{1}

can be obtained when specifications of the accelerometers in Table 3 are inserted into Table 2. By inserting these values into Equation (39), 1

σ

values of the initial heading errors to the accelerometer errors are in Table 4.

It can be seen from Table 4 that the initial alignment of GF-INS cannot be performed even when absolute quantum gravimeter which is the most precise accelerometer in the present technology level as well as navigation grade accelerometer are used since the heading error is very large. For the 1

σ

of the heading error in the arrangement of Figure 4a to be less than 5 deg, the precision of the accelerometer should be less than

σ_{δ y} = 6.696 \times 1 0^{- 11}

G. This value is 15 times more precise than the absolute quantum gravimeter in Table 3. It can be seen from these results that it is difficult to have a required performance in the heading coarse alignment of the GF-INS and these results are similar to the mentioning by Vaknin and Klein that the initial heading cannot be obtained [7,9].

In order to resolve this problem, it can be considered to add one gyroscope or two gyroscopes to the GF-MU as described in the next section.

4. Coarse Alignment of GF-INS with Gyro

According to the results in section 3, it can be considered to perform the coarse alignment after one or two gyroscopes are attached to the roll, pitch or yaw axes of the vehicle to the arrangement of the accelerometers since obtaining the initial heading is not feasible using only the arrangement of accelerometers.

The gyroscope output

{\tilde{g}}_{n}

can be expressed in Equation (41) in the body frame.

{\tilde{g}}_{n} = g_{n} + δ g_{n}

(41)

where

δ g_{n}, (n = x, y o r z)

denotes

n

axis gyroscope output error in the body frame.

Relationship between gyroscope output and

x

in Equation (18) is given in Equation (42).

\tilde{B} = {[\begin{matrix} b_{1} & b_{2} & b_{3} & b_{4} & b_{5} & b_{6} \end{matrix}]}^{T} = {[\begin{matrix} {\tilde{g}}_{x} {\tilde{g}}_{y} & {\tilde{g}}_{x} {\tilde{g}}_{z} & {\tilde{g}}_{y} {\tilde{g}}_{z} & {\tilde{g}}_{x}^{2} & {\tilde{g}}_{y}^{2} & {\tilde{g}}_{z}^{2} \end{matrix}]}^{T} = I_{6 \times 6} x

(42)

where

I_{6 \times 6}

denotes

6 \times 6

unit matrix. Inserting Equation (41) into Equation (42), error of

\tilde{B}

is given in Equation (43).

δ B = \tilde{B} - B = [\begin{matrix} δ b_{1} \\ δ b_{2} \\ δ b_{3} \\ δ b_{4} \\ δ b_{5} \\ δ b_{6} \end{matrix}] = [\begin{matrix} {\tilde{g}}_{x} {\tilde{g}}_{y} \\ {\tilde{g}}_{x} {\tilde{g}}_{z} \\ {\tilde{g}}_{y} {\tilde{g}}_{z} \\ {\tilde{g}}_{x}^{2} \\ {\tilde{g}}_{y}^{2} \\ {\tilde{g}}_{z}^{2} \end{matrix}] - [\begin{matrix} g_{x} g_{y} \\ g_{x} g_{z} \\ g_{y} g_{z} \\ g_{x}^{2} \\ g_{y}^{2} \\ g_{z}^{2} \end{matrix}] = [\begin{matrix} g_{x} δ g_{y} + g_{y} δ g_{x} + δ g_{x} δ g_{y} \\ g_{x} δ g_{z} + g_{z} δ g_{x} + δ g_{x} δ g_{z} \\ g_{y} δ g_{z} + g_{z} δ g_{y} + δ g_{y} δ g_{z} \\ 2 g_{x} δ g_{x} + δ g_{x}^{2} \\ 2 g_{y} δ g_{y} + δ g_{y}^{2} \\ 2 g_{z} δ g_{z} + δ g_{z}^{2} \end{matrix}]

(43)

It can be observed from Equation (43) that the error of

\tilde{B}

is proportional to the gyroscope outputs

g_{x}

g_{y}

, and

g_{z}

For simple description, consider the case that

L = 0

deg and the body frame is the same as the navigation frame. In this case, Equation (43) can be represented in Equation (44) since

{[\begin{matrix} g_{x} & g_{y} & g_{z} \end{matrix}]}^{T} = {[\begin{matrix} Ω & 0 & 0 \end{matrix}]}^{T}

δ B = \tilde{B} - B = [\begin{matrix} δ b_{1} \\ δ b_{2} \\ δ b_{3} \\ δ b_{4} \\ δ b_{5} \\ δ b_{6} \end{matrix}] = [\begin{matrix} Ω δ g_{y} + δ g_{x} δ g_{y} \\ Ω δ g_{z} + δ g_{x} δ g_{z} \\ δ g_{y} δ g_{z} \\ 2 Ω δ g_{x} + δ g_{x}^{2} \\ δ g_{y}^{2} \\ δ g_{z}^{2} \end{matrix}] ≅ [\begin{matrix} Ω δ g_{y} \\ Ω δ g_{z} \\ 0 \\ 2 Ω δ g_{x} \\ 0 \\ 0 \end{matrix}]

(44)

x

can be estimated in Equation (45) using

\hat{A}

calculated from accelerometer outputs and gyroscope outputs

\tilde{B}

\hat{x} = {(H^{T} W H)}^{- 1} H^{T} W [\begin{matrix} \hat{A} \\ \tilde{B} \end{matrix}]

(45)

where

W

denotes weight matrix given in Equation (46).

W = {(Σ_{δ C})}^{- 1} = {diag (\underset{N}{\underset{⏟}{σ_{δ a}^{2}, \dots, σ_{δ a}^{2}}}, σ_{δ b_{1}}^{2}, \dots, σ_{δ b_{6}}^{2})}^{- 1}

(46)

where

Σ_{δ C}

is covariance of

δ C

and

σ_{δ b_{k}}^{2}

is variance of

δ b_{k}

. Measurement matrix

H

is given in Equation (47).

H = [\begin{matrix} H_{A} \\ H_{G} \end{matrix}] = [\begin{matrix} \begin{matrix} {(h_{1})}_{1} & \dots & {(h_{1})}_{6} \\ ⋮ & ⋱ & ⋮ \\ {(h_{N})}_{1} & \dots & {(h_{N})}_{6} \end{matrix} \\ I_{6 \times 6} \end{matrix}]

(47)

where

H_{A}

and

H_{G}

are measurement matrices of accelerometer output and gyroscope output, respectively.

The number of arrangements of gyroscopes, in which the gyroscopes are located at one or two axes among roll, pitch, and yaw axes, is 6 in the body frame. One gyroscope can be located at the roll, pitch or yaw axis and two gyroscopes can be located at the roll and pitch axes, roll and yaw axes or pitch and yaw axes.

\tilde{B}

W

and

H_{G}

in Equation (45) for the gyroscope arrangements are listed in Table 5. Error covariance of the estimated

x

in Equation (45) is given in Equation (48).

Σ_{δ x} = {(H^{T} W H)}^{- 1}

(48)

For the accelerometer arrangement in Figure 5a, heading error can be checked when the initial heading is obtained using accelerometer outputs and added gyroscope outputs. Variances of

δ x_{1}

δ x_{2}

, and

δ x_{4}

from Equation (48) are listed in Table 6.

It can be seen from Table 6 that variance of

δ x_{1}

is the same as the case that only accelerometers are used except that the case when the added gyroscopes are located at the roll and pitch axes. Since the heading error is determined by

δ x_{1}

as shown in Equation (39), the additional gyroscopes should be located at the roll and pitch axes in order to have more accurate initial heading of the GF-INS.

Let us obtain variance of

δ x_{1}

to the grade of the gyroscope in order to have heading error. First, the variance of

δ b_{1}

in Equation (44) is given in Equation (49).

σ_{δ b_{1}}^{2} = var [δ b_{1}] = var [Ω δ g_{y}] = Ω^{2} var [δ g_{y}] = Ω^{2} σ_{δ g_{y}}^{2}

(49)

When the gyroscopes with the same error specifications are located at the roll and pitch axes, variance of

δ x_{1}

is in Equation (50) since

σ_{δ g_{x}}^{2} = σ_{δ g_{y}}^{2} = σ_{δ g}^{2}

σ_{δ x_{1}}^{2} = \frac{σ_{δ a}^{2} σ_{δ b_{1}}^{2}}{σ_{δ a}^{2} + 2 r^{2} σ_{δ b_{1}}^{2}} = \frac{Ω^{2} σ_{δ a}^{2} σ_{δ g}^{2}}{σ_{δ a}^{2} + 2 r^{2} Ω^{2} σ_{δ g}^{2}}

(50)

Since the variance of

δ x_{1}

becomes different to the gyroscope performance (

σ_{δ g}^{2}

) in Equation (50), the yaw errors can be investigated for the gyroscopes in Table 7 [21,22].

σ

values of the heading error in Equation (39) is listed in Table 8 for the accelerometer specifications in Table 3 and gyroscope specifications in Table 7 when

L = 0

deg and

r = 1

m as in section 3.4.

It can be seen from result in Table 8 that the heading error is determined by the grade of the gyroscope. This is the same result as that of the generic INS gyro-compassing [1,4]. Therefore, the initial heading can be determined after the leveling is completed when gyroscopes are additionally located at the roll and pitch axes.

5. Concluding Remarks

In this paper, feasibility of obtaining initial attitude of the GF-INS has been investigated by deriving equations to obtain initial attitude from accelerometer outputs and calculating error of the initial attitude. Initial roll and pitch have been obtained as the generic INS after neglecting the very small centripetal acceleration. Initial heading has been expressed in terms of accelerometer outputs and its error has been derived. It has been checked that it is possible to calculate initial heading in the two configurations among 15 configurations proposed in other researches. However, it has been seen that it is not feasible to get initial heading when accelerometer error is considered.

When gyroscopes are additionally located into one or two axes, the initial heading have been expressed in accelerometer and gyroscope outputs and the feasibility of obtaining initial heading has been examined by investigating the heading error. As a result of this, it can be seen that the initial heading is obtained when gyroscopes are additionally located at the roll and pitch axes as the generic INS.

Author Contributions

Conceptualization, S. H. Oh and D.-H. Hwang; methodology, S. H. Oh and D.-H. Hwang; software, H. Kim; validation, H. Kim and J. H. Son; writing—original draft preparation, H. Kim; writing—review and editing, D. H. Hwang; supervision, D. H. Hwang; All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT). (No.2019R1A2C1088134).

Conflicts of Interest

The authors declare no conflict of interest.

References

Titterton D., H.; Weston, J. L. , Strapdown inertial navigation technology,, 2nd ed.; The Institution of Electrical Engineers: Piscataway, New Jersey, US, 2004; pp. 17–301. [Google Scholar]
Groves P. D., Principles of GNSS, Inertial, and Multi sensor Integrated Navigation Systems, 2nd ed., Artech House: England, 2013; pp. 15-160.
Pitman G. R., Inertial Guidance, John Wiley & Sons Inc: New York, Hoboken, US, 1962; pp. 47-206.
Bar-Itzhack I. Y.; Berman N. Control Theoretic Approach to Inertial Navigation Systems. AIAA Journal of Guidance, Control, and Dynamics 1998, 11, 237–245. [Google Scholar]
Britting K. R., Inertial Navigation Systems Analysis, John Wiley & Sons Inc: New York, Hoboken, US, 1971; pp. 153-209.
Schuler A. R.; Grammatikos A.; Fegley K. A. Measuring Rotational Motion with Linear Accelerometers. IEEE Transactions on Aerospace and Electronic Systems 1967, AES-3, 465–472. [Google Scholar] [CrossRef]
Nusbaum, U.; Klein, I. Control Theoretic Approach to Gyro-Free Inertial Navigation Systems. IEEE Aerospace and Electronic Systems Magazine 2017, 32, 168–170. [Google Scholar] [CrossRef]
Pachter, M.; Welker, T.C.; Huffman, R.E. Gyro free INS theory. Journal of the Institute of Navigation 2013, 60, 85–96. [Google Scholar] [CrossRef]
Vaknin, E.; Klein, I. Coarse leveling of gyro-free INS. Journal of Gyroscopy and Navigation 2016, 7, 145–151. [Google Scholar] [CrossRef]
Padgaonkar A. J.; Krieger K, W.; A.I. King. Measurement of Angular Acceleration of a Rigid Body Using Linear Accelerometers. Journal of Applied Mechanics 1975, 42, 552–556. [Google Scholar] [CrossRef]
Park, S.; Tan, C.W.; Park, S. A scheme for improving the performance of a gyroscope-free inertial measurement unit. Sensors and Actuators A: Physical 2005, 121, 410–420. [Google Scholar] [CrossRef]
Fangjun Q.; Xu J.; Sai J., A New Scheme of Gyroscope Free Inertial Navigation System Using 9 Accelerometers, 2009 International Workshop on Intelligent Systems and Applications, Wuhan, China, 23-24 May 2009.
Shi Z.; Cheng Z.; Yang J., Study of Independent Initial Alignment Based on Gyroscope Free Strapdown Inertial Navigation System, 2010 Chinese Control and Decision Conference, Xuzhou, China, 26-28 May 2010, 2198-2202.
Edwan, E.; Knedlik, S.; Loffeld, O. Constrained Angular Motion Estimation in a Gyro-Free IMU. IEEE Transactions on Aerospace and Electronic systems 2011, 47, 596–610. [Google Scholar] [CrossRef]
Wang, X.; Xiao, L. Gyroscope-reduced inertial navigation system for flight vehicle motion estimation. Advances in Space Research 2017, 59, 413–424. [Google Scholar] [CrossRef]
Farrell J. A., Aided Navigation – GPS with High Rate Sensors, McGrawHill, New York, US, 2008; pp. 416-421.
Noureldin A.; Karamat T. B.; Georgy J. Fundamentals of Inertial Navigation Satellite-based Positioning and their Integration, Springer, New York, US, 2013; pp. 163-166.
Kayton, M.; Fried W. R. Avionics Navigation Systems, 2^nd Ed., John Wiley & Sons Inc: New York, US, 1997, pp. 382-386.
Honeywell, Q-FLEX QA-2000 ACCELEROMETER – The inertial navigation standard, Honeywell International, Inc. Defense and Space Electronic Systems Redmond: Redmond, US, 2020.
Muquans, Absolute Quantum Gravimeter – A free-fall absolute gravimeter based on laser-cooled atoms, Muquans: Rue François Mitterrand, France, 2022.
Honeywell, HG1700 INERTIAL MEASUREMENT UNIT – Proven technology for a wide range of guidance and control applications, Honeywell Aerospace: Minneapolis, US, 2022.
Honeywell, GG1320AN Digital Laser Gyro – Affordable and advanced sensing technology combined with unmatched production capabilities to meet the needs of customers throughout the world, Honeywell Aerospace: North America, US, 2015.

Figure 1. 6 accelerometers arrangements for GF-INS.

Figure 2. 7 accelerometers arrangement for GF-INS.

Figure 3. 9accelerometers arrangements for GF-INS.

Figure 4. 12 accelerometers arrangements for GF-INS.

Table 1. Rank of

H^{T} H

Table 1. Rank of

H^{T} H

Accelerometer Configuration	Number of Accelerometer	$rank (H^{T} H)$
Figure 1a	6	3
Figure 1b	6	3
Figure 1c	6	5
Figure 1d	6	2
Figure 1e	6	3
Figure 1f	6	3
Figure 2	7	4
Figure 3a	9	3
Figure 3b	9	3
Figure 3c	9	3
Figure 3d	9	3
Figure 3e	9	6
Figure 3f	9	5
Figure 4a	12	6
Figure 4b	12	3

Table 2. Variances of

δ x_{1}

δ x_{2}

, and

δ x_{4}

Table 2. Variances of

δ x_{1}

δ x_{2}

, and

δ x_{4}

	Figure 3e	Figure 4a
$Variance of δ x_{k}$	Figure 3e	Figure 4a
$σ_{δ x_{1}}^{2}$	$\frac{9}{11 r^{2}} σ_{δ a}^{2}$	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$
$σ_{δ x_{2}}^{2}$	$\frac{21}{22 r^{2}} σ_{δ a}^{2}$	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$
$σ_{δ x_{4}}^{2}$	$\frac{45}{44 r^{2}} σ_{δ a}^{2}$	$\frac{3}{4 r^{2}} σ_{δ a}^{2}$

Table 3. Specification of accelerometer

Model number	Manufacturer	Accuracy (1σ Bias Error)	Type
QA2000	Honeywell Inc., USA	$25 \times 1 0^{- 6}$ G (G = 9.8 m/s²)	Quartz Pendulum
Absolute QuantumGravimeter	Muquans, France	$1 0^{- 9}$ G	Laser Cooled Atom

Table 4. 1

σ

value of initial heading error.

Table 4. 1

σ

value of initial heading error.

	Figure 3e	Figure 4a
Model number	Figure 3e	Figure 4a
QA2000	$2.39 \times 1 0^{6}$ deg	$1.87 \times 1 0^{6}$ deg
Absolute Quantum Gravimeter	95.51 deg	74.67 deg

Table 5. Value of

\tilde{B}

W

, and

H_{G}

for gyro configurations.

Table 5. Value of

\tilde{B}

W

, and

H_{G}

for gyro configurations.

Gyro Axis	$\tilde{B}$	$W$	$H_{G}$
Roll	$b_{4}$	${diag (σ_{δ a_{1}}^{2}, \dots, σ_{δ a_{N}}^{2}, σ_{δ b_{4}}^{2})}^{- 1}$	$[\begin{matrix} 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}]$
Pitch	$b_{5}$	${diag (σ_{δ a_{1}}^{2}, \dots, σ_{δ a_{N}}^{2}, σ_{δ b_{5}}^{2})}^{- 1}$	$[\begin{matrix} 0 & 0 & 0 & 0 & 1 & 0 \end{matrix}]$
Yaw	$b_{6}$	${diag (σ_{δ a_{1}}^{2}, \dots, σ_{δ a_{N}}^{2}, σ_{δ b_{6}}^{2})}^{- 1}$	$[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}]$
Roll and Pitch	${[\begin{matrix} b_{1} & b_{4} & b_{5} \end{matrix}]}^{T}$	${diag (σ_{δ a_{1}}^{2}, \dots, σ_{δ a_{N}}^{2}, σ_{δ b_{1}}^{2}, σ_{δ b_{4}}^{2}, σ_{δ b_{5}}^{2})}^{- 1}$	$[\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{matrix}]$
Roll and Yaw	${[\begin{matrix} b_{2} & b_{4} & b_{6} \end{matrix}]}^{T}$	${diag (σ_{δ a_{1}}^{2}, \dots, σ_{δ a_{N}}^{2}, σ_{δ b_{2}}^{2}, σ_{δ b_{4}}^{2}, σ_{δ b_{6}}^{2})}^{- 1}$	$[\begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}]$
Pitch and Yaw	${[\begin{matrix} b_{3} & b_{5} & b_{6} \end{matrix}]}^{T}$	${diag (σ_{δ a_{1}}^{2}, \dots, σ_{δ a_{N}}^{2}, σ_{δ b_{3}}^{2}, σ_{δ b_{5}}^{2}, σ_{δ b_{6}}^{2})}^{- 1}$	$[\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}]$

Table 6. Variances of

δ x_{1}

δ x_{2}

and

δ x_{4}

Table 6. Variances of

δ x_{1}

δ x_{2}

and

δ x_{4}

	$σ_{δ x_{1}}^{2}$	$σ_{δ x_{2}}^{2}$	$σ_{δ x_{4}}^{2}$
Gyro Axis	$σ_{δ x_{1}}^{2}$	$σ_{δ x_{2}}^{2}$	$σ_{δ x_{4}}^{2}$
Roll	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{3 σ_{δ a}^{2} σ_{δ b_{4}}^{2}}{{3 σ}_{δ a}^{2} + 4 r^{2} σ_{δ b_{4}}^{2}}$
Pitch	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{σ_{δ a}^{2} (2 σ_{δ a}^{2} + 3 r^{2} σ_{δ b_{5}}^{2})}{r^{2} ({3 σ}_{δ a}^{2} + 4 r^{2} σ_{δ b_{5}}^{2})}$
Yaw	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{σ_{δ a}^{2} (2 σ_{δ a}^{2} + 3 r^{2} σ_{δ b_{6}}^{2})}{r^{2} ({3 σ}_{δ a}^{2} + 4 r^{2} σ_{δ b_{6}}^{2})}$
Roll and Pitch	$\frac{σ_{δ a}^{2} σ_{δ b_{1}}^{2}}{σ_{δ a}^{2} + 2 r^{2} σ_{δ b_{1}}^{2}}$	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{σ_{δ a}^{2} σ_{δ b_{4}}^{2} (2 σ_{δ a}^{2} + r^{2} 3 σ_{δ b_{5}}^{2})}{{3 σ}_{δ a}^{2} + r^{2} ({3 σ}_{δ a}^{2} σ_{δ b_{4}}^{2} + {3 σ}_{δ a}^{2} σ_{δ b_{5}}^{2} + 4 r^{2} σ_{δ b_{4}}^{2} σ_{δ b_{5}}^{2})}$
Roll and Yaw	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{σ_{δ a}^{2} σ_{δ b_{2}}^{2}}{σ_{δ a}^{2} + 2 r^{2} σ_{δ b_{2}}^{2}}$	$\frac{σ_{δ a}^{2} σ_{δ b_{4}}^{2} (2 σ_{δ a}^{2} + 3 r^{2} σ_{δ b_{6}}^{2})}{{2 σ}_{δ a}^{2} + r^{2} ({3 σ}_{δ a}^{2} σ_{δ b_{4}}^{2} + {3 σ}_{δ a}^{2} σ_{δ b_{6}}^{2} + 4 r^{2} σ_{δ b_{4}}^{2} σ_{δ b_{6}}^{2})}$
Pitch and Yaw	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{1}{2 r^{2}} σ_{δ a}^{2}$	$\frac{σ_{δ a}^{2} ({(σ_{δ a}^{2})}^{2} + 2 r^{2} σ_{δ a}^{2} σ_{δ b_{5}}^{2} + 2 r^{2} σ_{δ a}^{2} σ_{δ b_{6}}^{2} + 3 r^{4} σ_{δ b_{5}}^{2} σ_{δ b_{6}}^{2})}{r^{2} ({{2 (σ_{δ a}^{2})}^{2} + 3 r^{2} σ}_{δ a}^{2} σ_{δ b_{5}}^{2} + {3 r^{2} σ}_{δ a}^{2} σ_{δ b_{6}}^{2} + 4 r^{4} σ_{δ b_{5}}^{2} σ_{δ b_{6}}^{2})}$

Table 7. Specification of gyroscope

Gyro	Accuracy (1 σ Bias Error)	Type
RLG in HG1700AG58 (Honeywell Inc., USA)	1 deg/h	Tactical Grade RLG
GG1320AN (Honeywell Inc., USA)	0.003 deg/h	Navigation Grade RLG

Table 8. 1

σ

value of heading error.

Table 8. 1

σ

value of heading error.

	RLG in HG1700AG58	GG1320AN
Accelerometer	RLG in HG1700AG58	GG1320AN
QA3000	3.809 deg	0.011 deg
Absolute Quantum Gravimeter	3.804 deg	0.011 deg

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Coarse Alignment of Gyro-Free Inertial Navigation System

Abstract

1. Introduction

2. Coarse Alignment of INS

2.1. Leveling

2.2. Gyrocompassing

3. Coarse Alignment of GF-INS

3.1. Roll and pitch

3.2. Heading

3.3. Accelerometer configuration and possiblity of initial heading calculation

3.4. Initial heading error

4. Coarse Alignment of GF-INS with Gyro

5. Concluding Remarks

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe