Short-Term Load Forecasting of the Greek Power System Using a Dynamic Block-Diagonal Fuzzy Neural Network

A block-diagonal fuzzy neural network for short-term load forecasting is proposed. DBD-FELF consists of fuzzy rules with consequent parts that are neural networks with internal recurrence. These networks have a hidden layer which consists of pairs of neurons with feedback connections between them. The overall fuzzy model partitions the input space in partially overlapping fuzzy regions, where the recurrent neural networks of the respective rules operate. The partition of the input space and determination of the fuzzy rule base is performed by use of Fuzzy C-Means clustering algorithm and the RENNCOM constrained optimization method is applied for consequent parameter tuning. The electric load time-series of the Greek power system is examined, and hourly-based forecasting for the whole year is performed. The performance of DBD-FELF is tested via extensive experimental analysis and the results are promising, since an average percentage error of 1.18% is attained, along with an average yearly absolute error of 76.2 MW. Moreover, DBD-FELF is compared with Deep Learning, fuzzy and neurofuzzy rivals, such that its particular attributes are highlighted.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

During the third decade of the 21^st century, the issues of green energy and renewable sources penetration are pivotal worldwide. Power generation and coordination of power plants have been gaining considerable attention in economic policies of developed countries. Moreover, the impact of the recent war in the European continent and the fear for energy poverty contribute to the need for effective operation of energy management systems [1,2,3,4]. Therefore, accurate forecast in power demand constitutes a necessity for national operators and the power market.

Nowadays, Machine Learning and Computational Intelligence are two pillars of nonlinear identification and prediction. As far as electric load forecasting is concerned, the first intelligent tools were proposed more than thirty years ago, initially with feedforward neural networks [5,6] and in the sequel with fuzzy models or neurofuzzy schemes [7,8,9].

Machine learning methods like support vector machines, multiple linear regression or random forest regressors turned out to be promising forecasters [10,11,12,13]. Additionally, genetic algorithms and particle swarm optimization contributed to the arsenal of load forecasters [14,15].

The advent of Deep Learning has created a new path in many scientific fields, including smart energy management and power systems. All the established deep models have been used to perform accurate electric load prediction, leading to forecasters based on Convolutional Neural Networks (CNN), Long-Short-Term-Memory models (LSTM), Recurrent Neural Networks (RNN) and Gated Recurrent Unit schemes (GRU) [16,17,18,19,20].

One of the most challenging tasks in prediction problems is the formation of an appropriate and representative set of inputs, which will not lead to huge models with excessive computational burden. Since in STLF the inputs are usually past load values, climate variables and temperatures, it would be quite helpful to employ dimensionality reduction or transformation methods, in an attempt to provide a moderate input vector [21,22].

In light of the above, the DBD-FELF forecasting model (Dynamic Block-Diagonal Fuzzy Electric Load Forecaster) is proposed for the Greek power system. It is a modified fuzzy model, since the consequent parts of its fuzzy rules have internal recurrence; they are block-diagonal recurrent neural networks, where there are feedback connections only between pairs of neurons in the hidden layer. This local output feedback, though limited, is able to identify the dynamics of electric load time-series. The Fuzzy C-Means clustering algorithm is employed to perform input space partition and to determine the parameters of the premise parts of the fuzzy rules. The consequent parameters are tuned by use of RENNCOM, which is a constrained optimization algorithm that takes into account the temporal relations of the recurrent structures and overcomes the failings of the typical gradient-based methods. DBD-FELF is fed with a single input and performs quite effectively both on working days and weekends throughout the whole year, while having a significantly reduced structural complexity compared especially to Deep Learning approaches.

The rest of the paper proceeds as follows: the architecture and the structural attributes of DBD-FELF are presented in Section 2. Next section hosts the clustering and learning algorithms. The experimental results are detailed in Section 4, where a comparative analysis with established models is conducted. The pool of competing rivals includes static and recurrent fuzzy and neurofuzzy systems, along with LSTM, GRU and RNN schemes. In this analysis, the particular characteristics of DBD-FELF are highlighted and its performance on the load time-series of the Greek power system is evaluated. The closing remarks are given in the last section.

2. The Architecture of DBD-FELF

DBD-FELF belongs to a class of fuzzy models that can be considered as generalizations of the Takagi-Sugeno-Kang fuzzy model (TSK [23]). The forecaster’s fuzzy rule base consists of rules that contain fuzzy sets in the premise part, while the consequent parts are not linear functions of their inputs as in a classic TSK model, but they consist of neural structures. In the present case, the consequent parts are small neural networks with internal recurrence, comprising block-diagonal modules ([24]). The overall fuzzy scheme was introduced in [25] for biomedical system identification and is described as follows:

For the general case of a multiple-input-simple-output model, the fuzzy rules base has r fuzzy rules in the form:

\begin{array}{l} R^{(i)} : I F x_{1} (n) is A_{1}^{i} AND ... AND x_{m} (n) is A_{m}^{i} \\ T H E N g_{i} (n) = B D R N N_{i} (x (n)) \end{array}

(1)

where

R^{(i)}

denotes the i-th rule,

x (n) = {[x_{1} (n), ..., x_{m} (n)]}^{T}

is the input vector, n represents the sample index and

A_{j}^{i}

corresponds to the fuzzy set of the j-th input for the i-th rule.

The fuzzy sets are implemented by Gaussian membership functions:

μ_{A_{j}^{i}} (x_{j} (n)) = \exp \{- \frac{1}{2} \cdot \frac{{(x_{j} (n) - m_{i j})}^{2}}{σ_{i j}^{2}}\} i = 1, ..., r, j = 1, ..., m

(2)

The tuning parameters of the premise parts are the mean values, $m_{i j}$

, and the standard deviations,

σ_{i j}

, of the membership functions. It becomes evident from Equation (2) that the premise parts of the fuzzy rules are of static nature.

The degree of fulfilment of each rule is the algebraic product of the Gaussian membership functions:

\begin{array}{l} μ_{i} (n) = \prod_{j = 1}^{m} μ_{A_{j}^{i}} (x_{j} (n)) = \prod_{j = 1}^{m} \exp \{- \frac{1}{2} \cdot \frac{{(x_{j} (n) - m_{i j})}^{2}}{σ_{i j}^{2}}\} = \\ \exp \{- \frac{1}{2} \cdot \sum_{j = 1}^{m} \frac{{(x_{j} (n) - m_{i j})}^{2}}{σ_{i j}^{2}}\} = f (x (n), m_{i 1}, ..., m_{i m}, σ_{i 1}, ..., σ_{i m}) \end{array}

(3)

Equation (3) is an m-dimensional Gaussian function. Therefore, the degree of fulfilment corresponds to the membership function of a fuzzy hyper-region. The fuzzy rule-base partitions the input space to operating regions, where each rule can be considered as a local sub-model, which contributes to the overall fuzzy system’s output according to the degree of fulfilment, and produces its own output as a result of the operation of its BDRNN.
The consequent parts of the rules are block-diagonal recurrent neural networks. The structure of a two-block BDRNN is presented in Figure 1. The input signal is fed to the blocks of neurons, where each block contains a pair of neurons. There are no connections between neurons that belong to different blocks, while neurons of the same block feedback both to themselves and to each other, with unit delays. This network structure is of dynamic nature, having internal recurrence (local output feedback, [26]).

For a BDRNN with N neurons, the outputs of the neurons are given by state equations below:

s_{2 k - 1}^{(i)} (n) = f_{1} [\sum_{j = 1}^{m} a_{2 k - 1, j}^{(i)} \cdot x_{j} (n) + w_{1, k}^{(i)} \cdot s_{2 k - 1}^{(i)} (n - 1) + w_{2, k}^{(i)} \cdot s_{2 k}^{(i)} (n - 1)]

(4)

s_{2 k}^{(i)} (n) = f_{1} [\sum_{j = 1}^{m} a_{2 k, j}^{(i)} \cdot x_{j} (n) - w_{2, k}^{(i)} \cdot s_{2 k - 1}^{(i)} (n - 1) + w_{1, k}^{(i)} \cdot s_{2 k}^{(i)} (n - 1)]

(5)

i = 1, ..., r, k = 1, ..., \frac{N}{2}

The output of the BDRNN for the i-th fuzzy rule is calculated as follows:

g_{i} (n) = f_{2} [\sum_{j = 1}^{N} b_{i j} \cdot s_{j}^{(i)} (n)]

(6)

where the notation given below is used:

➢: the typical sigmoid function, $f (z) = \frac{1 - e^{- z}}{1 + e^{- z}}$ , implements the activation functions $f_{1}$ and $f_{2}$ .
➢: $s_{2 k - 1}^{(i)} (n)$ and $s_{2 k}^{(i)} (n)$ are the outputs of neurons that form the k-th block when the n-th sample is processed.
➢: $g_{i} (n)$ is the output of the i-th fuzzy rule.
➢: $g_{i} (n)$ is the output of the i-th fuzzy rule.
➢: $a_{2 k - 1, j}^{(i)}$ and $a_{2 k, j}^{(i)}$ are the synaptic weights of the neurons that form the k-th block and j is the dimension index of the input vector.
➢: $b_{i j}$ are the synaptic weights of the output neuron.
➢: $w_{1, k}^{(i)}, w_{2, k}^{(i)}$ are the feedback weights of the k-th block of neurons of BDRNN. In order to reduce the number of tuning parameters by half, the scaled orthogonal form is selected. As described in [24], the feedback weights of each block comprise the following feedback matrix:

$W_{k}^{(i)} = [\begin{matrix} w_{1, k}^{(i)} & w_{2, k}^{(i)} \\ - w_{2, k}^{(i)} & w_{1, k}^{(i)} \end{matrix}], k = 1, ..., \frac{N}{2}$

(7)

The defuzzification part of DBD-FELF produces the model’s output. The weighted average defuzzification scheme is employed, since it is the most popular in TSK fuzzy models, requiring a low computational burden as well:

y (n) = \frac{\sum_{i = 1}^{r} μ_{i} (n) \cdot g_{i} (n)}{\sum_{i = 1}^{r} μ_{i} (n)}

(8)

The architecture of DBD-FELF belongs to a class of dynamic fuzzy neural models where dynamics exist only at the consequent parts of the rules, leaving the premise and defuzzification parts static [27,28]. Moreover, there are no external feedback connections that blur the interpretability of the overall model. This class aims at preserving the local character of TSK modeling, since the rules in these models can be considered as local subsystems that are interconnected through the defuzzifier. The advantages of this class over models with (a) feedback of the total output [29], (b) recurrence in the premise parts of the fuzzy rules [30] or (c) recurrent modules in a cascade connection [31], are highlighted in [32,33,34]. In [35], such a recurrent neurofuzzy system was introduced as a very efficient load forecaster, with reduced complexity compared to Deep Learning counterparts. In this context, DBD-FELF is an alternative approach in this path.

3. The Model-Building Process

In the model-building process, the fuzzy rule base is constructed by partitioning the input space, and the forecaster’s parameters are calculated. In an attempt to create a moderate in size fuzzy rule base, the Fuzzy C-Means (FCM) (Dunn [36] and Bezdek [37]) clustering method is applied, in order to explore the input space and extract the most appropriate clusters that will determine (a) the number of fuzzy rules and (b) the fuzzy hyper-region of the premise parts.

FCM is a distance-based clustering method, which provides the most appropriate cluster centers in terms of minimum distances between the data samples that belong to each cluster. Since each cluster center corresponds to a fuzzy hyper-region, the resulting clustering produce fuzzy rules that each one of them is focused on a part of the data set. For a given number of clusters, r, and a data set of P m-dimensional samples, the cluster centers are derived as follows:

m_{i j} = \frac{\sum_{n = 1}^{P} {(u_{i n} (n))}^{c} \cdot x_{j} (n)}{\sum_{n = 1}^{P} {(u_{i n} (n))}^{c}}, i = 1, ..., r, j = 1, ..., m

(9)

c is a fuzziness parameter within

[1, + \infty]

and

u_{i n}

is the membership degree that the n-th data sample belongs to the i-th cluster:

u_{i n} = \frac{1}{{\sum_{k = 1}^{r} [\sqrt{\sum_{j = 1}^{m} {(m_{i j} - x_{j} (n))}^{2}} \cdot \sqrt{\sum_{j = 1}^{m} {(m_{k j} - x_{j} (n))}^{2}}]}^{\frac{2}{m - 1}}}

(10)

According to the above, the number of clusters, r, determines the size of the fuzzy rule base. Using Gaussian membership functions for each input axis, Equation (9) provides their mean values. The standard deviations are calculated as proposed in [38]:

σ_{i j} = \frac{\sum_{n = 1}^{P} u_{i n} \cdot {(m_{i j} - x_{j} (n))}^{2}}{\sum_{n = 1}^{P} u_{i n}}

(11)

Once the mean values and the standard deviations of the membership functions are determined, the premise parts of the fuzzy rules remain fixed. Thus, the weights of BDRNNs at the consequent parts remain to be tuned.

The training algorithm for the synaptic weights of BDRNN is RENNCOM [39]. It is a constrained optimization method, where various constraints regarding the learning process can be incorporated. In the present case, the methods based on gradient descent do not guarantee stable learning, since at the hidden layer of BDRNN there exist feedback connections. Therefore, a constraint relevant to stable learning can be introduced in the form of an appropriate function, which will be optimized simultaneously with the standard error function. Such an approach was followed in [25], where both the premise and consequent parameters were calculated by RENNCOM. In DBD-FELF, the algorithm is applied only to consequent weights and is briefly presented below.

According to the analysis given in [39], for the type of feedback matrices in Equation (7), their eigenvalues should fulfil the following constraint for stability to be ensured:

\begin{array}{l} |λ_{i k}| \leq 1 \Leftrightarrow \sqrt{{(w_{1, k}^{(i)})}^{2} + {(w_{2, k}^{(i)})}^{2}} \leq 1 \Leftrightarrow {(w_{1, k}^{(i)})}^{2} + {(w_{2, k}^{(i)})}^{2} \leq 1 \\ i = 1, ..., r, k = 1, ..., \frac{N}{2} \end{array}

(12)

A suitable stability function for incorporating Equation (12) is the sigmoid function, which is smooth and continuously differentiable, therefore robust to problems caused by parasitic oscillations. Thus, the stability function is written:

p_{i k} = f_{d} (z_{i k}) = \frac{1 - e^{- a_{s} z_{i k}}}{1 + e^{- a_{s} z_{i k}}}, z_{i k} = {|λ_{i k}|}^{2} - 1 = {(w_{1, k}^{(i)})}^{2} + {(w_{2, k}^{(i)})}^{2} - 1

(13)

The model is stable when the eigenvalues lie within the unit circle. Since parameter

a_{s}

controls the slope of the sigmoid function in Equation (13) and, consequently, its active region,

a_{s}

takes a value within [4,8].

Let all the consequent parameters of Equations (4)-(6) comprise the parameter vector of each fuzzy rule,

θ_{c o n}

. The RENNCOM algorithm aims at achieving the following three objectives:

1): The error measure, E, should be minimized, such that the electric load time-series, $\hat{y} (n)$ , is identified. The Mean Squared Error is selected to be the error measure:

M S E = ⥄ \frac{1}{P} \cdot \sum_{n = 1}^{P} {[y (n) - \hat{y} (n)]}^{2}

(14)

The error measure is minimized through an iterative process, where at each iteration

E

is decremented by a certain amount,

δ E

. This change is selected in an adaptive way, so that after a succession of iterations the accumulated changes lead to the establishment of an accurate input-output representation.

2): A second function, called the pay-off function, Φ, should be minimized, such that stability during the learning process is preserved. In the present case, the pay-off function includes the constraints given by Equation (12) and has the following form:

Φ = \frac{1}{2} \cdot \sum_{i = 1}^{r} \sum_{k = 1}^{\frac{N}{2}} {(- 1 - p_{i k})}^{2}

(15)

3): An extra condition is imposed, that facilitates search in the weight space [39]:

Φ_{w} = d θ^{T} \cdot {(Δ^{2})}^{- 1} \cdot d θ - 1 = 0

(16)

d θ

is the amount by which the consequent parameter vector is changed at each iteration. Matrix Δ is a diagonal matrix that hosts the maximum parameter change (MPC) of each weight. Equation (16) describes a hyper-ellipsoid, that is centered on the current consequent weight vector and search for the new values of the weights is restricted by this hyper-ellipsoid. For given values of

δ E

and Δ, the optimal

d θ

is the vector that maximizes

d Φ

The analysis for the consequent parameters’ updates is fully described in [39]. The set of equations that implement the learning scheme is given in the sequel:

θ_{n e w} = θ_{o l d} + d θ

(17)

\begin{array}{l} d θ = - Δ^{2} \cdot \sqrt{\frac{[{(\frac{\partial E}{\partial θ})}^{T} \cdot Δ^{2} \cdot \frac{\partial E}{\partial θ}] - {(δ E)}^{2}}{[{(\frac{\partial Φ}{\partial θ})}^{T} \cdot Δ^{2} \cdot \frac{\partial Φ}{\partial θ}] \cdot [{(\frac{\partial E}{\partial θ})}^{T} \cdot Δ^{2} \cdot \frac{\partial E}{\partial θ}] - {[{(\frac{\partial Φ}{\partial θ})}^{T} \cdot Δ^{2} \cdot \frac{\partial E}{\partial θ}]}^{2}}} \\ \cdot [{(\frac{\partial Φ}{\partial θ})}^{T} - {(\frac{\partial E}{\partial θ})}^{T} \cdot \frac{{(\frac{\partial Φ}{\partial θ})}^{T} \cdot Δ^{2} \cdot \frac{\partial Φ}{\partial θ}}{{(\frac{\partial E}{\partial θ})}^{T} \cdot Δ^{2} \cdot \frac{\partial E}{\partial θ}}] + Δ^{2} \cdot {(\frac{\partial E}{\partial θ})}^{T} \cdot \frac{δ E}{{(\frac{\partial E}{\partial θ})}^{T} \cdot Δ^{2} \cdot \frac{\partial E}{\partial θ}} \end{array}

(18)

The decrement

δ E

is expressed as a function of the gradient

\frac{\partial E}{\partial θ}

, the MPC matrix and a constant ξ within [0,1]:

δ E = - ξ \cdot [{(\frac{\partial E}{\partial θ})}^{T} \cdot Δ^{2} \cdot \frac{\partial E}{\partial θ}]

(19)

Due to the dynamic nature of the neurons and the existence of temporal relations, the gradients

\frac{\partial E}{\partial θ}

and

\frac{\partial Φ}{\partial θ}

are extracted using ordered derivatives [40] and Lagrange multipliers, which facilitate the process. Moreover, the multipliers with respect to the feedback weights create difference equations ((21) and (23)) that are solved recursively, starting from the last data sample (Equations (22) and (24)):

λ_{g, i} (n) = \frac{2}{P} \cdot (y (n) - \hat{y} (n)) \cdot \frac{μ_{i} (n)}{\sum_{j = 1}^{r} μ_{j} (n)}

(20)

\begin{array}{l} λ_{s, 2 k - 1}^{(i)} (n) = λ_{g, i} (n) \cdot b_{i, 2 k - 1} \cdot {f^{'}}_{2} (n, i) + λ_{s, 2 k - 1}^{(i)} (n + 1) \cdot w_{1, k}^{(i)} \cdot {f^{'}}_{1} (n + 1, i, 2 k - 1) \\ - λ_{s, 2 k}^{(i)} (n + 1) \cdot w_{2, k}^{(i)} \cdot {f^{'}}_{1} (n + 1, i, 2 k) \end{array}

(21)

λ_{s, 2 k - 1}^{(i)} (P) = λ_{g, i} (P) \cdot b_{i, 2 k - 1} \cdot {f^{'}}_{2} (P, i)

(22)

\begin{array}{l} λ_{s, 2 k}^{(i)} (n) = λ_{g, i} (n) \cdot b_{i, 2 k} \cdot {f^{'}}_{2} (n, i) + λ_{s, 2 k - 1}^{(i)} (n + 1) \cdot w_{2, k}^{(i)} \cdot {f^{'}}_{1} (n + 1, i, 2 k - 1) \\ + λ_{s, 2 k}^{(i)} (n + 1) \cdot w_{1, k}^{(i)} \cdot {f^{'}}_{1} (n + 1, i, 2 k) \end{array}

(23)

λ_{s, 2 k}^{(i)} (P) = λ_{g, i} (P) \cdot b_{i, 2 k} \cdot {f^{'}}_{2} (P, i)

(24)

{f^{'}}_{1} (n + 1, i, 2 k - 1)

{f^{'}}_{1} (n + 1, i, 2 k)

and

{f^{'}}_{2} (n, i)

are the derivatives of the neurons of the hidden and output layers, with respect to their arguments.

At each iteration each consequent parameter update,

d θ_{i}

, varies from the other updates, since it fulfils the constraint

|d θ_{i}| \leq Δ_{i}

. The MPCs are adaptable and their values are changed via the following adaptation mechanism: Initially, all the consequent weights take a value

Δ_{0}

. The gradients of E with respect to each weight

d θ_{i}

at the present and the previous iterations are monitored and their product is calculated. If the product is positive, MPC increases by a factor

n^{+} \in [1.1, 1.3]

, else it diminishes by a factor

n^{+} \in [0.5, 0 . 8]

. The MPCs are bounded by a small positive number in the range

10^{- 5} - 10^{- 3}

such that the weights retain nonzero values.

According to the above, at each iteration the learning process has the following steps: First, the aforementioned adaptation mechanism calculates the new MPCs. Next, the consequent parameters are updated using Equations (17)-(24) and the current MSE is calculated. If a predefined threshold for MSE is attained, the learning process ends, otherwise it is repeated.

4. Experimental Results

4.1. Problem Statement—Data Preprocessing Phase

The DBD-FELF described in the previous section is applied to predict one day ahead hourly loads of the Greek power system. In an attempt to investigate whether a recurrent system is capable of identifying the temporal relations of the electric load time-series, two decisions were made with regard the forecasting scenario:

(a): The data set is not divided to seasons and the whole annual electric load time-series is examined. Moreover, there is no separation to working days and weekends.
(b): A single input is used: the actual load value at hour h of the previous day, ${\hat{L}}_{d - 1, h}$ (MW), with DBD-FELF predicting the load at the same hour of day d. In this way, the forecaster attempts to identify the mapping

$L_{d, h} = f ({\hat{L}}_{d - 1, h})$

(25)

without resorting to climate and temperature variables. d = 1,...,365 and h = 1,...,24 are the day and hour indices, respectively. This decision aims at providing a very economical model in terms of parameters and computational burden. Therefore, no feature selection is required, a rather demanding preprocessing step, based either on the expertise of system operators or on statistical methods and regression models [41]. DBD-FELF intends to model the dependence of current load on past loads by taking advantage of the recurrent nature of BDRNNs.

Two error measures are selected in order to evaluate the forecasting performance of DBD-FELF. The first one is the Root Mean Squared Error, which is the root of MSE (Equation (14)). It is the most common metric in the area of modeling, measuring in a quadratic manner the discrepancy between the actual data and the output of the forecaster.

The second metric is the Average Percentage Error (APE) with respect to the daily peak:

A P E = \frac{1}{M} \sum_{d = 1}^{M} [\frac{1}{24} \cdot \sum_{h = 1}^{24} \frac{|L_{d, h} - {\hat{L}}_{d, h}|}{L_{\max, d}}] \cdot 100 %

(26)

where M is the number of days in the data set and

{\hat{L}}_{\max, d}

is the maximum actual load of day d.

The data set contains hourly load values from four consecutive years, 2013-2016, which are publicly available on the web by the Greek Independent Power Transmission Operator [42]. The total number of 35064 data is split to training and testing data sets, with a ratio of 3 to 1, respectively. The first three years constitute the training data set (26280 samples) and the leap year 2016, which contains 8784 samples, is the testing set. A preprocessing stage was necessary, in order to deal with missing or irregular values, integrate the data in a common format and perform normalization such that they can be used by BDRNNs. When a missing or an irregular value occurred, it was filled by the average of the value at the same hour of previous day and the next one. When there were consecutive missing values, cubic spline interpolation was employed to fill the gaps.

As far as normalization is concerned, data within

[- 0.8, 0 . 8]

, such that load data fall within the slopes of the activation function of the neurons at the consequent parts of the fuzzy rules.

The final data file contains 1461 lines (three regular years and one leap year) and 25 feature columns (one for the data serial number and twenty-four for the hourly loads). Apart from these columns, some more were added, containing metadata like the day of the week and the season of the year. These additions were necessary in order to perform evaluation tests, partition to seasonal data or to working days and weekends, etc.

4.2. DBD-FELF’s Features

The tuning parameters of a DBD-FELF with Gaussian membership functions, r rules and N hidden neurons at each rule are hosted in Table 1.

FCM partition algorithm leads to a fuzzy rule base with 3 rules. It should be noticed that the same dataset used in [35] is employed, therefore the conclusions regarding the selection of the number of rules based on the Davies–Bouldin index [43] and the respective arguments, apply here as well. The reader is referred to [35] for a detailed analysis. Moreover, since a comparative analysis with the forecaster proposed in [35] is presented in the sequel, the same input partition facilitates the comparison. The input space partition is presented in Figure 2.

It is concluded from Figure 2 that the three fuzzy sets adequately cover the input space, centered at 4306, 5428 and 6751 MW, meaning that the three cluster centers are placed where the load values appear most of the time. The first and third fuzzy sets have Gaussian membership functions with higher standard deviations than the set in the middle, in an attempt to cover the lower and upper values of the universe of discourse. As far as overlapping is concerned, the first and second fuzzy sets have an overlapping factor of 65% and the second and third sets a factor of 59%. Moreover in the central region of loads, all three rules operate, with an overlapping factor of 22% between the first set and the third one. These high overlapping factors are necessary for the rules to operate cooperatively in a wide range of electric loads.

BDRNNs with 1 to 5 blocks were examined. As shown in Subsection 4.3, a single block is sufficient to accurately perform predictions. Therefore, N is set to 2 and the parameter set is limited to 24 parameters. Since the premise parameters are determined by Equations (9) and (11), only 18 consequent weights (75% of the total number of parameters) need to be tuned by RENNCOM.

The learning parameters of RENNCOM are shown in Table 2.

4.3. Experimental Results

In order to depict the effect of network complexity to forecasting performance, the yearly forecast APE and RMSE attained by DBD-FELFs with 1 to 5 blocks of recurrent neurons in their consequent parts of their rules are summarized in Table 3. The RMSE is calculated on the denormalized (actual) values and is expressed in MW. Taking into consideration that usually an electric load prediction is considered reliable when its APE value falls below 2%, it becomes evident that all five versions of DBD-FELF operate very effectively. Moreover, the existence of internal feedback at each rule and the efficient partition of the input space are reflected on the size of BDRNN necessary for a fuzzy rule to track the time-series dynamics. The simplest BDRNN performs practically the same compared to bigger networks, therefore in the sequel the DBD-FELF with a single block of recurrent neurons will be employed.

The seasonal forecasting results are reported in Table 4. Despite the fact that a single model is used for the whole year, DBD-FELF predicts well below 2% in all seasons, with Spring being the most difficult season, where the highest deviation between the training and the testing error values occurs. The behavior of the forecaster is very similar for the rest three seasons, with APE values vary in a very small range, 0.08%.

In terms of the absolute error for the testing data set, a yearly average of 76.2 MW is attained, with its standard deviation being 81.8 MW, which means that the forecast error is less than 158 MW for most of the hours in 2016 (8784 hours as it was a leap year). The absolute error duration curve is hosted in Table 5. This curve depicts the percentage of hours of the year in which the absolute value of the forecast error is greater than the values given in the first row. It becomes evident that DBD-FELF performs very efficiently, since for nearly 69.5% and 92% of the time the forecast error is less than 100 and 200 MW, respectively. Moreover, the forecast error exceeds 500 MW for 15 hours throughout the year. It should be noticed that 9 out of these 15 hours belong to Orthodox Easter and Assumption days, highly irregular days as will be discussed in the sequel.

The daily evolution of electric load for week-days and Sundays, regarding all seasons, is shown in Figure 3, Figure 4, Figure 5 and Figure 6 and a winter week is hosted in Figure 7. Moreover, Figure 8 presents the three major holidays in Greece: Christmas, Orthodox Easter and Assumption days. In these charts, the blue solid lines are the actual load data series, and the red dashed lines refer to the predictions made by DBD-FELF.

From Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, the following remarks are in order:

In the case of working days, the appearances of morning and evening peaks as well as the first minimum load, are similar at all seasons. During Spring and Autumn working days, the evening minimum is more discrete than during Winter and Summer.
As expected, the evolution of the load curve on Sundays is quite different from the one of working days. Additionally, the seasonal patterns are also different. Autumn and Spring Sundays follow the evolution of the respective working day load curves after 6p.m.
Even though there exist differences between seasonal patterns, as well as between types of days, the proposed forecaster models efficiently the actual load curves, since it identifies the peaks and the minimum loads, and accurately predicts the values at the slopes. As shown in Figure 7, the single-input forecaster is capable of tracking the transition from weekend days to working days and vice versa.
As far as Holidays are concerned, it can be seen in Figure 8a that the Christmas load curve is tracked by DBD-FELF very efficiently. The average percentage error for the Christmas day is 0.31%. This behavior can be attributed to the fact that during Christmas Greeks stay at home or pay visits, therefore the household loads compensate the industrial ones. The two minima occur at 5a.m. and 3p.m., and the first peak load at 10am, at the same hours as the previous day. Moreover, the load evolution is quite similar on these two days, leading to the conclusion that the temporal relation of past loads has been effectively identified.
On the contrary, the Easter and Assumption holidays are quite a different story: the Easter day is a highly irregular day, as shown in Figure 8b. There is no morning peak and there is a continuous decrease in load demand until 3p.m. Moreover, the load values are significantly reduced (2331 MW at 3p.m.) with respect to the previous day (3405 MW) and to the previous Sunday (3392 MW), leading to enormous errors: 735.9 MW at 2p.m., 770 MW at 3p.m. and 652.6 at 4p.m., and an average percentage error of 8.11%. This unusual load curve reflects the fact that during Easter no industrial activity takes place and Greek people leave their homes and celebrate outdoors. The evening peak attains 4500 MW, when in a typical Spring Sunday the respective peak is around 6500 MW (Figure 4b). In the case of August 15^th (Assumption day), DBD-FELF does not perform accurately at least until 6p.m. Even though it tracks the dynamics, the predicted load takes quite bigger values, leading to errors up to 507 MW. The load curve is quite similar to that of Easter: there is no morning peak as well, and load keeps more or less reducing to a minimum below 3000 MW around 3p.m. (lunch time). Assumption day is at the heart of summer vacations for Greek people; most are on leave and spend the morning at the beach, returning to their summer houses or to hotels late in the evening. However, the load profile returns to its normal around 6p.m. and DBD-FELF performance ameliorates significantly. The average percentage error for August 15^th is 3.53%.

DBD-FELF is tested in comparison to six Computational Intelligence-based static and dynamic models, namely, ANFIS [44], LSTM forecaster [45,46], GRU and RNN models [17], the DFNN [47] and the ReNFuzz-LF [35] neurofuzzy models. ANFIS is selected as a well-established static neurofuzzy system, LSTM is an effective Deep Learning model in modeling applications, GRU and Recurrent Neural Network are popular dynamic schemes with enhanced learning capabilities. The pool of competing rivals includes two dynamic neurofuzzy systems, DFNN and ReNFuzz-LF, that are based on generalized TSK fuzzy rules like DBD-FELF, but have different network structure of the consequent parts, as described in [35]. The criteria employed in the comparative analysis are the prediction accuracy and model complexity. All models are applied to the same data sets of the Greek power system. Several setups of the LSTM scheme are tested: networks with one and two layers, each layer consisting of 25, 50 or 500 units. The results from four of them are included below. A GRU with 2 layers and 500 units per layer, along with two RNNS with two hidden layers and 40/200 neurons per layer, respectively, are also included in the test pool. Their other hyperparameters are summarized in Table 6, where the structural and learning parameters of DFNN and ReNFuzz-LF are also given, taken from [35]. The FCM partition applied to DBD-FELF is used for DFNN and ReNFuzz-LF. The input vector of the ANFIS model comprises two inputs,

[L_{d - 1, h}, L_{d - 1, h - 1}]

, in an attempt to compensate its static nature. Among several ANFIS structures that were investigated, the one containing 9 fuzzy sets per input, grid partition and a fuzzy rule base of 81 rules is selected. All forecasters are trained for 1000 iterations. The results are reported in Table 7.

From the aforementioned results it becomes evident that all seven types of models and all eleven forecasters attained APE values below 2%, with six of them predicting with APE less than 1.40%. DBD-FELF, GRU and LSTM-1 exhibit a similar performance, with the proposed forecaster requiring a parameter set that is a fraction of those of the other two rivals. Moreover, all three dynamic neurofuzzy forecasters are proved to be very efficient, despite their small size.

Additionally, recurrent neural networks are the least effective, even with a very complex structure. These observations highlight: (a) the advantage that local recurrence offers to the task of identifying the temporal relations of data series, even with a limited number of units, and (b) the enhanced learning capabilities with low computational complexity that the fuzzy blending of small scale recurrent sub-systems can create. Moreover, DBD-FELF outperforms ReNFuzz-LF in terms of prediction accuracy and structure complexity. Hence, it can be stated that the block-diagonal feedback structure of the consequent parts of the fuzzy rules can model the internal dependencies of the load time-series better than the respective consequent parts of ReNFuzz-LF, which are recurrent neural networks with simple local output feedback. An interesting conclusion can be drawn from the forecast error duration curves of DBD-FELF and ReNFuzz-LF; in Figure 9 the reduction in terms of hours that DBD-FELF has produced over the curve of ReNFuzz-LF is shown. Even though in the area of 100 MW the value is very low (just 3.62%), which means that these forecasters practically operate in the same way where their prediction results are most accurate, the difference in the amount of hours become increasing as less accurate forecasts are produced. For instance, ReNFuzz-LF has 40 hours with a prediction error over 500 MW [35], while DBD-FELF has 15 hours, a reduction by 62.50%. The results in Figure 9 show that the proposed forecaster is more robust, preventing large errors.

In conclusion, DBD-FELF has the following characteristics:

It produces accurate forecasts for the electric load data of the Greek Power System.
It is an economical model, with reduced computational complexity with regard to its rivals.
The model-building process does not require a preprocessing step for selecting appropriate past load values.
The model operates effectively without climate variables.
A single model is applied for forecasting the whole year, independent of the nature of the day. The results justify this decision in general; however, the effect of highly irregular days as Easter day and August 15^th are clear.

5. Conclusions

A block-diagonal fuzzy neural network for short-term electric load forecasting of the Greek power system has been suggested. DBD-FELF is a fuzzy system with rules that have small-scale block-diagonal recurrent structures as consequent parts. Unit feedback connections exist between the pairs of neurons that constitute each block. The FCM clustering method performs the partition of the single input’s space, determining the size of the fuzzy rule base and the values of the premise parameters. The RENNCOM iterative method guarantees stable learning of the consequent weights. The experimental results have shown that DBD-FELF produces very accurate predictions, equal or superior to Computational Intelligence-based models of significantly higher complexity. In the future, the effect of highly irregular days should be dealt with, possibly by introducing some expert knowledge in the form of typical fuzzy rules that will be activated when such a day is recognized.

Author Contributions

Conceptualization, G.K., P.M., A.V. and C.H.; methodology, G.K., P.M., and C.H.; software, G.K. and P.M.; validation, G.K. and A.V.; formal analysis, G.K., P.M., and C.H.; investigation, G.K. and P.M; resources, G.K. and P.M.; data curation, G.K.; writing—original draft preparation, G.K., P.M., and A.V.; writing—review and editing, P.M. and C.H.; visualization, G.K. and P.M.; supervision, P.M.; project administration, P.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: [https://www.admie.gr/en/market/market-statistics/detail-data /18-4-2023]

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

$A_{j}^{i}$	fuzzy set of the j-th input for the i-th rule.
$μ_{A_{j}^{i}}$	membership function of the j-th input axis for the i-th fuzzy rule
$m_{i j}$	mean of a Gaussian membership function of the j-th input dimension for the i-th fuzzy rule
$σ_{i j}$	standard deviation of a Gaussian membership function of the j-th input dimension for the l-th fuzzy rule
$μ_{i}$	degree of fulfilment of the i-th fuzzy rule
N	number of neurons at the consequent parts of the fuzzy rules
RMSE	root mean squared error
APE	average percentage error
P	size of the electric load data set
${\hat{L}}_{\max, d}$	maximum actual load of day d
${\hat{L}}_{d - 1, h}$	actual load at the h-th hour d-1
$L_{d, h}$	predicted load at the h-th hour d-1
$W_{k}^{(i)}$	scaled-orthogonal feedback matrix for k-th block of the i-th fuzzy rule
$a_{2 k - 1}^{(i)}, a_{2 k}^{(i)}$	synaptic weights at the k-th block of the i-th fuzzy rule
$w_{2 k - 1}^{(i)}, w_{2 k}^{(i)}$	feedback synaptic weights at the k-th block of the i-th fuzzy rule
$b_{i j}$	synaptic weights at the output layer of the i-th fuzzy rule
$s_{2 k - 1}^{(i)}, s_{2 k}^{(i)}$	the outputs of the neurons that consist the k-th block of the i-th fuzzy rule
BDRNN_i	the block-diagonal recurrent neural network of the i-th fuzzy rule
$g_{i}$	the output of the i-th fuzzy rule
$θ_{c o n}$	weight vector for the consequents parts of the fuzzy rules
$p_{i k}$	stability function for the k-th block of the i-th rule
$δ E$	error decrement
$Φ$	pay-off function
MPC	maximum parameter change
$u_{i n}$	membership degree that the n-th data sample belongs to the i-th cluster
$\frac{\partial^{+} E}{\partial w_{i}}$	ordered partial derivative of the error measure with respect to a consequent weight $w_{i}$
$λ_{s, 2 k - 1}^{(i)}, λ_{s, 2 k}^{(i)}$	Lagrange multipliers for the outputs of the neurons that consist the k-th block of the i-th fuzzy rule
$λ_{g, i}$	Lagrange multiplier for the output of the i-th fuzzy rule
$n^{+}$	increase factor for maximum parameter change
$n^{-}$	decrease factor for maximum parameter change
$Δ_{\min}$	minimum parameter change
$Δ_{\max}$	maximum parameter change
$Δ_{0}$	initial parameter change

References

Hoang, A.; Vo, D. The balanced enegy mix for achieving environmental and economic goals in the long run. Energies 2020, 13, 3850. [CrossRef]
Sgouras, K.; Dimitrelos, D.; Bakirtzis, A.; Labridis, D. Quantitative risk management by demand response in distribution networks. IEEE Trans. Power Syst. 2018, 33, 1496-1506. [CrossRef]
Halkos, G.; Gkampoura, E. Assessing fossil fuels and renewable’s impact on energy poverty conditions in Europe. Energies 2023, 16, 560. [CrossRef]
Marneris, I.; Ntomaris, A.; Biskas, P.; Basilis, C.; Chatzigiannis, D.; Demoulias, C.; Oureilidis, K.; Bakirtzis, A. Optimal Participation of RES aggregators in energy and ancillary services markets. IEEE Trans. Ind. Appl. 2022, 59, 232-243. https://10.1109/TIA.2022.3204863.
Park, D.C.; El-Sharkawi, M.; Marks, R.; Atlas, L.; Damborg, M. Electric load forecasting using an artificial neural network. IEEE Trans. Power Syst. 1991, 6, 442–449. [CrossRef]
Papalexopoulos, A.; How, S.; Peng, T. An implementation of a neural network based load forecasting model for the EMS. IEEE Trans. Power Syst. 1994, 9, 1956–1962. [CrossRef]
Bansal, R. Bibliography on the fuzzy set theory applications in power systems. IEEE Trans. Power Syst. 2003, 18, 1291–1299. [CrossRef]
Dash, P.; Liew, A.; Rahman, S.; Dash, S. Fuzzy and neuro-fuzzy computing models for electric load forecasting. Eng. Appl. Artif. Intell. 1995, 8, 423–433. [CrossRef]
Shah, S.; Nagraja, H.; Chakravorty, J. ANN and ANFIS for short term load forecasting. Eng. Technol. Appl. Sci. Res. 2018, 8, 2818–2820. [CrossRef]
Ibrahim, B.; Rabelo, L.; Gutierrez-Franco, E.; Clavijo-Buritica, N. Machine learning for short-term load forecasting in smart grids. Energies 2022, 15, 8079. [CrossRef]
Lahouar, A.; Ben Hadj Slama, J. Day-ahead Load forecast using Random Forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [CrossRef]
Madrid, E.; Nuno, A. Short-term electricity load forecasting with machine learning. Information 2021, 12, 50. [CrossRef]
Zhang, S.; Zhang, N.; Zhang, Z.; Chen, Y. Electric power load forecasting method based on a support vector machine optimized by the improved seagull optimization algorithm. Energies 2022, 15, 9197. [CrossRef]
Giasemidis, G.; Haben, S.; Lee, T.; Singleton, C.; Grindrod, P. A genetic algorithm approach for modelling low voltage network demands. Appl. Energy 2017, 203, 463–473. [CrossRef]
Yang, Y.; Shang, Z.; Chen, Y.; Chen, Y. Multi-objective particle swarm optimization algorithm for multi-step electric load forecasting. Energies 2020, 13, 532. [CrossRef]
Shohan, J.; Faruque, O.; Foo, S. Forecasting of electric load using a hybrid LSTM – neural prophet model. Energies 2022, 15, 2158. [CrossRef]
Abumohse, M.; Owda, A.; Owda, M. Electrical load forecasting using LSTM, GRU, and RNN algorithms. Energies 2023, 16, 2283. [CrossRef]
Bianchi, F.; Maiorino, E.; Kampffmeyer, M.; Rizzi, A.; Jenssen, R. Recurrent neural networks for short-term load forecasting – An overview and comparative analysis; Springer: Cham, Switzerland, 2017. [CrossRef]
Vanting, N.; Ma, Z.; Jorgensen, B. A scoping review of deep neural networks for electric load forecasting. Energy Inform. 2021, 4, 49. [CrossRef]
Farsi, B.; Amayri, M.; Bouguila, N.; Eicker, U. On short-term load forecasting using machine learning techniques and a novel parallel deep LSTM-CNN approach. IEEE Access 2021, 9. [CrossRef]
Pirbazari, A.; Chakravorty, A.; Rong, C. Evaluating feature selection methods for short-term load forecasting. In Proceedings of 2019 IEEE International Conference on Big Data and Smart Computing, Kyoto, Japan, 2019. [CrossRef]
Yang, Y.; Wang, Z.; Gao, Y.; Wu, J.; Zhao, S.; Ding, Z. An effective dimensionality reduction approach for short-term load forecasting. Electr. Power Syst. Res. 2022, 210, 108150. [CrossRef]
Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [CrossRef]
Sivakumar, S.; Robertson, W.; Phillips, W. On-line stabilization of block-diagonal recurrent neural networks. IEEE Trans. Neural Netw. 1999, 10, 167-175. [CrossRef]
Mastorocostas, P.; Hilas, C. A block-diagonal recurrent fuzzy neural network for system identification. Neural Comput. Applic. 2009, 18, 707-717. [CrossRef]
Tsoi, A.; Back, A. Locally recurrent Ggobally feedforward networks: A critical review of architectures. IEEE Trans. Neural Netw. 1994, 5, 229–239. [CrossRef]
Shihabudheen, K.; Pillai, G. Recent advances in neuro-fuzzy system: A Survey. Knowl. Based Syst. 2018, 152, 136–162. [CrossRef]
Ojha, V.; Abraham, A.; Snasel, V. Heuristic design of fuzzy inference systems: A review of three decades of research. Eng. Appl. Artif. Intel. 2019, 85, 845–864. [CrossRef]
Jassar, S.; Liao, Z.; Zhao, L. A recurrent neuro-fuzzy system and its application in inferential sensing. Appl. Soft Comput. 2011, 11, 2935–2945. [CrossRef]
Juang, C.-F.; Lin, Y.-Y.; Tu, C.-C. A recurrent self-evolving fuzzy neural network with local feedbacks and its application to dynamic system processing. Fuzzy Sets Syst. 2010, 161, 2552–2568. [CrossRef]
Stavrakoudis, D.; Theocharis, J. Pipelined recurrent fuzzy networks for nonlinear adaptive speech prediction. IEEE Trans. Syst. Man Cybern. B. Cybern. 2007, 37, 1305–1320. [CrossRef]
Mastorocostas, P.; Theocharis, J. A Recurrent fuzzy neural model for dynamic system identification. IEEE Trans. Syst. Man Cybern. B. Cybern. 2002, 32, 176–190. [CrossRef]
Samanta, S.; Suresh, S.; Senthilnath, J.; Sundararajan, N. A new neuro-fuzzy inference system with dynamic neurons (NFIS-DN) for system identification and time series forecasting. Appl. Soft Comput. 2019, 82, 105567. [CrossRef]
Mastorocostas, P.; Hilas, C. ReNFFor: A recurrent neurofuzzy forecaster for telecommunications data. Neural Comput. Appl. 2013, 22, 1727–1734. [CrossRef]
Kandilogiannakis, G; Mastorocostas, P; Voulodimos, A. ReNFuzz-LF: A recurrent neurofuzzy system for short-term load forecasting. Energies 2022, 15, 3637. [CrossRef]
Dunn, J. A fuzzy relative of the ISODATA process and its use in detecting compact, well-separated clusters. J. Cybernet. 1974, 3, 32–57. [CrossRef]
Bezdek, J. Cluster validity with fuzzy sets, J. Cybernet. 1973, 3, 58–73. [CrossRef]
Zhou, T.; Chung, F.-L.; Wang, S. Deep TSK fuzzy classifier with stacked generalization and triplely concise interpretability guarantee for large data. IEEE Trans. Fuzzy Syst. 2017, 25, 1207–1221. [CrossRef]
Mastorocostas, P.; Theocharis, J. A stable learning method for block-diagonal recurrent neural networks: application to the analysis of lung sounds. IEEE Trans. Syst. Man. Cybern. B Cybern. 2006, 36, 242-254. [CrossRef]
Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974.
Veeramsetty, V.; Chandra, D.R.; Grimaccia, F.; Mussetta, M. Short term electric load forecasting using principal component analysis and recurrent neural networks. Forecasting 2022, 4, 149–164. [CrossRef]
42. Greek Independent Power Transmission Operator. Available online: https://www.admie.gr/en/market/market-statistics/detail-data (accessed on 22 April 2023).
Davies, D.; Bouldin, D. A clustering separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [CrossRef]
Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man, Cybern. 1993, 23, 665–685. [CrossRef]
Veeramsetty, V.; Chandra, D.R.; Salkuti, S.R. Short-term electric power load forecasting using factor analysis and long short-term memory for smart cities. Int. J. Circuit Theory Appl. 2021, 49, 1678–1703. [CrossRef]
Veeramsetty, V.; Chandra, D.R.; Grimaccia, F.; Mussetta, M. Short term electric load forecasting using principal component analysis and recurrent neural networks. Forecasting 2022, 4, 149–164. [CrossRef]
Mastorocostas, P.; Theocharis, J. A Recurrent fuzzy neural model for dynamic system identification. IEEE Trans. Syst. Man Cybern. B. Cybern. 2002, 32, 176–190. [CrossRef]

Figure 1. A two-block BDRNN as the consequent part of the i-th fuzzy rule.

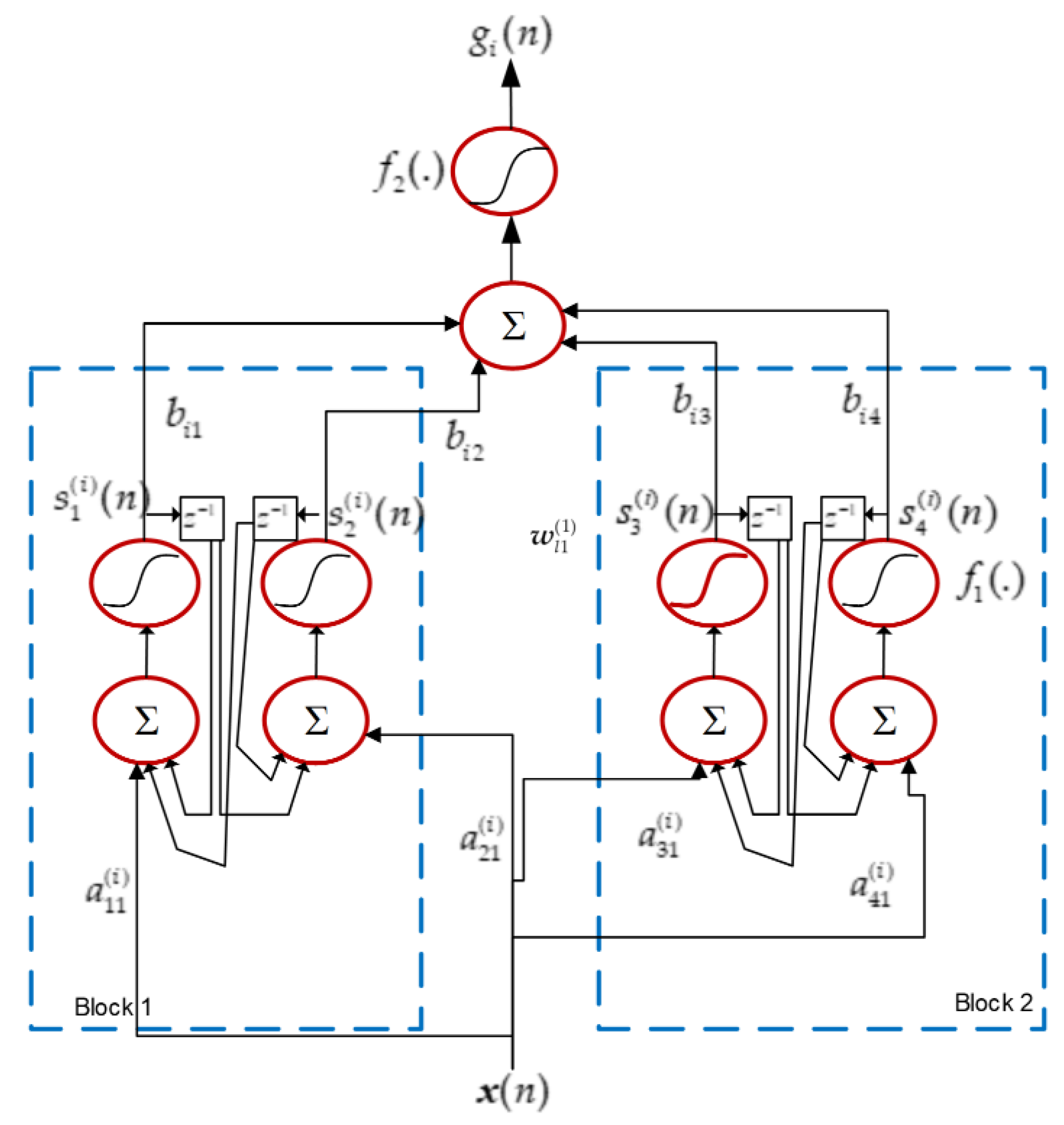
Figure 2. Input space partition with FCM.

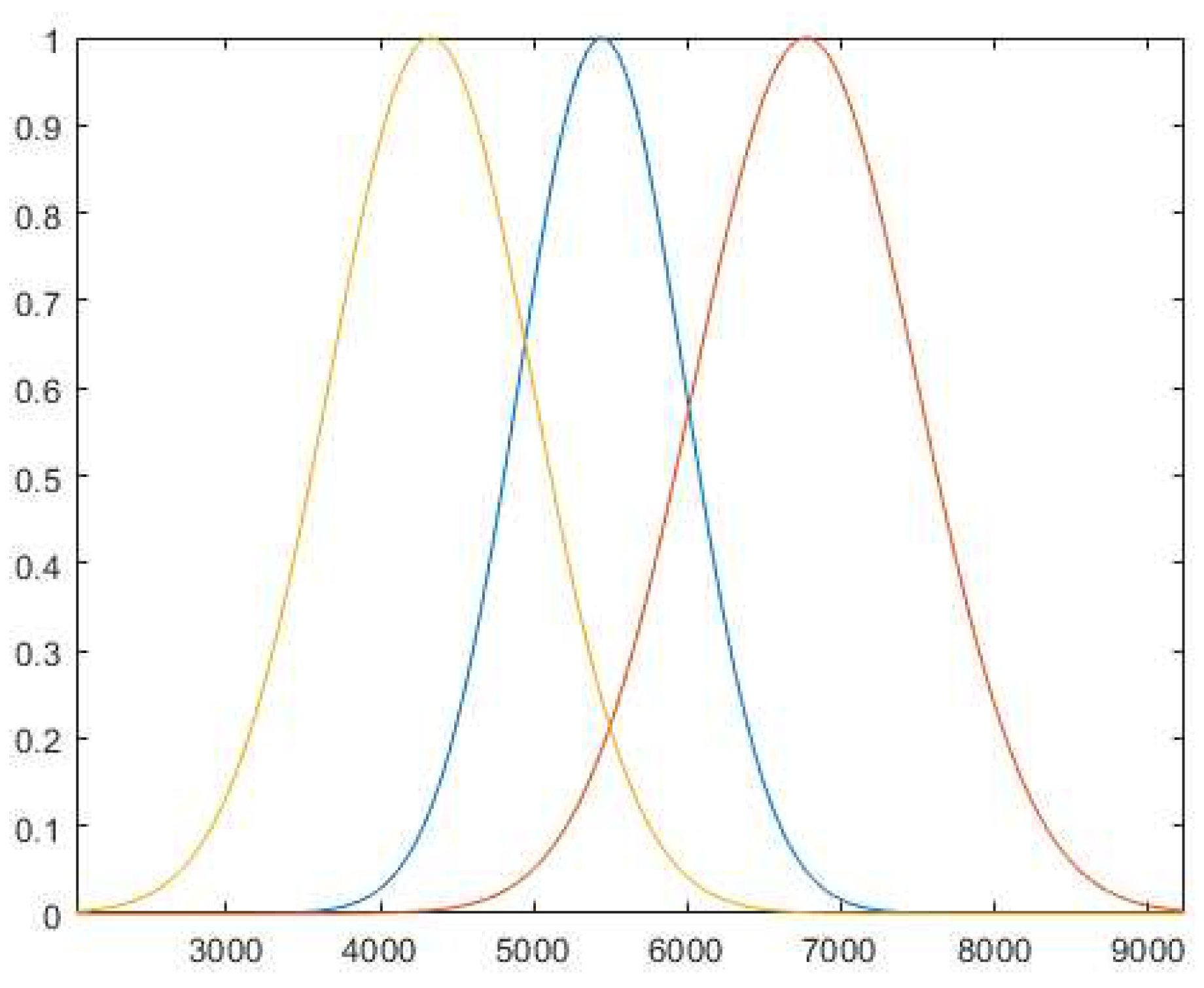
Figure 3. Presentation of winter days: (a) working day; (b) Sunday.

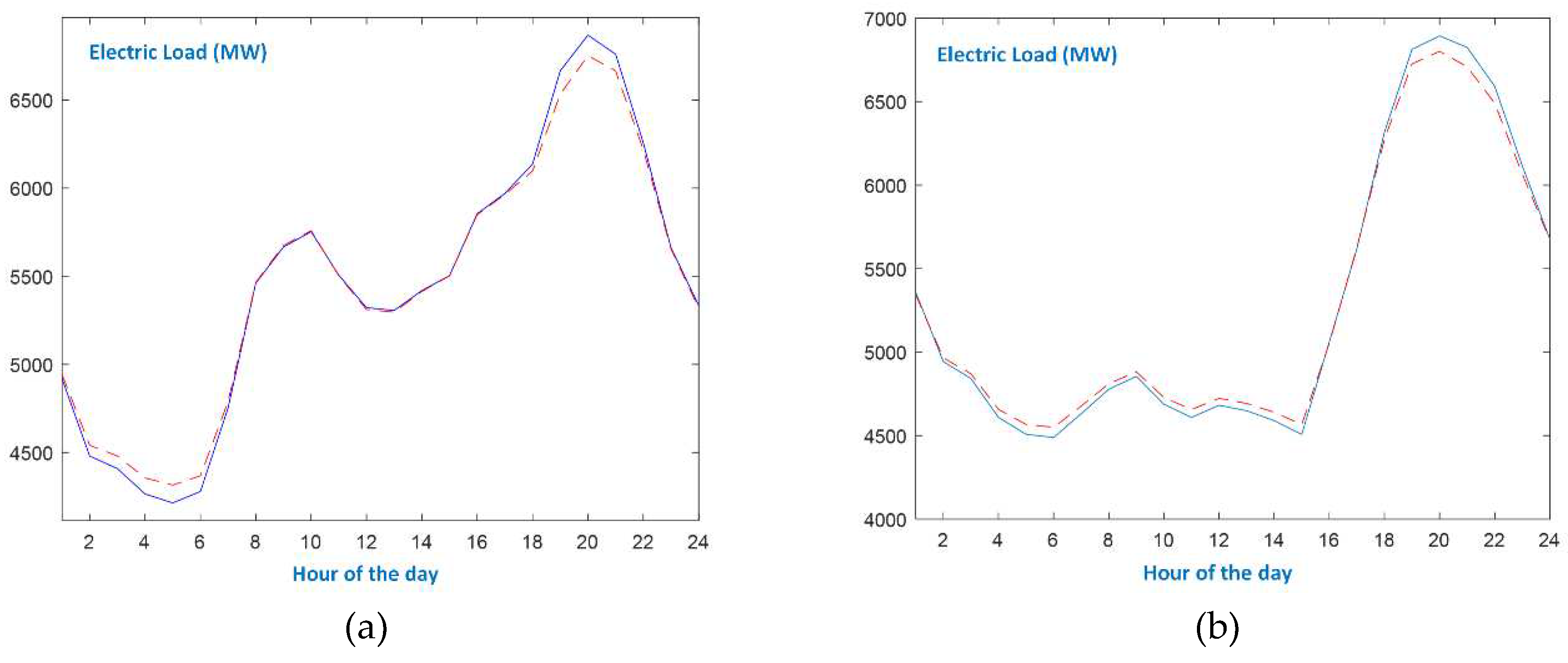
Figure 4. Presentation of spring days: (a) working day; (b) Sunday.

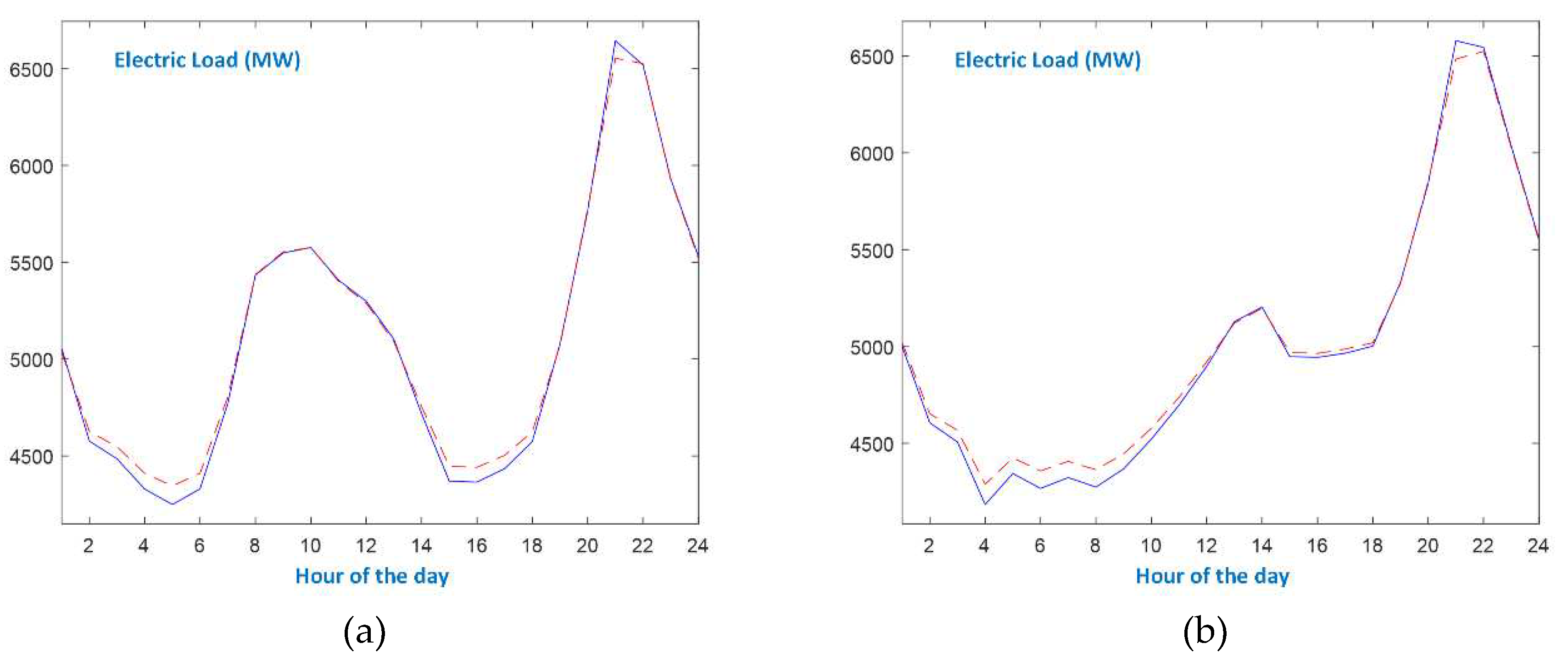
Figure 5. Presentation of summer days: (a) working day; (b) Sunday.

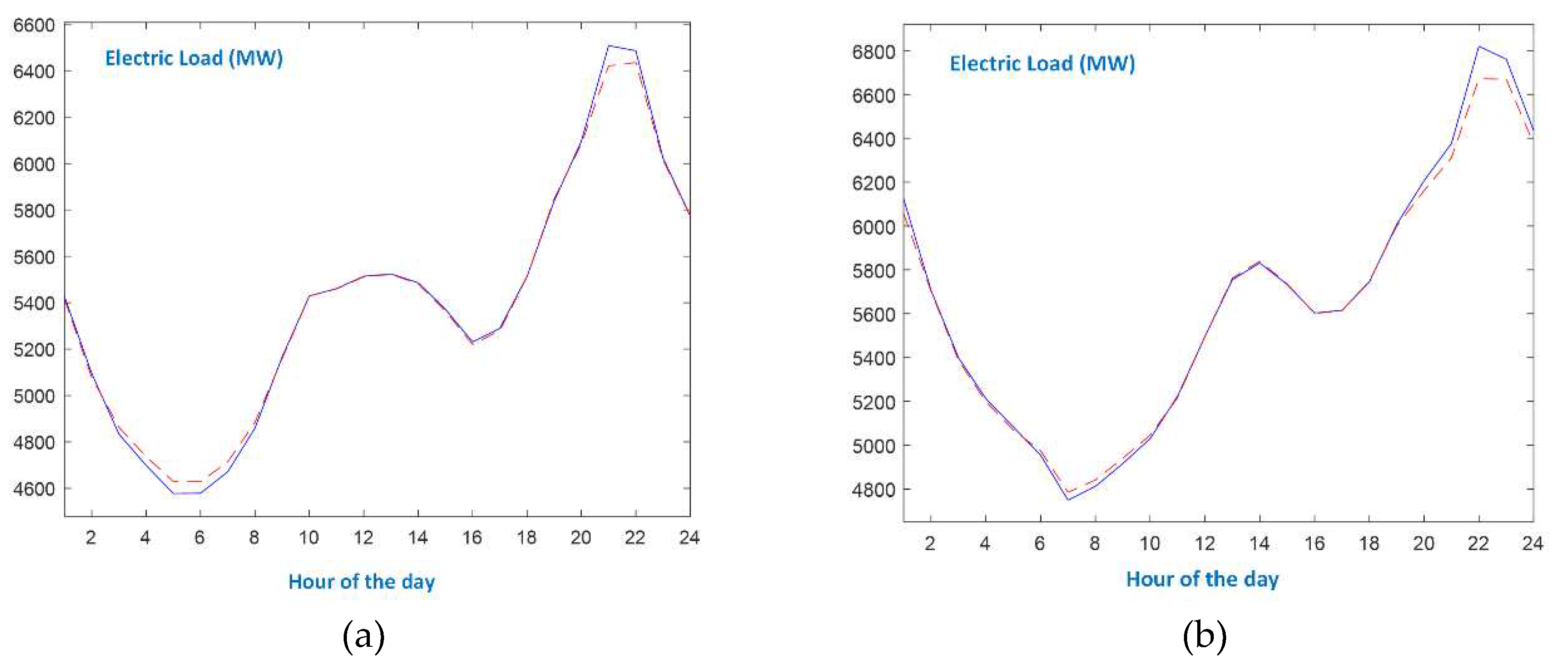
Figure 6. Presentation of autumn days: (a) working day; (b) Sunday.

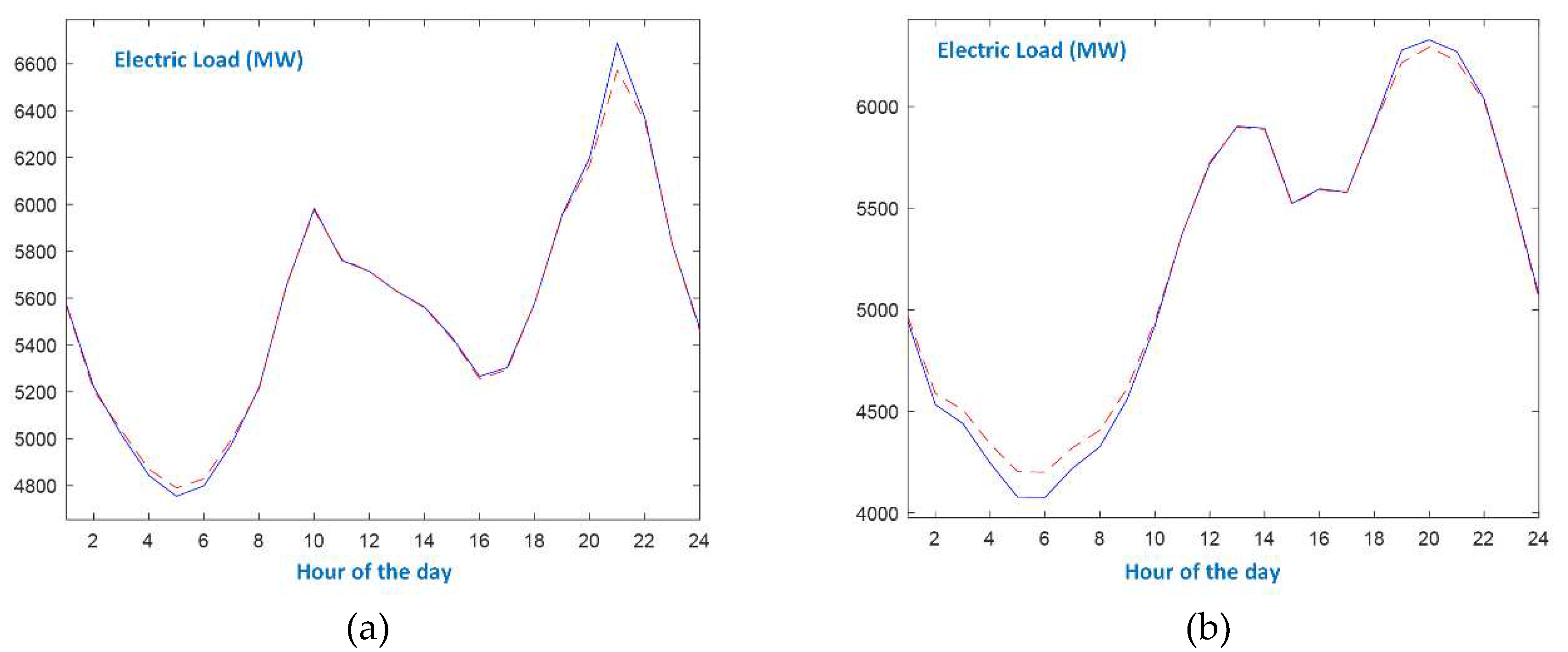
Figure 7. A winter week.

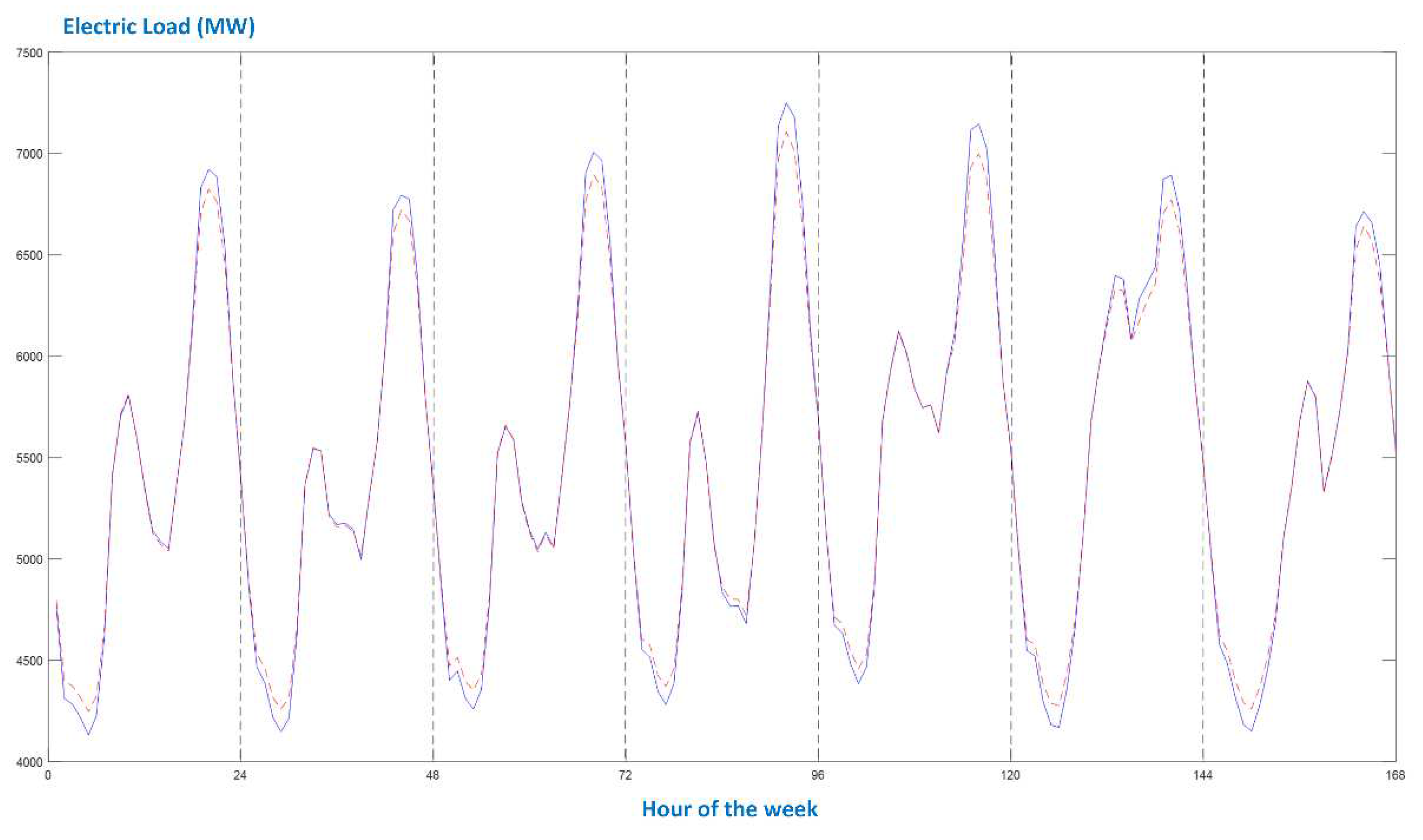
Figure 8. Presentation of holidays: (a) Christmas day; (b) Easter day; (c) Assumption day.

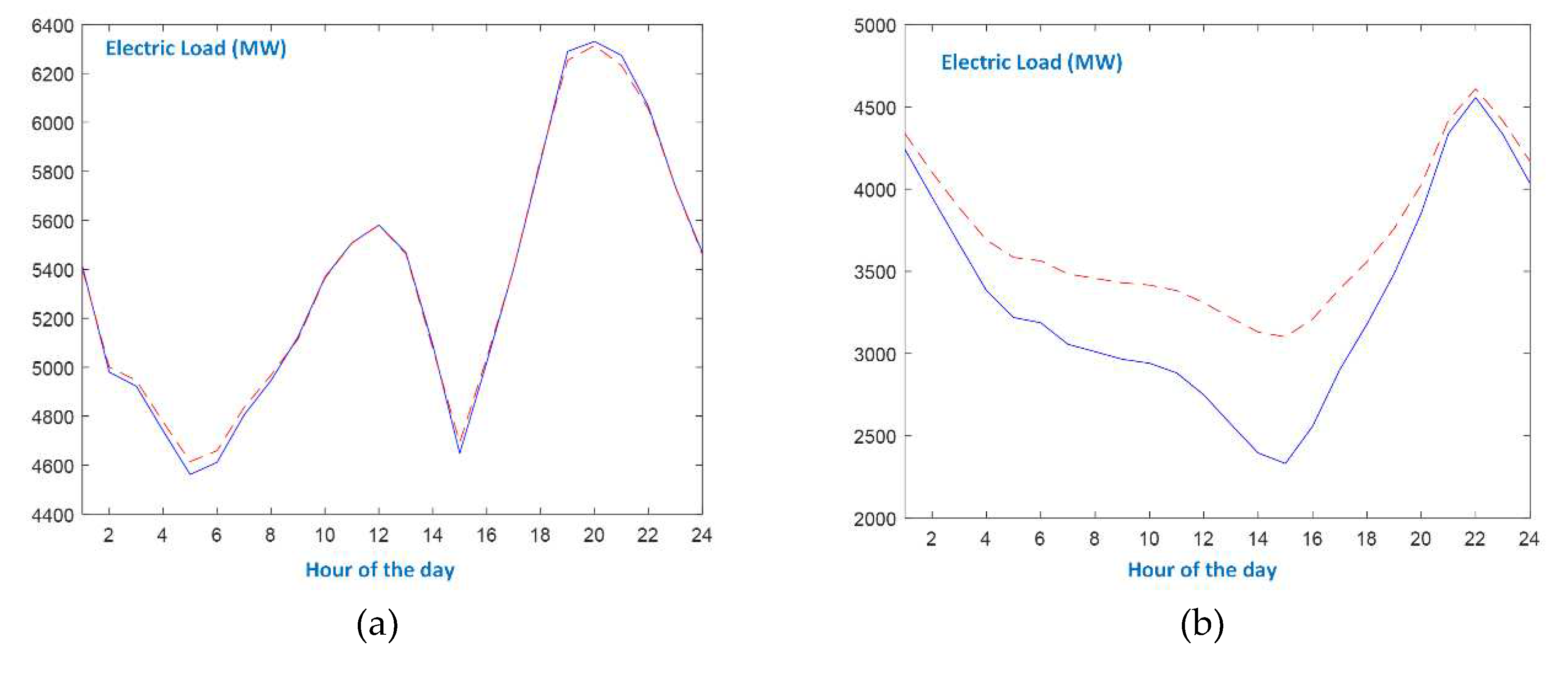
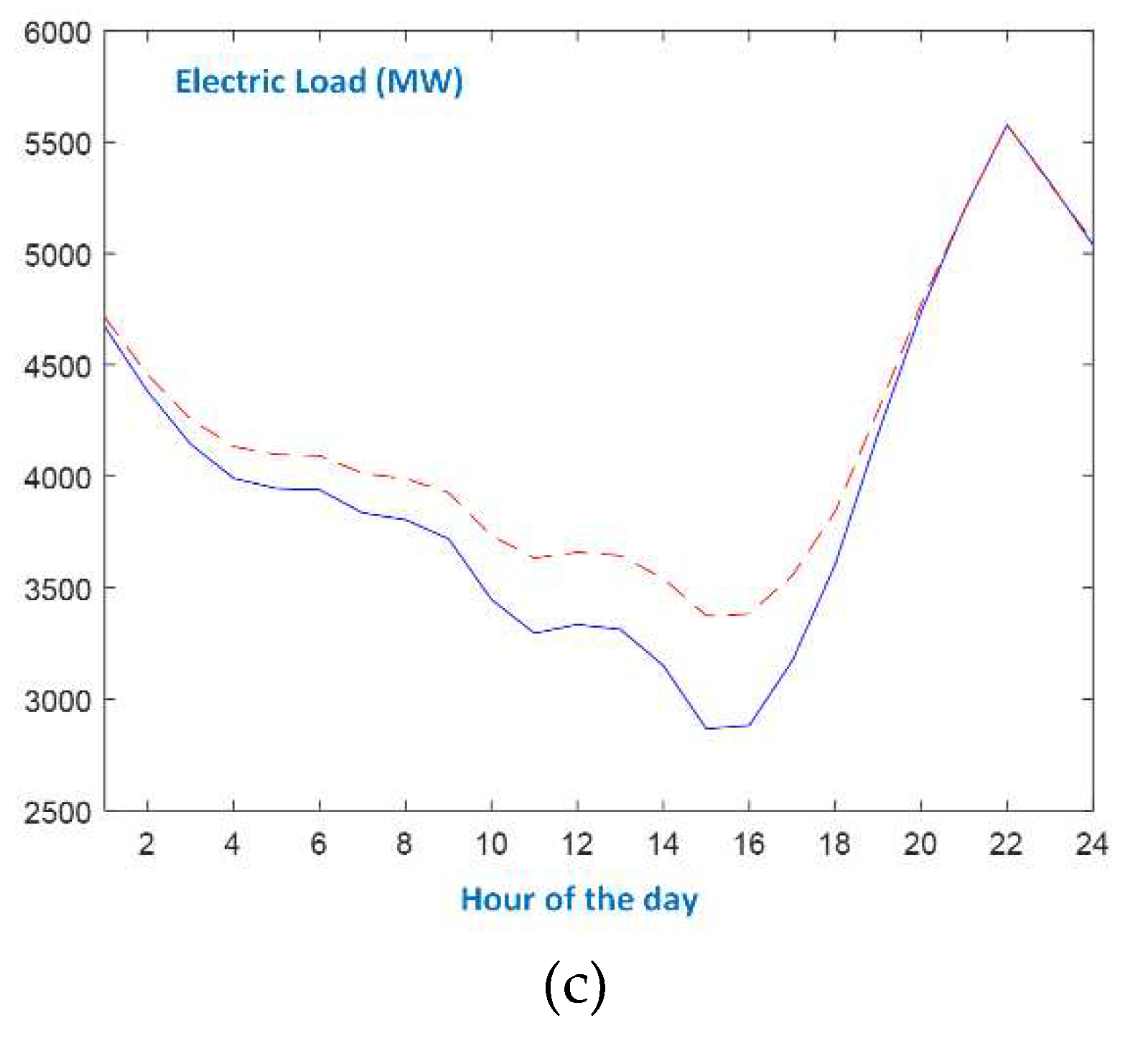
Figure 9. Comparison of DBD-FELF’s and ReNFuzz-LF’s error duration curves.

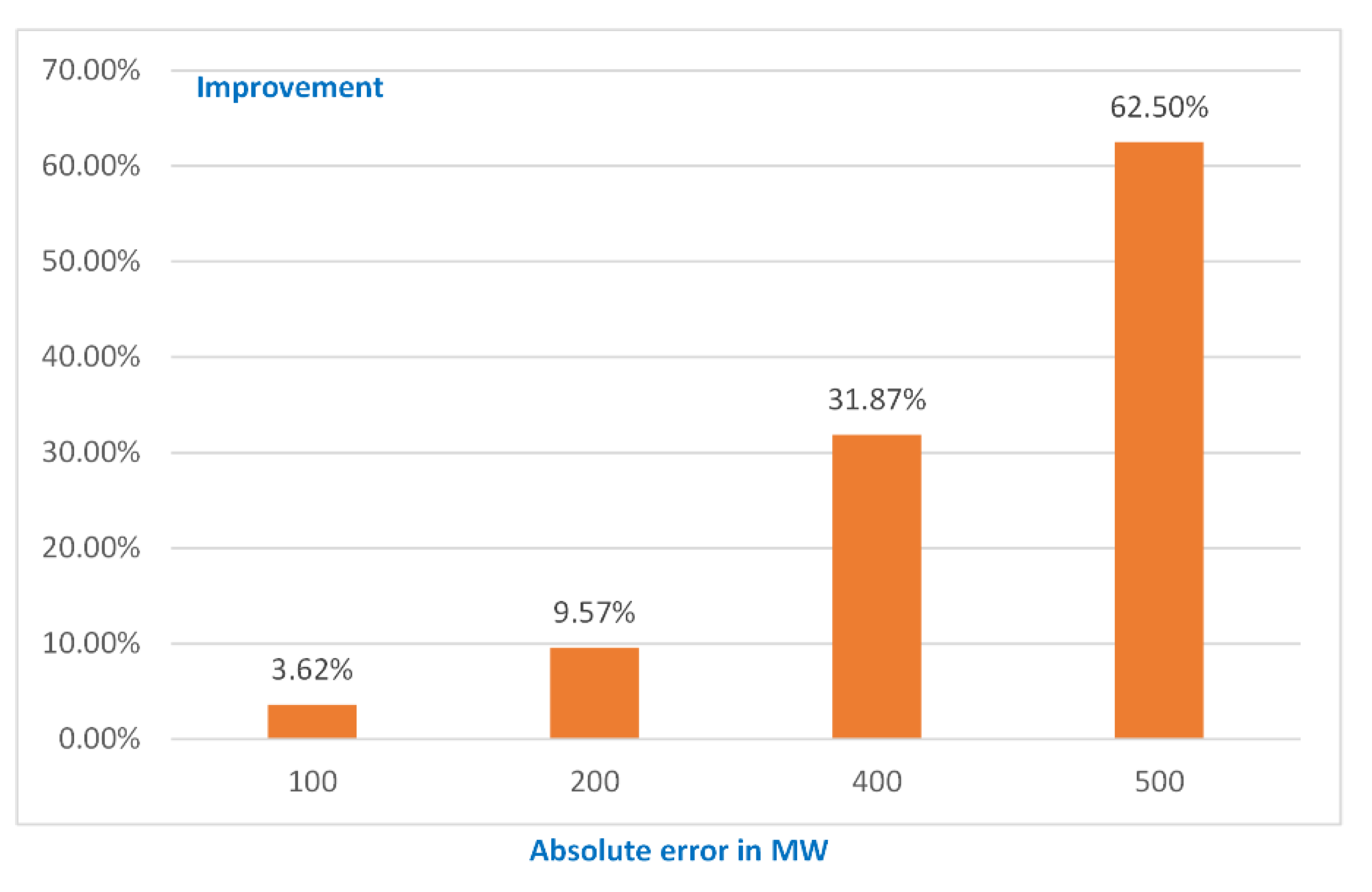
Table 1. Parameters of DBD-FELF.

Parameter	Number
m	r
σ	r
a	r·N
b	r·N
w	r·N
Premise	2·r
Consequent	3·r·N
Total	2·r +3·r·N

Table 2. Learning parameters of RENNCOM.

$n^{+}$	$n^{-}$	$Δ_{\min}$	$Δ_{\max}$	$Δ_{0}$	$a_{s}$	$ξ$	Iterations
1.05	0.5	1E-4	0.5	1E-2	6	0.9	1000

Table 3. Yearly APE and RMSE.

No of blocks	APE Training	RMSE Training	APE Testing	RMSE Testing	No of Param.
1	1.05%	107	1.18%	112	24
2	1.10%	104	1.22%	110	42
3	1.09%	107	1.20%	110	60
4	1.05%	107	1.18%	111	78
5	1.13%	108	1.18%	108	96

Table 4. Seasonal APE and RMSE.

Season	APE Training	RMSE Training	APE Testing	RMSE Testing
Winter	1.03%	125	1.04%	121
Spring	1.36%	118	1.66%	131
Summer	0.81%	90	0.96%	104
Autumn	1.00%	88	1.03%	88

Table 5. Absolute error duration curve.

Electric Load	>100 MW	>200 MW	>400 MW	>500 MW
Hours	2686	718	62	15
Time	30.58%	8.17%	0.70%	0.18%

Table 6. Parameters of the competing forecasters.

DFNN

Structural Parameters

O_{u}

O_{y_{1}}

O_{y_{2}}

O_{y_{3}}

Membership function

Activation function

Gaussian

tanh

Learning parameters

n^{+}

n^{-}

Δ_{\min}

Δ_{0}

ξ

1.05

0.5

0.0001

0.01

0.85

ReNFuzz-LF

Structural Parameters

Membership function

Activationfunction

Gaussian

tanh

Learning parameters

Temp

a_{1}

a_{2}

n^{+}

n^{-}

Δ_{\min}

Δ_{0}

1.2

0.01

0.4

1.05

0.5

0.0001

0.01

ANFIS

Learning parameters

Initial Step size

Step size increase rate

Step size decrease rate

0.01

1.1

0.9

Membership function: Gaussian

GRU

Hyperparameters

Activation
function

Bias

Dropout

Batch size

Optimizer

learning rate

tanh

Yes

0.35

Adam

0.001

LSTM-1

Hyperparameters

Activation
function

Bias

Dropout

Batch size

Optimizer

learning rate

tanh

Yes

0.35

Adam

0.001

LSTM-2,3,4

Hyperparameters

Activation
function

Bias

Dropout

Batch size

Optimizer

learning rate

tanh

Yes

0.2

Adam

0.001

RNN-1

Hyperparameters

Activation
function

Bias

Dropout

Batch size

Optimizer

learning rate

tanh

Yes

0.35

Adam

0.001

RNN-2

Hyperparameters

Activation
function

Bias

Dropout

Batch size

Optimizer

learning rate

tanh

Yes

0.35

Adam

0.001

Table 7. Results of the competing forecasters.

Model	APE (Testing)	No. of Parameters
DBD-FELF	1.18%	24
ReNFuzz-LF	1.35%	33
DFNN	1.36%	48
ANFIS	1.48%	279
LSTM-4 (1 layer, 25 units)	1.73%	2726
RNN-2 (40 neurons)	1.72%	4961
LSTM-3 (1 layer, 50 units)	1.51%	10451
LSTM-2 (2 layers, 50 units)	1.23%	30651
RNN-1 (200 neurons)	1.71%	120801
GRU	1.17%	3006501
LSTM-1 (2 layers, 500 units)	1.18%	3006501

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Short-Term Load Forecasting of the Greek Power System Using a Dynamic Block-Diagonal Fuzzy Neural Network

Abstract

1. Introduction

2. The Architecture of DBD-FELF

3. The Model-Building Process

4. Experimental Results

4.1. Problem Statement—Data Preprocessing Phase

4.2. DBD-FELF’s Features

4.3. Experimental Results

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Nomenclature

References

MDPI Initiatives

Important Links

Subscribe