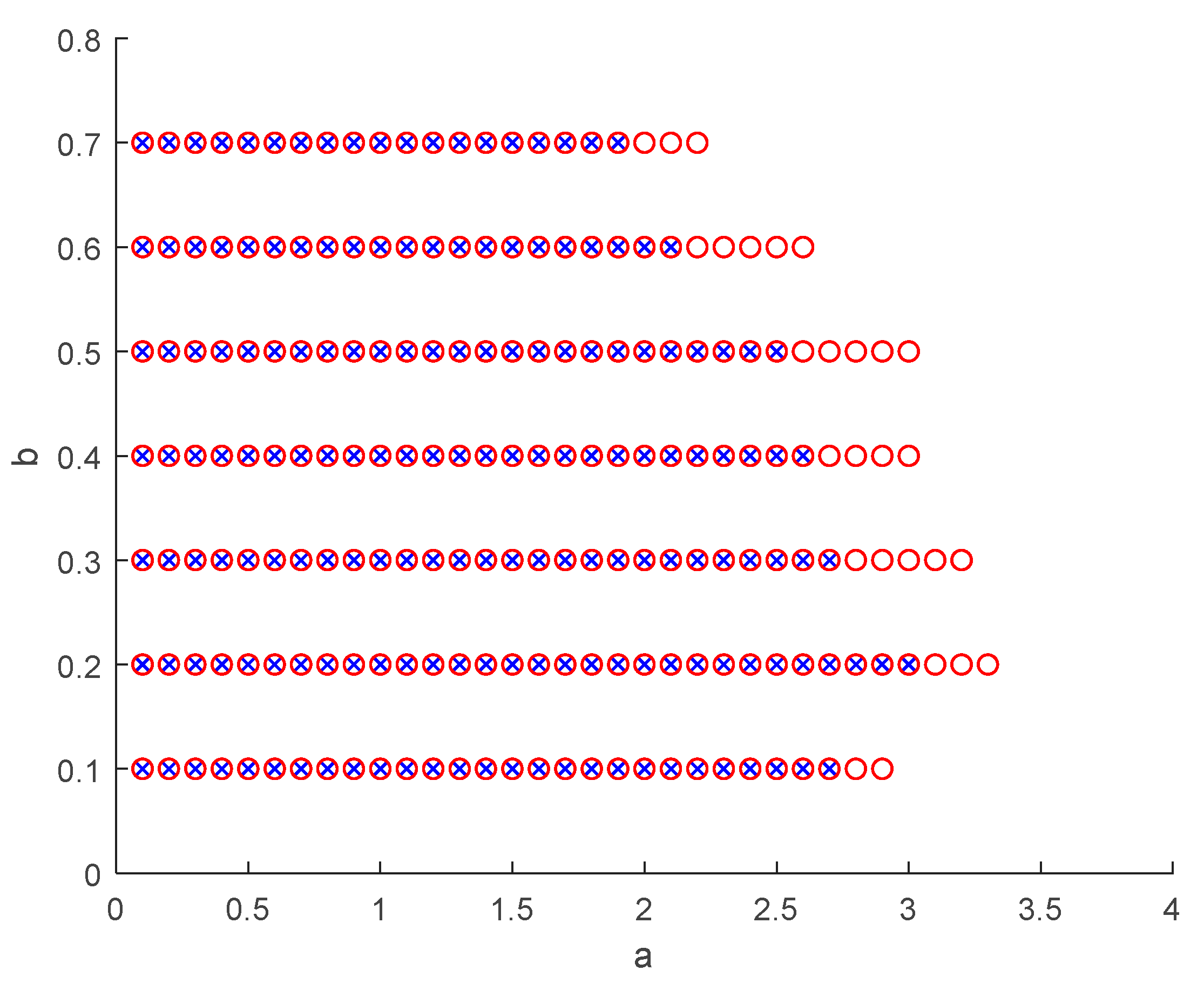Passive Fuzzy Controller Design for Parameter-Dependent Polynomial Fuzzy Model

1. Introduction

Based on convex optimization algorithm [1], many control problems [2-4] have been effectively investigated and solved for guaranteeing stability and control performance. It is well known that those control problems have to be converted into Linear Matrix Inequality (LMI) form for applying the convex optimization algorithm. In general, the control issue formulated as LMI condition is the definite problem to guarantee the stability and performance. To solve the definite problem, some technologies [3] have been proposed such that the semidefinite problem becomes as LMI form. It should be noted that the definite problem possesses conservatism in calculation processes according to the strict inequality. Thus, several relaxed technologies [4-5] have been proposed to reduce the conservatism caused by the LMI-based conditions can be effectively and derived solved. One of technologies is Sum-Of-Square (SOS) technology [5-6] that provides polynomial optimization algorithm. Referring to [6], the polynomial optimization algorithm uses semidefinite programing solver to deal with the control problems. Comparing with standard LMI condition, the polynomial condition solved by SOS is more general and relax for discussing the control problems. Furthermore, polynomial Lyapunov function is usually applied to derive the corresponding sufficient condition depending on states. Therefore, the SOS technology is widely applied to develop several relaxed stability criteria [7-8].

Referring to [8], the SOS technology was first utilized to deal with the stability criterion of nonlinear systems represented by a polynomial Takagi-Sugeno (T-S) fuzzy model. The local behavior of nonlinear systems can be expressed by subsystems whose structure is consisted of a polynomial matrix. Subsequently, the overall polynomial T-S fuzzy model is obtained by blending those subsystems and the membership function to describe the nonlinear dynamics. On the basis of the polynomial description, the reduction of fuzzy rule number [9] is quite significant when the nonlinearity is constructed by monomials in the state. Therefore, the control problem of nonlinear systems is simplified by using the polynomial T-S fuzzy model since the fewer fuzzy rules. For the polynomial T-S fuzzy model, some relaxed stability criteria have been furtherly developed by using the polynomial membership function [10], non-convex condition [11], and improved Lyapunov function [12]. With the development of those relaxed stability criteria, the corresponding fuzzy controllers constructed by polynomial feedback gains were respectively designed via Parallel Distributed Compensation (PDC) [13] and non-PDC [14] schemes. Extending the polynomial fuzzy controller design methods, the issues of sliding mode control [15], even-trigged control [16], static output control [17] and observer-based control [18] have been investigated for the nonlinear systems. Therefore, the SOS technology recently becomes a general and relaxed method for discussing the stability and stabilization problems of polynomial systems.

Besides, Linear Parameter Varying (LPV) model [19] was established to represent linear time-varying systems. Similar to the structure of T-S fuzzy model, the linear time-invarying systems and weighting functions comprise a convex combination [20-26] to build the LPV model and to interpret time-varying behaviors. With the LPV model, linear theories for time-invarying systems can be applied to achieve robust stability [21] of linear time-varying systems. Furthermore, some stability issues of a Nonlinear Time-Varying (NTV) system interpreted by merging the LPV model and T-S fuzzy model were researched by [22]. The above robust results were also formulated in terms of LMI to apply the convex optimization algorithm. It is well known as the number of sufficient conditions influencing the conservatism of stability criterion that is obviously appeared by applying the result [23] for NTV systems. Besides, an LPV model constructed by polynomial linear systems and weighting function was built by [24] to represent the NTV systems. Thus, the relaxed stability criteria for NTV systems were proposed via applying the SOS technology. Although the results in [24] are less conservative than one in [23], a limitation on the applications is indeed produced by that the nonlinearity in NTV systems is only consisted of polynomials term. Besides, a Parameter-Dependent Polynomial Fuzzy (PDPF) model was proposed by [25] to represent the NTV systems. In the T-S fuzzy model in [25], the linear sub-systems are built as parameter-dependent polynomial cases. Compared with [24], the nonlinearity in [22] is not restricted to polynomials since the structure of T-S fuzzy model. Furthermore, a relaxed stability criterion for the PDPF model was developed by [25] through considering the information on system parameters. However, a requirement that the limit values of the time-varying parameters are not the opposite sign exists to guarantee the positive of the Lyapunov function and the feasibility of the criterion. It is thus an interesting issue for providing a stability criterion for the NTV systems.

According to the above motivation, the T-S fuzzy model and LPV model are respectively applied to describe the nonlinearity and time-varying parameters of NTV systems. Based on the T-S fuzzy model, the nonlinearity can be expressed as several polynomial sub-systems and membership functions. Moreover, the polynomial description is used to reduce the number of fuzzy rules for increasing the relaxation of the proposed stability criterion. Besides, the LPV model is used to represent the time-varying parameters. Due to the convex combination of LPV model [26], the opposite sign of the time-varying function can be avoided to hold the positive definition of Lyapunov function. Thus, the limitation as the values of time-varying parameters is not required by the proposed criterion. Besides, the passivity in [27] is considered in this paper to constrain the effect of external disturbance on the NTV systems. Referring to [27], the passivity theory is usually employed to constrain the external disturbance effect on systems. To guarantee the stability and passivity of systems, some sufficient conditions are derived by choosing a parameter-dependent polynomial Lyapunov function. On the other hand, the relaxed technique in [25] is also applied to develop another PDPF controller design method for PDPF system. Although the limitation on the opposite sign influences the description of time-varying parameters, the conservatism of the proposed design method can be furtherly reduced. Thus, two methods are proposed for the general control issues of NTV systems. And, those conditions are also transformed into SOS decompositions which can be solved by SOSTOOLS [28]. Based on the proposed stability criteria, the PDPF controller can be designed to guarantee the stability and passivity of the NTV systems.

The structure of the paper is shown as follows: Section Ⅱ provides the system description and problem statement of the PDPF model. Section Ⅲ introduces the PDPF controller design method. The simulation results are presented in Section Ⅳ and the conclusions are stated in Section Ⅴ.

Notations: $\mathbf{I}$ denotes the identity matrix with appropriate dimension. $\ast$ denotes the transposed elements of matrices for the symmetric position. $sym\left\{\eta \right\}$ denotes the shorthand notation for $\eta +{\eta }^{\mathrm{T}}$. $diag\left[\begin{array}{cc}\eta {}_1& {\eta }_2\end{array}\right]$ denotes the two blocks in a diagonal matrix with the elements $\eta {}_1$ and $\eta {}_2$, such as $diag\left[\begin{array}{cc}\eta {}_1& {\eta }_2\end{array}\right]=\left[\begin{array}{cc}\eta {}_1& 0\\ 0& {\eta }_2\end{array}\right]$. ${\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$ denotes a set of SOS polynomials.

2. System Descriptions and Problem Statements

In this section, the following disturbed PDPF model is introduced for representing the NTV systems.

Plant Rule i :

IF $z_1\left(t\right)$ is $M_{i1}$ and … and $z_w\left(t\right)$ is $M_{iw}$ THEN

$$\dot{x}\left(t\right)=A_i\left(x\left(t\right),\theta \left(t\right)\right)\widehat{x}\left(x\left(t\right)\right)+B_i\left(x\left(t\right),\theta \left(t\right)\right)u\left(t\right)+{\mathbf{G}}_i\left(x\left(t\right),\theta \left(t\right)\right)\omega \left(t\right)$$

(1a)

$$y\left(t\right)={\mathbf{C}}_i\left(x\left(t\right),\theta \left(t\right)\right)\widehat{x}\left(x\left(t\right)\right)+{\mathbf{H}}_i\left(x\left(t\right),\theta \left(t\right)\right)\omega \left(t\right)$$

(1b)

where $i=1,2,\dots ,r$ and r denotes the number of fuzzy rules, the fuzzy set is denoted by $M_{i\mu }$, $z_{\mu }\left(t\right)$ is the premise variable, $\mu =1,2,\dots ,w$ is the number of premise variables. $x\left(t\right)\in {\Re }^n$ is the state vector, $\omega \left(t\right)\in {\Re }^v$ is the external disturbance, $y\left(t\right)\in {\Re }^l$ is the system output, system matrices are represented as$A_i\left(x\left(t\right),\theta \left(t\right)\right)\in {\Re }^{n\times N}$, input matrices are represented as $B_i\left(x\left(t\right),\theta \left(t\right)\right)\in {\Re }^{n\times m}$, ${\mathbf{G}}_i\left(x\left(t\right),\theta \left(t\right)\right)\in {\Re }^{n\times v}$ are disturbance matrices, ${\mathbf{C}}_i\left(x\left(t\right),\theta \left(t\right)\right)\in {\Re }^{l\times N}$ are output matrices, ${\mathbf{H}}_i\left(x\left(t\right),\theta \left(t\right)\right)\in {\Re }^{1\times v}$ are disturbance matrices, $\mathit{\theta }\left(t\right)\in {\Re }^e$ is the time-varying parameter, $u\left(t\right)\in {\Re }^m$ is the control input vector, the term $\widehat{x}\left(x\left(t\right)\right)$ is composed of all monomials in $x\left(t\right)$ which can be represented as $\widehat{x}\left(x\left(t\right)\right)={\left[\begin{array}{cccc}{\widehat{x}}_1\left(x\left(t\right)\right)& {\widehat{x}}_2\left(x\left(t\right)\right)& \cdots & {\widehat{x}}_N\left(x\left(t\right)\right)\end{array}\right]}^{\mathrm{T}}\in {\Re }^N$, N is the number of monomial terms in degree $\varpi$ which is a nonnegative integer, $N=n$ when $\varpi =1$ and $\widehat{x}\left(x\right)=0$ if and only if $x=0$ is assumed.

Based on the above expression, the PDPF model (1) is furtherly described as follows.

$$\dot{x}\left(t\right)={\displaystyle \sum }_{i=1}^r{h}_i\left(z\left(t\right)\right)\left(A_i\left(x\left(t\right),\theta \left(t\right)\right)\widehat{x}\left(x\left(t\right)\right)+B_i\left(x\left(t\right),\theta \left(t\right)\right)u\left(t\right)+{\mathbf{G}}_i\left(x\left(t\right),\theta \left(t\right)\right)\omega \left(t\right)\right)$$

(2a)

$$y\left(t\right)={\displaystyle \sum }_{i=1}^r{h}_i\left(z\left(t\right)\right)\left({\mathbf{C}}_i\left(x\left(t\right),\theta \left(t\right)\right)\widehat{x}\left(x\right)+{\mathbf{H}}_i\left(x\left(t\right),\theta \left(t\right)\right)\omega \left(t\right)\right)$$

(2b)

where $z\left(t\right)={\left[z_1\left(t\right)z_2\left(t\right)\cdots z_w\left(t\right)\right]}^{\mathrm{T}}$, $h_i\left(z\left(t\right)\right)={\displaystyle \prod _{\mu =1}^w{\mathrm{M}}_{i\mu }\left(z_{\mu }\left(t\right)\right)}/\left({\displaystyle \sum _{i=1}^r{\displaystyle \prod _{\mu =1}^w{\mathrm{M}}_{i\mu }\left(z_{\mu }\left(t\right)\right)}}\right)$, $h_i\left(z\left(t\right)\right)\ge 0$, ${\displaystyle \sum _{i=1}^r{h}_i\left(z\left(t\right)\right)=1}$ and ${\mathrm{M}}_{i\mu }\left(z_{\mu }\left(t\right)\right)$ is the grade of the membership of $z_{\mu }\left(t\right)$.

Generally, the parameter-dependent polynomial matrices in the PDPF model (2) can be expressed as follows by the convex combination [20].

$$A_i\left(x\left(t\right),\theta \left(t\right)\right)={\displaystyle \sum _{p=1}^s{\alpha }_p\left(t\right)A_{ip}\left(x\left(t\right)\right)}$$

(3a)

$$B_i\left(x\left(t\right),\theta \left(t\right)\right)={\displaystyle \sum _{p=1}^s{\alpha }_p\left(t\right)B_{ip}\left(x\left(t\right)\right)}$$

(3b)

$${\mathbf{G}}_i\left(x\left(t\right),\theta \left(t\right)\right)={\displaystyle \sum _{p=1}^s{\alpha }_p\left(t\right){\mathbf{G}}_{ip}\left(x\left(t\right)\right)}$$

(3c)

$${\mathbf{C}}_i\left(x\left(t\right),\theta \left(t\right)\right)={\displaystyle \sum _{p=1}^s{\alpha }_p\left(t\right){\mathbf{C}}_{ip}\left(x\left(t\right)\right)}$$

(3d)

$${\mathbf{H}}_i\left(x\left(t\right),\theta \left(t\right)\right)={\displaystyle \sum _{p=1}^s{\alpha }_p\left(t\right){\mathbf{H}}_{ip}\left(x\left(t\right)\right)}$$

(3e)

where ${\alpha }_p\left(t\right)\ge 0$, ${\displaystyle \sum _{p=1}^s{\alpha }_p\left(t\right)}=1$, $s=2^e$ and $e$ is the number of time-varying parameters.

For the stabilization problem of (2), the following PDPF controller can be designed by the PDC method [13].

Controller Rule i:

IF $z_1\left(t\right)$ is $M_{i1}$ and … and $z_w\left(t\right)$ is $M_{iw}$ THEN

$$u\left(t\right)={\mathbf{F}}_i\left(x\left(t\right),\theta \left(t\right)\right)\widehat{x}\left(x\left(t\right)\right)$$

(4)

Moreover, the controller (4) can be also expressed into the following form.

$$u\left(t\right)={\displaystyle \sum }_{i=1}^r{h}_i\left(z\left(t\right)\right){\mathbf{F}}_i\left(x\left(t\right),\theta \left(t\right)\right)\widehat{x}\left(x\left(t\right)\right)$$

(5)

Substituting (5) into (2), the following closed-loop system is inferred by using description (3).

$$\dot{x}\left(t\right)={\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{j=1}^r{\displaystyle \sum }_{p=1}^s{h}_i\left(z\left(t\right)\right)h_j\left(z\left(t\right)\right){\alpha }_p\left(t\right)\left(\left(A_{ip}\left(x\left(t\right)\right)+B_{ip}\left(x\left(t\right)\right){\mathbf{F}}_j\left(x\left(t\right),\theta \left(t\right)\right)\right)\widehat{x}\left(x\right)\right.$$

$$\left.+{\mathbf{G}}_{ip}\left(x\left(t\right)\right)\omega \left(t\right)\right)$$

(6a)

$$y\left(t\right)={\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{p=1}^s{h}_i\left(z\left(t\right)\right){\alpha }_p\left(t\right)\left({\mathbf{C}}_{ip}\left(x\left(t\right)\right)\widehat{x}\left(x\right)+{\mathbf{H}}_{ip}\left(x\left(t\right)\right)\omega \left(t\right)\right)$$

(6b)

Some notation respecting to time $t$ are used for brevity such as $x\triangleq x\left(t\right)$, $u\triangleq u\left(t\right)$, $\theta \triangleq \theta \left(t\right)$, ${\alpha }_p\triangleq {\alpha }_p\left(t\right)$ and $z_j\triangleq z_j\left(t\right)$. Next, the following definitions and lemma are introduced to be benefit for stability analysis. Firstly, due to the proposed method is based on SOS, the stability conditions should be transformed into the SOS form so that the semidefinite programming algorithm can be applied. Therefore, the SOS-related definition is introduced below.

Definition 1: [29].$f^{2\mathit{\kappa }}\left(x\right)$  is called SOS if and only if there exists a positive semidefinite matrix$\mathit{Q}\in {\Re }^{\xi \times \xi }$  such that the following equation holds.

$$f^{2\kappa }\left(x\right)={\mathit{Z}}^{\mathrm{T}}\left(x\right)\mathit{Q}\mathit{Z}\left(x\right)$$

(7)

where $f^{2\kappa }\left(x\right)$ is polynomial which is the even number degree and $\mathit{\kappa }$ is the positive integer number. The vector $\mathit{Z}\left(x\right)\in {\Re }^{\xi }$ is comprised of monomial in $x$ with degree $\lambda$ where $0<\lambda \le \mathit{\kappa }$.

According to [5], the result $f\left(x\right)\ge 0\forall x\in {\Re }^n$ can be inferred if $f\left(x\right)\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$ but the converse may not always be true. Furthermore, the state vector in (6) comprises the vector $\widehat{x}\left(x\right)$ instead of $x$ to be suitable to the definition of SOS. Based on [27], the following passivity performance for constraining external disturbance theory is exhibited.

Definition 2: [27]. If there exists the known real constant matrices ${\mathbf{S}}_1$, ${\mathbf{S}}_2\ge 0$ and ${\mathbf{S}}_3$ for satisfying the following inequality, the closed-loop system (6) is called passive with the external disturbance $\omega \left(t\right)$ and output $y\left(t\right)$ for all terminal time $t_p>0$.

$$2{\displaystyle {\int }_0^{t_p}{y}^{\mathrm{T}}\left(t\right){\mathbf{S}}_1\omega \left(t\right)dt}>{\displaystyle {\int }_0^{t_p}{y}^{\mathrm{T}}\left(t\right){\mathbf{S}}_{2}y\left(t\right)dt}+{\displaystyle {\int }_0^{t_p}{\omega }^{\mathrm{T}}\left(t\right){\mathbf{S}}_3\omega \left(t\right)dt}$$

(8)

Referring to [27], several performance constraints are reduced by setting ${\mathbf{S}}_1$, ${\mathbf{S}}_2$ and ${\mathbf{S}}_3$. Next, the following lemma is utilized to facilitate the procedure of deriving the stability conditions.

Lemma 1: [1]. For the arbitrary polynomial matrix $\mathbf{X}\left(x\right)$ which is invertible, the following equality holds.

$$\frac{\partial \mathbf{X}\left(x\right)}{\partial x_i}=-\mathbf{X}\left(x\right)\frac{\partial {\mathbf{X}}^{-1}\left(x\right)}{\partial x_i}\mathbf{X}\left(x\right)\forall i=1,2,\cdots ,n$$

(9)

Based on the above definitions and lemma, the stability criteria in the next section are proposed to guarantee stability of closed-loop system (6). Otherwise, the proposed stability conditions are derived as the SOS form for applying semidefinite programming.

3. PDPF-based Stability Analysis and Controller Design

In this section, the Lyapunov function, aforementioned definitions and lemma are utilized in deriving the stability conditions such that the closed-loop system (6) achieves robustly stable and passive.

Theorem 1. Given the matrices $\mathbf{\Omega }\left(x\right)$, ${\mathbf{S}}_1$, ${\mathbf{S}}_2\ge 0$ and ${\mathbf{S}}_3$, polynomials ${\epsilon }_1\left(\tilde{x}\right)>0$ and ${\epsilon }_2\left(x\right)>0$ and scalar $\varphi$, the closed-loop system (6) is robustly stable and passive if there exists polynomial matrices ${\mathbf{K}}_{jq}\left(x\right)$ and symmetric polynomial matrices ${\mathbf{P}}_q\left(\tilde{x}\right)$ and ${\mathbf{U}}_q\left(\tilde{x}\right)$ such that

$${\mathit{\nu }}^{\mathrm{T}}\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\epsilon }_1\left(\tilde{x}\right)\mathbf{I}\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(10)

$${\mathit{\nu }}^{\mathrm{T}}\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{U}}_q\left(\tilde{x}\right)\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(11)

$$-{\mathit{\nu }}^{\mathrm{T}}\left(\left[\begin{array}{ccc}{\mathbf{\Omega }}_{ijpq}^{11}-{\displaystyle \sum }_{q=1}^s\varphi \left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{U}}_q\left(\tilde{x}\right)\right)+{\epsilon }_2\left(x\right)\mathbf{I}& {\mathbf{\Omega }}_{ipq}^{12}& {\mathbf{P}}_q\left(\tilde{x}\right)C_{ip}^{\mathrm{T}}\left(x\right)\sqrt{{\mathbf{S}}_2}\\ \ast & {\mathbf{\Omega }}_{ip}^{22}& {\mathbf{H}}_{ip}^{\mathrm{T}}\left(x\right)\sqrt{{\mathbf{S}}_2}\\ \ast & \ast & -\mathbf{I}\end{array}\right]\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(12)

$\forall p,q=1,2,\dots ,s$ and $i,j=1,2,\dots ,r$

where $\mathit{\nu }$ is a vector independent of $x$ with the appropriate dimension, $D=\left\{d_1,d_2,\cdots ,d_k\right\}$ denotes the row indices of $B_{ip}\left(x\right)$ whose corresponding row is equal to zero, $A_{ip}^d\left(x\right)$and $B_{ip}^d\left(x\right)$ respectively denotes the d-th row of $A_{ip}\left(x\right)$and $B_{ip}\left(x\right)$, $\tilde{x}=\left(x_{d_1},x_{d_2},\cdots ,x_{d_k}\right)$ denotes the state $x_{d_k}$ corresponding to $B_{ip}^{d_k}\left(x\right)=0$, ${\mathbf{\Omega }}_{ijpq}^{11}=sym\left\{\mathbf{\Omega }\left(x\right)\left(A_{ip}\left(x\right){\mathbf{P}}_q\left(\tilde{x}\right)+B_{ip}\left(x\right){\mathbf{K}}_{jq}\left(x\right)\right)\right\}-{\displaystyle \sum _{d\in D}\frac{\partial {\mathbf{P}}_q\left(\tilde{x}\right)}{\partial x_d}{A}_{ip}^d\left(x\right)\widehat{x}\left(x\right)}$, ${\mathbf{\Omega }}_{ipq}^{12}=-{\mathbf{P}}_q\left(\tilde{x}\right)C_{ip}^{\mathrm{T}}\left(x\right){\mathbf{S}}_1+\mathbf{\Omega }\left(x\right){\mathbf{G}}_{ip}\left(x\right)$ and ${\mathbf{\Omega }}_{ip}^{22}={\mathbf{S}}_3-sym\left\{{\mathbf{H}}_{ip}^{\mathrm{T}}\left(x\right){\mathbf{S}}_1\right\}$.

Proof of Theorem 1.

Choosing the following parameter-dependent polynomial Lyapunov function.

$$V\left(x,\theta \right)={\widehat{x}}^{\mathrm{T}}\left(x\right){\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\widehat{x}\left(x\right)$$

(13)

The following time derivative of $V\left(x,\theta \right)$ is inferred by using $\dot{\widehat{x}}\left(x\right)=\mathbf{\Omega }\left(x\right)\dot{x}$. The elements of polynomial matrix $\mathbf{\Omega }\left(x\right)$ are obtained by ${\mathbf{\Omega }}_{\sigma \delta }\left(x\right)=\frac{\partial {\widehat{x}}_{\sigma }\left(x\right)}{\partial x_{\delta }}$.

$$\dot{V}\left(x,\theta \right)={\widehat{x}}^{\mathrm{T}}\left(x\right){\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\dot{\widehat{x}}\left(x\right)+{\dot{\widehat{x}}}^{\mathrm{T}}\left(x\right){\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\widehat{x}\left(x\right)+{\widehat{x}}^{\mathrm{T}}\left(x\right){\dot{\mathbf{P}}}^{-1}\left(\tilde{x},\theta \right)\widehat{x}\left(x\right)$$

$$={\widehat{x}}^{\mathrm{T}}\left(x\right){\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\mathbf{\Omega }\left(x\right)\dot{x}+{\mathbf{\Omega }}^{\mathrm{T}}\left(x\right){\dot{x}}^{\mathrm{T}}\left(x\right){\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\widehat{x}\left(x\right)+{\widehat{x}}^{\mathrm{T}}\left(x\right){\dot{\mathbf{P}}}^{-1}\left(\tilde{x},\theta \right)\widehat{x}\left(x\right)$$

$$={\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{j=1}^r{h}_i\left(z\right)h_j\left(z\right)\left({\widehat{x}}^{\mathrm{T}}\left(x\right)\left(sym\left\{{\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\mathbf{\Omega }\left(x\right)\left(A_i\left(x,\theta \right)+B_i\left(x,\theta \right){\mathbf{F}}_j\left(x,\theta \right)\right)\right\}\right.\right.$$

$$\left.\left.+{\dot{\mathbf{P}}}^{-1}\left(\tilde{x},\theta \right)\right)\widehat{x}\left(x\right)+sym\left\{{\widehat{x}}^{\mathrm{T}}\left(x\right)\left({\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\mathbf{\Omega }\left(x\right){\mathbf{G}}_i\left(x,\theta \right)\right)\omega \left(t\right)\right\}\right)$$

(14)

The cost function is defined with zero initial condition as follows.

$$\mathbf{\Xi }\left(x,\omega ,t\right)={\displaystyle {\int }_0^{t_p}\left(y^{\mathrm{T}}\left(t\right){\mathbf{S}}_{2}y\left(t\right)+{\omega }^{\mathrm{T}}\left(t\right){\mathbf{S}}_3\omega \left(t\right)-2y^{\mathrm{T}}\left(t\right){\mathbf{S}}_1\omega \left(t\right)\right)dt}$$

$$={\displaystyle {\int }_0^{t_p}\left(y^{\mathrm{T}}\left(t\right){\mathbf{S}}_{2}y\left(t\right)+{\omega }^{\mathrm{T}}\left(t\right){\mathbf{S}}_3\omega \left(t\right)-2y^{\mathrm{T}}\left(t\right){\mathbf{S}}_1\omega \left(t\right)+\dot{V}\left(x,\theta \right)\right)dt}-V\left(x\left(t_p\right),\theta \left(t_p\right)\right)$$

$$\le {\displaystyle {\int }_0^J\mathbf{\Phi }\left(x,\omega ,t\right)}dt$$

(15)

where $\mathbf{\Phi }\left(x,\omega ,t\right)=y^{\mathrm{T}}\left(t\right){\mathbf{S}}_{2}y\left(t\right)+{\omega }^{\mathrm{T}}\left(t\right){\mathbf{S}}_3\omega \left(t\right)-2y^{\mathrm{T}}\left(t\right){\mathbf{S}}_1\omega \left(t\right)+\dot{V}\left(x,\theta \right)$Substituting (6b) and (14) into (15), one has

$$\mathbf{\Phi }\left(x,\omega ,t\right)={\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{j=1}^r{h}_i\left(z\right)h_j\left(z\right){\left[\begin{array}{c}\widehat{x}\left(x\right)\\ \omega \left(t\right)\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{cc}{\mathbf{\Phi }}_{ij}^{11}& {\mathbf{\Phi }}_i^{12}\\ \ast & {\mathbf{\Phi }}_i^{22}\end{array}\right]\left[\begin{array}{c}\widehat{x}\left(x\right)\\ \omega \left(t\right)\end{array}\right]$$

(16)

where ${\mathbf{\Phi }}_{ij}^{11}=sym\left\{{\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\mathbf{\Omega }\left(x\right)\left(A_i\left(x,\theta \right)+B_i\left(x,\theta \right){\mathbf{F}}_j\left(x,\theta \right)\right)\right\}+{\dot{\mathbf{P}}}^{-1}\left(\tilde{x},\theta \right)+C_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_2{C}_i\left(x,\theta \right)$, ${\mathbf{\Phi }}_i^{12}=-C_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_1-C_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_2{\mathbf{H}}_i\left(x,\theta \right)+{\mathbf{P}}^{-1}\left(\tilde{x},\theta \right)\mathbf{\Omega }\left(x\right){\mathbf{G}}_i\left(x,\theta \right)$ and ${\mathbf{\Phi }}_i^{22}={\mathbf{S}}_3-{\mathbf{H}}_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_2{\mathbf{H}}_i\left(x,\theta \right)-sym\left\{{\mathbf{H}}_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_1\right\}$.

After multiplying $diag\left[\begin{array}{cc}\mathbf{P}\left(\tilde{x},\theta \right)& \mathbf{I}\end{array}\right]$ on both sides of $\left[\begin{array}{cc}{\mathbf{\Phi }}_{ij}^{11}& {\mathbf{\Phi }}_i^{12}\\ \ast & {\mathbf{\Phi }}_i^{22}\end{array}\right]$ and applying Lemma 1, the following equality can be easily obtained.

$${\Delta }_{ij}={\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{j=1}^r{h}_i\left(z\right)h_j\left(z\right)\left[\begin{array}{cc}{\Delta }_{ij}^{11}-\dot{\mathbf{P}}\left(\tilde{x},\theta \right)& {\Delta }_i^{12}\\ \ast & {\Delta }_i^{22}\end{array}\right]$$

where ${\mathbf{K}}_j\left(x,\theta \right)={\mathbf{F}}_j\left(x,\theta \right)\mathbf{P}\left(\tilde{x},\theta \right)$, ${\Delta }_i^{22}={\mathbf{S}}_3-{\mathbf{H}}_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_2{\mathbf{H}}_i\left(x,\theta \right)-sym\left\{{\mathbf{H}}_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_1\right\}$, ${\Delta }_{ij}^{11}=sym\left\{\mathbf{\Omega }\left(x\right)\left(A_i\left(x,\theta \right)\mathbf{P}\left(\tilde{x},\theta \right)+B_i\left(x,\theta \right){\mathbf{K}}_j\left(x,\theta \right)\right)\right\}+{\mathbf{P}}^{\mathrm{T}}\left(\tilde{x},\theta \right)C_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_2{C}_i\left(x,\theta \right)\mathbf{P}\left(\tilde{x},\theta \right)$ and ${\Delta }_i^{12}=-\mathbf{P}\left(\tilde{x},\theta \right)C_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_1+\mathbf{P}\left(\tilde{x},\theta \right)C_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_2{\mathbf{H}}_i\left(x,\theta \right)+\mathbf{\Omega }\left(x\right){\mathbf{G}}_i\left(x,\theta \right)$.

One can obtain the following result by the concept of the convex combination.

$${\Delta }_{ij}={\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{j=1}^r{\displaystyle \sum }_{p=1}^s{\displaystyle \sum }_{q=1}^s{h}_i\left(z\right)h_j\left(z\right){\alpha }_p{\alpha }_q{\mathbf{\Lambda }}_{ijpq}$$

(17)

where ${\mathbf{\Lambda }}_{ijpq}=\left[\begin{array}{cc}{\mathbf{\Lambda }}_{ijpq}^{11}-{\displaystyle \sum }_{q=1}^s{\dot{\alpha }}_q{\mathbf{P}}_q\left(\tilde{x}\right)& {\mathbf{\Lambda }}_{ipq}^{12}\\ \ast & {\mathbf{\Lambda }}_{ip}^{22}\end{array}\right]$, ${\mathbf{\Lambda }}_{ip}^{22}={\mathbf{S}}_3-{\mathbf{H}}_{ip}^{\mathrm{T}}\left(x\right){\mathbf{S}}_2{\mathbf{H}}_{ip}\left(x\right)-sym\left\{{\mathbf{H}}_{ip}^{\mathrm{T}}\left(x\right){\mathbf{S}}_1\right\}$, ${\mathbf{\Lambda }}_{ipq}^{12}=-{\mathbf{P}}_q\left(\tilde{x}\right)C_{ip}^{\mathrm{T}}\left(x\right){\mathbf{S}}_1+{\mathbf{P}}_q\left(\tilde{x}\right)C_{ip}^{\mathrm{T}}\left(x\right){\mathbf{S}}_2{\mathbf{H}}_{ip}\left(x\right)+\mathbf{\Omega }\left(x\right){\mathbf{G}}_{ip}\left(x\right)$ and ${\mathbf{\Lambda }}_{ijpq}^{11}=sym\left\{\mathbf{\Omega }\left(x\right)\left(A_{ip}\left(x\right){\mathbf{P}}_q\left(\tilde{x}\right)+B_{ip}\left(x\right){\mathbf{K}}_q\left(x\right)\right)\right\}+{\mathbf{P}}_q^{\mathrm{T}}\left(\tilde{x}\right)C_{ip}^{\mathrm{T}}\left(x\right){\mathbf{S}}_2{C}_{ip}\left(x\right){\mathbf{P}}_q\left(\tilde{x}\right)-{\displaystyle \sum _{d\in D}\frac{\partial {\mathbf{P}}_q\left(\tilde{x}\right)}{\partial x_d}}$$\times A_{ip}^d\left(x\right)\widehat{x}\left(x\right)$Since ${\displaystyle \sum }_{q=1}^s{\dot{\alpha }}_q=0$, ${\displaystyle \sum }_{q=1}^s{\dot{\alpha }}_q{\mathbf{U}}_q\left(\tilde{x}\right)=0$ can be obtained with any symmetric matrices ${\mathbf{U}}_q\left(\tilde{x}\right)$ that brings the following relation.

$${\displaystyle \sum }_{q=1}^s{\dot{\alpha }}_q{\mathbf{P}}_q\left(\tilde{x}\right)={\displaystyle \sum }_{q=1}^s{\dot{\alpha }}_q\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{U}}_q\left(\tilde{x}\right)\right)$$

(18)

By setting $\min \left\{{\dot{\alpha }}_q\right\}\ge \varphi$, one can obtain the following inequality via holding (11).

$$-\left({\displaystyle \sum }_{q=1}^s{\dot{\alpha }}_q\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{U}}_q\left(\tilde{x}\right)\right)\right)\le -\left({\displaystyle \sum }_{q=1}^s\varphi \left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{U}}_q\left(\tilde{x}\right)\right)\right)$$

(19)

Since (19), the following inequality can be obtained from (17).

$${\mathbf{\Lambda }}_{ijpq}\le \left[\begin{array}{cc}{\mathbf{\Lambda }}_{ijpq}^{11}-{\displaystyle \sum }_{q=1}^s\varphi \left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{U}}_q\left(\tilde{x}\right)\right)& {\mathbf{\Lambda }}_{ipq}^{12}\\ \ast & {\mathbf{\Lambda }}_{ip}^{22}\end{array}\right]$$

Based on Schur complement, the following inequality can be obtained from (12).

$$\left[\begin{array}{ccc}{\mathbf{\Omega }}_{ijpq}^{11}-{\displaystyle \sum }_{q=1}^s\varphi \left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{U}}_q\left(\tilde{x}\right)\right)+{\epsilon }_2\left(x\right)\mathbf{I}& {\mathbf{\Omega }}_{ipq}^{12}& {\mathbf{P}}_q\left(\tilde{x}\right)C_{ip}^{\mathrm{T}}\left(x\right)\sqrt{{\mathbf{S}}_2}\\ \ast & {\mathbf{\Omega }}_{ip}^{22}& {\mathbf{H}}_{ip}^{\mathrm{T}}\left(x\right)\sqrt{{\mathbf{S}}_2}\\ \ast & \ast & -\mathbf{I}\end{array}\right]<0$$

(20)

It can be seen that if (12) holds, $\mathbf{\Phi }\left(x,\omega ,t\right)<0$ can be inferred from (20). Furthermore, $\Xi \left(x,\omega ,t\right)<0$ is implied by $\mathbf{\Phi }\left(x,\omega ,t\right)<0$ from (15) and (20). According to $\Xi \left(x,\omega ,t\right)<0$, the passivity of the closed-loop system (6) is achieved via Definition 2 because of $\mathbf{\Phi }\left(x,\omega ,t\right)<0$. Afterward, it is necessary to check that the system is robustly stable. By holding the conditions in Theorem 1 and assuming the $\omega \left(t\right)=0$, one can obtain the following inequality because of $\mathbf{\Phi }\left(x,\omega ,t\right)<0$.

$$\dot{V}\left(x,\theta \right)+{\widehat{x}}^{\mathrm{T}}\left(x\right)C_i^{\mathrm{T}}\left(x,\theta \right){\mathbf{S}}_2{C}_i\left(x,\theta \right)\widehat{x}\left(x\right)<0$$

(21)

Since ${\mathbf{S}}_2={\mathbf{S}}_2^{\mathrm{T}}\ge 0$, $\dot{V}\left(x,\theta \right)<0$ can be found from (21). Referring to the Lyapunov stability, the closed-loop system (6) is robustly stable according to $\dot{V}\left(x,\theta \right)<0$ with time-varying parameters. The proof is complete.

By convex combination, the positive definition of Lyapunov function can be achieved even if the weighting functions are opposite sign. Therefore, the constraint on the time-varying parameters is not required in Theorem 1. However, the conservatism reduces the application of Theorem 1. Thus, the relaxed technology in [25] is applied to introduce the slack matrices. Although the constraint on opposite sign influences the description of time-varying parameter, the application of Theorem 1 can be extended for design PDPF controller. Thus, the relaxed stability criterion for closed-loop system (6) is proposed in the following theorem.

Theorem 2. Given the matrices $\mathbf{\Omega }\left(x\right)$, ${\mathbf{S}}_1$, ${\mathbf{S}}_2\ge 0$ and ${\mathbf{S}}_3$, scalars $h_i\left(z\right)$, ${\overline{h}}_i$, ${\underset{\_}{h}}_i$, ${\alpha }_p$, ${\overline{\gamma }}_q$, ${\underset{\_}{\gamma }}_q$, ${\overline{\phi }}_q$ and ${\underset{\_}{\phi }}_q$ and polynomials ${\epsilon }_i\left(\tilde{x}\right)>0$ $\left(i=1,2,\dots ,5\right)$ and ${\epsilon }_6\left(x\right)>0$, the closed-loop system (6) is robustly stable and passive if there exists polynomial matrices ${\mathbf{K}}_{jq}\left(x\right)$ and symmetric polynomial matrices ${\mathbf{R}}_q\left(\tilde{x}\right)$, ${\mathit{Q}}_q\left(\tilde{x}\right)$, ${\mathbf{P}}_q\left(\tilde{x}\right)$, ${\mathbf{W}}_{ij}\left(x\right)$, ${\mathbf{L}}_{pq}\left(x\right)$ and ${\mathbf{M}}_{ij}\left(x\right)$ such that

$$-{\mathit{\nu }}^{\mathrm{T}}\left({\mathbf{R}}_q\left(\tilde{x}\right)+{\epsilon }_1\left(\tilde{x}\right)\mathbf{I}\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(22)

$$-{\mathit{\nu }}^{\mathrm{T}}\left({\mathit{Q}}_q\left(\tilde{x}\right)+{\epsilon }_2\left(\tilde{x}\right)\mathbf{I}\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(23)

$${\mathit{\nu }}^{\mathrm{T}}\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{R}}_q\left(\tilde{x}\right)-{\epsilon }_3\left(\tilde{x}\right)\mathbf{I}\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(24)

$${\mathit{\nu }}^{\mathrm{T}}\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathit{Q}}_q\left(\tilde{x}\right)-{\epsilon }_4\left(\tilde{x}\right)\mathbf{I}\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(25)

$${\mathit{\nu }}^{\mathrm{T}}\left({\displaystyle \sum }_{q=1}^s\left({\overline{\gamma }}_q{\mathbf{R}}_q\left(\tilde{x}\right)+{\underset{\_}{\gamma }}_q\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{R}}_q\left(\tilde{x}\right)\right)\right)-{\epsilon }_5\left(\tilde{x}\right)\mathbf{I}\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(26)

$${\mathit{\nu }}^{\mathrm{T}}\left({\mathbf{L}}_{pq}\left(x\right)\right){\mathit{\nu }}^{\mathrm{T}}\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(27)

$${\mathit{\nu }}^{\mathrm{T}}\left({\mathbf{M}}_{ij}\left(x\right)\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}$$

(28)

$$-{\mathit{\nu }}^{\mathrm{T}}\left({\mathbf{\Omega }}_{ijpq}+{\mathbf{\Upsilon }}_q+{\mathbf{\Gamma }}_{ijpq}+{\epsilon }_6\left(x\right)\mathbf{I}\right)\mathit{\nu }\in {\mathbf{\Theta }}_{\mathbf{S}\mathbf{O}\mathbf{S}}\forall p,q=1,2,\dots ,s\mathrm{and}i,j=1,2,\dots ,r$$

(29)

where ${\mathbf{\Omega }}_{ijpq}={\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{j=1}^r{\displaystyle \sum }_{p=1}^s{\displaystyle \sum }_{q=1}^s{h}_i\left(z\right)h_j\left(z\right){\alpha }_p{\alpha }_q\left[\begin{array}{ccc}{\mathbf{\Omega }}_{ijpq}^{11}& {\mathbf{\Omega }}_{ipq}^{12}& {\mathbf{P}}_q\left(\tilde{x}\right)C_{ip}^{\mathrm{T}}\left(x\right)\sqrt{{\mathbf{S}}_2}\\ \ast & {\mathbf{\Omega }}_{ip}^{22}& {\mathbf{H}}_{ip}^{\mathrm{T}}\left(x\right)\sqrt{{\mathbf{S}}_2}\\ \ast & \ast & -\mathbf{I}\end{array}\right]$, ${\mathbf{W}}_{ij}\left(x,h\right)={\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{j=1}^r\left(h_i\left(z\right)-{\underset{\_}{h}}_i\left(z\right)\right)\left({\overline{h}}_j\left(z\right)-h_j\left(z\right)\right){\mathbf{W}}_{ij}\left(x\right)$, ${\underset{\_}{\gamma }}_q\le {\alpha }_q\le {\overline{\gamma }}_q$, ${\underset{\_}{\phi }}_q\le {\dot{\alpha }}_q\le {\overline{\phi }}_q$, ${\mathbf{\Gamma }}_{ijpq}={\mathbf{L}}_{pq}\left(x,\alpha \right)+{\mathbf{W}}_{ij}\left(x,h\right)+{\mathbf{M}}_{ij}\left(x,h\right)$, ${\mathbf{\Upsilon }}_q=\left[\begin{array}{ccc}-{\displaystyle \sum }_{q=1}^s\left({\overline{\phi }}_q{\mathbf{Q}}_q\left(\tilde{x}\right)+{\underset{\_}{\phi }}_q\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{Q}}_q\left(\tilde{x}\right)\right)\right)& 0& 0\\ \ast & 0& 0\\ \ast & \ast & 0\end{array}\right]$, ${\mathbf{L}}_{pq}\left(x,\alpha \right)={\displaystyle \sum }_{p=1}^s{\displaystyle \sum }_{q=1}^s\left({\alpha }_p-{\underset{\_}{\gamma }}_p\right)\left({\overline{\gamma }}_q-{\alpha }_q\right){\mathbf{L}}_{pq}\left(x\right)$ and ${\mathbf{M}}_{ij}\left(x,h\right)=\left({\displaystyle \sum }_{i=1}^r{h}_i\left(z\right)-1\right){\mathbf{M}}_{ij}\left(x\right)$.

Proof of Theorem 2.

The proof of Theorem 2 is following the same Lyapunov function $V\left(x,\theta \right)$ and cost function $\mathbf{\Phi }\left(x,\omega ,t\right)$ in Theorem 1. Referring to [25], one has the following inequality.

$${\displaystyle \sum }_{q=1}^s\left({\overline{\phi }}_q{\mathbf{Q}}_q\left(\tilde{x}\right)+{\underset{\_}{\phi }}_q\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{Q}}_q\left(\tilde{x}\right)\right)\right)\le {\displaystyle \sum }_{q=1}^s{\dot{\alpha }}_q{\mathbf{P}}_q\left(\tilde{x}\right)$$

(30)

The following inequality is inferred from (17) and (30).

$${\Delta }_{ij}\le {\displaystyle \sum }_{i=1}^r{\displaystyle \sum }_{j=1}^r{\displaystyle \sum }_{p=1}^s{\displaystyle \sum }_{q=1}^s{h}_i\left(z\right)h_j\left(z\right){\alpha }_p{\alpha }_q\left[\begin{array}{cc}{\mathbf{\Lambda }}_{ijpq}^{11}-{\displaystyle \sum }_{q=1}^s\left({\overline{\phi }}_q{\mathbf{Q}}_q\left(\tilde{x}\right)+{\underset{\_}{\phi }}_q\left({\mathbf{P}}_q\left(\tilde{x}\right)-{\mathbf{Q}}_q\left(\tilde{x}\right)\right)\right)& {\mathbf{\Lambda }}_{ipq}^{12}\\ \ast & {\mathbf{\Lambda }}_{ip}^{22}\end{array}\right]$$

Based on Schur complement, the following inequality can be obtained from (29).

$${\mathbf{\Omega }}_{ijpq}+{\mathbf{\gamma }}_q<0$$

(31)

Next, the symmetric matrix ${\mathbf{M}}_{ij}\left(x,h\right)$ and semidefinite positive matrices ${\mathbf{L}}_{pq}\left(x,\alpha \right)$, ${\mathbf{M}}_{ij}\left(x,h\right)$ are introduced. Considering the properties of ${\displaystyle \sum }_{i=1}^r{h}_i\left(z\right)=1$, ${\underset{\_}{\gamma }}_p\le {\alpha }_p\le {\overline{\gamma }}_p$ and ${\underset{\_}{h}}_i\le h_i\left(z\right)\le {\overline{h}}_i$, one can obtain ${\mathbf{M}}_{ij}\left(x,h\right)=0$, ${\mathbf{L}}_{pq}\left(x,\alpha \right)\ge 0$ and ${\mathbf{M}}_{ij}\left(x,h\right)\ge 0$. Adding the ${\mathbf{M}}_{ij}\left(x,h\right)$, ${\mathbf{L}}_{pq}\left(x,\alpha \right)$ and ${\mathbf{M}}_{ij}\left(x,h\right)$ into (31), the following inequality can be inferred.

$${\mathbf{\Omega }}_{ijpq}+{\mathbf{\gamma }}_q\le {\mathbf{\Omega }}_{ijpq}+{\mathbf{\gamma }}_q+{\mathbf{\Gamma }}_{ijpq}$$

(32)

As the same proof procedure of Theorem 1, via holding the conditions in Theorem 2, one can find that the $\Xi \left(x,\omega ,t\right)<0$ is held from ${\mathbf{\Omega }}_{ijpq}+{\mathbf{\gamma }}_q+{\mathbf{\Gamma }}_{ijpq}<0$ and the stability can be checked from inequality (21) by assuming the $\omega \left(t\right)=0$. The proof is complete.

Remark 1. Since the time-varying functions are not always be positive, the positive definition of parameter-dependent polynomial Lyapunov function cannot be guaranteed. Thus, the additional matrices ${\mathbf{R}}_q\left(\tilde{x}\right)$ is employed to achieve $\mathbf{P}\left(\tilde{x},\theta \right)>0$. Besides, referring to [25], stability analysis can be relaxed via considering membership function and time-varying function into the stability conditions. Therefore, the slack matrices ${\mathbf{M}}_{ij}\left(x,h\right)$, ${\mathbf{L}}_{pq}\left(x,\alpha \right)$ and ${\mathbf{W}}_{ij}\left(x,h\right)$ are employed for relaxing the stability conditions.

In order to demonstrate the applicability of the proposed controller, a numerical simulation is introduced in the next section. The SOSTOOLS is utilized to obtain the feasible solution by solving the conditions in Theorem 1 and 2.

4. Simulation Results

In this section, the following NTV system with external disturbance is considered to verify the proposed controller designed method.

$${\dot{x}}_1=\left(a\theta -1\right)x_1+x_1^2+x_1^3+x_1^2{x}_2-x_1{x}_2^2+\left(b\theta +1\right)u+\omega \left(t\right)$$

(33a)

$${\dot{x}}_2=-\sin \left(x_1\right)-x_2$$

(33b)

$$y\left(t\right)=x_1+\omega \left(t\right)$$

(33c)

Through the modelling approaches, the NTV system (33) can be represented by the following PDPF model.

$$\dot{x}={\displaystyle \sum }_{i=1}^2{\displaystyle \sum }_{j=1}^2{\displaystyle \sum }_{p=1}^2{\displaystyle \sum }_{q=1}^2{h}_i\left(x_1\right)h_j\left(x_1\right){\alpha }_p{\alpha }_q\left(\left(A_{ip}\left(x\right)+B_{ip}\left(x\right){\mathbf{F}}_j\left(x,\theta \right)\right)\widehat{x}\left(x\right)+\mathbf{G}\omega \left(t\right)\right)$$

(34a)

$$y\left(t\right)=\mathbf{C}\widehat{x}\left(x\right)+\mathbf{H}\omega \left(t\right)$$

(34b)

where $A_{11}\left(x\right)=\left[\begin{array}{cc}a-1+x_1+x_1^2+x_1{x}_2+x_2^2& 1\\ -1& -1\end{array}\right]$, $A_{12}\left(x\right)=\left[\begin{array}{cc}-a-1+x_1+x_1^2+x_1{x}_2+x_2^2& 1\\ -1& -1\end{array}\right]$, $A_{21}\left(x\right)=\left[\begin{array}{cc}a-1+x_1+x_1^2+x_1{x}_2+x_2^2& 1\\ 0.2172& -1\end{array}\right]$, $A_{22}\left(x\right)=\left[\begin{array}{cc}-a-1+x_1+x_1^2+x_1{x}_2+x_2^2& 1\\ 0.2172& -1\end{array}\right]$ , $B_{11}\left(x\right)=B_{21}\left(x\right)=\left[\begin{array}{c}\left(b+1\right)\\ 0\end{array}\right]$, $B_{12}\left(x\right)=B_{22}\left(x\right)=\left[\begin{array}{c}\left(-b+1\right)\\ 0\end{array}\right]$, $\mathbf{G}=\left[\begin{array}{c}1\\ 0\end{array}\right]$, $\mathbf{C}=\left[\begin{array}{cc}1& 0\end{array}\right]$, $\mathbf{H}=1$, ${\alpha }_1=\frac{1+\sin \left(t\right)}{2}$ , ${\alpha }_2=1-{\alpha }_1$, $h_1\left(x_1\right)=\frac{\sin \left(x_1\right)+0.2172x_1}{1.2172x_1}$ and $h_2\left(x_1\right)=1-h_1\left(x_1\right)$.

For the PDPF model (34), the proposed design methods are applied in the following cases to show their applicability and effectiveness. In the first case, the relaxation of the proposed theorems is discussed by setting two scalars $a$ and $b$ in (34). The other case is provided to show the effectiveness of the proposed PDPF controller design methods.

Case 1:

In this case, the theorems are respectively applied to find the maximum allowable scalars as $a$ and $b$ in (34) to discuss the relaxation. To apply the theorems, the required parameters are given as ${\mathbf{S}}_1=\mathbf{I}$, ${\mathbf{S}}_2=\eta \mathbf{I}$, ${\mathbf{S}}_3=\eta \mathbf{I}$, $\eta =0.9$, $\mathbf{T}\left(x\right)=\mathbf{I}$, $\varphi =-0.501$, ${\overline{h}}_1={\overline{h}}_2=1$, ${\underset{\_}{h}}_1={\underset{\_}{h}}_2=0$, ${\overline{\gamma }}_1={\overline{\gamma }}_2=1$, ${\underset{\_}{\gamma }}_1={\underset{\_}{\gamma }}_2=0$, ${\overline{\phi }}_1={\overline{\phi }}_2=0.5$, ${\underset{\_}{\phi }}_1={\underset{\_}{\phi }}_2=-0.5$ and ${\epsilon }_i=0.00001$ $\left(i=1,2,\dots ,6\right)$. In this case, ${\epsilon }_i=0.00001$ is chosen for simplifying the calculation. It can also be chosen as polynomials for finding the feasible solutions. Using SOSTOOLS, the allowable scalar $b$ satisfying the theorems are respectively obtained by setting the different $a$. And, the results of finding the scalars are concluded in Figure 1.

Based on the results, Theorem 2 provides less conservative solution than Theorem 1 for discussing the stability issue of PDPF model (34). The difference between them is that the number of variables in Theorem 2 is 22 that is more than one in Theorem 1. Furthermore, the information of system containing time-varying parameters and membership function is introduced into the stability conditions of Theorem 2. Thus, the number of inequalities can be reduced and the information is set as symbolic variables that facilitates the solutions seeking using SOSTOOLS. However, huge number of variables brings computational burn and heavy load on searching solutions. Besides, Theorem 2 cannot be applied to discuss the stability of the PDPF model with the weighting function who possesses opposite sign. Although Theorem 2 provides relaxed stability criterion, there is none limitation on description of time-varying parameters in applying Theorem 1 to design the PDPF controller for the NTV systems. Therefore, one can choose the proper PDPF controller design method for the encountered stability problem of NTV systems.

Case 2:

In this case, the effectiveness of Theorem 2 is respectively verified to design the corresponding PDPF controller such that the NTV system (33) is robust stable and passive. Also, the required parameters for applying theorems are the same as one in Case 1. Besides, the scalars as $a=0.1$ and $b=0.1$ are set. By using Theorem 1 to PDPF model (34), the feasible solutions can be found via SOSTOOLS to build the following PDPF controller.

$$u_{\mathbf{\Omega }1}\left(t\right)={\displaystyle \sum }_{j=1}^2{h}_j\left(z\right){\displaystyle \sum }_{q=1}^2{\alpha }_q{\mathbf{K}}_{jq}\left(x\right){\left({\displaystyle \sum }_{q=1}^2{\alpha }_q{\mathbf{P}}_q\left(\tilde{x}\right)\right)}^{-1}\widehat{x}\left(x\right)$$

(35)

where ${\mathbf{P}}_q\left(\tilde{x}\right)=\left[\begin{array}{cc}{p}_q^{11}& p_q^{12}\\ *& p_q^{22}\end{array}\right]$, ${\mathbf{K}}_{jq}=\left[\begin{array}{cc}{k}_{jq}^1& k_{jq}^2\end{array}\right]$, $p_1^{11}=7.812\times {10}^{-10}{x}_2^2+4.709\times {10}^{-9}{x}_2+0.8668$,

$p_1^{12}=-2.949\times {10}^{-10}{x}_2^2-2.385\times {10}^{-8}{x}_2+0.02548$, $p_1^{22}=0.0001064x_2^2-2.835\times {10}^{-8}{x}_2+3.177$,

$p_2^{11}=-8.615\times {10}^{-10}{x}_2^2+7.416\times {10}^{-9}{x}_2+0.8671$, $p_2^{12}=3.865\times {10}^{-11}{x}_2^2-8.116\times {10}^{-9}{x}_2+0.02085$,

$p_2^{22}=0.0001062x_2^2-2.887\times {10}^{-8}{x}_2+3.142$,

$k_{11}^1=-1.65x_1^2-0.7562x_1{x}_2-0.7645x_1-0.8087x_2^2-0.002728x_2-3.639$,

$k_{11}^2=-0.02316x_1^2-0.02315x_1{x}_2-0.02303x_1+0.02309x_2^2+1.056\times {10}^{-5}{x}_2-1.946$,

$k_{12}^1=-1.995x_1^2-0.9909x_1{x}_2-0.9229x_1-0.9781x_2^2-0.000677x_2-4.201$,

$k_{12}^2=-0.02316x_1^2-0.02315x_1{x}_2-0.02262x_1+0.02307x_2^2+0.0001143x_2-2.383$,

$k_{21}^1=-1.65x_1^2-0.7563x_1{x}_2-0.7647x_1-0.8088x_2^2-0.002741x_2-3.672$,

$k_{21}^2=-0.02316x_1^2-0.02316x_1{x}_2-0.02346x_1+0.02308x_2^2-0.0001555x_2-2.499$,

$k_{22}^1=-1.995x_1^2-0.91x_1{x}_2-0.9227x_1-0.9782x_2^2-0.0007129x_2-4.249$ and

$k_{22}^2=-0.02316x_1^2-0.02316x_1{x}_2-0.0265x_1+0.02306x_2^2-9.322\times {10}^{-5}{x}_2-2.872$.

Besides, the following PDPF controller is designed by the corresponding feasible solutions satisfying Theorem 2.

$$u_{\mathbf{\Omega }2}\left(t\right)={\displaystyle \sum }_{j=1}^2{h}_j\left(z\right){\displaystyle \sum }_{q=1}^2{\alpha }_q{\mathbf{K}}_{jq}\left(x\right){\left({\displaystyle \sum }_{q=1}^2{\alpha }_q{\mathbf{P}}_q\left(\tilde{x}\right)\right)}^{-1}\widehat{x}\left(x\right)$$

(36)

where ${\mathbf{P}}_q\left(\tilde{x}\right)=\left[\begin{array}{cc}{p}_q^{11}& p_q^{12}\\ *& p_q^{22}\end{array}\right]$, ${\mathbf{K}}_{jq}=\left[\begin{array}{cc}{k}_{jq}^1& k_{jq}^2\end{array}\right]$, $p_1^{11}=9.56\times {10}^{-9}{x}_2^2+9.496\times {10}^{-8}{x}_2+1.667$,

$p_1^{12}=-2.338\times {10}^{-9}{x}_2^2-1.859\times {10}^{-7}{x}_2+0.1034$, $p_1^{22}=0.0003701x_2^2-3.033\times {10}^{-9}{x}_2+4.769$,

$p_2^{11}=-3.566\times {10}^{-9}{x}_2^2+4.036\times {10}^{-8}{x}_2+0.8926$, $p_2^{12}=1.565\times {10}^{-10}{x}_2^2-4.628\times {10}^{-8}{x}_2+0.06893$,

$p_2^{22}=0.0001508x_2^2-5.953\times {10}^{-9}{x}_2+3.551$,

$k_{11}^1=-2.166x_1^2-1.284x_1{x}_2-1.266x_1+0.4864x_2^2-0.003187x_2-4.817$,

$k_{11}^2=-0.08617x_1^2-0.08617x_1{x}_2-0.08265x_1+0.08589x_2^2+0.001326x_2-2.335$,

$k_{12}^1=-2.026x_1^2-1.009x_1{x}_2-0.9912x_1+0.09688x_2^2-0.003313x_2-5.117$,

$k_{12}^2=-0.08617x_1^2-0.08617x_1{x}_2-0.08482x_1+0.08596x_2^2+0.0002182x_2-2.799$,

$k_{21}^1=-2.166x_1^2-1.284x_1{x}_2-1.266x_1+0.4864x_2^2-0.0032x_2-4.828$,

$k_{21}^2=-0.08617x_1^2-0.08617x_1{x}_2-0.08687x_1+0.08588x_2^2+0.000964x_2-3.823$,

$k_{22}^1=-2.026x_1^2-1.01x_1{x}_2-0.9907x_1+0.09694x_2^2-0.003375x_2-5.128$ and

$k_{22}^2=-0.08617x_1^2-0.8616x_1{x}_2-0.08721x_1+0.08595x_2^2+0.0002025x_2-4.066$.

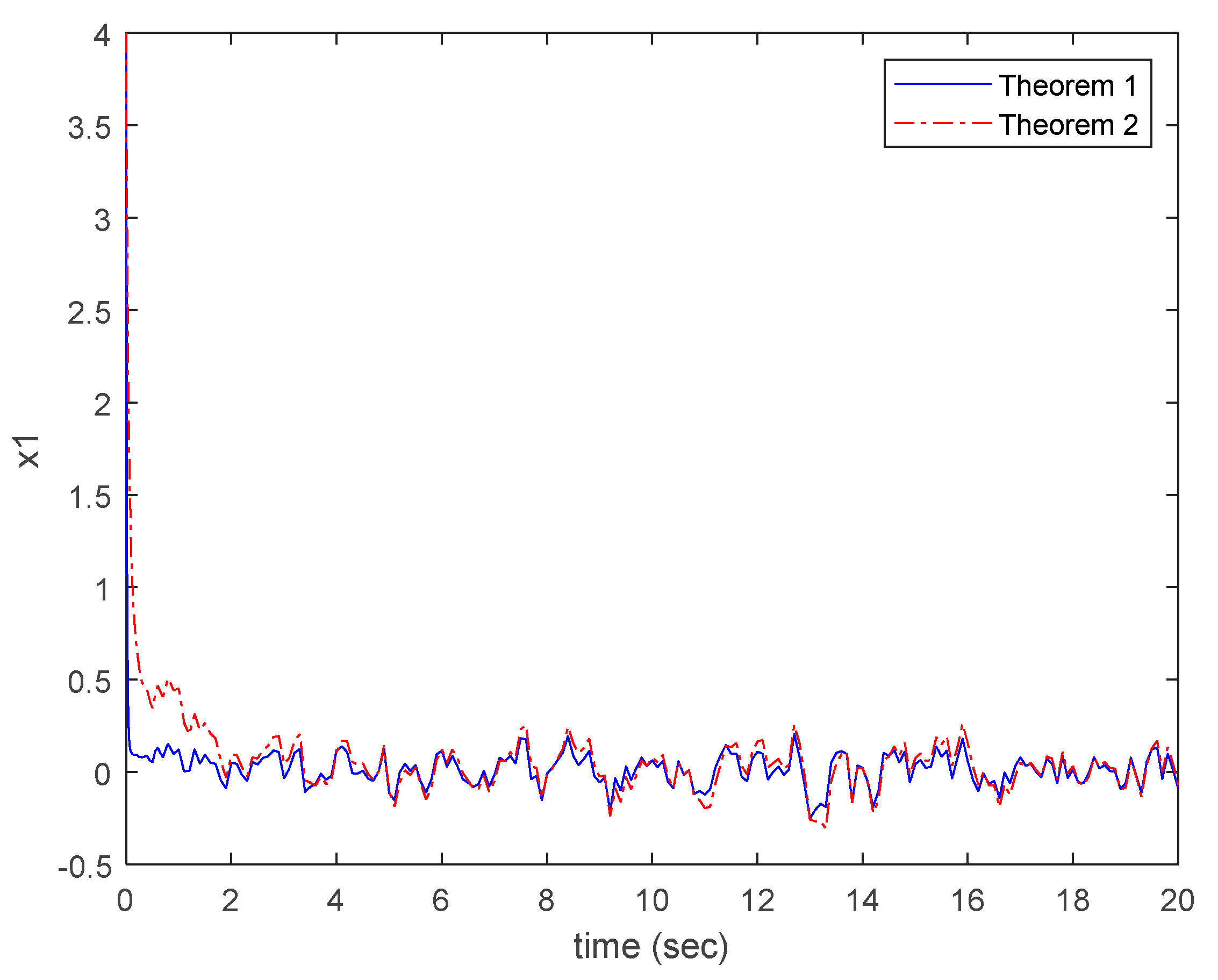
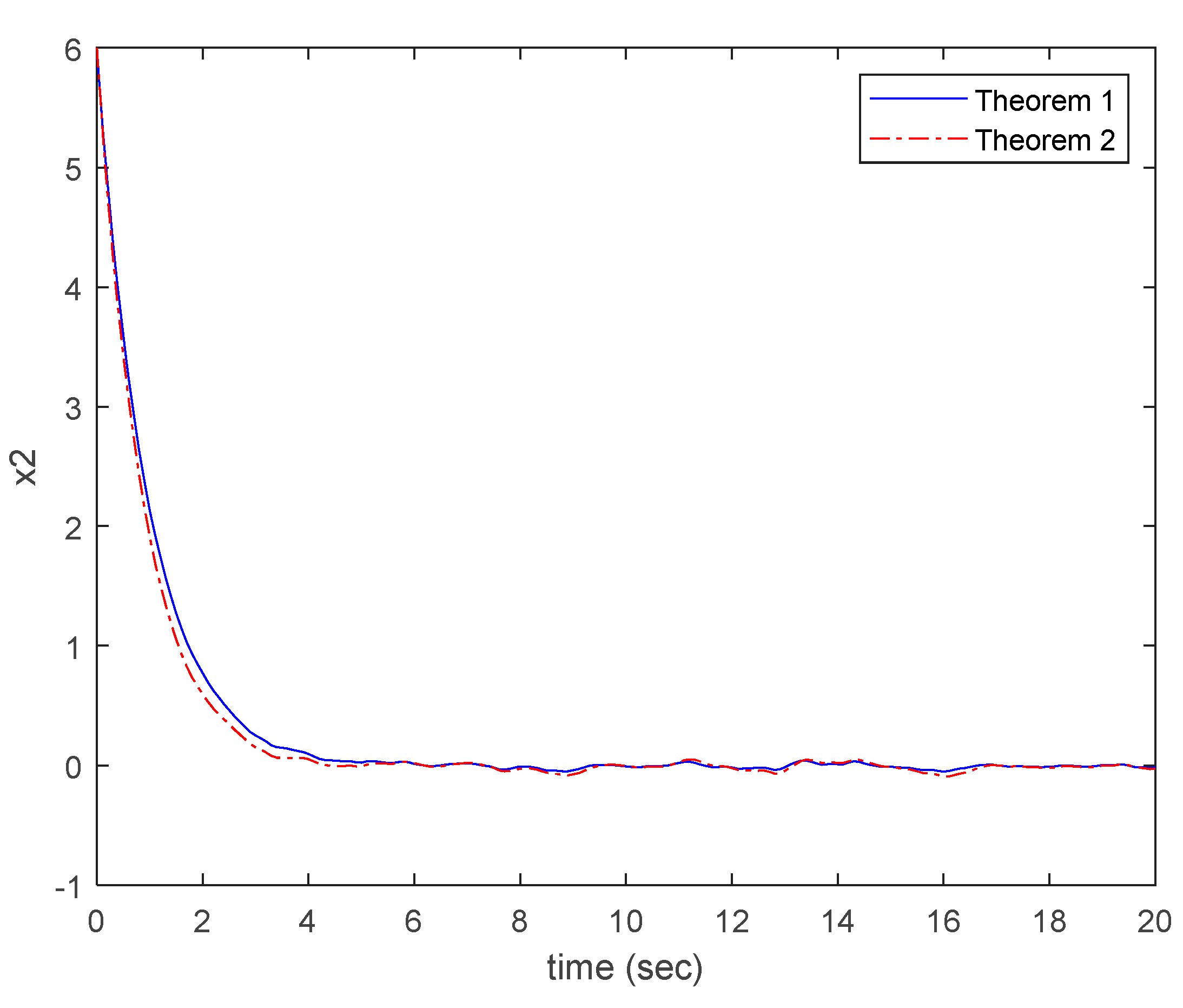
With the designed PDPF controllers $u_{\mathbf{\Omega }1}\left(t\right)$ and $u_{\mathbf{\Omega }2}\left(t\right)$, the responses of (33) are respectively sated in Figure 2 and Figure 3 with the same initial condition as $x\left(0\right)={\left[\begin{array}{cc}4& 6\end{array}\right]}^{\mathrm{T}}$. And, the external disturbance is chosen as zero mean white noise with unit variance.

Referring to the figures, all states are converged to zero in the simulation time. Although the vibration caused by external disturbance is not eliminated, the responses of (33) driven by the controllers are kept around the zero. Thus, the robust stability of PDPF model (33) is achieved by the designed controller. By introducing the simulation results into the passivity inequality in Definition 2, the following values can be respectively obtained.

$$\frac{0.9{\displaystyle {\int }_0^{20}\left(y^{\mathrm{T}}\left(t\right)y\left(t\right)\right)}dt+0.9{\displaystyle {\int }_0^{20}\left({\omega }^{\mathrm{T}}\left(t\right)\omega \left(t\right)\right)}dt}{2{\displaystyle {\int }_0^{20}\left(y^{\mathrm{T}}\left(t\right)\omega \left(t\right)\right)}dt}=0.9048$$

(37)

and

$$\frac{0.9{\displaystyle {\int }_0^{20}\left(y^{\mathrm{T}}\left(t\right)y\left(t\right)\right)}dt+0.9{\displaystyle {\int }_0^{20}\left({\omega }^{\mathrm{T}}\left(t\right)\omega \left(t\right)\right)}dt}{2{\displaystyle {\int }_0^{20}\left(y^{\mathrm{T}}\left(t\right)\omega \left(t\right)\right)}dt}=0.9159$$

(38)

The value in (37) is obtained by the responses of (33) driven by (35). Besides, the value in (38) is obtained by the responses of (33) driven by (36). Those values are smaller than 1 that satisfies the inequality in Definition 2. It should be mentioned that the passivity of NTV system (33) driven by the controllers designed by the proposed design methods is verified. Thus, the effectiveness of the proposed design methods for guaranteeing the robust stability and passivity of NTV system (33) From Fig. 2, it easily finds that the vibration in (33) driven by (35) is smaller than one driven by (36). That means Theorem 1 provides better controller performance than Theorem 2 because the information of system is not considered by the conditions in Theorem 1. Although Theorem 1 provides conservative solution in searching feasible solutions, the PDPF controller designed by Theorem 1 possesses better performance in stabilizing NTV system (33).

5. Conclusions

In this paper, the stabilization and constraining disturbance effect issue for NTV systems represented by PDPF model was studied via designing the PDPF controller. Based on the modelling approach, the time-varying parameters were interpreted via the convex combination for general description. Owning to the convex combination, the positive definition of parameter-dependent polynomial Lyapunov function can be held. Moreover, the limitation as opposite sign of time-varying function can also be ignored for the constraint of time-varying parameters. Furthermore, the passivity was considered to constrain the effect of external disturbance on the system. To discuss the issue, some sufficient conditions were derived into SOS form to find the parameter-dependent polynomial gains. Besides, the other stability criterion was proposed by introducing some slack variables to furtherly increase relaxation on discuss the issue. Both proposed criteria can be used to design the corresponding PDPF controller such that the NTV system achieves stability and attenuation performance. It should be noted that one can apply the proposed design method for the proper NTV systems. At last, the simulation results were provided to show the effectiveness and application of this paper.