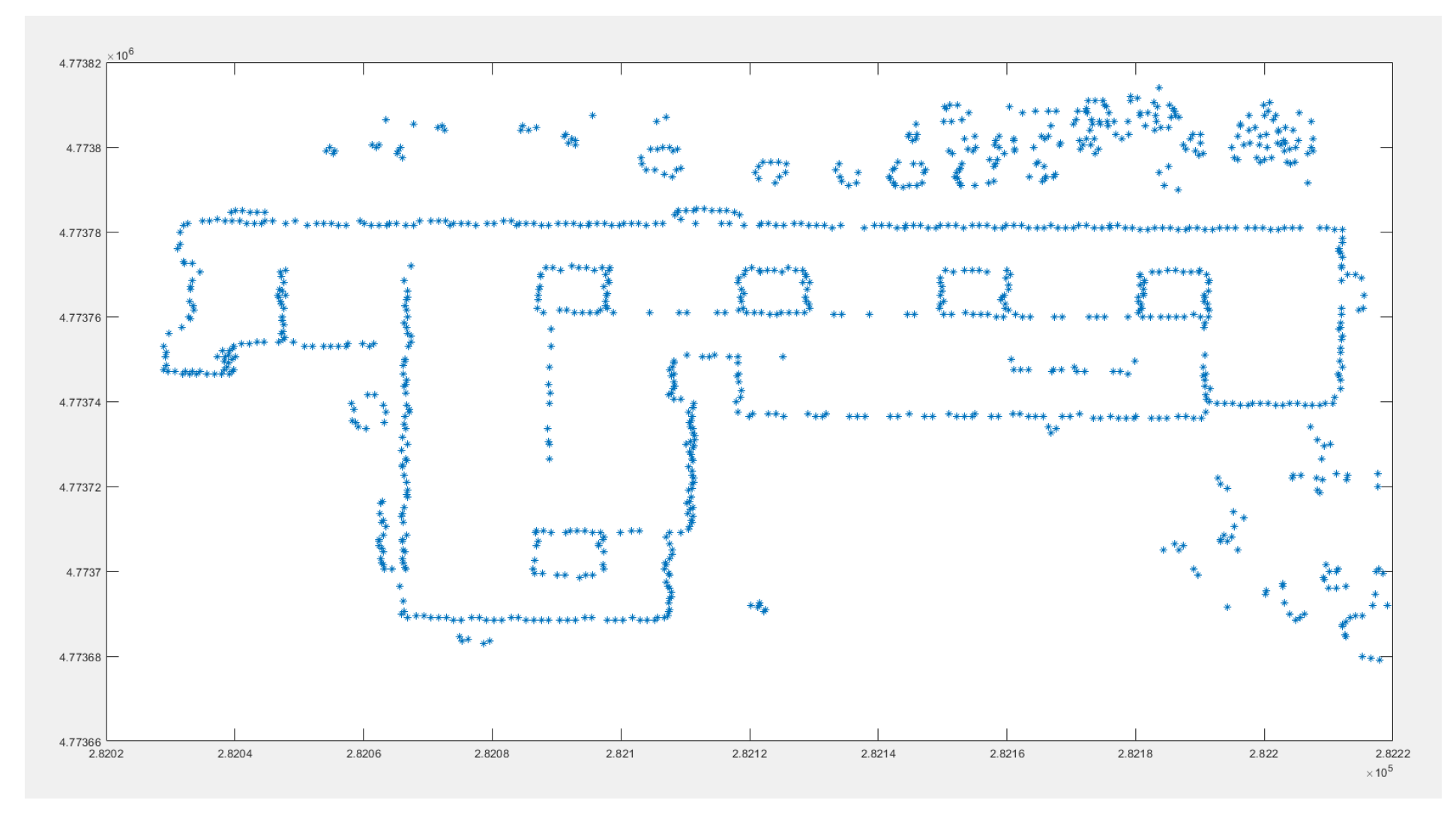
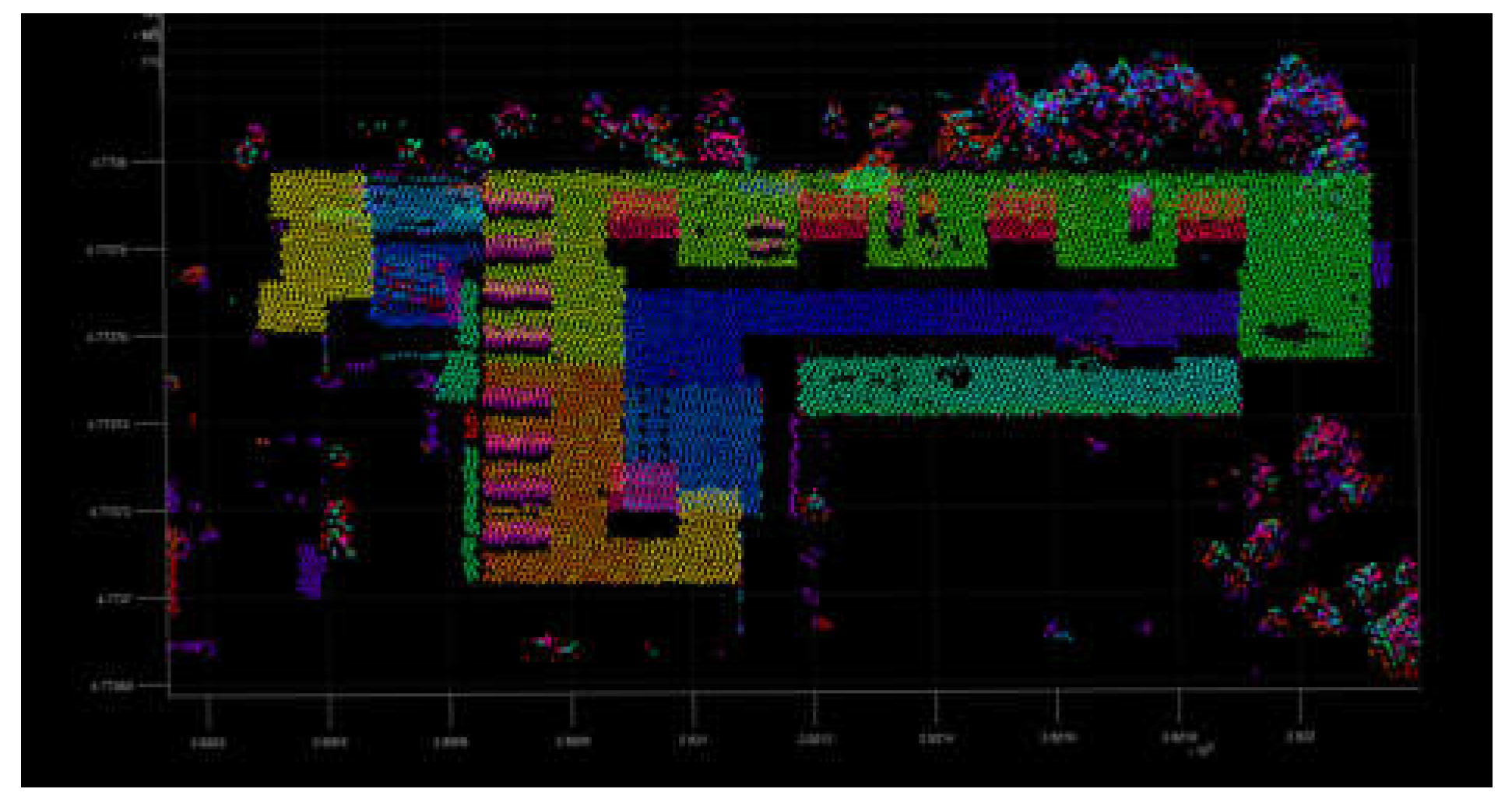
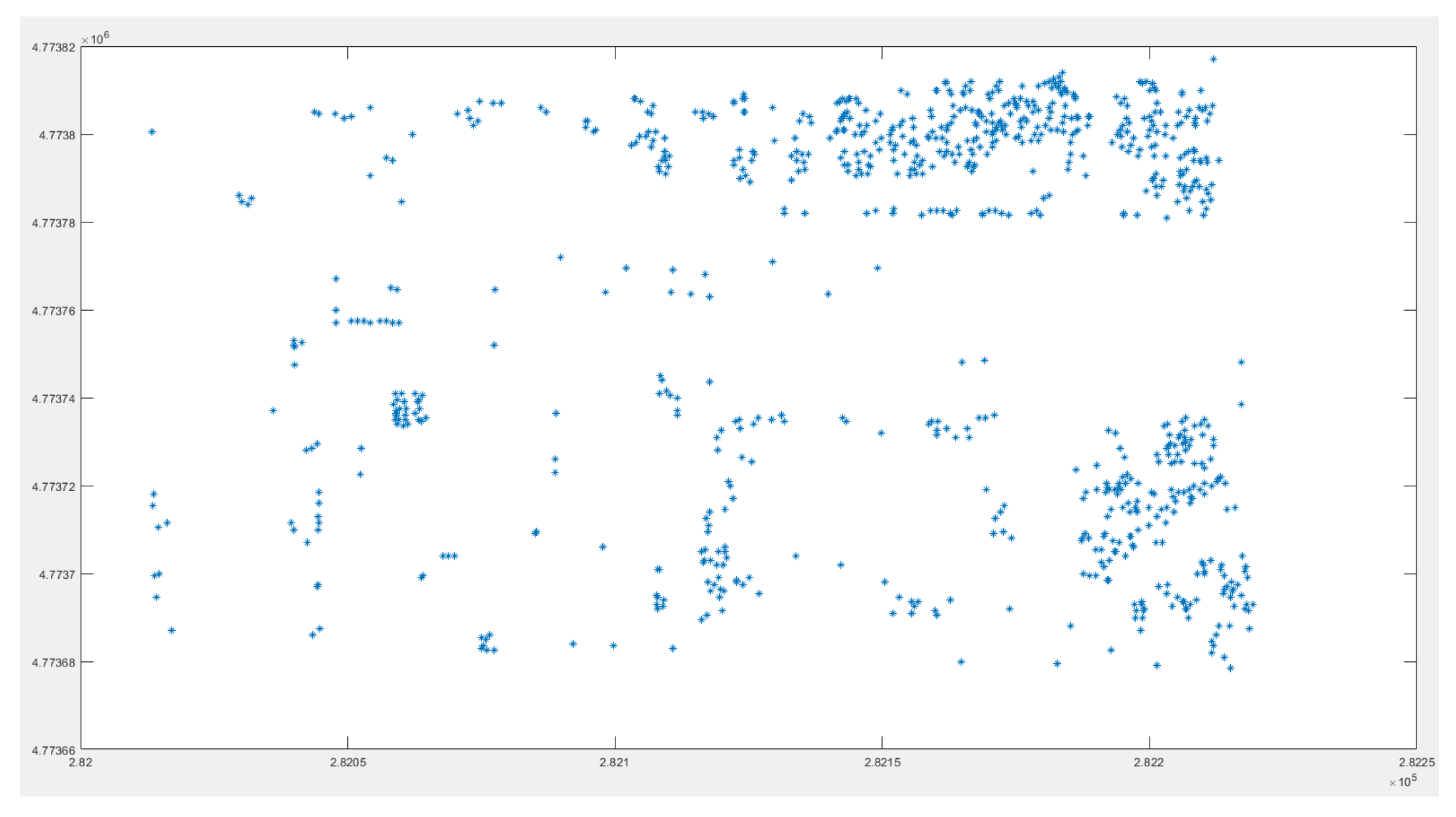
1. Introduction
Airborne Lidar technology combines global positioning system, laser scanner and inertial navigation system, which can obtain high-precision ground point cloud data quickly and efficiently [
1]. Airborne Lidar point cloud data are an important data source for obtaining spatial three-dimensional information. Their ability to accurately express the location of ground objects means that they are widely used in many fields, such as constructing a digital elevation model (DEM), contour production, and three-dimensional model generation. However, due to the massive and disordered characteristics of point cloud data, the classification and feature extraction of point cloud data is particularly important; therefore, a point cloud filter is undoubtedly an important process.
Various studies have compared the current mainstream filter algorithms. Sithole used eight filter algorithms to filter different point cloud data and compared their errors, concluding that the adaptive irregular triangulation filter method has the best filter effect [
2]. Zou compared and analyzed three commonly used filter methods from both qualitative and quantitative aspects and obtained the most suitable point cloud filter algorithm for different terrain data [
3]. These studies demonstrate that the point cloud filter algorithm has received extensive attention from scholars.
At present, the commonly used point cloud filter algorithms mainly include Segmentation-Based Filtering, the Cloth Simulation Filter, and the Slope Filter algorithm [
4]. The progressive triangulation filter algorithm is proposed by Lin, the principle is to select the lowest point in the local area as the seed point of TIN, and then use the remaining points to iteratively encrypt the triangular mesh [
5]. However, this method cannot usually preserve the points on the scarp when meeting steep slopes, misjudging the non-ground points close to the ground as ground points. The Cloth Simulation Filter, proposed by Zhang, flips the original point cloud data up and down, and then projects the flipped point cloud data and the simulated cloth node to the same horizontal plane. Following this it finds the point corresponding to each node in the cloth, and records the height of the corresponding point before projection; finally, comparing the distance between the laser point cloud and the cloth node in the same horizontal coordinate, if the distance exceeds the set threshold, and marks it as a non-ground point, otherwise it is marked as a ground point [
6]. The Cloth Simulation Filter has five adjustable parameters to complete the point cloud filter process. In the actual filter process, the filter effect is mainly improved by modifying the two parameters of grid resolution and cloth hardness, but the Cloth Simulation Filter has a poor filter effect with multi-storey buildings. The Slope Filter is proposed by Vosselman, the principle is to distinguish ground points and non-ground points according to the difference of slope [
7]; however, the method of a fixed slope is not accurate enough to be applied to the whole situation. Improvements to the three commonly used filter methods, have also been proposed. Sithole improves the Slope Filter so that the slope threshold can change with the terrain, which enhances the applicability of the algorithm[
2]; however this method requires multiple parameters to be set manually. In order to improve the accuracy, efficiency, and adaptability of the point cloud filter, Zhu also proposed an adaptive threshold point cloud filter method based on multi-level moving surface fitting [
8]. This algorithm can obtain a good filter effect in complex and continuous terrain areas, but the filter effect in discontinuous terrain areas needs to be improved. Wang also proposed a Multi-scale Adaptive Point Cloud Slope Filter method based on the Slope Filter. This method referenced the idea of the multi-scale virtual network and used distance weighting to realize a multi-scale adaptive point cloud slope filter[
9]; however, this method is less stable than a triangulation filter in urban scene areas.
The present study determined the non-ground points by finding the violation points and using these points for KD-Tree-Based Euclidean Clustering, the non-ground features are expressed in the form of cluster points. Various scholars have investigated the extraction of objects by clustering methods, and region growing [
10] and K-means algorithms [
11] have been employed for direct clustering in the 3-D model [
12].Rodriguez and Laio proposed a clustering by the rapid search and identification of density peaks [
13], Chen applied the exponential function density clustering method to indoor objects extraction and achieved good results [
14]. These studies showed that it is feasible to use a clustering algorithm for objects extraction. Sun used the hierarchical Euclidean Clustering to extract the building rooftop patches [
15], Guo used KD-Tree-Based Euclidean Clustering for point cloud extraction and segmentation[
12], and Gamal used DGCNN and Euclidean Clustering to finish the segmentation of Lidar buildings[
16]. These studies prove that the Euclidean Clustering method is feasible for the extraction of regular buildings, and KD-Tree-Based Euclidean Clustering can increase the clustering operation speed. This method can be applied to the segmentation of large scene point clouds; consequently, this study proposed an extraction method for regular landmarks by using KD-Tree-Based Euclidean Clustering, by calculating the violation point and collinear judgment to reduce the number of seeds that need indexing, and reducing the calculation amount .
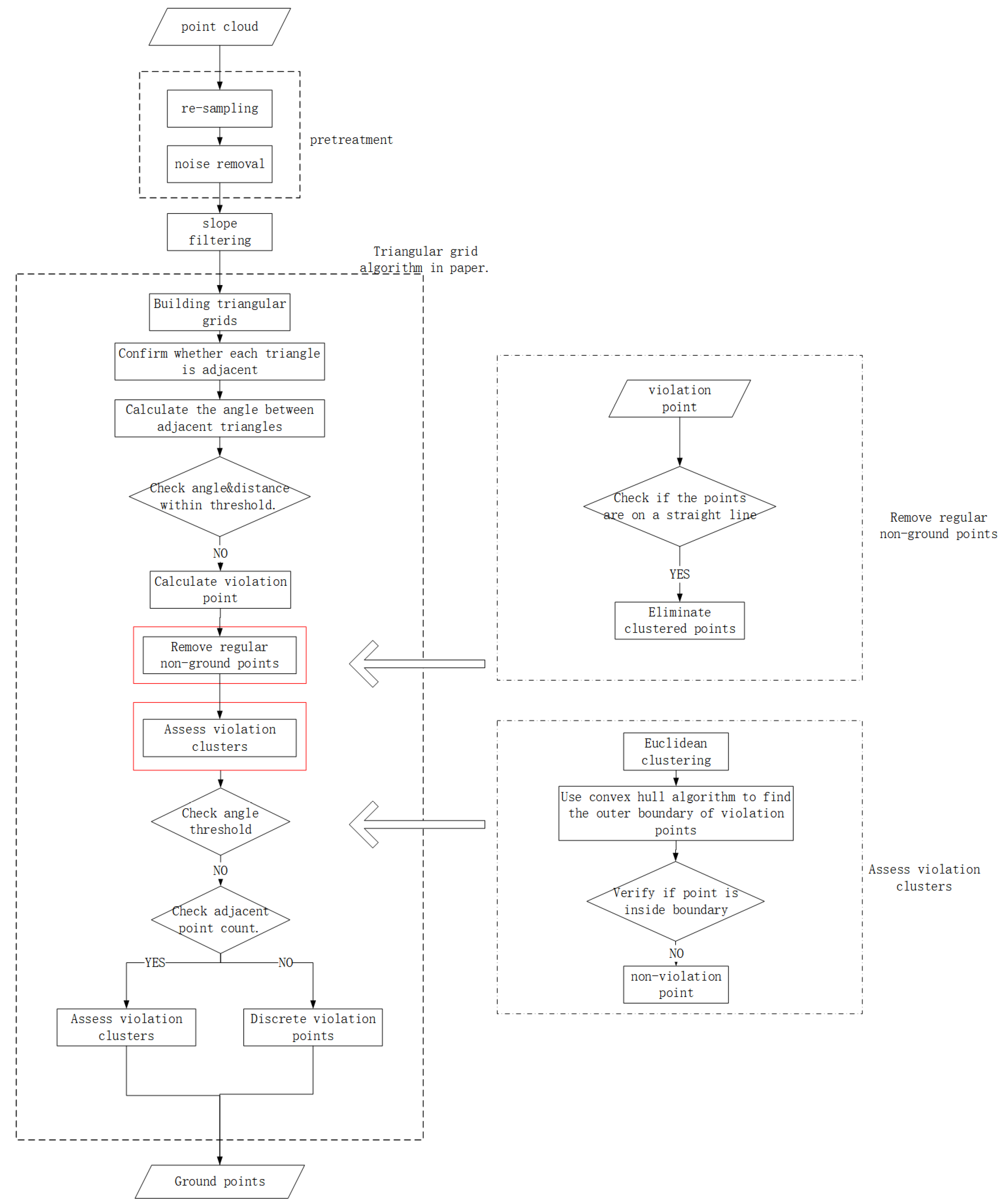
In summary, the current ground point filtering methods have certain limitations. Most of the filtering methods still use the grid method, the filtering effect of the grid method is easily affected by the size of the grid, and it is difficult to achieve better results for the complex building point cloud scene. The method of adaptively adjusting the size of the grid is also more complex and inefficient. Therefore, it is necessary to propose a filtering method that is not bound by the size of the grid. The present study proposed a triangular mesh filter method based on the Slope Filter(
Figure 1). This method find the violation points based on the distance and angle relationship in the triangular grid, subsequently, it uses the KD-Tree-Based Euclidean Clustering to find the non-ground points block through the spatial distance relationship.
4. Discussion
As an effective tool of the point cloud filter, the Slope Filter has been widely used in the classification of ground points and non-ground points, dividing the study area into grids, which is the first key step in this method. The ground grids and non-ground grids are distinguished by these grids, and the slope is, calculated separately to determine the lower points as the ground points. This article proposed a filter method based on the Slope Filter, which obtained the adjacent state between each point, determining the distances and angles of each point, and calculating the violation points. The principle is that there must be a certain violation area between the non-ground area and the ground area. Simply speaking, there will be an unnatural angle and distance area, unlike the ground slope which will rise slowly at a certain natural angle. Therefore, this article establishes a triangular grid to obtain the violation area, selecting two adjacent triangles in the grid. When the angle of these planes is too large, and the length of any edge in the two planes exceeds the threshold, it can be determined that the triangle with the longest edge is the unnatural area; thus, the violation point is identified from this triangle.
An airborne radar usually obtains the point cloud data from a large area. The characteristics of this method are that the horizontal of the points presents a certain distance distribution, it can be thought that if there is no contact with other objects in scanning, the points of the same object often appear as a cluster point, based on this idea, this article adds the KD-Tree-Based clustering algorithm to classify the objects in the scene. This method can express the distance relationship of each point, and is applied to the extraction of the building point cloud; however, there are still some problems in the point cloud filter. When the point cloud has near-ground scattered points, such as in a forest, it is easy to eliminate the ground points near the scattered points as non-ground points using a large clustering threshold. Therefore, this article proposed the use of a large threshold to extract higher non-ground points; most of these non-ground points are buildings. This article used a three-point collinear method because these violation points show a regular distribution and can be clustered and eliminated using the lower threshold to eliminate the scatter points. In the process of airborne radar scanning, it is inevitable to scan the building façade; therefore, this study added a height threshold to avoid the mutual conduction between the points in the clustering process and the elimination of the ground points.
Compared with using the grid, the triangular grid can more accurately express the relationship between each point, it can filter non-ground points when facing multiple buildings with different heights, as well as determine whether the points are the ground points in the face of discontinuous areas. This method is accurate, efficient, and can be applied to a variety of scenarios. The total error of the point cloud filter algorithm is only 3. 68%, which is smaller than most algorithms, and the error source is mainly due to a Type I error, the source of which can be explained as follows. (1) In the process of judging the violation point, the ground points are in the area with a significant change in slope; therefore, these points were judged as violation points. However, with the development of LiDAR technology, the density and quality of the point cloud will be improved, and the subsequent misjudgment of the violation point will be reduced. (2) Due to the limitation of the clustering algorithm, some ground points close to non-ground points will be judged as non-ground points. This is illustrated by the process of calculating the sample data from ISPRS, where there is a situation that the Type I error is too large. The reason for this is that the number of the non-ground points in the sample data is too small, and if using this method repeatedly to separate the point cloud, the total error will be too large. However, in order to confirm the practicability of the algorithm in a variety of areas, the Type II error is reduced as much as possible. In summary, this algorithm provided a new idea for the point cloud filter, and its efficiency can be improved with the development of the point cloud quality and clustering algorithm.
The research content of this article still has limitations:
- (1)
The clustering algorithm is still not perfect, as it fails to adjust the distance threshold by the point cloud distribution in the relevant scene being studied;
- (2)
This method needs to construct a triangular grid for each point in the point cloud, so the processing speed of point cloud data with large scenes is relatively slow, and complex scenes require repeated operations;
- (3)
The filter effect is poor when the slope on discontinuous ground changes significantly.
Figure 1.
The algorithm flowchart.
Figure 1.
The algorithm flowchart.
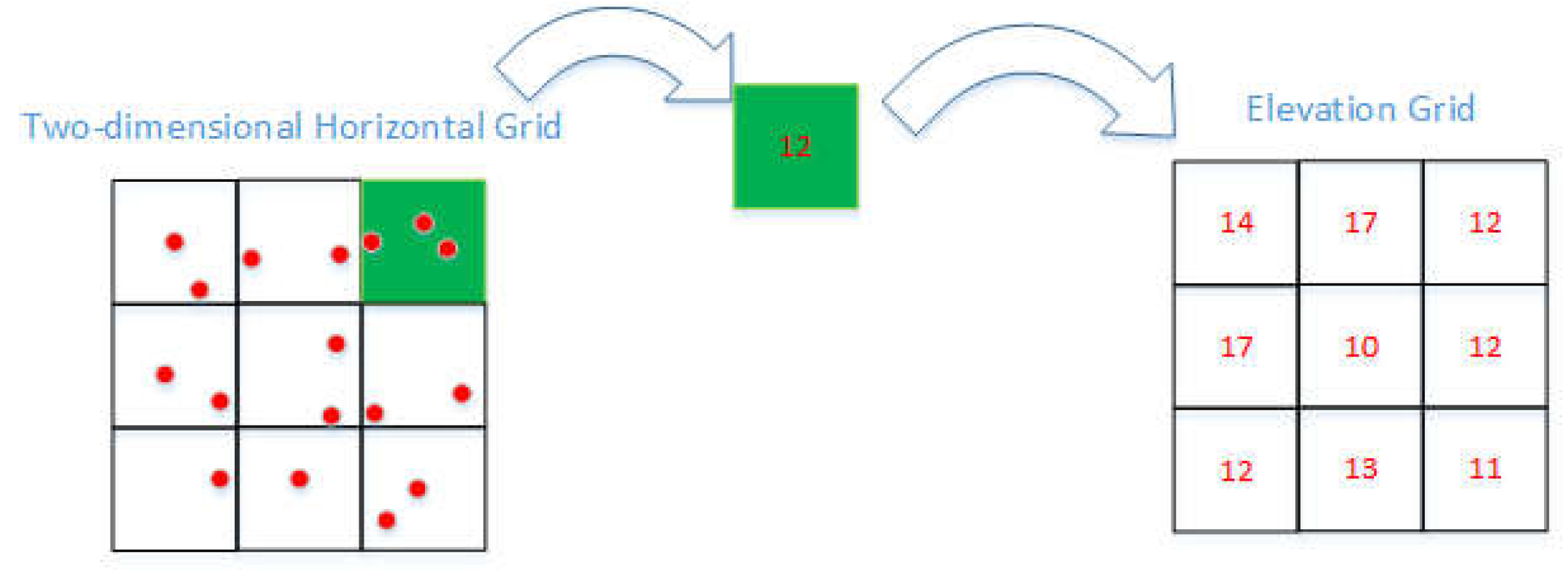
Figure 2.
How to obtain elevation grid.
Figure 2.
How to obtain elevation grid.
Figure 3.
How to obtain slope grid.
Figure 3.
How to obtain slope grid.
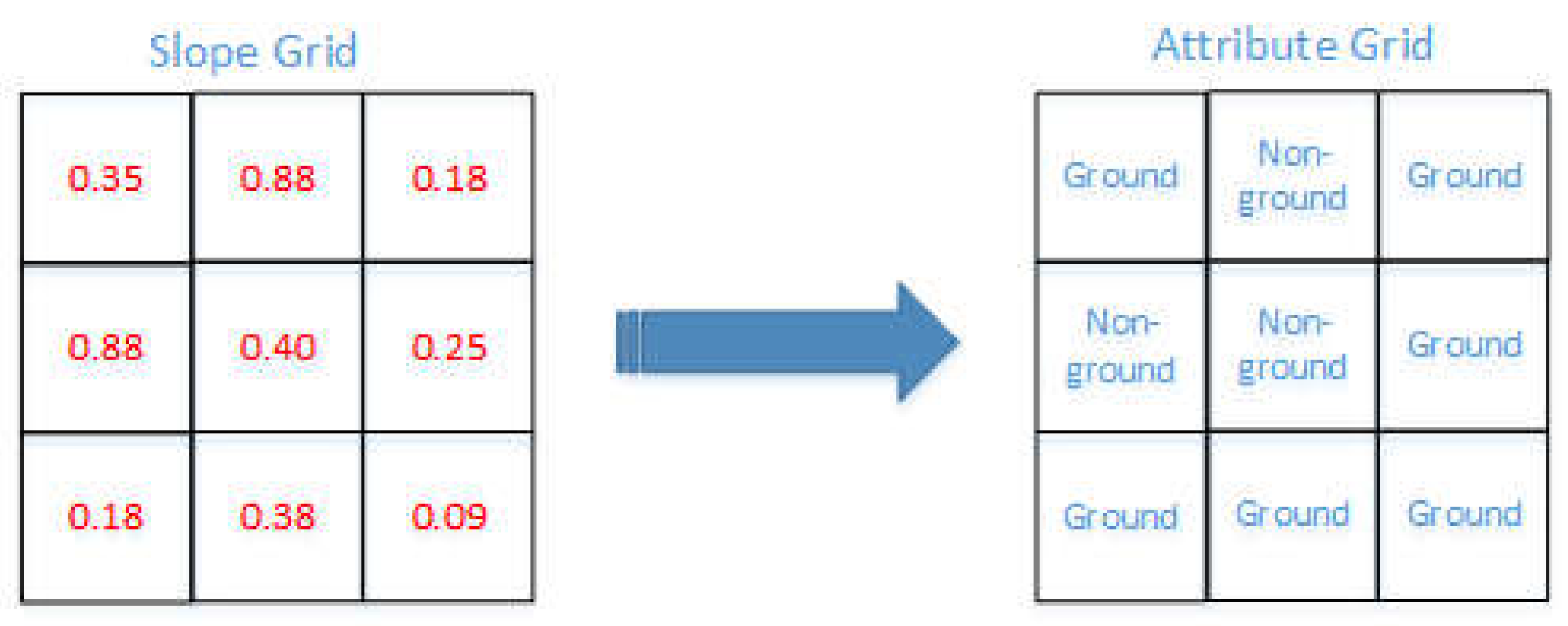
Figure 4.
How to obtain attribute grid.
Figure 4.
How to obtain attribute grid.
Figure 5.
Triangular grid.
Figure 5.
Triangular grid.
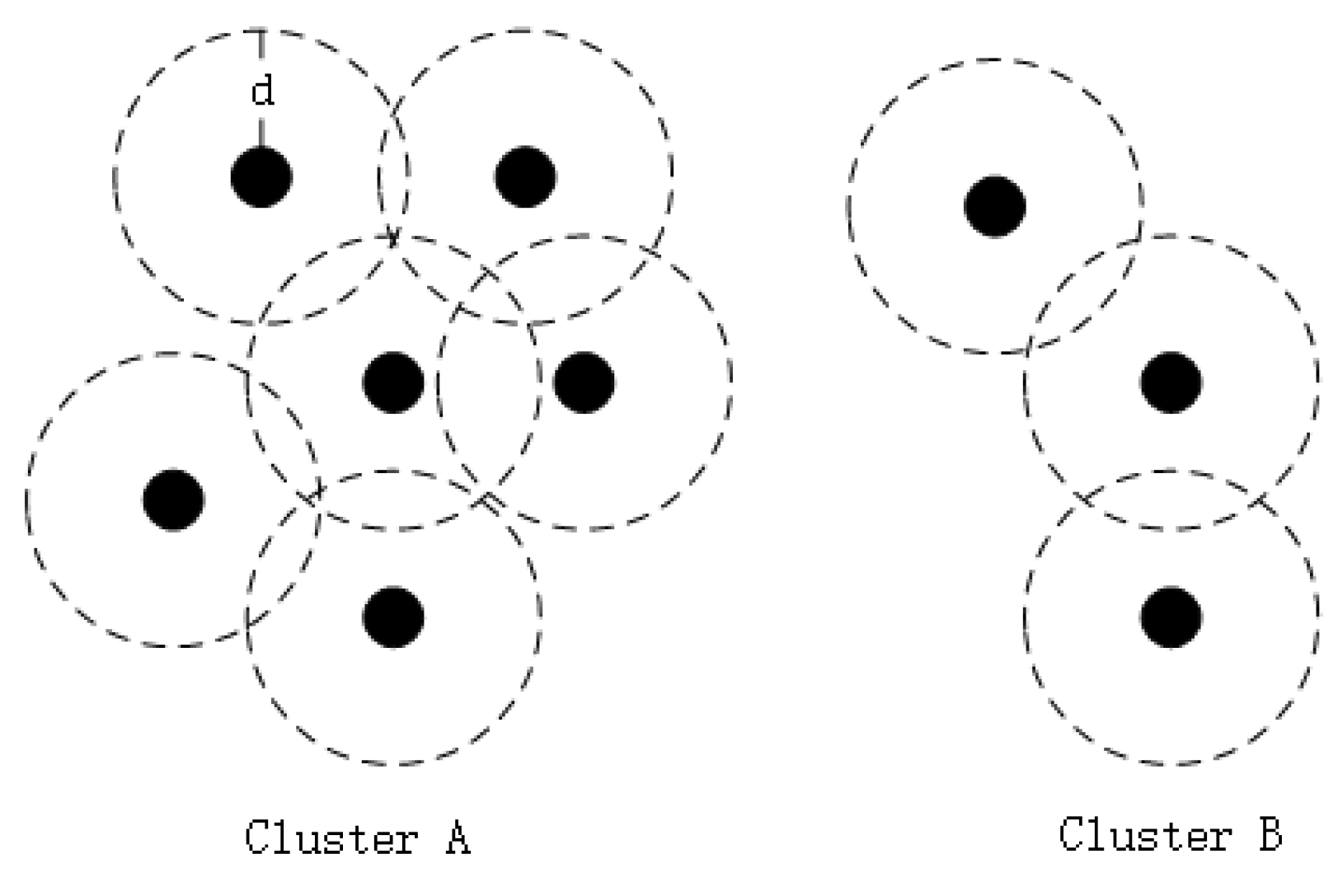
Figure 6.
The Euclidean Clustering.
Figure 6.
The Euclidean Clustering.
Figure 7.
The Euclidean Clustering process.
Figure 7.
The Euclidean Clustering process.
Figure 8.
The whole study point cloud.
Figure 8.
The whole study point cloud.
Figure 9.
The study area point cloud.
Figure 9.
The study area point cloud.
Figure 10.
The violation points.
Figure 10.
The violation points.
Figure 11.
The regular violation point.
Figure 11.
The regular violation point.
Figure 12.
The clustering result (Different color points represent different point sets after clustering.).
Figure 12.
The clustering result (Different color points represent different point sets after clustering.).
Figure 13.
The boundary of the clustering points (Different color boundary represent the corresponding boundary of different point sets after clustering.).
Figure 13.
The boundary of the clustering points (Different color boundary represent the corresponding boundary of different point sets after clustering.).
Figure 14.
The violation points of the second round.
Figure 14.
The violation points of the second round.
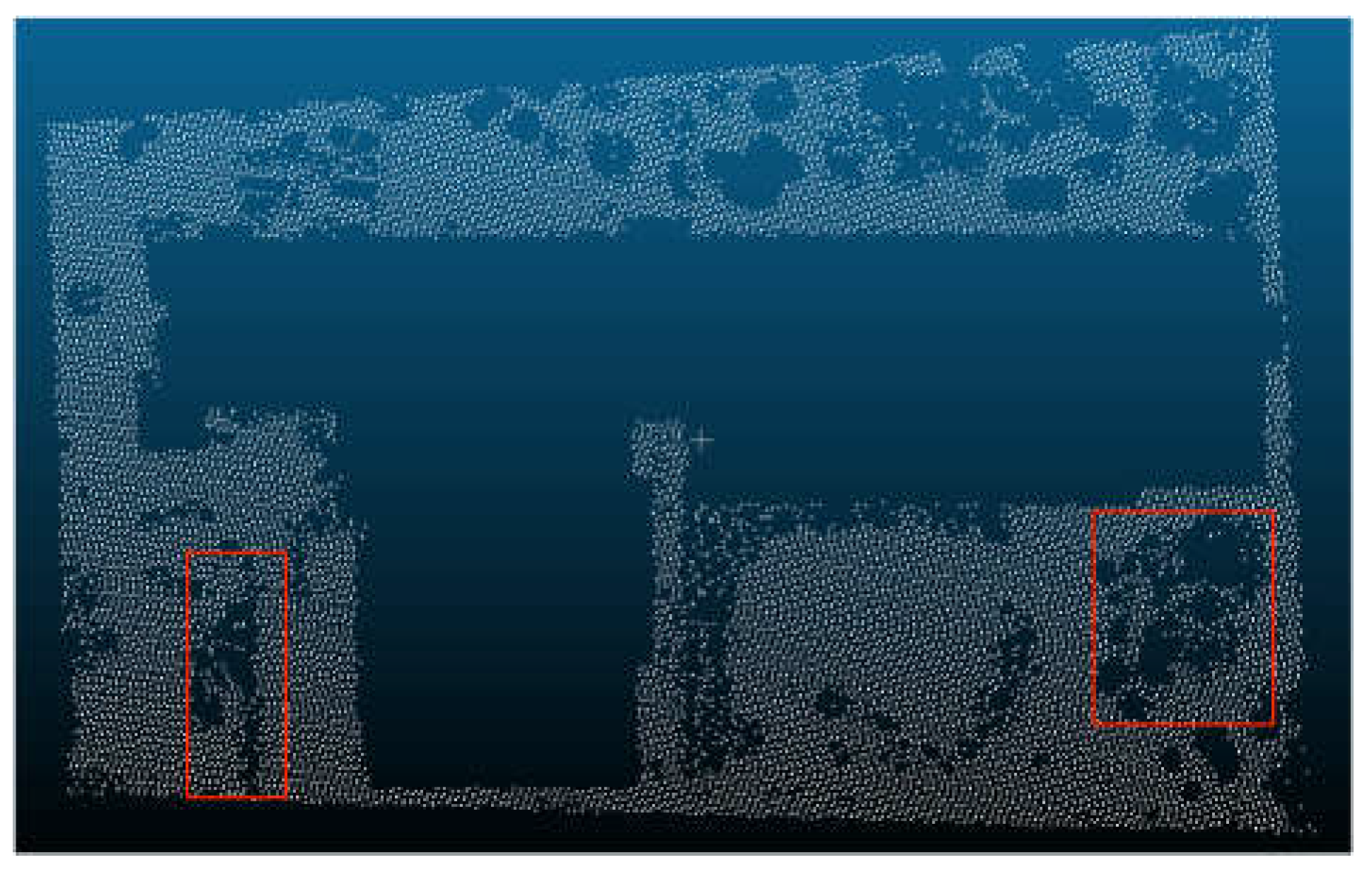
Figure 15.
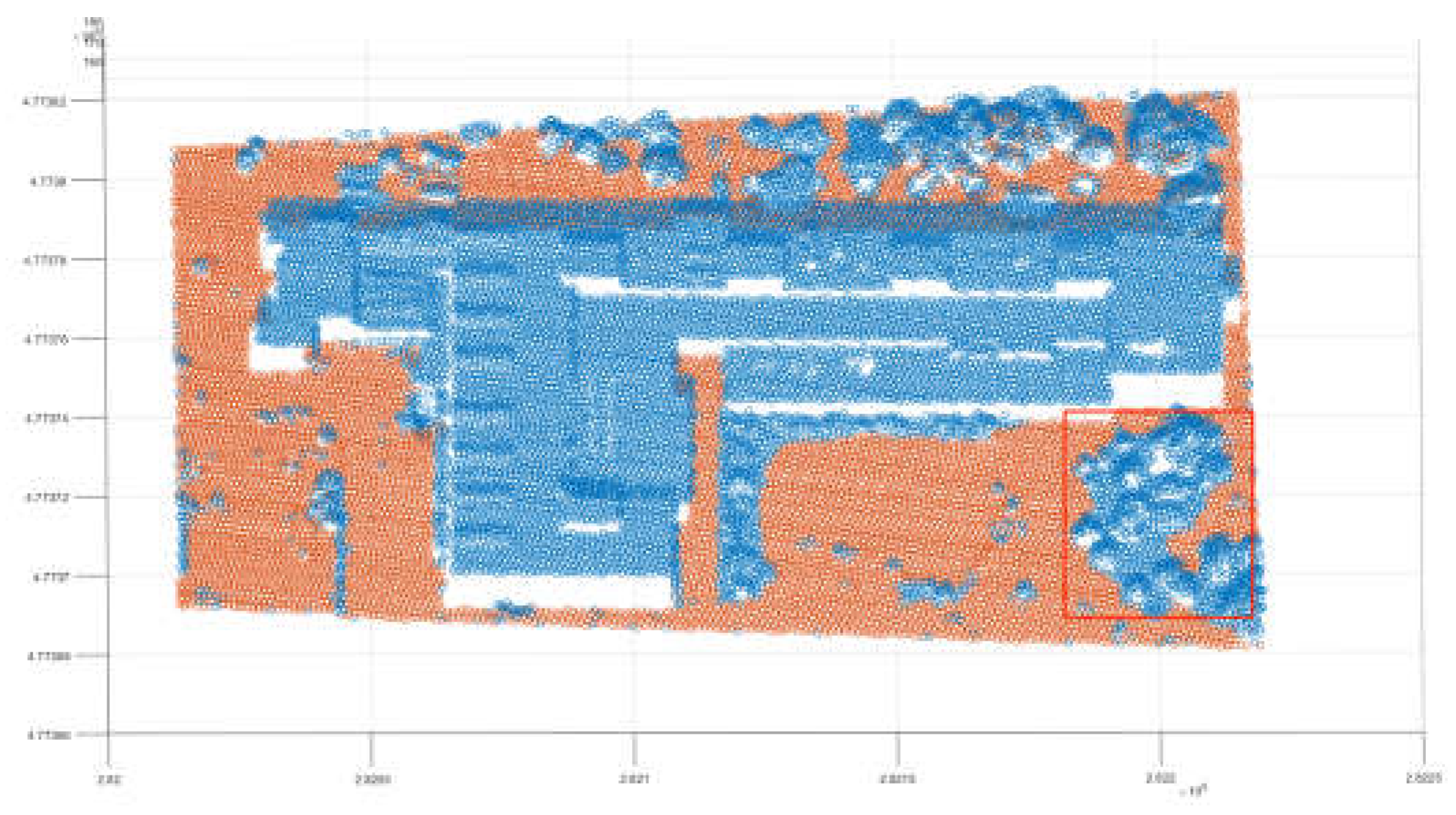
The study area after the triangular grid filter (The blue dot indicates the non-ground point, the red dot indicates the ground point, and the red box indicates the ineffective area.).
Figure 15.
The study area after the triangular grid filter (The blue dot indicates the non-ground point, the red dot indicates the ground point, and the red box indicates the ineffective area.).
Figure 16.
The study area after the Slope Filter with a high threshold.
Figure 16.
The study area after the Slope Filter with a high threshold.
Figure 17.
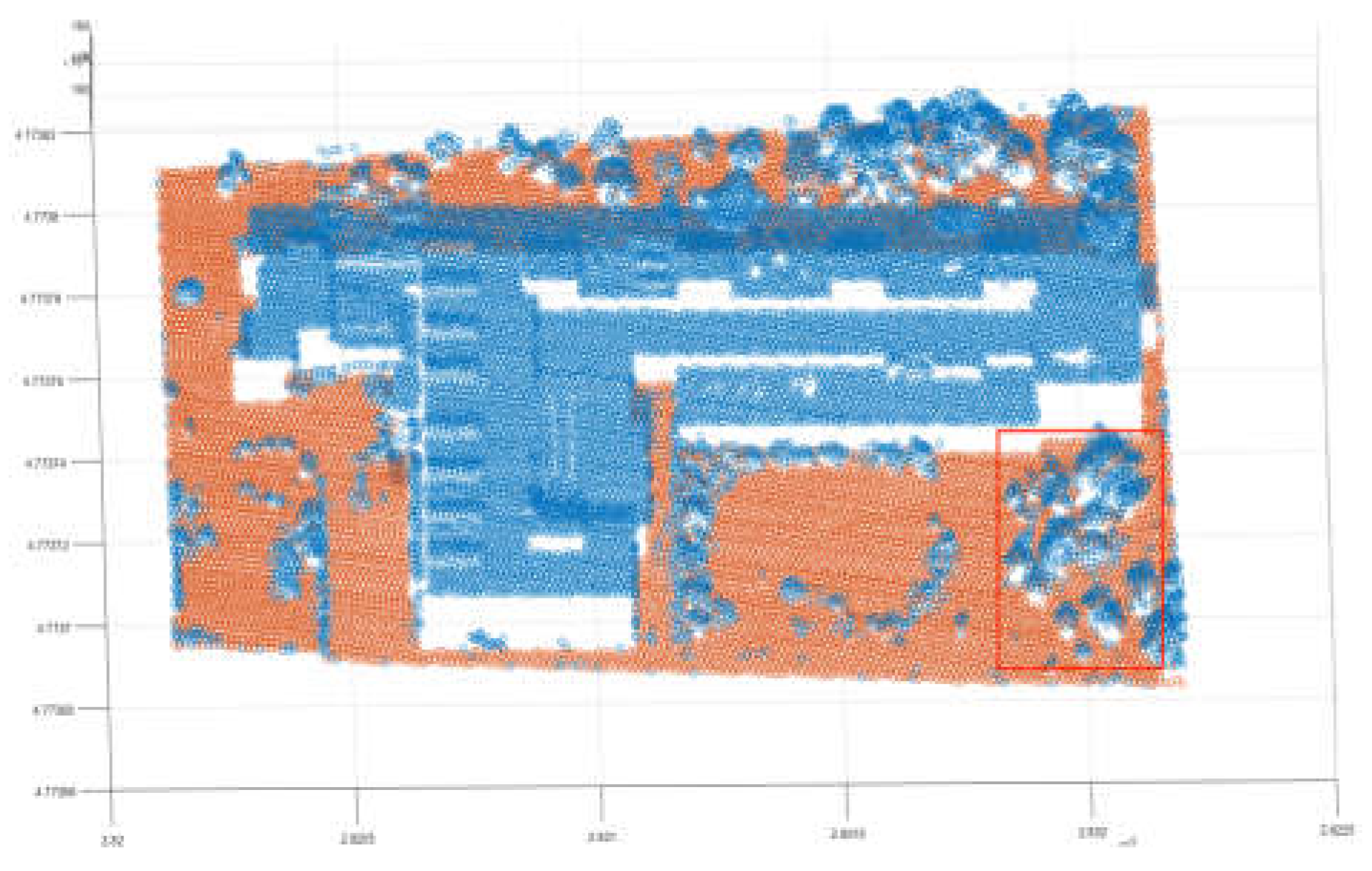
The study area after the filtering process combining two methods (The blue dot indicates the non-ground point, the red dot indicates the ground point, and the red box indicates the same area effect after the improvement.).
Figure 17.
The study area after the filtering process combining two methods (The blue dot indicates the non-ground point, the red dot indicates the ground point, and the red box indicates the same area effect after the improvement.).
Figure 18.
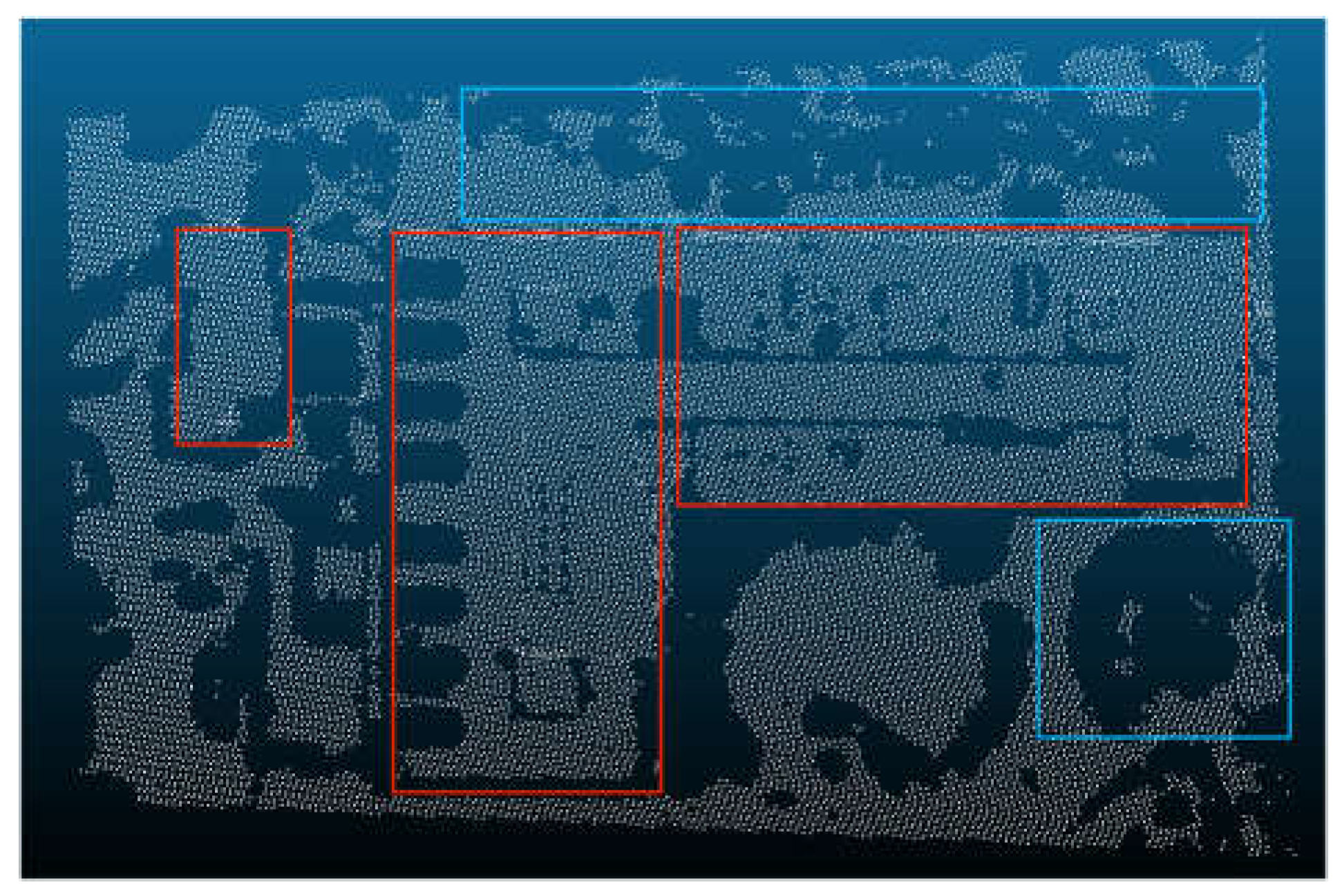
The EMD Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area.).
Figure 18.
The EMD Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area.).
Figure 19.
The SMRF Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area.).
Figure 19.
The SMRF Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area.).
Figure 20.
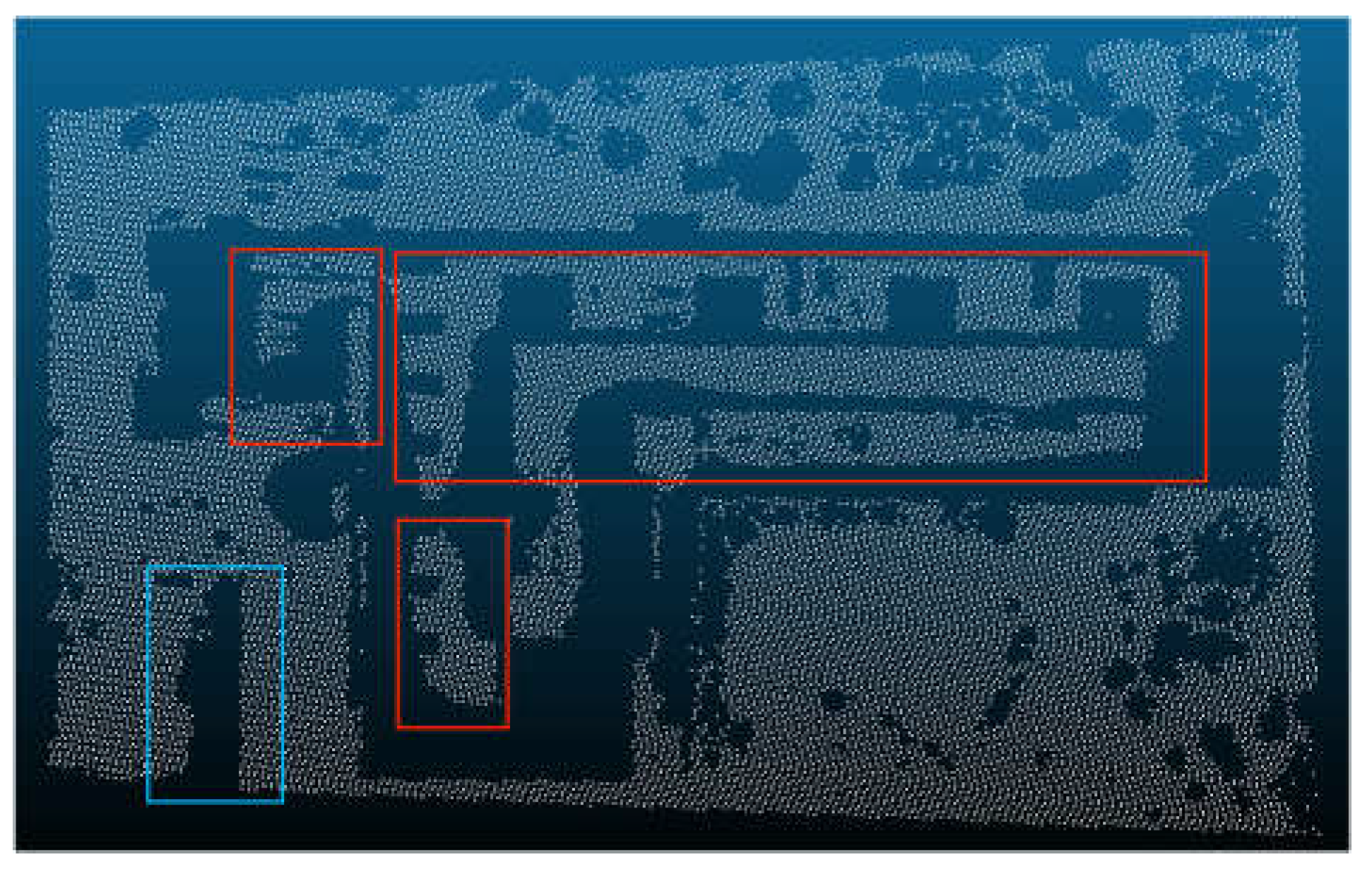
The Progressive Triangular Mesh Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area.).
Figure 20.
The Progressive Triangular Mesh Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area.).
Figure 21.
Slope Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area, and the blue box selection area indicates that the ground point is used as the non-ground point removal area.).
Figure 21.
Slope Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area, and the blue box selection area indicates that the ground point is used as the non-ground point removal area.).
Figure 22.
Cloth Simulation Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area, and the blue box selection area indicates that the ground point is used as the non-ground point removal area.).
Figure 22.
Cloth Simulation Filter (The red box selection area indicates that the non-ground point is used as the ground point retention area, and the blue box selection area indicates that the ground point is used as the non-ground point removal area.).
Figure 23.
Combining the Slope Filter and triangular grid filter (The red box selected area indicates that the filtering effect is improved.).
Figure 23.
Combining the Slope Filter and triangular grid filter (The red box selected area indicates that the filtering effect is improved.).
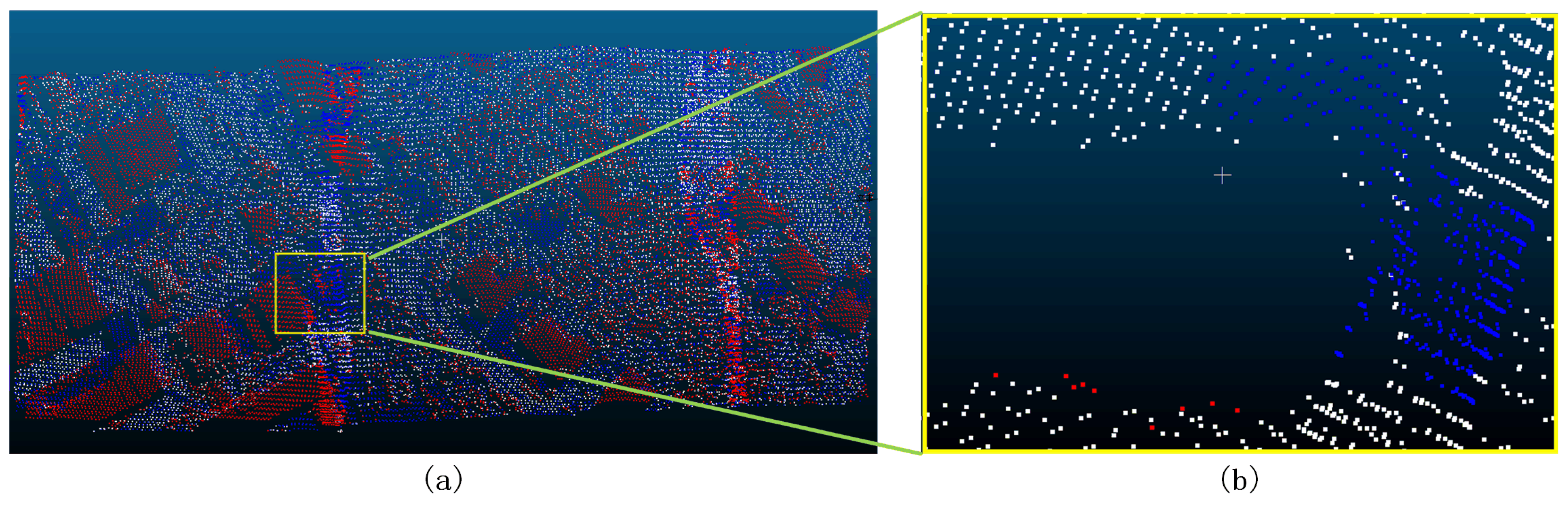
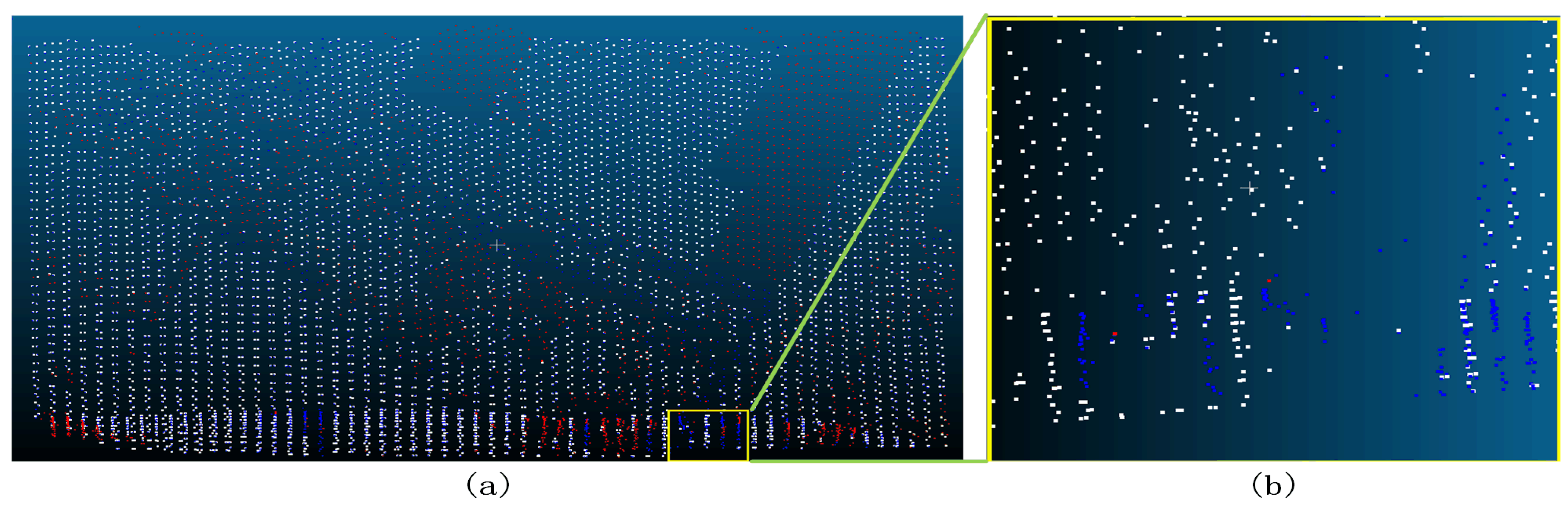
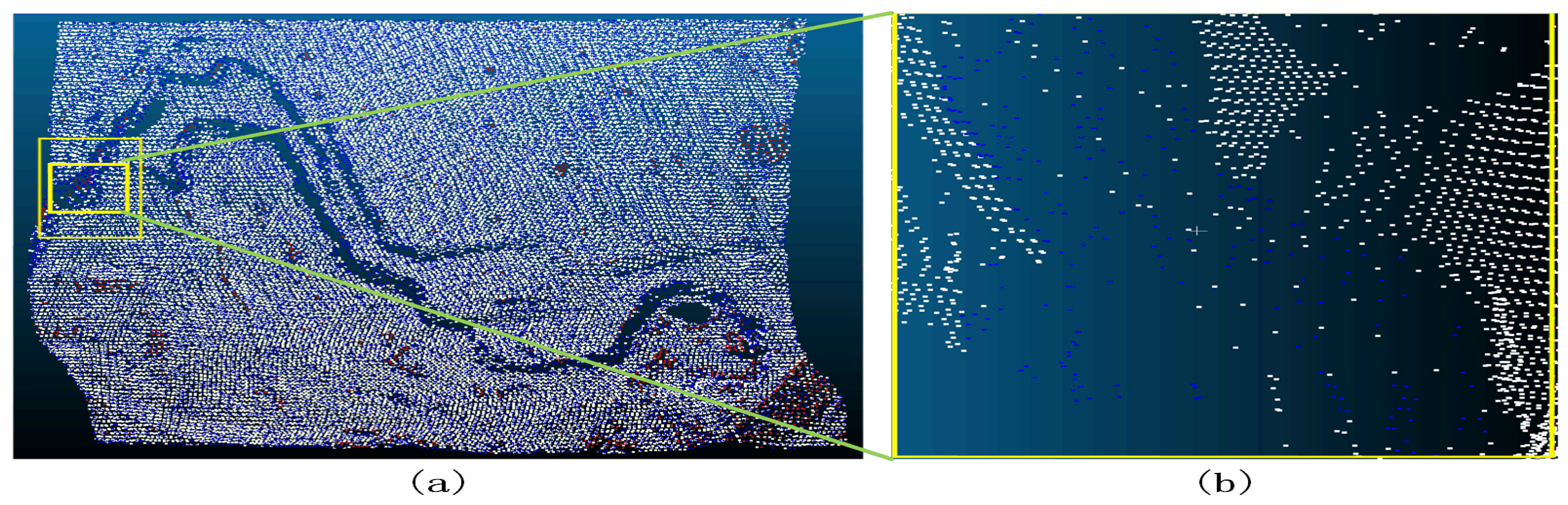
Figure 24.
Sample 1-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 24.
Sample 1-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
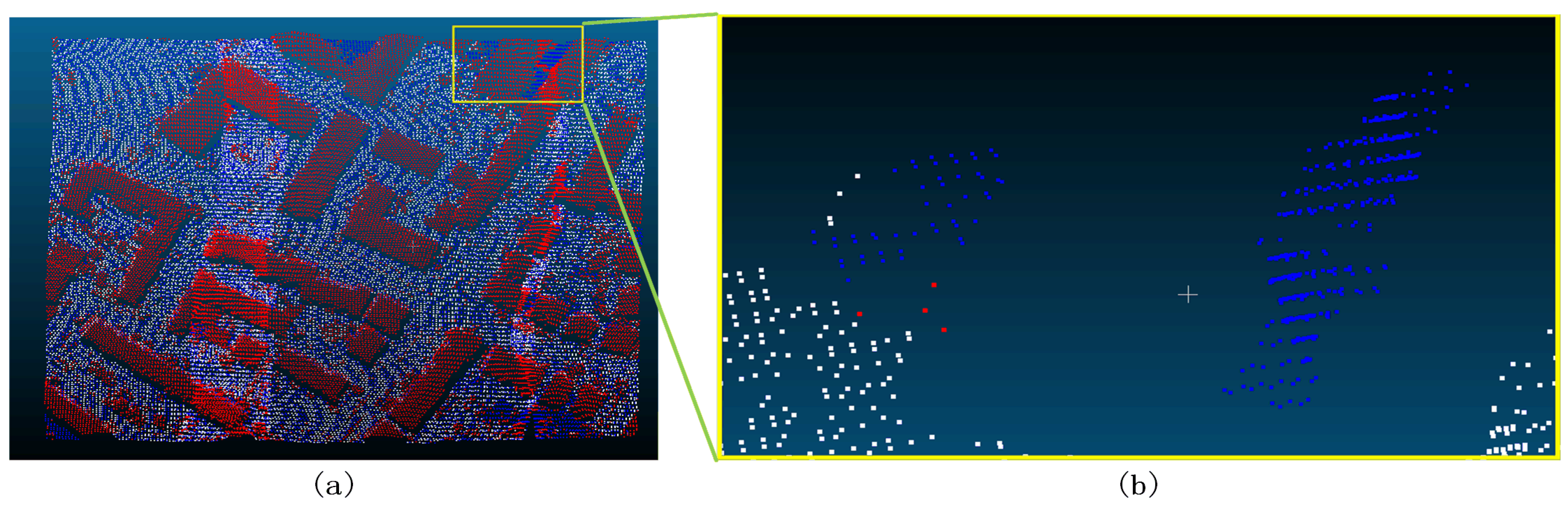
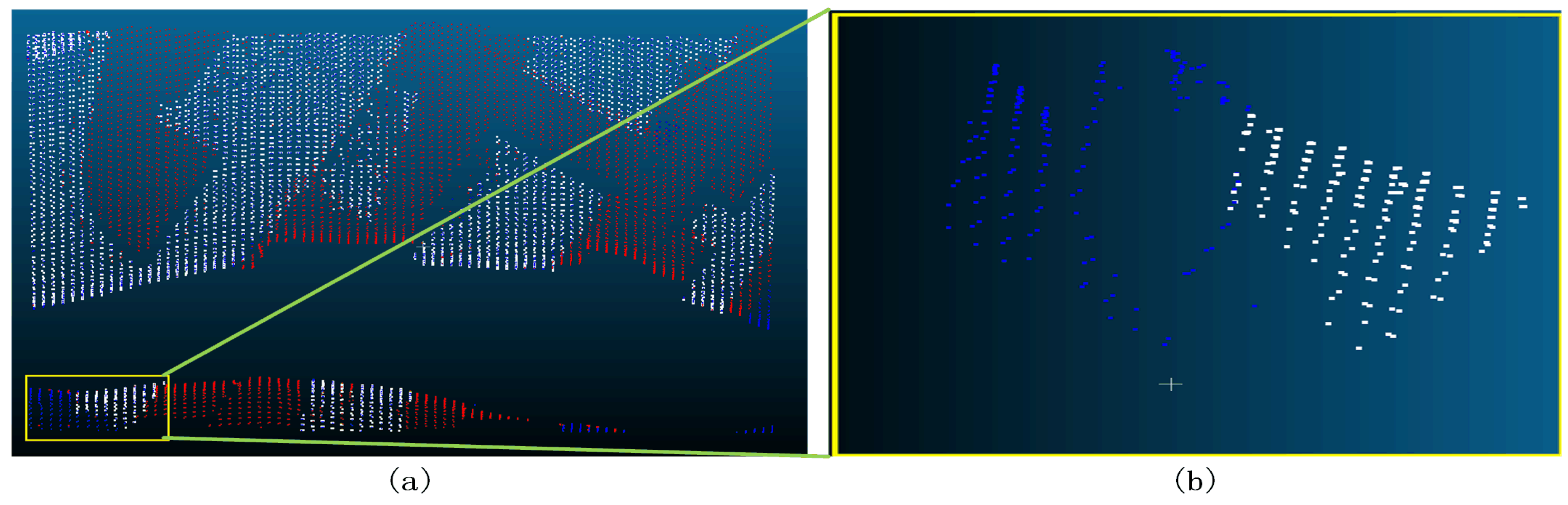
Figure 25.
Sample 1-2 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 25.
Sample 1-2 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
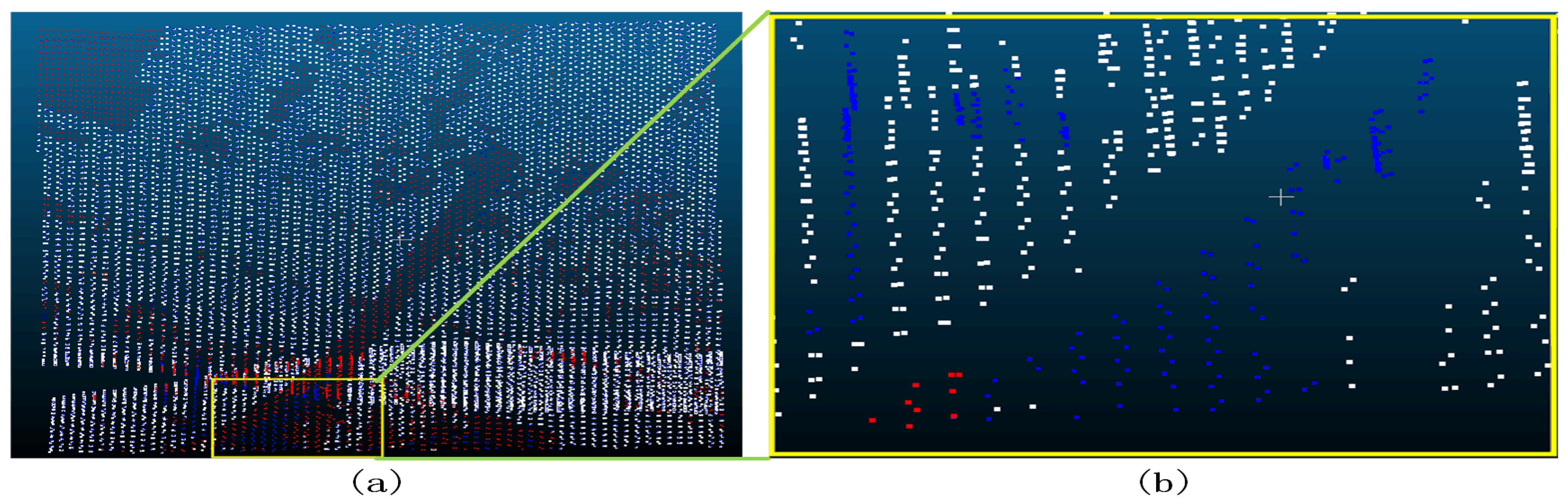
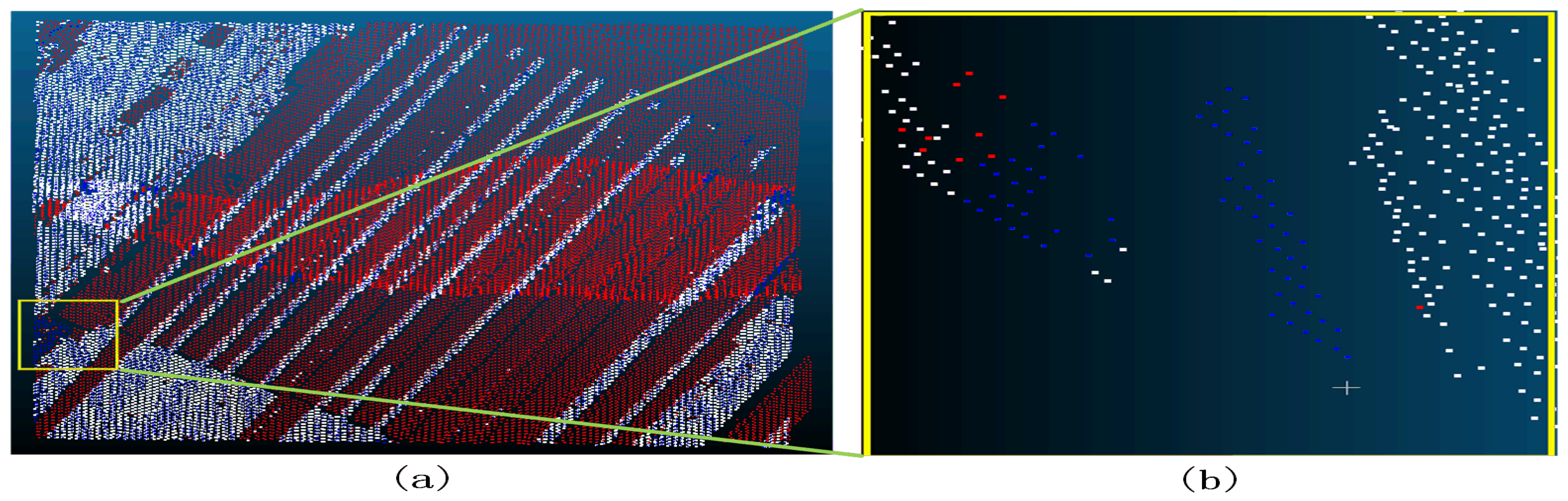
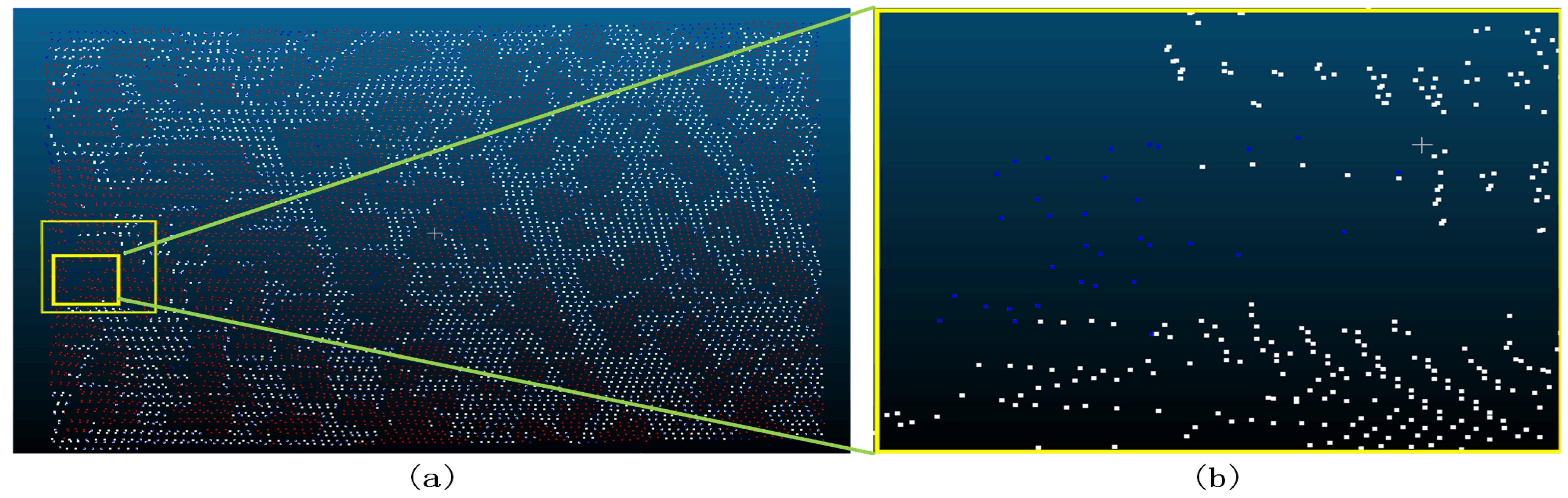
Figure 26.
Sample 2-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 26.
Sample 2-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
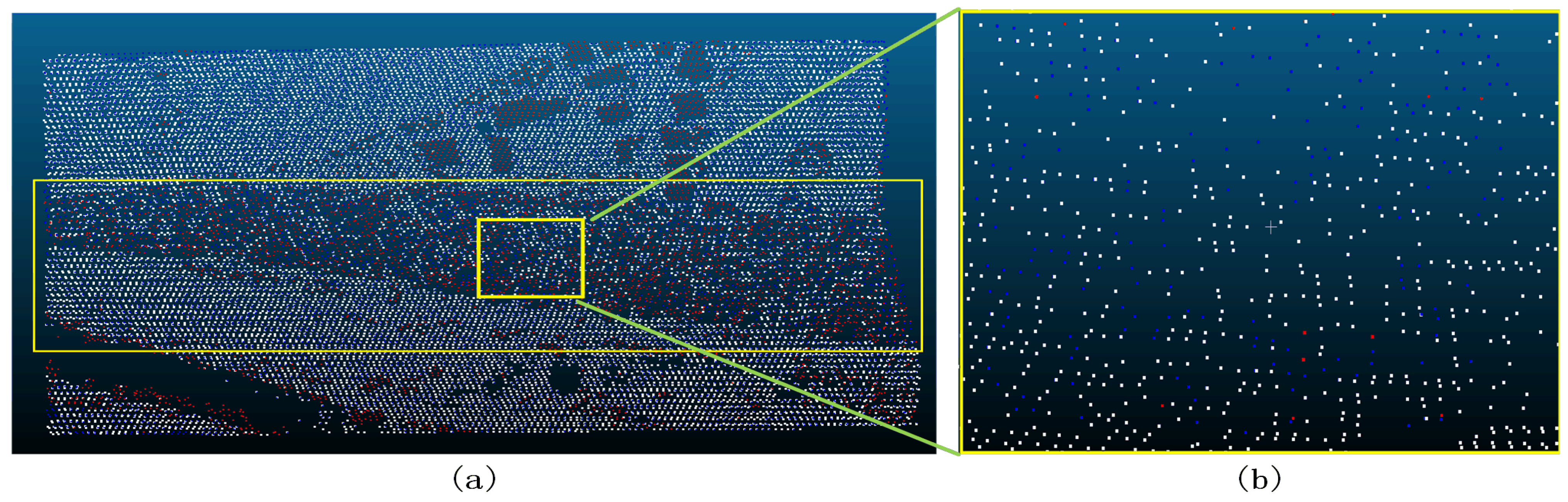
Figure 27.
Sample 2-2 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 27.
Sample 2-2 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 28.
Sample 2-3 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 28.
Sample 2-3 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 29.
Sample 2-4 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 29.
Sample 2-4 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 30.
Sample 3-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 30.
Sample 3-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 31.
Sample 4-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 31.
Sample 4-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 32.
Sample 4-2 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.)).
Figure 32.
Sample 4-2 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.)).
Figure 33.
Sample 5-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 33.
Sample 5-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 34.
Sample 5-2 after filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 34.
Sample 5-2 after filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 35.
Sample 5-3 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 35.
Sample 5-3 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 36.
Sample 5-4 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 36.
Sample 5-4 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
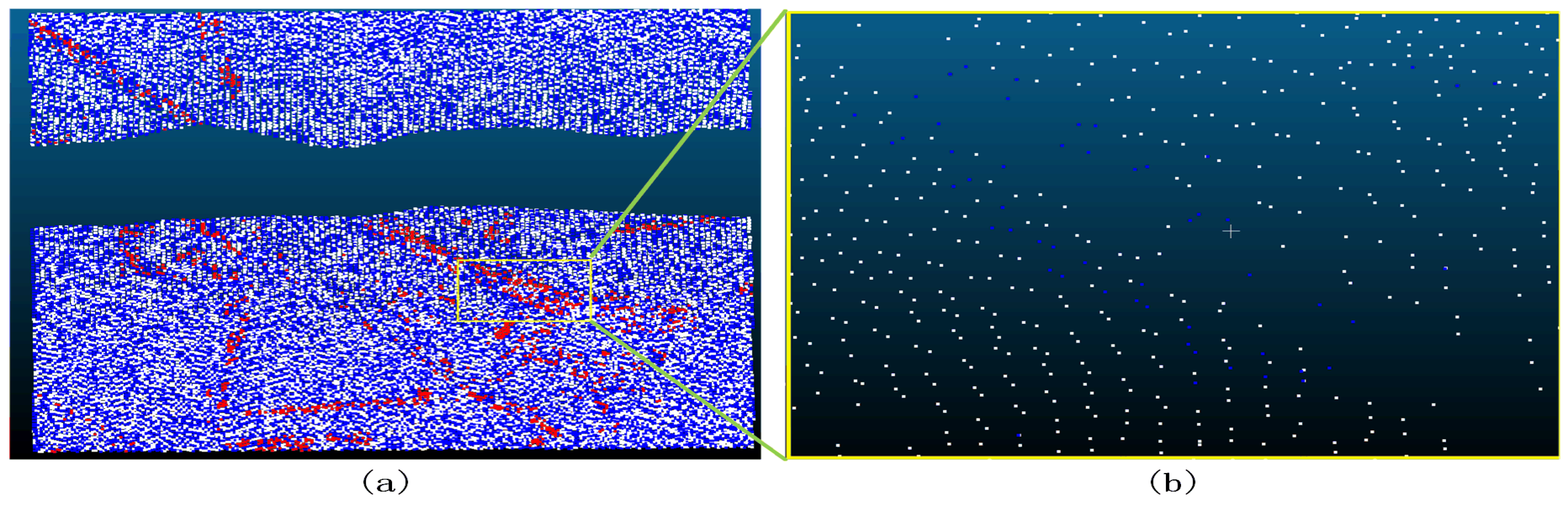
Figure 37.
Sample 6-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 37.
Sample 6-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 38.
Sample 7-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
Figure 38.
Sample 7-1 after the filter (a represents the overview of the filtering effect, the red dot in a indicates that the original data is not ground point, the blue dot indicates ground point, and the white dot indicates the remaining point after filtering as ground point; b represents the poor filtering effect, the red dot indicates Type II error, the blue dot indicates Type I error, and the white dot indicates the correct point.).
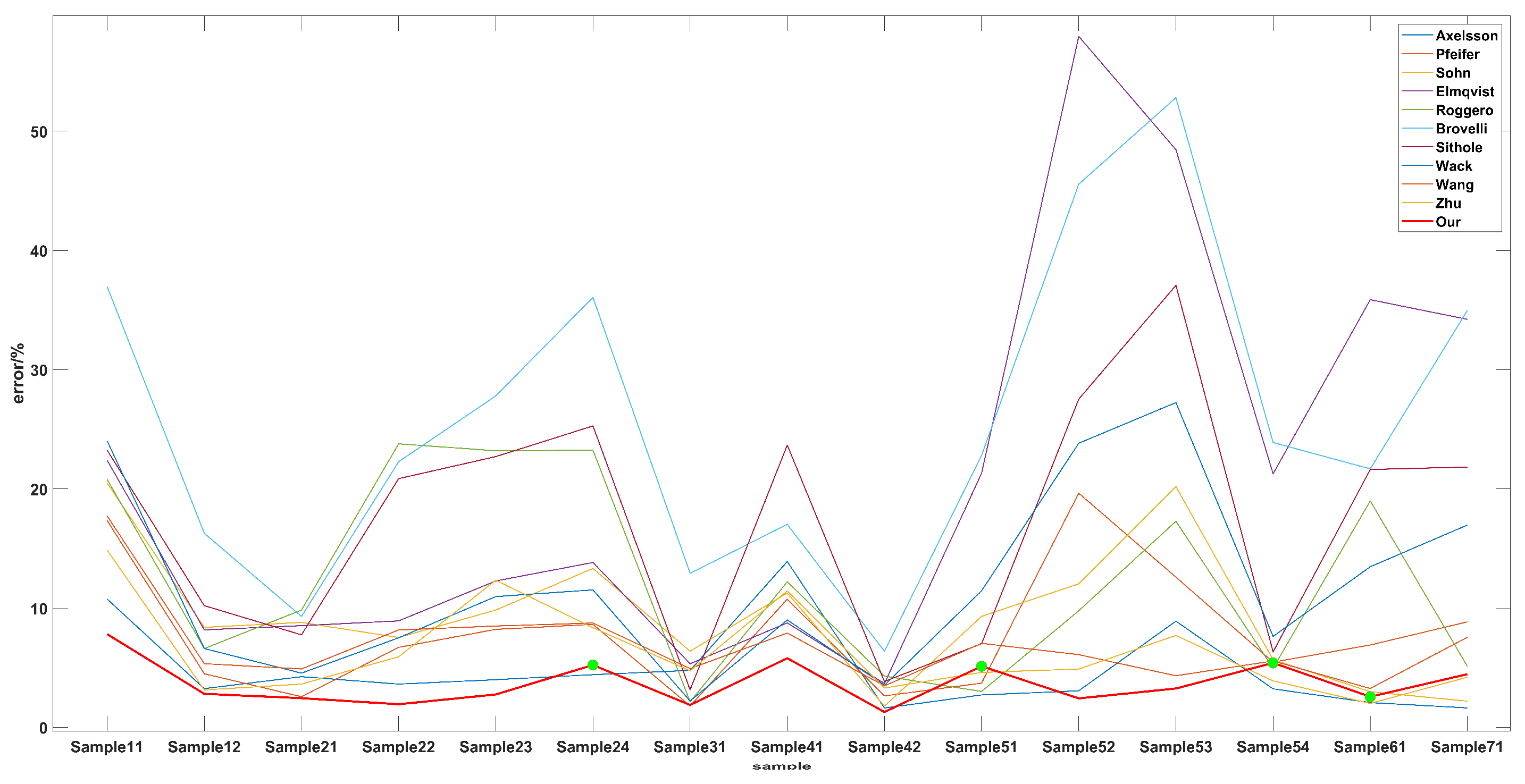
Figure 39.
The error of different methods in each sample.
Figure 39.
The error of different methods in each sample.
Figure 40.
Sample 3-1 surface reconstruction (a represents the original point cloud to construct the surface model, b represents the original ground point cloud to construct the surface model, c represents the filtered ground point to construct the surface model.).
Figure 40.
Sample 3-1 surface reconstruction (a represents the original point cloud to construct the surface model, b represents the original ground point cloud to construct the surface model, c represents the filtered ground point to construct the surface model.).
Figure 41.
Sample 5-4 surface reconstruction (a represents the original point cloud to construct the surface model, b represents the original ground point cloud to construct the surface model, c represents the filtered ground point to construct the surface model.).
Figure 41.
Sample 5-4 surface reconstruction (a represents the original point cloud to construct the surface model, b represents the original ground point cloud to construct the surface model, c represents the filtered ground point to construct the surface model.).
Table 1.
Filter Error Definition.
Table 1.
Filter Error Definition.
| Reference Data |
Filtered data |
Reference Data |
| The point of ground |
The point of non-ground |
| The point of ground |
a |
b |
e = a + b |
| The point of non-ground |
c |
d |
f = c + d |
| The point after filter |
g = a + c |
h = b + d |
n = a + b + c + d |
Table 2.
Three error types within the different methods (%).
Table 2.
Three error types within the different methods (%).
| Filter approach |
Type I error |
Type II error |
Total Error |
| EMD Filter[22] |
3. 5 |
33. 2 |
15. 4 |
| SMRF Filter[23] |
2. 4 |
35. 4 |
15. 8 |
| Segmentation-Based Filtering[5] |
1. 66 |
1. 64 |
1. 65 |
| Slope Filter[7] |
8. 5 |
23. 8 |
14. 7 |
| Cloth Simulation Filter[6] |
4. 57 |
2. 61 |
3. 77 |
| Our |
0. 76 |
0. 39 |
0. 55 |
Table 3.
Three error types within the Different Samples(%).
Table 3.
Three error types within the Different Samples(%).
| Sample |
Type I error |
Type II error |
Total Error |
| 1-1 |
10.76 |
3.86 |
7. 82 |
| 1-2 |
4.68 |
2.32 |
2. 81 |
| 2-1 |
2.70 |
1.57 |
2. 45 |
| 2-2 |
2.10 |
0. 72 |
1. 94 |
| 2-3 |
3.32 |
2.14 |
2. 76 |
| 2-4 |
5.26 |
5.15 |
5. 23 |
| 3-1 |
1.90 |
1.87 |
1. 88 |
| 4-1 |
10.64 |
0. 98 |
5. 80 |
| 4-2 |
3.76 |
0.26 |
1. 29 |
| 5-1 |
5.74 |
2.93 |
5. 13 |
| 5-2 |
2.14 |
4.91 |
2. 43 |
| 5-3 |
2.41 |
23. 47 |
3. 26 |
| 5-4 |
5.72 |
5.15 |
5. 41 |
| 6-1 |
1.05 |
31.76 |
2. 57 |
| 7-1 |
1.77 |
25.59 |
4. 46 |
| average |
4.26 |
7.51 |
3. 68 |
Table 4.
The Total Error Of the Different Methods(%).
Table 4.
The Total Error Of the Different Methods(%).
| Site |
Sample |
Axelsson
[5] |
Pfeifer
[24] |
Sohn
[25] |
Elmqvist
[26] |
Roggero
[27] |
Brovelli
[28] |
Sithole
[2] |
Wack
[29] |
Wang
[9] |
Zhu
[8] |
Our |
| Urban |
1-1 |
10. 76 |
17. 35 |
20. 49 |
22. 40 |
20. 80 |
36. 96 |
23. 25 |
24. 02 |
17. 74 |
14. 87 |
7. 82 |
| 1-2 |
3. 25 |
4. 50 |
8. 39 |
8. 18 |
6. 61 |
16. 28 |
10. 21 |
6. 61 |
5. 34 |
3. 14 |
2. 81 |
| 2-1 |
4. 25 |
2. 57 |
8. 8 |
8. 53 |
9. 84 |
9. 30 |
7. 76 |
4. 55 |
4. 90 |
3. 63 |
2. 45 |
| 2-2 |
3. 63 |
6. 71 |
7. 54 |
8. 93 |
23. 78 |
22. 28 |
20. 86 |
7. 51 |
8. 17 |
5. 92 |
1. 94 |
| 2-3 |
4. 00 |
8. 22 |
9. 84 |
12. 28 |
23. 20 |
27. 80 |
22. 71 |
10. 97 |
8. 50 |
12. 34 |
2. 76 |
| 2-4 |
4. 42 |
8. 64 |
13. 33 |
13. 83 |
23. 25 |
36. 06 |
25. 28 |
11. 53 |
8. 75 |
8. 36 |
5. 23 |
| 3-1 |
4. 78 |
1. 80 |
6. 39 |
5. 34 |
2. 14 |
12. 92 |
3. 15 |
2. 21 |
4. 93 |
4. 74 |
1. 88 |
| 4-1 |
13. 91 |
10. 75 |
11. 27 |
8. 76 |
12. 21 |
17. 03 |
23. 67 |
9. 01 |
7. 91 |
11. 44 |
5. 80 |
| 4-2 |
1. 62 |
2. 64 |
1. 78 |
3. 68 |
4. 30 |
6. 38 |
3. 85 |
3. 54 |
3. 48 |
3. 30 |
1. 29 |
| Rural |
5-1 |
2. 72 |
3. 71 |
9. 31 |
21. 31 |
3. 01 |
22. 81 |
7. 02 |
11. 45 |
7. 05 |
4. 61 |
5. 13 |
| 5-2 |
3. 07 |
19. 64 |
12. 04 |
57. 95 |
9. 78 |
45. 56 |
27. 53 |
23. 83 |
6. 10 |
4. 89 |
2. 43 |
| 5-3 |
8. 91 |
12. 60 |
20. 19 |
48. 45 |
17. 29 |
52. 81 |
37. 07 |
27. 24 |
4. 33 |
7. 71 |
3. 26 |
| 5-4 |
3. 23 |
5. 47 |
5. 68 |
21. 26 |
4. 96 |
23. 89 |
6. 33 |
7. 63 |
5. 57 |
3. 90 |
5. 41 |
| 6-1 |
2. 08 |
6. 91 |
2. 99 |
35. 87 |
18. 99 |
21. 68 |
21. 63 |
13. 47 |
3. 26 |
2. 01 |
2. 57 |
| 7-1 |
1. 63 |
8. 85 |
2. 20 |
34. 22 |
5. 11 |
34. 98 |
21. 83 |
16. 97 |
7. 56 |
4. 21 |
4. 46 |
| average |
4. 82 |
8. 02 |
9. 35 |
20. 73 |
12. 34 |
25. 78 |
17. 48 |
12. 04 |
6. 91 |
6. 34 |
3. 68 |