1. Introduction and Motivation
Car-following and lane change behaviour are far from being fully understood. This is illustrated by lack of consensus when it comes to explanatory mechanisms for many of the characteristics we can observe in data. For example, the capacity drop has been attributed to many plausible mechanisms, from reaction time dynamics (Yuan et al., 2017), a memory effect of obtaining larger headways in congestion (Treiber and Helbing, 2003), limited vehicle acceleration (Lebacque, 2003), and lane changes (Laval and Daganzo, 2006), to dynamics in task difficulty (Saifuzzaman et al., 2017). Microscopic traffic simulation models are widely used tools for the assessment of driver behaviour, road design, Intelligent Transport Systems (ITS) and autonomous vehicles. That many possible mechanisms may result in similar macroscopic phenomena underlines that, depending on the application of microscopic simulation models, more sophisticated mechanisms are needed to shed light on the underlying meso- and microscopic dynamics of traffic flow. This paper introduces a sophistication to shed light on social interactions in traffic flow.
A move towards more sophistication is particularly relevant, given the increasing importance of understanding the consequences of many different ITS and autonomous driving capabilities which are likely (and already) changing traffic flow dynamics in fundamental ways. Recent literature suggests, for example, that (Cooperative) Adaptive Cruise Control ((C)ACC) not only directly controls car-following but may indirectly also change important underlying driver traits such as desired headway (Gouy et al., 2014), reduce the number of lane changes and cluster desired speed (Schakel et al., 2017) and may also reduce a drivers’ attentiveness or willingness to for instance cooperate with merging drivers (Nowakowski et al., 2015). That cooperation between drivers—a form of social interaction—is key in explaining traffic dynamics, is widely acknowledged by many authors, particularly for lane changing (Treiber and Kesting, 2009; Farah and Toledo, 2010). As Zheng (2014) puts it “in heavy traffic, a typical LC (lane change) decision-making process involves at least two players – the lane changer and the follower in the target lane”.
A second crucial ingredient for adding more sophistication relates to heterogeneity in terms of driver traits and capabilities (and thus their behaviour). That heterogeneity is key to understanding traffic dynamics is also widely acknowledged (Chen et al., 2012; Leclercq et al., 2016; Ossen and Hoogendoorn, 2011; Treiber et al., 2006). As argued by van Lint and Calvert (2018), in most cases this heterogeneity is conceptualized exogenously (to the core car-following and/or lane change logic) by drawing key parameters (driver traits such as desired speed, or sensitivity to stimuli) from a presumed distribution over the population of drivers. To describe inter-driver heterogeneity (differences between drivers) this descriptive method is an effective approach. To describe intra-driver heterogeneity, e.g. the dynamics in the traits and preferences of a single driver along his trip, this approach is not effective, simply because it requires an a priori understanding of how these dynamics emerge. The logical alternative is to conceptualise these dynamics endogenously, so that driver heterogeneity emerges from the driver interactions and the prevailing circumstances themselves. For car-following, an increasing body of work seeks to explain driver heterogeneity in terms of the underlying cognition, e.g. by using the dynamics in task difficulty (van Lint and Calvert, 2018; Saifuzzaman et al., 2017) or in risk taking propensity (Hamdar et al., 2015). In this paper we aim to contribute to explaining intra-driver heterogeneity in driver behaviour, with a focus on social (i.e. multi-player) interactions, in which drivers willingly or unwillingly influence each other in their behaviour.
The literature on these social interactions in driving is limited, which is likely due to the inherent difficulty of observing and quantifying the phenomenon. Nonetheless, this is not a new topic. Juhlin (1999) observed driving lessons and concluded from conversations between drivers and instructors that in traffic informal rules are applied leading to cooperation between drivers. The hypothesis here is that interactions between drivers rely on communicating intent. One such informal rule taught to drivers in many countries is to conform to ‘flow priority’ (i.e. “go with the flow”), which may go against formal priority in certain circumstances. Some research is available on cooperative (or courtesy) behaviour at motorway merges, where drivers create room for another driver to change lane. This can be achieved either by changing lane or by yielding (Knoop et al., 2018). Research is lacking, however, on the different strategies involving social interactions that drivers apply. A key assumption underlying most car-following and lane change models is that drivers—aside from preventing collisions—egoistically aim to drive at their desired speed, which is usually considered a stochastic variable, i.e. a different constant for each driver.
Keyvan-Ekbatani et al. (2016) and Knoop et al. (2018) make a case that adapting desired speed—and possibly other personal traits—may be related to lane changing, or more specifically, to lane change strategies which drivers adhere to for longer time periods. Their key finding—based on interviews and empirical observations—is that lane change behaviour might be categorized into four strategies that essentially differ in terms of how much drivers are affected by their own preferences and by the preferences and behaviour of other drivers. Other researchers have argued from a game-theoretical point of view that in traffic, social dilemmas play an important role (Iwamura and Tanimoto, 2018). These authors also classify driver behaviour into four strategies along two dimensions: ‘lane changing if possible’ vs. ‘never lane changing’, and ‘hampering’ vs. ‘cooperating’ for lane changes of others. This creates strategies very similar to those proposed by Keyvan-Ekbatani et al. (2016). With these concepts they show how “chicken-type” dilemmas occur near critical densities (one has to concede, and the one who does is worse off); and likewise, “prisoner-type” dilemmas occur at higher densities (both could be better off, but at the risk of being worse off due to the other). The game-theoretical perspective has also been applied concerning cooperation for lane changing (Lütteken et al., 2016).
1.1. Contributions
In this paper, we introduce a behavioural theory that explains the lane change strategies proposed by Keyvan-Ekbatani et al. (2016) in terms of dynamics in driver traits (desired speed, desired headway and lane change desire) and the resulting social interactions. As these strategies are intricately related to longitudinal aspects of driving, we refer to the strategies as
driving strategies rather than lane change strategies. Moreover, this term fits better with the taxonomy of driving tasks by Michon (1985) as lane change strategies may be understood to be strategies for changing lane, whereas they are strategies in the social domain with lane changing being the primary tactical result assessed. The term driving strategies reflects this fact better; they are strategies for driving on the road, which is an inherently social context. The proposed theory is explored through simulation, to fill the research gap between empirical findings as shown in
Figure 1. The proposed theory improves the understanding of car-following and lane changing, in particular the variability thereof. The scope of this theory is driving strategies
on multi-lane motorways. The contributions of this paper are:
Empirically derived lane change strategies as discussed in literature (Iwamura and Tanimoto, 2018; Keyvan-Ekbatani et al., 2016) are conceptualized in a continuous 2-dimensional plane. One dimension explicitly adds social context to driving theory.
Endogenous mechanisms create inter-driver and intra-driver heterogeneity, that is dependent on prevailing circumstances in a social context.
Driver traits of desired speed, desired headway and lane change desire are explained as dynamic and dependent on social interactions, including social pressure and tailgating.
The social interactions, and correlated dynamic driver traits, are shown to influence mesoscopic traffic flow characteristics such as the number of lane changes, platoon lengths and headway distributions.
The resulting mesoscopic traffic flow characteristics are consistent with empirical findings from literature. The presented theory thus creates a link between empirical driver behaviour and empirical traffic flow characteristics.
This paper will explore the research gap by adding a plausible sophistication to the varied and growing body of explanations on nuanced traffic flow phenomena and driver behaviour. Through simulation, impacts on traffic flow are explored and found to be consistent with empirical findings. This brings our understanding further towards a theory on social interactions, and provides plausible hypotheses for future research to investigate and further validate.
1.2. Reading Guide
This paper is organised as follows. We discuss the starting points and requirements for the theory of driving strategies in section 2, and the theory itself in section 3. A modelling implementation of the theory is given in section 4.
Section 5 presents the methodology by which we assess the impacts of the theory, the results of which are presented in section 6. Finally, section 7 provides discussion and conclusions.
2. Starting Points and Requirements for a Theory of Driving Strategies
In this section we discuss the starting points of our theory (assumption and hypotheses of behaviour) and the requirements in terms of emerging micro- and mesoscopic traffic phenomena. This section lists 13 considerations that are referred to later in the paper. The considerations are largely based on empirical findings from literature that prescribe the social mechanisms to be present in the theory, and provide the relevant quantitative outcomes the theory can be tested against.
2.1. Starting Points: Behavioural Strategies and Dynamics
2.1.1. Lane Change Strategies
Our objective is to describe a quantitative theory of driving strategies in line with the four lane change strategies described and empirically underpinned by Keyvan-Ekbatani et al. (2016):
Speed leading; Drivers who adhere to their desired speed and are not easily persuaded to deviate from it.
Speed leading with speed increase at overtaking (socio-speed leading); Drivers who adhere to their desired speed but are willing to increase speed or get out of the way by changing lane for drivers that want to drive faster. For brevity and easier reference we will refer to this strategy as socio-speed leading.
Lane leading; Drivers who stay at a preferred lane so long as the speed does not deviate too much from the desired speed. This may be in a band of up to 40 km/h (Knoop et al., 2018). These drivers may dislike frequent lane changing, which also makes them less prone to change lanes for others.
Traffic leading; Drivers who are similar to lane leading drivers but may increase speed or change lane to get out of the way. These are typically novice or insecure drivers.
Clearly, these strategies govern the type of social interactions that may occur between drivers.
2.1.2. Behavioural Dynamics (Intra-Driver Heterogeneity)
Our key hypothesis is that these four driving strategies can be explained by dynamic settings of driver traits, and specifically, by the dynamics in desired speed, desired headway and lane change desire. We choose these traits, because they can be found in most conceptualisations of lane changing, and generally—regardless of how they are conceptualised—affect (a) the eagerness of drivers to change lane and (b) gap availability for lane changing, i.e. how gaps and platoons are distributed over lanes. We discuss the presumed dynamics of these driver traits in relation to the social interactions below:
- 5.
Desired headway. The dynamics in desired headways are relevant for social interactions through a phenomenon that we will call tailgating. Put simply, over shorter time periods, drivers are willing to maintain very short headways to communicate intent (Juhlin, 1999), i.e. to pressure drivers to get out of the way. There is empirical evidence that the tailgating mechanism indeed takes place. Portouli et al. (2012) found empirically that close following is used to indicate overtake desire on undivided roads. There is anecdotal evidence that close following is a means to prevent other drivers from merging in front. This is similar to the ‘hampering’ strategy by Iwamura and Tanimoto (2018). In this regard, tailgating is part of the chicken-type social dilemma.
- 6.
Desired speed. In relation to social interactions the hypothesis is that drivers may increase speed beyond their “regular” or “comfortable” desired speed during overtaking, which may have multiple effects. Increasing desired speed may close gaps for other vehicles wanting to cut in, or, it may do the opposite, that is, create gaps for vehicles to merge into. Decreasing desired speed affects the desire to overtake of the “ego-vehicle” and at the same time increases the desire to overtake of followers.
- 7.
Lane change desire. Although the desire to change lane can be conceptualised very differently (e.g. using trade-offs in discrete choice models (e.g. Farah and Toledo, 2010), or using thresholds in continuous incentive-based models (e.g. Schakel et al., 2012; Kesting et al., 2007)), our hypotheses in relation to social interactions can be tested in all such frameworks. We propose that, on top of many other reasons to change lanes, drivers have an explicit and dynamically changing desire to either get out of the way of (tailgating) followers, or to stay out of way of drivers closing in quickly on the target lane (i.e. to postpone a lane change). This desire is a function of other driver traits (e.g. desired speed) and circumstances.
2.2. Requirements: Social Interactions and Mesoscopic Characteristics
2.2.1. Social interactions
Consider a hypothetical example of a rather slow-moving personal car overtaking a truck. Before commencing the lane change movement, the driver in this car may allow a few fast-approaching vehicles to overtake the truck first. When overtaking the truck, the driver may increase speed beyond his/her regular desired speed as more fast driving (tailgating) vehicles are approaching. Finally, as soon as a suitable gap is available, the driver changes back to the slower lane after which the process may repeat itself.
- 8.
The theory should predict plausible and explainable social interactions (such as the truck overtaking process described above).
- 9.
Anisotropic traffic flow due to social interactions. As mentioned by Keyvan-Ekbatani et al. (2016) on speed leading with speed increase at overtaking: “This type of drivers seems to take the progress of other drivers more into account. However, note that none of the drivers commented explicitly on the driver following them. In the interviews of the non-test-drive participants, most participants mentioned that they did not want to hinder other traffic too much. Additionally, in other interviews, possible tailgating was mentioned as a reason.”
2.2.2. Mesoscopic Traffic Flow Characteristics
The key idea is that these microscopic behaviours (dynamics in desired speed, desired headway and lane change desire) affect mesoscopic traffic flow characteristics such as lane change frequency, platoon lengths and headway distributions. Fortunately, empirical findings on these mesoscopic traffic flow characteristics can be found in literature, as pointed out in considerations 10–12. This allows the theory to be tested against empirical findings. The behaviours also increase the realism and descriptive power of microscopic driving models. Depending on the implementation and parameter values, macroscopic traffic flow characteristics such as capacity and the capacity drop may also be affected. However, since existing models are already able to reproduce many macroscopic effects and phenomena, we focus on requirements at the mesoscopic scale.
- 10.
The theory should predict realistic lane change frequencies. As this depends heavily on the network and traffic density this is a circumstance-specific requirement. Knoop et al. (2012) found an average of 2.0-2.5km between lane changes, whereas Schakel et al. (2017) found an average of around 1.35-1.55km.
- 11.
Similarly, the theory should predict plausible headway distributions and platoon lengths. Also these depend heavily on traffic density. Several researchers have found that the headway distribution has a peak around 1.5s and a bulk between 1.0-2.0s (e.g. van Beinum, 2018). A wider headway distribution implies (more) short and compact platoons.
- 12.
Disturbances should be caused by lane changes, as Ahn and Cassidy (2007) found empirically to be the case.
- 13.
The theory should be parsimonious. We aim for the minimally required conceptualisation that reproduces plausible social interactions on multi-lane motorways and meets these requirements.
2.3. Summary
In summary, the starting points for our theory are four lane change strategies, which we aim to conceptualise using mechanisms that describe the dynamics of desired speed, desired headway, and lane change desire. These dynamics should result in social interactions (tailgating, get/stay out of the way behaviour) and in realistic mesoscopic traffic flow phenomena, in particular lane change frequency, headway distributions and platoon lengths.
3. Theory of Driving Strategies
The theoretical consideration in the previous section are conceptualized in a theory. We first discuss two new driver traits, and then describe a quantitative mechanism that uses these to reproduce the behaviours discussed in the previous section.
3.1. Ego-Speed and Socio-Speed Sensitivity
We conceptualise the four driving strategies using two new key driver traits, ego-speed sensitivity and socio-speed sensitivity. We define:
Ego-speed sensitivity; the extent to which drivers are willing (to act) to increase their speed. The value may for example be a product of risk-aversion, lane change aversion, and being in a hurry.
Socio-speed sensitivity; the extent to which drivers are willing (to act) to escape social pressure of following traffic that wants to drive faster. The value may be a product of risk-aversion, aversion to social pressure, and being in a hurry.
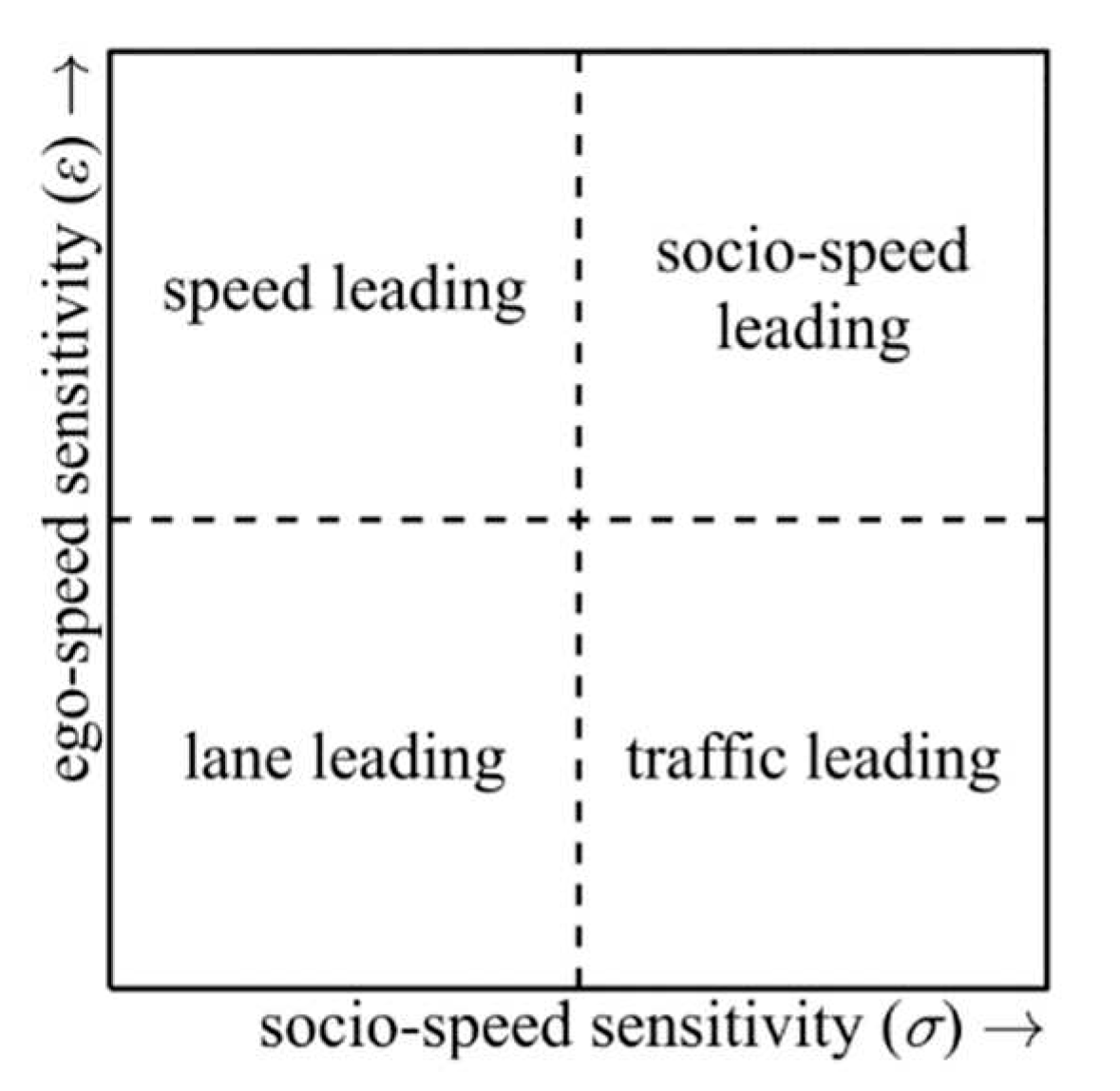
The traits ego-speed sensitivity and socio-speed sensitivity create a plane as in
Figure 2, in which we describe ego-speed sensitivity with parameter
, and socio-speed sensitivity with parameter
. The plane is divided into four quadrants, which coincide with the lane change strategies of Keyvan-Ekbatani et al. (2016), and also correlate to the strategies by Iwamura and Tanimoto (2018).
The population of drivers is distributed over this plane by their individual values of and . Speed leading drivers have high ego-speed sensitivity and low socio-speed sensitivity. In the case of socio-speed leading there is notable response to social pressure, by speeding up and changing lane out of the way. Lane leading drivers have low sensitivity overall and tend to stay in a lane. Finally traffic leading drivers have low ego-speed sensitivity and high socio-speed sensitivity, and are thus novice or insecure drivers.
3.2. Social Pressure and Tailgating
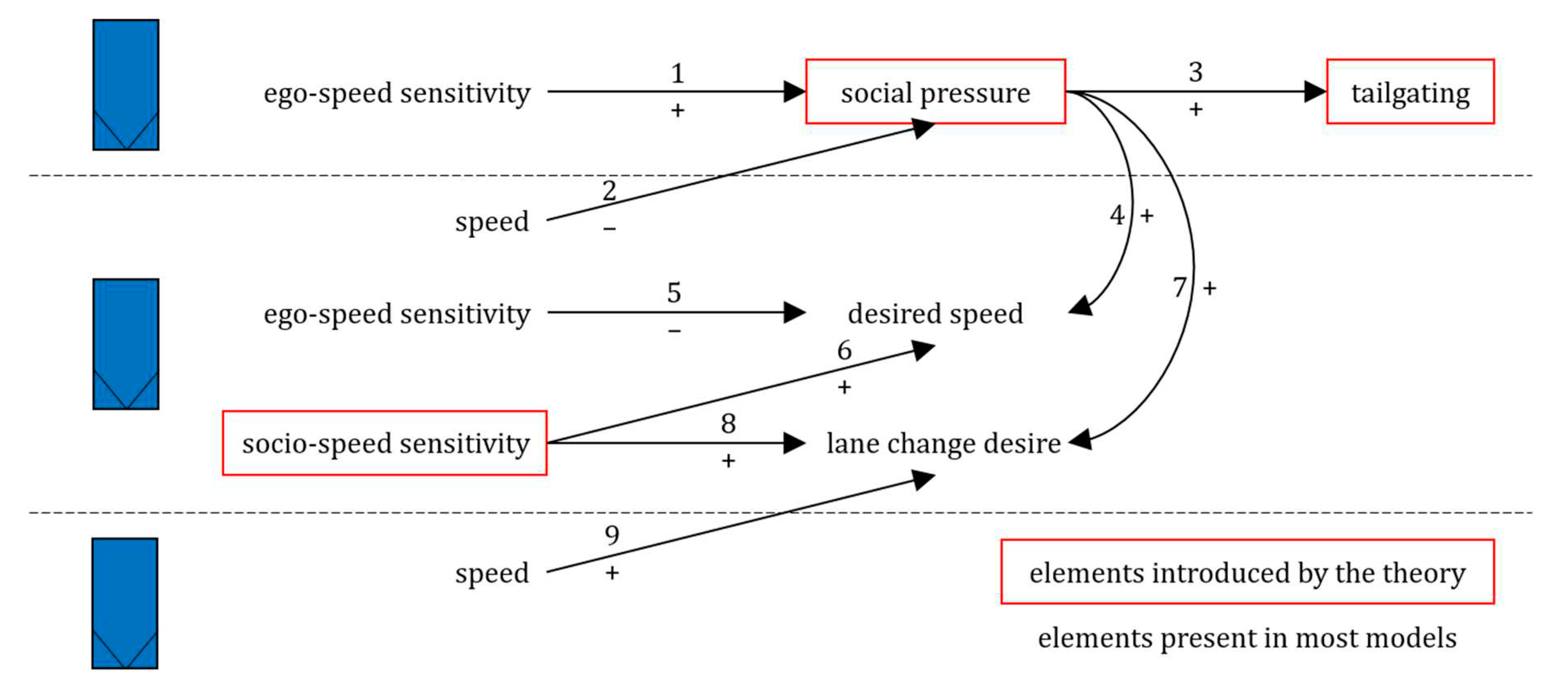
Social interactions are formalized with a dynamic state variable for social pressure. The perceived level of social pressure depends on the context but it is assumed to be mainly communicated to the leader and through lowering the headway, i.e. tailgating. The theory assumes a number of mechanisms based on social pressure. These are described in two parts, from the viewpoint of a driver applying social pressure, and from the viewpoint of a driver experiencing social pressure.
If a driver desires to drive faster than the leading vehicle, a social pressure arises. The extent of which depends on the ego-speed sensitivity (relation 1 in
Figure 3), and how much the driver wants to go faster than the leader (relation 2). The social pressure is communicated through increased tailgating (relation 3). However, the leader has a circumstantial perception of social pressure that is not directly related to the tailgating, as short headways may have other causes such as lane changing.
The leading driver has two strategies to alleviate the social pressure. The first strategy is to increase speed (relation 4). In Knoop et al. (2018) participants showed to be willing to increase speed by some extent. We assume the extent is hampered by the ego-speed sensitivity of the leader (relation 5), and enhanced by the socio-speed sensitivity of the leader (relation 6). Another strategy to alleviate social pressure is to change lane (relation 7). The extent of the resulting lane change desire relates to the socio-speed sensitivity (relation 8). Finally, if the leader itself is hampered by its leader, the lane change desire is less affected (relation 9). In this way, the leader does not give up a spot on the lane if that provides little utility given the circumstances.
It should be mentioned that relations 7, 8 and 9 obtain an opposite sign if a hypothetical situation on a potential target lane is assessed by a driver.
Figure 4 shows typical cases of social interactions between drivers.
Figure 4a shows a driver following a truck who may feel considerably suppressed in overtaking this truck in case of high social pressure
.
Figure 4b shows a driver who has just overtaken a truck and may feel considerably incentivised in changing to the slow lane in case of high social pressure
.
3.3. Driving Strategy Prevalence
Knoop et al. (2018) show drivers adopt a number of strategies. They find that 96% of drivers (at some point) adopt speed leading, 53% adopt socio-speed leading, 74% adopt lane leading, and (only) 1% adopt traffic leading. Note these percentages do not add up to 100%, since it is unknown for what percentage of time and under what circumstances drivers follow what strategy. Drivers may adopt all of them, or a selection, under specific circumstances. Either way, we conceive both ego-speed sensitivity and socio-speed sensitivity as (abstractions of) driver traits that may vary between drivers and that may even dynamically change as drivers encounter different conditions. Some drivers may simply have sensitivities which places them close to multiple quadrants, associating their behaviour with multiple strategies. Moreover, it is unclear at what value of
and
the behaviour can be considered to belong to one strategy or another. It is likely that the distribution should be weighted towards the upper left corner (speed leading) in
Figure 2, while the plane as a whole should cover values in a feasible range. Finally, the findings in Knoop et al. (2018) need not be representative. Note that in this paper we will apply 4 different 2-dimensional distributions, each designed to favour one of the strategies, to assess the impacts of each strategy more clearly.
4. Model for Verification
To assess the effects of driving strategies as proposed in the theory, this section explains a quantitative implementation for simulation.
4.1. Simulation Framework
Although multiple methodologies are possible to implement the framework for driving strategies, we apply LMRS (i.e. previously developed by the authors) as a main platform for the mathematical implementation of the novel model proposed in this paper. This choice is based on the fact that LMRS in combination with IDM+ for car-following has been shown to accurately describe speed differences between lanes, as well as the distribution of traffic over the lanes for various density levels (Schakel et al., 2012). Moreover, the model can be easily extended with additional lane change incentives and other modules. Finally an efficient implementation is available in OpenTrafficSim (van Lint et al., 2016). In the discussion section we discuss how the framework presented may also be used in conjunction with other lane change and car-following models. The changes we make to the model serve to relate quantitatively the empirically found driving strategies with the empirically found mesoscopic traffic flow characteristics. Such changes can be implemented in other models in similar quantitative fashion. This results in similar changes in mesoscopic traffic flow characteristics. For instance, the tailgating phenomenon varies the desired headway, and hence influences the measured headway distribution, irrespective of the car-following model. For convenience, we list the variables and parameters used in the ensuing sections in
Table 1.
4.2. Original LMRS Model
This section recalls some of the main principles and parameters of the applied base model. The Lane change Model with Relaxation and Synchronization (LMRS) (Schakel et al., 2012) was developed to accurately match lane speeds and distribution of traffic over lanes by considering a number of lane change incentives that result in a lane change desire
. Equation (1) shows that a balance is found between desire to follow the route and infrastructure
, to gain or maintain speed
, and a bias for a right-keeping rule
. Each of the three incentives is determined based on circumstances. For details the reader is referred to Schakel et al. (2012). The voluntary incentives
and
are included with a factor
, which approaches 0 as
increases such that a balance between all incentives is made based on urgency.
The level of lane change desire determines resulting lane change behaviour. Four regions are distinguished by thresholds as in equation (2). Below
, no lane change is considered. Free lane changes (FLC) may be performed for
, to the degree it is possible. Synchronized lane changes (SLC) are performed for
, meaning that a driver synchronizes speed and position to a gap in the target lane to enhance lane change opportunities. Finally, for
the potential follower in the target lane additionally cooperates (CLC) to create a gap. Both synchronization and cooperation are modelled by applying the car-following model to the leader in the appropriate adjacent lane, albeit with limited maximum deceleration.
Additionally, the level of lane change desire determines risk taking in gap-acceptance. For larger lane change desire, the acceptable deceleration increases, and the acceptable headway decreases. Accepting short headways during a lane change, and relaxing the headway back to normal values afterwards, is known as the relaxation effect (Laval and Leclercq, 2008). The key parameters here are the regular headway and the minimum acceptable headway (at maximum lane change desire) , we return to these below, because they play an important role in the tailgating principle. The maximum acceptable deceleration at full lane change desire is , which is also explained below. Other parameters used to determine the desire from the three incentives are also used in the model extensions described in the next section. These are anticipation distance , which can be regarded as a look-ahead distance; a threshold speed below which drivers consider traffic as congested ; and , which is a speed difference between lanes for which lane change desire is maximal.
The IDM+ car-following model (Schakel et al., 2010) is an adaptation of the original IDM model (Treiber et al., 2000), in which free driving and car-following are decoupled, so that more realistic capacity distributions emerge (Schakel et al., 2012)—see equation (3). Acceleration is a function of incentives ego-speed
, speed difference with the leader
and net distance headway
, with parameters desired speed
, maximum acceleration
, maximum comfortable deceleration
, stopping distance
and desired headway
. Note that
is dynamic in our case and between
and
. The value of
describes how slowly acceleration reduces as speed increases, and usually a value of 4 is used (Treiber et al., 2000).
4.3. Implementation of Social Driving Strategies in LMRS
In this section we introduce new elements to the LMRS which capture the behaviour of the driving strategies introduced above. First, we introduce the ego-speed sensitivity () dimension, which is already present in the LMRS, after which the socio-speed sensitivity () dimension is elaborated.
In the LMRS model, the parameter
describes at what speed difference between lanes a maximum lane change desire arises. The lower
, the more sensitive a driver is to ego-speed, since lower speed differences between lanes already result in maximum lane change desire. Equation (4) thus describes a suitable linkage of
to the LMRS.
A new variable is required for the inclusion of socio-speed sensitivity , which is the only new LMRS parameter we introduce. This satisfies parsimony (consideration 13, section 2)
4.3.1. The Social Pressure Construct
A key effect we aim to establish is that
social pressure is perceived by a leader and exerted by a follower
1,
2. In this section we refer back to the relations indicated in
Figure 3. We construct the social pressure exerted by a follower as proportional to
, with
the speed of the leader and
the
desired speed of the follower (relation 2). For drivers with larger ego-speed sensitivity
, the applied pressure is larger (relation 1). Equation (5) describes a mechanism that establishes this. First, Equation (5) includes a distance factor
, such that social pressure diminishes for leaders far away (recall
represents a max-look-ahead distance in the LMRS model). Secondly, we use an exponential function such that behaviours from social pressure quickly arise but stabilise fairly quickly as well. So, for
(i.e. large speed differences and/or small gaps combined with high ego-speed sensitivity of the follower) drivers show behaviour that is as risky as they are willing to allow.
To ensure that tailgating takes place, we require a mechanism that enables followers to “pressure” leaders (also those not sensitive to this pressure) with short following time headways. The LMRS provides a natural way to do this. To model relaxation, the desired headway
is already dynamic between
and
in the relaxation case. When a lane change is initiated, the current value of
T is set to some lower value, whereas every consecutive time step the headway is relaxed towards
. Similarly, in case of social pressure, the desired headway of the follower
can be kept low by setting it according to equation (6) (relation 3). Here,
is the desired headway according to the relaxation phenomenon. Should social pressure disappear, for instance because the leader changes lane, the value will then relax to
by
, the restrictive term in equation (6) for low values of
.
With these ingredients we can now affect the leaders’ driving behaviour by the social pressure from the follower. For this behaviour we use parameter as a value in the range [0…1], where 0 means a driver is not sensitive to the social pressure of other drivers, while 1 means the driver is very sensitive. We explain how these mechanisms work below.
4.3.2. Adapting LMRS Lane Change Incentives and Desired Speed Model
We first discuss how we alter lane change desire. The basic idea of our implementation is to include an
additional lane change incentive
for socio-speed sensitivity to the LMRS, changing Equation (1) into Equation (7).
This incentive may
reduce lane change desire towards the faster lane (to stay out of the way of faster “followers” on that lane), and/or it may increase lane change desire towards the slower lane (to get out of the way).
Figure 5 and
Table 2 show the same two cases as
Figure 4, now annotated with the LMRS lane change desire. The two cases are essentially mirrored, except that in the “stay out of the way” case (
Figure 5a), the follower of the truck in the slow lane considers a hypothetical situation in which it drives on the faster lane. This hypothetical situation is denoted by prime (
) where relevant.
We first explain the increased desire to change to the right lane in order to get out of the way (
Figure 5b). Recall that the extent of the lane change desire depends on
such that socio-speed sensitive drivers are more prone to get out of the way. Hence, we model the extent of this new lane change desire with
, which is a value between 0 and 1 as the LMRS requires. The incentive is more complex in terms of the conditions that need to apply for the socio-speed incentive (and the associated behaviour) to be considered by a driver. These conditions (in order of priority) are:
; a lane change to the right lane is possible and legal.
; lane change desire dictated by infrastructure/route does not conflict.
; there’s no congestion (there is no point as traffic is constrained then).
; this implements relation 9 in
Figure 3 by considering the social pressure from the follower (with sensitivity), and comparing it to the social pressure of the leader.
If these four conditions apply, we set
, otherwise “0”. These conditions and the resulting incentive to move towards the right (slow) lane are summarized in the right most column of
Table 2. The other case, that is, a decreased desire to move to the left (the fast lane), is essentially the mirror image of the increased desire to move to the right (the slow lane). As a result, it differs in sign only.
We now finally discuss how we increase the desired speed during overtaking for socio-speed sensitive drivers. The resulting desired speed model is given in equation (8). The increase of the desired speed relative to the base model can be up to
depending on
. With
this results in
specifically for the LMRS. In illustration, in case of high social pressure (e.g.
) and the strategy socio-speed leading (e.g.
,
) the speed is increased by 14km/h.
To summarize, we extend the LMRS with a notion of social pressure applied to the leader which depends on the ego-speed sensitivity . This leads to tailgating of the follower, which in turn has two behavioural effects on the leader. The leader has increased lane change desire and increased desired speed, depending on its socio-speed sensitivity and its ego-speed sensitivity . As a final note: for readability purposes we will further below refer to different settings for rather than for , since these translate to speeds and are more easily interpretable.
5. Evaluation Methodology
This section describes the methodology to evaluate the effects of driving strategies on traffic flow. We first describe the simulation setup, and then the scenarios and performance indicators.
5.1. Simulation Setup
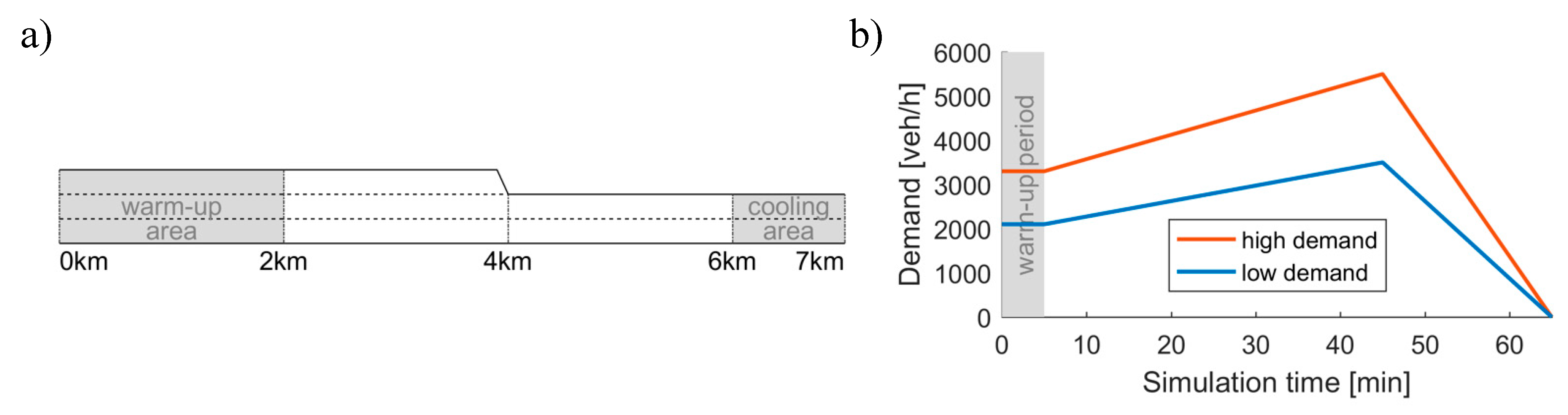
The strategies are tested on a 7km long motorway stretch depicted in
Figure 6 and simulated in OpenTrafficSim (van Lint et al., 2016), with a lane-drop from 3 to 2 lanes after 4km. This is the simplest network to create all situations the theory is sensitive to. The lane-drop causes mandatory lane changes and allows the strategies to be tested in case of congestion and free flow. The speed limit is set to 120km/h. All strategies are tested for a low and a high demand scenario, with peak demands of 3500veh/h and 5500veh/h respectively. During a 5-minute warm-up period, demand is at 60%. In the next 40 minutes demand increases linearly to peak demand, to reduce to 0 at the end of simulation after 65 minutes. The simulation time step is 0.5s.
The percentage of trucks is fixed at 10%. Trucks are simulated with socio-speed sensitivity and . This assures that trucks are mostly driving on the right-hand lane. Note that we are simplifying here, since trucks of course do overtake for marginal speed gains in reality. This is beyond the scope of this paper. Due to the stochastic nature of the simulation environment, each scenario is run 30 times (with 30 different seeds) to obtain reliable indicators.
5.2. Simulation Scenarios
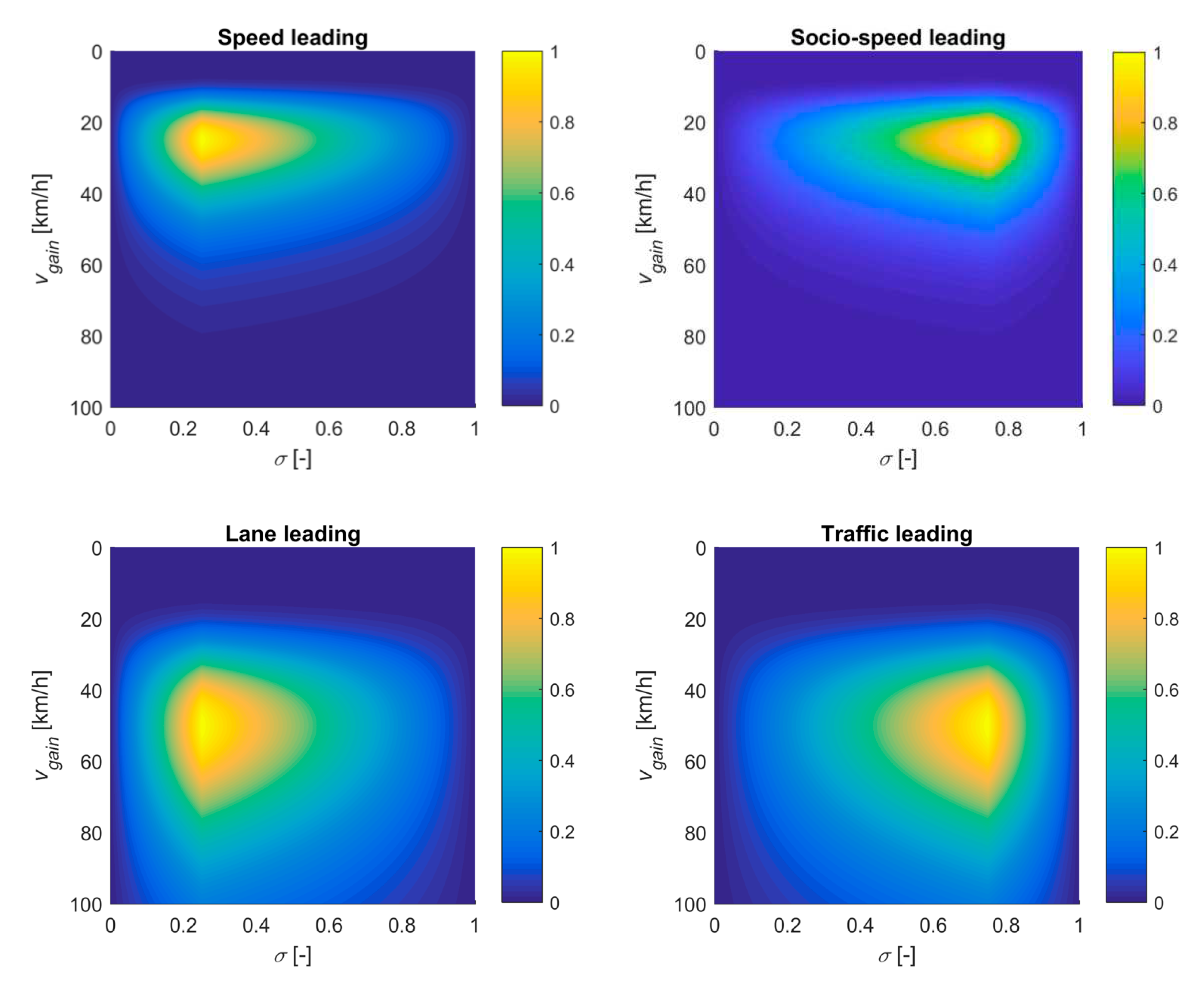
The strategies are compared by defining a scenario for each driving strategy, where the weight of the ego-speed sensitivity and socio-speed sensitivity distribution is in one of the four quadrants of
Figure 2. By comparing the four strategies the influence of parameters describing ego-speed sensitivity and socio-speed sensitivity can be inferred. Additionally, we include a base scenario of the LMRS without extensions. We assume drivers may have different ego- and socio-speed sensitivities, so we model these differences by drawing
(
) and
from distributions. For the ego-speed sensitivity we use a log-normal distribution to provide positive values of
. The standard deviation of the underlying normal distribution is 0.4, chosen for a reasonable spread. The chosen mode values of 25km/h and 50km/h are chosen to be distinct but below the value in the base scenario as to increase the number of lane changes relative to the base model, which section 6.2 shows to be necessary. Socio-speed sensitivity
is distributed with a triangular distribution with strict minimum and maximum of 0 and 1, with the mode in either the middle of the lower or upper half. The defined scenarios along with the parameters’ distributions are listed as follows (shown in
Figure 7):
Base; base LMRS without extensions
Speed leading; mode of 25km/h, mode of 0.25
Lane leading; mode of 50km/h, mode of 0.25
Socio-speed leading; mode of 25km/h, mode of 0.75
Traffic leading; mode of 50km/h, mode of 0.75
Since tailgating is applied in the four strategy scenarios, should be increased to reach an effective headway value similar to the base LMRS, and hence similar capacity. Given that speed leading is the most prevalent strategy, we have chosen to match mean maximum flow and mean saturation flow in the speed leading scenario with the base LMRS, and hence choose a parameter value of . For the base scenario equals 1.2s since no tailgating applies. Other important default parameters, which are shared among all five scenarios for good comparison, are: , , , , , , , and . All the parameter values are based on the calibration efforts in (Schakel et al., 2012).
5.3. Assessment Indicators
We assess the effects in 4 ways: (1) qualitative assessment of the trajectories, (2) quantitative assessment of the number of lane changes, (3) quantitative assessment of the distribution of platoon length and headways and (4) an assessment in to the number of lane changes as we introduce separate parts of the model.
So first, the social interactions of the driving strategies are qualitatively illustrated by comparing the base scenario and the speed leading scenarios (both with low demand). We show the vehicle positions. For visualization purposes, we show them relative to a subject vehicle by subtracting its position from all trajectories, resulting in gross headway to the subject vehicle. A truck is selected for the analysis, as trucks are moving slowly. Other traffic will generally move faster (hence traffic moves forward also in this frame of reference) and trucks form moving bottlenecks around which cars manoeuvre according to the strategies. All other performance measures are computed with (densely spaced simulated) loop detectors.
The number of lane changes (left and right) categorized by the largest incentive causing them is derived on the section from 2km to 6km for each lane. We also include the average distance between two consecutive lane changes of a single vehicle by dividing total vehicle mileages over the total number of lane changes. Here, total vehicle mileage is approximated by taking 70% of the peak demand (which is average demand) and multiplying by the section length of 4km (and by 1-hour simulation time).
Platoon distribution and headway distribution are derived. Platoon distribution is derived as the probability a vehicle is found in a platoon of specific size (not the probability a given platoon has a certain size). Two consecutive vehicles are considered to be part of the same platoon if their gross headway is less than 3s, as measured by their nose moving over the detector. Headway distributions are given by counting the number of measurements in bins of 0.1s width, up to 5s.
Finally, the number of lane changes is assessed as we introduce separate parts of the model: ego-speed sensitivity, socio-speed sensitivity and tailgating. To this end we define two additional scenarios:
Ego-speed sensitive; base scenario with . This scenario introduces to the base scenario an ego-speed sensitivity at a comparable level to the speed leading scenario.
No tailgating; Speed leading scenario without tailgating and with . This scenario introduces socio-speed sensitivity. As tailgating is still excluded, comparison with the speed leading scenario allows to assess the impact of tailgating.
6. Results
This section presents and discusses important findings from simulating the novel driving behaviour, proposed in this paper. We start with a qualitative analysis in which we demonstrate and face-validate that the addition of socio-sensitivities leads to new realistic behaviours in line with our theoretical framework. This is followed by a comparative quantitative appraisal of the proposed simulation scenarios by looking at the number of lane changes and the distributions of headways and platoon lengths. Note that by comparing the scenarios we explicitly compare the impact of different parameter values (distributions) regarding ego-speed sensitivity and socio-speed sensitivity. At the end, analysis is carried out to distinct individual contributions of the social phenomena to the number of lane changes. This sections refers to the theoretical considerations from section 2.
6.1. Qualitative Evaluation
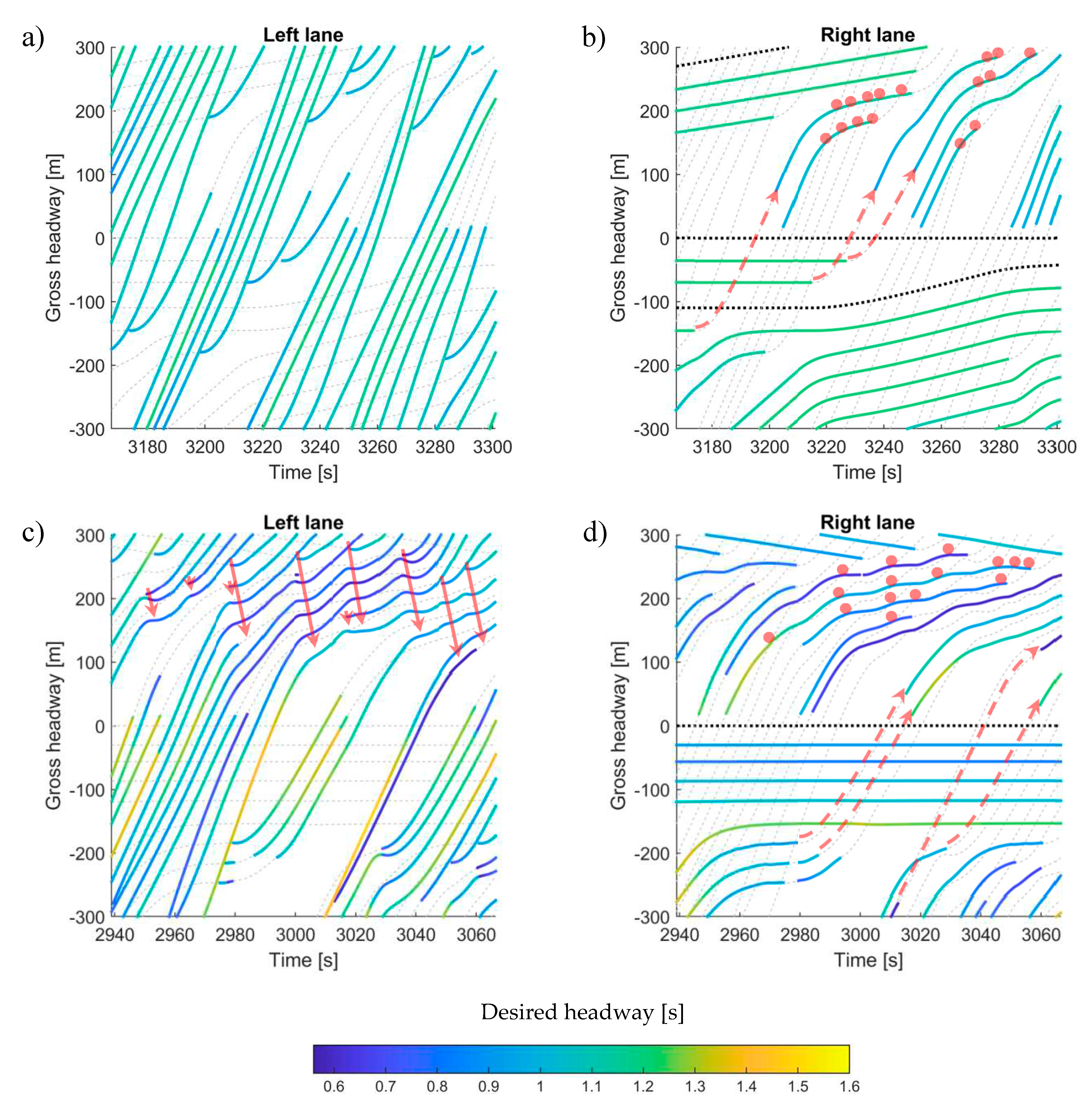
A qualitative analysis of the behaviours implied by driving strategies is shown in
Figure 8 for a run of the base scenario (
Figure 8a,b) and the speed leading scenario (
Figure 8c,d). In each graph, on the vertical axes, distance gaps between trajectories are given relative to a truck driving on the right lane during the time it moved from 4km to 7km (in the two-lane section). The colouring of each relative trajectory is informative of the driver’s desired headway
. Trucks are represented as black dotted lines. Trajectories of vehicles on the other lane are shown as grey dashed lines.
Let us first note that in both scenarios (
Figure 8a–d) social phenomena can be observed (consideration 8). Clearly, in the base scenario (
Figure 8a,b), drivers—incentivised by the three standard LMRS components—overtake other drivers by changing left and changing right again after the act (red dashed arrows). Conversely, drivers are being overtaken by other drivers by changing right and—at some point—by changing back left again (dots in figure). There are however also social phenomena occurring in the speed leading scenario, that
do not occur in the base scenario (consideration 7), but do arise in the other (three) driving strategies as well, albeit with different frequencies. These are:
Disturbances on the left lane due to lane changes, indicated by continuous arrows in
Figure 8 (consideration 12).
Circumstantial change of desired headway due to social pressure, i.e. tailgating and preventing lane changes in front (consideration 5). For instance, small desired headways (where trajectories are coloured blue) are seen where the left lane is disturbed (slow). For some vehicles the same is found on the right lane, while experiencing difficulty in changing left due to short headways on the left lane.
Circumstantial change of desired speed, which is inferred by the change in desired headway due to social pressure (consideration 6).
These phenomena show that the resulting traffic dynamics, in terms of desired headway and desired speed, are anisotropic (consideration 9), i.e. influenced by following traffic.
To further understand the behaviours we looked at the values of
,
and
of some of the individual drivers. We start with four vehicles that during the timespan shown, remain behind the truck in the speed leading scenario, indicated by the four horizontal trajectories underneath the (black) truck trajectory in
Figure 8d. The first two are socio-speed leading (consideration 2), where the socio aspect determines behaviour due to low desired speed or sensitivities more towards socio. The other two drivers tend much more to lane or traffic leading (considerations 3 and 4).
We now focus on four other vehicles in the speed leading scenario (i.e. in
Figure 8d) indicated by dashed arrows that change left from behind the slow vehicles and the truck, to overtake and then change back to the right lane. These drivers are speed leading (consideration 1), which explains the lane change to the fast lane. The lane changes back to the slower lane are due to disturbances (i.e. temporary lower speeds) on the fast lane.
6.2. Number of Lane Changes
Table 3 shows the number of lane changes performed for each scenario, categorized by lane, direction and by the largest of the four incentives involved. This results in nine sensible categories. For instance for the first lane changes column ‘3>’ indicates lane changes from the left lane (3
rd as counted from the right) to the middle lane. The symbol
dr indicates that the route incentive had the largest desire for this lane change.
In the low demand scenarios, the lane leading and traffic leading strategies reduce the number of lane changes compared to the base scenario. The negative socio-speed incentive reduces the number of lane changes made from the right lane to the middle lane (<1) for speed (
ds). With fewer slow drivers on the middle lane, also less lane changes from the middle to the right lane (2>) to keep-right (
db) are performed. In the high demand scenario, we see a significant increase in all lane changes caused by all lane change incentives. This is emphasized in the right-most two columns of
Table 3, which show the totals over all incentives and the average travelled distance between lane changes. The resulting distance between lane changes is similar to empirical findings (consideration 10) of 2.0-2.5km (Knoop et al., 2012) and 1.35-1.55km (Schakel et al., 2017).
6.3. Platoon and Headway Distribution
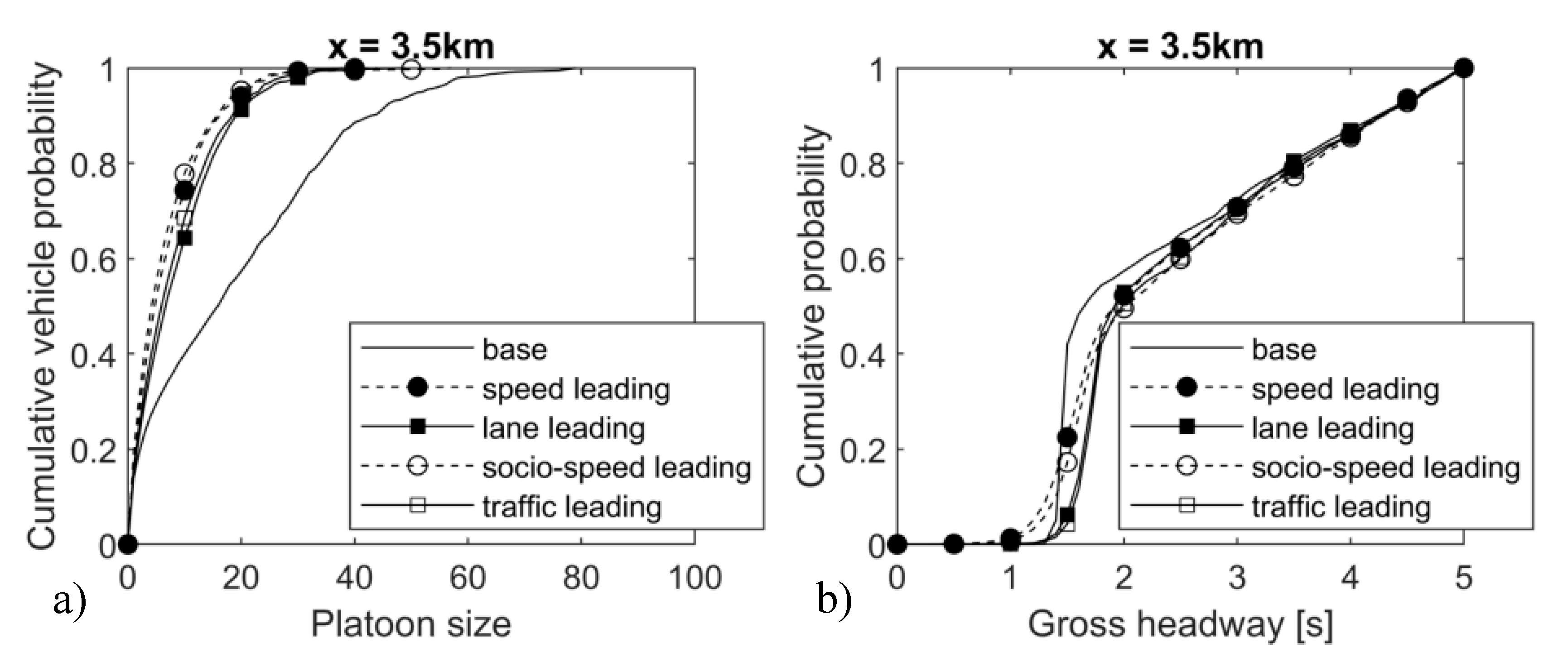
There appears to be a clear relation between distribution of platoon sizes and the four driving strategies (consideration 11). This is shown in
Figure 9a which shows platoon sizes of platoons passing at 500m before the lane-drop under high demand—but this phenomenon is also found on other cross-sections and under low demand. The results indicate the order of equation (8) in resulting platoon sizes, where
L i is the platoon size for scenario
i in vehicles at any given cumulative probability.
In other words, high ego-speed sensitivity leads to traffic flows with the smallest platoon sizes, followed by low ego-speed sensitivity, and the base case without social interactions. Socio-speed sensitivity
by itself seems to have a limited effect on platoon sizes or on headway distributions. This is illustrated by the fact that speed leading and socio-speed leading, as well as lane leading and traffic leading, have very similar curves in
Figure 9. Particularly on the left lane (
Figure 9a) the difference between the base scenario and all other scenarios is remarkable, which is likely due to much fewer lane changes between the left and middle lane.
Headway distributions are affected by the driving strategies as well, as
Figure 9b shows. All strategies have the effect of dispersing the headway distribution wider than in the base case, where the (socio-)speed leading strategies result in the largest variance. With a peak around 1.5s and a bulk between 1.0-2.0s, this is in line with empirical (consideration 11). We also found that platoon size distributions and headway distributions look more similar between the different driving strategies (including base) on the middle lane, as this lane is much more saturated.
To shed more light on the separate contributions of ego-speed sensitivity; socio-speed sensitivity and tailgating on the results we discuss the two additional scenarios introduced in section 5.2 in the next section. In particular, we will test the number of lane changes resulting from introducing these three components.
6.4. Sensitivity Analysis on Social Phenomena
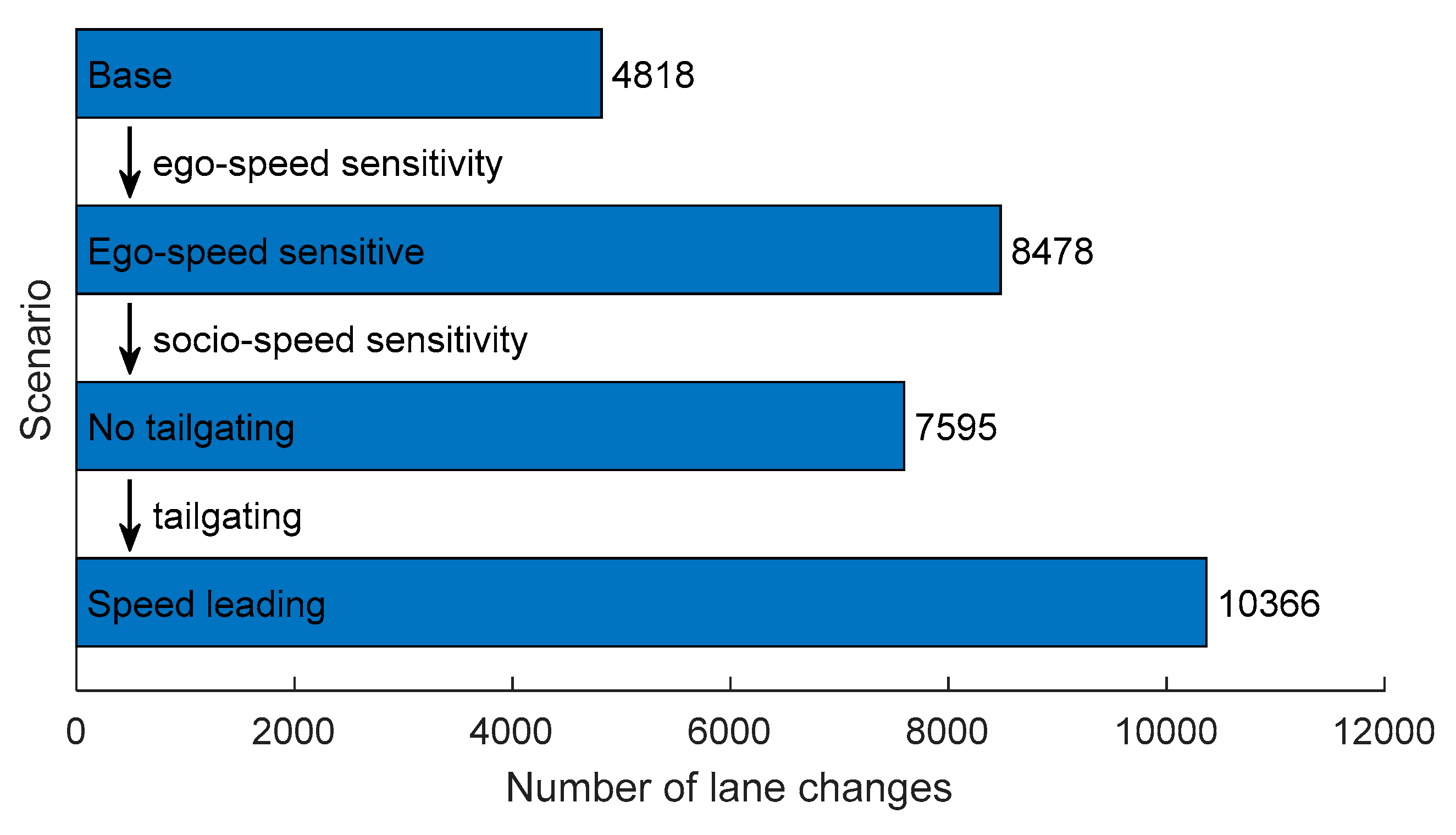
By introducing the separate social components of the model, the effects of the separate components on the number of lane changes can be assessed. This starts with the base scenario (no components) and ends with the speed leading scenario (all components). Two additional intermediate scenarios are used to introduce individual components, see
Figure 10.
A comparison between the ‘base’ scenario and ‘ego-speed sensitive’ scenario shows that introduction of ego-speed sensitivity (by means of a lower value) considerably increases the number of lane changes. However, the higher value of in the base scenario is a calibrated value and lowering it introduces disturbances and hence lowers capacity. Such disturbances are reduced by introducing socio-speed sensitivity, which the ‘no tailgating’ scenario does. The number of lane changes is somewhat reduced, but the socio-speed sensitivity seems to mostly reallocate lane changes to more appropriate times. Finally, comparison of the ‘no tailgating’ and ‘speed leading’ scenarios shows that introducing the tailgating phenomenon increases the number of lane changes once more. This may appear counter-intuitive, but note that the tailgating phenomenon mainly widens the distribution of headways (as we have selected in the speed leading scenario to result in a similar mean). The occurrence of larger headways allows more lane changes.
These findings can be summarized as follows. The ego-speed sensitivity makes drivers want to change lane more. The socio-speed sensitivity makes them wait for more appropriate times. And tailgating creates platoons between which available gaps are present. One could even postulate that without such gaps, drivers would likely not develop socio-speed sensitivity to the extent that they actually do in the first place.
7. Discussion and Conclusions
In this paper we discussed the fact that there are social interactions on multi-lane motorways and formulated a theory. The theory conceptualizes four empirically found lane change strategies on a two-dimensional plane of ego-speed sensitivity and socio-speed sensitivity. Using the concept of social pressure, the theory proposes several behaviours: tailgating, increasing speed, lane changing or delaying a lane change.
7.1. Discussion
The theory introduces endogenous mechanisms of social interactions that affect desired headway, desired speed and lane change desire. It is likely though that the desired headway is the result of many factors, including the modelled relaxation phenomenon and social pressure, but also other factors. This includes more social interactions. For example, the leading driver may slow down to communicate disapproval of tailgating. Reason to (not) change lane and the desired speed are similarly complex and multi-facetted. The theory does however introduce prominent social interactions that result in mesoscopic traffic flow characteristics in line with empirical data, regarding lane change frequency and headway distributions. Primarily the theory adds a social dimension to models. It should be noted that none of the drivers in the study of Keyvan-Ekbatani et al. (2016) mentioned the follower as a direct influence on their lane change strategy and a reason to change lane. However, survey participants did mention their reluctance to hinder other traffic too much and also addressed that being followed too closely could be a reason to change lanes, as a source of annoyance.
This paper applied the theory into a model, for which we chose the LMRS (Schakel et al., 2012). The theory can be implemented in other models as well. Microscopic simulation models typically have a parameter that reflects ego-speed sensitivity in the quantification of changing lane for speed. This parameter should be set to reflect the different driving strategies, and should drive the number of resulting lane changes to reflect empirical findings. Not many models however have a social parameter. An exception to this is MOBIL (Treiber and Kesting, 2009), which has a politeness factor regarding the acceleration of surrounding drivers. Gipps (1986) uses a speed threshold to persuade drivers to change back to a slower lane after overtaking. At the moment this is independent of following traffic, but a dynamic extension can be conceived. The same holds for Toledo et al. (2003) who include within the lane utility a negative term in case of tailgating, encouraging drivers to change from the current lane. In any case, social mechanisms need to be operationalized based on such parameters that reflect the relations from
Figure 3. In most cases a new parameter for socio-speed sensitivity will be required. Only then are mesoscopic traffic flow phenomena endogenously modelled, allowing research in developments that may affect them. For the implementation of the theory in any model, the 13 considerations from section 2 are key. Socio-speed sensitivity may also be related to courtesy lane changes; lane changes by which drivers create space for the lane change of another vehicle, typically for merging on the motorway. For future work it would be interesting to explore how the theory can be implemented in other models, and to verify similar changes in mesoscopic traffic flow characteristics.
In terms of road layouts, it should be investigated whether the social interactions can also successfully be applied on more complex networks with multiple discontinuities, like weaving areas, ramps, or diverges, meaning that macroscopic traffic flow characteristics are unaltered or improved, while introducing social interactions on the micro- and mesoscopic scale. More research is required into the circumstances under which drivers tailgate, and to what extent they do this, including in congestion and in the vicinity of bottlenecks. This may also shed light on why the capacity drop is different between bottlenecks. The relationship between local density and the number of lane changes from different lanes should also be further investigated for different networks. Our simulations show promising effects and differences between low and high demand on the investigated network, with higher density both increasing and decreasing the local number of lane changes. Such effects will have to be validated against empirical data.
Social interactions pave the way for many more relationships that are interesting topics for future research. This includes lane usage as a function of density, average speeds on different lanes as a function of density, local changes in the desired speed due to social pressure around e.g. a lane-drop, etc. Regarding lane usage and average speed on lanes, the base model has been calibrated and validated for this (Schakel et al., 2012), and the introduced lane change strategies do not change the overall patterns.
Finally, the proposed social interactions are quantified for exploratory purposes of their effects on desired speed, desired headway and lane change desire, and consequently the effect on mesoscopic traffic flow characteristics. The underlying ego-speed sensitivity and socio-speed sensitivity have been quantified in several scenarios. More research is needed on quantifying these traits and social interactions, and to further support the existence of the proposed social interactions, at least as a conceptual approximation of reality. Only with this knowledge can models be designed that capture essential social interactions on the one hand, while maintaining sufficient simplicity on the other hand. But already the theory allows to conceptually assess impacts of for instance self-driving cars, of which it is unclear how socially aware they will be.
7.2. Conclusions
Social interactions are an important part of driving behaviour on motorways that partake in determining mesoscopic traffic flow characteristics such as lane change frequencies, headway distributions and platoon lengths. The introduction of social interactions outperforms theories without them in explaining emerging mesoscopic traffic flow characteristics, as comparison of the scenarios with social interactions with the base scenario shows. The theory we propose explains this by connecting driver traits ego-speed sensitivity and socio-speed sensitivity to endogenously affect desired headway, desired speed and lane change desire, which in term affect mesoscopic traffic flow characteristics. The endogenous mechanism is based on social pressure, and includes tailgating as a behaviour. The theory provides understanding in such mechanisms, and hence partially explains the occurrence of heterogeneity in desired speed, desired headway and lane change desire. In particular, it correlates circumstances, such as following traffic with specific traits, to variability in such behaviour, not only between drivers, but also for one driver over time.
Important conclusions that follow from the quantification of the theory are:
Ego-speed sensitivity increases the number of lane changes.
Ego-speed sensitivity reduces the size of platoons, and disperses headway distribution. This effect diminishes as a lane becomes saturated.
Tailgating, as a result of ego-speed sensitivity, explains the above conclusion. Moreover it is shown vital to provide lane change opportunities in the form of larger gaps (between platoons) to further increase the number of lane changes.
Higher socio-speed sensitivity reduces the number of lane changes slightly, but mostly postpones them to more appropriate times.
At microscopic level the social interactions show typical behaviours such as overtaking trucks and re-ordering based on desired speed whenever the slower lane allows.
Ego-speed sensitivity makes lane changes a more pronounced disturbance.
These insights are important for a wide range of research and applications. Studies around driving styles can be focussed around these themes and theory. This might give a better insight on the elements to study in further research projects. The findings thereof are also relevant for the future of traffic systems when drivers are more and more interacting with machines (self-driving vehicles). The interaction with them can also be placed within the framework provided here and consequences of the changing system can in this way be systematically analysed.
| 1 |
In principle, social pressure may also be conceived as a more complex function of behaviours from vehicles upstream (in the simplest case a summation ), but we leave this generalisation for
future work. As it turns out, considering social pressures between single pairs of leaders and
followers (either on the same or different lanes) already leads to rich improvement of lane change
dynamics. |
| 2 |
Note that denotes the social pressure that a leader exerts on its leader. |
References
- Ahn, S. and Cassidy, M. (2007) 'Freeway Traffic Oscillations and Vehicle Lane-Change Maneuvers'. Proceedings of the International Symposium of Transportation and Traffic Theory, Amsterdam: Elsevier, pp. 691-710.
- Chen, D.; Laval, J.; Zheng, Z.; Ahn, S. A behavioral car-following model that captures traffic oscillations. Transp. Res. Part B: Methodol. 2012, 46, 744–761. [CrossRef]
- Farah, H. and Toledo, T. (2010) 'Passing behavior on two-lane highways', Transportation research part F: traffic psychology and behaviour, 13(6), pp. 355-364. [CrossRef]
- Gipps, P. A model for the structure of lane-changing decisions. Transp. Res. Part B: Methodol. 1986, 20, 403–414. [CrossRef]
- Gouy, M.; Wiedemann, K.; Stevens, A.; Brunett, G.; Reed, N. Driving next to automated vehicle platoons: How do short time headways influence non-platoon drivers’ longitudinal control?. Transp. Res. Part F: Traffic Psychol. Behav. 2014, 27, 264–273. [CrossRef]
- Hamdar, S. H., Mahmassani, H. S. and Treiber, M. (2015) 'From behavioral psychology to acceleration modeling: Calibration, validation, and exploration of drivers' cognitive and safety parameters in a risk-taking environment', Transportation Research Part B: Methodological, 78, pp. 32-53. [CrossRef]
- Iwamura, Y.; Tanimoto, J. Complex traffic flow that allows as well as hampers lane-changing intrinsically contains social-dilemma structures. J. Stat. Mech. Theory Exp. 2018, 2018, 023408. [CrossRef]
- Juhlin, O. (1999) 'Traffic behavior as social interaction – implications for the design of artificial drivers', Proceedings of the 6th World Congress on Intelligent Transportation Systems.
- Kesting, A., Treiber, M. and Helbing, D. (2007) 'General Lane changing Model MOBIL for Car-Following Models', Transportation Research Record: Journal of the Transportation Research Board, 1999, pp. 86-94. [CrossRef]
- Keyvan-Ekbatani, M.; Knoop, V.L.; Daamen, W. Categorization of the lane change decision process on freeways. Transp. Res. Part C: Emerg. Technol. 2016, 69, 515–526. [CrossRef]
- Knoop, V. L., Hoogendoorn, S. P., Siomi, Y. and Buisson, C. (2012) 'Quantifying the Number of Lane Changes in Traffic: Empirical Analysis', Transportation Research Records: Journal of the Transportation Research Board, 2278, pp. 31-41. [CrossRef]
- Knoop, V.L.; Keyvan-Ekbatani, M.; de Baat, M.; Taale, H.; Hoogendoorn, S.P. Lane Change Behavior on Freeways: An Online Survey Using Video Clips. J. Adv. Transp. 2018, 2018, 1–11. [CrossRef]
- Laval, J. A. and Daganzo, C. F. (2006) 'Lane-changing in Traffic Streams', Transportation Research Part B: Methodological, 40(3), pp. 251-264. [CrossRef]
- Laval, J.A.; Leclercq, L. Microscopic modeling of the relaxation phenomenon using a macroscopic lane-changing model. Transp. Res. Part B: Methodol. 2008, 42, 511–522. [CrossRef]
- Lebacque, J.P. Two-Phase Bounded-Acceleration Traffic Flow Model: Analytical Solutions and Applications. Transp. Res. Rec. J. Transp. Res. Board 2003, 1852, 220–230. [CrossRef]
- Leclercq, L.; Knoop, V.L.; Marczak, F.; Hoogendoorn, S.P. Capacity drops at merges: New analytical investigations. Transp. Res. Part C: Emerg. Technol. 2016, 62, 171–181. [CrossRef]
- Lütteken, N., Zimmermann, M. and Bengler, K. J. (2016) 'Using gamification to motivate human cooperation in a lane-change scenario'. Proceedings of the IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janiero, Brazil, 1-4 Nov. 2016. [CrossRef]
- Michon, J. A. (1985) 'A Critical View of Driver Behavior Models: What Do We Know, What Should We Do?'. Human Behavior and Traffic Safety. New York: Plenum Press, pp. 485-520.
- Nowakowski, C., Shladover, S. E., Lu, X.-Y., Thompson, D. and Kailas, A. (2015) Cooperative adaptive cruise control (CACC) for truck platooning: Operational concept alternatives.
- Ossen, S.; Hoogendoorn, S.P. Heterogeneity in car-following behavior: Theory and empirics. Transp. Res. Part C: Emerg. Technol. 2011, 19, 182–195. [CrossRef]
- Portouli, E.; Nathanael, D.; Marmaras, N.; Papakostopoulos, V. Naturalistic observation of drivers’ interactions while overtaking on an undivided road. Work 2012, 41, 4185–4191. [CrossRef]
- Saifuzzaman, M.; Zheng, Z.; Haque, M.; Washington, S. Understanding the mechanism of traffic hysteresis and traffic oscillations through the change in task difficulty level. Transp. Res. Part B: Methodol. 2017, 105, 523–538. [CrossRef]
- Schakel, W. J., Gorter, C. M., de Winter, J. C. F. and van Arem, B. (2017) 'Driving Characteristics and Adaptive Cruise Control: A Naturalistic Driving Study', IEEE Intelligent Transportation Systems Magazine, 9(2), pp. 17-24. [CrossRef]
- Schakel, W. J., Knoop, V. L. and van Arem, B. (2012) 'Integrated Lane Change Model with Relaxation and Synchronization', Transportation Research Record: Journal of the Transportation Research Board, 2316, pp. 47-57. [CrossRef]
- Schakel, W. J., Van Arem, B. and Netten, B. D. (2010) 'Effects of cooperative adaptive cruise control on traffic flow stability'. Proceedings 13th international IEEE conference on intelligent transportation systems, Funchal, Madeira, pp. 759-764. [CrossRef]
- Toledo, T., Koutsopoulos, H. N. and Ben-Akiva, M. E. (2003) 'Modeling Integrated Lane-Changing Behavior', Transportation Research Record: Journal of the Transportation Research Board, 1857, pp. 30-38. [CrossRef]
- Treiber, M.; Helbing, D. Memory effects in microscopic traffic models and wide scattering in flow-density data. Phys. Rev. E 2003, 68, 046119–046119. [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805–1824. [CrossRef]
- Treiber, M.; Kesting, A. Modeling Lane-Changing Decisions with MOBIL.CONFERENCE NAME, LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE; pp. 211–221.
- Treiber, M.; Kesting, A.; Helbing, D. Delays, inaccuracies and anticipation in microscopic traffic models. Phys. A: Stat. Mech. its Appl. 2005, 360, 71–88. [CrossRef]
- van Beinum, A. (2018) Turbulence in traffic at motorway ramps and its impact on traffic operations and safety. Delft University of Technology, Delft.
- van Lint, J.; Calvert, S. A generic multi-level framework for microscopic traffic simulation—Theory and an example case in modelling driver distraction. Transp. Res. Part B: Methodol. 2018, 117, 63–86. [CrossRef]
- van Lint, H.; Schakel, W.; Tamminga, G.; Knoppers, P.; Verbraeck, A. Getting the Human Factor into Traffic Flow Models: New Open-Source Design to Simulate Next Generation of Traffic Operations. Transp. Res. Rec. J. Transp. Res. Board 2016, 2561, 25–33. [CrossRef]
- Yuan, K.; Knoop, V.L.; Hoogendoorn, S.P. A Microscopic Investigation Into the Capacity Drop: Impacts of Longitudinal Behavior on the Queue Discharge Rate. Transp. Sci. 2017, 51, 852–862. [CrossRef]
- Zheng, Z. Recent developments and research needs in modeling lane changing. Transp. Res. Part B: Methodol. 2014, 60, 16–32. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
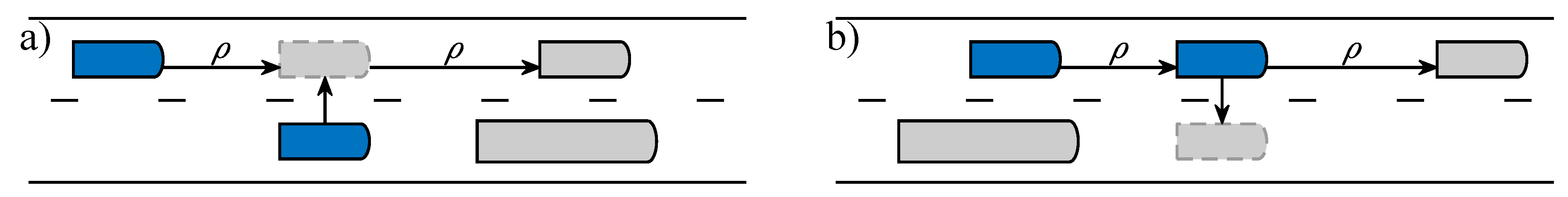
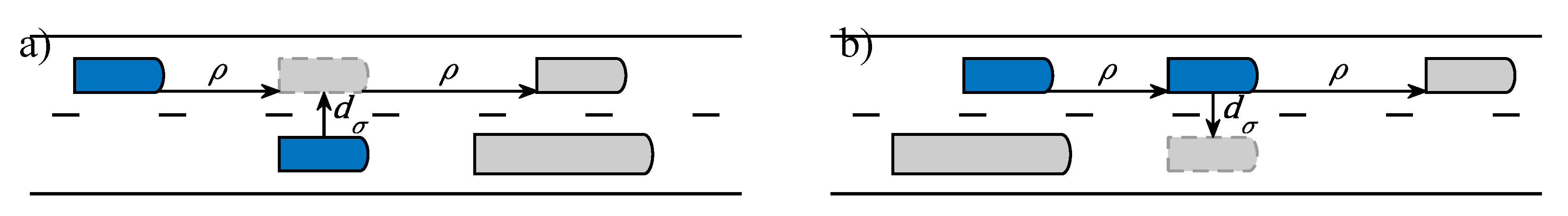
 Vehicle being overtaken just after having changed right, and just before changing back left;
Vehicle being overtaken just after having changed right, and just before changing back left;
 Vehicle changing left to overtake and changing back right after the overtake(s);
Vehicle changing left to overtake and changing back right after the overtake(s);
 Disturbance caused by a vehicle changing to the left lane.
Disturbance caused by a vehicle changing to the left lane.
 Vehicle being overtaken just after having changed right, and just before changing back left;
Vehicle being overtaken just after having changed right, and just before changing back left;
 Vehicle changing left to overtake and changing back right after the overtake(s);
Vehicle changing left to overtake and changing back right after the overtake(s);
 Disturbance caused by a vehicle changing to the left lane.
Disturbance caused by a vehicle changing to the left lane.