Tailoring Carbene-Metal-Amides for Thermally Activated Delayed Fluorescence: A Computationally Guided Study on the Effect of Cyclic (Alkyl)(amino)carbenes

1. Introduction

Organic light-emitting diodes (OLEDs) are widely employed in display technology due to their low power consumption and high efficiency in light production, along with other desirable properties. The efficiency of OLEDs relies on the selection of appropriate materials, especially the emitting layer, which converts electrical energy into light [1]. To develop efficient and stable materials for OLEDs, thermally activated delayed fluorescence (TADF) emitters have been extensively studied, as they have the potential to achieve high internal quantum efficiencies and long lifetimes [2]. Carbene-Metal-Amides (CMAs) [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] have emerged as a promising class of TADF emitters, thanks to their exceptional photoluminescence (PL) behaviors. These complexes are composed of carbene and amide ligands bridged by a coinage metal, such that the carbene acts as an electron acceptor and the amide as an electron donor. The two-coordinate metal center mediates the electron transfer between the donor and acceptor moieties, while inducing rotational flexibility [3]. TADF mechanism manifests in CMAs when the singlet excitons decay radiatively with prompt fluorescence and transform into triplet excitons via an intersystem crossing (ISC) process. Simultaneously, low-energy triplet excitons undergo a fast reverse ISC (RISC) to the emissive singlet level, followed by a delayed fluorescence to the ground (S0) state. The efficiency of TADF emitters depends on the energy difference between the lowest excited singlet (S1) and triplet (T1) states, referred to as exchange energy or singlet-triplet energy gap (ΔE_ST) [19].

Cyclic (alkyl)(amino)carbenes (CAACs), which were originally developed by Bertrand et al. [20], have recently attracted attention as effective acceptors in CMAs for TADF [3,4,5,6,7,8,9,10,11,12,13,14]. The most prominent is the 5-membered CAAC gold carbazolide (CMA1), which demonstrates a considerably short emission lifetime of 0.35 µs at ambient temperature. The OLED made from CMA1 emits green light with an external quantum efficiency surpassing 25% [4]. Inspired by CMA1, similar coinage metals complexes have been recently reported [3,5,6,7,8,9,10,11,12,13,14], including CMA-based emitters with CAAC substituted by groups such as methyl, ethyl (Et), menthyl, adamantly (Ad), and 2,6-diisopropylphenyl (Dipp) [5,6,7]. For example, the menthyl-CAAC copper complex exhibits broad emission with near unity quantum efficiency of 100% and 2.5 µs lifetime, resulting in an efficient blue-emitting OLED device [5], whereas the silver analogue exhibits significantly shorter emission lifetime (0.33 µs) [6]. Furthermore, CMAs of Cu, Ag and Au metals based on 6-membered monocyclic and bicyclic CAACs have been reported to manifest quantum yields of up to 100%. Among these, the gold complex of the bicyclic carbene moiety displays remarkable photostability when subjected to hard and soft UV-light [8].

This paper reports a systematic computational study on the effect of CAACs on the PL properties of CMAs. We focus on the design and optimization of new TADF emitters based on carbene-gold-carbazolide complexes, employing density functional theory (DFT) calculations to explore the electronic structures of ground and excited states of the molecules as a function of the structure of CAAC. We describe how the structural modifications of the CAACs affect the calculated parameters that directly relate to PL quantum yield (PLQY), thereby ending up making proposals for new promising TADF emitters for the CMA family, as well as synthesizing one.

2. Results and Discussion

We begin from CMA1 (Figure 1), the archetypical emitter in the CMA family exhibiting high PLQY (80-90%) [4]. This molecule has been thoroughly studied elsewhere, both experimentally and computationally [4,21,22,23,24]. We consider CMA1 as our reference structure, summarizing the relevant parameters for evaluation of its PL behavior, which are recomputed here for this purpose using MN15 [25]/ def2-TZVP [26,27] method with Tamm-Dancoff approximation [28] for time-dependent DFT (TD-DFT) calculations.

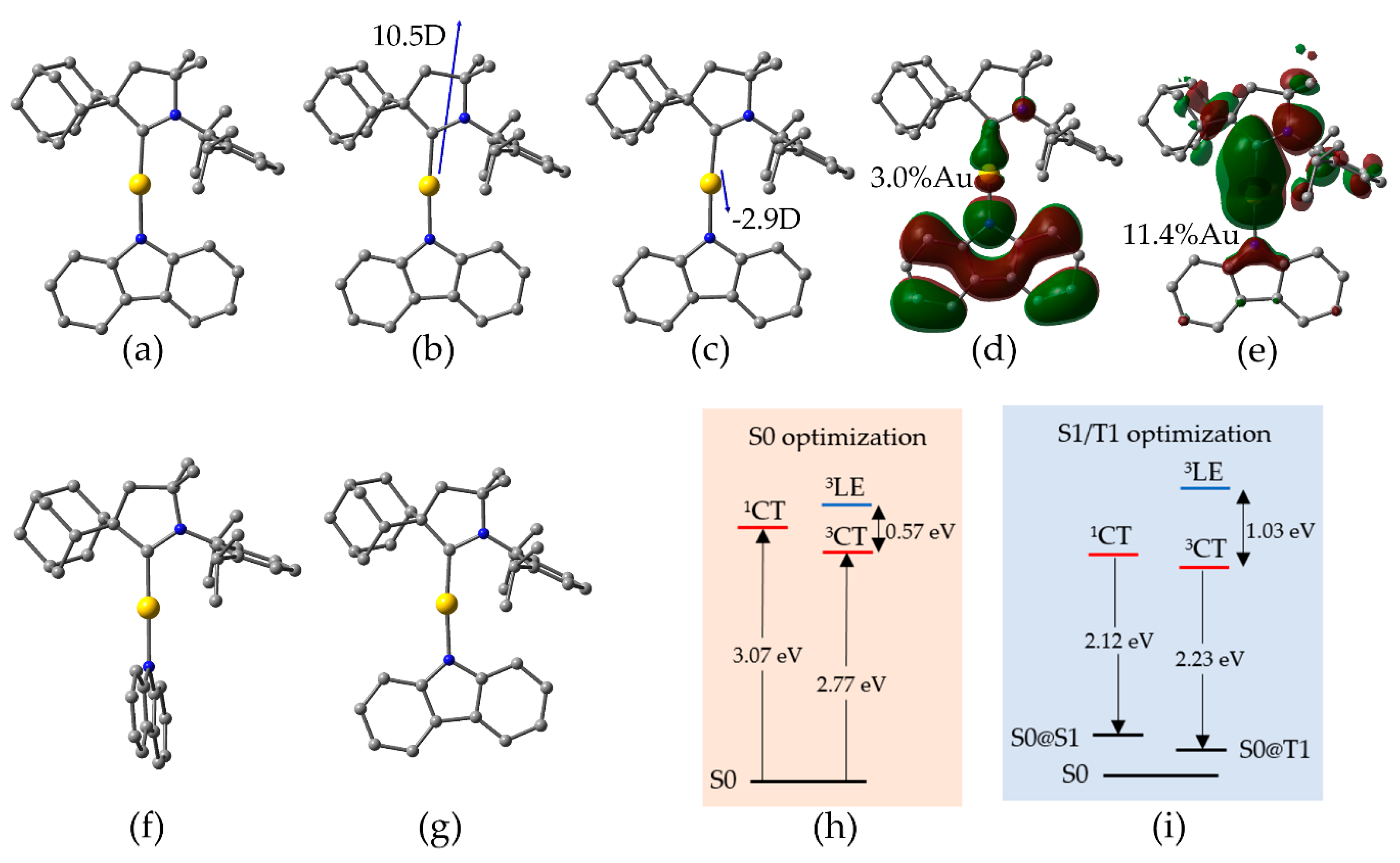
The HOMO and LUMO orbitals of CMA1 are visualized in Figure 1 with the percentage of calculated Au contributions to the frontier orbitals, illustrating localization of HOMO on carbazole (Cz) and LUMO on Au-carbene. These two orbitals mainly contribute to the charge transfer (CT) between the S0 state and the excited S1 and T1 states, as indicated by Natural Transition Orbitals (NTOs) of the S0-S1 and S0-T1 excitations having HOMO-LUMO character of 97% and 95%, for S0-S1 and S0-T1 transfer, respectively.

Overlap integral of the HOMO and LUMO orbitals provides a quantitative measure of the spatial separation of the orbitals participating in CT, which is connected to the ΔE_ST, such that a smaller overlap integral indicates smaller gap [29]. For CMA1, the HOMO and LUMO overlap integral is calculated 0.36, which appears small enough for efficient TADF mechanism [30], as is observed by the experiments. Vertical excitation energies on optimized S0 geometry are calculated 3.07 eV for S1 and 2.77 eV for T1, such that to give ΔE_ST = 0.30 eV. The calculations are consistent with broad peaks in steady-state absorption spectra, namely, at 390 nm (3.15 eV) for amorphous or crystallized CMA1 thin film and 405 nm (3.06 eV) for CMA1 in toluene solution [24].

The localized triplet excitation (³LE) within Cz ligand, ³LE(A), corresponds to the T2 state, with 92% HOMO-LUMO+3 character, and is calculated having vertical excitation energy of 3.34 eV – in agreement with the experimental peak at 370 nm (3.35 eV) [24]. The energy of the ³LE state relative to the CT states is of major importance, as it contributes to the emission mechanism. For the sake of efficient TADF, the ³LE state should lie well above the CT states [3].

Upon geometry optimization of the S1 and T1 states of CMA1, the calculated ΔE_ST decreases from 0.3 eV to 0.16 eV, which is small enough for RISC [19]. Due to the Stokes shift [31], the calculated energies for fluorescence (S1-S0@S1) and phosphorescence (T1-S0@T1) are lower than the corresponding absorption energies: 2.12 eV vs 3.07 eV and 2.23 eV vs 2.77 eV for S1 and T1, respectively. Like the S0 state, the carbene and amide remain nearly coplanar in the relaxed T1 geometry but adopt a perpendicular orientation in the relaxed S1 geometry (Figure 1). The rotation is associated with lowering of oscillator strength representing the probability of absorption or emission of electromagnetic radiation in transitions between energy levels. High PLQY requires high oscillator strength for the radiative decay to outpace the nonradiative decay [32], which is hence compromised on rotation. In the nearly coplanar S0 geometry, the S0-S1 oscillator strength is calculated 0.1927. In S1 geometry, the maximum S1-S0 oscillator strength (0.1110) is obtained, when carbene and amide are fixed coplanar, with energy cost of 0.13 eV, such that ΔE_ST increases from 0.16 eV to 0.29 eV, which is comparable to ΔE_ST in the S0 geometry.

Two more measures are useful to add for the purpose of this work, namely electrostatic dipole moments together with Au-C and Au-N bond dissociation energies. In the S0 ground state of CMA1, a dipole of 10.5D is calculated roughly along the C(carbene)-Au-N(amide) axis towards the carbene, reversing its direction in the S1@S0 state, while decreasing in magnitude down to 2.9D. The change arises from the CT character of the S1 state, leading to the electron displacement from the Cz moiety to the carbene moiety [22]. The bond dissociation energies provide measures for the stability of the complexes. For CMA1, the dissociation energies are 4.09 eV vs 3.90 eV for Au-C and Au-N bond, respectively.

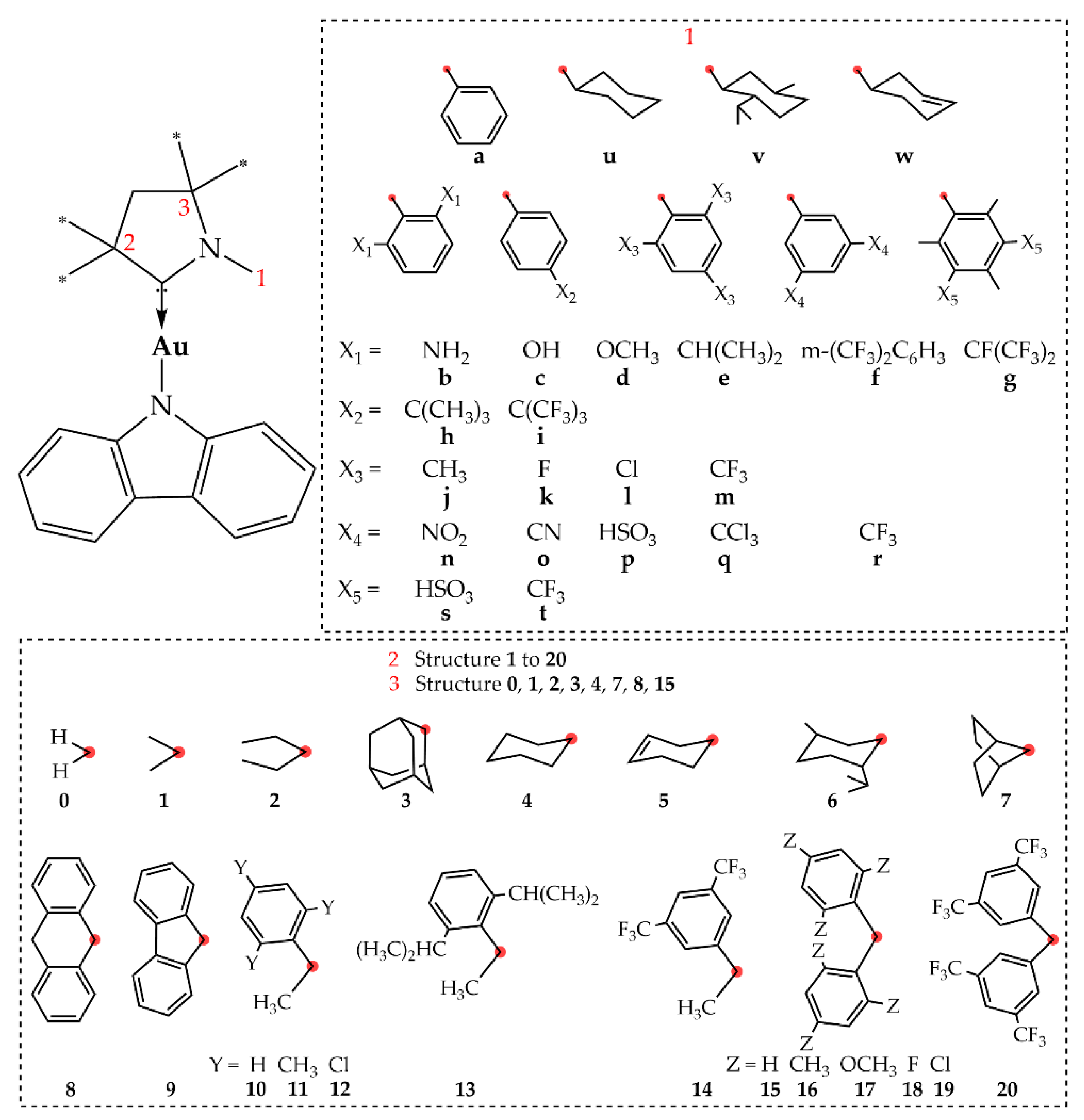
Targeting molecular design strategies for improved PLQY via structure-property relationships, we systematically modified the CAAC ligand of CMA1 as detailed in Figure 2. Since our primary focus was on experimental synthetic prospects, we made the structure selection based on experimentally available carbenes, extending the dataset by hypothetical structures for the sake of a more throughout structural analysis. The structures were modified at positions 1, 2, and 3, while retaining the CAAC-5 backbone.

Regarding position 1, much of the previous work on CAACs have focused on the Dipp structure [4,5,6,9,10,11,12,13,33,34], while 1,3,5-trimethylphenyl group (Mes) has been reported for N-heterocyclic carbenes (NHC) [15] and for diamidocarbenes [35]. Li et al. [15] synthesized a two-coordinate NHC(Mes)-Cu-Cz complex, which displays unique dual-emissive features from fluorescence (11.24 ns) and long-lived phosphorescence (32 ms) with total PLQY of 12.7%. Therefore, we included aromatic C₆-ring at position 1, substituted with various electron withdrawing and/or electron donating groups to evaluate the influence of electron density on the calculated parameters. We also included cyclohexanyl and cyclohexenyl substituents in the same position to compare with the aromatic ring. Regarding position 2, carbene-metal-Cz emitters with groups such as methyl, Et, menthyl, and Ad substituted on CAAC have been reported [5,6,7]. Particularly, the experimentally synthesized e-6-1 gold complex in 2-MeTHF solution exhibits high PLQY of 95% and 1.2 µs lifetime [6]. In our work, we supplemented the previously reported functional groups with various others so that to evaluate e.g. π systems at this position. Correspondingly, we evaluated a smaller subset of substituents at position 3, where previous reports concerning CAACs have focused on substituent 1 [3,4,5,6,7,9,10,11,12,13,14].

2.1. Composition of the frontier orbitals

All the studied molecules have nearly identical HOMO orbitals, which are localized on the Cz moiety, and hence are not much affected by the studied variations in the CAAC moiety, where the calculated Au contributions are around 3%, as in case of CMA1. The effect is strongest for position 1, where combining the phenyl group with m-(CF₃)₂C₆H₃ substituents at ortho-position (f-1-1) gives the lowest (2.5%), and HSO₃ groups at meta-positions (p-1-1 and s-1-1) the second highest (3.4%) contribution of Au.

HOMO remaining nearly unchanged, the spatial separation of the frontier orbitals, measured in terms of HOMO-LUMO overlap integral, depends mainly on the LUMO orbital. Since the LUMO is localized on Au-carbene, the percentage of Au contribution varies strongly as a function of CAAC, ranging from 1% to 16%, and consequently the overlap integral ranges between 0.14 and 0.38. It follows that the Au contribution of LUMO and the overlap integral are strongly correlated – decreasing Au contribution indicates localization of LUMO towards CAAC and hence farther away from the Cz-localized HOMO, increasing spatial separation of the orbitals. Therefore, we simplify the discussion of the effects of structural variations so that to focus on HOMO-LUMO overlap integrals. The results are tabulated in Tables S1-S3.

Position 1 has the strongest influence on the overlap integral, followed by position 2, while position 3 makes little contribution to the LUMO orbital and hence to the orbital overlap as it is located far from the N$-\ddot{\mathrm{C}}\to$ Au center. Concerning position 1, electron-withdrawing and electron donating substituents play a major role, as expected. The former has a stronger effect than the latter, arising from electron withdrawal from Au such that LUMO becomes primarily localized on CAAC at position 1. Combining the phenyl group with electron-withdrawing meta-substituents leads to a reduction in the overlap integral from 0.31 to 0.14 in the order CF₃ (r-1-1) > CCl₃ (q-1-1) HSO₃ > (p-1-1) > CN (o-1-1) > NO₂ ( n-1-1), due to the gradual shift in the LUMO distribution from N$-\ddot{\mathrm{C}}$ to the substituted phenyl ring (Figure S1). The order of CF₃ > HSO₃ is reproduced in the presence of methyl-substituents (t-1-1 vs s-1-1). Electron-donating ortho-NH₂-substituents (b-1-1) increase the overlap integral to its maximum value of 0.38 for this dataset. Ortho-substituents, being closest to the CAAC-5 backbone, have a stronger impact than the para-substituents. This is best exemplified by electron-withdrawing fluoroalkyl groups in ortho vs para positions, where the two ortho-substituents decrease the overlap integral from 0.36 of CMA1 down to 0.23 (f-1-1) or 0.20 (g-1-1), while remaining at 0.33 with the para-substituent (i-1-1), the combination of ortho- and para-substituents (m-1-1) giving an overlap integral of 0.21. Direct comparison of CF₃ substituents (m-1-1, r-1-1) indicates stronger effect for ortho- than for meta-position. Chloride (l-1-1) has a weaker withdrawing effect, while fluoride (k-1-1) hydroxyl (c-1-1), methoxy (d-1-1) and alkyl groups (e-1-1, h-1-1, j-1-1) have little effect on the overlap integral, and the same holds for saturation of the phenyl ring (u-1-1, v-1-1, w-1-1).

Concerning position 2, alkyl (1,2) and cycloalkyl (3-7) groups have no significant effect on the overlap integral. A modest effect arises from the bulky adamantyl (3) at position 2 canceling some of the electron withdrawal at position 1. This is best exemplified by f-1-1 vs f-3-1, where the overlap integral consequently increases from 0.23 to 0.27. More notable effects are seen for the conjugated rings at position 2, which we explored in conjunction with substituent e at position 1. These substituents tend to shift the LUMO orbital towards position 2, hence lowering the overlap integral, and the effect can be strengthened by ring substitutions. The effect is particularly strong for chlorides, where the maximum effect among the dataset is obtained for e-19-1, the resulting electron withdrawal decreasing the orbital overlap from 0.36 to 0.21. A similar but weaker effect is seen for e-12-1 having fewer chlorides.

2.2. Vertical excitations

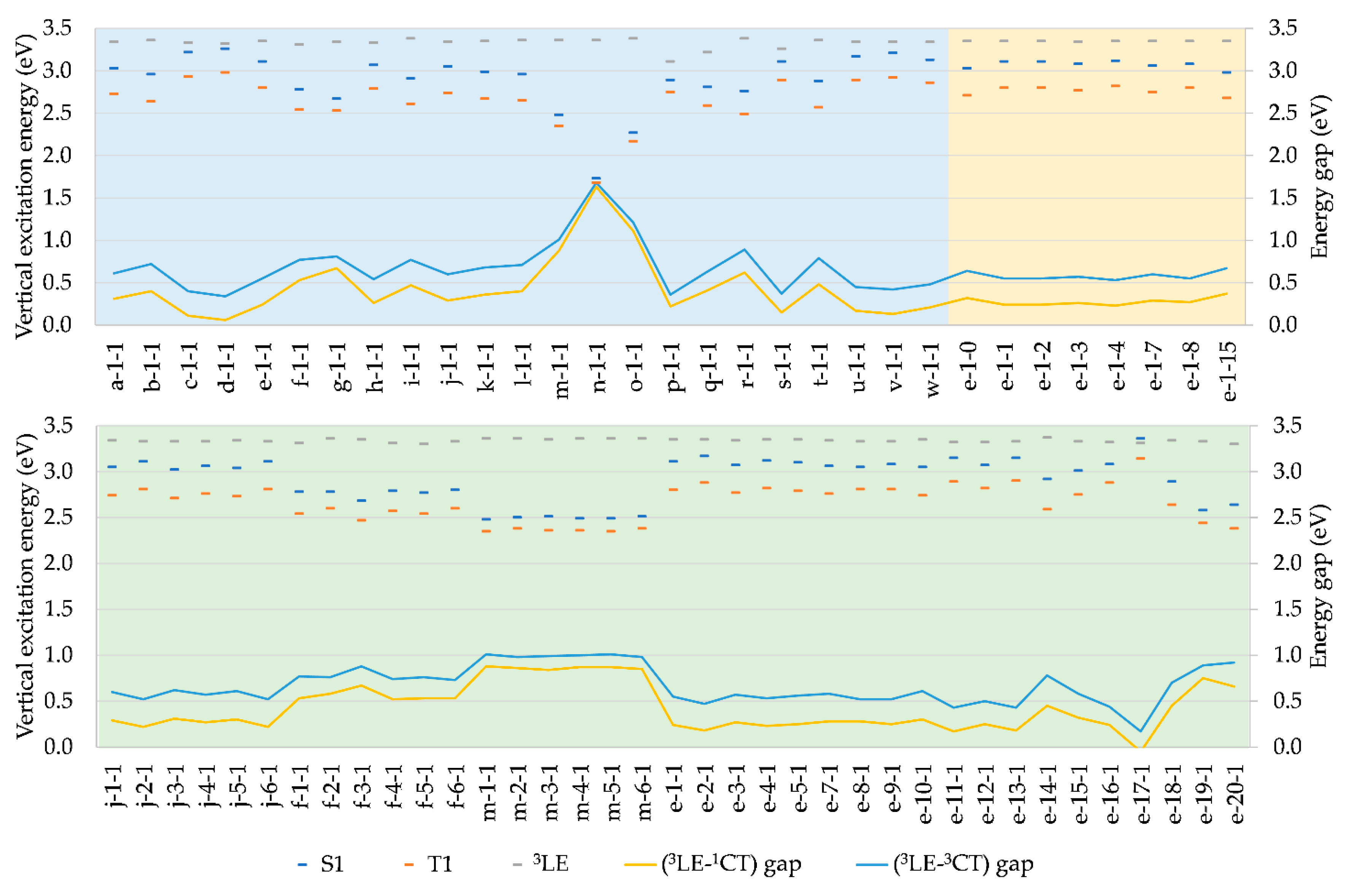
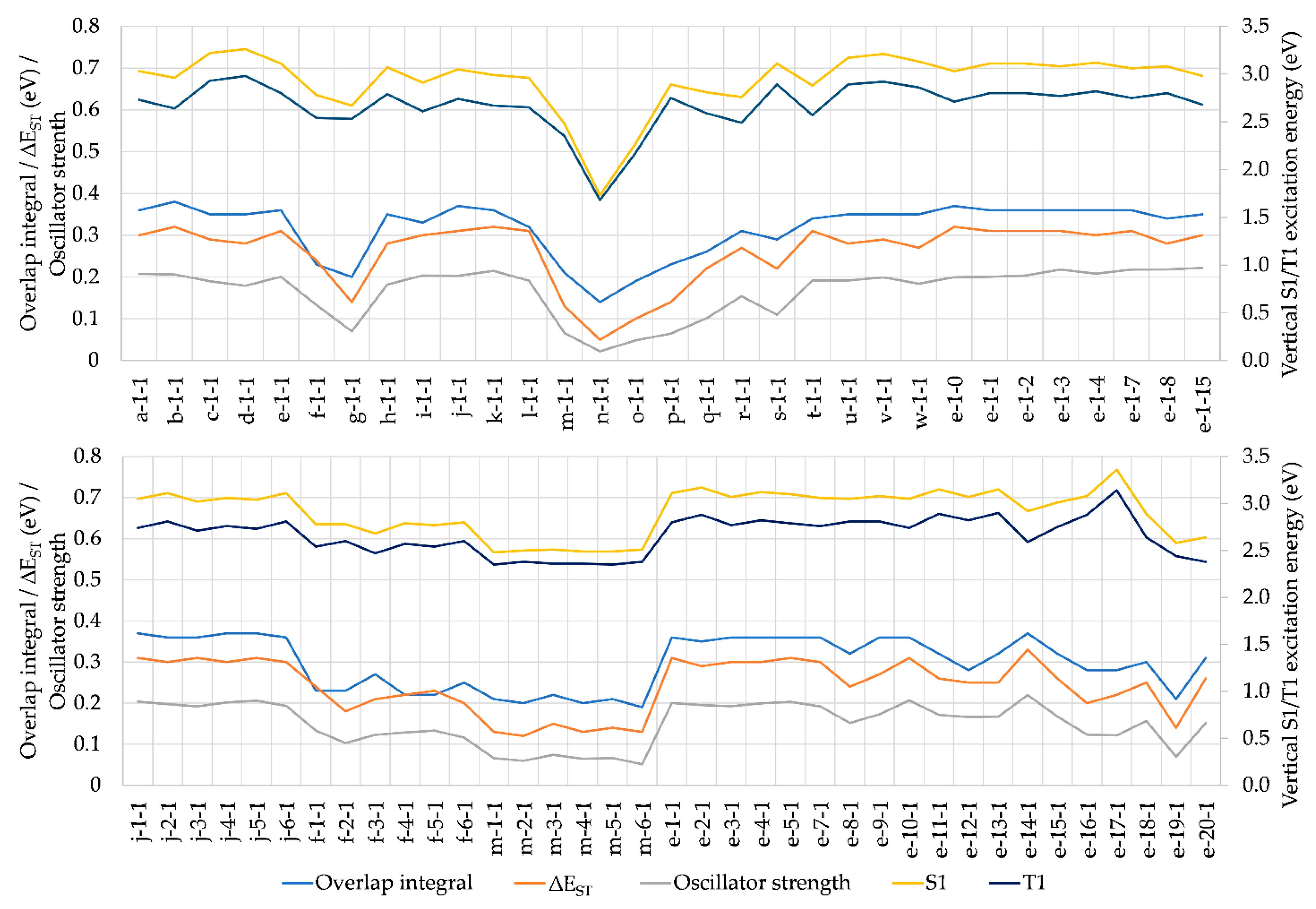
As summarized in Tables S1-S3, vertical S0-S1 excitation energies at optimized S0 geometries are within the visible region, ranging from 1.73 eV to 3.36 eV, i.e. ca. 400-700 nm, while the corresponding S0-T1 energies range from 1.68 eV to 3.14 eV. Based on the NTOs, both the S0-S1 and S0-T1 excitations are characterized primarily as CT from HOMO to LUMO. For S1, HOMO-LUMO accounts for 97±2% of CT in most cases, vs 97% for CMA1, hence remaining practically unaffected by any of the structural modifications employed in this dataset. T1 shows little more variation, but only concerning position 1, where the range of HOMO-LUMO character is 70-95%, the upper limit roughly representing the contribution in CMA1 and in any of its employed structural modifications at positions 2 and 3. Hence, the effects of structural modifications are limited to the possibility of substitutions at position 1 lowering the HOMO-LUMO character of the S0-T1 excitation, where the lower limit of 70% is obtained for f-1-1.

A general overview of S0-S1 and S0-T1 vertical excitation energies is given in Figure 3. Structural modifications at positions 1, 2, and 3 generally result in S1 states being above the T1 states approximately by a factor of 1.1, indicating that excitation energies are directly proportional to the S1-T1 energy gap. Hence, a small ΔE_ST, which is desirable for efficient TADF, is most easily achieved when the excitation energies are at the lower end of the desired color range. For our dataset, ΔE_ST ranges between 0.05-0.33 eV, vs 0.30 eV for CMA1, which shows TADF. From that point of view, TADF cannot be excluded for any of the molecules included here.

As illustrated in Figure 4, ΔE_ST is strongly correlated with the orbital integral discussed above, so that it is unnecessary to repeat the discussion of the effects of structural modifications in this context. Likewise, ΔE_ST is strongly correlated with S0-S1 and S0-T1 excitation energies, as well as with S0-S1 oscillator strength, with a major implication of the desired low ΔE_ST being unachievable with a desired high oscillator strength. Therefore, compromises are necessary in molecular design for improved PLQY.

In addition, one needs to consider the ³LE(A) due to its interference of TADF. This usually corresponds to the T2 state but is in some cases found at higher triplet states, T3-T6. The employed modifications of CAAC have little effect on ³LE(A), the energies averaging at 3.34 eV with standard deviation of 0.04 eV, and thus being much higher than the energy of S1 (Figure 3, Tables S1-S3), which is beneficial for the TADF mechanism [3]. The few exceptions are those having high S1 energy, while for e-17-1 having the highest S1 energy, the order becomes reversed. The ³LE-¹CT (and ³LE-³CT) gap is hence strongly correlated to vertical S0-S1 (and S0-T1) excitation energies, as illustrated in Figure 3 – the larger the excitation energy, the smaller the gap.

2.3. Electrostatic dipole moments

In the S0 ground state, the dipole moment vector points toward the carbene roughly along the $\ddot{\mathrm{C}}\to$ Au$-$N axis, with magnitude ranging between 8.7D and 12.7D for this dataset. The direction reverses for the S1@S0 state, originating from the amide-carbene electron rearrangement due to the CT character of the S1 state, as was discussed for CMA1 [22]. At the same time, the magnitude extends over a wider range, 2.5D-14.3D, (Tables S1-S3), but it is usually below 6D, and therefore smaller than in the S0 state. Exceptions where S1@S0 is above 6D and comparable in magnitude to S0 arise from ortho-substitution of the phenyl group at position 1 by electron-withdrawing fluoroalkyls (f-1-1, g-1-1, and m-1-1). In case of strongly electron-withdrawing meta-substituents on the phenyl group at position 1, the magnitude of the S1@S0 dipole reaches its maximum within the dataset of over 13D, hence exceeding the magnitude of the opposite S0 dipole (n-1-1, o-1-1, and p-1-1). Regarding position 2, ca. equal magnitudes of S0 and of S1@S0 dipoles are calculated for Cl- and CF₃-substituted e-19-1 and e-20-1, while substitutions at position 3 have in practice no effect.

2.4. Au-C and Au-N bond dissociation energies

The calculated bond dissociation energy of the Au-N bond varies between 355 and 398 kJ/mol, while the corresponding range for the Au-C bond is somewhat wider, 365-420 kJ/mol, which is due to focus of this work on modification of CAAC rather than the amide ligand. The both bonds are stabilized particularly by HSO₃ groups on the phenyl ring at position 1 (p-1-1 and s-1-1) and OCH₃ groups on the aromatic rings at position 2 (e-17-1), and correspondingly destabilized by halogens and electron-withdrawing fluoroalkyls substituted to the rings. Comparing the Au-C and Au-N bond dissociation energies, the former are systematically higher in average by 5%.

2.5. S1 and T1 excited state optimizations

Next, we selected promising candidates for the study of emission by fluorescence and phosphorescence, requiring geometry optimizations of the excited S1 and T1 states, respectively. The selection was made based on consideration of ∆E_ST, oscillator strength and HOMO-LUMO overlap integral, while the fourth decisive criterion, that ³LE must not interfere with the charge transfer, is satisfied by almost all studied complexes (Figure 3). For ∆E_ST, we set a threshold of 0.27 eV so that to be measurably lower than for our reference, CMA1 (0.30 eV). The threshold for oscillator strength was set at 0.13, which is lower than for CMA1 (0.1927), thus compromising oscillator strength in favor of ∆E_ST. 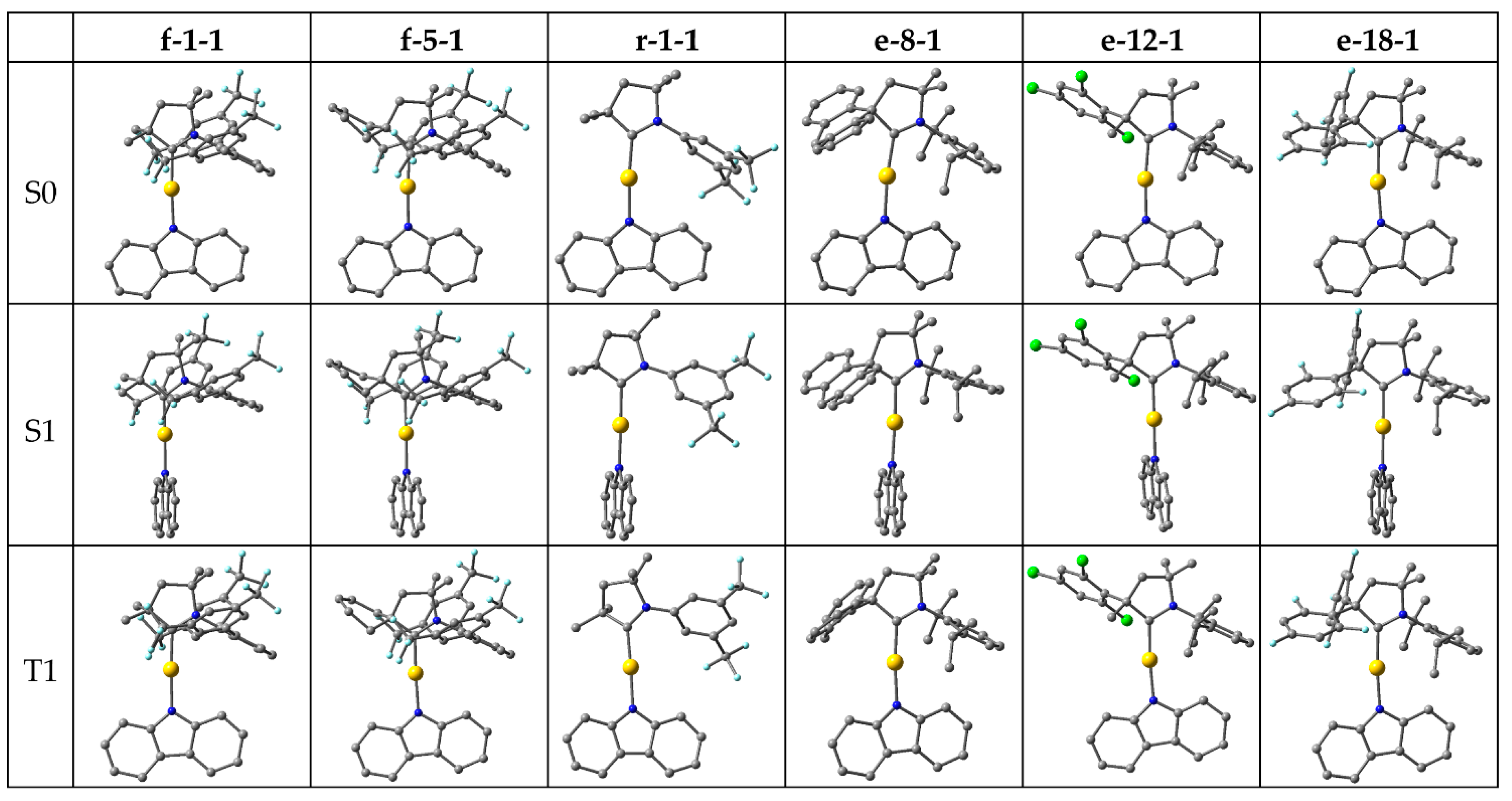For the overlap integral, strongly correlating with ∆E_ST, the threshold was set at 0.32, and hence measurably lower than for CMA1 (0.36). Based on these three criteria, six complexes were selected for excited state geometry optimizations: f-1-1, f-5-1, r-1-1, e-8-1, e-12-1, and e-18-1 (Figure 5).

The optimized excited state energies are summarized in Table 1, with corresponding vertical excitations included for comparison. The carbene and amide ligands remain nearly coplanar in the optimized T1 geometries, analogous to the S0 ground state, but rotate perpendicular to each other in the S1 geometries. The rotation significantly lowers the S1 energy so that to bring S1 and T1 energy levels to degeneracy for f-1-1, f-5-1 and r-1-1 and to near-degeneracy for e-8-1, e-12-1 and e-18-1, where ΔE_ST ranges from 0.10 eV to 0.14 eV and is thus lower than for the reference CMA1 (0.16 eV). The ³LE energy remains nearly constant and desirably high above the CT states. The S1-S0 oscillator strength decreases to almost zero at full rotation, while reaching its maximum value at a fixed coplanar orientation of carbene and amide, such that rotation towards coplanarity is required for efficient fluorescence. Among the studied complexes, full rotation to coplanarity requires 0.12-0.27 eV energy, thus bringing ΔE_ST to the range of 0.2-0.3 eV, i.e. the magnitude calculated for the vertical excitations, which is low enough for efficient TADF.

For complexes lacking a bulky group in position 2 (f-1-1, f-5-1, and r-1-1), the oscillator strength remains lower at the coplanar orientation, while for the bulky e-substituents (e-8-1, e-12-1, and e-18-1), the maximum oscillator strength is calculated being comparable or even higher than for CMA1 (0.1110). The latter are calculated to emit fluorescence well within the visible region, 2.0-2.3 eV, corresponding to ca. orange-green color.

2.6. Synthesis, Structure and Photophysical Properties for e-2-1

Finally, we develop our discussion and focus more on the factor of the steric protection of the metal atom in CMA complexes. We and others have recently demonstrated the importance of the bulky groups in position 2 to obtain bright CMA emitters [4,5,36]. It was demonstrated that increase in the steric protection of position 2 (methyl < ethyl < cyclohexyl < adamantyl < menthyl) results in increase of the PLQY values from 30% up to 100% in a series copper CMA complex analogous to CMA1. It’s a distortion of the linear geometry around metal atom (or Renner-Teller distortion [8,16]) originates poor quantum yields in case of the less sterically protected CMA-copper complexes. We synthesized and fully characterized gold complex e-2-1, with two ethyl groups in position 2 and compared with archetype complex CMA1 containing bulky adamantyle, ^AdCAAC-carbene. Complex e-2-1 is obtained from the (^Et2CAAC)AuCl and carbazole in the presence of the KO^tBu base in 82% yield. It’s fully spectroscopically characterized and demonstrates stability in air for months. The molecular structure of e-2-1 was confirmed by single crystal X-ray diffraction (Figure 6). Complexes e-2-1 and CMA1 have a similar two-coordinate geometry for the gold atom with negligible deviation from linearity with differences in Au-C and Au-N bond lengths laying within the error of the experiment. The torsion angle (C1-N1-N2-C23, Figure 6) between carbene and carbazole ligands for e-2-1 is ca. 15.1(1)º which is close to 17.7(2)º of CMA1, indicating near co-planar orientation of the ligands.

The redox behaviour of e-2-1 was analysed in THF solution using [ⁿBu₄N]PF₆ as the supporting electrolyte (Figure S5, Table S5). Complex e-2-1 shows a quasi-reversible, carbene ligand-centred reduction process at E_1/2 value –2.72 V. All oxidation processes are centered on the carbazole (similar to CMA1) and irreversible with E_p values at +0.15, +0.37 and +0.93 V (Table S5). The redox potentials and energy level of HOMO (–5.61 eV) and LUMO (–2.67 eV) for e-2-1 are similar to CMA1. The UV-vis absorption spectra in solvents with different polarity (Figure 6b) show a broad L(M)L charge transfer absorption. Negative solvatochromism for L(M)L CT band is characteristic for the CMA complexes, we measure a 65 nm blue shift upon increase of the solvent polarity from methylcyclohexane (MCH) to dichloromethane (DCM, Figure 6b).

The PL spectra were measured in toluene solution and polystyrene (PS) matrix at 295 and 77K (Table 2 and Figure 6c,d). Compound e-2-1 shows a broad CT PL profile with up to 14 nm blue-shift in both toluene (484 nm) and PS matrix (518 nm) compared to CMA1 (Table 2). The excited state lifetime is ca. 1.1 µs which is only slightly shorter compared to CMA1 (ca. 1.2 µs). Upon cooling to 77K, the e-2-1 PL spectra is blue-shifted to 425 nm while exhibiting a vibronically resolved profile indicative for a significant contribution in PL from the ³LE(A) states. The frozen toluene solution for e-2-1 excited state lifetime is increasing to several hundred of microseconds although it’s less compared to CMA1 (301 µs at 77K). The energy difference between CT and ³LE(A) states is slightly smaller for compound e-2-1 (0.16 eV) compared with CMA1 (0.19 eV), while ³LE(A) state is higher in energy compared with CT state for both complexes. The steric protection of the metal center in CMA complexes is usually considered as an important factor to rationalize high observed PLQY (Φ) values in solutions. However, the less sterically protected complex e-2-1 shows unity PLQY values in toluene solution similar to the archetype CMA1 complex (Table 2) or three-fold higher PLQY values compared to copper-based analog for e-2-1 [5]. Unity PLQY values together with shorter excited state lifetime for e-2-1 complex results in spectacular radiative rates approaching 10⁶ s⁻¹. Such difference in PL performance for e-2-1 can be associated with stronger preference of the gold(I) complexes to retain a linear geometry thus avoiding a Renner-Teller distortion. This together with the higher spin-orbit coupling values for gold compared with copper complexes may outcompete the importance of the steric protection for particular gold complexes. This enables the use of much more affordable CAAC carbenes with smaller substituents compared with bulky and expensive adamantyle substituted CAAC carbene.

3. Materials and Methods

3.1. Computational Details

Gas-phase DFT calculations of CMAs were carried out by the global hybrid MN15 functional by Truhlar and coworkers [25] in combination with the def2-TZVP basis set by Ahlrichs and coworkers [26,27]. The relativistic effective core potential of 60 electrons was used to describe the core electron of Au [37]. The ground states were studied by DFT and the excited states by TD-DFT [38]. The employed method provides excited state energies that do not suffer from underestimation typical for TD-DFT [39,40], as indicated by previous calculations of CMAs [5,9,14] as well as by earlier comparison to T1 energies calculated by unrestricted DFT, such that the unrestricted and TD-DFT T1 energies differed by only 0.004eV [23]. All calculations were carried out by Gaussian 16 [41]. Metal contributions to HOMO and LUMO were calculated by Mulliken population analysis, and HOMO-LUMO overlap integrals were calculated using Multiwfn program [42].

3.2. Experimental Details

Synthesis of e-2-1. In a Schlenk flask, (^Et2CAAC)AuCl [36] (1 mmol, 545 mg), carbazole (1 mmol, 168 mg), and tBuOK (1 mmol, 112 mg) in THF (20 mL) were stirred for 8 h. The mixture was evaporated, extracted with CH₂Cl₂ and filtered through Celite®. The filtrate was concentrated and washed with hexane to afford the pure product as an off-white solid. Yield: 554 mg (0.82 mmol; 82%).

¹H NMR (500 MHz, CD₂Cl₂): δ 7.94 (d, J = 7.6 Hz, 2H, CH Cz), 7.65 (t, J = 7.8 Hz, 1H, CH-aromatic CAAC), 7.45 (d, J = 7.6 Hz, 2H, CH-aromatic CAAC), 7.12 (t, J = 9 Hz, 2H, CH Cz), 6.94–6.91 (m, 4H, overlapping CH Cz), 2.97 (sept, J = 6.7 Hz, 2H, CH(CH₃)₂), 2.17 (s, 2H, CH₂), 2.13–2.00 (m, 4H, CH₂CH₃), 1.48 (s, 6H, 2CH₃), 1.38 (d, J = 6.7 Hz, 6H, CH(CH₃)₂), 1.35 (d, J = 6.7 Hz, 6H, CH(CH₃)₂), 1.22 (t, J = 7.5 Hz, 6H, CH₂CH₃) ppm. ¹³C NMR (125 MHz, CD₂Cl₂): δ 242.2 (C carbene), 150.0 (C_ipso, Cz), 146.2 (C_ipso), 135.6 (C_ipso), 130.1 (p-CH CAAC), 125.6 (m-CH), 124.3 (C_ipso, Cz), 123.7 (CH, Cz), 119.5 (CH, Cz), 116.2 (CH, Cz), 114.1 (CH, Cz), 80.5 (C_q), 62.7 (C_q), 42.7 (CH₂), 32.2 (CH₂), 29.6 (CH₃), 29.5 (CH₃), 26.7 (CH), 23.1 (CH₃), 9.8 (CH₂CH₃) ppm. Anal. Calcd. for C₃₄H₄₃AuN₂ (676.70): C, 60.35; H, 6.41; N, 4.14. Found: C, 60.61; H, 6.53; N, 4.20. C₃₄H₄₄AuN₂ theoretical [M+H⁺] = 677.3165, HRMS (APCI(ASAP)) = 677.3172.

4. Conclusions

In summary, we have carried out a DFT study of over 60 CMA complexes to evaluate their potential as TADF emitters, focusing on specific effects of the CAAC ligand. Several parameters that have been previously shown to be important for the PL properties of this family of complexes were studied as a function of CAAC, where the choice of its structural modifications was primarily based on experimental synthesis prospects.

We demonstrated that the properties of the CMAs are governed by the overlap of HOMO and LUMO orbitals, where the HOMO is localized on amide and the LUMO on metal-carbene, HOMO-LUMO accounting for nearly 100% of the charge transfer between the ground state and the lowest excited states. The states corresponding to localized triplet excitations usually lie well above the CT states and are therefore unlikely to interfere much with TADF. The HOMO-LUMO overlap was shown to be strongly correlated to vertical S0-S1 and S0-T1 excitation energies, exchange energy, and S0-S1 oscillator strength. Consequently, the optimal combination of low exchange energy and high oscillator strength is a compromise.

Prioritizing low exchange energy over oscillator strength in making the compromise, we selected six CMAs for geometry optimization of T1 and S1 states. The former relax to geometry analogous to S0, having carbene and amide nearly coplanar, while the latter rotate to perpendicular orientation, lowering both exchange energy and oscillator strength near zero. Efficient fluorescence thus requires rotation toward coplanarity, which comes at a cost of increasing exchange energy. Highest oscillator strengths are obtained with bulky substituents on CAAC.

Guided by the computational results, we synthesized and obtained a novel CMA complex e-2-1 with spectacular luminescence properties (up to unity PLQY values and one microsecond excited state lifetime). We demonstrated that we could use much more affordable CAAC ligands with small steric protection. For instance, ethyl-substituted CAAC-carbene is already sufficient to obtain gold-based CMA complexes with excellent performance. This paves the way towards more environmentally friendly and more sustainable production of the CMA complexes by eliminating the need of complex, multistep synthesis and use of the CAAC-carbenes with bulky substituents (adamantyle, menthyl and others).