Prerpints.org logo
Preprint
Article

Structure and Optical Anisotropy of Spider Scales and Silk: Use of Chromaticity and Azimuth Colors

Altmetrics

Downloads

173

Views

157

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 April 2023

Posted:

04 May 2023

You are already at the latest version

Alerts
Abstract
In this perspective, we give an overview of several less explored structural and optical characterisation techniques useful for biomaterials. New insights into the structure of natural fibres such as spider silk can be gained with minimal sample preparation. Electromagnetic radiation (EMR) over a broad range of wavelengths (from X-ray to THz) provides information of the structure of the material at cor- respondingly different length scales (nm-to-mm). When the sample features, such as the alignment of certain fibres, cannot be characterised optically, polarisation analysis of the optical images can provide further information on feature alignment. The 3D complexity of biological samples necessitates that there be feature measure- ments and characterisation over a large range of length scales. We discuss the issue of characterising complex shapes by analysis of the link between the color and struc- ture of spider scales and silk. For example, it is shown that the green-blue color of a spider scale is dominated by the chitin slab’s Fabry-P ́erot type reflectivity rather than the surface nanostructure. The use of a chromaticity plot simplifies complex spectra and enables quantification of the apparent colors. All the experimental data presented herein are used to support the discussion on the structure-color link in the characterisation of materials.
Keywords: 
Subject: Biology and Life Sciences  -   Biophysics

1. Introduction

It is well known that color and structure are closely linked. This link is established via the feature size and its pattern (organisation and alignment) [1]. Structural color, or the structural basis of color responsible for the vibrant shades observed on various insect species, can be endowed by the interaction of light (scattering and reflectance) with specific nano- and microstructures. The particular micro-nano surface structures (surface topography) also impart biomaterials with additional functionality, e.g., stronger light reflection or absorption due to the layered surface architecture of the feature arrangement along the height (a conifer or Christmas tree arrangement). Randomness, together with well-defined gratings, films, and cavities are key to the formation of structure-defined colors in Nature [1] in addition to pigment (chemical) based coloration. The lateral and axial dimensions of the absorbers and reflectors are discussed in electromagnetic (EM) antenna nomenclature. The portion of absorbed, reflected and transmitted parts of light energy obeys energy conservation A + R + T = 100 % . One of the most relevant examples found in nature is the structural colouration of arachnid species such as Theraphosidae (tarantulas) and Salticidae (jumping spiders) [2] Some spiders are vividly coloured by using a combination of chemical and structural colouration strategies, providing unique examples for the design of photonic devices. With approximately 47,500 described species of spider from ∼100 different taxonomic groups [3], the understanding of the origin and their function of structural colouration is still relatively unexplored. Furthermore, the correlation between specific feature alignment and color is obvious for characterisation techniques using light within the visible spectral range. However, characterisation of physical structures using different wavelengths (short UV and long IR- to-THz or sub-mm waves) allows us to confer new spectral properties. For example, recently, Kariko et al., established the origin of the red, silver and black color phenomona observed on the theridiid spider, Phoroncidia rubroargentea from Madagascar using complementary optical, structural and chemical analysis [4]. Correlative structural analysis of complex 3D samples, such as spiders, is integral to defining the compositional origins of color. Specifically, surface topography at the nano-and micro-scales can be investigated via surface sensitive optical techniques such as scanning electron and atomic force microscopy. Compositional features important for the structural colour phenomena that lie beneath the surface (e.g., the red color of the therediid spider was found to be facilitated by a combined effect of multiple structural layers including the thick sclerotized exoskeleton, guanine crystal microplates, and the chambered pigment-containing microspheres) are often investigated using artefact introducing, preparation intensive techniques like serial block face scanning electron microscopy, transmission electron microscopy and confocal scanning laser microscopy. However, simpler optical characterisation techniques, such as X-ray computed tomography and THz imaging may be incredibly useful for structural characterisation of colour complexity. Indeed, the penetration depth is directly related to the wavelength. Currently, longer (mm) wavelengths being used for telecommunication networks and their interference, diffraction, and multiple reflections with materials are defined according to the optical properties (complex refractive index n + i k ) of materials at those wavelengths.
Here, we overview several characterisation techniques for the optical and X-ray characterisation of natural materials. Specifically, we focus on the optical characterisation techniques of the spectral properties of peacock spider (Maratus volans) scales and silk (spider silk and silk from the silk worm). The anisotropic nature of the microstructure of silk fibres is notoriously difficult to study [5]. Often transmission studies of fibres suffer from reproducibility issues given the complexity of sample preparation and presentation. For example, cutting the fibres introduces microstructural changes [6,7,8,9,10]. The thickness of the fibres may result in absorbance peak distortion, loss of resolution, and low signal to noise ratio. The orientation of the fibres relative to the beam also influences the spectral data, ensuring that all materials must be analysed in the same orientation for reproducibility. Nevertheless, the optical and structural characterisation of these natural materials is important to inform the design of biomimetic polymers/materials that possess enhanced structural and optical properties. Indeed, the superior features of silk produced by spiders in comparison to silk produced by silkworms may be informed by their specific nano- and micro-structures, although both silks are composed of similar glycine-rich proteins. Due to the complexity of studying natural samples (shape and size complexity), the ability to achieve optical and structural characterisation over several orders of magnitude of the features of interest is important from multiple aspects: 1) resolution and 2) composition/structure. The complexity of 3D surfaces and structures should be described in its entirety for in-depth/comprehensive understanding of color and structure since geometry and dimensions of 3D structures are of paramount importance for their color/spectral response and linked to mechanical and thermal properties [11].

2. Materials and Methods

The peacock spider specimens were kindly donated by Jürgen C. Otto. Spider preparation for scanning electron microscopy (SEM) observation involved the removal of the abdomen from the main body using a surgical grade stainless steel scalpel. The abdomen was then immobilised on a Al stub using double-sided carbon tape. The spider was then fixed in 2.5% glutaraldehyde overnight at 4 ∘ C, followed by washing with double-distilled H2O ( 3 × 5 min) and further fixation with 1% aqueous osmium tetroxide for 2 h. Routine ethanol (EtOH) dehydration was followed using 20%, 50%, 70%, 80%, 90%, 95%, 100% ×2 EtOH. The abdomen was stored in EtOH prior to experiments. For SEM imaging, the fixed sample was placed in a critical point dryer (CPD; Polaron, E3100, Quorum Technologies Ltd.). The ethanol was gradually replaced with liquid CO2, which was then placed under supercritical conditions (1100 psi and 36 ∘ C). Once dried, the sample was then coated with approximately 10 nm of gold prior to SEM imaging. SEM imaging was performed under high vacuum using the Raith direct write electron beam lithography (EBL) system with high resolution (HR) field-emission imaging capabilities. Images of the abdomen were acquired at an accelerating voltage of 10 kV (Figure 1, Figure 2, Figure 3).
Garden spiders (Eriophora transmarina) were collected during the night from locations in Sydney, Australia. Their major ampullate (dragline) silk was collected by forcible spooling, as described by Blamires et al. [12]. The silks of this spider appear white to the naked eye, a consequence of high reflectance across the visible waveband outside of the UV [13]. Spiders were anaesthetized using CO2, placed them ventral side up on a foam platform, immobilized using non-adhesive tape and pins. A single silk thread from the spinnerets was collected under a dissecting microscope. An electronic spool rotating at 1 m/min was used to reel silk threads from spider [14].
Sericin cladding free silkworm fibers used for optical imaging were prepared by established washing protocol in basic solution [15].
Focused ion beam (FIB) milling of the abdominal platelets was applied to characterise the internal structure (Figure 3) (IonLine, Raith). Rectangular sections were milled using a gallium (Ga) ion beam at 30 kV, 0.5 nA to a depth of sub- 1 μ m. The FIB cross-sections were then imaged by SEM for detailed observation of the internal structure of the platelets/scales (Figure 3).

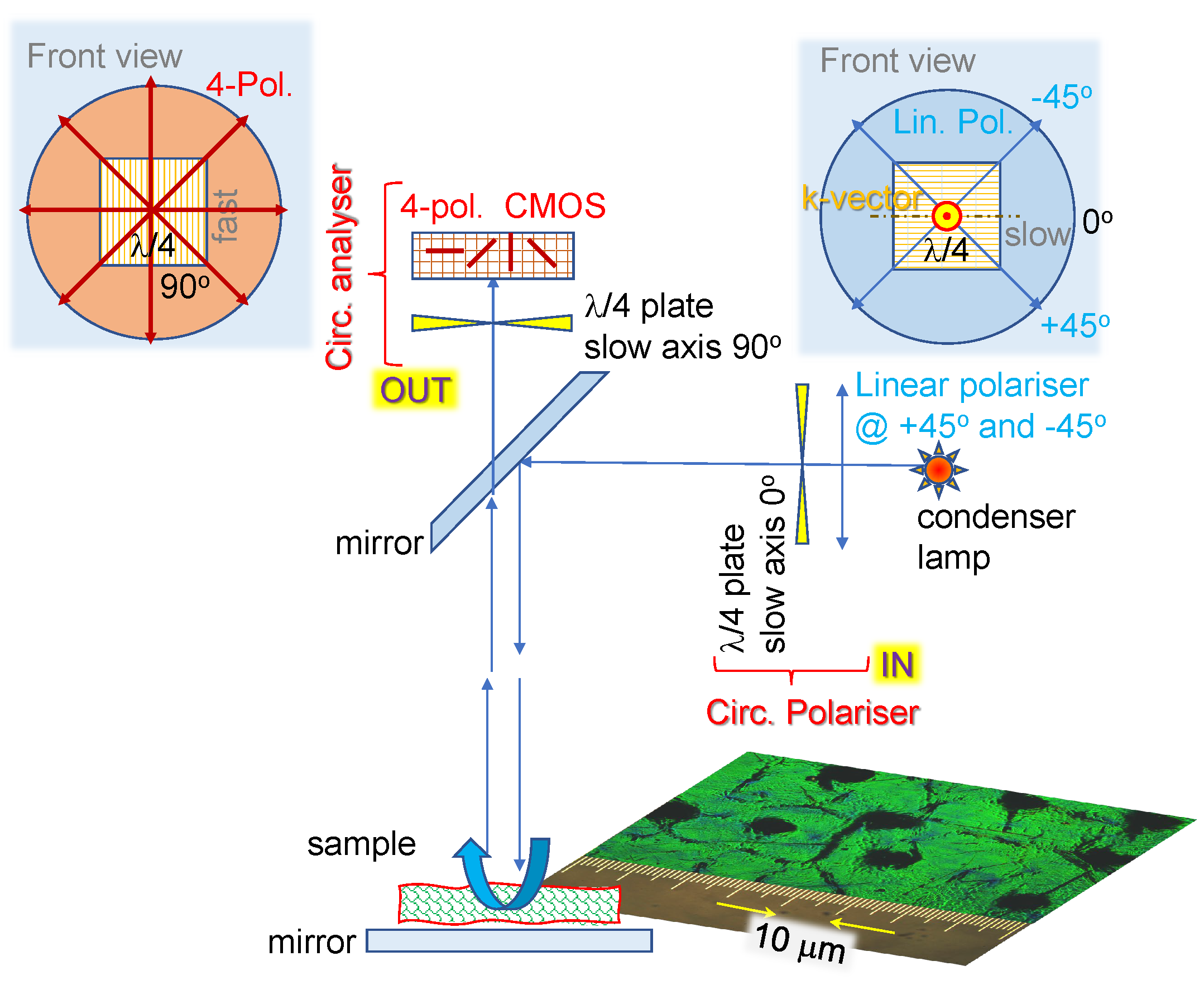
2.1. Optical imaging techniques

Optical microscopy with polarisation analysis was used for the optical characterisation of the nano-structured surfaces of the spider scales and for silk samples. Emphasis was placed on imaging of the orientation azimuth [16]. A 4-polarisation (4.pol) camera was used for the detection of anisotropy in absorbance and retardance. For mapping the slow axis orientation, we employed a recently invented polychromatic polarizing module (PPM; US patent 9625369). The PPM consist of a source of white light, polychromatic polarization state generator, and circular analyzer. While a traditional polarizing microscope generates the Newton interference colors if the specimen retardance lies from 300 nm to 2100 nm, PPM creates the interference colors if the specimen retardance is from a few tenths-of-nm to 300 nm. The hue in PPM mostly depends on the slow axis orientation rather than the retardance. This is in contrast to the traditional microscope, where the hue is determined by the retardance, but not on the slow axis orientation.
For reflection analysis of spider silk using a 4-pol. camera, a Au (60 nm thin film) mirror on a 5 nm Cr adhesion layer was thermally evaporated on cover glass at 60 A and 20 A currents, respectively, using LA-V5050L, Labotec evaporator at ∼ 4 × 10 − 4 Torr. We also used plastic λ / 4 -waveplates (Edmund Optics) as sample holders for transmission and reflection modes using the 4-pol. camera (Thorlabs).

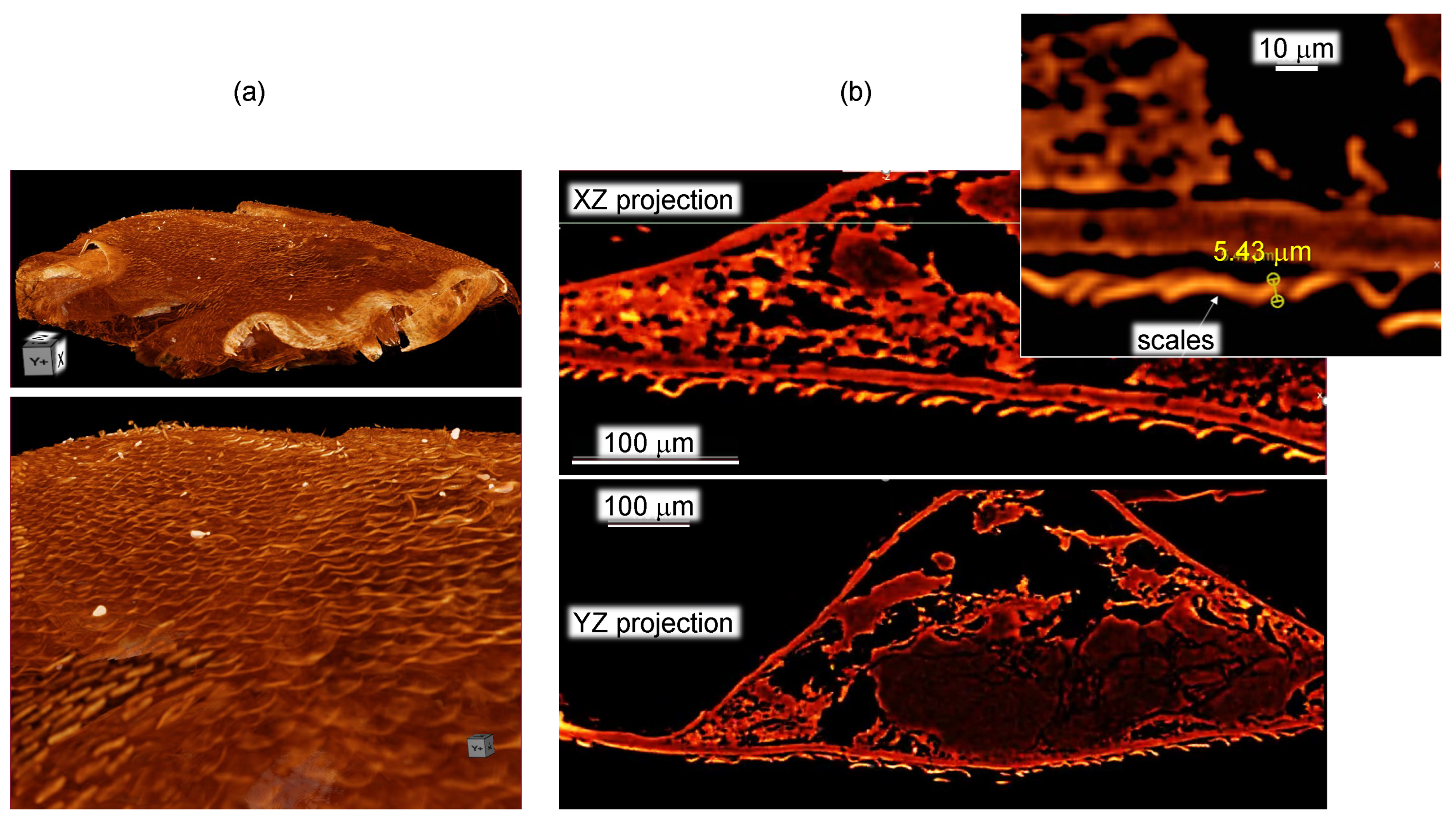
2.2. X-ray tomography

Hard X-ray micro-Computed Tomography ( μ -XCT) was used for virtual sectioning of the reconstructed 3D volume of spider. The μ -XCT experiment was carried out using ZEISS/Xradia Versa 520 X-ray microscope at the Stanford Nano-Shared Facilities, Stanford, CA. Both low and high low resolution x-ray tomography volumes of the spider were collected with voxel sizes of 1.23 μ m and 0.38 μ m, respectively (Figure 4). The 3200 sample projection images were acquired in absorption mode using geometrical together with 4 × and 20 × optical magnification for low and high resolution modes, respectively. In order to remove the high-energy part of the x-ray spectrum, the X-ray source voltage was set to 30 kV, minimum allowable for this instrument. To achieve the optimal signal-to-noise level (intensities of >5000 grey value over low transmission regions), the exposure time of 25 sec was chosen. The μ -XCT datasets were reconstructed using the proprietary ZEISS Reconstructor software.

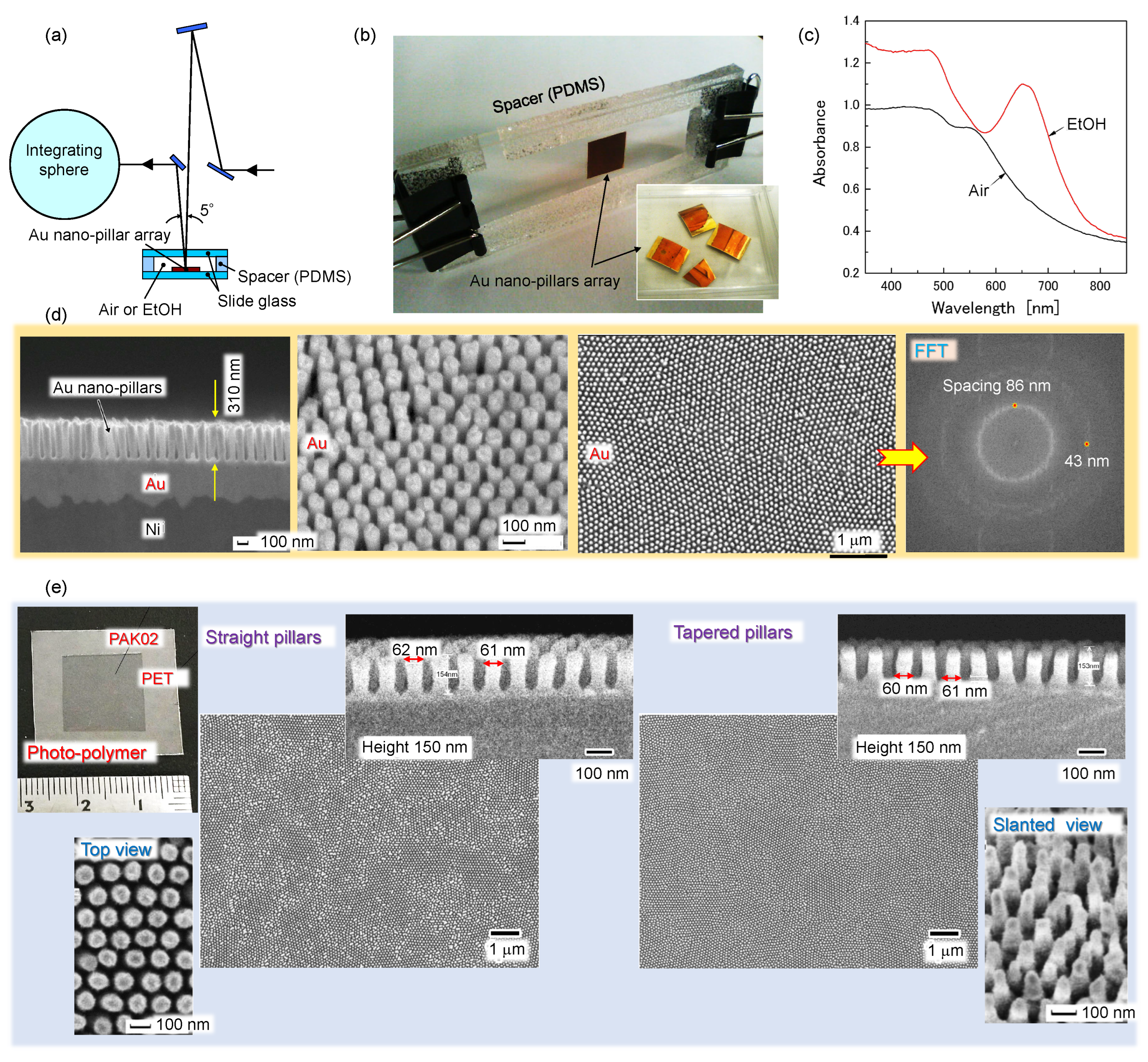
2.3. Sub-100 nm surface texturing

Metallic nano-pillars. Anodic porous alumina [17,18,19] was prepared using anodization of Al under a constant voltage of 40 V at 16 ∘ C for 1 hour. The through hole membrane of porous alumina was obtained by removing the Al substrate and the bottom part of the porous alumina [17,18]. An anodic porous alumina membrane with nano-holes was prepared by selectively dissolving the Al part of the sample in a saturated methanol solution of iodine at 50 ∘ C for 12 h. For the formation of Au nano-pillars, a thin Au layer, which acts as conducting layer during Au electrodeposition, was coated onto the alumina membrane by sputtering. The Au electrodeposition was carried out in the commercial electrolyte (EFC-60; N.E. Chemcat) at a constant voltage of -1 V for 2-4 min. The length of Au nanowires was controlled by changing the deposition time (Figure 12(d)). To reinforce the sample, Ni electrodeposition was carried out at constant voltage of –1 V [19]. Au nanowire array was obtained by dissolving the anodic porous alumina template and Al in 10 wt% NaOH solution. Hexagonal shape distribution of nano-pillars has center to center distance equal to 100 nm. Length an diameter of nano-pillars were 310 nm and 70 nm, respectively.
Polymer nano-pillars. The polymer straight or tapered nanopillar arrays were prepared by photo-nanoimprint process using a AAO mold (Figure 12(e)). Prior to photo-nanoimprint process, two types of AAO molds were prepared. One has straight nanoholes and the other has tapered nanoholes. The AAO molds were prepared by two-step anodization process [17,20]. First, an Al plate was anodized in 0.3 M oxalic acid solution by applying volage of 40 V for 12 h. A AAO layer formed on surface of an Al was selectively dissolved in mixture solution of chromic acid and phosphoric acid. A AAO mold having straight nanoholes was prepared by anodizing the Al in 0.3 M oxalic acid solution at 16 ∘ C by applying voltage of 40 V. Duration of the anodization was 1 min 40 sec. The sample was immersed in 5 wt% phosphoric acid solution at 30 ∘ C to adjust pore diameter by dissolving wall of nanoholes. Duration of the pore widening treatment was 31 min. A AAO mold having tapered nanoholes was prepared by alternately implementing anodization and pore widening treatment to the sample. Total durations of the anodization and the pore widening treatment were 1 min 40 sec and 21 min, respectively.
Next, polymer straight/tapered nanopillar arrays were obtained by photo-nanoimprint process using the obtained AAO molds. A photocurable polymer (PAK-02; Toyo Gosei) was coated on a surface of poly(ethylene terephthalate) (PET) substrate. The AAO mold was placed on the PET substrate, then, UV light was irradiated to the sample for 10 min. A polymer nanopillar array was obtained by removing the AAO mold from the substrate.

3. Results

3.1. Spider scales: peacock spider

The male Australian Peacock (jumping) spider Maratus volans is ∼1 mm in size and shows very strong coloration. The abdomen of the tiny arachnid displays a striking pattern of red, blue, and black. The abdomen possesses microscopic scales that contain three dimensional reflective diffraction grating structures. Some male peacock spiders are able to change their scales from red to green to violet with slight movements. In the family of structural color, the Morpho blue butterfly is the most well known example of color being independent of the observation angle [21]. Structural color comes from the interference of light scattered from a surface array of nanostructures. Ordered nanostructures (such as grating patterns) produce small angle colour changes (iridescence) whereas disordered nanostructures produce structural colors that are independent of the observation angle, similar to pigmented materials [22] . For the Morpho blue butterly, its wide angle colour is attributed to a mixture of both ordered and disordered nanostructures in a hierarchical (multilayered) display [23].
The peacock spider has a distinct red pattern; its color being defined by the absorption of xanthommatin [24] contained within the brush-like structures, hence coloration of a chemical origin (Figure 2(a)). The black color observed in some species is due to combination of both chemical and structural coloration [25]. For M. volans, the green-blue scales are composed of a colorless and transparent chitin with a refractive index of n ≈ 1.5 [24] (Figure 2(b)).
Numerical simulations using the effective medium approach showed that the surface nano-grating of ∼ 50 nm modulation depth and period ∼ 200 nm (Figure 2(c,d)) is mainly contributing as an anti-reflection structure, while the blue color is defined by the thickness of chitin membrane ∼ 360 nm and the gap ∼ 160 nm between the two sides of the scale and the fibre structure of diameter 100 nm (with a surface filling ratio of 0.25) inside the air gap [24]. Figure 3 shows the green-blue scale membrane milled by Ga-ions to different depths. It reveals the fiber mesh on the inside section. In a separate experiment, the form-birefringent nature of the surface nano-grating was revealed by the angular dependence of reflectance under illumination by linearly polarised light [24]. The medium theory of refractive index used in the modeling was not predictive of the polarisation dependence [24]. There was no polarisation dependence for the red brush structure whereby the color originated from a chemical pigment (xanthommatin).
Figure 4 shows a 3D reconstruction of the micro-CT scan of the surface of the spider abdomen and respective cross sections in the XZ and YZ axis. The cross-sections do not reveal structures below ∼ 2 μ m, however, micro-CT is able to show the actual pattern of the scales on the abdominal surface. The scales cover all the surface. In Figure 5, where the cross-sectional X-ray image are paired with the optical reflection image, the edges of the scales are well defined while the middle parts have lesser brightness and, in the case of the optical image, clear interference patterns are recognisable. The central part of some of the scales is flatter (see Figure 3(a)) and the air gap inside the scale is smaller or absent. The high vacuum environment in the SEM and FIB chambers may have contributed to the flattening of the scales (Figure 1(a)).
The origin of the blue-green color appearance of the spider scales can be explained by the Fabry-Pérot (FP) etalon and its spectral selectivity. An FP plate of thickness d at a tilt angle β defines the effective thickness of the FP etalon which becomes larger with tilt d / cos β ; the effective thickness and retardance is increased at an angle. The tilt angle tunes the phase delay δ = 2 π n d / λ . The transmission and reflection coefficients of the FP etalon are dependent on the reflectivity R of the FP film (chitin in the case of spider scales) interfaces; both interfaces are assumed to have the same reflectivity. The FP transmittance and reflectance spectra are given by:
T F P = ( 1 − R ) 2 ( 1 − R ) 2 + 4 R sin 2 δ ,
and complimentary reflectance (without absorbance A = 0 ):
R F P = 4 R sin 2 δ ( 1 − R ) 2 + 4 R sin 2 δ ,
respectively (widely used from visible to far-IR wavelengths [26]). The FP etalon imparts its reflectance/transmittance spectrum. The FP reflectance is maximum for a given R (of the single interface), when the phase delay corresponds to the λ / 4 or δ ≈ π / 2 .
Next, the spider scale was modelled as two FP etalons separated by a sub-wavelength gap. The model was used to investigate the effect of color reflectance (Figure 2(b)). The scale itself is oriented at an angle to the exoskeleton, which can also contribute as a back-reflector (hence the transmitted spectrum is partially back-reflected). The twin FP structure of the scale and air-gap is apparent from SEM images but is even better revealed using X-ray 3D tomography. Finite difference time domain (FDTD) calculations were implemented to explore predictions of the spider scale model.
Figure 6 shows the results of reflectance R ( λ ) and transmittance T ( λ ) spectra for the two FP chitin slabs separated with an air g a p = 160 nm and 50 nm (simulating a flattened scale), which are a closely matching model used in more elaborated calculations based on the actual structure of the spider scale and accounting for the effective refractive index on nano-corrugated surfaces [24]. The refractive index of chitin over the visible spectral range was calculated by Cauchy’s equation n c = A + B / λ 2 , where A = 1.517 and B = 8.8 × 10 3 [nm 2 ] [24]. Calculations were carried out by finite difference time domain (FDTD) method using Lumerical software package (Ansys). The total field scattered field monitors were setup to calculate the spectra; the incident field was linearly polarised and E-field strength was E = 1 (Figure 6(a)). At the normal incidence there is no difference for the s- and p-pol., which would change at a tilted angle (see Sec. Appendix B). The s-/p-pol. reflected and transmitted spectra becomes more complex, there are spectral regions where interference is causing intensity increase. However, all those complex spectra can be mapped onto a 2D chromaticity diagram as shown next for the simpler case of normal incidence.
The R ( λ ) plotted on the chromaticity coordinates ( x , y ) shows color change upon the thickness of chitin increasing from 300 to 360 nm, which is consistent with the SEM and FIB analysis discussed above (Figure 6(c)). The two slabs of chitin define the color without sub-wavelength patterns on the outer and inner chitin walls. The polarisation effect in R ( λ ) observed experimentally [24] is consistent with the pattern of nanogratings on the surface and the reflected light has a larger component of polarisation normal to the scattering plane as follows from the Fresnel rules for the s- and p-polarisations. Spectra of R ( λ ) and T ( λ ) are complimentary in terms of energy conservation (Figure 6(b)). The transmitted portion of light is larger than the reflected, understandably due to the low refractive index of chitin (close to that of window glass). This implies that the back-reflected light after transmission of a spider scale can produce the color appearance which is shown in (c). It is also noteworthy, that the R and T points are located on the chromaticity ( x , y ) coordinates in such a way that they are on the opposite sides of the “white” central point (the highest color temperature) as shown in the inset of (c). This is another representation of the complimentarity of R and T via the energy conservation A + R + T = 100 % in the absence of absorbance A = 0 .

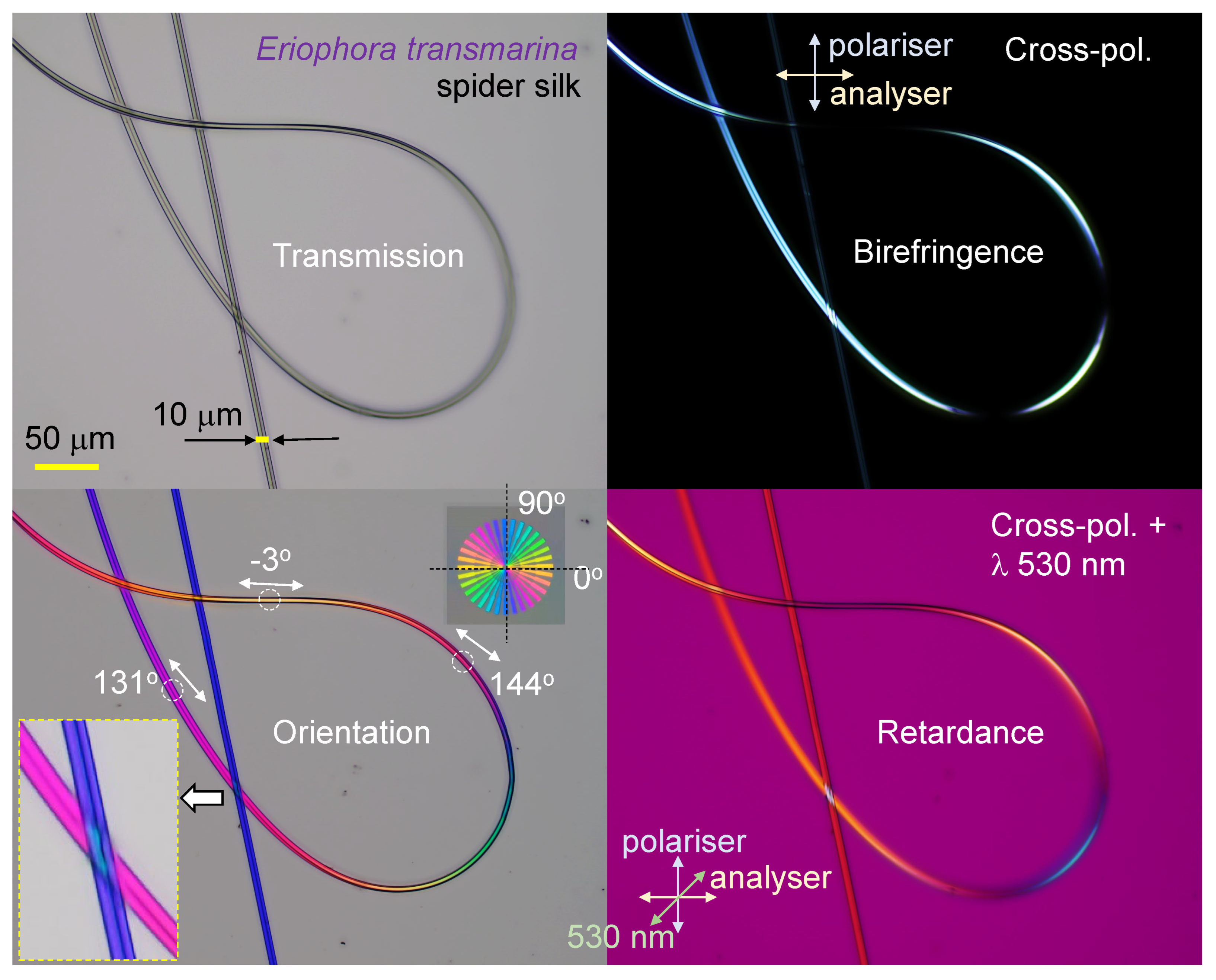
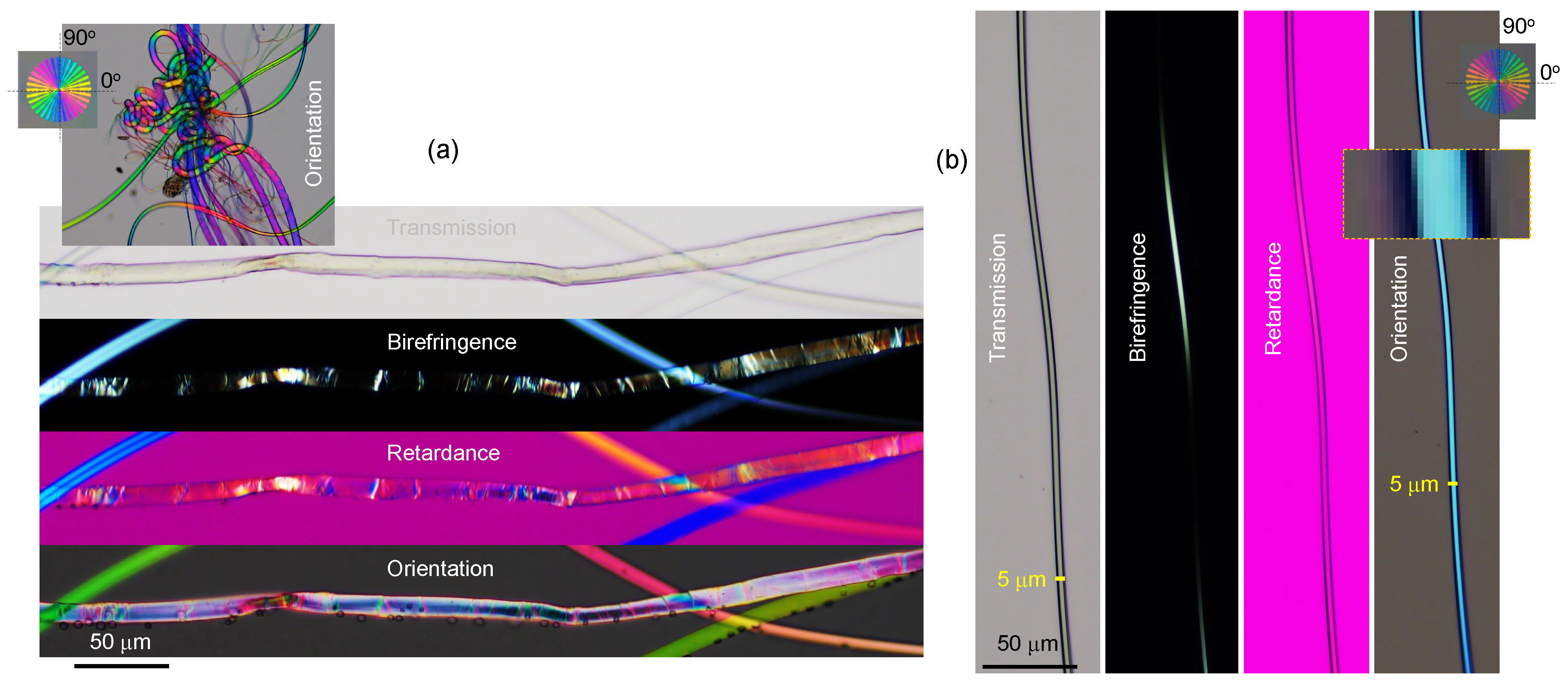
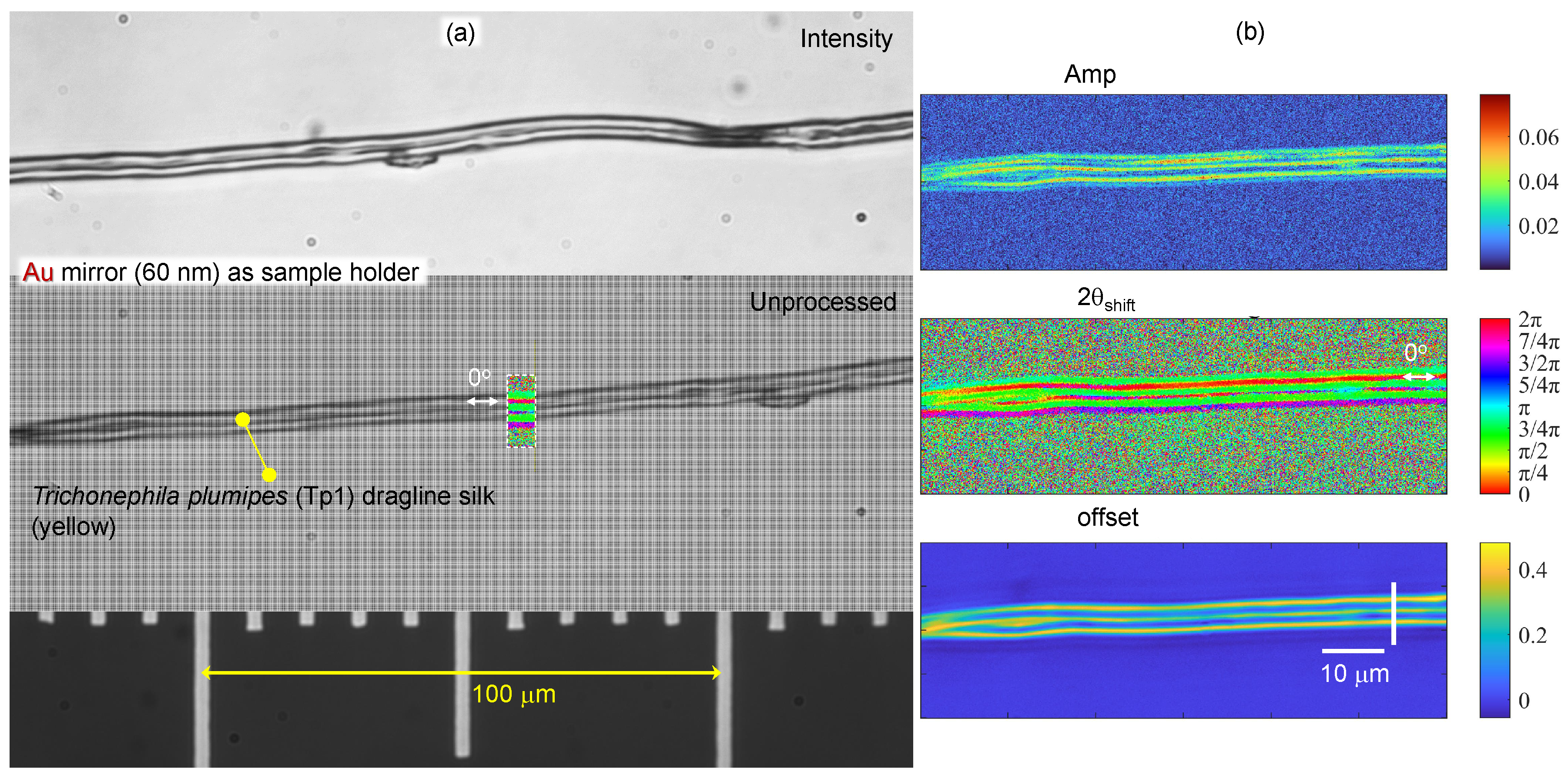
3.2. Spider silk

Spider silk, which is an excellent example of naturally occurring birefringence and alignment [27] was analysed by polarisation imaging techniques. Silk has a high ∼ 80 % crystallinity [10] and is much less common in the water soluble amorphous state [8], which is only attainable via a very fast thermal quenching of the disordered molten phase. Investigation of the light absorbance and scattering of spider silks over a broad UV-visible spectral range showed reduced absorbance at UV wavelengths [13]. Thus, the strong correlation between the glass transition temperature and the thermal degradation of silk with its color was experimentally established [14]. Spider silks are among the most mechanically resilient fibres known to man. Experimental stability testing of spider silks in outer space conditions (e.g., exposure to microgravity, cosmic radiation) will be performed and the evaluation will be based on its high refractive index and waveguiding properties (Suppl. Appendix C). We hypothesise, that the degradation of hydrogen-bonded molecules can be monitored via color and intensity mapping using simple observation methods during the harsh outer space environment. Figure 7 displays several possible optical imaging methods including the usual transmission mode for intensity to cross-polarised imaging, which can be rendered into a color map of retardance, as well as mapping of the orientation azimuth [16]. Silk fibers with structural defects that change the alignment of fibroin along the fiber direction can be observed using transmission mode imaging (Figure 8(a)), however, more detailed structural changes can be revealed using cross-polarised imaging showing localised changes of birefringence and retardance patterns. The color-azimuth map is an additional useful presentation of structural changes, as discussed in this perspective article.

4. Discussion

Optical anisotropies related to the real and imaginary parts of the refractive index ( n + i k ) are linked to the birefringence Δ n and dichroism Δ k . Both Δ n and Δ k occur for circular and linearly polarised light, depending on the material order and structure. The simplest measurement of absorption anisotropy can be made by using one linear polariser which is used to control polarisation of the incident light. For the birefringence, two polarisers (a pair of polariser and analyser) must be used. In such case, the transmitted intensity follows θ -azimuthal dependance when absorbance and reflectance are negligible ( R ≈ 0 , A ≈ 0 ):
T ( θ ) = sin 2 [ 2 ( θ − θ r e t ) ] sin 2 ( π Δ n d / λ ) ,
where θ is the orientation angle, θ r e t is the slow or fast axis direction (i.e., the slow axis is usually aligned to the main molecular chain or along a polymer stretch direction), Δ n is the birefringence of the sample/object at the wavelength λ for the thickness d. This equation defines the Maltese-cross with the dark intensity positions at θ = θ r e t and θ = θ r e t ± π / 2 , while the most bright regions are at θ = θ r e t ± π / 4 . The phase retardance δ = 2 π Δ n d / λ is defined by the second sin-term in Eqn. 3.

4.1. Polychromatic polarizing module

The PPM is an add-on that can be used with a regular benchtop optical microscope. The uniqueness of the device is that it allows for visualization of the birefringence instantly and independently of the specimen orientation. In the image, the hue represents the orientation of the slow axis, and the saturation depicts the retardance amount. The main component of the PPM is a polychromatic polarisation state generator, which produces polarized light with the polarization ellipse orientation determined by the wavelength. A set of ellipses corresponding to different wavelengths is called a spectral polarization fan. All polarization ellipses have the same ellipticity angle. If there is no alteration of the beam polarization by a specimen, then all wavelengths are transmitted the circular analyzer evenly. As a result, we see a gray background. If the major axis of the polarization ellipse is at 45 ∘ or 135 ∘ to the slow axis of a birefringent specimen, the intensity of light transmitted by the circular polariser will be minimal or maximal, respectively. For example, if the major axes of red and green polarization ellipses are oriented at 135 ∘ and 45 ∘ , respectively, and the specimen slow axis is oriented at 0 ∘ , then transmission of red wavelength will be maximal, and transmission of green wavelength will be minimal. As the result, the specimen will be red. In the case of rotation of the specimen by 90 ∘ , the situation will be reversed, and the specimen will be green. The dependence of the hue on orientation of the slow axis φ can be approximate by a linear function H u e = 2 ( φ + φ 0 ) , where 0 ∘ ≤ H u e < 360 ∘ with 0 ∘ ≤ φ < 180 ∘ and φ 0 is a constant defined by a reference angle, which depends on the mutual orientation of the polarization state generator and the camera. In order to find φ 0 we can use a birefringent structure with retardance of approximately 30 nm and the slow axis oriented at 0 ∘ . It is convenient to employ a calibration test target, which was developed by Prof. Peter G. Kazansky (University of Southampton). The test target has a birefringent star pattern with slow axes oriented in the radial direction. The birefringent star is shown in the right top corner of the polychromatic polarization image in Figure 7. The reference angle φ 0 equals to the half of hue of the horizontal wedge. Then we can compute a map of the slow axis distribution as φ = H u e / 2 − φ 0 . It is necessary to mention that the linear approximation can introduce an error of measured slow axis orientation, about 3 ∘ . In order to suppress the error, we can build a calibration curve by measuring the hue of each wedge. Another option is to mechanically rotate the birefringent specimen and measure the hue at each azimuthal position.

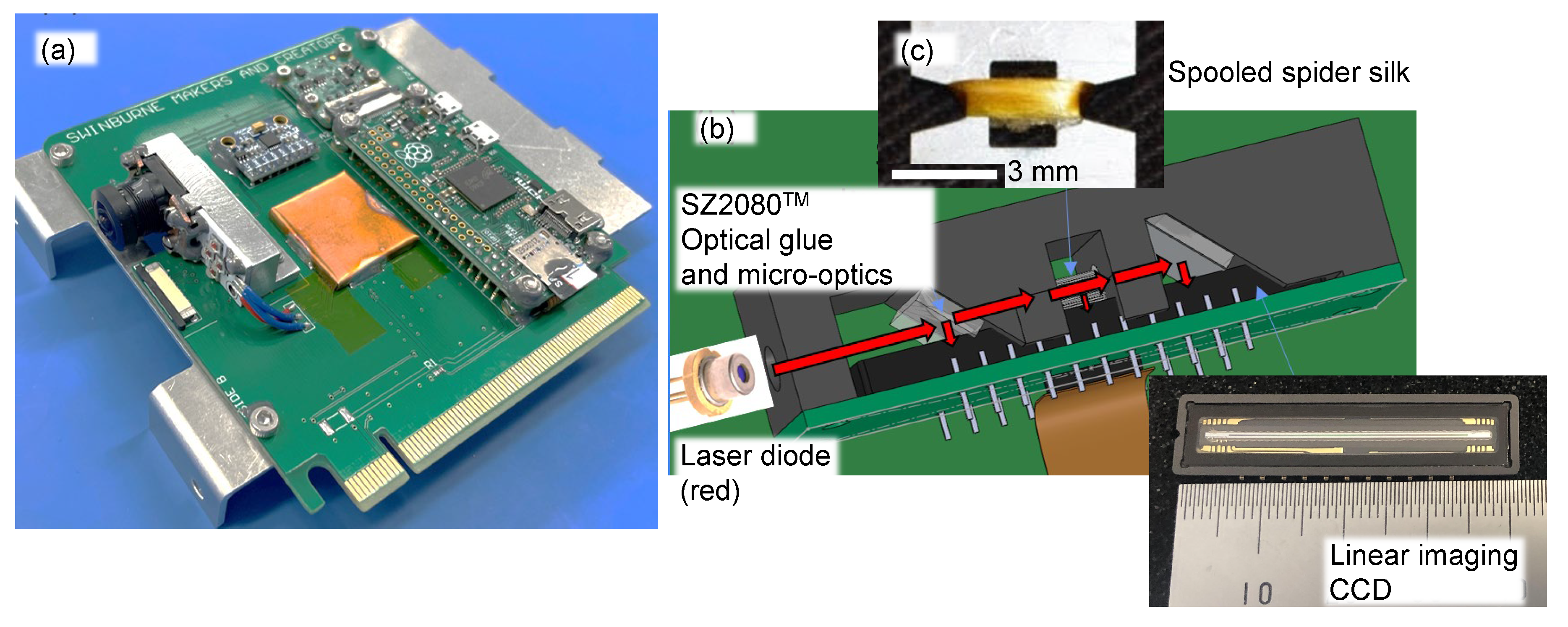
4.2. Four-polarisation camera

Biomaterials, such as silk, can exhibit not only linear but also circular dichroism due to specific protein structures. Measuring optical anisotropy using linear as well as circularly polarised light can be carried out with a simple setup assembled on the microscope, as shown in Figure 10. Setting of the circular right-/left-pol. is performed by orientation of the linear polariser at the IN-port. If the transmission axis (orientation of the E-field) of the linear polariser is aligned with the slow axis of the λ / 4 waveplate, a linearly polarised light is launched from the IN-port. Depending on the polarisation elements at the detection OUT-port, different optical characterisations can be possible, as discussed next. In all cases we consider the 4-pol. camera as a detector, that already provides four orientation analysis of the sample (reflection and absorption for transparent samples, Figure 10).
By capturing an image with a camera (e.g., CS505MUP1 Thorlabs) that has four directional wire grid arrays integrated into the CMOS sensor, polarisation analysis can be made faster. Even more importantly, the image shifts and distortions when the polariser (or sample) are rotated are significantly reduced to acquire several images to fit transmittance T (or absorbance A) by a harmonic function [29]. For the absorber oriented at angle θ a b s , the absorbance A = − log 10 T is defined [30]:
A ( θ ) = A m a x − A m i n 2 cos ( 2 θ − 2 θ a b s ) + A m a x + A m i n 2 ,
where measurement is carried out with incident light at four selected polarisations and detection is not discriminated in polarisation. With a 4-pol. camera, four images are directly acquired in a single acquisition while the incident light is non-polarised (isotropic random). The setup is shown in Figure 10 without λ / 4 waveplates at the IN and OUT-ports; polarisation homogenisers used at the IN-port of some microscopes can be useful for polarisation-isotropic illumination and are made with circular polarisers ( λ / 4 plates based on optical activity; not shown in Figure 10). The fit can also be modelled by sin-function with freely chosen phase sign ± θ a b s , without loss of generality ( ± cos θ = sin [ θ ± π / 2 ] ). Such measurement reveal the anisotropy of absorption for linearly polarised light (it can also be measured in transmission rather than reflection mode, as shown in Figure 10). Since polarisation is only set at one of the two IN/OUT ports, such measurements are not sensitive to polarisation changes due to retardance Δ n × d , where d is the thickness of the sample.
By setting circular polarisation at the IN-port (RHC or LHC) and without λ / 4 waveplate before 4-pol. camera it is possible to measure absorbance A image using Eqn. 4.
With linear polarisation at the IN-port ( λ / 4 and linear polarisers are both aligned at 0 ∘ ) and no λ / 4 plate at the OUT-port, a setup to measure birefringence and absorbance anisotropies is realised [31]; i.e., a typical polariser-analyser arrangement (Eqn. 3) only using 4-pol. camera. Since absorbance is π -fold (equal absorbance at 0 and π ), while birefringence has a twice high angular dependence, the fit function to account for the two contributions in transmittance is conveniently chosen:
T ( θ ) = [ a κ cos 2 ( θ − b κ ) + o κ ] + [ a n cos 2 2 ( θ − b n ) + o n ] ≡ A b s + R e t ,
where a κ and a n are the amplitudes related to absorbance A b s and retardance R e t contributions, b κ and b n are the orientation dependent angles (which can be different for the two anisotropies), o κ and o n are their corresponding offsets. The first term [ . . . ] is equivalent to the Eqn. 4 by use of the identity cos 2 θ = 2 cos 2 θ − 1 and both define anisotropy of absorbance (the π -folding in angular dependence). Three separate measurements are required to fit function with three fit parameters, i.e., three polarisation angles from 4-pol. camera image are required and are sufficient.
The second [ . . . ] term is due to retardance (birefringence) and has a twice larger angular frequency, i.e., π / 2 -folding (Eqn. 3). Also, three separate angles of polarisation are enough for the fit function, however, such a fit usually returns a lower confidence range due to the larger angular frequency for retardance. In many practical cases, one of the two A b s or R e t parts dominate the measured transmittance T ( θ ) . For example, at the infrared (IR) molecular fingerprinting spectral range, absorption bands tend to dominate and the retardance effects are small [32]. It is also clear from Eqn. 5 that by fitting one of the two θ ( A b s ) or 2 θ ( R e t ) dependencies the other is ignored, while the measured one is usually overestimated.
Next, experimental determination of the absorbance (Eqn. 4) of spider (Trichonephila plumipes) silk (yellow) using a 4-pol. camera at the OUT-port (Figure 10) and the transmittance T ( θ ) fit by Eqn. 5 (without retardance contribution) was performed with the same setup and the same number of optical elements in the beam, only changing their azimuthal orientation (Figure 10). For the non-polarised incident illumination, the spider silk was placed on an Au mirror (Figure 11(a)). Three polariser positions on the 4-pol. camera were used for the fit of reflected light using R ( θ ) = A m p × cos ( 2 θ − 2 θ s h i f t ) + O f f s e t ; normalisation of the reflected signal with silk was carried out using the reflection from the Au mirror for the reflectance R ( θ ) at four individual orientations (Figure 11(b)). The 4-pol. camera image at crossed Nicol position ( 0 ∘ -segment) was not used for the fit due to low intensity. It is noteworthy to add that simultaneous fit by Eqn. 5 would require at least six independent data points (six polarisation orientations). This is not possible without rotation of the sample or polarisers, since only four orientations are measured instantaneously with a 4-pol. camera. Such rotations cause an image shift and strongly compromise the fidelity of the fit [29]. Figure 11(b) shows maps of the three best fit parameters. The phase map 2 θ s h i f t shows that the main part of the fiber has the 0 ∘ -azimuth along the length direction as expected. Cross-polarised imaging was also carried out (not shown) since such setup is sensitive to the retardance anisotropy and birefringence. However, the fit was not conclusive, most probably due to the larger angular frequency of the signal, which was poorly resolved by the three point fit.

4.3. Stokes parameters from 4-pol. imaging

Four Stokes parameters define the state of polarisation and aim to fully characterise the detected light (coherent and incoherent). Firstly, three Stokes parameters per pixel can be calculated from the measured intensity 4-pol. images using simple image algebra. The intensity or S 0 = ( I 0 + I π / 4 + I π / 2 + I 3 π / 4 ) / 2 , S 1 = I 0 − I π / 2 , S 2 = I π / 4 − I 3 π / 4 . The azimuth then is θ s h i f t = arctan 2 ( S 2 , S 1 ) / 2 , where arctan 2 is the four quadrants inverse tangent. Also, the degree of linear polarisation can be calculated as D o L P = S 1 2 + S 2 2 / S 0 . The D o L P is widely used for edge detection in machine vision.
The intensity of transmitted light through a λ / 4 -waveplate at angle ϕ and a polariser/analyser at θ is given by [34]:
I T ( θ , ϕ ) = [ S 0 + S 1 cos ( 2 θ ) + S 2 sin ( 2 θ ) cos ϕ − S 3 sin ( 2 θ ) sin ϕ ] / 2 .
From four independent measurements all Stokes parameters are obtained [34]:
S 0 = I ( 0 , 0 ) + I ( π / 2 , 0 ) ,
S 1 = I ( 0 , 0 ) − I ( π / 2 , 0 ) ,
S 2 = 2 I ( π / 4 , 0 ) − S 0 ,
S 3 = S 0 − 2 I ( π / 4 , π / 2 ) .
For determination of the last S 3 , a circularly polarised light is required and can be generated by adding a λ / 4 waveplate with slow/fast axis at π / 4 degrees to the incident linear polarised light S 3 = I π / 4 λ / 4 − I − π / 4 λ / 4 . Yet a simpler method to obtain all four stokes parameters S 0 , 1 , 2 , 3 is useful with four independent measurements. First, the polariser is set at θ = 0 , π / 4 , π / 2 and then a λ / 4 -waveplate is added at π / 4 -orientation for the fourth measurement of intensity. The fourth Stokes component can be calculated as S 3 = S 2 × tan δ , where δ is the phase retardance δ ( λ ) = 2 π d λ [ n e − n o ] for thickness d. The first three are directly measured from 4-pol. images using simple image algebra. The intensity or S 0 = ( I 0 + I π / 4 + I π / 2 + I 3 π / 4 ) / 2 , S 1 = I 0 − I π / 2 , S 2 = I π / 4 − I 3 π / 4 .

4.4. Nanotextured surfaces for analysis of polarisation anisotropy in reflection

Finally, the demonstrated polarisation and color analysis of R and T spectra can be harnessed in the currently active area of research on "mechano-biocidal surfaces” [35,36,37,38]. Mechano-biocidal surfaces are so named because they have been demonstrated to mechanically rupture microbes that encounter the surfaces. The contact-killing surfaces usually exhibit an array of high-aspect-ratio nanofeatures (nanotopography). An image of a mechano-bactericidal surface in reflection mode (Figure 12(a)) can be analysed for optical anisotropies by the method outlined above. Real-time monitoring of cell attachment, growth, or mechanical rupture of the cell membranes can be monitored by a 4-pol. camera. Shape changes of the observed object contribute to optical changes (anisotropy) that can be determined by the 4-pol. method. Time-dependent evolution of changes in optical anisotropies using a 4-pol. camera are advantageous since all four images at each separate 45 ∘ degree change in polarisation are obtained in one acquisition. Such anisotropy azimuth can be calculated from Stokes parameters S 1 and S 2 as well as D o L P which shows the edge and is widely used in machine vision.
Moreover, the polarisation analysis can resolve the orientation and alignment of features within spectral regions which are up to 20 × smaller than the diffraction limit, as was demonstrated for the IR spectral range using microscopy [39]. Also, the same principle of discerning orientation when spatial resolution is beyond the required feature size was demonstrated with a 4-pol. camera attached to a drone from 20-140 m height [40]. Figure S2(d) shows another example where the sub-wavelength (nanoscale) feature of a diatom is not resolved and is beyond the diffraction limit e.g., ∼ 0.5 μ m; however, using a 4.pol camera the nanofeatures are resolved by color. The nano-slots (rectangular voids ∼ 5 μ m in length, ∼ 1 μ m in diameter) show strong polarisation anisotropy in transmission [41]. The azimuth of the colored regions in diatoms was only 13 ∘ for each separate and distinct color.
By using anodic aluminium oxide (AAO) templates, it is possible to electrochemically grow high aspect ratio metal nanopillars. The same AAO templates can also be used for nanoimprint lithography of polymeric materials, as shown in Figure 12. The AAO templated nanopillar spacing can be smaller than 100 nm, dependent on the anodisation conditions during growth whereas control of the height is achieved by controlling the time of electrochemical deposition (Figure 12(d)). The very same AAO template can also be used for nanoimprinting of UV sensitive polymer resist. The shape of the polymer nanopillars (from cylindrical to tapered-trapezoidal (Figure 12(e)) can be changed by tailoring AAO molds (see Sec. Section 2.3). Both metal and polymeric pillars have demonstrated bactericidal effect [38]. The conjecture we present here is that 4-pol. imaging can be used to trace changes to the shape of bacteria and other cell types attached onto nano-textured surfaces and to correlate those changes to their biocidal action. 4-pol. imaging of the biocidal action of nanotextured surfaces can be additionally supported by the antireflection property of such surfaces [42]. A gradual change of refractive index at the liquid-material interface decreases light reflection, which is valuable for achieving better contrast in imaging. Nano-textured silicon (Si; black-Si [43]) alters the gradient forces acting on polymeric and gel chains within focal spots comparable with bacteria size [44] and could potentially be used for color mapping using a chromaticity plot, as introduced earlier.

5. Conclusions and Outlook

In this perspective we present analysis of experimental results showing intuitive color visualisation of the 3D complex structures of natural materials such as spider scales and silk retrieved from polarisation analysis using optical microscopy. Chromaticity coordinates ( x , y ) are useful to trace (and quantify) minute color changes. We show that the simple sub-wavelength grating on twin slabs of chitin, that compose the spider cuticle, can produce vivid colors as demonstrated using a simple model linking reflectance and transmittance spectra. Visualisation using a chromaticity diagram shows the trends of color changes according to geometrical structure parameters in the ( x , y ) chromaticity presentation. Additionally, polarisation effects due to s- and p- polarisations can be more intuitively understood using a chromaticity plot as compared with the spectral presentation of T or R.
We present an optical characterisation method by which the differences in the orientation of anisotropic structures are proportional to the perceived differences in color. It is shown that a 4-pol. camera allows acquisition of simultaneous images for calculating three Stokes parameters S 0 , 1 , 2 and the azimuth of retardance, which can also be directly imaged by a polychromatic polarisation method using a standard optical microscope. The 4-pol. method has inherent capability to determine structure orientation and its anisotropy below the spatial resolution [45]. It was shown that this technique is applicable not only to the optical far-fields [31] but to the non-propagating near-fields widely adopted for attenuated total reflection (ATR) spectroscopy. Imaging of the orientation of absorbers and retardance below the surface of the samples, including biological tissues, has broad application potential, especially at the long IR and THz spectral range [46].
The polarisation analysis of the nano-micro features on nano-textured surfaces is still relatively unexplored. However, (auto)fluorescence, and absorbance changes, which can be plotted onto chromaticity color maps, can reveal new structural information in addition to the standard topographic analysis currently performed for nano-microstructured surfaces.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Acknowledgments

S.J. and S-H.N. acknowledges funding via the ARC Linkage LP190100505 project. J.M. and M.R. were funded by JSPS KAKENHI Grant No. 22H02137 and JST CREST Grant No. JPMJCR19I3. M.R. was funded by JSPS KAKENHI Grant No. 22K14200. M.S. acknowledges financial support via NIH/NIGMS grant R01GM101701. S.J. was supported via IdEx International Chair project at Bordeaux University, France. D.L acknowledges support of the McKenzie Postdoctoral Fellowships Program. We are grateful to Prof. Etienne Brasselet for discussions on polarisation and anisotropy.

Appendix A. Complex and larger fibers

Preprints 72089 g0s1
Figure S1. Detailed images of the inset shown in Figure 8(a). Spider (Eriophora transmarina) silk behaves as positive birefringent crystal judging from the retardance map with full-wave λ = 530 nm waveplate, similarly to the moth Bombyx mori silk [27].
Figure S1. Detailed images of the inset shown in Figure 8(a). Spider (Eriophora transmarina) silk behaves as positive birefringent crystal judging from the retardance map with full-wave λ = 530 nm waveplate, similarly to the moth Bombyx mori silk [27].
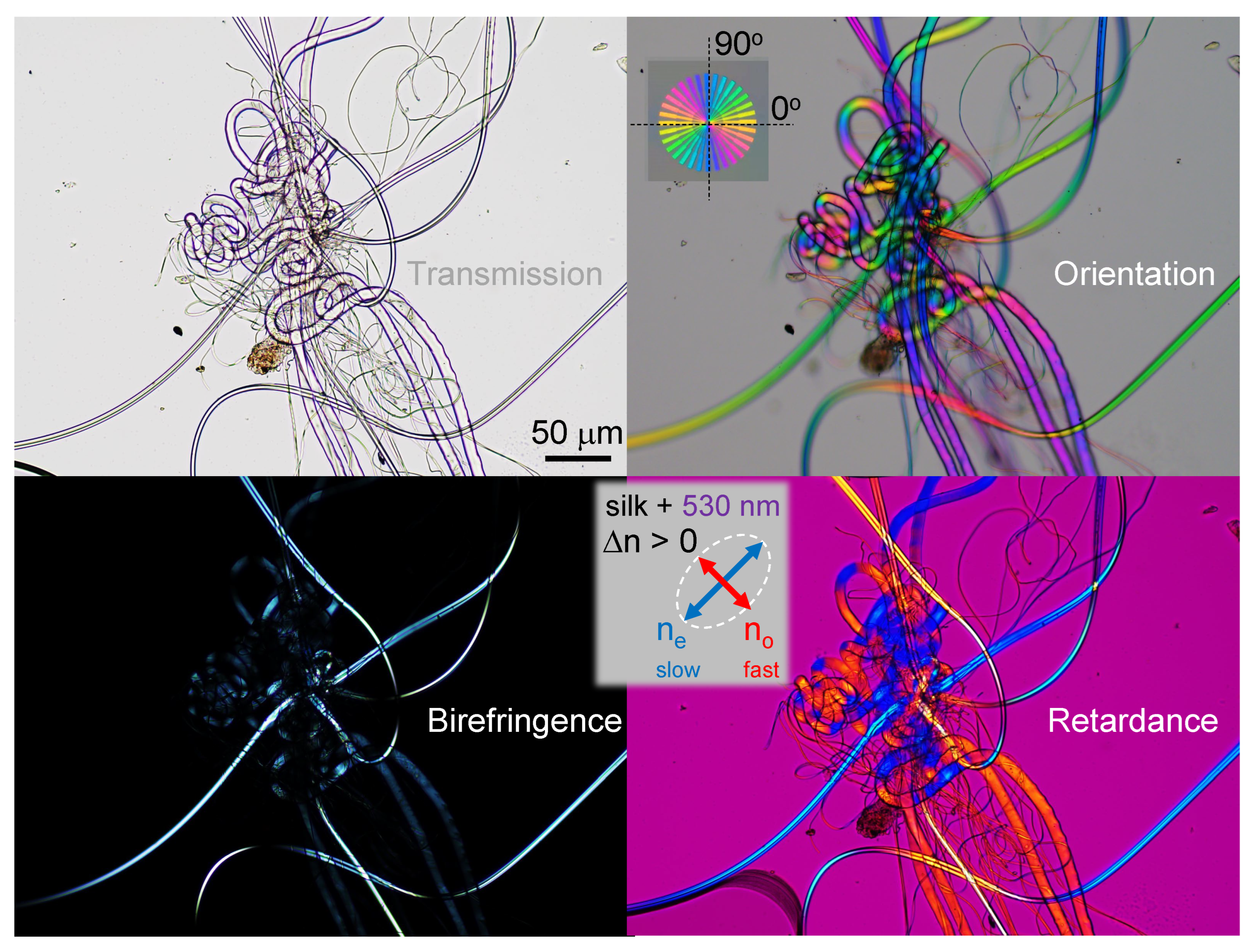
Preprints 72089 g0s1
Complex patterns with bending radius comparable with the diameter of the fiber can be reliably traced using orientation-sensitive microscopy as illustrated for the spider silk case in Figure S1. Spider silk shows positive birefringent crystal response Δ n ≡ n e − n o > 0 as revealed in the retardance visualisation with a full-wave λ = 530 nm plate (at SW-NE orientation in the image). Structure inside larger silk fibers can also be visualised using azimuth color (Figure S2(a,b)). Residual water droplets, which were still not evaporated after drying on cover glass, showed no color as expected (a). The most dark regions in the water droplet image are those which are at the circumference of the micro-sphere due to less collected light from those areas during imaging; water was used to fix silk to the glass during sample preparation. The most tiny peel-off fibers from spider silk showed faint color in accordance to molecular orientation (c). Example of color-azimuth from regions where nanoscale structures are not resolved is shown in (d), where images of diatom (bio-silica) was taken with an objective lens of N A = 0.6 , hence the resolution is ∼ 0.61 λ / N A ≈ λ . The regions which show azimuth-colors have sub-wavelength structures [47] which are not resolved, however, their alignment is visualised. The angular azimuth difference between the colored radial rays structure in the center of the pattern is Δ θ ≈ 13 ∘ .
Preprints 72089 g0s2
Figure S2. (a,b) Orientation of optical slow axis of brown silk (Antheraea pernyi moth). Water droplets and structural cracks are visualised. Inset in (b) shows the optical transmission, birefringence and retardance of the corresponding orientation image. Averaging of orientations at the two fiber junction takes place where magenta crossed with green results in yellow. Images taken by: UPLFLN20XP/0.5NA Olympus lens, color CMOS camera Olympus DP74 with pixel size 5.86 μ m and sensor size 1920 × 1200 . (c) Sub-micrometer fibers attached to the spider (Eriophora transmarina) silk are detached in some areas. (d) Orientation image of diatom reveals nanoscale slits by color. Images (c,d) were made with an objective lens LUCPLFLN40 × , Olympus ( N A = 0.6 ) and color CCD camera Lumenera Infinity 3-1C with pixel size 6.45 μ m and sensor 1392 × 1040 pixels.
Figure S2. (a,b) Orientation of optical slow axis of brown silk (Antheraea pernyi moth). Water droplets and structural cracks are visualised. Inset in (b) shows the optical transmission, birefringence and retardance of the corresponding orientation image. Averaging of orientations at the two fiber junction takes place where magenta crossed with green results in yellow. Images taken by: UPLFLN20XP/0.5NA Olympus lens, color CMOS camera Olympus DP74 with pixel size 5.86 μ m and sensor size 1920 × 1200 . (c) Sub-micrometer fibers attached to the spider (Eriophora transmarina) silk are detached in some areas. (d) Orientation image of diatom reveals nanoscale slits by color. Images (c,d) were made with an objective lens LUCPLFLN40 × , Olympus ( N A = 0.6 ) and color CCD camera Lumenera Infinity 3-1C with pixel size 6.45 μ m and sensor 1392 × 1040 pixels.
Preprints 72089 g0s2
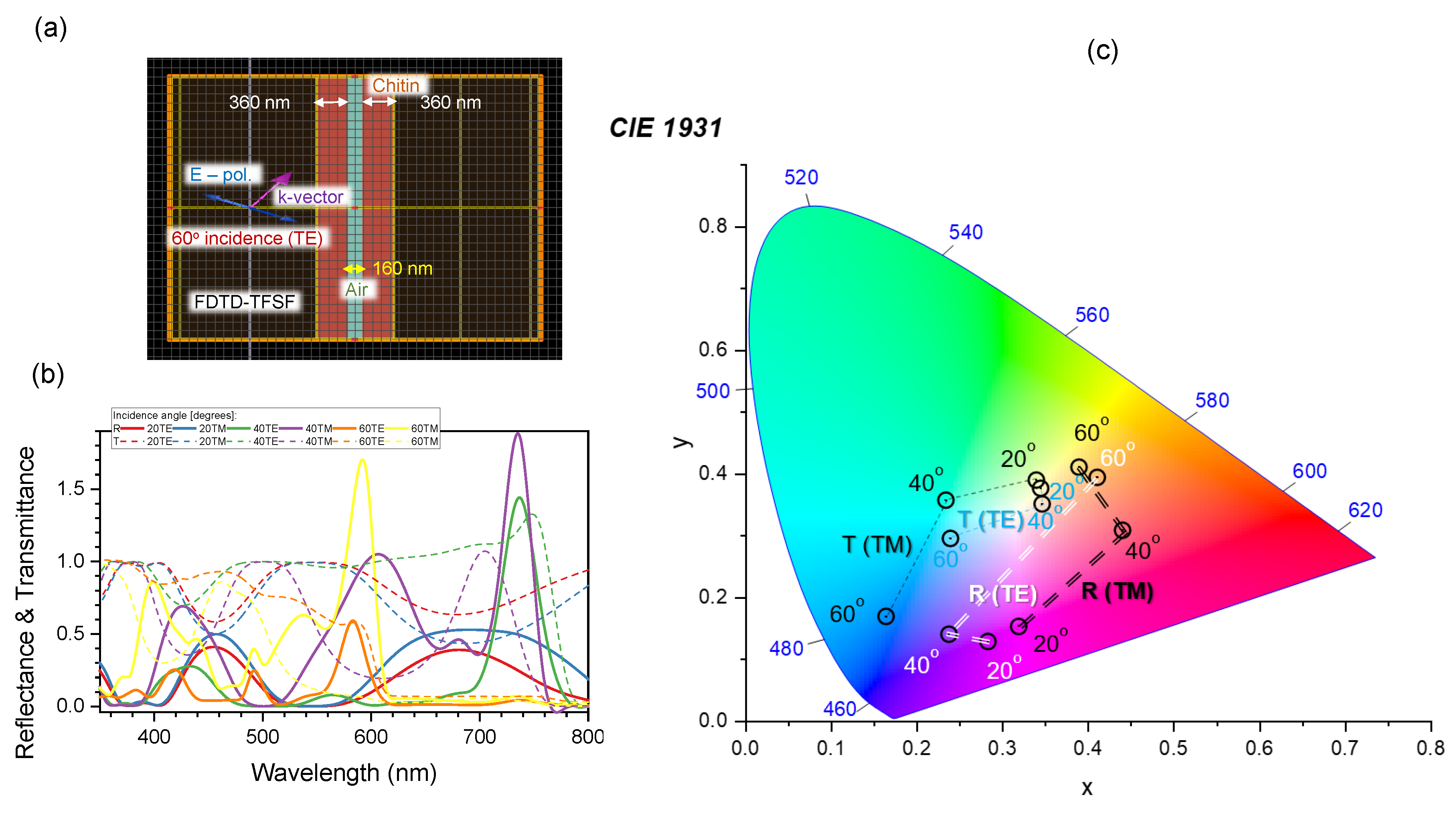
Preprints 72089 g0s3
Figure S3. FDTD simulations of two FP-slabs with an air nanogap for angle of incidence θ i = 20 , 40 , 60 ∘ . (a) Schematics of FDTD model. (b) Family of spectra for reflectance and transmittance. The values larger than 1 is due to interference; E-field of incidennt light E = 1 . (c) Spectra shown in (b) are plotted in chromaticity diagram. Figure 6 shows results for normal incidence θ i = 0 ∘ .
Figure S3. FDTD simulations of two FP-slabs with an air nanogap for angle of incidence θ i = 20 , 40 , 60 ∘ . (a) Schematics of FDTD model. (b) Family of spectra for reflectance and transmittance. The values larger than 1 is due to interference; E-field of incidennt light E = 1 . (c) Spectra shown in (b) are plotted in chromaticity diagram. Figure 6 shows results for normal incidence θ i = 0 ∘ .
Preprints 72089 g0s3
Preprints 72089 g0s4
Figure S4. (a) A payload card developed by partnership between Swinburne Makers and SkyKraft (2022). This technology demonstrator has payloads of a camera, accelerometer and dual 4 W LED array at 625nm, and a split array with wavelengths at 730 and 590nm. It was integrated into SkyKraft satellite at SkyKraft’s headquarters in Canberra, Dec. 2022 and scheduled to launch on SpaceX Transporter 8 in June 2023. (b) Schematics of an experiment planned on degradation of spider silk in outer space at low Earth orbit (LEO) by CCD monitoring its image using hardware shown in (a) and infrastructure developed by SkyKraft and Swinburne Makers (c) Spider silk spool [14] to be used for experimentation in space.
Figure S4. (a) A payload card developed by partnership between Swinburne Makers and SkyKraft (2022). This technology demonstrator has payloads of a camera, accelerometer and dual 4 W LED array at 625nm, and a split array with wavelengths at 730 and 590nm. It was integrated into SkyKraft satellite at SkyKraft’s headquarters in Canberra, Dec. 2022 and scheduled to launch on SpaceX Transporter 8 in June 2023. (b) Schematics of an experiment planned on degradation of spider silk in outer space at low Earth orbit (LEO) by CCD monitoring its image using hardware shown in (a) and infrastructure developed by SkyKraft and Swinburne Makers (c) Spider silk spool [14] to be used for experimentation in space.
Preprints 72089 g0s4
Color appearance of the surface depends on angle of incidence, as well understood for grating structures. Also, a flat thin films show colors at different angles of incidence since their effective thickness is changing depending on the angle d / cos θ i . Fresnel reflection coefficients control portions of the reflected and transmitted light at different θ i . Figure S3 shows s- and p-polarised light (TM and TE modes, respectively) for the pair of FP slabs with air nano-gap (for the normal incidence θ i = 0 see Figure 6). Color trends of complex and non-intuitive R ( λ ) and T ( λ ) spectra (Figure S3(b)) are presented onto chromaticity ( x , y ) -map in (c) and reveals tendencies of color appearance vs. structural parameters.

Appendix B. Model: spider scale illuminated at an angle

Figure S3 shows FDTD simulations of R and T spectra for incidence on a pair of FP slabs with the air gap. Complex spectra are mapped onto chromaticity diagram for the two polarisations or the TE and TM modes. Those modes are shown on ( x , y ) -map by connected lines for T and R spectra at different angles of incidence θ i . Complimentarity of T and R spectra are well discernible similarly to the case of normal incidence.

Appendix C. Spider silk test in outer space

Swinburne’s Nanotechnology (Nanolab) group is preparing an experiment at low Earth orbit (LEO) in 2023 with already developed and approved payload card (Figure S4(a)). Spider silk collected by a newly developed industrial process will be used to spool spider silk into a bundle (Figure S4(b)), which will act as an optical fiber for visible light. We aim to monitor degradation of silk, which is a prototype bio-material with hydrogen bonding over extended period of time (2 months) at LEO. Degradation of H-bonded bio materials at outer space environment is important and underlying mechanisms should be well understood. Time-lapse monitoring of the optical image changes due to light scattering from the bundle of silk fibers (Figure S4(b)) will indicate either alteration of internal structural integrity or/and surface erosion of spider silk. Visible light from a laser diode (LD) will be coupled into a bundle of silk fibers and light’s transmission will be measured using an onboard visible linear CCD camera (Figure S4(b)). Light from LD will be coupled into spooled bundle of spider silk fibers using optical resist SZ2080 T M and mm-diameter glass lens mounted on the output window of red-color LD. The bundle will be fixed to the linear CCD by the same resist. This project uses the Swinburne’s student team developed and tested electronics solutions for LD power supply, linear CCD imaging and data compression transfer to Earth through SkyKraft’s space infrastructure. (Figure S4(a)).
Swinburne’s student lead team, Swinburne Makers And Creators (SMACC) developed the SMACCSAT1 (Figure S4(a)) in 2022 to expand technical capability and discover the unique challenges of designing space payloads. This new understanding will be used to develop template hardware and software designs to accelerate development of space research payloads and integrate them with SkyKraft’s satellites to be launched to space. SkyKraft’s SkyRide program provide an efficient, cost effective method to launch small science experiments to space. SkyKards are allowed an active area of 90 × 90 × 15 mm 3 with a maximum weight of 200 g. SkyKraft’s satillite systems provide the SkyKards with 5 V, 1 A power and UART communication through the PCIE connector. SkyKrafts OBC allocates a 64 Kb buffer for each SkyKard that when filled, will be transmitted to Earth when the satellite is within range of a ground station. Earth side SkyKards are allowed an Earth facing aperture of 44 × 15 mm 2 . This allows Earth observation and optical transmission by SkyKards. Additional payload card slots next to each other can be purchased to expand size, weight, power budget and downlink bandwidth.
We aim to expand our capability to develop and launch space payloads by developing and testing standard reference designs compatible with SkyKrafts infrastructure to reduce the custom development to the specific research payload only. Hardware standard reference design based on the NXP MIMXRT1062, will be highly capable with the flexibility to control a wide range of experiments. Pin to pin compatibility with the Teensy4.1 T M will have an efficient development pipe line from breadboard prototype through to final space payload while enabling software teams to develop required software concurrently with hardware.
For materials to be suitable to use on space hardware, they need to meet specifications for material outgassing, vibration and mechanical stability and electronical specifications. The primary standard that covers space hardware templates is General Environmental Verification Standard (GEVS) for GSFC Flight Programs and Projects (GSFC-STD-7000B)
1. Material outgassing. Materials to make up payload cards to fly on SkyKraft are required to meet the specification of Total Mass Loss (TML) of <1% and Collected Volatile Condensable Material (CVCM) <0.1% with testing according to ASTM E595 standard. Where possible materials with prior flight heritage will simplify development, documentaiton and testing.
2. Vibration and mechanical stability. Payloads will be exposed to significant vibrational loading when launched to space. Exact specifics of the loading experienced my the payload card varies and will not be known at the design stage
3. Electronics. Electronics for SkyKraft payload cards have simpler specifications than many space hardware applications due to their relatively short operational life in space. Automotive rated parts, flight heritage and standard electronics design techniques to minimise Electro-magnetic Interference (EMI) will be the primary design considerations to meet required specifications.
This space hardware development capacity will facilitate the prototyping, manufacture, space certification and space launch spider silk to study the degradation from the space environment.

References

  1. M. Rothammer, C. Zollfrank, K. Busch, and G. von Freymann, “Tailored disorder in photonics: Learning from nature,” Adv. Optical Mater. 9, 2100787 (2021). [CrossRef]
  2. A. Parker and Z. Hegedus, “Diffractive optics in spiders,” J. Opt. A: Pure Appl. Opt. 5, S111 (2003). [CrossRef]
  3. Natural History Museum Bern, “World spider catalog. version 24,” Online; accessed on. 26 March 2023.
  4. S. Kariko, J. Timonen, J. Weaver, D. Gur, C. Marks, L. Leiserowitz, M. Kolle, and L. Li, “Structural origins of coloration in the spider phoroncidia rubroargentea berland, 1913 (araneae: Theridiidae) from madagascar,” J. R. Soc. Interface 15, 20170930 (2018).
  5. M. John and S. Thomas, “Biofibres and biocomposites,” Carbohydrate polymers 71, 343–364 (2008). [CrossRef]
  6. M. Ryu, R. Honda, A. Reich, A. Cernescu, J.-L. Li, J. Hu, S. Juodkazis, and J. Morikawa, “Near-field IR orientational spectroscopy of silk,” Appl. Sci. 9, 3991 (2019). [CrossRef]
  7. H. Fujisawa, M. Ryu, S. Lundgaard, D. Linklater, E. Ivanova, Y. Nishijima, S. Juodkazis, and J. Morikawa, “Direct measurement of temperature diffusivity of nanocellulose-doped biodegradable composite films,” Micromachines 11, 738 (2020). [CrossRef]
  8. M. Ryu, A. Balčytis, X. Wang, J. Vongsvivut, Y. Hikima, J. Li, M. J. Tobin, S. Juodkazis, and J. Morikawa, “Orientational mapping augmented sub-wavelength hyper-spectral imaging of silk,” Sci. Reports 7, 7419 (2017). [CrossRef]
  9. M. Ryu, H. Kobayashi, A. Balcytis, X. Wang, J. Vongsvivut, J. Li, N. Urayama, V. Mizeikis, M. Tobin, and S. Juodkazis, “Nanoscale chemical mapping of laser-solubilized silk,” Mater. Res. Express 4, 115028 (2017). [CrossRef]
  10. M. Ryu, R. Honda, A. Cernescu, A. Vailionis, A. Balcytis, J. Vongsvivut, J.-L. Li, D. Linklater, E. Ivanova, V. Mizeikis, M. Tobin, and J. M. S. Juodkazis, “Nanoscale optical and structural characterisation of silk,” Beilstein J. Nanotechnol. 10, 922–929 (2019). [CrossRef]
  11. W. P. Moestopo, S. Shaker, W. Deng, and J. R. Greer, “Knots are not for naught: Design, properties, and topology of hierarchical intertwined microarchitected materials,” Science Advances 9, eade6725 (2023). [CrossRef]
  12. S. Blamires, M. Nobbs, P. Martens, I. Tso, W. Chuang, C. Chang, and H. Sheu, “Multiscale mechanisms of nutritionally-induced property variation in spider silk,” PLoS One 13, e0192005 (2018). [CrossRef]
  13. S. Blamires, D. Little, T. White, and D. Kane, “Photoreflectance/scattering measurements of spider silks informed by standard optics,” Royal Society Open Science 7, 192174 (2020). [CrossRef]
  14. S. Blamires, G. Cerexhe, T. White, M. Herberstein, and M. Kasumovic, “Spider silk colouration co-varies with thermal properties but not protein structure,” J. Royal Society Interface 16, 20190199 (2019).
  15. A. Balčytis, M. Ryu, X. Wang, F. Novelli, G. Seniutinas, S. Du, X. Wang, J. Li, J. Davis, D. Appadoo, J. Morikawa, and S. Juodkazis, “Silk: Optical properties over 12.6 octaves THz-IR-Visible-UV range,” Materials 10, 356 (2017).
  16. M. Rajabi, O. Lavrentovich, and M. Shribak, “Instantaneous mapping of liquid crystal orientation using a polychromatic polarizing microscope,” Liquid Crystals, 1–10 (2023). [CrossRef]
  17. H. Masuda and K. Fukuda, “Ordered metal nanohole arrays made by a two-step replication of honeycomb structures of anodic alumina,” Science 268, 1466 (1995). [CrossRef]
  18. H. Masuda and M. Satoh, “Fabrication of gold nanodot array using anodic porous alumina as an evaporation mask,” Jpn. J. Appl. Phys.-Part 2 Lett. 35, 126 (1996). [CrossRef]
  19. T. Kondo, T. Fukushima, K. Nishio, and H. Masuda, “Surface-enhanced raman scattering in hierarchical structures of au formed using templates by site-controlled tunnel etching of Al,” Applied Physics Express 2, 125001 (2009). [CrossRef]
  20. H. Masuda, T. Yanagishita, and T. Kondo, “Encyclopedia of interfacial chemistry: Surface science and electrochemistry,” (Elsevier, 2018) Chap. Fabrication of Anodic Porous Alumina, pp. 226–235, 1st ed.
  21. A. Ingram and A. Parker, “Diffractive optics in spiders,” Philos Trans R Soc Lond B Biol Sci. 363, 2465–2480 (2008).
  22. A. Saito, M. Yonezawa, J. Murase, S. Juodkazis, V. Mizeikis, M. Akai-Kasaya, and Y. Kuwahara, “Numerical analysis on the optical role of nanometer scale randomness on the morpho butterfly’s scale,” J. Nanosci. Nanotechnol. 11, 2785–2792 (2011).
  23. A. Saito, K. Yamashita1, T. Hattori, and Y. Kuwahara, “Novel optical applications inspired by the morpho butterfly’s coloration: technology transfer from reflection to transmission,” Jpn. J. Appl. Phys. 61, SD0801 (2022). [CrossRef]
  24. D. Stavenga, J. Otto, and B. Wilts, “Splendid coloration of the peacock spider Maratus splendens,” J. R. Soc. Interface 2016, 20160437 (2016).
  25. D. McCoy, V. McCoy, N. Mandsberg, A. Shneidman, J. Aizenberg, R. Prum, and D. Haig, “Structurally assisted super black in colourful peacock spiders,” Proc Biol Sci. 286, 20190589 (2019). [CrossRef]
  26. M. Han, D. Smith, S.-H. Ng, Z. Vilagosh, V. Anand, T. Katkus, I. Reklaitis, H. Mu, M. Ryu, J. Morikawa, J. Vongsvivut, D. Appadoo, and S. Juodkazis, “THz filters made by laser ablation of stainless steel and kapton film,” Micromachines 13, 1170 (2022).
  27. R. Honda, M. Ryu, J.-L. Li, V. Mizeikis, S. Juodkazis, and J. Morikawa, “Simple multi-wavelength imaging of birefringence:case study of silk,” Sci. Rep. 8, 17652 (2018). [CrossRef]
  28. Y. Shimotsuma, P. Kazansky, J. Qiu, and K. Hirao, “Self-organized nanogratings in glass irradiated by ultrashort light pulses,” Phys. Rev. Lett. 91, 247405 (2003). [CrossRef]
  29. M. Ryu, Y. Nishijima, S. M. N. To, T. Hashizume, R. Matsubara, A. Kubono, J. Hu, S. Ng, S. Juodkazis, and J. Morikawa, “Hyperspectral molecular orientation mapping in metamaterials,” Appl. Sci. 11, 1544 (2021). [CrossRef]
  30. Y. Hikima, J. Morikawa, and T. Hashimoto, “FT-IR image processing algorithms for in-plane orientation function and azimuth angle of uniaxially drawn polyethylene composite film,” Macromolecules 44, 3950–3957 (2011). [CrossRef]
  31. R. Honda, M. Ryu, M. Moritake, A. Balcytis, V. Mizeikis, J. Vongsvivut, M. J. Tobin, D. Appadoo, J.-L. Li, S. H. Ng, S. Juodkazis, and J. Morikawa, “Hyperspectral mapping of anisotropy,” Nanoscale Horizons 4, 1443–1449 (2019).
  32. R. Honda, M. Ryu, A. Balcytis, J. Vongsvivut, M. J. Tobin, S. Juodkazis, and J. Morikawa, “Paracetamol micro-structure analysis by optical mapping,” Appl.Surf. Sci. 473, 127–132 (2019).
  33. G. Stavenga, B. Wilts, H. Leertouwer, and T. Hariyama, “Polarized iridescence of the multilayered elytra of the japanese jewel beetle, Chrysochroa fulgidissima,” Philos. Trans. R. Soc. Lond. B Biol. Sci. 366, 709–723 (2011).
  34. E. Collett, Polarization, 3rd ed. (SPIE Press, Field guides, Bellingham, 2005).
  35. D. Linklater, S. Juodkazis, and E. Ivanova, “Nanofabrication of mechano-bactericidal surfaces,” Nanoscale 9, 16564–16585 (2017). [CrossRef]
  36. D. Linklater, H. Nguyen, C. Bhadra, S. Juodkazis, and E. Ivanova, “Influence of nanoscale topology on bactericidal efficiency of black silicon surfaces,” Nanotechnology 28, 469501 (2017). [CrossRef]
  37. D. Linklater, V. Baulin, S. Juodkazis, R. Crawford, P. Stoodley, and E. Ivanova, “Mechano-bactericidal actions of nanostructured surfaces,” Nature Reviews Microbiology 19, 8–22 (2021). [CrossRef]
  38. D. Linklater, S. Saita, T. Murata, T. Yanagishita, C. Dekiwadia, R. Crawford, H. Masuda, H. Kusaka, and E. Ivanova, “Nanopillar polymer films as antibacterial packaging materials,” ACS Appl. Nano Mater. 5, 2578–2591 (2022). [CrossRef]
  39. R. Honda, M. Ryu, M. Moritake, A. Balcytis, V. Mizeikis, J. Vongsvivut, M. J. Tobin, D. Appadoo, J.-L. Li, S. H. Ng, S. Juodkazis, and J. Morikawa, “Infrared polariscopy imaging of linear polymeric patterns with a focal plane array,” Nanomaterials 9, 732 (2019). [CrossRef]
  40. S. Ng, B. Allan, D. Ierodiaconou, V. Anand, A. Babanin, and S. Juodkazis, “Drone polariscopy—towards remote sensing applications,” Eng. Proc. 11, 46 (2021).
  41. E. Brasselet, G. Gervinskas, G. Seniutinas, and S. Juodkazis, “Topological shaping of light by closed-path nanoslits,” Phys. Rev. Lett. 111, 193901 (2013). [CrossRef]
  42. Y. Nishijima, R. Komatsu, S. Ota, G. Seniutinas, A. Balčytis, and S. Juodkazis, “Anti-reflective surfaces: Cascading nano/microstructuring,” Appl. Phys. Lett.: Photonics 1, 076104 (2016). [CrossRef]
  43. E. P. Ivanova, J. Hasan, H. K. Webb, G. Gervinskas, S. Juodkazis, V. K. Truong, A. H. F. Wu, R. N. Lamb, V. Baulin, G. S. Watson, J. A. Watson, D. E. Mainwaring, and R. J. Crawford, “Bactericidal activity of nanostructured black silicon,” Nature Commun. 4, 2838 (2013).
  44. T. Nagai, K.-I. Yuyama, T. Shoji, Y. Matsumura, D. Linklater, E. Ivanova, S. Juodkazis, and Y. Tsuboi, “Wavelength-sensitive optical tweezers using black-si nanospikes for controlling the internal polarity of a polymer droplet,” ACS Appl. Nano Mater. 6, 180–189 (2023). [CrossRef]
  45. M. Ryu, S. Ng, M. Han, V. Anand, T. Katkus, J. Vongsvivut, D. Appadoo, Y. Nishijima, S. Juodkazis, and J. Morikawa, “Polariscopy with optical near-fields,” Nanoscale Horiz. 7, 1047–1053 (2022). [CrossRef]
  46. M. Ryu, S. Ng, V. Anand, S. Lundgaard, J. Hu, T. Katkus, D. Appadoo, Z. Vilagosh, A. Wood, S. Juodkazis, and J. Morikawa, “Attenuated total reflection at thz wavelengths: Prospective use of total internal reflection and polariscopy,” Applied Sciences 11, 7632 (2021). [CrossRef]
  47. “A mini-atlas of diatom frustule electron microscopy images at different magnifications,” Materials Today: Proceedings 33, 1924–1933 (2020), 10th International Conference on Key Engineering Materials 2020.
Preprints 72089 g001
Figure 1. Peacock (jumping) spider. (a) Low magnification optical and SEM images of the excised spider abdomen. Inset image shows the dissected spider abdomen fixed onto carbon tape for SEM imaging. The vibrant array of colours (blue-green and red) are produced by structural colouration, and pigment, respectively. (b) low magnification SEM image of the scales which possess the structural green-blue color. The image was taken along the central long-axis of the abdomen, showing the changing orientation of the scales toward the centre of the spider abdomen. (c) high magnification SEM image of the green-blue scales. (d) SEM image of the red brushes (pigment coloration). Inset image shows a high resolution optical image, revealing the vibrant red color.
Figure 1. Peacock (jumping) spider. (a) Low magnification optical and SEM images of the excised spider abdomen. Inset image shows the dissected spider abdomen fixed onto carbon tape for SEM imaging. The vibrant array of colours (blue-green and red) are produced by structural colouration, and pigment, respectively. (b) low magnification SEM image of the scales which possess the structural green-blue color. The image was taken along the central long-axis of the abdomen, showing the changing orientation of the scales toward the centre of the spider abdomen. (c) high magnification SEM image of the green-blue scales. (d) SEM image of the red brushes (pigment coloration). Inset image shows a high resolution optical image, revealing the vibrant red color.
Preprints 72089 g001
Preprints 72089 g002
Figure 2. Peacock (jumping) spider. (a) SEM images of brushes with red coloration. (b) SEM image of the green-blue scales. (c-d) High magnification SEM images of the individual scales and the surface grating structure that causes the blue-green structural color.
Figure 2. Peacock (jumping) spider. (a) SEM images of brushes with red coloration. (b) SEM image of the green-blue scales. (c-d) High magnification SEM images of the individual scales and the surface grating structure that causes the blue-green structural color.
Preprints 72089 g002
Preprints 72089 g003
Figure 3. SEM images of FIB milled green-blue scales at different magnifications. Chitin membrane of the green-blue scale has thickness ∼ 350 nm and an air gap inside.
Figure 3. SEM images of FIB milled green-blue scales at different magnifications. Chitin membrane of the green-blue scale has thickness ∼ 350 nm and an air gap inside.
Preprints 72089 g003
Preprints 72089 g004
Figure 4. X-ray tomography of Peacock spider abdomen region. Large scale (a) and 3D tomography cross sections (b). Movies of the 3D sectioning XZ and YZ are added in Supplement.
Figure 4. X-ray tomography of Peacock spider abdomen region. Large scale (a) and 3D tomography cross sections (b). Movies of the 3D sectioning XZ and YZ are added in Supplement.
Preprints 72089 g004
Preprints 72089 g005
Figure 5. Optical reflection (a) and X-ray (b) resolved green-blue scales of Peacock spider (same specimen as in Figure 4 only projection is showing flat cross section of the scales). Movies of the 3D sectioning shown in (b) is added in Supplement.
Figure 5. Optical reflection (a) and X-ray (b) resolved green-blue scales of Peacock spider (same specimen as in Figure 4 only projection is showing flat cross section of the scales). Movies of the 3D sectioning shown in (b) is added in Supplement.
Preprints 72089 g005
Preprints 72089 g006
Figure 6. (a) Finite difference time domain (FDTD) 2D model of two Fabry-Pérot (FP) slabs of chitin of thickness d with nano-gap of g a p = 160 nm. Total field scattered field (TFSF) model was setup for calculation of the reflectance R and transmittance T spectra shown in (b). The color appearance of the reflection from the chitin FP slabs separated by d = 160 nm gap are shown by white d-labels and line in (c). Absorbtance A = 0 , which defines R + T = 100 % . (c) Shows chromaticity diagram for the color appearance of reflection spectra of two coupled FP slabs with air gap of 50 (black lines) and 160 nm (white lines). Also the transmittance T for d = 160 nm gap are shown in the dashed-line encircled region. Inset shows R - T points connected by lines for the same d when air gap was 50 nm (see Suppl. for different angles of incidence in Figure S3).
Figure 6. (a) Finite difference time domain (FDTD) 2D model of two Fabry-Pérot (FP) slabs of chitin of thickness d with nano-gap of g a p = 160 nm. Total field scattered field (TFSF) model was setup for calculation of the reflectance R and transmittance T spectra shown in (b). The color appearance of the reflection from the chitin FP slabs separated by d = 160 nm gap are shown by white d-labels and line in (c). Absorbtance A = 0 , which defines R + T = 100 % . (c) Shows chromaticity diagram for the color appearance of reflection spectra of two coupled FP slabs with air gap of 50 (black lines) and 160 nm (white lines). Also the transmittance T for d = 160 nm gap are shown in the dashed-line encircled region. Inset shows R - T points connected by lines for the same d when air gap was 50 nm (see Suppl. for different angles of incidence in Figure S3).
Preprints 72089 g006
Preprints 72089 g007
Figure 7. Optical microscopy images of spider (Eriophora transmarina) silk harvested at constant mechanical pulling force. Images were taken in transmission and shows intensity, birefringence, retardance and azimuth (of the slow axis). For the retardance image the ful wavelength 530 nm λ -plate was at the orientation (looking at the image) from SW-NE. The slow axis orientation is calculated as A z i m u t h = [ H u e / 2 ] − 20 ∘ , where 0 ∘ < H u e < 360 ∘ . The slow-axis color reference shows the orientation angles; the reference sample was with fs-laser inscribed nanogratings inside silica without surface damage [28] was made by Prof. P. G. Kazansky’s team.
Figure 7. Optical microscopy images of spider (Eriophora transmarina) silk harvested at constant mechanical pulling force. Images were taken in transmission and shows intensity, birefringence, retardance and azimuth (of the slow axis). For the retardance image the ful wavelength 530 nm λ -plate was at the orientation (looking at the image) from SW-NE. The slow axis orientation is calculated as A z i m u t h = [ H u e / 2 ] − 20 ∘ , where 0 ∘ < H u e < 360 ∘ . The slow-axis color reference shows the orientation angles; the reference sample was with fs-laser inscribed nanogratings inside silica without surface damage [28] was made by Prof. P. G. Kazansky’s team.
Preprints 72089 g007
Preprints 72089 g008
Figure 8. Optical microscopy images in transmission showing intensity, birefringence, retardance and azimuth (of slow axis) at complex (a) and homogeneous (b) sections of spider silk. Inset in (a) shows entangled region of silk fiber and wishers shedding off the fiber (see Figure S1 for detailed optical analysis).
Figure 8. Optical microscopy images in transmission showing intensity, birefringence, retardance and azimuth (of slow axis) at complex (a) and homogeneous (b) sections of spider silk. Inset in (a) shows entangled region of silk fiber and wishers shedding off the fiber (see Figure S1 for detailed optical analysis).
Preprints 72089 g008
Preprints 72089 g009
Figure 9. Optical characterisation of Antheraea pernyi moth produced silk after degumming [15]. Single fibroin strands were imaged. Silk samples were kindly provided by Prof. Jingliang Li.
Figure 9. Optical characterisation of Antheraea pernyi moth produced silk after degumming [15]. Single fibroin strands were imaged. Silk samples were kindly provided by Prof. Jingliang Li.
Preprints 72089 g009
Preprints 72089 g010
Figure 10. Universal setup for detection of absorption and reflection/scattering differences between the left and right-hand circular polarisations (LHC/RHC), the optical activity and circular dichroism, using a 4-pol. camera (see text for discussion). The front-view insets show orientations by looking into the beam. The two λ / 4 waveplates have slow-axis crossed and imparts canceling contributions to the beam phase ± π / 2 and ∓ π / 2 , correspondingly to the position of the linear polariser at the input with ± 45 ∘ angle with slow-axis of λ / 4 plate at the first polariser plate. The inset shown as a sample’s image is from wing of Japanese jewlery bug (Chrysochroa fulgidissima, which has anisotropy for RHC and LHC polarisations [33]).
Figure 10. Universal setup for detection of absorption and reflection/scattering differences between the left and right-hand circular polarisations (LHC/RHC), the optical activity and circular dichroism, using a 4-pol. camera (see text for discussion). The front-view insets show orientations by looking into the beam. The two λ / 4 waveplates have slow-axis crossed and imparts canceling contributions to the beam phase ± π / 2 and ∓ π / 2 , correspondingly to the position of the linear polariser at the input with ± 45 ∘ angle with slow-axis of λ / 4 plate at the first polariser plate. The inset shown as a sample’s image is from wing of Japanese jewlery bug (Chrysochroa fulgidissima, which has anisotropy for RHC and LHC polarisations [33]).
Preprints 72089 g010
Preprints 72089 g011
Figure 11. Trichonephila plumipes (Tp1) dragline silk. (a) Optical images captured by the 4-pol. camera as average (intensity) and unprocessed (intensity of separate pixels without averaging) using an objective lens with 40 × magnification and N A = 0.74 (Olympus). Illumination was non-polarised. Silk fibers were placed directly on the Au-mirror (60 nm thickness was evaporated on cover glass with 5 nm Cr adhesion layer). The overlaid color segment on the fiber shows the corresponding phase 2 θ s h i f t structure. (b) Selected region was fitted by A m p × cos ( 2 θ − 2 θ s h i f t ) + O f f s e t . The fit parameters’ maps A m p , 2 θ s h i f t , O f f s e t . See Figure S2(c) for structure of the spider silk.
Figure 11. Trichonephila plumipes (Tp1) dragline silk. (a) Optical images captured by the 4-pol. camera as average (intensity) and unprocessed (intensity of separate pixels without averaging) using an objective lens with 40 × magnification and N A = 0.74 (Olympus). Illumination was non-polarised. Silk fibers were placed directly on the Au-mirror (60 nm thickness was evaporated on cover glass with 5 nm Cr adhesion layer). The overlaid color segment on the fiber shows the corresponding phase 2 θ s h i f t structure. (b) Selected region was fitted by A m p × cos ( 2 θ − 2 θ s h i f t ) + O f f s e t . The fit parameters’ maps A m p , 2 θ s h i f t , O f f s e t . See Figure S2(c) for structure of the spider silk.
Preprints 72089 g011
Preprints 72089 g012
Figure 12. Nano-pillar array surfaces fabricated using an anodic aluminium oxide (AAO) template. (a) Absorbance spectroscopy A ( λ ) at near-normal incidence. (b) Sample chamber for A ( λ ) measurements in air and liquid. (c) Absorbance spectra measured in reflectance mode using the setup shown in (a).(d) SEM images os Au grown inside AAO template; Fast Fourier Transform (FFT) image showing random spacing of 86 nm between pillars. (e) SEM images of nano-imprinted pillars of acrylic photo-polymer (PAK02, Toyo Gosei Ltd.) made using AAO tempate; top-left photo shows the sample made on poly(ethylene terephthalate) (PET). Straight cylindrical and tapered nano-pillars can be made using small protocol changes of the AAO mold formation (Sec. Section 2.3).
Figure 12. Nano-pillar array surfaces fabricated using an anodic aluminium oxide (AAO) template. (a) Absorbance spectroscopy A ( λ ) at near-normal incidence. (b) Sample chamber for A ( λ ) measurements in air and liquid. (c) Absorbance spectra measured in reflectance mode using the setup shown in (a).(d) SEM images os Au grown inside AAO template; Fast Fourier Transform (FFT) image showing random spacing of 86 nm between pillars. (e) SEM images of nano-imprinted pillars of acrylic photo-polymer (PAK02, Toyo Gosei Ltd.) made using AAO tempate; top-left photo shows the sample made on poly(ethylene terephthalate) (PET). Straight cylindrical and tapered nano-pillars can be made using small protocol changes of the AAO mold formation (Sec. Section 2.3).
Preprints 72089 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated