Prerpints.org logo
Preprint
Article

Laser-Metal Interaction with a Pulse Shorter the Ion Period: Ablation Threshold, Electrons Emission and Ions Explosion

Altmetrics

Downloads

124

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 May 2023

Posted:

04 May 2023

You are already at the latest version

Alerts
Abstract
Laser energy per unit surface, necessary to trigger the material removal, decreases with the pulse shortening becoming the pulse-time independent in the sub-picosecond range. These pulses are shorter the electron-to-ion energy transfer time and electronic heat conduction time minimizing the energy losses. The electrons receiving the energy larger than the threshold, drag the ions off the surface in the mode of electrostatic ablation. We show that the pulse shorter than the ion period (Shorter-the-Limit (StL)) ejects conduction electrons with the energy larger than the work function (from a metal) leaving the bare ions immobile in a few atomic layers. The electrons emission is followed by the bare ion’s explosion, ablation, and THz radiation from expanding plasma. We compare this phenomenon to the classic photo effect, nanocluster Coulomb explosions, show differences and consider possibilities for detecting the new mode of ablation experimentally by emitted THz radiation and consider applications of high-precision nano-machining with this low intensity irradiation.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

The Coulomb forces are entirely responsible for the keeping the solid intact. Quantum effects in solids significantly modify the Coulomb interactions. In the unperturbed metal the conduction electrons’ wave functions are periodic (Bloch waves) allowing the conductivity electrons propagate through a metal being not affected by the ions’ cores attraction. Intense ( ∼ 10 14 W/cm 2 ) sub-picosecond laser pulse excites electrons while the ions cores remain unperturbed. The conductivity electrons oscillate with the energy comparable to the Fermi energy, violating the Braggs conditions, destroying the Bloch wave function, and converting a metal into plasma. The multi-particle Coulomb interaction between electrons and ions is restored during the time depending on the electron-to-ion mass ratio. This time is in a range from few fs to a few tens of femtosecond depending on ion’s mass.
Sub-picosecond pulse duration (from few tens of picoseconds to few tens of femtoseconds) is shorter than the electron-to-ion energy transfer time and electronic heat conduction time. It is established experimentally [1,2] that the energy density per unit area triggering the material ejection (threshold fluence) does not depend on the pulse duration. The analysis shows that the collective electrostatic field of hot electrons drags cold ions off the skin layer of laser-excited solid [3]. The electron’s energy is proportional to the absorbed energy per unit surface. The threshold achieved when the absorbed energy per electron in the outmost surface layer is equal to the sum of the work function of electron and the cohesion energy of atom. The calculated threshold coincides well with the measured data. Hence, it is obvious that the laser-matter interaction in this mode occurs during the longer time than necessary for the collective electrostatic field restoration.
The subject of this paper is the analysis of the laser-metal interaction with a pulse duration shorter than that necessary for the collective electrostatic field restoration. First, we identify the limit of the restoration time in a solid and in plasma. Then, we analyse the electrostatic ablation mode and compare it to the shorter-the-limit (StL) pulse-metal interaction. The laser excited conduction electrons in this mode have no time to affect the ion’s cores. Therefore, an electron getting energy larger than the work function leaves the surface with the kinetic energy, ϵ k i n = ϵ e − w e , like in the classical photo-effect ( ϵ e is the energy of electron and w e is its work function; Figure 1).
However, in the Millikan’s experiments [4] (Nobel’s prize 1923) the intensity of the UV photons, ℏ ω > w e (the energy of photons per unit surface/unit time) was very low 10 − 7 − 10 − 3 W/cm 2 . Hence a photon interacted with electron as a particle swiftly knocking it off the potential well, the work function’s deep. The number density of affected ions was much lower the initial density, ions’ spatial separation very big preventing any ion/ion interaction. The long interaction time (minutes) allowed the weak electric currents from the bulk of metal restoring the neutrality.
Unlike the photo-effect, during more intense StL-metal interaction the electrons get energy larger than work function from flow of photons, as electro-magnetic wave, at, ℏ ω ≪ w e , while the unperturbed positively charged ions remain immobile inside a few close-to-surface atomic layers during the interaction time shorter than that necessary for restoring the collective Coulomb force of ions. After the end of the pulse the joint electric field of the positive charges ejects the surface ions. The acceleration of ions (proportional to the surface charge density) exceeds that of electrostatic ablation by two orders of magnitude. The electrons emission is followed by the ions’ explosion, ablation, and THz radiation from the expanding plasma. We discuss the experiments for the possible verification of the STL pulses action and consider applications of the high precision nano/ micro-machining.

2. Hierarchy of the time scales in the electron-ion interactions

There are two domains of the electron-ion Coulomb interactions. First domain includes particle-to-particle collisions of momentum and energy exchange in plasma. Second group deals with the collective electrons-ions interactions in plasma and solids when a particle is under the action of multiple fields of surrounding positive/negative charges.
Time scales in plasma are straightforward. The shortest is the electron-electron (e-e) and electron-ion (e-i) momentum exchange time, t m = ν e i − 1 ∝ ϵ e 3 / 2 n e > ω p e − 1 , where ν e i is the frequency of e-i collisions, n e the electrons’ number density, and ω p e is the electron plasma frequency. Maximum momentum exchange rate is around electron plasma frequency. Hence the momentum exchange time is around ∼ 0.1 fs for the solid density plasma. The energy exchange time is larger on the ratio of ion mass M i o n to the electron mass m e : t m = ν e i − 1 M i o n m e . It is of a few-ps range for the mass ratio of 10 5 . We start with the collective interactions in plasma where physics is straightforward.
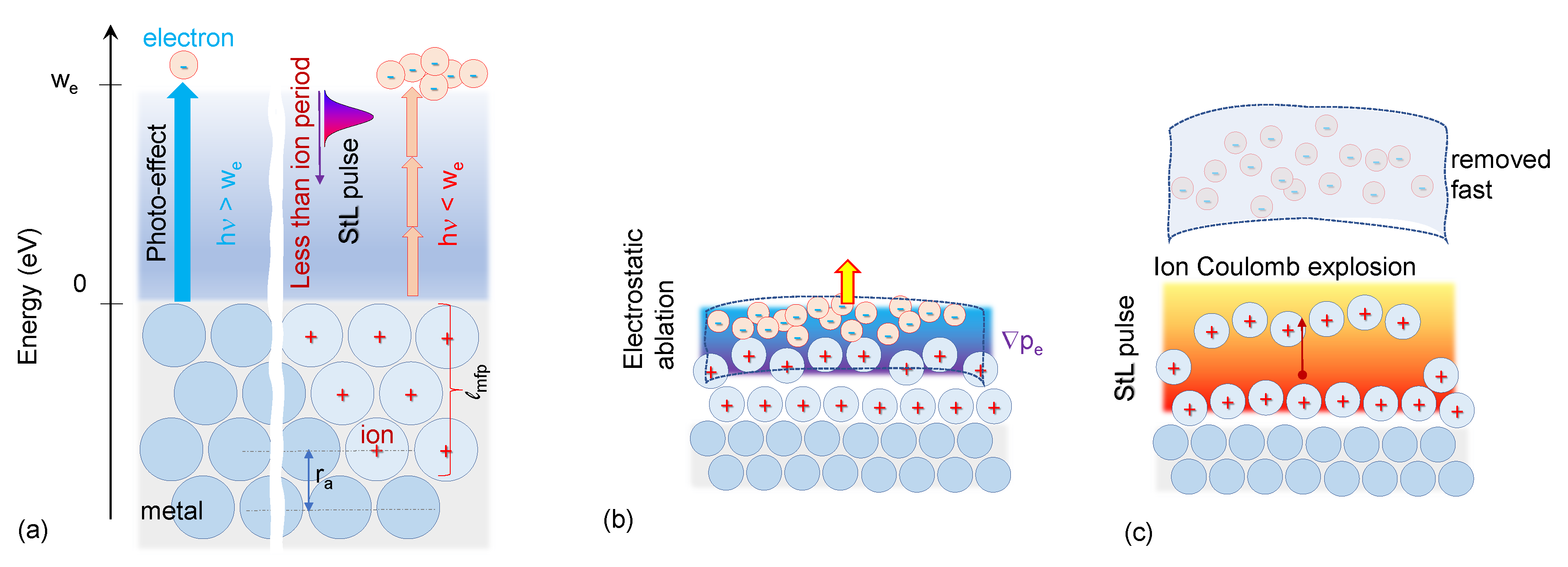
Preprints 72551 g001
Figure 1. The schemes of the different interaction regimes. (a) Left: knock off electron by single UV photon in classic photo-effect; Right: absorption of the multiple photons of StL laser pulse followed by an electron ejection. (b) In electrostatic ablation, the ions are driven by the gradient of the electronic pressure, ∇ p e . (c) In StL interaction mode the ions are driven by the Coulomb repulsion layer by layer with the outmost surface layer moving first and fastest. The energy scale is the work function, w e ; the space scales are the mean free path of an electron, l m f p , and inter-atomic distance, r a .
Figure 1. The schemes of the different interaction regimes. (a) Left: knock off electron by single UV photon in classic photo-effect; Right: absorption of the multiple photons of StL laser pulse followed by an electron ejection. (b) In electrostatic ablation, the ions are driven by the gradient of the electronic pressure, ∇ p e . (c) In StL interaction mode the ions are driven by the Coulomb repulsion layer by layer with the outmost surface layer moving first and fastest. The energy scale is the work function, w e ; the space scales are the mean free path of an electron, l m f p , and inter-atomic distance, r a .
Preprints 72551 g001

2.1. Time scales for the electron-ion collective coupling in plasma

In the cold, non-magnetic quasi-neutral plasma (equal number of positive and negative charges) on each charge always acts an unbalanced force from the neighbours making any charge moving and therefore the electrons density fluctuating (direct consequence of the Gauss theorem). The sum of electro-static fields forces the electrons oscillate with the electron plasma frequency, ω p e 2 = ( 4 π e 2 n e ) / m e after the time, t C , e ≈ ω p e − 1 ; in SI units ω p e 2 = e 2 n e / ( ε 0 m e ) with ε 0 ≡ 1 μ 0 c 2 1. Thus, the electrons start oscillating after the time, t C , e , from the moment the electronic plasma is instantaneously created ( ∼ 10 − 16 s). The sum of the electro-static fields of the oscillating electrons forces heavy ions oscillating with the ions’ plasma frequency, ω p i 2 = ( 4 π e 2 n e ) / M i . The time when the Coulomb fields of the multiple electrons starts affecting the ions is t C , i ≈ ω p i − 1 = t C , e M i / m e ( ∼ 10 − 14 s). Electron plasma frequency from Al to Ag is in a range ( 1.97 − 1.21 ) × 10 16 s − 1 making the time when ion’s motion begins, t C , i ≈ ( 0.5 − 0.82 ) × 10 − 16 M i / m e [s].

2.2. Time for the perturbation of ion core positions in a cold solid

At zero approximation the ions are assumed immobile, and electrons are moving in the Coulomb field of the stationary ions. The full energy of a solid (nonrelativistic Hamiltonian in the quantum treatment) includes the kinetic energy of electrons and ions, electron-electron and ion-ion Coulomb interaction, and electron-ion interactions [5]. The effective potential energy as well as the energy of the Coulomb interaction between the nuclei in equilibrium approximates well by the energy of two charges interaction, U 0 ≈ e 2 2 r B = m e e 4 2 ℏ 2 , here r B is the Bohr radius. The ion core motion under the action of the electron’s Coulomb field in a cold solid can be considered as a perturbation. It is the second term in the expansion of the core’s potential energy into the series on the deviation of ion core’s position from the equilibrium, δ R . The expansion of the potential near the equilibrium reads:
U = U 0 + δ U 0 ≈ U 0 + 1 2 ∂ 2 U ( R ) ∂ R 2 δ R 2 .
The second term is the potential energy of nucleus oscillations:
δ U 0 ≈ U 0 δ R 2 2 r B 2 .
The minimum momentum of a nucleus estimates from the uncertainty relations, p i ≥ ℏ / δ R . Then the ion’s kinetic energy follows, p i 2 / 2 M i ≥ ℏ 2 / ( 2 M i δ R 2 ) . Equalising the potential energy to the kinetic energy of the core (the Virial theorem) one obtains the nucleus displacement, δ R ≈ ( 2 m / M i ) 1 / 4 × r B . Hence the ions energy increase from Eqn. 2 is:
δ U 0 = ϵ i o n ≈ U 0 2 2 m e M i .
The minimum time when ion starts moving after receiving the energy from the electrons Coulomb field follows from the uncertainty relation:
t i o n ≈ ℏ ϵ i o n = 2 ℏ U 0 M i m e = 2 t a t M i m e ,
here, the characteristic atomic time is, t a t = ℏ / U 0 = 0.48 × 10 − 16 [s] for U 0 = 13.6 eV. Thus, t i o n ≈ M i m e × 0.68 × 10 − 16 [s]. This estimate based only on the fundamental constants and mass ratio. Therefore, it sets the minimum time for electron affect an ion by its electric field in a solid.
One can see the proximity of this result to the estimate for the solid density plasma, t C , i ≈ ( 0.5 − 0.82 ) × 10 − 16 M i m e [s]. In plasma this time depends on the electrons number density explicitly reflecting the collective nature of the effect that is in the above estimate implicit. It is legitimate assuming that in a shorter time the sum of forces of chaotically directed fields of the multiple charges do not build yet, i.e., ions are not moving. Hence the electrons excited during the period shorter than t C , i have not interacting with the core ions.

3. Ablation of metal by different pulses: long (electrostatic mode) and short (StL mode)

Let us compare the ablation of a metal in two different experiments by two pulses (both shorter the electron-to-ion energy transfer time) of different duration delivering the same energy per pulse at the same focal spot (same fluence). The longer pulse interacts in the regime of electrostatic ablation, while the shorter pulse ablates the same metal in the StL interaction mode. The electron temperature distribution in the skin layer depends on the absorbed fluence. The number of conduction electrons remains practically unchanged in the considered intensity range. Therefore, assumption that the absorption coefficient and skin length at two different intensities is approximately the same is reasonable. The processes in the considered experiments depend only on the ablation mode (pulse duration). The pulses are of the high contrast (no pre-plasma, step-like density gradient to the end of the pulse) incident along the normal to the surface. The laser energy is absorbed on the conduction electrons in the skin layer. Solution of 1D Maxwell equation in a metal allows calculation of absorbed energy density through the Poynting vector. Then, from the energy equation for electrons follows the electron energy space and time dependence in the form:
ϵ e ( x , t ) = ϵ e ( 0 , t ) × e − 2 x l s ,
where ϵ e ( 0 , t ) = 2 A n e l s F ( 0 , t ) and the fluence is a time integral of intensity F ( 0 , t ) = ∫ 0 t I ( 0 , τ ) d τ . Here A is the Fresnel absorption coefficient (ratio of the absorbed to the incident energy), l s is the skin length (for E-field), n e is the electron number density (see details in Appendix).

3.1. Electrostatic ablation

Pulse duration for the electrostatic ablation should be in a range, t C , i < t p u l s e < t e i e n , larger than that for building the collective Coulomb force and much less the electron-to-ion energy transfer time. Electrostatic ablation of metal surface has been experimentally verified by 15 fs laser pulses [6]. The threshold fluence from Eqn. 5 is defined as the electron energy necessary for removal of ion from the outmost surface layer. This energy equals to the sum of the cohesion energy and work function, ϵ e ( 0 , t p ) = ϵ b + w e . The threshold for metals, F t h ( 0 , t p ) = ( ϵ b + w e ) n e l s 2 A , agrees well with the measurements [1,2]. Let us define the ablation depth l a b l from the similar condition, ϵ e ( l a b l , t p ) = ϵ b + w e . Then the energy of electron in the outmost surface layer is ϵ e ( 0 , t p ) = ( ϵ b + w e ) e 2 as well as the incident laser fluence F = e 2 F t h ( 0 , t p ) ; e = 2.71 is the Napier’s number.
The momentum equations for electrons and ions are the following:
m e ∂ v e ∂ t = e E e l s t + 1 n e ∇ p e ,
M i ∂ v i ∂ t = e E e l s t ,
where p e is the electron pressure. Here the electric field is the coarse-grained field associated with the collective interaction of plasma charges [7]. In considering the ions motion the electron’s inertia can be ignored, n e e E e l s t ≈ − ∇ p e . The collective action of hot electrons drives the cold ions motion off the metal:
M i ∂ v i ∂ t = e E e l s t = − ∇ ϵ e = 2 ϵ e l s .
Electronic heat conduction smoothing the gradient well after the end of the pulse. The cooling time, when the gradient along with the ions acceleration goes to zero, is t c o o l = l s 2 / D h e a t where the diffusion coefficient is defined by the e-i momentum exchange rate ν e i m o m as D h e a t = v e 2 / [ 3 ν e i m o m ] . It is in picoseconds range. Thus, the number of ablated ions (focal area is known), their acceleration and final velocity can be calculated.

3.2. Ultra-short pulse t C , i > t p u l s e interaction

Let us now consider much shorter pulse, t C , i > t p u l s e , interaction with the same metal and the same absorbed surface energy density. The electrons energy space distribution created by the long and short pulse is the same. Now, the conduction electrons can get the energy larger the work function during the period shorter that necessary for building the link to ions. The state is very similar to that in the classical photo-effect with the difference that this state has been created by the multiple photon’s absorption by electrons (Figure 1). The electrons in a few atomic layers at the distance of the electronic mean free path from the metal-vacuum boundary can escape a metal with the kinetic energy, ϵ k i n = ϵ e − w e , leaving N atomic layers with the positively charged ions. This number equals to the electron’s mean free path by the atomic monolayer thickness, N = l m f p / r a . The focal spot area, S f , with the depth, l m f p , atomic number density, n a , became positively charged with the surface charge density, σ = e n a N × r a (Figure 1). In accord to electrostatics [8] the charged thin infinite plate creates the equal electric fields perpendicular to the plane in the positive and negative directions. Each field is proportional to the surface charge density, E e l s = 2 π σ . Thus, the single charged ion of mass M i is under action of this force pulling ion off:
d v i o n d t = 2 π e 2 n a N × r a M i = N ω p i 2 r a / 2 .
Note, that maximum acceleration of two repelling ions (at the small displacements, ζ ≪ r a equals to ω p i 2 r a / 3 [9], while in the ideal case of electrostatic charged plate acceleration is constant in space. The acceleration by charged plate is enhanced by the multiple contribution of the surface charges. However, the acceleration is not constant in space in the reality. The force has a maximum in the central part of the focal spot decreasing with the distance to the focal boundary.
For the finite plate and in plasma the space scale, where this acceleration is reasonable to consider constant, must be much less the size of the plate (focal spot). Taking conservatively this scale as r a one gets the maximum velocity as, v i , m a x ≈ N ω p i 2 r a 2 . For Ag ( ω p i = 2.53 × 10 13 s − 1 , r a = 1.59 × 10 − 8 cm, N ∼ 9 ) the velocity range is v i , m a x = ( 12 − 4 ) × 10 5 cm/s; and the acceleration range ( 5 − 0.45 ) × 10 19 cm/s 2 , orders of magnitude larger than in electrostatic ablation.
Hence there are few major differences with the electrostatic ablation. First, part of electrons is ejected most probably isotropic. Second, part of bare ions is accelerated by the Coulomb repulsion with acceleration couple of orders of magnitude higher than during the electrostatic ablation. Third, the ablation threshold reached at the electron’s energy slightly above the work function making electrons from couple of the outmost surface layer to leave letting an ion to be repulsed.

4. Radiation from the ablated plasma

The ablated plasma is a current flowing mainly perpendicular to the sample surface decelerating slowly before attending the constant velocity. Let us compare the radiation of plasma flow in two ablation modes. We consider ablation of Ag target with the same incident (and absorbed) surface energy density producing the identical space energy distribution and ablation depth equal to the skin depth. The total number of ablating particles in both cases is the same. However, in the case of StL pulse there are two groups of ions with different accelerations.

4.1. Radiation from the electrostatically ablated plasma

Frequency spectrum and total power of radiation emitted by the time-dependent current depends on the full number of emitting charges, their acceleration, and its duration. Ag ions’ acceleration in the electrostatic ablation mode is, ∂ v i ∂ t = 2 ϵ e M i l s = 2.3 × 10 17 cm/s 2 while the number of ablated ions constitutes, N a b l = 2.5 × 10 11 ions (see Appendix for details).
The Fourier transform of the time-dependent current defines the frequency spectrum of the emitted radiation: j ω = ∫ j ( t ) e i ω t d t . The acceleration of ions decreases because the electronic heat conduction leads to the flattening the electronic pressure gradient. The acceleration decreases from the maximum to zero due to the skin layer cooling, the characteristic time, T ∼ 1 ps and inverse is a characteristic frequency of emitted radiation ∼ 1 THz. The direction of the emission is perpendicular to the direction of nonrelativistic acceleration. The power of the radiation emitted by the current is given by the Larmor formula [10]:
P = 2 3 c 3 ( d ¨ ) 2 ,
here d ¨ = ∑ e v ˙ is the sum taken over all dipoles’ acceleration v ˙ in the current. The power of the emitted radiation is proportional to the square of the particles number and their deceleration. One can estimate the total energy emitted by the current as the following:
ϵ R a d = T × P ≈ 2 T 3 c 3 e N a b l d v i d t 2 .
Taking acceleration 2.3 × 10 17 cm/s 2 , N a b l = 2.5 × 10 11 ions, T ∼ 10 − 12 s one gets total energy of radiation 1.88 × 10 − 12 J (the power of 1.88 W). Hence, the ratio of the total emitted energy to laser energy of 3 μ J constitutes ∼ 6 × 10 − 7 .

4.2. Radiation from the plasma ablated by StL pulse

The total number of ablated atoms remains the same. However, the structure of the plasma outflow is different. First, the electrons from a few atomic layers with thickness of electronic mean free path are moving out. Then the bare ions abandoned by electrons are expelled by repulsion. Finally, the bulk of the ablated material are removed with low velocity and the features like considered in the previous paragraph.
The number of ions in layers from where electron escaped is N e x p = ( l m f p / l s ) N a b l ∼ 7.5 × 10 9 . The mean free path of an electron l m f p = ν e / ν e i m o m ∼ 1.48 × 10 − 7 cm extends to 9 monolayers. The electrons from these layers are emitted during the STL pulse. The removal of ions by repulsion occurs layer by layer with gradually decreasing acceleration in accord with diminishing number of layers:
d v i o n d t = N ω p i 2 r a / 2 .
For Ag, the acceleration range of exploding ions is 10 19 − 10 20 cm/s 2 , while the velocity range is v i , m a x = ( 12 − 4 ) × 10 5 cm/s. The time for reaching the constant velocity of expansion is a few hundred fs (100-400 fs). Therefore, the frequency of radiation is in a range (10-2.5) THz. Now estimates for the power and total energy of radiation are straightforward by Eqs. 10-11: P = ( 3.2 − 320 ) W, the total energy (taking T = 2.5 × 10 − 13 s) is around 2.5 × 10 − 11 J. Hence, only 3% of ablated ions emit by the order of magnitude larger energy in a bit higher frequency range. The plasma plume produced by the StL pulse contains major part of slow ions emitting less than 10% radiation in THz range. About ∼3% of total ablated fast ions emit the major radiation in a slightly higher frequency range. Two radiation peaks of different height are separated in time.

5. Discussion and conclusion

The non-relativistic StL laser pulse (ponderomotive potential 10-20 eV) excites free electrons in the conduction band of metal during the time shorter that for restoring electron-ion Coulomb coupling. Excited electrons escape from a few close to surface atomic layers after getting energy larger the work function. These layers become positively charged creating electrostatic field perpendicular to the surface accelerating and ejecting ions by the Coulomb explosion. Let’s discuss the proximity and difference of this phenomenon to the classic photo effect and the Coulomb explosion of nanoclusters.
In the classic photo-effect, the UV photon with the energy larger the work function knocks the conduction electron off the surface in the single photon-electron collision (Figure 1). To consider a photon as a quantum particle the number of photons per cube of photons wavelength should be less than one [11]. The intensity in the Millikan’s experiments [4] has been in a range 10 − 7 − 10 − 3 W/cm 2 well in accord with the above criterion leaving the rest of conduction electrons in a free state (not affected by the ions cores). Therefore, an electron after collision escaped the metal with the kinetic energy in accord to the Einstein formula ϵ k i n = ℏ ω − w e .
In the StL pulse-metal interaction the high-frequency laser field convert electrons into plasma state thus destroying free electron-ion core relations of metal in contrast to the classic photo-effect. However, an electron absorbs energy during the period shorter that needed for the restoration of the collective electron-ion coupling. The electron which received energy more than the work function escapes a metal not being affected by ions cores due to the extremely rapid nature of interaction. Ions in a few atomic layers left immobile and charged. Then the Coulomb repulsion drives ions out of metal.
The phenomenon of the Coulomb explosion of small [12] and large molecules [13] and nanoclusters [14,15,16] has been studied more than three decades. The relativistic laser beam with the ponderomotive potential around MeV ionises nanocluster up to several electrons per atom. Electrons are accelerated and swiftly ejected from a cluster with the energy comparable to the ponderomotive potential leaving ions immobile and positively charged. The cluster acquires a big total positive charge resulting in the Coulomb explosion. Kinetic energy of exploded ions reaches MeV depending on the total charge of the cluster. Recent studies provides new insights into ablation at ultra-relativistic intensities showing a steplike electrostatic potential which drives disassembly of the solid [17]. In the StL-metal interaction the similar events develop on the much smaller energy scale and on the similar short time scale. The laser ejected electrons are followed by fast ions (few percent) accelerated by explosion and followed by the slow ions of conventional ablation. Analysis shows that ablated flow of fast ions is much intense source of THz radiation than that of slow current. Using the light metals (like Al) and energetic lasers one can create StL-pulse-generated point source of THz radiation (controlled by choice of metal, pulse duration, laser energy, focal spot size).
Summing up the presented analysis suggests that the intense laser pulse with duration less than the ion period (few tens fs) is capable swiftly eject the conduction electrons from a few near-surface atomic layers followed by the flow of energetic ions ejected by the Coulomb repulsion and emission of THz radiation. As it follows from the above in this interaction regime (StL) is possible to remove a few atomic layers from a metal by the action of a single laser pulse (see Sec. H). The number of the atomic layers removed by explosion, i.e., the electron’s mean free path, is controlled by the absorbed surface energy density delivered by laser. Indeed, mean free path of electron in the Coulomb collisions is, l m f p ∝ ϵ e 2 , while ϵ e ∝ F . For experimental realisation and monitoring the StL pulse ablation, detection of THz emission reported for generation of single-cycle circularly polarised pulses under 40 fs pulsed irradiation of water micro-flow [18] can be used.

Author Contributions

Conceptualization, E.G.G; methodology, E.G.G; E.G.G; writing—original draft preparation, E.G.G; writing—review and editing, E.G.G and S.J.

Funding

This research received no external funding.

Data Availability Statement

All data are provided within the main text and supplemental sections.

Acknowledgments

E.G.G. thanks Prof. Vladimir Tikhonchuk for reading the paper, discussions, comments and suggestions. S.J. is grateful for funding by the ARC Linkage LP190100505 project.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Classical photo-effect

In the Millikan’s experiments (1916) photo effect has been induced by UV radiation of the mercury discharge. Intensity at 365 nm (3.4 eV) was 10 − 10 4 erg/cm 2 s ( 10 − 7 − 10 − 3 W/cm 2 ). Flow of photons maximum was 1.8 × 10 15 photons/cm 2 /s. UV photon swiftly knocks electron out of the surface layer. Positive charges are equalising by the slow currents from the bulk. The quantum description of the photon as a particle is necessary when the number density of photons is less one photon per cubic of photon’s wavelength [11].

Appendix B. Properties of metals at room temperature

Conduction electrons density n e is in 10 23 cm − 3 , inter atomic distance, r a = ( 4 π n e / 3 ) − 1 / 3 in 10 − 8 cm (Å), plasma frequency in 10 16 s − 1 , effective electron’s mass is in units of free electron mass. Ion frequency: Ag, m e / M i = 5 . 08 − 6 , ω p i = 2.53 × 10 13 s − 1 ( t C i = 36.7 fs).
Table A1. Parameters of metals which can be used for experiments with StL pulses. The maximum value of w e is shown and for which crystallographic plane [19].
Table A1. Parameters of metals which can be used for experiments with StL pulses. The maximum value of w e is shown and for which crystallographic plane [19].
Metal: n e M i r a ω p e m e f C e ϵ F ϵ b w e
units 10 23  cm − 3 at.mass Å 10 16  s − 1 m e 3 2 k B eV eV eV; (max)
Al 1.806 26.982 1.09 1.97 1.48 0.46 11.63 3.065 4.2; (100)-plane
Cu 0.845 63.546 1.41 1.395 1.38 0.70 7.0 3.173 4.48-4.98
Au 0.59 196.97 1.38 1.126 1.14 0.69 5.52 3.81 5.47; (100)-plane
Ag 0.585 107.86 1.59 1.121 1.0 0.79 5.48 2.95 4.52-4.74
The electron heat capacity is estimated from C e ≈ 3 2 k B T e ( 2 x − x 2 ) , where x = k B T e / ϵ F attains the ideal gas value at x = 1 [20]; the Fermi energy ϵ F . The electron heat capacity near the ablation threshold k B T e = ϵ b , where ϵ b is the binding energy defined as the potential barrier against free motion of atoms through the solid. For example, for Au ϵ b = 3.81 eV/atom (the cohesive energy per atom), ϵ F = 5.52 eV, x ≈ ϵ b / ϵ F = 0.69 and C e = 1.355 [ k B ], close to 1.5 as for the ideal gas.

Appendix C. Optical properties of the electronic plasma

The Drude-like dielectric permittivity reads [20]:
ε r e = 1 − ω p e 2 ω 2 + ν e i 2 , ε i m = ω p e 2 ω 2 + ν e i 2 × ν e i ω ,
and is related to the real and imaginary parts of the complex refractive index n ˜ ≡ n + i κ via ε r e = n 2 − κ 2 and ε i m = 2 n κ ; κ 2 = ( | ε r e | − ε r e ) / 2 and n 2 = ( | ε r e | + ε r e ) / 2 , where the complex modulus | ε r e | = ε r e 2 + ε i m 2 . The Fresnel absorption coefficient reads A = 4 n ( n + 1 ) 2 + κ 2 .Electron-ion momentum and energy transfer rates. Near the maximum it defines as, ν e i ≈ v e / r a . Taking the electron velocity on the atomic scale, 2 × 10 8 cm/s, one gets the rate of the order of the electron plasma frequency. We consider conditions when electrons energy is of the same order of magnitude as the Coulomb energy and Fermi energy. The plasma is non-ideal, unscreened and collision rate decreases. Cauble and Rozmus predicted [21] that in the solid density non-ideal plasma the e-i collision rate estimates as the following:
ν e i m o m ≈ ω e i ln Λ 10 N D ,
where the logarithm ln Λ and the number of particles in the Debye sphere N D for the ideal plasma are [7]:
Λ ≈ ( 9 N D ) / Z , N D = 1.7 × 10 9 θ e 3 / n e ,
where θ e is the electron temperature, Z is the charge state. Taking ϵ e = 10 eV and n e = 0.585 × 10 23 cm − 3 (Ag), one obtains Λ = 2 (the ref. [10] gives 0.69), N D = 0.22 and ν e i m o m ≈ 0.3 ω e i ∼ 3 × 10 15 s − 1 .
The electron-to-ions energy transfer time is, t e i e n = ν e i m o m × m e M i − 1 ; for Ag, it is 65 ps.
At ω = 1.88 × 10 15 s − 1 (wavelength of 1002 nm), ω p e = 1.21 × 10 16 s − 1 , ν e i m o m ≈ 3 × 10 15 s − 1 , one gets ε i m = 16 and ε r e = − 9 , i.e., n = 2.16 , κ = 3.7 and A = 0.365 ; the skin depth l s = 43 nm; the constant C 0 = 2 A n e l s = 3 × 10 − 18 cm 2 is used in calculation of electron energy (see below).
Oscillation energy (ponderomotive potential) is given by [22]: ε o s c = 9.375 ( 1 + α 2 ) × I 10 14 [ W / cm 2 ] × λ μ m 2 [eV]; here α = ± 1 for circular polarisation and α = 0 for linear polarisation. Intensity I is averaged over many laser pulse periods.

Appendix D. The electron’s energy space and time dependence in the skin layer

The electron’s energy time/space dependence in the skin layer (normal skin) in 1D approximation follows from the energy equation under assumption that the electron’s density and optical properties are time/space independent, and the pulse duration is much shorter the electron-to-ions energy transfer time, t e i e n = ν e i m o m × m e M i − 1 . The electrons contain all the absorbed energy. Energy equation for electrons (no losses) is:
n e ∂ ϵ e ∂ t = Q a b s ( x , t ) .
Here the absorbed energy density reads:
Q a b s ( x , t ) = 2 A I ( t , 0 ) l s e − 2 x / l s [ W / cm 3 ] .
The Fresnel absorption coefficient A and skin depth l s are the following:
2 A l s = 4 ω ε i m c × | 1 + ε | 2 , l s = c ω κ ,
c is the speed of light. Integration the electron energy equation by time gives the electron energy:
ϵ e ( x , t ) = C 0 × F ( 0 , t ) × e − 2 x / l s ,
where C 0 = 2 A n e l s , F ( 0 , t ) = ∫ 0 t I ( 0 , τ ) d τ . Threshold for Ag ϵ e ( 0 ) = ϵ b + w e = 7.5 eV at wavelength λ = 1 μ m, has fluence F t h = 0.4 J/cm 2 .

Appendix E. Electrostatic Ablation of Ag

Ablation depth, number of ablated atoms, cooling time for the skin layer for Ag target. For, F = 7.39 × F t h = 2.96 J/cm 2 at laser pulse energy ∼ 3 μ J, ϵ e ( 0 ) = 55.8 eV, v e = 4.43 × 10 8 cm/s, ablation depth x a b l = l s 2 ln ϵ e ϵ b + w e equals to l s . The ablation volume assuming S f o c = 10 − 6 cm 2 is V a b l = 4.3 × 10 − 12 cm 3 , N a b l = 2.5 × 10 11 ions ν e i m o m ≈ 0.3 ω e i ∼ 3 × 10 15 s − 1 . Heat diffusion coefficient for Ag D h e a t = v e 2 / 3 ν e i m o m = 21.8 cm 2 /s, cooling time t c o o l = l s 2 / D h e a t = 0.85 ps. The ions removal from these layers occurs under the electrostatic force of hot electrons acting as a gradient of the electronic energy.
Electrostatic ablated Ag ions’ acceleration. ∂ v i ∂ t = 2 ϵ e M i l s = 2.3 × 10 17 cm/s 2 (for ϵ e = 55.8 eV, l s = 43 nm, M i = 107.86 ). The average electrons’ velocity is around 10 8 cm/s and the motion of electrons is chaotic after a few electron-electron collisions. The ions motion is directional (along the electron pressure gradient when exciting beam is at the normal to the target surface). Thus, for the Gauss intensity distribution across the focal spot, the main current is directed at the normal at ions’ velocity more than two orders of magnitude lower than that of electrons.

Appendix F. Radiation from the ablated plasma

Unit vector along the current is r , direction to the detector located at the distance R 0 , is n . The size of the emitter, r, is much smaller than the distance to observation, r ≪ R 0 . The emitted wave arrives at detector as a plane wave. The vector potential of the emitted field reads:
A = 1 c R 0 ∫ j × d V .
The polarisation of the emitted field depends on the mutual directions of the current and the direction to the observation point:
H = d A d t × n / c , E = d A d t × n × n / c ,
where × is the sign of the vector product. Power of the emitted radiation at the observation point located at the distance, R 0 , into the unit of the solid angle Ω is d I = c E 2 4 π R 0 2 d Ω . Distance from the source to the measurement point is larger than the wavelength of emitted radiation and much larger than the size of the source.
Radiation of the ablated ion current. Estimate of the vector potential for the ablation case:
A ≈ 1 c R 0 e Z N a b l v i ,
here N a b l = ∫ n i d V is the full number of ablated ions, V a b l = l a b l · S f o c is the total ablated volume, N a b l = 2.5 × 10 11 ions of an ionisation number of an atom Z = 1 (for the conditions introduced above in Sec. E for Ag). Estimate for the electric field:
E ≈ 1 c R 0 e Z N a b l d v i d t .
Ions’ acceleration ∂ v i ∂ t = 2 ϵ e M i l s = 1.45 × 10 17 cm/s 2 . Taking for the estimate the distance to observation point R 0 = 1 cm one gets the field E = 580 V/m ( 1.93 × 10 − 2 CGSE).

Appendix G. Absence of the Debye screening

During the interaction time shorter the ion period (StL) the space and time dependence of the electron temperature is strong while the electron density remains practically unperturbed, e n e E ≈ − n e ∇ T e . Therefore, assumptions of the static limit and space independence of the electron temperature (isothermal equation of state [7]; see Kruer, p.14 [7]), essential for deriving the Debye screening, are both inapplicable, e n e E ≠ − T e ∇ n e . The absence of screening is due to lack of collective interaction of multiple charges.

Appendix H. Nanomachining: removal of a few mono-atomic layers

To remove few atomic layers with a thickness equal to the mean free path of electron, energy of electrons should be slightly above the work function ( l m f p ≈ nanometre) the laser shall deliver to the Ag surface the energy density (see Sec. D): F = w e C 0 × exp 2 l m f p l s J/cm 2 . For Ag hit by 1000 nm light only 5% of the surface energy density of 0.247 J/cm 2 is spent for a few atomic layers’ removal. The number of the atomic layers removed by explosion, i.e., the electron’s mean free path, is controlled by the absorbed surface energy density delivered by laser. Indeed, mean free path of electron in the Coulomb collisions is, l m f p ∝ ϵ e 2 , while ϵ e ∝ F .
Volume and speed of ablation demonstrated with bursts of t p ≥ 300 fs pulses [23] can potentially be improved using ablation by StL pulses, which are an order of magnitude shorter and cause energetic ion explosion from the laser-affected surface. Ablation by high repetition rate (bursts) of StL pulses harness the Coulomb explosion of the surface occurring at higher speed and can potentially improve throughput of material processing.

References

  1. Stuart, B.; Feit, M.; Shore, B.; Perry, M. Laser-induced damage in dielectrics with nanosecond to picosecond pulses. Phys. Rev. Lett. 1995, 74, 2248–2251. [Google Scholar] [CrossRef] [PubMed]
  2. Stuart, B.; Feit, M.; Herman, S.; Rubenchik, A.; Shore, B.; Perry, M. Optical ablation by high-power short-pulse lasers. J. Opt. Soc. Am. B 1996, 13, 459–468. [Google Scholar] [CrossRef]
  3. Gamaly, E.; Rode, A.; Luther-Davies, B.; Tikhonchuk, V. Ablation of solids by femtosecond lasers: Ablation mechanism and ablation thresholds for metals and dielectrics. Phys. Plasmas 2002, 9, 949–957. [Google Scholar] [CrossRef]
  4. Millikan, R. A Direct Photoelectric Determination of Planck’s ‘h. Phys. Rev. 1916, 7, 355–388. [Google Scholar] [CrossRef]
  5. Il’inskii, Y.; Keldysh, L. Electromagnetic response of Material Media; Plenum Press: New York and London, 1994. [Google Scholar]
  6. Genieys, T.; Sentis, M.; Utéza, O. Investigation of ultra-short laser excitation of aluminum and tungsten by reflectivity measurements. Appl. Phys. A 2019, 126, 263. [Google Scholar] [CrossRef]
  7. Kruer, W. The Physics of Laser Plasma Interactions; Addison-Wesley: Reading, 1988. [Google Scholar]
  8. Tamm, I. Basics of the Electricity Theory, 8 ed.; Mir Publishers: Moscow, 1976 (in Russ.).
  9. Mourou, G.; Tajima, T.; SV Bulanov, S. Optics in the relativistic regime. Rev. Mod. Phys. 2006, 78, 309. [Google Scholar] [CrossRef]
  10. Landau, L.; Lifshitz, E. Teoriya Polya (The Classical Theory of Fields), 5 ed.; Nauka: Moscow, 1967 (in Russ.).
  11. Landau, L.; Pitaevskii, L.; Lifshitz, E. Electrodynamics of Continuous Media; Vol. 5, Butterworth-Heinemann: Oxford, 1984. [Google Scholar]
  12. Codling, K.; Frasinski, L.; Hatherly, P.; Barr, J. On the major mode of multiphoton multiple ionisation. J. Phys. B: Atomic and Molecular Physics 1987, 20, L525. [Google Scholar] [CrossRef]
  13. Boll, R.; Schäfer, J.; Richard, B.; et al. . X-ray multiphoton-induced Coulomb explosion images complex single molecules. Nat. Phys. 2022, 18, 423–428. [Google Scholar] [CrossRef]
  14. Purnell, J.; Snyder, E.; Wei, S.; Castleman, A. Ultrafast laser-induced Coulomb explosion of clusters with high charge states. Chem. Phys. Lett. 1994, 229, 333–339. [Google Scholar] [CrossRef]
  15. Ditmire, T.; Donnelly, T.; Rubenchik, A.; Falcone, R.; Perry, M. Interaction of intense laser pulses with atomic clusters. Phys. Rev. A 1996, 53, 3379. [Google Scholar] [CrossRef] [PubMed]
  16. Ditmire, T.; Tisch, J.; Springate, E.; Mason, M.; Hay, N.; Smith, R.; Marangos, J.; Hutchinson, M. High-energy ions produced in explosions of super-heated atomic clusters. Nature 1997, 386, 54–56. [Google Scholar] [CrossRef]
  17. Kraus, B.F.; Gao, L.; Fox, W.; Hill, K.W.; Bitter, M.; Efthimion, P.C.; Moreau, A.; Hollinger, R.; Wang, S.; Song, H.; et al. Ablating Ion Velocity Distributions in Short-Pulse-Heated Solids via X-Ray Doppler Shifts. Phys. Rev. Lett. 2022, 129, 235001. [Google Scholar] [CrossRef] [PubMed]
  18. Huang, H.H.; Juodkazis, S.; Gamaly, E.; Nagashima, T.; Yonezawa, T.; Hatanaka, K. Spatio-temporal control of THz emission. Communications Physics 2022, 5, 134. [Google Scholar] [CrossRef]
  19. Weast, R.C. (Ed.) CRC handbook of chemistry and physics, 69 ed.; CRC Press: Boca Raton, Florida, 1989. [Google Scholar]
  20. Gamaly, E. Femtosecond Laser Matter Interactions: Solid-Plasma-Solid transformations at the Extreme Energy Density, 2 ed.; Jenny Stanford Publishing: Singapore, 2022. [Google Scholar]
  21. Cauble, R.; Rozmus, W. Two-temperature frequency-dependent electrical resistivity in solid density plasmas produced by ultrashort laser pulses. Phys. Rev. E 1995, 52, 2974–2981. [Google Scholar] [CrossRef] [PubMed]
  22. Gamaly, E. Femtosecond Laser Matter Interactions: Theory, Experiments, and Applications; Pan Stanford: Singapore, 2011. [Google Scholar]
  23. Kerse, C.; Kalaycıoğlu, H.; Elahi, P.; Çetin, B.; Kesim, D.; Akçaalan, Ö.; Yavaş, S.; Aşık, M.; Öktem, B.; Hoogland, H.; et al. Ablation-cooled material removal with ultrafast bursts of pulses. Nature 2016, 537, 84–89. [Google Scholar] [CrossRef]
1
Conversion between proportionality constants of the Coulomb’s force acting on separated electric charges and magnetic force between currents is 2 k e l = c 2 k m a g , where the electric and magnetic constants k e l , m a g depend on definition (units) of charge and current, respectively, k e l = 1 (CGS) and k e l = μ 0 c 2 4 π (SI).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated