Study of the Feasibility of Decoupling Temperature and Strainfrom a ϕ-PA-OFDR over an SMF Using Neural Networks

Abstract: Despite existing several techniques for distributed sensing (temperature and strain) using standard Single Mode optical Fiber (SMF), compensating or decoupling both effects is mandatory for many applications. Currently, most of the decoupling techniques require special optical fibers and are difficult to implement with high spatial resolution distributed techniques, such as ϕ-PA-OFDR. So, this work’s objective is to study the feasibility of decoupling temperature and strain out of a ϕ-PA-OFDR readouts taken over an SMF. For this purpose, the readouts will be subjected to a study using several Machine Learning algorithms, among them, Deep Neural Networks. The motivation which underlies this target is the current blockage in the widespread use of Fiber Optic Sensors in situations where both strain and temperature change, due to the coupled dependence of currently developed sensing methods. Instead of using other types of sensors or even other interrogation methods, the objective of this work is to analyze the available information in order to develop a sensing method capable of providing information about strain and temperature simultaneously.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

The general interest in Distribute Optical Fiber Sensors (DOFS) has increased in the past few decades [9,19,24]. Due to the huge variety of phenomena related to light propagation along an optical fiber and depending on the interrogator and the fiber used, there are more than 60 types of sensors [3]. This technology has been applied in several fields such as Structural Health Monitoring [23], Geo-Hydrological applications [2], Acoustic sensing [22] or even medicine [16].

Basically, a Distributed Optical Fiber Sensor consists of a segment of optical fiber within which monochromatic light is propagated forward (transmission) and backward (backscattering). The fiber core shape is varied, going from a simple circle up to the polarization-maintaining configurations shown in Figure 1. The dimension of this core determines the number of modes that can be propagated. In the present work, light propagation into an SMF is studied. This type of fiber is preferred due to its lower cost and reduced size when compared with other types of optical fiber (PMF), where, moreover, the decoupling has been achieved currently.

Commonly, light propagated within the fiber is emitted by a tunable laser source; and the backscatter radiation is analyzed by a photodetector after passing through some filters and beamsplitters [12]. Both photonic systems are usually integrated into the same equipment, the emitted and analyzed light wavelength determines the type of interrogator: Raman, Rayleigh, or Brillouin [24]; and with the appropriate beamsplitters and filters both States Of Polarization (SOP) can be studied separately. The phase analysis needs a special configuration in the photodetector to compare the signal received with a local oscillator [21]. For the present work, a Phase-sensitive and Polarization Analyzer Optical Frequency Domain Reflectometer (

ϕ

-PA-OFDR) was used.

Light backscattering is sensible to both temperature and strain changes and is nowadays the principal limitation when implementing this technology. The solutions are diverse and depend on the type of DOFS chosen, but two main groups can be distinguished. The first type of solution is to integrate sensors in parallel, which are usually either strain gauges or thermocouples along with Optical Fiber Sensors (OFS) in order to obtain one independent measure. The second type of solution consists of a signal treatment which requires either a second type of interrogator or a signal post-processing. In Table 1 some of the methods developed for different OFS are listed.

More specifically, the last one is the most similar to the present work. In it [10], Froggat et al. use a

ϕ

-PA-OFDR over a PMF. However, in the present work, the fiber studied is an SMF because of its higher availability and lower price (around two magnitude orders [30,31]). The behavior of SOP in an SMF is different and the same technique used by Froggat et al. cannot be implemented. More specifically, the birefringence vector’s randomness causes fast and slow polarization modes to have different time arrivals. Besides that, they will decompose into both the fast and slow modes of the next segment, leading to polarization-mode coupling [17].

Artificial Intelligence has been applied successfully to Optical Fiber Sensors [18]. Because of that, before trying to find an analytical approach to the SOP evolution through the fiber or any statistical analysis of the signals acquired, Artificial Intelligence (AI) methods have been applied to the problem in the present work, in order to determine the feasibility of decoupling temperature and strain from a

ϕ

-PA-OFDR readout.

2. Materials and Methods

2.1. Resources used

The optical fiber and interrogator used are described in Table 2. Moreover, the signal was analyzed using Python open libraries as Scipy [29] and Numpy [28].

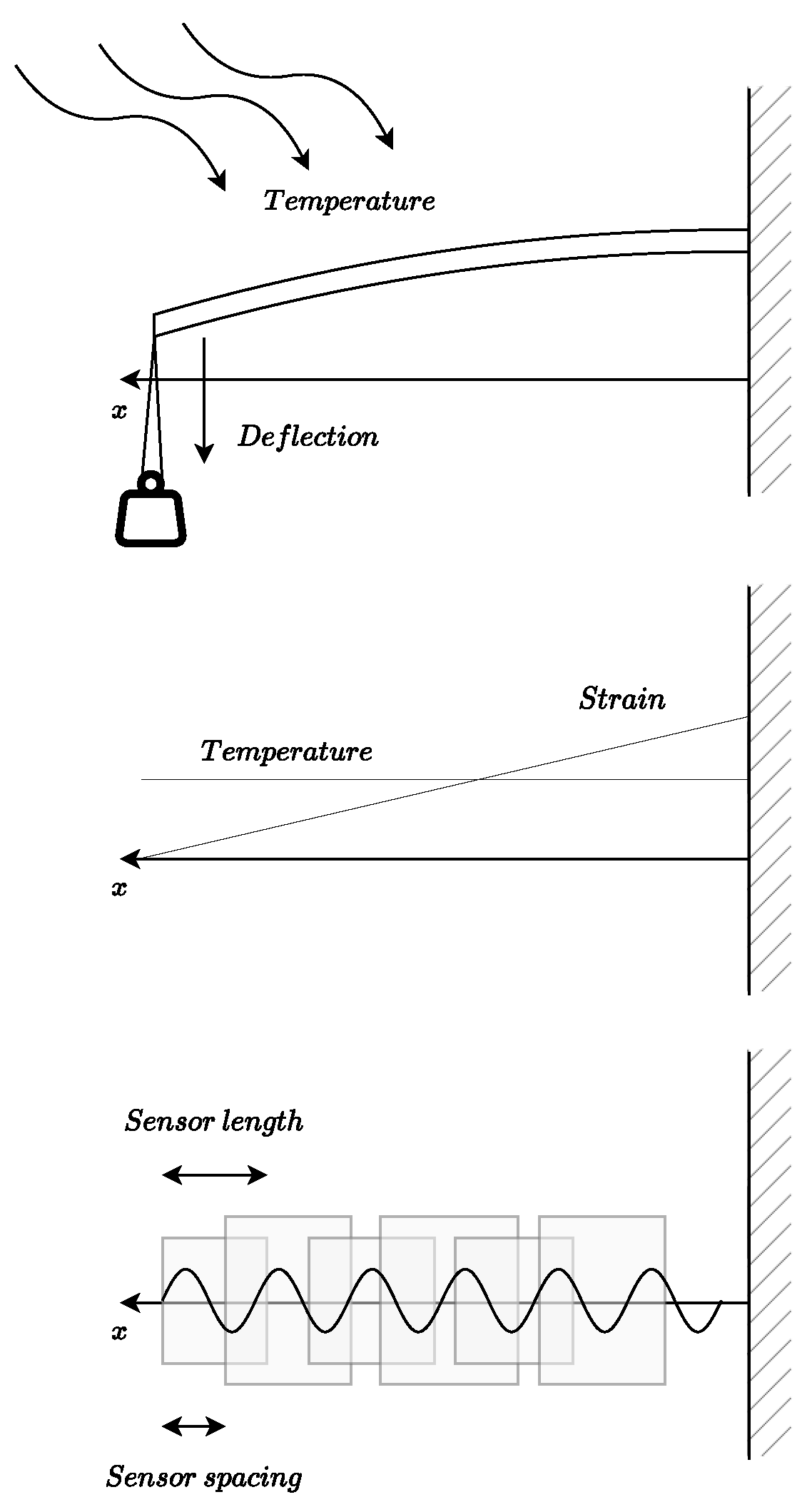
2.2. Experimental data acquisition

For a proper creation of an Artificial Intelligence model, it is imperative to have a huge and reliable experimental dataset [14,20]. For this purpose, the optical fiber was subjected to mechano-thermal tests where the longitudinal fiber strain and temperature were varied. The SMF was converted into a succession of overlapping sensors with a sensor length of 20 mm and a sensor spacing of 2 mm. This is possible because of the interferometer used that provides 2000 samples per sensor which allows signal processing calculations.

In Figure 2 the experimental setup is illustrated.

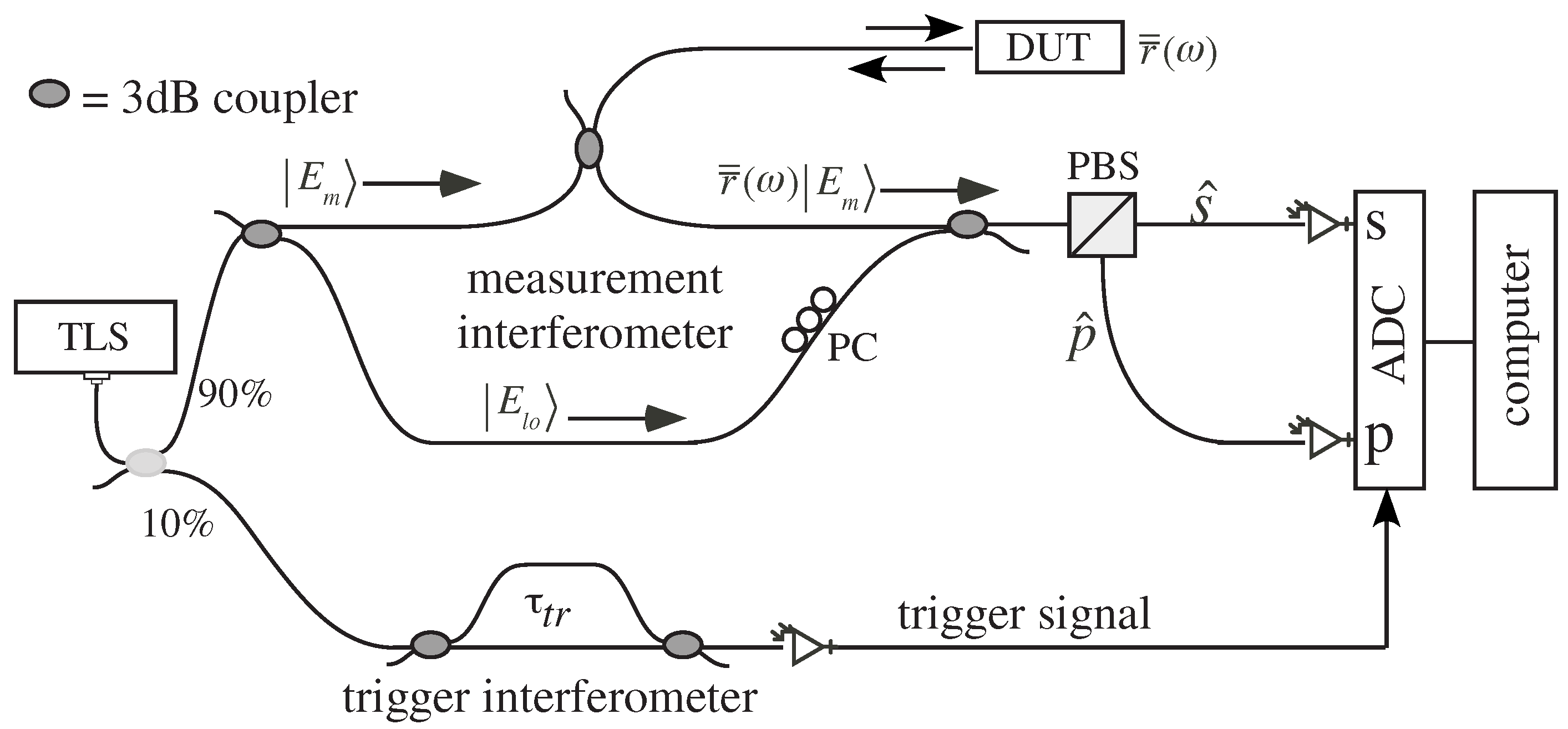
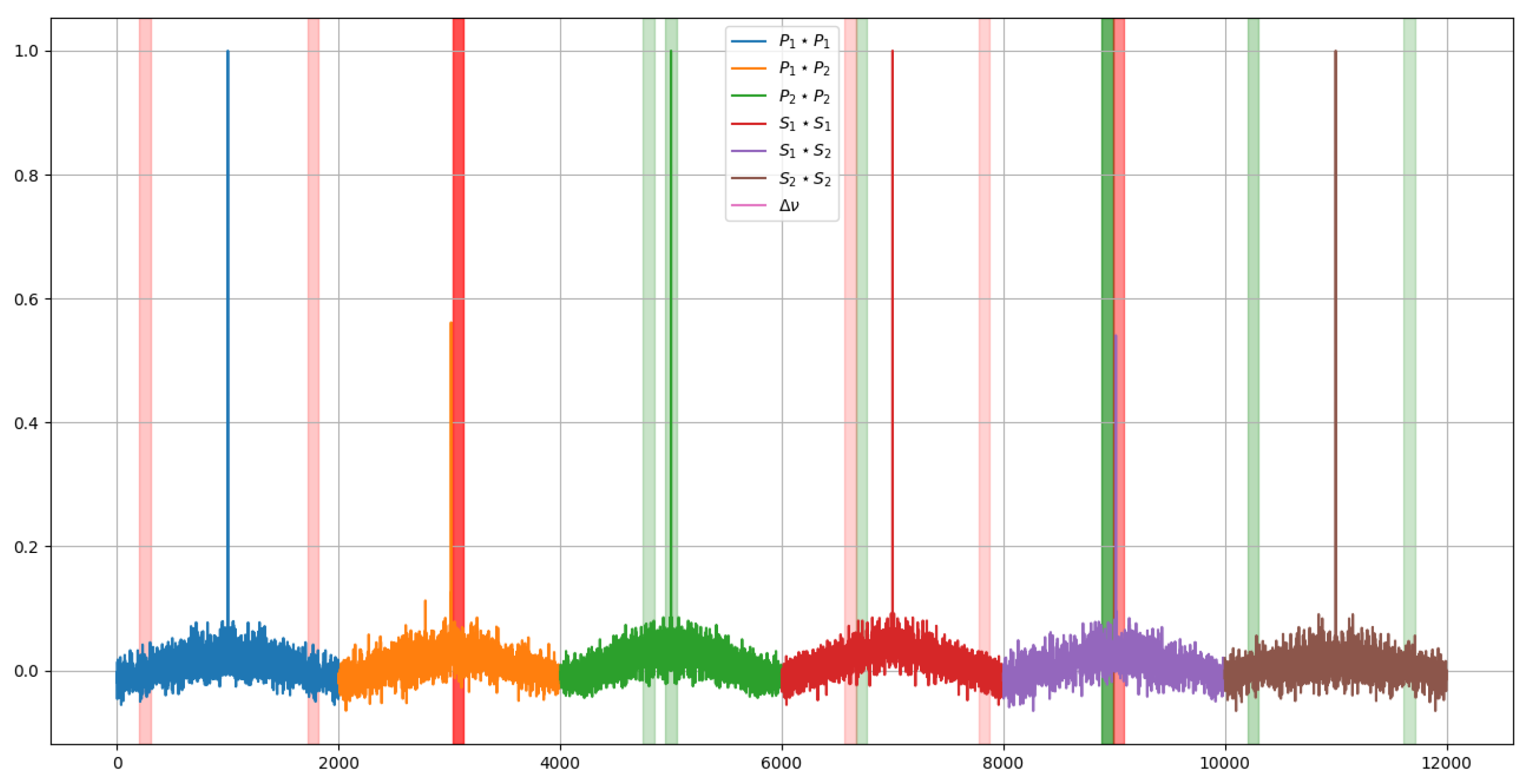
2.3. Interferometer readouts

ϕ

-PA-OFDR provides information about the two SOP of the interference between the backscattered electromagnetic field

E_{m}

and the one generated by a local oscillator

E_{l o}

(see Figure 3 or [12] for more details). This means that two complex measures

i_{s}

and

i_{p}

are received by the photo-detectors every time that the optical fiber is interrogated

\begin{matrix} i_{s} (ω) = 2 Re \{〈E_{l o} |{\bar{\bar{T}}}_{s}^{†} {\bar{\bar{T}}}_{s} \bar{\bar{r}} (ω)| E_{m}〉 exp [j ω (t) Δ τ]\}, \\ i_{p} (ω) = 2 Re \{〈E_{l o} |{\bar{\bar{T}}}_{p}^{†} {\bar{\bar{T}}}_{p} \bar{\bar{r}} (ω)| E_{m}〉 exp [j ω (t) Δ τ]\}, \end{matrix}

(1)

where the matrix operators

{\bar{\bar{T}}}_{s}

and

{\bar{\bar{T}}}_{p}

represent the beam splitter action.

By means of a Discrete Inverse Fourier Transform (DIFT) the time-domain response of the Device Under Test (DUT) can be obtained. Then, knowing the speed of light into the fiber, obtaining the spatial distribution is trivial.

3. Results

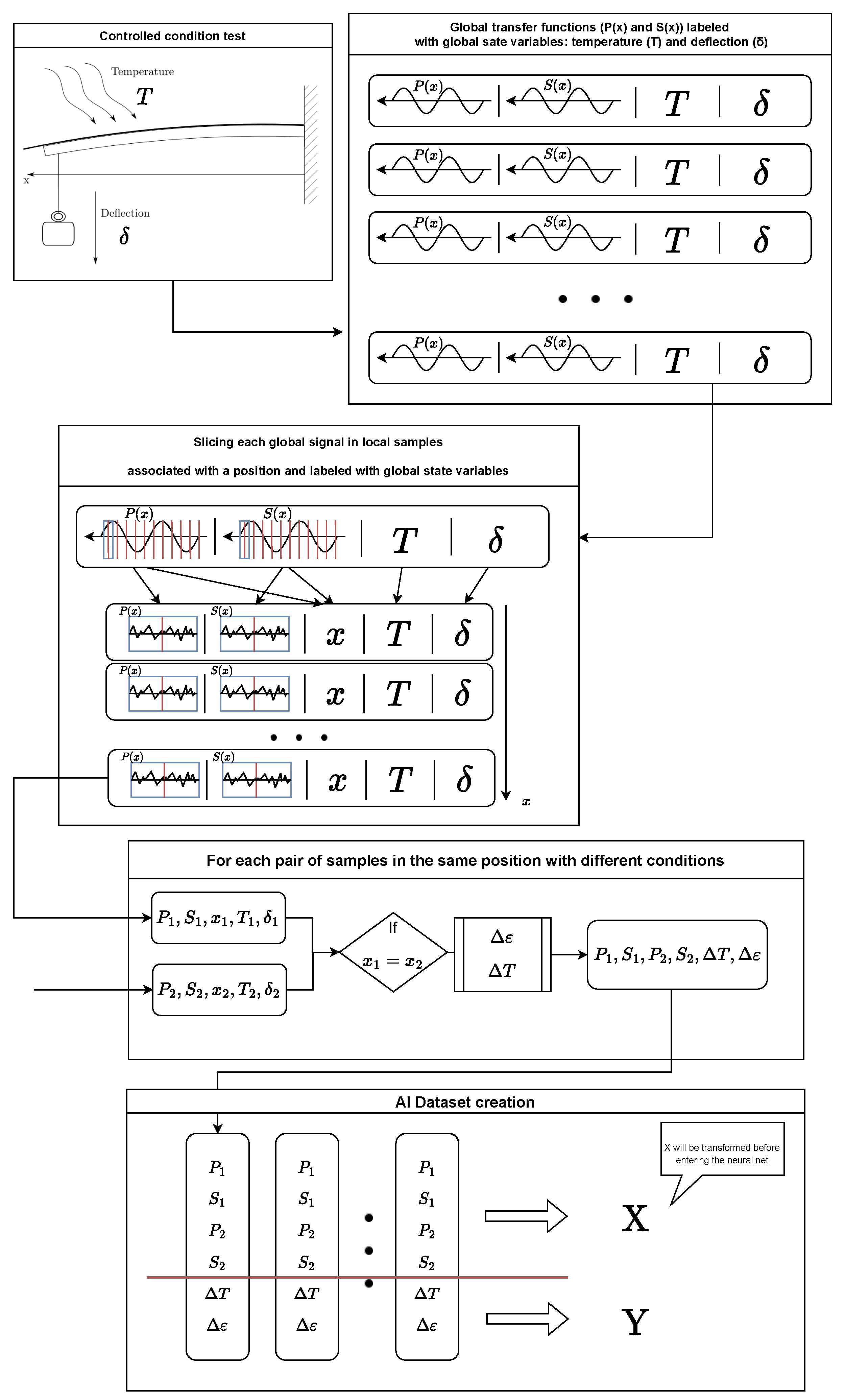
3.1. Dataset

The process carried out to create the dataset is illustrated in Figure 4. The readings obtained from the test under controlled conditions have been labeled with the test conditions themselves. Then each of these signals has been taken and divided into segments that act as a point sensor, i.e. they can be assigned a single temperature and a single strain value. Finally, these segments have been taken two by two and the temperature and strain increment corresponding to the pair has been computed, thus storing the two segment signals (P and S) and the difference of states. As a priori the most suitable pre-treatment of the signals was not known, it was decided to keep both signals (

P_{1}, S_{1}, P_{2}, S_{2}

) in full in order to evaluate the performance of the different transformations.

From the test performed, data have been obtained at four temperatures: 20, 30, 40, and 50 ^oC; and five strain states associated with an end deflection of: 0, 3.11, 6.22, 9.33, and 12.45 mm. These combined states result in 20 different states which, combined two by two, amount up to 190 possible combinations. By means of the optical interrogator used, the optical fiber was converted into a succession of overlapping sensors with a sensor length of 20 mm (with a sampling period of 10

μ

m) and a sensor spacing of 2 mm (see Figure 2). Then, for a fiber length of 300 mm of which only measurements between 100 and 280 mm have been selected (to avoid possible errors). Taking randomly a percentage of the number of combinations, a dataset of 13950 samples has been created by taking, randomly again, a 60 % for training, 20 % for validation and the remaining 20 % for testing.

The temperature range has been determined by the room temperature at the time of the test (since the oven does not have refrigeration) and the characteristics of the adhesive used, cyanoacrylate, to adhere the optical fiber to the aluminum plate.

3.2. Pre-processing

Sometimes, when talking about Artificial Intelligence, it is presented as a tool capable of solving any problem with just the corresponding training time. Nothing could be further from the truth, the proper dataset pre-processing is key not only in the success or failure of the model but also in its accuracy and efficiency [4,8].

In this case, several signal treatment options were considered, but finally the correlation between signals,

X = [P_{1} ★ P_{1}, P_{1} ★ P_{2}, P_{2} ★ P_{2}, S_{1} ★ S_{1}, S_{1} ★ S_{2}, S_{2} ★ S_{2}],

has been chosen. The decision was made using an unsupervised machine learning model aimed at dimensionality reduction for the reasons explained in the next subsection (SubSection 3.3).

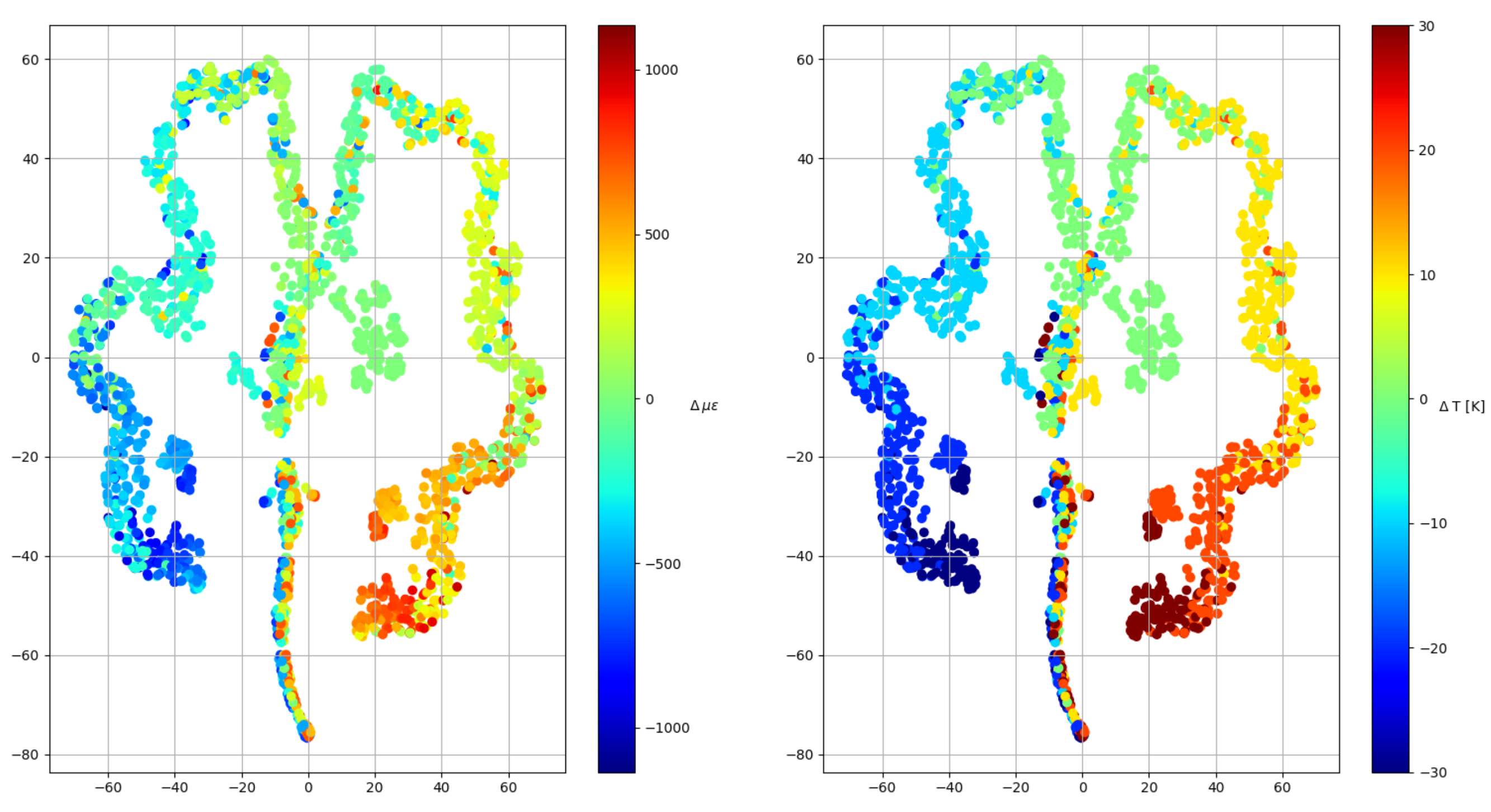
3.3. Clustering

Before starting to apply machine learning models, a clustering algorithm was used to determine if the pre-processed data is capable of being classified into groups that somehow could be related to strain and temperature increments. Note that this is an iterative process where the dataset was exposed to different pre-processing methods, however, only the final results of the clustering algorithm are shown in Figure 5. As can be seen, the algorithm (TSNE) spontaneously generates temperature groups and orders the deformations within them, which means that, although there is some confusion within some groups, an artificial intelligence model is able to differentiate both variables.

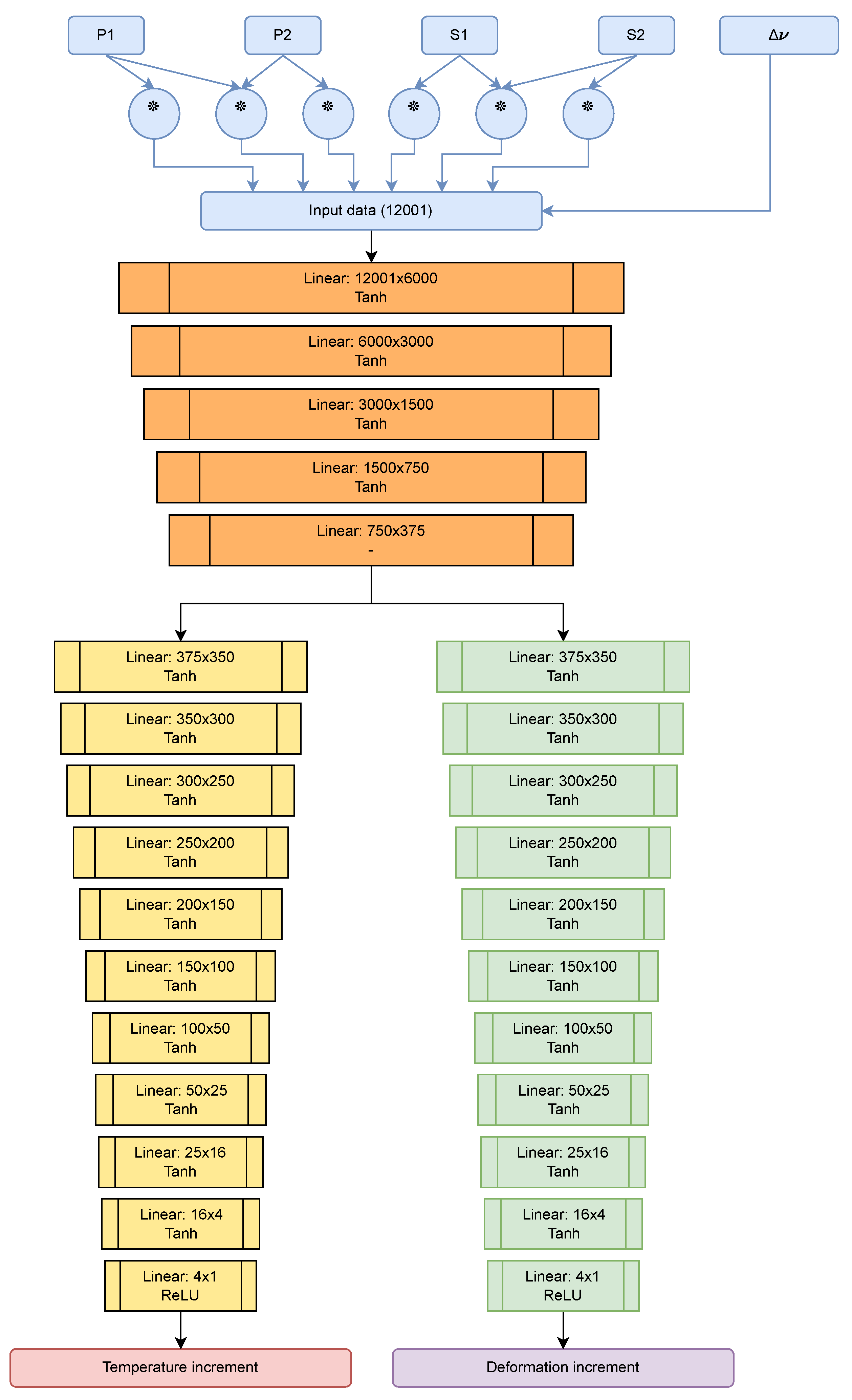
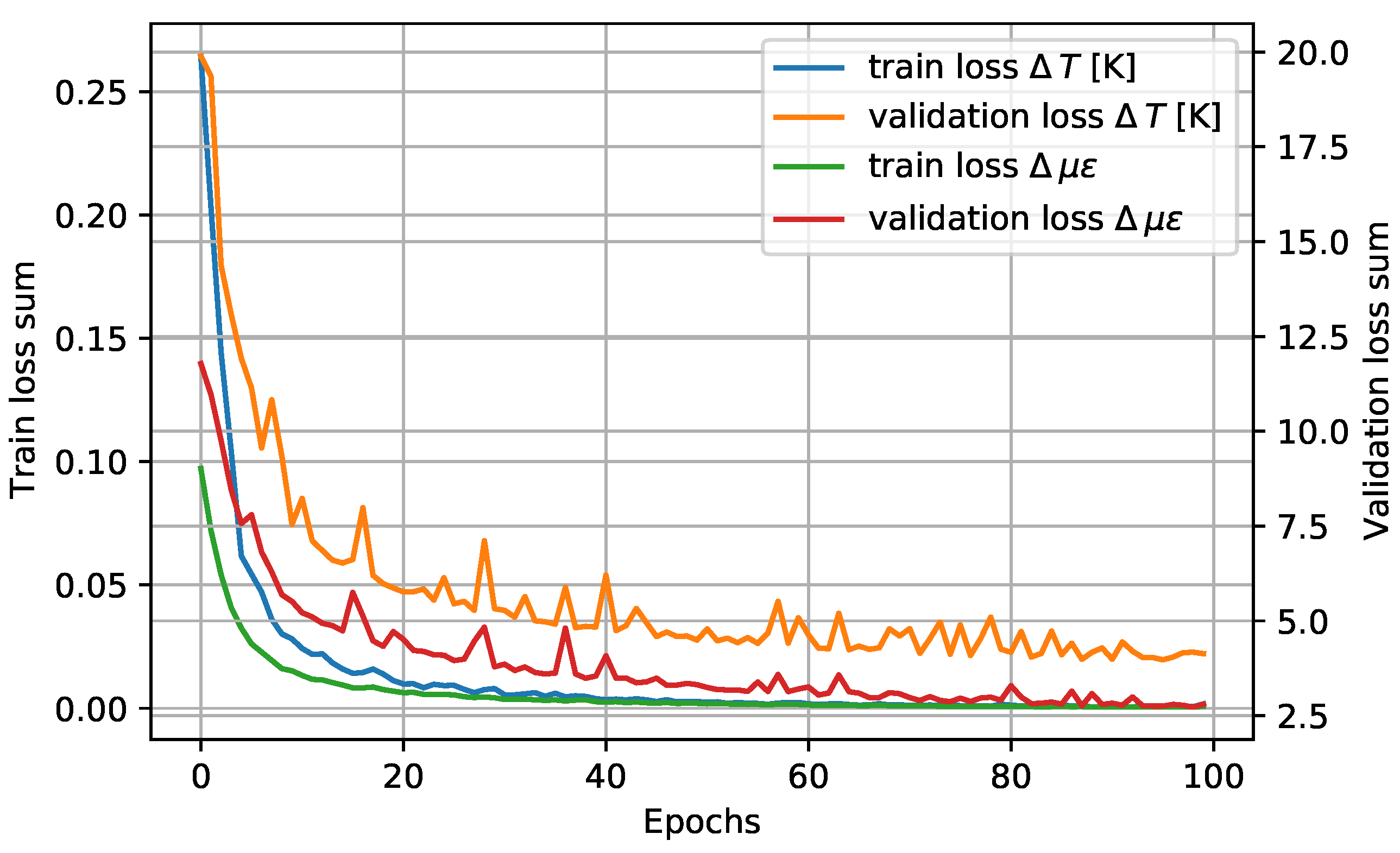
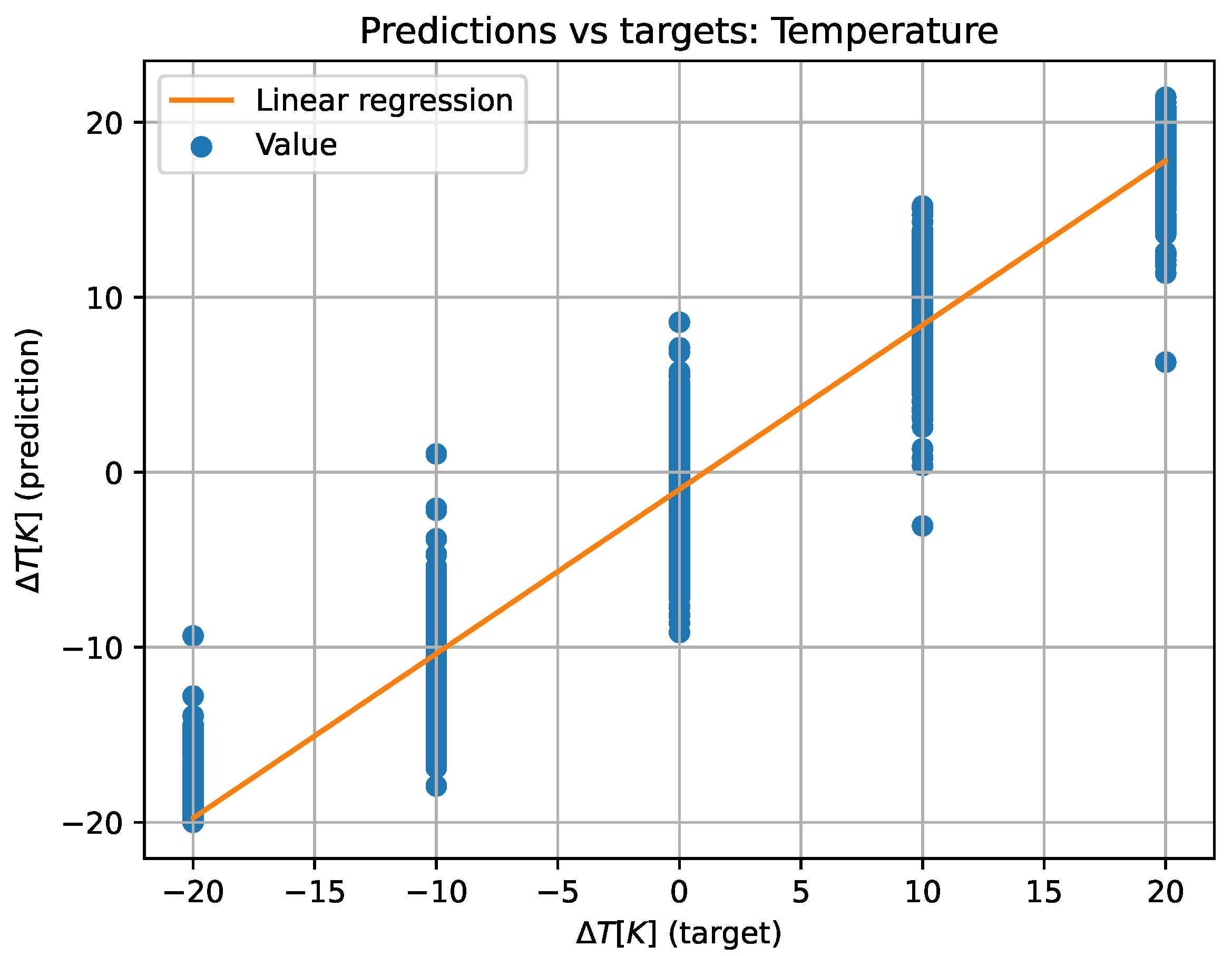
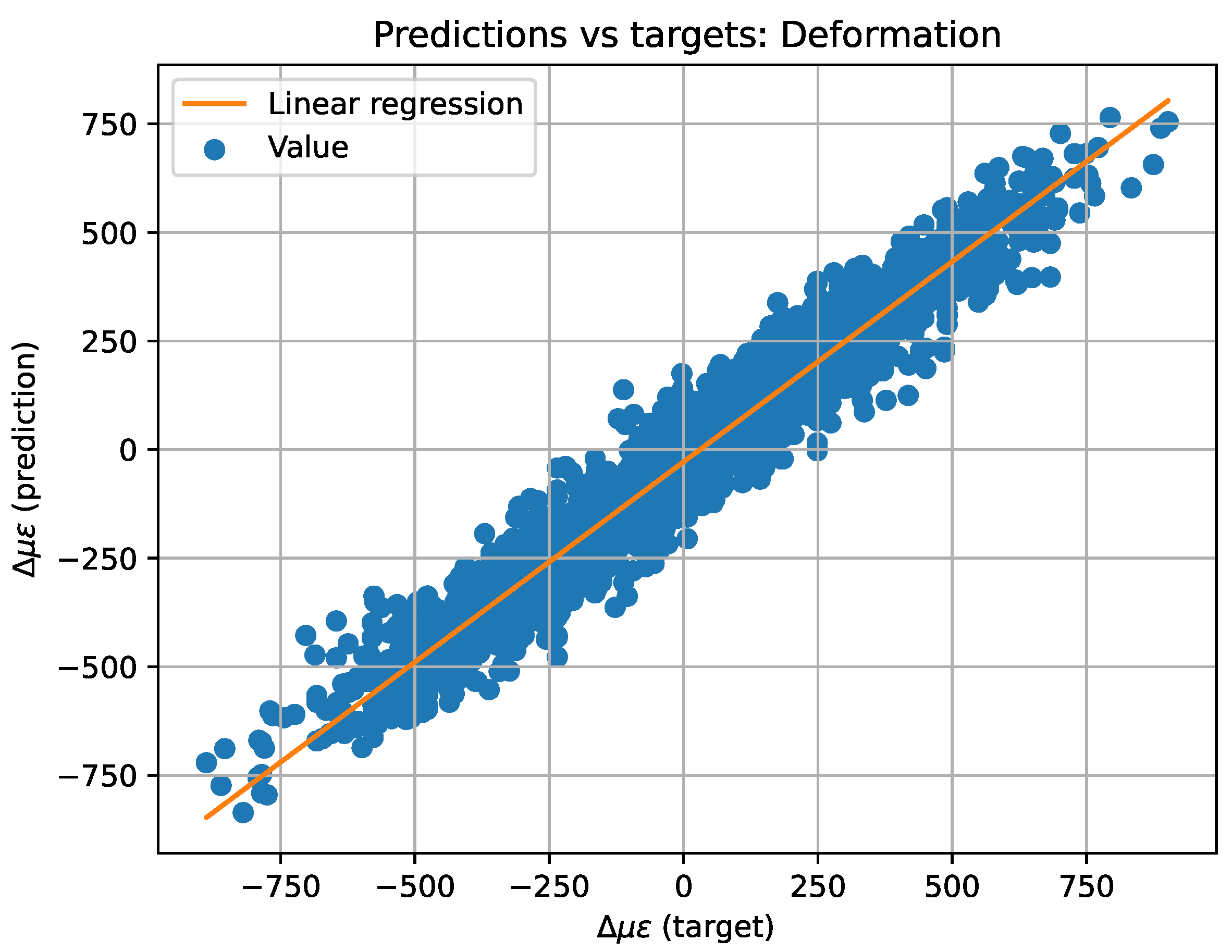
3.4. Neural Network

Input data

Once this check has been carried out, the artificial intelligence model capable of discerning between temperature increase and deformation from the signals of the different polarizations is designed. After trying several options to train the model, an input vector, composed of the cross-correlation of the two polarization states and the four auto-correlations of the four available measurements, is selected due to the clustering algorithm results. The input to the network is finally as follows:

x_{j} = [P_{1} ★ P_{1}, P_{1} ★ P_{2}, P_{2} ★ P_{2}, S_{1} ★ S_{1}, S_{1} ★ S_{2}, S_{2} ★ S_{2}, Δ ν],

where the frequency increment

Δ ν

has been added to provide scaling information (since the same equipment can operate in different frequency ranges).

Normalization

These input vectors have been previously normalized since training is much more efficient with normalized values. In this case, the normalization of each variable separately has been finally selected as it is the only one with which the model has been able to fit the data:

\begin{matrix} X = & (\begin{matrix} x_{1} \\ x_{2} \\ \dots \\ x_{n_{s} - 1} \\ x_{n_{s}} \end{matrix}) \to \begin{matrix} X_{\max i} = \max ({X_{0 i}, \dots, X_{j i}, \dots X_{n_{s} i}}) \\ X_{\min i} = \min ({X_{0 i}, \dots, X_{j i}, \dots X_{n_{s} i}}) \end{matrix} \to \\ \to {\hat{X}}_{j i} = \frac{X_{j i} - X_{\min i}}{X_{\max i} - X_{\min i}}, \end{matrix}

(2)

where index i refers to the column index, that is, to each of the items that make up the vector

x_{j}

; on the other hand, index j refers to the sample number.

Architecture

The network architecture is as shown in Figure 6 and is basically a compendium of densely connected layers with hyperbolic tangent-type activation functions that add to its nonlinearity.

Training

The results of the network training are shown in Figure 7. The training has been carried out with an Adam-type optimizer with a learning rate of

10^{- 6}

, and computing the error with the mean squared error (MSE) criterion.

As can be seen at the 100 training epochs, the behavior is asymptotic, which indicates that the model is not able to fit the data. On the other hand, from the behavior of the validation curves, it can be determined that the model has not undergone overfitting.

Results

Once the model has been trained, it is evaluated with the test data. In Figure 8 and Figure 9 error histograms for the target variables are shown together with an approximation of normal distribution, whose coefficients are shown in Table . In addition, confidence intervals of 99% and 95% have been computed and the limits of these intervals are also shown in Table 3.

For a better comprehension, the predicted versus target values have also been plotted on a plane (see Figure 10 and Figure 11) to create the equivalent of a confusion matrix but with continuous data. If the model worked perfectly, the predicted and target data would be the same, thus plotting a diagonal. For this reason, a least squares regression line has been plotted over the plane. The regression line has the form

y = m x + n

where x represents the target value and y the predicted one, m the slope of the straight line and n the ordinate at the origin. Additionally, the value of

r^{2}

has also been computed to determine the dispersion of the values. All of the above values can be also found in Table 3.

Explainable Artificial Intelligence (XAI)

Explainable Artificial Intelligence (XAI) consists of a series of methods aimed at converting the results provided by an Artificial Intelligence (AI) in a way that can be understood by humans. It contrasts with the ”black box” concept of machine learning, where even its designers cannot explain why an AI arrived at a particular decision. Thanks to XAI methods, features can be extracted that allow existing knowledge to be confirmed, existing knowledge to be questioned, and new hypotheses to be generated.

In this case, the XAI allows explaining how the developed model interprets the correlations of the signals to reveal the information on which the actions are based. To implement the XAI methods on this model, the Lime-For-Time repository (see [11]) has been used, in which the LIME library ([1]) is used to analyze time series.

The analysis consists of taking an example signal and dividing it into segments, which in this case have been 120, given the composition of the signal. Next, the neural network is studied as a classifier in which each segment constitutes a class and which contributes, to a greater or lesser extent, to the final decision. From the example signal, multiple variations of the parameters are made to interpret how the model behaves to the different inputs. From these data, the relevance of each of the segments can be determined. Taking the 12 most relevant segments and displaying their weights in a histogram, the images shown in Figure 12 and Figure 13 are produced.

If these segments are displayed over the signal, it can be seen which regions are the most relevant. In this case, to represent the importance, an opacity has been assigned according to the weights previously shown in the histograms. The result of this graphical representation is the one shown in Figure 14 and Figure 15.

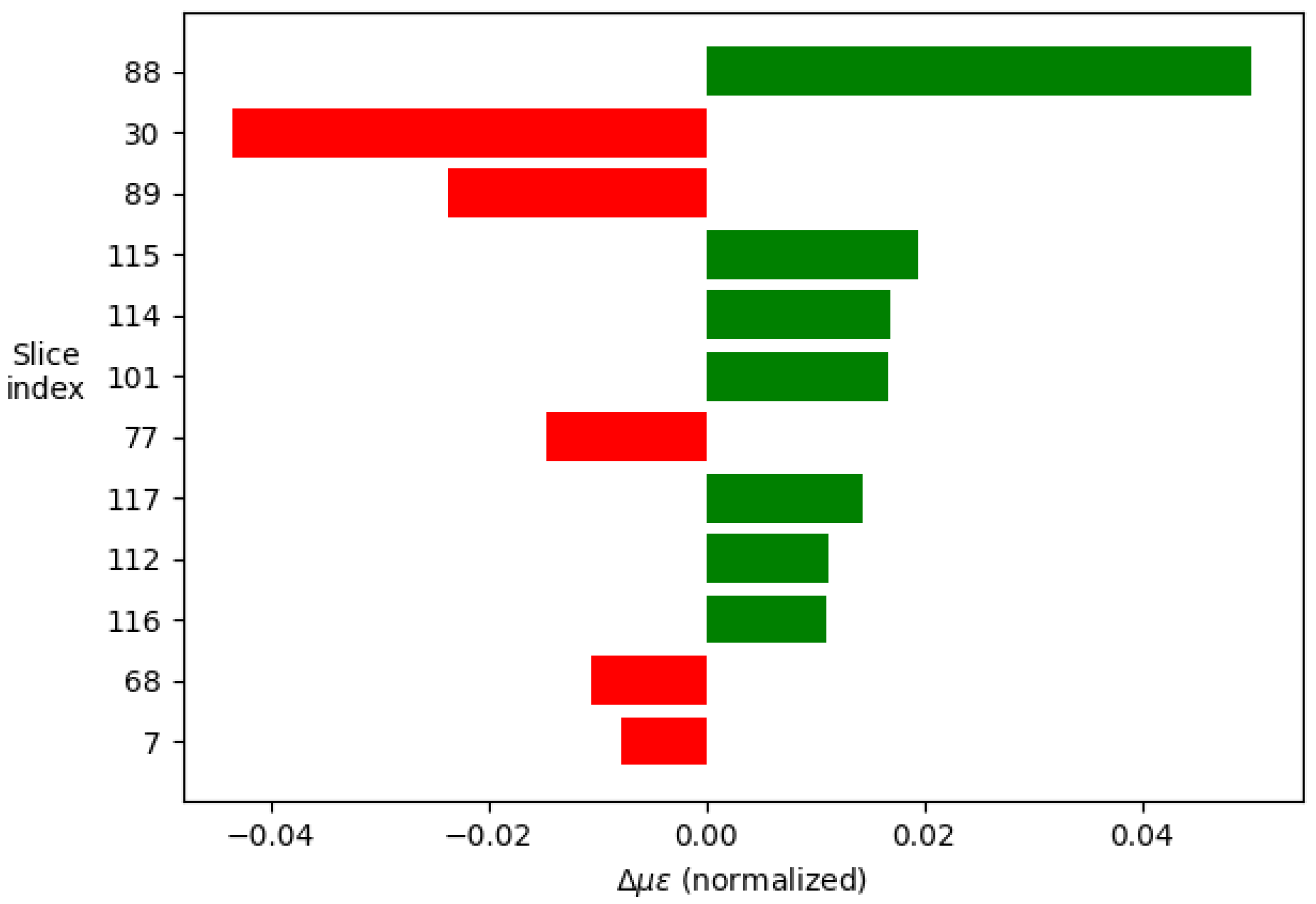
4. Discussion

From the results shown in the previous section (Section 3.4), it can be said that an Artificial Intelligence capable of distinguishing between strain and temperature readings has been trained successfully and so, the readout of the

ϕ

-PA-OFDR contains enough information to obtain the measure of the two magnitudes (strain and temperature) even when an SMF is used for sensing.

The results show how the artificial intelligence recognizes the spectral shift by comparing the values of segments 88, 30, and 89; which correspond to the central area of the cross-correlations between the two compared signals. On the other hand, studying the rest of the values is interesting as this is where the ability to discern between thermal and mechanical effects lies.

Comparing the two images in Figure 14 and Figure 15 it can be seen how, to determine the temperature, the model takes two symmetrical regions of the autocorrelation of the polarization state P of the first signal and similar regions of the autocorrelation of the polarization state S of the second one. Besides that, to determine the deformations, it is observed that the last values of the autocorrelation of the polarization state S of the second signal are interpreted by some kind of integral.

Additionally, the temperature-related decision seems to focus more on the behavior of the peak of the autocorrelation of the P polarization state of the second signal whereas the deformations focus on the peak of the autocorrelation of the S polarization state of the first one.

This information allows us to determine that the autocorrelation of the signals does provide additional information that can be key in determining unequivocally at what temperature and state of deformation the optical fiber is.

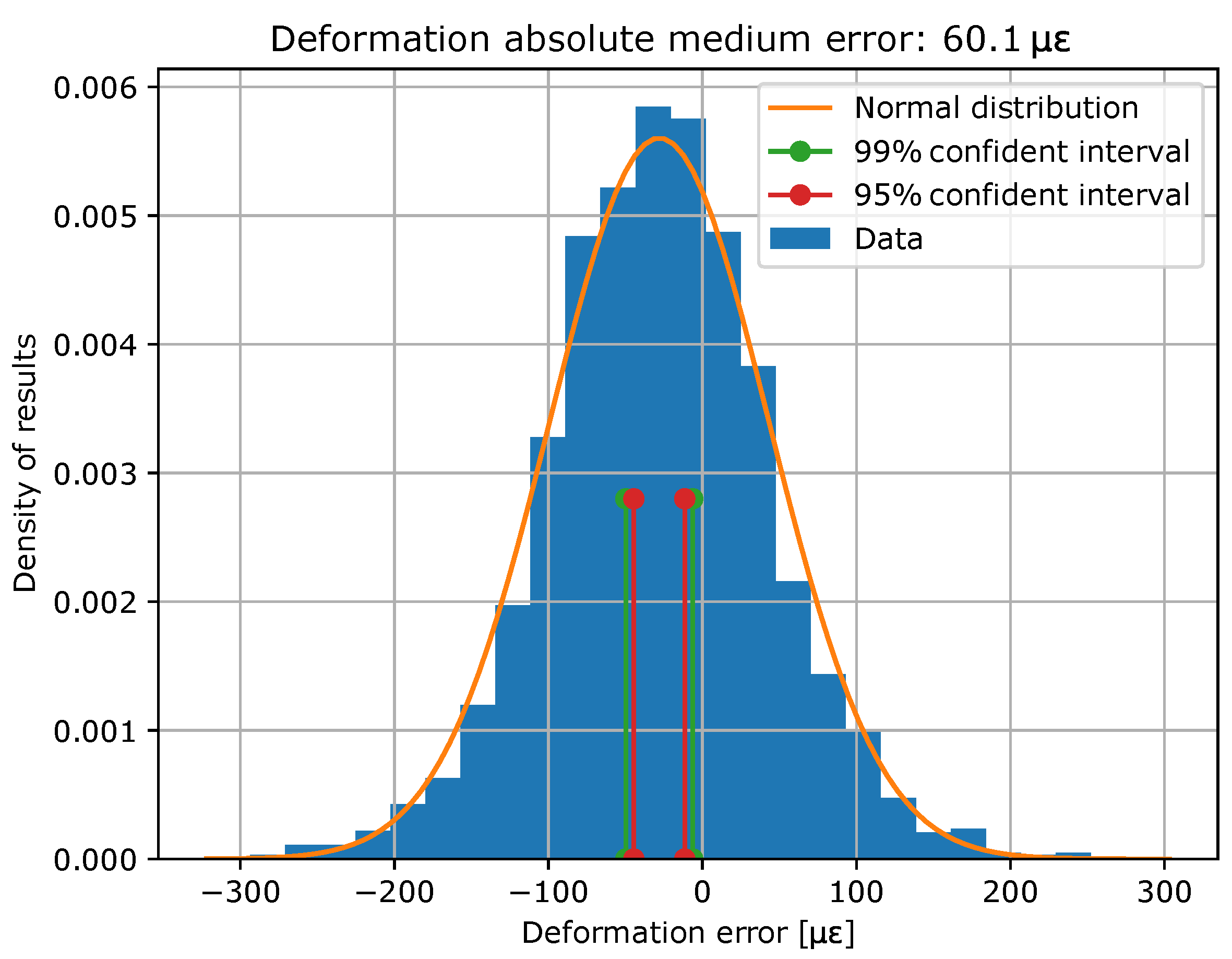
5. Conclusions

From these results, the following conclusions can be drawn:

Readouts provided by a $ϕ$ -PA-OFDR (as OBR-4800 is) contains are capable of providing more information than what nowadays is used.
Artificial Intelligence methods are suitable for analyzing DOFS data in order to decouple temperature and strain phenomena.
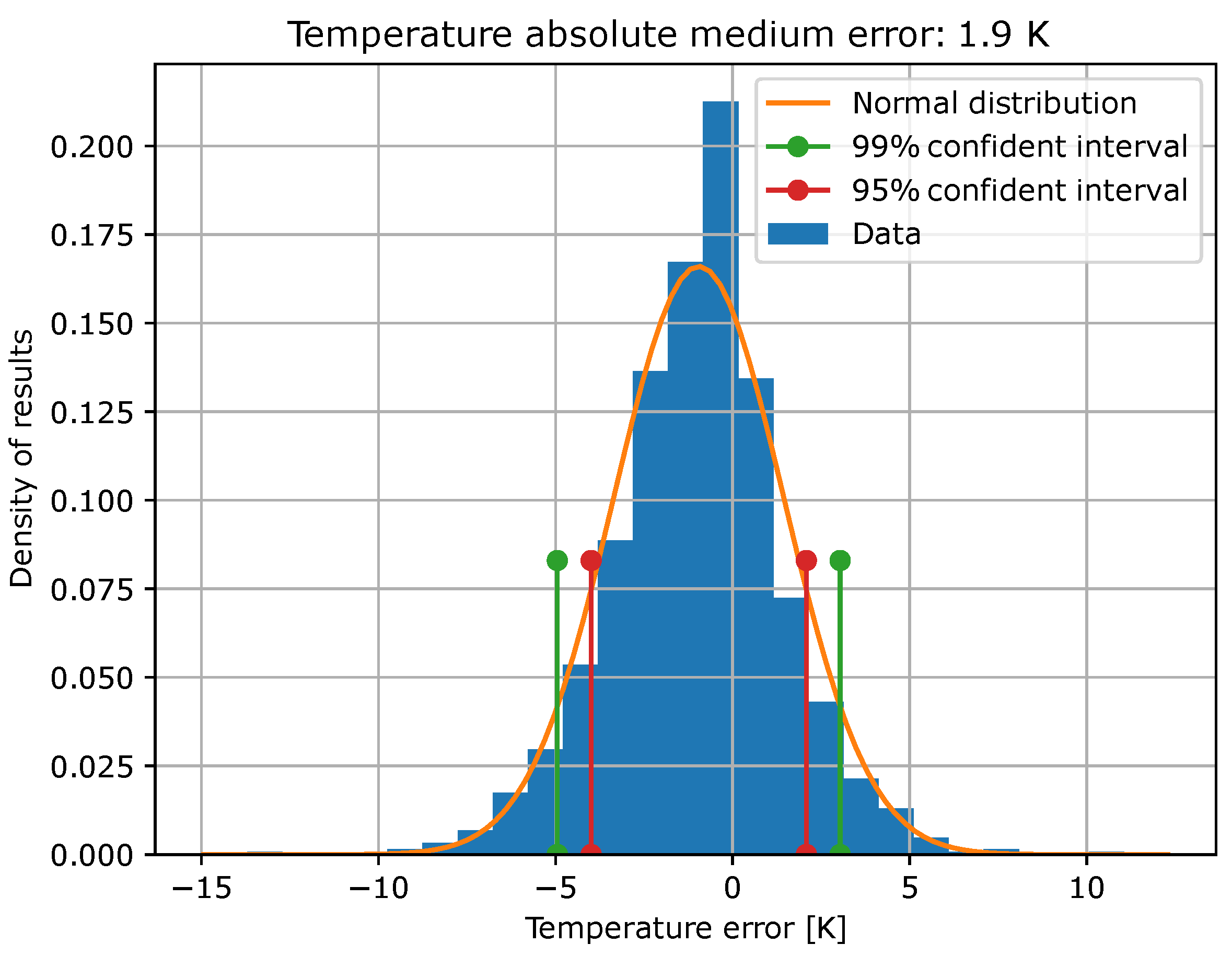
More specifically, the Neural Network model designed and trained for this purpose in the present work has reached the precision and accuracy shown in Table 4.
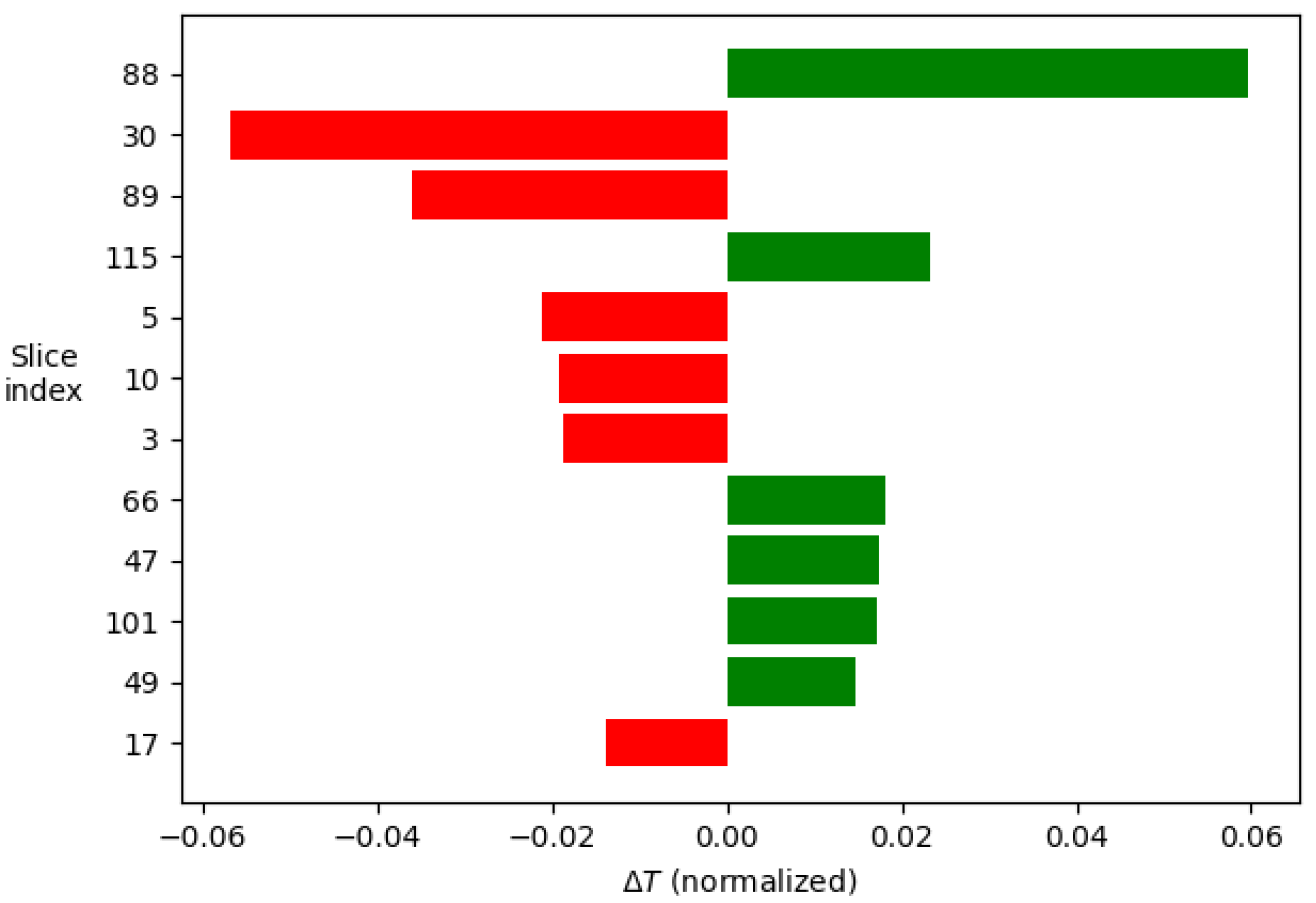
In addition, explainable AI offers a deeper analysis of the AI model, which can be used to chart the course for future research.

Acknowledgments

This project has received funding from the national research program Retos de la Sociedad under the Project STARGATE: Desarrollo de un sistema de monitorización estructural basado en un microinterrogador y redes neuronales (reference PID2019-105293RB-C21).

References

Guestrin, C.; Ribeiro, M.T.; Singh, S. "Why Should I Trust You?": Explaining the Predictions of Any Classifier Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 2016.
Schenato, L. A Review of Distributed Fibre Optic Sensors for Geo-Hydrological Applications Applied Sciences 2017.
Lasn, K.; Wang, S. Accurate non-linear calculation model for decoupling thermal and mechanical loading effects in the OBR measurements Optics Express 2021.
An Introduction to Preprocessing Data for Machine Learning. Available online: https://towardsdatascience.com/an-introduction-to-preprocessing-data-for-machine-learning-8325427f07ab.
Chen, L.; Li, W.; Bao, X. Compensation of temperature and strain coefficients due to local birefringence using optical frequency domain reflectometry Optics Communications 2013.
Cross-spectral analysis. Available online: https://nbviewer.org/github/mattijn/pynotebook/blob/master/2016/2016-05-25%20cross-spectral%20analysis.ipynb (accessed on 15/02/2023).
Cross-spectrum. Available online: https://en.wikipedia.org/wiki/Cross-spectrum (accessed on 15/02/2023).
Data Preprocessing in Machine learning. Available online: https://www.javatpoint.com/data-preprocessing-machine-learning.
Palmieri, L.; Schenato, L. Distributed Optical Fiber Sensing Based on Rayleigh Scattering The Open Optics Journal 2013.
Soller, B.J.; Gifford, D.K.; Froggatt, M.E.; Wolfe, M.S.; Kreger, S.T. Distributed Strain and Temperature Discrimination in Unaltered Polarization Maintaining Fiber Optical Fiber Sensors - OSA Technical Digest 2006.
emanuel-metzenthin/Lime-For-Time: Application of the LIME algorithm by Marco Tulio Ribeiro, Sameer Singh, Carlos Guestrin to the domain of time series classification. Available online: https://github.com/emanuel-metzenthin/Lime-For-Time (accessed on 15/02/2023).
Soller, B.J.; Gifford, D.K.; Froggatt, M.E.; Wolfe, M.S. High resolution optical frequency domain reflectometry for characterization of components and assemblies Optics Express 2005.
Moore, J.; Froggatt, M.E. High-spatial-resolution distributed strain measurement in optical fiber with Rayleigh scatter OSA - Applied Optics 1998.
How Much Training Data is Required for Machine Learning?. Available online: https://machinelearningmastery.com/much-training-data-required-machine-learning/ (accessed on 15/02/2023).
How to use the cross-spectral density to calculate the phase shift of two related signals. Available online: https://stackoverflow.com/questions/21647120/how-to-use-the-cross-spectral-density-to-calculate-the-phase-shift-of-two-relate (accessed on 15/02/2023).
Bellone, A.. Optical fibre sensors for distributed temperature monitoring during mini-invasive tumour treatments with laser ablation, Politecnico di Torino, 2020.
Muga, N.J.. Polarization Effects in Fiber-Optic Communication Systems, Universidade de Aveiro, 2011.
Venketeswaran, A.; Chorpening, B.; Wuenschell, J.; Chen, K.P.; Buric, M.; Badar, M.; Lalam, N.; Jr., P.R.O.; Lu, P.; Duan, Y. Recent Advances in Machine Learning for Fiber Optic Sensor Applications Advanced Intelligent Systems 2021.
Chen, L.; Bao, X. Recent Progress in Distributed Fiber Optic Sensors Sensors 2012.
Sample Size in Machine Learning and Artificial Intelligence. Available online: https://sites.uab.edu/periop-datascience/2021/06/28/sample-size-in-machine-learning-and-artificial-intelligence/ (accessed on 15/02/2023).
Luo, B.; He, H.; Shao, L.; Yan, L.; Pan, W.; Zhang, Z.; Li, Z. Self-Mixing Demodulation for Coherent Phase-Sensitive OTDR System Sensors 2016.
Eyal, A.; Shiloh, L. Sinusoidal frequency scan OFDR with fast processing algorithm for distributed acoustic sensing Optics Express 2017.
Güemes, A.; López, A.F.; Pérez, J.S.; Pozo, Á.R. Structural Health Monitoring for Advanced Composite Structures: A Review Journal of Composites Science 2020.
Ferdinand, P. The Evolution of Optical Fiber Sensors Technologies During the 35 Last Years and Their Applications in Structure Health Monitoring. In Proceedings of the European Workshop on Structural Health Monitoring.
SMF-28e+ by Corning: Corning SMF-28e+ Optical Fiber. Available online: https://www.corning.com/optical-communications/worldwide/en/home/products/fiber/optical-fiber-products/smf-28e-.html.
OBR-4600 by LUNA: Optical Frequency Domain Reflectometer. Available online: https://lunainc.com/product/obr-4600.
OBR-4600 by LUNA: Optical Frequency Domain Reflectometer (User Guide). Available online: https://lunainc.com/sites/default/files/assets/files/resource-library/OBR-4600-UG6_SW3.10.1.pdf.
Numpy. Available online: https://numpy.org/.
Scipy. Available online: https://scipy.org/.
SMF-28e+ by Corning: Corning SMF-28e+ 9/125/250µm OS2 Single Mode Fiber with NexCor Technology (G.652). Available online: https://www.fiberoptics4sale.com/products/smf-28e.
Polarization-Maintaining Single Mode Optical Fiber. Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=1596.
Sklearn. Available online: github.com/scikit-learn/scikit-learn.

Figure 1. Different existing core shapes for optical fiber.

Figure 2. Test configuration: aluminium plate (E = 70.3 GPa,

α

=24

μ

m/(m·K) ) with dimensions 300x30x2 mm. Up to four 50 g weights have been added at the end (since the weight is maintained with temperature).

Figure 2. Test configuration: aluminium plate (E = 70.3 GPa,

α

=24

μ

m/(m·K) ) with dimensions 300x30x2 mm. Up to four 50 g weights have been added at the end (since the weight is maintained with temperature).

Figure 3. Measurement network for a PA-OFDR. TLS = Tunable Laser Source, ADC = Analog to Digital Converter, PC = Polarization Controller, PBS = Polarization Beam Splitter,

τ_{t r}

= differential time delay of the two paths in the trigger interferometer. See [12] for further information.

Figure 3. Measurement network for a PA-OFDR. TLS = Tunable Laser Source, ADC = Analog to Digital Converter, PC = Polarization Controller, PBS = Polarization Beam Splitter,

τ_{t r}

= differential time delay of the two paths in the trigger interferometer. See [12] for further information.

Figure 4. Process carried out to obtain the dataset with which the model has been trained.

Figure 5. Clustering algorithm results.

Figure 6. Diagram of the neural network used. In the upper part, in blue, the pre-processing of the signal prior to the neural network is shown; the operation marked with the * denotes correlation between two input signals.

Figure 7. Training and validation of the network for both target variables.

Figure 8. Histogram of temperature errors and their normal distributions, as well as its confidence interval limits.

Figure 9. Histogram of strain errors and their normal distributions, as well as its confidence interval limits.

Figure 10. 2D representation of predicted versus target values and linear regression for temperature data.

Figure 11. 2D representation of predicted versus target values and linear regression for strain data.

Figure 12. Weight in the final decision of each of the segments in order of importance for the temperature decision.

Figure 13. Weight in the final decision of each of the segments in order of importance for the strain decision.

Figure 14. Most relevant regions of the signal for each of the model predictions, above for the temperature prediction.

Figure 15. Most relevant regions of the signal for each of the model predictions for the strain prediction.

Table 1. A summary of the strain/temperature discrimination methods using DOFS configurations (see [5] for more information, note that the last method’s configuration is not properly described there).

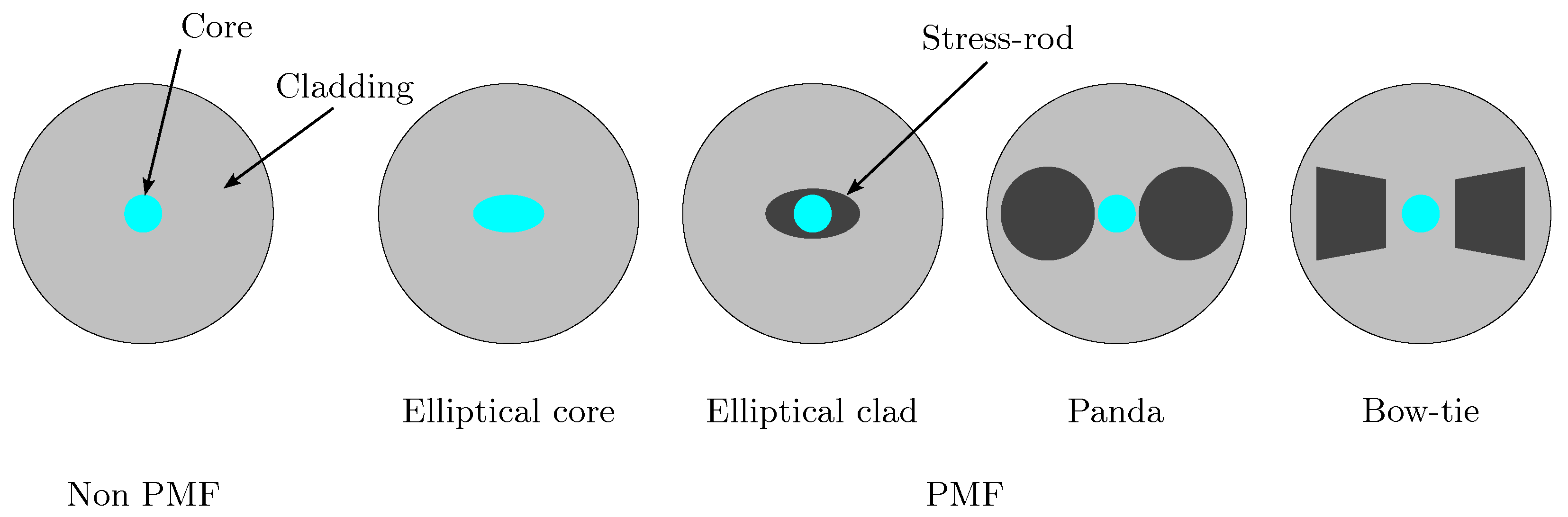
Method	Configuration
Brillouin	Brillouin frequency shift Brillouin amplitude effects with LEAF fiber
Brillouin and Raman hybrid	Raman-Brillouin gains
Photonic crystal fiber (PCF)	Brillouin
FBG	Dual wavelength
FBG on PMF	Polarization Maintaining Fiber analysis
OFDR	PMF, Rayleigh scattering, autocorrelation function

Table 2. Resources used.

Resource	Supplier	Model	Reference
Single Mode Fiber	Corning	SMF-28e+	[25]
Optical Frequency Domain Reflectometer	LUNA	OBR-4600	[26,27]

Table 3. Deep Learning AI model error metrics.

Table 4. Deep Learning AI model error metrics.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer