Aircraft Failures Prediction via Adaptive Neuro-Fuzzy Inference System

Preprint

Article

Aircraft Failures Prediction via Adaptive Neuro-Fuzzy Inference System

Altmetrics

Downloads

141

Views

Comments

This version is not peer-reviewed

Submitted:

04 May 2023

Posted:

05 May 2023

You are already at the latest version

Alerts

Abstract

Safety is very important in aviation since a loss of safety frequently results in both fatalities and financially damaging situations that are typically unrecoverable. Thus, achieving safety as much as possible is the primary goal of practically all aviation technology work. In this study, an Adaptive Neuro-Fuzzy Inference System (ANFIS)-based classifier is created to estimate the fault risk factor of airplanes. Five categories of real fleet data belonging to structure, electrical, avionic, motor systems, and incident statistics of the planes have been used for classifier development. A risk factor determination for each plane is the output of the developed intelligent classifier, and it can be used to identify general overhaul candidate planes and stop defects and crashes before they happen. The obtained results show that using ANFIS provides a great capability in processing many inputs and outputs depending on different types and classes in the aviation industry and thus predicting the failure risk of the airplane efficiently.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

As is well-known, the aviation industry, which is very competitive, wide-reaching, and enlarging over the globe, plays a key role in the inflating economy (Belobaba et al., 2015). As a substantial economic might through its wide range and pushing impacts in all aspects on almost all branches of industries, aviation technology extensively contributes to the growing global economy. Several factors, such as safety, reliability, convenience, cost, distance proximity, time, etc., impose aviation to always keep on enhancing further. Here, the cost is one of the foremost driving ingredients which propel all the associated stakeholders to manage cost-effectively. For a more efficient industry in all facets, one should first note that the main characteristic of the aviation industry is to use high and innovative technologies which are predominantly based on information and data analysis. However, dealing with the existing data is not such an easy task: more precisely, due to the existence of a great diversity of alternatives and discordant effects and parameters, experts generally encounter the obstacle pertaining to decision-making in processing the data associated with humans, technical or environmental factors. Specifically, for the sake of safety, which is the other foremost ingredient in aviation, these hindrances inevitably require to be overcome and resolved satisfactorily. Hence, utilizing distinct decision-making approaches is essential to guide experts for better resolution of all kinds of troubles encountered in aviation. Of course, such approaches are supposed to supply key succors to experts as they cope with all the decision-making problems commonly emerging throughout the aviation industry. Those approaches should assist the experts to compile, process, and generate data from different sources such that it will bring an adequate level of assurance in making decisions by processing all the presence parameters properly. For example, as one of the foremost decision-making methods which are broadly used to assemble and integrate data properly by considering the presence of multiple factors in the system, the Multi-Criteria Decision Making (MCDM) methods are commonly used to predict and analyze the failures in aircraft systems (Belton & Stewart, 2002; Dožić, 2019). As another leading artificial intelligence decision-making method, the Big Data Method is also extensively utilized in aviation as in the various branches of science. The Big Data Method coherently works with countless amounts of exponentially growing information to determine the appropriateness of the parameters and variables of data associated with given configurations (Esposito et al., 2015; Kolaitis, 2005; Kasturi et al., 2016). Alternatively, since most accidents in aviation are mainly due to the lack of right-decision-making judgment, together with analytical skills, Naturalistic Decision Making (NDM) is also broadly used in aviation to enhance the abilities of the aircrew and maintenance expeexpertsson to avoid systematic failures, accidents and thus increase the system performance. NDM is an internal experiential decision-making technique that expresses how an expert person makes decisions in dynamic and risky conditions within a limited time during challenging goals and complex processes. These behavioral reflexes are experienced in all processes of aviation (Zsambok & Klein, 2014; Simpson, 2001; Orasanu, 1995). For more details on decision-making methods, see (Harris, 2017).

As was mentioned above, safety is specifically vital in aviation since the loss of safety often ends up with both losses of lives and economical damages which generally cannot be compensated. Thus, the premier task of almost all the work in aviation technology is to achieve safety as much as possible. The attempt to boost safety is gaining new inferences and facets day after day in all branches of aviation since it is a dynamic industry depending on various effects. Generally, safety management is to analyze the system and identify the failures which adversely affect the aerial vehicles to eliminate the existing failures by taking the essential and required precautions. Here, the challenge is how to optimally describe and alleviate the interdependent succession of incidents associated with human, technical, and environmental factors to promote safety to the furthest extent. All these necessities in aviation require new ways of processing information and data to enable enhanced decision-making, insight discovery, and process optimization to deal with failures in all aspects.

The challenge in aviation is that the system principally consists of many inputs and outputs depending on the massive variety of parameters. As a result of the fact that the aviation industry is managed with an information-intensive management method where the decision-making procedure is based on information analysis, this dynamic information should be analyzed frequently aiming to guarantee that the aircraft fleet is managed, particularly in the safety and cost-effective perspectives.

When we look at the maintenance, sustainment, and operation methods currently carried out in the institutions operating in the aviation sector, the problems that affect the full capacity of the system, such as malfunctions in aircraft systems, inadequacies caused by fatigue resulting from wear, and performance errors, are determined by diagnostic monitoring methods. The decision-making procedure considering the collected data by the mentioned diagnostic methods is mostly based on the experience and knowledge of managers and technicians. With the further development of data processing techniques, predictive maintenance has come to the fore, and artificial intelligence is used to detect the factors that cause malfunctions in the early period and provide the detection and elimination of wear and fatigue before the occurrence. These techniques supply a more sensitive analysis. By using intelligent methods, it has been concluded that the control and monitoring of fault formation processes can be carried out with a higher capacity instead of humans. For example, wear in bearings used in engine systems can only be detected by the conventional method by the analysis of metal chips accumulated in engine oil. This detection process can sometimes be too late. Because the metal shavings accumulate very quickly and clogging the oil filters can cause possible accidents and crashes. However, it is considered that accidents and crashes can be prevented before occurring, by recording the wear life of the metal elements used in the engine bearings with the assistance of artificial intelligence techniques and ensuring that the metal elements are replaced at the end of a certain flight hour before the chip formation. In this study, an artificial intelligence-based classifier using an Adaptive Neuro-Fuzzy Inference System (ANFIS) is developed to predict the fault risk factor of airplanes. For this purpose, five categories of data have been used. These data categories are the structure, electrical, avionic, motor systems, and incident statistics of the planes. The mentioned dataset has been collected for the Turkish Aeronautical Association Cessna 172 fleet which are flying since 2010. The special and valuable side of this study is that all the data included in the analysis and classification model development are real data collected under the supervision of the Directorate General of Civil Aviation of Turkey. The output of the developed intelligent classifier is a risk factor determination for each plane that can be used for identifying general overhaul candidate planes and preventing faults and crashes before occurring. The outcome of this research results in the standardization of the knowledge extraction from raw data. Such a standardization improves the user’s fast and right decision-making ability. Also, it supplies the same decisions made by different stakeholders that prevent individual interpretation effects. The overall benefit of the developed algorithm will be increasing the safety and reliability level of the aviation systems by standardization of information, personnel data management, air vehicles operation safety, and aviation of the theatre.

The layout of the paper is as follows: In Section 2, the data collection procedure and weights calculation process are explained. Also, the ANFIS classifier details and its theory are briefly described. In Section 3, the model development steps, and their results are evaluated and discussed. In Section 4, the conclusion and innovative sides of the research are presented.

2. Method

2.1. Database Generation

All flights operated by our aircraft fleet since 2010 have been recorded in the Maintenance Data Collection System (MDCS) used by authorized and professional teams according to NDM and analytical abilities after each flight sorties (Zsambok & Klein, 2014; Simpson, 2001; Orasanu, 1995).

In the classification of aircraft systems, the main systems and the subsystems that make up these systems are defined in aircraft maintenance manuals. Failures in these sub-system units are obtained as a result of dynamic flight activities and a database is generated accordingly.

By monthly and annual analysis, the classified flight and maintenance failure record information collected in MDCS, failures, and incompatibilities occurring in aircraft systems are examined, and appropriately necessary corrective measures are taken so that aircraft can fly safely.

These data recorded in MDCS have been analyzed and classified at an academic level to be used in this study. This work is aimed at planning maintenance and troubleshooting activities of Cessna 172 aircraft operating within the body of THK Flight Academy in an optimum way via the preventive maintenance method to detect malfunctions and incompatibilities that may occur in the aircraft and to take necessary corrective measures. In addition, we also aim to contribute to the aviation literature by presenting the results in this paper.

2.2. Weight Calculation

The method which is used to determine the failure weights is as follows: Using a realistic data set of flight activities of our Cessna 172 fleet with 18 airplanes collected over the years, anomalies and dangers caused by the failures that have emerged in the aircraft systems are elaborately examined. Accordingly, the adverse effects of these failures on the system performances are classified as 1st degree, 2nd degree, and 3^rd according to the level of risk factors that each failure creates on the aircraft determined by experts’ knowledge at the Turkish Aeronautical Association.:

1^st-degree failures (Weight 1 (w1)): these are the low-level failures that do not seriously affect the performance of the belonging systems

2^nd-degree failures (Weight 2 (w2)): These are middle-level failures that have manifest negative effects on the performance of the existing system but do not cause any fatal accidents.

3^rd-degree failures (Weight 3 (w3)): these mainly occur in the engine and flight control system and generally cause the loss of the total power of the aircraft and fatal accidents.

In this work, we study the aircraft system in five main categories. By calculating the ratio of the failures occurring in the units belonging to the subsystems that make up the systems of these five main categories, to the system to which they belong, and the ratio to the total aircraft system. In doing so, the assigned weights which give the effect of any individual category within the total aircraft systems have been computed as follows: The Avionics System weight is 0.12, the Electrical System weight is 0.07, the Structural System weight is 0.23 and the Motor System weight is 0.57 and the Incidents weight is 0.01. Note that the total of the weights is 1 as expected.

F R_{s u b_{i j}} = \frac{f_{i j}}{\sum f_{i j}},

(1)

where indices

i

and

j

denote subsystem and category, respectively;

f_{i j}

represents a particular failure and

\sum f_{i j}

denotes the total failures of

i^{t h}

subsystem belonging to

j^{t h}

category;

F R_{s u b_{i j}}

is the ratio of the subsystem failure. The weighted amount of failures for each subsystem (

{WS}_{i j}

) is defined as

{WS}_{i j} = f_{i j} \times w_{i j}

(2)

where

w_{i j}

is the individual weight of

i j

subsystem. Furthermore, the weighted failure rate (

{WSR}_{i j}

) is defined as follows

{WSR}_{i j} = \frac{{WS}_{i j}}{\sum {WS}_{i j}} .

(3)

Finally, the assigned weight (

{AW}_{j}

) is computed as follows:

{AW}_{j} = \frac{{WSR}_{i j}}{\sum {WSR}_{i j}} .

(4)

2.3. Adaptive-Neuro Fuzzy Inference System (ANFIS)

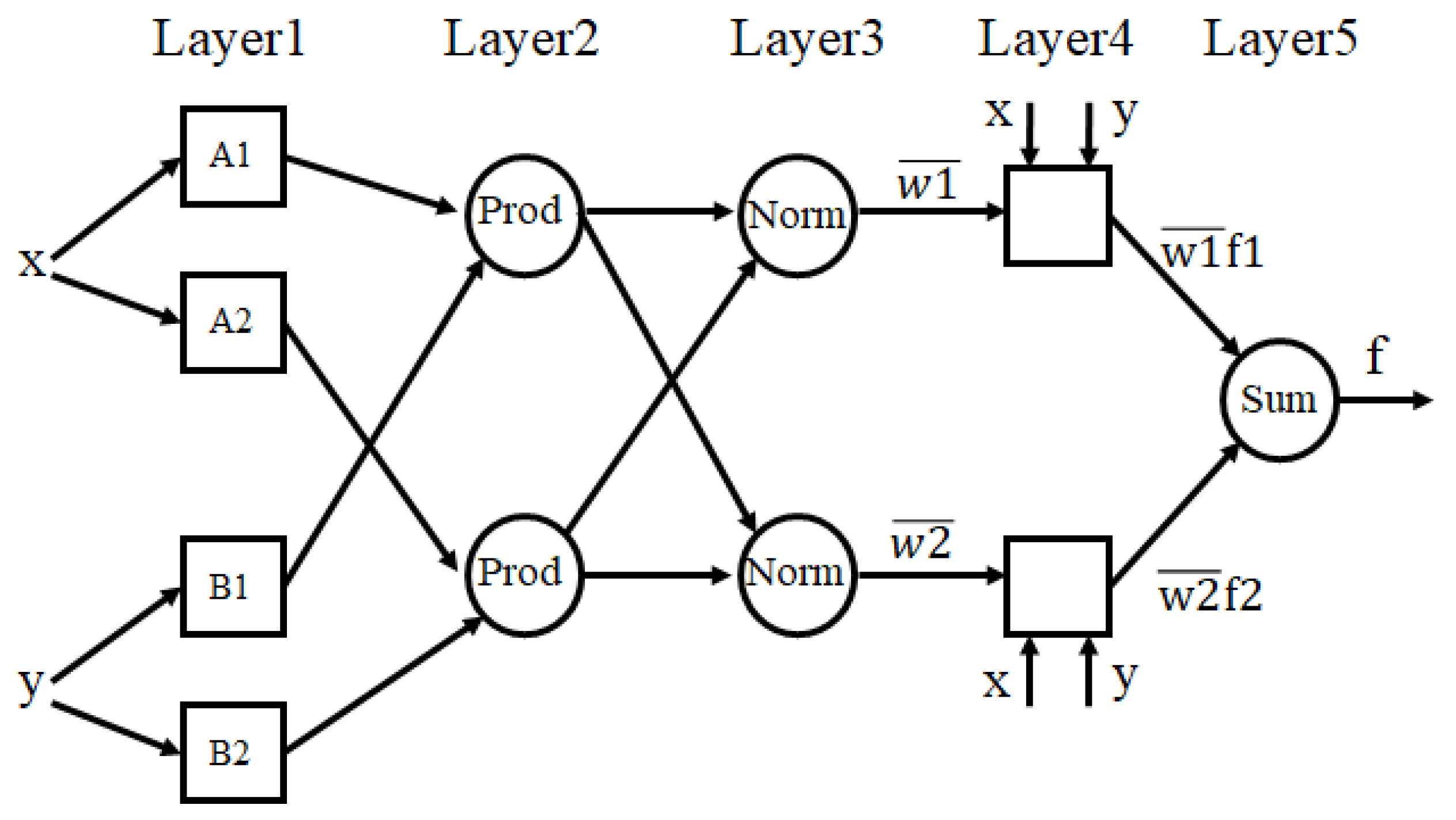
Neural networks are highly effective technique processes due to their versatile capabilities to process and learn data (Bensaber et al., 2020; Zadeh, 1996). The adaptive network is a multi-layer process wherein nodes operate specific functions on the input signals (Bensaber et al., 2020; Suparta & Alhasa, 2013). The Adaptive Neuro-Fuzzy Inference System (ANFIS) is a hybrid system that combines the benefits of neural networks and fuzzy logic to produce a potent tool for system identification and control. An artificial neural network-based fuzzy inference system, or ANFIS, models and learns the parameters of fuzzy inference systems. It is possible to reason with ambiguous or inaccurate data using the mathematical framework of fuzzy logic. It is predicated on the notion of membership functions, which define the extent to which an input value belongs to a given set. Fuzzy sets, which are fuzzy representations of the crisp sets employed in conventional logic, are frequently used to graphically describe these membership functions. A set of fuzzy rules that translate the input variables to the output variables make up the fuzzy inference system in ANFIS. There are antecedent and consequent sentences for each rule. The consequent clause is made up of an output variable and a weighting factor, whereas the antecedent clause is made up of a combination of input variables and the membership functions that correspond to them (Bensaber et al., 2020; Jang, 1993). The Takagi-Sugeno-Kang (TSK) fuzzy model serves as the foundation for the ANFIS model's structure (Takagi & Sugeno, 1983; Sugeno & Kang, 1988). The TSK fuzzy model is a particular kind of fuzzy system that approximates the output using a linear combination of fuzzy sets. By utilizing a neural network to learn the parameters of the fuzzy sets, the ANFIS model advances the TSK fuzzy model. In the ANFIS, the characteristic of the system is described via cultivating the IF-ELSE rule and does not require any preliminary information. Here, each output possesses its characteristic function, and the total numbers of rules and functions are identical (Al-Hmouz et al., 2012; Jang, 1993).

There are five layers in the ANFIS model. The input layer, which is the top layer, is where the input variables are sent. The input variables are subjected to the Gaussian membership functions in the second layer, which is the fuzzy layer. The outputs of the fuzzy layer are normalized in the third layer, which is the normalization layer. The ruling layer, which is the fourth layer, applies fuzzy rules to the outputs that have been normalized. The output layer, which computes the ANFIS model's ultimate output, is the fifth and last layer. ANFIS's learning algorithm is based on a combination of least squares estimation and gradient descent. The hybrid learning algorithm alternates between the two techniques to modify the parameters of the membership functions and the weights in the neural network. The fuzzy system's parameters can be learned using the hybrid learning algorithm rapidly and effectively.

To sum up, the ANFIS model is a potent tool for system identification and control. ANFIS model is a potent tool for system identification and control, to sum up. It creates a hybrid system that can quickly and effectively learn the parameters of fuzzy inference systems by combining the benefits of neural networks and fuzzy logic. The ANFIS model is widely employed in many industries, including engineering, finance, and medicine, and there is still active research being done in this area (Takagi & Sugeno, 1983; Sugeno & Kang, 1988).

Figure 1. ANFIS network architecture.

3. Results and Discussion

In this study, the last ten years’ data bank of the CESSNA 172S planes has been investigated. Here the aim is to develop an ANFIS model aiming to predict the general condition of the plane and classify them into two groups. The first group is the planes that need a fundamental overhaul and the second group is the planes that only need a routine overhaul. Such a model can help the aviation industry to have a more realistic evaluation of airplane squadrons. Also, it can help to predict the planes that need a fundamental overhaul and prevent the disaster of an airplane crash. The structure of the intelligent classification system that will be shown in this chapter is suitable to be extended for various airplane fleets.

In this study, a CESSNA 172S fleet (Figure 2) composed of 18 airplanes has been investigated. For this purpose, the last ten years’ failure data of the planes were categorized into five main categories. These categories are listed below:

Avionics

Electronics

Structure

Motor

Incidents

Figure 2. Overhaul process of Turkish Aeronautical Association CESSNA 172S fleet.

To develop a classification model, it is necessary to make a training dataset with inputs and outputs. Based on the nine decades of knowledge and experiences of the Turkish Aeronautical Association, and based on the expert evaluations and the statistical methods explained in the previous chapter, a weight is assigned to each five mentioned categories, considering their importance in the general condition of the airplane. The assigned weights are shown in Table 1.

As shown in Table 1 the motor and structural failures have the greatest effects on the general condition of the airplane. Each category includes a various number of features and each feature has its id code and an assigned weight value. The category features, their id number, and their descriptions are shown in Table 2, Table 3, Table 4, Table 5 and Table 6 respectively.

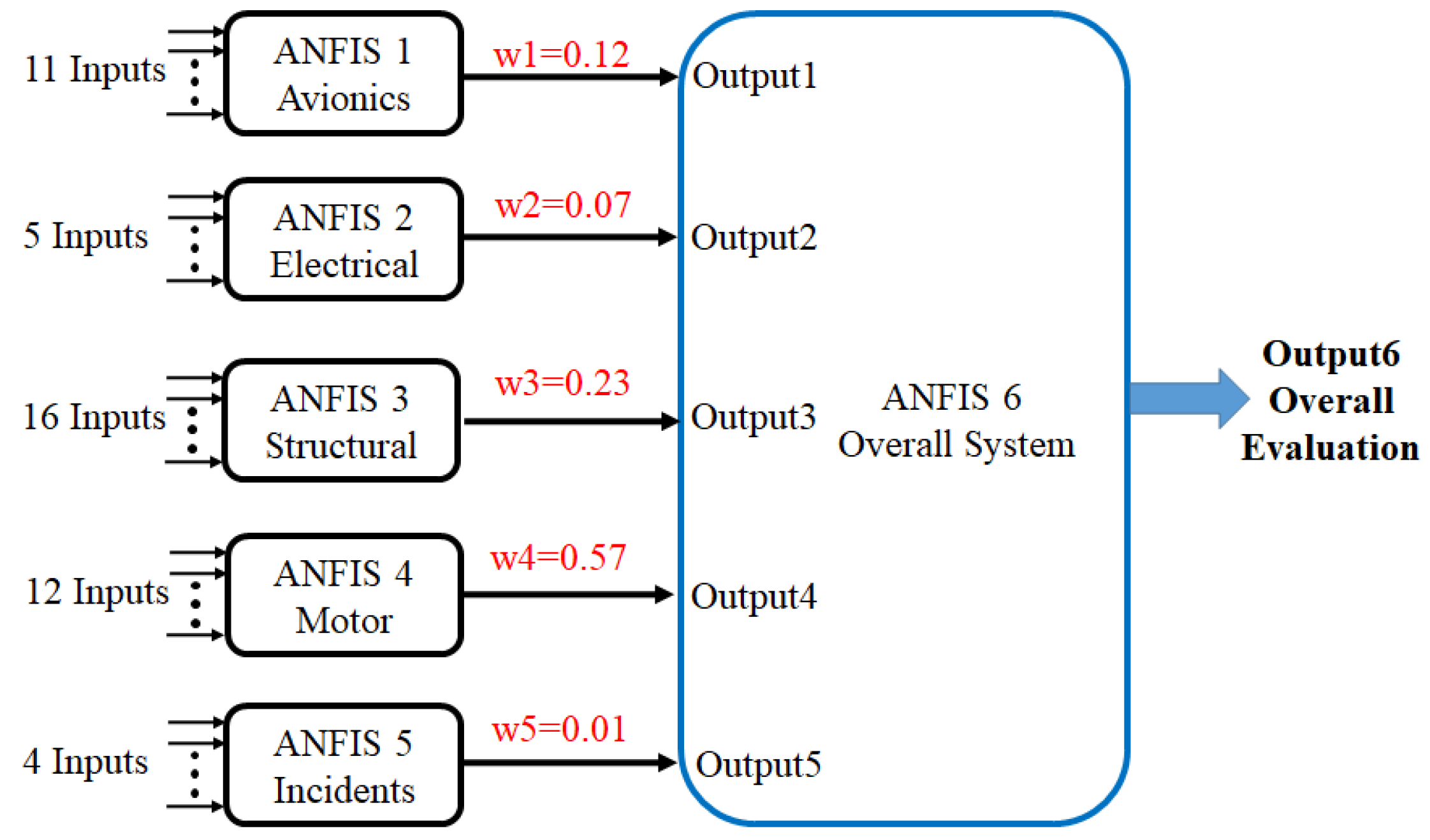
Considering the data and weights that are mentioned in Table 2, Table 3, Table 4, Table 5 and Table 6 six ANFIS models are developed and trained. The overall scheme of the developed system is shown in Figure 3. The first ANFIS model belongs to the avionics failure data. As mentioned in Table 2 there are 11 subsystem inputs and one output with a weight of 0.12 on the overall system. The second ANFIS model belongs to the electrical failure data where based on Table 3 there are 5 subsystem inputs and one output with a weight of 0.07 on the overall system. The third ANFIS model belongs to the structural failure data where based on Table 4 there are 16 subsystem inputs and one output with a weight of 0.23 on the overall system. The fourth ANFIS model belongs to the motor failure data where based on Table 5 there are 12 subsystem inputs and one output with a weight of 0.57 on the overall system. The fifth ANFIS model belongs to the data of the incidents where based on Table 6 there are 4 subsystem inputs and one output with a weight of 0.01 on the overall system. The mentioned subsystem inputs are the number of failures in each subsystem. The last ANFIS model belongs to the overall condition of the system.

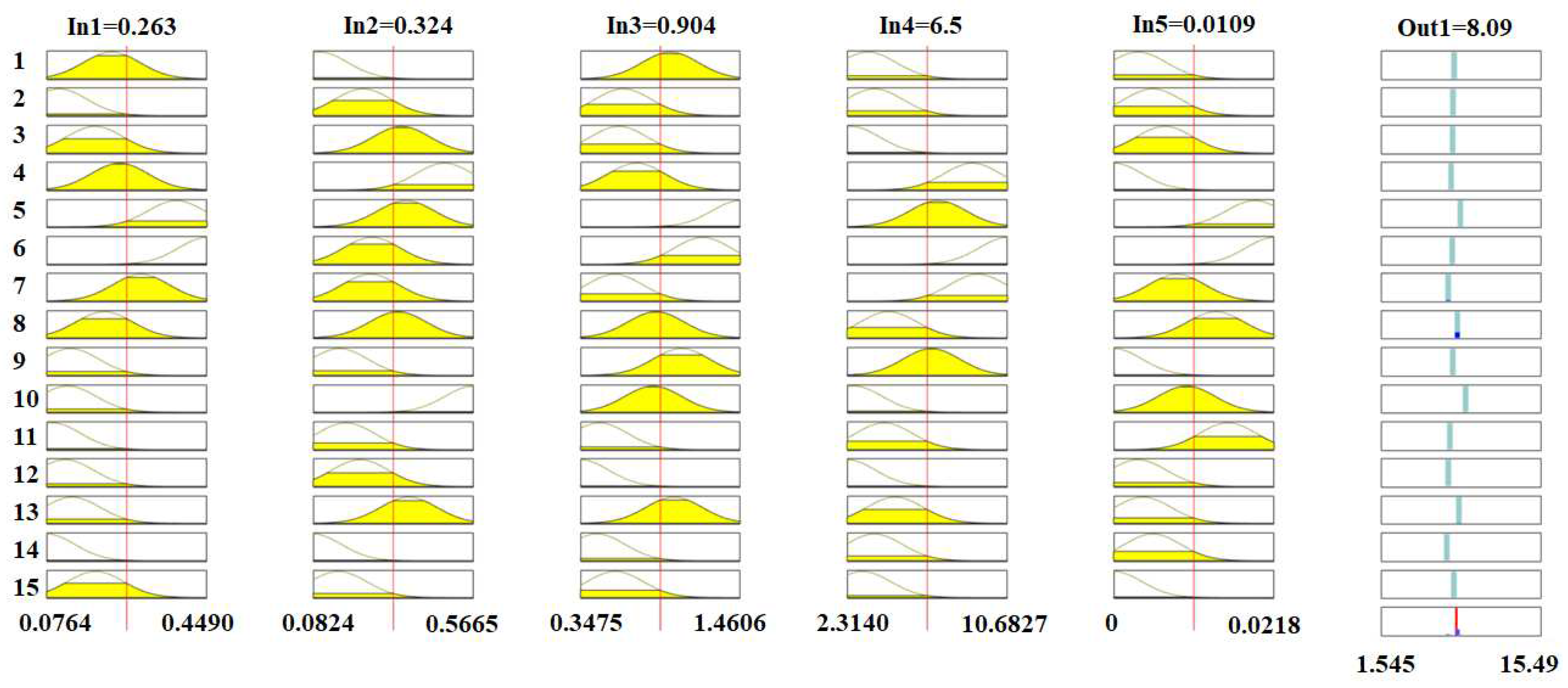
In this study, MATLAB Fuzzy Toolbox is used for the development of the ANFIS models. As an example, the architecture of the overall system ANFIS model developed in the MATLAB Fuzzy Toolbox is shown in Figure 4.

The membership functions and their ranges related to Figure 4 are shown in Figure 5. The example of the numeric values of 5 inputs and the resultant output values are shown in Figure 5 either.

3.1. Leave One out Evaluation Method

Even the Turkish Aeronautical Association has one of the biggest Cessna 172 fleets, but the number of airplanes is still limited. So there is a need to use a suitable method for benefiting the maximum number of training data. For this purpose, in this study leave-one-out evaluation method is used. Leave-one-out is a straightforward n-fold cross-validation, where n is the same as the dataset's instance count. Each case is excluded from the evaluation circle before the classifier is trained using the remaining examples. After then, the left instance is used as test data to determine whether the classification was successful. The accuracy of the n judgment outcomes serves as a proxy for the categorization procedure's success rate. The leave-one-out evaluation approach is more effective for two key reasons, which are detailed below.

1. To train the classifier and produce more accurate classification results, only one example of the training set is used as the test set in each stage, and the largest dataset is chosen.

2. All of the cases are evaluated as a test set in this type of evaluation, which does not rely on random sampling. As a result, its deterministic quality improves evaluation precision (Cruz & Mestrado, 2009; Witten, & Frank, 2005).

3.2. ANFIS Model Results Evaluation

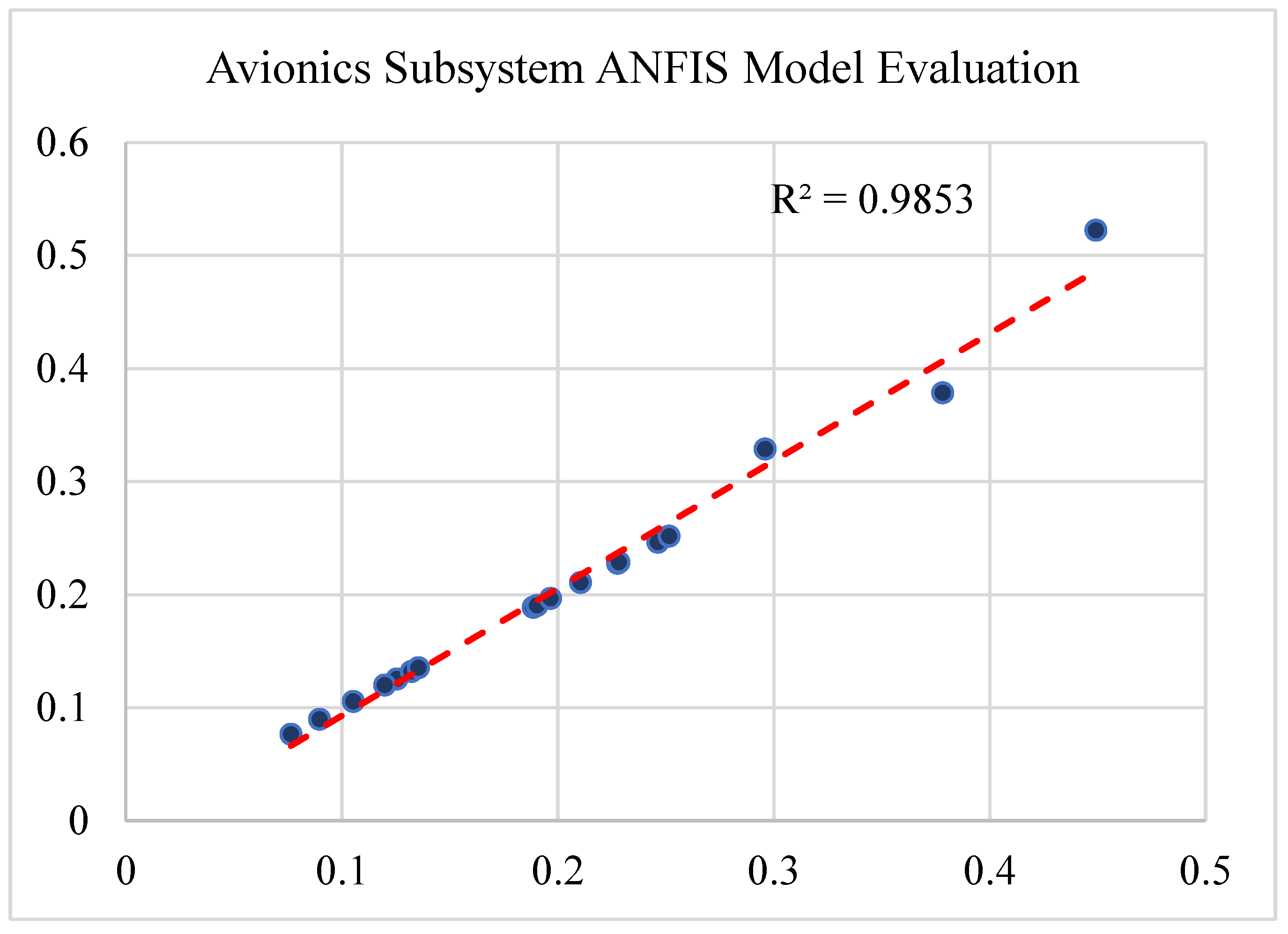
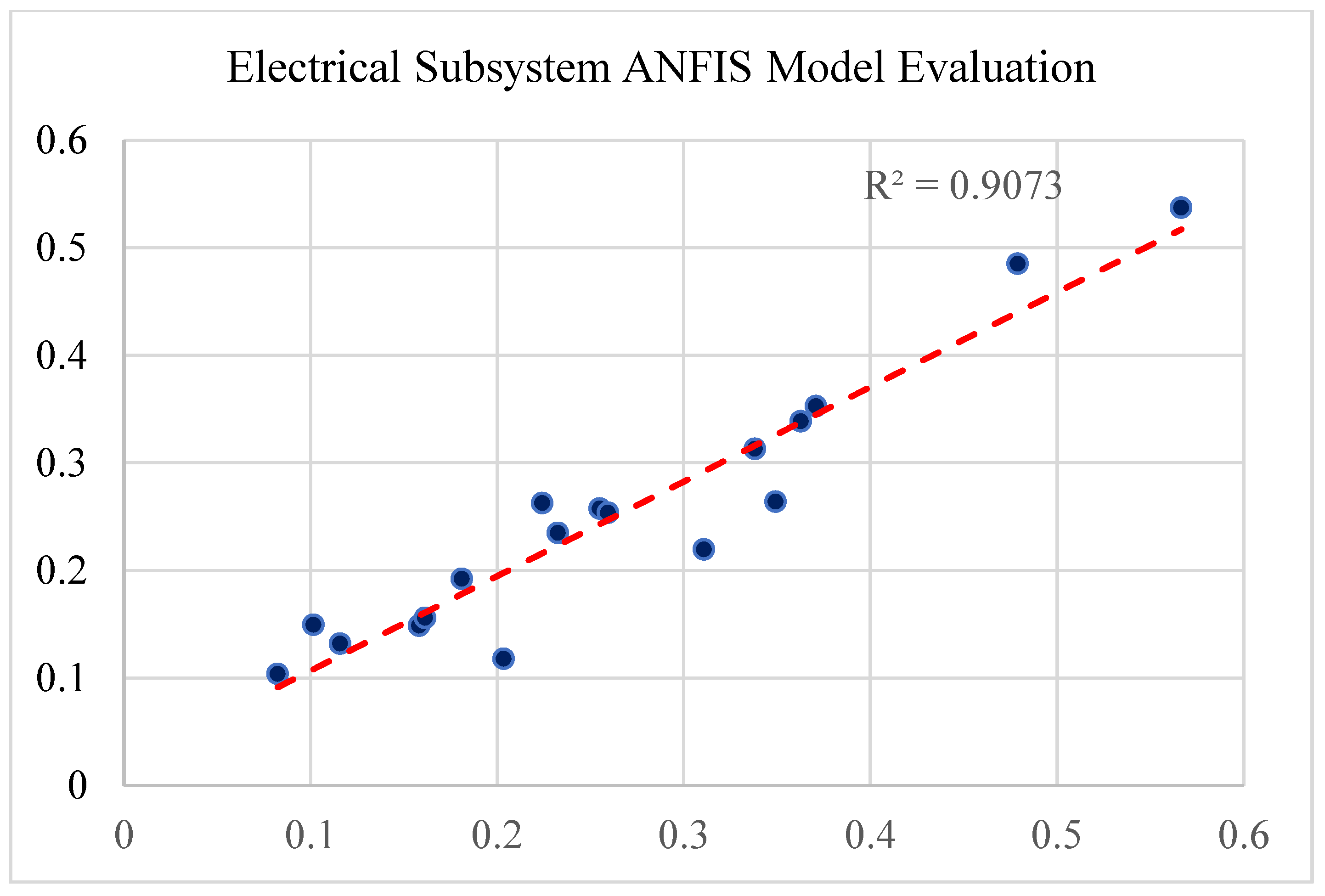
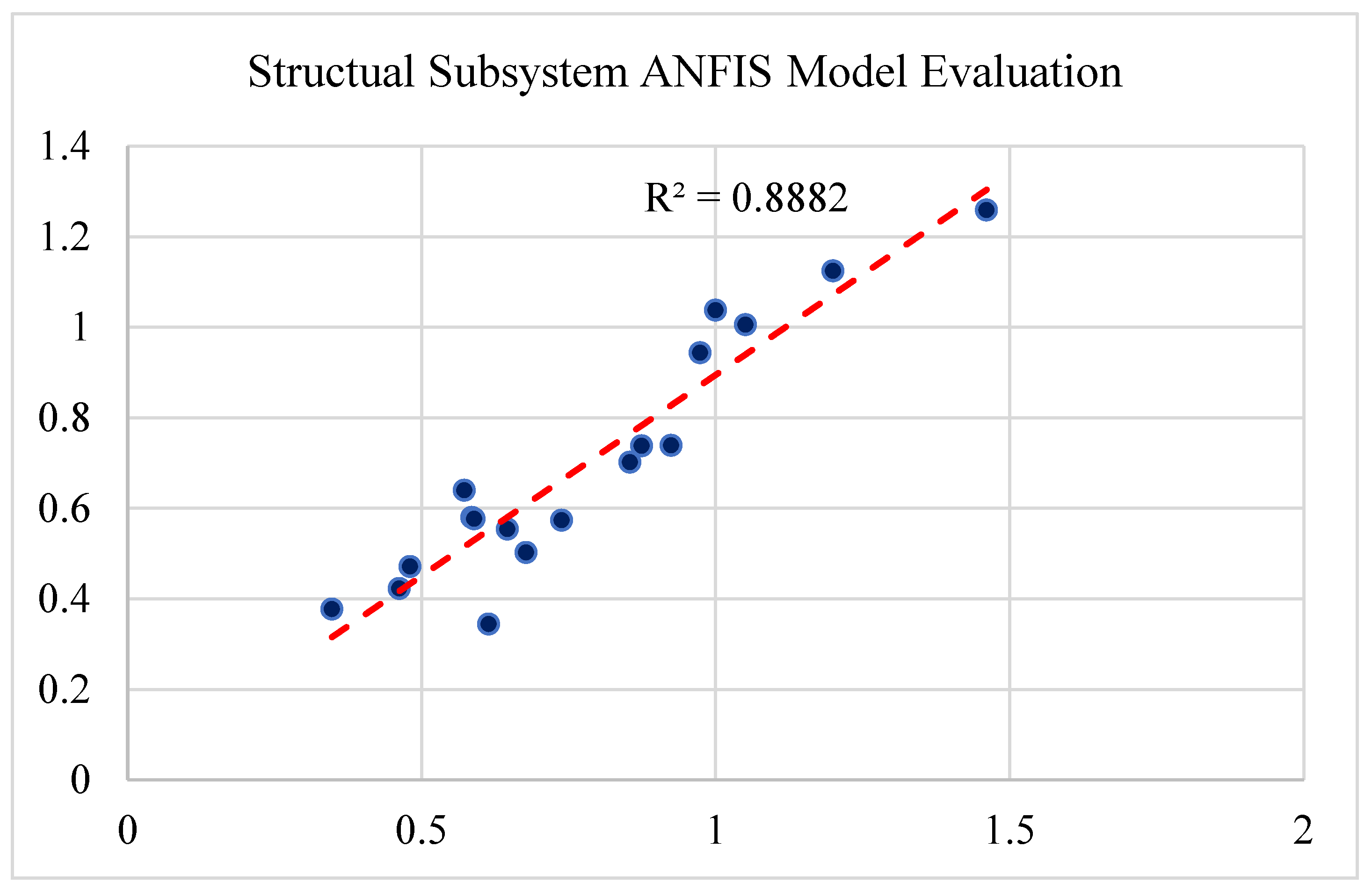
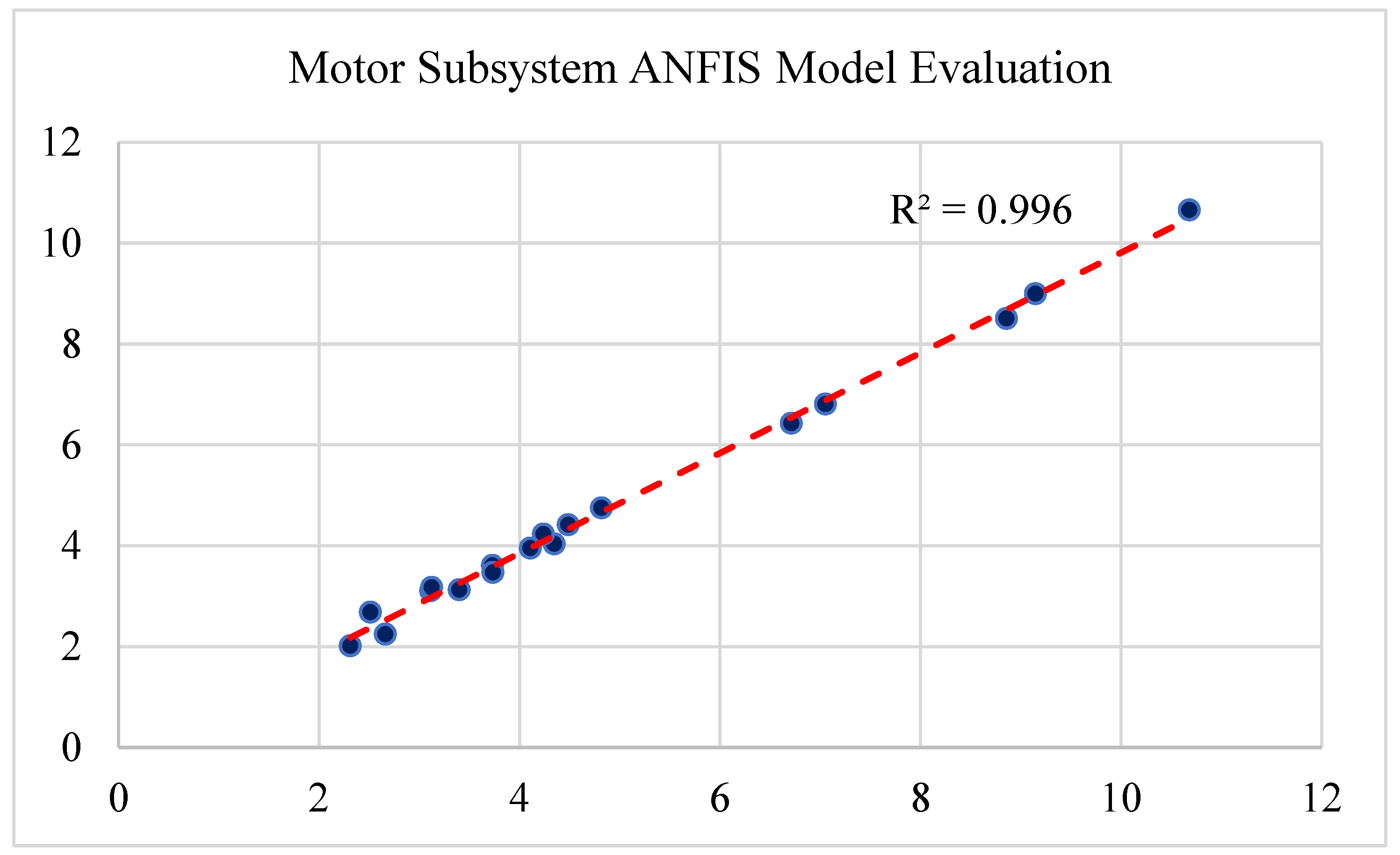
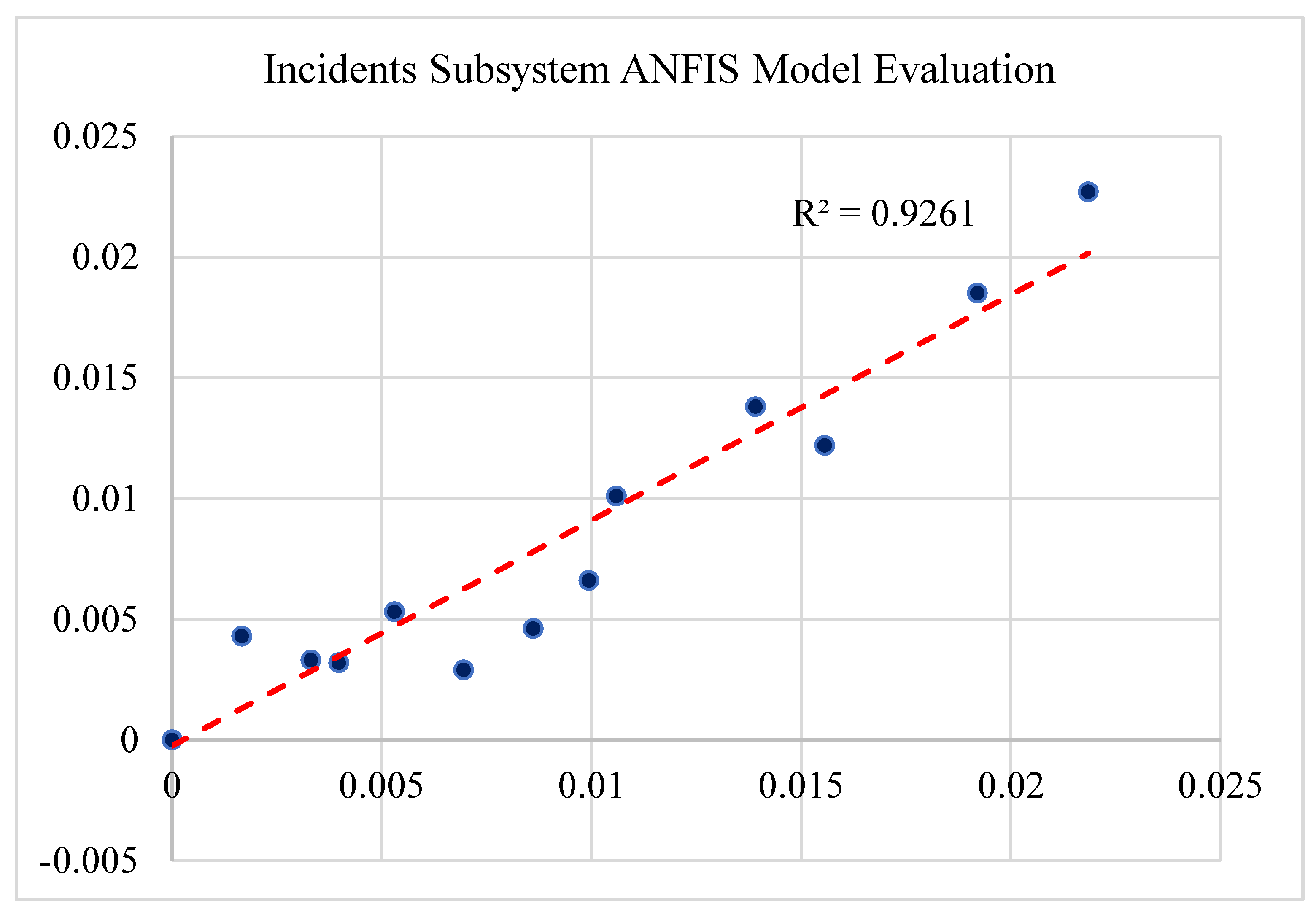
The details of each model and its performance statistics are mentioned as followings. For each model, the output values are shown versus the model output values. Also, R-Squared values are calculated for each model. In an ANFIS model, R-Squared (also known as R2 or the coefficient of determination) is a statistical metric that quantifies how much of the variance in the dependent variable can be accounted for by the independent variable. R-squared, thus, displays how well the data match the ANFIS model. The range of R-squared values is 0 to 1. R-squared is most frequently used to determine how well a model explains observed data. A greater r-squared typically means the model is better at explaining the variability. The results shown in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 reflect the high performance of the developed models.

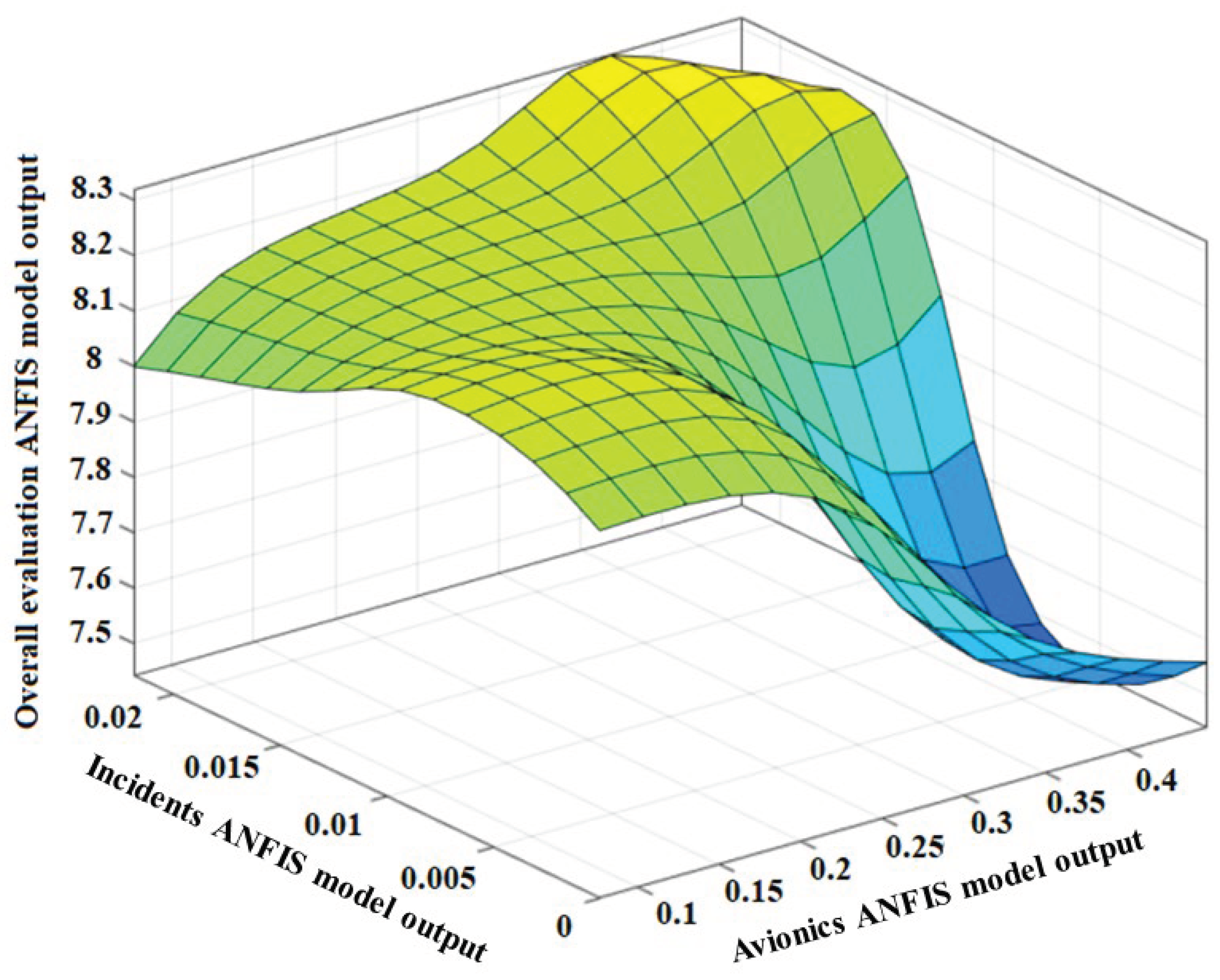
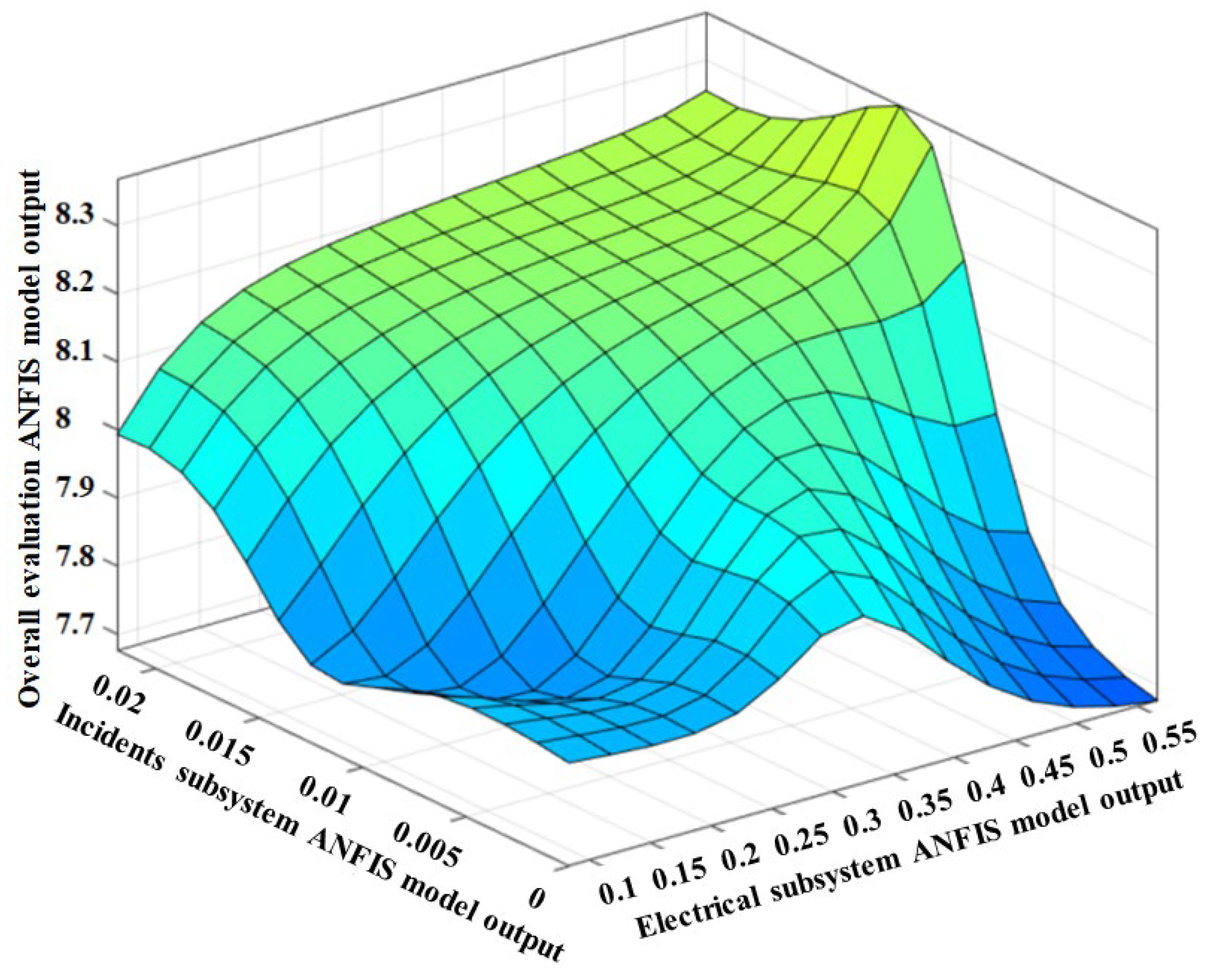
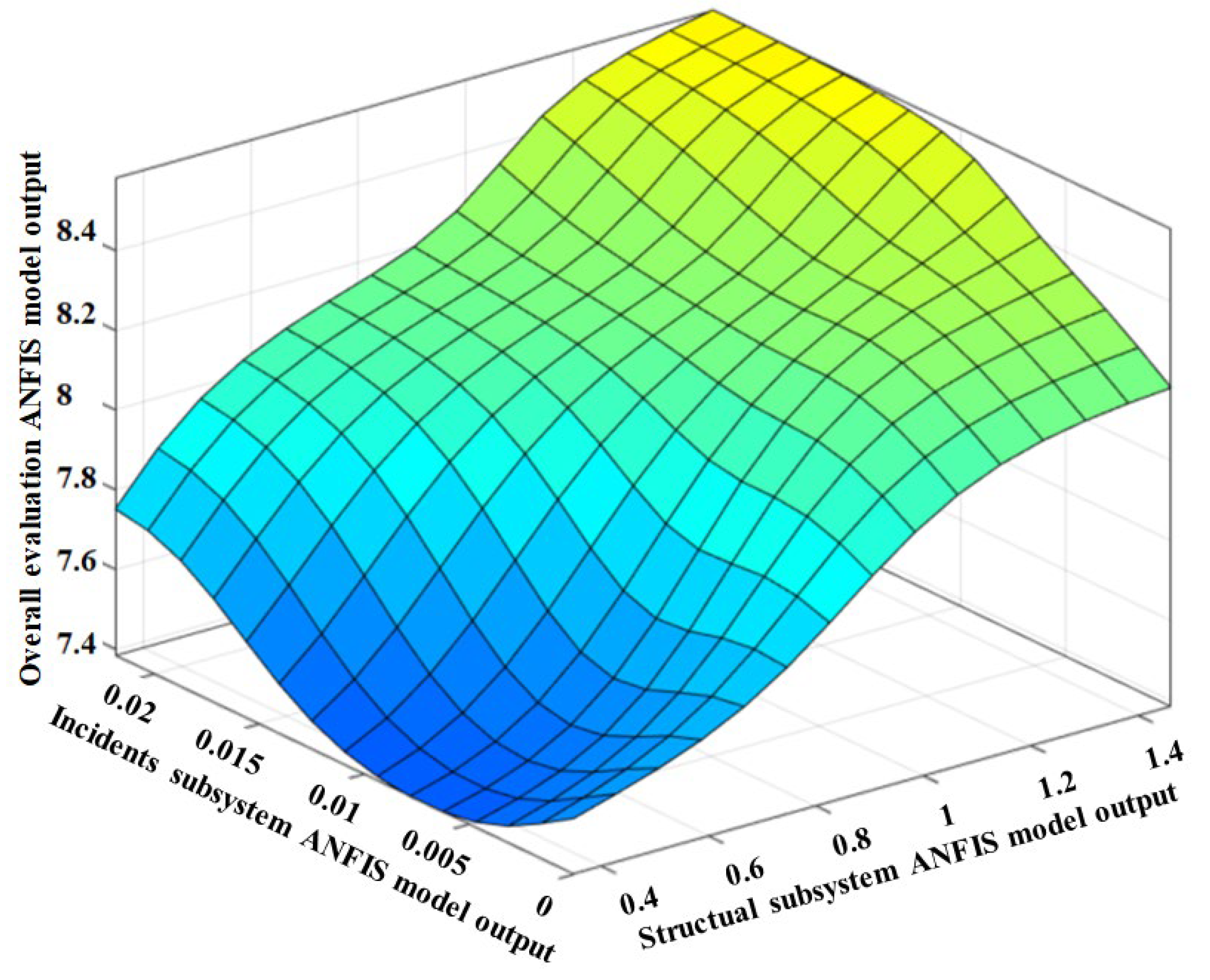
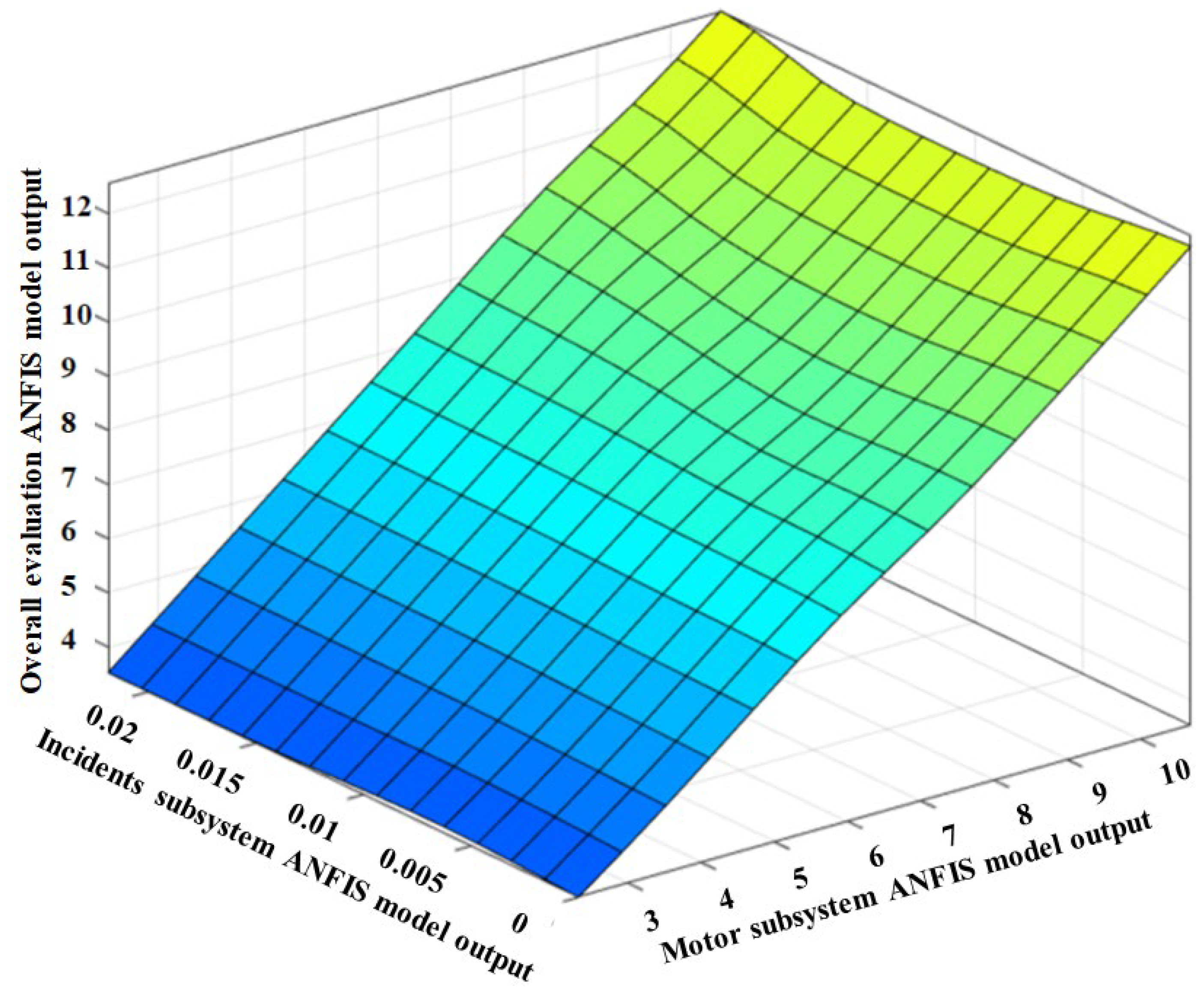
For a better understanding of the relationship between developed model outputs, the overall evaluation model outputs, and incidents model outputs are plotted in parallel with the other model outputs (Figure 11, Figure 12, Figure 13 and Figure 14). This is because of the incidents model has high merit in the overall evaluation model.

The evaluation of the 3-D graphs indicates that motor subsystem outputs have an almost linear relationship with the incident subsystem outputs. This result is the expected fact in airplane maintenance. Also, a semi-linear relationship is observed between the motor subsystem outputs, incident subsystem outputs, and the overall evaluation model outputs. This relationship shows the high impact of both model outputs on the overall condition evaluation of the aircraft.

Considering the output range of the overall evaluation model outputs and based on expert evaluations, it is recommended to consider the main overhaul for a plane with an overall evaluation value of more than 65-70.

4. Conclusions

Dealing with the data is not an easy task in the aviation industry. More specifically, because there are so many different options and conflicting effects and parameters, decision-makers frequently face challenges when processing data related to human, technical, or environmental factors. The difficulty in aviation is that the system is primarily knowledge-based and made up of several inputs and outputs that depend on a huge range of parameters. Particularly, these parameters must be conquered and satisfactorily handled appropriately for the sake of safety, which is the other essential component of aviation. To support improved decision-making, insight discovery, and process optimization to address problems in every part of aviation, all these demands call for new methods of information and data processing. Different decision-making methodologies can be used to direct professionals toward a better resolution of all issues encountered in aviation.

This study focuses on investigating the fault risk factor of CESSNA 172S airplanes of the Turkish Aeronautical Association fleet using the Adaptive Neuro-Fuzzy Inference System (ANFIS) classifier. For the creation of the classifier, five categories of real fleet data from the planes' motor, electrical, avionic, and structural systems as well as incident statistics were employed. The proposed intelligent classifier produces a risk factor determination for each plane, which can be utilized to identify general overhaul candidate planes and avert errors and crashes. As a result of this study, knowledge extraction from raw data has been standardized. A standardization like this helps users make good decisions quickly. Additionally, it provides the same decisions made by many stakeholders, preventing the impacts of individual interpretation. By standardizing information, level of data management, and air vehicle operating safety, the proposed algorithm will ultimately increase the level of safety and reliability of aviation systems. The results obtained demonstrate that using ANFIS offers a significant capability in processing numerous inputs and outputs based on various types and classes in the aviation industry and hence accurately predicting the failure risk of the aircraft. Also, the developed model is very flexible and to be extended for all types of airplane fleets and aviation systems such as fixed-wing and rotary-wing air vehicles.

References

Abbas, M.Z., Sajjad, I.A., Hussain, B., Liaqat, R., Rasool, A., Padmanaban, S., & Khan, B. (2022). An adaptive-neuro fuzzy inference system based-hybrid technique for performing load disaggregation for residential customers. Scientific Reports, 12, 2384. [CrossRef]
Al-Hmouz, A., Shen, J., Al-Hmouz, R., & Yan, J. (2012). Modeling and simulation of an adaptive neuro-fuzzy inference system (ANFIS) for mobile learning. IEEE Transactions on Learning Technologies, 5(3), 226–237. [CrossRef]
Belobaba, P., Odoni, A., & Barnhart, C. (Eds.). (2015). The global airline industry. John Wiley & Sons.
Belton, V., & Stewart, T. (2002). Multiple criteria decision analysis: An integrated approach. Springer Science & Business Media.
Bensaber B. A., Diaz, C. G. P., & Lahrouni Y (2020). Design and modeling an Adaptive Neuro-Fuzzy Inference System (ANFIS) for the prediction of a security index in VANET. Journal of Computational Science, 47, 101234. [CrossRef]
Cruz, A. O., & Mestrado, N. (2009). ANFIS: Adaptive neuro-fuzzy inference systems. IM, UFRJ, Mestrado NCE.
Dožić, S. (2019). Multi-criteria decision making methods: application in the aviation industry. Journal of Air Transport Management, 79, 101683. [CrossRef]
Esposito, C., Ficco, M., Palmieri, F., & Castiglione, A. (2015). A knowledge-based platform for Big Data analytics based on publish/ subscribe services and stream processing. Knowledge-Based Systems, 79, 3-17. [CrossRef]
Harris, D. (2017). Decision making in aviation (1st ed.). Routledge.
Jang, J.S.R. (1993). ANFIS: Adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, Man, and Cybernetics, 23(3), 665-685. [CrossRef]
Kasturi, E., Devi, S. P., Kiran, S. V., & Manivannan, S. (2016). Airline route profitability analysis and optimization using BIG DATA analytics on aviation data sets under heuristic techniques. Procedia Computer Science, 87, 86-92. [CrossRef]
Kolaitis, P. G. (2005, June). Schema mappings, data exchange, and metadata management. In Proceedings of the 24th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems (PODS’05). Association for Computing Machinery, New York, NY, 61–75. doi/10.1145/1065167.1065176.
Orasanu, J. (1995). Training for Aviation Decision Making: The Naturalistic Decision Making Perspective. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 39(20), 1258–1262. [CrossRef]
Simpson, P. A. (2001). Naturalistic decision making in aviation environments. Aeronautical and Maritime Research Laboratory Industry, DSTO, 1-40.
Suparta, W., & Alhasa, K.M. (2013). A comparison of ANFIS and MLP models for the prediction of precipitable water vapor. In: Proceedings of 2013 3rd IEEE international conference on space science and communication (IconSpace2013), pp 243–247. [CrossRef]
Takagi, T. & Sugeno. M. (1983). Derivation of fuzzy control rules from human operator's control actions. Proceedings of IFAC Symposium on Fuzzy Information, Knowledge Representation and Decision Analysis, 55-60.
Sugeno, M., & Kang, G.T. (1988). Structure Identification of Fuzzy Model. Journal of Fuzzy Sets and Systems, 28, 15-33. [CrossRef]
Zadeh, L.A. (1996). On fuzzy algorithms. In: Fuzzy sets, fuzzy logic, and fuzzy systems: Selected papers By Lotfi A Zadeh, pp 127–147. World Scientific.
Zsambok, C. E., & Klein, G. (2014). Naturalistic decision making (2nd ed.). Psychology Press.
Witten, I. H., & Frank, E. (2005). Data Mining: Practical machine learning tools and techniques (2nd ed.). San Francisco, CA: Morgan Kaufmann.

Figure 3. Developed six ANFIS models for Avionics, Electrical, Structural, Motor, and Incidents subsystems and one ANFIS model for the Overall evaluation of the plane.

Figure 4. Overall system ANFIS model developed in the MATLAB Fuzzy Toolbox.

Figure 5. Membership functions and their ranges related to the overall system ANFIS model are shown in Figure 4.

Figure 6. Performance evaluation of the Avionics Subsystem ANFIS Model.

Figure 7. Performance evaluation of the Electrical Subsystem ANFIS Model.

Figure 8. Performance Evaluation of the Structural Subsystem ANFIS Model.

Figure 9. Performance evaluation of the Motor Subsystem ANFIS Model.

Figure 10. Performance evaluation of the Incidents Subsystem ANFIS Model.

Figure 11. The avionics subsystem model outputs variation vs incidents model and the overall evaluation model outputs.

Figure 12. The electrical subsystem model outputs variation vs incidents model and the overall evaluation model outputs.

Figure 13. The structural subsystem model outputs variation vs incidents model and the overall evaluation model outputs.

Figure 14. The motor subsystem model outputs variation vs incidents model and the overall evaluation model outputs.

Table 1. Assigned weights to each category based on their importance in the general condition of the airplanes.

Category	Assigned Weights
Avionics	0.12
Electronics	0.07
Structure	0.23
Motor	0.57
Incidents	0.01

Table 2. Avionics features, their descriptions, and assigned weights to each feature.

Avionics Features
No	Feature ID	Description	Assigned Feature Weight
1	22-10-00	Autopilot System Failures	0.0059563
2	23-10-00	Communication System Failures	0.0291198
3	28-40-00	Fuel Quantity Indication System	0.0006618
4	31-00-00	Instrument and Control Panels Failures	0.0033091
5	33-40-00	Navigation System and Strobe Failures	0.0016545
6	34-00-00	Navigation System Failures	0.0026473
7	34-11-00	Pitot Static System Altimeter Failures	0.0125745
8	34-20-00	Attitude and Direction System Failures	0.0264725
9	34-52-00	ADF System Failures	0.0049636
10	34-60-10	Garmin Display Unit (GDU) Failures	0.0218398
11	37-10-00	Vacuum System Failures	0.0105890

Table 3. Electronics features, their descriptions, and assigned weights to each feature.

Electric Features
No	Feature ID	Description	Assigned Feature Weight
1	24-00-00	Electrical Power Failures on Aircraft	0.0046327
2	24-20-00	Alternator Failures in Electrical Power Systems	0.0509596
3	24-30-00	Battery Failures in Electrical Power System	0.0142290
4	24-60-00	Power Junction Failures in Distribution System	0.0006618
5	33-00-00	Lighting System Failures on Aircraft	0.0039709

Table 4. Structural features, their descriptions, and assigned weights to each feature.

Structural Features
No	Feature ID	Description	Assigned Feature Weight
1	21-00-00	Air Conditioning Failures in Structural System	0.0013236
2	21-40-00	Heating and Defrosting System Failures	0.0039709
3	25-10-00	Flight Compartment Failures on Aircraft	0.0023163
4	25-10-10	Inflatable Restrained Failures in Structural System	0.0000000
5	25-20-00	Passenger Compartment Failures on Aircraft	0.0023163
6	27-00-00	Flight Control System Failures	0.0675050
7	27-00-01	Dismantling or Installed of the Wing Failures	0.0006618
8	27-32-00	Stall Warning System Failures	0.0023163
9	28-20-00	Fuel Storage and Distribution System Failures	0.0264725
10	32-00-00	General Landing Gears System Failures	0.0277962
11	32-20-00	Nose Landing Gear System Failures	0.0145599
12	32-40-00	Main Landing Gear Wheel Failures	0.0423561
13	32-41-00	Nose Landing Gear Wheel Failures	0.0043018
14	32-42-00	Brake System Failures in Structure	0.0284580
15	52-10-10	Cabin Doors Failures on Aircraft	0.0039709
16	57-10-00	Left and Right Leading-Edge Flaps Failures	0.0006618

Table 5. Motor features, their descriptions, and assigned weights to each feature.

Motor Features
No	Feature ID	Description	Assigned Feature Weight
1	71-00-01	General Engine System Failures	0.2561218
2	71-20-00	Engine Mounting System Failures	0.0039709
3	71-60-00	Air Indication System Failures	0.0059563
4	73-00-00	Engine Fuel and Control System Failures	0.0327598
5	74-10-00	Engine Ignition System Failures	0.1360026
6	78-00-00	Engine Exhaust System Failures	0.0079418
7	80-10-00	Engine Starter Failures	0.0059563
8	61-10-00	Propeller System Failures	0.0009927
9	79-30-00	Engine Oil Pressure Indication System Failures	0.0287889
10	79-31-00	Engine Oil Temperature Control System Failures	0.0178690
11	73-30-00	Fuel Flow Indication System Failures	0.0089345
12	77-20-00	Engine Temperature Indication System Failures	0.0605559

Table 6. Incidents features, their descriptions, and assigned weights to each feature.

Incidents Features
No	Feature ID	Description	Assigned Feature Weight
1	05-50-00-2A	Hard and Overweight Landings	0.0033091
2	05-50-00-2B	Airframe Damages	0.0016545
3	05-50-00-2E	Foreign Object Damage (FOD) and Birds Strike	0.0052945
4	05-50-00-2F	Engine Stopping	0.0006618

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Aircraft Failures Prediction via Adaptive Neuro-Fuzzy Inference System

Abstract

1. Introduction

2. Method

2.1. Database Generation

2.2. Weight Calculation

2.3. Adaptive-Neuro Fuzzy Inference System (ANFIS)

3. Results and Discussion

3.1. Leave One out Evaluation Method

3.2. ANFIS Model Results Evaluation

4. Conclusions

References

MDPI Initiatives

Important Links

Subscribe