Prerpints.org logo
Preprint
Article

Large-Eddy Simulations of a Hypersonic Re-entry Capsule Coupled With the Supersonic Disk-Gap-Band Parachute

Altmetrics

Downloads

147

Views

76

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 May 2023

Posted:

05 May 2023

You are already at the latest version

Alerts
Abstract
The goal of this paper is to investigate the aerodynamic and aerothermodynamic behaviour of the Schiaparelli capsule after the deployment of the supersonic disk-gap-band (DGB) parachute during its re-entry phase into the Martian atmosphere. Large-Eddy Simulations of compressible flows have been performed over the capsule and the flexible DGB parachute to analyse the behaviour of the turbulent wake behind the capsule and its interaction with the parachute flow-field. The simulations are performed at an altitude of 10 km and a Mach number around 2, i.e., a regime in which large canopy-area oscillations are observed. These simulations have shown a strong interaction between the bow shock, the recompression and expansion waves, high pressure, density and temperature gradients, heat flux towards the airstream and the body implying turbulence generation, ingestion, and amplification through the shock waves. This nonlinear turbulence flowfield explains the non-axisymmetric behaviour around and behind the parachute that caused the uncontrolled capsule oscillation and the mission failure.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

For over a period of 60 years, both the experimental and computational studies have been conducted on the aerothermodynamics of the re-entry vehicles [1,2]. Mercury and Apollo programs levied a path for the experimental studies on the blunt body hypersonics while the computational studies began with the Apollo and Space Shuttle programs. Preliminary designs of atmospheric re-entry vehicles require in-depth knowledge of hypersonic flow characteristics [3]. Brian R. Holli in his book "Experimental and Computational Aerothermodynamics of a Mars Entry Vehicle" [4] presents a rapid history of studies on hypersonic flows around a 70° sphere cone geometry. Although this book was written in 1996, regarding the Mars Pathfinder Mission, the experimental and computational methods that are illustrated there are still used today, since the shape of the capsule is almost unchanged. Viking 1, Viking 2, Pathfinder, Spirit, Opportunity, Phoenix, Curiosity, and other successful spacecraft have been launched on Mars. In addition, ESA, in collaboration with Russia’s Roscosmos space agency, launched an ExoMars program consisting of two phases. The first phase of the ExoMars mission, including the TGO (Trace Gas Orbiter) satellite with scientific equipment and the ESA Schiaparelli descent module in the second phase, was launched in 2016. The Schiaparelli descent module's mission was to test the method of a controlled landing using the propulsion system. Schiaparelli, however, crashed into the surface of Mars due to onboard computer errors.
The entry, descent and landing phase (EDL) plays a crucial role during the re-entry phase of the capsule into the planet's atmosphere that undergoes complex interactions that are not yet completely understood: the entrance, which beginning at an attitude of 200 kms, where the aerodynamic resistance of the capsule is being used to decelerate; the descent, about 10 km from the surface, where the parachute/canopy is deployed and the landing. An intense shock wave is desired during the re-entry into the atmosphere, as the vehicle uses aerodynamic drag to control its speed. The shock layer near the nose is subjected to high temperatures as the kinetic energy in the hypersonic flow is converted into internal energy of the gas through the shock waves. Due to this loss of kinetic energy, it results in the deceleration of the vehicle. [5] Allen and Eggers discovery shows that an intense heating is observed due to the creation of very strong waves from the blunt body which is mostly carried away into the stream while the originating boundary layer acts as an insulator.
Due to their low mass and high packing efficiency, DGB (disk-gap-band) parachutes provide a very efficient aerodynamic method of decelerating an incoming vehicle from supersonic to subsonic speeds [6]. The primary uncertainty associated with the deceleration performance of a DGB parachute is inflation in a supersonic environment [7]. For the supersonic deceleration process, the parachute setup must be specially designed to achieve high aerodynamic efficiency. Parachute performance depends on Mach number, capsule shape and size, capsule-to-parachute distance, canopy shape and size, material properties, cables, and capsule angle of attack [8].
Modelling the dynamics of parachute accurately is difficult due to its complexity in the descent phase as they are governed by a coupling between the structural dynamics of the parachute and the surrounding flow both during the inflation process and the terminal descent phase. While the parachute is in its steady-state, the air flowing around the decelerator will separate at some point on the canopy. The shedding of vortices from the canopy can affect stability causing both the parachute and payload to oscillate on a regular basis. The wake of a porous parachute is made up of air flowing around and through the canopy.
In the operating speed range of the parachute, part of the flow entering the parachute is turbulent in nature and must be accounted for in the aerodynamic performance of the parachute [9] as the payload fairing produces a very turbulent wake.
Even at low speeds, the prediction of parachute aerodynamic properties is difficult due to the nonlinear nature of structural deformations, especially for parachutes with complex arrangements such as slots or gaps [10,11]. The supersonic behaviour of these parachutes involves complex, interdependent phenomena in fluid-structure interaction (FSI) studies which includes bluff and porous body aerodynamics, nonlinear structural dynamics, and the fully coupled interaction between compressible flow and shocks and a membrane structure undergoing large deformations.
The structural integrity and drag characteristics of the parachutes are impacted due to the rapid oscillatory movement of the inflated parachute in some flight regimes which is caused due to the inevitability of a close coupling between the parachute structure and the surrounding flow. This complex dynamics observed are related to the oscillatory axial motion of the bow shock originated in-front of the parachute canopy. This is due to over/under pressurization, an imbalance in the tension and compression stiffness of the suspension lines that are connected between the parachute and the capsule (re-entry vehicle), expansion instability caused by the imbalance of fluid forces with structural forces, which is exacerbated by the parachute's very low inertia, and contact forces [12].
In recent advances, Karagiozis et al. [13,14,15] used structural membrane-coupled large-eddy simulation (LES) to investigate the supersonic performance of a flexible DGB parachute. Therefore, basic theoretical research on supersonic capsule or parachute systems is urgently needed in the aerospace field. In this paper, we study the effects of the turbulent wake behind the capsule on a rigid DGB parachute at Mach 2 and investigate the causes of fluid instabilities in a supersonic capsule/rigid DGB parachute system.

2. Numerical Simulations of the Schiaparelli Capsule and Parachute

2.1. Geometry of the Capsule with Parachute system

The sketch of the Schiaparelli capsule blunt body along with the DGB supersonic parachute is shown in Figure 1.
The capsule (see Figure 2, right) consists of a diameter of D=2.4 m, a front body cone angle of 70º, a rear cone angle of 47º and an overall height of H=1.276m. The projected diameter of the parachute is Dp=8.640m, the disk diameter is Dd=8.223m, the gap height is of Hg=0.957m, the band height is of Hb=1.357m, and the vent diameter is of Do=0.848m.
The rigid DGB parachute (see Figure 2 left) is suspended at a length of 24m from the rear-end of the capsule. The bridle, raiser and bridle attachment lengths all included to be 4.011m.

2.2. Numerical Set-up

Large-Eddy Simulations (LES) have been performed by means of ANSYS Fluent. A density-based (coupled), implicit, second-order upwind scheme with an AUSM (advection upstream splitting method) flux vector has been implemented for LES simulations. The WALE (wall-adapting local eddy-viscosity) subgrid-scale model has been chosen.

2.2.1. Finite element model

A computational domain of about 2.1 million node, enclosing the parachute and the capsule has been designed, to carry out the numerical analysis. A three-dimensional structured grid has been generated by the ANSYS Workbench to simulate the flow field inside the computational domain. Due to computational capacity limitations, the suspension lines were neglected.
In order to investigate the pressure distribution along the Schiaparelli Capsule and Parachute, data are collected and processed at five different locations (L1, L2, L3, L4, L5) as shown in Figure 3.
L1 is the axisymmetric line of the domain. L2 and L3 are equidistant from L1, and pass through the shoulders of the capsule. L4 and L5 are still equidistant from L2 and L3, and axisymmetric with respect to L1.

2.2.2. Boundary conditions

The boundary conditions are summarised in Table 1.
The time step is 1.0×10−4 s and the overall runtime of numerical simulations conducted is 0.126 seconds.

3. Numerical Validation with reference work and theoretical results

In order to validate numerical simulations, theoretical and numerical results from [14] have been used as reference. Theoretical data have been calculated by implementing the normal shock equations reported below:
M 2 2 = 1 + M 1 2 ( γ − 1 ) / 2 γ M 1 2 − ( γ − 1 ) / 2
ρ 2 ρ 1 = ( γ + 1 ) M 1 2 2 + ( γ − 1 ) M 1 2
p 2 p 1 = 1 + 2 γ γ + 1 M 1 2 − 1
T 2 T 1 = p 2 p 1 · ρ 1 ρ 2
Results are reported in Table 2.
A good agreement between the three works has been observed. In particular, the error of the simulations with respect to the theoretical data is 1.06% for pressure and 0.22% for the temperature.

3.1. Numerical Results

In this section, numerical results of the Schiaparelli casule are shown. Figure 4 shows the Mach flow field around the capsule and the rigid DGB parachute at their axisymmetric plane. A strong bow shock is detached in front of the capsule at a distance of 0.7 m, and another in front of the canopy at a distance of approximately 1.8 m. Due to the strong bow shock ahead of the capsule and ahead of the canopy, there is a sudden decrease in the Mach number and increase in the pressure and temperature (see Figure 5). Because of the large deflection angle of the afterbody, the flow begins to expand after the shoulder; the expansion waves intersect at the back of the capsule generating recompression waves that are responsible for the pressure increase and Mach decrease.
Figure 4 showed that the parachute canopy's inner and outer flow fields are low-velocity regions: the Mach number is subsonic. When the supersonic flow enters the parachute canopy and reaches the saturation, it over pressurizes the canopy, and part of the flow moves in the opposite direction, interacting with the shock wave ahead of the canopy, as shown in Figure 6 (right).
Due to pressure decrease at the leeside of the afterbody, the flow separates and recirculating flow is generated at the back of the vehicle (see Figure 6). When the separating shear layer merges, this forms a "neck", which compresses the flow, causing a pressure increase. Behind the neck, there is a far wake that extends several body diameters downstream.
Eddies are axisymmetric behind the capsule, while these are non-axisymmetric in the front and behind the parachute. The instantaneous pressure at the bottom inner wall of the canopy is higher than that at the inner upper walls of the canopy, while the mean pressure field in Figure 5, is shown to be axisymmetric, this explaining the oscillatory movement of the system and its failure.
The maximum averaged pressure is approximately 14400 Pa in front of the capsule and approximately 14900 Pa at the inner surface of the canopy. The maximum instantaneous pressure, at t= 0.126 s, is nearly 14800 Pa in front of the capsule and nearly 6300 Pa near the inner surface of the canopy. Thereafter, the pressure drops drastically from 14,800 Pa to respectively 1,170 Pa immediately downstream of the capsule and to 1,370 Pa downstream of the canopy and tends to rise due to the vortex structures in the flow. A pressure variation of 5130 Pa within the canopy (as shown in Figure 6) confirms the inflation behaviour observed experimentally. Another portion of the flow ejects from the parachute band structure, forming an expansion wave that gradually merges with the bow shock in front of the canopy. The remaining fluid flows through the gap and along the disk structure into the turbulent wake region behind the canopy: there, the flow is characterized by complex and turbulent structures, containing eddies, and the supersonic jet flow.
Figure 7a shows that downstream of the capsule, the instantaneous field of the Mach number has a oscillatory behaviour in the wake region, while, in the same region, the mean field is completely axisymmetric. This means that in the wake, the flow field is not steady, but it starts to oscillate with a radius of oscillation of the order of the capsule diameter. Within the neck downstream of the capsule, as shown in Figure 7c, due to the eddies structures, the flow alternates sonic and supersonic regions. In front of the parachute, the velocity of the flow again drops drastically due to the second bow shock. Downstream of this shock, in front of the canopy, the Mach number in not axisymmetric both in the instantaneous and in the mean flow field: the Mach number at the wind side of the body is 50% higher than in the leeside (see Figure 7a,b).
Figure 8 shows respectively the vorticity and the x, y, z vorticity components contours.
This figure shows that the flow field is completely laminar at the inlet of the computational domain, i.e. the vorticity is nil. Downstream of the bow shock, it suddenly rise to 1500 Hz. Non dimensional eq. of vorticity (Eq. 1) shows that if the vorticity is zero, it remains nil unless there are strong density and pressure gradients, which cause the baroclinic term to inject eddies into the flow.
1 M ∂ ω _ ∂ t + ∇ _ × ω _ × u _ = ∇ ρ _ × ∇ p _ ρ 2 + 1 R e v ∇ 2 ω _ + 1 R e − 1 ρ 2 ∇ ρ _ × ∇ _ · σ _ _ + 1 ρ ∇ μ _ × ∇ 2 u _ + ∇ _ ∇ _ · u _ + 2 ∇ _ × E _ _   ∇ μ _
Since the non-dimensional inertial term is proportional to 1/M, downstream of the capsule, where the Mach number is subsonic, the inertial term is responsible for the “fluctuations” due to the vorticity structures. Once these structure are created, they are transported downstream and interact with the bow shock upstream of the canopy. The x-vorticity field shows that two counter-rotating structures generate just upstream of the capsule and are transported downstream for about 3 capsule radius. The spanwise x and z components of the vorticity are the highest, respectively of the order of 640 Hz and 1800 Hz. The streamline component is negligible with respect to the others, being of order of 40 Hz.
Figure 9 and Figure 10 show that the strong interaction of the flow field with the bow shock is responsible for the pressure and density gradients, that in turn are responsible for the vorticity generation by means of the baroclinic term [16]. Peaks of X-density gradients are of order of 3x10-2 kg/m3/m in the x direction, 1.7x10-1 kg/m3/m in the y direction and 2x10-2 kg/m3/m in the z direction. The density gradients are axisymmetric in the X and Y direction, and not in the z direction, where these are higher on the leeside and lower on the wind side.
As for the pressure gradients, the peaks are of order of 9800 Pa/m in the X-direction, 23000 Pa/m in the Y direction and 2000 Pa/m in the Z direction.
Figure 11a,b show the instantaneous cell Reynolds number contour. The maximum Reynolds number is 1.439*106 upstream of the capsule, then it suddenly reduces approximately to 4.98*102 downstream of the bow shock. Since the Reynolds number is the ratio between diffusive and inertial times, this means that times required to dissipate the eddies is about 500 times longer than inertial times, therefore eddies are transported downstream, where, these are swallowed by the second bow shock. After the second bow shock, due to the density increase, as shown in Figure 13, the Reynolds number also increases to an approximate value of 5.96*104. Crossing this second bow shock, the eddies are strengthened, and the viscous terms are not sufficient to dissipate the turbulence structures.
Figure 12 shows the mean static temperature contour. Due to the sudden decrease in Mach number and rise in the pressure around the vehicle body, a sudden rise in the temperature from 219 K to an approximate value of 382 K can be observed in front of the capsule. The temperature of the flow drops to an average approximate value of 222 K in the wake region, and it again raises at a distance of 0.7m in front of the parachute reaching the maximum value of 404 K inside the canopy region.
Figure 13 shows the density reaches the maximum at the nose of the vehicle with a mean value of 0.1304 kg/m3 and an instantaneous value of 0.1342 kg/m3 which immediately drops at the leeside of the afterbody. In the wake region, the instantaneous density flow field has a non-axisymmetric behaviour, while it is axisymmetric in the mean field. In the wake, the density keeps low for several body diameters and it rises when approaching the parachute. The instantaneous density contour shows that the density gradually decreases inside the canopy increasing the drag area behind the canopy and accordingly the turbulence.

4. Conclusion

In this article, the aerothermodynamic flow characteristics of the rigid capsule/DGB parachute system for Mach number 2.0 are investigated in order to explain the failure of Schiaparelli’s re-entry. LES numerical simulations are performed to compare the instantaneous and mean flow field. These simulations showed that the turbulence generated by the baroclinic term due to the first shock is transported downstream, where it is then swallowed and strengthened by the second bow shock. Due to the generation of these vortices, the wake exhibits non-axisymmetric behaviour in the instantaneous contours, which explains the beginning of capsule fluctuations. The instantaneous pressure, density and velocity flow fields are symmetrical in front of the capsule, while they are not axisymmetric downstream of the capsule, and in particular in the wake. The mean field, on the other hand, is axisymmetric also in the wake region behind the capsule, confirming the oscillatory behaviour of these variables that is responsible for the oscillatory motion of the capsule and the parachute system. Simulations showed the importance of LES with respect to RANS in order to predict the non-stationary flow behaviour. LES simulations are therefore mandatory to explain the reason for the oscillations and to predict this behaviour in order to propose solutions to dampen them.

Author Contributions

All the authors have contributed equally to this paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not Applicable.

Informed Consent Statement

Not Applicable.

Data Availability Statement

Not Applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

DGB Disk-Gap-Band
LES Large Eddy Simulations
TGO Trace Gas Orbiter
ESA European Space Agency
EDL Entry, Descent & Landing
FSI Fluid Structure Interactions
k Turbulent kinetic energy
ω Specific dissipation rate
SST Shear Stress Transport
Li; (1,2,3,4,5) Data points

References

  1. NASA (2017). Mars planet facts news & images | NASA Mars rover + mission info. [online] Available at: https://mars.nasa.gov/ [Accessed 15 May 2017].
  2. Pezzella, G., Viviani, A., 2011, “Aerodynamic Analysis of a Manned Space Vehicle for Missions to Mars”, Journal of Thermodynamics, Volume 2011, Article ID 857061. [CrossRef]
  3. Hamilton, H. H., II, 2000, “Approximate Method of Predicting Heating on the Windward Side of the Space Shuttle Orbiter and Comparisons with Flight Data,” Entry Vehicle Heating and Thermal Protection Systems: Space Shuttle, Solar Starprobe, Jupiter Galileo Probe, Progress in Astronautics and Aeronautics. P. Bauer, and H. Collicott, eds., American Institute of Aeronautics and Astronautics, New York, NY, pp. 21- 53. [CrossRef]
  4. Hollis, Brian Ray. Experimental and computational aerothermodynamics of a Mars entry vehicle. North Carolina State University, 1996.
  5. Anderson Jr, John D. Hypersonic and High-Temperature Gas Dynamics. 2006.
  6. Sengupta, A., Steltzner, A., Witkowski, A., et al., 2007b. An overview of the Mars science laboratory parachute decelerator system. In: Aero- space Conference, 2007 IEEE. pp. 1–8.
  7. Li, S., Peng, Y., 2011. Mars entry trajectory optimisation using DOC and DCNLP. Adv. Space Res. 47, 440–452. [CrossRef]
  8. M. L. Accorsi, J. W. Leonard, R. J. Benney, and K. R. Stein, “Structural modeling of parachute dynamics,” AIAA Journal, vol. 38, no. 1, pp. 139–146, 2000. [CrossRef]
  9. M. L. Accorsi, R. J. Benney, V. Kalro, J. W. Leonard, K. R. Stein, and T. E. Tezduyar, “Parachute fluid-structure interactions: 3- D computation,” Computer Methods in Applied Mechanics and Engineering, vol. 190, no. 3-4, pp. 373–386, 2000. [CrossRef]
  10. M.L.Accorsi, R.J.Benney, J.W.Leonard, K.R.Stein, and T.E.Tezduyar, “Fluid-structure interactions of a round parachute: modelling and simulation techniques,” Journal of Aircraft, vol. 38, no. 5, pp. 800–808, 2001. [CrossRef]
  11. Gao, X.L., Zhang, Q.B., Tang, Q.G., et al., 2013. Numerical study on fluid-structure interaction of slot-parachute’s inflation process. Acta Aeronaut. Astronaut. Sin. 34, 2265–2276. [CrossRef]
  12. Tezduyar, T.E., Kenji, T., Creighton, M., et al., 2010. Space–time finite element computation of complex fluid–structure interactions. Int. J. Numer. Methods Fluids 64, 1201–1218. [CrossRef]
  13. Peterson, C., Strickland, J., 1996. The fluid dynamics of parachute inflation. Annual Reviews of Fluid Mechanics 28, 361–387. [CrossRef]
  14. KARAGIOZIS, K., KAMAKOTI, R., CRIAK, F., and PANTANO, C. A computational study of supersonic disk-gap-band parachutes using large-eddy simulation coupled to a structural membrane. Journal of Fluids and Structures, 27(2), 175–192 (2011). [CrossRef]
  15. Giulio, S. Numerical investigation of the parachute-capsule aerodynamics in a Mars atmosphere reentry. Master of Science, Università Degli Studi Di Padova, Italy, 2022.
  16. JOHARI, H. and DESABRAIS, K. J. Vortex shedding in the near wake of a parachute canopy. Journal of Fluid Mechanics, 536, 185–207 (2005).
Preprints 72778 g001
Figure 1. Geometric configuration of a rigid disk-gap-band (DGB) supersonic parachute along with the Schiaparelli capsule.
Figure 1. Geometric configuration of a rigid disk-gap-band (DGB) supersonic parachute along with the Schiaparelli capsule.
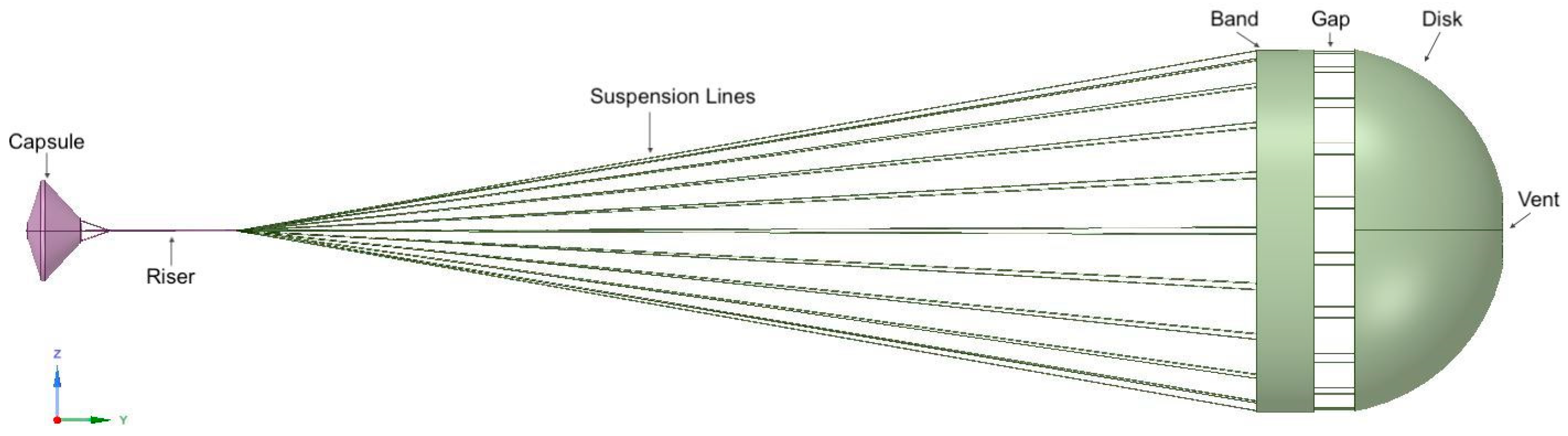
Preprints 72778 g001
Preprints 72778 g002
Figure 2. Geometry of the parachute (left) and Schiaparelli capsule (right).
Figure 2. Geometry of the parachute (left) and Schiaparelli capsule (right).
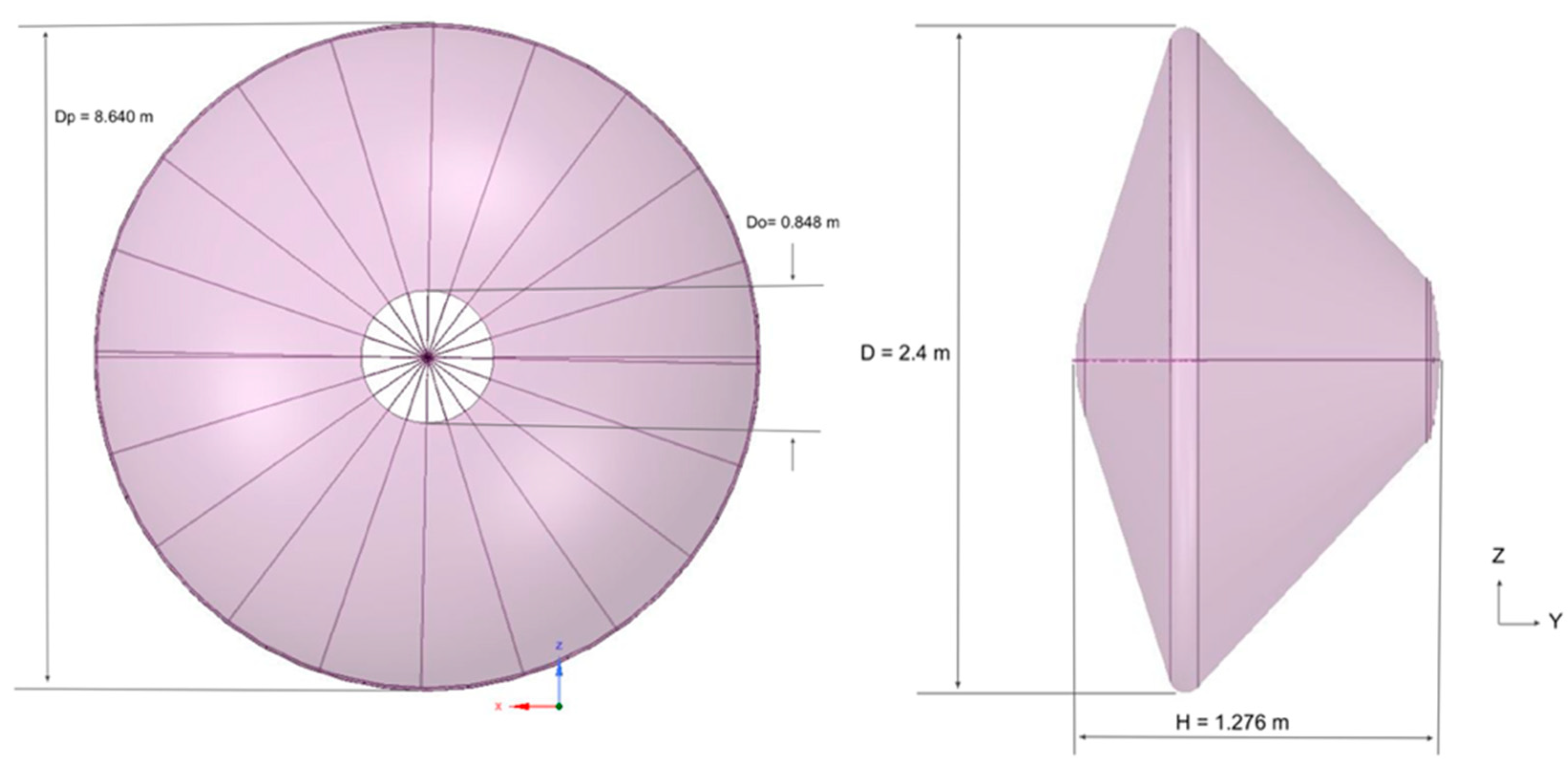
Preprints 72778 g002
Preprints 72778 g003
Figure 3. Data set locations L1, L2, L3, L4, L5 along the computational domain symmetric plane.
Figure 3. Data set locations L1, L2, L3, L4, L5 along the computational domain symmetric plane.
Preprints 72778 g003
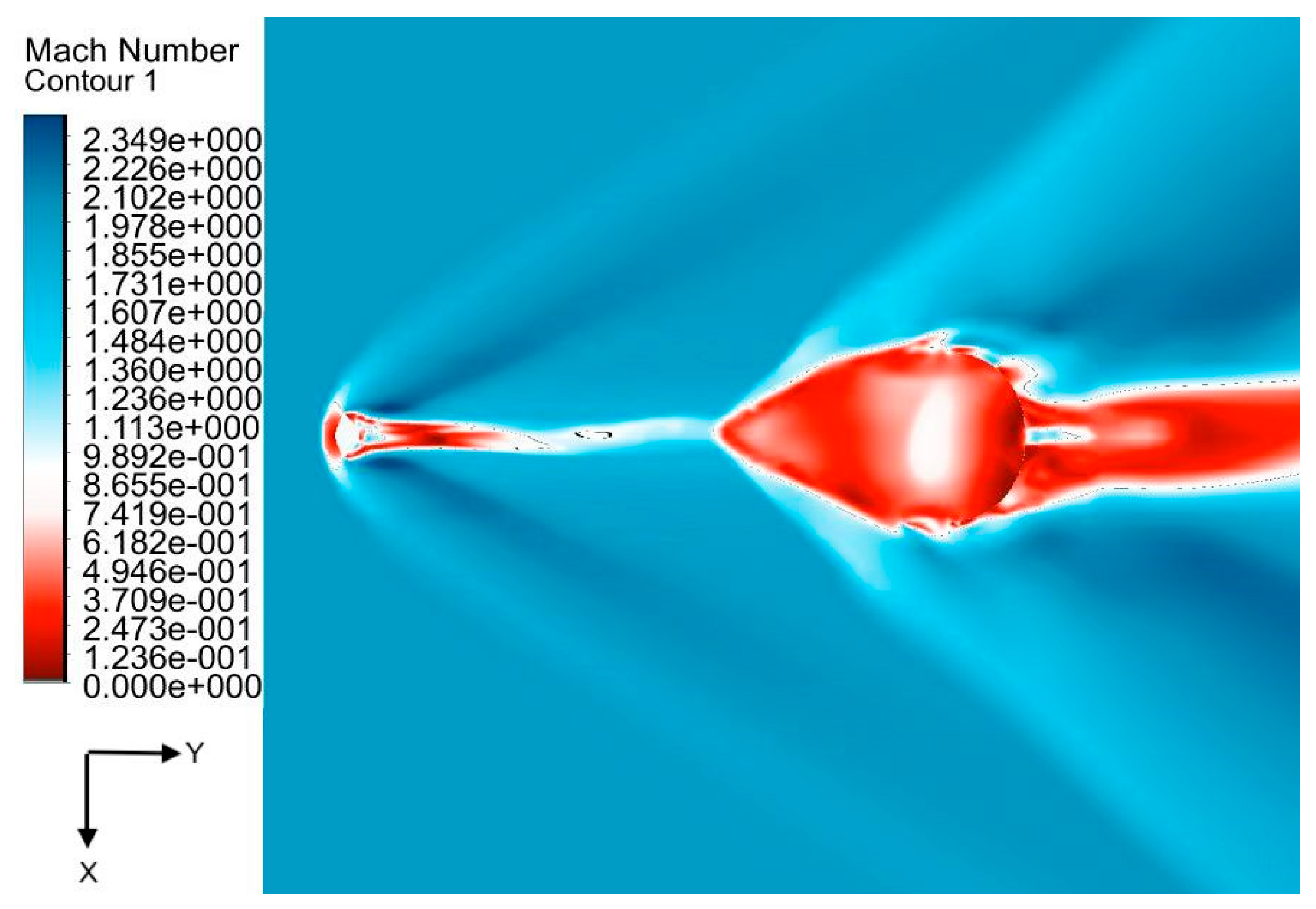
Preprints 72778 g004
Figure 4. Mach number contour in the midplane of the computational domain.
Figure 4. Mach number contour in the midplane of the computational domain.
Preprints 72778 g004
Preprints 72778 g005
Figure 5. Static pressure contours of capsule and rigid DGB parachute system at Mach number 2.0: (a) mean static pressure, (b) instantaneous static pressure.
Figure 5. Static pressure contours of capsule and rigid DGB parachute system at Mach number 2.0: (a) mean static pressure, (b) instantaneous static pressure.
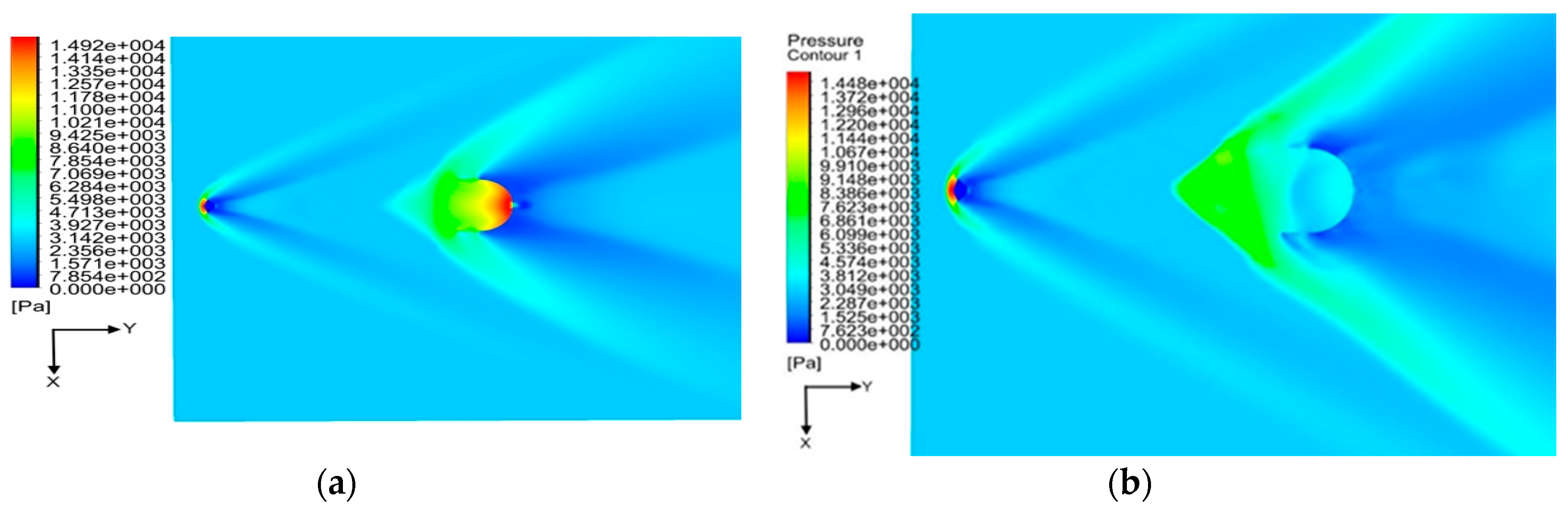
Preprints 72778 g005
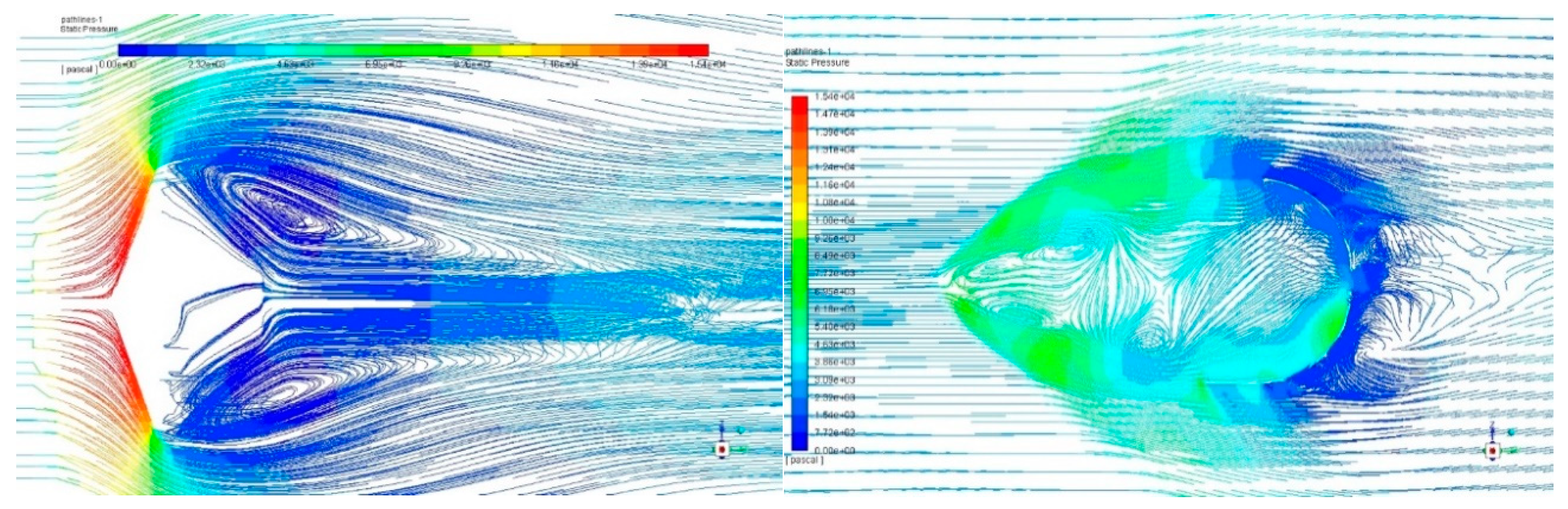
Preprints 72778 g006
Figure 6. Path lines coloured by the static pressure: (left) around the capsule, (right) around the parachute.
Figure 6. Path lines coloured by the static pressure: (left) around the capsule, (right) around the parachute.
Preprints 72778 g006
Preprints 72778 g007
Figure 7. (a) Instantaneous Mach number (b) Mean Mach number (c) instantaneous Mach number variation along the computational domain (d) mean Mach number variation along the computational domain.
Figure 7. (a) Instantaneous Mach number (b) Mean Mach number (c) instantaneous Mach number variation along the computational domain (d) mean Mach number variation along the computational domain.
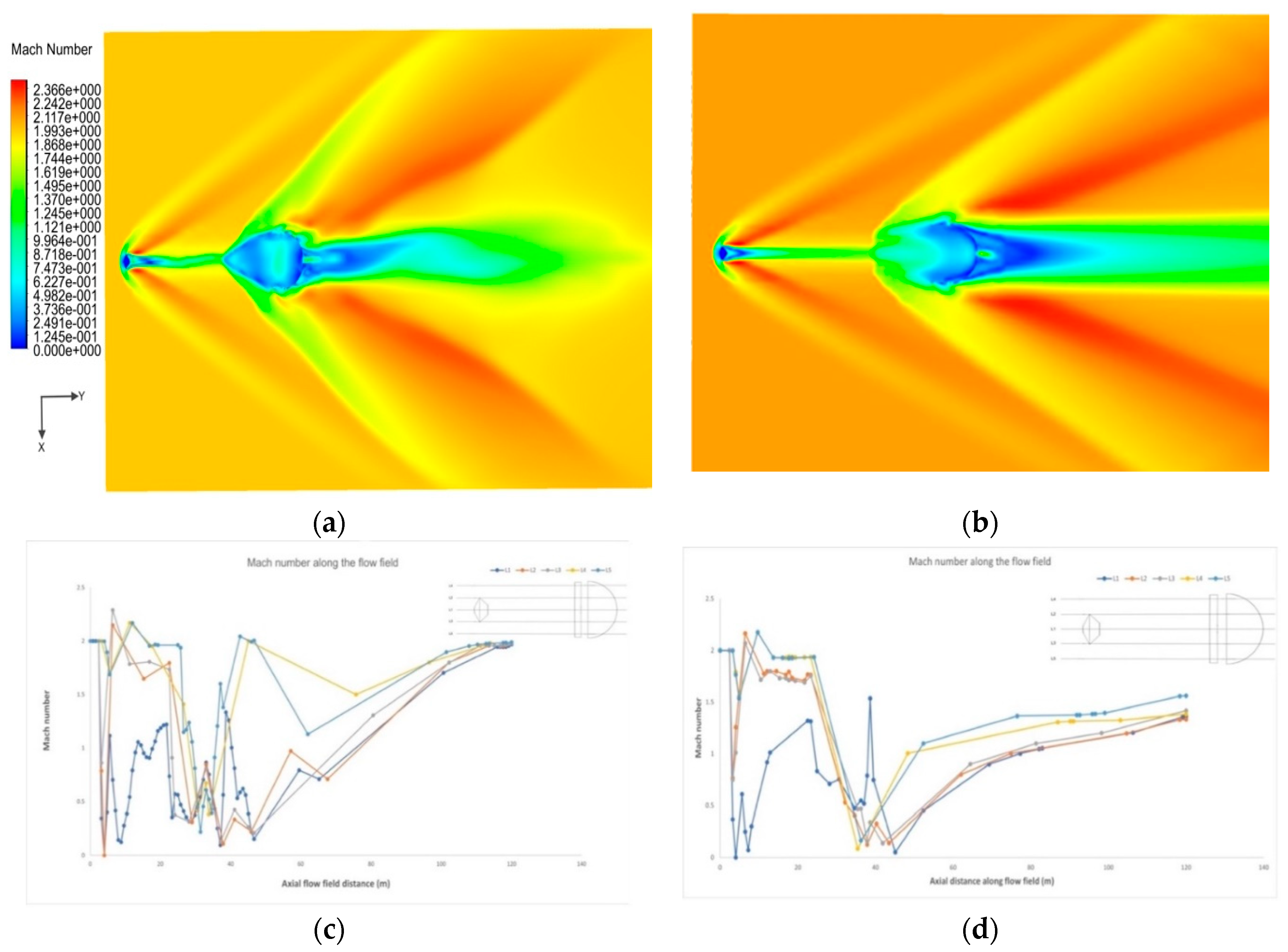
Preprints 72778 g007
Preprints 72778 g008aPreprints 72778 g008b
Figure 8. Instantaneous contours: (a) vorticity, (b) x-vorticity, (c) y-vorticity, (d) z-vorticity.
Figure 8. Instantaneous contours: (a) vorticity, (b) x-vorticity, (c) y-vorticity, (d) z-vorticity.
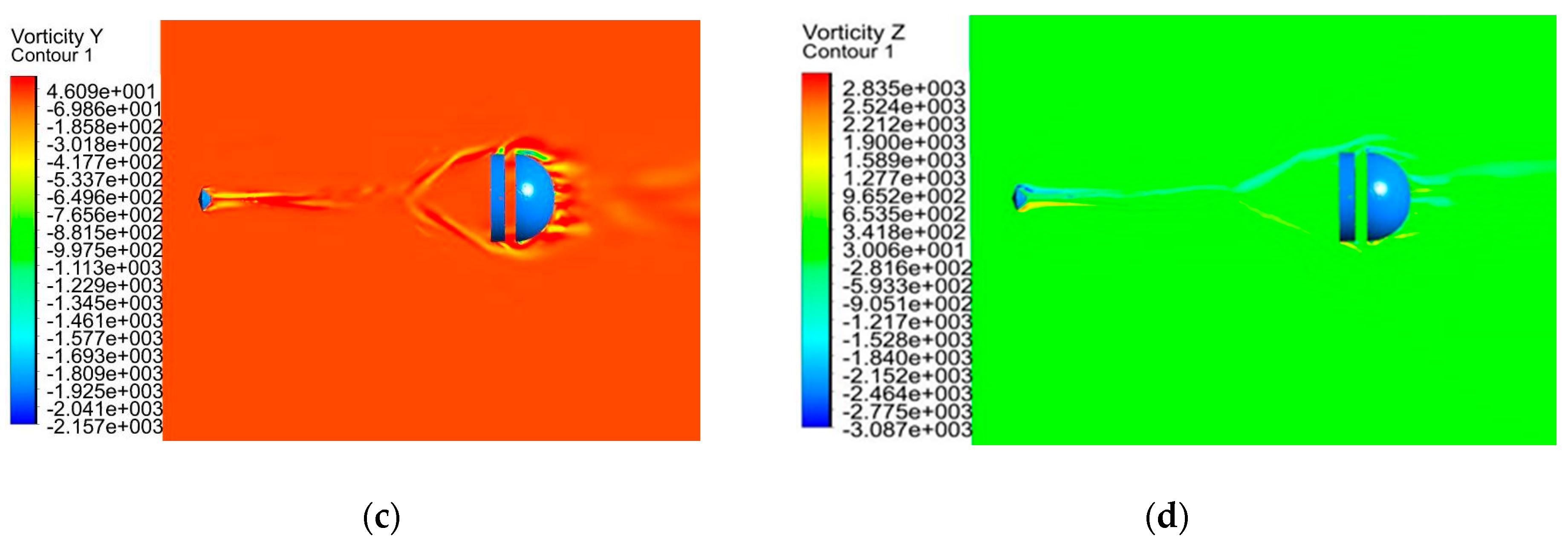
Preprints 72778 g008aPreprints 72778 g008b
Preprints 72778 g009
Figure 9. Instantaneous density gradient contours: (a) x-density gradient contour, (b) y-density gradient contour, (c) z-density gradient contour.
Figure 9. Instantaneous density gradient contours: (a) x-density gradient contour, (b) y-density gradient contour, (c) z-density gradient contour.
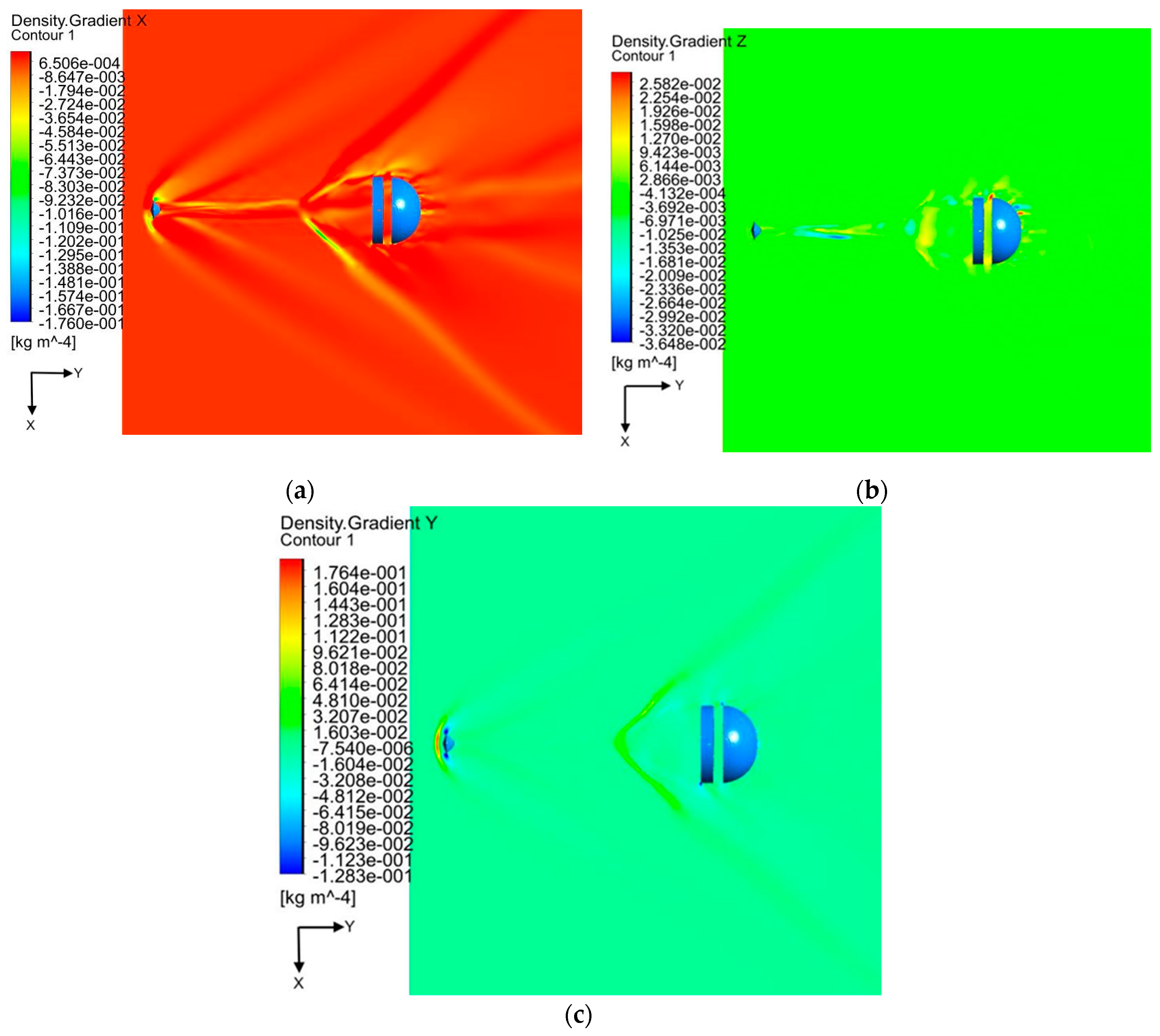
Preprints 72778 g009
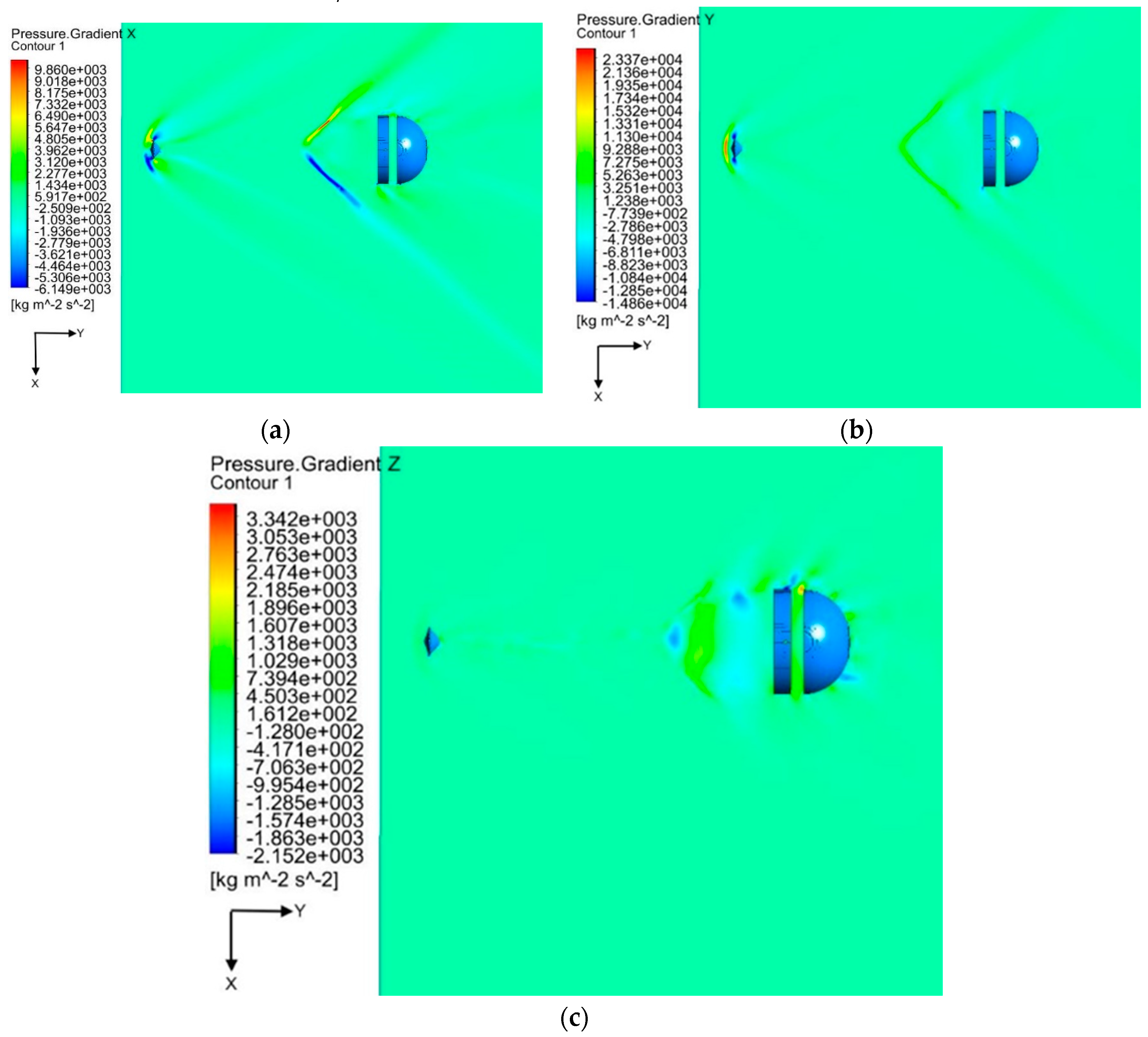
Preprints 72778 g010
Figure 10. Instantaneous pressure gradient: (a) x-pressure gradient contour, (b) y-pressure gradient, (c) z-pressure gradient contour.
Figure 10. Instantaneous pressure gradient: (a) x-pressure gradient contour, (b) y-pressure gradient, (c) z-pressure gradient contour.
Preprints 72778 g010
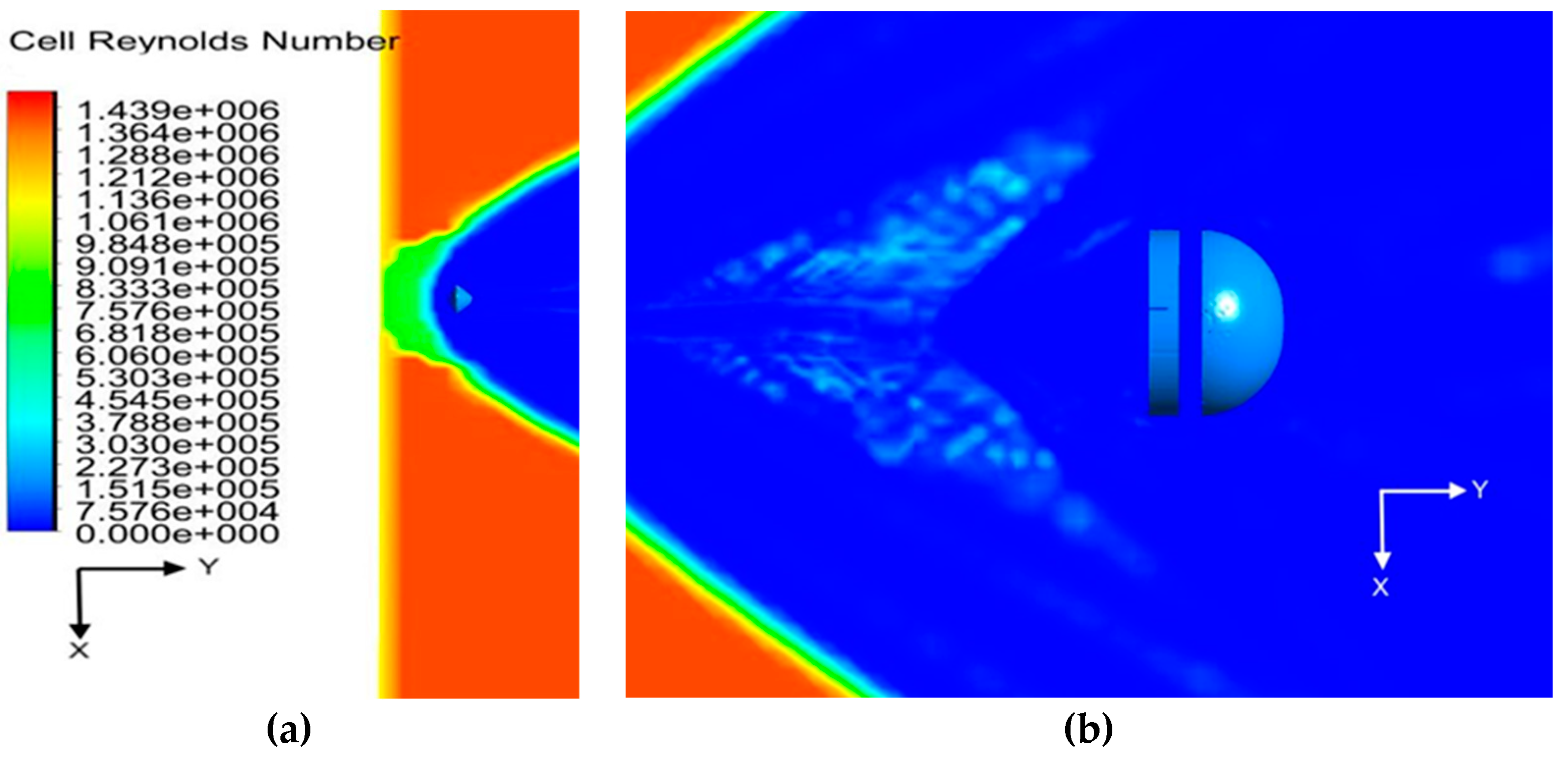
Preprints 72778 g011
Figure 11. Instantaneous Cell Reynolds number contour of: (a) the capsule, (b) the parachute for along the computational domain centre plane.
Figure 11. Instantaneous Cell Reynolds number contour of: (a) the capsule, (b) the parachute for along the computational domain centre plane.
Preprints 72778 g011
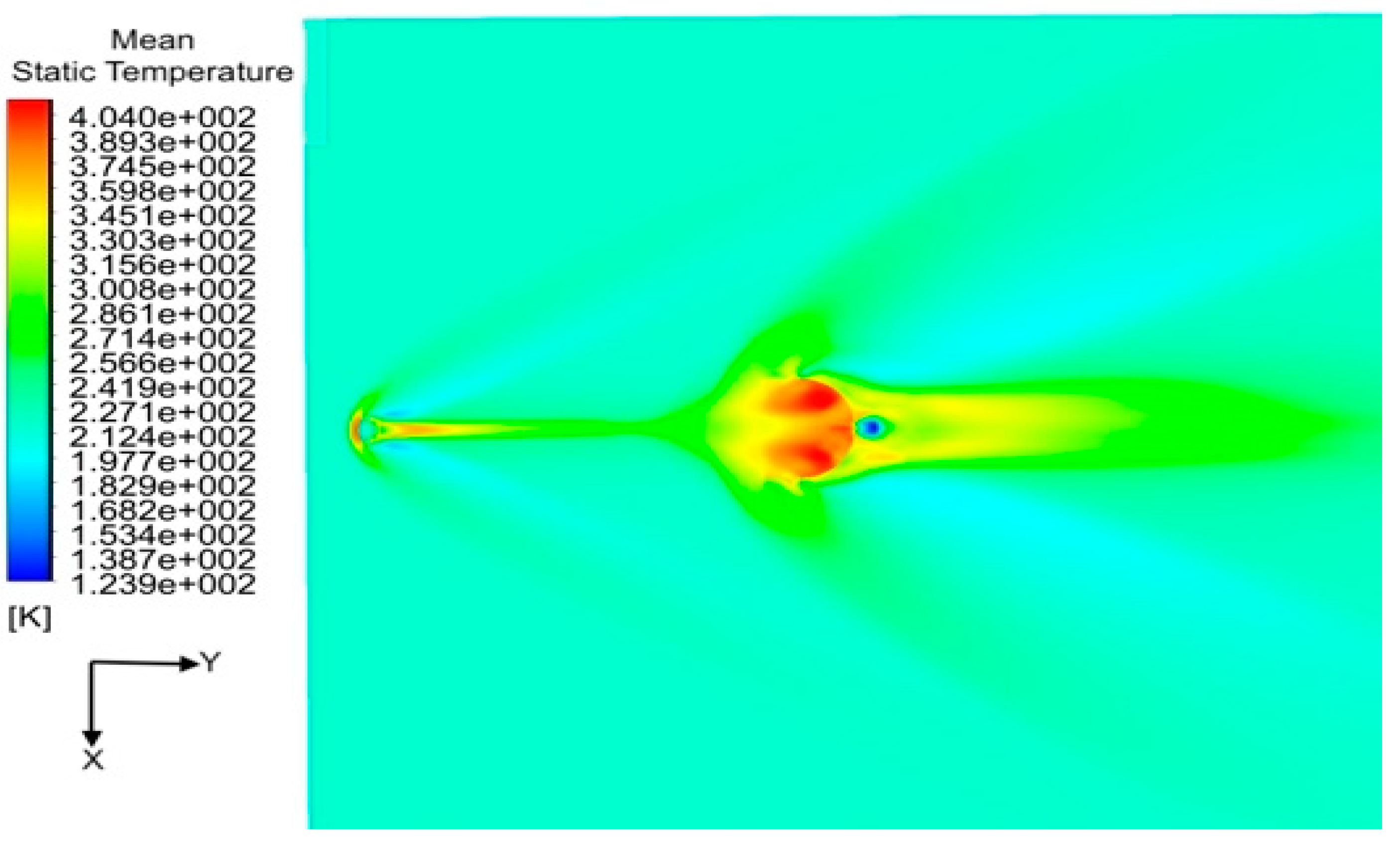
Preprints 72778 g012
Figure 12. Mean static temperature contour.
Figure 12. Mean static temperature contour.
Preprints 72778 g012
Preprints 72778 g013
Figure 13. Instantaneous and Mean density contours.
Figure 13. Instantaneous and Mean density contours.
Preprints 72778 g013
Table 1. Boundary Conditions.
Table 1. Boundary Conditions.
Gauge Pressure (Pa) Temperature (K) Mach number Angle of attack
2891 219 2 0º
Table 2. Analytical and simulated values of flow variables downstream of the capsule bow shock. Upstream values are computed from the simulation.
Table 2. Analytical and simulated values of flow variables downstream of the capsule bow shock. Upstream values are computed from the simulation.
Upstream Analytical Reference [14] Reference Error % Simulations Simulation error %
M1 = 2.00 M2 = 0.56 M2 = 0.56 0% 0.56 0%
ρ1 = 0.044 ρ2 = 0.126 ρ2 = 0.126 0% 0.126 0%
p1 = 2891 p2 = 12695.26 p2 = 12691.49 0.02% 12559.85 1.06%
T1 = 219 T2 = 335.83 T2 = 335.07 0.22% 335.06 0.22%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated