Prerpints.org logo
Preprint
Article

Point-MDA: Progressive Point Cloud Analysis for Extreme Multi-Scale Detail Activation

Altmetrics

Downloads

163

Views

53

Comments

0

This version is not peer-reviewed

Submitted:

03 May 2023

Posted:

06 May 2023

You are already at the latest version

Alerts
Abstract
The point cloud is a form of three-dimensional data that comprises various detailed features at multiple scales. Due to this characteristic and its irregularity, point cloud analysis based on deep learning is challenging. While previous works utilize the sampling-grouping operation of PointNet++ for feature description and then explore geometry by means of sophisticated feature extractors or deep networks, such operations fail to describe multi-scale features effectively. Additionally, these techniques have led to performance saturation. And it is difficult for standard MLPs to directly "mine" point cloud. To address above problems, we propose the Detail Activation (DA) module, which encodes data based on Fourier transform after sampling and grouping. We activate the channels at different frequency levels from low to high in the DA module to gradually recover finer point cloud details. As training progresses, the proposed Point-MDA can uncover local and global geometries of point cloud progressively. Our experiments show that Point-MDA achieves superior classification accuracy, outperforming PointNet++ by 3.3% and 7.9% in terms of overall accuracy on the ModelNet40 and ScanObjectNN dataset, respectively. Furthermore, it accomplishes this without employing complicated operations, while exploring the full potential of PointNet++.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

The point cloud is a data set of points in 3D space, where each point possesses its own distinct attributes like color, normal direction or light intensity. This data is commonly acquired through sensors such as laser radar or camera, and is ideal for preserving the geometric structure and surface features of objects, making it very suitable for 3D scene understanding. Point cloud classification has been active in the research fields such as photogrammetry and remote sensing for decades. It has become an important part of intelligent vehicles [1], automatic driving [2], 3D reconstruction [3], forest monitoring [4], robot perception [5], traffic signage extraction [6] and so on. Due to factors like irregularity and disorder, high sensor noise, complex scenes and non-homogeneous density, point cloud classification is still challenging. Most previous works focuse on manually designing point cloud features [7], which are limited to specific tasks and cannot be optimized easily for new tasks. Nowadays, deep learning has become the leading method of point cloud classification because of its high efficiency in processing large data sets and the autonomy of extracting features.
PointNet, proposed by Charles [8], is the first groundbreaking deep neural network directly processing unordered point clouds. PointNet mainly utilizes multi-layer perceptions (MLPs) to elevate the coordinate space of point clouds to a high-dimensional feature space, and then obtain representative global feature vectors of point clouds by global pooling. However, PointNet pays too much attention to the global features of point clouds, and its ability to exploit local features is poor. The subsequently proposed method, PointNet++ [9], is a layered network. Its abstraction layer consists of a sampling layer, a grouping layer, and a PointNet layer for nonlinear mapping. PointNet++ can better learn local features.
Inspired by PointNet++, some works attempt to extract local geometric features of point clouds by using convolution [10,11,12], graph convolution [13,14], and transformer [15,16] in the non-linear mapping layers. Some methods are also proposed to improve classification performance by deepening the network [17,18,19] or stacking network structures [20,21,22]. In addition, many researchers choose to convert irregular point clouds into regular data before processing [23,24], such as converting point clouds into grids for uniform distribution and then using 3D-CNN [25] to process grid data. These approaches have the disadvantages of high computational complexity and quantization noise, resulting in low accuracy and efficiency of point cloud classification.
Furthermore, the sampling-grouping operation can lead to the loss of point cloud information and the neglect of various detail regions. Using complex feature extractors in the non-linear mapping layer cannot also solve the sampling-grouping operation’s failure to capture multi-scale detailed features well. Meanwhile, [26] proves that the standard MLP is more suitable for low-dimensional visual and graphics tasks, and cannot learn high-frequency information in theory and practice. Deepening or stacking network structures can lead to network degradation, model performance saturation, and inference delay.
To address the above issues, this paper proposes a simple and intuitive point cloud analysis network without any delicate local feature exploration algorithms or deepening networks: a detail activation operation, similar to positional encoding, is added between the sampling-grouping operation and the non-linear mapping layer, so that subsequent coordinated-based MLPs can learn higher frequency features. We develop a novel Detail Activation (DA) module based on the corroborating theory using Neural Tangent Kernels [26]. The strategy we adopt is to gradually activate the high-frequency channels of the DA module’s inputs and successively unfold more complex details as the training proceeds. Specifically, after sampling and grouping, the DA module first recovers the detailed features of the point cloud at a low-frequency level. Then, in different network layers, we recover the feature information at different scales by activating channels at different frequency levels in the DA module. In this way, we progressively expand more intricate details as the training continues, which is more conducive to the subsequent MLP layer to learn detailed features.
Additionally, inspired by ResNet [27], DenseNet [28], and PointMLP [18], we develop an improved MLP module that integrates the design concepts of residual connection and dense connection. We call the module ResDMLP. Ablation experiments show that our network, coupling these two designs (ResDMLP and DA), can more efficiently learn and process point clouds than standard MLPs.
Finally, to enable the current layer to retain the details activated by the previous layers ultimately, we introduce residual connections between the network layers so that the entire feature extraction process can be jointly supervised with the details from the farthest scale to the current scale. In this paper, the following is achieved:
(1) We propose a new framework named Point-MDA, which can progressively expand more intricate details as training progresses. Point-MDA can jointly monitor the entire feature extraction process through the activated details from the farthest scale to the current scale.
(2) We introduce a novel Detail Activation (DA) module. In different layers of Point-MDA, we activate different frequency levels in the DA module. By progressively recovering detailed features at different scales, we aim to address the issue of information loss caused by the conventional sampling-grouping operation failing to fully explore the geometry of irregular point clouds. Additionally, the DA module enables subsequent MLPs to better learn high-frequency information, thereby improving the accuracy and robustness of point cloud classification.
(3) We design a plug-and-play style MLP-based module (ResDMLP) that combines ideas of residual connection and dense connection, aiming to reuse features, alleviate gradient disappearance, and help conduct training more intensely, accurately, and effectively.
Our method achieves superior overall and class-average accuracy on the point cloud classification task on ModelNet40 [29] and ScanObjectNN [30] datasets without complex feature extraction algorithms or deepening and stacking network structures, extensively tapping the potential of PointNet++.

2. Related Works and Proposed Methods

2.1. Related Works

The point cloud analysis tasks based on deep learning have always been challenging. Recent studies have shifted their focus towards achieving good performance by simplifying methods, rather than designing complex feature extraction algorithms. Some works considers improving the related modules in non-linear mapping layers to overcome model performance bottlenecks. In this section, we first review the development of point cloud analysis networks and compare them with our proposed method. Our method utilizes a progressive point cloud classification network structure that can extract point cloud details at different scales, without involving complex network design and module stacking. Our basic strategy is to gradually activate the high-frequency channels in the DA module and gradually unfold more complex details as the training progresses.

2.1.1. Point Cloud Analysis

Since the point cloud is irregular, previous works usually consider converting the raw point cloud into regular data before processing [23,24,31]. However, these transformations are accompanied by complex computation and loss of details, which leads to low accuracy and efficiency of point cloud analysis. Processing the original point cloud data directly can reduce the heavy computation, fully consider the characteristics of point clouds and retain data information more thoroughly. PointNet [8] pioneered using deep learning directly for 3D point cloud analysis tasks. Due to the disorder of point clouds, it is impossible to directly use convolution and other operations on the original point cloud. PointNet proposes to exploit the symmetric function to solve this problem and designs a network structure that can perform classification and segmentation tasks. PointNet++ [9] is one of the most influential hierarchical neural architectures for analyzing point clouds. Its architecture is simple, but its full potential remains to be tapped. PointNet++’s principal operations are composed of sampling, grouping, and shared MLPs. It can better obtain the local features of point clouds. Based on PointNet++, subsequent researchers propose a variety of point cloud analysis networks, such as SO-Net [32] and PointWeb [33]. Our Point-MDA also follows the design concept of PointNet++ that applies the sampling-grouping operation with an MLP-based architecture. Nevertheless, Point-MDA performs the encoding operation of activating the point cloud detailed features after the sampling-grouping layers but before the MLP layers. Moreover, Point-MDA deactivates point cloud features at different detail scales from low to high among different layers of the network and introduces the identity mapping between layers of the network to achieve the reuse of details activated.

2.1.2. Point Cloud Local Geometry Exploration

Owing to the success of PointNet++, the recent research focus is shifted to point cloud local geometry exploration. The methods of local geometry exploration can be broadly divided into four categories: convolution-based [10,12], graph-based [13,34,35], transformer-based [15,16], and geometry-based [18,36]. One of the most prominent convolution-based methods is PointConv [12], which regards the convolution kernel as a non-linear function composed of weight and density functions. The weight functions are learned through MLPs, and the density functions are learned through kernel density estimation. Unlike convolution-based methods, graph-based methods use graph edges to study the correlation between points. For example, Zhou [35] proposed the adaptive graph convolution (AdaptConv), which can generate an adaptive kernel for points according to their dynamic learning features. In this way, AdaptConv improves the flexibility of graph convolution and captures various relationships of points from different semantic parts effectively. Transformer-based methods emphasize the enhancement of connections between point cloud Surface Representation ds like Point-BERT [15] and Point Transformer [16]. Different from other categories, geometry-based methods are more customized. For example, PointMLP [18] proposes a lightweight geometric affine module to transform the local points to a normal distribution adaptively. At the same time, Repsurf [36] exploits representative surfaces to explicitly describe the points in local areas. With the development of local geometry exploration, the performance on various tasks tends to be saturated. Continuing this orbit will bring slight improvement. Unlike these methods demanding sophisticated local feature extractors, Point-MDA, proposed in this paper, succeeds in tapping the potential of point cloud analysis networks considerably by mainly utilizing simple encoding operations based on Fourier feature transform.

2.1.3. Shared MLP Improvement for Point Cloud Analysis

The essence of shared MLPs is generally known as multi-layer perceptrons (MLPs), which use a 1x1 convolution kernel to make convolution operations, aiming to reduce network training parameters and achieve a weight-sharing mechanism similar to CNN. Shared MLPs have been widely used in point cloud analysis networks. In recent years, point cloud analysis tasks have noticed that complex feature extractors for local geometric exploration of point clouds are not the key to point cloud analysis [17,18]. To better match the network structure, some works have upgraded the MLP module in the non-linear mapping layer to improve network performance. For example, PointMLP [18] builds a deep network for point cloud analysis using only residual feed-forward MLPs and abandons the use of delicate local geometric extractors. PointNorm [17] combines the advantages of InvResBlock [37] and SEBlock [38] to design a new controllable residual block (C-ResBlock) aimed at improving computational efficiency. PointNeXT [19] proposes an inverted residual bottleneck design and separable MLPs into PointNet++ to achieve efficient and effective model scaling. In contrast, the proposed ResDMLP module combines residual and dense connections principles. We aim not to deepen the network or reduce model parameters but to achieve feature reuse and help with more accurate and practical training. In ablation experiments, it has been proven that our developed ResDMLP module is more suitable for Point-MDA.

2.2. Proposed Methods

In this section, we first explain the significance and principle of the proposed Detail Activation module from the theory and formulas and how to use the DA module to activate point cloud details at different scales hierarchically. Then we introduce the ResDMLP module from the perspective of the module structure, which combines the concepts of residual and dense connections. Finally, based on the proposed DA and ResDMLP modules, we propose the specific framework of Point-MDA, as shown in Figure 2. It is worth noting that Point-MDA can utilize information from the farthest scale to the current scale to jointly supervise the entire feature extraction process, achieving progressive training.

2.2.1. Detail Activation Module

Point cloud data contains detailed information at different scales. For example, when we acquire point cloud data through laser scanning, the obtained data is usually incomplete and uneven due to factors such as low surface reflectivity of some materials and cluttered urban background. Such data typically has detailed information at different scales. However, even if the point cloud data is sampled and grouped hierarchically, the detailed information of the point cloud cannot be well excavated. In addition, [26] indicates that deep networks tend to learn functions with lower frequencies. It also suggests that before feeding data into a neural network, it is possible to better capture patterns and structures containing high-frequency variations by mapping the data from its original dimensionality to a higher dimensionality using high-frequency functions.
In the context of implementing point cloud classification based on deep learning, we utilize these findings and develope the Detail Activation (DA) module to encode and activate point cloud details for the sampled-grouped point cloud coordinates, while also helping subsequent MLPs represent high-frequency functions, significantly improving classification accuracy. The core implementation of the DA module is based on the basic principles of Fourier transform and can be expressed in formula as follows:
γ p = sin ⁡ 2 0 π p , cos ⁡ 2 0 π p , … , sin ⁡ 2 L − 1 π p , cos ⁡ 2 L − 1 π p ,
where p = p i i = 1 , … , N ∈ R N X 3 , represents a set of points, N indicates the number of points in an x , y , z Cartesian space and L represents different Fourier feature frequencies activated in the Detail Activation module. Specifically, L means the scales of detailed features we want to activate. γ · works as a mapping from R into a higher dimensional space R2L. The DA module is applied separately to each of the three coordinate values in the sampled-grouped point cloud.
The characteritics of point clouds imply varying degrees of learning difficulty and focal points. Therefore, we suggest building and training models in a progressive manner to encourage division of labor between network layers and fully utilize the power of the DA module across all frequency bands. The success of [39] has strengthened our motivation to construct a progressive layered network structure. We do not activate all detail scales at once. we gradually expand the training sets of point clouds by one closer scale at each model layer. Different network layers activate different Fourier feature frequencies of the DetailActivation module. For instance, in the shallow layers of the network, only low-frequency channels in the DA module are activated, thereby facilitating the learning of features that are matched with low-level details. Furthermore, in most existing hierarchical point cloud analysis networks, more information reuse is required between model layers. Despite attempts to restore point cloud details by activating channels of varying frequencies in DetailActivation through layer activation, earlier layers are unable to retain the details of previous layers. To address this challenge, we introduce skip connections between layers of the network, serving as a joint supervision mechanism that encompasses the entire feature extraction process for details from the farthest to the current scale. As a result, the final layer of the network is under the supervision of all the layers, whereas the earliest layer only exposes the point cloud features on the coarsest detail scale.

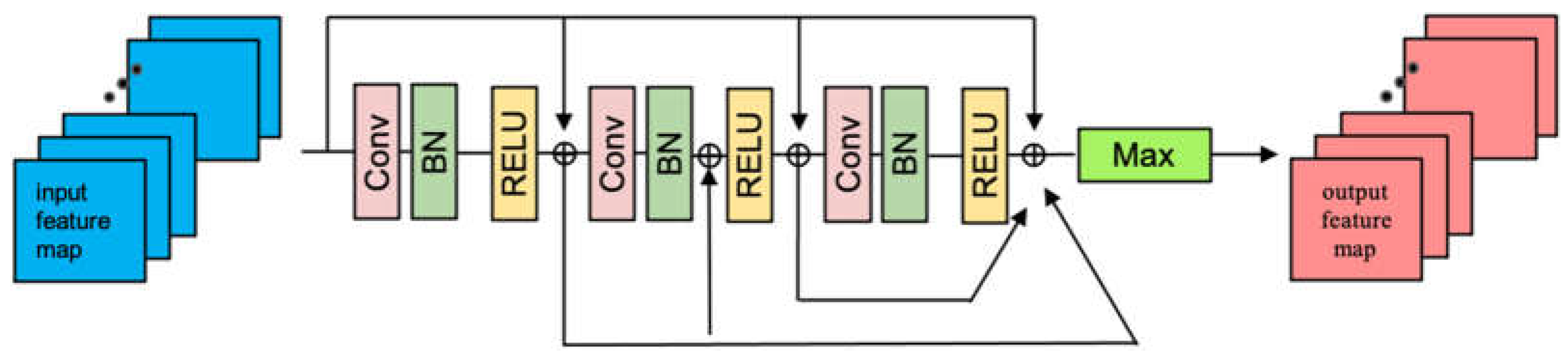
2.2.2. ResDMLP Module

To capture the non-linear characteristics of point cloud data, the multi-layer perceptron (MLP) is introduced as a non-linear mapping layer in the point cloud classification network for feature extraction and abstraction. A novel MLP module, named ResDMLP, is designed by combining the ideas of ResNet [27] and DenseNet [28] to enhance the performance of the network in conjunction with the Point-MDA structure.
ResNet was originally intended for 2D image classification tasks to cope with the degradation problem in deep networks via cross-layer connections. DenseNet introduces dense blocks, where each layer within each block is connected to all previous layers, producing a network that can effectively utilize the previous layers’ features. Recently, PointMLP [18] proposed a deep network using residual feedforward MLP. Following PointMLP’s approach, we merge residual blocks and dense blocks to the MLP module aimed at non-linear mapping layers. The ResDMLP module resembles DenseNet’s structure but utilizes ResNet’s “addition” functionality. Rather than intensifying the network, the ResDMLP module is intended to complement the entire progressive network structure, promote feature reuse, decelerate gradient disappearance, and facilitate more accurate training. Figure 1 depicts the ResDMLP module overview.
Preprints 72523 g001
Figure 1. Overview of the proposed ResDMLP module which combines the concepts of residual connection and dense connection. The ResDMLP module resembles the architecture of DenseNet, but it diffes in that addition is used instead of concatenation. “⨁” means that the corresponding elements of features are summed rather than concatenated.
Figure 1. Overview of the proposed ResDMLP module which combines the concepts of residual connection and dense connection. The ResDMLP module resembles the architecture of DenseNet, but it diffes in that addition is used instead of concatenation. “⨁” means that the corresponding elements of features are summed rather than concatenated.
Preprints 72523 g001

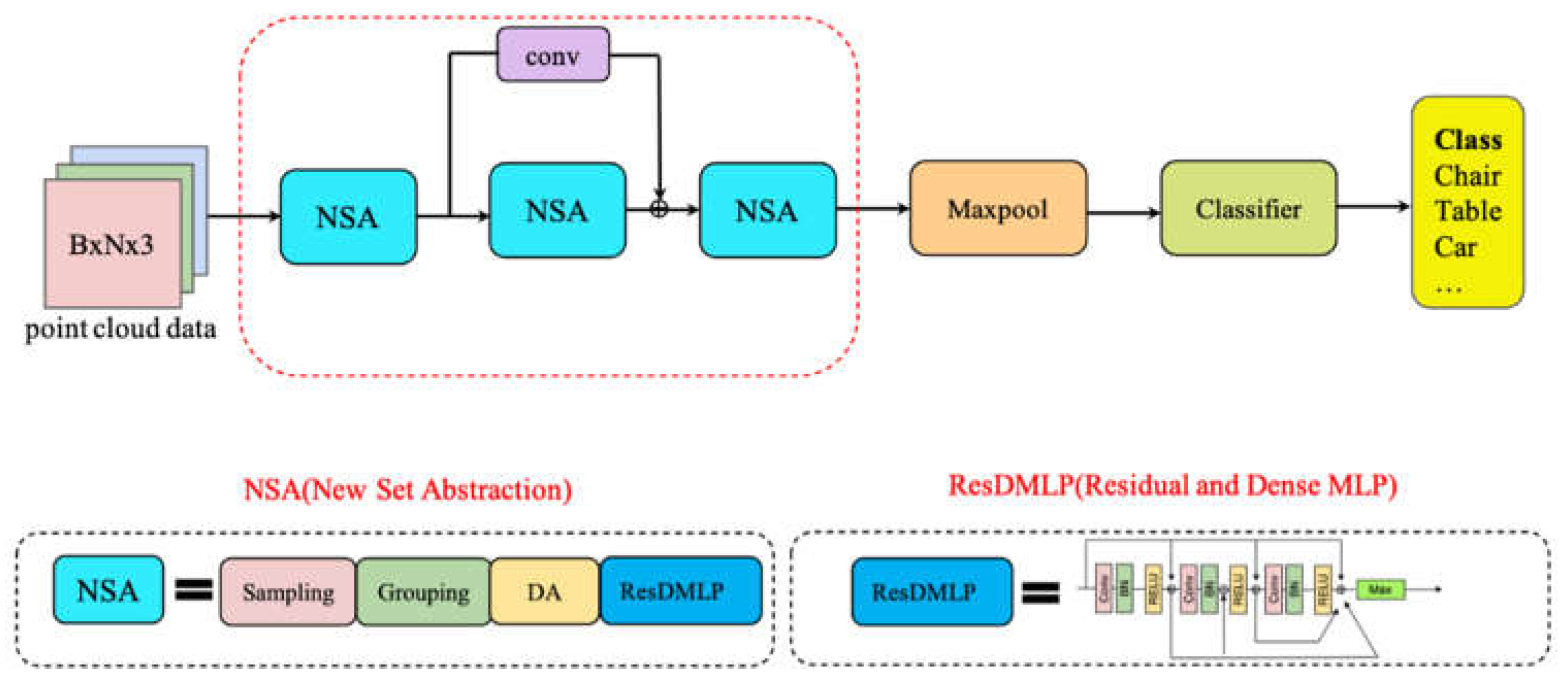
2.2.3. Framework of Point-MDA

The framework of Point-MDA is illustrated in Figure 2, which is a simple yet powerful MLP-based network designed for point cloud analysis by avoiding complex operations and deepening of the network. Given a set of points P =   p i i = 1 ,   … , N   ∈   R N X 3 , where N indicates the number of points in an x , y , z Cartesian space. The workflow of Point-MDA can be formulated as follows:
f n = ∑ i = 1 n − 2 E ( f i ) + R e s D M L P ( γ L i ( G ( S ( P ) ) ) ) ,
where S ( ⋅ ) is the sampling function and G ⋅ is the grouping function. Additionally, γ L i represents the DA module, which activates L frequency level initiated in network layer i. Furthermore, Ε ( ⋅ ) refers to 1 × 1 convolutions that adjust data dimensions. For this study, we set n = 3.
Point-MDA can be divided into four steps: sampling-grouping, DetailActivation, non-linear mapping, and classification. Drawing inspiration from PointNet++, we develope a new set abstraction layer composed of three modules: sampling-grouping, DetailActivation, and non-linear mapping. We repeat this new set abstraction layer three times to progressively capture and highlight point cloud details of differing scales, ranging from coarse to fine. For point sampling, we utilize Farthest Point Sampling (FPS), and for point grouping, we use K-Nearest Neighbors (KNN). After sampling and grouping, we utilize the Detail Activation (DA) module to activate the details at a coarse scale and gradually activate finer details. Following the DA module, Point-MDA enters a non-linear mapping layer, consisting of the ResDMLP module proposed. Notably, we introduce residual connections among the layers of Point-MDA to coordinate the whole progressive workflow, enable feature reuse, and facilitate deeper and more accurate training. Finally, we perform max pooling before the classifier to output the classification results.
In general, Point-MDA, which is a progressive point cloud layered classification network for extreme multi-scale detail activation, is a simple yet efficient neural network primarily used for recognizing and classifying point cloud data. The significant feature of this network is gradually introducing higher-level features into the network, processing point clouds in layers at different levels to identify features with varying levels of details without the need for complex feature extraction algorithms.
Preprints 72523 g002
Figure 2. The workflow of Point-MDA for classification tasks. Given an input point cloud, Point-MDA first uses the sampling-grouping operation and then exploits the Detail Activation module to activate the details of the point cloud and progressively activate different scales. The ResDMLP module will then process the activated features. Meanwhile, the feature extraction process is jointly supervised by the details captured from the farthest scale to the current scale through residual connections, thus promoting information reuse.
Figure 2. The workflow of Point-MDA for classification tasks. Given an input point cloud, Point-MDA first uses the sampling-grouping operation and then exploits the Detail Activation module to activate the details of the point cloud and progressively activate different scales. The ResDMLP module will then process the activated features. Meanwhile, the feature extraction process is jointly supervised by the details captured from the farthest scale to the current scale through residual connections, thus promoting information reuse.
Preprints 72523 g002

3. Results

In Section 3.1, we first introduce the two datasets utilized for the experiments, namely ModelNet40 [29] and ScanObjectNN [30], followed by a description of the specific implementation details. In Section 3.2, we evaluate the classification performance of Point-MDA on two benchmarks in point cloud classification and compare it with state-of-the-art networks in the field. Lastly, in Section 3.3, detailed ablation studies are conducted to demonstrate the effectiveness of the proposed modules and the appropriateness of the current hyperparameter selection.

3.1. Experiments

3.1.1. Experimental Data

We evaluate our Point-MDA on the ModelNet40 [29] dataset and ScanObjectNN [30] dataset. The ModelNet40 dataset is a large-scale synthetic dataset that consists of more than 12,000 3D models covering 40 different categories such as tables, chairs, sofas, cars, lamps and others. It comprises a total of 9843 training samples and 581 testing samples. The dataset is superior in quality as it is free from significant noise and defects. It is significantly diverse as it encompasses a wide range of categories, each with multiple variations. Additionally, it is easily accessible and available to the public through online platforms.
The ScanObjectNN dataset is a public dataset used for 3D object detection and classification. It consists of 200 3D scanning scenes covering various types of objects, which are categorized into 15 classes, such as tables, chairs, sofas, beds, bookcases, boxes, cabinets, and cutlery. This dataset exhibits high diversity, covering different scene types and object shapes. Additionally, the dataset contains over 15,000 annotated object instances, making it one of the largest-scale 3D object detection and classification datasets currently available. However, due to occlusion and noise, this dataset presents significant challenges to existing point cloud analysis methods.

3.1.2. Implementation Details

For the experiments conducted on the ModelNet40 dataset, PyTorch framework [40] is utilized along with AdamW optimizer [41]. In simple terms, AdamW introduces weight decay on top of Adam optimizer. Point-MDA is trained for 250 epochs to achieve convergence. The initial learning rate is set to 0.001 and gradually decreases to 0.000 by applying cosine annealing scheduler [42]. The batch size is set to 32. Based on experimental and theoretical analysis, the activation frequency of DA modules in each layer of the network is set to 2, 6, and 10. Following previous research [18,19,43], cross-entropy loss with label smoothing [44] is employed as the loss function. Scaling and translation are used as data augmentation techniques.
For the experiments conducted on the ScanObjectNN dataset, different implementation details are used, where the activation frequency of each layer is set to 3, 7, and 11, the initial learning rate is set to 0.002, and random rotation and scaling are used as data augmentation techniques.

3.2. Classification Results

3.2.1. Shape Classification on ModelNet40

We report the class-average accuracy (mAcc) and overall accuracy (OA) on the testing set. In Table 1, we present the results of shape classification experiments of Point-MDA on the ModelNet40 dataset. Point-MDA achieves excellent OA of 94.0% and best mAcc of 91.9%, outperforming PointNet++ by 3.3% and 3.5% in these two evaluation metrics, respectively.
We also report the class-average accuracy (mAcc) and overall accuracy (OA) on the testing set. The experimental results of Point-MDA on the ScanObjectNN dataset are presented in Table 2. Point-MDA achieves a reasonable OA of 85.8%, and an mAcc of 83.6%. These two evaluation metrics outperform those of PointNet++ by 7.9% and 8.2%, respectively.

3.3. Ablation Studies

Extensive ablation studies have been conducted to establish the efficacy of the proposed modules in Point-MDA. Two aspects are investigated using Table 3 and Table 4, including the activation of detail scales in different network layers and component studies.

3.3.1. Detail Scales Activated in Different Network Layers

The Detail Activation module is situated after the sampling-grouping operation and before the non-linear mapping layer in Point-MDA. During the training process, different frequency levels within the DA module need to be activated. For the ModelNet40 and ScanObjectNN datasets, we test various combinations of detail scales activated in different layers. The experimental results are presented in Table 3. Optimal results are achieved for the ModelNet40 dataset with the three scales set to 2, 6, and 10, respectively, with Point-MDA achieving the best OA and mAcc. For the ScanObjectNN dataset, the three scales set to 3, 7, and 11, respectively, yielded the best OA and mAcc.
Point-MDA comprises of two primary constituents: the Detail Activation module and the ResDMLP module. Additionally, to enhance the feature extraction process, we have introduced residual connections between network layers to jointly supervise the detail activation from the farthest scale to the current one. In this study, we perform ablation studies to evaluate the effectiveness of each of the three Point-MDA components mentioned above. Table 4 displays the experimental outcomes on the ModelNet40 and ScanObjectNN datasets.

4. Discussion

We further discuss and analyze the results in Table 1 and Table 2. In terms of classification accuracy on the ModelNet40 dataset, PointNeXt [19], Point-MAE [47] and P2P [48] are comparable to Point-MDA. However, in comparison to Point-MAE and P2P, Point-MDA has the advantage of not using additional training data. In comparison to PointNeXt, Point-MDA has a shallower network architecture and simpler structure. Although the classification accuracy of Point-MDA on the ModelNet40 dataset is not as high as RepSurf-U [36], on the ScanObjectNN dataset, Point-MDA outperforms RepSurf-U in both OA and mAcc. These findings suggest that Point-MDA is a network with strong overall performance.

5. Conclusions and Future Research Directions

This paper proposes Point-MDA, a simple MLP-based point cloud analysis network. Point-MDA discards complex feature extractors and does not require deepening or stacking network structures to improve performance. The key component of Point-MDA is the Detail Activation module, which revolves around Fourier feature transformation to recover detailed features of point clouds. For point cloud analysis tasks, Point-MDA’s biggest innovation is introducing a progressive activation strategy, gradually introducing higher-level features to the network and processing point clouds on different levels to identify features with varying levels of detail. Comprehensive experiments and ablation studies show that our model achieves competitive performance in point cloud classification tasks.
Our inspiration comes from computer graphics. We also hope that the point cloud community can rethink some classical network designs and pay more attention to standard works from other fields, rather than always focusing on complex feature extractors and more complex architectures. We plan to embed the DA module and progressive training ideas into other architectures, such as PointMLP and PointNorm. We also hope to apply Point-MDA to object detection (e.g., SUN RGB-D) [55], partial segmentation (e.g., ShapeNetpart) [56], and semantic segmentation (e.g., S3DIS) [57].

Author Contributions

Conceptualization, M.L. and Y.Z.; methodology, M.L. and Y.Z.; software, M.L.; validation, M.L. and Y.Z.; formal analysis, M.L.; investigation, M.L.; resources, Y.Z. and W.J.; data curation, M.L. and Y.Z.; writing—original draft preparation, M.L. and Y.Z.; writing—review and editing, M.L. and Y.Z.; visualization, M.L.; supervision, Y.Z. and W.J.; project administration, ,Y.Z. and W.J.; funding acquisition, Y.Z. and W.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Technologies Research and Development Program of China, grant number 2018YFB1404100.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: [https://shapenet.cs.stanford.edu/media].

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shao, Y.; Fan, Z.; Zhu, B.; Zhou, M.; Chen, Z.; Lu, J. A Novel Pallet Detection Method for Automated Guided Vehicles Based on Point Cloud Data. Sensors 2022, 22 (20), 8019. [CrossRef]
  2. Wan, R.; Zhao, T.; Zhao, W. PTA-Det: Point Transformer Associating Point Cloud and Image for 3D Object Detection. Sensors 2023, 23 (6), 3229. [CrossRef]
  3. Barranquero, M.; Olmedo, A.; Gómez, J.; Tayebi, A.; Hellín, C. J.; Saez de Adana, F. Automatic 3D Building Reconstruction from OpenStreetMap and LiDAR Using Convolutional Neural Networks. Sensors 2023, 23 (5), 2444. [CrossRef]
  4. Comesaña-Cebral, L.; Martínez-Sánchez, J.; Lorenzo, H.; Arias, P. Individual Tree Segmentation Method Based on Mobile Backpack LiDAR Point Clouds. Sensors 2021, 21 (18), 6007. [CrossRef]
  5. Bhandari, V.; Phillips, T. G.; McAree, P. R. Real-Time 6-DOF Pose Estimation of Known Geometries in Point Cloud Data. Sensors 2023, 23 (6), 3085. [CrossRef]
  6. Zhang, F.; Zhang, J.; Xu, Z.; Tang, J.; Jiang, P.; Zhong, R. Extracting Traffic Signage by Combining Point Clouds and Images. Sensors 2023, 23 (4), 2262. [CrossRef]
  7. Influence of Colour and Feature Geometry on Multi-modal 3D Point Clouds Data Registration. https://ieeexplore.ieee.org/abstract/document/7035827/ (accessed 2023-04-02).
  8. Qi, C. R.; Su, H.; Mo, K.; Guibas, L. J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation; 2017; pp 652–660.
  9. Qi, C. R.; Yi, L.; Su, H.; Guibas, L. J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Advances in Neural Information Processing Systems; Curran Associates, Inc., 2017; Vol. 30.
  10. Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN: Convolution On X-Transformed Points. Advances in Neural Information Processing Systems 2018, 31.
  11. Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-Shape Convolutional Neural Network for Point Cloud Analysis; 2019; pp 8895–8904.
  12. Wu, W.; Qi, Z.; Fuxin, L. PointConv: Deep Convolutional Networks on 3D Point Clouds; 2019; pp 9621–9630.
  13. Li, G.; Mueller, M.; Qian, G.; Delgadillo Perez, I. C.; Abualshour, A.; Thabet, A. K.; Ghanem, B. DeepGCNs: Making GCNs Go as Deep as CNNs. IEEE Transactions on Pattern Analysis and Machine Intelligence 2021, 1–1. [CrossRef]
  14. Zheng, Y.; Gao, C.; Chen, L.; Jin, D.; Li, Y. DGCN: Diversified Recommendation with Graph Convolutional Networks. In Proceedings of the Web Conference 2021; WWW ’21; Association for Computing Machinery: New York, NY, USA, 2021; pp 401–412. [CrossRef]
  15. Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-BERT: Pre-Training 3D Point Cloud Transformers With Masked Point Modeling; 2022; pp 19313–19322.
  16. Zhao, H.; Jiang, L.; Jia, J.; Torr, P. H. S.; Koltun, V. Point Transformer; 2021; pp 16259–16268.
  17. Zheng, S.; Pan, J.; Lu, C.; Gupta, G. PointNorm: Dual Normalization Is All You Need for Point Cloud Analysis. arXiv October 2, 2022. [CrossRef]
  18. Ma, X.; Qin, C.; You, H.; Ran, H.; Fu, Y. Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual MLP Framework. arXiv November 29, 2022. [CrossRef]
  19. Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.; Elhoseiny, M.; Ghanem, B. PointNeXt: Revisiting PointNet++ with Improved Training and Scaling Strategies. Advances in Neural Information Processing Systems 2022, 35, 23192–23204.
  20. Yan, X.; Zhan, H.; Zheng, C.; Gao, J.; Zhang, R.; Cui, S.; Li, Z. Let Images Give You More:Point Cloud Cross-Modal Training for Shape Analysis. arXiv October 9, 2022. [CrossRef]
  21. Xue, L.; Gao, M.; Xing, C.; Martín-Martín, R.; Wu, J.; Xiong, C.; Xu, R.; Niebles, J. C.; Savarese, S. ULIP: Learning a Unified Representation of Language, Images, and Point Clouds for 3D Understanding. arXiv March 30, 2023. [CrossRef]
  22. Yan, S.; Yang, Z.; Li, H.; Guan, L.; Kang, H.; Hua, G.; Huang, Q. IAE: Implicit Autoencoder for Point Cloud Self-Supervised Representation Learning. arXiv November 22, 2022. [CrossRef]
  23. Esteves, C.; Xu, Y.; Allen-Blanchette, C.; Daniilidis, K. Equivariant Multi-View Networks; 2019; pp 1568–1577.
  24. Wei, X.; Yu, R.; Sun, J. View-GCN: View-Based Graph Convolutional Network for 3D Shape Analysis; 2020; pp 1850–1859.
  25. Alakwaa, W.; Nassef, M.; Badr, A. Lung Cancer Detection and Classification with 3D Convolutional Neural Network (3D-CNN). ijacsa 2017, 8 (8). [CrossRef]
  26. Tancik, M.; Srinivasan, P.; Mildenhall, B.; Fridovich-Keil, S.; Raghavan, N.; Singhal, U.; Ramamoorthi, R.; Barron, J.; Ng, R. Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains. In Advances in Neural Information Processing Systems; Curran Associates, Inc., 2020; Vol. 33, pp 7537–7547.
  27. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition; 2016; pp 770–778.
  28. Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K. Q. Densely Connected Convolutional Networks; 2017; pp 4700–4708.
  29. Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A Deep Representation for Volumetric Shapes; 2015; pp 1912–1920.
  30. Uy, M. A.; Pham, Q.-H.; Hua, B.-S.; Nguyen, T.; Yeung, S.-K. Revisiting Point Cloud Classification: A New Benchmark Dataset and Classification Model on Real-World Data; 2019; pp 1588–1597.
  31. Woo, S.; Lee, D.; Lee, J.; Hwang, S.; Kim, W.; Lee, S. CKConv: Learning Feature Voxelization for Point Cloud Analysis. arXiv July 27, 2021. [CrossRef]
  32. Li, J.; Chen, B. M.; Lee, G. H. SO-Net: Self-Organizing Network for Point Cloud Analysis; 2018; pp 9397–9406.
  33. Zhao, H.; Jiang, L.; Fu, C.-W.; Jia, J. PointWeb: Enhancing Local Neighborhood Features for Point Cloud Processing; 2019; pp 5565–5573.
  34. Phan, A. V.; Nguyen, M. L.; Nguyen, Y. L. H.; Bui, L. T. DGCNN: A Convolutional Neural Network over Large-Scale Labeled Graphs. Neural Networks 2018, 108, 533–543. [CrossRef]
  35. Zhou, H.; Feng, Y.; Fang, M.; Wei, M.; Qin, J.; Lu, T. Adaptive Graph Convolution for Point Cloud Analysis; 2021; pp 4965–4974.
  36. Ran, H.; Liu, J.; Wang, C. Surface Representation for Point Clouds; 2022; pp 18942–18952.
  37. Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks; 2018; pp 4510–4520.
  38. Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks; 2018; pp 7132–7141.
  39. Xiangli, Y.; Xu, L.; Pan, X.; Zhao, N.; Rao, A.; Theobalt, C.; Dai, B.; Lin, D. BungeeNeRF: Progressive Neural Radiance Field for Extreme Multi-Scale Scene Rendering. In Computer Vision – ECCV 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G. M., Hassner, T., Eds.; Lecture Notes in Computer Science; Springer Nature Switzerland: Cham, 2022; pp 106–122. [CrossRef]
  40. Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; Desmaison, A.; Kopf, A.; Yang, E.; DeVito, Z.; Raison, M.; Tejani, A.; Chilamkurthy, S.; Steiner, B.; Fang, L.; Bai, J.; Chintala, S. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems; Curran Associates, Inc., 2019; Vol. 32.
  41. Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv January 4, 2019. [CrossRef]
  42. Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. arXiv May 3, 2017. [CrossRef]
  43. Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S. E.; Bronstein, M. M.; Solomon, J. M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. 2019, 38 (5), 146:1-146:12. [CrossRef]
  44. Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision; 2016; pp 2818–2826.
  45. Yan, X.; Zheng, C.; Li, Z.; Wang, S.; Cui, S. PointASNL: Robust Point Clouds Processing Using Nonlocal Neural Networks With Adaptive Sampling; 2020; pp 5589–5598.
  46. Muzahid, A. A. M.; Wan, W.; Sohel, F.; Wu, L.; Hou, L. CurveNet: Curvature-Based Multitask Learning Deep Networks for 3D Object Recognition. IEEE/CAA Journal of Automatica Sinica 2021, 8 (6), 1177–1187. [CrossRef]
  47. Pang, Y.; Wang, W.; Tay, F. E. H.; Liu, W.; Tian, Y.; Yuan, L. Masked Autoencoders for Point Cloud Self-Supervised Learning. In Computer Vision – ECCV 2022; Springer, Cham, 2022; pp 604–621. [CrossRef]
  48. Wang, Z.; Yu, X.; Rao, Y.; Zhou, J.; Lu, J. P2P: Tuning Pre-Trained Image Models for Point Cloud Analysis with Point-to-Pixel Prompting. arXiv October 12, 2022. [CrossRef]
  49. Zhang, R.; Wang, L.; Wang, Y.; Gao, P.; Li, H.; Shi, J. Parameter Is Not All You Need: Starting from Non-Parametric Networks for 3D Point Cloud Analysis. arXiv March 14, 2023. [CrossRef]
  50. Liu, Y.; Tian, B.; Lv, Y.; Li, L.; Wang, F.-Y. Point Cloud Classification Using Content-Based Transformer via Clustering in Feature Space. IEEE/CAA Journal of Automatica Sinica 2023, 1–9. [CrossRef]
  51. Wu, C.; Zheng, J.; Pfrommer, J.; Beyerer, J. Attention-Based Point Cloud Edge Sampling. arXiv March 26, 2023. [CrossRef]
  52. Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. SpiderCNN: Deep Learning on Point Sets with Parameterized Convolutional Filters; 2018; pp 87–102.
  53. Qiu, S.; Anwar, S.; Barnes, N. Dense-Resolution Network for Point Cloud Classification and Segmentation; 2021; pp 3813–3822.
  54. Cheng, S.; Chen, X.; He, X.; Liu, Z.; Bai, X. PRA-Net: Point Relation-Aware Network for 3D Point Cloud Analysis. IEEE Transactions on Image Processing 2021, 30, 4436–4448. [CrossRef]
  55. Song, S.; Lichtenberg, S. P.; Xiao, J. SUN RGB-D: A RGB-D Scene Understanding Benchmark Suite; 2015; pp 567–576.
  56. Yi, L.; Kim, V. G.; Ceylan, D.; Shen, I.-C.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A Scalable Active Framework for Region Annotation in 3D Shape Collections. ACM Trans. Graph. 2016, 35 (6), 210:1-210:12. [CrossRef]
  57. Armeni, I.; Sener, O.; Zamir, A. R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D Semantic Parsing of Large-Scale Indoor Spaces; 2016; pp 1534–1543.
Table 1. Shape Classification Results on the ModelNet40 dataset. All methods except PointASNL are tested without the voting strategy. ‘-’ indicates a result is unavailable. ‘Etra Training Data’ indicates whether the model uses additional training data, and ‘Deep’ indicates whether the model needs to improve performance by deepening the network. We use bold to indicate the best score, and blue for the second-best score.
Table 1. Shape Classification Results on the ModelNet40 dataset. All methods except PointASNL are tested without the voting strategy. ‘-’ indicates a result is unavailable. ‘Etra Training Data’ indicates whether the model uses additional training data, and ‘Deep’ indicates whether the model needs to improve performance by deepening the network. We use bold to indicate the best score, and blue for the second-best score.
Method Publication ModelNet40 Extra Training Data Deep
OA(%) mAcc(%)
PointNet [8] CVPR 2017 89.2 86.0 × ×
PointNet++ [9] NeurIPS 2017 90.7 88.4 × ×
PointCNN [10] NeurIPS 2018 92.5 88.1 × ×
RS-CNN [11] CVPR 2019 92.9 - × ×
PointConv [12] CVPR 2019 92.5 - × ×
DeepGCN [13] PAMI 2019 93.6 90.9 × √
PointASNL [45] CVPR 2020 93.2 - × ×
CurveNet [46] ICCV 2021 93.8 - × ×
Point-BERT [15] CVPR 2022 93.8 - √ ×
PointNorm [17] CVPR 2022 93.7 91.3 × √
PointMLP [18] ICLR 2022 93.7 90.9 × √
PointNeXT [19] NeurIPS 2022 94.4 91.1 × √
RepSurf-U [36] CVPR 2022 94.4 91.4 × ×
Point-MAE [47] CVPR 2022 94.0 - √ ×
P2P [48] CVPR 2022 94.0 91.6 √ √
Point-PN [49] CVPR 2023 93.8 - × ×
PointConT [50] IEEE 2023 93.5 - × ×
APES [51] CVPR 2023 93.5 - × ×
Point-MDA 2023 94.0 91.9 × ×
Table 2. Shape Classification Results on ScanObjectNN dataset. All methods are tested without the voting strategy. ‘-’ indicates a result is unavailable. ‘Etra Training Data’ indicates whether the model uses additional training data, and ‘Deep’ indicates whether the model needs to improve performance by deepening the network.
Table 2. Shape Classification Results on ScanObjectNN dataset. All methods are tested without the voting strategy. ‘-’ indicates a result is unavailable. ‘Etra Training Data’ indicates whether the model uses additional training data, and ‘Deep’ indicates whether the model needs to improve performance by deepening the network.
Method Publication ScanObjectNN Extra Training Data Deep
OA(%) mAcc(%)
PointNet [8] CVPR 2017 68.2 63.4 × ×
PointNet++ [9]
PointCNN [10]		 NeurIPS 2017
NeurIPS 2018		 77.9
78.5		 75.4
75.1		 ×
×		 ×
×
DGCNN [34]
SpiderCNN [52]
DRNet [53]
PRA-Net [54]		 ELSEVIER 2018
ECCV 2018
WACV 2021
IEEE 2021		 78.1
73.7
80.3
82.1		 73.6
69.8
78.0
79.1		 ×
×
×
×		 ×
×
×
×
Point-BERT [15]
PointNorm [17]
PointMLP [18]
PointNeXt [19]
RepSurf-U [36]		 CVPR 2022
CVPR 2022
ICLR 2022
NeurIPS 2022
CVPR 2022		 83.1
86.8
85.4
88.2
84.6		 -
85.6
83.9
86.8
81.9		 √
×
×
×
×		 ×
√
√
√
×
Point-MAE [47] CVPR 2022 85.2 - √ ×
P2P [48] CVPR 2022 89.3 88.5 √ ×
Point-PN [49]
PointConT [50]		 CVPR 2023
IEEE 2023		 87.1
88.0		 -
86.0		 ×
×		 ×
×
Point-MDA 2023 85.8 83.6 × ×
Table 3. Classification accuracy of Point-MDA using different combinations of detail scales activated in different layers on the ModelNet40 and ScanObjectNN dataset.
Table 3. Classification accuracy of Point-MDA using different combinations of detail scales activated in different layers on the ModelNet40 and ScanObjectNN dataset.
Dataset Activation Frequency Level OA(%) mAcc(%)
ModelNet40 L1=1,L2=5,L3=9 93.7 91.4
L1=2,L2=6,L3=10 94.0 91.9
L1=3,L2=7,L3=11
L1=4,L2=8,L3=12		 93.9
93.7		 91.7
91.3
ScanObjectNN L1=1,L2=5,L3=9 85.4 82.9
L1=2,L2=6,L3=10 85.7 83.2
L1=3,L2=7,L3=11 85.8 83.6
L1=4,L2=8,L3=12 85.4 83.3
Table 4. Component ablation studies on ModelNet40 and ScanObjectNN datasets. ‘DA’ indicates the DetailActivation module. ‘Reuse’ indicates the residual connection between network layers.
Table 4. Component ablation studies on ModelNet40 and ScanObjectNN datasets. ‘DA’ indicates the DetailActivation module. ‘Reuse’ indicates the residual connection between network layers.
Dataset DA ResDMLP Reuse OA(%) mAcc(%)
ModelNet40 √ √ √ 94.0 91.9
√ × √ 93.7 91.4
×
×		 √
√		 ×
√		 93.7
93.6		 91.2
91.2
ScanObjectNN √ √ √ 85.8 83.6
√ × √ 84.7 82.8
× √ × 85.3 83.2
× √ √ 84.8 82.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated