Prerpints.org logo
Preprint
Article

A New Type of Misaligned Journal Bearing with Flexible Structure

Altmetrics

Downloads

142

Views

51

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

05 May 2023

Posted:

06 May 2023

You are already at the latest version

Alerts
Abstract
A flexible structure is applied to improve the lubrication performance of a misaligned journal bearing. The journal bearing is representative sliding bearing and there are damages due to metal-to-metal contact by misalignment. Since misalignment is an unavoidable phenomenon, a journal bearing with a flexible structure was proposed as a way to improve it. The lubrication characteristics of the bearing are evaluated numerically under steady-state condition. EHL (elastohydrodynamic lubrication) analysis considering elastic deformation was performed. The lubrication performance is compared in accordance with variation of the geometry of the flexible structure and evaluated based on the minimum film thickness. Moreover, the results of the journal bearing with flexible structure are compared with those of the journal bearing without the flexible structure. The flexible structure is then applied in the form of a groove to the area supporting high load on the journal bearing; it is elastically deformed by the generated oil-film pressure, which helps to obscure a larger oil film. Through numerical analysis, it is found that the journal bearing with flexible structure can improve the lubrication performance in the misaligned condition.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Hydrodynamic journal bearings are one of the representative types of sliding bearings. They are broadly used in high-speed rotating machinery and equipment [1]. The journal’s axis is often misaligned in the bearing, and the film thickness for bearing clearance is distributed unevenly along the axial direction because of factors such as asymmetric loads or installation errors [2,3,4]. The axial asymmetric hydrodynamic pressure causes the location of the equivalent supporting point to deviate from the bearing axial mid-plane [5,6]. In recent years, misaligned journal bearings have been investigated with a great deal of interest. Jang and Khonsari [7] researched the cause of misalignments in journal bearings and studied their effects on the static and dynamic performances of the bearing. Pigott [8] showed that the load carrying capacity of the journal bearing decreases by 40% for a misalignment about 0.0002 rad. Sun and Gui [9] showed that the oil film thickness is minimized at the bearing ends by the misalignment; they also reported that the minimum film thickness of a misaligned journal bearing was smaller than that of the aligned journal because of decrease in the load carrying capacity [10]. When the film thickness between the bearing and misaligned shaft decreases below a certain level, metal-to-metal contact can occur, which may cause a malfunction or breakdown of the system [11,12]. Shenoy and Pai [13] as well as Ram and Sharma [14,15] reported the combined effect of journal misalignment and wear on the bearing performance. In addition, Nikolakopoulos and Papadopoulos [12] constructed a numerical model to investigate the relationship between inclination angle and friction force, providing that misalignment of the journal in the rotating machinery is one of the most important factors influencing bearing performance. These studies generally assume that the temperature of the lubricant is constant. However, thermal effects need to be considered because increase in eccentricity, rotating speed and friction loss can lead to a larger temperature rise of the lubricant [16]. He et al. [17] and Xu et al. [18] presented comprehensive analyses of the journal bearing performance considering the thermal effects; moreover, they found that the thermal effect had a major influence on the performance of the misaligned journal bearing when the eccentricity ratio was large. Sun et al. [9,10,19] reported the misalignment, thermal, and surface topography effects on bearing performance by experimental and theoretical methods.
Many studies have been conducted on preventing the contact problem by misalignment of the journal bearing from various engineering perspectives. In terms of bearing material, Sharma et al. [20] applied graphite particles to ZA-27 alloy for the material of the journal bearing; as a result, the misaligned journal bearing could run without seizure. Kim et al. [21] presented reduction in the wear and friction coefficients using carbon-fiber phenolic composite as the material of the journal bearing. Moreover, lubricant development and profile applications to bearings were conducted to prevent contact problem in misaligned journal bearing. Das et al. [2] applied a micropolar fluid as the lubricant to the journal bearing to increase its load carrying capacity and reduce the frictional force. Bouyer et al. [22] applied different profiles to the lubrication area at the bearing ends; they showed that the minimum film thickness increased by up to 60% in comparison with the journal bearing without the profile when the shaft was misaligned.
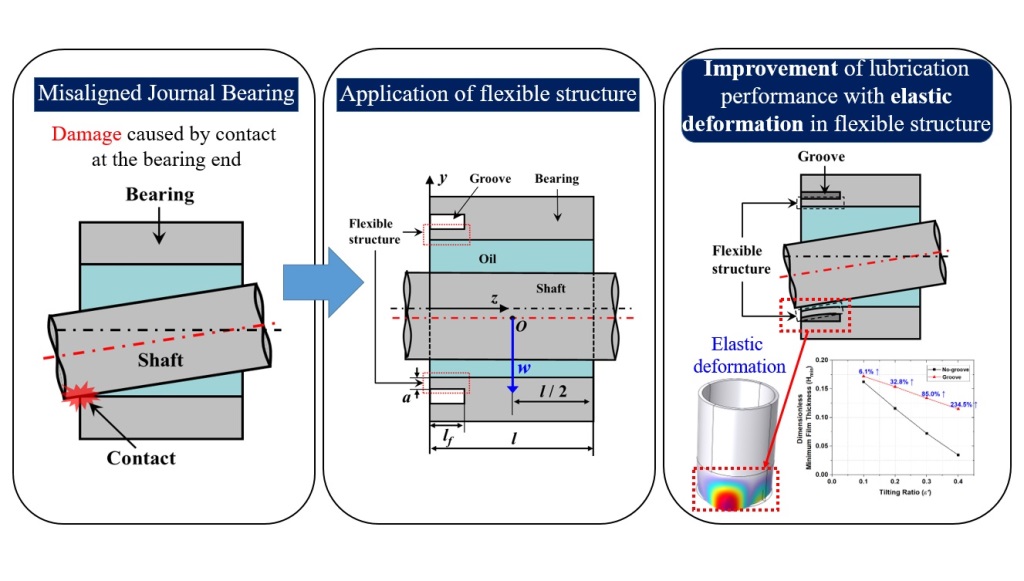
Furthermore, application of a flexible structure to the journal bearing is one of methods of preventing contact problems by a misalignment because the film thickness at the bearing end increases by elastic deformation. The flexible structure is applied using a ring-shaped groove in the dotted region shown in Figure 1 (b). Elastic deformation occurs in the grooved zone by the oil-film pressure acting on the bearing surface, so it is possible to obtain a larger oil-film thickness. Finally, the metal-to-metal contact by misalignment of the journal bearing can be prevented [23,24]. However, the flexible structure with an inappropriate geometry may decrease the minimum film thickness [25].
Therefore, the design of an appropriate flexible structure is crucial for the misaligned journal bearing for preventing contact problems and improving the lubrication performance effectively. However, studies on the flexible structure of the misaligned journal bearing are not varied, and the results are only useful to specific applications, such as rotary and scroll compressors. Furthermore, guidelines are not provided for appropriate flexible structure of the journal bearing. Thus, it is difficult to design appropriate flexible structures to improve the lubrication characteristics of misaligned journal bearings. Numerical research on the various flexible structure geometries of misaligned journal bearings can be useful for designing appropriate flexible structures in various engineering fields.
In the present research, the influence of the flexible structure of the misaligned journal bearing is investigated under various misalignment conditions to provide guidelines regarding the flexible structure design. The dimensionless minimum film thickness is used to estimate the lubrication performances of misaligned journal bearings are compared with and without flexible structures.

2. Numerical model and method

The elastohydrodynamic lubrication(EHL) analysis is conducted to investigate the lubrication performance of the misaligned journal bearing considering deformation in the flexible structure. In this study, the commercial software COMSOL 6.0 Version is used for performing multi-physics analysis. The software uses a finite element method to discretize the non-linear governing equations to algebraic equations that can be solved iteratively. In the numerical analysis, the hydrodynamic bearing module is used for hydrodynamic lubrication analysis, solid mechanics module is used for elastic deformation analysis of the bearing, and the solid-bearing coupling module is used for interworking between these two modules. Figure 2 shows the schematic of the journal bearing with radius r and length l. The shaft is rigid and rotates around the z-axis with an angular velocity ω. The z and x axes represent the axial and radial directions, respectively. The load w is applied in the direction of θw to the center of the shaft at the location where z is equal to l/2. A ring shape groove is applied to the given section as shown in Figure 2 (a) and (b). The flexible structure, which is shown in the dotted regions in Figure 2 (b) and (c), is applied to the bearing by the groove to obtain the elastic deformation. The geometry of the flexible structure is defined by the length (lf), inner end thickness (d), and outer end thickness (a). The sectional shape in the axial direction of the flexible structure depends on γ (= d/a), and is rectangle (for γ = 1) or taper (for γ >1) shaped. The bearing surface where the groove is not applied is rigid because the thickness is large; therefore, elastic deformation does not occur. The dimensionless parameters for the geometries of the journal bearing and flexible structure are defined as in Equation (1).
  A = a r ,   L = l r ,   L f = l f l ,   β = c r ,   γ = d a
The Reynolds equation shown in Equation (2) is used to solve the oil-film pressure p.
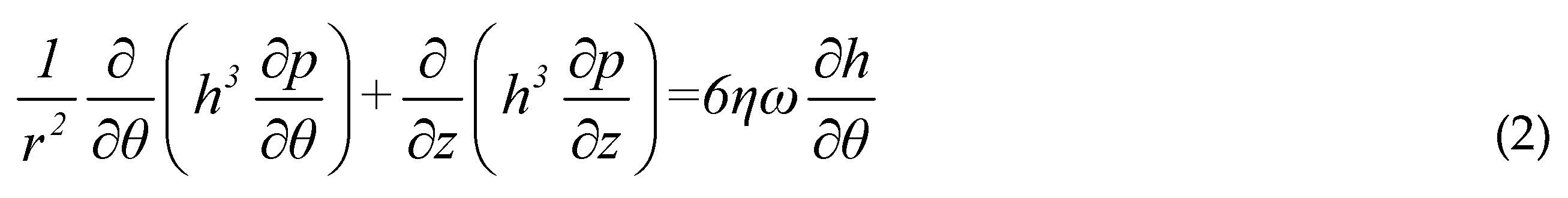
Preprints 72781 i002
The dimensionless form of Equation (2) can be written as:
∂ ∂ θ ( H 3 ∂ P ∂ θ ) + ∂ ∂ Z ( H 3 ∂ P ∂ Z ) = ∂ H ∂ θ
where
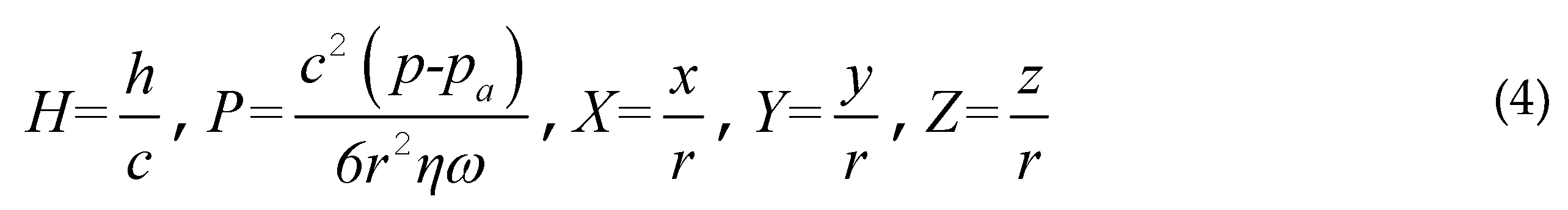
Preprints 72781 i004
The parameter, pa is the atmospheric pressure.
The oil-film thickness h between the bearing and shaft should be obtained to calculate the oil-film pressure in Eq. (2). The shaft rotates the bearing with eccentric and tilted motions, as shown in Figure 3; O is the center of the shaft at the location where z is equal to l/2. O1, O2 are the centers of the shaft at both ends of the bearing, respectively. Two circles in Figure 3(a) are cross sections of the shaft projected onto the x – y plane, and O1, O2 are their centers. The eccentric amount, e is a distance on the x – y plane between O and the center of the bearing. The altitude angle ψ is an angle on x – y plane between the load direction and straight line passing through O and the bearing center. The tilting direction of the shaft is equal to θw, and the tilting amount e’ is equal to half the distance between O1 and O2 on the x –y plane. When tilting amount is equal to zero, shaft rotates in the bearing under the aligned condition. The oil film thickness between the shaft and bearing is calculated using Equation (5).
h = c + e ⋅ cos { θ - ( θ W - π + ψ ) } + e ’ ( 1 - 2 l z ) cos { θ - ( θ W - π ) } + h e
The dimensionless form of Equation (5) can be written as:
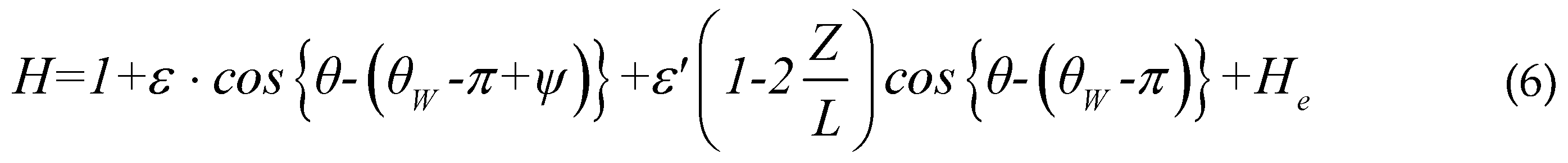
Preprints 72781 i006
where
H e = h e c ,   ε = e c ,   ε ’ = e ’ c
The parameters ε and ε’ in Equation (7) are the eccentricity and tilting ratios of the shaft, respectively. The oil-film thickness change by elastic deformation of the flexible structure he should also be obtained to calculate Equation (5). The elastic deformation of the bearing is calculated using the solid mechanics module, and the numerical results are interworked with the hydrodynamic bearing module for hydrodynamic lubrication analysis. Figure 4 shows the hexahedral mesh of the finite element model. The hexahedral mesh is used for numerical calculations owing to its higher resolution and faster calculation in comparison to the tetrahedral mesh [26]. In the analysis, 52 elements are applied in the circumferential direction and 53 elements are applied in the axial direction, except in the groove region. In the groove region, 108 elements are applied in the circumferential direction. The total number of elements is thus 50,220. The value of the convergence criteria is given as 10-3 for continuity, velocity and deformation.
The boundary conditions to solve Equations. (2), (8) are defined as follows:
▪ Boundary condition for the oil film fracture zone
▪ Pressure in the cavitation region, p = p a w h e r e   p < p a , (8)
▪ Pressure at bearing ends and oil feeding groove p ( 0 ,   z ) = p b ,   p ( θ ,   0 ) = p b ,   p ( θ ,   l ) = p b
▪ Displacement at the inner end of the flexible structure u(x,y,lf)=0.
The direction of n, which is shown in Equation (8), is perpendicular to the oil film fracture boundary line. Periodic conditions of pressure and displacement are also used for the ring shape of the bearing. Equation (8) in the dimensionless form can be written as Equation (9).
▪ Boundary condition for the oil film fracture zone
▪ Pressure in the cavitation region P = 0   w h e r e   P < 0 (9)
▪ Pressure at the bearing ends and oil feeding groove P ( 0 ,   Z ) = P b ,   P ( θ ,   0 ) = P b ,   P ( θ ,   L ) = P b
▪ Displacement at the inner end of the flexible structure U(X,Y,Lf)=0.
The oil film force fo is generated by the oil-film pressure, and is used to calculate the motion of the shaft by comparing with the load. Figure 5 shows the oil-film force acting on the shaft. The parameters fox, foy are components of the oil film force in the x, y directions, and calculates using Equation (10), (11), respectively. The oil-film force calculates with Equation (12).
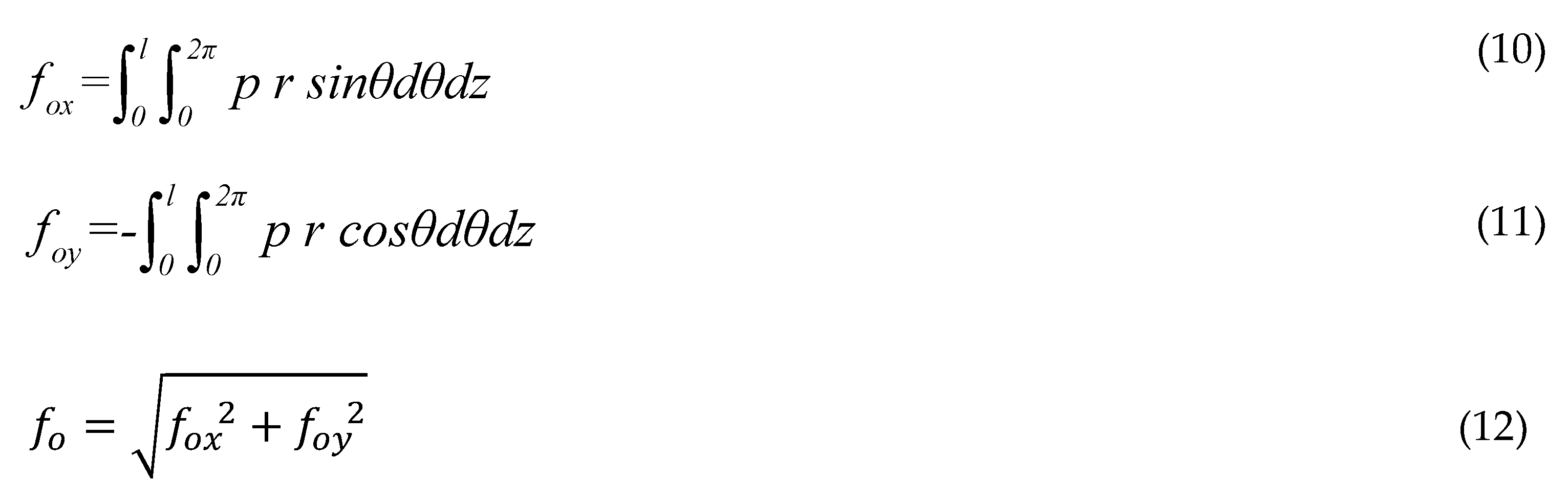
Preprints 72781 i008
Equations (10) - (12) are written in dimensionless form as follows:
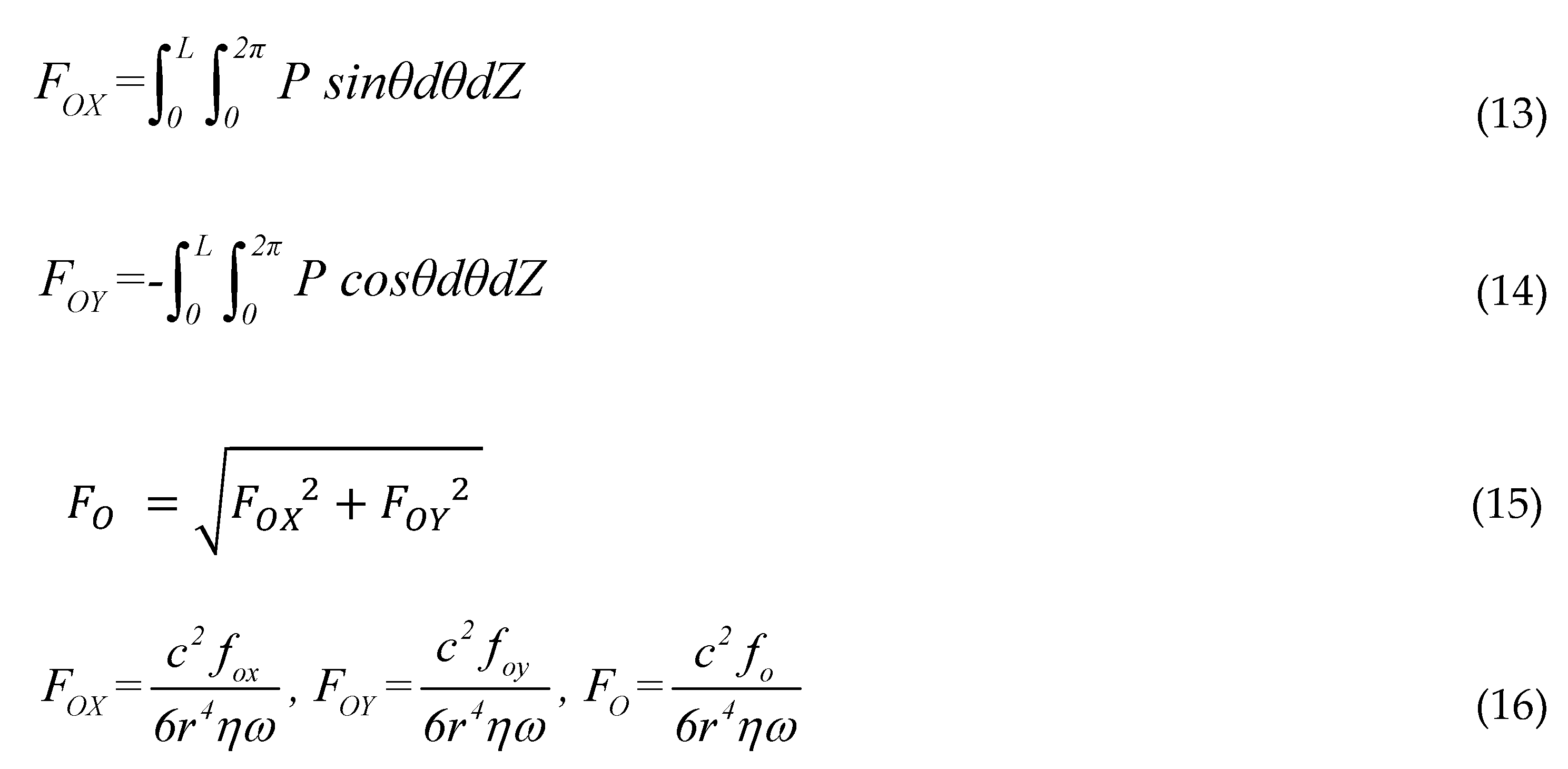
Preprints 72781 i009

3. Numerical results and discussion

EHL analysis [27,28,29] was conducted to estimate the lubrication characteristics of the misaligned journal bearing with flexible structure under the specifications shown in Table 1. Figure 6 and Figure 7 show the dimensionless film thickness and oil-film pressure characteristics of the no-groove and grooved journal bearings, respectively. The grooved journal bearing includes the flexible structure, and the dimensionless length of the structure is equal to Lf. This means that the flexible structure does not apply when the dimensionless length is equal to zero because the bearing is not grooved. Figure 6 (a) and Figure 7(a) show the dimensionless oil film thickness distributions of the no-groove and grooved journal bearings, respectively. Elastic deformation occurs and the dimensionless oil-film thickness increases by the flexible structure in the region between 0 and 1 in the Z direction, as shown in Figure 7 (a) when compared with the results of the no-groove journal bearing in Figure 6 (a). The dimensionless oil-film pressure distributions of the no-groove and grooved journal bearings are shown in Figure 6 (b) and Figure 7(b), respectively. Moreover, the dark-blue areas represent the cavitation regions in these figures. The dimensionless oil-film pressure in the flexible region of the grooved journal bearing decreases by the elastic deformation owing to the larger film thickness, and the location of the peak pressure in the Z direction moves to the inside of the bearing in comparison to the no-groove one. Figure 66 (c) and Figure 7 (c) are the circumferential distributions of the dimensionless film thickness and pressure at three lined locations in Figure 6(a, b) and Figure 7(a, b), respectively. When the flexible structure is applied to the misaligned journal bearing, the film thickness increases and oil-film pressure decreases in the flexible region owing to elastic deformation, as shown in Figure 7 (c) in comparison to Figure 6 (c). In addition, the eccentricity ratio ε’ increases when the flexible structure is applied under a constant load because the load capacity decreases with increase in oil film thickness.
The main purpose of the flexible structure is to prevent contact at the misaligned journal bearing end. Therefore, the minimum film thicknesses required for various misalignments and flexible structure geometries need to be compared. First, the minimum film thicknesses for different tilting ratios are compared with those of the no-groove journal bearing under a constant flexible structure geometry, and these specifications are shown in Table 2. Figure 8 shows the dimensionless minimum film thickness (Hmin) with variation of the tilting ratio ε’. The dimensionless minimum film thickness decreases when the tilting ratio increases under a constant load. The no-groove journal bearing has a dimensionless minimum film thickness of about 0.03 when the tilting ratio is equal to 0.4. This value is 3% of the clearance and may cause metal-to-metal contact at the bearing end because the minimum film thickness is significantly small. The journal bearing with flexible structure obtains a larger dimensionless minimum film thickness owing to increase in the film thickness by elastic deformation as compared the no-groove one. Moreover, the amount of increase in the dimensionless minimum film thickness by the flexible structure is proportional to the tilting ratio. The dimensionless minimum film thickness of the bearing with flexible structure is about 2.3 times that of the no-groove one for the case where the tilting ratio is equal to 0.4.
The dimensionless minimum film thickness of the misaligned journal bearing increases with application of the flexible structure. In addition, the minimum film thickness increases more when the shaft is more misaligned. That is, the flexible structure of the misaligned journal bearing can prevent metal-to-metal at the bearing end effectively.
The influences of the flexible structure geometry change can also be estimated to suggest a guideline for appropriate flexible structure design. Therefore, analysis of variations of the flexible structure geometry is carried out. The geometry of the flexible structure is varied by changing the dimensionless thickness (A), length (Lf), and thickness ratio (γ).
The elastic deformation is a function of the thickness of the flexible structure and influences the lubrication performance of the misaligned journal bearing. Figure 9 shows the dimensionless minimum film thickness with variation of the dimensionless thickness of the flexible structure, as shown in Table 3. The analysis also is performed for different tilting ratios as shown in Figure 9 (a) - (c).
The values of Z in Figure 9 indicate the locations along the Z direction of the dimensionless minimum film thickness. The location is the bearing end when Z is equal to zero, and the inner end of the flexible structure between the flexible and rigid regions of the bearing surface is represented when Z is not zero. When the tilting ratio is equal to 0.2 and dimensionless thickness of the flexible structure (A) is equal to 0.4, the dimensionless minimum film thickness is maximized. Compared to the case without the flexible structure, the difference in the dimensionless minimum film thickness is about 32%. The dimensionless minimum film thickness is also maximized when the dimensionless thickness of the flexible structure is equal to 0.4 for other tilting ratios as shown in Figure 9 - (b) and (c). When the tilting ratio increases, the ratio of increase in minimum film thickness by the flexible structure is greater than that for the case without the flexible structure. That is, it can be seen that as the shaft of the bearing tilts more, the lubrication performance by the flexible structure is improved.
Figure 10 shows the circumferential distributions of the dimensionless film thickness along three different lines, such as the results in Figure 6 and Figure 7 when the tilting ratio is equal to 0.3. In the dotted areas of these figures, the oil film pressure generation and deformation occurs mainly. The dimensionless minimum film thickness is maximized when the dimensionless thickness of the flexible structure is equal to 0.4. Moreover, the distributions of the dimensionless film thickness in the dotted areas are almost constant along the axial direction and the dimensionless film thicknesses are relatively large when the dimensionless thickness of the flexible structure is equal to 0.4.
When the dimensionless thickness of the flexible structure is less than 0.4, the eccentricity ratio increases owing to the decrease in load capacity from the larger elastic deformation, as shown in Figure 10 - (b), and the film thickness is minimized at the inner end (Z = 0.8) of the flexible structure. When an excessively large elastic deformation occurs by the significantly small thickness of the flexible structure, the eccentricity ratio increases, and film thickness at the inner end of the flexible structure may be significantly small. In this case, the dimensionless minimum film thickness cannot be increased effectively or may be smaller than that of the no-groove journal bearing. On the other hand, when the dimensionless thickness of the flexible structure is larger than 0.4, the elastic deformation amount decreases and dimensionless oil film thickness is minimized at the bearing end (Z = 0). In addition, the amount of increase in the dimensionless minimum film thickness becomes slightly smaller owing to decrease in the elastic deformation amount at the bearing end when the thickness of the flexible structure increases.
The appropriate dimensionless thickness of the flexible structure can be used to maximize the dimensionless minimum film thickness. Moreover, to obtain a larger film thickness, it is necessary to find an appropriate thickness of the flexible structure that can be used as a reference because the location of the minimum film thickness in the Z direction changes when the thickness of the flexible structure varies.
The influence on lubrication performance with variation in the dimensionless length of the flexible structure (Lf) is also investigated. Figure 11 shows the dimensionless minimum film thickness with variation in the dimensionless length of the flexible structure and tilting ratios. The geometries and their specifications are shown in Table 4.
As the dimensionless length of the flexible structure increases, the dimensionless minimum film thickness increases up to a certain point and then decreases, as shown in Figure 11 (a). When the dimensionless length of the flexible structure is 0.6 for ε’ = 0.2, the dimensionless minimum film thickness with the flexible structure is smaller than that of without. Moreover, as the dimensionless length of the flexible structure increases, the dimensionless minimum film thickness for A = 0.4 is generally larger than that for A = 0.8. When the tilting ratio increase, the dimensionless length of the flexible structure corresponding to the region where the dimensionless minimum film thickness in case with the flexible structure is larger than that without is longer. Figure 12 and Figure 13 show the dimensionless pressure distributions and deformations for six cases, respectively. These six cases are marked with green circles in Figure 11 (a), showing the results for a tilting ratio of 0.2. In Figure 12 (a) to (c) and Figure 13 (a) to (c), as the dimensionless length of the flexible structure increases, the oil pressure increases and amount of elastic displacement accordingly increases. Such a tendency is also shown in Figure 12 (d) to (f) and Figure 13 (d) to (f). This means that as the length of flexible structure increases beyond a certain level, the amount of elastic deformation also increases but minimum film thickness decreases. In other words, if the length of the flexible structure is inappropriate or excessive, the lubrication performance is worse than that without the flexible structure. Therefore, to improve the lubrication performance in the misaligned journal bearing, it is necessary to find and apply the appropriate length of the flexible structure.
The Dimensionless minimum film thickness is maximized when the film thickness distribution in the area that is flexible and where the oil-film pressure is generated is almost constant along the axial direction. Then, the elastic deformation amount at the outer region of the flexible structure should be larger than that of the inner region for the misaligned journal bearing. Therefore, the analysis results for various cross-sectional shapes of the flexible structure are also estimated for the specifications shown in Table 5. The minimum film thicknesses for various thickness ratios of the flexible structure ends (γ) are compared with those of the no-groove journal bearing, and the results are shown in Figure 14.
When the dimensionless thickness of the flexible structure is equal to 0.2, the dimensionless minimum film thicknesses are larger than those for A = 0.4. The reason for this is that the smaller dimensionless thickness of the flexible structure enables a larger oil-film thickness owing to deformation by oil-film pressure. When γ changes, the dimensionless minimum film thicknesses in the case of ε’ = 0.2 is larger than those for ε’ = 0.3 and ε’ = 0.4. However, when the flexible structure is applied, the dimensionless minimum film thickness increases by 18.2% (ε’ = 0.2), 39.5% (ε’ = 0.3), and 103.9% (ε’ = 0.4) compared to those of the no-groove journal bearing. That is, the increase in the dimensionless minimum film thicknesses with the flexible structure relative to those without the flexible structure is relatively large when the tilting ratio is 0.4. In addition, the rectangular flexible structure is more effective for increasing the minimum film thickness than the taper-shaped one for all tilting ratio. The reason for this is that it is not easy to increase the oil-film thickness owing to elastic deformation of the inside of the flexible structure when γ increases. Therefore, to improve the lubrication characteristics in the misaligned journal bearing, the shape of flexible structure should be designed such that the elastic deformation of the outer region of the flexible structure is larger than that of the inner region.

4. Conclusions

This study suggests the application of a flexible structure to misaligned journal bearings to improve their lubrication performances. EHL analysis was conducted to consider the deformation of the groove region using commercial software that can perform multi-physics analysis. The lubrication performance is estimated by comparing the minimum film thickness of the journal bearing with flexible structure for variation of the dimensionless thickness, length, ends thickness ratios of the flexible structure at both ends, and tilting ratio. In addition, these results are compared with those of the journal bearing without the flexible structure. The numerical analysis results indicate the following:
1. The flexible structure of the misaligned journal bearing increases the minimum film thickness effectively, because the film thicknesses in the flexible structure increase by elastic deformation. However, additional researches is needed to suggest the general guidelines for optimal design if the flexible structure.
2. The minimum film thickness is the largest when the film thickness distribution in the area that is flexible and where the oil-film pressure is generated is almost constant along the axial direction.
3. The minimum film thickness increases effectively when the thickness of the flexible structure is about 0.4 times the shaft radius under a constant load.
4. As the dimensionless length of the flexible structure increases, the minimum film thickness increases up to a certain length and then decreases. The reason for this is that an appropriate length of the flexible structure is advantageous for obtaining the oil film thickness based on the elastic deformation region.
5. The rectangular-shaped flexible structure is more effective for increasing the minimum film thickness than the taper shaped one for all tilting ratios. The reason for this is that it is not easy to increase the oil-film thickness based on elastic deformation of the inside of the flexible structure
6. This study also showed that application of the flexible structure can improve the lubrication characteristics of misaligned journal bearing; however further studies are needed on the analyses of abnormal operating conditions, such as shock or fluctuating load conditions and optimization of the flexible structure.

Author Contributions

Conceptualization, S.H., W.J.; literature review and formal analysis, W.J.; writing-original draft preparation, methodology, W.J.; review and editing, S.H. funding acquisition, S.H. (All authors have read and agreed to the published version of the manuscript.).

Funding

This work was supported by Korea Hydro & Nuclear Power Co. (2022).

Data Availability Statement

Not applicable.

Acknowledgments

This work was supported by Korea Hydro & Nuclear Power Co. (2022).

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

A : Dimensionless thickness of the flexible the structure (= a/r)
E : Young’s modulus [GPa]
E* : Dimensionless Young’s modulus (= c2E/(6r2ηω))
F : Dimensionless force (= c2f/(6r4ηω))
FO : Dimensionless oil film force (= c2fo/(6r4ηω))
FX : Component of dimensionless force in the X direction
FY : Component of dimensionless force in the Y direction
FZ : Component of dimensionless force in the Z direction
FOX : Component of dimensionless oil film force in the X direction
FOY : Component of dimensionless oil film force in the Y direction
H : Dimensionless oil film thickness (= h/c)
He : Dimensionless oil film thickness variation by elastic deformation (= he/c)
Hmin : Dimensionless minimum film thickness (= hmin /c)
L : Ratio of length to radius of the bearing (= l/r)
Lf : Dimensionless length of the flexible structure (= lf /l)
O : Center of the shaft at the middle of the bearing
O1, O2 : Centers of the shaft at both ends of the bearing
P : Dimensionless oil film pressure (= c2(p-pa)/(6r2 ηω))
Pb : Dimensionless pressure at the bearing ends and oil feeding groove (= c2(pb-pa)/(6r2ηω))
U : Dimensionless displacement in the element (= u/r)
W : Dimensionless load acting on the shaft (= c2w/ (6r4ηω))
X, Y, Z : Dimensionless rectangular coordinate system (X= x/r, Y= y/r, Z= z/r)
a : Thickness at the outer end of the flexible structure [mm]
c : Clearance [μm]
d : Thickness at the inner end of the flexible structure [mm]
e : Tilting amount of the shaft [μm]
e’ : Tilting amount of the shaft [μm]
f : Force [N]
fo : Oil film force [N]
fx : Component of force in the x direction [N]
fy : Component of force in the y direction [N]
fz : Component of force in the z direction [N]
fox : Component of oil film force in the x direction [N]
foy : Component of oil film force in the y direction [N]
h : Oil film thickness [μm]
he : Change in oil film thickness due to elastic deformation [μm]
hmin : Minimum film thickness [μm]
l : Length of the bearing [mm]
lf : Length of the flexible structure [mm]
p : Oil-film pressure [MPa]
pa : Atmospheric pressure [MPa]
pb : Pressure at bearing ends and oil feeding groove [MPa]
r : Radius of the bearing [mm]
u : Displacement in the element [mm]
w : Load acting on the shaft [N]
x, y, z : Rectangular coordinate system [mm]
β : Ratio of clearance to bearing radius (= c/r)
ε : Eccentricity ratio (= e/c)
ε’ : Tilting ratio (= e’/c)
γ : Ratio of thickness at both ends of the flexible structure (= d/a)
η : Absolute viscosity of the lubricant [Pa∙s]
ν : Poisson’s ratio
θ : Cylindrical coordinate [rad]
θw : Direction of the load in the cylindrical coordinate system [rad]
ω : Angular velocity [rad/s]

References

  1. Huang, Y.; Cao, H.; Tian, Z. Stability analysis of long hydrodynamic journal bearings based on the journal center trajectory. Friction, 2021, 9, 1776–1783. [Google Scholar] [CrossRef]
  2. Das, S.; Guha, S. K.; Chattopadhyay, A. K. On the steady-state performance of misaligned hydrodynamic journal bearings lubricated with micropolar fluids. Tribol. Int., 2002, 35, 201–210. [Google Scholar] [CrossRef]
  3. Zhang, Z. S.; Dai, X. D.; Zhang, Z. N.; Xie, Y. B. Thermoelastohydrodynamic behavior of misaligned plain journal bearings. Proc. Inst. Mech. Eng. Part C J Mech. Eng. Sci. 2013, 227, 2582–2599. [Google Scholar] [CrossRef]
  4. Zheng, L.; Zhu, H.; Zhu, J.; Deng, Y. Effects of oil film thickness and viscosity on the performance of misaligned journal bearings with couple stress lubricants. Tribol. Int., 2020, 146, 106229–11. [Google Scholar] [CrossRef]
  5. Murawski, I. Shaft line whirling vibrations: effects of numerical assumptions on analysis results. Mar. Technol., 2005, 42, 53–60. [Google Scholar] [CrossRef]
  6. Lv, F.; Ta, N.; Rao, Z. Analysis of equivalent supporting point location and carrying capacity of misaligned journal bearing. Tribol. Int., 2017, 116, 26–38. [Google Scholar] [CrossRef]
  7. Jang, J. Y.; Khonsari, M.M. On the characteristics of misaligned journal bearing. Lubricants, 2015, 3, 27–53. [Google Scholar] [CrossRef]
  8. Pigott, R. J. S. Bearings and lubricant-bearing troubles traceable to design can be avoided by engineering study. Mech. Eng., 1942, 64, 259–269. [Google Scholar]
  9. Sun, J.; Gui, C. Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation. Tribol. Int., 2004, 37, 841–848. [Google Scholar] [CrossRef]
  10. Sun, J.; Gui, C.; Li, Z. An experimental study of journal bearing lubrication effected by journal bearing misalignment as a result of shaft deformation under load. J. Tribol., 2005, 127, 813–819. [Google Scholar] [CrossRef]
  11. Etsion, I.; Gommed, K. Improved design with noncylindrical profiles of gas-lubricated ringless pistons. J. Tribol., 1995, 117, 143–147. [Google Scholar] [CrossRef]
  12. Nikolakopoulos, P. G.; Papadoulos, C. A. A study of friction in worn misaligned journal bearing under severe hydrodynamic lubrication. Tribol. Int., 2008, 41, 461–472. [Google Scholar] [CrossRef]
  13. Shenoy, S. B.; Pai, R. Theoretical investigations on the performance of an externally adjustable fluid-film bearing including misalignment and turbulence effects. Tribol. Int., 2009, 42, 1088–1100. [Google Scholar] [CrossRef]
  14. Ram, N.; Sharma, S. C. Influence of wear on the performance of hole-entry hybrid misaligned journal bearing in turbulent regime. Ind. Lubr. Tribol., 2014, 66, 509–519. [Google Scholar] [CrossRef]
  15. Ram, N.; Sharma, S. C. A study of misaligned hole-entry worn journal bearing operating in turbulent regime. Ind. Lubr. Tribol., 2013, 65, 108–118. [Google Scholar] [CrossRef]
  16. Li, B.; Sun, J.; Zhu, S.; et al. Thermohydrodynamic lubrication analysis of misaligned journal bearing considering the axial movement of journal. Tribol. Int., 2019, 135, 397–407. [Google Scholar] [CrossRef]
  17. He, Z. P.; Zhang, J. H.; Xie, W. S. Misalignment analysis of journal bearing influenced by asymmetric deflection, based on a simple stepped shaft model. J. Zhejiang Univ –Sci A, 2012, 13, 647–664. [Google Scholar] [CrossRef]
  18. Xu, G.; Zhou, J.; Geng, H. Research on the static and dynamic characteristics of misaligned journal bearing considering the turbulent and thermohydrodynamic effect. ASME J. Tribol., 2015, 137, 024504–8. [Google Scholar] [CrossRef]
  19. Sun, J.; Gui, C.; Li, Z. Influence of journal misalignment caused by shaft deformation under rotational load on performance of journal bearing. Proc. Inst. Mech. Eng Part J J. Eng. Tribol., 2005, 219, 275–283. [Google Scholar] [CrossRef]
  20. Sharma, S. C.; Girish, B. M.; Kamath, R.; Satish, B. M. Graphite particles reinforced ZA-27 alloy composite materials for journal applications. Wear, 1998, 219, 162–168. [Google Scholar] [CrossRef]
  21. Kim, S. S.; Park, D. C.; Lee, D. G. Characteristics of carbon fiber phenolic composite for journal bearing materials. Compos. Struct., 2004, 66, 359–366. [Google Scholar] [CrossRef]
  22. Bouyer, J.; Fillon, M. Improvement of the THD performance of a misaligned plain journal bearing. J. Tribol., 2003, 125, 334–342. [Google Scholar] [CrossRef]
  23. Hattori, H. EHL analysis of a journal bearing for rotary compressors under dynamic loading: effect of flexible structure at bearing end. Trans. Jap. Soc. Mech. Eng., 1998, 64, 3171–3178. [Google Scholar] [CrossRef]
  24. Ito. Y.; Hattori, H.; Miura, K. Mixed lubrication analysis of vane sliding surface in rotary compressor mechanisms. Tribol. Online, 2009, 4, 96–102. [Google Scholar] [CrossRef]
  25. Ikeda, A.; Satodate, K.; Aoki, T.; Miura, K. Development of the rotary compressor which is high performance in the wide range, and has high refrigerating capacity. In Proceedings of the JSRAE Annual Conference, Tokyo, Japan, 12-14, September 2012. [Google Scholar]
  26. Hong, S. H.; Kim, K. W. A new type groove for hydraulic spool valve. Tribol. Int., 2016, 103, 629–640. [Google Scholar] [CrossRef]
  27. Oh, K. P.; Huebner, K. H. Solution of the elastohydrodynamic finite journal bearing problem. ASME Lubr. Technol., 1973, 95, 342–351. [Google Scholar] [CrossRef]
  28. Kalin, M.; Kus, M. New strategy for reducing the EHL friction in steel contacts using additive-formed oleophobic boundary film. Friction, 2021, 9, 1346–1360. [Google Scholar] [CrossRef]
  29. Wang, Y.; Wang, Q. J.; Lin, C. A mixed-EHL analysis of effects of misalignments and elastic deformations on the performance of a coupled journal-thrust bearing system. Tribol. Int., 2006, 39, 281–289. [Google Scholar] [CrossRef]
Preprints 72781 g001
Figure 1. Application of the flexible structure to the misaligned journal bearing (a) without flexible structure; (b) with flexible structure.
Figure 1. Application of the flexible structure to the misaligned journal bearing (a) without flexible structure; (b) with flexible structure.
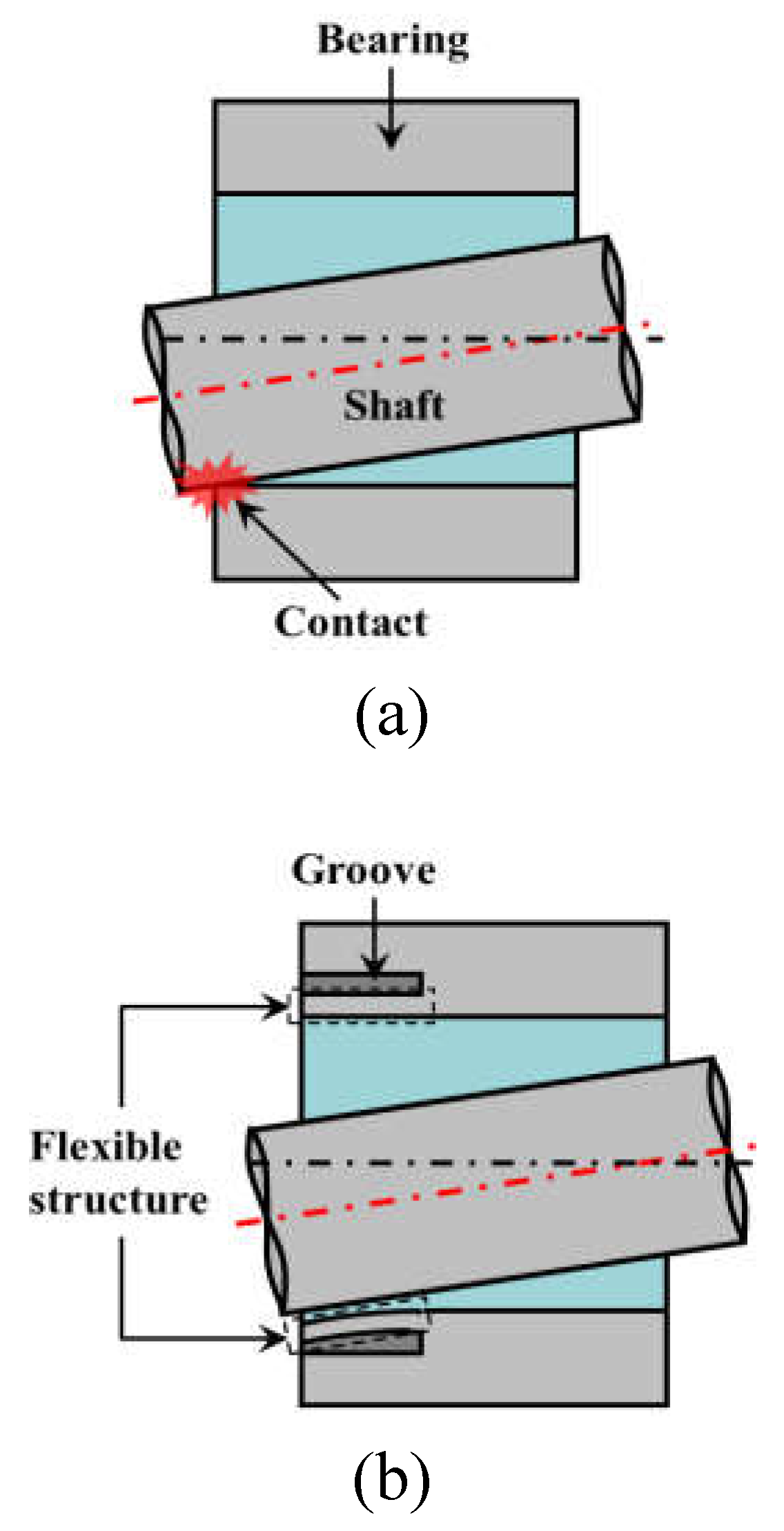
Preprints 72781 g001
Preprints 72781 g002
Figure 2. Schematic of journal bearing system (a) x-y plane; (b) y-z plane; (c) θ - z plane; (d) shapes of the flexible structure.
Figure 2. Schematic of journal bearing system (a) x-y plane; (b) y-z plane; (c) θ - z plane; (d) shapes of the flexible structure.
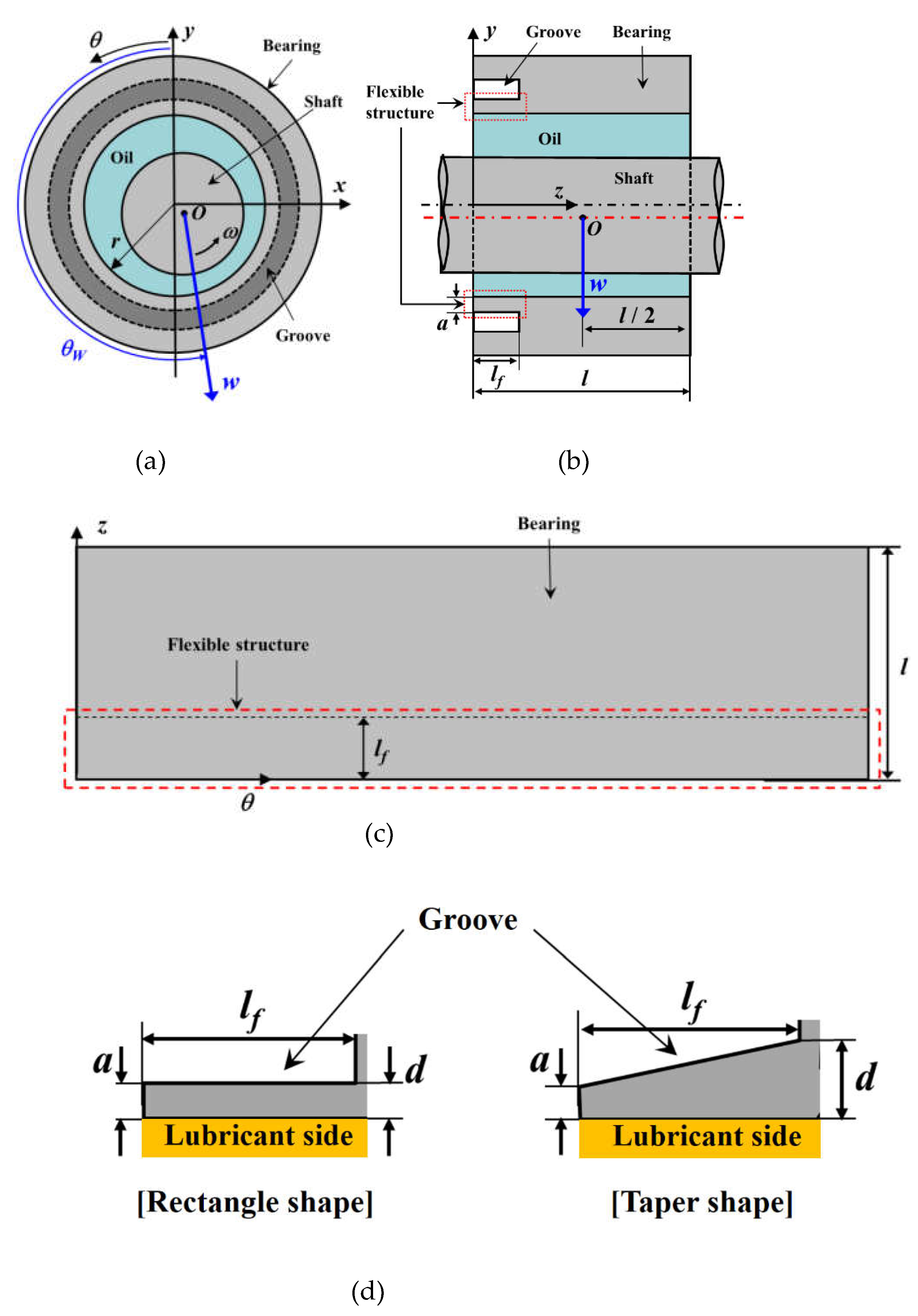
Preprints 72781 g002
Preprints 72781 g003
Figure 3. The shaft in bearing with eccentric and tilted motion (a) x-y plane; (b) y-z plane.
Figure 3. The shaft in bearing with eccentric and tilted motion (a) x-y plane; (b) y-z plane.
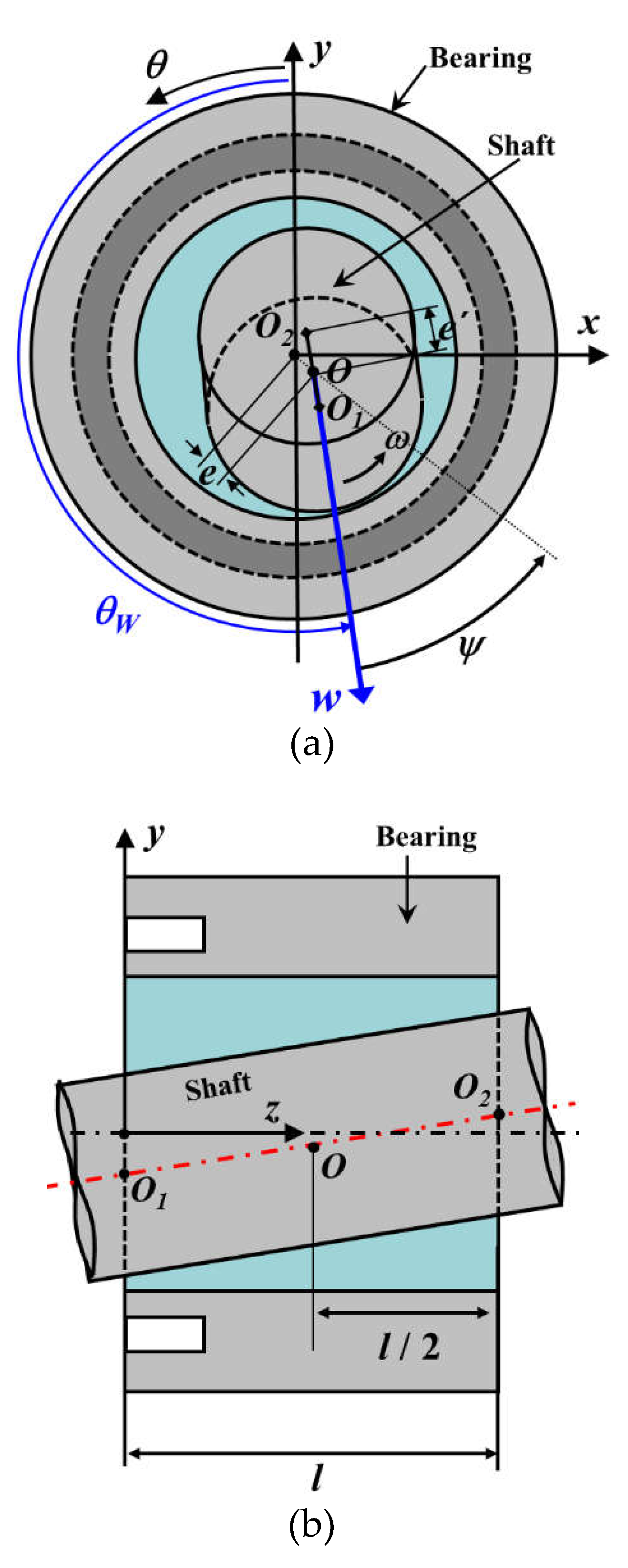
Preprints 72781 g003
Preprints 72781 g004
Figure 4. 3-dimensional finite element analysis model.
Figure 4. 3-dimensional finite element analysis model.
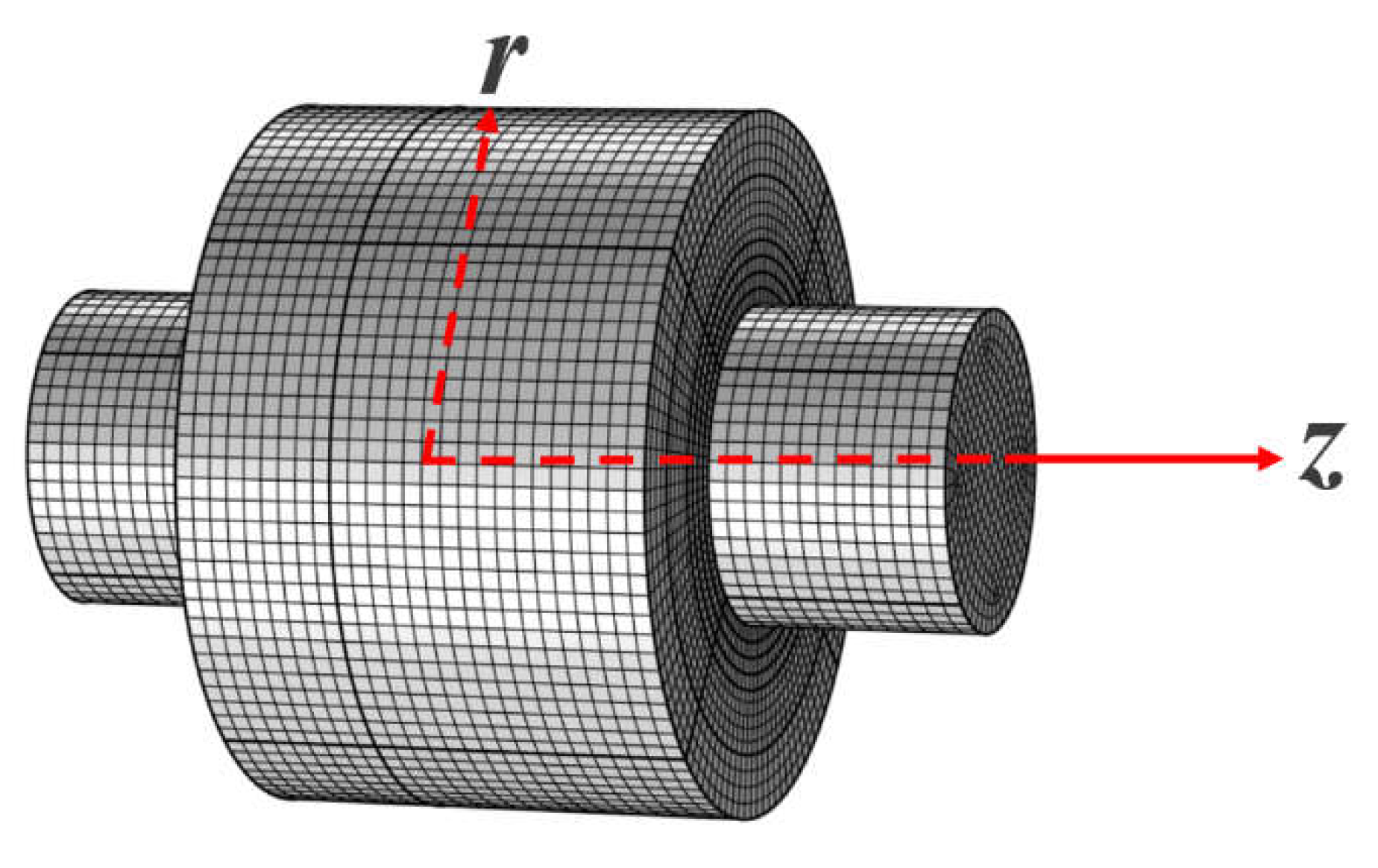
Preprints 72781 g004
Preprints 72781 g005
Figure 5. Oil-film force working on the shaft.
Figure 5. Oil-film force working on the shaft.
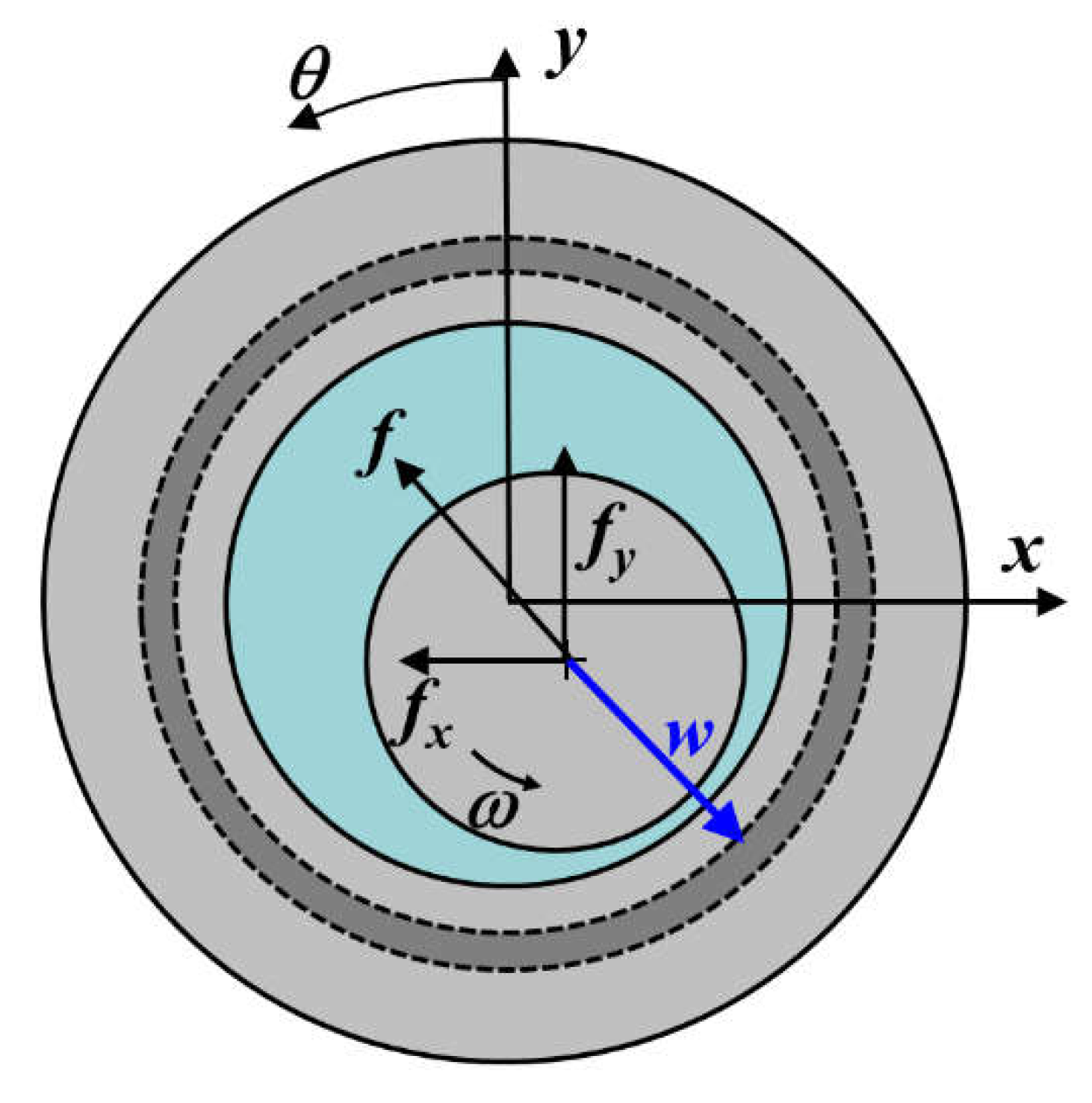
Preprints 72781 g005
Preprints 72781 g006
Figure 6. Dimensionless results for journal bearing without flexible structure (L = 3.0, W = 4.4, γ =1.0, ε’ = 0.2) (a) film thickness; (b) pressure distribution; (c) circumferential distribution of film thickness and pressure.
Figure 6. Dimensionless results for journal bearing without flexible structure (L = 3.0, W = 4.4, γ =1.0, ε’ = 0.2) (a) film thickness; (b) pressure distribution; (c) circumferential distribution of film thickness and pressure.
Preprints 72781 g006
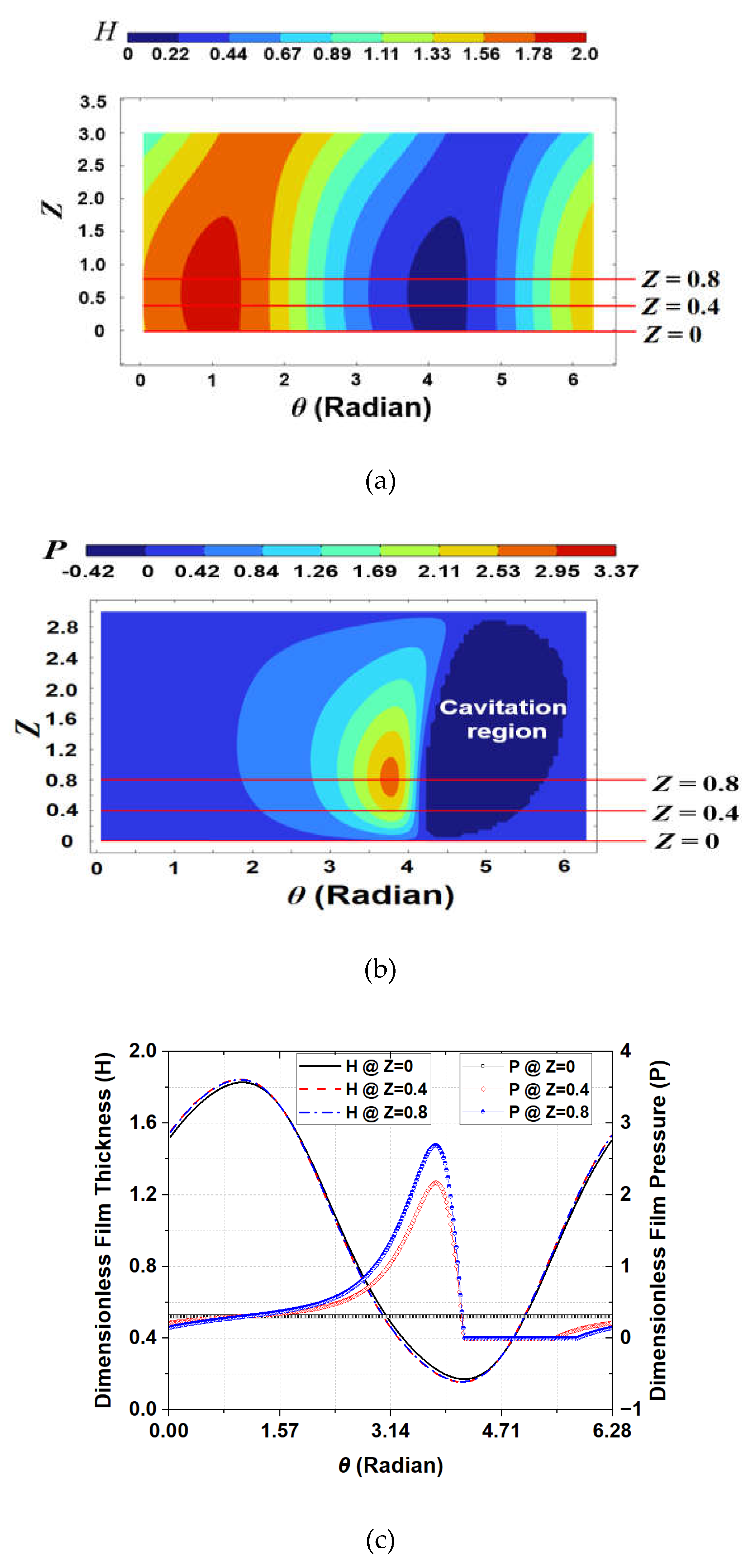
Preprints 72781 g007
Figure 7. Dimensionless results for journal bearing with flexible structure (L = 3.0, A =0.4, W = 4.4, γ =1.0, ε’ = 0.2) (a) film thickness; (b) pressure distribution; (c) circumferential distribution of film thickness and pressure.
Figure 7. Dimensionless results for journal bearing with flexible structure (L = 3.0, A =0.4, W = 4.4, γ =1.0, ε’ = 0.2) (a) film thickness; (b) pressure distribution; (c) circumferential distribution of film thickness and pressure.
Preprints 72781 g007
Preprints 72781 g008
Figure 8. Dimensionless minimum film thickness with shaft tilting ratio (L = 3.0, A =0.4, Lf = 1/3, W = 4.4, γ =1.0).
Figure 8. Dimensionless minimum film thickness with shaft tilting ratio (L = 3.0, A =0.4, Lf = 1/3, W = 4.4, γ =1.0).
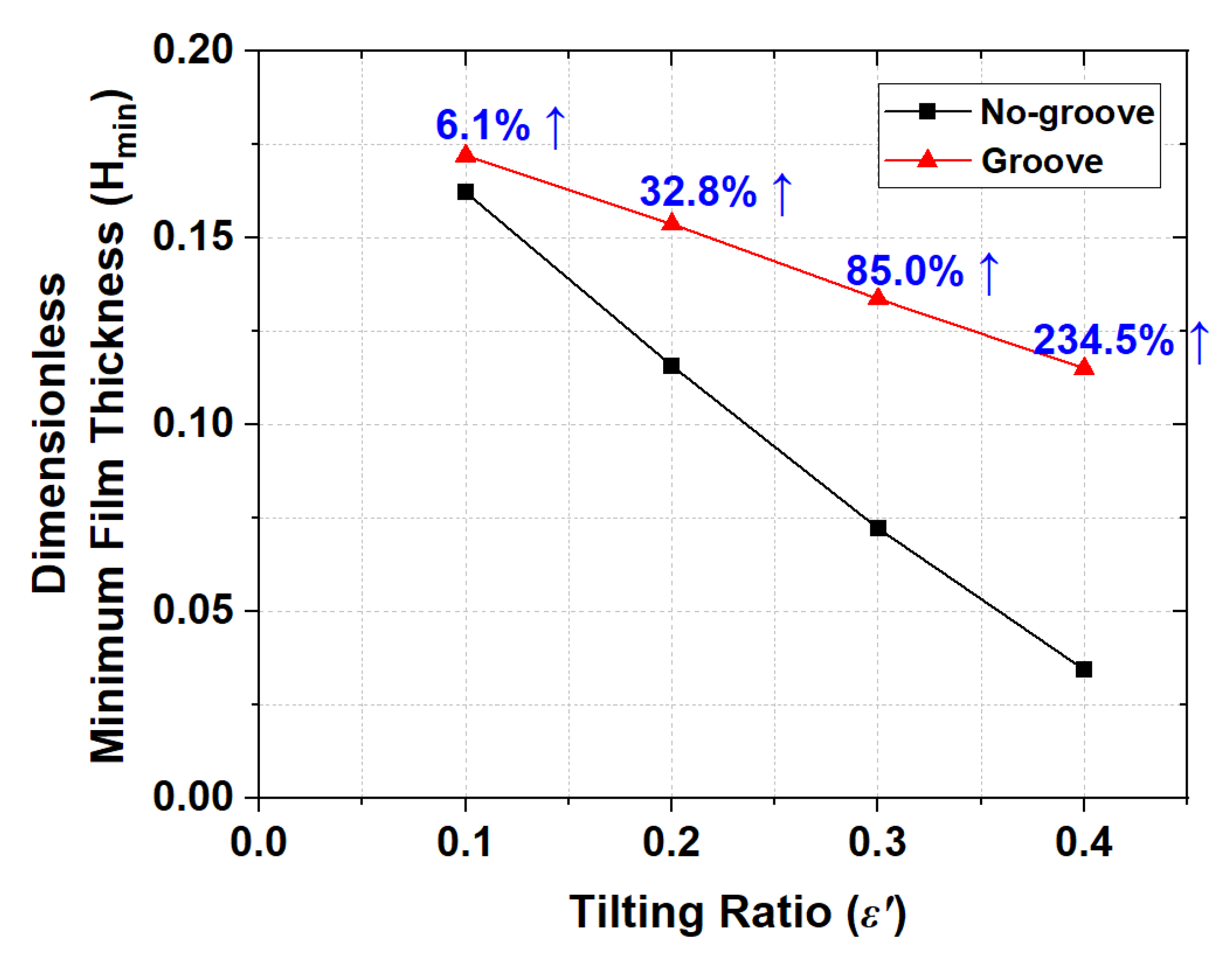
Preprints 72781 g008
Preprints 72781 g009
Figure 9. Dimensionless minimum film thickness with A (L = 3.0, Lf = 1/3, W = 4.4, γ =1.0). (a) ε’ = 0.2; (b) ε’ = 0.3; (c) ε’ = 0.4.
Figure 9. Dimensionless minimum film thickness with A (L = 3.0, Lf = 1/3, W = 4.4, γ =1.0). (a) ε’ = 0.2; (b) ε’ = 0.3; (c) ε’ = 0.4.
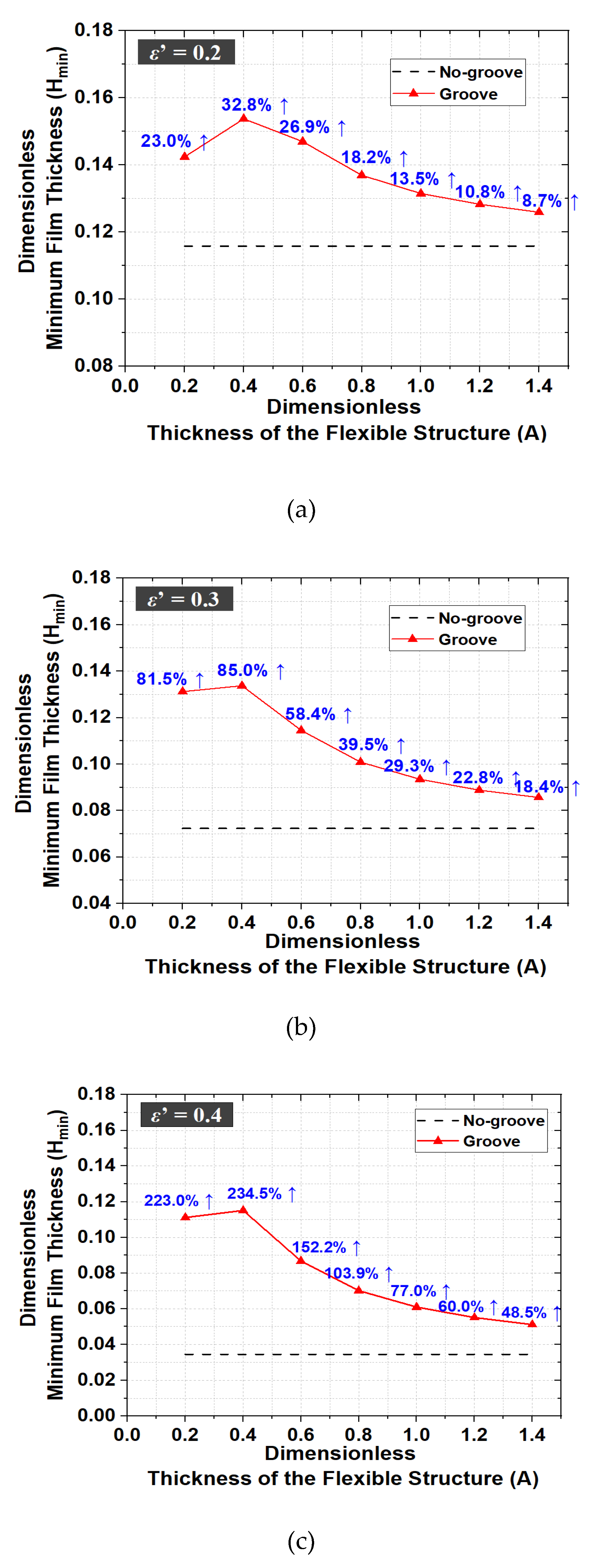
Preprints 72781 g009
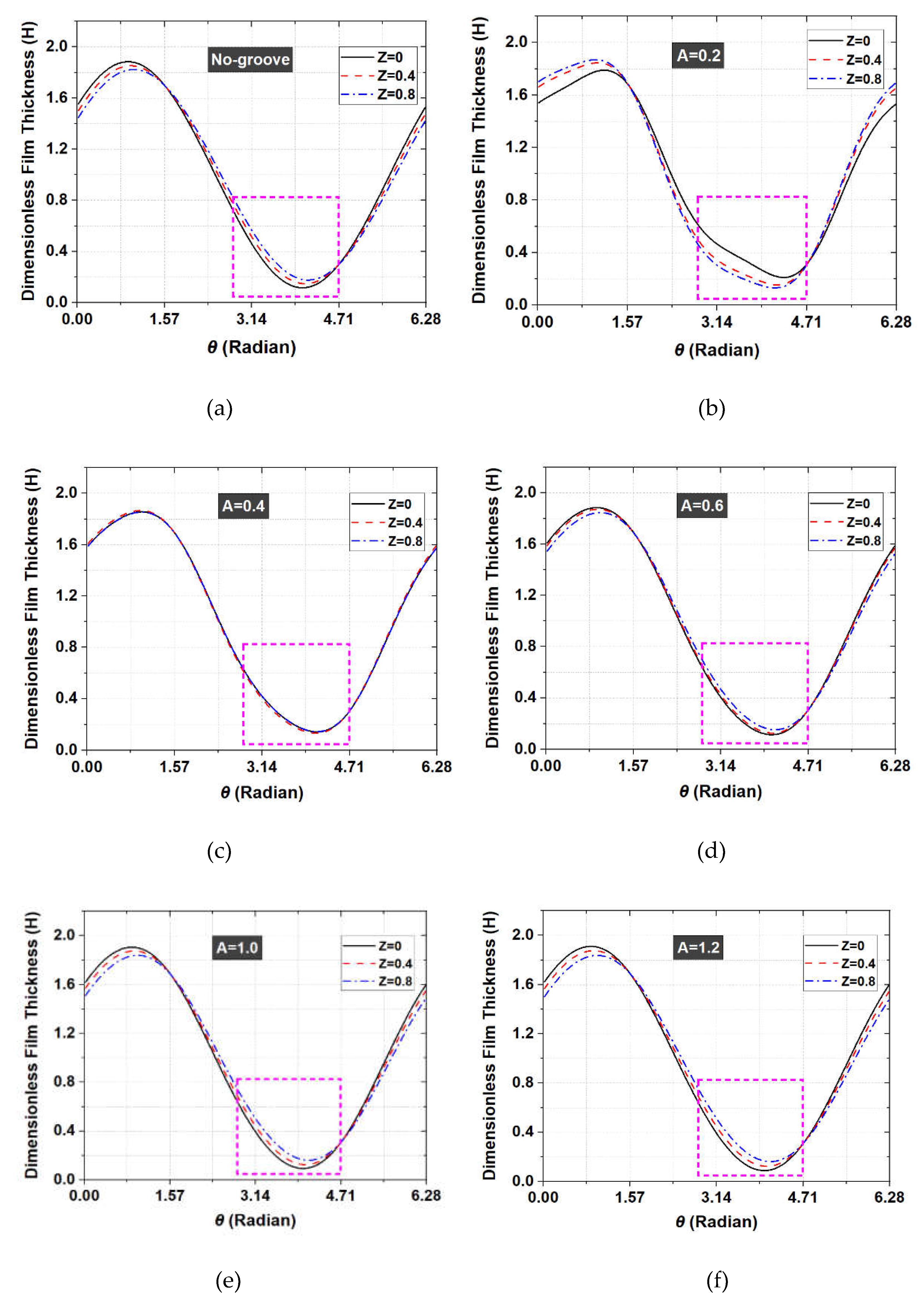
Preprints 72781 g010
Figure 10. Circumferential distributions of the dimensionless film thickness for different A (L = 3.0, Lf = 1/3, W = 4.4, γ =1.0, ε’ = 0.3) (a) No-groove; (b) A = 0.2; (c) A = 0.4; (d) A = 0.6; (e) A = 1.0; (f) A = 1.2.
Figure 10. Circumferential distributions of the dimensionless film thickness for different A (L = 3.0, Lf = 1/3, W = 4.4, γ =1.0, ε’ = 0.3) (a) No-groove; (b) A = 0.2; (c) A = 0.4; (d) A = 0.6; (e) A = 1.0; (f) A = 1.2.
Preprints 72781 g010
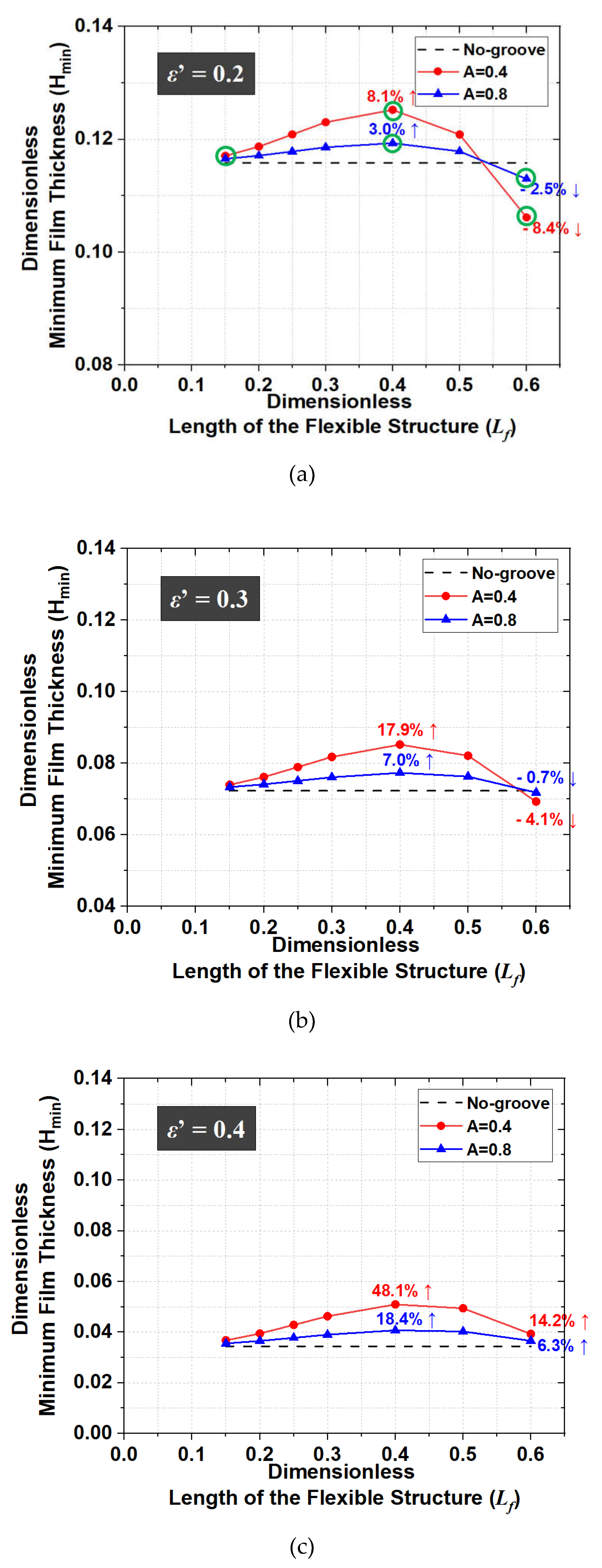
Preprints 72781 g011
Figure 11. Dimensionless minimum film thickness with Lf (L = 3.0, W = 4.4, γ =1.0). (a) ε’ = 0.2; (b) ε’ = 0.3; (c) ε’ = 0.4.
Figure 11. Dimensionless minimum film thickness with Lf (L = 3.0, W = 4.4, γ =1.0). (a) ε’ = 0.2; (b) ε’ = 0.3; (c) ε’ = 0.4.
Preprints 72781 g011
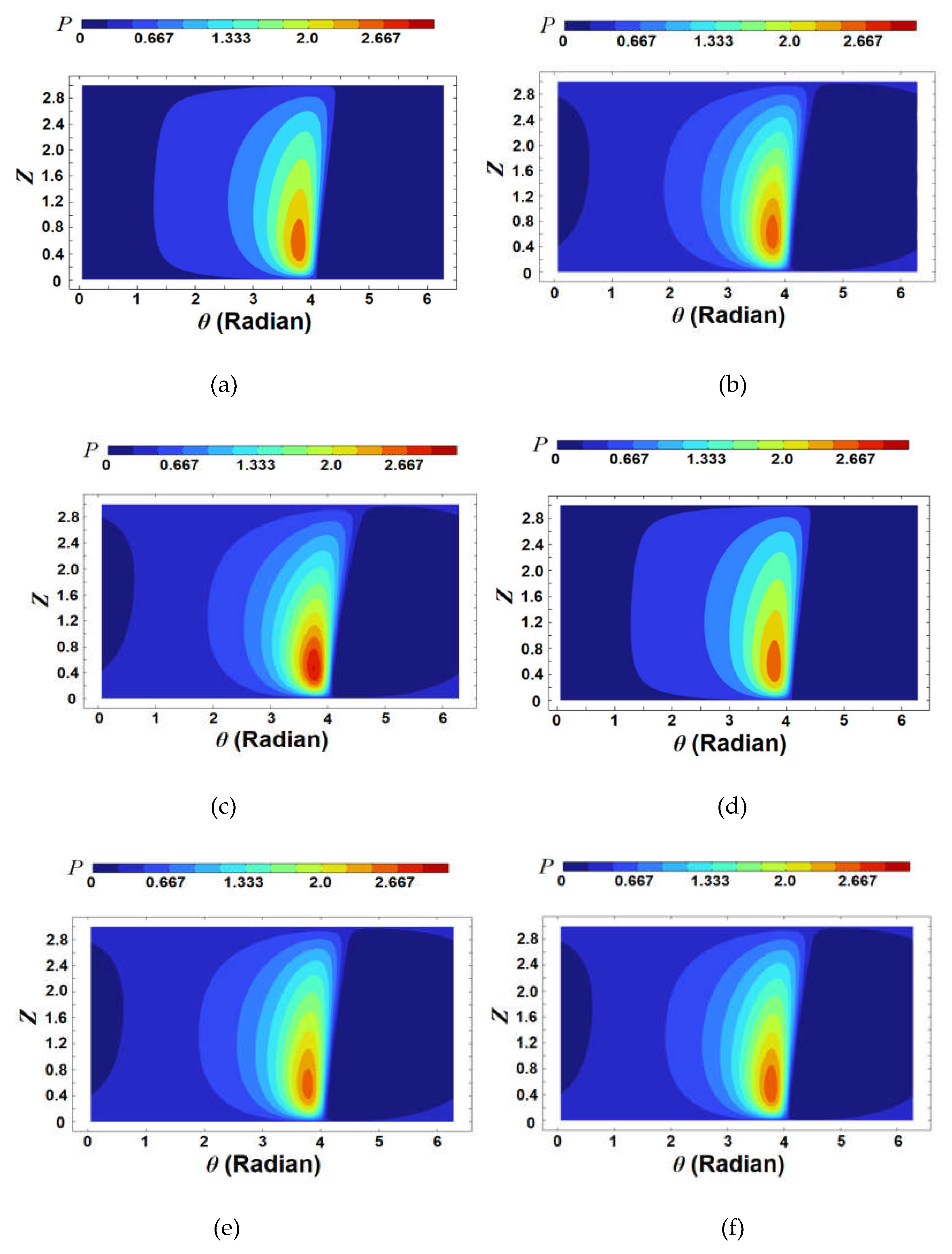
Preprints 72781 g012
Figure 12. Distributions of the dimensionless oil pressure for ε’ = 0.2. (a) A = 0.4, Lf = 0.15; (b) A = 0.4, Lf = 0.4; (c) A = 0.4, Lf = 0.6; (d) A = 0.8, Lf = 0.15; (e) A = 0.8, Lf = 0.4; (f) A = 0.8, Lf = 0.6.
Figure 12. Distributions of the dimensionless oil pressure for ε’ = 0.2. (a) A = 0.4, Lf = 0.15; (b) A = 0.4, Lf = 0.4; (c) A = 0.4, Lf = 0.6; (d) A = 0.8, Lf = 0.15; (e) A = 0.8, Lf = 0.4; (f) A = 0.8, Lf = 0.6.
Preprints 72781 g012
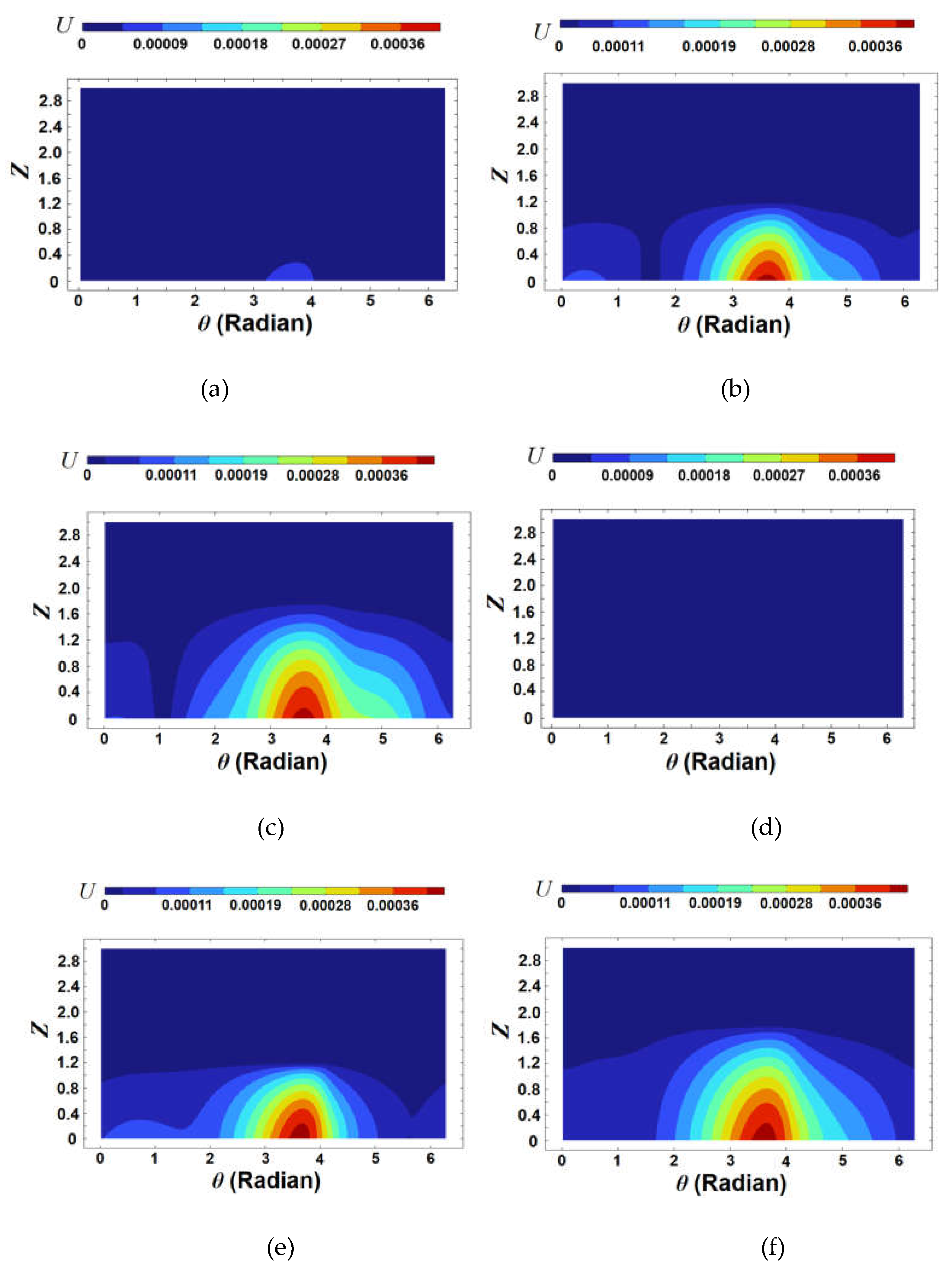
Preprints 72781 g013
Figure 13. Distributions of the dimensionless deformation for ε’ = 0.2. (a) A = 0.4, Lf = 0.15; (b) A = 0.4, Lf = 0.4; (c) A = 0.4, Lf = 0.6; (d) A = 0.8, Lf = 0.15; (e) A = 0.8, Lf = 0.4; (f) A = 0.8, Lf = 0.6.
Figure 13. Distributions of the dimensionless deformation for ε’ = 0.2. (a) A = 0.4, Lf = 0.15; (b) A = 0.4, Lf = 0.4; (c) A = 0.4, Lf = 0.6; (d) A = 0.8, Lf = 0.15; (e) A = 0.8, Lf = 0.4; (f) A = 0.8, Lf = 0.6.
Preprints 72781 g013
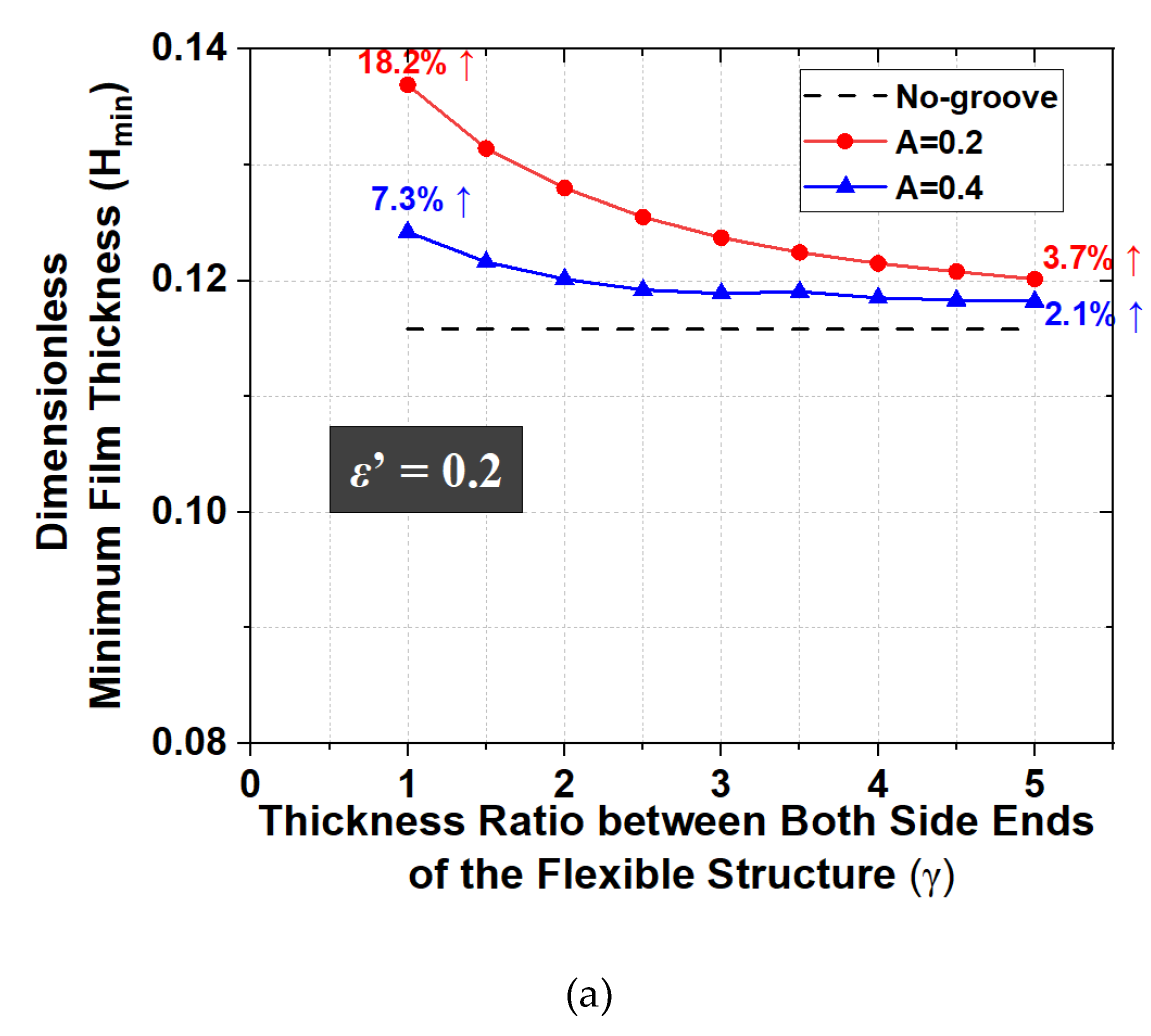
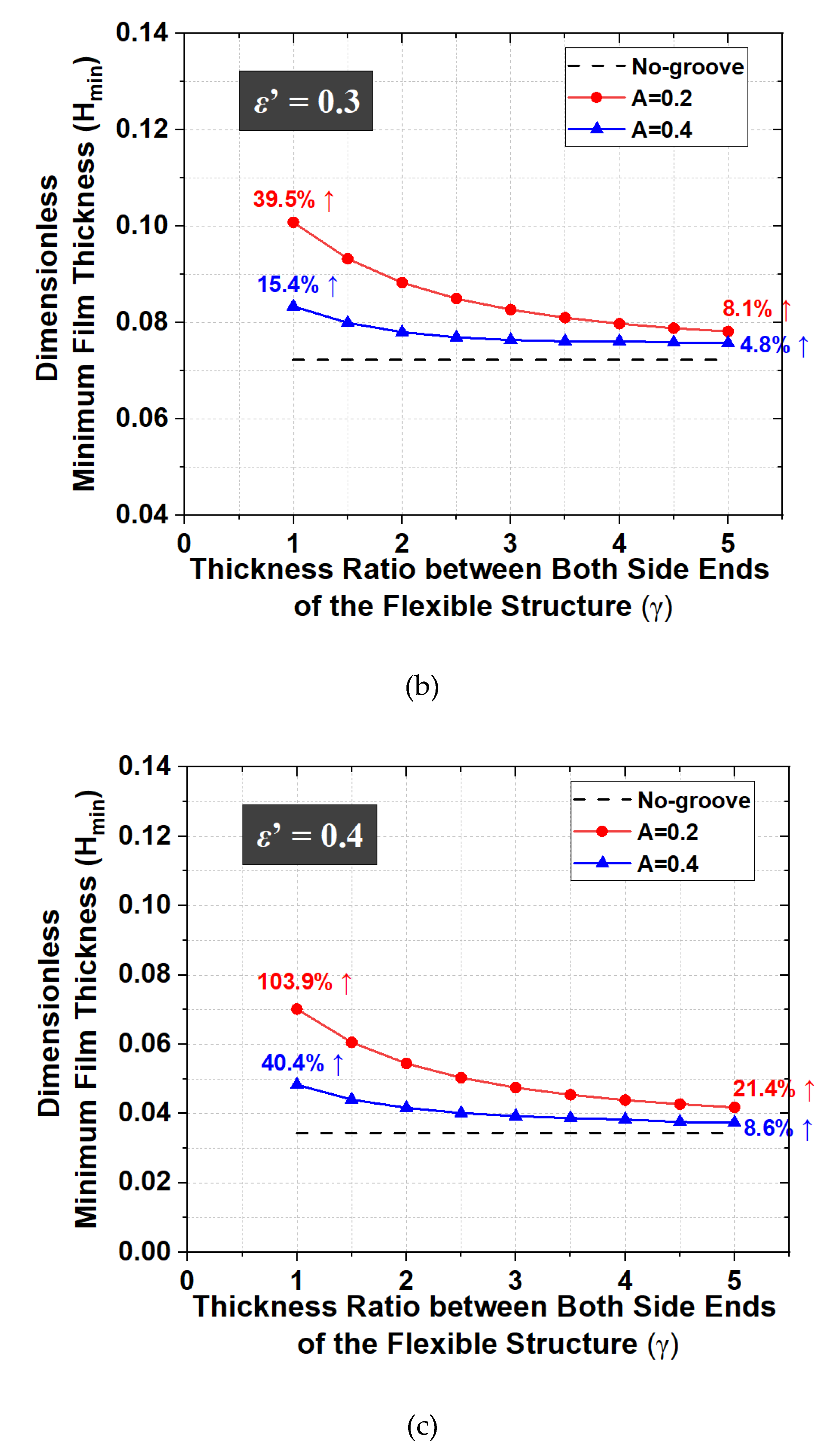
Preprints 72781 g014aPreprints 72781 g014b
Figure 14. Dimensionless minimum film thickness with γ (L = 3.0, W = 4.4, γ =1.0). (a) ε’ = 0.2; (b) ε’ = 0.3; (c) ε’ = 0.4.
Figure 14. Dimensionless minimum film thickness with γ (L = 3.0, W = 4.4, γ =1.0). (a) ε’ = 0.2; (b) ε’ = 0.3; (c) ε’ = 0.4.
Preprints 72781 g014aPreprints 72781 g014b
Table 1. Specification of the analysis model (application of flexible structure).
Table 1. Specification of the analysis model (application of flexible structure).
Parameter Value Parameter Value
A 0.4 W 4.4
E* 2.2 × 104 β 10-3
L 3.0 γ 1.0
Lf 0, 1/3 ε’ 0.2
Pb 0.3
Table 2. Specification of the analysis model (variation of ε’).
Table 2. Specification of the analysis model (variation of ε’).
Parameter Value Parameter Value
A 0.4 W 4.4
E* 2.2 × 104 β 10-3
L 3.0 γ 1.0
Lf 0, 1/3 ε’ 0.1, 0.2, 0.3, 0.4
Pb 0.3 θw π
ν 0.3
Table 3. Specification of the analysis model (variation of A).
Table 3. Specification of the analysis model (variation of A).
Parameter Value Parameter Value
A 0.2~1.2 W 4.4
E* 2.2 × 104 β 10-3
L 3.0 γ 1.0
Lf 0, 1/3 ε’ 0.2, 0.3, 0.4
Pb 0.3 θw π
ν 0.3
Table 4. Specification of the analysis model (variation of Lf).
Table 4. Specification of the analysis model (variation of Lf).
Parameter Value Parameter Value
A 0.4, 0.8 W 4.4
E* 2.2 × 104 β 10-3
L 3.0 γ 1.0
Lf 0 ~ 1/3 ε’ 0.2, 0.3, 0.4
Pb 0.3 θw π
ν 0.3
Table 5. Specification of the analysis model (variation of γ).
Table 5. Specification of the analysis model (variation of γ).
Parameter Value Parameter Value
A 0.2, 0.4 W 4.4
E* 2.2 × 104 β 10-3
L 3.0 γ 1.0 ~ 5.0
Lf 0 ~ 1/3 ε’ 0.2, 0.3, 0.4
Pb 0.3 θw π
ν 0.3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated