Prerpints.org logo
Preprint
Article

Effect of Hot Spot within Combustion Liner on YSZ Crack Propagation Mode

Altmetrics

Downloads

124

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

  † These authors contributed equally to this work.

This version is not peer-reviewed

Submitted:

26 April 2023

Posted:

08 May 2023

You are already at the latest version

Alerts
Abstract
On the aero-engine combustor liner, a phenomenon of overheating resembling a hot spot exists, accompanied by a preferential peeling of the YSZ thermal barrier coating that will negatively affect the service life of the component. The temperature gradient of the hot spot may affect the YSZ fracture pattern.In this paper, the morphological and property changes of YSZ sintering is investigated experimentally, and a coupled analysis of the YSZ Crack Propagation Mode under the hot spot is performed using ABAQUS. The results show that the pore fractal size D of YSZ increases by 15%. Inside the hot spot region, the coating has a shear stress of 75MPa. By inserting Cohesive units globally in the model to simulate the random crack initiation and propagation, unlike the thinning of YSZ layered peeling caused by uniform superheating, hot spot will cause the crack initiation at the tip of the pores inside the coating and the oblique propagation, eventually forming an oblique crack connection through the pores. When the temperature gradient reaches 30K/mm, the crack propagation is 40% greater than in a uniform temperature field; consequently, the YSZ in the hot spot boundary region with a greater temperature gradient results in more severe bulk peeling.
Keywords: 
Subject: Chemistry and Materials Science  -   Surfaces, Coatings and Films

1. Introduction

Thermal barrier coatings systems (TBCs) are utilized to increase the operating temperatures of advanced gas turbine engines and the thermal protection capacity of the engine’s hot section components. The principle is to isolate a portion of the temperature transmission via porous YSZ (primarily 6%-8% Y2O3 partially stabilized by ZrO2). However, TBCs will have a shorter lifespan in environments with elevated temperatures. Statistical analysis of a particular type of aero-engine combustion chamber hole probe images reveals that there is preferential shedding of thermal barrier coating between the cooling holes of the flame barrel wall insulation tiles, accompanied by the ablation point phenomenon, and that it is one of the primary causes of wall failure [1,2,3]. The analysis of the temperature field of the combustion chamber of the aero-engine and the flow field around the cooling holes reveals that, due to the admixture of hot gas and cooling gas, the temperature can reach 1573K in some areas and there is a large temperature gradient, which has an effect on the stress distribution and failure law of the coating [4,5,6].
Several factors, such as TGO and morphology at the interface, sintering of TC layers, creep and plasticity, interact to cause the failure of TBCs due to high temperature, and for the hot spot high temperature region, the sintering effect of the coating is more pronounced [7,8]. The strain difference caused by the disparity in thermal expansion of the layers under temperature loading as a result of the change in material toughness brought about by coating sintering must be compensated for by crack propagation within the coating [9,10,11]. SiKyaw et al. concluded that the increased modulus of YSZ due to sintering would result in a stress increase of approximately twofold, which contributes to crack propagation [12]. Wei et al. concluded that the emergence of coating fractures is closely related to the alteration of the material’s properties caused by high temperature.The sintering of the coating promotes the accumulation of strain energy at the fracture tip of the TC layer, thereby facilitating crack initiation and propagation [13]. And as a result of the lower fracture toughness and pore morphology, coating cracking occurs primarily within the ceramic layer and extends along the path of pores and brittle plate boundaries [14,15]. A.G. Evans et al. discovered that the longitudinal temperature gradient within the coating will produce a corresponding stress gradient. In addition, the temperature gradient distribution of the hot spot has an influence on the coating failure [16]. Yang et al. came to the conclusion that fractures within the ceramic layer are more likely to appear in regions with a greater temperature gradient [17]. It can be inferred that the sintering action of YSZ under the influence of high temperature will alter the structure and properties of the original coating, and that the temperature gradient distribution will generate new stress concentration points and crack propagation patterns; however, the transverse temperature gradient of the hot spot is not considered in the current study [18,19,20]. Therefore, the original life prediction method based on interfacial fracture is no longer used in environments where hot spots are heated. Therefore, it is necessary to study the effect of hot spots on crack extension under sintered morphology and evaluate the relationship between thermal concentration and crack patterns to provide a basis for life prediction under complex temperature conditions.
In investigations on cracking, the finite element method (FEM) is commonly used to simulate the formation and growth of cracks.Kadam and Koushali et al. used the finite element method to perform failure analysis in the context of YSZ and concluded that the internal stresses causing coating cracking are typically interlayer positive stresses and shear forces, which correspond to type I and type II fracture modes, respectively [21,22]. Using the finite element method, Zhi-Y et al. explained the YSZ coating peel fractures as the connection between the interface peak and the cracks within the YSZ [23]. Kai et al. came to the conclusion that the connection of the fractures within the YSZ would result in a rupture region later in the coating’s lifetime, thereby accelerating the coating’s peeling [24]. Consequently, the crack extension and connection problem will be a significant factor in coating failure; however, previous studies on thermal barrier coatings focused on the analysis of internal stress and interface morphology of the coating, concentrating on the TBC failure mode and the corresponding failure mechanism, while simplifying or ignoring the effect of the morphology of the porous YSZ on crack extension. Xie L. et al., for instance, utilized the residual stress equation related to thermal mismatch to explain that a change in thermal load will lead to a difference in thermal expansion of the coating, resulting in tensile stresses that cause microcracks in the TC [25]. However, the effect of the actual morphology of the sparse and porous APS TBC on the stress distribution of the coating cannot be captured. Therefore, it is necessary to model using the actual coating morphology, which can explain the failure mechanism more thoroughly.
Due to internal defects and sintering, hot barrier coatings will have more complex stress states in hot spot environments and will generate novel crack propagation patterns. This study focuses on the crack propagation process of TBCs with sintering characteristics subjected to cyclic hot spot loading. By preparing hot barrier coating specimens and obtaining YSZ samples with varying degrees of sintering, we summarize the changes of coating morphology and properties caused by sintering, extract typical sintering morphology features to establish a numerical model of the coating with real pores, analyze the stress distribution within the coating under hot spot loading, and simulate the random cracking process under temperature cycling by inserting cohesive units globally. And compare with the actual thermal barrier coating morphology of the combustion liner to validate the hot spot-influenced crack propagation process.

2. Materials and Methods

In this paper, the sintering behavior of YSZ is investigated using an experimental method, and a numerical method is used to simulate the crack extension behavior of YSZ under the influence of hot spot.

2.1. Experimental procedure

Sandblasting was used to prepare the hastelloy X specimens prior to the deposition of a 150um NiCoCrAlY bond coat and a 300um YSZ top coat using a Praxair 3710 atmospheric plasma spraying (APS) system and an SG100 spray gun. Table 1 outlines the deposition parameters.
The TBCs samples were treated at 1373K(1100℃) in 10h, 20h, 50h, 100h, and 150h cycles. This method employs a high-temperature furnace with a heating rate of 350K/h and a cooling rate of less than 90K/h to inhibit the propagation of YSZ fractures.Comparatively, another specimen with the same holding duration at 1423K(1150℃) was collected.
The layers were investigated using an OLYMPUS LASER and TESCAN MIRA LMS electron scanning microscope. The effect of sintering behavior on pore variation was described by applying fractal theory to the processing of pore morphology using image software. Individual pore areas S and perimeters L were measured, and the fractal dimension D of the pores was correlated as follows with the pore areas S and perimeters L [26]:
L = A S D 2 ,
log L = D 2 log S + log A ,
Where L is the pore diameter in microns, S is the pore area in micrometer squared, and A and D are dimensionless. Using equations (1) and (2), the fractal dimension distribution of the pores in each sintered morphology was inputted, and a linear regression equation was fitted. The value of D ranges from 1 to 2 and is dependent on the morphology of the pores; the flatter the morphology of the pores, the greater the fractal dimension D [27].
The YSZ modulus was measured with a holding duration, and the indentation method was chosen due to its ease of use and small sample size requirement, as well as its extensive use in measuring the performance of TC layers. Diamond indenter indentation process utilizing constant load rate method, the loading load is 50N, loading time is 15s, to eliminate the effect of creep set load retention time is 10s, sink speed is 0.10nm/s, the load-displacement relationship obtained after the formula (3), (4) to calculate the elastic modulus.
E r = π 2 S A ,
Where Er is the equivalent modulus of elasticity, S is the stiffness, which can be obtained by unloading the load to the depth by derivation. A is dimensionless. The modulus of elasticity of the material under test is calculated by equation (4):
1 E r = 1 − v 2 E + 1 − v i 2 E i ,
Where Ei, νi is the indenter modulus and Poisson’s ratio, take the value of 1140GPa and 0.07, assume the Poisson’s ratio of 8YSZ is constant 0.2 for calculation.
As seen on the image of the combuster liner borescope, there are areas of concentrated ablation between the cooling openings, along with preferential peeling of the TBCs. (Figure 1). Using a confocal microscope to produce cross-sectional 3D morphology to characterize the cracks, the cross-sectional position of the ablated part is determined as depicted in Figure 1.(b).

2.2. Numerical model

2.2.1. Model geometry

The simulation modeling of the thermal barrier coating system is performed using the ABAQUS finite element software, and the coating structure is simplified to a two-dimensional axisymmetric model in consideration of the coating’s geometry and thermal load symmetry. As depicted in Figure 2, the cross-sectional micrographs of the experimental specimens were binarized and the characteristic parameters of the pore morphology were extracted by the graphics processing software and sent to ABAQUS to establish TBCs. (a). Since the purpose of this paper is to examine the effect of ceramic layer sintering on the internal crack pattern of ceramic layer and previous research indicates that the coating is dominated by sintering failure in high temperature environments, the impact of interfacial TGO is disregarded [28,29]. The TC layer is conFig.d with a finite element (FE) mesh that is encrypted. Given that the volume of pores is significantly greater than that of microcracks, only the pore effect is considered in the modeling, and micrographs with a complete TC layer are chosen to more accurately model the effect of pore changes on the macroscopic modulus of YSZ, while directly characterizing the macroscopic condition of the coating represented by the pores.
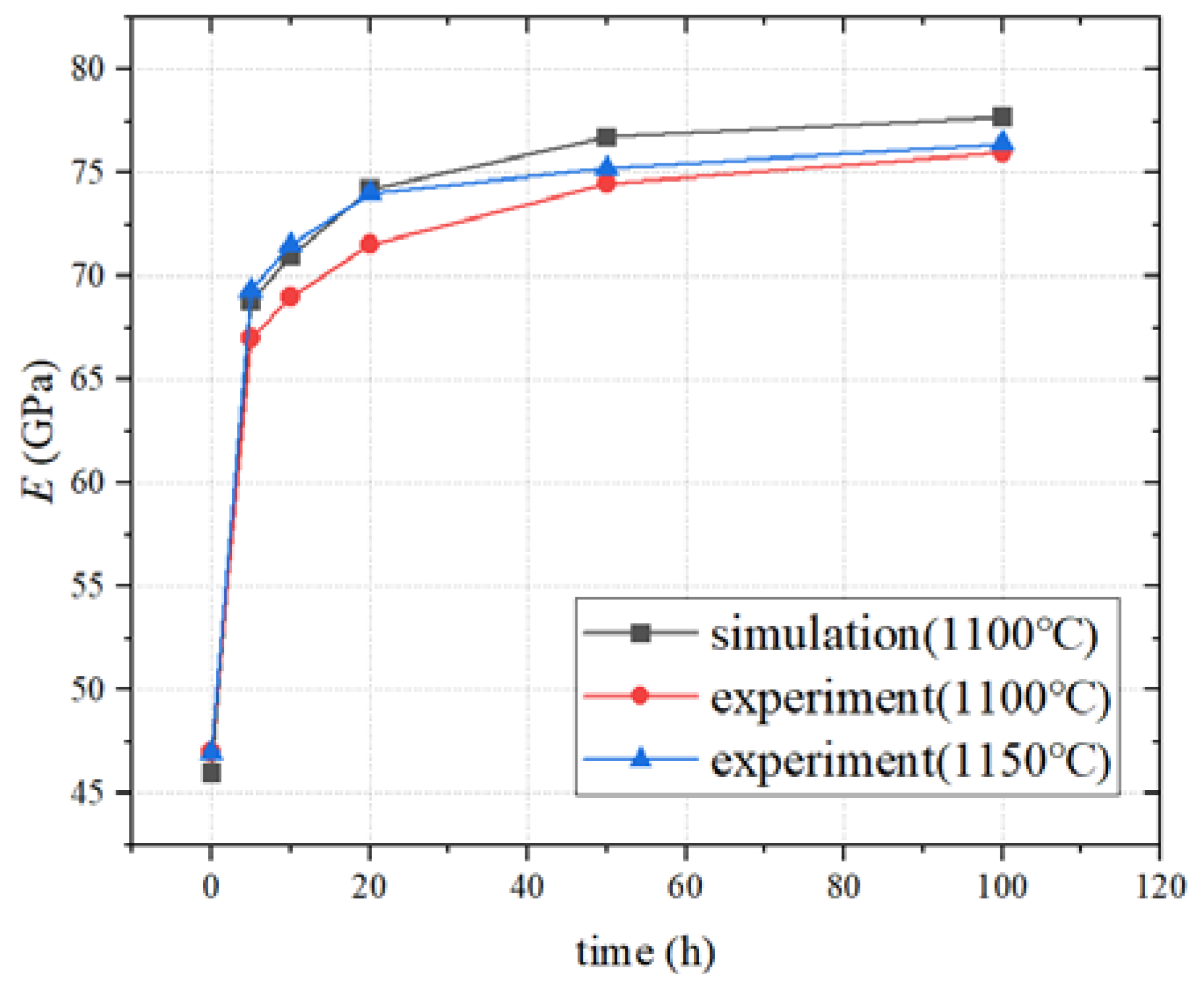
In order to verify the validity of the actual modeling, the YSZ grid cell density was set to 220 GPa to reflect the degree of sintering caused by the real pore morphology [30]. The YSZ elastic modulus was computed using the steady-state mechanical simulation Eq. 5, and the comparison to real-world measurements is depicted in Figure 3. The difference between the modulus E obtained by simulation and experimental methods is less than 6% of the measured value, demonstrating that the image-based model captures the main microstructural features contributing to the variation of the YSZ elastic modulus, and that ignoring finer cracks and pores is acceptable.
where E is the modulus of elasticity, P is the applied load, A is the cross-sectional area, and ε is the strain.
E r = P A 1 ε ,

2.2.2. Materials and boundary conditions

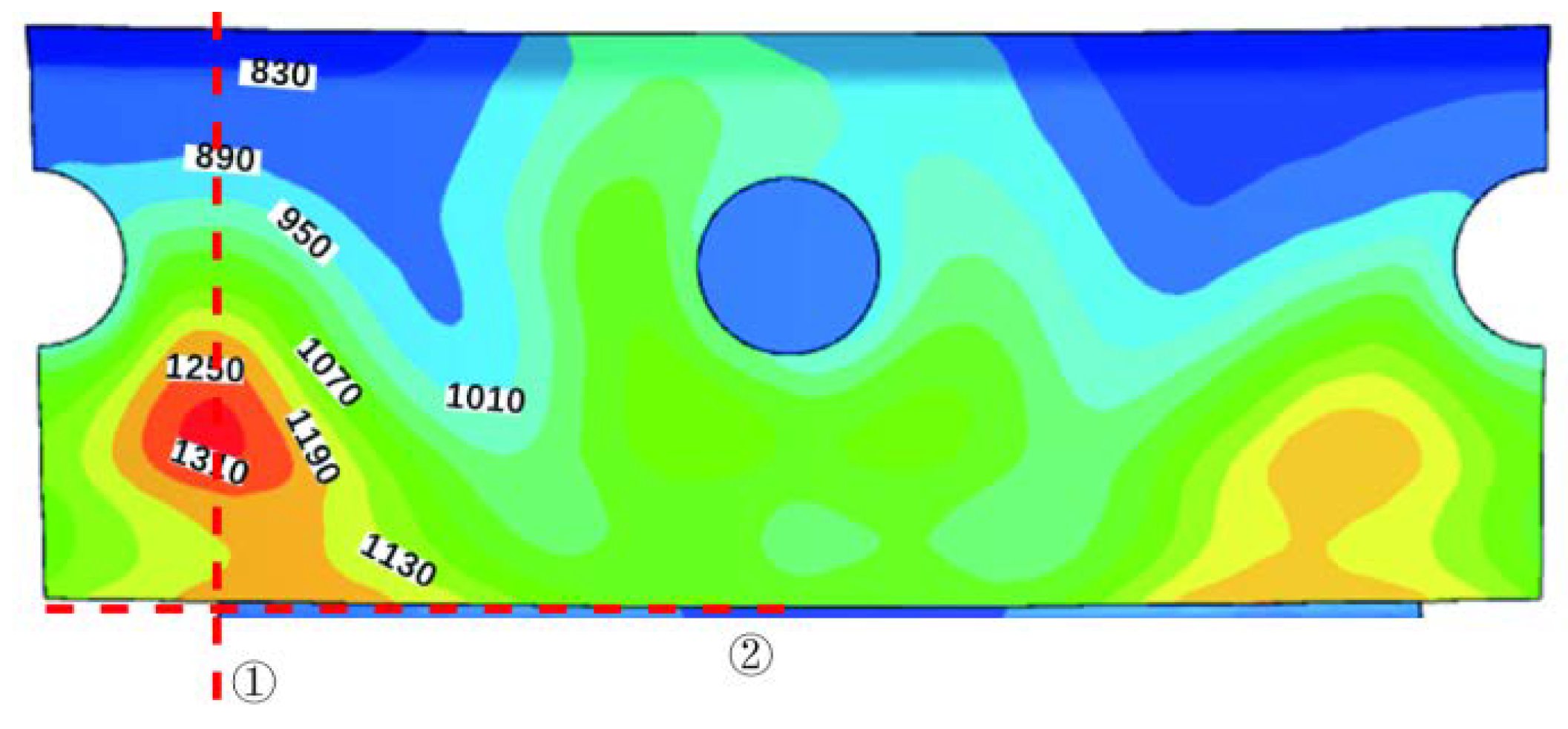
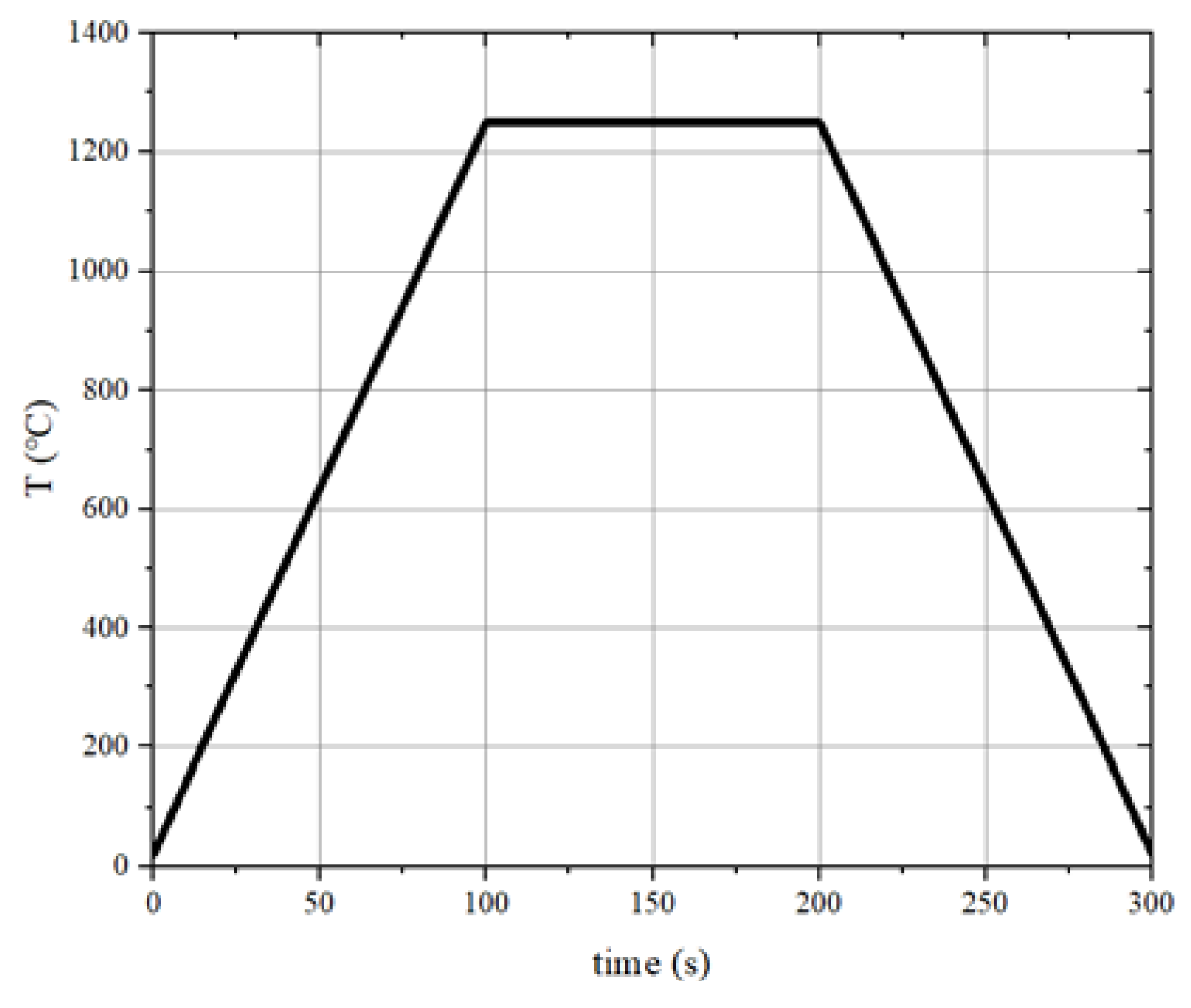
The material property parameters are shown in Table 2 based on the results of previous measurements [31]. As calculated by the combustion chamber flow field simulation method in the prior study, the wall tile hot spot temperature can reach 1583K(1310°C), as depicted in Figure 4, and the maximum temperature gradient in the hot spot edge region can reach 60°C/mm, so the heat condition is determined as the model upper surface applied 1523K~1463K hot spot gradient heat load, and the loading temperature variation with time is depicted in Figure 5 [32].In the model cell, set TC layer as triangular mesh with approximate mesh size 0.003mm to improve the calculation accuracy. BC layer as quadrilateral mesh with approximate size 0.006mm. SUB as quadrilateral mesh and divide 0.006~0.04mm mesh size over to improve the calculation speed. Model mesh property CPS4T, inserted Cohesive cell mesh property COH2D4T, which can be temperature and stress transfer.
In addition, surface convective heat transfer at room temperature is applied to the model’s top and bottom surfaces, and the convective heat transfer coefficient is calculated using Newton’s cooling equation6. To simulate the coating degrees of freedom, periodic boundary conditions are applied to the remaining three edges except the surface, with the left boundary having 0 degrees of freedom along the x-axis; coupling constraints are applied to the right boundary to ensure that all nodes have the same x-displacement; and the bottom boundary has 0 degrees of freedom along the y-axis to simulate frictionless support. Self-contact is set for the pores to prevent cell penetration when heated, and the characteristics are longitudinal firm contact and tangential frictionlessness.
q = α Δ T ,
Where ΔT is the temperature difference between the solid and the room, the reference experimental parameters can be derived from the convective heat transfer coefficients of 125W/(m2K) on the coating surface and 75W/(m2K) on the rear of the substrate.

2.2.3. Crack propagation simulation

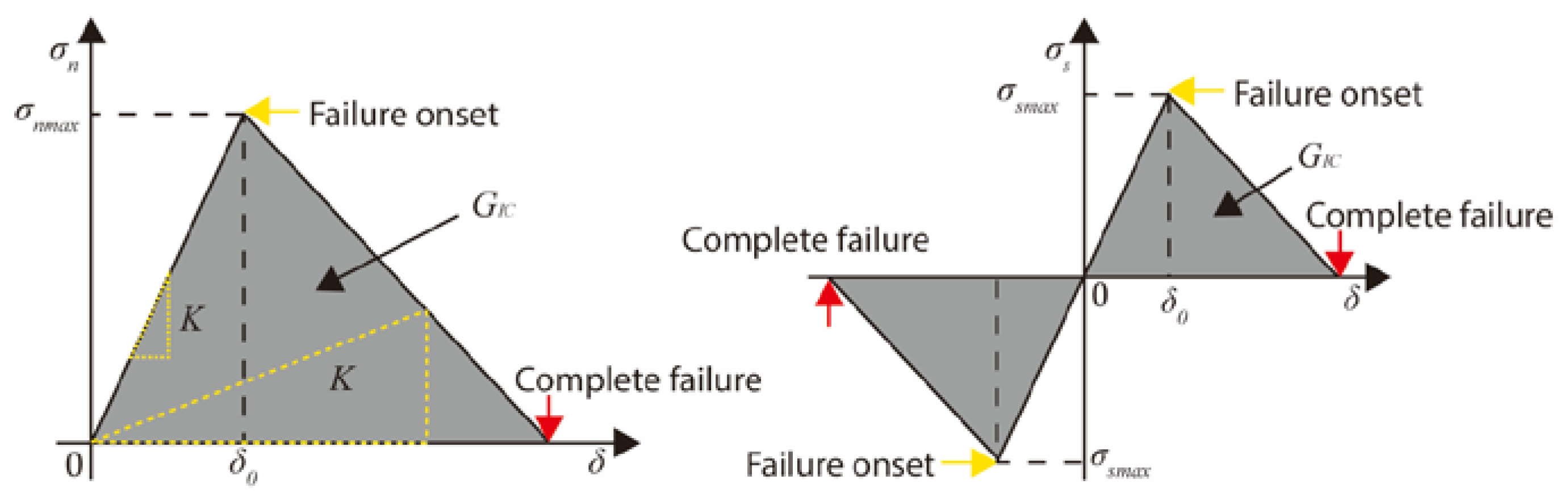
Cohesive is based on the premise that there is a small fracture process area at the fissure tip. As the tension between the crack surfaces increases, the material reaches its cohesion strength value and then begins to lose stiffness. fissure propagation occurs when the distance between fissure surfaces increases to the point where the fracture energy is satisfied. By inserting the cohesive cell globally in the TC layer (Figure 2(b)), it is possible to simulate the crack propagation characteristics of the TC layer under the influence of a hot spot by simulating the random initiation and propagation of cracks. As shown in Figure 6, the relationship between the traction force and displacement of the cohesive cell is governed by a bilinear law.
Crack propagation is usually divided into two stages: damage initiation and damage evolution. In the first stage, i.e., δ <δ0, the quadratic stress criterion is used as the damage criterion, as shown in Eq. 7, where only normal and tangential stresses are considered in the two-dimensional model. The material stiffness K is the ratio of the hardening factor En to the effective thickness heff, as shown in Eq. 8:
( σ n σ n max ) 2 + ( σ s σ s max ) 2 = 1 ,
K = E n h e f f ,
As the load increases, the normal stress σn and tangential stress σs on the surface of the cohesive unit reach the damage criterion, respectively. With reference to the previous toughness measurements of YSZ, the cohesive strength σnmax and σsmax of the cohesive unit of YSZ were taken to be 50 MPa with a fracture energy of 20 J/m2. The normal cohesive strength σnmax of the interfacial cohesive unit was taken to be 200 MPa with a fracture energy of 20 J/m2, and the tangential cohesive strength σsmax was taken to be 100 MPa with a fracture energy of 60 J/m2 [24~25]. After the starting criterion is reached, δ0 <δ, the material stiffness K begins to degrade, expressed using the damage evolution criterion as follows:
K = { K ( 1 − D )           δ > δ 0 K                                           δ < δ 0 ,
Where D is the total material damage, an initial value of 0 indicates that no damage has occurred, and its monotonic increase to 1 after the onset of damage indicates that the unit has failed completely.

3. Results

3.1. Thermal insulation experiment results

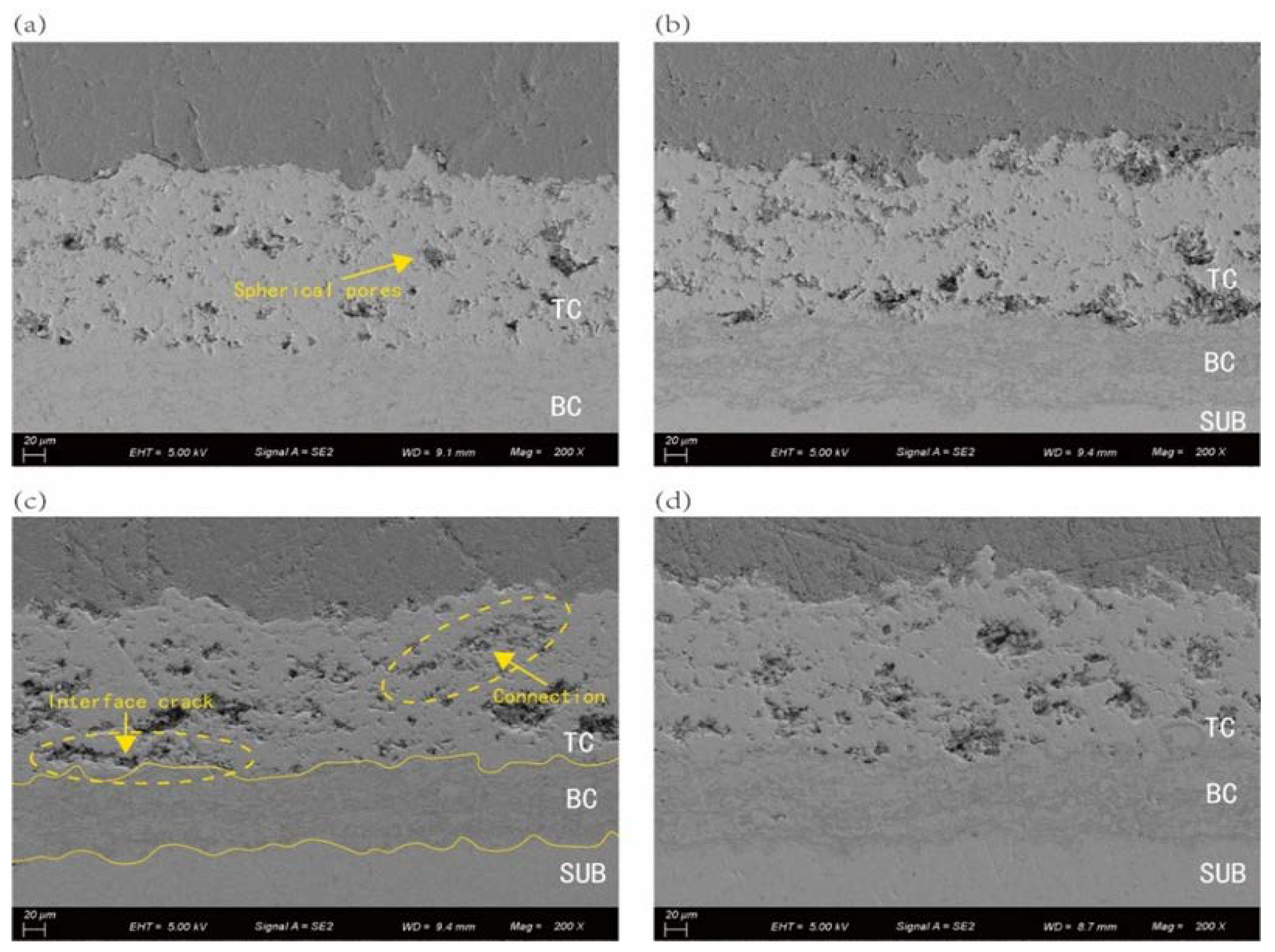
Figure 7 depicts the morphology of the APS TBC ceramic layer at 1373K(1100°C) with varying holding times. Figure 7(a) depicts the initial morphology of the coating layer, which consists of narrow microcracks with spherical pores of 1~5μm in diameter, with some pores intersecting with the fractures. Figure 7(b) demonstrates that after 10h of holding, healing occurs in the middle of the microcracks, and the crack length and density diminish, while the spherical pores remain essentially unchanged. After 20h, as depicted in Figure 7(c), the microcracks healed and the number of spherical apertures diminished. Figure 7(d) demonstrates that after 50h of heat preservation, crack propagation occurs in the TC layer, and the crack width and length are significantly larger than the microcracks in the initial morphology of Figure 7(a). Figure 7(e,f) reveal that after 100h of heat preservation, the crack propagation and pores are connected, and the morphological characteristics are essentially fixed.
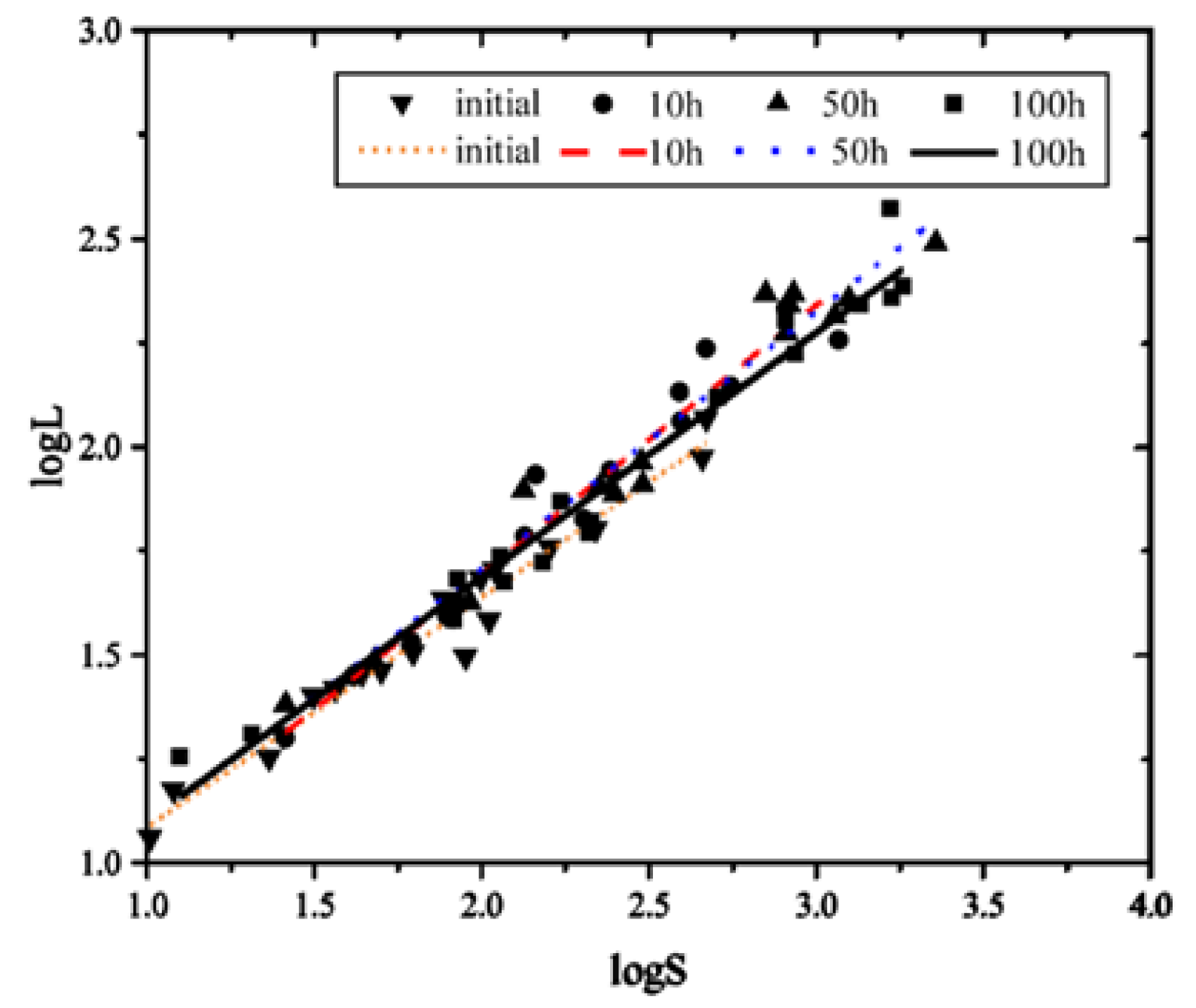
Figure 8 illustrates the morphological alterations of APS TBC during heat treatment. In its initial configuration, the TC layer has a large number of microporous openings and fissures. As shown in Figure 9, the fragmentation theory is used to quantitatively characterize the form of the gap. It is known that the concentration of the loop in its initial form is distributed in the region logL<2.0, logS<2.5. The linear regression equation for the distribution point of the gap is established, and the fragmentary dimension D is 1.10, indicating that the inner permeable gap in the TC layer is currently a smaller circle. After 10 hours at 1373K(1100°C), the radius of the opening in the shape depicted in Figure 8(b) increased. In conjunction with Figure 7(b), it is known that the microcracks heal swiftly, the spherical cavity is maintained, and the cavity concentration is distributed in the region logL<2.5, logS<3.0. The splitting dimension D is 1.29, indicating that the 10h thermal treatment widened the gap while making it flatter.In the shape of Figure 8(c) temperature 50h, observed in the midst of the TC layer and the interface, the gap larger than 10μm in diameter is linked to horizontal and vertical cracks, and a portion of the gap has logL>2.5, logS>3.0. The splitting dimension D is 1.24, which indicates that when the heating time is increased to 50 hours, the degree of foaming of the gap is delayed and the size of the loop, with the exception of a few gap connections, remains relatively constant. Figure 8(d) depicts the coating’s morphology after 100 hours of warming, with the gap remaining essentially unchanged. The splitting dimension of D is 1.20, and when combined with the YSZ module in Figure 7 and the known changes in the heat retention time, the microcracks of the early coating heal rapidly. At this time, the growth rate of the module is higher, but as the duration of the thermal retention increases, the growth rate of the modulus decreases. When the insulation duration reaches 50 hours, the gap’s size and flatness are essentially fixed.
Observably, the higher temperature causes the modulus E value to rise more rapidly, but the modulus E difference is only 1.4% of the measured value after 50 hours of insulation. Since the temperature difference is only 60K, the hot spot temperature gradient is disregarded for the ceramic layer properties and structure, the 50h coating morphology with stable sintering characteristics is selected in Figure 8(c), and the morphological features are extracted to develop the numerical geometric model.

3.2. Numerical simulation results

3.2.1. Stress distribution

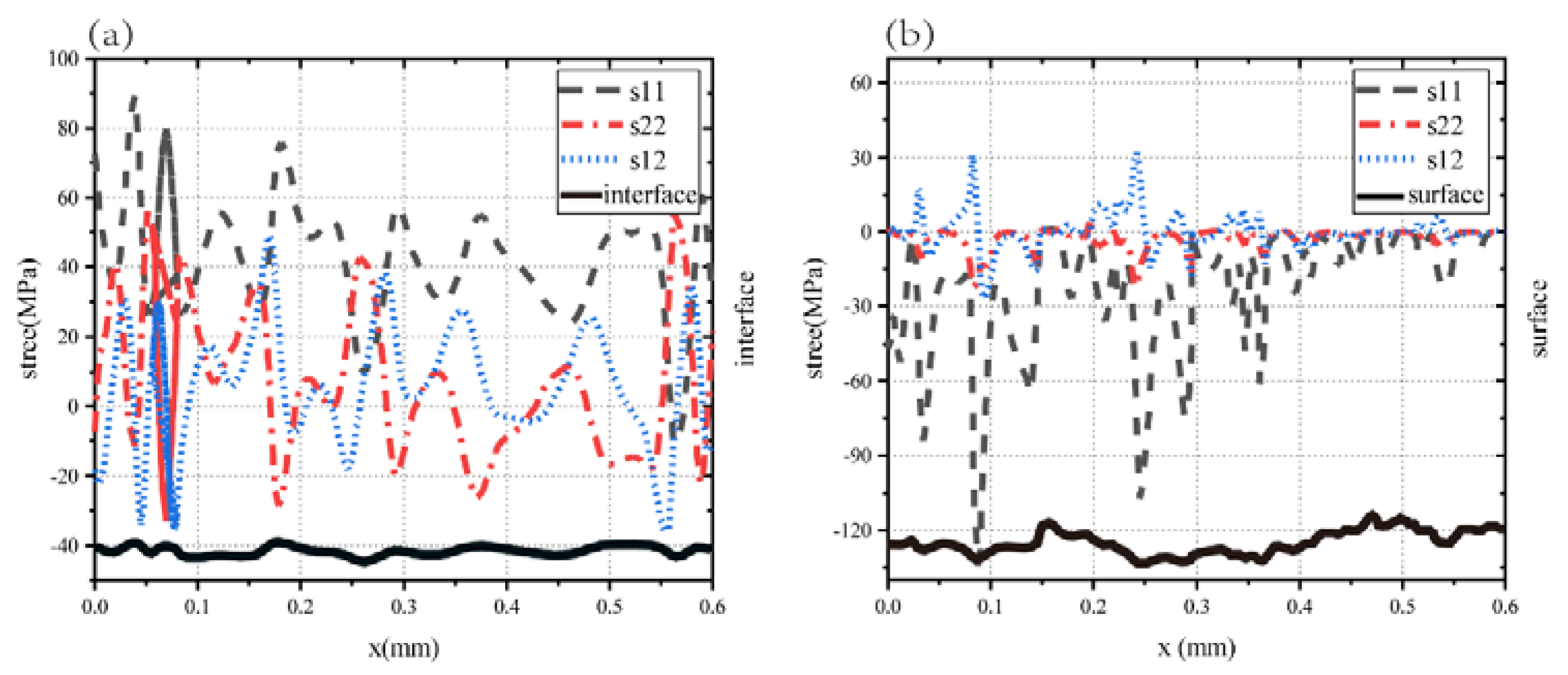
Failure of the TC layer to spall originates from the internal crack propagation, and the type I and type II crack extensions present in the TC layer are influenced by the principal stresses and shear stresses. Therefore, the analysis of transverse stress parallel to the interface (S11), normal positive stress perpendicular to the interface direction (S22), and shear direction stress (S12) can serve as a guide for locating the danger zone and predicting fractures.
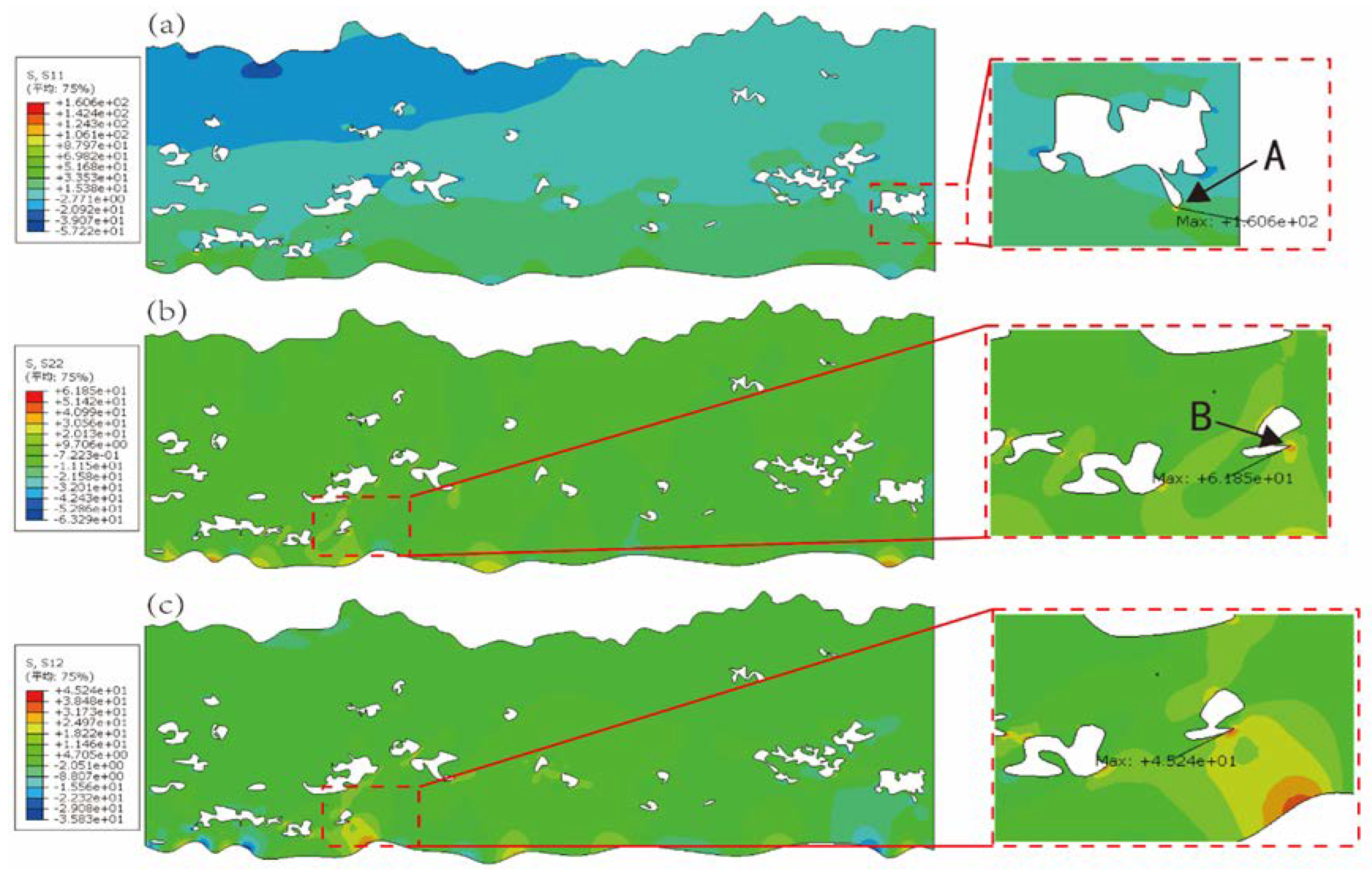
The stress analysis of YSZ is carried out by taking the stress cloud map at the early stage of cooling, as shown in Figure 10(a), due to the large number of pore defects existing in the real morphology of TC layer affects the stress distribution, the positive stress S11 has a concentrated stress distribution at the bottom of the pore, and the stress gradient between the 2μm radius zone can reach 90MPa; as shown in Figure 10(b), the positive stress S22 is tensile in the TC layer, and is concentrated at the interface valley with TC layer defects on both sides, and the stress value on the side away from the hot spot is greater than that on the side near the hot spot, and the stress gradient is less than S11, and the stress gradient between the radius 8μm zone is 50MPa; shear stress s12 is distributed as shown in Figure 10(c), and is affected by the hot spot in the interface crest near the hot spot side (left side) is positive, away from the hot spot side (right side) is negative, and the shear stress is distributed around the defects in the TC layer However, there is a larger stress area in the interface region at the edge of the hot spot, but the shear stress S12 gradient is lesser compared to the positive stress, and it is known from simulation results that the maximum shear stress can reach 75MPa during the initial stage of insulation.
The stress concentration point at the apex of the pore causes coating damage, and the stresses that dominate the damage vary depending on the location of the pore. As depicted in Figure 11, the S11 direction stress profile at the bottom point A of the defect is greater than the remainder of the stress, with a maximum value of 145MPa, causing the crack to grow along the vertical interface direction. The S22 stress at the right point B of the defect is greater than the remainder of the stress, with a maximum of 79MPa, causing the crack to expand laterally. In addition, the entire process of temperature cycling is accompanied by shear stress S12, which will affect the crack propagation angle.
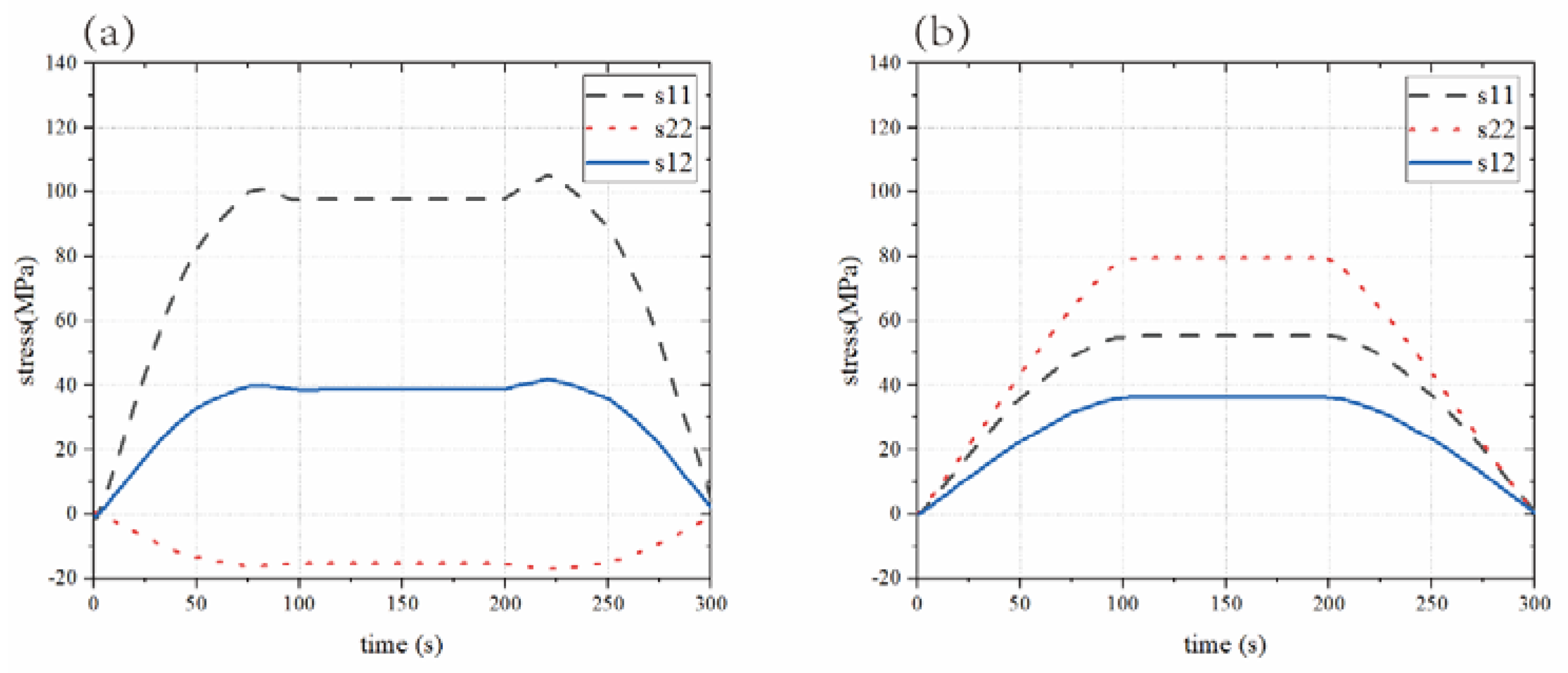
The stress magnitude at the interface is also sufficient to induce interfacial damage, as shown in Figure 12a, where the variation law of each stress with the interface can be seen, in the tip of the crest is accompanied by a concentrated distribution of positive stress S11, and constant for the tensile effect, which is the same as the simulation results of the simplified model with the cosine as the interface, and the stress magnitude decreases with the increase in the distance from the interface [33]. The maximal peak of S12 exists on the side of the interface wave crest away from the hot spot in the edge region of the hot spot, i.e., at an x-coordinate of 0.17mm. There is a concentrated distribution of positive stress S22 at the trough, and the magnitude of the stress is dependent on the amplitude of the interface; the larger the amplitude, the greater the value of S22 in the trough distribution.
The stress distribution pattern of the surface is depicted in Figure 11b, where the positive stress is predominantly compressive and the shear stress S12 is concentrated at the surface trough, with a maximum value of 32MPa at the edge of the hot spot, or 0.24 mm at the x-coordinate, indicating that the transverse temperature gradient of the hot spot and the undulating shape of the surface jointly affect the stress distribution of the coating surface, causing the surface trough. At the boundary of the hot area, the surface valley is subject to a substantial shearing effect.

3.2.2. Crack propagation simulation results

As Figure 13a depicts the crack budding stage under hot spot heating, it can be observed that cracks are preferentially budded at the pores within the TC layer, and when combined with the stress law in Figure 10, it can be observed that the pore cracks are deflected and expanded obliquely toward the surface and interface due to shear force. Figure 13b depicts the crack extension stage. During this stage, the crack extends from the previous pore crack to the connection between the pores and continues to expand after passing through the pores. Furthermore, due to the concentration of shear stress S12, crack initiation occurs at the surface groove and extends along the oblique direction. Figure 13c depicts the failure stage of the fracture, which occurs when pores sprouting from the middle of the coating connect to other pores, the crest of the interface, and the trough of the surface, resulting in a severe crack connection phenomenon that leads to the bulk peeling of YSZ. bulk peeling occurs at the boundary of the hot region because it has a high temperature gradient.
In a uniformly heated environment at 1473K(1200°C), Figure 14(a) depicts the crack initiation process of the TC layer, and when combined with Figure 12(b), it is clear that the high temperature will cause shear stress at the surface valley, and that crack initiation occurs at all valleys with a large surface amplitude due to the uniform heat. In addition, the interior of the TC layer lacks crack initiation, which is a result of the layer’s low shear tension. Unlike the shear stresses within the coating caused by hot areas, YSZ exhibits greater resistance to positive stresses than shear stresses. Figure 14(b) depicts the crack extension stage, in which surface cracks extend toward the interface and new cracks sprout in the remaining surface troughs. In comparison to the hot spot results at the same loading time, the TC layer has a greater number of surface cracks, but the extension depth is limited and does not reach the peel crack length.
In conclusion, under hot spot heating, cracks sprouted in the TC layer in the order of pore, surface, and interface, eventually forming oblique severe connection failure cracks in the hot spot’s edge region. In contrast, under uniform heating, multiple cracks sprouted at the surface trough of the TC layer, and a comparison of the results with the same loading time of the hot spot reveals that the number of cracks sprouted under uniform heating was greater, but the propagation depth of a single crack was limited, and it was unable to peel off YSZ.

3.3. Combustion chamber ablation part shape

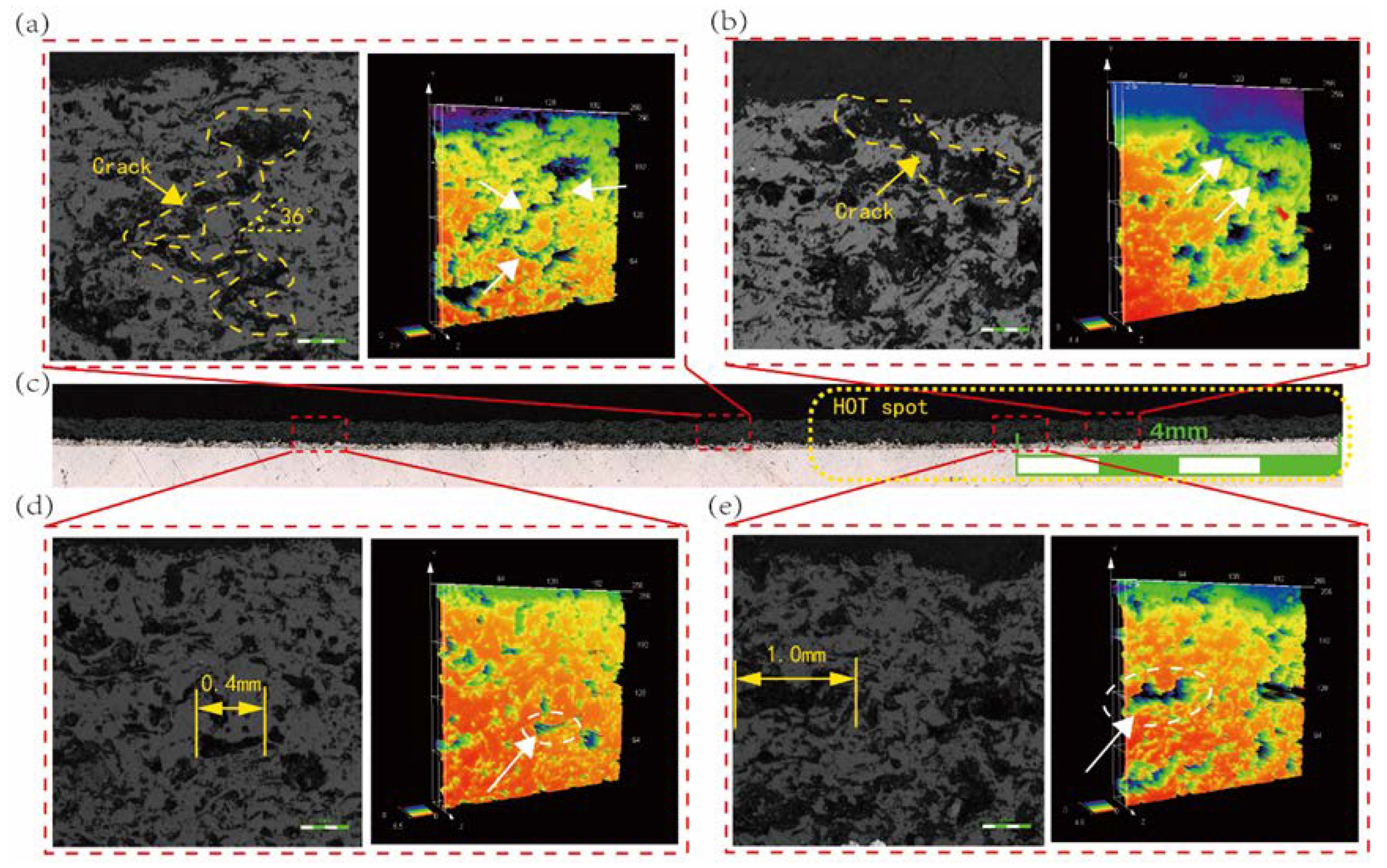
The cross-sectional coating morphology of the hot spot ablation area on the real aero-engine combustor liner is shown in Figure 15.
Comparatively, the pore length in the TC layer of Figure 15(e) can reach 1 mm, which is greater than the pore length of 0.40mm in Figure 15(d). Combined with the morphological change law of the TC layer in the insulation sintering experiment, it can be concluded that the region in Figure 15(e) between the two cooling holes of the tile has more severe sintering characteristics, which is related to the higher temperature experienced in the center of the hot spot during the service process, and the hot spot area is consistent with the one observed in Figure 1.(a) The area of concentrated ablation observed in Figure 1 coincides with the hot spot region.(a). Taking the coating morphology of the hot spot edge area as shown in Figure 15(a), cracks inside the YSZ are observed, and the cracks start from the pores in the middle of the TC layer and expand obliquely to the coating surface and the interface at an angle of 30°~45° with the interface direction, which demonstrates that this area is accompanied by a large temperature gradient and is consistent with the internal crack budding process illustrated in Figure 13. In the center of the hot spot, as depicted in Figure 15(b), multiple surface cracks are observed to sprout, and the crack location and propagation direction are consistent with the uniform superheat simulation process depicted in Figure 14, indicating that the center of the hot spot is more uniformly distributed, although the temperature is higher, and the coating is affected by uniform superheat during the service process.

4. Discussion

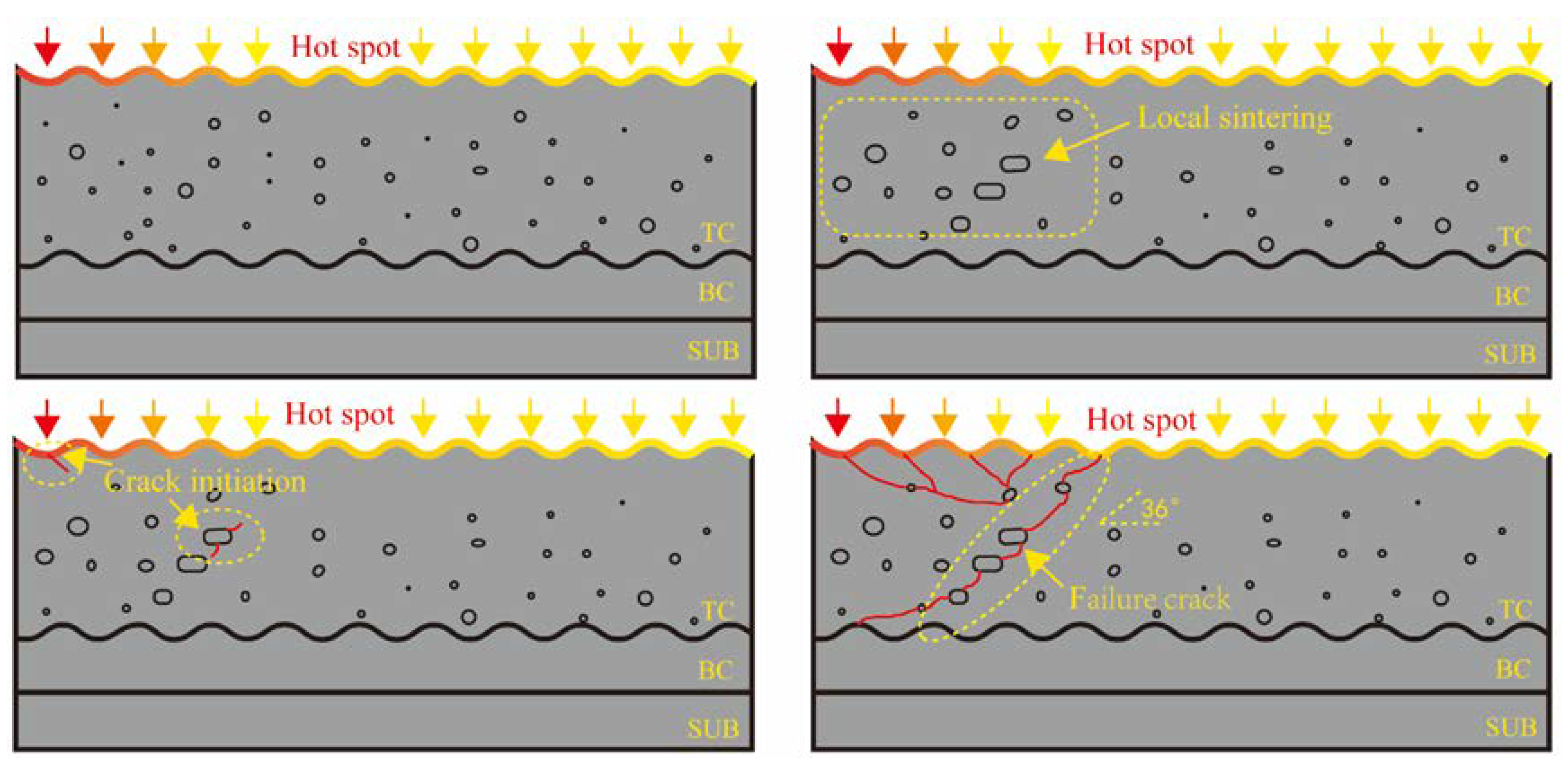
By comparing the above numerical simulation of the hot barrier coating with the real ablated part morphology, it can be concluded that the schematic diagram of YSZ crack propagation under hot spot heating is depicted in Figure 16: due to the influence of the APS process, there are a large number of pore defects in the initial coating morphology, as depicted in Figure 16(a), primarily spherical pores with a cross-sectional area of 300m2 or less. The lateral temperature gradient of the hot spot causes the YSZ beneath the hot spot to exhibit more pronounced sintering characteristics, as depicted in Figure 16(b), which demonstrates an increase in the volume and uniformity of the pores. Referring to the thermal insulation experiments, the fractal dimension D value of the pores increases by 13% due to the effect of sintering, which causes the pore tips to accumulate more tension. Since the pores redistribute stresses within the coating, local sintering of the coating will promote local stress concentration, which contributes to the initiation and growth of macroscopic cracks under the influence of cyclic thermal stresses. As a result of thermal expansion, a concentration of shear tension exists in the valley region of the coating’s surface, leading to the emergence of cracks. As depicted in Figure 16(c), the emergence of cracks occurs most frequently at the flattened relatively large apertures in the center of the TC layer and at the surface trough of the hot spot region, where the temperature is higher. Due to the shear tension in the coating caused by the transverse temperature gradient of the hot spot, the transverse and longitudinal cracks initiation at the tip of the pore are deflected in the propagation direction due to the shear effect. The crack propagation path is approximately 30°~45° from the horizontal angle, as determined by simulation and comparison to the actual shape. As depicted in Figure 16(d), once the cracks have penetrated the remaining pore defects within the coating along the oblique direction, they connect with the cracks at the surface and interface, thereby promoting the bulk spalling of the TC layer. And the central region of the hot spot with a small temperature gradient will instigate multiple surface cracks and cause crack connections, which will manifest as laminar spalling.
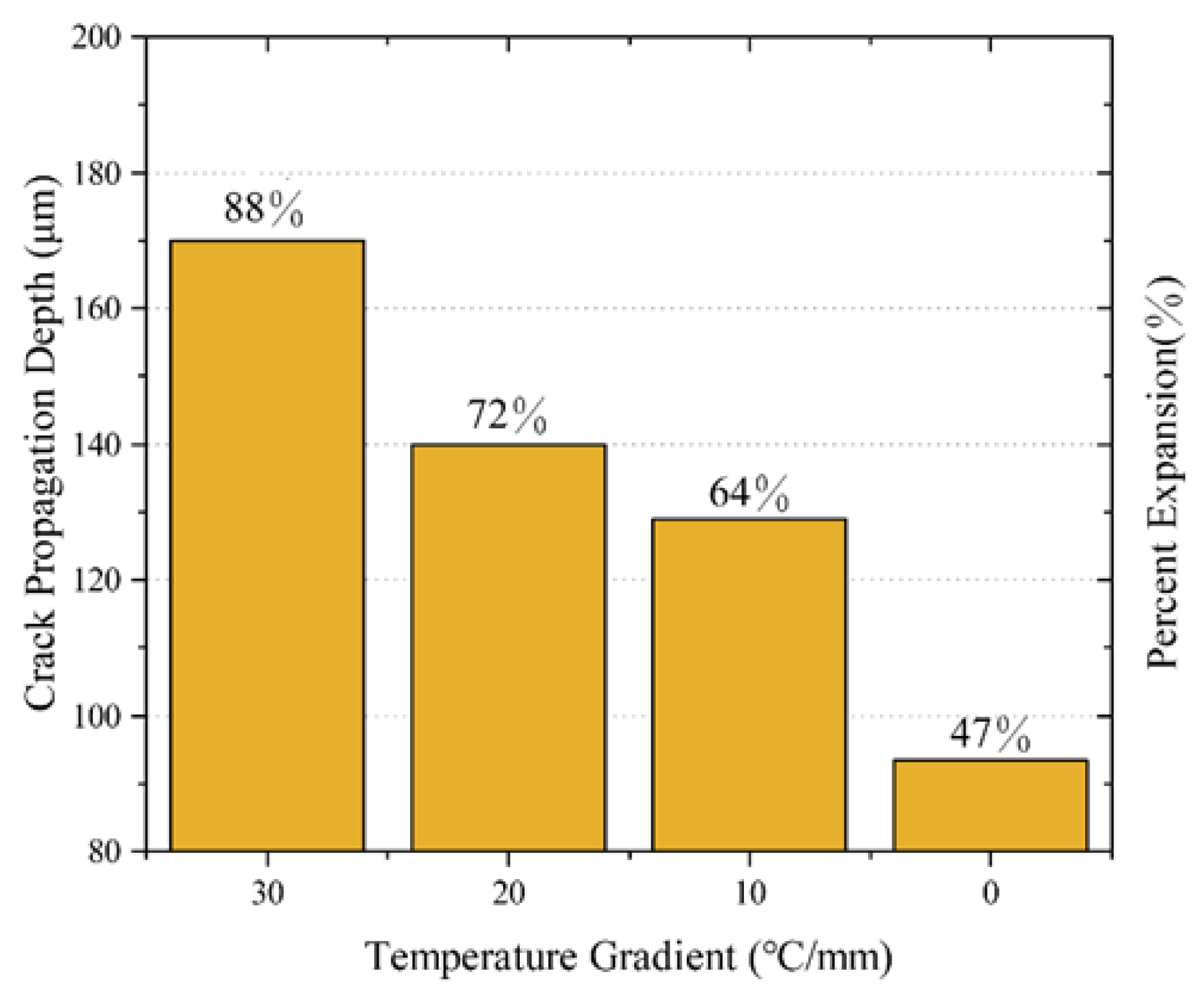
The studies on the splitting form of YSZ are divided into two forms: layered peeling and partial peeling. Among these two forms, partial peeling with a larger extension depth will be the predominant form causing the rapid failure of YSZ. The law of temperature gradient and crack extension depth for the same loading time as shown in Figure 17, which demonstrates that the depth of crack extension due to the mismatch of thermal expansion coefficient between layers of the coating decreases monotonically with the temperature gradient, and that the temperature gradient accelerates crack propagation and connection along the coating thickness direction. Therefore, the influence of hot spot on YSZ failure is manifested primarily as bulk peeling caused by crack extension in the edge region of the hot spot.

5. Conclusions

In this paper, a numerical model of TBCs is devised to describe the distribution of complex stresses within the YSZ and the crack extension process under hot spot heating. The advantage of this model is that the realistic morphology of YSZ sintering is taken into account in the numerical model, allowing for the random initiation and propagation of multiple cracks within the TBC. The following is a summary of the research on the pattern of crack propagation under hot spot heating.
(a) In addition to the longitudinal temperature gradient, the hot spot has a transverse temperature gradient, which results in a more complex stress distribution inside the YSZ. The pore morphology inside the YSZ also has an effect on each stress inside the coating, as demonstrated by the shear stress of 75MPa inside the coating at the edge region of the hot spot with the largest temperature gradient under hot spot heating, which is concentrated at the protruding tip of the hot spot.
(b) The concentrated hyperthermia of the hot spot imparts sintering characteristics to the internal YSZ, with the sintering degree being greater in the central region of the hot spot than in the non-hot spot region. In conjunction with the insulation experiments, it is known that the fractal dimension of the pores D within the YSZ increases by 13% under the influence of sintering, which increases the stress concentration at the tip of the pores and makes the pores in the local sintering area affected by the hot spot a hazardous point.
(c) Unlike the layered peeling caused by multiple surface cracks due to uniform heating, the YSZ coating failure caused by hot spot heating will be most severe in the hot spot edge region due to bulk peeling. In addition to surface cracks, the cracks take the internal pores of YSZ as the sprouting point, penetrate the remaining pores along the direction of 30°~45° angle with the interface, and expand in the thickness direction. cof the cracks in the thickness direction, and when the temperature gradient reaches 30K/mm, the cracks expand more than 40% along the thickness direction.

References

  1. Lv F, Li Q, Fu G. Failure analysis of an aero-engine combustor liner[J]. Engineering Failure Analysis, 2010, 17(5): 1094-1101. [CrossRef]
  2. Mondal K, Nuñez III L, Downey C M, et al. Recent advances in the thermal barrier coatings for extreme environments[J]. Materials Science for Energy Technologies, 2021, 4: 208-210. [CrossRef]
  3. Mishra R, K. Life Enhancement of Gas Turbine Combustor Liner through Thermal Barrier Coating [J]. Journal of Failure Analysis and Prevention, 2017, 17(5): 914-918. [CrossRef]
  4. Jiang J, Jiang L, Cai Z, et al. Numerical stress analysis of the TBC-film cooling system under operating conditions considering the effects of thermal gradient and TGO growth[J]. Surface and Coatings Technology, 2019, 357: 433-444. [CrossRef]
  5. Zhang J, Dai H, Lin J, et al. Cracking analysis of an aero-engine combustor[J]. Engineering Failure Analysis, 2020, 115: 104640. [CrossRef]
  6. Kim K M, Shin S, Lee D H, et al. Influence of material properties on temperature and thermal stress of thermal barrier coating near a normal cooling hole[J]. International journal of heat and mass transfer, 2011, 54(25-26): 5192-5199. [CrossRef]
  7. Xiao B, Huang X, Robertson T, et al. Sintering resistance of suspension plasma sprayed 7YSZ TBC under isothermal and cyclic oxidation[J]. Journal of the European Ceramic Society, 2020, 40(5): 2030-2041. [CrossRef]
  8. Li G R, Yang G J, Li C X, et al. Sintering characteristics of plasma-sprayed TBCs: Experimental analysis and an overall modelling[J]. Ceramics International, 2018, 44(3): 2982-2990. [CrossRef]
  9. Cheng B, Wang Y, Zhang X, et al. Sintering governing the cracking behaviors of different La2Zr2O7/YSZ ceramic layer combination TBCs at 1150° C[J]. Surface and Coatings Technology, 2021, 428: 127910. [CrossRef]
  10. Huang J B, Wang W Z, Li Y J, et al. Improve durability of plasma-splayed thermal barrier coatings by decreasing sintering-induced stiffening in ceramic coatings[J]. Journal of the European Ceramic Society, 2020, 40(4): 1433-1442. [CrossRef]
  11. Cheng B, Wang Y, Zhang X, et al. Sintering governing the cracking behaviors of different La2Zr2O7/YSZ ceramic layer combination TBCs at 1150° C[J]. Surface and Coatings Technology, 2021, 428: 127910. [CrossRef]
  12. Kyaw S, Jones A, Hyde T. Predicting failure within TBC system: Finite element simulation of stress within TBC system as affected by sintering of APS TBC, geometry of substrate and creep of TGO[J]. Engineering Failure Analysis, 2013, 27: 150-164. [CrossRef]
  13. Wei Z Y, Cai H N, Zhao S D, et al. Dynamic multi-crack evolution and coupling TBC failure together induced by continuous TGO growth and ceramic sintering[J]. Ceramics International, 2022, 48(11): 15913-15924. [CrossRef]
  14. Wei Z Y, Dong X X, Cai H N, et al. Influences of the near-spherical 3D pore on failure mechanism of atmospheric plasma spraying TBCs using a macro-micro integrated model[J]. Surface and Coatings Technology, 2022, 437: 128375. [CrossRef]
  15. Weng W X, Zheng Z H, Li Q. Cracking evolution of atmospheric plasma-sprayed YSZ thermal barrier coatings subjected to isothermal heat treatment[J]. Surface and Coatings Technology, 2020, 402: 125924. [CrossRef]
  16. Evans A G, Hutchinson J W. The mechanics of coating delamination in thermal gradients[J]. Surface and Coatings Technology, 2007, 201(18): 7905-7916. [CrossRef]
  17. Yang J, Wang L, Li D, et al. Stress analysis and failure mechanisms of plasma-sprayed thermal barrier coatings[J]. Journal of Thermal Spray Technology, 2017, 26(5): 890-901. [CrossRef]
  18. Erk K A, Deschaseaux C, Trice R W. Grain-boundary grooving of plasma-sprayed yttria-stabilized zirconia thermal barrier coatings[J]. Journal of the American Ceramic Society, 2006, 89(5): 1673-1678. [CrossRef]
  19. Cipitria A, Golosnoy I O, Clyne T W. A sintering model for plasma-sprayed zirconia TBCs. Part I: Free-standing coatings[J]. Acta Materialia, 2009, 57(4): 980-992. [CrossRef]
  20. Cocks A C F, Fleck N A. Constrained sintering of an air-plasma-sprayed thermal barrier coating[J]. Acta materialia, 2010, 58(12): 4233-4244. [CrossRef]
  21. Kadam P J, Damale A, Kadam N. Fracture analysis of Pre-cracked 8YSZ TBCs with edge and internal cracks under Thermo-mechanical load: A numerical approach[J]. Materials Today: Proceedings, 2022, 59: 1839-1845. [CrossRef]
  22. Koushali A G, Sameezadeh M, Vaseghi M, et al. Modeling and simulation of thermal fatigue crack in EB-PVD TBCs under non-uniform temperature[J]. Ceramics International, 2017, 43(16): 13140-13145. [CrossRef]
  23. Wei Z Y, Cai H N, Li C J. Comprehensive dynamic failure mechanism of thermal barrier coatings based on a novel crack propagation and TGO growth coupling model[J]. Ceramics International, 2018, 44(18): 22556-22566. [CrossRef]
  24. Yan K, Xiang Y, Yu H, et al. Effect of irregular microcracks on the hot corrosion behavior and thermal shock resistance of YSZ thermal barrier coatings[J]. Surface and Coatings Technology, 2022, 431: 128038. [CrossRef]
  25. Xie L, Dorfman M R, Cipitria A, et al. Properties and performance of high-purity thermal barrier coatings[J]. Journal of thermal spray technology, 2007, 16: 804-808. [CrossRef]
  26. Wang Y, Ma C, Liu Y, et al. A model for the effective thermal conductivity of moist porous building materials based on fractal theory[J]. International Journal of Heat and Mass Transfer, 2018, 125: 387-399. [CrossRef]
  27. SR Nayak, J Mishra, A Khandual, et al. Fractal dimension of RGB color images[J]. Optik, 2018, 162: 196-205. [CrossRef]
  28. Dai H, Zhang J, Ren Y, et al. Failure mechanism of thermal barrier coatings of an ex-service aero-engine combustor[J]. Surface and Coatings Technology, 2019, 380: 125030. [CrossRef]
  29. Xiao B, Huang X, Robertson T, et al. Sintering resistance of suspension plasma sprayed 7YSZ TBC under isothermal and cyclic oxidation[J]. Journal of the European Ceramic Society, 2020, 40(5): 2030-2041. [CrossRef]
  30. Ma K, Zhu J, Xie H, et al. Effect of porous microstructure on the elastic modulus of plasma-sprayed thermal barrier coatings: Experiment and numerical analysis[J]. Surface and Coatings Technology, 2013, 235: 589-595. [CrossRef]
  31. Li Z, Yu j, Li Q, Finite element simulation of ceramic layer/TGO interfacial crack on thermal barrier coating[J]. surface technology, 2017,46(07):70-76. [CrossRef]
  32. Zhang J, Dai H, Lin J, et al. Cracking analysis of an aero-engine combustor[J]. Engineering Failure Analysis, 2020, 115: 104640. [CrossRef]
  33. Song J, Li S, Yang X, et al. Numerical study on the competitive cracking behavior in TC and interface for thermal barrier coatings under thermal cycle fatigue loading[J]. Surface and Coatings Technology, 2019, 358: 850-857. [CrossRef]
Preprints 71924 g001
Figure 1. Ablation of combustion liner (a) borehole exploration photos (b) ablative specimen.
Figure 1. Ablation of combustion liner (a) borehole exploration photos (b) ablative specimen.
Preprints 71924 g001
Preprints 71924 g002
Figure 2. Establishment of numerical model (a) Cross-section of the TBCs (b) grid of numerical geometric model.
Figure 2. Establishment of numerical model (a) Cross-section of the TBCs (b) grid of numerical geometric model.
Preprints 71924 g002
Preprints 71924 g003
Figure 3. Variation pattern of coating elastic modulus with heat treatment time.
Figure 3. Variation pattern of coating elastic modulus with heat treatment time.
Preprints 71924 g003
Preprints 71924 g004
Figure 4. Temperature cloud of combustion liner.
Figure 4. Temperature cloud of combustion liner.
Preprints 71924 g004
Preprints 71924 g005
Figure 5. Load-thermal process.
Figure 5. Load-thermal process.
Preprints 71924 g005
Preprints 71924 g006
Figure 6. Cohesive element constitutive model.
Figure 6. Cohesive element constitutive model.
Preprints 71924 g006
Preprints 71924 g007
Figure 7. Micromorphology of YSZ sintering at 1100°C (a) 0h (b) 10h (c) 20h (d) 50h (d) 100h (e) 150h.
Figure 7. Micromorphology of YSZ sintering at 1100°C (a) 0h (b) 10h (c) 20h (d) 50h (d) 100h (e) 150h.
Preprints 71924 g007
Preprints 71924 g008
Figure 8. Sintering morphology of TBCs at 1100°C (a) 0h (b) 10h (c) 50h (d) 100h.
Figure 8. Sintering morphology of TBCs at 1100°C (a) 0h (b) 10h (c) 50h (d) 100h.
Preprints 71924 g008
Preprints 71924 g009
Figure 9. D calculated by power low method.
Figure 9. D calculated by power low method.
Preprints 71924 g009
Preprints 71924 g010
Figure 10. Stress distribution under the action of hot spot (a) S11 (b) S22 (c) S12.
Figure 10. Stress distribution under the action of hot spot (a) S11 (b) S22 (c) S12.
Preprints 71924 g010
Preprints 71924 g011
Figure 11. Stress change with time (a) point A (b) point B.
Figure 11. Stress change with time (a) point A (b) point B.
Preprints 71924 g011
Preprints 71924 g012
Figure 12. Stress distribution law during cooling (a) interface (b) surface.
Figure 12. Stress distribution law during cooling (a) interface (b) surface.
Preprints 71924 g012
Preprints 71924 g013
Figure 13. Crack propagation under hot spot load (a) crack initiation (b) crack propagation (c) failure crack.
Figure 13. Crack propagation under hot spot load (a) crack initiation (b) crack propagation (c) failure crack.
Preprints 71924 g013
Preprints 71924 g014
Figure 14. Crack growth under uniform thermal load(a) crack initiation (b) crack propagation (c) end of cycle.
Figure 14. Crack growth under uniform thermal load(a) crack initiation (b) crack propagation (c) end of cycle.
Preprints 71924 g014
Preprints 71924 g015
Figure 15. Cross section morphology of ablated parts (a) cracks at the edge of hot spot (b) cracks at hot spot (c) complete morphology of coating in ablated area (d) morphology of coating in non hot spot area (e) morphology of coating in hot spot area.
Figure 15. Cross section morphology of ablated parts (a) cracks at the edge of hot spot (b) cracks at hot spot (c) complete morphology of coating in ablated area (d) morphology of coating in non hot spot area (e) morphology of coating in hot spot area.
Preprints 71924 g015
Preprints 71924 g016
Figure 16. Schematic diagram of hot spot crack propagate (a) initial morphology (b) sintering morphology (c) crack initiation (d) crack propagation.
Figure 16. Schematic diagram of hot spot crack propagate (a) initial morphology (b) sintering morphology (c) crack initiation (d) crack propagation.
Preprints 71924 g016
Preprints 71924 g017
Figure 17. Relationship between temperature gradient of the hot spot and crack propagation depth.
Figure 17. Relationship between temperature gradient of the hot spot and crack propagation depth.
Preprints 71924 g017
Table 1. Process parameters of atmospheric plasma spraying thermal barrier coating.
Table 1. Process parameters of atmospheric plasma spraying thermal barrier coating.
Coat U/V I/A L/mm Argon flow
QAr/(L/min) 		Helium flow
QHe/(L/min) 		Nitrogen flow
QN/(L/min)
Top coat 37.9 845 85 60 110 40
Bond coat 38 850 72 66 30 30
Table 2. Material properties of each layer.
Table 2. Material properties of each layer.
Material Density (kg/m3) Thermal conductivity (W/m K) Specific heat(J/kg K) Thermal expansion coefficient(10-6/K) Poisson’s ratio Young’s modulus (GPa)
Top coat 5.28×103 1.7 640 10.9 0.2 220
Bond coat 8.10×103 10.2 781 12.5 0.31 17.5
Substrate 8.15×103 10.2 696 14.0 0.33 18.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated