Prerpints.org logo
Preprint
Article

Multi-Country and Multi-Horizon GDP Forecasting Using Temporal Fusion Transformers

Altmetrics

Downloads

95

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

05 May 2023

Posted:

08 May 2023

You are already at the latest version

Alerts
Abstract
This paper applies a new artificial intelligence architecture, the Temporal Fusion Transformer (TFT), for the joint GDP forecasting of 25 OECD countries at different time horizons. This new attention-based architecture offers significant advantages over other deep learning methods. First, results are interpretable since the impact of each explanatory variable on each forecast can be calculated. Second, it allows to visualize persistent temporal patterns and to identify significant events and different regimes. Third, it provides quantile regressions and permits to train the model on multiple time series from different distributions. Results suggest that TFTs outperform regression models, especially in periods of turbulence such as the COVID-19 shock. Interesting economic interpretations are obtained depending on whether the country is domestic demand-led or export-led growth. In essence, TFT is revealed as a new tool that artificial intelligence provides to economists and policy makers, with enormous prospects for the future.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

The Great Recession, the COVID-19 pandemic, and the war in Ukraine have increased the uncertainty surrounding the economic cycle. Preceding these crises, the world economy underwent a process of financialization over the preceding two decades, characterized by a broad range of shifts in the relationship between the financial and real sectors. This phenomenon elevated the significance of financial actors in the economy ([1]). It had altered the aspects of micro and macro dynamics. This has translated the dynamics of financial markets, in particular nonlinearities and long-term dependencies ([2,3]), into features of different business cycle indicators, including real GDP. Consequently, forecasting macroeconomic data, such as real GDP growth, has become a more complex task.
The effect of an explanatory variable on real GDP depends on how it is interrelated with other explanatory variables, which, in addition, can vary over time. An example of that is the evidence that we obtain in this study on the loss of the predictive power of the slope of the yield curve to anticipate the business cycle. In different previous studies, the yield curve had been revealed as an extremely powerful predictor of recessions ([4,5,6,7,8,9]).
The existence of long-range dependence and non-linearities in business cycle time series ([10,11,12,13]) opens the door to the use of artificial intelligence (AI) techniques to forecast real GDP. AI is the development of computer-based algorithms that can perform tasks similar to human intelligence being able to modify their actions, thus maximizing their chances of success. Such algorithms are increasingly capable of solving extremely complex problems, such as helping in decision-making processes; including the classification and evaluation of large amounts of data.
This paper contributes to the real GDP forecasting literature by proposing the application of Temporal Fusion Transformers (TFTs). This state-of-the-art time series model, developed by [14], is encompassed within Deep Neural Networks (DNNs). This new attention-based architecture offers significant comparative advantages over regression models and other deep learning methods. First, it can be applied to univariate and multivariate time series. Second, three types of explanatory variables can be used: temporal data known only up to the present, temporal data with known inputs into the future, and/or exogenous static/categorical variables. Third, it allows working with heterogeneous time series, so that it can train on multiple time series from different distributions. Fourth, the TFT architecture splits processing into local preprocessing and global processing. The first one captures specific events and the second one the common features of all the time series. Fifth, the results are interpretable since the impact of each explanatory variable on each forecast can be calculated by analysing the variable selection weights. Sixth, it allows to visualize persistent temporal patterns and to identify significant events and different regimes. Finally, it provides quantile regressions and permits to compute simulations based on a known input into the future. This feature is especially valuable to evaluate macroeconomic policies.
We apply TFTs for the joint GDP forecasting of 25 OECD countries using macroeconomic and financial variables. Since TFTs allow multi-horizon forecasts, we will forecast at different time horizons -one, two, three, and four quarters-. It requires the data sample to be partitioned into three datasets: the training dataset, the validation dataset, and finally the test dataset. The obtained results are compared with those of a benchmark ARIMA model using two standard metrics, Mean Absolute Error (MAE) and Root Mean Square Error (RMSE).
TFT outperforms the standard ARIMA in the two proposed metrics, MAE and RMSE. The performance of TFT forecasts has been compared to that of the ARIMA model separately, in recession and expansion sub-periods, in order to give greater robustness to the results obtained at a global level. TFT outperforms ARIMA in periods of economic slowdown or global recession as well as in periods of stable growth; in this case. the improvement is marginal. Results suggest that TFTs outperform regression models, especially in periods of turbulence, such as the COVID-19 shock. Interesting economic interpretations are obtained depending on whether the country is domestic demand-led or export-led growth. The obtained results show that the TFT forecasts improvements are significantly greater in demand-driven growth countries.
The use of TFTs to predict real GDP yields very interesting results regarding the importance of the explanatory variables. While the slope of the curve has limited predictive power, it's worth noting that the variable measuring the indebtedness of non-financial private sectors demonstrates a remarkable ability to anticipate future trends. This variable played a catalytic role in the Great Recession, once the value of collateral began to deteriorate, in accordance with Hyman Minsky's financial instability hypothesis ([15,16]). In this regard, recent studies show the high persistence of the ratio of private debt to GDP for different OECD countries and the key importance of macroprudential policy, as one of the pillars of macroeconomic policy ([17]). Finally, it should be noted that the importance of the explanatory variables in predicting real GDP might vary somewhat depending on the phase of the economic cycle or the forecast time horizon. TFTs are capable of capturing this.
The rest of the paper is organized as follows. Section 2 discusses the theoretical framework that allows us to use financial variables, composite leading indicators, credit cycle, and international trade as predictors of economic growth. Section 3 reviews the literature on forecasting economic growth using deep learning and regression models. Section 4 formulates the methodology designed, using TFTs, for the joint forecasting of the GDPs of a substantial number of countries, and details the description of the sample and the variables used. Section 5 discusses the empirical results obtained. Finally, section 6 presents the conclusions, pointing out future lines of research.

2. Predictors of GDP Growth: A Literature Review.

Over decades, economists have devoted a substantial amount of effort to model economic growth. There exists a wide literature that supports the importance of different kind of variables to predict the evolution of GDP. Throughout this section, we review a list of variables from a broad array of candidates and describe how they are related to the business cycle.

2.1. Financial Variables and Leading Indicators

Financial variables, such as the prices of financial instruments, interest rates, interest rate spreads, stock price indexes, and monetary aggregates, have significant predictive content for economic activity since they are forward-looking variables and, therefore, are useful indicators in macroeconomic prediction. For a comprehensive literature review, see [18].
1. The Yield Curve. The spreads between interest rates for different maturities tend to be interpreted as the market expectations of future rates corresponding to the period between the two maturities. Intuitively, long-term rates incorporate the expectations of financial markets on future short-term rates. Consequently, a negative-sloped or flat curve means that markets prospect involve a decrease in future real interest rates, which is associated to weak economic activity or downturn.
Evidence on the predictive power of the spread between long-term and short-term government bond rates -called the slope of the yield curve- for inflation and real economic activity is wide and robust across countries and time periods ([4,5,19,20,21,22,23]).
[6] provides the theoretical basis for this statistical evidence. In particular, the main implication of the analytical rational expectations model is that the relationships are not structural since they are influenced by the monetary policy regime. In other words, the extent to which the yield curve is a good predictor depends on the form of the monetary policy reaction function, which, in turn, may depend on explicit policy objectives. The yield curve has predictive power, for example, if the monetary authority follows strict or flexible inflation targeting or if policy follows the [24] rule.
We hypothesize that the impact of the yield curve on economic growth will depend on how it interacts non-linearly with the global credit spread cycle and the official interest rates.
2. Corporate Bond Spreads. Asset purchase programs, forward guidance, and other unconventional monetary policies can lower long-term interest rates, altering the information content of the yield curve. However, even in such circumstances, the behavior of the corporate bond credit spread curve varies over the business cycle, potentially containing more information about the future.
Many studies have focused on corporate bond spreads ([25,26,27,28,29,30,31]) providing strong evidence on the link between this spread and the economic activity.
We include in our model the ratio of the Moody’s U.S. Baa corporate bond yields on that of Aaa as a global proxy for credit spread.
3. The Composite Leading Indicator. The combination of multiple leading variables in composite leading indicators (CLIs) pursue a more accurate prediction of the development of the reference series. CLIs are designed to predict the development of the business cycle, focusing on the identification of turning points that occur when the growth rate moves from an expansion period to a contraction period or vice versa. Empirical evidence supporting the usefulness of the CLI, both in-sample and out-of-sample real-time, in a real time context, is wide. Some examples are [32], [4], [33], [34] and [35].
We include in our model the CLI built by OECD (see [36]), which captures fluctuations of the economic activity around its long-term potential level. This CLI shows short-term economic movements in qualitative rather than quantitative terms. A CLI reading above (below) 100 precedes levels of GDP above (below) its long-term trend.
4. The Industrials Commodity Price Index. The CRB Raw Industrials Spot Index, drawn from Bloomberg, is a synthetic measure of price movements of 13 sensitive basic commodities whose markets are presumed to be among the first to be influenced by changes in economic conditions. As such, it serves as one early indication of imminent changes in business activity.
The criteria for the selection of commodities are: i) wide use for further processing (basic); ii) freely traded in an open market; iii) sensitive to changing conditions significant in those markets; and iv) sufficiently homogeneous or standardized so that uniform and representative price quotations can be obtained over a period of time.
Then, the Spot Market Index is defined as the unweighted geometric mean of the individual commodity price relatives (i.e. the ratios of the current prices to the base period prices).
Different papers empirically examine the interactions between commodity prices, money, interest rates, goods and economic growth ([37-41). In particular, [41] explores how the commodity market can predict GDP growth for countries worldwide, rather than a few specific countries or regions. They find commodity returns significantly predict the next quarter’s GDP growth, and thus can be considered as leading indicators of economic growth.

2.2. The credit cycle

The credit cycle and the economic cycle are closely related. Many studies provide empirical evidence supporting that endogenous credit supply expansions precede decline in real GDP (see [42], for a review). The intuition is that, in the supply side of financial markets, risk appetite and the debt accumulation evolves over the business cycle following a regular process and, ultimately, this credit cycle translates to the real economy through defaults, that materialize credit risk and, the end, financial constraints affecting real economy. In particular, the Minsky’s financial instability hypothesis ([15,16,43,44]) predicts that, for given microeconomic condition, the likelihood of facing credit constraints decreases in periods of GDP expansion and increases in periods of contraction.
We include in our model the measurement of private indebtedness at the country level developed and published by the Bank for International Settlements (BIS). Specifically, it is defined as the ratio of the total debt of non-financial private sectors at market value of one country over its nominal GDP.

2.3. World Trade and Economic Integration across countries

As was first stressed by the classics, Adam Smith and David Ricardo, trade promotes growth by allowing the optimal use of resources. Empirical evidence is profuse and supports that trade tends to favor development given that it stimulates technical progress, which is spread across countries through the importation of capital goods that incorporate innovations (for a survey, see [45]).
Particularly, exports promote economic growth through several channels: it enhances a better allocation of resources through specialization on goods that have an improved comparative advantage, favoring productivity gains through economies of scale, spillover effects and learning-by-doing. In this sense, trade integration enables a higher external demand that increases the probability and/or intensity of exporting and, therefore, of economic growth, especially in periods where domestic demand is under pressure ([46,47,48]).
International trade has also been identified as a channel through which shocks are internationally transmitted, contributing to the synchronization in business cycles across countries. In particular, countries joining a currency union may lose their ability to stabilize cyclical fluctuations through independent counter-cyclical monetary policy. In general, empirical research has found that pairs of countries with relatively strong economic linkages, not only in terms of trade intensity but also in terms of financial and institutional integration, tend to have highly correlated business cycles. For example, [49], [50] and [51] find that the closer the trade linkages are, the higher the correlation in countries’ business cycles are as well. Similarly, [52] shows that more financially integrated countries display more correlated business cycles.
We incorporate in our model the World Trade Volume Index that is monthly computed by the Netherlands Bureau for Economic Policy Analysis. This index, defined as the arithmetic average of world exports and imports of goods, constitutes an indicator of global economic activity. It covers United States, Japan, EU, and four groups of emerging countries: Asian excluding Japan, Eastern Europe and CIS countries, Latin America, and Africa and Middle East.
Here, we have to emphasize the ability of the Temporal Fusions Transformers methodology to capture cross-country business cycle co-movements even if the drivers of this synchronization are not explicitly introduced in the list of explanatory variables.

3. Forecasting Economic Growth Using Deep Learning and Regression Models: Literature Review

The Great Recession (2007-2009) and the COVID-19 pandemic have increased the uncertainty surrounding the economic cycle. This indetermination occurs in a context of financialization of the global economy in recent decades, understood as a broad set of changes in the relationship between the financial sector and the real sector, which has given greater weight than before to financial motives and actors, consequently affecting the different relationships between macroeconomic and/or financial variables.
The influence of macroeconomic and/or financial variables on the business cycle has been extensively detailed in the previous section. In this one, we collect the different technical contributions to the forecasting of the business cycle, measured by GDP in real terms, from advanced regression models, especially in time series analysis, to the use of artificial intelligence techniques.

3.1. The Use of Regression Models for Business Cycle Forecasting

There is a wide variety of regression models used in macroeconomic research in order to forecast economic activity. They range from the early ARIMA ([53,54,55]), or VAR models ([56,57]) to those more complex ones that analyze the cycle from an explicit nonlinear perspective. VAR models are particularly useful for forecasting purpose but suffer from a major drawback, as they require the estimation of many potentially non-significant parameters. This over-parametrization problem, resulting in multicolinearity and loss of degrees of freedom, leads to inefficient estimates and large out-of-sample forecast errors. To face this problem there are two main approaches. The first one consist in identifying non-significant lags through statistical tests, and estimating the restricted version of the model that incorporates the identified restrictions on the parameters of the model. The second approach uses quasi-VAR models, which specify an unequal number of lags for the different equations.
Alternatively, some authors ([58,59]) propose a Bayesian VAR or BVAR model. Instead of eliminating the longest lags, the Bayesian method imposes restrictions on the coefficients of the model assuming that these coefficients are more likely to approach zero than the coefficients of the shortest lags. Within the VAR family, in order to capture the systemic dimension while retaining the advantage of estimating a single equation, structural vector autoregressive (SVAR) models emerged ([60,61]). Finally, it is worth mentioning the time-varying parameter VAR models, which successfully model regime-switching time series ([62,63,64]).
Within business cycle modeling from an explicit nonlinear perspective the range is very broad. They include, for example, Smooth Transition Regression (STR) models, which are a general class of reduced-form, state-dependent, nonlinear time series models in which the transition between states is, generally, generated endogenously, and where Smooth Transition Autoregression (STAR) models are a particular case. See [65], [66], and [67].
[68] show that the STR models include as particular cases, in addition to the STAR, the Exponential Autoregressive (EAR), the Threshold Autoregressive (TAR) and the SETAR models. TAR and SETAR models are those which, maintaining the idea that the level and time structure in an economic phenomenon depend on the cyclical phase in which it is found, provide a relatively simple way of introducing non-linear elements in the econometric analysis of time series. See [69], [70], and [71].
Finally, within the nonlinear modeling of the business cycle, we distinguish those models where the state of the cycle can be represented by a binary state variable whose evolution is explicitly characterized by a Markov chain. This state variable conditions the parameters of a linear model that completes the representation of the observed dynamics. We refer to Markov-Switching Autoregression (MS-AR) models, see [57], [72], [73], [74], [75], [76], [77] and [78]. [79] further generalizes the MS-AR model to a MS-VAR time series model.
[80] use a small set of variables -real GDP, the inflation rate, and the short-term interest rate- to analyze atheoretical (time series) and theoretical (structural) regression models, as well as linear and nonlinear, to test whether the decline in U.S. real GDP during the Great Recession could have been predicted. Their results suggest that structural (theoretical) models, especially the nonlinear model, perform well on average at all forecast horizons in ex post, out-of-sample forecasts, although at certain forecast horizons certain nonlinear atheoretical models perform better. The nonlinear theoretical model also dominates in ex ante, out-of-sample forecasts of the Great Recession.

3.2. Forecasting Real GDP Using Artificial Intelligence Models

Forecasting real GDP growth, like other macroeconomic data, is a far from straightforward process. Starting from the causal relationship between dependent and independent variables, traditional economic models use predetermined relevant variables to make predictions, adopting top-down and theory-driven approaches ([81]). This process, in relation to the data and methods used, is founded on economic intuition and forecasters' judgment. If any of the forecasters' assumptions are not met, the models will produce inaccurate predictions.
The effect of an explanatory variable on real GDP depends on how it is interrelated with other explanatory ones, which, in addition, can vary over time. This feature cannot be modeled using the conventional regression framework, opening the door to the use of artificial intelligence techniques (AI). AI is the development of computer-based algorithms that can perform tasks similar to human intelligence, being able to modify their actions maximizing their chances of success. Such algorithms are increasingly capable of solving extremely complex problems, and can assist in decision-making, including the classification and evaluation of large amounts of data.
Unlike many traditional economic forecasting models, AI machine learning models focus on pure prediction ([82]). Being more flexible than traditional economic forecasting models, they produce predictions without predetermined assumptions or judgments. Therefore, thanks to the development of new algorithms and the increase in computing power, machine learning models have been actively applied in various fields, from forecasting transportation, traffic or electricity flows ([14,83,84]), to forecasting housing prices ([85]) or financial market volatility ([14,86]). In most of the fields analyzed, machine learning methods perform better than traditional econometric models, including cases with low-frequency data. Looking at their application to economics, such as the inflation forecasting studies of [87] and [88], they produce robust predictions.
[89] divide AI learning methods into four major groups: unsupervised, supervised, semi-supervised, and reinforcement learning.
Almost all the artificial intelligence models that have been applied for business cycle forecasting fall within the supervised learning models, although elements of reinforcement learning can also be incorporated. For real GDP forecasting, different AI models have been used: K-Nearest Neighbor ([90,91,92]); Decision Trees, Boosted Trees, Gradient Boosting and/or Random Forest ([91,93,94,95,96,97,98]); Artificial Neural Networks and its Deep Learning Extensions ([99-101); Ordinary and Alternative Support Vector Machines ([91,101,102,103]); Boltzmann Machines ([101]). These papers find that all these learning algorithms can outperform traditional statistical models, thus offering a relevant addition to the field of economic forecasting.
It is important to remark that most Machine Learning techniques, such as Random Forest or Gradient Boosting algorithms are not ideal for time series forecasting, since they ignore the time order of the features. They assume that the value of each feature at a certain time step is independent of the value of the same feature at the previous time step. This is violated in time series data, where serial correlations are essential.
Because of this, RNNs (GRUs and LSTMs), have been extensively used to solve time series forecasting problems since they are capable of capturing the dependencies between time steps. The problem of these DNNs is that they can´t correctly capture long-range dependencies. This issue is solved in the Transformer architecture, initially presented in [104]
This paper is a contribution to the real GDP forecasting literature based on the application of Artificial Intelligence. It proposes the application of Temporal Fusion Transformers (TFTs), recently developed by [14], which encompasses within Deep Neural Networks (DNNs). TFTs provide considerable advantages that will be detailed in the next section.

4. Methodology and Database

We will apply a new deep learning model, the Temporal Fusion Transformers, for forecasting jointly the real GDP on a quarterly basis for 25 OECD countries at different time horizons. We will detail the main features of TFTs, explaining both, the attributes that make them very suitable for forecasting macroeconomic variables and the different blocks of their architecture. We will then explain in detail the methodology we have designed for the joint forecasting of the GDPs of a substantial number of countries.

4.1. Temporal Fusion Transformers for Forecasting Real GDP

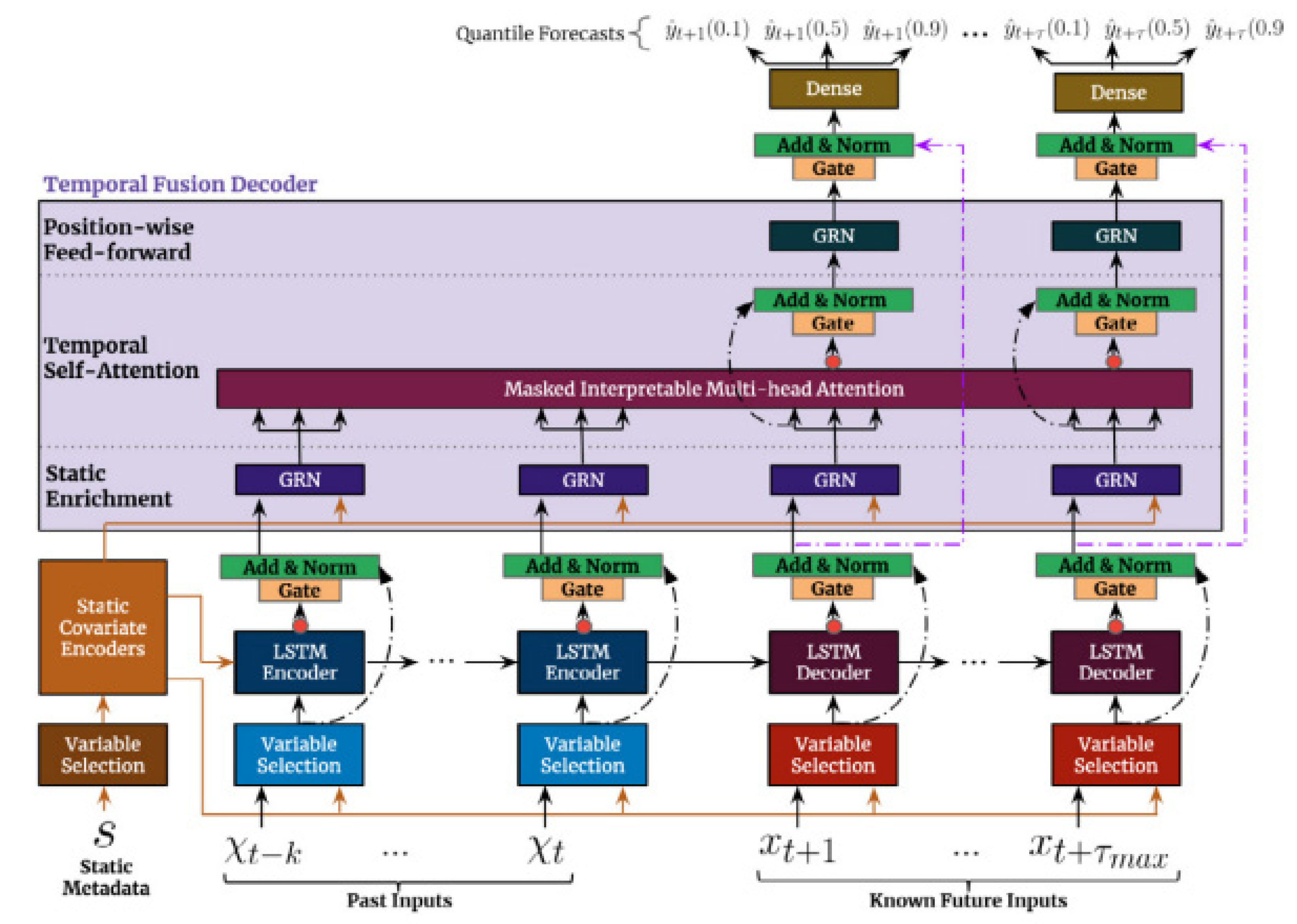
TFT ([14]) is the state-of-the-art model for interpretable, multi-horizon time-series forecasting. This attention-based architecture is specifically designed for time series prediction and provides several advantages over other deep learning models (Figure 1).
First, TFTs support different types of variables as inputs: time series that are only known up to the present (this is the type of data that most models work with); time series with known values in the future; and static or time-invariant variables. All these variables can be categorical or continuous. Due to its ability to process static variables, TFTs permit training on multiple time series, from different distributions. This is extremely important because it has enabled us to train the model with data from different countries, significantly increasing the size of the dataset, something essential for machine learning models.
Most models are not able to work with known future values and this is essential for certain time series problems. For example, from the perspective of a central bank, the model's ability to work with known future values of a given explanatory variable will allow for an analysis of the impact of monetary policy –interest rates and/or quantitative easing- on a given macroeconomic variable under study, be it inflation and/or real GDP.
Secondly, TFTs allow multi-horizon quantile prediction, through multi-step forecasts by calculating prediction intervals using the quantile loss function. The user can define these forecasting intervals.
Finally, one main property of TFTs is their interpretability. Most deep learning architectures are "black box" models and their predictions cannot be explained. Generally, AI explanatory methods obtain interpretability measures in a differentiated process from the estimation one. Common post-hoc machine learning explanatory techniques, such as SHAP or LIME, do not take into account the temporal order of the inputs, ignoring dependencies between time steps that are essential in time series. TFTs address this weakness incorporating Variable Selection Networks (VSN) that provide variable selection weights, which quantify the importance of each feature in the prediction of each observation in the dataset. Then, selection weights are collected for each variable across the entire test set to compute any statistic that characterizes each sampling distribution. In addition to quantify the importance of each input variable in prediction, TFTs permit us to visualize persistent temporal patterns, different regimes and significant events. For this purpose, TFTs employ a self-attention mechanism that estimates the attention weights that measure the importance of each period.
Having already explained the capabilities that make the TFT ideal for economic forecasting, we will now briefly explain its architecture, before detailing the methodology we have designed for the joint forecasting of real GDP for a considerable number of countries. See Figure 2.
TFT has a complex architecture, which gives it enormous flexibility and computing potential, the main blocks being:
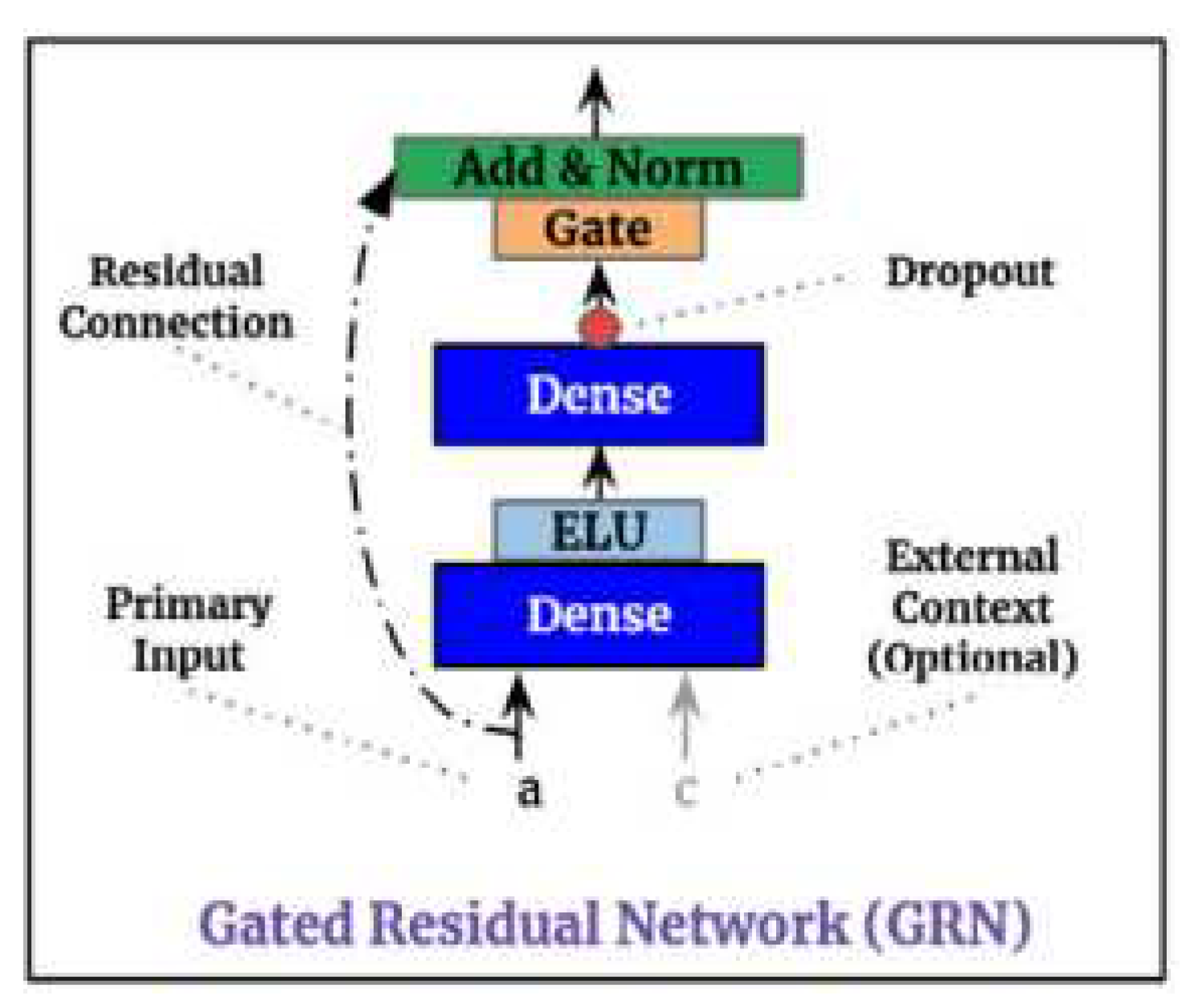
1-Gating mechanisms: Gating mechanisms give TFTs the ability to skip unused parts of the architecture. This is especially important in small or noisy datasets, where a simpler model can enhance performance (as the problem solved in this paper). This Gated Residual Network (GRN) is one of the main blocks of TFTs. The GRN takes in the main input and a context vector and decides whether additional dense layers are useful or these layers can be skipped through the residual connection.
2-Variable selection networks (VSN): In most prediction problems, we have variables that do not increase the prediction ability of the model. TFT has introduced variable selection networks: this part of the architecture removes irrelevant inputs that decrease the algorithm performance and provides information about the most relevant variables just by analyzing the weights assigned to each one.
3-Static covariate encoders: TFT is able to use information from static data thanks to separate GRN encoders that produce different context vectors that are connected to several parts of the architecture. These kinds of encoders are especially important for our problem since they allow the model to train with data from different countries.
4- LSTM Encoder-Decoder: This sequence-to-sequence layer is used for local processing; it captures short-term time dependencies. Known future inputs are directly connected to the decoder.
5- Interpretable multi-head self-attention: TFT has a self-attention mechanism that makes the model capable of learning long-term relationships: it integrates information from any time step. This transformer architecture presents some changes in comparison to standard transformers ([104]); these modifications allow interpretability studies by the analysis of attention weights.
6- Dense layers: Several dense layers are part of the model; these layers learn through different non-linear transformations. The final dense layer generates prediction intervals in addition to point forecasts.
7-Loss function: TFT is trained by minimizing the quantile loss of all quantile outputs. We use the following quantiles: {0.02, 0.1, 0.25, 0.5, 0.75, 0.9, 0.98}. The following equation represents the loss function:
L Ω , W = ∑ y t ∈ Ω .     ∑ q ∈ Q .     ∑ τ = 1 τ m a x   Q L ( y t , ŷ q , t − τ , τ , q ) M τ m a x
Q L y t , ŷ , q = q y − ŷ + + 1 − q ŷ − y +            

4.2. Methodology

In this section, we provide a brief explanation of the data used in the training, validation, and test datasets, the hyperparameter configuration, and the model specifications for each forecast horizon.
The target value (y) of our neural network is the GDP logarithmic growth rate, expressed as:
y = log ⁡ G D P ( t + s ) G D P ( t ) ,             s = 1 ,   2 ,   3   o r   4
where s denotes the number of quarters. For example, in the case of the annual growth rate forecast it would be:
y = log ⁡ G D P ( t + 4 ) G D P ( t )
This means that we will train our network with four different target values and different hyperparameters settings depending on the forecast horizon. We will measure the performance of the models using two different metrics, the RMSE and the MAE. For each date, the dataset is composed of the data from 25 OECD selected countries. Thus, we will simultaneously train and forecast for all of them.
The main disadvantage of machine learning models for macroeconomic forecasting is the lack of available data. We have used the Python library PyTorch Forecasting to implement the TFT; this package does not have stochastic gradient descent available. Because of this, we need to refit the model for each forecast to incorporate the data from the latest available observation. This is critical to forecast the GDP since the economic paradigm can change suddenly.
As shown in Figure 4, the first observation that belongs to the test dataset is the first quarter of 2009 and the last one is the third quarter of 2021. PyTorch Forecasting uses the last available quarter as the validation dataset, therefore the validation and test datasets will contain one observation per country in each forecast.
When we make predictions greater than one quarter (s=2, 3 or 4 quarters), the test dataset contains the GDP logarithmic growth rate that corresponds to those s periods. The forecast that we will use to check the model performance is the last one, in order to avoid overlapping data. We can see in Figure 5 how we may predict Q4 2009 when the last data available is Q4 2008. Even though our test dataset contains four annual growth rates, we only use the last one since it is the first prediction that does not contain any information from the test dataset.
The hyperparameters used to forecast at different time horizons are the same, with the only exception of the number of epochs. Main hyperparameters are shown in Table 1.
The GroupNormalizer scales by groups (in this application, countries). It means that for each group a scaler is fitted and applied

4.3. Sample data and variables

Database used in this paper comes from different combined sources corresponding to the period 1990–2021 for 25 OECD countries (See Table 2). (i) The Organization for Economic Co-operation and Development (OECD) for GDP in volume index, and main economic indicators ; (ii) The Bank for International Settlements (BIS) for the Total Debt Non Financial Private Sectors over GDP ; (iii) Federal Reserve Economic Data (FRED), Federal Reserve Bank of St. Louis for Credit Spreads ; (iv) Netherlands Bureau for Economic Policy Analysis (CPB) for World Trade data ; (v) Bloomberg for CRB Raw Industrials Spot Index. Table 3 shows detailed information about the variables, the reason of use, and the sources.

5. Results and Discussion

The TFT model is estimated for the 25 OECD countries listed in Table 2, focusing the analysis of the results on 10 representative countries that have been selected taking into account their heterogeneity in terms of size, growth pattern (demand-led or export-led growth) and monetary sovereignty.
In this section, we present and discuss the most important results. First, in subsection 5.1 we will discuss the results obtained over the entire test period for all forecast horizons and differentiating them across the 10 representative countries. Second, in subsection 5.2 we will present the results across different sub-periods defined to observe differences in performance, depending on the stage of the business cycle. Finally, we will provide some concrete examples of TFT forecasts and its interpretability.

5.1. Performance over the entire period

Table 4 shows how TFT outperforms the standard ARIMA over the entire test period for the selected countries in two metrics: Mean Absolute Error (MAE) and Root Mean Square Error (RMSE). Percentages reflect the error excess of ARIMA relative to TFT. For example, for an annual forecast, ARIMA RMSE is 188.27% higher than that of TFT. Improvements occur for all forecast time horizons.
To evaluate the statistical significance of the results we perform one-tailed hypothesis tests on the TFT error metrics. We compute the 99th percentile of the bootstrap distribution of the TFT error metrics and compare this critical value against the error metrics of the benchmark model. For the two metrics and across all forecast horizons’, except for one quarter, ARIMA error measures are higher than the 99th percentile of the TFT error metric distribution, confirming that TFT error metrics are statistically lower than the ARIMA ones, at the 1% significance level (see Appendix A).
Table 5 shows the increases of the two considered error metrics (MAE and RMSE), for the ARIMA model with respect to the TFT, in the 10 selected countries for the 1-quarter and 1-year forecasts. It shows that the TFT forecasts are usually more accurate than ARIMA, being these improvements greater in demand-driven growth countries.
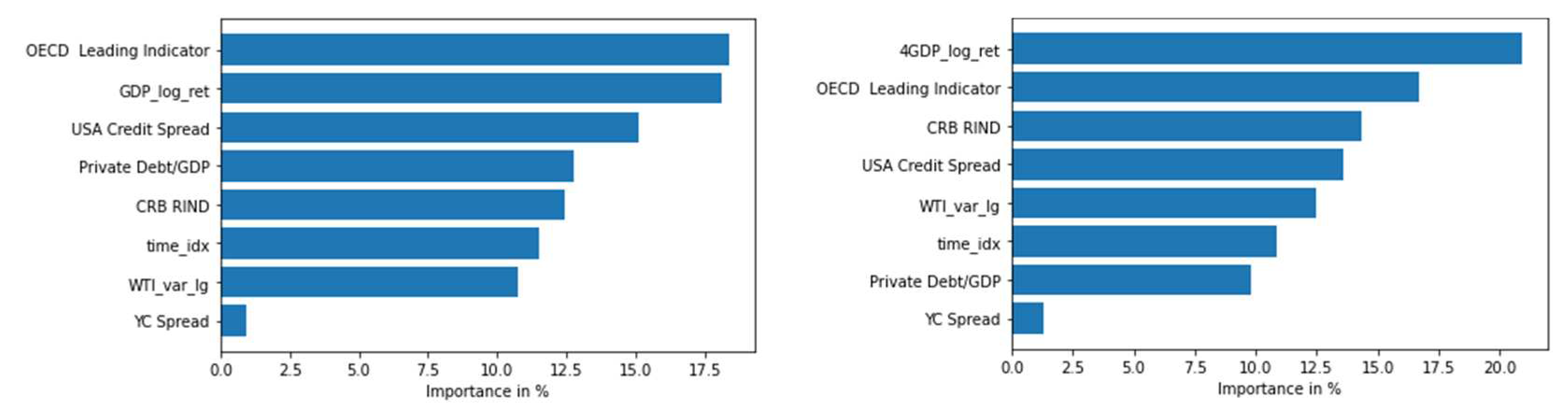
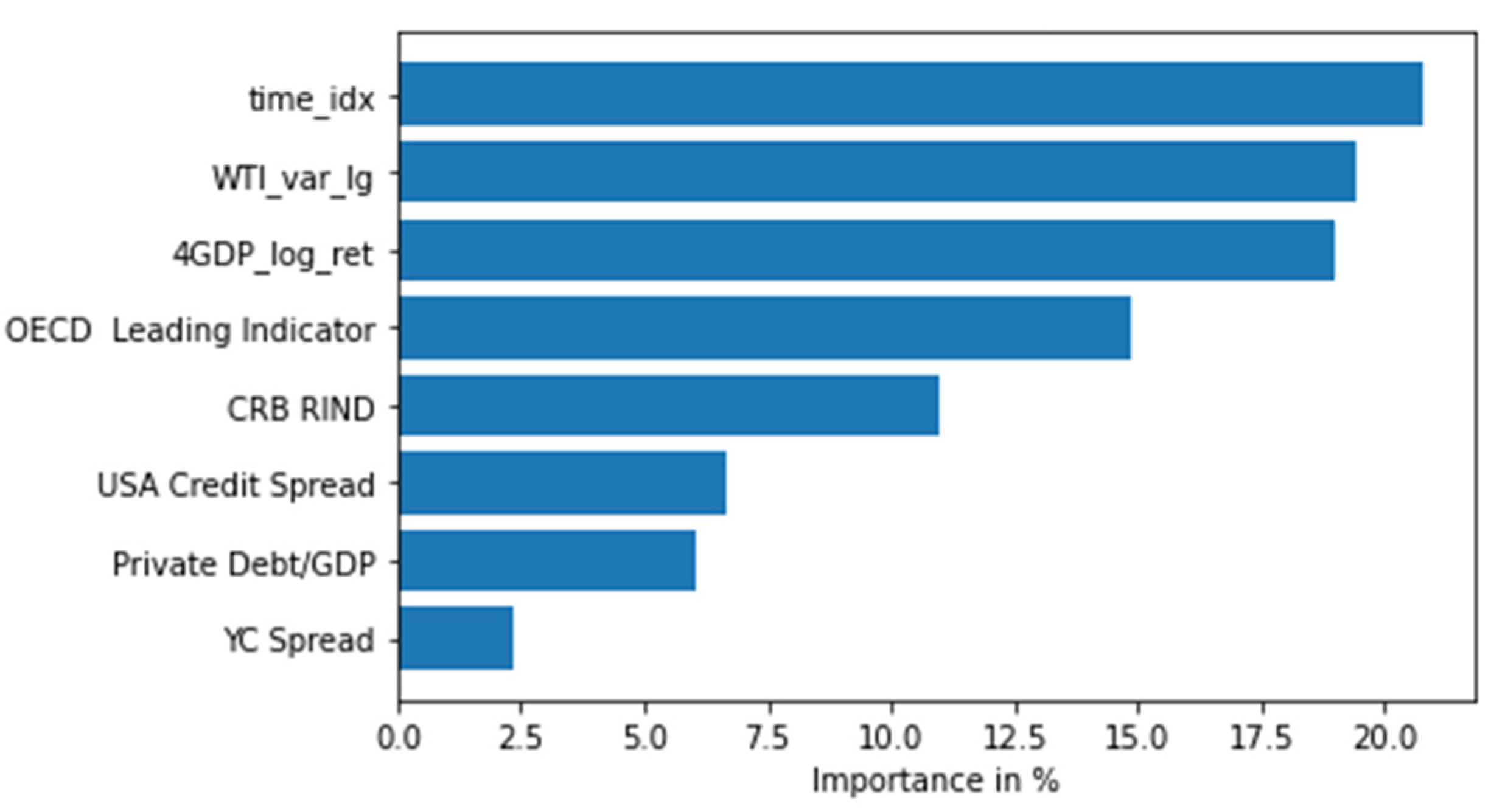
One of TFTs most interesting features is its interpretability. Figure 6 shows the encoder variables importance for one quarter (LHS) and annual (RHS) forecasts.
As expected, the most important predictor is the nearest lag of real GDP growth, which reflects the autoregressive behavior of the time series. Likewise, the OECD Leading Indicator index provides early signals of turning points in business cycles ([4,32,33,34,109]). The CRB Raw Industrial Spot Index’s relevance confirms it serves as an early indicator of impending changes in global business activity ([41]). The change in the World Trade Volume Index is an indicator of the global external demand, and its importance depicts how it affects countries’ business activity.
It is remarkable the predictive capacity of the variable that captures the indebtedness of the non-financial private sectors as a percentage of GDP, which played a catalytic role in the Great Recession once the value of collateral began to deteriorate, in accordance with Hyman Minsky's financial instability hypothesis ([15,16]). Recent studies provide evidence on the high persistence of the ratio of private debt to GDP for different OECD countries and the key importance of macroprudential policy in this area ([17]).
Related to this variable, our proxy of global credit spread cycle (USA Credit Spread) is economically important for predicting the business cycle ([25-31). In contrast, the limited forecasting capacity of the yield curve in TFT suggests that the slope of the sovereign debt interest rate curve has diminished its predictive power, compared to previous work ([4,5,6,7,8,9]), in anticipating the evolution of the business cycle. This loss of forecasting accuracy occurs in a context where quantitative easing policies have gained importance. More research is needed to understand the effects of quantitative easing on the yield curve’s predictive power.

5.2. Performance over expansive and recessive periods

A comparison of TFT versus ARIMA has been performed in both recession and expansion sub-periods, in order to give greater robustness to the results obtained at a global level. Table 6 shows how TFT clearly outperforms the standard ARIMA during the COVID-19 pandemic, and behaves almost equally in the rest of sub-periods. The difference in performance between both models increases in long-term forecasts, due the TFT ability to capture nonlinearities.
Table 7 exhibits the increases in the two considered error metrics (MAE and RMSE), for the ARIMA model with respect to the TFT, in the 10 selected countries for 1-year forecasts over the different sub-periods. In general, TFT forecasts are more accurate than those of the ARIMA, being these improvements greater in periods of economic slowdown or recession, in particular, in demand-driven growth countries.

5.3. Forecast examples

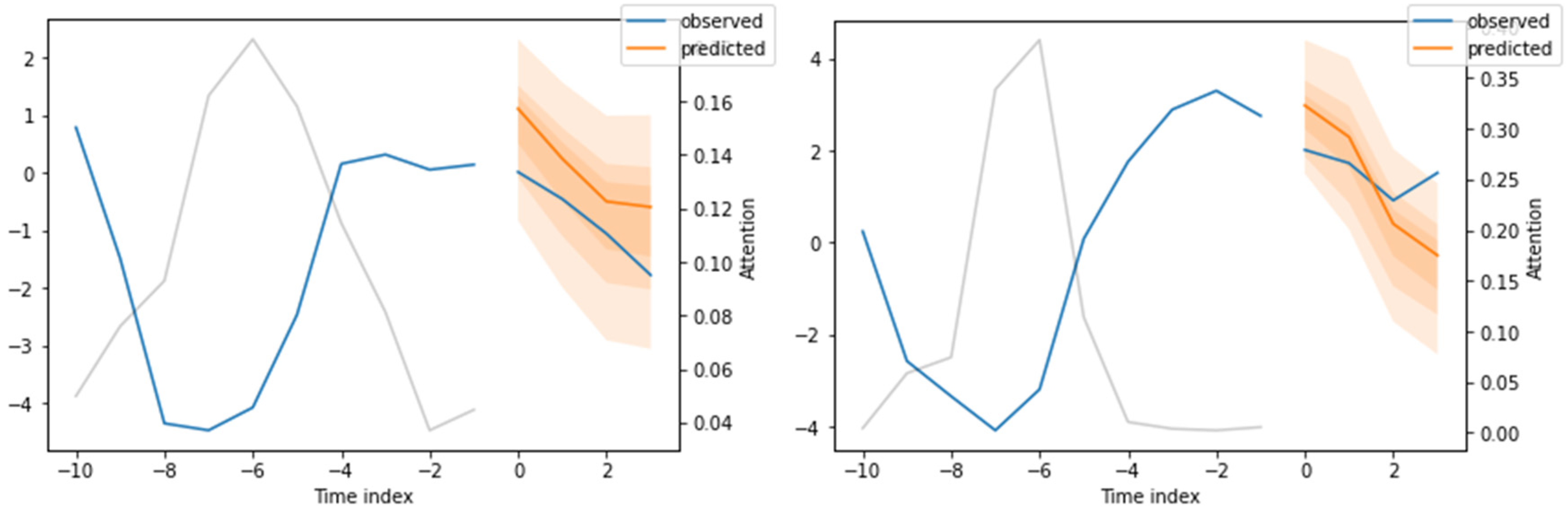
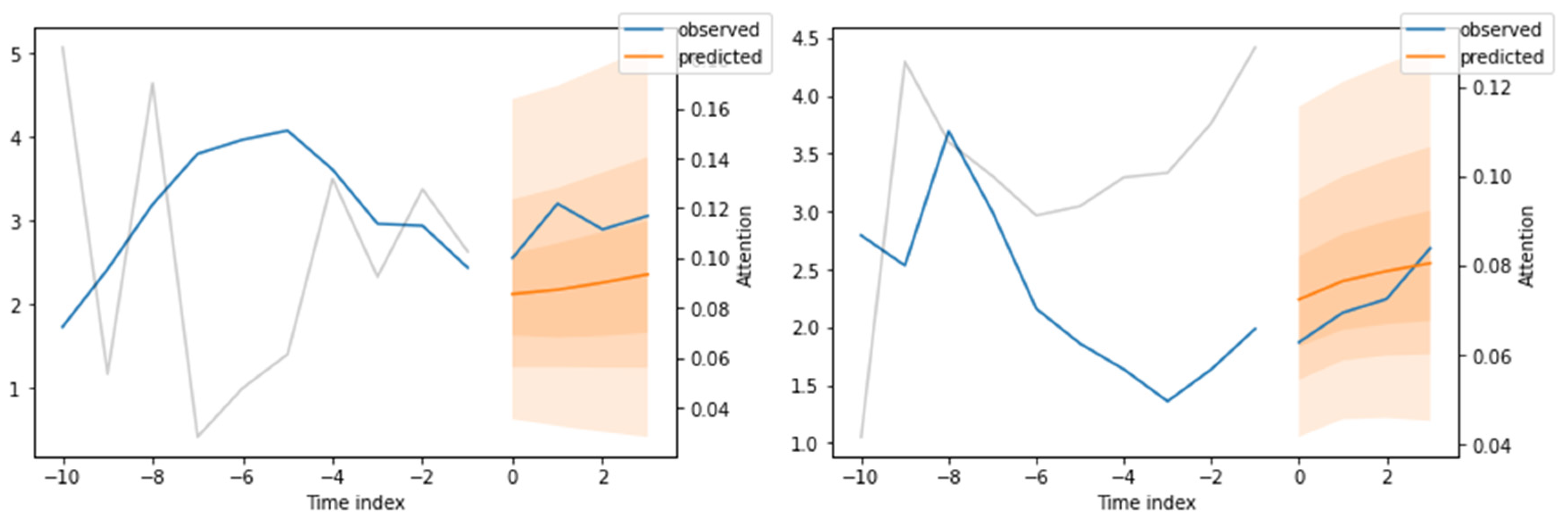
In order to provide a better understanding of the TFT, in this section, we present concrete examples of its predictions and their interpretability. We show the quantile forecast for Spain and United States for two years, 2011 and 2017. The first year displays how the model works in a period of turbulence, while the second presents its performance in a period of stable growth.
Figure 7 represents the quantile forecast for Spain (LHS) and USA (RHS) for year 2011. In addition to the point forecasts (orange line), the confidence intervals for different significance levels (2%, 10%, 25%, 50%, 75%, 90%, 98%) are plotted. The primary y-axis represents the accumulated logarithmic growth rate while the secondary y-axis provides information of which of the previous periods has more importance in each prediction. This aspect is obtained by analyzing the attention weights. As expected, the Great Recession has a great importance.
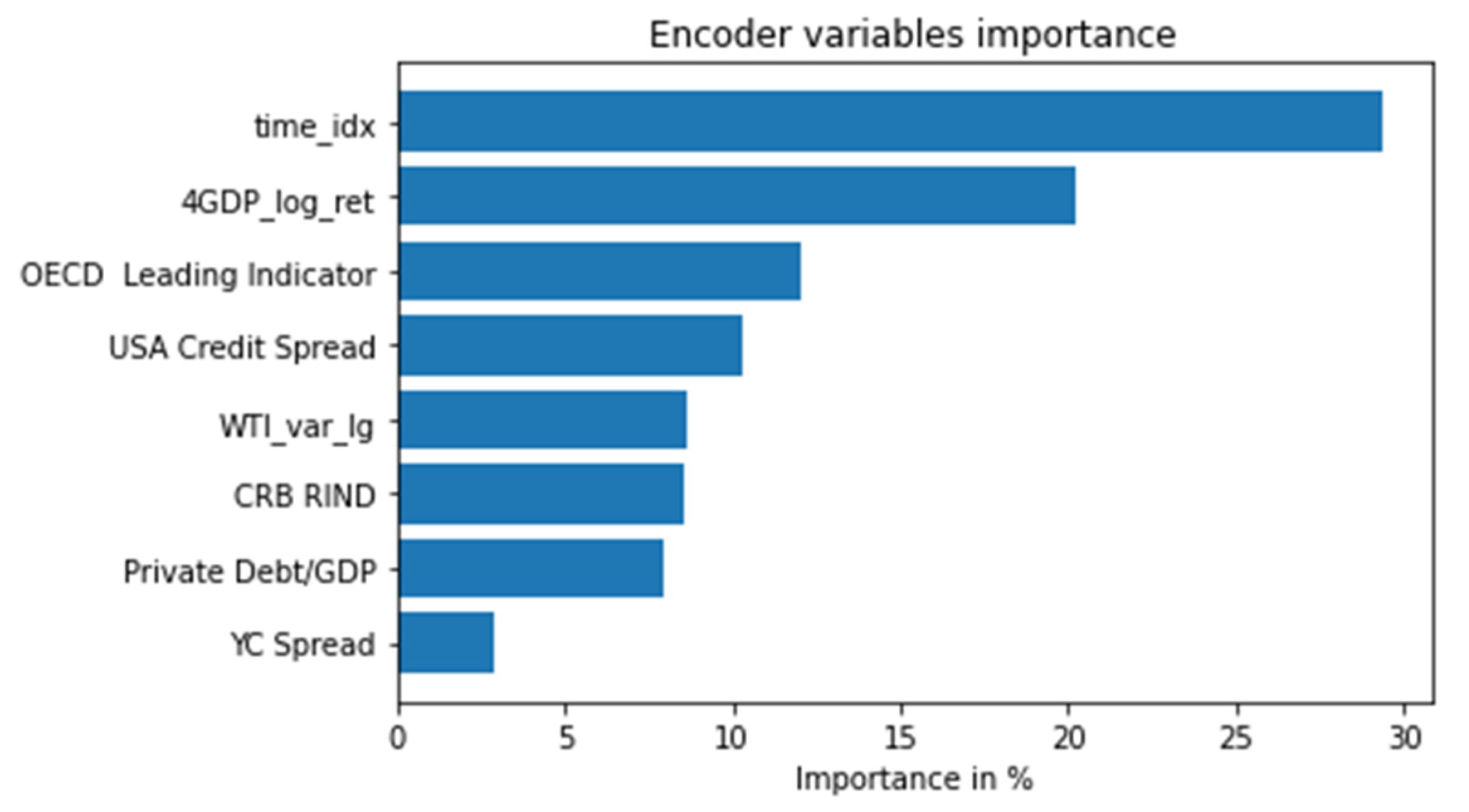
Figure 8 shows the encoder variables importance for the 2011 forecast. Variable time_idx, which represents the temporal sequence, is the most important one, followed by the World Trade Volume index, the autoregressive component, the OECD Leading Indicator, and the CRB Raw Industrial Spot Index’s. Otherwise, the private debt to GDP ratio, and our proxy of global credit spread cycle (USA Credit Spread) are not as relevant as most of private deleveraging process had already occurred. Finally, the yield curve spread predictive power is almost insignificant.
Figure 9 displays the quantile forecasting results for Spain (LHS) and USA (RHS) in 2017, including the predicted values compared to the observed ones, the prediction intervals and the relative importance of each lag in the forecast (grey line).
Figure 10 depicts the encoder variables importance for the 2017 forecast. The variable that captures the temporal sequence (time_idx) is revealed as the most important one, followed by the autoregressive component and the OECD Leading Indicator.

6. Concluding remarks

This paper applies the Temporal Fusion Transformers (TFTs), recently developed by [14], to the prediction of real GDP growth. This AI architecture offers significant comparative advantages over regression models and other deep learning methods in a context where the features of time series for business cycle indicators are affected by long-term nonlinearities. Mainly, it enables to train the model on multiple time series from different distributions; it allows to visualize persistent temporal patterns and to identify significant events and different regimes, providing quantile regressions for forecasts and interpretable results since the impact of each explanatory variable is quantified.
The results of the joint GDP forecasting of 25 OECD countries at different time horizons -one, two, three, and four quarters- using macroeconomic and financial variables outperform those obtained with the benchmark (ARIMA) in terms of both, the MAE and the RMSE, very especially in periods of turbulence, such as the COVID-19 shock. The obtained results show that TFT forecasts improvements are greater in the demand-driven growth countries than in export-led growth ones.
The use of TFTs to predict real GDP yields very interesting results regarding the importance of the explanatory variables. The relative importance of variables might vary somewhat, depending on the phase of the economic cycle or the forecast time horizon. It is remarkable the predictive capacity of the autoregressive component and the OECD Composite Leading Indicator, in addition to the CRB Raw Industrial Spot Index’s, as well as the variable that captures the indebtedness of the non-financial private sectors, which is related to our proxy of global credit spread cycle (USA Credit Spread), and the world trade indicator. On the opposite side, it is worth highlighting the low predictive power of the slope of the yield curve.
Future research should exploit one main ability of TFTs that is the possibility of incorporating the effects of known future inputs in the predictions. It allows policymakers to perform the impact assessment of changes in instrumental economic variables, such as, interest rates, taxes, etc. Given that one of the findings in this paper is the importance of private debt in forecasting real GDP, this framework could be used to simulate the effects of credit tightening measures.
Finally, it would be very interesting to exploit one of the most outstanding features of TFTs, the possibility of identifying different economic regimes. Several studies ([111,112,113]) suggest the hypothesis that, in the last decades, the only source of growth in the western countries is being bubble generation (financial or real estate). This new AI architecture would be useful to identify the blow-up periods and the subsequent bursting ones.
In short, TFTs are revealed as a new AI tool available to economists and policymakers, with enormous potential in the prediction of economic cycles.

Author Contributions

All authors have contributed equally. All authors have read and agreed to the published.

Funding

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Conflicts of Interest

The authors certify that they have not conflict of interest.

Appendix A. One sided tests for the outperforming of TFT GDP forecast with respect the benchmark ARIMA

We formally test the improvement of the MAE and RMSE metrics of TFT relative to ARIMA using the bootstrap one-sided test. The null hypothesis is that the difference between the metrics of both estimation procedures is not significant against the alternative hypothesis of the metric for the TFT is lower than that for the ARIMA. We compute the 99% critical value of the distribution of the TFT metric (MAE or RMSE) using bootstrap resampling. Then, we calculate the percentage difference of the ARIMA metric (MAE or RMSE, respectively) relative to this bootstrap critical value. As shown in Table A1, for both metrics, all the test-statistics for periods greater than one quarter are positive. Therefore, we can conclude that TFT outperforms ARIMA, at the 99% significance level, for most prediction horizons.
Table A1. Percentage difference of the ARIMA performance metric (MAE and RMSE) of ARIMA relative to the 99% critical value of the bootstrap distribution for the TFT metric.
Table A1. Percentage difference of the ARIMA performance metric (MAE and RMSE) of ARIMA relative to the 99% critical value of the bootstrap distribution for the TFT metric.
Metric t+1 t+2 t+3 t+4
MAE -18.59% 8.21% 25.02% 26.22%
RMSEa -20.05% 60.46% 118.43% 120.20%
a RMSE is the average of the RMSE calculated at country level.

References

  1. Stockhammer, E. Financialisation and the slowdown of accumulation. Camb. J. Econ. 2004, 28, 719–741. [Google Scholar] [CrossRef]
  2. Christodoulou-Volos, C.; Siokis, F.M. Long-range dependence in stock market returns. Appl. Financial Econ. 2006, 16, 1331–1338. [Google Scholar] [CrossRef]
  3. Murialdo, P; Ponta, L.; Carbone, A. Long-range dependence in financial markets: A moving average cluster entropy approach. Entropy. 2020, 22, 634. [CrossRef]
  4. Estrella, A.; Mishkin, F.S. Predicting U.S. recessions: Financial variables as leading indicators. Rev. Econ. Stat. 1998, 80, 45–61. [CrossRef]
  5. Chauvet, M.; Potter, S. Forecasting recessions using the yield curve. J. Forecast. 2005, 24, 77–103. [Google Scholar] [CrossRef]
  6. Estrella, A. Why does the yield curve predict output and inflation? Econ. J. 2005, 115 (July), 722–744. [Google Scholar] [CrossRef]
  7. Kauppi, H.; Saikkonen, P. Predicting US recessions with dynamic binary response models. Rev. Econ. Stat. 2008, 90, 777–791. [Google Scholar] [CrossRef]
  8. Katayama, M. Improving recession probability forecasts in the US economy; Working paper, Louisiana State University, 2009.
  9. Hamilton, J.D. Calling recessions in real time. Int. J. Forecast. 2011, 27, 1006–1026. [Google Scholar] [CrossRef]
  10. Van Dijk, D.; Franses, P.H.; Paap, R. A nonlinear long memory model, with an application to US unemployment. J. Econom. 2002, 110, 135–165. [Google Scholar] [CrossRef]
  11. Cuestas, J.C.; Garratt, D. Is real GDP per capita a stationary process? Smooth transitions, nonlinear trends and unit root testing. Empir. Econ. 2011, 41, 555–563. [Google Scholar] [CrossRef]
  12. Choudhry, T.; Papadimitriou, F.I.; Shabi, S. Stock market volatility and business cycle: Evidence from linear and nonlinear causality tests. J. Bank. Financ. 2016, 66, 89–101. [Google Scholar] [CrossRef]
  13. Cerra, M.V.; Fatás, A.; Saxena, M.S.C. Hysteresis and business cycles; International Monetary Fund, 2020.
  14. Lim, B.; Arık, S. Ö.; Loeff, N.; Pfister, T. Temporal Fusion Transformers for Interpretable Multi-Horizon Time Series Forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
  15. Minsky, H.P. Stabilizing an unstable economy; Yale University Press, New Haven, 1986.
  16. Minsky, H.P. The financial instability hypothesis; Working paper 74, The Jerome levy economics Institute of Bard College, 1992.
  17. Caporale, G.M.; Gil-Alana, L.A.; Malmierca, M. Persistence in the private debt-t-GDP ratio: evidence from 43 OECD countries. Appl. Econ. 2021, 53, 5018–5027. [Google Scholar] [CrossRef]
  18. Stock, J.H.; Watson, M.W. Forecasting output and inflation: the role of asset prices. J. Econ. Lit. 2003, 41, 788–829. [Google Scholar] [CrossRef]
  19. Harvey, C. The real term structure and consumption growth. J. Financ. Econ. 1988, 22, 305–333. [Google Scholar] [CrossRef]
  20. Laurent, R.D. An interest rate-based indicator of monetary policy. FRB Chic. Econ. Perspect. 1988, 12, 3–14. [Google Scholar]
  21. Estrella, A.; Hardouvelis, G. The term structure as a predictor of real economic activity. J. Finance. 1991, 46, 555–76. [Google Scholar] [CrossRef]
  22. Estrella, A.; Mishkin, F.S. The term structure of interest rates and its role in monetary policy in Europe and the United States: Implications for the European Central Bank. Eur. Econ. Rev. 1997, 41, 1375–1401. [Google Scholar] [CrossRef]
  23. Bernard, H.; Gerlach, S. Does the term structure predict recessions? The international evidence. Int. J. Finance Econ. 1998, 3, 195–215. [Google Scholar] [CrossRef]
  24. Taylor, J.B. Discretion versus policy rules in practice. J. Monet. Econ. 1993, 39, 195–214. [Google Scholar] [CrossRef]
  25. Gilchrist, S.; Yankov, V.; Zakrajšek, E. Credit market shocks and economic fluctuations: Evidence from corporate bond and stock markets. J. Monet. Econ. 2009, 56 (4) 471–493. [CrossRef]
  26. Gilchrist, S.; Zakrajšek, E. Credit spreads and business cycle fluctuations. Am. Econ. Rev. 2012, 102, 1692–1720. [Google Scholar] [CrossRef]
  27. Faust, J.; Gilchrist, S.; Wright, J.H.; Zakrajšek, E. Credit spreads as predictors of real-time economic activity: A Bayesian model-averaging approach. Rev. Econ. Stat. 2013, 95, 1501–1519. [Google Scholar] [CrossRef]
  28. Bleaney, M.; Mizen, P.; Veleanu, V. Bond spreads and economic activity in eight European economies. Econ. J. 2016, 126, 2257–2291. [Google Scholar] [CrossRef]
  29. Okimoto, T.; Takaoka, S. The term structure of credit spreads and business cycle in Japan. J. Jpn. Int. 2017, 45, 27–36. [Google Scholar] [CrossRef]
  30. Okimoto, T.; Takaoka, S. The credit spread curve distribution and economic fluctuations in Japan. J. Int. Money Finance. 2022, 122. [Google Scholar] [CrossRef]
  31. Gilchrist, S.; Mojon, B. Credit risk in the Euro area. Econ. J. 2018, 128, 118–158. [Google Scholar] [CrossRef]
  32. Hamilton, J.D.; Pérez-Quirós, G. Do the Leading Indicators Lead? J. Bus. 1996, 69, 27–49. https://www.jstor.org/stable/2353248.
  33. Banerjee, T. , Marcellino, M. Are there any reliable leading indicators for US inflation and GDP growth? Int. J. Forecast. 2006, 22, 137–151. [Google Scholar] [CrossRef]
  34. Kulendran, N.; Wong, K.F. Determinants versus Composite Leading Indicators in Predicting Turning Points in Growth Cycle. J. Travel Res. 2011, 50, 417–430. [Google Scholar] [CrossRef]
  35. Tkacova, A.; Gavurova, B.; Behun, M. The Composite Leading Indicator for German Business Cycle. J. Competitiv. 2017, 9, 114–133. [Google Scholar] [CrossRef]
  36. OECD, Composite leading indicator (CLI). https://data.oecd.org/leadind/composite-leading-indicator-cli.htm , 2023 (Accessed 02 May 2023).
  37. Hanson, M.S. The “price puzzle” reconsidered. J. Monet. Econ. 2004, 51, 1385–1413. [Google Scholar] [CrossRef]
  38. Beckmann, J.; Belke, A.; Czudaj, R. Does global liquidity drive commodity prices? J. Bank. Financ. 2014, 48, 224–234. [Google Scholar] [CrossRef]
  39. Belke, A., Bordon, I.; Hendricks, T.W. Monetary policy, global liquidity and commodity price dynamics. North Am. J. Econ. Finance. 2014, 28, 1–16. [CrossRef]
  40. Yardeni, E. Predicting the Markets; YRI Press: Brookville, NY, USA, 2018. [Google Scholar]
  41. Ge, Y.; Tang, K. Commodity prices and GDP growth. Int. Rev. Financial Anal. 2020, 71, 101512. [Google Scholar] [CrossRef]
  42. Mian, A.R.; Sufi, A. Finance and business cycles: The credit-driven household demand channel. J. Econ. Perspect. 2018, 32, 31–58. [Google Scholar] [CrossRef]
  43. insky, H.P. Can it happen again?; M.E. Sharpe, New York, 1984.
  44. Minsky, H.P. The financial instability process: a restatement, in: Arestis P, Shouras T (eds) Post Keynesian economic theory, Wheatsheaf Books, Sussex, 1985.
  45. Singh, T. Does International Trade Cause Economic Growth? A Survey. World Econ. 2010, 33, 1517–1564. [Google Scholar] [CrossRef]
  46. Esteves, P.S.; Rua, A. Is there a role for domestic demand pressure on export performance? Empir. Econ. 2015, 49, 1173–1189. [Google Scholar] [CrossRef]
  47. Bobeica, E.; Esteves, P.S.; Rua, A.; Staehr, K. Exports and domestic demand pressure: a dynamic panel data model for the euro area countries. Rev. World Econ. 2016, 152, 107–125. [Google Scholar] [CrossRef]
  48. Laborda, J.; Salas, V.; Suárez, C. Manufacturing firms’ export activity: Business and financial cycles overlaps! Int. Econ. 2020, 162, 1–14. [Google Scholar] [CrossRef]
  49. Frankel, J.A.; Rose, A.K. The endogeneity of the optimum currency area criteria. Econ. J. 1998, 108, 1009–1025. [Google Scholar] [CrossRef]
  50. Clark, T.E.; Van Wincoop, E. Borders and business cycle. J. Int. Econ. 2001, 55, 59–85. [Google Scholar] [CrossRef]
  51. De Soyres, F.; Gaillard, A. Global trade and GDP comovement. J. Econ. Dyn. Control. 2022, 138, 104353. [Google Scholar] [CrossRef]
  52. Imbs, J. Trade, finance, specialization and synchronization. Rev. Econ. Stat. 2004, 86, 723–34. [Google Scholar] [CrossRef]
  53. Box, G.; Jenkins, G.M. Time series analysis; forecasting and control; San Francisco: Holden-Day, 1970. [Google Scholar]
  54. Kirchgässner, G.; Wolters, J.; Hassler, U. Univariate stationary processes, in: Introduction to Modern Time Series Analysis; Springer, Berlin, Heidelberg, 2013, pp. 27–93. [CrossRef]
  55. Chatfield, C. The analysis of time series: An introduction; CRC Press, 2016.
  56. Sims, C.A. Macroeconomics and reality. Econometrica. 1980, 48, 1–48. [Google Scholar] [CrossRef]
  57. Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica. 1989, 57, 357–84. [Google Scholar] [CrossRef]
  58. Litterman, R.B. Forecasting with bayesian vector autoregressions-Five years of experience. J. Bus. Econ. Stat. 1986, 4, 25–38. [Google Scholar] [CrossRef]
  59. Spencer, D.E. Developing a bayesian vector autoregression forecasting model. Int. J. Forecast. 1993, 9, 407–421. [Google Scholar] [CrossRef]
  60. Bernanke, B.; Blinder, A. The Federal funds rate and the channels of monetary transmission. Am. Econ. Rev. 1992, 82, 901–921. https://www.jstor.org/stable/2117350.
  61. Sims, C.A. Interpreting the macroeconomic time series facts: The effects of monetary policy. Eur. Econ. Rev. 1992, 36, 975–1000. [Google Scholar] [CrossRef]
  62. D'Agostino, A.; Gambetti, L.; Giannone, D. Macroeconomic forecasting and structural change. J. Appl. Econ. 2013, 28, 82–101. [Google Scholar] [CrossRef]
  63. Korobilis, D. VAR forecasting using bayesian variable selection. J. Appl. Econ. 2013, 28, 204–230. [Google Scholar] [CrossRef]
  64. Koop, G.; Korobilis, D. Large time-varying parameter VARs. J. Econom. 2013, 177, 185–198. [Google Scholar] [CrossRef]
  65. Terasvirta, T.; Anderson, H.M. Characterizing nonlinearities in business cycles using smooth transition autoregressive models. J. Appl. Econ. 1992, 7 (S1), S119–S136. [Google Scholar] [CrossRef]
  66. Granger, C.W.; Teräsvirta, T.; Anderson, H.M. Modeling nonlinearity over the business cycle, in: Business Cycles, Indicators and Forecasting; University of Chicago Press, 1993, pp. 311–326. [CrossRef]
  67. Granger, C.W.; Terasvirta, T. Modelling non-linear economic relationships; OUP Catalogue, 1993.
  68. Escribano, A.; Jorda, O. Improved Testing and Specification of Smooth Transition Regression Models; in: Nonlinear Time Series Analysis of Economic and Financial Data, Springer, Boston, MA, 1999, pp. 289–319.
  69. Tsay, R.S. Testing and modelling threshold autoregressive processes. J. Am. Stat. Assoc. 1989, 84, 231–240. [Google Scholar] [CrossRef]
  70. Tiao, G.C.; Tsay, R.S. Some advances in non-linear and adaptive modelling in time series. J. Forecast. 1994, 13, 109–131. [Google Scholar] [CrossRef]
  71. Chen, R.; Langnau, A. Turning points detection of business cycles: A model comparison; Available at SSRN 1680828, 2010. [CrossRef]
  72. Hamilton, J.D. Specification testing in Markov-switching time-series models. J. Econom. 1996, 70, 127–157. [Google Scholar] [CrossRef]
  73. Filardo, A.J. Business-cycle phases and their transitional dynamics. J. Bus. Econ. Stat. 1994, 12, 299–308. [Google Scholar] [CrossRef]
  74. McCulloch, R.E.; Tsay, R.S. Statistical analysis of economic time series via Markov switching models. J. Time Ser. Anal. 1994, 15, 523–539. [Google Scholar] [CrossRef]
  75. Filardo, A.J.; Gordon, S.F. Business cycle durations. J. Econom. 1998, 85, 99–123. [Google Scholar] [CrossRef]
  76. Kim, C.J.; Nelson, C.R. State space models with regime switching: Classical and Gibbs-sampling approaches with applications; MIT Press. Cambridge, Massachusetts, 1999.
  77. Camacho, M.; Perez-Quiros, G.; Poncela, P. Extracting nonlinear signals from several economic indicators; Bank of Spain Working Paper 1202, 2012.
  78. Camacho, M.; Perez-Quiros, G.; Poncela, P. Markov-switching dynamic factor models in real time; Bank of Spain Working Paper 1205, 2012.
  79. Krolzig, H.M. Markov-switching vector autoregressions: Modelling, statistical inference, and application to business cycle analysis (Vol. 454); Springer Science & Business Media, 2013.
  80. Balcilar, M.; Gupta, R.; Majumdar, A.; Miller, S.M. Was the recent downturn in US real GDP predictable? Appl. Econ. 2015, 47, 2985–3007. [Google Scholar] [CrossRef]
  81. Mullainathan, S.; Spiess, J. Machine learning: An applied econometric approach. J. Econ. Perspect. 2017, 31, 87–106. [Google Scholar] [CrossRef]
  82. Varian, H.R. Big data: New tricks for econometrics. J. Econ. Perspect. 2014, 28, 3–28. [Google Scholar] [CrossRef]
  83. Yu, H.F.; Rao, N.; Dhillon, I.S. Temporal regularized matrix factorization for high-dimensional time series prediction, in: Advances in Neural Information Processing Systems NeurIPS Proceedings, 2016.
  84. Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
  85. Plakandaras, V.; Gupta, R.; Gogas, P.; Papadimitriou, T. Forecasting the US real house price index, Econ. Model. 2015, 45, 259–267. [Google Scholar] [CrossRef]
  86. Heber, G.; Lunde, A.; Shephard, N.; Sheppard, K. Oxford-Man Institute’s Realized Library, Version 0.1, 2009.
  87. Medeiros, M.C.; Vasconcelos, G.F.R.; Veiga, Á.; Zilberman, E. Forecasting inflation in a data-rich environment: The benefits of machine learning methods. J. Bus. Econ. Stat. 2019, 39 (1) (2019) 98-119. [CrossRef]
  88. Inoue, A. , Kilian, L. How useful is bagging in forecasting economic time series? A Case study of US consumer price inflation. J. Am. Stat. Assoc. 2008, 103, 511–522. [Google Scholar] [CrossRef]
  89. Rahmani, A.M. ; Yousefpoor, E,; Yousefpoor, M.S., Mehmood, Z., Haider, A., Hosseinzadeh, M., Eds.; Ali Naqvi, R. Machine Learning (ML) in medicine: Review, applications, and challenges. Mathematics. 2021, 9, 2970. [Google Scholar] [CrossRef]
  90. Jönsson, K. Machine Learning and Nowcasts of Swedish GDP. J. Bus. Cycle Res. 2020, 16, 123–134. [Google Scholar] [CrossRef]
  91. Cicceri, G.; Inserra, G.; Limosani, M. A machine learning approach to forecast economic recessions—an Italian case study. Mathematics. 2020, 8, 241. [Google Scholar] [CrossRef]
  92. Maccarrone, G.; Morelli, G.; Spadaccini, S. GDP forecasting: Machine learning, linear or autoregression? Front. Artif. Intell. 2021, 4. [Google Scholar] [CrossRef]
  93. Biau, O.; D ́Elia, A. Euro area GDP forecast using large survey dataset-A random forest approach; Euroindicators Working Paper 2011/002, 2011.
  94. Tiffin, M.A. Seeing in the dark: A machine-learning approach to nowcasting in Lebanon; International Monetary Fund, 2016.
  95. Behrens, C.; Pierdzioch, C.; Risse, M. A test of the joint efficiency of macroeconomic forecasts using multivariate random forests. J. Forecast. 2018, 37, 560–572. [Google Scholar] [CrossRef]
  96. Prüser, J. Forecasting with many predictors using bayesian additive regression trees. J. Forecast. 2019, 38, 621–631. [Google Scholar] [CrossRef]
  97. Foltas, A.; Pierdzioch, C. On the efficiency of German growth forecasts: An empirical analysis using quantile random forests and density forecasts. Appl. Econ. Lett. 2021, 1–10. [Google Scholar] [CrossRef]
  98. Yoon, J. Forecasting of real GDP growth using machine learning models: Gradient boosting and random forest approach. Comput. Econ. 2021, 57, 247–265. [Google Scholar] [CrossRef]
  99. Chai, S.H.; Lim, J.S. Forecasting business cycle with chaotic time series based on neural network with weighted fuzzy membership functions. Chaos Solitons Fractals. 2016, 90 118-126. [CrossRef]
  100. Jung, J.K.; Patnam, M.; Ter-Martirosyan, A. An algorithmic crystal ball: Forecasts-based on machine learning; International Monetary Fund, 2018.
  101. Alaminos, D.; Salas, M.B.; Fernández-Gámez, M.A. Quantum computing and deep learning methods for GDP growth forecasting. Comput. Econ. 2022, 59, 803–829. [Google Scholar] [CrossRef]
  102. Emsia, E.; Coskuner, C. Economic growth prediction using optimized support vector machines. Comput. Econ. 2016, 48, 453–462. [Google Scholar] [CrossRef]
  103. Kouziokas, G.N. A new W-SVM kernel combining PSO-neural network transformed vector and bayesian optimized SVM in GDP forecasting. Eng. Appl. Artif. Intell. 2020, 92, 103650. [Google Scholar] [CrossRef]
  104. Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need, in: Advances in Neural Information Processing Systems NeurIPS Proceedings, 2017.
  105. Koo, R. Balance Sheet Recession: Japan’s Struggle with Uncharted Economics and its Global Implications; Singapore, John Wiley & Sons, 2003.
  106. Koo, K. The Holy Grail of Macroeconomics: Lessons from Japan’s Great Recession; Singapore, John Wiley & Sons, 2009.
  107. Laborda, J.; Salas, V.; Suárez, C. Financial constraints on R&D projects and Minsky moments: Containing the credit cycle. J. Evol. Econ. 2021, 31, 1089–1111. [Google Scholar] [CrossRef]
  108. Mian, A.; Straub, L.; Sufi, A. Indebted demand. Q. J. Econ. 2021, 136, 2243–2307. [Google Scholar] [CrossRef]
  109. Andrea, T.; Beata, G.; Marcel, B. The composite leading indicator for German business cycle. J. Competitiv. 2017, 9, 114. [Google Scholar] [CrossRef]
  110. Armelius, H.; Belfrage, C.J.; Stenbacka, H. The mystery of the missing world trade growth after the global financial crisis, in: Sveriges Riksbank Economic Review, 3, 2014, pp. 7–22.
  111. Gordon, R.J. Is US economic growth over? Faltering innovation confronts the six headwinds; National Bureau of Economic Research, w18315, 2012. [CrossRef]
  112. Summers, L.H. US economic prospects: Secular stagnation, hysteresis, and the zero lower bound. Bus. Econ. 2014, 49, 65–73. [Google Scholar] [CrossRef]
  113. Summers, L.H. Demand side secular stagnation. Am. Econ. Rev. 2015, 105, 60–65. [Google Scholar] [CrossRef]
Preprints 72841 g001
Figure 1. The TFT advantages. Source: [14].
Figure 1. The TFT advantages. Source: [14].
Preprints 72841 g001
Preprints 72841 g002
Figure 2. TFT architecture. Source: [14].
Figure 2. TFT architecture. Source: [14].
Preprints 72841 g002
Preprints 72841 g003
Figure 3. GRN Scheme. Source: [14].
Figure 3. GRN Scheme. Source: [14].
Preprints 72841 g003
Preprints 72841 g004
Figure 4. Quarterly prediction methodology.
Figure 4. Quarterly prediction methodology.
Preprints 72841 g004
Preprints 72841 g005
Figure 5. Annual prediction methodology.
Figure 5. Annual prediction methodology.
Preprints 72841 g005
Preprints 72841 g006
Figure 6. Encoder variables importance for one quarter (left hand side) and annual predictions (right hand side).
Figure 6. Encoder variables importance for one quarter (left hand side) and annual predictions (right hand side).
Preprints 72841 g006
Preprints 72841 g007
Figure 7. 2011 quantile forecast for Spain (left hand side) and USA (right hand side).
Figure 7. 2011 quantile forecast for Spain (left hand side) and USA (right hand side).
Preprints 72841 g007
Preprints 72841 g008
Figure 8. Encoder variables importance for year 2011 forecast.
Figure 8. Encoder variables importance for year 2011 forecast.
Preprints 72841 g008
Preprints 72841 g009
Figure 9. 2017 quantile forecast for Spain (left hand side) and USA (right hand side).
Figure 9. 2017 quantile forecast for Spain (left hand side) and USA (right hand side).
Preprints 72841 g009
Preprints 72841 g010
Figure 10. Encoder variables importance for 2017 forecast.
Figure 10. Encoder variables importance for 2017 forecast.
Preprints 72841 g010
Table 1. Main hyperparameters.
Table 1. Main hyperparameters.
Main hyperparameters Forecast Horizon
1Q 2Q 3Q 4Q
Epochs 13 17 19 20
Learning rate 0.03
Dropout 0.1
Number of heads 1
State size 16
Batch size 64
Quantiles 0.02, 0.1, 0.25, 0.5, 0.75, 0.9, 0.98
Normalized GroupNormalizer
Table 2. Selected countries.
Table 2. Selected countries.
Australia Italy United Kingdom
Austria Japan United States
Belgium Korea South Africa
Canada Mexico
Denmark Netherlands
Finland New Zealand
France Norway
Germany Portugal
Greece Spain
Iceland Sweden
Ireland Switzerland
Table 3. Variables description.
Table 3. Variables description.
Variable Definition Reason of use Source
Dependent variable
GDP logarithmic growth rateit GDP in volume index, hundredths, 2015=100, of every country i in year t. Dependent variable for the country’ s economic growth OECD
Independent variables
Idiosyncratic variables
Yield Curve (YCit) It is the ratio of long-term interest rates on sovereign debt to short-term interest rates. The slope of the yield curve has been shown empirically to be a significant predictor of inflation and real economic activity. Quite a few academic studies have suggested that the slope of the yield curve seems to be extremely promising as a predictor of recessions. See [4,5,6,7,8,9]. We hypothesize that its impact on economic growth will depend on how it interacts non-linearly with the global credit spread cycle and official interest rates. OECD
Debt Non-Financial Private Sectors/GDP (Private Debt/GDP)it Ratio of the total debt of non-financial private sectors at market value of one country over its nominal GDP. It is developed, calculated and updated by the Bank for International Settlements (BIS). This index is regularly updated. It captures the progression of risk appetite and the debt accumulation process. During an economic expansion investors’ risk appetite tends to increase; the longer the expansion, without any major setback, the higher the risk appetite, indebtedness and economic growth. Exactly the opposite during periods of deleveraging and private balance sheet recessions ([15,16,43,44,48,105,106,107]). [108] found an increase in the household debt to GDP ratio predicts lower GDP growth and higher unemployment in the medium run for an unbalanced panel of 30 countries from 1960 to 2012. [17] found for almost all of 43 OECD countries analyzed that the private debt-to-GDP ratio is highly persistent. These results suggest long- lived effects of shocks to the private debt-to-GDP ratio, which require appropriate policy actions. BIS
OECD Composite Leading Indicator (CLIit) The OECD Composite Leading Indicator (CLI) is an aggregate time series displaying a reasonably consistent leading relationship with the reference series for the business cycle of a country (GDP). A CLI reading above (below) 100 is always an indication that anticipates levels of GDP above(below) long-term trend. The composite leading indicator (CLI) is designed to provide early signals of turning points in business cycles showing fluctuation of the economic activity around its long term potential level. Different research found that the composite leading indicators (CLI) are useful for forecasting gross demand product (GDP), both in sample and in an out- of-sample real-time exercise ([4,32,33,34,109]). OECD
Common variables
Global Credit Spread Cycle (GCSCt) The ratio of the Moody’s U.S. BAA corporate bond yields to that of AAA is taken as a proxy for the global credit spread cycle. Various researches indicate the usefulness of credit curve information to predict economic activity ([25-29, 31). Most unconventional monetary policies, such as asset purchase programs and forward guidance, aim to lower long-term rates, significantly affecting the information content of the yield curve. However, even in such circumstances, the behaviour of the corporate bond credit spread curve varies over the business cycle, potentially containing more information about the future economy. More recently research ([30]) find credit spread curve information in higher deciles (implying low credit quality) is statistically significant and economically important for predicting the business cycle. FRED, Federal Reserve Bank of St. Louis
CRB RIND Index (CRBRINDt) CRB Raw Industrials Spot Index It is a measure of price movements of 13 sensitive basic commodities whose markets are presumed to be among the first to be influenced by changes in economic conditions. As such, it serves as one early indication of impending changes in business activity. Bloomberg
World Trade Volume Index (WTVIt) The monthly world trade volume index is computed by the CPB (Netherlands Bureau for Economic Policy Analysis) and is defined as arithmetic average of world exports and world imports of goods. The series covers United States, Japan and EU and four groups of emerging countries: OPEC, Asian newly industrialised countries (Taiwan, Hong Kong, Singapore and South Korea), transition countries (central and eastern European countries including Turkey and ex-Soviet Union’s countries) and other emerging economies It is an indicator of global economic activity. Although after the financial crisis in 2008, the growth rate in world trade has been unusually low relative to growth in world GDP ([110]), a higher external demand increases the probability and/or intensity of exporting and, therefore, of economic growth, especially in periods where domestic demand is under pressure ([46,47,48]). CPB
Table 4. Improvement of the MAE and RMSE of TFT relative to ARIMA.
Table 4. Improvement of the MAE and RMSE of TFT relative to ARIMA.
Metric t+1 t+2 t+3 t+4
MAE 8.38% 33.89%*** 47.98%*** 48.53% ***
RMSEa 12.44% 88.80%*** 151.85%*** 157.07%***
aRMSE is the average of the RMSEs calculated at country level. Note: *** significant coefficient at 1%.
Table 5. Improvement of the MAE and RMSE of TFT relative to ARIMA by country.
Table 5. Improvement of the MAE and RMSE of TFT relative to ARIMA by country.
CAN GER DNK SPA FRA GBR ITA JPN POR USA
MAE t+1 3.0% -8.0% 11.0% 23.3% 20.8% 25.0% -5.8% 5.0% 1.1% -2.1%
t+4 17.0% 4.2% 12.0% 113.8% 78.3% 103.5% 41.6% 1.8% 49.1% 36.8%
RMSE t+1 9.1% -19.1% 16.9% 21.1% 20.6% 45.4% -0.7% -1.1% 1.4% 2.4%
t+4 63.3% 12.3% 7.6% 327.2% 205.2% 416.5% 92.0% 2.7% 127.1% 128.2%
Table 6. Improvement of the MAE and RMSEa of TFT relative to ARIMA by period.
Table 6. Improvement of the MAE and RMSEa of TFT relative to ARIMA by period.
Period Metric t+1 t+2 t+3 t+4
2008-2011 MAE 13.82% 10.04% -3.54% -5.85%
RMSEa 10.96% 5.31% -3.52% -4.14%
2012-2015 MAE 0.18% -2.42% 8.01% 26.59%
RMSEa -2.76% -0.99% 4.35% 21.72%
2016-2019 MAE -4.85% 6.56% -10.54% 0.67%
RMSEa -6.20% 4.83% -6.85% 0.01%
2020-2021 (Q3) MAE 9.43% 56.12% 116.82% 115.92%
RMSEa 12.47% 94.64% 190.81% 204.09%
aRMSE is the average of the RMSEs calculated at country level.
Table 7. Improvement of the MAE and RMSE of TFT relative to ARIMA by period and country in annual forecast.
Table 7. Improvement of the MAE and RMSE of TFT relative to ARIMA by period and country in annual forecast.
Period Metric CAN DEU DNK ESP FRA GBR ITA JPN POR USA
2008-2011 MAE -13.4% -14.2% 10.0% 9.0% -20.8% -31.0% -1.7% -2.1% 19.9% -7.4%
RMSEa -0.7% -13.0% 5.3% -0.2% -10.2% -18.5% 1.0% -2.2% 5.3% -5.9%
2012-2015 MAE 15.8% -10.2% 27.4% 49.4% 34.3% -27.8% 100.2% 3.2% 81.0% -17.7%
RMSEa 6.4% -5.8% 21.6% 32.9% 29.5% -26.6% 70.2% -2.3% 74.1% 7.4%
2016-2019 MAE -15.8% 80.5% 6.5% -11.7% 40.0% -24.0% -21.3% -17.2% -29.0% 40.2%
RMSEa -11.0% 77.6% -2.4% -21.0% 38.3% -23.3% -18.7% -22.5% -23.0% 41.8%
2020-2021 (Q3) MAE 61.6% 19.1% 11.6% 201.3% 140.6% 237.5% 68.6% 18.4% 79.1% 111.8%
RMSEa 94.9% 41.6% 12.3% 363.3% 219.7% 476.6% 105.7% 16.2% 149.7% 190.8%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Multi-Country and Multi-Horizon GDP Forecasting Using Temporal Fusion Transformers

Juan Laborda

et al.

,

2023

Deep Assessment Methodology Using Fractional Calculus on Mathematical Modeling and Prediction of Gross Domestic Product per Capita of Countries

Ertuğrul Karaçuha

et al.

,

2020

The Computation of the Output Gap in Polish Economy in the Light of the Secular Stagnation Scenario (Sustainability Antithesis)

Elżbieta Szaruga

,

2020

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated