Prerpints.org logo
Preprint
Article

Hybrid Off-Grid Energy Systems Optimal Sizing with Integrated Hydrogen Storage Based on Deterministic Balance Approach

Altmetrics

Downloads

379

Views

189

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 May 2023

Posted:

08 May 2023

You are already at the latest version

Alerts
Abstract
Integrating numerous renewable resources has been extensively researched and studied to create a dependable energy system. This study investigated the best techno-economical hybrid energy system configuration while using hydrogen energy to keep the system's energy balanced. Additionally, this study aims to determine the best hybrid system configuration for the location under investigation. A novel technique of DBM (Deterministic Balanced Method) was introduced to determine the total annual energy output for the project's lifetime. This approach is used to contrast the outcomes of other HOMER software tools. Then, using HOMER, it is possible to confirm the sizing optimization results for the suggested method by comparing the power ratings and yearly energy output. A detailed comparison between our proposed method and HOMER Pro has been conducted for validation and verification. Our method has been rigorously tested in various hybrid off-grid energy systems, ensuring its applicability and reliability across different scenarios and configurations. The results of our study indicate a high degree of similarity between the proposed approach and HOMER pro for computing annual energy power for the studied energy systems. Specifically, our analysis revealed that the difference between the approaches was within a range of 5%, indicating a high level of consistency and reliability in our method. These findings suggest that our approach can be confidently applied to determine the appropriate size of hybrid energy systems accurately. Overall, our study provides valuable insights into the development of effective sizing methodologies for hybrid energy systems. After considering the amount of solar radiation and wind speed gathered by global weather data platforms like NASA and METEONORM, this paper has also included a real case study of the Cairo International Airport's hybrid renewable energy production systems. To guarantee the viability of this study, the system design was founded on an actual load that was researched and simulated. A cluster of distributed networks was finally proposed to use the excess energy and enable energy conversion processes to be used in industry and transportation applications.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Hybrid off-grid systems are always challenging to design and optimize their operation for the project lifetime. The use of hydrogen as an energy storage carrier has made the sizing problem of energy systems become more complicated and need global optimal solutions for best techno-economical solution, Additionally, adverse nature of the wind-PV system can compensate the intermittency nature of each of system and therefore improve the overall reliability of the hybrid system. Hybrid energy systems are increasingly being used to provide sustainable and reliable power in off-grid and remote areas. These systems typically consist of a combination of renewable energy sources, such as solar and wind, and energy storage systems, such as batteries or hydrogen storage. While batteries have been widely used in hybrid energy systems, there is a growing interest in using hydrogen storage as a potential alternative due to its high energy density and the ability to produce hydrogen using renewable energy sources. A research conducted in (Gelma et al.,2011) described the design information of solar PV and wind turbine hybrid power generation systems to provide electricity to a model community of 100 households and health clinic and elementary school. The optimal simulation results in this study showed that PV/wind turbine/diesel generator/battery and converter is the best-configured system for their application with a renewable fraction of 84%. There are many research papers that had introduced different system configurations and comparative analysis for deciding the most economical feasible one. One of those researches was (Ghenai et al., 2015) which presented a case study in the desert region of United Arab of Emirates. It introduces a technical-economic analysis based on integrated modeling, simulation, and optimization approach to design an off-grid hybrid solar PV/Fuel Cell power system. This system is designed to meet the energy demand of 4500 kWh/day of the residential community (150 houses). The total power production from the distributed hybrid energy system was 52% from the solar PV, and 48% from the fuel cell with a 40.2 % renewable fraction which is a low value for renewable energy penetration of this system. Consequently, one of the main concerns of the paper research is how to achieve a renewable fraction of 100% in the simulated configurations of various hybrid off-grid systems. These given numbers of renewable fraction used to give a rough estimate for the previous research works that focused on the renewable resources’ penetration (increasing the renewable fraction percentage) and select the best configuration for the application targets.
Another approach for choosing the best size and location for off-grid hybrid systems was presented by (Cai et al., 2020). To discover the ideal capacity and location for continually meeting the load while reducing levelized cost of energy and overall life cycle cost, they considered economic, technical, social, and environmental factors. The hybrid algorithm based on geographic information system, simulated annealing, and enhanced harmony search is evaluated with real data for a genuine case study in South Khorasan, Iran, and the findings show that it provides more accurate results than those from previous heuristic approaches. As comparison to a standalone diesel system, the hybrid system saves 8948 L of diesel generator fuel and reduces pollutant emissions by 59.6% according to the IHS SA-GIS methodology (Cai et al., 2020). (Alberizzi et al., 2020) present a methodology based on Mixed Integer Linear Programming (MILP) and an algorithm implemented through Matlab software to determine the ideal size of a hybrid solar-wind system with battery storage to replace a diesel-fueled internal combustion engine (ICE) for a mountain lodge in South Tyrol, Italy.
(Mahmoudi et al., 2023) evaluates different combinations of photovoltaic panels and wind turbines with a backup system using a reliability-based analysis. The goal is to compare the sizing of three hybrid energy systems, namely PV/DG, Wind/DG, and PV/Wind/DG, under three scenarios: reducing carbon dioxide emissions, reducing total annual costs, and reducing both simultaneously. The proposed method uses the gravitational search algorithm and compares results with the simulated annealing method. The study examines 45 cases and includes economic and environmental analysis, as well as an examination of the damage caused by carbon dioxide emissions to human health. The results indicate that the optimal system is PV/Wind/DG, which reduces pollution by 27.2% and saves up to 4.76% of costs compared to a PV/DG system. By imposing carbon taxes on hybrid system designs, it is possible to prevent about 9% of CO2 emissions and reduce damage to human health by 8.9%.
(Özçelep et al., 2023) analyzed the electrical energy required for the heating system with a heat pump from a solar photovoltaic-hydrogen system and found that the 24 m² solar panel area and 0.08 m3 of hydrogen stored in 16 hydrogen cylinders is adequate for meeting energy demand. Using a solar-hydrogen-heat pump system reduces carbon emissions by 86.5 tons per 1000 m2 floor area greenhouse.
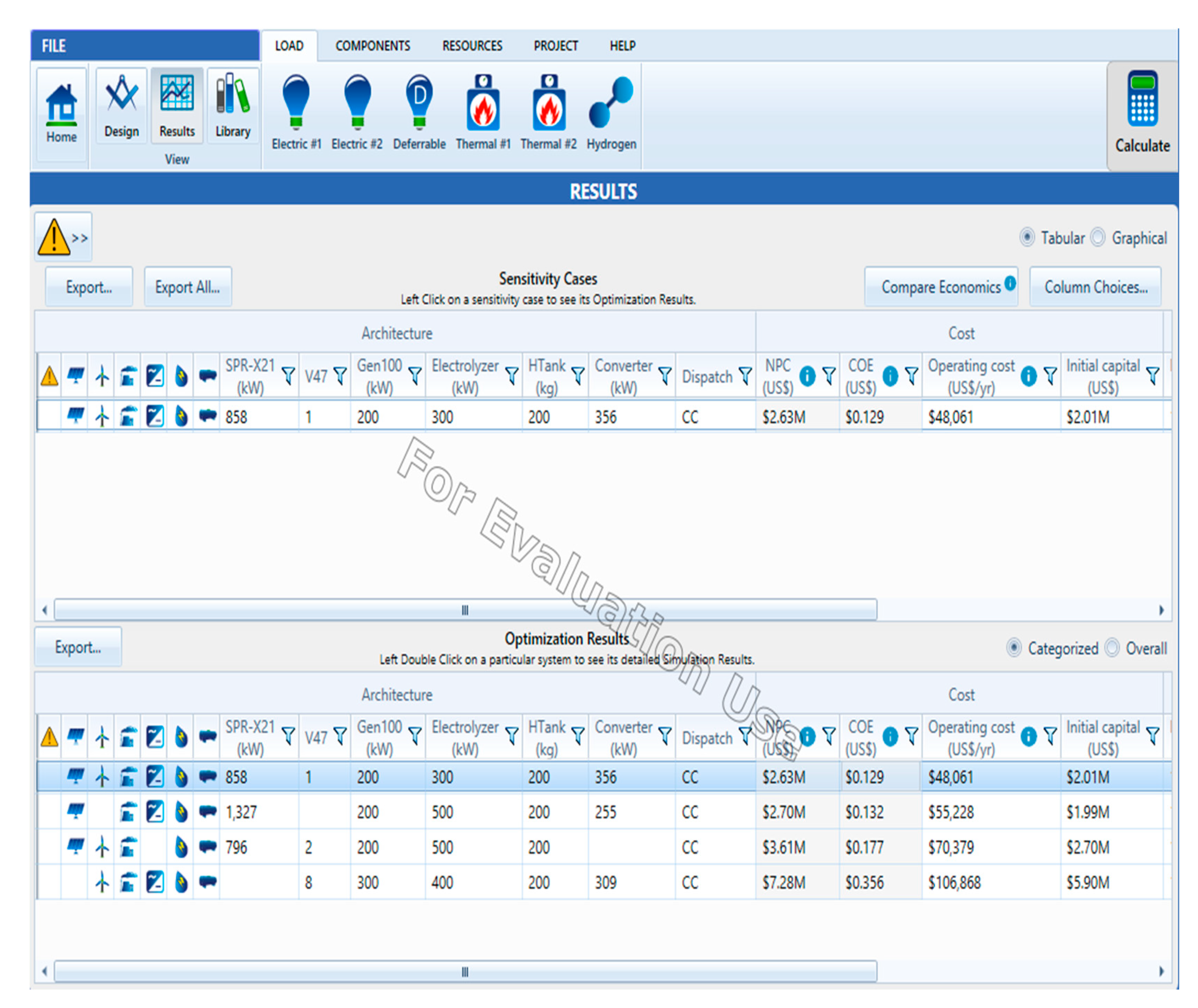
(Azad and Shateri, 2023) developed an approach to optimize power planning for an entirely renewable hybrid system that includes wind turbines, PV systems, bio-waste units, thermal energy storage, electric vehicle parking lots, and smart charging strategies. They have used a modified multi-objective function to minimize TANPC and LCOE and a modified cost model to increase modeling accuracy. Their results show that including bio-waste units can increase system efficiency and reduce greenhouse gas emissions, while implementing adaptive smart charging for electric vehicles can decrease LCOE and TANPC by load leveling and reducing the required storage capacity. They also considered uncertainties in renewable resources, loads, and electric vehicles' parameters to improve modeling accuracy. However, considering uncertainty leads to more resources and storage devices, which increases the system cost. They have used a modified combination of GWO and SCA to optimize the system, and their results show that their algorithm obtains the optimal solution with higher convergence speed and lower standard deviation compared to SEAs. Furthermore, this paper reviews the recent advancements in these methodologies, focusing on research published in the last few years in Table 1 and we classified their solution complexity by color bar and its popularity by sector area in Figure 1. Also, we used an evaluation metric named “common usage” that shows the most abundant combination of hybrid energy systems and their rank as shown in Figure 2.
Sizing hybrid energy systems with hydrogen storage presents a unique set of challenges. Unlike batteries, hydrogen storage systems are more complex and require careful consideration of factors such as the size and type of the storage tank, the electrolyzer and fuel cell efficiency, and the overall system balance. Moreover, the intermittent nature of renewable energy sources such as wind and solar can further complicate the sizing of hybrid systems with hydrogen storage. A critical aspect of designing these systems is determining the optimal sizing of each component, which has prompted the development of various sizing methodologies. Starting from iterative methods are characterized by their trial-and-error approach to determining the optimal sizing of hybrid off-grid systems. Although intuitive and straightforward, these methods can be computationally intensive and may not guarantee the global optimum.
Optimization-based methods, including linear programming (LP), mixed-integer linear programming (MILP), and multi-objective optimization, employ mathematical algorithms to optimize the sizing of hybrid off-grid systems by minimizing cost, maximizing efficiency, or addressing multiple objectives simultaneously (Ben Seddik et al., 2022). These methods are effective in finding the global optimum but often require extensive computation and may be limited by the complexity of the mathematical models (Adedoja et al., 2023).
Simulation-based methods, such as Monte Carlo simulations, artificial neural networks (ANN), and machine learning algorithms, use statistical models to simulate the performance of hybrid off-grid systems under varying conditions and determine the optimal sizing accordingly (Al-Othman et al., 2022). These methods are advantageous in accounting for uncertainties and variability in input data, such as weather and load profiles, but may require significant computational resources and training data.
Based on the limitations discussed above, several research gaps can be identified:
  • Development of more efficient algorithms: There is a need to develop more efficient algorithms that can reduce the computational burden of iterative and optimization-based methods while still ensuring the global optimum solution.
  • Adaptive sizing methodologies: As hybrid off-grid energy systems evolve over time due to factors such as changing load demands and component degradation, there is a need for adaptive sizing methodologies that can account for these changes and optimize system performance throughout its lifecycle.
  • Scalability and applicability: As the demand for hybrid off-grid energy systems grows, there is a need to develop sizing methodologies that can be applied to various scales, from small residential systems to large-scale microgrids. Research should focus on developing scalable algorithms and techniques that can handle the increasing complexity and size of these systems.
  • Incorporation of new technologies and energy sources: The rapid development of renewable energy technologies and energy storage solutions, such as advanced battery systems and hydrogen storage, necessitates the integration of these new technologies into existing sizing methodologies. Future research should explore how these emerging technologies can be effectively incorporated into the sizing process to enhance the performance of hybrid off-grid energy systems.
  • Standardization and benchmarking: There are a lack of standardization and benchmarking in the field of sizing methodologies for hybrid off-grid energy systems. Developing standardized benchmarks and performance metrics can facilitate the comparison and evaluation of different sizing approaches, driving further improvements and innovation in the field.
By addressing these research gaps, the field of sizing methodologies for hybrid off-grid energy systems can continue to advance, leading to more efficient, reliable, and cost-effective systems. The development of novel algorithms, improved modeling techniques, and the incorporation of deterministic approaches will not only enhance the performance of these methodologies but also contribute to the broader adoption of sustainable energy solutions in remote and off-grid areas
Deterministic methods for sizing hybrid off-grid energy systems rely on fixed input parameters and deterministic mathematical models to determine the optimal sizing of system components. These methods have several advantages:
  • Simplicity: Deterministic methods often involve simpler mathematical models and algorithms compared to stochastic or simulation-based approaches, making them easier to implement, understand, and interpret.
  • Computational efficiency: Due to their simplicity, deterministic methods generally require less computational resources and time compared to other approaches, such as stochastic or simulation-based methods.
  • Reproducibility: Deterministic methods, by their nature, provide consistent results for the same input data, ensuring reproducibility and comparability across different applications and scenarios.
  • Ease of integration: Deterministic methods can be more easily integrated into other optimization or decision-making frameworks, such as linear programming, mixed-integer linear programming, and multi-objective optimization algorithms.
  • Lower uncertainty: By relying on fixed input parameters, deterministic methods eliminate the uncertainty associated with variable input data, such as weather conditions and load profiles, leading to more predictable and consistent results.
From this literature analysis, we come up with a conclusion that the proposed system in this work must follow certain techno-economical outlines that is mandatory to design an energy hub for electricity and fuel production. This system is considered to achieve a 100% renewable fraction with different system configurations as shown in figure below:
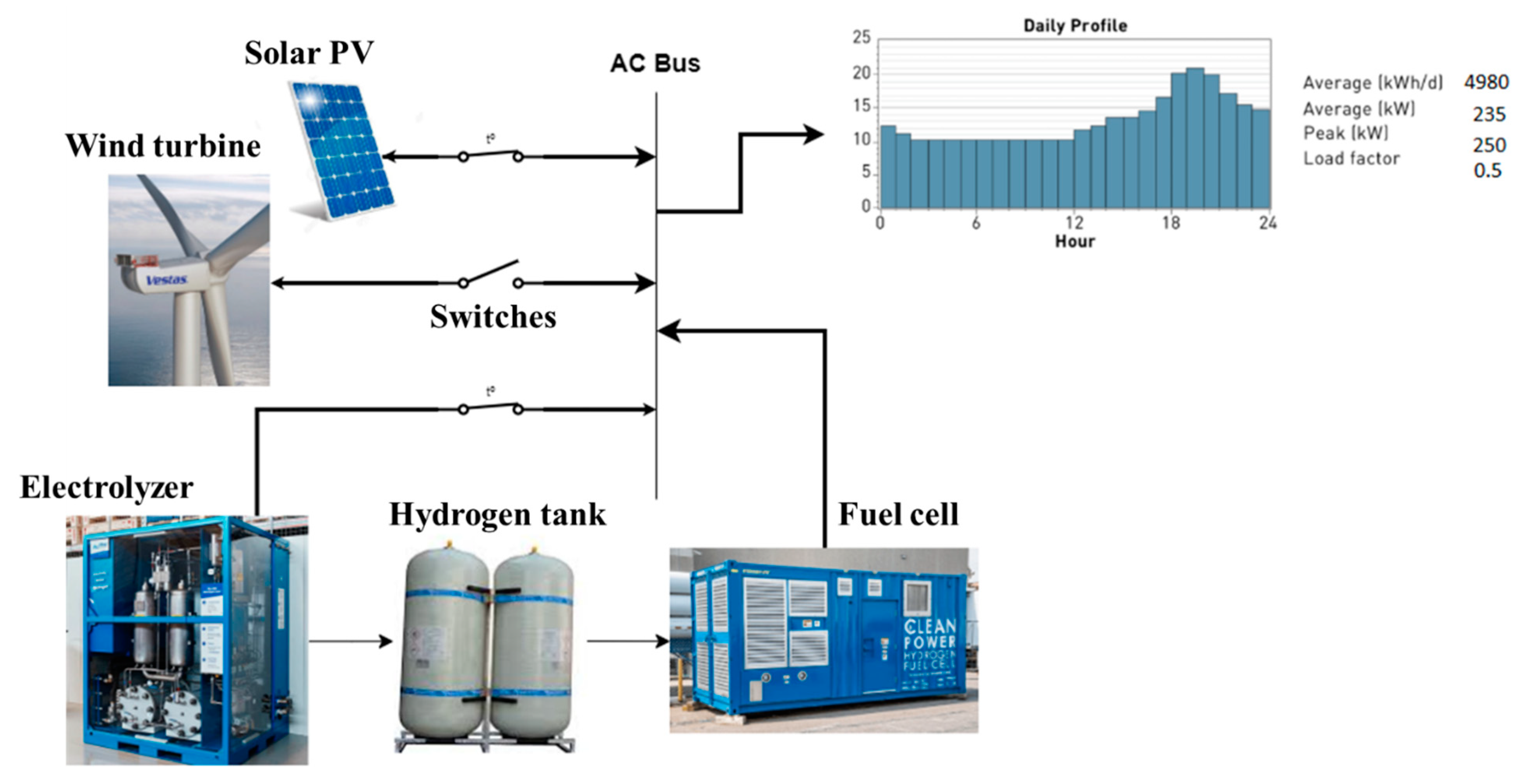
Preprints 72878 g003
Figure 3. Conceptual model for energy system based on hydrogen storage.
Figure 3. Conceptual model for energy system based on hydrogen storage.
Preprints 72878 g003
The primary objective of this endeavor is to develop a comprehensive model of an off-grid system composed of photovoltaic generators, wind turbines, fuel cells, electrolyzers, and hydrogen storage tanks. The meteorological data of Cairo International Airport as one of the data input files for the system model and the RTS load model as the current load profile for the design were both emphasized. Using the Deterministic Balance Method (DBM) for calculating the annual energy production for the system and then reflecting it on the load demand to ensure a balanced mode of generation, the system's sizing methodology is utilized to determine the system's design limitations. This method was then used to achieve the optimal dimensions of each system component. The hourly electricity and hydrogen balance must be satisfied by either converting excess electricity into hydrogen or storing hydrogen into electricity. The hourly simulation is performed for an entire year to size the system components so that there is no electricity curtailment. Another objective of the design of this energy system was to consider the optimal utilization of excess energy in relevant industrial and transportation domains. This strategy has paved the way for distrusted energy networks to be designed and regulated for sharing available energy based on demand analysis and forecasting.
The main contributions of this work can be summarized as follows:
  • A novel method named Deterministic Energy Balance Method (DBM) is proposed to find the optimal sizing of hybrid renewable energy sources (RESs) . This method is based on energy balance computation for system’s yearly profiles to avoid using any heuristic algorithms that are based on trial and error to find the global optima for system parameters and cost function.
  • Cost analysis model is computed for all studied systems for one-year simulation based on DBM method to come up with a techno-economical solution for fair comparison with commercial software.
  • 100% renewable energy system is introduced within different system setups and they are optimally sized using the DBM to achieve high reliability of energy supply. Additionally, seasonal variations’ impact on energy generation is utilized to manage the hydrogen production process for supplying the surplus energy in times of lack of generation.
  • Verification and validation of the proposed method are achieved by using HOMER to judge the Levelized cost of energy for different system configurations and justify the power ratings of installed components for different setups.

2. Modeling of the Hybrid Energy System

2.1. Solar Photovoltaic

The main objective functions were used to get the output power of the PV modules taking into consideration the efficiency of the modules and other derating factors. The first equation used in PV modeling is an output power function of Irradiance (Elshimy et al., 2015)
P p v = Y p v f p v G T t G T , S T C
Other factors that had been encountered during the literature view. Temperature and wind speed had significantly affected the model to get more accurate results that are feasible for execution. Consequently, another objective function for calculating the output power was then evolved providing a relation between the irradiance and temperature to deliver the actual output power shown in equation (Skoplaki et al., 2009)
p = η T r e f A G T 1 − 0.0045 T c − 298.15                          
After studying the behavior of temperature and irradiance throughout the meteorological model, the effect of this behavior was linked to the changes in each of the two parameters and the overall efficiency of the PV system (Skoplaki et al., 2009). This relation was supported by the following equation:
η = η T r e f [ 1 − B r e f T c , i − T r e f ]                                            

2.2. Wind Turbine Generators (WTGs)

  • The Wind Turbine Generator (WTG) hourly power output, at the studied location, depends on the hourly wind speed as shown in Figure 4. It can be expressed by following equations (Khiareddine et al.,2018):
P w i n d V V = P r A + B V V + C V V 2 ,       V D ≤ V V ≤ V N P r     ,         V N ≤ V V ≤ V R 0       E l s e w h e r e

2.3. Hydrogen System

Fuel cell can be defined as an electrochemical device that produces electrical power directly from a fuel like hydrogen, natural gas, diesel and propane. Its operation is similar to that of a conventional battery except in some parts that will be discussed in detail later in this paper and will affect the modeling of the hybrid off-grid system. Accordingly, their development has been much related to development of electrochemistry more than the power engineering and it is already studied as a distinct branch of physical chemistry (Larminie et al., 2003).
The second element in the hydrogen system is the electrolyzer, which is an electrochemical device that makes an electrolysis for the water molecules to produce hydrogen and oxygen. This process is powered by the excess electrically in the system. In other words, electrolyzer is used to convert the unused electrical energy into stored chemical energy inside hydrogen and then recall it back in the time of operation. The mathematical formula of the produced hydrogen from the electrolyzer can be expressed as follows (Fathy et al., 2016).
Energy required to produce one kilogram of hydrogen
=       η E l z X H 2 H e a t i n g   V a l u e H 2 d e n s i t y

2.4. Load Profile System

In this study, it is assumed that the DC and AC wiring losses are small enough to be neglected, due to the small geographic scatter of the study system. The Reliability Test System (RTS) load profile is used in this study ( IEE Standards et al., 1979) as shown in Figure 5 and the peak load is set to 250 kW. The load profile is then determined per hour for the 8760 hours of a year and illustrated in the appendix.

2.5. Economic Investigation for the Studied System

The economic study is what determines the feasibility of the hybrid renewable system. It reflects the whole image for the policy maker and decision makers to invest and work on these types of projects. The levelized cost of energy (LCOE), capital cost and cash flow study are what encourages the investor to direct the fund and grants to establish hybrid renewable system for remote areas. To start with, some definitions must be firstly explained to enable the researchers and engineers to apply optimizations techniques which satisfies the load demand with the minimum cost of energy. Levelized Cost of Energy is the annualized cost of producing electricity by the total electric load served for the entire life lime of the project. Net present cost is the present value of all the costs of installing and operating the system over the project lifetime. This analysis is performed using the cash flow table where it shows the operation & maintenance costs, salvage costs, replacement costs and fuel cost (if exists). Another factor which is added to the table to be multiplied by the costs discussed is the Discount factor. Discount factor is a direct reflection of the time value of money after a certain period. Additionally, there is a significant difference between the discount factor and the inflation rate. A factor named the real discount factor appears which compensates the effect of inflation analysis and represent the costs in year-zero dollars (HOMER et al., 2022)
Annualized cost is the cost that, if the investor pays every year would resemble the same net present cost at the end of the project when using the yearly cash flow sequence shown
Capital Recovery Factor (CRF) is a factor that converts the total net present cost into a total annualized cost. It depends on the inflation rate of the country and the lifetime of the project.
After defining the previous definitions, the cost objective function was elaborated where well-known optimization techniques could be applied in minimizing the function and obtaining the optimum configuration resulting in the least total annualized cost.
To optimally design the hybrid generation system, the optimization problem, defined by Equation (9) as in (HOMER et al., 2022), must be solved using any of the mentioned optimization techniques in the paper.
C c p t = [ N p v X C P V +
N T a n k X C T a n k + C F C / E L Z + N c o n v X C c o n v ]
Where CPV is unit cost of PV panel, Ntank is the number of storage tanks, CTankis unit cost of hydrogen storage tank and NConv/Invis the number of converter/inverter systems.
C M t n = ( i + 1 ) n − 1 i 1 + i n ( N P V X C P V , M t n + C F C , M t n + C E l z , M t n )
Where CPV.Mtn, CFC,Mtn and CElz,Mtn are the annual maintenance costs of PV, fuel cell and electrolyzer systems, respectively.
To minimize the total cost function,
C T = C c p t + C M t n
The economic model of the studied system was studied for the lifetime of the system using the following equations [33]
𝑂&𝑀 𝑐𝑜𝑠𝑡𝑠($/𝑦𝑒𝑎𝑟) =𝐴𝐸𝑃∗𝑂&𝑀 𝑐𝑜𝑠𝑡𝑠
𝐴𝑅=𝐴𝐸𝑃∗𝐸𝑆𝑃 𝐴𝑁𝐼=𝐴𝑅− 𝑂&𝑀 𝑐𝑜𝑠𝑡𝑠($/𝑦𝑒𝑎𝑟)
N P V = ∑ k = 1 n = 20 A N I ( 1 + R )           −     C I
P V M = ∑ k = 1 n = 20 N P V ( 1 + R )           −     C I
P V * = F V   1 ( 1 + R ) P
A C = − P V C * R ( 1 − ( 1 + R ) − P
𝑃𝑉𝐶 = 𝑃𝑉𝐷𝐶 + 𝑃𝑉𝑀 + 𝐶𝐼
L C O E = L A C A E P

3. Methodology: Deterministic Balance Method (DBM)

The deterministic Balance Method (DBM) application required determining PV output power, fuel cell size and efficiency, and hydrogen tank efficiency models. The accuracy of the PV model is crucial since it will be used to guide the overall layout of the system. To use the DBM, it is necessary to balance the energy needed to offset the time of zero PV output hour (usually at night) with the energy produced net by the PV (during sun hours after being absorbed through the load). Hydrogen tanks will store this surplus energy until needed; at this point, Fuel Cells will convert it to meet the day's energy needs. Power generated by PV and required by the load through Fuel Cells was determined using the area under graphs, as illustrated in Figure 6, which are computed using the Trapezium Rule. A discrete optimization was performed to find out how many PV modules would be ideal for striking this equilibrium.
In the first stage of the DBM design process, it was estimated that N solar PV modules would be sufficient to meet the required load and provide excess power at the end of the day. To begin computing energy Production values, this was founded on a random guess. This initial estimate was based on the energy balance equation discussed in the prior work [Selim et al., 2020] and was performed to estimate the surplus power supplied by PV to completely compensate the time of zero PV output power.
Using the data from NASA and METEONORM [34,35], the output PV power was calculated using equations (1,2) based on the irradiance profile of a specific day. Throughout the entirety of the model, the method of calculating energy production by obtaining the area under curves was the primary method employed. Numerous methods for calculating the area under curves, including the trapezium rule and the integration of curve functions in MATLAB. This model used the trapezium rule to calculate the area under curves in a 1 hour time step because it was challenging to obtain the function of each curve so that it could be integrated. In addition, the accuracy of the trapezium rule was deemed acceptable with minimal error ranges. As shown in Figure 6, Area under curve was calculated for the E+ E- and ED
E   − , 1 = ∫   ( P l − P p v )   d t ,   f o r     t s , 1 < t < t e , 1 ,   w h e r e   P p v < P l
E   − , 2 = ∫   ( P l − P p v )   d t ,   f o r     t s , 2 < t < t e , 2 ,   w h e r e   P p v < P l
E   + = ∫   ( P p v − P l )   d t ,   f o r     t s , + < t < t e . + ,   w h e r e   P l < P p v
E   D = ∫     P l     d t ,   f o r     0 < t < t e   ,   w h e r e   P l < P p v
E + h a s t o e q u a l o r g r e a t e r t h a n E − t o e n s u r e t h e e n e r g y b a l a n c e d o p e r a t i o n
Our target is to find the optimal sizing of   N P V as follows:
N P V = E + + E D E 1 , P V
Figure 7 depicts the computation of the optimal number of solar PVs. For equation (21), we used to iteratively compute the number of solar photovoltaics (PVs) given the energy provided by each PV module ( E 1 ) . This calculation is based on the premise that these are the maximum values required by the load during nighttime hours to obtain the optimal surplus of PV power capable of covering the load (considering the fuel cell's and hydrogen tank's efficiencies). It was also observed that the surplus energy the solar PV modules supplied must exceed the nighttime discharge power by a certain amount. This value primarily depends on the efficiency of the fuel cell, electrolyzer, and hydrogen tank. Consequently, system components with a higher efficiency yield a superior sizing optimization result. Equation (22) describes the effect of system component efficiencies on the surplus energy supplied and is a constraint for the optimization strategy.
E − = E + . η F C . η H 2 ,   T a n k
E D , 1 , E D . 2 resemble the Energy the load consumes via PV modules during the first hours between sunset and sunrise. In previous calculations, these two values should have been taken into account. Nevertheless, it is essential to analyze them, as they will account for the losses that occur during the conversion process via hydrogen tanks and fuel cells. Numerous factors prohibit solar PV arrays from operating at maximum efficiency. In addition to voltage drop and dust accumulation, one of these factors is the operating temperature of the PV module, which can contribute considerably to the most significant proportion of power loss. The effect of temperature on output varies by module and can be calculated using the temperature coefficients supplied on the manufacturer's data sheets and the following relationships:
T m = 20.4 + 1.2 × T a    
T x = 1 + α T m − T a    
In this model, it was assumed that AC losses are fixed at roughly 7% while array temperature losses range between 5% and 11% depending on the monthly temperature profile. We used the optimal N P V to calculate the cost analysis indicated in section 2.5.

4. Results and Discussion

4.1. a. Sizing Methodology of Hybrid PV/Hydrogen System: Case Study 1

In analyzing the annual system behavior for the examined location of Cairo International Airport, the production and energy consumption were investigated (same data as Selim et al., 2020). From October to March, hydrogen consumption exceeds production, and solar energy is the sole source of hydrogen production. During April through September, solar energy increases due to increased irradiance and moderate temperature ranges, causing hydrogen production to exceed consumption. The entire year's worth of excess solar electricity is stored in a hydrogen tank, yielding approximately 2,000 kg of hydrogen that will be exported to the grid upon application of the power management method during January and December, when there is no surplus power and end consumers consume all produced energy.
As shown in Figure 8, the net energy produced by PV modules is sufficient to cover the load demand for each month except for December which considered as the worst-case scenario. The PV contribution in that energy mix is found to be 50% or exceeding depending on the month of the year and this what proves the capability of the deterministic balance method for optimizing the generation and meeting the load requirement. In December, there was a lack of generation around 5% which are supplied by the stored hydrogen from the excess of the previous months. Finally, energy profiles for solar PVs, fuel cell, electrolyzer and hydrogen production were deduced for 8760 hours as shown in Figure 9a–e.
Referring to cost equations in paper and System cost per 1 kW as illustrated in Table 2, the economic model of the hybrid system will be evaluated as shown in Table 2 and Figure 10.
Consider Electrical selling price (ESP) =0.0788 $/kWhr (NREA et al.,2020), Project lifetime =25 years, Annual discount rate = 10% and assuming no decommissioning cost paid.

4.1. b. Evaluation Using HOMER Tool

HOMER -Pro [35] is an optimization model which performs thousands of simulations as discussed before and gives best possible design for the system. PV/FC configuration was set up as shown in in Figure 11. and simulated in the site of Cairo International Airport and load profile was inserted in the program for one year as shown in Appendix C.2. This simulation was performed on HP laptop with specs of Intel® Core™ i5 CPU with 2.20 GHz Processor with Installed memory 4.00 GB.
Detailed specs of the hybrid system components are being illustrated in Table 3, where data has been collected from commercial datasheets during the selection process.
An optimization analysis is used to find the best possible hybrid power system configuration based on the desired constraints at the lowest net present cost using the cycle charging control (CC). Cycle charging, combined dispatch and load following are three main controllers in HOMER where you apply the best controller that fits the application. It was found that cycle charging was the best controller to fully utilize the hydrogen system other than the other controllers which were not using the electrolyzer and hydrogen tank in simulation.
The optimized sizing results are illustrated in Table 4. The total electrical production from the hybrid power system the solar PV system (76.2%) and 748,235 kWh/year from the Genset (Fuel cell) (23,8%). This represents a renewable fraction of 100%. The proposed hybrid power system meets the AC primary load of 1,582,615 kWh/year (58% of the total production) The hybrid system is also used to power the electrolyzer 1,063, 082 kWh/year (42%) for hydrogen production and produces some excess power 214 kWh/year. As a result, the unmet electric load by Solar PV (main source of power) is235,003kWhr/yr. and the total excess electricity is 366,370 kWhr. This result is a crucial factor for determining the reliability criteria for the whole hybrid system. As shown in section 6.10, energy profiles were conducted to judge the performance of the system and check the accuracy of using DBM in evaluating annual energy production and hydrogen production. To validate these figures, HOMER pro was also used to conduct energy profiles for solar PV, fuel cell, electrolyzer and hydrogen tanks production/consumption as shown in Figure 12a–e.
Solar PV was operating in range of 0-1800 kW, Fuel Cell in range of 0 -250 kW, Electrolyzer in range of 0-700 kW. These ranges were found in the same ranges of operation that was conducted by DBM method as shown in Figure 13. However, hydrogen tank storage was found to be varying between -50 to 200 kg which is different than DBM results. This stems from the fact that there is no proper power management controller for utilizing the hydrogen production and preventing any stresses on the hydrogen tanks as shown in Figure 12d.

4.2. a. Sizing Methodology of Solar PV/Wind/Hydrogen system: Case Study 2

In this section, several cases have been discussed showing different renewable energy penetration percentages for WTGs and PVs. Adverse nature of wind-PV system can compensate the intermittency nature of each of system and therefore improve the overall reliability of the hybrid system. Hybrid PV, wind turbines, fuel cell and electrolyzer are being sized and utilized in serving the community load as discussed before in the previous sections. The methodology in this section is the DBM, where three different cases were sized and checked for their constraints and load demand satisfaction. Sizing methodology was applied as discussed before. Staring from 250 kW WTG to 750 kW WTGs on a step of 250 kW and calculating PV energy required to satisfy the balance of generation. During this study, critical month of design for this system was found to be on January, when there is no surplus energy production. This observation was used for applying DBM which uses the critical month for sizing optimization and calculating energy production. Figure 14, Figure 15, Figure 16, Figure 17 were conducted using DBM for different mixes between solar PV and wind turbines to get the monthly energy profile for each month and select the best configuration that yields the maximum energy production.
Figures below were used for selecting the configuration that yields the maximum energy production. System 1 in Figure 15 was found to have the highest annual energy production with higher ratio of solar PV installed capacity compared to the installed wind turbine. As a result, system 1 was used in this paper for full simulation for 8760 hours and conducting energy profiles for all system components as shown in Figure 18a–f.

4.2. b. Sensitivity Analysis

Sensitivity is a measure of how the optimal mix of components changes for any parametric variations in the lifelong of the system. Optimal system design depends on interplay with various necessary input variables. When these input cases change, it is good to know how the optimum system changes with variation of the variables. two separate sensitivity cases were carried out using variables of sensitivities like, design dependence on primary load, design dependence on diesel fuel, design dependence on maximum annual capacity shortage and minimum renewable fraction. The optimal system type, line graph and surface plot were used to make notes of the optimization results. In Figure 19 and Figure 20, surface plot graph showing PV array capacity and wind turbine quantity variations with primary load. Considering only two of the sensitivity cases (solar PV and wind turbines installed capacity).
By keeping the other two variables as fixed (load and price) at 100% and minimum renewable fraction).
Consider ESP =0.0788 $/kWhr (NREA-Egypt), Project lifetime =25 years, Annual discount rate = 10% and assuming no decommissioning cost paid. Additionally, a sensibility analysis was conducted as shown in Figure 21 for studying the effect of ratio of PV and wind installed capacity on the levelized cost of energy.
Table 4. Cost analysis of the hybrid system.
Table 4. Cost analysis of the hybrid system.
Month Solar PV Wind Turbine Electrolyzer Fuel Cell Hydrogen Tank
Capital Cost ($) 1,340,000 250,000 960,000 750,000 2000
Maintenance Cost ($) - 113,463 2,178,490 816,934
Replacement Cost ($) - - 960,000 750,000
Annual revenue ($) 263,678
Annual net income ($) 139,323
Net present Value ($) -2,037,360
Present value of O&M ($) 3,108,886
Present value of costs 6,410,886
Levelized annual cost ($) 706,275
Levelized Cost of energy ($/kWhr) 0.2116
Simulation of HOMER was conducted for 8760 hours as shown in Figure 22a–e to deduce the operation profiles of fuel cell, solar PV, wind turbine and hydrogen tanks respectively.
A final comparison for the hybrid systems discussed in three case studies is conducted in terms of the sizing of the system components and cost results as shown in Table 5.
Based on the comparison and cost analysis study conducted in Table 5., hybrid PV/Wind with high penetration of solar PV modules was selected for the implementation in the site of Cairo International Airport to supply the community load of 250 kW peak. Finally, a comparison of installed capacities deduced by DBM and HOMER in the selected site for implementation was conducted as shown in Figure 23 and Figure 24. It was observed that HOMER favors the wind energy penetration rather than solar PV. However, this penetration affects the utilization of the installed wind turbines resulting in a lower capacity factor of turbines.

Conclusion

Our work introduced a deterministic approach for sizing optimization of hybrid energy systems that serves as a reliable benchmark for comparison with existing methods. Unlike software tools like HOMER and other metaheuristic methods, which often require significant computational resources and longer convergence times, our proposed method offers a more efficient and time-effective solution. This deterministic balanced method not only streamlines the optimization process but also maintains accuracy and reliability, making it a valuable addition to the field of hybrid energy system design.
Additionally, this work discussed and simulated hybrid off-grid system to utilize excess of energy production in summer and spring times in the studied location. In fact, excess energy production in summer was due to solar PV modules and that was found in spring was due to WTGs. This means that optimal sizing methodologies have managed to sustain the balance of generation throughout the year and producing an excess of generation in certain times of the year due to the natural response of the renewable resources in the studied location towards the meteorological conditions. Consequently, this excess energy produced can be fully utilized in an energy storage element, in the proposed system that will be the hydrogen tanks. Hydrogen tanks can be then used as the infrastructure for hydrogen refueling stations for the city. Not only will these stations utilize the excess energy produced, but they will also introduce the power to gas concepts in the automotive industry, making the studied system an exemplar model for an energy hub for electricity and fuel production.
The best configuration found for this studied location was Solar PV/wind hybrid system with high penetration of solar PV. This configuration lead to the highest energy production with the minimum levelized cost of energy. HOMER software was the verification tool for DBM method, where the absolute difference between the two methods was in the range of 5%. However, HOMER in wind standalone system was exceeding energy production than DBM by 5.3% and given that the HOMER and DBM were having the same input data (weather data and load profile). Also, HOMER software was preferring the wind energy penetration rather than the solar energy and that was obvious in the hybrid mix of wind and PV modules, which was opposite to the DBM method which achieved a lower cost with the highest penetration of solar PV and maintaining the highest annual energy production.

Future Work

According to the previous results of the studied systems, it has been observed that the surplus power production, which is achieved in winter, spring and summer seasons based on system configurations has to be controlled and utilized to satisfy the power balance for other connected systems and avoid stresses on the current connected energy storage system. This approach has highlighted the concept of interconnectivity between clusters of DGs to achieve the optimal energy sharing and utilize the generated surplus power in all DGs. In future work, it was suggested to work on controlling the power sharing process between cluster of DGs and resolve the optimal power balance sharing problem on a larger scale as shown in Figure 25.

Conflicts of Interest

On behalf of all authors, the corresponding author states that there is no conflict of interest

Nomenclature

E-,1
Lack of energy from 12:00 a.m. till sunrise
E-,2
Lack of energy from sunset till 12:00 a.m.
AEP
Annual energy production (kWh)
AR
Annual revenue from selling the electricity ($/year)
ANI
Annual net income ($/year)
COE
Cost of energy ($)
CI
Capital investment ($)
DC
Decommissioning costs ($)
ESP
Electricity selling price ($/kWh)
E+
Surplus energy supplied by PV arrays
E-
Total lack of energy which will be supplied by fuel cell and electrolyzer
ED
Energy demanded by load and supplied by solar PV arrays
ED,1
Energy demanded by load and supplied by solar PV arrays during sunrise
ED,2
Energy demanded by load and supplied by solar PV arrays during sunset
ELZ
Electrolyzer
FC
Fuel cell
FV
Future value
GT
Irradiance power (W/m2)
LAC
Levelized annual cost ($)
LCOE
Levelized cost of energy ($/kWh)
LSCS
Lifespan cost of the hybrid system
LIP
Load interruption probability
NPV
Net present value ($)
O&M cost
Annual operating and maintenance cost ($/kWh)
PVDC
Present value of the cost of decommissioning ($)
PVC
Present value of all the costs ($)
PVM
Present value maintenance and repair cost
PV
Photovoltaics
P V *
Present value of the cost analysis
P
Period of years (years)
Ppv
Solar PV power (kW)
Pl
Load power (kW)
Pwind
Power of wind generator (kW)
Pr
Rated electrical power output (kW)
P-PMS
Predictive Power management strategies
R
Annual discount rate (%)
P-PMS
Reactive Power management strategies
TX
Temperature de-rating factor,
Tm
Module temperature (˚C)
Ta
Reference temperature (25˚C)
Te
End time of simulation
WTG
Wind turbine generator
VN
Rated speed (m/s)
VD
Cut-in speed (m/s)
VR
Cut-off speed (m/s)
VV
Wind speed (m/s)
α
Power temperature coefficient for module selected (-0.331% ˚C)

Appendix A. DBM methodology

As shown in Table A1, Table A2, Table A3, Table A4 and Table A5 The meteorological data, location and equation functions used in interoperating the methodology of calculating the energy production for one year.
Table A1. Wind Data
Table A1. Wind Data
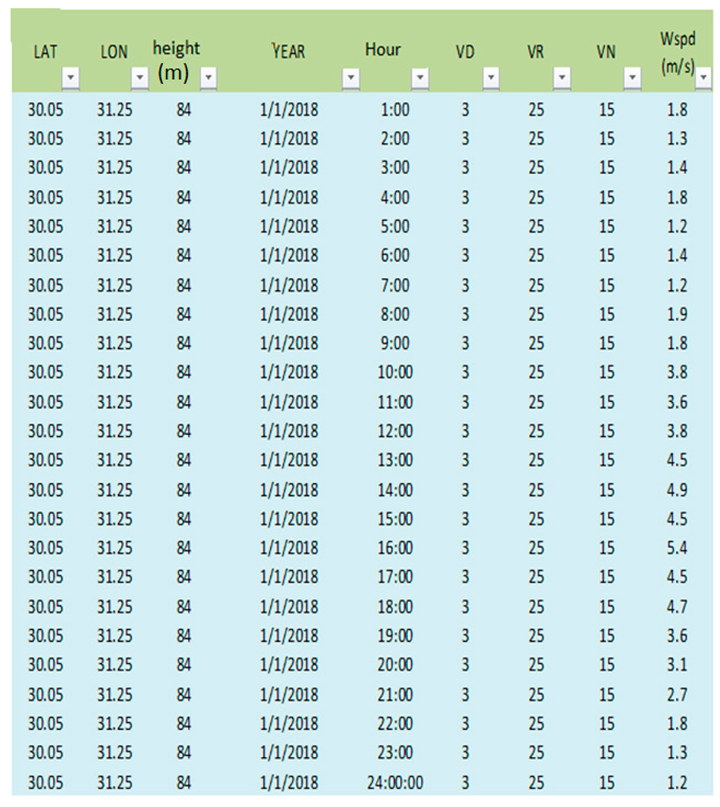Preprints 72878 i001
Table A2. Solar PV Data.
Table A2. Solar PV Data.
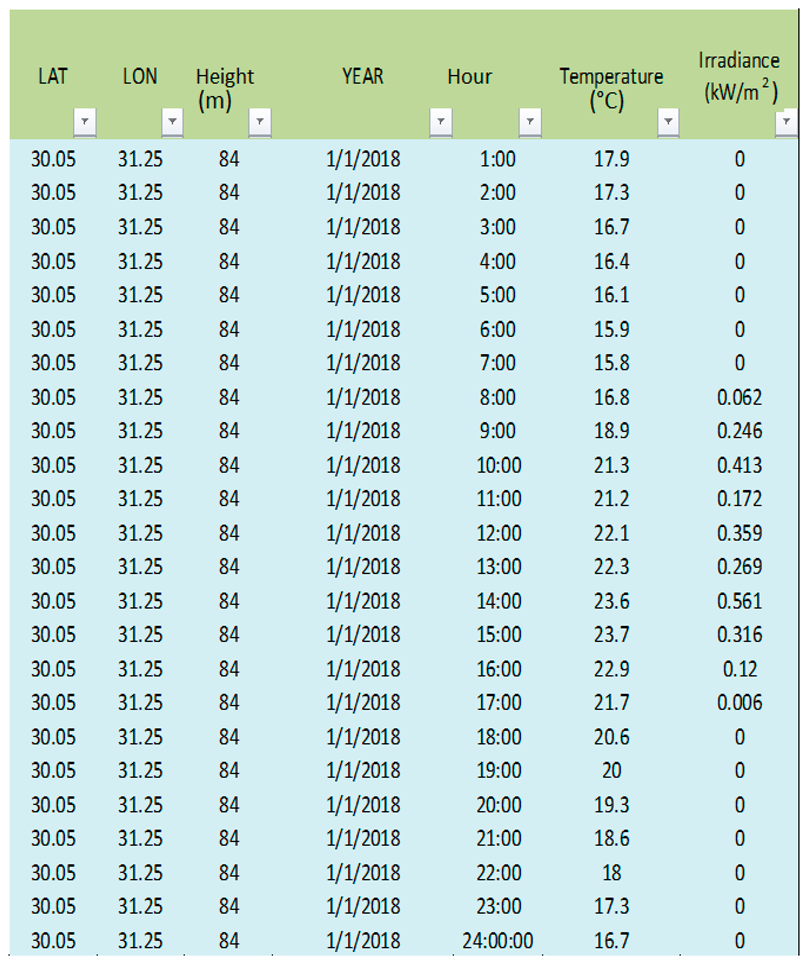Preprints 72878 i002
Table A3. Wind Energy Calculations.
Table A3. Wind Energy Calculations.
Preprints 72878 i003
Table A4. Solar PV Energy Calculations.
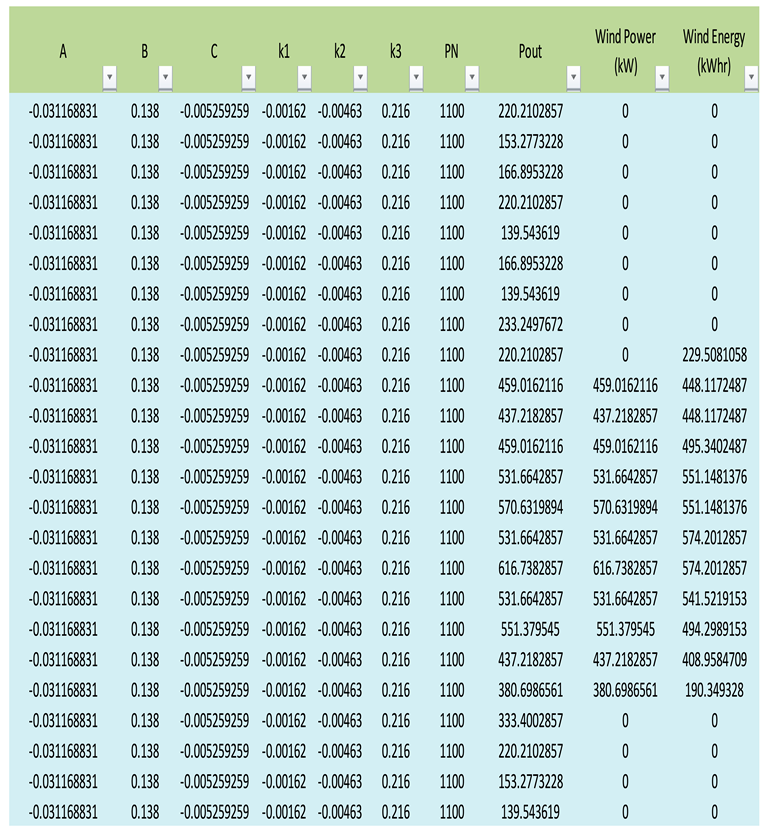Table A4. Solar PV Energy Calculations.
Preprints 72878 i004
Table A5. Hydrogen System Energy Calculations.
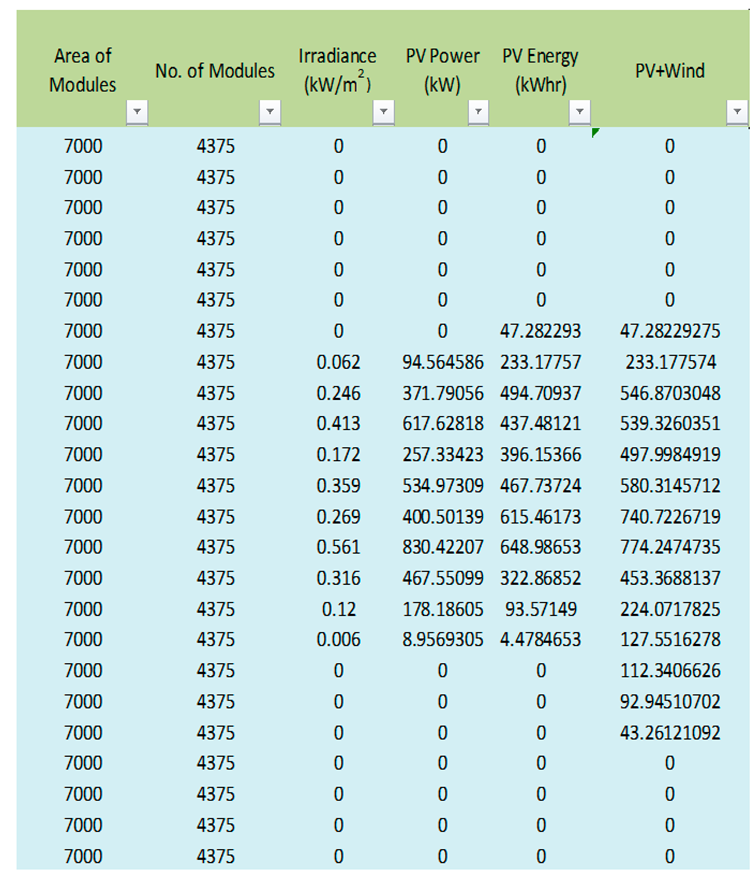Table A5. Hydrogen System Energy Calculations.
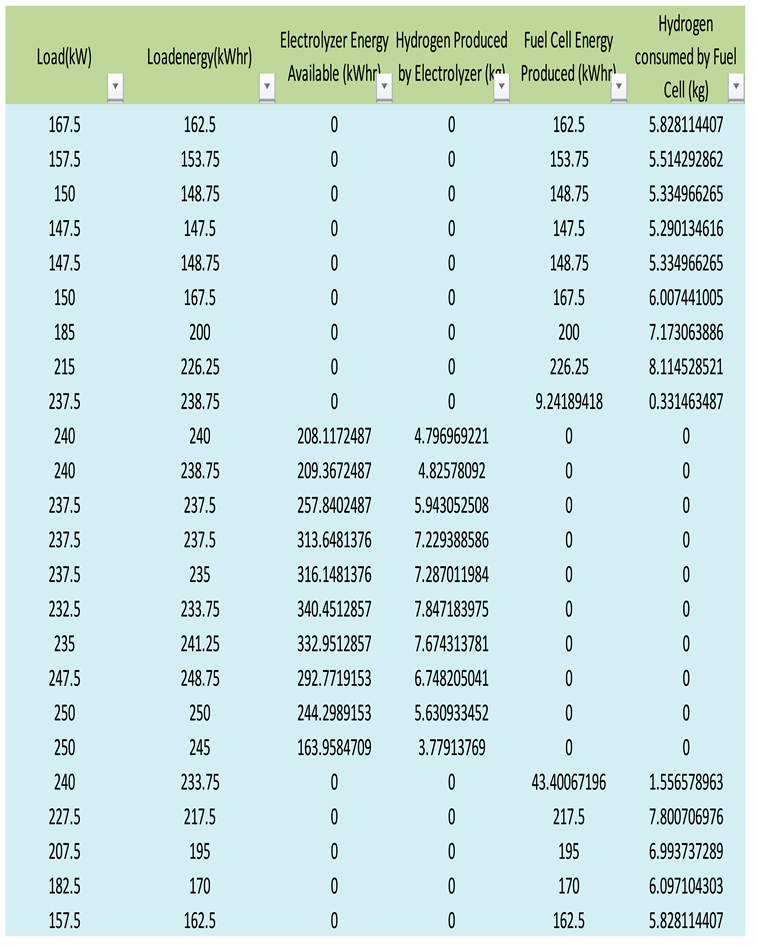Preprints 72878 i005

Appendix B. Load Profiles

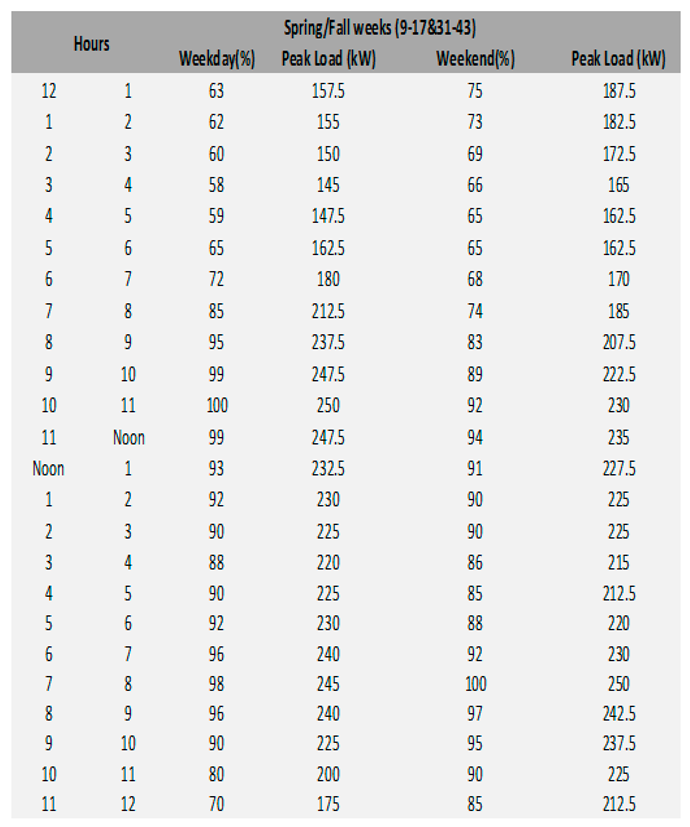
Based on RTS Model, the load profile was generated based on the percentages standards for the peak power for the system which is 250 kW in this analysis.
Table A6. RTS Load Profile.
Table A6. RTS Load Profile.
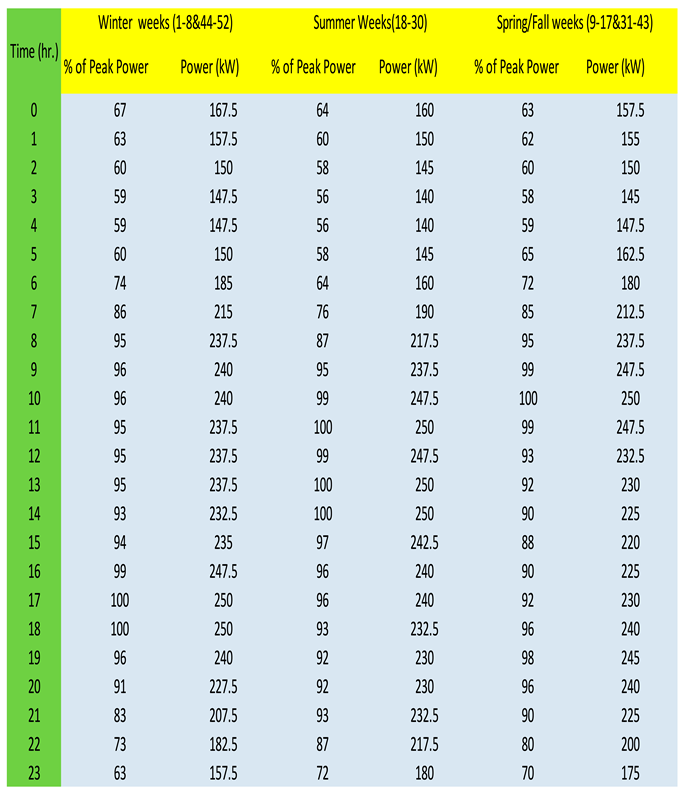Preprints 72878 i006
Table A7. Load Profile for Winter weeks.
Table A7. Load Profile for Winter weeks.
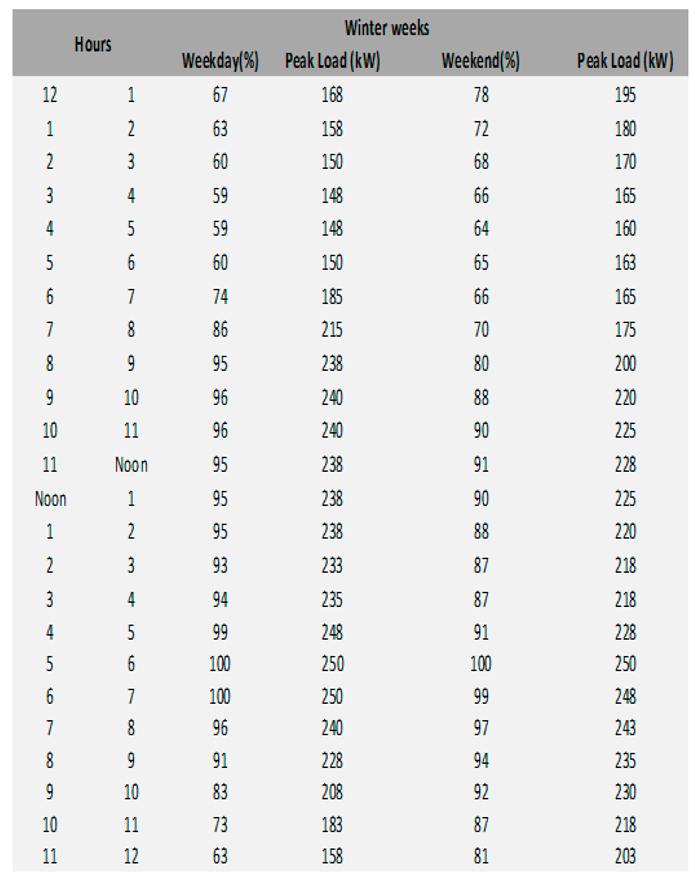Preprints 72878 i007
Table A8. Load Profile for Summer Weeks.
Table A8. Load Profile for Summer Weeks.
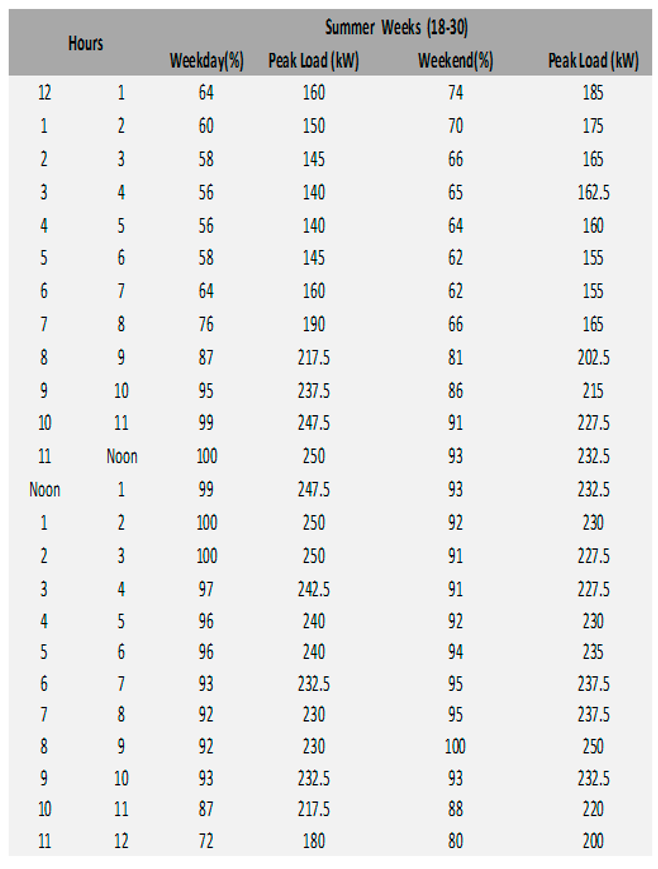Preprints 72878 i008
Table A9. Load Profile for Spring/Fall Weeks.
Table A9. Load Profile for Spring/Fall Weeks.
Preprints 72878 i009

Appendix C. Software Tools

Appendix C.1. METEONORM Model

Preprints 72878 g0a1
Figure A1. METEONORM software.
Figure A1. METEONORM software.
Preprints 72878 g0a1

Appendix C.2. HOMER Model

Preprints 72878 g0a2
Figure A2. HOMER Configuration.
Figure A2. HOMER Configuration.
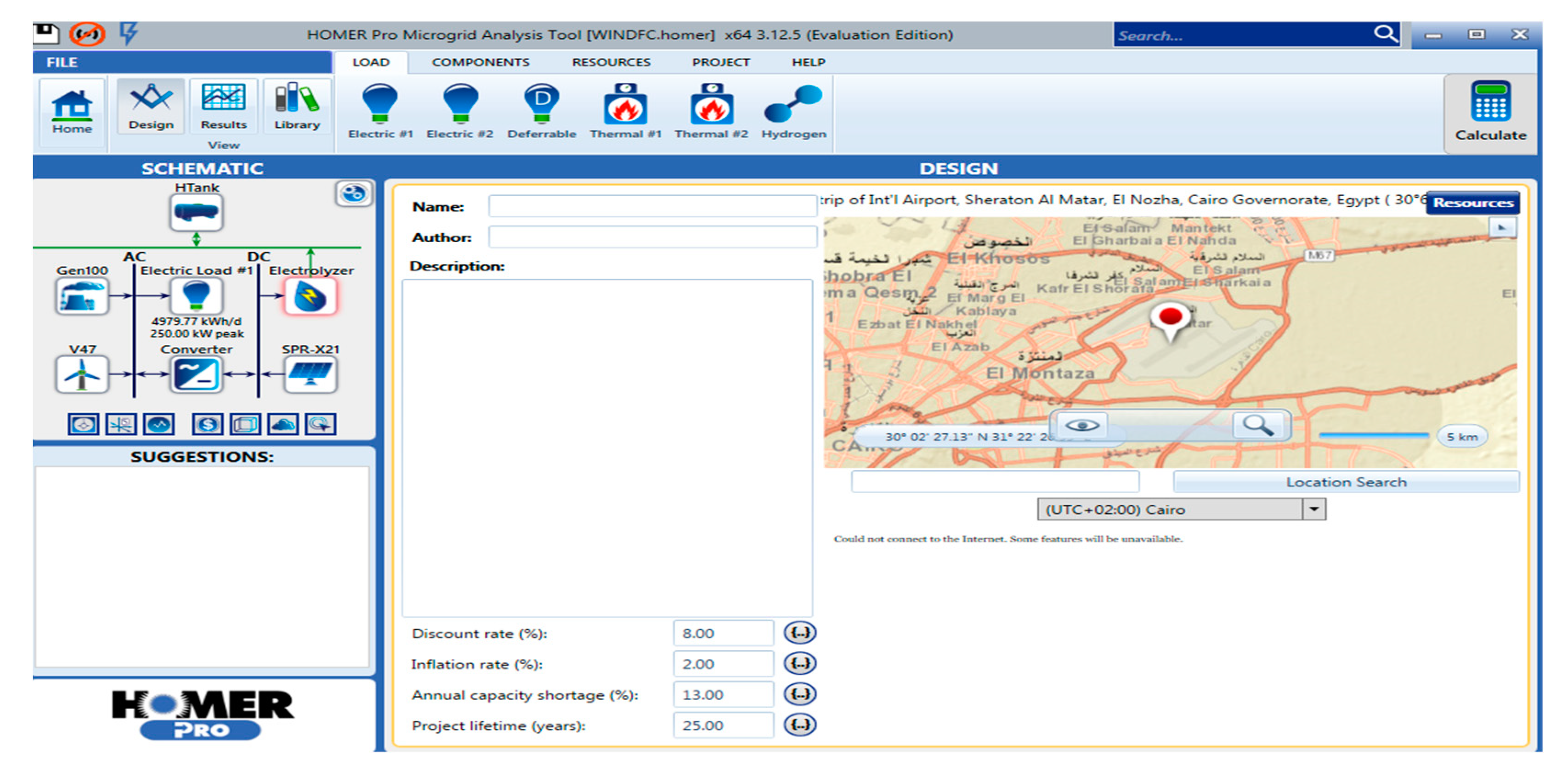
Preprints 72878 g0a2
Preprints 72878 g0a3
Figure A3. HOMER Results
Figure A3. HOMER Results
Preprints 72878 g0a3

References

  1. Gelma Boneya, Design of a photovoltaic-Wind Hybrid Power Generation System for Ethiopian Remote area, PhD thesis, Institue of Technology Department of Electrical and Computer Engineering, Addis Ababa University, 2011.
  2. Ghenai, C. , Salameh, T., & Merabet, A. (2018). Technico-economic analysis of off grid solar PV/Fuel cell energy system for residential community in desert region. International Journal of Hydrogen Energy.
  3. Adedoja, O.S. , Saleh, U.A., Alesinloye, A.R., Timiyo, T.-E.J., Onuigbo, I.F., Adejuwon, O.O., Josiah, E., 2023. An energy balance and multicriterial approach for the sizing of a hybrid renewable energy system with hydrogen storage. E-Prime - Adv. Electr. Eng. Electron. Energy 4, 100146. [CrossRef]
  4. Alberizzi, J.C. , Rossi, M., Renzi, M., 2020. A MILP algorithm for the optimal sizing of an off-grid​ hybrid renewable energy system in South Tyrol. Energy Rep. 6, 21–26. [CrossRef]
  5. Al-Othman, A. , Tawalbeh, M., Martis, R., Dhou, S., Orhan, M., Qasim, M., Ghani Olabi, A., 2022. Artificial intelligence and numerical models in hybrid renewable energy systems with fuel cells: Advances and prospects. Energy Convers. Manag. 253, 115154. [CrossRef]
  6. Arévalo, P. , Benavides, D., Lata-García, J., Jurado, F., 2020. Energy control and size optimization of a hybrid system (photovoltaic-hidrokinetic) using various storage technologies. Sustain. Cities Soc. 52, 101773. [CrossRef]
  7. Azad, A. , Shateri, H., 2023. Design and optimization of an entirely hybrid renewable energy system (WT/PV/BW/HS/TES/EVPL) to supply electrical and thermal loads with considering uncertainties in generation and consumption. Appl. Energy 336, 120782. [CrossRef]
  8. Ben Seddik, Z. , Ben Taher, M.A., Laknizi, A., Ahachad, M., Bahraoui, F., Mahdaoui, M., 2022. Hybridization of Taguchi method and genetic algorithm to optimize a PVT in different Moroccan climatic zones. Energy 250, 123802. [CrossRef]
  9. Brka, A. , Al-Abdeli, Y.M., Kothapalli, G., 2016. Predictive power management strategies for stand-alone hydrogen systems: Operational impact. Int. J. Hydrog. Energy 41, 6685–6698. [CrossRef]
  10. Cai, W. , Li, X., Maleki, A., Pourfayaz, F., Rosen, M.A., Alhuyi Nazari, M., Bui, D.T., 2020. Optimal sizing and location based on economic parameters for an off-grid application of a hybrid system with photovoltaic, battery and diesel technology. Energy 201, 117480. [CrossRef]
  11. Hadidian Moghaddam, M.J. , Kalam, A., Nowdeh, S.A., Ahmadi, A., Babanezhad, M., Saha, S., 2019. Optimal sizing and energy management of stand-alone hybrid photovoltaic/wind system based on hydrogen storage considering LOEE and LOLE reliability indices using flower pollination algorithm. Renew. Energy 135, 1412–1434. [CrossRef]
  12. Hassan, Q. , 2020. Optimisation of solar-hydrogen power system for household applications. Int. J. Hydrog. Energy 45, 33111–33127. [CrossRef]
  13. Jahannoosh, M. , Nowdeh, S.A., Naderipour, A., Kamyab, H., Davoudkhani, I.F., Klemeš, J.J., 2021. New hybrid meta-heuristic algorithm for reliable and cost-effective designing of photovoltaic/wind/fuel cell energy system considering load interruption probability. J. Clean. Prod. 278, 123406. [CrossRef]
  14. Mahmoudi, S.M. , Maleki, A., Rezaei Ochbelagh, D., 2023. Investigating the role of the carbon tax and loss of power supply probability in sizing a hybrid energy system, economically and environmentally. Energy Convers. Manag. 280, 116793. [CrossRef]
  15. Mokhtara, C. , Negrou, B., Settou, N., Bouferrouk, A., Yao, Y., 2021. Design optimization of grid-connected PV-Hydrogen for energy prosumers considering sector-coupling paradigm: Case study of a university building in Algeria. Int. J. Hydrog. Energy 46, 37564–37582. [CrossRef]
  16. Nazari-Heris, M. , Mirzaei, M.A., Asadi, S., Mohammadi-Ivatloo, B., Zare, K., Jebelli, H., 2021. A hybrid robust-stochastic optimization framework for optimal energy management of electric vehicles parking lots. Sustain. Energy Technol. Assess. 47, 101467. [CrossRef]
  17. Özçelep, Y. , Bekdaş, G., Apak, S., 2023. Meeting the electricity demand for the heating of greenhouses with hydrogen: Solar photovoltaic-hydrogen-heat pump system application in Turkey. Int. J. Hydrog. Energy 48, 2510–2517. [CrossRef]
  18. Pan, G. , Gu, W., Qiu, H., Lu, Y., Zhou, S., Wu, Z., 2020. Bi-level mixed-integer planning for electricity-hydrogen integrated energy system considering levelized cost of hydrogen. Appl. Energy 270, 115176. [CrossRef]
  19. Siddiqui, O. , Dincer, I., 2021. Optimization of a new renewable energy system for producing electricity, hydrogen and ammonia. Sustain. Energy Technol. Assess. 44, 101023. [CrossRef]
  20. Thirunavukkarasu, M. , Sawle, Y., Lala, H., 2023. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew. Sustain. Energy Rev. 176, 113192. [CrossRef]
  21. Vahid, M.Z. , hajivand, M., Moshkelgosha, M., Parsa, N., Mansoori, H., 2020. Optimal, reliable and economic designing of renewable energy photovoltaic/wind system considering different storage technology using intelligent improved salp swarm optimisation algorithm, commercial application for Iran country. Int. J. Sustain. Energy 39, 465–485. [CrossRef]
  22. Zhang, Y. , Hua, Q.S., Sun, L., Liu, Q., 2020. Life Cycle Optimization of Renewable Energy Systems Configuration with Hybrid Battery/Hydrogen Storage: A Comparative Study. J. Energy Storage 30, 101470. [CrossRef]
  23. Mohamed, E. S. (2015). Dynamic Security of Interconnected Electric Power Systems-Volume 2: Dynamics and stability of conventional and renewable energy systems. LAP LAMBERT Academic Publishing.
  24. Skoplaki, E. , & Palyvos, J. A. (2009). On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Solar energy 2009, 83, 614–624. [Google Scholar]
  25. Khiareddine, A. , Salah, C. B., Rekioua, D., &Mimouni, M. F. (2018). Sizing methodology for hybrid photovoltaic/wind/hydrogen/battery integrated to energy management strategy for pumping system. Energy 2018, 153, 743–762. [Google Scholar]
  26. New&Renewable Energy Authority-Annual Report2018,Accessed on 1 Jan.2020.
  27. New&Renewable Energy Authority official website http://www.nrea.gov.eg/, Accessed on : 1 sep.2020.
  28. Subcommittee, P.M. IEEE reliability test system. IEEE Transactions on power apparatus and systems 1979, 2047–2054. [Google Scholar] [CrossRef]
  29. Larminie, J., A. Dicks, and M.S. McDonald, Fuel cell systems explained. Vol. 2. 2003: J. Wiley Chichester, UK.
  30. Fathy, A. A reliable methodology based on mine blast optimization algorithm for optimal sizing of hybrid PV-wind-FC system for remote area in Egypt. Renewable energy 2016, 95, 367–380. [Google Scholar] [CrossRef]
  31. HOMER Support Guide, available online on https://www.homerenergy.com/support/ Accessed Apr 1, 2019.
  32. Global Atlas Wind, availabe online on https://globalwindatlas.info Accessed Apr 1, 2022.
  33. Meteonorm software platform, available online on https://meteonorm. 2022; 1.
  34. HOMER software program, available online on https://www.homerenergy.com/ Accessed Apr 1, 2022.
Preprints 72878 g001
Figure 1. Methods used for solving the sizing optimization of energy systems. Source: Self painted by the author
Figure 1. Methods used for solving the sizing optimization of energy systems. Source: Self painted by the author
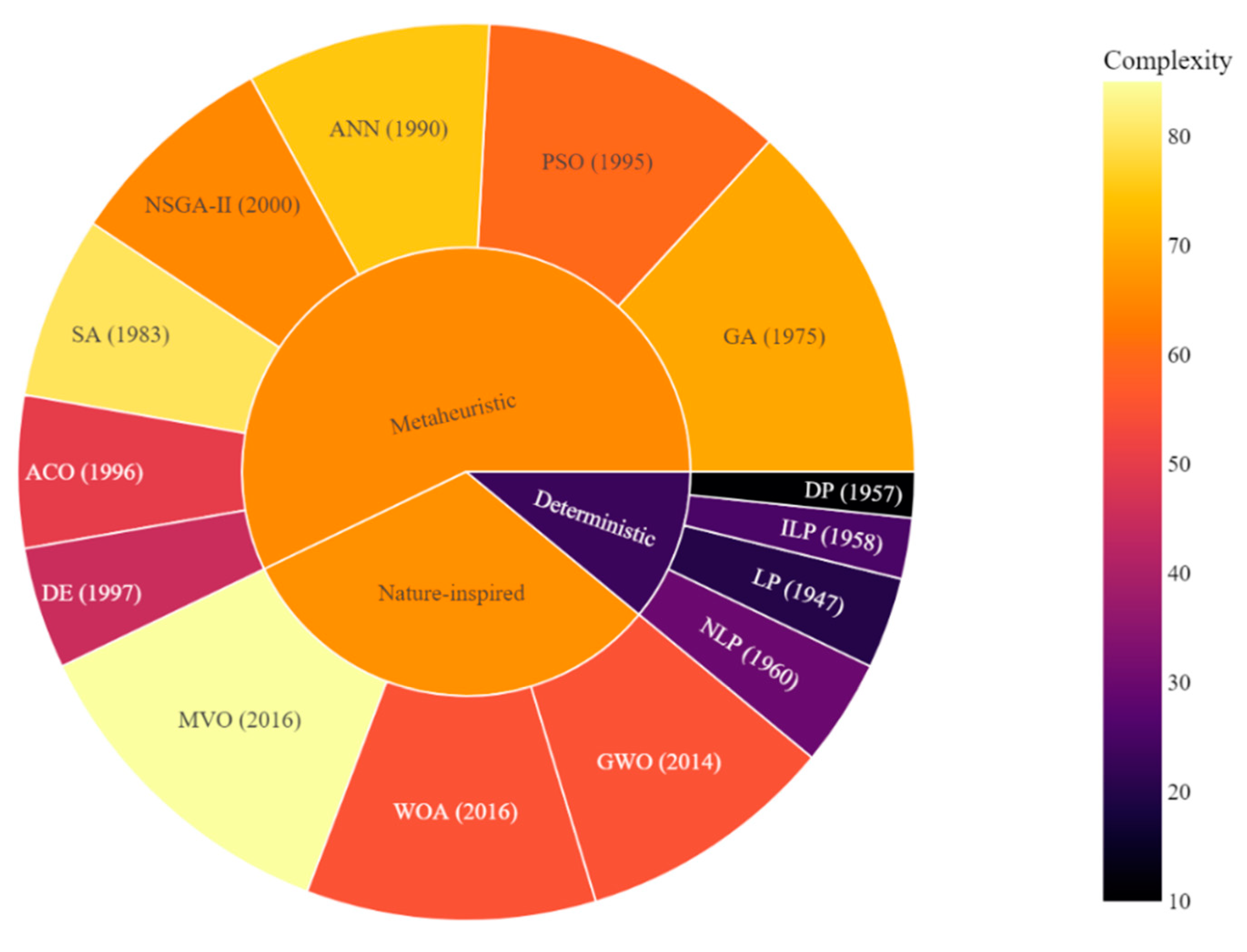
Preprints 72878 g001
Preprints 72878 g002
Figure 2. Common usage metric for energy resources and storages.
Figure 2. Common usage metric for energy resources and storages.
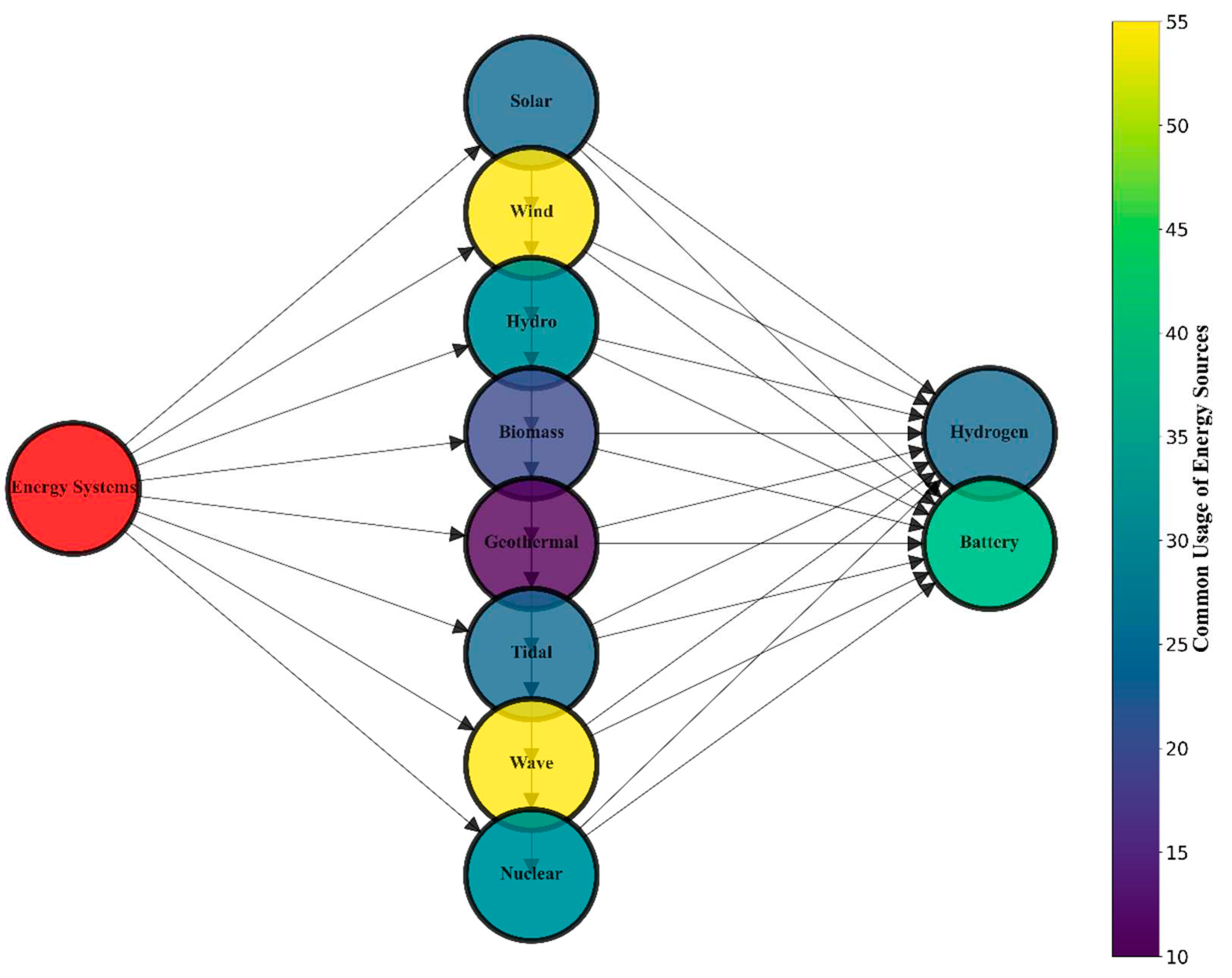
Preprints 72878 g002
Preprints 72878 g004
Figure 4. Power output curve of wind (Khiareddine et al., 2018).
Figure 4. Power output curve of wind (Khiareddine et al., 2018).
Preprints 72878 g004
Preprints 72878 g005
Figure 5. Load profile system based on RTS system.
Figure 5. Load profile system based on RTS system.
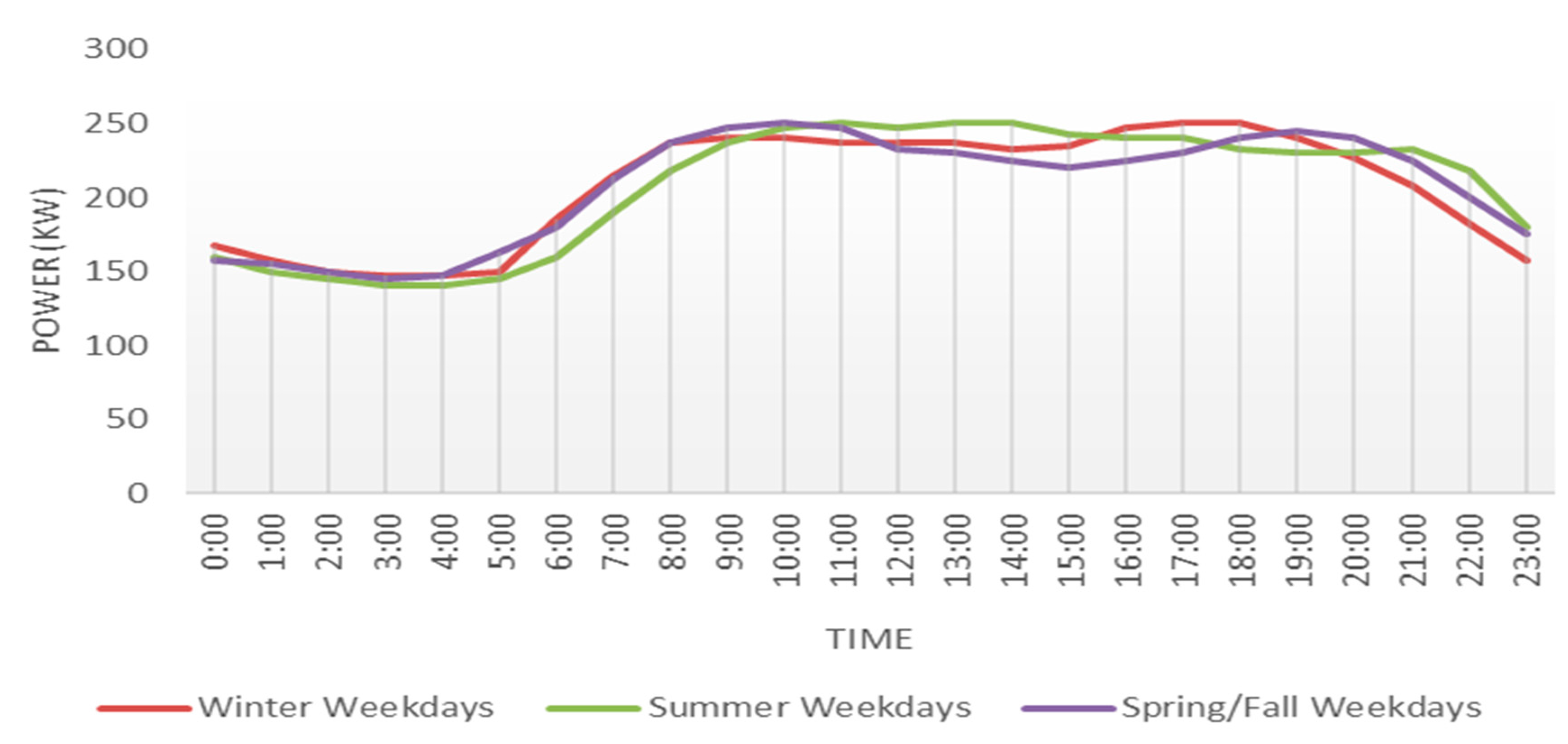
Preprints 72878 g005
Preprints 72878 g006
Figure 6. Area under curve for DBM.
Figure 6. Area under curve for DBM.
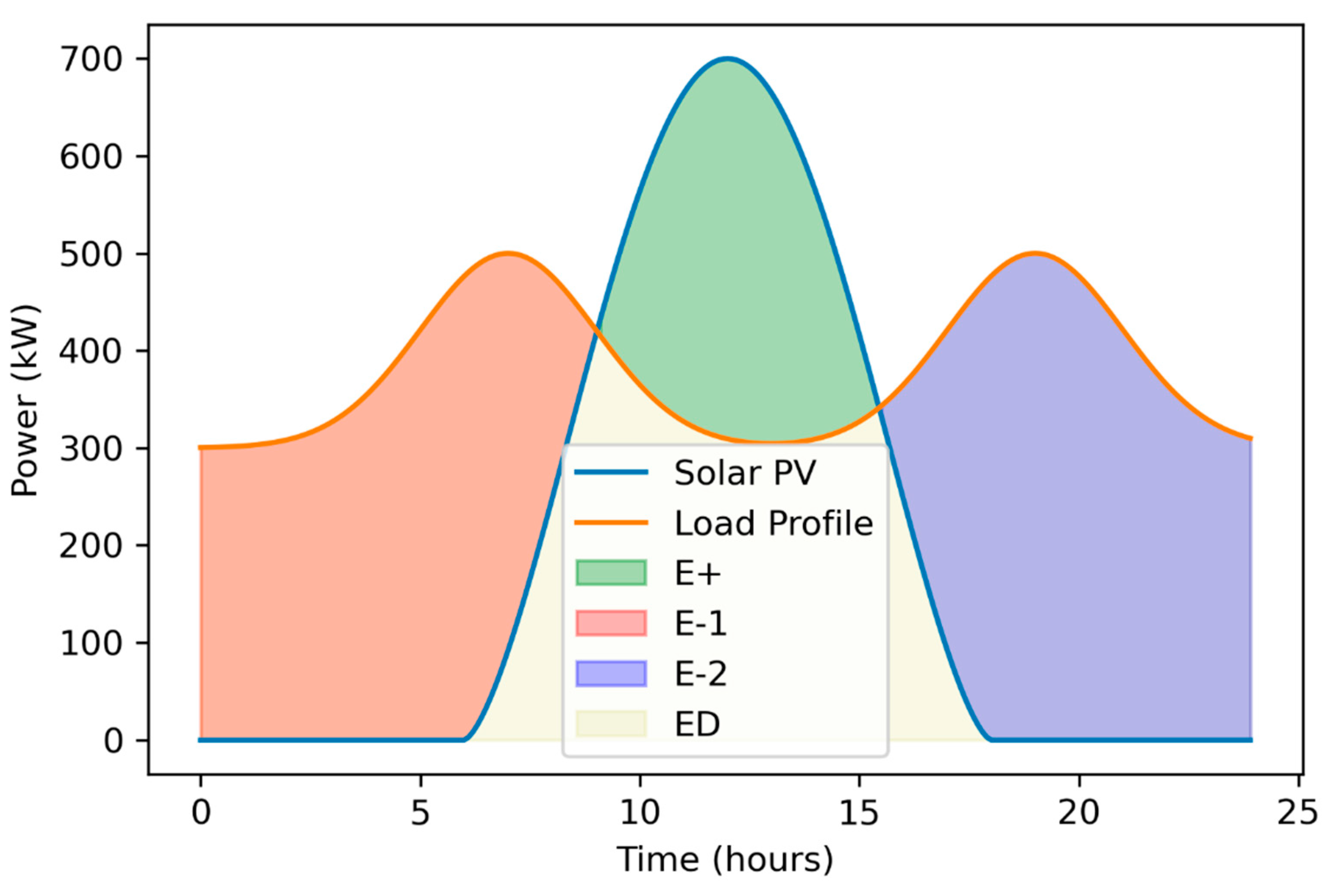
Preprints 72878 g006
Preprints 72878 g007
Figure 7. Flow chart of the DBM method.
Figure 7. Flow chart of the DBM method.
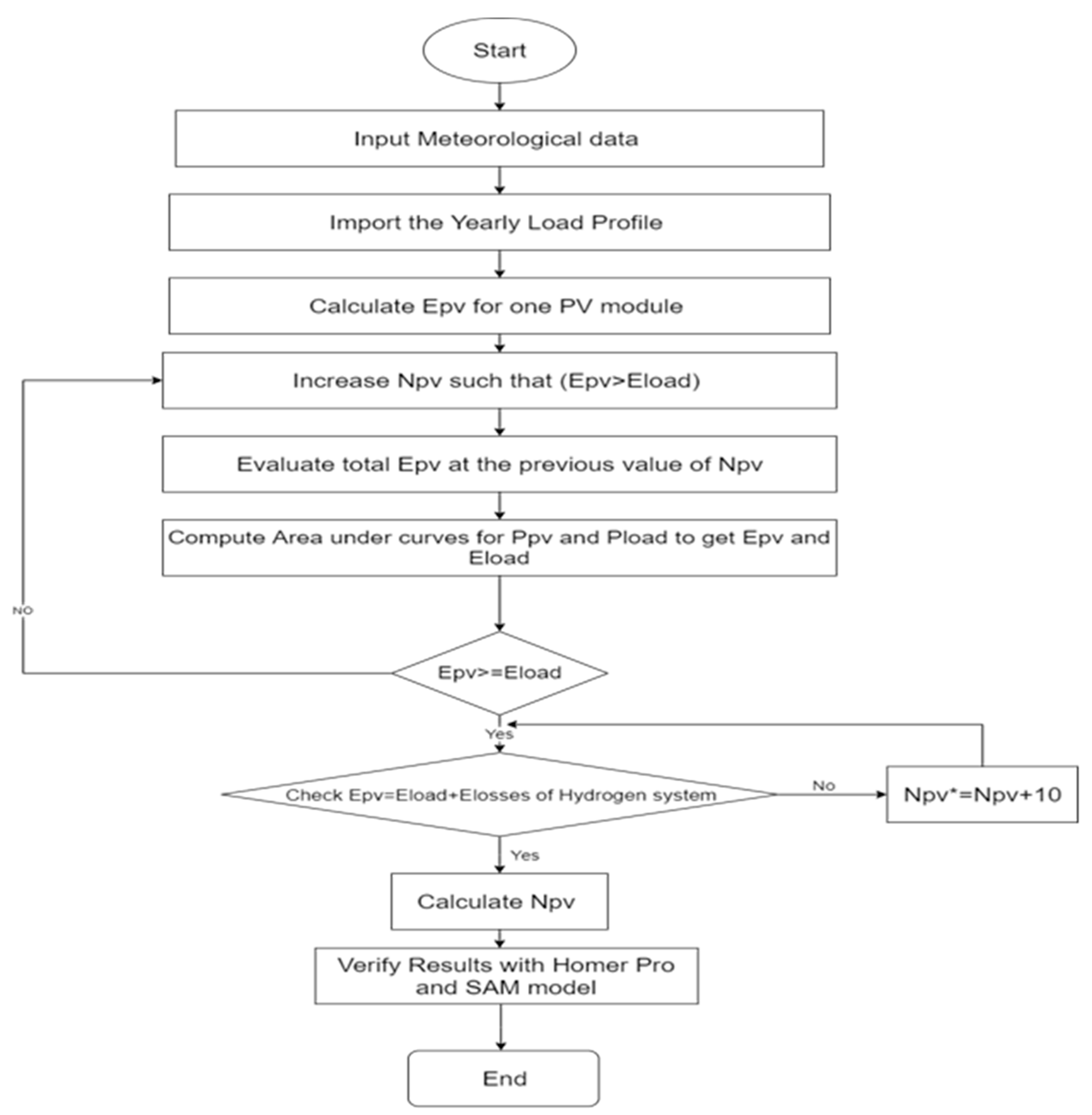
Preprints 72878 g007
Preprints 72878 g008
Figure 8. Net AC energy compared with load energy using DBM.
Figure 8. Net AC energy compared with load energy using DBM.
Preprints 72878 g008
Preprints 72878 g009aPreprints 72878 g009bPreprints 72878 g009c
Figure 9. e. Hydrogen Consumption using Fuel Cell.
Figure 9. e. Hydrogen Consumption using Fuel Cell.
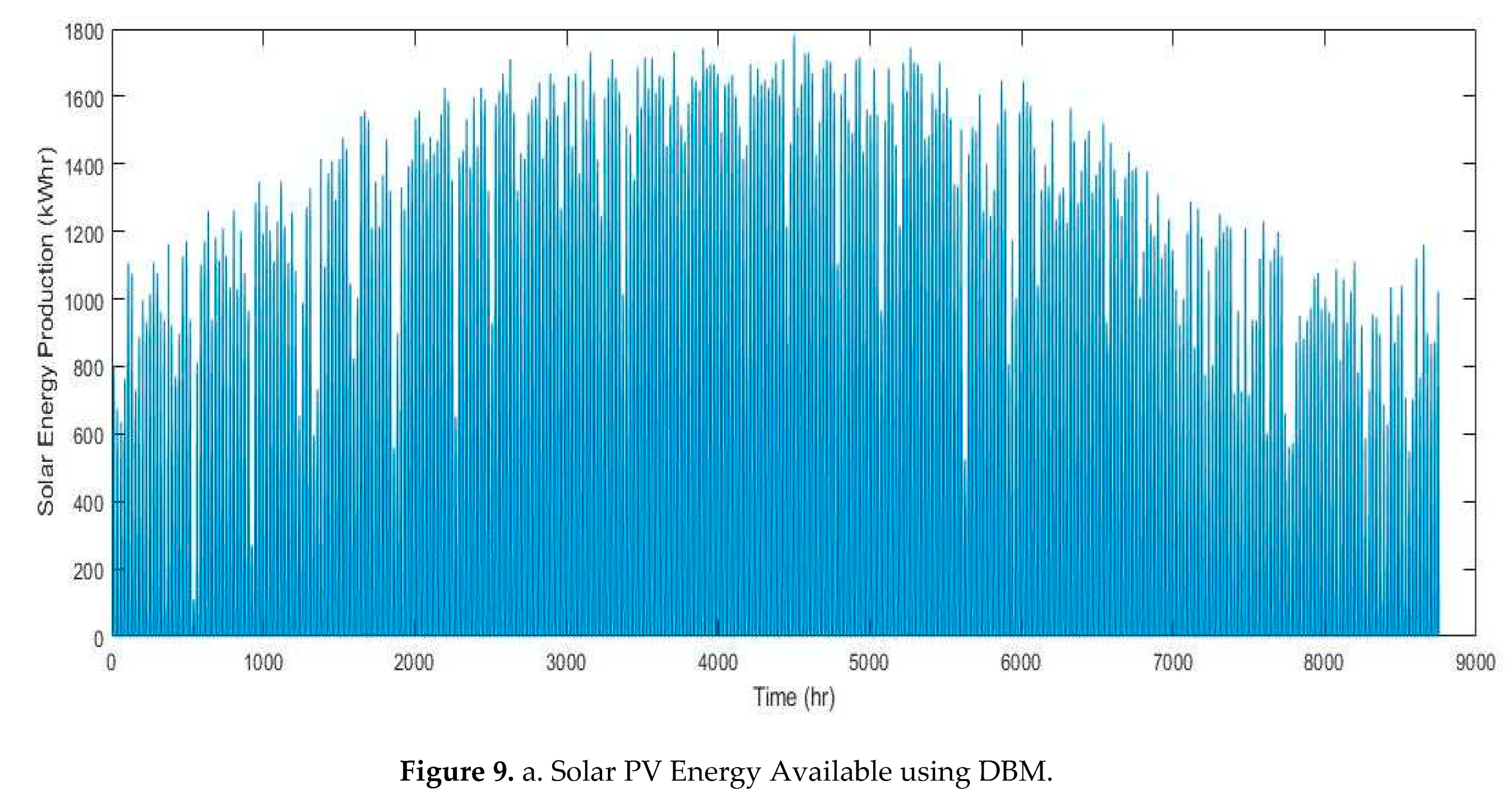
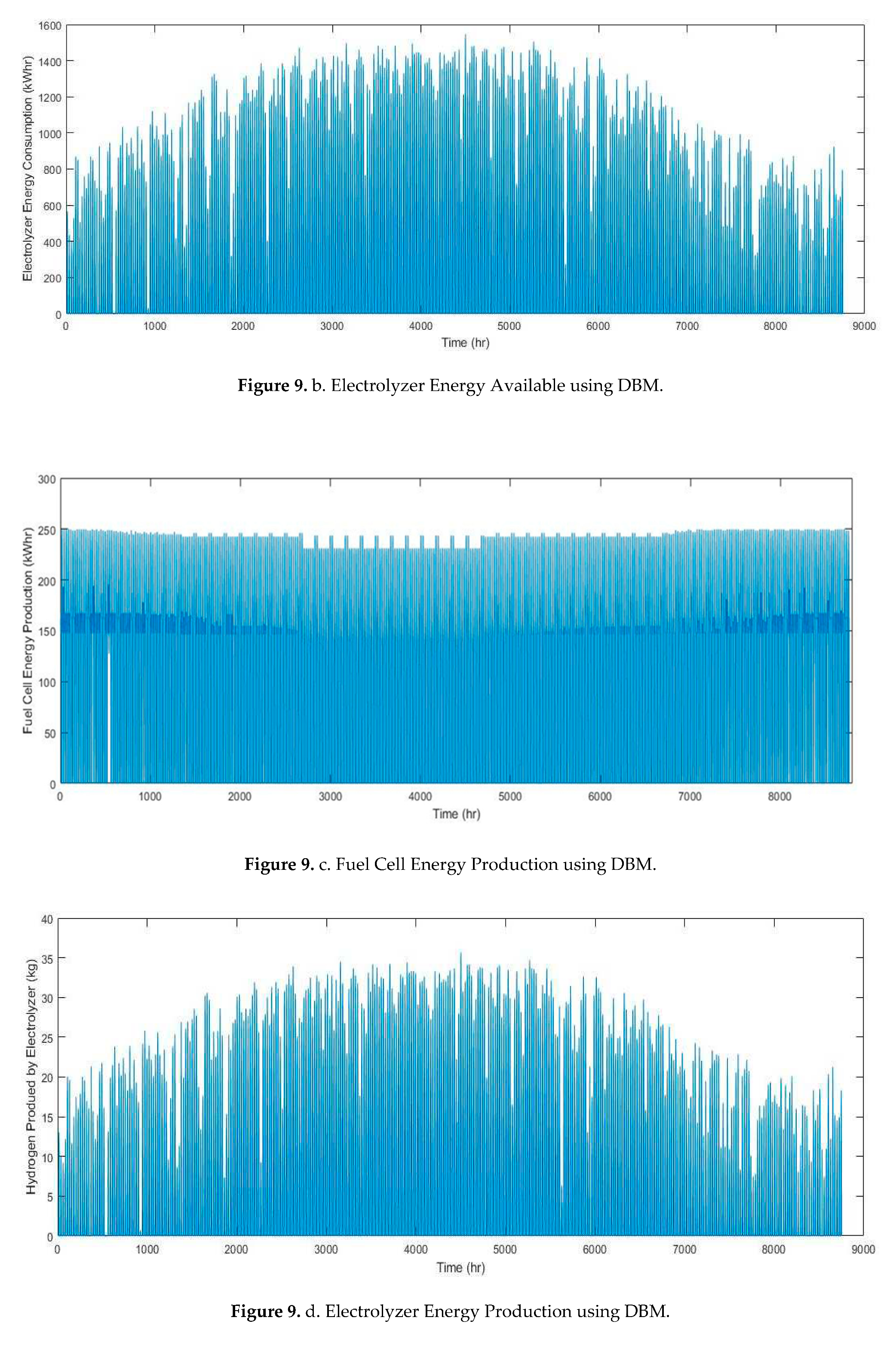
Preprints 72878 g009aPreprints 72878 g009bPreprints 72878 g009c
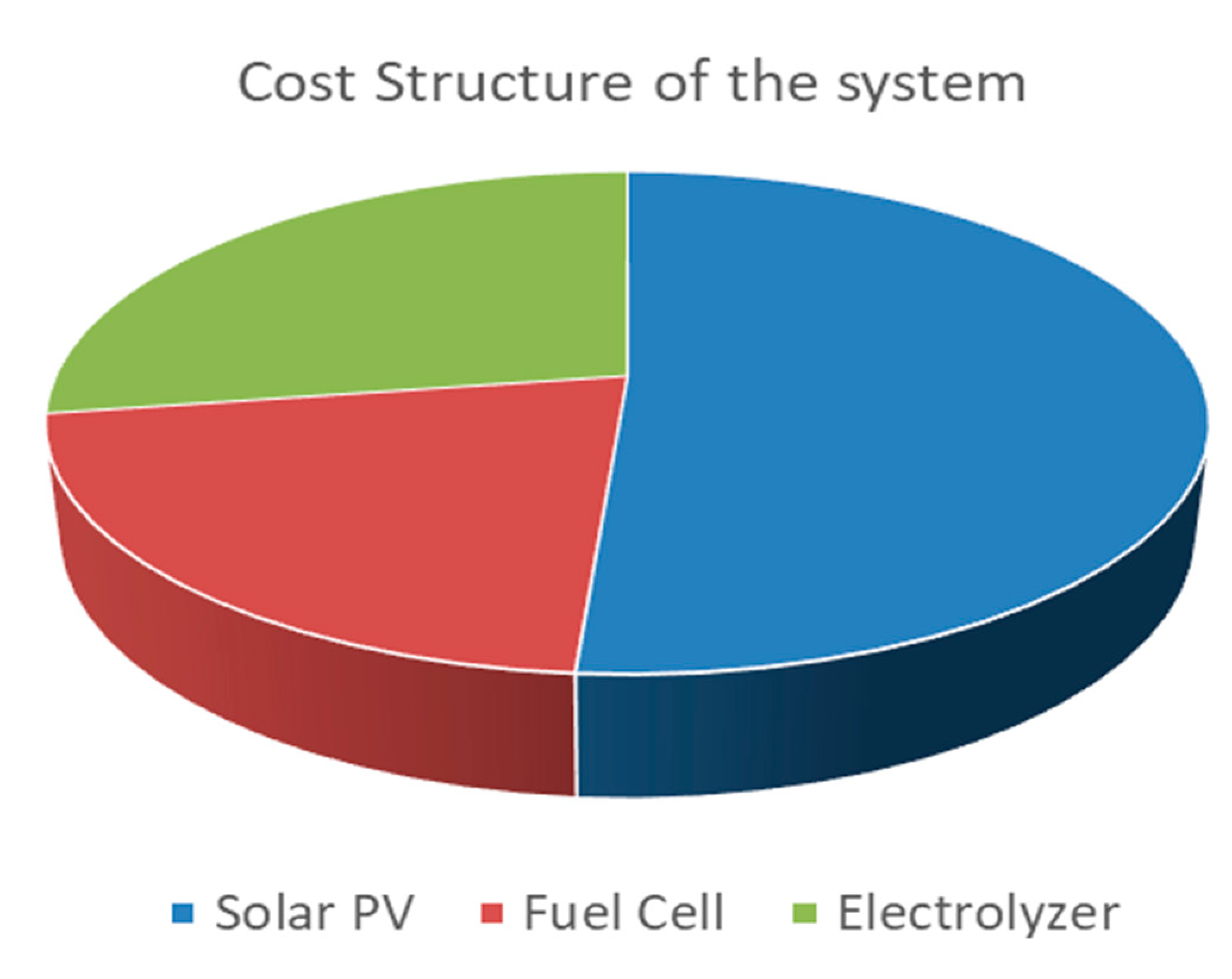
Preprints 72878 g010
Figure 10. Cost structure of hybrid solar PV/hydrogen system.
Figure 10. Cost structure of hybrid solar PV/hydrogen system.
Preprints 72878 g010
Preprints 72878 g011
Figure 11. HOMER configuration (Surplus Mode) [35].
Figure 11. HOMER configuration (Surplus Mode) [35].
Preprints 72878 g011
Preprints 72878 g012aPreprints 72878 g012b
Figure 12. e. Stored Hydrogen Consumption (kg/hr) [35].
Figure 12. e. Stored Hydrogen Consumption (kg/hr) [35].
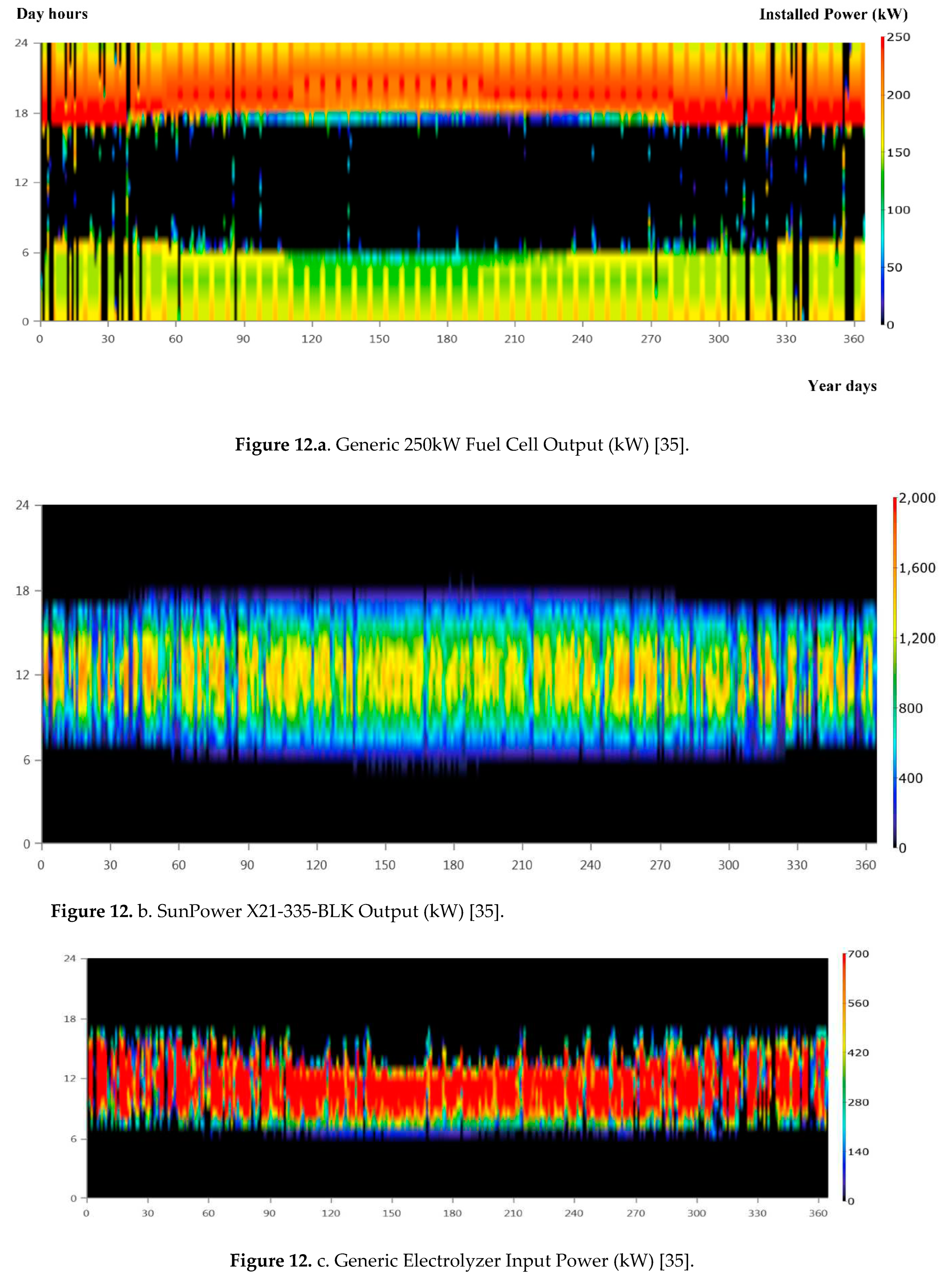
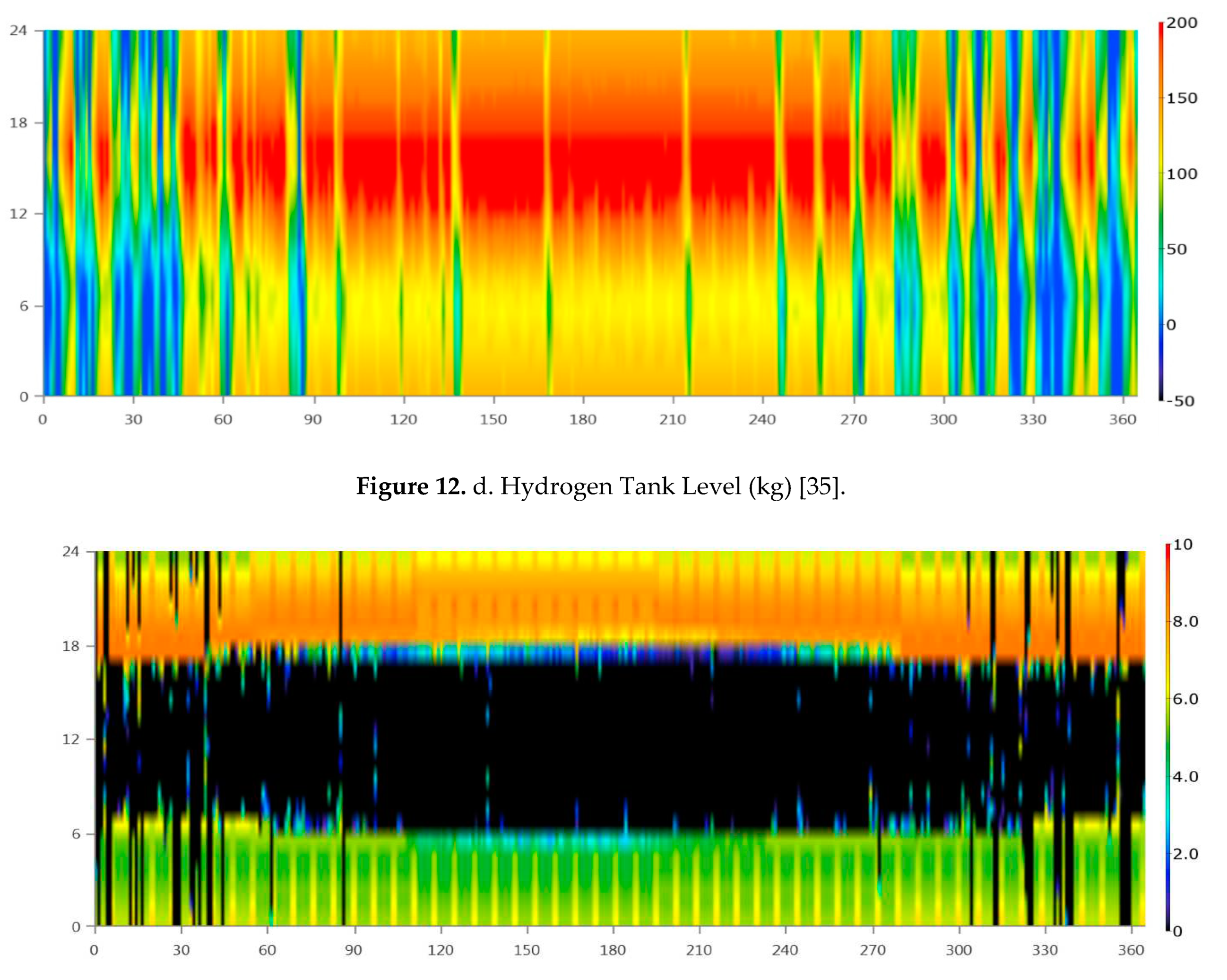
Preprints 72878 g012aPreprints 72878 g012b
Preprints 72878 g013
Figure 13. Comparison between DBM and HOMER Energy Results.
Figure 13. Comparison between DBM and HOMER Energy Results.
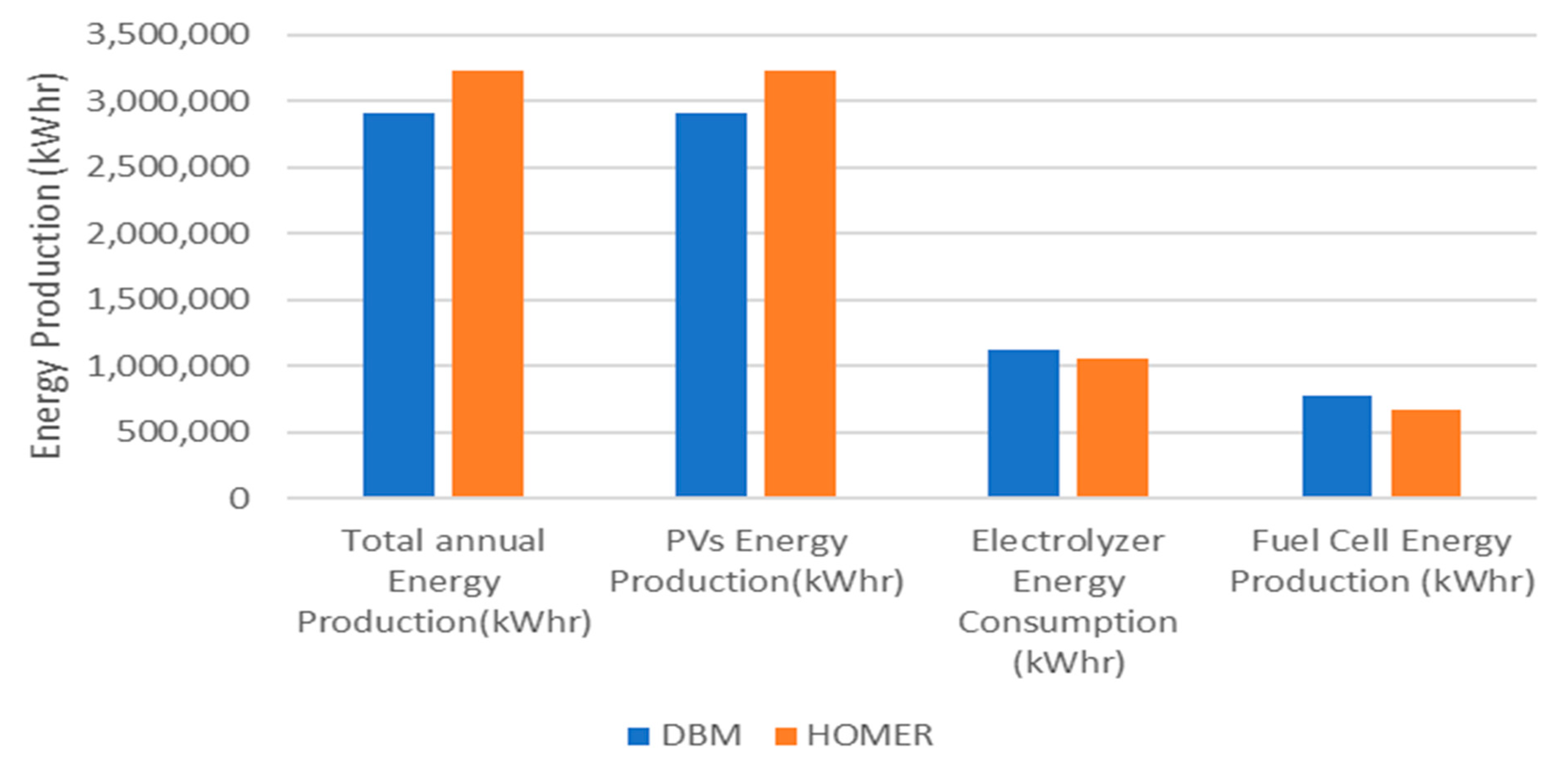
Preprints 72878 g013
Preprints 72878 g014
Figure 14. Power Curves for hybrid solar PV/Wind/Hydrogen system.
Figure 14. Power Curves for hybrid solar PV/Wind/Hydrogen system.
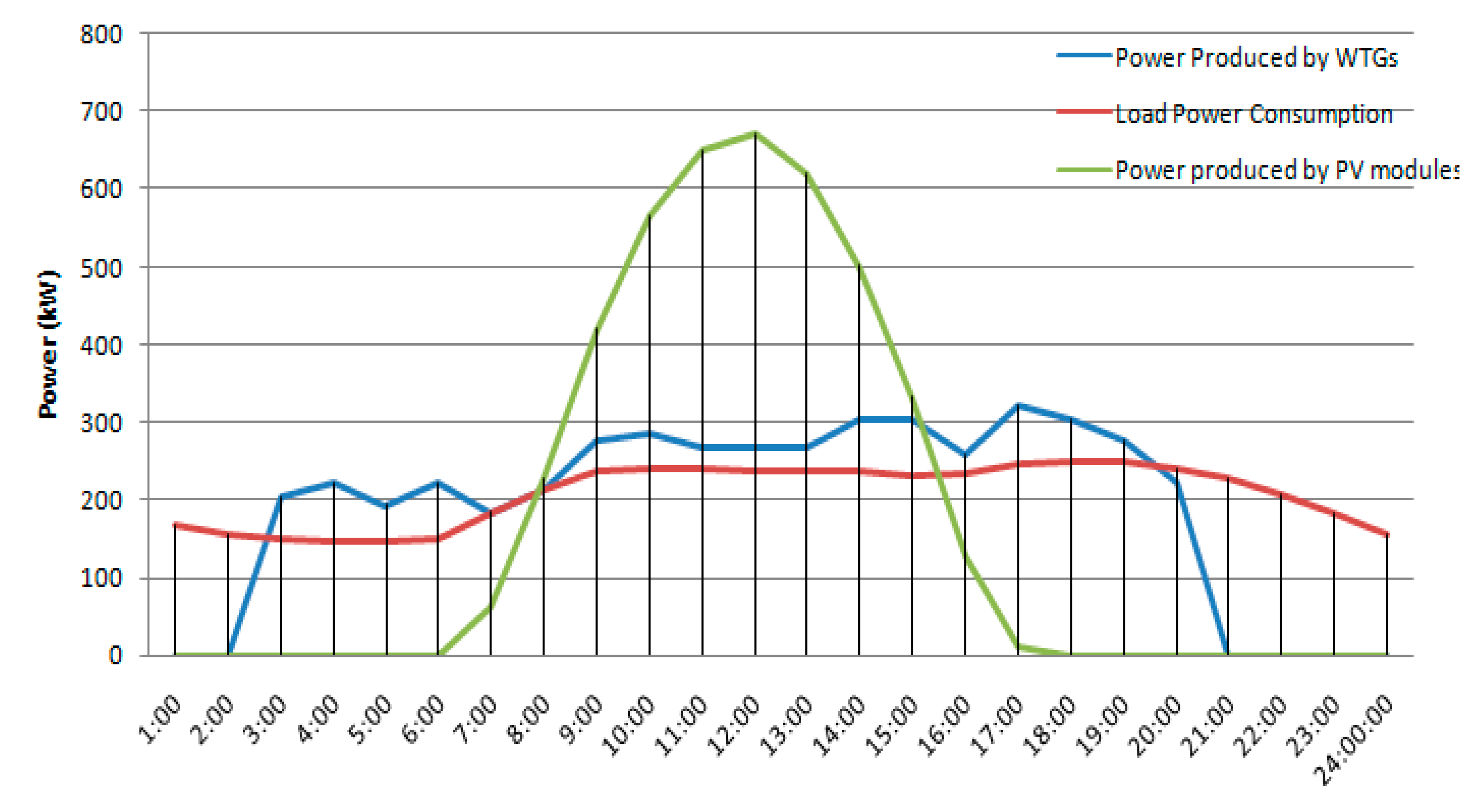
Preprints 72878 g014
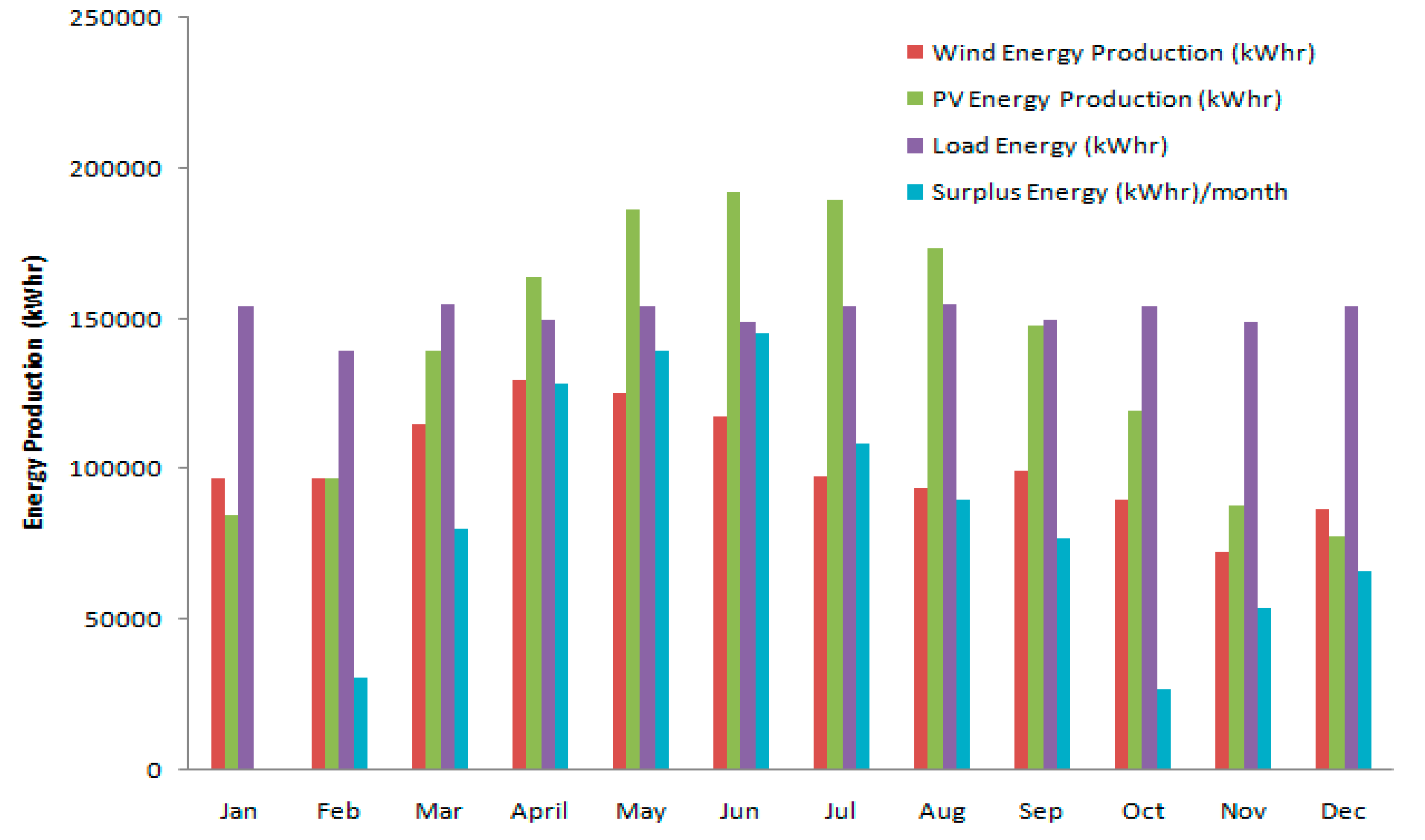
Preprints 72878 g015
Figure 15. Energy production using 500kW WTGs, 4200 m2 of PV modules.
Figure 15. Energy production using 500kW WTGs, 4200 m2 of PV modules.
Preprints 72878 g015
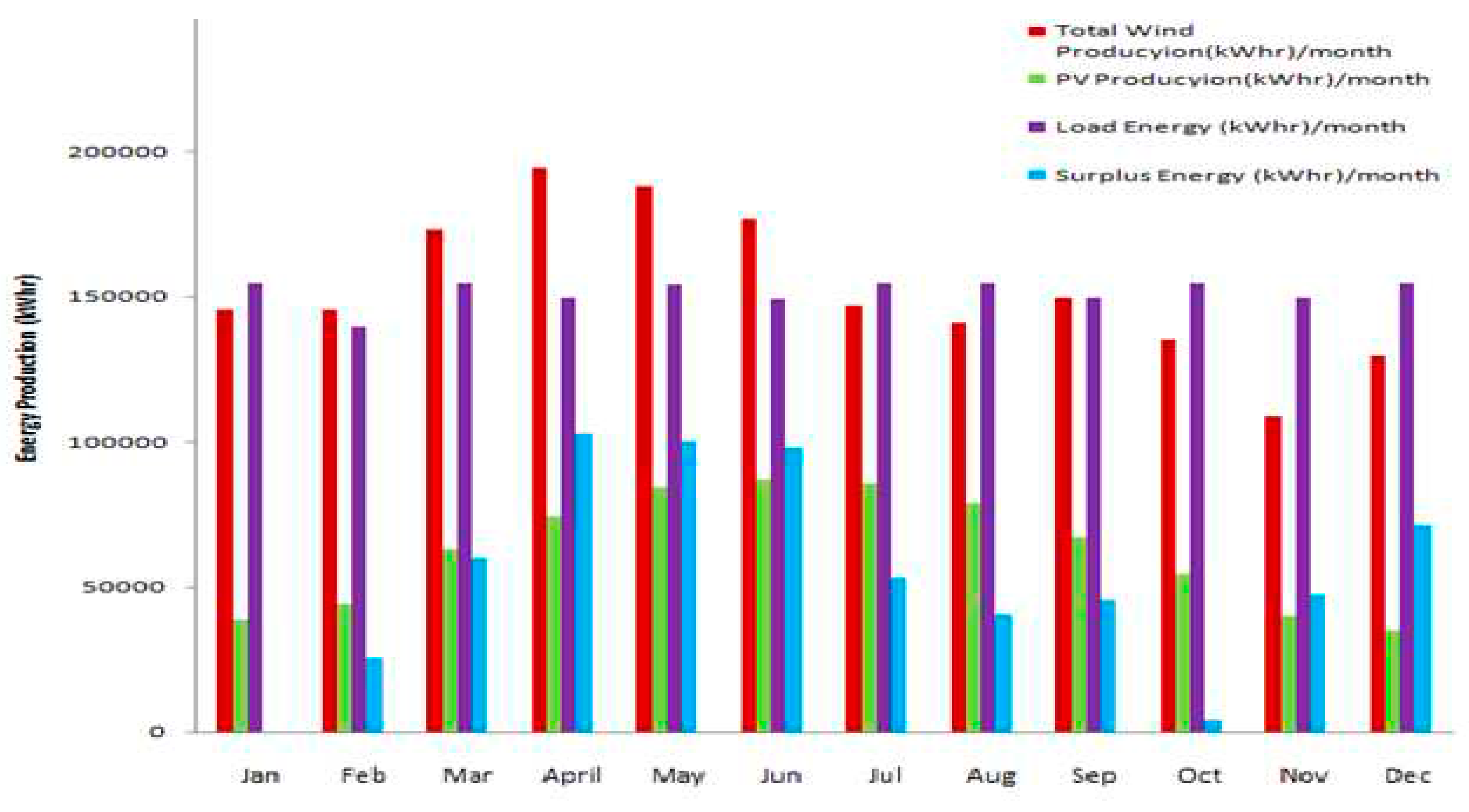
Preprints 72878 g016
Figure 16. Energy production using 750 kW WTGs, 1900 m2 of Solar modules.
Figure 16. Energy production using 750 kW WTGs, 1900 m2 of Solar modules.
Preprints 72878 g016
Preprints 72878 g017
Figure 17. Energy production using 250 kW WTGs, 7000 m2 of Solar module.
Figure 17. Energy production using 250 kW WTGs, 7000 m2 of Solar module.
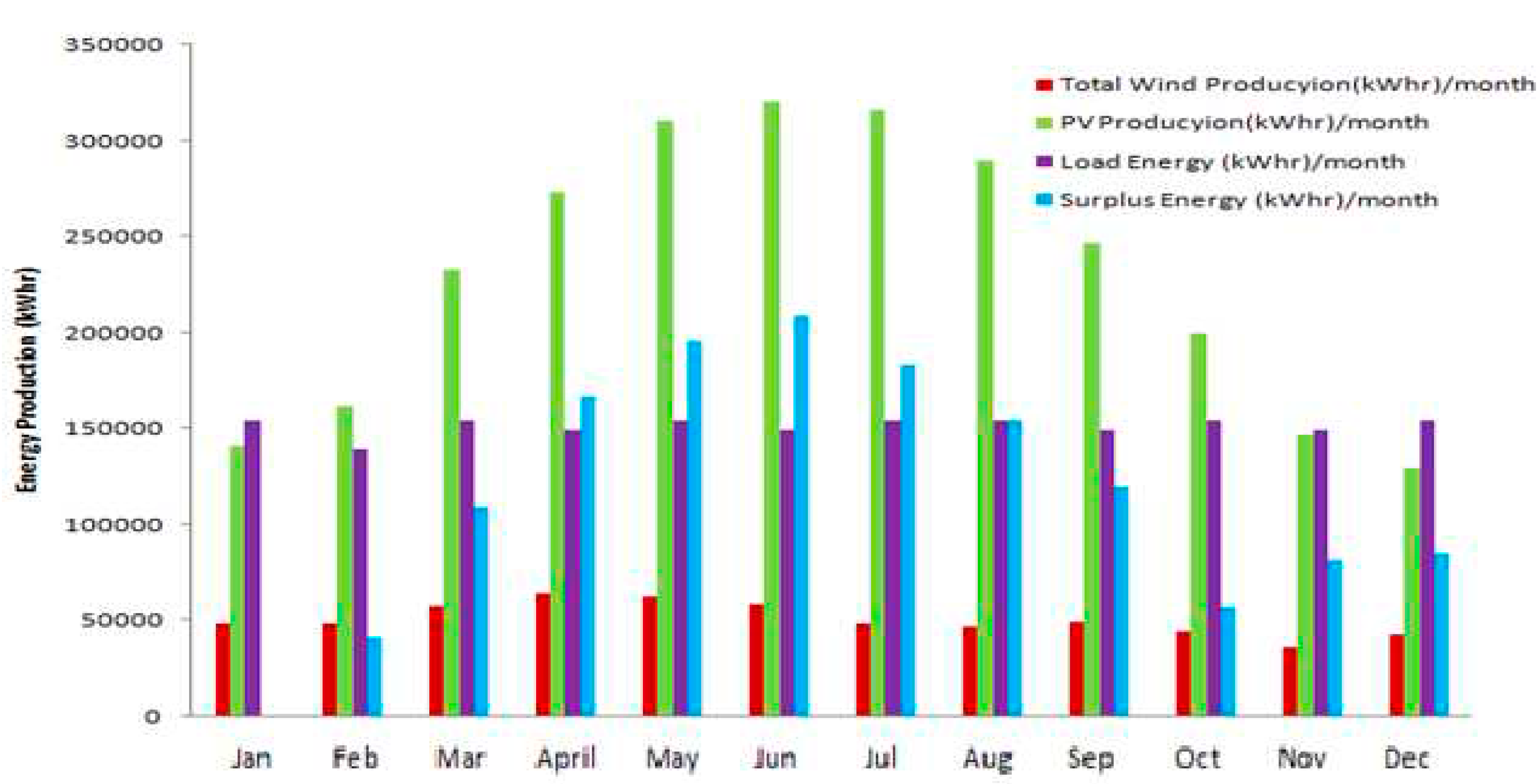
Preprints 72878 g017
Preprints 72878 g018aPreprints 72878 g018b
Figure 18. f. Hydrogen produced by Electrolyzer.
Figure 18. f. Hydrogen produced by Electrolyzer.
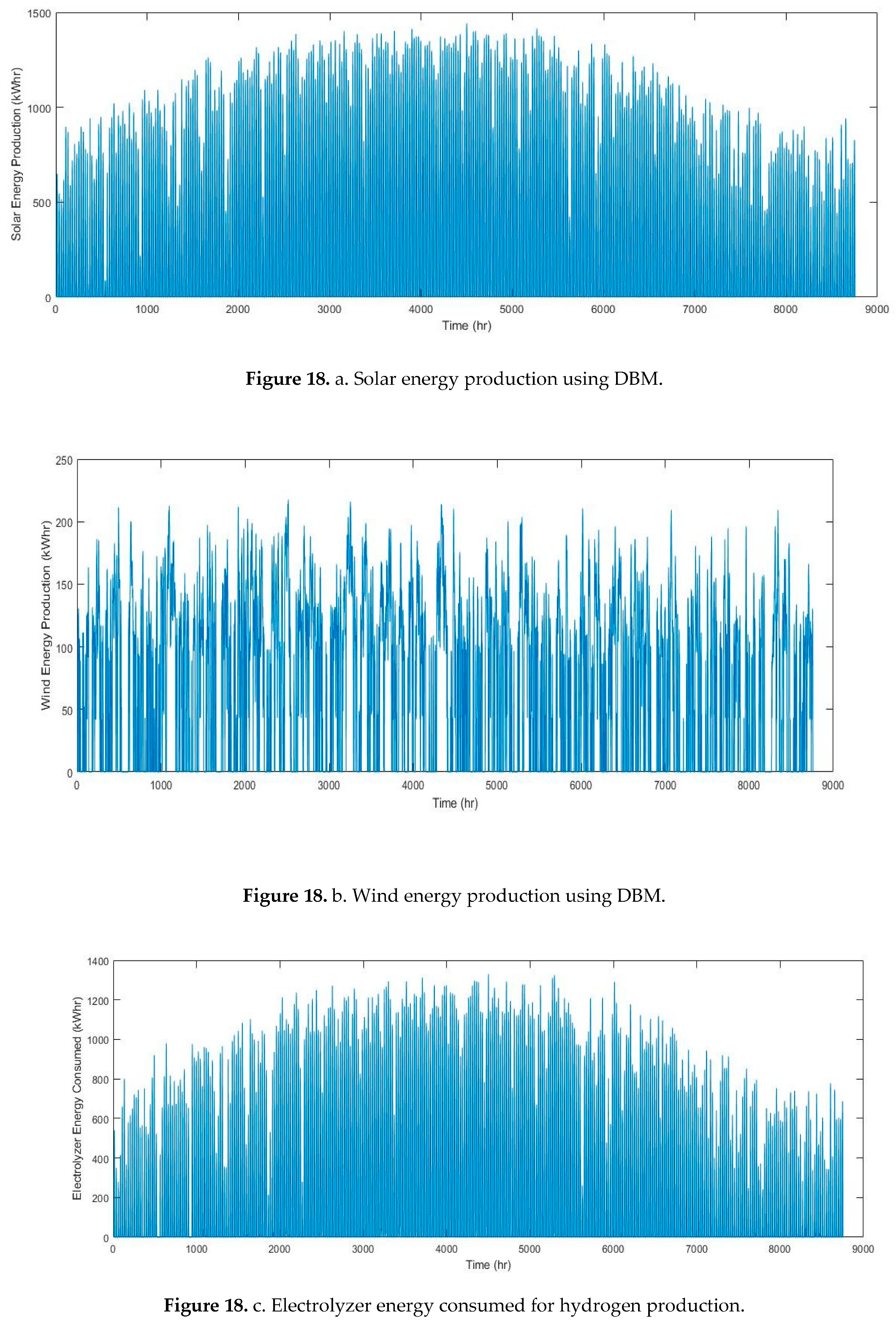
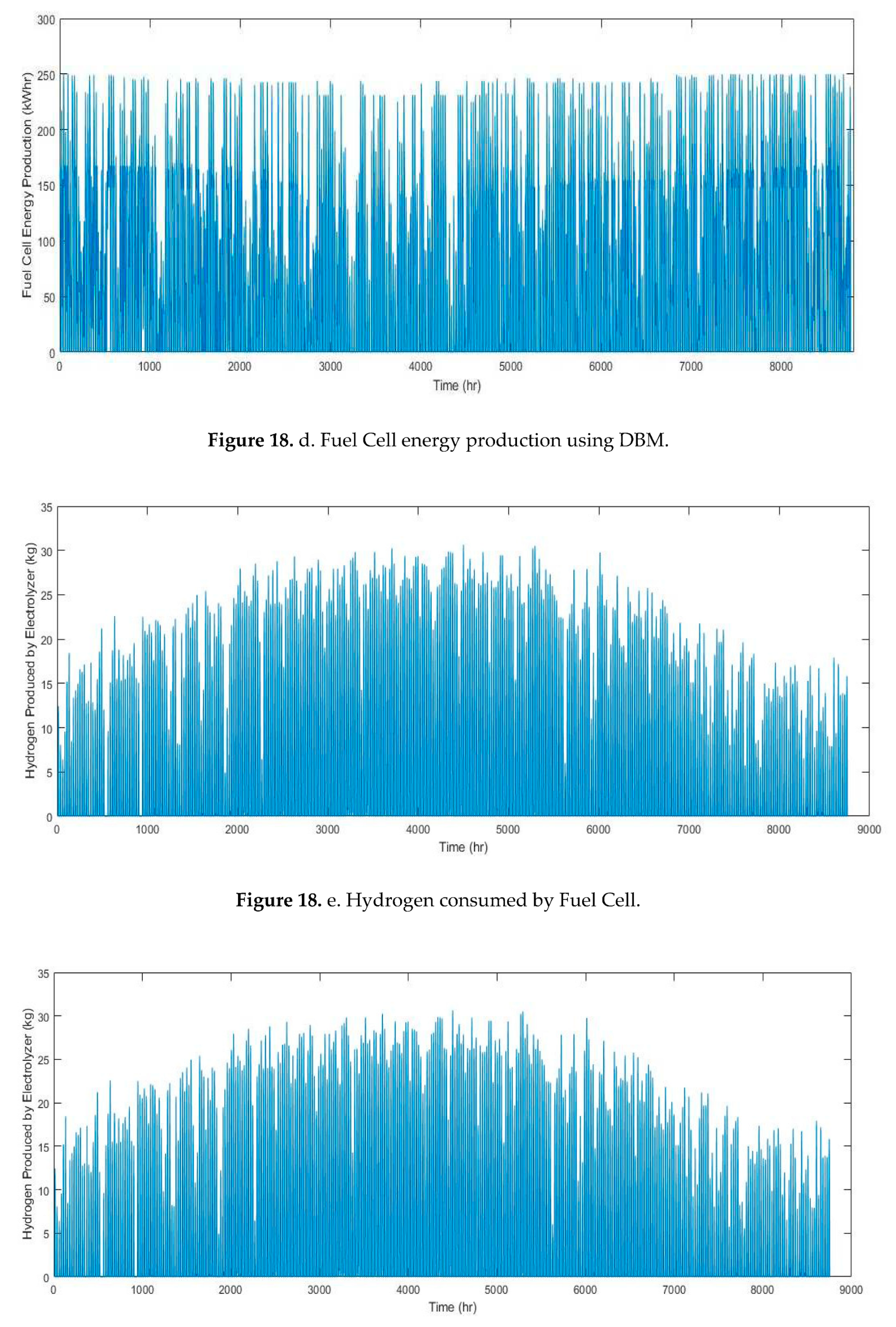
Preprints 72878 g018aPreprints 72878 g018b
Preprints 72878 g019
Figure 19. ratio of solar PV to wind turbines installed capacity
Figure 19. ratio of solar PV to wind turbines installed capacity
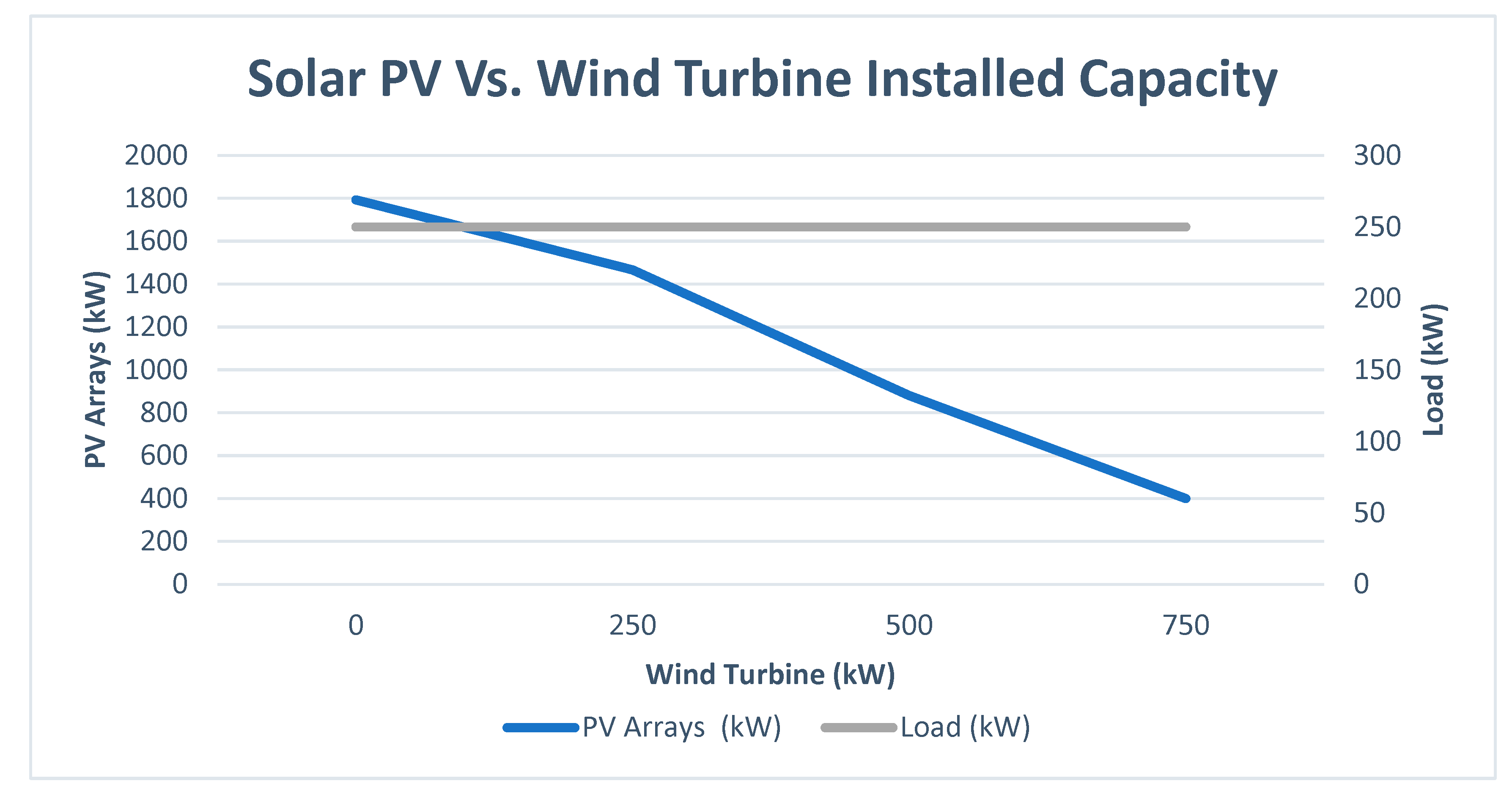
Preprints 72878 g019
Preprints 72878 g020
Figure 20. LCOE variation with PV to wind ratio.
Figure 20. LCOE variation with PV to wind ratio.
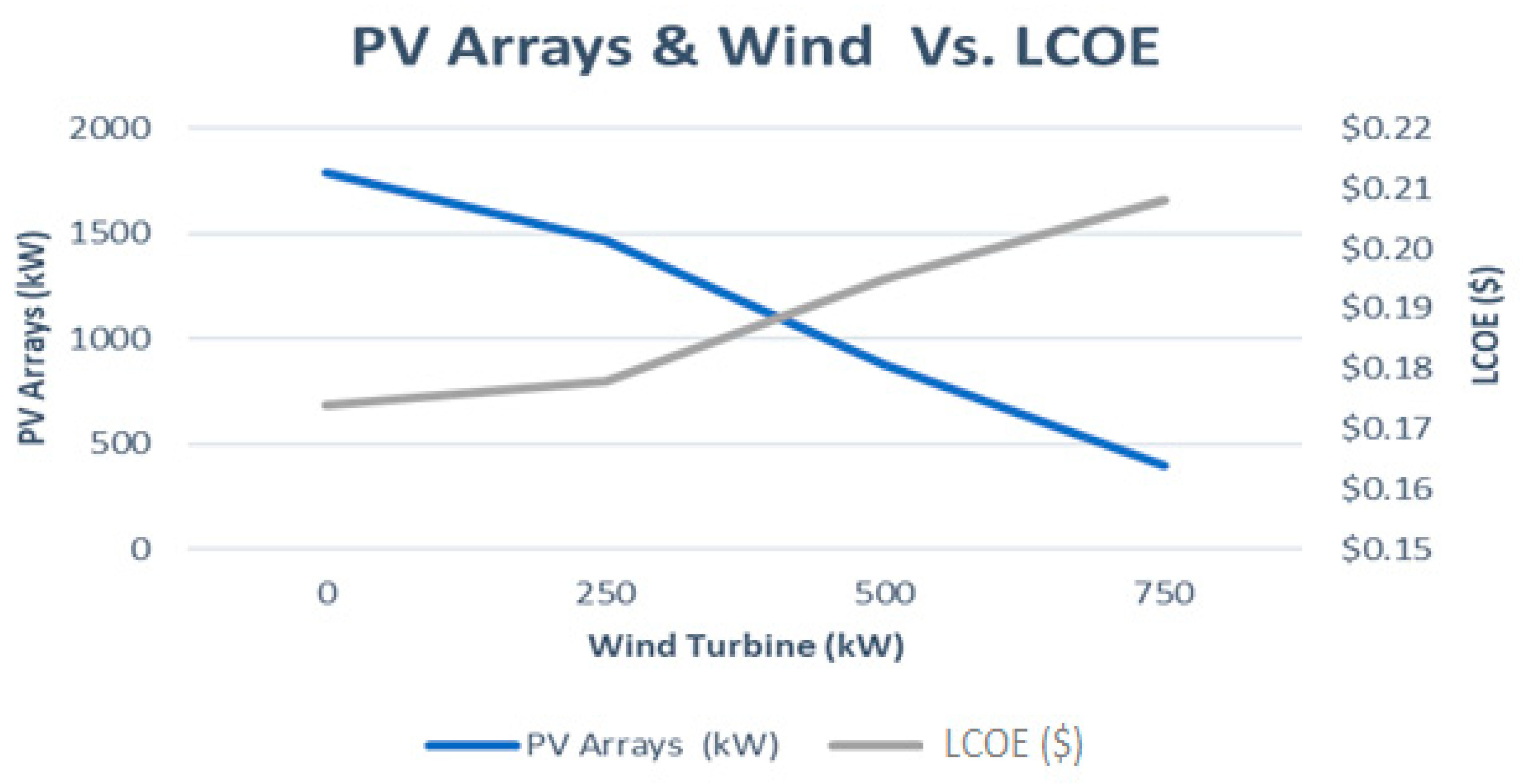
Preprints 72878 g020
Preprints 72878 g021
Figure 21. Cost structure of system 1.
Figure 21. Cost structure of system 1.
Preprints 72878 g021
Preprints 72878 g022aPreprints 72878 g022b
Figure 22. e. Hydrogen tanks storage level using HOMER [35].
Figure 22. e. Hydrogen tanks storage level using HOMER [35].
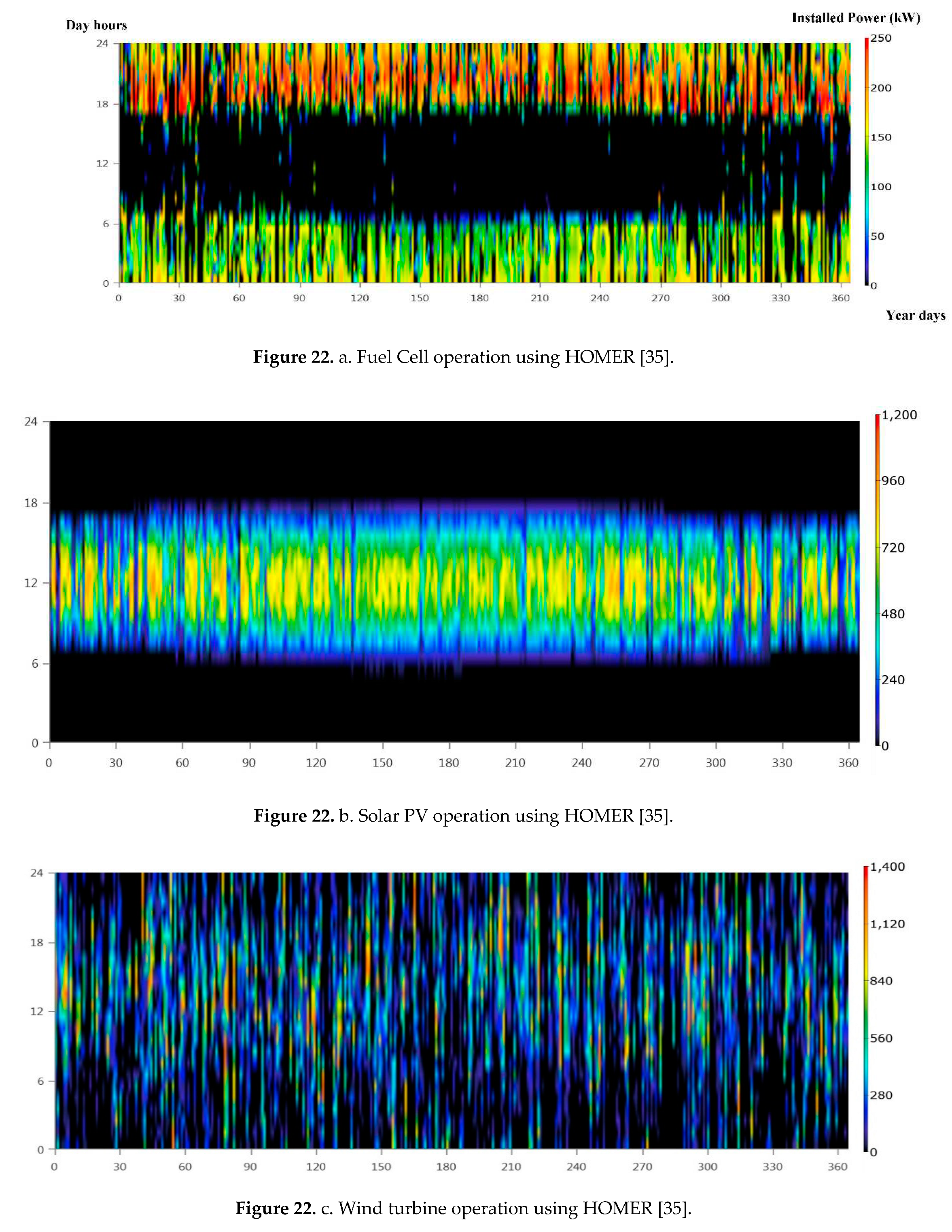
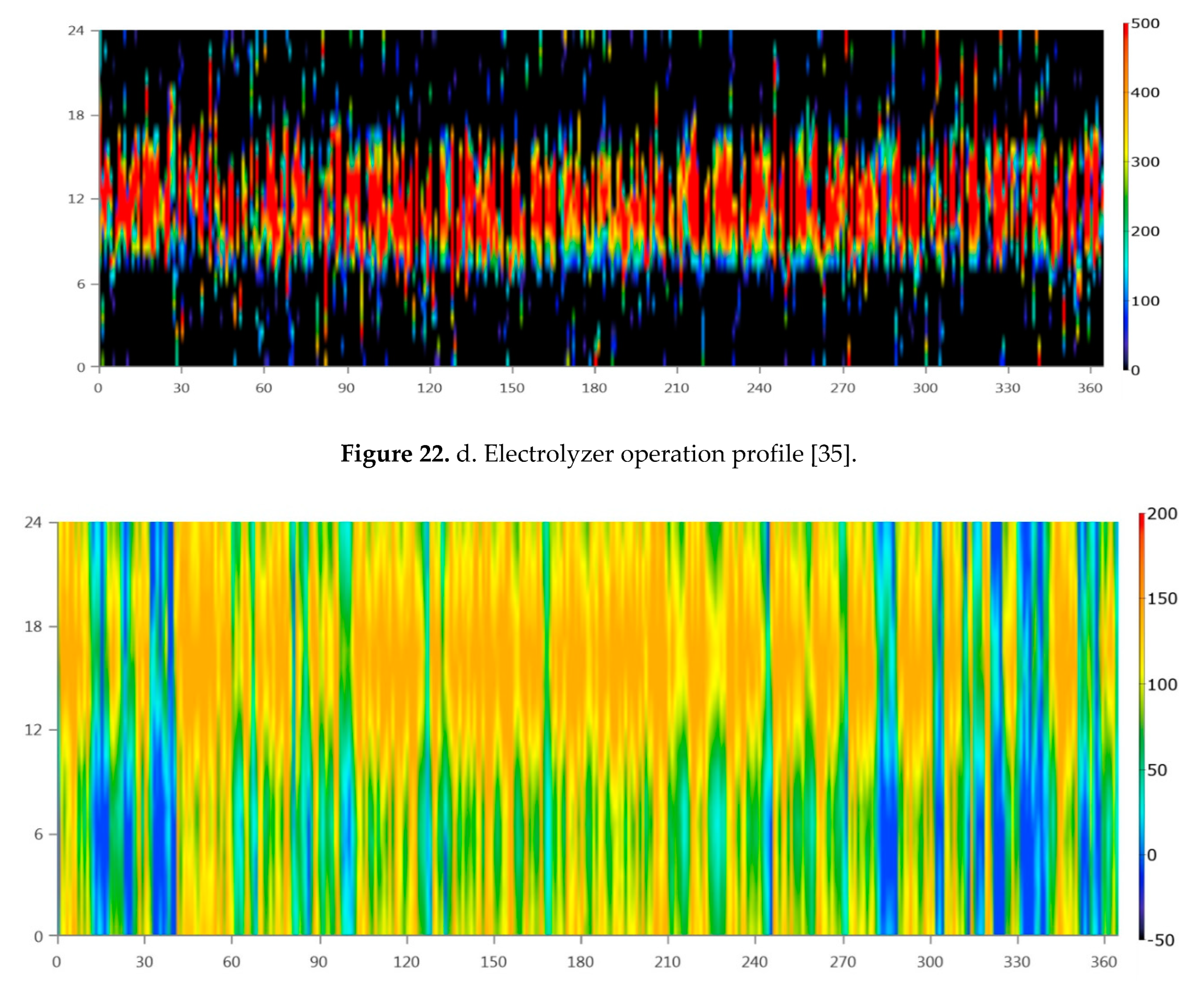
Preprints 72878 g022aPreprints 72878 g022b
Preprints 72878 g023
Figure 23. Comparing between installed capacities of hybrid system (PV/WTG/Hydrogen).
Figure 23. Comparing between installed capacities of hybrid system (PV/WTG/Hydrogen).
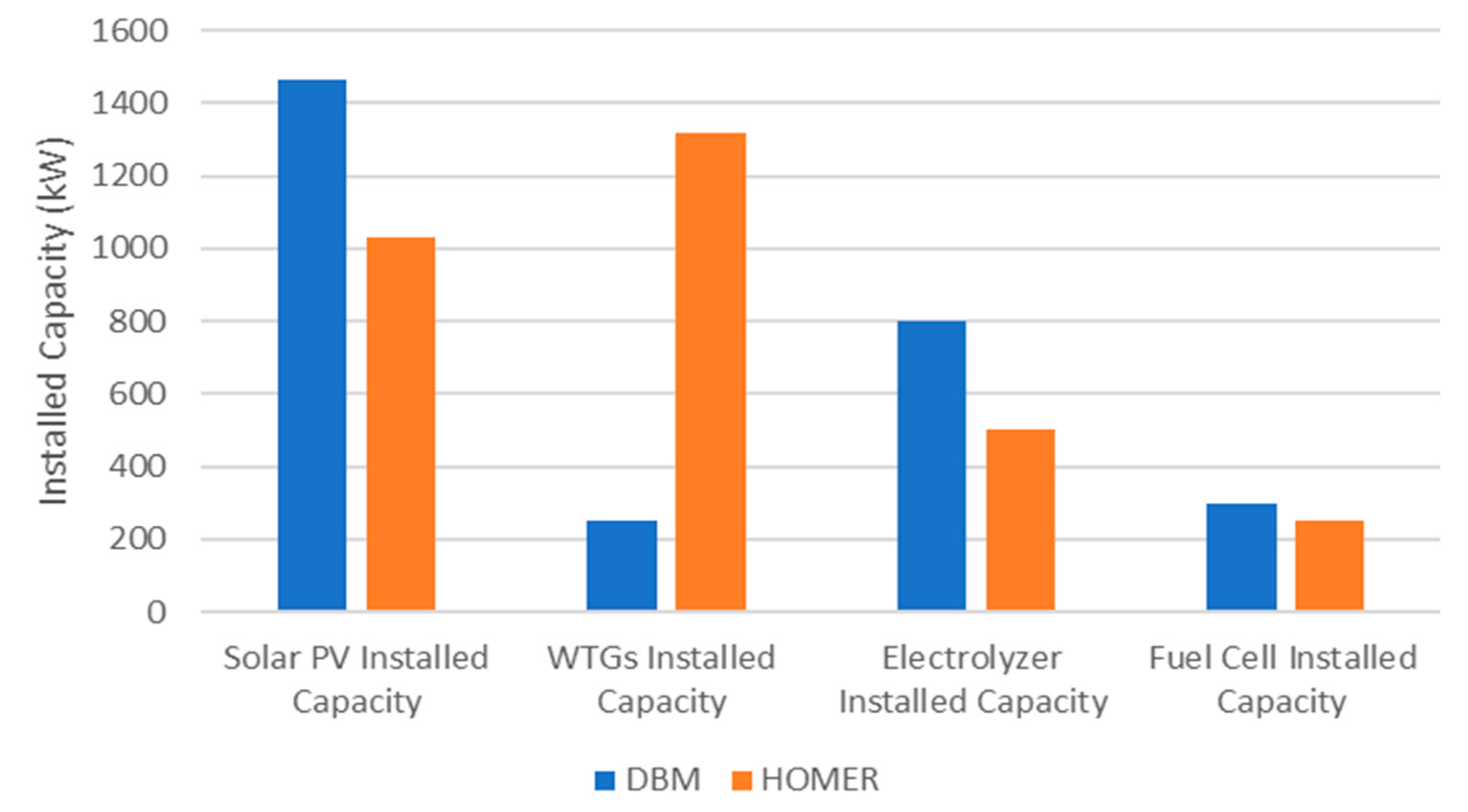
Preprints 72878 g023
Preprints 72878 g024
Figure 24. Comparing installed capacity for WTG standalone system.
Figure 24. Comparing installed capacity for WTG standalone system.
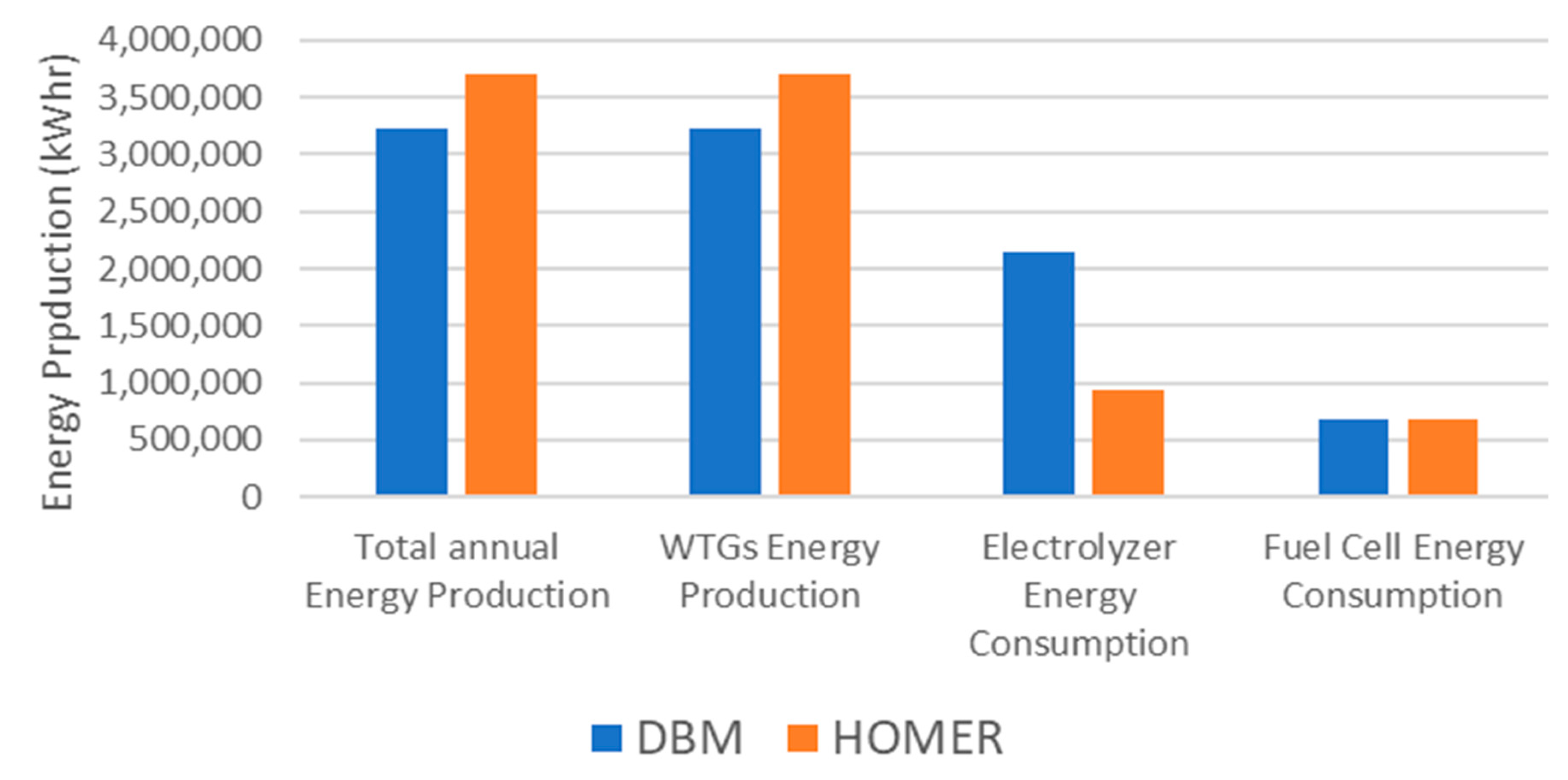
Preprints 72878 g024
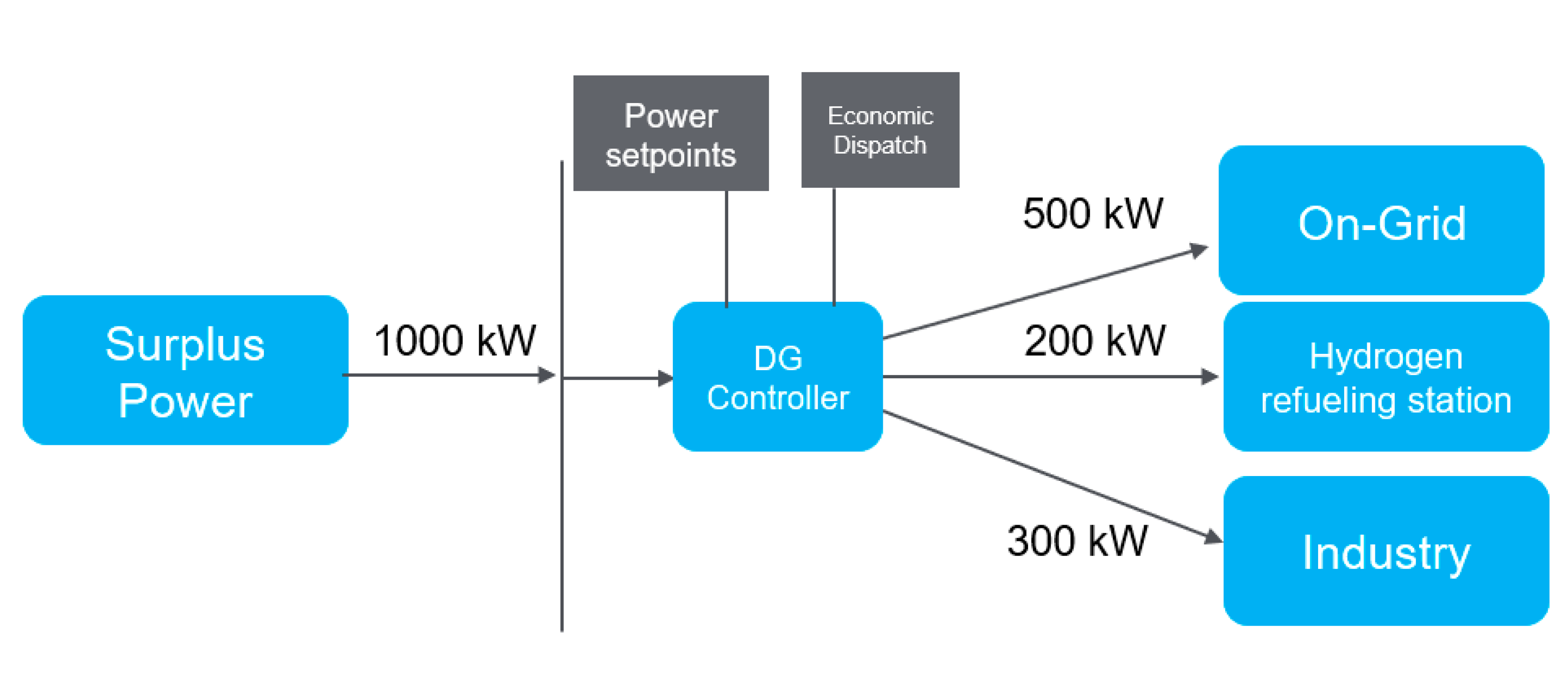
Preprints 72878 g025
Figure 25. Power sharing between cluster of DGs.
Figure 25. Power sharing between cluster of DGs.
Preprints 72878 g025
Table 1. Recent optimization research on HRES-H2 systems.
Table 1. Recent optimization research on HRES-H2 systems.
Hybrid system Method Discussion Authors/year
PV-WTG - battery - H2
storage 		Mixed-integer-linear programming The cogeneration model was created to regulate the energy repository system's two-way energy flow. The model can significantly reduce the cost of producing hydrogen overall, especially when the load profile is high. (Zhang et al., 2020)
WTG - PV-geothermal - H2
storage -battery		 Bi-level mixed-integer A model addressing the levelized cost of hydrogen was introduced in order to lower the cost of hydrogen generation. To address problems with system performance and dependability, the model includes a variety of continuous and discrete factors. (Pan et al., 2020)
Wind- PV – battery- H2
storage		 Particle swarm optimization The -constraint method minimizes the COE while constraining loss of power supply probability and non-renewable usage. Simulation and optimization use particle swarm optimization and HOMER software (Mokhtara et al., 2021)
PV – battery- H2
storage		 Iterative method Based on empirical data on electric power load, solar irradiation, and ambient temperature, the modeling process of the solar hydrogen energy system was examined using MATLAB. The cost of electricity was levelized by $0.195/kWh due to energy distribution, which is a financial consideration. (Hassan, 2020)
PV – battery- H2
storage 		Particle swarm optimization, genetic algorithm Systems operating in P-PMS mode outperformed R-PMS in terms of cost, renewable integration, and environmental impact. The efficiency of the chosen algorithms was found to be a significant determinant of P-PMS, though. P-PMS might greatly lessen how FC and ELZ instantaneous responses affect the size and operation of the energy system. (Brka et al., 2016)
WTG - PV - H2 storage -battery Multi-objective-genetic algorithm Using multi-objective optimization, a trigeneration system that produces ammonia, hydrogen, and electricity was examined. The measured range of the exergy efficiency was 10.9% to 38.2%, depending on the size of the meteorological data. (Siddiqui and Dincer, 2021)
WTG- PV – battery- H2
storage		 Flower pollination algorithm Renewable energy generation and hydrogen energy storage have an inverse relationship to the system's dependability restrictions. In some Iranian places, it was found that PV panels were more cost-effective than wind turbines. Moreover, wind turbines may be used as a reserve energy source to fulfill peak load requirements. (Hadidian Moghaddam et al., 2019)
WTG- PV – battery- H2
storage		 Improved salp swarm optimization algorithm (ISSOA) Dimensions of Hydrogen Tank and Battery storage In comparison to PV/WT with a battery storage system, H2 was shown to have a larger Cost of energy generation, while the latter exhibits superior system dependability. In terms of designing a hybrid system, ISSOA performed better than SSOA and PSO. (Vahid et al., 2020)
WTG- PV – H2 storage Hybrid grey wolf optimizer sine cosine algorithm When LSCS and LIP were taken into account, PV/WTG/FC was shown to be the best configuration to meet the load requirement. H2 was essential in reducing RE fluctuation, which helped the system achieve the highest level of dependability. The fuel cell's efficiency was shown to be inversely related to stored H2 and LSCS, while directly related (Jahannoosh et al., 2021)
WTG- PV – H2 storage HOMER The purpose of the study was to verify the effect of various storage technologies on HES. Minimum NPC and COE were supplied by the VRX battery system. The system made up of FC and H2 showed the fewest changes. By employing the load tracking control, it was discovered that the minimal SOC considering net cost fluctuated more than when using the load cycle control. (Arévalo et al., 2020)
Table 2. Cost analysis of the hybrid PV/hydrogen System.
Table 2. Cost analysis of the hybrid PV/hydrogen System.
Month Solar PV Fuel Cell Electrolyzer Hydrogen Tank
Capital Cost ($) 1,793,000 750,000 960,000 2000
Maintenance Cost ($) - 816,934 2,178,490
Replacement Cost ($) - 750,000 960,000
Annual revenue ($) 228,928
Annual net income ($) 109,111
Net present Value ($) -2,514,595*
Present value of O&M ($) 2,995,424
Present value of costs 6,500,424
Levelized annual cost ($) 716,139
Levelized Cost of energy ($/kWhr) 0.247
* net present cost was found to be with negative value indicating that the project will not be profitable with the currently selling prices for Solar PV plants announced by the government and the tariff prices will drastically increase in case of using hydrogen system as an energy storage system.
Table 3. System Components Specs.
Table 3. System Components Specs.
Photovoltaic Modules Hydrogen Tank
Rated Power (kW) 0.335 Capacity of hydrogen tank 100 kg
Type monocrystalline
Abbreviation: SPR-X21 Eefficiency 98%
Panel Type: Flat Type
Rated Capacity(kW): 0.335 Lifetime 15 years
`Temperature coefficient: -0.3
Operating temperature(C): 43 Initial tank level 10% relative to tank size
Efficiency (%): 21 Capital $14/kg
Manufacturer: Sun Power Replacement $14/kg
Model SunPower X21-335-BLK O&M $10/year/kg
Fuel Cell Electrolyzer
Nominal Power 250 kW Nominal Power 300 kW
H2 consumption rate 5800 Btu/kWhr H2 production rate 60 Nm3/hr
Input Pressure 15 psig Output pressure 10 barg-27barg
AC Power Production 5 AC power consumption 5 kWhr/Nm3
Nominal efficiency 90% Nominal efficiency 80%
Manufacturer ES5-EA2AAN Manufacturer Hydrogenics
Model Bloom Energy Model HySTAT-60-10
Capital $3000/kW Capital $1200/kW
Replacement $3000/kW Replacement $1200/kW
O&M $0.01/hour/kW O&M $100/year/kW
Table 5. Comparison between thesis sized hybrid systems.
Table 5. Comparison between thesis sized hybrid systems.
Point of Comparison PV/FC/ELZ WIND/FC/ELZ PV/WIND/FC/ELZ
Energy Production using DBM (kWhr) 2,905,172 3,223,807 3,377,699
Energy Production using HOMER (kWhr) 3,138,000 3,396,359 3,262,563
Absolute difference (%) -5% -5.3% +3.5%
Installed Capacity using DBM (kW) PV: 1793 kW
FC: 300 kW
ELZ:800 kW
H2 tank: 100 kg		 WTG: 1340 kW
FC:300 kW
ELZ:1000 kW
H2 tank: 100 kg		 PV: 1466 kW
WTG: 250 KW
FC: 300 kW
ELZ:800 kW
H2 tank: 100 kg
(best techno-economic config.)
Installed Capacity using HOMER PV: 1803 kW
FC: 200 Kw
ELZ:400 kW
H2 tank:100 kg		 WTG: 1980 kW
FC:200 kW
ELZ:500 kW
H2 tank:150 kg		 PV:1032 kW
WTG:1320 kW
FC:250 kW
ELZ:500 KW
H2 tank:150 kg
Levelized cost of energy-DBM $0.247 $0.237 $0.211
Levelized cost of energy-HOMER $0.332 $0.310 $0.232
Greenhouse emissions Only manufacturing material Only manufacturing material Only manufacturing material
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated