Prerpints.org logo
Preprint
Article

A Wheeler-DeWitt Quantum Approach to the Branch-cut Cosmology with Ordering Parameters

Altmetrics

Downloads

150

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 May 2023

Posted:

08 May 2023

You are already at the latest version

Alerts
Abstract
In this contribution to the Festschrift for Prof. Remo Ruffini, we investigated a formulation of quantum gravity based on the Wheeler-DeWitt (WDW) equation combined with the classical concepts of the branch-cut cosmology, which contemplates as a new scenario for the origin of the Universe, a smooth transition region between the contraction phase, prior to the primordial singularity, and the subsequent expansion phase. Through the introduction of an energy-dependent effective potential, which describes the space-time curvature associated with the embedding geometry and its coupling with the cosmological constant and matter fields, solutions of the WDW equation for the wave function of the Universe are obtained. The Lagrangian density is quantized through the standard procedure of raising the Hamiltonian, the helix-like complex scale factor of branched cosmology as well as the corresponding conjugate momentum to the category of quantum operators. As a novelty, ambiguities in the ordering of the quantum operators are overcome with the introduction of a set of ordering factors α, whose values are restricted to the integers α=[0,1,2], since non-integers have no physical meaning, allowing this way a broader class of solutions for the wave function of the Universe. As another novelty, additional energy-dependent parametrizations are considered, more specifically, in addition to a branched universe filled with underlying background vacuum energy, matter and radiation, in order to make contact with standard model calculations, we additionally supplement the formulation with baryon matter, dark matter and quintessence contributions. As an additional novelty, the boundary conditions for the wave function of the Universe are imposed by assuming the Bekenstein criterion. Our results indicate this way, as a novelty conclusion, the consistency of a topological quantum leap, or alternatively a quantum tunneling, for the transition region of the early universe in contrast to the classic branched cosmology view of a smooth transition.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

The equation developed by Wheeler and DeWitt, in 1967, represents a fundamental approach for describing quantum gravity [1]. This model, based on the Arnowitt-Deser-Misner decomposition of canonical general relativity in 3 + 1 dimensions, is additionally complemented by a boundary term proposed by the authors of Ref. [2,3,4,5]. Dirac’s canonical quantization procedure applied to the resulting Einstein-Hilbert action, then results in the equation developed by Wheeler and DeWitt (WDW), a second-order functional differential equation defined in a configuration superspace, whose functional solutions depend in general on a three-dimensional induced metric and matter fields [1,5,6,7].
Recently, we have proposed a topological canonical quantum approach [8] for the classical branch-cut cosmology [9,10,11] on basis of the WDW equation [1], whose solutions, represented by a geometric functional of compact manifolds and matter fields, describe the evolution of the quantum wave function of the Universe [6,7]. As a corollary of our approach, our expectations are that the WDW equation may provide the most complete dynamics of quantized gravity [12].
In this contribution we go beyond the previous formulation, overcoming ambiguities in the ordering of quantum operators by introducing a set of ordering factors α , whose values are restricted to the integers α = [ 0 , 1 , 2 ] , since non-integer values have no physical meaning, thus allowing a broader class of solutions for the wave function of the Universe. As another novelty, additional energy-dependent parameterizations are considered in the effective potential of the branched cosmology, with the incorporation, — in addition to the presence in the Universe of the background vacuum energy, matter and radiation —, of baryon matter, dark matter and quintessence contributions. Finally, as an additional novelty, boundary conditions for the wave function of the Universe are imposed by assuming the Bekenstein criterion [13], which indicates the existence of an universal upper bound of magnitude 2 π R / ℏ c to the entropy-to-energy ratio S / E of an arbitrary system of effective radius R. As a conclusion, as we will see, our results indicate the consistency of the proposition of a topological quantum leap, or alternatively, a quantum tunneling of the wave function of the Universe, in the primordial transition region in contrast with the classic view of the branched cosmology of a smooth transition between the contraction phase, before the primordial singularity, and the later phase of cosmic expansion.

2. Extended class of the branched quantum cosmological solutions

In what follows we investigate a branched quantum formulation of the WDW equation, whose dynamical variables, the helix-like scale factor analytically continued to the complex plane as well as the corresponding conjugate momentum are raised to the rank of quantum operators.

2.1. Branch-cut formulation of the Weeler-DeWitt Equation

The complex scale factor ln − 1 [ β ( t ) ] represents, in branched cosmology, the only dynamical variable1. The branched manifold M is in turn layered on hypersurfaces, Σ t , which are restricted to Riemann leaves characterized by a complex time parameter, t, with the normalized branching line element analytically continued in 4 dimensions and defined as [10,11]
d s [ ac ] 2 = − σ 2 N 2 ( t ) c 2 d t 2 + σ 2 ln − 1 [ β ( t ) ] 2 d r 2 1 − k r 2 ( t ) + r 2 ( t ) d θ 2 + s i n 2 θ d ϕ 2 .
In this expression, the variables r and t represent respectively, real and complex spacetime parameters and k the spatial curvature of the multiverse, more specifically, negatively curved (k=-1), flat (k = 0) or positively curved (k=1) spatial hypersurfaces. N ( t ) in turn represents the lapse2 function with σ 2 = 2 / 3 π denoting a normalisation factor.
In what follows, we consider as a starting point the renormalizable Hořava-Lifshitz theory of gravity whose action, given by S H L , employs terms dependent on the scalar curvature of the Universe and its derivatives, in different orders, defined in the form [14,15]:
S H L = M P 2 ∫ d 3 x d t N − g { K i j K i j − λ K 2 − η 0 M p 2 − η 1 R − η 2 M P − 2 R 2 − η 3 M − 2 R i j R i j − η 4 M P − 4 R 3 − η 5 M − 4 R ( R j i R i j ) − η 6 M − 4 R j i R k j R i k − η 7 M P − 4 R ∇ 2 R − η 8 M P − 4 ∇ i R j k ∇ i R j k } ;
in this expression η i denotes the coupling constants associated to the terms dependent on the curvature of the universe and its derivatives, M P represents the Planck mass, and ∇ i are the covariant derivatives. The branching Ricci components of the three dimensional metrics in equation (2) are determined by imposing a maximum symmetric surface foliation [8]. We then obtain
R i j = 2 σ 2 ln − 2 [ β ( t ) ] g i j , and R = 6 σ 2 ln − 2 [ β ( t ) ] ,
where R represents the branching scalar curvature. The trace of the extrinsic curvature tensor, K i j , which measures geometry modifications as well as deformation rates of the normal to a hypersurface as it is transported from one point to another, corresponds to a sub-manifold, which depends on the particular embedding and takes the form (for the details see [8])
K = K i j g i j = − 3 2 σ N d d t ln − 1 [ β ( t ) ] ln − 1 [ β ( t ) ] .
By means of canonical procedures, a Lagrangian density and the Hamiltonian of the model can be obtained (see [8,14,15]).

3. Spacetime topological quantization

The Lagrangian density of the model is quantized, trough a procedure called spacetime topological quantisation, by raising the Hamiltonian, the helix-like complex scale factor of branched cosmology as well as the corresponding conjugate momentum to the category of quantum operators. The resulting formulation describes the evolution of the wave function of the universe associated with hyper-surfaces Σ ln analytically continued to the complex plane.
Changing variable in the form u ( t ) ≡ ln − 1 [ β ( t ) ] , with d u ≡ d ln − 1 [ β ( t ) ] , the conjugate momentum p u of the original branching cosmology dynamical variable ln − 1 [ β ( t ) ] becomes
p u = − u ( t ) N d u ( t ) d t .
After applying standard procedures, the branching Hamiltonian is (for the details see [8,14,15])
H = 1 2 N u ( t ) − p u 2 + η k u 2 ( t ) − η Λ u 4 ( t ) − η r − η s u 2 ( t ) ,
with the dimensionless coupling constants redefined as [15,16]
η k ≡ 2 3 λ − 1 ; η Λ ≡ Λ M P I − 2 18 π 2 3 λ − 1 2 ; η r = 24 π 2 3 η 2 + η 3 ; η s ≡ 288 π 4 3 λ − 1 ( 9 η 4 + 3 η 5 + η 6 ) .
In this expression, η k , η Λ , η r , and η s represent respectively the curvature, cosmological constant, radiation, and stiff matter coupling constant contributions. The η r , and η s coupling constants can be positive or negative, without affecting the stability of the solutions. Stiff matter contribution in turn corresponds to the ρ = p condition in the corresponding equation of state.
The quantisation of the Lagrangian density is achieved by raising the Hamiltonian, the new dynamical variable u ( t ) and the corresponding conjugate momentum p u to the category of operators, represented respectively as H ^ ( t ) , u ^ ( t ) , and p ^ u :
H ( t ) → H ^ ( t ) ; u ( t ) → u ^ ( t ) ; a n d p u → p ^ u = − i ℏ ∂ u ( t ) ;
in what follows we simplify the notation by ignoring the use of the hat symbol in the operators u ^ and p ^ u as well as in most part of equations the time dependence on the new variable u ( t ) .
As a novelty, ambiguities in the ordering of the quantum operators are overcome with the introduction of a set of ordering factors, given by α = [ 0 , 1 , 2 ] , with p 2 defined as
p 2 ≡ − 1 u α ( t ) ∂ ∂ u ( t ) u α ( t ) ∂ ∂ u ( t ) ,
since intermediate non-integer values for α have no significance. This approach thus makes it possible to obtain a broader class of solutions for the wave function of the Universe.
Combining (6) and (9), we get the subsequent expression for the Wheeler-DeWitt equation for the wave function of the Universe, Ψ ( t ) :
− 1 u α d d u u α d d u + V ( u ) Ψ ( u ) = 0
with the effective potential
V ( u ) = − η r + η m u + η k u 2 + η q u 3 − η Λ u 4 − η s u 2 ,
which we supplemented as a novelty with two additional terms, η m u , that describes the contribution of baryon matter combined with dark matter, and η q u 3 , a quintessence-term. From this expression, for α = 0 , we obtain a Schrödinger-type equation under the action of a quantum real potential3 represented by V ( u ) :
− d 2 d u 2 + V ( u ) Ψ ( u ) = 0 .
For α = 1 , we get the equation
− 1 u d d u + d 2 d u 2 + V ( u ) Ψ ( u ) = 0 .
And for α = 2 , it results the equation
− 2 u d d u + d 2 d u 2 + V ( u ) Ψ ( u ) = 0 .
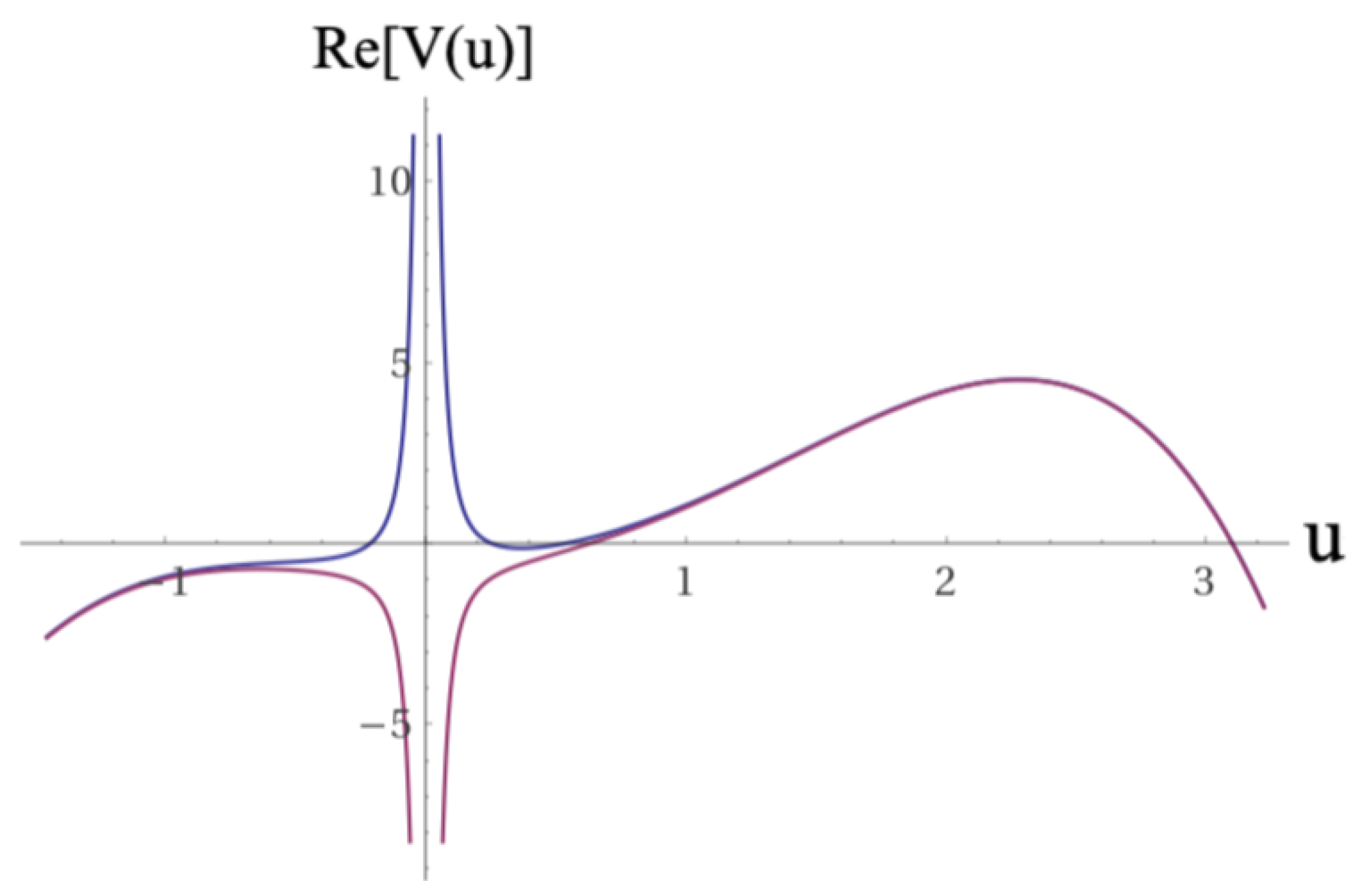
Preprints 72832 g001
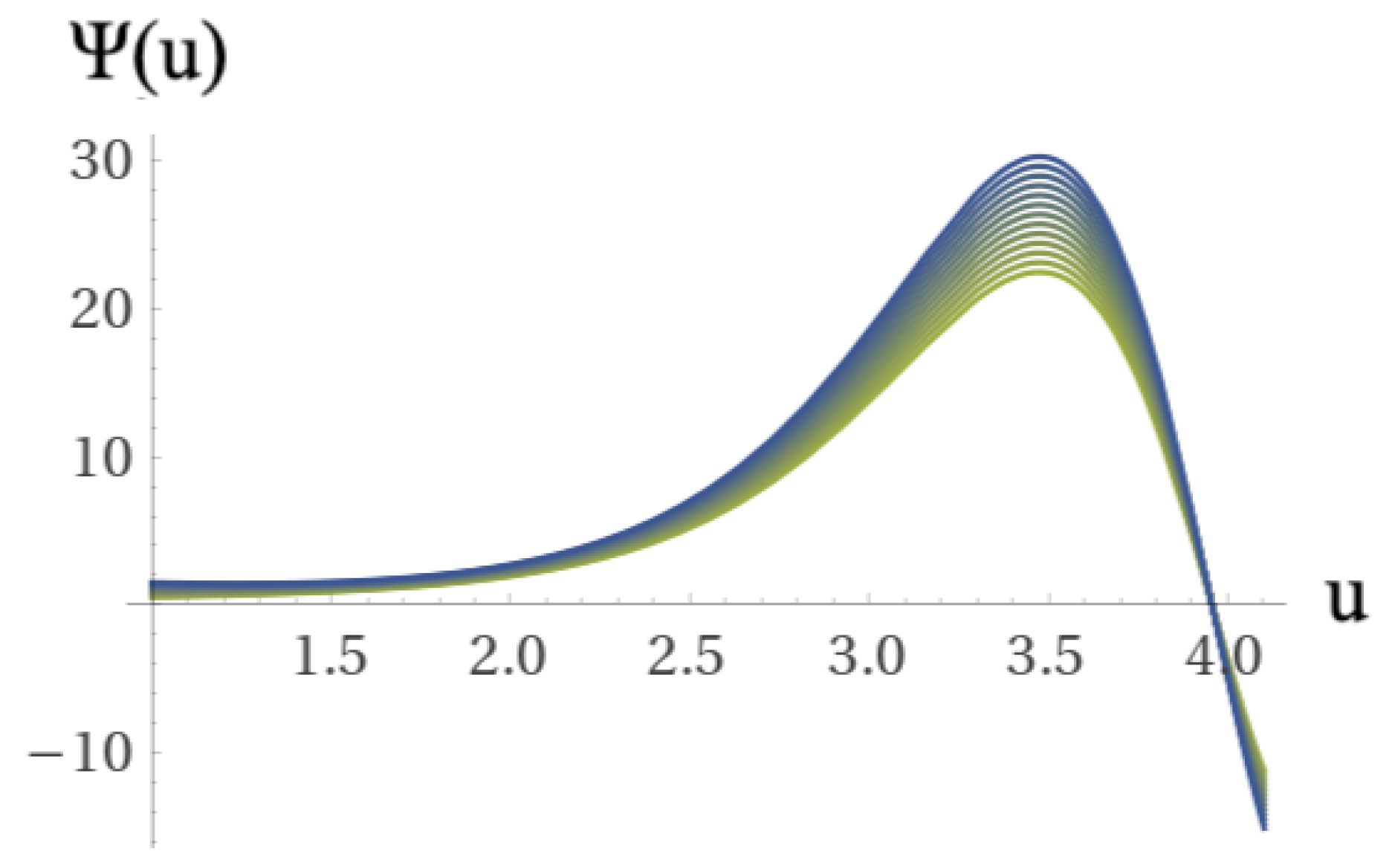
Figure 1. Plot of the real part of the potential defined in equation 11. In the top figure the coupling constants values are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . In the bottom figure the coupling constants values are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = + 0.03 . Values of parameters taken from [17,18,19].
Figure 1. Plot of the real part of the potential defined in equation 11. In the top figure the coupling constants values are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . In the bottom figure the coupling constants values are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = + 0.03 . Values of parameters taken from [17,18,19].
Preprints 72832 g001
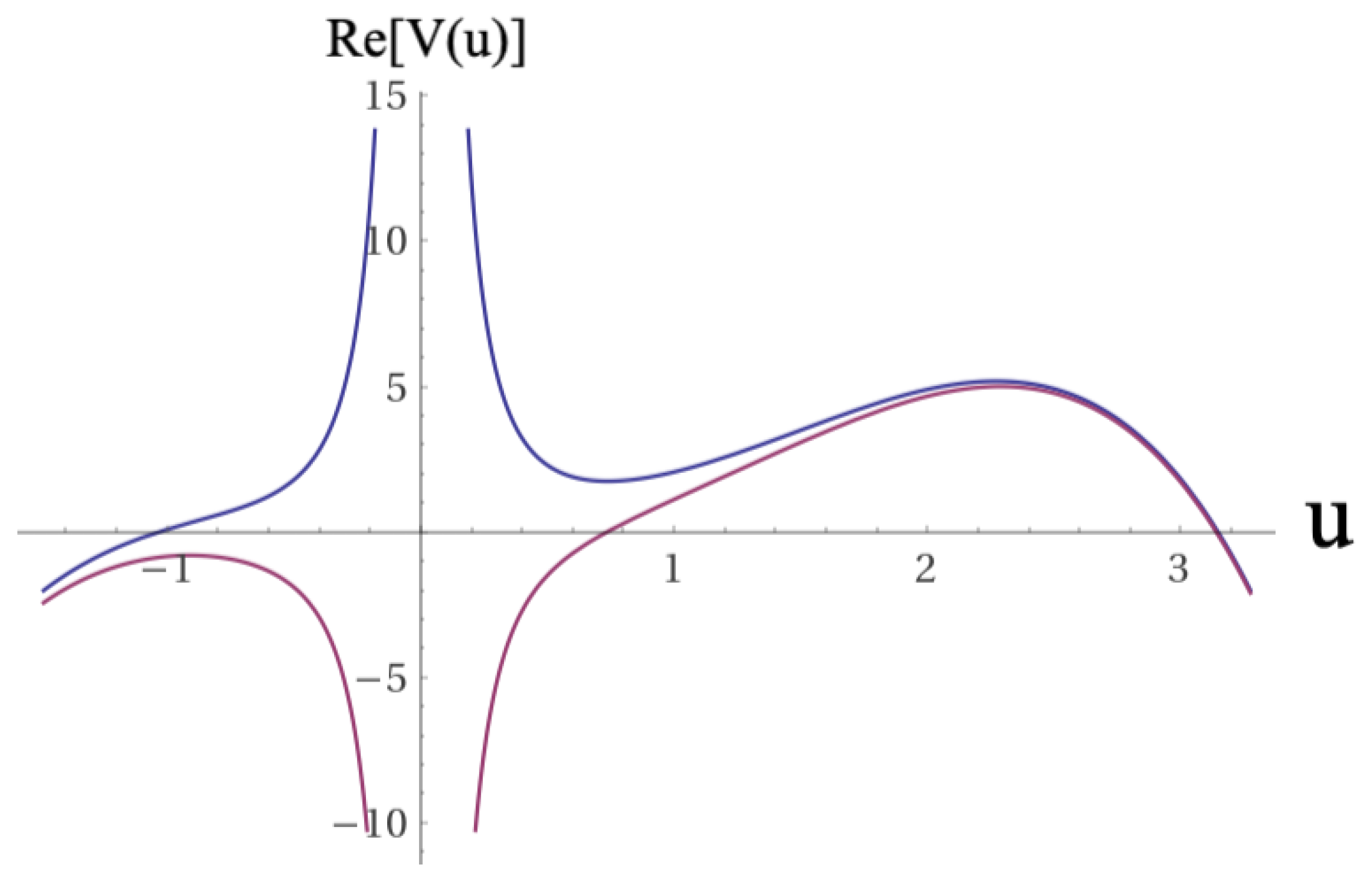
Preprints 72832 g002
Figure 2. Similar plot of the previous figure. Coupling constants values in the top figure: η r = 0.024 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.468 . Coupling constants values in the bottom figure: η r = 0.024 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = + 0.468 . Values of parameters taken from [17,18,19].
Figure 2. Similar plot of the previous figure. Coupling constants values in the top figure: η r = 0.024 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.468 . Coupling constants values in the bottom figure: η r = 0.024 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = + 0.468 . Values of parameters taken from [17,18,19].
Preprints 72832 g002
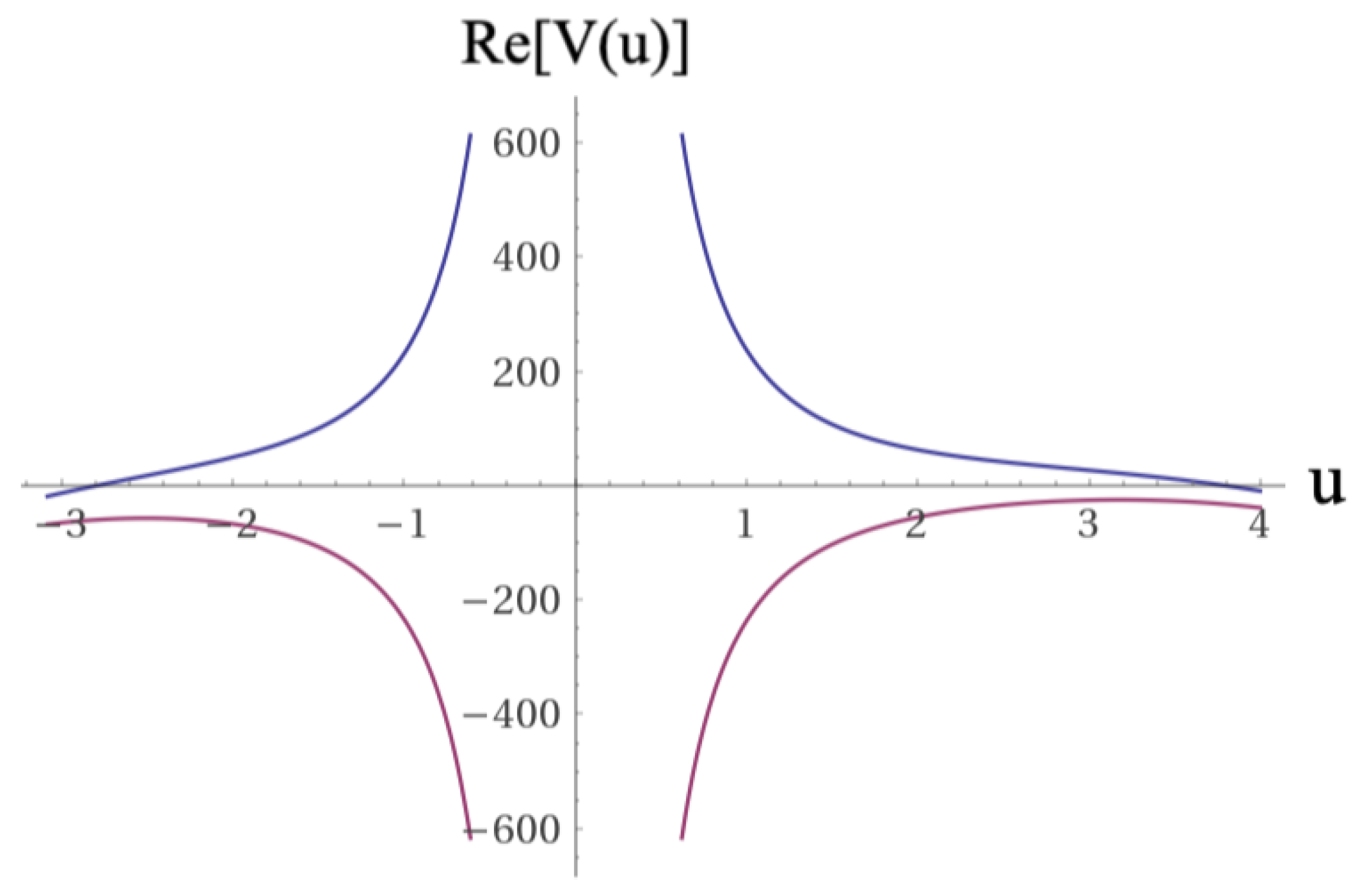
Preprints 72832 g003
Figure 3. Similar plot of the previous figure. Coupling constants values in the top figure: η r = 0.0 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 234.0 . Coupling constants values in the bottom figure: η r = 0.0 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = + 234.0 . Values of parameters taken from [17,18,19].
Figure 3. Similar plot of the previous figure. Coupling constants values in the top figure: η r = 0.0 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 234.0 . Coupling constants values in the bottom figure: η r = 0.0 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = + 234.0 . Values of parameters taken from [17,18,19].
Preprints 72832 g003
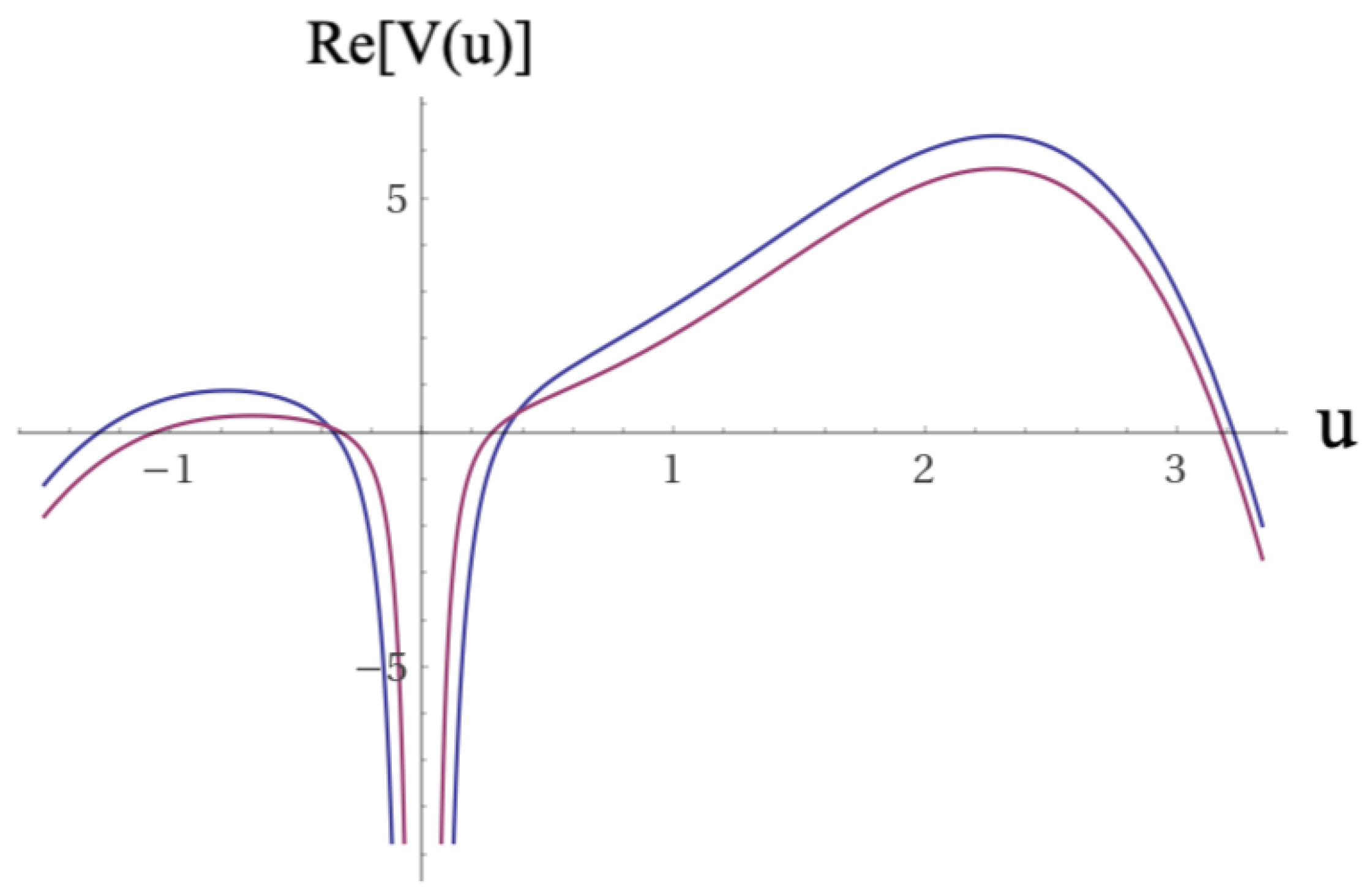
Preprints 72832 g004
Figure 4. Similar plot of the previous figure. Coupling constants values in the top figure: η r = − 1.22 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = 0.15 . Coupling constants values in the bottom figure: η r = − 0.5 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = 0.05 . Values of parameters taken from [17,18,19].
Figure 4. Similar plot of the previous figure. Coupling constants values in the top figure: η r = − 1.22 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = 0.15 . Coupling constants values in the bottom figure: η r = − 0.5 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = 0.05 . Values of parameters taken from [17,18,19].
Preprints 72832 g004
With a view to comparing results based on the standard formulation, in what follows, we set up the dimensionless coupling parameters of the effective potential with values found in the literature, complementing the coupling constants of baryon and dark matter and quintessence with a parametrization based on the total density parameter, Ω 0 , which describes the ratio between the total average density of matter and energy in the early Universe, ρ T and the critical density4, ρ c r i t . The most accepted value of the density parameter nowadays is:
Ω 0 ≡ ρ T ρ c r i t = Ω B + Ω D M + Ω Λ ∼ 0.04 + 0.23 + 0.73 ∼ 1 ,
where Ω B , Ω D M , and Ω Λ represent the baryon matter, dark matter and dark energy density parameters, respectively. At this stage of our investigation, we do not intend to obtain numerical data that may support future cosmological observations, but rather to seek first to establish a formal consistency in the treatment of the quantum branch-cut cosmology, with the aim of establishing observational predictions based on a consistent theoretical formulation in the future. There are numerous formulations in the literature, based on standard cosmology, that consistently deal with this problem, using improved technical models. Just to name a few of these, we indicate [12,15,17,20,21], among many others.
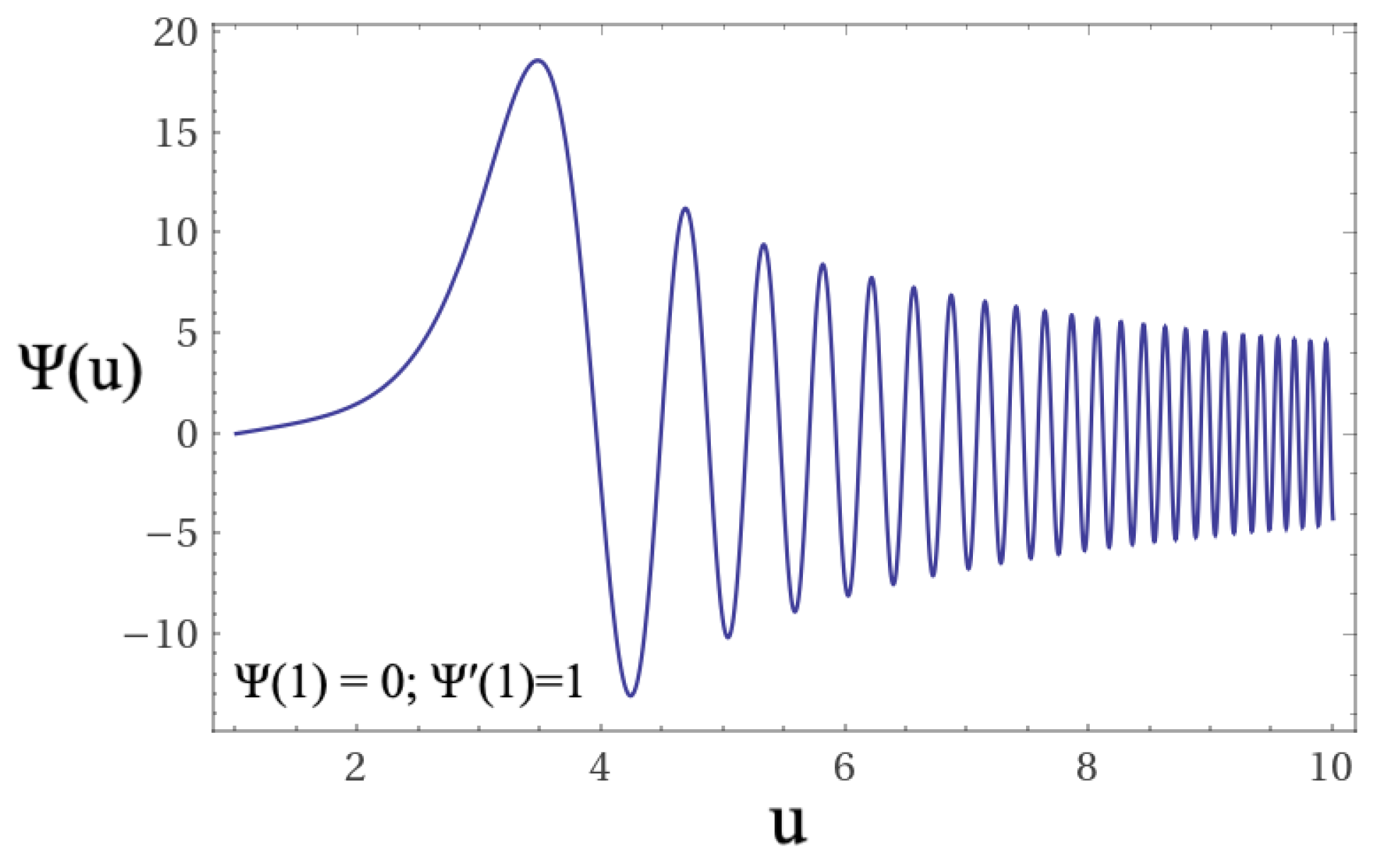
Figure 5 and Figure 6 show typical results of solving equation 12. Also typical results, but more systematized criteria of solutions of equations 12, 13, and 14 are presented in the following section.

3.1. Complex conjugation of the Friedmann’s-type wave equations

In the branching cosmology, the Friedmann’s-type equations, analytically continued to the complex plane, and expressed in terms of the new variables u ( t ) , are [9,10,11]:
d d t u ( t ) u ( t ) 2 = 8 π G 3 ρ ( t ) − k c 2 u ( t ) + 1 3 Λ ; d 2 d t 2 u ( t ) u ( t ) = − 4 π G 3 ρ ( t ) + 3 c 2 p ( t ) + 1 3 Λ ;
where Λ represents the cosmological constant. The corresponding complex conjugated Friedmann’s-type equations are:
d d t u * ( t * ) u * ( t * ) 2 = 8 π G 3 ρ * ( t * ) − k c 2 u * ( t * ) + 1 3 Λ * ; d 2 d t 2 u * ( t * ) u * ( t * ) = − 4 π G 3 ρ * ( t * ) + 3 c 2 p * ( t * ) + 1 3 Λ * .
These equations underlie the scenarios of branched cosmology in the imaginary sector: in the first scenario, in the region before the primordial singularity, there is a continuous evolution of the Universe around a branch-cut in the transition region as a function of an imaginary time parameter, conjugated to the corresponding time parameter of the later evolutionary region and no primordial singularity occurs; in the second scenario, the branch-cut and the branch point disappear after realization of the imaginary time by means of a Wick rotation, then this parameter is replaced by the real and continuous thermal time, the temperature. As a result, a parallel evolutionary mirror universe, adjacent to our own, is nested in the fabric of space and time, with its evolutionary process receding into the cosmological sector of negative thermal time. In the following, we adopt, as a consistent formal procedure, conjugated complex versions of expressions (12), (13), and (14). And as a consequence of this procedure, solutions of the wave function of the Universe that describe the quantum evolution of the scenarios described above can be obtained.

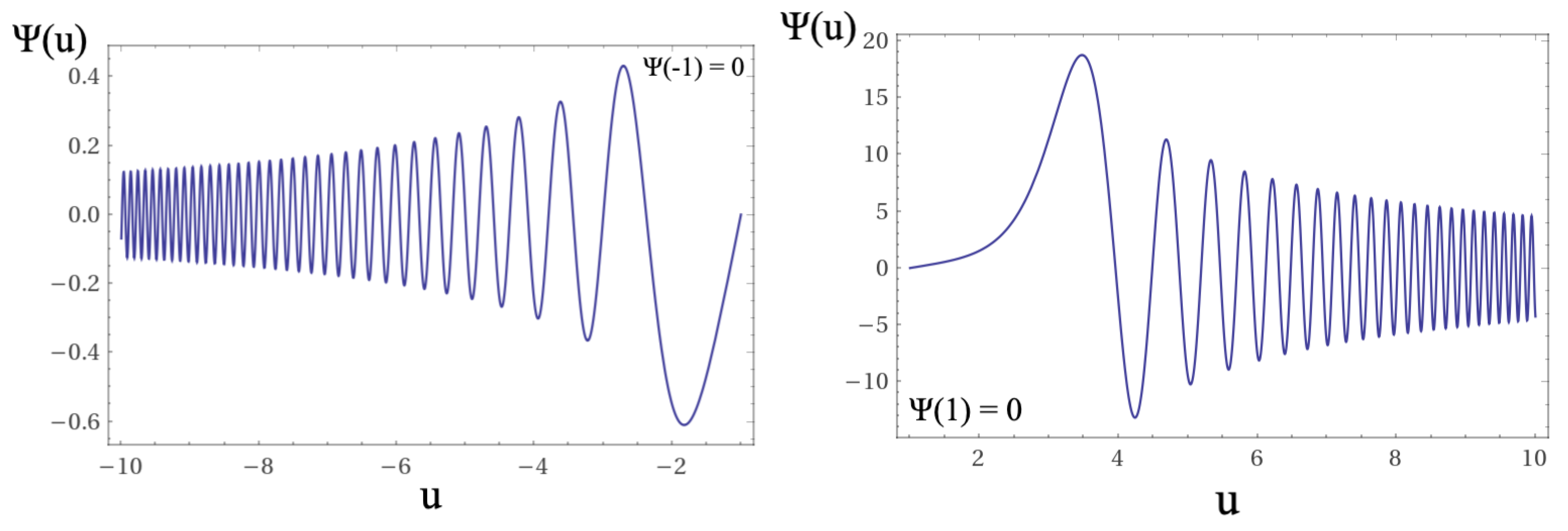
3.2. Solutions and Boundary Conditions

The boundary conditions adopted in this work follows the natural canons of convergence, as well as stability and continuity of the solutions of the differential equations. Moreover, as a novelty in this contribution, we analyze the boundary conditions of the wave function of the Universe in the light of the Bekenstein criterion.
The impossibility of packing the energy and entropy of the primordial Universe into finite dimensions considering spatially connected regions within the particle horizon of a given observer, locus of the most distant points that can be observed at a specific time t 0 in an event, made Bekenstein conjecture an upper bound, given by 2 π R ℏ c , for the entropy S and energy E of a system contained in a spherical region of radius R:
2 π R ℏ c ≥ S / E so S ≤ S B = 2 π ℏ c E R ,
in which S B denotes the upper limit of Bekenstein entropy.
Considering in a simplified way the proper distance d ( t ) of a pair of objects, in an arbitrary time t and its relationship with the proper distance d ( t 0 ) in a reference time t 0 , d ( t ) = u ( t ) d ( t 0 ) , this implies that for t = t 0 , u ( t 0 ) = 1 . We consider the condition | u ( t 0 ) = 1 | as a boundary condition in our calculation, assuming the time t 0 as the locus of the most distant points that can be observed, in tune with the Bekenstein criterion applied to the branched cosmology. With this assumption, due to the structural characteristics of the proposed effective potential and the extended class of solutions for the wave equations, the wave function of the Universe ‘naturally’ obeys the following boundary conditions in the expansion sector of the primordial Universe: Ψ ( 1 ) = 1 , Ψ ′ ( 1 ) = 0 and Ψ ( 1 ) = 0 , Ψ ′ ( 1 ) = 1 . Similarly, in the contraction sector of the primordial Universe, we have the boundary conditions: Ψ ( − 1 ) = − 1 , Ψ ′ ( − 1 ) = 0 and Ψ ( − 1 ) = 0 , Ψ ′ ( − 1 ) = − 1 , in opposition to the “no boundary” condition [6].
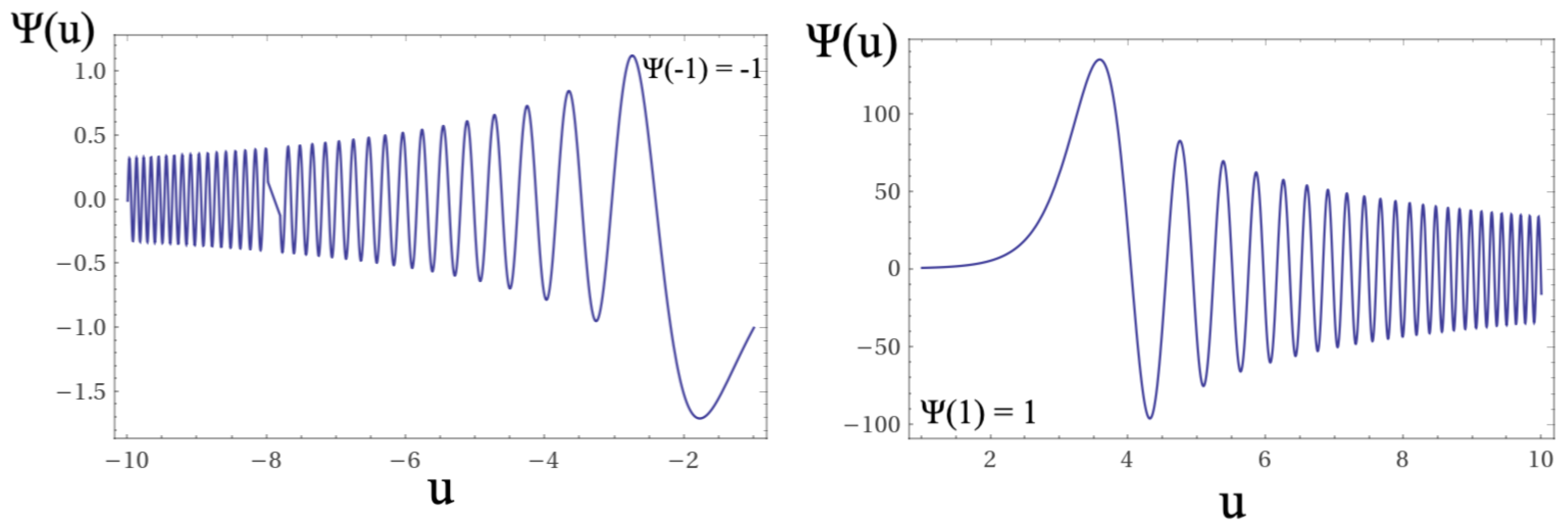
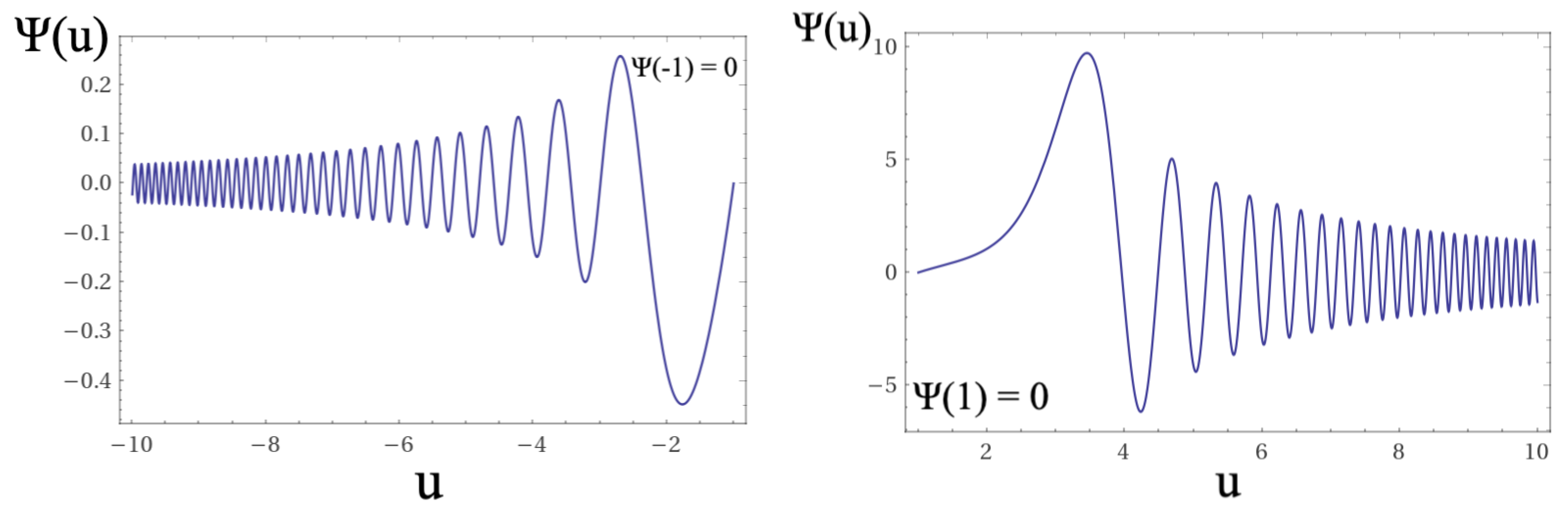
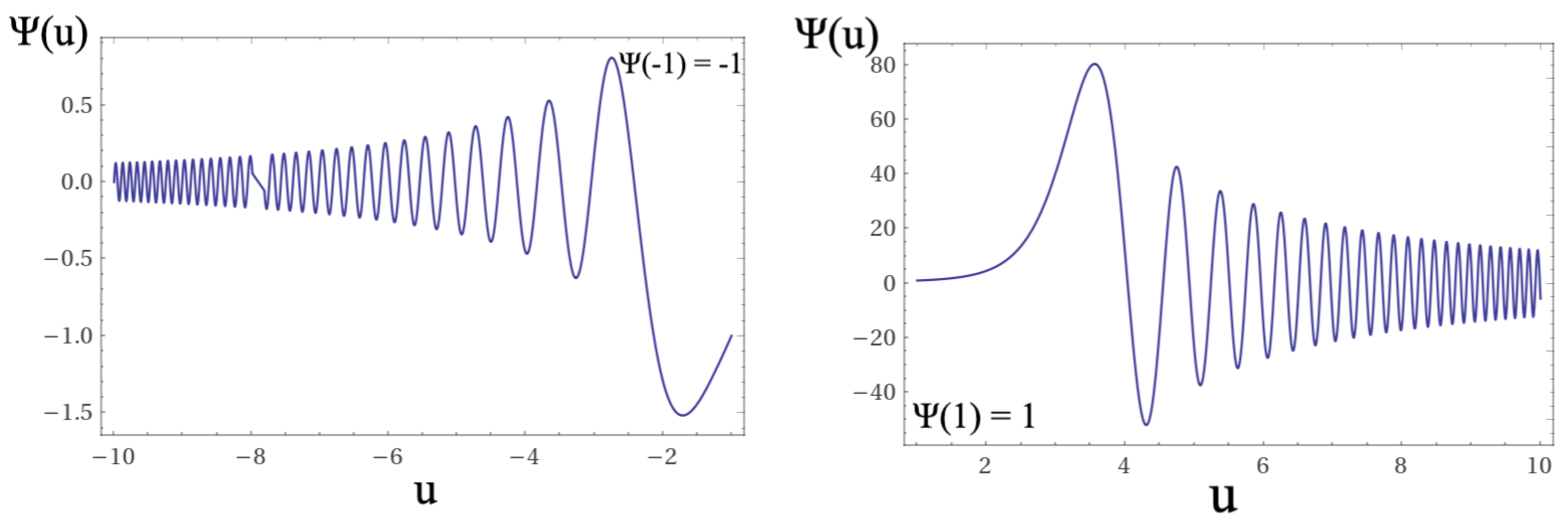
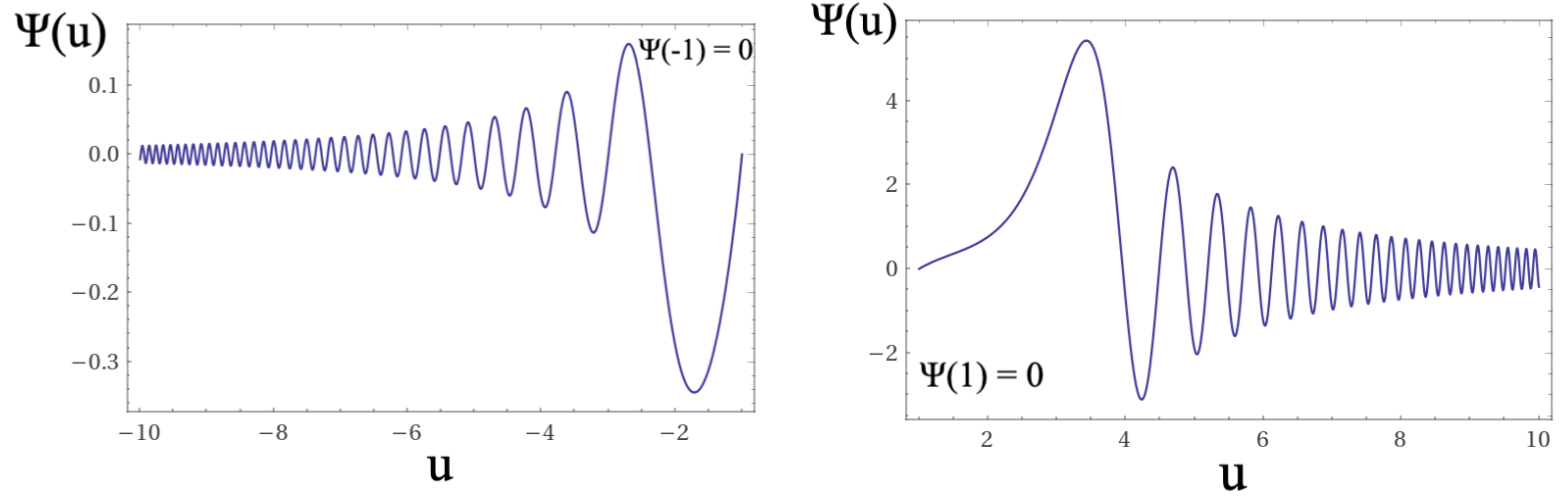
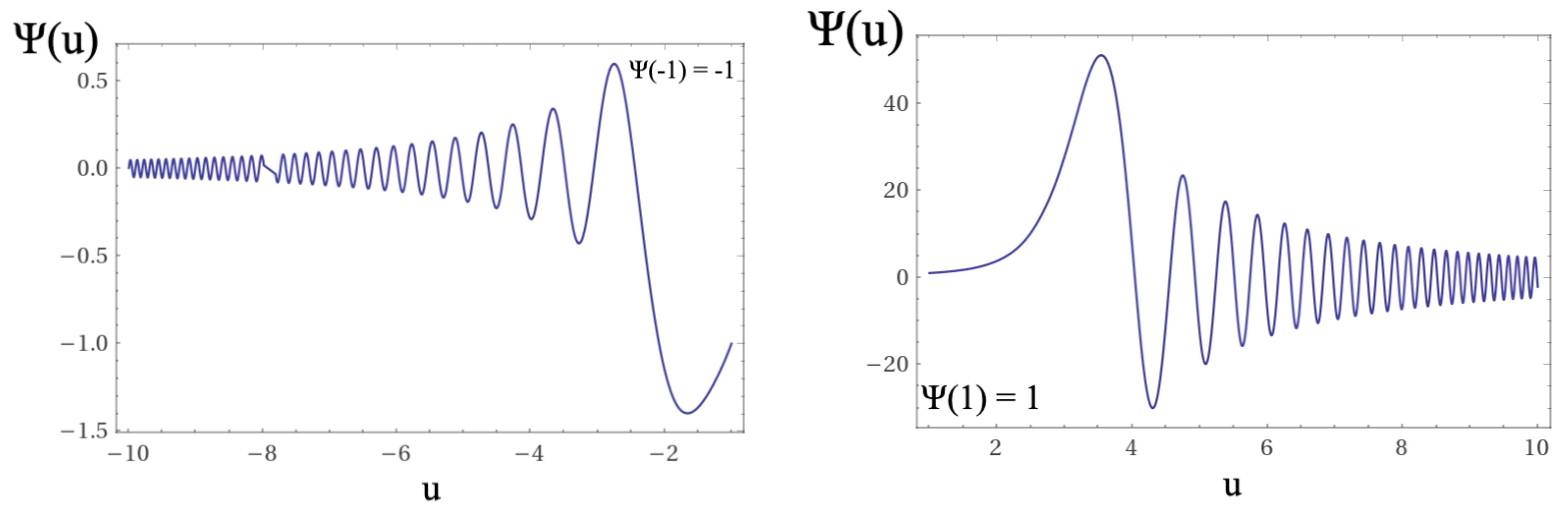
In Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 we show the solutions of equations 12, 13, and 14. As shown in the figures, for the region domains between u = − 1 and u = 1 the differential equations have no solutions. In our interpretation, this domain corresponds to the region in which a topological quantum leap occurs in accordance with the Bekenstein criterion [22,23].

4. Conclusions

Let’s summarize our propositions and our most relevant results. We adopted as underlying propositions in our approach a compact universe, filled with homogeneous matter, that exists forever in a quantum state, either static or oscillating, determined by the characteristics of the proposed model, without imposing in a ad hoc way a constraint limit for the cosmological scale factor and for the wave function of the Universe, such as its disappearance in any limit of the scale factor (see Ref. [24]. Although its disappearance ‘naturally’ occurs in the transition region of the branched model, as a structural consequence of the mathematical formulation, the results obtained indicate that the wave function of the Universe, in the expansion phase, oscillates downwards in a dumping way, while in the contraction phase, the opposite effect happens, suggesting the limit u ( t ) → ∞ (or ln − 1 [ β ( t ) ] → ∞ ) ‘naturally’ occurs, implying an Universe described by oscillating quantum states tending toward a stable ordering at some future time.
Our interpretation of the disappearance of the wave function of the Universe, in turn, in the region between u = − 1 and u = 1 , where a topological quantum leap or tunneling occurs according to Bekenstein’s criterion, although with a certain harmony with the Vilenkin’s quantum tunneling proposal [25], differs from most know proposals for the corresponding boundary conditions5. This is because these proposals, although based on different conceptions and assumptions, have in common the prediction of an inflationary stage of evolution of the Universe, in order to reconcile the causality problem of the Universe. In turn, causality involving the horizon size and the patch size may be accomplished in branch-cut cosmology through the accumulation of branches in the transition region between the present state of the Universe and the past events [26].
The presented proposal strengthens the idea of the transition region of the branched Universe acting as a ‘portal’ for cosmic material, playing the role this way of an ’eternal seed’ [28] for the expanding emergent cosmic scenario. The conclusions of this work lead to numerous underlying questions, whose understanding has motivated ongoing investigations.

Acknowledgments

P.O.H. acknowledges financial support from PAPIIT-DGAPA (IN100421).

References

  1. DeWitt, B. S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113. [Google Scholar] [CrossRef]
  2. Gibbons, G. and Hawking, S. W. Cosmological event horizons, thermodynamics, and particle creation. Phys.Rev. D 1977, 15, 2752–2756. [Google Scholar]
  3. York, J. W. Boundary terms in the action principles of general relativity. Foundations of Physics 1986, 16(3), 249–257. [Google Scholar] [CrossRef]
  4. York, J. W. Role of Conformal Three-Geometry in the Dynamics of Gravitation. Phys.Rev.Lett. 1972, 28, 1082–1085. [Google Scholar] [CrossRef]
  5. Lukasz, A. G. Novel Solution of Wheeler-DeWitt Theory. Applied Mathematics and Physics 2014, 2(3), 73–81. [Google Scholar]
  6. Hartle, J. B. and Hawking, S. W. Wave function of the Universe. Phys. Rev. D 1983, 28, 2960. [Google Scholar] [CrossRef]
  7. Hawking, S.W. The Boundary Conditions of the Universe. Pontif. Acad. Sci. Scr. Varia 1982, 48, 563. [Google Scholar]
  8. Hess, P. O.; Zen Vasconcellos, C. A.; de Freitas Pacheco, J.; Hadjimichef, H.; Bodmann, B. The branch-cut cosmology: A topological canonical quantum-mechanics approach. Astronomische Nachrichten 2022, e20220101. [Google Scholar] [CrossRef]
  9. Zen Vasconcellos, C. A.; Hadjimichef, D.; Razeira, M.; Volkmer, G.; Bodmann, B. Pushing the limits of General Relativity beyond the Big Bang singularity. Astronomische Nachrichten 2020, 340, 857. [Google Scholar] [CrossRef]
  10. Zen Vasconcellos, C. A.; Hess, P. O.; Hadjimichef, D.; Bodmann, B.; Razeira, M.; Volkmer, G. L. Pushing the limits of time beyond the Big Bang singularity: The branch cut universe. Astronomische Nachrichten 2021, 342 (5), 765–775. [Google Scholar] [CrossRef]
  11. Zen Vasconcellos, C. A.; Hess, P. O.; Hadjimichef, D.; Bodmann, B.; Razeira, M.; Volkmer, G. L. Pushing the limits of time beyond the Big Bang singularity: Scenarios for the branch cut universe. Astronomische Nachrichten 2021, 342 (5), 776–787. [Google Scholar] [CrossRef]
  12. Rovelli, C. The strange equation of quantum gravity. Classical and Quantum Gravity 2015, 32(12), 124005. [Google Scholar] [CrossRef]
  13. Bekenstein, J.D. Universal upper bound on the entropy-to-energy ratio for bounded systems. Phys. Rev. D 1081, 23, 287. [Google Scholar] [CrossRef]
  14. Hořava, P. Quantum gravity at a Lifshitz point. Phys. Rev. D 2009, 79, 084008. [Google Scholar] [CrossRef]
  15. Bertolami, O. and Carlos A.D. Zarro, C.A.D. Hořava-Lifshitz quantum cosmology. Phys. Rev. D 2011, 84, 044042. [Google Scholar] [CrossRef]
  16. Maeda, K.-i.; Misonoh, Y.; Kobayashi, T. Oscillating Bianchi IX Universe in Hořava-Lifshitz Gravity. Phys. Rev. D 2010, 82, 064024. [Google Scholar] [CrossRef]
  17. Cordero, R.; Garcia-Compean, H.; Turrubiates, F.J. Lorentzian Vacuum Transitions in Hořava–Lifshitz Gravity. General Relativity and Gravitation 2019, 51, 138. [Google Scholar] [CrossRef]
  18. Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. The Astrophysical Journal Supplement Series 2013, 208(2), 19. [Google Scholar] [CrossRef]
  19. França, U. and Rosenfeld, R. Quintessence Models with Exponential Potentials. JHEP 2002, 0210, 15. [Google Scholar]
  20. Vieira, H.S.; Bezerra, V.B.; Muniz, C.R.; Cunha, M.S.; Christiansen, H.R. Class of solutions of the Wheeler-DeWitt equation with ordering parameter. Phys. Lett. B 2020, 809, 135712. [Google Scholar] [CrossRef]
  21. R. Garattini, R. and Faizal, M. Cosmological constant from a deformation of the Wheeler–DeWitt equation. Nuclear Physics B 2016, 905, 313–326. [Google Scholar] [CrossRef]
  22. Zen Vasconcellos, C. A.; Hess, P. O.; de Freitas Pacheco, J.; Hadjimichef, H.; Bodmann, B. The branch-cut cosmology: evidences and open questions. Astronomische Nachrichten 2022. (Online Version of Record before inclusion in an issue e20220079). [Google Scholar] [CrossRef]
  23. de Freitas Pacheco, J.; Zen Vasconcellos, C. A.; Hess, P. O.; Hadjimichef, H.; Bodmann, B. The branch-cut cosmology: A topological canonical quantum-mechanics approach. Astronomische Nachrichten 2022. (Online Version of Record before inclusion in an issue e20220070). [Google Scholar]
  24. Damour, T. and Vilenkin, A. Quantum instability of an oscillating universe. Phys. Rev. D 2019, 100, 083525. [Google Scholar] [CrossRef]
  25. Vilenkin, A. Creation of universes from nothing. Phys. Lett. B 1982, 117, 25. [Google Scholar] [CrossRef]
  26. Bodmann, B.; Zen Vasconcellos, C.A.; de Freitas Pacheco, J.; Hess, P.O.; Hadjimichef, D. Causality and the arrow of time in the branch-cut cosmology. Astronomische Nachrichten 2022, 344, e220086. [Google Scholar] [CrossRef]
  27. Vilenkin, A. Boundary conditions in quantum cosmology. Phys. Rev. D 1986, 33, 3560. [Google Scholar] [CrossRef]
  28. Mulryne, D.J.; Tavakol, R.; Lidsey, J.E.; Ellis, G.F.R. An Emergent Universe from a loop. Phys. Rev. D 2005, 71, 123512. [Google Scholar] [CrossRef]
1
ln − 1 [ β ( t ) ] represents the reciprocal of ln [ β ( t ) ] and β ( t ) identifies the range and cuts of the helix-like cosmological factor in branched cosmology. ln − 1 [ β ( t ) ] characterizes complex topological leaves of singular foliations by means of Riemann surfaces.
2
N ( t ) does note represent a dynamical quantity; in turn it denotes a pure gauge variable.
3
Despite we consider only the real part of the effective potential, the variable u is complex, and the solutions still have a broader scope, describing the behavior of the wave function of the Universe both for the contraction region, prior to the primordial singularity, and for the later expansion cosmological region.
4
The critical density is the one at which the Universe would stop expanding only after an infinite amount of time.
5
The tunneling boundary condition of Vilenkin [27] in particular has two degrees of freedom: the scale factor and a homogeneous scalar field. A tunneling wave function then describes an ensemble of universes tunneling from ‘‘nothing’’ to a de Sitter space, and then evolving along the lines of an inflationary scenario and eventually collapsing to a singularity [27].
Preprints 72832 g005
Figure 5. Sampling solution family of equation 12 with the values of the coupling constants: η r = 0.6 , η m = 0.2855 ; η k = 1 ; η q = 0.7 ; η Λ = 1 / 3 ; η s = − 0.03 . Values of parameters taken from [17,18,19].
Figure 5. Sampling solution family of equation 12 with the values of the coupling constants: η r = 0.6 , η m = 0.2855 ; η k = 1 ; η q = 0.7 ; η Λ = 1 / 3 ; η s = − 0.03 . Values of parameters taken from [17,18,19].
Preprints 72832 g005
Preprints 72832 g006
Figure 6. Solutions of equation 12. The values of the coupling constants are similar to the ones in Figure 5: η r = 0.6 , η m = 0.2855 ; η k = 1 ; η q = 0.7 ; η Λ = 1 / 3 ; η s = − 0.03 . Values of parameters taken from [17,18,19].
Figure 6. Solutions of equation 12. The values of the coupling constants are similar to the ones in Figure 5: η r = 0.6 , η m = 0.2855 ; η k = 1 ; η q = 0.7 ; η Λ = 1 / 3 ; η s = − 0.03 . Values of parameters taken from [17,18,19].
Preprints 72832 g006
Preprints 72832 g007
Figure 7. Solutions of Equation 12. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Figure 7. Solutions of Equation 12. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Preprints 72832 g007
Preprints 72832 g008
Figure 8. Solutions of Equation 12. The values of the coupling constants are: η r = − 1.22 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = 0.15 . Values of parameters taken from [17,18,19].
Figure 8. Solutions of Equation 12. The values of the coupling constants are: η r = − 1.22 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = 0.15 . Values of parameters taken from [17,18,19].
Preprints 72832 g008
Preprints 72832 g009
Figure 9. Solutions of Equation 13. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Figure 9. Solutions of Equation 13. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Preprints 72832 g009
Preprints 72832 g010
Figure 10. Solutions of Equation 13. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Figure 10. Solutions of Equation 13. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Preprints 72832 g010
Preprints 72832 g011
Figure 11. Solutions of Equation 14. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Figure 11. Solutions of Equation 14. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Preprints 72832 g011
Preprints 72832 g012
Figure 12. Solutions of Equation 14. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Figure 12. Solutions of Equation 14. The values of the coupling constants are: η r = 0.6 , η m = 0.2855 , η k = 1 , η q = 0.7 , η Λ = 1 / 3 , and η s = − 0.03 . Values of parameters taken from [17,18,19].
Preprints 72832 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated