Preprint
Article
Critical Compactness Bound of a Select Class of Compact Stars
Altmetrics
Downloads
123
Views
45
Comments
0
This version is not peer-reviewed
Submitted:
05 May 2023
Posted:
08 May 2023
You are already at the latest version
Alerts
Abstract
Tolman VII solution \citep{ref-journal 2} is an exact analytic solution to the Einstein field equations describing the space-time of a static spherically symmetric distribution of matter. The solution has been shown to be capable of describing the interior of compact objects like neutron stars. Generalized \cite{ref-journal 13} and modified \cite{ref-journal 10} versions of the solution are also available in the literature, which have been subsequently developed to accommodate more realistic descriptions of neutron stars. The stability of the modified Tolman VII solution has recently been analyzed by Posada {\em et al} \cite{ref-journal 9 }, who evaluated a critical value of the adiabatic index above which the stellar configuration becomes unstable against radial oscillations. In this paper, making use of the generalized version of the Tolman VII solution, we prescribe an upper bound on the compactness ($M/R$) beyond which the star becomes unstable. Our investigation is based on the stability analysis of a star against radial oscillations developed by Chandrasekhar \cite{ref-journal 1}. The analysis brings out to attention the role of a particular model parameter in the generalized Tolman VII solution which can be linked to the inhomogeneity of the matter distribution vis-a-vis equation of state (EOS).
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
Compact stars are unique research laboratories in the sky for gaining insight into the nature of particle interactions in extreme conditions such as extreme density, pressure and gravity. Compact stars exist either in binaries or in isolation. In the era of multi-messenger astronomy, electromagnetic and gravitational wave signals and ground-based high-energy laboratory experiments provide valuable information that can constrain the compact star equation of state (EOS). Keeping in mind the systematic errors that might occur in the measurements of masses and radii of compact stars [6], an accurate estimation of the mass and radius of a compact star is crucial for gaining insight into the EOS of a compact star. Ideally, if the EOS is known, it is possible to numerically integrate the Tolman-Oppenheimer-Volkoff (TOV) equations to model a sequence of compact stars and the maximum compactness for any given EOS can be obtained from the plot. An alternative method to study compact stars is to develop meaningful exact solutions to Einstein field equations describing spherically symmetric compact objects. It is noteworthy that while the exterior solution to a static spherically symmetric distribution of uncharged matter is unique (the Schwarzschild solution), an infinite class of solutions can be obtained for the interior matter distribution. Corresponding to the Schwarzschild exterior solution, an interior solution was obtained by Schwarzschild [7] himself, which describes the interior geometry of a static spherically symmetric incompressible fluid distribution. Subsequently, numerous physically acceptable and well-behaved exact solutions have been developed to model compact stars like neutron and quark stars. Tolman provided one such solution [1], which is essentially a two-parameter [M, ] family of solutions where is the central density. The analytic solution was obtained for a specific fall-off behaviour of the energy density. Recently, for better agreement with more realistic neutron star EOS, Jiang and Yagi [8] introduced an additional parameter in the density profile thereby obtaining a three-parameter [M, , ] family of solutions.
An essential physical requirement of any stellar description is its stability. Hence, it becomes imperative to investigate the impact of the model parameters on the stability of the configuration. Internal thermodynamic processes and/or external tidal forces can influence the stability of a star. In a recent paper, Das et al [9] proposed a method to estimate the Tidal Love Number (TLN) of a spherically symmetric relativistic star which is a measure of tidal forces required to deform a star from its spherical distribution [10]. The question we want to address is - what could be the maximum bound on stellar model parameters beyond which the stellar configuration loses its equilibrium? Chandrasekhar [5], in 1964, proposed a method to study the stability of a spherically symmetric stellar configuration against radial oscillations. A catalogue to solve the dynamical equation governing the stellar equilibrium under radial oscillations was later provided by Bardeen [11]. Many investigators have extensively used the method to examine the stability of various stellar models. For example, the technique was used by Knutsen [12] to analyze the stability of a sub-class of the Vaidya-Tikekar [13] solution describing a relativistic superdense star. The method has also been extended to the case of an anisotropic stellar body by Dev and Gleiser [14]. It has been observed that anisotropy in the core region of a stellar configuration provides greater stability. Similarly, the stability of a general relativistic stellar model describing compact stars like was analyzed by Sharma et al [15]. Stability analysis of isentropic subclass of Buchdahl’s exact solution was carried out Negi [19] and it was reported that the solution is stable for all values of within the range . Detailed analysis on the role of the adiabatic index on stability was performed by Moustakidis [20]. Very recently, Posada et al [4] have analyzed the dynamical stability of the modified Tolman VII solution [3] and obtained a critical value of the adiabatic index at the onset of instability for specific values of the EOS parameter and compactness parameter .
The current investigation aims to provide the maximum compactness bound of a stellar configuration beyond which the star becomes unstable. Note that the Buchdahl bound provides the maximum compactness of a relativistic star. For a homogeneous distribution of matter, the bound provides obtainable from the Schwarzschild interior or Tolman III solutions. A more realistic description demands a departure from homogeneity. Hence, we take up the modified Tolman VII solution. The modified Tolman VII solution has an additional parameter which can be linked with the measure of departure from homogeneity. The parameter can also be identified as a tool to fix a certain EOS. In our work, using Chandrasekhar’s method, we intend to analyze the stability of a star for different values of the EOS parameter.
The paper is organized as follows: In Section 2, we lay down field equations corresponding to a static spherically symmetric relativistic compact star. The Tolman VII solution and its modified version are briefly introduced in Section 3. In Section 4, we outline Chandrasekhar’s method to study the stability of a stellar configuration. Physical analysis of our results is compiled in Section 5. Some concluding remarks are made in Section 6.
2. Einstein Field Equations
We assume the line element describing the interior of a static, spherically symmetric compact star in the standard form
The matter distribution inside the star is assumed to be a perfect fluid described by the energy-momentum tensor
where, is the energy density of the fluid, p the isotropic pressure and is the 4-velocity of the fluid. Using equations (1) and (2), we obtain the Einstein field equations
where a prime () denotes derivative with respect to radial coordinate r. The mass function can be written in terms of the metric potential as
In the above and hereafter, we set and .
3. Original and Modified Tolman VII Solutions
As the number of unknowns usually remains greater than the number of independent field equations, it is possible to generate an infinite class of solutions. However, often it is observed that not all the solutions become physically acceptable and well-behaved, as shown by Delgaty and Lake [16] and Finch and Skea [17]. Even though the Tolman VII solution fulfils most of the necessary conditions laid down in reference [16], a stellar configuration obtainable using the Tolman VII solution has some limitations in terms of its compatibility for a wide range of EOS. Raghoonundun and Hobill [2] developed a generalized version of the Tolman VII solution, which can accommodate a broader range of EOS. To get a more realistic description of a neutron star interior, Jiang and Yagi [3] also developed an improved version of the Tolman VII solution. The following sub-sections outline the Tolman VII solution and its subsequent modifications.
3.1. Original Tolman VII Solution
A stellar model is usually constructed by assuming a particular equation of state (EOS) and solving the equation of hydrostatic equilibrium, namely the Tolman-Oppenheimer-Volkoff (TOV) equations for the assumed EOS. However, Tolman [1] adopted a different technique to close the system (3)-(6). In this technique, one assumes a particular form of one of the metric potentials given by
where the parameter represents the stellar compactness and . The constant R represents the stellar radius and M is the total mass enclosed within a radius R so that .
The particular choice (7) of the metric potential is equivalent to choosing an energy density distribution inside the star as
where is the central energy density of the star.
Substitution of equation (8) in (5) and subsequent integration together with the regularity requirement yield
where the central density in terms of the total mass M and radius R is obtained in the form
Making use of equation (7) in (3) and integrating, one determines the unknown metric potential as
where
In equations (11) and (12), and are integration constants which can be determined from the boundary conditions (continuity of metric functions across the boundary and vanishing of pressure at the boundary)
as
Thus, we have a solution expressed in terms of total mass M and radius R.
3.2. Generalized Tolman VII solution
Raghoonundun and Hobill [2] extended the Tolman VII solution by considering the energy density in a more generalized form
where is a free parameter representing ‘stiffness’ of the EOS of the star [18] whose values may vary between . Note that in the extreme case of , we get an incompressible fluid sphere model and corresponds to the original Tolman VII solution. Interestingly, the case is similar to Schwarzschild’s incompressible fluid sphere solution, which readily provides the maximum compactness bound .
With the energy density profile (17), equation (5) can be integrated and applying the regularity requirement , one obtains
where is the mass function in this model. Since , we have
The isotropic pressure takes the form
with
The advantage of this solution is that the stiffness parameter can be suitably adjusted according to the requirement of a given EOS. Consequently, in this paper, we intend to take up this solution to analyze how the stiffness factor vis-a-vis EOS influences the stability of a stellar composition.
3.3. Improved Tolman VII Solution
Jiang and Yagi [3] have separately proposed an improved version of the Tolman VII solution for a more realistic description of neutron star interiors. In their approach, the energy density is assumed to be of the form
where is the central density, R is the stellar radius, is a free parameter which should be fixed so that the condition is always satisfied. Note that represents the original Tolman VII solution.
Posada et al [4] examined the dynamical stability of stellar configurations using this particular solution. Hence, we shall restrict our analysis to the case of generalized Tolman VII solution only.
4. Stability: Chandrasekhar’s Method
Chandrasekhar, in 1964, introduced the variational method to analyze the stability of a spherically symmetric star against radial oscillations. To obtain an upper bound on the physical variables beyond which instability might develop, in our calculation, we follow the same technique as proposed by Chandrasekhar. In this approach, for a spherically symmetric radially oscillating star, one assumes the line element in the standard form
where
are functions of r and t. In (28) and (29), and represent metric potentials corresponding to the equilibrium configuration and and represent functions due to perturbations from the equilibrium configuration. The physical variables like energy density and pressure are accordingly written as
The radial perturbation of the fluid from its equilibrium position is assumed to be of the form
where is the amplitude of nth mode of radial oscillation and is the characteristic frequency of oscillation.
The dynamical equation governing the stellar oscillation can be expressed in standard Sturm-Liouville’s differential equation form
where,
and
For the fundamental mode of oscillations, the pulsation equation takes the form
where the adiabatic index is defined as
A relativistic stellar model will be stable against radial oscillations if the fundamental frequency of oscillation is real and positive. In the following section, we shall perform numerical integration of equation(37) for specific stellar configurations to evaluate values of the fundamental frequencies.
To solve (37), we assume a trial solution with the following boundary conditions:
- Fluid at the star’s centre is not displaced during radial oscillation which implies
- The Lagrangian change in pressure () at the surface () must vanish which implies
5. Stability Range for Generalized Tolman VII Solution
To evaluate the maximum compactness bound, using generalized Tolman VII solution, we numerically integrate of equation (37) for specific stellar configurations and evaluate the values of the fundamental frequencies (). For a given radius and fixed value of the EOS parameter , we keep increasing the total mass till the fundamental frequency becomes a negative quantity. The procedure determines the maximum compactness bound beyond which the configuration becomes unstable. We would like to point out here that our procedure cannot be used to determine the frequency for case. However, for other values of , can be determined as shown in Table A1.
The subsequent maximum central density can also be determined using the relation
The results have been compiled in the Table (Table A1). In the table, the bold values indicate the maximum bounds. In Table 1, we have compiled the values of the maximum compactness bound for a wide range of values of . We note that the maximum compactness bound decreases as the inhomogeneity vis-a-vis the EOS parameter () increases. However, the central density increases with increasing values of . In Figure 1, we have shown the permissible compactness bound for different . Similarly, in Figure 2, we have graphically shown the permissible values of the central density for a star of a given radius (we have assumed km) by considering different values of . In Figure 3, we have plotted the values of the fundamental frequencies for different . Interestingly, the values of shift closer to zero with increasing values of . Since has the interpretation of departure from homogeneous matter distribution, this implies that the most stable configuration is the homogeneously distributed star.
6. Discussion
Our analysis shows that a departure from homogeneous matter distribution, characterized by the model parameter that appears in the Tolman VII solution, plays a crucial role in fixing the maximum compactness bound beyond which the star becomes dynamically unstable. Obviously, the most compact object has a homogeneous distribution of matter. As inhomogeneity in the matter distribution develops, the upper bound on compactness decreases. The subsequent maximum central density, in contrast, increases. It is to be stressed that the critical bound for the generalized Tolman VII solutions never exceeds the Buchdahl bound . In our calculation, the maximum compactness bound was obtained in two different ways: (i) For a given radius, the total mass was increased till the configuration became unstable and (ii) for a fixed mass star, the boundary was decreased till the configuration became unstable. In both the cases, we obtained the same compactness bound, as expected. We trust that this procedure has never been adopted in earlier analyses.
In the Tolman VII solution, since the parameters can also be linked with EOS, our results clearly show an intricate relationship between the maximum compactness bound and the EOS. Whether such an observation can help us in constraining the compact star EOS is a matter of further investigation and will be taken up elsewhere.
Author Contributions
Conceptualization, methodology, numerical computation, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation: RS and SB; Supervision: RS. All authors have read and agreed to the published version of the manuscript.
Funding
Not applicable.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data underlying this article is available in the public domain as cited in the references.
Acknowledgments
RS gratefully acknowledges support from the Inter-University Centre for Astronomy and Astrophysics (IUCAA), Pune, Govt. of India, under its Visiting Associateship Programme.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Table A1.
Maximum value of compactness and central density beyond which the stellar configuration becomes dynamically unstable in case of generalized Tolman VII solution (the radius is kept fixed at km).
Table A1.
Maximum value of compactness and central density beyond which the stellar configuration becomes dynamically unstable in case of generalized Tolman VII solution (the radius is kept fixed at km).
| mass (M) () | compactness(M/R) | central density (gm cm) | fundamental frequency () | |
|---|---|---|---|---|
| 0.1 | ||||
| 2 | ||||
| 3 | ||||
| 0.2 | 2 | |||
| 3 | ||||
| 0.3 | 1.4 | 0.2065 | ||
| 2.9 | 0.42775 | |||
| 2.9737 | 0.438621 | 1.72307 | 0.0144451 | |
| 2.9738 | 0.438636 | 1.72313 | ||
| 3 | 0.4425 | 1.73831 | ||
| 0.4 | 1.4 | 0.2065 | ||
| 2.9 | 0.42775 | |||
| 2.9545 | 0.435789 | 1.8471 | 0.00852387 | |
| 2.9546 | 0.435804 | |||
| 3 | 0.4425 | |||
| 0.5 | 1.4 | 0.2065 | ||
| 2.9 | 0.42775 | |||
| 2.9304 | 0.432234 | 1.98906 | 0.00502046 | |
| 2.9305 | 0.432249 | |||
| 3 | 0.4425 | |||
| 0.6 | 1.4 | 0.2065 | ||
| 2.5 | 0.36875 | |||
| 2.8996 | 0.427691 | 2.15267 | 0.00274282 | |
| 2.8997 | 0.427706 | |||
| 3 | 0.4425 | |||
| 0.7 | 1.4 | 0.2065 | ||
| 2.5 | 0.36875 | |||
| 2.8591 | 0.421717 | 2.34219 | 0.00118629 | |
| 2.8592 | 0.421732 | |||
| 3 | 0.4425 | |||
| 0.8 | 1.4 | 0.2065 | ||
| 2.5 | 0.36875 | |||
| 2.8042 | 0.41362 | 2.56227 | 0.00011319 | |
| 2.8043 | 0.413634 | |||
| 3 | 0.4425 | |||
| 0.9 | 2.5 | 0.36875 | ||
| 2.7277 | 0.402336 | 2.81747 | 0.00057973 | |
| 2.7278 | 0.402351 | |||
| 1 | 2.5 | 0.36875 | ||
| 2.6183 | 0.386199 | 3.11014 | 0.000892158 | |
| 2.6184 | 0.386214 | |||
| 3 | 0.4425 |
References
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364. [Google Scholar] [CrossRef]
- Raghoonundun, A.M.; Hobill, D.W. Possible physical realisations of the Tolman VII solution. Phys. Rev. D 2015, 92, 124005. [Google Scholar] [CrossRef]
- Jiang, N.; Yagi, K. Improved analytic modeling of neutron star interiors. Phys. Rev. D 2019, 99, 124029. [Google Scholar] [CrossRef]
- Posada, C.; Hladík, J.; Stuchlík, Z. Dynamical stability of the modified Tolman VII solution. Phys. Rev. D 2021, 103, 104067. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Dynamical Instability of Gaseous Masses Approaching the Schwarzschild Limit in General Relativity. Astrophys. J. 1964, 140, 417. [Google Scholar] [CrossRef]
- Miller, M.C.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. The Astrophysical Journal 2019, 887, L24. [Google Scholar] [CrossRef]
- Schwarzschild, K. On the gravitational field of a mass point according to Einstein’s theory, arXiv:physics/9905030 1999.
- Jiang, N.; Yagi, K. Improved analytic modeling of neutron star interiors. Phys. Rev. D 2019, 99, 124029. [Google Scholar] [CrossRef]
- Das, S.; Parida, B.K.; Sharma, R. Estimating tidal Love number of a class of Compact Stars. Eur. Phys. J C 2022, 82, 136. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I Love Q relations in neutron stars and their applications to astrophysics, gravitational waves, and fundamental physics. Phys. Rev. D 2013, 88, 023009. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Throne, K.S.; Meltzer, D.W. A Catalogue of Methods for Studying the Normal Modes of Radial Pulsation of General-Relativistic Stellar Models. Astrophys. J. 1966, 145, 508. [Google Scholar] [CrossRef]
- Knutsen, H. On the stability and physical properties of an exact relativistic model for a superdense star. Mon. Not. R. astr. Soc. 1988, 232, 163–174. [Google Scholar] [CrossRef]
- Vaidya, P.C.; Tikekar, R. Exact relativistic model for a superdense star. J. Astrophy. Astron. 1982, 3, 325–334. [Google Scholar] [CrossRef]
- Dev, K.; Gleiser, M. Anisotropic Stars: Exact Solutions and Stability. Int. J. Mod. Phys. D 2004, 13, 1389–1397. [Google Scholar]
- Sharma, R.; Mukherjee, S.; Dey, M.; Dey, J. A GENERAL RELATIVISTIC MODEL FOR SAX J1808.4-3658. Mod. Phys. Lett. A 2002, 17, 827–838. [Google Scholar] [CrossRef]
- Delgaty, M.S.R.; Lake, K. Physical Acceptability of Isolated, Static, Spherically Symmetric, Perfect Fluid Solutions of Einstein’s Equations. Comput. Phys. Commun. 1998, 115, 395–415. [Google Scholar] [CrossRef]
- Finch, M.R.; Skea, J.E.F. A realistic stellar model based on an ansatz of Duorah and Ray. Classical and Quantum Gravity 1989, 6, 467–476. [Google Scholar] [CrossRef]
- Chan, T.K.; Chan, A.P.O.; Leung, P.T. Multipolar universal relations between f-mode frequency and tidal deformability of compact stars. Phys. Rev. D 2016, 93, 24033. [Google Scholar] [CrossRef]
- Negi, P.S. The stability of an isentropic model for a gaseous relativistic star, gen. rel. grav. 2007, 39, 529–534. [Google Scholar] [CrossRef]
- Moustakidis, C.C. The stability of relativistic stars and the role of the adiabatic index, gen. rel. grav. 2017, 49, 68. [Google Scholar] [CrossRef]
Figure 1.
Upper bound on the maximum compactness bound for different values of in the generalized Tolman VII solution.
Figure 1.
Upper bound on the maximum compactness bound for different values of in the generalized Tolman VII solution.
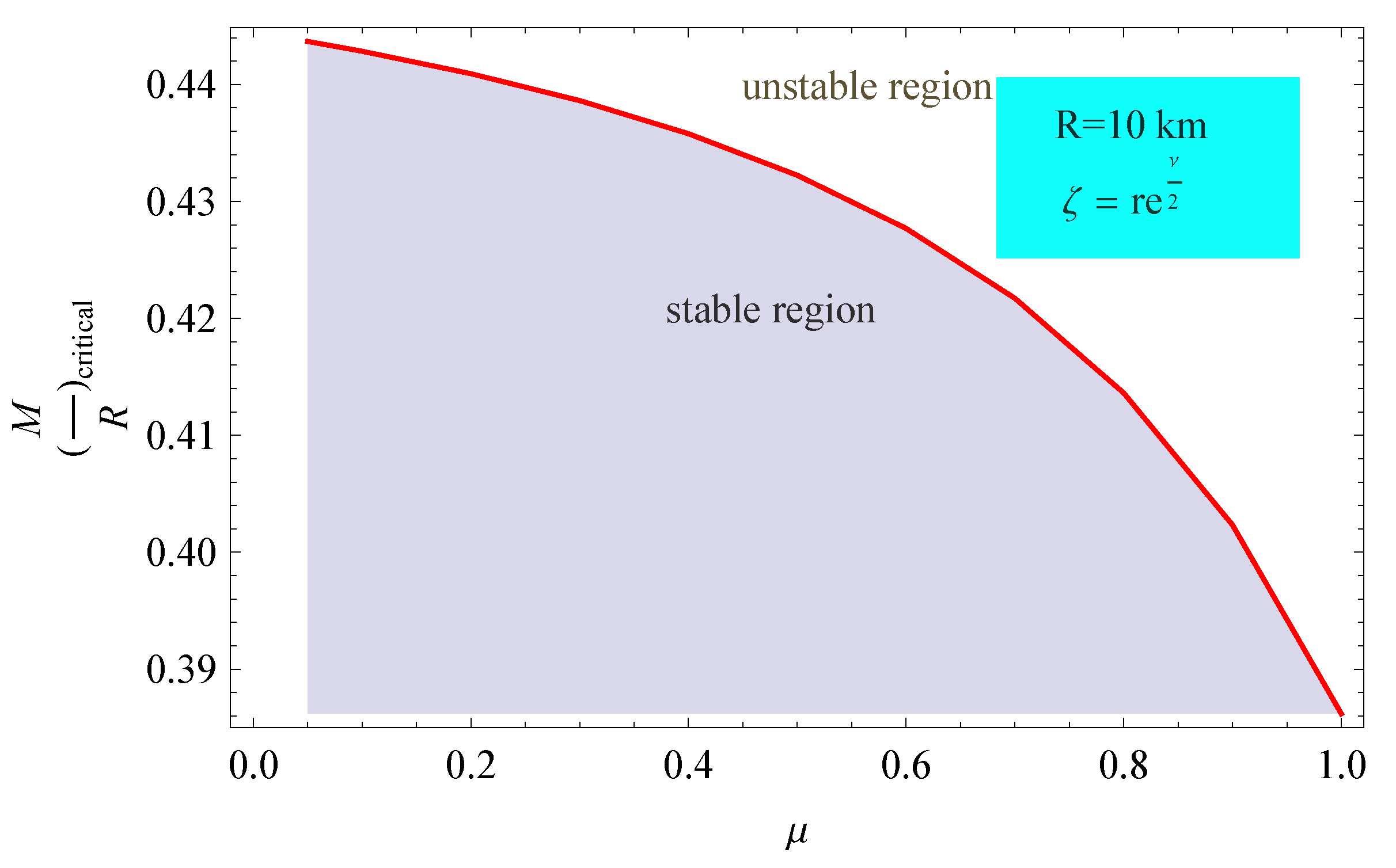
Figure 2.
Maximum central density for different values of in generalized Tolman VII solution (We have assumed km.
Figure 2.
Maximum central density for different values of in generalized Tolman VII solution (We have assumed km.
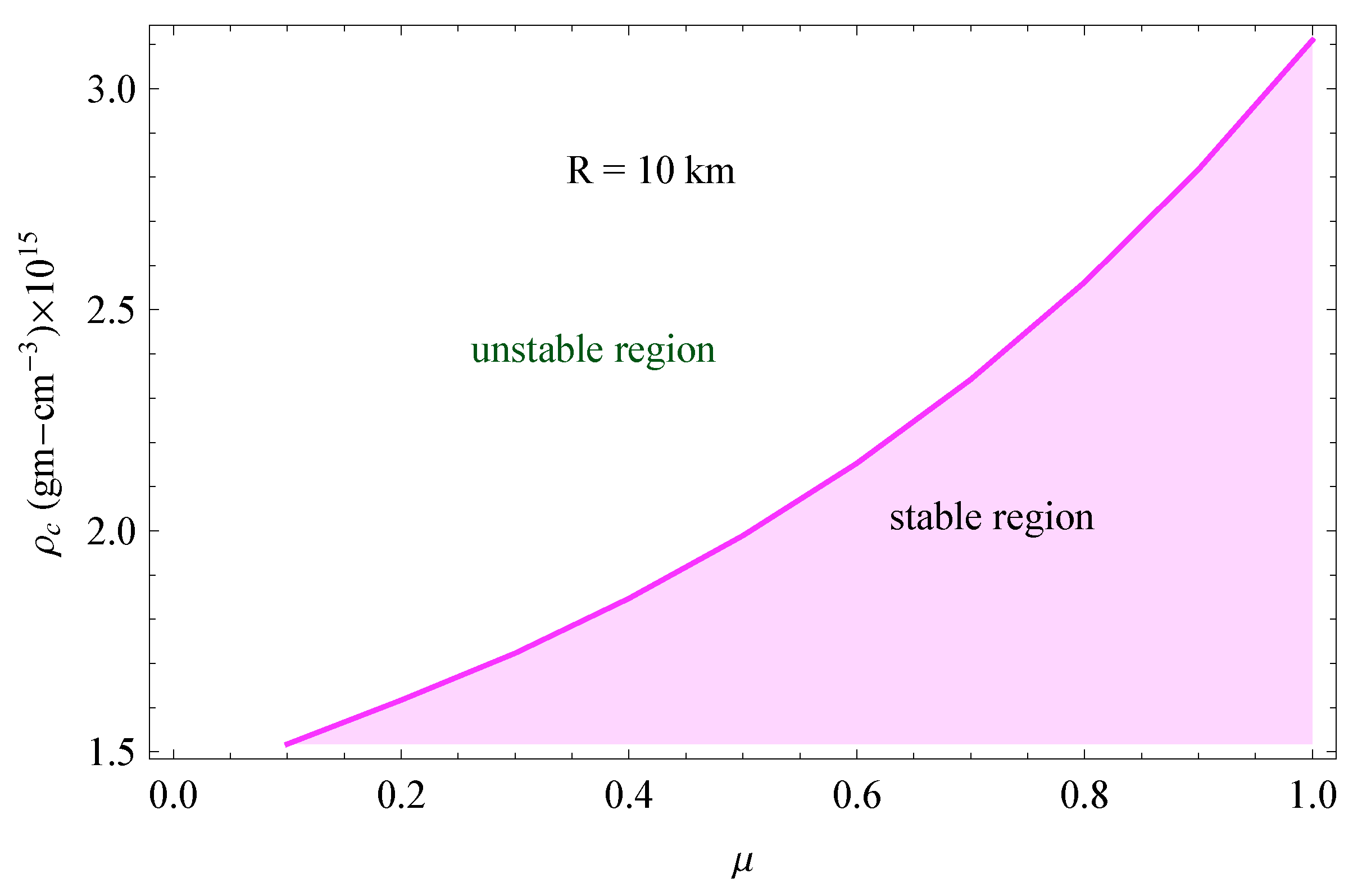
Figure 3.
Fundamental frequency () vs .
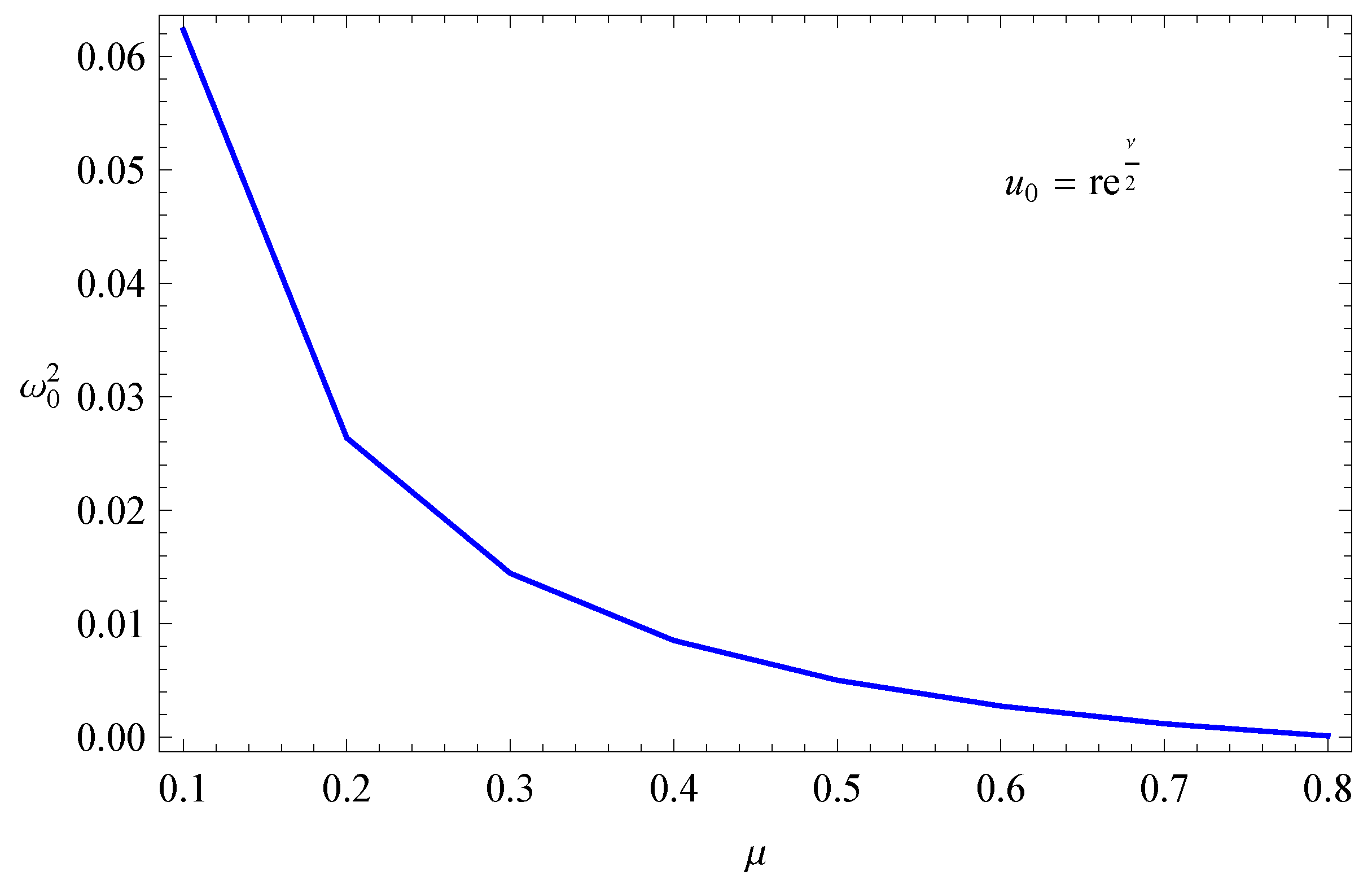
Table 1.
Variation of critical bound on compactness and maximum value of central density with in-homogeneous parameter .
Table 1.
Variation of critical bound on compactness and maximum value of central density with in-homogeneous parameter .
| central density | ||
|---|---|---|
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






