Description and Validation of Flow-Through Chambers of Respirometry for Measuring Gas Exchange in Animal Trials

Preprint

Technical Note

Description and Validation of Flow-Through Chambers of Respirometry for Measuring Gas Exchange in Animal Trials

This version is not peer-reviewed.

Rony Riveros

,Rosiane de Souza Camargos,Raully Lucas Silva,Bruno Leme,

Nilva Kazue Sakomura^*

Rony Riveros

,Rosiane de Souza Camargos,Raully Lucas Silva,Bruno Leme,

Nilva Kazue Sakomura^*

This version is not peer-reviewed.

Altmetrics

Downloads

129

Views

114

Comments

Submitted:

07 May 2023

Posted:

08 May 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

Indirect calorimetry (IC) is a widely used method to study animal energy metabolism by measuring gas exchange. The accuracy of IC depends on detecting variations in signals reflecting the metabolic response, which can be challenging due to measurement noise and external factors. In this study, we propose a methodology to validate IC systems, including an easy-to-use spreadsheet for data computing, to verify accuracy and detect whole-system leaks. We conducted a re-covery test using a simulation of CO2 dynamics in MS Excel and injecting a known CO2 concentration into four respirometry chambers. The clearance rate of CO2 was observed and compared to the expected clearance rate from the simulation. The results from the recovery test in our system show that the proposed methodology is accurate and precise. The proposed methodology and recovery test can be used to standardize the validation of IC systems, providing accurate measurements of animal energy metabolism in different environmental conditions and energy utilization from feeds.

Keywords:

Subject:

Biology and Life Sciences - Animal Science, Veterinary Science and Zoology

Supplementary Material

supplementary.rar (32.16MB )

Introduction

Indirect calorimetry (IC) is a widely used method to study the energy metabolism of animals and humans by directly measuring gas exchange (O₂ and CO₂). The heat production (HP) calculation is based on the principle of the volumetric stoichiometry of oxygen consumed (VO₂), carbon dioxide produced (VCO₂), and heat released from the oxidative process [1]. Recently, this method has gained interest from poultry researchers for supporting studies on energy metabolism and developing net energy systems [2,3,4,5].

IC accurately assesses the HP of animals under different environmental conditions, energy utilization from feeds, and other temporal measurements [2,3,6]. Over the years, advancements in gas analyzer technologies, data acquisition systems, and computing power have improved the accuracy of measurements [7,8]. However, to ensure the quality and accuracy of results, trained technicians are required to conduct biological trials, handle equipment properly, and acquire data adequately [9].

The accuracy of an IC system depends on the ability to detect and record variations in signals that reflect the metabolic or physiological animal response, which the researcher will later interpret [10,11]. Several procedures have been developed to check the accuracy of the IC, including alcohol or propane gas combustion, alcohol evaporation, continuous gas injection, and specific volume gas injection. However, some methods have limitations, such as low sensitivity, difficulty in the calculation, expensive materials or substances, and time-consuming procedures. Therefore, the recovery test should be flexible to accommodate the diversity of IC systems and the research objective. Still, it must simulate the experimental conditions of a biological trial, considering the flow used and the delta of CO₂ and O₂ observed when measurements were made in animals inside the chamber.

The open-circuit system integrated into the trough airflow of pull-mode calorimetric chambers is commonly used in farm animal trials [2,3,6,9,12]. This system measures the concentration of gases (O₂ and CO₂) and the rate of change when considering the flow of air from the atmosphere into the chamber, and the volume of gas exchanged (VO₂ and VCO₂) over time can be calculated. However, before obtaining the final value of HP, a set of computations aims to preserve the signals due to the metabolic animal response, identify atypical signals due to factors foreign to the investigation, and suppress measurement noise [12,13,14].

In this paper, we aim to standardize a methodology to validate the IC system to verify the accuracy and detect whole-system leaks. Additionally, we propose an easy-to-use spreadsheet to compute the data acquisition and final calculation of HP based on the fundamental equation of Brower [1], which yields an improved transient response and suppresses measurement noise.

General description of the flow-through IC system

We used an open-circuit IC system that could couple six chambers, as shown in Figure 1. Each chamber had the same geometric volume (Vch) of 980 m³ (dimensions 100 cm × 100 cm × 98 cm), implemented with a temperature control system inside (heater and cooler) that maintained a constant temperature set at 24±1.0°C and a humidity of 60% during the trials.

The experimental setup consisted of air conduction, analyzers, and data acquisition components. Mass flow pumps (FK-100, Sable System, Las Vegas) were coupled to each CH and set at a flow rate of 20 L/min. A sample of air at 160 ± 2.0 mL/min was carried from each flow pump using a sub-sampler pump (SS4, Sable System, Las Vegas) located at the end of the circuit, maintaining the sample flow constant through gas analyzers. The sampled air was subjected to water vapor pressure analysis (RH-100, Sable System, Las Vegas). The sample was passed through a drying column (>99.5% CaSO₄, Drierite®) to capture the humidity.

The O₂ and CO₂ concentrations were then analyzed using paramagnetic (PA-10, Sable System, Las Vegas) and infrared (CA-10, Sable System, Las Vegas) analyzers, respectively. The concentrations were measured as dry air. Finally, a universal interface (UI-3, Sable System, Las Vegas) was linked to the flowmeters and analyzers to record the signals at a frequency of one record per second. The signals from analyzers and flowmeters were extracted using ExpData software (Sable System, Las Vegas).

The atmospheric air was conducted using a diaphragm pump, and the concentrations of O₂ and CO₂ were measured to establish a baseline.

General calculations

The general calculations used here for the simulations of the dynamic of gas injection and the spreadsheet for data computing were described by Ligton [15] for an open-circuit system with negative pressure. The correction of the outgoing flow (Fout) by barometric (BP) and water vapor pressure (WVP) was calculated as

F o u t = {F o u t}_{(d y l)} * \frac{B P}{B P - W V P}

. The ingoing flow (Fin) was calculated by a nitrogen correction factor using the equation

F i n = F o u t * (\frac{N_{2} i n}{N_{2} o u t})

, where

N_{2} = 100 - O_{2} - {C O}_{2}

The volume of gases was determined as follows:

{V C O}_{2} i n = F i n \times {C O}_{2} i n

{V C O}_{2} o u t = F o u t \times {C O}_{2} o u t

. Furthermore,

{V C O}_{2} i n j = F i n j \times {C O}_{2} i n j

The HP was calculated using the Brower [1] equation:

H P (k c a l) = 3.866 \times {V O}_{2} + 1.200 \times {V C O}_{2}

Simulation of the dynamic of gas injection in a theoretical system

To conduct the recovery test, we developed a simulation of CO₂ dynamics in MS Excel when injected into the system (Suppl. 1). The simulation was based on a theoretical system that assumes constant flow (

F i n = F o u t

\frac{N_{2} i n}{N_{2} o u t} = 1

), and dry air (where

W V P = 0

), and it described the behavior of injected CO₂ concentration (CO₂inj) through the system over time (per minute). Parameters such as the volume of injected gas (Vinj), injection flow (Finj), and concentration of CO₂inj were assumed constant and can be modified for other gases and concentrations. Additional calculations are presented in Table 1. The simulation was conducted to determine the volume of CO₂ in three compartments: (1) ingoing rate (VCO₂in), (2) CO₂ volume in the chamber (VCO₂ch), and (3) outgoing rate (VCO₂out) (Figure 2A). The simulation was divided into two phases: injection phases (when Finj>0 and ti<tinj) and washing phases (when Vinj was empty and Finj=0) (Figure 2B).

The simulation began at ti = 0 (no injection of tested gas or baseline), where the concentration of CO₂ in all compartments was equal to the atmospheric air concentration. From that should establish the following volumetric concentration on each compartment:

{V C O}_{2}_{t i = 0} = \{\begin{matrix} V {C O}_{2} i n (\frac{L}{m i n}) = F i n \times {C O}_{2} i n; F i n j = 0; F o u t = F i n \\ V {C O}_{2} c h (L) = V c h \times {C O}_{2} i n \\ V {C O}_{2} o u t (\frac{L}{m i n}) = F o u t \times {C O}_{2} o u t; {C O}_{2} i n = {C O}_{2} o u t \end{matrix}

For the injection phases (ti = 1→tinj), the calculation was as follows:

{V C O}_{2}_{t i = 1 \dots t i n j} = \{\begin{matrix} V {C O}_{2} i n (\frac{L}{m i n}) = (F o u t - F i n j) \times {C O}_{2} i n \\ V {C O}_{2} c h (L) = {V {C O}_{2} c h}_{t i - 1} + {V C O}_{2} {i n}_{t i} + {V C O}_{2} {i n j}_{t i} - {{V C O}_{2} o u t}_{t i - 1}; {V C O}_{2} {i n j}_{t i} = F i n j \times {C O}_{2} i n j \\ V {C O}_{2} o u t (\frac{L}{m i n}) = F o u t \times {{C O}_{2} c h}_{t i}; {C O}_{2} c h = \frac{{V C O}_{2} {c h}_{t i}}{V c h} \end{matrix}

The VCO₂ch value for t=1 was calculated by adding the VCO₂ch value at t=i-1 to the VCO₂in value at t=i and the VCO₂inj value at t=i, and then subtracting the VCO₂out value at t=i-1. The VCO₂out rate at t=1 was utilized to determine the fractional concentration of CO₂ in the chamber (CO₂ch for t=i).

Finally, During the washing phases (ti = tinj…∞), the CO₂ volumes were calculated as follows:

{V C O}_{2}_{t i = t i n j \dots \infty} = \{\begin{matrix} V {C O}_{2} i n (\frac{L}{m i n}) = F i n \times {C O}_{2} i n \\ V {C O}_{2} c h (L) = {V {C O}_{2} c h}_{t i - 1} + {V C O}_{2} {i n}_{t i} - {{V C O}_{2} o u t}_{t i - 1} \\ V {C O}_{2} o u t (\frac{L}{m i n}) = F o u t \times {{C O}_{2} c h}_{t i}; {C O}_{2} c h = \frac{{V C O}_{2} {c h}_{t i}}{V c h} \end{matrix}

The outputs of interest from the simulation over time were CO₂out, the differential volume of CO₂ (

{∆ {V C O}_{2}}_{t i} = {{V C O}_{2} o u t}_{t i} - {{V C O}_{2} i n}_{t i}

), and the cumulative differential volume of CO₂ (

C u m u l a t i v e {∆ V C O}_{2} = \sum_{t i = 0}^{i} {∆ {V C O}_{2}}_{t i}

). These parameters (per minute) were used to compare with the result of each chamber.

Recovery test procedure

The recovery test was performed in four respirometry chambers by introducing a known concentration of CO₂ and measuring the rate of gas clearance over time as subjects exhaled. The recovery protocol was developed with the following considerations: (i) monitoring and controlling the concentration and injection flow of the gas every minute, (ii) ensuring that the concentration and injection flow is consistent with the expected range of metabolic rates in animal trials, and (iii) comparing the simulated clearance rate of CO₂ with the observed clearance rate in each chamber to assess accuracy and precision.

A non-diffusion medical bag was used to store 30 L of a known CO₂ concentration (65% analytical CO₂ and 35% compressed nitrogen, standard gas mixture with guaranteed concentration, Code: ONU-1013, White Martins, SP, Brazil), which was connected to a micro-diaphragm pump (Finj at 70 kPa of pressure on vacuum) and injected into the chamber at a controlled injection flow of 0.5 L/min, as monitored by a rotameter (Figure 1 and 2A). After that, the data collection was started by around 60 minutes (injection time) up to the bag empty and continued for another 60 minutes without injection (washing time). This process was repeated three times in each chamber, and the average of the three observations was compared with the expected clearance rate from the simulation.

Data analyses and recovery index calculation

The data analysis for the recovery test was carried out the same as was described in the simulation procedures. The data were recorded every second and averaged per minute. The parameters evaluated to assess the accuracy of the system for each chamber included the fractional concentration of CO₂out, ∆VCO₂, and cumulative ∆VCO₂. The error (ε) and residual standard deviation (RSD) were calculated for each chamber and each minute to assess the results. In addition, the recovery rate was calculated based on the expected volume of CO₂ and the observed volume in each chamber.

ε (k) = k_{o b s e r v e d} - k_{e x p e c t e d} R S D (k) = \sqrt{\sum \frac{{(k_{o b s e r v e d} - k_{e x p e c t e d})}^{2}}{n}} R e c o v e r y r a t e = \frac{\sum_{i = 0}^{120} ∆ {V C O}_{2} o b s e r v e d}{\sum_{i = 0}^{120} ∆ {V C O}_{2} e x p e c t e d}

Here, k represents CO₂out(ti), ΔVCO₂, or Cumulative ΔVCO₂. Observed values were recorded in each chamber, and expected values were calculated using the simulation.

Results of the recovery test

Figure 3 displays the dynamic behavior of each chamber per minute. All chambers exhibited similar behavior for all parameters compared with the model. However, chambers 2 and 3 showed different behavior and errors than chambers 1 and 4. Chamber 2 exhibited greater consistency and closeness to the expected behavior curve than the other chambers.

The injection phase results showed that chambers 2 and 3 reached their tinj values at approximately 60 minutes, which is consistent with the expected time for gas injection to finalize. However, chambers 1 and 4 took longer than expected, with a delay of around 15 minutes. During this period, all chambers exhibited slightly higher values for %CO₂out and ΔVCO₂ than expected. Additionally, the washing period showed a greater variation in the parameters of CO₂out(ti), ΔVCO₂, and Cumulative ΔVCO₂. In general, 1% of the variation in CO₂ resulted in a 0.05 L/min of the volumetric ΔVCO2 from the expected value. However, this did not affect the cumulative volumetric difference of CO₂, and it should not pose a problem during animal experimentation, as it only released less than 1 L of VCO₂ above the expected value. The variation in these parameters over time is related to the airflow (Finj or Fout). It can be calibrated on the flowmeter, which should exhibit greater precision during animal experimentation [15].

The recovery rates and relative standard deviation (RSD) for each chamber are presented in Table 2. As previously mentioned, chambers 2 and 3 exhibited similar behavior and higher RSD(ΔVCO₂) and lower RSD (Cumulative ΔVCO₂) than chambers 1 and 4. This resulted in a recovery rate below 1 for chambers 2 and 3, while chambers 1 and 4 had recovery rates above 1. These results fall within the system's inefficiency range, as McLean and Tobin [16] recommended, where a normal variation of 3% to 8% (from 0.92 to 1.08) is considered an acceptable range for recovery rates.

The procedure of data computing and filtering of IC system

An accurate description of the general steps involved in computing IC data is provided by Lighton [15] and Gerrits et. al. [9]. This methodology is suitable for data obtained from analyzers and chambers that have been checked and calibrated. In other words, the chamber should not have any defects or a recovery test should be conducted to establish the chamber's feasibility. Furthermore, the analyzer output signals should represent the variation over time during animal experimentation. Therefore, performing periodic calibration of the analyzer, verification of the recorded signals, and filtering to obtain coherent gas concentration values while disregarding some noise during recordings is recommended.

Here we used the IC data report by Camargos et. al., [17] on broiler chickens as an example to detail step-by-step the calculations of data management and is available the calculation spreadsheet developed in MS Excel with this data (Suppl. 2).

Oxygen and CO₂ signals calibration

The initial step in IC measurement involves verifying the recorded signal and ensuring coherent values of gas concentration. To achieve this, calibration must be performed at the start and end of each metabolic measurement period (daily).

For the data computing of the data from Camargos et. al., [17], we considered the calibration procedure carried out using two gases with known concentrations: gas A, which was pure nitrogen with approximately 99.99% N2 and 0% O₂ and CO₂ (White Martins, SP, Brazil), and gas B, which was a standard mixture of 21% O₂ and 1% CO₂ (White Martins, SP, Brazil).

The calibration curve was performed for each gases of interes (in this cases O₂ and CO₂) by extrapolationg along the time (ti) as:

{C O}_{2} e x t r a p o l a t e d f o r t i (f o r g a s A o r B) = {C O}_{2} t 0 + ({C O}_{2} (t n) - {C O}_{2} (t 0)) \times \frac{t i - t 0}{t n - t o}

Where O2ti is the fractional concentration for the gas A or gas B at the ti. O2t0 and O2tn is the concentration at the initial and the final register value by the analyzer, respectively. With the extrapoled concentration of O2 for each ti and each gases (A and B), is then linearized as:

s l o p e (t i) = \frac{{(C O}_{2} c e r t i f y f o r g a s A - {C O}_{2} c e r t i f y f o r g a s B)}{(C O_{2} e x t r a p o l a t e d a t t i f o r g a s A - {C O}_{2} e x t r a p o l a t e d a t t i f o r g a s B)}

i n t e r c e p t (t i) = {C O}_{2} c e r t i f y f o r g a s A - s l o p e (t i) \times {C O}_{2} e x t r a p o l a t e d a t t i f o r g a s A

Finally, the calibrated signals and expression of the concentration of both gases was expressed as:

{C O}_{2} c a l i b r a t e d (t i) = i n t e r c e p t (t i) + s l o p e \times {C O}_{2} r e g i s t e r (t i)

The same procedure was performed for O2.

Calibrated fractional concentration and filtering

The fractional concentration obtained through calibration is not sufficient for HP calculation. Thus, the reliability of the IC measurements depends on the metabolic signal detected by the system or the appropriate mathematical application to highlight these metabolic events.

The Bartholomew [18] data transformation is a widely used procedure for real-time gas exchange measurements [19]. This procedure is based on the relationship between Vch and Fout, which refers to the system's ability to detect the metabolic signal or, in the absence of it, to provide a delay for corrective action.

The fractional data for O₂ or CO₂ can be corrected by combining the exponential saturation of the chamber, which depends on the flow rate. The calibrated concentration of O₂ and CO₂ at a given time (i) can be corrected as follows:

{C O}_{2} (t i) t r a n s f o r m e d = \frac{{C O}_{2} c a l i b r a t e d (t i) - {C O}_{2} c a l i b r a t e d (t i - 1)}{1 - e^{- \frac{F o u t (t i)}{V c h} \times t i}}

After applying the Bartholomew transformation, the CO₂ concentration was transformed to the time ti. Since the signal recording was performed every second, a moving average (n=10) was used as a criterion to reduce noise and synchronize the O₂ and CO₂ analyzer signals.

{C O}_{2} (t = 0 \dots n) = \frac{1}{n} \sum_{i = 0}^{n} {C O}_{2} (t i) t r a n s f o r m e d

The same procedure was applied to O₂. The transformed and filtered signals were then used to calculate the HP based on the equation described by Lighton [15] and Gerrits et. al., [9].

The detailed step-by-step procedure for the data collection of an hour in a multichamber IC system is presented in Figure 4 and Supp 2.

Figure 5. The curve of recorded signal (A) calibration and Bartolomew transformation applied to individual data (B) and filtered data with moving average (C) of the fractional concentration of CO₂. In the same way, was applied to O₂.

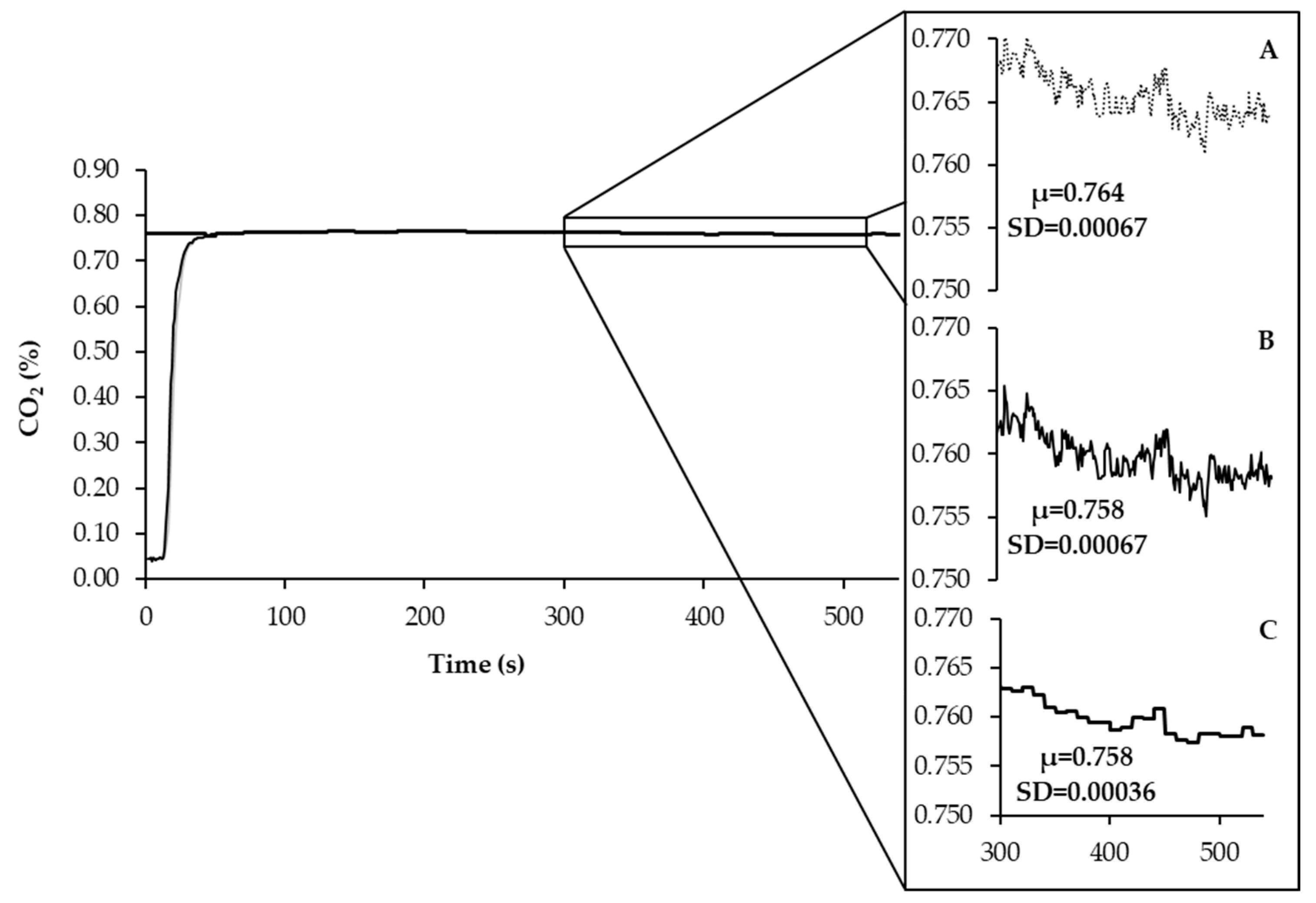
As illustrated in the figure, the average fractional concentration of CO₂ after calibration and Bartholomew transformation showed a slight reduction. This reduction was due to the volumetric contribution of CO₂ in the chamber, which is dependent on Vch, in addition to the CO₂out register by the analyzer. The variation in the recorded and calibrated-transformed data was similar at this point. To reduce noise in the data while maintaining the average of previously calibrated-transformed data, a moving average (n=10) was applied.

Implication

The implications of the described methodology for future research are significant, as it can enhance the accuracy and quality of measurements for indirect calorimetry (IC), which is crucial for investigating animal energy metabolism. This adaptable methodology can be tailored to diverse IC systems and research objectives, rendering it a valuable tool for researchers in various fields. Furthermore, the MS Excel spreadsheet can be customized for specific research purposes or serve as a didactic teaching aid. Thus, our proposal presents a valuable contribution to the field of IC and can significantly advance the precision and reliability of animal science research.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization, R.R.L.; methodology, R.R.L., and R.S.C.; spreadsheets development, R.R.L., R.S.C., R.L.S., and B.B.L; validation, R.R.L. and R.S.C.; formal analysis, R.R.L.; investigation, R.R.L., N.S.K.; resources, N.S.K.; simulation testing and data validation, R.R.L., R.S.C., B.B.L., R.L.S.; writing—original draft preparation, R.R.L.; writing—review and editing, R.R.L., and N.S.K.; project administration, N.S.K.; funding acquisition, N.S.K. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by FAPESP [Process 2019/26575-6] and scholarship (CNPq) – Finance Code Nº 88882.330298/2019-01.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Brower, E. Report of Sub-committee on Constants and Factors. In Symposium of Energy Metabolism Held at European Association for Animal Production; Eaap Academic: London, 1965; pp. 441–443. [Google Scholar]
Riveros, R.L. .; Camargos, R.S.; Macari, M.; Reis, M.P.; Leme, B.B.; Sakomura, N.S. Dynamic of Heat Production Partitioning in Rooster by Indirect Calorimetry. Anim Biosci. 2023, 36, 75–83. [Google Scholar] [CrossRef] [PubMed]
Martinez, D.A.; Suesuttajit, N.; Hilton, K.; Weil, J.T.; Umberson, C.; Scott, A.; Coon, C.N. The Fasting Heat Production of Broilersis a Function of their Body Composition. Anim.–Open Space 2022, 100029. [Google Scholar] [CrossRef]
Wu, S.B.; Swick, R.A.; Noblet, J.; Rodgers, N.; Cadogan, D.; Choct, M. Net Energy Prediction and Energy Efficiency of Feed for Broiler Chickens. Pult. Sci. 2019, 98, 1222–1234. [Google Scholar] [CrossRef] [PubMed]
Liu, W.; Lin, C.H.; Wu, Z.K.; Liu, G.H.; Yan, H.; Yang, H.; Cai, H. Estimation of the Net Energy Requirement for Maintenance in Broilers. Asian-Australas J. Anim. Sci. 2017, 30, 849–856. [Google Scholar] [CrossRef] [PubMed]
Caldas, J.V.; Hhilton, K.; Boonsinchai, N.; England, J.; Aauromoustakos, A.; Coon, C.N. Dynamics of Nutrient Utilization, Heat Production, and Body Composition in Broiler Breeder Hens During Egg Production. Poult. Sci. 2018, 97, 2845–2853. [Google Scholar] [CrossRef]
Takala, J. Handbook of Gas Exchange and Indirect Calorimetry; Detex, 1991. [Google Scholar]
Saathoff, A.J.; Welles, J. Gas Exchange Measurements in the Unsteady State. Plant Cell Environ. 2021, 44, 3509–3523. [Google Scholar] [CrossRef] [PubMed]
Gerrits, W.; Labussièr, E. Indirect Calorimetry, Techniques, Computations and Applications; Wageningen Academic Publishers: Wageningen, Netherlands, 2015. [Google Scholar]
Peppelenbos, H.W. The Use of Gas Exchange Characteristics to Optimize Ca Storage and Ma Packaging of Fruits and Vegetables. Ph.D. Thesis, Land Bouw Universiteit, Wageningen, 1996. [Google Scholar]
Staudacher, E.M; Huetteroth, W.; Schachtner, J.; Daly, K.C. 2009. A 4-Dimensional Representation of Antennal Lobe Out-put Based on an Ensemble of Characterized Projection Neurons. J. Neurosci. Methods. 2009, 180, 208–223. [Google Scholar] [CrossRef] [PubMed]
Fedak, M.A.; Rome, l.; Seeherman, H.J. One-step N2-Dilution Technique for Calibrating Open-Circuit VO2 Measuring Systems. J. Appl. Physiol., 1981, 51, 772–776. [Google Scholar] [CrossRef] [PubMed]
Ortigues; Dussap, C.G.; Aanglaret, Y. Comparison of Various Methods of Calculating the Instantaneous Respirato-RY Gaseous Exchanges from Discrete Measurements in Respiration Chambers. J. Theor. Biol.. 1997, 185, 489–501. [Google Scholar] [CrossRef]
Lighton, J.R.B. Instantaneous' Metabolic Measurement. J. Exp. Biol. 2013, 215, 1605–1606. [Google Scholar] [CrossRef] [PubMed]
Lighton, J.R.B. Measuring Metabolic Rates; Oxford Univ Press: Oxford, United Kindon, 2008. [Google Scholar]
McLean, J.; Tobin, G. Animal and Human Calorimetry; University Press: Cambridge, United Kindon, 1988. [Google Scholar]
Camargo, R.S.; Riveros, R.L.; Macari, M.; Freitas, L.F.V.; Zanetti, M.C.; Bicego, K.C.; Sakomura, N.S. Dynamic of the Energy Utilization of Broiler Chicks. In Proceedings of the Latin American Scientific Conference 2022, Foz do Iguaçú, Brasil, 4–6 October 2022. [Google Scholar]
Bartholomew, G.A.; Vleck, D.E.; Vleck, C.M. Instantaneous Measurements of Oxygen Consumption During Pre-flight Warm-up and Post-flight Cooling in Sphingid and Saturniid Moths. J. Exp. Biol. 1981, 90, 17–32. [Google Scholar] [CrossRef]
Pendar, H.; Socha, J.J. Estimation of Instantaneous Gas Exchange in Flow-Through Respirometry Systems: A Modern Revision of Bartholomew's Z-Transform Method. Plos One 2015, 10, e0139508. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Scheme of multiple flow-through respirometry systems and coupling to the gas for injection test. Fin: ingoing flow. Fout: outgoing flow. Finj: injection flow. CH_i: chambers (i = 1, 2, 3, 4). WVP: water vapor pressure analyzer. The arrows represent the airflow direction (→). Data transference line (●---●).

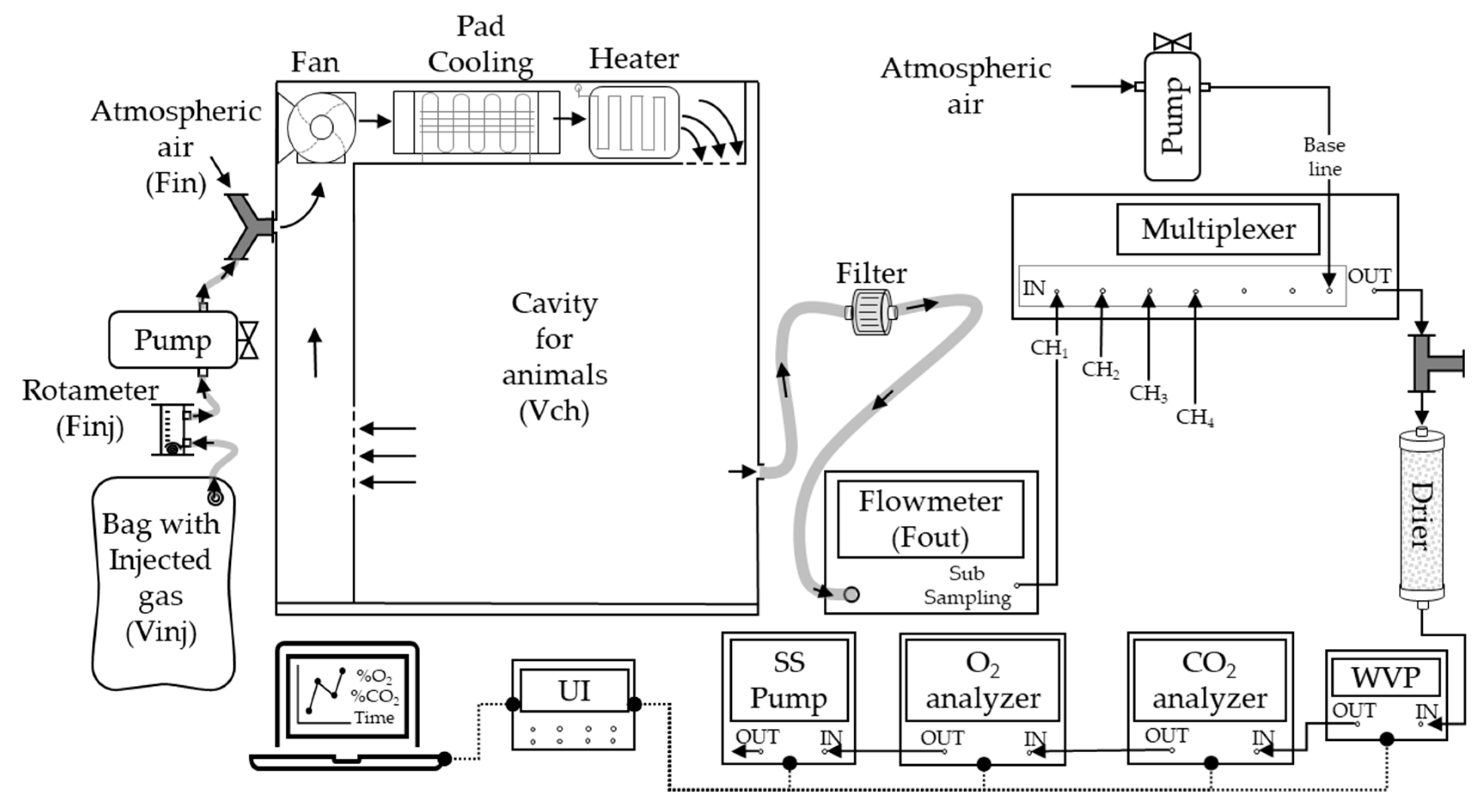
Figure 2. A. Illustrative scheme of the recovery procedure with an injection of a known gas concentration (65% CO₂). Fin: ingoing flow. Fout: outgoing flow. Finj: pure gas injection flow. V_CH: chamber volume. Vbag: volume of the bag that contains tested gas. → airflow direction. B. Phases of CO₂ recovery test and CO₂out behavior defined by the simulation. The tinj differentiates the injection and washing phases.

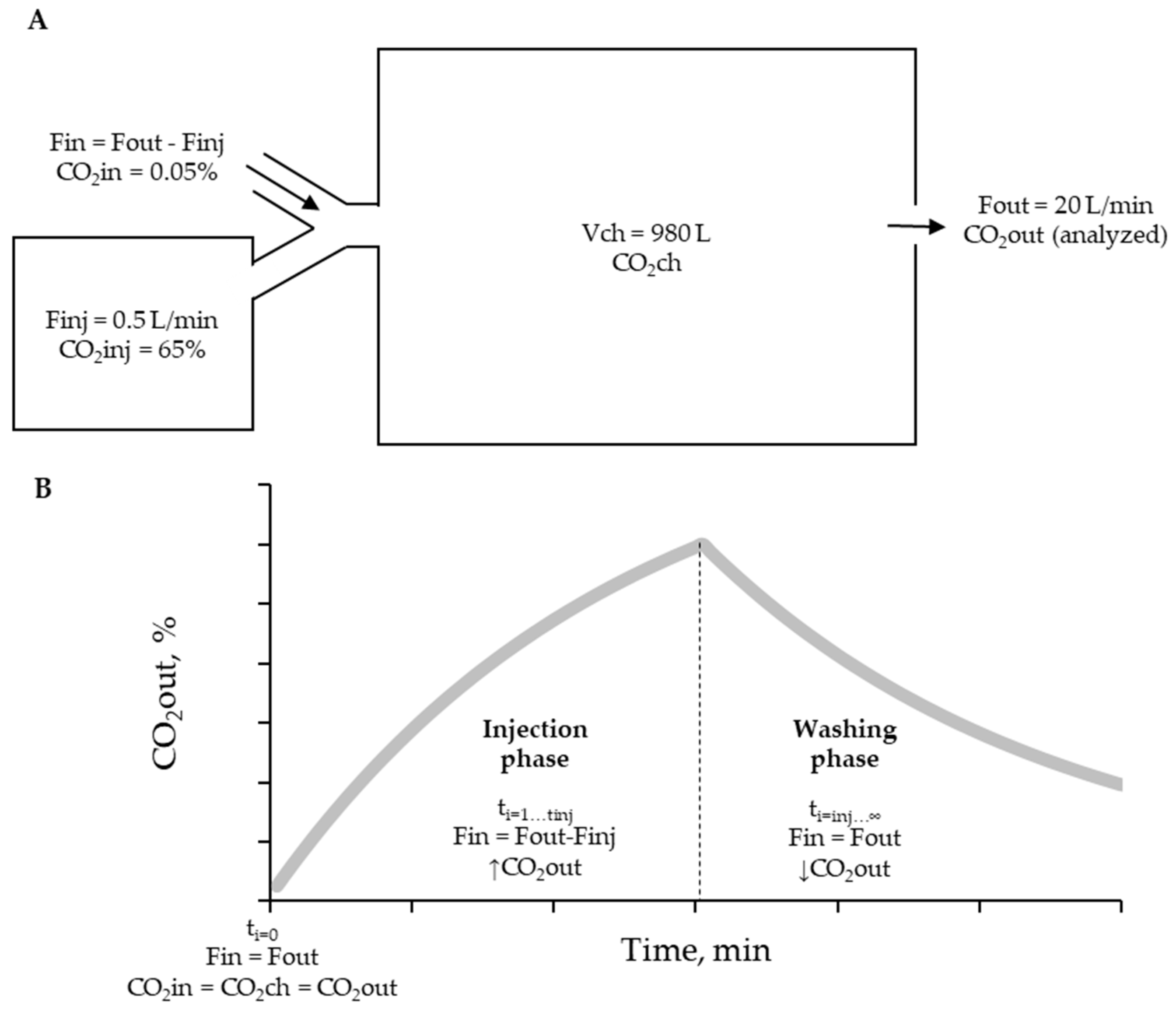
Figure 3. Dynamic (per minute) of the injection of know concentration of CO2 injected on each chamber and description on parameters of CO₂out(ti), ΔVCO₂, or Cumulative ΔVCO₂, and the error calculated for each time. Each line represents the behavior of each chamber (CHn, where n refers to different chambers). The shadow line describes the expected results per unit of time according to the simulation.

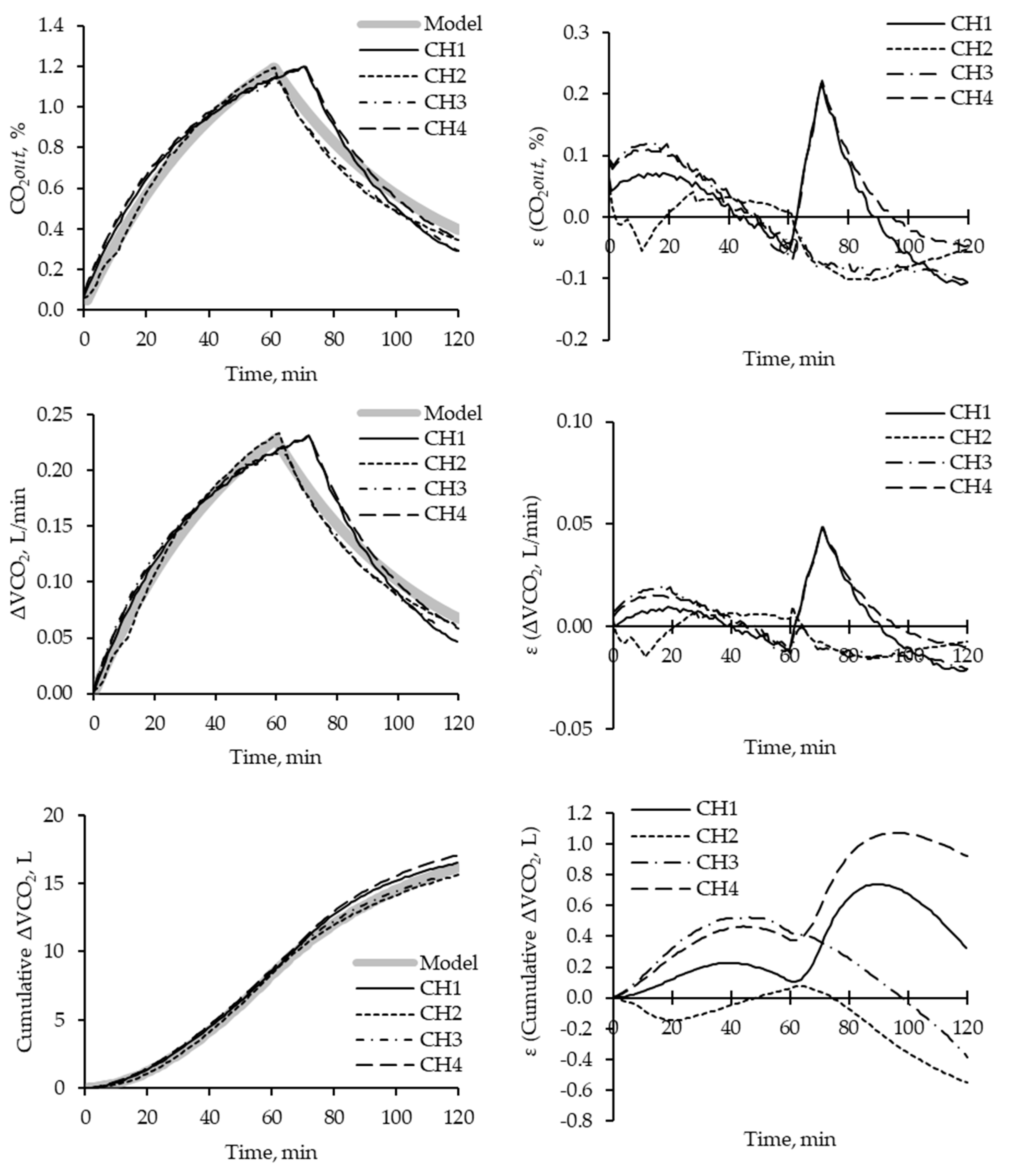
Table 1. Parameters and calculations used for the simulation of recovery test over time (ti).

Variable		Symbol	Parameter or calculation	Units
Initial parameters for the simulation
	Atmospheric CO₂ or fractional ingoing concentration	CO₂in	0.05	%
	Atmospheric oxygen or fractional ingoing concentration	O₂in	21	%
	Outgoing airflow (dry air)	Fout_(ti)	20	L/min
	Volume of injection	Vinj	30	L
	Fractional concentration of CO₂ injected	CO₂inj	65	%
	Injection flow for ti < tinj	Finj_(ti)	0.5	L/min
Intermediate calculations for t=i
	Injection time	tinj	Vinj/Finj = 60	min
	Ingoing volume of CO₂	VCO₂in_(ti)	Fin_(ti)*CO₂in_ti	L/min
	Injected volume of CO₂	VCO₂inj_(ti)	Finj_(ti)*CO₂inj_ti	L/min
	Volume of CO₂ on the chamber	VCO₂ch_(ti)	VCO₂ch_ti-1+VCO₂in_ti+VCO₂inj_ti-VCO₂out_ti-1	L
	Fractional concentration of CO₂ on the chamber	CO₂ch_(ti)	VCO₂ch/Vch	%
	Outgoing volume of CO₂	VCO₂out_(ti)	Fout_ti*CO₂ch_ti	L/min
Outputs
	Fractional concentration of outgoing CO₂	CO₂out_(ti)	CO₂ch_ti-1	%
	Differential volume of CO₂	ΔVCO₂	VCO₂out_ti - VCO₂in_ti	L/min
	Cumulative volume of differential CO₂	Cumulative ΔVCO₂	ΣΔVCO₂ti→∞	L

Table 2. Volumetric recovery of CO₂ (VCO₂ recovered (ti→120), L), recovery rate, and residual standard deviation calculated for the fractional concentration of CO₂, the volumetric difference of CO₂ (ΔVCO₂) and cumulative volumetric difference of CO₂ (Cumulative ΔVCO₂) describe for each chamber (CHn) during the recovery test.

Chamber	VCO₂ recovered (ti→120), L	Recovery rate	RSD_(%CO2out)	RSD_(ΔVCO2)	RSD_{(Cumulative ΔVCO2)}
CH₁	16.51	1.021	0.419	0.084	0.016
CH₂	14.87	0.920	0.730	0.172	0.032
CH₃	15.09	0.933	0.476	0.115	0.020
CH₄	17.09	1.057	0.693	0.081	0.015

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Description and Validation of Flow-Through Chambers of Respirometry for Measuring Gas Exchange in Animal Trials

Abstract

Keywords:

Subject:

Introduction

General description of the flow-through IC system

General calculations

Simulation of the dynamic of gas injection in a theoretical system

Recovery test procedure

Data analyses and recovery index calculation

Results of the recovery test

The procedure of data computing and filtering of IC system

Oxygen and CO2 signals calibration

Calibrated fractional concentration and filtering

Implication

Supplementary Materials

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

Oxygen and CO₂ signals calibration